prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
First we need to download the dataset. In this case we use a datasets containing poems. By doing so we train the model to create its own poems.
```
from datasets import load_dataset
dataset = load_dataset("poem_sentiment")
print(dataset)
```
Before training we need to preprocess the dataset. We tokenize the entries in the dataset and remove all columns we don't need to train the adapter.
```
from transformers import BertTokenizer, GPT2LMHeadModel, TextGenerationPipeline
tokenizer = BertTokenizer.from_pretrained("uer/gpt2-chinese-cluecorpussmall")
from transformers import GPT2Tokenizer
def encode_batch(batch):
"""Encodes a batch of input data using the model tokenizer."""
encoding = tokenizer(batch["verse_text"])
# For language modeling the labels need to be the input_ids
#encoding["labels"] = encoding["input_ids"]
return encoding
#tokenizer = GPT2Tokenizer.from_pretrained("gpt2")
#tokenizer.pad_token = tokenizer.eos_token
# The GPT-2 tokenizer does not have a padding token. In order to process the data
# in batches we set one here
column_names = dataset["train"].column_names
dataset = dataset.map(encode_batch, remove_columns=column_names, batched=True)
```
Next we concatenate the documents in the dataset and create chunks with a length of `block_size`. This is beneficial for language modeling.
```
block_size = 50
# Main data processing function that will concatenate all texts from our dataset and generate chunks of block_size.
def group_texts(examples):
# Concatenate all texts.
concatenated_examples = {k: sum(examples[k], []) for k in examples.keys()}
total_length = len(concatenated_examples[list(examples.keys())[0]])
# We drop the small remainder, we could add padding if the model supported it instead of this drop, you can
# customize this part to your needs.
total_length = (total_length // block_size) * block_size
# Split by chunks of max_len.
result = {
k: [t[i : i + block_size] for i in range(0, total_length, block_size)]
for k, t in concatenated_examples.items()
}
result["labels"] = result["input_ids"].copy()
return result
dataset = dataset.map(group_texts,batched=True,)
dataset.set_format(type="torch", columns=["input_ids", "attention_mask", "labels"])
```
Next we create the model and add our new adapter.Let's just call it `poem` since it is trained to create new poems. Then we activate it and prepare it for training.
```
from transformers import AutoModelForCausalLM
model = AutoModelForCausalLM.from_pretrained("uer/gpt2-chinese-cluecorpussmall")
# add new adapter
model.add_adapter("poem")
# activate adapter for training
model.train_adapter("poem")
```
The last thing we need to do before we can start training is create the trainer. As trainingsargumnénts we choose a learningrate of 1e-4. Feel free to play around with the paraeters and see how they affect the result.
```
from transformers import Trainer, TrainingArguments
training_args = TrainingArguments(
output_dir="./examples",
do_train=True,
remove_unused_columns=False,
learning_rate=5e-4,
num_train_epochs=3,
)
trainer = Trainer(
model=model,
args=training_args,
tokenizer=tokenizer,
train_dataset=dataset["train"],
eval_dataset=dataset["validation"],
)
trainer.train()
```
Now that we have a trained udapter we save it for future usage.
```
PREFIX = "what a "
encoding = tokenizer(PREFIX, return_tensors="pt")
encoding = encoding.to(model.device)
output_sequence = model.generate(
input_ids=encoding["input_ids"][:,:-1],
attention_mask=encoding["attention_mask"][:,:-1],
do_sample=True,
num_return_sequences=5,
max_length = 50,
)
```
Lastly we want to see what the model actually created. Too de this we need to decode the tokens from ids back to words and remove the end of sentence tokens. You can easily use this code with an other dataset. Don't forget to share your adapters at [AdapterHub](https://adapterhub.ml/).
```
for generated_sequence_idx, generated_sequence in enumerate(output_sequence):
print("=== GENERATED SEQUENCE {} ===".format(generated_sequence_idx + 1))
generated_sequence = generated_sequence.tolist()
# Decode text
text = tokenizer.decode(generated_sequence, clean_up_tokenization_spaces=True)
# Remove EndOfSentence Tokens
text = text[: text.find(tokenizer.pad_token)]
print(text)
```
| true |
code
| 0.768527 | null | null | null | null |
|
<a name="top"></a>
<div style="width:1000 px">
<div style="float:right; width:98 px; height:98px;">
<img src="https://raw.githubusercontent.com/Unidata/MetPy/master/metpy/plots/_static/unidata_150x150.png" alt="Unidata Logo" style="height: 98px;">
</div>
<h1>Advanced Pythonic Data Analysis</h1>
<h3>Unidata Python Workshop</h3>
<div style="clear:both"></div>
</div>
<hr style="height:2px;">
<div style="float:right; width:250 px"><img src="http://matplotlib.org/_images/date_demo.png" alt="METAR" style="height: 300px;"></div>
## Overview:
* **Teaching:** 45 minutes
* **Exercises:** 45 minutes
### Questions
1. How can we improve upon the versatility of the plotter developed in the basic time series notebook?
1. How can we iterate over all data file in a directory?
1. How can data processing functions be applied on a variable-by-variable basis?
### Objectives
1. <a href="#basicfunctionality">From Time Series Plotting Episode</a>
1. <a href="#parameterdict">Dictionaries of Parameters</a>
1. <a href="#multipledict">Multiple Dictionaries</a>
1. <a href="#functions">Function Application</a>
1. <a href="#glob">Glob and Multiple Files</a>
<a name="basicfunctionality"></a>
## From Time Series Plotting Episode
Here's the basic set of imports and data reading functionality that we established in the [Basic Time Series Plotting](../Time_Series/Basic%20Time%20Series%20Plotting.ipynb) notebook.
```
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter, DayLocator
from siphon.simplewebservice.ndbc import NDBC
%matplotlib inline
def format_varname(varname):
"""Format the variable name nicely for titles and labels."""
parts = varname.split('_')
title = parts[0].title()
label = varname.replace('_', ' ').title()
return title, label
def read_buoy_data(buoy, days=7):
# Read in some data
df = NDBC.realtime_observations(buoy)
# Trim to the last 7 days
df = df[df['time'] > (pd.Timestamp.utcnow() - pd.Timedelta(days=days))]
return df
```
<a href="#top">Top</a>
<hr style="height:2px;">
<a name="parameterdict"></a>
## Dictionaries of Parameters
When we left off last time, we had created dictionaries that stored line colors and plot properties in a key value pair. To further simplify things, we can actually pass a dictionary of arguements to the plot call. Enter the dictionary of dictionaries. Each key has a value that is a dictionary itself with it's key value pairs being the arguements to each plot call. Notice that different variables can have different arguements!
```
df = read_buoy_data('42039')
# Dictionary of plotting parameters by variable name
styles = {'wind_speed': dict(color='tab:orange'),
'wind_gust': dict(color='tab:olive', linestyle='None', marker='o', markersize=2),
'pressure': dict(color='black')}
plot_variables = [['wind_speed', 'wind_gust'], ['pressure']]
fig, axes = plt.subplots(1, len(plot_variables), sharex=True, figsize=(14, 5))
for col, var_names in enumerate(plot_variables):
ax = axes[col]
for var_name in var_names:
title, label = format_varname(var_name)
ax.plot(df.time, df[var_name], **styles[var_name])
ax.set_ylabel(title)
ax.set_title('Buoy 42039 {}'.format(title))
ax.grid(True)
ax.set_xlabel('Time')
ax.xaxis.set_major_formatter(DateFormatter('%m/%d'))
ax.xaxis.set_major_locator(DayLocator())
```
<a href="#top">Top</a>
<hr style="height:2px;">
<a name="multipledict"></a>
## Multiple Dictionaries
We can even use multiple dictionaries to define styles for types of observations and then specific observation properties such as levels, sources, etc. One common use case of this would be plotting all temperature data as red, but with different linestyles for an isobaric level and the surface.
```
type_styles = {'Temperature': dict(color='red', marker='o'),
'Relative humidity': dict(color='green', marker='s')}
level_styles = {'isobaric': dict(linestyle='-', linewidth=2),
'surface': dict(linestyle=':', linewidth=3)}
my_style = type_styles['Temperature']
print(my_style)
my_style.update(level_styles['isobaric'])
print(my_style)
```
If we look back at the original entry in `type_styles` we see it was updated too! That may not be the expected or even the desired behavior.
```
type_styles['Temperature']
```
We can use the `copy` method to make a copy of the element and avoid update the original.
```
type_styles = {'Temperature': dict(color='red', marker='o'),
'Relative humidity': dict(color='green', marker='s')}
level_styles = {'isobaric': dict(linestyle='-', linewidth=2),
'surface': dict(linestyle=':', linewidth=3)}
my_style = type_styles['Temperature'].copy() # Avoids altering the original entry
my_style.update(level_styles['isobaric'])
print(my_style)
type_styles['Temperature']
```
Since we don't have data from different levels, we'll work with wind measurements and pressure data. Our <code>format_varname</code> function returns a title and full variable name label.
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>Create a type styles dictionary of dictionaries with the variable title as the key that has styles for `Wind` and `Pressure` data. The pressure should be a solid black line. Wind should be a solid line.</li>
<li>Create a variable style dictionary of dictionaries with the variable name as the key that specifies an orange line of width 2 for wind speed, olive line of width 0.5 for gusts, and no additional information for pressure.</li>
<li>Update the plotting code below to use the new type and variable styles dictionary.
</ul>
</div>
```
# Your code goes here (modify the skeleton below)
type_styles = {}
variable_styles = {}
fig, axes = plt.subplots(1, len(plot_variables), sharex=True, figsize=(14, 5))
for col, var_names in enumerate(plot_variables):
ax = axes[col]
for var_name in var_names:
title, label = format_varname(var_name)
ax.plot(df.time, df[var_name], **styles[var_name])
ax.set_ylabel(title)
ax.set_title('Buoy 42039 {}'.format(title))
ax.grid(True)
ax.set_xlabel('Time')
ax.xaxis.set_major_formatter(DateFormatter('%m/%d'))
ax.xaxis.set_major_locator(DayLocator())
```
#### Solution
```
# %load solutions/dict_args.py
```
<a href="#top">Top</a>
<hr style="height:2px;">
<a name="functions"></a>
## Function Application
There are times where we might want to apply a certain amount of pre-processing to the data before they are plotted. Maybe we want to do a unit conversion, scale the data, or filter it. We can create a dictionary in which functions are the values and variable names are the keys.
For example, let's define a function that uses the running median to filter the wind data (effectively a low-pass). We'll also make a do nothing function for data we don't want to alter.
```
from scipy.signal import medfilt
def filter_wind(a):
return medfilt(a, 7)
def donothing(a):
return a
converters = {'Wind': filter_wind, 'Pressure': donothing}
type_styles = {'Pressure': dict(color='black'),
'Wind': dict(linestyle='-')}
variable_styles = {'pressure': dict(),
'wind_speed': dict(color='tab:orange', linewidth=2),
'wind_gust': dict(color='tab:olive', linewidth=0.5)}
fig, axes = plt.subplots(1, len(plot_variables), sharex=True, figsize=(14, 5))
for col, var_names in enumerate(plot_variables):
ax = axes[col]
for var_name in var_names:
title, label = format_varname(var_name)
# Apply our pre-processing
var_data = converters[title](df[var_name])
style = type_styles[title].copy() # So the next line doesn't change the original
style.update(variable_styles[var_name])
ax.plot(df.time, var_data, **style)
ax.set_ylabel(title)
ax.set_title('Buoy 42039 {}'.format(title))
ax.grid(True)
ax.set_xlabel('Time')
ax.xaxis.set_major_formatter(DateFormatter('%m/%d'))
ax.xaxis.set_major_locator(DayLocator())
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>Write a function to convert the pressure data to bars. (**Hint**: 1 bar = 100000 Pa)</li>
<li>Apply your converter in the code below and replot the data.</li>
</ul>
</div>
```
# Your code goes here (modify the code below)
converters = {'Wind': filter_wind, 'Pressure': donothing}
type_styles = {'Pressure': dict(color='black'),
'Wind': dict(linestyle='-')}
variable_styles = {'pressure': dict(),
'wind_speed': dict(color='tab:orange', linewidth=2),
'wind_gust': dict(color='tab:olive', linewidth=0.5)}
fig, axes = plt.subplots(1, len(plot_variables), sharex=True, figsize=(14, 5))
for col, var_names in enumerate(plot_variables):
ax = axes[col]
for var_name in var_names:
title, label = format_varname(var_name)
# Apply our pre-processing
var_data = converters[title](df[var_name])
style = type_styles[title].copy() # So the next line doesn't change the original
style.update(variable_styles[var_name])
ax.plot(df.time, var_data, **style)
ax.set_ylabel(title)
ax.set_title('Buoy 42039 {}'.format(title))
ax.grid(True)
ax.set_xlabel('Time')
ax.xaxis.set_major_formatter(DateFormatter('%m/%d'))
ax.xaxis.set_major_locator(DayLocator())
```
#### Solution
<div class="alert alert-info">
<b>REMINDER</b>:
You should be using the unit library to convert between various physical units, this is simply for demonstration purposes!
</div>
```
# %load solutions/function_application.py
```
<a href="#top">Top</a>
<hr style="height:2px;">
<a name="glob"></a>
## Multiple Buoys
We can now use the techniques we've seen before to make a plot of multiple buoys in a single figure.
```
buoys = ['42039', '42022']
type_styles = {'Pressure': dict(color='black'),
'Wind': dict(linestyle='-')}
variable_styles = {'pressure': dict(),
'wind_speed': dict(color='tab:orange', linewidth=2),
'wind_gust': dict(color='tab:olive', linewidth=0.5)}
fig, axes = plt.subplots(len(buoys), len(plot_variables), sharex=True, figsize=(14, 10))
for row, buoy in enumerate(buoys):
df = read_buoy_data(buoy)
for col, var_names in enumerate(plot_variables):
ax = axes[row, col]
for var_name in var_names:
title, label = format_varname(var_name)
style = type_styles[title].copy() # So the next line doesn't change the original
style.update(variable_styles[var_name])
ax.plot(df.time, df[var_name], **style)
ax.set_ylabel(title)
ax.set_title('Buoy {} {}'.format(buoy, title))
ax.grid(True)
ax.set_xlabel('Time')
ax.xaxis.set_major_formatter(DateFormatter('%m/%d'))
ax.xaxis.set_major_locator(DayLocator())
```
<a href="#top">Top</a>
<hr style="height:2px;">
<div class="alert alert-success">
<b>EXERCISE</b>: As a final exercise, use a dictionary to allow all of the plots to share common y axis limits based on the variable title.
</div>
```
# Your code goes here
```
#### Solution
```
# %load solutions/final.py
```
<a href="#top">Top</a>
<hr style="height:2px;">
| true |
code
| 0.61173 | null | null | null | null |
|
# Time Series Cross Validation
```
import pandas as pd
import numpy as np
#suppress ARIMA warnings
import warnings
warnings.filterwarnings('ignore')
```
Up till now we have used a single validation period to select our best model. The weakness of that approach is that it gives you a sample size of 1 (that's better than nothing, but generally poor statistics!). Time series cross validation is an approach to provide more data points when comparing models. In the classicial time series literature time series cross validation is called a **Rolling Forecast Origin**. There may also be benefit of taking a **sliding window** approach to cross validaiton. This second approach maintains a fixed sized training set. I.e. it drops older values from the time series during validation.
## Rolling Forecast Origin
The following code and output provide a simplified view of how rolling forecast horizons work in practice.
```
def rolling_forecast_origin(train, min_train_size, horizon):
'''
Rolling forecast origin generator.
'''
for i in range(len(train) - min_train_size - horizon + 1):
split_train = train[:min_train_size+i]
split_val = train[min_train_size+i:min_train_size+i+horizon]
yield split_train, split_val
full_series = [2502, 2414, 2800, 2143, 2708, 1900, 2333, 2222, 1234, 3456]
test = full_series[-2:]
train = full_series[:-2]
print('full training set: {0}'.format(train))
print('hidden test set: {0}'.format(test))
cv_rolling = rolling_forecast_origin(train, min_train_size=4, horizon=2)
cv_rolling
i = 0
for cv_train, cv_val in cv_rolling:
print(f'CV[{i+1}]')
print(f'Train:\t{cv_train}')
print(f'Val:\t{cv_val}')
print('-----')
i += 1
```
## Sliding Window Cross Validation
```
def sliding_window(train, window_size, horizon, step=1):
'''
sliding window generator.
Parameters:
--------
train: array-like
training data for time series method
window_size: int
lookback - how much data to include.
horizon: int
forecast horizon
step: int, optional (default=1)
step=1 means that a single additional data point is added to the time
series. increase step to run less splits.
Returns:
array-like, array-like
split_training, split_validation
'''
for i in range(0, len(train) - window_size - horizon + 1, step):
split_train = train[i:window_size+i]
split_val = train[i+window_size:window_size+i+horizon]
yield split_train, split_val
```
This code tests its with `step=1`
```
cv_sliding = sliding_window(train, window_size=4, horizon=1)
print('full training set: {0}\n'.format(train))
i = 0
for cv_train, cv_val in cv_sliding:
print(f'CV[{i+1}]')
print(f'Train:\t{cv_train}')
print(f'Val:\t{cv_val}')
print('-----')
i += 1
```
The following code tests it with `step=2`. Note that you get less splits. The code is less computationally expensive at the cost of less data. That is probably okay.
```
cv_sliding = sliding_window(train, window_size=4, horizon=1, step=2)
print('full training set: {0}\n'.format(train))
i = 0
for cv_train, cv_val in cv_sliding:
print(f'CV[{i+1}]')
print(f'Train:\t{cv_train}')
print(f'Val:\t{cv_val}')
print('-----')
i += 1
```
# Parallel Cross Validation Example using Naive1
```
from forecast_tools.baseline import SNaive, Naive1
from forecast_tools.datasets import load_emergency_dept
#optimised version of the functions above...
from forecast_tools.model_selection import (rolling_forecast_origin,
sliding_window,
cross_validation_score)
from sklearn.metrics import mean_absolute_error
train = load_emergency_dept()
model = Naive1()
#%%timeit runs the code multiple times to get an estimate of runtime.
#comment if out to run the code only once.
```
Run on a single core
```
%%time
cv = sliding_window(train, window_size=14, horizon=7, step=1)
results_1 = cross_validation_score(model, train, cv, mean_absolute_error,
n_jobs=1)
```
Run across multiple cores by setting `n_jobs=-1`
```
%%time
cv = sliding_window(train, window_size=14, horizon=7, step=1)
results_2 = cross_validation_score(model, train, cv, mean_absolute_error,
n_jobs=-1)
results_1.shape
results_2.shape
print(results_1.mean(), results_1.std())
```
just to illustrate that the results are the same - the difference is runtime.
```
print(results_2.mean(), results_2.std())
```
# Cross validation with multiple forecast horizons
```
horizons = [7, 14, 21]
cv = sliding_window(train, window_size=14, horizon=max(horizons), step=1)
#note that we now pass in the horizons list to cross_val_score
results_h = cross_validation_score(model, train, cv, mean_absolute_error,
horizons=horizons, n_jobs=-1)
#results are returned as numpy array - easy to cast to dataframe and display
pd.DataFrame(results_h, columns=['7days', '14days', '21days']).head()
```
## Cross validation example using ARIMA - does it speed up when CV run in Parallel?
```
#use ARIMA from pmdarima as that has a similar interface to baseline models.
from pmdarima import ARIMA, auto_arima
#ato_model = auto_arima(train, suppress_warnings=True, n_jobs=-1, m=7)
#auto_model
#create arima model - reasonably complex model
#order=(1, 1, 2), seasonal_order=(2, 0, 2, 7)
args = {'order':(1, 1, 2), 'seasonal_order':(2, 0, 2, 7)}
model = ARIMA(order=args['order'], seasonal_order=args['seasonal_order'],
enforce_stationarity=False, suppress_warnings=True)
%%time
cv = rolling_forecast_origin(train, min_train_size=320, horizon=7)
results_1 = cross_validation_score(model, train, cv, mean_absolute_error,
n_jobs=1)
```
comment out %%timeit to run the code only once!
you should see a big improvement in performance. mine went
from 12.3 seconds to 2.4 seconds.
```
%%time
cv = rolling_forecast_origin(train, min_train_size=320, horizon=7)
results_2 = cross_validation_score(model, train, cv, mean_absolute_error,
n_jobs=-1)
results_1.shape
results_2.shape
results_1.mean()
results_2.mean()
```
| true |
code
| 0.547041 | null | null | null | null |
|
# Exploratory data analysis
Exploratory data analysis is an important part of any data science projects. According to [Forbs](https://www.forbes.com/sites/gilpress/2016/03/23/data-preparation-most-time-consuming-least-enjoyable-data-science-task-survey-says/?sh=67e543e86f63), it accounts for about 80% of the work of data scientists. Thus, we are going to pay out attention to that part.
In the notebook are given data description, cleaning, variables preparation, and CTR calculation and visualization.
---
```
import pandas as pd
import random
import seaborn as sns
import matplotlib.pyplot as plt
import gc
%matplotlib inline
```
Given that file occupies 5.9G and has 40 mln rows we are going to read only a few rows to glimpse at data.
```
filename = 'data/train.csv'
!echo 'Number of lines in "train.csv":'
!wc -l {filename}
!echo '"train.csv" file size:'
!du -h {filename}
dataset_5 = pd.read_csv('data/train.csv', nrows=5)
dataset_5.head()
print("Number of columns: {}\n".format(dataset_5.shape[1]))
```
---
## Data preparation
* Column `Hour` has a format `YYMMDDHH` and has to be converted.
* It is necessary to load only `click` and `hour` columns for `CTR` calculation.
* For data exploration purposes we also calculate `hour` and build distributions of `CTR` by `hour` and `weekday`
---
```
pd.to_datetime(dataset_5['hour'], format='%y%m%d%H')
# custom_date_parser = lambda x: pd.datetime.strptime(x, '%y%m%d%H')
# The commented part is for preliminary analysis and reads only 10% of data
# row_num = 40428967
# to read 10% of data
# skip = sorted(random.sample(range(1, row_num), round(0.9 * row_num)))
# data_set = pd.read_csv('data/train.csv',
# header=0,
# skiprows=skip,
# usecols=['click', 'hour'])
data_set = pd.read_csv('data/train.csv',
header=0,
usecols=['click', 'hour'])
data_set['hour'] = pd.to_datetime(data_set['hour'], format='%y%m%d%H')
data_set.isna().sum()
data_set.shape
round(100 * data_set.click.value_counts() / data_set.shape[0])
data_set.hour.dt.date.unique()
```
### Data preparation for CTR time series graph
```
df_CTR = data_set.groupby('hour').agg({
'click': ['count', 'sum']
}).reset_index()
df_CTR.columns = ['hour', 'impressions', 'clicks']
df_CTR['CTR'] = df_CTR['clicks'] / df_CTR['impressions']
del data_set; gc.collect();
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
plt.figure(figsize=[16, 8])
sns.lineplot(x='hour', y='CTR', data=df_CTR, linewidth=3)
plt.title('Hourly CTR for period 2014/10/21 and 2014/10/30', fontsize=20)
```
### Data preparation for CTR by hours graph
```
df_CTR['h'] = df_CTR.hour.dt.hour
df_CTR_h = df_CTR[['h', 'impressions',
'clicks']].groupby('h').sum().reset_index()
df_CTR_h['CTR'] = df_CTR_h['clicks'] / df_CTR_h['impressions']
df_CTR_h_melt = pd.melt(df_CTR_h,
id_vars='h',
value_vars=['impressions', 'clicks'],
value_name='count',
var_name='type')
plt.figure(figsize=[16, 8])
sns.set_style("white")
g1 = sns.barplot(x='h',
y='count',
hue='type',
data=df_CTR_h_melt,
palette="deep")
g1.legend(loc=1).set_title(None)
ax2 = plt.twinx()
sns.lineplot(x='h',
y='CTR',
data=df_CTR_h,
palette="deep",
marker='o',
ax=ax2,
label='CTR',
linewidth=5,
color='lightblue')
plt.title('CTR, Number of Imressions and Clicks by hours', fontsize=20)
ax2.legend(loc=5)
plt.tight_layout()
```
### Data preparation for CTR by weekday graph
```
df_CTR['weekday'] = df_CTR.hour.dt.day_name()
df_CTR['weekday_num'] = df_CTR.hour.dt.weekday
df_CTR_w = df_CTR[['weekday', 'impressions',
'clicks']].groupby('weekday').sum().reset_index()
df_CTR_w['CTR'] = df_CTR_w['clicks'] / df_CTR_w['impressions']
df_CTR_w_melt = pd.melt(df_CTR_w,
id_vars='weekday',
value_vars=['impressions', 'clicks'],
value_name='count',
var_name='type')
plt.figure(figsize=[16, 8])
sns.set_style("white")
g1 = sns.barplot(x='weekday',
y='count',
hue='type',
data=df_CTR_w_melt.sort_values('weekday'),
palette="deep",
order=[
'Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday',
'Saturday', 'Sunday'
])
g1.legend(loc=1).set_title(None)
ax2 = plt.twinx()
sns.lineplot(x='weekday',
y='CTR',
data=df_CTR.sort_values(by='weekday_num'),
palette="deep",
marker='o',
ax=ax2,
label='CTR',
linewidth=5,
sort=False)
plt.title('CTR, Number of Imressions and Clicks by weekday', fontsize=20)
ax2.legend(loc=5)
plt.tight_layout()
```
### Normality test
```
from scipy.stats import normaltest, shapiro
def test_interpretation(stat, p, alpha=0.05):
"""
Outputs the result of statistical test comparing test-statistic and p-value
"""
print('Statistics=%.3f, p-value=%.3f, alpha=%.2f' % (stat, p, alpha))
if p > alpha:
print('Sample looks like from normal distribution (fail to reject H0)')
else:
print('Sample is not from Normal distribution (reject H0)')
stat, p = shapiro(df_CTR.CTR)
test_interpretation(stat, p)
stat, p = normaltest(df_CTR.CTR)
test_interpretation(stat, p)
```
---
## Summary
* Number of rows: 40428967
* Date duration: 10 days between 2014/10/21 and 2014/10/30. Each day has 24 hours
* No missing values in variables `click` and `hour`
* For simplicity, analysis is provided for 10% of the data. And as soon as the notebook is finalized, it will be re-run for all available data. And as soon as the hour aggregation takes place, the raw data source is deleted
* Three graphs are provided:
* CTR time serirs for all data duration
* CTR, impressions, and click counts by hour
* CTR, impressions, and click counts by weekday
* Average `CTR` value is **17%**
* Most of the `Impressions` and `Clicks` are appeared on Tuesday, Wednesday and Thursday. But highest `CTR` values is on Monday and Sunday
* The normality in `CTR` time-series is **rejected** by two tests
---
## Hypothesis:
There is a seasonality in `CTR` by an `hour` and `weekday`. For instance, `CTR` at hour 21 is lower than `CTR` at hour 14 which can be observed from graphs. Ideally, it is necessary to use 24-hour lag for anomaly detection. It can be implemented by comparing, for instance, hour 1 at day 10 with an average value of hour 1 at days 3, 4, 5, 6, 7, 8, 9 (one week), etc. One week is chosen because averaging of whole week smooth weekday seasonality: Monday and Sunday are different from Tuesday and Wednesday, but there is no big difference between whole weeks. Additional improvement can be done by the use of the median for central tendency instead of a simple averaging because averaging is biased towards abnormal values.
```
# save the final aggregated data frame to use for anomaly detection in the corresponding notebook
df_CTR.to_pickle('./data/CTR_aggregated.pkl')
```
| true |
code
| 0.317244 | null | null | null | null |
|
# TensorFlow Fold Quick Start
TensorFlow Fold is a library for turning complicated Python data structures into TensorFlow Tensors.
```
# boilerplate
import random
import tensorflow as tf
sess = tf.InteractiveSession()
import tensorflow_fold as td
```
The basic elements of Fold are *blocks*. We'll start with some blocks that work on simple data types.
```
scalar_block = td.Scalar()
vector3_block = td.Vector(3)
```
Blocks are functions with associated input and output types.
```
def block_info(block):
print("%s: %s -> %s" % (block, block.input_type, block.output_type))
block_info(scalar_block)
block_info(vector3_block)
```
We can use `eval()` to see what a block does with its input:
```
scalar_block.eval(42)
vector3_block.eval([1,2,3])
```
Not very exciting. We can compose simple blocks together with `Record`, like so:
```
record_block = td.Record({'foo': scalar_block, 'bar': vector3_block})
block_info(record_block)
```
We can see that Fold's type system is a bit richer than vanilla TF; we have tuple types! Running a record block does what you'd expect:
```
record_block.eval({'foo': 1, 'bar': [5, 7, 9]})
```
One useful thing you can do with blocks is wire them up to create pipelines using the `>>` operator, which performs function composition. For example, we can take our two tuple tensors and compose it with `Concat`, like so:
```
record2vec_block = record_block >> td.Concat()
record2vec_block.eval({'foo': 1, 'bar': [5, 7, 9]})
```
Note that because Python dicts are unordered, Fold always sorts the outputs of a record block by dictionary key. If you want to preserve order you can construct a Record block from an OrderedDict.
The whole point of Fold is to get your data into TensorFlow; the `Function` block lets you convert a TITO (Tensors In, Tensors Out) function to a block:
```
negative_block = record2vec_block >> td.Function(tf.negative)
negative_block.eval({'foo': 1, 'bar': [5, 7, 9]})
```
This is all very cute, but where's the beef? Things start to get interesting when our inputs contain sequences of indeterminate length. The `Map` block comes in handy here:
```
map_scalars_block = td.Map(td.Scalar())
```
There's no TF type for sequences of indeterminate length, but Fold has one:
```
block_info(map_scalars_block)
```
Right, but you've done the TF [RNN Tutorial](https://www.tensorflow.org/tutorials/recurrent/) and even poked at [seq-to-seq](https://www.tensorflow.org/tutorials/seq2seq/). You're a wizard with [dynamic rnns](https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn). What does Fold offer?
Well, how about jagged arrays?
```
jagged_block = td.Map(td.Map(td.Scalar()))
block_info(jagged_block)
```
The Fold type system is fully compositional; any block you can create can be composed with `Map` to create a sequence, or `Record` to create a tuple, or both to create sequences of tuples or tuples of sequences:
```
seq_of_tuples_block = td.Map(td.Record({'foo': td.Scalar(), 'bar': td.Scalar()}))
seq_of_tuples_block.eval([{'foo': 1, 'bar': 2}, {'foo': 3, 'bar': 4}])
tuple_of_seqs_block = td.Record({'foo': td.Map(td.Scalar()), 'bar': td.Map(td.Scalar())})
tuple_of_seqs_block.eval({'foo': range(3), 'bar': range(7)})
```
Most of the time, you'll eventually want to get one or more tensors out of your sequence, for wiring up to your particular learning task. Fold has a bunch of built-in reduction functions for this that do more or less what you'd expect:
```
((td.Map(td.Scalar()) >> td.Sum()).eval(range(10)),
(td.Map(td.Scalar()) >> td.Min()).eval(range(10)),
(td.Map(td.Scalar()) >> td.Max()).eval(range(10)))
```
The general form of such functions is `Reduce`:
```
(td.Map(td.Scalar()) >> td.Reduce(td.Function(tf.multiply))).eval(range(1,10))
```
If the order of operations is important, you should use `Fold` instead of `Reduce` (but if you can use `Reduce` you should, because it will be faster):
```
((td.Map(td.Scalar()) >> td.Fold(td.Function(tf.divide), tf.ones([]))).eval(range(1,5)),
(td.Map(td.Scalar()) >> td.Reduce(td.Function(tf.divide), tf.ones([]))).eval(range(1,5))) # bad, not associative!
```
Now, let's do some learning! This is the part where "magic" happens; if you want a deeper understanding of what's happening here you might want to jump right to our more formal [blocks tutorial](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/blocks.md) or learn more about [running blocks in TensorFlow](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/running.md)
```
def reduce_net_block():
net_block = td.Concat() >> td.FC(20) >> td.FC(1, activation=None) >> td.Function(lambda xs: tf.squeeze(xs, axis=1))
return td.Map(td.Scalar()) >> td.Reduce(net_block)
```
The `reduce_net_block` function creates a block (`net_block`) that contains a two-layer fully connected (FC) network that takes a pair of scalar tensors as input and produces a scalar tensor as output. This network gets applied in a binary tree to reduce a sequence of scalar tensors to a single scalar tensor.
One thing to notice here is that we are calling [`tf.squeeze`](https://www.tensorflow.org/versions/r1.0/api_docs/python/array_ops/shapes_and_shaping#squeeze) with `axis=1`, even though the Fold output type of `td.FC(1, activation=None)` (and hence the input type of the enclosing `Function` block) is a `TensorType` with shape `(1)`. This is because all Fold blocks actually run on TF tensors with an implicit leading batch dimension, which enables execution via [*dynamic batching*](https://arxiv.org/abs/1702.02181). It is important to bear this in mind when creating `Function` blocks that wrap functions that are not applied elementwise.
```
def random_example(fn):
length = random.randrange(1, 10)
data = [random.uniform(0,1) for _ in range(length)]
result = fn(data)
return data, result
```
The `random_example` function generates training data consisting of `(example, fn(example))` pairs, where `example` is a random list of numbers, e.g.:
```
random_example(sum)
random_example(min)
def train(fn, batch_size=100):
net_block = reduce_net_block()
compiler = td.Compiler.create((net_block, td.Scalar()))
y, y_ = compiler.output_tensors
loss = tf.nn.l2_loss(y - y_)
train = tf.train.AdamOptimizer().minimize(loss)
sess.run(tf.global_variables_initializer())
validation_fd = compiler.build_feed_dict(random_example(fn) for _ in range(1000))
for i in range(2000):
sess.run(train, compiler.build_feed_dict(random_example(fn) for _ in range(batch_size)))
if i % 100 == 0:
print(i, sess.run(loss, validation_fd))
return net_block
```
Now we're going to train a neural network to approximate a reduction function of our choosing. Calling `eval()` repeatedly is super-slow and cannot exploit batch-wise parallelism, so we create a [`Compiler`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#compiler). See our page on [running blocks in TensorFlow](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/running.md) for more on Compilers and how to use them effectively.
```
sum_block = train(sum)
sum_block.eval([1, 1])
```
Breaking news: deep neural network learns to calculate 1 + 1!!!!
Of course we've done something a little sneaky here by constructing a model that can only represent associative functions and then training it to compute an associative function. The technical term for being sneaky in machine learning is [inductive bias](https://en.wikipedia.org/wiki/Inductive_bias).
```
min_block = train(min)
min_block.eval([2, -1, 4])
```
Oh noes! What went wrong? Note that we trained our network to compute `min` on positive numbers; negative numbers are outside of its input distribution.
```
min_block.eval([0.3, 0.2, 0.9])
```
Well, that's better. What happens if you train the network on negative numbers as well as on positives? What if you only train on short lists and then evaluate the net on long ones? What if you used a `Fold` block instead of a `Reduce`? ... Happy Folding!
| true |
code
| 0.653376 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Image/connected_pixel_count.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Image/connected_pixel_count.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Image/connected_pixel_count.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Image/connected_pixel_count.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# Image.ConnectedPixelCount example.
# Split pixels of band 01 into "bright" (arbitrarily defined as
# reflectance > 0.3) and "dim". Highlight small (<30 pixels)
# standalone islands of "bright" or "dim" type.
img = ee.Image('MODIS/006/MOD09GA/2012_03_09') \
.select('sur_refl_b01') \
.multiply(0.0001)
# Create a threshold image.
bright = img.gt(0.3)
# Compute connected pixel counts stop searching for connected pixels
# once the size of the connected neightborhood reaches 30 pixels, and
# use 8-connected rules.
conn = bright.connectedPixelCount(**{
'maxSize': 30,
'eightConnected': True
})
# Make a binary image of small clusters.
smallClusters = conn.lt(30)
Map.setCenter(-107.24304, 35.78663, 8)
Map.addLayer(img, {'min': 0, 'max': 1}, 'original')
Map.addLayer(smallClusters.updateMask(smallClusters),
{'min': 0, 'max': 1, 'palette': 'FF0000'}, 'cc')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| true |
code
| 0.639905 | null | null | null | null |
|
# Experimental Mathimatics: Chronicle of Matlab code - 2008 - 2015
##### Whereas the discovery of Chaos, Fractal Geometry and Non-Linear Dynamical Systems falls outside the domain of analytic function in mathematical terms the path to discovery is taken as experimental computer-programming.
##### Whereas existing discoveries have been most delightfully difference equations this first effor concentrates on guided random search for equations and parameters of that type.
### equation and parameters data were saved in tiff file headers, matlab/python extracted to:
```
import os
import pandas as pd
spreadsheets_directory = '../data/Matlab_Chronicle_2008-2012/'
images_dataframe_filename = os.path.join(spreadsheets_directory, 'Of_tiff_headers.df')
equations_dataframe_filename = os.path.join(spreadsheets_directory, 'Of_m_files.df')
Images_Chronicle_df = pd.read_csv(images_dataframe_filename, sep='\t', index_col=0)
Equations_Chronicle_df = pd.read_csv(equations_dataframe_filename, sep='\t', index_col=0)
def get_number_of_null_parameters(df, print_out=True):
""" Usage good_null_bad_dict = get_number_of_null_parameters(df, print_out=True)
function to show the number of Images with missing or bad parameters
because they are only reproducable with both the equation and parameter set
Args:
df = dataframe in format of historical images - (not shown in this notebook)
Returns:
pars_contidtion_dict:
pars_contidtion_dict['good_pars']: number of good parametrs
pars_contidtion_dict['null_pars']: number of null parameters
pars_contidtion_dict['bad_list']: list of row numbers with bad parameters - for numeric indexing
"""
null_pars = 0
good_pars = 0
bad_list = []
for n, row in df.iterrows():
if row['parameters'] == []:
null_pars += 1
bad_list.append(n)
else:
good_pars += 1
if print_out:
print('good_pars', good_pars, '\nnull_pars', null_pars)
return {'good_pars': good_pars, 'null_pars': null_pars, 'bad_list': bad_list}
def display_images_df_columns_definition():
""" display an explanation of the images """
cols = {}
cols['image_filename'] = 'the file name as found in the header'
cols['function_name'] = 'm-file and function name'
cols['parameters'] = 'function parameters used to produce the image'
cols['max_iter'] = 'escape time algorithm maximum number of iterations'
cols['max_dist'] = 'escape time algorithm quit distance'
cols['Colormap'] = 'Name of colormap if logged'
cols['Center'] = 'center of image location on complex plane'
cols['bounds_box'] = '(upper left corner) ULC, URC, LLC, LRC'
cols['Author'] = 'author name if provied'
cols['location'] = 'file - subdirectory location'
cols['date'] = 'date the image file was written'
for k, v in cols.items():
print('%18s: %s'%(k,v))
def display_equations_df_columns_definition():
""" display an explanation of the images """
cols = {}
cols['arg_in'] = 'Input signiture of the m-file'
cols['arg_out'] = 'Output signiture of the m-file'
cols['eq_string'] = 'The equation as written in MATLAB'
cols['while_test'] = 'The loop test code'
cols['param_iterator'] = 'If parameters are iterated in the while loop'
cols['internal_vars'] = 'Variables that were set inside the m-file'
cols['while_lines'] = 'The actual code of the while loop'
for k, v in cols.items():
print('%15s: %s'%(k,v))
print('\n\tdisplay_images_df_columns_definition\n')
display_images_df_columns_definition()
print('\n\tdisplay_equations_df_columns_definition\n')
display_equations_df_columns_definition()
print('shape:',
Images_Chronicle_df.shape,
'Number of unique files:',
Images_Chronicle_df['image_filename'].nunique())
print('Number of unique functions used:',
Images_Chronicle_df['function_name'].nunique())
par_stats_dict = get_number_of_null_parameters(Images_Chronicle_df) # show parameters data
print('\nFirst 5 lines')
Images_Chronicle_df.head() # show top 5 lines
print(Equations_Chronicle_df.shape)
Equations_Chronicle_df.head()
cols = list(Equations_Chronicle_df.columns)
for c in cols:
print(c)
```
| true |
code
| 0.541288 | null | null | null | null |
|
**Author**: _Pradip Kumar Das_
**License:** https://github.com/PradipKumarDas/Competitions/blob/main/LICENSE
**Profile & Contact:** [LinkedIn](https://www.linkedin.com/in/daspradipkumar/) | [GitHub](https://github.com/PradipKumarDas) | [Kaggle](https://www.kaggle.com/pradipkumardas) | [email protected] (Email)
# Ugam Sentiment Analysis | MachineHack
**Dec. 22, 2021 - Jan. 10, 2022**
https://machinehack.com/hackathon/uhack_sentiments_20_decode_code_words/overview
**Sections:**
- Dependencies
- Exploratory Data Analysis (EDA) & Preprocessing
- Modeling & Evaluation
- Submission
NOTE: Running this notebook over CPU will be intractable as it uses Transformers, and hence it is recommended to use GPU.
# Dependencies
```
# The following packages may need to be first installed on cloud hosted Data Science platforms such as Google Colab.
!pip install transformers
# Imports required packages
import pandas as pd
import numpy as np
from sklearn.model_selection import StratifiedKFold
import tensorflow as tf
# from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint, TensorBoard
import transformers
from transformers import TFAutoModelForSequenceClassification, AutoTokenizer
import matplotlib.pyplot as plt
import seaborn as sns
import datetime, gc
```
# Initialization
```
# Connects drive in Google Colab
from google.colab import drive
drive.mount('/content/drive/')
# Changes working directory to the project directory
cd "/content/drive/MyDrive/Colab/Ugam_Sentiment_Analysis/"
# Configures styles for plotting runtime
plt.style.use("seaborn-whitegrid")
plt.rc(
"figure",
autolayout=True,
figsize=(11, 4),
titlesize=18,
titleweight='bold',
)
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=16,
titlepad=10,
)
%config InlineBackend.figure_format = 'retina'
# Sets Tranformer's level of verbosity to INFO level
transformers.logging.set_verbosity_error()
```
# Exploratory Data Analysis (EDA) & Preprocessing
```
# Loads train data set
train = pd.read_csv("./data/train.csv")
# Checks few rows from train data set
display(train)
# Sets dataframe's `Id` columns as its index
train.set_index("Id", drop=True, append=False, inplace=True)
# Loads test data set
test = pd.read_csv("./data/test.csv")
# Checks top few rows from test data set
display(test.head(5))
# Sets dataframe's `Id` columns as its index
test.set_index("Id", drop=True, append=False, inplace=True)
# Checks the distribution of review length (number of characters in review)
fig, ax = plt.subplots(1, 2, sharey=True)
fig.suptitle("Review Length")
train.Review.str.len().plot(kind='hist', bins=50, ax=ax[0])
ax[0].set_xlabel("Train Data")
ax[0].set_ylabel("No. of Reviews")
test.Review.str.len().plot(kind='hist', bins=50, ax=ax[1])
ax[1].set_xlabel("Test Data")
```
The above plot shows that lengthy reviews containing 1000+ characters are less compares to that of reviews having less than 1000 characters. Hence, first 512 characters from the reviews will be considered for analysis.
```
# Finds the distribution of each label
display(train.select_dtypes(["int"]).apply(pd.Series.value_counts))
# Let's find stratified cross validation on 'Polarity' label will have same distribution
sk_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
cv_generator = sk_fold.split(train, train.Polarity)
for fold, (idx_train, idx_val) in enumerate(cv_generator):
display(train.iloc[idx_train].select_dtypes(["int"]).apply(pd.Series.value_counts))
```
It shows the same distribution is available in cross validation.
# Modeling & Evaluation
The approach is to use pretrained **Transfomer** model and to fine-tune, if required. As fine-tuning over cross-validation is time consuming even on GPUs, let's avoid it, and hence prepare one stratified validation set first to check pretrained model's or fine-tuned model's performance.
```
# Creates data set splitter and gets indexes for train and validation rows
cv_generator = sk_fold.split(train, train.Polarity)
idx_train, idx_val = next(cv_generator)
# Sets parameters for Transformer model fine-tuning
model_config = {
"model_name": "distilbert-base-uncased-finetuned-sst-2-english", # selected pretrained model
"max_length": 512, # maximum number of review characters allowed to input to model
}
# Creates tokenizer from pre-trained transformer model
tokenizer = AutoTokenizer.from_pretrained(model_config["model_name"])
# Tokenize reviews for train, validation and test data set
train_encodings = tokenizer(
train.iloc[idx_train].Review.to_list(),
max_length=model_config["max_length"],
truncation=True,
padding=True,
return_tensors="tf"
)
val_encodings = tokenizer(
train.iloc[idx_val].Review.to_list(),
max_length=model_config["max_length"],
truncation=True,
padding=True,
return_tensors="tf"
)
test_encodings = tokenizer(
test.Review.to_list(),
max_length=model_config["max_length"],
truncation=True,
padding=True,
return_tensors="tf"
)
# Performs target specific model fine-tuning
"""
NOTE:
1) It was observed that increasing number of epochs more than one during model fine-tuning
does not improve model performance, and hence epochs is set to 1.
2) As pretrained model being used is already used for predicting sentiment polarity, that model
will not be fine-tuned any further, and will be used directly to predict sentimen polarity
against the test data. Fine-tuning was already experimented and found to be not useful as it
decreases performance with higher log loss and lower accuracy on validation data.
"""
columns = train.select_dtypes(["int"]).columns.tolist()
columns.remove("Polarity")
# Fine-tunes models except that of Polarity
for column in columns:
print(f"Fine tuning model for {column.upper()}...")
print("======================================================\n")
model = TFAutoModelForSequenceClassification.from_pretrained(model_config["model_name"])
# Prepares tensorflow dataset for both train, validation and test data
train_encodings_dataset = tf.data.Dataset.from_tensor_slices((
{"input_ids": train_encodings["input_ids"], "attention_mask": train_encodings["attention_mask"]},
train.iloc[idx_train][[column]]
)).batch(16).prefetch(tf.data.AUTOTUNE)
val_encodings_dataset = tf.data.Dataset.from_tensor_slices((
{"input_ids": val_encodings["input_ids"], "attention_mask": val_encodings["attention_mask"]},
train.iloc[idx_val][[column]]
)).batch(16).prefetch(tf.data.AUTOTUNE)
test_encodings_dataset = tf.data.Dataset.from_tensor_slices(
{"input_ids": test_encodings["input_ids"], "attention_mask": test_encodings["attention_mask"]}
).batch(16).prefetch(tf.data.AUTOTUNE)
predictions = tf.nn.softmax(model.predict(val_encodings_dataset).logits)
print("Pretrained model's perfomance on validation data before fine-tuning:",
tf.keras.metrics.binary_crossentropy(train.iloc[idx_val][column], predictions[:,1], from_logits=False).numpy(), "(log loss)",
tf.keras.metrics.binary_accuracy(train.iloc[idx_val][column], predictions[:,1]).numpy(), "(accuracy)\n"
)
del predictions
print("Starting fine tuning...")
# Freezes model configuration before starting fine-tuning
model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=5e-5),
loss=tf.keras.losses.binary_crossentropy,
metrics=[tf.keras.metrics.binary_crossentropy, tf.keras.metrics.binary_accuracy]
)
# Sets model file name to organize storing logs and fine-tuned models against
# model_filename = f"{column}" + "_" + datetime.datetime.now().strftime("%Y.%m.%d-%H:%M:%S")
# Fine tunes model
model.fit(
x=train_encodings_dataset,
validation_data=val_encodings_dataset,
batch_size=16,
epochs=1,
# callbacks=[
# EarlyStopping(monitor="val_loss", mode="min", patience=2, restore_best_weights=True, verbose=1),
# ModelCheckpoint(filepath=f"./models/{model_filename}", monitor="val_loss", mode="min", save_best_only=True, save_weights_only=True),
# TensorBoard(log_dir=f"./logs/{model_filename}", histogram_freq=1, update_freq='epoch')
# ],
use_multiprocessing=True)
print("\nFine tuning was completed.\n")
del train_encodings_dataset, val_encodings_dataset
print("Performing prediction on test data...", end="")
# Performs predictions on test data
predictions = tf.nn.softmax(model.predict(test_encodings_dataset).logits)
test[column] = predictions[:, 1]
del test_encodings_dataset
print("done\n")
del predictions, model
print("Skipping fine-tuning model for POLARITY (as it uses pretrained model) and continuing direct prediction on test data...")
print("======================================================================================================================\n")
print("Performing prediction on test data...", end="")
model = TFAutoModelForSequenceClassification.from_pretrained(model_config["model_name"])
# Prepares tensorflow dataset for test data
test_encodings_dataset = tf.data.Dataset.from_tensor_slices(
{"input_ids": test_encodings["input_ids"], "attention_mask": test_encodings["attention_mask"]}
).batch(16).prefetch(tf.data.AUTOTUNE)
# Performs predictions on test data
predictions = tf.nn.softmax(model.predict(test_encodings_dataset).logits)
test["Polarity"] = predictions[:, 1]
del test_encodings_dataset
del predictions, model
print("done\n")
print("Fine-tuning and test predictions were completed.")
```
# Submission
```
# Saves test predictions
test.select_dtypes(["float"]).to_csv("./submission.csv", index=False)
```
***Leaderboard score for this submission was 8.8942 as against highest of that was 2.74 on Jan 06, 2022 at 11:50 PM.***
| true |
code
| 0.727921 | null | null | null | null |
|
# SESSIONS ARE ALL YOU NEED
### Workshop on e-commerce personalization
This notebook showcases with working code the main ideas of our ML-in-retail workshop from June lst, 2021 at MICES (https://mices.co/). Please refer to the README in the repo for a bit of context!
While the code below is (well, should be!) fully functioning, please note we aim for functions which are pedagogically useful, more than terse code per se: it should be fairly easy to take these ideas and refactor the code to achieve more speed, better re-usability etc.
_If you want to use Google Colab, you can uncomment this cell:_
```
# if you need requirements....
# !pip install -r requirements.txt
# #from google.colab import drive
#drive.mount('/content/drive',force_remount=True)
#%cd drive/MyDrive/path_to_directory_containing_train_folder
#LOCAL_FOLDER = 'train'
```
## Basic import and some global vars to know where data is!
Here we import the libraries we need and set the working folders - make sure your current python interpreter has all the dependencies installed. If you want to use the same real-world data as I'm using, please download the open dataset you find at: https://github.com/coveooss/SIGIR-ecom-data-challenge.
```
import os
from random import choice
import time
import ast
import json
import numpy as np
import csv
from collections import Counter,defaultdict
# viz stuff
from sklearn.manifold import TSNE
from matplotlib import pyplot as plt
from IPython.display import Image
# gensim stuff for prod2vec
import gensim # gensim > 4
from gensim.similarities.annoy import AnnoyIndexer
# keras stuff for auto-encoder
from keras.layers.core import Dropout
from keras.layers.core import Dense
from keras.layers import Concatenate
from keras.models import Sequential
from keras.layers import Input
from keras.optimizers import SGD, Adam
from keras.models import Model
from keras.callbacks import EarlyStopping
from keras.utils import plot_model
from sklearn.model_selection import train_test_split
from keras import utils
import hashlib
from copy import deepcopy
%matplotlib inline
LOCAL_FOLDER = '/Users/jacopotagliabue/Documents/data_dump/train' # where is the dataset stored?
N_ROWS = 5000000 # how many rows we want to take (to avoid waiting too much for tutorial purposes)?
```
## Step 1: build a prod2vec space
For more information on prod2vec and its use, you can also check our blog post: https://blog.coveo.com/clothes-in-space-real-time-personalization-in-less-than-100-lines-of-code/ or latest NLP paper: https://arxiv.org/abs/2104.02061
```
def read_sessions_from_training_file(training_file: str, K: int = None):
"""
Read the training file containing product interactions, up to K rows.
:return: a list of lists, each list being a session (sequence of product IDs)
"""
user_sessions = []
current_session_id = None
current_session = []
with open(training_file) as csvfile:
reader = csv.DictReader(csvfile)
for idx, row in enumerate(reader):
# if a max number of items is specified, just return at the K with what you have
if K and idx >= K:
break
# just append "detail" events in the order we see them
# row will contain: session_id_hash, product_action, product_sku_hash
_session_id_hash = row['session_id_hash']
# when a new session begins, store the old one and start again
if current_session_id and current_session and _session_id_hash != current_session_id:
user_sessions.append(current_session)
# reset session
current_session = []
# check for the right type and append
if row['product_action'] == 'detail':
current_session.append(row['product_sku_hash'])
# update the current session id
current_session_id = _session_id_hash
# print how many sessions we have...
print("# total sessions: {}".format(len(user_sessions)))
# print first one to check
print("First session is: {}".format(user_sessions[0]))
assert user_sessions[0][0] == 'd5157f8bc52965390fa21ad5842a8502bc3eb8b0930f3f8eafbc503f4012f69c'
assert user_sessions[0][-1] == '63b567f4cef976d1411aecc4240984e46ebe8e08e327f2be786beb7ee83216d0'
return user_sessions
def train_product_2_vec_model(sessions: list,
min_c: int = 3,
size: int = 48,
window: int = 5,
iterations: int = 15,
ns_exponent: float = 0.75):
"""
Train CBOW to get product embeddings. We start with sensible defaults from the literature - please
check https://arxiv.org/abs/2007.14906 for practical tips on how to optimize prod2vec.
:param sessions: list of lists, as user sessions are list of interactions
:param min_c: minimum frequency of an event for it to be calculated for product embeddings
:param size: output dimension
:param window: window parameter for gensim word2vec
:param iterations: number of training iterations
:param ns_exponent: ns_exponent parameter for gensim word2vec
:return: trained product embedding model
"""
model = gensim.models.Word2Vec(sentences=sessions,
min_count=min_c,
vector_size=size,
window=window,
epochs=iterations,
ns_exponent=ns_exponent)
print("# products in the space: {}".format(len(model.wv.index_to_key)))
return model.wv
```
Get sessions from the training file, and train a prod2vec model with standard hyperparameters
```
# get sessions
sessions = read_sessions_from_training_file(
training_file=os.path.join(LOCAL_FOLDER, 'browsing_train.csv'),
K=N_ROWS)
# get a counter on all items for later use
sku_cnt = Counter([item for s in sessions for item in s])
# print out most common SKUs
sku_cnt.most_common(3)
# leave some sessions aside
idx = int(len(sessions) * 0.8)
train_sessions = sessions[0: idx]
test_sessions = sessions[idx:]
print("Train sessions # {}, test sessions # {}".format(len(train_sessions), len(test_sessions)))
# finally, train the p2vec, leaving all the default hyperparameters
prod2vec_model = train_product_2_vec_model(train_sessions)
```
Show how to get a prediction with knn
```
prod2vec_model.similar_by_word(sku_cnt.most_common(1)[0][0], topn=3)
```
Visualize the prod2vec space, color-coding for categories in the catalog
```
def plot_scatter_by_category_with_lookup(title,
skus,
sku_to_target_cat,
results,
custom_markers=None):
groups = {}
for sku, target_cat in sku_to_target_cat.items():
if sku not in skus:
continue
sku_idx = skus.index(sku)
x = results[sku_idx][0]
y = results[sku_idx][1]
if target_cat in groups:
groups[target_cat]['x'].append(x)
groups[target_cat]['y'].append(y)
else:
groups[target_cat] = {
'x': [x], 'y': [y]
}
# DEBUG print
print("Total of # groups: {}".format(len(groups)))
fig, ax = plt.subplots(figsize=(10, 10))
for group, data in groups.items():
ax.scatter(data['x'], data['y'],
alpha=0.3,
edgecolors='none',
s=25,
marker='o' if not custom_markers else custom_markers,
label=group)
plt.title(title)
plt.show()
return
def tsne_analysis(embeddings, perplexity=25, n_iter=1000):
tsne = TSNE(n_components=2, verbose=1, perplexity=perplexity, n_iter=n_iter)
return tsne.fit_transform(embeddings)
def get_sku_to_category_map(catalog_file, depth_index=1):
"""
For each SKU, get category from catalog file (if specified)
:return: dictionary, mapping SKU to a category
"""
sku_to_cats = dict()
with open(catalog_file) as csvfile:
reader = csv.DictReader(csvfile)
for row in reader:
_sku = row['product_sku_hash']
category_hash = row['category_hash']
if not category_hash:
continue
# pick only category at a certain depth in the tree
# e.g. x/xx/xxx, with depth=1, -> xx
branches = category_hash.split('/')
target_branch = branches[depth_index] if depth_index < len(branches) else None
if not target_branch:
continue
# if all good, store the mapping
sku_to_cats[_sku] = target_branch
return sku_to_cats
sku_to_category = get_sku_to_category_map(os.path.join(LOCAL_FOLDER, 'sku_to_content.csv'))
print("Total of # {} categories".format(len(set(sku_to_category.values()))))
print("Total of # {} SKU with a category".format(len(sku_to_category)))
# debug with a sample SKU
print(sku_to_category[sku_cnt.most_common(1)[0][0]])
skus = prod2vec_model.index_to_key
print("Total of # {} skus in the model".format(len(skus)))
embeddings = [prod2vec_model[s] for s in skus]
# print out tsne plot with standard params
tsne_results = tsne_analysis(embeddings)
assert len(tsne_results) == len(skus)
plot_scatter_by_category_with_lookup('Prod2vec', skus, sku_to_category, tsne_results)
# do a version with only top K categories
TOP_K = 5
cnt_categories = Counter(list(sku_to_category.values()))
top_categories = [c[0] for c in cnt_categories.most_common(TOP_K)]
# filter out SKUs outside of top categories
top_skus = []
top_tsne_results = []
for _s, _t in zip(skus, tsne_results):
if sku_to_category.get(_s, None) not in top_categories:
continue
top_skus.append(_s)
top_tsne_results.append(_t)
# re-plot tsne with filtered SKUs
print("Top SKUs # {}".format(len(top_skus)))
plot_scatter_by_category_with_lookup('Prod2vec (top {})'.format(TOP_K),
top_skus, sku_to_category, top_tsne_results)
```
### Bonus: faster inference
Gensim is awesome and support approximate, faster inference! You need to have installed ANNOY first, e.g. "pip install annoy". We re-run here on our prod space the original benchmark for word2vec from gensim!
See: https://radimrehurek.com/gensim/auto_examples/tutorials/run_annoy.html
```
# Set up the model and vector that we are using in the comparison
annoy_index = AnnoyIndexer(prod2vec_model, 100)
test_sku = sku_cnt.most_common(1)[0][0]
# test all is good
print(prod2vec_model.most_similar([test_sku], topn=2, indexer=annoy_index))
print(prod2vec_model.most_similar([test_sku], topn=2))
def avg_query_time(model, annoy_index=None, queries=5000):
"""Average query time of a most_similar method over random queries."""
total_time = 0
for _ in range(queries):
_v = model[choice(model.index_to_key)]
start_time = time.process_time()
model.most_similar([_v], topn=5, indexer=annoy_index)
total_time += time.process_time() - start_time
return total_time / queries
gensim_time = avg_query_time(prod2vec_model)
annoy_time = avg_query_time(prod2vec_model, annoy_index=annoy_index)
print("Gensim (s/query):\t{0:.5f}".format(gensim_time))
print("Annoy (s/query):\t{0:.5f}".format(annoy_time))
speed_improvement = gensim_time / annoy_time
print ("\nAnnoy is {0:.2f} times faster on average on this particular run".format(speed_improvement))
```
### Bonus: hyper tuning
For more info on hyper tuning in the context of product embeddings, please see our paper: https://arxiv.org/abs/2007.14906 and our data release: https://github.com/coveooss/fantastic-embeddings-sigir-2020.
We use the sessions we left out to simulate a small optimization loop...
```
def calculate_HR_on_NEP(model, sessions, k=10, min_length=3):
_count = 0
_hits = 0
for session in sessions:
# consider only decently-long sessions
if len(session) < min_length:
continue
# update the counter
_count += 1
# get the item to predict
target_item = session[-1]
# get model prediction using before-last item
query_item = session[-2]
# if model cannot make the prediction, it's a failure
if query_item not in model:
continue
predictions = model.similar_by_word(query_item, topn=k)
# debug
# print(target_item, query_item, predictions)
if target_item in [p[0] for p in predictions]:
_hits += 1
# debug
print("Total test cases: {}".format(_count))
return _hits / _count
# we simulate a test with 3 values for epochs in prod2ve
iterations_values = [1, 10]
# for each value we train a model, and use Next Event Prediction (NEP) to get a quality assessment
for i in iterations_values:
print("\n ======> Hyper value: {}".format(i))
cnt_model = train_product_2_vec_model(train_sessions, iterations=i)
# use hold-out to have NEP performance
_hr = calculate_HR_on_NEP(cnt_model, test_sessions)
print("HR: {}\n".format(_hr))
```
## Step 2: improving low-count vectors
For more information about prod2vec in the cold start scenario, please see our paper: https://dl.acm.org/doi/10.1145/3383313.3411477 and video: https://vimeo.com/455641121
```
def build_mapper(pro2vec_dims=48):
"""
Build a Keras model for content-based "fake" embeddings.
:return: a Keras model, mapping BERT-like catalog representations to the prod2vec space
"""
# input
description_input = Input(shape=(50,))
image_input = Input(shape=(50,))
# model
x = Dense(25, activation="relu")(description_input)
y = Dense(25, activation="relu")(image_input)
combined = Concatenate()([x, y])
combined = Dropout(0.3)(combined)
combined = Dense(25)(combined)
output = Dense(pro2vec_dims)(combined)
return Model(inputs=[description_input, image_input], outputs=output)
# get vectors representing text and images in the catalog
def get_sku_to_embeddings_map(catalog_file):
"""
For each SKU, get the text and image embeddings, as provided pre-computed by the dataset
:return: dictionary, mapping SKU to a tuple of embeddings
"""
sku_to_embeddings = dict()
with open(catalog_file) as csvfile:
reader = csv.DictReader(csvfile)
for row in reader:
_sku = row['product_sku_hash']
_description = row['description_vector']
_image = row['image_vector']
# skip when both vectors are not there
if not _description or not _image:
continue
# if all good, store the mapping
sku_to_embeddings[_sku] = (json.loads(_description), json.loads(_image))
return sku_to_embeddings
sku_to_embeddings = get_sku_to_embeddings_map(os.path.join(LOCAL_FOLDER, 'sku_to_content.csv'))
print("Total of # {} SKUs with embeddings".format(len(sku_to_embeddings)))
# print out an example
_d, _i = sku_to_embeddings['438630a8ba0320de5235ee1bedf3103391d4069646d640602df447e1042a61a3']
print(len(_d), len(_i), _d[:5], _i[:5])
# just make sure we have the SKUs in the model and a counter
skus = prod2vec_model.index_to_key
print("Total of # {} skus in the model".format(len(skus)))
print(sku_cnt.most_common(5))
# above which percentile of frequency we consider SKU popular enough to be our training set?
FREQUENT_PRODUCTS_PTILE = 80
_counts = [c[1] for c in sku_cnt.most_common()]
_counts[:3]
# make sure we have just SKUS in the prod2vec space for which we have embeddings
popular_threshold = np.percentile(_counts, FREQUENT_PRODUCTS_PTILE)
popular_skus = [s for s in skus if s in sku_to_embeddings and sku_cnt.get(s, 0) > popular_threshold]
product_embeddings = [prod2vec_model[s] for s in popular_skus]
description_embeddings = [sku_to_embeddings[s][0] for s in popular_skus]
image_embeddings = [sku_to_embeddings[s][1] for s in popular_skus]
# debug
print(popular_threshold, len(skus), len(popular_skus))
# print(description_embeddings[:1][:3])
# print(image_embeddings[:1][:3])
# train the mapper now
training_data_X = [np.array(description_embeddings), np.array(image_embeddings)]
training_data_y = np.array(product_embeddings)
es = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=20, restore_best_weights=True)
# build and display model
rare_net = build_mapper()
plot_model(rare_net, show_shapes=True, show_layer_names=True, to_file='rare_net.png')
Image('rare_net.png')
# train!
rare_net.compile(loss='mse', optimizer='rmsprop')
rare_net.fit(training_data_X,
training_data_y,
batch_size=200,
epochs=20000,
validation_split=0.2,
callbacks=[es])
# rarest_skus = [_[0] for _ in sku_cnt.most_common()[-500:]]
# test_skus = [s for s in rarest_skus if s in sku_to_embeddings]
# get to rare vectors
test_skus = [s for s in skus if s in sku_to_embeddings and sku_cnt.get(s, 0) < popular_threshold/2]
print(len(skus), len(test_skus))
# prepare embeddings for prediction
rare_description_embeddings = [sku_to_embeddings[s][0] for s in test_skus]
rare_image_embeddings = [sku_to_embeddings[s][1] for s in test_skus]
# prepare embeddings for prediction
test_data_X = [np.array(rare_description_embeddings), np.array(rare_image_embeddings)]
predicted_embeddings = rare_net.predict(test_data_X)
# debug
# print(len(predicted_embeddings))
# print(predicted_embeddings[0][:10])
def calculate_HR_on_NEP_rare(model, sessions, rare_skus, k=10, min_length=3):
_count = 0
_hits = 0
_rare_hits = 0
_rare_count = 0
for session in sessions:
# consider only decently-long sessions
if len(session) < min_length:
continue
# update the counter
_count += 1
# get the item to predict
target_item = session[-1]
# get model prediction using before-last item
query_item = session[-2]
# if model cannot make the prediction, it's a failure
if query_item not in model:
continue
# increment counter if rare sku
if query_item in rare_skus:
_rare_count+=1
predictions = model.similar_by_word(query_item, topn=k)
# debug
# print(target_item, query_item, predictions)
if target_item in [p[0] for p in predictions]:
_hits += 1
# track hits if query is rare sku
if query_item in rare_skus:
_rare_hits+=1
# debug
print("Total test cases: {}".format(_count))
print("Total rare test cases: {}".format(_rare_count))
return _hits / _count, _rare_hits/_rare_count
# make copy of original prod2vec model
prod2vec_rare_model = deepcopy(prod2vec_model)
# update model with new vectors
prod2vec_rare_model.add_vectors(test_skus, predicted_embeddings, replace=True)
prod2vec_rare_model.fill_norms(force=True)
# check
assert np.array_equal(predicted_embeddings[0], prod2vec_rare_model[test_skus[0]])
# test new model
calculate_HR_on_NEP_rare(prod2vec_rare_model, test_sessions, test_skus)
# test original model
calculate_HR_on_NEP_rare(prod2vec_model, test_sessions, test_skus)
```
## Step 3: query scoping
For more information about query scoping, please see our paper: https://www.aclweb.org/anthology/2020.ecnlp-1.2/ and repository: https://github.com/jacopotagliabue/session-path
```
# get vectors representing text and images in the catalog
def get_query_to_category_dataset(search_file, cat_2_id, sku_to_category):
"""
For each query, get a label representing the category in items clicked after the query.
It uses as input a mapping "sku_to_category" to join the search file with catalog meta-data!
:return: two lists, matching query vectors to a label
"""
query_X = list()
query_Y = list()
with open(search_file) as csvfile:
reader = csv.DictReader(csvfile)
for row in reader:
_click_products = row['clicked_skus_hash']
if not _click_products: # or _click_product not in sku_to_category:
continue
# clean the string and extract SKUs from array
cleaned_skus = ast.literal_eval(_click_products)
for s in cleaned_skus:
if s in sku_to_category:
query_X.append(json.loads(row['query_vector']))
target_category_as_int = cat_2_id[sku_to_category[s]]
query_Y.append(utils.to_categorical(target_category_as_int, num_classes=len(cat_2_id)))
return query_X, query_Y
sku_to_category = get_sku_to_category_map(os.path.join(LOCAL_FOLDER, 'sku_to_content.csv'))
print("Total of # {} categories".format(len(set(sku_to_category.values()))))
cats = list(set(sku_to_category.values()))
cat_2_id = {c: idx for idx, c in enumerate(cats)}
print(cat_2_id[cats[0]])
query_X, query_Y = get_query_to_category_dataset(os.path.join(LOCAL_FOLDER, 'search_train.csv'),
cat_2_id,
sku_to_category)
print(len(query_X))
print(query_Y[0])
x_train, x_test, y_train, y_test = train_test_split(np.array(query_X), np.array(query_Y), test_size=0.2)
def build_query_scoping_model(input_d, target_classes):
print('Shape tensor {}, target classes {}'.format(input_d, target_classes))
# define model
model = Sequential()
model.add(Dense(64, activation='relu', input_dim=input_d))
model.add(Dropout(0.5))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(target_classes, activation='softmax'))
return model
query_model = build_query_scoping_model(x_train[0].shape[0], y_train[0].shape[0])
# compile model
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
query_model.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
# train first
query_model.fit(x_train, y_train, epochs=10, batch_size=32)
# compute and print eval score
score = query_model.evaluate(x_test, y_test, batch_size=32)
score
# get vectors representing text and images in the catalog
def get_query_info(search_file):
"""
For each query, extract relevant metadata of query and to match with session data
:return: list of queries with metadata
"""
queries = list()
with open(search_file) as csvfile:
reader = csv.DictReader(csvfile)
for row in reader:
_click_products = row['clicked_skus_hash']
if not _click_products: # or _click_product not in sku_to_category:
continue
# clean the string and extract SKUs from array
cleaned_skus = ast.literal_eval(_click_products)
queries.append({'session_id_hash' : row['session_id_hash'],
'server_timestamp_epoch_ms' : int(row['server_timestamp_epoch_ms']),
'clicked_skus' : cleaned_skus,
'query_vector' : json.loads(row['query_vector'])})
print("# total queries: {}".format(len(queries)))
return queries
def get_session_info_for_queries(training_file: str, query_info: list, K: int = None):
"""
Read the training file containing product interactions for sessions with query, up to K rows.
:return: dict of lists with session_id as key, each list being a session (sequence of product events with metadata)
"""
user_sessions = dict()
current_session_id = None
current_session = []
query_session_ids = set([ _['session_id_hash'] for _ in query_info])
with open(training_file) as csvfile:
reader = csv.DictReader(csvfile)
for idx, row in enumerate(reader):
# if a max number of items is specified, just return at the K with what you have
if K and idx >= K:
break
# just append "detail" events in the order we see them
# row will contain: session_id_hash, product_action, product_sku_hash
_session_id_hash = row['session_id_hash']
# when a new session begins, store the old one and start again
if current_session_id and current_session and _session_id_hash != current_session_id:
user_sessions[current_session_id] = current_session
# reset session
current_session = []
# check for the right type and append event info
if row['product_action'] == 'detail' and _session_id_hash in query_session_ids :
current_session.append({'product_sku_hash': row['product_sku_hash'],
'server_timestamp_epoch_ms' : int(row['server_timestamp_epoch_ms'])})
# update the current session id
current_session_id = _session_id_hash
# print how many sessions we have...
print("# total sessions: {}".format(len(user_sessions)))
return dict(user_sessions)
query_info = get_query_info(os.path.join(LOCAL_FOLDER, 'search_train.csv'))
session_info = get_session_info_for_queries(os.path.join(LOCAL_FOLDER, 'browsing_train.csv'), query_info)
def get_contextual_query_to_category_dataset(query_info, session_info, prod2vec_model, cat_2_id, sku_to_category):
"""
For each query, get a label representing the category in items clicked after the query.
It uses as input a mapping "sku_to_category" to join the search file with catalog meta-data!
It also creates a joint embedding for input by concatenating query vector and average session vector up till
when query was made
:return: two lists, matching query vectors to a label
"""
query_X = list()
query_Y = list()
for row in query_info:
query_timestamp = row['server_timestamp_epoch_ms']
cleaned_skus = row['clicked_skus']
session_id_hash = row['session_id_hash']
if session_id_hash not in session_info or not cleaned_skus: # or _click_product not in sku_to_category:
continue
session_skus = session_info[session_id_hash]
context_skus = [ e['product_sku_hash'] for e in session_skus if query_timestamp > e['server_timestamp_epoch_ms']
and e['product_sku_hash'] in prod2vec_model]
if not context_skus:
continue
context_vector = np.mean([prod2vec_model[sku] for sku in context_skus], axis=0).tolist()
for s in cleaned_skus:
if s in sku_to_category:
query_X.append(row['query_vector'] + context_vector)
target_category_as_int = cat_2_id[sku_to_category[s]]
query_Y.append(utils.to_categorical(target_category_as_int, num_classes=len(cat_2_id)))
return query_X, query_Y
context_query_X, context_query_Y = get_contextual_query_to_category_dataset(query_info,
session_info,
prod2vec_model,
cat_2_id,
sku_to_category)
print(len(context_query_X))
print(context_query_Y[0])
x_train, x_test, y_train, y_test = train_test_split(np.array(context_query_X), np.array(context_query_Y), test_size=0.2)
contextual_query_model = build_query_scoping_model(x_train[0].shape[0], y_train[0].shape[0])
# compile model
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
contextual_query_model.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
# train first
contextual_query_model.fit(x_train, y_train, epochs=10, batch_size=32)
# compute and print eval score
score = contextual_query_model.evaluate(x_test, y_test, batch_size=32)
score
```
| true |
code
| 0.380759 | null | null | null | null |
|
## MIDI Generator
```
## Uncomment command below to kill current job:
#!neuro kill $(hostname)
import random
import sys
import subprocess
import torch
sys.path.append('../midi-generator')
%load_ext autoreload
%autoreload 2
import IPython.display as ipd
from model.dataset import MidiDataset
from utils.load_model import load_model
from utils.generate_midi import generate_midi
from utils.seed import set_seed
from utils.write_notes import write_notes
```
Each `*.mid` file can be thought of as a sequence where notes and chords follow each other with specified time offsets between them. So, following this model a next note can be predicted with a `seq2seq` model. In this work, a simple `GRU`-based model is used.
Note that the number of available notes and chord in vocabulary is not specified and depends on a dataset which a model was trained on.
To listen to MIDI files from Jupyter notebook, let's define help function which transforms `*.mid` file to `*.wav` file.
```
def mid2wav(mid_path, wav_path):
subprocess.check_output(['timidity', mid_path, '-OwS', '-o', wav_path])
```
The next step is loading the model from the checkpoint. To make experiments reproducible let's also specify random seed.
You can also try to use the model, which was trained with label smoothing (see `../results/smoothing.ch`).
```
seed = 1234
set_seed(seed)
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
print(device)
model, vocab = load_model(checkpoint_path='../results/test.ch', device=device)
```
Let's also specify additional help function to avoid code duplication.
```
def dump_result(file_preffix, vocab, note_seq, offset_seq=None):
note_seq = vocab.decode(note_seq)
notes = MidiDataset.decode_notes(note_seq, offset_seq=offset_seq)
mid_path = file_preffix + '.mid'
wav_path = file_preffix + '.wav'
write_notes(mid_path, notes)
mid2wav(mid_path, wav_path)
return wav_path
```
# MIDI file generation
Let's generate a new file. Note that the parameter `seq_len` specifies the length of the output sequence of notes.
Function `generate_midi` return sequence of generated notes and offsets between them.
## Nucleus (`top-p`) Sampling
Sample from the most probable tokens, which sum of probabilities gives `top-p`. If `top-p == 0` the most probable token is sampled.
## Temperature
As `temperature` → 0 this approaches greedy decoding, while `temperature` → ∞ asymptotically approaches uniform sampling from the vocabulary.
```
note_seq, offset_seq = generate_midi(model, vocab, seq_len=128, top_p=0, temperature=1, device=device)
```
Let's listen to result midi.
```
# midi with constant offsets
ipd.Audio(dump_result('../results/output_without_offsets', vocab, note_seq, offset_seq=None))
# midi with generated offsets
ipd.Audio(dump_result('../results/output_with_offsets.mid', vocab, note_seq, offset_seq))
```
The result with constant offsets sounds better, doesn't it? :)
Be free to try different generation parameters (`top-p` and `temperature`) to understand their impact on the resulting sound.
You can also train your own model with different specs (e.g. different hidden size) or use label smoothing during training.
# Continue existing file
## Continue sampled notes
For beginning, let's continue sound that consists of sampled from `vocab` notes.
```
seed = 4321
set_seed(seed)
history_notes = random.choices(range(len(vocab)), k=20)
history_offsets = len(history_notes) * [0.5]
ipd.Audio(dump_result('../results/random_history', vocab, history_notes, history_offsets))
```
It sounds a little bit chaotic. Let's try to continue this with our model.
```
history = [*zip(history_notes, history_offsets)]
note_seq, offset_seq = generate_midi(model, vocab, seq_len=128, top_p=0, temperature=1, device=device,
history=history)
# midi with constant offsets
ipd.Audio(dump_result('../results/random_without_offsets', vocab, note_seq, offset_seq=None))
```
After the sampled part ends, the generated melody starts to sound better.
## Continue existed melody
```
raw_notest = MidiDataset.load_raw_notes('../data/mining.mid')
org_note_seq, org_offset_seq = MidiDataset.encode_notes(raw_notest)
org_note_seq = vocab.encode(org_note_seq)
```
Let's listen to it
```
ipd.Audio(dump_result('../results/original_sound', vocab, org_note_seq, org_offset_seq))
```
and take 20 first elements from the sequence as out history sequence.
```
history_notes = org_note_seq[:20]
history_offsets = org_offset_seq[:20]
history = [*zip(history_notes, history_offsets)]
note_seq, offset_seq = generate_midi(model, vocab, seq_len=128, top_p=0, temperature=1, device=device,
history=history)
# result melody without generated offsets
ipd.Audio(dump_result('../results/continue_rand_without_offsets', vocab, note_seq, offset_seq=None))
# result melody with generated offsets
ipd.Audio(dump_result('../results/continue_rand_with_offsets', vocab, note_seq, offset_seq))
```
You can try to overfit your model on one melody to get better results. Otherwise, you can use already pretrained model (`../results/onemelody.ch`)
# Model overfitted on one melody
Let's try the same thing which we did before. Let's continue melody, but this time do it with the model,
which was overfitted with this melody.
```
seed = 1234
set_seed(seed)
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
model, vocab = load_model(checkpoint_path='../results/onemelody.ch', device=device)
raw_notest = MidiDataset.load_raw_notes('../data/Final_Fantasy_Matouyas_Cave_Piano.mid')
org_note_seq, org_offset_seq = MidiDataset.encode_notes(raw_notest)
org_note_seq = vocab.encode(org_note_seq)
```
Let's listen to it.
```
ipd.Audio(dump_result('../results/onemelody_original_sound', vocab, org_note_seq, org_offset_seq))
end = 60
history_notes = org_note_seq[:end]
history_offsets = org_offset_seq[:end]
```
Listen to history part of loaded melody.
```
ipd.Audio(dump_result('../results/onemelody_history', vocab, history_notes, history_offsets))
```
Now we can try to continue the original melody with our model. But firstly, you can listen to the original tail part of the melody do refresh it in the memory and have reference to compare with.
```
tail_notes = org_note_seq[end:]
tail_offsets = org_offset_seq[end:]
ipd.Audio(dump_result('../results/onemelody_tail', vocab, tail_notes, tail_offsets))
history = [*zip(history_notes, history_offsets)]
note_seq, offset_seq = generate_midi(model, vocab, seq_len=128, top_p=0, temperature=1, device=device,
history=history)
# delete history part
note_seq = note_seq[end:]
offset_seq = offset_seq[end:]
# result melody without generated offsets
ipd.Audio(dump_result('../results/continue_onemelody_without_offsets', vocab, note_seq, offset_seq=None))
# result melody with generated offsets
ipd.Audio(dump_result('../results/continue_onemelody_with_offsets', vocab, note_seq, offset_seq))
```
As you can hear, this time, the model generated better offsets and the result melody does not sound so chaostic.
| true |
code
| 0.524577 | null | null | null | null |
|
# Sandbox - Tutorial
## Building a fiber bundle
A [fiber bundle](https://github.com/3d-pli/fastpli/wiki/FiberModel) consit out of multiple individual nerve fibers.
A fiber bundle is a list of fibers, where fibers are represented as `(n,4)-np.array`.
This makes desining individually fiber of any shape possible.
However since nerve fibers are often in nerve fiber bundles, this toolbox allows to fill fiber_bundles from a pattern of fibers.
Additionally this toolbox also allows to build parallell cubic shapes as well as different kinds of cylindric shapes to allow a faster building experience.
## General imports
First, we prepair all necesarry modules and defining a function to euqalice all three axis of an 3d plot.
You can change the `magic ipython` line from `inline` to `qt`.
This generate seperate windows allowing us also to rotate the resulting plots and therfore to investigate the 3d models from different views.
Make sure you have `PyQt5` installed if you use it.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# %matplotlib qt
import fastpli.model.sandbox as sandbox
def set_3d_axes_equal(ax):
x_limits = ax.get_xlim3d()
y_limits = ax.get_ylim3d()
z_limits = ax.get_zlim3d()
x_range = abs(x_limits[1] - x_limits[0])
x_middle = np.mean(x_limits)
y_range = abs(y_limits[1] - y_limits[0])
y_middle = np.mean(y_limits)
z_range = abs(z_limits[1] - z_limits[0])
z_middle = np.mean(z_limits)
plot_radius = 0.5 * max([x_range, y_range, z_range])
ax.set_xlim3d([x_middle - plot_radius, x_middle + plot_radius])
ax.set_ylim3d([y_middle - plot_radius, y_middle + plot_radius])
ax.set_zlim3d([z_middle - plot_radius, z_middle + plot_radius])
```
## Designing a fiber bundle
The idea is to build design first a macroscopic struces, i. e. nerve fiber bundles, which can then at a later step be filled with individual nerve fibers.
We start by defining a fiber bundle as a trajectory of points (similar to fibers).
As an example we start with use a helical form.
```
t = np.linspace(0, 4 * np.pi, 50, True)
traj = np.array((42 * np.cos(t), 42 * np.sin(t), 10 * t)).T
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
ax.plot(
traj[:, 0],
traj[:, 1],
traj[:, 2],
)
plt.title("fb trajectory")
set_3d_axes_equal(ax)
plt.show()
```
### seed points
seed points are used to initialize the populating process of individual fibers inside the fiber bundle.
Seed points are a list of 3d points.
This toolbox provides two methods to build seed points pattern.
The first one is a 2d triangular grid.
It is defined by a `width`, `height` and an inside `spacing` between the seed point.
Additionally one can actiavte the `center` option so that the seed points are centered around a seed point at `(0,0,0)`.
The second method provides a circular shape instead of a rectangular.
However it can also be achievd by using an additional function `crop_circle` which returns only seed points along the first two dimensions with the defined `radius` around the center.
```
seeds = sandbox.seeds.triangular_grid(width=42,
height=42,
spacing=6,
center=True)
radius = 21
circ_seeds = sandbox.seeds.crop_circle(radius=radius, seeds=seeds)
fig, ax = plt.subplots(1, 1)
plt.title("seed points")
plt.scatter(seeds[:, 0], seeds[:, 1])
plt.scatter(circ_seeds[:, 0], circ_seeds[:, 1])
ax.set_aspect('equal', 'box')
# plot circle margin
t = np.linspace(0, 2 * np.pi, 42)
x = radius * np.cos(t)
y = radius * np.sin(t)
plt.plot(x, y)
plt.show()
```
### Generating a fiber bundle from seed points
The next step is to build a fiber bundle from the desined trajectory and seed points.
However one additional step is necesarry.
Since nerve fibers are not a line, but a 3d object, they need also a volume for the later `solving` and `simulation` steps of this toolbox.
This toolbox describes nerve fibers as tubes, which are defined by a list of points and radii, i. e. (n,4)-np.array).
The radii `[:,3]` can change along the fiber trajectories `[:,0:3]` allowiing for a change of thickness.
Now we have everything we need to build a fiber bundle from the desined trajectory and seed points.
The function `bundle` provides this funcionallity.
Additionally to the `traj` and `seeds` parameter the `radii` can be a single number if all fibers should have the same radii, or a list of numbers, if each fiber shell have a different radii.
An additional `scale` parameter allows to scale the seed points along the trajectory e. g. allowing for a fanning.
```
# populating fiber bundle
fiber_bundle = sandbox.build.bundle(
traj=traj,
seeds=circ_seeds,
radii=np.random.uniform(0.5, 0.8, circ_seeds.shape[0]),
scale=0.25 + 0.5 * np.linspace(0, 1, traj.shape[0]))
# plotting
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
for fiber in fiber_bundle:
ax.plot(fiber[:, 0], fiber[:, 1], fiber[:, 2])
plt.title("helical thinning out fiber bundle")
set_3d_axes_equal(ax)
plt.show()
```
## Additional macroscopic structures
In the development and using of this toolbox, it was found that it is usefull to have other patterns than filled fiber bundles to build macroscopic structures.
Depending on a brain sections, where the nerve fiber orientation is measured with the 3D-PLI technique, nerve fibers can be visibale as type of patterns.
### Cylindrical shapes
Radial shaped patterns can be quickly build with the following `cylinder` method.
A hollow cylinder is defined by a inner and outer radii `r_in` and `r_out`, along two points `p` and `q`.
Additionally the cylinder can be also only partial along its radius by defining two angles `alpha` and `beta`.
Again as for the `bundle` method, one needs seed points to defining a pattern.
Filling this cylindrig shape can be performed by three differet `mode`s:
- radial
- circular
- parallel
```
# plotting
seeds = sandbox.seeds.triangular_grid(width=200,
height=200,
spacing=5,
center=True)
fig, axs = plt.subplots(1, 3, figsize=(15,5), subplot_kw={'projection':'3d'}, constrained_layout=True)
for i, mode in enumerate(['radial', 'circular', 'parallel']):
# ax = fig.add_subplot(1, 1, 1, projection='3d')
fiber_bundle = sandbox.build.cylinder(p=(0, 80, 50),
q=(40, 80, 100),
r_in=20,
r_out=40,
seeds=seeds,
radii=1,
alpha=np.deg2rad(20),
beta=np.deg2rad(160),
mode=mode)
for fiber in fiber_bundle:
axs[i].plot(fiber[:, 0], fiber[:, 1], fiber[:, 2])
set_3d_axes_equal(axs[i])
axs[i].set_title(f'{mode}')
plt.show()
```
### Cubic shapes
The next method allows placing fibers inside a cube with a use definde direction.
The cube is definded by two 3d points `p` and `q`.
The direction of the fibers inside the cube is defined by spherical angels `phi` and `theta`.
Seed points again describe the pattern of fibers inside the cube.
The seed points (rotated its xy-plane according to `phi` and `theta`) are places at point `q` and `q`.
From the corresponding seed points are the starting and end point for each fiber.
```
# define cub corner points
p = np.array([0, 80, 50])
q = np.array([40, 180, 100])
# create seed points which will fill the cube
d = np.max(np.abs(p - q)) * np.sqrt(3)
seeds = sandbox.seeds.triangular_grid(width=d,
height=d,
spacing=10,
center=True)
# fill a cube with (theta, phi) directed fibers
fiber_bundle = sandbox.build.cuboid(p=p,
q=q,
phi=np.deg2rad(45),
theta=np.deg2rad(90),
seeds=seeds,
radii=1)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
for fiber in fiber_bundle:
ax.plot(fiber[:, 0], fiber[:, 1], fiber[:, 2])
plt.title('cubic shape')
set_3d_axes_equal(ax)
plt.show()
```
## next
from here further anatomical more interesting examples are presented in the solver tutorial and `examples/crossing.py` example.
| true |
code
| 0.70645 | null | null | null | null |
|
## 13.2 유가증권시장 12개월 모멘텀
최근 투자 기간 기준으로 12개월 모멘텀 계산 날짜 구하기
```
from pykrx import stock
import FinanceDataReader as fdr
df = fdr.DataReader(symbol='KS11', start="2019-11")
start = df.loc["2019-11"]
end = df.loc["2020-09"]
df.loc["2020-11"].head()
start
start_date = start.index[0]
end_date = end.index[-1]
print(start_date, end_date)
```
가격 모멘텀 계산 시작일 기준으로 등락률을 계산합니다.
```
df1 = stock.get_market_ohlcv_by_ticker("20191101")
df2 = stock.get_market_ohlcv_by_ticker("20200929")
kospi = df1.join(df2, lsuffix="_l", rsuffix="_r")
kospi
```
12개월 등락률(가격 모멘텀, 최근 1개월 제외)을 기준으로 상위 20종목의 종목 코드를 가져와봅시다.
```
kospi['모멘텀'] = 100 * (kospi['종가_r'] - kospi['종가_l']) / kospi['종가_l']
kospi = kospi[['종가_l', '종가_r', '모멘텀']]
kospi.sort_values(by='모멘텀', ascending=False)[:20]
kospi_momentum20 = kospi.sort_values(by='모멘텀', ascending=False)[:20]
kospi_momentum20.rename(columns={"종가_l": "매수가", "종가_r": "매도가"}, inplace=True)
kospi_momentum20
df3 = stock.get_market_ohlcv_by_ticker("20201102")
df4 = stock.get_market_ohlcv_by_ticker("20210430")
pct_df = df3.join(df4, lsuffix="_l", rsuffix="_r")
pct_df
pct_df = pct_df[['종가_l', '종가_r']]
kospi_momentum20_result = kospi_momentum20.join(pct_df)
kospi_momentum20_result
kospi_momentum20_result['수익률'] = (kospi_momentum20_result['종가_r'] /
kospi_momentum20_result['종가_l'])
kospi_momentum20_result
수익률평균 = kospi_momentum20_result['수익률'].fillna(0).mean()
수익률평균
mom20_cagr = 수익률평균 ** (1/0.5) - 1 # 6개월
mom20_cagr * 100
df_ref = fdr.DataReader(
symbol='KS11',
start="2020-11-02", # 첫번째 거래일
end="2021-04-30"
)
df_ref
CAGR = ((df_ref['Close'].iloc[-1] / df_ref['Close'].iloc[0]) ** (1/0.5)) -1
CAGR * 100
```
## 13.3 대형주 12개월 모멘텀
대형주(시가총액 200위) 기준으로 상대 모멘텀이 큰 종목을 20개 선정하는 전략
```
df1 = stock.get_market_ohlcv_by_ticker("20191101", market="ALL")
df2 = stock.get_market_ohlcv_by_ticker("20200929", market="ALL")
all = df1.join(df2, lsuffix="_l", rsuffix="_r")
all
# 기본 필터링
# 우선주 제외
all2 = all.filter(regex="0$", axis=0).copy()
all2
all2['모멘텀'] = 100 * (all2['종가_r'] - all2['종가_l']) / all2['종가_l']
all2 = all2[['모멘텀']]
all2
cap = stock.get_market_cap_by_ticker(date="20200929", market="ALL")
cap = cap[['시가총액']]
cap
all3 = all2.join(other=cap)
all3
# 대형주 필터링
big = all3.sort_values(by='시가총액', ascending=False)[:200]
big
big.sort_values(by='모멘텀', ascending=False)
big_pct20 = big.sort_values(by='모멘텀', ascending=False)[:20]
big_pct20
df3 = stock.get_market_ohlcv_by_ticker("20201102", market="ALL")
df4 = stock.get_market_ohlcv_by_ticker("20211015", market="ALL")
pct_df = df3.join(df4, lsuffix="_l", rsuffix="_r")
pct_df['수익률'] = pct_df['종가_r'] / pct_df['종가_l']
pct_df = pct_df[['종가_l', '종가_r', '수익률']]
pct_df
big_mom_result = big_pct20.join(pct_df)
big_mom_result
평균수익률 = big_mom_result['수익률'].mean()
big_mom_cagr = (평균수익률 ** 1/1) -1
big_mom_cagr * 100
```
## 13.4 장기 백테스팅
```
import pandas as pd
import datetime
from dateutil.relativedelta import relativedelta
year = 2010
month = 11
period = 6
inv_start = f"{year}-{month}-01"
inv_start = datetime.datetime.strptime(inv_start, "%Y-%m-%d")
inv_end = inv_start + relativedelta(months=period-1)
mom_start = inv_start - relativedelta(months=12)
mom_end = inv_start - relativedelta(months=2)
print(mom_start.strftime("%Y-%m"), mom_end.strftime("%Y-%m"), "=>",
inv_start.strftime("%Y-%m"), inv_end.strftime("%Y-%m"))
df = fdr.DataReader(symbol='KS11')
df
def get_business_day(df, year, month, index=0):
str_month = f"{year}-{month}"
return df.loc[str_month].index[index]
df = fdr.DataReader(symbol='KS11')
get_business_day(df, 2010, 1, 0)
def momentum(df, year=2010, month=11, period=12):
# 투자 시작일, 종료일
str_day = f"{year}-{month}-01"
start = datetime.datetime.strptime(str_day, "%Y-%m-%d")
end = start + relativedelta(months=period-1)
inv_start = get_business_day(df, start.year, start.month, 0) # 첫 번째 거래일의 종가
inv_end = get_business_day(df, end.year, end.month, -1)
inv_start = inv_start.strftime("%Y%m%d")
inv_end = inv_end.strftime("%Y%m%d")
#print(inv_start, inv_end)
# 모멘텀 계산 시작일, 종료일
end = start - relativedelta(months=2) # 역추세 1개월 제외
start = start - relativedelta(months=period)
mom_start = get_business_day(df, start.year, start.month, 0) # 첫 번째 거래일의 종가
mom_end = get_business_day(df, end.year, end.month, -1)
mom_start = mom_start.strftime("%Y%m%d")
mom_end = mom_end.strftime("%Y%m%d")
print(mom_start, mom_end, " | ", inv_start, inv_end)
# momentum 계산
df1 = stock.get_market_ohlcv_by_ticker(mom_start)
df2 = stock.get_market_ohlcv_by_ticker(mom_end)
mon_df = df1.join(df2, lsuffix="l", rsuffix="r")
mon_df['등락률'] = (mon_df['종가r'] - mon_df['종가l'])/mon_df['종가l']*100
# 우선주 제외
mon_df = mon_df.filter(regex="0$", axis=0)
mon20 = mon_df.sort_values(by="등락률", ascending=False)[:20]
mon20 = mon20[['등락률']]
#print(mon20)
# 투자 기간 수익률
df3 = stock.get_market_ohlcv_by_ticker(inv_start)
df4 = stock.get_market_ohlcv_by_ticker(inv_end)
inv_df = df3.join(df4, lsuffix="l", rsuffix="r")
inv_df['수익률'] = inv_df['종가r'] / inv_df['종가l'] # 수익률 = 매도가 / 매수가
inv_df = inv_df[['수익률']]
# join
result_df = mon20.join(inv_df)
result = result_df['수익률'].fillna(0).mean()
return year, result
import time
data = []
for year in range(2010, 2021):
ret = momentum(df, year, month=11, period=6)
data.append(ret)
time.sleep(1)
import pandas as pd
ret_df = pd.DataFrame(data=data, columns=['year', 'yield'])
ret_df.set_index('year', inplace=True)
ret_df
cum_yield = ret_df['yield'].cumprod()
cum_yield
CAGR = cum_yield.iloc[-1] ** (1/11) - 1
CAGR * 100
buy_price = df.loc["2010-11"].iloc[0, 0]
sell_price = df.loc["2021-04"].iloc[-1, 0]
kospi_yield = sell_price / buy_price
kospi_cagr = kospi_yield ** (1/11)-1
kospi_cagr * 100
```
| true |
code
| 0.288694 | null | null | null | null |
|
<h2> 25ppm - somehow more features detected than at 4ppm... I guess because more likely to pass over the #scans needed to define a feature </h2>
Enough retcor groups, loads of peak insertion problem (1000's). Does that mean data isn't centroided...?
```
import time
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn import preprocessing
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import StratifiedShuffleSplit
from sklearn.cross_validation import cross_val_score
#from sklearn.model_selection import StratifiedShuffleSplit
#from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import roc_curve, auc
from sklearn.utils import shuffle
from scipy import interp
%matplotlib inline
def remove_zero_columns(X, threshold=1e-20):
# convert zeros to nan, drop all nan columns, the replace leftover nan with zeros
X_non_zero_colum = X.replace(0, np.nan).dropna(how='all', axis=1).replace(np.nan, 0)
#.dropna(how='all', axis=0).replace(np.nan,0)
return X_non_zero_colum
def zero_fill_half_min(X, threshold=1e-20):
# Fill zeros with 1/2 the minimum value of that column
# input dataframe. Add only to zero values
# Get a vector of 1/2 minimum values
half_min = X[X > threshold].min(axis=0)*0.5
# Add the half_min values to a dataframe where everything that isn't zero is NaN.
# then convert NaN's to 0
fill_vals = (X[X < threshold] + half_min).fillna(value=0)
# Add the original dataframe to the dataframe of zeros and fill-values
X_zeros_filled = X + fill_vals
return X_zeros_filled
toy = pd.DataFrame([[1,2,3,0],
[0,0,0,0],
[0.5,1,0,0]], dtype=float)
toy_no_zeros = remove_zero_columns(toy)
toy_filled_zeros = zero_fill_half_min(toy_no_zeros)
print toy
print toy_no_zeros
print toy_filled_zeros
```
<h2> Import the dataframe and remove any features that are all zero </h2>
```
### Subdivide the data into a feature table
data_path = '/home/irockafe/Dropbox (MIT)/Alm_Lab/projects/revo_healthcare/data/processed/MTBLS315/'\
'uhplc_pos/xcms_result_25.csv'
## Import the data and remove extraneous columns
df = pd.read_csv(data_path, index_col=0)
df.shape
df.head()
# Make a new index of mz:rt
mz = df.loc[:,"mz"].astype('str')
rt = df.loc[:,"rt"].astype('str')
idx = mz+':'+rt
df.index = idx
df
# separate samples from xcms/camera things to make feature table
not_samples = ['mz', 'mzmin', 'mzmax', 'rt', 'rtmin', 'rtmax',
'npeaks', 'uhplc_pos',
]
samples_list = df.columns.difference(not_samples)
mz_rt_df = df[not_samples]
# convert to samples x features
X_df_raw = df[samples_list].T
# Remove zero-full columns and fill zeroes with 1/2 minimum values
X_df = remove_zero_columns(X_df_raw)
X_df_zero_filled = zero_fill_half_min(X_df)
print "original shape: %s \n# zeros: %f\n" % (X_df_raw.shape, (X_df_raw < 1e-20).sum().sum())
print "zero-columns repalced? shape: %s \n# zeros: %f\n" % (X_df.shape,
(X_df < 1e-20).sum().sum())
print "zeros filled shape: %s \n#zeros: %f\n" % (X_df_zero_filled.shape,
(X_df_zero_filled < 1e-20).sum().sum())
# Convert to numpy matrix to play nicely with sklearn
X = X_df.as_matrix()
print X.shape
```
<h2> Get mappings between sample names, file names, and sample classes </h2>
```
# Get mapping between sample name and assay names
path_sample_name_map = '/home/irockafe/Dropbox (MIT)/Alm_Lab/projects/revo_healthcare/data/raw/'\
'MTBLS315/metadata/a_UPLC_POS_nmfi_and_bsi_diagnosis.txt'
# Index is the sample name
sample_df = pd.read_csv(path_sample_name_map,
sep='\t', index_col=0)
sample_df = sample_df['MS Assay Name']
sample_df.shape
print sample_df.head(10)
# get mapping between sample name and sample class
path_sample_class_map = '/home/irockafe/Dropbox (MIT)/Alm_Lab/projects/revo_healthcare/data/raw/'\
'MTBLS315/metadata/s_NMFI and BSI diagnosis.txt'
class_df = pd.read_csv(path_sample_class_map,
sep='\t')
# Set index as sample name
class_df.set_index('Sample Name', inplace=True)
class_df = class_df['Factor Value[patient group]']
print class_df.head(10)
# convert all non-malarial classes into a single classes
# (collapse non-malarial febril illness and bacteremia together)
class_map_df = pd.concat([sample_df, class_df], axis=1)
class_map_df.rename(columns={'Factor Value[patient group]': 'class'}, inplace=True)
class_map_df
binary_class_map = class_map_df.replace(to_replace=['non-malarial febrile illness', 'bacterial bloodstream infection' ],
value='non-malarial fever')
binary_class_map
# convert classes to numbers
le = preprocessing.LabelEncoder()
le.fit(binary_class_map['class'])
y = le.transform(binary_class_map['class'])
```
<h2> Plot the distribution of classification accuracy across multiple cross-validation splits - Kinda Dumb</h2>
Turns out doing this is kind of dumb, because you're not taking into account the prediction score your classifier assigned. Use AUC's instead. You want to give your classifier a lower score if it is really confident and wrong, than vice-versa
```
def rf_violinplot(X, y, n_iter=25, test_size=0.3, random_state=1,
n_estimators=1000):
cross_val_skf = StratifiedShuffleSplit(y, n_iter=n_iter, test_size=test_size,
random_state=random_state)
clf = RandomForestClassifier(n_estimators=n_estimators, random_state=random_state)
scores = cross_val_score(clf, X, y, cv=cross_val_skf)
sns.violinplot(scores,inner='stick')
rf_violinplot(X,y)
# TODO - Switch to using caret for this bs..?
# Do multi-fold cross validation for adaboost classifier
def adaboost_violinplot(X, y, n_iter=25, test_size=0.3, random_state=1,
n_estimators=200):
cross_val_skf = StratifiedShuffleSplit(y, n_iter=n_iter, test_size=test_size, random_state=random_state)
clf = AdaBoostClassifier(n_estimators=n_estimators, random_state=random_state)
scores = cross_val_score(clf, X, y, cv=cross_val_skf)
sns.violinplot(scores,inner='stick')
adaboost_violinplot(X,y)
# TODO PQN normalization, and log-transformation,
# and some feature selection (above certain threshold of intensity, use principal components), et
def pqn_normalize(X, integral_first=False, plot=False):
'''
Take a feature table and run PQN normalization on it
'''
# normalize by sum of intensities in each sample first. Not necessary
if integral_first:
sample_sums = np.sum(X, axis=1)
X = (X / sample_sums[:,np.newaxis])
# Get the median value of each feature across all samples
mean_intensities = np.median(X, axis=0)
# Divde each feature by the median value of each feature -
# these are the quotients for each feature
X_quotients = (X / mean_intensities[np.newaxis,:])
if plot: # plot the distribution of quotients from one sample
for i in range(1,len(X_quotients[:,1])):
print 'allquotients reshaped!\n\n',
#all_quotients = X_quotients.reshape(np.prod(X_quotients.shape))
all_quotients = X_quotients[i,:]
print all_quotients.shape
x = np.random.normal(loc=0, scale=1, size=len(all_quotients))
sns.violinplot(all_quotients)
plt.title("median val: %f\nMax val=%f" % (np.median(all_quotients), np.max(all_quotients)))
plt.plot( title="median val: ")#%f" % np.median(all_quotients))
plt.xlim([-0.5, 5])
plt.show()
# Define a quotient for each sample as the median of the feature-specific quotients
# in that sample
sample_quotients = np.median(X_quotients, axis=1)
# Quotient normalize each samples
X_pqn = X / sample_quotients[:,np.newaxis]
return X_pqn
# Make a fake sample, with 2 samples at 1x and 2x dilutions
X_toy = np.array([[1,1,1,],
[2,2,2],
[3,6,9],
[6,12,18]], dtype=float)
print X_toy
print X_toy.reshape(1, np.prod(X_toy.shape))
X_toy_pqn_int = pqn_normalize(X_toy, integral_first=True, plot=True)
print X_toy_pqn_int
print '\n\n\n'
X_toy_pqn = pqn_normalize(X_toy)
print X_toy_pqn
```
<h2> pqn normalize your features </h2>
```
X_pqn = pqn_normalize(X)
print X_pqn
```
<h2>Random Forest & adaBoost with PQN-normalized data</h2>
```
rf_violinplot(X_pqn, y)
# Do multi-fold cross validation for adaboost classifier
adaboost_violinplot(X_pqn, y)
```
<h2> RF & adaBoost with PQN-normalized, log-transformed data </h2>
Turns out a monotonic transformation doesn't really affect any of these things.
I guess they're already close to unit varinace...?
```
X_pqn_nlog = np.log(X_pqn)
rf_violinplot(X_pqn_nlog, y)
adaboost_violinplot(X_pqn_nlog, y)
def roc_curve_cv(X, y, clf, cross_val,
path='/home/irockafe/Desktop/roc.pdf',
save=False, plot=True):
t1 = time.time()
# collect vals for the ROC curves
tpr_list = []
mean_fpr = np.linspace(0,1,100)
auc_list = []
# Get the false-positive and true-positive rate
for i, (train, test) in enumerate(cross_val):
clf.fit(X[train], y[train])
y_pred = clf.predict_proba(X[test])[:,1]
# get fpr, tpr
fpr, tpr, thresholds = roc_curve(y[test], y_pred)
roc_auc = auc(fpr, tpr)
#print 'AUC', roc_auc
#sns.plt.plot(fpr, tpr, lw=10, alpha=0.6, label='ROC - AUC = %0.2f' % roc_auc,)
#sns.plt.show()
tpr_list.append(interp(mean_fpr, fpr, tpr))
tpr_list[-1][0] = 0.0
auc_list.append(roc_auc)
if (i % 10 == 0):
print '{perc}% done! {time}s elapsed'.format(perc=100*float(i)/cross_val.n_iter, time=(time.time() - t1))
# get mean tpr and fpr
mean_tpr = np.mean(tpr_list, axis=0)
# make sure it ends up at 1.0
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(auc_list)
if plot:
# plot mean auc
plt.plot(mean_fpr, mean_tpr, label='Mean ROC - AUC = %0.2f $\pm$ %0.2f' % (mean_auc,
std_auc),
lw=5, color='b')
# plot luck-line
plt.plot([0,1], [0,1], linestyle = '--', lw=2, color='r',
label='Luck', alpha=0.5)
# plot 1-std
std_tpr = np.std(tpr_list, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
plt.fill_between(mean_fpr, tprs_lower, tprs_upper, color='grey', alpha=0.2,
label=r'$\pm$ 1 stdev')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve, {iters} iterations of {cv} cross validation'.format(
iters=cross_val.n_iter, cv='{train}:{test}'.format(test=cross_val.test_size, train=(1-cross_val.test_size)))
)
plt.legend(loc="lower right")
if save:
plt.savefig(path, format='pdf')
plt.show()
return tpr_list, auc_list, mean_fpr
rf_estimators = 1000
n_iter = 3
test_size = 0.3
random_state = 1
cross_val_rf = StratifiedShuffleSplit(y, n_iter=n_iter, test_size=test_size, random_state=random_state)
clf_rf = RandomForestClassifier(n_estimators=rf_estimators, random_state=random_state)
rf_graph_path = '''/home/irockafe/Dropbox (MIT)/Alm_Lab/projects/revolutionizing_healthcare/data/MTBLS315/\
isaac_feature_tables/uhplc_pos/rf_roc_{trees}trees_{cv}cviter.pdf'''.format(trees=rf_estimators, cv=n_iter)
print cross_val_rf.n_iter
print cross_val_rf.test_size
tpr_vals, auc_vals, mean_fpr = roc_curve_cv(X_pqn, y, clf_rf, cross_val_rf,
path=rf_graph_path, save=False)
# For adaboosted
n_iter = 3
test_size = 0.3
random_state = 1
adaboost_estimators = 200
adaboost_path = '''/home/irockafe/Dropbox (MIT)/Alm_Lab/projects/revolutionizing_healthcare/data/MTBLS315/\
isaac_feature_tables/uhplc_pos/adaboost_roc_{trees}trees_{cv}cviter.pdf'''.format(trees=adaboost_estimators,
cv=n_iter)
cross_val_adaboost = StratifiedShuffleSplit(y, n_iter=n_iter, test_size=test_size, random_state=random_state)
clf = AdaBoostClassifier(n_estimators=adaboost_estimators, random_state=random_state)
adaboost_tpr, adaboost_auc, adaboost_fpr = roc_curve_cv(X_pqn, y, clf, cross_val_adaboost,
path=adaboost_path)
```
<h2> Great, you can classify things. But make null models and do a sanity check to make
sure you arent just classifying garbage </h2>
```
# Make a null model AUC curve
def make_null_model(X, y, clf, cross_val, random_state=1, num_shuffles=5, plot=True):
'''
Runs the true model, then sanity-checks by:
Shuffles class labels and then builds cross-validated ROC curves from them.
Compares true AUC vs. shuffled auc by t-test (assumes normality of AUC curve)
'''
null_aucs = []
print y.shape
print X.shape
tpr_true, auc_true, fpr_true = roc_curve_cv(X, y, clf, cross_val)
# shuffle y lots of times
for i in range(0, num_shuffles):
#Iterate through the shuffled y vals and repeat with appropriate params
# Retain the auc vals for final plotting of distribution
y_shuffle = shuffle(y)
cross_val.y = y_shuffle
cross_val.y_indices = y_shuffle
print 'Number of differences b/t original and shuffle: %s' % (y == cross_val.y).sum()
# Get auc values for number of iterations
tpr, auc, fpr = roc_curve_cv(X, y_shuffle, clf, cross_val, plot=False)
null_aucs.append(auc)
#plot the outcome
if plot:
flattened_aucs = [j for i in null_aucs for j in i]
my_dict = {'true_auc': auc_true, 'null_auc': flattened_aucs}
df_poop = pd.DataFrame.from_dict(my_dict, orient='index').T
df_tidy = pd.melt(df_poop, value_vars=['true_auc', 'null_auc'],
value_name='auc', var_name='AUC_type')
#print flattened_aucs
sns.violinplot(x='AUC_type', y='auc',
inner='points', data=df_tidy)
# Plot distribution of AUC vals
plt.title("Distribution of aucs")
#sns.plt.ylabel('count')
plt.xlabel('AUC')
#sns.plt.plot(auc_true, 0, color='red', markersize=10)
plt.show()
# Do a quick t-test to see if odds of randomly getting an AUC that good
return auc_true, null_aucs
# Make a null model AUC curve & compare it to null-model
# Random forest magic!
rf_estimators = 1000
n_iter = 50
test_size = 0.3
random_state = 1
cross_val_rf = StratifiedShuffleSplit(y, n_iter=n_iter, test_size=test_size, random_state=random_state)
clf_rf = RandomForestClassifier(n_estimators=rf_estimators, random_state=random_state)
true_auc, all_aucs = make_null_model(X_pqn, y, clf_rf, cross_val_rf, num_shuffles=5)
# make dataframe from true and false aucs
flattened_aucs = [j for i in all_aucs for j in i]
my_dict = {'true_auc': true_auc, 'null_auc': flattened_aucs}
df_poop = pd.DataFrame.from_dict(my_dict, orient='index').T
df_tidy = pd.melt(df_poop, value_vars=['true_auc', 'null_auc'],
value_name='auc', var_name='AUC_type')
print df_tidy.head()
#print flattened_aucs
sns.violinplot(x='AUC_type', y='auc',
inner='points', data=df_tidy, bw=0.7)
plt.show()
```
<h2> Let's check out some PCA plots </h2>
```
from sklearn.decomposition import PCA
# Check PCA of things
def PCA_plot(X, y, n_components, plot_color, class_nums, class_names, title='PCA'):
pca = PCA(n_components=n_components)
X_pca = pca.fit(X).transform(X)
print zip(plot_color, class_nums, class_names)
for color, i, target_name in zip(plot_color, class_nums, class_names):
# plot one class at a time, first plot all classes y == 0
#print color
#print y == i
xvals = X_pca[y == i, 0]
print xvals.shape
yvals = X_pca[y == i, 1]
plt.scatter(xvals, yvals, color=color, alpha=0.8, label=target_name)
plt.legend(bbox_to_anchor=(1.01,1), loc='upper left', shadow=False)#, scatterpoints=1)
plt.title('PCA of Malaria data')
plt.show()
PCA_plot(X_pqn, y, 2, ['red', 'blue'], [0,1], ['malaria', 'non-malaria fever'])
PCA_plot(X, y, 2, ['red', 'blue'], [0,1], ['malaria', 'non-malaria fever'])
```
<h2> What about with all thre classes? </h2>
```
# convert classes to numbers
le = preprocessing.LabelEncoder()
le.fit(class_map_df['class'])
y_three_class = le.transform(class_map_df['class'])
print class_map_df.head(10)
print y_three_class
print X.shape
print y_three_class.shape
y_labels = np.sort(class_map_df['class'].unique())
print y_labels
colors = ['green', 'red', 'blue']
print np.unique(y_three_class)
PCA_plot(X_pqn, y_three_class, 2, colors, np.unique(y_three_class), y_labels)
PCA_plot(X, y_three_class, 2, colors, np.unique(y_three_class), y_labels)
```
| true |
code
| 0.369315 | null | null | null | null |
|
## 1. Inspecting transfusion.data file
<p><img src="https://assets.datacamp.com/production/project_646/img/blood_donation.png" style="float: right;" alt="A pictogram of a blood bag with blood donation written in it" width="200"></p>
<p>Blood transfusion saves lives - from replacing lost blood during major surgery or a serious injury to treating various illnesses and blood disorders. Ensuring that there's enough blood in supply whenever needed is a serious challenge for the health professionals. According to <a href="https://www.webmd.com/a-to-z-guides/blood-transfusion-what-to-know#1">WebMD</a>, "about 5 million Americans need a blood transfusion every year".</p>
<p>Our dataset is from a mobile blood donation vehicle in Taiwan. The Blood Transfusion Service Center drives to different universities and collects blood as part of a blood drive. We want to predict whether or not a donor will give blood the next time the vehicle comes to campus.</p>
<p>The data is stored in <code>datasets/transfusion.data</code> and it is structured according to RFMTC marketing model (a variation of RFM). We'll explore what that means later in this notebook. First, let's inspect the data.</p>
```
# Print out the first 5 lines from the transfusion.data file
!head -n 5 datasets/transfusion.data
```
## 2. Loading the blood donations data
<p>We now know that we are working with a typical CSV file (i.e., the delimiter is <code>,</code>, etc.). We proceed to loading the data into memory.</p>
```
# Import pandas
import pandas as pd
# Read in dataset
transfusion = pd.read_csv('datasets/transfusion.data')
# Print out the first rows of our dataset
transfusion.head()
```
## 3. Inspecting transfusion DataFrame
<p>Let's briefly return to our discussion of RFM model. RFM stands for Recency, Frequency and Monetary Value and it is commonly used in marketing for identifying your best customers. In our case, our customers are blood donors.</p>
<p>RFMTC is a variation of the RFM model. Below is a description of what each column means in our dataset:</p>
<ul>
<li>R (Recency - months since the last donation)</li>
<li>F (Frequency - total number of donation)</li>
<li>M (Monetary - total blood donated in c.c.)</li>
<li>T (Time - months since the first donation)</li>
<li>a binary variable representing whether he/she donated blood in March 2007 (1 stands for donating blood; 0 stands for not donating blood)</li>
</ul>
<p>It looks like every column in our DataFrame has the numeric type, which is exactly what we want when building a machine learning model. Let's verify our hypothesis.</p>
```
# Print a concise summary of transfusion DataFrame
transfusion.info()
```
## 4. Creating target column
<p>We are aiming to predict the value in <code>whether he/she donated blood in March 2007</code> column. Let's rename this it to <code>target</code> so that it's more convenient to work with.</p>
```
# Rename target column as 'target' for brevity
transfusion.rename(
columns={'whether he/she donated blood in March 2007':'target'},
inplace=True
)
# Print out the first 2 rows
transfusion.head(2)
```
## 5. Checking target incidence
<p>We want to predict whether or not the same donor will give blood the next time the vehicle comes to campus. The model for this is a binary classifier, meaning that there are only 2 possible outcomes:</p>
<ul>
<li><code>0</code> - the donor will not give blood</li>
<li><code>1</code> - the donor will give blood</li>
</ul>
<p>Target incidence is defined as the number of cases of each individual target value in a dataset. That is, how many 0s in the target column compared to how many 1s? Target incidence gives us an idea of how balanced (or imbalanced) is our dataset.</p>
```
# Print target incidence proportions, rounding output to 3 decimal places
transfusion.target.value_counts(normalize=True).round(3)
```
## 6. Splitting transfusion into train and test datasets
<p>We'll now use <code>train_test_split()</code> method to split <code>transfusion</code> DataFrame.</p>
<p>Target incidence informed us that in our dataset <code>0</code>s appear 76% of the time. We want to keep the same structure in train and test datasets, i.e., both datasets must have 0 target incidence of 76%. This is very easy to do using the <code>train_test_split()</code> method from the <code>scikit learn</code> library - all we need to do is specify the <code>stratify</code> parameter. In our case, we'll stratify on the <code>target</code> column.</p>
```
# Import train_test_split method
from sklearn.model_selection import train_test_split
# Split transfusion DataFrame into
# X_train, X_test, y_train and y_test datasets,
# stratifying on the `target` column
X_train, X_test, y_train, y_test = train_test_split(
transfusion.drop(columns='target'),
transfusion.target,
test_size=0.25,
random_state=42,
stratify=transfusion.target
)
# Print out the first 2 rows of X_train
X_train.head(2)
```
## 7. Selecting model using TPOT
<p><a href="https://github.com/EpistasisLab/tpot">TPOT</a> is a Python Automated Machine Learning tool that optimizes machine learning pipelines using genetic programming.</p>
<p><img src="https://assets.datacamp.com/production/project_646/img/tpot-ml-pipeline.png" alt="TPOT Machine Learning Pipeline"></p>
<p>TPOT will automatically explore hundreds of possible pipelines to find the best one for our dataset. Note, the outcome of this search will be a <a href="https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html">scikit-learn pipeline</a>, meaning it will include any pre-processing steps as well as the model.</p>
<p>We are using TPOT to help us zero in on one model that we can then explore and optimize further.</p>
```
# Import TPOTClassifier and roc_auc_score
from tpot import TPOTClassifier
from sklearn.metrics import roc_auc_score
# Instantiate TPOTClassifier
tpot = TPOTClassifier(
generations=5,
population_size=20,
verbosity=2,
scoring='roc_auc',
random_state=42,
disable_update_check=True,
config_dict='TPOT light'
)
tpot.fit(X_train, y_train)
# AUC score for tpot model
tpot_auc_score = roc_auc_score(y_test, tpot.predict_proba(X_test)[:, 1])
print(f'\nAUC score: {tpot_auc_score:.4f}')
# Print best pipeline steps
print('\nBest pipeline steps:', end='\n')
for idx, (name, transform) in enumerate(tpot.fitted_pipeline_.steps, start=1):
# Print idx and transform
print(f'{idx}. {transform}')
```
## 8. Checking the variance
<p>TPOT picked <code>LogisticRegression</code> as the best model for our dataset with no pre-processing steps, giving us the AUC score of 0.7850. This is a great starting point. Let's see if we can make it better.</p>
<p>One of the assumptions for linear regression models is that the data and the features we are giving it are related in a linear fashion, or can be measured with a linear distance metric. If a feature in our dataset has a high variance that's an order of magnitude or more greater than the other features, this could impact the model's ability to learn from other features in the dataset.</p>
<p>Correcting for high variance is called normalization. It is one of the possible transformations you do before training a model. Let's check the variance to see if such transformation is needed.</p>
```
# X_train's variance, rounding the output to 3 decimal places
X_train.var().round(3)
```
## 9. Log normalization
<p><code>Monetary (c.c. blood)</code>'s variance is very high in comparison to any other column in the dataset. This means that, unless accounted for, this feature may get more weight by the model (i.e., be seen as more important) than any other feature.</p>
<p>One way to correct for high variance is to use log normalization.</p>
```
# Import numpy
import numpy as np
# Copy X_train and X_test into X_train_normed and X_test_normed
X_train_normed, X_test_normed = X_train.copy(), X_test.copy()
# Specify which column to normalize
col_to_normalize = 'Monetary (c.c. blood)'
# Log normalization
for df_ in [X_train_normed, X_test_normed]:
# Add log normalized column
df_['monetary_log'] = np.log(df_[col_to_normalize])
# Drop the original column
df_.drop(columns=col_to_normalize, inplace=True)
# Check the variance for X_train_normed
X_train_normed.var().round(3)
```
## 10. Training the linear regression model
<p>The variance looks much better now. Notice that now <code>Time (months)</code> has the largest variance, but it's not the <a href="https://en.wikipedia.org/wiki/Order_of_magnitude">orders of magnitude</a> higher than the rest of the variables, so we'll leave it as is.</p>
<p>We are now ready to train the linear regression model.</p>
```
# Importing modules
from sklearn import linear_model.LogisticRegression
# Instantiate LogisticRegression
logreg = LogisticRegression(
solver='liblinear',
random_state=42
)
# Train the model
fit(X_train_normed, y_train)
# AUC score for tpot model
logreg_auc_score = roc_auc_score(y_test, logreg.predict_proba(X_test_normed)[:, 1])
print(f'\nAUC score: {logreg_auc_score:.4f}')
```
## 11. Conclusion
<p>The demand for blood fluctuates throughout the year. As one <a href="https://www.kjrh.com/news/local-news/red-cross-in-blood-donation-crisis">prominent</a> example, blood donations slow down during busy holiday seasons. An accurate forecast for the future supply of blood allows for an appropriate action to be taken ahead of time and therefore saving more lives.</p>
<p>In this notebook, we explored automatic model selection using TPOT and AUC score we got was 0.7850. This is better than simply choosing <code>0</code> all the time (the target incidence suggests that such a model would have 76% success rate). We then log normalized our training data and improved the AUC score by 0.5%. In the field of machine learning, even small improvements in accuracy can be important, depending on the purpose.</p>
<p>Another benefit of using logistic regression model is that it is interpretable. We can analyze how much of the variance in the response variable (<code>target</code>) can be explained by other variables in our dataset.</p>
```
# Importing itemgetter
from operator import itemgetter
# Sort models based on their AUC score from highest to lowest
sorted(
[('tpot', tpot_auc_score), ('logreg', logreg_auc_score)],
key=itemgetter(1),
reverse=True
)
```
| true |
code
| 0.684251 | null | null | null | null |
|
# A Table based Q-Learning Reinforcement Agent in A Grid World
This is a simple example of a Q-Learning agent. The Q function is a table, and each decision is made by sampling the Q-values for a particular state thermally.
```
import numpy as np
import random
import gym
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
from IPython.display import clear_output
from tqdm import tqdm
env = gym.make('FrozenLake-v0')
Q = np.zeros([env.observation_space.n, env.action_space.n])
# Set learning parameters
decision_temperature = 0.01
l_rate = 0.5
y = .99
e = 0.1
num_episodes = 900
# create lists to contain total rewawrds and steps per episode
epi_length = []
rs = []
for i in tqdm(range(num_episodes)):
s = env.reset()
r_total = 0
done = False
number_jumps = 0
# limit numerb of jumps
while number_jumps < 99:
number_jumps += 1
softmax = np.exp(Q[s]/decision_temperature)
rand_n = np.random.rand() * np.sum(softmax)
# pick the next action randomly
acc = 0
for ind in range(env.action_space.n):
acc += softmax[ind]
if acc >= rand_n:
a = ind
break
#print(a, softmax, rand_n)
# a = np.argmax(Q[s, :] + np.random.randn(1, env.action_space.n) * (1./(i+1)))
s_next, r, done, _ = env.step(a)
Q_next_value = Q[s_next]
max_Q_next = np.max(Q[s_next,:])
# now update Q
Q[s, a] += l_rate * (r + y * max_Q_next \
- Q[s, a])
r_total += r
s = s_next
if done:
# be more conservative as we learn more
e = 1./((i/50) + 10)
break
if i%900 == 899:
clear_output(wait=True)
print("success rate: " + str(sum(rs[-200:])/2) + "%")
plt.figure(figsize=(8, 8))
plt.subplot(211)
plt.title("Jumps Per Episode", fontsize=18)
plt.plot(epi_length[-200:], "#23aaff")
plt.subplot(212)
plt.title('Reward For Each Episode (0/1)', fontsize=18)
plt.plot(rs[-200:], "o", color='#23aaff', alpha=0.1)
plt.figure(figsize=(6, 6))
plt.title('Decision Table', fontsize=18)
plt.xlabel("States", fontsize=15)
plt.ylabel('Actions', fontsize=15)
plt.imshow(Q.T)
plt.show()
epi_length.append(number_jumps)
rs.append(r_total)
def mv_avg(xs, n):
return [sum(xs[i:i+n])/n for i in range(len(xs)-n)]
# plt.plot(mv_avg(rs, 200))
plt.figure(figsize=(8, 8))
plt.subplot(211)
plt.title("Jumps Per Episode", fontsize=18)
plt.plot(epi_length, "#23aaff", linewidth=0.1, alpha=0.7,
label="raw data")
plt.plot(mv_avg(epi_length, 200), color="blue", alpha=0.3, linewidth=4,
label="Moving Average")
plt.legend(loc=(1.05, 0), frameon=False, fontsize=15)
plt.subplot(212)
plt.title('Reward For Each Episode (0/1)', fontsize=18)
#plt.plot(rs, "o", color='#23aaff', alpha=0.2, markersize=0.4, label="Reward")
plt.plot(mv_avg(rs, 200), color="red", alpha=0.5, linewidth=4, label="Moving Average")
plt.ylim(-0.1, 1.1)
plt.legend(loc=(1.05, 0), frameon=False, fontsize=15)
plt.savefig('./figures/Frozen-Lake-v0-thermal-table.png', dpi=300, bbox_inches='tight')
```
| true |
code
| 0.41404 | null | null | null | null |
|
# Binary classification with Support Vector Machines (SVM)
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as widgets
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC, SVC
from ipywidgets import interact, interactive, fixed
from numpy.random import default_rng
plt.rcParams['figure.figsize'] = [9.5, 6]
rng = default_rng(seed=42)
```
## Two Gaussian distributions
Let's generate some data, two sets of Normally distributed points...
```
def plot_data():
plt.xlim(0.0, 1.0)
plt.ylim(0.0, 1.0)
plt.plot(x1, y1, 'bs', markersize=6)
plt.plot(x2, y2, 'rx', markersize=6)
s1=0.01
s2=0.01
n1=30
n2=30
x1, y1 = rng.multivariate_normal([0.5, 0.3], [[s1, 0], [0, s1]], n1).T
x2, y2 = rng.multivariate_normal([0.7, 0.7], [[s2, 0], [0, s2]], n2).T
plot_data()
plt.suptitle('generated data points')
plt.show()
```
## Separating hyperplane
Linear classifiers: separate the two distributions with a line (hyperplane)
```
def plot_line(slope, intercept, show_params=False):
x_vals = np.linspace(0.0, 1.0)
y_vals = slope*x_vals +intercept
plt.plot(x_vals, y_vals, '--')
if show_params:
plt.title('slope={:.4f}, intercept={:.4f}'.format(slope, intercept))
```
You can try out different parameters (slope, intercept) for the line. Note that there are many (in fact an infinite number) of lines that separate the two classes.
```
#plot_data()
#plot_line(-1.1, 1.1)
#plot_line(-0.23, 0.62)
#plot_line(-0.41, 0.71)
#plt.savefig('just_points2.png')
def do_plot_interactive(slope=-1.0, intercept=1.0):
plot_data()
plot_line(slope, intercept, True)
plt.suptitle('separating hyperplane (line)')
interactive_plot = interactive(do_plot_interactive, slope=(-2.0, 2.0), intercept=(0.5, 1.5))
output = interactive_plot.children[-1]
output.layout.height = '450px'
interactive_plot
```
## Logistic regression
Let's create a training set $\mathbf{X}$ with labels in $\mathbf{y}$ with our points (in shuffled order).
```
X = np.block([[x1, x2], [y1, y2]]).T
y = np.hstack((np.repeat(0, len(x1)), np.repeat(1, len(x2))))
rand_idx = rng.permutation(len(x1) + len(x2))
X = X[rand_idx]
y = y[rand_idx]
print(X.shape, y.shape)
print(X[:10,:])
print(y[:10].reshape(-1,1))
```
The task is now to learn a classification model $\mathbf{y} = f(\mathbf{X})$.
First, let's try [logistic regression](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html).
```
clf_lr = LogisticRegression(penalty='none')
clf_lr.fit(X, y)
w1 = clf_lr.coef_[0][0]
w2 = clf_lr.coef_[0][1]
b = clf_lr.intercept_[0]
plt.suptitle('Logistic regression')
plot_data()
plot_line(slope=-w1/w2, intercept=-b/w2, show_params=True)
```
## Linear SVM
```
clf_lsvm = SVC(C=1000, kernel='linear')
clf_lsvm.fit(X, y)
w1 = clf_lsvm.coef_[0][0]
w2 = clf_lsvm.coef_[0][1]
b = clf_lsvm.intercept_[0]
plt.suptitle('Linear SVM')
plot_data()
plot_line(slope=-w1/w2, intercept=-b/w2, show_params=True)
def plot_clf(clf):
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
# plot decision boundary and margins
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
```
Let's try different $C$ values. We'll also visualize the margins and support vectors.
```
def do_plot_svm(C=1000.0):
clf = SVC(C=C, kernel='linear')
clf.fit(X, y)
plot_data()
plot_clf(clf)
interactive_plot = interactive(do_plot_svm, C=widgets.FloatLogSlider(value=1000, base=10, min=-0.5, max=4, step=0.2))
output = interactive_plot.children[-1]
output.layout.height = '400px'
interactive_plot
#do_plot_svm()
#plt.savefig('linear-svm.png')
```
## Kernel SVM
```
clf_ksvm = SVC(C=10, kernel='rbf')
clf_ksvm.fit(X, y)
plot_data()
plot_clf(clf_ksvm)
plt.savefig('kernel-svm.png')
def do_plot_svm(C=1000.0):
clf = SVC(C=C, kernel='rbf')
clf.fit(X, y)
plot_data()
plot_clf(clf)
interactive_plot = interactive(do_plot_svm, C=widgets.FloatLogSlider(value=100, base=10, min=-1, max=3, step=0.2))
output = interactive_plot.children[-1]
output.layout.height = '400px'
interactive_plot
```
| true |
code
| 0.693213 | null | null | null | null |
|
We saw in this [journal entry](http://wiki.noahbrenowitz.com/doku.php?id=journal:2018-10:day-2018-10-24#run_110) that multiple-step trained neural network gives a very imbalanced estimate, but the two-step trained neural network gives a good answer. Where do these two patterns disagree?
```
%matplotlib inline
import matplotlib.pyplot as plt
import xarray as xr
import click
import torch
from uwnet.model import call_with_xr
import holoviews as hv
from holoviews.operation import decimate
hv.extension('bokeh')
def column_integrate(data_array, mass):
return (data_array * mass).sum('z')
def compute_apparent_sources(model_path, ds):
model = torch.load(model_path)
return call_with_xr(model, ds, drop_times=0)
def get_single_location(ds, location=(32,0)):
y, x = location
return ds.isel(y=slice(y,y+1), x=slice(x,x+1))
def dict_to_dataset(datasets, dim='key'):
"""Concatenate a dict of datasets along a new axis"""
keys, values = zip(*datasets.items())
idx = pd.Index(keys, name=dim)
return xr.concat(values, dim=idx)
def dataarray_to_table(dataarray):
return dataarray.to_dataset('key').to_dataframe().reset_index()
def get_apparent_sources(model_paths, data_path):
ds = xr.open_dataset(data_path)
location = get_single_location(ds, location=(32,0))
sources = {training_strategy: compute_apparent_sources(model_path, location)
for training_strategy, model_path in model_paths.items()}
return dict_to_dataset(sources)
model_paths = {
'multi': '../models/113/3.pkl',
'single': '../models/110/3.pkl'
}
data_path = "../data/processed/training.nc"
sources = get_apparent_sources(model_paths, data_path)
```
# Apparent moistening and heating
Here we scatter plot the apparent heating and moistening:
```
%%opts Scatter[width=500, height=500, color_index='z'](cmap='viridis', alpha=.2)
%%opts Curve(color='black')
lims = (-30, 40)
df = dataarray_to_table(sources.QT)
moisture_source = hv.Scatter(df, kdims=["multi", "single"]).groupby('z').redim.range(multi=lims, single=lims) \
*hv.Curve((lims, lims))
lims = (-30, 40)
df = dataarray_to_table(sources.SLI)
heating = hv.Scatter(df, kdims=["multi", "single"]).groupby('z').redim.range(multi=lims, single=lims) \
*hv.Curve((lims, lims))
moisture_source.relabel("Moistening (g/kg/day)") + heating.relabel("Heating (K/day)")
```
The multistep moistening is far too negative in the upper parts of the atmosphere, and the corresponding heating is too positive. Does this **happen because the moisture is negative in those regions**.
| true |
code
| 0.556821 | null | null | null | null |
|
# Logarithmic Regularization: Dataset 1
```
# Import libraries and modules
import numpy as np
import pandas as pd
import xgboost as xgb
from xgboost import plot_tree
from sklearn.metrics import r2_score, classification_report, confusion_matrix, \
roc_curve, roc_auc_score, plot_confusion_matrix, f1_score, \
balanced_accuracy_score, accuracy_score, mean_squared_error, \
log_loss
from sklearn.datasets import make_friedman1
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LogisticRegression, LinearRegression, SGDClassifier, \
Lasso, lasso_path
from sklearn.preprocessing import StandardScaler, LabelBinarizer
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn_pandas import DataFrameMapper
import scipy
from scipy import stats
import os
import shutil
from pathlib import Path
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import albumentations as A
from albumentations.pytorch import ToTensorV2
import cv2
import itertools
import time
import tqdm
import copy
import warnings
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision.models as models
from torch.utils.data import Dataset
import PIL
import joblib
import json
# import mysgd
# Import user-defined modules
import sys
import imp
sys.path.append('/Users/arbelogonzalezw/Documents/ML_WORK/LIBS/Lockdown')
import tools_general as tg
import tools_pytorch as tp
import lockdown as ld
imp.reload(tg)
imp.reload(tp)
imp.reload(ld)
```
## Read, clean, and save data
```
# Read X and y
X = pd.read_csv('/Users/arbelogonzalezw/Documents/ML_WORK/Project_Jerry_Lockdown/dataset_10LungCarcinoma/GDS3837_gene_profile.csv', index_col=0)
dfy = pd.read_csv('/Users/arbelogonzalezw/Documents/ML_WORK/Project_Jerry_Lockdown/dataset_10LungCarcinoma/GDS3837_output.csv', index_col=0)
# Change column names
cols = X.columns.tolist()
for i in range(len(cols)):
cols[i] = cols[i].lower()
cols[i] = cols[i].replace('-', '_')
cols[i] = cols[i].replace('.', '_')
cols[i] = cols[i].strip()
X.columns = cols
cols = dfy.columns.tolist()
for i in range(len(cols)):
cols[i] = cols[i].lower()
cols[i] = cols[i].replace('-', '_')
cols[i] = cols[i].replace('.', '_')
cols[i] = cols[i].strip()
dfy.columns = cols
# Set target
dfy['disease_state'] = dfy['disease_state'].str.replace(' ', '_')
dfy.replace({'disease_state': {"lung_cancer": 1, "control": 0}}, inplace=True)
Y = pd.DataFrame(dfy['disease_state'])
# Split and save data set
xtrain, xvalid, xtest, ytrain, yvalid, ytest = tg.split_data(X, Y)
tg.save_data(X, xtrain, xvalid, xtest, Y, ytrain, yvalid, ytest, 'dataset/')
tg.save_list(X.columns.to_list(), 'dataset/X.columns')
tg.save_list(Y.columns.to_list(), 'dataset/Y.columns')
#
print("- X size: {}\n".format(X.shape))
print("- xtrain size: {}".format(xtrain.shape))
print("- xvalid size: {}".format(xvalid.shape))
print("- xtest size: {}".format(xtest.shape))
```
## Load Data
```
# Select type of processor to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
if device == torch.device('cuda'):
print("-Type of precessor to be used: 'gpu'")
!nvidia-smi
else:
print("-Type of precessor to be used: 'cpu'")
# Choose device
# torch.cuda.set_device(6)
# Read data
X, x_train, x_valid, x_test, Y, ytrain, yvalid, ytest = tp.load_data_clf('dataset/')
cols_X = tg.read_list('dataset/X.columns')
cols_Y = tg.read_list('dataset/Y.columns')
# Normalize data
xtrain, xvalid, xtest = tp.normalize_x(x_train, x_valid, x_test)
# Create dataloaders
dl_train, dl_valid, dl_test = tp.make_DataLoaders(xtrain, xvalid, xtest, ytrain, yvalid, ytest,
tp.dataset_tabular, batch_size=10000)
# NN architecture with its corresponding forward method
class MyNet(nn.Module):
# .Network architecture
def __init__(self, features, layer_sizes):
super(MyNet, self).__init__()
self.classifier = nn.Sequential(
nn.Linear(features, layer_sizes[0], bias=True),
nn.ReLU(inplace=True),
nn.Linear(layer_sizes[0], layer_sizes[1], bias=True)
)
# .Forward function
def forward(self, x):
x = self.classifier(x)
return x
```
## Lockout (Log, beta=0.7)
```
# TRAIN WITH LOCKDOWN
model = MyNet(n_features, n_layers)
model.load_state_dict(torch.load('./model_forward_valid_min.pth'))
model.eval()
regul_type = [('classifier.0.weight', 2), ('classifier.2.weight', 2)]
regul_path = [('classifier.0.weight', True), ('classifier.2.weight', False)]
lockout_s = ld.lockdown(model, lr=1e-2,
regul_type=regul_type,
regul_path=regul_path,
loss_type=2, tol_grads=1e-2)
lockout_s.train(dl_train, dl_valid, dl_test, epochs=5000, early_stop=15, tol_loss=1e-5, epochs2=100000,
train_how="decrease_t0")
# Save model, data
tp.save_model(lockout_s.model_best_valid, 'model_lockout_valid_min_log7_path.pth')
tp.save_model(lockout_s.model_last, 'model_lockout_last_log7_path.pth')
lockout_s.path_data.to_csv('data_lockout_log7_path.csv')
# Relevant plots
df = pd.read_csv('data_lockout_log7_path.csv')
df.plot('iteration', y=['t0_calc__classifier.0.weight', 't0_used__classifier.0.weight'],
figsize=(8,6))
plt.show()
# L1
nn = int(1e2)
data_tmp = pd.read_csv('data_lockout_l1.csv', index_col=0)
data_lockout_l1 = pd.DataFrame(columns=['sparcity', 'train_accu', 'valid_accu', 'test_accu', 't0_used'])
xgrid, step = np.linspace(0., 1., num=nn,endpoint=True, retstep=True)
for x in xgrid:
msk = (data_tmp['sparcity__classifier.0.weight'] >= x) & \
(data_tmp['sparcity__classifier.0.weight'] < x+step)
train_accu = data_tmp.loc[msk, 'train_accu'].mean()
valid_accu = data_tmp.loc[msk, 'valid_accu'].mean()
test_accu = data_tmp.loc[msk, 'test_accu'].mean()
t0_used = data_tmp.loc[msk, 't0_used__classifier.0.weight'].mean()
data_lockout_l1 = data_lockout_l1.append({'sparcity': x,
'train_accu': train_accu,
'valid_accu': valid_accu,
'test_accu': test_accu,
't0_used': t0_used}, ignore_index=True)
data_lockout_l1.dropna(axis='index', how='any', inplace=True)
# Log, beta=0.7
nn = int(1e2)
data_tmp = pd.read_csv('data_lockout_log7_path.csv', index_col=0)
data_lockout_log7 = pd.DataFrame(columns=['sparcity', 'train_accu', 'valid_accu', 'test_accu', 't0_used'])
xgrid, step = np.linspace(0., 1., num=nn,endpoint=True, retstep=True)
for x in xgrid:
msk = (data_tmp['sparcity__classifier.0.weight'] >= x) & \
(data_tmp['sparcity__classifier.0.weight'] < x+step)
train_accu = data_tmp.loc[msk, 'train_accu'].mean()
valid_accu = data_tmp.loc[msk, 'valid_accu'].mean()
test_accu = data_tmp.loc[msk, 'test_accu'].mean()
t0_used = data_tmp.loc[msk, 't0_used__classifier.0.weight'].mean()
data_lockout_log7 = data_lockout_log7.append({'sparcity': x,
'train_accu': train_accu,
'valid_accu': valid_accu,
'test_accu': test_accu,
't0_used': t0_used}, ignore_index=True)
data_lockout_log7.dropna(axis='index', how='any', inplace=True)
# Plot
fig, axes = plt.subplots(figsize=(9,6))
axes.plot(n_features*data_lockout_l1.loc[2:, 'sparcity'],
1.0 - data_lockout_l1.loc[2:, 'valid_accu'],
"-", linewidth=4, markersize=10, label="Lockout(L1)",
color="tab:orange")
axes.plot(n_features*data_lockout_log7.loc[3:,'sparcity'],
1.0 - data_lockout_log7.loc[3:, 'valid_accu'],
"-", linewidth=4, markersize=10, label=r"Lockout(Log, $\beta$=0.7)",
color="tab:green")
axes.grid(True, zorder=2)
axes.set_xlabel("number of selected features", fontsize=16)
axes.set_ylabel("Validation Error", fontsize=16)
axes.tick_params(axis='both', which='major', labelsize=14)
axes.set_yticks(np.linspace(5e-3, 4.5e-2, 5, endpoint=True))
# axes.ticklabel_format(axis='y', style='sci', scilimits=(0,0))
axes.set_xlim(0, 54800)
axes.legend(fontsize=16)
plt.tight_layout()
plt.savefig('error_vs_features_log_dataset10.pdf', bbox_inches='tight')
plt.show()
```
| true |
code
| 0.694885 | null | null | null | null |
|
```
Copyright 2021 IBM Corporation
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
```
# Random Forest on Allstate Dataset
## Background
The goal of this competition is to predict Bodily Injury Liability Insurance claim payments based on the characteristics of the insured’s vehicle.
## Source
The raw dataset can be obtained directly from the [Allstate Claim Prediction Challenge](https://www.kaggle.com/c/ClaimPredictionChallenge).
In this example, we download the dataset directly from Kaggle using their API. In order for to work work, you must:
1. Login into Kaggle and accept the [competition rules](https://www.kaggle.com/c/ClaimPredictionChallenge/rules).
2. Folow [these instructions](https://www.kaggle.com/docs/api) to install your API token on your machine.
## Goal
The goal of this notebook is to illustrate how Snap ML can accelerate training of a random forest model on this dataset.
## Code
```
cd ../../
CACHE_DIR='cache-dir'
import numpy as np
import time
from datasets import Allstate
from sklearn.ensemble import RandomForestClassifier
from snapml import RandomForestClassifier as SnapRandomForestClassifier
from sklearn.metrics import roc_auc_score as score
dataset = Allstate(cache_dir=CACHE_DIR)
X_train, X_test, y_train, y_test = dataset.get_train_test_split()
print("Number of examples: %d" % (X_train.shape[0]))
print("Number of features: %d" % (X_train.shape[1]))
print("Number of classes: %d" % (len(np.unique(y_train))))
# the dataset is highly imbalanced
labels, sizes = np.unique(y_train, return_counts=True)
print("%6.2f %% of the training transactions belong to class 0" % (sizes[0]*100.0/(sizes[0]+sizes[1])))
print("%6.2f %% of the training transactions belong to class 1" % (sizes[1]*100.0/(sizes[0]+sizes[1])))
from sklearn.utils.class_weight import compute_sample_weight
w_train = compute_sample_weight('balanced', y_train)
w_test = compute_sample_weight('balanced', y_test)
model = RandomForestClassifier(max_depth=6, n_estimators=100, n_jobs=4, random_state=42)
t0 = time.time()
model.fit(X_train, y_train, sample_weight=w_train)
t_fit_sklearn = time.time()-t0
score_sklearn = score(y_test, model.predict_proba(X_test)[:,1], sample_weight=w_test)
print("Training time (sklearn): %6.2f seconds" % (t_fit_sklearn))
print("ROC AUC score (sklearn): %.4f" % (score_sklearn))
model = SnapRandomForestClassifier(max_depth=6, n_estimators=100, n_jobs=4, random_state=42, use_histograms=True)
t0 = time.time()
model.fit(X_train, y_train, sample_weight=w_train)
t_fit_snapml = time.time()-t0
score_snapml = score(y_test, model.predict_proba(X_test)[:,1], sample_weight=w_test)
print("Training time (snapml): %6.2f seconds" % (t_fit_snapml))
print("ROC AUC score (snapml): %.4f" % (score_snapml))
speed_up = t_fit_sklearn/t_fit_snapml
score_diff = (score_snapml-score_sklearn)/score_sklearn
print("Speed-up: %.1f x" % (speed_up))
print("Relative diff. in score: %.4f" % (score_diff))
```
## Disclaimer
Performance results always depend on the hardware and software environment.
Information regarding the environment that was used to run this notebook are provided below:
```
import utils
environment = utils.get_environment()
for k,v in environment.items():
print("%15s: %s" % (k, v))
```
## Record Statistics
Finally, we record the enviroment and performance statistics for analysis outside of this standalone notebook.
```
import scrapbook as sb
sb.glue("result", {
'dataset': dataset.name,
'n_examples_train': X_train.shape[0],
'n_examples_test': X_test.shape[0],
'n_features': X_train.shape[1],
'n_classes': len(np.unique(y_train)),
'model': type(model).__name__,
'score': score.__name__,
't_fit_sklearn': t_fit_sklearn,
'score_sklearn': score_sklearn,
't_fit_snapml': t_fit_snapml,
'score_snapml': score_snapml,
'score_diff': score_diff,
'speed_up': speed_up,
**environment,
})
```
| true |
code
| 0.858511 | null | null | null | null |
|
# Analytic center computation using a infeasible start Newton method
# The set-up
```
import numpy as np
import pandas as pd
import accpm
import accpm
from IPython.display import display
%load_ext autoreload
%autoreload 1
%aimport accpm
```
$\DeclareMathOperator{\domain}{dom}
\newcommand{\transpose}{\text{T}}
\newcommand{\vec}[1]{\begin{pmatrix}#1\end{pmatrix}}$
# Theory
To test the $\texttt{analytic_center}$ function we consider the following example. Suppose we want to find the analytic center $x_{ac} \in \mathbb{R}^2$ of the inequalities $x_1 \leq c_1, x_1 \geq 0, x_2 \leq c_2, x_2 \geq 0$. This is a rectange with dimensions $c_1 \times c_2$ centered at at $(\frac{c_1}{2}, \frac{c_2}{2})$ so we should have $x_{ac} = (\frac{c_1}{2}, \frac{c_2}{2})$. Now, $x_{ac}$ is the solution of the minimization problem
\begin{equation*}
\min_{\domain \phi} \phi(x) = - \sum_{i=1}^{4}{\log{(b_i - a_i^\transpose x)}}
\end{equation*}
where
\begin{equation*}
\domain \phi = \{x \;|\; a_i^\transpose x < b_i, i = 1, 2, 3, 4\}
\end{equation*}
with
\begin{align*}
&a_1 = \begin{bmatrix}1\\0\end{bmatrix}, &&b_1 = c_1, \\
&a_2 = \begin{bmatrix}-1\\0\end{bmatrix}, &&b_2 = 0, \\
&a_3 = \begin{bmatrix}0\\1\end{bmatrix}, &&b_3 = c_2, \\
&a_4 = \begin{bmatrix}0\\-1\end{bmatrix}, &&b_4 = 0.
\end{align*}
So we solve
\begin{align*}
&\phantom{iff}\nabla \phi(x) = \sum_{i=1}^{4
} \frac{1}{b_i - a_i^\transpose x}a_i = 0 \\
&\iff \frac{1}{c_1-x_1}\begin{bmatrix}1\\0\end{bmatrix} + \frac{1}{x_1}\begin{bmatrix}-1\\0\end{bmatrix} + \frac{1}{c_2-x_2}\begin{bmatrix}0\\1\end{bmatrix} + \frac{1}{x_2}\begin{bmatrix}0\\-1\end{bmatrix} = 0 \\
&\iff \frac{1}{c_1-x_1} - \frac{1}{x_1} = 0, \frac{1}{c_2-x_2} - \frac{1}{x_2} = 0 \\
&\iff x_1 = \frac{c_1}{2}, x_2 = \frac{c_2}{2},
\end{align*}
as expected.
# Testing
We test $\texttt{analytic_center}$ for varying values of $c_1, c_2$ and algorithm parameters $\texttt{alpha, beta}$:
```
def get_results(A, test_input, alpha, beta, tol=10e-8):
expected = []
actual = []
result = []
for (c1, c2) in test_input:
b = np.array([c1, 0, c2, 0])
ac_expected = np.asarray((c1/2, c2/2))
ac_actual = accpm.analytic_center(A, b, alpha = alpha, beta = beta)
expected.append(ac_expected)
actual.append(ac_actual)
# if np.array_equal(ac_expected, ac_actual):
if np.linalg.norm(ac_expected - ac_actual) <= tol:
result.append(True)
else:
result.append(False)
results = pd.DataFrame([test_input, expected, actual, result])
results = results.transpose()
results.columns = ['test_input', 'expected', 'actual', 'result']
print('alpha =', alpha, 'beta =', beta)
display(results)
```
Here we have results for squares of varying sizes and for varying values of $\texttt{alpha}$ and $\texttt{beta}$. In general, the algorithm performs worse on large starting polyhedrons than small starting polyhedrons. This seems acceptable given that we are most concerned with smaller polyhedrons.
```
A = np.array([[1, 0],[-1,0],[0,1],[0,-1]])
test_input = [(1, 1), (5, 5), (20, 20), (10e2, 10e2), (10e4, 10e4),
(10e6, 10e6), (10e8, 10e8), (10e10, 10e10),
(0.5, 0.5), (0.1, 0.1), (0.01, 0.01),
(0.005, 0.005), (0.001, 0.001),(0.0005, 0.0005), (0.0001, 0.0001),
(0.00005, 0.00005), (0.00001, 0.00001), (0.00001, 0.00001)]
get_results(A, test_input, alpha=0.01, beta=0.7)
get_results(A, test_input, alpha=0.01, beta=0.99)
get_results(A, test_input, alpha=0.49, beta=0.7)
get_results(A, test_input, alpha=0.25, beta=0.7)
```
| true |
code
| 0.345147 | null | null | null | null |
|
## Hyperparameter Tuning Design Pattern
In Hyperparameter Tuning, the training loop is itself inserted into an optimization method to find the optimal set of model hyperparameters.
```
import datetime
import os
import numpy as np
import pandas as pd
import tensorflow as tf
import time
from tensorflow import keras
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, f1_score
```
### Grid search in Scikit-learn
Here we'll look at how to implement hyperparameter tuning with the grid search algorithm, using Scikit-learn's built-in `GridSearchCV`. We'll do this by training a random forest model on the UCI mushroom dataset, which predicts whether a mushroom is edible or poisonous.
```
# First, download the data
# We've made it publicly available in Google Cloud Storage
!gsutil cp gs://ml-design-patterns/mushrooms.csv .
mushroom_data = pd.read_csv('mushrooms.csv')
mushroom_data.head()
```
To keep things simple, we'll first convert the label column to numeric and then
use `pd.get_dummies()` to covert the data to numeric.
```
# 1 = edible, 0 = poisonous
mushroom_data.loc[mushroom_data['class'] == 'p', 'class'] = 0
mushroom_data.loc[mushroom_data['class'] == 'e', 'class'] = 1
labels = mushroom_data.pop('class')
dummy_data = pd.get_dummies(mushroom_data)
# Split the data
train_size = int(len(mushroom_data) * .8)
train_data = dummy_data[:train_size]
test_data = dummy_data[train_size:]
train_labels = labels[:train_size].astype(int)
test_labels = labels[train_size:].astype(int)
```
Next, we'll build our Scikit-learn model and define the hyperparameters we want to optimize using grid serach.
```
model = RandomForestClassifier()
grid_vals = {
'max_depth': [5, 10, 100],
'n_estimators': [100, 150, 200]
}
grid_search = GridSearchCV(model, param_grid=grid_vals, scoring='accuracy')
# Train the model while running hyperparameter trials
grid_search.fit(train_data.values, train_labels.values)
```
Let's see which hyperparameters resulted in the best accuracy.
```
grid_search.best_params_
```
Finally, we can generate some test predictions on our model and evaluate its accuracy.
```
grid_predict = grid_search.predict(test_data.values)
grid_acc = accuracy_score(test_labels.values, grid_predict)
grid_f = f1_score(test_labels.values, grid_predict)
print('Accuracy: ', grid_acc)
print('F1-Score: ', grid_f)
```
### Hyperparameter tuning with `keras-tuner`
To show how this works we'll train a model on the MNIST handwritten digit dataset, which is available directly in Keras. For more details, see this [Keras tuner guide](https://www.tensorflow.org/tutorials/keras/keras_tuner).
```
!pip install keras-tuner --quiet
import kerastuner as kt
# Get the mnist data
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
def build_model(hp):
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(hp.Int('first_hidden', 128, 256, step=32), activation='relu'),
keras.layers.Dense(hp.Int('second_hidden', 16, 128, step=32), activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(
optimizer=tf.keras.optimizers.Adam(
hp.Float('learning_rate', .005, .01, sampling='log')),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
return model
tuner = kt.BayesianOptimization(
build_model,
objective='val_accuracy',
max_trials=30
)
tuner.search(x_train, y_train, validation_split=0.1, epochs=10)
best_hps = tuner.get_best_hyperparameters(num_trials = 1)[0]
```
### Hyperparameter tuning on Cloud AI Platform
In this section we'll show you how to scale your hyperparameter optimization by running it on Google Cloud's AI Platform. You'll need a Cloud account with AI Platform Training enabled to run this section.
We'll be using PyTorch to build a regression model in this section. To train the model we'll be the BigQuery natality dataset. We've made a subset of this data available in a public Cloud Storage bucket, which we'll download from within the training job.
```
from google.colab import auth
auth.authenticate_user()
```
In the cells below, replcae `your-project-id` with the ID of your Cloud project, and `your-gcs-bucket` with the name of your Cloud Storage bucket.
```
!gcloud config set project your-project-id
BUCKET_URL = 'gs://your-gcs-bucket'
```
To run this on AI Platform, we'll need to package up our model code in Python's package format, which includes an empty `__init__.py` file and a `setup.py` to install dependencies (in this case PyTorch, Scikit-learn, and Pandas).
```
!mkdir trainer
!touch trainer/__init__.py
%%writefile setup.py
from setuptools import find_packages
from setuptools import setup
REQUIRED_PACKAGES = ['torch>=1.5', 'scikit-learn>=0.20', 'pandas>=1.0']
setup(
name='trainer',
version='0.1',
install_requires=REQUIRED_PACKAGES,
packages=find_packages(),
include_package_data=True,
description='My training application package.'
)
```
Below, we're copying our model training code to a `model.py` file in our trainer package directory. This code runs training and after training completes, reports the model's final loss to Cloud HyperTune.
```
%%writefile trainer/model.py
import argparse
import hypertune
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.utils import shuffle
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import normalize
def get_args():
"""Argument parser.
Returns:
Dictionary of arguments.
"""
parser = argparse.ArgumentParser(description='PyTorch MNIST')
parser.add_argument('--job-dir', # handled automatically by AI Platform
help='GCS location to write checkpoints and export ' \
'models')
parser.add_argument('--lr', # Specified in the config file
type=float,
default=0.01,
help='learning rate (default: 0.01)')
parser.add_argument('--momentum', # Specified in the config file
type=float,
default=0.5,
help='SGD momentum (default: 0.5)')
parser.add_argument('--hidden-layer-size', # Specified in the config file
type=int,
default=8,
help='hidden layer size')
args = parser.parse_args()
return args
def train_model(args):
# Get the data
natality = pd.read_csv('https://storage.googleapis.com/ml-design-patterns/natality.csv')
natality = natality.dropna()
natality = shuffle(natality, random_state = 2)
natality.head()
natality_labels = natality['weight_pounds']
natality = natality.drop(columns=['weight_pounds'])
train_size = int(len(natality) * 0.8)
traindata_natality = natality[:train_size]
trainlabels_natality = natality_labels[:train_size]
testdata_natality = natality[train_size:]
testlabels_natality = natality_labels[train_size:]
# Normalize and convert to PT tensors
normalized_train = normalize(np.array(traindata_natality.values), axis=0)
normalized_test = normalize(np.array(testdata_natality.values), axis=0)
train_x = torch.Tensor(normalized_train)
train_y = torch.Tensor(np.array(trainlabels_natality))
test_x = torch.Tensor(normalized_test)
test_y = torch.Tensor(np.array(testlabels_natality))
# Define our data loaders
train_dataset = torch.utils.data.TensorDataset(train_x, train_y)
train_dataloader = torch.utils.data.DataLoader(train_dataset, batch_size=128, shuffle=True)
test_dataset = torch.utils.data.TensorDataset(test_x, test_y)
test_dataloader = torch.utils.data.DataLoader(test_dataset, batch_size=128, shuffle=False)
# Define the model, while tuning the size of our hidden layer
model = nn.Sequential(nn.Linear(len(train_x[0]), args.hidden_layer_size),
nn.ReLU(),
nn.Linear(args.hidden_layer_size, 1))
criterion = nn.MSELoss()
# Tune hyperparameters in our optimizer
optimizer = optim.SGD(model.parameters(), lr=args.lr, momentum=args.momentum)
epochs = 10
for e in range(epochs):
for batch_id, (data, label) in enumerate(train_dataloader):
optimizer.zero_grad()
y_pred = model(data)
label = label.view(-1,1)
loss = criterion(y_pred, label)
loss.backward()
optimizer.step()
val_mse = 0
num_batches = 0
# Evaluate accuracy on our test set
with torch.no_grad():
for i, (data, label) in enumerate(test_dataloader):
num_batches += 1
y_pred = model(data)
mse = criterion(y_pred, label.view(-1,1))
val_mse += mse.item()
avg_val_mse = (val_mse / num_batches)
# Report the metric we're optimizing for to AI Platform's HyperTune service
# In this example, we're mimizing loss on our test set
hpt = hypertune.HyperTune()
hpt.report_hyperparameter_tuning_metric(
hyperparameter_metric_tag='val_mse',
metric_value=avg_val_mse,
global_step=epochs
)
def main():
args = get_args()
print('in main', args)
train_model(args)
if __name__ == '__main__':
main()
%%writefile config.yaml
trainingInput:
hyperparameters:
goal: MINIMIZE
maxTrials: 10
maxParallelTrials: 5
hyperparameterMetricTag: val_mse
enableTrialEarlyStopping: TRUE
params:
- parameterName: lr
type: DOUBLE
minValue: 0.0001
maxValue: 0.1
scaleType: UNIT_LINEAR_SCALE
- parameterName: momentum
type: DOUBLE
minValue: 0.0
maxValue: 1.0
scaleType: UNIT_LINEAR_SCALE
- parameterName: hidden-layer-size
type: INTEGER
minValue: 8
maxValue: 32
scaleType: UNIT_LINEAR_SCALE
MAIN_TRAINER_MODULE = "trainer.model"
TRAIN_DIR = os.getcwd() + '/trainer'
JOB_DIR = BUCKET_URL + '/output'
REGION = "us-central1"
# Create a unique job name (run this each time you submit a job)
timestamp = str(datetime.datetime.now().time())
JOB_NAME = 'caip_training_' + str(int(time.time()))
```
The command below will submit your training job to AI Platform. To view the logs, and the results of each HyperTune trial visit your Cloud console.
```
# Configure and submit the training job
!gcloud ai-platform jobs submit training $JOB_NAME \
--scale-tier basic \
--package-path $TRAIN_DIR \
--module-name $MAIN_TRAINER_MODULE \
--job-dir $JOB_DIR \
--region $REGION \
--runtime-version 2.1 \
--python-version 3.7 \
--config config.yaml
```
Copyright 2020 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.679391 | null | null | null | null |
|
<p align="center">
<img src="https://github.com/GeostatsGuy/GeostatsPy/blob/master/TCG_color_logo.png?raw=true" width="220" height="240" />
</p>
## Bootstrap-based Hypothesis Testing Demonstration
### Boostrap and Methods for Hypothesis Testing, Difference in Means
* we calculate the hypothesis test for different in means with boostrap and compare to the analytical expression
* **Welch's t-test**: we assume the features are Gaussian distributed and the variance are unequal
#### Michael Pyrcz, Associate Professor, University of Texas at Austin
##### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1) | [GeostatsPy](https://github.com/GeostatsGuy/GeostatsPy)
#### Hypothesis Testing
Powerful methodology for spatial data analytics:
1. extracted sample set 1 and 2, the means look different, but are they?
2. should we suspect that the samples are in fact from 2 different populations?
Now, let's try the t-test, hypothesis test for difference in means. This test assumes that the variances are similar along with the data being Gaussian distributed (see the course notes for more on this). This is our test:
\begin{equation}
H_0: \mu_{X1} = \mu_{X2}
\end{equation}
\begin{equation}
H_1: \mu_{X1} \ne \mu_{X2}
\end{equation}
To test this we will calculate the t statistic with the bootstrap and analytical approaches.
#### The Welch's t-test for Difference in Means by Analytical and Empirical Methods
We work with the following test statistic, *t-statistic*, from the two sample sets.
\begin{equation}
\hat{t} = \frac{\overline{x}_1 - \overline{x}_2}{\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}}
\end{equation}
where $\overline{x}_1$ and $\overline{x}_2$ are the sample means, $s^2_1$ and $s^2_2$ are the sample variances and $n_1$ and $n_2$ are the numer of samples from the two datasets.
The critical value, $t_{critical}$ is calculated by the analytical expression by:
\begin{equation}
t_{critical} = \left|t(\frac{\alpha}{2},\nu)\right|
\end{equation}
The degrees of freedom, $\nu$, is calculated as follows:
\begin{equation}
\nu = \frac{\left(\frac{1}{n_1} + \frac{\mu}{n_2}\right)^2}{\frac{1}{n_1^2(n_1-1)} + \frac{\mu^2}{n_2^2(n_2-1)}}
\end{equation}
Alternatively, the sampling distribution of the $t_{statistic}$ and $t_{critical}$ may be calculated empirically with bootstrap.
The workflow proceeds as:
* shift both sample sets to have the mean of the combined data set, $x_1$ → $x^*_1$, $x_2$ → $x^*_2$, this makes the null hypothesis true.
* for each bootstrap realization, $\ell=1\ldots,L$
* perform $n_1$ Monte Carlo simulations, draws with replacement, from sample set $x^*_1$
* perform $n_2$ Monte Carlo simulations, draws with replacement, from sample set $x^*_2$
* calculate the t_{statistic} realization, $\hat{t}^{\ell}$ given the resulting sample means $\overline{x}^{*,\ell}_1$ and $\overline{x}^{*,\ell}_2$ and the sample variances $s^{*,2,\ell}_1$ and $s^{*,2,\ell}_2$
* pool the results to assemble the $t_{statistic}$ sampling distribution
* calculate the cumulative probability of the observed t_{statistic}m, $\hat{t}$, from the boostrap distribution based on $\hat{t}^{\ell}$, $\ell = 1,\ldots,L$.
Here's some prerequisite information on the boostrap.
#### Bootstrap
Bootstrap is a method to assess the uncertainty in a sample statistic by repeated random sampling with replacement.
Assumptions
* sufficient, representative sampling, identical, idependent samples
Limitations
1. assumes the samples are representative
2. assumes stationarity
3. only accounts for uncertainty due to too few samples, e.g. no uncertainty due to changes away from data
4. does not account for boundary of area of interest
5. assumes the samples are independent
6. does not account for other local information sources
The Bootstrap Approach (Efron, 1982)
Statistical resampling procedure to calculate uncertainty in a calculated statistic from the data itself.
* Does this work? Prove it to yourself, for uncertainty in the mean solution is standard error:
\begin{equation}
\sigma^2_\overline{x} = \frac{\sigma^2_s}{n}
\end{equation}
Extremely powerful - could calculate uncertainty in any statistic! e.g. P13, skew etc.
* Would not be possible access general uncertainty in any statistic without bootstrap.
* Advanced forms account for spatial information and sampling strategy (game theory and Journel’s spatial bootstrap (1993).
Steps:
1. assemble a sample set, must be representative, reasonable to assume independence between samples
2. optional: build a cumulative distribution function (CDF)
* may account for declustering weights, tail extrapolation
* could use analogous data to support
3. For $\ell = 1, \ldots, L$ realizations, do the following:
* For $i = \alpha, \ldots, n$ data, do the following:
* Draw a random sample with replacement from the sample set or Monte Carlo simulate from the CDF (if available).
6. Calculate a realization of the sammary statistic of interest from the $n$ samples, e.g. $m^\ell$, $\sigma^2_{\ell}$. Return to 3 for another realization.
7. Compile and summarize the $L$ realizations of the statistic of interest.
This is a very powerful method. Let's try it out and compare the result to the analytical form of the confidence interval for the sample mean.
#### Objective
Provide an example and demonstration for:
1. interactive plotting in Jupyter Notebooks with Python packages matplotlib and ipywidgets
2. provide an intuitive hands-on example of confidence intervals and compare to statistical boostrap
#### Getting Started
Here's the steps to get setup in Python with the GeostatsPy package:
1. Install Anaconda 3 on your machine (https://www.anaconda.com/download/).
2. Open Jupyter and in the top block get started by copy and pasting the code block below from this Jupyter Notebook to start using the geostatspy functionality.
#### Load the Required Libraries
The following code loads the required libraries.
```
%matplotlib inline
from ipywidgets import interactive # widgets and interactivity
from ipywidgets import widgets
from ipywidgets import Layout
from ipywidgets import Label
from ipywidgets import VBox, HBox
import matplotlib.pyplot as plt # plotting
import numpy as np # working with arrays
import pandas as pd # working with DataFrames
from scipy import stats # statistical calculations
import random # random drawing / bootstrap realizations of the data
```
#### Make a Synthetic Dataset
This is an interactive method to:
* select a parametric distribution
* select the distribution parameters
* select the number of samples and visualize the synthetic dataset distribution
```
# interactive calculation of the sample set (control of source parametric distribution and number of samples)
l = widgets.Text(value=' Interactive Hypothesis Testing, Difference in Means, Analytical & Bootstrap Methods, Michael Pyrcz, Associate Professor, The University of Texas at Austin',layout=Layout(width='950px', height='30px'))
n1 = widgets.IntSlider(min=0, max = 100, value = 10, step = 1, description = '$n_{1}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
n1.style.handle_color = 'red'
m1 = widgets.FloatSlider(min=0, max = 50, value = 3, step = 1.0, description = '$\overline{x}_{1}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
m1.style.handle_color = 'red'
s1 = widgets.FloatSlider(min=0, max = 10, value = 3, step = 0.25, description = '$s_1$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
s1.style.handle_color = 'red'
ui1 = widgets.VBox([n1,m1,s1],) # basic widget formatting
n2 = widgets.IntSlider(min=0, max = 100, value = 10, step = 1, description = '$n_{2}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
n2.style.handle_color = 'yellow'
m2 = widgets.FloatSlider(min=0, max = 50, value = 3, step = 1.0, description = '$\overline{x}_{2}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
m2.style.handle_color = 'yellow'
s2 = widgets.FloatSlider(min=0, max = 10, value = 3, step = 0.25, description = '$s_2$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
s2.style.handle_color = 'yellow'
ui2 = widgets.VBox([n2,m2,s2],) # basic widget formatting
L = widgets.IntSlider(min=10, max = 1000, value = 100, step = 1, description = '$L$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
L.style.handle_color = 'gray'
alpha = widgets.FloatSlider(min=0, max = 50, value = 3, step = 1.0, description = '$α$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
alpha.style.handle_color = 'gray'
ui3 = widgets.VBox([L,alpha],) # basic widget formatting
ui4 = widgets.HBox([ui1,ui2,ui3],) # basic widget formatting
ui2 = widgets.VBox([l,ui4],)
def f_make(n1, m1, s1, n2, m2, s2, L, alpha): # function to take parameters, make sample and plot
np.random.seed(73073)
x1 = np.random.normal(loc=m1,scale=s1,size=n1)
np.random.seed(73074)
x2 = np.random.normal(loc=m2,scale=s2,size=n2)
mu = (s2*s2)/(s1*s1)
nu = ((1/n1 + mu/n2)*(1/n1 + mu/n2))/(1/(n1*n1*(n1-1)) + ((mu*mu)/(n2*n2*(n2-1))))
prop_values = np.linspace(-8.0,8.0,100)
analytical_distribution = stats.t.pdf(prop_values,df = nu)
analytical_tcrit = stats.t.ppf(1.0-alpha*0.005,df = nu)
# Analytical Method with SciPy
t_stat_observed, p_value_analytical = stats.ttest_ind(x1,x2,equal_var=False)
# Bootstrap Method
global_average = np.average(np.concatenate([x1,x2])) # shift the means to be equal to the globla mean
x1s = x1 - np.average(x1) + global_average
x2s = x2 - np.average(x2) + global_average
t_stat = np.zeros(L); p_value = np.zeros(L)
random.seed(73075)
for l in range(0, L): # loop over realizations
samples1 = random.choices(x1s, weights=None, cum_weights=None, k=len(x1s))
#print(samples1)
samples2 = random.choices(x2s, weights=None, cum_weights=None, k=len(x2s))
#print(samples2)
t_stat[l], p_value[l] = stats.ttest_ind(samples1,samples2,equal_var=False)
bootstrap_lower = np.percentile(t_stat,alpha * 0.5)
bootstrap_upper = np.percentile(t_stat,100.0 - alpha * 0.5)
plt.subplot(121)
#print(t_stat)
plt.hist(x1,cumulative = False, density = True, alpha=0.4,color="red",edgecolor="black", bins = np.linspace(0,50,50), label = '$x_1$')
plt.hist(x2,cumulative = False, density = True, alpha=0.4,color="yellow",edgecolor="black", bins = np.linspace(0,50,50), label = '$x_2$')
plt.ylim([0,0.4]); plt.xlim([0.0,30.0])
plt.title('Sample Distributions'); plt.xlabel('Value'); plt.ylabel('Density')
plt.legend()
#plt.hist(x2)
plt.subplot(122)
plt.ylim([0,0.6]); plt.xlim([-8.0,8.0])
plt.title('Bootstrap and Analytical $t_{statistic}$ Sampling Distributions'); plt.xlabel('$t_{statistic}$'); plt.ylabel('Density')
plt.plot([t_stat_observed,t_stat_observed],[0.0,0.6],color = 'black',label='observed $t_{statistic}$')
plt.plot([bootstrap_lower,bootstrap_lower],[0.0,0.6],color = 'blue',linestyle='dashed',label = 'bootstrap interval')
plt.plot([bootstrap_upper,bootstrap_upper],[0.0,0.6],color = 'blue',linestyle='dashed')
plt.plot(prop_values,analytical_distribution, color = 'red',label='analytical $t_{statistic}$')
plt.hist(t_stat,cumulative = False, density = True, alpha=0.2,color="blue",edgecolor="black", bins = np.linspace(-8.0,8.0,50), label = 'bootstrap $t_{statistic}$')
plt.fill_between(prop_values, 0, analytical_distribution, where = prop_values <= -1*analytical_tcrit, facecolor='red', interpolate=True, alpha = 0.2)
plt.fill_between(prop_values, 0, analytical_distribution, where = prop_values >= analytical_tcrit, facecolor='red', interpolate=True, alpha = 0.2)
ax = plt.gca()
handles,labels = ax.get_legend_handles_labels()
handles = [handles[0], handles[2], handles[3], handles[1]]
labels = [labels[0], labels[2], labels[3], labels[1]]
plt.legend(handles,labels,loc=1)
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=1.2, wspace=0.2, hspace=0.2)
plt.show()
# connect the function to make the samples and plot to the widgets
interactive_plot = widgets.interactive_output(f_make, {'n1': n1, 'm1': m1, 's1': s1, 'n2': n2, 'm2': m2, 's2': s2, 'L': L, 'alpha': alpha})
interactive_plot.clear_output(wait = True) # reduce flickering by delaying plot updating
```
### Boostrap and Analytical Methods for Hypothesis Testing, Difference in Means
* including the analytical and bootstrap methods for testing the difference in means
* interactive plot demonstration with ipywidget, matplotlib packages
#### Michael Pyrcz, Associate Professor, University of Texas at Austin
##### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1) | [GeostatsPy](https://github.com/GeostatsGuy/GeostatsPy)
### The Problem
Let's simulate bootstrap, resampling with replacement from a hat with $n_{red}$ and $n_{green}$ balls
* **$n_1$**, **$n_2$** number of samples, **$\overline{x}_1$**, **$\overline{x}_2$** means and **$s_1$**, **$s_2$** standard deviation of the 2 sample sets
* **$L$**: number of bootstrap realizations
* **$\alpha$**: alpha level
```
display(ui2, interactive_plot) # display the interactive plot
```
#### Observations
Some observations:
* lower dispersion and higher difference in means increases the absolute magnitude of the observed $t_{statistic}$
* the bootstrap distribution closely matches the analytical distribution if $L$ is large enough
* it is possible to use bootstrap to calculate the sampling distribution instead of relying on the theoretical express distribution, in this case the Student's t distribution.
#### Comments
This was a demonstration of interactive hypothesis testing for the significance in difference in means aboserved between 2 sample sets in Jupyter Notebook Python with the ipywidgets and matplotlib packages.
I have many other demonstrations on data analytics and machine learning, e.g. on the basics of working with DataFrames, ndarrays, univariate statistics, plotting data, declustering, data transformations, trend modeling and many other workflows available at https://github.com/GeostatsGuy/PythonNumericalDemos and https://github.com/GeostatsGuy/GeostatsPy.
I hope this was helpful,
*Michael*
#### The Author:
### Michael Pyrcz, Associate Professor, University of Texas at Austin
*Novel Data Analytics, Geostatistics and Machine Learning Subsurface Solutions*
With over 17 years of experience in subsurface consulting, research and development, Michael has returned to academia driven by his passion for teaching and enthusiasm for enhancing engineers' and geoscientists' impact in subsurface resource development.
For more about Michael check out these links:
#### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#### Want to Work Together?
I hope this content is helpful to those that want to learn more about subsurface modeling, data analytics and machine learning. Students and working professionals are welcome to participate.
* Want to invite me to visit your company for training, mentoring, project review, workflow design and / or consulting? I'd be happy to drop by and work with you!
* Interested in partnering, supporting my graduate student research or my Subsurface Data Analytics and Machine Learning consortium (co-PIs including Profs. Foster, Torres-Verdin and van Oort)? My research combines data analytics, stochastic modeling and machine learning theory with practice to develop novel methods and workflows to add value. We are solving challenging subsurface problems!
* I can be reached at [email protected].
I'm always happy to discuss,
*Michael*
Michael Pyrcz, Ph.D., P.Eng. Associate Professor The Hildebrand Department of Petroleum and Geosystems Engineering, Bureau of Economic Geology, The Jackson School of Geosciences, The University of Texas at Austin
#### More Resources Available at: [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
| true |
code
| 0.656466 | null | null | null | null |
|
# Systems of Nonlinear Equations
## CH EN 2450 - Numerical Methods
**Prof. Tony Saad (<a>www.tsaad.net</a>) <br/>Department of Chemical Engineering <br/>University of Utah**
<hr/>
# Example 1
A system of nonlinear equations consists of several nonlinear functions - as many as there are unknowns. Solving a system of nonlinear equations means funding those points where the functions intersect each other. Consider for example the following system of equations
\begin{equation}
y = 4x - 0.5 x^3
\end{equation}
\begin{equation}
y = \sin(x)e^{-x}
\end{equation}
The first step is to write these in residual form
\begin{equation}
f_1 = y - 4x + 0.5 x^3,\\
f_2 = y - \sin(x)e^{-x}
\end{equation}
```
import numpy as np
from numpy import cos, sin, pi, exp
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
y1 = lambda x: 4 * x - 0.5 * x**3
y2 = lambda x: sin(x)*exp(-x)
x = np.linspace(-3.5,4,100)
plt.ylim(-8,6)
plt.plot(x,y1(x), 'k')
plt.plot(x,y2(x), 'r')
plt.grid()
plt.savefig('example1.pdf')
def F(xval):
x = xval[0] # let the first value in xval denote x
y = xval[1] # let the second value in xval denote y
f1 = y - 4.0*x + 0.5*x**3 # define f1
f2 = y - sin(x)*exp(-x) # define f2
return np.array([f1,f2]) # must return an array
def J(xval):
x = xval[0]
y = xval[1]
return np.array([[1.5*x**2 - 4.0 , 1.0 ],
[-cos(x)*exp(-x) + sin(x)*exp(-x) , 1.0]]) # Jacobian matrix J = [[df1/dx, df1/dy], [df2/dx,df2/dy]]
guess = np.array([1,3])
F(guess)
J(guess)
def newton_solver(F, J, x, tol): # x is nothing more than your initial guess
F_value = F(x)
err = np.linalg.norm(F_value, ord=2) # l2 norm of vector
# err = tol + 100
niter = 0
while abs(err) > tol and niter < 100:
J_value = J(x)
delta = np.linalg.solve(J_value, - F_value)
x = x + delta # update the solution
F_value = F(x) # compute new values for vector of residual functions
err = np.linalg.norm(F_value, ord=2) # compute error norm (absolute error)
niter += 1
# Here, either a solution is found, or too many iterations
if abs(err) > tol:
niter = -1
print('No Solution Found!!!!!!!!!')
return x, niter, err
```
Try to find the root less than [-2,-4]
```
tol = 1e-8
xguess = np.array([-3,0])
roots, n, err = newton_solver(F,J,xguess,tol)
print ('# of iterations', n, 'roots:', roots)
print ('Error Norm =',err)
F(roots)
```
Use Python's fsolve routine
```
fsolve(F,xguess)
```
# Example 2
Find the roots of the following system of equations
\begin{equation}
x^2 + y^2 = 1, \\
y = x^3 - x + 1
\end{equation}
First we assign $x_1 \equiv x$ and $x_2 \equiv y$ and rewrite the system in residual form
\begin{equation}
f_1(x_1,x_2) = x_1^2 + x_2^2 - 1, \\
f_2(x_1,x_2) = x_1^3 - x_1 - x_2 + 1
\end{equation}
```
x = np.linspace(-1,1)
y1 = lambda x: x**3 - x + 1
y2 = lambda x: np.sqrt(1 - x**2)
plt.plot(x,y1(x), 'k')
plt.plot(x,y2(x), 'r')
plt.grid()
def F(xval):
?
def J(xval):
?
tol = 1e-8
xguess = np.array([0.5,0.5])
x, n, err = newton_solver(F, J, xguess, tol)
print (n, x)
print ('Error Norm =',err)
fsolve(F,(0.5,0.5))
import urllib
import requests
from IPython.core.display import HTML
def css_styling():
styles = requests.get("https://raw.githubusercontent.com/saadtony/NumericalMethods/master/styles/custom.css")
return HTML(styles.text)
css_styling()
```
| true |
code
| 0.57678 | null | null | null | null |
|
(pandas_plotting)=
# Plotting
``` {index} Pandas: plotting
```
Plotting with pandas is very intuitive. We can use syntax:
df.plot.*
where * is any plot from matplotlib.pyplot supported by pandas. Full tutorial on pandas plots can be found [here](https://pandas.pydata.org/pandas-docs/stable/user_guide/visualization.html).
Alternatively, we can use other plots from matplotlib library and pass specific columns as arguments:
plt.scatter(df.col1, df.col2, c=df.col3, s=df.col4, *kwargs)
In this tutorial we will use both ways of plotting.
At first we will load New Zealand earthquake data and following date-time tutorial we will create date-time index:
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
nz_eqs = pd.read_csv("../../geosciences/data/nz_largest_eq_since_1970.csv")
nz_eqs.head(4)
nz_eqs["hour"] = nz_eqs["utc_time"].str.split(':').str.get(0).astype(float)
nz_eqs["minute"] = nz_eqs["utc_time"].str.split(':').str.get(1).astype(float)
nz_eqs["second"] = nz_eqs["utc_time"].str.split(':').str.get(2).astype(float)
nz_eqs["datetime"] = pd.to_datetime(nz_eqs[['year', 'month', 'day', 'hour', 'minute', 'second']])
nz_eqs.head(4)
nz_eqs = nz_eqs.set_index('datetime')
```
Let's plot magnitude data for all years and then for year 2000 only using pandas way of plotting:
```
plt.figure(figsize=(7,5))
nz_eqs['mag'].plot()
plt.xlabel('Date')
plt.ylabel('Magnitude')
plt.show()
plt.figure(figsize=(7,5))
nz_eqs['mag'].loc['2000-01':'2001-01'].plot()
plt.xlabel('Date')
plt.ylabel('Magnitude')
plt.show()
```
We can calculate how many earthquakes are within each year using:
df.resample('bintype').count()
For example, if we want to use intervals for year, month, minute and second we can use 'Y', 'M', 'T' and 'S' in the bintype argument.
Let's count our earthquakes in 4 month intervals and display it with xticks every 4 years:
```
figure, ax = plt.subplots(figsize=(7,5))
# Resample datetime index into 4 month bins
# and then count how many
nz_eqs['year'].resample("4M").count().plot(ax=ax, x_compat=True)
import matplotlib
# Change xticks to be every 4 years
ax.xaxis.set_major_locator(matplotlib.dates.YearLocator(base=4))
ax.xaxis.set_major_formatter(matplotlib.dates.DateFormatter("%Y"))
plt.xlabel('Date')
plt.ylabel('No. of earthquakes')
plt.show()
```
Suppose we would like to view the earthquake locations, places with largest earthquakes and their depths. To do that, we can use Cartopy library and create a scatter plot, passing magnitude column into size and depth column into colour.
```
import cartopy.crs as ccrs
import cartopy.feature as cfeature
from cartopy.mpl.gridliner import LONGITUDE_FORMATTER, LATITUDE_FORMATTER
import matplotlib.ticker as mticker
```
Let's plot this data passing columns into scatter plot:
```
plt.rcParams.update({'font.size': 14})
central_lon, central_lat = 170, -50
extent = [160,188,-48,-32]
fig, ax = plt.subplots(1, subplot_kw=dict(projection=ccrs.Mercator(central_lon, central_lat)), figsize=(7,7))
ax.set_extent(extent)
ax.coastlines(resolution='10m')
ax.set_title("Earthquakes in New Zealand since 1970")
# Create a scatter plot
scatplot = ax.scatter(nz_eqs.lon,nz_eqs.lat, c=nz_eqs.depth_km,
s=nz_eqs.depth_km/10, edgecolor="black",
cmap="PuRd", lw=0.1,
transform=ccrs.Geodetic())
# Create colourbar
cbar = plt.colorbar(scatplot, ax=ax, fraction=0.03, pad=0.1, label='Depth [km]')
# Sort out gridlines and their density
xticks_extent = list(np.arange(160, 180, 4)) + list(np.arange(-200,-170,4))
yticks_extent = list(np.arange(-60, -30, 2))
gl = ax.gridlines(linewidths=0.1)
gl.xlabels_top = False
gl.xlabels_bottom = True
gl.ylabels_left = True
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator(xticks_extent)
gl.ylocator = mticker.FixedLocator(yticks_extent)
gl.xformatter = LONGITUDE_FORMATTER
gl.yformatter = LATITUDE_FORMATTER
plt.show()
```
This way we can easily see that the deepest and largest earthquakes are in the North.
# References
The notebook was compiled based on:
* [Pandas official Getting Started tutorials](https://pandas.pydata.org/docs/getting_started/index.html#getting-started)
* [Kaggle tutorial](https://www.kaggle.com/learn/pandas)
| true |
code
| 0.810957 | null | null | null | null |
|
# Machine Learning with PyTorch and Scikit-Learn
# -- Code Examples
## Package version checks
Add folder to path in order to load from the check_packages.py script:
```
import sys
sys.path.insert(0, '..')
```
Check recommended package versions:
```
from python_environment_check import check_packages
d = {
'torch': '1.8.0',
}
check_packages(d)
```
Chapter 15: Modeling Sequential Data Using Recurrent Neural Networks (part 3/3)
========
**Outline**
- Implementing RNNs for sequence modeling in PyTorch
- [Project two -- character-level language modeling in PyTorch](#Project-two----character-level-language-modeling-in-PyTorch)
- [Preprocessing the dataset](#Preprocessing-the-dataset)
- [Evaluation phase -- generating new text passages](#Evaluation-phase----generating-new-text-passages)
- [Summary](#Summary)
Note that the optional watermark extension is a small IPython notebook plugin that I developed to make the code reproducible. You can just skip the following line(s).
```
from IPython.display import Image
%matplotlib inline
```
## Project two: character-level language modeling in PyTorch
```
Image(filename='figures/15_11.png', width=500)
```
### Preprocessing the dataset
```
import numpy as np
## Reading and processing text
with open('1268-0.txt', 'r', encoding="utf8") as fp:
text=fp.read()
start_indx = text.find('THE MYSTERIOUS ISLAND')
end_indx = text.find('End of the Project Gutenberg')
text = text[start_indx:end_indx]
char_set = set(text)
print('Total Length:', len(text))
print('Unique Characters:', len(char_set))
Image(filename='figures/15_12.png', width=500)
chars_sorted = sorted(char_set)
char2int = {ch:i for i,ch in enumerate(chars_sorted)}
char_array = np.array(chars_sorted)
text_encoded = np.array(
[char2int[ch] for ch in text],
dtype=np.int32)
print('Text encoded shape: ', text_encoded.shape)
print(text[:15], ' == Encoding ==> ', text_encoded[:15])
print(text_encoded[15:21], ' == Reverse ==> ', ''.join(char_array[text_encoded[15:21]]))
for ex in text_encoded[:5]:
print('{} -> {}'.format(ex, char_array[ex]))
Image(filename='figures/15_13.png', width=500)
Image(filename='figures/15_14.png', width=500)
seq_length = 40
chunk_size = seq_length + 1
text_chunks = [text_encoded[i:i+chunk_size]
for i in range(len(text_encoded)-chunk_size+1)]
## inspection:
for seq in text_chunks[:1]:
input_seq = seq[:seq_length]
target = seq[seq_length]
print(input_seq, ' -> ', target)
print(repr(''.join(char_array[input_seq])),
' -> ', repr(''.join(char_array[target])))
import torch
from torch.utils.data import Dataset
class TextDataset(Dataset):
def __init__(self, text_chunks):
self.text_chunks = text_chunks
def __len__(self):
return len(self.text_chunks)
def __getitem__(self, idx):
text_chunk = self.text_chunks[idx]
return text_chunk[:-1].long(), text_chunk[1:].long()
seq_dataset = TextDataset(torch.tensor(text_chunks))
for i, (seq, target) in enumerate(seq_dataset):
print(' Input (x):', repr(''.join(char_array[seq])))
print('Target (y):', repr(''.join(char_array[target])))
print()
if i == 1:
break
device = torch.device("cuda:0")
# device = 'cpu'
from torch.utils.data import DataLoader
batch_size = 64
torch.manual_seed(1)
seq_dl = DataLoader(seq_dataset, batch_size=batch_size, shuffle=True, drop_last=True)
```
### Building a character-level RNN model
```
import torch.nn as nn
class RNN(nn.Module):
def __init__(self, vocab_size, embed_dim, rnn_hidden_size):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embed_dim)
self.rnn_hidden_size = rnn_hidden_size
self.rnn = nn.LSTM(embed_dim, rnn_hidden_size,
batch_first=True)
self.fc = nn.Linear(rnn_hidden_size, vocab_size)
def forward(self, x, hidden, cell):
out = self.embedding(x).unsqueeze(1)
out, (hidden, cell) = self.rnn(out, (hidden, cell))
out = self.fc(out).reshape(out.size(0), -1)
return out, hidden, cell
def init_hidden(self, batch_size):
hidden = torch.zeros(1, batch_size, self.rnn_hidden_size)
cell = torch.zeros(1, batch_size, self.rnn_hidden_size)
return hidden.to(device), cell.to(device)
vocab_size = len(char_array)
embed_dim = 256
rnn_hidden_size = 512
torch.manual_seed(1)
model = RNN(vocab_size, embed_dim, rnn_hidden_size)
model = model.to(device)
model
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
num_epochs = 10000
torch.manual_seed(1)
for epoch in range(num_epochs):
hidden, cell = model.init_hidden(batch_size)
seq_batch, target_batch = next(iter(seq_dl))
seq_batch = seq_batch.to(device)
target_batch = target_batch.to(device)
optimizer.zero_grad()
loss = 0
for c in range(seq_length):
pred, hidden, cell = model(seq_batch[:, c], hidden, cell)
loss += loss_fn(pred, target_batch[:, c])
loss.backward()
optimizer.step()
loss = loss.item()/seq_length
if epoch % 500 == 0:
print(f'Epoch {epoch} loss: {loss:.4f}')
```
### Evaluation phase: generating new text passages
```
from torch.distributions.categorical import Categorical
torch.manual_seed(1)
logits = torch.tensor([[1.0, 1.0, 1.0]])
print('Probabilities:', nn.functional.softmax(logits, dim=1).numpy()[0])
m = Categorical(logits=logits)
samples = m.sample((10,))
print(samples.numpy())
torch.manual_seed(1)
logits = torch.tensor([[1.0, 1.0, 3.0]])
print('Probabilities:', nn.functional.softmax(logits, dim=1).numpy()[0])
m = Categorical(logits=logits)
samples = m.sample((10,))
print(samples.numpy())
def sample(model, starting_str,
len_generated_text=500,
scale_factor=1.0):
encoded_input = torch.tensor([char2int[s] for s in starting_str])
encoded_input = torch.reshape(encoded_input, (1, -1))
generated_str = starting_str
model.eval()
hidden, cell = model.init_hidden(1)
hidden = hidden.to('cpu')
cell = cell.to('cpu')
for c in range(len(starting_str)-1):
_, hidden, cell = model(encoded_input[:, c].view(1), hidden, cell)
last_char = encoded_input[:, -1]
for i in range(len_generated_text):
logits, hidden, cell = model(last_char.view(1), hidden, cell)
logits = torch.squeeze(logits, 0)
scaled_logits = logits * scale_factor
m = Categorical(logits=scaled_logits)
last_char = m.sample()
generated_str += str(char_array[last_char])
return generated_str
torch.manual_seed(1)
model.to('cpu')
print(sample(model, starting_str='The island'))
```
* **Predictability vs. randomness**
```
logits = torch.tensor([[1.0, 1.0, 3.0]])
print('Probabilities before scaling: ', nn.functional.softmax(logits, dim=1).numpy()[0])
print('Probabilities after scaling with 0.5:', nn.functional.softmax(0.5*logits, dim=1).numpy()[0])
print('Probabilities after scaling with 0.1:', nn.functional.softmax(0.1*logits, dim=1).numpy()[0])
torch.manual_seed(1)
print(sample(model, starting_str='The island',
scale_factor=2.0))
torch.manual_seed(1)
print(sample(model, starting_str='The island',
scale_factor=0.5))
```
...
# Summary
...
Readers may ignore the next cell.
```
! python ../.convert_notebook_to_script.py --input ch15_part3.ipynb --output ch15_part3.py
```
| true |
code
| 0.657841 | null | null | null | null |
|
<a id='Top'></a>
# MultiSurv results by cancer type<a class='tocSkip'></a>
C-index value results for each cancer type of the best MultiSurv model trained on all-cancer data.
```
%load_ext autoreload
%autoreload 2
%load_ext watermark
import sys
import os
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import torch
# Make modules in "src" dir visible
project_dir = os.path.split(os.getcwd())[0]
if project_dir not in sys.path:
sys.path.append(os.path.join(project_dir, 'src'))
import dataset
from model import Model
import utils
matplotlib.style.use('multisurv.mplstyle')
```
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Load-model" data-toc-modified-id="Load-model-1"><span class="toc-item-num">1 </span>Load model</a></span></li><li><span><a href="#Evaluate" data-toc-modified-id="Evaluate-2"><span class="toc-item-num">2 </span>Evaluate</a></span></li><li><span><a href="#Result-graph" data-toc-modified-id="Result-graph-3"><span class="toc-item-num">3 </span>Result graph</a></span><ul class="toc-item"><li><span><a href="#Save-to-files" data-toc-modified-id="Save-to-files-3.1"><span class="toc-item-num">3.1 </span>Save to files</a></span></li></ul></li><li><span><a href="#Metric-correlation-with-other-attributes" data-toc-modified-id="Metric-correlation-with-other-attributes-4"><span class="toc-item-num">4 </span>Metric correlation with other attributes</a></span><ul class="toc-item"><li><span><a href="#Collect-feature-representations" data-toc-modified-id="Collect-feature-representations-4.1"><span class="toc-item-num">4.1 </span>Collect feature representations</a></span></li><li><span><a href="#Compute-dispersion-and-add-to-selected-metric-table" data-toc-modified-id="Compute-dispersion-and-add-to-selected-metric-table-4.2"><span class="toc-item-num">4.2 </span>Compute dispersion and add to selected metric table</a></span></li><li><span><a href="#Plot" data-toc-modified-id="Plot-4.3"><span class="toc-item-num">4.3 </span>Plot</a></span></li></ul></li></ul></div>
```
DATA = utils.INPUT_DATA_DIR
MODELS = utils.TRAINED_MODEL_DIR
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
```
# Load model
```
dataloaders = utils.get_dataloaders(
data_location=DATA,
labels_file='../data/labels.tsv',
modalities=['clinical', 'mRNA'],
# exclude_patients=exclude_cancers,
return_patient_id=True
)
multisurv = Model(dataloaders=dataloaders, device=device)
multisurv.load_weights(os.path.join(MODELS, 'clinical_mRNA_lr0.005_epoch43_acc0.81.pth'))
```
# Evaluate
```
def get_patients_with(cancer_type, split_group='test'):
labels = pd.read_csv('../data/labels.tsv', sep='\t')
cancer_labels = labels[labels['project_id'] == cancer_type]
group_cancer_labels = cancer_labels[cancer_labels['group'] == split_group]
return list(group_cancer_labels['submitter_id'])
%%time
results = {}
minimum_n_patients = 0
cancer_types = pd.read_csv('../data/labels.tsv', sep='\t').project_id.unique()
for i, cancer_type in enumerate(cancer_types):
print('-' * 44)
print(' ' * 17, f'{i + 1}.', cancer_type)
print('-' * 44)
patients = get_patients_with(cancer_type)
if len(patients) < minimum_n_patients:
continue
exclude_patients = [p for p in dataloaders['test'].dataset.patient_ids
if not p in patients]
data = utils.get_dataloaders(
data_location=DATA,
labels_file='../data/labels.tsv',
modalities=['clinical', 'mRNA'],
exclude_patients=exclude_patients,
return_patient_id=True
)['test'].dataset
results[cancer_type] = utils.Evaluation(model=multisurv, dataset=data, device=device)
results[cancer_type].run_bootstrap()
print()
print()
print()
%%time
data = utils.get_dataloaders(
data_location=DATA,
labels_file='../data/labels.tsv',
modalities=['clinical', 'mRNA'],
return_patient_id=True
)['test'].dataset
results['All'] = utils.Evaluation(model=multisurv, dataset=data, device=device)
results['All'].run_bootstrap()
print()
```
In order to avoid very __noisy values__, establish a __minimum threshold__ for the number of patients in each given cancer type.
```
minimum_n_patients = 20
cancer_types = pd.read_csv('../data/labels.tsv', sep='\t').project_id.unique()
selected_cancer_types = ['All']
print('-' * 40)
print(' Cancer Ctd IBS # patients')
print('-' * 40)
for cancer_type in sorted(list(cancer_types)):
patients = get_patients_with(cancer_type)
if len(patients) > minimum_n_patients:
selected_cancer_types.append(cancer_type)
ctd = str(round(results[cancer_type].c_index_td, 3))
ibs = str(round(results[cancer_type].ibs, 3))
message = ' ' + cancer_type
message += ' ' * (11 - len(message)) + ctd
message += ' ' * (20 - len(message)) + ibs
message += ' ' * (32 - len(message)) + str(len(patients))
print(message)
# print(' ' + cancer_type + ' ' * (10 - len(cancer_type)) + \
# ctd + ' ' * (10 - len(ibs)) + ibs + ' ' * (13 - len(ctd)) \
# + str(len(patients)))
def format_bootstrap_output(evaluator):
results = evaluator.format_results()
for metric in results:
results[metric] = results[metric].split(' ')
val = results[metric][0]
ci_low, ci_high = results[metric][1].split('(')[1].split(')')[0].split('-')
results[metric] = val, ci_low, ci_high
results[metric] = [float(x) for x in results[metric]]
return results
formatted_results = {}
# for cancer_type in results:
for cancer_type in sorted(selected_cancer_types):
formatted_results[cancer_type] = format_bootstrap_output(results[cancer_type])
formatted_results
```
# Result graph
Exclude cancer types with less than a chosen minimum number of patients, to avoid extremely noisy results.
```
utils.plot.show_default_colors()
PLOT_SIZE = (15, 4)
default_colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
def get_metric_results(metric, data):
df = pd.DataFrame()
df['Cancer type'] = data.keys()
val, err = [], []
for cancer in formatted_results:
values = formatted_results[cancer][metric]
val.append(values[0])
err.append((values[0] - values[1], values[2] - values[0]))
df[metric] = val
err = np.swapaxes(np.array(err), 1, 0)
return df, err
def plot_results(metric, data, ci, y_lim=None, y_label=None, h_lines=[1, 0.5]):
fig = plt.figure(figsize=PLOT_SIZE)
ax = fig.add_subplot(1, 1, 1)
for y in h_lines:
ax.axhline(y, linestyle='--', color='grey')
ax.bar(df['Cancer type'][:1], df[metric][:1], yerr=err[:, :1],
align='center', ecolor=default_colors[0],
alpha=0.5, capsize=5)
ax.bar(df['Cancer type'][1:], df[metric][1:], yerr=err[:, 1:],
align='center', color=default_colors[6], ecolor=default_colors[6],
alpha=0.5, capsize=5)
if y_lim is None:
y_lim = (0, 1)
ax.set_ylim(y_lim)
ax.set_title('')
ax.set_xlabel('Cancer types')
if y_label is None:
ax.set_ylabel(metric + ' (95% CI)')
else:
ax.set_ylabel(y_label)
return fig
metric='Ctd'
df, err = get_metric_results(metric, formatted_results)
fig_ctd = plot_results(metric, df, err, y_label='$C^{td}$ (95% CI)')
metric='IBS'
df, err = get_metric_results(metric, formatted_results)
fig_ibs = plot_results(metric, df, err, y_lim=(0, 0.35), y_label=None, h_lines=[0.25])
```
## Save to files
```
%%javascript
IPython.notebook.kernel.execute('nb_name = "' + IPython.notebook.notebook_name + '"')
pdf_file = nb_name.split('.ipynb')[0] + '_Ctd'
utils.plot.save_plot_for_figure(figure=fig_ctd, file_name=pdf_file)
pdf_file = nb_name.split('.ipynb')[0] + '_IBS'
utils.plot.save_plot_for_figure(figure=fig_ibs, file_name=pdf_file)
pdf_file = nb_name.split('.ipynb')[0] + '_INBLL'
utils.plot.save_plot_for_figure(figure=fig_inbll, file_name=pdf_file)
```
# Watermark<a class='tocSkip'></a>
```
%watermark --iversions
%watermark -v
print()
%watermark -u -n
```
[Top of the page](#Top)
| true |
code
| 0.429669 | null | null | null | null |
|
# `model_hod` module tutorial notebook
```
%load_ext autoreload
%autoreload 2
%pylab inline
import logging
mpl_logger = logging.getLogger('matplotlib')
mpl_logger.setLevel(logging.WARNING)
pil_logger = logging.getLogger('PIL')
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.size'] = 18
plt.rcParams['axes.linewidth'] = 1.5
plt.rcParams['xtick.major.size'] = 5
plt.rcParams['ytick.major.size'] = 5
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['xtick.top'] = True
plt.rcParams['ytick.right'] = True
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['figure.figsize'] = (10,6)
from dark_emulator import model_hod
hod = model_hod.darkemu_x_hod({"fft_num":8})
```
## how to set cosmology and galaxy parameters (HOD, off-centering, satellite distribution, and incompleteness)
```
cparam = np.array([0.02225,0.1198,0.6844,3.094,0.9645,-1.])
hod.set_cosmology(cparam)
gparam = {"logMmin":13.13, "sigma_sq":0.22, "logM1": 14.21, "alpha": 1.13, "kappa": 1.25, # HOD parameters
"poff": 0.2, "Roff": 0.1, # off-centering parameters p_off is the fraction of off-centered galaxies. Roff is the typical off-centered scale with respect to R200m.
"sat_dist_type": "emulator", # satellite distribution. Chosse emulator of NFW. In the case of NFW, the c-M relation by Diemer & Kravtsov (2015) is assumed.
"alpha_inc": 0.44, "logM_inc": 13.57} # incompleteness parameters. For details, see More et al. (2015)
hod.set_galaxy(gparam)
```
## how to plot g-g lensing signal in DeltaSigma(R)
```
redshift = 0.55
r = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_ds(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_ds_cen(r, redshift), "--", color = "k", label = "central")
plt.loglog(r, hod.get_ds_cen_off(r, redshift), ":", color = "k", label = "central w/offset")
plt.loglog(r, hod.get_ds_sat(r, redshift), "-.", color = "k", label = "satellite")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$\Delta\Sigma$ [hM$_\odot$/pc$^2$]")
plt.legend()
```
## how to plot g-g lensing signal in xi
```
redshift = 0.55
r = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_xi_gm(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_xi_gm_cen(r, redshift), "--", color = "k", label = "central")
plt.loglog(r, hod.get_xi_gm_cen_off(r, redshift), ":", color = "k", label = "central w/offset")
plt.loglog(r, hod.get_xi_gm_sat(r, redshift), "-.", color = "k", label = "satellite")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$\xi_{\rm gm}$")
plt.legend()
```
## how to plot g-g clustering signal in wp
```
redshift = 0.55
rs = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_wp(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_wp_1hcs(r, redshift), "--", color = "k", label = "1-halo cen-sat")
plt.loglog(r, hod.get_wp_1hss(r, redshift), ":", color = "k", label = "1-halo sat-sat")
plt.loglog(r, hod.get_wp_2hcc(r, redshift), "-.", color = "k", label = "2-halo cen-cen")
plt.loglog(r, hod.get_wp_2hcs(r, redshift), dashes=[4,1,1,1,1,1], color = "k", label = "2-halo cen-sat")
plt.loglog(r, hod.get_wp_2hss(r, redshift), dashes=[4,1,1,1,4,1], color = "k", label = "2-halo sat-sat")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$w_p$ [Mpc/h]")
plt.legend()
plt.ylim(0.1, 6e3)
```
## how to plot g-g clustering signal in xi
```
redshift = 0.55
rs = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_xi_gg(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_xi_gg_1hcs(r, redshift), "--", color = "k", label = "1-halo cen-sat")
plt.loglog(r, hod.get_xi_gg_1hss(r, redshift), ":", color = "k", label = "1-halo sat-sat")
plt.loglog(r, hod.get_xi_gg_2hcc(r, redshift), "-.", color = "k", label = "2-halo cen-cen")
plt.loglog(r, hod.get_xi_gg_2hcs(r, redshift), dashes=[4,1,1,1,1,1], color = "k", label = "2-halo cen-sat")
plt.loglog(r, hod.get_xi_gg_2hss(r, redshift), dashes=[4,1,1,1,4,1], color = "k", label = "2-halo sat-sat")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$\xi$")
plt.legend()
plt.ylim(1e-3, 6e3)
```
| true |
code
| 0.692382 | null | null | null | null |
|
# Generic Integration With Credo AI's Governance App
Lens is primarily a framework for comprehensive assessment of AI models. However, in addition, it is the primary way to integrate assessment analysis with Credo AI's Governance App.
In this tutorial, we will take a model created and assessed _completely independently of Lens_ and send that data to Credo AI's Governance App
### Find the code
This notebook can be found on [github](https://github.com/credo-ai/credoai_lens/blob/develop/docs/notebooks/integration_demo.ipynb).
## Create an example ML Model
```
import numpy as np
from matplotlib import pyplot as plt
from pprint import pprint
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.metrics import classification_report
from sklearn.metrics import precision_recall_curve
```
### Load data and train model
For the purpose of this demonstration, we will be classifying digits after a large amount of noise has been added to each image.
We'll create some charts and assessment metrics to reflect our work.
```
# load data
digits = datasets.load_digits()
# add noise
digits.data += np.random.rand(*digits.data.shape)*16
# split into train and test
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target)
# create and fit model
clf = SVC(probability=True)
clf.fit(X_train, y_train)
```
### Visualize example images along with predicted label
```
examples_plot = plt.figure()
for i in range(8):
image_data = X_test[i,:]
prediction = digits.target_names[clf.predict(image_data[None,:])[0]]
label = f'Pred: "{prediction}"'
# plot
ax = plt.subplot(2,4,i+1)
ax.imshow(image_data.reshape(8,8), cmap='gray')
ax.set_title(label)
ax.tick_params(labelbottom=False, labelleft=False, length=0)
plt.suptitle('Example Images and Predictions', fontsize=16)
```
### Calculate performance metrics and visualize
As a multiclassification problem, we can calculate metrics per class, or overall. We record overall metrics, but include figures for individual class performance breakdown
```
metrics = classification_report(y_test, clf.predict(X_test), output_dict=True)
overall_metrics = metrics['macro avg']
del overall_metrics['support']
pprint(overall_metrics)
probs = clf.predict_proba(X_test)
pr_curves = plt.figure(figsize=(8,6))
# plot PR curve sper digit
for digit in digits.target_names:
y_true = y_test == digit
y_prob = probs[:,digit]
precisions, recalls, thresholds = precision_recall_curve(y_true, y_prob)
plt.plot(recalls, precisions, lw=3, label=f'Digit: {digit}')
plt.xlabel('Recall', fontsize=16)
plt.ylabel('Precision', fontsize=16)
# plot iso lines
f_scores = np.linspace(0.2, 0.8, num=4)
lines = []
labels = []
for f_score in f_scores:
label = label='ISO f1 curves' if f_score==f_scores[0] else ''
x = np.linspace(0.01, 1)
y = f_score * x / (2 * x - f_score)
l, = plt.plot(x[y >= 0], y[y >= 0], color='gray', alpha=0.2, label=label)
# final touches
plt.xlim([0.5, 1.0])
plt.ylim([0.0, 1.05])
plt.tick_params(labelsize=14)
plt.title('PR Curves per Digit', fontsize=20)
plt.legend(loc='lower left', fontsize=10)
from sklearn.metrics import plot_confusion_matrix
confusion_plot = plt.figure(figsize=(6,6))
plot_confusion_matrix(clf, X_test, y_test, \
normalize='true', ax=plt.gca(), colorbar=False)
plt.tick_params(labelsize=14)
```
## Sending assessment information to Credo AI
Now that we have completed training and assessing the model, we will demonstrate how information can be sent to the Credo AI Governance App. Metrics related to performance, fairness, or other governance considerations are the most important kind of evidence needed for governance.
In addition, figures are often produced that help communicate metrics better, understand the model, or other contextualize the AI system. Credo can ingest those as well.
**Which metrics to record?**
Ideally you will have decided on the most important metrics before building the model. We refer to this stage as `Metric Alignment`. This is the phase where your team explicitly determine how you will measure whether your model can be safely deployed. It is part of the more general `Alignment Stage`, which often requires input from multiple stakeholders outside of the team specifically involved in the development of the AI model.
Of course, you may want to record more metrics than those explicitly determined during `Metric Alignment`.
For instance, in this example let's say that during `Metric Alignment`, the _F1 Score_ is the primary metric used to evaluate model performance. However, we have decided that recall and precision would be helpful supporting. So we will send those three metrics.
To reiterate: You are always free to send more metrics - Credo AI will ingest them. It is you and your team's decision which metrics are tracked specifically for governance purposes.
```
import credoai.integration as ci
from credoai.utils import list_metrics
model_name = 'SVC'
dataset_name = 'sklearn_digits'
```
## Quick reference
Below is all the code needed to record a set of metrics and figures. We will unpack each part below.
```
# metrics
metric_records = ci.record_metrics_from_dict(overall_metrics,
model_label=model_name,
dataset_label=dataset_name)
#figures
example_figure_record = ci.Figure(examples_plot._suptitle.get_text(), examples_plot)
confusion_figure_record = ci.Figure(confusion_plot.axes[0].get_title(), confusion_plot)
pr_curve_caption="""Precision-recall curves are shown for each digit separately.
These are calculated by treating each class as a separate
binary classification problem. The grey lines are
ISO f1 curves - all points on each curve have identical
f1 scores.
"""
pr_curve_figure_record = ci.Figure(pr_curves.axes[0].get_title(),
figure=pr_curves,
caption=pr_curve_caption)
figure_records = ci.MultiRecord([example_figure_record, confusion_figure_record, pr_curve_figure_record])
# export to file
# ci.export_to_file(model_record, 'model_record.json')
```
## Metric Record
To record a metric you can either record each one manually or ingest a dictionary of metrics.
### Manually entering individual metrics
```
f1_description = """Harmonic mean of precision and recall scores.
Ranges from 0-1, with 1 being perfect performance."""
f1_record = ci.Metric(metric_type='f1',
value=overall_metrics['f1-score'],
model_label=model_name,
dataset_label=dataset_name)
precision_record = ci.Metric(metric_type='precision',
value=overall_metrics['precision'],
model_label=model_name,
dataset_label=dataset_name)
recall_record = ci.Metric(metric_type='recall',
value=overall_metrics['recall'],
model_label=model_name,
dataset_label=dataset_name)
metrics = [f1_record, precision_record, recall_record]
```
### Convenience to record multiple metrics
Multiple metrics can be recorded as long as they are described using a pandas dataframe.
```
metric_records = ci.record_metrics_from_dict(overall_metrics,
model_name=model_name,
dataset_name=dataset_name)
```
## Record figures
Credo can accept a path to an image file or a matplotlib figure. Matplotlib figures are converted to PNG images and saved.
A caption can be included for futher description. Included a caption is recommended when the image is not self-explanatory, which is most of the time!
```
example_figure_record = ci.Figure(examples_plot._suptitle.get_text(), examples_plot)
confusion_figure_record = ci.Figure(confusion_plot.axes[0].get_title(), confusion_plot)
pr_curve_caption="""Precision-recall curves are shown for each digit separately.
These are calculated by treating each class as a separate
binary classification problem. The grey lines are
ISO f1 curves - all points on each curve have identical
f1 scores.
"""
pr_curve_figure_record = ci.Figure(pr_curves.axes[0].get_title(),
figure=pr_curves,
description=pr_curve_caption)
figure_records = [example_figure_record, confusion_figure_record, pr_curve_figure_record]
```
## MultiRecords
To send all the information, we wrap the records in a MuliRecord, which wraps records of the same type.
```
metric_records = ci.MultiRecord(metric_records)
figure_records = ci.MultiRecord(figure_records)
```
## Export to Credo AI
The json object of the model record can be created by calling `MultiRecord.jsonify()`. The convenience function `export_to_file` can be called to export the json record to a file. This file can then be uploaded to Credo AI's Governance App.
```
# filename is the location to save the json object of the model record
# filename="XXX.json"
# ci.export_to_file(metric_records, filename)
```
MultiRecords can be directly uploaded to Credo AI's Governance App as well. A model (or data) ID must be known to do so. You use `export_to_credo` to accomplish this.
```
# model_id = "XXX"
# ci.export_to_credo(metric_records, model_id)
```
| true |
code
| 0.740717 | null | null | null | null |
|
# Supercritical Steam Cycle Example
This example uses Jupyter Lab or Jupyter notebook, and demonstrates a supercritical pulverized coal (SCPC) steam cycle model. See the ```supercritical_steam_cycle.py``` to see more information on how to assemble a power plant model flowsheet. Code comments in that file will guide you through the process.
## Model Description
The example model doesn't represent any particular power plant, but should be a reasonable approximation of a typical plant. The gross power output is about 620 MW. The process flow diagram (PFD) can be shown using the code below. The initial PFD contains spaces for model results, to be filled in later.
To get a more detailed look at the model structure, you may find it useful to review ```supercritical_steam_cycle.py``` first. Although there is no detailed boiler model, there are constraints in the model to complete the steam loop through the boiler and calculate boiler heat input to the steam cycle. The efficiency calculation for the steam cycle doesn't account for heat loss in the boiler, which would be a result of a more detailed boiler model.
```
# pkg_resources is used here to get the svg information from the
# installed IDAES package
import pkg_resources
from IPython.display import SVG, display
# Get the contents of the PFD (which is an svg file)
init_pfd = pkg_resources.resource_string(
"idaes.examples.power_generation.supercritical_steam_cycle",
"supercritical_steam_cycle.svg"
)
# Make the svg contents into an SVG object and display it.
display(SVG(init_pfd))
```
## Initialize the steam cycle flowsheet
This example is part of the ```idaes``` package, which you should have installed. To run the example, the example flowsheet is imported from the ```idaes``` package. When you write your own model, you can import and run it in whatever way is appropriate for you. The Pyomo environment is also imported as ```pyo```, providing easy access to Pyomo functions and classes.
The supercritical flowsheet example main function returns a Pyomo concrete mode (m) and a solver object (solver). The model is also initialized by the ```main()``` function.
```
import pyomo.environ as pyo
from idaes.examples.power_generation.supercritical_steam_cycle import (
main,
create_stream_table_dataframe,
pfd_result,
)
m, solver = main()
```
Inside the model, there is a subblock ```fs```. This is an IDAES flowsheet model, which contains the supercritical steam cycle model. In the flowsheet, the model called ```turb``` is a multistage turbine model. The turbine model contains an expression for total power, ```power```. In this case the model is steady-state, but all IDAES models allow for dynamic simulation, and contain time indexes. Power is indexed by time, and only the "0" time point exists. By convention, in the IDAES framework, power going into a model is positive, so power produced by the turbine is negative.
The property package used for this model uses SI (mks) units of measure, so the power is in Watts. Here a function is defined which can be used to report power output in MW.
```
# Define a function to report gross power output in MW
def gross_power_mw(model):
# pyo.value(m.fs.turb.power[0]) is the power consumed in Watts
return -pyo.value(model.fs.turb.power[0])/1e6
# Show the gross power
gross_power_mw(m)
```
## Change the model inputs
The turbine in this example simulates partial arc admission with four arcs, so there are four throttle valves. For this example, we will close one of the valves to 25% open, and observe the result.
```
m.fs.turb.throttle_valve[1].valve_opening[:].value = 0.25
```
Next, we re-solve the model using the solver created by the ```supercritical_steam_cycle.py``` script.
```
solver.solve(m, tee=True)
```
Now we can check the gross power output again.
```
gross_power_mw(m)
```
## Creating a PFD with results and a stream table
A more detailed look at the model results can be obtained by creating a stream table and putting key results on the PFD. Of course, any unit model or stream result can be obtained from the model.
```
# Create a Pandas dataframe with stream results
df = create_stream_table_dataframe(streams=m._streams, orient="index")
# Create a new PFD with simulation results
res_pfd = pfd_result(m, df, svg=init_pfd)
# Display PFD with results.
display(SVG(res_pfd))
# Display the stream table.
df
```
| true |
code
| 0.372905 | null | null | null | null |
|
# A canonical asset pricing job
Let's estimate, for each firm, for each year, the alpha, beta, and size and value loadings.
So we want a dataset that looks like this:
| Firm | Year | alpha | beta |
| --- | --- | --- | --- |
| GM | 2000 | 0.01 | 1.04 |
| GM | 2001 | -0.005 | 0.98 |
...but it will do this for every firm, every year!
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pandas_datareader as pdr
import seaborn as sns
# import statsmodels.api as sm
```
Load your stock returns. Here, I'll use this dataset, but you can use anything.
The returns don't even have to be firms.
**They can be any asset.** (Portfolios, mutual funds, crypto, ...)
```
crsp = pd.read_stata('https://github.com/LeDataSciFi/ledatascifi-2021/blob/main/data/3firm_ret_1990_2020.dta?raw=true')
crsp['ret'] = crsp['ret']*100 # convert to precentage to match FF's convention on scaling (daily % rets)
```
Then grab the market returns. Here, we will use one of the Fama-French datasets.
```
ff = pdr.get_data_famafrench('F-F_Research_Data_5_Factors_2x3_daily',start=1980,end=2010)[0] # the [0] is because the imported obect is a dictionary, and key=0 is the dataframe
ff = ff.reset_index().rename(columns={"Mkt-RF":"mkt_excess", "Date":"date"})
```
Merge the market returns into the stock returns.
```
crsp_ready = pd.merge(left=ff, right=crsp, on='date', how="inner",
indicator=True, validate="one_to_many")
```
So the data's basically ready. Again, the goal is to estimate, for each firm, for each year, the alpha, beta, and size and value loadings.
You caught that right? I have a dataframe, and **for each** firm, and **for each** year, I want to \<do stuff\> (run regressions).
**Pandas + "for each" = groupby!**
So we will _basically_ run `crsp.groupby([firm,year]).runregression()`. Except there is no "runregression" function that applies to pandas groupby objects. Small workaround: `crsp.groupby([firm,year]).apply(<our own reg fcn>)`.
We just need to write a reg function that works on groupby objects.
```
import statsmodels.api as sm
def reg_in_groupby(df,formula="ret_excess ~ mkt_excess + SMB + HML"):
'''
Want to run regressions after groupby?
This will do it!
Note: This defaults to a FF3 model assuming specific variable names. If you
want to run any other regression, just specify your model.
Usage:
df.groupby(<whatever>).apply(reg_in_groupby)
df.groupby(<whatever>).apply(reg_in_groupby,formula=<whatever>)
'''
return pd.Series(sm.formula.ols(formula,data = df).fit().params)
```
Let's apply that to our returns!
```
(
crsp_ready # grab the data
# Two things before the regressions:
# 1. need a year variable (to group on)
# 2. the market returns in FF are excess returns, so
# our stock returns need to be excess as well
.assign(year = crsp_ready.date.dt.year,
ret_excess = crsp_ready.ret - crsp_ready.RF)
# ok, run the regs, so easy!
.groupby(['permno','year']).apply(reg_in_groupby)
# and clean up - with better var names
.rename(columns={'Intercept':'alpha','mkt_excess':'beta'})
.reset_index()
)
```
How cool is that!
## Summary
This is all you need to do:
1. Set up the data like you would have to no matter what:
1. Load your stock prices.
1. Merge in the market returns and any factors you want to include in your model.
1. Make sure your returns are scaled like your factors (e.g., above, I converted to percentages to match the FF convention)
1. Make sure your asset returns and market returns are both excess returns (or both are not excess returns)
1. Create any variables you want to group on (e.g. above, I created a year variable)
3. `df.groupby(<whatever>).apply(reg_in_groupby)`
Holy smokes!
| true |
code
| 0.465327 | null | null | null | null |
|
# NYC PLUTO Data and Noise Complaints
Investigating how PLUTO data and zoning characteristics impact spatial, temporal and types of noise complaints through out New York City. Specifically looking at noise complaints that are handled by NYC's Department of Environmental Protection (DEP).
All work performed by Zoe Martiniak.
```
import os
import pandas as pd
import numpy as np
import datetime
import urllib
import requests
from sodapy import Socrata
import matplotlib
import matplotlib.pyplot as plt
import pylab as pl
from pandas.plotting import scatter_matrix
%matplotlib inline
%pylab inline
##Geospatial
import shapely
import geopandas as gp
from geopandas import GeoDataFrame
from fiona.crs import from_epsg
from shapely.geometry import Point, MultiPoint
import io
from geopandas.tools import sjoin
from shapely.ops import nearest_points
## Statistical Modelling
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.datasets.longley import load
import sklearn.preprocessing as preprocessing
from sklearn.ensemble import RandomForestRegressor as rfr
from sklearn.cross_validation import train_test_split
from sklearn.metrics import confusion_matrix
from APPTOKEN import myToken
## Save your SOTA API Token as variable myToken in a file titled SOTAPY_APPTOKEN.py
## e.g.
## myToken = 'XXXXXXXXXXXXXXXX'
```
# DATA IMPORTING
Applying domain knowledge to only read in columns of interest to reduce computing requirements.
### PLUTO csv file
```
pluto = pd.read_csv(os.getenv('MYDATA')+'/pluto_18v2.csv', usecols=['borocode','zonedist1',
'overlay1', 'bldgclass', 'landuse',
'ownertype','lotarea', 'bldgarea', 'comarea',
'resarea', 'officearea', 'retailarea', 'garagearea', 'strgearea',
'factryarea', 'otherarea', 'numfloors',
'unitsres', 'unitstotal', 'proxcode', 'lottype','lotfront',
'lotdepth', 'bldgfront', 'bldgdepth',
'yearalter1',
'assessland', 'yearbuilt','histdist', 'landmark', 'builtfar',
'residfar', 'commfar', 'facilfar','bbl', 'xcoord','ycoord'])
```
### 2010 Census Blocks
```
census = gp.read_file('Data/2010 Census Blocks/geo_export_56edaf68-bbe6-44a7-bd7c-81a898fb6f2e.shp')
```
### Read in 311 Complaints
```
complaints = pd.read_csv('Data/311DEPcomplaints.csv', usecols=['address_type','borough','city',
'closed_date', 'community_board','created_date',
'cross_street_1', 'cross_street_2', 'descriptor', 'due_date',
'facility_type', 'incident_address', 'incident_zip',
'intersection_street_1', 'intersection_street_2', 'latitude',
'location_type', 'longitude', 'resolution_action_updated_date',
'resolution_description', 'status', 'street_name' ])
## Many missing lat/lon values in complaints file
## Is it worth it to manually fill in NaN with geopy geocded laton/long?
len(complaints[(complaints.latitude.isna()) | (complaints.longitude.isna())])/len(complaints)
```
### Mannually Filling in Missing Lat/Long from Addresses
Very time and computationally expensive, so this step should be performed on a different machine.
For our intents and purposes, I will just be dropping rows with missing lat/long
```
complaints.dropna(subset=['longitude', 'latitude'],inplace=True)
complaints['createdate'] = pd.to_datetime(complaints['created_date'])
complaints = complaints[complaints.createdate >= datetime.datetime(2018,1,1)]
complaints = complaints[complaints.createdate < datetime.datetime(2019,1,1)]
complaints['lonlat']=list(zip(complaints.longitude.astype(float), complaints.latitude.astype(float)))
complaints['geometry']=complaints[['lonlat']].applymap(lambda x:shapely.geometry.Point(x))
crs = {'init':'epsg:4326', 'no_defs': True}
complaints = gp.GeoDataFrame(complaints, crs=crs, geometry=complaints['geometry'])
```
## NYC Zoning Shapefile
```
zoning = gp.GeoDataFrame.from_file('Data/nycgiszoningfeatures_201902shp/nyzd.shp')
zoning.to_crs(epsg=4326, inplace=True)
```
# PLUTO Shapefiles
## Load in PLUTO Shapefiles by Boro
The PLUTO shapefiles are incredibly large. I used ArcMAP to separate the pluto shapefiles by borough and saved them locally.
My original plan was to perform a spatial join of the complaints to the pluto shapefiles to find the relationship between PLUTO data on the building-scale and noise complaints.
While going through this exploratory analysis, I discovered that the 311 complaints are actually all located in the street and therefore the points do not intersect with the PLUTO shapefiles. This brings up some interesting questions, such as how the lat/long coordinates are assigned by the DEP.
I am including this step to showcase that the complaints do not intersect with the shapefiles, to justify my next step of simply aggregating by zoning type with the zoning shapefiles.
```
## PLUTO SHAPEFILES BY BORO
#files = ! ls Data/PLUTO_Split | grep '.shp'
boros= ['bronx','brooklyn','man','queens','staten']
columns_to_drop = ['FID_pluto_', 'Borough','CT2010', 'CB2010',
'SchoolDist', 'Council', 'FireComp', 'PolicePrct',
'HealthCent', 'HealthArea', 'Sanitboro', 'SanitDistr', 'SanitSub',
'Address','BldgArea', 'ComArea', 'ResArea', 'OfficeArea',
'RetailArea', 'GarageArea', 'StrgeArea', 'FactryArea', 'OtherArea',
'AreaSource','LotFront', 'LotDepth', 'BldgFront', 'BldgDepth', 'Ext', 'ProxCode',
'IrrLotCode', 'BsmtCode', 'AssessLand', 'AssessTot',
'ExemptLand', 'ExemptTot','ResidFAR', 'CommFAR', 'FacilFAR',
'BoroCode','CondoNo','XCoord', 'YCoord', 'ZMCode', 'Sanborn', 'TaxMap', 'EDesigNum', 'APPBBL',
'APPDate', 'PLUTOMapID', 'FIRM07_FLA', 'PFIRM15_FL', 'Version','BoroCode_1', 'BoroName']
bx_shp = gp.GeoDataFrame.from_file('Data/PLUTO_Split/Pluto_bronx.shp')
bx_311 = complaints[complaints.borough == 'BRONX']
bx_shp.to_crs(epsg=4326, inplace=True)
bx_shp.drop(columns_to_drop, axis=1, inplace=True)
```
## Mapping
```
f, ax = plt.subplots(figsize=(15,15))
#ax.get_xaxis().set_visible(False)
#ax.get_yaxis().set_visible(False)
ax.set_xlim(-73.91, -73.9)
ax.set_ylim(40.852, 40.86)
bx_shp.plot(ax=ax, color = 'w', edgecolor='k',alpha=0.5, legend=True)
plt.title("2018 Bronx Noise Complaints", size=20)
bx_311.plot(ax=ax,marker='.', color='red')#, markersize=.4, alpha=.4)
#fname = 'Bronx2018zoomed.png'
#plt.savefig(fname)
plt.show()
```
**Fig1:** This figure shows that the complaint points are located in the street, and therefore do not intersect with a tax lot. Therefore we cannot perform a spatial join on the two shapefiles.
# Data Cleaning & Simplifying
Here we apply our domain knowledge of zoning and Pluto data to do a bit of cleaning. This includes simplifying the zoning districts to extract the first letter, which can be one of the following five options:<br />
B: Ball Field, BPC<br />
P: Public Place, Park, Playground (all public areas)<br />
C: Commercial<br />
R: Residential<br />
M: Manufacturing<br />
```
print(len(zoning.ZONEDIST.unique()))
print(len(pluto.zonedist1.unique()))
def simplifying_zone(x):
if x in ['PLAYGROUND','PARK','PUBLIC PLACE','BALL FIELD' ,'BPC']:
return 'P'
if '/' in x:
return 'O'
if x[:3] == 'R10':
return x[:3]
else:
return x[:2]
def condensed_simple(x):
if x[:2] in ['R1','R2', 'R3','R4']:
return 'R1-R4'
if x[:2] in ['R5','R6', 'R7']:
return 'R5-R7'
if x[:2] in ['R8','R9', 'R10']:
return 'R8-R10'
if x[:2] in ['C1','C2']:
return 'C1-C2'
if x[:2] in ['C5','C6']:
return 'C5-C6'
if x[:2] in ['C3','C4','C7','C8']:
return 'C'
if x[:1] =='M':
return 'M'
else:
return x[:2]
cols_to_tidy = []
notcommon = []
for c in pluto.columns:
if type(pluto[c].mode()[0]) == str:
cols_to_tidy.append(c)
for c in cols_to_tidy:
pluto[c].fillna('U',inplace=True)
pluto.fillna(0,inplace=True)
pluto['bldgclass'] = pluto['bldgclass'].map(lambda x: x[0])
pluto['overlay1'] = pluto['overlay1'].map(lambda x: x[:2])
pluto['simple_zone'] = pluto['zonedist1'].map(simplifying_zone)
pluto['condensed'] = pluto['simple_zone'].map(condensed_simple)
```
```
zoning_analysis = pluto[['lotarea', 'bldgarea', 'comarea',
'resarea', 'officearea', 'retailarea', 'garagearea', 'strgearea',
'factryarea', 'otherarea', 'areasource', 'numbldgs', 'numfloors',
'unitsres', 'unitstotal', 'lotfront', 'lotdepth', 'bldgfront',
'bldgdepth','lotfront', 'lotdepth', 'bldgfront',
'bldgdepth','yearbuilt',
'yearalter1', 'yearalter2','builtfar','simple_zone']]
zoning_analysis.dropna(inplace=True)
## Cleaning the Complaint file for easier 1-hot-encoding
def TOD_shifts(x):
if x.hour <=7:
return 'M'
if x.hour >7 and x.hour<18:
return 'D'
if x.hour >= 18:
return 'E'
def DOW_(x):
weekdays = ['mon','tues','weds','thurs','fri','sat','sun']
for i in range(7):
if x.dayofweek == i:
return weekdays[i]
def resolution_(x):
descriptions = complaints.resolution_description.unique()
for a in [2,3,4,5,11,12,14,17,20,23,25]:
if x == descriptions[a]:
return 'valid_no_vio'
continue
next
if x == descriptions[1]:
return 'violation'
next
for b in [0,6,10,16,19,21,24]:
if x == descriptions[b]:
return 'further_investigation'
continue
next
for c in [7,8,9,13,15,18,22]:
if x == descriptions[c]:
return 'access_issue'
```
#### SIMPLIFIED COMPLAINT DESCRIPTIONS
0: Did not observe violation<br/>
1: Violation issued <br/>
No violation issued yet/canceled/resolved because:<br/>
2: Duplicate<br/>
3: Not warranted<br/>
4: Complainant canceled<br/>
5: Not warranted<br/>
6: Investigate further<br/>
7: Closed becuase complainant didnt respond<br/>
8: Incorrect complainant contact info (phone)<br/>
9: Incorrect complainant contact info (address)<br/>
10: Further investigation<br/>
11: NaN<br/>
12: Status unavailable<br/>
13: Could not gain access to location<br/>
14: NYPD<br/>
15: Sent letter to complainant after calling<br/>
16: Recieved letter from dog owner<br/>
17: Resolved with complainant<br/>
18: Incorrect address<br/>
19: An inspection is warranted<br/>
20: Hydrant<br/>
21: 2nd inspection<br/>
22: No complainant info<br/>
23: Refer to other agency (not nypd)<br/>
24: Inspection is scheduled<br/>
25: Call 311 for more info<br/>
Violation: [1]
not warranted/canceled/otheragency/duplicate: [2,3,4,5,11,12,14,17,20,23,25]
Complainant/access issue: [7,8,9,13,15,18,22]
Further investigtion: [0,6,10,16,19,21,24]
```
complaints['TOD']=complaints.createdate.map(TOD_shifts)
complaints['DOW']=complaints.createdate.map(DOW_)
```
## PLUTO/Zoning Feature Analysis
```
## Obtained this line of code from datascience.stackexchange @ the following link:
## https://datascience.stackexchange.com/questions/10459/calculation-and-visualization-of-correlation-matrix-with-pandas
def drange(start, stop, step):
r = start
while r <= stop:
yield r
r += step
def correlation_matrix(df):
from matplotlib import pyplot as plt
from matplotlib import cm as cm
fig = plt.figure(figsize=(10,10))
ax1 = fig.add_subplot(111)
cmap = cm.get_cmap('jet', 30)
cax = ax1.imshow(df.corr(), interpolation="nearest", cmap=cmap)
ax1.grid(True)
plt.title('PLUTO Correlation', size=20)
labels =[x for x in zoning_analysis.columns ]
ax1.set_yticklabels(labels,fontsize=14)
ax1.set_xticklabels(labels,fontsize=14, rotation='90')
# Add colorbar, make sure to specify tick locations to match desired ticklabels
fig.colorbar(cax, ticks = list(drange(-1, 1, 0.25)))
plt.show()
correlation_matrix(zoning_analysis)
zoning_analysis.sort_values(['simple_zone'],ascending=False, inplace=True)
y = zoning_analysis.groupby('simple_zone').mean()
f, axes = plt.subplots(figsize=(8,25), nrows=6, ncols=1)
cols = ['lotarea', 'bldgarea', 'comarea', 'resarea', 'officearea', 'retailarea']
for colind in range(6):
y[cols[colind]].plot(ax = plt.subplot(6,1,colind+1), kind='bar')
plt.ylabel('Avg. {} Units'.format(cols[colind]))
plt.title(cols[colind])
zoning['simple_zone'] = zoning['ZONEDIST'].map(simplifying_zone)
zoning['condensed'] = zoning['simple_zone'].map(condensed_simple)
zoning = zoning.reset_index().rename(columns={'index':'zdid'})
```
## Perform Spatial Joins
```
## Joining Census group shapefile to PLUTO shapefile
sjoin(census, plutoshp)
## Joining the zoning shapefile to complaints
zoning_joined = sjoin(zoning, complaints).reset_index()
zoning_joined.drop('index',axis=1, inplace=True)
print(zoning.shape)
print(complaints.shape)
print(zoning_joined.shape)
zoning_joined.drop(columns=['index_right', 'address_type', 'borough',
'city', 'closed_date', 'community_board', 'created_date',
'cross_street_1', 'cross_street_2', 'due_date',
'facility_type', 'incident_address', 'incident_zip',
'intersection_street_1', 'intersection_street_2',
'location_type', 'resolution_action_updated_date',
'resolution_description', 'status', 'street_name', 'lonlat'], inplace=True)
## Joining each borough PLUTO shapefile to zoning shapefile
bx_shp['centroid_colum'] = bx_shp.centroid
bx_shp = bx_shp.set_geometry('centroid_colum')
pluto_bx = sjoin(zoning, bx_shp).reset_index()
print(zoning.shape)
print(bx_shp.shape)
print(pluto_bx.shape)
pluto_bx = pluto_bx.groupby('zdid')['LandUse', 'LotArea', 'NumBldgs', 'NumFloors', 'UnitsRes',
'UnitsTotal', 'LotType', 'YearBuilt','YearAlter1', 'YearAlter2','BuiltFAR'].mean()
pluto_bx = zoning.merge(pluto_bx, on='zdid')
```
# ANALYSIS
## Visual Analysis
```
x = zoning_joined.groupby('simple_zone')['ZONEDIST'].count().index
y = zoning_joined.groupby('simple_zone')['ZONEDIST'].count()
f, ax = plt.subplots(figsize=(12,9))
plt.bar(x, y)
plt.ylabel('Counts', size=12)
plt.title('Noise Complaints by Zoning Districts (2018)', size=15)
```
**FIg 1** This shows the total counts of complaints by Zoning district. Clearly there are more complaints in middle/high-population density residential zoning districts. There are also high complaints in commercial districts C5 & C6. These commercial districts tend to have a residential overlay.
```
y.sort_values(ascending=False, inplace=True)
x = y.index
descriptors = zoning_joined.descriptor.unique()
df = pd.DataFrame(index=x)
for d in descriptors:
df[d] = zoning_joined[zoning_joined.descriptor == d].groupby('simple_zone')['ZONEDIST'].count()
df = df.div(df.sum(axis=1), axis=0)
ax = df.plot(kind="bar", stacked=True, figsize=(18,12))
df.sum(axis=1).plot(ax=ax, color="k")
plt.title('Noise Complaints by Descriptor', size=20)
plt.xlabel('Simplified Zone District (Decreasing Total Count -->)', size=12)
plt.ylabel('%', size=12)
fname = 'Descriptorpercent.jpeg'
#plt.savefig(fname)
plt.show()
```
**FIg 2** This figure shows the breakdown of the main noise complaint types per zoning district.
```
descriptors
complaints_by_zone = pd.get_dummies(zoning_joined, columns=['TOD','DOW'])
complaints_by_zone = complaints_by_zone.rename(columns={'TOD_D':'Day','TOD_E':'Night',
'TOD_M':'Morning','DOW_fri':'Friday','DOW_mon':'Monday','DOW_sat':'Saturday',
'DOW_sun':'Sunday','DOW_thurs':'Thursday','DOW_tues':'Tuesday','DOW_weds':'Wednesday'})
complaints_by_zone.drop(columns=['descriptor', 'latitude', 'longitude','createdate'],inplace=True)
complaints_by_zone = complaints_by_zone.groupby('zdid').sum()[['Day', 'Night', 'Morning', 'Friday',
'Monday', 'Saturday', 'Sunday', 'Thursday', 'Tuesday', 'Wednesday']].reset_index()
## Creating total counts of complaints by zoning district
complaints_by_zone['Count_TOD'] = (complaints_by_zone.Day +
complaints_by_zone.Night +
complaints_by_zone.Morning)
complaints_by_zone['Count_DOW'] = (complaints_by_zone.Monday +
complaints_by_zone.Tuesday +
complaints_by_zone.Wednesday +
complaints_by_zone.Thursday +
complaints_by_zone.Friday +
complaints_by_zone.Saturday +
complaints_by_zone.Sunday)
## Verifying the counts are the same
complaints_by_zone[complaints_by_zone.Count_TOD != complaints_by_zone.Count_DOW]
print(complaints_by_zone.shape)
print(zoning.shape)
complaints_by_zone = zoning.merge(complaints_by_zone, on='zdid')
print(complaints_by_zone.shape)
f, ax = plt.subplots(1,figsize=(13,13))
ax.set_axis_off()
ax.set_title('Avg # of Complaints',size=15)
complaints_by_zone.plot(ax=ax, column='Count_TOD', cmap='gist_earth', k=3, alpha=0.7, legend=True)
fname = 'AvgComplaintsbyZD.png'
plt.savefig(fname)
plt.show()
complaints_by_zone['Norm_count'] = complaints_by_zone.Count_TOD/complaints_by_zone.Shape_Area*1000000
f, ax = plt.subplots(1,figsize=(13,13))
ax.set_axis_off()
ax.set_title('Complaints Normalized by ZD Area',size=15)
complaints_by_zone[complaints_by_zone.Norm_count < 400].plot(ax=ax, column='Norm_count', cmap='gist_earth', k=3, alpha=0.7, legend=True)
fname = 'NormComplaintsbyZD.png'
plt.savefig(fname)
plt.show()
```
**Fig 3** This figure shows the spread of noise complaint density (complaints per unit area) of each zoning district.
```
complaints_by_zone.columns
TODcols = ['Day', 'Night', 'Morning']
fig = pl.figure(figsize=(30,20))
for x in range(1,8):
fig.add_subplot(2,3,x).set_axis_off()
fig.add_subplot(2,3,x).set_title(title[x-1], size=28)
pumashp.plot(column=column[x-1],cmap='Blues', alpha=1,
edgecolor='k', ax=fig.add_subplot(2,3,x), legend=True)
DOWcols = ['Friday', 'Monday', 'Saturday', 'Sunday', 'Thursday', 'Tuesday', 'Wednesday']
fig = pl.figure(figsize=(30,20))
for x in range(1,7):
fig.add_subplot(2,3,x).set_axis_off()
fig.add_subplot(2,3,x).set_title(DOWcols[x-1], size=28)
complaints_by_zone.plot(column=DOWcols[x-1],cmap='gist_stern', alpha=1,
ax=fig.add_subplot(2,3,x), legend=True)
```
## Regression
Define lat/long coordinates of zoning centroids for regression
```
complaints_by_zone.shape
complaints_by_zone['centerlong'] = complaints_by_zone.centroid.x
complaints_by_zone['centerlat'] = complaints_by_zone.centroid.y
mod = smf.ols(formula =
'Norm_count ~ centerlat + centerlong', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
len(complaints_by_zone.ZONEDIST.unique())
mod = smf.ols(formula =
'Norm_count ~ ZONEDIST', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
len(complaints_by_zone.simple_zone.unique())
mod = smf.ols(formula =
'Norm_count ~ simple_zone', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
complaints_by_zone.condensed.unique()
mod = smf.ols(formula =
'Norm_count ~ condensed', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
```
### PLAN
- JOIN ALL ZONE DIST TO PLUTO SHAPEFILES, AGGREGATE FEATURES
- PERFORM REGRESSION
COMPLEX CLASSIFIERS
- DECISION TREE AND CLUSTERING
```
import folium
from folium.plugins import HeatMap
hmap = folium.Map()
hm_wide = HeatMap( list(zip()))
f, ax = plt.subplots(figsize=(15,15))
#ax.get_xaxis().set_visible(False)
#ax.get_yaxis().set_visible(False)
zoning.plot(column='counts',ax=ax, cmap='plasma', alpha = 0.9, legend=True)
plt.title("Complaints by Zone", size=20)
```
| true |
code
| 0.372819 | null | null | null | null |
|
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Particle Filters
```
#format the book
%matplotlib notebook
from __future__ import division, print_function
from book_format import load_style
load_style()
```
## Motivation
Here is our problem. We have moving objects that we want to track. Maybe the objects are fighter jets and missiles, or maybe we are tracking people playing cricket in a field. It doesn't really matter. Which of the filters that we have learned can handle this problem? Unfortunately, none of them are ideal. Let's think about the characteristics of this problem.
* **multimodal**: We want to track zero, one, or more than one object simultaneously.
* **occlusions**: One object can hide another, resulting in one measurement for multiple objects.
* **nonlinear behavior**: Aircraft are buffeted by winds, balls move in parabolas, and people collide into each other.
* **nonlinear measurements**: Radar gives us the distance to an object. Converting that to an (x,y,z) coordinate requires a square root, which is nonlinear.
* **non-Gaussian noise:** as objects move across a background the computer vision can mistake part of the background for the object.
* **continuous:** the object's position and velocity (i.e. the state space) can smoothly vary over time.
* **multivariate**: we want to track several attributes, such as position, velocity, turn rates, etc.
* **unknown process model**: we may not know the process model of the system
None of the filters we have learned work well with all of these constraints.
* **Discrete Bayes filter**: This has most of the attributes. It is multimodal, can handle nonlinear measurements, and can be extended to work with nonlinear behavior. However, it is discrete and univariate.
* **Kalman filter**: The Kalman filter produces optimal estimates for unimodal linear systems with Gaussian noise. None of these are true for our problem.
* **Unscented Kalman filter**: The UKF handles nonlinear, continuous, multivariate problems. However, it is not multimodal nor does it handle occlusions. It can handle noise that is modestly non-Gaussian, but does not do well with distributions that are very non-Gaussian or problems that are very nonlinear.
* **Extended Kalman filter**: The EKF has the same strengths and limitations as the UKF, except that is it even more sensitive to strong nonlinearities and non-Gaussian noise.
## Monte Carlo Sampling
In the UKF chapter I generated a plot similar to this to illustrate the effects of nonlinear systems on Gaussians:
```
from code.book_plots import interactive_plot
import code.pf_internal as pf_internal
with interactive_plot():
pf_internal.plot_monte_carlo_ukf()
```
The left plot shows 3,000 points normally distributed based on the Gaussian
$$\mu = \begin{bmatrix}0\\0\end{bmatrix},\, \, \, \Sigma = \begin{bmatrix}32&15\\15&40\end{bmatrix}$$
The right plots shows these points passed through this set of equations:
$$\begin{aligned}x&=x+y\\
y &= 0.1x^2 + y^2\end{aligned}$$
Using a finite number of randomly sampled points to compute a result is called a [*Monte Carlo*](https://en.wikipedia.org/wiki/Monte_Carlo_method) (MC) method. The idea is simple. Generate enough points to get a representative sample of the problem, run the points through the system you are modeling, and then compute the results on the transformed points.
In a nutshell this is what particle filtering does. The Bayesian filter algorithm we have been using throughout the book is applied to thousands of particles, where each particle represents a *possible* state for the system. We extract the estimated state from the thousands of particles using weighted statistics of the particles.
## Generic Particle Filter Algorithm
1. **Randomly generate a bunch of particles**
Particles can have position, heading, and/or whatever other state variable you need to estimate. Each has a weight (probability) indicating how likely it matches the actual state of the system. Initialize each with the same weight.
2. **Predict next state of the particles**
Move the particles based on how you predict the real system is behaving.
3. **Update**
Update the weighting of the particles based on the measurement. Particles that closely match the measurements are weighted higher than particles which don't match the measurements very well.
4. **Resample**
Discard highly improbable particle and replace them with copies of the more probable particles.
5. **Compute Estimate**
Optionally, compute weighted mean and covariance of the set of particles to get a state estimate.
This naive algorithm has practical difficulties which we will need to overcome, but this is the general idea. Let's see an example. I wrote a particle filter for the robot localization problem from the UKF and EKF chapters. The robot has steering and velocity control inputs. It has sensors that measures distance to visible landmarks. Both the sensors and control mechanism have noise in them, and we need to track the robot's position.
Here I run a particle filter and plotted the positions of the particles. The plot on the left is after one iteration, and on the right is after 10. The red 'X' shows the actual position of the robot, and the large circle is the computed weighted mean position.
```
with interactive_plot():
pf_internal.show_two_pf_plots()
```
If you are viewing this in a browser, this animation shows the entire sequence:
<img src='animations/particle_filter_anim.gif'>
After the first iteration the particles are still largely randomly scattered around the map, but you can see that some have already collected near the robot's position. The computed mean is quite close to the robot's position. This is because each particle is weighted based on how closely it matches the measurement. The robot is near (1,1), so particles that are near (1, 1) will have a high weight because they closely match the measurements. Particles that are far from the robot will not match the measurements, and thus have a very low weight. The estimated position is computed as the weighted mean of positions of the particles. Particles near the robot contribute more to the computation so the estimate is quite accurate.
Several iterations later you can see that all the particles have clustered around the robot. This is due to the *resampling* step. Resampling discards particles that are very improbable (very low weight) and replaces them with particles with higher probability.
I haven't fully shown *why* this works nor fully explained the algorithms for particle weighting and resampling, but it should make intuitive sense. Make a bunch of random particles, move them so they 'kind of' follow the robot, weight them according to how well they match the measurements, only let the likely ones live. It seems like it should work, and it does.
## Probability distributions via Monte Carlo
Suppose we want to know the area under the curve $y= \mathrm{e}^{\sin(x)}$ in the interval [0, $\pi$]. The area is computed with the definite integral $\int_0^\pi \mathrm{e}^{\sin(x)}\, \mathrm{d}x$. As an exercise, go ahead and find the answer; I'll wait.
If you are wise you did not take that challenge; $\mathrm{e}^{\sin(x)}$ cannot be integrated analytically. The world is filled with equations which we cannot integrate. For example, consider calculating the luminosity of an object. An object reflects some of the light that strike it. Some of the reflected light bounces off of other objects and restrikes the original object, increasing the luminosity. This creates a *recursive integral*. Good luck with that one.
However, integrals are trivial to compute using a Monte Carlo technique. To find the area under a curve create a bounding box that contains the curve in the desired interval. Generate randomly positioned point within the box, and compute the ratio of points that fall under the curve vs the total number of points. For example, if 40% of the points are under the curve and the area of the bounding box is 1, then the area under the curve is approximately 0.4. As you tend towards infinite points you can achieve any arbitrary precision. In practice, a few thousand points will give you a fairly accurate result.
You can use this technique to numerically integrate a function of any arbitrary difficulty. this includes non-integrable and noncontinuous functions. This technique was invented by Stanley Ulam at Los Alamos National Laboratory to allow him to perform computations for nuclear reactions which were unsolvable on paper.
Let's compute $\pi$ by finding the area of a circle. We will define a circle with a radius of 1, and bound it in a square. The side of the square has length 2, so the area is 4. We generate a set of uniformly distributed random points within the box, and count how many fall inside the circle. The area of the circle is computed as the area of the box times the ratio of points inside the circle vs. the total number of points. Finally, we know that $A = \pi r^2$, so we compute $\pi = A / r^2$.
We start by creating the points.
```python
N = 20000
pts = uniform(-1, 1, (N, 2))
```
A point is inside a circle if its distance from the center of the circle is less than or equal to the radius. We compute the distance with `numpy.linalg.norm`, which computes the magnitude of a vector. Since vectors start at (0, 0) calling norm will compute the point's distance from the origin.
```python
dist = np.linalg.norm(pts, axis=1)
```
Next we compute which of this distances fit the criteria. This code returns a bool array that contains `True` if it meets the condition `dist <= 1`:
```python
in_circle = dist <= 1
```
All that is left is to count the points inside the circle, compute pi, and plot the results. I've put it all in one cell so you can experiment with alternative values for `N`, the number of points.
```
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import uniform
N = 20000 # number of points
radius = 1
area = (2*radius)**2
pts = uniform(-1, 1, (N, 2))
# distance from (0,0)
dist = np.linalg.norm(pts, axis=1)
in_circle = dist <= 1
pts_in_circle = np.count_nonzero(in_circle)
pi = area * (pts_in_circle / N)
# plot results
with interactive_plot():
plt.scatter(pts[in_circle,0], pts[in_circle,1],
marker=',', edgecolor='k', s=1)
plt.scatter(pts[~in_circle,0], pts[~in_circle,1],
marker=',', edgecolor='r', s=1)
plt.axis('equal')
print('mean pi(N={})= {:.4f}'.format(N, pi))
print('err pi(N={})= {:.4f}'.format(N, np.pi-pi))
```
This insight leads us to the realization that we can use Monte Carlo to compute the probability density of any probability distribution. For example, suppose we have this Gaussian:
```
from filterpy.stats import plot_gaussian_pdf
with interactive_plot():
plot_gaussian_pdf(mean=2, variance=3);
```
The probability density function (PDF) gives the probability that the random value falls between 2 values. For example, we may want to know the probability of x being between 0 and 2 in the graph above. This is a continuous function, so we need to take the integral to find the area under the curve, as the area is equal to the probability for that range of values to occur.
$$P[a \le X \le b] = \int_a^b f_X(x) \, dx$$
It is easy to compute this integral for a Gaussian. But real life is not so easy. For example, the plot below shows a probability distribution. There is no way to analytically describe an arbitrary curve, let alone integrate it.
```
with interactive_plot():
pf_internal.plot_random_pd()
```
We can use Monte Carlo methods to compute any integral. The PDF is computed with an integral, hence we can compute the PDF of this curve using Monte Carlo.
## The Particle Filter
All of this brings us to the particle filter. Consider tracking a robot or a car in an urban environment. For consistency I will use the robot localization problem from the EKF and UKF chapters. In this problem we tracked a robot that has a sensor which measures the range and bearing to known landmarks.
Particle filters are a family of algorithms. I'm presenting a specific form of a particle filter that is intuitive to grasp and relates to the problems we have studied in this book. This will leave a few of the steps seeming a bit 'magical' since I haven't offered a full explanation. That will follow later in the chapter.
Taking insight from the discussion in the previous section we start by creating several thousand *particles*. Each particle has a position that represents a possible belief of where the robot is in the scene, and perhaps a heading and velocity. Suppose that we have no knowledge of the location of the robot. We would want to scatter the particles uniformly over the entire scene. If you think of all of the particles representing a probability distribution, locations where there are more particles represent a higher belief, and locations with fewer particles represents a lower belief. If there was a large clump of particles near a specific location that would imply that we were more certain that the robot is there.
Each particle needs a weight - ideally the probability that it represents the true position of the robot. This probability is rarely computable, so we only require it be *proportional* to that probability, which is computable. At initialization we have no reason to favor one particle over another, so we assign a weight of $1/N$, for $N$ particles. We use $1/N$ so that the sum of all probabilities equals one.
The combination of particles and weights forms the *probability distribution* for our problem. Think back to the *Discrete Bayes* chapter. In that chapter we modeled positions in a hallway as discrete and uniformly spaced. This is very similar except the particles are randomly distributed in a continuous space rather than constrained to discrete locations. In this problem the robot can move on a plane of some arbitrary dimension, with the lower right corner at (0,0).
To track our robot we need to maintain states for x, y, and heading. We will store `N` particles in a `(N, 3)` shaped array. The three columns contain x, y, and heading, in that order.
If you are passively tracking something (no control input), then you would need to include velocity in the state and use that estimate to make the prediction. More dimensions requires exponentially more particles to form a good estimate, so we always try to minimize the number of random variables in the state.
This code creates a uniform and Gaussian distribution of particles over a region:
```
from numpy.random import uniform
def create_uniform_particles(x_range, y_range, hdg_range, N):
particles = np.empty((N, 3))
particles[:, 0] = uniform(x_range[0], x_range[1], size=N)
particles[:, 1] = uniform(y_range[0], y_range[1], size=N)
particles[:, 2] = uniform(hdg_range[0], hdg_range[1], size=N)
particles[:, 2] %= 2 * np.pi
return particles
def create_gaussian_particles(mean, std, N):
particles = np.empty((N, 3))
particles[:, 0] = mean[0] + (randn(N) * std[0])
particles[:, 1] = mean[1] + (randn(N) * std[1])
particles[:, 2] = mean[2] + (randn(N) * std[2])
particles[:, 2] %= 2 * np.pi
return particles
```
For example:
```
create_uniform_particles((0,1), (0,1), (0, np.pi*2), 4)
```
### Predict Step
The predict step in the Bayes algorithm uses the process model to update the belief in the system state. How would we do that with particles? Each particle represents a possible position for the robot. Suppose we send a command to the robot to move 0.1 meters while turning by 0.007 radians. We could move each particle by this amount. If we did that we would soon run into a problem. The robot's controls are not perfect so it will not move exactly as commanded. Therefore we need to add noise to the particle's movements to have a reasonable chance of capturing the actual movement of the robot. If you do not model the uncertainty in the system the particle filter will not correctly model the probability distribution of our belief in the robot's position.
```
def predict(particles, u, std, dt=1.):
""" move according to control input u (heading change, velocity)
with noise Q (std heading change, std velocity)`"""
N = len(particles)
# update heading
particles[:, 2] += u[0] + (randn(N) * std[0])
particles[:, 2] %= 2 * np.pi
# move in the (noisy) commanded direction
dist = (u[1] * dt) + (randn(N) * std[1])
particles[:, 0] += np.cos(particles[:, 2]) * dist
particles[:, 1] += np.sin(particles[:, 2]) * dist
```
### Update Step
Next we get a set of measurements - one for each landmark currently in view. How should these measurements be used to alter our probability distribution as modeled by the particles?
Think back to the **Discrete Bayes** chapter. In that chapter we modeled positions in a hallway as discrete and uniformly spaced. We assigned a probability to each position which we called the *prior*. When a new measurement came in we multiplied the current probability of that position (the *prior*) by the *likelihood* that the measurement matched that location:
```python
def update(likelihood, prior):
posterior = prior * likelihood
return normalize(posterior)
```
which is an implementation of the equation
$$x = \| \mathcal L \bar x \|$$
which is a realization of Bayes theorem:
$$\begin{aligned}P(x \mid z) &= \frac{P(z \mid x)\, P(x)}{P(z)} \\
&= \frac{\mathtt{likelihood}\times \mathtt{prior}}{\mathtt{normalization}}\end{aligned}$$
We do the same with our particles. Each particle has a position and a weight which estimates how well it matches the measurement. Normalizing the weights so they sum to one turns them into a probability distribution. The particles those that are closest to the robot will generally have a higher weight than ones far from the robot.
```
def update(particles, weights, z, R, landmarks):
weights.fill(1.)
for i, landmark in enumerate(landmarks):
distance = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
weights *= scipy.stats.norm(distance, R).pdf(z[i])
weights += 1.e-300 # avoid round-off to zero
weights /= sum(weights) # normalize
```
In the literature this part of the algorithm is called *Sequential Importance Sampling*, or SIS. The equation for the weights is called the *importance density*. I will give these theoretical underpinnings in a following section. For now I hope that this makes intuitive sense. If we weight the particles according to how how they match the measurements they are probably a good sample for the probability distribution of the system after incorporating the measurements. Theory proves this is so. The weights are the *likelihood* in Bayes theorem. Different problems will need to tackle this step in slightly different ways but this is the general idea.
### Computing the State Estimate
In most applications you will want to know the estimated state after each update, but the filter consists of nothing but a collection of particles. Assuming that we are tracking one object (i.e. it is unimodal) we can compute the mean of the estimate as the sum of the weighted values of the particles.
$$ \mu = \frac{1}{N}\sum\limits_{i=1}^N w^ix^i$$
Here I adopt the notation $x^i$ to indicate the i$^{th}$ particle. A superscript is used because we often need to use subscripts to denote time steps the k$^{th}$ or k+1$^{th}$ particle, yielding the unwieldy $x^i_{k+1}$.
This function computes both the mean and variance of the particles:
```
def estimate(particles, weights):
"""returns mean and variance of the weighted particles"""
pos = particles[:, 0:2]
mean = np.average(pos, weights=weights, axis=0)
var = np.average((pos - mean)**2, weights=weights, axis=0)
return mean, var
```
If we create a uniform distribution of points in a 1x1 square with equal weights we get a mean position very near the center of the square at (0.5, 0.5) and a small variance.
```
particles = create_uniform_particles((0,1), (0,1), (0, 5), 1000)
weights = np.array([.25]*1000)
estimate(particles, weights)
```
### Particle Resampling
The SIS algorithm suffers from the *degeneracy problem*. It starts with uniformly distributed particles with equal weights. There may only be a handful of particles near the robot. As the algorithm runs any particle that does not match the measurements will acquire an extremely low weight. Only the particles which are near the robot will have an appreciable weight. We could have 5,000 particles with only 3 contributing meaningfully to the state estimate! We say the filter has *degenerated*.
This problem is usually solved by some form of *resampling* of the particles. Particles with very small weights do not meaningfully describe the probability distribution of the robot.
The resampling algorithm discards particles with very low probability and replaces them with new particles with higher probability. It does that by duplicating particles with relatively high probability. The duplicates are slightly dispersed by the noise added in the predict step. This results in a set of points in which a large majority of the particles accurately represent the probability distribution.
There are many resampling algorithms. For now let's look at one of the simplest, *simple random resampling*, also called *multinomial resampling*. It samples from the current particle set $N$ times, making a new set of particles from the sample. The probability of selecting any given particle should be proportional to its weight.
We accomplish this with NumPy's `cumsum` function. `cumsum` computes the cumulative sum of an array. That is, element one is the sum of elements zero and one, element two is the sum of elements zero, one and two, etc. Then we generate random numbers in the range of 0.0 to 1.0 and do a binary search to find the weight that most closely matches that number:
```
def simple_resample(particles, weights):
N = len(particles)
cumulative_sum = np.cumsum(weights)
cumulative_sum[-1] = 1. # avoid round-off error
indexes = np.searchsorted(cumulative_sum, random(N))
# resample according to indexes
particles[:] = particles[indexes]
weights[:] = weights[indexes]
weights /= np.sum(weights) # normalize
```
We don't resample at every epoch. For example, if you received no new measurements you have not received any information from which the resample can benefit. We can determine when to resample by using something called the *effective N*, which approximately measures the number of particles which meaningfully contribute to the probability distribution. The equation for this is
$$\hat{N}_\text{eff} = \frac{1}{\sum w^2}$$
and we can implement this in Python with
```
def neff(weights):
return 1. / np.sum(np.square(weights))
```
If $\hat{N}_\text{eff}$ falls below some threshold it is time to resample. A useful starting point is $N/2$, but this varies by problem. It is also possible for $\hat{N}_\text{eff} = N$, which means the particle set has collapsed to one point (each has equal weight). It may not be theoretically pure, but if that happens I create a new distribution of particles in the hopes of generating particles with more diversity. If this happens to you often, you may need to increase the number of particles, or otherwise adjust your filter. We will talk more of this later.
## SIR Filter - A Complete Example
There is more to learn, but we know enough to implement a full particle filter. We will implement the *Sampling Importance Resampling filter*, or SIR.
I need to introduce a more sophisticated resampling method than I gave above. FilterPy provides several resampling methods. I will describe them later. They take an array of weights and returns indexes to the particles that have been chosen for the resampling. We just need to write a function that performs the resampling from these indexes:
```
def resample_from_index(particles, weights, indexes):
particles[:] = particles[indexes]
weights[:] = weights[indexes]
weights /= np.sum(weights)
```
To implement the filter we need to create the particles and the landmarks. We then execute a loop, successively calling `predict`, `update`, resampling, and then computing the new state estimate with `estimate`.
```
from filterpy.monte_carlo import systematic_resample
from numpy.linalg import norm
from numpy.random import randn
import scipy.stats
def run_pf1(N, iters=18, sensor_std_err=.1,
do_plot=True, plot_particles=False,
xlim=(0, 20), ylim=(0, 20),
initial_x=None):
landmarks = np.array([[-1, 2], [5, 10], [12,14], [18,21]])
NL = len(landmarks)
plt.figure()
# create particles and weights
if initial_x is not None:
particles = create_gaussian_particles(
mean=initial_x, std=(5, 5, np.pi/4), N=N)
else:
particles = create_uniform_particles((0,20), (0,20), (0, 6.28), N)
weights = np.zeros(N)
if plot_particles:
alpha = .20
if N > 5000:
alpha *= np.sqrt(5000)/np.sqrt(N)
plt.scatter(particles[:, 0], particles[:, 1],
alpha=alpha, color='g')
xs = []
robot_pos = np.array([0., 0.])
for x in range(iters):
robot_pos += (1, 1)
# distance from robot to each landmark
zs = (norm(landmarks - robot_pos, axis=1) +
(randn(NL) * sensor_std_err))
# move diagonally forward to (x+1, x+1)
predict(particles, u=(0.00, 1.414), std=(.2, .05))
# incorporate measurements
update(particles, weights, z=zs, R=sensor_std_err,
landmarks=landmarks)
# resample if too few effective particles
if neff(weights) < N/2:
indexes = systematic_resample(weights)
resample_from_index(particles, weights, indexes)
mu, var = estimate(particles, weights)
xs.append(mu)
if plot_particles:
plt.scatter(particles[:, 0], particles[:, 1],
color='k', marker=',', s=1)
p1 = plt.scatter(robot_pos[0], robot_pos[1], marker='+',
color='k', s=180, lw=3)
p2 = plt.scatter(mu[0], mu[1], marker='s', color='r')
xs = np.array(xs)
#plt.plot(xs[:, 0], xs[:, 1])
plt.legend([p1, p2], ['Actual', 'PF'], loc=4, numpoints=1)
plt.xlim(*xlim)
plt.ylim(*ylim)
print('final position error, variance:\n\t', mu, var)
from numpy.random import seed
seed(2)
run_pf1(N=5000, plot_particles=False)
```
Most of this code is devoted to initialization and plotting. The entirety of the particle filter processing consists of these lines:
```python
# move diagonally forward to (x+1, x+1)
predict(particles, u=(0.00, 1.414), std=(.2, .05))
# incorporate measurements
update(particles, weights, z=zs, R=sensor_std_err,
landmarks=landmarks)
# resample if too few effective particles
if neff(weights) < N/2:
indexes = systematic_resample(weights)
resample_from_index(particles, weights, indexes)
mu, var = estimate(particles, weights)
```
The first line predicts the position of the particles with the assumption that the robot is moving in a straight line (`u[0] == 0`) and moving 1 unit in both the x and y axis (`u[1]==1.414`). The standard deviation for the error in the turn is 0.2, and the standard deviation for the distance is 0.05. When this call returns the particles will all have been moved forward, but the weights are no longer correct as they have not been updated.
The next line incorporates the measurement into the filter. This does not alter the particle positions, it only alters the weights. If you recall the weight of the particle is computed as the probability that it matches the Gaussian of the sensor error model. The further the particle from the measured distance the less likely it is to be a good representation.
The final two lines example the effective particle count ($\hat{N}_\text{eff})$. If it falls below $N/2$ we perform resampling to try to ensure our particles form a good representation of the actual probability distribution.
Now let's look at this with all the particles plotted. Seeing this happen interactively is much more instructive, but this format still gives us useful information. I plotted the original random distribution of points in a very pale green and large circles to help distinguish them from the subsequent iterations where the particles are plotted with black pixels. The number of particles makes it hard to see the details, so I limited the number of iterations to 8 so we can zoom in and look more closely.
```
seed(2)
run_pf1(N=5000, iters=8, plot_particles=True,
xlim=(0,8), ylim=(0,8))
```
From the plot it looks like there are only a few particles at the first two robot positions. This is not true; there are 5,000 particles, but due to resampling most are duplicates of each other. The reason for this is the Gaussian for the sensor is very narrow. This is called *sample impoverishment* and can lead to filter divergence. I'll address this in detail below. For now, looking at the second step at x=2 we can see that the particles have dispersed a bit. This dispersion is due to the motion model noise. All particles are projected forward according to the control input `u`, but noise is added to each particle proportional to the error in the control mechanism in the robot. By the third step the particles have dispersed enough to make a convincing cloud of particles around the robot.
The shape of the particle cloud is an ellipse. This is not a coincidence. The sensors and robot control are both modeled as Gaussian, so the probability distribution of the system is also a Gaussian. The particle filter is a sampling of the probability distribution, so the cloud should be an ellipse.
It is important to recognize that the particle filter algorithm *does not require* the sensors or system to be Gaussian or linear. Because we represent the probability distribution with a cloud of particles we can handle any probability distribution and strongly nonlinear problems. There can be discontinuities and hard limits in the probability model.
### Effect of Sensor Errors on the Filter
The first few iterations of the filter resulted in many duplicate particles. This happens because the model for the sensors is Gaussian, and we gave it a small standard deviation of $\sigma=0.1$. This is counterintuitive at first. The Kalman filter performs better when the noise is smaller, yet the particle filter can perform worse.
We can reason about why this is true. If $\sigma=0.1$, the robot is at (1, 1) and a particle is at (2, 2) the particle is 14 standard deviations away from the robot. This gives it a near zero probability. It contributes nothing to the estimate of the mean, and it is extremely unlikely to survive after the resampling. If $\sigma=1.4$ then the particle is only $1\sigma$ away and thus it will contribute to the estimate of the mean. During resampling it is likely to be copied one or more times.
This is *very important* to understand - a very accurate sensor can lead to poor performance of the filter because few of the particles will be a good sample of the probability distribution. There are a few fixes available to us. First, we can artificially increase the sensor noise standard deviation so the particle filter will accept more points as matching the robots probability distribution. This is non-optimal because some of those points will be a poor match. The real problem is that there aren't enough points being generated such that enough are near the robot. Increasing `N` usually fixes this problem. This decision is not cost free as increasing the number of particles significantly increase the computation time. Still, let's look at the result of using 100,000 particles.
```
seed(2)
run_pf1(N=100000, iters=8, plot_particles=True,
xlim=(0,8), ylim=(0,8))
```
There are many more particles at x=1, and we have a convincing cloud at x=2. Clearly the filter is performing better, but at the cost of large memory usage and long run times.
Another approach is to be smarter about generating the initial particle cloud. Suppose we guess that the robot is near (0, 0). This is not exact, as the simulation actually places the robot at (1, 1), but it is close. If we create a normally distributed cloud near (0, 0) there is a much greater chance of the particles matching the robot's position.
`run_pf1()` has an optional parameter `initial_x`. Use this to specify the initial position guess for the robot. The code then uses `create_gaussian_particles(mean, std, N)` to create particles distributed normally around the initial guess. We will use this in the next section.
### Filter Degeneracy From Inadequate Samples
The filter as written is far from perfect. Here is how it performs with a different random seed.
```
seed(6)
run_pf1(N=5000, plot_particles=True, ylim=(-20, 20))
```
Here the initial sample of points did not generate any points near the robot. The particle filter does not create new points during the resample operation, so it ends up duplicating points which are not a representative sample of the probability distribution. As mentioned earlier this is called *sample impoverishment*. The problem quickly spirals out of control. The particles are not a good match for the landscape measurement so they become dispersed in a highly nonlinear, curved distribution, and the particle filter diverges from reality. No particles are available near the robot, so it cannot ever converge.
Let's make use of the `create_gaussian_particles()` method to try to generate more points near the robot. We can do this by using the `initial_x` parameter to specify a location to create the particles.
```
seed(6)
run_pf1(N=5000, plot_particles=True, initial_x=(1,1, np.pi/4))
```
This works great. You should always try to create particles near the initial position if you have any way to roughly estimate it. Do not be *too* careful - if you generate all the points very near a single position the particles may not be dispersed enough to capture the nonlinearities in the system. This is a fairly linear system, so we could get away with a smaller variance in the distribution. Clearly this depends on your problem. Increasing the number of particles is always a good way to get a better sample, but the processing cost may be a higher price than you are willing to pay.
## Importance Sampling
I've hand waved a difficulty away which we must now confront. There is some probability distribution that describes the position and movement of our robot. We want to draw a sample of particles from that distribution and compute the integral using MC methods.
Our difficulty is that in many problems we don't know the distribution. For example, the tracked object might move very differently than we predicted with our state model. How can we draw a sample from a probability distribution that is unknown?
There is a theorem from statistics called [*importance sampling*](https://en.wikipedia.org/wiki/Importance_sampling)[1]. Remarkably, it gives us a way to draw samples from a different and known probability distribution and use those to compute the properties of the unknown one. It's a fantastic theorem that brings joy to my heart.
The idea is simple, and we already used it. We draw samples from the known probability distribution, but *weight the samples* according to the distribution we are interested in. We can then compute properties such as the mean and variance by computing the weighted mean and weighted variance of the samples.
For the robot localization problem we drew samples from the probability distribution that we computed from our state model prediction step. In other words, we reasoned 'the robot was there, it is perhaps moving at this direction and speed, hence it might be here'. Yet the robot might have done something completely different. It may have fell off a cliff or been hit by a mortar round. In each case the probability distribution is not correct. It seems like we are stymied, but we are not because we can use importance sampling. We drew particles from that likely incorrect probability distribution, then weighted them according to how well the particles match the measurements. That weighting is based on the true probability distribution, so according to the theory the resulting mean, variance, etc, will be correct!
How can that be true? I'll give you the math; you can safely skip this if you don't plan to go beyond the robot localization problem. However, other particle filter problems require different approaches to importance sampling, and a bit of math helps. Also, the literature and much of the content on the web uses the mathematical formulation in favor of my rather imprecise "imagine that..." exposition. If you want to understand the literature you will need to know the following equations.
We have some probability distribution $\pi(x)$ which we want to take samples from. However, we don't know what $\pi(x)$ is; instead we only know an alternative probability distribution $q(x)$. In the context of robot localization, $\pi(x)$ is the probability distribution for the robot, but we don't know it, and $q(x)$ is the probability distribution of our measurements, which we do know.
The expected value of a function $f(x)$ with probability distribution $\pi(x)$ is
$$\mathbb{E}\big[f(x)\big] = \int f(x)\pi(x)\, dx$$
We don't know $\pi(x)$ so we cannot compute this integral. We do know an alternative distribution $q(x)$ so we can add it into the integral without changing the value with
$$\mathbb{E}\big[f(x)\big] = \int f(x)\pi(x)\frac{q(x)}{q(x)}\, dx$$
Now we rearrange and group terms
$$\mathbb{E}\big[f(x)\big] = \int f(x)q(x)\, \, \cdot \, \frac{\pi(x)}{q(x)}\, dx$$
$q(x)$ is known to us, so we can compute $\int f(x)q(x)$ using MC integration. That leaves us with $\pi(x)/q(x)$. That is a ratio, and we define it as a *weight*. This gives us
$$\mathbb{E}\big[f(x)\big] = \sum\limits_{i=1}^N f(x^i)w(x^i)$$
Maybe that seems a little abstract. If we want to compute the mean of the particles we would compute
$$\mu = \sum\limits_{i=1}^N x^iw^i$$
which is the equation I gave you earlier in the chapter.
It is required that the weights be proportional to the ratio $\pi(x)/q(x)$. We normally do not know the exact value, so in practice we normalize the weights by dividing them by $\sum w(x^i)$.
When you formulate a particle filter algorithm you will have to implement this step depending on the particulars of your situation. For robot localization the best distribution to use for $q(x)$ is the particle distribution from the `predict()` step of the filter. Let's look at the code again:
```python
def update(particles, weights, z, R, landmarks):
weights.fill(1.)
for i, landmark in enumerate(landmarks):
dist = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
weights *= scipy.stats.norm(dist, R).pdf(z[i])
weights += 1.e-300 # avoid round-off to zero
weights /= sum(weights) # normalize
```
The reason for `self.weights.fill(1.)` might have confused you. In all the Bayesian filters up to this chapter we started with the probability distribution created by the `predict` step, and this appears to discard that information by setting all of the weights to 1. Well, we are discarding the weights, but we do not discard the particles. That is a direct result of applying importance sampling - we draw from the known distribution, but weight by the unknown distribution. In this case our known distribution is the uniform distribution - all are weighted equally.
Of course if you can compute the posterior probability distribution from the prior you should do so. If you cannot, then importance sampling gives you a way to solve this problem. In practice, computing the posterior is incredibly difficult. The Kalman filter became a spectacular success because it took advantage of the properties of Gaussians to find an analytic solution. Once we relax the conditions required by the Kalman filter (Markov property, Gaussian measurements and process) importance sampling and monte carlo methods make the problem tractable.
## Resampling Methods
The resampling algorithm effects the performance of the filter. For example, suppose we resampled particles by picking particles at random. This would lead us to choosing many particles with a very low weight, and the resulting set of particles would be a terrible representation of the problem's probability distribution.
Research on the topic continues, but a handful of algorithms work well in practice across a wide variety of situations. We desire an algorithm that has several properties. It should preferentially select particles that have a higher probability. It should select a representative population of the higher probability particles to avoid sample impoverishment. It should include enough lower probability particles to give the filter a chance of detecting strongly nonlinear behavior.
FilterPy implements several of the popular algorithms. FilterPy doesn't know how your particle filter is implemented, so it cannot generate the new samples. Instead, the algorithms create a `numpy.array` containing the indexes of the particles that are chosen. Your code needs to perform the resampling step. For example, I used this for the robot:
```
def resample_from_index(particles, weights, indexes):
particles[:] = particles[indexes]
weights[:] = weights[indexes]
weights /= np.sum(weights)
```
### Multinomial Resampling
Multinomial resampling is the algorithm that I used while developing the robot localization example. The idea is simple. Compute the cumulative sum of the normalized weights. This gives you an array of increasing values from 0 to 1. Here is a plot which illustrates how this spaces out the weights. The colors are meaningless, they just make the divisions easier to see.
```
from code.pf_internal import plot_cumsum
print('cumulative sume is', np.cumsum([.1, .2, .1, .6]))
plot_cumsum([.1, .2, .1, .6])
```
To select a weight we generate a random number uniformly selected between 0 and 1 and use binary search to find its position inside the cumulative sum array. Large weights occupy more space than low weights, so they will be more likely to be selected.
This is very easy to code using NumPy's [ufunc](http://docs.scipy.org/doc/numpy/reference/ufuncs.html) support. Ufuncs apply functions to every element of an array, returning an array of the results. `searchsorted` is NumPy's binary search algorithm. If you provide is with an array of search values it will return an array of answers; one answer for each search value.
```
def multinomal_resample(weights):
cumulative_sum = np.cumsum(weights)
cumulative_sum[-1] = 1. # avoid round-off errors
return np.searchsorted(cumulative_sum, random(len(weights)))
```
Here is an example:
```
from code.pf_internal import plot_multinomial_resample
plot_multinomial_resample([.1, .2, .3, .4, .2, .3, .1])
```
This is an $O(n \log(n))$ algorithm. That is not terrible, but there are $O(n)$ resampling algorithms with better properties with respect to the uniformity of the samples. I'm showing it because you can understand the other algorithms as variations on this one. There is a faster implementation of this multinomial resampling that uses the inverse of the CDF of the distribution. You can search on the internet if you are interested.
Import the function from FilterPy using
```python
from filterpy.monte_carlo import multinomal_resample
```
### Residual Resampling
Residual resampling both improves the run time of multinomial resampling, and ensures that the sampling is uniform across the population of particles. It's fairly ingenious: the normalized weights are multiplied by *N*, and then the integer value of each weight is used to define how many samples of that particle will be taken. For example, if the weight of a particle is 0.0012 and $N$=3000, the scaled weight is 3.6, so 3 samples will be taken of that particle. This ensures that all higher weight particles are chosen at least once. The running time is $O(N)$, making it faster than multinomial resampling.
However, this does not generate all *N* selections. To select the rest, we take the *residual*: the weights minus the integer part, which leaves the fractional part of the number. We then use a simpler sampling scheme such as multinomial, to select the rest of the particles based on the residual. In the example above the scaled weight was 3.6, so the residual will be 0.6 (3.6 - int(3.6)). This residual is very large so the particle will be likely to be sampled again. This is reasonable because the larger the residual the larger the error in the round off, and thus the particle was relatively under sampled in the integer step.
```
def residual_resample(weights):
N = len(weights)
indexes = np.zeros(N, 'i')
# take int(N*w) copies of each weight
num_copies = (N*np.asarray(weights)).astype(int)
k = 0
for i in range(N):
for _ in range(num_copies[i]): # make n copies
indexes[k] = i
k += 1
# use multinormial resample on the residual to fill up the rest.
residual = w - num_copies # get fractional part
residual /= sum(residual) # normalize
cumulative_sum = np.cumsum(residual)
cumulative_sum[-1] = 1. # ensures sum is exactly one
indexes[k:N] = np.searchsorted(cumulative_sum, random(N-k))
return indexes
```
You may be tempted to replace the inner for loop with a slice `indexes[k:k + num_copies[i]] = i`, but very short slices are comparatively slow, and the for loop usually runs faster.
Let's look at an example:
```
from code.pf_internal import plot_residual_resample
plot_residual_resample([.1, .2, .3, .4, .2, .3, .1])
```
You may import this from FilterPy using
```python
from filterpy.monte_carlo import residual_resample
```
### Stratified Resampling
This scheme aims to make selections relatively uniformly across the particles. It works by dividing the cumulative sum into $N$ equal sections, and then selects one particle randomly from each section. This guarantees that each sample is between 0 and $\frac{2}{N}$ apart.
The plot below illustrates this. The colored bars show the cumulative sum of the array, and the black lines show the $N$ equal subdivisions. Particles, shown as black circles, are randomly placed in each subdivision.
```
from pf_internal import plot_stratified_resample
plot_stratified_resample([.1, .2, .3, .4, .2, .3, .1])
```
The code to perform the stratification is quite straightforward.
```
def stratified_resample(weights):
N = len(weights)
# make N subdivisions, chose a random position within each one
positions = (random(N) + range(N)) / N
indexes = np.zeros(N, 'i')
cumulative_sum = np.cumsum(weights)
i, j = 0, 0
while i < N:
if positions[i] < cumulative_sum[j]:
indexes[i] = j
i += 1
else:
j += 1
return indexes
```
Import it from FilterPy with
```python
from filterpy.monte_carlo import stratified_resample
```
### Systematic Resampling
The last algorithm we will look at is systemic resampling. As with stratified resampling the space is divided into $N$ divisions. We then choose a random offset to use for all of the divisions, ensuring that each sample is exactly $\frac{1}{N}$ apart. It looks like this.
```
from pf_internal import plot_systematic_resample
plot_systematic_resample([.1, .2, .3, .4, .2, .3, .1])
```
Having seen the earlier examples the code couldn't be simpler.
```
def systematic_resample(weights):
N = len(weights)
# make N subdivisions, choose positions
# with a consistent random offset
positions = (np.arange(N) + random()) / N
indexes = np.zeros(N, 'i')
cumulative_sum = np.cumsum(weights)
i, j = 0, 0
while i < N:
if positions[i] < cumulative_sum[j]:
indexes[i] = j
i += 1
else:
j += 1
return indexes
```
Import from FilterPy with
```python
from filterpy.monte_carlo import systematic_resample
```
### Choosing a Resampling Algorithm
Let's look at the four algorithms at once so they are easier to compare.
```
a = [.1, .2, .3, .4, .2, .3, .1]
np.random.seed(4)
plot_multinomial_resample(a)
plot_residual_resample(a)
plot_systematic_resample(a)
plot_stratified_resample(a)
```
The performance of the multinomial resampling is quite bad. There is a very large weight that was not sampled at all. The largest weight only got one resample, yet the smallest weight was sample was sampled twice. Most tutorials on the net that I have read use multinomial resampling, and I am not sure why. Multinomial resampling is rarely used in the literature or for real problems. I recommend not using it unless you have a very good reason to do so.
The residual resampling algorithm does excellently at what it tries to do: ensure all the largest weights are resampled multiple times. It doesn't evenly distribute the samples across the particles - many reasonably large weights are not resampled at all.
Both systematic and stratified perform very well. Systematic sampling does an excellent job of ensuring we sample from all parts of the particle space while ensuring larger weights are proportionality resampled more often. Stratified resampling is not quite as uniform as systematic resampling, but it is a bit better at ensuring the higher weights get resampled more.
Plenty has been written on the theoretical performance of these algorithms, and feel free to read it. In practice I apply particle filters to problems that resist analytic efforts, and so I am a bit dubious about the validity of a specific analysis to these problems. In practice both the stratified and systematic algorithms perform well and similarly across a variety of problems. I say try one, and if it works stick with it. If performance of the filter is critical try both, and perhaps see if there is literature published on your specific problem that will give you better guidance.
## Summary
This chapter only touches the surface of what is a vast topic. My goal was not to teach you the field, but to expose you to practical Bayesian Monte Carlo techniques for filtering.
Particle filters are a type of *ensemble* filtering. Kalman filters represents state with a Gaussian. Measurements are applied to the Gaussian using Bayes Theorem, and the prediction is done using state-space methods. These techniques are applied to the Gaussian - the probability distribution.
In contrast, ensemble techniques represent a probability distribution using a discrete collection of points and associated probabilities. Measurements are applied to these points, not the Gaussian distribution. Likewise, the system model is applied to the points, not a Gaussian. We then compute the statistical properties of the resulting ensemble of points.
These choices have many trade-offs. The Kalman filter is very efficient, and is an optimal estimator if the assumptions of linearity and Gaussian noise are true. If the problem is nonlinear than we must linearize the problem. If the problem is multimodal (more than one object being tracked) then the Kalman filter cannot represent it. The Kalman filter requires that you know the state model. If you do not know how your system behaves the performance is poor.
In contrast, particle filters work with any arbitrary, non-analytic probability distribution. The ensemble of particles, if large enough, form an accurate approximation of the distribution. It performs wonderfully even in the presence of severe nonlinearities. Importance sampling allows us to compute probabilities even if we do not know the underlying probability distribution. Monte Carlo techniques replace the analytic integrals required by the other filters.
This power comes with a cost. The most obvious costs are the high computational and memory burdens the filter places on the computer. Less obvious is the fact that they are fickle. You have to be careful to avoid particle degeneracy and divergence. It can be very difficult to prove the correctness of your filter. If you are working with multimodal distributions you have further work to cluster the particles to determine the paths of the multiple objects. This can be very difficult when the objects are close to each other.
There are many different classes of particle filter; I only described the naive SIS algorithm, and followed that with a SIR algorithm that performs well. There are many classes of filters, and many examples of filters in each class. It would take a small book to describe them all.
When you read the literature on particle filters you will find that it is strewn with integrals. We perform computations on probability distributions using integrals, so using integrals gives the authors a powerful and compact notation. You must recognize that when you reduce these equations to code you will be representing the distributions with particles, and integrations are replaced with sums over the particles. If you keep in mind the core ideas in this chapter the material shouldn't be daunting.
## References
[1] *Importance Sampling*, Wikipedia.
https://en.wikipedia.org/wiki/Importance_sampling
| true |
code
| 0.699639 | null | null | null | null |
|
# Fine-tuning and deploying ProtBert Model for Protein Classification using Amazon SageMaker
## Contents
1. [Motivation](#Motivation)
2. [What is ProtBert?](#What-is-ProtBert?)
3. [Notebook Overview](#Notebook-Overview)
- [Setup](#Setup)
4. [Dataset](#Dataset)
- [Download Data](#Download-Data)
5. [Data Exploration](#Data-Exploration)
- [Upload Data to S3](#Upload-Data-to-S3)
6. [Training script](#Training-script)
7. [Train on Amazon SageMaker](#Train-on-Amazon-SageMaker)
8. [Deploy the Model on Amazon SageMaker](#Deploy-the-model-on-Amazon-SageMaker)
- [Create a model object](#Create-a-model-object)
- [Deploy the model on an endpoint](#Deploy-the-model-on-an-endpoint)
9. [Predicting SubCellular Localization of Protein Sequences](#Predicting-SubCellular-Localization-of-Protein-Sequences)
10. [References](#References)
---
## Motivation
<img src="https://upload.wikimedia.org/wikipedia/commons/6/60/Myoglobin.png"
alt="Protein Sequence"
style="float: left;"
height = 100
width = 250/>
**Proteins** are the key fundamental macromolecules governing in biological bodies. The study of protein localization is important to comprehend the function of protein and has great importance for drug design and other applications. It also plays an important role in characterizing the cellular function of hypothetical and newly discovered proteins [1]. There are several research endeavours that aim to localize whole proteomes by using high-throughput approaches [2–4]. These large datasets provide important information about protein function, and more generally global cellular processes. However, they currently do not achieve 100% coverage of proteomes, and the methodology used can in some cases cause mislocalization of subsets of proteins [5,6]. Therefore, complementary methods are necessary to address these problems. In this notebook, we will leverage Natural Language Processing (NLP) techniques for protein sequence classification. The idea is to interpret protein sequences as sentences and their constituent – amino acids –
as single words [7]. More specifically we will fine tune Pytorch ProtBert model from Hugging Face library.
## What is ProtBert?
ProtBert is a pretrained model on protein sequences using a masked language modeling (MLM) objective. It is based on Bert model which is pretrained on a large corpus of protein sequences in a self-supervised fashion. This means it was pretrained on the raw protein sequences only, with no humans labelling them in any way (which is why it can use lots of publicly available data) with an automatic process to generate inputs and labels from those protein sequences [8]. For more information about ProtBert, see [`ProtTrans: Towards Cracking the Language of Life’s Code Through Self-Supervised Deep Learning and High Performance Computing`](https://www.biorxiv.org/content/10.1101/2020.07.12.199554v2.full).
---
## Notebook Overview
This example notebook focuses on fine-tuning the Pytorch ProtBert model and deploying it using Amazon SageMaker, which is the most comprehensive and fully managed machine learning service. With SageMaker, data scientists and developers can quickly and easily build and train machine learning models, and then directly deploy them into a production-ready hosted environment.
During the training, we will leverage SageMaker distributed data parallel (SDP) feature which extends SageMaker’s training capabilities on deep learning models with near-linear scaling efficiency, achieving fast time-to-train with minimal code changes.
_**Note**_: Please select the Kernel as ` Python 3 (Pytorch 1.6 Python 3.6 CPU Optimized)`.
---
### Setup
To start, we import some Python libraries and initialize a SageMaker session, S3 bucket and prefix, and IAM role.
```
!pip install --upgrade pip -q
!pip install -U boto3 sagemaker -q
!pip install seaborn -q
```
Next let us import the common libraries needed for the operations done later.
```
import re
import json
import pandas as pd
from tqdm import tqdm
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import time
import os
import numpy as np
import pandas as pd
import sagemaker
import torch
import seaborn as sns
import matplotlib.pyplot as plt
from torch import nn, optim
from torch.utils.data import Dataset, DataLoader
```
Next, let's verify the version, create a SageMaker session and get the execution role which is the IAM role arn used to give training and hosting access to your data.
```
import sagemaker
print(sagemaker.__version__)
sagemaker_session = sagemaker.Session()
role = sagemaker.get_execution_role()
```
Now we will specify the S3 bucket and prefix where you will store your training data and model artifacts. This should be within the same region as the Notebook Instance, training, and hosting.
```
bucket = sagemaker_session.default_bucket()
prefix = "sagemaker/DEMO-pytorch-bert"
```
As the last step of setting up the enviroment lets set a value to a random seed so that we can reproduce the same results later.
```
RANDOM_SEED = 43
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)
```
---
## Dataset
We are going to use a opensource public dataset of protein sequences available [here](http://www.cbs.dtu.dk/services/DeepLoc-1.0/data.php). The dataset is a `fasta file` composed by header and protein sequence. The header is composed by the accession number from Uniprot, the annotated subcellular localization and possibly a description field indicating if the protein was part of the test set. The subcellular localization includes an additional label, where S indicates soluble, M membrane and U unknown[9].
Sample of the data is as follows :
```
>Q9SMX3 Mitochondrion-M test
MVKGPGLYTEIGKKARDLLYRDYQGDQKFSVTTYSSTGVAITTTGTNKGSLFLGDVATQVKNNNFTADVKVST
DSSLLTTLTFDEPAPGLKVIVQAKLPDHKSGKAEVQYFHDYAGISTSVGFTATPIVNFSGVVGTNGLSLGTDV
AYNTESGNFKHFNAGFNFTKDDLTASLILNDKGEKLNASYYQIVSPSTVVGAEISHNFTTKENAITVGTQHAL>
DPLTTVKARVNNAGVANALIQHEWRPKSFFTVSGEVDSKAIDKSAKVGIALALKP"
```
A sequence in FASTA format begins with a single-line description, followed by lines of sequence data. The definition line (defline) is distinguished from the sequence data by a greater-than (>) symbol at the beginning. The word following the ">" symbol is the identifier of the sequence, and the rest of the line is the description.
### Download Data
```
!wget http://www.cbs.dtu.dk/services/DeepLoc-1.0/deeploc_data.fasta -P ./data -q
```
Since the data is in fasta format, we can leverage `Bio.SeqIO.FastaIO` library to read the dataset. Let us install the Bio package.
```
!pip install Bio -q
import Bio
```
Using the Bio package we will read the data directly by filtering out the columns that are of interest. We will also add a space seperater between each character in the sequence field which will be useful during model training.
```
def read_fasta(file_path, columns) :
from Bio.SeqIO.FastaIO import SimpleFastaParser
with open('./data/deeploc_data.fasta') as fasta_file: # Will close handle cleanly
records = []
for title, sequence in SimpleFastaParser(fasta_file):
record = []
title_splits = title.split(None)
record.append(title_splits[0]) # First word is ID
sequence = " ".join(sequence)
record.append(sequence)
record.append(len(sequence))
location_splits = title_splits[1].split("-")
record.append(location_splits[0]) # Second word is Location
record.append(location_splits[1]) # Second word is Membrane
if(len(title_splits) > 2):
record.append(0)
else:
record.append(1)
records.append(record)
return pd.DataFrame(records, columns = columns)
data = read_fasta("./tmp/deeploc_data.fasta", columns=["id", "sequence", "sequence_length", "location", "membrane", "is_train"])
data.head()
```
### Data Exploration
Dataset consists of 14K sequences and 6 columns in total. We will only use the following columns during training:
* _**id**_ : Unique identifier given each sequence in the dataset.
* _**sequence**_ : Protein sequence. Each character is seperated by a "space". Will be useful for BERT tokernizer.
* _**sequence_length**_ : Character length of each protein sequence.
* _**location**_ : Classification given each sequence.
* _**is_train**_ : Indicates whether the record be used for training or test. Will be used to seperate the dataset for traning and validation.
First, let's verify if there are any missing values in the dataset.
```
data.info()
data.isnull().values.any()
```
As you can see, there are **no** missing values in this dataset.
Second, we will see the number of available classes (subcellular localization), which will be used for protein classification.
```
unique_classes = data.location.unique()
print("Number of classes: ", len(unique_classes))
unique_classes
```
We can see that there are 10 unique classes in the dataset.
Third, lets check the sequence length.
```
%matplotlib inline
%config InlineBackend.figure_format='retina'
sns.set(style='whitegrid', palette='muted', font_scale=1.2)
ax = sns.distplot(data['sequence_length'].values)
ax.set_xlim(0, 3000)
plt.title(f'sequence length distribution')
plt.grid(True)
```
This is an important observation as PROTBERT model receives a fixed length of sentence as input. Usually the maximum length of a sentence depends on the data we are working on. For sentences that are shorter than this maximum length, we will have to add paddings (empty tokens) to the sentences to make up the length.
As you can see from the above plot that most of the sequences lie under the length of around 1500, therefore, its a good idea to select the `max_length = 1536` but that will increase the training time for this sample notebook, therefore, we will use `max_length = 512`. You can experiment it with the bigger length and it does improves the accuracy as most of the subcellular localization information of protiens is stored at the end of the sequence.
Next let's factorize the protein classes.
```
categories = data.location.astype('category').cat
data['location'] = categories.codes
class_names = categories.categories
num_classes = len(class_names)
print(class_names)
```
Next, let's devide the dataset into training and test. We can leverage the `is_train` column to do the split.
```
df_train = data[data.is_train == 1]
df_train = df_train.drop(["is_train"], axis = 1)
df_train.shape[0]
df_test = data[data.is_train == 0]
df_test = df_test.drop(["is_train"], axis = 1)
df_test.shape[0]
```
We got **11231** records as training set and **2773** records as the test set which is about 75:25 data split between the train and test. Also, the composition between multiple classes remains uniform between both datasets.
### Upload Data to S3
In order to accomodate model training on SageMaker we need to upload the data to s3 location. We are going to use the `sagemaker.Session.upload_data` function to upload our datasets to an S3 location. The return value inputs identifies the location -- we will use later when we start the training job.
```
train_dataset_path = './data/deeploc_per_protein_train.csv'
test_dataset_path = './data/deeploc_per_protein_test.csv'
df_train.to_csv(train_dataset_path)
df_test.to_csv(test_dataset_path)
inputs_train = sagemaker_session.upload_data(train_dataset_path, bucket=bucket, key_prefix=prefix)
inputs_test = sagemaker_session.upload_data(test_dataset_path, bucket=bucket, key_prefix=prefix)
print("S3 location for training data: ", inputs_train )
print("S3 location for testing data: ", inputs_test )
```
## Training script
We use the [PyTorch-Transformers library](https://pytorch.org/hub/huggingface_pytorch-transformers), which contains PyTorch implementations and pre-trained model weights for many NLP models, including BERT. As mentioned above, we will use `ProtBert model` which is pre-trained on protein sequences.
Our training script should save model artifacts learned during training to a file path called `model_dir`, as stipulated by the SageMaker PyTorch image. Upon completion of training, model artifacts saved in `model_dir` will be uploaded to S3 by SageMaker and will be used for deployment.
We save this script in a file named `train.py`, and put the file in a directory named `code/`. The full training script can be viewed under `code/`.
It also has the code required for distributed data parallel (DDP) training using SMDataParallel. It is very similar to a PyTorch training script you might run outside of SageMaker, but modified to run with SMDataParallel, which is a new capability in Amazon SageMaker to train deep learning models faster and cheaper. SMDataParallel's PyTorch client provides an alternative to PyTorch's native DDP. For details about how to use SMDataParallel's DDP in your native PyTorch script, see the [Getting Started with SMDataParallel tutorials](https://docs.aws.amazon.com/sagemaker/latest/dg/distributed-training.html#distributed-training-get-started).
```
!pygmentize code/train.py
```
### Train on Amazon SageMaker
We use Amazon SageMaker to train and deploy a model using our custom PyTorch code. The Amazon SageMaker Python SDK makes it easier to run a PyTorch script in Amazon SageMaker using its PyTorch estimator. After that, we can use the SageMaker Python SDK to deploy the trained model and run predictions. For more information on how to use this SDK with PyTorch, see [the SageMaker Python SDK documentation](https://sagemaker.readthedocs.io/en/stable/using_pytorch.html).
To start, we use the `PyTorch` estimator class to train our model. When creating our estimator, we make sure to specify a few things:
* `entry_point`: the name of our PyTorch script. It contains our training script, which loads data from the input channels, configures training with hyperparameters, trains a model, and saves a model. It also contains code to load and run the model during inference.
* `source_dir`: the location of our training scripts and requirements.txt file. "requirements.txt" lists packages you want to use with your script.
* `framework_version`: the PyTorch version we want to use.
The PyTorch estimator supports both single-machine & multi-machine, distributed PyTorch training using SMDataParallel. _Our training script supports distributed training for only GPU instances_.
#### Instance types
SMDataParallel supports model training on SageMaker with the following instance types only:
- ml.p3.16xlarge
- ml.p3dn.24xlarge [Recommended]
- ml.p4d.24xlarge [Recommended]
#### Instance count
To get the best performance and the most out of SMDataParallel, you should use at least 2 instances, but you can also use 1 for testing this example.
#### Distribution strategy
Note that to use DDP mode, you update the the distribution strategy, and set it to use smdistributed dataparallel.
After creating the estimator, we then call fit(), which launches a training job. We use the Amazon S3 URIs where we uploaded the training data earlier.
```
# Training job will take around 20-25 mins to execute.
from sagemaker.pytorch import PyTorch
TRAINING_JOB_NAME="protbert-training-pytorch-{}".format(time.strftime("%m-%d-%Y-%H-%M-%S"))
print('Training job name: ', TRAINING_JOB_NAME)
estimator = PyTorch(
entry_point="train.py",
source_dir="code",
role=role,
framework_version="1.6.0",
py_version="py36",
instance_count=1, # this script support distributed training for only GPU instances.
instance_type="ml.p3.16xlarge",
distribution={'smdistributed':{
'dataparallel':{
'enabled': True
}
}
},
debugger_hook_config=False,
hyperparameters={
"epochs": 3,
"num_labels": num_classes,
"batch-size": 4,
"test-batch-size": 4,
"log-interval": 100,
"frozen_layers": 15,
},
metric_definitions=[
{'Name': 'train:loss', 'Regex': 'Training Loss: ([0-9\\.]+)'},
{'Name': 'test:accuracy', 'Regex': 'Validation Accuracy: ([0-9\\.]+)'},
{'Name': 'test:loss', 'Regex': 'Validation loss: ([0-9\\.]+)'},
]
)
estimator.fit({"training": inputs_train, "testing": inputs_test}, job_name=TRAINING_JOB_NAME)
```
With `max_length=512` and running the model for only 3 epochs we get the validation accuracy of around 65%, which is pretty decent. You can optimize it further by trying bigger sequence length, increasing the number of epochs and tuning other hyperparamters. For details you can refer to the research paper:
[`ProtTrans: Towards Cracking the Language of Life’s Code Through Self-Supervised Deep Learning and High Performance Computing`](https://arxiv.org/pdf/2007.06225.pdf).
Before, we deploy the model to an endpoint, let's first store the model to S3.
```
model_data = estimator.model_data
print("Storing {} as model_data".format(model_data))
%store model_data
%store -r model_data
# If no model was found, set it manually here.
# model_data = 's3://sagemaker-{region}-XXX/protbert-training-pytorch-XX-XX-XXXX-XX-XX-XX/output/model.tar.gz'
print("Using this model: {}".format(model_data))
```
## Deploy the model on Amazon SageMaker
After training our model, we host it on an Amazon SageMaker Endpoint. To make the endpoint load the model and serve predictions, we implement a few methods in inference.py.
- `model_fn()`: function defined to load the saved model and return a model object that can be used for model serving. The SageMaker PyTorch model server loads our model by invoking model_fn.
- `input_fn()`: deserializes and prepares the prediction input. In this example, our request body is first serialized to JSON and then sent to model serving endpoint. Therefore, in input_fn(), we first deserialize the JSON-formatted request body and return the input as a torch.tensor, as required for BERT.
- `predict_fn()`: performs the prediction and returns the result.
To deploy our endpoint, we call deploy() on our PyTorch estimator object, passing in our desired number of instances and instance type:
### Create a model object
You define the model object by using SageMaker SDK's PyTorchModel and pass in the model from the estimator and the entry_point. The function loads the model and sets it to use a GPU, if available.
```
import sagemaker
from sagemaker.pytorch import PyTorchModel
ENDPOINT_NAME = "protbert-inference-pytorch-1-{}".format(time.strftime("%m-%d-%Y-%H-%M-%S"))
print("Endpoint name: ", ENDPOINT_NAME)
model = PyTorchModel(model_data=model_data, source_dir='code',
entry_point='inference.py', role=role, framework_version='1.6.0', py_version='py3')
```
### Deploy the model on an endpoint
You create a predictor by using the model.deploy function. You can optionally change both the instance count and instance type.
```
%%time
predictor = model.deploy(initial_instance_count=1, instance_type='ml.m5.2xlarge', endpoint_name=ENDPOINT_NAME)
```
## Predicting SubCellular Localization of Protein Sequences
```
import boto3
runtime= boto3.client('runtime.sagemaker')
client = boto3.client('sagemaker')
endpoint_desc = client.describe_endpoint(EndpointName=ENDPOINT_NAME)
print(endpoint_desc)
print('---'*30)
```
We then configure the predictor to use application/json for the content type when sending requests to our endpoint:
```
predictor.serializer = sagemaker.serializers.JSONSerializer()
predictor.deserializer = sagemaker.deserializers.JSONDeserializer()
```
Finally, we use the returned predictor object to call the endpoint:
```
protein_sequence = 'M G K K D A S T T R T P V D Q Y R K Q I G R Q D Y K K N K P V L K A T R L K A E A K K A A I G I K E V I L V T I A I L V L L F A F Y A F F F L N L T K T D I Y E D S N N'
prediction = predictor.predict(protein_sequence)
print(prediction)
print(f'Protein Sequence: {protein_sequence}')
print("Sequence Localization Ground Truth is: {} - prediction is: {}".format('Endoplasmic.reticulum', class_names[prediction[0]]))
protein_sequence = 'M S M T I L P L E L I D K C I G S N L W V I M K S E R E F A G T L V G F D D Y V N I V L K D V T E Y D T V T G V T E K H S E M L L N G N G M C M L I P G G K P E'
prediction = predictor.predict(protein_sequence)
print(prediction)
print(f'Protein Sequence: {protein_sequence}')
print("Sequence Localization Ground Truth is: {} - prediction is: {}".format('Nucleus', class_names[prediction[0]]))
seq = 'M G G P T R R H Q E E G S A E C L G G P S T R A A P G P G L R D F H F T T A G P S K A D R L G D A A Q I H R E R M R P V Q C G D G S G E R V F L Q S P G S I G T L Y I R L D L N S Q R S T C C C L L N A G T K G M C'
prediction = predictor.predict(seq)
print(prediction)
print(f'Protein Sequence: {seq}')
print("Sequence Localization Ground Truth is: {} - prediction is: {}".format('Cytoplasm',class_names[prediction[0]]))
```
# Cleanup
Lastly, please remember to delete the Amazon SageMaker endpoint to avoid charges:
```
predictor.delete_endpoint()
```
## References
- [1] Refining Protein Subcellular Localization (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1289393/)
- [2] Kumar A, Agarwal S, Heyman JA, Matson S, Heidtman M, et al. Subcellular localization of the yeast proteome. Genes Dev. 2002;16:707–719. [PMC free article] [PubMed] [Google Scholar]
- [3] Huh WK, Falvo JV, Gerke LC, Carroll AS, Howson RW, et al. Global analysis of protein localization in budding yeast. Nature. 2003;425:686–691. [PubMed] [Google Scholar]
- [4] Wiemann S, Arlt D, Huber W, Wellenreuther R, Schleeger S, et al. From ORFeome to biology: A functional genomics pipeline. Genome Res. 2004;14:2136–2144. [PMC free article] [PubMed] [Google Scholar]
- [5] Davis TN. Protein localization in proteomics. Curr Opin Chem Biol. 2004;8:49–53. [PubMed] [Google Scholar]
- [6] Scott MS, Thomas DY, Hallett MT. Predicting subcellular localization via protein motif co-occurrence. Genome Res. 2004;14:1957–1966. [PMC free article] [PubMed] [Google Scholar]
- [7] ProtTrans: Towards Cracking the Language of Life's Code Through Self-Supervised Deep Learning and High Performance Computing (https://www.biorxiv.org/content/10.1101/2020.07.12.199554v2.full.pdf)
- [8] ProtBert Hugging Face (https://huggingface.co/Rostlab/prot_bert)
- [9] DeepLoc-1.0: Eukaryotic protein subcellular localization predictor (http://www.cbs.dtu.dk/services/DeepLoc-1.0/data.php)
| true |
code
| 0.289378 | null | null | null | null |
|
# The Autodiff Cookbook
[](https://colab.sandbox.google.com/github/google/jax/blob/master/docs/notebooks/autodiff_cookbook.ipynb)
*alexbw@, mattjj@*
JAX has a pretty general automatic differentiation system. In this notebook, we'll go through a whole bunch of neat autodiff ideas that you can cherry pick for your own work, starting with the basics.
```
import jax.numpy as jnp
from jax import grad, jit, vmap
from jax import random
key = random.PRNGKey(0)
```
## Gradients
### Starting with `grad`
You can differentiate a function with `grad`:
```
grad_tanh = grad(jnp.tanh)
print(grad_tanh(2.0))
```
`grad` takes a function and returns a function. If you have a Python function `f` that evaluates the mathematical function $f$, then `grad(f)` is a Python function that evaluates the mathematical function $\nabla f$. That means `grad(f)(x)` represents the value $\nabla f(x)$.
Since `grad` operates on functions, you can apply it to its own output to differentiate as many times as you like:
```
print(grad(grad(jnp.tanh))(2.0))
print(grad(grad(grad(jnp.tanh)))(2.0))
```
Let's look at computing gradients with `grad` in a linear logistic regression model. First, the setup:
```
def sigmoid(x):
return 0.5 * (jnp.tanh(x / 2) + 1)
# Outputs probability of a label being true.
def predict(W, b, inputs):
return sigmoid(jnp.dot(inputs, W) + b)
# Build a toy dataset.
inputs = jnp.array([[0.52, 1.12, 0.77],
[0.88, -1.08, 0.15],
[0.52, 0.06, -1.30],
[0.74, -2.49, 1.39]])
targets = jnp.array([True, True, False, True])
# Training loss is the negative log-likelihood of the training examples.
def loss(W, b):
preds = predict(W, b, inputs)
label_probs = preds * targets + (1 - preds) * (1 - targets)
return -jnp.sum(jnp.log(label_probs))
# Initialize random model coefficients
key, W_key, b_key = random.split(key, 3)
W = random.normal(W_key, (3,))
b = random.normal(b_key, ())
```
Use the `grad` function with its `argnums` argument to differentiate a function with respect to positional arguments.
```
# Differentiate `loss` with respect to the first positional argument:
W_grad = grad(loss, argnums=0)(W, b)
print('W_grad', W_grad)
# Since argnums=0 is the default, this does the same thing:
W_grad = grad(loss)(W, b)
print('W_grad', W_grad)
# But we can choose different values too, and drop the keyword:
b_grad = grad(loss, 1)(W, b)
print('b_grad', b_grad)
# Including tuple values
W_grad, b_grad = grad(loss, (0, 1))(W, b)
print('W_grad', W_grad)
print('b_grad', b_grad)
```
This `grad` API has a direct correspondence to the excellent notation in Spivak's classic *Calculus on Manifolds* (1965), also used in Sussman and Wisdom's [*Structure and Interpretation of Classical Mechanics*](http://mitpress.mit.edu/sites/default/files/titles/content/sicm_edition_2/book.html) (2015) and their [*Functional Differential Geometry*](https://mitpress.mit.edu/books/functional-differential-geometry) (2013). Both books are open-access. See in particular the "Prologue" section of *Functional Differential Geometry* for a defense of this notation.
Essentially, when using the `argnums` argument, if `f` is a Python function for evaluating the mathematical function $f$, then the Python expression `grad(f, i)` evaluates to a Python function for evaluating $\partial_i f$.
### Differentiating with respect to nested lists, tuples, and dicts
Differentiating with respect to standard Python containers just works, so use tuples, lists, and dicts (and arbitrary nesting) however you like.
```
def loss2(params_dict):
preds = predict(params_dict['W'], params_dict['b'], inputs)
label_probs = preds * targets + (1 - preds) * (1 - targets)
return -jnp.sum(jnp.log(label_probs))
print(grad(loss2)({'W': W, 'b': b}))
```
You can [register your own container types](https://github.com/google/jax/issues/446#issuecomment-467105048) to work with not just `grad` but all the JAX transformations (`jit`, `vmap`, etc.).
### Evaluate a function and its gradient using `value_and_grad`
Another convenient function is `value_and_grad` for efficiently computing both a function's value as well as its gradient's value:
```
from jax import value_and_grad
loss_value, Wb_grad = value_and_grad(loss, (0, 1))(W, b)
print('loss value', loss_value)
print('loss value', loss(W, b))
```
### Checking against numerical differences
A great thing about derivatives is that they're straightforward to check with finite differences:
```
# Set a step size for finite differences calculations
eps = 1e-4
# Check b_grad with scalar finite differences
b_grad_numerical = (loss(W, b + eps / 2.) - loss(W, b - eps / 2.)) / eps
print('b_grad_numerical', b_grad_numerical)
print('b_grad_autodiff', grad(loss, 1)(W, b))
# Check W_grad with finite differences in a random direction
key, subkey = random.split(key)
vec = random.normal(subkey, W.shape)
unitvec = vec / jnp.sqrt(jnp.vdot(vec, vec))
W_grad_numerical = (loss(W + eps / 2. * unitvec, b) - loss(W - eps / 2. * unitvec, b)) / eps
print('W_dirderiv_numerical', W_grad_numerical)
print('W_dirderiv_autodiff', jnp.vdot(grad(loss)(W, b), unitvec))
```
JAX provides a simple convenience function that does essentially the same thing, but checks up to any order of differentiation that you like:
```
from jax.test_util import check_grads
check_grads(loss, (W, b), order=2) # check up to 2nd order derivatives
```
### Hessian-vector products with `grad`-of-`grad`
One thing we can do with higher-order `grad` is build a Hessian-vector product function. (Later on we'll write an even more efficient implementation that mixes both forward- and reverse-mode, but this one will use pure reverse-mode.)
A Hessian-vector product function can be useful in a [truncated Newton Conjugate-Gradient algorithm](https://en.wikipedia.org/wiki/Truncated_Newton_method) for minimizing smooth convex functions, or for studying the curvature of neural network training objectives (e.g. [1](https://arxiv.org/abs/1406.2572), [2](https://arxiv.org/abs/1811.07062), [3](https://arxiv.org/abs/1706.04454), [4](https://arxiv.org/abs/1802.03451)).
For a scalar-valued function $f : \mathbb{R}^n \to \mathbb{R}$ with continuous second derivatives (so that the Hessian matrix is symmetric), the Hessian at a point $x \in \mathbb{R}^n$ is written as $\partial^2 f(x)$. A Hessian-vector product function is then able to evaluate
$\qquad v \mapsto \partial^2 f(x) \cdot v$
for any $v \in \mathbb{R}^n$.
The trick is not to instantiate the full Hessian matrix: if $n$ is large, perhaps in the millions or billions in the context of neural networks, then that might be impossible to store.
Luckily, `grad` already gives us a way to write an efficient Hessian-vector product function. We just have to use the identity
$\qquad \partial^2 f (x) v = \partial [x \mapsto \partial f(x) \cdot v] = \partial g(x)$,
where $g(x) = \partial f(x) \cdot v$ is a new scalar-valued function that dots the gradient of $f$ at $x$ with the vector $v$. Notice that we're only ever differentiating scalar-valued functions of vector-valued arguments, which is exactly where we know `grad` is efficient.
In JAX code, we can just write this:
```
def hvp(f, x, v):
return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)
```
This example shows that you can freely use lexical closure, and JAX will never get perturbed or confused.
We'll check this implementation a few cells down, once we see how to compute dense Hessian matrices. We'll also write an even better version that uses both forward-mode and reverse-mode.
### Jacobians and Hessians using `jacfwd` and `jacrev`
You can compute full Jacobian matrices using the `jacfwd` and `jacrev` functions:
```
from jax import jacfwd, jacrev
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
J = jacfwd(f)(W)
print("jacfwd result, with shape", J.shape)
print(J)
J = jacrev(f)(W)
print("jacrev result, with shape", J.shape)
print(J)
```
These two functions compute the same values (up to machine numerics), but differ in their implementation: `jacfwd` uses forward-mode automatic differentiation, which is more efficient for "tall" Jacobian matrices, while `jacrev` uses reverse-mode, which is more efficient for "wide" Jacobian matrices. For matrices that are near-square, `jacfwd` probably has an edge over `jacrev`.
You can also use `jacfwd` and `jacrev` with container types:
```
def predict_dict(params, inputs):
return predict(params['W'], params['b'], inputs)
J_dict = jacrev(predict_dict)({'W': W, 'b': b}, inputs)
for k, v in J_dict.items():
print("Jacobian from {} to logits is".format(k))
print(v)
```
For more details on forward- and reverse-mode, as well as how to implement `jacfwd` and `jacrev` as efficiently as possible, read on!
Using a composition of two of these functions gives us a way to compute dense Hessian matrices:
```
def hessian(f):
return jacfwd(jacrev(f))
H = hessian(f)(W)
print("hessian, with shape", H.shape)
print(H)
```
This shape makes sense: if we start with a function $f : \mathbb{R}^n \to \mathbb{R}^m$, then at a point $x \in \mathbb{R}^n$ we expect to get the shapes
* $f(x) \in \mathbb{R}^m$, the value of $f$ at $x$,
* $\partial f(x) \in \mathbb{R}^{m \times n}$, the Jacobian matrix at $x$,
* $\partial^2 f(x) \in \mathbb{R}^{m \times n \times n}$, the Hessian at $x$,
and so on.
To implement `hessian`, we could have used `jacfwd(jacrev(f))` or `jacrev(jacfwd(f))` or any other composition of the two. But forward-over-reverse is typically the most efficient. That's because in the inner Jacobian computation we're often differentiating a function wide Jacobian (maybe like a loss function $f : \mathbb{R}^n \to \mathbb{R}$), while in the outer Jacobian computation we're differentiating a function with a square Jacobian (since $\nabla f : \mathbb{R}^n \to \mathbb{R}^n$), which is where forward-mode wins out.
## How it's made: two foundational autodiff functions
### Jacobian-Vector products (JVPs, aka forward-mode autodiff)
JAX includes efficient and general implementations of both forward- and reverse-mode automatic differentiation. The familiar `grad` function is built on reverse-mode, but to explain the difference in the two modes, and when each can be useful, we need a bit of math background.
#### JVPs in math
Mathematically, given a function $f : \mathbb{R}^n \to \mathbb{R}^m$, the Jacobian of $f$ evaluated at an input point $x \in \mathbb{R}^n$, denoted $\partial f(x)$, is often thought of as a matrix in $\mathbb{R}^m \times \mathbb{R}^n$:
$\qquad \partial f(x) \in \mathbb{R}^{m \times n}$.
But we can also think of $\partial f(x)$ as a linear map, which maps the tangent space of the domain of $f$ at the point $x$ (which is just another copy of $\mathbb{R}^n$) to the tangent space of the codomain of $f$ at the point $f(x)$ (a copy of $\mathbb{R}^m$):
$\qquad \partial f(x) : \mathbb{R}^n \to \mathbb{R}^m$.
This map is called the [pushforward map](https://en.wikipedia.org/wiki/Pushforward_(differential)) of $f$ at $x$. The Jacobian matrix is just the matrix for this linear map in a standard basis.
If we don't commit to one specific input point $x$, then we can think of the function $\partial f$ as first taking an input point and returning the Jacobian linear map at that input point:
$\qquad \partial f : \mathbb{R}^n \to \mathbb{R}^n \to \mathbb{R}^m$.
In particular, we can uncurry things so that given input point $x \in \mathbb{R}^n$ and a tangent vector $v \in \mathbb{R}^n$, we get back an output tangent vector in $\mathbb{R}^m$. We call that mapping, from $(x, v)$ pairs to output tangent vectors, the *Jacobian-vector product*, and write it as
$\qquad (x, v) \mapsto \partial f(x) v$
#### JVPs in JAX code
Back in Python code, JAX's `jvp` function models this transformation. Given a Python function that evaluates $f$, JAX's `jvp` is a way to get a Python function for evaluating $(x, v) \mapsto (f(x), \partial f(x) v)$.
```
from jax import jvp
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
key, subkey = random.split(key)
v = random.normal(subkey, W.shape)
# Push forward the vector `v` along `f` evaluated at `W`
y, u = jvp(f, (W,), (v,))
```
In terms of Haskell-like type signatures, we could write
```haskell
jvp :: (a -> b) -> a -> T a -> (b, T b)
```
where we use `T a` to denote the type of the tangent space for `a`. In words, `jvp` takes as arguments a function of type `a -> b`, a value of type `a`, and a tangent vector value of type `T a`. It gives back a pair consisting of a value of type `b` and an output tangent vector of type `T b`.
The `jvp`-transformed function is evaluated much like the original function, but paired up with each primal value of type `a` it pushes along tangent values of type `T a`. For each primitive numerical operation that the original function would have applied, the `jvp`-transformed function executes a "JVP rule" for that primitive that both evaluates the primitive on the primals and applies the primitive's JVP at those primal values.
That evaluation strategy has some immediate implications about computational complexity: since we evaluate JVPs as we go, we don't need to store anything for later, and so the memory cost is independent of the depth of the computation. In addition, the FLOP cost of the `jvp`-transformed function is about 3x the cost of just evaluating the function (one unit of work for evaluating the original function, for example `sin(x)`; one unit for linearizing, like `cos(x)`; and one unit for applying the linearized function to a vector, like `cos_x * v`). Put another way, for a fixed primal point $x$, we can evaluate $v \mapsto \partial f(x) \cdot v$ for about the same marginal cost as evaluating $f$.
That memory complexity sounds pretty compelling! So why don't we see forward-mode very often in machine learning?
To answer that, first think about how you could use a JVP to build a full Jacobian matrix. If we apply a JVP to a one-hot tangent vector, it reveals one column of the Jacobian matrix, corresponding to the nonzero entry we fed in. So we can build a full Jacobian one column at a time, and to get each column costs about the same as one function evaluation. That will be efficient for functions with "tall" Jacobians, but inefficient for "wide" Jacobians.
If you're doing gradient-based optimization in machine learning, you probably want to minimize a loss function from parameters in $\mathbb{R}^n$ to a scalar loss value in $\mathbb{R}$. That means the Jacobian of this function is a very wide matrix: $\partial f(x) \in \mathbb{R}^{1 \times n}$, which we often identify with the Gradient vector $\nabla f(x) \in \mathbb{R}^n$. Building that matrix one column at a time, with each call taking a similar number of FLOPs to evaluating the original function, sure seems inefficient! In particular, for training neural networks, where $f$ is a training loss function and $n$ can be in the millions or billions, this approach just won't scale.
To do better for functions like this, we just need to use reverse-mode.
### Vector-Jacobian products (VJPs, aka reverse-mode autodiff)
Where forward-mode gives us back a function for evaluating Jacobian-vector products, which we can then use to build Jacobian matrices one column at a time, reverse-mode is a way to get back a function for evaluating vector-Jacobian products (equivalently Jacobian-transpose-vector products), which we can use to build Jacobian matrices one row at a time.
#### VJPs in math
Let's again consider a function $f : \mathbb{R}^n \to \mathbb{R}^m$.
Starting from our notation for JVPs, the notation for VJPs is pretty simple:
$\qquad (x, v) \mapsto v \partial f(x)$,
where $v$ is an element of the cotangent space of $f$ at $x$ (isomorphic to another copy of $\mathbb{R}^m$). When being rigorous, we should think of $v$ as a linear map $v : \mathbb{R}^m \to \mathbb{R}$, and when we write $v \partial f(x)$ we mean function composition $v \circ \partial f(x)$, where the types work out because $\partial f(x) : \mathbb{R}^n \to \mathbb{R}^m$. But in the common case we can identify $v$ with a vector in $\mathbb{R}^m$ and use the two almost interchageably, just like we might sometimes flip between "column vectors" and "row vectors" without much comment.
With that identification, we can alternatively think of the linear part of a VJP as the transpose (or adjoint conjugate) of the linear part of a JVP:
$\qquad (x, v) \mapsto \partial f(x)^\mathsf{T} v$.
For a given point $x$, we can write the signature as
$\qquad \partial f(x)^\mathsf{T} : \mathbb{R}^m \to \mathbb{R}^n$.
The corresponding map on cotangent spaces is often called the [pullback](https://en.wikipedia.org/wiki/Pullback_(differential_geometry))
of $f$ at $x$. The key for our purposes is that it goes from something that looks like the output of $f$ to something that looks like the input of $f$, just like we might expect from a transposed linear function.
#### VJPs in JAX code
Switching from math back to Python, the JAX function `vjp` can take a Python function for evaluating $f$ and give us back a Python function for evaluating the VJP $(x, v) \mapsto (f(x), v^\mathsf{T} \partial f(x))$.
```
from jax import vjp
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
y, vjp_fun = vjp(f, W)
key, subkey = random.split(key)
u = random.normal(subkey, y.shape)
# Pull back the covector `u` along `f` evaluated at `W`
v = vjp_fun(u)
```
In terms of Haskell-like type signatures, we could write
```haskell
vjp :: (a -> b) -> a -> (b, CT b -> CT a)
```
where we use `CT a` to denote the type for the cotangent space for `a`. In words, `vjp` takes as arguments a function of type `a -> b` and a point of type `a`, and gives back a pair consisting of a value of type `b` and a linear map of type `CT b -> CT a`.
This is great because it lets us build Jacobian matrices one row at a time, and the FLOP cost for evaluating $(x, v) \mapsto (f(x), v^\mathsf{T} \partial f(x))$ is only about three times the cost of evaluating $f$. In particular, if we want the gradient of a function $f : \mathbb{R}^n \to \mathbb{R}$, we can do it in just one call. That's how `grad` is efficient for gradient-based optimization, even for objectives like neural network training loss functions on millions or billions of parameters.
There's a cost, though: though the FLOPs are friendly, memory scales with the depth of the computation. Also, the implementation is traditionally more complex than that of forward-mode, though JAX has some tricks up its sleeve (that's a story for a future notebook!).
For more on how reverse-mode works, see [this tutorial video from the Deep Learning Summer School in 2017](http://videolectures.net/deeplearning2017_johnson_automatic_differentiation/).
### Vector-valued gradients with VJPs
If you're interested in taking vector-valued gradients (like `tf.gradients`):
```
from jax import vjp
def vgrad(f, x):
y, vjp_fn = vjp(f, x)
return vjp_fn(jnp.ones(y.shape))[0]
print(vgrad(lambda x: 3*x**2, jnp.ones((2, 2))))
```
### Hessian-vector products using both forward- and reverse-mode
In a previous section, we implemented a Hessian-vector product function just using reverse-mode (assuming continuous second derivatives):
```
def hvp(f, x, v):
return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)
```
That's efficient, but we can do even better and save some memory by using forward-mode together with reverse-mode.
Mathematically, given a function $f : \mathbb{R}^n \to \mathbb{R}$ to differentiate, a point $x \in \mathbb{R}^n$ at which to linearize the function, and a vector $v \in \mathbb{R}^n$, the Hessian-vector product function we want is
$(x, v) \mapsto \partial^2 f(x) v$
Consider the helper function $g : \mathbb{R}^n \to \mathbb{R}^n$ defined to be the derivative (or gradient) of $f$, namely $g(x) = \partial f(x)$. All we need is its JVP, since that will give us
$(x, v) \mapsto \partial g(x) v = \partial^2 f(x) v$.
We can translate that almost directly into code:
```
from jax import jvp, grad
# forward-over-reverse
def hvp(f, primals, tangents):
return jvp(grad(f), primals, tangents)[1]
```
Even better, since we didn't have to call `jnp.dot` directly, this `hvp` function works with arrays of any shape and with arbitrary container types (like vectors stored as nested lists/dicts/tuples), and doesn't even have a dependence on `jax.numpy`.
Here's an example of how to use it:
```
def f(X):
return jnp.sum(jnp.tanh(X)**2)
key, subkey1, subkey2 = random.split(key, 3)
X = random.normal(subkey1, (30, 40))
V = random.normal(subkey2, (30, 40))
ans1 = hvp(f, (X,), (V,))
ans2 = jnp.tensordot(hessian(f)(X), V, 2)
print(jnp.allclose(ans1, ans2, 1e-4, 1e-4))
```
Another way you might consider writing this is using reverse-over-forward:
```
# reverse-over-forward
def hvp_revfwd(f, primals, tangents):
g = lambda primals: jvp(f, primals, tangents)[1]
return grad(g)(primals)
```
That's not quite as good, though, because forward-mode has less overhead than reverse-mode, and since the outer differentiation operator here has to differentiate a larger computation than the inner one, keeping forward-mode on the outside works best:
```
# reverse-over-reverse, only works for single arguments
def hvp_revrev(f, primals, tangents):
x, = primals
v, = tangents
return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)
print("Forward over reverse")
%timeit -n10 -r3 hvp(f, (X,), (V,))
print("Reverse over forward")
%timeit -n10 -r3 hvp_revfwd(f, (X,), (V,))
print("Reverse over reverse")
%timeit -n10 -r3 hvp_revrev(f, (X,), (V,))
print("Naive full Hessian materialization")
%timeit -n10 -r3 jnp.tensordot(hessian(f)(X), V, 2)
```
## Composing VJPs, JVPs, and `vmap`
### Jacobian-Matrix and Matrix-Jacobian products
Now that we have `jvp` and `vjp` transformations that give us functions to push-forward or pull-back single vectors at a time, we can use JAX's `vmap` [transformation](https://github.com/google/jax#auto-vectorization-with-vmap) to push and pull entire bases at once. In particular, we can use that to write fast matrix-Jacobian and Jacobian-matrix products.
```
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
# Pull back the covectors `m_i` along `f`, evaluated at `W`, for all `i`.
# First, use a list comprehension to loop over rows in the matrix M.
def loop_mjp(f, x, M):
y, vjp_fun = vjp(f, x)
return jnp.vstack([vjp_fun(mi) for mi in M])
# Now, use vmap to build a computation that does a single fast matrix-matrix
# multiply, rather than an outer loop over vector-matrix multiplies.
def vmap_mjp(f, x, M):
y, vjp_fun = vjp(f, x)
outs, = vmap(vjp_fun)(M)
return outs
key = random.PRNGKey(0)
num_covecs = 128
U = random.normal(key, (num_covecs,) + y.shape)
loop_vs = loop_mjp(f, W, M=U)
print('Non-vmapped Matrix-Jacobian product')
%timeit -n10 -r3 loop_mjp(f, W, M=U)
print('\nVmapped Matrix-Jacobian product')
vmap_vs = vmap_mjp(f, W, M=U)
%timeit -n10 -r3 vmap_mjp(f, W, M=U)
assert jnp.allclose(loop_vs, vmap_vs), 'Vmap and non-vmapped Matrix-Jacobian Products should be identical'
def loop_jmp(f, W, M):
# jvp immediately returns the primal and tangent values as a tuple,
# so we'll compute and select the tangents in a list comprehension
return jnp.vstack([jvp(f, (W,), (mi,))[1] for mi in M])
def vmap_jmp(f, W, M):
_jvp = lambda s: jvp(f, (W,), (s,))[1]
return vmap(_jvp)(M)
num_vecs = 128
S = random.normal(key, (num_vecs,) + W.shape)
loop_vs = loop_jmp(f, W, M=S)
print('Non-vmapped Jacobian-Matrix product')
%timeit -n10 -r3 loop_jmp(f, W, M=S)
vmap_vs = vmap_jmp(f, W, M=S)
print('\nVmapped Jacobian-Matrix product')
%timeit -n10 -r3 vmap_jmp(f, W, M=S)
assert jnp.allclose(loop_vs, vmap_vs), 'Vmap and non-vmapped Jacobian-Matrix products should be identical'
```
### The implementation of `jacfwd` and `jacrev`
Now that we've seen fast Jacobian-matrix and matrix-Jacobian products, it's not hard to guess how to write `jacfwd` and `jacrev`. We just use the same technique to push-forward or pull-back an entire standard basis (isomorphic to an identity matrix) at once.
```
from jax import jacrev as builtin_jacrev
def our_jacrev(f):
def jacfun(x):
y, vjp_fun = vjp(f, x)
# Use vmap to do a matrix-Jacobian product.
# Here, the matrix is the Euclidean basis, so we get all
# entries in the Jacobian at once.
J, = vmap(vjp_fun, in_axes=0)(jnp.eye(len(y)))
return J
return jacfun
assert jnp.allclose(builtin_jacrev(f)(W), our_jacrev(f)(W)), 'Incorrect reverse-mode Jacobian results!'
from jax import jacfwd as builtin_jacfwd
def our_jacfwd(f):
def jacfun(x):
_jvp = lambda s: jvp(f, (x,), (s,))[1]
Jt =vmap(_jvp, in_axes=1)(jnp.eye(len(x)))
return jnp.transpose(Jt)
return jacfun
assert jnp.allclose(builtin_jacfwd(f)(W), our_jacfwd(f)(W)), 'Incorrect forward-mode Jacobian results!'
```
Interestingly, [Autograd](https://github.com/hips/autograd) couldn't do this. Our [implementation](https://github.com/HIPS/autograd/blob/96a03f44da43cd7044c61ac945c483955deba957/autograd/differential_operators.py#L60) of reverse-mode `jacobian` in Autograd had to pull back one vector at a time with an outer-loop `map`. Pushing one vector at a time through the computation is much less efficient than batching it all together with `vmap`.
Another thing that Autograd couldn't do is `jit`. Interestingly, no matter how much Python dynamism you use in your function to be differentiated, we could always use `jit` on the linear part of the computation. For example:
```
def f(x):
try:
if x < 3:
return 2 * x ** 3
else:
raise ValueError
except ValueError:
return jnp.pi * x
y, f_vjp = vjp(f, 4.)
print(jit(f_vjp)(1.))
```
## Complex numbers and differentiation
JAX is great at complex numbers and differentiation. To support both [holomorphic and non-holomorphic differentiation](https://en.wikipedia.org/wiki/Holomorphic_function), it helps to think in terms of JVPs and VJPs.
Consider a complex-to-complex function $f: \mathbb{C} \to \mathbb{C}$ and identify it with a corresponding function $g: \mathbb{R}^2 \to \mathbb{R}^2$,
```
def f(z):
x, y = jnp.real(z), jnp.imag(z)
return u(x, y) + v(x, y) * 1j
def g(x, y):
return (u(x, y), v(x, y))
```
That is, we've decomposed $f(z) = u(x, y) + v(x, y) i$ where $z = x + y i$, and identified $\mathbb{C}$ with $\mathbb{R}^2$ to get $g$.
Since $g$ only involves real inputs and outputs, we already know how to write a Jacobian-vector product for it, say given a tangent vector $(c, d) \in \mathbb{R}^2$, namely
$\begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix}
\begin{bmatrix} c \\ d \end{bmatrix}$.
To get a JVP for the original function $f$ applied to a tangent vector $c + di \in \mathbb{C}$, we just use the same definition and identify the result as another complex number,
$\partial f(x + y i)(c + d i) =
\begin{matrix} \begin{bmatrix} 1 & i \end{bmatrix} \\ ~ \end{matrix}
\begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix}
\begin{bmatrix} c \\ d \end{bmatrix}$.
That's our definition of the JVP of a $\mathbb{C} \to \mathbb{C}$ function! Notice it doesn't matter whether or not $f$ is holomorphic: the JVP is unambiguous.
Here's a check:
```
def check(seed):
key = random.PRNGKey(seed)
# random coeffs for u and v
key, subkey = random.split(key)
a, b, c, d = random.uniform(subkey, (4,))
def fun(z):
x, y = jnp.real(z), jnp.imag(z)
return u(x, y) + v(x, y) * 1j
def u(x, y):
return a * x + b * y
def v(x, y):
return c * x + d * y
# primal point
key, subkey = random.split(key)
x, y = random.uniform(subkey, (2,))
z = x + y * 1j
# tangent vector
key, subkey = random.split(key)
c, d = random.uniform(subkey, (2,))
z_dot = c + d * 1j
# check jvp
_, ans = jvp(fun, (z,), (z_dot,))
expected = (grad(u, 0)(x, y) * c +
grad(u, 1)(x, y) * d +
grad(v, 0)(x, y) * c * 1j+
grad(v, 1)(x, y) * d * 1j)
print(jnp.allclose(ans, expected))
check(0)
check(1)
check(2)
```
What about VJPs? We do something pretty similar: for a cotangent vector $c + di \in \mathbb{C}$ we define the VJP of $f$ as
$(c + di)^* \; \partial f(x + y i) =
\begin{matrix} \begin{bmatrix} c & -d \end{bmatrix} \\ ~ \end{matrix}
\begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix}
\begin{bmatrix} 1 \\ -i \end{bmatrix}$.
What's with the negatives? They're just to take care of complex conjugation, and the fact that we're working with covectors.
Here's a check of the VJP rules:
```
def check(seed):
key = random.PRNGKey(seed)
# random coeffs for u and v
key, subkey = random.split(key)
a, b, c, d = random.uniform(subkey, (4,))
def fun(z):
x, y = jnp.real(z), jnp.imag(z)
return u(x, y) + v(x, y) * 1j
def u(x, y):
return a * x + b * y
def v(x, y):
return c * x + d * y
# primal point
key, subkey = random.split(key)
x, y = random.uniform(subkey, (2,))
z = x + y * 1j
# cotangent vector
key, subkey = random.split(key)
c, d = random.uniform(subkey, (2,))
z_bar = jnp.array(c + d * 1j) # for dtype control
# check vjp
_, fun_vjp = vjp(fun, z)
ans, = fun_vjp(z_bar)
expected = (grad(u, 0)(x, y) * c +
grad(v, 0)(x, y) * (-d) +
grad(u, 1)(x, y) * c * (-1j) +
grad(v, 1)(x, y) * (-d) * (-1j))
assert jnp.allclose(ans, expected, atol=1e-5, rtol=1e-5)
check(0)
check(1)
check(2)
```
What about convenience wrappers like `grad`, `jacfwd`, and `jacrev`?
For $\mathbb{R} \to \mathbb{R}$ functions, recall we defined `grad(f)(x)` as being `vjp(f, x)[1](1.0)`, which works because applying a VJP to a `1.0` value reveals the gradient (i.e. Jacobian, or derivative). We can do the same thing for $\mathbb{C} \to \mathbb{R}$ functions: we can still use `1.0` as the cotangent vector, and we just get out a complex number result summarizing the full Jacobian:
```
def f(z):
x, y = jnp.real(z), jnp.imag(z)
return x**2 + y**2
z = 3. + 4j
grad(f)(z)
```
For geneneral $\mathbb{C} \to \mathbb{C}$ functions, the Jacobian has 4 real-valued degrees of freedom (as in the 2x2 Jacobian matrices above), so we can't hope to represent all of them with in a complex number. But we can for holomorphic functions! A holomorphic function is precisely a $\mathbb{C} \to \mathbb{C}$ function with the special property that its derivative can be represented as a single complex number. (The [Cauchy-Riemann equations](https://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations) ensure that the above 2x2 Jacobians have the special form of a scale-and-rotate matrix in the complex plane, i.e. the action of a single complex number under multiplication.) And we can reveal that one complex number using a single call to `vjp` with a covector of `1.0`.
Because this only works for holomorphic functions, to use this trick we need to promise JAX that our function is holomorphic; otherwise, JAX will raise an error when `grad` is used for a complex-output function:
```
def f(z):
return jnp.sin(z)
z = 3. + 4j
grad(f, holomorphic=True)(z)
```
All the `holomorphic=True` promise does is disable the error when the output is complex-valued. We can still write `holomorphic=True` when the function isn't holomorphic, but the answer we get out won't represent the full Jacobian. Instead, it'll be the Jacobian of the function where we just discard the imaginary part of the output:
```
def f(z):
return jnp.conjugate(z)
z = 3. + 4j
grad(f, holomorphic=True)(z) # f is not actually holomorphic!
```
There are some useful upshots for how `grad` works here:
1. We can use `grad` on holomorphic $\mathbb{C} \to \mathbb{C}$ functions.
2. We can use `grad` to optimize $f : \mathbb{C} \to \mathbb{R}$ functions, like real-valued loss functions of complex parameters `x`, by taking steps in the dierction of the conjugate of `grad(f)(x)`.
3. If we have an $\mathbb{R} \to \mathbb{R}$ function that just happens to use some complex-valued operations internally (some of which must be non-holomorphic, e.g. FFTs used in covolutions) then `grad` still works and we get the same result that an implementation using only real values would have given.
In any case, JVPs and VJPs are always unambiguous. And if we wanted to compute the full Jacobian matrix of a non-holomorphic $\mathbb{C} \to \mathbb{C}$ function, we can do it with JVPs or VJPs!
You should expect complex numbers to work everywhere in JAX. Here's differentiating through a Cholesky decomposition of a complex matrix:
```
A = jnp.array([[5., 2.+3j, 5j],
[2.-3j, 7., 1.+7j],
[-5j, 1.-7j, 12.]])
def f(X):
L = jnp.linalg.cholesky(X)
return jnp.sum((L - jnp.sin(L))**2)
grad(f, holomorphic=True)(A)
```
## More advanced autodiff
In this notebook, we worked through some easy, and then progressively more complicated, applications of automatic differentiation in JAX. We hope you now feel that taking derivatives in JAX is easy and powerful.
There's a whole world of other autodiff tricks and functionality out there. Topics we didn't cover, but hope to in a "Advanced Autodiff Cookbook" include:
- Gauss-Newton Vector Products, linearizing once
- Custom VJPs and JVPs
- Efficient derivatives at fixed-points
- Estimating the trace of a Hessian using random Hessian-vector products.
- Forward-mode autodiff using only reverse-mode autodiff.
- Taking derivatives with respect to custom data types.
- Checkpointing (binomial checkpointing for efficient reverse-mode, not model snapshotting).
- Optimizing VJPs with Jacobian pre-accumulation.
| true |
code
| 0.705633 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/airctic/icevision-gradio/blob/master/IceApp_pets.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# IceVision Deployment App Example: PETS Dataset
This example uses Faster RCNN trained weights using the [PETS dataset](https://airctic.github.io/icedata/pets/)
[IceVision](https://github.com/airctic/IceVision) features:
✔ Data curation/cleaning with auto-fix
✔ Exploratory data analysis dashboard
✔ Pluggable transforms for better model generalization
✔ Access to hundreds of neural net models (Torchvision, MMDetection, EfficientDet, Timm)
✔ Access to multiple training loop libraries (Pytorch-Lightning, Fastai)
✔ Multi-task training to efficiently combine object
detection, segmentation, and classification models
## Installing packages
```
!wget https://raw.githubusercontent.com/airctic/icevision/master/install_icevision_inference.sh
!bash install_icevision_inference.sh colab
!echo "- Installing gradio"
!pip install gradio -U -q
# Restart kernel
import IPython
IPython.Application.instance().kernel.do_shutdown(True)
```
## Imports
```
from icevision.all import *
import icedata
import PIL, requests
import torch
from torchvision import transforms
import gradio as gr
```
## Loading trained model
```
_CLASSES = sorted(
{
"Abyssinian",
"great_pyrenees",
"Bombay",
"Persian",
"samoyed",
"Maine_Coon",
"havanese",
"beagle",
"yorkshire_terrier",
"pomeranian",
"scottish_terrier",
"saint_bernard",
"Siamese",
"chihuahua",
"Birman",
"american_pit_bull_terrier",
"miniature_pinscher",
"japanese_chin",
"British_Shorthair",
"Bengal",
"Russian_Blue",
"newfoundland",
"wheaten_terrier",
"Ragdoll",
"leonberger",
"english_cocker_spaniel",
"english_setter",
"staffordshire_bull_terrier",
"german_shorthaired",
"Egyptian_Mau",
"boxer",
"shiba_inu",
"keeshond",
"pug",
"american_bulldog",
"basset_hound",
"Sphynx",
}
)
class_map = ClassMap(_CLASSES)
class_map
# Loading model from IceZoo (IceVision Hub)
model = icedata.pets.trained_models.faster_rcnn_resnet50_fpn()
# Transforms
image_size = 384
valid_tfms = tfms.A.Adapter([*tfms.A.resize_and_pad(image_size), tfms.A.Normalize()])
```
## Defining the `show_preds` method: called by `gr.Interface(fn=show_preds, ...)`
```
# Setting the model type: used in end2end_detect() method here below
model_type = models.torchvision.faster_rcnn
def show_preds(input_image, display_label, display_bbox, detection_threshold):
if detection_threshold==0: detection_threshold=0.5
img = PIL.Image.fromarray(input_image, 'RGB')
pred_dict = model_type.end2end_detect(img, valid_tfms, model, class_map=class_map, detection_threshold=detection_threshold,
display_label=display_label, display_bbox=display_bbox, return_img=True,
font_size=40, label_color="#FF59D6")
return pred_dict['img']
```
## Gradio User Interface
```
display_chkbox_label = gr.inputs.Checkbox(label="Label", default=True)
display_chkbox_box = gr.inputs.Checkbox(label="Box", default=True)
detection_threshold_slider = gr.inputs.Slider(minimum=0, maximum=1, step=0.1, default=0.5, label="Detection Threshold")
outputs = gr.outputs.Image(type="pil")
gr_interface = gr.Interface(fn=show_preds, inputs=["image", display_chkbox_label, display_chkbox_box, detection_threshold_slider], outputs=outputs, title='IceApp - PETS')
gr_interface.launch(inline=False, share=True, debug=True)
```
| true |
code
| 0.654702 | null | null | null | null |
|
# Amazon SageMaker Multi-Model Endpoints using XGBoost
With [Amazon SageMaker multi-model endpoints](https://docs.aws.amazon.com/sagemaker/latest/dg/multi-model-endpoints.html), customers can create an endpoint that seamlessly hosts up to thousands of models. These endpoints are well suited to use cases where any one of a large number of models, which can be served from a common inference container to save inference costs, needs to be invokable on-demand and where it is acceptable for infrequently invoked models to incur some additional latency. For applications which require consistently low inference latency, an endpoint deploying a single model is still the best choice.
At a high level, Amazon SageMaker manages the loading and unloading of models for a multi-model endpoint, as they are needed. When an invocation request is made for a particular model, Amazon SageMaker routes the request to an instance assigned to that model, downloads the model artifacts from S3 onto that instance, and initiates loading of the model into the memory of the container. As soon as the loading is complete, Amazon SageMaker performs the requested invocation and returns the result. If the model is already loaded in memory on the selected instance, the downloading and loading steps are skipped and the invocation is performed immediately.
To demonstrate how multi-model endpoints are created and used, this notebook provides an example using a set of XGBoost models that each predict housing prices for a single location. This domain is used as a simple example to easily experiment with multi-model endpoints.
The Amazon SageMaker multi-model endpoint capability is designed to work across with Mxnet, PyTorch and Scikit-Learn machine learning frameworks (TensorFlow coming soon), SageMaker XGBoost, KNN, and Linear Learner algorithms.
In addition, Amazon SageMaker multi-model endpoints are also designed to work with cases where you bring your own container that integrates with the multi-model server library. An example of this can be found [here](https://github.com/awslabs/amazon-sagemaker-examples/tree/master/advanced_functionality/multi_model_bring_your_own) and documentation [here.](https://docs.aws.amazon.com/sagemaker/latest/dg/build-multi-model-build-container.html)
### Contents
1. [Generate synthetic data for housing models](#Generate-synthetic-data-for-housing-models)
1. [Train multiple house value prediction models](#Train-multiple-house-value-prediction-models)
1. [Create the Amazon SageMaker MultiDataModel entity](#Create-the-Amazon-SageMaker-MultiDataModel-entity)
1. [Create the Multi-Model Endpoint](#Create-the-multi-model-endpoint)
1. [Deploy the Multi-Model Endpoint](#deploy-the-multi-model-endpoint)
1. [Get Predictions from the endpoint](#Get-predictions-from-the-endpoint)
1. [Additional Information](#Additional-information)
1. [Clean up](#Clean-up)
# Generate synthetic data
The code below contains helper functions to generate synthetic data in the form of a `1x7` numpy array representing the features of a house.
The first entry in the array is the randomly generated price of a house. The remaining entries are the features (i.e. number of bedroom, square feet, number of bathrooms, etc.).
These functions will be used to generate synthetic data for training, validation, and testing. It will also allow us to submit synthetic payloads for inference to test our multi-model endpoint.
```
import numpy as np
import pandas as pd
import time
NUM_HOUSES_PER_LOCATION = 1000
LOCATIONS = ['NewYork_NY', 'LosAngeles_CA', 'Chicago_IL', 'Houston_TX', 'Dallas_TX',
'Phoenix_AZ', 'Philadelphia_PA', 'SanAntonio_TX', 'SanDiego_CA', 'SanFrancisco_CA']
PARALLEL_TRAINING_JOBS = 4 # len(LOCATIONS) if your account limits can handle it
MAX_YEAR = 2019
def gen_price(house):
_base_price = int(house['SQUARE_FEET'] * 150)
_price = int(_base_price + (10000 * house['NUM_BEDROOMS']) + \
(15000 * house['NUM_BATHROOMS']) + \
(15000 * house['LOT_ACRES']) + \
(15000 * house['GARAGE_SPACES']) - \
(5000 * (MAX_YEAR - house['YEAR_BUILT'])))
return _price
def gen_random_house():
_house = {'SQUARE_FEET': int(np.random.normal(3000, 750)),
'NUM_BEDROOMS': np.random.randint(2, 7),
'NUM_BATHROOMS': np.random.randint(2, 7) / 2,
'LOT_ACRES': round(np.random.normal(1.0, 0.25), 2),
'GARAGE_SPACES': np.random.randint(0, 4),
'YEAR_BUILT': min(MAX_YEAR, int(np.random.normal(1995, 10)))}
_price = gen_price(_house)
return [_price, _house['YEAR_BUILT'], _house['SQUARE_FEET'],
_house['NUM_BEDROOMS'], _house['NUM_BATHROOMS'],
_house['LOT_ACRES'], _house['GARAGE_SPACES']]
def gen_houses(num_houses):
_house_list = []
for i in range(num_houses):
_house_list.append(gen_random_house())
_df = pd.DataFrame(_house_list,
columns=['PRICE', 'YEAR_BUILT', 'SQUARE_FEET', 'NUM_BEDROOMS',
'NUM_BATHROOMS','LOT_ACRES', 'GARAGE_SPACES'])
return _df
```
# Train multiple house value prediction models
In the follow section, we are setting up the code to train a house price prediction model for each of 4 different cities.
As such, we will launch multiple training jobs asynchronously, using the XGBoost algorithm.
In this notebook, we will be using the AWS Managed XGBoost Image for both training and inference - this image provides native support for launching multi-model endpoints.
```
import sagemaker
from sagemaker import get_execution_role
from sagemaker.amazon.amazon_estimator import image_uris
import boto3
from sklearn.model_selection import train_test_split
s3 = boto3.resource('s3')
sagemaker_session = sagemaker.Session()
role = get_execution_role()
BUCKET = sagemaker_session.default_bucket()
# This is references the AWS managed XGBoost container
XGBOOST_IMAGE = image_uris.retrieve(region=boto3.Session().region_name, framework='xgboost', version='1.0-1')
DATA_PREFIX = 'XGBOOST_BOSTON_HOUSING'
MULTI_MODEL_ARTIFACTS = 'multi_model_artifacts'
TRAIN_INSTANCE_TYPE = 'ml.m4.xlarge'
ENDPOINT_INSTANCE_TYPE = 'ml.m4.xlarge'
ENDPOINT_NAME = 'mme-xgboost-housing'
MODEL_NAME = ENDPOINT_NAME
```
### Split a given dataset into train, validation, and test
The code below will generate 3 sets of data. 1 set to train, 1 set for validation and 1 for testing.
```
SEED = 7
SPLIT_RATIOS = [0.6, 0.3, 0.1]
def split_data(df):
# split data into train and test sets
seed = SEED
val_size = SPLIT_RATIOS[1]
test_size = SPLIT_RATIOS[2]
num_samples = df.shape[0]
X1 = df.values[:num_samples, 1:] # keep only the features, skip the target, all rows
Y1 = df.values[:num_samples, :1] # keep only the target, all rows
# Use split ratios to divide up into train/val/test
X_train, X_val, y_train, y_val = \
train_test_split(X1, Y1, test_size=(test_size + val_size), random_state=seed)
# Of the remaining non-training samples, give proper ratio to validation and to test
X_test, X_test, y_test, y_test = \
train_test_split(X_val, y_val, test_size=(test_size / (test_size + val_size)),
random_state=seed)
# reassemble the datasets with target in first column and features after that
_train = np.concatenate([y_train, X_train], axis=1)
_val = np.concatenate([y_val, X_val], axis=1)
_test = np.concatenate([y_test, X_test], axis=1)
return _train, _val, _test
```
### Launch a single training job for a given housing location
There is nothing specific to multi-model endpoints in terms of the models it will host. They are trained in the same way as all other SageMaker models. Here we are using the XGBoost estimator and not waiting for the job to complete.
```
def launch_training_job(location):
# clear out old versions of the data
s3_bucket = s3.Bucket(BUCKET)
full_input_prefix = f'{DATA_PREFIX}/model_prep/{location}'
s3_bucket.objects.filter(Prefix=full_input_prefix + '/').delete()
# upload the entire set of data for all three channels
local_folder = f'data/{location}'
inputs = sagemaker_session.upload_data(path=local_folder, key_prefix=full_input_prefix)
print(f'Training data uploaded: {inputs}')
_job = 'xgb-{}'.format(location.replace('_', '-'))
full_output_prefix = f'{DATA_PREFIX}/model_artifacts/{location}'
s3_output_path = f's3://{BUCKET}/{full_output_prefix}'
xgb = sagemaker.estimator.Estimator(XGBOOST_IMAGE, role,
instance_count=1, instance_type=TRAIN_INSTANCE_TYPE,
output_path=s3_output_path, base_job_name=_job,
sagemaker_session=sagemaker_session)
xgb.set_hyperparameters(max_depth=5, eta=0.2, gamma=4, min_child_weight=6, subsample=0.8, silent=0,
early_stopping_rounds=5, objective='reg:linear', num_round=25)
DISTRIBUTION_MODE = 'FullyReplicated'
train_input = sagemaker.inputs.TrainingInput(s3_data=inputs+'/train',
distribution=DISTRIBUTION_MODE, content_type='csv')
val_input = sagemaker.inputs.TrainingInput(s3_data=inputs+'/val',
distribution=DISTRIBUTION_MODE, content_type='csv')
remote_inputs = {'train': train_input, 'validation': val_input}
xgb.fit(remote_inputs, wait=False)
# Return the estimator object
return xgb
```
### Kick off a model training job for each housing location
```
def save_data_locally(location, train, val, test):
os.makedirs(f'data/{location}/train')
np.savetxt( f'data/{location}/train/{location}_train.csv', train, delimiter=',', fmt='%.2f')
os.makedirs(f'data/{location}/val')
np.savetxt(f'data/{location}/val/{location}_val.csv', val, delimiter=',', fmt='%.2f')
os.makedirs(f'data/{location}/test')
np.savetxt(f'data/{location}/test/{location}_test.csv', test, delimiter=',', fmt='%.2f')
import shutil
import os
estimators = []
shutil.rmtree('data', ignore_errors=True)
for loc in LOCATIONS[:PARALLEL_TRAINING_JOBS]:
_houses = gen_houses(NUM_HOUSES_PER_LOCATION)
_train, _val, _test = split_data(_houses)
save_data_locally(loc, _train, _val, _test)
estimator = launch_training_job(loc)
estimators.append(estimator)
print()
print(f'{len(estimators)} training jobs launched: {[x.latest_training_job.job_name for x in estimators]}')
```
### Wait for all model training to finish
```
def wait_for_training_job_to_complete(estimator):
job = estimator.latest_training_job.job_name
print(f'Waiting for job: {job}')
status = estimator.latest_training_job.describe()['TrainingJobStatus']
while status == 'InProgress':
time.sleep(45)
status = estimator.latest_training_job.describe()['TrainingJobStatus']
if status == 'InProgress':
print(f'{job} job status: {status}')
print(f'DONE. Status for {job} is {status}\n')
for est in estimators:
wait_for_training_job_to_complete(est)
```
# Create the multi-model endpoint with the SageMaker SDK
### Create a SageMaker Model from one of the Estimators
```
estimator = estimators[0]
model = estimator.create_model(role=role, image_uri=XGBOOST_IMAGE)
```
### Create the Amazon SageMaker MultiDataModel entity
We create the multi-model endpoint using the [```MultiDataModel```](https://sagemaker.readthedocs.io/en/stable/api/inference/multi_data_model.html) class.
You can create a MultiDataModel by directly passing in a `sagemaker.model.Model` object - in which case, the Endpoint will inherit information about the image to use, as well as any environmental variables, network isolation, etc., once the MultiDataModel is deployed.
In addition, a MultiDataModel can also be created without explictly passing a `sagemaker.model.Model` object. Please refer to the documentation for additional details.
```
from sagemaker.multidatamodel import MultiDataModel
# This is where our MME will read models from on S3.
model_data_prefix = f's3://{BUCKET}/{DATA_PREFIX}/{MULTI_MODEL_ARTIFACTS}/'
mme = MultiDataModel(name=MODEL_NAME,
model_data_prefix=model_data_prefix,
model=model,# passing our model - passes container image needed for the endpoint
sagemaker_session=sagemaker_session)
```
# Deploy the Multi Model Endpoint
You need to consider the appropriate instance type and number of instances for the projected prediction workload across all the models you plan to host behind your multi-model endpoint. The number and size of the individual models will also drive memory requirements.
```
predictor = mme.deploy(initial_instance_count=1,
instance_type=ENDPOINT_INSTANCE_TYPE,
endpoint_name=ENDPOINT_NAME)
```
### Our endpoint has launched! Let's look at what models are available to the endpoint!
By 'available', what we mean is, what model artfiacts are currently stored under the S3 prefix we defined when setting up the `MultiDataModel` above i.e. `model_data_prefix`.
Currently, since we have no artifacts (i.e. `tar.gz` files) stored under our defined S3 prefix, our endpoint, will have no models 'available' to serve inference requests.
We will demonstrate how to make models 'available' to our endpoint below.
```
# No models visible!
list(mme.list_models())
```
### Lets deploy model artifacts to be found by the endpoint
We are now using the `.add_model()` method of the `MultiDataModel` to copy over our model artifacts from where they were initially stored, during training, to where our endpoint will source model artifacts for inference requests.
`model_data_source` refers to the location of our model artifact (i.e. where it was deposited on S3 after training completed)
`model_data_path` is the **relative** path to the S3 prefix we specified above (i.e. `model_data_prefix`) where our endpoint will source models for inference requests.
Since this is a **relative** path, we can simply pass the name of what we wish to call the model artifact at inference time (i.e. `Chicago_IL.tar.gz`)
### Dynamically deploying additional models
It is also important to note, that we can always use the `.add_model()` method, as shown below, to dynamically deploy more models to the endpoint, to serve up inference requests as needed.
```
for est in estimators:
artifact_path = est.latest_training_job.describe()['ModelArtifacts']['S3ModelArtifacts']
model_name = artifact_path.split('/')[-4]+'.tar.gz'
# This is copying over the model artifact to the S3 location for the MME.
mme.add_model(model_data_source=artifact_path, model_data_path=model_name)
```
## We have added the 4 model artifacts from our training jobs!
We can see that the S3 prefix we specified when setting up `MultiDataModel` now has 4 model artifacts. As such, the endpoint can now serve up inference requests for these models.
```
list(mme.list_models())
```
# Get predictions from the endpoint
Recall that ```mme.deploy()``` returns a [RealTimePredictor](https://github.com/aws/sagemaker-python-sdk/blob/master/src/sagemaker/predictor.py#L35) that we saved in a variable called ```predictor```.
We will use ```predictor``` to submit requests to the endpoint.
XGBoost supports ```text/csv``` for the content type and accept type. For more information on XGBoost Input/Output Interface, please see [here.](https://docs.aws.amazon.com/sagemaker/latest/dg/xgboost.html#InputOutput-XGBoost)
Since the default RealTimePredictor does not have a serializer or deserializer set for requests, we will also set these.
This will allow us to submit a python list for inference, and get back a float response.
```
from sagemaker.serializers import CSVSerializer
from sagemaker.deserializers import JSONDeserializer
predictor.serializer = CSVSerializer()
predictor.deserializer = JSONDeserializer()
#predictor.content_type =predictor.content_type , removed as mentioned https://github.com/aws/sagemaker-python-sdk/blob/e8d16f8bc4c570f763f1129afc46ba3e0b98cdad/src/sagemaker/predictor.py#L82
#predictor.accept = "text/csv" # removed also : https://github.com/aws/sagemaker-python-sdk/blob/e8d16f8bc4c570f763f1129afc46ba3e0b98cdad/src/sagemaker/predictor.py#L83
```
### Invoking models on a multi-model endpoint
Notice the higher latencies on the first invocation of any given model. This is due to the time it takes SageMaker to download the model to the Endpoint instance and then load the model into the inference container. Subsequent invocations of the same model take advantage of the model already being loaded into the inference container.
```
start_time = time.time()
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Chicago_IL.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
start_time = time.time()
#Invoke endpoint
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Chicago_IL.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
start_time = time.time()
#Invoke endpoint
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Houston_TX.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
start_time = time.time()
#Invoke endpoint
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Houston_TX.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
```
### Updating a model
To update a model, you would follow the same approach as above and add it as a new model. For example, if you have retrained the `NewYork_NY.tar.gz` model and wanted to start invoking it, you would upload the updated model artifacts behind the S3 prefix with a new name such as `NewYork_NY_v2.tar.gz`, and then change the `target_model` field to invoke `NewYork_NY_v2.tar.gz` instead of `NewYork_NY.tar.gz`. You do not want to overwrite the model artifacts in Amazon S3, because the old version of the model might still be loaded in the containers or on the storage volume of the instances on the endpoint. Invocations to the new model could then invoke the old version of the model.
Alternatively, you could stop the endpoint and re-deploy a fresh set of models.
## Using Boto APIs to invoke the endpoint
While developing interactively within a Jupyter notebook, since `.deploy()` returns a `RealTimePredictor` it is a more seamless experience to start invoking your endpoint using the SageMaker SDK. You have more fine grained control over the serialization and deserialization protocols to shape your request and response payloads to/from the endpoint.
This is great for iterative experimentation within a notebook. Furthermore, should you have an application that has access to the SageMaker SDK, you can always import `RealTimePredictor` and attach it to an existing endpoint - this allows you to stick to using the high level SDK if preferable.
Additional documentation on `RealTimePredictor` can be found [here.](https://sagemaker.readthedocs.io/en/stable/api/inference/predictors.html?highlight=RealTimePredictor#sagemaker.predictor.RealTimePredictor)
The lower level Boto3 SDK may be preferable if you are attempting to invoke the endpoint as a part of a broader architecture.
Imagine an API gateway frontend that uses a Lambda Proxy in order to transform request payloads before hitting a SageMaker Endpoint - in this example, Lambda does not have access to the SageMaker Python SDK, and as such, Boto3 can still allow you to interact with your endpoint and serve inference requests.
Boto3 allows for quick injection of ML intelligence via SageMaker Endpoints into existing applications with minimal/no refactoring to existing code.
Boto3 will submit your requests as a binary payload, while still allowing you to supply your desired `Content-Type` and `Accept` headers with serialization being handled by the inference container in the SageMaker Endpoint.
Additional documentation on `.invoke_endpoint()` can be found [here.](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/sagemaker-runtime.html)
```
import boto3
import json
runtime_sm_client = boto3.client(service_name='sagemaker-runtime')
def predict_one_house_value(features, model_name):
print(f'Using model {model_name} to predict price of this house: {features}')
# Notice how we alter the list into a string as the payload
body = ','.join(map(str, features)) + '\n'
start_time = time.time()
response = runtime_sm_client.invoke_endpoint(
EndpointName=ENDPOINT_NAME,
ContentType='text/csv',
TargetModel=model_name,
Body=body)
predicted_value = json.loads(response['Body'].read())[0]
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value, int(duration * 1000)))
predict_one_house_value(gen_random_house()[1:], 'Chicago_IL.tar.gz')
```
## Clean up
Here, to be sure we are not billed for endpoints we are no longer using, we clean up.
```
predictor.delete_endpoint()
predictor.delete_model()
```
| true |
code
| 0.426262 | null | null | null | null |
|
```
import xarray as xr
import xroms
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import cmocean.cm as cmo
import cartopy
```
# How to select data
The [load_data](load_data.ipynb) notebook demonstrates how to load in data, but now how to select out parts of it?
### Load in data
More information at in [load_data notebook](load_data.ipynb)
```
loc = 'http://barataria.tamu.edu:8080/thredds/dodsC/forecast_latest/txla2_his_f_latest.nc'
chunks = {'ocean_time':1}
ds = xr.open_dataset(loc, chunks=chunks)
# set up grid
ds, grid = xroms.roms_dataset(ds)
```
## Select
### Slices by index or keyword
#### Surface layer slice
The surface in ROMS is given by the last index in the vertical dimension. The easiest way to access this is by indexing into `s_rho`. While normally it is better to access coordinates through keywords to be human-readable, it's not easy to tell what value of `s_rho` gives the surface. In this instance, it's easier to just go by index.
```
ds.salt.isel(s_rho=-1)
```
#### x/y index slice
For a curvilinear ROMS grid, selecting by the dimensions `xi_rho` or `eta_rho` (or for whichever is the relevant grid) is not very meaningful because they are given by index. Thus the following is possible to get a slice along the index, but it cannot be used to find a slice based on the lon/lat values.
```
ds.temp.sel(xi_rho=20)
```
#### Single time
Find the forecast model output available that is closest to now. Note that the `method` keyword argument is not necessary if the desired date/time is exactly a model output time.
```
now = pd.Timestamp.today()
ds.salt.isel(s_rho=-1).sel(ocean_time=now, method='nearest')
```
#### Range of time
```
ds.salt.sel(ocean_time=slice(now,now+pd.Timedelta('2 days')))
```
### Calculate slice
#### Cross-section along a longitude value
Because the example grid is curvilinear, a slice along a grid dimension is not the same as a slice along a longitude or latitude (or projected $x$/$y$) value. This needs to be calculated and we can use the `xisoslice` function to do this. The calculation is done lazily. We calculate only part of the slice, on the continental shelf. Renaming the subsetted dataset (below, as `dss`) is convenient because this variable can be used in place of `ds` for all related function calls to be consistent and only have to subset one time.
```
# want salinity along this constant value
lon0 = -91.5
# This is the array we want projected onto the longitude value.
# Note that we are requesting multiple times at once.
dss = ds.isel(ocean_time=slice(0,10), eta_rho=slice(50,-1))
# Projecting 3rd input onto constant value lon0 in iso_array ds.lon_rho
sl = xroms.xisoslice(dss.lon_rho, lon0, dss.salt, 'xi_rho')
sl
fig, axes = plt.subplots(1, 2, figsize=(15,6))
sl.isel(ocean_time=0).plot(ax=axes[0])
sl.isel(ocean_time=-1).plot(ax=axes[1])
```
Better plot: use coordinates and one colorbar to compare.
```
# calculate z values (s_rho)
slz = xroms.xisoslice(dss.lon_rho, lon0, dss.z_rho, 'xi_rho')
# calculate latitude values (eta_rho)
sllat = xroms.xisoslice(dss.lon_rho, lon0, dss.lat_rho, 'xi_rho')
# assign these as coords to be used in plot
sl = sl.assign_coords(z=slz, lat=sllat)
# points that should be masked
slmask = xroms.xisoslice(dss.lon_rho, lon0, dss.mask_rho, 'xi_rho')
# drop masked values
sl = sl.where(slmask==1, drop=True)
# find min and max of the slice itself (without values that should be masked)
vmin = sl.min().values
vmax = sl.max().values
fig, axes = plt.subplots(1, 2, figsize=(15,6), sharey=True)
sl.isel(ocean_time=0).plot(x='lat', y='z', ax=axes[0], vmin=vmin, vmax=vmax, add_colorbar=False)
mappable = sl.isel(ocean_time=-1).plot(x='lat', y='z', ax=axes[1], vmin=vmin, vmax=vmax, add_colorbar=False)
fig.colorbar(ax=axes, mappable=mappable, orientation='horizontal').set_label('salt')
```
Verify performance of isoslice by comparing slice at surface with planview surface plot.
```
vmin = dss.salt.min().values
vmax = dss.salt.max().values
fig, ax = plt.subplots(1, 1, figsize=(15,15))
ds.salt.isel(ocean_time=0, s_rho=-1).plot(ax=ax, x='lon_rho', y='lat_rho')
ax.scatter(lon0*np.ones_like(sl.lat[::10]), sl.lat[::10], c=sl.isel(ocean_time=0, s_rho=-1)[::10],
s=100, vmin=vmin, vmax=vmax, zorder=10, edgecolor='k')
```
#### Variable at constant z value
```
# want temperature along this constant depth value
z0 = -10
# This is the array we want projected
dss = ds.isel(ocean_time=0)
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
sl = xroms.xisoslice(dss.z_rho, z0, dss.temp, 's_rho')
sl
sl.plot(cmap=cmo.thermal, x='lon_rho', y='lat_rho')
```
#### Variable at constant z depth, in time
```
# want temperature along this constant depth value
z0 = -10
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
sl = xroms.xisoslice(ds.z_rho, z0, ds.temp, 's_rho')
sl
```
#### zeta at constant z depth, in time
... to verify that xisoslice does act in time across zeta.
```
# want temperature along this constant depth value
z0 = -10
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
zeta_s_rho = ds.zeta.expand_dims({'s_rho': ds.s_rho}).transpose('ocean_time','s_rho',...)
sl = xroms.xisoslice(ds.z_rho, z0, zeta_s_rho, 's_rho')
sl.sel(eta_rho=30,xi_rho=20).plot()
```
#### Depth of isohaline surface
Calculate the depth of a specific isohaline.
Note that in this case there are a few wonky values, so we should filter them out or control the vmin/vmax values on the plot.
```
# want the depth of this constant salinity value
S0 = 33
# This is the array we want projected
dss = ds.isel(ocean_time=0)
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
sl = xroms.xisoslice(dss.salt, S0, dss.z_rho, 's_rho')
sl.plot(cmap=cmo.deep, x='lon_rho', y='lat_rho', vmin=-20, vmax=0, figsize=(10, 10))
```
### Select region
Select a boxed region by min/max lon and lat values.
```
# want model output only within the box defined by these lat/lon values
lon = np.array([-97, -96])
lat = np.array([28, 29])
# this condition defines the region of interest
box = ((lon[0] < ds.lon_rho) & (ds.lon_rho < lon[1]) & (lat[0] < ds.lat_rho) & (ds.lat_rho < lat[1])).compute()
```
Plot the model output in the box at the surface
```
dss = ds.where(box).salt.isel(s_rho=-1, ocean_time=0)
dss.plot(x='lon_rho', y='lat_rho')
```
Can calculate a metric within the box:
```
dss.mean().values
```
### Find nearest model output in two dimensions
This matters for a curvilinear grid.
Can't use `sel` because it will only search in one coordinate for the nearest value and the coordinates are indices which are not necessarily geographic distance. Instead need to use a search for distance and use that for the `where` condition from the previous example.
Find the model output at the grid node nearest the point (lon0, lat0). You can create the projection to use for the distance calculation in `sel2d` and input it into the function, or you can let it choose a default for you.
```
lon0, lat0 = -96, 27
dl = 0.05
proj = cartopy.crs.LambertConformal(central_longitude=-98, central_latitude=30)
dssub = xroms.sel2d(ds, lon0, lat0, proj)
```
Or, if you instead want the indices of the nearest grid node returned, you can call `argsel2d`:
```
ix, iy = xroms.argsel2d(ds, lon0, lat0, proj)
```
Check this function, just to be sure:
```
box = (ds.lon_rho>lon0-dl) & (ds.lon_rho<lon0+dl) & (ds.lat_rho>lat0-dl) & (ds.lat_rho<lat0+dl)
dss = ds.where(box).salt.isel(ocean_time=0, s_rho=-1)
vmin = dss.min().values
vmax = dss.max().values
dss.plot(x='lon_rho', y='lat_rho')
plt.scatter(lon0, lat0, c=dssub.salt.isel(s_rho=-1, ocean_time=0), s=200, edgecolor='k', vmin=vmin, vmax=vmax)
plt.xlim(lon0-dl,lon0+dl)
plt.ylim(lat0-dl, lat0+dl)
```
Note that the `sel2d` function returned a time series since that was input, and it worked fine. Getting the numbers take time.
```
dssub.salt.isel(s_rho=-1, ocean_time=slice(0,5)).plot()
```
| true |
code
| 0.608012 | null | null | null | null |
|
This notebook was prepared by [Donne Martin](https://github.com/donnemartin). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# Solution Notebook
## Problem: Given two 16 bit numbers, n and m, and two indices i, j, insert m into n such that m starts at bit j and ends at bit i.
* [Constraints](#Constraints)
* [Test Cases](#Test-Cases)
* [Algorithm](#Algorithm)
* [Code](#Code)
* [Unit Test](#Unit-Test)
## Constraints
* Can we assume j > i?
* Yes
* Can we assume i through j have enough space for m?
* Yes
* Can we assume the inputs are valid?
* No
* Can we assume this fits memory?
* Yes
## Test Cases
* None as an input -> Exception
* Negative index for i or j -> Exception
* General case
<pre>
i = 2, j = 6
j i
n = 0000 0100 0011 1101
m = 0000 0000 0001 0011
result = 0000 0100 0100 1101
</pre>
## Algorithm
<pre>
j i
n = 0000 0100 0011 1101
m = 0000 0000 0001 0011
lmask = 1111 1111 1111 1111 -1
lmask = 1111 1111 1000 0000 -1 << (j + 1)
rmask = 0000 0000 0000 0001 1
rmask = 0000 0000 0000 0100 1 << i
rmask = 0000 0000 0000 0011 (1 << i) -1
mask = 1111 1111 1000 0011 lmask | rmask
n = 0000 0100 0011 1101
mask = 1111 1111 1000 0011 n & mask
--------------------------------------------------
n2 = 0000 0100 0000 0001
n2 = 0000 0100 0000 0001
mask2 = 0000 0000 0100 1100 m << i
--------------------------------------------------
result = 0000 0100 0100 1101 n2 | mask2
</pre>
Complexity:
* Time: O(b), where b is the number of bits
* Space: O(b), where b is the number of bits
## Code
```
class Bits(object):
def insert_m_into_n(self, m, n, i, j):
if None in (m, n, i, j):
raise TypeError('Argument cannot be None')
if i < 0 or j < 0:
raise ValueError('Index cannot be negative')
left_mask = -1 << (j + 1)
right_mask = (1 << i) - 1
n_mask = left_mask | right_mask
# Clear bits from j to i, inclusive
n_cleared = n & n_mask
# Shift m into place before inserting it into n
m_mask = m << i
return n_cleared | m_mask
```
## Unit Test
```
%%writefile test_insert_m_into_n.py
import unittest
class TestBit(unittest.TestCase):
def test_insert_m_into_n(self):
n = int('0000010000111101', base=2)
m = int('0000000000010011', base=2)
expected = int('0000010001001101', base=2)
bits = Bits()
self.assertEqual(bits.insert_m_into_n(m, n, i=2, j=6), expected)
print('Success: test_insert_m_into_n')
def main():
test = TestBit()
test.test_insert_m_into_n()
if __name__ == '__main__':
main()
%run -i test_insert_m_into_n.py
```
| true |
code
| 0.574992 | null | null | null | null |
|
#### SageMaker Pipelines Tuning Step
This notebook illustrates how a Hyperparameter Tuning Job can be run as a step in a SageMaker Pipeline.
The steps in this pipeline include -
* Preprocessing the abalone dataset
* Running a Hyperparameter Tuning job
* Creating the 2 best models
* Evaluating the performance of the top performing model of the HPO step
* Registering the top model in the model registry using a conditional step based on evaluation metrics
```
import sys
!{sys.executable} -m pip install "sagemaker>=2.48.0"
import os
import boto3
import sagemaker
from sagemaker.estimator import Estimator
from sagemaker.inputs import TrainingInput
from sagemaker.processing import (
ProcessingInput,
ProcessingOutput,
Processor,
ScriptProcessor,
)
from sagemaker import Model
from sagemaker.xgboost import XGBoostPredictor
from sagemaker.sklearn.processing import SKLearnProcessor
from sagemaker.model_metrics import (
MetricsSource,
ModelMetrics,
)
from sagemaker.workflow.parameters import (
ParameterInteger,
ParameterString,
)
from sagemaker.workflow.pipeline import Pipeline
from sagemaker.workflow.properties import PropertyFile
from sagemaker.workflow.steps import (
ProcessingStep,
CacheConfig,
TuningStep,
)
from sagemaker.workflow.step_collections import RegisterModel, CreateModelStep
from sagemaker.workflow.conditions import ConditionLessThanOrEqualTo
from sagemaker.workflow.condition_step import ConditionStep
from sagemaker.workflow.functions import Join, JsonGet
from sagemaker.workflow.execution_variables import ExecutionVariables
from sagemaker.tuner import (
ContinuousParameter,
HyperparameterTuner,
WarmStartConfig,
WarmStartTypes,
)
# Create the SageMaker Session
region = sagemaker.Session().boto_region_name
sm_client = boto3.client("sagemaker")
boto_session = boto3.Session(region_name=region)
sagemaker_session = sagemaker.session.Session(boto_session=boto_session, sagemaker_client=sm_client)
# Define variables and parameters needed for the Pipeline steps
role = sagemaker.get_execution_role()
default_bucket = sagemaker_session.default_bucket()
base_job_prefix = "tuning-step-example"
model_package_group_name = "tuning-job-model-packages"
processing_instance_count = ParameterInteger(name="ProcessingInstanceCount", default_value=1)
processing_instance_type = ParameterString(
name="ProcessingInstanceType", default_value="ml.m5.xlarge"
)
training_instance_type = ParameterString(name="TrainingInstanceType", default_value="ml.m5.xlarge")
model_approval_status = ParameterString(
name="ModelApprovalStatus", default_value="PendingManualApproval"
)
input_data = ParameterString(
name="InputDataUrl",
default_value=f"s3://sagemaker-servicecatalog-seedcode-{region}/dataset/abalone-dataset.csv",
)
model_approval_status = ParameterString(
name="ModelApprovalStatus", default_value="PendingManualApproval"
)
# Cache Pipeline steps to reduce execution time on subsequent executions
cache_config = CacheConfig(enable_caching=True, expire_after="30d")
```
#### Data Preparation
An SKLearn processor is used to prepare the dataset for the Hyperparameter Tuning job. Using the script `preprocess.py`, the dataset is featurized and split into train, test, and validation datasets.
The output of this step is used as the input to the TuningStep
```
%%writefile preprocess.py
"""Feature engineers the abalone dataset."""
import argparse
import logging
import os
import pathlib
import requests
import tempfile
import boto3
import numpy as np
import pandas as pd
from sklearn.compose import ColumnTransformer
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OneHotEncoder
logger = logging.getLogger()
logger.setLevel(logging.INFO)
logger.addHandler(logging.StreamHandler())
# Since we get a headerless CSV file we specify the column names here.
feature_columns_names = [
"sex",
"length",
"diameter",
"height",
"whole_weight",
"shucked_weight",
"viscera_weight",
"shell_weight",
]
label_column = "rings"
feature_columns_dtype = {
"sex": str,
"length": np.float64,
"diameter": np.float64,
"height": np.float64,
"whole_weight": np.float64,
"shucked_weight": np.float64,
"viscera_weight": np.float64,
"shell_weight": np.float64,
}
label_column_dtype = {"rings": np.float64}
def merge_two_dicts(x, y):
"""Merges two dicts, returning a new copy."""
z = x.copy()
z.update(y)
return z
if __name__ == "__main__":
logger.debug("Starting preprocessing.")
parser = argparse.ArgumentParser()
parser.add_argument("--input-data", type=str, required=True)
args = parser.parse_args()
base_dir = "/opt/ml/processing"
pathlib.Path(f"{base_dir}/data").mkdir(parents=True, exist_ok=True)
input_data = args.input_data
bucket = input_data.split("/")[2]
key = "/".join(input_data.split("/")[3:])
logger.info("Downloading data from bucket: %s, key: %s", bucket, key)
fn = f"{base_dir}/data/abalone-dataset.csv"
s3 = boto3.resource("s3")
s3.Bucket(bucket).download_file(key, fn)
logger.debug("Reading downloaded data.")
df = pd.read_csv(
fn,
header=None,
names=feature_columns_names + [label_column],
dtype=merge_two_dicts(feature_columns_dtype, label_column_dtype),
)
os.unlink(fn)
logger.debug("Defining transformers.")
numeric_features = list(feature_columns_names)
numeric_features.remove("sex")
numeric_transformer = Pipeline(
steps=[
("imputer", SimpleImputer(strategy="median")),
("scaler", StandardScaler()),
]
)
categorical_features = ["sex"]
categorical_transformer = Pipeline(
steps=[
("imputer", SimpleImputer(strategy="constant", fill_value="missing")),
("onehot", OneHotEncoder(handle_unknown="ignore")),
]
)
preprocess = ColumnTransformer(
transformers=[
("num", numeric_transformer, numeric_features),
("cat", categorical_transformer, categorical_features),
]
)
logger.info("Applying transforms.")
y = df.pop("rings")
X_pre = preprocess.fit_transform(df)
y_pre = y.to_numpy().reshape(len(y), 1)
X = np.concatenate((y_pre, X_pre), axis=1)
logger.info("Splitting %d rows of data into train, validation, test datasets.", len(X))
np.random.shuffle(X)
train, validation, test = np.split(X, [int(0.7 * len(X)), int(0.85 * len(X))])
logger.info("Writing out datasets to %s.", base_dir)
pd.DataFrame(train).to_csv(f"{base_dir}/train/train.csv", header=False, index=False)
pd.DataFrame(validation).to_csv(
f"{base_dir}/validation/validation.csv", header=False, index=False
)
pd.DataFrame(test).to_csv(f"{base_dir}/test/test.csv", header=False, index=False)
# Process the training data step using a python script.
# Split the training data set into train, test, and validation datasets
# When defining the ProcessingOutput destination as a dynamic value using the
# Pipeline Execution ID, caching will not be in effect as each time the step runs,
# the step definition changes resulting in new execution. If caching is required,
# the ProcessingOutput definition should be status
sklearn_processor = SKLearnProcessor(
framework_version="0.23-1",
instance_type=processing_instance_type,
instance_count=processing_instance_count,
base_job_name=f"{base_job_prefix}/sklearn-abalone-preprocess",
sagemaker_session=sagemaker_session,
role=role,
)
step_process = ProcessingStep(
name="PreprocessAbaloneDataForHPO",
processor=sklearn_processor,
outputs=[
ProcessingOutput(
output_name="train",
source="/opt/ml/processing/train",
destination=Join(
on="/",
values=[
"s3:/",
default_bucket,
base_job_prefix,
ExecutionVariables.PIPELINE_EXECUTION_ID,
"PreprocessAbaloneDataForHPO",
],
),
),
ProcessingOutput(
output_name="validation",
source="/opt/ml/processing/validation",
destination=Join(
on="/",
values=[
"s3:/",
default_bucket,
base_job_prefix,
ExecutionVariables.PIPELINE_EXECUTION_ID,
"PreprocessAbaloneDataForHPO",
],
),
),
ProcessingOutput(
output_name="test",
source="/opt/ml/processing/test",
destination=Join(
on="/",
values=[
"s3:/",
default_bucket,
base_job_prefix,
ExecutionVariables.PIPELINE_EXECUTION_ID,
"PreprocessAbaloneDataForHPO",
],
),
),
],
code="preprocess.py",
job_arguments=["--input-data", input_data],
)
```
#### Hyperparameter Tuning
Amazon SageMaker automatic model tuning, also known as hyperparameter tuning, finds the best version of a model by running many training jobs on your dataset using the algorithm and ranges of hyperparameters that you specify. It then chooses the hyperparameter values that result in a model that performs the best, as measured by a metric that you choose.
[Valid metrics](https://github.com/dmlc/xgboost/blob/master/doc/parameter.rst#learning-task-parameters) for XGBoost Tuning Job
You can learn more about [Hyperparameter Tuning](https://docs.aws.amazon.com/sagemaker/latest/dg/automatic-model-tuning-how-it-works.html) in the SageMaker docs.
```
# Define the output path for the model artifacts from the Hyperparameter Tuning Job
model_path = f"s3://{default_bucket}/{base_job_prefix}/AbaloneTrain"
image_uri = sagemaker.image_uris.retrieve(
framework="xgboost",
region=region,
version="1.0-1",
py_version="py3",
instance_type=training_instance_type,
)
xgb_train = Estimator(
image_uri=image_uri,
instance_type=training_instance_type,
instance_count=1,
output_path=model_path,
base_job_name=f"{base_job_prefix}/abalone-train",
sagemaker_session=sagemaker_session,
role=role,
)
xgb_train.set_hyperparameters(
eval_metric="rmse",
objective="reg:squarederror", # Define the object metric for the training job
num_round=50,
max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.7,
silent=0,
)
objective_metric_name = "validation:rmse"
hyperparameter_ranges = {
"alpha": ContinuousParameter(0.01, 10, scaling_type="Logarithmic"),
"lambda": ContinuousParameter(0.01, 10, scaling_type="Logarithmic"),
}
tuner_log = HyperparameterTuner(
xgb_train,
objective_metric_name,
hyperparameter_ranges,
max_jobs=3,
max_parallel_jobs=3,
strategy="Random",
objective_type="Minimize",
)
step_tuning = TuningStep(
name="HPTuning",
tuner=tuner_log,
inputs={
"train": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs["train"].S3Output.S3Uri,
content_type="text/csv",
),
"validation": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs[
"validation"
].S3Output.S3Uri,
content_type="text/csv",
),
},
cache_config=cache_config,
)
```
#### Warm start for Hyperparameter Tuning Job
Use warm start to start a hyperparameter tuning job using one or more previous tuning jobs as a starting point. The results of previous tuning jobs are used to inform which combinations of hyperparameters to search over in the new tuning job. Hyperparameter tuning uses either Bayesian or random search to choose combinations of hyperparameter values from ranges that you specify.
Find more information on [Warm Starts](https://docs.aws.amazon.com/sagemaker/latest/dg/automatic-model-tuning-warm-start.html) in the SageMaker docs.
In a training pipeline, the parent tuning job name can be provided as a pipeline parameter if there is an already complete Hyperparameter tuning job that should be used as the basis for the warm start.
This step is left out of the pipeline steps in this notebook. It can be added into the steps while defining the pipeline and the appropriate parent tuning job should be specified.
```
# This is an example to illustrate how a the name of the tuning job from the previous step can be used as the parent tuning job, in practice,
# it is unlikely to have the parent job run before the warm start job on each run. Typically the first tuning job would run and the pipeline
# would be altered to use tuning jobs with a warm start using the first job as the parent job.
parent_tuning_job_name = (
step_tuning.properties.HyperParameterTuningJobName
) # Use the parent tuning job specific to the use case
warm_start_config = WarmStartConfig(
WarmStartTypes.IDENTICAL_DATA_AND_ALGORITHM, parents={parent_tuning_job_name}
)
tuner_log_warm_start = HyperparameterTuner(
xgb_train,
objective_metric_name,
hyperparameter_ranges,
max_jobs=3,
max_parallel_jobs=3,
strategy="Random",
objective_type="Minimize",
warm_start_config=warm_start_config,
)
step_tuning_warm_start = TuningStep(
name="HPTuningWarmStart",
tuner=tuner_log_warm_start,
inputs={
"train": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs["train"].S3Output.S3Uri,
content_type="text/csv",
),
"validation": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs[
"validation"
].S3Output.S3Uri,
content_type="text/csv",
),
},
cache_config=cache_config,
)
```
#### Creating and Registering the best models
After successfully completing the Hyperparameter Tuning job. You can either create SageMaker models from the model artifacts created by the training jobs from the TuningStep or register the models into the Model Registry.
When using the model Registry, if you register multiple models from the TuningStep, they will be registered as versions within the same model package group unless unique model package groups are specified for each RegisterModelStep that is part of the pipeline.
In this example, the two best models from the TuningStep are added to the same model package group in the Model Registry as v0 and v1.
You use the `get_top_model_s3_uri` method of the TuningStep class to get the model artifact from one of the top performing model versions
```
# Creating 2 SageMaker Models
model_bucket_key = f"{default_bucket}/{base_job_prefix}/AbaloneTrain"
best_model = Model(
image_uri=image_uri,
model_data=step_tuning.get_top_model_s3_uri(top_k=0, s3_bucket=model_bucket_key),
sagemaker_session=sagemaker_session,
role=role,
predictor_cls=XGBoostPredictor,
)
step_create_first = CreateModelStep(
name="CreateTopModel",
model=best_model,
inputs=sagemaker.inputs.CreateModelInput(instance_type="ml.m4.large"),
)
second_best_model = Model(
image_uri=image_uri,
model_data=step_tuning.get_top_model_s3_uri(top_k=1, s3_bucket=model_bucket_key),
sagemaker_session=sagemaker_session,
role=role,
predictor_cls=XGBoostPredictor,
)
step_create_second = CreateModelStep(
name="CreateSecondBestModel",
model=second_best_model,
inputs=sagemaker.inputs.CreateModelInput(instance_type="ml.m4.large"),
)
```
#### Evaluate the top model
Use a processing job to evaluate the top model from the tuning step
```
%%writefile evaluate.py
"""Evaluation script for measuring mean squared error."""
import json
import logging
import pathlib
import pickle
import tarfile
import numpy as np
import pandas as pd
import xgboost
from sklearn.metrics import mean_squared_error
logger = logging.getLogger()
logger.setLevel(logging.INFO)
logger.addHandler(logging.StreamHandler())
if __name__ == "__main__":
logger.debug("Starting evaluation.")
model_path = "/opt/ml/processing/model/model.tar.gz"
with tarfile.open(model_path) as tar:
tar.extractall(path=".")
logger.debug("Loading xgboost model.")
model = pickle.load(open("xgboost-model", "rb"))
logger.debug("Reading test data.")
test_path = "/opt/ml/processing/test/test.csv"
df = pd.read_csv(test_path, header=None)
logger.debug("Reading test data.")
y_test = df.iloc[:, 0].to_numpy()
df.drop(df.columns[0], axis=1, inplace=True)
X_test = xgboost.DMatrix(df.values)
logger.info("Performing predictions against test data.")
predictions = model.predict(X_test)
logger.debug("Calculating mean squared error.")
mse = mean_squared_error(y_test, predictions)
std = np.std(y_test - predictions)
report_dict = {
"regression_metrics": {
"mse": {"value": mse, "standard_deviation": std},
},
}
output_dir = "/opt/ml/processing/evaluation"
pathlib.Path(output_dir).mkdir(parents=True, exist_ok=True)
logger.info("Writing out evaluation report with mse: %f", mse)
evaluation_path = f"{output_dir}/evaluation.json"
with open(evaluation_path, "w") as f:
f.write(json.dumps(report_dict))
# A ProcessingStep is used to evaluate the performance of a selected model from the HPO step. In this case, the top performing model
# is evaluated. Based on the results of the evaluation, the model is registered into the Model Registry using a ConditionStep.
script_eval = ScriptProcessor(
image_uri=image_uri,
command=["python3"],
instance_type=processing_instance_type,
instance_count=1,
base_job_name=f"{base_job_prefix}/script-tuning-step-eval",
sagemaker_session=sagemaker_session,
role=role,
)
evaluation_report = PropertyFile(
name="BestTuningModelEvaluationReport",
output_name="evaluation",
path="evaluation.json",
)
# This can be extended to evaluate multiple models from the HPO step
step_eval = ProcessingStep(
name="EvaluateTopModel",
processor=script_eval,
inputs=[
ProcessingInput(
source=step_tuning.get_top_model_s3_uri(top_k=0, s3_bucket=model_bucket_key),
destination="/opt/ml/processing/model",
),
ProcessingInput(
source=step_process.properties.ProcessingOutputConfig.Outputs["test"].S3Output.S3Uri,
destination="/opt/ml/processing/test",
),
],
outputs=[
ProcessingOutput(output_name="evaluation", source="/opt/ml/processing/evaluation"),
],
code="evaluate.py",
property_files=[evaluation_report],
cache_config=cache_config,
)
model_metrics = ModelMetrics(
model_statistics=MetricsSource(
s3_uri="{}/evaluation.json".format(
step_eval.arguments["ProcessingOutputConfig"]["Outputs"][0]["S3Output"]["S3Uri"]
),
content_type="application/json",
)
)
# Register the model in the Model Registry
# Multiple models can be registered into the Model Registry using multiple RegisterModel steps. These models can either be added to the
# same model package group as different versions within the group or the models can be added to different model package groups.
step_register_best = RegisterModel(
name="RegisterBestAbaloneModel",
estimator=xgb_train,
model_data=step_tuning.get_top_model_s3_uri(top_k=0, s3_bucket=model_bucket_key),
content_types=["text/csv"],
response_types=["text/csv"],
inference_instances=["ml.t2.medium", "ml.m5.large"],
transform_instances=["ml.m5.large"],
model_package_group_name=model_package_group_name,
approval_status=model_approval_status,
)
# condition step for evaluating model quality and branching execution
cond_lte = ConditionLessThanOrEqualTo(
left=JsonGet(
step_name=step_eval.name,
property_file=evaluation_report,
json_path="regression_metrics.mse.value",
),
right=6.0,
)
step_cond = ConditionStep(
name="CheckMSEAbaloneEvaluation",
conditions=[cond_lte],
if_steps=[step_register_best],
else_steps=[],
)
pipeline = Pipeline(
name="tuning-step-pipeline",
parameters=[
processing_instance_type,
processing_instance_count,
training_instance_type,
input_data,
model_approval_status,
],
steps=[
step_process,
step_tuning,
step_create_first,
step_create_second,
step_eval,
step_cond,
],
sagemaker_session=sagemaker_session,
)
```
#### Execute the Pipeline
```
import json
definition = json.loads(pipeline.definition())
definition
pipeline.upsert(role_arn=role)
pipeline.start()
```
#### Cleaning up resources
Users are responsible for cleaning up resources created when running this notebook. Specify the ModelName, ModelPackageName, and ModelPackageGroupName that need to be deleted. The model names are generated by the CreateModel step of the Pipeline and the property values are available only in the Pipeline context. To delete the models created by this pipeline, navigate to the Model Registry and Console to find the models to delete.
```
# # Create a SageMaker client
# sm_client = boto3.client("sagemaker")
# # Delete SageMaker Models
# sm_client.delete_model(ModelName="...")
# # Delete Model Packages
# sm_client.delete_model_package(ModelPackageName="...")
# # Delete the Model Package Group
# sm_client.delete_model_package_group(ModelPackageGroupName="...")
# # Delete the Pipeline
# sm_client.delete_pipeline(PipelineName="tuning-step-pipeline")
```
| true |
code
| 0.588889 | null | null | null | null |
|
# Ensembles
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
sns.set_theme()
rng = np.random.default_rng(42)
x = rng.uniform(size=(150, 1), low=0.0, high=10.0)
x_train, x_test = x[:100], x[100:]
x_plot = np.linspace(0, 10, 500).reshape(-1, 1)
def lin(x):
return 0.85 * x - 1.5
def fun(x):
return 2 * np.sin(x) + 0.1 * x ** 2 - 2
def randomize(fun, x, scale=0.5):
return fun(x) + rng.normal(size=x.shape, scale=scale)
def evaluate_non_random_regressor(reg_type, f_y, *args, **kwargs):
reg = reg_type(*args, **kwargs)
y_train = f_y(x_train).reshape(-1)
y_test = f_y(x_test).reshape(-1)
reg.fit(x_train, y_train)
y_pred = reg.predict(x_test)
x_plot = np.linspace(0, 10, 500).reshape(-1, 1)
fig, ax = plt.subplots(figsize=(20, 8))
sns.lineplot(x=x_plot[:, 0], y=reg.predict(x_plot), ax=ax)
sns.lineplot(x=x_plot[:, 0], y=f_y(x_plot[:, 0]), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_train, ax=ax)
plt.show()
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print(
"\nNo randomness: " f"MAE = {mae:.2f}, MSE = {mse:.2f}, RMSE = {rmse:.2f}"
)
return reg
def plot_graphs(f_y, reg, reg_rand, reg_chaos, y_train, y_rand_train, y_chaos_train):
x_plot = np.linspace(0, 10, 500).reshape(-1, 1)
fig, ax = plt.subplots(figsize=(20, 12))
sns.lineplot(x=x_plot[:, 0], y=reg.predict(x_plot), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_train, ax=ax)
sns.lineplot(x=x_plot[:, 0], y=reg_rand.predict(x_plot), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_rand_train, ax=ax)
sns.lineplot(x=x_plot[:, 0], y=reg_chaos.predict(x_plot), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_chaos_train, ax=ax)
sns.lineplot(x=x_plot[:, 0], y=f_y(x_plot[:, 0]), ax=ax)
plt.show()
def print_evaluation(y_test, y_pred, y_rand_test, y_rand_pred, y_chaos_test, y_chaos_pred):
mae = mean_absolute_error(y_test, y_pred)
mae_rand = mean_absolute_error(y_rand_test, y_rand_pred)
mae_chaos = mean_absolute_error(y_chaos_test, y_chaos_pred)
mse = mean_squared_error(y_test, y_pred)
mse_rand = mean_squared_error(y_rand_test, y_rand_pred)
mse_chaos = mean_squared_error(y_chaos_test, y_chaos_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
rmse_rand = np.sqrt(mean_squared_error(y_rand_test, y_rand_pred))
rmse_chaos = np.sqrt(mean_squared_error(y_chaos_test, y_chaos_pred))
print(
"\nNo randomness: " f"MAE = {mae:.2f}, MSE = {mse:.2f}, RMSE = {rmse:.2f}"
)
print(
"Some randomness: "
f"MAE = {mae_rand:.2f}, MSE = {mse_rand:.2f}, RMSE = {rmse_rand:.2f}"
)
print(
"Lots of randomness: "
f"MAE = {mae_chaos:.2f}, MSE = {mse_chaos:.2f}, RMSE = {rmse_chaos:.2f}"
)
def evaluate_regressor(reg_type, f_y, *args, **kwargs):
reg = reg_type(*args, **kwargs)
reg_rand = reg_type(*args, **kwargs)
reg_chaos = reg_type(*args, **kwargs)
y_train = f_y(x_train).reshape(-1)
y_test = f_y(x_test).reshape(-1)
y_pred = reg.fit(x_train, y_train).predict(x_test)
y_rand_train = randomize(f_y, x_train).reshape(-1)
y_rand_test = randomize(f_y, x_test).reshape(-1)
y_rand_pred = reg_rand.fit(x_train, y_rand_train).predict(x_test)
y_chaos_train = randomize(f_y, x_train, 1.5).reshape(-1)
y_chaos_test = randomize(f_y, x_test, 1.5).reshape(-1)
y_chaos_pred = reg_chaos.fit(x_train, y_chaos_train).predict(x_test)
plot_graphs(f_y, reg, reg_rand, reg_chaos, y_train, y_rand_train, y_chaos_train)
print_evaluation(y_test, y_pred, y_rand_test, y_rand_pred, y_chaos_test, y_chaos_pred)
```
# Ensembles, Random Forests, Gradient Boosted Trees
## Ensemble Methods
Idea: combine several estimators to improve their overal performance.
- Averaging methods:
- Independent estimators, average predictions
- Reduces variance (overfitting)
- Bagging, random forests
- Boosting methods:
- Train estimators sequentially
- Each estimator is trained to reduce the bias of its (combined) predecessors
### Bagging
- Averaging method: build several estimators of the same type, average their results
- Needs some way to introduce differences between estimators
- Otherwise variance is not reduced
- Train on random subsets of the training data
- Reduce overfitting
- Work best with strong estimators (e.g., decision trees with (moderately) large depth)
### Random Forests
- Bagging classifier/regressor using decision trees
- For each tree in the forest:
- Subset of training data
- Subset of features
- Often significant reduction in variance (overfitting)
- Sometimes increase in bias
```
from sklearn.ensemble import RandomForestRegressor
evaluate_non_random_regressor(RandomForestRegressor, lin, random_state=42);
evaluate_non_random_regressor(RandomForestRegressor, fun, random_state=42);
evaluate_non_random_regressor(
RandomForestRegressor, fun, n_estimators=25, criterion="absolute_error", random_state=42
);
evaluate_regressor(RandomForestRegressor, lin, random_state=42);
evaluate_regressor(
RandomForestRegressor, lin, n_estimators=500, max_depth=3, random_state=42
)
evaluate_regressor(
RandomForestRegressor, lin, n_estimators=500, min_samples_leaf=6, random_state=42
)
evaluate_regressor(RandomForestRegressor, fun, random_state=42)
evaluate_regressor(
RandomForestRegressor,
fun,
n_estimators=1000,
min_samples_leaf=6,
random_state=43,
n_jobs=-1,
)
```
## Gradient Boosted Trees
- Boosting method for both regression and classification
- Requires differentiable loss function
```
from sklearn.ensemble import GradientBoostingRegressor
evaluate_non_random_regressor(GradientBoostingRegressor, lin);
evaluate_non_random_regressor(GradientBoostingRegressor, fun);
evaluate_regressor(GradientBoostingRegressor, lin);
evaluate_regressor(GradientBoostingRegressor, lin, n_estimators=200, learning_rate=0.05, loss="absolute_error");
evaluate_regressor(GradientBoostingRegressor, lin, n_estimators=500, learning_rate=0.01,
loss="absolute_error", subsample=0.1, random_state=46);
evaluate_regressor(GradientBoostingRegressor, fun, n_estimators=500, learning_rate=0.01,
loss="absolute_error", subsample=0.1, random_state=44);
```
### Multiple Features
```
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
np.set_printoptions(precision=1)
x, y, coef = make_regression(n_samples=250, n_features=4, n_informative=1, coef=True, random_state=42)
x.shape, y.shape, coef
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(20, 12))
for i, ax in enumerate(axs.reshape(-1)):
sns.scatterplot(x=x[:, i], y=y, ax=ax)
x, y, coef = make_regression(n_samples=250, n_features=20, n_informative=10, coef=True, random_state=42)
x.shape, y.shape, coef
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4)
x_train.shape, x_test.shape, y_train.shape, y_test.shape
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(20, 12))
for i in range(2):
sns.scatterplot(x=x[:, i], y=y, ax=axs[0, i]);
for i in range(2):
sns.scatterplot(x=x[:, i + 6], y=y, ax=axs[1, i]);
lr_clf = LinearRegression()
lr_clf.fit(x_train, y_train)
y_lr_pred = lr_clf.predict(x_test)
mean_absolute_error(y_test, y_lr_pred), mean_squared_error(y_test, y_lr_pred)
lr_clf.coef_.astype(np.int32), coef.astype(np.int32)
dt_clf = DecisionTreeRegressor()
dt_clf.fit(x_train, y_train)
y_dt_pred = dt_clf.predict(x_test)
mean_absolute_error(y_test, y_dt_pred), mean_squared_error(y_test, y_dt_pred)
rf_clf = RandomForestRegressor()
rf_clf.fit(x_train, y_train)
y_rf_pred = rf_clf.predict(x_test)
mean_absolute_error(y_test, y_rf_pred), mean_squared_error(y_test, y_rf_pred)
gb_clf = GradientBoostingRegressor()
gb_clf.fit(x_train, y_train)
y_gb_pred = gb_clf.predict(x_test)
mean_absolute_error(y_test, y_gb_pred), mean_squared_error(y_test, y_gb_pred)
x, y, coef = make_regression(n_samples=250, n_features=20, n_informative=10, noise=100.0, coef=True, random_state=42)
x.shape, y.shape, coef
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4)
x_train.shape, x_test.shape, y_train.shape, y_test.shape
lr_clf = LinearRegression()
lr_clf.fit(x_train, y_train)
y_lr_pred = lr_clf.predict(x_test)
mean_absolute_error(y_test, y_lr_pred), mean_squared_error(y_test, y_lr_pred)
dt_clf = DecisionTreeRegressor()
dt_clf.fit(x_train, y_train)
y_dt_pred = dt_clf.predict(x_test)
mean_absolute_error(y_test, y_dt_pred), mean_squared_error(y_test, y_dt_pred)
rf_clf = RandomForestRegressor()
rf_clf.fit(x_train, y_train)
y_rf_pred = rf_clf.predict(x_test)
mean_absolute_error(y_test, y_rf_pred), mean_squared_error(y_test, y_rf_pred)
gb_clf = GradientBoostingRegressor()
gb_clf.fit(x_train, y_train)
y_gb_pred = gb_clf.predict(x_test)
mean_absolute_error(y_test, y_gb_pred), mean_squared_error(y_test, y_gb_pred)
x, y, coef = make_regression(n_samples=250, n_features=20, n_informative=10, noise=100.0,
coef=True, random_state=42)
y += (20 * x[:, 1]) ** 2
x.shape, y.shape, coef
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4)
x_train.shape, x_test.shape, y_train.shape, y_test.shape
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(20, 12))
for i in range(2):
sns.scatterplot(x=x[:, i], y=y, ax=axs[0, i]);
for i in range(2):
sns.scatterplot(x=x[:, i + 6], y=y, ax=axs[1, i]);
lr_clf = LinearRegression()
lr_clf.fit(x_train, y_train)
y_lr_pred = lr_clf.predict(x_test)
mean_absolute_error(y_test, y_lr_pred), mean_squared_error(y_test, y_lr_pred)
dt_clf = DecisionTreeRegressor()
dt_clf.fit(x_train, y_train)
y_dt_pred = dt_clf.predict(x_test)
mean_absolute_error(y_test, y_dt_pred), mean_squared_error(y_test, y_dt_pred)
rf_clf = RandomForestRegressor()
rf_clf.fit(x_train, y_train)
y_rf_pred = rf_clf.predict(x_test)
mean_absolute_error(y_test, y_rf_pred), mean_squared_error(y_test, y_rf_pred)
gb_clf = GradientBoostingRegressor()
gb_clf.fit(x_train, y_train)
y_gb_pred = gb_clf.predict(x_test)
mean_absolute_error(y_test, y_gb_pred), mean_squared_error(y_test, y_gb_pred)
```
## Feature Engineering
```
x = rng.uniform(size=(150, 1), low=0.0, high=10.0)
x_train, x_test = x[:100], x[100:]
x_plot = np.linspace(0, 10, 500)
x_train[:3]
y_lin_train = lin(x_train).reshape(-1)
y_lin_test = lin(x_test).reshape(-1)
y_fun_train = fun(x_train.reshape(-1))
y_fun_test = fun(x_test).reshape(-1)
x_squares = x * x
x_squares[:3]
x_sins = np.sin(x)
x_sins[:3]
x_train_aug = np.concatenate([x_train, x_train * x_train, np.sin(x_train)], axis=1)
x_train_aug[:3]
x_test_aug = np.concatenate([x_test, x_test * x_test, np.sin(x_test)], axis=1)
# from sklearn.linear_model import Ridge
# lr_aug_lin = Ridge()
lr_aug_lin = LinearRegression()
lr_aug_lin.fit(x_train_aug, y_lin_train);
lr_aug_lin.coef_, lr_aug_lin.intercept_
y_aug_lin_pred = lr_aug_lin.predict(x_test_aug)
mean_absolute_error(y_lin_test, y_aug_lin_pred), mean_squared_error(
y_lin_test, y_aug_lin_pred
)
x_test.shape, x_plot.shape
def train_and_plot_aug(f_y, scale=0.5):
y_plot = f_y(x_plot)
f_r = lambda x: randomize(f_y, x, scale=scale)
y_train = f_r(x_train_aug[:, 0])
y_test = f_r(x_test)
lr_aug = LinearRegression() # Try with Ridge() as well...
lr_aug.fit(x_train_aug, y_train)
y_pred_test = lr_aug.predict(
np.concatenate([x_test, x_test * x_test, np.sin(x_test)], axis=1)
)
x_plot2 = x_plot.reshape(-1, 1)
y_pred_plot = lr_aug.predict(
np.concatenate([x_plot2, x_plot2 * x_plot2, np.sin(x_plot2)], axis=1)
)
fig, ax = plt.subplots(figsize=(12, 6))
sns.scatterplot(x=x_plot2[:, 0], y=y_plot, color="orange")
sns.scatterplot(x=x_plot2[:, 0], y=y_pred_plot, color="red")
sns.scatterplot(x=x_train_aug[:, 0], y=y_train, color="green")
plt.show()
mae_in = mean_absolute_error(y_test, y_pred_test)
mse_in = mean_absolute_error(y_test, y_pred_test)
rmse_in = np.sqrt(mse_in)
y_nr = f_y(x_test)
mae_true = mean_absolute_error(y_nr, y_pred_test)
mse_true = mean_absolute_error(y_nr, y_pred_test)
rmse_true = np.sqrt(mse_true)
print(f"Vs. input: MAE: {mae_in:.2f}, MSE: {mse_in:.2f}, RMSE: {rmse_in:.2f}")
print(f"True: MAE: {mae_true:.2f}, MSE: {mse_true:.2f}, RMSE: {rmse_true:.2f}")
print(f"Parameters: {lr_aug.coef_}, {lr_aug.intercept_}")
train_and_plot_aug(lin)
train_and_plot_aug(fun, scale=0.0)
train_and_plot_aug(fun, scale=0.5)
train_and_plot_aug(fun, scale=1.5)
train_and_plot_aug(fun, scale=3)
def fun2(x): return 2.8 * np.sin(x) + 0.3 * x + 0.08 * x ** 2 - 2.5
train_and_plot_aug(fun2, scale=1.5)
train_and_plot_aug(lambda x: np.select([x<=6, x>6], [-0.5, 3.5]))
```
| true |
code
| 0.765221 | null | null | null | null |
|
# Image Classification with Logistic Regression from Scratch with NumPy
Welcome to another jupyter notebook of implementing machine learning algorithms from scratch using only NumPy. This time we will be implementing a different version of logistic regression for a simple image classification task. I've already done a basic version of logistic regression before [here](https://github.com/leventbass/logistic_regression). This time, we will use logistic regression to classify images. I will show all necessary mathematical equations of logistic regression and how to vectorize the summations in the equations. We will be working with a subset of the famous handwritten digit dataset called MNIST. In the subset, there will only be images of digit 1 and 5. Therefore, we will be solving a binary classification problem.
This notebook includes feature extraction, model training, and evaluation steps. Let's see what we will achieve in this post in steps:
* First, we wil load and visualize the dataset and extract two different set of features to build a classifier on.
* We will run our logistic regression algorithm with gradient descent the representations to classify digits into 1 and 5.
* We will experiment with different learning rates to find the best one.
* Finally, we will evaluate the implemented models, decide which is the best performing one and visualize a decision boundary.
* Once again, let's remind ourselves that we won't be using any function or library that accomplishes the task itself. For instance, we won't use scikit-learn to implement cross validation, we will use numpy for that and for all of the other tasks.
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
```
## Feature Extraction
Let's load the training/test data and labels as numpy arrays. All data that is used is provided in the repository in data folder. Train and test data are 1561x256 and 424x256 dimensional matrices, respectively. Each row in the aforementioned matrices corresponds to an image of a digit. The 256 pixels correspond to a 16x16 image. Label 1 is assigned to digit 1 and label -1 is assigned to digit 5.
```
train_x = np.load('data/train_data.npy')
train_y = np.load('data/train_labels.npy')
test_x = np.load('data/test_data.npy')
test_y = np.load('data/test_labels.npy')
```
Now, let's display two of the digit images, one for digit 1 and one for digit 5. We will use `imshow` function of `matplotlib` library with a suitable colormap. We will first need to reshape 256 pixels to a 16x16 matrix.
```
digit_1 = train_x[0].reshape((16,16))
digit_5 = train_x[-1].reshape((16,16))
plt.subplot(121, title='Digit 1')
plt.imshow(digit_1, cmap='gray');
plt.subplot(122, title='Digit 5')
plt.imshow(digit_5, cmap='gray');
```
**Implementing Representation 1:**
Now, we will extract the **symmetry** and **average intensity** features to use in the model. To compute the intensity features, we compute the average pixel value of the image, and for the symmetry feature, we compute the negative of the norm of the difference between the image and its y-axis symmetrical. We will extract these two features for each image in the training and test sets. As a result, we should obtain a training data matrix of size 1561x2 and test data matrix of size 424x2.
Throughout the notebook, we will refer the representation with these two features as **Representation 1**
```
train_feature_1 = np.mean(train_x, axis=1)
test_feature_1 = np.mean(test_x, axis=1)
mirrored_image_train = np.flip(train_x.reshape((train_x.shape[0],16,16)), axis=2)
mirrored_image_test = np.flip(test_x.reshape((test_x.shape[0],16,16)), axis=2)
plt.subplot(121, title='Image')
plt.imshow(train_x[-1].reshape((16,16)), cmap='gray');
plt.subplot(122, title='Mirrored Image')
plt.imshow(mirrored_image_train[-1], cmap='gray');
train_diff = train_x - mirrored_image_train.reshape((mirrored_image_train.shape[0],256))
test_diff = test_x - mirrored_image_test.reshape((mirrored_image_test.shape[0],256))
norm_train_diff = np.linalg.norm(train_diff, axis=1)
norm_test_diff = np.linalg.norm(test_diff, axis=1)
train_feature_2 = -(norm_train_diff)
test_feature_2 = -(norm_test_diff)
train_X_1 = np.concatenate((train_feature_1[:,np.newaxis], train_feature_2[:,np.newaxis]), axis=1)
test_X_1 = np.concatenate((test_feature_1[:,np.newaxis], test_feature_2[:,np.newaxis]), axis=1)
```
Now, let's provide two scatter plots, one for training and one for test data. The plots will contain the average intensity values in the x-axis and symmetry values in the y-axis. We will denote the data points of label 1 with blue marker shaped <font color='blue'>o</font> and the data points of label -1 with a red marker shaped <font color='red'>x</font>.
```
plt.figure(figsize=(6,6))
plt.scatter(train_X_1[(train_y==1),0], train_X_1[(train_y==1),1], marker='o', color='blue', s=16)
plt.scatter(train_X_1[(train_y==-1),0], train_X_1[(train_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Training Data for Representation 1')
plt.xlabel('Average Intensity')
plt.ylabel('Symmetry')
plt.figure(figsize=(6,6))
plt.scatter(test_X_1[(test_y==1),0], test_X_1[(test_y==1),1], marker='o', color='blue', s=16)
plt.scatter(test_X_1[(test_y==-1),0], test_X_1[(test_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Test Data for Representation 1')
plt.xlabel('Average Intensity')
plt.ylabel('Symmetry');
```
**Implementing Representation 2:** We will come up with an alternative feature extraction approach and we will refer this representation as **Representation 2**.
```
train_rep2_fet1 = np.array([(i>-1).sum() for i in train_x])/(train_x.shape[0]) # feature 1 for representation 2
test_rep2_fet1 = np.array([(i>-1).sum() for i in test_x])/(test_x.shape[0])
train_rep2_fet2 = np.std(train_x, axis=1) # feature 2 for representation 2
test_rep2_fet2 = np.std(test_x, axis=1)
train_X_2 = np.concatenate((train_rep2_fet1[:,np.newaxis], train_rep2_fet2[:,np.newaxis]), axis=1)
test_X_2 = np.concatenate((test_rep2_fet1[:,np.newaxis], test_rep2_fet2[:,np.newaxis]), axis=1)
```
To create the first feature of representation 2, we sum up all of the pixel values that are higher than -1 since pixel values of -1 represent the surrounding area of the image and not itself. By summing up those values we get a number that would be clearly distinctive for image of number 5 and 1, because evidently number 5 would take up more space than number 1 when it is drawn.
To add another feature to representation 2, let's calculate the standard deviation of the images. Image of number 5 will obviously have more standard deviation than image of number 1 because of the fact that it is more dispersed throughtout the area than number 1, while pixel values of number 1 are more confined and closer to each other than the image of number 5. Hence, taking the standard deviation of pixel values would be a differentiating factor for our images.
```
plt.figure(figsize=(9,5))
plt.scatter(train_X_2[(train_y==1),0], train_X_2[(train_y==1),1], marker='o', color='blue', s=16)
plt.scatter(train_X_2[(train_y==-1),0], train_X_2[(train_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Training Data for Representation 2')
plt.xlabel('Average Intensity')
plt.ylabel('Symmetry')
plt.figure(figsize=(9,5))
plt.scatter(test_X_2[(test_y==1),0], test_X_2[(test_y==1),1], marker='o', color='blue', s=16)
plt.scatter(test_X_2[(test_y==-1),0], test_X_2[(test_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Test Data for Representation 2')
plt.xlabel('Length of non-white Pixels')
plt.ylabel('Standard Deviation');
```
## Logistic Regression
Let's implement the logistic regression classifier from scratch with gradient descent and train it using Representation 1 and Representation 2 as inputs. We will concatenate 1 to our features for the intercept term, such that one data point will look like for 2-D features [1,$x_1$,$x_2$], and the model vector will be [$w_0, w_1, w_2$], where $w_0$ is the intercept parameter.
```
def data_init(X, y):
y = y[:,np.newaxis]
m = len(y)
X = np.hstack((np.ones((m,1)),X))
n = np.size(X,1)
params = np.zeros((n,1))
return (X, y, params)
```
To implement the gradient of the logistic loss with respect to $w$, first let's derive its expression:
Total cost is:
$E(w) = \frac{1}{N} \sum_{n=1}^{N} \ln \left(1 + \exp \left(-y^{\left(n\right)} w^T x^{\left(n\right)}\right)\right)$
Cost for one sample is:
$E \left(w^{\left(1\right)} \right) = \ln \left(1 + \exp \left(-y^{\left(1\right)} w^T x^{\left(1\right)} \right) \right)$
where;
$y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \end{bmatrix}_{N\times 1}$
$x = \begin{bmatrix} 1 & {x_1}^{\left(1\right)} & {x_2}^{\left(1\right)} \\
1 & {x_1}^{\left(2\right)} & {x_2}^{\left(2\right)} \\
\vdots & \vdots & \vdots \\
1 & {x_1}^{\left(N\right)} & {x_2}^{\left(N\right)}\end{bmatrix}_{N\times 3}$
$w = \begin{bmatrix}w_0 \\ w_1 \\ w_2 \end{bmatrix}_{3\times 1}$
Let $z = -y^{\left(1\right)} w^T x^{\left(1\right)}$:
$\begin{aligned}
\frac{\partial E}{\partial w_0} &= \frac{\partial \ln(1 + \exp(z))}{\partial w_0} \\
&=\frac{\exp(z) \frac{\partial z}{\partial w_0}}{1 + \exp(z)}
\quad \left( \theta(z) = \frac{\exp(z)}{1 + \exp(z)} \right)\\
&= \theta(z) \frac{\partial z}{\partial w_0} \\
&= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right)
\frac{\partial \left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right)}{\partial w_0} \\
&= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right)
\frac{\partial \left(-y^{\left(1\right)} \left(w_0 + w_1 {x_1}^{\left(1\right)} + w_2 {x_2}^{\left(1\right)}\right)\right)}{\partial w_0}\\
\frac{\partial E}{\partial w_0} &= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right) \left( -y^{\left(1\right)} \right) \\
\frac{\partial E}{\partial w_1} &= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right) \left( -y^{\left(1\right)} {x_1}^{\left(1\right)} \right)\\
\frac{\partial E}{\partial w_2} &= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right) \left( -y^{\left(1\right)} {x_2}^{\left(1\right)} \right)\\
\end{aligned}$
$\begin{aligned}
\nabla E (w) &= \frac{1}{N} \sum_{n=1}^{N} -\theta \left(-y^{\left(n\right)} w^T x^{\left(n\right)}\right) y^{\left(n\right)} x^{\left(n\right)}\\
&= \frac{1}{N} {\left( - \textbf{y} \circ \textbf{x} \right)}^T \cdot \theta \left( -\textbf{y} \circ \textbf{x w} \right)
\end{aligned}$
To prove that our implementation is converging, we will keep the loss values at each gradient descent iteration in a numpy array. To decide when to terminate the gradient descent iterations, we will check the absolute difference between the current loss value and the loss value of the previous step. If the difference is less than a small number, such as $10^{-5}$, we will exit the loop.
```
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def gradient_descent(X, y, params, learning_rate):
m = len(y)
cost_history = []
i=0
while(True):
params = params - (learning_rate/m) * ((-y * X).T @ sigmoid(-y * (X @ params)))
cost_history.append(compute_cost(X, y, params))
if(i!=0 and abs(cost_history[i] - cost_history[i-1]) < 10**-5):
break;
i+=1
cost_history = np.array(cost_history)
return (cost_history, params)
def compute_cost(X, y, theta):
N = len(y)
cost = np.sum(np.log(1+np.exp(-y * (X @ theta)))) / N
return cost
```
After the training is finalized, we will plot the loss values with respect to iteration count. Obviously, we should observe a decreasing loss as the number of iterations increases. Also, we will experiment with 5 different learning rates between 0 and 1, and plot the convergence curves for each learning rate in the same plot to observe the effect of the learning rate (step size) on the convergence.
```
(X, y, params) = data_init(train_X_1, train_y)
lr_list = [0.001, 0.003, 0.01, 0.03, 0.1]
c_list = ['red', 'green', 'yellow', 'blue','black']
plt.figure()
for lr, color in zip(lr_list, c_list):
(cost_history, params_optimal) = gradient_descent(X, y, params, lr)
plt.plot(range(len(cost_history)),cost_history, c=color);
plt.title("Convergence Graph of Cost Function")
plt.xlabel("Number of Iterations")
plt.ylabel("Cost")
plt.show()
```
## Evaluation
Now, let's train the logistic regression classifier on Representation 1 and 2 with the best learning rate we have used so far. We will report the training and test classification accuracy as:
\begin{align*}
\frac{\text{number of correctly classified samples}}{\text{total number of samples}}x100
\end{align*}
```
def predict(X, params):
y_pred_dummy = np.round(sigmoid(X @ params))
y_pred = np.where(y_pred_dummy==0,-1,1)
return y_pred
def get_accuracy(y_pred, y):
score = float(sum(y_pred == y))/ float(len(y)) * 100
return score
def evaluate(train_X, train_y, test_X, test_y, learning_rate, lambda_param):
(X, y, params) = data_init(train_X, train_y)
(_, params_optimal_1) = gradient_descent(X, y, params, learning_rate)
X_normalized = test_X
X_test = np.hstack((np.ones((X_normalized.shape[0],1)),X_normalized))
y_pred_train = predict(X, params_optimal_1)
train_score = get_accuracy(y_pred_train, y)
print('Training Score:',train_score)
y_pred_test = predict(X_test, params_optimal_1)
test_score = get_accuracy(y_pred_test, test_y[:,np.newaxis])
print('Test Score:',test_score)
print('Evaluation results for Representation 1:')
print('-'*50)
evaluate(train_X_1, train_y, test_X_1, test_y, 0.1, 0.0003)
print('\nEvaluation results for Representation 2:')
print('-'*50)
evaluate(train_X_2, train_y, test_X_2, test_y, 0.1, 0.0001)
```
Last but not least, we will visualize the decision boundary (the line that is given by $\mathbf{w}^{T}x=0$) obtained from the logistic regression classifier learned. For this purpose, we will only use Representation 1. Below, two scatter plots can be seen for training and test data points with the decision boundary shown on each of the plots.
```
(X, y, params) = data_init(train_X_1,train_y)
learning_rate = 0.1
(_, params_optimal_1) = gradient_descent(X, y, params, learning_rate)
slope = -(params_optimal_1[1] / params_optimal_1[2])
intercept = -(params_optimal_1[0] / params_optimal_1[2])
titles = ['Training Data with Decision Boundary', 'Test Data with Decision Boundary']
for X, y, title in [(train_X_1, y, titles[0]), (test_X_1, test_y, titles[1])]:
plt.figure(figsize=(7,7))
plt.scatter(X[:,0],X[:,1],c=y.reshape(-1), s=14, cmap='bwr')
ax = plt.gca()
ax.autoscale(False)
x_vals = np.array(ax.get_xlim())
y_vals = intercept + (slope * x_vals)
plt.title(title);
plt.plot(x_vals, y_vals, c='k')
```
| true |
code
| 0.439206 | null | null | null | null |
|
# Machine Learning application: Forecasting wind power. Using alternative energy for social & enviromental Good
<table>
<tr><td>
<img src="https://github.com/dmatrix/mlflow-workshop-part-3/raw/master/images/wind_farm.jpg"
alt="Keras NN Model as Logistic regression" width="800">
</td></tr>
</table>
In this notebook, we will use the MLflow Model Registry to build a machine learning application that forecasts the daily power output of a [wind farm](https://en.wikipedia.org/wiki/Wind_farm).
Wind farm power output depends on weather conditions: generally, more energy is produced at higher wind speeds. Accordingly, the machine learning models used in the notebook predicts power output based on weather forecasts with three features: `wind direction`, `wind speed`, and `air temperature`.
* This notebook uses altered data from the [National WIND Toolkit dataset](https://www.nrel.gov/grid/wind-toolkit.html) provided by NREL, which is publicly available and cited as follows:*
* Draxl, C., B.M. Hodge, A. Clifton, and J. McCaa. 2015. Overview and Meteorological Validation of the Wind Integration National Dataset Toolkit (Technical Report, NREL/TP-5000-61740). Golden, CO: National Renewable Energy Laboratory.*
* Draxl, C., B.M. Hodge, A. Clifton, and J. McCaa. 2015. "The Wind Integration National Dataset (WIND) Toolkit." Applied Energy 151: 355366.*
* Lieberman-Cribbin, W., C. Draxl, and A. Clifton. 2014. Guide to Using the WIND Toolkit Validation Code (Technical Report, NREL/TP-5000-62595). Golden, CO: National Renewable Energy Laboratory.*
* King, J., A. Clifton, and B.M. Hodge. 2014. Validation of Power Output for the WIND Toolkit (Technical Report, NREL/TP-5D00-61714). Golden, CO: National Renewable Energy Laboratory.*
Google's DeepMind publised a [AI for Social Good: 7 Inspiring Examples](https://www.springboard.com/blog/ai-for-good/) blog. One of example was
how Wind Farms can predict expected power ouput based on wind conditions and temperature, hence mitigating the burden from consuming
energy from fossil fuels.
<table>
<tr><td>
<img src="https://github.com/dmatrix/ds4g-workshop/raw/master/notebooks/images/deepmind_system-windpower.gif"
alt="Deep Mind ML Wind Power" width="400">
<img src="https://github.com/dmatrix/ds4g-workshop/raw/master/notebooks/images/machine_learning-value_wind_energy.max-1000x1000.png"
alt="Deep Mind ML Wind Power" width="400">
</td></tr>
</table>
```
import warnings
warnings.filterwarnings("ignore")
import mlflow
mlflow.__version__
```
## Run some class and utility notebooks
This defines and allows us to use some Python model classes and utility functions
```
%run ./rfr_class.ipynb
%run ./utils_class.ipynb
```
## Load our training data
Ideally, you would load it from a Feature Store or Delta Lake table
```
# Load and print dataset
csv_path = "https://raw.githubusercontent.com/dmatrix/olt-mlflow/master/model_registery/notebooks/data/windfarm_data.csv"
# Use column 0 (date) as the index
wind_farm_data = Utils.load_data(csv_path, index_col=0)
wind_farm_data.head(5)
```
## Get Training and Validation data
```
X_train, y_train = Utils.get_training_data(wind_farm_data)
val_x, val_y = Utils.get_validation_data(wind_farm_data)
```
## Initialize a set of hyperparameters for the training and try three runs
```
# Initialize our model hyperparameters
params_list = [{"n_estimators": 100},
{"n_estimators": 200},
{"n_estimators": 300}]
mlflow.set_tracking_uri("sqlite:///mlruns.db")
model_name = "WindfarmPowerForecastingModel"
for params in params_list:
rfr = RFRModel.new_instance(params)
print("Using paramerts={}".format(params))
runID = rfr.mlflow_run(X_train, y_train, val_x, val_y, model_name, register=True)
print("MLflow run_id={} completed with MSE={} and RMSE={}".format(runID, rfr.mse, rfr.rsme))
```
## Let's Examine the MLflow UI
1. Let's examine some models and start comparing their metrics
2. **mlflow ui --backend-store-uri sqlite:///mlruns.db**
# Integrating Model Registry with CI/CD Forecasting Application
<table>
<tr><td>
<img src="https://github.com/dmatrix/mlflow-workshop-part-3/raw/master/images/forecast_app.png"
alt="Keras NN Model as Logistic regression" width="800">
</td></tr>
</table>
1. Use the model registry fetch different versions of the model
2. Score the model
3. Select the best scored model
4. Promote model to production, after testing
# Define a helper function to load PyFunc model from the registry
<table>
<tr><td> Save a Built-in MLflow Model Flavor and load as PyFunc Flavor</td></tr>
<tr><td>
<img src="https://raw.githubusercontent.com/dmatrix/mlflow-workshop-part-2/master/images/models_2.png"
alt="" width="600">
</td></tr>
</table>
```
def score_model(data, model_uri):
model = mlflow.pyfunc.load_model(model_uri)
return model.predict(data)
```
## Load scoring data
Again, ideally you would load it from on-line or off-line FeatureStore
```
# Load the score data
score_path = "https://raw.githubusercontent.com/dmatrix/olt-mlflow/master/model_registery/notebooks/data/score_windfarm_data.csv"
score_df = Utils.load_data(score_path, index_col=0)
score_df.head()
# Drop the power column since we are predicting that value
actual_power = pd.DataFrame(score_df.power.values, columns=['power'])
score = score_df.drop("power", axis=1)
```
## Score the version 1 of the model
```
# Formulate the model URI to fetch from the model registery
model_uri = "models:/{}/{}".format(model_name, 1)
# Predict the Power output
pred_1 = pd.DataFrame(score_model(score, model_uri), columns=["predicted_1"])
pred_1
```
#### Combine with the actual power
```
actual_power["predicted_1"] = pred_1["predicted_1"]
actual_power
```
## Score the version 2 of the model
```
# Formulate the model URI to fetch from the model registery
model_uri = "models:/{}/{}".format(model_name, 2)
# Predict the Power output
pred_2 = pd.DataFrame(score_model(score, model_uri), columns=["predicted_2"])
pred_2
```
#### Combine with the actual power
```
actual_power["predicted_2"] = pred_2["predicted_2"]
actual_power
```
## Score the version 3 of the model
```
# Formulate the model URI to fetch from the model registery
model_uri = "models:/{}/{}".format(model_name, 3)
# Formulate the model URI to fetch from the model registery
pred_3 = pd.DataFrame(score_model(score, model_uri), columns=["predicted_3"])
pred_3
```
#### Combine the values into a single pandas DataFrame
```
actual_power["predicted_3"] = pred_3["predicted_3"]
actual_power
```
## Plot the combined predicited results vs the actual power
```
%matplotlib inline
actual_power.plot.line()
```
| true |
code
| 0.520557 | null | null | null | null |
|
# Building a Classifier from Lending Club Data
**An end-to-end machine learning example using Pandas and Scikit-Learn**
## Data Ingestion
```
%matplotlib inline
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from pandas.tools.plotting import scatter_matrix
names = [
#Lending Club features
"funded_amnt",
"term",
"int_rate",
"emp_length",
"home_ownership",
"annual_inc",
"verification_status",
"purpose",
"dti",
"delinq_2yrs",
"inq_last_6mths",
"open_acc",
"pub_rec",
"revol_bal",
"revol_util",
# Macroeconomical data
"ilc_mean",
"ilc_LSFT",
"gdp_mean",
"gdp_LSFT",
"Tbill_mean",
"Tbill_LSFT",
"cc_rate",
"unemp",
"unemp_LSFT",
"spread",
# Label
"loan_status"
]
Fnames = names[:-1]
label = names[-1]
# Open up the earlier CSV to determine how many different types ofentries there are in the column 'loan_status'
data_with_all_csv_features = pd.read_csv("./data/dfaWR4F.csv")
full_data = data_with_all_csv_features[names];
data = full_data.copy()[names]
data.head(3)
```
# Data Exploration
The very first thing to do is to explore the dataset and see what's inside.
```
# Shape of the full dataset
print data.shape
import matplotlib.pyplot as plt
%matplotlib inline
data.boxplot(column="annual_inc",by="loan_status")
from pandas.tools.plotting import radviz
import matplotlib.pyplot as plt
fig = plt.figure()
radviz(data, 'loan_status')
plt.show()
areas = full_data[['funded_amnt','term','int_rate', 'loan_status']]
scatter_matrix(areas, alpha=0.2, figsize=(18,18), diagonal='kde')
sns.set_context("poster")
sns.countplot(x='home_ownership', hue='loan_status', data=full_data,)
sns.set_context("poster")
sns.countplot(x='emp_length', hue='loan_status', data=full_data,)
sns.set_context("poster")
sns.countplot(x='term', hue='loan_status', data=full_data,)
sns.set_context("poster")
sns.countplot(y='purpose', hue='loan_status', data=full_data,)
sns.set_context("poster", font_scale=0.8)
plt.figure(figsize=(15, 15))
plt.ylabel('Loan Originating State')
sns.countplot(y='verification_status', hue='loan_status', data=full_data)
pd.crosstab(data["term"],data["loan_status"],margins=True)
def percConvert(ser):
return ser/float(ser[-1])
pd.crosstab(data["term"],data["loan_status"],margins=True).apply(percConvert, axis=1)
data.hist(column="annual_inc",by="loan_status",bins=30)
# Balancing the data so that we have 50/50 class balancing (underbalancing reducing one class)
paid_data = data.loc[(data['loan_status'] == "Paid")]
default_data = data.loc[(data['loan_status'] == "Default")]
# Reduce the Fully Paid data to the same number as Defaulted
num_of_paid = default_data.shape[0]
reduce_paid_data = paid_data.sample(num_of_paid)
# This is the smaller sample data with 50-50 Defaulted and Fully aod loan
balanced_data = reduce_paid_data.append(default_data,ignore_index = True )
#Now shuffle several times
data = balanced_data.sample(balanced_data.shape[0])
data = data.sample(balanced_data.shape[0])
print "Fully Paid data size was {}".format(paid_data.shape[0])
print "Default data size was {}".format(default_data.shape[0])
print "Updated new Data size is {}".format(data.shape[0])
pd.crosstab(data["term"],data["loan_status"],margins=True).apply(percConvert, axis=1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(paid_data['int_rate'], bins = 50, alpha = 0.4, label='Fully_Paid', color = 'blue', range = (paid_data['int_rate'].min(),reduce_paid_data['int_rate'].max()))
ax.hist(default_data['int_rate'], bins = 50, alpha = 0.4, label='Default', color = 'red', range = (default_data['int_rate'].min(),default_data['int_rate'].max()))
plt.title('Interest Rate vs Number of Loans')
plt.legend(loc='upper right')
plt.xlabel('Interest Rate')
plt.axis([0, 25, 0, 8000])
plt.ylabel('Number of Loans')
plt.show()
```
The countplot function accepts either an x or a y argument to specify if this is a bar plot or a column plot. I chose to use the y argument so that the labels were readable. The hue argument specifies a column for comparison; in this case we're concerned with the relationship of our categorical variables to the target income.
## Data Management
In order to organize our data on disk, we'll need to add the following files:
- `README.md`: a markdown file containing information about the dataset and attribution. Will be exposed by the `DESCR` attribute.
- `meta.json`: a helper file that contains machine readable information about the dataset like `target_names` and `feature_names`.
```
import json
meta = {
'target_names': list(full_data.loan_status.unique()),
'feature_names': list(full_data.columns),
'categorical_features': {
column: list(full_data[column].unique())
for column in full_data.columns
if full_data[column].dtype == 'object'
},
}
with open('data/ls_meta.json', 'wb') as f:
json.dump(meta, f, indent=2)
```
This code creates a `meta.json` file by inspecting the data frame that we have constructued. The `target_names` column, is just the two unique values in the `data.loan_status` series; by using the `pd.Series.unique` method - we're guarenteed to spot data errors if there are more or less than two values. The `feature_names` is simply the names of all the columns.
Then we get tricky — we want to store the possible values of each categorical field for lookup later, but how do we know which columns are categorical and which are not? Luckily, Pandas has already done an analysis for us, and has stored the column data type, `data[column].dtype`, as either `int64` or `object`. Here I am using a dictionary comprehension to create a dictionary whose keys are the categorical columns, determined by checking the object type and comparing with `object`, and whose values are a list of unique values for that field.
Now that we have everything we need stored on disk, we can create a `load_data` function, which will allow us to load the training and test datasets appropriately from disk and store them in a `Bunch`:
```
from sklearn import cross_validation
from sklearn.cross_validation import train_test_split
from sklearn.datasets.base import Bunch
def load_data(root='data'):
# Load the meta data from the file
with open(os.path.join(root, 'meta.json'), 'r') as f:
meta = json.load(f)
names = meta['feature_names']
# Load the readme information
with open(os.path.join(root, 'README.md'), 'r') as f:
readme = f.read()
X = data[Fnames]
# Remove the target from the categorical features
meta['categorical_features'].pop(label)
y = data[label]
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X,y,test_size = 0.2,random_state=10)
# Return the bunch with the appropriate data chunked apart
return Bunch(
#data = train[names[:-1]],
data = X_train,
#target = train[names[-1]],
target = y_train,
#data_test = test[names[:-1]],
data_test = X_test,
#target_test = test[names[-1]],
target_test = y_test,
target_names = meta['target_names'],
feature_names = meta['feature_names'],
categorical_features = meta['categorical_features'],
DESCR = readme,
)
dataset = load_data()
print meta['target_names']
dataset.data_test.head()
```
The primary work of the `load_data` function is to locate the appropriate files on disk, given a root directory that's passed in as an argument (if you saved your data in a different directory, you can modify the root to have it look in the right place). The meta data is included with the bunch, and is also used split the train and test datasets into `data` and `target` variables appropriately, such that we can pass them correctly to the Scikit-Learn `fit` and `predict` estimator methods.
## Feature Extraction
Now that our data management workflow is structured a bit more like Scikit-Learn, we can start to use our data to fit models. Unfortunately, the categorical values themselves are not useful for machine learning; we need a single instance table that contains _numeric values_. In order to extract this from the dataset, we'll have to use Scikit-Learn transformers to transform our input dataset into something that can be fit to a model. In particular, we'll have to do the following:
- encode the categorical labels as numeric data
- impute missing values with data (or remove)
We will explore how to apply these transformations to our dataset, then we will create a feature extraction pipeline that we can use to build a model from the raw input data. This pipeline will apply both the imputer and the label encoders directly in front of our classifier, so that we can ensure that features are extracted appropriately in both the training and test datasets.
### Label Encoding
Our first step is to get our data out of the object data type land and into a numeric type, since nearly all operations we'd like to apply to our data are going to rely on numeric types. Luckily, Sckit-Learn does provide a transformer for converting categorical labels into numeric integers: [`sklearn.preprocessing.LabelEncoder`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html). Unfortunately it can only transform a single vector at a time, so we'll have to adapt it in order to apply it to multiple columns.
Like all Scikit-Learn transformers, the `LabelEncoder` has `fit` and `transform` methods (as well as a special all-in-one, `fit_transform` method) that can be used for stateful transformation of a dataset. In the case of the `LabelEncoder`, the `fit` method discovers all unique elements in the given vector, orders them lexicographically, and assigns them an integer value. These values are actually the indices of the elements inside the `LabelEncoder.classes_` attribute, which can also be used to do a reverse lookup of the class name from the integer value.
For example, if we were to encode the `home_ownership` column of our dataset as follows:
```
from sklearn.preprocessing import LabelEncoder
ownership = LabelEncoder()
ownership.fit(dataset.data.home_ownership)
print(ownership.classes_)
from sklearn.preprocessing import LabelEncoder
purpose = LabelEncoder()
purpose.fit(dataset.data.purpose)
print(purpose.classes_)
```
Obviously this is very useful for a single column, and in fact the `LabelEncoder` really was intended to encode the target variable, not necessarily categorical data expected by the classifiers.
In order to create a multicolumn LabelEncoder, we'll have to extend the `TransformerMixin` in Scikit-Learn to create a transformer class of our own, then provide `fit` and `transform` methods that wrap individual `LabelEncoders` for our columns.
```
from sklearn.base import BaseEstimator, TransformerMixin
class EncodeCategorical(BaseEstimator, TransformerMixin):
"""
Encodes a specified list of columns or all columns if None.
"""
def __init__(self, columns=None):
self.columns = columns
self.encoders = None
def fit(self, data, target=None):
"""
Expects a data frame with named columns to encode.
"""
# Encode all columns if columns is None
if self.columns is None:
self.columns = data.columns
# Fit a label encoder for each column in the data frame
self.encoders = {
column: LabelEncoder().fit(data[column])
for column in self.columns
}
return self
def transform(self, data):
"""
Uses the encoders to transform a data frame.
"""
output = data.copy()
for column, encoder in self.encoders.items():
output[column] = encoder.transform(data[column])
return output
encoder = EncodeCategorical(dataset.categorical_features.keys())
#data = encoder.fit_transform(dataset.data)
```
This specialized transformer now has the ability to label encode multiple columns in a data frame, saving information about the state of the encoders. It would be trivial to add an `inverse_transform` method that accepts numeric data and converts it to labels, using the `inverse_transform` method of each individual `LabelEncoder` on a per-column basis.
### Imputation
Scikit-Learn provides a transformer for dealing with missing values at either the column level or at the row level in the `sklearn.preprocessing` library called the [Imputer](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.Imputer.html).
The `Imputer` requires information about what missing values are, either an integer or the string, `Nan` for `np.nan` data types, it then requires a strategy for dealing with it. For example, the `Imputer` can fill in the missing values with the mean, median, or most frequent values for each column. If provided an axis argument of 0 then columns that contain only missing data are discarded; if provided an axis argument of 1, then rows which contain only missing values raise an exception. Basic usage of the `Imputer` is as follows:
```python
imputer = Imputer(missing_values='Nan', strategy='most_frequent')
imputer.fit(dataset.data)
```
```
from sklearn.preprocessing import Imputer
class ImputeCategorical(BaseEstimator, TransformerMixin):
"""
Encodes a specified list of columns or all columns if None.
"""
def __init__(self, columns=None):
self.columns = columns
self.imputer = None
def fit(self, data, target=None):
"""
Expects a data frame with named columns to impute.
"""
# Encode all columns if columns is None
if self.columns is None:
self.columns = data.columns
# Fit an imputer for each column in the data frame
#self.imputer = Imputer(strategy='most_frequent')
self.imputer = Imputer(strategy='mean')
self.imputer.fit(data[self.columns])
return self
def transform(self, data):
"""
Uses the encoders to transform a data frame.
"""
output = data.copy()
output[self.columns] = self.imputer.transform(output[self.columns])
return output
imputer = ImputeCategorical(Fnames)
#data = imputer.fit_transform(data)
data.head(5)
```
Our custom imputer, like the `EncodeCategorical` transformer takes a set of columns to perform imputation on. In this case we only wrap a single `Imputer` as the `Imputer` is multicolumn — all that's required is to ensure that the correct columns are transformed.
I had chosen to do the label encoding first, assuming that because the `Imputer` required numeric values, I'd be able to do the parsing in advance. However, after requiring a custom imputer, I'd say that it's probably best to deal with the missing values early, when they're still a specific value, rather than take a chance.
## Model Build
To create classifier, we're going to create a [`Pipeline`](http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html) that uses our feature transformers and ends in an estimator that can do classification. We can then write the entire pipeline object to disk with the `pickle`, allowing us to load it up and use it to make predictions in the future.
A pipeline is a step-by-step set of transformers that takes input data and transforms it, until finally passing it to an estimator at the end. Pipelines can be constructed using a named declarative syntax so that they're easy to modify and develop.
# PCA
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
%matplotlib inline
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#print yencode
# construct the pipeline
pca = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
#('classifier', PCA(n_components=20))
('classifier', PCA())
])
# fit the pipeline
pca.fit(dataset.data, yencode.transform(dataset.target))
#print dataset.target
import numpy as np
#The amount of variance that each PC explains
var= pca.named_steps['classifier'].explained_variance_ratio_
#Cumulative Variance explains
var1=np.cumsum(np.round(pca.named_steps['classifier'].explained_variance_ratio_, decimals=4)*100)
print var1
plt.plot(var1)
```
# LDA
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.lda import LDA
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
%matplotlib inline
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#print yencode
# construct the pipeline
lda = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', LDA())
])
# fit the pipeline
lda.fit(dataset.data, yencode.transform(dataset.target))
#print dataset.target
import numpy as np
#The amount of variance that each PC explains
var= lda.named_steps['classifier']
print var
#Cumulative Variance explains
#var1=np.cumsum(np.round(lda.named_steps['classifier'], decimals=4)*100)
print var1
plt.plot(var1)
```
# Logistic Regression
Fits a logistic model to data and makes predictions about the probability of a categorical event (between 0 and 1). Logistic regressions make predictions between 0 and 1, so in order to classify multiple classes a one-vs-all scheme is used (one model per class, winner-takes-all).
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import Normalizer
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#normalizer = Normalizer(copy=False)
# construct the pipeline
lr = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
#('normalizer', Normalizer(copy=False)),
#('classifier', LogisticRegression(class_weight='{0:.5, 1:.3}'))
('classifier', LogisticRegression())
])
# fit the pipeline
lr.fit(dataset.data, yencode.transform(dataset.target))
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = lr.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = lr.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#lr.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = lr.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## Chaining PCA and Logistic Regression
The PCA does an unsupervised dimensionality reduction, while the logistic regression does the prediction.
Here we are using default values for all component of the pipeline.
```
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn import linear_model, decomposition
yencode = LabelEncoder().fit(dataset.target)
logistic = linear_model.LogisticRegression()
pca = decomposition.PCA()
pipe = Pipeline(steps=[
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('logistic', logistic)
])
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#print yencode
# construct the pipeline
lda = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', LDA())
])
# fit the pipeline
lda.fit(dataset.data, yencode.transform(dataset.target))
# Running the test
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = lda.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = lda.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#lda.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = lda.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## Random Forest
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error as mse
from sklearn.metrics import r2_score
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
rf = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', RandomForestClassifier(n_estimators=20, oob_score=True, max_depth=7))
])
# ...and then run the 'fit' method to build a forest of trees
rf.fit(dataset.data, yencode.transform(dataset.target))
# Running the test
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = rf.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = rf.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#rf.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = rf.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## ElasticNet
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import ElasticNet
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
lelastic = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', ElasticNet(alpha=0.01, l1_ratio =0.1))
])
# fit the pipeline
lelastic.fit(dataset.data, yencode.transform(dataset.target))
#A helper method for pretty-printing linear models
def pretty_print_linear(coefs, names = None, sort = False):
if names == None:
names = ["X%s" % x for x in range(len(coefs))]
lst = zip(coefs[0], names)
if sort:
lst = sorted(lst, key = lambda x:-np.abs(x[0]))
return " + ".join("%s * %s" % (round(coef, 3), name)
for coef, name in lst)
coefs = lelastic.named_steps['classifier'].coef_
print coefs
#print "Linear model:", pretty_print_linear(coefs, Fnames)
#Naive Bayes
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB
from sklearn.pipeline import Pipeline
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
nb = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
# ('classifier', GaussianNB())
# ('classifier', MultinomialNB(alpha=0.7, class_prior=[0.5, 0.5], fit_prior=True))
('classifier', BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=False))
])
# Next split up the data with the 'train test split' method in the Cross Validation module
#X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2)
# ...and then run the 'fit' method to build a model
nb.fit(dataset.data, yencode.transform(dataset.target))
# Running the test
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = nb.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = nb.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#rf.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = nb.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## Gradient Boosting Classifier
```
from sklearn.ensemble import GradientBoostingClassifier
clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
max_depth=1, random_state=0).fit(dataset.data, dataset.target)
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = clf.predict(dataset.data_test)
# execute classification report
clf.score(dataset.data_test, y_true)
```
## Voting Classifier
1xLogistic, 4xRandom Forest, 1xgNB, 1xDecisionTree, 2xkNeighbors
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
from sklearn import linear_model, decomposition
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
clf1 = LogisticRegression(random_state=12)
clf2 = RandomForestClassifier(max_features=5, min_samples_leaf=4, min_samples_split=9,
bootstrap=False, criterion='entropy', max_depth=None, n_estimators=24, random_state=12)
clf3 = GaussianNB()
clf4 = DecisionTreeClassifier(max_depth=4)
clf5 = KNeighborsClassifier(n_neighbors=7)
#clf6 = SVC(kernel='rbf', probability=True)
pca = decomposition.PCA(n_components=24)
# construct the pipeline
pipe = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('eclf_classifier', VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3),
('dtc', clf4),('knc', clf5)],
voting='soft',
weights=[1, 4, 1, 1, 2])),
])
# fit the pipeline
pipe.fit(dataset.data, yencode.transform(dataset.target))
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), pipe.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), pipe.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), pipe.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
```
## Parameter Tuning for Logistic regression inside pipeline
A grid search or feature analysis may lead to a higher scoring model than the one we quickly put together.
```
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn import linear_model, decomposition
yencode = LabelEncoder().fit(dataset.target)
logistic = LogisticRegression(penalty='l2', dual=False, solver='newton-cg')
clf2 = RandomForestClassifier(max_features=5, min_samples_leaf=4, min_samples_split=9,
bootstrap=False, criterion='entropy', max_depth=None, n_estimators=24, random_state=12)
clf3 = GaussianNB()
clf4 = DecisionTreeClassifier(max_depth=4)
clf5 = KNeighborsClassifier(n_neighbors=7)
#clf6 = SVC(kernel='rbf', probability=True)
pca = decomposition.PCA(n_components=24)
# construct the pipeline
pipe = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('logistic', logistic),
])
tuned_parameters = {
#'pca__n_components':[5, 7, 13, 24],
'logistic__fit_intercept':(False, True),
#'logistic__C':(0.1, 1, 10),
'logistic__class_weight':({0:.5, 1:.5},{0:.7, 1:.3},{0:.6, 1:.4},{0:.55, 1:.45},None),
}
scores = ['precision', 'recall', 'f1']
for score in scores:
print("# Tuning hyper-parameters for %s" % score)
print()
clf = GridSearchCV(pipe, tuned_parameters, scoring='%s_weighted' % score)
clf.fit(dataset.data, yencode.transform(dataset.target))
print("Best parameters set found on development set:")
print()
print(clf.best_params_)
print()
print("Grid scores on development set:")
print()
for params, mean_score, scores in clf.grid_scores_:
print("%0.3f (+/-%0.03f) for %r"
% (mean_score, scores.std() * 2, params))
print()
print("Detailed classification report:")
print()
print("The model is trained on the full development set.")
print("The scores are computed on the full evaluation set.")
print()
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), clf.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), clf.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), clf.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
```
## Parameter Tuning for classifiers inside VotingClassifier
A grid search or feature analysis may lead to a higher scoring model than the one we quickly put together.
```
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn import linear_model, decomposition
yencode = LabelEncoder().fit(dataset.target)
logistic = LogisticRegression(penalty='l2', dual=False, solver='newton-cg')
clf2 = RandomForestClassifier(max_features=5, min_samples_leaf=4, min_samples_split=9,
bootstrap=False, criterion='entropy', max_depth=None, n_estimators=24, random_state=12)
clf3 = GaussianNB()
clf4 = DecisionTreeClassifier(max_depth=4)
clf5 = KNeighborsClassifier(n_neighbors=7)
#clf6 = SVC(kernel='rbf', probability=True)
pca = decomposition.PCA(n_components=24)
# construct the pipeline
pipe = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('eclf_classifier', VotingClassifier(estimators=[('logistic', logistic), ('randomf', clf2), ('nb', clf3),
('decisiontree', clf4),('kn', clf5)],
voting='soft',
weights=[1, 4, 1, 1, 2])),
])
tuned_parameters = {
#'pca__n_components':[5, 7, 13, 20, 24],
#'eclf_classifier__logistic__fit_intercept':(False, True),
#'logistic__C':(0.1, 1, 10),
'eclf_classifier__logistic__class_weight':({0:.5, 1:.5},{0:.7, 1:.3},{0:.6, 1:.4},{0:.55, 1:.45},None),
#'randomf__max_depth': [3, None],
#'randomf__max_features': sp_randint(1, 11),
#'randomf__min_samples_split': sp_randint(1, 11),
#'randomf__min_samples_leaf': sp_randint(1, 11),
#'randomf__bootstrap': [True, False],
#'randomf__criterion': ['gini', 'entropy']
}
scores = ['precision', 'recall', 'f1']
for score in scores:
print("# Tuning hyper-parameters for %s" % score)
print()
clf = GridSearchCV(pipe, tuned_parameters, scoring='%s_weighted' % score)
clf.fit(dataset.data, yencode.transform(dataset.target))
print("Best parameters set found on development set:")
print()
print(clf.best_params_)
print()
print("Grid scores on development set:")
print()
for params, mean_score, scores in clf.grid_scores_:
print("%0.3f (+/-%0.03f) for %r"
% (mean_score, scores.std() * 2, params))
print()
print("Detailed classification report:")
print()
print("The model is trained on the full development set.")
print("The scores are computed on the full evaluation set.")
print()
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), clf.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), clf.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), clf.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
```
## Tuning the weights in the VotingClassifier
```
from sklearn.base import BaseEstimator
from sklearn.base import ClassifierMixin
import numpy as np
import operator
class EnsembleClassifier(BaseEstimator, ClassifierMixin):
"""
Ensemble classifier for scikit-learn estimators.
Parameters
----------
clf : `iterable`
A list of scikit-learn classifier objects.
weights : `list` (default: `None`)
If `None`, the majority rule voting will be applied to the predicted class labels.
If a list of weights (`float` or `int`) is provided, the averaged raw probabilities (via `predict_proba`)
will be used to determine the most confident class label.
"""
def __init__(self, clfs, weights=None):
self.clfs = clfs
self.weights = weights
def fit(self, X, y):
"""
Fit the scikit-learn estimators.
Parameters
----------
X : numpy array, shape = [n_samples, n_features]
Training data
y : list or numpy array, shape = [n_samples]
Class labels
"""
for clf in self.clfs:
clf.fit(X, y)
def predict(self, X):
"""
Parameters
----------
X : numpy array, shape = [n_samples, n_features]
Returns
----------
maj : list or numpy array, shape = [n_samples]
Predicted class labels by majority rule
"""
self.classes_ = np.asarray([clf.predict(X) for clf in self.clfs])
if self.weights:
avg = self.predict_proba(X)
maj = np.apply_along_axis(lambda x: max(enumerate(x), key=operator.itemgetter(1))[0], axis=1, arr=avg)
else:
maj = np.asarray([np.argmax(np.bincount(self.classes_[:,c])) for c in range(self.classes_.shape[1])])
return maj
def predict_proba(self, X):
"""
Parameters
----------
X : numpy array, shape = [n_samples, n_features]
Returns
----------
avg : list or numpy array, shape = [n_samples, n_probabilities]
Weighted average probability for each class per sample.
"""
self.probas_ = [clf.predict_proba(X) for clf in self.clfs]
avg = np.average(self.probas_, axis=0, weights=self.weights)
return avg
y_true = yencode.transform(full_data[label])
df = pd.DataFrame(columns=('w1', 'w2', 'w3','w4','w5', 'mean', 'std'))
i = 0
for w1 in range(0,2):
for w2 in range(0,2):
for w3 in range(0,2):
for w4 in range(0,2):
for w5 in range(0,2):
if len(set((w1,w2,w3,w4,w5))) == 1: # skip if all weights are equal
continue
eclf = EnsembleClassifier(clfs=[clf1, clf2, clf3, clf4, clf5], weights=[w1,w2,w3,w4,w5])
eclf.fit(dataset.data, yencode.transform(dataset.target))
print "w1"
print w1
print "w2"
print w2
print "w3"
print w3
print "w4"
print w4
print "w5"
print w5
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), eclf.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), eclf.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), eclf.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
#scores = cross_validation.cross_val_score(
# estimator=eclf,
# X=full_data[Fnames],
# y=y_true,
# cv=5,
# scoring='f1',
# n_jobs=1)
#df.loc[i] = [w1, w2, w3, w4, w5, scores.mean(), scores.std()]
i += 1
#print i
#print scores.mean()
#df.sort(columns=['mean', 'std'], ascending=False)
```
The pipeline first passes data through our encoder, then to the imputer, and finally to our classifier. In this case, I have chosen a `LogisticRegression`, a regularized linear model that is used to estimate a categorical dependent variable, much like the binary target we have in this case. We can then evaluate the model on the test data set using the same exact pipeline.
The last step is to save our model to disk for reuse later, with the `pickle` module:
# Model Pickle
```
import pickle
def dump_model(model, path='data', name='classifier.pickle'):
with open(os.path.join(path, name), 'wb') as f:
pickle.dump(model, f)
dump_model(lr)
import pickle
def dump_model(model, path='data', name='encodert.pickle'):
with open(os.path.join(path, name), 'wb') as f:
pickle.dump(model, f)
dump_model(yencode)
```
# SVMs
Support Vector Machines (SVM) uses points in transformed problem space that separates the classes into groups.
```
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error as mse
from sklearn.metrics import r2_score
from sklearn.svm import SVC
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
svm = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', SVC(kernel='linear'))
])
svm.fit(dataset.data, yencode.transform(dataset.target))
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), svm.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), svm.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), svm.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
#kernels = ['linear', 'poly', 'rbf']
#for kernel in kernels:
# if kernel != 'poly':
# model = SVC(kernel=kernel)
# else:
# model = SVC(kernel=kernel, degree=3)
```
We can also dump meta information about the date and time your model was built, who built the model, etc. But we'll skip that step here.
## Model Operation
Now it's time to explore how to use the model. To do this, we'll create a simple function that gathers input from the user on the command line, and returns a prediction with the classifier model. Moreover, this function will load the pickled model into memory to ensure the latest and greatest saved model is what's being used.
```
def load_model(path='data/classifier.pickle'):
with open(path, 'rb') as f:
return pickle.load(f)
def predict(model, meta=meta):
data = {} # Store the input from the user
for column in meta['feature_names'][:-1]:
# Get the valid responses
valid = meta['categorical_features'].get(column)
# Prompt the user for an answer until good
while True:
val = "" + raw_input("enter {} >".format(column))
print val
# if valid and val not in valid:
# print "Not valid, choose one of {}".format(valid)
# else:
data[column] = val
break
# Create prediction and label
# yhat = model.predict(pd.DataFrame([data]))
yhat = model.predict_proba(pd.DataFrame([data]))
print yhat
return yencode.inverse_transform(yhat)
# Execute the interface
#model = load_model()
#predict(model)
#print data
#yhat = model.predict_proba(pd.DataFrame([data]))
```
## Conclusion
| true |
code
| 0.52902 | null | null | null | null |
|
# Asymmetric Loss
This documentation is based on the paper "[Asymmetric Loss For Multi-Label Classification](https://arxiv.org/abs/2009.14119)".
## Asymetric Single-Label Loss
```
import timm
import torch
import torch.nn.functional as F
from timm.loss import AsymmetricLossMultiLabel, AsymmetricLossSingleLabel
import matplotlib.pyplot as plt
from PIL import Image
from pathlib import Path
```
Let's create a example of the `output` of a model, and our `labels`.
```
output = F.one_hot(torch.tensor([0,9,0])).float()
labels=torch.tensor([0,0,0])
labels, output
```
If we set all the parameters to 0, the loss becomes `F.cross_entropy` loss.
```
asl = AsymmetricLossSingleLabel(gamma_pos=0,gamma_neg=0,eps=0.0)
asl(output,labels)
F.cross_entropy(output,labels)
```
Now lets look at the asymetric part. ASL is Asymetric in how it handles positive and negative examples. Positive examples being the labels that are present in the image, and negative examples being labels that are not present in the image. The idea being that an image has a lot of easy negative examples, few hard negative examples and very few positive examples. Getting rid of the influence of easy negative examples, should help emphasize the gradients of the positive examples.
```
Image.open(Path()/'images/cat.jpg')
```
Notice this image contains a cat, that would be a positive label. This images does not contain a dog, elephant bear, giraffe, zebra, banana or many other of the labels found in the coco dataset, those would be negative examples. It is very easy to see that a giraffe is not in this image.
```
output = (2*F.one_hot(torch.tensor([0,9,0]))-1).float()
labels=torch.tensor([0,9,0])
losses=[AsymmetricLossSingleLabel(gamma_neg=i*0.04+1,eps=0.1,reduction='mean')(output,labels) for i in range(int(80))]
plt.plot([ i*0.04+1 for i,l in enumerate(losses)],[loss for loss in losses])
plt.ylabel('Loss')
plt.xlabel('Change in gamma_neg')
plt.show()
```
$$L_- = (p)^{\gamma-}\log(1-p) $$
The contibution of small negative examples quickly decreases as gamma_neg is increased as $\gamma-$ is an exponent and $p$ should be a small number close to 0.
Below we set `eps=0`, this has the effect of completely flattening out the above graph, we are no longer applying label smoothing, so negative examples end up not contributing to the loss.
```
losses=[AsymmetricLossSingleLabel(gamma_neg=0+i*0.02,eps=0.0,reduction='mean')(output,labels) for i in range(100)]
plt.plot([ i*0.04 for i in range(len(losses))],[loss for loss in losses])
plt.ylabel('Loss')
plt.xlabel('Change in gamma_neg')
plt.show()
```
## AsymmetricLossMultiLabel
`AsymmetricLossMultiLabel` allows for working on multi-label problems.
```
labels=F.one_hot(torch.LongTensor([0,0,0]),num_classes=10)+F.one_hot(torch.LongTensor([1,9,1]),num_classes=10)
labels
AsymmetricLossMultiLabel()(output,labels)
```
For `AsymmetricLossMultiLabel` another parameter exists called `clip`. This clamps smaller inputs to 0 for negative examples. This is called Asymmetric Probability Shifting.
```
losses=[AsymmetricLossMultiLabel(clip=i/100)(output,labels) for i in range(100)]
plt.plot([ i/100 for i in range(len(losses))],[loss for loss in losses])
plt.ylabel('Loss')
plt.xlabel('Clip')
plt.show()
```
| true |
code
| 0.670406 | null | null | null | null |
|
# 0. Dependências
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
%matplotlib inline
pd.options.display.max_rows = 10
```
# 1. Introdução
**O objetivo principal do PCA é analisar os dados para identificar padrões visando reduzir a dimensionalidade dos dados com uma perda mínima de informação**. Uma possível aplicação seria o reconhecimento de padrões, onde queremos reduzir os custos computacionais e o erro da estimação de parâmetros pela redução da dimensionalidade do nosso espaço de atributos extraindo um subespaço que descreve os nosso dados "de forma satisfatória". **A redução de dimensionalidade se torna importante quando temos um número de atributos significativamente maior que o número de amostras de treinamento**.
Nós aplicamos o PCA para projetar todos os nossos dados (sem rótulos de classe) em um subespaço diferente, procurando encontrar os eixos com a máxima variância onde os dados são mais distribuídos. A questão principal é: **"Qual o subespaço que representa *bem* os nossos dados?"**.
**Primeiramente, calculamos os autovetores (componentes principais) dos nossos dados e organizamos em uma matriz de projeção. Cada autovetor (*eigenvector*) é associada a um autovalor (*eigenvalue*) que pode ser interpretado como o "tamanho" ou "magnitude" do autovetor correspondente**. Em geral, consideramos apenas o autovalores que tem uma magnitude significativamente maior que os outros e desconsideramos os autopares (autovetores-autovalores) que consideramos *menos informativos*.
Se observamos que todos os autovalores tem uma magnitude similar, isso pode ser um bom indicador que nossos dados já estão em um *bom* subespaço. Por outro lado, **se alguns autovalores tem a magnitude muito maior que a dos outros, devemos escolher seus autovetores já que eles contém mais informação sobre a distribuição dos nossos dados**. Da mesma forma, autovalores próximos a zero são menos informativos e devemos desconsiderá-los na construção do nosso subespaço.
Em geral, a aplicação do PCA envolve os seguintes passos:
1. Padronização dos dados
2. Obtenção dos autovetores e autovalores através da:
- Matriz de Covariância; ou
- Matriz de Correlação; ou
- *Singular Vector Decomposition*
3. Construção da matriz de projeção a partir dos autovetores selecionados
4. Transformação dos dados originais X via a matriz de projeção para obtenção do subespaço Y
## 1.1 PCA vs LDA
Ambos PCA e LDA (*Linear Discrimant Analysis*) são métodos de transformação linear. Por uma lado, o PCA fornece as direções (autovetores ou componentes principais) que maximiza a variância dos dados, enquanto o LDA visa as direções que maximizam a separação (ou discriminação) entre classes diferentes. Maximizar a variância, no caso do PCA, também significa reduzir a perda de informação, que é representada pela soma das distâncias de projeção dos dados nos eixos dos componentes principais.
Enquanto o PCA projeta os dados em um subespaço diferente, o LDA tenta determinar um subespaço adequado para distinguir os padrões pertencentes as classes diferentes.
<img src="images/PCAvsLDA.png" width=600>
## 1.2 Autovetores e autovalores
Os autovetores e autovalores de uma matriz de covariância (ou correlação) representam a base do PCA: os autovetores (componentes principais) determinam a direção do novo espaço de atributos, e os autovalores determinam sua magnitude. Em outras palavras, os autovalores explicam a variância dos dados ao longo dos novos eixos de atributos.
### 1.2.1 Matriz de Covariância
A abordagem clássica do PCA calcula a matriz de covariância, onde cada elemento representa a covariância entre dois atributos. A covariância entre dois atributos é calculada da seguinte forma:
$$\sigma_{jk} = \frac{1}{n-1}\sum_{i=1}^N(x_{ij}-\overline{x}_j)(x_{ik}-\overline{x}_k)$$
Que podemos simplificar na forma vetorial através da fórmula:
$$S=\frac{1}{n-1}((x-\overline{x})^T(x-\overline{x}))$$
onde $\overline{x}$ é um vetor d-dimensional onde cada valor representa a média de cada atributo, e $n$ representa o número de atributos por amostra. Vale ressaltar ainda que x é um vetor onde cada amostra está organizada em linhas e cada coluna representa um atributo. Caso se tenha um vetor onde as amostras estão organizadas em colunas e cada linha representa um atributo, a transposta passa para o segundo elemento da multiplicação.
Na prática, o resultado da matriz de covariância representa basicamente a seguinte estrutura:
$$\begin{bmatrix}var(1) & cov(1,2) & cov(1,3) & cov(1,4)
\\ cov(1,2) & var(2) & cov(2,3) & cov(2,4)
\\ cov(1,3) & cov(2,3) & var(3) & cov(3,4)
\\ cov(1,4) & cov(2,4) & cov(3,4) & var(4)
\end{bmatrix}$$
Onde a diagonal principal representa a variância em cada dimensão e os demais elementos são a covariância entre cada par de dimensões.
Para se calcular os autovalores e autovetores, só precisamos chamar a função *np.linalg.eig*, onde cada autovetor estará representado por uma coluna.
> Uma propriedade interessante da matriz de covariância é que **a soma da diagonal principal da matriz (variância para cada dimensão) é igual a soma dos autovalores**.
### 1.2.2 Matriz de Correlação
Outra maneira de calcular os autovalores e autovetores é utilizando a matriz de correlação. Apesar das matrizes serem diferentes, elas vão resultar nos mesmos autovalores e autovetores (mostrado mais a frente) já que a matriz de correlação é dada pela normalização da matriz de covariância.
$$corr(x,y) = \frac{cov(x,y)}{\sigma_x \sigma_y}$$
### 1.2.3 Singular Vector Decomposition
Apesar da autodecomposição (cálculo dos autovetores e autovalores) efetuada pelas matriz de covariância ou correlação ser mais intuitiva, a maior parte das implementações do PCA executam a *Singular Vector Decomposition* (SVD) para melhorar o desempenho computacional. Para calcular a SVD, podemos utilizar a biblioteca numpy, através do método *np.linalg.svd*.
Note que a autodecomposição resulta nos mesmos autovalores e autovetores utilizando qualquer uma das matrizes abaixo:
- Matriz de covariânca após a padronização dos dados
- Matriz de correlação
- Matriz de correlação após a padronização dos dados
Mas qual a relação entre a SVD e o PCA? Dado que a matriz de covariância $C = \frac{X^TX}{n-1}$ é uma matriz simétrica, ela pode ser diagonalizada da seguinte forma:
$$C = VLV^T$$
onde $V$ é a matriz de autovetores (cada coluna é um autovetor) e $L$ é a matriz diagonal com os autovalores $\lambda_i$ na ordem decrescente na diagonal. Se executarmos o SVD em X, nós obtemos a seguinte decomposição:
$$X = USV^T$$
onde $U$ é a matriz unitária e $S$ é a matriz diagonal de *singular values* $s_i$. A partir disso, pode-se calcular que:
$$C = VSU^TUSV^T = V\frac{S^2}{n-1}V^T$$
Isso significa que os *right singular vectors* V são as *principal directions* e que os *singular values* estão relacionados aos autovalores da matriz de covariância via $\lambda_i = \frac{s_i^2}{n-1}$. Os componentes principais são dados por $XV = USV^TV = US$
Resumindo:
1. Se $X = USV^T$, então as colunas de V são as direções/eixos principais;
2. As colunas de $US$ são os componentes principais;
3. *Singular values* estão relacionados aos autovalores da matriz de covariância via $\lambda_i = \frac{s_i^2}{n-1}$;
4. Scores padronizados (*standardized*) são dados pelas colunas de $\sqrt{n-1}U$ e *loadings* são dados pelas colunas de $\frac{VS}{\sqrt{n-1}}$. Veja [este link](https://stats.stackexchange.com/questions/125684) e [este](https://stats.stackexchange.com/questions/143905) para entender as diferenças entre *loadings* e *principal directions*;
5. As fórmulas acima só são válidas se $X$ está centralizado, ou seja, somente quando a matriz de covariância é igual a $\frac{X^TX}{n-1}$;
6. As proposições acima estão corretas somente quando $X$ for representado por uma matriz onde as linhas são amostras e as colunas são atributos. Caso contrário, $U$ e $V$ tem interpretações contrárias. Isto é, $U, V = V, U$;
7. Para reduzir a dimensionalidade com o PCA baseado no SVD, selecione as *k*-ésimas primeiras colunas de U, e $k\times k$ parte superior de S. O produto $U_kS_k$ é a matriz $n \times k$ necessária para conter os primeiros $k$ PCs.
8. Para reconstruir os dados originais a partir dos primeiros $k$ PCs, multiplicá-los pelo eixos principais correspondentes $V_k^T$ produz a matriz $X_k = U_kS_kV_k^T$ que tem o tamanho original $n \times p$. Essa forma gera a matriz reconstruída com o menor erro de reconstrução possível dos dados originais. [Veja esse link](https://stats.stackexchange.com/questions/130721);
9. Estritamente falando, $U$ é de tamanho $n \times n$ e $V$ é de tamanho $p \times p$. Entretanto, se $n > p$ então as últimas $n-p$ colunas de $U$ são arbitrárias (e as linhas correspondentes de $S$ são constantes e iguais a zero).
### 1.2.4 Verificação dos autovetores e autovalores
Para verificar se os autovetores e autovalores calculados na autodecomposição estão corretos, devemos verificar se eles satisfazem a equação para cada autovetor e autovalor correspondente:
$$\Sigma \overrightarrow{v} = \lambda \overrightarrow{v}$$
onde:
$$\Sigma = Matriz\,de\,Covariância$$
$$\overrightarrow{v} = autovetor$$
$$\lambda = autovalor$$
### 1.2.5 Escolha dos autovetores e autovalores
Como dito, o objetivo típico do PCA é reduzir a dimensionalidade dos dados pela projeção em um subespaço menor, onde os autovetores formam os eixos. Entretando, os autovetores definem somente as direções dos novos eixos, já que todos eles tem tamanho 1. Logo, para decidir qual(is) autovetor(es) podemos descartar sem perder muita informação na construção do nosso subespaço, precisamos verificar os autovalores correspondentes. **Os autovetores com os maiores valores são os que contém mais informação sobre a distribuição dos nossos dados**. Esse são os autovetores que queremos.
Para fazer isso, devemos ordenar os autovalores em ordem decrescente para escolher o top k autovetores.
### 1.2.6 Cálculo da Informação
Após ordenar os autovalores, o próximo passo é **definir quantos componentes principais serão escolhidos para o nosso novo subespaço**. Para fazer isso, podemos utilizar o método da *variância explicada*, que calcula quanto de informação (variância) é atribuida a cada componente principal.
## 1. 3 Matriz de Projeção
Na prática, a matriz de projeção nada mais é que os top k autovetores concatenados. Portanto, se queremos reduzir o nosso espaço 4-dimensional para um espaço 2-dimensional, devemos escolher os 2 autovetores com os 2 maiores autovalores para construir nossa matriz W (d$\times$k).
## 1.4 Projeção no novo subespaço
O último passo do PCA é utilizar a nossa matriz de projeção dimensional W (4x2, onde cada coluna representa um autovetor) para transformar nossas amostras em um novo subespaço. Para isso, basta aplicar a seguinte equação:
$$S = (X-\mu_X) \times W$$
Onde cada linha em S contém os pesos para cada atributo (coluna da matriz) no novo subespaço.
A título de curiosidade, repare que se W representasse todos os autovetores - e não somente os escolhidos -, poderíamos recompor cada instância em X pela seguinte fórmula:
$$X = (S \times W^{-1}) + \mu_X$$
Novamente, cada linha em S representa os pesos para cada atributo, só que dessa vez seria possível representar X pela soma de cada autovetor multiplicado por um peso.
## 1.5 Recomendações
- Sempre normalize os atributos antes de aplicar o PCA (StandarScaler);
- Lembre-se de armazenar a média para efetuar a ida e volta;
- Não aplique o PCA após outros algoritmos de seleção de atributos ([fonte](https://www.quora.com/Should-I-apply-PCA-before-or-after-feature-selection));
- O número de componentes principais que você quer manter deve ser escolhido através da análise entre o número de componentes e a precisão do sistema. Nem sempre mais componentes principais ocasionam em melhor precisão!
# 2. Dados
```
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['class'] = iris.target
df
df.describe()
x = df.drop(labels='class', axis=1).values
y = df['class'].values
print(x.shape, y.shape)
```
# 3. Implementação
```
class MyPCACov():
def __init__(self, n_components=None):
self.n_components = n_components
self.eigen_values = None
self.eigen_vectors = None
def fit(self, x):
self.n_components = x.shape[1] if self.n_components is None else self.n_components
self.mean_ = np.mean(x, axis=0)
cov_matrix = np.cov(x - self.mean_, rowvar=False)
self.eigen_values, self.eigen_vectors = np.linalg.eig(cov_matrix)
self.eigen_vectors = self.eigen_vectors.T
self.sorted_components_ = np.argsort(self.eigen_values)[::-1]
self.projection_matrix_ = self.eigen_vectors[self.sorted_components_[:self.n_components]]
self.explained_variance_ = self.eigen_values[self.sorted_components_]
self.explained_variance_ratio_ = self.explained_variance_ / self.eigen_values.sum()
def transform(self, x):
return np.dot(x - self.mean_, self.projection_matrix_.T)
def inverse_transform(self, x):
return np.dot(x, self.projection_matrix_) + self.mean_
class MyPCASVD():
def __init__(self, n_components=None):
self.n_components = n_components
self.eigen_values = None
self.eigen_vectors = None
def fit(self, x):
self.n_components = x.shape[1] if self.n_components is None else self.n_components
self.mean_ = np.mean(x, axis=0)
U, s, Vt = np.linalg.svd(x - self.mean_, full_matrices=False) # a matriz s já retorna ordenada
# S = np.diag(s)
self.eigen_vectors = Vt
self.eigen_values = s
self.projection_matrix = self.eigen_vectors[:self.n_components]
self.explained_variance_ = (self.eigen_values ** 2) / (x.shape[0] - 1)
self.explained_variance_ratio_ = self.explained_variance_ / self.explained_variance_.sum()
def transform(self, x):
return np.dot(x - self.mean_, self.projection_matrix.T)
def inverse_transform(self, x):
return np.dot(x, self.projection_matrix) + self.mean_
```
# 4. Teste
```
std = StandardScaler()
x_std = StandardScaler().fit_transform(x)
```
### PCA implementado pela matriz de covariância
```
pca_cov = MyPCACov(n_components=2)
pca_cov.fit(x_std)
print('Autovetores: \n', pca_cov.eigen_vectors)
print('Autovalores: \n', pca_cov.eigen_values)
print('Variância explicada: \n', pca_cov.explained_variance_)
print('Variância explicada (ratio): \n', pca_cov.explained_variance_ratio_)
print('Componentes ordenados: \n', pca_cov.sorted_components_)
x_std_proj = pca_cov.transform(x_std)
plt.figure()
plt.scatter(x_std_proj[:, 0], x_std_proj[:, 1], c=y)
x_std_back = pca_cov.inverse_transform(x_std_proj)
print(x_std[:5])
print(x_std_back[:5])
```
### PCA implementado pela SVD
```
pca_svd = MyPCASVD(n_components=2)
pca_svd.fit(x_std)
print('Autovetores: \n', pca_svd.eigen_vectors)
print('Autovalores: \n', pca_svd.eigen_values)
print('Variância explicada: \n', pca_svd.explained_variance_)
print('Variância explicada (ratio): \n', pca_svd.explained_variance_ratio_)
x_std_proj = pca_svd.transform(x_std)
plt.figure()
plt.scatter(x_std_proj[:, 0], x_std_proj[:, 1], c=y)
x_std_back = pca_svd.inverse_transform(x_std_proj)
print(x_std[:5])
print(x_std_back[:5])
```
## Comparação com o Scikit-learn
```
pca_sk = PCA(n_components=2)
pca_sk.fit(x_std)
print('Autovetores: \n', pca_sk.components_)
print('Autovalores: \n', pca_sk.singular_values_)
print('Variância explicada: \n', pca_sk.explained_variance_)
print('Variância explicada (ratio): \n', pca_sk.explained_variance_ratio_)
x_std_proj_sk = pca_sk.transform(x_std)
plt.figure()
plt.scatter(x_std_proj_sk[:, 0], x_std_proj_sk[:, 1], c=y)
x_std_back_sk = pca_sk.inverse_transform(x_std_proj_sk)
print(x_std[:5])
print(x_std_back_sk[:5])
```
### Observação sobre a implementação do Scikit-learn
Por algum motivo (que não sei qual), a [implementação do scikit-learn](https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/decomposition/pca.py) inverte os sinais de alguns valores na matriz de autovetores. Na implementação, as matrizes $U$ e $V$ são passada para um método ```svd_flip``` (implementada [nesse arquivo](https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/utils/extmath.py)):
```py
U, V = svd_flip(U[:, ::-1], V[::-1])
```
Repare que isso muda apenas os dados projetados. No gráfico, isso inverte os eixos correspondentes apenas. No entanto, os **autovalores**, a ```explained_variance```, ```explained_variance_ratio``` e os dados reprojetados ao espaço original são exatamente iguais.
## 5. Referências
- [Antigo notebook do PCA com explicações passo-a-passo](https://github.com/arnaldog12/Machine_Learning/blob/62b628bd3c37ec2fa52e349f38da24751ef67313/PCA.ipynb)
- [Principal Component Analysis in Python](https://plot.ly/ipython-notebooks/principal-component-analysis/)
- [Implementing a Principal Component Analysis (PCA)](https://sebastianraschka.com/Articles/2014_pca_step_by_step.html)
- [Relationship between SVD and PCA. How to use SVD to perform PCA?](https://stats.stackexchange.com/questions/134282/relationship-between-svd-and-pca-how-to-use-svd-to-perform-pca)
- [How to reverse PCA and reconstruct original variables from several principal components?](https://stats.stackexchange.com/questions/229092/how-to-reverse-pca-and-reconstruct-original-variables-from-several-principal-com)
- [Everything you did and didn't know about PCA](http://alexhwilliams.info/itsneuronalblog/2016/03/27/pca/)
- [Unpacking (** PCA )](https://towardsdatascience.com/unpacking-pca-b5ea8bec6aa5)
| true |
code
| 0.667107 | null | null | null | null |
|
# Predictions with Pyro + GPyTorch (High-Level Interface)
## Overview
In this example, we will give an overview of the high-level Pyro-GPyTorch integration - designed for predictive models.
This will introduce you to the key GPyTorch objects that play with Pyro. Here are the key benefits of the integration:
**Pyro provides:**
- The engines for performing approximate inference or sampling
- The ability to define additional latent variables
**GPyTorch provides:**
- A library of kernels/means/likelihoods
- Mechanisms for efficient GP computations
```
import math
import torch
import pyro
import tqdm
import gpytorch
from matplotlib import pyplot as plt
%matplotlib inline
```
In this example, we will be doing simple variational regression to learn a monotonic function. This example is doing the exact same thing as [GPyTorch's native approximate inference](../04_Variational_and_Approximate_GPs/SVGP_Regression_CUDA.ipynb), except we're now using Pyro's variational inference engine.
In general - if this was your dataset, you'd be better off using GPyTorch's native exact or approximate GPs.
(We're just using a simple example to introduce you to the GPyTorch/Pyro integration).
```
train_x = torch.linspace(0., 1., 21)
train_y = torch.pow(train_x, 2).mul_(3.7)
train_y = train_y.div_(train_y.max())
train_y += torch.randn_like(train_y).mul_(0.02)
fig, ax = plt.subplots(1, 1, figsize=(3, 2))
ax.plot(train_x.numpy(), train_y.numpy(), 'bo')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(['Training data'])
```
## The PyroGP model
In order to use Pyro with GPyTorch, your model must inherit from `gpytorch.models.PyroGP` (rather than `gpytorch.modelks.ApproximateGP`). The `PyroGP` extends the `ApproximateGP` class and differs in a few key ways:
- It adds the `model` and `guide` functions which are used by Pyro's inference engine.
- It's constructor requires two additional arguments beyond the variational strategy:
- `likelihood` - the model's likelihood
- `num_data` - the total amount of training data (required for minibatch SVI training)
- `name_prefix` - a unique identifier for the model
```
class PVGPRegressionModel(gpytorch.models.PyroGP):
def __init__(self, train_x, train_y, likelihood):
# Define all the variational stuff
variational_distribution = gpytorch.variational.CholeskyVariationalDistribution(
num_inducing_points=train_y.numel(),
)
variational_strategy = gpytorch.variational.VariationalStrategy(
self, train_x, variational_distribution
)
# Standard initializtation
super(PVGPRegressionModel, self).__init__(
variational_strategy,
likelihood,
num_data=train_y.numel(),
name_prefix="simple_regression_model"
)
self.likelihood = likelihood
# Mean, covar
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(
gpytorch.kernels.MaternKernel(nu=1.5)
)
def forward(self, x):
mean = self.mean_module(x) # Returns an n_data vec
covar = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean, covar)
model = PVGPRegressionModel(train_x, train_y, gpytorch.likelihoods.GaussianLikelihood())
```
## Performing inference with Pyro
Unlike all the other examples in this library, `PyroGP` models use Pyro's inference and optimization classes (rather than the classes provided by PyTorch).
If you are unfamiliar with Pyro's inference tools, we recommend checking out the [Pyro SVI tutorial](http://pyro.ai/examples/svi_part_i.html).
```
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
num_iter = 2 if smoke_test else 200
num_particles = 1 if smoke_test else 256
def train(lr=0.01):
optimizer = pyro.optim.Adam({"lr": 0.1})
elbo = pyro.infer.Trace_ELBO(num_particles=num_particles, vectorize_particles=True, retain_graph=True)
svi = pyro.infer.SVI(model.model, model.guide, optimizer, elbo)
model.train()
iterator = tqdm.tqdm_notebook(range(num_iter))
for i in iterator:
model.zero_grad()
loss = svi.step(train_x, train_y)
iterator.set_postfix(loss=loss)
%time train()
```
In this example, we are only performing inference over the GP latent function (and its associated hyperparameters). In later examples, we will see that this basic loop also performs inference over any additional latent variables that we define.
## Making predictions
For some problems, we simply want to use Pyro to perform inference over latent variables. However, we can also use the models' (approximate) predictive posterior distribution. Making predictions with a PyroGP model is exactly the same as for standard GPyTorch models.
```
fig, ax = plt.subplots(1, 1, figsize=(4, 3))
train_data, = ax.plot(train_x.cpu().numpy(), train_y.cpu().numpy(), 'bo')
model.eval()
with torch.no_grad():
output = model.likelihood(model(train_x))
mean = output.mean
lower, upper = output.confidence_region()
line, = ax.plot(train_x.cpu().numpy(), mean.detach().cpu().numpy())
ax.fill_between(train_x.cpu().numpy(), lower.detach().cpu().numpy(),
upper.detach().cpu().numpy(), color=line.get_color(), alpha=0.5)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend([train_data, line], ['Train data', 'Prediction'])
```
## Next steps
This was a pretty boring example, and it wasn't really all that different from GPyTorch's native SVGP implementation! The real power of the Pyro integration comes when we have additional latent variables to infer over. We will see an example of this in the [next example](./Clustered_Multitask_GP_Regression.ipynb), which learns a clustering over multiple time series using multitask GPs and Pyro.
| true |
code
| 0.781028 | null | null | null | null |
|
# Module 10 - Regression Algorithms - Linear Regression
Welcome to Machine Learning (ML) in Python!
We're going to use a dataset about vehicles and their respective miles per gallon (mpg) to explore the relationships between variables.
The first thing to be familiar with is the data preprocessing workflow. Data needs to be prepared in order for us to successfully use it in ML. This is where a lot of the actual work is going to take place!
I'm going to use this dataset for each of the regression algorithms, so we can see how each one differs.
The next notebooks with the dataset will be:
- Linear Regression w/ Transformed Target (Logarithmic)
- Ridge Regression with Standardized Inputs
- Ridge and LASSO Regression with Polynomial Features
These four notebooks are designed to be a part of a series, with this one being the first.
We're going to start by importing our usual packages and then some IPython settings to get more output:
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
```
## Part A: Data Exploration
The first thing to do is import and explore our mpg dataset!
There's a few things to note in the dataset description: na values are denoted by `?` and column names are in a separate doc.
I added the column names so we don't have to worry about them:
```
loc = "https://raw.githubusercontent.com/mhall-simon/python/main/data/car-mpg/auto-mpg.data"
df = pd.read_csv(loc, sep="\s+", header=None, na_values="?")
cols = {0:"mpg", 1:"cylinders", 2:"displacement", 3:"horsepower", 4:"weight", 5:"accel", 6:"year", 7:"origin", 8:"model"}
df = df.rename(columns=cols)
df.head(15)
```
When starting, it's always good to have a look at how complete our data set is.
Let's see just how many na values were brought into the dataset per column:
```
df.isna().sum()
```
We have 6 missing values for horsepower!
A safe assumption for imputing missing values is to insert the column mean, let's do that! (Feature engineering is somewhere that we can go into this more in depth.)
*Note:* Imputing values is something that's not always objective, as it introduces some biases. We could also drop those 6 rows out of our dataset, however, I think imputing average hp isn't too serious of an issue.
```
df = df.replace(np.nan, df.horsepower.mean())
df.isna().sum()
```
Now, there's no more missing values!
Let's get some descriptive statistics running for our numerical columns (non-numerical are automatically dropped):
```
df.describe()
```
Another thing we can look at is the number of unique car models in the dataset:
```
df.nunique(axis=0)
```
For the ML analysis, there's too many models to worry about, so we're going to have them drop off the dataset! We're trying to predict mpg, and with our data the model name will have practically no predictive power!
One Hot Encoding the makes/models would make the dataset have almost more columns than rows!
```
df = df.drop("model", axis=1)
df.head()
```
### Train-Test Split
We're getting closer to starting our analysis! The first major consideration is the train/test split, where we reserve a chunk of our dataset to validate the model.
Remember, no peeking into the results with testing to train our model! That'll introduce a bias!
Let's separate our data into X and y, and then run the split:
```
X = df.iloc[:,1:]
y = df.iloc[:,0]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=97)
```
Another important thing to look at is the distributions of continuous variables and their pairwise relationships.
Seaborn has a really cool pairplot function that allows us to easily visualize this automatically! We just need to pass in columns of continuous variables.
Note: This is a marginal dependence, and does not keep all other variables fixed! We should only analyze this after our split!
```
train_dataset = X_train.copy()
train_dataset.insert(0, "mpg", y_train)
sns.pairplot(train_dataset[['mpg','displacement','horsepower','weight','accel']], kind='reg', diag_kind='kde')
```
When looking at this, there's two things to takeaway:
1. `mpg` is close to being normal, but there's a long tail. This means we may be better taking the log of mpg when running our analysis - something to explore in the next notebook.
2. Some relationships are not quite linear! We will work on this more in the following notebooks!
Let's now get into the ML aspects!
## Part B: Data Preprocessing & Pipeline
There's a lot of online tutorials that show the SKLearn models and how to call them in one line, and not much else.
A really powerful tool is to leverage the pipelines, as you can adjsut easily on the fly and not rewrite too much code!
Pipelines also reduce the potential for errors, as we only define preprocessing steps, and don't actually need to manipulate our tables. When we transform the target with a log later, we also don't need to worry about switching between log and normal values! It'll be handled for us.
It's also not as bad as it seems!
The first main step is to separate our data into:
- categorical columns that need to be one-hot encoded
- continuous columns (no changes - for now)
- other processing subsets (none in these examples, but binary columns would be handled a bit differently.)
- label encoding the response (y) variable when we get into classification models
Let's get right to it! We can split apart the explanatory column names into the two categories with basic lists:
```
categorical_columns = ['cylinders','origin','year']
numerical_columns = ['displacement','horsepower','weight','accel']
```
*Discussion:* Why is Year Categorical, even though it's a numerical year?
In Linear Regression, the year 70 (1970) would appear to be a factor of 80 (1980) by about 9/10ths, and it would be scaled that way. This would not make sense, as we expect only marginal increases in mpg year-over-year. To prevent a relationship like this, we're going to one-hot encode the years into categories.
Now, let's put together our preprocessing pipeline.
We'll need to:
1. OneHot Encode Categorical
2. Leave Continuous Alone
Let's build our preprocessor:
```
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import make_column_transformer
preprocessor = make_column_transformer((OneHotEncoder(drop="first"), categorical_columns), remainder="passthrough")
```
Why are we dropping the first category in each categorical column?
Our regression can imply the first one with zeros for all the encoded variables, and by not including it we are preventing colinearity from being introduced!
A potential issue that can arise is when you encounter new labels in the test/validation sets that are not one-hot encoded. Right now, this would toss an error if it happens! Later notebooks will go into how to handle these errors.
Now, let's build the pipeline:
```
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
model = make_pipeline(preprocessor, LinearRegression())
```
And now we can easily train our model and preprocess our data all in one step:
```
model.fit(X_train, y_train)
```
Before we start evaluating the model, I'll show you some useful features with the pipeline:
1. View Named Steps
```
model.named_steps
```
2. View Coefficients and Intercept (Expanded Later)
```
model.named_steps['linearregression'].coef_
model.named_steps['linearregression'].intercept_
```
3. Generate Predictions
*Viewing First 10*
```
model.predict(X_train)[:10]
```
## Part C: Evaluating Machine Learning Model
So, now we have an ML model, but how do we know if it's good?
Also, what's our criteria for good?
This changes depending upon what you're doing!
Let's bring in some metrics, and look at our "in sample" performance. This is the performance valuation in sample, without looking at any test data yet!
- $r^2$: coefficient of determination
- mean absolute error
- mean squared error
Let's generate our in-sample predictions based upon the model:
```
y_pred_in = model.predict(X_train)
```
And now let's generate some metrics:
This compares the training (truth) values, to the ones predicted by the line of best fit.
```
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
r2_score(y_train, y_pred_in)
mean_squared_error(y_train, y_pred_in)
mean_absolute_error(y_train, y_pred_in)
```
We're explaining about 87.5% of the variation in our in-sample dataset! That's pretty good, but will it hold when analyzing out of sample?
Also, we now know that our average absolute error is 2.09 mpg! That's not too bad, considering the range of the dataset and STD from the data:
```
y_train.std()
y_train.max() - y_train.min()
```
Let's now visualize our predictions! As a note, we want all of our datapoints to be along the line!
*Tip:* If you're reproducing this graph, ensure that the diagonal goes through the origin of the plot. The red line is setup to draw from corner to corner, and if you move your axes this may not work out!
```
fig, ax = plt.subplots(figsize=(5,5))
plt.scatter(y_train, y_pred_in)
ax.plot([0,1],[0,1], transform=ax.transAxes, ls="--", c="red")
plt.xlim([0,50])
plt.ylim([0,50])
plt.ylabel("Model Predictions")
plt.xlabel("Truth Values")
plt.title("In Sample Performance")
plt.show();
```
Our predictions are pretty good!
A few things to note:
- It's a really good fit, but it appears that there's a slight curve to this dataset.
- This is still in sample (we trained the model on this data)
- If we're making predictions, what regions are we confident in?
I think average mpg we'll be accurate, however, at the edges we're missing some of the trend.
Let's plot our residual error to see the shape:
```
plt.scatter(y_train, y_train-y_pred_in)
plt.xlabel("Truth Values - In Sample")
plt.ylabel("Residual Error")
plt.xlim([5,50])
plt.plot([5,50],[0,0], color='black', alpha=0.6)
plt.show();
```
Our errors definitely have curvature in them! We'll improve upon this in the next module!
For now...
Let's start looking at the coefficients in our model while it's simple.
We can grab coefficients out of the preprocessor to ensure that the coefficients line up with labels.
It'll always be in order of the preprocessor, so we can first fetch the feature names from the one hot encoded, and then just concatenate our numerical columns as there were no changes!
```
feature_names = (model.named_steps['columntransformer']
.named_transformers_['onehotencoder']
.get_feature_names(input_features=categorical_columns))
feature_names = np.concatenate([feature_names, numerical_columns])
coefs = pd.DataFrame(
model.named_steps['linearregression'].coef_,
columns=['Coefficients'],
index=feature_names
)
coefs
```
Let's plot the coefficients to see if there's anything we can learn out of it!
```
coefs.Coefficients.plot(kind='barh', figsize=(9,7))
plt.title("Unscaled Linear Regression Coefficients")
plt.show();
```
Woah, it looks like weight in unimportant at first glance, even though it would probably impact mpg quite a bit!
A word of caution! We just can't compare the coefficients, as they're in a different scale!
If we scale them with their standard deviation, then we can compare them. However, some meaning is lost!
Currently, the coefficient `-0.034440` for `horsepower` means that while holding all else equal, increasing the horsepower by 1 unit decreases mpg by about 0.034 mpg!
So, if we add 100 hp to the car, mileage decreases by about 3.4 mpg if we hold all else equal!
Let's scale these coefficients to compare them better! Just keep in mind that the 1hp:-0.34mpg relationship will no longer be interpretable from the scaled coefficients. But, we will be able to compare between coefficients.
Using the model pipeline, we can easily transform our data using the built in transformer, and then take the std:
`model.named_steps['columntransformer'].transform(DATASET)` is how we can use the transformer we built above.
When training the model, this dataset transformation happened all behind the scenes!! However, we can reproduce it with our training sample to work with it manually:
**NOTE:** The pipeline transformation is better than manual, because we know for certain the order of the columns that are being outputted. We fetched them above! The preprocessor in this instance returned a SciPy sparse matrix, which we can import with a new DataFrame constructor:
```
X_train_preprocessed = pd.DataFrame.sparse.from_spmatrix(
model.named_steps['columntransformer'].transform(X_train),
columns=feature_names
)
X_train_preprocessed.head(10)
```
By plotting the standard deviations, we can see for certain that the coeffs are definitely in a different scale!
Weight varies in the thousands, while acceleration is usually around 10-20 seconds!!
```
X_train_preprocessed.std(axis=0).plot(kind='barh', figsize=(9,7))
plt.title("Features Std Dev")
plt.show();
```
As you can probably see, the standard deviation of weight is far higher than any other variable!
This makes it impossible to compare.
Now, let's scale everything.
This scale works because very large continuous variables have a large standard deviation, but very small coefficients, which brings them down. The opposite is true for very small continuous variables for standard deviations, their coefficient is usually much larger. By multiplying the two together, we're bringing everything in towrads the middle, and with the same units of measurement.
```
coefs['coefScaled'] = coefs.Coefficients * X_train_preprocessed.std(axis=0)
coefs
```
Now, let's plot the scaled coefs:
```
coefs.coefScaled.plot(kind="barh", figsize=(9,7))
plt.title("Scaled Linear Coefficients")
plt.show();
```
Earlier, weight had almost no impact on the model at first glance! Now, we can see that it's the most important explanatory variable for mpg.
Let's now do our final validations for the model by bringing in the test data!!
The first is going to be done using the test (reserved) dataset, which we can make predictions with easily:
```
y_pred_out = model.predict(X_test)
```
And now let's generate a small DataFrame to compare metrics from in sample and out of sample!
Out of sample performance is usually worse, it's usually a question of how much!
```
metrics = pd.DataFrame(index=['r2','mse','mae'],columns=['in','out'])
metrics['in'] = (r2_score(y_train, y_pred_in), mean_squared_error(y_train, y_pred_in), mean_absolute_error(y_train, y_pred_in))
metrics['out'] = (r2_score(y_test, y_pred_out), mean_squared_error(y_test, y_pred_out), mean_absolute_error(y_test, y_pred_out))
metrics
```
When looking at the data, we see that the $r^2$ value decreased slightly from 0.875 to 0.854! This is still fairly significant!
And let's do a similar graph for out of sample performance:
```
fig, ax = plt.subplots(figsize=(5,5))
plt.scatter(y_test, y_pred_out)
ax.plot([0,1],[0,1], transform=ax.transAxes, ls="--", c="red")
plt.xlim([0,50])
plt.ylim([0,50])
plt.ylabel("Model Predictions")
plt.xlabel("Truth Values")
plt.title("Out of Sample Performance")
plt.show();
```
We're doing pretty good! There's stil some curvature that we'll work on fixing in the next notebooks.
Let's plot our residuals one more time:
```
plt.scatter(y_test, y_test-y_pred_out)
plt.xlabel("Truth Values - Out of Sample")
plt.ylabel("Residual Error")
plt.xlim([5,50])
plt.plot([5,50],[0,0], color='black', alpha=0.6)
plt.show();
```
Our model is pretty good, except for when we go above 32-ish mpg. Our model is predicting values far too high.
We'll solve this in a later notebook.
Another key question for ML is...
How do we know if the performance is due to just our sample selected? How much would our model change depending upon the sample selected?
We can solve for this using cross validation!
Cross validation takes different samples from our dataset, runs the regression, and then outputs the results!
We can easily cut the dataset into chunks and see how it behaves.
We're going to plot the distributions of coefficients throughout the folds to see how stable the model is:
```
from sklearn.model_selection import cross_validate
from sklearn.model_selection import RepeatedKFold
# Part 1: Defining Cross Validation Model
cv_model = cross_validate(
model, X, y, cv=RepeatedKFold(n_splits=5, n_repeats=5),
return_estimator=True, n_jobs=-1
)
# Part 2: Analyzing Each Model's Coefficients, and Setting Them In DataFrame:
cv_coefs = pd.DataFrame(
[est.named_steps['linearregression'].coef_ * X_train_preprocessed.std(axis=0) for est in cv_model['estimator']],
columns=feature_names
)
# Part 3: Plotting the Distribution of Coefficients
plt.figure(figsize=(9,7))
sns.stripplot(data=cv_coefs, orient='h', color='k', alpha=0.5)
sns.boxplot(data=cv_coefs, orient='h', color='cyan', saturation=0.5)
plt.axvline(x=0, color='.5')
plt.xlabel('Coefficient importance')
plt.title('Coefficient importance and its variability')
plt.subplots_adjust(left=.3)
plt.show();
```
What are the takeaways from this plot?
Our model doesn't appear to be too sensitive to the splits in training and testing!
This is a signal that our model is robust, and we should have confidence that our findings weren't due to choosing a "good" sample!
If we saw a variable changing from -6 to +2, that would be a sign it is not stable!
Now, we're ready to start exploring the second notebook! Which starts working towards a fix in the curvature!
## Bonus Box: Easily Checking for Variable Colinearity
If we suspect two variables are colinear, we can easily check for it with the following code:
```
plt.scatter(cv_coefs['weight'], cv_coefs['displacement'])
plt.ylabel('Displacement coefficient')
plt.xlabel('Weight coefficient')
plt.grid(True)
plt.title('Co-variations of variables across folds');
```
These are not colinear across folds, which is good for the model!
If they *were* colinear across folds, it would look something like this:
<div>
<img src=https://github.com/mhall-simon/python/blob/main/data/screenshots/Screen%20Shot%202021-03-22%20at%206.38.12%20PM.png?raw=True width="400"/>
</div>
If you notice strong colinearlity, then one should be removed and you can run the model again!
| true |
code
| 0.683829 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/isaacmg/task-vt/blob/biobert_finetune/drug_treatment_extraction/notebooks/BioBERT_RE.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Finetuning BioBERT for RE
This is a fine-tuning notebook that we used to finetune BioBERT for relation classification (on our own data, GAD and Euadr) and then convert the resulting model checkpoint to PyTorch HuggingFace library for model inference. This was done for the vaccine and therapeutics task in order to identify drug treatment relations.
```
!git clone https://github.com/dmis-lab/biobert
from google.colab import auth
from datetime import datetime
auth.authenticate_user()
!pip install tensorflow==1.15
import os
os.chdir('biobert')
```
### Downloading data
```
!./download.sh
!fileid="1GJpGjQj6aZPV-EfbiQELpBkvlGtoKiyA"
!wget --load-cookies /tmp/cookies.txt "https://docs.google.com/uc?export=download&confirm=$(wget --quiet --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://docs.google.com/uc?export=download&id=1GJpGjQj6aZPV-EfbiQELpBkvlGtoKiyA' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=1GJpGjQj6aZPV-EfbiQELpBkvlGtoKiyA" -O biobert_w.tar.gz && rm -rf /tmp/cookies.txt
!tar -xvf biobert_w.tar.gz
%set_env RE_DIR datasets/RE/GAD/1
%set_env TASK_NAME=gad
%set_env OUTPUT_DIR=./re_outputs_1
%set_env BIOBERT_DIR=biobert_large
!python run_re.py --task_name=$TASK_NAME --do_train=true --do_eval=true --do_predict=true --vocab_file=$BIOBERT_DIR/vocab_cased_pubmed_pmc_30k.txt --bert_config_file=$BIOBERT_DIR/bert_config_bio_58k_large.json --init_checkpoint=$BIOBERT_DIR/bio_bert_large_1000k.ckpt.index --max_seq_length=128 --train_batch_size=32 --learning_rate=2e-5 --num_train_epochs=3.0 --do_lower_case=false --data_dir=$RE_DIR --output_dir=$OUTPUT_DIR
#Uncomment this if you want to temporarily stash weights on GCS also collect garbage
#!gsutil -m cp -r ./re_outputs_1/model.ckpt-0.data-00000-of-00001 gs://coronaviruspublicdata/new_data .
#import gc
#gc.collect()
```
### Converting the model to HuggingFace
```
!pip install transformers
import logging
import torch
logger = logging.getLogger('spam_application')
def load_tf_weights_in_bert(model, config, tf_checkpoint_path):
""" Load tf checkpoints in a pytorch model.
"""
try:
import re
import numpy as np
import tensorflow as tf
except ImportError:
logger.error(
"Loading a TensorFlow model in PyTorch, requires TensorFlow to be installed. Please see "
"https://www.tensorflow.org/install/ for installation instructions."
)
raise
tf_path = os.path.abspath(tf_checkpoint_path)
logger.info("Converting TensorFlow checkpoint from {}".format(tf_path))
# Load weights from TF model
init_vars = tf.train.list_variables(tf_path)
excluded = ['BERTAdam','_power','global_step']
init_vars = list(filter(lambda x:all([True if e not in x[0] else False for e in excluded]),init_vars))
names = []
arrays = []
for name, shape in init_vars:
logger.info("Loading TF weight {} with shape {}".format(name, shape))
array = tf.train.load_variable(tf_path, name)
names.append(name)
arrays.append(array)
print("A name",names)
for name, array in zip(names, arrays):
if name in ['output_weights', 'output_bias']:
name = 'classifier/' + name
name = name.split("/")
# if name in ['output_weights', 'output_bias']:
# name = 'classifier/' + name
# adam_v and adam_m are variables used in AdamWeightDecayOptimizer to calculated m and v
# which are not required for using pretrained model
if any(
n in ["adam_v", "adam_m", "AdamWeightDecayOptimizer", "AdamWeightDecayOptimizer_1", "global_step"]
for n in name
):
logger.info("Skipping {}".format("/".join(name)))
continue
pointer = model
# if name in ['output_weights' , 'output_bias']:
# name = 'classifier/' + name
for m_name in name:
print("model",m_name)
#print(scope_names)
if re.fullmatch(r"[A-Za-z]+_\d+", m_name):
scope_names = re.split(r"_(\d+)", m_name)
else:
scope_names = [m_name]
if scope_names[0] == "kernel" or scope_names[0] == "gamma":
print(scope_names)
pointer = getattr(pointer, "weight")
elif scope_names[0] == "output_bias" or scope_names[0] == "beta":
# elif scope_names[0] == "beta":
# print(scope_names)
pointer = getattr(pointer, "bias")
# elif scope_names[0] == "output_bias":
# print(scope_names)
# pointer = getattr(pointer, "cls")
elif scope_names[0] == "output_weights":
print(scope_names)
pointer = getattr(pointer, "weight")
elif scope_names[0] == "squad":
print(scope_names)
pointer = getattr(pointer, "classifier")
else:
try:
pointer = getattr(pointer, scope_names[0])
except AttributeError:
logger.info("Skipping {}".format("/".join(name)))
continue
if len(scope_names) >= 2:
num = int(scope_names[1])
pointer = pointer[num]
if m_name[-11:] == "_embeddings":
pointer = getattr(pointer, "weight")
elif m_name == "kernel":
array = np.transpose(array)
try:
assert pointer.shape == array.shape
except AssertionError as e:
e.args += (pointer.shape, array.shape)
raise
logger.info("Initialize PyTorch weight {}".format(name))
pointer.data = torch.from_numpy(array)
return model
from transformers import BertConfig, BertForSequenceClassification, BertForPreTraining
def convert_tf_checkpoint_to_pytorch(tf_checkpoint_path, bert_config_file, pytorch_dump_path):
# Initialise PyTorch model
config = BertConfig.from_json_file(bert_config_file)
print("Building PyTorch model from configuration: {}".format(str(config)))
config.num_labels = 2
model = BertForSequenceClassification(config)
#model = BertForSequenceClassification(config)
# Load "weights from tf checkpoint
load_tf_weights_in_bert(model, config, tf_checkpoint_path)
# Save pytorch-model
print("Save PyTorch model to {}".format(pytorch_dump_path))
model.save_pretrained(pytorch_dump_path)
return model
# Alternatevely you can download existing stashed data
#!gsutil cp -r gs://coronaviruspublicdata/re_outputs_1 .
import os
!mkdir pytorch_output_temp
model2 = convert_tf_checkpoint_to_pytorch("re_outputs_1", "biobert_large/bert_config_bio_58k_large.json", "pytorch_output_temp")
```
### Upload converted checkpoint and test inference
If everything goes smoothly we should be able to upload weights and use the converted model.
```
from transformers import BertTokenizer
tokenizer = BertTokenizer.from_pretrained('biobert_large/vocab_cased_pubmed_pmc_30k.txt')
model2.eval()
input_ids = torch.tensor(tokenizer.encode("Hello, my dog is cute", add_special_tokens=True)).unsqueeze(0) # Batch size 1
labels = torch.tensor([1]).unsqueeze(0) # Batch size 1
outputs = model2(input_ids)
outputs = model2(input_ids)
outputs
input_ids = torch.tensor(tokenizer.encode("All our results indicate that the presence of the @GENE$ genotype (++) in patients with structural @DISEASE$, severe left ventricular dysfunction and malignant ventricular arrhythmias increases the risk for these patients of hemodynamic collapse during these arrhythmias"))
outputs = model2(input_ids.unsqueeze(0))
outputs
values, indices = torch.max(outputs[0], 1, keepdim=False)
indices
```
**Lets refactor this into something nicer**
```
from transformers import BertConfig, BertForSequenceClassification, BertForPreTraining
from transformers import BertTokenizer
class InferSequenceClassifier(object):
def __init__(self, pytorch_model_path, token_path, add_special_tokens=False):
self.tokenizer = BertTokenizer.from_pretrained(token_path)
self.model = BertForSequenceClassification.from_pretrained(pytorch_model_path)
self.add_special_tokens = add_special_tokens
def make_prediction(self, text):
input_ids = torch.tensor(self.tokenizer.encode(text, add_special_tokens=self.add_special_tokens))
outputs = self.model(input_ids.unsqueeze(0))
print(outputs)
values, indices = torch.max(outputs[0], 1, keepdim=False)
return indices
!cp biobert_large/vocab_cased_pubmed_pmc_30k.txt pytorch_output_temp/vocab.txt
!cp biobert_large/bert_config_bio_58k_large.json pytorch_output_temp/config.json
seq_infer = InferSequenceClassifier("pytorch_output_temp", "pytorch_output_temp", True)
seq_infer.make_prediction("@GENE$ influences brain beta-@DISEASE$ load, cerebrospinal fluid levels of beta-amyloid peptides and phosphorylated tau, and the genetic risk of late-onset sporadic AD.")
seq_infer.make_prediction("All our results indicate that the presence of the @GENE$ genotype (++) in patients with structural @DISEASE$, severe left ventricular dysfunction and malignant ventricular arrhythmias increases the risk for these patients of hemodynamic collapse during these arrhythmias")
seq_infer.make_prediction("Functional studies to unravel the biological significance of this region in regulating @GENE$ production is clearly indicated, which may lead to new strategies to modify the disease course of severe @DISEASE$.")
!gsutil cp -r pytorch_output_temp gs://coronavirusqa/re_convert
```
| true |
code
| 0.425426 | null | null | null | null |
|
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
from sqlalchemy import inspect
```
# Reflect Tables into SQLAlchemy ORM
```
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflecting an existing database into a new model
Base = automap_base()
# reflecting the tables
Base.prepare(engine, reflect=True)
# Displaying classes
Base.classes.keys()
# Saving data bases to variables
Measurement = Base.classes.measurement
Station = Base.classes.station
# Starting session from Python to the DB
session = Session(engine)
```
# Exploratory Climate Analysis
```
#Getting the last date in Measurment DB
max_date = session.query(func.max(Measurement.date)).first()
max_date
# Calculating the date 1 year ago from the last data point in the database
begin_date = dt.date(2017, 8, 23) - dt.timedelta(days=365)
begin_date
# Querying the Base tables returns results in a list
data = session.query(Measurement.date, Measurement.prcp).filter(Measurement.date >= begin_date).order_by(Measurement.date).all()
data
# Getting names and types of columns in "measurement" data set
inspector = inspect(engine)
columns = inspector.get_columns("measurement")
for column in columns:
print(column["name"], column["type"])
# Getting names and types of columns in "station" data set
inspector = inspect(engine)
columns = inspector.get_columns("station")
for column in columns:
print(column["name"], column["type"])
# Save the query results as a Pandas DataFrame and setting the index to the date column
precip_df = pd.DataFrame(data, columns=["Date", "Precipitation"])
precip_df["Date"] = pd.to_datetime(precip_df["Date"])
#Resettinng index to Date column
precip_df = precip_df.set_index("Date")
#Dropping all N/As
precip_df = precip_df.dropna(how = "any")
#Sorting by Date colummn - ascending
precip_df = precip_df.sort_values(by="Date", ascending=True)
precip_df
# Use Pandas Plotting with Matplotlib to plot the data
plt.figure(figsize=(10,5))
plt.plot(precip_df, label="Precipitation by Date")
plt.xlabel("Date")
plt.ylabel("Precipitation(in)")
plt.xticks(rotation="45")
plt.legend(loc="upper center")
plt.savefig("Output/Precipitation_plot.png")
plt.show()
```

```
#calcualting the summary statistics for the precipitation data
precip_df.describe()
```

```
# Query to count the number of stations in "Stations" data
session.query(func.count(Station.id)).all()
# What are the most active stations? (i.e. what stations have the most rows)?
# List the stations and the counts in descending order.
stations = session.query(Measurement.station, func.count(Measurement.station)).group_by(Measurement.station).order_by(func.count(Measurement.station).desc()).all()
stations
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature of the most active station?
session.query(Measurement.station, func.min(Measurement.tobs),
func.max(Measurement.tobs), func.avg(Measurement.tobs)). filter(Measurement.station == "USC00519281").\
group_by(Measurement.station).all()
# Choose the station with the highest number of temperature observations.
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
#Filtering data by date and by station
data_2 = session.query(Measurement.date, Measurement.tobs).filter(Measurement.station == "USC00519281").\
filter(func.strftime( Measurement.date) >= begin_date).all()
data_2
# Cleaning temp.data and setting index to date
temp_df = pd.DataFrame(data_2, columns=["Date", "Temperature"])
temp_df = temp_df.sort_values(by="Date", ascending=True)
temp_df.set_index("Date", inplace=True)
temp_df.head()
plt.figure(figsize=[8,5])
#Ploting the results as a histogram with 12 bins
plt.hist(x=temp_df["Temperature"], bins=12, label="tobs")
# Labeling figure
plt.grid
plt.xlabel("Temperature (F)")
plt.ylabel("Frequency")
plt.title("Temperature Frequency Histogram")
plt.legend()
# Saving Plot
plt.savefig("Output/Temp Frequency Histogram");
plt.show()
```

```
# This function called `calc_temps` will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
# function usage example
print(calc_temps('2011-02-28', '2011-03-05'))
# using the example to calculate min, max and average tempreture for my vacation date
# Vacation Dates
start_date = "2020-04-01"
end_date = "2020-04-11"
# Previous Year Dates
hst_start_date = "2017-04-01"
hst_end_date = "2017-04-11"
# Min,average and max temp calculation
temp_min = calc_temps(hst_start_date, hst_end_date)[0][0]
temp_avg = calc_temps(hst_start_date, hst_end_date)[0][1]
temp_max = calc_temps(hst_start_date, hst_end_date)[0][2]
print(temp_min, temp_avg, temp_max)
# Ploting the results from your previous query as a bar chart.
# Use "Trip Avg Temp" as your Title
# Use the average temperature for the y value
# Use the peak-to-peak (tmax-tmin) value as the y error bar (yerr)
x_axis = 1
y_axis = temp_avg
error = temp_max-temp_min
# Defining Bar and Error paramaters
plt.bar(x_axis, y_axis, yerr=error, align='center', color = "r")
plt.tick_params(bottom=False,labelbottom=False)
# Labeling, tickers and grids
plt.ylabel("Temperature (F)")
plt.title("Trip Avg Temperature")
plt.grid(b=None, which="major", axis="x")
plt.margins(1.5, 1.5)
plt.ylim(0, 90)
plt.savefig("Output/Trip Average Temperature")
#Show the Plot
plt.show();
```
## Optional Challenge Assignment
```
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("04-01")
# calculate the daily normals for your trip
# push each tuple of calculations into a list called `normals`
# Seting the start and end date of the trip from historic dates
hst_start_date # defined above
hst_end_date
# Useing the start and end date to create a range of dates
dates = session.query(Measurement.date).filter(Measurement.date >= hst_start_date).filter(Measurement.date <= hst_end_date).group_by(Measurement.date).all()
#saving trip dates into array
arr_dates = [x[0] for x in dates]
# Reformating dates to mm-dd format and getting data ion a list
arr_dates_mm_dd= [x[5:] for x in arr_dates]
start_mmdd = arr_dates_mm_dd[0]
end_mmdd = arr_dates_mm_dd[10]
# Looping through the list of mm-dd and getting max,ave, min temp averages
temps_by_dates = [session.query(func.min(Measurement.tobs),
func.avg(Measurement.tobs),
func.max(Measurement.tobs)).filter(func.strftime("%m-%d", Measurement.date) >= start_mmdd).filter(func.strftime("%m-%d", Measurement.date) <= end_mmdd).group_by(func.strftime("%m-%d", Measurement.date)).all()]
temps_by_dates = temps_by_dates[0]
#displaying averages for each date of the trip
temps_by_dates
# reformating list of temp into Pandas DataFrame
temps_by_dates_df= pd.DataFrame(temps_by_dates,columns=["min_t","avg_t","max_t"])
#Adding date column
temps_by_dates_df["date"]= arr_dates_mm_dd
# Seting index to date
temps_by_dates_df.set_index("date",inplace=True)
temps_by_dates_df
# Ploting the daily normals as an area plot with `stacked=False`
temps_by_dates_df.plot(kind='area', stacked=False, x_compat=True, title="Daily Normals for Trip Dates")
plt.xticks(rotation="45")
plt.savefig(("Output/Temp Frequency"))
plt.show()
```
| true |
code
| 0.742066 | null | null | null | null |
|
# Mislabel detection using influence function with all of layers on Cifar-10, ResNet
### Author
[Neosapience, Inc.](http://www.neosapience.com)
### Pre-train model conditions
---
- made mis-label from 1 percentage dog class to horse class
- augumentation: on
- iteration: 80000
- batch size: 128
#### cifar-10 train dataset
| | horse | dog | airplane | automobile | bird | cat | deer | frog | ship | truck |
|----------:|:-----:|:----:|:--------:|:----------:|:----:|:----:|:----:|:----:|:----:|:-----:|
| label | 5000 | **4950** | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 |
| mis-label | **50** | | | | | | | | | |
| total | **5050** | 4950 | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 |
### License
---
Apache License 2.0
### References
---
- Darkon Documentation: <http://darkon.io>
- Darkon Github: <https://github.com/darkonhub/darkon>
- Resnet code: <https://github.com/wenxinxu/resnet-in-tensorflow>
- More examples: <https://github.com/darkonhub/darkon-examples>
### Index
- [Load results and analysis](#Load-results-and-analysis)
- [How to use upweight influence function for mis-label](#How-to-use-upweight-influence-function-for-mis-label)
## Load results and analysis
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
scores = np.load('mislabel-result-all.npy')
print('num tests: {}'.format(len(scores)))
begin_mislabel_idx = 5000
sorted_indices = np.argsort(scores)
print('dogs in helpful: {} / 100'.format(np.sum(sorted_indices[-100:] >= begin_mislabel_idx)))
print('mean for all: {}'.format(np.mean(scores)))
print('mean for horse: {}'.format(np.mean(scores[:begin_mislabel_idx])))
print('mean for dogs: {}'.format(np.mean(scores[begin_mislabel_idx:])))
mis_label_ranking = np.where(sorted_indices >= begin_mislabel_idx)[0]
print('all of mis-labels: {}'.format(mis_label_ranking))
total = scores.size
total_pos = mis_label_ranking.size
total_neg = total - total_pos
tpr = np.zeros([total_pos])
fpr = np.zeros([total_pos])
for idx in range(total_pos):
tpr[idx] = float(total_pos - idx)
fpr[idx] = float(total - mis_label_ranking[idx] - tpr[idx])
tpr /= total_pos
fpr /= total_neg
histogram = sorted_indices >= begin_mislabel_idx
histogram = histogram.reshape([10, -1])
histogram = np.sum(histogram, axis=1)
acc = np.cumsum(histogram[::-1])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].set_ylabel('true positive rate')
ax[0].set_xlabel('false positive rate')
ax[0].set_ylim(0.0, 1.0)
ax[0].set_xlim(0.0, 1.0)
ax[0].grid(True)
ax[0].plot(fpr, tpr)
ax[1].set_ylabel('num of mis-label')
ax[1].set_xlabel('threshold')
ax[1].grid(True)
ax[1].bar(range(10), acc)
plt.sca(ax[1])
plt.xticks(range(10), ['{}~{}%'.format(p, p + 10) for p in range(0, 100, 10)])
fig, ax = plt.subplots(figsize=(20, 5))
ax.grid(True)
ax.plot(scores)
```
<br><br><br><br>
## How to use upweight influence function for mis-label
### Import packages
```
# resnet: implemented by wenxinxu
from cifar10_input import *
from cifar10_train import Train
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import darkon
# to enable specific GPU
%set_env CUDA_VISIBLE_DEVICES=0
# cifar-10 classes
_classes = (
'airplane',
'automobile',
'bird',
'cat',
'deer',
'dog',
'frog',
'horse',
'ship',
'truck'
)
```
### Download/Extract cifar10 dataset
```
maybe_download_and_extract()
```
### Implement dataset feeder
```
class MyFeeder(darkon.InfluenceFeeder):
def __init__(self):
# load train data
# for ihvp
data, label = prepare_train_data(padding_size=0)
# update some label
label = self.make_mislabel(label)
self.train_origin_data = data / 256.
self.train_label = label
self.train_data = whitening_image(data)
self.train_batch_offset = 0
def make_mislabel(self, label):
target_class_idx = 7
correct_indices = np.where(label == target_class_idx)[0]
self.correct_indices = correct_indices[:]
# 1% dogs to horses.
# In the mis-label model training, I used this script to choose random dogs.
labeled_dogs = np.where(label == 5)[0]
np.random.shuffle(labeled_dogs)
mislabel_indices = labeled_dogs[:int(labeled_dogs.shape[0] * 0.01)]
label[mislabel_indices] = 7.0
self.mislabel_indices = mislabel_indices
print('target class: {}'.format(_classes[target_class_idx]))
print(self.mislabel_indices)
return label
def test_indices(self, indices):
return self.train_data[indices], self.train_label[indices]
def train_batch(self, batch_size):
# for recursion part
# calculate offset
start = self.train_batch_offset
end = start + batch_size
self.train_batch_offset += batch_size
return self.train_data[start:end, ...], self.train_label[start:end, ...]
def train_one(self, idx):
return self.train_data[idx, ...], self.train_label[idx, ...]
def reset(self):
self.train_batch_offset = 0
# to fix shuffled data
np.random.seed(75)
feeder = MyFeeder()
```
### Restore pre-trained model
```
# tf model checkpoint
check_point = 'pre-trained-mislabel/model.ckpt-79999'
net = Train()
net.build_train_validation_graph()
saver = tf.train.Saver(tf.global_variables())
sess = tf.InteractiveSession()
saver.restore(sess, check_point)
```
### Upweight influence options
```
approx_params = {
'scale': 200,
'num_repeats': 3,
'recursion_depth': 50,
'recursion_batch_size': 100
}
# targets
test_indices = list(feeder.correct_indices) + list(feeder.mislabel_indices)
print('num test targets: {}'.format(len(test_indices)))
```
### Run upweight influence function
```
# choose all of trainable layers
trainable_variables = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES)
# initialize Influence function
inspector = darkon.Influence(
workspace='./influence-workspace',
feeder=feeder,
loss_op_train=net.full_loss,
loss_op_test=net.loss_op,
x_placeholder=net.image_placeholder,
y_placeholder=net.label_placeholder,
trainable_variables=trainable_variables)
scores = list()
for i, target in enumerate(test_indices):
score = inspector.upweighting_influence(
sess,
[target],
1,
approx_params,
[target],
10000000,
force_refresh=True
)
scores += list(score)
print('done: [{}] - {}'.format(i, score))
print(scores)
np.save('mislabel-result-all.npy', scores)
```
### License
---
<pre>
Copyright 2017 Neosapience, Inc.
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
</pre>
---
| true |
code
| 0.634458 | null | null | null | null |
|
## CIFAR 10
```
%matplotlib inline
%reload_ext autoreload
%autoreload 2
```
You can get the data via:
wget http://pjreddie.com/media/files/cifar.tgz
**Important:** Before proceeding, the student must reorganize the downloaded dataset files to match the expected directory structure, so that there is a dedicated folder for each class under 'test' and 'train', e.g.:
```
* test/airplane/airplane-1001.png
* test/bird/bird-1043.png
* train/bird/bird-10018.png
* train/automobile/automobile-10000.png
```
The filename of the image doesn't have to include its class.
```
from fastai.conv_learner import *
PATH = "data/cifar10/"
os.makedirs(PATH,exist_ok=True)
!ls {PATH}
if not os.path.exists(f"{PATH}/train/bird"):
raise Exception("expecting class subdirs under 'train/' and 'test/'")
!ls {PATH}/train
classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
stats = (np.array([ 0.4914 , 0.48216, 0.44653]), np.array([ 0.24703, 0.24349, 0.26159]))
def get_data(sz,bs):
tfms = tfms_from_stats(stats, sz, aug_tfms=[RandomFlip()], pad=sz//8)
return ImageClassifierData.from_paths(PATH, val_name='test', tfms=tfms, bs=bs)
bs=256
```
### Look at data
```
data = get_data(32,4)
x,y=next(iter(data.trn_dl))
plt.imshow(data.trn_ds.denorm(x)[0]);
plt.imshow(data.trn_ds.denorm(x)[1]);
```
## Fully connected model
```
data = get_data(32,bs)
lr=1e-2
```
From [this notebook](https://github.com/KeremTurgutlu/deeplearning/blob/master/Exploring%20Optimizers.ipynb) by our student Kerem Turgutlu:
```
class SimpleNet(nn.Module):
def __init__(self, layers):
super().__init__()
self.layers = nn.ModuleList([
nn.Linear(layers[i], layers[i + 1]) for i in range(len(layers) - 1)])
def forward(self, x):
x = x.view(x.size(0), -1)
for l in self.layers:
l_x = l(x)
x = F.relu(l_x)
return F.log_softmax(l_x, dim=-1)
learn = ConvLearner.from_model_data(SimpleNet([32*32*3, 40,10]), data)
learn, [o.numel() for o in learn.model.parameters()]
learn.summary()
learn.lr_find()
learn.sched.plot()
%time learn.fit(lr, 2)
%time learn.fit(lr, 2, cycle_len=1)
```
## CNN
```
class ConvNet(nn.Module):
def __init__(self, layers, c):
super().__init__()
self.layers = nn.ModuleList([
nn.Conv2d(layers[i], layers[i + 1], kernel_size=3, stride=2)
for i in range(len(layers) - 1)])
self.pool = nn.AdaptiveMaxPool2d(1)
self.out = nn.Linear(layers[-1], c)
def forward(self, x):
for l in self.layers: x = F.relu(l(x))
x = self.pool(x)
x = x.view(x.size(0), -1)
return F.log_softmax(self.out(x), dim=-1)
learn = ConvLearner.from_model_data(ConvNet([3, 20, 40, 80], 10), data)
learn.summary()
learn.lr_find(end_lr=100)
learn.sched.plot()
%time learn.fit(1e-1, 2)
%time learn.fit(1e-1, 4, cycle_len=1)
```
## Refactored
```
class ConvLayer(nn.Module):
def __init__(self, ni, nf):
super().__init__()
self.conv = nn.Conv2d(ni, nf, kernel_size=3, stride=2, padding=1)
def forward(self, x): return F.relu(self.conv(x))
class ConvNet2(nn.Module):
def __init__(self, layers, c):
super().__init__()
self.layers = nn.ModuleList([ConvLayer(layers[i], layers[i + 1])
for i in range(len(layers) - 1)])
self.out = nn.Linear(layers[-1], c)
def forward(self, x):
for l in self.layers: x = l(x)
x = F.adaptive_max_pool2d(x, 1)
x = x.view(x.size(0), -1)
return F.log_softmax(self.out(x), dim=-1)
learn = ConvLearner.from_model_data(ConvNet2([3, 20, 40, 80], 10), data)
learn.summary()
%time learn.fit(1e-1, 2)
%time learn.fit(1e-1, 2, cycle_len=1)
```
## BatchNorm
```
class BnLayer(nn.Module):
def __init__(self, ni, nf, stride=2, kernel_size=3):
super().__init__()
self.conv = nn.Conv2d(ni, nf, kernel_size=kernel_size, stride=stride,
bias=False, padding=1)
self.a = nn.Parameter(torch.zeros(nf,1,1))
self.m = nn.Parameter(torch.ones(nf,1,1))
def forward(self, x):
x = F.relu(self.conv(x))
x_chan = x.transpose(0,1).contiguous().view(x.size(1), -1)
if self.training:
self.means = x_chan.mean(1)[:,None,None]
self.stds = x_chan.std (1)[:,None,None]
return (x-self.means) / self.stds *self.m + self.a
class ConvBnNet(nn.Module):
def __init__(self, layers, c):
super().__init__()
self.conv1 = nn.Conv2d(3, 10, kernel_size=5, stride=1, padding=2)
self.layers = nn.ModuleList([BnLayer(layers[i], layers[i + 1])
for i in range(len(layers) - 1)])
self.out = nn.Linear(layers[-1], c)
def forward(self, x):
x = self.conv1(x)
for l in self.layers: x = l(x)
x = F.adaptive_max_pool2d(x, 1)
x = x.view(x.size(0), -1)
return F.log_softmax(self.out(x), dim=-1)
learn = ConvLearner.from_model_data(ConvBnNet([10, 20, 40, 80, 160], 10), data)
learn.summary()
%time learn.fit(3e-2, 2)
%time learn.fit(1e-1, 4, cycle_len=1)
```
## Deep BatchNorm
```
class ConvBnNet2(nn.Module):
def __init__(self, layers, c):
super().__init__()
self.conv1 = nn.Conv2d(3, 10, kernel_size=5, stride=1, padding=2)
self.layers = nn.ModuleList([BnLayer(layers[i], layers[i+1])
for i in range(len(layers) - 1)])
self.layers2 = nn.ModuleList([BnLayer(layers[i+1], layers[i + 1], 1)
for i in range(len(layers) - 1)])
self.out = nn.Linear(layers[-1], c)
def forward(self, x):
x = self.conv1(x)
for l,l2 in zip(self.layers, self.layers2):
x = l(x)
x = l2(x)
x = F.adaptive_max_pool2d(x, 1)
x = x.view(x.size(0), -1)
return F.log_softmax(self.out(x), dim=-1)
learn = ConvLearner.from_model_data(ConvBnNet2([10, 20, 40, 80, 160], 10), data)
%time learn.fit(1e-2, 2)
%time learn.fit(1e-2, 2, cycle_len=1)
```
## Resnet
```
class ResnetLayer(BnLayer):
def forward(self, x): return x + super().forward(x)
class Resnet(nn.Module):
def __init__(self, layers, c):
super().__init__()
self.conv1 = nn.Conv2d(3, 10, kernel_size=5, stride=1, padding=2)
self.layers = nn.ModuleList([BnLayer(layers[i], layers[i+1])
for i in range(len(layers) - 1)])
self.layers2 = nn.ModuleList([ResnetLayer(layers[i+1], layers[i + 1], 1)
for i in range(len(layers) - 1)])
self.layers3 = nn.ModuleList([ResnetLayer(layers[i+1], layers[i + 1], 1)
for i in range(len(layers) - 1)])
self.out = nn.Linear(layers[-1], c)
def forward(self, x):
x = self.conv1(x)
for l,l2,l3 in zip(self.layers, self.layers2, self.layers3):
x = l3(l2(l(x)))
x = F.adaptive_max_pool2d(x, 1)
x = x.view(x.size(0), -1)
return F.log_softmax(self.out(x), dim=-1)
learn = ConvLearner.from_model_data(Resnet([10, 20, 40, 80, 160], 10), data)
wd=1e-5
%time learn.fit(1e-2, 2, wds=wd)
%time learn.fit(1e-2, 3, cycle_len=1, cycle_mult=2, wds=wd)
%time learn.fit(1e-2, 8, cycle_len=4, wds=wd)
```
## Resnet 2
```
class Resnet2(nn.Module):
def __init__(self, layers, c, p=0.5):
super().__init__()
self.conv1 = BnLayer(3, 16, stride=1, kernel_size=7)
self.layers = nn.ModuleList([BnLayer(layers[i], layers[i+1])
for i in range(len(layers) - 1)])
self.layers2 = nn.ModuleList([ResnetLayer(layers[i+1], layers[i + 1], 1)
for i in range(len(layers) - 1)])
self.layers3 = nn.ModuleList([ResnetLayer(layers[i+1], layers[i + 1], 1)
for i in range(len(layers) - 1)])
self.out = nn.Linear(layers[-1], c)
self.drop = nn.Dropout(p)
def forward(self, x):
x = self.conv1(x)
for l,l2,l3 in zip(self.layers, self.layers2, self.layers3):
x = l3(l2(l(x)))
x = F.adaptive_max_pool2d(x, 1)
x = x.view(x.size(0), -1)
x = self.drop(x)
return F.log_softmax(self.out(x), dim=-1)
learn = ConvLearner.from_model_data(Resnet2([16, 32, 64, 128, 256], 10, 0.2), data)
wd=1e-6
%time learn.fit(1e-2, 2, wds=wd)
%time learn.fit(1e-2, 3, cycle_len=1, cycle_mult=2, wds=wd)
%time learn.fit(1e-2, 8, cycle_len=4, wds=wd)
learn.save('tmp3')
log_preds,y = learn.TTA()
preds = np.mean(np.exp(log_preds),0)
metrics.log_loss(y,preds), accuracy_np(preds,y)
```
### End
| true |
code
| 0.803887 | null | null | null | null |
|
# Generative Spaces (ABM)
In this workshop we will lwarn how to construct a ABM (Agent Based Model) with spatial behaviours, that is capable of configuring the space. This file is a simplified version of Generative Spatial Agent Based Models. For further information, you can find more advanced versions here:
* [Object Oriented version](https://github.com/shervinazadi/spatial_computing_workshops/blob/master/notebooks/w3_generative_spaces.ipynb)
* [Vectorized version](https://topogenesis.readthedocs.io/notebooks/random_walker)
## 0. Initialization
### 0.1. Load required libraries
```
# !pip install pyvista==0.28.1 ipyvtklink
import os
import topogenesis as tg
import pyvista as pv
import trimesh as tm
import pandas as pd
import numpy as np
np.random.seed(0)
```
### 0.2. Define the Neighborhood (Stencil)
```
# creating neighborhood definition
stencil = tg.create_stencil("von_neumann", 1, 1)
# setting the center to zero
stencil.set_index([0,0,0], 0)
print(stencil)
```
### 0.3 Visualize the Stencil
```
# initiating the plotter
p = pv.Plotter(notebook=True)
# Create the spatial reference
grid = pv.UniformGrid()
# Set the grid dimensions: shape because we want to inject our values
grid.dimensions = np.array(stencil.shape) + 1
# The bottom left corner of the data set
grid.origin = [0,0,0]
# These are the cell sizes along each axis
grid.spacing = [1,1,1]
# Add the data values to the cell data
grid.cell_arrays["values"] = stencil.flatten(order="F") # Flatten the stencil
threshed = grid.threshold([0.9, 1.1])
# adding the voxels: light red
p.add_mesh(threshed, show_edges=True, color="#ff8fa3", opacity=0.3)
# plotting
# p.show(use_ipyvtk=True)
```
## 1. Setup the Environment
### 1.1. Load the envelope lattice as the avialbility lattice
```
# loading the lattice from csv
lattice_path = os.path.relpath('../data/voxelized_envelope.csv')
avail_lattice = tg.lattice_from_csv(lattice_path)
init_avail_lattice = tg.to_lattice(np.copy(avail_lattice), avail_lattice)
```
### 1.2 Load Program
```
program_complete = pd.read_csv("../data/program_small.csv")
program_complete
program_prefs = program_complete.drop(["space_name","space_id"], 1)
program_prefs
```
### 1.2 Load the value fields
```
# loading the lattice from csv
fields = {}
for f in program_prefs.columns:
lattice_path = os.path.relpath('../data/' + f + '.csv')
fields[f] = tg.lattice_from_csv(lattice_path)
```
### 1.3. Initialize the Agents
```
# initialize the occupation lattice
occ_lattice = avail_lattice * 0 - 1
# Finding the index of the available voxels in avail_lattice
avail_flat = avail_lattice.flatten()
avail_index = np.array(np.where(avail_lattice == 1)).T
# Randomly choosing three available voxels
agn_num = len(program_complete)
select_id = np.random.choice(len(avail_index), agn_num)
agn_origins = avail_index[select_id]
# adding the origins to the agents locations
agn_locs = []
# for each agent origin ...
for a_id, a_origin in enumerate(agn_origins):
# add the origin to the list of agent locations
agn_locs.append([a_origin])
# set the origin in availablity lattice as 0 (UNavailable)
avail_lattice[tuple(a_origin)] = 0
# set the origin in occupation lattice as the agent id (a_id)
occ_lattice[tuple(a_origin)] = a_id
```
### 1.4. Visualize the environment
```
p = pv.Plotter(notebook=True)
# Set the grid dimensions: shape + 1 because we want to inject our values on the CELL data
grid = pv.UniformGrid()
grid.dimensions = np.array(occ_lattice.shape) + 1
# The bottom left corner of the data set
grid.origin = occ_lattice.minbound - occ_lattice.unit * 0.5
# These are the cell sizes along each axis
grid.spacing = occ_lattice.unit
# adding the boundingbox wireframe
p.add_mesh(grid.outline(), color="grey", label="Domain")
# adding axes
p.add_axes()
p.show_bounds(grid="back", location="back", color="#777777")
# Add the data values to the cell data
grid.cell_arrays["Agents"] = occ_lattice.flatten(order="F").astype(int) # Flatten the array!
# filtering the voxels
threshed = grid.threshold([-0.1, agn_num - 0.9])
# adding the voxels
p.add_mesh(threshed, show_edges=True, opacity=1.0, show_scalar_bar=False)
# adding the availability lattice
init_avail_lattice.fast_vis(p)
# p.show(use_ipyvtk=True)
```
## 2. ABM Simulation (Agent Based Space Occupation)
### 2.1. Running the simulation
```
# make a deep copy of occupation lattice
cur_occ_lattice = tg.to_lattice(np.copy(occ_lattice), occ_lattice)
# initialzing the list of frames
frames = [cur_occ_lattice]
# setting the time variable to 0
t = 0
n_frames = 30
# main feedback loop of the simulation (for each time step ...)
while t<n_frames:
# for each agent ...
for a_id, a_prefs in program_complete.iterrows():
# retrieve the list of the locations of the current agent
a_locs = agn_locs[a_id]
# initialize the list of free neighbours
free_neighs = []
# for each location of the agent
for loc in a_locs:
# retrieve the list of neighbours of the agent based on the stencil
neighs = avail_lattice.find_neighbours_masked(stencil, loc = loc)
# for each neighbour ...
for n in neighs:
# compute 3D index of neighbour
neigh_3d_id = np.unravel_index(n, avail_lattice.shape)
# if the neighbour is available...
if avail_lattice[neigh_3d_id]:
# add the neighbour to the list of free neighbours
free_neighs.append(neigh_3d_id)
# check if found any free neighbour
if len(free_neighs)>0:
# convert free neighbours to a numpy array
fns = np.array(free_neighs)
# find the value of neighbours
# init the agent value array
a_eval = np.ones(len(fns))
# for each field...
for f in program_prefs.columns:
# find the raw value of free neighbours...
vals = fields[f][fns[:,0], fns[:,1], fns[:,2]]
# raise the the raw value to the power of preference weight of the agent
a_weighted_vals = vals ** a_prefs[f]
# multiply them to the previous weighted values
a_eval *= a_weighted_vals
# select the neighbour with highest evaluation
selected_int = np.argmax(a_eval)
# find 3D integer index of selected neighbour
selected_neigh_3d_id = free_neighs[selected_int]
# find the location of the newly selected neighbour
selected_neigh_loc = np.array(selected_neigh_3d_id).flatten()
# add the newly selected neighbour location to agent locations
agn_locs[a_id].append(selected_neigh_loc)
# set the newly selected neighbour as UNavailable (0) in the availability lattice
avail_lattice[selected_neigh_3d_id] = 0
# set the newly selected neighbour as OCCUPIED by current agent
# (-1 means not-occupied so a_id)
occ_lattice[selected_neigh_3d_id] = a_id
# constructing the new lattice
new_occ_lattice = tg.to_lattice(np.copy(occ_lattice), occ_lattice)
# adding the new lattice to the list of frames
frames.append(new_occ_lattice)
# adding one to the time counter
t += 1
```
### 2.2. Visualizing the simulation
```
p = pv.Plotter(notebook=True)
base_lattice = frames[0]
# Set the grid dimensions: shape + 1 because we want to inject our values on the CELL data
grid = pv.UniformGrid()
grid.dimensions = np.array(base_lattice.shape) + 1
# The bottom left corner of the data set
grid.origin = base_lattice.minbound - base_lattice.unit * 0.5
# These are the cell sizes along each axis
grid.spacing = base_lattice.unit
# adding the boundingbox wireframe
p.add_mesh(grid.outline(), color="grey", label="Domain")
# adding the availability lattice
init_avail_lattice.fast_vis(p)
# adding axes
p.add_axes()
p.show_bounds(grid="back", location="back", color="#aaaaaa")
def create_mesh(value):
f = int(value)
lattice = frames[f]
# Add the data values to the cell data
grid.cell_arrays["Agents"] = lattice.flatten(order="F").astype(int) # Flatten the array!
# filtering the voxels
threshed = grid.threshold([-0.1, agn_num - 0.9])
# adding the voxels
p.add_mesh(threshed, name='sphere', show_edges=True, opacity=1.0, show_scalar_bar=False)
return
p.add_slider_widget(create_mesh, [0, n_frames], title='Time', value=0, event_type="always", style="classic")
p.show(use_ipyvtk=True)
```
### 2.3. Saving lattice frames in CSV
```
for i, lattice in enumerate(frames):
csv_path = os.path.relpath('../data/abm_animation/abm_f_'+ f'{i:03}' + '.csv')
lattice.to_csv(csv_path)
```
### Credits
```
__author__ = "Shervin Azadi "
__license__ = "MIT"
__version__ = "1.0"
__url__ = "https://github.com/shervinazadi/spatial_computing_workshops"
__summary__ = "Spatial Computing Design Studio Workshop on Agent Based Models for Generative Spaces"
```
| true |
code
| 0.499756 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/NielsRogge/Transformers-Tutorials/blob/master/TrOCR/Evaluating_TrOCR_base_handwritten_on_the_IAM_test_set.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Set-up environment
```
!pip install -q git+https://github.com/huggingface/transformers.git
!pip install -q datasets jiwer
```
## Load IAM test set
```
import pandas as pd
df = pd.read_fwf('/content/drive/MyDrive/TrOCR/Tutorial notebooks/IAM/gt_test.txt', header=None)
df.rename(columns={0: "file_name", 1: "text"}, inplace=True)
del df[2]
df.head()
import torch
from torch.utils.data import Dataset
from PIL import Image
class IAMDataset(Dataset):
def __init__(self, root_dir, df, processor, max_target_length=128):
self.root_dir = root_dir
self.df = df
self.processor = processor
self.max_target_length = max_target_length
def __len__(self):
return len(self.df)
def __getitem__(self, idx):
# get file name + text
file_name = self.df['file_name'][idx]
text = self.df['text'][idx]
# some file names end with jp instead of jpg, the two lines below fix this
if file_name.endswith('jp'):
file_name = file_name + 'g'
# prepare image (i.e. resize + normalize)
image = Image.open(self.root_dir + file_name).convert("RGB")
pixel_values = self.processor(image, return_tensors="pt").pixel_values
# add labels (input_ids) by encoding the text
labels = self.processor.tokenizer(text,
padding="max_length",
max_length=self.max_target_length).input_ids
# important: make sure that PAD tokens are ignored by the loss function
labels = [label if label != self.processor.tokenizer.pad_token_id else -100 for label in labels]
encoding = {"pixel_values": pixel_values.squeeze(), "labels": torch.tensor(labels)}
return encoding
from transformers import TrOCRProcessor
processor = TrOCRProcessor.from_pretrained("microsoft/trocr-base-handwritten")
test_dataset = IAMDataset(root_dir='/content/drive/MyDrive/TrOCR/Tutorial notebooks/IAM/image/',
df=df,
processor=processor)
from torch.utils.data import DataLoader
test_dataloader = DataLoader(test_dataset, batch_size=8)
batch = next(iter(test_dataloader))
for k,v in batch.items():
print(k, v.shape)
from transformers import TrOCRProcessor
processor = TrOCRProcessor.from_pretrained("microsoft/trocr-base-handwritten")
labels = batch["labels"]
labels[labels == -100] = processor.tokenizer.pad_token_id
label_str = processor.batch_decode(labels, skip_special_tokens=True)
label_str
```
## Run evaluation
```
from transformers import VisionEncoderDecoderModel
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = VisionEncoderDecoderModel.from_pretrained("microsoft/trocr-base-handwritten")
model.to(device)
from datasets import load_metric
cer = load_metric("cer")
from tqdm.notebook import tqdm
print("Running evaluation...")
for batch in tqdm(test_dataloader):
# predict using generate
pixel_values = batch["pixel_values"].to(device)
outputs = model.generate(pixel_values)
# decode
pred_str = processor.batch_decode(outputs, skip_special_tokens=True)
labels = batch["labels"]
labels[labels == -100] = processor.tokenizer.pad_token_id
label_str = processor.batch_decode(labels, skip_special_tokens=True)
# add batch to metric
cer.add_batch(predictions=pred_str, references=label_str)
final_score = cer.compute()
print("Character error rate on test set:", final_score)
```
| true |
code
| 0.722151 | null | null | null | null |
|
# Implementing a one-layer Neural Network
We will illustrate how to create a one hidden layer NN
We will use the iris data for this exercise
We will build a one-hidden layer neural network to predict the fourth attribute, Petal Width from the other three (Sepal length, Sepal width, Petal length).
```
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
iris = datasets.load_iris()
x_vals = np.array([x[0:3] for x in iris.data])
y_vals = np.array([x[3] for x in iris.data])
# Create graph session
sess = tf.Session()
# make results reproducible
seed = 2
tf.set_random_seed(seed)
np.random.seed(seed)
# Split data into train/test = 80%/20%
train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices)))
x_vals_train = x_vals[train_indices]
x_vals_test = x_vals[test_indices]
y_vals_train = y_vals[train_indices]
y_vals_test = y_vals[test_indices]
# Normalize by column (min-max norm)
def normalize_cols(m):
col_max = m.max(axis=0)
col_min = m.min(axis=0)
return (m-col_min) / (col_max - col_min)
x_vals_train = np.nan_to_num(normalize_cols(x_vals_train))
x_vals_test = np.nan_to_num(normalize_cols(x_vals_test))
# Declare batch size
batch_size = 50
# Initialize placeholders
x_data = tf.placeholder(shape=[None, 3], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# Create variables for both NN layers
hidden_layer_nodes = 10
A1 = tf.Variable(tf.random_normal(shape=[3,hidden_layer_nodes])) # inputs -> hidden nodes
b1 = tf.Variable(tf.random_normal(shape=[hidden_layer_nodes])) # one biases for each hidden node
A2 = tf.Variable(tf.random_normal(shape=[hidden_layer_nodes,1])) # hidden inputs -> 1 output
b2 = tf.Variable(tf.random_normal(shape=[1])) # 1 bias for the output
# Declare model operations
hidden_output = tf.nn.relu(tf.add(tf.matmul(x_data, A1), b1))
final_output = tf.nn.relu(tf.add(tf.matmul(hidden_output, A2), b2))
# Declare loss function (MSE)
loss = tf.reduce_mean(tf.square(y_target - final_output))
# Declare optimizer
my_opt = tf.train.GradientDescentOptimizer(0.005)
train_step = my_opt.minimize(loss)
# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)
# Training loop
loss_vec = []
test_loss = []
for i in range(500):
rand_index = np.random.choice(len(x_vals_train), size=batch_size)
rand_x = x_vals_train[rand_index]
rand_y = np.transpose([y_vals_train[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(np.sqrt(temp_loss))
test_temp_loss = sess.run(loss, feed_dict={x_data: x_vals_test, y_target: np.transpose([y_vals_test])})
test_loss.append(np.sqrt(test_temp_loss))
if (i+1)%50==0:
print('Generation: ' + str(i+1) + '. Loss = ' + str(temp_loss))
%matplotlib inline
# Plot loss (MSE) over time
plt.plot(loss_vec, 'k-', label='Train Loss')
plt.plot(test_loss, 'r--', label='Test Loss')
plt.title('Loss (MSE) per Generation')
plt.legend(loc='upper right')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()
```
| true |
code
| 0.703066 | null | null | null | null |
|
# Logic: `logic.py`; Chapters 6-8
This notebook describes the [logic.py](https://github.com/aimacode/aima-python/blob/master/logic.py) module, which covers Chapters 6 (Logical Agents), 7 (First-Order Logic) and 8 (Inference in First-Order Logic) of *[Artificial Intelligence: A Modern Approach](http://aima.cs.berkeley.edu)*. See the [intro notebook](https://github.com/aimacode/aima-python/blob/master/intro.ipynb) for instructions.
We'll start by looking at `Expr`, the data type for logical sentences, and the convenience function `expr`. We'll be covering two types of knowledge bases, `PropKB` - Propositional logic knowledge base and `FolKB` - First order logic knowledge base. We will construct a propositional knowledge base of a specific situation in the Wumpus World. We will next go through the `tt_entails` function and experiment with it a bit. The `pl_resolution` and `pl_fc_entails` functions will come next. We'll study forward chaining and backward chaining algorithms for `FolKB` and use them on `crime_kb` knowledge base.
But the first step is to load the code:
```
from utils import *
from logic import *
```
## Logical Sentences
The `Expr` class is designed to represent any kind of mathematical expression. The simplest type of `Expr` is a symbol, which can be defined with the function `Symbol`:
```
Symbol('x')
```
Or we can define multiple symbols at the same time with the function `symbols`:
```
(x, y, P, Q, f) = symbols('x, y, P, Q, f')
```
We can combine `Expr`s with the regular Python infix and prefix operators. Here's how we would form the logical sentence "P and not Q":
```
P & ~Q
```
This works because the `Expr` class overloads the `&` operator with this definition:
```python
def __and__(self, other): return Expr('&', self, other)```
and does similar overloads for the other operators. An `Expr` has two fields: `op` for the operator, which is always a string, and `args` for the arguments, which is a tuple of 0 or more expressions. By "expression," I mean either an instance of `Expr`, or a number. Let's take a look at the fields for some `Expr` examples:
```
sentence = P & ~Q
sentence.op
sentence.args
P.op
P.args
Pxy = P(x, y)
Pxy.op
Pxy.args
```
It is important to note that the `Expr` class does not define the *logic* of Propositional Logic sentences; it just gives you a way to *represent* expressions. Think of an `Expr` as an [abstract syntax tree](https://en.wikipedia.org/wiki/Abstract_syntax_tree). Each of the `args` in an `Expr` can be either a symbol, a number, or a nested `Expr`. We can nest these trees to any depth. Here is a deply nested `Expr`:
```
3 * f(x, y) + P(y) / 2 + 1
```
## Operators for Constructing Logical Sentences
Here is a table of the operators that can be used to form sentences. Note that we have a problem: we want to use Python operators to make sentences, so that our programs (and our interactive sessions like the one here) will show simple code. But Python does not allow implication arrows as operators, so for now we have to use a more verbose notation that Python does allow: `|'==>'|` instead of just `==>`. Alternately, you can always use the more verbose `Expr` constructor forms:
| Operation | Book | Python Infix Input | Python Output | Python `Expr` Input
|--------------------------|----------------------|-------------------------|---|---|
| Negation | ¬ P | `~P` | `~P` | `Expr('~', P)`
| And | P ∧ Q | `P & Q` | `P & Q` | `Expr('&', P, Q)`
| Or | P ∨ Q | `P`<tt> | </tt>`Q`| `P`<tt> | </tt>`Q` | `Expr('`|`', P, Q)`
| Inequality (Xor) | P ≠ Q | `P ^ Q` | `P ^ Q` | `Expr('^', P, Q)`
| Implication | P → Q | `P` <tt>|</tt>`'==>'`<tt>|</tt> `Q` | `P ==> Q` | `Expr('==>', P, Q)`
| Reverse Implication | Q ← P | `Q` <tt>|</tt>`'<=='`<tt>|</tt> `P` |`Q <== P` | `Expr('<==', Q, P)`
| Equivalence | P ↔ Q | `P` <tt>|</tt>`'<=>'`<tt>|</tt> `Q` |`P <=> Q` | `Expr('<=>', P, Q)`
Here's an example of defining a sentence with an implication arrow:
```
~(P & Q) |'==>'| (~P | ~Q)
```
## `expr`: a Shortcut for Constructing Sentences
If the `|'==>'|` notation looks ugly to you, you can use the function `expr` instead:
```
expr('~(P & Q) ==> (~P | ~Q)')
```
`expr` takes a string as input, and parses it into an `Expr`. The string can contain arrow operators: `==>`, `<==`, or `<=>`, which are handled as if they were regular Python infix operators. And `expr` automatically defines any symbols, so you don't need to pre-define them:
```
expr('sqrt(b ** 2 - 4 * a * c)')
```
For now that's all you need to know about `expr`. If you are interested, we explain the messy details of how `expr` is implemented and how `|'==>'|` is handled in the appendix.
## Propositional Knowledge Bases: `PropKB`
The class `PropKB` can be used to represent a knowledge base of propositional logic sentences.
We see that the class `KB` has four methods, apart from `__init__`. A point to note here: the `ask` method simply calls the `ask_generator` method. Thus, this one has already been implemented, and what you'll have to actually implement when you create your own knowledge base class (though you'll probably never need to, considering the ones we've created for you) will be the `ask_generator` function and not the `ask` function itself.
The class `PropKB` now.
* `__init__(self, sentence=None)` : The constructor `__init__` creates a single field `clauses` which will be a list of all the sentences of the knowledge base. Note that each one of these sentences will be a 'clause' i.e. a sentence which is made up of only literals and `or`s.
* `tell(self, sentence)` : When you want to add a sentence to the KB, you use the `tell` method. This method takes a sentence, converts it to its CNF, extracts all the clauses, and adds all these clauses to the `clauses` field. So, you need not worry about `tell`ing only clauses to the knowledge base. You can `tell` the knowledge base a sentence in any form that you wish; converting it to CNF and adding the resulting clauses will be handled by the `tell` method.
* `ask_generator(self, query)` : The `ask_generator` function is used by the `ask` function. It calls the `tt_entails` function, which in turn returns `True` if the knowledge base entails query and `False` otherwise. The `ask_generator` itself returns an empty dict `{}` if the knowledge base entails query and `None` otherwise. This might seem a little bit weird to you. After all, it makes more sense just to return a `True` or a `False` instead of the `{}` or `None` But this is done to maintain consistency with the way things are in First-Order Logic, where an `ask_generator` function is supposed to return all the substitutions that make the query true. Hence the dict, to return all these substitutions. I will be mostly be using the `ask` function which returns a `{}` or a `False`, but if you don't like this, you can always use the `ask_if_true` function which returns a `True` or a `False`.
* `retract(self, sentence)` : This function removes all the clauses of the sentence given, from the knowledge base. Like the `tell` function, you don't have to pass clauses to remove them from the knowledge base; any sentence will do fine. The function will take care of converting that sentence to clauses and then remove those.
## Wumpus World KB
Let us create a `PropKB` for the wumpus world with the sentences mentioned in `section 7.4.3`.
```
wumpus_kb = PropKB()
```
We define the symbols we use in our clauses.<br/>
$P_{x, y}$ is true if there is a pit in `[x, y]`.<br/>
$B_{x, y}$ is true if the agent senses breeze in `[x, y]`.<br/>
```
P11, P12, P21, P22, P31, B11, B21 = expr('P11, P12, P21, P22, P31, B11, B21')
```
Now we tell sentences based on `section 7.4.3`.<br/>
There is no pit in `[1,1]`.
```
wumpus_kb.tell(~P11)
```
A square is breezy if and only if there is a pit in a neighboring square. This has to be stated for each square but for now, we include just the relevant squares.
```
wumpus_kb.tell(B11 | '<=>' | ((P12 | P21)))
wumpus_kb.tell(B21 | '<=>' | ((P11 | P22 | P31)))
```
Now we include the breeze percepts for the first two squares leading up to the situation in `Figure 7.3(b)`
```
wumpus_kb.tell(~B11)
wumpus_kb.tell(B21)
```
We can check the clauses stored in a `KB` by accessing its `clauses` variable
```
wumpus_kb.clauses
```
We see that the equivalence $B_{1, 1} \iff (P_{1, 2} \lor P_{2, 1})$ was automatically converted to two implications which were inturn converted to CNF which is stored in the `KB`.<br/>
$B_{1, 1} \iff (P_{1, 2} \lor P_{2, 1})$ was split into $B_{1, 1} \implies (P_{1, 2} \lor P_{2, 1})$ and $B_{1, 1} \Longleftarrow (P_{1, 2} \lor P_{2, 1})$.<br/>
$B_{1, 1} \implies (P_{1, 2} \lor P_{2, 1})$ was converted to $P_{1, 2} \lor P_{2, 1} \lor \neg B_{1, 1}$.<br/>
$B_{1, 1} \Longleftarrow (P_{1, 2} \lor P_{2, 1})$ was converted to $\neg (P_{1, 2} \lor P_{2, 1}) \lor B_{1, 1}$ which becomes $(\neg P_{1, 2} \lor B_{1, 1}) \land (\neg P_{2, 1} \lor B_{1, 1})$ after applying De Morgan's laws and distributing the disjunction.<br/>
$B_{2, 1} \iff (P_{1, 1} \lor P_{2, 2} \lor P_{3, 2})$ is converted in similar manner.
## Inference in Propositional Knowledge Base
In this section we will look at two algorithms to check if a sentence is entailed by the `KB`. Our goal is to decide whether $\text{KB} \vDash \alpha$ for some sentence $\alpha$.
### Truth Table Enumeration
It is a model-checking approach which, as the name suggests, enumerates all possible models in which the `KB` is true and checks if $\alpha$ is also true in these models. We list the $n$ symbols in the `KB` and enumerate the $2^{n}$ models in a depth-first manner and check the truth of `KB` and $\alpha$.
```
%psource tt_check_all
```
Note that `tt_entails()` takes an `Expr` which is a conjunction of clauses as the input instead of the `KB` itself. You can use the `ask_if_true()` method of `PropKB` which does all the required conversions. Let's check what `wumpus_kb` tells us about $P_{1, 1}$.
```
wumpus_kb.ask_if_true(~P11), wumpus_kb.ask_if_true(P11)
```
Looking at Figure 7.9 we see that in all models in which the knowledge base is `True`, $P_{1, 1}$ is `False`. It makes sense that `ask_if_true()` returns `True` for $\alpha = \neg P_{1, 1}$ and `False` for $\alpha = P_{1, 1}$. This begs the question, what if $\alpha$ is `True` in only a portion of all models. Do we return `True` or `False`? This doesn't rule out the possibility of $\alpha$ being `True` but it is not entailed by the `KB` so we return `False` in such cases. We can see this is the case for $P_{2, 2}$ and $P_{3, 1}$.
```
wumpus_kb.ask_if_true(~P22), wumpus_kb.ask_if_true(P22)
```
### Proof by Resolution
Recall that our goal is to check whether $\text{KB} \vDash \alpha$ i.e. is $\text{KB} \implies \alpha$ true in every model. Suppose we wanted to check if $P \implies Q$ is valid. We check the satisfiability of $\neg (P \implies Q)$, which can be rewritten as $P \land \neg Q$. If $P \land \neg Q$ is unsatisfiable, then $P \implies Q$ must be true in all models. This gives us the result "$\text{KB} \vDash \alpha$ <em>if and only if</em> $\text{KB} \land \neg \alpha$ is unsatisfiable".<br/>
This technique corresponds to <em>proof by <strong>contradiction</strong></em>, a standard mathematical proof technique. We assume $\alpha$ to be false and show that this leads to a contradiction with known axioms in $\text{KB}$. We obtain a contradiction by making valid inferences using inference rules. In this proof we use a single inference rule, <strong>resolution</strong> which states $(l_1 \lor \dots \lor l_k) \land (m_1 \lor \dots \lor m_n) \land (l_i \iff \neg m_j) \implies l_1 \lor \dots \lor l_{i - 1} \lor l_{i + 1} \lor \dots \lor l_k \lor m_1 \lor \dots \lor m_{j - 1} \lor m_{j + 1} \lor \dots \lor m_n$. Applying the resolution yeilds us a clause which we add to the KB. We keep doing this until:
* There are no new clauses that can be added, in which case $\text{KB} \nvDash \alpha$.
* Two clauses resolve to yield the <em>empty clause</em>, in which case $\text{KB} \vDash \alpha$.
The <em>empty clause</em> is equivalent to <em>False</em> because it arises only from resolving two complementary
unit clauses such as $P$ and $\neg P$ which is a contradiction as both $P$ and $\neg P$ can't be <em>True</em> at the same time.
```
%psource pl_resolution
pl_resolution(wumpus_kb, ~P11), pl_resolution(wumpus_kb, P11)
pl_resolution(wumpus_kb, ~P22), pl_resolution(wumpus_kb, P22)
```
## First-Order Logic Knowledge Bases: `FolKB`
The class `FolKB` can be used to represent a knowledge base of First-order logic sentences. You would initialize and use it the same way as you would for `PropKB` except that the clauses are first-order definite clauses. We will see how to write such clauses to create a database and query them in the following sections.
## Criminal KB
In this section we create a `FolKB` based on the following paragraph.<br/>
<em>The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American.</em><br/>
The first step is to extract the facts and convert them into first-order definite clauses. Extracting the facts from data alone is a challenging task. Fortunately, we have a small paragraph and can do extraction and conversion manually. We'll store the clauses in list aptly named `clauses`.
```
clauses = []
```
<em>“... it is a crime for an American to sell weapons to hostile nations”</em><br/>
The keywords to look for here are 'crime', 'American', 'sell', 'weapon' and 'hostile'. We use predicate symbols to make meaning of them.
* `Criminal(x)`: `x` is a criminal
* `American(x)`: `x` is an American
* `Sells(x ,y, z)`: `x` sells `y` to `z`
* `Weapon(x)`: `x` is a weapon
* `Hostile(x)`: `x` is a hostile nation
Let us now combine them with appropriate variable naming to depict the meaning of the sentence. The criminal `x` is also the American `x` who sells weapon `y` to `z`, which is a hostile nation.
$\text{American}(x) \land \text{Weapon}(y) \land \text{Sells}(x, y, z) \land \text{Hostile}(z) \implies \text{Criminal} (x)$
```
clauses.append(expr("(American(x) & Weapon(y) & Sells(x, y, z) & Hostile(z)) ==> Criminal(x)"))
```
<em>"The country Nono, an enemy of America"</em><br/>
We now know that Nono is an enemy of America. We represent these nations using the constant symbols `Nono` and `America`. the enemy relation is show using the predicate symbol `Enemy`.
$\text{Enemy}(\text{Nono}, \text{America})$
```
clauses.append(expr("Enemy(Nono, America)"))
```
<em>"Nono ... has some missiles"</em><br/>
This states the existence of some missile which is owned by Nono. $\exists x \text{Owns}(\text{Nono}, x) \land \text{Missile}(x)$. We invoke existential instantiation to introduce a new constant `M1` which is the missile owned by Nono.
$\text{Owns}(\text{Nono}, \text{M1}), \text{Missile}(\text{M1})$
```
clauses.append(expr("Owns(Nono, M1)"))
clauses.append(expr("Missile(M1)"))
```
<em>"All of its missiles were sold to it by Colonel West"</em><br/>
If Nono owns something and it classifies as a missile, then it was sold to Nono by West.
$\text{Missile}(x) \land \text{Owns}(\text{Nono}, x) \implies \text{Sells}(\text{West}, x, \text{Nono})$
```
clauses.append(expr("(Missile(x) & Owns(Nono, x)) ==> Sells(West, x, Nono)"))
```
<em>"West, who is American"</em><br/>
West is an American.
$\text{American}(\text{West})$
```
clauses.append(expr("American(West)"))
```
We also know, from our understanding of language, that missiles are weapons and that an enemy of America counts as “hostile”.
$\text{Missile}(x) \implies \text{Weapon}(x), \text{Enemy}(x, \text{America}) \implies \text{Hostile}(x)$
```
clauses.append(expr("Missile(x) ==> Weapon(x)"))
clauses.append(expr("Enemy(x, America) ==> Hostile(x)"))
```
Now that we have converted the information into first-order definite clauses we can create our first-order logic knowledge base.
```
crime_kb = FolKB(clauses)
```
## Inference in First-Order Logic
In this section we look at a forward chaining and a backward chaining algorithm for `FolKB`. Both aforementioned algorithms rely on a process called <strong>unification</strong>, a key component of all first-order inference algorithms.
### Unification
We sometimes require finding substitutions that make different logical expressions look identical. This process, called unification, is done by the `unify` algorithm. It takes as input two sentences and returns a <em>unifier</em> for them if one exists. A unifier is a dictionary which stores the substitutions required to make the two sentences identical. It does so by recursively unifying the components of a sentence, where the unification of a variable symbol `var` with a constant symbol `Const` is the mapping `{var: Const}`. Let's look at a few examples.
```
unify(expr('x'), 3)
unify(expr('A(x)'), expr('A(B)'))
unify(expr('Cat(x) & Dog(Dobby)'), expr('Cat(Bella) & Dog(y)'))
```
In cases where there is no possible substitution that unifies the two sentences the function return `None`.
```
print(unify(expr('Cat(x)'), expr('Dog(Dobby)')))
```
We also need to take care we do not unintentionally use the same variable name. Unify treats them as a single variable which prevents it from taking multiple value.
```
print(unify(expr('Cat(x) & Dog(Dobby)'), expr('Cat(Bella) & Dog(x)')))
```
### Forward Chaining Algorithm
We consider the simple forward-chaining algorithm presented in <em>Figure 9.3</em>. We look at each rule in the knoweldge base and see if the premises can be satisfied. This is done by finding a substitution which unifies each of the premise with a clause in the `KB`. If we are able to unify the premises, the conclusion (with the corresponding substitution) is added to the `KB`. This inferencing process is repeated until either the query can be answered or till no new sentences can be added. We test if the newly added clause unifies with the query in which case the substitution yielded by `unify` is an answer to the query. If we run out of sentences to infer, this means the query was a failure.
The function `fol_fc_ask` is a generator which yields all substitutions which validate the query.
```
%psource fol_fc_ask
```
Let's find out all the hostile nations. Note that we only told the `KB` that Nono was an enemy of America, not that it was hostile.
```
answer = fol_fc_ask(crime_kb, expr('Hostile(x)'))
print(list(answer))
```
The generator returned a single substitution which says that Nono is a hostile nation. See how after adding another enemy nation the generator returns two substitutions.
```
crime_kb.tell(expr('Enemy(JaJa, America)'))
answer = fol_fc_ask(crime_kb, expr('Hostile(x)'))
print(list(answer))
```
<strong><em>Note</em>:</strong> `fol_fc_ask` makes changes to the `KB` by adding sentences to it.
### Backward Chaining Algorithm
This algorithm works backward from the goal, chaining through rules to find known facts that support the proof. Suppose `goal` is the query we want to find the substitution for. We find rules of the form $\text{lhs} \implies \text{goal}$ in the `KB` and try to prove `lhs`. There may be multiple clauses in the `KB` which give multiple `lhs`. It is sufficient to prove only one of these. But to prove a `lhs` all the conjuncts in the `lhs` of the clause must be proved. This makes it similar to <em>And/Or</em> search.
#### OR
The <em>OR</em> part of the algorithm comes from our choice to select any clause of the form $\text{lhs} \implies \text{goal}$. Looking at all rules's `lhs` whose `rhs` unify with the `goal`, we yield a substitution which proves all the conjuncts in the `lhs`. We use `parse_definite_clause` to attain `lhs` and `rhs` from a clause of the form $\text{lhs} \implies \text{rhs}$. For atomic facts the `lhs` is an empty list.
```
%psource fol_bc_or
```
#### AND
The <em>AND</em> corresponds to proving all the conjuncts in the `lhs`. We need to find a substitution which proves each <em>and</em> every clause in the list of conjuncts.
```
%psource fol_bc_and
```
Now the main function `fl_bc_ask` calls `fol_bc_or` with substitution initialized as empty. The `ask` method of `FolKB` uses `fol_bc_ask` and fetches the first substitution returned by the generator to answer query. Let's query the knowledge base we created from `clauses` to find hostile nations.
```
# Rebuild KB because running fol_fc_ask would add new facts to the KB
crime_kb = FolKB(clauses)
crime_kb.ask(expr('Hostile(x)'))
```
You may notice some new variables in the substitution. They are introduced to standardize the variable names to prevent naming problems as discussed in the [Unification section](#Unification)
## Appendix: The Implementation of `|'==>'|`
Consider the `Expr` formed by this syntax:
```
P |'==>'| ~Q
```
What is the funny `|'==>'|` syntax? The trick is that "`|`" is just the regular Python or-operator, and so is exactly equivalent to this:
```
(P | '==>') | ~Q
```
In other words, there are two applications of or-operators. Here's the first one:
```
P | '==>'
```
What is going on here is that the `__or__` method of `Expr` serves a dual purpose. If the right-hand-side is another `Expr` (or a number), then the result is an `Expr`, as in `(P | Q)`. But if the right-hand-side is a string, then the string is taken to be an operator, and we create a node in the abstract syntax tree corresponding to a partially-filled `Expr`, one where we know the left-hand-side is `P` and the operator is `==>`, but we don't yet know the right-hand-side.
The `PartialExpr` class has an `__or__` method that says to create an `Expr` node with the right-hand-side filled in. Here we can see the combination of the `PartialExpr` with `Q` to create a complete `Expr`:
```
partial = PartialExpr('==>', P)
partial | ~Q
```
This [trick](http://code.activestate.com/recipes/384122-infix-operators/) is due to [Ferdinand Jamitzky](http://code.activestate.com/recipes/users/98863/), with a modification by [C. G. Vedant](https://github.com/Chipe1),
who suggested using a string inside the or-bars.
## Appendix: The Implementation of `expr`
How does `expr` parse a string into an `Expr`? It turns out there are two tricks (besides the Jamitzky/Vedant trick):
1. We do a string substitution, replacing "`==>`" with "`|'==>'|`" (and likewise for other operators).
2. We `eval` the resulting string in an environment in which every identifier
is bound to a symbol with that identifier as the `op`.
In other words,
```
expr('~(P & Q) ==> (~P | ~Q)')
```
is equivalent to doing:
```
P, Q = symbols('P, Q')
~(P & Q) |'==>'| (~P | ~Q)
```
One thing to beware of: this puts `==>` at the same precedence level as `"|"`, which is not quite right. For example, we get this:
```
P & Q |'==>'| P | Q
```
which is probably not what we meant; when in doubt, put in extra parens:
```
(P & Q) |'==>'| (P | Q)
```
## Examples
```
from notebook import Canvas_fol_bc_ask
canvas_bc_ask = Canvas_fol_bc_ask('canvas_bc_ask', crime_kb, expr('Criminal(x)'))
```
# Authors
This notebook by [Chirag Vartak](https://github.com/chiragvartak) and [Peter Norvig](https://github.com/norvig).
| true |
code
| 0.767178 | null | null | null | null |
|
# Classification algorithms
In the context of record linkage, classification refers to the process of dividing record pairs into matches and non-matches (distinct pairs). There are dozens of classification algorithms for record linkage. Roughly speaking, classification algorithms fall into two groups:
- **supervised learning algorithms** - These algorithms make use of trainings data. If you do have trainings data, then you can use supervised learning algorithms. Most supervised learning algorithms offer good accuracy and reliability. Examples of supervised learning algorithms in the *Python Record Linkage Toolkit* are *Logistic Regression*, *Naive Bayes* and *Support Vector Machines*.
- **unsupervised learning algorithms** - These algorithms do not need training data. The *Python Record Linkage Toolkit* supports *K-means clustering* and an *Expectation/Conditional Maximisation* classifier.
```
%precision 5
from __future__ import print_function
import pandas as pd
pd.set_option('precision',5)
pd.options.display.max_rows = 10
```
**First things first**
The examples below make use of the [Krebs register](http://recordlinkage.readthedocs.org/en/latest/reference.html#recordlinkage.datasets.krebsregister_cmp_data) (German for cancer registry) dataset. The Krebs register dataset contains comparison vectors of a large set of record pairs. For each record pair, it is known if the records represent the same person (match) or not (non-match). This was done with a massive clerical review. First, import the recordlinkage module and load the Krebs register data. The dataset contains 5749132 compared record pairs and has the following variables: first name, last name, sex, birthday, birth month, birth year and zip code. The Krebs register contains `len(krebs_true_links) == 20931` matching record pairs.
```
import recordlinkage as rl
from recordlinkage.datasets import load_krebsregister
krebs_X, krebs_true_links = load_krebsregister(missing_values=0)
krebs_X
```
Most classifiers can not handle comparison vectors with missing values. To prevent issues with the classification algorithms, we convert the missing values into disagreeing comparisons (using argument missing_values=0). This approach for handling missing values is widely used in record linkage applications.
```
krebs_X.describe().T
```
## Supervised learning
As described before, supervised learning algorithms do need training data. Training data is data for which the true match status is known for each comparison vector. In the example in this section, we consider that the true match status of the first 5000 record pairs of the Krebs register data is known.
```
golden_pairs = krebs_X[0:5000]
golden_matches_index = golden_pairs.index & krebs_true_links # 2093 matching pairs
```
### Logistic regression
The ``recordlinkage.LogisticRegressionClassifier`` classifier is an application of the logistic regression model. This supervised learning method is one of the oldest classification algorithms used in record linkage. In situations with enough training data, the algorithm gives relatively good results.
```
# Initialize the classifier
logreg = rl.LogisticRegressionClassifier()
# Train the classifier
logreg.fit(golden_pairs, golden_matches_index)
print ("Intercept: ", logreg.intercept)
print ("Coefficients: ", logreg.coefficients)
# Predict the match status for all record pairs
result_logreg = logreg.predict(krebs_X)
len(result_logreg)
rl.confusion_matrix(krebs_true_links, result_logreg, len(krebs_X))
# The F-score for this prediction is
rl.fscore(krebs_true_links, result_logreg)
```
The predicted number of matches is not much more than the 20931 true matches. The result was achieved with a small training dataset of 5000 record pairs.
In (older) literature, record linkage procedures are often divided in **deterministic record linkage** and **probabilistic record linkage**. The Logistic Regression Classifier belongs to deterministic record linkage methods. Each feature/variable has a certain importance (named weight). The weight is multiplied with the comparison/similarity vector. If the total sum exceeds a certain threshold, it as considered to be a match.
```
intercept = -9
coefficients = [2.0, 1.0, 3.0, 1.0, 1.0, 1.0, 1.0, 2.0, 3.0]
logreg = rl.LogisticRegressionClassifier(coefficients, intercept)
# predict without calling LogisticRegressionClassifier.fit
result_logreg_pretrained = logreg.predict(krebs_X)
print (len(result_logreg_pretrained))
rl.confusion_matrix(krebs_true_links, result_logreg_pretrained, len(krebs_X))
# The F-score for this classification is
rl.fscore(krebs_true_links, result_logreg_pretrained)
```
For the given coefficients, the F-score is better than the situation without trainings data. Surprising? No (use more trainings data and the result will improve)
### Naive Bayes
In contrast to the logistic regression classifier, the Naive Bayes classifier is a probabilistic classifier. The probabilistic record linkage framework by Fellegi and Sunter (1969) is the most well-known probabilistic classification method for record linkage. Later, it was proved that the Fellegi and Sunter method is mathematically equivalent to the Naive Bayes method in case of assuming independence between comparison variables.
```
# Train the classifier
nb = rl.NaiveBayesClassifier(binarize=0.3)
nb.fit(golden_pairs, golden_matches_index)
# Predict the match status for all record pairs
result_nb = nb.predict(krebs_X)
len(result_nb)
rl.confusion_matrix(krebs_true_links, result_nb, len(krebs_X))
# The F-score for this classification is
rl.fscore(krebs_true_links, result_nb)
```
### Support Vector Machines
Support Vector Machines (SVM) have become increasingly popular in record linkage. The algorithm performs well there is only a small amount of training data available. The implementation of SVM in the Python Record Linkage Toolkit is a linear SVM algorithm.
```
# Train the classifier
svm = rl.SVMClassifier()
svm.fit(golden_pairs, golden_matches_index)
# Predict the match status for all record pairs
result_svm = svm.predict(krebs_X)
len(result_svm)
rl.confusion_matrix(krebs_true_links, result_svm, len(krebs_X))
# The F-score for this classification is
rl.fscore(krebs_true_links, result_svm)
```
## Unsupervised learning
In situations without training data, unsupervised learning can be a solution for record linkage problems. In this section, we discuss two unsupervised learning methods. One algorithm is K-means clustering, and the other algorithm is an implementation of the Expectation-Maximisation algorithm. Most of the time, unsupervised learning algorithms take more computational time because of the iterative structure in these algorithms.
### K-means clustering
The K-means clustering algorithm is well-known and widely used in big data analysis. The K-means classifier in the Python Record Linkage Toolkit package is configured in such a way that it can be used for linking records. For more info about the K-means clustering see [Wikipedia](https://en.wikipedia.org/wiki/K-means_clustering).
```
kmeans = rl.KMeansClassifier()
result_kmeans = kmeans.fit_predict(krebs_X)
# The predicted number of matches
len(result_kmeans)
```
The classifier is now trained and the comparison vectors are classified.
```
rl.confusion_matrix(krebs_true_links, result_kmeans, len(krebs_X))
rl.fscore(krebs_true_links, result_kmeans)
```
### Expectation/Conditional Maximization Algorithm
The ECM-algorithm is an Expectation-Maximisation algorithm with some additional constraints. This algorithm is closely related to the Naive Bayes algorithm. The ECM algorithm is also closely related to estimating the parameters in the Fellegi and Sunter (1969) framework. The algorithms assume that the attributes are independent of each other. The Naive Bayes algorithm uses the same principles.
```
# Train the classifier
ecm = rl.ECMClassifier(binarize=0.8)
result_ecm = ecm.fit_predict(krebs_X)
len(result_ecm)
rl.confusion_matrix(krebs_true_links, result_ecm, len(krebs_X))
# The F-score for this classification is
rl.fscore(krebs_true_links, result_ecm)
```
| true |
code
| 0.624923 | null | null | null | null |
|
# Consumption Equivalent Variation (CEV)
1. Use the model in the **ConsumptionSaving.pdf** slides and solve it using **egm**
2. This notebooks estimates the *cost of income risk* through the Consumption Equivalent Variation (CEV)
We will here focus on the cost of income risk, but the CEV can be used to estimate the value of many different aspects of an economy. For eaxample, [Oswald (2019)](http://qeconomics.org/ojs/index.php/qe/article/view/701 "The option value of homeownership") estimated the option value of homeownership using a similar strategy as described below.
**Goal:** To estimate the CEV by comparing the *value of life* under the baseline economy and an alternative economy with higher permanent income shock variance along with a consumption compensation.
**Value of Life:**
1. Let the *utility function* be a generalized version of the CRRA utility function with $\delta$ included as a potential consumption compensation.
\begin{equation}
{u}(c,\delta) = \frac{(c\cdot(1+\delta))^{1-\rho}}{1-\rho}
\end{equation}
2. Let the *value of life* of a synthetic consumer $s$ for a given level of permanent income shock varaince, $\sigma_{\psi}$, and $\delta$, be
\begin{equation}
{V}_{s}({\sigma}_{\psi},\delta)=\sum_{t=1}^T \beta ^{t-1}{u}({c}^{\star}_{s,t}({\sigma}_{\psi},\delta),\delta)
\end{equation}
where ${c}^{\star}_{s,t}({\sigma}_{\psi},\delta)$ is optimal consumption found using the **egm**. The value of life is calcualted in the function `value_of_life(.)` defined below.
**Consumption Equivalent Variation:**
1. Let $V=\frac{1}{S}\sum_{s=1}^SV(\sigma_{\psi},0)$ be the average value of life under the *baseline* economy with the baseline value of $\sigma_{\psi}$ and $\delta=0$.
2. Let $\tilde{V}(\delta)=\frac{1}{S}\sum_{s=1}^SV(\tilde{\sigma}_{\psi},\delta)$ be the average value of life under the *alternative* economy with $\tilde{\sigma}_{\psi} > \sigma_{\psi}$.
The CEV is the value of $\delta$ that sets $V=\tilde{V}(\delta)$ and can be estimated as
\begin{equation}
\hat{\delta} = \arg\min_\delta (V-\tilde{V}(\delta))^2
\end{equation}
where the objective function is calculated in `obj_func_cev(.)` defined below.
# Setup
```
%matplotlib inline
%load_ext autoreload
%autoreload 2
import time
import numpy as np
import scipy.optimize as optimize
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
import sys
sys.path.append('../')
import ConsumptionSavingModel as csm
from ConsumptionSavingModel import ConsumptionSavingModelClass
```
# Setup the baseline model and the alternative model
```
par = {'simT':40}
model = ConsumptionSavingModelClass(name='baseline',solmethod='egm',**par)
# increase the permanent income with 100 percent and allow for consumption compensation
par_cev = {'sigma_psi':0.2,'do_cev':1,'simT':40}
model_cev = ConsumptionSavingModelClass(name='cev',solmethod='egm',**par_cev)
model.solve()
model.simulate()
```
# Average value of life
**Define Functions:** value of life and objective function used to estimate "cev"
```
def value_of_life(model):
# utility associated with consumption for all N and T
util = csm.utility(model.sim.c,model.par)
# discounted sum of utility
disc = np.ones(model.par.simT)
disc[1:] = np.cumprod(np.ones(model.par.simT-1)*model.par.beta)
disc_util = np.sum(disc*util,axis=1)
# return average of discounted sum of utility
return np.mean(disc_util)
def obj_func_cev(theta,model_cev,value_of_life_baseline):
# update cev-parameter
setattr(model_cev.par,'cev',theta)
# re-solve and simulate alternative model
model_cev.solve(do_print=False)
model_cev.simulate(do_print=False)
# calculate value of life
value_of_life_cev = value_of_life(model_cev)
# return squared difference to baseline
return (value_of_life_cev - value_of_life_baseline)*(value_of_life_cev - value_of_life_baseline)
```
**Baseline value of life and objective function at cev=0**
```
value_of_life_baseline = value_of_life(model)
obj_func_cev(0.0,model_cev,value_of_life_baseline)
# plot the objective function
grid_cev = np.linspace(0.0,0.2,20)
grid_obj = np.empty(grid_cev.size)
for j,cev in enumerate(grid_cev):
grid_obj[j] = obj_func_cev(cev,model_cev,value_of_life_baseline)
plt.plot(grid_cev,grid_obj);
```
# Estimate the Consumption Equivalent Variation (CEV)
```
res = optimize.minimize_scalar(obj_func_cev, bounds=[-0.01,0.5],
args=(model_cev,value_of_life_baseline),method='golden')
res
```
The estimated CEV suggests that consumers would be indifferent between the baseline economy and a 100% increase in the permanent income shock variance along with a 10% increase in consumption in all periods.
| true |
code
| 0.523603 | null | null | null | null |
|
# Facial Expression Recognizer
```
#The OS module in Python provides a way of using operating system dependent functionality.
#import os
# For array manipulation
import numpy as np
#For importing data from csv and other manipulation
import pandas as pd
#For displaying images
import matplotlib.pyplot as plt
import matplotlib.cm as cm
%matplotlib inline
#For displaying graph
#import seaborn as sns
#For constructing and handling neural network
import tensorflow as tf
#Constants
LEARNING_RATE = 1e-4
TRAINING_ITERATIONS = 10000 #increase iteration to improve accuracy
DROPOUT = 0.5
BATCH_SIZE = 50
IMAGE_TO_DISPLAY = 3
VALIDATION_SIZE = 2000
#Reading data from csv file
data = pd.read_csv('Train_updated_six_emotion.csv')
#Seperating images data from labels ie emotion
images = data.iloc[:,1:].values
images = images.astype(np.float)
#Normalizaton : convert from [0:255] => [0.0:1.0]
images = np.multiply(images, 1.0 / 255.0)
image_size = images.shape[1]
image_width = image_height = 48
#Displaying an image from 20K images
def display(img):
#Reshaping,(1*2304) pixels into (48*48)
one_image = img.reshape(image_width,image_height)
plt.axis('off')
#Show image
plt.imshow(one_image, cmap=cm.binary)
display(images[IMAGE_TO_DISPLAY])
#Creating an array of emotion labels using dataframe 'data'
labels_flat = data[['label']].values.ravel()
labels_count = np.unique(labels_flat).shape[0]
# convert class labels from scalars to one-hot vectors
# 0 => [1 0 0]
# 1 => [0 1 0]
# 2 => [0 0 1]
def dense_to_one_hot(labels_dense, num_classes = 7):
num_labels = labels_dense.shape[0]
index_offset = np.arange(num_labels) * num_classes
labels_one_hot = np.zeros((num_labels, num_classes))
labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1
return labels_one_hot
labels = dense_to_one_hot(labels_flat, labels_count)
labels = labels.astype(np.uint8)
#Printing example hot-dense label
print ('labels[{0}] => {1}'.format(IMAGE_TO_DISPLAY,labels[IMAGE_TO_DISPLAY]))
#Using data for training & cross validation
validation_images = images[:2000]
validation_labels = labels[:2000]
train_images = images[2000:]
train_labels = labels[2000:]
```
#Next is the neural network structure.
#Weights and biases are created.
#The weights should be initialised with a small a amount of noise
#for symmetry breaking, and to prevent 0 gradients. Since we are using
#rectified neurones (ones that contain rectifier function *f(x)=max(0,x)*),
#we initialise them with a slightly positive initial bias to avoid "dead neurones.
```
# initialization of weight
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
# We use zero padded convolution neural network with a stride of 1 and the size of the output is same as that of input.
# The convolution layer finds the features in the data the number of filter denoting the number of features to be detected.
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
# Pooling downsamples the data. 2x2 max-pooling splits the image into square 2-pixel blocks and only keeps the maximum value
# for each of the blocks.
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# images
x = tf.placeholder('float', shape=[None, image_size])
# labels (0, 1 or 2)
y_ = tf.placeholder('float', shape=[None, labels_count])
BATCH_SIZE
```
### VGG-16 architecture
```
W_conv1 = weight_variable([3, 3, 1, 8])
b_conv1 = bias_variable([8])
# we reshape the input data to a 4d tensor, with the first dimension corresponding to the number of images,
# second and third - to image width and height, and the final dimension - to the number of colour channels.
# (20000,2304) => (20000,48,48,1)
image = tf.reshape(x, [-1,image_width , image_height,1])
print (image.get_shape())
h_conv1 = tf.nn.relu(conv2d(image, W_conv1) + b_conv1)
print (h_conv1)
W_conv2 = weight_variable([3, 3, 8, 8])
b_conv2 = bias_variable([8])
h_conv2 = tf.nn.relu(conv2d(h_conv1, W_conv2) + b_conv2)
print (h_conv2)
# pooling reduces the size of the output from 48x48 to 24x24.
h_pool1 = max_pool_2x2(h_conv2)
#print (h_pool1.get_shape()) => (20000, 24, 24, 8)
# Prepare for visualization
# display 8 features in 4 by 2 grid
layer1 = tf.reshape(h_conv1, (-1, image_height, image_width, 4 ,2))
# reorder so the channels are in the first dimension, x and y follow.
layer1 = tf.transpose(layer1, (0, 3, 1, 4,2))
layer1 = tf.reshape(layer1, (-1, image_height*4, image_width*2))
# The second layer has 16 features for each 5x5 patch. Its weight tensor has a shape of [5, 5, 8, 16].
# The first two dimensions are the patch size. the next is the number of input channels (8 channels correspond to 8
# features that we got from previous convolutional layer).
W_conv3 = weight_variable([3, 3, 8, 16])
b_conv3 = bias_variable([16])
h_conv3 = tf.nn.relu(conv2d(h_pool1, W_conv3) + b_conv3)
print(h_conv3)
W_conv4 = weight_variable([3, 3, 16, 16])
b_conv4 = bias_variable([16])
h_conv4 = tf.nn.relu(conv2d(h_conv3, W_conv4) + b_conv4)
print(h_conv4)
h_pool2 = max_pool_2x2(h_conv4)
#print (h_pool2.get_shape()) => (20000, 12, 12, 16)
# The third layer has 16 features for each 5x5 patch. Its weight tensor has a shape of [5, 5, 16, 32].
# The first two dimensions are the patch size. the next is the number of input channels (16 channels correspond to 16
# features that we got from previous convolutional layer)
W_conv5 = weight_variable([3, 3, 16, 32])
b_conv5 = bias_variable([32])
h_conv5 = tf.nn.relu(conv2d(h_pool2, W_conv5) + b_conv5)
print(h_conv5)
W_conv6 = weight_variable([3, 3, 32, 32])
b_conv6 = bias_variable([32])
h_conv6 = tf.nn.relu(conv2d(h_conv5, W_conv6) + b_conv6)
print(h_conv6)
W_conv7 = weight_variable([3, 3, 32, 32])
b_conv7 = bias_variable([32])
h_conv7 = tf.nn.relu(conv2d(h_conv6, W_conv7) + b_conv7)
print(h_conv7)
h_pool3 = max_pool_2x2(h_conv7)
#print (h_pool2.get_shape()) => (20000, 6, 6, 32)
W_conv8 = weight_variable([3, 3, 32, 32])
b_conv8 = bias_variable([32])
h_conv8 = tf.nn.relu(conv2d(h_pool3, W_conv8) + b_conv8)
print(h_conv8)
W_conv9 = weight_variable([3, 3, 32, 32])
b_conv9 = bias_variable([32])
h_conv9 = tf.nn.relu(conv2d(h_conv8, W_conv9) + b_conv9)
print(h_conv9)
W_conv10 = weight_variable([3, 3, 32, 32])
b_conv10 = bias_variable([32])
h_conv10 = tf.nn.relu(conv2d(h_conv9, W_conv10) + b_conv10)
print(h_conv10)
h_pool4 = max_pool_2x2(h_conv10)
print (h_pool4.get_shape())
# Now that the image size is reduced to 3x3, we add a Fully_Connected_layer) with 1024 neurones
# to allow processing on the entire image (each of the neurons of the fully connected layer is
# connected to all the activations/outpus of the previous layer)
W_conv11 = weight_variable([3, 3, 32, 32])
b_conv11 = bias_variable([32])
h_conv11 = tf.nn.relu(conv2d(h_pool4, W_conv11) + b_conv11)
print(h_conv11)
W_conv12 = weight_variable([3, 3, 32, 32])
b_conv12 = bias_variable([32])
h_conv12 = tf.nn.relu(conv2d(h_conv11, W_conv12) + b_conv12)
print(h_conv12)
W_conv13 = weight_variable([3, 3, 32, 32])
b_conv13 = bias_variable([32])
h_conv13 = tf.nn.relu(conv2d(h_conv12, W_conv13) + b_conv13)
print(h_conv13)
# densely connected layer
W_fc1 = weight_variable([3 * 3 * 32, 512])
b_fc1 = bias_variable([512])
# (20000, 6, 6, 32) => (20000, 1152 )
h_pool2_flat = tf.reshape(h_conv13, [-1, 3*3*32])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
print (h_fc1.get_shape()) # => (20000, 1024)
W_fc2 = weight_variable([512, 512])
b_fc2 = bias_variable([512])
h_fc2 = tf.nn.relu(tf.matmul(h_fc1, W_fc2) + b_fc2)
print (h_fc2.get_shape()) # => (20000, 1024)
W_fc3 = weight_variable([512, 512])
b_fc3 = bias_variable([512])
h_fc3 = tf.nn.relu(tf.matmul(h_fc2, W_fc3) + b_fc3)
print (h_fc3.get_shape()) # => (20000, 1024)
# To prevent overfitting, we apply dropout before the readout layer.
# Dropout removes some nodes from the network at each training stage. Each of the nodes is either kept in the
# network with probability (keep_prob) or dropped with probability (1 - keep_prob).After the training stage
# is over the nodes are returned to the NN with their original weights.
keep_prob = tf.placeholder('float')
h_fc1_drop = tf.nn.dropout(h_fc2, keep_prob)
# readout layer 1024*3
W_fc4 = weight_variable([512, labels_count])
b_fc4 = bias_variable([labels_count])
# Finally, we add a softmax layer
y = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc4) + b_fc4)
#print (y.get_shape()) # => (20000, 3)
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
train_step = tf.train.AdamOptimizer(LEARNING_RATE).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float'))
predict = tf.argmax(y,1)
epochs_completed = 0
index_in_epoch = 0
num_examples = train_images.shape[0]
# serve data by batches
def next_batch(batch_size):
global train_images
global train_labels
global index_in_epoch
global epochs_completed
start = index_in_epoch
index_in_epoch += batch_size
# when all trainig data have been already used, it is reorder randomly
if index_in_epoch > num_examples:
# finished epoch
epochs_completed += 1
# shuffle the data
perm = np.arange(num_examples)
np.random.shuffle(perm)
train_images = train_images[perm]
train_labels = train_labels[perm]
# start next epoch
start = 0
index_in_epoch = batch_size
assert batch_size <= num_examples
end = index_in_epoch
return train_images[start:end], train_labels[start:end]
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
# visualisation variables
train_accuracies = []
validation_accuracies = []
x_range = []
display_step=1
for i in range(TRAINING_ITERATIONS):
#get new batch
batch_xs, batch_ys = next_batch(BATCH_SIZE)
# check progress on every 1st,2nd,...,10th,20th,...,100th... step
if i%display_step == 0 or (i+1) == TRAINING_ITERATIONS:
train_accuracy = accuracy.eval(feed_dict={x:batch_xs,
y_: batch_ys,
keep_prob: 1.0})
if(VALIDATION_SIZE):
validation_accuracy = accuracy.eval(feed_dict={ x: validation_images[0:BATCH_SIZE],
y_: validation_labels[0:BATCH_SIZE],
keep_prob: 1.0})
print('training_accuracy / validation_accuracy => %.2f / %.2f for step %d'%(train_accuracy, validation_accuracy, i))
validation_accuracies.append(validation_accuracy)
else:
print('training_accuracy => %.4f for step %d'%(train_accuracy, i))
train_accuracies.append(train_accuracy)
x_range.append(i)
# increase display_step
if i%(display_step*10) == 0 and i:
display_step *= 10
# train on batch
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys, keep_prob: DROPOUT})
if(VALIDATION_SIZE):
validation_accuracy = accuracy.eval(feed_dict={x: validation_images,
y_: validation_labels,
keep_prob: 1.0})
print('validation_accuracy => %.4f'%validation_accuracy)
plt.plot(x_range, train_accuracies,'-b', label='Training')
plt.plot(x_range, validation_accuracies,'-g', label='Validation')
plt.legend(loc='lower right', frameon=False)
plt.ylim(ymax = 1.1, ymin = 0.0)
plt.ylabel('accuracy')
plt.xlabel('step')
plt.show()
```
| true |
code
| 0.668177 | null | null | null | null |
|
<h1>Demand forecasting with BigQuery and TensorFlow</h1>
In this notebook, we will develop a machine learning model to predict the demand for taxi cabs in New York.
To develop the model, we will need to get historical data of taxicab usage. This data exists in BigQuery. Let's start by looking at the schema.
```
import google.datalab.bigquery as bq
import pandas as pd
import numpy as np
import shutil
%bq tables describe --name bigquery-public-data.new_york.tlc_yellow_trips_2015
```
<h2> Analyzing taxicab demand </h2>
Let's pull the number of trips for each day in the 2015 dataset using Standard SQL.
```
%bq query
SELECT
EXTRACT (DAYOFYEAR from pickup_datetime) AS daynumber
FROM `bigquery-public-data.new_york.tlc_yellow_trips_2015`
LIMIT 5
```
<h3> Modular queries and Pandas dataframe </h3>
Let's use the total number of trips as our proxy for taxicab demand (other reasonable alternatives are total trip_distance or total fare_amount). It is possible to predict multiple variables using Tensorflow, but for simplicity, we will stick to just predicting the number of trips.
We will give our query a name 'taxiquery' and have it use an input variable '$YEAR'. We can then invoke the 'taxiquery' by giving it a YEAR. The to_dataframe() converts the BigQuery result into a <a href='http://pandas.pydata.org/'>Pandas</a> dataframe.
```
%bq query -n taxiquery
WITH trips AS (
SELECT EXTRACT (DAYOFYEAR from pickup_datetime) AS daynumber
FROM `bigquery-public-data.new_york.tlc_yellow_trips_*`
where _TABLE_SUFFIX = @YEAR
)
SELECT daynumber, COUNT(1) AS numtrips FROM trips
GROUP BY daynumber ORDER BY daynumber
query_parameters = [
{
'name': 'YEAR',
'parameterType': {'type': 'STRING'},
'parameterValue': {'value': 2015}
}
]
trips = taxiquery.execute(query_params=query_parameters).result().to_dataframe()
trips[:5]
```
<h3> Benchmark </h3>
Often, a reasonable estimate of something is its historical average. We can therefore benchmark our machine learning model against the historical average.
```
avg = np.mean(trips['numtrips'])
print('Just using average={0} has RMSE of {1}'.format(avg, np.sqrt(np.mean((trips['numtrips'] - avg)**2))))
```
The mean here is about 400,000 and the root-mean-square-error (RMSE) in this case is about 52,000. In other words, if we were to estimate that there are 400,000 taxi trips on any given day, that estimate is will be off on average by about 52,000 in either direction.
Let's see if we can do better than this -- our goal is to make predictions of taxicab demand whose RMSE is lower than 52,000.
What kinds of things affect people's use of taxicabs?
<h2> Weather data </h2>
We suspect that weather influences how often people use a taxi. Perhaps someone who'd normally walk to work would take a taxi if it is very cold or rainy.
One of the advantages of using a global data warehouse like BigQuery is that you get to mash up unrelated datasets quite easily.
```
%bq query
SELECT * FROM `bigquery-public-data.noaa_gsod.stations`
WHERE state = 'NY' AND wban != '99999' AND name LIKE '%LA GUARDIA%'
```
<h3> Variables </h3>
Let's pull out the minimum and maximum daily temperature (in Fahrenheit) as well as the amount of rain (in inches) for La Guardia airport.
```
%bq query -n wxquery
SELECT EXTRACT (DAYOFYEAR FROM CAST(CONCAT(@YEAR,'-',mo,'-',da) AS TIMESTAMP)) AS daynumber,
MIN(EXTRACT (DAYOFWEEK FROM CAST(CONCAT(@YEAR,'-',mo,'-',da) AS TIMESTAMP))) dayofweek,
MIN(min) mintemp, MAX(max) maxtemp, MAX(IF(prcp=99.99,0,prcp)) rain
FROM `bigquery-public-data.noaa_gsod.gsod*`
WHERE stn='725030' AND _TABLE_SUFFIX = @YEAR
GROUP BY 1 ORDER BY daynumber DESC
query_parameters = [
{
'name': 'YEAR',
'parameterType': {'type': 'STRING'},
'parameterValue': {'value': 2015}
}
]
weather = wxquery.execute(query_params=query_parameters).result().to_dataframe()
weather[:5]
```
<h3> Merge datasets </h3>
Let's use Pandas to merge (combine) the taxi cab and weather datasets day-by-day.
```
data = pd.merge(weather, trips, on='daynumber')
data[:5]
```
<h3> Exploratory analysis </h3>
Is there a relationship between maximum temperature and the number of trips?
```
j = data.plot(kind='scatter', x='maxtemp', y='numtrips')
```
The scatterplot above doesn't look very promising. There appears to be a weak downward trend, but it's also quite noisy.
Is there a relationship between the day of the week and the number of trips?
```
j = data.plot(kind='scatter', x='dayofweek', y='numtrips')
```
Hurrah, we seem to have found a predictor. It appears that people use taxis more later in the week. Perhaps New Yorkers make weekly resolutions to walk more and then lose their determination later in the week, or maybe it reflects tourism dynamics in New York City.
Perhaps if we took out the <em>confounding</em> effect of the day of the week, maximum temperature will start to have an effect. Let's see if that's the case:
```
j = data[data['dayofweek'] == 7].plot(kind='scatter', x='maxtemp', y='numtrips')
```
Removing the confounding factor does seem to reflect an underlying trend around temperature. But ... the data are a little sparse, don't you think? This is something that you have to keep in mind -- the more predictors you start to consider (here we are using two: day of week and maximum temperature), the more rows you will need so as to avoid <em> overfitting </em> the model.
<h3> Adding 2014 and 2016 data </h3>
Let's add in 2014 and 2016 data to the Pandas dataframe. Note how useful it was for us to modularize our queries around the YEAR.
```
data2 = data # 2015 data
for year in [2014, 2016]:
query_parameters = [
{
'name': 'YEAR',
'parameterType': {'type': 'STRING'},
'parameterValue': {'value': year}
}
]
weather = wxquery.execute(query_params=query_parameters).result().to_dataframe()
trips = taxiquery.execute(query_params=query_parameters).result().to_dataframe()
data_for_year = pd.merge(weather, trips, on='daynumber')
data2 = pd.concat([data2, data_for_year])
data2.describe()
j = data2[data2['dayofweek'] == 7].plot(kind='scatter', x='maxtemp', y='numtrips')
```
The data do seem a bit more robust. If we had even more data, it would be better of course. But in this case, we only have 2014-2016 data for taxi trips, so that's what we will go with.
<h2> Machine Learning with Tensorflow </h2>
We'll use 80% of our dataset for training and 20% of the data for testing the model we have trained. Let's shuffle the rows of the Pandas dataframe so that this division is random. The predictor (or input) columns will be every column in the database other than the number-of-trips (which is our target, or what we want to predict).
The machine learning models that we will use -- linear regression and neural networks -- both require that the input variables are numeric in nature.
The day of the week, however, is a categorical variable (i.e. Tuesday is not really greater than Monday). So, we should create separate columns for whether it is a Monday (with values 0 or 1), Tuesday, etc.
Against that, we do have limited data (remember: the more columns you use as input features, the more rows you need to have in your training dataset), and it appears that there is a clear linear trend by day of the week. So, we will opt for simplicity here and use the data as-is. Try uncommenting the code that creates separate columns for the days of the week and re-run the notebook if you are curious about the impact of this simplification.
```
import tensorflow as tf
shuffled = data2.sample(frac=1, random_state=13)
# It would be a good idea, if we had more data, to treat the days as categorical variables
# with the small amount of data, we have though, the model tends to overfit
#predictors = shuffled.iloc[:,2:5]
#for day in range(1,8):
# matching = shuffled['dayofweek'] == day
# key = 'day_' + str(day)
# predictors[key] = pd.Series(matching, index=predictors.index, dtype=float)
predictors = shuffled.iloc[:,1:5]
predictors[:5]
shuffled[:5]
targets = shuffled.iloc[:,5]
targets[:5]
```
Let's update our benchmark based on the 80-20 split and the larger dataset.
```
trainsize = int(len(shuffled['numtrips']) * 0.8)
avg = np.mean(shuffled['numtrips'][:trainsize])
rmse = np.sqrt(np.mean((targets[trainsize:] - avg)**2))
print('Just using average={0} has RMSE of {1}'.format(avg, rmse))
```
<h2> Linear regression with tf.contrib.learn </h2>
We scale the number of taxicab rides by 400,000 so that the model can keep its predicted values in the [0-1] range. The optimization goes a lot faster when the weights are small numbers. We save the weights into ./trained_model_linear and display the root mean square error on the test dataset.
```
SCALE_NUM_TRIPS = 600000.0
trainsize = int(len(shuffled['numtrips']) * 0.8)
testsize = len(shuffled['numtrips']) - trainsize
npredictors = len(predictors.columns)
noutputs = 1
tf.logging.set_verbosity(tf.logging.WARN) # change to INFO to get output every 100 steps ...
shutil.rmtree('./trained_model_linear', ignore_errors=True) # so that we don't load weights from previous runs
estimator = tf.contrib.learn.LinearRegressor(model_dir='./trained_model_linear',
feature_columns=tf.contrib.learn.infer_real_valued_columns_from_input(predictors.values))
print("starting to train ... this will take a while ... use verbosity=INFO to get more verbose output")
def input_fn(features, targets):
return tf.constant(features.values), tf.constant(targets.values.reshape(len(targets), noutputs)/SCALE_NUM_TRIPS)
estimator.fit(input_fn=lambda: input_fn(predictors[:trainsize], targets[:trainsize]), steps=10000)
pred = np.multiply(list(estimator.predict(predictors[trainsize:].values)), SCALE_NUM_TRIPS )
rmse = np.sqrt(np.mean(np.power((targets[trainsize:].values - pred), 2)))
print('LinearRegression has RMSE of {0}'.format(rmse))
```
The RMSE here (57K) is lower than the benchmark (62K) indicates that we are doing about 10% better with the machine learning model than we would be if we were to just use the historical average (our benchmark).
<h2> Neural network with tf.contrib.learn </h2>
Let's make a more complex model with a few hidden nodes.
```
SCALE_NUM_TRIPS = 600000.0
trainsize = int(len(shuffled['numtrips']) * 0.8)
testsize = len(shuffled['numtrips']) - trainsize
npredictors = len(predictors.columns)
noutputs = 1
tf.logging.set_verbosity(tf.logging.WARN) # change to INFO to get output every 100 steps ...
shutil.rmtree('./trained_model', ignore_errors=True) # so that we don't load weights from previous runs
estimator = tf.contrib.learn.DNNRegressor(model_dir='./trained_model',
hidden_units=[5, 5],
feature_columns=tf.contrib.learn.infer_real_valued_columns_from_input(predictors.values))
print("starting to train ... this will take a while ... use verbosity=INFO to get more verbose output")
def input_fn(features, targets):
return tf.constant(features.values), tf.constant(targets.values.reshape(len(targets), noutputs)/SCALE_NUM_TRIPS)
estimator.fit(input_fn=lambda: input_fn(predictors[:trainsize], targets[:trainsize]), steps=10000)
pred = np.multiply(list(estimator.predict(predictors[trainsize:].values)), SCALE_NUM_TRIPS )
rmse = np.sqrt(np.mean((targets[trainsize:].values - pred)**2))
print('Neural Network Regression has RMSE of {0}'.format(rmse))
```
Using a neural network results in similar performance to the linear model when I ran it -- it might be because there isn't enough data for the NN to do much better. (NN training is a non-convex optimization, and you will get different results each time you run the above code).
<h2> Running a trained model </h2>
So, we have trained a model, and saved it to a file. Let's use this model to predict taxicab demand given the expected weather for three days.
Here we make a Dataframe out of those inputs, load up the saved model (note that we have to know the model equation -- it's not saved in the model file) and use it to predict the taxicab demand.
```
input = pd.DataFrame.from_dict(data =
{'dayofweek' : [4, 5, 6],
'mintemp' : [60, 40, 50],
'maxtemp' : [70, 90, 60],
'rain' : [0, 0.5, 0]})
# read trained model from ./trained_model
estimator = tf.contrib.learn.LinearRegressor(model_dir='./trained_model_linear',
feature_columns=tf.contrib.learn.infer_real_valued_columns_from_input(input.values))
pred = np.multiply(list(estimator.predict(input.values)), SCALE_NUM_TRIPS )
print(pred)
```
Looks like we should tell some of our taxi drivers to take the day off on Thursday (day=5). No wonder -- the forecast calls for extreme weather fluctuations on Thursday.
Copyright 2017 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.515742 | null | null | null | null |
|
# Building Autonomous Trader using mt5se
## How to setup and use mt5se
### 1. Install Metatrader 5 (https://www.metatrader5.com/)
### 2. Install python package Metatrader5 using pip
#### Use: pip install MetaTrader5 ... or Use sys package
### 3. Install python package mt5se using pip
#### Use: pip install mt5se ... or Use sys package
#### For documentation, check : https://paulo-al-castro.github.io/mt5se/
```
# installing Metatrader5 using sys
import sys
# python MetaTrader5
#!{sys.executable} -m pip install MetaTrader5
#mt5se
!{sys.executable} -m pip install mt5se --upgrade
```
<hr>
## Connecting and getting account information
```
import mt5se as se
connected=se.connect()
if connected:
print('Ok!! It is connected to the Stock exchange!!')
else:
print('Something went wrong! It is NOT connected to se!!')
ti=se.terminal_info()
print('Metatrader program file path: ', ti.path)
print('Metatrader path to data folder: ', ti.data_path )
print('Metatrader common data path: ',ti.commondata_path)
```
<hr>
### Getting information about the account
```
acc=se.account_info() # it returns account's information
print('login=',acc.login) # Account id
print('balance=',acc.balance) # Account balance in the deposit currency using buy price of assets (margin_free+margin)
print('equity=',acc.equity) # Account equity in the deposit currency using current price of assets (capital liquido) (margin_free+margin+profit)
print('free margin=',acc.margin_free) # Free margin ( balance in cash ) of an account in the deposit currency(BRL)
print('margin=',acc.margin) #Account margin used in the deposit currency (equity-margin_free-profit )
print('client name=',acc.name) #Client name
print('Server =',acc.server) # Trade server name
print('Currency =',acc.currency) # Account currency, BRL for Brazilian Real
```
<hr>
### Getting info about asset's prices quotes (a.k.a bars)
```
import pandas as pd
# Some example of Assets in Nasdaq
assets=[
'AAL', # American Airlines Group, Inc.
'GOOG', # Apple Inc.
'UAL', # United Airlines Holdings, Inc.
'AMD', # Advanced Micro Devices, Inc.
'MSFT' # MICROSOFT
]
asset=assets[0]
df=se.get_bars(asset,10) # it returns the last 10 days
print(df)
```
<hr>
### Getting information about current position
```
print('Position=',se.get_positions()) # return the current value of assets (not include balance or margin)
symbol_id='MSFT'
print('Position on paper ',symbol_id,' =',se.get_position_value(symbol_id)) # return the current position in a given asset (symbol_id)
pos=se.get_position_value(symbol_id)
print(pos)
```
<hr>
### Creating, checking and sending orders
```
###Buying three hundred shares of AAPL !!
symbol_id='AAPL'
bars=se.get_bars(symbol_id,2)
price=se.get_last(bars)
volume=300
b=se.buyOrder(symbol_id,volume, price ) # price, sl and tp are optional
if se.is_market_open(symbol_id):
print('Market is Open!!')
else:
print('Market is closed! Orders will not be accepted!!')
if se.checkOrder(b):
print('Buy order seems ok!')
else:
print('Error : ',se.getLastError())
# if se.sendOrder(b):
# print('Order executed!)
```
### Direct Control Robots using mt5se
```
import mt5se as se
import pandas as pd
import time
asset='AAPL'
def run(asset):
if se.is_market_open(asset): # change 'if' for 'while' for running until the end of the market session
print("getting information")
bars=se.get_bars(asset,14)
curr_shares=se.get_shares(asset)
# number of shares that you can buy
price=se.get_last(bars)
free_shares=se.get_affor_shares(asset,price)
rsi=se.tech.rsi(bars)
print("deliberating")
if rsi>=70 and free_shares>0:
order=se.buyOrder(asset,free_shares)
elif rsi<70 and curr_shares>0:
order=se.sellOrder(asset,curr_shares)
else:
order=None
print("sending order")
# check and send (it is sent only if check is ok!)
if order!=None:
if se.checkOrder(order) and se.sendOrder(order):
print('order sent to se')
else:
print('Error : ',se.getLastError())
else:
print("No order at the moment for asset=",asset )
time.sleep(1) # waits one second
print('Trader ended operation!')
if se.connect()==False:
print('Error when trying to connect to se')
exit()
else:
run(asset) # trade asset PETR4
```
### Multiple asset Trading Robot
```
#Multiple asset Robot (Example), single strategy for multiple assets, where the resources are equally shared among the assets
import time
def runMultiAsset(assets):
if se.is_market_open(assets[0]): # change 'if' for 'while' for running until the end of the market session
for asset in assets:
bars=se.get_bars(asset,14) #get information
curr_shares=se.get_shares(asset)
money=se.account_info().margin_free/len(assets) # number of shares that you can buy
price=se.get_last(bars)
free_shares=se.get_affor_shares(asset,price,money)
rsi=se.tech.rsi(bars)
if rsi>=70 and free_shares>0:
order=se.buyOrder(asset,free_shares)
elif rsi<70 and curr_shares>0:
order=se.sellOrder(asset,curr_shares)
else:
order=None
if order!=None: # check and send if it is Ok
if se.checkOrder(order) and se.sendOrder(order):
print('order sent to se')
else:
print('Error : ',se.getLastError())
else:
print("No order at the moment for asset=",asset)
time.sleep(1)
print('Trader ended operation!')
```
## Running multiple asset direct control code!
```
assets=['GOOG','AAPL']
runMultiAsset(assets) # trade asset
```
### Processing Financial Data - Return Histogram Example
```
import mt5se as se
from datetime import datetime
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
asset='MSFT'
se.connect()
bars=se.get_bars(asset,252) # 252 business days (basically one year)
x=se.get_returns(bars) # calculate daily returns given the bars
#With a small change we can see the historgram of weekly returns
#x=se.getReturns(bars,offset=5)
plt.hist(x,bins=16) # creates a histogram graph with 16 bins
plt.grid()
plt.show()
```
### Robots based on Inversion of control
You may use an alternative method to build your robots, that may reduce your workload. It is called inverse control robots. You receive the most common information requrired by robots and returns your orders
Let's some examples of Robots based on Inversion of Control including the multiasset strategy presented before in a inverse control implementation
### Trader class
Inversion of control Traders are classes that inherint from se.Trader and they have to implement just one function:
trade: It is called at each moment, with dbars. It should returns the list of orders to be executed or None if there is no order at the moment
Your trader may also implement two other function if required:
setup: It is called once when the operation starts. It receives dbars ('mem' bars from each asset) . See the operation setup, for more information
ending: It is called one when the sheculed operation reaches its end time.
Your Trader class may also implement a constructor function
Let's see an Example!
### A Random Trader
```
import numpy.random as rand
class RandomTrader(se.Trader):
def __init__(self):
pass
def setup(self,dbars):
print('just getting started!')
def trade(self,dbars):
orders=[]
assets=ops['assets']
for asset in assets:
if rand.randint(2)==1:
order=se.buyOrder(asset,100)
else:
order=se.sellOrder(asset,100)
orders.append(order)
return orders
def ending(self,dbars):
print('Ending stuff')
if issubclass(RandomTrader,se.Trader):
print('Your trader class seems Ok!')
else:
print('Your trader class should a subclass of se.Trader')
trader=RandomTrader() # DummyTrader class also available in se.sampleTraders.DummyTrader()
```
### Another Example of Trader class
```
class MultiAssetTrader(se.Trader):
def trade(self,dbars):
assets=dbars.keys()
orders=[]
for asset in assets:
bars=dbars[asset]
curr_shares=se.get_shares(asset)
money=se.get_balance()/len(assets) # divide o saldo em dinheiro igualmente entre os ativos
# number of shares that you can buy of asset
price=se.get_last(bars)
free_shares=se.get_affor_shares(asset,price,money)
rsi=se.tech.rsi(bars)
if rsi>=70 and free_shares>0:
order=se.buyOrder(asset,free_shares)
elif rsi<70 and curr_shares>0:
order=se.sellOrder(asset,curr_shares)
else:
order=None
if order!=None:
orders.append(order)
return orders
if issubclass(MultiAssetTrader,se.Trader):
print('Your trader class seems Ok!')
else:
print('Your trader class should a subclass of se.Trader')
trader=MultiAssetTrader()
```
### Testing your Trader!!!
The evaluation for trading robots is usually called backtesting. That means that a trading robot executes with historical price series , and its performance is computed
In backtesting, time is discretized according with bars and the package mt5se controls the information access to the Trader according with the simulated time.
To backtest one strategy, you just need to create a subclass of Trader and implement one function:
trade
You may implement function setup, to prepare the Trader Strategy if it is required and a function ending to clean up after the backtest is done
The simulation time advances and in function 'trade' the Trader class receives the new bar info and decides wich orders to send
## Let's create a Simple Algorithmic Trader and Backtest it
```
## Defines the Trader
class MonoAssetTrader(se.Trader):
def trade(self,dbars):
assets=dbars.keys()
asset=list(assets)[0]
orders=[]
bars=dbars[asset]
curr_shares=se.get_shares(asset)
# number of shares that you can buy
price=se.get_last(bars)
free_shares=se.get_affor_shares(asset,price)
rsi=se.tech.rsi(bars)
if rsi>=70:
order=se.buyOrder(asset,free_shares)
else:
order=se.sellOrder(asset,curr_shares)
if rsi>=70 and free_shares>0:
order=se.buyOrder(asset,free_shares)
elif rsi<70 and curr_shares>0:
order=se.sellOrder(asset,curr_shares)
if order!=None:
orders.append(order)
return orders
trader=MonoAssetTrader() # also available in se.sampleTraders.MonoAssetTrader()
print(trader)
```
## Setup and check a backtest!
```
# sets Backtest options
prestart=se.date(2018,12,10)
start=se.date(2019,1,10)
end=se.date(2019,2,27)
capital=1000000
results_file='data_equity_file.csv'
verbose=False
assets=['AAPL']
# Use True if you want debug information for your Trader
#sets the backtest setup
period=se.DAILY
# it may be se.INTRADAY (one minute interval)
bts=se.backtest.set(assets,prestart,start,end,period,capital,results_file,verbose)
# check if the backtest setup is ok!
if se.backtest.checkBTS(bts):
print('Backtest Setup is Ok!')
else:
print('Backtest Setup is NOT Ok!')
```
## Run the Backtest
```
# Running the backtest
df= se.backtest.run(trader,bts)
# run calls the Trader. setup and trade (once for each bar)
```
## Evaluate the Backtest result
```
#print the results
print(df)
# evaluates the backtest results
se.backtest.evaluate(df)
```
## Evaluating Backtesting results
The method backtest.run creates a data file with the name given in the backtest setup (bts)
This will give you a report about the trader performance
We need ot note that it is hard to perform meaningful evaluations using backtest. There are many pitfalls to avoid and it may be easier to get trading robots with great performance in backtest, but that perform really badly in real operations.
More about that in mt5se backtest evaluation chapter.
For a deeper discussion, we suggest:
Is it a great Autonomous Trading Strategy or you are just fooling yourself Bernardini,M. and Castro, P.A.L
In order to analyze the trader's backtest, you may use :
se.backtest.evaluateFile(fileName) #fileName is the name of file generated by the backtest
or
se.bactest.evaluate(df) # df is the dataframe returned by se.backtest.run
# Another Example: Multiasset Trader
```
import mt5se as se
class MultiAssetTrader(se.Trader):
def trade(self,dbars):
assets=dbars.keys()
orders=[]
for asset in assets:
bars=dbars[asset]
curr_shares=se.get_shares(asset)
money=se.get_balance()/len(assets) # divide o saldo em dinheiro igualmente entre os ativos
# number of shares that you can buy of asset
price=se.get_last(bars)
free_shares=se.get_affor_shares(asset,price,money)
rsi=se.tech.rsi(bars)
if rsi>=70 and free_shares>0:
order=se.buyOrder(asset,free_shares)
elif rsi<70 and curr_shares>0:
order=se.sellOrder(asset,curr_shares)
else:
order=None
if order!=None:
orders.append(order)
return orders
trader=MultiAssetTrader() # also available in se.sampleTraders.MultiAssetTrader()
print(trader)
```
## Setuping Backtest for Multiple Assets
```
# sets Backtest options
prestart=se.date(2020,5,4)
start=se.date(2020,5,6)
end=se.date(2020,6,21)
capital=10000000
results_file='data_equity_file.csv'
verbose=False
assets=[
'AAL', # American Airlines Group, Inc.
'GOOG', # Apple Inc.
'UAL', # United Airlines Holdings, Inc.
'AMD', # Advanced Micro Devices, Inc.
'MSFT' # MICROSOFT
]
# Use True if you want debug information for your Trader
#sets the backtest setup
period=se.DAILY
bts=se.backtest.set(assets,prestart,start,end,period,capital,results_file,verbose)
if se.backtest.checkBTS(bts): # check if the backtest setup is ok!
print('Backtest Setup is Ok!')
else:
print('Backtest Setup is NOT Ok!')
```
## Run and evaluate the backtest
```
se.connect()
# Running the backtest
df= se.backtest.run(trader,bts)
# run calls the Trader. setup and trade (once for each bar)
# evaluates the backtest results
se.backtest.evaluate(df)
```
## Next Deploying Autonomous Trader powered by mt5se
### You have seen how to:
install and import mt5se and MetaTrader5
get financial data
create direct control trading robots
create [Simple] Trader classes based on inversion of control
backtest Autonomous Traders
### Next, We are going to show how to:
deploy autonomous trader to run on simulated or real Stock Exchange accounts
create Autonomous Traders based on Artifical Intelligence and Machine Learning
| true |
code
| 0.223758 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Lambda-School-Labs/bridges-to-prosperity-ds-d/blob/SMOTE_model_building%2Ftrevor/notebooks/Modeling_off_original_data_smote_gridsearchcv.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
This notebook is for problem 2 as described in `B2P Dataset_2020.10.xlsx` Contextual Summary tab:
## Problem 2: Predicting which sites will be technically rejected in future engineering reviews
> Any sites with a "Yes" in the column AQ (`Senior Engineering Review Conducted`) have undergone a full technical review, and of those, the Stage (column L) can be considered to be correct. (`Bridge Opportunity: Stage`)
> Any sites without a "Yes" in Column AQ (`Senior Engineering Review Conducted`) have not undergone a full technical review, and the Stage is based on the assessor's initial estimate as to whether the site was technically feasible or not.
> We want to know if we can use the sites that have been reviewed to understand which of the sites that haven't yet been reviewed are likely to be rejected by the senior engineering team.
> Any of the data can be used, but our guess is that Estimated Span, Height Differential Between Banks, Created By, and Flag for Rejection are likely to be the most reliable predictors.
### Load the data
```
import pandas as pd
url = 'https://github.com/Lambda-School-Labs/bridges-to-prosperity-ds-d/blob/main/Data/B2P%20Dataset_2020.10.xlsx?raw=true'
df = pd.read_excel(url, sheet_name='Data')
```
### Define the target
```
# Any sites with a "Yes" in the column "Senior Engineering Review Conducted"
# have undergone a full technical review, and of those, the
# "Bridge Opportunity: Stage" column can be considered to be correct.
positive = (
(df['Senior Engineering Review Conducted']=='Yes') &
(df['Bridge Opportunity: Stage'].isin(['Complete', 'Prospecting', 'Confirmed']))
)
negative = (
(df['Senior Engineering Review Conducted']=='Yes') &
(df['Bridge Opportunity: Stage'].isin(['Rejected', 'Cancelled']))
)
# Any sites without a "Yes" in column Senior Engineering Review Conducted"
# have not undergone a full technical review ...
# So these sites are unknown and unlabeled
unknown = df['Senior Engineering Review Conducted'].isna()
# Create a new column named "Good Site." This is the target to predict.
# Assign a 1 for the positive class and 0 for the negative class.
df.loc[positive, 'Good Site'] = 1
df.loc[negative, 'Good Site'] = 0
# Assign -1 for unknown/unlabled observations.
# Scikit-learn's documentation for "Semi-Supervised Learning" says,
# "It is important to assign an identifier to unlabeled points ...
# The identifier that this implementation uses is the integer value -1."
# We'll explain this soon!
df.loc[unknown, 'Good Site'] = -1
```
### Drop columns used to derive the target
```
# Because these columns were used to derive the target,
# We can't use them as features, or it would be leakage.
df = df.drop(columns=['Senior Engineering Review Conducted', 'Bridge Opportunity: Stage'])
```
### Look at target's distribution
```
df['Good Site'].value_counts()
```
So we have 65 labeled observations for the positive class, 24 labeled observations for the negative class, and almost 1,400 unlabeled observations.
### 4 recommendations:
- Use **semi-supervised learning**, which "combines a small amount of labeled data with a large amount of unlabeled data". See Wikipedia notes below. Python implementations are available in [scikit-learn](https://scikit-learn.org/stable/modules/label_propagation.html) and [pomegranate](https://pomegranate.readthedocs.io/en/latest/semisupervised.html). Another way to get started: feature engineering + feature selection + K-Means Clustering + PCA in 2 dimensions. Then visualize the clusters on a scatterplot, with colors for the labels.
- Use [**leave-one-out cross-validation**](https://en.wikipedia.org/wiki/Cross-validation_(statistics)#Leave-one-out_cross-validation), without an independent test set, because we have so few labeled observations. It's implemented in [scikit-learn](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.LeaveOneOut.html). Or maybe 10-fold cross-validation with stratified sampling (and no independent test set).
- Consider **"over-sampling"** techniques for imbalanced classification. Python implementations are available in [imbalanced-learn](https://github.com/scikit-learn-contrib/imbalanced-learn).
- Consider using [**Snorkel**](https://www.snorkel.org/) to write "labeling functions" for "weakly supervised learning." The site has many [tutorials](https://www.snorkel.org/use-cases/).
### [Semi-supervised learning - Wikipedia](https://en.wikipedia.org/wiki/Semi-supervised_learning)
> Semi-supervised learning is an approach to machine learning that combines a small amount of labeled data with a large amount of unlabeled data during training. Semi-supervised learning falls between unsupervised learning (with no labeled training data) and supervised learning (with only labeled training data).
> Unlabeled data, when used in conjunction with a small amount of labeled data, can produce considerable improvement in learning accuracy. The acquisition of labeled data for a learning problem often requires a skilled human agent ... The cost associated with the labeling process thus may render large, fully labeled training sets infeasible, whereas acquisition of unlabeled data is relatively inexpensive. In such situations, semi-supervised learning can be of great practical value.

> An example of the influence of unlabeled data in semi-supervised learning. The top panel shows a decision boundary we might adopt after seeing only one positive (white circle) and one negative (black circle) example. The bottom panel shows a decision boundary we might adopt if, in addition to the two labeled examples, we were given a collection of unlabeled data (gray circles). This could be viewed as performing clustering and then labeling the clusters with the labeled data, pushing the decision boundary away from high-density regions ...
See also:
- “Positive-Unlabeled Learning”
- https://en.wikipedia.org/wiki/One-class_classification
# Model attempt - Smaller Dataset Not utilizing world data
- Here I am attempting to build a model using less "created" data than we did in previous attempts using the world data set. This had more successful bridge builds but those bridge builds did not include pertainant feature for building a predictive model.
```
df.info()
# Columns suggeested bt stakeholder to utilize while model building
keep_list = ['Bridge Opportunity: Span (m)',
'Bridge Opportunity: Individuals Directly Served',
'Form: Created By',
'Height differential between banks', 'Flag for Rejection',
'Good Site']
# isolating the dataset to just the modelset
modelset = df[keep_list]
modelset.head()
# built modelset based off of original dataset - not much cleaning here.
# further cleaning could be an area for improvement.
modelset['Good Site'].value_counts()
!pip install category_encoders
# Imports:
from collections import Counter
from sklearn.pipeline import make_pipeline
from imblearn.pipeline import make_pipeline as make_pipeline_imb
from imblearn.over_sampling import SMOTE
from imblearn.metrics import classification_report_imbalanced
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.ensemble import RandomForestClassifier
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.metrics import precision_score, recall_score, f1_score, roc_auc_score, accuracy_score, classification_report
# split data - intial split eliminated all of the "unlabeled" sites
data = modelset[(modelset['Good Site']== 0) | (modelset['Good Site']== 1)]
test = modelset[modelset['Good Site']== -1]
train, val = train_test_split(data, test_size=.2, random_state=42)
# splitting our labeled sites into a train and validation set for model building
X_train = train.drop('Good Site', axis=1)
y_train = train['Good Site']
X_val = val.drop('Good Site', axis=1)
y_val = val['Good Site']
X_train.shape, y_train.shape, X_val.shape, y_val.shape
# Building a base model without SMOTE
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
kf = KFold(n_splits=5, shuffle=False)
base_pipe = make_pipeline(ce.OrdinalEncoder(),
SimpleImputer(strategy = 'mean'),
RandomForestClassifier(n_estimators=100, random_state=42))
cross_val_score(base_pipe, X_train, y_train, cv=kf, scoring='precision')
```
From the results above we can see the variety of the precision scores, looks like we have some overfit values when it comes to different cross validations
```
# use of imb_learn pipeline
imba_pipe = make_pipeline_imb(ce.OrdinalEncoder(),
SimpleImputer(strategy = 'mean'),
SMOTE(random_state=42),
RandomForestClassifier(n_estimators=100, random_state=42))
cross_val_score(imba_pipe, X_train, y_train, cv=kf, scoring='precision')
```
Using an imbalanced Pipeline with SMOTE we still see the large variety in precision 1.0 as a high and .625 as a low.
```
# using grid search to attempt to further validate the model to use on predicitions
new_params = {'randomforestclassifier__n_estimators': [100, 200, 50],
'randomforestclassifier__max_depth': [4, 6, 10, 12],
'simpleimputer__strategy': ['mean', 'median']
}
imba_grid_1 = GridSearchCV(imba_pipe, param_grid=new_params, cv=kf,
scoring='precision',
return_train_score=True)
imba_grid_1.fit(X_train, y_train);
# Params used and best score on a basis of precision
print(imba_grid_1.best_params_, imba_grid_1.best_score_)
# Working with more folds for validation
more_kf = KFold(n_splits=15)
imba_grid_2 = GridSearchCV(imba_pipe, param_grid=new_params, cv=more_kf,
scoring='precision',
return_train_score=True)
imba_grid_2.fit(X_train, y_train);
print(imba_grid_2.best_score_, imba_grid_2.best_estimator_)
imba_grid_2.cv_results_
# muted output because it was lenghty
# during output we did see a lot of 1s... Is this a sign of overfitting?
# Now looking to the val set to get some more numbers
y_val_predict = imba_grid_2.predict(X_val)
precision_score(y_val, y_val_predict)
```
The best score from above was .87, now running the model on the val set, it looks like we end with 92% precision score.
```
```
| true |
code
| 0.605741 | null | null | null | null |
|
<a href="https://cognitiveclass.ai"><img src = "https://ibm.box.com/shared/static/9gegpsmnsoo25ikkbl4qzlvlyjbgxs5x.png" width = 400> </a>
<h1 align=center><font size = 5>Waffle Charts, Word Clouds, and Regression Plots</font></h1>
## Introduction
In this lab, we will learn how to create word clouds and waffle charts. Furthermore, we will start learning about additional visualization libraries that are based on Matplotlib, namely the library *seaborn*, and we will learn how to create regression plots using the *seaborn* library.
## Table of Contents
<div class="alert alert-block alert-info" style="margin-top: 20px">
1. [Exploring Datasets with *p*andas](#0)<br>
2. [Downloading and Prepping Data](#2)<br>
3. [Visualizing Data using Matplotlib](#4) <br>
4. [Waffle Charts](#6) <br>
5. [Word Clouds](#8) <br>
7. [Regression Plots](#10) <br>
</div>
<hr>
# Exploring Datasets with *pandas* and Matplotlib<a id="0"></a>
Toolkits: The course heavily relies on [*pandas*](http://pandas.pydata.org/) and [**Numpy**](http://www.numpy.org/) for data wrangling, analysis, and visualization. The primary plotting library we will explore in the course is [Matplotlib](http://matplotlib.org/).
Dataset: Immigration to Canada from 1980 to 2013 - [International migration flows to and from selected countries - The 2015 revision](http://www.un.org/en/development/desa/population/migration/data/empirical2/migrationflows.shtml) from United Nation's website
The dataset contains annual data on the flows of international migrants as recorded by the countries of destination. The data presents both inflows and outflows according to the place of birth, citizenship or place of previous / next residence both for foreigners and nationals. In this lab, we will focus on the Canadian Immigration data.
# Downloading and Prepping Data <a id="2"></a>
Import Primary Modules:
```
import numpy as np # useful for many scientific computing in Python
import pandas as pd # primary data structure library
from PIL import Image # converting images into arrays
```
Let's download and import our primary Canadian Immigration dataset using *pandas* `read_excel()` method. Normally, before we can do that, we would need to download a module which *pandas* requires to read in excel files. This module is **xlrd**. For your convenience, we have pre-installed this module, so you would not have to worry about that. Otherwise, you would need to run the following line of code to install the **xlrd** module:
```
!conda install -c anaconda xlrd --yes
```
Download the dataset and read it into a *pandas* dataframe:
```
df_can = pd.read_excel('https://ibm.box.com/shared/static/lw190pt9zpy5bd1ptyg2aw15awomz9pu.xlsx',
sheet_name='Canada by Citizenship',
skiprows=range(20),
skip_footer=2)
print('Data downloaded and read into a dataframe!')
```
Let's take a look at the first five items in our dataset
```
df_can.head()
```
Let's find out how many entries there are in our dataset
```
# print the dimensions of the dataframe
print(df_can.shape)
```
Clean up data. We will make some modifications to the original dataset to make it easier to create our visualizations. Refer to *Introduction to Matplotlib and Line Plots* and *Area Plots, Histograms, and Bar Plots* for a detailed description of this preprocessing.
```
# clean up the dataset to remove unnecessary columns (eg. REG)
df_can.drop(['AREA','REG','DEV','Type','Coverage'], axis = 1, inplace = True)
# let's rename the columns so that they make sense
df_can.rename (columns = {'OdName':'Country', 'AreaName':'Continent','RegName':'Region'}, inplace = True)
# for sake of consistency, let's also make all column labels of type string
df_can.columns = list(map(str, df_can.columns))
# set the country name as index - useful for quickly looking up countries using .loc method
df_can.set_index('Country', inplace = True)
# add total column
df_can['Total'] = df_can.sum (axis = 1)
# years that we will be using in this lesson - useful for plotting later on
years = list(map(str, range(1980, 2014)))
print ('data dimensions:', df_can.shape)
```
# Visualizing Data using Matplotlib<a id="4"></a>
Import `matplotlib`:
```
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches # needed for waffle Charts
mpl.style.use('ggplot') # optional: for ggplot-like style
# check for latest version of Matplotlib
print ('Matplotlib version: ', mpl.__version__) # >= 2.0.0
```
# Waffle Charts <a id="6"></a>
A `waffle chart` is an interesting visualization that is normally created to display progress toward goals. It is commonly an effective option when you are trying to add interesting visualization features to a visual that consists mainly of cells, such as an Excel dashboard.
Let's revisit the previous case study about Denmark, Norway, and Sweden.
```
# let's create a new dataframe for these three countries
df_dsn = df_can.loc[['Denmark', 'Norway', 'Sweden'], :]
# let's take a look at our dataframe
df_dsn
```
Unfortunately, unlike R, `waffle` charts are not built into any of the Python visualization libraries. Therefore, we will learn how to create them from scratch.
**Step 1.** The first step into creating a waffle chart is determing the proportion of each category with respect to the total.
```
# compute the proportion of each category with respect to the total
total_values = sum(df_dsn['Total'])
category_proportions = [(float(value) / total_values) for value in df_dsn['Total']]
# print out proportions
for i, proportion in enumerate(category_proportions):
print (df_dsn.index.values[i] + ': ' + str(proportion))
```
**Step 2.** The second step is defining the overall size of the `waffle` chart.
```
width = 40 # width of chart
height = 10 # height of chart
total_num_tiles = width * height # total number of tiles
print ('Total number of tiles is ', total_num_tiles)
```
**Step 3.** The third step is using the proportion of each category to determe it respective number of tiles
```
# compute the number of tiles for each catagory
tiles_per_category = [round(proportion * total_num_tiles) for proportion in category_proportions]
# print out number of tiles per category
for i, tiles in enumerate(tiles_per_category):
print (df_dsn.index.values[i] + ': ' + str(tiles))
```
Based on the calculated proportions, Denmark will occupy 129 tiles of the `waffle` chart, Norway will occupy 77 tiles, and Sweden will occupy 194 tiles.
**Step 4.** The fourth step is creating a matrix that resembles the `waffle` chart and populating it.
```
# initialize the waffle chart as an empty matrix
waffle_chart = np.zeros((height, width))
# define indices to loop through waffle chart
category_index = 0
tile_index = 0
# populate the waffle chart
for col in range(width):
for row in range(height):
tile_index += 1
# if the number of tiles populated for the current category is equal to its corresponding allocated tiles...
if tile_index > sum(tiles_per_category[0:category_index]):
# ...proceed to the next category
category_index += 1
# set the class value to an integer, which increases with class
waffle_chart[row, col] = category_index
print ('Waffle chart populated!')
```
Let's take a peek at how the matrix looks like.
```
waffle_chart
```
As expected, the matrix consists of three categories and the total number of each category's instances matches the total number of tiles allocated to each category.
**Step 5.** Map the `waffle` chart matrix into a visual.
```
# instantiate a new figure object
fig = plt.figure()
# use matshow to display the waffle chart
colormap = plt.cm.coolwarm
plt.matshow(waffle_chart, cmap=colormap)
plt.colorbar()
```
**Step 6.** Prettify the chart.
```
# instantiate a new figure object
fig = plt.figure()
# use matshow to display the waffle chart
colormap = plt.cm.coolwarm
plt.matshow(waffle_chart, cmap=colormap)
plt.colorbar()
# get the axis
ax = plt.gca()
# set minor ticks
ax.set_xticks(np.arange(-.5, (width), 1), minor=True)
ax.set_yticks(np.arange(-.5, (height), 1), minor=True)
# add gridlines based on minor ticks
ax.grid(which='minor', color='w', linestyle='-', linewidth=2)
plt.xticks([])
plt.yticks([])
```
**Step 7.** Create a legend and add it to chart.
```
# instantiate a new figure object
fig = plt.figure()
# use matshow to display the waffle chart
colormap = plt.cm.coolwarm
plt.matshow(waffle_chart, cmap=colormap)
plt.colorbar()
# get the axis
ax = plt.gca()
# set minor ticks
ax.set_xticks(np.arange(-.5, (width), 1), minor=True)
ax.set_yticks(np.arange(-.5, (height), 1), minor=True)
# add gridlines based on minor ticks
ax.grid(which='minor', color='w', linestyle='-', linewidth=2)
plt.xticks([])
plt.yticks([])
# compute cumulative sum of individual categories to match color schemes between chart and legend
values_cumsum = np.cumsum(df_dsn['Total'])
total_values = values_cumsum[len(values_cumsum) - 1]
# create legend
legend_handles = []
for i, category in enumerate(df_dsn.index.values):
label_str = category + ' (' + str(df_dsn['Total'][i]) + ')'
color_val = colormap(float(values_cumsum[i])/total_values)
legend_handles.append(mpatches.Patch(color=color_val, label=label_str))
# add legend to chart
plt.legend(handles=legend_handles,
loc='lower center',
ncol=len(df_dsn.index.values),
bbox_to_anchor=(0., -0.2, 0.95, .1)
)
```
And there you go! What a good looking *delicious* `waffle` chart, don't you think?
Now it would very inefficient to repeat these seven steps every time we wish to create a `waffle` chart. So let's combine all seven steps into one function called *create_waffle_chart*. This function would take the following parameters as input:
> 1. **categories**: Unique categories or classes in dataframe.
> 2. **values**: Values corresponding to categories or classes.
> 3. **height**: Defined height of waffle chart.
> 4. **width**: Defined width of waffle chart.
> 5. **colormap**: Colormap class
> 6. **value_sign**: In order to make our function more generalizable, we will add this parameter to address signs that could be associated with a value such as %, $, and so on. **value_sign** has a default value of empty string.
```
def create_waffle_chart(categories, values, height, width, colormap, value_sign=''):
# compute the proportion of each category with respect to the total
total_values = sum(values)
category_proportions = [(float(value) / total_values) for value in values]
# compute the total number of tiles
total_num_tiles = width * height # total number of tiles
print ('Total number of tiles is', total_num_tiles)
# compute the number of tiles for each catagory
tiles_per_category = [round(proportion * total_num_tiles) for proportion in category_proportions]
# print out number of tiles per category
for i, tiles in enumerate(tiles_per_category):
print (df_dsn.index.values[i] + ': ' + str(tiles))
# initialize the waffle chart as an empty matrix
waffle_chart = np.zeros((height, width))
# define indices to loop through waffle chart
category_index = 0
tile_index = 0
# populate the waffle chart
for col in range(width):
for row in range(height):
tile_index += 1
# if the number of tiles populated for the current category
# is equal to its corresponding allocated tiles...
if tile_index > sum(tiles_per_category[0:category_index]):
# ...proceed to the next category
category_index += 1
# set the class value to an integer, which increases with class
waffle_chart[row, col] = category_index
# instantiate a new figure object
fig = plt.figure()
# use matshow to display the waffle chart
colormap = plt.cm.coolwarm
plt.matshow(waffle_chart, cmap=colormap)
plt.colorbar()
# get the axis
ax = plt.gca()
# set minor ticks
ax.set_xticks(np.arange(-.5, (width), 1), minor=True)
ax.set_yticks(np.arange(-.5, (height), 1), minor=True)
# add dridlines based on minor ticks
ax.grid(which='minor', color='w', linestyle='-', linewidth=2)
plt.xticks([])
plt.yticks([])
# compute cumulative sum of individual categories to match color schemes between chart and legend
values_cumsum = np.cumsum(values)
total_values = values_cumsum[len(values_cumsum) - 1]
# create legend
legend_handles = []
for i, category in enumerate(categories):
if value_sign == '%':
label_str = category + ' (' + str(values[i]) + value_sign + ')'
else:
label_str = category + ' (' + value_sign + str(values[i]) + ')'
color_val = colormap(float(values_cumsum[i])/total_values)
legend_handles.append(mpatches.Patch(color=color_val, label=label_str))
# add legend to chart
plt.legend(
handles=legend_handles,
loc='lower center',
ncol=len(categories),
bbox_to_anchor=(0., -0.2, 0.95, .1)
)
```
Now to create a `waffle` chart, all we have to do is call the function `create_waffle_chart`. Let's define the input parameters:
```
width = 40 # width of chart
height = 10 # height of chart
categories = df_dsn.index.values # categories
values = df_dsn['Total'] # correponding values of categories
colormap = plt.cm.coolwarm # color map class
```
And now let's call our function to create a `waffle` chart.
```
create_waffle_chart(categories, values, height, width, colormap)
```
There seems to be a new Python package for generating `waffle charts` called [PyWaffle](https://github.com/ligyxy/PyWaffle), but the repository has barely any documentation on the package. Accordingly, I couldn't use the package to prepare enough content to incorporate into this lab. But feel free to check it out and play with it. In the event that the package becomes complete with full documentation, then I will update this lab accordingly.
# Word Clouds <a id="8"></a>
`Word` clouds (also known as text clouds or tag clouds) work in a simple way: the more a specific word appears in a source of textual data (such as a speech, blog post, or database), the bigger and bolder it appears in the word cloud.
Luckily, a Python package already exists in Python for generating `word` clouds. The package, called `word_cloud` was developed by **Andreas Mueller**. You can learn more about the package by following this [link](https://github.com/amueller/word_cloud/).
Let's use this package to learn how to generate a word cloud for a given text document.
First, let's install the package.
```
# install wordcloud
!conda install -c conda-forge wordcloud==1.4.1 --yes
# import package and its set of stopwords
from wordcloud import WordCloud, STOPWORDS
print ('Wordcloud is installed and imported!')
```
`Word` clouds are commonly used to perform high-level analysis and visualization of text data. Accordinly, let's digress from the immigration dataset and work with an example that involves analyzing text data. Let's try to analyze a short novel written by **Lewis Carroll** titled *Alice's Adventures in Wonderland*. Let's go ahead and download a _.txt_ file of the novel.
```
# download file and save as alice_novel.txt
!wget --quiet https://ibm.box.com/shared/static/m54sjtrshpt5su20dzesl5en9xa5vfz1.txt -O alice_novel.txt
# open the file and read it into a variable alice_novel
alice_novel = open('alice_novel.txt', 'r').read()
print ('File downloaded and saved!')
```
Next, let's use the stopwords that we imported from `word_cloud`. We use the function *set* to remove any redundant stopwords.
```
stopwords = set(STOPWORDS)
```
Create a word cloud object and generate a word cloud. For simplicity, let's generate a word cloud using only the first 2000 words in the novel.
```
# instantiate a word cloud object
alice_wc = WordCloud(
background_color='white',
max_words=2000,
stopwords=stopwords
)
# generate the word cloud
alice_wc.generate(alice_novel)
```
Awesome! Now that the `word` cloud is created, let's visualize it.
```
# display the word cloud
plt.imshow(alice_wc, interpolation='bilinear')
plt.axis('off')
plt.show()
```
Interesting! So in the first 2000 words in the novel, the most common words are **Alice**, **said**, **little**, **Queen**, and so on. Let's resize the cloud so that we can see the less frequent words a little better.
```
fig = plt.figure()
fig.set_figwidth(14) # set width
fig.set_figheight(18) # set height
# display the cloud
plt.imshow(alice_wc, interpolation='bilinear')
plt.axis('off')
plt.show()
```
Much better! However, **said** isn't really an informative word. So let's add it to our stopwords and re-generate the cloud.
```
stopwords.add('said') # add the words said to stopwords
# re-generate the word cloud
alice_wc.generate(alice_novel)
# display the cloud
fig = plt.figure()
fig.set_figwidth(14) # set width
fig.set_figheight(18) # set height
plt.imshow(alice_wc, interpolation='bilinear')
plt.axis('off')
plt.show()
```
Excellent! This looks really interesting! Another cool thing you can implement with the `word_cloud` package is superimposing the words onto a mask of any shape. Let's use a mask of Alice and her rabbit. We already created the mask for you, so let's go ahead and download it and call it *alice_mask.png*.
```
# download image
!wget --quiet https://ibm.box.com/shared/static/3mpxgaf6muer6af7t1nvqkw9cqj85ibm.png -O alice_mask.png
# save mask to alice_mask
alice_mask = np.array(Image.open('alice_mask.png'))
print('Image downloaded and saved!')
```
Let's take a look at how the mask looks like.
```
fig = plt.figure()
fig.set_figwidth(14) # set width
fig.set_figheight(18) # set height
plt.imshow(alice_mask, cmap=plt.cm.gray, interpolation='bilinear')
plt.axis('off')
plt.show()
```
Shaping the `word` cloud according to the mask is straightforward using `word_cloud` package. For simplicity, we will continue using the first 2000 words in the novel.
```
# instantiate a word cloud object
alice_wc = WordCloud(background_color='white', max_words=2000, mask=alice_mask, stopwords=stopwords)
# generate the word cloud
alice_wc.generate(alice_novel)
# display the word cloud
fig = plt.figure()
fig.set_figwidth(14) # set width
fig.set_figheight(18) # set height
plt.imshow(alice_wc, interpolation='bilinear')
plt.axis('off')
plt.show()
```
Really impressive!
Unfortunately, our immmigration data does not have any text data, but where there is a will there is a way. Let's generate sample text data from our immigration dataset, say text data of 90 words.
Let's recall how our data looks like.
```
df_can.head()
```
And what was the total immigration from 1980 to 2013?
```
total_immigration = df_can['Total'].sum()
total_immigration
```
Using countries with single-word names, let's duplicate each country's name based on how much they contribute to the total immigration.
```
max_words = 90
word_string = ''
for country in df_can.index.values:
# check if country's name is a single-word name
if len(country.split(' ')) == 1:
repeat_num_times = int(df_can.loc[country, 'Total']/float(total_immigration)*max_words)
word_string = word_string + ((country + ' ') * repeat_num_times)
# display the generated text
word_string
```
We are not dealing with any stopwords here, so there is no need to pass them when creating the word cloud.
```
# create the word cloud
wordcloud = WordCloud(background_color='white').generate(word_string)
print('Word cloud created!')
# display the cloud
fig = plt.figure()
fig.set_figwidth(14)
fig.set_figheight(18)
plt.imshow(wordcloud, interpolation='bilinear')
plt.axis('off')
plt.show()
```
According to the above word cloud, it looks like the majority of the people who immigrated came from one of 15 countries that are displayed by the word cloud. One cool visual that you could build, is perhaps using the map of Canada and a mask and superimposing the word cloud on top of the map of Canada. That would be an interesting visual to build!
# Regression Plots <a id="10"></a>
> Seaborn is a Python visualization library based on matplotlib. It provides a high-level interface for drawing attractive statistical graphics. You can learn more about *seaborn* by following this [link](https://seaborn.pydata.org/) and more about *seaborn* regression plots by following this [link](http://seaborn.pydata.org/generated/seaborn.regplot.html).
In lab *Pie Charts, Box Plots, Scatter Plots, and Bubble Plots*, we learned how to create a scatter plot and then fit a regression line. It took ~20 lines of code to create the scatter plot along with the regression fit. In this final section, we will explore *seaborn* and see how efficient it is to create regression lines and fits using this library!
Let's first install *seaborn*
```
# install seaborn
!pip install seaborn
# import library
import seaborn as sns
print('Seaborn installed and imported!')
```
Create a new dataframe that stores that total number of landed immigrants to Canada per year from 1980 to 2013.
```
# we can use the sum() method to get the total population per year
df_tot = pd.DataFrame(df_can[years].sum(axis=0))
# change the years to type float (useful for regression later on)
df_tot.index = map(float,df_tot.index)
# reset the index to put in back in as a column in the df_tot dataframe
df_tot.reset_index(inplace = True)
# rename columns
df_tot.columns = ['year', 'total']
# view the final dataframe
df_tot.head()
```
With *seaborn*, generating a regression plot is as simple as calling the **regplot** function.
```
import seaborn as sns
ax = sns.regplot(x='year', y='total', data=df_tot)
```
This is not magic; it is *seaborn*! You can also customize the color of the scatter plot and regression line. Let's change the color to green.
```
import seaborn as sns
ax = sns.regplot(x='year', y='total', data=df_tot, color='green')
```
You can always customize the marker shape, so instead of circular markers, let's use '+'.
```
import seaborn as sns
ax = sns.regplot(x='year', y='total', data=df_tot, color='green', marker='+')
```
Let's blow up the plot a little bit so that it is more appealing to the sight.
```
plt.figure(figsize=(15, 10))
ax = sns.regplot(x='year', y='total', data=df_tot, color='green', marker='+')
```
And let's increase the size of markers so they match the new size of the figure, and add a title and x- and y-labels.
```
plt.figure(figsize=(15, 10))
ax = sns.regplot(x='year', y='total', data=df_tot, color='green', marker='+', scatter_kws={'s': 200})
ax.set(xlabel='Year', ylabel='Total Immigration') # add x- and y-labels
ax.set_title('Total Immigration to Canada from 1980 - 2013') # add title
```
And finally increase the font size of the tickmark labels, the title, and the x- and y-labels so they don't feel left out!
```
plt.figure(figsize=(15, 10))
sns.set(font_scale=1.5)
ax = sns.regplot(x='year', y='total', data=df_tot, color='green', marker='+', scatter_kws={'s': 200})
ax.set(xlabel='Year', ylabel='Total Immigration')
ax.set_title('Total Immigration to Canada from 1980 - 2013')
```
Amazing! A complete scatter plot with a regression fit with 5 lines of code only. Isn't this really amazing?
If you are not a big fan of the purple background, you can easily change the style to a white plain background.
```
plt.figure(figsize=(15, 10))
sns.set(font_scale=1.5)
sns.set_style('ticks') # change background to white background
ax = sns.regplot(x='year', y='total', data=df_tot, color='green', marker='+', scatter_kws={'s': 200})
ax.set(xlabel='Year', ylabel='Total Immigration')
ax.set_title('Total Immigration to Canada from 1980 - 2013')
```
Or to a white background with gridlines.
```
plt.figure(figsize=(15, 10))
sns.set(font_scale=1.5)
sns.set_style('whitegrid')
ax = sns.regplot(x='year', y='total', data=df_tot, color='green', marker='+', scatter_kws={'s': 200})
ax.set(xlabel='Year', ylabel='Total Immigration')
ax.set_title('Total Immigration to Canada from 1980 - 2013')
```
**Question**: Use seaborn to create a scatter plot with a regression line to visualize the total immigration from Denmark, Sweden, and Norway to Canada from 1980 to 2013.
```
### type your answer here
```
Double-click __here__ for the solution.
<!-- The correct answer is:
\\ # create df_countries dataframe
df_countries = df_can.loc[['Denmark', 'Norway', 'Sweden'], years].transpose()
-->
<!--
\\ # create df_total by summing across three countries for each year
df_total = pd.DataFrame(df_countries.sum(axis=1))
-->
<!--
\\ # reset index in place
df_total.reset_index(inplace=True)
-->
<!--
\\ # rename columns
df_total.columns = ['year', 'total']
-->
<!--
\\ # change column year from string to int to create scatter plot
df_total['year'] = df_total['year'].astype(int)
-->
<!--
\\ # define figure size
plt.figure(figsize=(15, 10))
-->
<!--
\\ # define background style and font size
sns.set(font_scale=1.5)
sns.set_style('whitegrid')
-->
<!--
\\ # generate plot and add title and axes labels
ax = sns.regplot(x='year', y='total', data=df_total, color='green', marker='+', scatter_kws={'s': 200})
ax.set(xlabel='Year', ylabel='Total Immigration')
ax.set_title('Total Immigrationn from Denmark, Sweden, and Norway to Canada from 1980 - 2013')
-->
### Thank you for completing this lab!
This notebook was created by [Alex Aklson](https://www.linkedin.com/in/aklson/). I hope you found this lab interesting and educational. Feel free to contact me if you have any questions!
This notebook is part of a course on **Coursera** called *Data Visualization with Python*. If you accessed this notebook outside the course, you can take this course online by clicking [here](http://cocl.us/DV0101EN_Coursera_Week3_LAB1).
<hr>
Copyright © 2018 [Cognitive Class](https://cognitiveclass.ai/?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu). This notebook and its source code are released under the terms of the [MIT License](https://bigdatauniversity.com/mit-license/).
| true |
code
| 0.396886 | null | null | null | null |
|
<h2>Factorization Machines - Movie Recommendation Model</h2>
Input Features: [userId, moveId] <br>
Target: rating <br>
```
import numpy as np
import pandas as pd
# Define IAM role
import boto3
import re
import sagemaker
from sagemaker import get_execution_role
# SageMaker SDK Documentation: http://sagemaker.readthedocs.io/en/latest/estimators.html
```
## Upload Data to S3
```
# Specify your bucket name
bucket_name = 'chandra-ml-sagemaker'
training_file_key = 'movie/user_movie_train.recordio'
test_file_key = 'movie/user_movie_test.recordio'
s3_model_output_location = r's3://{0}/movie/model'.format(bucket_name)
s3_training_file_location = r's3://{0}/{1}'.format(bucket_name,training_file_key)
s3_test_file_location = r's3://{0}/{1}'.format(bucket_name,test_file_key)
# Read Dimension: Number of unique users + Number of unique movies in our dataset
dim_movie = 0
# Update movie dimension - from file used for training
with open(r'ml-latest-small/movie_dimension.txt','r') as f:
dim_movie = int(f.read())
dim_movie
print(s3_model_output_location)
print(s3_training_file_location)
print(s3_test_file_location)
# Write and Reading from S3 is just as easy
# files are referred as objects in S3.
# file name is referred as key name in S3
# Files stored in S3 are automatically replicated across 3 different availability zones
# in the region where the bucket was created.
# http://boto3.readthedocs.io/en/latest/guide/s3.html
def write_to_s3(filename, bucket, key):
with open(filename,'rb') as f: # Read in binary mode
return boto3.Session().resource('s3').Bucket(bucket).Object(key).upload_fileobj(f)
write_to_s3(r'ml-latest-small/user_movie_train.recordio',bucket_name,training_file_key)
write_to_s3(r'ml-latest-small/user_movie_test.recordio',bucket_name,test_file_key)
```
## Training Algorithm Docker Image
### AWS Maintains a separate image for every region and algorithm
```
sess = sagemaker.Session()
role = get_execution_role()
# This role contains the permissions needed to train, deploy models
# SageMaker Service is trusted to assume this role
print(role)
# https://sagemaker.readthedocs.io/en/stable/api/utility/image_uris.html#sagemaker.image_uris.retrieve
# SDK 2 uses image_uris.retrieve the container image location
# Use factorization-machines
container = sagemaker.image_uris.retrieve("factorization-machines",sess.boto_region_name)
print (f'Using FM Container {container}')
container
```
## Build Model
```
# Configure the training job
# Specify type and number of instances to use
# S3 location where final artifacts needs to be stored
# Reference: http://sagemaker.readthedocs.io/en/latest/estimators.html
# SDK 2.x version does not require train prefix for instance count and type
estimator = sagemaker.estimator.Estimator(container,
role,
instance_count=1,
instance_type='ml.m4.xlarge',
output_path=s3_model_output_location,
sagemaker_session=sess,
base_job_name ='fm-movie-v4')
```
### New Configuration after Model Tuning
### Refer to Hyperparameter Tuning Lecture on how to optimize hyperparameters
```
estimator.set_hyperparameters(feature_dim=dim_movie,
num_factors=8,
predictor_type='regressor',
mini_batch_size=994,
epochs=91,
bias_init_method='normal',
bias_lr=0.21899531189430518,
factors_init_method='normal',
factors_lr=5.357593337770278e-05,
linear_init_method='normal',
linear_lr=0.00021524948053767607)
estimator.hyperparameters()
```
### Train the model
```
# New Hyperparameters
# Reference: Supported channels by algorithm
# https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-algo-docker-registry-paths.html
estimator.fit({'train':s3_training_file_location, 'test': s3_test_file_location})
```
## Deploy Model
```
# Ref: http://sagemaker.readthedocs.io/en/latest/estimators.html
predictor = estimator.deploy(initial_instance_count=1,
instance_type='ml.m4.xlarge',
endpoint_name = 'fm-movie-v4')
```
## Run Predictions
### Dense and Sparse Formats
https://docs.aws.amazon.com/sagemaker/latest/dg/cdf-inference.html
```
import json
def fm_sparse_serializer(data):
js = {'instances': []}
for row in data:
column_list = row.tolist()
value_list = np.ones(len(column_list),dtype=int).tolist()
js['instances'].append({'data':{'features': { 'keys': column_list, 'shape':[dim_movie], 'values': value_list}}})
return json.dumps(js)
# SDK 2
from sagemaker.deserializers import JSONDeserializer
# https://github.com/aws/amazon-sagemaker-examples/blob/master/introduction_to_amazon_algorithms/factorization_machines_mnist/factorization_machines_mnist.ipynb
# Specify custom serializer
predictor.serializer.serialize = fm_sparse_serializer
predictor.serializer.content_type = 'application/json'
predictor.deserializer = JSONDeserializer()
import numpy as np
fm_sparse_serializer([np.array([341,1416])])
# Let's test with few entries from test file
# Movie dataset is updated regularly...so, instead of hard coding userid and movie id, let's
# use actual values
# Each row is in this format: ['2.5', '426:1', '943:1']
# ActualRating, UserID, MovieID
with open(r'ml-latest-small/user_movie_test.svm','r') as f:
for i in range(3):
rating = f.readline().split()
print(f"Movie {rating}")
userID = rating[1].split(':')[0]
movieID = rating[2].split(':')[0]
predicted_rating = predictor.predict([np.array([int(userID),int(movieID)])])
print(f' Actual Rating:\t{rating[0]}')
print(f" Predicted Rating:\t{predicted_rating['predictions'][0]['score']}")
print()
```
## Summary
1. Ensure Training, Test and Validation data are in S3 Bucket
2. Select Algorithm Container Registry Path - Path varies by region
3. Configure Estimator for training - Specify Algorithm container, instance count, instance type, model output location
4. Specify algorithm specific hyper parameters
5. Train model
6. Deploy model - Specify instance count, instance type and endpoint name
7. Run Predictions
| true |
code
| 0.545286 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ymoslem/OpenNMT-Tutorial/blob/main/2-NMT-Training.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
# Install OpenNMT-py 2.x
!pip3 install OpenNMT-py
```
# Prepare Your Datasets
Please make sure you have completed the [first exercise](https://colab.research.google.com/drive/1rsFPnAQu9-_A6e2Aw9JYK3C8mXx9djsF?usp=sharing).
```
# Open the folder where you saved your prepapred datasets from the first exercise
%cd drive/MyDrive/nmt/
!ls
```
# Create the Training Configuration File
The following config file matches most of the recommended values for the Transformer model [Vaswani et al., 2017](https://arxiv.org/abs/1706.03762). As the current dataset is small, we reduced the following values:
* `train_steps` - for datasets with a few millions of sentences, consider using a value between 100000 and 200000, or more! Enabling the option `early_stopping` can help stop the training when there is no considerable improvement.
* `valid_steps` - 10000 can be good if the value `train_steps` is big enough.
* `warmup_steps` - obviously, its value must be less than `train_steps`. Try 4000 and 8000 values.
Refer to [OpenNMT-py training parameters](https://opennmt.net/OpenNMT-py/options/train.html) for more details. If you are interested in further explanation of the Transformer model, you can check this article, [Illustrated Transformer](https://jalammar.github.io/illustrated-transformer/).
```
# Create the YAML configuration file
# On a regular machine, you can create it manually or with nano
# Note here we are using some smaller values because the dataset is small
# For larger datasets, consider increasing: train_steps, valid_steps, warmup_steps, save_checkpoint_steps, keep_checkpoint
config = '''# config.yaml
## Where the samples will be written
save_data: run
# Training files
data:
corpus_1:
path_src: UN.en-fr.fr-filtered.fr.subword.train
path_tgt: UN.en-fr.en-filtered.en.subword.train
transforms: [filtertoolong]
valid:
path_src: UN.en-fr.fr-filtered.fr.subword.dev
path_tgt: UN.en-fr.en-filtered.en.subword.dev
transforms: [filtertoolong]
# Vocabulary files, generated by onmt_build_vocab
src_vocab: run/source.vocab
tgt_vocab: run/target.vocab
# Vocabulary size - should be the same as in sentence piece
src_vocab_size: 50000
tgt_vocab_size: 50000
# Filter out source/target longer than n if [filtertoolong] enabled
#src_seq_length: 200
#src_seq_length: 200
# Tokenization options
src_subword_model: source.model
tgt_subword_model: target.model
# Where to save the log file and the output models/checkpoints
log_file: train.log
save_model: models/model.fren
# Stop training if it does not imporve after n validations
early_stopping: 4
# Default: 5000 - Save a model checkpoint for each n
save_checkpoint_steps: 1000
# To save space, limit checkpoints to last n
# keep_checkpoint: 3
seed: 3435
# Default: 100000 - Train the model to max n steps
# Increase for large datasets
train_steps: 3000
# Default: 10000 - Run validation after n steps
valid_steps: 1000
# Default: 4000 - for large datasets, try up to 8000
warmup_steps: 1000
report_every: 100
decoder_type: transformer
encoder_type: transformer
word_vec_size: 512
rnn_size: 512
layers: 6
transformer_ff: 2048
heads: 8
accum_count: 4
optim: adam
adam_beta1: 0.9
adam_beta2: 0.998
decay_method: noam
learning_rate: 2.0
max_grad_norm: 0.0
# Tokens per batch, change if out of GPU memory
batch_size: 4096
valid_batch_size: 4096
batch_type: tokens
normalization: tokens
dropout: 0.1
label_smoothing: 0.1
max_generator_batches: 2
param_init: 0.0
param_init_glorot: 'true'
position_encoding: 'true'
# Number of GPUs, and IDs of GPUs
world_size: 1
gpu_ranks: [0]
'''
with open("config.yaml", "w+") as config_yaml:
config_yaml.write(config)
# [Optional] Check the content of the configuration file
!cat config.yaml
```
# Build Vocabulary
For large datasets, it is not feasable to use all words/tokens found in the corpus. Instead, a specific set of vocabulary is extracted from the training dataset, usually betweeen 32k and 100k words. This is the main purpose of the vocabulary building step.
```
# Find the number of CPUs/cores on the machine
!nproc --all
# Build Vocabulary
# -config: path to your config.yaml file
# -n_sample: use -1 to build vocabulary on all the segment in the training dataset
# -num_threads: change it to match the number of CPUs to run it faster
!onmt_build_vocab -config config.yaml -n_sample -1 -num_threads 2
```
From the **Runtime menu** > **Change runtime type**, make sure that the "**Hardware accelerator**" is "**GPU**".
```
# Check if the GPU is active
!nvidia-smi -L
# Check if the GPU is visable to PyTorch
import torch
print(torch.cuda.is_available())
print(torch.cuda.get_device_name(0))
```
# Training
Now, start training your NMT model! 🎉 🎉 🎉
```
# Train the NMT model
!onmt_train -config config.yaml
```
# Translation
Translation Options:
* `-model` - specify the last model checkpoint name; try testing the quality of multiple checkpoints
* `-src` - the subworded test dataset, source file
* `-output` - give any file name to the new translation output file
* `-gpu` - GPU ID, usually 0 if you have one GPU. Otherwise, it will translate on CPU, which would be slower.
* `-min_length` - [optional] to avoid empty translations
* `-verbose` - [optional] if you want to print translations
Refer to [OpenNMT-py translation options](https://opennmt.net/OpenNMT-py/options/translate.html) for more details.
```
# Translate - change the model name
!onmt_translate -model models/model.fren_step_3000.pt -src UN.en-fr.fr-filtered.fr.subword.test -output UN.en.translated -gpu 0 -min_length 1
# Check the first 5 lines of the translation file
!head -n 5 UN.en.translated
# Desubword the translation file
!python3 MT-Preparation/subwording/3-desubword.py target.model UN.en.translated
# Check the first 5 lines of the desubworded translation file
!head -n 5 UN.en.translated.desubword
# Desubword the source test
# Note: You might as well have split files *before* subwording during dataset preperation,
# but sometimes datasets have tokeniztion issues, so this way you are sure the file is really untokenized.
!python3 MT-Preparation/subwording/3-desubword.py target.model UN.en-fr.en-filtered.en.subword.test
# Check the first 5 lines of the desubworded source
!head -n 5 UN.en-fr.en-filtered.en.subword.test.desubword
```
# MT Evaluation
There are several MT Evaluation metrics such as BLEU, TER, METEOR, COMET, BERTScore, among others.
Here we are using BLEU. Files must be detokenized/desubworded beforehand.
```
# Download the BLEU script
!wget https://raw.githubusercontent.com/ymoslem/MT-Evaluation/main/BLEU/compute-bleu.py
# Install sacrebleu
!pip3 install sacrebleu
# Evaluate the translation (without subwording)
!python3 compute-bleu.py UN.en-fr.en-filtered.en.subword.test.desubword UN.en.translated.desubword
```
# More Features and Directions to Explore
Experiment with the following ideas:
* Icrease `train_steps` and see to what extent new checkpoints provide better translation, in terms of both BLEU and your human evaluation.
* Check other MT Evaluation mentrics other than BLEU such as [TER](https://github.com/mjpost/sacrebleu#ter), [WER](https://blog.machinetranslation.io/compute-wer-score/), [METEOR](https://blog.machinetranslation.io/compute-bleu-score/#meteor), [COMET](https://github.com/Unbabel/COMET), and [BERTScore](https://github.com/Tiiiger/bert_score). What are the conceptual differences between them? Is there there special cases for using a specific metric?
* Continue training from the last model checkpoint using the `-train_from` option, only if the training stopped and you want to continue it. In this case, `train_steps` in the config file should be larger than the steps of the last checkpoint you train from.
```
!onmt_train -config config.yaml -train_from models/model.fren_step_3000.pt
```
* **Ensemble Decoding:** During translation, instead of adding one model/checkpoint to the `-model` argument, add multiple checkpoints. For example, try the two last checkpoints. Does it improve quality of translation? Does it affect translation seepd?
* **Averaging Models:** Try to average multiple models into one model using the [average_models.py](https://github.com/OpenNMT/OpenNMT-py/blob/master/onmt/bin/average_models.py) script, and see how this affects translation quality.
```
python3 average_models.py -models model_step_xxx.pt model_step_yyy.pt -output model_avg.pt
```
* **Release the model:** Try this command and see how it reduce the model size.
```
onmt_release_model --model "model.pt" --output "model_released.pt
```
* **Use CTranslate2:** For efficient translation, consider using [CTranslate2](https://github.com/OpenNMT/CTranslate2), a fast inference engine. Check out an [example](https://gist.github.com/ymoslem/60e1d1dc44fe006f67e130b6ad703c4b).
* **Work on low-resource languages:** Find out more details about [how to train NMT models for low-resource languages](https://blog.machinetranslation.io/low-resource-nmt/).
* **Train a multilingual model:** Find out helpful notes about [training multilingual models](https://blog.machinetranslation.io/multilingual-nmt).
* **Publish a demo:** Show off your work through a [simple demo with CTranslate2 and Streamlit](https://blog.machinetranslation.io/nmt-web-interface/).
| true |
code
| 0.687079 | null | null | null | null |
|
```
try:
from openmdao.utils.notebook_utils import notebook_mode
except ImportError:
!python -m pip install openmdao[notebooks]
```
# NonlinearBlockGS
NonlinearBlockGS applies Block Gauss-Seidel (also known as fixed-point iteration) to the
components and subsystems in the system. This is mainly used to solve cyclic connections. You
should try this solver for systems that satisfy the following conditions:
1. System (or subsystem) contains a cycle, though subsystems may.
2. System does not contain any implicit states, though subsystems may.
NonlinearBlockGS is a block solver, so you can specify different nonlinear solvers in the subsystems and they
will be utilized to solve the subsystem nonlinear problem.
Note that you may not know if you satisfy the second condition, so choosing a solver can be a trial-and-error proposition. If
NonlinearBlockGS doesn't work, then you will need to use [NewtonSolver](../../../_srcdocs/packages/solvers.nonlinear/newton).
Here, we choose NonlinearBlockGS to solve the Sellar problem, which has two components with a
cyclic dependency, has no implicit states, and works very well with Gauss-Seidel.
```
from openmdao.utils.notebook_utils import get_code
from myst_nb import glue
glue("code_src33", get_code("openmdao.test_suite.components.sellar.SellarDis1withDerivatives"), display=False)
```
:::{Admonition} `SellarDis1withDerivatives` class definition
:class: dropdown
{glue:}`code_src33`
:::
```
from openmdao.utils.notebook_utils import get_code
from myst_nb import glue
glue("code_src34", get_code("openmdao.test_suite.components.sellar.SellarDis2withDerivatives"), display=False)
```
:::{Admonition} `SellarDis2withDerivatives` class definition
:class: dropdown
{glue:}`code_src34`
:::
```
import numpy as np
import openmdao.api as om
from openmdao.test_suite.components.sellar import SellarDis1withDerivatives, SellarDis2withDerivatives
prob = om.Problem()
model = prob.model
model.add_subsystem('d1', SellarDis1withDerivatives(), promotes=['x', 'z', 'y1', 'y2'])
model.add_subsystem('d2', SellarDis2withDerivatives(), promotes=['z', 'y1', 'y2'])
model.add_subsystem('obj_cmp', om.ExecComp('obj = x**2 + z[1] + y1 + exp(-y2)',
z=np.array([0.0, 0.0]), x=0.0),
promotes=['obj', 'x', 'z', 'y1', 'y2'])
model.add_subsystem('con_cmp1', om.ExecComp('con1 = 3.16 - y1'), promotes=['con1', 'y1'])
model.add_subsystem('con_cmp2', om.ExecComp('con2 = y2 - 24.0'), promotes=['con2', 'y2'])
model.nonlinear_solver = om.NonlinearBlockGS()
prob.setup()
prob.set_val('x', 1.)
prob.set_val('z', np.array([5.0, 2.0]))
prob.run_model()
print(prob.get_val('y1'))
print(prob.get_val('y2'))
from openmdao.utils.assert_utils import assert_near_equal
assert_near_equal(prob.get_val('y1'), 25.58830273, .00001)
assert_near_equal(prob.get_val('y2'), 12.05848819, .00001)
```
This solver runs all of the subsystems each iteration, passing data along all connections
including the cyclic ones. After each iteration, the iteration count and the residual norm are
checked to see if termination has been satisfied.
You can control the termination criteria for the solver using the following options:
# NonlinearBlockGS Options
```
om.show_options_table("openmdao.solvers.nonlinear.nonlinear_block_gs.NonlinearBlockGS")
```
## NonlinearBlockGS Constructor
The call signature for the `NonlinearBlockGS` constructor is:
```{eval-rst}
.. automethod:: openmdao.solvers.nonlinear.nonlinear_block_gs.NonlinearBlockGS.__init__
:noindex:
```
## Aitken relaxation
This solver implements Aitken relaxation, as described in Algorithm 1 of this paper on aerostructual design [optimization](http://www.umich.edu/~mdolaboratory/pdf/Kenway2014a.pdf).
The relaxation is turned off by default, but it may help convergence for more tightly coupled models.
## Residual Calculation
The `Unified Derivatives Equations` are formulated so that explicit equations (via `ExplicitComponent`) are also expressed
as implicit relationships, and their residual is also calculated in "apply_nonlinear", which runs the component a second time and
saves the difference in the output vector as the residual. However, this would require an extra call to `compute`, which is
inefficient for slower components. To eliminate the inefficiency of running the model twice every iteration the NonlinearBlockGS
driver saves a copy of the output vector and uses that to calculate the residual without rerunning the model. This does require
a little more memory, so if you are solving a model where memory is more of a concern than execution time, you can set the
"use_apply_nonlinear" option to True to use the original formulation that calls "apply_nonlinear" on the subsystem.
## NonlinearBlockGS Option Examples
**maxiter**
`maxiter` lets you specify the maximum number of Gauss-Seidel iterations to apply. In this example, we
cut it back from the default, ten, down to two, so that it terminates a few iterations earlier and doesn't
reach the specified absolute or relative tolerance.
```
from openmdao.test_suite.components.sellar import SellarDis1withDerivatives, SellarDis2withDerivatives
prob = om.Problem()
model = prob.model
model.add_subsystem('d1', SellarDis1withDerivatives(), promotes=['x', 'z', 'y1', 'y2'])
model.add_subsystem('d2', SellarDis2withDerivatives(), promotes=['z', 'y1', 'y2'])
model.add_subsystem('obj_cmp', om.ExecComp('obj = x**2 + z[1] + y1 + exp(-y2)',
z=np.array([0.0, 0.0]), x=0.0),
promotes=['obj', 'x', 'z', 'y1', 'y2'])
model.add_subsystem('con_cmp1', om.ExecComp('con1 = 3.16 - y1'), promotes=['con1', 'y1'])
model.add_subsystem('con_cmp2', om.ExecComp('con2 = y2 - 24.0'), promotes=['con2', 'y2'])
prob.setup()
nlbgs = model.nonlinear_solver = om.NonlinearBlockGS()
#basic test of number of iterations
nlbgs.options['maxiter'] = 1
prob.run_model()
print(model.nonlinear_solver._iter_count)
assert(model.nonlinear_solver._iter_count == 1)
nlbgs.options['maxiter'] = 5
prob.run_model()
print(model.nonlinear_solver._iter_count)
assert(model.nonlinear_solver._iter_count == 5)
#test of number of iterations AND solution after exit at maxiter
prob.set_val('x', 1.)
prob.set_val('z', np.array([5.0, 2.0]))
nlbgs.options['maxiter'] = 3
prob.set_solver_print()
prob.run_model()
print(prob.get_val('y1'))
print(prob.get_val('y2'))
print(model.nonlinear_solver._iter_count)
assert_near_equal(prob.get_val('y1'), 25.58914915, .00001)
assert_near_equal(prob.get_val('y2'), 12.05857185, .00001)
assert(model.nonlinear_solver._iter_count == 3)
```
**atol**
Here, we set the absolute tolerance to a looser value that will trigger an earlier termination. After
each iteration, the norm of the residuals is calculated one of two ways. If the "use_apply_nonlinear" option
is set to False (its default), then the norm is calculated by subtracting a cached previous value of the
outputs from the current value. If "use_apply_nonlinear" is True, then the norm is calculated by calling
apply_nonlinear on all of the subsystems. In this case, `ExplicitComponents` are executed a second time.
If this norm value is lower than the absolute tolerance `atol`, the iteration will terminate.
```
from openmdao.test_suite.components.sellar import SellarDis1withDerivatives, SellarDis2withDerivatives
prob = om.Problem()
model = prob.model
model.add_subsystem('d1', SellarDis1withDerivatives(), promotes=['x', 'z', 'y1', 'y2'])
model.add_subsystem('d2', SellarDis2withDerivatives(), promotes=['z', 'y1', 'y2'])
model.add_subsystem('obj_cmp', om.ExecComp('obj = x**2 + z[1] + y1 + exp(-y2)',
z=np.array([0.0, 0.0]), x=0.0),
promotes=['obj', 'x', 'z', 'y1', 'y2'])
model.add_subsystem('con_cmp1', om.ExecComp('con1 = 3.16 - y1'), promotes=['con1', 'y1'])
model.add_subsystem('con_cmp2', om.ExecComp('con2 = y2 - 24.0'), promotes=['con2', 'y2'])
nlbgs = model.nonlinear_solver = om.NonlinearBlockGS()
nlbgs.options['atol'] = 1e-4
prob.setup()
prob.set_val('x', 1.)
prob.set_val('z', np.array([5.0, 2.0]))
prob.run_model()
print(prob.get_val('y1'))
print(prob.get_val('y2'))
assert_near_equal(prob.get_val('y1'), 25.5882856302, .00001)
assert_near_equal(prob.get_val('y2'), 12.05848819, .00001)
```
**rtol**
Here, we set the relative tolerance to a looser value that will trigger an earlier termination. After
each iteration, the norm of the residuals is calculated one of two ways. If the "use_apply_nonlinear" option
is set to False (its default), then the norm is calculated by subtracting a cached previous value of the
outputs from the current value. If "use_apply_nonlinear" is True, then the norm is calculated by calling
apply_nonlinear on all of the subsystems. In this case, `ExplicitComponents` are executed a second time.
If the ratio of the currently calculated norm to the initial residual norm is lower than the relative tolerance
`rtol`, the iteration will terminate.
```
from openmdao.utils.notebook_utils import get_code
from myst_nb import glue
glue("code_src35", get_code("openmdao.test_suite.components.sellar.SellarDerivatives"), display=False)
```
:::{Admonition} `SellarDerivatives` class definition
:class: dropdown
{glue:}`code_src35`
:::
```
from openmdao.test_suite.components.sellar import SellarDis1withDerivatives, SellarDis2withDerivatives, SellarDerivatives
prob = om.Problem()
model = prob.model
model.add_subsystem('d1', SellarDis1withDerivatives(), promotes=['x', 'z', 'y1', 'y2'])
model.add_subsystem('d2', SellarDis2withDerivatives(), promotes=['z', 'y1', 'y2'])
model.add_subsystem('obj_cmp', om.ExecComp('obj = x**2 + z[1] + y1 + exp(-y2)',
z=np.array([0.0, 0.0]), x=0.0),
promotes=['obj', 'x', 'z', 'y1', 'y2'])
model.add_subsystem('con_cmp1', om.ExecComp('con1 = 3.16 - y1'), promotes=['con1', 'y1'])
model.add_subsystem('con_cmp2', om.ExecComp('con2 = y2 - 24.0'), promotes=['con2', 'y2'])
nlbgs = model.nonlinear_solver = om.NonlinearBlockGS()
nlbgs.options['rtol'] = 1e-3
prob.setup()
prob.set_val('x', 1.)
prob.set_val('z', np.array([5.0, 2.0]))
prob.run_model()
print(prob.get_val('y1'), 25.5883027, .00001)
print(prob.get_val('y2'), 12.05848819, .00001)
assert_near_equal(prob.get_val('y1'), 25.5883027, .00001)
assert_near_equal(prob.get_val('y2'), 12.05848819, .00001)
```
| true |
code
| 0.613671 | null | null | null | null |
|
## Search algorithms within Optuna
In this notebook, I will demo how to select the search algorithm with Optuna. We will compare the use of:
- Grid Search
- Randomized search
- Tree-structured Parzen Estimators
- CMA-ES
We can select the search algorithm from the [optuna.study.create_study()](https://optuna.readthedocs.io/en/stable/reference/generated/optuna.study.create_study.html#optuna.study.create_study) class.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.metrics import accuracy_score, roc_auc_score
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.ensemble import RandomForestClassifier
import optuna
# load dataset
breast_cancer_X, breast_cancer_y = load_breast_cancer(return_X_y=True)
X = pd.DataFrame(breast_cancer_X)
y = pd.Series(breast_cancer_y).map({0:1, 1:0})
X.head()
# the target:
# percentage of benign (0) and malign tumors (1)
y.value_counts() / len(y)
# split dataset into a train and test set
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
X_train.shape, X_test.shape
```
## Define the objective function
This is the hyperparameter response space, the function we want to minimize.
```
# the objective function takes the hyperparameter space
# as input
def objective(trial):
rf_n_estimators = trial.suggest_int("rf_n_estimators", 100, 1000)
rf_criterion = trial.suggest_categorical("rf_criterion", ['gini', 'entropy'])
rf_max_depth = trial.suggest_int("rf_max_depth", 1, 4)
rf_min_samples_split = trial.suggest_float("rf_min_samples_split", 0.01, 1)
model = RandomForestClassifier(
n_estimators=rf_n_estimators,
criterion=rf_criterion,
max_depth=rf_max_depth,
min_samples_split=rf_min_samples_split,
)
score = cross_val_score(model, X_train, y_train, cv=3)
accuracy = score.mean()
return accuracy
```
## Randomized Search
RandomSampler()
```
study = optuna.create_study(
direction="maximize",
sampler=optuna.samplers.RandomSampler(),
)
study.optimize(objective, n_trials=5)
study.best_params
study.best_value
study.trials_dataframe()
```
## TPE
TPESampler is the default
```
study = optuna.create_study(
direction="maximize",
sampler=optuna.samplers.TPESampler(),
)
study.optimize(objective, n_trials=5)
study.best_params
study.best_value
```
## CMA-ES
CmaEsSampler
```
study = optuna.create_study(
direction="maximize",
sampler=optuna.samplers.CmaEsSampler(),
)
study.optimize(objective, n_trials=5)
study.best_params
study.best_value
```
## Grid Search
GridSampler()
We are probably not going to perform GridSearch with Optuna, but in case you wanted to, you need to add a variable with the space, with the exact values that you want to be tested.
```
search_space = {
"rf_n_estimators": [100, 500, 1000],
"rf_criterion": ['gini', 'entropy'],
"rf_max_depth": [1, 2, 3],
"rf_min_samples_split": [0.1, 1.0]
}
study = optuna.create_study(
direction="maximize",
sampler=optuna.samplers.GridSampler(search_space),
)
study.optimize(objective)
study.best_params
study.best_value
```
| true |
code
| 0.616705 | null | null | null | null |
|
This notebook was prepared by [Donne Martin](https://github.com/donnemartin). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# Solution Notebook
## Problem: Generate a list of primes.
* [Constraints](#Constraints)
* [Test Cases](#Test-Cases)
* [Algorithm](#Algorithm)
* [Code](#Code)
* [Unit Test](#Unit-Test)
## Constraints
* Is it correct that 1 is not considered a prime number?
* Yes
* Can we assume the inputs are valid?
* No
* Can we assume this fits memory?
* Yes
## Test Cases
* None -> Exception
* Not an int -> Exception
* 20 -> [False, False, True, True, False, True, False, True, False, False, False, True, False, True, False, False, False, True, False, True]
## Algorithm
For a number to be prime, it must be 2 or greater and cannot be divisible by another number other than itself (and 1).
We'll use the Sieve of Eratosthenes. All non-prime numbers are divisible by a prime number.
* Use an array (or bit array, bit vector) to keep track of each integer up to the max
* Start at 2, end at sqrt(max)
* We can use sqrt(max) instead of max because:
* For each value that divides the input number evenly, there is a complement b where a * b = n
* If a > sqrt(n) then b < sqrt(n) because sqrt(n^2) = n
* "Cross off" all numbers divisible by 2, 3, 5, 7, ... by setting array[index] to False
Complexity:
* Time: O(n log log n)
* Space: O(n)
Wikipedia's animation:

## Code
```
import math
class PrimeGenerator(object):
def generate_primes(self, max_num):
if max_num is None:
raise TypeError('max_num cannot be None')
array = [True] * max_num
array[0] = False
array[1] = False
prime = 2
while prime <= math.sqrt(max_num):
self._cross_off(array, prime)
prime = self._next_prime(array, prime)
return array
def _cross_off(self, array, prime):
for index in range(prime*prime, len(array), prime):
# Start with prime*prime because if we have a k*prime
# where k < prime, this value would have already been
# previously crossed off
array[index] = False
def _next_prime(self, array, prime):
next = prime + 1
while next < len(array) and not array[next]:
next += 1
return next
```
## Unit Test
```
%%writefile test_generate_primes.py
import unittest
class TestMath(unittest.TestCase):
def test_generate_primes(self):
prime_generator = PrimeGenerator()
self.assertRaises(TypeError, prime_generator.generate_primes, None)
self.assertRaises(TypeError, prime_generator.generate_primes, 98.6)
self.assertEqual(prime_generator.generate_primes(20), [False, False, True,
True, False, True,
False, True, False,
False, False, True,
False, True, False,
False, False, True,
False, True])
print('Success: generate_primes')
def main():
test = TestMath()
test.test_generate_primes()
if __name__ == '__main__':
main()
%run -i test_generate_primes.py
```
| true |
code
| 0.517632 | null | null | null | null |
|
# BUSINESS ANALYTICS
You are the business owner of the retail firm and want to see how your company is performing. You are interested in finding out the weak areas where you can work to make more profit. What all business problems you can derive by looking into the data?
```
# Importing certain libraries
import pandas as pd
import numpy as np
import seaborn as sb
import matplotlib.pyplot as plt
%matplotlib inline
```
## Understanding the data
```
# Importing the dataset
data = pd.read_csv(r"D:/TSF/Task 5/SampleSuperstore.csv")
# Displaying the Dataset
data.head()
# Gathering the basic Information
data.describe()
# Learning about differnet datatypes present in the dataset
data.dtypes
# Checking for any null or misssing values
data.isnull().sum()
```
Since, there are no null or missing values present, therefore we can move further for data exploration
## Exploratory Data Analysis
```
# First, using seaborn pairplot for data visualisation
sb.set(style = "whitegrid")
plt.figure(figsize = (20, 10))
sb.pairplot(data, hue = "Quantity")
```
We can clearly see that in our dataset, there are total of 14 different quantities in which our business deals.
```
# Second, using seaborn heatmap for data visualization
plt.figure(figsize = (7, 5))
sb.heatmap(data.corr(), annot = True, fmt = ".2g", linewidth = 0.5, linecolor = "Black", cmap = "YlOrRd")
```
Here, We can see that Sales and Profit are highly corelated as obvious.
```
# Third, using seaborn countplot for data visualization
sb.countplot(x = data["Country"])
plt.show()
```
Our dataset only contains data from United States only.
```
sb.countplot(x = data["Segment"])
plt.show()
```
Maximum Segment is of Consumer & Minimum segment is of Home Office
```
sb.countplot(x = data["Region"])
plt.show()
```
Maximum entries are from West region of United States, followed by East, Central & South respectively.
```
sb.countplot(x = data["Ship Mode"])
plt.show()
```
This shows that the mostly our business uses Standard class for shipping as compared to other classes.
```
plt.figure(figsize = (8, 8))
sb.countplot(x = data["Quantity"])
plt.show()
```
Out of total 14 quantites present, Maximum are number 2 and 3 respectively.
```
plt.figure(figsize = (10, 8))
sb.countplot(x = data["State"])
plt.xticks(rotation = 90)
plt.show()
```
If we watch carefully, we can clearly see that maximum sales happened in California, followed by New York & the Texas.
Lowest sales happened North Dakota, West Virginea.
```
sb.countplot(x = data["Category"])
plt.show()
```
So, Our business deals maximum in Office Supplies category, followed by Furniture & then Tech products.
```
plt.figure(figsize = (10, 8))
sb.countplot(x = data['Sub-Category'])
plt.xticks(rotation = 90)
plt.show()
```
If we define Sub Categories section, maximum profit is earned through Binders, followed by Paper & Furnishing. Minimum Profit is earned through Copiers, Machines etc.
```
# Forth, using Seaborn barplot for data visualization
plt.figure(figsize = (12, 10))
sb.barplot(x = data["Sub-Category"], y = data["Profit"], capsize = .1, saturation = .5)
plt.xticks(rotation = 90)
plt.show()
```
In this Sub-categories, Bookcases, Tables and Supplies are facing losses on the business level as compared to ther categories. So, Business owner needs to pay attention towards these 3 categories.
### Now, to compare specific features of Business, We have to use certain different Exploration operations
```
# Fifth, using regression plot for data visualization
plt.figure(figsize = (10, 8))
sb.regplot(data["Sales"], data["Profit"], marker = "X", color = "r")
plt.show()
```
This Relationship does not seem to be Linear. So, this relationship doesn't help much.
```
plt.figure(figsize = (10, 8))
sb.regplot(data["Quantity"], data["Profit"], color = "black", y_jitter=.1)
plt.show()
```
This Relationship happens to be linear. The quantity '5' has the maximum profit as compared to others.
```
plt.figure(figsize = (10, 8))
sb.regplot(data["Quantity"], data["Sales"], color = "m", marker = "+", y_jitter=.1)
plt.show()
```
This Relationship is also linear. The quantity '6' has the maximum sales as compared to others.
```
# Sixth, using seaborn lineplot for data visualisation
plt.figure(figsize = (10, 8))
sb.lineplot(data["Discount"], data["Profit"], color = "orange", label = "Discount")
plt.legend()
plt.show()
```
As expected, we can see at 50% discount, the profit is very much negligible or we can say that there are losses. But, on the other hand, at 10% discount, there is a profit at a very good level.
```
plt.figure(figsize = (10, 8))
sb.lineplot(data["Sub-Category"], data["Profit"], color = "blue", label = "Sales")
plt.xticks(rotation = 90)
plt.legend()
plt.show()
```
With Copiers, Business makes the largest Profit.
```
plt.figure(figsize = (10, 8))
sb.lineplot(data["Quantity"], data["Profit"], color = "red", label = "Quantity")
plt.legend()
plt.show()
```
Quantity '13' has the maximum profit.
### WHAT CAN BE DERIVED FROM ABOVE VISUALIZATIONS :
* Improvements should be made for same day shipment mode.
* We have to work more in the Southern region of USA for better business.
* Office Supplies are good. We have to work more on Technology and Furniture Category of business.
* There are very less people working as Copiers.
* Maximum number of people are from California and New York. It should expand in other parts of USA as well.
* Company is facing losses in sales of bookcases and tables products.
* Company have a lots of profit in the sale of copier but the number of sales is very less so there is a need of increase innumber of sales of copier.
* When the profits of a state are compared with the discount provided in each state, the states which has allowed more discount, went into loss.
* Profit and discount show very weak and negative relationship. This should be kept in mind that before taking any other decision related to business.
# ASSIGNMENT COMPLETED !!
| true |
code
| 0.61832 | null | null | null | null |
|
# Canonical correlation analysis in python
In this notebook, we will walk through the solution to the basic algrithm of canonical correlation analysis and compare that to the output of implementations in existing python libraries `statsmodels` and `scikit-learn`.
```
import numpy as np
from scipy.linalg import sqrtm
from statsmodels.multivariate.cancorr import CanCorr as smCCA
from sklearn.cross_decomposition import CCA as skCCA
import matplotlib.pyplot as plt
from seaborn import heatmap
```
Let's define a plotting functon for the output first.
```
def plot_cca(a, b, U, V, s):
# plotting
plt.figure()
heatmap(a, square=True, center=0)
plt.title("Canonical vector - x")
plt.figure()
heatmap(b, square=True, center=0)
plt.title("Canonical vector - y")
plt.figure(figsize=(9, 6))
for i in range(N):
plt.subplot(221 + i)
plt.scatter(np.array(X_score[:, i]).reshape(100),
np.array(Y_score[:, i]).reshape(100),
marker="o", c="b", s=25)
plt.xlabel("Canonical variate of X")
plt.ylabel("Canonical variate of Y")
plt.title('Mode %i (corr = %.2f)' %(i + 1, s[i]))
plt.xticks(())
plt.yticks(())
```
## Create data based on some latent variables
First generate some test data.
The code below is modified based on the scikit learn example of CCA.
The aim of using simulated data is that we can have complete control over the structure of the data and help us see the utility of CCA.
Let's create a dataset with 100 observations with two hidden variables:
```
n = 100
# fix the random seed so this tutorial will always create the same results
np.random.seed(42)
l1 = np.random.normal(size=n)
l2 = np.random.normal(size=n)
```
For each observation, there are two domains of data.
Six and four variables are measured in each of the domain.
In domain 1 (x), the first latent structure 1 is underneath the first 3 variables and latent strucutre 2 for the rest.
In domain 2 (y), the first latent structure 1 is underneath every other variable and for latent strucutre 2 as well.
```
latents_x = np.array([l1, l1, l1, l2, l2, l2]).T
latents_y = np.array([l1, l2, l1, l2]).T
```
Now let's add some random noise on this latent structure.
```
X = latents_x + np.random.normal(size=6 * n).reshape((n, 6))
Y = latents_y + np.random.normal(size=4 * n).reshape((n, 4))
```
The aim of CCA is finding the correlated latent features in the two domains of data.
Therefore, we would expect to find the hidden strucure is laid out in the latent components.
## SVD algebra solution
SVD solution is the most implemented way of CCA solution. For the proof of standard eigenvalue solution and the proof SVD solution demonstrated below, see [Uurtio wt. al, (2018)](https://dl.acm.org/citation.cfm?id=3136624).
The first step is getting the covariance matrixes of X and Y.
```
Cx, Cy = np.corrcoef(X.T), np.corrcoef(Y.T)
Cxy = np.corrcoef(X.T, Y.T)[:X.shape[1], X.shape[1]:]
Cyx = Cxy.T
```
We first retrieve the identity form of the covariance matix of X and Y.
```
sqrt_x, sqrt_y = np.matrix(sqrtm(Cx)), np.matrix(sqrtm(Cy))
isqrt_x, isqrt_y = sqrt_x.I, sqrt_y.I
```
According to the proof, we leared that the canonical correlation can be retrieved from SVD on Cx^-1/2 Cxy Cy^-1/2.
```
W = isqrt_x * Cxy * isqrt_y
u, s, v = np.linalg.svd(W)
```
The columns of the matrices U and V correspond to the sets of orthonormal left and right singular vectors respectively. The singular values of matrix S correspond to
the canonical correlations. The positions w a and w b are obtained from:
```
N = np.min([X.shape[1], Y.shape[1]])
a = np.dot(u, isqrt_x.T[:, :N]) / np.std(X) # scaling because we didn't standardise the input
b = np.dot(v, isqrt_y).T / np.std(Y)
```
Now compute the score.
```
X_score, Y_score = X.dot(a), Y.dot(b)
plot_cca(a, b, X_score, Y_score, s) # predefined plotting function
```
## Solution Using SVD Only
The solution above can be further simplified by conducting SVD on the two domains.
The algorithm SVD X and Y. This step is similar to doing principle component analysis on the two domains.
```
ux, sx, vx = np.linalg.svd(X, 0)
uy, sy, vy = np.linalg.svd(Y, 0)
```
Then take the unitary bases and form UxUy^T and SVD it. S would be the canonical correlation of the two domanins of features.
```
u, s, v = np.linalg.svd(ux.T.dot(uy), 0)
```
We can yield the canonical vectors by transforming the unitary basis in the hidden space back to the original space.
```
a = (vx.T).dot(u) # no scaling here as SVD handled it.
b = (vy.T).dot(v.T)
X_score, Y_score = X.dot(a), Y.dot(b)
```
Now we can plot the results. It shows very similar results to solution 1.
```
plot_cca(a, b, X_score, Y_score, s) # predefined plotting function
```
The method above has been implemented in `Statsmodels`. The results are almost identical:
```
sm_cca = smCCA(Y, X)
sm_s = sm_cca.cancorr
sm_a = sm_cca.x_cancoef
sm_b = sm_cca.y_cancoef
sm_X_score = X.dot(a)
sm_Y_score = Y.dot(b)
plot_cca(a, b, X_score, Y_score, s)
```
## Scikit learn
Scikit learn implemented [a different algorithm](https://www.stat.washington.edu/sites/default/files/files/reports/2000/tr371.pdf).
The outcome of the Scikit learn implementation yield very similar results.
The first mode capture the hidden structure in the simulated data.
```
cca = skCCA(n_components=4)
cca.fit(X, Y)
s = np.corrcoef(cca.x_scores_.T, cca.y_scores_.T).diagonal(offset=cca.n_components)
a = cca.x_weights_
b = cca.y_weights_
X_score, Y_score = cca.x_scores_, cca.y_scores_
plot_cca(a, b, X_score, Y_score, s) # predefined plotting function
```
| true |
code
| 0.619011 | null | null | null | null |
|
# Debugging Numba problems
## Common problems
Numba is a compiler, if there's a problem, it could well be a "compilery" problem, the dynamic interpretation that comes with the Python interpreter is gone! As with any compiler toolchain there's a bit of a learning curve but once the basics are understood it becomes easy to write quite complex applications.
```
from numba import njit
import numpy as np
```
### Type inference problems
A very large set of problems can be classed as type inference problems. These are problems which appear when Numba can't work out the types of all the variables in your code. Here's an example:
```
@njit
def type_inference_problem():
a = {}
return a
type_inference_problem()
```
Things to note in the above, Numba has said that:
1. It has encountered a typing error.
2. It cannot infer (work out) the type of the variable named `a`.
3. It has an imprecise type for `a` of `DictType[undefined, undefined]`.
4. It's pointing to where the problem is in the source
5. It's giving you things to look at for help
Numba's response is reasonable, how can it possibly compile a specialisation of an empty dictionary, it cannot work out what to use for a key or value type.
### Type unification problems
Another common issue is that of type unification, this is due to Numba needing the inferred variable types for the code it's compiling to be statically determined and type stable. What this usually means is something like the type of a variable is being changed in a loop or there's two (or more) possible return types. Example:
```
@njit
def foo(x):
if x > 10:
return (1,)
else:
return 1
foo(1)
```
Things to note in the above, Numba has said that:
1. It has encountered a typing error.
2. It cannot unify the return types and then lists the offending types.
3. It pointis to the locations in the source that are the cause of the problem.
4. It's giving you things to look at for help.
Numba's response due to it not being possible to compile a function that returns a tuple or an integer? You couldn't do that in C/Fortran, same here!
### Unsupported features
Numba supports a subset of Python and NumPy, it's possible to run into something that hasn't been implemented. For example `str(int)` has not been written yet (this is a rather tricky thing to write :)). This is what it looks like:
```
@njit
def foo():
return str(10)
foo()
```
Things to note in the above, Numba has said that:
1. It has encountered a typing error.
2. It's an invalid use of a `Function` of type `(<class 'str'>)` with argument(s) of type(s): `(Literal[int](10))`
3. It points to the location in the source that is the cause of the problem.
4. It's giving you things to look at for help.
What's this bit about?
```
* parameterized
In definition 0:
All templates rejected with literals.
In definition 1:
All templates rejected without literals.
In definition 2:
All templates rejected with literals.
In definition 3:
All templates rejected without literals.
```
Internally Numba does something akin to "template matching" to try and find something to do the functionality requested with the types requested, it's looking through the definitions see if any match and reporting what they say (which in this case is "rejected").
Here's a different one, Numba's `np.mean` implementation doesn't support `axis`:
```
@njit
def foo():
x = np.arange(100).reshape((10, 10))
return np.mean(x, axis=1)
foo()
```
Things to note in the above, Numba has said that:
1. It has encountered a typing error.
2. It's an invalid use of a `Function` "mean" with argument(s) of type(s): `(array(float64, 2d, C), axis=Literal[int](1))`
3. It's reporting what the various template defintions are responding with: e.g.
"TypingError: numba doesn't support kwarg for mean", which is correct!
4. It points to the location in the source that is the cause of the problem.
5. It's giving you things to look at for help.
A common workaround for the above is to just unroll the loop over the axis, for example:
```
@njit
def foo():
x = np.arange(100).reshape((10, 10))
lim, _ = x.shape
buf = np.empty((lim,), x.dtype)
for i in range(lim):
buf[i] = np.mean(x[i])
return buf
foo()
```
### Lowering errors
"Lowering" is the process of translating the Numba IR to LLVM IR to machine code. Numba tries really hard to prevent lowering errors, but sometimes you might see them, if you do please tell us:
https://github.com/numba/numba/issues/new
A lowering error means that there's a problem in Numba internals. The most common cause is that it worked out that it could compile a function as all the variable types were statically determined, but when it tried to find an implementation for some operation in the function to translate to machine code, it couldn't find one.
<h3><span style="color:blue"> Task 1: Debugging practice</span></h3>
The following code has a couple of issues, see if you can work them out and fix them.
```
x = np.arange(20.).reshape((4, 5))
@njit
def problem_factory(x):
nrm_x = np.linalg.norm(x, ord=2, axis=1) # axis not supported, manual unroll
nrm_total = np.sum(nrm_x)
ret = {} # dict type requires float->int cast, true branch is int and it sets the dict type
if nrm_total > 87:
ret[nrm_total] = 1
else:
ret[nrm_total] = nrm_total
return ret
# This is a fixed version
@njit
def problem_factory_fixed(x):
lim, _ = x.shape
nrm_x = np.empty(lim, x.dtype)
for i in range(lim):
nrm_x[i] = np.linalg.norm(x[i])
nrm_total = np.sum(nrm_x)
ret = {}
if nrm_total > 87:
ret[nrm_total] = 1.0
else:
ret[nrm_total] = nrm_total
return ret
fixed = problem_factory_fixed(x)
expected = problem_factory.py_func(x)
# will pass if "fixed" correctly
for k, v in zip(fixed.items(), expected.items()):
np.testing.assert_allclose(k[0], k[1])
np.testing.assert_allclose(v[0], v[1])
```
## Debugging compiled code
In Numba compiled code debugging typically takes one of a few forms.
1. Temporarily disabling the JIT compiler so that the code just runs in Python and the usual Python debugging tools can be used. Either remove the Numba JIT decorators or set the environment variable `NUMBA_DISABLE_JIT`, to disable JIT compilation globally, [docs](http://numba.pydata.org/numba-doc/latest/reference/envvars.html#envvar-NUMBA_DISABLE_JIT).
2. Traditional "print-to-stdout" debugging, Numba supports the use of `print()` (without interpolation!) so it's relatively easy to inspect values and control flow. e.g.
```
@njit
def demo_print(x):
print("function entry")
if x > 1:
print("branch 1, x = ", x)
else:
print("branch 2, x = ", x)
print("function exit")
demo_print(5)
```
3. Debugging with `gdb` (the GNU debugger). This is not going to be demonstrated here as it does not work with notebooks. However, the gist is to supply the Numba JIT decorator with the kwarg `debug=True` and then Numba has a special function `numba.gdb()` that can be used in your program to automatically launch and attach `gdb` at the call site. For example (and **remember not to run this!**):
```
from numba import gdb
@njit(debug=True)
def _DO_NOT_RUN_gdb_demo(x):
if x > 1:
y = 3
gdb()
else:
y = 5
return y
```
Extensive documentation on using `gdb` with Numba is available [here](http://numba.pydata.org/numba-doc/latest/user/troubleshoot.html#debugging-jit-compiled-code-with-gdb).
| true |
code
| 0.414484 | null | null | null | null |
|
# Naive Bayes Classifier (Self Made)
### 1. Importing Libraries
```
import numpy as np
import matplotlib.pyplot as plt
import os
import pandas as pd
from sklearn.metrics import r2_score
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from collections import defaultdict
```
### 2. Data Preprocessing
```
pima = pd.read_csv("diabetes.csv")
pima.head()
pima.info()
#normalizing the dataset
scalar = preprocessing.MinMaxScaler()
pima = scalar.fit_transform(pima)
#split dataset in features and target variable
X = pima[:,:8]
y = pima[:, 8]
X_train, X_test, Y_train, Y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print(X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
```
### 3. Required Functions
```
def normal_distr(x, mean, dev):
#finding the value through the normal distribution formula
return (1/(np.sqrt(2 * np.pi) * dev)) * (np.exp(- (((x - mean) / dev) ** 2) / 2))
def finding_mean(X):
return np.mean(X)
def finding_std_dev(X):
return np.std(X)
#def pred(X_test):
def train(X_train,Y_train):
labels = set(Y_train)
cnt_table = defaultdict(list)
for row in range(X_train.shape[0]):
for col in range(X_train.shape[1]):
cnt_table[(col, Y_train[row])].append(X_train[row][col])
lookup_list = defaultdict(list)
for item in cnt_table.items():
X_category = np.asarray(item[1])
lookup_list[(item[0][0], item[0][1])].append(finding_mean(X_category))
lookup_list[(item[0][0], item[0][1])].append(finding_std_dev(X_category))
return lookup_list
def pred(X_test, lookup_list):
Y_pred = []
for row in range(X_test.shape[0]):
prob_yes = 1
prob_no = 1
for col in range(X_test.shape[1]):
prob_yes = prob_yes * normal_distr(X_test[row][col], lookup_list[(col, 1)][0], lookup_list[(col, 1)][1])
prob_no = prob_no * normal_distr(X_test[row][col], lookup_list[(col, 0)][0], lookup_list[(col, 1)][1])
if(prob_yes >= prob_no):
Y_pred.append(1)
else:
Y_pred.append(0)
return np.asarray(Y_pred)
def score(Y_pred, Y_test):
correct_pred = np.sum(Y_pred == Y_test)
return correct_pred / Y_pred.shape[0]
def naive_bayes(X_train,Y_train, X_test, Y_test):
lookup_list = train(X_train, Y_train)
Y_pred = pred(X_test, lookup_list)
return score(Y_pred, Y_test)
score = naive_bayes(X_train, Y_train, X_test, Y_test)
print("The accuracy of the model is : {0}".format(score))
```
| true |
code
| 0.601184 | null | null | null | null |
|
Let's load the data from the csv just as in `dataset.ipynb`.
```
import pandas as pd
import numpy as np
raw_data_file_name = "../dataset/fer2013.csv"
raw_data = pd.read_csv(raw_data_file_name)
```
Now, we separate and clean the data a little bit. First, we create an array of only the training data. Then, we create an array of only the private test data (referred to in the code with the prefix `first_test`). The `reset_index` call re-aligns the `first_test_data` to index from 0 instead of wherever it starts in the set.
```
train_data = raw_data[raw_data["Usage"] == "Training"]
first_test_data = raw_data[raw_data["Usage"] == "PrivateTest"]
first_test_data.reset_index(inplace=True)
second_test_data = raw_data[raw_data["Usage"] == "PublicTest"]
second_test_data.reset_index(inplace=True)
import keras
train_expected = keras.utils.to_categorical(train_data["emotion"], num_classes=7, dtype='int32')
first_test_expected = keras.utils.to_categorical(first_test_data["emotion"], num_classes=7, dtype='int32')
second_test_expected = keras.utils.to_categorical(second_test_data["emotion"], num_classes=7, dtype='int32')
def process_pixels(array_input):
output = np.empty([int(len(array_input)), 2304])
for index, item in enumerate(output):
item[:] = array_input[index].split(" ")
output /= 255
return output
train_pixels = process_pixels(train_data["pixels"])
train_pixels = train_pixels.reshape(train_pixels.shape[0], 48, 48, 1)
first_test_pixels = process_pixels(first_test_data["pixels"])
first_test_pixels = first_test_pixels.reshape(first_test_pixels.shape[0], 48, 48, 1)
second_test_pixels = process_pixels(second_test_data["pixels"])
second_test_pixels = second_test_pixels.reshape(second_test_pixels.shape[0], 48, 48, 1)
from keras.preprocessing.image import ImageDataGenerator
datagen = ImageDataGenerator(
featurewise_center=False,
featurewise_std_normalization=False,
rotation_range=10,
width_shift_range=0.1,
height_shift_range=0.1,
horizontal_flip=True
)
```
Here, we create our own top-level network to load on top of VGG16.
```
from keras.models import Sequential
from keras.layers import Dense, Dropout, MaxPooling2D, Conv2D, Flatten
from keras.optimizers import Adam
def gen_model(size):
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape = (48, 48, 1)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(size, activation='relu'))
model.add(Dense(7, activation='softmax'))
optimizer = Adam(learning_rate=0.0009)
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
return model
from keras.callbacks.callbacks import EarlyStopping, ReduceLROnPlateau
early_stop = EarlyStopping('val_loss', patience=50)
reduce_lr = ReduceLROnPlateau('val_loss', factor=0.1, patience=int(50/4), verbose=1)
callbacks = [early_stop, reduce_lr]
sizes = [32, 64, 128, 256]
results = [None] * len(sizes)
for i in range(len(sizes)):
model = gen_model(sizes[i])
model.fit_generator(datagen.flow(train_pixels, train_expected, batch_size=32),
steps_per_epoch=len(train_pixels) / 32,
epochs=10, verbose=1, callbacks=callbacks,
validation_data=(first_test_pixels,first_test_expected))
results[i] = model.evaluate(second_test_pixels, second_test_pixels, batch_size=32)
```
| true |
code
| 0.646879 | null | null | null | null |
|
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
#all_slow
#export
from fastai.basics import *
from fastai.learner import Callback
#hide
from nbdev.showdoc import *
#default_exp callback.azureml
```
# AzureML Callback
Track fastai experiments with the azure machine learning plattform.
## Prerequisites
Install the azureml SDK:
```python
pip install azureml-core
```
## How to use it?
Import and use `AzureMLCallback` during model fitting.
If you are submitting your training run with azureml SDK [ScriptRunConfig](https://docs.microsoft.com/en-us/azure/machine-learning/how-to-set-up-training-targets), the callback will automatically detect the run and log metrics. For example:
```python
from fastai.callback.azureml import AzureMLCallback
learn.fit_one_cycle(epoch, lr, cbs=AzureMLCallback())
```
If you are running an experiment manually and just want to have interactive logging of the run, use azureml's `Experiment.start_logging` to create the interactive `run`, and pass that into `AzureMLCallback`. For example:
```python
from azureml.core import Experiment
experiment = Experiment(workspace=ws, name='experiment_name')
run = experiment.start_logging(outputs=None, snapshot_directory=None)
from fastai.callback.azureml import AzureMLCallback
learn.fit_one_cycle(epoch, lr, cbs=AzureMLCallback(run))
```
If you are running an experiment on your local machine (i.e. not using `ScriptRunConfig` and not passing an azureml `run` into the callback), it will recognize that there is no AzureML run to log to, and print the log attempts instead.
To save the model weights, use the usual fastai methods and save the model to the `outputs` folder, which is a "special" (for Azure) folder that is automatically tracked in AzureML.
As it stands, note that if you pass the callback into your `Learner` directly, e.g.:
```python
learn = Learner(dls, model, cbs=AzureMLCallback())
```
…some `Learner` methods (e.g. `learn.show_results()`) might add unwanted logging into your azureml experiment runs. Adding further checks into the callback should help eliminate this – another PR needed.
```
#export
from azureml.core.run import Run
# export
class AzureMLCallback(Callback):
"Log losses, metrics, model architecture summary to AzureML"
order = Recorder.order+1
def __init__(self, azurerun=None):
if azurerun:
self.azurerun = azurerun
else:
self.azurerun = Run.get_context()
def before_fit(self):
self.azurerun.log("n_epoch", self.learn.n_epoch)
self.azurerun.log("model_class", str(type(self.learn.model)))
try:
summary_file = Path("outputs") / 'model_summary.txt'
with summary_file.open("w") as f:
f.write(repr(self.learn.model))
except:
print('Did not log model summary. Check if your model is PyTorch model.')
def after_batch(self):
# log loss and opt.hypers
if self.learn.training:
self.azurerun.log('batch__loss', self.learn.loss.item())
self.azurerun.log('batch__train_iter', self.learn.train_iter)
for i, h in enumerate(self.learn.opt.hypers):
for k, v in h.items():
self.azurerun.log(f'batch__opt.hypers.{k}', v)
def after_epoch(self):
# log metrics
for n, v in zip(self.learn.recorder.metric_names, self.learn.recorder.log):
if n not in ['epoch', 'time']:
self.azurerun.log(f'epoch__{n}', v)
if n == 'time':
# split elapsed time string, then convert into 'seconds' to log
m, s = str(v).split(':')
elapsed = int(m)*60 + int(s)
self.azurerun.log(f'epoch__{n}', elapsed)
```
| true |
code
| 0.630486 | null | null | null | null |
|
# Multiple Qubits & Entangled States
Single qubits are interesting, but individually they offer no computational advantage. We will now look at how we represent multiple qubits, and how these qubits can interact with each other. We have seen how we can represent the state of a qubit using a 2D-vector, now we will see how we can represent the state of multiple qubits.
## Contents
1. [Representing Multi-Qubit States](#represent)
1.1 [Exercises](#ex1)
2. [Single Qubit Gates on Multi-Qubit Statevectors](#single-qubit-gates)
2.1 [Exercises](#ex2)
3. [Multi-Qubit Gates](#multi-qubit-gates)
3.1 [The CNOT-gate](#cnot)
3.2 [Entangled States](#entangled)
3.3 [Visualizing Entangled States](#visual)
3.4 [Exercises](#ex3)
## 1. Representing Multi-Qubit States <a id="represent"></a>
We saw that a single bit has two possible states, and a qubit state has two complex amplitudes. Similarly, two bits have four possible states:
`00` `01` `10` `11`
And to describe the state of two qubits requires four complex amplitudes. We store these amplitudes in a 4D-vector like so:
$$ |a\rangle = a_{00}|00\rangle + a_{01}|01\rangle + a_{10}|10\rangle + a_{11}|11\rangle = \begin{bmatrix} a_{00} \\ a_{01} \\ a_{10} \\ a_{11} \end{bmatrix} $$
The rules of measurement still work in the same way:
$$ p(|00\rangle) = |\langle 00 | a \rangle |^2 = |a_{00}|^2$$
And the same implications hold, such as the normalisation condition:
$$ |a_{00}|^2 + |a_{01}|^2 + |a_{10}|^2 + |a_{11}|^2 = 1$$
If we have two separated qubits, we can describe their collective state using the tensor product:
$$ |a\rangle = \begin{bmatrix} a_0 \\ a_1 \end{bmatrix}, \quad |b\rangle = \begin{bmatrix} b_0 \\ b_1 \end{bmatrix} $$
$$
|ba\rangle = |b\rangle \otimes |a\rangle = \begin{bmatrix} b_0 \times \begin{bmatrix} a_0 \\ a_1 \end{bmatrix} \\ b_1 \times \begin{bmatrix} a_0 \\ a_1 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} b_0 a_0 \\ b_0 a_1 \\ b_1 a_0 \\ b_1 a_1 \end{bmatrix}
$$
And following the same rules, we can use the tensor product to describe the collective state of any number of qubits. Here is an example with three qubits:
$$
|cba\rangle = \begin{bmatrix} c_0 b_0 a_0 \\ c_0 b_0 a_1 \\ c_0 b_1 a_0 \\ c_0 b_1 a_1 \\
c_1 b_0 a_0 \\ c_1 b_0 a_1 \\ c_1 b_1 a_0 \\ c_1 b_1 a_1 \\
\end{bmatrix}
$$
If we have $n$ qubits, we will need to keep track of $2^n$ complex amplitudes. As we can see, these vectors grow exponentially with the number of qubits. This is the reason quantum computers with large numbers of qubits are so difficult to simulate. A modern laptop can easily simulate a general quantum state of around 20 qubits, but simulating 100 qubits is too difficult for the largest supercomputers.
Let's look at an example circuit:
```
from qiskit import QuantumCircuit, Aer, assemble
from math import pi
import numpy as np
from qiskit.visualization import plot_histogram, plot_bloch_multivector
qc = QuantumCircuit(3)
# Apply H-gate to each qubit:
for qubit in range(3):
qc.h(qubit)
# See the circuit:
qc.draw()
```
Each qubit is in the state $|+\rangle$, so we should see the vector:
$$
|{+++}\rangle = \frac{1}{\sqrt{8}}\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\
1 \\ 1 \\ 1 \\ 1 \\
\end{bmatrix}
$$
```
# Let's see the result
svsim = Aer.get_backend('statevector_simulator')
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
# In Jupyter Notebooks we can display this nicely using Latex.
# If not using Jupyter Notebooks you may need to remove the
# array_to_latex function and use print(final_state) instead.
from qiskit_textbook.tools import array_to_latex
array_to_latex(final_state, pretext="\\text{Statevector} = ")
```
And we have our expected result.
### 1.2 Quick Exercises: <a id="ex1"></a>
1. Write down the tensor product of the qubits:
a) $|0\rangle|1\rangle$
b) $|0\rangle|+\rangle$
c) $|+\rangle|1\rangle$
d) $|-\rangle|+\rangle$
2. Write the state:
$|\psi\rangle = \tfrac{1}{\sqrt{2}}|00\rangle + \tfrac{i}{\sqrt{2}}|01\rangle $
as two separate qubits.
## 2. Single Qubit Gates on Multi-Qubit Statevectors <a id="single-qubit-gates"></a>
We have seen that an X-gate is represented by the matrix:
$$
X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}
$$
And that it acts on the state $|0\rangle$ as so:
$$
X|0\rangle = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1\end{bmatrix}
$$
but it may not be clear how an X-gate would act on a qubit in a multi-qubit vector. Fortunately, the rule is quite simple; just as we used the tensor product to calculate multi-qubit statevectors, we use the tensor product to calculate matrices that act on these statevectors. For example, in the circuit below:
```
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.draw()
```
we can represent the simultaneous operations (H & X) using their tensor product:
$$
X|q_1\rangle \otimes H|q_0\rangle = (X\otimes H)|q_1 q_0\rangle
$$
The operation looks like this:
$$
X\otimes H = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \otimes \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} = \frac{1}{\sqrt{2}}
\begin{bmatrix} 0 \times \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
& 1 \times \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\\
1 \times \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
& 0 \times \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\end{bmatrix} = \frac{1}{\sqrt{2}}
\begin{bmatrix} 0 & 0 & 1 & 1 \\
0 & 0 & 1 & -1 \\
1 & 1 & 0 & 0 \\
1 & -1 & 0 & 0 \\
\end{bmatrix}
$$
Which we can then apply to our 4D statevector $|q_1 q_0\rangle$. This can become quite messy, you will often see the clearer notation:
$$
X\otimes H =
\begin{bmatrix} 0 & H \\
H & 0\\
\end{bmatrix}
$$
Instead of calculating this by hand, we can use Qiskit’s `unitary_simulator` to calculate this for us. The unitary simulator multiplies all the gates in our circuit together to compile a single unitary matrix that performs the whole quantum circuit:
```
usim = Aer.get_backend('unitary_simulator')
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
```
and view the results:
```
# In Jupyter Notebooks we can display this nicely using Latex.
# If not using Jupyter Notebooks you may need to remove the
# array_to_latex function and use print(unitary) instead.
from qiskit_textbook.tools import array_to_latex
array_to_latex(unitary, pretext="\\text{Circuit = }\n")
```
If we want to apply a gate to only one qubit at a time (such as in the circuit below), we describe this using tensor product with the identity matrix, e.g.:
$$ X \otimes I $$
```
qc = QuantumCircuit(2)
qc.x(1)
qc.draw()
# Simulate the unitary
usim = Aer.get_backend('unitary_simulator')
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
# Display the results:
array_to_latex(unitary, pretext="\\text{Circuit = } ")
```
We can see Qiskit has performed the tensor product:
$$
X \otimes I =
\begin{bmatrix} 0 & I \\
I & 0\\
\end{bmatrix} =
\begin{bmatrix} 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\end{bmatrix}
$$
### 2.1 Quick Exercises: <a id="ex2"></a>
1. Calculate the single qubit unitary ($U$) created by the sequence of gates: $U = XZH$. Use Qiskit's unitary simulator to check your results.
2. Try changing the gates in the circuit above. Calculate their tensor product, and then check your answer using the unitary simulator.
**Note:** Different books, softwares and websites order their qubits differently. This means the tensor product of the same circuit can look very different. Try to bear this in mind when consulting other sources.
## 3. Multi-Qubit Gates <a id="multi-qubit-gates"></a>
Now we know how to represent the state of multiple qubits, we are now ready to learn how qubits interact with each other. An important two-qubit gate is the CNOT-gate.
### 3.1 The CNOT-Gate <a id="cnot"></a>
You have come across this gate before in _[The Atoms of Computation](../ch-states/atoms-computation.html)._ This gate is a conditional gate that performs an X-gate on the second qubit (target), if the state of the first qubit (control) is $|1\rangle$. The gate is drawn on a circuit like this, with `q0` as the control and `q1` as the target:
```
qc = QuantumCircuit(2)
# Apply CNOT
qc.cx(0,1)
# See the circuit:
qc.draw()
```
When our qubits are not in superposition of $|0\rangle$ or $|1\rangle$ (behaving as classical bits), this gate is very simple and intuitive to understand. We can use the classical truth table:
| Input (t,c) | Output (t,c) |
|:-----------:|:------------:|
| 00 | 00 |
| 01 | 11 |
| 10 | 10 |
| 11 | 01 |
And acting on our 4D-statevector, it has one of the two matrices:
$$
\text{CNOT} = \begin{bmatrix} 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
\end{bmatrix}, \quad
\text{CNOT} = \begin{bmatrix} 1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
$$
depending on which qubit is the control and which is the target. Different books, simulators and papers order their qubits differently. In our case, the left matrix corresponds to the CNOT in the circuit above. This matrix swaps the amplitudes of $|01\rangle$ and $|11\rangle$ in our statevector:
$$
|a\rangle = \begin{bmatrix} a_{00} \\ a_{01} \\ a_{10} \\ a_{11} \end{bmatrix}, \quad \text{CNOT}|a\rangle = \begin{bmatrix} a_{00} \\ a_{11} \\ a_{10} \\ a_{01} \end{bmatrix} \begin{matrix} \\ \leftarrow \\ \\ \leftarrow \end{matrix}
$$
We have seen how this acts on classical states, but let’s now see how it acts on a qubit in superposition. We will put one qubit in the state $|+\rangle$:
```
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
qc.draw()
# Let's see the result:
svsim = Aer.get_backend('statevector_simulator')
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
# Print the statevector neatly:
array_to_latex(final_state, pretext="\\text{Statevector = }")
```
As expected, this produces the state $|0\rangle \otimes |{+}\rangle = |0{+}\rangle$:
$$
|0{+}\rangle = \tfrac{1}{\sqrt{2}}(|00\rangle + |01\rangle)
$$
And let’s see what happens when we apply the CNOT gate:
```
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
# Apply a CNOT:
qc.cx(0,1)
qc.draw()
# Let's get the result:
qobj = assemble(qc)
result = svsim.run(qobj).result()
# Print the statevector neatly:
final_state = result.get_statevector()
array_to_latex(final_state, pretext="\\text{Statevector = }")
```
We see we have the state:
$$
\text{CNOT}|0{+}\rangle = \tfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle)
$$
This state is very interesting to us, because it is _entangled._ This leads us neatly on to the next section.
### 3.2 Entangled States <a id="entangled"></a>
We saw in the previous section we could create the state:
$$
\tfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle)
$$
This is known as a _Bell_ state. We can see that this state has 50% probability of being measured in the state $|00\rangle$, and 50% chance of being measured in the state $|11\rangle$. Most interestingly, it has a **0%** chance of being measured in the states $|01\rangle$ or $|10\rangle$. We can see this in Qiskit:
```
plot_histogram(result.get_counts())
```
This combined state cannot be written as two separate qubit states, which has interesting implications. Although our qubits are in superposition, measuring one will tell us the state of the other and collapse its superposition. For example, if we measured the top qubit and got the state $|1\rangle$, the collective state of our qubits changes like so:
$$
\tfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle) \quad \xrightarrow[]{\text{measure}} \quad |11\rangle
$$
Even if we separated these qubits light-years away, measuring one qubit collapses the superposition and appears to have an immediate effect on the other. This is the [‘spooky action at a distance’](https://en.wikipedia.org/wiki/Quantum_nonlocality) that upset so many physicists in the early 20th century.
It’s important to note that the measurement result is random, and the measurement statistics of one qubit are **not** affected by any operation on the other qubit. Because of this, there is **no way** to use shared quantum states to communicate. This is known as the no-communication theorem.[1]
### 3.3 Visualizing Entangled States<a id="visual"></a>
We have seen that this state cannot be written as two separate qubit states, this also means we lose information when we try to plot our state on separate Bloch spheres:
```
plot_bloch_multivector(final_state)
```
Given how we defined the Bloch sphere in the earlier chapters, it may not be clear how Qiskit even calculates the Bloch vectors with entangled qubits like this. In the single-qubit case, the position of the Bloch vector along an axis nicely corresponds to the expectation value of measuring in that basis. If we take this as _the_ rule of plotting Bloch vectors, we arrive at this conclusion above. This shows us there is _no_ single-qubit measurement basis for which a specific measurement is guaranteed. This contrasts with our single qubit states, in which we could always pick a single-qubit basis. Looking at the individual qubits in this way, we miss the important effect of correlation between the qubits. We cannot distinguish between different entangled states. For example, the two states:
$$\tfrac{1}{\sqrt{2}}(|01\rangle + |10\rangle) \quad \text{and} \quad \tfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$$
will both look the same on these separate Bloch spheres, despite being very different states with different measurement outcomes.
How else could we visualize this statevector? This statevector is simply a collection of four amplitudes (complex numbers), and there are endless ways we can map this to an image. One such visualization is the _Q-sphere,_ here each amplitude is represented by a blob on the surface of a sphere. The size of the blob is proportional to the magnitude of the amplitude, and the colour is proportional to the phase of the amplitude. The amplitudes for $|00\rangle$ and $|11\rangle$ are equal, and all other amplitudes are 0:
```
from qiskit.visualization import plot_state_qsphere
plot_state_qsphere(final_state)
```
Here we can clearly see the correlation between the qubits. The Q-sphere's shape has no significance, it is simply a nice way of arranging our blobs; the number of `0`s in the state is proportional to the states position on the Z-axis, so here we can see the amplitude of $|00\rangle$ is at the top pole of the sphere, and the amplitude of $|11\rangle$ is at the bottom pole of the sphere.
### 3.4 Exercise: <a id="ex3"></a>
1. Create a quantum circuit that produces the Bell state: $\tfrac{1}{\sqrt{2}}(|01\rangle + |10\rangle)$.
Use the statevector simulator to verify your result.
2. The circuit you created in question 1 transforms the state $|00\rangle$ to $\tfrac{1}{\sqrt{2}}(|01\rangle + |10\rangle)$, calculate the unitary of this circuit using Qiskit's simulator. Verify this unitary does in fact perform the correct transformation.
3. Think about other ways you could represent a statevector visually. Can you design an interesting visualization from which you can read the magnitude and phase of each amplitude?
## 4. References
[1] Asher Peres, Daniel R. Terno, _Quantum Information and Relativity Theory,_ 2004, https://arxiv.org/abs/quant-ph/0212023
```
import qiskit
qiskit.__qiskit_version__
```
| true |
code
| 0.726765 | null | null | null | null |
|
# A Transformer based Language Model from scratch
> Building transformer with simple building blocks
- toc: true
- branch: master
- badges: true
- comments: true
- author: Arto
- categories: [fastai, pytorch]
```
#hide
import sys
if 'google.colab' in sys.modules:
!pip install -Uqq fastai
```
In this notebook i'm going to construct transformer based language model from scratch starting with the simplest building blocks. This is inspired by Chapter 12 of [Deep Learning for Coders book](https://www.amazon.com/Deep-Learning-Coders-fastai-PyTorch/dp/1492045527) in which it's demonstrated how to create a Recurrent Neural Network. It provides a strong intuition of how RNNs relate to regular feed-forward neural nets and why certain design choices were made. Here we aim to aquire similar kind of intuition about Transfomer based architectures.
But as always we should start with the data to be modeled, 'cause without data any model makes no particular sense.
## Data
Similar to authors of the book I'll use simple Human numbers dataset which is specifically designed to prototyping model fast and straightforward. For more details on the data one can refer to the aforemantioned book chapter which is also available for free as [a notebook](https://github.com/fastai/fastbook/blob/master/12_nlp_dive.ipynb) (isn't that awesome?!)
```
from fastai.text.all import *
path = untar_data(URLs.HUMAN_NUMBERS)
Path.BASE_PATH = path
path.ls()
```
The data consists of consecutive numbers from 1 to 9999 inclusive spelled as words.
```
lines = L()
with open(path/'train.txt') as f: lines += L(*f.readlines())
with open(path/'valid.txt') as f: lines += L(*f.readlines())
lines
text = ' . '.join([l.strip() for l in lines])
tokens = text.split(' ')
tokens[:10]
vocab = L(*tokens).unique()
vocab
word2idx = {w:i for i,w in enumerate(vocab)}
nums = L(word2idx[i] for i in tokens)
nums
```
The task will be to predict subsequent token given preceding three. This kind of tasks when the goal is to predict next token from previous ones is called autoregresive language modeling.
```
L((tokens[i:i+3], tokens[i+3]) for i in range(0,len(tokens)-4,3))
seqs = L((tensor(nums[i:i+3]), nums[i+3]) for i in range(0,len(nums)-4,3))
seqs
bs = 64
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], bs=64, shuffle=False)
x, y = dls.one_batch()
x.shape, y.shape
```
## Dot product attention

The core idea behind Transformers is Attention. Since the release of famous paper [Attention is All You Need](https://arxiv.org/abs/1706.03762) transformers has become most popular architecture for language modelling.
There are a lot of great resourses explaining transformers architecture. I'll list some of those I found useful and comprehensive:
1. [The Annotated Transformer](http://nlp.seas.harvard.edu/2018/04/03/attention.html) completes the original paper with code
2. [Encoder-Decoder Model](https://colab.research.google.com/github/patrickvonplaten/notebooks/blob/master/Encoder_Decoder_Model.ipynb) notebook by huggingface gives mathemetically grounded explanation of how transformer encoder-decoder models work
3. [The Illustrated GPT-2](https://jalammar.github.io/illustrated-gpt2/) one of the great blogposts by Jay Alammar visualizing generative language modelling on exaple of GPT-2
4. [minGPT](https://github.com/karpathy/minGPT) cool repo by A. Karpathy providing clear minimal implementation of GPT model
There exist multiple attention mechanisms. The particular one used in the original transformer paper is Scaled Dot Product attention.
Given query vector for particular token we will compare it with a key vector for each token in a sequence and decide how much value vectors of those will effect resulting representetion of the token of interest. One way to view this from a linguistic prospective is: a key is a question each word respondes to, value is information that word represent and a query is related to what every word was looking to combine with.
Mathemetically we can compute attention for all _q_, _k_, _v_ in a matrix form:
$$\textbf {Attention}(Q,K,V) = \textbf {softmax}({QK^T\over\sqrt d_k})V $$
Note that dot product $QK^T$ results in matrix of shape (seq_len x seq_len). Then it is devided by $ \sqrt d_k$ to compensate the fact, that longer sequences will have larger dot product. $ \textbf{softmax}$ is applied to rescale the attention matrix to be betwin 0 and 1. When multiplied by $V$ it produces a matrix of the same shape as $V$ (seq_len x dv).
So where those _q_, _k_, _v_ come from. Well that's fairly straitforward queries are culculated from the embeddings of tokens we want to find representation for by simple linear projection. Keys and values are calculated from the embeddings of context tokens. In case of self attention all of them come from the original sequence.
```
class SelfAttention(Module):
def __init__(self, d_in, d_qk, d_v=None):
d_v = ifnone(d_v, d_qk)
self.iq = nn.Linear(d_in, d_qk)
self.ik = nn.Linear(d_in, d_qk)
self.iv = nn.Linear(d_in, d_v)
self.out = nn.Linear(d_v, d_in)
self.scale = d_qk**-0.5
def forward(self, x):
q, k, v = self.iq(x), self.ik(x), self.iv(x)
q *= self.scale
return self.out(F.softmax([email protected](-2,-1), -1)@v)
```
Even though self attention mechanism is extremely useful it posseses limited expressive power. Essentially we are computing weighted some of the input modified by single affine transformation, shared across the whole sequence. To add more computational power to the model we can introduce fully connected feedforward network on top of the SelfAttention layer.
Curious reader can find detailed formal analysis of the roles of SelfAttention and FeedForward layers in transformer architecture in [this paper](https://arxiv.org/pdf/1912.10077.pdf) by C. Yun et al.
In brief the authors state that SelfAttention layers compute precise contextual maps and FeedForward layers then assign the results of these contextual maps to the desired output values.
```
class FeedForward(Module):
def __init__(self, d_in, d_ff):
self.lin1 = nn.Linear(d_in, d_ff)
self.lin2 = nn.Linear(d_ff, d_in)
self.act = nn.ReLU()
def forward(self, x):
out = self.lin2(self.act(self.lin1(x)))
return out
```
The output would be of shape (bs, seq_len, d) which then may be mapped to (bs, seq_len, vocab_sz) using linear layer. But we have only one target. To adress this issue we can simply do average pooling over seq_len dimention.
The resulting model is fairly simple:
```
class Model1(Module):
def __init__(self, vocab_sz, d_model, d_qk, d_ff):
self.emb = Embedding(vocab_sz, d_model)
self.attn = SelfAttention(d_model, d_qk)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.ff(self.attn(x))
x = x.mean(1)
return self.out(x)
model = Model1(len(vocab), 64, 64, 128)
out = model(x)
out.shape
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.lr_find()
learn.fit_one_cycle(5, 5e-3)
```
To evaluete the model performance we need to compare it to some baseline. Let's see what would be the accuracy if of the model which would always predict most common token.
```
n,counts = 0,torch.zeros(len(vocab))
for x,y in dls.valid:
n += y.shape[0]
for i in range_of(vocab): counts[i] += (y==i).long().sum()
idx = torch.argmax(counts)
idx, vocab[idx.item()], counts[idx].item()/n
```
As you can see, always predicting "thousand" which turn out to be the most common token in the dataset would result in ~15% accuracy. Our simple transformer does much better then that. It feels promising, so let's try to improve the architecture and check if we can get better results.
### Multihead attention
A structured sequence may comprise multiple distinctive kinds of relationships. Our model is forced to learn only one way in which queries, keys and values are constructed from the original token embedding. To remove this limitation we can modify attention layer include multiple heads which would correspond to extracting different kinds of relationships between tokens. The MultiHeadAttention layer consits of several heads each of those is similar to SelfAttention layer we made before. To keep computational cost of the multi-head layer we set $d_k = d_v = d_{model}/n_h$, where $n_h$ is number of heads.
```
class SelfAttention(Module):
def __init__(self, d_in, d_qk, d_v=None):
d_v = ifnone(d_v, d_qk)
self.iq = nn.Linear(d_in, d_qk)
self.ik = nn.Linear(d_in, d_qk)
self.iv = nn.Linear(d_in, d_v)
self.scale = d_qk**-0.5
def forward(self, x):
q, k, v = self.iq(x), self.ik(x), self.iv(x)
return F.softmax([email protected](-2,-1)*self.scale, -1)@v
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads, d_qk=None, d_v=None):
d_qk = ifnone(d_qk, d_model//n_heads)
d_v = ifnone(d_v, d_qk)
self.heads = nn.ModuleList([SelfAttention(d_model, d_qk) for _ in range(n_heads)])
self.out = nn.Linear(d_v*n_heads, d_model)
def forward(self, x):
out = [m(x) for m in self.heads]
return self.out(torch.cat(out, -1))
inp = torch.randn(8, 10, 64)
mha = MultiHeadAttention(64, 8)
out = mha(inp)
out.shape
class Model2(Module):
def __init__(self, vocab_sz, d_model=64, n_heads=4, d_ff=64*4):
self.emb = nn.Embedding(vocab_sz, d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.ff(self.attn(x))
x = x.mean(1)
return self.out(x)
learn = Learner(dls, Model2(len(vocab)), loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.fit_one_cycle(5, 5e-4)
```
### MultiHead Attention Refactor
Python `for` loops are slow, therefore it is better to refactor the MultiHeadAttention module to compute Q, K, V for all heads in batch.
```
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads):
assert d_model%n_heads == 0
self.n_heads = n_heads
#d_qk, d_v = d_model//n_heads, d_model//n_heads
self.iq = nn.Linear(d_model, d_model, bias=False)
self.ik = nn.Linear(d_model, d_model, bias=False)
self.iv = nn.Linear(d_model, d_model, bias=False)
self.out = nn.Linear(d_model, d_model, bias=False)
self.scale = d_model//n_heads
def forward(self, x):
bs, seq_len, d = x.size()
# (bs,sl,d) -> (bs,sl,nh,dh) -> (bs,nh,sl,dh)
q = self.iq(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
k = self.ik(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
v = self.iv(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
q*= self.scale
att = F.softmax([email protected](-2,-1), -1)
out = att @ v # (bs, nh, sl, sl) x (bs, nh, sl, dh) -> (bs, nh, sl, dh)
out = out.transpose(1, 2).contiguous().view(bs, seq_len, d) # back to original shape
return self.out(out)
learn = Learner(dls, Model2(len(vocab)), loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.fit_one_cycle(5, 1e-3)
```
Note that some speedup is observed even on such a tiny dataset and small model.
## More signal
Similarly to the RNN case considered in the book, we can take the next step and create more signal for the model to learn from. To adapt to the modified objective we need to make couple of steps. First let's rearrange data to proper input-target pairs for the new task.
### Arranging data
Unlike RNN the tranformer is not a stateful model. This means it treats each sequence indepently and can only attend within fixed length context. This limitation was addressed by authors of [Transformer-XL paper](https://arxiv.org/abs/1901.02860) where adding a segment-level recurrence mechanism and a novel positional encoding scheme were proposed to enable capturing long-term dependencies. I will not go into details of TransformerXL architecture here. As we shell see stateless transformer can also learn a lot about the structure of our data.
One thing to note in this case is that we don't need to maintain the structure of the data outside of the sequences, so we can shuffle the sequences randomly in the dataloader.
```
sl = 16
seqs = L((tensor(nums[i:i+sl]), tensor(nums[i+1:i+sl+1]))
for i in range(0,len(nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:],
bs=bs, drop_last=True, shuffle=True)
xb, yb = dls.one_batch()
xb.shape, yb.shape
[L(vocab[o] for o in s) for s in seqs[0]]
```
### Positional encoding
Before we did average pooling over seq_len dimension. Our model didn't care about the order of the tokens at all. But actually order of the tokens in a sentence matter a lot. In our case `one hundred two` and `two hundred one` are pretty different and `hundred one two` doesn't make sense.
To encorporate positional information into the model authors of the transformer architecture proposed to use positional encodings in addition to regular token embeddings. Positional encodings may be learned, but it's also possible to use hardcoded encodings. For instance encodings may be composed of sin and cos.
In this way each position in a sequence will get unique vector associated with it.
```
class PositionalEncoding(Module):
def __init__(self, d):
self.register_buffer('freq', 1/(10000 ** (torch.arange(0., d, 2.)/d)))
self.scale = d**0.5
def forward(self, x):
device = x.device
pos_enc = torch.cat([torch.sin(torch.outer(torch.arange(x.size(1), device=device), self.freq)),
torch.cos(torch.outer(torch.arange(x.size(1), device=device), self.freq))],
axis=-1)
return x*self.scale + pos_enc
#collapse-hide
x = torch.zeros(1, 16, 64)
encs = PositionalEncoding(64)(x)
plt.matshow(encs.squeeze())
plt.xlabel('Embedding size')
plt.ylabel('Sequence length')
plt.show()
class TransformerEmbedding(Module):
def __init__(self, emb_sz, d_model):
self.emb = nn.Embedding(emb_sz, d_model)
self.pos_enc = PositionalEncoding(d_model)
def forward(self, x):
return self.pos_enc(self.emb(x))
class Model3(Module):
def __init__(self, vocab_sz, d_model=64, n_heads=4, d_ff=64*4):
self.emb = TransformerEmbedding(vocab_sz, d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.ff(self.attn(x))
return self.out(x)
model = Model3(len(vocab))
out = model(xb)
out.shape
def loss_func(inp, targ):
return F.cross_entropy(inp.view(-1, len(vocab)), targ.view(-1))
learn = Learner(dls, Model3(len(vocab)), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(5, 1e-2)
```
Wow! That's a great accuracy! So the problem is solved and we only needed one attention layer and 2 layer deep feed-forward block? Don't you feel somewhat skeptical about this result?
Well, you should be! Think about what we did here: the goal was to predict a target sequence, say `['.','two','.','three','.','four']` from an input `['one','.','two','.','three','.']`. These two sequences intersect on all positions except the first and the last one. So models needs to learn simply to copy input tokens starting from the second one to the outputs. In our case this will result in 15 correct predictions of total 16 positions, that's almost 94% accuracy. This makes the task very simple but not very useful to learn. To train proper autoregressive language model, as we did with RNNs, a concept of masking is to be introduced.
### Causal Masking
So we want to allow the model for each token to attend only to itself and those prior to it. To acomplish this we can set all the values of attention matrix above the main diagonal to $-\infty$. After softmax this values will effectively turn to 0 thus disabling attention to the "future".
```
def get_subsequent_mask(x):
sz = x.size(1)
mask = (torch.triu(torch.ones(sz, sz, device=x.device)) == 1).transpose(0, 1)
mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
return mask
inp = torch.randn(8, 10, 64)
mask = get_subsequent_mask(inp)
plt.matshow(mask);
q, k = torch.rand(1,10,32), torch.randn(1,10,32)
att_ = F.softmax(([email protected](0,2,1)+mask), -1)
plt.matshow(att_[0].detach());
```
We should also modify the attention layer to accept mask:
```
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads):
assert d_model%n_heads == 0
self.n_heads = n_heads
d_qk, d_v = d_model//n_heads, d_model//n_heads
self.iq = nn.Linear(d_model, d_model, bias=False)
self.ik = nn.Linear(d_model, d_model, bias=False)
self.iv = nn.Linear(d_model, d_model, bias=False)
self.scale = d_qk**-0.5
self.out = nn.Linear(d_model, d_model, bias=False)
def forward(self, x, mask=None):
bs, seq_len, d = x.size()
mask = ifnone(mask, 0)
q = self.iq(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
k = self.ik(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
v = self.iv(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
q*= self.scale
att = F.softmax([email protected](-2,-1) + mask, -1)
out = att @ v # (bs, nh, sl, sl) x (bs, nh, sl, dh) -> (bs, nh, sl, dh)
out = out.transpose(1, 2).contiguous().view(bs, seq_len, d) # back to original shape
return self.out(out)
class Model4(Module):
def __init__(self, vocab_sz, d_model=64, n_heads=8, d_ff=64*4):
self.emb = TransformerEmbedding(vocab_sz, d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
mask = get_subsequent_mask(x)
x = self.ff(self.attn(x, mask))
return self.out(x)
learn = Learner(dls, Model4(len(vocab)), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(5, 3e-3)
```
Now we get somewhat lower accuracy, which is expected given that the task has become more difficult. Also training loss is significantly lower than validation loss, which means the model is overfitting. Let's see if the same approaches as was applied to RNNs can help.
### Multilayer transformer
To solve a more difficult task we ussualy need a deeper model. For convenience let's make a TransformerLayer which will combine self-attention and feed-forward blocks.
```
class TransformerLayer(Module):
def __init__(self, d_model, n_heads=8, d_ff=None, causal=True):
d_ff = ifnone(d_ff, 4*d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.causal = causal
def forward(self, x, mask=None):
if self.causal:
mask = get_subsequent_mask(x)
return self.ff(self.attn(x, mask))
class Model5(Module):
def __init__(self, vocab_sz, d_model=64, n_layer=4, n_heads=8):
self.emb = TransformerEmbedding(vocab_sz, d_model)
self.encoder = nn.Sequential(*[TransformerLayer(d_model, n_heads) for _ in range(n_layer)])
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.encoder(x)
return self.out(x)
learn = Learner(dls, Model5(len(vocab), n_layer=4), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(5, 1e-2)
```
That's not good! 4 layer deep Transformer strugles to learn anything. But there are good news, this problem has been already resolved in the original transformer.
### Residual connections and Regularization
If you are familiar with ResNets the proposed solution will not surprise you much. The idea is simple yet very effective. Instead of returning modified output $f(x)$ each transformer sublayer will return $x + f(x)$. This allows the original input to propagate freely through the model. So the model learns not an entirely new representation of $x$ but how to modify $x$ to add some useful information to the original representation.
As we modify layers to include the residual connections let's also add some regularization by inserting Dropout layers.
```
class TransformerEmbedding(Module):
def __init__(self, emb_sz, d_model, p=0.1):
self.emb = Embedding(emb_sz, d_model)
nn.init.trunc_normal_(self.emb.weight, std=d_model**-0.5)
self.pos_enc = PositionalEncoding(d_model)
self.drop = nn.Dropout(p)
def forward(self, x):
return self.drop(self.pos_enc(self.emb(x)))
```
Another modification is to add layer normalization which is intended to improve learning dynamics of the network by reparametrising data statistics and is generally used in transformer based architectures.
```
class FeedForward(Module):
def __init__(self, d_model, d_ff, p=0.2):
self.lin1 = nn.Linear(d_model, d_ff)
self.lin2 = nn.Linear(d_ff, d_model)
self.act = nn.ReLU()
self.norm = nn.LayerNorm(d_model)
self.drop = nn.Dropout(p)
def forward(self, x):
x = self.norm(x)
out = self.act(self.lin1(x))
out = self.lin2(out)
return x + self.drop(out)
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads, p=0.1):
assert d_model%n_heads == 0
self.n_heads = n_heads
d_qk, d_v = d_model//n_heads, d_model//n_heads
self.iq = nn.Linear(d_model, d_model, bias=False)
self.ik = nn.Linear(d_model, d_model, bias=False)
self.iv = nn.Linear(d_model, d_model, bias=False)
self.scale = d_qk**0.5
self.out = nn.Linear(d_model, d_model, bias=False)
self.norm = nn.LayerNorm(d_model)
self.drop = nn.Dropout(p)
def forward(self, x, mask=None):
bs, seq_len, d = x.size()
mask = ifnone(mask, 0)
x = self.norm(x)
k = self.ik(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
q = self.iq(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
v = self.iv(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
att = F.softmax([email protected](-2,-1)/self.scale + mask, -1)
out = att @ v # (bs, nh, sl, sl) x (bs, nh, sl, dh) -> (bs, nh, sl, dh)
out = out.transpose(1, 2).contiguous().view(bs, seq_len, d) # back to original shape
return x + self.drop(self.out(out))
class TransformerLayer(Module):
def __init__(self, d_model, n_heads=8, d_ff=None, causal=True,
p_att=0.1, p_ff=0.1):
d_ff = ifnone(d_ff, 4*d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff, p=p_ff)
self.causal = causal
self._init()
def forward(self, x, mask=None):
if self.causal:
mask = get_subsequent_mask(x)
return self.ff(self.attn(x, mask))
def _init(self):
for p in self.parameters():
if p.dim()>1: nn.init.xavier_uniform_(p)
class Model6(Module):
def __init__(self, vocab_sz, d_model=64, n_layer=4, n_heads=8,
p_emb=0.1, p_att=0.1, p_ff=0.2, tie_weights=True):
self.emb = TransformerEmbedding(vocab_sz, d_model, p=p_emb)
self.encoder = nn.Sequential(*[TransformerLayer(d_model, n_heads,
p_att=p_att, p_ff=p_ff)
for _ in range(n_layer)],
nn.LayerNorm(d_model))
self.out = nn.Linear(d_model, vocab_sz)
if tie_weights: self.out.weight = self.emb.emb.weight
def forward(self, x):
x = self.emb(x)
x = self.encoder(x)
return self.out(x)
learn = Learner(dls, Model6(len(vocab), n_layer=2), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(8, 1e-2)
```
## Bonus - Generation example
```
#hide
from google.colab import drive
drive.mount('/content/drive')
path = Path('/content/drive/MyDrive/char_model')
```
Learning to predict numbers is great, but let's try something more entertaining. We can train a language model to generate texts. For example let's try to generate some text in style of Lewis Carroll. For this we'll fit a language model on "Alice in Wonderland" and "Through the looking glass".
```
#collapse-hide
def parse_txt(fns):
txts = []
for fn in fns:
with open(fn) as f:
tmp = ''
for line in f.readlines():
line = line.strip('\n')
if line:
tmp += ' ' + line
elif tmp:
txts.append(tmp.strip())
tmp = ''
return txts
texts = parse_txt([path/'11-0.txt', path/'12-0.txt'])
len(texts)
texts[0:2]
#collapse-hide
class CharTokenizer(Transform):
"Simple charecter level tokenizer"
def __init__(self, vocab=None):
self.vocab = ifnone(vocab, ['', 'xxbos', 'xxeos'] + list(string.printable))
self.c2i = defaultdict(int, [(c,i) for i, c in enumerate(self.vocab)])
def encodes(self, s, add_bos=False, add_eos=False):
strt = [self.c2i['xxbos']] if add_bos else []
end = [self.c2i['xxeos']] if add_eos else []
return LMTensorText(strt + [self.c2i[c] for c in s] + end)
def decodes(self, s, remove_special=False):
return TitledStr(''.join([self.decode_one(i) for i in s]))
def decode_one(self, i):
if i == 2: return '\n'
elif i == 1: return ''
else: return self.vocab[i]
@property
def vocab_sz(self):
return len(self.vocab)
tok = CharTokenizer()
def add_bos_eos(x:list, bos_id=1, eos_id=2):
return [bos_id] + x + [eos_id]
nums = [add_bos_eos(tok(t.lower()).tolist()) for t in texts]
len(nums)
all_nums = []
for n in nums: all_nums.extend(n)
all_nums[:15]
print(tok.decode(all_nums[:100]))
sl = 512
seqs = L((tensor(all_nums[i:i+sl]), tensor(all_nums[i+1:i+sl+1]))
for i in range(0,len(all_nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], device='cuda',
bs=8, drop_last=True, shuffle=True)
xb, yb = dls.one_batch()
xb.shape, yb.shape
model = Model6(tok.vocab_sz, 512, 6, p_emb=0.1, p_ff=0.1, tie_weights=True)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=[accuracy, perplexity]).to_native_fp16()
learn.lr_find()
#collapse_output
learn.fit_one_cycle(50, 5e-4, cbs=EarlyStoppingCallback(patience=5))
```
### Text generation
Text generation is a big topic on it's own. One can refer to great posts [by Patrick von Platen from HuggingFace](https://huggingface.co/blog/how-to-generate) and [Lilian Weng](https://lilianweng.github.io/lil-log/2021/01/02/controllable-neural-text-generation.html) for more details on various approaches. Here I will use nucleus sampling. This method rallies on sampling from candidates compounding certain value of probability mass. Intuitively this approach should work for character level generation: when there is only one grammatically correct option for continuation we always want to select it, but when starting a new word some diversity in outputs is desirable.
```
#collapse-hide
def expand_dim1(x):
if len(x.shape) == 1:
return x[None, :]
else: return x
def top_p_filter(logits, top_p=0.9):
sorted_logits, sorted_indices = torch.sort(logits, descending=True)
cum_probs = torch.cumsum(F.softmax(sorted_logits, dim=-1), dim=-1)
sorted_indices_to_remove = cum_probs > top_p
sorted_indices_to_remove[..., 1:] = sorted_indices_to_remove[..., :-1].clone()
sorted_indices_to_remove[..., 0] = 0
indices_to_remove = sorted_indices_to_remove.scatter(1, sorted_indices, sorted_indices_to_remove)
logits[indices_to_remove] = float('-inf')
return logits
@torch.no_grad()
def generate(model, inp,
max_len=50,
temperature=1.,
top_k = 20,
top_p = 0.9,
early_stopping=False, #need eos_idx to work
eos_idx=None):
model.to(inp.device)
model.eval()
thresh = top_p
inp = expand_dim1(inp)
b, t = inp.shape
out = inp
for _ in range(max_len):
x = out
logits = model(x)[:, -1, :]
filtered_logits = top_p_filter(logits)
probs = F.softmax(filtered_logits / temperature, dim=-1)
sample = torch.multinomial(probs, 1)
out = torch.cat((out, sample), dim=-1)
if early_stopping and (sample == eos_idx).all():
break
return out
out = generate(learn.model, tok('Alice said '), max_len=200, early_stopping=True, eos_idx=tok.c2i['xxeos'])
print(tok.decode(out[0]))
```
Our relatively simple model learned to generate mostly grammatically plausible text, but it's not entirely coherent. But it would be too much to ask from the model to learn language from scratch by "reading" only two novels (however great those novels are). To get more from the model let's feed it larger corpus of data.
### Pretraining on larger dataset
```
#hide
import sys
if 'google.colab' in sys.modules:
!pip install -Uqq datasets
from datasets import load_dataset
```
For this purpose I will use a sample from [bookcorpus dataset](https://huggingface.co/datasets/bookcorpus).
```
#hide_ouput
dataset = load_dataset("bookcorpus", split='train')
df = pd.DataFrame(dataset[:10_000_000])
df.head()
df['len'] = df['text'].str.len()
cut = int(len(df)*0.8)
splits = range_of(df)[:cut], range_of(df[cut:])
tfms = Pipeline([ColReader('text'), tok])
dsets = Datasets(df, tfms=tfms, dl_type=LMDataLoader, splits=splits)
#collapse
@patch
def create_item(self:LMDataLoader, seq):
if seq>=self.n: raise IndexError
sl = self.last_len if seq//self.bs==self.n_batches-1 else self.seq_len
st = (seq%self.bs)*self.bl + (seq//self.bs)*self.seq_len
txt = self.chunks[st : st+sl+1]
return LMTensorText(txt[:-1]),txt[1:]
%%time
dl_kwargs = [{'lens':df['len'].values[splits[0]]}, {'val_lens':df['len'].values[splits[1]]}]
dls = dsets.dataloaders(bs=32, seq_len=512, dl_kwargs=dl_kwargs, shuffle_train=True, num_workers=2)
dls.show_batch(max_n=2)
model = Model6(tok.vocab_sz, 512, 8, p_emb=0.1, p_ff=0.1, tie_weights=True)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=[accuracy, perplexity]).to_native_fp16()
learn.lr_find()
learn = learn.load(path/'char_bookcorpus_10m')
learn.fit_one_cycle(1, 1e-4)
learn.save(path/'char_bookcorpus_10m')
```
### Finetune on Carrolls' books
Finally we can finetune the pretrained bookcorpus model on Carroll's books. This will determine the style of generated text.
```
sl = 512
seqs = L((tensor(all_nums[i:i+sl]), tensor(all_nums[i+1:i+sl+1]))
for i in range(0,len(all_nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], device='cuda',
bs=16, drop_last=True, shuffle=True)
model = Model6(tok.vocab_sz, 512, 8, p_emb=0.1, p_ff=0.1, tie_weights=True)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=[accuracy, perplexity]).to_native_fp16()
learn = learn.load(path/'char_bookcorpus_10m')
learn.lr_find()
learn.fit_one_cycle(10, 1e-4)
```
As you see pretraining model on large corpus followed by finetuning helped to reduce validation loss from arount 1.53 to 1.037 and improve accuracy in predicting next character to 68% (compared to 56.7% before). Let's see how it effects sampled text:
```
out = generate(learn.model, tok('Alice said '), max_len=200, early_stopping=True, eos_idx=tok.c2i['xxeos'])
#collapse-hide
print(tok.decode(out[0]))
#hide
learn.save(path/'char_alice')
```
| true |
code
| 0.681859 | null | null | null | null |
|
## <span style="color:purple">ArcGIS API for Python: Real-time Person Detection</span>
<img src="../img/webcam_detection.PNG" style="width: 100%"></img>
## Integrating ArcGIS with TensorFlow Deep Learning using the ArcGIS API for Python
This notebook provides an example of integration between ArcGIS and deep learning frameworks like TensorFlow using the ArcGIS API for Python.
<img src="../img/ArcGIS_ML_Integration.png" style="width: 75%"></img>
We will leverage a model to detect objects on your device's video camera, and use these to update a feature service on a web GIS in real-time. As people are detected on your camera, the feature will be updated to reflect the detection.
### Notebook Requirements:
#### 1. TensorFlow and Object Detection API
This demonstration is designed to run using the TensorFlow Object Detection API (https://github.com/tensorflow/models/tree/master/research/object_detection)
Please follow the instructions found in that repository to install TensorFlow, clone the repository, and test a pre-existing model.
Once you have followed those instructions, this notebook should be placed within the "object_detection" folder of that repository. Alternatively, you may leverage this notebook from another location but reference paths to the TensorFlow model paths and utilities will need to be adjusted.
#### 2. Access to ArcGIS Online or ArcGIS Enterprise
This notebook will make a connection to an ArcGIS Enterprise or ArcGIS Online organization to provide updates to a target feature service.
Please ensure you have access to an ArcGIS Enterprise or ArcGIS Online account with a feature service to serve as the target of your detection updates. The feature service should have a record with an boolean attribute (i.e. column with True or False possible options) named "Person_Found".
# Import needed modules
```
import numpy as np
import os
import six.moves.urllib as urllib
import sys
import tarfile
import tensorflow as tf
import zipfile
from collections import defaultdict
from io import StringIO
from matplotlib import pyplot as plt
from PIL import Image
import cv2
```
We will use VideoCapture to connect to the device's web camera feed. The cv2 module helps here.
```
# Set our caption
cap = cv2.VideoCapture(0)
# This is needed since the notebook is meant to be run in the object_detection folder.
sys.path.append("..")
```
## Object detection imports
Here are the imports from the object detection module.
```
from utils import label_map_util
from utils import visualization_utils as vis_util
```
# Model preparation
## Variables
Any model exported using the `export_inference_graph.py` tool can be loaded here simply by changing `PATH_TO_CKPT` to point to a new .pb file.
By default we use an "SSD with Mobilenet" model here. See the [detection model zoo](https://github.com/tensorflow/models/blob/master/object_detection/g3doc/detection_model_zoo.md) for a list of other models that can be run out-of-the-box with varying speeds and accuracies.
```
# What model to download.
MODEL_NAME = 'ssd_mobilenet_v1_coco_11_06_2017'
MODEL_FILE = MODEL_NAME + '.tar.gz'
DOWNLOAD_BASE = 'http://download.tensorflow.org/models/object_detection/'
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_CKPT = MODEL_NAME + '/frozen_inference_graph.pb'
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = os.path.join('data', 'mscoco_label_map.pbtxt')
NUM_CLASSES = 90
```
## Download Model
```
opener = urllib.request.URLopener()
opener.retrieve(DOWNLOAD_BASE + MODEL_FILE, MODEL_FILE)
tar_file = tarfile.open(MODEL_FILE)
for file in tar_file.getmembers():
file_name = os.path.basename(file.name)
if 'frozen_inference_graph.pb' in file_name:
tar_file.extract(file, os.getcwd())
```
## Load a (frozen) Tensorflow model into memory.
```
detection_graph = tf.Graph()
with detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_CKPT, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
```
## Loading label map
Label maps map indices to category names, so that when our convolution network predicts `5`, we know that this corresponds to `airplane`. Here we use internal utility functions, but anything that returns a dictionary mapping integers to appropriate string labels would be fine
```
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=NUM_CLASSES, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
category_index
```
## Helper code
```
def load_image_into_numpy_array(image):
(im_width, im_height) = image.size
return np.array(image.getdata()).reshape(
(im_height, im_width, 3)).astype(np.uint8)
```
This is a helper function that takes the detection graph output tensor (np arrays), stacks the classes and scores, and determines if the class for a person (1) is available within a certain score and within a certain amount of objects
```
def person_in_image(classes_arr, scores_arr, obj_thresh=5, score_thresh=0.5):
stacked_arr = np.stack((classes_arr, scores_arr), axis=-1)
person_found_flag = False
for ix in range(obj_thresh):
if 1.00000000e+00 in stacked_arr[ix]:
if stacked_arr[ix][1] >= score_thresh:
person_found_flag = True
return person_found_flag
```
# Establish Connection to GIS via ArcGIS API for Python
### Authenticate
```
import arcgis
gis_url = "" # Replace with gis URL
username = "" # Replace with username
gis = arcgis.gis.GIS(gis_url, username)
```
### Retrieve the Object Detection Point Layer
```
target_service_name = "" # Replace with name of target service
object_point_srvc = gis.content.search(target_service_name)[0]
object_point_srvc
# Convert our existing service into a pandas dataframe
object_point_lyr = object_point_srvc.layers[0]
obj_fset = object_point_lyr.query() #querying without any conditions returns all the features
obj_df = obj_fset.df
obj_df.head()
all_features = obj_fset.features
all_features
from copy import deepcopy
original_feature = all_features[0]
feature_to_be_updated = deepcopy(original_feature)
feature_to_be_updated
```
### Test of Manual Update
```
feature_to_be_updated.attributes['Person_Found']
features_for_update = []
feature_to_be_updated.attributes['Person_Found'] = "False"
features_for_update.append(feature_to_be_updated)
object_point_lyr.edit_features(updates=features_for_update)
```
# Detection
```
with detection_graph.as_default():
with tf.Session(graph=detection_graph) as sess:
# Definite input and output Tensors for detection_graph
image_tensor = detection_graph.get_tensor_by_name('image_tensor:0')
# Each box represents a part of the image where a particular object was detected.
detection_boxes = detection_graph.get_tensor_by_name('detection_boxes:0')
# Each score represent how level of confidence for each of the objects.
# Score is shown on the result image, together with the class label.
detection_scores = detection_graph.get_tensor_by_name('detection_scores:0')
detection_classes = detection_graph.get_tensor_by_name('detection_classes:0')
num_detections = detection_graph.get_tensor_by_name('num_detections:0')
while True:
ret, image_np = cap.read()
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
# Actual detection.
(boxes, scores, classes, num) = sess.run(
[detection_boxes, detection_scores, detection_classes, num_detections],
feed_dict={image_tensor: image_np_expanded})
# Visualization of the results of a detection.
vis_util.visualize_boxes_and_labels_on_image_array(
image_np,
np.squeeze(boxes),
np.squeeze(classes).astype(np.int32),
np.squeeze(scores),
category_index,
use_normalized_coordinates=True,
line_thickness=8, min_score_thresh=0.5)
cv2.imshow('object detection', cv2.resize(image_np, (800,600)))
if cv2.waitKey(25) & 0xFF == ord('q'):
cv2.destroyAllWindows()
break
person_found = person_in_image(np.squeeze(classes).astype(np.int32),
np.squeeze(scores),
obj_thresh=2)
features_for_update = []
feature_to_be_updated.attributes['Person_Found'] = str(person_found)
features_for_update.append(feature_to_be_updated)
object_point_lyr.edit_features(updates=features_for_update)
```
| true |
code
| 0.426501 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/dlmacedo/starter-academic/blob/master/3The_ultimate_guide_to_Encoder_Decoder_Models_3_4.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
%%capture
!pip install -qq git+https://github.com/huggingface/transformers.git
```
# **Transformer-based Encoder-Decoder Models**
The *transformer-based* encoder-decoder model was introduced by Vaswani et al. in the famous [Attention is all you need paper](https://arxiv.org/abs/1706.03762) and is today the *de-facto* standard encoder-decoder architecture in natural language processing (NLP).
Recently, there has been a lot of research on different *pre-training* objectives for transformer-based encoder-decoder models, *e.g.* T5, Bart, Pegasus, ProphetNet, Marge, *etc*..., but the model architecture has stayed largely the same.
The goal of the blog post is to give an **in-detail** explanation of **how** the transformer-based encoder-decoder architecture models *sequence-to-sequence* problems. We will focus on the mathematical model defined by the architecture and how the model can be used in inference. Along the way, we will give some background on sequence-to-sequence models in NLP and break down the *transformer-based* encoder-decoder architecture into its **encoder** and **decoder** part. We provide many illustrations and establish the link
between the theory of *transformer-based* encoder-decoder models and their practical usage in 🤗Transformers for inference.
Note that this blog post does *not* explain how such models can be trained - this will be the topic of a future blog post.
Transformer-based encoder-decoder models are the result of years of research on *representation learning* and *model architectures*.
This notebook provides a short summary of the history of neural encoder-decoder models. For more context, the reader is advised to read this awesome [blog post](https://ruder.io/a-review-of-the-recent-history-of-nlp/) by Sebastion Ruder. Additionally, a basic understanding of the *self-attention architecture* is recommended.
The following blog post by Jay Alammar serves as a good refresher on the original Transformer model [here](http://jalammar.github.io/illustrated-transformer/).
At the time of writing this notebook, 🤗Transformers comprises the encoder-decoder models *T5*, *Bart*, *MarianMT*, and *Pegasus*, which are summarized in the docs under [model summaries](https://huggingface.co/transformers/model_summary.html#sequence-to-sequence-models).
The notebook is divided into four parts:
- **Background** - *A short history of neural encoder-decoder models is given with a focus on on RNN-based models.* - [click here](https://colab.research.google.com/drive/18ZBlS4tSqSeTzZAVFxfpNDb_SrZfAOMf?usp=sharing)
- **Encoder-Decoder** - *The transformer-based encoder-decoder model is presented and it is explained how the model is used for inference.* - [click here](https://colab.research.google.com/drive/1XpKHijllH11nAEdPcQvkpYHCVnQikm9G?usp=sharing)
- **Encoder** - *The encoder part of the model is explained in detail.*
- **Decoder** - *The decoder part of the model is explained in detail.* - to be published on *Thursday, 08.10.2020*
Each part builds upon the previous part, but can also be read on its own.
## **Encoder**
As mentioned in the previous section, the *transformer-based* encoder maps the input sequence to a contextualized encoding sequence:
$$ f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n}. $$
Taking a closer look at the architecture, the transformer-based encoder is a stack of residual *encoder blocks*.
Each encoder block consists of a **bi-directional** self-attention layer, followed by two feed-forward layers. For simplicity, we disregard the normalization layers in this notebook. Also, we will not further discuss the role of the two feed-forward layers, but simply see it as a final vector-to-vector mapping required in each encoder block ${}^1$.
The bi-directional self-attention layer puts each input vector $\mathbf{x'}_j, \forall j \in \{1, \ldots, n\}$ into relation with all input vectors $\mathbf{x'}_1, \ldots, \mathbf{x'}_n$ and by doing so transforms the input vector $\mathbf{x'}_j$ to a more "refined" contextual representation of itself, defined as $\mathbf{x''}_j$.
Thereby, the first encoder block transforms each input vector of the input sequence $\mathbf{X}_{1:n}$ (shown in light green below) from a *context-independent* vector representation to a *context-dependent* vector representation, and the following encoder blocks further refine this contextual representation until the last encoder block outputs the final contextual encoding $\mathbf{\overline{X}}_{1:n}$ (shown in darker green below).
Let's visualize how the encoder processes the input sequence "I want to buy a car EOS" to a contextualized encoding sequence. Similar to RNN-based encoders, transformer-based encoders also add a special "end-of-sequence" input vector to the input sequence to hint to the model that the input vector sequence is finished ${}^2$.
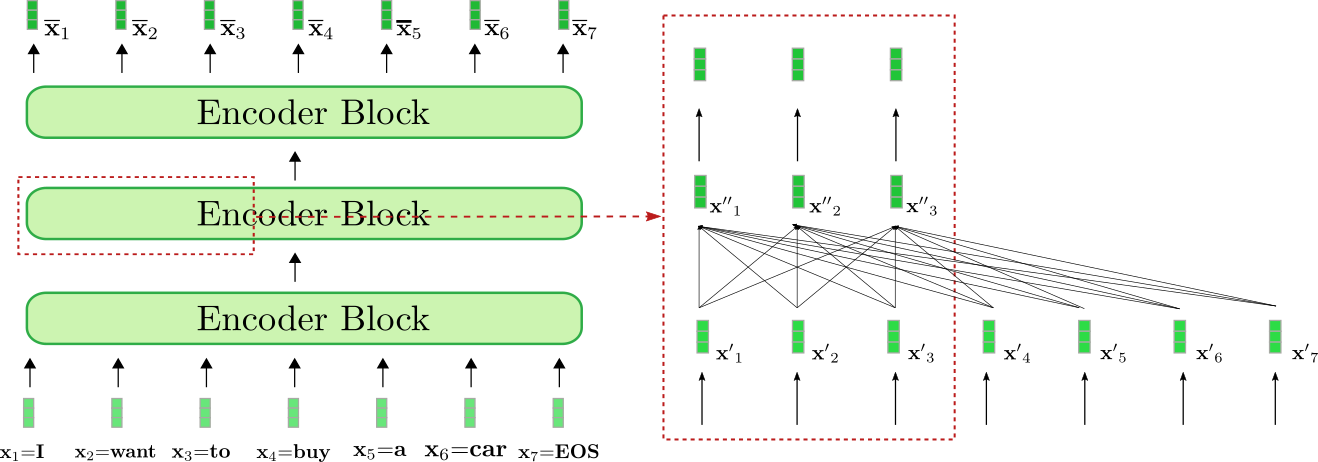
Our exemplary *transformer-based* encoder is composed of three encoder blocks, whereas the second encoder block is shown in more detail in the red box on the right for the first three input vectors $\mathbf{x}_1, \mathbf{x}_2 and \mathbf{x}_3$.
The bi-directional self-attention mechanism is illustrated by the fully-connected graph in the lower part of the red box and the two feed-forward layers are shown in the upper part of the red box. As stated before, we will focus only on the bi-directional self-attention mechanism.
As can be seen each output vector of the self-attention layer $\mathbf{x''}_i, \forall i \in \{1, \ldots, 7\}$ depends *directly* on *all* input vectors $\mathbf{x'}_1, \ldots, \mathbf{x'}_7$. This means, *e.g.* that the input vector representation of the word "want", *i.e.* $\mathbf{x'}_2$, is put into direct relation with the word "buy", *i.e.* $\mathbf{x'}_4$, but also with the word "I",*i.e.* $\mathbf{x'}_1$. The output vector representation of "want", *i.e.* $\mathbf{x''}_2$, thus represents a more refined contextual representation for the word "want".
Let's take a deeper look at how bi-directional self-attention works.
Each input vector $\mathbf{x'}_i$ of an input sequence $\mathbf{X'}_{1:n}$ of an encoder block is projected to a key vector $\mathbf{k}_i$, value vector $\mathbf{v}_i$ and query vector $\mathbf{q}_i$ (shown in orange, blue, and purple respectively below) through three trainable weight matrices $\mathbf{W}_q, \mathbf{W}_v, \mathbf{W}_k$:
$$ \mathbf{q}_i = \mathbf{W}_q \mathbf{x'}_i,$$
$$ \mathbf{v}_i = \mathbf{W}_v \mathbf{x'}_i,$$
$$ \mathbf{k}_i = \mathbf{W}_k \mathbf{x'}_i, $$
$$ \forall i \in \{1, \ldots n \}.$$
Note, that the **same** weight matrices are applied to each input vector $\mathbf{x}_i, \forall i \in \{i, \ldots, n\}$. After projecting each input vector $\mathbf{x}_i$ to a query, key, and value vector, each query vector $\mathbf{q}_j, \forall j \in \{1, \ldots, n\}$ is compared to all key vectors $\mathbf{k}_1, \ldots, \mathbf{k}_n$. The more similar one of the key vectors $\mathbf{k}_1, \ldots \mathbf{k}_n$ is to a query vector $\mathbf{q}_j$, the more important is the corresponding value vector $\mathbf{v}_j$ for the output vector $\mathbf{x''}_j$. More specifically, an output vector $\mathbf{x''}_j$ is defined as the weighted sum of all value vectors $\mathbf{v}_1, \ldots, \mathbf{v}_n$ plus the input vector $\mathbf{x'}_j$. Thereby, the weights are proportional to the cosine similarity between $\mathbf{q}_j$ and the respective key vectors $\mathbf{k}_1, \ldots, \mathbf{k}_n$, which is mathematically expressed by $\textbf{Softmax}(\mathbf{K}_{1:n}^\intercal \mathbf{q}_j)$ as illustrated in the equation below.
For a complete description of the self-attention layer, the reader is advised to take a look at [this](http://jalammar.github.io/illustrated-transformer/) blog post or the original [paper](https://arxiv.org/abs/1706.03762).
Alright, this sounds quite complicated. Let's illustrate the bi-directional self-attention layer for one of the query vectors of our example above. For simplicity, it is assumed that our exemplary *transformer-based* decoder uses only a single attention head `config.num_heads = 1` and that no normalization is applied.
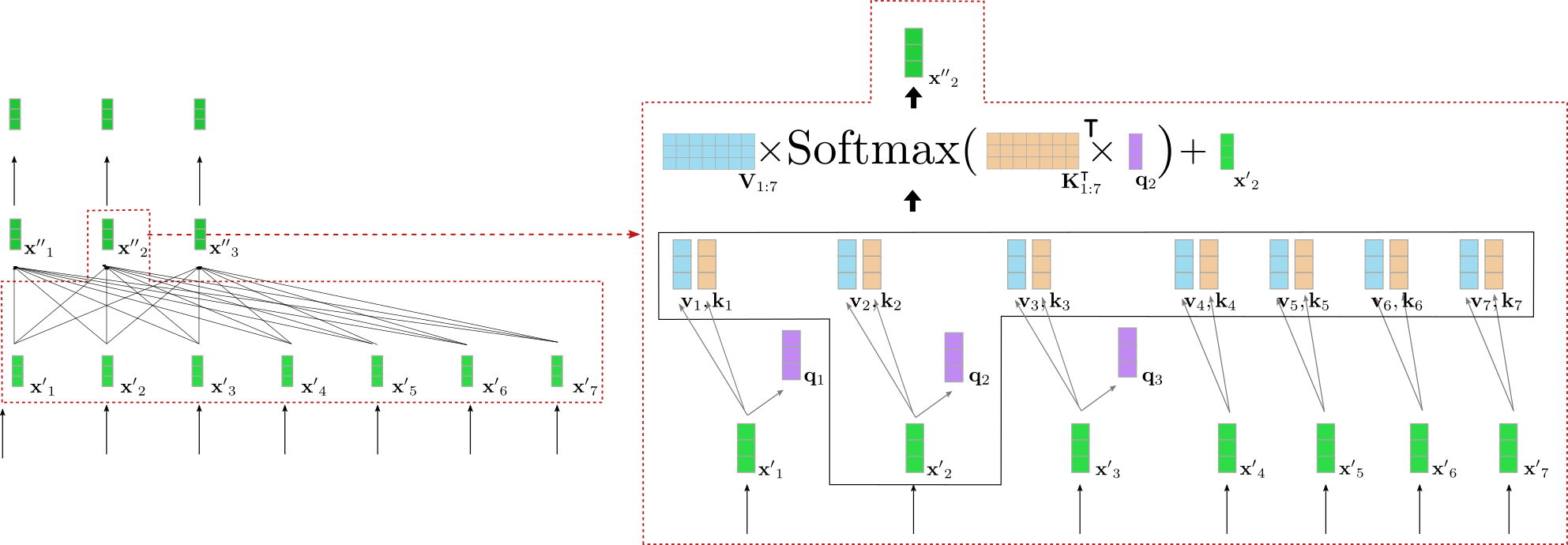
On the left, the previously illustrated second encoder block is shown again and on the right, an in detail visualization of the bi-directional self-attention mechanism is given for the second input vector $\mathbf{x'}_2$ that corresponds to the input word "want".
At first all input vectors $\mathbf{x'}_1, \ldots, \mathbf{x'}_7$ are projected to their respective query vectors $\mathbf{q}_1, \ldots, \mathbf{q}_7$ (only the first three query vectors are shown in purple above), value vectors $\mathbf{v}_1, \ldots, \mathbf{v}_7$ (shown in blue), and key vectors $\mathbf{k}_1, \ldots, \mathbf{k}_7$ (shown in orange). The query vector $\mathbf{q}_2$ is then multiplied by the transpose of all key vectors, *i.e.* $\mathbf{K}_{1:7}^{\intercal}$ followed by the softmax operation to yield the *self-attention weights*. The self-attention weights are finally multiplied by the respective value vectors and the input vector $\mathbf{x'}_2$ is added to output the "refined" representation of the word "want", *i.e.* $\mathbf{x''}_2$ (shown in dark green on the right).
The whole equation is illustrated in the upper part of the box on the right.
The multiplication of $\mathbf{K}_{1:7}^{\intercal}$ and $\mathbf{q}_2$ thereby makes it possible to compare the vector representation of "want" to all other input vector representations "I", "to", "buy", "a", "car", "EOS" so that the self-attention weights mirror the importance each of the other input vector representations $\mathbf{x'}_j \text{, with } j \ne 2$ for the refined representation $\mathbf{x''}_2$ of the word "want".
To further understand the implications of the bi-directional self-attention layer, let's assume the following sentence is processed: "*The house is beautiful and well located in the middle of the city where it is easily accessible by public transport*". The word "it" refers to "house", which is 12 "positions away". In transformer-based encoders, the bi-directional self-attention layer performs a single mathematical operation to put the input vector of "house" into relation with the input vector of "it" (compare to the first illustration of this section). In contrast, in an RNN-based encoder, a word that is 12 "positions away", would require at least 12 mathematical operations meaning that in an RNN-based encoder a linear number of mathematical operations are required. This makes it much harder for an RNN-based encoder to model long-range contextual representations.
Also, it becomes clear that a transformer-based encoder is much less prone to lose important information than an RNN-based encoder-decoder model because the sequence length of the encoding is kept the same, *i.e.* $\textbf{len}(\mathbf{X}_{1:n}) = \textbf{len}(\mathbf{\overline{X}}_{1:n}) = n$, while an RNN compresses the length from $\textbf{len}((\mathbf{X}_{1:n}) = n$ to just $\textbf{len}(\mathbf{c}) = 1$, which makes it very difficult for RNNs to effectively encode long-range dependencies between input words.
In addition to making long-range dependencies more easily learnable, we can see that the Transformer architecture is able to process text in parallel.Mathematically, this can easily be shown by writing the self-attention formula as a product of query, key, and value matrices:
$$\mathbf{X''}_{1:n} = \mathbf{V}_{1:n} \text{Softmax}(\mathbf{Q}_{1:n}^\intercal \mathbf{K}_{1:n}) + \mathbf{X'}_{1:n}. $$
The output $\mathbf{X''}_{1:n} = \mathbf{x''}_1, \ldots, \mathbf{x''}_n$ is computed via a series of matrix multiplications and a softmax operation, which can be parallelized effectively.
Note, that in an RNN-based encoder model, the computation of the hidden state $\mathbf{c}$ has to be done sequentially: Compute hidden state of the first input vector $\mathbf{x}_1$, then compute the hidden state of the second input vector that depends on the hidden state of the first hidden vector, etc. The sequential nature of RNNs prevents effective parallelization and makes them much more inefficient compared to transformer-based encoder models on modern GPU hardware.
Great, now we should have a better understanding of a) how transformer-based encoder models effectively model long-range contextual representations and b) how they efficiently process long sequences of input vectors.
Now, let's code up a short example of the encoder part of our `MarianMT` encoder-decoder models to verify that the explained theory holds in practice.
---
${}^1$ An in-detail explanation of the role the feed-forward layers play in transformer-based models is out-of-scope for this notebook. It is argued in [Yun et. al, (2017)](https://arxiv.org/pdf/1912.10077.pdf) that feed-forward layers are crucial to map each contextual vector $\mathbf{x'}_i$ individually to the desired output space, which the *self-attention* layer does not manage to do on its own. It should be noted here, that each output token $\mathbf{x'}$ is processed by the same feed-forward layer. For more detail, the reader is advised to read the paper.
${}^2$ However, the EOS input vector does not have to be appended to the input sequence, but has been shown to improve performance in many cases. In contrast to the *0th* $\text{BOS}$ target vector of the transformer-based decoder is required as a starting input vector to predict a first target vector.
```
%%capture
from transformers import MarianMTModel, MarianTokenizer
import torch
tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
embeddings = model.get_input_embeddings()
# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids
# pass input_ids to encoder
encoder_hidden_states = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state
# change the input slightly and pass to encoder
input_ids_perturbed = tokenizer("I want to buy a house", return_tensors="pt").input_ids
encoder_hidden_states_perturbed = model.base_model.encoder(input_ids_perturbed, return_dict=True).last_hidden_state
# compare shape and encoding of first vector
print(f"Length of input embeddings {embeddings(input_ids).shape[1]}. Length of encoder_hidden_states {encoder_hidden_states.shape[1]}")
# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `I` equal to its perturbed version?: ", torch.allclose(encoder_hidden_states[0, 0], encoder_hidden_states_perturbed[0, 0], atol=1e-3))
```
We compare the length of the input word embeddings, *i.e.* `embeddings(input_ids)` corresponding to $\mathbf{X}_{1:n}$, with the length of the `encoder_hidden_states`, corresponding to $\mathbf{\overline{X}}_{1:n}$.
Also, we have forwarded the word sequence "I want to buy a car" and a slightly perturbated version "I want to buy a house" through the encoder to check if the first output encoding, corresponding to "I", differs when only the last word is changed in the input sequence.
As expected the output length of the input word embeddings and encoder output encodings, *i.e.* $\textbf{len}(\mathbf{X}_{1:n})$ and $\textbf{len}(\mathbf{\overline{X}}_{1:n})$, is equal.
Second, it can be noted that the values of the encoded output vector of $\mathbf{\overline{x}}_1 = \text{"I"}$ are different when the last word is changed from "car" to "house". This however should not come as a surprise if one has understood bi-directional self-attention.
On a side-note, *autoencoding* models, such as BERT, have the exact same architecture as *transformer-based* encoder models. *Autoencoding* models leverage this architecture for massive self-supervised pre-training on open-domain text data so that they can map any word sequence to a deep bi-directional representation. In [Devlin et al. (2018)](https://arxiv.org/abs/1810.04805), the authors show that a pre-trained BERT model with a single task-specific classification layer on top can achieve SOTA results on eleven NLP tasks. All *autoencoding* models of 🤗Transformers can be found [here](https://huggingface.co/transformers/model_summary.html#autoencoding-models).
| true |
code
| 0.623692 | null | null | null | null |
|
# Simple Go-To-Goal for Cerus
The following code implements a simple go-to-goal behavior for Cerus. It uses a closed feedback loop to continuously asses Cerus' state (position and heading) in the world using data from two wheel encoders. It subsequently calculates the error between a given goal location and its current pose and will attempt to minimize the error until it reaches the goal location. A P-regulator (see PID regulator) script uses the error as an input and outputs the angular velocity for the Arduino and motor controllers that drive the robot.
All models used in this program are adapted from Georgia Tech's "Control of Mobile Robots" by Dr. Magnus Egerstedt.
```
#Import useful libraries
import serial
import time
import math
import numpy as np
from traitlets import HasTraits, List
#Open a serial connection with the Arduino Mega
#Opening a serial port on the Arduino resets it, so our encoder count is also reset to 0,0
ser = serial.Serial('COM3', 115200)
#Defining our goal location. Units are metric, real-world coordinates in an X/Y coordinate system
goal_x = 1
goal_y = 0
#Create a class for our Cerus robot
class Cerus():
def __init__(self, pose_x, pose_y, pose_phi, R_wheel, N_ticks, L_track):
self.pose_x = pose_x #X Position
self.pose_y = pose_y #Y Position
self.pose_phi = pose_phi #Heading
self.R_wheel = R_wheel #wheel radius in meters
self.N_ticks = N_ticks #encoder ticks per wheel revolution
self.L_track = L_track #wheel track in meters
#Create a Cerus instance and initialize it to a 0,0,0 world position and with some physical dimensions
cerus = Cerus(0,0,0,0.03,900,0.23)
```
We'll use the Traitlets library to implement an observer pattern that will recalculate the pose of the robot every time an update to the encoder values is detected and sent to the Jetson nano by the Arduino.
```
#Create an encoder class with traits
class Encoders(HasTraits):
encoderValues = List() #We store the left and right encoder value in a list
def __init__(self, encoderValues, deltaTicks):
self.encoderValues = encoderValues
self.deltaTicks = deltaTicks
#Create an encoder instance
encoders = Encoders([0,0], [0,0])
#Create a function that is triggered when a change to encoders is detected
def monitorEncoders(change):
if change['new']:
oldVals = np.array(change['old'])
newVals = np.array(change['new'])
deltaTicks = newVals - oldVals
#print("Old values: ", oldVals)
#print("New values: ", newVals)
#print("Delta values: ", deltaTicks)
calculatePose(deltaTicks)
encoders.observe(monitorEncoders, names = "encoderValues")
```
The functions below are helpers and will be called through our main loop.
```
#Create a move function that sends move commands to the Arduino
def move(linearVelocity, angularVelocity):
command = f"<{linearVelocity},{angularVelocity}>"
ser.write(str.encode(command))
#Create a function that calculates an updated pose of Cerus every time it is called
def calculatePose(deltaTicks):
#Calculate the centerline distance moved
distanceLeft = 2 * math.pi * cerus.R_wheel * (deltaTicks[0] / cerus.N_ticks)
distanceRight = 2 * math.pi * cerus.R_wheel * (deltaTicks[1] / cerus.N_ticks)
distanceCenter = (distanceLeft + distanceRight) / 2
#Update the position and heading
cerus.pose_x = round((cerus.pose_x + distanceCenter * math.cos(cerus.pose_phi)), 4)
cerus.pose_y = round((cerus.pose_y + distanceCenter * math.sin(cerus.pose_phi)), 4)
cerus.pose_phi = round((cerus.pose_phi + ((distanceRight - distanceLeft) / cerus.L_track)), 4)
print(f"The new position is {cerus.pose_x}, {cerus.pose_y} and the new heading is {cerus.pose_phi}.")
#Calculate the error between Cerus' heading and the goal point
def calculateError():
phi_desired = math.atan((goal_y - cerus.pose_y)/(goal_x - cerus.pose_x))
temp = phi_desired - cerus.pose_phi
error_heading = round((math.atan2(math.sin(temp), math.cos(temp))), 4) #ensure that error is within [-pi, pi]
error_x = round((goal_x - cerus.pose_x), 4)
error_y = round((goal_y - cerus.pose_y), 4)
#print("The heading error is: ", error_heading)
#print("The X error is: ", error_x)
#print("The Y error is: ", error_y)
return error_x, error_y, error_heading
atGoal = False
constVel = 0.2
K = 1 #constant for our P-regulator below
#Functions to read and format encoder data received from the Serial port
def formatData(data):
delimiter = "x"
leftVal = ""
rightVal = ""
for i in range(len(data)):
if data[i] == ",":
delimiter = ","
elif delimiter != "," and data[i].isdigit():
leftVal += data[i]
elif delimiter == "," and data[i].isdigit():
rightVal += data[i]
leftVal, rightVal = int(leftVal), int(rightVal)
encoders.encoderValues = [leftVal, rightVal]
print("Encoders: ", encoders.encoderValues)
def handleSerial():
#ser.readline() waits for the next line of encoder data, which is sent by Arduino every 50 ms
if ser.inWaiting():
#Get the serial data and format it
temp = ser.readline()
data = temp.decode()
formatData(data)
#Calculate the current pose to goal error
error_x, error_y, error_heading = calculateError()
print(f"Error X: {error_x}, Error Y: {error_y}")
#If we're within 5 cm of the goal
if error_x <= 0.05:# and error_y <= 0.05:
print("Goal reached!")
move(0.0,0.0)
time.sleep(0.1)
atGoal = True
#Otherwise keep driving
else:
omega = - (K * error_heading)
handleSerial()
move(constVel, 0.0)
print("Moving at angular speed: ", omega)
def moveRobot():
#The Arduino sends data every 50ms, we first check if data is in the buffer
if ser.inWaiting():
#Get the serial data and format it if data is in the buffer
temp = ser.readline()
data = temp.decode()
formatData(data)
#Calculate the current pose to goal error
error_x, error_y, error_heading = calculateError()
print(f"Error X: {error_x}, Error Y: {error_y}")
#If we're within 5 cm of the goal
if error_x <= 0.05:# and error_y <= 0.05:
print("Goal reached!")
move(0.0,0.0)
time.sleep(0.1)
atGoal = True
#Otherwise keep driving
else:
omega = - (K * error_heading)
handleSerial()
move(constVel, 0.0)
print("Moving at angular speed: ", omega)
```
This is the main part for our program that will loop over and over until Cerus has reached its goal. For our simple go-to-goal behavior, we will drive the robot at a constant speed and only adjust our heading so that we reach the goal location.
__WARNING: This will move the robot!__
```
while not atGoal:
try:
moveRobot()
except(KeyboardInterrupt):
print("Program interrupted by user!")
move(0.0,0.0) #Stop motors
break
"Loop exited..."
move(0.0,0.0) #Stop motors
#Close the serial connection when done
ser.close()
atGoal = False
constVel = 0.2
K = 1 #constant for our P-regulator below
while not atGoal:
try:
#Calculate the current pose to goal error
error_x, error_y, error_heading = calculateError()
print(f"Error X: {error_x}, Error Y: {error_y}")
#If we're within 5 cm of the goal
if error_x <= 0.05 and error_y <= 0.05:
print("Goal reached!")
move(0.0,0.0)
time.sleep(0.1)
atGoal = True
#Otherwise keep driving
else:
omega = - (K * error_heading)
handleSerial()
move(constVel, 0.0)
print("Moving at angular speed: ", omega)
except(KeyboardInterrupt):
print("Program interrupted by user!")
move(0.0,0.0) #Stop motors
break
"Loop exited..."
move(0.0,0.0) #Stop motors
```
| true |
code
| 0.458531 | null | null | null | null |
|
# SARK-110 Time Domain and Gating Example
Example adapted from: https://scikit-rf.readthedocs.io/en/latest/examples/networktheory/Time%20Domain.html
- Measurements with a 2.8m section of rg58 coax cable not terminated at the end
This notebooks demonstrates how to use scikit-rf for time-domain analysis and gating. A quick example is given first, followed by a more detailed explanation.
S-parameters are measured in the frequency domain, but can be analyzed in time domain if you like. In many cases, measurements are not made down to DC. This implies that the time-domain transform is not complete, but it can be very useful non-theless. A major application of time-domain analysis is to use gating to isolate a single response in space. More information about the details of time domain analysis.
Please ensure that the analyzer is connected to the computer using the USB cable and in Computer Control mode.
```
from sark110 import *
import skrf as rf
rf.stylely()
from pylab import *
```
Enter frequency limits:
```
fr_start = 100000 # Frequency start in Hz
fr_stop = 230000000 # Frequency stop in Hz
points = 401 # Number of points
```
## Utility functions
```
def z2vswr(rs: float, xs: float, z0=50 + 0j) -> float:
gamma = math.sqrt((rs - z0.real) ** 2 + xs ** 2) / math.sqrt((rs + z0.real) ** 2 + xs ** 2)
if gamma > 0.980197824:
return 99.999
swr = (1 + gamma) / (1 - gamma)
return swr
def z2mag(r: float, x: float) -> float:
return math.sqrt(r ** 2 + x ** 2)
def z2gamma(rs: float, xs: float, z0=50 + 0j) -> complex:
z = complex(rs, xs)
return (z - z0) / (z + z0)
```
## Connect to the device
```
sark110 = Sark110()
sark110.open()
sark110.connect()
if not sark110.is_connected:
print("Device not connected")
exit(-1)
else:
print("Device connected")
sark110.buzzer()
print(sark110.fw_protocol, sark110.fw_version)
```
## Acquire and plot the data
```
y = []
x = []
rs = [0]
xs = [0]
for i in range(points):
fr = int(fr_start + i * (fr_stop - fr_start) / (points - 1))
sark110.measure(fr, rs, xs)
x.append(fr / 1e9) # Units in GHz
y.append(z2gamma(rs[0][0], xs[0][0]))
probe = rf.Network(frequency=x, s=y, z0=50)
probe.frequency.unit = 'mhz'
print (probe)
```
# Quick example
```
# we will focus on s11
s11 = probe.s11
# time-gate the first largest reflection
s11_gated = s11.time_gate(center=0, span=50)
s11_gated.name='gated probe'
# plot frequency and time-domain s-parameters
figure(figsize=(8,4))
subplot(121)
s11.plot_s_db()
s11_gated.plot_s_db()
title('Frequency Domain')
subplot(122)
s11.plot_s_db_time()
s11_gated.plot_s_db_time()
title('Time Domain')
tight_layout()
```
# Interpreting Time Domain
Note there are two time-domain plotting functions in scikit-rf:
- Network.plot_s_db_time()
- Network.plot_s_time_db()
The difference is that the former, plot_s_db_time(), employs windowing before plotting to enhance impluse resolution. Windowing will be discussed in a bit, but for now we just use plot_s_db_time().
Plotting all four s-parameters of the probe in both frequency and time-domain.
```
# plot frequency and time-domain s-parameters
figure(figsize=(8,4))
subplot(121)
probe.plot_s_db()
title('Frequency Domain')
subplot(122)
probe.plot_s_db_time()
title('Time Domain')
tight_layout()
```
Focusing on the reflection coefficient from the waveguide port (s11), you can see there is an interference pattern present.
```
probe.plot_s_db(0,0)
title('Reflection Coefficient From \nWaveguide Port')
```
This ripple is evidence of several discrete reflections. Plotting s11 in the time-domain allows us to see where, or when, these reflections occur.
```
probe_s11 = probe.s11
probe_s11.plot_s_db_time(0,0)
title('Reflection Coefficient From \nWaveguide Port, Time Domain')
ylim(-100,0)
```
# Gating The Reflection of Interest
To isolate the reflection from the waveguide port, we can use time-gating. This can be done by using the method Network.time_gate(), and provide it an appropriate center and span (in ns). To see the effects of the gate, both the original and gated reponse are compared.
```
probe_s11_gated = probe_s11.time_gate(center=0, span=50)
probe_s11_gated.name='gated probe'
s11.plot_s_db_time()
s11_gated.plot_s_db_time()
```
Next, compare both responses in frequency domain to see the effect of the gate.
```
s11.plot_s_db()
s11_gated.plot_s_db()
```
# Auto-gate
The time-gating method in skrf has an auto-gating feature which can also be used to gate the largest reflection. When no gate parameters are provided, time_gate() does the following:
find the two largest peaks
center the gate on the tallest peak
set span to distance between two tallest peaks
You may want to plot the gated network in time-domain to see what the determined gate shape looks like.
```
title('Waveguide Interface of Probe')
s11.plot_s_db(label='original')
s11.time_gate().plot_s_db(label='autogated') #autogate on the fly
```
# Determining Distance
To make time-domain useful as a diagnostic tool, one would like to convert the x-axis to distance. This requires knowledge of the propagation velocity in the device. skrf provides some transmission-line models in the module skrf.media, which can be used for this.
However...
For dispersive media, such as rectangular waveguide, the phase velocity is a function of frequency, and transforming time to distance is not straightforward. As an approximation, you can normalize the x-axis to the speed of light.
Alternatively, you can simulate the a known device and compare the two time domain responses. This allows you to attribute quantatative meaning to the axes. For example, you could create an ideal delayed load as shown below. Note: the magnitude of a response behind a large impulse doesn not have meaningful units.
```
from skrf.media import DistributedCircuit
# create a Media object for RG-58, based on distributed ckt values
rg58 = DistributedCircuit(
frequency = probe.frequency,
C =93.5e-12,#F/m
L =273e-9, #H/m
R =0, #53e-3, #Ohm/m
G =0, #S/m
)
# create an ideal delayed load, parameters are adjusted until the
# theoretical response agrees with the measurement
theory = rg58.delay_load(Gamma0=rf.db_2_mag(-20),
d=280, unit='cm')
probe.plot_s_db_time(0,0, label = 'Measurement')
theory.plot_s_db_time(label='-20dB @ 280cm from test-port')
ylim(-100,0)
xlim(-500,500)
```
This plot demonstrates a few important points:
the theortical delayed load is not a perfect impulse in time. This is due to the dispersion in waveguide.
the peak of the magnitude in time domain is not identical to that specified, also due to disperison (and windowing).
# What the hell is Windowing?
The 'plot_s_db_time()' function does a few things.
windows the s-parameters.
converts to time domain
takes magnitude component, convert to dB
calculates time-axis s
plots
A word about step 1: windowing. A FFT represents a signal with a basis of periodic signals (sinusoids). If your frequency response is not periodic, which in general it isnt, taking a FFT will introduces artifacts in the time-domain results. To minimize these effects, the frequency response is windowed. This makes the frequency response more periodic by tapering off the band-edges.
Windowing is just applied to improve the plot appearance,d it does not affect the original network.
In skrf this can be done explicitly using the 'windowed()' function. By default this function uses the hamming window, but can be adjusted through arguments. The result of windowing is show below.
```
probe_w = probe.windowed()
probe.plot_s_db(0,0, label = 'Original')
probe_w.plot_s_db(0,0, label = 'Windowed')
```
Comparing the two time-domain plotting functions, we can see the difference between windowed and not.
```
probe.plot_s_time_db(0,0, label = 'Original')
probe_w.plot_s_time_db(0,0, label = 'Windowed')
```
# The end!
```
sark110.close()
```
| true |
code
| 0.51812 | null | null | null | null |
|
### Introduction
The `Lines` object provides the following features:
1. Ability to plot a single set or multiple sets of y-values as a function of a set or multiple sets of x-values
2. Ability to style the line object in different ways, by setting different attributes such as the `colors`, `line_style`, `stroke_width` etc.
3. Ability to specify a marker at each point passed to the line. The marker can be a shape which is at the data points between which the line is interpolated and can be set through the `markers` attribute
The `Lines` object has the following attributes
| Attribute | Description | Default Value |
|:-:|---|:-:|
| `colors` | Sets the color of each line, takes as input a list of any RGB, HEX, or HTML color name | `CATEGORY10` |
| `opacities` | Controls the opacity of each line, takes as input a real number between 0 and 1 | `1.0` |
| `stroke_width` | Real number which sets the width of all paths | `2.0` |
| `line_style` | Specifies whether a line is solid, dashed, dotted or both dashed and dotted | `'solid'` |
| `interpolation` | Sets the type of interpolation between two points | `'linear'` |
| `marker` | Specifies the shape of the marker inserted at each data point | `None` |
| `marker_size` | Controls the size of the marker, takes as input a non-negative integer | `64` |
|`close_path`| Controls whether to close the paths or not | `False` |
|`fill`| Specifies in which way the paths are filled. Can be set to one of `{'none', 'bottom', 'top', 'inside'}`| `None` |
|`fill_colors`| `List` that specifies the `fill` colors of each path | `[]` |
| **Data Attribute** | **Description** | **Default Value** |
|`x` |abscissas of the data points | `array([])` |
|`y` |ordinates of the data points | `array([])` |
|`color` | Data according to which the `Lines` will be colored. Setting it to `None` defaults the choice of colors to the `colors` attribute | `None` |
## pyplot's plot method can be used to plot lines with meaningful defaults
```
import numpy as np
from pandas import date_range
import bqplot.pyplot as plt
from bqplot import *
security_1 = np.cumsum(np.random.randn(150)) + 100.
security_2 = np.cumsum(np.random.randn(150)) + 100.
```
## Basic Line Chart
```
fig = plt.figure(title='Security 1')
axes_options = {'x': {'label': 'Index'}, 'y': {'label': 'Price'}}
# x values default to range of values when not specified
line = plt.plot(security_1, axes_options=axes_options)
fig
```
**We can explore the different attributes by changing each of them for the plot above:**
```
line.colors = ['DarkOrange']
```
In a similar way, we can also change any attribute after the plot has been displayed to change the plot. Run each of the cells below, and try changing the attributes to explore the different features and how they affect the plot.
```
# The opacity allows us to display the Line while featuring other Marks that may be on the Figure
line.opacities = [.5]
line.stroke_width = 2.5
```
To switch to an area chart, set the `fill` attribute, and control the look with `fill_opacities` and `fill_colors`.
```
line.fill = 'bottom'
line.fill_opacities = [0.2]
line.line_style = 'dashed'
line.interpolation = 'basis'
```
While a `Lines` plot allows the user to extract the general shape of the data being plotted, there may be a need to visualize discrete data points along with this shape. This is where the `markers` attribute comes in.
```
line.marker = 'triangle-down'
```
The `marker` attributes accepts the values `square`, `circle`, `cross`, `diamond`, `square`, `triangle-down`, `triangle-up`, `arrow`, `rectangle`, `ellipse`. Try changing the string above and re-running the cell to see how each `marker` type looks.
## Plotting a Time-Series
The `DateScale` allows us to plot time series as a `Lines` plot conveniently with most `date` formats.
```
# Here we define the dates we would like to use
dates = date_range(start='01-01-2007', periods=150)
fig = plt.figure(title='Time Series')
axes_options = {'x': {'label': 'Date'}, 'y': {'label': 'Security 1'}}
time_series = plt.plot(dates, security_1,
axes_options=axes_options)
fig
```
## Plotting multiples sets of data
The `Lines` mark allows the user to plot multiple `y`-values for a single `x`-value. This can be done by passing an `ndarray` or a list of the different `y`-values as the y-attribute of the `Lines` as shown below.
```
dates_new = date_range(start='06-01-2007', periods=150)
```
We pass each data set as an element of a `list`
```
fig = plt.figure()
axes_options = {'x': {'label': 'Date'}, 'y': {'label': 'Price'}}
line = plt.plot(dates, [security_1, security_2],
labels=['Security 1', 'Security 2'],
axes_options=axes_options,
display_legend=True)
fig
```
Similarly, we can also pass multiple `x`-values for multiple sets of `y`-values
```
line.x, line.y = [dates, dates_new], [security_1, security_2]
```
### Coloring Lines according to data
The `color` attribute of a `Lines` mark can also be used to encode one more dimension of data. Suppose we have a portfolio of securities and we would like to color them based on whether we have bought or sold them. We can use the `color` attribute to encode this information.
```
fig = plt.figure()
axes_options = {'x': {'label': 'Date'},
'y': {'label': 'Security 1'},
'color' : {'visible': False}}
# add a custom color scale to color the lines
plt.scales(scales={'color': ColorScale(colors=['Red', 'Green'])})
dates_color = date_range(start='06-01-2007', periods=150)
securities = 100. + np.cumsum(np.random.randn(150, 10), axis=0)
# we generate 10 random price series and 10 random positions
positions = np.random.randint(0, 2, size=10)
# We pass the color scale and the color data to the plot method
line = plt.plot(dates_color, securities.T, color=positions,
axes_options=axes_options)
fig
```
We can also reset the colors of the Line to their defaults by setting the `color` attribute to `None`.
```
line.color = None
```
## Patches
The `fill` attribute of the `Lines` mark allows us to fill a path in different ways, while the `fill_colors` attribute lets us control the color of the `fill`
```
fig = plt.figure(animation_duration=1000)
patch = plt.plot([],[],
fill_colors=['orange', 'blue', 'red'],
fill='inside',
axes_options={'x': {'visible': False}, 'y': {'visible': False}},
stroke_width=10,
close_path=True,
display_legend=True)
patch.x = [[0, 2, 1.2, np.nan, np.nan, np.nan, np.nan], [0.5, 2.5, 1.7 , np.nan, np.nan, np.nan, np.nan], [4, 5, 6, 6, 5, 4, 3]],
patch.y = [[0, 0, 1 , np.nan, np.nan, np.nan, np.nan], [0.5, 0.5, -0.5, np.nan, np.nan, np.nan, np.nan], [1, 1.1, 1.2, 2.3, 2.2, 2.7, 1.0]]
fig
patch.opacities = [0.1, 0.2]
patch.x = [[2, 3, 3.2, np.nan, np.nan, np.nan, np.nan], [0.5, 2.5, 1.7, np.nan, np.nan, np.nan, np.nan], [4,5,6, 6, 5, 4, 3]]
patch.close_path = False
```
| true |
code
| 0.608827 | null | null | null | null |
|
# Draw an isochrone map with OSMnx
How far can you travel on foot in 15 minutes?
- [Overview of OSMnx](http://geoffboeing.com/2016/11/osmnx-python-street-networks/)
- [GitHub repo](https://github.com/gboeing/osmnx)
- [Examples, demos, tutorials](https://github.com/gboeing/osmnx-examples)
- [Documentation](https://osmnx.readthedocs.io/en/stable/)
- [Journal article/citation](http://geoffboeing.com/publications/osmnx-complex-street-networks/)
```
import geopandas as gpd
import matplotlib.pyplot as plt
import networkx as nx
import osmnx as ox
from descartes import PolygonPatch
from shapely.geometry import Point, LineString, Polygon
ox.config(log_console=True, use_cache=True)
ox.__version__
# configure the place, network type, trip times, and travel speed
place = 'Berkeley, CA, USA'
network_type = 'walk'
trip_times = [5, 10, 15, 20, 25] #in minutes
travel_speed = 4.5 #walking speed in km/hour
```
## Download and prep the street network
```
# download the street network
G = ox.graph_from_place(place, network_type=network_type)
# find the centermost node and then project the graph to UTM
gdf_nodes = ox.graph_to_gdfs(G, edges=False)
x, y = gdf_nodes['geometry'].unary_union.centroid.xy
center_node = ox.get_nearest_node(G, (y[0], x[0]))
G = ox.project_graph(G)
# add an edge attribute for time in minutes required to traverse each edge
meters_per_minute = travel_speed * 1000 / 60 #km per hour to m per minute
for u, v, k, data in G.edges(data=True, keys=True):
data['time'] = data['length'] / meters_per_minute
```
## Plots nodes you can reach on foot within each time
How far can you walk in 5, 10, 15, 20, and 25 minutes from the origin node? We'll use NetworkX to induce a subgraph of G within each distance, based on trip time and travel speed.
```
# get one color for each isochrone
iso_colors = ox.get_colors(n=len(trip_times), cmap='Reds', start=0.3, return_hex=True)
# color the nodes according to isochrone then plot the street network
node_colors = {}
for trip_time, color in zip(sorted(trip_times, reverse=True), iso_colors):
subgraph = nx.ego_graph(G, center_node, radius=trip_time, distance='time')
for node in subgraph.nodes():
node_colors[node] = color
nc = [node_colors[node] if node in node_colors else 'none' for node in G.nodes()]
ns = [20 if node in node_colors else 0 for node in G.nodes()]
fig, ax = ox.plot_graph(G, fig_height=8, node_color=nc, node_size=ns, node_alpha=0.8, node_zorder=2)
```
## Plot the time-distances as isochrones
How far can you walk in 5, 10, 15, 20, and 25 minutes from the origin node? We'll use a convex hull, which isn't perfectly accurate. A concave hull would be better, but shapely doesn't offer that.
```
# make the isochrone polygons
isochrone_polys = []
for trip_time in sorted(trip_times, reverse=True):
subgraph = nx.ego_graph(G, center_node, radius=trip_time, distance='time')
node_points = [Point((data['x'], data['y'])) for node, data in subgraph.nodes(data=True)]
bounding_poly = gpd.GeoSeries(node_points).unary_union.convex_hull
isochrone_polys.append(bounding_poly)
# plot the network then add isochrones as colored descartes polygon patches
fig, ax = ox.plot_graph(G, fig_height=8, show=False, close=False, edge_color='k', edge_alpha=0.2, node_color='none')
for polygon, fc in zip(isochrone_polys, iso_colors):
patch = PolygonPatch(polygon, fc=fc, ec='none', alpha=0.6, zorder=-1)
ax.add_patch(patch)
plt.show()
```
## Or, plot isochrones as buffers to get more faithful isochrones than convex hulls can offer
in the style of http://kuanbutts.com/2017/12/16/osmnx-isochrones/
```
def make_iso_polys(G, edge_buff=25, node_buff=50, infill=False):
isochrone_polys = []
for trip_time in sorted(trip_times, reverse=True):
subgraph = nx.ego_graph(G, center_node, radius=trip_time, distance='time')
node_points = [Point((data['x'], data['y'])) for node, data in subgraph.nodes(data=True)]
nodes_gdf = gpd.GeoDataFrame({'id': subgraph.nodes()}, geometry=node_points)
nodes_gdf = nodes_gdf.set_index('id')
edge_lines = []
for n_fr, n_to in subgraph.edges():
f = nodes_gdf.loc[n_fr].geometry
t = nodes_gdf.loc[n_to].geometry
edge_lines.append(LineString([f,t]))
n = nodes_gdf.buffer(node_buff).geometry
e = gpd.GeoSeries(edge_lines).buffer(edge_buff).geometry
all_gs = list(n) + list(e)
new_iso = gpd.GeoSeries(all_gs).unary_union
# try to fill in surrounded areas so shapes will appear solid and blocks without white space inside them
if infill:
new_iso = Polygon(new_iso.exterior)
isochrone_polys.append(new_iso)
return isochrone_polys
isochrone_polys = make_iso_polys(G, edge_buff=25, node_buff=0, infill=True)
fig, ax = ox.plot_graph(G, fig_height=8, show=False, close=False, edge_color='k', edge_alpha=0.2, node_color='none')
for polygon, fc in zip(isochrone_polys, iso_colors):
patch = PolygonPatch(polygon, fc=fc, ec='none', alpha=0.6, zorder=-1)
ax.add_patch(patch)
plt.show()
```
| true |
code
| 0.529993 | null | null | null | null |
|
## 1. Regression discontinuity: banking recovery
<p>After a debt has been legally declared "uncollectable" by a bank, the account is considered "charged-off." But that doesn't mean the bank <strong><em>walks away</em></strong> from the debt. They still want to collect some of the money they are owed. The bank will score the account to assess the expected recovery amount, that is, the expected amount that the bank may be able to receive from the customer in the future. This amount is a function of the probability of the customer paying, the total debt, and other factors that impact the ability and willingness to pay.</p>
<p>The bank has implemented different recovery strategies at different thresholds (\$1000, \$2000, etc.) where the greater the expected recovery amount, the more effort the bank puts into contacting the customer. For low recovery amounts (Level 0), the bank just adds the customer's contact information to their automatic dialer and emailing system. For higher recovery strategies, the bank incurs more costs as they leverage human resources in more efforts to obtain payments. Each additional level of recovery strategy requires an additional \$50 per customer so that customers in the Recovery Strategy Level 1 cost the company \$50 more than those in Level 0. Customers in Level 2 cost \$50 more than those in Level 1, etc. </p>
<p><strong>The big question</strong>: does the extra amount that is recovered at the higher strategy level exceed the extra \$50 in costs? In other words, was there a jump (also called a "discontinuity") of more than \$50 in the amount recovered at the higher strategy level? We'll find out in this notebook.</p>
<p>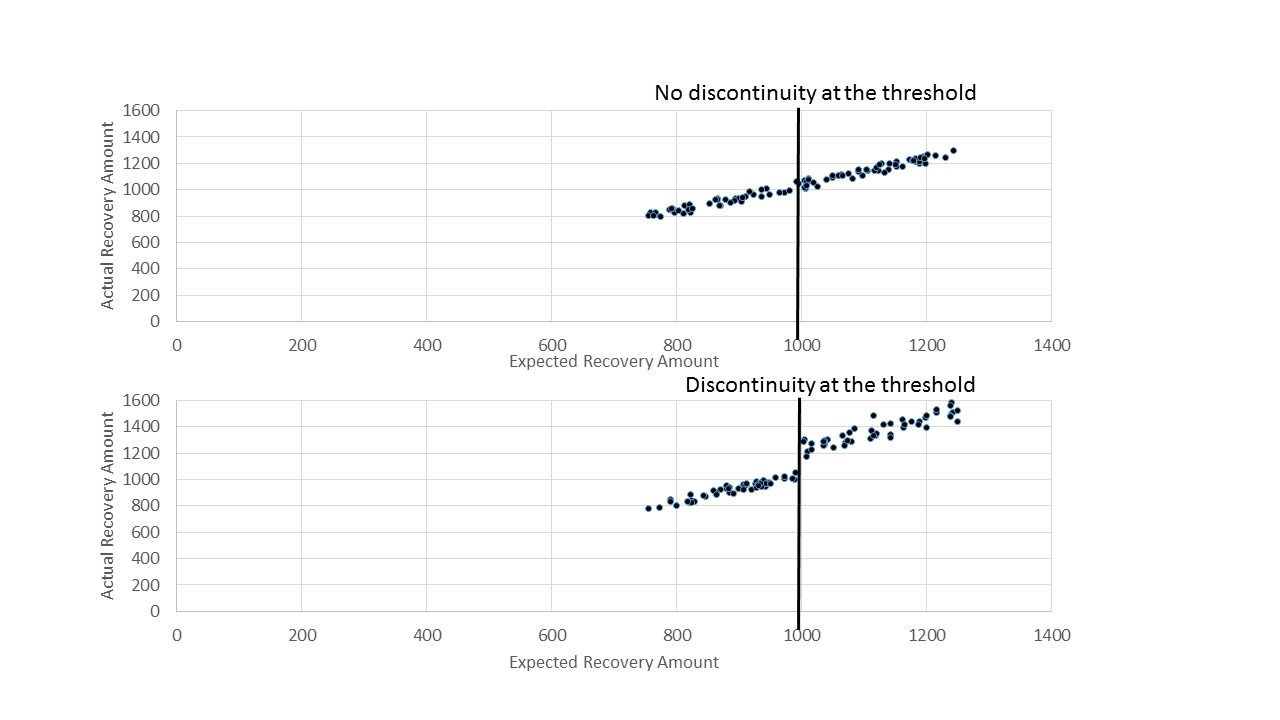</p>
<p>First, we'll load the banking dataset and look at the first few rows of data. This lets us understand the dataset itself and begin thinking about how to analyze the data.</p>
```
# Import modules
import pandas as pd
import numpy as np
# Read in dataset
df = pd.read_csv("datasets/bank_data.csv")
# Print the first few rows of the DataFrame
df.head()
```
## 2. Graphical exploratory data analysis
<p>The bank has implemented different recovery strategies at different thresholds (\$1000, \$2000, \$3000 and \$5000) where the greater the Expected Recovery Amount, the more effort the bank puts into contacting the customer. Zeroing in on the first transition (between Level 0 and Level 1) means we are focused on the population with Expected Recovery Amounts between \$0 and \$2000 where the transition between Levels occurred at \$1000. We know that the customers in Level 1 (expected recovery amounts between \$1001 and \$2000) received more attention from the bank and, by definition, they had higher Expected Recovery Amounts than the customers in Level 0 (between \$1 and \$1000).</p>
<p>Here's a quick summary of the Levels and thresholds again:</p>
<ul>
<li>Level 0: Expected recovery amounts >\$0 and <=\$1000</li>
<li>Level 1: Expected recovery amounts >\$1000 and <=\$2000</li>
<li>The threshold of \$1000 separates Level 0 from Level 1</li>
</ul>
<p>A key question is whether there are other factors besides Expected Recovery Amount that also varied systematically across the \$1000 threshold. For example, does the customer age show a jump (discontinuity) at the \$1000 threshold or does that age vary smoothly? We can examine this by first making a scatter plot of the age as a function of Expected Recovery Amount for a small window of Expected Recovery Amount, \$0 to \$2000. This range covers Levels 0 and 1.</p>
```
# Scatter plot of Age vs. Expected Recovery Amount
from matplotlib import pyplot as plt
%matplotlib inline
plt.scatter(x=df['expected_recovery_amount'], y=df['age'], c="g", s=2)
plt.xlim(0, 2000)
plt.ylim(0, 60)
plt.xlabel("Expected Recovery Amount")
plt.ylabel("Age")
plt.legend(loc=2)
plt.show()
```
## 3. Statistical test: age vs. expected recovery amount
<p>We want to convince ourselves that variables such as age and sex are similar above and below the \$1000 Expected Recovery Amount threshold. This is important because we want to be able to conclude that differences in the actual recovery amount are due to the higher Recovery Strategy and not due to some other difference like age or sex.</p>
<p>The scatter plot of age versus Expected Recovery Amount did not show an obvious jump around \$1000. We will now do statistical analysis examining the average age of the customers just above and just below the threshold. We can start by exploring the range from \$900 to \$1100.</p>
<p>For determining if there is a difference in the ages just above and just below the threshold, we will use the Kruskal-Wallis test, a statistical test that makes no distributional assumptions.</p>
```
# Import stats module
from scipy import stats
# Compute average age just below and above the threshold
era_900_1100 = df.loc[(df['expected_recovery_amount']<1100) &
(df['expected_recovery_amount']>=900)]
by_recovery_strategy = era_900_1100.groupby(['recovery_strategy'])
by_recovery_strategy['age'].describe().unstack()
# Perform Kruskal-Wallis test
Level_0_age = era_900_1100.loc[df['recovery_strategy']=="Level 0 Recovery"]['age']
Level_1_age = era_900_1100.loc[df['recovery_strategy']=="Level 1 Recovery"]['age']
stats.kruskal(Level_0_age,Level_1_age)
```
## 4. Statistical test: sex vs. expected recovery amount
<p>We have seen that there is no major jump in the average customer age just above and just
below the \$1000 threshold by doing a statistical test as well as exploring it graphically with a scatter plot. </p>
<p>We want to also test that the percentage of customers that are male does not jump across the \$1000 threshold. We can start by exploring the range of \$900 to \$1100 and later adjust this range.</p>
<p>We can examine this question statistically by developing cross-tabs as well as doing chi-square tests of the percentage of customers that are male vs. female.</p>
```
# Number of customers in each category
crosstab = pd.crosstab(df.loc[(df['expected_recovery_amount']<1100) &
(df['expected_recovery_amount']>=900)]['recovery_strategy'],
df['sex'])
print(crosstab)
# Chi-square test
chi2_stat, p_val, dof, ex = stats.chi2_contingency(crosstab)
print(p_val)
```
## 5. Exploratory graphical analysis: recovery amount
<p>We are now reasonably confident that customers just above and just below the \$1000 threshold are, on average, similar in their average age and the percentage that are male. </p>
<p>It is now time to focus on the key outcome of interest, the actual recovery amount.</p>
<p>A first step in examining the relationship between the actual recovery amount and the expected recovery amount is to develop a scatter plot where we want to focus our attention at the range just below and just above the threshold. Specifically, we will develop a scatter plot of Expected Recovery Amount (X) versus Actual Recovery Amount (Y) for Expected Recovery Amounts between \$900 to \$1100. This range covers Levels 0 and 1. A key question is whether or not we see a discontinuity (jump) around the \$1000 threshold.</p>
```
# Scatter plot of Actual Recovery Amount vs. Expected Recovery Amount
plt.scatter(x=df['expected_recovery_amount'], y=df['actual_recovery_amount'], c="g", s=2)
plt.xlim(900, 1100)
plt.ylim(0, 2000)
plt.xlabel("Expected Recovery Amount")
plt.ylabel("Actual Recovery Amount")
plt.legend(loc=2)
# ... YOUR CODE FOR TASK 5 ...
```
## 6. Statistical analysis: recovery amount
<p>As we did with age, we can perform statistical tests to see if the actual recovery amount has a discontinuity above the \$1000 threshold. We are going to do this for two different windows of the expected recovery amount \$900 to \$1100 and for a narrow range of \$950 to \$1050 to see if our results are consistent.</p>
<p>Again, we will use the Kruskal-Wallis test.</p>
<p>We will first compute the average actual recovery amount for those customers just below and just above the threshold using a range from \$900 to \$1100. Then we will perform a Kruskal-Wallis test to see if the actual recovery amounts are different just above and just below the threshold. Once we do that, we will repeat these steps for a smaller window of \$950 to \$1050.</p>
```
# Compute average actual recovery amount just below and above the threshold
by_recovery_strategy['actual_recovery_amount'].describe().unstack()
# Perform Kruskal-Wallis test
Level_0_actual = era_900_1100.loc[df['recovery_strategy']=='Level 0 Recovery']['actual_recovery_amount']
Level_1_actual = era_900_1100.loc[df['recovery_strategy']=='Level 1 Recovery']['actual_recovery_amount']
stats.kruskal(Level_0_actual,Level_1_actual)
# Repeat for a smaller range of $950 to $1050
era_950_1050 = df.loc[(df['expected_recovery_amount']<1050) &
(df['expected_recovery_amount']>=950)]
Level_0_actual = era_950_1050.loc[df['recovery_strategy']=='Level 0 Recovery']['actual_recovery_amount']
Level_1_actual = era_950_1050.loc[df['recovery_strategy']=='Level 1 Recovery']['actual_recovery_amount']
stats.kruskal(Level_0_actual,Level_1_actual)
```
## 7. Regression modeling: no threshold
<p>We now want to take a regression-based approach to estimate the program impact at the \$1000 threshold using data that is just above and below the threshold. </p>
<p>We will build two models. The first model does not have a threshold while the second will include a threshold.</p>
<p>The first model predicts the actual recovery amount (dependent variable) as a function of the expected recovery amount (independent variable). We expect that there will be a strong positive relationship between these two variables. </p>
<p>We will examine the adjusted R-squared to see the percent of variance explained by the model. In this model, we are not representing the threshold but simply seeing how the variable used for assigning the customers (expected recovery amount) relates to the outcome variable (actual recovery amount).</p>
```
# Import statsmodels
import statsmodels.api as sm
# Define X and y
X = era_900_1100['expected_recovery_amount']
y = era_900_1100['actual_recovery_amount']
X = sm.add_constant(X)
# Build linear regression model
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
# Print out the model summary statistics
model.summary()
```
## 8. Regression modeling: adding true threshold
<p>From the first model, we see that the expected recovery amount's regression coefficient is statistically significant. </p>
<p>The second model adds an indicator of the true threshold to the model (in this case at \$1000). </p>
<p>We will create an indicator variable (either a 0 or a 1) that represents whether or not the expected recovery amount was greater than \$1000. When we add the true threshold to the model, the regression coefficient for the true threshold represents the additional amount recovered due to the higher recovery strategy. That is to say, the regression coefficient for the true threshold measures the size of the discontinuity for customers just above and just below the threshold.</p>
<p>If the higher recovery strategy helped recovery more money, then the regression coefficient of the true threshold will be greater than zero. If the higher recovery strategy did not help recovery more money, then the regression coefficient will not be statistically significant.</p>
```
#Create indicator (0 or 1) for expected recovery amount >= $1000
df['indicator_1000'] = np.where(df['expected_recovery_amount']<1000, 0, 1)
era_900_1100 = df.loc[(df['expected_recovery_amount']<1100) &
(df['expected_recovery_amount']>=900)]
# Define X and y
X = era_900_1100[['expected_recovery_amount','indicator_1000']]
y = era_900_1100['actual_recovery_amount']
X = sm.add_constant(X)
# Build linear regression model
model = sm.OLS(y,X).fit()
# Print the model summary
model.summary()
```
## 9. Regression modeling: adjusting the window
<p>The regression coefficient for the true threshold was statistically significant with an estimated impact of around \$278. This is much larger than the \$50 per customer needed to run this higher recovery strategy. </p>
<p>Before showing this to our manager, we want to convince ourselves that this result wasn't due to choosing an expected recovery amount window of \$900 to \$1100. Let's repeat this analysis for the window from \$950 to \$1050 to see if we get similar results.</p>
<p>The answer? Whether we use a wide (\$900 to \$1100) or narrower window (\$950 to \$1050), the incremental recovery amount at the higher recovery strategy is much greater than the \$50 per customer it costs for the higher recovery strategy. So we conclude that the higher recovery strategy is worth the extra cost of \$50 per customer.</p>
```
# Redefine era_950_1050 so the indicator variable is included
era_950_1050 = df.loc[(df['expected_recovery_amount']<1050) &
(df['expected_recovery_amount']>=950)]
# Define X and y
X = era_950_1050[['expected_recovery_amount','indicator_1000']]
y = era_950_1050['actual_recovery_amount']
X = sm.add_constant(X)
# Build linear regression model
model = sm.OLS(y,X).fit()
# Print the model summary
model.summary()
```
| true |
code
| 0.678806 | null | null | null | null |
|
# Self DCGAN
<table class="tfo-notebook-buttons" align="left" >
<td>
<a target="_blank" href="https://colab.research.google.com/github/HighCWu/SelfGAN/blob/master/implementations/dcgan/self_dcgan.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/HighCWu/SelfGAN/blob/master/implementations/dcgan/self_dcgan.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
## Datasets
```
import glob
import random
import os
import numpy as np
from torch.utils.data import Dataset
from PIL import Image
import torchvision.transforms as transforms
class ImageDataset(Dataset):
def __init__(self, root, transforms_=None):
self.transform = transforms.Compose(transforms_)
self.files = sorted(glob.glob(root + '/**/*.*', recursive=True))
def __getitem__(self, index):
img = Image.open(self.files[index % len(self.files)]).convert('RGB')
w, h = img.size
img = self.transform(img)
return img
def __len__(self):
return len(self.files)
```
## Prepare
```
import argparse
import os
import sys
import numpy as np
import math
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
os.makedirs('images', exist_ok=True)
os.makedirs('images_normal', exist_ok=True)
parser = argparse.ArgumentParser()
parser.add_argument('--n_epochs', type=int, default=200, help='number of epochs of training')
parser.add_argument('--batch_size', type=int, default=64, help='size of the batches')
parser.add_argument('--lr', type=float, default=2e-4, help='adam: learning rate')
parser.add_argument('--b1', type=float, default=0.5, help='adam: decay of first order momentum of gradient')
parser.add_argument('--b2', type=float, default=0.999, help='adam: decay of first order momentum of gradient')
parser.add_argument('--n_cpu', type=int, default=8, help='number of cpu threads to use during batch generation')
parser.add_argument('--latent_dim', type=int, default=100, help='dimensionality of the latent space')
parser.add_argument('--img_size', type=int, default=64, help='size of each image dimension')
parser.add_argument('--channels', type=int, default=3, help='number of image channels')
parser.add_argument('--sample_interval', type=int, default=200, help='interval betwen image samples')
parser.add_argument('--data_use', type=str, default='bedroom', help='datasets:[mnist]/[bedroom]')
opt, _ = parser.parse_known_args()
if opt.data_use == 'mnist':
opt.img_size = 32
opt.channels = 1
print(opt)
import os, zipfile
from google.colab import files
if opt.data_use == 'bedroom':
os.makedirs('data/bedroom', exist_ok=True)
print('Please upload your kaggle api json.')
files.upload()
! mkdir /root/.kaggle
! mv ./kaggle.json /root/.kaggle
! chmod 600 /root/.kaggle/kaggle.json
! kaggle datasets download -d jhoward/lsun_bedroom
out_fname = 'lsun_bedroom.zip'
zip_ref = zipfile.ZipFile(out_fname)
zip_ref.extractall('./')
zip_ref.close()
os.remove(out_fname)
out_fname = 'sample.zip'
zip_ref = zipfile.ZipFile(out_fname)
zip_ref.extractall('data/bedroom/')
zip_ref.close()
os.remove(out_fname)
else:
os.makedirs('data/mnist', exist_ok=True)
img_shape = (opt.channels, opt.img_size, opt.img_size)
cuda = True if torch.cuda.is_available() else False
def weights_init_normal(m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
torch.nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm2d') != -1:
torch.nn.init.normal_(m.weight.data, 1.0, 0.02)
torch.nn.init.constant_(m.bias.data, 0.0)
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.init_size = opt.img_size // 4
self.l1 = nn.Sequential(nn.Linear(opt.latent_dim, 128*self.init_size**2))
self.conv_blocks = nn.Sequential(
nn.BatchNorm2d(128),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 128, 3, stride=1, padding=1),
nn.BatchNorm2d(128, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 64, 3, stride=1, padding=1),
nn.BatchNorm2d(64, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64, opt.channels, 3, stride=1, padding=1),
nn.Tanh()
)
def forward(self, z):
out = self.l1(z)
out = out.view(out.shape[0], 128, self.init_size, self.init_size)
img = self.conv_blocks(out)
return img
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
def discriminator_block(in_filters, out_filters, bn=True):
block = [ nn.Conv2d(in_filters, out_filters, 3, 2, 1),
nn.LeakyReLU(0.2, inplace=True),
nn.Dropout2d(0.25)]
if bn:
block.append(nn.BatchNorm2d(out_filters, 0.8))
return block
self.model = nn.Sequential(
*discriminator_block(opt.channels, 16, bn=False),
*discriminator_block(16, 32),
*discriminator_block(32, 64),
*discriminator_block(64, 128),
)
# The height and width of downsampled image
ds_size = opt.img_size // 2**4
self.adv_layer = nn.Sequential( nn.Linear(128*ds_size**2, 1),
nn.Sigmoid())
def forward(self, img):
out = self.model(img)
out = out.view(out.shape[0], -1)
validity = self.adv_layer(out)
return validity
class SelfGAN(nn.Module):
def __init__(self):
super(SelfGAN, self).__init__()
# Initialize generator and discriminator
self.generator = Generator()
self.discriminator = Discriminator()
def forward(self, z, real_img, fake_img):
gen_img = self.generator(z)
validity_gen = self.discriminator(gen_img)
validity_real = self.discriminator(real_img)
validity_fake = self.discriminator(fake_img)
return gen_img, validity_gen, validity_real, validity_fake
```
## SelfGAN Part
```
# Loss function
adversarial_loss = torch.nn.BCELoss()
shard_adversarial_loss = torch.nn.BCELoss(reduction='none')
# Initialize SelfGAN model
self_gan = SelfGAN()
if cuda:
self_gan.cuda()
adversarial_loss.cuda()
shard_adversarial_loss.cuda()
# Initialize weights
self_gan.apply(weights_init_normal)
# Configure data loader
dataloader = torch.utils.data.DataLoader(
ImageDataset('data/bedroom',
transforms_=[
transforms.Resize((opt.img_size, opt.img_size)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
]) if opt.data_use == 'bedroom' else
datasets.MNIST('data/mnist', train=True, download=True,
transform=transforms.Compose([
transforms.Resize(opt.img_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])),
batch_size=opt.batch_size, shuffle=True, drop_last=True)
# Optimizers
optimizer = torch.optim.Adam(self_gan.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
last_imgs = Tensor(opt.batch_size, *img_shape)*0.0
```
### Standard performance on the GPU
```
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, imgs in enumerate(dataloader):
if opt.data_use != 'bedroom':
imgs = imgs[0]
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train SelfGAN
# -----------------
optimizer.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs, validity_gen, validity_real, validity_fake = self_gan(z, real_imgs, last_imgs)
# Loss measures generator's ability to fool the discriminator and measure discriminator's ability to classify real from generated samples at the same time
gen_loss = adversarial_loss(validity_gen, valid)
real_loss = adversarial_loss(validity_real, valid)
fake_loss = adversarial_loss(validity_fake, fake)
v_g = 1 - torch.mean(validity_gen)
v_f = torch.mean(validity_fake)
s_loss = (real_loss + v_g*gen_loss*0.1 + v_f*fake_loss*0.9) / 2
s_loss.backward()
optimizer.step()
last_imgs = gen_imgs.detach()
sys.stdout.flush()
print ("\r[Epoch %d/%d] [Batch %d/%d] [S loss: %f R loss: %f F loss: %f G loss: %f]" % (epoch, opt.n_epochs, i, len(dataloader),
s_loss.item(), real_loss.item(), fake_loss.item(), gen_loss.item()),
end='')
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], 'images/%d.png' % batches_done, nrow=5, normalize=True)
```
### Running on the GPU with similar performance of running on the TPU (Maybe)
```
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, imgs in enumerate(dataloader):
if opt.data_use != 'bedroom':
imgs = imgs[0]
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train SelfGAN
# -----------------
optimizer.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
s = opt.batch_size//8
for k in range(8):
# Generate a batch of images
gen_imgs, validity_gen, validity_real, validity_fake = self_gan(z[k*s:k*s+s], real_imgs[k*s:k*s+s], last_imgs[k*s:k*s+s])
# Loss measures generator's ability to fool the discriminator and measure discriminator's ability to classify real from generated samples at the same time
gen_loss = shard_adversarial_loss(validity_gen, valid[k*s:k*s+s])
real_loss = shard_adversarial_loss(validity_real, valid[k*s:k*s+s])
fake_loss = shard_adversarial_loss(validity_fake, fake[k*s:k*s+s])
v_g = 1 - torch.mean(validity_gen)
v_r = 1 - torch.mean(validity_real)
v_f = torch.mean(validity_fake)
v_sum = v_g + v_r + v_f
s_loss = v_r*real_loss/v_sum + v_g*gen_loss/v_sum + v_f*fake_loss/v_sum
gen_loss = torch.mean(gen_loss)
real_loss = torch.mean(real_loss)
fake_loss = torch.mean(fake_loss)
s_loss = torch.mean(s_loss)
s_loss.backward()
last_imgs[k*s:k*s+s] = gen_imgs.detach()
optimizer.step()
sys.stdout.flush()
print ("\r[Epoch %d/%d] [Batch %d/%d] [S loss: %f R loss: %f F loss: %f G loss: %f]" % (epoch, opt.n_epochs, i, len(dataloader),
s_loss.item(), real_loss.item(), fake_loss.item(), gen_loss.item()),
end='')
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(last_imgs.data[:25], 'images/%d.png' % batches_done, nrow=5, normalize=True)
```
## Normal GAN Part
```
# Loss function
adversarial_loss = torch.nn.BCELoss()
# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()
if cuda:
generator.cuda()
discriminator.cuda()
adversarial_loss.cuda()
# Initialize weights
generator.apply(weights_init_normal)
discriminator.apply(weights_init_normal)
# Configure data loader
dataloader = torch.utils.data.DataLoader(
ImageDataset('data/bedroom',
transforms_=[
transforms.Resize((opt.img_size, opt.img_size)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
]) if opt.data_use == 'bedroom' else
datasets.MNIST('data/mnist', train=True, download=True,
transform=transforms.Compose([
transforms.Resize(opt.img_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])),
batch_size=opt.batch_size, shuffle=True)
# Optimizers
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, imgs in enumerate(dataloader):
if opt.data_use != 'bedroom':
imgs = imgs[0]
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs = generator(z)
# Loss measures generator's ability to fool the discriminator
g_loss = adversarial_loss(discriminator(gen_imgs), valid)
g_loss.backward()
optimizer_G.step()
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad()
# Measure discriminator's ability to classify real from generated samples
real_loss = adversarial_loss(discriminator(real_imgs), valid)
fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake)
d_loss = (real_loss + fake_loss) / 2
d_loss.backward()
optimizer_D.step()
sys.stdout.flush()
print ("\r[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]" % (epoch, opt.n_epochs, i, len(dataloader),
d_loss.item(), g_loss.item()),
end='')
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], 'images_normal/%d.png' % batches_done, nrow=5, normalize=True)
```
| true |
code
| 0.781529 | null | null | null | null |
|
# Diagramas de Cortante e Momento em Vigas
Exemplo disponível em https://youtu.be/MNW1-rB46Ig
<img src="viga1.jpg">
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
from matplotlib import rc
# Set the font dictionaries (for plot title and axis titles)
rc('font', **{'family': 'serif', 'serif': ['Computer Modern'],'size': '18'})
rc('text', usetex=True)
q = 10
L = 1
N=10
# Reações de Apoio
VA=3*q*L/4
VB=q*L/4
print("Reação de Apoio em A (kN) =",VA)
print("Reação de Apoio em B (kN) =",VB)
```
Cálculo da Cortante pela integração do carregamento usando a Regra do Trapézio
```
def Cortante(q,x,V0):
# Entro com o carregamento, comprimento do trecho e cortante em x[0]
V = np.zeros(len(x)) # inicializa
dx=x[1] # passo
V[0]=V0 # Valor inicial da cortante
for i in range(1,N):
V[i]=V[i-1]+dx*(q[i-1]+q[i])/2
return np.array(V)
```
Cálculo do Momento Fletor pela integração do carregamento usando a Regra do Trapézio
```
def Momento(V,x,M0):
# Entro com a cortante, comprimento do trecho e momento em x[0]
M = np.zeros(len(x)) # inicializa
dx=x[1] # passo
M[0]=M0 # Valor inicial da cortante
for i in range(1,N):
M[i]=M0+M[i-1]+dx*(V[i-1]+V[i])/2
return np.array(M)
carregamento1 = q*np.ones(N)
carregamento2 =0*np.ones(N)
x1=np.linspace(0,L,N)
x2=np.linspace(L,2*L,N)
# Carregamento
plt.figure(figsize=(15,5))
plt.plot(x1,carregamento1,color='r',linewidth=2)
plt.fill_between(x1,carregamento1, facecolor='b', alpha=0.5)
plt.plot(x2,carregamento2,color='r',linewidth=2)
plt.fill_between(x2,carregamento2, facecolor='b', alpha=0.5)
plt.xlabel("Comprimento (m)")
plt.ylabel("Carregamento (kN/m)")
plt.grid(which='major', axis='both')
plt.title("Carregamento")
plt.show()
# Trecho I - 0<x<L
V1=-q*x1+VA # Cortante Teórica
M1=VA*x1-q*(x1*x1)/2 # Momento Teórico
# por integração numérica
V1int = Cortante(-carregamento1,x1,VA)
M1int = Momento(V1int,x1,0)
# Trecho II - L<x<2L
V2=VA-q*np.ones(N)*L # Cortante Teórico
M2=VA*x2-q*L*(x2-L/2) # Momento Teórico
# por integração numérica
V2int=Cortante(-carregamento2,x2,V1int[N-1])
M2int=Momento(V2int,x2,M1int[N-1])
# Cortante
plt.figure(figsize=(15,5))
plt.plot(x1,V1,color='r',linewidth=2)
plt.fill_between(x1, V1, facecolor='b', alpha=0.5)
plt.plot(x2,V2,color='r',linewidth=2,label="Método das Seções")
plt.fill_between(x2, V2, facecolor='b', alpha=0.5)
plt.plot(x1,V1int,color='k',linestyle = 'dotted', linewidth=5,label="Integração")
plt.plot(x2,V2int,color='k',linestyle = 'dotted', linewidth=5)
plt.legend(loc ="upper right")
plt.xlabel("Comprimento (m)")
plt.ylabel("Cortante (kN)")
plt.grid(which='major', axis='both')
plt.title("Diagrama de Cortante")
plt.show()
# Momento Fletor
plt.figure(figsize=(15,5))
plt.plot(x1,M1,color='r',linewidth=2)
plt.fill_between(x1, M1, facecolor='b', alpha=0.5)
plt.plot(x2,M2,color='r',linewidth=2,label="Método das Seções")
plt.fill_between(x2, M2, facecolor='b', alpha=0.5)
plt.plot(x1,M1int,color='k',linestyle = 'dotted', linewidth=5,label="Integração")
plt.plot(x2,M2int,color='k',linestyle = 'dotted', linewidth=5)
plt.legend(loc ="upper right")
plt.xlabel("Comprimento (m)")
plt.ylabel("Momento (kN.m)")
plt.grid(which='major', axis='both')
plt.title("Diagrama de Momento Fletor")
plt.show()
```
| true |
code
| 0.435841 | null | null | null | null |
|
```
import mxnet as mx
import numpy as np
import random
import bisect
# set up logging
import logging
reload(logging)
logging.basicConfig(format='%(asctime)s %(levelname)s:%(message)s', level=logging.DEBUG, datefmt='%I:%M:%S')
```
# A Glance of LSTM structure and embedding layer
We will build a LSTM network to learn from char only. At each time, input is a char. We will see this LSTM is able to learn words and grammers from sequence of chars.
The following figure is showing an unrolled LSTM network, and how we generate embedding of a char. The one-hot to embedding operation is a special case of fully connected network.
<img src="http://data.dmlc.ml/mxnet/data/char-rnn_1.png">
<img src="http://data.dmlc.ml/mxnet/data/char-rnn_2.png">
```
from lstm import lstm_unroll, lstm_inference_symbol
from bucket_io import BucketSentenceIter
from rnn_model import LSTMInferenceModel
# Read from doc
def read_content(path):
with open(path) as ins:
content = ins.read()
return content
# Build a vocabulary of what char we have in the content
def build_vocab(path):
content = read_content(path)
content = list(content)
idx = 1 # 0 is left for zero-padding
the_vocab = {}
for word in content:
if len(word) == 0:
continue
if not word in the_vocab:
the_vocab[word] = idx
idx += 1
return the_vocab
# We will assign each char with a special numerical id
def text2id(sentence, the_vocab):
words = list(sentence)
words = [the_vocab[w] for w in words if len(w) > 0]
return words
# Evaluation
def Perplexity(label, pred):
label = label.T.reshape((-1,))
loss = 0.
for i in range(pred.shape[0]):
loss += -np.log(max(1e-10, pred[i][int(label[i])]))
return np.exp(loss / label.size)
```
# Get Data
```
import os
data_url = "http://data.dmlc.ml/mxnet/data/lab_data.zip"
os.system("wget %s" % data_url)
os.system("unzip -o lab_data.zip")
```
Sample training data:
```
all to Renewal Keynote Address Call to Renewal Pt 1Call to Renewal Part 2 TOPIC: Our Past, Our Future & Vision for America June
28, 2006 Call to Renewal' Keynote Address Complete Text Good morning. I appreciate the opportunity to speak here at the Call to R
enewal's Building a Covenant for a New America conference. I've had the opportunity to take a look at your Covenant for a New Ame
rica. It is filled with outstanding policies and prescriptions for much of what ails this country. So I'd like to congratulate yo
u all on the thoughtful presentations you've given so far about poverty and justice in America, and for putting fire under the fe
et of the political leadership here in Washington.But today I'd like to talk about the connection between religion and politics a
nd perhaps offer some thoughts about how we can sort through some of the often bitter arguments that we've been seeing over the l
ast several years.I do so because, as you all know, we can affirm the importance of poverty in the Bible; and we can raise up and
pass out this Covenant for a New America. We can talk to the press, and we can discuss the religious call to address poverty and
environmental stewardship all we want, but it won't have an impact unless we tackle head-on the mutual suspicion that sometimes
```
# LSTM Hyperparameters
```
# The batch size for training
batch_size = 32
# We can support various length input
# For this problem, we cut each input sentence to length of 129
# So we only need fix length bucket
buckets = [129]
# hidden unit in LSTM cell
num_hidden = 512
# embedding dimension, which is, map a char to a 256 dim vector
num_embed = 256
# number of lstm layer
num_lstm_layer = 3
# we will show a quick demo in 2 epoch
# and we will see result by training 75 epoch
num_epoch = 2
# learning rate
learning_rate = 0.01
# we will use pure sgd without momentum
momentum = 0.0
# we can select multi-gpu for training
# for this demo we only use one
devs = [mx.context.gpu(i) for i in range(1)]
# build char vocabluary from input
vocab = build_vocab("./obama.txt")
# generate symbol for a length
def sym_gen(seq_len):
return lstm_unroll(num_lstm_layer, seq_len, len(vocab) + 1,
num_hidden=num_hidden, num_embed=num_embed,
num_label=len(vocab) + 1, dropout=0.2)
# initalize states for LSTM
init_c = [('l%d_init_c'%l, (batch_size, num_hidden)) for l in range(num_lstm_layer)]
init_h = [('l%d_init_h'%l, (batch_size, num_hidden)) for l in range(num_lstm_layer)]
init_states = init_c + init_h
# we can build an iterator for text
data_train = BucketSentenceIter("./obama.txt", vocab, buckets, batch_size,
init_states, seperate_char='\n',
text2id=text2id, read_content=read_content)
# the network symbol
symbol = sym_gen(buckets[0])
```
# Train model
```
# Train a LSTM network as simple as feedforward network
model = mx.model.FeedForward(ctx=devs,
symbol=symbol,
num_epoch=num_epoch,
learning_rate=learning_rate,
momentum=momentum,
wd=0.0001,
initializer=mx.init.Xavier(factor_type="in", magnitude=2.34))
# Fit it
model.fit(X=data_train,
eval_metric = mx.metric.np(Perplexity),
batch_end_callback=mx.callback.Speedometer(batch_size, 50),
epoch_end_callback=mx.callback.do_checkpoint("obama"))
```
# Inference from model
```
# helper strcuture for prediction
def MakeRevertVocab(vocab):
dic = {}
for k, v in vocab.items():
dic[v] = k
return dic
# make input from char
def MakeInput(char, vocab, arr):
idx = vocab[char]
tmp = np.zeros((1,))
tmp[0] = idx
arr[:] = tmp
# helper function for random sample
def _cdf(weights):
total = sum(weights)
result = []
cumsum = 0
for w in weights:
cumsum += w
result.append(cumsum / total)
return result
def _choice(population, weights):
assert len(population) == len(weights)
cdf_vals = _cdf(weights)
x = random.random()
idx = bisect.bisect(cdf_vals, x)
return population[idx]
# we can use random output or fixed output by choosing largest probability
def MakeOutput(prob, vocab, sample=False, temperature=1.):
if sample == False:
idx = np.argmax(prob, axis=1)[0]
else:
fix_dict = [""] + [vocab[i] for i in range(1, len(vocab) + 1)]
scale_prob = np.clip(prob, 1e-6, 1 - 1e-6)
rescale = np.exp(np.log(scale_prob) / temperature)
rescale[:] /= rescale.sum()
return _choice(fix_dict, rescale[0, :])
try:
char = vocab[idx]
except:
char = ''
return char
# load from check-point
_, arg_params, __ = mx.model.load_checkpoint("obama", 75)
# build an inference model
model = LSTMInferenceModel(num_lstm_layer, len(vocab) + 1,
num_hidden=num_hidden, num_embed=num_embed,
num_label=len(vocab) + 1, arg_params=arg_params, ctx=mx.gpu(), dropout=0.2)
# generate a sequence of 1200 chars
seq_length = 1200
input_ndarray = mx.nd.zeros((1,))
revert_vocab = MakeRevertVocab(vocab)
# Feel free to change the starter sentence
output ='The joke'
random_sample = True
new_sentence = True
ignore_length = len(output)
for i in range(seq_length):
if i <= ignore_length - 1:
MakeInput(output[i], vocab, input_ndarray)
else:
MakeInput(output[-1], vocab, input_ndarray)
prob = model.forward(input_ndarray, new_sentence)
new_sentence = False
next_char = MakeOutput(prob, revert_vocab, random_sample)
if next_char == '':
new_sentence = True
if i >= ignore_length - 1:
output += next_char
# Let's see what we can learned from char in Obama's speech.
print(output)
```
| true |
code
| 0.443781 | null | null | null | null |
|
This notebook is designed to run in a IBM Watson Studio default runtime (NOT the Watson Studio Apache Spark Runtime as the default runtime with 1 vCPU is free of charge). Therefore, we install Apache Spark in local mode for test purposes only. Please don't use it in production.
In case you are facing issues, please read the following two documents first:
https://github.com/IBM/skillsnetwork/wiki/Environment-Setup
https://github.com/IBM/skillsnetwork/wiki/FAQ
Then, please feel free to ask:
https://coursera.org/learn/machine-learning-big-data-apache-spark/discussions/all
Please make sure to follow the guidelines before asking a question:
https://github.com/IBM/skillsnetwork/wiki/FAQ#im-feeling-lost-and-confused-please-help-me
If running outside Watson Studio, this should work as well. In case you are running in an Apache Spark context outside Watson Studio, please remove the Apache Spark setup in the first notebook cells.
```
from IPython.display import Markdown, display
def printmd(string):
display(Markdown('# <span style="color:red">'+string+'</span>'))
if ('sc' in locals() or 'sc' in globals()):
printmd('<<<<<!!!!! It seems that you are running in a IBM Watson Studio Apache Spark Notebook. Please run it in an IBM Watson Studio Default Runtime (without Apache Spark) !!!!!>>>>>')
!pip install pyspark==2.4.5
try:
from pyspark import SparkContext, SparkConf
from pyspark.sql import SparkSession
except ImportError as e:
printmd('<<<<<!!!!! Please restart your kernel after installing Apache Spark !!!!!>>>>>')
sc = SparkContext.getOrCreate(SparkConf().setMaster("local[*]"))
spark = SparkSession \
.builder \
.getOrCreate()
```
# Exercise 3.2
Welcome to the last exercise of this course. This is also the most advanced one because it somehow glues everything together you've learned.
These are the steps you will do:
- load a data frame from cloudant/ApacheCouchDB
- perform feature transformation by calculating minimal and maximal values of different properties on time windows (we'll explain what a time windows is later in here)
- reduce these now twelve dimensions to three using the PCA (Principal Component Analysis) algorithm of SparkML (Spark Machine Learning) => We'll actually make use of SparkML a lot more in the next course
- plot the dimensionality reduced data set
Now it is time to grab a PARQUET file and create a dataframe out of it. Using SparkSQL you can handle it like a database.
```
!wget https://github.com/IBM/coursera/blob/master/coursera_ds/washing.parquet?raw=true
!mv washing.parquet?raw=true washing.parquet
df = spark.read.parquet('washing.parquet')
df.createOrReplaceTempView('washing')
df.show()
```
This is the feature transformation part of this exercise. Since our table is mixing schemas from different sensor data sources we are creating new features. In other word we use existing columns to calculate new ones. We only use min and max for now, but using more advanced aggregations as we've learned in week three may improve the results. We are calculating those aggregations over a sliding window "w". This window is defined in the SQL statement and basically reads the table by a one by one stride in direction of increasing timestamp. Whenever a row leaves the window a new one is included. Therefore this window is called sliding window (in contrast to tubling, time or count windows). More on this can be found here: https://flink.apache.org/news/2015/12/04/Introducing-windows.html
```
result = spark.sql("""
SELECT * from (
SELECT
min(temperature) over w as min_temperature,
max(temperature) over w as max_temperature,
min(voltage) over w as min_voltage,
max(voltage) over w as max_voltage,
min(flowrate) over w as min_flowrate,
max(flowrate) over w as max_flowrate,
min(frequency) over w as min_frequency,
max(frequency) over w as max_frequency,
min(hardness) over w as min_hardness,
max(hardness) over w as max_hardness,
min(speed) over w as min_speed,
max(speed) over w as max_speed
FROM washing
WINDOW w AS (ORDER BY ts ROWS BETWEEN CURRENT ROW AND 10 FOLLOWING)
)
WHERE min_temperature is not null
AND max_temperature is not null
AND min_voltage is not null
AND max_voltage is not null
AND min_flowrate is not null
AND max_flowrate is not null
AND min_frequency is not null
AND max_frequency is not null
AND min_hardness is not null
AND min_speed is not null
AND max_speed is not null
""")
```
Since this table contains null values also our window might contain them. In case for a certain feature all values in that window are null we obtain also null. As we can see here (in my dataset) this is the case for 9 rows.
```
df.count()-result.count()
```
Now we import some classes from SparkML. PCA for the actual algorithm. Vectors for the data structure expected by PCA and VectorAssembler to transform data into these vector structures.
```
from pyspark.ml.feature import PCA
from pyspark.ml.linalg import Vectors
from pyspark.ml.feature import VectorAssembler
```
Let's define a vector transformation helper class which takes all our input features (result.columns) and created one additional column called "features" which contains all our input features as one single column wrapped in "DenseVector" objects
```
assembler = VectorAssembler(inputCols=result.columns, outputCol="features") ###columns of n features into a column of n_d row vector
```
Now we actually transform the data, note that this is highly optimized code and runs really fast in contrast if we had implemented it.
```
features = assembler.transform(result)
```
Let's have a look at how this new additional column "features" looks like:
```
features.rdd.map(lambda r : r.features).take(10)
```
Since the source data set has been prepared as a list of DenseVectors we can now apply PCA. Note that the first line again only prepares the algorithm by finding the transformation matrices (fit method)
```
pca = PCA(k=3, inputCol="features", outputCol="pcaFeatures") ###computes the transformation matrix
model = pca.fit(features)
```
Now we can actually transform the data. Let's have a look at the first 20 rows
```
result_pca = model.transform(features).select("pcaFeatures") ###performs the transformation
result_pca.show(truncate=False)
```
So we obtained three completely new columns which we can plot now. Let run a final check if the number of rows is the same.
```
result_pca.count()
```
Cool, this works as expected. Now we obtain a sample and read each of the three columns into a python list
```
rdd = result_pca.rdd.sample(False,0.8)
x = rdd.map(lambda a : a.pcaFeatures).map(lambda a : a[0]).collect()
y = rdd.map(lambda a : a.pcaFeatures).map(lambda a : a[1]).collect()
z = rdd.map(lambda a : a.pcaFeatures).map(lambda a : a[2]).collect()
```
Finally we plot the three lists and name each of them as dimension 1-3 in the plot
```
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x,y,z, c='r', marker='o')
ax.set_xlabel('dimension1')
ax.set_ylabel('dimension2')
ax.set_zlabel('dimension3')
plt.show()
```
Congratulations, we are done! We can see two clusters in the data set. We can also see a third cluster which either can be outliers or a real cluster. In the next course we will actually learn how to compute clusters automatically. For now we know that the data indicates that there are two semi-stable states of the machine and sometime we see some anomalies since those data points don't fit into one of the two clusters.
| true |
code
| 0.519582 | null | null | null | null |
|
# Dowloading data
We'll use a shell command to download the zipped data, unzip it into are working directory (folder).
```
!wget "https://docs.google.com/uc?export=download&id=1h3YjfecYS8vJ4yXKE3oBwg3Am64kN4-x" -O temp.zip && unzip -o temp.zip && rm temp.zip
```
# Importing and Cleaning the Data
```
import pandas as pd # aliasing for convenience
```
## Importing data one file at a time
### Importing 2015 data
```
df = pd.read_csv('happiness_report/2015.csv') # loading the data to a variable called "df"
df.head(3) # looking at the first 3 rows
df.tail(2) # looking at the last 2 rows
```
#### adding a year column
To add a column we can use the syntax:
`df['new_col_name'] = values`
**note**: if there was a column with the same name, it would be overwritten
```
df['year'] = 2015 # adding a column
df
```
### Importing 2016 data
```
df_2016 = pd.read_csv('happiness_report/2016.csv')
df_2016['year'] = 2016
```
### merging (stacking vertically) the two dataframes
**note** if a column exists in one dataframe but not in the other, the values for the latter will be set to NaN (empty value)
```
list_of_df_to_merge = [df, df_2016]
df_merged = pd.concat(list_of_df_to_merge)
df_merged
```
## Interaction with the filesystem
```
# python library for OperatingSystem interaction
import os
# list of files under the speficied folder
os.listdir('happiness_report')
# getting the full path given the folder and file
os.path.join('happiness_report','2019.csv')
```
## Loading and combining data from all files
We will:
- initialise an empty list of dataframes
- loop over the content of the `happiness_report` folder
- get the filepath from the filename and folder name
- load the data from the filepath
- add a column to the dataframe so we can keep track of which file the data belongs to
- add the dataframe to the list
- merge all the dataframes (vertically)
```
fld_name = 'happiness_report'
df_list = []
for filename in os.listdir(fld_name):
filepath = os.path.join(fld_name, filename)
df = pd.read_csv(filepath)
print(filename, ':', df.columns) # printing the column name for the file
df['filename'] = filename
df_list.append(df)
df_merged = pd.concat(df_list)
```
## Data cleaning
Because of inconsistency over the years of reporting, we need to do some data cleaning:
- we want a `year` column which we can get from the filename
- there are different naming for the Happiness score over the years: `Happiness Score`, `Happiness.Score`, `Score`. We want to unify them into one column.
- the country column has the same issue: `Country`, `Country or region`
```
# `filename` column is a text (string) column, so we can use string methods to edit it
column_of_string_pairs = df_merged['filename'].str.split('.') # '2015.csv' is now ['2015', 'csv']
# selecting only the fist element for each list
column_year_string = column_of_string_pairs.str[0] # ['2015', 'csv'] is now '2015'
# converting the string to an integer (number)
column_of_years = (column_year_string).astype(int) # '2015' (string) is now 2015 (number)
df_merged['year'] = column_of_years
```
To fix the issue of change in naming, we can use:
`colA.fillna(colB)`
which checks if there are any empty valus in `colA` and fills them with the values in `colB` for the same row.
```
# checks if there are any empty valus in colA and fills them with the values in colB for the same row
df_merged['Happiness Score'] = df_merged['Happiness Score'].fillna(df_merged['Happiness.Score']).fillna(df_merged['Score'])
df_merged['Country'] = df_merged['Country or region'].fillna(df_merged['Country'])
```
## Data Reshaping and Plotting
### Trends of Happiness and Generosity over the years
We'll:
- select only the columns we care about
- group the data by `year` and take the mean
- plot the Happiness and Generosity (in separate plots)
```
df_subset = df_merged[['year', 'Happiness Score', 'Generosity']]
mean_by_year = df_subset.groupby('year').mean()
mean_by_year
mean_by_year.plot(subplots=True, grid=True)
# `subplots=True` will plot the two columns in two separate charts
# `grid=True` will add the axis grid in the background
```
### Average Generosity and Happiness by year AND Country
We'll:
- select only the columns we care about
- group the data by `Country` and `year`
- take the mean
```
df = df_merged[['year', 'Happiness Score', 'Generosity', 'Country']]
mean_by_country_and_year = df.groupby(['Country', 'year']).mean()
mean_by_country_and_year
```
#### Finding the countries and years with highest and lowest Happiness
```
mean_by_country_and_year['Happiness Score'].idxmax() # highest
mean_by_country_and_year['Happiness Score'].idxmin() # lowest
```
#### Happiness by Country and Year
```
happiness_column = mean_by_country_and_year['Happiness Score']
# turning the single column with 2d-index into a table by moving the inner index to columns
happiness_table = happiness_column.unstack()
happiness_table
# for each year, plotting the values in each country
happiness_table.plot(figsize=(20,5),grid=True)
```
# (FYI) Interactive Chart
You can also create interactive charts by using a different library (bokeh).
for more examples: https://colab.research.google.com/notebooks/charts.ipynb
```
uk_happiness = happiness_column['United Kingdom']
from bokeh.plotting import figure, output_notebook, show
output_notebook()
x = uk_happiness.index
y = uk_happiness.values
fig = figure(title="UK Happiness", x_axis_label='x', y_axis_label='y')
fig.line(x, y, legend_label="UK", line_width=2)
show(fig)
```
| true |
code
| 0.606644 | null | null | null | null |
|
# Rejection Sampling
Rejection sampling, or "accept-reject Monte Carlo" is a Monte Carlo method used to generate obsrvations from distributions. As it is a Monte Carlo it can also be used for numerical integration.
## Monte Carlo Integration
### Example: Approximation of $\pi$
Enclose a quadrant of a circle of radius $1$ in a square of side length $1$. Then uniformly sample points inside the bounds of the square in Cartesian coordinates. If the point lies inside the circle quadrant record this information. At the ends of many throws the ratio of points inside the circle to all points thrown will approximate the ratio of the area of the cricle quadrant to the area of the square
$$
\frac{\text{points inside circle}}{\text{all points thrown}} \approx \frac{\text{area of circle quadrant}}{\text{area of square}} = \frac{\pi r^2}{4\, l^2} = \frac{\pi}{4},
$$
thus, an approximation of $\pi$ can be found to be
$$
\pi \approx 4 \cdot \frac{\text{points inside circle}}{\text{all points thrown}}.
$$
```
import numpy as np
import matplotlib.pyplot as plt
def approximate_pi(n_throws=10000, draw=True):
n_circle_points = 0
x_coord = np.random.uniform(0, 1, n_throws)
y_coord = np.random.uniform(0, 1, n_throws)
circle_x = []
circle_y = []
outside_x = []
outside_y = []
for x, y in zip(x_coord, y_coord):
radius = np.sqrt(x ** 2 + y ** 2)
if 1 > radius:
n_circle_points += 1
circle_x.append(x)
circle_y.append(y)
else:
outside_x.append(x)
outside_y.append(y)
approx_pi = 4 * (n_circle_points / n_throws)
print(f"The approximation of pi after {n_throws} throws is: {approx_pi}")
if draw:
plt.plot(circle_x, circle_y, "ro")
plt.plot(outside_x, outside_y, "bo")
plt.xlabel(r"$x$")
plt.ylabel(r"$y$")
plt.show()
approximate_pi()
```
## Sampling Distributions
To approximate a statistical distribution one can also use accept-reject Monte Carlo to approximate the distribution.
### Example: Approximation of Gaussian Distribution
```
import scipy.stats as stats
```
The Gaussian has a known analytic form
$$
f\left(\vec{x}\,\middle|\,\mu, \sigma\right) = \frac{1}{\sqrt{2\pi}\, \sigma} e^{-\left(x-\mu\right)^2/2\sigma^2}
$$
```
x = np.linspace(-5.0, 5.0, num=10000)
plt.plot(x, stats.norm.pdf(x, 0, 1), linewidth=2, color="black")
# Axes
# plt.title('Plot of $f(x;\mu,\sigma)$')
plt.xlabel(r"$x$")
plt.ylabel(r"$f(\vec{x}|\mu,\sigma)$")
# dist_window_w = sigma * 2
plt.xlim([-5, 5])
plt.show()
```
Given this it is seen that the Gaussian's maximum is at its mean. For the standard Gaussian this is at $\mu = 0$, and so it has a maximum at $1/\sqrt{2\pi}\,\sigma \approx 0.39$. Thus, this can be the maximum height of a rectangle that we need to throw our points in.
```
def approximate_Guassian(n_throws=10000, x_range=[-5, 5], draw=True):
n_accept = 0
x_coord = np.random.uniform(x_range[0], x_range[1], n_throws)
y_coord = np.random.uniform(0, stats.norm.pdf(0, 0, 1), n_throws)
# Use Freedman–Diaconis rule
# https://en.wikipedia.org/wiki/Freedman%E2%80%93Diaconis_rule
h = 2 * stats.iqr(x_coord) / np.cbrt([n_throws])
n_bins = int((x_range[1] - x_range[0]) / h)
accept_x = []
accept_y = []
reject_x = []
reject_y = []
for x, y in zip(x_coord, y_coord):
if stats.norm.pdf(x, 0, 1) > y:
n_accept += 1
accept_x.append(x)
accept_y.append(y)
else:
reject_x.append(x)
reject_y.append(y)
if draw:
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(1.2 * 14, 1.2 * 4.5))
x_space = np.linspace(x_range[0], x_range[1], num=10000)
axes[0].plot(accept_x, accept_y, "ro")
axes[0].plot(reject_x, reject_y, "bo")
axes[0].plot(x_space, stats.norm.pdf(x_space, 0, 1), linewidth=2, color="black")
axes[0].set_xlabel(r"$x$")
axes[0].set_ylabel(r"$y$")
axes[0].set_title(r"Sampled space of $f(\vec{x}|\mu,\sigma)$")
hist_count, bins, _ = axes[1].hist(accept_x, n_bins, density=True)
axes[1].set_xlabel(r"$x$")
axes[1].set_ylabel("Arbitrary normalized units")
axes[1].set_title(r"Normalized binned distribution of accepted toys")
plt.xlim(x_range)
plt.show()
approximate_Guassian()
```
This exercise is trivial but for more complex functional forms with more difficult integrals it can be a powerful numerical technique.
| true |
code
| 0.631992 | null | null | null | null |
|
# Simple training tutorial
The objective of this tutorial is to show you the basics of the library and how it can be used to simplify the audio processing pipeline.
This page is generated from the corresponding jupyter notebook, that can be found on [this folder](https://github.com/fastaudio/fastaudio/tree/master/docs)
To install the library, uncomment and run this cell:
```
# !pip install git+https://github.com/fastaudio/fastaudio.git
```
**COLAB USERS: Before you continue and import the lib, go to the `Runtime` menu and select `Restart Runtime`.**
```
from fastai.vision.all import *
from fastaudio.core.all import *
from fastaudio.augment.all import *
```
# ESC-50: Dataset for Environmental Sound Classification
```
#The first time this will download a dataset that is ~650mb
path = untar_data(URLs.ESC50, dest="ESC50")
```
The audio files are inside a subfolder `audio/`
```
(path/"audio").ls()
```
And there's another folder `meta/` with some metadata about all the files and the labels
```
(path/"meta").ls()
```
Opening the metadata file
```
df = pd.read_csv(path/"meta"/"esc50.csv")
df.head()
```
## Datablock and Basic End to End Training
```
# Helper function to split the data
def CrossValidationSplitter(col='fold', fold=1):
"Split `items` (supposed to be a dataframe) by fold in `col`"
def _inner(o):
assert isinstance(o, pd.DataFrame), "ColSplitter only works when your items are a pandas DataFrame"
col_values = o.iloc[:,col] if isinstance(col, int) else o[col]
valid_idx = (col_values == fold).values.astype('bool')
return IndexSplitter(mask2idxs(valid_idx))(o)
return _inner
```
Creating the Audio to Spectrogram transform from a predefined config.
```
cfg = AudioConfig.BasicMelSpectrogram(n_fft=512)
a2s = AudioToSpec.from_cfg(cfg)
```
Creating the Datablock
```
auds = DataBlock(blocks=(AudioBlock, CategoryBlock),
get_x=ColReader("filename", pref=path/"audio"),
splitter=CrossValidationSplitter(fold=1),
batch_tfms = [a2s],
get_y=ColReader("category"))
dbunch = auds.dataloaders(df, bs=64)
```
Visualizing one batch of data. Notice that the title of each Spectrogram is the corresponding label.
```
dbunch.show_batch(figsize=(10, 5))
```
# Learner and Training
While creating the learner, we need to pass a special cnn_config to indicate that our input spectrograms only have one channel. Besides that, it's the usual vision learner.
```
learn = cnn_learner(dbunch,
resnet18,
config={"n_in":1}, #<- Only audio specific modification here
loss_func=CrossEntropyLossFlat(),
metrics=[accuracy])
from fastaudio.ci import skip_if_ci
@skip_if_ci
def learn():
learn.fine_tune(10)
```
| true |
code
| 0.692967 | null | null | null | null |
|
<h3 align=center> Combining Datasets: Merge and Join</h3>
One essential feature offered by Pandas is its high-performance, in-memory join and merge operations.
If you have ever worked with databases, you should be familiar with this type of data interaction.
The main interface for this is the ``pd.merge`` function, and we'll see few examples of how this can work in practice.
For convenience, we will start by redefining the ``display()`` functionality from the previous section:
```
import pandas as pd
import numpy as np
class display(object):
"""Display HTML representation of multiple objects"""
template = """<div style="float: left; padding: 10px;">
<p style='font-family:"Courier New", Courier, monospace'>{0}</p>{1}
</div>"""
def __init__(self, *args):
self.args = args
def _repr_html_(self):
return '\n'.join(self.template.format(a, eval(a)._repr_html_())
for a in self.args)
def __repr__(self):
return '\n\n'.join(a + '\n' + repr(eval(a))
for a in self.args)
```
## Relational Algebra
The behavior implemented in ``pd.merge()`` is a subset of what is known as *relational algebra*, which is a formal set of rules for manipulating relational data, and forms the conceptual foundation of operations available in most databases.
The strength of the relational algebra approach is that it proposes several primitive operations, which become the building blocks of more complicated operations on any dataset.
With this lexicon of fundamental operations implemented efficiently in a database or other program, a wide range of fairly complicated composite operations can be performed.
Pandas implements several of these fundamental building-blocks in the ``pd.merge()`` function and the related ``join()`` method of ``Series`` and ``Dataframe``s.
As we will see, these let you efficiently link data from different sources.
## Categories of Joins
The ``pd.merge()`` function implements a number of types of joins: the
1. *one-to-one*,
2. *many-to-one*, and
3. *many-to-many* joins.
All three types of joins are accessed via an identical call to the ``pd.merge()`` interface; the type of join performed depends on the form of the input data.
Here we will show simple examples of the three types of merges, and discuss detailed options further below.
### One-to-one joins
Perhaps the simplest type of merge expresion is the one-to-one join, which is in many ways very similar to the column-wise concatenation seen in [Combining Datasets: Concat & Append](03.06-Concat-And-Append.ipynb).
As a concrete example, consider the following two ``DataFrames`` which contain information on several employees in a company:
```
df1 = pd.DataFrame({'employee': ['Raju', 'Rani', 'Ramesh', 'Ram'],
'group': ['Accounting', 'Engineering', 'Engineering', 'HR']})
df2 = pd.DataFrame({'employee': ['Raju', 'Rani', 'Ramesh', 'Ram'],
'hire_date': [2004, 2008, 2012, 2014]})
display('df1', 'df2','pd.merge(df1, df2)')
```
To combine this information into a single ``DataFrame``, we can use the ``pd.merge()`` function:
```
df3 = pd.merge(df1, df2)
df3
```
The ``pd.merge()`` function recognizes that each ``DataFrame`` has an "employee" column, and automatically joins using this column as a key.
The result of the merge is a new ``DataFrame`` that combines the information from the two inputs.
Notice that the order of entries in each column is not necessarily maintained: in this case, the order of the "employee" column differs between ``df1`` and ``df2``, and the ``pd.merge()`` function correctly accounts for this.
Additionally, keep in mind that the merge in general discards the index, except in the special case of merges by index (see the ``left_index`` and ``right_index`` keywords, discussed momentarily).
### Many-to-one joins
Many-to-one joins are joins in which one of the two key columns contains duplicate entries.
For the many-to-one case, the resulting ``DataFrame`` will preserve those duplicate entries as appropriate.
Consider the following example of a many-to-one join:
```
df4 = pd.DataFrame({'group': ['Accounting', 'Engineering', 'HR'],
'supervisor': ['Carly', 'Guido', 'Steve']})
df4
pd.merge(df3, df4)
display('df3', 'df4', 'pd.merge(df3, df4)')
```
The resulting ``DataFrame`` has an aditional column with the "supervisor" information, where the information is repeated in one or more locations as required by the inputs.
### Many-to-many joins
Many-to-many joins are a bit confusing conceptually, but are nevertheless well defined.
If the key column in both the left and right array contains duplicates, then the result is a many-to-many merge.
This will be perhaps most clear with a concrete example.
Consider the following, where we have a ``DataFrame`` showing one or more skills associated with a particular group.
By performing a many-to-many join, we can recover the skills associated with any individual person:
```
df5 = pd.DataFrame({'group': ['Accounting', 'Accounting',
'Engineering', 'Engineering', 'HR', 'Hdf4'],
'skills': ['math', 'spreadsheets', 'coding', 'linux',
'spreadsheets', 'organization']})
df5
display('df1', 'df5', "pd.merge(df1, df5)")
pd.merge(df1, df5)
```
These three types of joins can be used with other Pandas tools to implement a wide array of functionality.
But in practice, datasets are rarely as clean as the one we're working with here.
In the following section we'll consider some of the options provided by ``pd.merge()`` that enable you to tune how the join operations work.
## Specification of the Merge Key
We've already seen the default behavior of ``pd.merge()``: it looks for one or more matching column names between the two inputs, and uses this as the key.
However, often the column names will not match so nicely, and ``pd.merge()`` provides a variety of options for handling this.
### The ``on`` keyword
Most simply, you can explicitly specify the name of the key column using the ``on`` keyword, which takes a column name or a list of column names:
```
display('df1', 'df2', "pd.merge(df1, df2, on='employee')")
pd.merge(df1, df2, on='employee')
```
This option works only if both the left and right ``DataFrame``s have the specified column name.
### The ``left_on`` and ``right_on`` keywords
At times you may wish to merge two datasets with different column names; for example, we may have a dataset in which the employee name is labeled as "name" rather than "employee".
In this case, we can use the ``left_on`` and ``right_on`` keywords to specify the two column names:
```
df3 = pd.DataFrame({'name': ['Raju', 'Rani', 'Ramesh', 'Ram'],
'salary': [70000, 80000, 120000, 90000]})
display('df1', 'df3', 'pd.merge(df1, df3, left_on="employee", right_on="name")')
```
The result has a redundant column that we can drop if desired–for example, by using the ``drop()`` method of ``DataFrame``s:
```
pd.merge(df1, df3, left_on="employee", right_on="name").drop('name', axis=1) #Duplicat Col
```
### The ``left_index`` and ``right_index`` keywords
Sometimes, rather than merging on a column, you would instead like to merge on an index.
For example, your data might look like this:
```
df1a = df1.set_index('employee')
df2a = df2.set_index('employee')
display('df1a', 'df2a')
```
You can use the index as the key for merging by specifying the ``left_index`` and/or ``right_index`` flags in ``pd.merge()``:
```
display('df1a', 'df2a',
"pd.merge(df1a, df2a, left_index=True, right_index=True)")
pd.merge(df1a, df2a, left_index=True, right_index=True)
```
For convenience, ``DataFrame``s implement the ``join()`` method, which performs a merge that defaults to joining on indices:
```
display('df1a', 'df2a', 'df1a.join(df2a)')
```
If you'd like to mix indices and columns, you can combine ``left_index`` with ``right_on`` or ``left_on`` with ``right_index`` to get the desired behavior:
```
display('df1a', 'df3', "pd.merge(df1a, df3, left_index=True, right_on='name')")
```
All of these options also work with multiple indices and/or multiple columns; the interface for this behavior is very intuitive.
For more information on this, see the ["Merge, Join, and Concatenate" section](http://pandas.pydata.org/pandas-docs/stable/merging.html) of the Pandas documentation.
## Specifying Set Arithmetic for Joins
In all the preceding examples we have glossed over one important consideration in performing a join: the type of set arithmetic used in the join.
This comes up when a value appears in one key column but not the other. Consider this example:
```
df6 = pd.DataFrame({'name': ['Peter', 'Paul', 'Mary'],
'food': ['fish', 'beans', 'bread']},
columns=['name', 'food'])
df7 = pd.DataFrame({'name': ['Mary', 'Joseph','Paul'],
'drink': ['wine', 'beer','Water']},
columns=['name', 'drink'])
display('df6', 'df7', 'pd.merge(df6, df7)')
```
Here we have merged two datasets that have only a single "name" entry in common: Mary.
By default, the result contains the *intersection* of the two sets of inputs; this is what is known as an *inner join*.
We can specify this explicitly using the ``how`` keyword, which defaults to ``"inner"``:
```
pd.merge(df6, df7, how='inner') # by Defautl inner to join the data
pd.merge(df6, df7, how='outer')
```
Other options for the ``how`` keyword are ``'outer'``, ``'left'``, and ``'right'``.
An *outer join* returns a join over the union of the input columns, and fills in all missing values with NAs:
```
display('df6', 'df7', "pd.merge(df6, df7, how='outer')")
```
The *left join* and *right join* return joins over the left entries and right entries, respectively.
For example:
```
display('df6', 'df7', "pd.merge(df6, df7, how='left')")
display('df6', 'df7', "pd.merge(df6, df7, how='right')")
```
The output rows now correspond to the entries in the left input. Using
``how='right'`` works in a similar manner.
All of these options can be applied straightforwardly to any of the preceding join types.
## Overlapping Column Names: The ``suffixes`` Keyword
Finally, you may end up in a case where your two input ``DataFrame``s have conflicting column names.
Consider this example:
```
df8 = pd.DataFrame({'name': ['Bob', 'Jake', 'Lisa', 'Sue'],
'rank': [1, 2, 3, 4]})
df9 = pd.DataFrame({'name': ['Bob', 'Jake', 'Lisa', 'Sue'],
'rank': [3, 1, 4, 2]})
display('df8', 'df9', 'pd.merge(df8, df9, on="name")')
```
Because the output would have two conflicting column names, the merge function automatically appends a suffix ``_x`` or ``_y`` to make the output columns unique.
If these defaults are inappropriate, it is possible to specify a custom suffix using the ``suffixes`` keyword:
```
display('df8', 'df9', 'pd.merge(df8, df9, on="name", suffixes=["_L", "_R"])')
```
These suffixes work in any of the possible join patterns, and work also if there are multiple overlapping columns.
For more information on these patterns, see [Aggregation and Grouping](03.08-Aggregation-and-Grouping.ipynb) where we dive a bit deeper into relational algebra.
Also see the [Pandas "Merge, Join and Concatenate" documentation](http://pandas.pydata.org/pandas-docs/stable/merging.html) for further discussion of these topics.
## Example: US States Data
Merge and join operations come up most often when combining data from different sources.
Here we will consider an example of some data about US states and their populations.
The data files can be found at [DataSet](https://github.com/reddyprasade/Data-Sets-For-Machine-Learnig-and-Data-Science/tree/master/DataSets)
Let's take a look at the three datasets, using the Pandas ``read_csv()`` function:
```
pop = pd.read_csv('data/state-population.csv')
areas = pd.read_csv('data/state-areas.csv')
abbrevs = pd.read_csv('data/state-abbrevs.csv')
display('pop.head()', 'areas.head()', 'abbrevs.head()')
pop.shape,areas.shape,abbrevs.shape
pop.isna().sum()
areas.isna().sum()
abbrevs.isna().sum()
```
Given this information, say we want to compute a relatively straightforward result: rank US states and territories by their 2010 population density.
We clearly have the data here to find this result, but we'll have to combine the datasets to find the result.
We'll start with a many-to-one merge that will give us the full state name within the population ``DataFrame``.
We want to merge based on the ``state/region`` column of ``pop``, and the ``abbreviation`` column of ``abbrevs``.
We'll use ``how='outer'`` to make sure no data is thrown away due to mismatched labels.
```
merged = pd.merge(pop, abbrevs, how='outer',
left_on='state/region', right_on='abbreviation')
merged.head()
merged.isna().sum()
merged.tail()
merged = merged.drop('abbreviation', 1) # drop duplicate info
merged.head()
```
Let's double-check whether there were any mismatches here, which we can do by looking for rows with nulls:
```
merged.isnull().any()
merged.isnull().sum()
```
Some of the ``population`` info is null; let's figure out which these are!
```
merged['population'].isnull().sum()
merged['state'].isnull().sum()
merged[merged['population'].isnull()]
merged[merged['state'].isnull()]
```
It appears that all the null population values are from Puerto Rico prior to the year 2000; this is likely due to this data not being available from the original source.
More importantly, we see also that some of the new ``state`` entries are also null, which means that there was no corresponding entry in the ``abbrevs`` key!
Let's figure out which regions lack this match:
```
merged.loc[merged['state'].isnull(), 'state/region'].unique()
```
We can quickly infer the issue: our population data includes entries for Puerto Rico (PR) and the United States as a whole (USA), while these entries do not appear in the state abbreviation key.
We can fix these quickly by filling in appropriate entries:
```
merged.loc[merged['state/region'] == 'PR', 'state'] = 'Puerto Rico'
merged.loc[merged['state/region'] == 'USA', 'state'] = 'United States'
merged.isnull().any()
merged.isnull().sum()
```
No more nulls in the ``state`` column: we're all set!
Now we can merge the result with the area data using a similar procedure.
Examining our results, we will want to join on the ``state`` column in both:
```
final = pd.merge(merged, areas, on='state', how='left')
final.head()
```
Again, let's check for nulls to see if there were any mismatches:
```
final.isnull().any()
final.isna().sum()
```
There are nulls in the ``area`` column; we can take a look to see which regions were ignored here:
```
final['state'][final['area (sq. mi)'].isnull()].unique()
```
We see that our ``areas`` ``DataFrame`` does not contain the area of the United States as a whole.
We could insert the appropriate value (using the sum of all state areas, for instance), but in this case we'll just drop the null values because the population density of the entire United States is not relevant to our current discussion:
```
final.dropna(inplace=True)
final.head()
final.shape
final.isnull().info()
final.isna().sum()
```
Now we have all the data we need. To answer the question of interest, let's first select the portion of the data corresponding with the year 2000, and the total population.
We'll use the ``query()`` function to do this quickly (this requires the ``numexpr`` package to be installed; see [High-Performance Pandas: ``eval()`` and ``query()``](03.12-Performance-Eval-and-Query.ipynb)):
```
data2010 = final.query("year == 2010 & ages == 'total'") # SQL Select Stastement
data2010.head()
```
Now let's compute the population density and display it in order.
We'll start by re-indexing our data on the state, and then compute the result:
```
data2010.set_index('state', inplace=True)
data2010
density = data2010['population'] / data2010['area (sq. mi)']
density.head()
density.sort_values(ascending=True, inplace=True)
density.head()
```
The result is a ranking of US states plus Washington, DC, and Puerto Rico in order of their 2010 population density, in residents per square mile.
We can see that by far the densest region in this dataset is Washington, DC (i.e., the District of Columbia); among states, the densest is New Jersey.
We can also check the end of the list:
```
density.tail()
final.isnull().describe()
```
Converting the Data Frame into Pickle File Formate
```
Data = pd.to_pickle(final,'Data/US_States_Data.plk')# Save the Data in the from of Pickled
final.to_csv('Data/US_States_Data.csv')# Save the Data Csv
unpickled_df = pd.read_pickle("Data/US_States_Data.plk")
unpickled_df
```
We see that the least dense state, by far, is Alaska, averaging slightly over one resident per square mile.
This type of messy data merging is a common task when trying to answer questions using real-world data sources.
I hope that this example has given you an idea of the ways you can combine tools we've covered in order to gain insight from your data!
| true |
code
| 0.459986 | null | null | null | null |
|
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import os
os.chdir('../../')
from musicautobot.numpy_encode import *
from musicautobot.utils.file_processing import process_all, process_file
from musicautobot.config import *
from musicautobot.music_transformer import *
from musicautobot.multitask_transformer import *
from musicautobot.utils.stacked_dataloader import StackedDataBunch
from fastai.text import *
```
## MultitaskTransformer Training
Multitask Training is an extension of [MusicTransformer](../music_transformer/Train.ipynb).
Instead a basic language model that predicts the next word...
We train on multiple tasks
* [Next Word](../music_transformer/Train.ipynb)
* [Bert Mask](https://arxiv.org/abs/1810.04805)
* [Sequence to Sequence Translation](http://jalammar.github.io/illustrated-transformer/)
This gives a more generalized model and also let's you do some really cool [predictions](Generate.ipynb)
## End to end training pipeline
1. Create and encode dataset
2. Initialize Transformer MOdel
3. Train
4. Predict
```
# Location of your midi files
midi_path = Path('data/midi/examples')
midi_path.mkdir(parents=True, exist_ok=True)
# Location to save dataset
data_path = Path('data/numpy')
data_path.mkdir(parents=True, exist_ok=True)
data_save_name = 'musicitem_data_save.pkl'
s2s_data_save_name = 'multiitem_data_save.pkl'
```
## 1. Gather midi dataset
Make sure all your midi data is in `musicautobot/data/midi` directory
Here's a pretty good dataset with lots of midi data:
https://www.reddit.com/r/datasets/comments/3akhxy/the_largest_midi_collection_on_the_internet/
Download the folder and unzip it to `data/midi`
## 2. Create dataset from MIDI files
```
midi_files = get_files(midi_path, '.mid', recurse=True); len(midi_files)
```
### 2a. Create NextWord/Mask Dataset
```
processors = [Midi2ItemProcessor()]
data = MusicDataBunch.from_files(midi_files, data_path, processors=processors,
encode_position=True, dl_tfms=mask_lm_tfm_pitchdur,
bptt=5, bs=2)
data.save(data_save_name)
xb, yb = data.one_batch(); xb
```
Key:
* 'msk' = masked input
* 'lm' = next word input
* 'pos' = timestepped postional encoding. This is in addition to relative positional encoding
Note: MultitaskTransformer trains on both the masked input ('msk') and next word input ('lm') at the same time.
The encoder is trained on the 'msk' data, while the decoder is trained on 'lm' data.
### 2b. Create sequence to sequence dataset
```
processors = [Midi2MultitrackProcessor()]
s2s_data = MusicDataBunch.from_files(midi_files, data_path, processors=processors,
preloader_cls=S2SPreloader, list_cls=S2SItemList,
dl_tfms=melody_chord_tfm,
bptt=5, bs=2)
s2s_data.save(s2s_data_save_name)
```
Structure
```
xb, yb = s2s_data.one_batch(); xb
```
Key:
* 'c2m' = chord2melody translation
* enc = chord
* dec = melody
* 'm2c' = next word input
* enc = melody
* dec = chord
* 'pos' = timestepped postional encoding. Gives the model a better reference when translating
Note: MultitaskTransformer trains both translations ('m2c' and 'c2m') at the same time.
## 3. Initialize Model
```
# Load Data
batch_size = 2
bptt = 128
lm_data = load_data(data_path, data_save_name,
bs=batch_size, bptt=bptt, encode_position=True,
dl_tfms=mask_lm_tfm_pitchdur)
s2s_data = load_data(data_path, s2s_data_save_name,
bs=batch_size//2, bptt=bptt,
preloader_cls=S2SPreloader, dl_tfms=melody_chord_tfm)
# Combine both dataloaders so we can train multiple tasks at the same time
data = StackedDataBunch([lm_data, s2s_data])
# Create Model
config = multitask_config(); config
learn = multitask_model_learner(data, config.copy())
# learn.to_fp16(dynamic=True) # Enable for mixed precision
learn.model
```
# 4. Train
```
learn.fit_one_cycle(4)
learn.save('example')
```
## Predict
---
See [Generate.ipynb](Generate.ipynb) to use a pretrained model and generate better predictions
---
```
# midi_files = get_files(midi_path, '.mid', recurse=True)
midi_file = Path('data/midi/notebook_examples/single_bar_example.mid'); midi_file
next_word = nw_predict_from_midi(learn, midi_file, n_words=20, seed_len=8); next_word.show()
pred_melody = s2s_predict_from_midi(learn, midi_file, n_words=20, seed_len=4, pred_melody=True); pred_melody.show()
pred_notes = mask_predict_from_midi(learn, midi_file, predict_notes=True); pred_notes.show()
```
| true |
code
| 0.612281 | null | null | null | null |
|
# Gaussian Process (GP) smoothing
This example deals with the case when we want to **smooth** the observed data points $(x_i, y_i)$ of some 1-dimensional function $y=f(x)$, by finding the new values $(x_i, y'_i)$ such that the new data is more "smooth" (see more on the definition of smoothness through allocation of variance in the model description below) when moving along the $x$ axis.
It is important to note that we are **not** dealing with the problem of interpolating the function $y=f(x)$ at the unknown values of $x$. Such problem would be called "regression" not "smoothing", and will be considered in other examples.
If we assume the functional dependency between $x$ and $y$ is **linear** then, by making the independence and normality assumptions about the noise, we can infer a straight line that approximates the dependency between the variables, i.e. perform a linear regression. We can also fit more complex functional dependencies (like quadratic, cubic, etc), if we know the functional form of the dependency in advance.
However, the **functional form** of $y=f(x)$ is **not always known in advance**, and it might be hard to choose which one to fit, given the data. For example, you wouldn't necessarily know which function to use, given the following observed data. Assume you haven't seen the formula that generated it:
```
%pylab inline
figsize(12, 6);
import numpy as np
import scipy.stats as stats
x = np.linspace(0, 50, 100)
y = (np.exp(1.0 + np.power(x, 0.5) - np.exp(x/15.0)) +
np.random.normal(scale=1.0, size=x.shape))
plot(x, y);
xlabel("x");
ylabel("y");
title("Observed Data");
```
### Let's try a linear regression first
As humans, we see that there is a non-linear dependency with some noise, and we would like to capture that dependency. If we perform a linear regression, we see that the "smoothed" data is less than satisfactory:
```
plot(x, y);
xlabel("x");
ylabel("y");
lin = stats.linregress(x, y)
plot(x, lin.intercept + lin.slope * x);
title("Linear Smoothing");
```
### Linear regression model recap
The linear regression assumes there is a linear dependency between the input $x$ and output $y$, sprinkled with some noise around it so that for each observed data point we have:
$$ y_i = a + b\, x_i + \epsilon_i $$
where the observation errors at each data point satisfy:
$$ \epsilon_i \sim N(0, \sigma^2) $$
with the same $\sigma$, and the errors are independent:
$$ cov(\epsilon_i, \epsilon_j) = 0 \: \text{ for } i \neq j $$
The parameters of this model are $a$, $b$, and $\sigma$. It turns out that, under these assumptions, the maximum likelihood estimates of $a$ and $b$ don't depend on $\sigma$. Then $\sigma$ can be estimated separately, after finding the most likely values for $a$ and $b$.
### Gaussian Process smoothing model
This model allows departure from the linear dependency by assuming that the dependency between $x$ and $y$ is a Brownian motion over the domain of $x$. This doesn't go as far as assuming a particular functional dependency between the variables. Instead, by **controlling the standard deviation of the unobserved Brownian motion** we can achieve different levels of smoothness of the recovered functional dependency at the original data points.
The particular model we are going to discuss assumes that the observed data points are **evenly spaced** across the domain of $x$, and therefore can be indexed by $i=1,\dots,N$ without the loss of generality. The model is described as follows:
\begin{equation}
\begin{aligned}
z_i & \sim \mathcal{N}(z_{i-1} + \mu, (1 - \alpha)\cdot\sigma^2) \: \text{ for } i=2,\dots,N \\
z_1 & \sim ImproperFlat(-\infty,\infty) \\
y_i & \sim \mathcal{N}(z_i, \alpha\cdot\sigma^2)
\end{aligned}
\end{equation}
where $z$ is the hidden Brownian motion, $y$ is the observed data, and the total variance $\sigma^2$ of each ovservation is split between the hidden Brownian motion and the noise in proportions of $1 - \alpha$ and $\alpha$ respectively, with parameter $0 < \alpha < 1$ specifying the degree of smoothing.
When we estimate the maximum likelihood values of the hidden process $z_i$ at each of the data points, $i=1,\dots,N$, these values provide an approximation of the functional dependency $y=f(x)$ as $\mathrm{E}\,[f(x_i)] = z_i$ at the original data points $x_i$ only. Therefore, again, the method is called smoothing and not regression.
### Let's describe the above GP-smoothing model in PyMC3
```
import pymc3 as pm
from theano import shared
from pymc3.distributions.timeseries import GaussianRandomWalk
from scipy import optimize
```
Let's create a model with a shared parameter for specifying different levels of smoothing. We use very wide priors for the "mu" and "tau" parameters of the hidden Brownian motion, which you can adjust according to your application.
```
LARGE_NUMBER = 1e5
model = pm.Model()
with model:
smoothing_param = shared(0.9)
mu = pm.Normal("mu", sigma=LARGE_NUMBER)
tau = pm.Exponential("tau", 1.0/LARGE_NUMBER)
z = GaussianRandomWalk("z",
mu=mu,
tau=tau / (1.0 - smoothing_param),
shape=y.shape)
obs = pm.Normal("obs",
mu=z,
tau=tau / smoothing_param,
observed=y)
```
Let's also make a helper function for inferring the most likely values of $z$:
```
def infer_z(smoothing):
with model:
smoothing_param.set_value(smoothing)
res = pm.find_MAP(vars=[z], fmin=optimize.fmin_l_bfgs_b)
return res['z']
```
Please note that in this example, we are only looking at the MAP estimate of the unobserved variables. We are not really interested in inferring the posterior distributions. Instead, we have a control parameter $\alpha$ which lets us allocate the variance between the hidden Brownian motion and the noise. Other goals and/or different models may require sampling to obtain the posterior distributions, but for our goal a MAP estimate will suffice.
### Exploring different levels of smoothing
Let's try to allocate 50% variance to the noise, and see if the result matches our expectations.
```
smoothing = 0.5
z_val = infer_z(smoothing)
plot(x, y);
plot(x, z_val);
title("Smoothing={}".format(smoothing));
```
It appears that the variance is split evenly between the noise and the hidden process, as expected.
Let's try gradually increasing the smoothness parameter to see if we can obtain smoother data:
```
smoothing = 0.9
z_val = infer_z(smoothing)
plot(x, y);
plot(x, z_val);
title("Smoothing={}".format(smoothing));
```
### Smoothing "to the limits"
By increading the smoothing parameter, we can gradually make the inferred values of the hidden Brownian motion approach the average value of the data. This is because as we increase the smoothing parameter, we allow less and less of the variance to be allocated to the Brownian motion, so eventually it aproaches the process which almost doesn't change over the domain of $x$:
```
fig, axes = subplots(2, 2)
for ax, smoothing in zip(axes.ravel(), [0.95, 0.99, 0.999, 0.9999]):
z_val = infer_z(smoothing)
ax.plot(x, y)
ax.plot(x, z_val)
ax.set_title('Smoothing={:05.4f}'.format(smoothing))
```
This example originally contributed by: Andrey Kuzmenko, http://github.com/akuz
| true |
code
| 0.679378 | null | null | null | null |
|
```
# %load /Users/facai/Study/book_notes/preconfig.py
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import SVG
```
逻辑回归在scikit-learn中的实现简介
==============================
分析用的代码版本信息:
```bash
~/W/g/scikit-learn ❯❯❯ git log -n 1
commit d161bfaa1a42da75f4940464f7f1c524ef53484f
Author: John B Nelson <[email protected]>
Date: Thu May 26 18:36:37 2016 -0400
Add missing double quote (#6831)
```
### 0. 总纲
下面是sklearn中逻辑回归的构成情况:
```
SVG("./res/sklearn_lr.svg")
```
如[逻辑回归在spark中的实现简介](./spark_ml_lr.ipynb)中分析一样,主要把精力定位到算法代码上,即寻优算子和损失函数。
### 1. 寻优算子
sklearn支持liblinear, sag, lbfgs和newton-cg四种寻优算子,其中lbfgs属于scipy包,liblinear属于LibLinear库,剩下两种由sklearn自己实现。代码很好定位,逻辑也很明了,不多说:
```python
704 if solver == 'lbfgs':
705 try:
706 w0, loss, info = optimize.fmin_l_bfgs_b(
707 func, w0, fprime=None,
708 args=(X, target, 1. / C, sample_weight),
709 iprint=(verbose > 0) - 1, pgtol=tol, maxiter=max_iter)
710 except TypeError:
711 # old scipy doesn't have maxiter
712 w0, loss, info = optimize.fmin_l_bfgs_b(
713 func, w0, fprime=None,
714 args=(X, target, 1. / C, sample_weight),
715 iprint=(verbose > 0) - 1, pgtol=tol)
716 if info["warnflag"] == 1 and verbose > 0:
717 warnings.warn("lbfgs failed to converge. Increase the number "
718 "of iterations.")
719 try:
720 n_iter_i = info['nit'] - 1
721 except:
722 n_iter_i = info['funcalls'] - 1
723 elif solver == 'newton-cg':
724 args = (X, target, 1. / C, sample_weight)
725 w0, n_iter_i = newton_cg(hess, func, grad, w0, args=args,
726 maxiter=max_iter, tol=tol)
727 elif solver == 'liblinear':
728 coef_, intercept_, n_iter_i, = _fit_liblinear(
729 X, target, C, fit_intercept, intercept_scaling, None,
730 penalty, dual, verbose, max_iter, tol, random_state,
731 sample_weight=sample_weight)
732 if fit_intercept:
733 w0 = np.concatenate([coef_.ravel(), intercept_])
734 else:
735 w0 = coef_.ravel()
736
737 elif solver == 'sag':
738 if multi_class == 'multinomial':
739 target = target.astype(np.float64)
740 loss = 'multinomial'
741 else:
742 loss = 'log'
743
744 w0, n_iter_i, warm_start_sag = sag_solver(
745 X, target, sample_weight, loss, 1. / C, max_iter, tol,
746 verbose, random_state, False, max_squared_sum, warm_start_sag)
```
### 2. 损失函数
#### 2.1 二分类
二分类的损失函数和导数由`_logistic_loss_and_grad`实现,运算逻辑和[逻辑回归算法简介和Python实现](./demo.ipynb)是相同的,不多说。
#### 2.2 多分类
sklearn的多分类支持ovr (one vs rest,一对多)和multinominal两种方式。
##### 2.2.0 ovr
默认是ovr,它会对毎个标签训练一个二分类的分类器,即总共$K$个。训练代码在
```python
1230 fold_coefs_ = Parallel(n_jobs=self.n_jobs, verbose=self.verbose,
1231 backend=backend)(
1232 path_func(X, y, pos_class=class_, Cs=[self.C],
1233 fit_intercept=self.fit_intercept, tol=self.tol,
1234 verbose=self.verbose, solver=self.solver, copy=False,
1235 multi_class=self.multi_class, max_iter=self.max_iter,
1236 class_weight=self.class_weight, check_input=False,
1237 random_state=self.random_state, coef=warm_start_coef_,
1238 max_squared_sum=max_squared_sum,
1239 sample_weight=sample_weight)
1240 for (class_, warm_start_coef_) in zip(classes_, warm_start_coef))
```
注意,1240L的`for class_ in classes`配合1232L的`pos_class=class`,就是逐个取标签来训练的逻辑。
##### 2.2.1 multinominal
前面讲到ovr会遍历标签,逐个训练。为了兼容这段逻辑,真正的二分类问题需要做变化:
```python
1201 if len(self.classes_) == 2:
1202 n_classes = 1
1203 classes_ = classes_[1:]
```
同样地,multinominal需要一次对全部标签做处理,也需要做变化:
```python
1217 # Hack so that we iterate only once for the multinomial case.
1218 if self.multi_class == 'multinomial':
1219 classes_ = [None]
1220 warm_start_coef = [warm_start_coef]
```
好,接下来,我们看multinoinal的损失函数和导数计算代码,它是`_multinomial_loss_grad`这个函数。
sklearn里多分类的代码使用的公式和[逻辑回归算法简介和Python实现](./demo.ipynb)里一致,即:
\begin{align}
L(\beta) &= \log(\sum_i e^{\beta_{i0} + \beta_i x)}) - (\beta_{k0} + \beta_k x) \\
\frac{\partial L}{\partial \beta} &= x \left ( \frac{e^{\beta_{k0} + \beta_k x}}{\sum_i e^{\beta_{i0} + \beta_i x}} - I(y = k) \right ) \\
\end{align}
具体到损失函数:
```python
244 def _multinomial_loss(w, X, Y, alpha, sample_weight):
245 #+-- 37 lines: """Computes multinomial loss and class probabilities.---
282 n_classes = Y.shape[1]
283 n_features = X.shape[1]
284 fit_intercept = w.size == (n_classes * (n_features + 1))
285 w = w.reshape(n_classes, -1)
286 sample_weight = sample_weight[:, np.newaxis]
287 if fit_intercept:
288 intercept = w[:, -1]
289 w = w[:, :-1]
290 else:
291 intercept = 0
292 p = safe_sparse_dot(X, w.T)
293 p += intercept
294 p -= logsumexp(p, axis=1)[:, np.newaxis]
295 loss = -(sample_weight * Y * p).sum()
296 loss += 0.5 * alpha * squared_norm(w)
297 p = np.exp(p, p)
298 return loss, p, w
```
+ 292L-293L是计算$\beta_{i0} + \beta_i x$。
+ 294L是计算 $L(\beta)$。注意,这里防止计算溢出,是在`logsumexp`函数里作的,原理和[逻辑回归在spark中的实现简介](./spark_ml_lr.ipynb)一样。
+ 295L是加总(注意,$Y$毎列是单位向量,所以起了选标签对应$k$的作用)。
+ 296L加上L2正则。
+ 注意,297L是p变回了$\frac{e^{\beta_{k0} + \beta_k x}}{\sum_i e^{\beta_{i0} + \beta_i x}}$,为了计算导数时直接用。
好,再看导数的计算:
```python
301 def _multinomial_loss_grad(w, X, Y, alpha, sample_weight):
302 #+-- 37 lines: """Computes the multinomial loss, gradient and class probabilities.---
339 n_classes = Y.shape[1]
340 n_features = X.shape[1]
341 fit_intercept = (w.size == n_classes * (n_features + 1))
342 grad = np.zeros((n_classes, n_features + bool(fit_intercept)))
343 loss, p, w = _multinomial_loss(w, X, Y, alpha, sample_weight)
344 sample_weight = sample_weight[:, np.newaxis]
345 diff = sample_weight * (p - Y)
346 grad[:, :n_features] = safe_sparse_dot(diff.T, X)
347 grad[:, :n_features] += alpha * w
348 if fit_intercept:
349 grad[:, -1] = diff.sum(axis=0)
350 return loss, grad.ravel(), p
```
+ 345L-346L,对应了导数的计算式;
+ 347L是加上L2的导数;
+ 348L-349L,是对intercept的计算。
#### 2.3 Hessian
注意,sklearn支持牛顿法,需要用到Hessian阵,定义见维基[Hessian matrix](https://en.wikipedia.org/wiki/Hessian_matrix),
\begin{equation}
{\mathbf H}={\begin{bmatrix}{\dfrac {\partial ^{2}f}{\partial x_{1}^{2}}}&{\dfrac {\partial ^{2}f}{\partial x_{1}\,\partial x_{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{1}\,\partial x_{n}}}\\[2.2ex]{\dfrac {\partial ^{2}f}{\partial x_{2}\,\partial x_{1}}}&{\dfrac {\partial ^{2}f}{\partial x_{2}^{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{2}\,\partial x_{n}}}\\[2.2ex]\vdots &\vdots &\ddots &\vdots \\[2.2ex]{\dfrac {\partial ^{2}f}{\partial x_{n}\,\partial x_{1}}}&{\dfrac {\partial ^{2}f}{\partial x_{n}\,\partial x_{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{n}^{2}}}\end{bmatrix}}.
\end{equation}
其实就是各点位的二阶偏导。具体推导就不写了,感兴趣可以看[Logistic Regression - Jia Li](http://sites.stat.psu.edu/~jiali/course/stat597e/notes2/logit.pdf)或[Logistic regression: a simple ANN Nando de Freitas](https://www.cs.ox.ac.uk/people/nando.defreitas/machinelearning/lecture6.pdf)。
基本公式是$\mathbf{H} = \mathbf{X}^T \operatorname{diag}(\pi_i (1 - \pi_i)) \mathbf{X}$,其中$\pi_i = \operatorname{sigm}(x_i \beta)$。
```python
167 def _logistic_grad_hess(w, X, y, alpha, sample_weight=None):
168 #+-- 33 lines: """Computes the gradient and the Hessian, in the case of a logistic loss.
201 w, c, yz = _intercept_dot(w, X, y)
202 #+-- 4 lines: if sample_weight is None:---------
206 z = expit(yz)
207 #+-- 8 lines: z0 = sample_weight * (z - 1) * y---
215 # The mat-vec product of the Hessian
216 d = sample_weight * z * (1 - z)
217 if sparse.issparse(X):
218 dX = safe_sparse_dot(sparse.dia_matrix((d, 0),
219 shape=(n_samples, n_samples)), X)
220 else:
221 # Precompute as much as possible
222 dX = d[:, np.newaxis] * X
223
224 if fit_intercept:
225 # Calculate the double derivative with respect to intercept
226 # In the case of sparse matrices this returns a matrix object.
227 dd_intercept = np.squeeze(np.array(dX.sum(axis=0)))
228
229 def Hs(s):
230 ret = np.empty_like(s)
231 ret[:n_features] = X.T.dot(dX.dot(s[:n_features]))
232 ret[:n_features] += alpha * s[:n_features]
233
234 # For the fit intercept case.
235 if fit_intercept:
236 ret[:n_features] += s[-1] * dd_intercept
237 ret[-1] = dd_intercept.dot(s[:n_features])
238 ret[-1] += d.sum() * s[-1]
239 return ret
240
241 return grad, Hs
```
+ 201L, 206L, 和216L是计算中间的$\pi_i (1 - \pi_i)$。
+ 217L-222L,对中间参数变为对角阵后,预算公式后半部份,配合231L就是整个式子了。
这里我也只知其然,以后有时间再深挖下吧。
### 3. 小结
本文简单介绍了sklearn中逻辑回归的实现,包括二分类和多分类的具体代码和公式对应。
| true |
code
| 0.550728 | null | null | null | null |
|
# Basic functionality tests.
If the notebook cells complete with no exception the tests have passed.
The tests must be run in the full `jupyter notebook` or `jupyter lab` environment.
*Note:* I couldn't figure out to make the validation tests run correctly
at top level cell evaluation using `Run all`
because the widgets initialize after later cells have executed, causing spurious
failures. Consequently the automated validation steps involve an extra round trip using
a widget at the bottom of the notebook which is guaranteed to render last.
```
# Some test artifacts used below:
import jp_proxy_widget
from jp_proxy_widget import notebook_test_helpers
validators = notebook_test_helpers.ValidationSuite()
import time
class PythonClass:
class_attribute = "initial class attribute value"
def __init__(self):
self.set_instance_attribute("initial instance attribute value")
def set_instance_attribute(self, value):
self.instance_attribute = value
@classmethod
def set_class_attribute(cls, value):
cls.class_attribute = value
notebook_test_helpers
jp_proxy_widget
python_instance = PythonClass()
def python_function(value1, value2):
python_instance.new_attribute = "value1=%s and value2=%s" % (value1, value2)
```
# pong: test that a proxy widget can call back to Python
```
import jp_proxy_widget
pong = jp_proxy_widget.JSProxyWidget()
def validate_pong():
# check that the Python callbacks were called.
assert python_instance.instance_attribute == "instance"
assert PythonClass.class_attribute == "class"
assert python_instance.new_attribute == 'value1=1 and value2=3'
assert pong.error_msg == 'No error'
print ("pong says", pong.error_msg)
print ("Pong callback test succeeded!")
pong.js_init("""
//debugger;
instance_method("instance");
class_method("class");
python_function(1, 3);
element.html("<b>Callback test widget: nothing interesting to see here</b>")
//validate()
""",
instance_method=python_instance.set_instance_attribute,
class_method=PythonClass.set_class_attribute,
python_function=python_function,
#validate=validate_pong
)
#widget_validator_list.append([pong, validate_pong])
validators.add_validation(pong, validate_pong)
#pong.debugging_display()
pong
# set the mainloop check to True if running cells one at a time
mainloop_check = False
if mainloop_check:
# At this time this fails on "run all"
validate_pong()
```
# pingpong: test that Python can call in to a widget
... use a widget callback to pass the value back
```
pingpong_list = "just some strings".split()
def pingpong_python_fn(argument1, argument2):
print("called pingpong_python_fn") # this print goes nowhere?
pingpong_list[:] = [argument1, argument2]
def validate_pingpong():
# check that the callback got the right values
assert pingpong_list == ["testing", 123]
print ("ping pong test callback got ", pingpong_list)
print ("ping pong test succeeded!")
pingpong = jp_proxy_widget.JSProxyWidget()
pingpong.js_init("""
element.html("<em>Ping pong test -- no call yet.</em>")
element.call_in_to_the_widget = function (argument1, argument2) {
element.html("<b> Call in sent " + argument1 + " and " + argument2 + "</b>")
call_back_to_python(argument1, argument2);
}
element.validate = validate;
""", call_back_to_python=pingpong_python_fn, validate=validate_pingpong)
#widget_validator_list.append([pingpong, validate_pingpong])
validators.add_validation(pingpong, validate_pingpong)
#pingpong.debugging_display()
pingpong
# call in to javascript
pingpong.element.call_in_to_the_widget("testing", 123)
# call in to javascript and back to python to validate
pingpong.element.validate()
if mainloop_check:
validate_pingpong()
```
# roundtrip: datatype round trip
Test that values can be passed in to the proxy widget and back out again.
```
binary = bytearray(b"\x12\xff binary bytes")
string_value = "just a string"
int_value = -123
float_value = 45.6
json_dictionary = {"keys": None, "must": 321, "be": [6, 12], "strings": "values", "can": ["be", "any json"]}
list_value = [9, string_value, json_dictionary]
roundtrip_got_values = []
from jp_proxy_widget import hex_codec
from pprint import pprint
def get_values_back(binary, string_value, int_value, float_value, json_dictionary, list_value):
# NOTE: binary values must be converted explicitly from hex string encoding!
binary = hex_codec.hex_to_bytearray(binary)
roundtrip_got_values[:] = [binary, string_value, int_value, float_value, json_dictionary, list_value]
print ("GOT VALUES BACK")
pprint(roundtrip_got_values)
roundtrip_names = "binary string_value int_value float_value json_dictionary list_value".split()
def validate_roundtrip():
#assert roundtrip_got_values == [string_value, int_value, float_value, json_dictionary, list_value]
expected_values = [binary, string_value, int_value, float_value, json_dictionary, list_value]
if len(expected_values) != len(roundtrip_got_values):
print ("bad lengths", len(expected_values), len(roundtrip_got_values))
pprint(expected_values)
pprint(roundtrip_got_values)
assert len(expected_values) == len(roundtrip_got_values)
for (name, got, expected) in zip(roundtrip_names, roundtrip_got_values, expected_values):
if (got != expected):
print(name, "BAD MATCH got")
pprint(got)
print(" ... expected")
pprint(expected)
assert got == expected, "values don't match: " + repr((name, got, expected))
print ("roundtrip values match!")
roundtrip = jp_proxy_widget.JSProxyWidget()
roundtrip.js_init(r"""
element.all_values = [binary, string_value, int_value, float_value, json_dictionary, list_value];
html = ["<pre> Binary values sent as bytearrays appear in Javascript as Uint8Arrays"]
for (var i=0; i<names.length; i++) {
html.push(names[i]);
var v = element.all_values[i];
if (v instanceof Uint8Array) {
html.push(" Uint8Array")
} else {
html.push(" type: " + (typeof v))
}
html.push(" value: " + v);
}
html.push("</pre>");
element.html(html.join("\n"));
// send the values back
callback(binary, string_value, int_value, float_value, json_dictionary, list_value);
""",
binary=binary,
string_value=string_value,
int_value=int_value,
float_value=float_value,
json_dictionary=json_dictionary,
list_value=list_value,
names=roundtrip_names,
callback=get_values_back,
# NOTE: must up the callable level!
callable_level=4
)
roundtrip.debugging_display()
validators.add_validation(roundtrip, validate_roundtrip)
if mainloop_check:
validate_roundtrip()
#validate_roundtrip()
```
# loadCSS -- test load of simple CSS file.
We want to load this css file
```
from jp_proxy_widget import js_context
style_fn="js/simple.css"
print(js_context.get_text_from_file_name(style_fn))
loadCSS = jp_proxy_widget.JSProxyWidget()
# load the file
loadCSS.load_css(style_fn)
# callback for storing the styled element color
loadCSSstyle = {}
def color_callback(color):
loadCSSstyle["color"] = color
# initialize the element using the style and callback to report the color.
loadCSS.js_init("""
element.html('<div><em class="random-style-for-testing" id="loadCSSelement">Styled widget element.</em></div>')
var e = document.getElementById("loadCSSelement");
var style = window.getComputedStyle(e);
color_callback(style["color"]);
""", color_callback=color_callback)
def validate_loadCSS():
expect = 'rgb(216, 50, 61)'
assert expect == loadCSSstyle["color"], repr((expect, loadCSSstyle))
print ("Loaded CSS color is correct!")
loadCSS
validators.add_validation(loadCSS, validate_loadCSS)
if mainloop_check:
validate_loadCSS()
```
# loadJS -- load a javascript file (once only per interpreter)
We want to load this javascript file:
```
js_fn="js/simple.js"
print(js_context.get_text_from_file_name(js_fn))
loadJS = jp_proxy_widget.JSProxyWidget()
# load the file
loadJS.load_js_files([js_fn], force=True)
# callback for storing the styled element color
loadJSinfo = {}
def answer_callback(answer):
loadJSinfo["answer"] = answer
loadJS.js_init("""
element.html('<b>The answer is ' + window.the_answer + '</b>')
answer_callback(window.the_answer);
""", answer_callback=answer_callback, js_fn=js_fn)
def validate_loadJS():
expect = 42
assert expect == loadJSinfo["answer"], repr((expect, loadJSinfo))
print ("Loaded JS value is correct!")
loadJS
validators.add_validation(loadJS, validate_loadJS)
if mainloop_check:
validate_loadJS()
loadJS.print_status()
delay_ms = 1000
validators.run_all_in_widget(delay_ms=delay_ms)
```
| true |
code
| 0.461138 | null | null | null | null |
|
## 範例重點
* 學習如何在 keras 中加入 EarlyStop
* 知道如何設定監控目標
* 比較有無 earlystopping 對 validation 的影響
```
import os
from tensorflow import keras
# 本範例不需使用 GPU, 將 GPU 設定為 "無"
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
train, test = keras.datasets.cifar10.load_data()
## 資料前處理
def preproc_x(x, flatten=True):
x = x / 255.
if flatten:
x = x.reshape((len(x), -1))
return x
def preproc_y(y, num_classes=10):
if y.shape[-1] == 1:
y = keras.utils.to_categorical(y, num_classes)
return y
x_train, y_train = train
x_test, y_test = test
# 資料前處理 - X 標準化
x_train = preproc_x(x_train)
x_test = preproc_x(x_test)
# 資料前處理 -Y 轉成 onehot
y_train = preproc_y(y_train)
y_test = preproc_y(y_test)
from tensorflow.keras.layers import BatchNormalization
"""
建立神經網路,並加入 BN layer
"""
def build_mlp(input_shape, output_units=10, num_neurons=[256, 128, 64]):
input_layer = keras.layers.Input(input_shape)
for i, n_units in enumerate(num_neurons):
if i == 0:
x = keras.layers.Dense(units=n_units,
activation="relu",
name="hidden_layer"+str(i+1))(input_layer)
x = BatchNormalization()(x)
else:
x = keras.layers.Dense(units=n_units,
activation="relu",
name="hidden_layer"+str(i+1))(x)
x = BatchNormalization()(x)
out = keras.layers.Dense(units=output_units, activation="softmax", name="output")(x)
model = keras.models.Model(inputs=[input_layer], outputs=[out])
return model
## 超參數設定
LEARNING_RATE = 1e-3
EPOCHS = 50
BATCH_SIZE = 1024
MOMENTUM = 0.95
"""
# 載入 Callbacks, 並將 monitor 設定為監控 validation loss
"""
from tensorflow.keras.callbacks import EarlyStopping
earlystop = EarlyStopping(monitor="val_loss",
patience=5,
verbose=1
)
model = build_mlp(input_shape=x_train.shape[1:])
model.summary()
optimizer = keras.optimizers.SGD(lr=LEARNING_RATE, nesterov=True, momentum=MOMENTUM)
model.compile(loss="categorical_crossentropy", metrics=["accuracy"], optimizer=optimizer)
model.fit(x_train, y_train,
epochs=EPOCHS,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
shuffle=True,
callbacks=[earlystop]
)
# Collect results
train_loss = model.history.history["loss"]
valid_loss = model.history.history["val_loss"]
train_acc = model.history.history["accuracy"]
valid_acc = model.history.history["val_accuracy"]
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(range(len(train_loss)), train_loss, label="train loss")
plt.plot(range(len(valid_loss)), valid_loss, label="valid loss")
plt.legend()
plt.title("Loss")
plt.show()
plt.plot(range(len(train_acc)), train_acc, label="train accuracy")
plt.plot(range(len(valid_acc)), valid_acc, label="valid accuracy")
plt.legend()
plt.title("Accuracy")
plt.show()
```
## Work
1. 試改變 monitor "Validation Accuracy" 並比較結果
2. 調整 earlystop 的等待次數至 10, 25 並比較結果
| true |
code
| 0.739707 | null | null | null | null |
|
# Performance analysis of a uniform linear array
We compare the MSE of MUSIC with the CRB for a uniform linear array (ULA).
```
import numpy as np
import doatools.model as model
import doatools.estimation as estimation
import doatools.performance as perf
import matplotlib.pyplot as plt
%matplotlib inline
wavelength = 1.0 # normalized
d0 = wavelength / 2
# Create a 12-element ULA.
ula = model.UniformLinearArray(12, d0)
# Place 8 sources uniformly within (-pi/3, pi/4)
sources = model.FarField1DSourcePlacement(
np.linspace(-np.pi/3, np.pi/4, 8)
)
# All sources share the same power.
power_source = 1 # Normalized
source_signal = model.ComplexStochasticSignal(sources.size, power_source)
# 200 snapshots.
n_snapshots = 200
# We use root-MUSIC.
estimator = estimation.RootMUSIC1D(wavelength)
```
We vary the SNR from -20 dB to 20 dB. Here the SNR is defined as:
\begin{equation}
\mathrm{SNR} = 10\log_{10}\frac{\min_i p_i}{\sigma^2_{\mathrm{n}}},
\end{equation}
where $p_i$ is the power of the $i$-th source, and $\sigma^2_{\mathrm{n}}$ is the noise power.
```
snrs = np.linspace(-20, 10, 20)
# 300 Monte Carlo runs for each SNR
n_repeats = 300
mses = np.zeros((len(snrs),))
crbs_sto = np.zeros((len(snrs),))
crbs_det = np.zeros((len(snrs),))
crbs_stouc = np.zeros((len(snrs),))
for i, snr in enumerate(snrs):
power_noise = power_source / (10**(snr / 10))
noise_signal = model.ComplexStochasticSignal(ula.size, power_noise)
# The squared errors and the deterministic CRB varies
# for each run. We need to compute the average.
cur_mse = 0.0
cur_crb_det = 0.0
for r in range(n_repeats):
# Stochastic signal model.
A = ula.steering_matrix(sources, wavelength)
S = source_signal.emit(n_snapshots)
N = noise_signal.emit(n_snapshots)
Y = A @ S + N
Rs = (S @ S.conj().T) / n_snapshots
Ry = (Y @ Y.conj().T) / n_snapshots
resolved, estimates = estimator.estimate(Ry, sources.size, d0)
# In practice, you should check if `resolved` is true.
# We skip the check here.
cur_mse += np.mean((estimates.locations - sources.locations)**2)
B_det = perf.ecov_music_1d(ula, sources, wavelength, Rs, power_noise,
n_snapshots)
cur_crb_det += np.mean(np.diag(B_det))
# Update the results.
B_sto = perf.crb_sto_farfield_1d(ula, sources, wavelength, power_source,
power_noise, n_snapshots)
B_stouc = perf.crb_stouc_farfield_1d(ula, sources, wavelength, power_source,
power_noise, n_snapshots)
mses[i] = cur_mse / n_repeats
crbs_sto[i] = np.mean(np.diag(B_sto))
crbs_det[i] = cur_crb_det / n_repeats
crbs_stouc[i] = np.mean(np.diag(B_stouc))
print('Completed SNR = {0:.2f} dB'.format(snr))
```
We plot the results below.
* The MSE should approach the stochastic CRBs in high SNR regions.
* The stochastic CRB should be tighter than the deterministic CRB.
* With the additional assumption of uncorrelated sources, we expect a even lower CRB.
* All three CRBs should converge together as the SNR approaches infinity.
```
plt.figure(figsize=(8, 6))
plt.semilogy(
snrs, mses, '-x',
snrs, crbs_sto, '--',
snrs, crbs_det, '--',
snrs, crbs_stouc, '--'
)
plt.xlabel('SNR (dB)')
plt.ylabel(r'MSE / $\mathrm{rad}^2$')
plt.grid(True)
plt.legend(['MSE', 'Stochastic CRB', 'Deterministic CRB',
'Stochastic CRB (Uncorrelated)'])
plt.title('MSE vs. CRB')
plt.margins(x=0)
plt.show()
```
| true |
code
| 0.815435 | null | null | null | null |
|
# Fast Bernoulli: Benchmark Python
In this notebooks we will measure performance of generating sequencies of Bernoulli-distributed random varibales in Python without and within LLVM JIT compiler. The baseline generator is based on top of expression `random.uniform() < p`.
```
import numpy as np
import matplotlib.pyplot as plt
from random import random
from typing import List
from bernoulli import LLVMBernoulliGenerator, PyBernoulliGenerator
from tqdm import tqdm
```
## Benchmarking
As it was mentioned above, the baseline generator is just thresholding a uniform-distributed random variable.
```
class BaselineBernoulliGenerator:
def __init__(self, probability: float, tolerance: float = float('nan'), seed: int = None):
self.prob = probability
def __call__(self, nobits: int = 32):
return [int(random() <= self.prob) for _ in range(nobits)]
```
Here we define some routines for benchmarking.
```
def benchmark(cls, nobits_list: List[int], probs: List[float], tol: float = 1e-6) -> np.ndarray:
timings = np.empty((len(probs), len(nobits_list)))
with tqdm(total=timings.size, unit='bench') as progress:
for i, prob in enumerate(probs):
generator = cls(prob, tol)
for j, nobits in enumerate(nobits_list):
try:
timing = %timeit -q -o generator(nobits)
timings[i, j] = timing.average
except Exception as e:
# Here we catch the case when number of bits is not enough
# to obtain desirable precision.
timings[i, j] = float('nan')
progress.update()
return timings
```
The proposed Bernoulli generator has two parameters. The first one is well-known that is probability of success $p$. The second one is precision of quantization.
```
NOBITS = [1, 2, 4, 8, 16, 32]
PROBAS = [1 / 2 ** n for n in range(1, 8)]
```
Now, start benchmarking!
```
baseline = benchmark(BaselineBernoulliGenerator, NOBITS, PROBAS)
py = benchmark(PyBernoulliGenerator, NOBITS, PROBAS)
llvm = benchmark(LLVMBernoulliGenerator, NOBITS, PROBAS)
```
Multiplication by factor $10^6$ corresponds to changing units from seconds to microseconds.
```
baseline *= 1e6
py *= 1e6
llvm *= 1e6
```
Save timings for the future.
```
np.save('../data/benchmark-data-baseline.npy', baseline)
np.save('../data/benchmark-data-py.npy', py)
np.save('../data/benchmark-data-llvm.npy', llvm)
```
## Visualization
On the figures below we depics how timings (or bitrate) depends on algorithm parameters.
```
fig = plt.figure(figsize=(14, 6))
ax = fig.add_subplot(1, 1, 1)
ax.grid()
for i, proba in enumerate(PROBAS):
ax.loglog(NOBITS, baseline[i, :], '-x',label=f'baseline p={proba}')
ax.loglog(NOBITS, py[i, :], '-+',label=f'python p={proba}')
ax.loglog(NOBITS, llvm[i, :], '-o',label=f'llvm p={proba}')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set_xlabel('Sequence length, bit')
ax.set_ylabel('Click time, $\mu s$')
plt.show()
fig = plt.figure(figsize=(14, 6))
ax = fig.add_subplot(1, 1, 1)
ax.grid()
for i, proba in enumerate(PROBAS):
ax.loglog(NOBITS, NOBITS / baseline[i, :], '-x',label=f'baseline p={proba}')
ax.loglog(NOBITS, NOBITS / py[i, :], '-+',label=f'python p={proba}')
ax.loglog(NOBITS, NOBITS / llvm[i, :], '-o',label=f'llvm p={proba}')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set_xlabel('Sequence length, bit')
ax.set_ylabel('Bit rate, Mbit per s')
plt.show()
fig = plt.figure(figsize=(14, 6))
ax = fig.add_subplot(1, 1, 1)
ax.grid()
for j, nobits in enumerate(NOBITS):
ax.loglog(PROBAS, nobits / baseline[:, j], '-x',label=f'baseline block={nobits}')
ax.loglog(PROBAS, nobits / py[:, j], '-+',label=f'python block={nobits}')
ax.loglog(PROBAS, nobits / llvm[:, j], '-o',label=f'llvm block={nobits}')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set_xlabel('Bernoulli parameter')
ax.set_ylabel('Bitrate, Mbit / sec')
plt.show()
```
## Comments and Discussions
On the figures above one can see that direct implementation of the algorithm does not improve bitrate. Also, we can see that the statement is true for implementaion with LLVM as well as without LLVM. This means that overhead is too large.
Nevertheless, the third figure is worth to note that bitrate scales note very well for baseline generator. The bitrate of baseline drops dramatically while the bitrates of the others decrease much lesser.
Such benchmarking like this has unaccounted effects like different implementation levels (IR and Python), expansion of bit block to list of bits, overhead of Python object system.
| true |
code
| 0.663587 | null | null | null | null |
|
```
import numpy as np
import lqrpols
import matplotlib.pyplot as plt
```
Here is a link to [lqrpols.py](http://www.argmin.net/code/lqrpols.py)
```
np.random.seed(1337)
# state transition matrices for linear system:
# x(t+1) = A x (t) + B u(t)
A = np.array([[1,1],[0,1]])
B = np.array([[0],[1]])
d,p = B.shape
# LQR quadratic cost per state
Q = np.array([[1,0],[0,0]])
# initial condition for system
z0 = -1 # initial position
v0 = 0 # initial velocity
x0 = np.vstack((z0,v0))
R = np.array([[1.0]])
# number of time steps to simulate
T = 10
# amount of Gaussian noise in dynamics
eq_err = 1e-2
# N_vals = np.floor(np.linspace(1,75,num=7)).astype(int)
N_vals = [1,2,5,7,12,25,50,75]
N_trials = 10
### Bunch of matrices for storing costs
J_finite_nom = np.zeros((N_trials,len(N_vals)))
J_finite_nomK = np.zeros((N_trials,len(N_vals)))
J_finite_rs = np.zeros((N_trials,len(N_vals)))
J_finite_ur = np.zeros((N_trials,len(N_vals)))
J_finite_pg = np.zeros((N_trials,len(N_vals)))
J_inf_nom = np.zeros((N_trials,len(N_vals)))
J_inf_rs = np.zeros((N_trials,len(N_vals)))
J_inf_ur = np.zeros((N_trials,len(N_vals)))
J_inf_pg = np.zeros((N_trials,len(N_vals)))
# cost for finite time horizon, true model
J_finite_opt = lqrpols.cost_finite_model(A,B,Q,R,x0,T,A,B)
### Solve for optimal infinite time horizon LQR controller
K_opt = -lqrpols.lqr_gain(A,B,Q,R)
# cost for infinite time horizon, true model
J_inf_opt = lqrpols.cost_inf_K(A,B,Q,R,K_opt)
# cost for zero control
baseline = lqrpols.cost_finite_K(A,B,Q,R,x0,T,np.zeros((p,d)))
# model for nominal control with 1 rollout
A_nom1,B_nom1 = lqrpols.lsqr_estimator(A,B,Q,R,x0,eq_err,1,T)
print(A_nom1)
print(B_nom1)
# cost for finite time horizon, one rollout, nominal control
one_rollout_cost = lqrpols.cost_finite_model(A,B,Q,R,x0,T,A_nom1,B_nom1)
K_nom1 = -lqrpols.lqr_gain(A_nom1,B_nom1,Q,R)
one_rollout_cost_inf = lqrpols.cost_inf_K(A,B,Q,R,K_nom1)
for N in range(len(N_vals)):
for trial in range(N_trials):
# nominal model, N x 40 to match sample budget of policy gradient
A_nom,B_nom = lqrpols.lsqr_estimator(A,B,Q,R,x0,eq_err,N_vals[N]*40,T);
# finite time horizon cost with nominal model
J_finite_nom[trial,N] = lqrpols.cost_finite_model(A,B,Q,R,x0,T,A_nom,B_nom)
# Solve for infinite time horizon nominal LQR controller
K_nom = -lqrpols.lqr_gain(A_nom,B_nom,Q,R)
# cost of using the infinite time horizon solution for finite time horizon
J_finite_nomK[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_nom)
# infinite time horizon cost of nominal model
J_inf_nom[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_nom)
# policy gradient, batchsize 40 per iteration
K_pg = lqrpols.policy_gradient_adam_linear_policy(A,B,Q,R,x0,eq_err,N_vals[N]*5,T)
J_finite_pg[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_pg)
J_inf_pg[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_pg)
# random search, batchsize 4, so uses 8 rollouts per iteration
K_rs = lqrpols.random_search_linear_policy(A,B,Q,R,x0,eq_err,N_vals[N]*5,T)
J_finite_rs[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_rs)
J_inf_rs[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_rs)
# uniformly random sampling, N x 40 to match sample budget of policy gradient
K_ur = lqrpols.uniform_random_linear_policy(A,B,Q,R,x0,eq_err,N_vals[N]*40,T)
J_finite_ur[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_ur)
J_inf_ur[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_ur)
colors = [ '#2D328F', '#F15C19',"#81b13c","#ca49ac"]
label_fontsize = 18
tick_fontsize = 14
linewidth = 3
markersize = 10
tot_samples = 40*np.array(N_vals)
plt.plot(tot_samples,np.amin(J_finite_pg,axis=0),'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.plot(tot_samples,np.amin(J_finite_ur,axis=0),'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.plot(tot_samples,np.amin(J_finite_rs,axis=0),'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.plot([tot_samples[0],tot_samples[-1]],[baseline, baseline],color='#000000',linewidth=linewidth,
linestyle='--',label='zero control')
plt.plot([tot_samples[0],tot_samples[-1]],[J_finite_opt, J_finite_opt],color='#000000',linewidth=linewidth,
linestyle=':',label='optimal')
plt.axis([0,2000,0,12])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('cost',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
plt.plot(tot_samples,np.median(J_finite_pg,axis=0),'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.fill_between(tot_samples, np.amin(J_finite_pg,axis=0), np.amax(J_finite_pg,axis=0), alpha=0.25)
plt.plot(tot_samples,np.median(J_finite_ur,axis=0),'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.fill_between(tot_samples, np.amin(J_finite_ur,axis=0), np.amax(J_finite_ur,axis=0), alpha=0.25)
plt.plot(tot_samples,np.median(J_finite_rs,axis=0),'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.fill_between(tot_samples, np.amin(J_finite_rs,axis=0), np.amax(J_finite_rs,axis=0), alpha=0.25)
plt.plot([tot_samples[0],tot_samples[-1]],[baseline, baseline],color='#000000',linewidth=linewidth,
linestyle='--',label='zero control')
plt.plot([tot_samples[0],tot_samples[-1]],[J_finite_opt, J_finite_opt],color='#000000',linewidth=linewidth,
linestyle=':',label='optimal')
plt.axis([0,2000,0,12])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('cost',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
plt.plot(tot_samples,np.median(J_inf_pg,axis=0),'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.fill_between(tot_samples, np.amin(J_inf_pg,axis=0), np.minimum(np.amax(J_inf_pg,axis=0),15), alpha=0.25)
plt.plot(tot_samples,np.median(J_inf_ur,axis=0),'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.fill_between(tot_samples, np.amin(J_inf_ur,axis=0), np.minimum(np.amax(J_inf_ur,axis=0),15), alpha=0.25)
plt.plot(tot_samples,np.median(J_inf_rs,axis=0),'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.fill_between(tot_samples, np.amin(J_inf_rs,axis=0), np.minimum(np.amax(J_inf_rs,axis=0),15), alpha=0.25)
plt.plot([tot_samples[0],tot_samples[-1]],[J_inf_opt, J_inf_opt],color='#000000',linewidth=linewidth,
linestyle=':',label='optimal')
plt.axis([0,3000,5,10])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('cost',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
plt.plot(tot_samples,1-np.sum(np.isinf(J_inf_pg),axis=0)/10,'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.plot(tot_samples,1-np.sum(np.isinf(J_inf_ur),axis=0)/10,'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.plot(tot_samples,1-np.sum(np.isinf(J_inf_rs),axis=0)/10,'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.axis([0,3000,0,1])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('fraction stable',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
one_rollout_cost-J_finite_opt
one_rollout_cost_inf-J_inf_opt
```
| true |
code
| 0.675256 | null | null | null | null |
|
# Encoding of categorical variables
In this notebook, we will present typical ways of dealing with
**categorical variables** by encoding them, namely **ordinal encoding** and
**one-hot encoding**.
Let's first load the entire adult dataset containing both numerical and
categorical data.
```
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
# drop the duplicated column `"education-num"` as stated in the first notebook
adult_census = adult_census.drop(columns="education-num")
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=[target_name])
```
## Identify categorical variables
As we saw in the previous section, a numerical variable is a
quantity represented by a real or integer number. These variables can be
naturally handled by machine learning algorithms that are typically composed
of a sequence of arithmetic instructions such as additions and
multiplications.
In contrast, categorical variables have discrete values, typically
represented by string labels (but not only) taken from a finite list of
possible choices. For instance, the variable `native-country` in our dataset
is a categorical variable because it encodes the data using a finite list of
possible countries (along with the `?` symbol when this information is
missing):
```
data["native-country"].value_counts().sort_index()
```
How can we easily recognize categorical columns among the dataset? Part of
the answer lies in the columns' data type:
```
data.dtypes
```
If we look at the `"native-country"` column, we observe its data type is
`object`, meaning it contains string values.
## Select features based on their data type
In the previous notebook, we manually defined the numerical columns. We could
do a similar approach. Instead, we will use the scikit-learn helper function
`make_column_selector`, which allows us to select columns based on
their data type. We will illustrate how to use this helper.
```
from sklearn.compose import make_column_selector as selector
categorical_columns_selector = selector(dtype_include=object)
categorical_columns = categorical_columns_selector(data)
categorical_columns
```
Here, we created the selector by passing the data type to include; we then
passed the input dataset to the selector object, which returned a list of
column names that have the requested data type. We can now filter out the
unwanted columns:
```
data_categorical = data[categorical_columns]
data_categorical.head()
print(f"The dataset is composed of {data_categorical.shape[1]} features")
```
In the remainder of this section, we will present different strategies to
encode categorical data into numerical data which can be used by a
machine-learning algorithm.
## Strategies to encode categories
### Encoding ordinal categories
The most intuitive strategy is to encode each category with a different
number. The `OrdinalEncoder` will transform the data in such manner.
We will start by encoding a single column to understand how the encoding
works.
```
from sklearn.preprocessing import OrdinalEncoder
education_column = data_categorical[["education"]]
encoder = OrdinalEncoder()
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
We see that each category in `"education"` has been replaced by a numeric
value. We could check the mapping between the categories and the numerical
values by checking the fitted attribute `categories_`.
```
encoder.categories_
```
Now, we can check the encoding applied on all categorical features.
```
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The dataset encoded contains {data_encoded.shape[1]} features")
```
We see that the categories have been encoded for each feature (column)
independently. We also note that the number of features before and after the
encoding is the same.
However, be careful when applying this encoding strategy:
using this integer representation leads downstream predictive models
to assume that the values are ordered (0 < 1 < 2 < 3... for instance).
By default, `OrdinalEncoder` uses a lexicographical strategy to map string
category labels to integers. This strategy is arbitrary and often
meaningless. For instance, suppose the dataset has a categorical variable
named `"size"` with categories such as "S", "M", "L", "XL". We would like the
integer representation to respect the meaning of the sizes by mapping them to
increasing integers such as `0, 1, 2, 3`.
However, the lexicographical strategy used by default would map the labels
"S", "M", "L", "XL" to 2, 1, 0, 3, by following the alphabetical order.
The `OrdinalEncoder` class accepts a `categories` constructor argument to
pass categories in the expected ordering explicitly. You can find more
information in the
[scikit-learn documentation](https://scikit-learn.org/stable/modules/preprocessing.html#encoding-categorical-features)
if needed.
If a categorical variable does not carry any meaningful order information
then this encoding might be misleading to downstream statistical models and
you might consider using one-hot encoding instead (see below).
### Encoding nominal categories (without assuming any order)
`OneHotEncoder` is an alternative encoder that prevents the downstream
models to make a false assumption about the ordering of categories. For a
given feature, it will create as many new columns as there are possible
categories. For a given sample, the value of the column corresponding to the
category will be set to `1` while all the columns of the other categories
will be set to `0`.
We will start by encoding a single feature (e.g. `"education"`) to illustrate
how the encoding works.
```
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(sparse=False)
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p><tt class="docutils literal">sparse=False</tt> is used in the <tt class="docutils literal">OneHotEncoder</tt> for didactic purposes, namely
easier visualization of the data.</p>
<p class="last">Sparse matrices are efficient data structures when most of your matrix
elements are zero. They won't be covered in detail in this course. If you
want more details about them, you can look at
<a class="reference external" href="https://scipy-lectures.org/advanced/scipy_sparse/introduction.html#why-sparse-matrices">this</a>.</p>
</div>
We see that encoding a single feature will give a NumPy array full of zeros
and ones. We can get a better understanding using the associated feature
names resulting from the transformation.
```
feature_names = encoder.get_feature_names_out(input_features=["education"])
education_encoded = pd.DataFrame(education_encoded, columns=feature_names)
education_encoded
```
As we can see, each category (unique value) became a column; the encoding
returned, for each sample, a 1 to specify which category it belongs to.
Let's apply this encoding on the full dataset.
```
print(
f"The dataset is composed of {data_categorical.shape[1]} features")
data_categorical.head()
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The encoded dataset contains {data_encoded.shape[1]} features")
```
Let's wrap this NumPy array in a dataframe with informative column names as
provided by the encoder object:
```
columns_encoded = encoder.get_feature_names_out(data_categorical.columns)
pd.DataFrame(data_encoded, columns=columns_encoded).head()
```
Look at how the `"workclass"` variable of the 3 first records has been
encoded and compare this to the original string representation.
The number of features after the encoding is more than 10 times larger than
in the original data because some variables such as `occupation` and
`native-country` have many possible categories.
### Choosing an encoding strategy
Choosing an encoding strategy will depend on the underlying models and the
type of categories (i.e. ordinal vs. nominal).
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">In general <tt class="docutils literal">OneHotEncoder</tt> is the encoding strategy used when the
downstream models are <strong>linear models</strong> while <tt class="docutils literal">OrdinalEncoder</tt> is often a
good strategy with <strong>tree-based models</strong>.</p>
</div>
Using an `OrdinalEncoder` will output ordinal categories. This means
that there is an order in the resulting categories (e.g. `0 < 1 < 2`). The
impact of violating this ordering assumption is really dependent on the
downstream models. Linear models will be impacted by misordered categories
while tree-based models will not.
You can still use an `OrdinalEncoder` with linear models but you need to be
sure that:
- the original categories (before encoding) have an ordering;
- the encoded categories follow the same ordering than the original
categories.
The **next exercise** highlights the issue of misusing `OrdinalEncoder` with
a linear model.
One-hot encoding categorical variables with high cardinality can cause
computational inefficiency in tree-based models. Because of this, it is not recommended
to use `OneHotEncoder` in such cases even if the original categories do not
have a given order. We will show this in the **final exercise** of this sequence.
## Evaluate our predictive pipeline
We can now integrate this encoder inside a machine learning pipeline like we
did with numerical data: let's train a linear classifier on the encoded data
and check the generalization performance of this machine learning pipeline using
cross-validation.
Before we create the pipeline, we have to linger on the `native-country`.
Let's recall some statistics regarding this column.
```
data["native-country"].value_counts()
```
We see that the `Holand-Netherlands` category is occurring rarely. This will
be a problem during cross-validation: if the sample ends up in the test set
during splitting then the classifier would not have seen the category during
training and will not be able to encode it.
In scikit-learn, there are two solutions to bypass this issue:
* list all the possible categories and provide it to the encoder via the
keyword argument `categories`;
* use the parameter `handle_unknown`.
Here, we will use the latter solution for simplicity.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">Be aware the <tt class="docutils literal">OrdinalEncoder</tt> exposes as well a parameter
<tt class="docutils literal">handle_unknown</tt>. It can be set to <tt class="docutils literal">use_encoded_value</tt> and by setting
<tt class="docutils literal">unknown_value</tt> to handle rare categories. You are going to use these
parameters in the next exercise.</p>
</div>
We can now create our machine learning pipeline.
```
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
model = make_pipeline(
OneHotEncoder(handle_unknown="ignore"), LogisticRegression(max_iter=500)
)
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">Here, we need to increase the maximum number of iterations to obtain a fully
converged <tt class="docutils literal">LogisticRegression</tt> and silence a <tt class="docutils literal">ConvergenceWarning</tt>. Contrary
to the numerical features, the one-hot encoded categorical features are all
on the same scale (values are 0 or 1), so they would not benefit from
scaling. In this case, increasing <tt class="docutils literal">max_iter</tt> is the right thing to do.</p>
</div>
Finally, we can check the model's generalization performance only using the
categorical columns.
```
from sklearn.model_selection import cross_validate
cv_results = cross_validate(model, data_categorical, target)
cv_results
scores = cv_results["test_score"]
print(f"The accuracy is: {scores.mean():.3f} +/- {scores.std():.3f}")
```
As you can see, this representation of the categorical variables is
slightly more predictive of the revenue than the numerical variables
that we used previously.
In this notebook we have:
* seen two common strategies for encoding categorical features: **ordinal
encoding** and **one-hot encoding**;
* used a **pipeline** to use a **one-hot encoder** before fitting a logistic
regression.
| true |
code
| 0.621455 | null | null | null | null |
|
This notebook is part of the orix documentation https://orix.readthedocs.io. Links to the documentation won’t work from the notebook.
## Visualizing point groups
Point group symmetry operations are shown here in the stereographic projection.
Vectors located on the upper (`z >= 0`) hemisphere are displayed as points (`o`), whereas vectors on the lower hemisphere are reprojected onto the upper hemisphere and shown as crosses (`+`) by default. For more information about plot formatting and visualization, see [Vector3d.scatter()](reference.rst#orix.vector.Vector3d.scatter).
More explanation of these figures is provided at http://xrayweb.chem.ou.edu/notes/symmetry.html#point.
```
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
from orix import plot
from orix.quaternion import Rotation, symmetry
from orix.vector import Vector3d
plt.rcParams.update({"font.size": 15})
```
For example, the `O (432)` point group:
```
symmetry.O.plot()
```
The stereographic projection of all point groups is shown below:
```
# fmt: off
schoenflies = [
"C1", "Ci", # triclinic,
"C2x", "C2y", "C2z", "Csx", "Csy", "Csz", "C2h", # monoclinic
"D2", "C2v", "D2h", # orthorhombic
"C4", "S4", "C4h", "D4", "C4v", "D2d", "D4h", # tetragonal
"C3", "S6", "D3x", "D3y", "D3", "C3v", "D3d", "C6", # trigonal
"C3h", "C6h", "D6", "C6v", "D3h", "D6h", # hexagonal
"T", "Th", "O", "Td", "Oh", # cubic
]
# fmt: on
assert len(symmetry._groups) == len(schoenflies)
schoenflies = [s for s in schoenflies if not (s.endswith("x") or s.endswith("y"))]
assert len(schoenflies) == 32
orientation = Rotation.from_axes_angles((-1, 8, 1), np.deg2rad(65))
fig, ax = plt.subplots(
nrows=8, ncols=4, figsize=(10, 20), subplot_kw=dict(projection="stereographic")
)
ax = ax.ravel()
for i, s in enumerate(schoenflies):
sym = getattr(symmetry, s)
ori_sym = sym.outer(orientation)
v = ori_sym * Vector3d.zvector()
# reflection in the projection plane (x-y) is performed internally in
# Symmetry.plot() or when using the `reproject=True` argument for
# Vector3d.scatter()
v_reproject = Vector3d(v.data.copy())
v_reproject.z *= -1
# the Symmetry marker formatting for vectors on the upper and lower hemisphere
# can be set using `kwargs` and `reproject_scatter_kwargs`, respectively, for
# Symmetry.plot()
# vectors on the upper hemisphere are shown as open circles
ax[i].scatter(v, marker="o", fc="None", ec="k", s=150)
# vectors on the lower hemisphere are reprojected onto the upper hemisphere and
# shown as crosses
ax[i].scatter(v_reproject, marker="+", ec="C0", s=150)
ax[i].set_title(f"${s}$ $({sym.name})$")
ax[i].set_labels("a", "b", None)
fig.tight_layout()
```
| true |
code
| 0.791136 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.