prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
```
%cd -q data/actr_reco
import matplotlib.pyplot as plt
import tqdm
import numpy as np
with open("users.txt", "r") as f:
users = f.readlines()
hist = []
for user in tqdm.tqdm(users):
user = user.strip()
ret = !wc -l user_split/listening_events_2019_{user}.tsv
lc, _ = ret[0].split(" ")
hist.append(int(lc))
len(hist), sum(hist)
plt.hist(hist, bins=100)
plt.show()
subset = [x for x in hist if x < 30_000 and x >= 1_000]
len(subset)
plt.hist(subset, bins=100)
plt.show()
plt.hist(subset, bins=5)
plt.show()
plt.hist(subset, bins=10)
plt.show()
plt.hist(subset, bins=10)
```
# Stratification
```
def stratification_numbers(data, min_value, max_value, bins, num_samples):
subset = [x for x in data if x >= min_value and x < max_value]
percentage = num_samples / len(subset)
bin_size = int((max_value-min_value)/bins)
num_per_bin = []
old_boundary = min_value
for new_boundary in range(min_value+bin_size, max_value+1, bin_size):
data_in_bin = [x for x in subset if x >= old_boundary and x < new_boundary]
num_per_bin.append(len(data_in_bin))
old_boundary = new_boundary
assert sum(num_per_bin) == len(subset)
samples_per_bin = np.array(num_per_bin)*percentage
floor_samples_per_bin = np.floor(samples_per_bin)
error = int(round(sum(samples_per_bin) - sum(floor_samples_per_bin)))
if error == 0:
assert sum(floor_samples_per_bin) == num_samples
return floor_samples_per_bin
remainders = np.remainder(samples_per_bin, 1)
to_adjust = np.argsort(remainders)[::-1][:error]
for ta in to_adjust:
floor_samples_per_bin[ta] += 1
assert sum(floor_samples_per_bin) == num_samples
return floor_samples_per_bin
samples_per_bin = stratification_numbers(hist, 1_000, 30_000, 10, num_samples=100)
samples_per_bin, sum(samples_per_bin)
stratification_numbers(hist, 1_000, 30_000, 10, 2)
```
# Iterative Stratified Sampling
```
test_hist = hist[len(test_users):]
assert len(test_hist) == len(test_users)
test_user_interaction = list(zip(test_users, test_hist))
test_user_interaction[:2]
!wc -l user_split/listening_events_2019_61740.tsv
def get_bin_boundaries_from_config(bin_config=None):
if not bin_config:
bin_config = {"min_value": 1_000, "max_value": 30_000, "bins": 10}
bin_size = int((bin_config["max_value"]-bin_config["min_value"])/bin_config["bins"])
return list(range(bin_config["min_value"], bin_config["max_value"]+1, bin_size))
def check_in_bin(item_value, target_bin, bin_config=None):
bin_boundaries = get_bin_boundaries_from_config()
return item_value >= bin_boundaries[target_bin] and item_value < bin_boundaries[target_bin+1]
assert check_in_bin(2400, 0)
assert not check_in_bin(5000, 0)
assert check_in_bin(29_000, 9)
def get_next_for_bin(user_interactions, target_bin):
iterlist = user_interactions.copy()
for ui in user_interactions:
if check_in_bin(ui[1], target_bin):
iterlist.remove(ui)
return ui[0], iterlist
raise StopIteration("No remaing items for bin.")
def list_index_difference(list1, list2):
changed_indices = []
for index, (first, second) in enumerate(zip(list1, list2)):
if first != second:
changed_indices.append(index)
return changed_indices
assert list_index_difference([0,1], [0,0]) == [1]
def iterative_sampling(user_interactions, max_size=1000, num_bins=10):
iterlist = user_interactions.copy()
bins = num_bins*[0]
sampled_list = []
mult_index_changes = []
for i in tqdm.tqdm(range(1, max_size+1)):
updated_bins = stratification_numbers(hist, 1_000, 30_000, 10, num_samples=i)
changed_indices = list_index_difference(bins, updated_bins)
if len(changed_indices) != 1:
mult_index_changes.append(i)
# print(f"Multi-index change at pos {i}: {changed_indices} (old: {bins} vs new: {updated_bins}")
target_bin = changed_indices[0] # empirically increase the first change index, assuming items are in descending order
bins[target_bin] += 1
item, iterlist = get_next_for_bin(iterlist, target_bin)
sampled_list.append(item)
print(len(mult_index_changes))
print(mult_index_changes[-3:])
print(bins)
return sampled_list
sampled_list = iterative_sampling(test_user_interaction, 150)
len(sampled_list)
# overlap
len(set(test_users[:300]).intersection(set(sampled_list[:150])))
with open("sampled.txt", "w") as f:
f.write("".join(sampled_list))
!head sampled.txt
!wc -l sampled.txt
```
| true |
code
| 0.27762 | null | null | null | null |
|
# Assignment Submission for FMUP
## Kishlaya Jaiswal
### Chennai Mathematical Institute - MCS201909
---
# Solution 1
I have choosen the following stocks from Nifty50:
- Kotak Mahindra Bank Ltd (KOTAKBANK)
- Hindustan Unilever Ltd (HINDUNILVR)
- Nestle India Limited (NESTLEIND)
Note:
- I am doing these computations on Apr 2, 2021, and hence using the closing price for this day as my strike price.
- I am using the historical data for the month of February to find the volatility of each of these stocks (volatility computation is done at the end)
```
import QuantLib as ql
# function to find the price and greeks for a given option
# with it's strike/spot price and it's volatility
def find_price_greeks(spot_price, strike_price, volatility, option_type):
# construct the European Option
payoff = ql.PlainVanillaPayoff(option_type, strike_price)
exercise = ql.EuropeanExercise(maturity_date)
european_option = ql.VanillaOption(payoff, exercise)
# quote the spot price
spot_handle = ql.QuoteHandle(
ql.SimpleQuote(spot_price)
)
flat_ts = ql.YieldTermStructureHandle(
ql.FlatForward(calculation_date, risk_free_rate, day_count)
)
dividend_yield = ql.YieldTermStructureHandle(
ql.FlatForward(calculation_date, dividend_rate, day_count)
)
flat_vol_ts = ql.BlackVolTermStructureHandle(
ql.BlackConstantVol(calculation_date, calendar, volatility, day_count)
)
# create the Black Scholes process
bsm_process = ql.BlackScholesMertonProcess(spot_handle,
dividend_yield,
flat_ts,
flat_vol_ts)
# set the engine to use the above process
european_option.setPricingEngine(ql.AnalyticEuropeanEngine(bsm_process))
return european_option
tickers = ["KOTAKBANK", "HINDUNILVR", "NESTLEIND"]
# spot price = closing price as on Mar 1, 2021
spot = {"KOTAKBANK":1845.35,
"HINDUNILVR":2144.70,
"NESTLEIND":16288.20}
# strike price = closing price as on Apr 2, 2021
strike = {"KOTAKBANK":1804.45,
"HINDUNILVR":2399.45,
"NESTLEIND":17102.15}
# historical volatility from the past month's data
vol = {"KOTAKBANK":0.38,
"HINDUNILVR":0.15,
"NESTLEIND":0.18}
# date of option purchase
calculation_date = ql.Date(1,3,2021)
# exercise date
# this excludes the holidays in the Indian calendar
calendar = ql.India()
period = ql.Period(65, ql.Days)
maturity_date = calendar.advance(calculation_date, period)
# rate of interest
risk_free_rate = 0.06
# other settings
dividend_rate = 0.0
day_count = ql.Actual365Fixed()
ql.Settings.instance().evaluationDate = calculation_date
# store final variables for future calculations
delta = {}
gamma = {}
vega = {}
# print settings
format_type_head = "{:<15}" + ("{:<12}" * 7)
format_type = "{:<15}{:<12}" + ("{:<12.2f}" * 6)
print(format_type_head.format("Name", "Type", "Price", "Delta", "Gamma", "Rho", "Theta", "Vega"))
print()
for ticker in tickers:
option = find_price_greeks(spot[ticker], strike[ticker], vol[ticker], ql.Option.Call)
print(format_type.format(ticker, "Call", option.NPV(),
option.delta(), option.gamma(),
option.rho(), option.theta(), option.vega()))
delta[ticker] = option.delta()
gamma[ticker] = option.gamma()
vega[ticker] = option.vega()
option = find_price_greeks(spot[ticker], strike[ticker], vol[ticker], ql.Option.Put)
print(format_type.format(ticker, "Put", option.NPV(),
option.delta(), option.gamma(),
option.rho(), option.theta(), option.vega()))
print()
```
### Delta Gamma Vega neutrality
First we make the Gamma and Vega neutral by taking
- x units of KOTAKBANK
- y units of HINDUNILVR
- 1 unit of NESTLEIND
To solve for x,y we have the following:
```
import numpy as np
G1, G2, G3 = gamma["KOTAKBANK"], gamma["HINDUNILVR"], gamma["NESTLEIND"]
V1, V2, V3 = vega["KOTAKBANK"], vega["HINDUNILVR"], vega["NESTLEIND"]
# Solve the following equation:
# G1 x + G2 y + G3 = 0
# V1 x + V2 y + V3 = 0
A = np.array([[G1, G2], [V1, V2]])
b = np.array([-G3, -V3])
z = np.linalg.solve(A, b)
print("x = {:.2f}".format(z[0]))
print("y = {:.2f}".format(z[1]))
print()
final_delta = z[0]*delta["KOTAKBANK"] + z[1]*delta["HINDUNILVR"] + delta["NESTLEIND"]
print("Delta of portfolio is {:.2f}".format(final_delta))
```
## Final Strategy
- Take a short position of 18.46 units of Kotak Mahindra Bank Ltd Call Option
- Take a long position of 17.34 units of Hindustan Unilever Ltd Call Option
- Take a long position of 1 unit of Nestle India Limited Call Option
- Take a long position of 9.13 units of Nestle India Limited Stock
This will yield a portfolio with Delta, Gamma and Vega neutral.
# Solution 2
Using Taylor expansion, we get
$$\Delta P = \frac{\partial P}{\partial y} \Delta y + \frac12 \frac{\partial^2 P}{\partial y^2}(\Delta y)^2$$
$$\implies \frac{\Delta P}{P} = -D \Delta y + \frac12 C (\Delta y)^2$$
where $D$ denotes duration and $C$ denotes convexity of a bond.
We remark that the duration of the bonds we are comparing are same and fixed.
---
<p>With that being said, let's say the interest rates fall, then we have $$\Delta y < 0 \implies - D \Delta y + C \Delta y^2 > 0 \implies \Delta P > 0$$
Now for the bond with greater convexity, $C \Delta y^2$ has a large value hence $\Delta P$ has to be large and so we get that "Greater convexity translates into greater price gains as interest rates fall"
</p>
---
Now suppose interest rates rise that is $\Delta y > 0$, then we $-D \Delta y < 0$, that is the price of the bonds decreases but the bond with greater convexity will add up for a large $C \Delta y^2$ also and so the price decrease will be less for bond with high convexity.
This explains "Lessened price declines as interest rates rise"
# Solution 3
```
import QuantLib as ql
# function to calculate coupon value
def find_coupon(pv, r, m, n):
discount_factor = (r/m) / (1 - (1 + r/m)**(-n*m))
C = pv * discount_factor
return C
# loan settings
loan_amt = 0.8*1000000
rate = 0.12
pay = find_coupon(loan_amt, rate, 12, 5)
month = ql.Date(15,8,2021)
period = ql.Period('1m')
# print settings
print("Monthly coupon is: {:.2f}".format(pay))
print()
format_type = "{:<15}" * 4
print(format_type.format("Date", "Interest", "Principal", "Remaining"))
while loan_amt > 0:
interest = loan_amt * rate / 12
principal = pay - interest
loan_amt = loan_amt - principal
print(format_type.format(month.ISO(), "{:.2f}".format(interest), "{:.2f}".format(principal), "{:.2f}".format(loan_amt)))
if round(loan_amt) == 0:
break
month = month + period
```
### Volatility Computation for Problem 1
```
import math
def get_volatility(csv):
data = csv.split('\n')[1:]
data = map(lambda x: x.split(','), data)
closing_prices = list(map(lambda x: float(x[-2]), data))
n = len(closing_prices)
log_returns = []
for i in range(1,n):
log_returns.append(math.log(closing_prices[i]/closing_prices[i-1]))
mu = sum(log_returns)/(n-1)
tmp = map(lambda x: (x-mu)**2, log_returns)
vol = math.sqrt(sum(tmp)/(n-1)) * math.sqrt(252)
return vol
kotak_csv = '''Date,Open,High,Low,Close,Adj Close,Volume
2021-02-01,1730.000000,1810.000000,1696.250000,1801.349976,1801.349976,220763
2021-02-02,1825.000000,1878.650024,1801.349976,1863.500000,1863.500000,337556
2021-02-03,1875.000000,1882.349976,1820.099976,1851.849976,1851.849976,147146
2021-02-04,1857.900024,1914.500000,1831.050049,1911.250000,1911.250000,188844
2021-02-05,1921.000000,1997.900024,1915.000000,1982.550049,1982.550049,786773
2021-02-08,1995.000000,2029.949951,1951.949951,1956.300049,1956.300049,212114
2021-02-09,1950.000000,1975.000000,1938.000000,1949.199951,1949.199951,62613
2021-02-10,1954.550049,1961.849976,1936.300049,1953.650024,1953.650024,143830
2021-02-11,1936.000000,1984.300049,1936.000000,1961.300049,1961.300049,120121
2021-02-12,1966.000000,1974.550049,1945.599976,1951.449951,1951.449951,86860
2021-02-15,1954.000000,1999.000000,1954.000000,1986.199951,1986.199951,135074
2021-02-16,1995.000000,2048.949951,1995.000000,2021.650024,2021.650024,261589
2021-02-17,2008.500000,2022.400024,1969.500000,1989.150024,1989.150024,450365
2021-02-18,1980.000000,1982.349976,1938.000000,1945.300049,1945.300049,193234
2021-02-19,1945.000000,1969.599976,1925.050049,1937.300049,1937.300049,49189
2021-02-22,1941.000000,1961.650024,1921.650024,1948.550049,1948.550049,44651
2021-02-23,1955.000000,1961.900024,1867.000000,1873.150024,1873.150024,118138
2021-02-24,1875.199951,1953.949951,1852.000000,1919.000000,1919.000000,454695
2021-02-25,1935.000000,1964.949951,1886.900024,1895.349976,1895.349976,195212
2021-02-26,1863.000000,1868.000000,1773.099976,1782.349976,1782.349976,180729'''
hind_csv = '''Date,Open,High,Low,Close,Adj Close,Volume
2021-02-01,2265.000000,2286.000000,2226.550049,2249.149902,2249.149902,130497
2021-02-02,2271.000000,2275.000000,2207.699951,2231.850098,2231.850098,327563
2021-02-03,2234.000000,2256.699951,2218.199951,2232.600098,2232.600098,121232
2021-02-04,2234.000000,2258.449951,2226.949951,2247.050049,2247.050049,533609
2021-02-05,2252.000000,2285.000000,2241.000000,2270.350098,2270.350098,254911
2021-02-08,2275.000000,2287.000000,2233.000000,2237.800049,2237.800049,211465
2021-02-09,2247.000000,2254.000000,2211.199951,2216.649902,2216.649902,171285
2021-02-10,2216.649902,2240.000000,2213.449951,2235.899902,2235.899902,185915
2021-02-11,2245.000000,2267.500000,2235.000000,2262.399902,2262.399902,121168
2021-02-12,2270.000000,2270.649902,2232.199951,2241.899902,2241.899902,33016
2021-02-15,2252.000000,2261.500000,2212.100098,2215.850098,2215.850098,91240
2021-02-16,2225.000000,2228.399902,2190.500000,2196.899902,2196.899902,101652
2021-02-17,2191.000000,2200.000000,2160.300049,2164.649902,2164.649902,138504
2021-02-18,2165.000000,2168.449951,2143.050049,2147.750000,2147.750000,110272
2021-02-19,2150.000000,2193.649902,2148.000000,2181.149902,2181.149902,150398
2021-02-22,2200.000000,2201.699951,2161.100098,2167.250000,2167.250000,98782
2021-02-23,2173.550049,2192.000000,2169.399902,2177.949951,2177.949951,22743
2021-02-24,2179.000000,2183.949951,2104.250000,2181.600098,2181.600098,329265
2021-02-25,2190.000000,2190.000000,2160.000000,2163.600098,2163.600098,357853
2021-02-26,2151.149902,2182.000000,2122.000000,2132.050049,2132.050049,158925'''
nestle_csv = '''Date,Open,High,Low,Close,Adj Close,Volume
2021-02-01,17162.099609,17277.000000,16996.449219,17096.949219,17096.949219,3169
2021-02-02,17211.000000,17328.099609,16800.000000,17189.349609,17189.349609,3852
2021-02-03,17247.449219,17284.000000,17064.349609,17155.400391,17155.400391,2270
2021-02-04,17250.000000,17250.000000,17054.800781,17073.199219,17073.199219,13193
2021-02-05,17244.000000,17244.000000,17019.949219,17123.300781,17123.300781,2503
2021-02-08,17199.949219,17280.000000,17107.349609,17213.550781,17213.550781,7122
2021-02-09,17340.000000,17510.699219,17164.050781,17325.800781,17325.800781,2714
2021-02-10,17396.900391,17439.300781,17083.800781,17167.699219,17167.699219,3341
2021-02-11,17167.699219,17442.000000,17165.550781,17416.650391,17416.650391,2025
2021-02-12,17449.849609,17500.000000,17241.000000,17286.099609,17286.099609,3486
2021-02-15,17290.000000,17500.000000,17280.000000,17484.500000,17484.500000,1927
2021-02-16,17600.000000,17634.599609,17141.250000,17222.449219,17222.449219,7901
2021-02-17,16900.000000,16900.000000,16360.000000,16739.900391,16739.900391,28701
2021-02-18,17050.000000,17050.000000,16307.000000,16374.150391,16374.150391,13711
2021-02-19,16395.000000,16477.599609,16214.450195,16386.099609,16386.099609,5777
2021-02-22,16400.000000,16531.050781,16024.599609,16099.200195,16099.200195,9051
2021-02-23,16123.000000,16250.000000,16003.000000,16165.250000,16165.250000,6261
2021-02-24,16249.000000,16800.000000,15900.000000,16369.950195,16369.950195,18003
2021-02-25,16394.699219,16394.699219,16102.000000,16114.349609,16114.349609,18735
2021-02-26,16075.000000,16287.200195,16010.000000,16097.700195,16097.700195,13733'''
print("Annualized Volatility of KOTAKBANK is {:.2f}%".format(get_volatility(kotak_csv)*100))
print("Annualized Volatility of HINDUNILVR is {:.2f}%".format(get_volatility(hind_csv)*100))
print("Annualized Volatility of NESTLEIND is {:.2f}%".format(get_volatility(nestle_csv)*100))
```
| true |
code
| 0.388212 | null | null | null | null |
|
# QCoDeS Example with Lakeshore 325
Here provided is an example session with model 325 of the Lakeshore temperature controller
```
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
from qcodes.instrument_drivers.Lakeshore.Model_325 import Model_325
lake = Model_325("lake", "GPIB0::12::INSTR")
```
## Sensor commands
```
# Check that the sensor is in the correct status
lake.sensor_A.status()
# What temperature is it reading?
lake.sensor_A.temperature()
lake.sensor_A.temperature.unit
# We can access the sensor objects through the sensor list as well
assert lake.sensor_A is lake.sensor[0]
```
## Heater commands
```
# In a closed loop configuration, heater 1 reads from...
lake.heater_1.input_channel()
lake.heater_1.unit()
# Get the PID values
print("P = ", lake.heater_1.P())
print("I = ", lake.heater_1.I())
print("D = ", lake.heater_1.D())
# Is the heater on?
lake.heater_1.output_range()
```
## Loading and updating sensor calibration values
```
curve = lake.sensor_A.curve
curve_data = curve.get_data()
curve_data.keys()
fig, ax = plt.subplots()
ax.plot(curve_data["Temperature (K)"], curve_data['log Ohm'], '.')
plt.show()
curve.curve_name()
curve_x = lake.curve[23]
curve_x_data = curve_x.get_data()
curve_x_data.keys()
temp = np.linspace(0, 100, 200)
new_data = {"Temperature (K)": temp, "log Ohm": 1/(temp+1)+2}
fig, ax = plt.subplots()
ax.plot(new_data["Temperature (K)"], new_data["log Ohm"], '.')
plt.show()
curve_x.format("log Ohm/K")
curve_x.set_data(new_data)
curve_x.format()
curve_x_data = curve_x.get_data()
fig, ax = plt.subplots()
ax.plot(curve_x_data["Temperature (K)"], curve_x_data['log Ohm'], '.')
plt.show()
```
## Go to a set point
```
import time
import numpy
from IPython.display import display
from ipywidgets import interact, widgets
from matplotlib import pyplot as plt
def live_plot_temperature_reading(channel_to_read, read_period=0.2, n_reads=1000):
"""
Live plot the temperature reading from a Lakeshore sensor channel
Args:
channel_to_read
Lakeshore channel object to read the temperature from
read_period
time in seconds between two reads of the temperature
n_reads
total number of reads to perform
"""
# Make a widget for a text display that is contantly being updated
text = widgets.Text()
display(text)
fig, ax = plt.subplots(1)
line, = ax.plot([], [], '*-')
ax.set_xlabel('Time, s')
ax.set_ylabel(f'Temperature, {channel_to_read.temperature.unit}')
fig.show()
plt.ion()
for i in range(n_reads):
time.sleep(read_period)
# Update the text field
text.value = f'T = {channel_to_read.temperature()}'
# Add new point to the data that is being plotted
line.set_ydata(numpy.append(line.get_ydata(), channel_to_read.temperature()))
line.set_xdata(numpy.arange(0, len(line.get_ydata()), 1)*read_period)
ax.relim() # Recalculate limits
ax.autoscale_view(True, True, True) # Autoscale
fig.canvas.draw() # Redraw
lake.heater_1.control_mode("Manual PID")
lake.heater_1.output_range("Low (2.5W)")
lake.heater_1.input_channel("A")
# The following seem to be good settings for our setup
lake.heater_1.P(400)
lake.heater_1.I(40)
lake.heater_1.D(10)
lake.heater_1.setpoint(15.0) # <- temperature
live_plot_temperature_reading(lake.sensor_a, n_reads=400)
```
## Querying the resistance and heater output
```
# to get the resistance of the system (25 or 50 Ohm)
lake.heater_1.resistance()
# to set the resistance of the system (25 or 50 Ohm)
lake.heater_1.resistance(50)
lake.heater_1.resistance()
# output in percent (%) of current or power, depending on setting, which can be queried by lake.heater_1.output_metric()
lake.heater_1.heater_output() # in %, 50 means 50%
```
| true |
code
| 0.668366 | null | null | null | null |
|
# Capstone Part 2a - Classical ML Models (MFCCs with Offset)
___
## Setup
```
# Basic packages
import numpy as np
import pandas as pd
# For splitting the data into training and test sets
from sklearn.model_selection import train_test_split
# For scaling the data as necessary
from sklearn.preprocessing import StandardScaler
# For doing principal component analysis as necessary
from sklearn.decomposition import PCA
# For visualizations
import matplotlib.pyplot as plt
%matplotlib inline
# For building a variety of models
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from sklearn.neighbors import KNeighborsClassifier
# For hyperparameter optimization
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
# For caching pipeline and grid search results
from tempfile import mkdtemp
# For model evaluation
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
# For getting rid of warning messages
import warnings
warnings.filterwarnings('ignore')
# For pickling models
import joblib
# Loading in the finished dataframe from part 1
ravdess_mfcc_df = pd.read_csv('C:/Users/Patrick/Documents/Capstone Data/ravdess_mfcc.csv')
```
___
# Building Models for Classifying Gender (Regardless of Emotion)
```
# Splitting the dataframe into features and target
X = ravdess_mfcc_df.iloc[:, :-2]
g = ravdess_mfcc_df['Gender']
```
The convention is to name the target variable 'y', but I will be declaring many different target variables throughout the notebook, so I opted for 'g' for simplicity instead of 'y_g' or 'y_gen', for example.
```
# # Encoding the genders
# gender_encoder = LabelEncoder()
# g = gender_encoder.fit_transform(g)
# # Checking the results
# g
# # Which number represents which gender?
# for num in np.unique(g):
# print(f'{num} represents {gender_encoder.inverse_transform([num])[0]}.')
```
Note: I realized that encoding the target is unnecessary; it is done automatically by the models.
```
# What test size should I use?
print(f'Length of g: {len(g)}')
print(f'30% of {len(g)} is {len(g)*0.3}')
```
I will use 30%.
```
# Splitting the data into training and test sets
X_train, X_test, g_train, g_test = train_test_split(X, g, test_size=0.3, stratify=g, random_state=1)
# Checking the shapes
print(X_train.shape)
print(X_test.shape)
print(g_train.shape)
print(g_test.shape)
```
I want to build a simple, initial classifier to get a sense of the performances I might get in more optimized models. To this end, I will build a logistic regression model without doing any cross-validation or hyperparameter optimization.
```
# Instantiate the model
initial_logreg = LogisticRegression()
# Fit to training set
initial_logreg.fit(X_train, g_train)
# Score on training set
print(f'Model accuracy on training set: {initial_logreg.score(X_train, g_train)*100}%')
# Score on test set
print(f'Model accuracy on test set: {initial_logreg.score(X_test, g_test)*100}%')
```
These are extremely high accuracies. The model has most likely overfit to the training set, but the accuracy on the test set is still surprisingly high.
Here are some possible explanations:
- The dataset (RAVDESS) is relatively small, with only 1440 data points (1438 if I do not count the two very short clips that I excluded). This model is likely not very robust and has easily overfit to the training set.
- The features I have extracted could be excellent predictors of gender.
- This could be a very simple classification task. After all, there are only two classes, and theoretically, features extracted from male and female voice clips should have distinguishable patterns.
I had originally planned to build more gender classification models for this dataset, but I will forgo this for now. In part 4, I will try using this model to classify clips from another dataset and examine its performance.
```
# Pickling the model for later use
joblib.dump(initial_logreg, 'pickle1_gender_logreg.pkl')
```
___
# Building Models for Classifying Emotion for Males
```
# Making a new dataframe that contains only male recordings
ravdess_mfcc_m_df = ravdess_mfcc_df[ravdess_mfcc_df['Gender'] == 'male'].reset_index().drop('index', axis=1)
ravdess_mfcc_m_df
# Splitting the dataframe into features and target
Xm = ravdess_mfcc_m_df.iloc[:, :-2]
em = ravdess_mfcc_m_df['Emotion']
# # Encoding the emotions
# emotion_encoder = LabelEncoder()
# em = emotion_encoder.fit_transform(em)
# # Checking the results
# em
# # Which number represents which emotion?
# for num in np.unique(em):
# print(f'{num} represents {emotion_encoder.inverse_transform([num])[0]}.')
```
Note: I realized that encoding the target is unnecessary; it is done automatically by the models.
```
# Splitting the data into training and test sets
Xm_train, Xm_test, em_train, em_test = train_test_split(Xm, em, test_size=0.3, stratify=em, random_state=1)
# Checking the shapes
print(Xm_train.shape)
print(Xm_test.shape)
print(em_train.shape)
print(em_test.shape)
```
As before, I will try building an initial model.
```
# Instantiate the model
initial_logreg_em = LogisticRegression()
# Fit to training set
initial_logreg_em.fit(Xm_train, em_train)
# Score on training set
print(f'Model accuracy on training set: {initial_logreg_em.score(Xm_train, em_train)*100}%')
# Score on test set
print(f'Model accuracy on test set: {initial_logreg_em.score(Xm_test, em_test)*100}%')
```
The model has overfit to the training set yet again, and this time the accuracy on the test set leaves a lot to be desired. Let's evaluate the model further using a confusion matrix and a classification report.
```
# Having initial_logreg_em make predictions based on the test set features
em_pred = initial_logreg_em.predict(Xm_test)
# Building the confusion matrix as a dataframe
emotions = ['angry', 'calm', 'disgusted', 'fearful', 'happy', 'neutral', 'sad', 'surprised']
em_confusion_df = pd.DataFrame(confusion_matrix(em_test, em_pred))
em_confusion_df.columns = [f'Predicted {emotion}' for emotion in emotions]
em_confusion_df.index = [f'Actual {emotion}' for emotion in emotions]
em_confusion_df
# Classification report
print(classification_report(em_test, em_pred))
```
In a binary classification problem, there is one negative class and one positive class. This is not the case here, because this is a multiclass classification problem. In the table above, each row of precision and recall scores assumes the corresponding emotion is the positive class, and groups all other emotions as the negative class.
Precision is the following measure: Of all the data points that the model classified as belonging to the positive class (i.e., the true and false positives), what proportion is correct (i.e., truly positive)?
Recall is the following measure: Of all the data points that are truly positive (i.e., the true positives and false negatives as classified by the model), what proportion did the model correctly classify (i.e., the true positives)?
It appears that the initial model is strongest at classifying calm voice clips, and weakest at classifying neutral voice clips. In order of strongest to weakest: calm, angry, fearful, disgusted, surprised, happy, sad, and neutral.
I will now try building new models and optimizing hyperparameters to obtain better performance. I will use a pipeline and multiple grid searches to accomplish this.
Before I build all my models in bulk, I want to see if doing principal component analysis (PCA) could be beneficial. I will do PCA on both unscaled and scaled features, and plot the resulting explained variance ratios. I have two goals here:
- Get a sense of whether scaling would be beneficial for model performance
- Get a sense of how many principal components I should use
```
# PCA on unscaled features
# Instantiate PCA and fit to Xm_train
pca = PCA().fit(Xm_train)
# Transform Xm_train
Xm_train_pca = pca.transform(Xm_train)
# Transform Xm_test
Xm_test_pca = pca.transform(Xm_test)
# Standard scaling
# Instantiate the scaler and fit to Xm_train
scaler = StandardScaler().fit(Xm_train)
# Transform Xm_train
Xm_train_scaled = scaler.transform(Xm_train)
# Transform Xm_test
Xm_test_scaled = scaler.transform(Xm_test)
# PCA on scaled features
# Instantiate PCA and fit to Xm_train_scaled
pca_scaled = PCA().fit(Xm_train_scaled)
# Transform Xm_train_scaled
Xm_train_scaled_pca = pca_scaled.transform(Xm_train_scaled)
# Transform Xm_test_scaled
Xm_test_scaled_pca = pca_scaled.transform(Xm_test_scaled)
# Plot the explained variance ratios
plt.subplots(1, 2, figsize = (15, 5))
# Unscaled
plt.subplot(1, 2, 1)
plt.bar(np.arange(1, len(pca.explained_variance_ratio_)+1), pca.explained_variance_ratio_)
plt.xlabel('Principal Component')
plt.ylabel('Explained Variance Ratio')
plt.title('PCA on Unscaled Features')
plt.ylim(top = 0.5) # Equalizing the y-axes
# Scaled
plt.subplot(1, 2, 2)
plt.bar(np.arange(1, len(pca_scaled.explained_variance_ratio_)+1), pca_scaled.explained_variance_ratio_)
plt.xlabel('Principal Component')
plt.ylabel('Explained Variance Ratio')
plt.title('PCA on Scaled Features')
plt.ylim(top = 0.5) # Equalizing the y-axes
plt.tight_layout()
plt.show()
```
Principal components are linear combinations of the original features, ordered by how much of the dataset's variance they explain. Looking at the two plots above, it appears that for the same number of principal components, those using unscaled features are able to explain more variance (i.e., capture more information) than those using scaled features. For example, looking at the first ~25 principal components of each plot, the bars of the left plot (unscaled) are higher and skewed more to the left than those of the right plot (scaled). Since the purpose of PCA is to reduce dimensionality of the data by keeping the components that explain the most variance and discarding the rest, the unscaled principal components might benefit my models more than the scaled principal components will.
However, I have to be mindful of the underlying variance in my features. Some features have values in the -800s, while others are close to 0.
```
# Examining the variances
var_df = pd.DataFrame(ravdess_mfcc_m_df.var()).T
var_df
```
Since PCA is looking for high variance directions, it can become biased by the underlying variance in a given feature if I do not scale it down first. I can see that some features have much higher variance than others do, so there is likely a lot of bias in the unscaled principal components above.
How much variance is explained by certain numbers of unscaled and scaled principal components? This will help me determine how many principal components to try in my grid searches later.
```
# Unscaled
num_components = [503, 451, 401, 351, 301, 251, 201, 151, 101, 51]
for n in num_components:
print(f'Variance explained by {n-1} unscaled principal components: {np.round(np.sum(pca.explained_variance_ratio_[:n])*100, 2)}%')
# Scaled
num_components = [503, 451, 401, 351, 301, 251, 201, 151, 101, 51]
for n in num_components:
print(f'Variance explained by {n-1} scaled principal components: {np.round(np.sum(pca_scaled.explained_variance_ratio_[:n])*100, 2)}%')
```
I will now build a pipeline and multiple grid searches with five-fold cross-validation to optimize the hyperparameters. I will try five types of classifiers: logistic regression, support vector machine, random forest, XGBoost, and k-nearest neighbours. To get a better sense of how each type performs, I will make a grid search for each one. I will also try different numbers of principal components for unscaled and scaled features.
```
# Cache
cachedir = mkdtemp()
# Pipeline (these values are placeholders)
my_pipeline = Pipeline(steps=[('scaler', StandardScaler()), ('dim_reducer', PCA()), ('model', LogisticRegression())], memory=cachedir)
# Parameter grid for log reg
logreg_param_grid = [
# l1 without PCA
# unscaled and scaled * 9 regularization strengths = 18 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [LogisticRegression(penalty='l1', n_jobs=-1)],
'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l1 unscaled with PCA
# 5 PCAs * 9 regularization strengths = 45 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 251, 50),
'model': [LogisticRegression(penalty='l1', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l1 scaled with PCA
# 4 PCAs * 9 regularization strengths = 36 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50),
'model': [LogisticRegression(penalty='l1', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l2 (default) without PCA
# unscaled and scaled * 9 regularization strengths = 18 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [LogisticRegression(solver='lbfgs', n_jobs=-1)],
'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l2 (default) unscaled with PCA
# 5 PCAs * 9 regularization strengths = 45 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 251, 50),
'model': [LogisticRegression(solver='lbfgs', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l2 (default) scaled with PCA
# 4 PCAs * 9 regularization strengths = 36 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50),
'model': [LogisticRegression(solver='lbfgs', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]}
]
# Instantiate the log reg grid search
logreg_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=logreg_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the log reg grid search
fitted_logreg_grid_em = logreg_grid_search.fit(Xm_train, em_train)
# What was the best log reg?
fitted_logreg_grid_em.best_estimator_
print(f"The best log reg's accuracy on the training set: {fitted_logreg_grid_em.score(Xm_train, em_train)*100}%")
print(f"The best log reg's accuracy on the test set: {fitted_logreg_grid_em.score(Xm_test, em_test)*100}%")
# Pickling the best log reg for later use
joblib.dump(fitted_logreg_grid_em.best_estimator_, 'pickle2_male_emotion_logreg.pkl')
# Parameter grid for SVM
svm_param_grid = [
# unscaled and scaled * 9 regularization strengths = 18 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [SVC()], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# unscaled
# 5 PCAs * 9 regularization strengths = 45 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 251, 50), 'model': [SVC()],
'model__C':[0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# scaled
# 4 PCAs * 9 regularization strengths = 36 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50), 'model': [SVC()],
'model__C':[0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]}
]
# Instantiate the SVM grid search
svm_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=svm_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the SVM grid search
fitted_svm_grid_em = svm_grid_search.fit(Xm_train, em_train)
# What was the best SVM?
fitted_svm_grid_em.best_estimator_
print(f"The best SVM's accuracy on the training set: {fitted_svm_grid_em.score(Xm_train, em_train)*100}%")
print(f"The best SVM's accuracy on the test set: {fitted_svm_grid_em.score(Xm_test, em_test)*100}%")
# Pickling the best SVM for later use
joblib.dump(fitted_svm_grid_em.best_estimator_, 'pickle3_male_emotion_svm.pkl')
# Parameter grid for random forest (scaling is unnecessary)
rf_param_grid = [
# 5 numbers of estimators * 5 max depths = 25 models
{'scaler': [None], 'dim_reducer': [None], 'model': [RandomForestClassifier(n_jobs=-1)], 'model__n_estimators': np.arange(100, 501, 100),
'model__max_depth': np.arange(5, 26, 5)},
# 5 PCAs * 5 numbers of estimators * 5 max depths = 150 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 251, 50), 'model': [RandomForestClassifier(n_jobs=-1)],
'model__n_estimators': np.arange(100, 501, 100), 'model__max_depth': np.arange(5, 26, 5)}
]
# Instantiate the rf grid search
rf_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=rf_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the rf grid search
fitted_rf_grid_em = rf_grid_search.fit(Xm_train, em_train)
# What was the best rf?
fitted_rf_grid_em.best_estimator_
print(f"The best random forest's accuracy on the training set: {fitted_rf_grid_em.score(Xm_train, em_train)*100}%")
print(f"The best random forest's accuracy on the test set: {fitted_rf_grid_em.score(Xm_test, em_test)*100}%")
# # Parameter grid for XGBoost (scaling is unnecessary)
# xgb_param_grid = [
# # 5 numbers of estimators * 5 max depths = 25 models
# {'scaler': [None], 'dim_reducer': [None], 'model': [XGBClassifier(n_jobs=-1)], 'model__n_estimators': np.arange(100, 501, 100),
# 'model__max_depth': np.arange(5, 26, 5)},
# # 3 PCAs * 5 numbers of estimators * 5 max depths = 75 models
# # I am trying fewer PCAs for XGBoost
# {'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': [200, 250, 300], 'model': [XGBClassifier(n_jobs=-1)],
# 'model__n_estimators': np.arange(100, 501, 100), 'model__max_depth': np.arange(5, 26, 5)}
# ]
# # Instantiate the XGB grid search
# xgb_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=xgb_param_grid, cv=5, n_jobs=-1, verbose=5)
# # Fit the XGB grid search
# fitted_xgb_grid_em = xgb_grid_search.fit(Xm_train, em_train)
```
The above never finished so I decided to comment it out. I will try again without passing `n_jobs=-1` into `XGBClassifier()`, and with a higher number (10 instead of 5) for `verbose` in `GridSearchCV()`.
```
# Parameter grid for XGBoost (scaling is unnecessary)
xgb_param_grid = [
# 5 numbers of estimators * 5 max depths = 25 models
{'scaler': [None], 'dim_reducer': [None], 'model': [XGBClassifier()], 'model__n_estimators': np.arange(100, 501, 100),
'model__max_depth': np.arange(5, 26, 5)},
# 3 PCAs * 5 numbers of estimators * 5 max depths = 75 models
# I am trying fewer PCAs for XGBoost
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': [200, 250, 300], 'model': [XGBClassifier()],
'model__n_estimators': np.arange(100, 501, 100), 'model__max_depth': np.arange(5, 26, 5)}
]
# Instantiate the XGB grid search
xgb_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=xgb_param_grid, cv=5, n_jobs=-1, verbose=10)
# Fit the XGB grid search
fitted_xgb_grid_em = xgb_grid_search.fit(Xm_train, em_train)
# What was the best XGB model?
fitted_xgb_grid_em.best_estimator_
print(f"The best XGB model's accuracy on the training set: {fitted_xgb_grid_em.score(Xm_train, em_train)*100}%")
print(f"The best XGB model's accuracy on the test set: {fitted_xgb_grid_em.score(Xm_test, em_test)*100}%")
# Parameter grid for KNN
knn_param_grid = [
# unscaled and scaled * 10 Ks = 20 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [KNeighborsClassifier(n_jobs=-1)], 'model__n_neighbors': np.arange(3, 22, 2)},
# unscaled
# 5 PCAs * 10 Ks = 50 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 251, 50), 'model': [KNeighborsClassifier(n_jobs=-1)],
'model__n_neighbors': np.arange(3, 22, 2)},
# scaled
# 4 PCAs * 10 Ks = 40 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50), 'model': [KNeighborsClassifier(n_jobs=-1)],
'model__n_neighbors': np.arange(3, 22, 2)}
]
# Instantiate the grid search
knn_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=knn_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the KNN grid search
fitted_knn_grid_em = knn_grid_search.fit(Xm_train, em_train)
# What was the best KNN model?
fitted_knn_grid_em.best_estimator_
print(f"The best KNN model's accuracy on the training set: {fitted_knn_grid_em.score(Xm_train, em_train)*100}%")
print(f"The best KNN model's accuracy on the test set: {fitted_knn_grid_em.score(Xm_test, em_test)*100}%")
```
### Conclusions for classifying emotions for males
- Of the five classifier types I tried in my grid searches, SVM had the highest accuracy on the test set (60.19%), followed by logistic regression (58.80%), XGBoost (51.39%), random forest (46.76%), and lastly, KNN (45.37%).
- Based on these results, I have pickled the best SVM and logistic regression. In part 4, I will try them on a new, male-only dataset.
- Except for the best KNN model, all the best models found in the grid searches had training accuracies of 100%, indicating that they overfit to the training set.
- The best KNN model had a training accuracy of 76.29%, but this was still much higher than its test accuracy of 45.37%.
- For the classifier types in which scaling the features matters (logistic regression, SVM, and KNN), all the best models made use of the standard scaler.
- Of the five best-in-type models, random forest and KNN were the only two which made use of principal components.
___
# Building Models for Classifying Emotion for Females
I will follow the same steps I took in classifying emotions for males, with one difference: This time I will not try XGBoost, due to its long computation time and comparatively low performance.
```
# Making a new dataframe that contains only female recordings
ravdess_mfcc_f_df = ravdess_mfcc_df[ravdess_mfcc_df['Gender'] == 'female'].reset_index().drop('index', axis=1)
ravdess_mfcc_f_df
# Splitting the dataframe into features and target
Xf = ravdess_mfcc_f_df.iloc[:, :-2]
ef = ravdess_mfcc_f_df['Emotion']
# Splitting the data into training and test sets
Xf_train, Xf_test, ef_train, ef_test = train_test_split(Xf, ef, test_size=0.3, stratify=ef, random_state=1)
# Checking the shapes
print(Xf_train.shape)
print(Xf_test.shape)
print(ef_train.shape)
print(ef_test.shape)
```
Here is an initial model:
```
# Instantiate the model
initial_logreg_ef = LogisticRegression()
# Fit to training set
initial_logreg_ef.fit(Xf_train, ef_train)
# Score on training set
print(f'Model accuracy on training set: {initial_logreg_ef.score(Xf_train, ef_train)*100}%')
# Score on test set
print(f'Model accuracy on test set: {initial_logreg_ef.score(Xf_test, ef_test)*100}%')
```
The model has overfit to the training set yet again. Interestingly, this initial accuracy on the female test set is noticeably higher than the initial accuracy on the male test set, which was 56.48%. Again, let's evaluate the model further using a confusion matrix and a classification report.
```
# Having initial_logreg_ef make predictions based on the test set features
ef_pred = initial_logreg_ef.predict(Xf_test)
# Building the confusion matrix as a dataframe
emotions = ['angry', 'calm', 'disgusted', 'fearful', 'happy', 'neutral', 'sad', 'surprised']
ef_confusion_df = pd.DataFrame(confusion_matrix(ef_test, ef_pred))
ef_confusion_df.columns = [f'Predicted {emotion}' for emotion in emotions]
ef_confusion_df.index = [f'Actual {emotion}' for emotion in emotions]
ef_confusion_df
# Classification report
print(classification_report(ef_test, ef_pred))
```
It appears that the initial model is strongest at classifying calm voice clips, and weakest at classifying fearful voice clips. In order of strongest to weakest: calm, neutral, happy, surprised, angry, disgusted, sad, and fearful.
There is not as much variance in performance across the emotions when compared to that of the initial model for male emotions.
Although I found that none of the best male emotion classifiers made use of PCA, I will still examine the explained variance ratios like I did before.
```
# PCA on unscaled features
# Instantiate PCA and fit to Xf_train
pca = PCA().fit(Xf_train)
# Transform Xf_train
Xf_train_pca = pca.transform(Xf_train)
# Transform Xf_test
Xf_test_pca = pca.transform(Xf_test)
# Standard scaling
# Instantiate the scaler and fit to Xf_train
scaler = StandardScaler().fit(Xf_train)
# Transform Xf_train
Xf_train_scaled = scaler.transform(Xf_train)
# Transform Xf_test
Xf_test_scaled = scaler.transform(Xf_test)
# PCA on scaled features
# Instantiate PCA and fit to Xf_train_scaled
pca_scaled = PCA().fit(Xf_train_scaled)
# Transform Xf_train_scaled
Xf_train_scaled_pca = pca_scaled.transform(Xf_train_scaled)
# Transform Xf_test_scaled
Xf_test_scaled_pca = pca_scaled.transform(Xf_test_scaled)
# Plot the explained variance ratios
plt.subplots(1, 2, figsize = (15, 5))
# Unscaled
plt.subplot(1, 2, 1)
plt.bar(np.arange(1, len(pca.explained_variance_ratio_)+1), pca.explained_variance_ratio_)
plt.xlabel('Principal Component')
plt.ylabel('Explained Variance Ratio')
plt.title('PCA on Unscaled Features')
plt.ylim(top = 0.5) # Equalizing the y-axes
# Scaled
plt.subplot(1, 2, 2)
plt.bar(np.arange(1, len(pca_scaled.explained_variance_ratio_)+1), pca_scaled.explained_variance_ratio_)
plt.xlabel('Principal Component')
plt.ylabel('Explained Variance Ratio')
plt.title('PCA on Scaled Features')
plt.ylim(top = 0.5) # Equalizing the y-axes
plt.tight_layout()
plt.show()
```
These are the same trends I saw previously for male emotions.
How much variance is explained by certain numbers of unscaled and scaled principal components? This will help me determine how many principal components to try in my grid searches later.
```
# Unscaled
num_components = [503, 451, 401, 351, 301, 251, 201, 151, 101, 51]
for n in num_components:
print(f'Variance explained by {n-1} unscaled principal components: {np.round(np.sum(pca.explained_variance_ratio_[:n])*100, 2)}%')
# Scaled
num_components = [503, 451, 401, 351, 301, 251, 201, 151, 101, 51]
for n in num_components:
print(f'Variance explained by {n-1} scaled principal components: {np.round(np.sum(pca_scaled.explained_variance_ratio_[:n])*100, 2)}%')
```
Like before, I will now do a grid search for each classifier type, with five-fold cross-validation to optimize the hyperparameters.
```
# Cache
cachedir = mkdtemp()
# Pipeline (these values are placeholders)
my_pipeline = Pipeline(steps=[('scaler', StandardScaler()), ('dim_reducer', PCA()), ('model', LogisticRegression())], memory=cachedir)
# Parameter grid for log reg
logreg_param_grid = [
# l1 without PCA
# unscaled and scaled * 9 regularization strengths = 18 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [LogisticRegression(penalty='l1', n_jobs=-1)],
'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l1 unscaled with PCA
# 6 PCAs * 9 regularization strengths = 54 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 301, 50),
'model': [LogisticRegression(penalty='l1', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l1 scaled with PCA
# 4 PCAs * 9 regularization strengths = 36 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50),
'model': [LogisticRegression(penalty='l1', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l2 (default) without PCA
# unscaled and scaled * 9 regularization strengths = 18 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [LogisticRegression(solver='lbfgs', n_jobs=-1)],
'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l2 (default) unscaled with PCA
# 6 PCAs * 9 regularization strengths = 54 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 301, 50),
'model': [LogisticRegression(solver='lbfgs', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# l2 (default) scaled with PCA
# 4 PCAs * 9 regularization strengths = 36 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50),
'model': [LogisticRegression(solver='lbfgs', n_jobs=-1)], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]}
]
# Instantiate the log reg grid search
logreg_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=logreg_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the log reg grid search
fitted_logreg_grid_ef = logreg_grid_search.fit(Xf_train, ef_train)
# What was the best log reg?
fitted_logreg_grid_ef.best_estimator_
print(f"The best log reg's accuracy on the training set: {fitted_logreg_grid_ef.score(Xf_train, ef_train)*100}%")
print(f"The best log reg's accuracy on the test set: {fitted_logreg_grid_ef.score(Xf_test, ef_test)*100}%")
# Parameter grid for SVM
svm_param_grid = [
# unscaled and scaled * 9 regularization strengths = 18 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [SVC()], 'model__C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# unscaled
# 6 PCAs * 9 regularization strengths = 54 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 301, 50), 'model': [SVC()],
'model__C':[0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]},
# scaled
# 4 PCAs * 9 regularization strengths = 36 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50), 'model': [SVC()],
'model__C':[0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000]}
]
# Instantiate the SVM grid search
svm_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=svm_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the SVM grid search
fitted_svm_grid_ef = svm_grid_search.fit(Xf_train, ef_train)
# What was the best SVM?
fitted_svm_grid_ef.best_estimator_
print(f"The best SVM's accuracy on the training set: {fitted_svm_grid_ef.score(Xf_train, ef_train)*100}%")
print(f"The best SVM's accuracy on the test set: {fitted_svm_grid_ef.score(Xf_test, ef_test)*100}%")
# Parameter grid for random forest (scaling is unnecessary)
rf_param_grid = [
# 5 numbers of estimators * 5 max depths = 25 models
{'scaler': [None], 'dim_reducer': [None], 'model': [RandomForestClassifier(n_jobs=-1)], 'model__n_estimators': np.arange(100, 501, 100),
'model__max_depth': np.arange(5, 26, 5)},
# 6 PCAs * 5 numbers of estimators * 5 max depths = 150 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 301, 50), 'model': [RandomForestClassifier(n_jobs=-1)],
'model__n_estimators': np.arange(100, 501, 100), 'model__max_depth': np.arange(5, 26, 5)}
]
# Instantiate the rf grid search
rf_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=rf_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the rf grid search
fitted_rf_grid_ef = rf_grid_search.fit(Xf_train, ef_train)
# What was the best rf?
fitted_rf_grid_ef.best_estimator_
print(f"The best random forest's accuracy on the training set: {fitted_rf_grid_ef.score(Xf_train, ef_train)*100}%")
print(f"The best random forest's accuracy on the test set: {fitted_rf_grid_ef.score(Xf_test, ef_test)*100}%")
# Parameter grid for KNN
knn_param_grid = [
# unscaled and scaled * 10 Ks = 20 models
{'scaler': [None, StandardScaler()], 'dim_reducer': [None], 'model': [KNeighborsClassifier(n_jobs=-1)], 'model__n_neighbors': np.arange(3, 22, 2)},
# unscaled
# 6 PCAs * 10 Ks = 60 models
{'scaler': [None], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(50, 301, 50), 'model': [KNeighborsClassifier(n_jobs=-1)],
'model__n_neighbors': np.arange(3, 22, 2)},
# scaled
# 4 PCAs * 10 Ks = 40 models
{'scaler': [StandardScaler()], 'dim_reducer': [PCA()], 'dim_reducer__n_components': np.arange(200, 351, 50), 'model': [KNeighborsClassifier(n_jobs=-1)],
'model__n_neighbors': np.arange(3, 22, 2)}
]
# Instantiate the grid search
knn_grid_search = GridSearchCV(estimator=my_pipeline, param_grid=knn_param_grid, cv=5, n_jobs=-1, verbose=5)
# Fit the KNN grid search
fitted_knn_grid_ef = knn_grid_search.fit(Xf_train, ef_train)
# What was the best KNN model?
fitted_knn_grid_ef.best_estimator_
print(f"The best KNN model's accuracy on the training set: {fitted_knn_grid_ef.score(Xf_train, ef_train)*100}%")
print(f"The best KNN model's accuracy on the test set: {fitted_knn_grid_ef.score(Xf_test, ef_test)*100}%")
```
### Conclusions for classifying emotions for females
- Of the four classifier types I tried in my grid searches, logistic regression had the highest accuracy on the test set (71.29%), followed by SVM (70.83%), random forest (61.57%), and lastly, KNN (55.56%).
- Except for the best KNN model, all the best models found in the grid searches had training accuracies of 100%, indicating that they overfit to the training set.
- The best KNN model had a training accuracy of 59.33%, which was not much higher than its test accuracy of 55.56%. A much wider gap was found in the best KNN model for male emotions.
- For the classifier types in which scaling the features matters (logistic regression, SVM, and KNN), the best logistic regression and SVM models made use of the standard scaler, while the best KNN model did not.
- All the best-in-type models made use of principal components, except SVM.
- Interestingly, the female emotion classifiers achieved higher accuracies than their male counterparts. It appears that for the RAVDESS dataset, the differences between female emotions are greater the differences between male emotions.
- Based on this alone, I cannot extrapolate and conclude that women are more socially more expressive than men are, although this is an interesting thought.
| true |
code
| 0.62157 | null | null | null | null |
|
```
from mplsoccer import Pitch, VerticalPitch
from mplsoccer.dimensions import valid, size_varies
import matplotlib.pyplot as plt
import numpy as np
import random
np.random.seed(42)
```
# Test five points are same in both orientations
```
for pitch_type in valid:
if pitch_type in size_varies:
kwargs = {'pitch_length': 105, 'pitch_width': 68}
else:
kwargs = {}
pitch = Pitch(pitch_type=pitch_type, line_zorder=2, **kwargs)
pitch_vertical = VerticalPitch(pitch_type=pitch_type, line_zorder=2, **kwargs)
fig, ax = plt.subplots(ncols=2, figsize=(12, 7))
fig.suptitle(pitch_type)
x = np.random.uniform(low=pitch.dim.pitch_extent[0], high=pitch.dim.pitch_extent[1], size=5)
y = np.random.uniform(low=pitch.dim.pitch_extent[2], high=pitch.dim.pitch_extent[3], size=5)
pitch.draw(ax[0])
pitch.scatter(x, y, ax=ax[0], color='red', zorder=3)
stats = pitch.bin_statistic(x, y)
stats['statistic'][stats['statistic'] == 0] = np.nan
hm = pitch.heatmap(stats, ax=ax[0])
txt = pitch.label_heatmap(stats, color='white', ax=ax[0])
pitch_vertical.draw(ax[1])
pitch_vertical.scatter(x, y, ax=ax[1], color='red', zorder=3)
stats_vertical = pitch_vertical.bin_statistic(x, y)
stats_vertical['statistic'][stats_vertical['statistic'] == 0] = np.nan
hm_vertical = pitch_vertical.heatmap(stats_vertical, ax=ax[1])
txt_vertical = pitch_vertical.label_heatmap(stats, color='white', ax=ax[1])
```
# Test five points are same in both orientations - positional
```
for pitch_type in valid:
if pitch_type in size_varies:
kwargs = {'pitch_length': 105, 'pitch_width': 68}
else:
kwargs = {}
pitch = Pitch(pitch_type=pitch_type, line_zorder=2, **kwargs)
pitch_vertical = VerticalPitch(pitch_type=pitch_type, line_zorder=2, **kwargs)
fig, ax = plt.subplots(ncols=2, figsize=(12, 7))
fig.suptitle(pitch_type)
x = np.random.uniform(low=pitch.dim.pitch_extent[0], high=pitch.dim.pitch_extent[1], size=5)
y = np.random.uniform(low=pitch.dim.pitch_extent[2], high=pitch.dim.pitch_extent[3], size=5)
pitch.draw(ax[0])
pitch.scatter(x, y, ax=ax[0], color='red', zorder=3)
stats = pitch.bin_statistic_positional(x, y)
hm = pitch.heatmap_positional(stats, ax=ax[0])
txt = pitch.label_heatmap(stats, color='white', ax=ax[0])
pitch_vertical.draw(ax[1])
pitch_vertical.scatter(x, y, ax=ax[1], color='red', zorder=3)
stats_vertical = pitch_vertical.bin_statistic_positional(x, y)
hm_vertical = pitch_vertical.heatmap_positional(stats_vertical, ax=ax[1])
txt_vertical = pitch_vertical.label_heatmap(stats, color='white', ax=ax[1])
```
# Test edges - positional x
```
for pitch_type in valid:
if pitch_type in size_varies:
kwargs = {'pitch_length': 105, 'pitch_width': 68}
else:
kwargs = {}
pitch = Pitch(pitch_type=pitch_type, line_zorder=2, pitch_color='None', axis=True, label=True, **kwargs)
pitch_vertical = VerticalPitch(pitch_type=pitch_type, line_zorder=2, pitch_color='None', axis=True, label=True, **kwargs)
fig, ax = plt.subplots(ncols=2, figsize=(12, 7))
fig.suptitle(pitch_type)
x = pitch.dim.positional_x
y = np.random.uniform(low=pitch.dim.pitch_extent[2], high=pitch.dim.pitch_extent[3], size=x.size)
pitch.draw(ax[0])
pitch.scatter(x, y, ax=ax[0], color='red', zorder=3)
stats = pitch.bin_statistic_positional(x, y)
hm = pitch.heatmap_positional(stats, ax=ax[0], edgecolors='yellow')
txt = pitch.label_heatmap(stats, color='white', ax=ax[0])
pitch_vertical.draw(ax[1])
pitch_vertical.scatter(x, y, ax=ax[1], color='red', zorder=3)
stats_vertical = pitch_vertical.bin_statistic_positional(x, y)
hm_vertical = pitch_vertical.heatmap_positional(stats_vertical, ax=ax[1], edgecolors='yellow')
txt_vertical = pitch_vertical.label_heatmap(stats_vertical, color='white', ax=ax[1])
```
# Test edges - positional y
```
for pitch_type in valid:
if pitch_type in size_varies:
kwargs = {'pitch_length': 105, 'pitch_width': 68}
else:
kwargs = {}
pitch = Pitch(pitch_type=pitch_type, line_zorder=2, pitch_color='None', axis=True, label=True, **kwargs)
pitch_vertical = VerticalPitch(pitch_type=pitch_type, line_zorder=2, pitch_color='None', axis=True, label=True, **kwargs)
fig, ax = plt.subplots(ncols=2, figsize=(12, 7))
fig.suptitle(pitch_type)
y = pitch.dim.positional_y
x = np.random.uniform(low=pitch.dim.pitch_extent[0], high=pitch.dim.pitch_extent[1], size=y.size)
pitch.draw(ax[0])
pitch.scatter(x, y, ax=ax[0], color='red', zorder=3)
stats = pitch.bin_statistic_positional(x, y)
hm = pitch.heatmap_positional(stats, ax=ax[0], edgecolors='yellow')
txt = pitch.label_heatmap(stats, color='white', ax=ax[0])
pitch_vertical.draw(ax[1])
pitch_vertical.scatter(x, y, ax=ax[1], color='red', zorder=3)
stats_vertical = pitch_vertical.bin_statistic_positional(x, y)
hm_vertical = pitch_vertical.heatmap_positional(stats_vertical, ax=ax[1], edgecolors='yellow')
txt_vertical = pitch_vertical.label_heatmap(stats_vertical, color='white', ax=ax[1])
```
| true |
code
| 0.637115 | null | null | null | null |
|
# Pipelines for classifiers using Balanced Accuracy
For each dataset, classifier and folds:
- Robust scaling
- 2, 3, 5, 10-fold outer CV
- balanced accurary as score
We will use folders *datasets2* and *results2*.
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
# remove warnings
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
import numpy as np
import pandas as pd
import time
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score, GridSearchCV, StratifiedKFold, LeaveOneOut
from sklearn.metrics import confusion_matrix,accuracy_score, roc_auc_score,f1_score, recall_score, precision_score
from sklearn.utils import class_weight
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression, LassoCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from xgboost import XGBClassifier
from sklearn.svm import SVC
from sklearn.gaussian_process.kernels import RBF
from sklearn.svm import LinearSVC
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler
from sklearn.feature_selection import RFECV, VarianceThreshold, SelectKBest, chi2
from sklearn.feature_selection import SelectFromModel, SelectPercentile, f_classif
import os
!ls ./datasets2/*
!ls ./results2/*
# get list of files in datasets2 = all datasets
dsList = os.listdir('./datasets2')
print('--> Found', len(dsList), 'dataset files')
# create a list with all output variable names
outVars = []
for eachdsFile in dsList:
outVars.append( (eachdsFile[:-4])[3:] )
```
### Define script parameters
```
# define list of folds
foldTypes = [2,3,5,10]
# define a label for output files
targetName = '_Outer'
seed = 42
```
### Function definitions
```
def set_weights(y_data, option='balanced'):
"""Estimate class weights for umbalanced dataset
If ‘balanced’, class weights will be given by n_samples / (n_classes * np.bincount(y)).
If a dictionary is given, keys are classes and values are corresponding class weights.
If None is given, the class weights will be uniform """
cw = class_weight.compute_class_weight(option, np.unique(y_data), y_data)
w = {i:j for i,j in zip(np.unique(y_data), cw)}
return w
def getDataFromDataset(sFile, OutVar):
# read details file
print('\n-> Read dataset', sFile)
df = pd.read_csv(sFile)
#df = feather.read_dataframe(sFile)
print('Shape', df.shape)
# print(list(df.columns))
# select X and Y
ds_y = df[OutVar]
ds_X = df.drop(OutVar,axis = 1)
Xdata = ds_X.values # get values of features
Ydata = ds_y.values # get output values
print('Shape X data:', Xdata.shape)
print('Shape Y data:',Ydata.shape)
# return data for X and Y, feature names as list
return (Xdata, Ydata, list(ds_X.columns))
def Pipeline_OuterCV(Xdata, Ydata, label = 'my', class_weights = {0: 1, 1: 1}, folds = 3, seed = 42):
# inputs:
# data for X, Y; a label about data, number of folds, seeed
# default: 3-fold CV
# define classifiers
names = ['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']
classifiers = [KNeighborsClassifier(3),
SVC(kernel="linear",random_state=seed,gamma='scale'),
SVC(kernel = 'rbf', random_state=seed,gamma='auto'),
LogisticRegression(solver='lbfgs',random_state=seed),
DecisionTreeClassifier(random_state = seed),
RandomForestClassifier(n_estimators=50,n_jobs=-1,random_state=seed),
XGBClassifier(n_jobs=-1,seed=seed)
]
# results dataframe: each column for a classifier
df_res = pd.DataFrame(columns=names)
# build each classifier
print('* Building scaling+feature selection+outer '+str(folds)+'-fold CV for '+str(len(names))+' classifiers:', str(names))
total = time.time()
# define a fold-CV for all the classifier
outer_cv = StratifiedKFold(n_splits=folds,shuffle=True,random_state=seed)
# use each ML
for name, clf in zip(names, classifiers):
start = time.time()
# create pipeline: scaler + classifier
estimators = []
# SCALER
estimators.append(('Scaler', RobustScaler() ))
# add Classifier
estimators.append(('Classifier', clf))
# create pipeline
model = Pipeline(estimators)
# evaluate pipeline
scores = cross_val_score(model, Xdata, Ydata, cv=outer_cv, scoring='balanced_accuracy', n_jobs=-1)
df_res[name] = scores
print('%s, MeanScore=%0.2f, Time:%0.1f mins' % (name, scores.mean(), (time.time() - start)/60))
# save results
resFile = './results2/'+str(label)+str(targetName)+'_Outer-'+str(folds)+'-foldCV.csv'
df_res.to_csv(resFile, index=False)
print('* Scores saved', resFile)
print('Total time:', (time.time() - total)/60, ' mins')
# return scores for all classifiers as dataframe (each column a classifier)
return df_res
```
### Calculations
```
df_results = None # all results
# apply MLs to each data
for OutVar in outVars:
sFile = './datasets2/ds.'+str(OutVar)+'.csv'
# get data from file
Xdata, Ydata, Features = getDataFromDataset(sFile,OutVar)
# Calculate class weights
class_weights = set_weights(Ydata)
print("Class weights = ", class_weights)
# try different folds for each subset -> box plots
for folds in foldTypes:
# calculate outer CV for different binary classifiers
df_fold = Pipeline_OuterCV(Xdata, Ydata, label = OutVar, class_weights = class_weights, folds = folds, seed = seed)
df_fold['Dataset'] = OutVar
df_fold['folds'] = folds
# add each result to a summary dataframe
df_results = pd.concat([df_results,df_fold])
# save the results to file
resFile = './results2/'+'ML_Outer-n-foldCV.csv'
df_results.to_csv(resFile, index=False)
```
### Mean scores
```
# calculate means of ACC scores for each ML
df_means =df_results.groupby(['Dataset','folds'], as_index = False).mean()[['Dataset', 'folds','KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']]
# save averaged values
resFile_means = './results2/'+'ML_Outer-n-foldCV_means.csv'
df_means.to_csv(resFile_means, index=False)
```
### Best ML results
```
# find the maximum value rows for all MLs
bestMLs = df_means[['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']].idxmax()
print(bestMLs)
# get the best score by ML method
for ML in ['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']:
print(ML, '\t', list(df_means.iloc[df_means[ML].idxmax()][['Dataset', 'folds', ML]]))
# Add a new column with the original output name (get first 2 characters from Dataset column)
getOutOrig = []
for each in df_means['Dataset']:
getOutOrig.append(each[:2])
df_means['Output'] = getOutOrig
df_means
# save new results including extra column with output variable name
resFile_means2 = './results2/'+'ML_Outer-n-foldCV_means2.csv'
df_means.to_csv(resFile_means2, index=False)
```
### Get the best ML for each type of output
We are checking all 2, 3, 5, 10-fold CV results:
```
for outName in list(set(df_means['Output'])):
print('*********************')
print('OUTPUT =', outName)
df_sel = df_means[df_means['Output'] == outName].copy()
for ML in ['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']:
print(ML, '\t', list(df_sel.loc[df_sel[ML].idxmax(),:][['Dataset', 'folds', ML]]))
df_sel.loc[df_sel[ML].idxmax(),:]
```
### Get the best ML for each type of output for 10-fold CV
```
df_10fold = df_means[df_means['folds']==10].copy()
df_10fold.head()
for outName in list(set(df_10fold['Output'])):
print('*********************')
print('OUTPUT =', outName)
df_sel = df_10fold[df_10fold['Output'] == outName].copy()
print('MAX =',df_sel[['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']].max().max())
for ML in ['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']:
print(ML, '\t', list(df_sel.loc[df_sel[ML].idxmax(),:][['Dataset', 'folds', ML]]))
```
### Get the best ML for each type of output for 5-fold CV
```
df_5fold = df_means[df_means['folds']==5].copy()
df_5fold.head()
for outName in list(set(df_5fold['Output'])):
print('*********************')
print('OUTPUT =', outName)
df_sel = df_5fold[df_5fold['Output'] == outName].copy()
print('MAX =',df_sel[['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']].max().max())
for ML in ['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']:
print(ML, '\t', list(df_sel.loc[df_sel[ML].idxmax(),:][['Dataset', 'folds', ML]]))
```
Get only the best values from all MLs for 5- and 10-fold CV:
```
print('5-fold CV')
for outName in list(set(df_5fold['Output'])):
df_sel = df_5fold[df_5fold['Output'] == outName].copy()
print(outName,df_sel[['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']].max().max())
print('10-fold CV')
for outName in list(set(df_10fold['Output'])):
df_sel = df_10fold[df_10fold['Output'] == outName].copy()
print(outName,df_sel[['KNN', 'SVM linear', 'SVM', 'LR', 'DT', 'RF', 'XGB']].max().max())
```
**Conclusion**: even with **5,10-CV** we are able to obtain classification models with **ACC > 0.70** and in one case with **ACC > 0.81**.
| true |
code
| 0.475118 | null | null | null | null |
|
Week 7 Notebook: Optimizing Other Objectives
===============================================================
This week, we will look at optimizing multiple objectives simultaneously. In particular, we will look at pivoting with adversarial neural networks {cite:p}`Louppe:2016ylz,ganin2014unsupervised,Sirunyan:2019nfw`.
We will borrow the implementation from: <https://github.com/glouppe/paper-learning-to-pivot>
```
import tensorflow.keras as keras
import numpy as np
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
import uproot
from tqdm.notebook import tqdm
import yaml
with open('definitions.yml') as file:
# The FullLoader parameter handles the conversion from YAML
# scalar values to Python the dictionary format
definitions = yaml.load(file, Loader=yaml.FullLoader)
features = definitions['features']
spectators = definitions['spectators']
labels = definitions['labels']
nfeatures = definitions['nfeatures']
nspectators = definitions['nspectators']
nlabels = definitions['nlabels']
ntracks = definitions['ntracks']
```
## Define discriminator, regression, and combined adversarial models
The combined loss function is $$L = L_\mathrm{class} - \lambda L_\mathrm{reg}$$
- $L_\mathrm{class}$ is the loss function for the classification part (categorical cross entropy)
- $L_\mathrm{reg}$ is the loss function for the adversarial part (in this case a regression)
- $\lambda$ is a hyperparamter that controls how important the adversarial part of the loss is compared to the classification part, which we nominally set to 1
```
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense, BatchNormalization, Concatenate, GlobalAveragePooling1D
import tensorflow.keras.backend as K
# define Deep Sets model with Dense Keras layer
inputs = Input(shape=(ntracks, nfeatures,), name='input')
x = BatchNormalization(name='bn_1')(inputs)
x = Dense(64, name='dense_1', activation='relu')(x)
x = Dense(32, name='dense_2', activation='relu')(x)
x = Dense(32, name='dense_3', activation='relu')(x)
# sum over tracks
x = GlobalAveragePooling1D(name='pool_1')(x)
x = Dense(100, name='dense_4', activation='relu')(x)
output = Dense(nlabels, name = 'output', activation='softmax')(x)
keras_model_disc = Model(inputs=inputs, outputs=output)
keras_model_disc.compile(optimizer='adam',
loss='categorical_crossentropy')
# regressor
x = Dense(100, name='dense_5', activation='relu')(keras_model_disc(inputs))
x = Dense(100, name='dense_6', activation='relu')(x)
output_reg = Dense(2, activation='linear', name='mass_pt_reg')(x)
sgd_opt = keras.optimizers.SGD(momentum=0)
keras_model_reg = Model(inputs=inputs, outputs=output_reg)
keras_model_reg.compile(optimizer=sgd_opt,
loss='mse')
# combined model
lam = 1
keras_model_adv = Model(inputs=inputs, outputs=[keras_model_disc(inputs), keras_model_reg(inputs)])
keras_model_adv.compile(optimizer=sgd_opt,
loss=['categorical_crossentropy', 'mse'],
loss_weights = [1, -lam])
print(keras_model_disc.summary())
print(keras_model_reg.summary())
print(keras_model_adv.summary())
```
## Load data
```
from DataGenerator import DataGenerator
# load training and validation generators
train_files = ['root://eospublic.cern.ch//eos/opendata/cms/datascience/HiggsToBBNtupleProducerTool/HiggsToBBNTuple_HiggsToBB_QCD_RunII_13TeV_MC/train/ntuple_merged_10.root']
val_files = ['root://eospublic.cern.ch//eos/opendata/cms/datascience/HiggsToBBNtupleProducerTool/HiggsToBBNTuple_HiggsToBB_QCD_RunII_13TeV_MC/train/ntuple_merged_11.root']
train_generator = DataGenerator(train_files, features, labels, spectators, batch_size=1024, n_dim=ntracks,
remove_mass_pt_window=False,
remove_unlabeled=True, max_entry=5000,
return_spectators=True, scale_mass_pt=[100., 10000.])
val_generator = DataGenerator(val_files, features, labels, spectators, batch_size=1024, n_dim=ntracks,
remove_mass_pt_window=False,
remove_unlabeled=True, max_entry=5000,
return_spectators=True, scale_mass_pt=[100., 10000.])
```
## Pretrain discriminator and regressor models
```
# pretrain discriminator
keras_model_disc.trainable = True
keras_model_disc.compile(optimizer='adam',
loss='categorical_crossentropy')
for n_epoch in tqdm(range(20)):
for t in tqdm(train_generator, total=len(train_generator), leave=bool(n_epoch==19)):
keras_model_disc.fit(t[0], t[1][0],verbose=0)
# pretrain regressor
keras_model_reg.trainable = True
keras_model_disc.trainable = False
keras_model_reg.compile(optimizer=sgd_opt, loss='mse')
for n_epoch in tqdm(range(20)):
for t in tqdm(train_generator, total=len(train_generator), leave=bool(n_epoch==19)):
keras_model_reg.fit(t[0], t[1][1], verbose=0)
```
## Main training loop
During the main training loop, we do two things:
1. Train the discriminator model with the combined loss function $$L = L_\mathrm{class} - \lambda L_\mathrm{reg}$$
1. Train the regression model to learn the mass from with the standard MSE loss function $$L_\mathrm{reg}$$
```
# alternate training discriminator and regressor
for n_epoch in tqdm(range(40)):
for t in tqdm(train_generator, total=len(train_generator), leave=bool(n_epoch==39)):
# train discriminator
keras_model_reg.trainable = False
keras_model_disc.trainable = True
keras_model_adv.compile(optimizer=sgd_opt,
loss=['categorical_crossentropy', 'mse'],
loss_weights=[1, -lam])
keras_model_adv.fit(t[0], t[1], verbose=0)
# train regressor
keras_model_reg.trainable = True
keras_model_disc.trainable = False
keras_model_reg.compile(optimizer=sgd_opt, loss='mse')
keras_model_reg.fit(t[0], t[1][1],verbose=0)
keras_model_adv.save_weights('keras_model_adv_best.h5')
```
## Test
```
# load testing file
test_files = ['root://eospublic.cern.ch//eos/opendata/cms/datascience/HiggsToBBNtupleProducerTool/HiggsToBBNTuple_HiggsToBB_QCD_RunII_13TeV_MC/test/ntuple_merged_0.root']
test_generator = DataGenerator(test_files, features, labels, spectators, batch_size=8192, n_dim=ntracks,
remove_mass_pt_window=True,
remove_unlabeled=True,
return_spectators=True,
max_entry=200000) # basically, no maximum
# run model inference on test data set
predict_array_adv = []
label_array_test = []
spec_array_test = []
for t in tqdm(test_generator, total=len(test_generator)):
label_array_test.append(t[1][0])
spec_array_test.append(t[1][1])
predict_array_adv.append(keras_model_adv.predict(t[0])[0])
predict_array_adv = np.concatenate(predict_array_adv, axis=0)
label_array_test = np.concatenate(label_array_test, axis=0)
spec_array_test = np.concatenate(spec_array_test, axis=0)
# create ROC curves
print(label_array_test.shape)
print(spec_array_test.shape)
print(predict_array_adv.shape)
fpr_adv, tpr_adv, threshold_adv = roc_curve(label_array_test[:,1], predict_array_adv[:,1])
# plot ROC curves
plt.figure()
plt.plot(tpr_adv, fpr_adv, lw=2.5, label="Adversarial, AUC = {:.1f}%".format(auc(fpr_adv,tpr_adv)*100))
plt.xlabel(r'True positive rate')
plt.ylabel(r'False positive rate')
plt.semilogy()
plt.ylim(0.001, 1)
plt.xlim(0, 1)
plt.grid(True)
plt.legend(loc='upper left')
plt.show()
from utils import find_nearest
plt.figure()
for wp in [1.0, 0.5, 0.3, 0.1, 0.05]:
idx, val = find_nearest(fpr_adv, wp)
plt.hist(spec_array_test[:,0], bins=np.linspace(40, 200, 21),
weights=label_array_test[:,0]*(predict_array_adv[:,1] > threshold_adv[idx]),
alpha=0.4, density=True, label='QCD, {}% FPR cut'.format(int(wp*100)),linestyle='-')
plt.legend()
plt.xlabel(r'$m_{SD}$')
plt.ylabel(r'Normalized probability')
plt.xlim(40, 200)
plt.figure()
for wp in [1.0, 0.5, 0.3, 0.1, 0.05]:
idx, val = find_nearest(fpr_adv, wp)
plt.hist(spec_array_test[:,0], bins=np.linspace(40, 200, 21),
weights=label_array_test[:,1]*(predict_array_adv[:,1] > threshold_adv[idx]),
alpha=0.4, density=True, label='H(bb), {}% FPR cut'.format(int(wp*100)),linestyle='-')
plt.legend()
plt.xlabel(r'$m_{SD}$')
plt.ylabel(r'Normalized probability')
plt.xlim(40, 200)
plt.show()
plt.figure()
plt.hist(predict_array_adv[:,1], bins = np.linspace(0, 1, 21),
weights=label_array_test[:,1]*0.1,
alpha=0.4, linestyle='-', label='H(bb)')
plt.hist(predict_array_adv[:,1], bins = np.linspace(0, 1, 21),
weights=label_array_test[:,0],
alpha=0.4, linestyle='-', label='QCD')
plt.legend()
plt.show()
plt.figure()
plt.hist(spec_array_test[:,0], bins = np.linspace(40, 200, 21),
weights = label_array_test[:,1]*0.1,
alpha=0.4, linestyle='-', label='H(bb)')
plt.hist(spec_array_test[:,0], bins = np.linspace(40, 200, 21),
weights = label_array_test[:,0],
alpha=0.4, linestyle='-', label='QCD')
plt.legend()
plt.show()
```
| true |
code
| 0.681912 | null | null | null | null |
|
## TASK-1: Make a class to calculate the range, time of flight and horizontal range of the projectile fired from the ground.
## TASK-2: Use the list to find the range, time of flight and horizontal range for varying value of angle from 1 degree to 90 dergree.
## TASK-3: Make a plot to show the variation of range, time of flight and horizontal range with angle of projection.
## TASK-4: Change the list of [angle], [range], [time of flight] and [horizontal range] into dictionary and finely into dataframe using pandas. Save the file in your PC in csv file.
### Required formula:
### Horizontal range: $R=u^2sin2A/g$
### Time of flight: $T = 2usinA/g$
### Maximum Height: $H = u^2*sin^2A/2g$
```
import math
import numpy as np
class Projectile():
def __init__(self,u,A,g):
self.u=u
self.A=A
self.g=g
def HorizontalRange(self):
R= (self.u^2) * math.sin(2 * self.A * math.pi/180)/ (self.g)
return R
def TimeofFlight(self):
T= (self.u*2) * math.sin(self.A* math.pi/180) / (self.g)
return T
def MaximumHeight(self):
H=(self.u * math.sin(self.A* math.pi/180))**2 / (self.g*2)
return H
def update_A(self,A):
self.A=A
u=36 #in m/s
g=9.8 #in m/s^2
P = Projectile(36, 0, 9.8 )
R=[] #empty list to collect horizontal range
T=[] #empty list to collect the time of flight
H=[] #empty list to collect the maximum height
N=[] #empty list to collect angle of projection
x=np.arange(0,90+0.1,0.1)
for i in x:
N.append(i)
P.update_A(i)
r=P.HorizontalRange()
t=P.TimeofFlight()
h=P.MaximumHeight()
R.append(i)
T.append(t)
H.append(h)
import matplotlib.pyplot as plt
plt.subplot(2,2,1)
plt.plot(N,R)
plt.xlabel('N')
plt.ylabel('R')
plt.title("Angle of projection with Horizontal Range")
plt.subplot(2,2,2)
plt.plot(N,T)
plt.xlabel('N')
plt.ylabel('T')
plt.title("Angle of projection with Time of Flight")
plt.subplot(2,2,3)
plt.plot(N,H)
plt.xlabel('N')
plt.ylabel('H')
plt.title("Angle of projection with Maximum Distance")
data={} #empty list
data.update({"Angle_of_projection":N,"Horizontal_Range":R,"Time_of_Flight":T,"Maximum_Distance":H})
print(data)
import pandas as pd
Df=pd.DataFrame(data)
print(Df)
Df.to_csv('Projectile.csv')
df=pd.read_csv('Projectile.csv')
df.head()
plt.figure(figsize=[10,10])
plt.subplot(2,2,1)
plt.semilogy(df.Angle_of_projection,df.Horizontal_Range)
plt.xlabel('N')
plt.ylabel('R')
plt.title('Angle of projection with Horizontal Range')
plt.subplot(2,2,2)
plt.semilogy(df.Angle_of_projection,df.Time_of_Flight)
plt.xlabel('N')
plt.ylabel('T')
plt.title('Angle of projecton with Time of Flight')
plt.subplot(2,2,3)
plt.semilogy(df.Angle_of_projection,df.Maximum_Distance)
plt.xlabel('N')
plt.ylabel('H')
plt.title('Angle of projection with Maximum Distance')
```
| true |
code
| 0.514095 | null | null | null | null |
|
#Improving Computer Vision Accuracy using Convolutions
In the previous lessons you saw how to do fashion recognition using a Deep Neural Network (DNN) containing three layers -- the input layer (in the shape of the data), the output layer (in the shape of the desired output) and a hidden layer. You experimented with the impact of different sized of hidden layer, number of training epochs etc on the final accuracy.
For convenience, here's the entire code again. Run it and take a note of the test accuracy that is printed out at the end.
```
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images / 255.0
test_images=test_images / 255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
test_loss = model.evaluate(test_images, test_labels)
```
Your accuracy is probably about 89% on training and 87% on validation...not bad...But how do you make that even better? One way is to use something called Convolutions. I'm not going to details on Convolutions here, but the ultimate concept is that they narrow down the content of the image to focus on specific, distinct, details.
If you've ever done image processing using a filter (like this: https://en.wikipedia.org/wiki/Kernel_(image_processing)) then convolutions will look very familiar.
In short, you take an array (usually 3x3 or 5x5) and pass it over the image. By changing the underlying pixels based on the formula within that matrix, you can do things like edge detection. So, for example, if you look at the above link, you'll see a 3x3 that is defined for edge detection where the middle cell is 8, and all of its neighbors are -1. In this case, for each pixel, you would multiply its value by 8, then subtract the value of each neighbor. Do this for every pixel, and you'll end up with a new image that has the edges enhanced.
This is perfect for computer vision, because often it's features that can get highlighted like this that distinguish one item for another, and the amount of information needed is then much less...because you'll just train on the highlighted features.
That's the concept of Convolutional Neural Networks. Add some layers to do convolution before you have the dense layers, and then the information going to the dense layers is more focussed, and possibly more accurate.
Run the below code -- this is the same neural network as earlier, but this time with Convolutional layers added first. It will take longer, but look at the impact on the accuracy:
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(64, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.summary()
model.fit(training_images, training_labels, epochs=5)
test_loss = model.evaluate(test_images, test_labels)
```
It's likely gone up to about 93% on the training data and 91% on the validation data.
That's significant, and a step in the right direction!
Try running it for more epochs -- say about 20, and explore the results! But while the results might seem really good, the validation results may actually go down, due to something called 'overfitting' which will be discussed later.
(In a nutshell, 'overfitting' occurs when the network learns the data from the training set really well, but it's too specialised to only that data, and as a result is less effective at seeing *other* data. For example, if all your life you only saw red shoes, then when you see a red shoe you would be very good at identifying it, but blue suade shoes might confuse you...and you know you should never mess with my blue suede shoes.)
Then, look at the code again, and see, step by step how the Convolutions were built:
Step 1 is to gather the data. You'll notice that there's a bit of a change here in that the training data needed to be reshaped. That's because the first convolution expects a single tensor containing everything, so instead of 60,000 28x28x1 items in a list, we have a single 4D list that is 60,000x28x28x1, and the same for the test images. If you don't do this, you'll get an error when training as the Convolutions do not recognize the shape.
```
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
```
Next is to define your model. Now instead of the input layer at the top, you're going to add a Convolution. The parameters are:
1. The number of convolutions you want to generate. Purely arbitrary, but good to start with something in the order of 32
2. The size of the Convolution, in this case a 3x3 grid
3. The activation function to use -- in this case we'll use relu, which you might recall is the equivalent of returning x when x>0, else returning 0
4. In the first layer, the shape of the input data.
You'll follow the Convolution with a MaxPooling layer which is then designed to compress the image, while maintaining the content of the features that were highlighted by the convlution. By specifying (2,2) for the MaxPooling, the effect is to quarter the size of the image. Without going into too much detail here, the idea is that it creates a 2x2 array of pixels, and picks the biggest one, thus turning 4 pixels into 1. It repeats this across the image, and in so doing halves the number of horizontal, and halves the number of vertical pixels, effectively reducing the image by 25%.
You can call model.summary() to see the size and shape of the network, and you'll notice that after every MaxPooling layer, the image size is reduced in this way.
```
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
```
Add another convolution
```
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2)
```
Now flatten the output. After this you'll just have the same DNN structure as the non convolutional version
```
tf.keras.layers.Flatten(),
```
The same 128 dense layers, and 10 output layers as in the pre-convolution example:
```
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
```
Now compile the model, call the fit method to do the training, and evaluate the loss and accuracy from the test set.
```
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(test_acc)
```
# Visualizing the Convolutions and Pooling
This code will show us the convolutions graphically. The print (test_labels[;100]) shows us the first 100 labels in the test set, and you can see that the ones at index 0, index 23 and index 28 are all the same value (9). They're all shoes. Let's take a look at the result of running the convolution on each, and you'll begin to see common features between them emerge. Now, when the DNN is training on that data, it's working with a lot less, and it's perhaps finding a commonality between shoes based on this convolution/pooling combination.
```
print(test_labels[:100])
import matplotlib.pyplot as plt
f, axarr = plt.subplots(3,4)
FIRST_IMAGE=0
SECOND_IMAGE=7
THIRD_IMAGE=26
CONVOLUTION_NUMBER = 1
from tensorflow.keras import models
layer_outputs = [layer.output for layer in model.layers]
activation_model = tf.keras.models.Model(inputs = model.input, outputs = layer_outputs)
for x in range(0,4):
f1 = activation_model.predict(test_images[FIRST_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[0,x].imshow(f1[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[0,x].grid(False)
f2 = activation_model.predict(test_images[SECOND_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[1,x].imshow(f2[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[1,x].grid(False)
f3 = activation_model.predict(test_images[THIRD_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[2,x].imshow(f3[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[2,x].grid(False)
```
EXERCISES
1. Try editing the convolutions. Change the 32s to either 16 or 64. What impact will this have on accuracy and/or training time.
2. Remove the final Convolution. What impact will this have on accuracy or training time?
3. How about adding more Convolutions? What impact do you think this will have? Experiment with it.
4. Remove all Convolutions but the first. What impact do you think this will have? Experiment with it.
5. In the previous lesson you implemented a callback to check on the loss function and to cancel training once it hit a certain amount. See if you can implement that here!
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=10)
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(test_acc)
```
| true |
code
| 0.833274 | null | null | null | null |
|
# Edge Computing using Tensorflow and Neural Compute Stick
## " Generate piano sounds using EEG capturing rhythmic activity of brain"
### Contents
#### 1. Motivation
#### 2. Signal acquisition
#### 3. Signal postprocessing
#### 4. Synthesize music
##### 4.1 Training Data
##### 4.2 Training data preprocessing
##### 4.3 Neural Network architecture
##### 4.4 Training methodology
#### 5. Error definition and Further development
### 1. Motivation
The following work is inspired by EEG. EEG can be described in terms of rhythmic cortical electrical activity of brain triggered by perceived sensory stimuli , where those rythmic activity falls in certain frequency bands(delta to gamma). In sound engineering, signals with dominant frequencies makes a pitch and sequences of pitches creates rhythm. Combining this concepts intuitively shows, by detecting those dominant frequencies, it is possible to listen to our brain using the signals it generates for different stimuli. Using principles of sound synthesis and sampling along with deep neural networks(DNN), in this project, i made an attempt to extract the rhythm or pitch hidding within brain waves and reproduce it as piano music.
### 2. Signal acquisition: (Not available)
EEG/EOG recordings are not available. For the sake of simplicity and bring general working prototype of the model, used some random auto generated signal for test. This is because, the trained DNN is not constrained within brain waves, but to any kind of signal with dominant frequencies. Piano data set available for none commercial use is used during training and evaluation phase.
### 3. Signal Postprocessing (idea proposed)
Enough researches proved, "brain waves are rhytmic"[2] and they falls in frequency bandwidth from Delta(<4Hz) to Gamma (>30-100Hz). Human audible frequecy range 20 - 20KHz. Hence, increasing the acquired EEG freuencies by certain constant value and preprocess with sampling rate 44100 makes it resembles piano sounds (fundamental frequency range 27.5 - 4186.01Hz), which itself within human audible range. Later, save the processed brain signals as numpy arrays and convert them as .wav files to reproduce the sound. Using the .wav files to extract brain signal (now sound) informations (frequencies, sampling rate and pitch). In case, we succeed to regenerate the sounds, since we increased the signal frequency by constant (to fit our piano data), the sounds plays faster. Hence we need to reduce the frequency by the same value while replaying the sound that fits the original brain signal.
### 4. Synthesize music
#### 4.1 Training data
Piano chords dataset available to public for non commercial purposes
[3]. Each piano .wav files in the data set are sampled at 44100 and have varying data length. Data is analysed and studied further in detail from the code blocks below.
#### 4.2 Training data preprocessing
###### Import required python libraries and add the current working directory to python path and system paths
Directory structure
<br>
<br>
Wavenet/
-/dataset (downloaded piano chords)
- /UMAPiano-DB-Poly-1/UMAPiano-DB-A0-NO-F.wav
-/clipped_data (clipped paino sounds are here)
-/wavenet_logs (tensorflow checkpoints and logs)
```
%matplotlib inline
from __future__ import division
import numpy as np
import tensorflow as tf
import scipy.io
import matplotlib
import matplotlib.pyplot as plt
import os
import sys
import random
import scipy.io.wavfile
import scipy
matplotlib.rcParams['figure.figsize'] = (8.0, 6.0)
#-------------------------------------Add working directory to path-----------------------------------------------
cwd = os.getcwd()
sys.path.append(cwd)
sys.path.insert(0,'E:/!CogSci/!!!WS2017/Edge_computing/Wavenet')
sys.path.insert(0,'C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/dataset')
sys.path.insert(0,'E:/!CogSci/!!!WS2017/Edge_computing/Wavenet/clipped_data')
# Save the variables in a log/directory during training
save_path = "C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/wavenet_logs"
if not os.path.exists(save_path):
os.makedirs(save_path)
```
Each piano file from the dataset is approximately 1-2 seconds in length. We used the scipy to read each music file and get their sampling rate and data as array and found that all audio files has sampling rate 44100 and the data length varies based on length of audio. To train DNN, we need all training data with same length and increase the sampling rate to prevent signal loss/corruption. Below code shows the acquisition of first information about the piano dataset.
```
# Location of the wav file in the file system.
fileName1 = 'E:/!CogSci/!!!WS2017/Edge_computing/Wavenet/dataset/UMAPiano-DB-Poly-1/UMAPiano-DB-A0-NO-F.wav'
fileName2 = 'E:/!CogSci/!!!WS2017/Edge_computing/Wavenet/dataset/UMAPiano-DB-Poly-1/UMAPiano-DB-A0-NO-M.wav'
# Loads sample rate (bps) and signal data (wav).
sample_rate1, data1 = scipy.io.wavfile.read(fileName1)
sample_rate2, data2 = scipy.io.wavfile.read(fileName2)
# Print in sdout the sample rate, number of items and duration in seconds of the wav file
print("Sample rate1 %s data size1 %s duration1: %s seconds"%(sample_rate1,data1.shape,len(data1)/sample_rate1))
print("Sample rate2 %s data size2 %s duration2: %s seconds"%(sample_rate2,data2.shape,len(data2)/sample_rate2))
print("DATA SIZES ARE DIFFERENT NEEDS TO BE CONSIDERED")
# Plot the wave file and get insight about the sample. Here we test first 100 samples of the wav file
plt.plot(data1)
plt.plot(data2)
plt.show()
```
Looking at the plot above, it is clear that there is no signal informations at the head and tail of the piano data. We can clip them safely and that reduces computation and memory resources. Also, i changed all the data file names with numbers for convenient. Later, i checked the files with shortest and longest length to fix varying length problem in the code block below.
```
"""
dataset_path = 'E:/!CogSci/!!!WS2017/Edge_computing/Wavenet/dataset/UMAPiano-DB-Poly-1'
dir_list_len = len(os.listdir(dataset_path))
print("Number of files in the Dataset ",dir_list_len)
# Change file names to be easily recognized
def change_filenames(dataset_path):
i = 0 # Counter and target filename
for old_name in os.listdir(dataset_path):
# os.rename(dataset_path + "/" + old_name, dataset_path + "/" + str(i) + '.wav')
os.rename(os.path.join(dataset_path, old_name), os.path.join(dataset_path, str(i) + '.wav'))
i+=1
change_filenames(dataset_new)
list_sizes_new =[]
for data_new in os.listdir(dataset_new):
_,data_new = scipy.io.wavfile.read(dataset_new+'/'+data_new)
list_sizes_new.append(data_new.shape[0])
print("Maximum size %s and the music file is",np.argmax(list_sizes_new))
"""
dataset_new = 'C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/dataset'
list_sizes =[]
for datas in os.listdir(dataset_new):
_,data_new = scipy.io.wavfile.read(os.path.join(dataset_new,datas))
list_sizes.append(data_new.shape[0])
if data_new.shape[0]== 39224:
print("Minimum sized file is",datas)
if data_new.shape[0] == 181718:
print("Max sized file is",datas)
print("Maximum size %s "%(max(list_sizes)))
print("Minimum size %s "%(min(list_sizes)))
print("Dataset is in C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/dataset and all the files are numbered")
# -------------------------Get some insights and information about the max and min sized data-----------------------------
# Location of the wav file in the file system.
fileName3 = 'C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/dataset/356.wav'
fileName4 = 'C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/dataset/722.wav'
# Loads sample rate (bps) and signal data (wav).
sample_rate3, data3 = scipy.io.wavfile.read(fileName3)
sample_rate4, data4 = scipy.io.wavfile.read(fileName4)
# Print in sdout the sample rate, number of items and duration in seconds of the wav file
print("Sample rate3 %s data size3 %s duration3: %s seconds"%(sample_rate3,data3.shape,len(data3)/sample_rate3))
print("Sample rate4 %s data size4 %s duration4: %s seconds"%(sample_rate4,data4.shape,len(data4)/sample_rate4))
print("Data sizes are different")
# Plot the wave file and get insight about the sample. Here we test first 100 samples of the wav file
plt.plot(data4)
plt.show()
print("Safe to clip first 10000 sample points out from the array and convert them back to .wav file")
```
As we can see that even the smallest piano file has 20k values of zeros at head and tail combined. Hence it is safe to clip the first and last 10k indices from all files and save them back to .wav files. We can also add small amount of noise to the training data at this step using the code below. We will discuss the reason later briefly.
```
#----------------------- .WAV training data preprocessing steps ----------------------
import IPython
# Clip the first and last 10000 values which doesn't show any informations
"""
def clip_write_wav(dataset_path):
i = 0 # Counter and target filename
for datas in os.listdir(dataset_path):
_,data = scipy.io.wavfile.read(dataset_path+'/'+datas)
data= data[:-10000] # Slice out last 10000 elements in data
data= data[10000:] # Slice out first 10000 elements in the data
#IF ADD NOISE DO it here in the data which is an array.
scipy.io.wavfile.write('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/clipped_data/%i.wav'%i, 44100, data)
i+=1
"""
_dataset = 'C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/dataset'
_target = 'C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/clipped_data'
clip_points = 10000
_sampling_rate = 44100
# clip_write_wav(_dataset) # Uncomment this line to clip and write the wav files again
# Verify required informations again
sample_rate3, data3 = scipy.io.wavfile.read('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/clipped_data/3.wav')
print("Sample rate %s data size %s duration: %s seconds"%(sample_rate3,data3.shape,len(data3)/sample_rate3))
plt.plot(data3)
plt.show()
#Play the audio inline
IPython.display.Audio('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/clipped_data/3.wav')
```
The data are clipped and they have shorter neck and tail now. Now we will increase the sampling rate (using "write_wav" function below) and fix the varying length in data by choosing the data with longest length as reference and zero padd other data until their length matches the length of the largest file done while feeding DNN using "get_training_data" function below .
<br>
But the scipy read module doesn't preserve the indices of the files in the dataset, as we can see that the largest and smallest file names from code block above and below are different. So, i hard coded the size of smallest and largest and search for the corresponding files.
```
# ------------- Search for the largest and smallest files --------------
_dataset_new = 'C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/clipped_data'
_list_sizes =[]
for datas in os.listdir(_dataset_new):
_,_data_new = scipy.io.wavfile.read(os.path.join(_dataset_new,datas))
_list_sizes.append(_data_new.shape[0])
if _data_new.shape[0]== 19224:
print("Minimum sized file is",datas)
if _data_new.shape[0] == 161718:
print("Max sized file is",datas)
print("Maximum size %s "%(max(_list_sizes)))
print("Minimum size %s "%(min(_list_sizes)))
print("Notice that io read and write doesnt preserve the index of files in the directory")
# ------------------------ Upsample the data -----------------------------
"""
def write_wav(dataset_path):
i=0
for datas in os.listdir(dataset_path):
_,data = scipy.io.wavfile.read(dataset_path+'/'+datas)
#IF ADD NOISE DO it here in the data which is an array.
scipy.io.wavfile.write('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/upsampled_data/%i.wav'%i, 88000, data)
i+=1
write_wav(_dataset_new)
"""
# ----------------- Verifying data integrity again -----------------------
sampled_datapath ='C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/upsampled_data'
_list_sizes =[]
for datas in os.listdir(sampled_datapath):
sampling_rate,_data_new = scipy.io.wavfile.read(os.path.join(sampled_datapath,datas))
_list_sizes.append(_data_new.shape[0])
if _data_new.shape[0]== 19224:
print("Minimum sized file is %s and sampling rate"%datas,sampling_rate)
elif _data_new.shape[0] == 161718:
print("Max sized file is %s and sampling rate"%datas,sampling_rate)
print("Maximum size %s "%(max(_list_sizes)))
print("Minimum size %s "%(min(_list_sizes)))
# Verify required informations again
sample_rate5, data5 = scipy.io.wavfile.read('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/upsampled_data/3.wav')
print("Sample rate %s data size %s duration: %s seconds"%(sample_rate5,data5.shape,len(data5)/sample_rate5))
plt.plot(data5)
plt.show()
#Play the audio inline
IPython.display.Audio('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/clipped_data/3.wav')
```
Since, we use stacks of CNN in the encoder, i decided to convert the data as matrix of size 512*512 for which
we need each file to have 262144 entries. So, instead of using largest file as reference, i opted 262144 as a length limit for all files. Function "get_training_data" serve this purpose for us.
```
# Each audio file should have 262144 entries. Extend them all with zeros in the tail
# Convert all audio files as matrices of 512x512 shape
def get_training_data(dataset_path):
training_data = []
for datas in os.listdir(dataset_path):
_,data = scipy.io.wavfile.read(dataset_path+'/'+datas)
# Add Zeros at the tail until 262144
temp_zeros = [0]*262144
temp_zeros[:len(data)] = data # Slice temp_zeros and add the data into the slice
# Reshape the data as square matrix of 512*512 of size 262144
data_ = np.reshape(temp_zeros,(512,512))
training_data.append(data_)
return training_data
training_data = get_training_data('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/upsampled_data')
print(training_data[0].shape)
# Expand the dims # The third dimension represents number of channels
for i in range(len(training_data)):
training_data[i] = training_data[i][:,:,np.newaxis]
print(training_data[0].shape)
```
The training data is ready to be fed into the network. But we still require the pitch info about each training data, since the network architecture we use require them while training. Class "HarmonicPowerSpectrum" and the nesxt two code blocks are bandpass filtering the signal that ease pitch detection.
```
# Get pitch of corresponding data
"""
Steps to extract the pitches of input signal:
Reference:
https://stackoverflow.com/questions/43946112/slicing-audio-signal-to-detect-pitch
1. Detect the fundamental frequencies "f0 estimation" (For piano, lowest freq - 27.5 and highest - 4186.01 Hz)
2. Get ride of garbage transients and low frequency noise using bandpass filter
3. After filtering do the peak detection using fft to find the pitches
"""
# 1. Fundamental frequencies [27.5,4186.01] Hz
# 2. Build bandpass fileter
from scipy.signal import butter, lfilter
def butter_bandpass(f0, fs, order):
"""Give the Sampling freq(fs),Bandpass window(f0) of filter, build the bandpass filter"""
nyq = 0.5 * fs
low = f0[0] / nyq
high = f0[1] / nyq
b, a = butter(order, [low, high], btype='band') # Numerator (b) and denominator (a) polynomials of the IIR filter
return b, a
def butter_bandpass_filter(sig, f0, fs, order):
""" Apply bandpass filter to the given signal"""
b, a = butter_bandpass(f0, fs,order)
y = lfilter(b, a, sig) # Apply the filter to the signal
return y
# Verify filter signal
sig = data5
f0= (27.5, 4186.01) # Fundamental freq of piano
fs = sample_rate5 # sampling rate of .wav files in the preprocessed training dataset
order = 1
b, a = butter_bandpass(f0, fs, order=1) # Numerator (b) and denominator (a) polynomials of the IIR filter
filtered_sig= butter_bandpass_filter(sig, f0,fs,order=1)
# Plot some range of samples from both raw signal and bandpass fitered signal.
plt.plot(sig[10000:10500], label='training signal')
plt.plot(filtered_sig[10000:10500], label='Bandpass filtered signal with order %d'% order)
plt.legend(loc='upper left')
# orders = [1,2,3,4,5]
# for order in orders:
# filtered_sig= butter_bandpass_filter(sig, f0,fs,order) # Bandpass filtered signal
# plt.plot(data5[10000:10500], label='training signal')
# plt.plot(filtered_sig[10000:10500], label='Bandpass filtered signal with order %d'% order)
# plt.legend(loc='upper left')
print("Bandpass filter with order 1 looks okay. We do not want to loose much informations in the data by filter it with higher orders")
# Reference :https://github.com/pydanny/pydanny-event-notes/blob/master/Pycon2008/intro_to_numpy/files/pycon_demos/windowed_fft/short_time_fft_solution.py
# Get frequency components of the data using Short time fourier transform
from scipy.fftpack import fft, fftfreq, fftshift
from scipy.signal import get_window
from math import ceil
from pylab import figure, imshow, clf, gray, xlabel, ylabel
sig = data5
f0= (27.5, 4186.01) # Fundamental freq of piano
fs = sample_rate5 # sampling rate of .wav files in the preprocessed training dataset
def freq_comp(signal,sample_rate):
# Define the sample spacing and window size.
dT = 1.0/sample_rate
T_window = 50e-3 # 50ms ; window time frame
N_window = int(T_window * sample_rate) # 440
N_data = len(signal)
# 1. Get the window profile
window = get_window('hamming', N_window) # Multiply the segments of data using hamming window func
# 2. Set up the FFT
result = []
start = 0
while (start < N_data - N_window):
end = start + N_window
result.append(fftshift(fft(window*signal[start:end])))
start = end
result.append(fftshift(fft(window*signal[-N_window:])))
result = np.array(result,result[0].dtype)
return result
freq_comp_unfiltered = freq_comp(sig,fs)
freq_comp_filtered = freq_comp(filtered_sig,fs)
plt.figure(1)
plt.plot(freq_comp_unfiltered)
plt.title("Unfiltered Frequency componenets of the training signal")
plt.show()
plt.figure(2)
plt.plot(freq_comp_filtered)
plt.title("Filtered frequency component of the training signal")
plt.show()
# # Display results
# freqscale = fftshift(fftfreq(N_window,dT))[150:-150]/1e3
# figure(1)
# clf()
# imshow(abs(result[:,150:-150]),extent=(freqscale[-1],freqscale[0],(N_data*dT-T_window/2.0),T_window/2.0))
# xlabel('Frequency (kHz)')
# ylabel('Time (sec.)')
# gray()
# Reference: http://musicweb.ucsd.edu/~trsmyth/analysis/Harmonic_Product_Spectrum.html
# Get the fundamental frequency(peak frequency) of the training data
import parabolic
from pylab import subplot, plot, log, copy, show
# def hps(sig,fs,maxharms):
# """
# Estimate peak frequency using harmonic product spectrum (HPS)
# """
# window = sig * scipy.signal.blackmanharris(len(sig))
# # Harmonic product spectrum: Measures the maximum coincidence for harmonics for each spectral frame
# c = abs(np.fft.rfft(window)) # Compute the one-dimensional discrete Fourier Transform for real input.
# plt.plot(c)
# plt.title("Discrete fourier transform of signal")
# plt.figure()
# pitch = np.log(c)
# plt.plot(pitch)
# plt.title("Max Harmonics for the range same as fundamental frequencies")
# # Search for a maximum value of a range of possible fundamental frequencies
# # for x in range(2, maxharms):
# # a = copy(c[::x]) # Should average or maximum instead of decimating
# # c = c[:len(a)]
# # i = np.argmax(abs(c))
# # c *= a
# # plt.title("Max Harmonics for the range of %d times the fundamental frequencies"%x)
# # plt.plot(maxharms, x)
# # plt.plot(np.log(c))
# # show()
# hps(butter_bandpass_filter(sig,f0, fs,order = 1),fs,maxharms=0)
# print(" As usual we opt to choose the same range as fundamental frequecies to make sure we dont loss much informations")
# Wrap them all in one class HarmonicPowerSpectrum
class HarmonicPowerSpectrum(object):
def __init__(self,sig,f0,fs,order,maxharms):
self.sig = sig
self.f0 = f0
self.fs = fs
self.order = order
self.maxharms = maxharms
@property
def butter_bandpass(self):
"""Give the Sampling freq(fs),Bandpass window(f0) of filter, build the bandpass filter"""
nyq = 0.5 * fs # Nyquist frequency
low = self.f0[0] / nyq
high = self.f0[1] / nyq
b, a = butter(self.order, [low, high], btype='band') # Numerator (b) and denominator (a) polynomials of the IIR filter
return b, a
@property
def butter_bandpass_filter(self):
""" Apply bandpass filter to the given signal"""
b, a = self.butter_bandpass
y = lfilter(b, a, self.sig) # Apply the filter to the signal
return y
@property
def hps(self):
"""Estimate peak frequency using harmonic product spectrum (HPS)"""
y = self.butter_bandpass_filter
window = y * scipy.signal.blackmanharris(len(y)) #Create window to search harmonics in signal slices
# Harmonic product spectrum: Measures the maximum coincidence for harmonics for each spectral frame
c = abs(np.fft.rfft(window)) # Compute the one-dimensional discrete Fourier Transform for real input.
z = np.log(c) # Fundamental frequency or pitch of the given signal
return z
z = HarmonicPowerSpectrum(sig, f0, fs, order = 1,maxharms=0)
harm_pow_spec = z.hps
plt.figure(1)
plt.plot(harm_pow_spec)
plt.title("Max Harmonics for the range same as fundamental frequencies Bp filtered in Order 0 and max harmonic psectum 0")
freq_comp_hps = freq_comp(harm_pow_spec,fs)
plt.figure(2)
plt.plot(freq_comp_hps)
plt.title("""Frequency components(in logarithmix scale) of harmonic spectrum of filtered training data.
A harmonic set of two pitches contributing significantly to this piano chord""")
plt.show()
```
Hence, i updated the get_training_data function to perform pitch detection using the HarmonicPowerSpectrum analyser
as seen below.
```
# Each audio file should have 262144 entries. Extend them all with zeros in the tail
# Convert all audio files as matrices of 512x512 shape
def get_training_data(dataset_path, f0, fs, order = 1,maxharms=0):
training_data = []
pitch_data = []
for datas in os.listdir(dataset_path):
_,data = scipy.io.wavfile.read(dataset_path+'/'+datas)
# Add Zeros at the tail until 162409
temp_zeros_data = [0]*262144
# print("Unpadded data len",len(data))
# print(len(temp_zeros))
temp_zeros_data[:len(data)] = data # Slice temp_zeros and add the data into the slice
# print("Padded data len",len(temp_zeros))
# print(np.shape(temp_zeros))
# Reshape the data as square matrix of 403*403 of size 162409
data_ = np.reshape(temp_zeros_data,(512,512))
# Get pitch of the signal
z = HarmonicPowerSpectrum(temp_zeros_data, f0, fs, order = 1,maxharms=0)
harm_pow_spec = z.hps
training_data.append(data_)
pitch_data.append(harm_pow_spec)
return training_data,pitch_data
training_data,pitch_data = get_training_data('C:/Users/Saran/!!!!!!!!!!!!!Edge_computing/Wavenet/upsampled_data',f0, fs, order = 1,maxharms=0)
print(training_data[0].shape)
# Expand the dims # The third dimension represents number of channels
for i in range(len(training_data)):
training_data[i] = training_data[i][:,:,np.newaxis]
print(training_data[0].shape)
```
| true |
code
| 0.299528 | null | null | null | null |
|
# Customizing and controlling xclim
xclim's behaviour can be controlled globally or contextually through `xclim.set_options`, which acts the same way as `xarray.set_options`. For the extension of xclim with the addition of indicators, see the [Extending xclim](extendxclim.ipynb) notebook.
```
import xarray as xr
import xclim
from xclim.testing import open_dataset
```
Let's create fake data with some missing values and mask every 10th, 20th and 30th of the month.This represents 9.6-10% of masked data for all months except February where it is 7.1%.
```
tasmax = (
xr.tutorial.open_dataset("air_temperature")
.air.resample(time="D")
.max(keep_attrs=True)
)
tasmax = tasmax.where(tasmax.time.dt.day % 10 != 0)
```
## Checks
Above, we created fake temperature data from a xarray tutorial dataset that doesn't have all the standard CF attributes. By default, when triggering a computation with an Indicator from xclim, warnings will be raised:
```
tx_mean = xclim.atmos.tx_mean(tasmax=tasmax, freq="MS") # compute monthly max tasmax
```
Setting `cf_compliance` to `'log'` mutes those warnings and sends them to the log instead.
```
xclim.set_options(cf_compliance="log")
tx_mean = xclim.atmos.tx_mean(tasmax=tasmax, freq="MS") # compute monthly max tasmax
```
## Missing values
For example, one can globally change the missing method.
Change the default missing method to "pct" and set its tolerance to 8%:
```
xclim.set_options(check_missing="pct", missing_options={"pct": {"tolerance": 0.08}})
tx_mean = xclim.atmos.tx_mean(tasmax=tasmax, freq="MS") # compute monthly max tasmax
tx_mean.sel(time="2013", lat=75, lon=200)
```
Only February has non-masked data. Let's say we want to use the "wmo" method (and its default options), but only once, we can do:
```
with xclim.set_options(check_missing="wmo"):
tx_mean = xclim.atmos.tx_mean(
tasmax=tasmax, freq="MS"
) # compute monthly max tasmax
tx_mean.sel(time="2013", lat=75, lon=200)
```
This method checks that there is less than `nm=5` invalid values in a month and that there are no consecutive runs of `nc>=4` invalid values. Thus, every month is now valid.
Finally, it is possible for advanced users to register their own method. Xclim's missing methods are in fact based on class instances. Thus, to create a custom missing class, one should implement a subclass based on `xclim.core.checks.MissingBase` and overriding at least the `is_missing` method. The method should take a `null` argument and a `count` argument.
- `null` is a `DataArrayResample` instance of the resampled mask of invalid values in the input dataarray.
- `count` is the number of days in each resampled periods and any number of other keyword arguments.
The `is_missing` method should return a boolean mask, at the same frequency as the indicator output (same as `count`), where True values are for elements that are considered missing and masked on the output.
When registering the class with the `xclim.core.checks.register_missing_method` decorator, the keyword arguments will be registered as options for the missing method. One can also implement a `validate` static method that receives only those options and returns whether they should be considered valid or not.
```
from xclim.core.missing import register_missing_method
from xclim.core.missing import MissingBase
from xclim.indices.run_length import longest_run
@register_missing_method("consecutive")
class MissingConsecutive(MissingBase):
"""Any period with more than max_n consecutive missing values is considered invalid"""
def is_missing(self, null, count, max_n=5):
return null.map(longest_run, dim="time") >= max_n
@staticmethod
def validate(max_n):
return max_n > 0
```
The new method is now accessible and usable with:
```
with xclim.set_options(
check_missing="consecutive", missing_options={"consecutive": {"max_n": 2}}
):
tx_mean = xclim.atmos.tx_mean(
tasmax=tasmax, freq="MS"
) # compute monthly max tasmax
tx_mean.sel(time="2013", lat=75, lon=200)
```
| true |
code
| 0.67338 | null | null | null | null |
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/figures/PDSH-cover-small.png?raw=1">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
<!--NAVIGATION-->
< [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb) | [Contents](Index.ipynb) | [In-Depth: Manifold Learning](05.10-Manifold-Learning.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.09-Principal-Component-Analysis.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
# In Depth: Principal Component Analysis
Up until now, we have been looking in depth at supervised learning estimators: those estimators that predict labels based on labeled training data.
Here we begin looking at several unsupervised estimators, which can highlight interesting aspects of the data without reference to any known labels.
In this section, we explore what is perhaps one of the most broadly used of unsupervised algorithms, principal component analysis (PCA).
PCA is fundamentally a dimensionality reduction algorithm, but it can also be useful as a tool for visualization, for noise filtering, for feature extraction and engineering, and much more.
After a brief conceptual discussion of the PCA algorithm, we will see a couple examples of these further applications.
We begin with the standard imports:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
```
## Introducing Principal Component Analysis
Principal component analysis is a fast and flexible unsupervised method for dimensionality reduction in data, which we saw briefly in [Introducing Scikit-Learn](05.02-Introducing-Scikit-Learn.ipynb).
Its behavior is easiest to visualize by looking at a two-dimensional dataset.
Consider the following 200 points:
```
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal');
```
By eye, it is clear that there is a nearly linear relationship between the x and y variables.
This is reminiscent of the linear regression data we explored in [In Depth: Linear Regression](05.06-Linear-Regression.ipynb), but the problem setting here is slightly different: rather than attempting to *predict* the y values from the x values, the unsupervised learning problem attempts to learn about the *relationship* between the x and y values.
In principal component analysis, this relationship is quantified by finding a list of the *principal axes* in the data, and using those axes to describe the dataset.
Using Scikit-Learn's ``PCA`` estimator, we can compute this as follows:
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
```
The fit learns some quantities from the data, most importantly the "components" and "explained variance":
```
print(pca.components_)
print(pca.explained_variance_)
```
To see what these numbers mean, let's visualize them as vectors over the input data, using the "components" to define the direction of the vector, and the "explained variance" to define the squared-length of the vector:
```
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca()
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
# plot data
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');
```
These vectors represent the *principal axes* of the data, and the length of the vector is an indication of how "important" that axis is in describing the distribution of the data—more precisely, it is a measure of the variance of the data when projected onto that axis.
The projection of each data point onto the principal axes are the "principal components" of the data.
If we plot these principal components beside the original data, we see the plots shown here:

[figure source in Appendix](06.00-Figure-Code.ipynb#Principal-Components-Rotation)
This transformation from data axes to principal axes is an *affine transformation*, which basically means it is composed of a translation, rotation, and uniform scaling.
While this algorithm to find principal components may seem like just a mathematical curiosity, it turns out to have very far-reaching applications in the world of machine learning and data exploration.
### PCA as dimensionality reduction
Using PCA for dimensionality reduction involves zeroing out one or more of the smallest principal components, resulting in a lower-dimensional projection of the data that preserves the maximal data variance.
Here is an example of using PCA as a dimensionality reduction transform:
```
pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape: ", X.shape)
print("transformed shape:", X_pca.shape)
```
The transformed data has been reduced to a single dimension.
To understand the effect of this dimensionality reduction, we can perform the inverse transform of this reduced data and plot it along with the original data:
```
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');
```
The light points are the original data, while the dark points are the projected version.
This makes clear what a PCA dimensionality reduction means: the information along the least important principal axis or axes is removed, leaving only the component(s) of the data with the highest variance.
The fraction of variance that is cut out (proportional to the spread of points about the line formed in this figure) is roughly a measure of how much "information" is discarded in this reduction of dimensionality.
This reduced-dimension dataset is in some senses "good enough" to encode the most important relationships between the points: despite reducing the dimension of the data by 50%, the overall relationship between the data points are mostly preserved.
### PCA for visualization: Hand-written digits
The usefulness of the dimensionality reduction may not be entirely apparent in only two dimensions, but becomes much more clear when looking at high-dimensional data.
To see this, let's take a quick look at the application of PCA to the digits data we saw in [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb).
We start by loading the data:
```
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
```
Recall that the data consists of 8×8 pixel images, meaning that they are 64-dimensional.
To gain some intuition into the relationships between these points, we can use PCA to project them to a more manageable number of dimensions, say two:
```
pca = PCA(2) # project from 64 to 2 dimensions
projected = pca.fit_transform(digits.data)
print(digits.data.shape)
print(projected.shape)
```
We can now plot the first two principal components of each point to learn about the data:
```
plt.scatter(projected[:, 0], projected[:, 1],
c=digits.target, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('spectral', 10))
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar();
```
Recall what these components mean: the full data is a 64-dimensional point cloud, and these points are the projection of each data point along the directions with the largest variance.
Essentially, we have found the optimal stretch and rotation in 64-dimensional space that allows us to see the layout of the digits in two dimensions, and have done this in an unsupervised manner—that is, without reference to the labels.
### What do the components mean?
We can go a bit further here, and begin to ask what the reduced dimensions *mean*.
This meaning can be understood in terms of combinations of basis vectors.
For example, each image in the training set is defined by a collection of 64 pixel values, which we will call the vector $x$:
$$
x = [x_1, x_2, x_3 \cdots x_{64}]
$$
One way we can think about this is in terms of a pixel basis.
That is, to construct the image, we multiply each element of the vector by the pixel it describes, and then add the results together to build the image:
$$
{\rm image}(x) = x_1 \cdot{\rm (pixel~1)} + x_2 \cdot{\rm (pixel~2)} + x_3 \cdot{\rm (pixel~3)} \cdots x_{64} \cdot{\rm (pixel~64)}
$$
One way we might imagine reducing the dimension of this data is to zero out all but a few of these basis vectors.
For example, if we use only the first eight pixels, we get an eight-dimensional projection of the data, but it is not very reflective of the whole image: we've thrown out nearly 90% of the pixels!

[figure source in Appendix](06.00-Figure-Code.ipynb#Digits-Pixel-Components)
The upper row of panels shows the individual pixels, and the lower row shows the cumulative contribution of these pixels to the construction of the image.
Using only eight of the pixel-basis components, we can only construct a small portion of the 64-pixel image.
Were we to continue this sequence and use all 64 pixels, we would recover the original image.
But the pixel-wise representation is not the only choice of basis. We can also use other basis functions, which each contain some pre-defined contribution from each pixel, and write something like
$$
image(x) = {\rm mean} + x_1 \cdot{\rm (basis~1)} + x_2 \cdot{\rm (basis~2)} + x_3 \cdot{\rm (basis~3)} \cdots
$$
PCA can be thought of as a process of choosing optimal basis functions, such that adding together just the first few of them is enough to suitably reconstruct the bulk of the elements in the dataset.
The principal components, which act as the low-dimensional representation of our data, are simply the coefficients that multiply each of the elements in this series.
This figure shows a similar depiction of reconstructing this digit using the mean plus the first eight PCA basis functions:

[figure source in Appendix](06.00-Figure-Code.ipynb#Digits-PCA-Components)
Unlike the pixel basis, the PCA basis allows us to recover the salient features of the input image with just a mean plus eight components!
The amount of each pixel in each component is the corollary of the orientation of the vector in our two-dimensional example.
This is the sense in which PCA provides a low-dimensional representation of the data: it discovers a set of basis functions that are more efficient than the native pixel-basis of the input data.
### Choosing the number of components
A vital part of using PCA in practice is the ability to estimate how many components are needed to describe the data.
This can be determined by looking at the cumulative *explained variance ratio* as a function of the number of components:
```
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
```
This curve quantifies how much of the total, 64-dimensional variance is contained within the first $N$ components.
For example, we see that with the digits the first 10 components contain approximately 75% of the variance, while you need around 50 components to describe close to 100% of the variance.
Here we see that our two-dimensional projection loses a lot of information (as measured by the explained variance) and that we'd need about 20 components to retain 90% of the variance. Looking at this plot for a high-dimensional dataset can help you understand the level of redundancy present in multiple observations.
## PCA as Noise Filtering
PCA can also be used as a filtering approach for noisy data.
The idea is this: any components with variance much larger than the effect of the noise should be relatively unaffected by the noise.
So if you reconstruct the data using just the largest subset of principal components, you should be preferentially keeping the signal and throwing out the noise.
Let's see how this looks with the digits data.
First we will plot several of the input noise-free data:
```
def plot_digits(data):
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plot_digits(digits.data)
```
Now lets add some random noise to create a noisy dataset, and re-plot it:
```
np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)
```
It's clear by eye that the images are noisy, and contain spurious pixels.
Let's train a PCA on the noisy data, requesting that the projection preserve 50% of the variance:
```
pca = PCA(0.50).fit(noisy)
pca.n_components_
```
Here 50% of the variance amounts to 12 principal components.
Now we compute these components, and then use the inverse of the transform to reconstruct the filtered digits:
```
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
```
This signal preserving/noise filtering property makes PCA a very useful feature selection routine—for example, rather than training a classifier on very high-dimensional data, you might instead train the classifier on the lower-dimensional representation, which will automatically serve to filter out random noise in the inputs.
## Example: Eigenfaces
Earlier we explored an example of using a PCA projection as a feature selector for facial recognition with a support vector machine (see [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb)).
Here we will take a look back and explore a bit more of what went into that.
Recall that we were using the Labeled Faces in the Wild dataset made available through Scikit-Learn:
```
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)
```
Let's take a look at the principal axes that span this dataset.
Because this is a large dataset, we will use ``RandomizedPCA``—it contains a randomized method to approximate the first $N$ principal components much more quickly than the standard ``PCA`` estimator, and thus is very useful for high-dimensional data (here, a dimensionality of nearly 3,000).
We will take a look at the first 150 components:
```
from sklearn.decomposition import RandomizedPCA
pca = RandomizedPCA(150)
pca.fit(faces.data)
```
In this case, it can be interesting to visualize the images associated with the first several principal components (these components are technically known as "eigenvectors,"
so these types of images are often called "eigenfaces").
As you can see in this figure, they are as creepy as they sound:
```
fig, axes = plt.subplots(3, 8, figsize=(9, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(pca.components_[i].reshape(62, 47), cmap='bone')
```
The results are very interesting, and give us insight into how the images vary: for example, the first few eigenfaces (from the top left) seem to be associated with the angle of lighting on the face, and later principal vectors seem to be picking out certain features, such as eyes, noses, and lips.
Let's take a look at the cumulative variance of these components to see how much of the data information the projection is preserving:
```
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
```
We see that these 150 components account for just over 90% of the variance.
That would lead us to believe that using these 150 components, we would recover most of the essential characteristics of the data.
To make this more concrete, we can compare the input images with the images reconstructed from these 150 components:
```
# Compute the components and projected faces
pca = RandomizedPCA(150).fit(faces.data)
components = pca.transform(faces.data)
projected = pca.inverse_transform(components)
# Plot the results
fig, ax = plt.subplots(2, 10, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(10):
ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r')
ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r')
ax[0, 0].set_ylabel('full-dim\ninput')
ax[1, 0].set_ylabel('150-dim\nreconstruction');
```
The top row here shows the input images, while the bottom row shows the reconstruction of the images from just 150 of the ~3,000 initial features.
This visualization makes clear why the PCA feature selection used in [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb) was so successful: although it reduces the dimensionality of the data by nearly a factor of 20, the projected images contain enough information that we might, by eye, recognize the individuals in the image.
What this means is that our classification algorithm needs to be trained on 150-dimensional data rather than 3,000-dimensional data, which depending on the particular algorithm we choose, can lead to a much more efficient classification.
## Principal Component Analysis Summary
In this section we have discussed the use of principal component analysis for dimensionality reduction, for visualization of high-dimensional data, for noise filtering, and for feature selection within high-dimensional data.
Because of the versatility and interpretability of PCA, it has been shown to be effective in a wide variety of contexts and disciplines.
Given any high-dimensional dataset, I tend to start with PCA in order to visualize the relationship between points (as we did with the digits), to understand the main variance in the data (as we did with the eigenfaces), and to understand the intrinsic dimensionality (by plotting the explained variance ratio).
Certainly PCA is not useful for every high-dimensional dataset, but it offers a straightforward and efficient path to gaining insight into high-dimensional data.
PCA's main weakness is that it tends to be highly affected by outliers in the data.
For this reason, many robust variants of PCA have been developed, many of which act to iteratively discard data points that are poorly described by the initial components.
Scikit-Learn contains a couple interesting variants on PCA, including ``RandomizedPCA`` and ``SparsePCA``, both also in the ``sklearn.decomposition`` submodule.
``RandomizedPCA``, which we saw earlier, uses a non-deterministic method to quickly approximate the first few principal components in very high-dimensional data, while ``SparsePCA`` introduces a regularization term (see [In Depth: Linear Regression](05.06-Linear-Regression.ipynb)) that serves to enforce sparsity of the components.
In the following sections, we will look at other unsupervised learning methods that build on some of the ideas of PCA.
<!--NAVIGATION-->
< [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb) | [Contents](Index.ipynb) | [In-Depth: Manifold Learning](05.10-Manifold-Learning.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.09-Principal-Component-Analysis.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
| true |
code
| 0.690755 | null | null | null | null |
|
```
"""
Today we will be looking at the 2 Naive Bayes classification algorithms SeaLion has to offer - gaussian and multinomial (more common).
Both of them use the same underlying principles and as usual we'll explain them step by step.
"""
# first import
import sealion as sl
from sealion.naive_bayes import GaussianNaiveBayes, MultinomialNaiveBayes
"""
We'll first start with gaussian naive bayes. The way it works is by creating a normal (gaussian) curve to measure the
probability of any certain feature occuring for a given class. It looks at the probability for a feature to be on
each class possible. The way it makes its predictions on a given data point is by just looking at the probability of
each feature in the point for each class, and as it after aggregating all of the probabilities for all of the features
will predict the class with the highest probability.
"""
# we will use the iris dataset for this
from sklearn.datasets import load_iris
X, y = load_iris()['data'], load_iris()['target']
# and let's split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4, random_state = 3) # another thing to note :
# with naive bayes, try to always have as balanced data for all classes as possible.
# we can now setup the model
gnb = GaussianNaiveBayes()
gnb.fit(X_train, y_train) # fit the model
gnb.evaluate(X_test, y_test) # we can evaluate it
# WOAH! Looks like we do pretty well with this model. Let's see how much we got wrong.
y_pred = gnb.predict(X_test)
y_pred == y_test
# 1 wrong. Super simple, right?
# onto multinomial naive bayes
"""
Multinomial Naive Bayes is a type of naive bayes that will work with stuff like text classification, where you have
a dataset where each observation/data point is just a word. This could look like : ["hello", "what", "do", "you", "want", "from", "me"]
for a given data point. Each feature is the exact same here, so what if a model could look split all data into its classes,
and then see the probability of finding a feature (i.e. "hello") for that class. For example if you have a dataset of 100 emails,
50 spam and 50 ham - you can split the 100 into a dataset of 50 spam and 50 ham and then count the number of
times "hello" and all other features show up in each of those 50 class-datasets (doesn't matter where.) Then if you are given a new
data point you can see the probability of seeing each of its features for each class, and choose the class with the
highest probability. This is the underlying idea behind multinomial naive bayes.
"""
# let's get started
# the spam dataset is available here : https://www.kaggle.com/uciml/sms-spam-collection-dataset
import pandas as pd
spam_df = pd.read_csv("spam.csv", engine = "python", encoding='ISO-8859-1') # we need to manually define the encoding
spam_df # print it out
# as usual data manipulation is honestly not as fun as the algorithms, so we're going to have to get our hands dirty
X, y = spam_df['v2'], spam_df['v1']
X, y # let's print this stuff out
# it looks like we have plenty of data
# the first step is tokenize, where we take those strings in each data point and turn them into unique numbers. This
# will apply throughout, so "hello" as 100 in one data point is the same for another
VOCAB_SIZE = 10000 # we allow 10000 words
from tensorflow.keras.preprocessing.text import Tokenizer
tokenizer = Tokenizer(num_words = VOCAB_SIZE)
tokenizer.fit_on_texts(X)
X_seq = tokenizer.texts_to_sequences(X)
from tensorflow.keras.preprocessing.sequence import pad_sequences
# we'll also want to pad it, meaning that we make sure everything is the same length
X_pad = pad_sequences(X_seq, maxlen = 100, truncating = "post", padding = "post")
# and we will want to split it up now
from sklearn.model_selection import train_test_split
import numpy as np
y = np.array(y)
y[np.where(y == "ham")] = 0
y[np.where(y == "spam")] = 1 # spam is 1
X_train, X_test, y_train, y_test = train_test_split(X_pad, y, test_size = 0.15, random_state = 3)
# let's print out X_train
X_train
# time to start using Multinomial Naive Bayes
mnb = MultinomialNaiveBayes()
mnb.fit(X_train, y_train)
# time to evaluate
mnb.evaluate(X_test, y_test)
# dang ... but hmmm is it just predicting 0s? Is that why?
mnb.predict(X_test)[:10]
# looks like it did phenomenal. And of course, we're going to use a confusion matrix.
from sealion.utils import confusion_matrix
confusion_matrix(mnb.predict(X_test), y_test)
# The only thing we get wrong is thinking something is fine when its not. I think that's better than
# the opposite, where you miss something important and it goes into your spam folder...
# Look's like that's the end for us. As usual, I hope you enjoyed this tutorial!
```
| true |
code
| 0.64738 | null | null | null | null |
|
<h1><center>Deep Learning Helping Navigate Robots</center></h1>
<img src="https://storage.googleapis.com/kaggle-competitions/kaggle/13242/logos/thumb76_76.png?t=2019-03-12-23-33-31" width="300"></img>
### Dependencies
```
import warnings
import cufflinks
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from keras import optimizers
from keras.layers import Dense
from keras.utils import to_categorical
from keras.models import Sequential, Model
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
%matplotlib inline
warnings.filterwarnings("ignore")
cufflinks.go_offline(connected=True)
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
from numpy.random import seed
set_random_seed(0)
seed(0)
```
### Load data
```
train = pd.read_csv('../input/X_train.csv')
labels = pd.read_csv('../input/y_train.csv')
test = pd.read_csv('../input/X_test.csv')
print('Train features shape', train.shape)
display(train.head())
print('Train labels shape', labels.shape)
display(labels.head())
print('Test shape', test.shape)
display(test.head())
```
### Join train features with labels
```
train = train.join(labels, on='series_id', rsuffix='_')
train.drop('series_id_', axis=1, inplace=True)
print(train.shape)
display(train.head())
```
### Plotly graphs may take a while to load.
# EDA
## Surface distribution
- Let's see what's the label distribution of our data
```
f, ax = plt.subplots(figsize=(12, 8))
ax = sns.countplot(y='surface', data=train, palette="rocket", order=reversed(train['surface'].value_counts().index))
ax.set_ylabel("Surface type")
plt.show()
```
### Surface distribution by "group_id"
```
group_df = train.groupby(['group_id', 'surface'])['surface'].agg({'surface':['count']}).reset_index()
group_df.columns = ['group_id', 'surface', 'count']
f, ax = plt.subplots(figsize=(18, 8))
ax = sns.barplot(x="group_id", y="count", data=group_df, palette="GnBu_d")
for index, row in group_df.iterrows():
ax.text(row.name, row['count'], row['surface'], color='black', ha="center", rotation=60)
plt.show()
```
## Features distribution
- Now would be a good idea to see how each other type of features behavior
### Orientation distribution
```
orientation_features = ['orientation_X', 'orientation_Y', 'orientation_Z', 'orientation_W']
train[orientation_features].iplot(kind='histogram', bins=200, subplots=True, shape=(len(orientation_features), 1))
train[orientation_features].iplot(kind='histogram', barmode='overlay', bins=200)
train[orientation_features].iplot(kind='box')
```
The interesting part here is that "orientation_Y" and "orientation_X" are far more spread than the other two.
### Angular velocity distribution
```
velocity_features = ['angular_velocity_X', 'angular_velocity_Y', 'angular_velocity_Z']
train[velocity_features].iplot(kind='histogram', bins=200, subplots=True, shape=(len(velocity_features), 1))
train[velocity_features].iplot(kind='histogram', barmode='overlay', bins=200)
train[velocity_features].iplot(kind='box')
```
Here all the angular velocity features seem to be centered around 0, but "angular_velocity_Y" is less spread than the others.
### Linear acceleration distribution
```
acceleration_features = ['linear_acceleration_X', 'linear_acceleration_Y', 'linear_acceleration_Z']
train[acceleration_features].iplot(kind='histogram', bins=200, subplots=True, shape=(len(acceleration_features), 1))
train[acceleration_features].iplot(kind='histogram', barmode='overlay', bins=200)
train[acceleration_features].iplot(kind='box')
```
The linear acceleration features seem to be the most different between itself, all 3 features have different mean and spread.
### Preprocess the labels
```
target = train['surface']
n_labels = target.nunique()
labels_names = target.unique()
le = LabelEncoder()
target = le.fit_transform(target.values)
target = to_categorical(target)
train.drop('surface', axis=1, inplace=True)
```
### Train/validation split
```
features = ['orientation_X', 'orientation_Y', 'orientation_Z', 'orientation_W',
'angular_velocity_X', 'angular_velocity_Y', 'angular_velocity_Z',
'linear_acceleration_X', 'linear_acceleration_Y', 'linear_acceleration_Z']
X_train, X_val, Y_train, Y_val = train_test_split(train[features], target, test_size=0.2, random_state=0)
print('Train shape', X_train.shape)
print('Validation shape', X_val.shape)
display(X_train.head())
```
### Model
```
epochs = 70
batch = 128
lr = 0.001
adam = optimizers.Adam(lr)
model = Sequential()
model.add(Dense(20, activation='relu', input_dim=X_train.shape[1]))
model.add(Dense(20, activation='relu'))
model.add(Dense(n_labels, activation="softmax"))
model.compile(loss='categorical_crossentropy', optimizer=adam)
model.summary()
history = model.fit(X_train.values, Y_train, validation_data=(X_val.values, Y_val), epochs=epochs, verbose=2)
```
#### Model loss plot
```
history_pd = pd.DataFrame.from_dict(history.history)
history_pd.iplot(kind='line')
```
#### Model confusion matrix
```
cnf_matrix = confusion_matrix(np.argmax(Y_train, axis=1), model.predict_classes(X_train))
cnf_matrix_norm = cnf_matrix.astype('float') / cnf_matrix.sum(axis=1)[:, np.newaxis]
df_cm = pd.DataFrame(cnf_matrix_norm, index=labels_names, columns=labels_names)
plt.figure(figsize=(20, 7))
ax = plt.axes()
ax.set_title('Train')
sns.heatmap(df_cm, annot=True, fmt='.2f', cmap="Blues", ax=ax)
plt.show()
cnf_matrix = confusion_matrix(np.argmax(Y_val, axis=1), model.predict_classes(X_val))
cnf_matrix_norm = cnf_matrix.astype('float') / cnf_matrix.sum(axis=1)[:, np.newaxis]
df_cm = pd.DataFrame(cnf_matrix_norm, index=labels_names, columns=labels_names)
plt.figure(figsize=(20, 7))
ax = plt.axes()
ax.set_title('Validation')
sns.heatmap(df_cm, annot=True, fmt='.2f', cmap="Blues", ax=ax)
plt.show()
```
### Test predictions
```
predictions = model.predict_classes(test[features].values)
test['surface'] = le.inverse_transform(predictions)
df = test[['series_id', 'surface']]
df = df.groupby('series_id', as_index=False).agg(lambda x:x.value_counts().index[0])
df.to_csv('submission.csv', index=False)
df.head(10)
```
| true |
code
| 0.680839 | null | null | null | null |
|
# Predicting Review rating from review text
# <span style="color:dodgerblue"> Naive Bayes Classifier Using 5 Classes (1,2,3,4 and 5 Rating)</span>
```
%pylab inline
import warnings
warnings.filterwarnings('ignore')
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import nltk
from nltk.corpus import stopwords
# Importing the reviews dataset
reviews_dataset = pd.read_csv('reviews_restaurants_text.csv')
# Creating X and Y for the classifier. X is the review text and Y is the rating
x = reviews_dataset['text']
y = reviews_dataset['stars']
# Text preprocessing
import string
def text_preprocessing(text):
no_punctuation = [ch for ch in text if ch not in string.punctuation]
no_punctuation = ''.join(no_punctuation)
return [w for w in no_punctuation.split() if w.lower() not in stopwords.words('english')]
%%time
# Estimated time: 30 min
# Vectorization
# Converting each review into a vector using bag-of-words approach
from sklearn.feature_extraction.text import CountVectorizer
vector = CountVectorizer(analyzer=text_preprocessing).fit(x)
x = vector.transform(x)
# Spitting data into training and test set
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(x, y, test_size=0.20, random_state=0, shuffle =False)
# Building Multinomial Naive Bayes modle and fit it to our training set
from sklearn.naive_bayes import MultinomialNB
classifier = MultinomialNB()
classifier.fit(X_train, Y_train)
# Using our trained classifier to predict the ratings from text
# Testing our model on the test set
preds = classifier.predict(X_test)
print("Actual Ratings(Stars): ",end = "")
display(Y_test[:15])
print("Predicted Ratings: ",end = "")
print(preds[:15])
```
## Evaluating the model
## <span style="color:orangered"> Accuracy </span>
```
# Accuracy of the model
from sklearn.metrics import accuracy_score
accuracy_score(Y_test, preds)
```
## <span style="color:orangered"> Precision and Recall of the model</span>
```
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
print ('Precision: ' + str(precision_score(Y_test, preds, average='weighted')))
print ('Recall: ' + str(recall_score(Y_test,preds, average='weighted')))
```
## <span style="color:orangered"> Classification Report </span>
```
# Evaluating the model
from sklearn.metrics import confusion_matrix, classification_report
print(confusion_matrix(Y_test, preds))
print('\n')
print(classification_report(Y_test, preds))
```
## <span style="color:orangered">Confusion Matrix of the model</span>
```
# citation: http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
from sklearn import metrics
class_names = ['1','2','3','4','5']
# Compute confusion matrix
cnf_matrix = metrics.confusion_matrix(Y_test, preds
)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
# Plot normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
title='Normalized confusion matrix')
plt.show()
```
# <span style="color:dodgerblue"> Naive Bayes Classifier Using 2 Classes <span style="color:dodgerblue"> (1 and 5 Rating: Positive & Negative Reviews)</span>
```
# Importing the datasets
reviews = pd.read_csv('reviews_restaurants_text.csv')
reviews['text'] = reviews['text'].str[2:-2]
# Reducing the dataset to 2 classes i.e 1 and 5 star rating
reviews['stars'][reviews.stars == 3] = 1
reviews['stars'][reviews.stars == 2] = 1
reviews['stars'][reviews.stars == 4] = 5
#Undersampling of the dataset to get a balanced dataset
review1 = reviews[reviews['stars'] == 1]
review5 = reviews[reviews['stars'] == 5][0:34062]
frames = [review1, review5]
reviews = pd.concat(frames)
# Creating X and Y for the classifier. X is the review text and Y is the rating
x2 = reviews['text']
y2 = reviews['stars']
# Vectorization
# Converting each review into a vector using bag-of-words approach
from sklearn.feature_extraction.text import CountVectorizer
vector2 = CountVectorizer(analyzer=text_preprocessing).fit(x2)
x2 = vector.transform(x2)
# Spitting data into training and test set
from sklearn.model_selection import train_test_split
X2_train, X2_test, Y2_train, Y2_test = train_test_split(x2, y2, test_size=0.20, random_state=0)
# Building Multinomial Naive Bayes modle and fit it to our training set
from sklearn.naive_bayes import MultinomialNB
classifier2 = MultinomialNB()
classifier2.fit(X2_train, Y2_train)
# Testing our model on the test set
Y2_pred = classifier2.predict(X2_test)
```
## <span style="color:orangered"> Classification Report </span>
```
# Evaluating the model
from sklearn.metrics import confusion_matrix, classification_report
print(confusion_matrix(Y2_test, Y2_pred))
print('\n')
print(classification_report(Y2_test, Y2_pred))
```
## <span style="color:orangered"> Accuracy of the model </span>
```
# Accuracy of the model
from sklearn.metrics import accuracy_score
accuracy_score(Y2_test, Y2_pred)
```
## <span style="color:orangered"> Precision and Recall of the model</span>
```
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
print ('Precision: ' + str(precision_score(Y2_test, Y2_pred, average='weighted')))
print ('Recall: ' + str(recall_score(Y2_test, Y2_pred, average='weighted')))
```
## <span style="color:orangered"> Confusion Matrix of the model </font>
```
class_names = ['Negative','Positive']
# Compute confusion matrix
cnf_matrix = metrics.confusion_matrix(Y2_test, Y2_pred)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
# Plot normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
title='Normalized confusion matrix')
plt.show()
```
| true |
code
| 0.652186 | null | null | null | null |
|
# Introduction to optimization
The basic components
* The objective function (also called the 'cost' function)
```
import numpy as np
objective = np.poly1d([1.3, 4.0, 0.6])
print(objective)
```
* The "optimizer"
```
import scipy.optimize as opt
x_ = opt.fmin(objective, [3])
print("solved: x={}".format(x_))
%matplotlib notebook
x = np.linspace(-4,1,101)
import matplotlib.pylab as mpl
mpl.plot(x, objective(x))
mpl.plot(x_, objective(x_), 'ro')
```
Additional components
* "Box" constraints
```
import scipy.special as ss
import scipy.optimize as opt
import numpy as np
import matplotlib.pylab as mpl
x = np.linspace(2, 7, 200)
# 1st order Bessel
j1x = ss.j1(x)
mpl.plot(x, j1x)
# use scipy.optimize's more modern "results object" interface
result = opt.minimize_scalar(ss.j1, method="bounded", bounds=[2, 4])
j1_min = ss.j1(result.x)
mpl.plot(result.x, j1_min,'ro')
```
* The gradient and/or hessian
```
import mystic.models as models
print(models.rosen.__doc__)
import mystic
mystic.model_plotter(mystic.models.rosen, kwds='-f -d -x 1 -b "-3:3:.1, -1:5:.1, 1"')
import scipy.optimize as opt
import numpy as np
# initial guess
x0 = [1.3, 1.6, -0.5, -1.8, 0.8]
result = opt.minimize(opt.rosen, x0)
print(result.x)
# number of function evaluations
print(result.nfev)
# again, but this time provide the derivative
result = opt.minimize(opt.rosen, x0, jac=opt.rosen_der)
print(result.x)
# number of function evaluations and derivative evaluations
print(result.nfev, result.njev)
print('')
# however, note for a different x0...
for i in range(5):
x0 = np.random.randint(-20,20,5)
result = opt.minimize(opt.rosen, x0, jac=opt.rosen_der)
print("{} @ {} evals".format(result.x, result.nfev))
```
* The penalty functions
$\psi(x) = f(x) + k*p(x)$
```
# http://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html#tutorial-sqlsp
'''
Maximize: f(x) = 2*x0*x1 + 2*x0 - x0**2 - 2*x1**2
Subject to: x0**3 - x1 == 0
x1 >= 1
'''
import numpy as np
def objective(x, sign=1.0):
return sign*(2*x[0]*x[1] + 2*x[0] - x[0]**2 - 2*x[1]**2)
def derivative(x, sign=1.0):
dfdx0 = sign*(-2*x[0] + 2*x[1] + 2)
dfdx1 = sign*(2*x[0] - 4*x[1])
return np.array([ dfdx0, dfdx1 ])
# unconstrained
result = opt.minimize(objective, [-1.0,1.0], args=(-1.0,),
jac=derivative, method='SLSQP', options={'disp': True})
print("unconstrained: {}".format(result.x))
cons = ({'type': 'eq',
'fun' : lambda x: np.array([x[0]**3 - x[1]]),
'jac' : lambda x: np.array([3.0*(x[0]**2.0), -1.0])},
{'type': 'ineq',
'fun' : lambda x: np.array([x[1] - 1]),
'jac' : lambda x: np.array([0.0, 1.0])})
# constrained
result = opt.minimize(objective, [-1.0,1.0], args=(-1.0,), jac=derivative,
constraints=cons, method='SLSQP', options={'disp': True})
print("constrained: {}".format(result.x))
```
Optimizer classifications
* Constrained versus unconstrained (and importantly LP and QP)
```
# from scipy.optimize.minimize documentation
'''
**Unconstrained minimization**
Method *Nelder-Mead* uses the Simplex algorithm [1]_, [2]_. This
algorithm has been successful in many applications but other algorithms
using the first and/or second derivatives information might be preferred
for their better performances and robustness in general.
Method *Powell* is a modification of Powell's method [3]_, [4]_ which
is a conjugate direction method. It performs sequential one-dimensional
minimizations along each vector of the directions set (`direc` field in
`options` and `info`), which is updated at each iteration of the main
minimization loop. The function need not be differentiable, and no
derivatives are taken.
Method *CG* uses a nonlinear conjugate gradient algorithm by Polak and
Ribiere, a variant of the Fletcher-Reeves method described in [5]_ pp.
120-122. Only the first derivatives are used.
Method *BFGS* uses the quasi-Newton method of Broyden, Fletcher,
Goldfarb, and Shanno (BFGS) [5]_ pp. 136. It uses the first derivatives
only. BFGS has proven good performance even for non-smooth
optimizations. This method also returns an approximation of the Hessian
inverse, stored as `hess_inv` in the OptimizeResult object.
Method *Newton-CG* uses a Newton-CG algorithm [5]_ pp. 168 (also known
as the truncated Newton method). It uses a CG method to the compute the
search direction. See also *TNC* method for a box-constrained
minimization with a similar algorithm.
Method *Anneal* uses simulated annealing, which is a probabilistic
metaheuristic algorithm for global optimization. It uses no derivative
information from the function being optimized.
Method *dogleg* uses the dog-leg trust-region algorithm [5]_
for unconstrained minimization. This algorithm requires the gradient
and Hessian; furthermore the Hessian is required to be positive definite.
Method *trust-ncg* uses the Newton conjugate gradient trust-region
algorithm [5]_ for unconstrained minimization. This algorithm requires
the gradient and either the Hessian or a function that computes the
product of the Hessian with a given vector.
**Constrained minimization**
Method *L-BFGS-B* uses the L-BFGS-B algorithm [6]_, [7]_ for bound
constrained minimization.
Method *TNC* uses a truncated Newton algorithm [5]_, [8]_ to minimize a
function with variables subject to bounds. This algorithm uses
gradient information; it is also called Newton Conjugate-Gradient. It
differs from the *Newton-CG* method described above as it wraps a C
implementation and allows each variable to be given upper and lower
bounds.
Method *COBYLA* uses the Constrained Optimization BY Linear
Approximation (COBYLA) method [9]_, [10]_, [11]_. The algorithm is
based on linear approximations to the objective function and each
constraint. The method wraps a FORTRAN implementation of the algorithm.
Method *SLSQP* uses Sequential Least SQuares Programming to minimize a
function of several variables with any combination of bounds, equality
and inequality constraints. The method wraps the SLSQP Optimization
subroutine originally implemented by Dieter Kraft [12]_. Note that the
wrapper handles infinite values in bounds by converting them into large
floating values.
'''
```
The typical optimization algorithm (local or global) is unconstrained. Constrained algorithms tend strongly to be local, and also often use LP/QP approximations. Hence, most optimization algorithms are good either for quick linear/quadratic approximation under some constraints, or are intended for nonlinear functions without constraints. Any information about the problem that impacts the potential solution can be seen as constraining information. Constraining information is typically applied as a penatly, or as a box constraint on an input. The user is thus typically forced to pick whether they want to apply constraints but treat the problem as a LP/QP approximation, or to ignore the constraining information in exchange for a nonliear solver.
```
import scipy.optimize as opt
# constrained: linear (i.e. A*x + b)
print(opt.cobyla.fmin_cobyla)
print(opt.linprog)
# constrained: quadratic programming (i.e. up to x**2)
print(opt.fmin_slsqp)
# http://cvxopt.org/examples/tutorial/lp.html
'''
minimize: f = 2*x0 + x1
subject to:
-x0 + x1 <= 1
x0 + x1 >= 2
x1 >= 0
x0 - 2*x1 <= 4
'''
import cvxopt as cvx
from cvxopt import solvers as cvx_solvers
A = cvx.matrix([ [-1.0, -1.0, 0.0, 1.0], [1.0, -1.0, -1.0, -2.0] ])
b = cvx.matrix([ 1.0, -2.0, 0.0, 4.0 ])
cost = cvx.matrix([ 2.0, 1.0 ])
sol = cvx_solvers.lp(cost, A, b)
print(sol['x'])
# http://cvxopt.org/examples/tutorial/qp.html
'''
minimize: f = 2*x1**2 + x2**2 + x1*x2 + x1 + x2
subject to:
x1 >= 0
x2 >= 0
x1 + x2 == 1
'''
import cvxopt as cvx
from cvxopt import solvers as cvx_solvers
Q = 2*cvx.matrix([ [2, .5], [.5, 1] ])
p = cvx.matrix([1.0, 1.0])
G = cvx.matrix([[-1.0,0.0],[0.0,-1.0]])
h = cvx.matrix([0.0,0.0])
A = cvx.matrix([1.0, 1.0], (1,2))
b = cvx.matrix(1.0)
sol = cvx_solvers.qp(Q, p, G, h, A, b)
print(sol['x'])
```
Notice how much nicer it is to see the optimizer "trajectory". Now, instead of a single number, we have the path the optimizer took in finding the solution. `scipy.optimize` has a version of this, with `options={'retall':True}`, which returns the solver trajectory.
**EXERCISE:** Solve the constrained programming problem by any of the means above.
Minimize: f = -1*x[0] + 4*x[1]
Subject to: <br>
-3*x[0] + 1*x[1] <= 6 <br>
1*x[0] + 2*x[1] <= 4 <br>
x[1] >= -3 <br>
where: -inf <= x[0] <= inf
* Local versus global
```
import scipy.optimize as opt
# probabilstic solvers, that use random hopping/mutations
print(opt.differential_evolution)
print(opt.basinhopping)
import scipy.optimize as opt
# bounds instead of an initial guess
bounds = [(-10., 10)]*5
for i in range(10):
result = opt.differential_evolution(opt.rosen, bounds)
# result and number of function evaluations
print(result.x, '@ {} evals'.format(result.nfev))
```
Global optimizers tend to be much slower than local optimizers, and often use randomness to pick points within some box constraints instead of starting with an initial guess. The choice then is between algorithms that are non-deterministic and algorithms that are deterministic but depend very strongly on the selected starting point.
Local optimization algorithms have names like "gradient descent" and "steepest descent", while global optimizations tend to use things like "stocastic" and "genetic" algorithms.
* Not covered: other exotic types
Other important special cases:
* Least-squares fitting
```
import scipy.optimize as opt
import scipy.stats as stats
import numpy as np
# Define the function to fit.
def function(x, a, b, f, phi):
result = a * np.exp(-b * np.sin(f * x + phi))
return result
# Create a noisy data set around the actual parameters
true_params = [3, 2, 1, np.pi/4]
print("target parameters: {}".format(true_params))
x = np.linspace(0, 2*np.pi, 25)
exact = function(x, *true_params)
noisy = exact + 0.3*stats.norm.rvs(size=len(x))
# Use curve_fit to estimate the function parameters from the noisy data.
initial_guess = [1,1,1,1]
estimated_params, err_est = opt.curve_fit(function, x, noisy, p0=initial_guess)
print("solved parameters: {}".format(estimated_params))
# err_est is an estimate of the covariance matrix of the estimates
print("covarance: {}".format(err_est.diagonal()))
import matplotlib.pylab as mpl
mpl.plot(x, noisy, 'ro')
mpl.plot(x, function(x, *estimated_params))
```
Least-squares tends to be chosen when the user wants a measure of the covariance, typically as an error estimate.
* Integer programming
Integer programming (IP) or Mixed-integer programming (MIP) requires special optimizers that only select parameter values from the set of integers. These optimizers are typically used for things like cryptography, or other optimizations over a discrete set of possible solutions.
Typical uses
* Function minimization
* Data fitting
* Root finding
```
import numpy as np
import scipy.optimize as opt
def system(x,a,b,c):
x0, x1, x2 = x
eqs= [
3 * x0 - np.cos(x1*x2) + a, # == 0
x0**2 - 81*(x1+0.1)**2 + np.sin(x2) + b, # == 0
np.exp(-x0*x1) + 20*x2 + c # == 0
]
return eqs
# coefficients
a = -0.5
b = 1.06
c = (10 * np.pi - 3.0) / 3
# initial guess
x0 = [0.1, 0.1, -0.1]
# Solve the system of non-linear equations.
result = opt.root(system, x0, args=(a, b, c))
print("root:", result.x)
print("solution:", result.fun)
```
* Parameter estimation
```
import numpy as np
import scipy.stats as stats
# Create clean data.
x = np.linspace(0, 4.0, 100)
y = 1.5 * np.exp(-0.2 * x) + 0.3
# Add a bit of noise.
noise = 0.1 * stats.norm.rvs(size=100)
noisy_y = y + noise
# Fit noisy data with a linear model.
linear_coef = np.polyfit(x, noisy_y, 1)
linear_poly = np.poly1d(linear_coef)
linear_y = linear_poly(x)
# Fit noisy data with a quadratic model.
quad_coef = np.polyfit(x, noisy_y, 2)
quad_poly = np.poly1d(quad_coef)
quad_y = quad_poly(x)
import matplotlib.pylab as mpl
mpl.plot(x, noisy_y, 'ro')
mpl.plot(x, linear_y)
mpl.plot(x, quad_y)
#mpl.plot(x, y)
```
Standard diagnostic tools
* Eyeball the plotted solution against the objective
* Run several times and take the best result
* Analyze a log of intermediate results, per iteration
* Rare: look at the covariance matrix
* Issue: how can you really be sure you have the results you were looking for?
**EXERCISE:** Use any of the solvers we've seen thus far to find the minimum of the `zimmermann` function (i.e. use `mystic.models.zimmermann` as the objective). Use the bounds suggested below, if your choice of solver allows it.
```
import mystic.models as models
print(models.zimmermann.__doc__)
```
**EXERCISE:** Do the same for the `fosc3d` function found at `mystic.models.fosc3d`, using the bounds suggested by the documentation, if your chosen solver accepts bounds or constraints.
More to ponder: what about high-dimenstional and nonlinear constraints?
Let's look at optimization "redesigned" in [mystic](mystic.ipynb)...
| true |
code
| 0.606498 | null | null | null | null |
|
# Other programming languages
**Today we talk about various programming languages:** If you have learned one programming language, it is easy to learn the next.
**Different kinds** of programming languages:
1. **Low-level, compiled (C/C++, Fortran):** You are in full control, but need to specify types, allocate memory and clean up after your-self
2. **High-level, interpreted (MATLAB, Python, Julia, R):** Types are inferred, memory is allocated automatically, and there is automatic garbage collection
**Others:**
1. **[Wolfram Mathematica](https://www.wolfram.com/mathematica/)**: A mathematical programming langauge. The inspiration for **sympy**.
2. **[STATA](https://www.stata.com/)**: For many economists still the prefered statistical program, because it is so good at panel data and provides standard errors for a lot of the commonly used estimators.
> **Note:** Data cleaning and structuring is increasingly done in **R** or **Python**, and **STATA** is then only used for estimation.
**Comparison:** We solve the same Simulated Minimum Distance (SMD) problem in MATLAB, Python and Julia.
**Observations:**
1. Any language can typically be used to solve a task. But some have a **comparative advantage**.
2. If a **syntax** in a language irritates you, you will write worse code.
3. A **community** in your field around a language is important.
4. **No language is the best at everything**.
**Comparisons:**
- Coleman et al. (2020): MATLAB, [Python and Julia: What to choose in economics?](https://lmaliar.ws.gc.cuny.edu/files/2019/01/CEPR-DP13210.pdf)
- Fernández-Villaverde and Valencia (2019): [A Practical Guide to Parallization in Economics](https://www.sas.upenn.edu/~jesusfv/Guide_Parallel.pdf)
# High-level programming languages
## MATLAB
The **godfather** of high-level scientific programming. *The main source of inspiration for numpy and Julia*.
The **good** things:
1. Full scientific programming langauge
2. Especially good at optimization and (sparse) matrix algebra
3. Well-developed interface (IDE) and debugger
4. Integration with C++ through mex functions
The **bad** things:
1. Not open source and costly outside of academia
2. Not always easy to parallelize natively
3. Not complete programming langauge
4. Not in JupyterLab
**Download:** Available in the Absalon software library.
**Example:** `SMD_MATLAB.mlx`
**More:**
1. **Mini-course in MATLAB:** See the folder `\MATLAB_course`
2. [NumPy for Matlab users](https://docs.scipy.org/doc/numpy/user/numpy-for-matlab-users.html)
## Python
The **swiss-knife** of programming languages.
The **good** things:
1. Allround programming language
2. Full scientific programming (numpy+scipy)
3. Good at statistics (in particular data handling and machine learning)
4. Just-in-time (jit) compilation availible (numba)
4. Easy to integrate with C++ (ctypes, cffi)
The **bad** things:
1. Messy package system at times
2. Sometimes hard to jit-compile and parallelize
**Example:** `SMD_Python.ipynb`
## Julia
The **newcomer** of scientific programming languages.
1. All-round programming language
2. Automatic just-in-time compilation with native parallization - almost as fast as C++
3. Focused on scientific computing and high performance computing
The **bad** things:
1. Young language, with smallish, but growing, community
2. Sometimes hard to ensure that the just-in-time compliation works efficiently
**Example:** `SMD_Julia.ipynb`
**Download Julia:**
- [Open source version](https://julialang.org/downloads/)
- [JuliaPro from Julia Computing (bundled with IDE and notebook support)](https://juliacomputing.com/products/juliapro)
- [Documentation (language and about 1900 packages)](https://pkg.julialang.org/docs/)
**Julia community:**
- [Discourse](https://discourse.julialang.org)
- [Slack](https://julialang.slack.com)
For **introductory material on Julia for economists**, see [https://lectures.quantecon.org/jl/](https://lectures.quantecon.org/jl/).
## R
The **statistician favorite choice** of programming language.
1. Great package system
2. The best statistical packages
3. Well-developed interface (IDE) (Rstudio)
4. Easy to integrate with C++ (Rcpp)
The **bad** things:
1. Not designed to be a scientific programming langauge
2. Not a complete programming langauge
**Download:** https://www.rstudio.com/
# Low-level programming languages
## Fortran
What I have nightmares about...
In the old days, it was a bit faster than C++. This is no longer true.
## C/C++
**The fastest you can get.** A very powerfull tool, but hard to learn, and impossible to master.
```
import numpy as np
import ctypes as ct
import callcpp # local library
import psutil
CPUs = psutil.cpu_count()
CPUs_list = set(np.sort([1,2,4,*np.arange(8,CPUs+1,4)]))
print(f'this computer has {CPUs} CPUs')
```
## Calling C++ from Python
> **Note I:** This section can only be run on a Windows computer with the free **Microsoft Visual Studio 2017 Community Edition** ([download here](https://visualstudio.microsoft.com/downloads/)) installed.
>
> **Note II:** Learning C++ is somewhat hard. These [tutorials](http://www.cplusplus.com/doc/tutorial/) are helpful.
Pyton contains multiple ways of calling functions written in C++. Here I use **ctypes**.
**C++ file:** example.cpp in the current folder.
**Step 1:** Compile C++ to a .dll file
```
callcpp.compile_cpp('example') # compiles example.cpp
```
> **Details:** Write a file called ``compile.bat`` and run it in a terminal under the hood.
**Step 2:** Link to .dll file
```
# funcs (list): list of functions with elements (functionname,[argtype1,argtype2,etc.])
funcs = [('myfun_cpp',[ct.POINTER(ct.c_double),ct.POINTER(ct.c_double),ct.POINTER(ct.c_double),
ct.c_long,ct.c_long,ct.c_long])]
# ct.POINTER(ct.c_double) to a double
# ct.c_long interger
cppfile = callcpp.link_cpp('example',funcs)
```
**Step 3:** Call function
```
def myfun_numpy_vec(x1,x2):
y = np.empty((1,x1.size))
I = x1 < 0.5
y[I] = np.sum(np.exp(x2*x1[I]),axis=0)
y[~I] = np.sum(np.log(x2*x1[~I]),axis=0)
return y
# setup
x1 = np.random.uniform(size=10**6)
x2 = np.random.uniform(size=np.int(100*CPUs/8)) # adjust the size of the problem
x1_np = x1.reshape((1,x1.size))
x2_np = x2.reshape((x2.size,1))
# timing
%timeit myfun_numpy_vec(x1_np,x2_np)
def myfun_cpp(x1,x2,threads):
y = np.empty(x1.size)
p_x1 = np.ctypeslib.as_ctypes(x1) # pointer to x1
p_x2 = np.ctypeslib.as_ctypes(x2) # pointer to x2
p_y = np.ctypeslib.as_ctypes(y) # pointer to y
cppfile.myfun_cpp(p_x1,p_x2,p_y,x1.size,x2.size,threads)
return y
assert np.allclose(myfun_numpy_vec(x1_np,x2_np),myfun_cpp(x1,x2,1))
for threads in CPUs_list:
print(f'threads = {threads}')
%timeit myfun_cpp(x1,x2,threads)
print('')
```
**Observation:** Compare with results in lecture 12. Numba is roughly as fast as C++ here (I get different results across different computers). In larger problems, C++ is usually faster, and while Numba is limited in terms of which Python and Numpy features it supports, everything can be coded in C++.
**Step 4:** Delink .dll file
```
callcpp.delink_cpp(cppfile,'example')
```
**More information:** See the folder "Numba and C++" in the [ConsumptionSavingNotebooks](https://github.com/NumEconCopenhagen/ConsumptionSavingNotebooks) repository. Incudes, an explanation on how to use the **NLopt optimizers** in C++.
| true |
code
| 0.295776 | null | null | null | null |
|
```
import matplotlib.pyplot as plt
import numpy as np
import os
import PIL
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.models import Sequential
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import pathlib
from tqdm import tqdm
from abc import ABCMeta, abstractmethod
```
I have downloaded the dataset locally and mentioned paths below. Since dataset is huge (~30 GB), I am not pushing it to the repository. You can put the `data` dir inside dataset adjacent to this jupyter notebook in order to run it successfully.
```
train_data_dir = 'data/train'
test_data_dir = 'data/test'
train_data_path = pathlib.Path(train_data_dir)
test_data_path = pathlib.Path(test_data_dir)
```
Below are all the classes given for tissue samples in `train` and `test` dataset.
```
tissue_classes = [
'spleen',
'skin_1',
'skin_2',
'pancreas',
'lymph_node',
'small_intestine',
'endometrium_1',
'endometrium_2',
'liver',
'kidney',
'lung',
'colon'
]
```
Let us display an example image from each of the `12` classes of tissues in our dataset.
```
fig, ax = plt.subplots(nrows=4, ncols=3, figsize=(10, 10))
counter = 0
for row in ax:
for col in row:
images = list(train_data_path.glob(tissue_classes[counter] + '/*'))
image = np.array(PIL.Image.open(str(images[0])))
col.set_title(tissue_classes[counter])
col.imshow(image)
counter += 1
fig.tight_layout()
plt.show()
```
From dataset, we have **1119** unique images for **training** and **600** unique images for **testing** data.
Since we are working with very large dataset, it is not advisable to load all the data at once. It is not possible to do that since the data is huge. That is why, we have created data generator which will generate training/testing examples on demand. It will only generate a batch of examples at a time.
Below class is the custom data generator we have created in order to ingest images into ML pipeline.
```
class TissueDataGenerator(tf.keras.utils.Sequence):
def __init__(self,
data_dir,
batch_size,
class_labels,
img_height=128,
img_width=128,
img_channels=3,
preprocess_func=None,
shuffle=True):
self.file_ds = tf.data.Dataset.list_files(str(data_dir + '/*/*'))
self.batch_size = batch_size
self.class_labels = class_labels
self.n_classes = len(class_labels)
self.img_size = (img_height, img_width)
self.img_n_channels = img_channels
self.shuffle = shuffle
self.preprocess_func = preprocess_func
self.label_mapping = self.find_label_mappings()
self.labeled_ds = self.file_ds.map(lambda f: tf.py_function(func=self.process_example,
inp=[f],
Tout=[tf.float32, tf.int32]))
self.labeled_ds = self.labeled_ds.batch(self.batch_size)
self.on_epoch_end()
def find_label_mappings(self):
mp = {}
for i, label in enumerate(self.class_labels):
mp[label] = i
return mp
def process_example(self, file_path):
label = tf.strings.split(file_path, os.sep)[-2]
label_map = self.label_mapping[str(label.numpy().decode('utf-8'))]
label_encode = tf.keras.utils.to_categorical(label_map, self.n_classes)
image = np.array(PIL.Image.open(str(file_path.numpy().decode('utf-8'))))
image = tf.image.resize(image, self.img_size)
if self.preprocess_func is not None:
image = self.preprocess_func(image)
return image, label_encode
def __getitem__(self, index):
'Generate one batch of data'
batch = next(self.iterator, None)
if batch is None:
self.on_epoch_end()
batch = next(self.iterator)
return batch
def on_epoch_end(self):
self.iterator = iter(self.labeled_ds)
def __len__(self):
return len(self.file_ds) // self.batch_size
```
During our research of finding best model for image classification, we usually experiment on various different kinds of models. Because of that, we usually rewrite some of the code redundantly. To prevent that, we have created abstract model class below. Whatever models we want to experiment on can inherit this class to get access to some of the common features we will use for all the model classes like compiling & training model, testing model, plotting metrics etc.
```
class ModifiedModel:
__metaclass__ = ABCMeta
def __init__(self,
input_shape,
num_classes,
optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'],
verbose=True):
if not isinstance(input_shape, list) and not isinstance(input_shape, tuple):
raise TypeError('input_shape must be of type list or tuple.')
input_shape = tuple(input_shape)
if len(input_shape) != 3:
raise TypeError('input_shape must contain exactly 3 dimensions.')
self.input_shape = input_shape
self.num_classes = num_classes
self.optimizer = optimizer
self.loss = loss
self.metrics = metrics
self.verbose = verbose
self.history = None
self.model = None
@abstractmethod
def build_model(self):
pass
def compile_model(self, **kwargs):
self.raise_if_not_built()
self.model.compile(optimizer=self.optimizer,
loss=self.loss,
metrics=self.metrics, **kwargs)
def raise_if_not_built(self):
if self.model is None:
raise ValueError('object of model class has not created instance yet.')
def train(self, train_generator, epochs, **kwargs):
self.raise_if_not_built()
self.history = self.model.fit(train_generator, epochs=epochs, **kwargs)
def test(self, test_generator, **kwargs):
self.raise_if_not_built()
return self.model.evaluate(test_generator, **kwargs)
def plot_metrics(self):
if self.history is None:
raise ValueError('model must be trained to generate metric plot.')
if 'loss' not in self.history.history:
raise ValueError('history must contain loss information.')
if 'accuracy' not in self.history.history:
raise ValueError('history must contain accuracy information')
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
attrs = ['loss', 'accuracy']
counter = 0
for col in ax:
info = self.history.history[attrs[counter]]
col.plot(range(len(info)), info)
col.set_title(attrs[counter])
col.set_xlabel('Epochs')
col.set_ylabel(attrs[counter])
counter += 1
fig.tight_layout()
plt.show()
def display_score(self, score):
if len(score) < 2:
raise ValueError('score must have atleast 2 values')
print('Loss: {}, Accuracy: {}'.format(score[0], score[1]))
```
Below are some of the parameters which will be common across all the experiments and that is why we have decided to initialize them at the top and all other experiments will consume these three parameters.
**Note:** We haven't fixed shape of input images because the input image shape may differ based on the model we experiment on. Also, We haven't used original dimension `(3000, 3000, 3)` because of computational power restrictions. We are using smaller shapes of images as input as per the model requirements
```
batch_size = 4
num_channels = 3
epochs = 15
```
## Training Custom CNN model for image classification
Custom model inherits the `ModifiedModel` class defined above. We have used multiple Conv - Max pooling blocks following softmax output. The input images resized to shape `(128, 128, 3)`.
```
custom_img_height = 128
custom_img_width = 128
custom_train_gen = TissueDataGenerator(train_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=custom_img_height,
img_width=custom_img_width)
custom_test_gen = TissueDataGenerator(test_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=custom_img_height,
img_width=custom_img_width)
class CustomModel(ModifiedModel):
def __init__(self,
input_shape,
num_classes,
optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'],
verbose=True):
super().__init__(input_shape,
num_classes,
optimizer,
loss,
metrics,
verbose)
self.build_model()
self.compile_model()
def build_model(self):
self.model = Sequential([
layers.Rescaling(1./255, input_shape=self.input_shape),
layers.Conv2D(16, 3, padding='same', activation='relu'),
layers.MaxPooling2D(),
layers.Conv2D(32, 3, padding='same', activation='relu'),
layers.MaxPooling2D(),
layers.Conv2D(64, 3, padding='same', activation='relu'),
layers.MaxPooling2D(),
layers.Flatten(),
layers.Dense(128, activation='relu'),
layers.Dense(self.num_classes, activation = 'softmax')
])
customModel = CustomModel(input_shape=(custom_img_height, custom_img_width, num_channels),
num_classes=len(tissue_classes))
customModel.model.summary()
customModel.train(custom_train_gen, epochs=epochs)
customModel.plot_metrics()
custom_score = customModel.test(custom_test_gen)
customModel.display_score(custom_score)
```
Now, we also are experimenting on some of the pretrained models like VGG, InceptionNet and EfficientNet. We have defined single class `PretrainedModel` below which will take instance of pretrained model and define it as functional unit in the classification model followed by multiple fully connected layers and softmax output.
```
class PretrainedModel(ModifiedModel):
def __init__(self,
input_shape,
num_classes,
pretrainedModel,
optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'],
verbose=True):
super().__init__(input_shape,
num_classes,
optimizer,
loss,
metrics,
verbose)
self.pretrained = pretrainedModel
self.build_model()
self.compile_model()
def build_model(self):
for layer in self.pretrained.layers:
layer.trainable = False
self.model = Sequential([
self.pretrained,
layers.Flatten(),
layers.Dense(512, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(self.num_classes, activation = 'softmax')
])
```
## Transfer Learning on VGG16
We are using pretrained `VGG16` model as the first layer in our model and retraing only the layers which are added. The input images resized to shape `(224, 224, 3)`.
```
vgg_img_height = 224
vgg_img_width = 224
vgg_train_gen = TissueDataGenerator(train_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=vgg_img_height,
img_width=vgg_img_width,
preprocess_func=tf.keras.applications.vgg16.preprocess_input)
vgg_test_gen = TissueDataGenerator(test_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=vgg_img_height,
img_width=vgg_img_width,
preprocess_func=tf.keras.applications.vgg16.preprocess_input)
vggModel = PretrainedModel(input_shape=(vgg_img_height, vgg_img_width, num_channels),
num_classes=len(tissue_classes),
pretrainedModel=tf.keras.applications.vgg16.VGG16())
vggModel.model.summary()
vggModel.train(vgg_train_gen, epochs=epochs)
vggModel.plot_metrics()
vgg_score = vggModel.test(vgg_test_gen)
vggModel.display_score(vgg_score)
```
## Transfer Learning on InceptionV3
We are using pretrained `InceptionV3` model as the first layer in our model and retraing only the layers which are added. The input images resized to shape `(299, 299, 3)`.
```
inception_img_height = 299
inception_img_width = 299
inception_train_gen = TissueDataGenerator(train_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=inception_img_height,
img_width=inception_img_width,
preprocess_func=tf.keras.applications.inception_v3.preprocess_input)
inception_test_gen = TissueDataGenerator(test_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=inception_img_height,
img_width=inception_img_width,
preprocess_func=tf.keras.applications.inception_v3.preprocess_input)
inceptionModel = PretrainedModel(input_shape=(inception_img_height, inception_img_width, num_channels),
num_classes=len(tissue_classes),
pretrainedModel=tf.keras.applications.inception_v3.InceptionV3())
inceptionModel.model.summary()
inceptionModel.train(inception_train_gen, epochs=epochs)
inceptionModel.plot_metrics()
inception_score = inceptionModel.test(inception_test_gen)
inceptionModel.display_score(inception_score)
```
## Transfer Learning on EfficientNetB7
We are using pretrained `EfficientNetB7` model as the first layer in our model and retraing only the layers which are added. The input images resized to shape `(128, 128, 3)`.
```
effnet_img_height = 128
effnet_img_width = 128
effnet_train_gen = TissueDataGenerator(train_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=effnet_img_height,
img_width=effnet_img_width,
preprocess_func=tf.keras.applications.efficientnet.preprocess_input)
effnet_test_gen = TissueDataGenerator(test_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=effnet_img_height,
img_width=effnet_img_width,
preprocess_func=tf.keras.applications.efficientnet.preprocess_input)
effnetModel = PretrainedModel(input_shape=(effnet_img_height, effnet_img_width, num_channels),
num_classes=len(tissue_classes),
pretrainedModel=tf.keras.applications.efficientnet.EfficientNetB7())
effnetModel.model.summary()
effnetModel.train(effnet_train_gen, epochs=epochs)
effnetModel.plot_metrics()
effnet_score = effnetModel.test(effnet_test_gen)
effnetModel.display_score(effnet_score)
```
Note that above three pretrained model accuracy will improve on training for more epochs but we were not able to do that because of less computational power and time constraint.
## t-SNE plot for visualizing data distributions
Let us draw t-SNE plot of image features w.r.t. `customModel` that we created.
```
img_height = 128
img_width = 128
model = customModel
label2int = {}
for i, t in enumerate(tissue_classes):
label2int[t] = i
def process_path(file_path):
label = tf.strings.split(file_path, os.sep)[-2]
label_map = label2int[str(label.numpy().decode('utf-8'))]
image = np.array(PIL.Image.open(str(file_path.numpy().decode('utf-8'))))
image = tf.image.resize(image, (img_height, img_width))
feature = model.model(np.array([image]))
return feature.numpy()[0], label_map
train_gen = TissueDataGenerator(train_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=img_height,
img_width=img_width)
train_ds = train_gen.file_ds.map(lambda f: tf.py_function(func=process_path,
inp=[f],
Tout=[tf.float32, tf.int32]))
test_gen = TissueDataGenerator(test_data_dir,
batch_size=batch_size,
class_labels=tissue_classes,
img_height=img_height,
img_width=img_width)
test_ds = test_gen.file_ds.map(lambda f: tf.py_function(func=process_path,
inp=[f],
Tout=[tf.float32, tf.int32]))
def extract_data(ds):
images = None
labels = None
for img, lab in tqdm(ds):
if images is None:
images = np.array([img])
labels = np.array([lab])
else:
images = np.append(images, [img], axis=0)
labels = np.append(labels, [lab], axis=0)
return images, labels
train_images, train_labels = extract_data(train_ds)
test_images, test_labels = extract_data(test_ds)
from sklearn.manifold import TSNE
import seaborn as sns
import matplotlib.patheffects as PathEffects
train_tsne = TSNE(n_components=2, random_state=41).fit_transform(train_images)
test_tsne = TSNE(n_components=2, random_state=41).fit_transform(test_images)
def tissue_scatter(x, colors):
num_classes = len(np.unique(colors))
palette = np.array(sns.color_palette("hls", num_classes))
# create a scatter plot.
f = plt.figure(figsize=(8, 8))
ax = plt.subplot(aspect='equal')
sc = ax.scatter(x[:,0], x[:,1], lw=0, s=40, c=palette[colors.astype(np.int)])
plt.xlim(-25, 25)
plt.ylim(-25, 25)
ax.axis('off')
ax.axis('tight')
# add the labels for each digit corresponding to the label
txts = []
for i in range(num_classes):
# Position of each label at median of data points.
xtext, ytext = np.median(x[colors == i, :], axis=0)
txt = ax.text(xtext, ytext, str(i), fontsize=24)
txt.set_path_effects([
PathEffects.Stroke(linewidth=5, foreground="w"),
PathEffects.Normal()])
txts.append(txt)
return f, ax, sc, txts
tissue_scatter(train_tsne, train_labels)
tissue_scatter(test_tsne, test_labels)
```
## Reasons behind missclassification
- One possible reason might be mixed pixels. The composition of the various objects in a single pixel makes identification of genuine class more difficult.
- Original size of images are `(3000, 3000, 3)` but we have resized them down to very small size `(128, 128, 3)` for the model because which many details in image data might be lost.
- We trained image only for 15 epochs becuase of limited time and computational power restriction.
| true |
code
| 0.755473 | null | null | null | null |
|
# 📃 Solution for Exercise M2.01
The aim of this exercise is to make the following experiments:
* train and test a support vector machine classifier through
cross-validation;
* study the effect of the parameter gamma of this classifier using a
validation curve;
* study if it would be useful in term of classification if we could add new
samples in the dataset using a learning curve.
To make these experiments we will first load the blood transfusion dataset.
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">If you want a deeper overview regarding this dataset, you can refer to the
Appendix - Datasets description section at the end of this MOOC.</p>
</div>
```
import pandas as pd
blood_transfusion = pd.read_csv("../datasets/blood_transfusion.csv")
data = blood_transfusion.drop(columns="Class")
target = blood_transfusion["Class"]
```
We will use a support vector machine classifier (SVM). In its most simple
form, a SVM classifier is a linear classifier behaving similarly to a
logistic regression. Indeed, the optimization used to find the optimal
weights of the linear model are different but we don't need to know these
details for the exercise.
Also, this classifier can become more flexible/expressive by using a
so-called kernel making the model becomes non-linear. Again, no requirement
regarding the mathematics is required to accomplish this exercise.
We will use an RBF kernel where a parameter `gamma` allows to tune the
flexibility of the model.
First let's create a predictive pipeline made of:
* a [`sklearn.preprocessing.StandardScaler`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html)
with default parameter;
* a [`sklearn.svm.SVC`](https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html)
where the parameter `kernel` could be set to `"rbf"`. Note that this is the
default.
```
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
model = make_pipeline(StandardScaler(), SVC())
```
Evaluate the statistical performance of your model by cross-validation with a
`ShuffleSplit` scheme. Thus, you can use
[`sklearn.model_selection.cross_validate`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_validate.html)
and pass a [`sklearn.model_selection.ShuffleSplit`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.ShuffleSplit.html)
to the `cv` parameter. Only fix the `random_state=0` in the `ShuffleSplit`
and let the other parameters to the default.
```
from sklearn.model_selection import cross_validate, ShuffleSplit
cv = ShuffleSplit(random_state=0)
cv_results = cross_validate(model, data, target, cv=cv, n_jobs=-1)
cv_results = pd.DataFrame(cv_results)
cv_results
print(
f"Accuracy score of our model:\n"
f"{cv_results['test_score'].mean():.3f} +/- "
f"{cv_results['test_score'].std():.3f}"
)
```
As previously mentioned, the parameter `gamma` is one of the parameter
controlling under/over-fitting in support vector machine with an RBF kernel.
Compute the validation curve to evaluate the effect of the parameter `gamma`.
You can vary its value between `10e-3` and `10e2` by generating samples on a
logarithmic scale. Thus, you can use `np.logspace(-3, 2, num=30)`.
Since we are manipulating a `Pipeline` the parameter name will be set to
`svc__gamma` instead of only `gamma`. You can retrieve the parameter name
using `model.get_params().keys()`. We will go more into details regarding
accessing and setting hyperparameter in the next section.
```
import numpy as np
from sklearn.model_selection import validation_curve
gammas = np.logspace(-3, 2, num=30)
param_name = "svc__gamma"
train_scores, test_scores = validation_curve(
model, data, target, param_name=param_name, param_range=gammas, cv=cv,
n_jobs=-1)
```
Plot the validation curve for the train and test scores.
```
import matplotlib.pyplot as plt
plt.errorbar(gammas, train_scores.mean(axis=1),
yerr=train_scores.std(axis=1), label='Training error')
plt.errorbar(gammas, test_scores.mean(axis=1),
yerr=test_scores.std(axis=1), label='Testing error')
plt.legend()
plt.xscale("log")
plt.xlabel(r"Value of hyperparameter $\gamma$")
plt.ylabel("Accuracy score")
_ = plt.title("Validation score of support vector machine")
```
Looking at the curve, we can clearly identify the over-fitting regime of
the SVC classifier when `gamma > 1`.
The best setting is around `gamma = 1` while for `gamma < 1`,
it is not very clear if the classifier is under-fitting but the
testing score is worse than for `gamma = 1`.
Now, you can perform an analysis to check whether adding new samples to the
dataset could help our model to better generalize. Compute the learning curve
(using [`sklearn.model_selection.learning_curve`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.learning_curve.html))
by computing the train and test scores for different training dataset size.
Plot the train and test scores with respect to the number of samples.
```
from sklearn.model_selection import learning_curve
train_sizes = np.linspace(0.1, 1, num=10)
results = learning_curve(
model, data, target, train_sizes=train_sizes, cv=cv, n_jobs=-1)
train_size, train_scores, test_scores = results[:3]
plt.errorbar(train_size, train_scores.mean(axis=1),
yerr=train_scores.std(axis=1), label='Training error')
plt.errorbar(train_size, test_scores.mean(axis=1),
yerr=test_scores.std(axis=1), label='Testing error')
plt.legend()
plt.xlabel("Number of samples in the training set")
plt.ylabel("Accuracy")
_ = plt.title("Learning curve for support vector machine")
```
We observe that adding new samples in the dataset does not improve the
testing score. We can only conclude that the standard deviation of
the training error is decreasing when adding more samples which is not a
surprise.
| true |
code
| 0.605303 | null | null | null | null |
|
# Improve accuracy of pdf batch processing with Amazon Textract and Amazon A2I
In this chapter and this accompanying notebook learn with an example on how you can use Amazon Textract in asynchronous mode by extracting content from multiple PDF files in batch, and sending specific content from these PDF documents to an Amazon A2I human review loop to review and modify the values, and send them to an Amazon DynamoDB table for downstream processing.
**Important Note:** This is an accompanying notebook for Chapter 16 - Improve accuracy of pdf batch processing with Amazon Textract and Amazon A2I from the Natural Language Processing with AWS AI Services book. Please make sure to read the instructions provided in the book prior to attempting this notebook.
### Step 0 - Create a private human review workforce
This step requires you to use the AWS Console. However, we highly recommend that you follow it, especially when creating your own task with a custom template we will use for this notebook. We will create a private workteam and add only one user (you) to it.
To create a private team:
1. Go to AWS Console > Amazon SageMaker > Labeling workforces
1. Click "Private" and then "Create private team".
1. Enter the desired name for your private workteam.
1. Enter your own email address in the "Email addresses" section.
1. Enter the name of your organization and a contact email to administer the private workteam.
1. Click "Create Private Team".
1. The AWS Console should now return to AWS Console > Amazon SageMaker > Labeling workforces. Your newly created team should be visible under "Private teams". Next to it you will see an ARN which is a long string that looks like arn:aws:sagemaker:region-name-123456:workteam/private-crowd/team-name. Please copy this ARN to paste in the cell below.
1. You should get an email from [email protected] that contains your workforce username and password.
1. In AWS Console > Amazon SageMaker > Labeling workforces, click on the URL in Labeling portal sign-in URL. Use the email/password combination from Step 8 to log in (you will be asked to create a new, non-default password).
1. This is your private worker's interface. When we create a verification task in Verify your task using a private team below, your task should appear in this window. You can invite your colleagues to participate in the labeling job by clicking the "Invite new workers" button.
Please refer to the [Amazon SageMaker documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/sms-workforce-management.html) if you need more details.
### Step 1 - Import libraries and initiliaze variables
```
# Step 1 - Cell 1
import urllib
import boto3
import os
import json
import time
import uuid
import sagemaker
import pandas as pd
from sagemaker import get_execution_role
from sagemaker.s3 import S3Uploader, S3Downloader
textract = boto3.client('textract')
s3 = boto3.resource('s3')
bucket = "<S3-bucket-name>"
prefix = 'chapter16/input'
# Enter the Workteam ARN you created from point 7 in Step 0 above
WORKTEAM_ARN= '<your-private-workteam-arn>'
# Step 1 - Cell 2
# Upload the SEC registration documents
s3_client = boto3.client('s3')
for secfile in os.listdir():
if secfile.endswith('pdf'):
response = s3_client.upload_file(secfile, bucket, prefix+'/'+secfile)
print("Uploaded {} to S3 bucket {} in folder {}".format(secfile, bucket, prefix))
```
### Step 2 - Start Amazon Textract Text Detection Job
```
# Step 2 - Cell 1
input_bucket = s3.Bucket(bucket)
jobids = {}
# Step 2 - Cell 2
for doc in input_bucket.objects.all():
if doc.key.startswith(prefix) and doc.key.endswith('pdf'):
tres = textract.start_document_text_detection(
DocumentLocation={
"S3Object": {
"Bucket": bucket,
"Name": doc.key
}
}
)
jobids[doc.key.split('/')[2]] = tres['JobId']
# Step 2 - Cell 3
for j in jobids:
print("Textract detection Job ID for {} is {}".format(j,str(jobids[j])))
```
### Step 3 - Get Amazon Textract Text Detection Results
```
# Step 3 - Cell 1
class TextExtractor():
def extract_text(self, jobId):
""" Extract text from document corresponding to jobId and
generate a list of pages containing the text
"""
textract_result = self.__get_textract_result(jobId)
pages = {}
self.__extract_all_pages(jobId, textract_result, pages, [])
return pages
def __get_textract_result(self, jobId):
""" retrieve textract result with job Id """
result = textract.get_document_text_detection(
JobId=jobId
)
return result
def __extract_all_pages(self, jobId, textract_result, pages, page_numbers):
""" extract page content: build the pages array,
recurse if response is too big (when NextToken is provided by textract)
"""
blocks = [x for x in textract_result['Blocks'] if x['BlockType'] == "LINE"]
content = {}
line = 0
for block in blocks:
line += 1
content['Text'+str(line)] = block['Text']
content['Confidence'+str(line)] = block['Confidence']
if block['Page'] not in page_numbers:
page_numbers.append(block['Page'])
pages[block['Page']] = {
"Number": block['Page'],
"Content": content
}
else:
pages[block['Page']]['Content'] = content
nextToken = textract_result.get("NextToken", "")
if nextToken != '':
textract_result = textract.get_document_text_detection(
JobId=jobId,
NextToken=nextToken
)
self.__extract_all_pages(jobId,
textract_result,
pages,
page_numbers)
# Step 3 - Cell 2
text_extractor = TextExtractor()
indoc = {}
df_indoc = pd.DataFrame(columns = ['DocName','LineNr','DetectedText','Confidence', 'CorrectedText', 'Comments'])
for x in jobids:
pages = text_extractor.extract_text(jobids[x])
contdict =pages[1]['Content']
for row in range(1,(int(len(contdict)/2))+1):
df_indoc.loc[len(df_indoc.index)] = [x, row, contdict['Text'+str(row)], round(contdict['Confidence'+str(row)],1),'','']
# Uncomment the line below if you want to review the contents of this dataframe
#df_indoc.to_csv('extract.csv')
# Step 3 - Cell 3
# The lines in each document that are of importance for the human loop to review
bounding_dict = {'lines': '9:11:12:13:15:16:17:18:19:20:21:22:23:24:25'}
# Step 3 - Cell 4
# Let us now create a new dataframe that only contains the subset of lines we need from the bounding_dict
df_newdoc = pd.DataFrame(columns = ['DocName','LineNr','DetectedText','Confidence','CorrectedText','Comments'])
for idx, row in df_indoc.iterrows():
if str(row['LineNr']) in bounding_dict['lines'].split(':'):
df_newdoc.loc[len(df_newdoc.index)] = [row['DocName'],row['LineNr'], row['DetectedText'], row['Confidence'], row['CorrectedText'],row['Comments']]
df_newdoc
```
### Step 4 - Create the Amazon A2I human review Task UI
We will customize a sample tabular template from the Amazon A2I sample Task UI template page - https://github.com/aws-samples/amazon-a2i-sample-task-uis
```
# Step 4 - Cell 1
# Initialize A2I variables
a2i_prefix = "chapter16/a2i-results"
# Define IAM role
role = get_execution_role()
print("RoleArn: {}".format(role))
timestamp = time.strftime("%Y-%m-%d-%H-%M-%S", time.gmtime())
# Amazon SageMaker client
sagemaker_client = boto3.client('sagemaker')
# Amazon Augment AI (A2I) client
a2i = boto3.client('sagemaker-a2i-runtime')
# Flow definition name - this value is unique per account and region. You can also provide your own value here.
flowDefinitionName = 'fd-pdf-docs-' + timestamp
# Task UI name - this value is unique per account and region. You can also provide your own value here.
taskUIName = 'ui-pdf-docs-' + timestamp
# Flow definition outputs
OUTPUT_PATH = f's3://' + bucket + '/' + a2i_prefix
# Step 4 - Cell 2
# We will use the tabular liquid template and customize it for our requirements
template = r"""
<script src="https://assets.crowd.aws/crowd-html-elements.js"></script>
<style>
table, tr, th, td {
border: 1px solid black;
border-collapse: collapse;
padding: 5px;
}
</style>
<crowd-form>
<div>
<h1>Instructions</h1>
<p>Please review the SEC registration form inputs, and make corrections where appropriate. </p>
</div>
<div>
<h3>Original Registration Form - Page 1</h3>
<classification-target>
<img style="width: 70%; max-height: 40%; margin-bottom: 10px" src="{{ task.input.image | grant_read_access }}"/>
</classification-target>
</div>
<br>
<h1> Please enter your modifications below </h1>
<table>
<tr>
<th>Line Nr</th>
<th style="width:500px">Detected Text</th>
<th style="width:500px">Confidence</th>
<th>Change Required</th>
<th style="width:500px">Corrected Text</th>
<th>Comments</th>
</tr>
{% for pair in task.input.document %}
<tr>
<td>{{ pair.linenr }}</td>
<td><crowd-text-area name="predicteddoc{{ pair.linenr }}" value="{{ pair.detectedtext }}"></crowd-text-area></td>
<td><crowd-text-area name="confidence{{ pair.linenr }}" value="{{ pair.confidence }}"></crowd-text-area></td>
<td>
<p>
<input type="radio" id="agree{{ pair.linenr }}" name="rating{{ pair.linenr }}" value="agree" required>
<label for="agree{{ pair.linenr }}">Correct</label>
</p>
<p>
<input type="radio" id="disagree{{ pair.linenr }}" name="rating{{ pair.linenr }}" value="disagree" required>
<label for="disagree{{ pair.linenr }}">Incorrect</label>
</p>
</td>
<td>
<p>
<input style="width:500px" rows="3" type="text" name="correcteddoc{{ pair.linenr }}" value="{{pair.detectedtext}}" required/>
</p>
</td>
<td>
<p>
<input style="width:500px" rows="3" type="text" name="comments{{ pair.linenr }}" placeholder="Explain why you changed the value"/>
</p>
</td>
</tr>
{% endfor %}
</table>
<br>
<br>
</crowd-form>
"""
# Step 4 - Cell 2
# Define the method to initialize and create the Task UI
def create_task_ui():
response = sagemaker_client.create_human_task_ui(
HumanTaskUiName=taskUIName,
UiTemplate={'Content': template})
return response
# Step 4 - Cell 3
# Execute the method to create the Task UI
humanTaskUiResponse = create_task_ui()
humanTaskUiArn = humanTaskUiResponse['HumanTaskUiArn']
print(humanTaskUiArn)
```
### Step 5 - Create the Amazon A2I flow definition
In this section, we're going to create a flow definition definition. Flow Definitions allow us to specify:
* The workforce that your tasks will be sent to.
* The instructions that your workforce will receive. This is called a worker task template.
* Where your output data will be stored.
This notebook is going to use the API, but you can optionally create this workflow definition in the console as well.
For more details and instructions, see: https://docs.aws.amazon.com/sagemaker/latest/dg/a2i-create-flow-definition.html.
```
# Step 5 - Cell 1
create_workflow_definition_response = sagemaker_client.create_flow_definition(
FlowDefinitionName=flowDefinitionName,
RoleArn=role,
HumanLoopConfig= {
"WorkteamArn": WORKTEAM_ARN,
"HumanTaskUiArn": humanTaskUiArn,
"TaskCount": 1,
"TaskDescription": "Review the contents and correct values as indicated",
"TaskTitle": "SEC Registration Form Review"
},
OutputConfig={
"S3OutputPath" : OUTPUT_PATH
}
)
flowDefinitionArn = create_workflow_definition_response['FlowDefinitionArn'] # let's save this ARN for future use
# Step 5 - Cell 2
for x in range(60):
describeFlowDefinitionResponse = sagemaker_client.describe_flow_definition(FlowDefinitionName=flowDefinitionName)
print(describeFlowDefinitionResponse['FlowDefinitionStatus'])
if (describeFlowDefinitionResponse['FlowDefinitionStatus'] == 'Active'):
print("Flow Definition is active")
break
time.sleep(2)
```
### Step 6 - Activate the Amazon A2I flow definition
```
# Step 6 - Cell 1
# We will display the PDF first page for reference on what is being edited by the human loop
reg_images = {}
for image in os.listdir():
if image.endswith('png'):
reg_images[image.split('_')[0]] = S3Uploader.upload(image, 's3://{}/{}'.format(bucket, prefix))
# Step 6 - Cell 2
# Activate human loops for all the three documents. These will be delivered for review sequentially in the Task UI.
# We will also send only low confidence detections to A2I so the human team can update the text for what is should actually be
humanLoopName = {}
docs = df_newdoc.DocName.unique()
# confidence threshold
confidence_threshold = 95
for doc in docs:
doc_list = []
humanLoopName[doc] = str(uuid.uuid4())
for idx, line in df_newdoc.iterrows():
# Send only those lines whose confidence score is less than threshold
if line['DocName'] == doc and line['Confidence'] <= confidence_threshold:
doc_list.append({'linenr': line['LineNr'], 'detectedtext': line['DetectedText'], 'confidence':line['Confidence']})
ip_content = {"document": doc_list,
'image': reg_images[doc.split('.')[0]]
}
start_loop_response = a2i.start_human_loop(
HumanLoopName=humanLoopName[doc],
FlowDefinitionArn=flowDefinitionArn,
HumanLoopInput={
"InputContent": json.dumps(ip_content)
}
)
# Step 6 - Cell 3
completed_human_loops = []
for doc in humanLoopName:
resp = a2i.describe_human_loop(HumanLoopName=humanLoopName[doc])
print(f'HumanLoop Name: {humanLoopName[doc]}')
print(f'HumanLoop Status: {resp["HumanLoopStatus"]}')
print(f'HumanLoop Output Destination: {resp["HumanLoopOutput"]}')
print('\n')
# Step 6 - Cell 4
workteamName = WORKTEAM_ARN[WORKTEAM_ARN.rfind('/') + 1:]
print("Navigate to the private worker portal and do the tasks. Make sure you've invited yourself to your workteam!")
print('https://' + sagemaker_client.describe_workteam(WorkteamName=workteamName)['Workteam']['SubDomain'])
# Step 6 - Cell 5
completed_human_loops = []
for doc in humanLoopName:
resp = a2i.describe_human_loop(HumanLoopName=humanLoopName[doc])
print(f'HumanLoop Name: {humanLoopName[doc]}')
print(f'HumanLoop Status: {resp["HumanLoopStatus"]}')
print(f'HumanLoop Output Destination: {resp["HumanLoopOutput"]}')
print('\n')
if resp["HumanLoopStatus"] == "Completed":
completed_human_loops.append(resp)
# Step 6 - Cell 7
import re
import pandas as pd
for resp in completed_human_loops:
splitted_string = re.split('s3://' + bucket + '/', resp['HumanLoopOutput']['OutputS3Uri'])
output_bucket_key = splitted_string[1]
response = s3_client.get_object(Bucket=bucket, Key=output_bucket_key)
content = response["Body"].read()
json_output = json.loads(content)
loop_name = json_output['humanLoopName']
for i in json_output['humanAnswers']:
x = i['answerContent']
docname = list(humanLoopName.keys())[list(humanLoopName.values()).index(loop_name)]
for i, r in df_newdoc.iterrows():
if r['DocName'] == docname:
df_newdoc.at[i,'CorrectedText'] = x['correcteddoc'+str(r['LineNr'])] if 'correcteddoc'+str(r['LineNr']) in x else ''
df_newdoc.at[i,'Comments'] = x['comments'+str(r['LineNr'])] if 'comments'+str(r['LineNr']) in x else ''
# Step 6 - Cell 8
df_newdoc.head(30)
```
### Step 7 - Save changes to Amazon DynamoDB
```
# Step 7 - Cell 1
# Create the Amazon DynamoDB table - note that a new DynamoDB table is created everytime you execute this cell
# Get the service resource.
dynamodb = boto3.resource('dynamodb')
tablename = "SEC-registration-"+str(uuid.uuid4())
# Create the DynamoDB table.
table = dynamodb.create_table(
TableName=tablename,
KeySchema=[
{
'AttributeName': 'row_nr',
'KeyType': 'HASH'
}
],
AttributeDefinitions=[
{
'AttributeName': 'row_nr',
'AttributeType': 'N'
},
],
ProvisionedThroughput={
'ReadCapacityUnits': 5,
'WriteCapacityUnits': 5
}
)
# Wait until the table exists, this will take a minute or so
table.meta.client.get_waiter('table_exists').wait(TableName=tablename)
# Print out some data about the table.
print("Table successfully created")
# Step 7 - Cell 2
# Load the Amazon DynamoDB table
for idx, row in df_newdoc.iterrows():
table.put_item(
Item={
'row_nr': idx,
'doc_name': str(row['DocName']) ,
'line_nr': str(row['LineNr']),
'detected_line': str(row['DetectedText']),
'confidence': str(row['Confidence']),
'corrected_line': str(row['CorrectedText']),
'change_comments': str(row['Comments'])
}
)
print("Items were successfully created in DynamoDB table")
```
### End of Notebook
Please go back to Chapter 16 - Improve accuracy of pdf batch processing with Amazon Textract and Amazon A2I from the Natural Language Processing with AWS AI Services book to proceed further.
| true |
code
| 0.319961 | null | null | null | null |
|
import modules and get command-line parameters if running as script
```
from probrnn import models, data, inference
import numpy as np
import json
from matplotlib import pyplot as plt
from IPython.display import clear_output
```
parameters for the model and training
```
params = \
{
"N_ITERATIONS": 10 ** 5,
"VALIDATE_EACH": 100,
"SAVE_EACH": 1000,
"LOG_EVERY": 50,
"LEARNING_RATE": 0.0001,
"N_HIDDEN": 256,
"N_BINS": 50,
"BATCH_SIZE": 50,
}
```
Get some correlated toy data
```
datastruct = data.CoupledToyData(n_bins=params["N_BINS"])
x, _ = datastruct._gen(1).next()
x = datastruct.get_readable(x)
plt.figure()
plt.plot(x)
plt.show()
```
do some training
```
model = models.NADE(datastruct, params=params)
training = models.Training(
model,
"../models/toy_nade_bivariate",
"../models/toy_nade_bivariate_training.json",
)
def print_function(trer, i, batch):
if i % 10 == 0:
clear_output()
print "loss: {}; iteration {}".format(np.mean(trer[-100:]), i)
training.train(print_function)
```
visualize the training errors
```
with open("../models/toy_nade_bivariate_training.json") as f:
errs = json.load(f)
plt.figure()
plt.plot(np.array(errs["training_error"])[:, 0],
np.array(errs["training_error"])[:, 1])
plt.plot(np.array(errs["validation_error"])[:, 0],
np.array(errs["validation_error"])[:, 1], 'r')
plt.legend(["training", "validation"])
plt.show()
```
plot some weight traces
```
for x in errs.keys():
if x != "training_error" and x != "validation_error" and "train" not in x:
plt.figure()
for key in errs[x].keys():
if key == "mean":
plt.plot(errs[x][key], 'b', linewidth=5.0)
elif key == "random":
plt.plot(errs[x][key], 'c')
else:
plt.plot(errs[x][key], 'b', linestyle='--')
plt.title("variable: {}".format(x))
plt.show()
```
load trained model
```
load_name = "../models/toy_nade_bivariate_12000"
model = models.NADE(datastruct, fn=load_name)
print json.dumps(model.params, indent=4)
```
try some sampling
```
x = model.sample(200)
plt.plot(x[::2])
plt.plot(x[1::2])
plt.show()
```
try some imputation
```
x = datastruct.simulate()
x_missing = np.zeros(x.shape[0] * 2)
x_missing[::2] = x[:, 0]
x_missing[1::2] = np.nan
estimate = inference.NaiveSIS(model, x_missing, 1000, binned=False, quiet=False).estimate()
plt.figure()
plt.plot(estimate[::2])
plt.plot(estimate[1::2])
plt.show()
```
| true |
code
| 0.564579 | null | null | null | null |
|
# Inference and Validation
Now that you have a trained network, you can use it for making predictions. This is typically called **inference**, a term borrowed from statistics. However, neural networks have a tendency to perform *too well* on the training data and aren't able to generalize to data that hasn't been seen before. This is called **overfitting** and it impairs inference performance. To test for overfitting while training, we measure the performance on data not in the training set called the **validation** set. We avoid overfitting through regularization such as dropout while monitoring the validation performance during training. In this notebook, I'll show you how to do this in PyTorch.
As usual, let's start by loading the dataset through torchvision. You'll learn more about torchvision and loading data in a later part. This time we'll be taking advantage of the test set which you can get by setting `train=False` here:
```python
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
```
The test set contains images just like the training set. Typically you'll see 10-20% of the original dataset held out for testing and validation with the rest being used for training.
```
import torch
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here I'll create a model like normal, using the same one from my solution for part 4.
```
from torch import nn, optim
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
The goal of validation is to measure the model's performance on data that isn't part of the training set. Performance here is up to the developer to define though. Typically this is just accuracy, the percentage of classes the network predicted correctly. Other options are [precision and recall](https://en.wikipedia.org/wiki/Precision_and_recall#Definition_(classification_context)) and top-5 error rate. We'll focus on accuracy here. First I'll do a forward pass with one batch from the test set.
```
model = Classifier()
images, labels = next(iter(testloader))
# Get the class probabilities
ps = torch.exp(model(images))
# Make sure the shape is appropriate, we should get 10 class probabilities for 64 examples
print(ps.shape)
```
With the probabilities, we can get the most likely class using the `ps.topk` method. This returns the $k$ highest values. Since we just want the most likely class, we can use `ps.topk(1)`. This returns a tuple of the top-$k$ values and the top-$k$ indices. If the highest value is the fifth element, we'll get back 4 as the index.
```
top_p, top_class = ps.topk(1, dim=1)
# Look at the most likely classes for the first 10 examples
print(top_class[:10,:])
```
Now we can check if the predicted classes match the labels. This is simple to do by equating `top_class` and `labels`, but we have to be careful of the shapes. Here `top_class` is a 2D tensor with shape `(64, 1)` while `labels` is 1D with shape `(64)`. To get the equality to work out the way we want, `top_class` and `labels` must have the same shape.
If we do
```python
equals = top_class == labels
```
`equals` will have shape `(64, 64)`, try it yourself. What it's doing is comparing the one element in each row of `top_class` with each element in `labels` which returns 64 True/False boolean values for each row.
```
equals = top_class == labels.view(*top_class.shape)
```
Now we need to calculate the percentage of correct predictions. `equals` has binary values, either 0 or 1. This means that if we just sum up all the values and divide by the number of values, we get the percentage of correct predictions. This is the same operation as taking the mean, so we can get the accuracy with a call to `torch.mean`. If only it was that simple. If you try `torch.mean(equals)`, you'll get an error
```
RuntimeError: mean is not implemented for type torch.ByteTensor
```
This happens because `equals` has type `torch.ByteTensor` but `torch.mean` isn't implement for tensors with that type. So we'll need to convert `equals` to a float tensor. Note that when we take `torch.mean` it returns a scalar tensor, to get the actual value as a float we'll need to do `accuracy.item()`.
```
accuracy = torch.mean(equals.type(torch.FloatTensor))
print(f'Accuracy: {accuracy.item()*100}%')
```
The network is untrained so it's making random guesses and we should see an accuracy around 10%. Now let's train our network and include our validation pass so we can measure how well the network is performing on the test set. Since we're not updating our parameters in the validation pass, we can speed up the by turning off gradients using `torch.no_grad()`:
```python
# turn off gradients
with torch.no_grad():
# validation pass here
for images, labels in testloader:
...
```
>**Exercise:** Implement the validation loop below. You can largely copy and paste the code from above, but I suggest typing it in because writing it out yourself is essential for building the skill. In general you'll always learn more by typing it rather than copy-pasting.
```
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
accuracy = 0
# Turn off gradients for validation, saves memory and computations
with torch.no_grad():
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running_loss/len(trainloader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(testloader)),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
```
## Overfitting
If we look at the training and validation losses as we train the network, we can see a phenomenon known as overfitting.
<img src='assets/overfitting.png' width=450px>
The network learns the training set better and better, resulting in lower training losses. However, it starts having problems generalizing to data outside the training set leading to the validation loss increasing. The ultimate goal of any deep learning model is to make predictions on new data, so we should strive to get the lowest validation loss possible. One option is to use the version of the model with the lowest validation loss, here the one around 8-10 training epochs. This strategy is called *early-stopping*. In practice, you'd save the model frequently as you're training then later choose the model with the lowest validation loss.
The most common method to reduce overfitting (outside of early-stopping) is *dropout*, where we randomly drop input units. This forces the network to share information between weights, increasing it's ability to generalize to new data. Adding dropout in PyTorch is straightforward using the [`nn.Dropout`](https://pytorch.org/docs/stable/nn.html#torch.nn.Dropout) module.
```python
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# Now with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
During training we want to use dropout to prevent overfitting, but during inference we want to use the entire network. So, we need to turn off dropout during validation, testing, and whenever we're using the network to make predictions. To do this, you use `model.eval()`. This sets the model to evaluation mode where the dropout probability is 0. You can turn dropout back on by setting the model to train mode with `model.train()`. In general, the pattern for the validation loop will look like this, where you turn off gradients, set the model to evaluation mode, calculate the validation loss and metric, then set the model back to train mode.
```python
# turn off gradients
with torch.no_grad():
# set model to evaluation mode
model.eval()
# validation pass here
for images, labels in testloader:
...
# set model back to train mode
model.train()
```
> **Exercise:** Add dropout to your model and train it on Fashion-MNIST again. See if you can get a lower validation loss.
```
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# Now with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
accuracy = 0
# Turn off gradients for validation, saves memory and computations
with torch.no_grad():
model.eval()
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
model.train()
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(train_losses[-1]),
"Test Loss: {:.3f}.. ".format(test_losses[-1]),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
```
## Inference
Now that the model is trained, we can use it for inference. We've done this before, but now we need to remember to set the model in inference mode with `model.eval()`. You'll also want to turn off autograd with the `torch.no_grad()` context.
```
# Import helper module (should be in the repo)
import helper
# Test out your network!
model.eval()
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.view(1, 784)
# Calculate the class probabilities (softmax) for img
with torch.no_grad():
output = model.forward(img)
ps = torch.exp(output)
# Plot the image and probabilities
helper.view_classify(img.view(1, 28, 28), ps, version='Fashion')
```
## Next Up!
In the next part, I'll show you how to save your trained models. In general, you won't want to train a model everytime you need it. Instead, you'll train once, save it, then load the model when you want to train more or use if for inference.
| true |
code
| 0.87925 | null | null | null | null |
|
# Point Spread Function Photometry with Photutils
The PSF photometry module of photutils is intended to be a fully modular tool such that users are able to completly customise the photometry procedure, e.g., by using different source detection algorithms, background estimators, PSF models, etc. Photutils provides implementations for each subtask involved in the photometry process, however, users are still able to include their own implementations without having to touch into the photutils core classes!
This modularity characteristic is accomplished by using the object oriented programming approach which provides a more convient user experience while at the same time allows the developers to think in terms of classes and objects rather than isolated functions.
Photutils provides three basic classes to perform PSF photometry: `BasicPSFPhotometry`, `IterativelySubtractedPSFPhotometry`, and `DAOPhotPSFPhotometry`. In this notebook, we will go through them, explaining their differences and particular uses.
# Artificial Starlist
First things first! Let's create an artifical list of stars using photutils in order to explain the PSF procedures through examples.
```
from photutils.datasets import make_random_gaussians
from photutils.datasets import make_noise_image
from photutils.datasets import make_gaussian_sources
num_sources = 150
min_flux = 500
max_flux = 5000
min_xmean = 16
max_xmean = 240
sigma_psf = 2.0
starlist = make_random_gaussians(num_sources, [min_flux, max_flux],
[min_xmean, max_xmean],
[min_xmean, max_xmean],
[sigma_psf, sigma_psf],
[sigma_psf, sigma_psf],
random_state=1234)
shape = (256, 256)
image = (make_gaussian_sources(shape, starlist) +
make_noise_image(shape, type='poisson', mean=6., random_state=1234) +
make_noise_image(shape, type='gaussian', mean=0., stddev=2., random_state=1234))
```
Note that we also added Poisson and Gaussian background noises with the function `make_noise_image`.
Let's keep in mind this fact:
```
type(starlist)
starlist
```
Pretty much all lists of sources in `photutils` are returned or passed in as `astropy` `Table` objects, so this is something to get used to.
Let's also plot our list of stars.
```
%matplotlib inline
from matplotlib import rcParams
import matplotlib.pyplot as plt
rcParams['image.cmap'] = 'magma'
rcParams['image.aspect'] = 1 # to get images with square pixels
rcParams['figure.figsize'] = (20,10)
rcParams['image.interpolation'] = 'nearest'
rcParams['image.origin'] = 'lower'
rcParams['font.size'] = 14
plt.imshow(image)
plt.title('Simulated data')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04)
```
# The `BasicPSFPhotometry` class
As the name suggests, this is a basic class which provides the minimum tools necessary to perform photometry in crowded fields (or non crowded fields). Let's take a look into its attributes and methods.
BasicPSFPhotometry has the following mandatory attributes:
* group_maker : callable or instance of any GroupStarsBase subclass
* bkg_estimator : callable, instance of any BackgroundBase subclass, or None
* psf_model : astropy.modeling.Fittable2DModel instance
* fitshape : integer or length-2 array-like
And the following optional attributes:
* finder : callable or instance of any StarFinderBase subclasses or None
* fitter : Astropy Fitter instance
* aperture_radius : float or int
## Group Maker
`group_maker` can be instantiated using any GroupStarBase subclass, such as `photutils.psf.DAOGroup` or `photutils.psf.DBSCANGroup`, or even using a `callable` provided by the user.
`photutils.psf.DAOGroup` is a class which implements the `GROUP` algorithm proposed by Stetson which is used in DAOPHOT. This class takes one attribute to be initialized namely:
* crit_separation : int or float
Distance, in units of pixels, such that any two stars separated by less than this distance will be placed in the same group.
As it is shown in its description, `crit_separation` plays a crucial role in deciding whether or not a given star belong to some group of stars. Usually, `crit_separation` is set to be a positive real number multiplied by the FWHM of the PSF.
`photutils.psf.DBSCANGroup` is a generalized case of `photutils.psf.DAOGroup`, in fact, it is a wrapper around the `sklearn.cluster.DBSCAN` class. Its usage is very similar to `photutils.psf.DAOGroup` and we refer the photutils API doc page for more information: https://photutils.readthedocs.io/en/latest/api/photutils.psf.DBSCANGroup.html#photutils.psf.DBSCANGroup
The user is welcome to check the narrative docs on the photutils RTD webpage: https://photutils.readthedocs.io/en/latest/photutils/grouping.html
Now, let's instantiate a `group_maker` from `DAOGroup`:
```
from photutils import psf
from astropy.stats import gaussian_sigma_to_fwhm
daogroup = psf.DAOGroup(crit_separation=2.*sigma_psf*gaussian_sigma_to_fwhm)
```
Now, the object `daogroup` is ready to be passed to `BasicPSFPhotometry`.
## Background Estimation
Background estimation is needed in the photometry process in order to reduce the bias added primarily by Poisson noise background into the flux estimation.
Photutils provides several classes to perform both scalar background estimation, i.e., when the background is flat and does not vary strongly across the image, and spatial varying background estimation, i.e., when there exist a gradient field associated with the background.
The user is welcome to refer to the Background Esimation narrative docs in the photutils webpage for a detailed explanation. https://photutils.readthedocs.io/en/latest/photutils/background.html
In this notebook, we will use the class `MMMBackground` which is intended to estimate scalar background. This class is based on the background estimator used in `DAOPHOT`.
`MMMBackground` gets a `SigmaClip` object as an attribute. It's basically used to perform sigma clip on the image before performing background estimation. For our scenario, we will just instatiate a object of `MMMBackground` with default attribute values:
```
from photutils import MMMBackground
mmm_bkg = MMMBackground()
mmm_bkg.sigma_clip.sigma
mmm_bkg.sigma_clip.iters
```
## PSF Models
The attribute ``psf_model`` represents an analytical function with unkwon parameters (e.g., peak center and flux) which describes the underlying point spread function. ``psf_model`` is usually a subclass of `astropy.modeling.Fittable2DModel`. In this notebook, we will use `photutils.psf.IntegratedGaussianPRF` as our underlying PSF model.
Note that the underlying PSF model has to have parameters with the following names ``x_0``, ``y_0``, and ``flux``, to describe the center peak position and the flux, respectively.
```
from photutils.psf import IntegratedGaussianPRF
gaussian_psf = IntegratedGaussianPRF(sigma=2.0)
```
## Finder
Finder is an optional attribute, meaning that if it is `None`, then the user should provide a table with the center positions of each star when calling the `BasicPSFPhotometry` object.
Later, we will see examples of both cases, i.e., when Finder is `None` and when it is not.
The finder attribute is used to perform source detection. It can be any subclass of `photutils.StarFinderBase` such as `photutils.DAOStarFinder` or `photutils.IRAFStarFinder`, which implement a DAOPHOT-like or IRAF-like source detection algorithms, respectively. The user can also set her/his own source detection algorithm as long as the input/output formats are compatible with `photutils.StarFinderBase`.
`photutils.DAOStarFinder`, for instance, receives the following mandatory attributes:
* threshold : float
The absolute image value above which to select sources.
* fwhm : float
The full-width half-maximum (FWHM) of the major axis of the Gaussian kernel in units of pixels.
Now, let's instantiate our `DAOStarFinder` object:
```
from photutils.detection import DAOStarFinder
daofinder = DAOStarFinder(threshold=2.5*mmm_bkg(image), fwhm=sigma_psf*gaussian_sigma_to_fwhm)
```
Note that we choose the `threshold` to be a multiple of the background level and we assumed the `fwhm` to be known from our list of stars.
More details about source detection can be found on the `photutils.detection` narrative docs: https://photutils.readthedocs.io/en/latest/photutils/detection.html
## Fitter
Fitter should be an instance of a fitter implemented in `astropy.modeling.fitting`. Since the PSF model is almost always nonlinear, the fitter should be able to handle nonlinear optimization problems. In this notebook, we will use the `LevMarLSQFitter`, which combines the Levenberg-Marquardt optimization algorithm with the least-squares statistic. The default value for fitter is `LevMarLSQFitter()`.
Look at http://docs.astropy.org/en/stable/modeling/index.html for more details on fitting.
NOTE: At this point it should be stated tha photutils do not have a standard way to compute uncertainties on the fitted parameters. However, this will change in the near future with the addition of a new affiliated package to the Astropy environment, namely, `SABA: Sherpa-Astropy Bridge` which made possible to use astropy models together with Sherpa Fitters.
## Fitshape and Aperture Radius
There are two attributes left: `fitshape` (mandatory) and `aperture_radius` (optional).
`fitshape` corresponds to the size of the rectangular region necessary to enclose one single source. The pixels inside that region will be used in the fitting process. `fitshape` should be an odd integer or a tuple of odd integers.
```
import numpy as np
fitshape = 11
```
The aperture radius corresponds to the radius used to compute initial guesses for the fluxes of the sources. If this value is `None`, then one fwhm will be used if it can be determined by the `psf_model`.
## Example with unknown positions and unknown fluxes
Now we are ready to take a look at an actual example. Let's first create our `BasicPSFPhotometry` object putting together the pieces that we defined along the way:
```
from photutils.psf import BasicPSFPhotometry
basic_photometry = BasicPSFPhotometry(group_maker=daogroup, bkg_estimator=mmm_bkg,
psf_model=gaussian_psf, fitshape=fitshape,
finder=daofinder)
```
To actually perform photometry on our image that we defined previously, we should use `basic_photometry` as a function call:
```
photometry_results = basic_photometry(image)
photometry_results
```
Let's plot the residual image along with the original image:
```
fig, (ax1, ax2) = plt.subplots(1,2)
im1 = ax1.imshow(basic_photometry.get_residual_image())
ax1.set_title('Residual Image')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04,
ax=ax1, mappable=im1)
im2 = ax2.imshow(image)
ax2.set_title('Simulated data')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04,
ax=ax2, mappable=im2)
```
Looking at the residual image we observe that the photometry process was able to fit many stars but not all. This is probably due to inability of the source detection algorithm to decide the number of sources in every crowded group. Therefore, let's play with the source detection classes to see whether we can improve the photometry process.
Let's use the `IRAFStarFinder` and play with the optional parameters. A complete description of these parameters can be seen at the `photutils.dection` API documentation: https://photutils.readthedocs.io/en/latest/api/photutils.detection.IRAFStarFinder.html#photutils.detection.IRAFStarFinder
```
from photutils.detection import IRAFStarFinder
iraffind = IRAFStarFinder(threshold=2.5*mmm_bkg(image),
fwhm=sigma_psf*gaussian_sigma_to_fwhm,
minsep_fwhm=0.01, roundhi=5.0, roundlo=-5.0,
sharplo=0.0, sharphi=2.0)
```
Now let's set the `finder` attribute of our `BasicPSFPhotometry` object with `iraffind`:
```
basic_photometry.finder = iraffind
```
Let's repeat the photometry process:
```
photometry_results = basic_photometry(image)
photometry_results
plt.subplot(1,2,1)
plt.imshow(basic_photometry.get_residual_image())
plt.title('Residual Image')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04)
plt.subplot(1,2,2)
plt.imshow(image)
plt.title('Simulated data')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04)
```
As we can see, the residual presents a better Gaussianity with only three groups that were not fitted well. The reason for that is that the sources may be too close to be distinguishable by the source detection algorithm.
## Example with known positions and unknwon fluxes
Let's assume that somehow we know the true positions of the stars and we only would like to perform fitting on the fluxes. Then we should use the optional argument `positions` when calling the photometry object:
```
from astropy.table import Table
positions = Table(names=['x_0', 'y_0'], data=[starlist['x_mean'], starlist['y_mean']])
photometry_results = basic_photometry(image=image, positions=positions)
plt.subplot(1,2,1)
plt.imshow(basic_photometry.get_residual_image())
plt.title('Residual Image')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04)
plt.subplot(1,2,2)
plt.imshow(image)
plt.title('Simulated data')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04)
```
Let's do a scatter plot between ground-truth fluxes and estimated fluxes:
```
photometry_results.sort('id')
plt.scatter(starlist['flux'], photometry_results['flux_fit'])
plt.xlabel('Ground-truth fluxes')
plt.ylabel('Estimated fluxes')
```
Let's also plot the relative error on the fluxes estimation as a function of the ground-truth fluxes.
```
plt.scatter(starlist['flux'], (photometry_results['flux_fit'] - starlist['flux'])/starlist['flux'])
plt.xlabel('Ground-truth flux')
plt.ylabel('Estimate Relative Error')
```
As we can see, the relative error becomes smaller as the flux increase.
# `IterativelySubtractedPSFPhotometry`
`IterativelySubtractedPSFPhotometry` is a subclass of `BasicPSFPhotometry` which adds iteration functionality to the photometry procedure. It has the same attributes as `BasicPSFPhotometry`, except that it includes an additional `niters` which represents the number of of times to loop through the photometry process, subtracting the best-fit stars each time.
Hence, the process implemented in `IterativelySubtractedPSFPhotometry` resembles the loop used by DAOPHOT: `FIND`, `GROUP`, `NSTAR`, `SUBTRACT`, `FIND`. On its own `IterativelySubtractedPSFPhotometry` doesn't implement the specific algorithms used in DAOPHOT, but it does implement the *structure* to enambe this (and `DAOPhotPSFPhotometry`, discussed below, does).
The attribute `niters` can be `None`, which means that the photometry procedure will continue until no more sources are detected.
One final detail: the attribute `finder` (specifying the star-finder algorithm) for `IterativelySubtractedPSFPhotometry` cannot be `None` (as it can be for `BasicPSFPhotometry`). This is because it would not make sense to have an iterative process where the star finder changes completely at each step. If you want to do that you're better off manually looping over a series of calls to different `BasicPSFPhotometry` objects.
## Example with unknwon positions and unknown fluxes
Let's instantiate an object of `IterativelySubtractedPSFPhotometry`:
```
from photutils.psf import IterativelySubtractedPSFPhotometry
itr_phot = IterativelySubtractedPSFPhotometry(group_maker=daogroup, bkg_estimator=mmm_bkg,
psf_model=gaussian_psf, fitshape=fitshape,
finder=iraffind, niters=2)
```
Let's now perform photometry on our artificil image:
```
photometry_results = itr_phot(image)
photometry_results
```
Observe that there is a new column namely `iter_detected` which shows the number of the iteration in which that source was detected.
Let's plot the residual image:
```
plt.subplot(1,2,1)
plt.imshow(itr_phot.get_residual_image())
plt.title('Residual Image')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04)
plt.subplot(1,2,2)
plt.imshow(image)
plt.title('Simulated data')
plt.colorbar(orientation='horizontal', fraction=0.046, pad=0.04)
```
# `DAOPhotPSFPhotometry`
There is also a class called `DAOPhotPSFPhotometry` that is a subclass of `IterativelySubtractedPSFPhotometry`. `DAOPhotPSFPhotometry` essentially implements the DAOPHOT photometry algorithm using `IterativelySubtractedPSFPhotometry`. So instead of giving it arguments like `finder`, you provide parameters specific for the DAOPhot-like sub-tasks (e.g., the FWHM the star-finder is optimized for).
We leave the use of this class as an exercise to the user to play with the parameters which would optimize the photometry procedure.
```
from photutils.psf import DAOPhotPSFPhotometry
dao_phot = DAOPhotPSFPhotometry(...)
photometry_results = dao_phot(image)
photometry_results
```
## Documentation
Narrative and API docs of the classes used here can be found in https://photutils.readthedocs.io/en/latest/
# Future Works
The PSF Photometry module in photutils is still under development and feedback from users is much appreciated. Please open an issue on the github issue tracker of photutils with any suggestions for improvement, functionalities wanted, bugs, etc.
Near future implementations in the photutils.psf module include:
* FWHM estimation: a Python equivalent to DAOPHOT psfmeasure.
* Uncertainties computation: uncertainties are very critical and it's very likely that we are going to use astropy saba package to integrate uncertainty computation into photutils.psf.
| true |
code
| 0.843235 | null | null | null | null |
|
# 1 - Sequence to Sequence Learning with Neural Networks
In this series we'll be building a machine learning model to go from once sequence to another, using PyTorch and torchtext. This will be done on German to English translations, but the models can be applied to any problem that involves going from one sequence to another, such as summarization, i.e. going from a sequence to a shorter sequence in the same language.
In this first notebook, we'll start simple to understand the general concepts by implementing the model from the [Sequence to Sequence Learning with Neural Networks](https://arxiv.org/abs/1409.3215) paper.
## Introduction
The most common sequence-to-sequence (seq2seq) models are *encoder-decoder* models, which commonly use a *recurrent neural network* (RNN) to *encode* the source (input) sentence into a single vector. In this notebook, we'll refer to this single vector as a *context vector*. We can think of the context vector as being an abstract representation of the entire input sentence. This vector is then *decoded* by a second RNN which learns to output the target (output) sentence by generating it one word at a time.

The above image shows an example translation. The input/source sentence, "guten morgen", is passed through the embedding layer (yellow) and then input into the encoder (green). We also append a *start of sequence* (`<sos>`) and *end of sequence* (`<eos>`) token to the start and end of sentence, respectively. At each time-step, the input to the encoder RNN is both the embedding, $e$, of the current word, $e(x_t)$, as well as the hidden state from the previous time-step, $h_{t-1}$, and the encoder RNN outputs a new hidden state $h_t$. We can think of the hidden state as a vector representation of the sentence so far. The RNN can be represented as a function of both of $e(x_t)$ and $h_{t-1}$:
$$h_t = \text{EncoderRNN}(e(x_t), h_{t-1})$$
We're using the term RNN generally here, it could be any recurrent architecture, such as an *LSTM* (Long Short-Term Memory) or a *GRU* (Gated Recurrent Unit).
Here, we have $X = \{x_1, x_2, ..., x_T\}$, where $x_1 = \text{<sos>}, x_2 = \text{guten}$, etc. The initial hidden state, $h_0$, is usually either initialized to zeros or a learned parameter.
Once the final word, $x_T$, has been passed into the RNN via the embedding layer, we use the final hidden state, $h_T$, as the context vector, i.e. $h_T = z$. This is a vector representation of the entire source sentence.
Now we have our context vector, $z$, we can start decoding it to get the output/target sentence, "good morning". Again, we append start and end of sequence tokens to the target sentence. At each time-step, the input to the decoder RNN (blue) is the embedding, $d$, of current word, $d(y_t)$, as well as the hidden state from the previous time-step, $s_{t-1}$, where the initial decoder hidden state, $s_0$, is the context vector, $s_0 = z = h_T$, i.e. the initial decoder hidden state is the final encoder hidden state. Thus, similar to the encoder, we can represent the decoder as:
$$s_t = \text{DecoderRNN}(d(y_t), s_{t-1})$$
Although the input/source embedding layer, $e$, and the output/target embedding layer, $d$, are both shown in yellow in the diagram they are two different embedding layers with their own parameters.
In the decoder, we need to go from the hidden state to an actual word, therefore at each time-step we use $s_t$ to predict (by passing it through a `Linear` layer, shown in purple) what we think is the next word in the sequence, $\hat{y}_t$.
$$\hat{y}_t = f(s_t)$$
The words in the decoder are always generated one after another, with one per time-step. We always use `<sos>` for the first input to the decoder, $y_1$, but for subsequent inputs, $y_{t>1}$, we will sometimes use the actual, ground truth next word in the sequence, $y_t$ and sometimes use the word predicted by our decoder, $\hat{y}_{t-1}$. This is called *teacher forcing*, see a bit more info about it [here](https://machinelearningmastery.com/teacher-forcing-for-recurrent-neural-networks/).
When training/testing our model, we always know how many words are in our target sentence, so we stop generating words once we hit that many. During inference it is common to keep generating words until the model outputs an `<eos>` token or after a certain amount of words have been generated.
Once we have our predicted target sentence, $\hat{Y} = \{ \hat{y}_1, \hat{y}_2, ..., \hat{y}_T \}$, we compare it against our actual target sentence, $Y = \{ y_1, y_2, ..., y_T \}$, to calculate our loss. We then use this loss to update all of the parameters in our model.
## Preparing Data
We'll be coding up the models in PyTorch and using torchtext to help us do all of the pre-processing required. We'll also be using spaCy to assist in the tokenization of the data.
```
import torch
import torch.nn as nn
import torch.optim as optim
from torchtext.datasets import Multi30k
from torchtext.data import Field, BucketIterator
import spacy
import numpy as np
import random
import math
import time
```
We'll set the random seeds for deterministic results.
```
SEED = 1234
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deterministic = True
```
Next, we'll create the tokenizers. A tokenizer is used to turn a string containing a sentence into a list of individual tokens that make up that string, e.g. "good morning!" becomes ["good", "morning", "!"]. We'll start talking about the sentences being a sequence of tokens from now, instead of saying they're a sequence of words. What's the difference? Well, "good" and "morning" are both words and tokens, but "!" is a token, not a word.
spaCy has model for each language ("de_core_news_sm" for German and "en_core_web_sm" for English) which need to be loaded so we can access the tokenizer of each model.
**Note**: the models must first be downloaded using the following on the command line:
```
python -m spacy download en_core_web_sm
python -m spacy download de_core_news_sm
```
We load the models as such:
```
spacy_de = spacy.load('de_core_news_sm')
spacy_en = spacy.load('en_core_web_sm')
```
Next, we create the tokenizer functions. These can be passed to torchtext and will take in the sentence as a string and return the sentence as a list of tokens.
In the paper we are implementing, they find it beneficial to reverse the order of the input which they believe "introduces many short term dependencies in the data that make the optimization problem much easier". We copy this by reversing the German sentence after it has been transformed into a list of tokens.
```
def tokenize_de(text):
"""
Tokenizes German text from a string into a list of strings (tokens) and reverses it
"""
return [tok.text for tok in spacy_de.tokenizer(text)][::-1]
def tokenize_en(text):
"""
Tokenizes English text from a string into a list of strings (tokens)
"""
return [tok.text for tok in spacy_en.tokenizer(text)]
```
torchtext's `Field`s handle how data should be processed. All of the possible arguments are detailed [here](https://github.com/pytorch/text/blob/master/torchtext/data/field.py#L61).
We set the `tokenize` argument to the correct tokenization function for each, with German being the `SRC` (source) field and English being the `TRG` (target) field. The field also appends the "start of sequence" and "end of sequence" tokens via the `init_token` and `eos_token` arguments, and converts all words to lowercase.
```
SRC = Field(tokenize = tokenize_de,
init_token = '<sos>',
eos_token = '<eos>',
lower = True)
TRG = Field(tokenize = tokenize_en,
init_token = '<sos>',
eos_token = '<eos>',
lower = True)
```
Next, we download and load the train, validation and test data.
The dataset we'll be using is the [Multi30k dataset](https://github.com/multi30k/dataset). This is a dataset with ~30,000 parallel English, German and French sentences, each with ~12 words per sentence.
`exts` specifies which languages to use as the source and target (source goes first) and `fields` specifies which field to use for the source and target.
```
train_data, valid_data, test_data = Multi30k.splits(exts = ('.de', '.en'),
fields = (SRC, TRG))
```
We can double check that we've loaded the right number of examples:
```
print(f"Number of training examples: {len(train_data.examples)}")
print(f"Number of validation examples: {len(valid_data.examples)}")
print(f"Number of testing examples: {len(test_data.examples)}")
```
We can also print out an example, making sure the source sentence is reversed:
```
print(vars(train_data.examples[0]))
```
The period is at the beginning of the German (src) sentence, so it looks like the sentence has been correctly reversed.
Next, we'll build the *vocabulary* for the source and target languages. The vocabulary is used to associate each unique token with an index (an integer). The vocabularies of the source and target languages are distinct.
Using the `min_freq` argument, we only allow tokens that appear at least 2 times to appear in our vocabulary. Tokens that appear only once are converted into an `<unk>` (unknown) token.
It is important to note that our vocabulary should only be built from the training set and not the validation/test set. This prevents "information leakage" into our model, giving us artifically inflated validation/test scores.
```
SRC.build_vocab(train_data, min_freq = 2)
TRG.build_vocab(train_data, min_freq = 2)
print(f"Unique tokens in source (de) vocabulary: {len(SRC.vocab)}")
print(f"Unique tokens in target (en) vocabulary: {len(TRG.vocab)}")
```
The final step of preparing the data is to create the iterators. These can be iterated on to return a batch of data which will have a `src` attribute (the PyTorch tensors containing a batch of numericalized source sentences) and a `trg` attribute (the PyTorch tensors containing a batch of numericalized target sentences). Numericalized is just a fancy way of saying they have been converted from a sequence of readable tokens to a sequence of corresponding indexes, using the vocabulary.
We also need to define a `torch.device`. This is used to tell torchText to put the tensors on the GPU or not. We use the `torch.cuda.is_available()` function, which will return `True` if a GPU is detected on our computer. We pass this `device` to the iterator.
When we get a batch of examples using an iterator we need to make sure that all of the source sentences are padded to the same length, the same with the target sentences. Luckily, torchText iterators handle this for us!
We use a `BucketIterator` instead of the standard `Iterator` as it creates batches in such a way that it minimizes the amount of padding in both the source and target sentences.
```
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
BATCH_SIZE = 128
train_iterator, valid_iterator, test_iterator = BucketIterator.splits(
(train_data, valid_data, test_data),
batch_size = BATCH_SIZE,
device = device)
```
## Building the Seq2Seq Model
We'll be building our model in three parts. The encoder, the decoder and a seq2seq model that encapsulates the encoder and decoder and will provide a way to interface with each.
### Encoder
First, the encoder, a 2 layer LSTM. The paper we are implementing uses a 4-layer LSTM, but in the interest of training time we cut this down to 2-layers. The concept of multi-layer RNNs is easy to expand from 2 to 4 layers.
For a multi-layer RNN, the input sentence, $X$, after being embedded goes into the first (bottom) layer of the RNN and hidden states, $H=\{h_1, h_2, ..., h_T\}$, output by this layer are used as inputs to the RNN in the layer above. Thus, representing each layer with a superscript, the hidden states in the first layer are given by:
$$h_t^1 = \text{EncoderRNN}^1(e(x_t), h_{t-1}^1)$$
The hidden states in the second layer are given by:
$$h_t^2 = \text{EncoderRNN}^2(h_t^1, h_{t-1}^2)$$
Using a multi-layer RNN also means we'll also need an initial hidden state as input per layer, $h_0^l$, and we will also output a context vector per layer, $z^l$.
Without going into too much detail about LSTMs (see [this](https://colah.github.io/posts/2015-08-Understanding-LSTMs/) blog post to learn more about them), all we need to know is that they're a type of RNN which instead of just taking in a hidden state and returning a new hidden state per time-step, also take in and return a *cell state*, $c_t$, per time-step.
$$\begin{align*}
h_t &= \text{RNN}(e(x_t), h_{t-1})\\
(h_t, c_t) &= \text{LSTM}(e(x_t), h_{t-1}, c_{t-1})
\end{align*}$$
We can just think of $c_t$ as another type of hidden state. Similar to $h_0^l$, $c_0^l$ will be initialized to a tensor of all zeros. Also, our context vector will now be both the final hidden state and the final cell state, i.e. $z^l = (h_T^l, c_T^l)$.
Extending our multi-layer equations to LSTMs, we get:
$$\begin{align*}
(h_t^1, c_t^1) &= \text{EncoderLSTM}^1(e(x_t), (h_{t-1}^1, c_{t-1}^1))\\
(h_t^2, c_t^2) &= \text{EncoderLSTM}^2(h_t^1, (h_{t-1}^2, c_{t-1}^2))
\end{align*}$$
Note how only our hidden state from the first layer is passed as input to the second layer, and not the cell state.
So our encoder looks something like this:

We create this in code by making an `Encoder` module, which requires we inherit from `torch.nn.Module` and use the `super().__init__()` as some boilerplate code. The encoder takes the following arguments:
- `input_dim` is the size/dimensionality of the one-hot vectors that will be input to the encoder. This is equal to the input (source) vocabulary size.
- `emb_dim` is the dimensionality of the embedding layer. This layer converts the one-hot vectors into dense vectors with `emb_dim` dimensions.
- `hid_dim` is the dimensionality of the hidden and cell states.
- `n_layers` is the number of layers in the RNN.
- `dropout` is the amount of dropout to use. This is a regularization parameter to prevent overfitting. Check out [this](https://www.coursera.org/lecture/deep-neural-network/understanding-dropout-YaGbR) for more details about dropout.
We aren't going to discuss the embedding layer in detail during these tutorials. All we need to know is that there is a step before the words - technically, the indexes of the words - are passed into the RNN, where the words are transformed into vectors. To read more about word embeddings, check these articles: [1](https://monkeylearn.com/blog/word-embeddings-transform-text-numbers/), [2](http://p.migdal.pl/2017/01/06/king-man-woman-queen-why.html), [3](http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/), [4](http://mccormickml.com/2017/01/11/word2vec-tutorial-part-2-negative-sampling/).
The embedding layer is created using `nn.Embedding`, the LSTM with `nn.LSTM` and a dropout layer with `nn.Dropout`. Check the PyTorch [documentation](https://pytorch.org/docs/stable/nn.html) for more about these.
One thing to note is that the `dropout` argument to the LSTM is how much dropout to apply between the layers of a multi-layer RNN, i.e. between the hidden states output from layer $l$ and those same hidden states being used for the input of layer $l+1$.
In the `forward` method, we pass in the source sentence, $X$, which is converted into dense vectors using the `embedding` layer, and then dropout is applied. These embeddings are then passed into the RNN. As we pass a whole sequence to the RNN, it will automatically do the recurrent calculation of the hidden states over the whole sequence for us! Notice that we do not pass an initial hidden or cell state to the RNN. This is because, as noted in the [documentation](https://pytorch.org/docs/stable/nn.html#torch.nn.LSTM), that if no hidden/cell state is passed to the RNN, it will automatically create an initial hidden/cell state as a tensor of all zeros.
The RNN returns: `outputs` (the top-layer hidden state for each time-step), `hidden` (the final hidden state for each layer, $h_T$, stacked on top of each other) and `cell` (the final cell state for each layer, $c_T$, stacked on top of each other).
As we only need the final hidden and cell states (to make our context vector), `forward` only returns `hidden` and `cell`.
The sizes of each of the tensors is left as comments in the code. In this implementation `n_directions` will always be 1, however note that bidirectional RNNs (covered in tutorial 3) will have `n_directions` as 2.
```
class Encoder(nn.Module):
def __init__(self, input_dim, emb_dim, hid_dim, n_layers, dropout):
super().__init__()
self.hid_dim = hid_dim
self.n_layers = n_layers
self.embedding = nn.Embedding(input_dim, emb_dim)
self.rnn = nn.LSTM(emb_dim, hid_dim, n_layers, dropout = dropout)
self.dropout = nn.Dropout(dropout)
def forward(self, src):
#src = [src len, batch size]
embedded = self.dropout(self.embedding(src))
#embedded = [src len, batch size, emb dim]
outputs, (hidden, cell) = self.rnn(embedded)
#outputs = [src len, batch size, hid dim * n directions]
#hidden = [n layers * n directions, batch size, hid dim]
#cell = [n layers * n directions, batch size, hid dim]
#outputs are always from the top hidden layer
return hidden, cell
```
### Decoder
Next, we'll build our decoder, which will also be a 2-layer (4 in the paper) LSTM.

The `Decoder` class does a single step of decoding, i.e. it ouputs single token per time-step. The first layer will receive a hidden and cell state from the previous time-step, $(s_{t-1}^1, c_{t-1}^1)$, and feeds it through the LSTM with the current embedded token, $y_t$, to produce a new hidden and cell state, $(s_t^1, c_t^1)$. The subsequent layers will use the hidden state from the layer below, $s_t^{l-1}$, and the previous hidden and cell states from their layer, $(s_{t-1}^l, c_{t-1}^l)$. This provides equations very similar to those in the encoder.
$$\begin{align*}
(s_t^1, c_t^1) = \text{DecoderLSTM}^1(d(y_t), (s_{t-1}^1, c_{t-1}^1))\\
(s_t^2, c_t^2) = \text{DecoderLSTM}^2(s_t^1, (s_{t-1}^2, c_{t-1}^2))
\end{align*}$$
Remember that the initial hidden and cell states to our decoder are our context vectors, which are the final hidden and cell states of our encoder from the same layer, i.e. $(s_0^l,c_0^l)=z^l=(h_T^l,c_T^l)$.
We then pass the hidden state from the top layer of the RNN, $s_t^L$, through a linear layer, $f$, to make a prediction of what the next token in the target (output) sequence should be, $\hat{y}_{t+1}$.
$$\hat{y}_{t+1} = f(s_t^L)$$
The arguments and initialization are similar to the `Encoder` class, except we now have an `output_dim` which is the size of the vocabulary for the output/target. There is also the addition of the `Linear` layer, used to make the predictions from the top layer hidden state.
Within the `forward` method, we accept a batch of input tokens, previous hidden states and previous cell states. As we are only decoding one token at a time, the input tokens will always have a sequence length of 1. We `unsqueeze` the input tokens to add a sentence length dimension of 1. Then, similar to the encoder, we pass through an embedding layer and apply dropout. This batch of embedded tokens is then passed into the RNN with the previous hidden and cell states. This produces an `output` (hidden state from the top layer of the RNN), a new `hidden` state (one for each layer, stacked on top of each other) and a new `cell` state (also one per layer, stacked on top of each other). We then pass the `output` (after getting rid of the sentence length dimension) through the linear layer to receive our `prediction`. We then return the `prediction`, the new `hidden` state and the new `cell` state.
**Note**: as we always have a sequence length of 1, we could use `nn.LSTMCell`, instead of `nn.LSTM`, as it is designed to handle a batch of inputs that aren't necessarily in a sequence. `nn.LSTMCell` is just a single cell and `nn.LSTM` is a wrapper around potentially multiple cells. Using the `nn.LSTMCell` in this case would mean we don't have to `unsqueeze` to add a fake sequence length dimension, but we would need one `nn.LSTMCell` per layer in the decoder and to ensure each `nn.LSTMCell` receives the correct initial hidden state from the encoder. All of this makes the code less concise - hence the decision to stick with the regular `nn.LSTM`.
```
class Decoder(nn.Module):
def __init__(self, output_dim, emb_dim, hid_dim, n_layers, dropout):
super().__init__()
self.output_dim = output_dim
self.hid_dim = hid_dim
self.n_layers = n_layers
self.embedding = nn.Embedding(output_dim, emb_dim)
self.rnn = nn.LSTM(emb_dim, hid_dim, n_layers, dropout = dropout)
self.fc_out = nn.Linear(hid_dim, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, input, hidden, cell):
#input = [batch size]
#hidden = [n layers * n directions, batch size, hid dim]
#cell = [n layers * n directions, batch size, hid dim]
#n directions in the decoder will both always be 1, therefore:
#hidden = [n layers, batch size, hid dim]
#context = [n layers, batch size, hid dim]
input = input.unsqueeze(0)
#input = [1, batch size]
embedded = self.dropout(self.embedding(input))
#embedded = [1, batch size, emb dim]
output, (hidden, cell) = self.rnn(embedded, (hidden, cell))
#output = [seq len, batch size, hid dim * n directions]
#hidden = [n layers * n directions, batch size, hid dim]
#cell = [n layers * n directions, batch size, hid dim]
#seq len and n directions will always be 1 in the decoder, therefore:
#output = [1, batch size, hid dim]
#hidden = [n layers, batch size, hid dim]
#cell = [n layers, batch size, hid dim]
prediction = self.fc_out(output.squeeze(0))
#prediction = [batch size, output dim]
return prediction, hidden, cell
```
### Seq2Seq
For the final part of the implemenetation, we'll implement the seq2seq model. This will handle:
- receiving the input/source sentence
- using the encoder to produce the context vectors
- using the decoder to produce the predicted output/target sentence
Our full model will look like this:

The `Seq2Seq` model takes in an `Encoder`, `Decoder`, and a `device` (used to place tensors on the GPU, if it exists).
For this implementation, we have to ensure that the number of layers and the hidden (and cell) dimensions are equal in the `Encoder` and `Decoder`. This is not always the case, we do not necessarily need the same number of layers or the same hidden dimension sizes in a sequence-to-sequence model. However, if we did something like having a different number of layers then we would need to make decisions about how this is handled. For example, if our encoder has 2 layers and our decoder only has 1, how is this handled? Do we average the two context vectors output by the decoder? Do we pass both through a linear layer? Do we only use the context vector from the highest layer? Etc.
Our `forward` method takes the source sentence, target sentence and a teacher-forcing ratio. The teacher forcing ratio is used when training our model. When decoding, at each time-step we will predict what the next token in the target sequence will be from the previous tokens decoded, $\hat{y}_{t+1}=f(s_t^L)$. With probability equal to the teaching forcing ratio (`teacher_forcing_ratio`) we will use the actual ground-truth next token in the sequence as the input to the decoder during the next time-step. However, with probability `1 - teacher_forcing_ratio`, we will use the token that the model predicted as the next input to the model, even if it doesn't match the actual next token in the sequence.
The first thing we do in the `forward` method is to create an `outputs` tensor that will store all of our predictions, $\hat{Y}$.
We then feed the input/source sentence, `src`, into the encoder and receive out final hidden and cell states.
The first input to the decoder is the start of sequence (`<sos>`) token. As our `trg` tensor already has the `<sos>` token appended (all the way back when we defined the `init_token` in our `TRG` field) we get our $y_1$ by slicing into it. We know how long our target sentences should be (`max_len`), so we loop that many times. The last token input into the decoder is the one **before** the `<eos>` token - the `<eos>` token is never input into the decoder.
During each iteration of the loop, we:
- pass the input, previous hidden and previous cell states ($y_t, s_{t-1}, c_{t-1}$) into the decoder
- receive a prediction, next hidden state and next cell state ($\hat{y}_{t+1}, s_{t}, c_{t}$) from the decoder
- place our prediction, $\hat{y}_{t+1}$/`output` in our tensor of predictions, $\hat{Y}$/`outputs`
- decide if we are going to "teacher force" or not
- if we do, the next `input` is the ground-truth next token in the sequence, $y_{t+1}$/`trg[t]`
- if we don't, the next `input` is the predicted next token in the sequence, $\hat{y}_{t+1}$/`top1`, which we get by doing an `argmax` over the output tensor
Once we've made all of our predictions, we return our tensor full of predictions, $\hat{Y}$/`outputs`.
**Note**: our decoder loop starts at 1, not 0. This means the 0th element of our `outputs` tensor remains all zeros. So our `trg` and `outputs` look something like:
$$\begin{align*}
\text{trg} = [<sos>, &y_1, y_2, y_3, <eos>]\\
\text{outputs} = [0, &\hat{y}_1, \hat{y}_2, \hat{y}_3, <eos>]
\end{align*}$$
Later on when we calculate the loss, we cut off the first element of each tensor to get:
$$\begin{align*}
\text{trg} = [&y_1, y_2, y_3, <eos>]\\
\text{outputs} = [&\hat{y}_1, \hat{y}_2, \hat{y}_3, <eos>]
\end{align*}$$
```
class Seq2Seq(nn.Module):
def __init__(self, encoder, decoder, device):
super().__init__()
self.encoder = encoder
self.decoder = decoder
self.device = device
assert encoder.hid_dim == decoder.hid_dim, \
"Hidden dimensions of encoder and decoder must be equal!"
assert encoder.n_layers == decoder.n_layers, \
"Encoder and decoder must have equal number of layers!"
def forward(self, src, trg, teacher_forcing_ratio = 0.5):
#src = [src len, batch size]
#trg = [trg len, batch size]
#teacher_forcing_ratio is probability to use teacher forcing
#e.g. if teacher_forcing_ratio is 0.75 we use ground-truth inputs 75% of the time
batch_size = trg.shape[1]
trg_len = trg.shape[0]
trg_vocab_size = self.decoder.output_dim
#tensor to store decoder outputs
outputs = torch.zeros(trg_len, batch_size, trg_vocab_size).to(self.device)
#last hidden state of the encoder is used as the initial hidden state of the decoder
hidden, cell = self.encoder(src)
#first input to the decoder is the <sos> tokens
input = trg[0,:]
for t in range(1, trg_len):
#insert input token embedding, previous hidden and previous cell states
#receive output tensor (predictions) and new hidden and cell states
output, hidden, cell = self.decoder(input, hidden, cell)
#place predictions in a tensor holding predictions for each token
outputs[t] = output
#decide if we are going to use teacher forcing or not
teacher_force = random.random() < teacher_forcing_ratio
#get the highest predicted token from our predictions
top1 = output.argmax(1)
#if teacher forcing, use actual next token as next input
#if not, use predicted token
input = trg[t] if teacher_force else top1
return outputs
```
# Training the Seq2Seq Model
Now we have our model implemented, we can begin training it.
First, we'll initialize our model. As mentioned before, the input and output dimensions are defined by the size of the vocabulary. The embedding dimesions and dropout for the encoder and decoder can be different, but the number of layers and the size of the hidden/cell states must be the same.
We then define the encoder, decoder and then our Seq2Seq model, which we place on the `device`.
```
INPUT_DIM = len(SRC.vocab)
OUTPUT_DIM = len(TRG.vocab)
ENC_EMB_DIM = 256
DEC_EMB_DIM = 256
HID_DIM = 512
N_LAYERS = 2
ENC_DROPOUT = 0.5
DEC_DROPOUT = 0.5
enc = Encoder(INPUT_DIM, ENC_EMB_DIM, HID_DIM, N_LAYERS, ENC_DROPOUT)
dec = Decoder(OUTPUT_DIM, DEC_EMB_DIM, HID_DIM, N_LAYERS, DEC_DROPOUT)
model = Seq2Seq(enc, dec, device).to(device)
```
Next up is initializing the weights of our model. In the paper they state they initialize all weights from a uniform distribution between -0.08 and +0.08, i.e. $\mathcal{U}(-0.08, 0.08)$.
We initialize weights in PyTorch by creating a function which we `apply` to our model. When using `apply`, the `init_weights` function will be called on every module and sub-module within our model. For each module we loop through all of the parameters and sample them from a uniform distribution with `nn.init.uniform_`.
```
def init_weights(m):
for name, param in m.named_parameters():
nn.init.uniform_(param.data, -0.08, 0.08)
model.apply(init_weights)
```
We also define a function that will calculate the number of trainable parameters in the model.
```
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f'The model has {count_parameters(model):,} trainable parameters')
```
We define our optimizer, which we use to update our parameters in the training loop. Check out [this](http://ruder.io/optimizing-gradient-descent/) post for information about different optimizers. Here, we'll use Adam.
```
optimizer = optim.Adam(model.parameters())
```
Next, we define our loss function. The `CrossEntropyLoss` function calculates both the log softmax as well as the negative log-likelihood of our predictions.
Our loss function calculates the average loss per token, however by passing the index of the `<pad>` token as the `ignore_index` argument we ignore the loss whenever the target token is a padding token.
```
TRG_PAD_IDX = TRG.vocab.stoi[TRG.pad_token]
criterion = nn.CrossEntropyLoss(ignore_index = TRG_PAD_IDX)
```
Next, we'll define our training loop.
First, we'll set the model into "training mode" with `model.train()`. This will turn on dropout (and batch normalization, which we aren't using) and then iterate through our data iterator.
As stated before, our decoder loop starts at 1, not 0. This means the 0th element of our `outputs` tensor remains all zeros. So our `trg` and `outputs` look something like:
$$\begin{align*}
\text{trg} = [<sos>, &y_1, y_2, y_3, <eos>]\\
\text{outputs} = [0, &\hat{y}_1, \hat{y}_2, \hat{y}_3, <eos>]
\end{align*}$$
Here, when we calculate the loss, we cut off the first element of each tensor to get:
$$\begin{align*}
\text{trg} = [&y_1, y_2, y_3, <eos>]\\
\text{outputs} = [&\hat{y}_1, \hat{y}_2, \hat{y}_3, <eos>]
\end{align*}$$
At each iteration:
- get the source and target sentences from the batch, $X$ and $Y$
- zero the gradients calculated from the last batch
- feed the source and target into the model to get the output, $\hat{Y}$
- as the loss function only works on 2d inputs with 1d targets we need to flatten each of them with `.view`
- we slice off the first column of the output and target tensors as mentioned above
- calculate the gradients with `loss.backward()`
- clip the gradients to prevent them from exploding (a common issue in RNNs)
- update the parameters of our model by doing an optimizer step
- sum the loss value to a running total
Finally, we return the loss that is averaged over all batches.
```
def train(model, iterator, optimizer, criterion, clip):
model.train()
epoch_loss = 0
for i, batch in enumerate(iterator):
src = batch.src
trg = batch.trg
optimizer.zero_grad()
output = model(src, trg)
#trg = [trg len, batch size]
#output = [trg len, batch size, output dim]
output_dim = output.shape[-1]
output = output[1:].view(-1, output_dim)
trg = trg[1:].view(-1)
#trg = [(trg len - 1) * batch size]
#output = [(trg len - 1) * batch size, output dim]
loss = criterion(output, trg)
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), clip)
optimizer.step()
epoch_loss += loss.item()
return epoch_loss / len(iterator)
```
Our evaluation loop is similar to our training loop, however as we aren't updating any parameters we don't need to pass an optimizer or a clip value.
We must remember to set the model to evaluation mode with `model.eval()`. This will turn off dropout (and batch normalization, if used).
We use the `with torch.no_grad()` block to ensure no gradients are calculated within the block. This reduces memory consumption and speeds things up.
The iteration loop is similar (without the parameter updates), however we must ensure we turn teacher forcing off for evaluation. This will cause the model to only use it's own predictions to make further predictions within a sentence, which mirrors how it would be used in deployment.
```
def evaluate(model, iterator, criterion):
model.eval()
epoch_loss = 0
with torch.no_grad():
for i, batch in enumerate(iterator):
src = batch.src
trg = batch.trg
output = model(src, trg, 0) #turn off teacher forcing
#trg = [trg len, batch size]
#output = [trg len, batch size, output dim]
output_dim = output.shape[-1]
output = output[1:].view(-1, output_dim)
trg = trg[1:].view(-1)
#trg = [(trg len - 1) * batch size]
#output = [(trg len - 1) * batch size, output dim]
loss = criterion(output, trg)
epoch_loss += loss.item()
return epoch_loss / len(iterator)
```
Next, we'll create a function that we'll use to tell us how long an epoch takes.
```
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
```
We can finally start training our model!
At each epoch, we'll be checking if our model has achieved the best validation loss so far. If it has, we'll update our best validation loss and save the parameters of our model (called `state_dict` in PyTorch). Then, when we come to test our model, we'll use the saved parameters used to achieve the best validation loss.
We'll be printing out both the loss and the perplexity at each epoch. It is easier to see a change in perplexity than a change in loss as the numbers are much bigger.
```
N_EPOCHS = 10
CLIP = 1
best_valid_loss = float('inf')
for epoch in range(N_EPOCHS):
start_time = time.time()
train_loss = train(model, train_iterator, optimizer, criterion, CLIP)
valid_loss = evaluate(model, valid_iterator, criterion)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'tut1-model.pt')
print(f'Epoch: {epoch+1:02} | Time: {epoch_mins}m {epoch_secs}s')
print(f'\tTrain Loss: {train_loss:.3f} | Train PPL: {math.exp(train_loss):7.3f}')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. PPL: {math.exp(valid_loss):7.3f}')
```
We'll load the parameters (`state_dict`) that gave our model the best validation loss and run it the model on the test set.
```
model.load_state_dict(torch.load('tut1-model.pt'))
test_loss = evaluate(model, test_iterator, criterion)
print(f'| Test Loss: {test_loss:.3f} | Test PPL: {math.exp(test_loss):7.3f} |')
```
In the following notebook we'll implement a model that achieves improved test perplexity, but only uses a single layer in the encoder and the decoder.
| true |
code
| 0.82226 | null | null | null | null |
|
# mlforecast
> Scalable machine learning based time series forecasting.
**mlforecast** is a framework to perform time series forecasting using machine learning models, with the option to scale to massive amounts of data using remote clusters.
[](https://github.com/Nixtla/mlforecast/actions/workflows/ci.yaml)
[](https://github.com/Nixtla/mlforecast/actions/workflows/lint.yaml)
[](https://pypi.org/project/mlforecast/)
[](https://pypi.org/project/mlforecast/)
[](https://anaconda.org/conda-forge/mlforecast)
[](https://codecov.io/gh/Nixtla/mlforecast)
[](https://github.com/Nixtla/mlforecast/blob/main/LICENSE)
## Install
### PyPI
`pip install mlforecast`
#### Optional dependencies
If you want more functionality you can instead use `pip install mlforecast[extra1,extra2,...]`. The current extra dependencies are:
* **aws**: adds the functionality to use S3 as the storage in the CLI.
* **cli**: includes the validations necessary to use the CLI.
* **distributed**: installs [dask](https://dask.org/) to perform distributed training. Note that you'll also need to install either [LightGBM](https://github.com/microsoft/LightGBM/tree/master/python-package) or [XGBoost](https://xgboost.readthedocs.io/en/latest/install.html#python).
For example, if you want to perform distributed training through the CLI using S3 as your storage you'll need all three extras, which you can get using: `pip install mlforecast[aws,cli,distributed]`.
### conda-forge
`conda install -c conda-forge mlforecast`
Note that this installation comes with the required dependencies for the local interface. If you want to:
* Use s3 as storage: `conda install -c conda-forge s3path`
* Perform distributed training: `conda install -c conda-forge dask` and either [LightGBM](https://github.com/microsoft/LightGBM/tree/master/python-package) or [XGBoost](https://xgboost.readthedocs.io/en/latest/install.html#python).
## How to use
The following provides a very basic overview, for a more detailed description see the [documentation](https://nixtla.github.io/mlforecast/).
### Programmatic API
```
#hide
import os
import shutil
from pathlib import Path
from IPython.display import display, Markdown
os.chdir('..')
def display_df(df):
display(Markdown(df.to_markdown()))
```
Store your time series in a pandas dataframe with an index named **unique_id** that identifies each time serie, a column **ds** that contains the datestamps and a column **y** with the values.
```
from mlforecast.utils import generate_daily_series
series = generate_daily_series(20)
display_df(series.head())
```
Then create a `TimeSeries` object with the features that you want to use. These include lags, transformations on the lags and date features. The lag transformations are defined as [numba](http://numba.pydata.org/) *jitted* functions that transform an array, if they have additional arguments you supply a tuple (`transform_func`, `arg1`, `arg2`, ...).
```
from mlforecast.core import TimeSeries
from window_ops.expanding import expanding_mean
from window_ops.rolling import rolling_mean
ts = TimeSeries(
lags=[7, 14],
lag_transforms={
1: [expanding_mean],
7: [(rolling_mean, 7), (rolling_mean, 14)]
},
date_features=['dayofweek', 'month']
)
ts
```
Next define a model. If you want to use the local interface this can be any regressor that follows the scikit-learn API. For distributed training there are `LGBMForecast` and `XGBForecast`.
```
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(random_state=0)
```
Now instantiate your forecast object with the model and the time series. There are two types of forecasters, `Forecast` which is local and `DistributedForecast` which performs the whole process in a distributed way.
```
from mlforecast.forecast import Forecast
fcst = Forecast(model, ts)
```
To compute the features and train the model using them call `.fit` on your `Forecast` object.
```
fcst.fit(series)
```
To get the forecasts for the next 14 days call `.predict(14)` on the forecaster. This will update the target with each prediction and recompute the features to get the next one.
```
predictions = fcst.predict(14)
display_df(predictions.head())
```
### CLI
If you're looking for computing quick baselines, want to avoid some boilerplate or just like using CLIs better then you can use the `mlforecast` binary with a configuration file like the following:
```
!cat sample_configs/local.yaml
```
The configuration is validated using `FlowConfig`.
This configuration will use the data in `data.prefix/data.input` to train and write the results to `data.prefix/data.output` both with `data.format`.
```
data_path = Path('data')
data_path.mkdir()
series.to_parquet(data_path/'train')
!mlforecast sample_configs/local.yaml
list((data_path/'outputs').iterdir())
#hide
shutil.rmtree(data_path)
```
| true |
code
| 0.403156 | null | null | null | null |
|
Author: Xi Ming.
## Build a Multilayer Perceptron from Scratch based on PyTorch.
PyTorch's automatic differentiation mechanism can help quickly implement multilayer perceptrons.
### Import Packages.
```
import torch
import torchvision
import torch.nn as nn
from torchvision import datasets,transforms
from torch.utils.data import DataLoader
import numpy as np
print('pytorch version:',torch.__version__,'\ntorchvision version: ',torchvision.__version__,'\nnumpy version:' ,np.__version__)
```
### Settings
```
# model runs on GPU or CPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# Hyperparameters
learning_rate = 1e-2
momentum = 0.9
num_epochs = 10
batch_size = 128
# Architecture
num_features = 784
num_hidden_1 = 400
num_hidden_2 = 200
num_classes = 10
```
### Dataset: MNIST
```
train_dataset = datasets.MNIST(root='data',
train=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))]),
download=True)
test_dataset = datasets.MNIST(root='data',
train=False,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))]))
train_loader = DataLoader(dataset=train_dataset,
batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset,
batch_size=batch_size, shuffle=False)
# Checking the dataset
for images, labels in train_loader:
print('Image batch dimensions:', images.shape)
print('Image label dimensions:', labels.shape)
break
```
### Define model
```
class MultilayerPerceptron(nn.Module):
def __init__(self, num_features, num_classes):
super(MultilayerPerceptron, self).__init__()
self.model = nn.Sequential(
nn.Linear(num_features, num_hidden_1),
nn.Sigmoid(),
nn.Linear(num_hidden_1, num_hidden_2),
nn.Sigmoid(),
nn.Linear(num_hidden_2, num_classes)
)
def forward(self, x):
x = self.model(x)
return x
```
### Init model, define optimizer and loss function
```
model = MultilayerPerceptron(num_features=num_features,
num_classes=num_classes)
model = model.to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, momentum=momentum)
criterion = nn.CrossEntropyLoss()
```
### Training model
```
train_loss_list = []
test_acc_list = []
for epoch in range(num_epochs):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
data = data.view(-1, 28*28)
# forward
logits = model(data)
loss = criterion(logits, target)
# backprop
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch_idx % 100 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.data.item()))
train_loss_list.append(loss.data.item())
test_loss = 0
correct = 0
model.eval()
with torch.no_grad():
# test
total_correct = 0
total_num = 0
for data, target in test_loader:
data, target = data.to(device), target.to(device)
data = data.view(-1, 28*28)
logits = model(data)
test_loss += criterion(logits, target).item()
pred = logits.data.max(1)[1]
correct += pred.eq(target.data).sum()
test_loss /= len(test_loader.dataset)
test_acc = 100. * correct / len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset), test_acc))
test_acc_list.append(test_acc)
```
### Plot Training index curve
```
import matplotlib
import matplotlib.pyplot as plt
x = np.arange(0, num_epochs)
plt.title("Training index curve")
plt.plot(x, train_loss_list, label='train loss')
plt.xlabel('epochs')
plt.ylabel('train loss')
plt.show()
plt.title("Training index curve")
plt.plot(x, test_acc_list, label='test accuracy')
plt.xlabel('epochs')
plt.ylabel('train acc')
plt.show()
```
### Visual Inspection
```
for features, targets in test_loader:
break
fig, ax = plt.subplots(1, 4)
data = data.to('cpu')
for i in range(4):
ax[i].imshow(data[i].view(28, 28), cmap=matplotlib.cm.binary)
plt.show()
data = data.to(device)
predictions = model.forward(data[:4].view(-1, 28*28))
predictions = torch.argmax(predictions, dim=1)
print('Predicted labels', predictions)
```
| true |
code
| 0.8618 | null | null | null | null |
|
# Fuzzing APIs
So far, we have always generated _system input_, i.e. data that the program as a whole obtains via its input channels. However, we can also generate inputs that go directly into individual functions, gaining flexibility and speed in the process. In this chapter, we explore the use of grammars to synthesize code for function calls, which allows you to generate _program code that very efficiently invokes functions directly._
```
from bookutils import YouTubeVideo
YouTubeVideo('U842dC2R3V0')
```
**Prerequisites**
* You have to know how grammar fuzzing work, e.g. from the [chapter on grammars](Grammars.ipynb).
* We make use of _generator functions_, as discussed in the [chapter on fuzzing with generators](GeneratorGrammarFuzzer.ipynb).
* We make use of probabilities, as discussed in the [chapter on fuzzing with probabilities](ProbabilisticGrammarFuzzer.ipynb).
## Synopsis
<!-- Automatically generated. Do not edit. -->
To [use the code provided in this chapter](Importing.ipynb), write
```python
>>> from fuzzingbook.APIFuzzer import <identifier>
```
and then make use of the following features.
This chapter provides *grammar constructors* that are useful for generating _function calls_.
The grammars are [probabilistic](ProbabilisticGrammarFuzzer.ipynb) and make use of [generators](GeneratorGrammarFuzzer.ipynb), so use `ProbabilisticGeneratorGrammarFuzzer` as a producer.
```python
>>> from GeneratorGrammarFuzzer import ProbabilisticGeneratorGrammarFuzzer
```
`INT_GRAMMAR`, `FLOAT_GRAMMAR`, `ASCII_STRING_GRAMMAR` produce integers, floats, and strings, respectively:
```python
>>> fuzzer = ProbabilisticGeneratorGrammarFuzzer(INT_GRAMMAR)
>>> [fuzzer.fuzz() for i in range(10)]
['-51', '9', '0', '0', '0', '0', '32', '0', '0', '0']
>>> fuzzer = ProbabilisticGeneratorGrammarFuzzer(FLOAT_GRAMMAR)
>>> [fuzzer.fuzz() for i in range(10)]
['0e0',
'-9.43e34',
'-7.3282e0',
'-9.5e-9',
'0',
'-30.840386e-5',
'3',
'-4.1e0',
'-9.7',
'413']
>>> fuzzer = ProbabilisticGeneratorGrammarFuzzer(ASCII_STRING_GRAMMAR)
>>> [fuzzer.fuzz() for i in range(10)]
['"#vYV*t@I%KNTT[q~}&-v+[zAzj[X-z|RzC$(g$Br]1tC\':5<F-"',
'""',
'"^S/"',
'"y)QDs_9"',
'")dY~?WYqMh,bwn3\\"A!02Pk`gx"',
'"01n|(dd$-d.sx\\"83\\"h/]qx)d9LPNdrk$}$4t3zhC.%3VY@AZZ0wCs2 N"',
'"D\\6\\xgw#TQ}$\'3"',
'"LaM{"',
'"\\"ux\'1H!=%;2T$.=l"',
'"=vkiV~w.Ypt,?JwcEr}Moc>!5<U+DdYAup\\"N 0V?h3x~jFN3"']
```
`int_grammar_with_range(start, end)` produces an integer grammar with values `N` such that `start <= N <= end`:
```python
>>> int_grammar = int_grammar_with_range(100, 200)
>>> fuzzer = ProbabilisticGeneratorGrammarFuzzer(int_grammar)
>>> [fuzzer.fuzz() for i in range(10)]
['154', '149', '185', '117', '182', '154', '131', '194', '147', '192']
```
`float_grammar_with_range(start, end)` produces a floating-number grammar with values `N` such that `start <= N <= end`.
```python
>>> float_grammar = float_grammar_with_range(100, 200)
>>> fuzzer = ProbabilisticGeneratorGrammarFuzzer(float_grammar)
>>> [fuzzer.fuzz() for i in range(10)]
['121.8092479227325',
'187.18037169119634',
'127.9576486784452',
'125.47768739781723',
'151.8091820472274',
'117.864410860742',
'187.50918008379483',
'119.29335112884749',
'149.2637029583114',
'126.61818995939146']
```
All such values can be immediately used for testing function calls:
```python
>>> from math import sqrt
>>> fuzzer = ProbabilisticGeneratorGrammarFuzzer(int_grammar)
>>> call = "sqrt(" + fuzzer.fuzz() + ")"
>>> call
'sqrt(143)'
>>> eval(call)
11.958260743101398
```
These grammars can also be composed to form more complex grammars. `list_grammar(object_grammar)` returns a grammar that produces lists of objects as defined by `object_grammar`.
```python
>>> int_list_grammar = list_grammar(int_grammar)
>>> fuzzer = ProbabilisticGeneratorGrammarFuzzer(int_list_grammar)
>>> [fuzzer.fuzz() for i in range(5)]
['[118, 111, 188, 137, 129]',
'[170, 172]',
'[171, 161, 117, 191, 175, 183, 164]',
'[189]',
'[129, 110, 178]']
>>> some_list = eval(fuzzer.fuzz())
>>> some_list
[172, 120, 106, 192, 124, 191, 161, 100, 117]
>>> len(some_list)
9
```
In a similar vein, we can construct arbitrary further data types for testing individual functions programmatically.
## Fuzzing a Function
Let us start with our first problem: How do we fuzz a given function? For an interpreted language like Python, this is pretty straight-forward. All we need to do is to generate _calls_ to the function(s) we want to test. This is something we can easily do with a grammar.
As an example, consider the `urlparse()` function from the Python library. `urlparse()` takes a URL and decomposes it into its individual components.
```
import bookutils
from urllib.parse import urlparse
urlparse('https://www.fuzzingbook.com/html/APIFuzzer.html')
```
You see how the individual elements of the URL – the _scheme_ (`"http"`), the _network location_ (`"www.fuzzingbook.com"`), or the path (`"//html/APIFuzzer.html"`) are all properly identified. Other elements (like `params`, `query`, or `fragment`) are empty, because they were not part of our input.
To test `urlparse()`, we'd want to feed it a large set of different URLs. We can obtain these from the URL grammar we had defined in the ["Grammars"](Grammars.ipynb) chapter.
```
from Grammars import URL_GRAMMAR, is_valid_grammar, START_SYMBOL
from Grammars import opts, extend_grammar, Grammar
from GrammarFuzzer import GrammarFuzzer
url_fuzzer = GrammarFuzzer(URL_GRAMMAR)
for i in range(10):
url = url_fuzzer.fuzz()
print(urlparse(url))
```
This way, we can easily test any Python function – by setting up a scaffold that runs it. How would we proceed, though, if we wanted to have a test that can be re-run again and again, without having to generate new calls every time?
## Synthesizing Code
The "scaffolding" method, as sketched above, has an important downside: It couples test generation and test execution into a single unit, disallowing running both at different times, or for different languages. To decouple the two, we take another approach: Rather than generating inputs and immediately feeding this input into a function, we _synthesize code_ instead that invokes functions with a given input.
For instance, if we generate the string
```
call = "urlparse('http://www.example.com/')"
```
we can execute this string as a whole (and thus run the test) at any time:
```
eval(call)
```
To systematically generate such calls, we can again use a grammar:
```
URLPARSE_GRAMMAR: Grammar = {
"<call>":
['urlparse("<url>")']
}
# Import definitions from URL_GRAMMAR
URLPARSE_GRAMMAR.update(URL_GRAMMAR)
URLPARSE_GRAMMAR["<start>"] = ["<call>"]
assert is_valid_grammar(URLPARSE_GRAMMAR)
```
This grammar creates calls in the form `urlparse(<url>)`, where `<url>` comes from the "imported" URL grammar. The idea is to create many of these calls and to feed them into the Python interpreter.
```
URLPARSE_GRAMMAR
```
We can now use this grammar for fuzzing and synthesizing calls to `urlparse)`:
```
urlparse_fuzzer = GrammarFuzzer(URLPARSE_GRAMMAR)
urlparse_fuzzer.fuzz()
```
Just as above, we can immediately execute these calls. To better see what is happening, we define a small helper function:
```
# Call function_name(arg[0], arg[1], ...) as a string
def do_call(call_string):
print(call_string)
result = eval(call_string)
print("\t= " + repr(result))
return result
call = urlparse_fuzzer.fuzz()
do_call(call)
```
If `urlparse()` were a C function, for instance, we could embed its call into some (also generated) C function:
```
URLPARSE_C_GRAMMAR: Grammar = {
"<cfile>": ["<cheader><cfunction>"],
"<cheader>": ['#include "urlparse.h"\n\n'],
"<cfunction>": ["void test() {\n<calls>}\n"],
"<calls>": ["<call>", "<calls><call>"],
"<call>": [' urlparse("<url>");\n']
}
URLPARSE_C_GRAMMAR.update(URL_GRAMMAR)
URLPARSE_C_GRAMMAR["<start>"] = ["<cfile>"]
assert is_valid_grammar(URLPARSE_C_GRAMMAR)
urlparse_fuzzer = GrammarFuzzer(URLPARSE_C_GRAMMAR)
print(urlparse_fuzzer.fuzz())
```
## Synthesizing Oracles
In our `urlparse()` example, both the Python as well as the C variant only check for _generic_ errors in `urlparse()`; that is, they only detect fatal errors and exceptions. For a full test, we need to set up a specific *oracle* as well that checks whether the result is valid.
Our plan is to check whether specific parts of the URL reappear in the result – that is, if the scheme is `http:`, then the `ParseResult` returned should also contain a `http:` scheme. As discussed in the [chapter on fuzzing with generators](GeneratorGrammarFuzzer.ipynb), equalities of strings such as `http:` across two symbols cannot be expressed in a context-free grammar. We can, however, use a _generator function_ (also introduced in the [chapter on fuzzing with generators](GeneratorGrammarFuzzer.ipynb)) to automatically enforce such equalities.
Here is an example. Invoking `geturl()` on a `urlparse()` result should return the URL as originally passed to `urlparse()`.
```
from GeneratorGrammarFuzzer import GeneratorGrammarFuzzer, ProbabilisticGeneratorGrammarFuzzer
URLPARSE_ORACLE_GRAMMAR: Grammar = extend_grammar(URLPARSE_GRAMMAR,
{
"<call>": [("assert urlparse('<url>').geturl() == '<url>'",
opts(post=lambda url_1, url_2: [None, url_1]))]
})
urlparse_oracle_fuzzer = GeneratorGrammarFuzzer(URLPARSE_ORACLE_GRAMMAR)
test = urlparse_oracle_fuzzer.fuzz()
print(test)
exec(test)
```
In a similar way, we can also check individual components of the result:
```
URLPARSE_ORACLE_GRAMMAR: Grammar = extend_grammar(URLPARSE_GRAMMAR,
{
"<call>": [("result = urlparse('<scheme>://<host><path>?<params>')\n"
# + "print(result)\n"
+ "assert result.scheme == '<scheme>'\n"
+ "assert result.netloc == '<host>'\n"
+ "assert result.path == '<path>'\n"
+ "assert result.query == '<params>'",
opts(post=lambda scheme_1, authority_1, path_1, params_1,
scheme_2, authority_2, path_2, params_2:
[None, None, None, None,
scheme_1, authority_1, path_1, params_1]))]
})
# Get rid of unused symbols
del URLPARSE_ORACLE_GRAMMAR["<url>"]
del URLPARSE_ORACLE_GRAMMAR["<query>"]
del URLPARSE_ORACLE_GRAMMAR["<authority>"]
del URLPARSE_ORACLE_GRAMMAR["<userinfo>"]
del URLPARSE_ORACLE_GRAMMAR["<port>"]
urlparse_oracle_fuzzer = GeneratorGrammarFuzzer(URLPARSE_ORACLE_GRAMMAR)
test = urlparse_oracle_fuzzer.fuzz()
print(test)
exec(test)
```
The use of generator functions may feel a bit cumbersome. Indeed, if we uniquely stick to Python, we could also create a _unit test_ that directly invokes the fuzzer to generate individual parts:
```
def fuzzed_url_element(symbol):
return GrammarFuzzer(URLPARSE_GRAMMAR, start_symbol=symbol).fuzz()
scheme = fuzzed_url_element("<scheme>")
authority = fuzzed_url_element("<authority>")
path = fuzzed_url_element("<path>")
query = fuzzed_url_element("<params>")
url = "%s://%s%s?%s" % (scheme, authority, path, query)
result = urlparse(url)
# print(result)
assert result.geturl() == url
assert result.scheme == scheme
assert result.path == path
assert result.query == query
```
Using such a unit test makes it easier to express oracles. However, we lose the ability to systematically cover individual URL elements and alternatives as with [`GrammarCoverageFuzzer`](GrammarCoverageFuzzer.ipynb) as well as the ability to guide generation towards specific elements as with [`ProbabilisticGrammarFuzzer`](ProbabilisticGrammarFuzzer.ipynb). Furthermore, a grammar allows us to generate tests for arbitrary programming languages and APIs.
## Synthesizing Data
For `urlparse()`, we have used a very specific grammar for creating a very specific argument. Many functions take basic data types as (some) arguments, though; we therefore define grammars that generate precisely those arguments. Even better, we can define functions that _generate_ grammars tailored towards our specific needs, returning values in a particular range, for instance.
### Integers
We introduce a simple grammar to produce integers.
```
from Grammars import convert_ebnf_grammar, crange
from ProbabilisticGrammarFuzzer import ProbabilisticGrammarFuzzer
INT_EBNF_GRAMMAR: Grammar = {
"<start>": ["<int>"],
"<int>": ["<_int>"],
"<_int>": ["(-)?<leaddigit><digit>*", "0"],
"<leaddigit>": crange('1', '9'),
"<digit>": crange('0', '9')
}
assert is_valid_grammar(INT_EBNF_GRAMMAR)
INT_GRAMMAR = convert_ebnf_grammar(INT_EBNF_GRAMMAR)
INT_GRAMMAR
int_fuzzer = GrammarFuzzer(INT_GRAMMAR)
print([int_fuzzer.fuzz() for i in range(10)])
```
If we need integers in a specific range, we can add a generator function that does right that:
```
from Grammars import set_opts
import random
def int_grammar_with_range(start, end):
int_grammar = extend_grammar(INT_GRAMMAR)
set_opts(int_grammar, "<int>", "<_int>",
opts(pre=lambda: random.randint(start, end)))
return int_grammar
int_fuzzer = GeneratorGrammarFuzzer(int_grammar_with_range(900, 1000))
[int_fuzzer.fuzz() for i in range(10)]
```
### Floats
The grammar for floating-point values closely resembles the integer grammar.
```
FLOAT_EBNF_GRAMMAR: Grammar = {
"<start>": ["<float>"],
"<float>": [("<_float>", opts(prob=0.9)), "inf", "NaN"],
"<_float>": ["<int>(.<digit>+)?<exp>?"],
"<exp>": ["e<int>"]
}
FLOAT_EBNF_GRAMMAR.update(INT_EBNF_GRAMMAR)
FLOAT_EBNF_GRAMMAR["<start>"] = ["<float>"]
assert is_valid_grammar(FLOAT_EBNF_GRAMMAR)
FLOAT_GRAMMAR = convert_ebnf_grammar(FLOAT_EBNF_GRAMMAR)
FLOAT_GRAMMAR
float_fuzzer = ProbabilisticGrammarFuzzer(FLOAT_GRAMMAR)
print([float_fuzzer.fuzz() for i in range(10)])
def float_grammar_with_range(start, end):
float_grammar = extend_grammar(FLOAT_GRAMMAR)
set_opts(float_grammar, "<float>", "<_float>", opts(
pre=lambda: start + random.random() * (end - start)))
return float_grammar
float_fuzzer = ProbabilisticGeneratorGrammarFuzzer(
float_grammar_with_range(900.0, 900.9))
[float_fuzzer.fuzz() for i in range(10)]
```
### Strings
Finally, we introduce a grammar for producing strings.
```
ASCII_STRING_EBNF_GRAMMAR: Grammar = {
"<start>": ["<ascii-string>"],
"<ascii-string>": ['"<ascii-chars>"'],
"<ascii-chars>": [
("", opts(prob=0.05)),
"<ascii-chars><ascii-char>"
],
"<ascii-char>": crange(" ", "!") + [r'\"'] + crange("#", "~")
}
assert is_valid_grammar(ASCII_STRING_EBNF_GRAMMAR)
ASCII_STRING_GRAMMAR = convert_ebnf_grammar(ASCII_STRING_EBNF_GRAMMAR)
string_fuzzer = ProbabilisticGrammarFuzzer(ASCII_STRING_GRAMMAR)
print([string_fuzzer.fuzz() for i in range(10)])
```
## Synthesizing Composite Data
From basic data, as discussed above, we can also produce _composite data_ in data structures such as sets or lists. We illustrate such generation on lists.
### Lists
```
LIST_EBNF_GRAMMAR: Grammar = {
"<start>": ["<list>"],
"<list>": [
("[]", opts(prob=0.05)),
"[<list-objects>]"
],
"<list-objects>": [
("<list-object>", opts(prob=0.2)),
"<list-object>, <list-objects>"
],
"<list-object>": ["0"],
}
assert is_valid_grammar(LIST_EBNF_GRAMMAR)
LIST_GRAMMAR = convert_ebnf_grammar(LIST_EBNF_GRAMMAR)
```
Our list generator takes a grammar that produces objects; it then instantiates a list grammar with the objects from these grammars.
```
def list_grammar(object_grammar, list_object_symbol=None):
obj_list_grammar = extend_grammar(LIST_GRAMMAR)
if list_object_symbol is None:
# Default: Use the first expansion of <start> as list symbol
list_object_symbol = object_grammar[START_SYMBOL][0]
obj_list_grammar.update(object_grammar)
obj_list_grammar[START_SYMBOL] = ["<list>"]
obj_list_grammar["<list-object>"] = [list_object_symbol]
assert is_valid_grammar(obj_list_grammar)
return obj_list_grammar
int_list_fuzzer = ProbabilisticGrammarFuzzer(list_grammar(INT_GRAMMAR))
[int_list_fuzzer.fuzz() for i in range(10)]
string_list_fuzzer = ProbabilisticGrammarFuzzer(
list_grammar(ASCII_STRING_GRAMMAR))
[string_list_fuzzer.fuzz() for i in range(10)]
float_list_fuzzer = ProbabilisticGeneratorGrammarFuzzer(list_grammar(
float_grammar_with_range(900.0, 900.9)))
[float_list_fuzzer.fuzz() for i in range(10)]
```
Generators for dictionaries, sets, etc. can be defined in a similar fashion. By plugging together grammar generators, we can produce data structures with arbitrary elements.
## Synopsis
This chapter provides *grammar constructors* that are useful for generating _function calls_.
The grammars are [probabilistic](ProbabilisticGrammarFuzzer.ipynb) and make use of [generators](GeneratorGrammarFuzzer.ipynb), so use `ProbabilisticGeneratorGrammarFuzzer` as a producer.
```
from GeneratorGrammarFuzzer import ProbabilisticGeneratorGrammarFuzzer
```
`INT_GRAMMAR`, `FLOAT_GRAMMAR`, `ASCII_STRING_GRAMMAR` produce integers, floats, and strings, respectively:
```
fuzzer = ProbabilisticGeneratorGrammarFuzzer(INT_GRAMMAR)
[fuzzer.fuzz() for i in range(10)]
fuzzer = ProbabilisticGeneratorGrammarFuzzer(FLOAT_GRAMMAR)
[fuzzer.fuzz() for i in range(10)]
fuzzer = ProbabilisticGeneratorGrammarFuzzer(ASCII_STRING_GRAMMAR)
[fuzzer.fuzz() for i in range(10)]
```
`int_grammar_with_range(start, end)` produces an integer grammar with values `N` such that `start <= N <= end`:
```
int_grammar = int_grammar_with_range(100, 200)
fuzzer = ProbabilisticGeneratorGrammarFuzzer(int_grammar)
[fuzzer.fuzz() for i in range(10)]
```
`float_grammar_with_range(start, end)` produces a floating-number grammar with values `N` such that `start <= N <= end`.
```
float_grammar = float_grammar_with_range(100, 200)
fuzzer = ProbabilisticGeneratorGrammarFuzzer(float_grammar)
[fuzzer.fuzz() for i in range(10)]
```
All such values can be immediately used for testing function calls:
```
from math import sqrt
fuzzer = ProbabilisticGeneratorGrammarFuzzer(int_grammar)
call = "sqrt(" + fuzzer.fuzz() + ")"
call
eval(call)
```
These grammars can also be composed to form more complex grammars. `list_grammar(object_grammar)` returns a grammar that produces lists of objects as defined by `object_grammar`.
```
int_list_grammar = list_grammar(int_grammar)
fuzzer = ProbabilisticGeneratorGrammarFuzzer(int_list_grammar)
[fuzzer.fuzz() for i in range(5)]
some_list = eval(fuzzer.fuzz())
some_list
len(some_list)
```
In a similar vein, we can construct arbitrary further data types for testing individual functions programmatically.
## Lessons Learned
* To fuzz individual functions, one can easily set up grammars that produce function calls.
* Fuzzing at the API level can be much faster than fuzzing at the system level, but brings the risk of false alarms by violating implicit preconditions.
## Next Steps
This chapter was all about manually writing test and controlling which data gets generated. [In the next chapter](Carver.ipynb), we will introduce a much higher level of automation:
* _Carving_ automatically records function calls and arguments from program executions.
* We can turn these into _grammars_, allowing to test these functions with various combinations of recorded values.
With these techniques, we automatically obtain grammars that already invoke functions in application contexts, making our work of specifying them much easier.
## Background
The idea of using generator functions to generate input structures was first explored in QuickCheck \cite{Claessen2000}. A very nice implementation for Python is the [hypothesis package](https://hypothesis.readthedocs.io/en/latest/) which allows to write and combine data structure generators for testing APIs.
## Exercises
The exercises for this chapter combine the above techniques with fuzzing techniques introduced earlier.
### Exercise 1: Deep Arguments
In the example generating oracles for `urlparse()`, important elements such as `authority` or `port` are not checked. Enrich `URLPARSE_ORACLE_GRAMMAR` with post-expansion functions that store the generated elements in a symbol table, such that they can be accessed when generating the assertions.
**Solution.** Left to the reader.
### Exercise 2: Covering Argument Combinations
In the chapter on [configuration testing](ConfigurationFuzzer.ipynb), we also discussed _combinatorial testing_ – that is, systematic coverage of _sets_ of configuration elements. Implement a scheme that by changing the grammar, allows all _pairs_ of argument values to be covered.
**Solution.** Left to the reader.
### Exercise 3: Mutating Arguments
To widen the range of arguments to be used during testing, apply the _mutation schemes_ introduced in [mutation fuzzing](MutationFuzzer.ipynb) – for instance, flip individual bytes or delete characters from strings. Apply this either during grammar inference or as a separate step when invoking functions.
**Solution.** Left to the reader.
| true |
code
| 0.248124 | null | null | null | null |
|
# Creating a class
```
class Student: # created a class "Student"
name = "Tom"
grade = "A"
age = 15
def display(self):
print(self.name,self.grade,self.age)
# There will be no output here, because we are not invoking (calling) the "display" function to print
```
## Creating an object
```
class Student:
name = "Tom"
grade = "A"
age = 15
def display(self):
print(self.name,self.grade,self.age)
s1 = Student() # created an object "s1" of class "Student"
s1.display() # displaying the details through the "display" finction
```
## Creating a constructor
> If we give parameters inside the constructor (inside __init__) then that type of representation is called "Parameterized constructor"
> If we don't give parameters inside the constructor (inside __init__) then that type of representation is called "Non-Parameterized constructor"

```
# This is a parameterized constructor
class Student:
def __init__(self,name,study,occupation): # intializing all the parameters we need i.e, name, study, occupation in the constructor
self.name = name
self.study = study
self.occupation = occupation
def output(self):
print(self.name + " completed " + self.study + " and working as a " + self.occupation)
s1 = Student('Tom', 'Btech' ,'software engineer') # creating two objects and giving the
s2 = Student('Jerry', "MBBS", 'doctor') # input as the order mentioned in the " __init__ " function
s1.output()
s2.output()
# This is a non-parameterized constructor
class Student:
def __init__(self):
print(" This is a Non parameterized constructor")
s1 = Student()
```
## Python in-built class functions
```
class Student:
def __init__(self,name,grade,age):
self.name = name
self.grade = grade
self.age = age
s1 = Student("Tom","A",15)
print(getattr(s1,'name')) # we get the value of the particular attribute
print(getattr(s1,"age")) # Here,we are asking for attributes "name","age" and the value of those attributes are "Tom",15 respectively
setattr(s1,"age",20) # setting the attribute (changing)
print("Age of the tom is changed using 'setattr' ")
print(getattr(s1,"age"))
print("Checking whether the particular attribute is there or not")
print(hasattr(s1,"name")) # Returns "True" if the attribute is intialized on our class
print(hasattr(s1,"school")) # or else gives "False"
```
## Built-in class attributes
```
class Student:
'''This is doc string where we mention,what's the idea of this progam '''
def __init__(self,name,grade,age):
self.name = name
self.grade = grade
self.age = age
s1 = Student("Tom","A",15)
print(Student.__doc__) # printing the doc string
print(s1.__dict__) # printing the attributes in a dictionary data type way
```
# Inheritance
```
class Parent:
print("This is the parent class")
def dog(self):
print("Dog barks")
class Child(Parent): # Inheriting the "parent" class using "child" class
def lion(self):
print("Lion roars")
c1 = Child() # "c1" is the object of "Child" class
c1.lion()
c1.dog() # because of inheritance, the print statement inside the "dog" function , which is inside the "Parent" class is also printed.
```
## Multi-level inheritance
```
class Parent:
print("This is the parent class")
def dog(self):
print("Dog barks")
class Child(Parent): # Inheriting the "parent" class using "child" class
def lion(self):
print("Lion roars")
class Grandchild(Child): # Inheriting the "Child" class
def pegion(self):
print("pegion coos")
c1 = Grandchild() # "c1" is the object of "Grandchild" class
c1.lion()
c1.dog() # because of inheritance, the print statement inside the "dog" function , which is inside the "Parent" class is also printed.
c1.pegion() # because of inheritance, the print statement inside the "lion" function , which is inside the "Child" class is also printed.
```
# Multiple inheritance
```
class Calculator1:
def sum(self,a,b):
return a + b
class Calculator2:
def mul(self,a,b):
return a * b
class Derived(Calculator1,Calculator2): # Multiple inheritance, since it is having multiple (in this case 2) class arguments.
def div(self,a,b):
return a / b
d = Derived()
print(d.sum(20,30))
print(d.mul(20,30))
print(d.div(20,30))
```
# Polymorphism
```
class Teacher:
def intro(self):
print("I am a teacher")
def experience(self):
print("3 to 4 years")
class Lecturer:
def intro(self):
print("I am a lecturer")
def experience(self):
print("5 to 6 years")
class Professor:
def intro(self):
print("I am a professor")
def experience(self):
print("8 to 10 years")
# Common Interface for all persons
def category(person):
person.intro() # only intros are printed
# type "person.experience" instead of "person.intro", we get only experience. If we type both "person.intro" and "person.experience" , then both statements are printed.
# instantiate objects
t = Teacher()
l = Lecturer()
p = Professor()
# passing the object
category(t)
category(l)
category(p)
```
# Encapsulation
```
class Computer:
def __init__(self):
self.__maxprice = 900 # maxprice is a private data bcz, it is starting with " __ " underscores
def sell(self):
print("Selling Price: {}".format(self.__maxprice))
def setMaxPrice(self, price): # This method is used to set the private data
self.__maxprice = price
c = Computer() # c is an object of "Computer" class
c.sell()
# change the price
c.__maxprice = 1000 # Here, we are modifying our data directly "__maxprice" to 1000. But the data is not modified because it is a private data
c.sell()
# using setter function
c.setMaxPrice(1000) # In order to change the private data, we have to take help of the method "setMaxPrice" and then now the data is modified
c.sell() # Invoking (calling) the "sell" method (function)
```
## Data abstraction
```
from abc import ABC,abstractclassmethod
class Company(ABC): # this is the abstract class and "ABC" is called as "Abstract Base Class" which is imported from module "abc"
# this is the abstact class method and that "@" is called as decorators. With the help of the decorator only we can make the method as abstract class method
@abstractclassmethod
def developer(self):
pass
class Jr_developer(Company):
def developer(self):
print("I am a jr.developer and develops small applications")
class Sr_developer(Company):
def developer(self):
print("I am a sr.developer and develops large applications")
j = Jr_developer()
s = Sr_developer()
j.developer()
s.developer()
```
| true |
code
| 0.4953 | null | null | null | null |
|
<a href="http://cocl.us/pytorch_link_top">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/Pytochtop.png" width="750" alt="IBM Product " />
</a>
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/cc-logo-square.png" width="200" alt="cognitiveclass.ai logo" />
<h1>Linear Regression Multiple Outputs</h1>
<h2>Table of Contents</h2>
<p>In this lab, you will create a model the PyTroch way. This will help you more complicated models.</p>
<ul>
<li><a href="#Makeup_Data">Make Some Data</a></li>
<li><a href="#Model_Cost">Create the Model and Cost Function the PyTorch way</a></li>
<li><a href="#BGD">Train the Model: Batch Gradient Descent</a></li>
</ul>
<p>Estimated Time Needed: <strong>20 min</strong></p>
<hr>
<h2>Preparation</h2>
We'll need the following libraries:
```
# Import the libraries we need for this lab
from torch import nn,optim
import torch
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from torch.utils.data import Dataset, DataLoader
```
Set the random seed:
```
# Set the random seed.
torch.manual_seed(1)
```
Use this function for plotting:
```
# The function for plotting 2D
def Plot_2D_Plane(model, dataset, n=0):
w1 = model.state_dict()['linear.weight'].numpy()[0][0]
w2 = model.state_dict()['linear.weight'].numpy()[0][0]
b = model.state_dict()['linear.bias'].numpy()
# Data
x1 = data_set.x[:, 0].view(-1, 1).numpy()
x2 = data_set.x[:, 1].view(-1, 1).numpy()
y = data_set.y.numpy()
# Make plane
X, Y = np.meshgrid(np.arange(x1.min(), x1.max(), 0.05), np.arange(x2.min(), x2.max(), 0.05))
yhat = w1 * X + w2 * Y + b
# Plotting
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(x1[:, 0], x2[:, 0], y[:, 0],'ro', label='y') # Scatter plot
ax.plot_surface(X, Y, yhat) # Plane plot
ax.set_xlabel('x1 ')
ax.set_ylabel('x2 ')
ax.set_zlabel('y')
plt.title('estimated plane iteration:' + str(n))
ax.legend()
plt.show()
```
<!--Empty Space for separating topics-->
<h2 id="Makeup_Data"r>Make Some Data </h2>
Create a dataset class with two-dimensional features:
```
# Create a 2D dataset
class Data2D(Dataset):
# Constructor
def __init__(self):
self.x = torch.zeros(20, 2)
self.x[:, 0] = torch.arange(-1, 1, 0.1)
self.x[:, 1] = torch.arange(-1, 1, 0.1)
self.w = torch.tensor([[1.0], [1.0]])
self.b = 1
self.f = torch.mm(self.x, self.w) + self.b
self.y = self.f + 0.1 * torch.randn((self.x.shape[0],1))
self.len = self.x.shape[0]
# Getter
def __getitem__(self, index):
return self.x[index], self.y[index]
# Get Length
def __len__(self):
return self.len
```
Create a dataset object:
```
# Create the dataset object
data_set = Data2D()
```
<h2 id="Model_Cost">Create the Model, Optimizer, and Total Loss Function (Cost)</h2>
Create a customized linear regression module:
```
# Create a customized linear
class linear_regression(nn.Module):
# Constructor
def __init__(self, input_size, output_size):
super(linear_regression, self).__init__()
self.linear = nn.Linear(input_size, output_size)
# Prediction
def forward(self, x):
yhat = self.linear(x)
return yhat
```
Create a model. Use two features: make the input size 2 and the output size 1:
```
# Create the linear regression model and print the parameters
model = linear_regression(2,1)
print("The parameters: ", list(model.parameters()))
```
Create an optimizer object. Set the learning rate to 0.1. <b>Don't forget to enter the model parameters in the constructor.</b>
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter2/2.6.2paramater_hate.png" width = "100" alt="How the optimizer works" />
```
# Create the optimizer
optimizer = optim.SGD(model.parameters(), lr=0.1)
```
Create the criterion function that calculates the total loss or cost:
```
# Create the cost function
criterion = nn.MSELoss()
```
Create a data loader object. Set the batch_size equal to 2:
```
# Create the data loader
train_loader = DataLoader(dataset=data_set, batch_size=2)
```
<!--Empty Space for separating topics-->
<h2 id="BGD">Train the Model via Mini-Batch Gradient Descent</h2>
Run 100 epochs of Mini-Batch Gradient Descent and store the total loss or cost for every iteration. Remember that this is an approximation of the true total loss or cost:
```
# Train the model
LOSS = []
print("Before Training: ")
Plot_2D_Plane(model, data_set)
epochs = 100
def train_model(epochs):
for epoch in range(epochs):
for x,y in train_loader:
yhat = model(x)
loss = criterion(yhat, y)
LOSS.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_model(epochs)
print("After Training: ")
Plot_2D_Plane(model, data_set, epochs)
# Plot out the Loss and iteration diagram
plt.plot(LOSS)
plt.xlabel("Iterations ")
plt.ylabel("Cost/total loss ")
```
<h3>Practice</h3>
Create a new <code>model1</code>. Train the model with a batch size 30 and learning rate 0.1, store the loss or total cost in a list <code>LOSS1</code>, and plot the results.
```
# Practice create model1. Train the model with batch size 30 and learning rate 0.1, store the loss in a list <code>LOSS1</code>. Plot the results.
data_set = Data2D()
model1=linear_regression(2,1)
trainloader=DataLoader(dataset=data_set, batch_size=30)
optimizer1=optim.SGD(model.parameters(),lr=0.1)
LOSS1=[]
for epoch in range(epochs):
for x,y in trainloader:
yhat=model1(x)
loss=criterion(yhat,y)
LOSS1.append(loss)
optimizer1.zero_grad()
loss.backward()
optimizer.step()
print("After Training: ")
Plot_2D_Plane(model, data_set, epochs)
```
Double-click <b>here</b> for the solution.
<!-- Your answer is below:
train_loader = DataLoader(dataset = data_set, batch_size = 30)
model1 = linear_regression(2, 1)
optimizer = optim.SGD(model1.parameters(), lr = 0.1)
LOSS1 = []
epochs = 100
def train_model(epochs):
for epoch in range(epochs):
for x,y in train_loader:
yhat = model1(x)
loss = criterion(yhat,y)
LOSS1.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_model(epochs)
Plot_2D_Plane(model1 , data_set)
plt.plot(LOSS1)
plt.xlabel("iterations ")
plt.ylabel("Cost/total loss ")
-->
Use the following validation data to calculate the total loss or cost for both models:
```
torch.manual_seed(2)
validation_data = Data2D()
Y = validation_data.y
X = validation_data.x
print("For model:")
totalloss=criterion(model(X),Y)
print(totalloss)
print("For model1:")
totalloss=criterion(model1(X),Y)
print(totalloss)
```
Double-click <b>here</b> for the solution.
<!-- Your answer is below:
print("total loss or cost for model: ",criterion(model(X),Y))
print("total loss or cost for model: ",criterion(model1(X),Y))
-->
<!--Empty Space for separating topics-->
<a href="http://cocl.us/pytorch_link_bottom">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/notebook_bottom%20.png" width="750" alt="PyTorch Bottom" />
</a>
<h2>About the Authors:</h2>
<a href="https://www.linkedin.com/in/joseph-s-50398b136/">Joseph Santarcangelo</a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/">Michelle Carey</a>, <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
<hr>
Copyright © 2018 <a href="cognitiveclass.ai?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu">cognitiveclass.ai</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.
| true |
code
| 0.816223 | null | null | null | null |
|
# Loading and Checking Data
## Importing Libraries
```
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
use_cuda = torch.cuda.is_available()
```
## Loading Data
```
batch_size = 4
# These are the mean and standard deviation values for all pictures in the training set.
mean = (0.4914 , 0.48216, 0.44653)
std = (0.24703, 0.24349, 0.26159)
# Class to denormalize images to display later.
class DeNormalize(object):
def __init__(self, mean, std):
self.mean = mean
self.std = std
def __call__(self, tensor):
for t, m, s in zip(tensor, self.mean, self.std):
t.mul_(s).add_(m)
return tensor
# Creating instance of Functor
denorm = DeNormalize(mean, std)
# Load data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize(mean, std)])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=True, num_workers=4)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
# Do NOT shuffle the test set or else the order will be messed up
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=4)
# Classes in order
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
```
## Sample Images and Labels
```
# functions to show an image
def imshow(img):
img = denorm(img) # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
# Defining Model
## Fully-Connected DNN
```
class Net_DNN(nn.Module):
def __init__(self, architecture):
super().__init__()
self.layers = nn.ModuleList([
nn.Linear(architecture[layer], architecture[layer + 1])
for layer in range(len(architecture) - 1)])
def forward(self, data):
# Flatten the Tensor (i.e., dimensions 3 x 32 x 32) to a single column
data = data.view(data.size(0), -1)
for layer in self.layers:
layer_data = layer(data)
data = F.relu(layer_data)
return F.log_softmax(layer_data, dim=-1)
```
## Fully-CNN
```
class Net_CNN(nn.Module):
# Padding is set to 2 and stride to 2
# Padding ensures all edge pixels are exposed to the filter
# Stride = 2 is common practice
def __init__(self, layers, c, stride=2):
super().__init__()
self.layers = nn.ModuleList([
nn.Conv2d(layers[i], layers[i + 1], kernel_size=3, padding=2, stride=stride)
for i in range(len(layers) - 1)])
self.pool = nn.AdaptiveMaxPool2d(1) # Simply takes the maximum value from the Tensor
self.out = nn.Linear(layers[-1], c)
def forward(self, data):
for layer in self.layers:
data = F.relu(layer(data))
data = self.pool(data)
data = data.view(data.size(0), -1)
return F.log_softmax(self.out(data), dim=-1)
```
## Chained CNN and NN
```
class Net_CNN_NN(nn.Module):
# Padding is set to 2 and stride to 2
# Padding ensures all edge pixels are exposed to the filter
# Stride = 2 is common practice
def __init__(self, layers, architecture, stride=2):
super().__init__()
# Fully Convolutional Layers
self.layers = nn.ModuleList([
nn.Conv2d(layers[i], layers[i + 1], kernel_size=3, padding=2,stride=stride)
for i in range(len(layers) - 1)])
# Fully Connected Neural Network to map to output
self.layers_NN = nn.ModuleList([
nn.Linear(architecture[layer], architecture[layer + 1])
for layer in range(len(architecture) - 1)])
self.pool = nn.AdaptiveMaxPool2d(1) # Simply takes the maximum value from the Tensor
def forward(self, data):
for layer in self.layers:
data = F.relu(layer(data))
data = self.pool(data)
data = data.view(data.size(0), -1)
for layer in self.layers_NN:
layer_data = layer(data)
data = F.relu(layer_data)
return F.log_softmax(layer_data, dim=-1)
```
## Defining the NN, Loss Function and Optimizer
```
# ---------------------------------------------
# Uncomment the architecture you want to use
# ---------------------------------------------
# # DNN
# architecture = [32*32*3, 100, 100, 100, 100, 10]
# net = Net_DNN(architecture)
# # CNN
# architecture = [3, 20, 40, 80, 160]
# num_outputs = 10
# net = Net_CNN(architecture, num_outputs)
# # CNN with NN
# architecture = [3, 20, 40, 80]
# architecture_NN = [80, 40, 20, 10]
# num_outputs = 10
# net = Net_CNN_NN(architecture, architecture_NN)
if use_cuda:
net = net.cuda() # Training on the GPU
criterion = nn.CrossEntropyLoss()
```
## Loading Model
```
# ---------------------------------------------
# Uncomment the architecture you want to use
# ---------------------------------------------
# # DNN
# architecture = [32*32*3, 100, 100, 10]
# net = Net_DNN(architecture)
# # CNN
# architecture = [3, 20, 40, 80, 160]
# num_outputs = 10
# net = Net_CNN(architecture, num_outputs)
# criterion = nn.CrossEntropyLoss()
if use_cuda:
net = net.cuda() # Training on the GPU
# ---------------------------------------------
# Uetermine the path for the saved weights
# ---------------------------------------------
PATH = './checkpoints_CNN_v2/5'
# Load weights
net.load_state_dict(torch.load(PATH))
```
## Recording Loss
```
# Initialize a list of loss_results
loss_results = []
```
# Training Manual
```
# Set the Learning rate and epoch start and end points
start_epoch = 11
end_epoch = 15
lr = 0.0001
# Define the optimizer
optimizer = optim.SGD(net.parameters(), lr=lr, momentum=0.9)
for epoch in range(start_epoch, end_epoch+1): # loop over the dataset multiple times
print("Epoch:", epoch)
running_loss = 0.0
for i, (inputs, labels) in enumerate(trainloader, 0):
# get the inputs
if use_cuda:
inputs, labels = inputs.cuda(), labels.cuda()
# wrap them in Variable
inputs, labels = Variable(inputs), Variable(labels) # Inputs and Target values to GPU
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.data[0]
if i % 2000 == 1999: # print every 2000 mini-batches
print(running_loss / 2000)
loss_results.append(running_loss / 2000)
running_loss = 0.0
PATH = './checkpoints_hybrid/' + str(epoch)
torch.save(net.state_dict(), PATH)
```
## Sample of the Results
```
# load a min-batch of the images
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
## Sample of Predictions
```
# For the images shown above, show the predictions
# first activate GPU processing
images, labels = images.cuda(), labels.cuda()
# Feed forward
outputs = net(Variable(images))
_, predicted = torch.max(outputs.data, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
for j in range(4)))
```
## Total Test Set Accuracy
```
# Small code snippet to determine test accuracy
correct = 0
total = 0
for data in testloader:
# load images
images, labels = data
if use_cuda:
images, labels = images.cuda(), labels.cuda()
# feed forward
outputs = net(Variable(images))
# perform softmax regression
_, predicted = torch.max(outputs.data, 1)
# update stats
total += labels.size(0)
correct += (predicted == labels).sum()
# print the results
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
```
## Accuracy per Class for Test Set
```
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
for data in testloader:
images, labels = data
if use_cuda:
images, labels = images.cuda(), labels.cuda()
outputs = net(Variable(images))
_, predicted = torch.max(outputs.data, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i]
class_total[label] += 1
# Print the accuracy per class
for i in range(10):
print(classes[i], 100 * class_correct[i] / class_total[i])
```
# Plot Loss
```
batch_size = 4
loss_samples_per_epoch = 6
num_epochs = 15
epochs_list = [(i/loss_samples_per_epoch) for i in range(1, num_epochs*loss_samples_per_epoch + 1)]
plt.semilogy(epochs_list, loss_results[:-6])
plt.ylabel('Loss')
plt.xlabel('Epoch Number')
plt.savefig('./DNN_v2.png', format='png', pad_inches=1, dpi=1200)
```
| true |
code
| 0.824126 | null | null | null | null |
|
## Apprentissage supervisé: Forêts d'arbres aléatoires (Random Forests)
Intéressons nous maintenant à un des algorithmes les plus popualires de l'état de l'art. Cet algorithme est non-paramétrique et porte le nom de **forêts d'arbres aléatoires**
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
plt.style.use('seaborn')
```
## A l'origine des forêts d'arbres aléatoires : l'arbre de décision
Les fôrets aléatoires appartiennent à la famille des méthodes d'**apprentissage ensembliste** et sont construits à partir d'**arbres de décision**. Pour cette raison, nous allons tout d'abord présenter les arbres de décisions.
Un arbre de décision est une manière très intuitive de résoudre un problème de classification. On se contente de définir un certain nombre de questions qui vont permetre d'identifier la classe adéquate.
```
import fig_code.figures as fig
fig.plot_example_decision_tree()
```
Le découpage binaire des données est rapide a mettre en oeuvre. La difficulté va résider dans la manière de déterminer quelle est la "bonne" question à poser.
C'est tout l'enjeu de la phase d'apprentissage d'un arbre de décision. L'algorithme va déterminer, au vue d'un ensemble de données, quelle question (ou découpage...) va apporter le plus gros gain d'information.
### Construction d'un arbre de décision
Voici un exemple de classifieur à partir d'un arbre de décision en utlisiant la libraire scikit-learn.
Nous commencons par définir un jeu de données en 2 dimensions avec des labels associés:
```
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=300, centers=4,
random_state=0, cluster_std=1.0)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='rainbow');
```
Nous avons précemment défini une fonction qui va faciliter la visualisation du processus :
```
from fig_code.figures import visualize_tree, plot_tree_interactive
```
On utilise maintenant le module ``interact`` dans Ipython pour visualiser les découpages effectués par l'arbre de décision en fonction de la profondeur de l'arbre (*depth* en anglais), i.e. le nombre de questions que l'arbre peut poser :
```
plot_tree_interactive(X, y);
```
**Remarque** : à chaque augmentation de la profondeur de l'arbre, chaque branche est découpée en deux **à l'expection** des branches qui contiennent uniquement des points d'une unique classe.
L'arbre de décision est une méthode de classification non paramétrique facile à mettre en oeuvre
**Question: Observez-vous des problèmes avec cette modélisation ?**
## Arbre de décision et sur-apprentissage
Un problème avec les arbres de décision est qu'ils ont tendance à **sur-apprendre** rapidement sur les données d'apprentissage. En effet, ils ont une forte tendance à capturer le bruit présent dans les données plutôt que la vraie distribution recherchée. Par exemple, si on construit 2 arbres à partir de sous ensembles des données définies précédemment, on obtient les deux classifieurs suivants:
```
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
plt.figure()
visualize_tree(clf, X[:200], y[:200], boundaries=False)
plt.figure()
visualize_tree(clf, X[-200:], y[-200:], boundaries=False)
```
Les 2 classifieurs ont des différences notables si on regarde en détails les figures. Lorsque'on va prédire la classe d'un nouveau point, cela risque d'être impacté par le bruit dans les données plus que par le signal que l'on cherche à modéliser.
## Prédictions ensemblistes: Forêts aléatoires
Une façon de limiter ce problème de sur-apprentissage est d'utiliser un **modèle ensembliste**: un méta-estimateur qui va aggréger les predictions de mutliples estimateurs (qui peuvent sur-apprendre individuellement). Grace à des propriétés mathématiques plutôt magiques (!), la prédiction aggrégée de ces estimateurs s'avère plus performante et robuste que les performances des estimateurs considérés individuellement.
Une des méthodes ensemblistes les plus célèbres est la méthode des **forêts d'arbres aléatoires** qui aggrège les prédictions de multiples arbres de décision.
Il y a beaucoup de littératures scientifiques pour déterminer la façon de rendre aléatoires ces arbres mais donner un exemple concret, voici un ensemble de modèle qui utilise seulement un sous échantillon des données :
```
X, y = make_blobs(n_samples=300, centers=4,
random_state=0, cluster_std=2.0)
def fit_randomized_tree(random_state=0):
rng = np.random.RandomState(random_state)
i = np.arange(len(y))
rng.shuffle(i)
clf = DecisionTreeClassifier(max_depth=5)
#on utilise seulement 250 exemples choisis aléatoirement sur les 300 disponibles
visualize_tree(clf, X[i[:250]], y[i[:250]], boundaries=False,
xlim=(X[:, 0].min(), X[:, 0].max()),
ylim=(X[:, 1].min(), X[:, 1].max()))
from ipywidgets import interact
interact(fit_randomized_tree, random_state=(0, 100));
```
On peut observer dans le détail les changements du modèle en fonction du tirage aléatoire des données qu'il utilise pour l'apprentissage, alors que la distribution des données est figée !
La forêt aléatoire va faire des caluls similaires, mais va aggréger l'ensemble des arbres aléatoires générés pour construire une unique prédiction:
```
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=0)
visualize_tree(clf, X, y, boundaries=False);
from sklearn.svm import SVC
clf = SVC(kernel='linear')
clf.fit(X, y)
visualize_tree(clf,X, y, boundaries=False)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=200, facecolors='none');
```
En moyennant 100 arbres de décision "perturbés" aléatoirement, nous obtenons une prédiction aggrégé qui modélise avec plus de précision nos données.
*(Remarque: ci dessus, notre perturbation aléatoire est effectué en echantillonant de manière aléatoire nos données... Les arbres aléatoires utilisent des techniques plus sophistiquées, pour plus de détails voir la [documentation de scikit-learn](http://scikit-learn.org/stable/modules/ensemble.html#forest)*)
## Exemple 1 : utilisation en régression
On considère pour cet exemple un cas d'tétude différent des exemples précédent de classification. Les arbres aléatoires peuvent être également utilisés sur des problèmes de régression (c'est à dire la prédiction d'une variable continue plutôt que discrète).
L'estimateur que nous utiliserons est le suivant: ``sklearn.ensemble.RandomForestRegressor``.
Nous présentons rapidement comment il peut être utilisé:
```
from sklearn.ensemble import RandomForestRegressor
# On commence par créer un jeu de données d'apprentissage
x = 10 * np.random.rand(100)
def model(x, sigma=0.):
# sigma controle le bruit
# sigma=0 pour avoir une distribution "parfaite"
oscillation_rapide = np.sin(5 * x)
oscillation_lente = np.sin(0.5 * x)
bruit = sigma * np.random.randn(len(x))
return oscillation_rapide + oscillation_lente + bruit
y = model(x)
plt.figure(figsize=(10,5))
plt.scatter(x, y);
xfit = np.linspace(0, 10, num=1000)
# yfit contient les prédictions de la forêt aléatoire à partir des données bruités
yfit = RandomForestRegressor(100).fit(x[:, None], y).predict(xfit[:, None])
# ytrue contient les valuers du modèle qui génèrent nos données avec un bruit nul
ytrue = model(xfit, sigma=0)
plt.figure(figsize=(10,5))
#plt.scatter(x, y)
plt.plot(xfit, yfit, '-r', label = 'forêt aléatoire')
plt.plot(xfit, ytrue, '-g', alpha=0.5, label = 'distribution non bruitée')
plt.legend();
```
On observe que les forêts aléatoires, de manière non-paramétrique, arrivent à estimer une distribution avec de mutliples périodicités sans aucune intervention de notre part pour définir ces périodicités !
---
**Hyperparamètres**
Utilisons l'outil d'aide inclus dans Ipython pour explorer la classe ``RandomForestRegressor``. Pour cela on rajoute un ? à la fin de l'objet
```
RandomForestRegressor?
```
Quelle sont les options disponibles pour le ``RandomForestRegressor``?
Quelle influence sur le graphique précédent si on modifie ces valeurs?
Ces paramètres de classe sont appelés les **hyperparamètres** d'un modèle.
---
```
# Exercice : proposer un modèle de régression à vecteur support permettant de modéliser le phénomène
from sklearn.svm import SVR
SVMreg = SVR().fit(x[:, None], y)
yfit_SVM = SVMreg.predict(xfit[:, None])
plt.figure(figsize=(10,5))
plt.scatter(x, y)
plt.plot(xfit, yfit_SVM, '-r', label = 'SVM')
plt.plot(xfit, ytrue, '-g', alpha=0.5, label = 'distribution non bruitée')
plt.legend();
SVR?
```
| true |
code
| 0.644197 | null | null | null | null |
|
[Sascha Spors](https://orcid.org/0000-0001-7225-9992),
Professorship Signal Theory and Digital Signal Processing,
[Institute of Communications Engineering (INT)](https://www.int.uni-rostock.de/),
Faculty of Computer Science and Electrical Engineering (IEF),
[University of Rostock, Germany](https://www.uni-rostock.de/en/)
# Tutorial Signals and Systems (Signal- und Systemtheorie)
Summer Semester 2021 (Bachelor Course #24015)
- lecture: https://github.com/spatialaudio/signals-and-systems-lecture
- tutorial: https://github.com/spatialaudio/signals-and-systems-exercises
WIP...
The project is currently under heavy development while adding new material for the summer semester 2021
Feel free to contact lecturer [[email protected]](https://orcid.org/0000-0002-3010-0294)
## Fourier Series Right Time Shift <-> Phase Mod
```
import numpy as np
import matplotlib.pyplot as plt
def my_sinc(x): # we rather use definition sinc(x) = sin(x)/x, thus:
return np.sinc(x/np.pi)
Th_des = [1, 0.2]
om = np.linspace(-100, 100, 1000)
plt.figure(figsize=(10, 8))
plt.subplot(2,1,1)
for idx, Th in enumerate(Th_des):
A = 1/Th # such that sinc amplitude is always 1
# Fourier transform for single rect pulse
Xsinc = A*Th * my_sinc(om*Th/2)
Xsinc_phase = Xsinc*np.exp(-1j*om*Th/2)
plt.plot(om, Xsinc, 'C7', lw=1)
plt.plot(om, np.abs(Xsinc_phase), label=r'$T_h$=%1.0e s' % Th, lw=5-idx)
plt.legend()
plt.title(r'Fourier transform of single rectangular impulse with $A=1/T_h$ right-shifted by $\tau=T_h/2$')
plt.ylabel(r'magnitude $|X(\mathrm{j}\omega)|$')
plt.xlim(om[0], om[-1])
plt.grid(True)
plt.subplot(2,1,2)
for idx, Th in enumerate(Th_des):
Xsinc = A*Th * my_sinc(om*Th/2)
Xsinc_phase = Xsinc*np.exp(-1j*om*Th/2)
plt.plot(om, np.angle(Xsinc_phase), label=r'$T_h$=%1.0e s' % Th, lw=5-idx)
plt.legend()
plt.xlabel(r'$\omega$ / (rad/s)')
plt.ylabel(r'phase $\angle X(\mathrm{j}\omega)$')
plt.xlim(om[0], om[-1])
plt.ylim(-4, +4)
plt.grid(True)
plt.savefig('A8A2DEE53A.pdf')
```
## Copyright
This tutorial is provided as Open Educational Resource (OER), to be found at
https://github.com/spatialaudio/signals-and-systems-exercises
accompanying the OER lecture
https://github.com/spatialaudio/signals-and-systems-lecture.
Both are licensed under a) the Creative Commons Attribution 4.0 International
License for text and graphics and b) the MIT License for source code.
Please attribute material from the tutorial as *Frank Schultz,
Continuous- and Discrete-Time Signals and Systems - A Tutorial Featuring
Computational Examples, University of Rostock* with
``main file, github URL, commit number and/or version tag, year``.
| true |
code
| 0.590248 | null | null | null | null |
|
# Histograms of time-mean surface temperature
## Import the libraries
```
# Data analysis and viz libraries
import aeolus.plot as aplt
import matplotlib.pyplot as plt
import numpy as np
import xarray as xr
# Local modules
from calc import sfc_temp
import mypaths
from names import names
from commons import MODELS
import const_ben1_hab1 as const
from plot_func import (
KW_MAIN_TTL,
KW_SBPLT_LABEL,
figsave,
)
plt.style.use("paper.mplstyle")
```
## Load the data
Load the time-averaged data previously preprocessed.
```
THAI_cases = ["Hab1", "Hab2"]
# Load data
datasets = {} # Create an empty dictionary to store all data
# for each of the THAI cases, create a nested directory for models
for THAI_case in THAI_cases:
datasets[THAI_case] = {}
for model_key in MODELS.keys():
datasets[THAI_case][model_key] = xr.open_dataset(
mypaths.datadir / model_key / f"{THAI_case}_time_mean_{model_key}.nc"
)
bin_step = 10
bins = np.arange(170, 321, bin_step)
bin_mid = (bins[:-1] + bins[1:]) * 0.5
t_sfc_step = abs(bins - const.t_melt).max()
ncols = 1
nrows = 2
width = 0.75 * bin_step / len(MODELS)
fig, axs = plt.subplots(ncols=ncols, nrows=nrows, figsize=(ncols * 8, nrows * 4.5))
iletters = aplt.subplot_label_generator()
for THAI_case, ax in zip(THAI_cases, axs.flat):
ax.set_title(f"{next(iletters)}", **KW_SBPLT_LABEL)
ax.set_xlim(bins[0], bins[-1])
ax.set_xticks(bins)
ax.grid(axis="x")
if ax.get_subplotspec().is_last_row():
ax.set_xlabel("Surface temperature [$K$]")
ax.set_title(THAI_case, **KW_MAIN_TTL)
# ax2 = ax.twiny()
# ax2.set_xlim(bins[0], bins[-1])
# ax2.axvline(const.t_melt, color="k", linestyle="--")
# ax2.set_xticks([const.t_melt])
# ax2.set_xticklabels([const.t_melt])
# ax.vlines(const.t_melt, ymin=0, ymax=38.75, color="k", linestyle="--")
# ax.vlines(const.t_melt, ymin=41.5, ymax=45, color="k", linestyle="--")
# ax.text(const.t_melt, 40, f"{const.t_melt:.2f}", ha="center", va="center", fontsize="small")
ax.imshow(
np.linspace(0, 1, 100).reshape(1, -1),
extent=[const.t_melt - t_sfc_step, const.t_melt + t_sfc_step, 0, 45],
aspect="auto",
cmap="seismic",
alpha=0.25,
)
ax.set_ylim([0, 45])
if ax.get_subplotspec().is_first_col():
ax.set_ylabel("Area fraction [%]")
for i, (model_key, model_dict) in zip([-3, -1, 1, 3], MODELS.items()):
model_names = names[model_key]
ds = datasets[THAI_case][model_key]
arr = sfc_temp(ds, model_key, const)
weights = xr.broadcast(np.cos(np.deg2rad(arr.latitude)), arr)[0].values.ravel()
# tot_pnts = arr.size
hist, _ = np.histogram(
arr.values.ravel(), bins=bins, weights=weights, density=True
)
hist *= 100 * bin_step
# hist = hist / tot_pnts * 100
# hist[hist==0] = np.nan
ax.bar(
bin_mid + (i * width / 2),
hist,
width=width,
facecolor=model_dict["color"],
edgecolor="none",
alpha=0.8,
label=model_dict["title"],
)
ax.legend(loc="upper left")
fig.tight_layout()
fig.align_labels()
figsave(
fig,
mypaths.plotdir / f"{'_'.join(THAI_cases)}__hist__t_sfc_weighted",
)
```
| true |
code
| 0.659871 | null | null | null | null |
|
# Near to far field transformation
See on [github](https://github.com/flexcompute/tidy3d-notebooks/blob/main/Near2Far_ZonePlate.ipynb), run on [colab](https://colab.research.google.com/github/flexcompute/tidy3d-notebooks/blob/main/Near2Far_ZonePlate.ipynb), or just follow along with the output below.
This tutorial will show you how to solve for electromagnetic fields far away from your structure using field information stored on a nearby surface.
This technique is called a 'near field to far field transformation' and is very useful for reducing the simulation size needed for structures involving lots of empty space.
As an example, we will simulate a simple zone plate lens with a very thin domain size to get the transmitted fields measured just above the structure. Then, we'll show how to use the `Near2Far` feature from `tidy3D` to extrapolate to the fields at the focal plane above the lens.
```
# get the most recent version of tidy3d
!pip install -q --upgrade tidy3d
# make sure notebook plots inline
%matplotlib inline
# standard python imports
import numpy as np
import matplotlib.pyplot as plt
import sys
# import client side tidy3d
import tidy3d as td
from tidy3d import web
```
## Problem Setup
Below is a rough sketch of the setup of a near field to far field transformation.
The transmitted near fields are measured just above the metalens on the blue line, and the near field to far field transformation is then used to project the fields to the focal plane above at the red line.
<img src="img/n2f_diagram.png" width=800>
## Define Simulation Parameters
As always, we first need to define our simulation parameters. As a reminder, all length units in `tidy3D` are specified in microns.
```
# 1 nanometer in units of microns (for conversion)
nm = 1e-3
# free space central wavelength
wavelength = 1.0
# numerical aperture
NA = 0.8
# thickness of lens features
H = 200 * nm
# space between bottom PML and substrate (-z)
# and the space between lens structure and top pml (+z)
space_below_sub = 1.5 * wavelength
# thickness of substrate (um)
thickness_sub = wavelength / 2
# side length (xy plane) of entire metalens (um)
length_xy = 40 * wavelength
# Lens and substrate refractive index
n_TiO2 = 2.40
n_SiO2 = 1.46
# define material properties
air = td.Medium(epsilon=1.0)
SiO2 = td.Medium(epsilon=n_SiO2**2)
TiO2 = td.Medium(epsilon=n_TiO2**2)
# resolution of simulation (15 or more grids per wavelength is adequate)
grids_per_wavelength = 20
# Number of PML layers to use around edges of simulation, choose thickness of one wavelength to be safe
npml = grids_per_wavelength
```
## Process Geometry
Next we perform some conversions based on these parameters to define the simulation.
```
# grid size (um)
dl = wavelength / grids_per_wavelength
# because the wavelength is in microns, use builtin td.C_0 (um/s) to get frequency in Hz
f0 = td.C_0 / wavelength
# Define PML layers, for this application we surround the whole structure in PML to isolate the fields
pml_layers = [npml, npml, npml]
# domain size in z, note, we're just simulating a thin slice: (space -> substrate -> lens thickness -> space)
length_z = space_below_sub + thickness_sub + H + space_below_sub
# construct simulation size array
sim_size = np.array([length_xy, length_xy, length_z])
```
## Create Geometry
Now we create the ring metalens programatically
```
# define substrate
substrate = td.Box(
center=[0, 0, -length_z/2 + space_below_sub + thickness_sub / 2.0],
size=[td.inf, td.inf, thickness_sub],
material=SiO2)
# create a running list of structures
geometry = [substrate]
# focal length
focal_length = length_xy / 2 / NA * np.sqrt(1 - NA**2)
# location from center for edge of the n-th inner ring, see https://en.wikipedia.org/wiki/Zone_plate
def edge(n):
return np.sqrt(n * wavelength * focal_length + n**2 * wavelength**2 / 4)
# loop through the ring indeces until it's too big and add each to geometry list
n = 1
r = edge(n)
while r < 2 * length_xy:
# progressively wider cylinders, material alternating between air and TiO2
cyl = td.Cylinder(
center = [0,0,-length_z/2 + space_below_sub + thickness_sub + H / 2],
axis='z',
radius=r,
height=H,
material=TiO2 if n % 2 == 0 else air,
name=f'cylinder_n={n}'
)
geometry.append(cyl)
n += 1
r = edge(n)
# reverse geometry list so that inner, smaller rings are added last and therefore override larger rings.
geometry.reverse()
```
## Create Source
Create a plane wave incident from below the metalens
```
# Bandwidth in Hz
fwidth = f0 / 10.0
# Gaussian source offset; the source peak is at time t = offset/fwidth
offset = 4.
# time dependence of source
gaussian = td.GaussianPulse(f0, fwidth, offset=offset, phase=0)
source = td.PlaneWave(
source_time=gaussian,
injection_axis='+z',
position=-length_z/2 + space_below_sub / 2, # halfway between PML and substrate
polarization='x')
# Simulation run time
run_time = 40 / fwidth
```
## Create Monitor
Create a near field monitor to measure the fields just above the metalens
```
# place it halfway between top of lens and PML
monitor_near = td.FreqMonitor(
center=[0., 0., -length_z/2 + space_below_sub + thickness_sub + H + space_below_sub / 2],
size=[length_xy, length_xy, 0],
freqs=[f0],
name='near_field')
```
## Create Simulation
Put everything together and define a simulation object
```
sim = td.Simulation(size=sim_size,
mesh_step=[dl, dl, dl],
structures=geometry,
sources=[source],
monitors=[monitor_near],
run_time=run_time,
pml_layers=pml_layers)
```
## Visualize Geometry
Lets take a look and make sure everything is defined properly
```
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(24, 8))
# Time the visualization of the 2D plane
sim.viz_eps_2D(normal='x', position=0.1, ax=ax1);
sim.viz_eps_2D(normal='z', position=-length_z/2 + space_below_sub + thickness_sub + H / 2, ax=ax2);
```
## Run Simulation
Now we can run the simulation and download the results
```
# Run simulation
project = web.new_project(sim.export(), task_name='near2far_docs')
web.monitor_project(project['taskId'])
# download and load the results
print('Downloading results')
web.download_results(project['taskId'], target_folder='output')
sim.load_results('output/monitor_data.hdf5')
# print stats from the logs
with open("output/tidy3d.log") as f:
print(f.read())
```
## Visualization
Let's inspect the near field using the Tidy3D builtin field visualization methods.
For more details see the documentation of [viz_field_2D](https://simulation.cloud/docs/html/generated/tidy3d.Simulation.viz_field_2D.html#tidy3d.Simulation.viz_field_2D).
```
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
for ax, val in zip(axes, ('re', 'abs', 'int')):
im = sim.viz_field_2D(monitor_near, eps_alpha=0, comp='x', val=val, cbar=True, ax=ax)
plt.show()
```
## Setting Up Near 2 Far
To set up near to far, we first need to grab the data from the nearfield monitor.
```
# near field monitor data dictionary
monitor_data = sim.data(monitor_near)
# grab the raw data for plotting later
xs = monitor_data['xmesh']
ys =monitor_data['ymesh']
E_near = np.squeeze(monitor_data['E'])
```
Then, we create a `td.Near2Far` object using the monitor data dictionary as follows.
This object just stores near field data and provides [various methods](https://simulation.cloud/docs/html/generated/tidy3d.Near2Far.html#tidy3d.Near2Far) for looking at various far field quantities.
```
# from near2far_tidy3d import Near2Far
n2f = td.Near2Far(monitor_data)
```
## Getting Far Field Data
With the `Near2Far` object initialized, we just need to call one of it's methods to get a far field quantity.
For this example, we use `Near2Far.get_fields_cartesian(x,y,z)` to get the fields at an `x,y,z` point relative to the monitor center.
Below, we scan through x and y points in a plane located at `z=z0` and record the far fields.
```
# points to project to
num_far = 40
xs_far = 4 * wavelength * np.linspace(-0.5, 0.5, num_far)
ys_far = 4 * wavelength * np.linspace(-0.5, 0.5, num_far)
# get a mesh in cartesian, convert to spherical
Nx, Ny = len(xs), len(ys)
# initialize the far field values
E_far = np.zeros((3, num_far, num_far), dtype=complex)
H_far = np.zeros((3, num_far, num_far), dtype=complex)
# loop through points in the output plane
for i in range(num_far):
sys.stdout.write(" \rGetting far fields, %2d%% done"%(100*i/(num_far + 1)))
sys.stdout.flush()
x = xs_far[i]
for j in range(num_far):
y = ys_far[j]
# compute and store the outputs from projection function at the focal plane
E, H = n2f.get_fields_cartesian(x, y, focal_length)
E_far[:, i, j] = E
H_far[:, i, j] = H
sys.stdout.write("\nDone!")
```
## Plot Results
Now we can plot the near and far fields together
```
# plot everything
f, ((ax1, ax2, ax3),
(ax4, ax5, ax6)) = plt.subplots(2, 3, tight_layout=True, figsize=(10, 5))
def pmesh(xs, ys, array, ax, cmap):
im = ax.pcolormesh(xs, ys, array.T, cmap=cmap, shading='auto')
return im
im1 = pmesh(xs, ys, np.real(E_near[0]), ax=ax1, cmap='RdBu')
im2 = pmesh(xs, ys, np.real(E_near[1]), ax=ax2, cmap='RdBu')
im3 = pmesh(xs, ys, np.real(E_near[2]), ax=ax3, cmap='RdBu')
im4 = pmesh(xs_far, ys_far, np.real(E_far[0]), ax=ax4, cmap='RdBu')
im5 = pmesh(xs_far, ys_far, np.real(E_far[1]), ax=ax5, cmap='RdBu')
im6 = pmesh(xs_far, ys_far, np.real(E_far[2]), ax=ax6, cmap='RdBu')
ax1.set_title('near field $E_x(x,y)$')
ax2.set_title('near field $E_y(x,y)$')
ax3.set_title('near field $E_z(x,y)$')
ax4.set_title('far field $E_x(x,y)$')
ax5.set_title('far field $E_y(x,y)$')
ax6.set_title('far field $E_z(x,y)$')
plt.colorbar(im1, ax=ax1)
plt.colorbar(im2, ax=ax2)
plt.colorbar(im3, ax=ax3)
plt.colorbar(im4, ax=ax4)
plt.colorbar(im5, ax=ax5)
plt.colorbar(im6, ax=ax6)
plt.show()
# we can also use the far field data and plot the field intensity to see the focusing effect
intensity_far = np.sum(np.square(np.abs(E_far)), axis=0)
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
im1 = pmesh(xs_far, ys_far, intensity_far, ax=ax1, cmap='magma')
im2 = pmesh(xs_far, ys_far, np.sqrt(intensity_far), ax=ax2, cmap='magma')
ax1.set_title('$|E(x,y)|^2$')
ax2.set_title('$|E(x,y)|$')
plt.colorbar(im1, ax=ax1)
plt.colorbar(im2, ax=ax2)
plt.show()
```
| true |
code
| 0.68658 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/AWH-GlobalPotential-X/AWH-Geo/blob/master/notebooks/AWH-Geo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Welcome to AWH-Geo
This tool requires a [Google Drive](https://drive.google.com/drive/my-drive) and [Earth Engine](https://developers.google.com/earth-engine/) Account.
[Start here](https://drive.google.com/drive/u/1/folders/1EzuqsbADrtdXChcpHqygTh7SuUw0U_QB) to create a new Output Table from the template:
1. Right-click on "OutputTable_TEMPLATE" file > Make a Copy to your own Drive folder
2. Rename the new file "OuputTable_CODENAME" with CODENAME (max 83 characters!) as a unique output table code. If including a date in the code, use the YYYYMMDD date format.
3. Enter in the output values in L/hr to each cell in each of the 10%-interval rH bins... interpolate in Sheets as necessary.
Then, click "Connect" at the top right of this notebook.
Then run each of the code blocks below, following instructions. For "OutputTableCode" inputs, use the CODENAME you created in Sheets.
```
#@title Basic setup and earthengine access.
print('Welcome to AWH-Geo')
# import, authenticate, then initialize EarthEngine module ee
# https://developers.google.com/earth-engine/python_install#package-import
import ee
print('Make sure the EE version is v0.1.215 or greater...')
print('Current EE version = v' + ee.__version__)
print('')
ee.Authenticate()
ee.Initialize()
worldGeo = ee.Geometry.Polygon( # Created for some masking and geo calcs
coords=[[-180,-90],[-180,0],[-180,90],[-30,90],[90,90],[180,90],
[180,0],[180,-90],[30,-90],[-90,-90],[-180,-90]],
geodesic=False,
proj='EPSG:4326'
)
#@title Test Earth Engine connection (see Mt Everest elev and a green map)
# Print the elevation of Mount Everest.
dem = ee.Image('USGS/SRTMGL1_003')
xy = ee.Geometry.Point([86.9250, 27.9881])
elev = dem.sample(xy, 30).first().get('elevation').getInfo()
print('Mount Everest elevation (m):', elev)
# Access study assets
from IPython.display import Image
jmpGeofabric_image = ee.Image('users/awhgeoglobal/jmpGeofabric_image') # access to study folder in EE
Image(url=jmpGeofabric_image.getThumbUrl({'min': 0, 'max': 1, 'dimensions': 512,
'palette': ['006633', 'E5FFCC', '662A00', 'D8D8D8', 'F5F5F5']}))
#@title Set up access to Google Sheets (follow instructions)
from google.colab import auth
auth.authenticate_user()
# gspread is module to access Google Sheets through python
# https://gspread.readthedocs.io/en/latest/index.html
import gspread
from oauth2client.client import GoogleCredentials
gc = gspread.authorize(GoogleCredentials.get_application_default()) # get credentials
#@title STEP 1: Export timeseries for given OutputTable: enter CODENAME (without "OutputTable_" prefix) below
OutputTableCode = "" #@param {type:"string"}
StartYear = 2010 #@param {type:"integer"}
EndYear = 2020 #@param {type:"integer"}
ExportWeekly_1_or_0 = 0#@param {type:"integer"}
ee_username = ee.String(ee.Dictionary(ee.List(ee.data.getAssetRoots()).get(0)).get('id'))
ee_username = ee_username.getInfo()
years = list(range(StartYear,EndYear))
print('Time Period: ', years)
def timeseriesExport(outputTable_code):
"""
This script runs the output table value over the climate variables using the
nearest lookup values, worldwide, every three hours during a user-determined
period. It then resamples the temporal interval by averaging the hourly output
over semi-week periods. It then converts the resulting image collection into a
single image with several bands, each of which representing one (hourly or
semi-week) interval. Finally, it exports this image over 3-month tranches and
saves each as an EE Image Assets with appropriate names corresponding to the
tranche's time period.
"""
# print the output table code from user input for confirmation
print('outputTable code:', outputTable_code)
# CLIMATE DATA PRE-PROCESSING
# ERA5-Land climate dataset used for worldwide (derived) climate metrics
# https://www.ecmwf.int/en/era5-land
# era5-land HOURLY images in EE catalog
era5Land = ee.ImageCollection('ECMWF/ERA5_LAND/HOURLY')
# print('era5Land',era5Land.limit(50)) # print some data for inspection (debug)
era5Land_proj = era5Land.first().projection() # get ERA5-Land projection & scale for export
era5Land_scale = era5Land_proj.nominalScale()
print('era5Land_scale (should be ~11132):',era5Land_scale.getInfo())
era5Land_filtered = era5Land.filterDate( # ERA5-Land climate data
str(StartYear-1) + '-12-31', str(EndYear) + '-01-01').select( # filter by date
# filter by ERA5-Land image collection bands
[
'dewpoint_temperature_2m', # K (https://apps.ecmwf.int/codes/grib/param-db?id=168)
'surface_solar_radiation_downwards', # J/m^2 (Accumulated value. Divide by 3600 to get W/m^2 over hourly interval https://apps.ecmwf.int/codes/grib/param-db?id=176)
'temperature_2m' # K
])
# print('era5Land_filtered',era5Land_filtered.limit(50))
print('Wait... retrieving data from sheets takes a couple minutes')
# COLLECT OUTPUT TABLE DATA FROM SHEETS INTO PYTHON ARRAYS
# gspread function which will look in list of gSheets accessible to user
# in Earth Engine, an array is a list of lists.
# loop through worksheet tabs and build a list of lists of lists (3 dimensional)
# to organize output values [L/hr] by the 3 physical variables in the following
# order: by temperature (first nesting leve), ghi (second nesting level), then
# rH (third nesting level).
spreadsheet = gc.open('OutputTable_' + outputTable_code)
outputArray = list() # create empty array
rH_labels = ['rH0','rH10','rH20','rH30','rH40','rH50', # worksheet tab names
'rH60','rH70','rH80','rH90','rH100']
for rH in rH_labels: # loop to create 3-D array (list of lists of lists)
rH_interval_array = list()
worksheet = spreadsheet.worksheet(rH)
for x in list(range(7,26)): # relevant ranges in output table sheet
rH_interval_array.append([float(y) for y in worksheet.row_values(x)])
outputArray.append(rH_interval_array)
# print('Output Table values:', outputArray) # for debugging
# create an array image in EE (each pixel is a multi-dimensional matrix)
outputImage_arrays = ee.Image(ee.Array(outputArray)) # values are in [L/hr]
def processTimeseries(i): # core processing algorithm with lookups to outputTable
"""
This is the core AWH-Geo algorithm to convert image-based input climate data
into an image of AWG device output [L/time] based on a given output lookup table.
It runs across the ERA5-Land image collection timeseries and runs the lookup table
on each pixel of each image representing each hourly climate timestep.
"""
i = ee.Image(i) # cast as image
i = i.updateMask(i.select('temperature_2m').mask()) # ensure mask is applied to all bands
timestamp_millis = ee.Date(i.get('system:time_start'))
i_previous = ee.Image(era5Land_filtered.filterDate(
timestamp_millis.advance(-1,'hour')).first())
rh = ee.Image().expression( # relative humidity calculation [%]
# from http://bmcnoldy.rsmas.miami.edu/Humidity.html
'100 * (e**((17.625 * Td) / (To + Td)) / e**((17.625 * T) / (To + T)))', {
'e': 2.718281828459045, # Euler's constant
'T': i.select('temperature_2m').subtract(273.15), # temperature K converted to Celsius [°C]
'Td': i.select('dewpoint_temperature_2m').subtract(273.15), # dewpoint temperature K converted to Celsius [°C]
'To': 243.04 # reference temperature [K]
}).rename('rh')
ghi = ee.Image(ee.Algorithms.If( # because this parameter in ERA5 is cumulative in J/m^2...
condition=ee.Number(timestamp_millis.get('hour')).eq(1), # ...from last obseration...
trueCase=i.select('surface_solar_radiation_downwards'), # ...current value must be...
falseCase=i.select('surface_solar_radiation_downwards').subtract( # ...subtracted from last...
i_previous.select('surface_solar_radiation_downwards')) # ... then divided by seconds
)).divide(3600).rename('ghi') # solar global horizontal irradiance [W/m^2]
temp = i.select('temperature_2m'
).subtract(273.15).rename('temp') # temperature K converted to Celsius [°C]
rhClamp = rh.clamp(0.1,100) # relative humdity clamped to output table range [%]
ghiClamp = ghi.clamp(0.1,1300) # global horizontal irradiance clamped to range [W/m^2]
tempClamp = temp.clamp(0.1,45) # temperature clamped to output table range [°C]
# convert climate variables to lookup integers
rhLookup = rhClamp.divide(10
).round().int().rename('rhLookup') # rH lookup interval
tempLookup = tempClamp.divide(2.5
).round().int().rename('tempLookup') # temp lookup interval
ghiLookup = ghiClamp.divide(100
).add(1).round().int().rename('ghiLookup') # ghi lookup interval
# combine lookup values in a 3-band image
xyzLookup = ee.Image(rhLookup).addBands(tempLookup).addBands(ghiLookup)
# lookup values in 3D array for each pixel to return AWG output from table [L/hr]
# set output to 0 if temperature is less than 0 deg C
output = outputImage_arrays.arrayGet(xyzLookup).multiply(temp.gt(0))
nightMask = ghi.gt(0.5) # mask pixels which have no incident sunlight
return ee.Image(output.rename('O').addBands( # return image of output labeled "O" [L/hr]
rh.updateMask(nightMask)).addBands(
ghi.updateMask(nightMask)).addBands(
temp.updateMask(nightMask)).setMulti({ # add physical variables as bands
'system:time_start': timestamp_millis # set time as property
})).updateMask(1) # close partial masks at continental edges
def outputHourly_export(timeStart, timeEnd, year):
"""
Run the lookup processing function (from above) across the entire climate
timeseries at the finest temporal interval (1 hr for ERA5-Land). Convert the
resulting image collection as a single image with a band for each timestep
to allow for export as an Earth Engine asset (you cannot export/save image
collections as assets).
"""
# filter ERA5-Land climate data by time
era5Land_filtered_section = era5Land_filtered.filterDate(timeStart, timeEnd)
# print('era5Land_filtered_section',era5Land_filtered_section.limit(1).getInfo())
outputHourly = era5Land_filtered_section.map(processTimeseries)
# outputHourly_toBands_pre = outputHourly.select(['ghi']).toBands()
outputHourly_toBands_pre = outputHourly.select(['O']).toBands()
outputHourly_toBands = outputHourly_toBands_pre.select(
# input climate variables as multiband image with each band representing timestep
outputHourly_toBands_pre.bandNames(),
# rename bands by timestamp
outputHourly_toBands_pre.bandNames().map(
lambda name: ee.String('H').cat( # "H" for hourly
ee.String(name).replace('T','')
)
)
)
# notify user of export
print('Exporting outputHourly year:', year)
task = ee.batch.Export.image.toAsset(
image=ee.Image(outputHourly_toBands),
region=worldGeo,
description='O_hourly_' + outputTable_code + '_' + year,
assetId=ee_username + '/O_hourly_' + outputTable_code + '_' + year,
scale=era5Land_scale.getInfo(),
crs='EPSG:4326',
crsTransform=[0.1,0,-180.05,0,-0.1,90.05],
maxPixels=1e10,
maxWorkers=2000
)
task.start()
# run timeseries export on entire hourly ERA5-Land for each yearly tranche
for y in years:
y = str(y)
outputHourly_export(y + '-01-01', y + '-04-01', y + 'a')
outputHourly_export(y + '-04-01', y + '-07-01', y + 'b')
outputHourly_export(y + '-07-01', y + '-10-01', y + 'c')
outputHourly_export(y + '-10-01', str(int(y)+1) + '-01-01', y + 'd')
def outputWeekly_export(timeStart, timeEnd, year):
era5Land_filtered_section = era5Land_filtered.filterDate(timeStart, timeEnd) # filter ERA5-Land climate data by time
outputHourly = era5Land_filtered_section.map(processTimeseries)
# resample values over time by 2-week aggregations
# Define a time interval
start = ee.Date(timeStart)
end = ee.Date(timeEnd)
# Number of years, in DAYS_PER_RANGE-day increments.
DAYS_PER_RANGE = 14
# DateRangeCollection, which contains the ranges we're interested in.
drc = ee.call("BetterDateRangeCollection",
start,
end,
DAYS_PER_RANGE,
"day",
True)
# This filter will join images with the date range that contains their start time.
filter = ee.Filter.dateRangeContains("date_range", None, "system:time_start")
# Save all of the matching values under "matches".
join = ee.Join.saveAll("matches")
# Do the join.
joinedResult = join.apply(drc, outputHourly, filter)
# print('joinedResult',joinedResult)
# Map over the functions, and add the mean of the matches as "meanForRange".
joinedResult = joinedResult.map(
lambda e: e.set("meanForRange", ee.ImageCollection.fromImages(e.get("matches")).mean())
)
# print('joinedResult',joinedResult)
# roll resampled images into new image collection
outputWeekly = ee.ImageCollection(joinedResult.map(
lambda f: ee.Image(f.get('meanForRange'))
))
# print('outputWeekly',outputWeekly.getInfo())
# convert image collection into image with many bands which can be saved as EE asset
outputWeekly_toBands_pre = outputWeekly.toBands()
outputWeekly_toBands = outputWeekly_toBands_pre.select(
outputWeekly_toBands_pre.bandNames(), # input climate variables as multiband image with each band representing timestep
outputWeekly_toBands_pre.bandNames().map(
lambda name: ee.String('W').cat(name)
)
)
task = ee.batch.Export.image.toAsset(
image=ee.Image(outputWeekly_toBands),
region=worldGeo,
description='O_weekly_' + outputTable_code + '_' + year,
assetId=ee_username + '/O_weekly_' + outputTable_code + '_' + year,
scale=era5Land_scale.getInfo(),
crs='EPSG:4326',
crsTransform=[0.1,0,-180.05,0,-0.1,90.05],
maxPixels=1e10,
maxWorkers=2000
)
if ExportWeekly_1_or_0 == 1:
task.start() # remove comment hash if weekly exports are desired
print('Exporting outputWeekly year:', year)
# run semi-weekly timeseries export on ERA5-Land by year
for y in years:
y = str(y)
outputWeekly_export(y + '-01-01', y + '-04-01', y + 'a')
outputWeekly_export(y + '-04-01', y + '-07-01', y + 'b')
outputWeekly_export(y + '-07-01', y + '-10-01', y + 'c')
outputWeekly_export(y + '-10-01', str(int(y)+1) + '-01-01', y + 'd')
timeseriesExport(OutputTableCode)
print('Complete! Read instructions below')
```
# *Before moving on to the next step... Wait until above tasks are complete in the task manager: https://code.earthengine.google.com/*
(right pane, tab "tasks", click "refresh"; the should show up once the script prints "Exporting...")
```
#@title Re-instate earthengine access (follow instructions)
print('Welcome Back to AWH-Geo')
print('')
# import, authenticate, then initialize EarthEngine module ee
# https://developers.google.com/earth-engine/python_install#package-import
import ee
print('Make sure the EE version is v0.1.215 or greater...')
print('Current EE version = v' + ee.__version__)
print('')
ee.Authenticate()
ee.Initialize()
worldGeo = ee.Geometry.Polygon( # Created for some masking and geo calcs
coords=[[-180,-90],[-180,0],[-180,90],[-30,90],[90,90],[180,90],
[180,0],[180,-90],[30,-90],[-90,-90],[-180,-90]],
geodesic=False,
proj='EPSG:4326'
)
#@title STEP 2: Export statistical results for given OutputTable: enter CODENAME (without "OutputTable_" prefix) below
ee_username = ee.String(ee.Dictionary(ee.List(ee.data.getAssetRoots()).get(0)).get('id'))
ee_username = ee_username.getInfo()
OutputTableCode = "" #@param {type:"string"}
StartYear = 2010 #@param {type:"integer"}
EndYear = 2020 #@param {type:"integer"}
SuffixName_optional = "" #@param {type:"string"}
ExportMADP90s_1_or_0 = 0#@param {type:"integer"}
years = list(range(StartYear,EndYear))
print('Time Period: ', years)
def generateStats(outputTable_code):
"""
This function generates single images which contain time-aggregated output
statistics including overall mean and shortfall metrics such as MADP90s.
"""
# CLIMATE DATA PRE-PROCESSING
# ERA5-Land climate dataset used for worldwide (derived) climate metrics
# https://www.ecmwf.int/en/era5-land
# era5-land HOURLY images in EE catalog
era5Land = ee.ImageCollection('ECMWF/ERA5_LAND/HOURLY')
# print('era5Land',era5Land.limit(50)) # print some data for inspection (debug)
era5Land_proj = era5Land.first().projection() # get ERA5-Land projection & scale for export
era5Land_scale = era5Land_proj.nominalScale()
# setup the image collection timeseries to chart
# unravel and concatenate all the image stages into a single image collection
def unravel(i): # function to "unravel" image bands into an image collection
def setDate(bandName): # loop over band names in image and return a LIST of ...
dateCode = ee.Date.parse( # ... images, one for each band
format='yyyyMMddHH',
date=ee.String(ee.String(bandName).split('_').get(0)).slice(1) # get date periods from band name
)
return i.select([bandName]).rename('O').set('system:time_start',dateCode)
i = ee.Image(i)
return i.bandNames().map(setDate) # returns a LIST of images
yearCode_list = ee.List(sum([[ # each image units in [L/hr]
unravel(ee.Image(ee_username + '/O_hourly_' + outputTable_code + '_' + str(y)+'a')),
unravel(ee.Image(ee_username + '/O_hourly_' + outputTable_code + '_' + str(y)+'b')),
unravel(ee.Image(ee_username + '/O_hourly_' + outputTable_code + '_' + str(y)+'c')),
unravel(ee.Image(ee_username + '/O_hourly_' + outputTable_code + '_' + str(y)+'d'))
] for y in years], [])).flatten()
outputTimeseries = ee.ImageCollection(yearCode_list)
Od_overallMean = outputTimeseries.mean().multiply(24).rename('Od') # hourly output x 24 = mean daily output [L/day]
# export overall daily mean
task = ee.batch.Export.image.toAsset(
image=Od_overallMean,
region=worldGeo,
description='Od_overallMean_' + outputTable_code + SuffixName_optional,
assetId=ee_username + '/Od_overallMean_' + outputTable_code + SuffixName_optional,
scale=era5Land_scale.getInfo(),
crs='EPSG:4326',
crsTransform=[0.1,0,-180.05,0,-0.1,90.05],
maxPixels=1e10,
maxWorkers=2000
)
task.start()
print('Exporting Od_overallMean_' + outputTable_code + SuffixName_optional)
## run the moving average function over the timeseries using DAILY averages
# start and end dates over which to calculate aggregate statistics
startDate = ee.Date(str(StartYear) + '-01-01')
endDate = ee.Date(str(EndYear) + '-01-01')
# resample values over time by daily aggregations
# Number of years, in DAYS_PER_RANGE-day increments.
DAYS_PER_RANGE = 1
# DateRangeCollection, which contains the ranges we're interested in.
drc = ee.call('BetterDateRangeCollection',
startDate,
endDate,
DAYS_PER_RANGE,
'day',
True)
# This filter will join images with the date range that contains their start time.
filter = ee.Filter.dateRangeContains('date_range', None, 'system:time_start')
# Save all of the matching values under "matches".
join = ee.Join.saveAll('matches')
# Do the join.
joinedResult = join.apply(drc, outputTimeseries, filter)
# print('joinedResult',joinedResult)
# Map over the functions, and add the mean of the matches as "meanForRange".
joinedResult = joinedResult.map(
lambda e: e.set('meanForRange', ee.ImageCollection.fromImages(e.get('matches')).mean())
)
# print('joinedResult',joinedResult)
# roll resampled images into new image collection
outputDaily = ee.ImageCollection(joinedResult.map(
lambda f: ee.Image(f.get('meanForRange')).set(
'system:time_start',
ee.Date.parse('YYYYMMdd',f.get('system:index')).millis()
)
))
# print('outputDaily',outputDaily.getInfo())
outputDaily_p90 = ee.ImageCollection( # collate rolling periods into new image collection of rolling average values
outputDaily.toList(outputDaily.size())).reduce(
ee.Reducer.percentile( # reduce image collection by percentile
[10] # 100% - 90% = 10%
)).multiply(24).rename('Od')
task = ee.batch.Export.image.toAsset(
image=outputDaily_p90,
region=worldGeo,
description='Od_DailyP90_' + outputTable_code + SuffixName_optional,
assetId=ee_username + '/Od_DailyP90_' + outputTable_code + SuffixName_optional,
scale=era5Land_scale.getInfo(),
crs='EPSG:4326',
crsTransform=[0.1,0,-180.05,0,-0.1,90.05],
maxPixels=1e10,
maxWorkers=2000
)
if ExportMADP90s_1_or_0 == 1:
task.start()
print('Exporting Od_DailyP90_' + outputTable_code + SuffixName_optional)
def rollingStats(period): # run rolling stat function for each rolling period scenerio
# collect neighboring time periods into a join
timeFilter = ee.Filter.maxDifference(
difference=float(period)/2 * 24 * 60 * 60 * 1000, # mid-centered window
leftField='system:time_start',
rightField='system:time_start'
)
rollingPeriod_join = ee.ImageCollection(ee.Join.saveAll('images').apply(
primary=outputDaily, # apply the join on itself to collect images
secondary=outputDaily,
condition=timeFilter
))
def rollingPeriod_mean(i): # get the mean across each collected periods
i = ee.Image(i) # collected images stored in "images" property of each timestep image
return ee.ImageCollection.fromImages(i.get('images')).mean()
outputDaily_rollingMean = rollingPeriod_join.filterDate(
startDate.advance(float(period)/2,'days'),
endDate.advance(float(period)/-2,'days')
).map(rollingPeriod_mean,True)
Od_p90_rolling = ee.ImageCollection( # collate rolling periods into new image collection of rolling average values
outputDaily_rollingMean.toList(outputDaily_rollingMean.size())).reduce(
ee.Reducer.percentile( # reduce image collection by percentile
[10] # 100% - 90% = 10%
)).multiply(24).rename('Od') # hourly output x 24 = mean daily output [L/day]
task = ee.batch.Export.image.toAsset(
image=Od_p90_rolling,
region=worldGeo,
description='Od_MADP90_'+ period + 'day_' + outputTable_code + SuffixName_optional,
assetId=ee_username + '/Od_MADP90_'+ period + 'day_' + outputTable_code + SuffixName_optional,
scale=era5Land_scale.getInfo(),
crs='EPSG:4326',
crsTransform=[0.1,0,-180.05,0,-0.1,90.05],
maxPixels=1e10,
maxWorkers=2000
)
if ExportMADP90s_1_or_0 == 1:
task.start()
print('Exporting Od_MADP90_' + period + 'day_' + outputTable_code + SuffixName_optional)
rollingPeriods = [
'007',
'030',
# '060',
'090',
# '180',
] # define custom rolling periods over which to calc MADP90 [days]
for period in rollingPeriods: # execute the calculations & export
# print(period)
rollingStats(period)
generateStats(OutputTableCode) # run stats function
print('Complete! Go to next step.')
```
Wait until these statistics are completed processing. Track them in the task manager: https://code.earthengine.google.com/
When they are finished.... [Go here to see maps](https://code.earthengine.google.com/fac0cc72b2ac2e431424cbf45b2852cf)
| true |
code
| 0.544862 | null | null | null | null |
|
# Chapter 7
```
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
import statsmodels.api as sm
import statsmodels.formula.api as smf
from patsy import dmatrix
from scipy import stats
from scipy.special import logsumexp
%config Inline.figure_format = 'retina'
az.style.use("arviz-darkgrid")
az.rcParams["stats.hdi_prob"] = 0.89 # set credible interval for entire notebook
np.random.seed(0)
```
#### Code 7.1
```
brains = pd.DataFrame.from_dict(
{
"species": [
"afarensis",
"africanus",
"habilis",
"boisei",
"rudolfensis",
"ergaster",
"sapiens",
],
"brain": [438, 452, 612, 521, 752, 871, 1350], # volume in cc
"mass": [37.0, 35.5, 34.5, 41.5, 55.5, 61.0, 53.5], # mass in kg
}
)
brains
# Figure 7.2
plt.scatter(brains.mass, brains.brain)
# point labels
for i, r in brains.iterrows():
if r.species == "afarensis":
plt.text(r.mass + 0.5, r.brain, r.species, ha="left", va="center")
elif r.species == "sapiens":
plt.text(r.mass, r.brain - 25, r.species, ha="center", va="top")
else:
plt.text(r.mass, r.brain + 25, r.species, ha="center")
plt.xlabel("body mass (kg)")
plt.ylabel("brain volume (cc)");
```
#### Code 7.2
```
brains.loc[:, "mass_std"] = (brains.loc[:, "mass"] - brains.loc[:, "mass"].mean()) / brains.loc[
:, "mass"
].std()
brains.loc[:, "brain_std"] = brains.loc[:, "brain"] / brains.loc[:, "brain"].max()
```
#### Code 7.3
This is modified from [Chapter 6 of 1st Edition](https://nbviewer.jupyter.org/github/pymc-devs/resources/blob/master/Rethinking/Chp_06.ipynb) (6.2 - 6.6).
```
m_7_1 = smf.ols("brain_std ~ mass_std", data=brains).fit()
m_7_1.summary()
```
#### Code 7.4
```
p, cov = np.polyfit(brains.loc[:, "mass_std"], brains.loc[:, "brain_std"], 1, cov=True)
post = stats.multivariate_normal(p, cov).rvs(1000)
az.summary({k: v for k, v in zip("ba", post.T)}, kind="stats")
```
#### Code 7.5
```
1 - m_7_1.resid.var() / brains.brain_std.var()
```
#### Code 7.6
```
def R2_is_bad(model):
return 1 - model.resid.var() / brains.brain_std.var()
R2_is_bad(m_7_1)
```
#### Code 7.7
```
m_7_2 = smf.ols("brain_std ~ mass_std + I(mass_std**2)", data=brains).fit()
m_7_2.summary()
```
#### Code 7.8
```
m_7_3 = smf.ols("brain_std ~ mass_std + I(mass_std**2) + I(mass_std**3)", data=brains).fit()
m_7_4 = smf.ols(
"brain_std ~ mass_std + I(mass_std**2) + I(mass_std**3) + I(mass_std**4)",
data=brains,
).fit()
m_7_5 = smf.ols(
"brain_std ~ mass_std + I(mass_std**2) + I(mass_std**3) + I(mass_std**4) + I(mass_std**5)",
data=brains,
).fit()
```
#### Code 7.9
```
m_7_6 = smf.ols(
"brain_std ~ mass_std + I(mass_std**2) + I(mass_std**3) + I(mass_std**4) + I(mass_std**5) + I(mass_std**6)",
data=brains,
).fit()
```
#### Code 7.10
The chapter gives code to produce the first panel of Figure 7.3. Here, produce the entire figure by looping over models 7.1-7.6.
To sample the posterior predictive on a new independent variable we make use of theano SharedVariable objects, as outlined [here](https://docs.pymc.io/notebooks/data_container.html)
```
models = [m_7_1, m_7_2, m_7_3, m_7_4, m_7_5, m_7_6]
names = ["m_7_1", "m_7_2", "m_7_3", "m_7_4", "m_7_5", "m_7_6"]
mass_plot = np.linspace(33, 62, 100)
mass_new = (mass_plot - brains.mass.mean()) / brains.mass.std()
fig, axs = plt.subplots(3, 2, figsize=[6, 8.5], sharex=True, sharey="row")
for model, name, ax in zip(models, names, axs.flat):
prediction = model.get_prediction({"mass_std": mass_new})
pred = prediction.summary_frame(alpha=0.11) * brains.brain.max()
ax.plot(mass_plot, pred["mean"])
ax.fill_between(mass_plot, pred["mean_ci_lower"], pred["mean_ci_upper"], alpha=0.3)
ax.scatter(brains.mass, brains.brain, color="C0", s=15)
ax.set_title(f"{name}: R^2: {model.rsquared:.2f}", loc="left", fontsize=11)
if ax.is_first_col():
ax.set_ylabel("brain volume (cc)")
if ax.is_last_row():
ax.set_xlabel("body mass (kg)")
if ax.is_last_row():
ax.set_ylim(-500, 2100)
ax.axhline(0, ls="dashed", c="k", lw=1)
ax.set_yticks([0, 450, 1300])
else:
ax.set_ylim(300, 1600)
ax.set_yticks([450, 900, 1300])
fig.tight_layout()
```
#### Code 7.11 - this is R specific notation for dropping rows
```
brains_new = brains.drop(brains.index[-1])
# Figure 7.4
# this code taken from PyMC3 port of Rethinking/Chp_06.ipynb
f, (ax1, ax2) = plt.subplots(1, 2, sharey=True, figsize=(8, 3))
ax1.scatter(brains.mass, brains.brain, alpha=0.8)
ax2.scatter(brains.mass, brains.brain, alpha=0.8)
for i in range(len(brains)):
d_new = brains.drop(brains.index[-i]) # drop each data point in turn
# first order model
m0 = smf.ols("brain ~ mass", d_new).fit()
# need to calculate regression line
# need to add intercept term explicitly
x = sm.add_constant(d_new.mass) # add constant to new data frame with mass
x_pred = pd.DataFrame(
{"mass": np.linspace(x.mass.min() - 10, x.mass.max() + 10, 50)}
) # create linspace dataframe
x_pred2 = sm.add_constant(x_pred) # add constant to newly created linspace dataframe
y_pred = m0.predict(x_pred2) # calculate predicted values
ax1.plot(x_pred, y_pred, "gray", alpha=0.5)
ax1.set_ylabel("body mass (kg)", fontsize=12)
ax1.set_xlabel("brain volume (cc)", fontsize=12)
ax1.set_title("Underfit model")
# fifth order model
m1 = smf.ols(
"brain ~ mass + I(mass**2) + I(mass**3) + I(mass**4) + I(mass**5)", data=d_new
).fit()
x = sm.add_constant(d_new.mass) # add constant to new data frame with mass
x_pred = pd.DataFrame(
{"mass": np.linspace(x.mass.min() - 10, x.mass.max() + 10, 200)}
) # create linspace dataframe
x_pred2 = sm.add_constant(x_pred) # add constant to newly created linspace dataframe
y_pred = m1.predict(x_pred2) # calculate predicted values from fitted model
ax2.plot(x_pred, y_pred, "gray", alpha=0.5)
ax2.set_xlim(32, 62)
ax2.set_ylim(-250, 2200)
ax2.set_ylabel("body mass (kg)", fontsize=12)
ax2.set_xlabel("brain volume (cc)", fontsize=12)
ax2.set_title("Overfit model")
```
#### Code 7.12
```
p = np.array([0.3, 0.7])
-np.sum(p * np.log(p))
# Figure 7.5
p = np.array([0.3, 0.7])
q = np.arange(0.01, 1, 0.01)
DKL = np.sum(p * np.log(p / np.array([q, 1 - q]).T), 1)
plt.plot(q, DKL)
plt.xlabel("q[1]")
plt.ylabel("Divergence of q from p")
plt.axvline(0.3, ls="dashed", color="k")
plt.text(0.315, 1.22, "q = p");
```
#### Code 7.13 & 7.14
```
n_samples = 3000
intercept, slope = stats.multivariate_normal(m_7_1.params, m_7_1.cov_params()).rvs(n_samples).T
pred = intercept + slope * brains.mass_std.values.reshape(-1, 1)
n, ns = pred.shape
# PyMC3 does not have a way to calculate LPPD directly, so we use the approach from 7.14
sigmas = (np.sum((pred - brains.brain_std.values.reshape(-1, 1)) ** 2, 0) / 7) ** 0.5
ll = np.zeros((n, ns))
for s in range(ns):
logprob = stats.norm.logpdf(brains.brain_std, pred[:, s], sigmas[s])
ll[:, s] = logprob
lppd = np.zeros(n)
for i in range(n):
lppd[i] = logsumexp(ll[i]) - np.log(ns)
lppd
```
#### Code 7.15
```
# make an lppd function that can be applied to all models (from code above)
def lppd(model, n_samples=1e4):
n_samples = int(n_samples)
pars = stats.multivariate_normal(model.params, model.cov_params()).rvs(n_samples).T
dmat = dmatrix(
model.model.data.design_info, brains, return_type="dataframe"
).values # get model design matrix
pred = dmat.dot(pars)
n, ns = pred.shape
# this approach for calculating lppd isfrom 7.14
sigmas = (np.sum((pred - brains.brain_std.values.reshape(-1, 1)) ** 2, 0) / 7) ** 0.5
ll = np.zeros((n, ns))
for s in range(ns):
logprob = stats.norm.logpdf(brains.brain_std, pred[:, s], sigmas[s])
ll[:, s] = logprob
lppd = np.zeros(n)
for i in range(n):
lppd[i] = logsumexp(ll[i]) - np.log(ns)
return lppd
# model 7_6 does not work with OLS because its covariance matrix is not finite.
lppds = np.array(list(map(lppd, models[:-1], [1000] * len(models[:-1]))))
lppds.sum(1)
```
#### Code 7.16
This relies on the `sim.train.test` function in the `rethinking` package. [This](https://github.com/rmcelreath/rethinking/blob/master/R/sim_train_test.R) is the original function.
The python port of this function below is from [Rethinking/Chp_06](https://nbviewer.jupyter.org/github/pymc-devs/resources/blob/master/Rethinking/Chp_06.ipynb) Code 6.12.
```
def sim_train_test(N=20, k=3, rho=[0.15, -0.4], b_sigma=100):
n_dim = 1 + len(rho)
if n_dim < k:
n_dim = k
Rho = np.diag(np.ones(n_dim))
Rho[0, 1:3:1] = rho
i_lower = np.tril_indices(n_dim, -1)
Rho[i_lower] = Rho.T[i_lower]
x_train = stats.multivariate_normal.rvs(cov=Rho, size=N)
x_test = stats.multivariate_normal.rvs(cov=Rho, size=N)
mm_train = np.ones((N, 1))
np.concatenate([mm_train, x_train[:, 1:k]], axis=1)
# Using pymc3
with pm.Model() as m_sim:
vec_V = pm.MvNormal(
"vec_V",
mu=0,
cov=b_sigma * np.eye(n_dim),
shape=(1, n_dim),
testval=np.random.randn(1, n_dim) * 0.01,
)
mu = pm.Deterministic("mu", 0 + pm.math.dot(x_train, vec_V.T))
y = pm.Normal("y", mu=mu, sd=1, observed=x_train[:, 0])
with m_sim:
trace_m_sim = pm.sample(return_inferencedata=True)
vec = az.summary(trace_m_sim)["mean"][:n_dim]
vec = np.array([i for i in vec]).reshape(n_dim, -1)
dev_train = -2 * sum(stats.norm.logpdf(x_train, loc=np.matmul(x_train, vec), scale=1))
mm_test = np.ones((N, 1))
mm_test = np.concatenate([mm_test, x_test[:, 1 : k + 1]], axis=1)
dev_test = -2 * sum(stats.norm.logpdf(x_test[:, 0], loc=np.matmul(mm_test, vec), scale=1))
return np.mean(dev_train), np.mean(dev_test)
n = 20
tries = 10
param = 6
r = np.zeros(shape=(param - 1, 4))
train = []
test = []
for j in range(2, param + 1):
print(j)
for i in range(1, tries + 1):
tr, te = sim_train_test(N=n, k=param)
train.append(tr), test.append(te)
r[j - 2, :] = (
np.mean(train),
np.std(train, ddof=1),
np.mean(test),
np.std(test, ddof=1),
)
```
#### Code 7.17
Does not apply because multi-threading is automatic in PyMC3.
#### Code 7.18
```
num_param = np.arange(2, param + 1)
plt.figure(figsize=(10, 6))
plt.scatter(num_param, r[:, 0], color="C0")
plt.xticks(num_param)
for j in range(param - 1):
plt.vlines(
num_param[j],
r[j, 0] - r[j, 1],
r[j, 0] + r[j, 1],
color="mediumblue",
zorder=-1,
alpha=0.80,
)
plt.scatter(num_param + 0.1, r[:, 2], facecolors="none", edgecolors="k")
for j in range(param - 1):
plt.vlines(
num_param[j] + 0.1,
r[j, 2] - r[j, 3],
r[j, 2] + r[j, 3],
color="k",
zorder=-2,
alpha=0.70,
)
dist = 0.20
plt.text(num_param[1] - dist, r[1, 0] - dist, "in", color="C0", fontsize=13)
plt.text(num_param[1] + dist, r[1, 2] - dist, "out", color="k", fontsize=13)
plt.text(num_param[1] + dist, r[1, 2] + r[1, 3] - dist, "+1 SD", color="k", fontsize=10)
plt.text(num_param[1] + dist, r[1, 2] - r[1, 3] - dist, "+1 SD", color="k", fontsize=10)
plt.xlabel("Number of parameters", fontsize=14)
plt.ylabel("Deviance", fontsize=14)
plt.title(f"N = {n}", fontsize=14)
plt.show()
```
These uncertainties are a *lot* larger than in the book... MCMC vs OLS again?
#### Code 7.19
7.19 to 7.25 transcribed directly from 6.15-6.20 in [Chapter 6 of 1st Edition](https://nbviewer.jupyter.org/github/pymc-devs/resources/blob/master/Rethinking/Chp_06.ipynb).
```
data = pd.read_csv("Data/cars.csv", sep=",", index_col=0)
with pm.Model() as m:
a = pm.Normal("a", mu=0, sd=100)
b = pm.Normal("b", mu=0, sd=10)
sigma = pm.Uniform("sigma", 0, 30)
mu = pm.Deterministic("mu", a + b * data["speed"])
dist = pm.Normal("dist", mu=mu, sd=sigma, observed=data["dist"])
m = pm.sample(5000, tune=10000)
```
#### Code 7.20
```
n_samples = 1000
n_cases = data.shape[0]
logprob = np.zeros((n_cases, n_samples))
for s in range(0, n_samples):
mu = m["a"][s] + m["b"][s] * data["speed"]
p_ = stats.norm.logpdf(data["dist"], loc=mu, scale=m["sigma"][s])
logprob[:, s] = p_
```
#### Code 7.21
```
n_cases = data.shape[0]
lppd = np.zeros(n_cases)
for a in range(1, n_cases):
lppd[a] = logsumexp(logprob[a]) - np.log(n_samples)
```
#### Code 7.22
```
pWAIC = np.zeros(n_cases)
for i in range(1, n_cases):
pWAIC[i] = np.var(logprob[i])
```
#### Code 7.23
```
-2 * (sum(lppd) - sum(pWAIC))
```
#### Code 7.24
```
waic_vec = -2 * (lppd - pWAIC)
(n_cases * np.var(waic_vec)) ** 0.5
```
#### Setup for Code 7.25+
Have to reproduce m6.6-m6.8 from Code 6.13-6.17 in Chapter 6
```
# number of plants
N = 100
# simulate initial heights
h0 = np.random.normal(10, 2, N)
# assign treatments and simulate fungus and growth
treatment = np.repeat([0, 1], N / 2)
fungus = np.random.binomial(n=1, p=0.5 - treatment * 0.4, size=N)
h1 = h0 + np.random.normal(5 - 3 * fungus, size=N)
# compose a clean data frame
d = pd.DataFrame.from_dict({"h0": h0, "h1": h1, "treatment": treatment, "fungus": fungus})
with pm.Model() as m_6_6:
p = pm.Lognormal("p", 0, 0.25)
mu = pm.Deterministic("mu", p * d.h0)
sigma = pm.Exponential("sigma", 1)
h1 = pm.Normal("h1", mu=mu, sigma=sigma, observed=d.h1)
m_6_6_trace = pm.sample(return_inferencedata=True)
with pm.Model() as m_6_7:
a = pm.Normal("a", 0, 0.2)
bt = pm.Normal("bt", 0, 0.5)
bf = pm.Normal("bf", 0, 0.5)
p = a + bt * d.treatment + bf * d.fungus
mu = pm.Deterministic("mu", p * d.h0)
sigma = pm.Exponential("sigma", 1)
h1 = pm.Normal("h1", mu=mu, sigma=sigma, observed=d.h1)
m_6_7_trace = pm.sample(return_inferencedata=True)
with pm.Model() as m_6_8:
a = pm.Normal("a", 0, 0.2)
bt = pm.Normal("bt", 0, 0.5)
p = a + bt * d.treatment
mu = pm.Deterministic("mu", p * d.h0)
sigma = pm.Exponential("sigma", 1)
h1 = pm.Normal("h1", mu=mu, sigma=sigma, observed=d.h1)
m_6_8_trace = pm.sample(return_inferencedata=True)
```
#### Code 7.25
```
az.waic(m_6_7_trace, m_6_7, scale="deviance")
```
#### Code 7.26
```
compare_df = az.compare(
{
"m_6_6": m_6_6_trace,
"m_6_7": m_6_7_trace,
"m_6_8": m_6_8_trace,
},
method="pseudo-BMA",
ic="waic",
scale="deviance",
)
compare_df
```
#### Code 7.27
```
waic_m_6_7 = az.waic(m_6_7_trace, pointwise=True, scale="deviance")
waic_m_6_8 = az.waic(m_6_8_trace, pointwise=True, scale="deviance")
# pointwise values are stored in the waic_i attribute.
diff_m_6_7_m_6_8 = waic_m_6_7.waic_i - waic_m_6_8.waic_i
n = len(diff_m_6_7_m_6_8)
np.sqrt(n * np.var(diff_m_6_7_m_6_8)).values
```
#### Code 7.28
```
40.0 + np.array([-1, 1]) * 10.4 * 2.6
```
#### Code 7.29
```
az.plot_compare(compare_df);
```
#### Code 7.30
```
waic_m_6_6 = az.waic(m_6_6_trace, pointwise=True, scale="deviance")
diff_m6_6_m6_8 = waic_m_6_6.waic_i - waic_m_6_8.waic_i
n = len(diff_m6_6_m6_8)
np.sqrt(n * np.var(diff_m6_6_m6_8)).values
```
#### Code 7.31
dSE is calculated by compare above, but `rethinking` produces a pairwise comparison. This is not implemented in `arviz`, but we can hack it together:
```
dataset_dict = {"m_6_6": m_6_6_trace, "m_6_7": m_6_7_trace, "m_6_8": m_6_8_trace}
# compare all models
s0 = az.compare(dataset_dict, ic="waic", scale="deviance")["dse"]
# the output compares each model to the 'best' model - i.e. two models are compared to one.
# to complete a pair-wise comparison we need to compare the remaining two models.
# to do this, remove the 'best' model from the input data
del dataset_dict[s0.index[0]]
# re-run compare with the remaining two models
s1 = az.compare(dataset_dict, ic="waic", scale="deviance")["dse"]
# s0 compares two models to one model, and s1 compares the remaining two models to each other
# now we just nee to wrangle them together!
# convert them both to dataframes, setting the name to the 'best' model in each `compare` output.
# (i.e. the name is the model that others are compared to)
df_0 = s0.to_frame(name=s0.index[0])
df_1 = s1.to_frame(name=s1.index[0])
# merge these dataframes to create a pairwise comparison
pd.merge(df_0, df_1, left_index=True, right_index=True)
```
**Note:** this work for three models, but will get increasingly hack-y with additional models. The function below can be applied to *n* models:
```
def pairwise_compare(dataset_dict, metric="dse", **kwargs):
"""
Calculate pairwise comparison of models in dataset_dict.
Parameters
----------
dataset_dict : dict
A dict containing two ore more {'name': pymc3.backends.base.MultiTrace}
items.
metric : str
The name of the matric to be calculated. Can be any valid column output
by `arviz.compare`. Note that this may change depending on the **kwargs
that are specified.
kwargs
Arguments passed to `arviz.compare`
"""
data_dict = dataset_dict.copy()
dicts = []
while len(data_dict) > 1:
c = az.compare(data_dict, **kwargs)[metric]
dicts.append(c.to_frame(name=c.index[0]))
del data_dict[c.index[0]]
return pd.concat(dicts, axis=1)
dataset_dict = {"m_6_6": m_6_6_trace, "m_6_7": m_6_7_trace, "m_6_8": m_6_8_trace}
pairwise_compare(dataset_dict, metric="dse", ic="waic", scale="deviance")
```
#### Code 7.32
```
d = pd.read_csv("Data/WaffleDivorce.csv", delimiter=";")
d["A"] = stats.zscore(d["MedianAgeMarriage"])
d["D"] = stats.zscore(d["Divorce"])
d["M"] = stats.zscore(d["Marriage"])
with pm.Model() as m_5_1:
a = pm.Normal("a", 0, 0.2)
bA = pm.Normal("bA", 0, 0.5)
mu = a + bA * d["A"]
sigma = pm.Exponential("sigma", 1)
D = pm.Normal("D", mu, sigma, observed=d["D"])
m_5_1_trace = pm.sample(return_inferencedata=True)
with pm.Model() as m_5_2:
a = pm.Normal("a", 0, 0.2)
bM = pm.Normal("bM", 0, 0.5)
mu = a + bM * d["M"]
sigma = pm.Exponential("sigma", 1)
D = pm.Normal("D", mu, sigma, observed=d["D"])
m_5_2_trace = pm.sample(return_inferencedata=True)
with pm.Model() as m_5_3:
a = pm.Normal("a", 0, 0.2)
bA = pm.Normal("bA", 0, 0.5)
bM = pm.Normal("bM", 0, 0.5)
mu = a + bA * d["A"] + bM * d["M"]
sigma = pm.Exponential("sigma", 1)
D = pm.Normal("D", mu, sigma, observed=d["D"])
m_5_3_trace = pm.sample(return_inferencedata=True)
```
#### Code 7.33
```
az.compare(
{"m_5_1": m_5_1_trace, "m_5_2": m_5_2_trace, "m_5_3": m_5_3_trace},
scale="deviance",
)
```
#### Code 7.34
```
psis_m_5_3 = az.loo(m_5_3_trace, pointwise=True, scale="deviance")
waic_m_5_3 = az.waic(m_5_3_trace, pointwise=True, scale="deviance")
# Figure 7.10
plt.scatter(psis_m_5_3.pareto_k, waic_m_5_3.waic_i)
plt.xlabel("PSIS Pareto k")
plt.ylabel("WAIC");
# Figure 7.11
v = np.linspace(-4, 4, 100)
g = stats.norm(loc=0, scale=1)
t = stats.t(df=2, loc=0, scale=1)
fig, (ax, lax) = plt.subplots(1, 2, figsize=[8, 3.5])
ax.plot(v, g.pdf(v), color="b")
ax.plot(v, t.pdf(v), color="k")
lax.plot(v, -g.logpdf(v), color="b")
lax.plot(v, -t.logpdf(v), color="k");
```
#### Code 7.35
```
with pm.Model() as m_5_3t:
a = pm.Normal("a", 0, 0.2)
bA = pm.Normal("bA", 0, 0.5)
bM = pm.Normal("bM", 0, 0.5)
mu = a + bA * d["A"] + bM * d["M"]
sigma = pm.Exponential("sigma", 1)
D = pm.StudentT("D", 2, mu, sigma, observed=d["D"])
m_5_3t_trace = pm.sample(return_inferencedata=True)
az.loo(m_5_3t_trace, pointwise=True, scale="deviance")
az.plot_forest([m_5_3_trace, m_5_3t_trace], model_names=["m_5_3", "m_5_3t"], figsize=[6, 3.5]);
%load_ext watermark
%watermark -n -u -v -iv -w
```
| true |
code
| 0.586464 | null | null | null | null |
|
# Data Cleaning
For each IMU file, clean the IMU data, adjust the labels, and output these as CSV files.
```
%load_ext autoreload
%autoreload 2
%matplotlib notebook
import numpy as np
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import GradientBoostingClassifier
from matplotlib.lines import Line2D
import joblib
from src.data.labels_util import load_labels, LabelCol, get_labels_file, load_clean_labels, get_workouts
from src.data.imu_util import (
get_sensor_file, ImuCol, load_imu_data, Sensor, fix_epoch, resample_uniformly, time_to_row_range, get_data_chunk,
normalize_with_bounds, data_to_features, list_imu_abspaths, clean_imu_data
)
from src.data.util import find_nearest, find_nearest_index, shift, low_pass_filter, add_col
from src.data.workout import Activity, Workout
from src.data.data import DataState
from src.data.clean_dataset import main as clean_dataset
from src.data.clean_labels import main as clean_labels
from src.visualization.visualize import multiplot
# import data types
from pandas import DataFrame
from numpy import ndarray
from typing import List, Tuple, Optional
```
## Clean IMU data
```
# Clean data (UNCOMMENT when needed)
# clean_dataset()
# Test
cleaned_files = list_imu_abspaths(sensor_type=Sensor.Accelerometer, data_state=DataState.Clean)
def plot_helper(idx, plot):
imu_data = np.load(cleaned_files[idx])
plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.XACCEL])
# plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.YACCEL])
# plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.ZACCEL])
multiplot(len(cleaned_files), plot_helper)
```
## Adjust Labels
A few raw IMU files seems to have corrupted timestamps, causing some labels to not properly map to their data point. We note these labels in the cleaned/adjusted labels. They'll be handled in the model fitting.
```
# Adjust labels (UNCOMMENT when needed)
# clean_labels()
# Test
raw_boot_labels: ndarray = load_labels(get_labels_file(Activity.Boot, DataState.Raw), Activity.Boot)
raw_pole_labels: ndarray = load_labels(get_labels_file(Activity.Pole, DataState.Raw), Activity.Pole)
clean_boot_labels: ndarray = load_clean_labels(Activity.Boot)
clean_pole_labels: ndarray = load_clean_labels(Activity.Pole)
# Check cleaned data content
# print('Raw Boot')
# print(raw_boot_labels[:50,])
# print('Clean Boot')
# print(clean_boot_labels[:50,])
# print('Raw Pole')
# print(raw_pole_labels[:50,])
# print('Clean Pole')
# print(clean_pole_labels[:50,])
```
## Examine Data Integrity
Make sure that labels for steps are still reasonable after data cleaning.
**Something to consider**: one area of concern are the end steps labels for poles labels. Pole lift-off (end of step) occurs at a min-peak. Re-sampling, interpolation, and the adjustment of labels may cause the end labels to deviate slightly from the min-peak. (The graph seems okay, with some points slightly off the peak, but it's not too common.) We can make the reasonable assumption that data points are sampled approximately uniformly. This may affect the accuracy of using a low-pass filter and (for workout detection) FFT.
```
# CHOOSE a workout and test type (pole or boot) to examine
workout_idx = 5
selected_labels = clean_boot_labels
workouts: List[Workout] = get_workouts(selected_labels)
print('Number of workouts: %d' % len(workouts))
workout = workouts[workout_idx]
print('Sensor %s' % workout.sensor)
def plot_helper(idx, plot):
# Plot IMU data
imu_data: ndarray = np.load(
get_sensor_file(sensor_name=workout.sensor, sensor_type=Sensor.Accelerometer, data_state=DataState.Clean))
plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.XACCEL])
# plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.YACCEL])
# plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.ZACCEL])
plot.set_xlabel('Epoch Time')
# Plot step labels
for i in range(workout.labels.shape[0]):
start_row, end_row = workout.labels[i, LabelCol.START], workout.labels[i, LabelCol.END]
plot.axvline(x=imu_data[start_row, ImuCol.TIME], color='green', linestyle='dashed')
plot.axvline(x=imu_data[end_row, ImuCol.TIME], color='red', linestyle='dotted')
legend_items = [Line2D([], [], color='green', linestyle='dashed', label='Step start'),
Line2D([], [], color='red', linestyle='dotted', label='Step end')]
plot.legend(handles=legend_items)
# Zoom (REMOVE to see the entire graph)
# plot.set_xlim([1597340600000, 1597340615000])
multiplot(1, plot_helper)
```
Let's compare the cleaned labels to the original labels.
```
# CHOOSE a workout and test type (pole or boot) to examine
workout_idx = 5
selected_labels = raw_pole_labels
workouts: List[Workout] = get_workouts(selected_labels)
print('Number of workouts: %d' % len(workouts))
workout = workouts[workout_idx]
print('Sensor %s' % workout.sensor)
def plot_helper(idx, plot):
# Plot IMU data
imu_data: ndarray = load_imu_data(
get_sensor_file(sensor_name=workout.sensor, sensor_type=Sensor.Accelerometer, data_state=DataState.Raw))
plot.plot(imu_data[:, ImuCol.XACCEL])
# plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.YACCEL])
# plot.plot(imu_data[:, ImuCol.TIME], imu_data[:, ImuCol.ZACCEL])
plot.set_xlabel('Row Index')
# Plot step labels
for i in range(workout.labels.shape[0]):
# find labels rows
start_epoch, end_epoch = workout.labels[i, LabelCol.START], workout.labels[i, LabelCol.END]
start_row = np.where(imu_data[:, ImuCol.TIME].astype(int) == int(start_epoch))[0]
end_row = np.where(imu_data[:, ImuCol.TIME].astype(int) == int(end_epoch))[0]
if len(start_row) != 1 or len(end_row) != 1:
print('Bad workout')
return
start_row, end_row = start_row[0], end_row[0]
plot.axvline(x=start_row, color='green', linestyle='dashed')
plot.axvline(x=end_row, color='red', linestyle='dotted')
legend_items = [Line2D([], [], color='green', linestyle='dashed', label='Step start'),
Line2D([], [], color='red', linestyle='dotted', label='Step end')]
plot.legend(handles=legend_items)
# Zoom (REMOVE to see the entire graph)
plot.set_xlim([124500, 125000])
multiplot(1, plot_helper)
```
Make sure NaN labels were persisted during the label data's save/load process.
```
def count_errors(labels: ndarray):
for workout in get_workouts(labels):
boot: ndarray = workout.labels
num_errors = np.count_nonzero(
np.isnan(boot[:, LabelCol.START].astype(np.float64)) | np.isnan(boot[:, LabelCol.END].astype(np.float64)))
if num_errors != 0:
print('Number of labels that could not be mapped for sensor %s: %d' % (workout.sensor, num_errors))
clean_boot_labels: ndarray = load_clean_labels(Activity.Boot)
clean_pole_labels: ndarray = load_clean_labels(Activity.Pole)
print('Boot labels')
count_errors(clean_boot_labels)
print('Pole labels')
count_errors(clean_pole_labels)
```
| true |
code
| 0.582907 | null | null | null | null |
|
# Getting Started with *pyFTracks* v 1.0
**Romain Beucher, Roderick Brown, Louis Moresi and Fabian Kohlmann**
The Australian National University
The University of Glasgow
Lithodat
*pyFTracks* is a Python package that can be used to predict Fission Track ages and Track lengths distributions for some given thermal-histories and kinetic parameters.
*pyFTracks* is an open-source project licensed under the MiT license. See LICENSE.md for details.
The functionalities provided are similar to Richard Ketcham HeFTy sofware.
The main advantage comes from its Python interface which allows users to easily integrate *pyFTracks* with other Python libraries and existing scientific applications.
*pyFTracks* is available on all major operating systems.
For now, *pyFTracks* only provide forward modelling functionalities. Integration with inverse problem schemes is planned for version 2.0.
# Installation
*pyFTracks* is availabe on pypi. The code should work on all major operating systems (Linux, MaxOSx and Windows)
`pip install pyFTracks`
# Importing *pyFTracks*
The recommended way to import pyFTracks is to run:
```
import pyFTracks as FT
```
# Input
## Specifying a Thermal history
```
thermal_history = FT.ThermalHistory(name="My Thermal History",
time=[0., 43., 44., 100.],
temperature=[283., 283., 403., 403.])
import matplotlib.pyplot as plt
plt.figure(figsize=(15, 5))
plt.plot(thermal_history.input_time, thermal_history.input_temperature, label=thermal_history.name, marker="o")
plt.xlim(100., 0.)
plt.ylim(150. + 273.15, 0.+273.15)
plt.ylabel("Temperature in degC")
plt.xlabel("Time in (Ma)")
plt.legend()
```
## Predefined thermal histories
We provide predefined thermal histories for convenience.
```
from pyFTracks.thermal_history import WOLF1, WOLF2, WOLF3, WOLF4, WOLF5, FLAXMANS1, VROLIJ
thermal_histories = [WOLF1, WOLF2, WOLF3, WOLF4, WOLF5, FLAXMANS1, VROLIJ]
plt.figure(figsize=(15, 5))
for thermal_history in thermal_histories:
plt.plot(thermal_history.input_time, thermal_history.input_temperature, label=thermal_history.name, marker="o")
plt.xlim(100., 0.)
plt.ylim(150. + 273.15, 0.+273.15)
plt.ylabel("Temperature in degC")
plt.xlabel("Time in (Ma)")
plt.legend()
```
## Annealing Models
```
annealing_model = FT.Ketcham1999(kinetic_parameters={"ETCH_PIT_LENGTH": 1.65})
annealing_model.history = WOLF1
annealing_model.calculate_age()
annealing_model = FT.Ketcham2007(kinetic_parameters={"ETCH_PIT_LENGTH": 1.65})
annealing_model.history = WOLF1
annealing_model.calculate_age()
FT.Viewer(history=WOLF1, annealing_model=annealing_model)
```
# Simple Fission-Track data Predictions
```
Ns = [31, 19, 56, 67, 88, 6, 18, 40, 36, 54, 35, 52, 51, 47, 27, 36, 64, 68, 61, 30]
Ni = [41, 22, 63, 71, 90, 7, 14, 41, 49, 79, 52, 76, 74, 66, 39, 44, 86, 90, 91, 41]
zeta = 350.
zeta_err = 10. / 350.
rhod = 1.304
rhod_err = 0.
Nd = 2936
FT.central_age(Ns, Ni, zeta, zeta_err, rhod, Nd)
FT.pooled_age(Ns, Ni, zeta, zeta_err, rhod, Nd)
FT.single_grain_ages(Ns, Ni, zeta, zeta_err, rhod, Nd)
FT.chi2_test(Ns, Ni)
```
# Included datasets
*pyFTracks* comes with some sample datasets that can be used for testing and designing general code.
```
from pyFTracks.ressources import Gleadow
from pyFTracks.ressources import Miller
Gleadow
FT.central_age(Gleadow.Ns,
Gleadow.Ni,
Gleadow.zeta,
Gleadow.zeta_error,
Gleadow.rhod,
Gleadow.nd)
Miller
FT.central_age(Miller.Ns,
Miller.Ni,
Miller.zeta,
Miller.zeta_error,
Miller.rhod,
Miller.nd)
Miller.calculate_central_age()
Miller.calculate_pooled_age()
Miller.calculate_ages()
```
| true |
code
| 0.608303 | null | null | null | null |
|
# Preliminary instruction
To follow the code in this chapter, the `yfinance` package must be installed in your environment. If you do not have this installed yet, review Chapter 4 for instructions on how to do so.
# Chapter 9: Risk is a Number
```
# Chapter 9: Risk is a Number
import pandas as pd
import numpy as np
import yfinance as yf
%matplotlib inline
import matplotlib.pyplot as plt
```
#### Mock Strategy: Turtle for dummies
```
# Chapter 9: Risk is a Number
def regime_breakout(df,_h,_l,window):
hl = np.where(df[_h] == df[_h].rolling(window).max(),1,
np.where(df[_l] == df[_l].rolling(window).min(), -1,np.nan))
roll_hl = pd.Series(index= df.index, data= hl).fillna(method= 'ffill')
return roll_hl
def turtle_trader(df, _h, _l, slow, fast):
'''
_slow: Long/Short direction
_fast: trailing stop loss
'''
_slow = regime_breakout(df,_h,_l,window = slow)
_fast = regime_breakout(df,_h,_l,window = fast)
turtle = pd. Series(index= df.index,
data = np.where(_slow == 1,np.where(_fast == 1,1,0),
np.where(_slow == -1, np.where(_fast ==-1,-1,0),0)))
return turtle
```
#### Run the strategy with Softbank in absolute
Plot: Softbank turtle for dummies, positions, and returns
Plot: Softbank cumulative returns and Sharpe ratios: rolling and cumulative
```
# Chapter 9: Risk is a Number
ticker = '9984.T' # Softbank
start = '2017-12-31'
end = None
df = round(yf.download(tickers= ticker,start= start, end = end,
interval = "1d",group_by = 'column',auto_adjust = True,
prepost = True, treads = True, proxy = None),0)
slow = 50
fast = 20
df['tt'] = turtle_trader(df, _h= 'High', _l= 'Low', slow= slow,fast= fast)
df['stop_loss'] = np.where(df['tt'] == 1, df['Low'].rolling(fast).min(),
np.where(df['tt'] == -1, df['High'].rolling(fast).max(),np.nan))
df['tt_chg1D'] = df['Close'].diff() * df['tt'].shift()
df['tt_PL_cum'] = df['tt_chg1D'].cumsum()
df['tt_returns'] = df['Close'].pct_change() * df['tt'].shift()
tt_log_returns = np.log(df['Close']/df['Close'].shift()) * df['tt'].shift()
df['tt_cumul'] = tt_log_returns.cumsum().apply(np.exp) - 1
df[['Close','stop_loss','tt','tt_cumul']].plot(secondary_y=['tt','tt_cumul'],
figsize=(20,8),style= ['k','r--','b:','b'],
title= str(ticker)+' Close Price, Turtle L/S entries, cumulative returns')
df[['tt_PL_cum','tt_chg1D']].plot(secondary_y=['tt_chg1D'],
figsize=(20,8),style= ['b','c:'],
title= str(ticker) +' Daily P&L & Cumulative P&L')
```
#### Sharpe ratio: the right mathematical answer to the wrong question
Plot: Softbank cumulative returns and Sharpe ratios: rolling and cumulative
```
# Chapter 9: Risk is a Number
r_f = 0.00001 # risk free returns
def rolling_sharpe(returns, r_f, window):
avg_returns = returns.rolling(window).mean()
std_returns = returns.rolling(window).std(ddof=0)
return (avg_returns - r_f) / std_returns
def expanding_sharpe(returns, r_f):
avg_returns = returns.expanding().mean()
std_returns = returns.expanding().std(ddof=0)
return (avg_returns - r_f) / std_returns
window= 252
df['sharpe_roll'] = rolling_sharpe(returns= tt_log_returns, r_f= r_f, window= window) * 252**0.5
df['sharpe']= expanding_sharpe(returns=tt_log_returns,r_f= r_f) * 252**0.5
df[window:][['tt_cumul','sharpe_roll','sharpe'] ].plot(figsize = (20,8),style = ['b','c-.','c'],grid=True,
title = str(ticker)+' cumulative returns, Sharpe ratios: rolling & cumulative')
```
### Grit Index
This formula was originally invented by Peter G. Martin in 1987 and published as the Ulcer Index in his book The Investor's Guide to Fidelity Funds. Legendary trader Ed Seykota recycled it into the Seykota Lake ratio.
Investors react to drawdowns in three ways:
1. Magnitude: never test the stomach of your investors
2. Frequency: never test the nerves of your investors
3. Duration: never test the patience of your investors
The Grit calculation sequence is as follows:
1. Calculate the peak cumulative returns using rolling().max() or expanding().max()
2. Calculate the squared drawdown from the peak and square them
3. Calculate the least square sum by taking the square root of the squared drawdowns
4. Divide the cumulative returns by the surface of losses
Plot: Softbank cumulative returns and Grit ratios: rolling and cumulative
```
# Chapter 9: Risk is a Number
def rolling_grit(cumul_returns, window):
tt_rolling_peak = cumul_returns.rolling(window).max()
drawdown_squared = (cumul_returns - tt_rolling_peak) ** 2
ulcer = drawdown_squared.rolling(window).sum() ** 0.5
return cumul_returns / ulcer
def expanding_grit(cumul_returns):
tt_peak = cumul_returns.expanding().max()
drawdown_squared = (cumul_returns - tt_peak) ** 2
ulcer = drawdown_squared.expanding().sum() ** 0.5
return cumul_returns / ulcer
window = 252
df['grit_roll'] = rolling_grit(cumul_returns= df['tt_cumul'] , window = window)
df['grit'] = expanding_grit(cumul_returns= df['tt_cumul'])
df[window:][['tt_cumul','grit_roll', 'grit'] ].plot(figsize = (20,8),
secondary_y = 'tt_cumul',style = ['b','g-.','g'],grid=True,
title = str(ticker) + ' cumulative returns & Grit Ratios: rolling & cumulative '+ str(window) + ' days')
```
### Common Sense Ratio
1. Risk metric for trend following strategies: profit ratio, gain-to-pain ratio
2. Risk metric for trend following strategies: tail ratio
3. Combined risk metric: profit ratio * tail ratio
Plot: Cumulative returns and common sense ratios: cumulative and rolling
```
# Chapter 9: Risk is a Number
def rolling_profits(returns,window):
profit_roll = returns.copy()
profit_roll[profit_roll < 0] = 0
profit_roll_sum = profit_roll.rolling(window).sum().fillna(method='ffill')
return profit_roll_sum
def rolling_losses(returns,window):
loss_roll = returns.copy()
loss_roll[loss_roll > 0] = 0
loss_roll_sum = loss_roll.rolling(window).sum().fillna(method='ffill')
return loss_roll_sum
def expanding_profits(returns):
profit_roll = returns.copy()
profit_roll[profit_roll < 0] = 0
profit_roll_sum = profit_roll.expanding().sum().fillna(method='ffill')
return profit_roll_sum
def expanding_losses(returns):
loss_roll = returns.copy()
loss_roll[loss_roll > 0] = 0
loss_roll_sum = loss_roll.expanding().sum().fillna(method='ffill')
return loss_roll_sum
def profit_ratio(profits, losses):
pr = profits.fillna(method='ffill') / abs(losses.fillna(method='ffill'))
return pr
def rolling_tail_ratio(cumul_returns, window, percentile,limit):
left_tail = np.abs(cumul_returns.rolling(window).quantile(percentile))
right_tail = cumul_returns.rolling(window).quantile(1-percentile)
np.seterr(all='ignore')
tail = np.maximum(np.minimum(right_tail / left_tail,limit),-limit)
return tail
def expanding_tail_ratio(cumul_returns, percentile,limit):
left_tail = np.abs(cumul_returns.expanding().quantile(percentile))
right_tail = cumul_returns.expanding().quantile(1 - percentile)
np.seterr(all='ignore')
tail = np.maximum(np.minimum(right_tail / left_tail,limit),-limit)
return tail
def common_sense_ratio(pr,tr):
return pr * tr
```
#### Plot: Cumulative returns and profit ratios: cumulative and rolling
```
# Chapter 9: Risk is a Number
window = 252
df['pr_roll'] = profit_ratio(profits= rolling_profits(returns = tt_log_returns,window = window),
losses= rolling_losses(returns = tt_log_returns,window = window))
df['pr'] = profit_ratio(profits= expanding_profits(returns= tt_log_returns),
losses= expanding_losses(returns = tt_log_returns))
df[window:] [['tt_cumul','pr_roll','pr'] ].plot(figsize = (20,8),secondary_y= ['tt_cumul'],
style = ['r','y','y:'],grid=True)
```
#### Plot: Cumulative returns and common sense ratios: cumulative and rolling
```
# Chapter 9: Risk is a Number
window = 252
df['tr_roll'] = rolling_tail_ratio(cumul_returns= df['tt_cumul'],
window= window, percentile= 0.05,limit=5)
df['tr'] = expanding_tail_ratio(cumul_returns= df['tt_cumul'], percentile= 0.05,limit=5)
df['csr_roll'] = common_sense_ratio(pr= df['pr_roll'],tr= df['tr_roll'])
df['csr'] = common_sense_ratio(pr= df['pr'],tr= df['tr'])
df[window:] [['tt_cumul','csr_roll','csr'] ].plot(secondary_y= ['tt_cumul'],style = ['b','r-.','r'], figsize = (20,8),
title= str(ticker)+' cumulative returns, Common Sense Ratios: cumulative & rolling '+str(window)+ ' days')
```
### T-stat of gain expectancy, Van Tharp's System Quality Number (SQN)
Plot: Softbank cumulative returns and t-stat (Van Tharp's SQN): cumulative and rolling
```
# Chapter 9: Risk is a Number
def expectancy(win_rate,avg_win,avg_loss):
# win% * avg_win% - loss% * abs(avg_loss%)
return win_rate * avg_win + (1-win_rate) * avg_loss
def t_stat(signal_count, trading_edge):
sqn = (signal_count ** 0.5) * trading_edge / trading_edge.std(ddof=0)
return sqn
# Trade Count
df['trades'] = df.loc[(df['tt'].diff() !=0) & (pd.notnull(df['tt'])),'tt'].abs().cumsum()
signal_count = df['trades'].fillna(method='ffill')
signal_roll = signal_count.diff(window)
# Rolling t_stat
window = 252
win_roll = tt_log_returns.copy()
win_roll[win_roll < 0] = np.nan
win_rate_roll = win_roll.rolling(window,min_periods=0).count() / window
avg_win_roll = rolling_profits(returns = tt_log_returns,window = window) / window
avg_loss_roll = rolling_losses(returns = tt_log_returns,window = window) / window
edge_roll= expectancy(win_rate= win_rate_roll,avg_win=avg_win_roll,avg_loss=avg_loss_roll)
df['sqn_roll'] = t_stat(signal_count= signal_roll, trading_edge=edge_roll)
# Cumulative t-stat
tt_win_count = tt_log_returns[tt_log_returns>0].expanding().count().fillna(method='ffill')
tt_count = tt_log_returns[tt_log_returns!=0].expanding().count().fillna(method='ffill')
win_rate = (tt_win_count / tt_count).fillna(method='ffill')
avg_win = expanding_profits(returns= tt_log_returns) / tt_count
avg_loss = expanding_losses(returns= tt_log_returns) / tt_count
trading_edge = expectancy(win_rate,avg_win,avg_loss).fillna(method='ffill')
df['sqn'] = t_stat(signal_count, trading_edge)
df[window:][['tt_cumul','sqn','sqn_roll'] ].plot(figsize = (20,8),
secondary_y= ['tt_cumul'], grid= True,style = ['b','y','y-.'],
title= str(ticker)+' Cumulative Returns and SQN: cumulative & rolling'+ str(window)+' days')
```
### Robustness score
Combined risk metric:
1. The Grit Index integrates losses throughout the period
2. The CSR combines risks endemic to the two types of strategies in a single measure
3. The t-stat SQN incorporates trading frequency into the trading edge formula to show the most efficient use of capital.
```
# Chapter 9: Risk is a Number
def robustness_score(grit,csr,sqn):
start_date = max(grit[pd.notnull(grit)].index[0],
csr[pd.notnull(csr)].index[0],
sqn[pd.notnull(sqn)].index[0])
score = grit * csr * sqn / (grit[start_date] * csr[start_date] * sqn[start_date])
return score
df['score_roll'] = robustness_score(grit = df['grit_roll'], csr = df['csr_roll'],sqn= df['sqn_roll'])
df['score'] = robustness_score(grit = df['grit'],csr = df['csr'],sqn = df['sqn'])
df[window:][['tt_cumul','score','score_roll']].plot(
secondary_y= ['score'],figsize=(20,6),style = ['b','k','k-.'],
title= str(ticker)+' Cumulative Returns and Robustness Score: cumulative & rolling '+ str(window)+' days')
```
| true |
code
| 0.575349 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/iamsoroush/DeepEEGAbstractor/blob/master/cv_rnr_8s_proposed_gap.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title # Clone the repository and upgrade Keras {display-mode: "form"}
!git clone https://github.com/iamsoroush/DeepEEGAbstractor.git
!pip install --upgrade keras
#@title # Imports {display-mode: "form"}
import os
import pickle
import sys
sys.path.append('DeepEEGAbstractor')
import numpy as np
from src.helpers import CrossValidator
from src.models import SpatioTemporalWFB, TemporalWFB, TemporalDFB, SpatioTemporalDFB
from src.dataset import DataLoader, Splitter, FixedLenGenerator
from google.colab import drive
drive.mount('/content/gdrive')
#@title # Set data path {display-mode: "form"}
#@markdown ---
#@markdown Type in the folder in your google drive that contains numpy _data_ folder:
parent_dir = 'soroush'#@param {type:"string"}
gdrive_path = os.path.abspath(os.path.join('gdrive/My Drive', parent_dir))
data_dir = os.path.join(gdrive_path, 'data')
cv_results_dir = os.path.join(gdrive_path, 'cross_validation')
if not os.path.exists(cv_results_dir):
os.mkdir(cv_results_dir)
print('Data directory: ', data_dir)
print('Cross validation results dir: ', cv_results_dir)
#@title ## Set Parameters
batch_size = 80
epochs = 50
k = 10
t = 10
instance_duration = 8 #@param {type:"slider", min:3, max:10, step:0.5}
instance_overlap = 2 #@param {type:"slider", min:0, max:3, step:0.5}
sampling_rate = 256 #@param {type:"number"}
n_channels = 20 #@param {type:"number"}
task = 'rnr'
data_mode = 'cross_subject'
#@title ## Spatio-Temporal WFB
model_name = 'ST-WFB-GAP'
train_generator = FixedLenGenerator(batch_size=batch_size,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=True)
test_generator = FixedLenGenerator(batch_size=8,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=False)
params = {'task': task,
'data_mode': data_mode,
'main_res_dir': cv_results_dir,
'model_name': model_name,
'epochs': epochs,
'train_generator': train_generator,
'test_generator': test_generator,
't': t,
'k': k,
'channel_drop': True}
validator = CrossValidator(**params)
dataloader = DataLoader(data_dir,
task,
data_mode,
sampling_rate,
instance_duration,
instance_overlap)
data, labels = dataloader.load_data()
input_shape = (sampling_rate * instance_duration,
n_channels)
model_obj = SpatioTemporalWFB(input_shape,
model_name=model_name,
spatial_dropout_rate=0.2,
dropout_rate=0.4)
scores = validator.do_cv(model_obj,
data,
labels)
#@title ## Temporal WFB
model_name = 'T-WFB-GAP'
train_generator = FixedLenGenerator(batch_size=batch_size,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=True)
test_generator = FixedLenGenerator(batch_size=8,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=False)
params = {'task': task,
'data_mode': data_mode,
'main_res_dir': cv_results_dir,
'model_name': model_name,
'epochs': epochs,
'train_generator': train_generator,
'test_generator': test_generator,
't': t,
'k': k,
'channel_drop': True}
validator = CrossValidator(**params)
dataloader = DataLoader(data_dir,
task,
data_mode,
sampling_rate,
instance_duration,
instance_overlap)
data, labels = dataloader.load_data()
input_shape = (sampling_rate * instance_duration,
n_channels)
model_obj = TemporalWFB(input_shape,
model_name=model_name,
spatial_dropout_rate=0.2,
dropout_rate=0.4)
scores = validator.do_cv(model_obj,
data,
labels)
#@title ## Spatio-Temporal DFB
model_name = 'ST-DFB-GAP'
train_generator = FixedLenGenerator(batch_size=batch_size,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=True)
test_generator = FixedLenGenerator(batch_size=8,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=False)
params = {'task': task,
'data_mode': data_mode,
'main_res_dir': cv_results_dir,
'model_name': model_name,
'epochs': epochs,
'train_generator': train_generator,
'test_generator': test_generator,
't': t,
'k': k,
'channel_drop': True}
validator = CrossValidator(**params)
dataloader = DataLoader(data_dir,
task,
data_mode,
sampling_rate,
instance_duration,
instance_overlap)
data, labels = dataloader.load_data()
input_shape = (sampling_rate * instance_duration,
n_channels)
model_obj = SpatioTemporalDFB(input_shape,
model_name=model_name,
spatial_dropout_rate=0.2,
dropout_rate=0.4)
scores = validator.do_cv(model_obj,
data,
labels)
#@title ## Spatio-Temporal DFB (Normalized Kernels)
model_name = 'ST-DFB-NK-GAP'
train_generator = FixedLenGenerator(batch_size=batch_size,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=True)
test_generator = FixedLenGenerator(batch_size=8,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=False)
params = {'task': task,
'data_mode': data_mode,
'main_res_dir': cv_results_dir,
'model_name': model_name,
'epochs': epochs,
'train_generator': train_generator,
'test_generator': test_generator,
't': t,
'k': k,
'channel_drop': True}
validator = CrossValidator(**params)
dataloader = DataLoader(data_dir,
task,
data_mode,
sampling_rate,
instance_duration,
instance_overlap)
data, labels = dataloader.load_data()
input_shape = (sampling_rate * instance_duration,
n_channels)
model_obj = SpatioTemporalDFB(input_shape,
model_name=model_name,
spatial_dropout_rate=0.2,
dropout_rate=0.4,
normalize_kernels=True)
scores = validator.do_cv(model_obj,
data,
labels)
#@title ## Temporal DFB
model_name = 'T-DFB-GAP'
train_generator = FixedLenGenerator(batch_size=batch_size,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=True)
test_generator = FixedLenGenerator(batch_size=8,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=False)
params = {'task': task,
'data_mode': data_mode,
'main_res_dir': cv_results_dir,
'model_name': model_name,
'epochs': epochs,
'train_generator': train_generator,
'test_generator': test_generator,
't': t,
'k': k,
'channel_drop': True}
validator = CrossValidator(**params)
dataloader = DataLoader(data_dir,
task,
data_mode,
sampling_rate,
instance_duration,
instance_overlap)
data, labels = dataloader.load_data()
input_shape = (sampling_rate * instance_duration,
n_channels)
model_obj = TemporalDFB(input_shape,
model_name=model_name,
spatial_dropout_rate=0.2,
dropout_rate=0.4)
scores = validator.do_cv(model_obj,
data,
labels)
#@title ## Temporal DFB (Normalized Kernels)
model_name = 'T-DFB-NK-GAP'
train_generator = FixedLenGenerator(batch_size=batch_size,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=True)
test_generator = FixedLenGenerator(batch_size=8,
duration=instance_duration,
overlap=instance_overlap,
sampling_rate=sampling_rate,
is_train=False)
params = {'task': task,
'data_mode': data_mode,
'main_res_dir': cv_results_dir,
'model_name': model_name,
'epochs': epochs,
'train_generator': train_generator,
'test_generator': test_generator,
't': t,
'k': k,
'channel_drop': True}
validator = CrossValidator(**params)
dataloader = DataLoader(data_dir,
task,
data_mode,
sampling_rate,
instance_duration,
instance_overlap)
data, labels = dataloader.load_data()
input_shape = (sampling_rate * instance_duration,
n_channels)
model_obj = TemporalDFB(input_shape,
model_name=model_name,
spatial_dropout_rate=0.2,
dropout_rate=0.4,
normalize_kernels=True)
scores = validator.do_cv(model_obj,
data,
labels)
```
| true |
code
| 0.658692 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Yoshibansal/ML-practical/blob/main/Cat_vs_Dog_Part-1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
##Cat vs Dog (Binary class classification)
ImageDataGenerator
(Understanding overfitting)
Download dataset
```
!wget --no-check-certificate \
https://storage.googleapis.com/mledu-datasets/cats_and_dogs_filtered.zip \
-O /tmp/cats_and_dogs_filtered.zip
#importing libraries
import os
import zipfile
import tensorflow as tf
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
#unzip
local_zip = '/tmp/cats_and_dogs_filtered.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp')
zip_ref.close()
base_dir = '/tmp/cats_and_dogs_filtered'
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'validation')
# Directory with our training cat pictures
train_cats_dir = os.path.join(train_dir, 'cats')
# Directory with our training dog pictures
train_dogs_dir = os.path.join(train_dir, 'dogs')
# Directory with our validation cat pictures
validation_cats_dir = os.path.join(validation_dir, 'cats')
# Directory with our validation dog pictures
validation_dogs_dir = os.path.join(validation_dir, 'dogs')
INPUT_SHAPE = (150, 150)
MODEL_INPUT_SHAPE = INPUT_SHAPE + (3,)
#HYPERPARAMETERS
LEARNING_RATE = 1e-4
BATCH_SIZE = 20
EPOCHS = 50
#model architecture
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape = MODEL_INPUT_SHAPE),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy',
optimizer=RMSprop(lr=LEARNING_RATE),
metrics=['accuracy'])
#summary of model (including type of layer, Ouput shape and number of parameters)
model.summary()
#plotting model and saving it architecture picture
dot_img_file = '/tmp/model_1.png'
tf.keras.utils.plot_model(model, to_file=dot_img_file, show_shapes=True)
# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(rescale=1./255)
test_datagen = ImageDataGenerator(rescale=1./255)
# Flow training images in batches of 20 using train_datagen generator
train_generator = train_datagen.flow_from_directory(
train_dir, # This is the source directory for training images
target_size=INPUT_SHAPE, # All images will be resized to 150x150
batch_size=BATCH_SIZE,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
# Flow validation images in batches of 20 using test_datagen generator
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=INPUT_SHAPE,
batch_size=BATCH_SIZE,
class_mode='binary')
#Fitting data into model -> training model
history = model.fit(
train_generator,
steps_per_epoch=100, # steps = 2000 images / batch_size
epochs=EPOCHS,
validation_data=validation_generator,
validation_steps=50, # steps = 1000 images / batch_size
verbose=1)
#PLOTTING model performance
import matplotlib.pyplot as plt
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.figure()
plt.plot(epochs, loss, 'ro', label='Training Loss')
plt.plot(epochs, val_loss, 'r', label='Validation Loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
The Training Accuracy is close to 100%, and the validation accuracy is in the 70%-80% range. This is a great example of overfitting -- which in short means that it can do very well with images it has seen before, but not so well with images it hasn't.
next we see how we can do better to avoid overfitting -- and one simple method is to **augment** the images a bit.
```
```
| true |
code
| 0.757909 | null | null | null | null |
|
# Approximate q-learning
In this notebook you will teach a __tensorflow__ neural network to do Q-learning.
__Frameworks__ - we'll accept this homework in any deep learning framework. This particular notebook was designed for tensorflow, but you will find it easy to adapt it to almost any python-based deep learning framework.
```
import sys, os
if 'google.colab' in sys.modules:
%tensorflow_version 1.x
if not os.path.exists('.setup_complete'):
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/setup_colab.sh -O- | bash
!touch .setup_complete
# This code creates a virtual display to draw game images on.
# It will have no effect if your machine has a monitor.
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
!bash ../xvfb start
os.environ['DISPLAY'] = ':1'
import gym
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
env = gym.make("CartPole-v0").env
env.reset()
n_actions = env.action_space.n
state_dim = env.observation_space.shape
plt.imshow(env.render("rgb_array"))
```
# Approximate (deep) Q-learning: building the network
To train a neural network policy one must have a neural network policy. Let's build it.
Since we're working with a pre-extracted features (cart positions, angles and velocities), we don't need a complicated network yet. In fact, let's build something like this for starters:
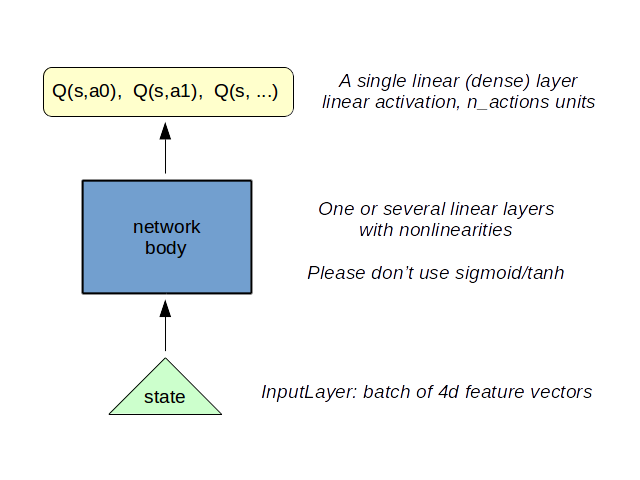
For your first run, please only use linear layers (`L.Dense`) and activations. Stuff like batch normalization or dropout may ruin everything if used haphazardly.
Also please avoid using nonlinearities like sigmoid & tanh: since agent's observations are not normalized, sigmoids might be saturated at initialization. Instead, use non-saturating nonlinearities like ReLU.
Ideally you should start small with maybe 1-2 hidden layers with < 200 neurons and then increase network size if agent doesn't beat the target score.
```
import tensorflow as tf
import keras
import keras.layers as L
tf.reset_default_graph()
sess = tf.InteractiveSession()
keras.backend.set_session(sess)
assert not tf.test.is_gpu_available(), \
"Please complete this assignment without a GPU. If you use a GPU, the code " \
"will run a lot slower due to a lot of copying to and from GPU memory. " \
"To disable the GPU in Colab, go to Runtime → Change runtime type → None."
network = keras.models.Sequential()
network.add(L.InputLayer(state_dim))
<YOUR CODE: stack layers!!!1>
def get_action(state, epsilon=0):
"""
sample actions with epsilon-greedy policy
recap: with p = epsilon pick random action, else pick action with highest Q(s,a)
"""
q_values = network.predict(state[None])[0]
<YOUR CODE>
return <YOUR CODE: epsilon-greedily selected action>
assert network.output_shape == (None, n_actions), "please make sure your model maps state s -> [Q(s,a0), ..., Q(s, a_last)]"
assert network.layers[-1].activation == keras.activations.linear, "please make sure you predict q-values without nonlinearity"
# test epsilon-greedy exploration
s = env.reset()
assert np.shape(get_action(s)) == (), "please return just one action (integer)"
for eps in [0., 0.1, 0.5, 1.0]:
state_frequencies = np.bincount([get_action(s, epsilon=eps) for i in range(10000)], minlength=n_actions)
best_action = state_frequencies.argmax()
assert abs(state_frequencies[best_action] - 10000 * (1 - eps + eps / n_actions)) < 200
for other_action in range(n_actions):
if other_action != best_action:
assert abs(state_frequencies[other_action] - 10000 * (eps / n_actions)) < 200
print('e=%.1f tests passed'%eps)
```
### Q-learning via gradient descent
We shall now train our agent's Q-function by minimizing the TD loss:
$$ L = { 1 \over N} \sum_i (Q_{\theta}(s,a) - [r(s,a) + \gamma \cdot max_{a'} Q_{-}(s', a')]) ^2 $$
Where
* $s, a, r, s'$ are current state, action, reward and next state respectively
* $\gamma$ is a discount factor defined two cells above.
The tricky part is with $Q_{-}(s',a')$. From an engineering standpoint, it's the same as $Q_{\theta}$ - the output of your neural network policy. However, when doing gradient descent, __we won't propagate gradients through it__ to make training more stable (see lectures).
To do so, we shall use `tf.stop_gradient` function which basically says "consider this thing constant when doingbackprop".
```
# Create placeholders for the <s, a, r, s'> tuple and a special indicator for game end (is_done = True)
states_ph = keras.backend.placeholder(dtype='float32', shape=(None,) + state_dim)
actions_ph = keras.backend.placeholder(dtype='int32', shape=[None])
rewards_ph = keras.backend.placeholder(dtype='float32', shape=[None])
next_states_ph = keras.backend.placeholder(dtype='float32', shape=(None,) + state_dim)
is_done_ph = keras.backend.placeholder(dtype='bool', shape=[None])
#get q-values for all actions in current states
predicted_qvalues = network(states_ph)
#select q-values for chosen actions
predicted_qvalues_for_actions = tf.reduce_sum(predicted_qvalues * tf.one_hot(actions_ph, n_actions), axis=1)
gamma = 0.99
# compute q-values for all actions in next states
predicted_next_qvalues = <YOUR CODE: apply network to get q-values for next_states_ph>
# compute V*(next_states) using predicted next q-values
next_state_values = <YOUR CODE>
# compute "target q-values" for loss - it's what's inside square parentheses in the above formula.
target_qvalues_for_actions = <YOUR CODE>
# at the last state we shall use simplified formula: Q(s,a) = r(s,a) since s' doesn't exist
target_qvalues_for_actions = tf.where(is_done_ph, rewards_ph, target_qvalues_for_actions)
#mean squared error loss to minimize
loss = (predicted_qvalues_for_actions - tf.stop_gradient(target_qvalues_for_actions)) ** 2
loss = tf.reduce_mean(loss)
# training function that resembles agent.update(state, action, reward, next_state) from tabular agent
train_step = tf.train.AdamOptimizer(1e-4).minimize(loss)
assert tf.gradients(loss, [predicted_qvalues_for_actions])[0] is not None, "make sure you update q-values for chosen actions and not just all actions"
assert tf.gradients(loss, [predicted_next_qvalues])[0] is None, "make sure you don't propagate gradient w.r.t. Q_(s',a')"
assert predicted_next_qvalues.shape.ndims == 2, "make sure you predicted q-values for all actions in next state"
assert next_state_values.shape.ndims == 1, "make sure you computed V(s') as maximum over just the actions axis and not all axes"
assert target_qvalues_for_actions.shape.ndims == 1, "there's something wrong with target q-values, they must be a vector"
```
### Playing the game
```
sess.run(tf.global_variables_initializer())
def generate_session(env, t_max=1000, epsilon=0, train=False):
"""play env with approximate q-learning agent and train it at the same time"""
total_reward = 0
s = env.reset()
for t in range(t_max):
a = get_action(s, epsilon=epsilon)
next_s, r, done, _ = env.step(a)
if train:
sess.run(train_step,{
states_ph: [s], actions_ph: [a], rewards_ph: [r],
next_states_ph: [next_s], is_done_ph: [done]
})
total_reward += r
s = next_s
if done:
break
return total_reward
epsilon = 0.5
for i in range(1000):
session_rewards = [generate_session(env, epsilon=epsilon, train=True) for _ in range(100)]
print("epoch #{}\tmean reward = {:.3f}\tepsilon = {:.3f}".format(i, np.mean(session_rewards), epsilon))
epsilon *= 0.99
assert epsilon >= 1e-4, "Make sure epsilon is always nonzero during training"
if np.mean(session_rewards) > 300:
print("You Win!")
break
```
### How to interpret results
Welcome to the f.. world of deep f...n reinforcement learning. Don't expect agent's reward to smoothly go up. Hope for it to go increase eventually. If it deems you worthy.
Seriously though,
* __ mean reward__ is the average reward per game. For a correct implementation it may stay low for some 10 epochs, then start growing while oscilating insanely and converges by ~50-100 steps depending on the network architecture.
* If it never reaches target score by the end of for loop, try increasing the number of hidden neurons or look at the epsilon.
* __ epsilon__ - agent's willingness to explore. If you see that agent's already at < 0.01 epsilon before it's is at least 200, just reset it back to 0.1 - 0.5.
### Record videos
As usual, we now use `gym.wrappers.Monitor` to record a video of our agent playing the game. Unlike our previous attempts with state binarization, this time we expect our agent to act ~~(or fail)~~ more smoothly since there's no more binarization error at play.
As you already did with tabular q-learning, we set epsilon=0 for final evaluation to prevent agent from exploring himself to death.
```
# Record sessions
import gym.wrappers
with gym.wrappers.Monitor(gym.make("CartPole-v0"), directory="videos", force=True) as env_monitor:
sessions = [generate_session(env_monitor, epsilon=0, train=False) for _ in range(100)]
# Show video. This may not work in some setups. If it doesn't
# work for you, you can download the videos and view them locally.
from pathlib import Path
from IPython.display import HTML
video_names = sorted([s for s in Path('videos').iterdir() if s.suffix == '.mp4'])
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format(video_names[-1])) # You can also try other indices
```
| true |
code
| 0.598899 | null | null | null | null |
|
# Developing Advanced User Interfaces
*Using Jupyter Widgets, Pandas Dataframes and Matplotlib*
While BPTK-Py offers a number of high-level functions to quickly plot equations (such as `bptk.plot_scenarios`) or create a dashboard (e.g. `bptk.dashboard`), you may sometimes be in a situation when you want to create more sophisticated plots (e.g. plots with two axes) or a more sophisticated interface dashboard for your simulation.
This is actually quite easy, because BPTK-Py's high-level functions already utilize some very powerfull open source libraries for data management, plotting and dashboards: Pandas, Matplotlib and Jupyter Widgets.
In order to harness the full power of these libraries, you only need to understand how to make the data generated by BPTK-Py available to them. This _How To_ illustrates this using a neat little simulation of customer acquisition strategies. You don't need to understand the simulation to follow this document, but if you are interested you can read more about it on our [blog](https://www.transentis.com/an-example-to-illustrate-the-business-prototyping-methodology/).
## Advanced Plotting
We'll start with some advanced plotting of simulation results.
```
## Load the BPTK Package
from BPTK_Py.bptk import bptk
bptk = bptk()
```
BPTK-Py's workhorse for creating plots is the `bptk.plot_scenarios`function. The function generates all the data you would like to plot using the simulation defined by the scenario manager and the settings defined by the scenarios. The data are stored in a Pandas dataframe. When it comes to plotting the results, the framework uses Matplotlib. To illustrate this, we will recreate the plot below directly from the underlying data:
```
bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["base"],
equations=['customers'],
title="Base",
freq="M",
x_label="Time",
y_label="No. of Customers"
)
```
You can access the data generated by a scenario by saving it into a dataframe. You can do this by adding the `return_df` flag to `bptk.plot_scenario`:
```
df=bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["base"],
equations=['customers'],
title="Base",
freq="M",
x_label="Time",
y_label="No. of Customers",
return_df=True
)
```
The dataframe is indexed by time and stores the equations (in SD models) or agent properties (in Agent-based models) in the columns
```
df[0:10] # just show the first ten items
```
The frameworks `bptk.plot_scenarios` method first runs the simulation using the setting defined in the scenario and stores the data in a dataframe. It then plots the dataframe using Pandas `df.plot`method.
We can do the same:
```
subplot=df.plot(None,"customers")
```
The plot above doesn't look quite as neat as the plots created by `bptk.plot_scenarios`– this is because the framework applies some styling information. The styling information is stored in BPTK_Py.config, and you can access (and modify) it there.
Now let's apply the config to `df.plot`:
```
import BPTK_Py.config as config
subplot=df.plot(kind=config.configuration["kind"],
alpha=config.configuration["alpha"], stacked=config.configuration["stacked"],
figsize=config.configuration["figsize"],
title="Base",
color=config.configuration["colors"],
lw=config.configuration["linewidth"])
```
Yes! We've recreated the plot from the high level `btpk.plot_scenarios` method using basic plotting functions.
Now let's do something that currently isn't possible using the high-level BPTK-Py methods - let's create a graph that has two axes.
This is useful when you want to show the results of two equations at the same time, but they have different orders of magnitudes. For instance in the plot below, the number of customers is much smaller than the profit made, so the customer graph looks like a straight line. But it would still be intersting to be able to compare the two graphs.
```
bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["base"],
equations=['customers','profit'],
title="Base",
freq="M",
x_label="Time",
y_label="No. of Customers"
)
```
As before, we collect the data in a dataframe.
```
df=bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["base"],
equations=['customers','profit'],
title="Base",
freq="M",
x_label="Time",
y_label="No. of Customers",
return_df = True
)
df[0:10]
```
Plotting two axes is easy in Pandas (which itself uses the Matplotlib library):
```
ax = df.plot(None,'customers', kind=config.configuration["kind"],
alpha=config.configuration["alpha"], stacked=config.configuration["stacked"],
figsize=config.configuration["figsize"],
title="Profit vs. Customers",
color=config.configuration["colors"],
lw=config.configuration["linewidth"])
# ax is a Matplotlib Axes object
ax1 = ax.twinx()
# Matplotlib.axes.Axes.twinx creates a twin y-axis.
plot =df.plot(None,'profit',ax=ax1)
```
Voila! This is actually quite easy one you understand how to access the data (and of course a little knowledge of Pandas and Matplotlib is also useful). If you were writing a document that needed a lot of plots of this kind, you could create your own high-level function to avoide having to copy and paste the code above multiple times.
## Advanced interactive user interfaces
Now let's try something a little more challenging: Let's build a dashboard for our simulation that let's you manipulate some of the scenrio settings interactively and plots results in tabs.
> Note: You need to have widgets enabled in Jupyter for the following to work. Please check the [BPTK-Py installation instructions](https://bptk.transentis-labs.com/en/latest/docs/usage/installation.html) or refer to the [Jupyter Widgets](https://ipywidgets.readthedocs.io/en/latest/user_install.html) documentation
First, we need to understand how to create tabs. For this we need to import the `ipywidget` Library and we also need to access Matplotlib's `pyplot`
```
%matplotlib inline
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets
```
Then we can create some tabs that display scenario results as follows:
```
out1 = widgets.Output()
out2 = widgets.Output()
tab = widgets.Tab(children = [out1, out2])
tab.set_title(0, 'Customers')
tab.set_title(1, 'Profit')
display(tab)
with out1:
# turn of pyplot's interactive mode to ensure the plot is not created directly
plt.ioff()
# create the plot, but don't show it yet
bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["hereWeGo"],
equations=['customers'],
title="Here We Go",
freq="M",
x_label="Time",
y_label="No. of Customers"
)
# show the plot
plt.show()
# turn interactive mode on again
plt.ion()
with out2:
plt.ioff()
bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["hereWeGo"],
equations=['profit'],
title="Here We Go",
freq="M",
x_label="Time",
y_label="Euro"
)
plt.show()
plt.ion()
```
That was easy! The only thing you really need to understand is to turn interactive plotting in `pyplot` off before creating the tabs and then turn it on again to create the plots. If you forget to do that, the plots appear above the tabs (try it and see!).
In the next step, we need to add some sliders to manipulate the following scenario settings:
* Referrals
* Referral Free Months
* Referral Program Adoption %
* Advertising Success %
Creating a slider for the referrals is easy using the integer slider from the `ipywidgets` widget library:
```
widgets.IntSlider(
value=7,
min=0,
max=15,
step=1,
description='Referrals:',
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='d'
)
```
When manipulating a simulation model, we mostly want to start with a particular scenario and then manipulate some of the scenario settings using interactive widgets. Let's set up a new scenario for this purpose and call it `interactiveScenario`:
```
bptk.register_scenarios(scenario_manager="smCustomerAcquisition", scenarios=
{
"interactiveScenario":{
"constants":{
"referrals":0,
"advertisingSuccessPct":0.1,
"referralFreeMonths":3,
"referralProgamAdoptionPct":10
}
}
}
)
```
We can then access the scenario using `bptk.get_scenarios`:
```
scenario = bptk.get_scenario("smCustomerAcquisition","interactiveScenario")
scenario.constants
bptk.plot_scenarios(scenario_managers=["smCustomerAcquisition"],
scenarios=["interactiveScenario"],
equations=['profit'],
title="Interactive Scenario",
freq="M",
x_label="Time",
y_label="Euro"
)
```
The scenario constants can be accessed in the constants variable:
Now we have all the right pieces, we can put them together using the interact function.
```
@interact(advertising_success_pct=widgets.FloatSlider(
value=0.1,
min=0,
max=1,
step=0.01,
continuous_update=False,
description='Advertising Success Pct'
))
def dashboard(advertising_success_pct):
scenario= bptk.get_scenario("smCustomerAcquisition",
"interactiveScenario")
scenario.constants["advertisingSuccessPct"]=advertising_success_pct
bptk.reset_scenario_cache(scenario_manager="smCustomerAcquisition",
scenario="interactiveScenario")
bptk.plot_scenarios(scenario_managers=["smCustomerAcquisition"],
scenarios=["interactiveScenario"],
equations=['profit'],
title="Interactive Scenario",
freq="M",
x_label="Time",
y_label="Euro"
)
```
Now let's combine this with the tabs from above.
```
out1 = widgets.Output()
out2 = widgets.Output()
tab = widgets.Tab(children = [out1, out2])
tab.set_title(0, 'Customers')
tab.set_title(1, 'Profit')
display(tab)
@interact(advertising_success_pct=widgets.FloatSlider(
value=0.1,
min=0,
max=10,
step=0.01,
continuous_update=False,
description='Advertising Success Pct'
))
def dashboardWithTabs(advertising_success_pct):
scenario= bptk.get_scenario("smCustomerAcquisition","interactiveScenario")
scenario.constants["advertisingSuccessPct"]=advertising_success_pct
bptk.reset_scenario_cache(scenario_manager="smCustomerAcquisition",
scenario="interactiveScenario")
with out1:
# turn of pyplot's interactive mode to ensure the plot is not created directly
plt.ioff()
# clear the widgets output ... otherwise we will end up with a long list of plots, one for each change of settings
# create the plot, but don't show it yet
bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["interactiveScenario"],
equations=['customers'],
title="Interactive Scenario",
freq="M",
x_label="Time",
y_label="No. of Customers"
)
# show the plot
out1.clear_output()
plt.show()
# turn interactive mode on again
plt.ion()
with out2:
plt.ioff()
out2.clear_output()
bptk.plot_scenarios(
scenario_managers=["smCustomerAcquisition"],
scenarios=["interactiveScenario"],
equations=['profit'],
title="Interactive Scenario",
freq="M",
x_label="Time",
y_label="Euro"
)
plt.show()
plt.ion()
```
| true |
code
| 0.779637 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/kartikgill/The-GAN-Book/blob/main/Skill-08/Cycle-GAN-No-Outputs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Import Useful Libraries
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm_notebook
%matplotlib inline
import tensorflow
print (tensorflow.__version__)
```
# Download and Unzip Data
```
!wget https://people.eecs.berkeley.edu/~taesung_park/CycleGAN/datasets/horse2zebra.zip
!unzip horse2zebra.zip
!ls horse2zebra
import glob
path = ""
horses_train = glob.glob(path + 'horse2zebra/trainA/*.jpg')
zebras_train = glob.glob(path + 'horse2zebra/trainB/*.jpg')
horses_test = glob.glob(path + 'horse2zebra/testA/*.jpg')
zebras_test = glob.glob(path + 'horse2zebra/testB/*.jpg')
len(horses_train), len(zebras_train), len(horses_test), len(zebras_test)
import cv2
for file in horses_train[:10]:
img = cv2.imread(file)
print (img.shape)
```
# Display few Samples
```
print ("Horses")
for k in range(2):
plt.figure(figsize=(15, 15))
for j in range(6):
file = np.random.choice(horses_train)
img = cv2.imread(file)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.subplot(660 + 1 + j)
plt.imshow(img)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
print ("-"*80)
print ("Zebras")
for k in range(2):
plt.figure(figsize=(15, 15))
for j in range(6):
file = np.random.choice(zebras_train)
img = cv2.imread(file)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.subplot(660 + 1 + j)
plt.imshow(img)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
```
# Define Generator Model (Res-Net Like)
```
#Following function is taken from: https://keras.io/examples/generative/cyclegan/
class ReflectionPadding2D(tensorflow.keras.layers.Layer):
"""Implements Reflection Padding as a layer.
Args:
padding(tuple): Amount of padding for the
spatial dimensions.
Returns:
A padded tensor with the same type as the input tensor.
"""
def __init__(self, padding=(1, 1), **kwargs):
self.padding = tuple(padding)
super(ReflectionPadding2D, self).__init__(**kwargs)
def call(self, input_tensor, mask=None):
padding_width, padding_height = self.padding
padding_tensor = [
[0, 0],
[padding_height, padding_height],
[padding_width, padding_width],
[0, 0],
]
return tensorflow.pad(input_tensor, padding_tensor, mode="REFLECT")
import tensorflow_addons as tfa
# Weights initializer for the layers.
kernel_init = tensorflow.keras.initializers.RandomNormal(mean=0.0, stddev=0.02)
# Gamma initializer for instance normalization.
gamma_init = tensorflow.keras.initializers.RandomNormal(mean=0.0, stddev=0.02)
def custom_resnet_block(input_data, filters):
x = ReflectionPadding2D()(input_data)
x = tensorflow.keras.layers.Conv2D(filters, kernel_size=(3,3), padding='valid', kernel_initializer=kernel_init)(x)
x = tfa.layers.InstanceNormalization()(x)
x = tensorflow.keras.layers.Activation('relu')(x)
x = ReflectionPadding2D()(x)
x = tensorflow.keras.layers.Conv2D(filters, kernel_size=(3,3), padding='valid', kernel_initializer=kernel_init)(x)
x = tfa.layers.InstanceNormalization()(x)
x = tensorflow.keras.layers.Add()([x, input_data])
return x
def make_generator():
source_image = tensorflow.keras.layers.Input(shape=(256, 256, 3))
x = ReflectionPadding2D(padding=(3, 3))(source_image)
x = tensorflow.keras.layers.Conv2D(64, kernel_size=(7,7), kernel_initializer=kernel_init, use_bias=False)(x)
x = tfa.layers.InstanceNormalization()(x)
x = tensorflow.keras.layers.Activation('relu')(x)
x = tensorflow.keras.layers.Conv2D(128, kernel_size=(3,3), strides=(2,2), padding='same', kernel_initializer=kernel_init)(x)
x = tfa.layers.InstanceNormalization()(x)
x = tensorflow.keras.layers.Activation('relu')(x)
x = tensorflow.keras.layers.Conv2D(256, kernel_size=(3,3), strides=(2,2), padding='same', kernel_initializer=kernel_init)(x)
x = tfa.layers.InstanceNormalization()(x)
x = tensorflow.keras.layers.Activation('relu')(x)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = custom_resnet_block(x, 256)
x = tensorflow.keras.layers.Conv2DTranspose(128, kernel_size=(3,3), strides=(2,2), padding='same', kernel_initializer=kernel_init)(x)
x = tfa.layers.InstanceNormalization()(x)
x = tensorflow.keras.layers.Activation('relu')(x)
x = tensorflow.keras.layers.Conv2DTranspose(64, kernel_size=(3,3), strides=(2,2), padding='same', kernel_initializer=kernel_init)(x)
x = tfa.layers.InstanceNormalization()(x)
x = tensorflow.keras.layers.Activation('relu')(x)
x = ReflectionPadding2D(padding=(3, 3))(x)
x = tensorflow.keras.layers.Conv2D(3, kernel_size=(7,7), padding='valid')(x)
x = tfa.layers.InstanceNormalization()(x)
translated_image = tensorflow.keras.layers.Activation('tanh')(x)
return source_image, translated_image
source_image, translated_image = make_generator()
generator_network_AB = tensorflow.keras.models.Model(inputs=source_image, outputs=translated_image)
source_image, translated_image = make_generator()
generator_network_BA = tensorflow.keras.models.Model(inputs=source_image, outputs=translated_image)
print (generator_network_AB.summary())
```
# Define Discriminator Network
```
def my_conv_layer(input_layer, filters, strides, bn=True):
x = tensorflow.keras.layers.Conv2D(filters, kernel_size=(4,4), strides=strides, padding='same', kernel_initializer=kernel_init)(input_layer)
x = tensorflow.keras.layers.LeakyReLU(alpha=0.2)(x)
if bn:
x = tfa.layers.InstanceNormalization()(x)
return x
def make_discriminator():
target_image_input = tensorflow.keras.layers.Input(shape=(256, 256, 3))
x = my_conv_layer(target_image_input, 64, (2,2), bn=False)
x = my_conv_layer(x, 128, (2,2))
x = my_conv_layer(x, 256, (2,2))
x = my_conv_layer(x, 512, (1,1))
patch_features = tensorflow.keras.layers.Conv2D(1, kernel_size=(4,4), padding='same')(x)
return target_image_input, patch_features
target_image_input, patch_features = make_discriminator()
discriminator_network_A = tensorflow.keras.models.Model(inputs=target_image_input, outputs=patch_features)
target_image_input, patch_features = make_discriminator()
discriminator_network_B = tensorflow.keras.models.Model(inputs=target_image_input, outputs=patch_features)
print (discriminator_network_A.summary())
adam_optimizer = tensorflow.keras.optimizers.Adam(learning_rate=0.0002, beta_1=0.5)
discriminator_network_A.compile(loss='mse', optimizer=adam_optimizer, metrics=['accuracy'])
discriminator_network_B.compile(loss='mse', optimizer=adam_optimizer, metrics=['accuracy'])
```
# Define Cycle-GAN
```
source_image_A = tensorflow.keras.layers.Input(shape=(256, 256, 3))
source_image_B = tensorflow.keras.layers.Input(shape=(256, 256, 3))
# Domain Transfer
fake_B = generator_network_AB(source_image_A)
fake_A = generator_network_BA(source_image_B)
# Restoring original Domain
get_back_A = generator_network_BA(fake_B)
get_back_B = generator_network_AB(fake_A)
# Get back Identical/Same Image
get_same_A = generator_network_BA(source_image_A)
get_same_B = generator_network_AB(source_image_B)
discriminator_network_A.trainable=False
discriminator_network_B.trainable=False
# Tell Real vs Fake, for a given domain
verify_A = discriminator_network_A(fake_A)
verify_B = discriminator_network_B(fake_B)
cycle_gan = tensorflow.keras.models.Model(inputs = [source_image_A, source_image_B], \
outputs = [verify_A, verify_B, get_back_A, get_back_B, get_same_A, get_same_B])
cycle_gan.summary()
```
# Compiling Model
```
cycle_gan.compile(loss=['mse', 'mse', 'mae', 'mae', 'mae', 'mae'], loss_weights=[1, 1, 10, 10, 5, 5],\
optimizer=adam_optimizer)
```
# Define Data Generators
```
def horses_to_zebras(horses, generator_network):
generated_samples = generator_network.predict_on_batch(horses)
return generated_samples
def zebras_to_horses(zebras, generator_network):
generated_samples = generator_network.predict_on_batch(zebras)
return generated_samples
def get_horse_samples(batch_size):
random_files = np.random.choice(horses_train, size=batch_size)
images = []
for file in random_files:
img = cv2.imread(file)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
images.append((img-127.5)/127.5)
horse_images = np.array(images)
return horse_images
def get_zebra_samples(batch_size):
random_files = np.random.choice(zebras_train, size=batch_size)
images = []
for file in random_files:
img = cv2.imread(file)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
images.append((img-127.5)/127.5)
zebra_images = np.array(images)
return zebra_images
def show_generator_results_horses_to_zebras(generator_network_AB, generator_network_BA):
images = []
for j in range(5):
file = np.random.choice(horses_test)
img = cv2.imread(file)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
images.append(img)
print ('Input Horse Images')
plt.figure(figsize=(13, 13))
for j, img in enumerate(images):
plt.subplot(550 + 1 + j)
plt.imshow(img)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
print ('Translated (Horse -> Zebra) Images')
translated = []
plt.figure(figsize=(13, 13))
for j, img in enumerate(images):
img = (img-127.5)/127.5
output = horses_to_zebras(np.array([img]), generator_network_AB)[0]
translated.append(output)
output = (output+1.0)/2.0
plt.subplot(550 + 1 + j)
plt.imshow(output)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
print ('Translated reverse ( Fake Zebras -> Fake Horses)')
plt.figure(figsize=(13, 13))
for j, img in enumerate(translated):
output = zebras_to_horses(np.array([img]), generator_network_BA)[0]
output = (output+1.0)/2.0
plt.subplot(550 + 1 + j)
plt.imshow(output)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
def show_generator_results_zebras_to_horses(generator_network_AB, generator_network_BA):
images = []
for j in range(5):
file = np.random.choice(zebras_test)
img = cv2.imread(file)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
images.append(img)
print ('Input Zebra Images')
plt.figure(figsize=(13, 13))
for j, img in enumerate(images):
plt.subplot(550 + 1 + j)
plt.imshow(img)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
print ('Translated (Zebra -> Horse) Images')
translated = []
plt.figure(figsize=(13, 13))
for j, img in enumerate(images):
img = (img-127.5)/127.5
output = zebras_to_horses(np.array([img]), generator_network_BA)[0]
translated.append(output)
output = (output+1.0)/2.0
plt.subplot(550 + 1 + j)
plt.imshow(output)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
print ('Translated reverse (Fake Horse -> Fake Zebra)')
plt.figure(figsize=(13, 13))
for j, img in enumerate(translated):
output = horses_to_zebras(np.array([img]), generator_network_AB)[0]
output = (output+1.0)/2.0
plt.subplot(550 + 1 + j)
plt.imshow(output)
plt.axis('off')
#plt.title(trainY[i])
plt.show()
```
# Training Cycle-GAN
```
len(horses_train), len(zebras_train)
epochs = 500
batch_size = 1
steps = 1067
for i in range(0, epochs):
if i%5 == 0:
show_generator_results_horses_to_zebras(generator_network_AB, generator_network_BA)
print ("-"*100)
show_generator_results_zebras_to_horses(generator_network_AB, generator_network_BA)
for j in range(steps):
# A == Horses
# B == Zebras
domain_A_images = get_horse_samples(batch_size)
domain_B_images = get_zebra_samples(batch_size)
fake_patch = np.zeros((batch_size, 32, 32, 1))
real_patch = np.ones((batch_size, 32, 32, 1))
fake_B_images = generator_network_AB(domain_A_images)
fake_A_images = generator_network_BA(domain_B_images)
# Updating Discriminator A weights
discriminator_network_A.trainable=True
discriminator_network_B.trainable=False
loss_d_real_A = discriminator_network_A.train_on_batch(domain_A_images, real_patch)
loss_d_fake_A = discriminator_network_A.train_on_batch(fake_A_images, fake_patch)
loss_d_A = np.add(loss_d_real_A, loss_d_fake_A)/2.0
# Updating Discriminator B weights
discriminator_network_B.trainable=True
discriminator_network_A.trainable=False
loss_d_real_B = discriminator_network_B.train_on_batch(domain_B_images, real_patch)
loss_d_fake_B = discriminator_network_B.train_on_batch(fake_B_images, fake_patch)
loss_d_B = np.add(loss_d_real_B, loss_d_fake_B)/2.0
# Make the Discriminator belive that these are real samples and calculate loss to train the generator
discriminator_network_A.trainable=False
discriminator_network_B.trainable=False
# Updating Generator weights
loss_g = cycle_gan.train_on_batch([domain_A_images, domain_B_images],\
[real_patch, real_patch, domain_A_images, domain_B_images, domain_A_images, domain_B_images])
if j%100 == 0:
print ("Epoch:%.0f, Step:%.0f, DA-Loss:%.3f, DA-Acc:%.3f, DB-Loss:%.3f, DB-Acc:%.3f, G-Loss:%.3f"\
%(i,j,loss_d_A[0],loss_d_A[1]*100,loss_d_B[0],loss_d_B[1]*100,loss_g[0]))
```
| true |
code
| 0.748982 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/agemagician/Prot-Transformers/blob/master/Embedding/Advanced/Electra.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<h3> Extracting protein sequences' features using ProtElectra pretrained-model <h3>
<b>1. Load necessry libraries including huggingface transformers<b>
```
!pip install -q transformers
import torch
from transformers import ElectraTokenizer, ElectraForPreTraining, ElectraForMaskedLM, ElectraModel
import re
import os
import requests
from tqdm.auto import tqdm
```
<b>2. Set the url location of ProtElectra and the vocabulary file<b>
```
generatorModelUrl = 'https://www.dropbox.com/s/5x5et5q84y3r01m/pytorch_model.bin?dl=1'
discriminatorModelUrl = 'https://www.dropbox.com/s/9ptrgtc8ranf0pa/pytorch_model.bin?dl=1'
generatorConfigUrl = 'https://www.dropbox.com/s/9059fvix18i6why/config.json?dl=1'
discriminatorConfigUrl = 'https://www.dropbox.com/s/jq568evzexyla0p/config.json?dl=1'
vocabUrl = 'https://www.dropbox.com/s/wck3w1q15bc53s0/vocab.txt?dl=1'
```
<b>3. Download ProtElectra models and vocabulary files<b>
```
downloadFolderPath = 'models/electra/'
discriminatorFolderPath = os.path.join(downloadFolderPath, 'discriminator')
generatorFolderPath = os.path.join(downloadFolderPath, 'generator')
discriminatorModelFilePath = os.path.join(discriminatorFolderPath, 'pytorch_model.bin')
generatorModelFilePath = os.path.join(generatorFolderPath, 'pytorch_model.bin')
discriminatorConfigFilePath = os.path.join(discriminatorFolderPath, 'config.json')
generatorConfigFilePath = os.path.join(generatorFolderPath, 'config.json')
vocabFilePath = os.path.join(downloadFolderPath, 'vocab.txt')
if not os.path.exists(discriminatorFolderPath):
os.makedirs(discriminatorFolderPath)
if not os.path.exists(generatorFolderPath):
os.makedirs(generatorFolderPath)
def download_file(url, filename):
response = requests.get(url, stream=True)
with tqdm.wrapattr(open(filename, "wb"), "write", miniters=1,
total=int(response.headers.get('content-length', 0)),
desc=filename) as fout:
for chunk in response.iter_content(chunk_size=4096):
fout.write(chunk)
if not os.path.exists(generatorModelFilePath):
download_file(generatorModelUrl, generatorModelFilePath)
if not os.path.exists(discriminatorModelFilePath):
download_file(discriminatorModelUrl, discriminatorModelFilePath)
if not os.path.exists(generatorConfigFilePath):
download_file(generatorConfigUrl, generatorConfigFilePath)
if not os.path.exists(discriminatorConfigFilePath):
download_file(discriminatorConfigUrl, discriminatorConfigFilePath)
if not os.path.exists(vocabFilePath):
download_file(vocabUrl, vocabFilePath)
```
<b>4. Load the vocabulary and ProtElectra discriminator and generator Models<b>
```
tokenizer = ElectraTokenizer(vocabFilePath, do_lower_case=False )
discriminator = ElectraForPreTraining.from_pretrained(discriminatorFolderPath)
generator = ElectraForMaskedLM.from_pretrained(generatorFolderPath)
electra = ElectraModel.from_pretrained(discriminatorFolderPath)
```
<b>5. Load the model into the GPU if avilabile and switch to inference mode<b>
```
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
discriminator = discriminator.to(device)
discriminator = discriminator.eval()
generator = generator.to(device)
generator = generator.eval()
electra = electra.to(device)
electra = electra.eval()
```
<b>6. Create or load sequences and map rarely occured amino acids (U,Z,O,B) to (X)<b>
```
sequences_Example = ["A E T C Z A O","S K T Z P"]
sequences_Example = [re.sub(r"[UZOB]", "X", sequence) for sequence in sequences_Example]
```
<b>7. Tokenize, encode sequences and load it into the GPU if possibile<b>
```
ids = tokenizer.batch_encode_plus(sequences_Example, add_special_tokens=True, pad_to_max_length=True)
input_ids = torch.tensor(ids['input_ids']).to(device)
attention_mask = torch.tensor(ids['attention_mask']).to(device)
```
<b>8. Extracting sequences' features and load it into the CPU if needed<b>
```
with torch.no_grad():
discriminator_embedding = discriminator(input_ids=input_ids,attention_mask=attention_mask)[0]
discriminator_embedding = discriminator_embedding.cpu().numpy()
with torch.no_grad():
generator_embedding = generator(input_ids=input_ids,attention_mask=attention_mask)[0]
generator_embedding = generator_embedding.cpu().numpy()
with torch.no_grad():
electra_embedding = electra(input_ids=input_ids,attention_mask=attention_mask)[0]
electra_embedding = electra_embedding.cpu().numpy()
```
<b>9. Remove padding ([PAD]) and special tokens ([CLS],[SEP]) that is added by Electra model<b>
```
features = []
for seq_num in range(len(electra_embedding)):
seq_len = (attention_mask[seq_num] == 1).sum()
seq_emd = electra_embedding[seq_num][1:seq_len-1]
features.append(seq_emd)
print(features)
```
| true |
code
| 0.566798 | null | null | null | null |
|
```
library(keras)
```
**Loading MNIST dataset from the library datasets**
```
mnist <- dataset_mnist()
x_train <- mnist$train$x
y_train <- mnist$train$y
x_test <- mnist$test$x
y_test <- mnist$test$y
```
**Data Preprocessing**
```
# reshape
x_train <- array_reshape(x_train, c(nrow(x_train), 784))
x_test <- array_reshape(x_test, c(nrow(x_test), 784))
# rescale
x_train <- x_train / 255
x_test <- x_test / 255
```
The y data is an integer vector with values ranging from 0 to 9.
To prepare this data for training we one-hot encode the vectors into binary class matrices using the Keras to_categorical() function:
```
y_train <- to_categorical(y_train, 10)
y_test <- to_categorical(y_test, 10)
```
**Building model**
```
model <- keras_model_sequential()
model %>%
layer_dense(units = 256, activation = 'relu', input_shape = c(784)) %>%
layer_dropout(rate = 0.4) %>%
layer_dense(units = 128, activation = 'relu') %>%
layer_dropout(rate = 0.3) %>%
layer_dense(units = 10, activation = 'softmax')
# Use the summary() function to print the details of the model:
summary(model)
```
**Compiling the model**
```
model %>% compile(
loss = 'categorical_crossentropy',
optimizer = optimizer_rmsprop(),
metrics = c('accuracy')
)
```
**Training and Evaluation**
```
history <- model %>% fit(
x_train, y_train,
epochs = 30, batch_size = 128,
validation_split = 0.2
)
plot(history)
# Plot the accuracy of the training data
plot(history$metrics$acc, main="Model Accuracy", xlab = "epoch", ylab="accuracy", col="blue", type="l")
# Plot the accuracy of the validation data
lines(history$metrics$val_acc, col="green")
# Add Legend
legend("bottomright", c("train","test"), col=c("blue", "green"), lty=c(1,1))
# Plot the model loss of the training data
plot(history$metrics$loss, main="Model Loss", xlab = "epoch", ylab="loss", col="blue", type="l")
# Plot the model loss of the test data
lines(history$metrics$val_loss, col="green")
# Add legend
legend("topright", c("train","test"), col=c("blue", "green"), lty=c(1,1))
```
**Predicting for the test data**
```
model %>% predict_classes(x_test)
# Evaluate on test data and labels
score <- model %>% evaluate(x_test, y_test, batch_size = 128)
# Print the score
print(score)
```
## Hyperparameter tuning
```
# install.packages("tfruns")
library(tfruns)
runs <- tuning_run(file = "hyperparameter_tuning_model.r", flags = list(
dense_units1 = c(8,16),
dropout1 = c(0.2, 0.3, 0.4),
dense_units2 = c(8,16),
dropout2 = c(0.2, 0.3, 0.4)
))
runs
```
| true |
code
| 0.722148 | null | null | null | null |
|
## This notebook contains a sample code for the COMPAS data experiment in Section 5.2.
Before running the code, please check README.md and install LEMON.
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn import feature_extraction
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import stealth_sampling
```
### Functions
```
# split data to bins (s, y) = (1, 1), (1, 0), (0, 1), (0, 0)
def split_to_four(X, S, Y):
Z = np.c_[X, S, Y]
Z_pos_pos = Z[np.logical_and(S, Y), :]
Z_pos_neg = Z[np.logical_and(S, np.logical_not(Y)), :]
Z_neg_pos = Z[np.logical_and(np.logical_not(S), Y), :]
Z_neg_neg = Z[np.logical_and(np.logical_not(S), np.logical_not(Y)), :]
Z = [Z_pos_pos, Z_pos_neg, Z_neg_pos, Z_neg_neg]
return Z
# compute demographic parity
def demographic_parity(W):
p_pos = np.mean(np.concatenate(W[:2]))
p_neg = np.mean(np.concatenate(W[2:]))
return np.abs(p_pos - p_neg)
# compute the sampling size from each bin
def computeK(Z, Nsample, sampled_spos, sampled_ypos):
Kpp = Nsample*sampled_spos*sampled_ypos[0]
Kpn = Nsample*sampled_spos*(1-sampled_ypos[0])
Knp = Nsample*(1-sampled_spos)*sampled_ypos[1]
Knn = Nsample*(1-sampled_spos)*(1-sampled_ypos[1])
K = [Kpp, Kpn, Knp, Knn]
kratio = min([min(1, z.shape[0]/k) for (z, k) in zip(Z, K)])
Kpp = int(np.floor(Nsample*kratio*sampled_spos*sampled_ypos[0]))
Kpn = int(np.floor(Nsample*kratio*sampled_spos*(1-sampled_ypos[0])))
Knp = int(np.floor(Nsample*kratio*(1-sampled_spos)*sampled_ypos[1]))
Knn = int(np.floor(Nsample*kratio*(1-sampled_spos)*(1-sampled_ypos[1])))
K = [max([k, 1]) for k in [Kpp, Kpn, Knp, Knn]]
return K
# case-contrl sampling
def case_control_sampling(X, K):
q = [(K[i]/sum(K)) * np.ones(x.shape[0]) / x.shape[0] for i, x in enumerate(X)]
return q
# compute wasserstein distance
def compute_wasserstein(X1, S1, X2, S2, timeout=10.0):
dx = stealth_sampling.compute_wasserstein(X1, X2, path='./', prefix='compas', timeout=timeout)
dx_s1 = stealth_sampling.compute_wasserstein(X1[S1>0.5, :], X2[S2>0.5, :], path='./', prefix='compas', timeout=timeout)
dx_s0 = stealth_sampling.compute_wasserstein(X1[S1<0.5, :], X2[S2<0.5, :], path='./', prefix='compas', timeout=timeout)
return dx, dx_s1, dx_s0
```
### Fetch data and preprocess
We modified [https://github.com/mbilalzafar/fair-classification/blob/master/disparate_mistreatment/propublica_compas_data_demo/load_compas_data.py]
```
url = 'https://raw.githubusercontent.com/propublica/compas-analysis/master/compas-scores-two-years.csv'
feature_list = ['age_cat', 'race', 'sex', 'priors_count', 'c_charge_degree', 'two_year_recid']
sensitive = 'race'
label = 'score_text'
# fetch data
df = pd.read_table(url, sep=',')
df = df.dropna(subset=['days_b_screening_arrest'])
# convert to np array
data = df.to_dict('list')
for k in data.keys():
data[k] = np.array(data[k])
# filtering records
idx = np.logical_and(data['days_b_screening_arrest']<=30, data['days_b_screening_arrest']>=-30)
idx = np.logical_and(idx, data['is_recid'] != -1)
idx = np.logical_and(idx, data['c_charge_degree'] != 'O')
idx = np.logical_and(idx, data['score_text'] != 'NA')
idx = np.logical_and(idx, np.logical_or(data['race'] == 'African-American', data['race'] == 'Caucasian'))
for k in data.keys():
data[k] = data[k][idx]
# label Y
Y = 1 - np.logical_not(data[label]=='Low').astype(np.int32)
# feature X, sensitive feature S
X = []
for feature in feature_list:
vals = data[feature]
if feature == 'priors_count':
vals = [float(v) for v in vals]
vals = preprocessing.scale(vals)
vals = np.reshape(vals, (Y.size, -1))
else:
lb = preprocessing.LabelBinarizer()
lb.fit(vals)
vals = lb.transform(vals)
if feature == sensitive:
S = vals[:, 0]
X.append(vals)
X = np.concatenate(X, axis=1)
```
### Experiment
```
# parameter settings
seed = 0 # random seed
# parameter settings for sampling
Nsample = 2000 # number of data to sample
sampled_ypos = [0.5, 0.5] # the ratio of positive decisions '\alpha' in sampling
# parameter settings for complainer
Nref = 1278 # number of referential data
def sample_and_evaluate(X, S, Y, Nref=1278, Nsample=2000, sampled_ypos=[0.5, 0.5], seed=0):
# load data
Xbase, Xref, Sbase, Sref, Ybase, Yref = train_test_split(X, S, Y, test_size=Nref, random_state=seed)
N = Xbase.shape[0]
scaler = StandardScaler()
scaler.fit(Xbase)
Xbase = scaler.transform(Xbase)
Xref = scaler.transform(Xref)
# wasserstein distance between base and ref
np.random.seed(seed)
idx = np.random.permutation(Xbase.shape[0])[:Nsample]
dx, dx_s1, dx_s0 = compute_wasserstein(Xbase[idx, :], Sbase[idx], Xref, Sref, timeout=10.0)
# demographic parity
Z = split_to_four(Xbase, Sbase, Ybase)
parity = demographic_parity([z[:, -1] for z in Z])
# sampling
results = [[parity, dx, dx_s1, dx_s0]]
sampled_spos = np.mean(Sbase)
K = computeK(Z, Nsample, sampled_spos, sampled_ypos)
for i, sampling in enumerate(['case-control', 'stealth']):
#print('%s: sampling ...' % (sampling,), end='')
np.random.seed(seed+i)
if sampling == 'case-control':
p = case_control_sampling([z[:, :-1] for z in Z], K)
elif sampling == 'stealth':
p = stealth_sampling.stealth_sampling([z[:, :-1] for z in Z], K, path='./', prefix='compas', timeout=30.0)
idx = np.random.choice(N, sum(K), p=np.concatenate(p), replace=False)
Xs = np.concatenate([z[:, :-2] for z in Z], axis=0)[idx, :]
Ss = np.concatenate([z[:, -2] for z in Z], axis=0)[idx]
Ts = np.concatenate([z[:, -1] for z in Z], axis=0)[idx]
#print('done.')
# demographic parity of the sampled data
#print('%s: evaluating ...' % (sampling,), end='')
Zs = split_to_four(Xs, Ss, Ts)
parity = demographic_parity([z[:, -1] for z in Zs])
# wasserstein disttance
dx, dx_s1, dx_s0 = compute_wasserstein(Xs, Ss, Xref, Sref, timeout=10.0)
#print('done.')
results.append([parity, dx, dx_s1, dx_s0])
return results
```
#### Experiment (One Run)
```
result = sample_and_evaluate(X, S, Y, Nref=Nref, Nsample=Nsample, sampled_ypos=sampled_ypos, seed=seed)
df = pd.DataFrame(result)
df.index = ['Baseline', 'Case-control', 'Stealth']
df.columns = ['DP', 'WD on Pr[x]', 'WD on Pr[x|s=1]', 'WD on Pr[x|s=0]']
print('Result (alpha = %.2f, seed=%d)' % (sampled_ypos[0], seed))
df
```
#### Experiment (10 Runs)
```
num_itr = 10
result_all = []
for i in range(num_itr):
result_i = sample_and_evaluate(X, S, Y, Nref=Nref, Nsample=Nsample, sampled_ypos=sampled_ypos, seed=i)
result_all.append(result_i)
result_all = np.array(result_all)
df = pd.DataFrame(np.mean(result_all, axis=0))
df.index = ['Baseline', 'Case-control', 'Stealth']
df.columns = ['DP', 'WD on Pr[x]', 'WD on Pr[x|s=1]', 'WD on Pr[x|s=0]']
print('Average Result of %d runs (alpha = %.2f)' % (num_itr, sampled_ypos[0]))
df
```
| true |
code
| 0.511717 | null | null | null | null |
|
```
from collections import OrderedDict
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import scipy as sp
from theano import shared
%config InlineBackend.figure_format = 'retina'
az.style.use('arviz-darkgrid')
```
#### Code 11.1
```
trolley_df = pd.read_csv('Data/Trolley.csv', sep=';')
trolley_df.head()
```
#### Code 11.2
```
ax = (trolley_df.response
.value_counts()
.sort_index()
.plot(kind='bar'))
ax.set_xlabel("response", fontsize=14);
ax.set_ylabel("Frequency", fontsize=14);
```
#### Code 11.3
```
ax = (trolley_df.response
.value_counts()
.sort_index()
.cumsum()
.div(trolley_df.shape[0])
.plot(marker='o'))
ax.set_xlim(0.9, 7.1);
ax.set_xlabel("response", fontsize=14)
ax.set_ylabel("cumulative proportion", fontsize=14);
```
#### Code 11.4
```
resp_lco = (trolley_df.response
.value_counts()
.sort_index()
.cumsum()
.iloc[:-1]
.div(trolley_df.shape[0])
.apply(lambda p: np.log(p / (1. - p))))
ax = resp_lco.plot(marker='o')
ax.set_xlim(0.9, 7);
ax.set_xlabel("response", fontsize=14)
ax.set_ylabel("log-cumulative-odds", fontsize=14);
```
#### Code 11.5
```
with pm.Model() as m11_1:
a = pm.Normal(
'a', 0., 10.,
transform=pm.distributions.transforms.ordered,
shape=6, testval=np.arange(6) - 2.5)
resp_obs = pm.OrderedLogistic(
'resp_obs', 0., a,
observed=trolley_df.response.values - 1
)
with m11_1:
map_11_1 = pm.find_MAP()
```
#### Code 11.6
```
map_11_1['a']
daf
```
#### Code 11.7
```
sp.special.expit(map_11_1['a'])
```
#### Code 11.8
```
with m11_1:
trace_11_1 = pm.sample(1000, tune=1000)
az.summary(trace_11_1, var_names=['a'], credible_interval=.89, rount_to=2)
```
#### Code 11.9
```
def ordered_logistic_proba(a):
pa = sp.special.expit(a)
p_cum = np.concatenate(([0.], pa, [1.]))
return p_cum[1:] - p_cum[:-1]
ordered_logistic_proba(trace_11_1['a'].mean(axis=0))
```
#### Code 11.10
```
(ordered_logistic_proba(trace_11_1['a'].mean(axis=0)) \
* (1 + np.arange(7))).sum()
```
#### Code 11.11
```
ordered_logistic_proba(trace_11_1['a'].mean(axis=0) - 0.5)
```
#### Code 11.12
```
(ordered_logistic_proba(trace_11_1['a'].mean(axis=0) - 0.5) \
* (1 + np.arange(7))).sum()
```
#### Code 11.13
```
action = shared(trolley_df.action.values)
intention = shared(trolley_df.intention.values)
contact = shared(trolley_df.contact.values)
with pm.Model() as m11_2:
a = pm.Normal(
'a', 0., 10.,
transform=pm.distributions.transforms.ordered,
shape=6,
testval=trace_11_1['a'].mean(axis=0)
)
bA = pm.Normal('bA', 0., 10.)
bI = pm.Normal('bI', 0., 10.)
bC = pm.Normal('bC', 0., 10.)
phi = bA * action + bI * intention + bC * contact
resp_obs = pm.OrderedLogistic(
'resp_obs', phi, a,
observed=trolley_df.response.values - 1
)
with m11_2:
map_11_2 = pm.find_MAP()
```
#### Code 11.14
```
with pm.Model() as m11_3:
a = pm.Normal(
'a', 0., 10.,
transform=pm.distributions.transforms.ordered,
shape=6,
testval=trace_11_1['a'].mean(axis=0)
)
bA = pm.Normal('bA', 0., 10.)
bI = pm.Normal('bI', 0., 10.)
bC = pm.Normal('bC', 0., 10.)
bAI = pm.Normal('bAI', 0., 10.)
bCI = pm.Normal('bCI', 0., 10.)
phi = bA * action + bI * intention + bC * contact \
+ bAI * action * intention \
+ bCI * contact * intention
resp_obs = pm.OrderedLogistic(
'resp_obs', phi, a,
observed=trolley_df.response - 1
)
with m11_3:
map_11_3 = pm.find_MAP()
```
#### Code 11.15
```
def get_coefs(map_est):
coefs = OrderedDict()
for i, ai in enumerate(map_est['a']):
coefs[f'a_{i}'] = ai
coefs['bA'] = map_est.get('bA', np.nan)
coefs['bI'] = map_est.get('bI', np.nan)
coefs['bC'] = map_est.get('bC', np.nan)
coefs['bAI'] = map_est.get('bAI', np.nan)
coefs['bCI'] = map_est.get('bCI', np.nan)
return coefs
(pd.DataFrame.from_dict(
OrderedDict([
('m11_1', get_coefs(map_11_1)),
('m11_2', get_coefs(map_11_2)),
('m11_3', get_coefs(map_11_3))
]))
.astype(np.float64)
.round(2))
```
#### Code 11.16
```
with m11_2:
trace_11_2 = pm.sample(1000, tune=1000)
with m11_3:
trace_11_3 = pm.sample(1000, tune=1000)
comp_df = pm.compare({m11_1:trace_11_1,
m11_2:trace_11_2,
m11_3:trace_11_3})
comp_df.loc[:,'model'] = pd.Series(['m11.1', 'm11.2', 'm11.3'])
comp_df = comp_df.set_index('model')
comp_df
```
#### Code 11.17-19
```
pp_df = pd.DataFrame(np.array([[0, 0, 0],
[0, 0, 1],
[1, 0, 0],
[1, 0, 1],
[0, 1, 0],
[0, 1, 1]]),
columns=['action', 'contact', 'intention'])
pp_df
action.set_value(pp_df.action.values)
contact.set_value(pp_df.contact.values)
intention.set_value(pp_df.intention.values)
with m11_3:
pp_trace_11_3 = pm.sample_ppc(trace_11_3, samples=1500)
PP_COLS = [f'pp_{i}' for i, _ in enumerate(pp_trace_11_3['resp_obs'])]
pp_df = pd.concat((pp_df,
pd.DataFrame(pp_trace_11_3['resp_obs'].T, columns=PP_COLS)),
axis=1)
pp_cum_df = (pd.melt(
pp_df,
id_vars=['action', 'contact', 'intention'],
value_vars=PP_COLS, value_name='resp'
)
.groupby(['action', 'contact', 'intention', 'resp'])
.size()
.div(1500)
.rename('proba')
.reset_index()
.pivot_table(
index=['action', 'contact', 'intention'],
values='proba',
columns='resp'
)
.cumsum(axis=1)
.iloc[:, :-1])
pp_cum_df
for (plot_action, plot_contact), plot_df in pp_cum_df.groupby(level=['action', 'contact']):
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot([0, 1], plot_df, c='C0');
ax.plot([0, 1], [0, 0], '--', c='C0');
ax.plot([0, 1], [1, 1], '--', c='C0');
ax.set_xlim(0, 1);
ax.set_xlabel("intention");
ax.set_ylim(-0.05, 1.05);
ax.set_ylabel("probability");
ax.set_title(
"action = {action}, contact = {contact}".format(
action=plot_action, contact=plot_contact
)
);
```
#### Code 11.20
```
# define parameters
PROB_DRINK = 0.2 # 20% of days
RATE_WORK = 1. # average 1 manuscript per day
# sample one year of production
N = 365
drink = np.random.binomial(1, PROB_DRINK, size=N)
y = (1 - drink) * np.random.poisson(RATE_WORK, size=N)
```
#### Code 11.21
```
drink_zeros = drink.sum()
work_zeros = (y == 0).sum() - drink_zeros
bins = np.arange(y.max() + 1) - 0.5
plt.hist(y, bins=bins);
plt.bar(0., drink_zeros, width=1., bottom=work_zeros, color='C1', alpha=.5);
plt.xticks(bins + 0.5);
plt.xlabel("manuscripts completed");
plt.ylabel("Frequency");
```
#### Code 11.22
```
with pm.Model() as m11_4:
ap = pm.Normal('ap', 0., 1.)
p = pm.math.sigmoid(ap)
al = pm.Normal('al', 0., 10.)
lambda_ = pm.math.exp(al)
y_obs = pm.ZeroInflatedPoisson('y_obs', 1. - p, lambda_, observed=y)
with m11_4:
map_11_4 = pm.find_MAP()
map_11_4
```
#### Code 11.23
```
sp.special.expit(map_11_4['ap']) # probability drink
np.exp(map_11_4['al']) # rate finish manuscripts, when not drinking
```
#### Code 11.24
```
def dzip(x, p, lambda_, log=True):
like = p**(x == 0) + (1 - p) * sp.stats.poisson.pmf(x, lambda_)
return np.log(like) if log else like
```
#### Code 11.25
```
PBAR = 0.5
THETA = 5.
a = PBAR * THETA
b = (1 - PBAR) * THETA
p = np.linspace(0, 1, 100)
plt.plot(p, sp.stats.beta.pdf(p, a, b));
plt.xlim(0, 1);
plt.xlabel("probability");
plt.ylabel("Density");
```
#### Code 11.26
```
admit_df = pd.read_csv('Data/UCBadmit.csv', sep=';')
admit_df.head()
with pm.Model() as m11_5:
a = pm.Normal('a', 0., 2.)
pbar = pm.Deterministic('pbar', pm.math.sigmoid(a))
theta = pm.Exponential('theta', 1.)
admit_obs = pm.BetaBinomial(
'admit_obs',
pbar * theta, (1. - pbar) * theta,
admit_df.applications.values,
observed=admit_df.admit.values
)
with m11_5:
trace_11_5 = pm.sample(1000, tune=1000)
```
#### Code 11.27
```
pm.summary(trace_11_5, alpha=.11).round(2)
```
#### Code 11.28
```
np.percentile(trace_11_5['pbar'], [2.5, 50., 97.5])
```
#### Code 11.29
```
pbar_hat = trace_11_5['pbar'].mean()
theta_hat = trace_11_5['theta'].mean()
p_plot = np.linspace(0, 1, 100)
plt.plot(
p_plot,
sp.stats.beta.pdf(p_plot, pbar_hat * theta_hat, (1. - pbar_hat) * theta_hat)
);
plt.plot(
p_plot,
sp.stats.beta.pdf(
p_plot[:, np.newaxis],
trace_11_5['pbar'][:100] * trace_11_5['theta'][:100],
(1. - trace_11_5['pbar'][:100]) * trace_11_5['theta'][:100]
),
c='C0', alpha=0.1
);
plt.xlim(0., 1.);
plt.xlabel("probability admit");
plt.ylim(0., 3.);
plt.ylabel("Density");
```
#### Code 11.30
```
with m11_5:
pp_trace_11_5 = pm.sample_ppc(trace_11_5)
x_case = np.arange(admit_df.shape[0])
plt.scatter(
x_case,
pp_trace_11_5['admit_obs'].mean(axis=0) \
/ admit_df.applications.values
);
plt.scatter(x_case, admit_df.admit / admit_df.applications);
high = np.percentile(pp_trace_11_5['admit_obs'], 95, axis=0) \
/ admit_df.applications.values
plt.scatter(x_case, high, marker='x', c='k');
low = np.percentile(pp_trace_11_5['admit_obs'], 5, axis=0) \
/ admit_df.applications.values
plt.scatter(x_case, low, marker='x', c='k');
```
#### Code 11.31
```
mu = 3.
theta = 1.
x = np.linspace(0, 10, 100)
plt.plot(x, sp.stats.gamma.pdf(x, mu / theta, scale=theta));
import platform
import sys
import IPython
import matplotlib
import scipy
print("This notebook was createad on a computer {} running {} and using:\nPython {}\nIPython {}\nPyMC {}\nNumPy {}\nPandas {}\nSciPy {}\nMatplotlib {}\n".format(platform.machine(), ' '.join(platform.linux_distribution()[:2]), sys.version[:5], IPython.__version__, pm.__version__, np.__version__, pd.__version__, scipy.__version__, matplotlib.__version__))
```
| true |
code
| 0.503418 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/iesous-kurios/DS-Unit-2-Applied-Modeling/blob/master/module4/BuildWeekProject.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
!pip install category_encoders==2.*
!pip install eli5
# If you're working locally:
else:
DATA_PATH = '../data/'
# all imports needed for this sheet
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import category_encoders as ce
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.pipeline import make_pipeline
from sklearn.feature_selection import f_regression, SelectKBest
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve
from sklearn.tree import DecisionTreeRegressor
import xgboost as xgb
%matplotlib inline
import seaborn as sns
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
df = pd.read_excel('/content/pipeline_pickle.xlsx')
```
I chose "exit to permanent" housing as my target due to my belief that accurately predicting this feature would have the largest impact on actual people experiencing homelessness in my county. Developing and fine tuning an accurate model with our data could also lead to major improvements in our county's efforts at addressing the homelessness problem among singles as well (as our shelter only serves families)
```
exit_reasons = ['Rental by client with RRH or equivalent subsidy',
'Rental by client, no ongoing housing subsidy',
'Staying or living with family, permanent tenure',
'Rental by client, other ongoing housing subsidy',
'Permanent housing (other than RRH) for formerly homeless persons',
'Staying or living with friends, permanent tenure',
'Owned by client, with ongoing housing subsidy',
'Rental by client, VASH housing Subsidy'
]
# pull all exit destinations from main data file and sum up the totals of each destination,
# placing them into new df for calculations
exits = df['3.12 Exit Destination'].value_counts()
# create target column (multiple types of exits to perm)
df['perm_leaver'] = df['3.12 Exit Destination'].isin(exit_reasons)
# replace spaces with underscore
df.columns = df.columns.str.replace(' ', '_')
df = df.rename(columns = {'Length_of_Time_Homeless_(3.917_Approximate_Start)':'length_homeless', '4.2_Income_Total_at_Entry':'entry_income'
})
```
If a person were to guess "did not exit to permanent" housing every single time, they would be correct approximately 63 percent of the time. I am hoping that through this project, we will be able to provide more focused case management services to guests that displayed features which my model predicted as contributing negatively toward their chances of having an exit to permanent housing. It is my hope that a year from now, the base case will be flipped, and you would need to guess "did exit to permanent housing" to be correct approximately 63 percent of the time.
```
# base case
df['perm_leaver'].value_counts(normalize=True)
# see size of df prior to dropping empties
df.shape
# drop rows with no exit destination (current guests at time of report)
df = df.dropna(subset=['3.12_Exit_Destination'])
# shape of df after dropping current guests
df.shape
df.to_csv('/content/n_alltime.csv')
# verify no NaN in exit destination feature
df['3.12_Exit_Destination'].isna().value_counts()
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
train = df
# Split train into train & val
#train, val = train_test_split(train, train_size=0.80, test_size=0.20,
# stratify=train['perm_leaver'], random_state=42)
# Do train/test split
# Use data from Jan -March 2019 to train
# Use data from April 2019 to test
df['enroll_date'] = pd.to_datetime(df['3.10_Enroll_Date'], infer_datetime_format=True)
cutoff = pd.to_datetime('2019-01-01')
train = df[df.enroll_date < cutoff]
test = df[df.enroll_date >= cutoff]
def wrangle(X):
"""Wrangle train, validate, and test sets in the same way"""
# Prevent SettingWithCopyWarning
X = X.copy()
# drop any private information
X = X.drop(columns=['3.1_FirstName', '3.1_LastName', '3.2_SocSecNo',
'3.3_Birthdate', 'V5_Prior_Address'])
# drop unusable columns
X = X.drop(columns=['2.1_Organization_Name', '2.4_ProjectType',
'WorkSource_Referral_Most_Recent', 'YAHP_Referral_Most_Recent',
'SOAR_Enrollment_Determination_(Most_Recent)',
'R7_General_Health_Status', 'R8_Dental_Health_Status',
'R9_Mental_Health_Status', 'RRH_Date_Of_Move-In',
'RRH_In_Permanent_Housing', 'R10_Pregnancy_Due_Date',
'R10_Pregnancy_Status', 'R1_Referral_Source',
'R2_Date_Status_Determined', 'R2_Enroll_Status',
'R2_Reason_Why_No_Services_Funded', 'R2_Runaway_Youth',
'R3_Sexual_Orientation', '2.5_Utilization_Tracking_Method_(Invalid)',
'2.2_Project_Name', '2.6_Federal_Grant_Programs', '3.16_Client_Location',
'3.917_Stayed_Less_Than_90_Days',
'3.917b_Stayed_in_Streets,_ES_or_SH_Night_Before',
'3.917b_Stayed_Less_Than_7_Nights', '4.24_In_School_(Retired_Data_Element)',
'CaseChildren', 'ClientID', 'HEN-HP_Referral_Most_Recent',
'HEN-RRH_Referral_Most_Recent', 'Emergency_Shelter_|_Most_Recent_Enrollment',
'ProgramType', 'Days_Enrolled_Until_RRH_Date_of_Move-in',
'CurrentDate', 'Current_Age', 'Count_of_Bed_Nights_-_Entire_Episode',
'Bed_Nights_During_Report_Period'])
# drop rows with no exit destination (current guests at time of report)
X = X.dropna(subset=['3.12_Exit_Destination'])
# remove columns to avoid data leakage
X = X.drop(columns=['3.12_Exit_Destination', '5.9_Household_ID', '5.8_Personal_ID',
'4.2_Income_Total_at_Exit', '4.3_Non-Cash_Benefit_Count_at_Exit'])
# Drop needless feature
unusable_variance = ['Enrollment_Created_By', '4.24_Current_Status_(Retired_Data_Element)']
X = X.drop(columns=unusable_variance)
# Drop columns with timestamp
timestamp_columns = ['3.10_Enroll_Date', '3.11_Exit_Date',
'Date_of_Last_ES_Stay_(Beta)', 'Date_of_First_ES_Stay_(Beta)',
'Prevention_|_Most_Recent_Enrollment', 'PSH_|_Most_Recent_Enrollment',
'Transitional_Housing_|_Most_Recent_Enrollment', 'Coordinated_Entry_|_Most_Recent_Enrollment',
'Street_Outreach_|_Most_Recent_Enrollment', 'RRH_|_Most_Recent_Enrollment',
'SOAR_Eligibility_Determination_(Most_Recent)', 'Date_of_First_Contact_(Beta)',
'Date_of_Last_Contact_(Beta)', '4.13_Engagement_Date', '4.11_Domestic_Violence_-_When_it_Occurred',
'3.917_Homeless_Start_Date']
X = X.drop(columns=timestamp_columns)
# return the wrangled dataframe
return X
train.shape
test.shape
train = wrangle(train)
test = wrangle(test)
# Hand pick features only known at entry to avoid data leakage
features = ['CaseMembers',
'3.2_Social_Security_Quality', '3.3_Birthdate_Quality',
'Age_at_Enrollment', '3.4_Race', '3.5_Ethnicity', '3.6_Gender',
'3.7_Veteran_Status', '3.8_Disabling_Condition_at_Entry',
'3.917_Living_Situation', 'length_homeless',
'3.917_Times_Homeless_Last_3_Years', '3.917_Total_Months_Homeless_Last_3_Years',
'V5_Last_Permanent_Address', 'V5_State', 'V5_Zip', 'Municipality_(City_or_County)',
'4.1_Housing_Status', '4.4_Covered_by_Health_Insurance', '4.11_Domestic_Violence',
'4.11_Domestic_Violence_-_Currently_Fleeing_DV?', 'Household_Type',
'R4_Last_Grade_Completed', 'R5_School_Status',
'R6_Employed_Status', 'R6_Why_Not_Employed', 'R6_Type_of_Employment',
'R6_Looking_for_Work', 'entry_income',
'4.3_Non-Cash_Benefit_Count', 'Barrier_Count_at_Entry',
'Chronic_Homeless_Status', 'Under_25_Years_Old',
'4.10_Alcohol_Abuse_(Substance_Abuse)', '4.07_Chronic_Health_Condition',
'4.06_Developmental_Disability', '4.10_Drug_Abuse_(Substance_Abuse)',
'4.08_HIV/AIDS', '4.09_Mental_Health_Problem',
'4.05_Physical_Disability'
]
target = 'perm_leaver'
X_train = train[features]
y_train = train[target]
X_test = test[features]
y_test = test[target]
# base case
df['perm_leaver'].value_counts(normalize=True)
# fit linear model to get a 3 on Sprint
from sklearn.linear_model import LogisticRegression
encoder = ce.OneHotEncoder(use_cat_names=True)
X_train_encoded = encoder.fit_transform(X_train)
X_test_encoded = encoder.transform(X_test)
imputer = SimpleImputer()
X_train_imputed = imputer.fit_transform(X_train_encoded)
X_test_imputed = imputer.transform(X_test_encoded)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_imputed)
X_test_scaled = scaler.transform(X_test_imputed)
model = LogisticRegression(random_state=42, max_iter=5000)
model.fit(X_train_scaled, y_train)
print ('Validation Accuracy', model.score(X_test_scaled,y_test))
```
Linear model above beat the baseline model, now let's see if we can get even more accurate with a tree-based model
```
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import GradientBoostingClassifier
# Make pipeline!
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=100, n_jobs=-1,
random_state=42,
)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_test)
print('Validation Accuracy', accuracy_score(y_test, y_pred))
from joblib import dump
dump(pipeline, 'pipeline.joblib', compress=True)
# get and plot feature importances
# Linear models have coefficients whereas decision trees have "Feature Importances"
import matplotlib.pyplot as plt
model = pipeline.named_steps['randomforestclassifier']
encoder = pipeline.named_steps['ordinalencoder']
encoded_columns = encoder.transform(X_test).columns
importances = pd.Series(model.feature_importances_, encoded_columns)
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} features')
importances.sort_values()[-n:].plot.barh(color='grey');
# cross validation
k = 3
scores = cross_val_score(pipeline, X_train, y_train, cv=k,
scoring='accuracy')
print(f'MAE for {k} folds:', -scores)
-scores.mean()
```
Now that we have beaten the linear model with a tree based model, let us see if xgboost does a better job at predicting exit destination
```
from xgboost import XGBClassifier
pipeline = make_pipeline(
ce.OrdinalEncoder(),
XGBClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
print('Validation Accuracy:', pipeline.score(X_test, y_test))
```
xgboost failed to beat my tree-based model, so the tree-based model is what I will use for my prediction on my web-app
```
# get and plot feature importances
# Linear models have coefficients whereas decision trees have "Feature Importances"
import matplotlib.pyplot as plt
model = pipeline.named_steps['xgbclassifier']
encoder = pipeline.named_steps['ordinalencoder']
encoded_columns = encoder.transform(X_test).columns
importances = pd.Series(model.feature_importances_, encoded_columns)
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} features')
importances.sort_values()[-n:].plot.barh(color='grey');
history = pd.read_csv('/content/n_alltime.csv')
from plotly.tools import mpl_to_plotly
import seaborn as sns
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
# Assign to X, y to avoid data leakage
features = ['CaseMembers',
'3.2_Social_Security_Quality', '3.3_Birthdate_Quality',
'Age_at_Enrollment', '3.4_Race', '3.5_Ethnicity', '3.6_Gender',
'3.7_Veteran_Status', '3.8_Disabling_Condition_at_Entry',
'3.917_Living_Situation', 'length_homeless',
'3.917_Times_Homeless_Last_3_Years', '3.917_Total_Months_Homeless_Last_3_Years',
'V5_Last_Permanent_Address', 'V5_State', 'V5_Zip', 'Municipality_(City_or_County)',
'4.1_Housing_Status', '4.4_Covered_by_Health_Insurance', '4.11_Domestic_Violence',
'4.11_Domestic_Violence_-_Currently_Fleeing_DV?', 'Household_Type',
'R4_Last_Grade_Completed', 'R5_School_Status',
'R6_Employed_Status', 'R6_Why_Not_Employed', 'R6_Type_of_Employment',
'R6_Looking_for_Work', 'entry_income',
'4.3_Non-Cash_Benefit_Count', 'Barrier_Count_at_Entry',
'Chronic_Homeless_Status', 'Under_25_Years_Old',
'4.10_Alcohol_Abuse_(Substance_Abuse)', '4.07_Chronic_Health_Condition',
'4.06_Developmental_Disability', '4.10_Drug_Abuse_(Substance_Abuse)',
'4.08_HIV/AIDS', '4.09_Mental_Health_Problem',
'4.05_Physical_Disability', 'perm_leaver'
]
X = history[features]
X = X.drop(columns='perm_leaver')
y_pred = pipeline.predict(X)
fig, ax = plt.subplots()
sns.distplot(test['perm_leaver'], hist=False, kde=True, ax=ax, label='Actual')
sns.distplot(y_pred, hist=False, kde=True, ax=ax, label='Predicted')
ax.set_title('Distribution of Actual Exit compared to prediction')
ax.legend().set_visible(True)
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(),
RandomForestClassifier(random_state=42)
)
param_distributions = {
'simpleimputer__strategy': ['most_frequent', 'mean', 'median'],
'randomforestclassifier__bootstrap': [True, False],
'randomforestclassifier__max_depth': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, None],
'randomforestclassifier__max_features': ['auto', 'sqrt'],
'randomforestclassifier__min_samples_leaf': [1, 2, 4],
'randomforestclassifier__min_samples_split': [2, 5, 10],
'randomforestclassifier__n_estimators': [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000]}
# If you're on Colab, decrease n_iter & cv parameters
search = RandomizedSearchCV(
pipeline,
param_distributions=param_distributions,
n_iter=1,
cv=3,
scoring='accuracy',
verbose=10,
return_train_score=True,
n_jobs=-1
)
# Fit on train, score on val
search.fit(X_train, y_train)
print('Best hyperparameters', search.best_params_)
print('Cross-validation accuracy score', -search.best_score_)
print('Validation Accuracy', search.score(X_test, y_test))
y_pred.shape
history['perm_leaver'].value_counts()
1282+478
from joblib import dump
dump(pipeline, 'pipeline2.joblib', compress=True)
```
| true |
code
| 0.397734 | null | null | null | null |
|
## A track example
The file `times.dat` has made up data for 100-m races between Florence Griffith-Joyner and Shelly-Ann Fraser-Pryce.
We want to understand how often Shelly-Ann beats Flo-Jo.
```
%pylab inline --no-import-all
```
<!-- Secret comment:
How the data were generated
w = np.random.normal(0,.07,10000)
x = np.random.normal(10.65,.02,10000)+w
y = np.random.normal(10.7,.02,10000)+w
np.savetxt('times.dat', (x,y), delimiter=',')
-->
```
florence, shelly = np.loadtxt('times.dat', delimiter=',')
counts, bins, patches = plt.hist(florence,bins=50,alpha=0.2, label='Flo-Jo')
counts, bins, patches = plt.hist(shelly,bins=bins,alpha=0.2, label='Shelly-Ann')
plt.legend()
plt.xlabel('times (s)')
np.mean(florence), np.mean(shelly)
np.std(florence),np.std(shelly)
```
## let's make a prediction
Based on the mean and std. of their times, let's make a little simulation to predict how often Shelly-Ann beats Flo-Jo.
We can use propagation of errors to predict mean and standard deviation for $q=T_{shelly}-T_{Florence}$
```
mean_q = np.mean(shelly)-np.mean(florence)
sigma_q = np.sqrt(np.std(florence)**2+np.std(shelly)**2)
f_guess = np.random.normal(np.mean(florence),np.std(florence),10000)
s_guess = np.random.normal(np.mean(shelly),np.std(shelly),10000)
toy_difference = s_guess-f_guess
```
Make Toy data
```
#toy_difference = np.random.normal(mean_q, sigma_q, 10000)
counts, bins, patches = plt.hist(toy_difference,bins=50, alpha=0.2, label='toy data')
counts, bins, patches = plt.hist(toy_difference[toy_difference<0],bins=bins, alpha=0.2)
norm = (bins[1]-bins[0])*10000
plt.plot(bins,norm*mlab.normpdf(bins,mean_q,sigma_q), label='prediction')
plt.legend()
plt.xlabel('Shelly - Florence')
# predict fraction of wins
np.sum(toy_difference<0)/10000.
#check toy data looks like real data
counts, bins, patches = plt.hist(f_guess,bins=50,alpha=0.2)
counts, bins, patches = plt.hist(s_guess,bins=bins,alpha=0.2)
```
## How often does she actually win?
```
counts, bins, patches = plt.hist(shelly-florence,bins=50,alpha=0.2)
counts, bins, patches = plt.hist((shelly-florence)[florence-shelly>0],bins=bins,alpha=0.2)
plt.xlabel('Shelly - Florence')
1.*np.sum(florence-shelly>0)/florence.size
```
## What's gonig on?
```
plt.scatter(f_guess,s_guess, alpha=0.01)
plt.scatter(florence,shelly, alpha=0.01)
plt.hexbin(shelly,florence, alpha=1)
```
Previously we learned propagation of errors formula neglecting correlation:
$\sigma_q^2 = \left( \frac{\partial q}{ \partial x} \sigma_x \right)^2 + \left( \frac{\partial q}{ \partial y}\, \sigma_y \right)^2 = \frac{\partial q}{ \partial x} \frac{\partial q}{ \partial x} C_{xx} + \frac{\partial q}{ \partial y} \frac{\partial q}{ \partial y} C_{yy}$
Now we need to extend the formula to take into account correlation
$\sigma_q^2 = \frac{\partial q}{ \partial x} \frac{\partial q}{ \partial x} C_{xx} + \frac{\partial q}{ \partial y} \frac{\partial q}{ \partial y} C_{yy} + 2 \frac{\partial q}{ \partial x} \frac{\partial q}{ \partial y} C_{xxy} $
```
# covariance matrix
cov_matrix = np.cov(shelly,florence)
cov_matrix
# normalized correlation matrix
np.corrcoef(shelly,florence)
# q = T_shelly - T_florence
# x = T_shelly
# y = T_florence
# propagation of errors
cov_matrix[0,0]+cov_matrix[1,1]-2*cov_matrix[0,1]
mean_q = np.mean(shelly)-np.mean(florence)
sigma_q_with_corr = np.sqrt(cov_matrix[0,0]+cov_matrix[1,1]-2*cov_matrix[0,1])
sigma_q_no_corr = np.sqrt(cov_matrix[0,0]+cov_matrix[1,1])
counts, bins, patches = plt.hist(shelly-florence,bins=50,alpha=0.2)
counts, bins, patches = plt.hist((shelly-florence)[florence-shelly>0],bins=bins,alpha=0.2)
norm = (bins[1]-bins[0])*10000
plt.plot(bins,norm*mlab.normpdf(bins,mean_q,sigma_q_with_corr), label='prediction with correlation')
plt.plot(bins,norm*mlab.normpdf(bins,mean_q, sigma_q_no_corr), label='prediction without correlation')
plt.legend()
plt.xlabel('Shelly - Florence')
1.*np.sum(florence-shelly>0)/florence.size
np.std(florence-shelly)
np.sqrt(2.)*0.73
((np.sqrt(2.)*0.073)**2-0.028**2)/2.
.073**2
np.std(florence+shelly)
np.sqrt(2*(np.sqrt(2.)*0.073)**2 -0.028**2)
```
| true |
code
| 0.622775 | null | null | null | null |
|
## Load Python Packages
```
# --- load packages
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim import lr_scheduler
from torch.nn.modules.distance import PairwiseDistance
from torch.utils.data import Dataset
from torchvision import transforms
from torchsummary import summary
from torch.cuda.amp import GradScaler, autocast
from torch.nn import functional as F
import time
from collections import OrderedDict
import numpy as np
import os
from skimage import io
from PIL import Image
import cv2
import matplotlib.pyplot as plt
```
## Set parameters
```
# --- Set all Parameters
DatasetFolder = "./CASIA-WebFace" # path to Dataset folder
ResNet_sel = "18" # select ResNet type
NumberID = 10575 # Number of ID in dataset
batch_size = 256 # size of batch size
Triplet_size = 10000 * batch_size # size of total Triplets
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
loss_margin = 0.6 # Margin for Triplet loss
learning_rate = 0.075 # choose Learning Rate(note that this value will be change during training)
epochs = 200 # number of iteration over total dataset
```
## Download Datasets
#### In this section we download CASIA-WebFace and LFW-Dataset
#### we use CAISA-WebFace for Training and LFW for Evaluation
```
# --- Download CASIA-WebFace Dataset
print(40*"=" + " Download CASIA WebFace " + 40*'=')
! gdown --id 1Of_EVz-yHV7QVWQGihYfvtny9Ne8qXVz
! unzip CASIA-WebFace.zip
! rm CASIA-WebFace.zip
# --- Download LFW Dataset
print(40*"=" + " Download LFW " + 40*'=')
! wget http://vis-www.cs.umass.edu/lfw/lfw-deepfunneled.tgz
! tar -xvzf lfw-deepfunneled.tgz
! rm lfw-deepfunneled.tgz
```
# Define ResNet Parts
#### 1. Residual block
#### 2. Make ResNet by Prv. block
```
# --- Residual block
class ResidualBlock(nn.Module):
def __init__(self, in_channels, out_channels, downsample=1):
super().__init__()
# --- Variables
self.in_channels = in_channels
self.out_channels = out_channels
self.downsample = downsample
# --- Residual parts
# --- Conv part
self.blocks = nn.Sequential(OrderedDict(
{
# --- First Conv
'conv1' : nn.Conv2d(self.in_channels, self.out_channels, kernel_size=3, stride=self.downsample, padding=1, bias=False),
'bn1' : nn.BatchNorm2d(self.out_channels),
'Relu1' : nn.ReLU(),
# --- Secound Conv
'conv2' : nn.Conv2d(self.out_channels, self.out_channels, kernel_size=3, stride=1, padding=1, bias=False),
'bn2' : nn.BatchNorm2d(self.out_channels)
}
))
# --- shortcut part
self.shortcut = nn.Sequential(OrderedDict(
{
'conv' : nn.Conv2d(self.in_channels, self.out_channels, kernel_size=1, stride=self.downsample, bias=False),
'bn' : nn.BatchNorm2d(self.out_channels)
}
))
def forward(self, x):
residual = x
if (self.in_channels != self.out_channels) : residual = self.shortcut(x)
x = self.blocks(x)
x += residual
return x
# # --- Test Residual block
# dummy = torch.ones((1, 32, 140, 140))
# block = ResidualBlock(32, 64)
# block(dummy).shape
# print(block)
# --- Make ResNet18
class ResNet18(nn.Module):
def __init__(self):
super().__init__()
# --- Pre layers with 7*7 conv with stride2 and a max-pooling
self.PreBlocks = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=7, padding=3, stride=2, bias=False),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
# --- Define all Residual Blocks here
self.CoreBlocka = nn.Sequential(
ResidualBlock(64,64 ,downsample=1),
ResidualBlock(64,64 ,downsample=1),
# ResidualBlock(64,64 ,downsample=1),
ResidualBlock(64,128 ,downsample=2),
ResidualBlock(128,128 ,downsample=1),
# ResidualBlock(128,128 ,downsample=1),
# ResidualBlock(128,128 ,downsample=1),
ResidualBlock(128,256 ,downsample=2),
ResidualBlock(256,256 ,downsample=1),
# ResidualBlock(256,256 ,downsample=1),
# ResidualBlock(256,256 ,downsample=1),
# ResidualBlock(256,256 ,downsample=1),
# ResidualBlock(256,256 ,downsample=1),
ResidualBlock(256,512 ,downsample=2),
ResidualBlock(512,512 ,downsample=1),
# ResidualBlock(512,512 ,downsample=1)
)
# --- Make Average pooling
self.avg = nn.AdaptiveAvgPool2d((1,1))
# --- FC layer for output
self.fc = nn.Linear(512, 512, bias=False)
def forward(self, x):
x = self.PreBlocks(x)
x = self.CoreBlocka(x)
x = self.avg(x)
x = x.view(x.size(0), -1)
x = self.fc(x)
x = F.normalize(x, p=2, dim=1)
return x
# dummy = torch.ones((1, 3, 114, 144))
model = ResNet18()
# model
# res = model(dummy)
model.to(device)
summary(model, (3, 114, 114))
del model
```
# Make TripletLoss Class
```
# --- Triplet loss
"""
This code was imported from tbmoon's 'facenet' repository:
https://github.com/tbmoon/facenet/blob/master/utils.py
"""
import torch
from torch.autograd import Function
from torch.nn.modules.distance import PairwiseDistance
class TripletLoss(Function):
def __init__(self, margin):
super(TripletLoss, self).__init__()
self.margin = margin
self.pdist = PairwiseDistance(p=2)
def forward(self, anchor, positive, negative):
pos_dist = self.pdist.forward(anchor, positive)
neg_dist = self.pdist.forward(anchor, negative)
hinge_dist = torch.clamp(self.margin + pos_dist - neg_dist, min=0.0)
loss = torch.mean(hinge_dist)
# print(torch.mean(pos_dist).item(), torch.mean(neg_dist).item(), loss.item())
# print("pos_dist", pos_dist)
# print("neg_dist", neg_dist)
# print(self.margin + pos_dist - neg_dist)
return loss
```
# Make Triplet Dataset from CASIA-WebFace
##### 1. Make Triplet pairs
##### 2. Make them zip
##### 3. Make Dataset Calss
##### 4. Define Transform
```
# --- Create Triplet Datasets ---
# --- make a list of ids and folders
selected_ids = np.uint32(np.round((np.random.rand(int(Triplet_size))) * (NumberID-1)))
folders = os.listdir("./CASIA-WebFace/")
# --- Itrate on each id and make Triplets list
TripletList = []
for index,id in enumerate(selected_ids):
# --- find name of id faces folder
id_str = str(folders[id])
# --- find list of faces in this folder
number_faces = os.listdir("./CASIA-WebFace/"+id_str)
# --- Get two Random number for Anchor and Positive
while(True):
two_random = np.uint32(np.round(np.random.rand(2) * (len(number_faces)-1)))
if (two_random[0] != two_random[1]):
break
# --- Make Anchor and Positive image
Anchor = str(number_faces[two_random[0]])
Positive = str(number_faces[two_random[1]])
# --- Make Negative image
while(True):
neg_id = np.uint32(np.round(np.random.rand(1) * (NumberID-1)))
if (neg_id != id):
break
# --- number of images in negative Folder
neg_id_str = str(folders[neg_id[0]])
number_faces = os.listdir("./CASIA-WebFace/"+neg_id_str)
one_random = np.uint32(np.round(np.random.rand(1) * (len(number_faces)-1)))
Negative = str(number_faces[one_random[0]])
# --- insert Anchor, Positive and Negative image path to TripletList
TempList = ["","",""]
TempList[0] = id_str + "/" + Anchor
TempList[1] = id_str + "/" + Positive
TempList[2] = neg_id_str + "/" + Negative
TripletList.append(TempList)
# # --- Make dataset Triplets File
# f = open("CASIA-WebFace-Triplets.txt", "w")
# for index, triplet in enumerate(TripletList):
# f.write(triplet[0] + " " + triplet[1] + " " + triplet[2])
# if (index != len(TripletList)-1):
# f.write("\n")
# f.close()
# # --- Make zipFile if you need
# !zip -r CASIA-WebFace-Triplets.zip CASIA-WebFace-Triplets.txt
# # --- Read zip File and extract TripletList
# TripletList = []
# # !unzip CASIA-WebFace-Triplets.zip
# # --- Read text file
# with open('CASIA-WebFace-Triplets.txt') as f:
# lines = f.readlines()
# for line in lines:
# TripletList.append(line.split(' '))
# TripletList[-1][2] = TripletList[-1][2][0:-1]
# # --- Print some data
# print(TripletList[0:5])
# --- Make Pytorch Dataset Class for Triplets
class TripletFaceDatset(Dataset):
def __init__(self, list_of_triplets, transform=None):
# --- initializing values
print("Start Creating Triplets Dataset from CASIA-WebFace")
self.list_of_triplets = list_of_triplets
self.transform = transform
# --- getitem function
def __getitem__(self, index):
# --- get images path and read faces
anc_img_path, pos_img_path, neg_img_path = self.list_of_triplets[index]
anc_img = cv2.imread('./CASIA-WebFace/'+anc_img_path)
pos_img = cv2.imread('./CASIA-WebFace/'+pos_img_path)
neg_img = cv2.imread('./CASIA-WebFace/'+neg_img_path)
# anc_img = cv2.resize(anc_img, (114,114))
# pos_img = cv2.resize(pos_img, (114,114))
# neg_img = cv2.resize(neg_img, (114,114))
# --- set transform
if self.transform:
anc_img = self.transform(anc_img)
pos_img = self.transform(pos_img)
neg_img = self.transform(neg_img)
return {'anc_img' : anc_img,
'pos_img' : pos_img,
'neg_img' : neg_img}
# --- return len of triplets
def __len__(self):
return len(self.list_of_triplets)
# --- Define Transforms
transform_list =transforms.Compose([
transforms.ToPILImage(),
transforms.Resize((140,140)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std =[0.229, 0.224, 0.225])
])
# --- Test Dataset
triplet_dataset = TripletFaceDatset(TripletList, transform_list)
triplet_dataset[0]['anc_img'].shape
```
# LFW Evaluation
##### 1. Face detection function
##### 2. Load LFW Pairs .npy file
##### 3. Define Function for evaluation
```
# -------------------------- UTILS CELL -------------------------------
trained_face_data = cv2.CascadeClassifier(cv2.data.haarcascades+'haarcascade_frontalface_default.xml')
# --- define Functions
def face_detect(file_name):
flag = True
# Choose an image to detect faces in
img = cv2.imread(file_name)
# Must convert to greyscale
# grayscaled_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Detect Faces
# face_coordinates = trained_face_data.detectMultiScale(grayscaled_img)
# img_crop = []
# Draw rectangles around the faces
# for (x, y, w, h) in face_coordinates:
# img_crop.append(img[y-20:y+h+20, x-20:x+w+20])
# --- select only Biggest
# big_id = 0
# if len(img_crop) > 1:
# temp = 0
# for idx, img in enumerate(img_crop):
# if img.shape[0] > temp:
# temp = img.shape[0]
# big_id = idx
# elif len(img_crop) == 0:
# flag = False
# img_crop = [0]
# return image crop
# return [img_crop[big_id]], flag
return [img], flag
# --- LFW Dataset loading for test part
l2_dist = PairwiseDistance(2)
cos = nn.CosineSimilarity(dim=1, eps=1e-6)
# --- 1. Load .npy pairs path
lfw_pairs_path = np.load('lfw_pairs_path.npy', allow_pickle=True)
pairs_dist_list_mat = []
pairs_dist_list_unmat = []
valid_thresh = 0.96
def lfw_validation(model):
global valid_thresh
tot_len = len(lfw_pairs_path)
model.eval() # use model in evaluation mode
with torch.no_grad():
true_match = 0
for path in lfw_pairs_path:
# --- extracting
pair_one_path = path['pair_one']
# print(pair_one_path)
pair_two_path = path['pair_two']
# print(pair_two_path)
matched = int(path['matched'])
# --- detect face and resize it
pair_one_img, flag_one = face_detect(pair_one_path)
pair_two_img, flag_two = face_detect(pair_two_path)
if (flag_one==False) or (flag_two==False):
tot_len = tot_len-1
continue
# --- Model Predict
pair_one_img = transform_list(pair_one_img[0])
pair_two_img = transform_list(pair_two_img[0])
pair_one_embed = model(torch.unsqueeze(pair_one_img, 0).to(device))
pair_two_embed = model(torch.unsqueeze(pair_two_img, 0).to(device))
# print(pair_one_embed.shape)
# break
# print(pair_one_img)
# break
# --- find Distance
pairs_dist = l2_dist.forward(pair_one_embed, pair_two_embed)
if matched == 1: pairs_dist_list_mat.append(pairs_dist.item())
if matched == 0: pairs_dist_list_unmat.append(pairs_dist.item())
# --- thrsholding
if (matched==1 and pairs_dist.item() <= valid_thresh) or (matched==0 and pairs_dist.item() > valid_thresh):
true_match += 1
valid_thresh = (np.percentile(pairs_dist_list_unmat,25) + np.percentile(pairs_dist_list_mat,75)) /2
print("Thresh :", valid_thresh)
return (true_match/tot_len)*100
# img, _ = face_detect("./lfw-deepfunneled/Steve_Lavin/Steve_Lavin_0002.jpg")
# plt.imshow(img[0])
# plt.show()
temp = [0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
for i in temp:
valid_thresh = i
print(lfw_validation(model))
(np.mean(pairs_dist_list_mat) + np.mean(pairs_dist_list_unmat) )/2
ppairs_dist_list_unmat
# --- find best thresh
round_unmat = pairs_dist_list_unmat
round_mat = pairs_dist_list_mat
print("----- Unmatched statistical information -----")
print("len : ",len(round_unmat))
print("min : ", np.min(round_unmat))
print("Q1 : ", np.percentile(round_unmat, 15))
print("mean : ", np.mean(round_unmat))
print("Q3 : ", np.percentile(round_unmat, 75))
print("max : ", np.max(round_unmat))
print("\n")
print("----- matched statistical information -----")
print("len : ",len(round_mat))
print("min : ", np.min(round_mat))
print("Q1 : ", np.percentile(round_mat, 25))
print("mean : ", np.mean(round_mat))
print("Q3 : ", np.percentile(round_mat, 85))
print("max : ", np.max(round_mat))
```
## How to make Training Faster
```
# Make Trianing Faster in Pytorch(Cuda):
# 1. use number of worker
# 2. set pin_memory
# 3. Enable cuDNN for optimizing Conv
# 4. using AMP
# 5. set bias=False in conv layer if you set batch normalizing in model
# source: https://betterprogramming.pub/how-to-make-your-pytorch-code-run-faster-93079f3c1f7b
```
# DataLoader
```
# --- DataLoader
face_data = torch.utils.data.DataLoader(triplet_dataset,
batch_size= batch_size,
shuffle=True,
num_workers=4,
pin_memory= True)
# --- Enable cuDNN
torch.backends.cudnn.benchmark = True
```
# Save Model (best acc. and last acc.)
```
# --- saving model for best and last model
# --- Connect to google Drive for saving models
from google.colab import drive
drive.mount('/content/gdrive')
# --- some variable for saving models
BEST_MODEL_PATH = "./gdrive/MyDrive/best_trained.pth"
LAST_MODEL_PATH = "./gdrive/MyDrive/last_trained.pth"
def save_model(model_sv, loss_sv, epoch_sv, optimizer_state_sv, accuracy, accu_sv_list, loss_sv_list):
# --- Inputs:
# 1. model_sv : orginal model that trained
# 2. loss_sv : current loss
# 3. epoch_sv : current epoch
# 4. optimizer_state_sv : current value of optimizer
# 5. accuracy : current accuracy
# --- save last epoch
if accuracy >= max(accu_sv_list):
torch.save(model.state_dict(), BEST_MODEL_PATH)
# --- save this model for checkpoint
torch.save({
'epoch': epoch_sv,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer_state_sv.state_dict(),
'loss': loss_sv,
'accu_sv_list': accu_sv_list,
'loss_sv_list' : loss_sv_list
}, LAST_MODEL_PATH)
```
# Load prev. model for continue training
```
torch.cuda.empty_cache()
# --- training initialize and start
model = ResNet18().to(device) # load model
tiplet_loss = TripletLoss(loss_margin) # load Tripletloss
optimizer = optim.Adam(filter(lambda p: p.requires_grad, model.parameters()),
lr=learning_rate) # load optimizer
l2_dist = PairwiseDistance(2) # L2 distance loading # save loss values
epoch_check = 0
valid_arr = []
loss_arr = []
load_last_epoch = True
if (load_last_epoch == True):
# --- load last model
# define model objects before this
checkpoint = torch.load(LAST_MODEL_PATH, map_location=device) # load model path
model.load_state_dict(checkpoint['model_state_dict']) # load state dict
optimizer.load_state_dict(checkpoint['optimizer_state_dict']) # load optimizer
epoch_check = checkpoint['epoch'] # load epoch
loss = checkpoint['loss'] # load loss value
valid_arr = checkpoint['accu_sv_list'] # load Acc. values
loss_arr = checkpoint['loss_sv_list'] # load loss values
model.train()
epoch_check
loss
```
# Training Loop
```
model.train()
# --- Training loop based on number of epoch
temp = 0.075
for epoch in range(epoch_check,200):
print(80*'=')
# --- For saving imformation
triplet_loss_sum = 0.0
len_face_data = len(face_data)
# -- set starting time
time0 = time.time()
# --- make learning rate update
if 50 < len(loss_arr):
for g in optimizer.param_groups:
g['lr'] = 0.001
temp = 0.001
# --- loop on batches
for batch_idx, batch_faces in enumerate(face_data):
# --- Extract face triplets and send them to CPU or GPU
anc_img = batch_faces['anc_img'].to(device)
pos_img = batch_faces['pos_img'].to(device)
neg_img = batch_faces['neg_img'].to(device)
# --- Get embedded values for each triplet
anc_embed = model(anc_img)
pos_embed = model(pos_img)
neg_embed = model(neg_img)
# --- Find Distance
pos_dist = l2_dist.forward(anc_embed, pos_embed)
neg_dist = l2_dist.forward(anc_embed, neg_embed)
# --- Select hard triplets
all = (neg_dist - pos_dist < 0.8).cpu().numpy().flatten()
hard_triplets = np.where(all == 1)
if len(hard_triplets[0]) == 0: # --- Check number of hard triplets
continue
# --- select hard embeds
anc_hard_embed = anc_embed[hard_triplets]
pos_hard_embed = pos_embed[hard_triplets]
neg_hard_embed = neg_embed[hard_triplets]
# --- Loss
loss_value = tiplet_loss.forward(anc_hard_embed, pos_hard_embed, neg_hard_embed)
# --- backward path
optimizer.zero_grad()
loss_value.backward()
optimizer.step()
if (batch_idx % 200 == 0) : print("Epoch: [{}/{}] ,Batch index: [{}/{}], Loss Value:[{:.8f}]".format(epoch+1, epochs, batch_idx+1, len_face_data,loss_value))
# --- save information
triplet_loss_sum += loss_value.item()
print("Learning Rate: ", temp)
# --- Find Avg. loss value
avg_triplet_loss = triplet_loss_sum / len_face_data
loss_arr.append(avg_triplet_loss)
# --- Validation part besed on LFW Dataset
validation_acc = lfw_validation(model)
valid_arr.append(validation_acc)
model.train()
# --- Save model with checkpoints
save_model(model, avg_triplet_loss, epoch+1, optimizer, validation_acc, valid_arr, loss_arr)
# --- Print information for each epoch
print(" Train set - Triplet Loss = {:.8f}".format(avg_triplet_loss))
print(' Train set - Accuracy = {:.8f}'.format(validation_acc))
print(f' Execution time = {time.time() - time0}')
```
# plot and print some information
```
plt.plotvalid_arr(, 'b-',
label='Validation Accuracy',
)
plt.show()
plt.plot(loss_arr, 'b-',
label='loss values',
)
plt.show()
for param_group in optimizer.param_groups:
print(param_group['lr'])
valid_arr
print(40*"=" + " Download CASIA WebFace " + 40*'=')
! gdown --id 1Of_EVz-yHV7QVWQGihYfvtny9Ne8qXVz
! unzip CASIA-WebFace.zip
! rm CASIA-WebFace.zip
# --- LFW Dataset loading for test part
l2_dist = PairwiseDistance(2)
cos = nn.CosineSimilarity(dim=1, eps=1e-6)
valid_thresh = 0.96
model.eval()
with torch.no_grad():
# --- extracting
pair_one_path = "./3.jpg"
# print(pair_one_path)
pair_two_path = "./2.jpg"
# --- detect face and resize it
pair_one_img, flag_one = face_detect(pair_one_path)
pair_two_img, flag_two = face_detect(pair_two_path)
# --- Model Predict
pair_one_img = transform_list(pair_one_img[0])
pair_two_img = transform_list(pair_two_img[0])
pair_one_embed = model(torch.unsqueeze(pair_one_img, 0).to(device))
pair_two_embed = model(torch.unsqueeze(pair_two_img, 0).to(device))
# --- find Distance
pairs_dist = l2_dist.forward(pair_one_embed, pair_two_embed)
print(pairs_dist)
# --- Create Triplet Datasets ---
# --- make a list of ids and folders
selected_ids = np.uint32(np.round((np.random.rand(int(Triplet_size))) * (NumberID-1)))
folders = os.listdir("./CASIA-WebFace/")
# --- Itrate on each id and make Triplets list
TripletList = []
for index,id in enumerate(selected_ids):
# --- print info
# print(40*"=" + str(index) + 40*"=")
# print(index)
# --- find name of id faces folder
id_str = str(folders[id])
# --- find list of faces in this folder
number_faces = os.listdir("./CASIA-WebFace/"+id_str)
# --- Get two Random number for Anchor and Positive
while(True):
two_random = np.uint32(np.round(np.random.rand(2) * (len(number_faces)-1)))
if (two_random[0] != two_random[1]):
break
# --- Make Anchor and Positive image
Anchor = str(number_faces[two_random[0]])
Positive = str(number_faces[two_random[1]])
# --- Make Negative image
while(True):
neg_id = np.uint32(np.round(np.random.rand(1) * (NumberID-1)))
if (neg_id != id):
break
# --- number of images in negative Folder
neg_id_str = str(folders[neg_id[0]])
number_faces = os.listdir("./CASIA-WebFace/"+neg_id_str)
one_random = np.uint32(np.round(np.random.rand(1) * (len(number_faces)-1)))
Negative = str(number_faces[one_random[0]])
# --- insert Anchor, Positive and Negative image path to TripletList
TempList = ["","",""]
TempList[0] = id_str + "/" + Anchor
TempList[1] = id_str + "/" + Positive
TempList[2] = neg_id_str + "/" + Negative
TripletList.append(TempList)
# print(TripletList[-1])
```
| true |
code
| 0.800673 | null | null | null | null |
|
# Baby boy/girl classifier model preparation
*based on: Francisco Ingham and Jeremy Howard. Inspired by [Adrian Rosebrock](https://www.pyimagesearch.com/2017/12/04/how-to-create-a-deep-learning-dataset-using-google-images/)*
*by: Artyom Vorobyov*
Notebook execution and model training is made in Google Colab
```
from fastai.vision import *
from pathlib import Path
# Check if running in Google Colab and save it to bool variable
try:
import google.colab
IS_COLAB = True
except:
IS_COLAB = False
print("Is Colab:", IS_COLAB)
```
## Get a list of URLs
### How to get a dataset from Google Images
Go to [Google Images](http://images.google.com) and search for the images you are interested in. The more specific you are in your Google Search, the better the results and the less manual pruning you will have to do.
Scroll down until you've seen all the images you want to download, or until you see a button that says 'Show more results'. All the images you scrolled past are now available to download. To get more, click on the button, and continue scrolling. The maximum number of images Google Images shows is 700.
It is a good idea to put things you want to exclude into the search query, for instance if you are searching for the Eurasian wolf, "canis lupus lupus", it might be a good idea to exclude other variants:
"canis lupus lupus" -dog -arctos -familiaris -baileyi -occidentalis
You can also limit your results to show only photos by clicking on Tools and selecting Photos from the Type dropdown.
### How to download image URLs
Now you must run some Javascript code in your browser which will save the URLs of all the images you want for you dataset.
Press <kbd>Ctrl</kbd><kbd>Shift</kbd><kbd>J</kbd> in Windows/Linux and <kbd>Cmd</kbd><kbd>Opt</kbd><kbd>J</kbd> in Mac, and a small window the javascript 'Console' will appear. That is where you will paste the JavaScript commands.
You will need to get the urls of each of the images. Before running the following commands, you may want to disable ad blocking extensions (uBlock, AdBlockPlus etc.) in Chrome. Otherwise the window.open() command doesn't work. Then you can run the following commands:
```javascript
urls = Array.from(document.querySelectorAll('.rg_di .rg_meta')).map(el=>JSON.parse(el.textContent).ou);
window.open('data:text/csv;charset=utf-8,' + escape(urls.join('\n')));
```
### What to do with babies
For this particular application (baby boy/girl classifier) you can just search for "baby boys" and "baby girls". Then run the script mentioned above and save the URLs in "boys_urls.csv" and "girls_urls.csv".
## Download images
fast.ai has a function that allows you to do just that. You just have to specify the urls filename as well as the destination folder and this function will download and save all images that can be opened. If they have some problem in being opened, they will not be saved.
Let's download our images! Notice you can choose a maximum number of images to be downloaded. In this case we will not download all the urls.
```
class_boy = 'boys'
class_girl = 'girls'
classes = [class_boy, class_girl]
path = Path('./data')
path.mkdir(parents=True, exist_ok=True)
def download_dataset(is_colab):
if is_colab:
from google.colab import drive
import shutil
import zipfile
# You'll be asked to sign in Google Account and copy-paste a code here. Do it.
drive.mount('/content/gdrive')
# Copy this model from Google Drive after export and manually put it in the "ai_models" folder in the repository
# If there'll be an error during downloading the model - share it with some other Google account and download
# from this 2nd account - it should work fine.
zip_remote_path = Path('/content/gdrive/My Drive/Colab/boyorgirl/train.zip')
shutil.copy(str(zip_remote_path), str(path))
zip_local_path = path/'train.zip'
with zipfile.ZipFile(zip_local_path, 'r') as zip_ref:
zip_ref.extractall(path)
print("train folder contents:", (path/'train').ls())
else:
data_sources = [
('./boys_urls.csv', path/'train'/class_boy),
('./girls_urls.csv', path/'train'/class_girl)
]
# Download the images listed in URL's files
for urls_path, dest_path in data_sources:
dest = Path(dest_path)
dest.mkdir(parents=True, exist_ok=True)
download_images(urls_path, dest, max_pics=800)
# If you have problems download, try the code below with `max_workers=0` to see exceptions:
# download_images(urls_path, dest, max_pics=20, max_workers=0)
# Then we can remove any images that can't be opened:
for _, dest_path in data_sources:
verify_images(dest_path, delete=True, max_size=800)
# If running from colab - zip your train set (train folder) and put it to "Colab/boyorgirl/train.zip" in your Google Drive
download_dataset(IS_COLAB)
```
## Cleaning the data
Now it's a good moment to review the downloaded images and clean them. There will be some non-relevant images - photos of adults, photos of the baby clothes without the babies etc. Just review the images and remove non-relevant ones. For 2x400 images it'll take just 10-20 minutes in total.
There's also another way to clean the data - use the `fastiai.widgets.ImageCleaner`. It's used after you've trained your model. Even if you plan to use `ImageCleaner` later - it still makes sense to review the dataset briefly by yourself at the beginning.
## Load the data
```
np.random.seed(42)
data = ImageDataBunch.from_folder(path, train='train', valid_pct=0.2,
ds_tfms=get_transforms(), size=224, num_workers=4).normalize(imagenet_stats)
```
Good! Let's take a look at some of our pictures then.
```
# Check if all the classes were correctly read
print(data.classes)
print(data.classes == classes)
data.show_batch(rows=3, figsize=(7,8), ds_type=DatasetType.Train)
data.show_batch(rows=3, figsize=(7,8), ds_type=DatasetType.Valid)
print('Train set size: {}. Validation set size: {}'.format(len(data.train_ds), len(data.valid_ds)))
```
## Train model
```
learn = cnn_learner(data, models.resnet50, metrics=error_rate)
learn.fit_one_cycle(4)
learn.save('stage-1')
learn.unfreeze()
learn.lr_find()
# If the plot is not showing try to give a start and end learning rate
# learn.lr_find(start_lr=1e-5, end_lr=1e-1)
learn.recorder.plot()
learn.fit_one_cycle(2, max_lr=slice(1e-5,1e-3))
learn.save('stage-2')
```
## Interpretation
```
learn.load('stage-2');
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()
```
## Putting your model in production
First thing first, let's export the content of our `Learner` object for production. Below are 2 variants of export - for local environment and for colab environment:
```
# Use this cell to export model from local environment within the repository
def get_export_path(is_colab):
if is_colab:
from google.colab import drive
# You'll be asked to sign in Google Account and copy-paste a code here. Do it.
# force_remount=True is needed to write model if it was deleted from Google Drive, but remains in Colab local file system
drive.mount('/content/gdrive', force_remount=True)
# Copy this model from Google Drive after export and manually put it in the "ai_models" folder in the repository
# If there'll be an error during downloading the model - share it with some other Google account and download
# from this 2nd account - it should work fine.
return Path('/content/gdrive/My Drive/Colab/boyorgirl/ai_models/export.pkl')
else:
# Used in case when notebook is run from the repository, but not in the Colab
return Path('../backend/ai_models/export.pkl')
# In case of Colab - model will be exported to 'Colab/boyorgirl/ai_models/export.pkl'. Download and save it in your repository manually
# in the 'ai_models' folder
export_path = get_export_path(IS_COLAB)
# ensure folder exists
export_path.parents[0].mkdir(parents=True, exist_ok=True)
# absolute path is passed as learn object attaches relative path to it's data folder rather than to notebook folder
learn.export(export_path.absolute())
print("Export folder contents:", export_path.parents[0].ls())
```
This will create a file named 'export.pkl' in the given directory. This exported model contains everything we need to deploy our model (the model, the weights but also some metadata like the classes or the transforms/normalization used).
```
```
| true |
code
| 0.350116 | null | null | null | null |
|
```
from IPython.display import Markdown as md
### change to reflect your notebook
_nb_loc = "09_deploying/09c_changesig.ipynb"
_nb_title = "Changing signatures of exported model"
### no need to change any of this
_nb_safeloc = _nb_loc.replace('/', '%2F')
md("""
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://console.cloud.google.com/ai-platform/notebooks/deploy-notebook?name={1}&url=https%3A%2F%2Fgithub.com%2FGoogleCloudPlatform%2Fpractical-ml-vision-book%2Fblob%2Fmaster%2F{2}&download_url=https%3A%2F%2Fgithub.com%2FGoogleCloudPlatform%2Fpractical-ml-vision-book%2Fraw%2Fmaster%2F{2}">
<img src="https://raw.githubusercontent.com/GoogleCloudPlatform/practical-ml-vision-book/master/logo-cloud.png"/> Run in AI Platform Notebook</a>
</td>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/GoogleCloudPlatform/practical-ml-vision-book/blob/master/{0}">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/GoogleCloudPlatform/practical-ml-vision-book/blob/master/{0}">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://raw.githubusercontent.com/GoogleCloudPlatform/practical-ml-vision-book/master/{0}">
<img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
""".format(_nb_loc, _nb_title, _nb_safeloc))
```
# Changing signatures of exported model
In this notebook, we start from an already trained and saved model (as in Chapter 7).
For convenience, we have put this model in a public bucket in gs://practical-ml-vision-book/flowers_5_trained
## Enable GPU and set up helper functions
This notebook and pretty much every other notebook in this repository
will run faster if you are using a GPU.
On Colab:
- Navigate to Edit→Notebook Settings
- Select GPU from the Hardware Accelerator drop-down
On Cloud AI Platform Notebooks:
- Navigate to https://console.cloud.google.com/ai-platform/notebooks
- Create an instance with a GPU or select your instance and add a GPU
Next, we'll confirm that we can connect to the GPU with tensorflow:
```
import tensorflow as tf
print('TensorFlow version' + tf.version.VERSION)
print('Built with GPU support? ' + ('Yes!' if tf.test.is_built_with_cuda() else 'Noooo!'))
print('There are {} GPUs'.format(len(tf.config.experimental.list_physical_devices("GPU"))))
device_name = tf.test.gpu_device_name()
if device_name != '/device:GPU:0':
raise SystemError('GPU device not found')
print('Found GPU at: {}'.format(device_name))
```
## Exported model
We start from a trained and saved model from Chapter 7.
<pre>
model.save(...)
</pre>
```
MODEL_LOCATION='gs://practical-ml-vision-book/flowers_5_trained'
!gsutil ls {MODEL_LOCATION}
!saved_model_cli show --tag_set serve --signature_def serving_default --dir {MODEL_LOCATION}
```
## Passing through an input
Note that the signature doesn't tell us the input filename.
Let's add that.
```
import tensorflow as tf
import os, shutil
model = tf.keras.models.load_model(MODEL_LOCATION)
@tf.function(input_signature=[tf.TensorSpec([None,], dtype=tf.string)])
def predict_flower_type(filenames):
old_fn = model.signatures['serving_default']
result = old_fn(filenames) # has flower_type_int etc.
result['filename'] = filenames
return result
shutil.rmtree('export', ignore_errors=True)
os.mkdir('export')
model.save('export/flowers_model',
signatures={
'serving_default': predict_flower_type
})
!saved_model_cli show --tag_set serve --signature_def serving_default --dir export/flowers_model
import tensorflow as tf
serving_fn = tf.keras.models.load_model('export/flowers_model').signatures['serving_default']
filenames = [
'gs://cloud-ml-data/img/flower_photos/dandelion/9818247_e2eac18894.jpg',
'gs://cloud-ml-data/img/flower_photos/dandelion/9853885425_4a82356f1d_m.jpg',
'gs://cloud-ml-data/img/flower_photos/daisy/9299302012_958c70564c_n.jpg',
'gs://cloud-ml-data/img/flower_photos/tulips/8733586143_3139db6e9e_n.jpg',
'gs://cloud-ml-data/img/flower_photos/tulips/8713397358_0505cc0176_n.jpg'
]
pred = serving_fn(tf.convert_to_tensor(filenames))
print(pred)
```
## Multiple signatures
```
import tensorflow as tf
import os, shutil
model = tf.keras.models.load_model(MODEL_LOCATION)
old_fn = model.signatures['serving_default']
@tf.function(input_signature=[tf.TensorSpec([None,], dtype=tf.string)])
def pass_through_input(filenames):
result = old_fn(filenames) # has flower_type_int etc.
result['filename'] = filenames
return result
shutil.rmtree('export', ignore_errors=True)
os.mkdir('export')
model.save('export/flowers_model2',
signatures={
'serving_default': old_fn,
'input_pass_through': pass_through_input
})
!saved_model_cli show --tag_set serve --dir export/flowers_model2
!saved_model_cli show --tag_set serve --dir export/flowers_model2 --signature_def serving_default
!saved_model_cli show --tag_set serve --dir export/flowers_model2 --signature_def input_pass_through
```
## Deploying multi-signature model as REST API
```
!./caip_deploy.sh --version multi --model_location ./export/flowers_model2
%%writefile request.json
{
"instances": [
{
"filenames": "gs://cloud-ml-data/img/flower_photos/dandelion/9818247_e2eac18894.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/dandelion/9853885425_4a82356f1d_m.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/daisy/9299302012_958c70564c_n.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/tulips/8733586143_3139db6e9e_n.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/tulips/8713397358_0505cc0176_n.jpg"
}
]
}
!gcloud ai-platform predict --model=flowers --version=multi --json-request=request.json
%%writefile request.json
{
"signature_name": "input_pass_through",
"instances": [
{
"filenames": "gs://cloud-ml-data/img/flower_photos/dandelion/9818247_e2eac18894.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/dandelion/9853885425_4a82356f1d_m.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/daisy/9299302012_958c70564c_n.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/tulips/8733586143_3139db6e9e_n.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/tulips/8713397358_0505cc0176_n.jpg"
}
]
}
!gcloud ai-platform predict --model=flowers --version=multi --json-request=request.json
```
that's a bug ... filed a bug report; hope it's fixed by the time you are reading the book.
```
from oauth2client.client import GoogleCredentials
import requests
import json
PROJECT = 'ai-analytics-solutions' # CHANGE
MODEL_NAME = 'flowers'
MODEL_VERSION = 'multi'
token = GoogleCredentials.get_application_default().get_access_token().access_token
api = 'https://ml.googleapis.com/v1/projects/{}/models/{}/versions/{}:predict' \
.format(PROJECT, MODEL_NAME, MODEL_VERSION)
headers = {'Authorization': 'Bearer ' + token }
data = {
"signature_name": "input_pass_through",
"instances": [
{
"filenames": "gs://cloud-ml-data/img/flower_photos/dandelion/9818247_e2eac18894.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/dandelion/9853885425_4a82356f1d_m.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/daisy/9299302012_958c70564c_n.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/tulips/8733586143_3139db6e9e_n.jpg"
},
{
"filenames": "gs://cloud-ml-data/img/flower_photos/tulips/8713397358_0505cc0176_n.jpg"
}
]
}
response = requests.post(api, json=data, headers=headers)
print(response.content.decode('utf-8'))
```
## License
Copyright 2020 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
| true |
code
| 0.50891 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Miseq/naive_imdb_reviews_model/blob/master/naive_imdb_model.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from keras.datasets import imdb
from keras import optimizers
from keras import losses
from keras import metrics
from keras import models
from keras import layers
import matplotlib.pyplot as plt
import numpy as np
def vectorize_data(data, dimension=10000):
result = np.zeros((len(data), dimension))
for i, seq in enumerate(data):
result[i, seq] = 1.
return result
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
x_train = vectorize_data(train_data)
x_test = vectorize_data(test_data)
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=0.001), loss=losses.binary_crossentropy, metrics=['accuracy'])
x_val = x_train[:20000]
partial_x_train = x_train[20000:]
y_val = y_train[:20000]
partial_y_train = y_train[20000:]
history = model.fit(partial_x_train, partial_y_train, epochs=20, batch_size=512, validation_data=(x_val, y_val))
history_dict = history.history
history_dict.keys()
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc)+1)
# Tworzenie wykresu start tenowania i walidacji
plt.plot(epochs, loss, 'bo', label='Strata trenowania')
plt.plot(epochs, val_loss, 'b', label='Strata walidacji')
plt.title('Strata renowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Strata')
plt.legend()
plt.show()
# Tworzenie wykresu dokładności trenowania i walidacji
plt.clf() # Czyszczenie rysunku(wazne)
acc_values = history_dict['acc']
val_acc_vales = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='Dokladnosc trenowania')
plt.plot(epochs, val_acc, 'b', label='Dokladnosc walidacji')
plt.title('Dokladnosc trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Strata')
plt.legend()
plt.show()
min_loss_val = min(val_loss)
max_acc_val = max(val_acc)
min_loss_ix = val_loss.index(min_loss_val)
max_acc_ix = val_acc.index(max_acc_val)
print(f'{min_loss_ix} --- {max_acc_ix}')
```
Po 7 epoce model zaczyna być przetrenowany
```
model.fit(x_train, y_train, epochs=7, batch_size=512, validation_data=(x_val, y_val))
results = model.evaluate(x_test, y_test)
results
```
## Wiecej warstw ukrytych
```
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(8, activation='relu'))
model.add(layers.Dense(4, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=0.001), loss=losses.binary_crossentropy, metrics=['accuracy'])
model.fit(x_train, y_train, epochs=10, batch_size=512, validation_data=(x_val, y_val))
results = model.evaluate(x_test, y_test)
results
```
## Wieksza ilosc jednostek ukrytych
```
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=0.001), loss=losses.binary_crossentropy, metrics=['accuracy'])
model.fit(x_train, y_train, epochs=10, batch_size=512, validation_data=(x_val, y_val))
results = model.evaluate(x_test, y_test)
results
```
## Funkcja straty mse
```
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=0.001), loss=losses.mse, metrics=['accuracy'])
model.fit(x_train, y_train, epochs=10, batch_size=512, validation_data=(x_val, y_val))
results = model.evaluate(x_test, y_test)
results
```
| true |
code
| 0.853272 | null | null | null | null |
|
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-59152712-8');
</script>
# Convert LaTeX Sentence to SymPy Expression
## Author: Ken Sible
## The following module will demonstrate a recursive descent parser for LaTeX.
### NRPy+ Source Code for this module:
1. [latex_parser.py](../edit/latex_parser.py); [\[**tutorial**\]](Tutorial-LaTeX_SymPy_Conversion.ipynb) The latex_parser.py script will convert a LaTeX sentence to a SymPy expression using the following function: parse(sentence).
<a id='toc'></a>
# Table of Contents
$$\label{toc}$$
1. [Step 1](#intro): Introduction: Lexical Analysis and Syntax Analysis
1. [Step 2](#sandbox): Demonstration and Sandbox (LaTeX Parser)
1. [Step 3](#tensor): Tensor Support with Einstein Notation (WIP)
1. [Step 4](#latex_pdf_output): $\LaTeX$ PDF Output
<a id='intro'></a>
# Step 1: Lexical Analysis and Syntax Analysis \[Back to [top](#toc)\]
$$\label{intro}$$
In the following section, we discuss [lexical analysis](https://en.wikipedia.org/wiki/Lexical_analysis) (lexing) and [syntax analysis](https://en.wikipedia.org/wiki/Parsing) (parsing). In the process of lexical analysis, a lexer will tokenize a character string, called a sentence, using substring pattern matching (or tokenizing). We implemented a regex-based lexer for NRPy+, which does pattern matching using a [regular expression](https://en.wikipedia.org/wiki/Regular_expression) for each token pattern. In the process of syntax analysis, a parser will receive a token iterator from the lexer and build a parse tree containing all syntactic information of the language, as specified by a [formal grammar](https://en.wikipedia.org/wiki/Formal_grammar). We implemented a [recursive descent parser](https://en.wikipedia.org/wiki/Recursive_descent_parser) for NRPy+, which will build a parse tree in [preorder](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order_(NLR)), starting from the root [nonterminal](https://en.wikipedia.org/wiki/Terminal_and_nonterminal_symbols), using a [right recursive](https://en.wikipedia.org/wiki/Left_recursion) grammar. The following right recursive, [context-free grammar](https://en.wikipedia.org/wiki/Context-free_grammar) was written for parsing [LaTeX](https://en.wikipedia.org/wiki/LaTeX), adhering to the canonical (extended) [BNF](https://en.wikipedia.org/wiki/Backus%E2%80%93Naur_form) notation used for describing a context-free grammar:
```
<ROOT> -> <EXPRESSION> | <STRUCTURE> { <LINE_BREAK> <STRUCTURE> }*
<STRUCTURE> -> <CONFIG> | <ENVIROMENT> | <ASSIGNMENT>
<ENVIROMENT> -> <BEGIN_ALIGN> <ASSIGNMENT> { <LINE_BREAK> <ASSIGNMENT> }* <END_ALIGN>
<ASSIGNMENT> -> <VARIABLE> = <EXPRESSION>
<EXPRESSION> -> <TERM> { ( '+' | '-' ) <TERM> }*
<TERM> -> <FACTOR> { [ '/' ] <FACTOR> }*
<FACTOR> -> <BASE> { '^' <EXPONENT> }*
<BASE> -> [ '-' ] ( <ATOM> | '(' <EXPRESSION> ')' | '[' <EXPRESSION> ']' )
<EXPONENT> -> <BASE> | '{' <BASE> '}'
<ATOM> -> <VARIABLE> | <NUMBER> | <COMMAND>
<VARIABLE> -> <ARRAY> | <SYMBOL> [ '_' ( <SYMBOL> | <INTEGER> ) ]
<NUMBER> -> <RATIONAL> | <DECIMAL> | <INTEGER>
<COMMAND> -> <SQRT> | <FRAC>
<SQRT> -> '\\sqrt' [ '[' <INTEGER> ']' ] '{' <EXPRESSION> '}'
<FRAC> -> '\\frac' '{' <EXPRESSION> '}' '{' <EXPRESSION> '}'
<CONFIG> -> '%' <ARRAY> '[' <INTEGER> ']' [ ':' <SYMMETRY> ] { ',' <ARRAY> '[' <INTEGER> ']' [ ':' <SYMMETRY> ] }*
<ARRAY> -> ( <SYMBOL | <TENSOR> )
[ '_' ( <SYMBOL> | '{' { <SYMBOL> }+ '}' ) [ '^' ( <SYMBOL> | '{' { <SYMBOL> }+ '}' ) ]
| '^' ( <SYMBOL> | '{' { <SYMBOL> }+ '}' ) [ '_' ( <SYMBOL> | '{' { <SYMBOL> }+ '}' ) ] ]
```
<small>**Source**: Robert W. Sebesta. Concepts of Programming Languages. Pearson Education Limited, 2016.</small>
```
from latex_parser import * # Import NRPy+ module for lexing and parsing LaTeX
from sympy import srepr # Import SymPy function for expression tree representation
lexer = Lexer(); lexer.initialize(r'\sqrt{5}(x + 2/3)^2')
print(', '.join(token for token in lexer.tokenize()))
expr = parse(r'\sqrt{5}(x + 2/3)^2', expression=True)
print(expr, ':', srepr(expr))
```
#### `Grammar Derivation: (x + 2/3)^2`
```
<EXPRESSION> -> <TERM>
-> <FACTOR>
-> <BASE>^<EXPONENT>
-> (<EXPRESSION>)^<EXPONENT>
-> (<TERM> + <TERM>)^<EXPONENT>
-> (<FACTOR> + <TERM>)^<EXPONENT>
-> (<BASE> + <TERM>)^<EXPONENT>
-> (<ATOM> + <TERM>)^<EXPONENT>
-> (<VARIABLE> + <TERM>)^<EXPONENT>
-> (<SYMBOL> + <TERM>)^<EXPONENT>
-> (x + <TERM>)^<EXPONENT>
-> (x + <FACTOR>)^<EXPONENT>
-> (x + <BASE>)^<EXPONENT>
-> (x + <ATOM>)^<EXPONENT>
-> (x + <NUMBER>)^<EXPONENT>
-> (x + <RATIONAL>)^<EXPONENT>
-> (x + 2/3)^<EXPONENT>
-> (x + 2/3)^<BASE>
-> (x + 2/3)^<ATOM>
-> (x + 2/3)^<NUMBER>
-> (x + 2/3)^<INTEGER>
-> (x + 2/3)^2
```
<a id='sandbox'></a>
# Step 2: Demonstration and Sandbox (LaTeX Parser) \[Back to [top](#toc)\]
$$\label{sandbox}$$
We implemented a wrapper function for the `parse()` method that will accept a LaTeX sentence and return a SymPy expression. Furthermore, the entire parsing module was designed for extendibility. We apply the following procedure for extending parser functionality to include an unsupported LaTeX command: append that command to the grammar dictionary in the Lexer class with the mapping regex:token, write a grammar abstraction (similar to a regular expression) for that command, add the associated nonterminal (the command name) to the command abstraction in the Parser class, and finally implement the straightforward (private) method for parsing the grammar abstraction. We shall demonstrate the extension procedure using the `\sqrt` LaTeX command.
```<SQRT> -> '\\sqrt' [ '[' <INTEGER> ']' ] '{' <EXPRESSION> '}'```
```
def _sqrt(self):
if self.accept('LEFT_BRACKET'):
integer = self.lexer.lexeme
self.expect('INTEGER')
root = Rational(1, integer)
self.expect('RIGHT_BRACKET')
else: root = Rational(1, 2)
self.expect('LEFT_BRACE')
expr = self.__expr()
self.expect('RIGHT_BRACE')
return Pow(expr, root)
```
```
print(parse(r'\sqrt[3]{\alpha_0}', expression=True))
```
In addition to expression parsing, we included support for equation parsing, which will produce a dictionary mapping LHS $\mapsto$ RHS, where LHS must be a symbol, and insert that mapping into the global namespace of the previous stack frame, as demonstrated below.
```
parse(r'x = n\sqrt{2}^n'); print(x)
```
We implemented robust error messaging using the custom `ParseError` exception, which should handle every conceivable case to identify, as detailed as possible, invalid syntax inside of a LaTeX sentence. The following are runnable examples of possible error messages (simply uncomment and run the cell):
```
# parse(r'\sqrt[*]{2}')
# ParseError: \sqrt[*]{2}
# ^
# unexpected '*' at position 6
# parse(r'\sqrt[0.5]{2}')
# ParseError: \sqrt[0.5]{2}
# ^
# expected token INTEGER at position 6
# parse(r'\command{}')
# ParseError: \command{}
# ^
# unsupported command '\command' at position 0
from warnings import filterwarnings # Import Python function for warning suppression
filterwarnings('ignore', category=OverrideWarning); del Parser.namespace['x']
```
In the sandbox code cell below, you can experiment with the LaTeX parser using the wrapper function `parse(sentence)`, where sentence must be a [raw string](https://docs.python.org/3/reference/lexical_analysis.html) to interpret a backslash as a literal character rather than an [escape sequence](https://en.wikipedia.org/wiki/Escape_sequence).
```
# Write Sandbox Code Here
```
<a id='tensor'></a>
# Step 3: Tensor Support with Einstein Notation (WIP) \[Back to [top](#toc)\]
$$\label{tensor}$$
In the following section, we demonstrate the current parser support for tensor notation using the Einstein summation convention. The first example will parse an equation for a tensor contraction, the second will parse an equation for raising an index using the metric tensor, and the third will parse an align enviroment with an equation dependency. In each example, every tensor should appear either on the LHS of an equation or inside of a configuration before appearing on the RHS of an equation. Moreover, the parser will raise an exception upon violation of the Einstein summation convention, i.e. an invalid free or bound index.
**Configuration Syntax** `% <TENSOR> [<DIMENSION>]: <SYMMETRY>, <TENSOR> [<DIMENSION>]: <SYMMETRY>, ... ;`
#### Example 1
LaTeX Source | Rendered LaTeX
:----------- | :-------------
<pre lang="latex"> h = h^\\mu{}_\\mu </pre> | $$ h = h^\mu{}_\mu $$
```
parse(r"""
% h^\mu_\mu [4]: nosym;
h = h^\mu{}_\mu
""")
print('h =', h)
```
#### Example 2
LaTeX Source | Rendered LaTeX
:----------- | :-------------
<pre lang="latex"> v^\\mu = g^{\\mu\\nu}v_\\nu </pre> | $$ v^\mu = g^{\mu\nu}v_\nu $$
```
parse(r"""
% g^{\mu\nu} [3]: metric, v_\nu [3];
v^\mu = g^{\mu\nu}v_\nu
""")
print('vU =', vU)
```
#### Example 3
LaTeX Source | Rendered LaTeX
:----------- | :-------------
<pre lang="latex"> \\begin{align\*}<br>    R &= g_{ab}R^{ab} \\\\ <br>    G^{ab} &= R^{ab} - \\frac{1}{2}g^{ab}R <br> \\end{align\*} </pre> | $$ \begin{align*} R &= g_{ab}R^{ab} \\ G^{ab} &= R^{ab} - \frac{1}{2}g^{ab}R \end{align*} $$
```
parse(r"""
% g_{ab} [2]: metric, R^{ab} [2]: sym01;
\begin{align*}
R &= g_{ab}R^{ab} \\
G^{ab} &= R^{ab} - \frac{1}{2}g^{ab}R
\end{align*}
""")
print('R =', R)
display(GUU)
```
The static variable `namespace` for the `Parser` class will provide access to the global namespace of the parser across each instance of the class.
```
Parser.namespace
```
We extended our robust error messaging using the custom `TensorError` exception, which should handle any inconsistent tensor dimension and any violation of the Einstein summation convention, specifically that a bound index must appear exactly once as a superscript and exactly once as a subscript in any single term and that a free index must appear in every term with the same position and cannot be summed over in any term. The following are runnable examples of possible error messages (simply uncomment and run the cell):
```
# parse(r"""
# % h^{\mu\mu}_{\mu\mu} [4]: nosym;
# h = h^{\mu\mu}_{\mu\mu}
# """)
# TensorError: illegal bound index
# parse(r"""
# % g^\mu_\nu [3]: sym01, v_\nu [3];
# v^\mu = g^\mu_\nu v_\nu
# """)
# TensorError: illegal bound index
# parse(r"""
# % g^{\mu\nu} [3]: sym01, v_\mu [3], w_\nu [3];
# u^\mu = g^{\mu\nu}(v_\mu + w_\nu)
# """)
# TensorError: unbalanced free index
```
<a id='latex_pdf_output'></a>
# Step 4: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-LaTeX_SymPy_Conversion.pdf](Tutorial-LaTeX_SymPy_Conversion.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-LaTeX_SymPy_Conversion")
```
| true |
code
| 0.385635 | null | null | null | null |
|
# Predicting NYC Taxi Fares with RAPIDS
Process 380 million rides in NYC from 2015-2017.
RAPIDS is a suite of GPU accelerated data science libraries with APIs that should be familiar to users of Pandas, Dask, and Scikitlearn.
This notebook focuses on showing how to use cuDF with Dask & XGBoost to scale GPU DataFrame ETL-style operations & model training out to multiple GPUs.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import cupy
import cudf
import dask
import dask_cudf
import xgboost as xgb
from dask.distributed import Client, wait
from dask.utils import parse_bytes
from dask_cuda import LocalCUDACluster
cluster = LocalCUDACluster(rmm_pool_size=parse_bytes("25 GB"),
scheduler_port=9888,
dashboard_address=9787,
)
client = Client(cluster)
client
```
# Inspecting the Data
Now that we have a cluster of GPU workers, we'll use [dask-cudf](https://github.com/rapidsai/dask-cudf/) to load and parse a bunch of CSV files into a distributed DataFrame.
```
base_path = "/raid/vjawa/nyc_taxi/data/"
import dask_cudf
df_2014 = dask_cudf.read_csv(base_path+'2014/yellow_*.csv', chunksize='256 MiB')
df_2014.head()
```
# Data Cleanup
As usual, the data needs to be massaged a bit before we can start adding features that are useful to an ML model.
For example, in the 2014 taxi CSV files, there are `pickup_datetime` and `dropoff_datetime` columns. The 2015 CSVs have `tpep_pickup_datetime` and `tpep_dropoff_datetime`, which are the same columns. One year has `rate_code`, and another `RateCodeID`.
Also, some CSV files have column names with extraneous spaces in them.
Worst of all, starting in the July 2016 CSVs, pickup & dropoff latitude and longitude data were replaced by location IDs, making the second half of the year useless to us.
We'll do a little string manipulation, column renaming, and concatenating of DataFrames to sidestep the problems.
```
#Dictionary of required columns and their datatypes
must_haves = {
'pickup_datetime': 'datetime64[s]',
'dropoff_datetime': 'datetime64[s]',
'passenger_count': 'int32',
'trip_distance': 'float32',
'pickup_longitude': 'float32',
'pickup_latitude': 'float32',
'rate_code': 'int32',
'dropoff_longitude': 'float32',
'dropoff_latitude': 'float32',
'fare_amount': 'float32'
}
def clean(ddf, must_haves):
# replace the extraneous spaces in column names and lower the font type
tmp = {col:col.strip().lower() for col in list(ddf.columns)}
ddf = ddf.rename(columns=tmp)
ddf = ddf.rename(columns={
'tpep_pickup_datetime': 'pickup_datetime',
'tpep_dropoff_datetime': 'dropoff_datetime',
'ratecodeid': 'rate_code'
})
ddf['pickup_datetime'] = ddf['pickup_datetime'].astype('datetime64[ms]')
ddf['dropoff_datetime'] = ddf['dropoff_datetime'].astype('datetime64[ms]')
for col in ddf.columns:
if col not in must_haves:
ddf = ddf.drop(columns=col)
continue
# if column was read as a string, recast as float
if ddf[col].dtype == 'object':
ddf[col] = ddf[col].str.fillna('-1')
ddf[col] = ddf[col].astype('float32')
else:
# downcast from 64bit to 32bit types
# Tesla T4 are faster on 32bit ops
if 'int' in str(ddf[col].dtype):
ddf[col] = ddf[col].astype('int32')
if 'float' in str(ddf[col].dtype):
ddf[col] = ddf[col].astype('float32')
ddf[col] = ddf[col].fillna(-1)
return ddf
```
<b> NOTE: </b>We will realize that some of 2015 data has column name as `RateCodeID` and others have `RatecodeID`. When we rename the columns in the clean function, it internally doesn't pass meta while calling map_partitions(). This leads to the error of column name mismatch in the returned data. For this reason, we will call the clean function with map_partition and pass the meta to it. Here is the link to the bug created for that: https://github.com/rapidsai/cudf/issues/5413
```
df_2014 = df_2014.map_partitions(clean, must_haves, meta=must_haves)
```
We still have 2015 and the first half of 2016's data to read and clean. Let's increase our dataset.
```
df_2015 = dask_cudf.read_csv(base_path+'2015/yellow_*.csv', chunksize='1024 MiB')
df_2015 = df_2015.map_partitions(clean, must_haves, meta=must_haves)
```
# Handling 2016's Mid-Year Schema Change
In 2016, only January - June CSVs have the columns we need. If we try to read base_path+2016/yellow_*.csv, Dask will not appreciate having differing schemas in the same DataFrame.
Instead, we'll need to create a list of the valid months and read them independently.
```
months = [str(x).rjust(2, '0') for x in range(1, 7)]
valid_files = [base_path+'2016/yellow_tripdata_2016-'+month+'.csv' for month in months]
#read & clean 2016 data and concat all DFs
df_2016 = dask_cudf.read_csv(valid_files, chunksize='512 MiB').map_partitions(clean, must_haves, meta=must_haves)
#concatenate multiple DataFrames into one bigger one
taxi_df = dask.dataframe.multi.concat([df_2014, df_2015, df_2016])
```
## Exploratory Data Analysis (EDA)
Here, we are checking out if there are any non-sensical records and outliers, and in such case, we need to remove them from the dataset.
```
# check out if there is any negative total trip time
taxi_df[taxi_df.dropoff_datetime <= taxi_df.pickup_datetime].head()
# check out if there is any abnormal data where trip distance is short, but the fare is very high.
taxi_df[(taxi_df.trip_distance < 10) & (taxi_df.fare_amount > 300)].head()
# check out if there is any abnormal data where trip distance is long, but the fare is very low.
taxi_df[(taxi_df.trip_distance > 50) & (taxi_df.fare_amount < 50)].head()
```
EDA visuals and additional analysis yield the filter logic below.
```
# apply a list of filter conditions to throw out records with missing or outlier values
query_frags = [
'fare_amount > 1 and fare_amount < 500',
'passenger_count > 0 and passenger_count < 6',
'pickup_longitude > -75 and pickup_longitude < -73',
'dropoff_longitude > -75 and dropoff_longitude < -73',
'pickup_latitude > 40 and pickup_latitude < 42',
'dropoff_latitude > 40 and dropoff_latitude < 42',
'trip_distance > 0 and trip_distance < 500',
'not (trip_distance > 50 and fare_amount < 50)',
'not (trip_distance < 10 and fare_amount > 300)',
'not dropoff_datetime <= pickup_datetime'
]
taxi_df = taxi_df.query(' and '.join(query_frags))
# reset_index and drop index column
taxi_df = taxi_df.reset_index(drop=True)
taxi_df.head()
```
# Adding Interesting Features
Dask & cuDF provide standard DataFrame operations, but also let you run "user defined functions" on the underlying data. Here we use [dask.dataframe's map_partitions](https://docs.dask.org/en/latest/dataframe-api.html#dask.dataframe.DataFrame.map_partitions) to apply user defined python function on each DataFrame partition.
We'll use a Haversine Distance calculation to find total trip distance, and extract additional useful variables from the datetime fields.
```
## add features
taxi_df['hour'] = taxi_df['pickup_datetime'].dt.hour
taxi_df['year'] = taxi_df['pickup_datetime'].dt.year
taxi_df['month'] = taxi_df['pickup_datetime'].dt.month
taxi_df['day'] = taxi_df['pickup_datetime'].dt.day
taxi_df['day_of_week'] = taxi_df['pickup_datetime'].dt.weekday
taxi_df['is_weekend'] = (taxi_df['day_of_week']>=5).astype('int32')
#calculate the time difference between dropoff and pickup.
taxi_df['diff'] = taxi_df['dropoff_datetime'].astype('int64') - taxi_df['pickup_datetime'].astype('int64')
taxi_df['diff']=(taxi_df['diff']/1000).astype('int64')
taxi_df['pickup_latitude_r'] = taxi_df['pickup_latitude']//.01*.01
taxi_df['pickup_longitude_r'] = taxi_df['pickup_longitude']//.01*.01
taxi_df['dropoff_latitude_r'] = taxi_df['dropoff_latitude']//.01*.01
taxi_df['dropoff_longitude_r'] = taxi_df['dropoff_longitude']//.01*.01
taxi_df = taxi_df.drop('pickup_datetime', axis=1)
taxi_df = taxi_df.drop('dropoff_datetime', axis=1)
import cupy as cp
def cudf_haversine_distance(lon1, lat1, lon2, lat2):
lon1, lat1, lon2, lat2 = map(cp.radians, [lon1, lat1, lon2, lat2])
newlon = lon2 - lon1
newlat = lat2 - lat1
haver_formula = cp.sin(newlat/2.0)**2 + cp.cos(lat1) * cp.cos(lat2) * cp.sin(newlon/2.0)**2
dist = 2 * cp.arcsin(cp.sqrt(haver_formula ))
km = 6367 * dist #6367 for distance in KM for miles use 3958
return km
def haversine_dist(df):
df['h_distance']= cudf_haversine_distance(
df['pickup_longitude'],
df['pickup_latitude'],
df['dropoff_longitude'],
df['dropoff_latitude']
)
df['h_distance']= df['h_distance'].astype('float32')
return df
taxi_df = taxi_df.map_partitions(haversine_dist)
taxi_df.head()
len(taxi_df)
%%time
taxi_df = taxi_df.persist()
x = wait(taxi_df);
```
# Pick a Training Set
Let's imagine you're making a trip to New York on the 25th and want to build a model to predict what fare prices will be like the last few days of the month based on the first part of the month. We'll use a query expression to identify the `day` of the month to use to divide the data into train and test sets.
The wall-time below represents how long it takes your GPU cluster to load data from the Google Cloud Storage bucket and the ETL portion of the workflow.
```
#since we calculated the h_distance let's drop the trip_distance column, and then do model training with XGB.
taxi_df = taxi_df.drop('trip_distance', axis=1)
# this is the original data partition for train and test sets.
X_train = taxi_df.query('day < 25')
# create a Y_train ddf with just the target variable
Y_train = X_train[['fare_amount']].persist()
# drop the target variable from the training ddf
X_train = X_train[X_train.columns.difference(['fare_amount'])].persist()
# # this wont return until all data is in GPU memory
a = wait([X_train, Y_train]);
```
# Train the XGBoost Regression Model
The wall time output below indicates how long it took your GPU cluster to train an XGBoost model over the training set.
```
dtrain = xgb.dask.DaskDMatrix(client, X_train, Y_train)
%%time
params = {
'learning_rate': 0.3,
'max_depth': 8,
'objective': 'reg:squarederror',
'subsample': 0.6,
'gamma': 1,
'silent': False,
'verbose_eval': True,
'tree_method':'gpu_hist'
}
trained_model = xgb.dask.train(
client,
params,
dtrain,
num_boost_round=12,
evals=[(dtrain, 'train')]
)
ax = xgb.plot_importance(trained_model['booster'], height=0.8, max_num_features=10, importance_type="gain")
ax.grid(False, axis="y")
ax.set_title('Estimated feature importance')
ax.set_xlabel('importance')
plt.show()
```
# How Good is Our Model?
Now that we have a trained model, we need to test it with the 25% of records we held out.
Based on the filtering conditions applied to this dataset, many of the DataFrame partitions will wind up having 0 rows. This is a problem for XGBoost which doesn't know what to do with 0 length arrays. We'll repartition the data.
```
def drop_empty_partitions(df):
lengths = df.map_partitions(len).compute()
nonempty = [length > 0 for length in lengths]
return df.partitions[nonempty]
X_test = taxi_df.query('day >= 25').persist()
X_test = drop_empty_partitions(X_test)
# Create Y_test with just the fare amount
Y_test = X_test[['fare_amount']].persist()
# Drop the fare amount from X_test
X_test = X_test[X_test.columns.difference(['fare_amount'])]
# this wont return until all data is in GPU memory
done = wait([X_test, Y_test])
# display test set size
len(X_test)
```
## Calculate Prediction
```
# generate predictions on the test set
booster = trained_model["booster"] # "Booster" is the trained model
booster.set_param({'predictor': 'gpu_predictor'})
prediction = xgb.dask.inplace_predict(client, booster, X_test).persist()
wait(prediction);
y = Y_test['fare_amount'].reset_index(drop=True)
# Calculate RMSE
squared_error = ((prediction-y)**2)
cupy.sqrt(squared_error.mean().compute())
```
## Save Trained Model for Later Use¶
We often need to store our models on a persistent filesystem for future deployment. Let's save our model.
```
trained_model
import joblib
# Save the booster to file
joblib.dump(trained_model, "xgboost-model")
len(taxi_df)
```
## Reload a Saved Model from Disk
You can also read the saved model back into a normal XGBoost model object.
```
with open("xgboost-model", 'rb') as fh:
loaded_model = joblib.load(fh)
# Generate predictions on the test set again, but this time using the reloaded model
loaded_booster = loaded_model["booster"]
loaded_booster.set_param({'predictor': 'gpu_predictor'})
new_preds = xgb.dask.inplace_predict(client, loaded_booster, X_test).persist()
# Verify that the predictions result in the same RMSE error
squared_error = ((new_preds - y)**2)
cp.sqrt(squared_error.mean().compute())
```
| true |
code
| 0.303945 | null | null | null | null |
|
```
```
# INTRODUCTION TO UNSUPERVISED LEARNING
Unsupervised learning is the training of a machine using information that is neither classified nor labeled and allowing the algorithm to act on that information without guidance. Here the task of the machine is to group unsorted information according to similarities, patterns, and differences without any prior training of data.
Unlike supervised learning, no teacher is provided that means no training will be given to the machine. Therefore the machine is restricted to find the hidden structure in unlabeled data by itself.
#Example of Unsupervised Machine Learning
For instance, suppose a image having both dogs and cats which it has never seen.
Thus the machine has no idea about the features of dogs and cats so we can’t categorize it as ‘dogs and cats ‘. But it can categorize them according to their similarities, patterns, and differences, i.e., we can easily categorize the picture into two parts. The first may contain all pics having dogs in it and the second part may contain all pics having cats in it. Here you didn’t learn anything before, which means no training data or examples.
It allows the model to work on its own to discover patterns and information that was previously undetected. It mainly deals with unlabelled data.
#Why Unsupervised Learning?
Here, are prime reasons for using Unsupervised Learning in Machine Learning:
>Unsupervised machine learning finds all kind of unknown patterns in data.
>Unsupervised methods help you to find features which can be useful for categorization.
>It is taken place in real time, so all the input data to be analyzed and labeled in the presence of learners.
>It is easier to get unlabeled data from a computer than labeled data, which needs manual intervention.
#Unsupervised Learning Algorithms
Unsupervised Learning Algorithms allow users to perform more complex processing tasks compared to supervised learning. Although, unsupervised learning can be more unpredictable compared with other natural learning methods. Unsupervised learning algorithms include clustering, anomaly detection, neural networks, etc.
#Unsupervised learning is classified into two categories of algorithms:
>Clustering: A clustering problem is where you want to discover the inherent groupings in the data, such as grouping customers by purchasing behavior.
>Association: An association rule learning problem is where you want to discover rules that describe large portions of your data, such as people that buy X also tend to buy Y.
#a)Clustering
Clustering is an important concept when it comes to unsupervised learning.
It mainly deals with finding a structure or pattern in a collection of uncategorized data.
Unsupervised Learning Clustering algorithms will process your data and find natural clusters(groups) if they exist in the data.
You can also modify how many clusters your algorithms should identify. It allows you to adjust the granularity of these groups.
#There are different types of clustering you can utilize:
#1.Exclusive (partitioning)
In this clustering method, Data are grouped in such a way that one data can belong to one cluster only.
Example: K-means
#2.Agglomerative
In this clustering technique, every data is a cluster. The iterative unions between the two nearest clusters reduce the number of clusters.
Example: Hierarchical clustering
#3.Overlapping
In this technique, fuzzy sets is used to cluster data. Each point may belong to two or more clusters with separate degrees of membership.
Here, data will be associated with an appropriate membership value.
Example: Fuzzy C-Means
#4.Probabilistic
This technique uses probability distribution to create the clusters
Example: Following keywords
“man’s shoe.”
“women’s shoe.”
“women’s glove.”
“man’s glove.”
can be clustered into two categories “shoe” and “glove” or “man” and “women.”
#Clustering Types
Following are the clustering types of Machine Learning:
Hierarchical clustering
K-means clustering
K-NN (k nearest neighbors)
Principal Component Analysis
Singular value decomposition
Independent Component Analysis
#1.Hierarchical Clustering
>Hierarchical clustering is an algorithm which builds a hierarchy of clusters. It begins with all the data which is assigned to a cluster of their own. Here, two close cluster are going to be in the same cluster. This algorithm ends when there is only one cluster left.
#2.K-means Clustering
>K-means it is an iterative clustering algorithm which helps you to find the highest value for every iteration. Initially, the desired number of clusters are selected. In this clustering method, you need to cluster the data points into k groups. A larger k means smaller groups with more granularity in the same way. A lower k means larger groups with less granularity.
>The output of the algorithm is a group of “labels.” It assigns data point to one of the k groups. In k-means clustering, each group is defined by creating a centroid for each group. The centroids are like the heart of the cluster, which captures the points closest to them and adds them to the cluster.
K-mean clustering further defines two subgroups:
Agglomerative clustering
Dendrogram
#Agglomerative clustering
>This type of K-means clustering starts with a fixed number of clusters. It allocates all data into the exact number of clusters. This clustering method does not require the number of clusters K as an input. Agglomeration process starts by forming each data as a single cluster.
>This method uses some distance measure, reduces the number of clusters (one in each iteration) by merging process. Lastly, we have one big cluster that contains all the objects.
#Dendrogram
>In the Dendrogram clustering method, each level will represent a possible cluster. The height of dendrogram shows the level of similarity between two join clusters. The closer to the bottom of the process they are more similar cluster which is finding of the group from dendrogram which is not natural and mostly subjective.
#K- Nearest neighbors
>K- nearest neighbour is the simplest of all machine learning classifiers. It differs from other machine learning techniques, in that it doesn’t produce a model. It is a simple algorithm which stores all available cases and classifies new instances based on a similarity measure.
It works very well when there is a distance between examples. The learning speed is slow when the training set is large, and the distance calculation is nontrivial.
#4.Principal Components Analysis
>In case you want a higher-dimensional space. You need to select a basis for that space and only the 200 most important scores of that basis. This base is known as a principal component. The subset you select constitute is a new space which is small in size compared to original space. It maintains as much of the complexity of data as possible.
#5.Singular value decomposition
>The singular value decomposition of a matrix is usually referred to as the SVD.
This is the final and best factorization of a matrix:
A = UΣV^T
where U is orthogonal, Σ is diagonal, and V is orthogonal.
In the decomoposition A = UΣV^T, A can be any matrix. We know that if A
is symmetric positive definite its eigenvectors are orthogonal and we can write
A = QΛQ^T. This is a special case of a SVD, with U = V = Q. For more general
A, the SVD requires two different matrices U and V.
We’ve also learned how to write A = SΛS^−1, where S is the matrix of n
distinct eigenvectors of A. However, S may not be orthogonal; the matrices U
and V in the SVD will be.
#6.Independent Component Analysis
>Independent Component Analysis (ICA) is a machine learning technique to separate independent sources from a mixed signal. Unlike principal component analysis which focuses on maximizing the variance of the data points, the independent component analysis focuses on independence, i.e. independent components.
#b)Association
>Association rules allow you to establish associations amongst data objects inside large databases. This unsupervised technique is about discovering interesting relationships between variables in large databases. For example, people that buy a new home most likely to buy new furniture.
>Other Examples:
>A subgroup of cancer patients grouped by their gene expression measurements
>Groups of shopper based on their browsing and purchasing histories
>Movie group by the rating given by movies viewers
#Applications of Unsupervised Machine Learning
Some application of Unsupervised Learning Techniques are:
1.Clustering automatically split the dataset into groups base on their similarities
2.Anomaly detection can discover unusual data points in your dataset. It is useful for finding fraudulent transactions
3.Association mining identifies sets of items which often occur together in your dataset
4.Latent variable models are widely used for data preprocessing. Like reducing the number of features in a dataset or decomposing the dataset into multiple components.
#Real-life Applications Of Unsupervised Learning
Machines are not that quick, unlike humans. It takes a lot of resources to train a model based on patterns in data. Below are a few of the wonderful real-life simulations of unsupervised learning.
1.Anomaly detection –The advent of technology and the internet has given birth to enormous anomalies in the past and is still growing. Unsupervised learning has huge scope when it comes to anomaly detection.
2.Segmentation – Unsupervised learning can be used to segment the customers based on certain patterns. Each cluster of customers is different whereas customers within a cluster share common properties. Customer segmentation is a widely opted approach used in devising marketing plans.
#Advantages of unsupervised learning
1.It can see what human minds cannot visualize.
2.It is used to dig hidden patterns which hold utmost importance in the industry and has widespread applications in real-time.
3.The outcome of an unsupervised task can yield an entirely new business vertical or venture.
4.There is lesser complexity compared to the supervised learning task. Here, no one is required to interpret the associated labels and hence it holds lesser complexities.
5.It is reasonably easier to obtain unlabeled data.
#Disadvantages of Unsupervised Learning
1.You cannot get precise information regarding data sorting, and the output as data used in unsupervised learning is labeled and not known.
2.Less accuracy of the results is because the input data is not known and not labeled by people in advance. This means that the machine requires to do this itself.
3.The spectral classes do not always correspond to informational classes.
The user needs to spend time interpreting and label the classes which follow that classification.
4.Spectral properties of classes can also change over time so you can’t have the same class information while moving from one image to another.
#How to use Unsupervised learning to find patterns in data
#CODE:
from sklearn import datasets
import matplotlib.pyplot as plt
iris_df = datasets.load_iris()
print(dir(iris_df)
print(iris_df.feature_names)
print(iris_df.target)
print(iris_df.target_names)
label = {0: 'red', 1: 'blue', 2: 'green'}
x_axis = iris_df.data[:, 0]
y_axis = iris_df.data[:, 2]
plt.scatter(x_axis, y_axis, c=iris_df.target)
plt.show()
#Explanation:
As the above code shows, we have used the Iris dataset to make predictions.The dataset contains a records under four attributes-petal length, petal width, sepal length, sepal width.And also it contains three iris classes:setosa, virginica and versicolor .We'll feed the four features of our flowers to the unsupervised algorithm and it will predict which class the iris belongs.For that we have used scikit-learn library in python to load the Iris dataset and matplotlib for data visualisation.
#OUTPUT:
As we can see here the violet colour represents setosa,green colour represents versicolor and yellow
colour represents virginica.

```
```
| true |
code
| 0.757944 | null | null | null | null |
|
```
import math
import numpy as np
import pandas as pd
```
### Initial conditions
```
initial_rating = 400
k = 100
things = ['Malted Milk','Rich Tea','Hobnob','Digestive']
```
### Elo Algos
```
def expected_win(r1, r2):
"""
Expected probability of player 1 beating player 2
if player 1 has rating 1 (r1) and player 2 has rating 2 (r2)
"""
return 1.0 / (1 + math.pow(10, (r2-r1)/400))
def update_rating(R, k, P, d):
"""
d = 1 = WIN
d = 0 = LOSS
"""
return R + k*(d-P)
def elo(Ra, Rb, k, d):
"""
d = 1 when player A wins
d = 0 when player B wins
"""
Pa = expected_win(Ra, Rb)
Pb = expected_win(Rb, Ra)
# update if A wins
if d == 1:
Ra = update_rating(Ra, k, Pa, d)
Rb = update_rating(Rb, k, Pb, d-1)
# update if B wins
elif d == 0:
Ra = update_rating(Ra, k, Pa, d)
Rb = update_rating(Rb, k, Pb, d+1)
return Pa, Pb, Ra, Rb
def elo_sequence(things, initial_rating, k, results):
"""
Initialises score dictionary, and runs through sequence of pairwise results, returning final dictionary of Elo rankings
"""
dic_scores = {i:initial_rating for i in things}
for result in results:
winner, loser = result
Ra, Rb = dic_scores[winner], dic_scores[loser]
_, _, newRa, newRb = elo(Ra, Rb, k, 1)
dic_scores[winner], dic_scores[loser] = newRa, newRb
return dic_scores
```
### Mean Elo
```
def mElo(things, initial_rating, k, results, numEpochs):
"""
Randomises the sequence of the pairwise comparisons, running the Elo sequence in a random
sequence for a number of epochs
Returns the mean Elo ratings over the randomised epoch sequences
"""
lst_outcomes = []
for i in np.arange(numEpochs):
np.random.shuffle(results)
lst_outcomes.append(elo_sequence(things, initial_rating, k, results))
return pd.DataFrame(lst_outcomes).mean().sort_values(ascending=False)
```
### Pairwise Outcomes from Christian's Taste Test
> **Format** (Winner, Loser)
```
results = np.array([('Malted Milk','Rich Tea'),('Malted Milk','Digestive'),('Malted Milk','Hobnob')\
,('Hobnob','Rich Tea'),('Hobnob','Digestive'),('Digestive','Rich Tea')])
jenResults = np.array([('Rich Tea','Malted Milk'),('Digestive','Malted Milk'),('Hobnob','Malted Milk')\
,('Hobnob','Rich Tea'),('Hobnob','Digestive'),('Digestive','Rich Tea')])
mElo(things, initial_rating, k, jenResults, 1000)
```
| true |
code
| 0.553023 | null | null | null | null |
|
This notebook contains an implementation of the third place result in the Rossman Kaggle competition as detailed in Guo/Berkhahn's [Entity Embeddings of Categorical Variables](https://arxiv.org/abs/1604.06737).
The motivation behind exploring this architecture is it's relevance to real-world application. Much of our focus has been computer-vision and NLP tasks, which largely deals with unstructured data.
However, most of the data informing KPI's in industry are structured, time-series data. Here we explore the end-to-end process of using neural networks with practical structured data problems.
```
%matplotlib inline
import math, keras, datetime, pandas as pd, numpy as np, keras.backend as K
import matplotlib.pyplot as plt, xgboost, operator, random, pickle
from utils2 import *
np.set_printoptions(threshold=50, edgeitems=20)
limit_mem()
from isoweek import Week
from pandas_summary import DataFrameSummary
%cd data/rossman/
```
## Create datasets
In addition to the provided data, we will be using external datasets put together by participants in the Kaggle competition. You can download all of them [here](http://files.fast.ai/part2/lesson14/rossmann.tgz).
For completeness, the implementation used to put them together is included below.
```
def concat_csvs(dirname):
os.chdir(dirname)
filenames=glob.glob("*.csv")
wrote_header = False
with open("../"+dirname+".csv","w") as outputfile:
for filename in filenames:
name = filename.split(".")[0]
with open(filename) as f:
line = f.readline()
if not wrote_header:
wrote_header = True
outputfile.write("file,"+line)
for line in f:
outputfile.write(name + "," + line)
outputfile.write("\n")
os.chdir("..")
# concat_csvs('googletrend')
# concat_csvs('weather')
```
Feature Space:
* train: Training set provided by competition
* store: List of stores
* store_states: mapping of store to the German state they are in
* List of German state names
* googletrend: trend of certain google keywords over time, found by users to correlate well w/ given data
* weather: weather
* test: testing set
```
table_names = ['train', 'store', 'store_states', 'state_names',
'googletrend', 'weather', 'test']
```
We'll be using the popular data manipulation framework pandas.
Among other things, pandas allows you to manipulate tables/data frames in python as one would in a database.
We're going to go ahead and load all of our csv's as dataframes into a list `tables`.
```
tables = [pd.read_csv(fname+'.csv', low_memory=False) for fname in table_names]
from IPython.display import HTML
```
We can use `head()` to get a quick look at the contents of each table:
* train: Contains store information on a daily basis, tracks things like sales, customers, whether that day was a holdiay, etc.
* store: general info about the store including competition, etc.
* store_states: maps store to state it is in
* state_names: Maps state abbreviations to names
* googletrend: trend data for particular week/state
* weather: weather conditions for each state
* test: Same as training table, w/o sales and customers
```
for t in tables: display(t.head())
```
This is very representative of a typical industry dataset.
The following returns summarized aggregate information to each table accross each field.
```
for t in tables: display(DataFrameSummary(t).summary())
```
## Data Cleaning / Feature Engineering
As a structured data problem, we necessarily have to go through all the cleaning and feature engineering, even though we're using a neural network.
```
train, store, store_states, state_names, googletrend, weather, test = tables
len(train),len(test)
```
Turn state Holidays to Bool
```
train.StateHoliday = train.StateHoliday!='0'
test.StateHoliday = test.StateHoliday!='0'
```
Define function for joining tables on specific fields.
By default, we'll be doing a left outer join of `right` on the `left` argument using the given fields for each table.
Pandas does joins using the `merge` method. The `suffixes` argument describes the naming convention for duplicate fields. We've elected to leave the duplicate field names on the left untouched, and append a "_y" to those on the right.
```
def join_df(left, right, left_on, right_on=None):
if right_on is None: right_on = left_on
return left.merge(right, how='left', left_on=left_on, right_on=right_on,
suffixes=("", "_y"))
```
Join weather/state names.
```
weather = join_df(weather, state_names, "file", "StateName")
```
In pandas you can add new columns to a dataframe by simply defining it. We'll do this for googletrends by extracting dates and state names from the given data and adding those columns.
We're also going to replace all instances of state name 'NI' with the usage in the rest of the table, 'HB,NI'. This is a good opportunity to highlight pandas indexing. We can use `.ix[rows, cols]` to select a list of rows and a list of columns from the dataframe. In this case, we're selecting rows w/ statename 'NI' by using a boolean list `googletrend.State=='NI'` and selecting "State".
```
googletrend['Date'] = googletrend.week.str.split(' - ', expand=True)[0]
googletrend['State'] = googletrend.file.str.split('_', expand=True)[2]
googletrend.loc[googletrend.State=='NI', "State"] = 'HB,NI'
```
The following extracts particular date fields from a complete datetime for the purpose of constructing categoricals.
You should always consider this feature extraction step when working with date-time. Without expanding your date-time into these additional fields, you can't capture any trend/cyclical behavior as a function of time at any of these granularities.
```
def add_datepart(df):
df.Date = pd.to_datetime(df.Date)
df["Year"] = df.Date.dt.year
df["Month"] = df.Date.dt.month
df["Week"] = df.Date.dt.week
df["Day"] = df.Date.dt.day
```
We'll add to every table w/ a date field.
```
add_datepart(weather)
add_datepart(googletrend)
add_datepart(train)
add_datepart(test)
trend_de = googletrend[googletrend.file == 'Rossmann_DE']
```
Now we can outer join all of our data into a single dataframe.
Recall that in outer joins everytime a value in the joining field on the left table does not have a corresponding value on the right table, the corresponding row in the new table has Null values for all right table fields.
One way to check that all records are consistent and complete is to check for Null values post-join, as we do here.
*Aside*: Why note just do an inner join?
If you are assuming that all records are complete and match on the field you desire, an inner join will do the same thing as an outer join. However, in the event you are wrong or a mistake is made, an outer join followed by a null-check will catch it. (Comparing before/after # of rows for inner join is equivalent, but requires keeping track of before/after row #'s. Outer join is easier.)
```
store = join_df(store, store_states, "Store")
len(store[store.State.isnull()])
joined = join_df(train, store, "Store")
len(joined[joined.StoreType.isnull()])
joined = join_df(joined, googletrend, ["State","Year", "Week"])
len(joined[joined.trend.isnull()])
joined = joined.merge(trend_de, 'left', ["Year", "Week"], suffixes=('', '_DE'))
len(joined[joined.trend_DE.isnull()])
joined = join_df(joined, weather, ["State","Date"])
len(joined[joined.Mean_TemperatureC.isnull()])
joined_test = test.merge(store, how='left', left_on='Store', right_index=True)
len(joined_test[joined_test.StoreType.isnull()])
```
Next we'll fill in missing values to avoid complications w/ na's.
```
joined.CompetitionOpenSinceYear = joined.CompetitionOpenSinceYear.fillna(1900).astype(np.int32)
joined.CompetitionOpenSinceMonth = joined.CompetitionOpenSinceMonth.fillna(1).astype(np.int32)
joined.Promo2SinceYear = joined.Promo2SinceYear.fillna(1900).astype(np.int32)
joined.Promo2SinceWeek = joined.Promo2SinceWeek.fillna(1).astype(np.int32)
```
Next we'll extract features "CompetitionOpenSince" and "CompetitionDaysOpen". Note the use of `apply()` in mapping a function across dataframe values.
```
joined["CompetitionOpenSince"] = pd.to_datetime(joined.apply(lambda x: datetime.datetime(
x.CompetitionOpenSinceYear, x.CompetitionOpenSinceMonth, 15), axis=1).astype(pd.datetime))
joined["CompetitionDaysOpen"] = joined.Date.subtract(joined["CompetitionOpenSince"]).dt.days
```
We'll replace some erroneous / outlying data.
```
joined.loc[joined.CompetitionDaysOpen<0, "CompetitionDaysOpen"] = 0
joined.loc[joined.CompetitionOpenSinceYear<1990, "CompetitionDaysOpen"] = 0
```
Added "CompetitionMonthsOpen" field, limit the maximum to 2 years to limit number of unique embeddings.
```
joined["CompetitionMonthsOpen"] = joined["CompetitionDaysOpen"]//30
joined.loc[joined.CompetitionMonthsOpen>24, "CompetitionMonthsOpen"] = 24
joined.CompetitionMonthsOpen.unique()
```
Same process for Promo dates.
```
joined["Promo2Since"] = pd.to_datetime(joined.apply(lambda x: Week(
x.Promo2SinceYear, x.Promo2SinceWeek).monday(), axis=1).astype(pd.datetime))
joined["Promo2Days"] = joined.Date.subtract(joined["Promo2Since"]).dt.days
joined.loc[joined.Promo2Days<0, "Promo2Days"] = 0
joined.loc[joined.Promo2SinceYear<1990, "Promo2Days"] = 0
joined["Promo2Weeks"] = joined["Promo2Days"]//7
joined.loc[joined.Promo2Weeks<0, "Promo2Weeks"] = 0
joined.loc[joined.Promo2Weeks>25, "Promo2Weeks"] = 25
joined.Promo2Weeks.unique()
```
## Durations
It is common when working with time series data to extract data that explains relationships across rows as opposed to columns, e.g.:
* Running averages
* Time until next event
* Time since last event
This is often difficult to do with most table manipulation frameworks, since they are designed to work with relationships across columns. As such, we've created a class to handle this type of data.
```
columns = ["Date", "Store", "Promo", "StateHoliday", "SchoolHoliday"]
```
We've defined a class `elapsed` for cumulative counting across a sorted dataframe.
Given a particular field `fld` to monitor, this object will start tracking time since the last occurrence of that field. When the field is seen again, the counter is set to zero.
Upon initialization, this will result in datetime na's until the field is encountered. This is reset every time a new store is seen.
We'll see how to use this shortly.
```
class elapsed(object):
def __init__(self, fld):
self.fld = fld
self.last = pd.to_datetime(np.nan)
self.last_store = 0
def get(self, row):
if row.Store != self.last_store:
self.last = pd.to_datetime(np.nan)
self.last_store = row.Store
if (row[self.fld]): self.last = row.Date
return row.Date-self.last
df = train[columns]
```
And a function for applying said class across dataframe rows and adding values to a new column.
```
def add_elapsed(fld, prefix):
sh_el = elapsed(fld)
df[prefix+fld] = df.apply(sh_el.get, axis=1)
```
Let's walk through an example.
Say we're looking at School Holiday. We'll first sort by Store, then Date, and then call `add_elapsed('SchoolHoliday', 'After')`:
This will generate an instance of the `elapsed` class for School Holiday:
* Instance applied to every row of the dataframe in order of store and date
* Will add to the dataframe the days since seeing a School Holiday
* If we sort in the other direction, this will count the days until another promotion.
```
fld = 'SchoolHoliday'
df = df.sort_values(['Store', 'Date'])
add_elapsed(fld, 'After')
df = df.sort_values(['Store', 'Date'], ascending=[True, False])
add_elapsed(fld, 'Before')
```
We'll do this for two more fields.
```
fld = 'StateHoliday'
df = df.sort_values(['Store', 'Date'])
add_elapsed(fld, 'After')
df = df.sort_values(['Store', 'Date'], ascending=[True, False])
add_elapsed(fld, 'Before')
fld = 'Promo'
df = df.sort_values(['Store', 'Date'])
add_elapsed(fld, 'After')
df = df.sort_values(['Store', 'Date'], ascending=[True, False])
add_elapsed(fld, 'Before')
display(df.head())
```
We're going to set the active index to Date.
```
df = df.set_index("Date")
```
Then set null values from elapsed field calculations to 0.
```
columns = ['SchoolHoliday', 'StateHoliday', 'Promo']
for o in ['Before', 'After']:
for p in columns:
a = o+p
df[a] = df[a].fillna(pd.Timedelta(0)).dt.days
```
Next we'll demonstrate window functions in pandas to calculate rolling quantities.
Here we're sorting by date (`sort_index()`) and counting the number of events of interest (`sum()`) defined in `columns` in the following week (`rolling()`), grouped by Store (`groupby()`). We do the same in the opposite direction.
```
bwd = df[['Store']+columns].sort_index().groupby("Store").rolling(7, min_periods=1).sum()
fwd = df[['Store']+columns].sort_index(ascending=False
).groupby("Store").rolling(7, min_periods=1).sum()
```
Next we want to drop the Store indices grouped together in the window function.
Often in pandas, there is an option to do this in place. This is time and memory efficient when working with large datasets.
```
bwd.drop('Store',1,inplace=True)
bwd.reset_index(inplace=True)
fwd.drop('Store',1,inplace=True)
fwd.reset_index(inplace=True)
df.reset_index(inplace=True)
```
Now we'll merge these values onto the df.
```
df = df.merge(bwd, 'left', ['Date', 'Store'], suffixes=['', '_bw'])
df = df.merge(fwd, 'left', ['Date', 'Store'], suffixes=['', '_fw'])
df.drop(columns,1,inplace=True)
df.head()
```
It's usually a good idea to back up large tables of extracted / wrangled features before you join them onto another one, that way you can go back to it easily if you need to make changes to it.
```
df.to_csv('df.csv')
df = pd.read_csv('df.csv', index_col=0)
df["Date"] = pd.to_datetime(df.Date)
df.columns
joined = join_df(joined, df, ['Store', 'Date'])
```
We'll back this up as well.
```
joined.to_csv('joined.csv')
```
We now have our final set of engineered features.
```
joined = pd.read_csv('joined.csv', index_col=0)
joined["Date"] = pd.to_datetime(joined.Date)
joined.columns
```
While these steps were explicitly outlined in the paper, these are all fairly typical feature engineering steps for dealing with time series data and are practical in any similar setting.
## Create features
Now that we've engineered all our features, we need to convert to input compatible with a neural network.
This includes converting categorical variables into contiguous integers or one-hot encodings, normalizing continuous features to standard normal, etc...
```
from sklearn_pandas import DataFrameMapper
from sklearn.preprocessing import LabelEncoder, Imputer, StandardScaler
```
This dictionary maps categories to embedding dimensionality. In generally, categories we might expect to be conceptually more complex have larger dimension.
```
cat_var_dict = {'Store': 50, 'DayOfWeek': 6, 'Year': 2, 'Month': 6,
'Day': 10, 'StateHoliday': 3, 'CompetitionMonthsOpen': 2,
'Promo2Weeks': 1, 'StoreType': 2, 'Assortment': 3, 'PromoInterval': 3,
'CompetitionOpenSinceYear': 4, 'Promo2SinceYear': 4, 'State': 6,
'Week': 2, 'Events': 4, 'Promo_fw': 1,
'Promo_bw': 1, 'StateHoliday_fw': 1,
'StateHoliday_bw': 1, 'SchoolHoliday_fw': 1,
'SchoolHoliday_bw': 1}
```
Name categorical variables
```
cat_vars = [o[0] for o in
sorted(cat_var_dict.items(), key=operator.itemgetter(1), reverse=True)]
"""cat_vars = ['Store', 'DayOfWeek', 'Year', 'Month', 'Day', 'StateHoliday',
'StoreType', 'Assortment', 'Week', 'Events', 'Promo2SinceYear',
'CompetitionOpenSinceYear', 'PromoInterval', 'Promo', 'SchoolHoliday', 'State']"""
```
Likewise for continuous
```
# mean/max wind; min temp; cloud; min/mean humid;
contin_vars = ['CompetitionDistance',
'Max_TemperatureC', 'Mean_TemperatureC', 'Min_TemperatureC',
'Max_Humidity', 'Mean_Humidity', 'Min_Humidity', 'Max_Wind_SpeedKm_h',
'Mean_Wind_SpeedKm_h', 'CloudCover', 'trend', 'trend_DE',
'AfterStateHoliday', 'BeforeStateHoliday', 'Promo', 'SchoolHoliday']
"""contin_vars = ['CompetitionDistance', 'Max_TemperatureC', 'Mean_TemperatureC',
'Max_Humidity', 'trend', 'trend_DE', 'AfterStateHoliday', 'BeforeStateHoliday']"""
```
Replace nulls w/ 0 for continuous, "" for categorical.
```
for v in contin_vars: joined.loc[joined[v].isnull(), v] = 0
for v in cat_vars: joined.loc[joined[v].isnull(), v] = ""
```
Here we create a list of tuples, each containing a variable and an instance of a transformer for that variable.
For categoricals, we use a label encoder that maps categories to continuous integers. For continuous variables, we standardize them.
```
cat_maps = [(o, LabelEncoder()) for o in cat_vars]
contin_maps = [([o], StandardScaler()) for o in contin_vars]
```
The same instances need to be used for the test set as well, so values are mapped/standardized appropriately.
DataFrame mapper will keep track of these variable-instance mappings.
```
cat_mapper = DataFrameMapper(cat_maps)
cat_map_fit = cat_mapper.fit(joined)
cat_cols = len(cat_map_fit.features)
cat_cols
contin_mapper = DataFrameMapper(contin_maps)
contin_map_fit = contin_mapper.fit(joined)
contin_cols = len(contin_map_fit.features)
contin_cols
```
Example of first five rows of zeroth column being transformed appropriately.
```
cat_map_fit.transform(joined)[0,:5], contin_map_fit.transform(joined)[0,:5]
```
We can also pickle these mappings, which is great for portability!
```
pickle.dump(contin_map_fit, open('contin_maps.pickle', 'wb'))
pickle.dump(cat_map_fit, open('cat_maps.pickle', 'wb'))
[len(o[1].classes_) for o in cat_map_fit.features]
```
## Sample data
Next, the authors removed all instances where the store had zero sale / was closed.
```
joined_sales = joined[joined.Sales!=0]
n = len(joined_sales)
```
We speculate that this may have cost them a higher standing in the competition. One reason this may be the case is that a little EDA reveals that there are often periods where stores are closed, typically for refurbishment. Before and after these periods, there are naturally spikes in sales that one might expect. Be ommitting this data from their training, the authors gave up the ability to leverage information about these periods to predict this otherwise volatile behavior.
```
n
```
We're going to run on a sample.
```
samp_size = 100000
np.random.seed(42)
idxs = sorted(np.random.choice(n, samp_size, replace=False))
joined_samp = joined_sales.iloc[idxs].set_index("Date")
samp_size = n
joined_samp = joined_sales.set_index("Date")
```
In time series data, cross-validation is not random. Instead, our holdout data is always the most recent data, as it would be in real application.
We've taken the last 10% as our validation set.
```
train_ratio = 0.9
train_size = int(samp_size * train_ratio)
train_size
joined_valid = joined_samp[train_size:]
joined_train = joined_samp[:train_size]
len(joined_valid), len(joined_train)
```
Here's a preprocessor for our categoricals using our instance mapper.
```
def cat_preproc(dat):
return cat_map_fit.transform(dat).astype(np.int64)
cat_map_train = cat_preproc(joined_train)
cat_map_valid = cat_preproc(joined_valid)
```
Same for continuous.
```
def contin_preproc(dat):
return contin_map_fit.transform(dat).astype(np.float32)
contin_map_train = contin_preproc(joined_train)
contin_map_valid = contin_preproc(joined_valid)
```
Grab our targets.
```
y_train_orig = joined_train.Sales
y_valid_orig = joined_valid.Sales
```
Finally, the authors modified the target values by applying a logarithmic transformation and normalizing to unit scale by dividing by the maximum log value.
Log transformations are used on this type of data frequently to attain a nicer shape.
Further by scaling to the unit interval we can now use a sigmoid output in our neural network. Then we can multiply by the maximum log value to get the original log value and transform back.
```
max_log_y = np.max(np.log(joined_samp.Sales))
y_train = np.log(y_train_orig)/max_log_y
y_valid = np.log(y_valid_orig)/max_log_y
```
Note: Some testing shows this doesn't make a big difference.
```
"""#y_train = np.log(y_train)
ymean=y_train_orig.mean()
ystd=y_train_orig.std()
y_train = (y_train_orig-ymean)/ystd
#y_valid = np.log(y_valid)
y_valid = (y_valid_orig-ymean)/ystd"""
```
Root-mean-squared percent error is the metric Kaggle used for this competition.
```
def rmspe(y_pred, targ = y_valid_orig):
pct_var = (targ - y_pred)/targ
return math.sqrt(np.square(pct_var).mean())
```
These undo the target transformations.
```
def log_max_inv(preds, mx = max_log_y):
return np.exp(preds * mx)
# - This can be used if ymean and ystd are calculated above (they are currently commented out)
def normalize_inv(preds):
return preds * ystd + ymean
```
## Create models
Now we're ready to put together our models.
Much of the following code has commented out portions / alternate implementations.
```
"""
1 97s - loss: 0.0104 - val_loss: 0.0083
2 93s - loss: 0.0076 - val_loss: 0.0076
3 90s - loss: 0.0071 - val_loss: 0.0076
4 90s - loss: 0.0068 - val_loss: 0.0075
5 93s - loss: 0.0066 - val_loss: 0.0075
6 95s - loss: 0.0064 - val_loss: 0.0076
7 98s - loss: 0.0063 - val_loss: 0.0077
8 97s - loss: 0.0062 - val_loss: 0.0075
9 95s - loss: 0.0061 - val_loss: 0.0073
0 101s - loss: 0.0061 - val_loss: 0.0074
"""
def split_cols(arr):
return np.hsplit(arr,arr.shape[1])
# - This gives the correct list length for the model
# - (list of 23 elements: 22 embeddings + 1 array of 16-dim elements)
map_train = split_cols(cat_map_train) + [contin_map_train]
map_valid = split_cols(cat_map_valid) + [contin_map_valid]
len(map_train)
# map_train = split_cols(cat_map_train) + split_cols(contin_map_train)
# map_valid = split_cols(cat_map_valid) + split_cols(contin_map_valid)
```
Helper function for getting categorical name and dim.
```
def cat_map_info(feat): return feat[0], len(feat[1].classes_)
cat_map_info(cat_map_fit.features[1])
# - In Keras 2 the "initializations" module is not available.
# - To keep here the custom initializer the code from Keras 1 "uniform" initializer is exploited
def my_init(scale):
# return lambda shape, name=None: initializations.uniform(shape, scale=scale, name=name)
return K.variable(np.random.uniform(low=-scale, high=scale, size=shape),
name=name)
# - In Keras 2 the "initializations" module is not available.
# - To keep here the custom initializer the code from Keras 1 "uniform" initializer is exploited
def emb_init(shape, name=None):
# return initializations.uniform(shape, scale=2/(shape[1]+1), name=name)
return K.variable(np.random.uniform(low=-2/(shape[1]+1), high=2/(shape[1]+1), size=shape),
name=name)
```
Helper function for constructing embeddings. Notice commented out codes, several different ways to compute embeddings at play.
Also, note we're flattening the embedding. Embeddings in Keras come out as an element of a sequence like we might use in a sequence of words; here we just want to concatenate them so we flatten the 1-vector sequence into a vector.
```
def get_emb(feat):
name, c = cat_map_info(feat)
#c2 = cat_var_dict[name]
c2 = (c+1)//2
if c2>50: c2=50
inp = Input((1,), dtype='int64', name=name+'_in')
# , kernel_regularizer=l2(1e-6) # Keras 2
u = Flatten(name=name+'_flt')(Embedding(c, c2, input_length=1, embeddings_initializer=emb_init)(inp)) # Keras 2
# u = Flatten(name=name+'_flt')(Embedding(c, c2, input_length=1)(inp))
return inp,u
```
Helper function for continuous inputs.
```
def get_contin(feat):
name = feat[0][0]
inp = Input((1,), name=name+'_in')
return inp, Dense(1, name=name+'_d', kernel_initializer=my_init(1.))(inp) # Keras 2
```
Let's build them.
```
contin_inp = Input((contin_cols,), name='contin')
contin_out = Dense(contin_cols*10, activation='relu', name='contin_d')(contin_inp)
#contin_out = BatchNormalization()(contin_out)
```
Now we can put them together. Given the inputs, continuous and categorical embeddings, we're going to concatenate all of them.
Next, we're going to pass through some dropout, then two dense layers w/ ReLU activations, then dropout again, then the sigmoid activation we mentioned earlier.
```
embs = [get_emb(feat) for feat in cat_map_fit.features]
#conts = [get_contin(feat) for feat in contin_map_fit.features]
#contin_d = [d for inp,d in conts]
x = concatenate([emb for inp,emb in embs] + [contin_out]) # Keras 2
#x = concatenate([emb for inp,emb in embs] + contin_d) # Keras 2
x = Dropout(0.02)(x)
x = Dense(1000, activation='relu', kernel_initializer='uniform')(x)
x = Dense(500, activation='relu', kernel_initializer='uniform')(x)
x = Dropout(0.2)(x)
x = Dense(1, activation='sigmoid')(x)
model = Model([inp for inp,emb in embs] + [contin_inp], x)
#model = Model([inp for inp,emb in embs] + [inp for inp,d in conts], x)
model.compile('adam', 'mean_absolute_error')
#model.compile(Adam(), 'mse')
```
### Start training
```
%%time
hist = model.fit(map_train, y_train, batch_size=128, epochs=25,
verbose=1, validation_data=(map_valid, y_valid))
hist.history
plot_train(hist)
preds = np.squeeze(model.predict(map_valid, 1024))
```
Result on validation data: 0.1678 (samp 150k, 0.75 trn)
```
log_max_inv(preds)
# - This will work if ymean and ystd are calculated in the "Data" section above (in this case uncomment)
# normalize_inv(preds)
```
## Using 3rd place data
```
pkl_path = '/data/jhoward/github/entity-embedding-rossmann/'
def load_pickle(fname):
return pickle.load(open(pkl_path+fname + '.pickle', 'rb'))
[x_pkl_orig, y_pkl_orig] = load_pickle('feature_train_data')
max_log_y_pkl = np.max(np.log(y_pkl_orig))
y_pkl = np.log(y_pkl_orig)/max_log_y_pkl
pkl_vars = ['Open', 'Store', 'DayOfWeek', 'Promo', 'Year', 'Month', 'Day',
'StateHoliday', 'SchoolHoliday', 'CompetitionMonthsOpen', 'Promo2Weeks',
'Promo2Weeks_L', 'CompetitionDistance',
'StoreType', 'Assortment', 'PromoInterval', 'CompetitionOpenSinceYear',
'Promo2SinceYear', 'State', 'Week', 'Max_TemperatureC', 'Mean_TemperatureC',
'Min_TemperatureC', 'Max_Humidity', 'Mean_Humidity', 'Min_Humidity', 'Max_Wind_SpeedKm_h',
'Mean_Wind_SpeedKm_h', 'CloudCover','Events', 'Promo_fw', 'Promo_bw',
'StateHoliday_fw', 'StateHoliday_bw', 'AfterStateHoliday', 'BeforeStateHoliday',
'SchoolHoliday_fw', 'SchoolHoliday_bw', 'trend_DE', 'trend']
x_pkl = np.array(x_pkl_orig)
gt_enc = StandardScaler()
gt_enc.fit(x_pkl[:,-2:])
x_pkl[:,-2:] = gt_enc.transform(x_pkl[:,-2:])
x_pkl.shape
x_pkl = x_pkl[idxs]
y_pkl = y_pkl[idxs]
x_pkl_trn, x_pkl_val = x_pkl[:train_size], x_pkl[train_size:]
y_pkl_trn, y_pkl_val = y_pkl[:train_size], y_pkl[train_size:]
x_pkl_trn.shape
xgb_parms = {'learning_rate': 0.1, 'subsample': 0.6,
'colsample_bylevel': 0.6, 'silent': True, 'objective': 'reg:linear'}
xdata_pkl = xgboost.DMatrix(x_pkl_trn, y_pkl_trn, feature_names=pkl_vars)
xdata_val_pkl = xgboost.DMatrix(x_pkl_val, y_pkl_val, feature_names=pkl_vars)
xgb_parms['seed'] = random.randint(0,1e9)
model_pkl = xgboost.train(xgb_parms, xdata_pkl)
model_pkl.eval(xdata_val_pkl)
#0.117473
importance = model_pkl.get_fscore()
importance = sorted(importance.items(), key=operator.itemgetter(1))
df = pd.DataFrame(importance, columns=['feature', 'fscore'])
df['fscore'] = df['fscore'] / df['fscore'].sum()
df.plot(kind='barh', x='feature', y='fscore', legend=False, figsize=(6, 10))
plt.title('XGBoost Feature Importance')
plt.xlabel('relative importance');
```
### Neural net
```
#np.savez_compressed('vars.npz', pkl_cats, pkl_contins)
#np.savez_compressed('deps.npz', y_pkl)
pkl_cats = np.stack([x_pkl[:,pkl_vars.index(f)] for f in cat_vars], 1)
pkl_contins = np.stack([x_pkl[:,pkl_vars.index(f)] for f in contin_vars], 1)
co_enc = StandardScaler().fit(pkl_contins)
pkl_contins = co_enc.transform(pkl_contins)
pkl_contins_trn, pkl_contins_val = pkl_contins[:train_size], pkl_contins[train_size:]
pkl_cats_trn, pkl_cats_val = pkl_cats[:train_size], pkl_cats[train_size:]
y_pkl_trn, y_pkl_val = y_pkl[:train_size], y_pkl[train_size:]
def get_emb_pkl(feat):
name, c = cat_map_info(feat)
c2 = (c+2)//3
if c2>50: c2=50
inp = Input((1,), dtype='int64', name=name+'_in')
u = Flatten(name=name+'_flt')(Embedding(c, c2, input_length=1, init=emb_init)(inp))
return inp,u
n_pkl_contin = pkl_contins_trn.shape[1]
contin_inp = Input((n_pkl_contin,), name='contin')
contin_out = BatchNormalization()(contin_inp)
map_train_pkl = split_cols(pkl_cats_trn) + [pkl_contins_trn]
map_valid_pkl = split_cols(pkl_cats_val) + [pkl_contins_val]
def train_pkl(bs=128, ne=10):
return model_pkl.fit(map_train_pkl, y_pkl_trn, batch_size=bs, nb_epoch=ne,
verbose=0, validation_data=(map_valid_pkl, y_pkl_val))
def get_model_pkl():
conts = [get_contin_pkl(feat) for feat in contin_map_fit.features]
embs = [get_emb_pkl(feat) for feat in cat_map_fit.features]
x = merge([emb for inp,emb in embs] + [contin_out], mode='concat')
x = Dropout(0.02)(x)
x = Dense(1000, activation='relu', init='uniform')(x)
x = Dense(500, activation='relu', init='uniform')(x)
x = Dense(1, activation='sigmoid')(x)
model_pkl = Model([inp for inp,emb in embs] + [contin_inp], x)
model_pkl.compile('adam', 'mean_absolute_error')
#model.compile(Adam(), 'mse')
return model_pkl
model_pkl = get_model_pkl()
train_pkl(128, 10).history['val_loss']
K.set_value(model_pkl.optimizer.lr, 1e-4)
train_pkl(128, 5).history['val_loss']
"""
1 97s - loss: 0.0104 - val_loss: 0.0083
2 93s - loss: 0.0076 - val_loss: 0.0076
3 90s - loss: 0.0071 - val_loss: 0.0076
4 90s - loss: 0.0068 - val_loss: 0.0075
5 93s - loss: 0.0066 - val_loss: 0.0075
6 95s - loss: 0.0064 - val_loss: 0.0076
7 98s - loss: 0.0063 - val_loss: 0.0077
8 97s - loss: 0.0062 - val_loss: 0.0075
9 95s - loss: 0.0061 - val_loss: 0.0073
0 101s - loss: 0.0061 - val_loss: 0.0074
"""
plot_train(hist)
preds = np.squeeze(model_pkl.predict(map_valid_pkl, 1024))
y_orig_pkl_val = log_max_inv(y_pkl_val, max_log_y_pkl)
rmspe(log_max_inv(preds, max_log_y_pkl), y_orig_pkl_val)
```
## XGBoost
Xgboost is extremely quick and easy to use. Aside from being a powerful predictive model, it gives us information about feature importance.
```
X_train = np.concatenate([cat_map_train, contin_map_train], axis=1)
X_valid = np.concatenate([cat_map_valid, contin_map_valid], axis=1)
all_vars = cat_vars + contin_vars
xgb_parms = {'learning_rate': 0.1, 'subsample': 0.6,
'colsample_bylevel': 0.6, 'silent': True, 'objective': 'reg:linear'}
xdata = xgboost.DMatrix(X_train, y_train, feature_names=all_vars)
xdata_val = xgboost.DMatrix(X_valid, y_valid, feature_names=all_vars)
xgb_parms['seed'] = random.randint(0,1e9)
model = xgboost.train(xgb_parms, xdata)
model.eval(xdata_val)
model.eval(xdata_val)
```
Easily, competition distance is the most important, while events are not important at all.
In real applications, putting together a feature importance plot is often a first step. Oftentimes, we can remove hundreds of thousands of features from consideration with importance plots.
```
importance = model.get_fscore()
importance = sorted(importance.items(), key=operator.itemgetter(1))
df = pd.DataFrame(importance, columns=['feature', 'fscore'])
df['fscore'] = df['fscore'] / df['fscore'].sum()
df.plot(kind='barh', x='feature', y='fscore', legend=False, figsize=(6, 10))
plt.title('XGBoost Feature Importance')
plt.xlabel('relative importance');
```
## End
| true |
code
| 0.214691 | null | null | null | null |
|
# mlrose Tutorial Examples - Genevieve Hayes
## Overview
mlrose is a Python package for applying some of the most common randomized optimization and search algorithms to a range of different optimization problems, over both discrete- and continuous-valued parameter spaces. This notebook contains the examples used in the mlrose tutorial.
### Import Libraries
```
import mlrose
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder
from sklearn.metrics import accuracy_score
```
### Example 1: 8-Queens Using Pre-Defined Fitness Function
```
# Initialize fitness function object using pre-defined class
fitness = mlrose.Queens()
# Define optimization problem object
problem = mlrose.DiscreteOpt(length = 8, fitness_fn = fitness, maximize=False, max_val=8)
# Define decay schedule
schedule = mlrose.ExpDecay()
# Solve using simulated annealing - attempt 1
np.random.seed(1)
init_state = np.array([0, 1, 2, 3, 4, 5, 6, 7])
best_state, best_fitness = mlrose.simulated_annealing(problem, schedule = schedule, max_attempts = 10,
max_iters = 1000, init_state = init_state)
print(best_state)
print(best_fitness)
# Solve using simulated annealing - attempt 2
np.random.seed(1)
best_state, best_fitness = mlrose.simulated_annealing(problem, schedule = schedule, max_attempts = 100,
max_iters = 1000, init_state = init_state)
print(best_state)
print(best_fitness)
```
### Example 2: 8-Queens Using Custom Fitness Function
```
# Define alternative N-Queens fitness function for maximization problem
def queens_max(state):
# Initialize counter
fitness = 0
# For all pairs of queens
for i in range(len(state) - 1):
for j in range(i + 1, len(state)):
# Check for horizontal, diagonal-up and diagonal-down attacks
if (state[j] != state[i]) \
and (state[j] != state[i] + (j - i)) \
and (state[j] != state[i] - (j - i)):
# If no attacks, then increment counter
fitness += 1
return fitness
# Check function is working correctly
state = np.array([1, 4, 1, 3, 5, 5, 2, 7])
# The fitness of this state should be 22
queens_max(state)
# Initialize custom fitness function object
fitness_cust = mlrose.CustomFitness(queens_max)
# Define optimization problem object
problem_cust = mlrose.DiscreteOpt(length = 8, fitness_fn = fitness_cust, maximize = True, max_val = 8)
# Solve using simulated annealing - attempt 1
np.random.seed(1)
best_state, best_fitness = mlrose.simulated_annealing(problem_cust, schedule = schedule,
max_attempts = 10, max_iters = 1000,
init_state = init_state)
print(best_state)
print(best_fitness)
# Solve using simulated annealing - attempt 2
np.random.seed(1)
best_state, best_fitness = mlrose.simulated_annealing(problem_cust, schedule = schedule,
max_attempts = 100, max_iters = 1000,
init_state = init_state)
print(best_state)
print(best_fitness)
```
### Example 3: Travelling Salesperson Using Coordinate-Defined Fitness Function
```
# Create list of city coordinates
coords_list = [(1, 1), (4, 2), (5, 2), (6, 4), (4, 4), (3, 6), (1, 5), (2, 3)]
# Initialize fitness function object using coords_list
fitness_coords = mlrose.TravellingSales(coords = coords_list)
# Define optimization problem object
problem_fit = mlrose.TSPOpt(length = 8, fitness_fn = fitness_coords, maximize = False)
# Solve using genetic algorithm - attempt 1
np.random.seed(2)
best_state, best_fitness = mlrose.genetic_alg(problem_fit)
print(best_state)
print(best_fitness)
# Solve using genetic algorithm - attempt 2
np.random.seed(2)
best_state, best_fitness = mlrose.genetic_alg(problem_fit, mutation_prob = 0.2, max_attempts = 100)
print(best_state)
print(best_fitness)
```
### Example 4: Travelling Salesperson Using Distance-Defined Fitness Function
```
# Create list of distances between pairs of cities
dist_list = [(0, 1, 3.1623), (0, 2, 4.1231), (0, 3, 5.8310), (0, 4, 4.2426), (0, 5, 5.3852), \
(0, 6, 4.0000), (0, 7, 2.2361), (1, 2, 1.0000), (1, 3, 2.8284), (1, 4, 2.0000), \
(1, 5, 4.1231), (1, 6, 4.2426), (1, 7, 2.2361), (2, 3, 2.2361), (2, 4, 2.2361), \
(2, 5, 4.4721), (2, 6, 5.0000), (2, 7, 3.1623), (3, 4, 2.0000), (3, 5, 3.6056), \
(3, 6, 5.0990), (3, 7, 4.1231), (4, 5, 2.2361), (4, 6, 3.1623), (4, 7, 2.2361), \
(5, 6, 2.2361), (5, 7, 3.1623), (6, 7, 2.2361)]
# Initialize fitness function object using dist_list
fitness_dists = mlrose.TravellingSales(distances = dist_list)
# Define optimization problem object
problem_fit2 = mlrose.TSPOpt(length = 8, fitness_fn = fitness_dists, maximize = False)
# Solve using genetic algorithm
np.random.seed(2)
best_state, best_fitness = mlrose.genetic_alg(problem_fit2, mutation_prob = 0.2, max_attempts = 100)
print(best_state)
print(best_fitness)
```
### Example 5: Travelling Salesperson Defining Fitness Function as Part of Optimization Problem Definition Step
```
# Create list of city coordinates
coords_list = [(1, 1), (4, 2), (5, 2), (6, 4), (4, 4), (3, 6), (1, 5), (2, 3)]
# Define optimization problem object
problem_no_fit = mlrose.TSPOpt(length = 8, coords = coords_list, maximize = False)
# Solve using genetic algorithm
np.random.seed(2)
best_state, best_fitness = mlrose.genetic_alg(problem_no_fit, mutation_prob = 0.2, max_attempts = 100)
print(best_state)
print(best_fitness)
```
### Example 6: Fitting a Neural Network to the Iris Dataset
```
# Load the Iris dataset
data = load_iris()
# Get feature values of first observation
print(data.data[0])
# Get feature names
print(data.feature_names)
# Get target value of first observation
print(data.target[0])
# Get target name of first observation
print(data.target_names[data.target[0]])
# Get minimum feature values
print(np.min(data.data, axis = 0))
# Get maximum feature values
print(np.max(data.data, axis = 0))
# Get unique target values
print(np.unique(data.target))
# Split data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size = 0.2,
random_state = 3)
# Normalize feature data
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# One hot encode target values
one_hot = OneHotEncoder()
y_train_hot = one_hot.fit_transform(y_train.reshape(-1, 1)).todense()
y_test_hot = one_hot.transform(y_test.reshape(-1, 1)).todense()
# Initialize neural network object and fit object - attempt 1
np.random.seed(3)
nn_model1 = mlrose.NeuralNetwork(hidden_nodes = [2], activation ='relu',
algorithm ='random_hill_climb',
max_iters = 1000, bias = True, is_classifier = True,
learning_rate = 0.0001, early_stopping = True,
clip_max = 5, max_attempts = 100)
nn_model1.fit(X_train_scaled, y_train_hot)
# Predict labels for train set and assess accuracy
y_train_pred = nn_model1.predict(X_train_scaled)
y_train_accuracy = accuracy_score(y_train_hot, y_train_pred)
print(y_train_accuracy)
# Predict labels for test set and assess accuracy
y_test_pred = nn_model1.predict(X_test_scaled)
y_test_accuracy = accuracy_score(y_test_hot, y_test_pred)
print(y_test_accuracy)
# Initialize neural network object and fit object - attempt 2
np.random.seed(3)
nn_model2 = mlrose.NeuralNetwork(hidden_nodes = [2], activation = 'relu',
algorithm = 'gradient_descent',
max_iters = 1000, bias = True, is_classifier = True,
learning_rate = 0.0001, early_stopping = True,
clip_max = 5, max_attempts = 100)
nn_model2.fit(X_train_scaled, y_train_hot)
# Predict labels for train set and assess accuracy
y_train_pred = nn_model2.predict(X_train_scaled)
y_train_accuracy = accuracy_score(y_train_hot, y_train_pred)
print(y_train_accuracy)
# Predict labels for test set and assess accuracy
y_test_pred = nn_model2.predict(X_test_scaled)
y_test_accuracy = accuracy_score(y_test_hot, y_test_pred)
print(y_test_accuracy)
```
### Example 7: Fitting a Logistic Regression to the Iris Data
```
# Initialize logistic regression object and fit object - attempt 1
np.random.seed(3)
lr_model1 = mlrose.LogisticRegression(algorithm = 'random_hill_climb', max_iters = 1000,
bias = True, learning_rate = 0.0001,
early_stopping = True, clip_max = 5, max_attempts = 100)
lr_model1.fit(X_train_scaled, y_train_hot)
# Predict labels for train set and assess accuracy
y_train_pred = lr_model1.predict(X_train_scaled)
y_train_accuracy = accuracy_score(y_train_hot, y_train_pred)
print(y_train_accuracy)
# Predict labels for test set and assess accuracy
y_test_pred = lr_model1.predict(X_test_scaled)
y_test_accuracy = accuracy_score(y_test_hot, y_test_pred)
print(y_test_accuracy)
# Initialize logistic regression object and fit object - attempt 2
np.random.seed(3)
lr_model2 = mlrose.LogisticRegression(algorithm = 'random_hill_climb', max_iters = 1000,
bias = True, learning_rate = 0.01,
early_stopping = True, clip_max = 5, max_attempts = 100)
lr_model2.fit(X_train_scaled, y_train_hot)
# Predict labels for train set and assess accuracy
y_train_pred = lr_model2.predict(X_train_scaled)
y_train_accuracy = accuracy_score(y_train_hot, y_train_pred)
print(y_train_accuracy)
# Predict labels for test set and assess accuracy
y_test_pred = lr_model2.predict(X_test_scaled)
y_test_accuracy = accuracy_score(y_test_hot, y_test_pred)
print(y_test_accuracy)
```
### Example 8: Fitting a Logistic Regression to the Iris Data using the NeuralNetwork() class
```
# Initialize neural network object and fit object - attempt 1
np.random.seed(3)
lr_nn_model1 = mlrose.NeuralNetwork(hidden_nodes = [], activation = 'sigmoid',
algorithm = 'random_hill_climb',
max_iters = 1000, bias = True, is_classifier = True,
learning_rate = 0.0001, early_stopping = True,
clip_max = 5, max_attempts = 100)
lr_nn_model1.fit(X_train_scaled, y_train_hot)
# Predict labels for train set and assess accuracy
y_train_pred = lr_nn_model1.predict(X_train_scaled)
y_train_accuracy = accuracy_score(y_train_hot, y_train_pred)
print(y_train_accuracy)
# Predict labels for test set and assess accuracy
y_test_pred = lr_nn_model1.predict(X_test_scaled)
y_test_accuracy = accuracy_score(y_test_hot, y_test_pred)
print(y_test_accuracy)
# Initialize neural network object and fit object - attempt 2
np.random.seed(3)
lr_nn_model2 = mlrose.NeuralNetwork(hidden_nodes = [], activation = 'sigmoid',
algorithm = 'random_hill_climb',
max_iters = 1000, bias = True, is_classifier = True,
learning_rate = 0.01, early_stopping = True,
clip_max = 5, max_attempts = 100)
lr_nn_model2.fit(X_train_scaled, y_train_hot)
# Predict labels for train set and assess accuracy
y_train_pred = lr_nn_model2.predict(X_train_scaled)
y_train_accuracy = accuracy_score(y_train_hot, y_train_pred)
print(y_train_accuracy)
# Predict labels for test set and assess accuracy
y_test_pred = lr_nn_model2.predict(X_test_scaled)
y_test_accuracy = accuracy_score(y_test_hot, y_test_pred)
print(y_test_accuracy)
```
| true |
code
| 0.535584 | null | null | null | null |
|
# SciPy를 이용한 최적화
- fun: 2.0
hess_inv: array([[ 0.5]])
jac: array([ 0.])
message: 'Optimization terminated successfully.'
nfev: 9 # SciPy는 Sympy가 아니라서, Symbolic을 활용하지 못하기에 수치 미분을 함 - 1위치에서 3번 계산됨 nit가 2 이라는거는 2번 뛰엇나느 것이며, 3곳에서 9번함수를돌림..
nit: 2
njev: 3
status: 0
success: True
x: array([ 1.99999999])
def f1p(x):
return 2 * (x - 2)
result = sp.optimize.minimize(f1, x0, jac=f1p) ## 여기 flp 값을 미리 설정해줘야 1자리에서 3번 계산안하게 됨, 더 빨리됨
print(result)
fun: 2.0
hess_inv: array([[ 0.5]])
jac: array([ 0.])
message: 'Optimization terminated successfully.'
nfev: 3
nit: 2
njev: 3
status: 0
success: True
x: array([ 2.])
```
# 연습문제 1
# 2차원 RosenBerg 함수에 대해
# 1) 최적해에 수렴할 수 있도록 초기점을 변경하여 본다.
# 2) 그레디언트 벡터 함수를 구현하여 jac 인수로 주는 방법으로 계산 속도를 향상시킨다.
# 1) 최적해에 수렴할 수 있도록 초기점을 변경하여 본다.
x0 = 1 # 초기값 설정
result = sp.optimize.minimize(f1, x0)
print(result)
%matplotlib inline
def f1(x):
return (x - 2) ** 2 + 2
xx = np.linspace(-1, 4, 100)
plt.plot(xx, f1(xx))
plt.plot(2, 2, 'ro', markersize=20)
plt.ylim(0, 10)
plt.show()
def f2(x, y):
return (1 - x)**2 + 100.0 * (y - x**2)**2
xx = np.linspace(-4, 4, 800)
yy = np.linspace(-3, 3, 600)
X, Y = np.meshgrid(xx, yy)
Z = f2(X, Y)
plt.contour(X, Y, Z, colors="gray", levels=[0.4, 3, 15, 50, 150, 500, 1500, 5000])
plt.plot(1, 1, 'ro', markersize=20)
plt.xlim(-4, 4)
plt.ylim(-3, 3)
plt.xticks(np.linspace(-4, 4, 9))
plt.yticks(np.linspace(-3, 3, 7))
plt.show()
def f1d(x):
"""derivative of f1(x)"""
return 2 * (x - 2.0)
xx = np.linspace(-1, 4, 100)
plt.plot(xx, f1(xx), 'k-')
# step size
mu = 0.4
# k = 0
x = 0
plt.plot(x, f1(x), 'go', markersize=10)
plt.plot(xx, f1d(x) * (xx - x) + f1(x), 'b--')
print("x = {}, g = {}".format(x, f1d(x)))
# k = 1
x = x - mu * f1d(x)
plt.plot(x, f1(x), 'go', markersize=10)
plt.plot(xx, f1d(x) * (xx - x) + f1(x), 'b--')
print("x = {}, g = {}".format(x, f1d(x)))
# k = 2
x = x - mu * f1d(x)
plt.plot(x, f1(x), 'go', markersize=10)
plt.plot(xx, f1d(x) * (xx - x) + f1(x), 'b--')
print("x = {}, g = {}".format(x, f1d(x)))
plt.ylim(0, 10)
plt.show()
# 1)
def f2g(x, y):
"""gradient of f2(x)"""
return np.array((2.0 * (x - 1) - 400.0 * x * (y - x**2), 200.0 * (y - x**2)))
xx = np.linspace(-4, 4, 800)
yy = np.linspace(-3, 3, 600)
X, Y = np.meshgrid(xx, yy)
Z = f2(X, Y)
levels=np.logspace(-1, 3, 10)
plt.contourf(X, Y, Z, alpha=0.2, levels=levels)
plt.contour(X, Y, Z, colors="green", levels=levels, zorder=0)
plt.plot(1, 1, 'ro', markersize=10)
mu = 8e-4 # step size
s = 0.95 # for arrowr head drawing
x, y = 0, 0 # x = 1 , y = 1 에서 시작
for i in range(5):
g = f2g(x, y)
plt.arrow(x, y, -s * mu * g[0], -s * mu * g[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw=2)
x = x - mu * g[0]
y = y - mu * g[1]
plt.xlim(-3, 3)
plt.ylim(-2, 2)
plt.xticks(np.linspace(-3, 3, 7))
plt.yticks(np.linspace(-2, 2, 5))
plt.show()
x0 = -0.5 # 초기값
result = sp.optimize.minimize(f1, x0)
print(result)
def f1p(x):
return 2 * (x - 2)
result = sp.optimize.minimize(f1, x0, jac=f1p)
print(result)
def f2(x):
return (1 - x[0])**2 + 400.0 * (x[1] - x[0]**2)**2
x0 = (0.7, 0.7)
result = sp.optimize.minimize(f2, x0)
print(result)
def f2p(x):
return np.array([2*x[0]-2-1600*x[0]*x[1]+1600*x[0]**3, 800*x[1]-800*x[0]**2])
result = sp.optimize.minimize(f2, x0, jac=f2p)
print(result)
```
| true |
code
| 0.440349 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Reinforcement Learning in Azure Machine Learning - Training a Minecraft agent using custom environments
This tutorial will show how to set up a more complex reinforcement
learning (RL) training scenario. It demonstrates how to train an agent to
navigate through a lava maze in the Minecraft game using Azure Machine
Learning.
**Please note:** This notebook trains an agent on a randomly generated
Minecraft level. As a result, on rare occasions, a training run may fail
to produce a model that can solve the maze. If this happens, you can
re-run the training step as indicated below.
**Please note:** This notebook uses 1 NC6 type node and 8 D2 type nodes
for up to 5 hours of training, which corresponds to approximately $9.06 (USD)
as of May 2020.
Minecraft is currently one of the most popular video
games and as such has been a study object for RL. [Project
Malmo](https://www.microsoft.com/en-us/research/project/project-malmo/) is
a platform for artificial intelligence experimentation and research built on
top of Minecraft. We will use Minecraft [gym](https://gym.openai.com) environments from Project
Malmo's 2019 MineRL competition, which are part of the
[MineRL](http://minerl.io/docs/index.html) Python package.
Minecraft environments require a display to run, so we will demonstrate
how to set up a virtual display within the docker container used for training.
Learning will be based on the agent's visual observations. To
generate the necessary amount of sample data, we will run several
instances of the Minecraft game in parallel. Below, you can see a video of
a trained agent navigating a lava maze. Starting from the green position,
it moves to the blue position by moving forward, turning left or turning right:
<table style="width:50%">
<tr>
<th style="text-align: center;">
<img src="./images/lava_maze_minecraft.gif" alt="Minecraft lava maze" align="middle" margin-left="auto" margin-right="auto"/>
</th>
</tr>
<tr style="text-align: center;">
<th>Fig 1. Video of a trained Minecraft agent navigating a lava maze.</th>
</tr>
</table>
The tutorial will cover the following steps:
- Initializing Azure Machine Learning resources for training
- Training the RL agent with Azure Machine Learning service
- Monitoring training progress
- Reviewing training results
## Prerequisites
The user should have completed the Azure Machine Learning introductory tutorial.
You will need to make sure that you have a valid subscription id, a resource group and a
workspace. For detailed instructions see [Tutorial: Get started creating
your first ML experiment.](https://docs.microsoft.com/en-us/azure/machine-learning/tutorial-1st-experiment-sdk-setup)
While this is a standalone notebook, we highly recommend going over the
introductory notebooks for RL first.
- Getting started:
- [RL using a compute instance with Azure Machine Learning service](../cartpole-on-compute-instance/cartpole_ci.ipynb)
- [Using Azure Machine Learning compute](../cartpole-on-single-compute/cartpole_sc.ipynb)
- [Scaling RL training runs with Azure Machine Learning service](../atari-on-distributed-compute/pong_rllib.ipynb)
## Initialize resources
All required Azure Machine Learning service resources for this tutorial can be set up from Jupyter.
This includes:
- Connecting to your existing Azure Machine Learning workspace.
- Creating an experiment to track runs.
- Setting up a virtual network
- Creating remote compute targets for [Ray](https://docs.ray.io/en/latest/index.html).
### Azure Machine Learning SDK
Display the Azure Machine Learning SDK version.
```
import azureml.core
print("Azure Machine Learning SDK Version: ", azureml.core.VERSION)
```
### Connect to workspace
Get a reference to an existing Azure Machine Learning workspace.
```
from azureml.core import Workspace
ws = Workspace.from_config()
print(ws.name, ws.location, ws.resource_group, sep=' | ')
```
### Create an experiment
Create an experiment to track the runs in your workspace. A
workspace can have multiple experiments and each experiment
can be used to track multiple runs (see [documentation](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.experiment.experiment?view=azure-ml-py)
for details).
```
from azureml.core import Experiment
exp = Experiment(workspace=ws, name='minecraft-maze')
```
### Create Virtual Network
If you are using separate compute targets for the Ray head and worker, a virtual network must be created in the resource group. If you have alraeady created a virtual network in the resource group, you can skip this step.
To do this, you first must install the Azure Networking API.
`pip install --upgrade azure-mgmt-network`
```
# If you need to install the Azure Networking SDK, uncomment the following line.
#!pip install --upgrade azure-mgmt-network
from azure.mgmt.network import NetworkManagementClient
# Virtual network name
vnet_name ="your_vnet"
# Default subnet
subnet_name ="default"
# The Azure subscription you are using
subscription_id=ws.subscription_id
# The resource group for the reinforcement learning cluster
resource_group=ws.resource_group
# Azure region of the resource group
location=ws.location
network_client = NetworkManagementClient(ws._auth_object, subscription_id)
async_vnet_creation = network_client.virtual_networks.create_or_update(
resource_group,
vnet_name,
{
'location': location,
'address_space': {
'address_prefixes': ['10.0.0.0/16']
}
}
)
async_vnet_creation.wait()
print("Virtual network created successfully: ", async_vnet_creation.result())
```
### Set up Network Security Group on Virtual Network
Depending on your Azure setup, you may need to open certain ports to make it possible for Azure to manage the compute targets that you create. The ports that need to be opened are described [here](https://docs.microsoft.com/en-us/azure/machine-learning/how-to-enable-virtual-network).
A common situation is that ports `29876-29877` are closed. The following code will add a security rule to open these ports. Or you can do this manually in the [Azure portal](https://portal.azure.com).
You may need to modify the code below to match your scenario.
```
import azure.mgmt.network.models
security_group_name = vnet_name + '-' + "nsg"
security_rule_name = "AllowAML"
# Create a network security group
nsg_params = azure.mgmt.network.models.NetworkSecurityGroup(
location=location,
security_rules=[
azure.mgmt.network.models.SecurityRule(
name=security_rule_name,
access=azure.mgmt.network.models.SecurityRuleAccess.allow,
description='Reinforcement Learning in Azure Machine Learning rule',
destination_address_prefix='*',
destination_port_range='29876-29877',
direction=azure.mgmt.network.models.SecurityRuleDirection.inbound,
priority=400,
protocol=azure.mgmt.network.models.SecurityRuleProtocol.tcp,
source_address_prefix='BatchNodeManagement',
source_port_range='*'
),
],
)
async_nsg_creation = network_client.network_security_groups.create_or_update(
resource_group,
security_group_name,
nsg_params,
)
async_nsg_creation.wait()
print("Network security group created successfully:", async_nsg_creation.result())
network_security_group = network_client.network_security_groups.get(
resource_group,
security_group_name,
)
# Define a subnet to be created with network security group
subnet = azure.mgmt.network.models.Subnet(
id='default',
address_prefix='10.0.0.0/24',
network_security_group=network_security_group
)
# Create subnet on virtual network
async_subnet_creation = network_client.subnets.create_or_update(
resource_group_name=resource_group,
virtual_network_name=vnet_name,
subnet_name=subnet_name,
subnet_parameters=subnet
)
async_subnet_creation.wait()
print("Subnet created successfully:", async_subnet_creation.result())
```
### Review the virtual network security rules
Ensure that the virtual network is configured correctly with required ports open. It is possible that you have configured rules with broader range of ports that allows ports 29876-29877 to be opened. Kindly review your network security group rules.
```
from files.networkutils import *
check_vnet_security_rules(ws._auth_object, ws.subscription_id, ws.resource_group, vnet_name, True)
```
### Create or attach an existing compute resource
A compute target is a designated compute resource where you
run your training script. For more information, see [What
are compute targets in Azure Machine Learning service?](https://docs.microsoft.com/en-us/azure/machine-learning/concept-compute-target).
#### GPU target for Ray head
In the experiment setup for this tutorial, the Ray head node
will run on a GPU-enabled node. A maximum cluster size
of 1 node is therefore sufficient. If you wish to run
multiple experiments in parallel using the same GPU
cluster, you may elect to increase this number. The cluster
will automatically scale down to 0 nodes when no training jobs
are scheduled (see `min_nodes`).
The code below creates a compute cluster of GPU-enabled NC6
nodes. If the cluster with the specified name is already in
your workspace the code will skip the creation process.
Note that we must specify a Virtual Network during compute
creation to allow communication between the cluster running
the Ray head node and the additional Ray compute nodes. For
details on how to setup the Virtual Network, please follow the
instructions in the "Prerequisites" section above.
**Note: Creation of a compute resource can take several minutes**
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
gpu_cluster_name = 'gpu-cl-nc6-vnet'
try:
gpu_cluster = ComputeTarget(workspace=ws, name=gpu_cluster_name)
print('Found existing compute target')
except ComputeTargetException:
print('Creating a new compute target...')
compute_config = AmlCompute.provisioning_configuration(
vm_size='Standard_NC6',
min_nodes=0,
max_nodes=1,
vnet_resourcegroup_name=ws.resource_group,
vnet_name=vnet_name,
subnet_name=subnet_name)
gpu_cluster = ComputeTarget.create(ws, gpu_cluster_name, compute_config)
gpu_cluster.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
print('Cluster created.')
```
#### CPU target for additional Ray nodes
The code below creates a compute cluster of D2 nodes. If the cluster with the specified name is already in your workspace the code will skip the creation process.
This cluster will be used to start additional Ray nodes
increasing the clusters CPU resources.
**Note: Creation of a compute resource can take several minutes**
```
cpu_cluster_name = 'cpu-cl-d2-vnet'
try:
cpu_cluster = ComputeTarget(workspace=ws, name=cpu_cluster_name)
print('Found existing compute target')
except ComputeTargetException:
print('Creating a new compute target...')
compute_config = AmlCompute.provisioning_configuration(
vm_size='STANDARD_D2',
min_nodes=0,
max_nodes=10,
vnet_resourcegroup_name=ws.resource_group,
vnet_name=vnet_name,
subnet_name=subnet_name)
cpu_cluster = ComputeTarget.create(ws, cpu_cluster_name, compute_config)
cpu_cluster.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
print('Cluster created.')
```
## Training the agent
### Training environments
This tutorial uses custom docker images (CPU and GPU respectively)
with the necessary software installed. The
[Environment](https://docs.microsoft.com/en-us/azure/machine-learning/how-to-use-environments)
class stores the configuration for the training environment. The docker
image is set via `env.docker.base_image` which can point to any
publicly available docker image. `user_managed_dependencies`
is set so that the preinstalled Python packages in the image are preserved.
Note that since Minecraft requires a display to start, we set the `interpreter_path`
such that the Python process is started via **xvfb-run**.
```
import os
from azureml.core import Environment
max_train_time = os.environ.get("AML_MAX_TRAIN_TIME_SECONDS", 5 * 60 * 60)
def create_env(env_type):
env = Environment(name='minecraft-{env_type}'.format(env_type=env_type))
env.docker.enabled = True
env.docker.base_image = 'akdmsft/minecraft-{env_type}'.format(env_type=env_type)
env.python.interpreter_path = "xvfb-run -s '-screen 0 640x480x16 -ac +extension GLX +render' python"
env.environment_variables["AML_MAX_TRAIN_TIME_SECONDS"] = str(max_train_time)
env.python.user_managed_dependencies = True
return env
cpu_minecraft_env = create_env('cpu')
gpu_minecraft_env = create_env('gpu')
```
### Training script
As described above, we use the MineRL Python package to launch
Minecraft game instances. MineRL provides several OpenAI gym
environments for different scenarios, such as chopping wood.
Besides predefined environments, MineRL lets its users create
custom Minecraft environments through
[minerl.env](http://minerl.io/docs/api/env.html). In the helper
file **minecraft_environment.py** provided with this tutorial, we use the
latter option to customize a Minecraft level with a lava maze
that the agent has to navigate. The agent receives a negative
reward of -1 for falling into the lava, a negative reward of
-0.02 for sending a command (i.e. navigating through the maze
with fewer actions yields a higher total reward) and a positive reward
of 1 for reaching the goal. To encourage the agent to explore
the maze, it also receives a positive reward of 0.1 for visiting
a tile for the first time.
The agent learns purely from visual observations and the image
is scaled to an 84x84 format, stacking four frames. For the
purposes of this example, we use a small action space of size
three: move forward, turn 90 degrees to the left, and turn 90
degrees to the right.
The training script itself registers the function to create training
environments with the `tune.register_env` function and connects to
the Ray cluster Azure Machine Learning service started on the GPU
and CPU nodes. Lastly, it starts a RL training run with `tune.run()`.
We recommend setting the `local_dir` parameter to `./logs` as this
directory will automatically become available as part of the training
run's files in the Azure Portal. The Tensorboard integration
(see "View the Tensorboard" section below) also depends on the files'
availability. For a list of common parameter options, please refer
to the [Ray documentation](https://docs.ray.io/en/latest/rllib-training.html#common-parameters).
```python
# Taken from minecraft_environment.py and minecraft_train.py
# Define a function to create a MineRL environment
def create_env(config):
mission = config['mission']
port = 1000 * config.worker_index + config.vector_index
print('*********************************************')
print(f'* Worker {config.worker_index} creating from mission: {mission}, port {port}')
print('*********************************************')
if config.worker_index == 0:
# The first environment is only used for checking the action and observation space.
# By using a dummy environment, there's no need to spin up a Minecraft instance behind it
# saving some CPU resources on the head node.
return DummyEnv()
env = EnvWrapper(mission, port)
env = TrackingEnv(env)
env = FrameStack(env, 2)
return env
def stop(trial_id, result):
return result["episode_reward_mean"] >= 1 \
or result["time_total_s"] > 5 * 60 * 60
if __name__ == '__main__':
tune.register_env("Minecraft", create_env)
ray.init(address='auto')
tune.run(
run_or_experiment="IMPALA",
config={
"env": "Minecraft",
"env_config": {
"mission": "minecraft_missions/lava_maze-v0.xml"
},
"num_workers": 10,
"num_cpus_per_worker": 2,
"rollout_fragment_length": 50,
"train_batch_size": 1024,
"replay_buffer_num_slots": 4000,
"replay_proportion": 10,
"learner_queue_timeout": 900,
"num_sgd_iter": 2,
"num_data_loader_buffers": 2,
"exploration_config": {
"type": "EpsilonGreedy",
"initial_epsilon": 1.0,
"final_epsilon": 0.02,
"epsilon_timesteps": 500000
},
"callbacks": {"on_train_result": callbacks.on_train_result},
},
stop=stop,
checkpoint_at_end=True,
local_dir='./logs'
)
```
### Submitting a training run
Below, you create the training run using a `ReinforcementLearningEstimator`
object, which contains all the configuration parameters for this experiment:
- `source_directory`: Contains the training script and helper files to be
copied onto the node running the Ray head.
- `entry_script`: The training script, described in more detail above..
- `compute_target`: The compute target for the Ray head and training
script execution.
- `environment`: The Azure machine learning environment definition for
the node running the Ray head.
- `worker_configuration`: The configuration object for the additional
Ray nodes to be attached to the Ray cluster:
- `compute_target`: The compute target for the additional Ray nodes.
- `node_count`: The number of nodes to attach to the Ray cluster.
- `environment`: The environment definition for the additional Ray nodes.
- `max_run_duration_seconds`: The time after which to abort the run if it
is still running.
- `shm_size`: The size of docker container's shared memory block.
For more details, please take a look at the [online documentation](https://docs.microsoft.com/en-us/python/api/azureml-contrib-reinforcementlearning/?view=azure-ml-py)
for Azure Machine Learning service's reinforcement learning offering.
We configure 8 extra D2 (worker) nodes for the Ray cluster, giving us a total of
22 CPUs and 1 GPU. The GPU and one CPU are used by the IMPALA learner,
and each MineRL environment receives 2 CPUs allowing us to spawn a total
of 10 rollout workers (see `num_workers` parameter in the training script).
Lastly, the `RunDetails` widget displays information about the submitted
RL experiment, including a link to the Azure portal with more details.
```
from azureml.contrib.train.rl import ReinforcementLearningEstimator, WorkerConfiguration
from azureml.widgets import RunDetails
worker_config = WorkerConfiguration(
compute_target=cpu_cluster,
node_count=8,
environment=cpu_minecraft_env)
rl_est = ReinforcementLearningEstimator(
source_directory='files',
entry_script='minecraft_train.py',
compute_target=gpu_cluster,
environment=gpu_minecraft_env,
worker_configuration=worker_config,
max_run_duration_seconds=6 * 60 * 60,
shm_size=1024 * 1024 * 1024 * 30)
train_run = exp.submit(rl_est)
RunDetails(train_run).show()
# If you wish to cancel the run before it completes, uncomment and execute:
#train_run.cancel()
```
## Monitoring training progress
### View the Tensorboard
The Tensorboard can be displayed via the Azure Machine Learning service's
[Tensorboard API](https://docs.microsoft.com/en-us/azure/machine-learning/how-to-monitor-tensorboard).
When running locally, please make sure to follow the instructions in the
link and install required packages. Running this cell will output a URL
for the Tensorboard.
Note that the training script sets the log directory when starting RLlib
via the `local_dir` parameter. `./logs` will automatically appear in
the downloadable files for a run. Since this script is executed on the
Ray head node run, we need to get a reference to it as shown below.
The Tensorboard API will continuously stream logs from the run.
**Note: It may take a couple of minutes after the run is in "Running" state
before Tensorboard files are available and the board will refresh automatically**
```
import time
from azureml.tensorboard import Tensorboard
head_run = None
timeout = 60
while timeout > 0 and head_run is None:
timeout -= 1
try:
head_run = next(r for r in train_run.get_children() if r.id.endswith('head'))
except StopIteration:
time.sleep(1)
tb = Tensorboard([head_run], port=6007)
tb.start()
```
## Review results
Please ensure that the training run has completed before continuing with this section.
```
train_run.wait_for_completion()
print('Training run completed.')
```
**Please note:** If the final "episode_reward_mean" metric from the training run is negative,
the produced model does not solve the problem of navigating the maze well. You can view
the metric on the Tensorboard or in "Metrics" section of the head run in the Azure Machine Learning
portal. We recommend training a new model by rerunning the notebook starting from "Submitting a training run".
### Export final model
The key result from the training run is the final checkpoint
containing the state of the IMPALA trainer (model) upon meeting the
stopping criteria specified in `minecraft_train.py`.
Azure Machine Learning service offers the [Model.register()](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.model.model?view=azure-ml-py)
API which allows you to persist the model files from the
training run. We identify the directory containing the
final model written during the training run and register
it with Azure Machine Learning service. We use a Dataset
object to filter out the correct files.
```
import re
import tempfile
from azureml.core import Dataset
path_prefix = os.path.join(tempfile.gettempdir(), 'tmp_training_artifacts')
run_artifacts_path = os.path.join('azureml', head_run.id)
datastore = ws.get_default_datastore()
run_artifacts_ds = Dataset.File.from_files(datastore.path(os.path.join(run_artifacts_path, '**')))
cp_pattern = re.compile('.*checkpoint-\\d+$')
checkpoint_files = [file for file in run_artifacts_ds.to_path() if cp_pattern.match(file)]
# There should only be one checkpoint with our training settings...
final_checkpoint = os.path.dirname(os.path.join(run_artifacts_path, os.path.normpath(checkpoint_files[-1][1:])))
datastore.download(target_path=path_prefix, prefix=final_checkpoint.replace('\\', '/'), show_progress=True)
print('Download complete.')
from azureml.core.model import Model
model_name = 'final_model_minecraft_maze'
model = Model.register(
workspace=ws,
model_path=os.path.join(path_prefix, final_checkpoint),
model_name=model_name,
description='Model of an agent trained to navigate a lava maze in Minecraft.')
```
Models can be used through a varity of APIs. Please see the
[documentation](https://docs.microsoft.com/en-us/azure/machine-learning/how-to-deploy-and-where)
for more details.
### Test agent performance in a rollout
To observe the trained agent's behavior, it is a common practice to
view its behavior in a rollout. The previous reinforcement learning
tutorials explain rollouts in more detail.
The provided `minecraft_rollout.py` script loads the final checkpoint
of the trained agent from the model registered with Azure Machine Learning
service. It then starts a rollout on 4 different lava maze layouts, that
are all larger and thus more difficult than the maze the agent was trained
on. The script further records videos by replaying the agent's decisions
in [Malmo](https://github.com/microsoft/malmo). Malmo supports multiple
agents in the same environment, thus allowing us to capture videos that
depict the agent from another agent's perspective. The provided
`malmo_video_recorder.py` file and the Malmo Github repository have more
details on the video recording setup.
You can view the rewards for each rollout episode in the logs for the 'head'
run submitted below. In some episodes, the agent may fail to reach the goal
due to the higher level of difficulty - in practice, we could continue
training the agent on harder tasks starting with the final checkpoint.
```
script_params = {
'--model_name': model_name
}
rollout_est = ReinforcementLearningEstimator(
source_directory='files',
entry_script='minecraft_rollout.py',
script_params=script_params,
compute_target=gpu_cluster,
environment=gpu_minecraft_env,
shm_size=1024 * 1024 * 1024 * 30)
rollout_run = exp.submit(rollout_est)
RunDetails(rollout_run).show()
```
### View videos captured during rollout
To inspect the agent's training progress you can view the videos captured
during the rollout episodes. First, ensure that the training run has
completed.
```
rollout_run.wait_for_completion()
head_run_rollout = next(r for r in rollout_run.get_children() if r.id.endswith('head'))
print('Rollout completed.')
```
Next, you need to download the video files from the training run. We use a
Dataset to filter out the video files which are in tgz archives.
```
rollout_run_artifacts_path = os.path.join('azureml', head_run_rollout.id)
datastore = ws.get_default_datastore()
rollout_run_artifacts_ds = Dataset.File.from_files(datastore.path(os.path.join(rollout_run_artifacts_path, '**')))
video_archives = [file for file in rollout_run_artifacts_ds.to_path() if file.endswith('.tgz')]
video_archives = [os.path.join(rollout_run_artifacts_path, os.path.normpath(file[1:])) for file in video_archives]
datastore.download(
target_path=path_prefix,
prefix=os.path.dirname(video_archives[0]).replace('\\', '/'),
show_progress=True)
print('Download complete.')
```
Next, unzip the video files and rename them by the Minecraft mission seed used
(see `minecraft_rollout.py` for more details on how the seed is used).
```
import tarfile
import shutil
training_artifacts_dir = './training_artifacts'
video_dir = os.path.join(training_artifacts_dir, 'videos')
video_files = []
for tar_file_path in video_archives:
seed = tar_file_path[tar_file_path.index('rollout_') + len('rollout_'): tar_file_path.index('.tgz')]
tar = tarfile.open(os.path.join(path_prefix, tar_file_path).replace('\\', '/'), 'r')
tar_info = next(t_info for t_info in tar.getmembers() if t_info.name.endswith('mp4'))
tar.extract(tar_info, video_dir)
tar.close()
unzipped_folder = os.path.join(video_dir, next(f_ for f_ in os.listdir(video_dir) if not f_.endswith('mp4')))
video_file = os.path.join(unzipped_folder,'video.mp4')
final_video_path = os.path.join(video_dir, '{seed}.mp4'.format(seed=seed))
shutil.move(video_file, final_video_path)
video_files.append(final_video_path)
shutil.rmtree(unzipped_folder)
# Clean up any downloaded 'tmp' files
shutil.rmtree(path_prefix)
print('Local video files:\n', video_files)
```
Finally, run the cell below to display the videos in-line. In some cases,
the agent may struggle to find the goal since the maze size was increased
compared to training.
```
from IPython.core.display import display, HTML
index = 0
while index < len(video_files) - 1:
display(
HTML('\
<video controls alt="cannot display video" autoplay loop width=49%> \
<source src="{f1}" type="video/mp4"> \
</video> \
<video controls alt="cannot display video" autoplay loop width=49%> \
<source src="{f2}" type="video/mp4"> \
</video>'.format(f1=video_files[index], f2=video_files[index + 1]))
)
index += 2
if index < len(video_files):
display(
HTML('\
<video controls alt="cannot display video" autoplay loop width=49%> \
<source src="{f1}" type="video/mp4"> \
</video>'.format(f1=video_files[index]))
)
```
## Cleaning up
Below, you can find code snippets for your convenience to clean up any resources created as part of this tutorial you don't wish to retain.
```
# to stop the Tensorboard, uncomment and run
#tb.stop()
# to delete the gpu compute target, uncomment and run
#gpu_cluster.delete()
# to delete the cpu compute target, uncomment and run
#cpu_cluster.delete()
# to delete the registered model, uncomment and run
#model.delete()
# to delete the local video files, uncomment and run
#shutil.rmtree(training_artifacts_dir)
```
## Next steps
This is currently the last introductory tutorial for Azure Machine Learning
service's Reinforcement
Learning offering. We would love to hear your feedback to build the features
you need!
| true |
code
| 0.493409 | null | null | null | null |
|
# Learning Tree-augmented Naive Bayes (TAN) Structure from Data
In this notebook, we show an example for learning the structure of a Bayesian Network using the TAN algorithm. We will first build a model to generate some data and then attempt to learn the model's graph structure back from the generated data.
For comparison of Naive Bayes and TAN classifier, refer to the blog post [Classification with TAN and Pgmpy](https://loudly-soft.blogspot.com/2020/08/classification-with-tree-augmented.html).
## First, create a Naive Bayes graph
```
import networkx as nx
import matplotlib.pyplot as plt
from pgmpy.models import BayesianNetwork
# class variable is A and feature variables are B, C, D, E and R
model = BayesianNetwork([("A", "R"), ("A", "B"), ("A", "C"), ("A", "D"), ("A", "E")])
nx.draw_circular(
model, with_labels=True, arrowsize=30, node_size=800, alpha=0.3, font_weight="bold"
)
plt.show()
```
## Second, add interaction between the features
```
# feature R correlates with other features
model.add_edges_from([("R", "B"), ("R", "C"), ("R", "D"), ("R", "E")])
nx.draw_circular(
model, with_labels=True, arrowsize=30, node_size=800, alpha=0.3, font_weight="bold"
)
plt.show()
```
## Then, parameterize our graph to create a Bayesian network
```
from pgmpy.factors.discrete import TabularCPD
# add CPD to each edge
cpd_a = TabularCPD("A", 2, [[0.7], [0.3]])
cpd_r = TabularCPD(
"R", 3, [[0.6, 0.2], [0.3, 0.5], [0.1, 0.3]], evidence=["A"], evidence_card=[2]
)
cpd_b = TabularCPD(
"B",
3,
[
[0.1, 0.1, 0.2, 0.2, 0.7, 0.1],
[0.1, 0.3, 0.1, 0.2, 0.1, 0.2],
[0.8, 0.6, 0.7, 0.6, 0.2, 0.7],
],
evidence=["A", "R"],
evidence_card=[2, 3],
)
cpd_c = TabularCPD(
"C",
2,
[[0.7, 0.2, 0.2, 0.5, 0.1, 0.3], [0.3, 0.8, 0.8, 0.5, 0.9, 0.7]],
evidence=["A", "R"],
evidence_card=[2, 3],
)
cpd_d = TabularCPD(
"D",
3,
[
[0.3, 0.8, 0.2, 0.8, 0.4, 0.7],
[0.4, 0.1, 0.4, 0.1, 0.1, 0.1],
[0.3, 0.1, 0.4, 0.1, 0.5, 0.2],
],
evidence=["A", "R"],
evidence_card=[2, 3],
)
cpd_e = TabularCPD(
"E",
2,
[[0.5, 0.6, 0.6, 0.5, 0.5, 0.4], [0.5, 0.4, 0.4, 0.5, 0.5, 0.6]],
evidence=["A", "R"],
evidence_card=[2, 3],
)
model.add_cpds(cpd_a, cpd_r, cpd_b, cpd_c, cpd_d, cpd_e)
```
## Next, generate sample data from our Bayesian network
```
from pgmpy.sampling import BayesianModelSampling
# sample data from BN
inference = BayesianModelSampling(model)
df_data = inference.forward_sample(size=10000)
print(df_data)
```
## Now we are ready to learn the TAN structure from sample data
```
from pgmpy.estimators import TreeSearch
# learn graph structure
est = TreeSearch(df_data, root_node="R")
dag = est.estimate(estimator_type="tan", class_node="A")
nx.draw_circular(
dag, with_labels=True, arrowsize=30, node_size=800, alpha=0.3, font_weight="bold"
)
plt.show()
```
## To parameterize the learned graph from data, check out the other tutorials for more info
```
from pgmpy.estimators import BayesianEstimator
# there are many choices of parametrization, here is one example
model = BayesianNetwork(dag.edges())
model.fit(
df_data, estimator=BayesianEstimator, prior_type="dirichlet", pseudo_counts=0.1
)
model.get_cpds()
```
| true |
code
| 0.729526 | null | null | null | null |
|
**This notebook is an exercise in the [Intermediate Machine Learning](https://www.kaggle.com/learn/intermediate-machine-learning) course. You can reference the tutorial at [this link](https://www.kaggle.com/alexisbcook/introduction).**
---
As a warm-up, you'll review some machine learning fundamentals and submit your initial results to a Kaggle competition.
# Setup
The questions below will give you feedback on your work. Run the following cell to set up the feedback system.
```
# Set up code checking
import os
if not os.path.exists("../input/train.csv"):
os.symlink("../input/home-data-for-ml-course/train.csv", "../input/train.csv")
os.symlink("../input/home-data-for-ml-course/test.csv", "../input/test.csv")
from learntools.core import binder
binder.bind(globals())
from learntools.ml_intermediate.ex1 import *
print("Setup Complete")
```
You will work with data from the [Housing Prices Competition for Kaggle Learn Users](https://www.kaggle.com/c/home-data-for-ml-course) to predict home prices in Iowa using 79 explanatory variables describing (almost) every aspect of the homes.

Run the next code cell without changes to load the training and validation features in `X_train` and `X_valid`, along with the prediction targets in `y_train` and `y_valid`. The test features are loaded in `X_test`. (_If you need to review **features** and **prediction targets**, please check out [this short tutorial](https://www.kaggle.com/dansbecker/your-first-machine-learning-model). To read about model **validation**, look [here](https://www.kaggle.com/dansbecker/model-validation). Alternatively, if you'd prefer to look through a full course to review all of these topics, start [here](https://www.kaggle.com/learn/machine-learning).)_
```
import pandas as pd
from sklearn.model_selection import train_test_split
# Read the data
X_full = pd.read_csv('../input/train.csv', index_col='Id')
X_test_full = pd.read_csv('../input/test.csv', index_col='Id')
# Obtain target and predictors
y = X_full.SalePrice
features = ['LotArea', 'YearBuilt', '1stFlrSF', '2ndFlrSF', 'FullBath', 'BedroomAbvGr', 'TotRmsAbvGrd']
X = X_full[features].copy()
X_test = X_test_full[features].copy()
# Break off validation set from training data
X_train, X_valid, y_train, y_valid = train_test_split(X, y, train_size=0.8, test_size=0.2,
random_state=0)
```
Use the next cell to print the first several rows of the data. It's a nice way to get an overview of the data you will use in your price prediction model.
```
X_train.head()
```
The next code cell defines five different random forest models. Run this code cell without changes. (_To review **random forests**, look [here](https://www.kaggle.com/dansbecker/random-forests)._)
```
from sklearn.ensemble import RandomForestRegressor
# Define the models
model_1 = RandomForestRegressor(n_estimators=50, random_state=0)
model_2 = RandomForestRegressor(n_estimators=100, random_state=0)
model_3 = RandomForestRegressor(n_estimators=100, criterion='mae', random_state=0)
model_4 = RandomForestRegressor(n_estimators=200, min_samples_split=20, random_state=0)
model_5 = RandomForestRegressor(n_estimators=100, max_depth=7, random_state=0)
models = [model_1, model_2, model_3, model_4, model_5]
```
To select the best model out of the five, we define a function `score_model()` below. This function returns the mean absolute error (MAE) from the validation set. Recall that the best model will obtain the lowest MAE. (_To review **mean absolute error**, look [here](https://www.kaggle.com/dansbecker/model-validation).)_
Run the code cell without changes.
```
from sklearn.metrics import mean_absolute_error
# Function for comparing different models
def score_model(model, X_t=X_train, X_v=X_valid, y_t=y_train, y_v=y_valid):
model.fit(X_t, y_t)
preds = model.predict(X_v)
return mean_absolute_error(y_v, preds)
for i in range(0, len(models)):
mae = score_model(models[i])
print("Model %d MAE: %d" % (i+1, mae))
```
# Step 1: Evaluate several models
Use the above results to fill in the line below. Which model is the best model? Your answer should be one of `model_1`, `model_2`, `model_3`, `model_4`, or `model_5`.
```
# Fill in the best model
best_model = model_3
# Check your answer
step_1.check()
# Lines below will give you a hint or solution code
#step_1.hint()
#step_1.solution()
```
# Step 2: Generate test predictions
Great. You know how to evaluate what makes an accurate model. Now it's time to go through the modeling process and make predictions. In the line below, create a Random Forest model with the variable name `my_model`.
```
# Define a model
my_model = best_model
# Check your answer
step_2.check()
# Lines below will give you a hint or solution code
#step_2.hint()
#step_2.solution()
```
Run the next code cell without changes. The code fits the model to the training and validation data, and then generates test predictions that are saved to a CSV file. These test predictions can be submitted directly to the competition!
```
# Fit the model to the training data
my_model.fit(X, y)
# Generate test predictions
preds_test = my_model.predict(X_test)
# Save predictions in format used for competition scoring
output = pd.DataFrame({'Id': X_test.index,
'SalePrice': preds_test})
output.to_csv('submission.csv', index=False)
```
# Submit your results
Once you have successfully completed Step 2, you're ready to submit your results to the leaderboard! First, you'll need to join the competition if you haven't already. So open a new window by clicking on [this link](https://www.kaggle.com/c/home-data-for-ml-course). Then click on the **Join Competition** button.

Next, follow the instructions below:
1. Begin by clicking on the blue **Save Version** button in the top right corner of the window. This will generate a pop-up window.
2. Ensure that the **Save and Run All** option is selected, and then click on the blue **Save** button.
3. This generates a window in the bottom left corner of the notebook. After it has finished running, click on the number to the right of the **Save Version** button. This pulls up a list of versions on the right of the screen. Click on the ellipsis **(...)** to the right of the most recent version, and select **Open in Viewer**. This brings you into view mode of the same page. You will need to scroll down to get back to these instructions.
4. Click on the **Output** tab on the right of the screen. Then, click on the file you would like to submit, and click on the blue **Submit** button to submit your results to the leaderboard.
You have now successfully submitted to the competition!
If you want to keep working to improve your performance, select the blue **Edit** button in the top right of the screen. Then you can change your code and repeat the process. There's a lot of room to improve, and you will climb up the leaderboard as you work.
# Keep going
You've made your first model. But how can you quickly make it better?
Learn how to improve your competition results by incorporating columns with **[missing values](https://www.kaggle.com/alexisbcook/missing-values)**.
---
*Have questions or comments? Visit the [Learn Discussion forum](https://www.kaggle.com/learn-forum/161289) to chat with other Learners.*
| true |
code
| 0.446072 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/magenta/ddsp/blob/master/ddsp/colab/demos/timbre_transfer.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
##### Copyright 2020 Google LLC.
Licensed under the Apache License, Version 2.0 (the "License");
```
# Copyright 2020 Google LLC. All Rights Reserved.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================
```
# DDSP Timbre Transfer Demo
This notebook is a demo of timbre transfer using DDSP (Differentiable Digital Signal Processing).
The model here is trained to generate audio conditioned on a time series of fundamental frequency and loudness.
* [DDSP ICLR paper](https://openreview.net/forum?id=B1x1ma4tDr)
* [Audio Examples](http://goo.gl/magenta/ddsp-examples)
This notebook extracts these features from input audio (either uploaded files, or recorded from the microphone) and resynthesizes with the model.
<img src="https://magenta.tensorflow.org/assets/ddsp/ddsp_cat_jamming.png" alt="DDSP Tone Transfer" width="700">
By default, the notebook will download pre-trained models. You can train a model on your own sounds by using the [Train Autoencoder Colab](https://github.com/magenta/ddsp/blob/master/ddsp/colab/demos/train_autoencoder.ipynb).
Have fun! And please feel free to hack this notebook to make your own creative interactions.
### Instructions for running:
* Make sure to use a GPU runtime, click: __Runtime >> Change Runtime Type >> GPU__
* Press ▶️ on the left of each of the cells
* View the code: Double-click any of the cells
* Hide the code: Double click the right side of the cell
```
#@title #Install and Import
#@markdown Install ddsp, define some helper functions, and download the model. This transfers a lot of data and _should take a minute or two_.
%tensorflow_version 2.x
print('Installing from pip package...')
!pip install -qU ddsp
# Ignore a bunch of deprecation warnings
import warnings
warnings.filterwarnings("ignore")
import copy
import os
import time
import crepe
import ddsp
import ddsp.training
from ddsp.colab import colab_utils
from ddsp.colab.colab_utils import (
auto_tune, detect_notes, fit_quantile_transform,
get_tuning_factor, download, play, record,
specplot, upload, DEFAULT_SAMPLE_RATE)
import gin
from google.colab import files
import librosa
import matplotlib.pyplot as plt
import numpy as np
import pickle
import tensorflow.compat.v2 as tf
import tensorflow_datasets as tfds
# Helper Functions
sample_rate = DEFAULT_SAMPLE_RATE # 16000
print('Done!')
#@title Record or Upload Audio
#@markdown * Either record audio from microphone or upload audio from file (.mp3 or .wav)
#@markdown * Audio should be monophonic (single instrument / voice)
#@markdown * Extracts fundmanetal frequency (f0) and loudness features.
record_or_upload = "Record" #@param ["Record", "Upload (.mp3 or .wav)"]
record_seconds = 5#@param {type:"number", min:1, max:10, step:1}
if record_or_upload == "Record":
audio = record(seconds=record_seconds)
else:
# Load audio sample here (.mp3 or .wav3 file)
# Just use the first file.
filenames, audios = upload()
audio = audios[0]
audio = audio[np.newaxis, :]
print('\nExtracting audio features...')
# Plot.
specplot(audio)
play(audio)
# Setup the session.
ddsp.spectral_ops.reset_crepe()
# Compute features.
start_time = time.time()
audio_features = ddsp.training.metrics.compute_audio_features(audio)
audio_features['loudness_db'] = audio_features['loudness_db'].astype(np.float32)
audio_features_mod = None
print('Audio features took %.1f seconds' % (time.time() - start_time))
TRIM = -15
# Plot Features.
fig, ax = plt.subplots(nrows=3,
ncols=1,
sharex=True,
figsize=(6, 8))
ax[0].plot(audio_features['loudness_db'][:TRIM])
ax[0].set_ylabel('loudness_db')
ax[1].plot(librosa.hz_to_midi(audio_features['f0_hz'][:TRIM]))
ax[1].set_ylabel('f0 [midi]')
ax[2].plot(audio_features['f0_confidence'][:TRIM])
ax[2].set_ylabel('f0 confidence')
_ = ax[2].set_xlabel('Time step [frame]')
#@title Load a model
#@markdown Run for ever new audio input
model = 'Violin' #@param ['Violin', 'Flute', 'Flute2', 'Trumpet', 'Tenor_Saxophone', 'Upload your own (checkpoint folder as .zip)']
MODEL = model
def find_model_dir(dir_name):
# Iterate through directories until model directory is found
for root, dirs, filenames in os.walk(dir_name):
for filename in filenames:
if filename.endswith(".gin") and not filename.startswith("."):
model_dir = root
break
return model_dir
if model in ('Violin', 'Flute', 'Flute2', 'Trumpet', 'Tenor_Saxophone'):
# Pretrained models.
PRETRAINED_DIR = '/content/pretrained'
# Copy over from gs:// for faster loading.
!rm -r $PRETRAINED_DIR &> /dev/null
!mkdir $PRETRAINED_DIR &> /dev/null
GCS_CKPT_DIR = 'gs://ddsp/models/tf2'
model_dir = os.path.join(GCS_CKPT_DIR, 'solo_%s_ckpt' % model.lower())
!gsutil cp $model_dir/* $PRETRAINED_DIR &> /dev/null
model_dir = PRETRAINED_DIR
gin_file = os.path.join(model_dir, 'operative_config-0.gin')
else:
# User models.
UPLOAD_DIR = '/content/uploaded'
!mkdir $UPLOAD_DIR
uploaded_files = files.upload()
for fnames in uploaded_files.keys():
print("Unzipping... {}".format(fnames))
!unzip -o "/content/$fnames" -d $UPLOAD_DIR &> /dev/null
model_dir = find_model_dir(UPLOAD_DIR)
gin_file = os.path.join(model_dir, 'operative_config-0.gin')
# Load the dataset statistics.
DATASET_STATS = None
dataset_stats_file = os.path.join(model_dir, 'dataset_statistics.pkl')
print(f'Loading dataset statistics from {dataset_stats_file}')
try:
if tf.io.gfile.exists(dataset_stats_file):
with tf.io.gfile.GFile(dataset_stats_file, 'rb') as f:
DATASET_STATS = pickle.load(f)
except Exception as err:
print('Loading dataset statistics from pickle failed: {}.'.format(err))
# Parse gin config,
with gin.unlock_config():
gin.parse_config_file(gin_file, skip_unknown=True)
# Assumes only one checkpoint in the folder, 'ckpt-[iter]`.
ckpt_files = [f for f in tf.io.gfile.listdir(model_dir) if 'ckpt' in f]
ckpt_name = ckpt_files[0].split('.')[0]
ckpt = os.path.join(model_dir, ckpt_name)
# Ensure dimensions and sampling rates are equal
time_steps_train = gin.query_parameter('DefaultPreprocessor.time_steps')
n_samples_train = gin.query_parameter('Additive.n_samples')
hop_size = int(n_samples_train / time_steps_train)
time_steps = int(audio.shape[1] / hop_size)
n_samples = time_steps * hop_size
# print("===Trained model===")
# print("Time Steps", time_steps_train)
# print("Samples", n_samples_train)
# print("Hop Size", hop_size)
# print("\n===Resynthesis===")
# print("Time Steps", time_steps)
# print("Samples", n_samples)
# print('')
gin_params = [
'RnnFcDecoder.input_keys = ("f0_scaled", "ld_scaled")',
'Additive.n_samples = {}'.format(n_samples),
'FilteredNoise.n_samples = {}'.format(n_samples),
'DefaultPreprocessor.time_steps = {}'.format(time_steps),
]
with gin.unlock_config():
gin.parse_config(gin_params)
# Trim all input vectors to correct lengths
for key in ['f0_hz', 'f0_confidence', 'loudness_db']:
audio_features[key] = audio_features[key][:time_steps]
audio_features['audio'] = audio_features['audio'][:, :n_samples]
# Set up the model just to predict audio given new conditioning
model = ddsp.training.models.Autoencoder()
model.restore(ckpt)
# Build model by running a batch through it.
start_time = time.time()
_ = model(audio_features, training=False)
print('Restoring model took %.1f seconds' % (time.time() - start_time))
#@title Modify conditioning
#@markdown These models were not explicitly trained to perform timbre transfer, so they may sound unnatural if the incoming loudness and frequencies are very different then the training data (which will always be somewhat true).
#@markdown ## Note Detection
#@markdown You can leave this at 1.0 for most cases
threshold = 1 #@param {type:"slider", min: 0.0, max:2.0, step:0.01}
#@markdown ## Automatic
ADJUST = True #@param{type:"boolean"}
#@markdown Quiet parts without notes detected (dB)
quiet = 20 #@param {type:"slider", min: 0, max:60, step:1}
#@markdown Force pitch to nearest note (amount)
autotune = 0 #@param {type:"slider", min: 0.0, max:1.0, step:0.1}
#@markdown ## Manual
#@markdown Shift the pitch (octaves)
pitch_shift = 0 #@param {type:"slider", min:-2, max:2, step:1}
#@markdown Adjsut the overall loudness (dB)
loudness_shift = 0 #@param {type:"slider", min:-20, max:20, step:1}
audio_features_mod = {k: v.copy() for k, v in audio_features.items()}
## Helper functions.
def shift_ld(audio_features, ld_shift=0.0):
"""Shift loudness by a number of ocatves."""
audio_features['loudness_db'] += ld_shift
return audio_features
def shift_f0(audio_features, pitch_shift=0.0):
"""Shift f0 by a number of ocatves."""
audio_features['f0_hz'] *= 2.0 ** (pitch_shift)
audio_features['f0_hz'] = np.clip(audio_features['f0_hz'],
0.0,
librosa.midi_to_hz(110.0))
return audio_features
mask_on = None
if ADJUST and DATASET_STATS is not None:
# Detect sections that are "on".
mask_on, note_on_value = detect_notes(audio_features['loudness_db'],
audio_features['f0_confidence'],
threshold)
if np.any(mask_on):
# Shift the pitch register.
target_mean_pitch = DATASET_STATS['mean_pitch']
pitch = ddsp.core.hz_to_midi(audio_features['f0_hz'])
mean_pitch = np.mean(pitch[mask_on])
p_diff = target_mean_pitch - mean_pitch
p_diff_octave = p_diff / 12.0
round_fn = np.floor if p_diff_octave > 1.5 else np.ceil
p_diff_octave = round_fn(p_diff_octave)
audio_features_mod = shift_f0(audio_features_mod, p_diff_octave)
# Quantile shift the note_on parts.
_, loudness_norm = colab_utils.fit_quantile_transform(
audio_features['loudness_db'],
mask_on,
inv_quantile=DATASET_STATS['quantile_transform'])
# Turn down the note_off parts.
mask_off = np.logical_not(mask_on)
loudness_norm[mask_off] -= quiet * (1.0 - note_on_value[mask_off][:, np.newaxis])
loudness_norm = np.reshape(loudness_norm, audio_features['loudness_db'].shape)
audio_features_mod['loudness_db'] = loudness_norm
# Auto-tune.
if autotune:
f0_midi = np.array(ddsp.core.hz_to_midi(audio_features_mod['f0_hz']))
tuning_factor = get_tuning_factor(f0_midi, audio_features_mod['f0_confidence'], mask_on)
f0_midi_at = auto_tune(f0_midi, tuning_factor, mask_on, amount=autotune)
audio_features_mod['f0_hz'] = ddsp.core.midi_to_hz(f0_midi_at)
else:
print('\nSkipping auto-adjust (no notes detected or ADJUST box empty).')
else:
print('\nSkipping auto-adujst (box not checked or no dataset statistics found).')
# Manual Shifts.
audio_features_mod = shift_ld(audio_features_mod, loudness_shift)
audio_features_mod = shift_f0(audio_features_mod, pitch_shift)
# Plot Features.
has_mask = int(mask_on is not None)
n_plots = 3 if has_mask else 2
fig, axes = plt.subplots(nrows=n_plots,
ncols=1,
sharex=True,
figsize=(2*n_plots, 8))
if has_mask:
ax = axes[0]
ax.plot(np.ones_like(mask_on[:TRIM]) * threshold, 'k:')
ax.plot(note_on_value[:TRIM])
ax.plot(mask_on[:TRIM])
ax.set_ylabel('Note-on Mask')
ax.set_xlabel('Time step [frame]')
ax.legend(['Threshold', 'Likelihood','Mask'])
ax = axes[0 + has_mask]
ax.plot(audio_features['loudness_db'][:TRIM])
ax.plot(audio_features_mod['loudness_db'][:TRIM])
ax.set_ylabel('loudness_db')
ax.legend(['Original','Adjusted'])
ax = axes[1 + has_mask]
ax.plot(librosa.hz_to_midi(audio_features['f0_hz'][:TRIM]))
ax.plot(librosa.hz_to_midi(audio_features_mod['f0_hz'][:TRIM]))
ax.set_ylabel('f0 [midi]')
_ = ax.legend(['Original','Adjusted'])
#@title #Resynthesize Audio
af = audio_features if audio_features_mod is None else audio_features_mod
# Run a batch of predictions.
start_time = time.time()
audio_gen = model(af, training=False)
print('Prediction took %.1f seconds' % (time.time() - start_time))
# Plot
print('Original')
play(audio)
print('Resynthesis')
play(audio_gen)
specplot(audio)
plt.title("Original")
specplot(audio_gen)
_ = plt.title("Resynthesis")
```
| true |
code
| 0.715908 | null | null | null | null |
|
# SP LIME
## Regression explainer with boston housing prices dataset
```
from sklearn.datasets import load_boston
import sklearn.ensemble
import sklearn.linear_model
import sklearn.model_selection
import numpy as np
from sklearn.metrics import r2_score
np.random.seed(1)
#load example dataset
boston = load_boston()
#print a description of the variables
print(boston.DESCR)
#train a regressor
rf = sklearn.ensemble.RandomForestRegressor(n_estimators=1000)
train, test, labels_train, labels_test = sklearn.model_selection.train_test_split(boston.data, boston.target, train_size=0.80, test_size=0.20)
rf.fit(train, labels_train);
#train a linear regressor
lr = sklearn.linear_model.LinearRegression()
lr.fit(train,labels_train)
#print the R^2 score of the random forest
print("Random Forest R^2 Score: " +str(round(r2_score(rf.predict(test),labels_test),3)))
print("Linear Regression R^2 Score: " +str(round(r2_score(lr.predict(test),labels_test),3)))
# import lime tools
import lime
import lime.lime_tabular
# generate an "explainer" object
categorical_features = np.argwhere(np.array([len(set(boston.data[:,x])) for x in range(boston.data.shape[1])]) <= 10).flatten()
explainer = lime.lime_tabular.LimeTabularExplainer(train, feature_names=boston.feature_names, class_names=['price'], categorical_features=categorical_features, verbose=False, mode='regression',discretize_continuous=False)
#generate an explanation
i = 13
exp = explainer.explain_instance(test[i], rf.predict, num_features=14)
%matplotlib inline
fig = exp.as_pyplot_figure();
print("Input feature names: ")
print(boston.feature_names)
print('\n')
print("Input feature values: ")
print(test[i])
print('\n')
print("Predicted: ")
print(rf.predict(test)[i])
```
# SP-LIME pick step
### Maximize the 'coverage' function:
$c(V,W,I) = \sum_{j=1}^{d^{\prime}}{\mathbb{1}_{[\exists i \in V : W_{ij}>0]}I_j}$
$W = \text{Explanation Matrix, } n\times d^{\prime}$
$V = \text{Set of chosen explanations}$
$I = \text{Global feature importance vector, } I_j = \sqrt{\sum_i{|W_{ij}|}}$
```
import lime
import warnings
from lime import submodular_pick
sp_obj = submodular_pick.SubmodularPick(explainer, train, rf.predict, sample_size=20, num_features=14, num_exps_desired=5)
[exp.as_pyplot_figure() for exp in sp_obj.sp_explanations];
import pandas as pd
W=pd.DataFrame([dict(this.as_list()) for this in sp_obj.explanations])
W.head()
im=W.hist('NOX',bins=20)
```
## Text explainer using the newsgroups
```
# run the text explainer example notebook, up to single explanation
import sklearn
import numpy as np
import sklearn
import sklearn.ensemble
import sklearn.metrics
# from __future__ import print_function
from sklearn.datasets import fetch_20newsgroups
categories = ['alt.atheism', 'soc.religion.christian']
newsgroups_train = fetch_20newsgroups(subset='train', categories=categories)
newsgroups_test = fetch_20newsgroups(subset='test', categories=categories)
class_names = ['atheism', 'christian']
vectorizer = sklearn.feature_extraction.text.TfidfVectorizer(lowercase=False)
train_vectors = vectorizer.fit_transform(newsgroups_train.data)
test_vectors = vectorizer.transform(newsgroups_test.data)
rf = sklearn.ensemble.RandomForestClassifier(n_estimators=500)
rf.fit(train_vectors, newsgroups_train.target)
pred = rf.predict(test_vectors)
sklearn.metrics.f1_score(newsgroups_test.target, pred, average='binary')
from lime import lime_text
from sklearn.pipeline import make_pipeline
c = make_pipeline(vectorizer, rf)
from lime.lime_text import LimeTextExplainer
explainer = LimeTextExplainer(class_names=class_names)
idx = 83
exp = explainer.explain_instance(newsgroups_test.data[idx], c.predict_proba, num_features=6)
print('Document id: %d' % idx)
print('Probability(christian) =', c.predict_proba([newsgroups_test.data[idx]])[0,1])
print('True class: %s' % class_names[newsgroups_test.target[idx]])
sp_obj = submodular_pick.SubmodularPick(explainer, newsgroups_test.data, c.predict_proba, sample_size=2, num_features=6,num_exps_desired=2)
[exp.as_pyplot_figure(label=exp.available_labels()[0]) for exp in sp_obj.sp_explanations];
from sklearn.datasets import load_iris
iris=load_iris()
from sklearn.model_selection import train_test_split as tts
Xtrain,Xtest,ytrain,ytest=tts(iris.data,iris.target,test_size=.2)
from sklearn.ensemble import RandomForestClassifier
rf=RandomForestClassifier()
rf.fit(Xtrain,ytrain)
rf.score(Xtest,ytest)
explainer = lime.lime_tabular.LimeTabularExplainer(Xtrain,
feature_names=iris.feature_names,
class_names=iris.target_names,
verbose=False,
mode='classification',
discretize_continuous=False)
exp=explainer.explain_instance(Xtrain[i],rf.predict_proba,top_labels=3)
exp.available_labels()
sp_obj = submodular_pick.SubmodularPick(data=Xtrain,explainer=explainer,num_exps_desired=5,predict_fn=rf.predict_proba, sample_size=20, num_features=4, top_labels=3)
import pandas as pd
df=pd.DataFrame({})
for this_label in range(3):
dfl=[]
for i,exp in enumerate(sp_obj.sp_explanations):
l=exp.as_list(label=this_label)
l.append(("exp number",i))
dfl.append(dict(l))
dftest=pd.DataFrame(dfl)
df=df.append(pd.DataFrame(dfl,index=[iris.target_names[this_label] for i in range(len(sp_obj.sp_explanations))]))
df
```
| true |
code
| 0.605857 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/yukinaga/object_detection/blob/main/section_3/03_exercise.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 演習
RetinaNetで、物体の領域を出力する`regression_head`も訓練対象に加えてみましょう。
モデルを構築するコードに、追記を行なってください。
## 各設定
```
import torch
from torch.utils.data import DataLoader
import torchvision
import torchvision.transforms as transforms
from torchvision.utils import draw_bounding_boxes
import numpy as np
import matplotlib.pyplot as plt
import math
# インデックスを物体名に変換
index2name = [
"person",
"bird",
"cat",
"cow",
"dog",
"horse",
"sheep",
"aeroplane",
"bicycle",
"boat",
"bus",
"car",
"motorbike",
"train",
"bottle",
"chair",
"diningtable",
"pottedplant",
"sofa",
"tvmonitor",
]
print(index2name)
# 物体名をインデックスに変換
name2index = {}
for i in range(len(index2name)):
name2index[index2name[i]] = i
print(name2index)
```
## ターゲットを整える関数
```
def arrange_target(target):
objects = target["annotation"]["object"]
box_dics = [obj["bndbox"] for obj in objects]
box_keys = ["xmin", "ymin", "xmax", "ymax"]
# バウンディングボックス
boxes = []
for box_dic in box_dics:
box = [int(box_dic[key]) for key in box_keys]
boxes.append(box)
boxes = torch.tensor(boxes)
# 物体名
labels = [name2index[obj["name"]] for obj in objects] # 物体名はインデックスに変換
labels = torch.tensor(labels)
dic = {"boxes":boxes, "labels":labels}
return dic
```
## データセットの読み込み
```
dataset_train=torchvision.datasets.VOCDetection(root="./VOCDetection/2012",
year="2012",image_set="train",
download=True,
transform=transforms.ToTensor(),
target_transform=transforms.Lambda(arrange_target)
)
dataset_test=torchvision.datasets.VOCDetection(root="./VOCDetection/2012",
year="2012",image_set="val",
download=True,
transform=transforms.ToTensor(),
target_transform=transforms.Lambda(arrange_target)
)
```
## DataLoaderの設定
```
data_loader_train = DataLoader(dataset_train, batch_size=1, shuffle=True)
data_loader_test = DataLoader(dataset_test, batch_size=1, shuffle=True)
```
## ターゲットの表示
```
def show_boxes(image, boxes, names):
drawn_boxes = draw_bounding_boxes(image, boxes, labels=names)
plt.figure(figsize = (16,16))
plt.imshow(np.transpose(drawn_boxes, (1, 2, 0))) # チャンネルを一番後ろに
plt.tick_params(labelbottom=False, labelleft=False, bottom=False, left=False) # ラベルとメモリを非表示に
plt.show()
dataiter = iter(data_loader_train) # イテレータ
image, target = dataiter.next() # バッチを取り出す
print(target)
image = image[0]
image = (image*255).to(torch.uint8) # draw_bounding_boxes関数の入力は0-255
boxes = target["boxes"][0]
labels = target["labels"][0]
names = [index2name[label.item()] for label in labels]
show_boxes(image, boxes, names)
```
# モデルの構築
以下のセルのコードに追記を行い、物体領域の座標を出力する`regression_head`のパラメータも訓練可能にしましょう。
PyTorchの公式ドキュメントに記載されている、RetinaNetのコードを参考にしましょう。
https://pytorch.org/vision/stable/_modules/torchvision/models/detection/retinanet.html#retinanet_resnet50_fpn
```
model = torchvision.models.detection.retinanet_resnet50_fpn(pretrained=True)
num_classes=len(index2name)+1 # 分類数: 背景も含めて分類するため1を加える
num_anchors = model.head.classification_head.num_anchors # アンカーの数
# 分類数を設定
model.head.classification_head.num_classes = num_classes
# 分類結果を出力する層の入れ替え
cls_logits = torch.nn.Conv2d(256, num_anchors*num_classes, kernel_size=3, stride=1, padding=1)
torch.nn.init.normal_(cls_logits.weight, std=0.01) # RetinaNetClassificationHeadクラスより
torch.nn.init.constant_(cls_logits.bias, -math.log((1 - 0.01) / 0.01)) # RetinaNetClassificationHeadクラスより
model.head.classification_head.cls_logits = cls_logits # 層の入れ替え
# 全てのパラメータを更新不可に
for p in model.parameters():
p.requires_grad = False
# classification_headのパラメータを更新可能に
for p in model.head.classification_head.parameters():
p.requires_grad = True
# regression_headのパラメータを更新可能に
# ------- 以下にコードを書く -------
# ------- ここまで -------
model.cuda() # GPU対応
```
## 訓練
```
# 最適化アルゴリズム
params = [p for p in model.parameters() if p.requires_grad]
optimizer = torch.optim.SGD(params, lr=0.001, momentum=0.9)
model.train() # 訓練モード
epochs = 3
for epoch in range(epochs):
for i, (image, target) in enumerate(data_loader_train):
image = image.cuda() # GPU対応
boxes = target["boxes"][0].cuda()
labels = target["labels"][0].cuda()
target = [{"boxes":boxes, "labels":labels}] # ターゲットは辞書を要素に持つリスト
loss_dic = model(image, target)
loss = sum(loss for loss in loss_dic.values()) # 誤差の合計を計算
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i%100 == 0: # 100回ごとに経過を表示
print("epoch:", epoch, "iteration:", i, "loss:", loss.item())
```
## 訓練したモデルの使用
```
dataiter = iter(data_loader_test) # イテレータ
image, target = dataiter.next() # バッチを取り出す
image = image.cuda() # GPU対応
model.eval()
predictions = model(image)
print(predictions)
image = (image[0]*255).to(torch.uint8).cpu() # draw_bounding_boxes関数の入力は0-255
boxes = predictions[0]["boxes"].cpu()
labels = predictions[0]["labels"].cpu().detach().numpy()
labels = np.where(labels>=len(index2name), 0, labels) # ラベルが範囲外の場合は0に
names = [index2name[label.item()] for label in labels]
print(names)
show_boxes(image, boxes, names)
```
## スコアによる選別
```
boxes = []
names = []
for i, box in enumerate(predictions[0]["boxes"]):
score = predictions[0]["scores"][i].cpu().detach().numpy()
if score > 0.5: # スコアが0.5より大きいものを抜き出す
boxes.append(box.cpu().tolist())
label = predictions[0]["labels"][i].item()
if label >= len(index2name): # ラベルが範囲外の場合は0に
label = 0
name = index2name[label]
names.append(name)
boxes = torch.tensor(boxes)
show_boxes(image, boxes, names)
```
# 解答例
以下は、どうしても手がかりがないときのみ参考にしましょう。
```
model = torchvision.models.detection.retinanet_resnet50_fpn(pretrained=True)
num_classes=len(index2name)+1 # 分類数: 背景も含めて分類するため1を加える
num_anchors = model.head.classification_head.num_anchors # アンカーの数
# 分類数を設定
model.head.classification_head.num_classes = num_classes
# 分類結果を出力する層の入れ替え
cls_logits = torch.nn.Conv2d(256, num_anchors*num_classes, kernel_size=3, stride=1, padding=1)
torch.nn.init.normal_(cls_logits.weight, std=0.01) # RetinaNetClassificationHeadクラスより
torch.nn.init.constant_(cls_logits.bias, -math.log((1 - 0.01) / 0.01)) # RetinaNetClassificationHeadクラスより
model.head.classification_head.cls_logits = cls_logits # 層の入れ替え
# 全てのパラメータを更新不可に
for p in model.parameters():
p.requires_grad = False
# classification_headのパラメータを更新可能に
for p in model.head.classification_head.parameters():
p.requires_grad = True
# regression_headのパラメータを更新可能に
# ------- 以下にコードを書く -------
for p in model.head.regression_head.parameters():
p.requires_grad = True
# ------- ここまで -------
model.cuda() # GPU対応
```
| true |
code
| 0.50293 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
credit_df = pd.read_csv('German Credit Data.csv')
credit_df
credit_df.info()
X_features = list(credit_df.columns)
X_features.remove('status')
X_features
encoded_df = pd.get_dummies(credit_df[X_features],drop_first = True)
encoded_df
import statsmodels.api as sm
Y = credit_df.status
X = sm.add_constant(encoded_df)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,Y,test_size = 0.3,random_state = 42)
logit = sm.Logit(y_train,X_train)
logit_model =logit.fit()
logit_model.summary2()
```
## Models Diagnostics using CHI SQUARE TEST
The model summary suggests that as per the Wald's test, only 8 features are statistically significant at a significant value of alpha= 0.05 as p-values are less than 0.05.
p-value for liklelihood ratio test (almost 0.00) indicates that the overall model is statiscally significant.
```
def get_significant_vars(lm):
var_p_values_df = pd.DataFrame(lm.pvalues)
var_p_values_df['vars'] = var_p_values_df.index
var_p_values_df.columns = ['pvals','vars']
return list(var_p_values_df[var_p_values_df['pvals']<=0.05]['vars'])
significant_vars = get_significant_vars(logit_model)
significant_vars
final_logit = sm.Logit(y_train,sm.add_constant(X_train[significant_vars])).fit()
final_logit.summary2()
```
The negative sign in Coefficient value indicates that as the values of this variable increases, the probability of being a bad credit decreases.
A positive value indicates that the probability of a bad credit increases as the corresponding value of the variable increases.
```
y_pred_df = pd.DataFrame({'actual':y_test,'predicted_prob':final_logit.predict(sm.add_constant(X_test[significant_vars]))})
y_pred_df
```
To understand how many observations the model has classified correctly and how many not, a cut-off probability needs to be assumed.
let the assumption be 0.5 for now.
```
y_pred_df['predicted'] = y_pred_df['predicted_prob'].map(lambda x: 1 if x>0.5 else 0)
y_pred_df.sample(5)
```
## Creating a Confusion Matrix
```
from sklearn import metrics
def draw_cm(actual,predicted):
cm = metrics.confusion_matrix(actual,predicted,[1,0])
sns.heatmap(cm,annot=True,fmt= '.2f',
xticklabels=['Bad Credit','Good Credit'],
yticklabels=['Bad Credit','Good Credit'])
plt.ylabel('True Label')
plt.xlabel('Predicted Label')
plt.show()
draw_cm(y_pred_df['actual'],y_pred_df['predicted'])
```
# Building Decision Tree using Gini Criterion
```
Y = credit_df['status']
X = encoded_df
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,Y,test_size= 0.3,random_state=42)
from sklearn.tree import DecisionTreeClassifier
clf_tree = DecisionTreeClassifier(criterion= 'gini',max_depth = 3)
clf_tree.fit(X_train,y_train)
tree_predict = clf_tree.predict(X_test)
metrics.roc_auc_score(y_test,tree_predict)
```
# Displaying the Tree
```
Y = credit_df.status
X =encoded_df
from sklearn.tree import DecisionTreeClassifier,plot_tree
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,Y,test_size = 0.3,random_state = 42)
```
### Using Gini Criterion
```
clf_tree = DecisionTreeClassifier(criterion='gini',max_depth=3)
clf_tree.fit(X_train,y_train)
tree_predict = clf_tree.predict(X_test)
metrics.roc_auc_score(tree_predict,y_test)
## Displaying the Tree
plt.figure(figsize = (20,10))
plot_tree(clf_tree,feature_names=X.columns)
plt.show()
```
### Using Entropy criterion
```
clf_tree_ent = DecisionTreeClassifier(criterion='entropy',max_depth=3)
clf_tree_ent.fit(X_train,y_train)
tree_predict = clf_tree_ent.predict(X_test)
metrics.roc_auc_score(tree_predict,y_test)
## Displaying the Tree
plt.figure(figsize = (20,10))
plot_tree(clf_tree_ent,feature_names=X.columns)
plt.show()
from sklearn.model_selection import GridSearchCV
tuned_params = [{'criterion':['gini','entropy'],
'max_depth':range(2,10)}]
clf_ = DecisionTreeClassifier()
clf = GridSearchCV(clf_tree,
tuned_params,cv =10,
scoring='roc_auc')
clf.fit(X_train,y_train)
score = clf.best_score_*100
print("Best Score is:",score)
best_params = clf.best_params_
print("Best Params is:",best_params)
```
The tree with gini and max_depth = 4 is the best model. Finally, we can build a model with these params and measure the accuracy of the test.
| true |
code
| 0.51946 | null | null | null | null |
|
# Comparing Training and Test and Parking and Sensor Datasets
```
import sys
import pandas as pd
import numpy as np
import datetime as dt
import time
import matplotlib.pyplot as plt
sys.path.append('../')
from common import reorder_street_block, process_sensor_dataframe, get_train, \
feat_eng, add_tt_gps, get_parking, get_test, plot_dataset_overlay, \
parking_join_addr, tt_join_nh
%matplotlib inline
```
### Import City data
```
train = get_train()
train = feat_eng(train)
```
### Import Scraped City Data
```
city_stats = pd.read_csv('../ref_data/nh_city_stats.txt',delimiter='|')
city_stats.head()
```
### Import Parking data with Addresses
```
clean_park = parking_join_addr(True)
clean_park.min_join_dist.value_counts()
clean_park.head(25)
plot_dataset_overlay()
```
### Prototyping Below (joining and Mapping Code)
```
from multiprocessing import cpu_count, Pool
# simple example of parallelizing filling nulls
def parallelize(data, func):
cores = cpu_count()
data_split = np.array_split(data, cores)
pool = Pool(cores)
data = np.concatenate(pool.map(func, data_split), axis=0)
pool.close()
pool.join()
return data
def closest_point(park_dist):
output = np.zeros((park_dist.shape[0], 3), dtype=int)
for i, point in enumerate(park_dist):
x,y, id_ = point
dist = np.sqrt(np.power(gpspts.iloc[:,0]-x,2) + np.power(gpspts.iloc[:,1]-y,2))
output[i,:] = (id_,np.argmin(dist),np.min(dist))
return output
def parking_join_addr(force=False):
save_path = DATA_PATH + 'P_parking_clean.feather'
if os.path.isfile(save_path) and force==False:
print('loading cached copy')
join_parking_df = pd.read_feather(save_path)
return join_parking_df
else:
parking_df = get_parking()
park_dist = parking_df.groupby(['lat','lon'])[['datetime']].count().reset_index()[['lat','lon']]
park_dist['id'] =park_dist.index
gps2addr = pd.read_csv('../ref_data/clean_parking_gps2addr.txt', delimiter='|')
keep_cols = ['full_addr','jlat','jlon','nhood','road','zipcode']
gpspts = gps2addr[['lat','lon']]
lkup = parallelize(park_dist.values, closest_point)
lkup_df = pd.DataFrame(lkup)
lkup_df.columns = ['parking_idx','addr_idx','min_join_dist']
tmp = park_dist.merge(lkup_df, how='left', left_index=True, right_on='parking_idx')
tmp = tmp.merge(gps2addr[keep_cols], how='left', left_on='addr_idx', right_index=True)
join_parking_df = parking_df.merge(tmp, how='left', on=['lat','lon'])
join_parking_df.to_feather(save_path)
return join_parking_df
print("loading parking data 1.7M")
parking_df = get_parking()
park_dist = parking_df.groupby(['lat','lon'])[['datetime']].count().reset_index()[['lat','lon']]
park_dist['id'] =park_dist.index
print("loading address data 30K")
gps2addr = pd.read_csv('../ref_data/clean_parking_gps2addr.txt', delimiter='|')
keep_cols = ['full_addr','jlat','jlon','nhood','road','zipcode']
gpspts = gps2addr[['lat','lon']]
x,y,id_= park_dist.iloc[0,:]
dist = np.sqrt(np.power(gpspts.iloc[:,0]-x,2) + np.power(gpspts.iloc[:,1]-y,2))
np.log(dist)
dist = np.sqrt(np.power(gpspts.iloc[:,0]-x,2) + np.power(gpspts.iloc[:,1]-y,2))
join_parking_df
lkup_df = pd.DataFrame(lkup)
lkup_df.columns = ['parking_idx','addr_idx']
tmp = park_dist.merge(lkup_df, how='left', left_index=True, right_on='parking_idx')
keep_cols = ['full_addr','jlat','jlon','nhood','road','zipcode']
tmp = tmp.merge(gps2addr[keep_cols], how='left', left_on='addr_idx', right_index=True)
tmp = parking_df.merge(tmp, how='left', on=['lat','lon'])
tmp.isna().sum()
gpspts = gps2addr[['lat','lon']]
park_dist['id'] =park_dist.index
park_dist.head()
park_dist.shape, gpspts.shape
np.concatenate()
from multiprocessing import cpu_count, Pool
# simple example of parallelizing filling nulls
def parallelize(data, func):
cores = cpu_count()
data_split = np.array_split(data, cores)
pool = Pool(cores)
data = np.concatenate(pool.map(func, data_split), axis=0)
pool.close()
pool.join()
return data
def closest_point(park_dist):
output = np.zeros((park_dist.shape[0], 2), dtype=int)
for i, point in enumerate(park_dist):
x,y, id_ = point
dist = np.sqrt(np.power(gpspts.iloc[:,0]-x,2) + np.power(gpspts.iloc[:,1]-y,2))
output[i,:] = (id_,np.argmin(dist))
return output
lkup
122.465370178
gps2addr[(gps2addr['lon'] <= -122.46537) & (gps2addr['lon'] > -122.4654) ].sort_values('lon')
```
| true |
code
| 0.273186 | null | null | null | null |
|
# Introduction to Modeling Libraries
```
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
```
## Interfacing Between pandas and Model Code
```
import pandas as pd
import numpy as np
data = pd.DataFrame({
'x0': [1, 2, 3, 4, 5],
'x1': [0.01, -0.01, 0.25, -4.1, 0.],
'y': [-1.5, 0., 3.6, 1.3, -2.]})
data
data.columns
data.values
df2 = pd.DataFrame(data.values, columns=['one', 'two', 'three'])
df2
model_cols = ['x0', 'x1']
data.loc[:, model_cols].values
data['category'] = pd.Categorical(['a', 'b', 'a', 'a', 'b'],
categories=['a', 'b'])
data
dummies = pd.get_dummies(data.category, prefix='category')
data_with_dummies = data.drop('category', axis=1).join(dummies)
data_with_dummies
```
## Creating Model Descriptions with Patsy
y ~ x0 + x1
```
data = pd.DataFrame({
'x0': [1, 2, 3, 4, 5],
'x1': [0.01, -0.01, 0.25, -4.1, 0.],
'y': [-1.5, 0., 3.6, 1.3, -2.]})
data
import patsy
y, X = patsy.dmatrices('y ~ x0 + x1', data)
y
X
np.asarray(y)
np.asarray(X)
patsy.dmatrices('y ~ x0 + x1 + 0', data)[1]
coef, resid, _, _ = np.linalg.lstsq(X, y)
coef
coef = pd.Series(coef.squeeze(), index=X.design_info.column_names)
coef
```
### Data Transformations in Patsy Formulas
```
y, X = patsy.dmatrices('y ~ x0 + np.log(np.abs(x1) + 1)', data)
X
y, X = patsy.dmatrices('y ~ standardize(x0) + center(x1)', data)
X
new_data = pd.DataFrame({
'x0': [6, 7, 8, 9],
'x1': [3.1, -0.5, 0, 2.3],
'y': [1, 2, 3, 4]})
new_X = patsy.build_design_matrices([X.design_info], new_data)
new_X
y, X = patsy.dmatrices('y ~ I(x0 + x1)', data)
X
```
### Categorical Data and Patsy
```
data = pd.DataFrame({
'key1': ['a', 'a', 'b', 'b', 'a', 'b', 'a', 'b'],
'key2': [0, 1, 0, 1, 0, 1, 0, 0],
'v1': [1, 2, 3, 4, 5, 6, 7, 8],
'v2': [-1, 0, 2.5, -0.5, 4.0, -1.2, 0.2, -1.7]
})
y, X = patsy.dmatrices('v2 ~ key1', data)
X
y, X = patsy.dmatrices('v2 ~ key1 + 0', data)
X
y, X = patsy.dmatrices('v2 ~ C(key2)', data)
X
data['key2'] = data['key2'].map({0: 'zero', 1: 'one'})
data
y, X = patsy.dmatrices('v2 ~ key1 + key2', data)
X
y, X = patsy.dmatrices('v2 ~ key1 + key2 + key1:key2', data)
X
```
## Introduction to statsmodels
### Estimating Linear Models
```
import statsmodels.api as sm
import statsmodels.formula.api as smf
def dnorm(mean, variance, size=1):
if isinstance(size, int):
size = size,
return mean + np.sqrt(variance) * np.random.randn(*size)
# For reproducibility
np.random.seed(12345)
N = 100
X = np.c_[dnorm(0, 0.4, size=N),
dnorm(0, 0.6, size=N),
dnorm(0, 0.2, size=N)]
eps = dnorm(0, 0.1, size=N)
beta = [0.1, 0.3, 0.5]
y = np.dot(X, beta) + eps
X[:5]
y[:5]
X_model = sm.add_constant(X)
X_model[:5]
model = sm.OLS(y, X)
results = model.fit()
results.params
print(results.summary())
data = pd.DataFrame(X, columns=['col0', 'col1', 'col2'])
data['y'] = y
data[:5]
results = smf.ols('y ~ col0 + col1 + col2', data=data).fit()
results.params
results.tvalues
results.predict(data[:5])
```
### Estimating Time Series Processes
```
init_x = 4
import random
values = [init_x, init_x]
N = 1000
b0 = 0.8
b1 = -0.4
noise = dnorm(0, 0.1, N)
for i in range(N):
new_x = values[-1] * b0 + values[-2] * b1 + noise[i]
values.append(new_x)
MAXLAGS = 5
model = sm.tsa.AR(values)
results = model.fit(MAXLAGS)
results.params
```
## Introduction to scikit-learn
```
train = pd.read_csv('datasets/titanic/train.csv')
test = pd.read_csv('datasets/titanic/test.csv')
train[:4]
train.isnull().sum()
test.isnull().sum()
impute_value = train['Age'].median()
train['Age'] = train['Age'].fillna(impute_value)
test['Age'] = test['Age'].fillna(impute_value)
train['IsFemale'] = (train['Sex'] == 'female').astype(int)
test['IsFemale'] = (test['Sex'] == 'female').astype(int)
predictors = ['Pclass', 'IsFemale', 'Age']
X_train = train[predictors].values
X_test = test[predictors].values
y_train = train['Survived'].values
X_train[:5]
y_train[:5]
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
y_predict[:10]
```
(y_true == y_predict).mean()
```
from sklearn.linear_model import LogisticRegressionCV
model_cv = LogisticRegressionCV(10)
model_cv.fit(X_train, y_train)
from sklearn.model_selection import cross_val_score
model = LogisticRegression(C=10)
scores = cross_val_score(model, X_train, y_train, cv=4)
scores
```
## Continuing Your Education
```
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
```
| true |
code
| 0.449272 | null | null | null | null |
|
# This notebook is copied from [here](https://github.com/warmspringwinds/tensorflow_notes/blob/master/tfrecords_guide.ipynb) with some small changes
---
### Introduction
In this post we will cover how to convert a dataset into _.tfrecord_ file.
Binary files are sometimes easier to use, because you don't have to specify
different directories for images and groundtruth annotations. While storing your data
in binary file, you have your data in one block of memory, compared to storing
each image and annotation separately. Openning a file is a considerably
time-consuming operation especially if you use _hdd_ and not _ssd_, because it
involves moving the disk reader head and that takes quite some time. Overall,
by using binary files you make it easier to distribute and make
the data better aligned for efficient reading.
The post consists of tree parts:
* in the first part, we demonstrate how you can get raw data bytes of any image using _numpy_ which is in some sense similar to what you do when converting your dataset to binary format.
* Second part shows how to convert a dataset to _tfrecord_ file without defining a computational graph and only by employing some built-in _tensorflow_ functions.
* Third part explains how to define a model for reading your data from created binary file and batch it in a random manner, which is necessary during training.
### Getting raw data bytes in numpy
Here we demonstrate how you can get raw data bytes of an image (any ndarray)
and how to restore the image back.
One important note is that **during this operation
the information about the dimensions of the image is lost and we have to
use it to recover the original image. This is one of the reasons why
we will have to store the raw image representation along with the dimensions
of the original image.**
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
cat_img = plt.imread('data/imgs/cat.jpg')
plt.imshow(cat_img)
# io.imshow(cat_img)
# Let's convert the picture into string representation
# using the ndarray.tostring() function
cat_string = cat_img.tostring()
# Now let's convert the string back to the image
# Important: the dtype should be specified
# otherwise the reconstruction will be errorness
# Reconstruction is 1d, so we need sizes of image
# to fully reconstruct it.
reconstructed_cat_1d = np.fromstring(cat_string, dtype=np.uint8)
# Here we reshape the 1d representation
# This is the why we need to store the sizes of image
# along with its serialized representation.
reconstructed_cat_img = reconstructed_cat_1d.reshape(cat_img.shape)
# Let's check if we got everything right and compare
# reconstructed array to the original one.
np.allclose(cat_img, reconstructed_cat_img)
```
### Creating a _.tfrecord_ file and reading it without defining a graph
Here we show how to write a small dataset (three images/annotations from _PASCAL VOC_) to
_.tfrrecord_ file and read it without defining a computational graph.
We also make sure that images that we read back from _.tfrecord_ file are equal to
the original images. Pay attention that we also write the sizes of the images along with
the image in the raw format. We showed an example on why we need to also store the size
in the previous section.
```
# Get some image/annotation pairs for example
filename_pairs = [
('data/VOC2012/JPEGImages/2007_000032.jpg',
'data/VOC2012/SegmentationClass/2007_000032.png'),
('data/VOC2012/JPEGImages/2007_000039.jpg',
'data/VOC2012/SegmentationClass/2007_000039.png'),
('data/VOC2012/JPEGImages/2007_000033.jpg',
'data/VOC2012/SegmentationClass/2007_000033.png')
]
%matplotlib inline
# Important: We are using PIL to read .png files later.
# This was done on purpose to read indexed png files
# in a special way -- only indexes and not map the indexes
# to actual rgb values. This is specific to PASCAL VOC
# dataset data. If you don't want thit type of behaviour
# consider using skimage.io.imread()
from PIL import Image
import numpy as np
import skimage.io as io
import tensorflow as tf
def _bytes_feature(value):
return tf.train.Feature(bytes_list=tf.train.BytesList(value=[value]))
def _int64_feature(value):
return tf.train.Feature(int64_list=tf.train.Int64List(value=[value]))
tfrecords_filename = 'pascal_voc_segmentation.tfrecords'
writer = tf.python_io.TFRecordWriter(tfrecords_filename)
# Let's collect the real images to later on compare
# to the reconstructed ones
original_images = []
for img_path, annotation_path in filename_pairs:
img = np.array(Image.open(img_path))
annotation = np.array(Image.open(annotation_path))
# The reason to store image sizes was demonstrated
# in the previous example -- we have to know sizes
# of images to later read raw serialized string,
# convert to 1d array and convert to respective
# shape that image used to have.
height = img.shape[0]
width = img.shape[1]
# Put in the original images into array
# Just for future check for correctness
original_images.append((img, annotation))
img_raw = img.tostring()
annotation_raw = annotation.tostring()
example = tf.train.Example(features=tf.train.Features(feature={
'height': _int64_feature(height),
'width': _int64_feature(width),
'image_raw': _bytes_feature(img_raw),
'mask_raw': _bytes_feature(annotation_raw)}))
writer.write(example.SerializeToString())
writer.close()
reconstructed_images = []
record_iterator = tf.python_io.tf_record_iterator(path=tfrecords_filename)
for string_record in record_iterator:
example = tf.train.Example()
example.ParseFromString(string_record)
height = int(example.features.feature['height']
.int64_list
.value[0])
width = int(example.features.feature['width']
.int64_list
.value[0])
img_string = (example.features.feature['image_raw']
.bytes_list
.value[0])
annotation_string = (example.features.feature['mask_raw']
.bytes_list
.value[0])
img_1d = np.fromstring(img_string, dtype=np.uint8)
reconstructed_img = img_1d.reshape((height, width, -1))
annotation_1d = np.fromstring(annotation_string, dtype=np.uint8)
# Annotations don't have depth (3rd dimension)
reconstructed_annotation = annotation_1d.reshape((height, width))
reconstructed_images.append((reconstructed_img, reconstructed_annotation))
# Let's check if the reconstructed images match
# the original images
for original_pair, reconstructed_pair in zip(original_images, reconstructed_images):
img_pair_to_compare, annotation_pair_to_compare = zip(original_pair,
reconstructed_pair)
print(np.allclose(*img_pair_to_compare))
print(np.allclose(*annotation_pair_to_compare))
```
### Defining the graph to read and batch images from _.tfrecords_
Here we define a graph to read and batch images from the file that we have created
previously. It is very important to randomly shuffle images during training and depending
on the application we have to use different batch size.
It is very important to point out that if we use batching -- we have to define
the sizes of images beforehand. This may sound like a limitation, but actually in the
Image Classification and Image Segmentation fields the training is performed on the images
of the same size.
The code provided here is partially based on [this official example](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/examples/how_tos/reading_data/fully_connected_reader.py) and code from [this stackoverflow question](http://stackoverflow.com/questions/35028173/how-to-read-images-with-different-size-in-a-tfrecord-file).
Also if you want to know how you can control the batching according to your need read [these docs](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/g3doc/api_docs/python/functions_and_classes/shard2/tf.train.shuffle_batch.md)
.
```
%matplotlib inline
import tensorflow as tf
import skimage.io as io
IMAGE_HEIGHT = 384
IMAGE_WIDTH = 384
tfrecords_filename = 'pascal_voc_segmentation.tfrecords'
def read_and_decode(filename_queue):
reader = tf.TFRecordReader()
_, serialized_example = reader.read(filename_queue)
features = tf.parse_single_example(
serialized_example,
# Defaults are not specified since both keys are required.
features={
'height': tf.FixedLenFeature([], tf.int64),
'width': tf.FixedLenFeature([], tf.int64),
'image_raw': tf.FixedLenFeature([], tf.string),
'mask_raw': tf.FixedLenFeature([], tf.string)
})
# Convert from a scalar string tensor (whose single string has
# length mnist.IMAGE_PIXELS) to a uint8 tensor with shape
# [mnist.IMAGE_PIXELS].
image = tf.decode_raw(features['image_raw'], tf.uint8)
annotation = tf.decode_raw(features['mask_raw'], tf.uint8)
height = tf.cast(features['height'], tf.int32)
width = tf.cast(features['width'], tf.int32)
image_shape = tf.stack([height, width, 3])
annotation_shape = tf.stack([height, width, 1])
image = tf.reshape(image, image_shape)
annotation = tf.reshape(annotation, annotation_shape)
image_size_const = tf.constant((IMAGE_HEIGHT, IMAGE_WIDTH, 3), dtype=tf.int32)
annotation_size_const = tf.constant((IMAGE_HEIGHT, IMAGE_WIDTH, 1), dtype=tf.int32)
# Random transformations can be put here: right before you crop images
# to predefined size. To get more information look at the stackoverflow
# question linked above.
resized_image = tf.image.resize_image_with_crop_or_pad(image=image,
target_height=IMAGE_HEIGHT,
target_width=IMAGE_WIDTH)
resized_annotation = tf.image.resize_image_with_crop_or_pad(image=annotation,
target_height=IMAGE_HEIGHT,
target_width=IMAGE_WIDTH)
images, annotations = tf.train.shuffle_batch( [resized_image, resized_annotation],
batch_size=2,
capacity=30,
num_threads=2,
min_after_dequeue=10)
return images, annotations
filename_queue = tf.train.string_input_producer(
[tfrecords_filename], num_epochs=10)
# Even when reading in multiple threads, share the filename
# queue.
image, annotation = read_and_decode(filename_queue)
# The op for initializing the variables.
init_op = tf.group(tf.global_variables_initializer(),
tf.local_variables_initializer())
with tf.Session() as sess:
sess.run(init_op)
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(coord=coord)
# Let's read off 3 batches just for example
for i in range(3):
img, anno = sess.run([image, annotation])
print(img[0, :, :, :].shape)
print('current batch')
# We selected the batch size of two
# So we should get two image pairs in each batch
# Let's make sure it is random
io.imshow(img[0, :, :, :])
io.show()
io.imshow(anno[0, :, :, 0])
io.show()
io.imshow(img[1, :, :, :])
io.show()
io.imshow(anno[1, :, :, 0])
io.show()
coord.request_stop()
coord.join(threads)
```
### Conclusion and Discussion
In this post we covered how to convert a dataset into _.tfrecord_ format,
made sure that we have the same data and saw how to define a graph to
read and batch files from the created file.
| true |
code
| 0.615492 | null | null | null | null |
|
# Custom Models in pycalphad: Viscosity
## Viscosity Model Background
We are going to take a CALPHAD-based property model from the literature and use it to predict the viscosity of Al-Cu-Zr liquids.
For a binary alloy liquid under small undercooling, Gąsior suggested an entropy model of the form
$$\eta = (\sum_i x_i \eta_i ) (1 - 2\frac{S_{ex}}{R})$$
where $\eta_i$ is the viscosity of the element $i$, $x_i$ is the mole fraction, $S_{ex}$ is the excess entropy, and $R$ is the gas constant.
For more details on this model, see
1. M.E. Trybula, T. Gancarz, W. Gąsior, *Density, surface tension and viscosity of liquid binary Al-Zn and ternary Al-Li-Zn alloys*, Fluid Phase Equilibria 421 (2016) 39-48, [doi:10.1016/j.fluid.2016.03.013](http://dx.doi.org/10.1016/j.fluid.2016.03.013).
2. Władysław Gąsior, *Viscosity modeling of binary alloys: Comparative studies*, Calphad 44 (2014) 119-128, [doi:10.1016/j.calphad.2013.10.007](http://dx.doi.org/10.1016/j.calphad.2013.10.007).
3. Chenyang Zhou, Cuiping Guo, Changrong Li, Zhenmin Du, *Thermodynamic assessment of the phase equilibria and prediction of glass-forming ability of the Al–Cu–Zr system*, Journal of Non-Crystalline Solids 461 (2017) 47-60, [doi:10.1016/j.jnoncrysol.2016.09.031](https://doi.org/10.1016/j.jnoncrysol.2016.09.031).
```
from pycalphad import Database
```
## TDB Parameters
We can calculate the excess entropy of the liquid using the Al-Cu-Zr thermodynamic database from Zhou et al.
We add three new parameters to describe the viscosity (in Pa-s) of the pure elements Al, Cu, and Zr:
```
$ Viscosity test parameters
PARAMETER ETA(LIQUID,AL;0) 2.98150E+02 +0.000281*EXP(12300/(8.3145*T)); 6.00000E+03
N REF:0 !
PARAMETER ETA(LIQUID,CU;0) 2.98150E+02 +0.000657*EXP(21500/(8.3145*T)); 6.00000E+03
N REF:0 !
PARAMETER ETA(LIQUID,ZR;0) 2.98150E+02 +4.74E-3 - 4.97E-6*(T-2128) ; 6.00000E+03
N REF:0 !
```
Great! However, if we try to load the database now, we will get an error. This is because `ETA` parameters are not supported by default in pycalphad, so we need to tell pycalphad's TDB parser that "ETA" should be on the list of supported parameter types.
```
dbf = Database('alcuzr-viscosity.tdb')
```
### Adding the `ETA` parameter to the TDB parser
```
import pycalphad.io.tdb_keywords
pycalphad.io.tdb_keywords.TDB_PARAM_TYPES.append('ETA')
```
Now the database will load:
```
dbf = Database('alcuzr-viscosity.tdb')
```
## Writing the Custom Viscosity Model
Now that we have our `ETA` parameters in the database, we need to write a `Model` class to tell pycalphad how to compute viscosity. All custom models are subclasses of the pycalphad `Model` class.
When the `ViscosityModel` is constructed, the `build_phase` method is run and we need to construct the viscosity model after doing all the other initialization using a new method `build_viscosity`. The implementation of `build_viscosity` needs to do four things:
1. Query the Database for all the `ETA` parameters
2. Compute their weighted sum
3. Compute the excess entropy of the liquid
4. Plug all the values into the Gąsior equation and return the result
Since the `build_phase` method sets the attribute `viscosity` to the `ViscosityModel`, we can access the property using `viscosity` as the output in pycalphad caluclations.
```
from tinydb import where
import sympy
from pycalphad import Model, variables as v
class ViscosityModel(Model):
def build_phase(self, dbe):
super(ViscosityModel, self).build_phase(dbe)
self.viscosity = self.build_viscosity(dbe)
def build_viscosity(self, dbe):
if self.phase_name != 'LIQUID':
raise ValueError('Viscosity is only defined for LIQUID phase')
phase = dbe.phases[self.phase_name]
param_search = dbe.search
# STEP 1
eta_param_query = (
(where('phase_name') == phase.name) & \
(where('parameter_type') == 'ETA') & \
(where('constituent_array').test(self._array_validity))
)
# STEP 2
eta = self.redlich_kister_sum(phase, param_search, eta_param_query)
# STEP 3
excess_energy = self.GM - self.models['ref'] - self.models['idmix']
#liquid_mod = Model(dbe, self.components, self.phase_name)
## we only want the excess contributions to the entropy
#del liquid_mod.models['ref']
#del liquid_mod.models['idmix']
excess_entropy = -excess_energy.diff(v.T)
ks = 2
# STEP 4
result = eta * (1 - ks * excess_entropy / v.R)
self.eta = eta
return result
```
## Performing Calculations
Now we can create an instance of `ViscosityModel` for the liquid phase using the `Database` object we created earlier. We can verify this model has a `viscosity` attribute containing a symbolic expression for the viscosity.
```
mod = ViscosityModel(dbf, ['CU', 'ZR'], 'LIQUID')
print(mod.viscosity)
```
Finally we calculate and plot the viscosity.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from pycalphad import calculate
mod = ViscosityModel(dbf, ['CU', 'ZR'], 'LIQUID')
temp = 2100
# NOTICE: we need to tell pycalphad about our model for this phase
models = {'LIQUID': mod}
res = calculate(dbf, ['CU', 'ZR'], 'LIQUID', P=101325, T=temp, model=models, output='viscosity')
fig = plt.figure(figsize=(6,6))
ax = fig.gca()
ax.scatter(res.X.sel(component='ZR'), 1000 * res.viscosity.values)
ax.set_xlabel('X(ZR)')
ax.set_ylabel('Viscosity (mPa-s)')
ax.set_xlim((0,1))
ax.set_title('Viscosity at {}K'.format(temp));
```
We repeat the calculation for Al-Cu.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from pycalphad import calculate
temp = 1300
models = {'LIQUID': ViscosityModel} # we can also use Model class
res = calculate(dbf, ['CU', 'AL'], 'LIQUID', P=101325, T=temp, model=models, output='viscosity')
fig = plt.figure(figsize=(6,6))
ax = fig.gca()
ax.scatter(res.X.sel(component='CU'), 1000 * res.viscosity.values)
ax.set_xlabel('X(CU)')
ax.set_ylabel('Viscosity (mPa-s)')
ax.set_xlim((0,1))
ax.set_title('Viscosity at {}K'.format(temp));
```
| true |
code
| 0.479747 | null | null | null | null |
|
# "[Prob] Basics of the Poisson Distribution"
> "Some useful facts about the Poisson distribution"
- toc:false
- branch: master
- badges: false
- comments: true
- author: Peiyi Hung
- categories: [category, learning, probability]
# Introduction
The Poisson distribution is an important discrete probability distribution prevalent in a variety of fields. In this post, I will present some useful facts about the Poisson distribution. Here's the concepts I will discuss in the post:
* PMF, expectation and variance of Poisson
* In what situation we can use it?
* Sum of indepentent Poisson is also a Poisson
* Relationship with the Binomial distribution
# PMF, Expectation and Variance
First, we define what's Poisson distribution.
Let X be a Poisson random variable with a parameter $\lambda$, where $\lambda >0$. The pmf of X would be:
$$P(X=x) = \frac{e^{-\lambda}\lambda^{x}}{x!}, \quad \text{for } k = 0, 1,2,3,\dots$$
where $x$ can only be non-negative integer.
This is a valid pmf since
$$\sum_{k=0}^{\infty} \frac{e^{-\lambda}\lambda^{k}}{k!} = e^{-\lambda}\sum_{k=0}^{\infty} \frac{\lambda^{k}}{k!}= e^{-\lambda}e^{\lambda}=1$$
where $\displaystyle\sum_{k=0}^{\infty} \frac{\lambda^{k}}{k!}$ is the Taylor expansion of $e^{\lambda}$.
The expectation and the variance of the Poisson distribution are both $\lambda$. The derivation of this result is just some pattern recognition of $\sum_{k=0}^{\infty} \frac{\lambda^{k}}{k!}=e^{\lambda}$, so I omit it here.
# In what situation can we use it?
The Poisson distribution is often applied to the situation where we are counting the number of successes or an event happening in a time interval or a particular region, and there are a large number of trials with a small probability of success. The parameter $\lambda$ is the rate parameter which indicates the average number of successes in a time interval or a region.
Here are some examples:
* The number of emails you receive in an hour.
* The number of chips in a chocolate chip cookie.
* The number of earthquakes in a year in some region of the world.
Also, let's consider an example probability problem.
**Example problem 1**
> Raindrops are falling at an average rate of 20 drops per square inch per minute. Find the probability that the region has no rain drops in a given 1-minute time interval.
The success in this problem is one raindrop. The average rate is 20, so $\lambda=20$. Let $X$ be the raindrops that region has in a minute. We would model $X$ with Pois$(20)$, so the probability we concerned would be
$$P(X=0) = \frac{e^{-20}20^0}{0!}=e^{-20} \approx 2.0611\times 10 ^{-9}$$
If we are concerned with raindrops in a 3-second time interval in 5 square inches, then $$\lambda = 20\times\frac{1}{20} \text{ minutes} \times5 \text{ square inches} = 5$$
Let $Y$ be raindrops in a 3-second time interval. $Y$ would be Pois$(5)$, so $P(Y=0) = e^{-5} \approx 0.0067$.
# Sum of Independent Poisson
The sum of independent Poisson would also be Poisson. Let $X$ be Pois$(\lambda_1)$ and $Y$ be Pois$(\lambda_2)$. If $T=X+Y$, then $T \sim \text{Pois}(\lambda_1 + \lambda_2)$.
To get pmf of $T$, we should first apply the law of total probability:
$$
P(X+Y=t) = \sum_{k=0}^{t}P(X+Y=t|X=k)P(X=k)
$$
Since they are independent, we got
$$
\sum_{k=0}^{t}P(X+Y=t|X=k)P(X=k) = \sum_{k=0}^{t}P(Y=t-k)P(X=k)
$$
Next, we plug in the pmf of Poisson:
$$
\sum_{k=0}^{t}P(Y=t-k)P(X=k) = \sum_{k=0}^{t}\frac{e^{-\lambda_2}\lambda_2^{t-k}}{(t-k)!}\frac{e^{-\lambda_2}\lambda_1^k}{k!} = \frac{e^{-(\lambda_1+\lambda_2)}}{t!}\sum_{k=0}^{t} {t \choose k}\lambda_1^{k}\lambda_2^{t-k}
$$
Finally, by Binomial theorem, we got
$$
P(X+Y=t) = \frac{e^{-(\lambda_1+\lambda_2)}(\lambda_1+\lambda_2)^t}{t!}
$$
which is the pmf of Pois$(\lambda_1 + \lambda_2)$.
# Relationship with the Binomial distribution
We can obtain Poisson from Binomial and can also obtain Binomial to Poisson. Let's first see how we get the Binomial distribution from the Poisson distribution
**From Poisson to Binomial**
If $X \sim$ Pois$(\lambda_1)$ and $Y \sim$ Pois$(\lambda_2)$, and they are independent, then the conditional distribution of $X$ given $X+Y=n$ is Bin$(n, \lambda_1/(\lambda_1 + \lambda_2))$. Let's derive the pmf of $X$ given $X+Y=n$.
By Bayes' rule and the indenpendence between $X$ and $Y$:
$$
P(X=x|X+Y=n) = \frac{P(X+Y=n|X=x)P(X=x)}{P(X+Y=n)} = \frac{P(Y=n-k)P(X=x)}{P(X+Y=n)}
$$
From the previous section, we know $X+Y \sim$ Poin$(\lambda_1 + \lambda_2)$. Use this fact, we get
$$
P(X=x|X+Y=n) = \frac{ \big(\frac{e^{-\lambda_2}\lambda_2^{n-k}}{(n-k)!}\big) \big( \frac{e^{\lambda_1\lambda_1^k}}{k!} \big)}{ \frac{e^{-(\lambda_1 + \lambda_2)}(\lambda_1 + \lambda_2)^n}{n!}} = {n\choose k}\bigg(\frac{\lambda_1}{\lambda_1+\lambda_2}\bigg)^k \bigg(\frac{\lambda_2}{\lambda_1+\lambda_2}\bigg)^{n-k}
$$
which is the Bin$(n, \lambda_1/(\lambda_1 + \lambda_2))$ pmf.
**From Binomial to Poisson**
We can approximate Binomial by Poisson when $n \rightarrow \infty$ and $p \rightarrow 0$, and $\lambda = np$.
The pmf of Binomial is
$$
P(X=k) = {n \choose k}p^{k}(1-p)^{n-k} = {n \choose k}\big(\frac{\lambda}{n}\big)^{k}\big(1-\frac{\lambda}{n}\big)^n\big(1-\frac{\lambda}{n}\big)^{-k}
$$
By some algebra manipulation, we got
$$
P(X=k) = \frac{\lambda^{k}}{k!}\frac{n(n-1)\dots(n-k+1)}{n^k}\big(1-\frac{\lambda}{n}\big)^n\big(1-\frac{\lambda}{n}\big)^{-k}
$$
When $n \rightarrow \infty$, we got:
$$
\frac{n(n-1)\dots(n-k+1)}{n^k} \rightarrow 1,\\
\big(1-\frac{\lambda}{n}\big)^n \rightarrow e^{-\lambda}, \text{and}\\
\big(1-\frac{\lambda}{n}\big)^{-k} \rightarrow 1
$$
Therefore, $P(X=k) = \frac{e^{-\lambda}\lambda^k}{k!}$ when $n \rightarrow \infty$.
Let's see an example on how to use Poisson to approximate Binomial.
**Example problem 2**
>Ten million people enter a certain lottery. For each person, the chance of winning is one in ten million, independently. Find a simple, good approximation for the PMF of the number of people who win the lottery.
Let $X$ be the number of people winning the lottery. $X$ would be Bin$(10000000, 1/10000000)$ and $E(X) = 1$. We can approximate the pmf of $X$ by Pois$(1)$:
$$
P(X=k) \approx \frac{1}{e\cdot k!}
$$
Let's see if this approximation is accurate by Python code.
```
#collapse-hide
from scipy.stats import binom
from math import factorial, exp
import numpy as np
import matplotlib.pyplot as plt
def pois(k):
return 1 / (exp(1) * factorial(k))
n = 10000000
p = 1/10000000
k = np.arange(10)
binomial = binom.pmf(k, n, p)
poisson = [pois(i) for i in k]
fig, ax = plt.subplots(ncols=2, nrows=1, figsize=(15, 4), dpi=120)
ax[0].plot(k, binomial)
ax[0].set_title("PMF of Binomial")
ax[0].set_xlabel(r"$X=k$")
ax[0].set_xticks(k)
ax[1].plot(k, poisson)
ax[1].set_title("Approximation by Poisson")
ax[1].set_xlabel(r"X=k")
ax[1].set_xticks(k)
plt.tight_layout();
```
The approximation is quite accurate since these two graphs are almost identical.
**Reference**
1. *Introduction to Probability* by Joe Blitzstein and Jessica Hwang.
| true |
code
| 0.562597 | null | null | null | null |
|
# Facial Keypoint Detection
This project will be all about defining and training a convolutional neural network to perform facial keypoint detection, and using computer vision techniques to transform images of faces. The first step in any challenge like this will be to load and visualize the data you'll be working with.
Let's take a look at some examples of images and corresponding facial keypoints.
<img src='images/key_pts_example.png' width=50% height=50%/>
Facial keypoints (also called facial landmarks) are the small magenta dots shown on each of the faces in the image above. In each training and test image, there is a single face and **68 keypoints, with coordinates (x, y), for that face**. These keypoints mark important areas of the face: the eyes, corners of the mouth, the nose, etc. These keypoints are relevant for a variety of tasks, such as face filters, emotion recognition, pose recognition, and so on. Here they are, numbered, and you can see that specific ranges of points match different portions of the face.
<img src='images/landmarks_numbered.jpg' width=30% height=30%/>
---
## Load and Visualize Data
The first step in working with any dataset is to become familiar with your data; you'll need to load in the images of faces and their keypoints and visualize them! This set of image data has been extracted from the [YouTube Faces Dataset](https://www.cs.tau.ac.il/~wolf/ytfaces/), which includes videos of people in YouTube videos. These videos have been fed through some processing steps and turned into sets of image frames containing one face and the associated keypoints.
#### Training and Testing Data
This facial keypoints dataset consists of 5770 color images. All of these images are separated into either a training or a test set of data.
* 3462 of these images are training images, for you to use as you create a model to predict keypoints.
* 2308 are test images, which will be used to test the accuracy of your model.
The information about the images and keypoints in this dataset are summarized in CSV files, which we can read in using `pandas`. Let's read the training CSV and get the annotations in an (N, 2) array where N is the number of keypoints and 2 is the dimension of the keypoint coordinates (x, y).
---
```
# import the required libraries
import glob
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import cv2
key_pts_frame = pd.read_csv('data/training_frames_keypoints.csv')
n = 0
image_name = key_pts_frame.iloc[n, 0]
key_pts = key_pts_frame.iloc[n, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
print('Image name: ', image_name)
print('Landmarks shape: ', key_pts.shape)
print('First 4 key pts: {}'.format(key_pts[:4]))
# print out some stats about the data
print('Number of images: ', key_pts_frame.shape[0])
```
## Look at some images
Below, is a function `show_keypoints` that takes in an image and keypoints and displays them. As you look at this data, **note that these images are not all of the same size**, and neither are the faces! To eventually train a neural network on these images, we'll need to standardize their shape.
```
def show_keypoints(image, key_pts):
"""Show image with keypoints"""
plt.imshow(image)
plt.scatter(key_pts[:, 0], key_pts[:, 1], s=20, marker='.', c='m')
# Display a few different types of images by changing the index n
# select an image by index in our data frame
n = 0
image_name = key_pts_frame.iloc[n, 0]
key_pts = key_pts_frame.iloc[n, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
plt.figure(figsize=(5, 5))
show_keypoints(mpimg.imread(os.path.join('data/training/', image_name)), key_pts)
plt.show()
```
## Dataset class and Transformations
To prepare our data for training, we'll be using PyTorch's Dataset class. Much of this this code is a modified version of what can be found in the [PyTorch data loading tutorial](http://pytorch.org/tutorials/beginner/data_loading_tutorial.html).
#### Dataset class
``torch.utils.data.Dataset`` is an abstract class representing a
dataset. This class will allow us to load batches of image/keypoint data, and uniformly apply transformations to our data, such as rescaling and normalizing images for training a neural network.
Your custom dataset should inherit ``Dataset`` and override the following
methods:
- ``__len__`` so that ``len(dataset)`` returns the size of the dataset.
- ``__getitem__`` to support the indexing such that ``dataset[i]`` can
be used to get the i-th sample of image/keypoint data.
Let's create a dataset class for our face keypoints dataset. We will
read the CSV file in ``__init__`` but leave the reading of images to
``__getitem__``. This is memory efficient because all the images are not
stored in the memory at once but read as required.
A sample of our dataset will be a dictionary
``{'image': image, 'keypoints': key_pts}``. Our dataset will take an
optional argument ``transform`` so that any required processing can be
applied on the sample. We will see the usefulness of ``transform`` in the
next section.
```
from torch.utils.data import Dataset, DataLoader
class FacialKeypointsDataset(Dataset):
"""Face Landmarks dataset."""
def __init__(self, csv_file, root_dir, transform=None):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.key_pts_frame = pd.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.key_pts_frame)
def __getitem__(self, idx):
image_name = os.path.join(self.root_dir,
self.key_pts_frame.iloc[idx, 0])
image = mpimg.imread(image_name)
# if image has an alpha color channel, get rid of it
if(image.shape[2] == 4):
image = image[:,:,0:3]
key_pts = self.key_pts_frame.iloc[idx, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
sample = {'image': image, 'keypoints': key_pts}
if self.transform:
sample = self.transform(sample)
return sample
```
Now that we've defined this class, let's instantiate the dataset and display some images.
```
# Construct the dataset
face_dataset = FacialKeypointsDataset(csv_file='data/training_frames_keypoints.csv',
root_dir='data/training/')
# print some stats about the dataset
print('Length of dataset: ', len(face_dataset))
# Display a few of the images from the dataset
num_to_display = 3
for i in range(num_to_display):
# define the size of images
fig = plt.figure(figsize=(20,10))
# randomly select a sample
rand_i = np.random.randint(0, len(face_dataset))
sample = face_dataset[rand_i]
# print the shape of the image and keypoints
print(i, sample['image'].shape, sample['keypoints'].shape)
ax = plt.subplot(1, num_to_display, i + 1)
ax.set_title('Sample #{}'.format(i))
# Using the same display function, defined earlier
show_keypoints(sample['image'], sample['keypoints'])
```
## Transforms
Now, the images above are not of the same size, and neural networks often expect images that are standardized; a fixed size, with a normalized range for color ranges and coordinates, and (for PyTorch) converted from numpy lists and arrays to Tensors.
Therefore, we will need to write some pre-processing code.
Let's create four transforms:
- ``Normalize``: to convert a color image to grayscale values with a range of [0,1] and normalize the keypoints to be in a range of about [-1, 1]
- ``Rescale``: to rescale an image to a desired size.
- ``RandomCrop``: to crop an image randomly.
- ``ToTensor``: to convert numpy images to torch images.
We will write them as callable classes instead of simple functions so
that parameters of the transform need not be passed everytime it's
called. For this, we just need to implement ``__call__`` method and
(if we require parameters to be passed in), the ``__init__`` method.
We can then use a transform like this:
tx = Transform(params)
transformed_sample = tx(sample)
Observe below how these transforms are generally applied to both the image and its keypoints.
```
import torch
from torchvision import transforms, utils
# tranforms
class Normalize(object):
"""Convert a color image to grayscale and normalize the color range to [0,1]."""
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
image_copy = np.copy(image)
key_pts_copy = np.copy(key_pts)
# convert image to grayscale
image_copy = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
# scale color range from [0, 255] to [0, 1]
image_copy= image_copy/255.0
# scale keypoints to be centered around 0 with a range of [-1, 1]
# mean = 100, sqrt = 50, so, pts should be (pts - 100)/50
key_pts_copy = (key_pts_copy - 100)/50.0
return {'image': image_copy, 'keypoints': key_pts_copy}
class Rescale(object):
"""Rescale the image in a sample to a given size.
Args:
output_size (tuple or int): Desired output size. If tuple, output is
matched to output_size. If int, smaller of image edges is matched
to output_size keeping aspect ratio the same.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
self.output_size = output_size
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
h, w = image.shape[:2]
if isinstance(self.output_size, int):
if h > w:
new_h, new_w = self.output_size * h / w, self.output_size
else:
new_h, new_w = self.output_size, self.output_size * w / h
else:
new_h, new_w = self.output_size
new_h, new_w = int(new_h), int(new_w)
img = cv2.resize(image, (new_w, new_h))
# scale the pts, too
key_pts = key_pts * [new_w / w, new_h / h]
return {'image': img, 'keypoints': key_pts}
class RandomCrop(object):
"""Crop randomly the image in a sample.
Args:
output_size (tuple or int): Desired output size. If int, square crop
is made.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
if isinstance(output_size, int):
self.output_size = (output_size, output_size)
else:
assert len(output_size) == 2
self.output_size = output_size
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
h, w = image.shape[:2]
new_h, new_w = self.output_size
top = np.random.randint(0, h - new_h)
left = np.random.randint(0, w - new_w)
image = image[top: top + new_h,
left: left + new_w]
key_pts = key_pts - [left, top]
return {'image': image, 'keypoints': key_pts}
class ToTensor(object):
"""Convert ndarrays in sample to Tensors."""
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
# if image has no grayscale color channel, add one
if(len(image.shape) == 2):
# add that third color dim
image = image.reshape(image.shape[0], image.shape[1], 1)
# swap color axis because
# numpy image: H x W x C
# torch image: C X H X W
image = image.transpose((2, 0, 1))
return {'image': torch.from_numpy(image),
'keypoints': torch.from_numpy(key_pts)}
```
## Test out the transforms
Let's test these transforms out to make sure they behave as expected. As you look at each transform, note that, in this case, **order does matter**. For example, you cannot crop a image using a value smaller than the original image (and the orginal images vary in size!), but, if you first rescale the original image, you can then crop it to any size smaller than the rescaled size.
```
# test out some of these transforms
rescale = Rescale(100)
crop = RandomCrop(50)
composed = transforms.Compose([Rescale(250),
RandomCrop(224)])
# apply the transforms to a sample image
test_num = 500
sample = face_dataset[test_num]
fig = plt.figure()
for i, tx in enumerate([rescale, crop, composed]):
transformed_sample = tx(sample)
ax = plt.subplot(1, 3, i + 1)
plt.tight_layout()
ax.set_title(type(tx).__name__)
show_keypoints(transformed_sample['image'], transformed_sample['keypoints'])
plt.show()
```
## Create the transformed dataset
Apply the transforms in order to get grayscale images of the same shape. Verify that your transform works by printing out the shape of the resulting data (printing out a few examples should show you a consistent tensor size).
```
# define the data tranform
# order matters! i.e. rescaling should come before a smaller crop
data_transform = transforms.Compose([Rescale(250),
RandomCrop(224),
Normalize(),
ToTensor()])
# create the transformed dataset
transformed_dataset = FacialKeypointsDataset(csv_file='data/training_frames_keypoints.csv',
root_dir='data/training/',
transform=data_transform)
# print some stats about the transformed data
print('Number of images: ', len(transformed_dataset))
# make sure the sample tensors are the expected size
for i in range(5):
sample = transformed_dataset[i]
print(i, sample['image'].size(), sample['keypoints'].size())
```
## Data Iteration and Batching
Right now, we are iterating over this data using a ``for`` loop, but we are missing out on a lot of PyTorch's dataset capabilities, specifically the abilities to:
- Batch the data
- Shuffle the data
- Load the data in parallel using ``multiprocessing`` workers.
``torch.utils.data.DataLoader`` is an iterator which provides all these
features, and we'll see this in use in the *next* notebook, Notebook 2, when we load data in batches to train a neural network!
---
| true |
code
| 0.707127 | null | null | null | null |
|
# Parameterizing with Continuous Variables
```
from IPython.display import Image
```
## Continuous Factors
1. Base Class for Continuous Factors
2. Joint Gaussian Distributions
3. Canonical Factors
4. Linear Gaussian CPD
In many situations, some variables are best modeled as taking values in some continuous space. Examples include variables such as position, velocity, temperature, and pressure. Clearly, we cannot use a table representation in this case.
Nothing in the formulation of a Bayesian network requires that we restrict attention to discrete variables. The only requirement is that the CPD, P(X | Y1, Y2, ... Yn) represent, for every assignment of values y1 ∈ Val(Y1), y2 ∈ Val(Y2), .....yn ∈ val(Yn), a distribution over X. In this case, X might be continuous, in which case the CPD would need to represent distributions over a continuum of values; we might also have X’s parents continuous, so that the CPD would also need to represent a continuum of different probability distributions. There exists implicit representations for CPDs of this type, allowing us to apply all the network machinery for the continuous case as well.
### Base Class for Continuous Factors
This class will behave as a base class for the continuous factor representations. All the present and future factor classes will be derived from this base class. We need to specify the variable names and a pdf function to initialize this class.
```
import numpy as np
from scipy.special import beta
# Two variable drichlet ditribution with alpha = (1,2)
def drichlet_pdf(x, y):
return (np.power(x, 1)*np.power(y, 2))/beta(x, y)
from pgmpy.factors.continuous import ContinuousFactor
drichlet_factor = ContinuousFactor(['x', 'y'], drichlet_pdf)
drichlet_factor.scope(), drichlet_factor.assignment(5,6)
```
This class supports methods like **marginalize, reduce, product and divide** just like what we have with discrete classes. One caveat is that when there are a number of variables involved, these methods prove to be inefficient and hence we resort to certain Gaussian or some other approximations which are discussed later.
```
def custom_pdf(x, y, z):
return z*(np.power(x, 1)*np.power(y, 2))/beta(x, y)
custom_factor = ContinuousFactor(['x', 'y', 'z'], custom_pdf)
custom_factor.scope(), custom_factor.assignment(1, 2, 3)
custom_factor.reduce([('y', 2)])
custom_factor.scope(), custom_factor.assignment(1, 3)
from scipy.stats import multivariate_normal
std_normal_pdf = lambda *x: multivariate_normal.pdf(x, [0, 0], [[1, 0], [0, 1]])
std_normal = ContinuousFactor(['x1', 'x2'], std_normal_pdf)
std_normal.scope(), std_normal.assignment([1, 1])
std_normal.marginalize(['x2'])
std_normal.scope(), std_normal.assignment(1)
sn_pdf1 = lambda x: multivariate_normal.pdf([x], [0], [[1]])
sn_pdf2 = lambda x1,x2: multivariate_normal.pdf([x1, x2], [0, 0], [[1, 0], [0, 1]])
sn1 = ContinuousFactor(['x2'], sn_pdf1)
sn2 = ContinuousFactor(['x1', 'x2'], sn_pdf2)
sn3 = sn1 * sn2
sn4 = sn2 / sn1
sn3.assignment(0, 0), sn4.assignment(0, 0)
```
The ContinuousFactor class also has a method **discretize** that takes a pgmpy Discretizer class as input. It will output a list of discrete probability masses or a Factor or TabularCPD object depending upon the discretization method used. Although, we do not have inbuilt discretization algorithms for multivariate distributions for now, the users can always define their own Discretizer class by subclassing the pgmpy.BaseDiscretizer class.
### Joint Gaussian Distributions
In its most common representation, a multivariate Gaussian distribution over X1………..Xn is characterized by an n-dimensional mean vector μ, and a symmetric n x n covariance matrix Σ. The density function is most defined as -
$$
p(x) = \dfrac{1}{(2\pi)^{n/2}|Σ|^{1/2}} exp[-0.5*(x-μ)^TΣ^{-1}(x-μ)]
$$
The class pgmpy.JointGaussianDistribution provides its representation. This is derived from the class pgmpy.ContinuousFactor. We need to specify the variable names, a mean vector and a covariance matrix for its inialization. It will automatically comute the pdf function given these parameters.
```
from pgmpy.factors.distributions import GaussianDistribution as JGD
dis = JGD(['x1', 'x2', 'x3'], np.array([[1], [-3], [4]]),
np.array([[4, 2, -2], [2, 5, -5], [-2, -5, 8]]))
dis.variables
dis.mean
dis.covariance
dis.pdf([0,0,0])
```
This class overrides the basic operation methods **(marginalize, reduce, normalize, product and divide)** as these operations here are more efficient than the ones in its parent class. Most of these operation involve a matrix inversion which is O(n^3) with repect to the number of variables.
```
dis1 = JGD(['x1', 'x2', 'x3'], np.array([[1], [-3], [4]]),
np.array([[4, 2, -2], [2, 5, -5], [-2, -5, 8]]))
dis2 = JGD(['x3', 'x4'], [1, 2], [[2, 3], [5, 6]])
dis3 = dis1 * dis2
dis3.variables
dis3.mean
dis3.covariance
```
The others methods can also be used in a similar fashion.
### Canonical Factors
While the Joint Gaussian representation is useful for certain sampling algorithms, a closer look reveals that it can also not be used directly in the sum-product algorithms. Why? Because operations like product and reduce, as mentioned above involve matrix inversions at each step.
So, in order to compactly describe the intermediate factors in a Gaussian network without the costly matrix inversions at each step, a simple parametric representation is used known as the Canonical Factor. This representation is closed under the basic operations used in inference: factor product, factor division, factor reduction, and marginalization. Thus, we can define a set of simple data structures that allow the inference process to be performed. Moreover, the integration operation required by marginalization is always well defined, and it is guaranteed to produce a finite integral under certain conditions; when it is well defined, it has a simple analytical solution.
A canonical form C (X; K,h, g) is defined as:
$$C(X; K,h,g) = exp(-0.5X^TKX + h^TX + g)$$
We can represent every Gaussian as a canonical form. Rewriting the joint Gaussian pdf we obtain,
N (μ; Σ) = C (K, h, g) where:
$$
K = Σ^{-1}
$$
$$
h = Σ^{-1}μ
$$
$$
g = -0.5μ^TΣ^{-1}μ - log((2π)^{n/2}|Σ|^{1/2}
$$
Similar to the JointGaussainDistribution class, the CanonicalFactor class is also derived from the ContinuousFactor class but with its own implementations of the methods required for the sum-product algorithms that are much more efficient than its parent class methods. Let us have a look at the API of a few methods in this class.
```
from pgmpy.factors.continuous import CanonicalDistribution
phi1 = CanonicalDistribution(['x1', 'x2', 'x3'],
np.array([[1, -1, 0], [-1, 4, -2], [0, -2, 4]]),
np.array([[1], [4], [-1]]), -2)
phi2 = CanonicalDistribution(['x1', 'x2'], np.array([[3, -2], [-2, 4]]),
np.array([[5], [-1]]), 1)
phi3 = phi1 * phi2
phi3.variables
phi3.h
phi3.K
phi3.g
```
This class also has a method, to_joint_gaussian to convert the canoncial representation back into the joint gaussian distribution.
```
phi = CanonicalDistribution(['x1', 'x2'], np.array([[3, -2], [-2, 4]]),
np.array([[5], [-1]]), 1)
jgd = phi.to_joint_gaussian()
jgd.variables
jgd.covariance
jgd.mean
```
### Linear Gaussian CPD
A linear gaussian conditional probability distribution is defined on a continuous variable. All the parents of this variable are also continuous. The mean of this variable, is linearly dependent on the mean of its parent variables and the variance is independent.
For example,
$$
P(Y ; x1, x2, x3) = N(β_1x_1 + β_2x_2 + β_3x_3 + β_0 ; σ^2)
$$
Let Y be a linear Gaussian of its parents X1,...,Xk:
$$
p(Y | x) = N(β_0 + β^T x ; σ^2)
$$
The distribution of Y is a normal distribution p(Y) where:
$$
μ_Y = β_0 + β^Tμ
$$
$$
{{σ^2}_Y = σ^2 + β^TΣβ}
$$
The joint distribution over {X, Y} is a normal distribution where:
$$Cov[X_i; Y] = {\sum_{j=1}^{k} β_jΣ_{i,j}}$$
Assume that X1,...,Xk are jointly Gaussian with distribution N (μ; Σ). Then:
For its representation pgmpy has a class named LinearGaussianCPD in the module pgmpy.factors.continuous. To instantiate an object of this class, one needs to provide a variable name, the value of the beta_0 term, the variance, a list of the parent variable names and a list of the coefficient values of the linear equation (beta_vector), where the list of parent variable names and beta_vector list is optional and defaults to None.
```
# For P(Y| X1, X2, X3) = N(-2x1 + 3x2 + 7x3 + 0.2; 9.6)
from pgmpy.factors.continuous import LinearGaussianCPD
cpd = LinearGaussianCPD('Y', [0.2, -2, 3, 7], 9.6, ['X1', 'X2', 'X3'])
print(cpd)
```
A Gaussian Bayesian is defined as a network all of whose variables are continuous, and where all of the CPDs are linear Gaussians. These networks are of particular interest as these are an alternate form of representaion of the Joint Gaussian distribution.
These networks are implemented as the LinearGaussianBayesianNetwork class in the module, pgmpy.models.continuous. This class is a subclass of the BayesianModel class in pgmpy.models and will inherit most of the methods from it. It will have a special method known as to_joint_gaussian that will return an equivalent JointGuassianDistribution object for the model.
```
from pgmpy.models import LinearGaussianBayesianNetwork
model = LinearGaussianBayesianNetwork([('x1', 'x2'), ('x2', 'x3')])
cpd1 = LinearGaussianCPD('x1', [1], 4)
cpd2 = LinearGaussianCPD('x2', [-5, 0.5], 4, ['x1'])
cpd3 = LinearGaussianCPD('x3', [4, -1], 3, ['x2'])
# This is a hack due to a bug in pgmpy (LinearGaussianCPD
# doesn't have `variables` attribute but `add_cpds` function
# wants to check that...)
cpd1.variables = [*cpd1.evidence, cpd1.variable]
cpd2.variables = [*cpd2.evidence, cpd2.variable]
cpd3.variables = [*cpd3.evidence, cpd3.variable]
model.add_cpds(cpd1, cpd2, cpd3)
jgd = model.to_joint_gaussian()
jgd.variables
jgd.mean
jgd.covariance
```
| true |
code
| 0.766037 | null | null | null | null |
|
# Understanding Classification and Logistic Regression with Python
## Introduction
This notebook contains a short introduction to the basic principles of classification and logistic regression. A simple Python simulation is used to illustrate these principles. Specifically, the following steps are performed:
- A data set is created. The label has binary `TRUE` and `FALSE` labels. Values for two features are generated from two bivariate Normal distribion, one for each label class.
- A plot is made of the data set, using color and shape to show the two label classes.
- A plot of a logistic function is computed.
- For each of three data sets a logistic regression model is computed, scored and a plot created using color to show class and shape to show correct and incorrect scoring.
## Create the data set
The code in the cell below computes the two class data set. The feature values for each label level are computed from a bivariate Normal distribution. Run this code and examine the first few rows of the data frame.
```
def sim_log_data(x1, y1, n1, sd1, x2, y2, n2, sd2):
import pandas as pd
import numpy.random as nr
wx1 = nr.normal(loc = x1, scale = sd1, size = n1)
wy1 = nr.normal(loc = y1, scale = sd1, size = n1)
z1 = [1]*n1
wx2 = nr.normal(loc = x2, scale = sd2, size = n2)
wy2 = nr.normal(loc = y2, scale = sd2, size = n2)
z2 = [0]*n2
df1 = pd.DataFrame({'x': wx1, 'y': wy1, 'z': z1})
df2 = pd.DataFrame({'x': wx2, 'y': wy2, 'z': z2})
return pd.concat([df1, df2], axis = 0, ignore_index = True)
sim_data = sim_log_data(1, 1, 50, 1, -1, -1, 50, 1)
sim_data.head()
```
## Plot the data set
The code in the cell below plots the data set using color to show the two classes of the labels. Execute this code and examine the results. Notice that the posion of the points from each class overlap with each other.
```
%matplotlib inline
def plot_class(df):
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(5, 5))
fig.clf()
ax = fig.gca()
df[df.z == 1].plot(kind = 'scatter', x = 'x', y = 'y', ax = ax,
alpha = 1.0, color = 'Red', marker = 'x', s = 40)
df[df.z == 0].plot(kind = 'scatter', x = 'x', y = 'y', ax = ax,
alpha = 1.0, color = 'DarkBlue', marker = 'o', s = 40)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_title('Classes vs X and Y')
return 'Done'
plot_class(sim_data)
```
## Plot the logistic function
Logistic regression computes a binary {0,1} score using a logistic function. A value of the logistic function above the cutoff (typically 0.5) are scored as a 1 or true, and values less than the cutoff are scored as a 0 or false. Execute the code and examine the resulting logistic function.
```
def plot_logistic(upper = 6, lower = -6, steps = 100):
import matplotlib.pyplot as plt
import pandas as pd
import math as m
step = float(upper - lower) / float(steps)
x = [lower + x * step for x in range(101)]
y = [m.exp(z)/(1 + m.exp(z)) for z in x]
fig = plt.figure(figsize=(5, 4))
fig.clf()
ax = fig.gca()
ax.plot(x, y, color = 'r')
ax.axvline(0, 0.0, 1.0)
ax.axhline(0.5, lower, upper)
ax.set_xlabel('X')
ax.set_ylabel('Probabiltiy of positive response')
ax.set_title('Logistic function for two-class classification')
return 'done'
plot_logistic()
```
## Compute and score a logistic regression model
There is a considerable anount of code in the cell below.
The fist function uses scikit-learn to compute and scores a logsitic regression model. Notie that the features and the label must be converted to a numpy array which is required for scikit-learn.
The second function computes the evaluation of the logistic regression model in the following steps:
- Compute the elements of theh confusion matrix.
- Plot the correctly and incorrectly scored cases, using shape and color to identify class and classification correctness.
- Commonly used performance statistics are computed.
Execute this code and examine the results. Notice that most of the cases have been correctly classified. Classification errors appear along a boundary between those two classes.
```
def logistic_mod(df, logProb = 1.0):
from sklearn import linear_model
## Prepare data for model
nrow = df.shape[0]
X = df[['x', 'y']].as_matrix().reshape(nrow,2)
Y = df.z.as_matrix().ravel() #reshape(nrow,1)
## Compute the logistic regression model
lg = linear_model.LogisticRegression()
logr = lg.fit(X, Y)
## Compute the y values
temp = logr.predict_log_proba(X)
df['predicted'] = [1 if (logProb > p[1]/p[0]) else 0 for p in temp]
return df
def eval_logistic(df):
import matplotlib.pyplot as plt
import pandas as pd
truePos = df[((df['predicted'] == 1) & (df['z'] == df['predicted']))]
falsePos = df[((df['predicted'] == 1) & (df['z'] != df['predicted']))]
trueNeg = df[((df['predicted'] == 0) & (df['z'] == df['predicted']))]
falseNeg = df[((df['predicted'] == 0) & (df['z'] != df['predicted']))]
fig = plt.figure(figsize=(5, 5))
fig.clf()
ax = fig.gca()
truePos.plot(kind = 'scatter', x = 'x', y = 'y', ax = ax,
alpha = 1.0, color = 'DarkBlue', marker = '+', s = 80)
falsePos.plot(kind = 'scatter', x = 'x', y = 'y', ax = ax,
alpha = 1.0, color = 'Red', marker = 'o', s = 40)
trueNeg.plot(kind = 'scatter', x = 'x', y = 'y', ax = ax,
alpha = 1.0, color = 'DarkBlue', marker = 'o', s = 40)
falseNeg.plot(kind = 'scatter', x = 'x', y = 'y', ax = ax,
alpha = 1.0, color = 'Red', marker = '+', s = 80)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_title('Classes vs X and Y')
TP = truePos.shape[0]
FP = falsePos.shape[0]
TN = trueNeg.shape[0]
FN = falseNeg.shape[0]
confusion = pd.DataFrame({'Positive': [FP, TP],
'Negative': [TN, FN]},
index = ['TrueNeg', 'TruePos'])
accuracy = float(TP + TN)/float(TP + TN + FP + FN)
precision = float(TP)/float(TP + FP)
recall = float(TP)/float(TP + FN)
print(confusion)
print('accracy = ' + str(accuracy))
print('precision = ' + str(precision))
print('recall = ' + str(recall))
return 'Done'
mod = logistic_mod(sim_data)
eval_logistic(mod)
```
## Moving the decision boundary
The example above uses a cutoff at the midpoint of the logistic function. However, you can change the trade-off between correctly classifying the positive cases and correctly classifing the negative cases. The code in the cell below computes and scores a logistic regressiion model for three different cutoff points.
Run the code in the cell and carefully compare the results for the three cases. Notice, that as the logistic cutoff changes the decision boundary moves on the plot, with progressively more positive cases are correctly classified. In addition, accuracy and precision decrease and recall increases.
```
def logistic_demo_prob():
logt = sim_log_data(0.5, 0.5, 50, 1, -0.5, -0.5, 50, 1)
probs = [1, 2, 4]
for p in probs:
logMod = logistic_mod(logt, p)
eval_logistic(logMod)
return 'Done'
logistic_demo_prob()
```
| true |
code
| 0.582788 | null | null | null | null |
|
# Implementation of Softmax Regression from Scratch
:label:`chapter_softmax_scratch`
Just as we implemented linear regression from scratch,
we believe that multiclass logistic (softmax) regression
is similarly fundamental and you ought to know
the gory details of how to implement it from scratch.
As with linear regression, after doing things by hand
we will breeze through an implementation in Gluon for comparison.
To begin, let's import our packages.
```
import sys
sys.path.insert(0, '..')
%matplotlib inline
import d2l
import torch
from torch.distributions import normal
```
We will work with the Fashion-MNIST dataset just introduced,
cuing up an iterator with batch size 256.
```
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
```
## Initialize Model Parameters
Just as in linear regression, we represent each example as a vector.
Since each example is a $28 \times 28$ image,
we can flatten each example, treating them as $784$ dimensional vectors.
In the future, we'll talk about more sophisticated strategies
for exploiting the spatial structure in images,
but for now we treat each pixel location as just another feature.
Recall that in softmax regression,
we have as many outputs as there are categories.
Because our dataset has $10$ categories,
our network will have an output dimension of $10$.
Consequently, our weights will constitute a $784 \times 10$ matrix
and the biases will constitute a $1 \times 10$ vector.
As with linear regression, we will initialize our weights $W$
with Gaussian noise and our biases to take the initial value $0$.
```
num_inputs = 784
num_outputs = 10
W = normal.Normal(loc = 0, scale = 0.01).sample((num_inputs, num_outputs))
b = torch.zeros(num_outputs)
```
Recall that we need to *attach gradients* to the model parameters.
More literally, we are allocating memory for future gradients to be stored
and notifiying PyTorch that we want gradients to be calculated with respect to these parameters in the first place.
```
W.requires_grad_(True)
b.requires_grad_(True)
```
## The Softmax
Before implementing the softmax regression model,
let's briefly review how `torch.sum` work
along specific dimensions in a PyTorch tensor.
Given a matrix `X` we can sum over all elements (default) or only
over elements in the same column (`dim=0`) or the same row (`dim=1`).
Note that if `X` is an array with shape `(2, 3)`
and we sum over the columns (`torch.sum(X, dim=0`),
the result will be a (1D) vector with shape `(3,)`.
If we want to keep the number of axes in the original array
(resulting in a 2D array with shape `(1,3)`),
rather than collapsing out the dimension that we summed over
we can specify `keepdim=True` when invoking `torch.sum`.
```
X = torch.tensor([[1, 2, 3], [4, 5, 6]])
torch.sum(X, dim=0, keepdim=True), torch.sum(X, dim=1, keepdim=True)
```
We are now ready to implement the softmax function.
Recall that softmax consists of two steps:
First, we exponentiate each term (using `torch.exp`).
Then, we sum over each row (we have one row per example in the batch)
to get the normalization constants for each example.
Finally, we divide each row by its normalization constant,
ensuring that the result sums to $1$.
Before looking at the code, let's recall
what this looks expressed as an equation:
$$
\mathrm{softmax}(\mathbf{X})_{ij} = \frac{\exp(X_{ij})}{\sum_k \exp(X_{ik})}
$$
The denominator, or normalization constant,
is also sometimes called the partition function
(and its logarithm the log-partition function).
The origins of that name are in [statistical physics](https://en.wikipedia.org/wiki/Partition_function_(statistical_mechanics))
where a related equation models the distribution
over an ensemble of particles).
```
def softmax(X):
X_exp = torch.exp(X)
partition = torch.sum(X_exp, dim=1, keepdim=True)
return X_exp / partition # The broadcast mechanism is applied here
```
As you can see, for any random input, we turn each element into a non-negative number. Moreover, each row sums up to 1, as is required for a probability.
Note that while this looks correct mathematically,
we were a bit sloppy in our implementation
because failed to take precautions against numerical overflow or underflow
due to large (or very small) elements of the matrix,
as we did in
:numref:`chapter_naive_bayes`.
```
# X = nd.random.normal(shape=(2, 5))
X = normal.Normal(loc = 0, scale = 1).sample((2, 5))
X_prob = softmax(X)
X_prob, torch.sum(X_prob, dim=1)
```
## The Model
Now that we have defined the softmax operation,
we can implement the softmax regression model.
The below code defines the forward pass through the network.
Note that we flatten each original image in the batch
into a vector with length `num_inputs` with the `view` function
before passing the data through our model.
```
def net(X):
return softmax(torch.matmul(X.reshape((-1, num_inputs)), W) + b)
```
## The Loss Function
Next, we need to implement the cross entropy loss function,
introduced in :numref:`chapter_softmax`.
This may be the most common loss function
in all of deep learning because, at the moment,
classification problems far outnumber regression problems.
Recall that cross entropy takes the negative log likelihood
of the predicted probability assigned to the true label $-\log p(y|x)$.
Rather than iterating over the predictions with a Python `for` loop
(which tends to be inefficient), we can use the `gather` function
which allows us to select the appropriate terms
from the matrix of softmax entries easily.
Below, we illustrate the `gather` function on a toy example,
with 3 categories and 2 examples.
```
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.tensor([0, 2])
torch.gather(y_hat, 1, y.unsqueeze(dim=1)) # y has to be unsqueezed so that shape(y_hat) = shape(y)
```
Now we can implement the cross-entropy loss function efficiently
with just one line of code.
```
def cross_entropy(y_hat, y):
return -torch.gather(y_hat, 1, y.unsqueeze(dim=1)).log()
```
## Classification Accuracy
Given the predicted probability distribution `y_hat`,
we typically choose the class with highest predicted probability
whenever we must output a *hard* prediction. Indeed, many applications require that we make a choice. Gmail must catetegorize an email into Primary, Social, Updates, or Forums. It might estimate probabilities internally, but at the end of the day it has to choose one among the categories.
When predictions are consistent with the actual category `y`, they are correct. The classification accuracy is the fraction of all predictions that are correct. Although we cannot optimize accuracy directly (it is not differentiable), it's often the performance metric that we care most about, and we will nearly always report it when training classifiers.
To compute accuracy we do the following:
First, we execute `y_hat.argmax(dim=1)`
to gather the predicted classes
(given by the indices for the largest entires each row).
The result has the same shape as the variable `y`.
Now we just need to check how frequently the two match. The result is PyTorch tensor containing entries of 0 (false) and 1 (true). Since the attribute `mean` can only calculate the mean of floating types,
we also need to convert the result to `float`. Taking the mean yields the desired result.
```
def accuracy(y_hat, y):
return (y_hat.argmax(dim=1) == y).float().mean().item()
```
We will continue to use the variables `y_hat` and `y`
defined in the `gather` function,
as the predicted probability distribution and label, respectively.
We can see that the first example's prediction category is 2
(the largest element of the row is 0.6 with an index of 2),
which is inconsistent with the actual label, 0.
The second example's prediction category is 2
(the largest element of the row is 0.5 with an index of 2),
which is consistent with the actual label, 2.
Therefore, the classification accuracy rate for these two examples is 0.5.
```
accuracy(y_hat, y)
```
Similarly, we can evaluate the accuracy for model `net` on the data set
(accessed via `data_iter`).
```
# The function will be gradually improved: the complete implementation will be
# discussed in the "Image Augmentation" section
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).sum().item()
n += y.size()[0] # y.size()[0] = batch_size
return acc_sum / n
```
Because we initialized the `net` model with random weights,
the accuracy of this model should be close to random guessing,
i.e. 0.1 for 10 classes.
```
evaluate_accuracy(test_iter, net)
```
## Model Training
The training loop for softmax regression should look strikingly familiar
if you read through our implementation
of linear regression earlier in this chapter.
Again, we use the mini-batch stochastic gradient descent
to optimize the loss function of the model.
Note that the number of epochs (`num_epochs`),
and learning rate (`lr`) are both adjustable hyper-parameters.
By changing their values, we may be able to increase the classification accuracy of the model. In practice we'll want to split our data three ways
into training, validation, and test data, using the validation data to choose the best values of our hyperparameters.
```
num_epochs, lr = 5, 0.1
# This function has been saved in the d2l package for future use
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params=None, lr=None, trainer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
l.backward()
if trainer is None:
d2l.sgd(params, lr, batch_size)
else:
# This will be illustrated in the next section
trainer.step(batch_size)
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.size()[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)
```
## Prediction
Now that training is complete, our model is ready to classify some images.
Given a series of images, we will compare their actual labels
(first line of text output) and the model predictions
(second line of text output).
```
for X, y in test_iter:
break
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [truelabel + '\n' + predlabel for truelabel, predlabel in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[10:20], titles[10:20])
```
## Summary
With softmax regression, we can train models for multi-category classification. The training loop is very similar to that in linear regression: retrieve and read data, define models and loss functions,
then train models using optimization algorithms. As you'll soon find out, most common deep learning models have similar training procedures.
## Exercises
1. In this section, we directly implemented the softmax function based on the mathematical definition of the softmax operation. What problems might this cause (hint - try to calculate the size of $\exp(50)$)?
1. The function `cross_entropy` in this section is implemented according to the definition of the cross-entropy loss function. What could be the problem with this implementation (hint - consider the domain of the logarithm)?
1. What solutions you can think of to fix the two problems above?
1. Is it always a good idea to return the most likely label. E.g. would you do this for medical diagnosis?
1. Assume that we want to use softmax regression to predict the next word based on some features. What are some problems that might arise from a large vocabulary?
| true |
code
| 0.57081 | null | null | null | null |
|
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/ShopRunner/collie/blob/main/tutorials/05_hybrid_model.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/ShopRunner/collie/blob/main/tutorials/05_hybrid_model.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a>
</td>
<td>
<a target="_blank" href="https://raw.githubusercontent.com/ShopRunner/collie/main/tutorials/05_hybrid_model.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" /> Download notebook</a>
</td>
</table>
```
# for Collab notebooks, we will start by installing the ``collie`` library
!pip install collie --quiet
%reload_ext autoreload
%autoreload 2
%matplotlib inline
%env DATA_PATH data/
import os
import numpy as np
import pandas as pd
from pytorch_lightning.utilities.seed import seed_everything
from IPython.display import HTML
import joblib
import torch
from collie.metrics import mapk, mrr, auc, evaluate_in_batches
from collie.model import CollieTrainer, HybridPretrainedModel, MatrixFactorizationModel
from collie.movielens import get_movielens_metadata, get_recommendation_visualizations
```
## Load Data From ``01_prepare_data`` Notebook
If you're running this locally on Jupyter, you should be able to run the next cell quickly without a problem! If you are running this on Colab, you'll need to regenerate the data by running the cell below that, which should only take a few extra seconds to complete.
```
try:
# let's grab the ``Interactions`` objects we saved in the last notebook
train_interactions = joblib.load(os.path.join(os.environ.get('DATA_PATH', 'data/'),
'train_interactions.pkl'))
val_interactions = joblib.load(os.path.join(os.environ.get('DATA_PATH', 'data/'),
'val_interactions.pkl'))
except FileNotFoundError:
# we're running this notebook on Colab where results from the first notebook are not saved
# regenerate this data below
from collie.cross_validation import stratified_split
from collie.interactions import Interactions
from collie.movielens import read_movielens_df
from collie.utils import convert_to_implicit, remove_users_with_fewer_than_n_interactions
df = read_movielens_df(decrement_ids=True)
implicit_df = convert_to_implicit(df, min_rating_to_keep=4)
implicit_df = remove_users_with_fewer_than_n_interactions(implicit_df, min_num_of_interactions=3)
interactions = Interactions(
users=implicit_df['user_id'],
items=implicit_df['item_id'],
ratings=implicit_df['rating'],
allow_missing_ids=True,
)
train_interactions, val_interactions = stratified_split(interactions, test_p=0.1, seed=42)
print('Train:', train_interactions)
print('Val: ', val_interactions)
```
# Hybrid Collie Model Using a Pre-Trained ``MatrixFactorizationModel``
In this notebook, we will use this same metadata and incorporate it directly into the model architecture with a hybrid Collie model.
## Read in Data
```
# read in the same metadata used in notebooks ``03`` and ``04``
metadata_df = get_movielens_metadata()
metadata_df.head()
# and, as always, set our random seed
seed_everything(22)
```
## Train a ``MatrixFactorizationModel``
The first step towards training a Collie Hybrid model is to train a regular ``MatrixFactorizationModel`` to generate rich user and item embeddings. We'll use these embeddings in a ``HybridPretrainedModel`` a bit later.
```
model = MatrixFactorizationModel(
train=train_interactions,
val=val_interactions,
embedding_dim=30,
lr=1e-2,
)
trainer = CollieTrainer(model=model, max_epochs=10, deterministic=True)
trainer.fit(model)
mapk_score, mrr_score, auc_score = evaluate_in_batches([mapk, mrr, auc], val_interactions, model)
print(f'Standard MAP@10 Score: {mapk_score}')
print(f'Standard MRR Score: {mrr_score}')
print(f'Standard AUC Score: {auc_score}')
```
## Train a ``HybridPretrainedModel``
With our trained ``model`` above, we can now use these embeddings and additional side data directly in a hybrid model. The architecture essentially takes our user embedding, item embedding, and item metadata for each user-item interaction, concatenates them, and sends it through a simple feedforward network to output a recommendation score.
We can initially freeze the user and item embeddings from our previously-trained ``model``, train for a few epochs only optimizing our newly-added linear layers, and then train a model with everything unfrozen at a lower learning rate. We will show this process below.
```
# we will apply a linear layer to the metadata with ``metadata_layers_dims`` and
# a linear layer to the combined embeddings and metadata data with ``combined_layers_dims``
hybrid_model = HybridPretrainedModel(
train=train_interactions,
val=val_interactions,
item_metadata=metadata_df,
trained_model=model,
metadata_layers_dims=[8],
combined_layers_dims=[16],
lr=1e-2,
freeze_embeddings=True,
)
hybrid_trainer = CollieTrainer(model=hybrid_model, max_epochs=10, deterministic=True)
hybrid_trainer.fit(hybrid_model)
mapk_score, mrr_score, auc_score = evaluate_in_batches([mapk, mrr, auc], val_interactions, hybrid_model)
print(f'Hybrid MAP@10 Score: {mapk_score}')
print(f'Hybrid MRR Score: {mrr_score}')
print(f'Hybrid AUC Score: {auc_score}')
hybrid_model_unfrozen = HybridPretrainedModel(
train=train_interactions,
val=val_interactions,
item_metadata=metadata_df,
trained_model=model,
metadata_layers_dims=[8],
combined_layers_dims=[16],
lr=1e-4,
freeze_embeddings=False,
)
hybrid_model.unfreeze_embeddings()
hybrid_model_unfrozen.load_from_hybrid_model(hybrid_model)
hybrid_trainer_unfrozen = CollieTrainer(model=hybrid_model_unfrozen, max_epochs=10, deterministic=True)
hybrid_trainer_unfrozen.fit(hybrid_model_unfrozen)
mapk_score, mrr_score, auc_score = evaluate_in_batches([mapk, mrr, auc],
val_interactions,
hybrid_model_unfrozen)
print(f'Hybrid Unfrozen MAP@10 Score: {mapk_score}')
print(f'Hybrid Unfrozen MRR Score: {mrr_score}')
print(f'Hybrid Unfrozen AUC Score: {auc_score}')
```
Note here that while our ``MAP@10`` and ``MRR`` scores went down slightly from the frozen version of the model above, our ``AUC`` score increased. For implicit recommendation models, each evaluation metric is nuanced in what it represents for real world recommendations.
You can read more about each evaluation metric by checking out the [Mean Average Precision at K (MAP@K)](https://en.wikipedia.org/wiki/Evaluation_measures_(information_retrieval)#Mean_average_precision), [Mean Reciprocal Rank](https://en.wikipedia.org/wiki/Mean_reciprocal_rank), and [Area Under the Curve (AUC)](https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Area_under_the_curve) Wikipedia pages.
```
user_id = np.random.randint(0, train_interactions.num_users)
display(
HTML(
get_recommendation_visualizations(
model=hybrid_model_unfrozen,
user_id=user_id,
filter_films=True,
shuffle=True,
detailed=True,
)
)
)
```
The metrics and results look great, and we should only see a larger difference compared to a standard model as our data becomes more nuanced and complex (such as with MovieLens 10M data).
If we're happy with this model, we can go ahead and save it for later!
## Save and Load a Hybrid Model
```
# we can save the model with...
os.makedirs('models', exist_ok=True)
hybrid_model_unfrozen.save_model('models/hybrid_model_unfrozen')
# ... and if we wanted to load that model back in, we can do that easily...
hybrid_model_loaded_in = HybridPretrainedModel(load_model_path='models/hybrid_model_unfrozen')
hybrid_model_loaded_in
```
While our model works and the results look great, it's not always possible to be able to fully train two separate models like we've done in this tutorial. Sometimes, it's easier (and even better) to train a single hybird model up from scratch, no pretrained ``MatrixFactorizationModel`` needed.
In the next tutorial, we'll cover multi-stage models in Collie, tackling this exact problem and more! See you there!
-----
| true |
code
| 0.644449 | null | null | null | null |
|
# Implicit Georeferencing
This workbook sets explicit georeferences from implicit georeferencing through names of extents given in dataset titles or keywords.
A file `sources.py` needs to contain the CKAN and SOURCE config as follows:
```
CKAN = {
"dpaw-internal":{
"url": "http://internal-data.dpaw.wa.gov.au/",
"key": "API-KEY"
}
}
```
## Configure CKAN and source
```
import ckanapi
from harvest_helpers import *
from secret import CKAN
ckan = ckanapi.RemoteCKAN(CKAN["dpaw-internal"]["url"], apikey=CKAN["dpaw-internal"]["key"])
print("Using CKAN {0}".format(ckan.address))
```
## Spatial extent name-geometry lookup
The fully qualified names and GeoJSON geometries of relevant spatial areas are contained in our custom dataschema.
```
# Getting the extent dictionary e
url = "https://raw.githubusercontent.com/datawagovau/ckanext-datawagovautheme/dpaw-internal/ckanext/datawagovautheme/datawagovau_dataset.json"
ds = json.loads(requests.get(url).content)
choice_dict = [x for x in ds["dataset_fields"] if x["field_name"] == "spatial"][0]["choices"]
e = dict([(x["label"], json.dumps(x["value"])) for x in choice_dict])
print("Extents: {0}".format(e.keys()))
```
## Name lookups
Relevant areas are listed under different synonyms. We'll create a dictionary of synonymous search terms ("s") and extent names (index "i").
```
# Creating a search term - extent index lookup
# m is a list of keys "s" (search term) and "i" (extent index)
m = [
{"s":"Eighty", "i":"MPA Eighty Mile Beach"},
{"s":"EMBMP", "i":"MPA Eighty Mile Beach"},
{"s":"Camden", "i":"MPA Lalang-garram / Camden Sound"},
{"s":"LCSMP", "i":"MPA Lalang-garram / Camden Sound"},
{"s":"Rowley", "i":"MPA Rowley Shoals"},
{"s":"RSMP", "i":"MPA Rowley Shoals"},
{"s":"Montebello", "i":"MPA Montebello Barrow"},
{"s":"MBIMPA", "i":"MPA Montebello Barrow"},
{"s":"Ningaloo", "i":"MPA Ningaloo"},
{"s":"NMP", "i":"MPA Ningaloo"},
{"s":"Shark bay", "i":"MPA Shark Bay Hamelin Pool"},
{"s":"SBMP", "i":"MPA Shark Bay Hamelin Pool"},
{"s":"Jurien", "i":"MPA Jurien Bay"},
{"s":"JBMP", "i":"MPA Jurien Bay"},
{"s":"Marmion", "i":"MPA Marmion"},
{"s":"Swan Estuary", "i":"MPA Swan Estuary"},
{"s":"SEMP", "i":"MPA Swan Estuary"},
{"s":"Shoalwater", "i":"MPA Shoalwater Islands"},
{"s":"SIMP", "i":"MPA Shoalwater Islands"},
{"s":"Ngari", "i":"MPA Ngari Capes"},
{"s":"NCMP", "i":"MPA Ngari Capes"},
{"s":"Walpole", "i":"MPA Walpole Nornalup"},
{"s":"WNIMP", "i":"MPA Walpole Nornalup"}
]
def add_spatial(dsdict, extent_string, force=False, debug=False):
"""Adds a given spatial extent to a CKAN dataset dict if
"spatial" is None, "" or force==True.
Arguments:
dsdict (ckanapi.action.package_show()) CKAN dataset dict
extent_string (String) GeoJSON geometry as json.dumps String
force (Boolean) Whether to force overwriting "spatial"
debug (Boolean) Debug noise
Returns:
(dict) The dataset with spatial extent replaced per above rules.
"""
if not dsdict.has_key("spatial"):
overwrite = True
if debug:
msg = "Spatial extent not given"
elif dsdict["spatial"] == "":
overwrite = True
if debug:
msg = "Spatial extent is empty"
elif force:
overwrite = True
msg = "Spatial extent was overwritten"
else:
overwrite = False
msg = "Spatial extent unchanged"
if overwrite:
dsdict["spatial"] = extent_string
print(msg)
return dsdict
def restore_extents(search_mapping, extents, ckan, debug=False):
"""Restore spatial extents for datasets
Arguments:
search_mapping (list) A list of dicts with keys "s" for ckanapi
package_search query parameter "q", and key "i" for the name
of the extent
e.g.:
m = [
{"s":"tags:marinepark_80_mile_beach", "i":"MPA Eighty Mile Beach"},
...
]
extents (dict) A dict with key "i" (extent name) and
GeoJSON Multipolygon geometry strings as value, e.g.:
{u'MPA Eighty Mile Beach': '{"type": "MultiPolygon", "coordinates": [ .... ]', ...}
ckan (ckanapi) A ckanapi instance
debug (boolean) Debug noise
Returns:
A list of dictionaries returned by ckanapi's package_update
"""
for x in search_mapping:
if debug:
print("\nSearching CKAN with '{0}'".format(x["s"]))
found = ckan.action.package_search(q=x["s"])["results"]
if debug:
print("Found datasets: {0}\n".format([d["title"] for d in found]))
fixed = [add_spatial(d, extents[x["i"]], force=True, debug=True) for d in found]
if debug:
print(fixed, "\n")
datasets_updated = upsert_datasets(fixed, ckan, debug=False)
restore_extents(m, e, ckan)
d = [ckan.action.package_show(id = x) for x in ckan.action.package_list()]
fix = [x["title"] for x in d if not x.has_key("spatial")]
len(fix)
d[0]
fix
```
| true |
code
| 0.496033 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/xavoliva6/dpfl_pytorch/blob/main/experiments/exp_FedMNIST.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Experiments on FedMNIST
**Colab Support**<br/>
Only run the following lines if you want to run the code on Google Colab
```
# Enable access to files stored in Google Drive
from google.colab import drive
drive.mount('/content/gdrive/')
% cd /content/gdrive/My Drive/OPT4ML/src
```
# Main
```
# Install necessary requirements
!pip install -r ../requirements.txt
# Make sure cuda support is available
import torch
if torch.cuda.is_available():
device_name = "cuda:0"
else:
device_name = "cpu"
print("device_name: {}".format(device_name))
device = torch.device(device_name)
%load_ext autoreload
%autoreload 2
import sys
import warnings
warnings.filterwarnings("ignore")
from server import Server
from utils import plot_exp
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [6, 6]
plt.rcParams['figure.dpi'] = 100
```
### First experiment : impact of federated learning
```
LR = 0.01
EPOCHS = 1
NR_TRAINING_ROUNDS = 30
BATCH_SIZE = 128
RANGE_NR_CLIENTS = [1,5,10]
experiment_losses, experiment_accs = [], []
for nr_clients in RANGE_NR_CLIENTS:
print(f"### Number of clients : {nr_clients} ###\n\n")
server = Server(
nr_clients=nr_clients,
nr_training_rounds=NR_TRAINING_ROUNDS,
data='MNIST',
epochs=EPOCHS,
lr=LR,
batch_size=BATCH_SIZE,
is_private=False,
epsilon=None,
max_grad_norm=None,
noise_multiplier=None,
is_parallel=True,
device=device,
verbose='server')
test_losses, test_accs = server.train()
experiment_losses.append(test_losses)
experiment_accs.append(test_accs)
names = [f'{i} clients' for i in RANGE_NR_CLIENTS]
title = 'First experiment : MNIST database'
fig = plot_exp(experiment_losses, experiment_accs, names, title)
fig.savefig("MNIST_exp1.pdf")
```
### Second experiment : impact of differential privacy
```
NR_CLIENTS = 10
NR_TRAINING_ROUNDS = 30
EPOCHS = 1
LR = 0.01
BATCH_SIZE = 128
MAX_GRAD_NORM = 1.2
NOISE_MULTIPLIER = None
RANGE_EPSILON = [10,50,100]
experiment_losses, experiment_accs = [], []
for epsilon in RANGE_EPSILON:
print(f"### ε : {epsilon} ###\n\n")
server = Server(
nr_clients=NR_CLIENTS,
nr_training_rounds=NR_TRAINING_ROUNDS,
data='MNIST',
epochs=EPOCHS,
lr=LR,
batch_size=BATCH_SIZE,
is_private=True,
epsilon=epsilon,
max_grad_norm=MAX_GRAD_NORM,
noise_multiplier=NOISE_MULTIPLIER,
is_parallel=True,
device=device,
verbose='server')
test_losses, test_accs = server.train()
experiment_losses.append(test_losses)
experiment_accs.append(test_accs)
names = [f'ε = {i}' for i in RANGE_EPSILON]
title = 'Second experiment : MNIST database'
fig = plot_exp(experiment_losses, experiment_accs, names, title)
plt.savefig('MNIST_exp2.pdf')
```
| true |
code
| 0.636155 | null | null | null | null |
|
```
# for reading and validating data
import emeval.input.spec_details as eisd
import emeval.input.phone_view as eipv
import emeval.input.eval_view as eiev
# Visualization helpers
import emeval.viz.phone_view as ezpv
import emeval.viz.eval_view as ezev
import emeval.viz.geojson as ezgj
import pandas as pd
# Metrics helpers
import emeval.metrics.dist_calculations as emd
# For computation
import numpy as np
import math
import scipy.stats as stats
import matplotlib.pyplot as plt
import geopandas as gpd
import shapely as shp
import folium
DATASTORE_URL = "http://cardshark.cs.berkeley.edu"
AUTHOR_EMAIL = "[email protected]"
sd_la = eisd.SpecDetails(DATASTORE_URL, AUTHOR_EMAIL, "unimodal_trip_car_bike_mtv_la")
sd_sj = eisd.SpecDetails(DATASTORE_URL, AUTHOR_EMAIL, "car_scooter_brex_san_jose")
sd_ucb = eisd.SpecDetails(DATASTORE_URL, AUTHOR_EMAIL, "train_bus_ebike_mtv_ucb")
import importlib
importlib.reload(eisd)
pv_la = eipv.PhoneView(sd_la)
pv_sj = eipv.PhoneView(sd_sj)
pv_ucb = eipv.PhoneView(sd_ucb)
```
### Validate distance calculations
Our x,y coordinates are in degrees (lon, lat). So when we calculate the distance between two points, it is also in degrees. In order for this to be meaningful, we need to convert it to a regular distance metric such as meters.
This is a complicated problem in general because our distance calculation applies 2-D spatial operations to a 3-D curved space. However, as documented in the shapely documentation, since our areas of interest are small, we can use a 2-D approximation and get reasonable results.
In order to get distances from degree-based calculations, we can use the following options:
- perform the calculations in degrees and then convert them to meters. As an approximation, we can use the fact that 360 degrees represents the circumference of the earth. Therefore `dist = degree_dist * (C/360)`
- convert degrees to x,y coordinates using utm (https://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system) and then calculate the distance
- since we calculate the distance from the ground truth linestring, calculate the closest ground truth point in (lon,lat) and then use the haversine formula (https://en.wikipedia.org/wiki/Haversine_formula) to calculate the distance between the two points
Let us quickly all three calculations for three selected test cases and:
- check whether they are largely consistent
- compare with other distance calculators to see which are closer
```
test_cases = {
"commuter_rail_aboveground": {
"section": pv_ucb.map()["android"]["ucb-sdb-android-3"]["evaluation_ranges"][0]["evaluation_trip_ranges"][0]["evaluation_section_ranges"][2],
"ground_truth": sd_ucb.get_ground_truth_for_leg("mtv_to_berkeley_sf_bart", "commuter_rail_aboveground")
},
"light_rail_below_above_ground": {
"section": pv_ucb.map()["android"]["ucb-sdb-android-3"]["evaluation_ranges"][0]["evaluation_trip_ranges"][2]["evaluation_section_ranges"][7],
"ground_truth": sd_ucb.get_ground_truth_for_leg("berkeley_to_mtv_SF_express_bus", "light_rail_below_above_ground")
},
"express_bus": {
"section": pv_ucb.map()["ios"]["ucb-sdb-ios-3"]["evaluation_ranges"][1]["evaluation_trip_ranges"][2]["evaluation_section_ranges"][4],
"ground_truth": sd_ucb.get_ground_truth_for_leg("berkeley_to_mtv_SF_express_bus", "express_bus")
},
}
for t in test_cases.values():
t["gt_shapes"] = gpd.GeoSeries(eisd.SpecDetails.get_shapes_for_leg(t["ground_truth"]))
importlib.reload(emd)
dist_checks = []
pct_checks = []
for (k, t) in test_cases.items():
location_gpdf = emd.filter_geo_df(emd.to_geo_df(t["section"]["location_df"]), t["gt_shapes"].filter(["start_loc","end_loc"]))
gt_linestring = emd.filter_ground_truth_linestring(t["gt_shapes"])
dc = emd.dist_using_circumference(location_gpdf, gt_linestring)
dcrs = emd.dist_using_crs_change(location_gpdf, gt_linestring)
dmuc = emd.dist_using_manual_utm_change(location_gpdf, gt_linestring)
dmmc = emd.dist_using_manual_mercator_change(location_gpdf, gt_linestring)
dup = emd.dist_using_projection(location_gpdf, gt_linestring)
dist_compare = pd.DataFrame({"dist_circumference": dc, "dist_crs_change": dcrs,
"dist_manual_utm": dmuc, "dist_manual_mercator": dmmc,
"dist_project": dup})
dist_compare["diff_c_mu"] = (dist_compare.dist_circumference - dist_compare.dist_manual_utm).abs()
dist_compare["diff_mu_pr"] = (dist_compare.dist_manual_utm - dist_compare.dist_project).abs()
dist_compare["diff_mm_pr"] = (dist_compare.dist_manual_mercator - dist_compare.dist_project).abs()
dist_compare["diff_c_pr"] = (dist_compare.dist_circumference - dist_compare.dist_project).abs()
dist_compare["diff_c_mu_pct"] = dist_compare.diff_c_mu / dist_compare.dist_circumference
dist_compare["diff_mu_pr_pct"] = dist_compare.diff_mu_pr / dist_compare.dist_circumference
dist_compare["diff_mm_pr_pct"] = dist_compare.diff_mm_pr / dist_compare.dist_circumference
dist_compare["diff_c_pr_pct"] = dist_compare.diff_c_pr / dist_compare.dist_circumference
match_dist = lambda t: {"key": k,
"threshold": t,
"diff_c_mu": len(dist_compare.query('diff_c_mu > @t')),
"diff_mu_pr": len(dist_compare.query('diff_mu_pr > @t')),
"diff_mm_pr": len(dist_compare.query('diff_mm_pr > @t')),
"diff_c_pr": len(dist_compare.query('diff_c_pr > @t')),
"total_entries": len(dist_compare)}
dist_checks.append(match_dist(1))
dist_checks.append(match_dist(5))
dist_checks.append(match_dist(10))
dist_checks.append(match_dist(50))
match_pct = lambda t: {"key": k,
"threshold": t,
"diff_c_mu_pct": len(dist_compare.query('diff_c_mu_pct > @t')),
"diff_mu_pr_pct": len(dist_compare.query('diff_mu_pr_pct > @t')),
"diff_mm_pr_pct": len(dist_compare.query('diff_mm_pr_pct > @t')),
"diff_c_pr_pct": len(dist_compare.query('diff_c_pr_pct > @t')),
"total_entries": len(dist_compare)}
pct_checks.append(match_pct(0.01))
pct_checks.append(match_pct(0.05))
pct_checks.append(match_pct(0.10))
pct_checks.append(match_pct(0.15))
pct_checks.append(match_pct(0.20))
pct_checks.append(match_pct(0.25))
# t = "commuter_rail_aboveground"
# gt_gj = eisd.SpecDetails.get_geojson_for_leg(test_cases[t]["ground_truth"])
# print(gt_gj.features[2])
# gt_gj.features[2] = ezgj.get_geojson_for_linestring(emd.filter_ground_truth_linestring(test_cases[t]["gt_shapes"]))
# curr_map = ezgj.get_map_for_geojson(gt_gj)
# curr_map.add_child(ezgj.get_fg_for_loc_df(emd.linestring_to_geo_df(test_cases[t]["gt_shapes"].loc["route"]),
# name="gt_points", color="green"))
# curr_map
pd.DataFrame(dist_checks)
pd.DataFrame(pct_checks)
manual_check_points = pd.concat([location_gpdf, dist_compare], axis=1)[["latitude", "fmt_time", "longitude", "dist_circumference", "dist_manual_utm", "dist_manual_mercator", "dist_project"]].sample(n=3, random_state=10); manual_check_points
# curr_map = ezpv.display_map_detail_from_df(manual_check_points)
# curr_map.add_child(folium.GeoJson(eisd.SpecDetails.get_geojson_for_leg(t["ground_truth"])))
```
### Externally calculated distance for these points is:
Distance calculated manually using
1. https://www.freemaptools.com/measure-distance.htm
1. Google Maps
Note that the error of my eyes + hand is ~ 2-3 m
- 1213: within margin of error
- 1053: 3987 (freemaptools), 4km (google)
- 1107: 15799.35 (freemaptools), 15.80km (google)
```
manual_check_points
```
### Results and method choice
We find that the `manual_utm` and `project` methods are pretty consistent, and are significantly different from the `circumference` method. The `circumference` method appears to be consistently greater than the other two and the difference appears to be around 25%. The manual checks also appear to be closer to the `manual_utm` and `project` values. The `manual_utm` and `project` values are consistently within ~ 5% of each other, so we could really use either one.
**We will use the utm approach** since it is correct, is consistent with the shapely documentation (https://shapely.readthedocs.io/en/stable/manual.html#coordinate-systems) and applicable to operations beyond distance calculation
> Even though the Earth is not flat – and for that matter not exactly spherical – there are many analytic problems that can be approached by transforming Earth features to a Cartesian plane, applying tried and true algorithms, and then transforming the results back to geographic coordinates. This practice is as old as the tradition of accurate paper maps.
## Spatial error calculation
```
def get_spatial_errors(pv):
spatial_error_df = pd.DataFrame()
for phone_os, phone_map in pv.map().items():
for phone_label, phone_detail_map in phone_map.items():
for (r_idx, r) in enumerate(phone_detail_map["evaluation_ranges"]):
run_errors = []
for (tr_idx, tr) in enumerate(r["evaluation_trip_ranges"]):
trip_errors = []
for (sr_idx, sr) in enumerate(tr["evaluation_section_ranges"]):
# This is a Shapely LineString
section_gt_leg = pv.spec_details.get_ground_truth_for_leg(tr["trip_id_base"], sr["trip_id_base"])
section_gt_shapes = gpd.GeoSeries(eisd.SpecDetails.get_shapes_for_leg(section_gt_leg))
if len(section_gt_shapes) == 1:
print("No ground truth route for %s %s, must be polygon, skipping..." % (tr["trip_id_base"], sr["trip_id_base"]))
assert section_gt_leg["type"] != "TRAVEL", "For %s, %s, %s, %s, %s found type %s" % (phone_os, phone_label, r_idx, tr_idx, sr_idx, section_gt_leg["type"])
continue
if len(sr['location_df']) == 0:
print("No sensed locations found, role = %s skipping..." % (r["eval_role_base"]))
# assert r["eval_role_base"] == "power_control", "Found no locations for %s, %s, %s, %s, %s" % (phone_os, phone_label, r_idx, tr_idx, sr_idx)
continue
print("Processing travel leg %s, %s, %s, %s, %s" %
(phone_os, phone_label, r["eval_role_base"], tr["trip_id_base"], sr["trip_id_base"]))
# This is a GeoDataFrame
section_geo_df = emd.to_geo_df(sr["location_df"])
# After this point, everything is in UTM so that 2-D inside/filtering operations work
utm_section_geo_df = emd.to_utm_df(section_geo_df)
utm_section_gt_shapes = section_gt_shapes.apply(lambda s: shp.ops.transform(emd.to_utm_coords, s))
filtered_us_gpdf = emd.filter_geo_df(utm_section_geo_df, utm_section_gt_shapes.loc["start_loc":"end_loc"])
filtered_gt_linestring = emd.filter_ground_truth_linestring(utm_section_gt_shapes)
meter_dist = filtered_us_gpdf.geometry.distance(filtered_gt_linestring)
ne = len(meter_dist)
curr_spatial_error_df = gpd.GeoDataFrame({"error": meter_dist,
"ts": section_geo_df.ts,
"geometry": section_geo_df.geometry,
"phone_os": np.repeat(phone_os, ne),
"phone_label": np.repeat(phone_label, ne),
"role": np.repeat(r["eval_role_base"], ne),
"timeline": np.repeat(pv.spec_details.CURR_SPEC_ID, ne),
"run": np.repeat(r_idx, ne),
"trip_id": np.repeat(tr["trip_id_base"], ne),
"section_id": np.repeat(sr["trip_id_base"], ne)})
spatial_error_df = pd.concat([spatial_error_df, curr_spatial_error_df], axis="index")
return spatial_error_df
spatial_errors_df = pd.DataFrame()
spatial_errors_df = pd.concat([spatial_errors_df, get_spatial_errors(pv_la)], axis="index")
spatial_errors_df = pd.concat([spatial_errors_df, get_spatial_errors(pv_sj)], axis="index")
spatial_errors_df = pd.concat([spatial_errors_df, get_spatial_errors(pv_ucb)], axis="index")
spatial_errors_df.head()
r2q_map = {"power_control": 0, "HAMFDC": 1, "MAHFDC": 2, "HAHFDC": 3, "accuracy_control": 4}
q2r_map = {0: "power", 1: "HAMFDC", 2: "MAHFDC", 3: "HAHFDC", 4: "accuracy"}
spatial_errors_df["quality"] = spatial_errors_df.role.apply(lambda r: r2q_map[r])
spatial_errors_df["label"] = spatial_errors_df.role.apply(lambda r: r.replace('_control', ''))
timeline_list = ["train_bus_ebike_mtv_ucb", "car_scooter_brex_san_jose", "unimodal_trip_car_bike_mtv_la"]
spatial_errors_df.head()
```
## Overall stats
```
ifig, ax_array = plt.subplots(nrows=1,ncols=2,figsize=(8,2), sharey=True)
spatial_errors_df.query("phone_os == 'android' & quality > 0").boxplot(ax = ax_array[0], column=["error"], by=["quality"], showfliers=False)
ax_array[0].set_title('android')
spatial_errors_df.query("phone_os == 'ios' & quality > 0").boxplot(ax = ax_array[1], column=["error"], by=["quality"], showfliers=False)
ax_array[1].set_title("ios")
for i, ax in enumerate(ax_array):
# print([t.get_text() for t in ax.get_xticklabels()])
ax.set_xticklabels([q2r_map[int(t.get_text())] for t in ax.get_xticklabels()])
ax.set_xlabel("")
ax_array[0].set_ylabel("Spatial error (meters)")
# ax_array[1][0].set_ylabel("Spatial error (meters)")
ifig.suptitle("Spatial trajectory error v/s quality (excluding outliers)", y = 1.1)
# ifig.tight_layout()
ifig, ax_array = plt.subplots(nrows=1,ncols=2,figsize=(8,2), sharey=True)
spatial_errors_df.query("phone_os == 'android' & quality > 0").boxplot(ax = ax_array[0], column=["error"], by=["quality"])
ax_array[0].set_title('android')
spatial_errors_df.query("phone_os == 'ios' & quality > 0").boxplot(ax = ax_array[1], column=["error"], by=["quality"])
ax_array[1].set_title("ios")
for i, ax in enumerate(ax_array):
# print([t.get_text() for t in ax.get_xticklabels()])
ax.set_xticklabels([q2r_map[int(t.get_text())] for t in ax.get_xticklabels()])
ax.set_xlabel("")
ax_array[0].set_ylabel("Spatial error (meters)")
# ax_array[1][0].set_ylabel("Spatial error (meters)")
ifig.suptitle("Spatial trajectory error v/s quality", y = 1.1)
# ifig.tight_layout()
```
### Split out results by timeline
```
ifig, ax_array = plt.subplots(nrows=2,ncols=3,figsize=(12,6), sharex=False, sharey=False)
timeline_list = ["train_bus_ebike_mtv_ucb", "car_scooter_brex_san_jose", "unimodal_trip_car_bike_mtv_la"]
for i, tl in enumerate(timeline_list):
spatial_errors_df.query("timeline == @tl & phone_os == 'android' & quality > 0").boxplot(ax = ax_array[0][i], column=["error"], by=["quality"])
ax_array[0][i].set_title(tl)
spatial_errors_df.query("timeline == @tl & phone_os == 'ios' & quality > 0").boxplot(ax = ax_array[1][i], column=["error"], by=["quality"])
ax_array[1][i].set_title("")
for i, ax in enumerate(ax_array[0]):
ax.set_xticklabels([q2r_map[int(t.get_text())] for t in ax.get_xticklabels()])
ax.set_xlabel("")
for i, ax in enumerate(ax_array[1]):
ax.set_xticklabels([q2r_map[int(t.get_text())] for t in ax.get_xticklabels()])
ax.set_xlabel("")
ax_array[0][0].set_ylabel("Spatial error (android)")
ax_array[1][0].set_ylabel("Spatial error (iOS)")
ifig.suptitle("Spatial trajectory error v/s quality over multiple timelines")
# ifig.tight_layout()
```
### Split out results by section for the most complex timeline (train_bus_ebike_mtv_ucb)
```
ifig, ax_array = plt.subplots(nrows=2,ncols=4,figsize=(25,10), sharex=True, sharey=True)
timeline_list = ["train_bus_ebike_mtv_ucb"]
for i, tl in enumerate(timeline_list):
for q in range(1,5):
sel_df = spatial_errors_df.query("timeline == @tl & phone_os == 'android' & quality == @q")
if len(sel_df) > 0:
sel_df.boxplot(ax = ax_array[2*i][q-1], column=["error"], by=["section_id"])
ax_array[2*i][q-1].tick_params(axis="x", labelrotation=45)
sel_df = spatial_errors_df.query("timeline == @tl & phone_os == 'ios' & quality == @q")
if len(sel_df) > 0:
sel_df.boxplot(ax = ax_array[2*i+1][q-1], column=["error"], by=["section_id"])
# ax_array[i][].set_title("")
def make_acronym(s):
ssl = s.split("_")
# print("After splitting %s, we get %s" % (s, ssl))
if len(ssl) == 0 or len(ssl[0]) == 0:
return ""
else:
return "".join([ss[0] for ss in ssl])
for q in range(1,5):
ax_array[0][q-1].set_title(q2r_map[q])
curr_ticks = [t.get_text() for t in ax_array[1][q-1].get_xticklabels()]
new_ticks = [make_acronym(t) for t in curr_ticks]
ax_array[1][q-1].set_xticklabels(new_ticks)
print(list(zip(curr_ticks, new_ticks)))
# fig.text(0,0,"%s"% list(zip(curr_ticks, new_ticks)))
timeline_list = ["train_bus_ebike_mtv_ucb"]
for i, tl in enumerate(timeline_list):
unique_sections = spatial_errors_df.query("timeline == @tl").section_id.unique()
ifig, ax_array = plt.subplots(nrows=2,ncols=len(unique_sections),figsize=(40,10), sharex=True, sharey=False)
for sid, s_name in enumerate(unique_sections):
sel_df = spatial_errors_df.query("timeline == @tl & phone_os == 'android' & section_id == @s_name & quality > 0")
if len(sel_df) > 0:
sel_df.boxplot(ax = ax_array[2*i][sid], column=["error"], by=["quality"])
ax_array[2*i][sid].set_title(s_name)
sel_df = spatial_errors_df.query("timeline == @tl & phone_os == 'ios' & section_id == @s_name & quality > 0")
if len(sel_df) > 0:
sel_df.boxplot(ax = ax_array[2*i+1][sid], column=["error"], by=["quality"])
ax_array[2*i+1][sid].set_title("")
# ax_array[i][].set_title("")
```
### Focus only on sections where the max error is > 1000 meters
```
timeline_list = ["train_bus_ebike_mtv_ucb"]
for i, tl in enumerate(timeline_list):
unique_sections = pd.Series(spatial_errors_df.query("timeline == @tl").section_id.unique())
sections_with_outliers_mask = unique_sections.apply(lambda s_name: spatial_errors_df.query("timeline == 'train_bus_ebike_mtv_ucb' & section_id == @s_name").error.max() > 1000)
sections_with_outliers = unique_sections[sections_with_outliers_mask]
ifig, ax_array = plt.subplots(nrows=2,ncols=len(sections_with_outliers),figsize=(17,4), sharex=True, sharey=False)
for sid, s_name in enumerate(sections_with_outliers):
sel_df = spatial_errors_df.query("timeline == @tl & phone_os == 'android' & section_id == @s_name & quality > 0")
if len(sel_df) > 0:
sel_df.boxplot(ax = ax_array[2*i][sid], column=["error"], by=["quality"])
ax_array[2*i][sid].set_title(s_name)
ax_array[2*i][sid].set_xlabel("")
sel_df = spatial_errors_df.query("timeline == @tl & phone_os == 'ios' & section_id == @s_name & quality > 0")
if len(sel_df) > 0:
sel_df.boxplot(ax = ax_array[2*i+1][sid], column=["error"], by=["quality"])
ax_array[2*i+1][sid].set_title("")
print([t.get_text() for t in ax_array[2*i+1][sid].get_xticklabels()])
ax_array[2*i+1][sid].set_xticklabels([q2r_map[int(t.get_text())] for t in ax_array[2*i+1][sid].get_xticklabels() if len(t.get_text()) > 0])
ax_array[2*i+1][sid].set_xlabel("")
ifig.suptitle("")
```
### Validation of outliers
#### (express bus iOS, MAHFDC)
ok, so it looks like the error is non-trivial across all runs, but run #1 is the worst and is responsible for the majority of the outliers. And this is borne out by the map, where on run #1, we end up with points in San Leandro!!
```
spatial_errors_df.query("phone_os == 'ios' & quality == 2 & section_id == 'express_bus' & error > 500").run.unique()
spatial_errors_df.query("phone_os == 'ios' & quality == 2 & section_id == 'express_bus'").boxplot(column="error", by="run")
gt_leg = sd_ucb.get_ground_truth_for_leg("berkeley_to_mtv_SF_express_bus", "express_bus"); print(gt_leg["id"])
curr_map = ezgj.get_map_for_geojson(sd_ucb.get_geojson_for_leg(gt_leg), name="ground_truth")
ezgj.get_fg_for_loc_df(emd.linestring_to_geo_df(eisd.SpecDetails.get_shapes_for_leg(gt_leg)["route"]),
name="gt_points", color="green").add_to(curr_map)
name_err_time = lambda lr: "%d: %d, %s, %s" % (lr["index"], lr["df_idx"], lr["error"], sd_ucb.fmt(lr["ts"], "MM-DD HH:mm:ss"))
error_df = emd.to_loc_df(spatial_errors_df.query("phone_os == 'ios' & quality == 2 & section_id == 'express_bus' & run == 1"))
gt_16k = lambda lr: lr["error"] == error_df.error.max()
folium.GeoJson(ezgj.get_geojson_for_loc_df(error_df, color="red"), name="sensed_values").add_to(curr_map)
ezgj.get_fg_for_loc_df(error_df, name="sensed_points", color="red", popupfn=name_err_time, stickyfn=gt_16k).add_to(curr_map)
folium.LayerControl().add_to(curr_map)
curr_map
importlib.reload(ezgj)
gt_leg = sd_ucb.get_ground_truth_for_leg("berkeley_to_mtv_SF_express_bus", "express_bus"); print(gt_leg["id"])
curr_map = ezgj.get_map_for_geojson(sd_ucb.get_geojson_for_leg(gt_leg), name="ground_truth")
ezgj.get_fg_for_loc_df(emd.linestring_to_geo_df(eisd.SpecDetails.get_shapes_for_leg(gt_leg)["route"]),
name="gt_points", color="green").add_to(curr_map)
name_err_time = lambda lr: "%d: %d, %s, %s" % (lr["index"], lr["df_idx"], lr["error"], sd_ucb.fmt(lr["ts"], "MM-DD HH:mm:ss"))
colors = ["red", "yellow", "blue"]
for run in range(3):
error_df = emd.to_loc_df(spatial_errors_df.query("phone_os == 'ios' & quality == 2 & section_id == 'express_bus' & run == @run"))
gt_16k = lambda lr: lr["error"] == error_df.error.max()
print("max error for run %d is %s" % (run, error_df.error.max()))
folium.GeoJson(ezgj.get_geojson_for_loc_df(error_df, color=colors[run]), name="sensed_values").add_to(curr_map)
ezgj.get_fg_for_loc_df(error_df, name="sensed_points", color=colors[run], popupfn=name_err_time, stickyfn=gt_16k).add_to(curr_map)
folium.LayerControl().add_to(curr_map)
curr_map
```
#### (commuter rail aboveground android, HAMFDC)
Run 0: Multiple outliers at the start in San Jose. After that, everything is fine.
```
spatial_errors_df.query("phone_os == 'android' & quality == 1 & section_id == 'commuter_rail_aboveground' & error > 500").run.unique()
spatial_errors_df.query("phone_os == 'android' & quality == 1 & section_id == 'commuter_rail_aboveground' & error > 500").boxplot(column="error", by="run")
gt_leg = sd_ucb.get_ground_truth_for_leg("mtv_to_berkeley_sf_bart", "commuter_rail_aboveground"); print(gt_leg["id"])
curr_map = ezgj.get_map_for_geojson(sd_ucb.get_geojson_for_leg(gt_leg), name="ground_truth")
ezgj.get_fg_for_loc_df(emd.linestring_to_geo_df(eisd.SpecDetails.get_shapes_for_leg(gt_leg)["route"]),
name="gt_points", color="green").add_to(curr_map)
name_err_time = lambda lr: "%d: %d, %s, %s" % (lr["index"], lr["df_idx"], lr["error"], sd_ucb.fmt(lr["ts"], "MM-DD HH:mm:ss"))
error_df = emd.to_loc_df(spatial_errors_df.query("phone_os == 'android' & quality == 1 & section_id == 'commuter_rail_aboveground' & run == 0"))
maxes = [error_df.error.max(), error_df[error_df.error < 10000].error.max(), error_df[error_df.error < 1000].error.max()]
gt_16k = lambda lr: lr["error"] in maxes
folium.GeoJson(ezgj.get_geojson_for_loc_df(error_df, color="red"), name="sensed_values").add_to(curr_map)
ezgj.get_fg_for_loc_df(error_df, name="sensed_points", color="red", popupfn=name_err_time, stickyfn=gt_16k).add_to(curr_map)
folium.LayerControl().add_to(curr_map)
curr_map
spatial_errors_df.query("phone_os == 'android' & quality == 1 & section_id == 'commuter_rail_aboveground' & error > 10000")
```
#### (walk_to_bus android, HAMFDC, HAHFDC)
Huge zig zag when we get out of the BART station
```
spatial_errors_df.query("phone_os == 'android' & (quality == 1 | quality == 3) & section_id == 'walk_to_bus' & error > 500").run.unique()
spatial_errors_df.query("phone_os == 'android' & (quality == 1 | quality == 3) & section_id == 'walk_to_bus' & error > 500")
spatial_errors_df.query("phone_os == 'android' & (quality == 1 | quality == 3) & section_id == 'walk_to_bus'").boxplot(column="error", by="run")
spatial_errors_df.query("phone_os == 'android' & (quality == 1 | quality == 3) & section_id == 'walk_to_bus'").error.max()
error_df
ucb_and_back = pv_ucb.map()["android"]["ucb-sdb-android-2"]["evaluation_ranges"][0]; ucb_and_back["trip_id"]
to_trip = ucb_and_back["evaluation_trip_ranges"][0]; print(to_trip["trip_id"])
wb_leg = to_trip["evaluation_section_ranges"][6]; print(wb_leg["trip_id"])
gt_leg = sd_ucb.get_ground_truth_for_leg(to_trip["trip_id_base"], wb_leg["trip_id_base"]); gt_leg["id"]
importlib.reload(ezgj)
gt_leg = sd_ucb.get_ground_truth_for_leg("mtv_to_berkeley_sf_bart", "walk_to_bus"); print(gt_leg["id"])
curr_map = ezgj.get_map_for_geojson(sd_ucb.get_geojson_for_leg(gt_leg), name="ground_truth")
ezgj.get_fg_for_loc_df(emd.linestring_to_geo_df(eisd.SpecDetails.get_shapes_for_leg(gt_leg)["route"]),
name="gt_points", color="green").add_to(curr_map)
name_err_time = lambda lr: "%d: %d, %s, %s" % (lr["index"], lr["df_idx"], lr["error"], sd_ucb.fmt(lr["ts"], "MM-DD HH:mm:ss"))
error_df = emd.to_loc_df(spatial_errors_df.query("phone_os == 'android' & quality == 3 & section_id == 'walk_to_bus'").sort_index(axis="index"))
maxes = [error_df.error.max(), error_df[error_df.error < 16000].error.max(), error_df[error_df.error < 5000].error.max()]
gt_16k = lambda lr: lr["error"] in maxes
print("Checking errors %s" % maxes)
folium.GeoJson(ezgj.get_geojson_for_loc_df(error_df, color="red"), name="sensed_values").add_to(curr_map)
ezgj.get_fg_for_loc_df(error_df, name="sensed_points", color="red", popupfn=name_err_time, stickyfn=gt_16k).add_to(curr_map)
folium.LayerControl().add_to(curr_map)
curr_map
```
#### (light_rail_below_above_ground, android, accuracy_control)
ok, so it looks like the error is non-trivial across all runs, but run #1 is the worst and is responsible for the majority of the outliers. And this is borne out by the map, where on run #1, we end up with points in San Leandro!!
```
spatial_errors_df.query("phone_os == 'android' & quality == 4 & section_id == 'light_rail_below_above_ground' & error > 100").run.unique()
spatial_errors_df.query("phone_os == 'android' & (quality == 4) & section_id == 'light_rail_below_above_ground'").boxplot(column="error", by="run")
ucb_and_back = pv_ucb.map()["android"]["ucb-sdb-android-2"]["evaluation_ranges"][0]; ucb_and_back["trip_id"]
back_trip = ucb_and_back["evaluation_trip_ranges"][2]; print(back_trip["trip_id"])
lt_leg = back_trip["evaluation_section_ranges"][7]; print(lt_leg["trip_id"])
gt_leg = sd_ucb.get_ground_truth_for_leg(back_trip["trip_id_base"], lt_leg["trip_id_base"]); gt_leg["id"]
import folium
gt_leg = sd_ucb.get_ground_truth_for_leg("berkeley_to_mtv_SF_express_bus", "light_rail_below_above_ground"); print(gt_leg["id"])
curr_map = ezgj.get_map_for_geojson(sd_ucb.get_geojson_for_leg(gt_leg), name="ground_truth")
ezgj.get_fg_for_loc_df(emd.linestring_to_geo_df(eisd.SpecDetails.get_shapes_for_leg(gt_leg)["route"]),
name="gt_points", color="green").add_to(curr_map)
name_err_time = lambda lr: "%d: %d, %s, %s" % (lr["index"], lr["df_idx"], lr["error"], sd_ucb.fmt(lr["ts"], "MM-DD HH:mm:ss"))
colors = ["red", "yellow", "blue"]
for run in range(3):
error_df = emd.to_loc_df(spatial_errors_df.query("phone_os == 'android' & quality == 4 & section_id == 'light_rail_below_above_ground' & run == @run"))
gt_16k = lambda lr: lr["error"] == error_df.error.max()
print("max error for run %d is %s" % (run, error_df.error.max()))
folium.GeoJson(ezgj.get_geojson_for_loc_df(error_df, color=colors[run]), name="sensed_values").add_to(curr_map)
ezgj.get_fg_for_loc_df(error_df, name="sensed_points", color=colors[run], popupfn=name_err_time, stickyfn=gt_16k).add_to(curr_map)
folium.LayerControl().add_to(curr_map)
curr_map
```
#### (subway, android, HAMFDC)
This is the poster child for temporal accuracy tracking
```
bart_leg = pv_ucb.map()["android"]["ucb-sdb-android-3"]["evaluation_ranges"][0]["evaluation_trip_ranges"][0]["evaluation_section_ranges"][5]
gt_leg = sd_ucb.get_ground_truth_for_leg("mtv_to_berkeley_sf_bart", "subway_underground"); gt_leg["id"]
gt_leg = sd_ucb.get_ground_truth_for_leg("mtv_to_berkeley_sf_bart", "subway_underground"); print(gt_leg["id"])
curr_map = ezgj.get_map_for_geojson(sd_ucb.get_geojson_for_leg(gt_leg), name="ground_truth")
ezgj.get_fg_for_loc_df(emd.linestring_to_geo_df(eisd.SpecDetails.get_shapes_for_leg(gt_leg)["route"]),
name="gt_points", color="green").add_to(curr_map)
name_err_time = lambda lr: "%d: %d, %s, %s" % (lr["index"], lr["df_idx"], lr["error"], sd_ucb.fmt(lr["ts"], "MM-DD HH:mm:ss"))
error_df = emd.to_loc_df(spatial_errors_df.query("phone_os == 'android' & quality == 1 & section_id == 'subway_underground' & run == 0").sort_index(axis="index"))
maxes = [error_df.error.max(), error_df[error_df.error < 16000].error.max(), error_df[error_df.error < 5000].error.max()]
gt_16k = lambda lr: lr["error"] in maxes
print("Checking errors %s" % maxes)
folium.GeoJson(ezgj.get_geojson_for_loc_df(error_df, color="red"), name="sensed_values").add_to(curr_map)
ezgj.get_fg_for_loc_df(error_df, name="sensed_points", color="red", popupfn=name_err_time, stickyfn=gt_16k).add_to(curr_map)
folium.LayerControl().add_to(curr_map)
curr_map
gt_leg = sd_ucb.get_ground_truth_for_leg("mtv_to_berkeley_sf_bart", "subway_underground"); gt_leg["id"]
eisd.SpecDetails.get_shapes_for_leg(gt_leg)["route"].is_simple
pd.concat([
error_df.iloc[40:50],
error_df.iloc[55:60],
error_df.iloc[65:75],
error_df.iloc[70:75]])
import pyproj
latlonProj = pyproj.Proj(init="epsg:4326")
xyProj = pyproj.Proj(init="epsg:3395")
xy = pyproj.transform(latlonProj, xyProj, -122.08355963230133, 37.39091642895306); xy
pyproj.transform(xyProj, latlonProj, xy[0], xy[1])
import pandas as pd
df = pd.DataFrame({"a": [1,2,3], "b": [4,5,6]}); df
pd.concat([pd.DataFrame([{"a": 10, "b": 14}]), df, pd.DataFrame([{"a": 20, "b": 24}])], axis='index').reset_index(drop=True)
```
| true |
code
| 0.214856 | null | null | null | null |
|
# Examples for Bounded Innovation Propagation (BIP) MM ARMA parameter estimation
```
import numpy as np
import scipy.signal as sps
import robustsp as rsp
import matplotlib.pyplot as plt
import matplotlib
# Fix random number generator for reproducibility
np.random.seed(1)
```
## Example 1: AR(1) with 30 percent isolated outliers
```
# Generate AR(1) observations
N = 300
a = np.random.randn(N)
x = sps.lfilter([1],[1,-.8],a)
p = 1
q = 0
```
### Generate isolated Outliers
```
cont_prob = 0.3 # outlier contamination probability
outlier_ind = np.where(np.sign(np.random.rand(N)-cont_prob)<0)# outlier index
outlier = 100*np.random.randn(N) # contaminating process
v = np.zeros(N) # additive outlier signal
v[outlier_ind] = outlier[outlier_ind]
v[0] = 0 # first sample should not be an outlier
x_ao = x+v # 30% of isolated additive outliers
```
### BIP MM Estimation
```
result = rsp.arma_est_bip_mm(x_ao,p,q)
print('Example: AR(1) with ar_coeff = -0.8')
print('30% of isolated additive outliers')
print('estimaed coefficients: %.3f' % result['ar_coeffs'])
%matplotlib inline
matplotlib.rcParams['figure.figsize'] = [10, 10]
plt.subplot(2,1,1)
plt.plot(x_ao,'-',lw=2,label='outlier contaminated AR(1)')
plt.plot(result['cleaned_signal'],'-.',c='y',label='cleaned')
plt.xlabel('samples')
plt.ylabel('Amplitude')
plt.title('BIP-AR(1) cleaned signal')
plt.legend()
plt.subplot(2,1,2)
plt.plot(x,lw=2,label='original AR(1)')
plt.plot(result['cleaned_signal'],'-.',label='cleaned')
plt.xlabel('samples')
plt.ylabel('Amplitude')
plt.title('BIP-AR(1) cleaned signal')
plt.legend()
plt.show()
```
# Example 2: ARMA(1,1) with 10% patchy outliers
## Generate ARMA(1,1) observations
```
N = 1000
a = np.random.randn(N)
x = sps.lfilter([1, 0.2],[1, -.8],a)
p = 1
q = 1
```
## Generate a patch of outliers of length 101 samples
```
v = 1000*np.random.randn(101)
```
## 10% of patch additive outliers
```
x_ao = np.array(x)
x_ao[99:200] += v
```
### BIP-MM estimation
```
result = rsp.arma_est_bip_mm(x_ao,p,q)
print('''Example 2: ARMA(1,1) with ar_coeff = -0.8, ma_coeff 0.2' \n
10 percent patchy additive outliers \n
estimated coefficients: \n
ar_coeff_est = %.3f \n
ma_coeff_est = %.3f''' %(result['ar_coeffs'],result['ma_coeffs']))
plt.subplot(2,1,1)
plt.plot(x_ao,'-',lw=2,label='outlier contaminated AR(1)')
plt.plot(result['cleaned_signal'],label='cleaned')
plt.xlabel('samples')
plt.ylabel('Amplitude')
plt.title('BIP-ARMA(1,1) cleaned signal')
plt.legend()
plt.subplot(2,1,2)
plt.plot(x,lw=2,label='original ARMA(1,1)')
plt.plot(result['cleaned_signal'],label='cleaned')
plt.xlabel('samples')
plt.ylabel('Amplitude')
plt.title('BIP-ARMA(1,1) cleaned signal')
plt.legend()
plt.show()
```
# Example 3: MA(2) with 20 % isolated Outliers
## Generate MA(2) observations
```
N = 500
a = np.random.randn(N)
x = sps.lfilter([1,-.7,.5],[1],a)
p=0
q=2
```
## Generate isolated Outliers
```
cont_prob = 0.2
outlier_ind = np.where(np.sign(np.random.rand(N)-(cont_prob))<0)
outlier = 100*np.random.randn(N)
v = np.zeros(N)
v[outlier_ind] = outlier[outlier_ind]
v[:2] = 0
```
## 20 % of isolated additive Outliers
```
x_ao = x+v
```
## BIP MM estimation
```
result = rsp.arma_est_bip_mm(x_ao,p,q)
print('''Example 3: MA(2) ma_coeff [-0.7 0.5]' \n
20 % of isolated additive Outliers \n
estimated coefficients: \n
ma_coeff_est = ''',result['ma_coeffs'])
plt.subplot(2,1,1)
plt.plot(x_ao,'-',lw=2,label='outlier contaminated AR(1)')
plt.plot(result['cleaned_signal'],label='cleaned')
plt.xlabel('samples')
plt.ylabel('Amplitude')
plt.title('BIP-MA(2) cleaned signal')
plt.legend()
plt.subplot(2,1,2)
plt.plot(x,lw=2,label='original MA(2)')
plt.plot(result['cleaned_signal'],label='cleaned')
plt.xlabel('samples')
plt.ylabel('Amplitude')
plt.title('BIP-MA(2) cleaned signal')
plt.legend()
plt.show()
```
| true |
code
| 0.710691 | null | null | null | null |
|
# OneHotEncoder
Performs One Hot Encoding.
The encoder can select how many different labels per variable to encode into binaries. When top_categories is set to None, all the categories will be transformed in binary variables.
However, when top_categories is set to an integer, for example 10, then only the 10 most popular categories will be transformed into binary, and the rest will be discarded.
The encoder has also the possibility to create binary variables from all categories (drop_last = False), or remove the binary for the last category (drop_last = True), for use in linear models.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from feature_engine.encoding import OneHotEncoder
# Load titanic dataset from OpenML
def load_titanic():
data = pd.read_csv('https://www.openml.org/data/get_csv/16826755/phpMYEkMl')
data = data.replace('?', np.nan)
data['cabin'] = data['cabin'].astype(str).str[0]
data['pclass'] = data['pclass'].astype('O')
data['age'] = data['age'].astype('float')
data['fare'] = data['fare'].astype('float')
data['embarked'].fillna('C', inplace=True)
data.drop(labels=['boat', 'body', 'home.dest'], axis=1, inplace=True)
return data
data = load_titanic()
data.head()
X = data.drop(['survived', 'name', 'ticket'], axis=1)
y = data.survived
# we will encode the below variables, they have no missing values
X[['cabin', 'pclass', 'embarked']].isnull().sum()
''' Make sure that the variables are type (object).
if not, cast it as object , otherwise the transformer will either send an error (if we pass it as argument)
or not pick it up (if we leave variables=None). '''
X[['cabin', 'pclass', 'embarked']].dtypes
# let's separate into training and testing set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
X_train.shape, X_test.shape
```
One hot encoding consists in replacing the categorical variable by a
combination of binary variables which take value 0 or 1, to indicate if
a certain category is present in an observation.
Each one of the binary variables are also known as dummy variables. For
example, from the categorical variable "Gender" with categories 'female'
and 'male', we can generate the boolean variable "female", which takes 1
if the person is female or 0 otherwise. We can also generate the variable
male, which takes 1 if the person is "male" and 0 otherwise.
The encoder has the option to generate one dummy variable per category, or
to create dummy variables only for the top n most popular categories, that is,
the categories that are shown by the majority of the observations.
If dummy variables are created for all the categories of a variable, you have
the option to drop one category not to create information redundancy. That is,
encoding into k-1 variables, where k is the number if unique categories.
The encoder will encode only categorical variables (type 'object'). A list
of variables can be passed as an argument. If no variables are passed as
argument, the encoder will find and encode categorical variables (object type).
#### Note:
New categories in the data to transform, that is, those that did not appear
in the training set, will be ignored (no binary variable will be created for them).
### All binary, no top_categories
```
'''
Parameters
----------
top_categories: int, default=None
If None, a dummy variable will be created for each category of the variable.
Alternatively, top_categories indicates the number of most frequent categories
to encode. Dummy variables will be created only for those popular categories
and the rest will be ignored. Note that this is equivalent to grouping all the
remaining categories in one group.
variables : list
The list of categorical variables that will be encoded. If None, the
encoder will find and select all object type variables.
drop_last: boolean, default=False
Only used if top_categories = None. It indicates whether to create dummy
variables for all the categories (k dummies), or if set to True, it will
ignore the last variable of the list (k-1 dummies).
'''
ohe_enc = OneHotEncoder(top_categories=None,
variables=['pclass', 'cabin', 'embarked'],
drop_last=False)
ohe_enc.fit(X_train)
ohe_enc.encoder_dict_
train_t = ohe_enc.transform(X_train)
test_t = ohe_enc.transform(X_train)
test_t.head()
```
### Selecting top_categories to encode
```
ohe_enc = OneHotEncoder(top_categories=2,
variables=['pclass', 'cabin', 'embarked'],
drop_last=False)
ohe_enc.fit(X_train)
ohe_enc.encoder_dict_
train_t = ohe_enc.transform(X_train)
test_t = ohe_enc.transform(X_train)
test_t.head()
```
### Dropping the last category for linear models
```
ohe_enc = OneHotEncoder(top_categories=None,
variables=['pclass', 'cabin', 'embarked'],
drop_last=True)
ohe_enc.fit(X_train)
ohe_enc.encoder_dict_
train_t = ohe_enc.transform(X_train)
test_t = ohe_enc.transform(X_train)
test_t.head()
```
### Automatically select categorical variables
This encoder selects all the categorical variables, if None is passed to the variable argument when calling the encoder.
```
ohe_enc = OneHotEncoder(top_categories=None,
drop_last=True)
ohe_enc.fit(X_train)
train_t = ohe_enc.transform(X_train)
test_t = ohe_enc.transform(X_train)
test_t.head()
```
| true |
code
| 0.444324 | null | null | null | null |
|
# Cat Dog Classification
## 1. 下载数据
我们将使用包含猫与狗图片的数据集。它是Kaggle.com在2013年底计算机视觉竞赛提供的数据集的一部分,当时卷积神经网络还不是主流。可以在以下位置下载原始数据集: `https://www.kaggle.com/c/dogs-vs-cats/data`。
图片是中等分辨率的彩色JPEG。看起来像这样:

不出所料,2013年的猫狗大战的Kaggle比赛是由使用卷积神经网络的参赛者赢得的。最佳成绩达到了高达95%的准确率。在本例中,我们将非常接近这个准确率,即使我们将使用不到10%的训练集数据来训练我们的模型。
原始数据集的训练集包含25,000张狗和猫的图像(每个类别12,500张),543MB大(压缩)。
在下载并解压缩之后,我们将创建一个包含三个子集的新数据集:
* 每个类有1000个样本的训练集,
* 每个类500个样本的验证集,
* 最后是每个类500个样本的测试集。
数据已经提前处理好。
### 1.1 加载数据集目录
```
import os, shutil
# The directory where we will
# store our smaller dataset
base_dir = './data/cats_and_dogs_small'
# Directories for our training,
# validation and test splits
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'validation')
test_dir = os.path.join(base_dir, 'test')
# Directory with our training cat pictures
train_cats_dir = os.path.join(train_dir, 'cats')
# Directory with our training dog pictures
train_dogs_dir = os.path.join(train_dir, 'dogs')
# Directory with our validation cat pictures
validation_cats_dir = os.path.join(validation_dir, 'cats')
# Directory with our validation dog pictures
validation_dogs_dir = os.path.join(validation_dir, 'dogs')
# Directory with our validation cat pictures
test_cats_dir = os.path.join(test_dir, 'cats')
# Directory with our validation dog pictures
test_dogs_dir = os.path.join(test_dir, 'dogs')
```
## 2. 模型一
### 2.1 数据处理
```
from keras.preprocessing.image import ImageDataGenerator
# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(rescale=1./255)
validation_datagen = ImageDataGenerator(rescale=1./255)
test_datagen = ImageDataGenerator(rescale=1./255)
# 150*150
train_generator = train_datagen.flow_from_directory(
# This is the target directory
train_dir,
# All images will be resized to 150x150
target_size=(150, 150),
batch_size=20,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
validation_generator = validation_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
test_generator = test_datagen.flow_from_directory(
test_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
print('train_dir: ',train_dir)
print('validation_dir: ',validation_dir)
print('test_dir: ',test_dir)
for data_batch, labels_batch in train_generator:
print('data batch shape:', data_batch.shape)
print('labels batch shape:', labels_batch.shape)
break
labels_batch
```
### 2.2 构建模型
```
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=1e-4),
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit_generator(train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50)
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
plt.show()
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
plt.show()
val_loss_min = history.history['val_loss'].index(min(history.history['val_loss']))
val_acc_max = history.history['val_acc'].index(max(history.history['val_acc']))
print('validation set min loss: ', val_loss_min)
print('validation set max accuracy: ', val_acc_max)
from keras import layers
from keras import models
# vgg的做法
model = models.Sequential()
model.add(layers.Conv2D(32, 3, activation='relu', padding="same", input_shape=(64, 64, 3)))
model.add(layers.Conv2D(32, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(64, 3, activation='relu', padding="same"))
model.add(layers.Conv2D(64, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(128, 3, activation='relu', padding="same"))
model.add(layers.Conv2D(128, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(256, 3, activation='relu', padding="same"))
model.add(layers.Conv2D(256, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=2))
model.add(layers.Flatten())
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))
model.summary()
from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=1e-4),
loss='binary_crossentropy',
metrics=['acc'])
# model.compile(loss='binary_crossentropy',
# optimizer='adam',
# metrics=['accuracy'])
```
### 2.3 训练模型
```
history = model.fit_generator(train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50)
```
### 2.4 画出表现
```
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
val_loss_min = val_loss.index(min(val_loss))
val_acc_max = val_acc.index(max(val_acc))
print('validation set min loss: ', val_loss_min)
print('validation set max accuracy: ', val_acc_max)
```
### 2.5 测试集表现
```
scores = model.evaluate_generator(test_generator, verbose=0)
print("Large CNN Error: %.2f%%" % (100 - scores[1] * 100))
```
## 3. 模型二 使用数据增强来防止过拟合
### 3.1 数据增强示例
```
datagen = ImageDataGenerator(
rotation_range=40, # 角度值(在 0~180 范围内),表示图像随机旋转的角度范围
width_shift_range=0.2, # 图像在水平或垂直方向上平移的范围
height_shift_range=0.2, # (相对于总宽度或总高度的比例)
shear_range=0.2, # 随机错切变换的角度
zoom_range=0.2, # 图像随机缩放的范围
horizontal_flip=True, # 随机将一半图像水平翻转
fill_mode='nearest') # 用于填充新创建像素的方法,
# 这些新像素可能来自于旋转或宽度/高度平移
# This is module with image preprocessing utilities
from keras.preprocessing import image
fnames = [os.path.join(train_cats_dir, fname) for fname in os.listdir(train_cats_dir)]
# We pick one image to "augment"
img_path = fnames[3]
# Read the image and resize it
img = image.load_img(img_path, target_size=(150, 150))
imgplot_oringe = plt.imshow(img)
# Convert it to a Numpy array with shape (150, 150, 3)
x = image.img_to_array(img)
# Reshape it to (1, 150, 150, 3)
x = x.reshape((1,) + x.shape)
# The .flow() command below generates batches of randomly transformed images.
# It will loop indefinitely, so we need to `break` the loop at some point!
i = 0
for batch in datagen.flow(x, batch_size=1):
plt.figure(i)
imgplot = plt.imshow(image.array_to_img(batch[0]))
i += 1
if i % 4 == 0:
break
plt.show()
```
### 3.2 定义数据增强
```
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,)
# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1./255) # 注意,不能增强验证数据
train_generator = train_datagen.flow_from_directory(
# This is the target directory
train_dir,
# All images will be resized to 150x150
target_size=(150, 150),
batch_size=32,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=32,
class_mode='binary')
```
### 3.3 训练网络
```
model = models.Sequential()
model.add(layers.Conv2D(32, 3, activation='relu', padding="same", input_shape=(150, 150, 3)))
model.add(layers.Conv2D(32, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(64, 3, activation='relu', padding="same"))
model.add(layers.Conv2D(64, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(128, 3, activation='relu', padding="same"))
model.add(layers.Conv2D(128, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(256, 3, activation='relu', padding="same"))
model.add(layers.Conv2D(256, 3, activation='relu', padding="same"))
model.add(layers.MaxPooling2D(pool_size=2))
model.add(layers.Flatten())
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))
# model.compile(optimizer=optimizers.RMSprop(lr=1e-4),
# loss='binary_crossentropy',
# metrics=['acc'])
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
history = model.fit_generator(train_generator,
steps_per_epoch=100, # 训练集分成100批送进去,相当于每批送20个
epochs=100, # 循环100遍
validation_data=validation_generator,
validation_steps=50, # 验证集分50批送进去,每批20个
verbose=0)
```
### 3.4 画出表现
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
val_loss_min = val_loss.index(min(val_loss))
val_acc_max = val_acc.index(max(val_acc))
print('validation set min loss: ', val_loss_min)
print('validation set max accuracy: ', val_acc_max)
# train_datagen = ImageDataGenerator(rotation_range=40,
# width_shift_range=0.2,
# height_shift_range=0.2,
# shear_range=0.2,
# zoom_range=0.2,
# horizontal_flip=True,
# fill_mode='nearest')
# train_datagen.fit(train_X)
# train_generator = train_datagen.flow(train_X, train_y,
# batch_size = 64)
# history = model_vgg16.fit_generator(train_generator,
# validation_data = (test_X, test_y),
# steps_per_epoch = train_X.shape[0] / 100,
# epochs = 10)
```
## 4. 使用预训练的VGG-16
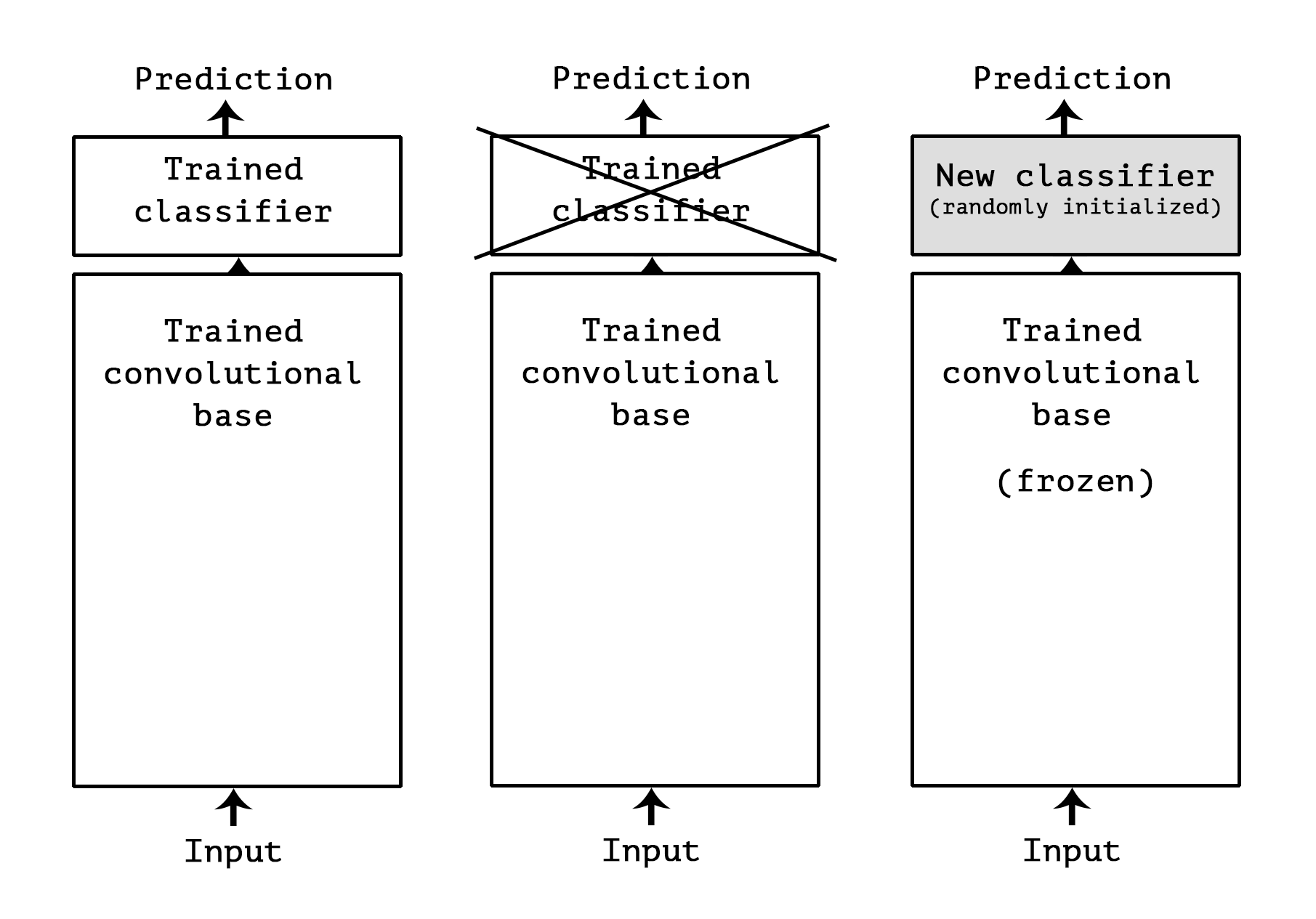
```
from keras.applications import VGG16
conv_base = VGG16(weights='imagenet',
include_top=False, # 不要分类层
input_shape=(150, 150, 3))
conv_base.summary()
from keras import models
from keras import layers
model = models.Sequential()
model.add(conv_base)
model.add(layers.Flatten())
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
# model = models.Sequential()
# model.add(conv_base)
# model.add(layers.Dense(256, activation='relu'))
# model.add(layers.Dropout(0.5))
# model.add(layers.Dense(256, activation='relu'))
# model.add(layers.Dropout(0.5))
# model.add(layers.Dense(1, activation='sigmoid'))
print('This is the number of trainable weights '
'before freezing the conv base:', len(model.trainable_weights))
conv_base.trainable = False
print('This is the number of trainable weights '
'after freezing the conv base:', len(model.trainable_weights))
from keras.preprocessing.image import ImageDataGenerator
from keras import optimizers
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
# This is the target directory
train_dir,
# All images will be resized to 150x150
target_size=(150, 150),
batch_size=20,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=2e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50,
verbose=2)
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
val_loss_min = val_loss.index(min(val_loss))
val_acc_max = val_acc.index(max(val_acc))
print('validation set min loss: ', val_loss_min)
print('validation set max accuracy: ', val_acc_max)
```
## Fine-tuning
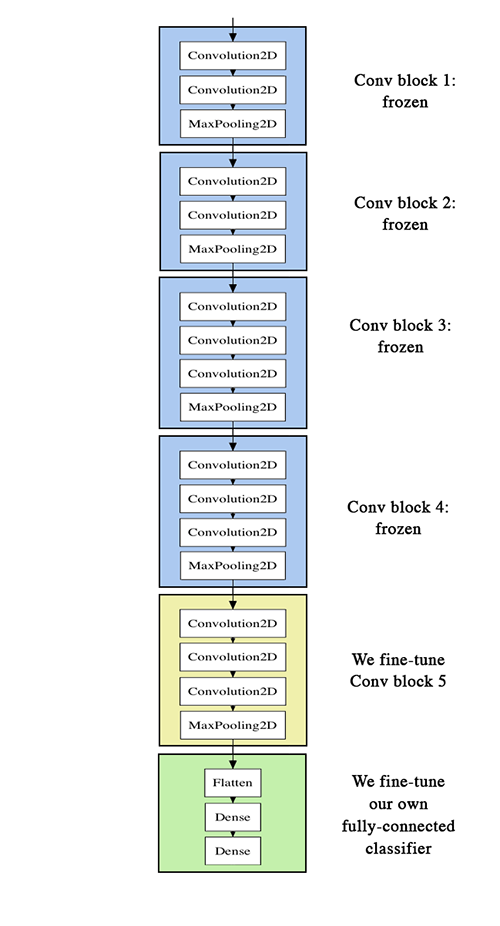
```
conv_base.summary()
conv_base.trainable = True
set_trainable = False
for layer in conv_base.layers:
if layer.name == 'block5_conv1':
set_trainable = True
if set_trainable:
layer.trainable = True
else:
layer.trainable = False
model.summary()
model.compile(optimizer=optimizers.RMSprop(lr=1e-5),
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit_generator(train_generator,
steps_per_epoch=100,
epochs=100,
validation_data=validation_generator,
validation_steps=50,
verbose=0)
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
def smooth_curve(points, factor=0.8):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
plt.plot(epochs,
smooth_curve(acc), 'bo', label='Smoothed training acc')
plt.plot(epochs,
smooth_curve(val_acc), 'b', label='Smoothed validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs,
smooth_curve(loss), 'bo', label='Smoothed training loss')
plt.plot(epochs,
smooth_curve(val_loss), 'b', label='Smoothed validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
smooth_val_loss = smooth_curve(val_loss)
smooth_val_loss.index(min(smooth_val_loss))
test_generator = test_datagen.flow_from_directory(test_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
test_loss, test_acc = model.evaluate_generator(test_generator, steps=50)
print('test acc:', test_acc)
# plt.plot(history.history['loss'])
# plt.plot(history.history['val_loss'])
# plt.title('model loss')
# plt.ylabel('loss')
# plt.xlabel('epoch')
# plt.legend(['train', 'test'], loc='upper right')
# plt.show()
# plt.plot(history.history['acc'])
# plt.plot(history.history['val_acc'])
# plt.title('model accuracy')
# plt.ylabel('accuracy')
# plt.xlabel('epoch')
# plt.legend(['train', 'test'], loc='upper right')
# plt.show()
```
| true |
code
| 0.709975 | null | null | null | null |
|
# Widget Events
In this lecture we will discuss widget events, such as button clicks!
## Special events
The `Button` is not used to represent a data type. Instead the button widget is used to handle mouse clicks. The `on_click` method of the `Button` can be used to register a function to be called when the button is clicked. The docstring of the `on_click` can be seen below.
```
import ipywidgets as widgets
print(widgets.Button.on_click.__doc__)
```
### Example #1 - on_click
Since button clicks are stateless, they are transmitted from the front-end to the back-end using custom messages. By using the `on_click` method, a button that prints a message when it has been clicked is shown below.
```
from IPython.display import display
button = widgets.Button(description="Click Me!")
display(button)
def on_button_clicked(b):
print("Button clicked.")
button.on_click(on_button_clicked)
```
### Example #2 - on_submit
The `Text` widget also has a special `on_submit` event. The `on_submit` event fires when the user hits <kbd>enter</kbd>.
```
text = widgets.Text()
display(text)
def handle_submit(sender):
print(text.value)
text.on_submit(handle_submit)
```
## Traitlet events
Widget properties are IPython traitlets and traitlets are eventful. To handle changes, the `observe` method of the widget can be used to register a callback. The docstring for `observe` can be seen below.
```
print(widgets.Widget.observe.__doc__)
```
### Signatures
Mentioned in the docstring, the callback registered must have the signature `handler(change)` where `change` is a dictionary holding the information about the change.
Using this method, an example of how to output an `IntSlider`’s value as it is changed can be seen below.
```
int_range = widgets.IntSlider()
display(int_range)
def on_value_change(change):
print(change['new'])
int_range.observe(on_value_change, names='value')
```
# Linking Widgets
Often, you may want to simply link widget attributes together. Synchronization of attributes can be done in a simpler way than by using bare traitlets events.
## Linking traitlets attributes in the kernel¶
The first method is to use the `link` and `dlink` functions from the `traitlets` module. This only works if we are interacting with a live kernel.
```
import traitlets
# Create Caption
caption = widgets.Label(value = 'The values of slider1 and slider2 are synchronized')
# Create IntSliders
slider1 = widgets.IntSlider(description='Slider 1')
slider2 = widgets.IntSlider(description='Slider 2')
# Use trailets to link
l = traitlets.link((slider1, 'value'), (slider2, 'value'))
# Display!
display(caption, slider1, slider2)
# Create Caption
caption = widgets.Label(value='Changes in source values are reflected in target1')
# Create Sliders
source = widgets.IntSlider(description='Source')
target1 = widgets.IntSlider(description='Target 1')
# Use dlink
dl = traitlets.dlink((source, 'value'), (target1, 'value'))
display(caption, source, target1)
```
Function `traitlets.link` and `traitlets.dlink` return a `Link` or `DLink` object. The link can be broken by calling the `unlink` method.
```
# May get an error depending on order of cells being run!
l.unlink()
dl.unlink()
```
### Registering callbacks to trait changes in the kernel
Since attributes of widgets on the Python side are traitlets, you can register handlers to the change events whenever the model gets updates from the front-end.
The handler passed to observe will be called with one change argument. The change object holds at least a `type` key and a `name` key, corresponding respectively to the type of notification and the name of the attribute that triggered the notification.
Other keys may be passed depending on the value of `type`. In the case where type is `change`, we also have the following keys:
* `owner` : the HasTraits instance
* `old` : the old value of the modified trait attribute
* `new` : the new value of the modified trait attribute
* `name` : the name of the modified trait attribute.
```
caption = widgets.Label(value='The values of range1 and range2 are synchronized')
slider = widgets.IntSlider(min=-5, max=5, value=1, description='Slider')
def handle_slider_change(change):
caption.value = 'The slider value is ' + (
'negative' if change.new < 0 else 'nonnegative'
)
slider.observe(handle_slider_change, names='value')
display(caption, slider)
```
## Linking widgets attributes from the client side
When synchronizing traitlets attributes, you may experience a lag because of the latency due to the roundtrip to the server side. You can also directly link widget attributes in the browser using the link widgets, in either a unidirectional or a bidirectional fashion.
Javascript links persist when embedding widgets in html web pages without a kernel.
```
# NO LAG VERSION
caption = widgets.Label(value = 'The values of range1 and range2 are synchronized')
range1 = widgets.IntSlider(description='Range 1')
range2 = widgets.IntSlider(description='Range 2')
l = widgets.jslink((range1, 'value'), (range2, 'value'))
display(caption, range1, range2)
# NO LAG VERSION
caption = widgets.Label(value = 'Changes in source_range values are reflected in target_range')
source_range = widgets.IntSlider(description='Source range')
target_range = widgets.IntSlider(description='Target range')
dl = widgets.jsdlink((source_range, 'value'), (target_range, 'value'))
display(caption, source_range, target_range)
```
Function `widgets.jslink` returns a `Link` widget. The link can be broken by calling the `unlink` method.
```
l.unlink()
dl.unlink()
```
### The difference between linking in the kernel and linking in the client
Linking in the kernel means linking via python. If two sliders are linked in the kernel, when one slider is changed the browser sends a message to the kernel (python in this case) updating the changed slider, the link widget in the kernel then propagates the change to the other slider object in the kernel, and then the other slider’s kernel object sends a message to the browser to update the other slider’s views in the browser. If the kernel is not running (as in a static web page), then the controls will not be linked.
Linking using jslink (i.e., on the browser side) means contructing the link in Javascript. When one slider is changed, Javascript running in the browser changes the value of the other slider in the browser, without needing to communicate with the kernel at all. If the sliders are attached to kernel objects, each slider will update their kernel-side objects independently.
To see the difference between the two, go to the [ipywidgets documentation](http://ipywidgets.readthedocs.io/en/latest/examples/Widget%20Events.html) and try out the sliders near the bottom. The ones linked in the kernel with `link` and `dlink` are no longer linked, but the ones linked in the browser with `jslink` and `jsdlink` are still linked.
## Continuous updates
Some widgets offer a choice with their `continuous_update` attribute between continually updating values or only updating values when a user submits the value (for example, by pressing Enter or navigating away from the control). In the next example, we see the “Delayed” controls only transmit their value after the user finishes dragging the slider or submitting the textbox. The “Continuous” controls continually transmit their values as they are changed. Try typing a two-digit number into each of the text boxes, or dragging each of the sliders, to see the difference.
```
import traitlets
a = widgets.IntSlider(description="Delayed", continuous_update=False)
b = widgets.IntText(description="Delayed", continuous_update=False)
c = widgets.IntSlider(description="Continuous", continuous_update=True)
d = widgets.IntText(description="Continuous", continuous_update=True)
traitlets.link((a, 'value'), (b, 'value'))
traitlets.link((a, 'value'), (c, 'value'))
traitlets.link((a, 'value'), (d, 'value'))
widgets.VBox([a,b,c,d])
```
Sliders, `Text`, and `Textarea` controls default to `continuous_update=True`. `IntText` and other text boxes for entering integer or float numbers default to `continuous_update=False` (since often you’ll want to type an entire number before submitting the value by pressing enter or navigating out of the box).
# Conclusion
You should now feel comfortable linking Widget events!
| true |
code
| 0.300951 | null | null | null | null |
|
# Broadcast Variables
We already saw so called *broadcast joins* which is a specific impementation of a join suitable for small lookup tables. The term *broadcast* is also used in a different context in Spark, there are also *broadcast variables*.
### Origin of Broadcast Variables
Broadcast variables where introduced fairly early with Spark and were mainly targeted at the RDD API. Nontheless they still have their place with the high level DataFrames API in conjunction with user defined functions (UDFs).
### Weather Example
As usual, we'll use the weather data example. This time we'll manually implement a join using a UDF (actually this would be again a manual broadcast join).
# 1 Load Data
First we load the weather data, which consists of the measurement data and some station metadata.
```
storageLocation = "s3://dimajix-training/data/weather"
```
## 1.1 Load Measurements
Measurements are stored in multiple directories (one per year). But we will limit ourselves to a single year in the analysis to improve readability of execution plans.
```
from pyspark.sql.functions import *
from functools import reduce
# Read in all years, store them in an Python array
raw_weather_per_year = [spark.read.text(storageLocation + "/" + str(i)).withColumn("year", lit(i)) for i in range(2003,2015)]
# Union all years together
raw_weather = reduce(lambda l,r: l.union(r), raw_weather_per_year)
```
Use a single year to keep execution plans small
```
raw_weather = spark.read.text(storageLocation + "/2003").withColumn("year", lit(2003))
```
### Extract Measurements
Measurements were stored in a proprietary text based format, with some values at fixed positions. We need to extract these values with a simple SELECT statement.
```
weather = raw_weather.select(
col("year"),
substring(col("value"),5,6).alias("usaf"),
substring(col("value"),11,5).alias("wban"),
substring(col("value"),16,8).alias("date"),
substring(col("value"),24,4).alias("time"),
substring(col("value"),42,5).alias("report_type"),
substring(col("value"),61,3).alias("wind_direction"),
substring(col("value"),64,1).alias("wind_direction_qual"),
substring(col("value"),65,1).alias("wind_observation"),
(substring(col("value"),66,4).cast("float") / lit(10.0)).alias("wind_speed"),
substring(col("value"),70,1).alias("wind_speed_qual"),
(substring(col("value"),88,5).cast("float") / lit(10.0)).alias("air_temperature"),
substring(col("value"),93,1).alias("air_temperature_qual")
)
```
## 1.2 Load Station Metadata
We also need to load the weather station meta data containing information about the geo location, country etc of individual weather stations.
```
stations = spark.read \
.option("header", True) \
.csv(storageLocation + "/isd-history")
```
### Convert Station Metadata
We convert the stations DataFrame to a normal Python map, since we want to discuss broadcast variables. This means that the variable `py_stations` contains a normal Python object which only lives on the driver. It has no connection to Spark any more.
The resulting map converts a given station id (usaf and wban) to a country.
```
py_stations = stations.select(concat(stations["usaf"], stations["wban"]).alias("key"), stations["ctry"]).collect()
py_stations = {key:value for (key,value) in py_stations}
# Inspect result
list(py_stations.items())[0:10]
```
# 2 Using Broadcast Variables
In the following section, we want to use a Spark broadcast variable inside a UDF. Technically this is not required, as Spark also has other mechanisms of distributing data, so we'll start with a simple implementation *without* using a broadcast variable.
## 2.1 Create a UDF
For the initial implementation, we create a simple Python UDF which looks up the country for a given station id, which consists of the usaf and wban code. This way we will replace the `JOIN` of our original solution with a UDF implemented in Python.
```
def lookup_country(usaf, wban):
return py_stations.get(usaf + wban)
# Test lookup with an existing station
print(lookup_country("007026", "99999"))
# Test lookup with a non-existing station (better should not throw an exception)
print(lookup_country("123", "456"))
```
## 2.2 Not using a broadcast variable
Now that we have a simple Python function providing the required functionality, we convert it to a PySpark UDF using a Python decorator.
```
@udf('string')
def lookup_country(usaf, wban):
return py_stations.get(usaf + wban)
```
### Replace JOIN by UDF
Now we can perform the lookup by using the UDF instead of the original `JOIN`.
```
result = weather.withColumn('country', lookup_country(weather["usaf"], weather["wban"]))
result.limit(10).toPandas()
```
### Remarks
Since the code is actually executed not on the driver, but istributed on the executors, the executors also require access to the Python map. PySpark automatically serializes the map and sends it to the executors on the fly.
### Inspect Plan
We can also inspect the execution plan, which is different from the original implementation. Instead of the broadcast join, it now contains a `BatchEvalPython` step which looks up the stations country from the station id.
```
result.explain()
```
## 2.2 Using a Broadcast Variable
Now let us change the implementation to use a so called *broadcast variable*. While the original implementation implicitly sent the Python map to all executors, a broadcast variable makes the process of sending (*broadcasting*) a Python variable to all executors more explicit.
A Python variable can be broadcast using the `broadcast` method of the underlying Spark context (the Spark session does not export this functionality). Once the data is encapsulated in the broadcast variable, all executors can access the original data via the `value` member variable.
```
# First create a broadcast variable from the original Python map
bc_stations = spark.sparkContext.broadcast(py_stations)
@udf('string')
def lookup_country(usaf, wban):
# Access the broadcast variables value and perform lookup
return bc_stations.value.get(usaf + wban)
```
### Replace JOIN by UDF
Again we replace the original `JOIN` by the UDF we just defined above
```
result = weather.withColumn('country', lookup_country(weather["usaf"], weather["wban"]))
result.limit(10).toPandas()
```
### Remarks
Actually there is no big difference to the original implementation. But Spark handles a broadcast variable slightly more efficiently, especially if the variable is used in multiple UDFs. In this case the data will be broadcast only a single time, while not using a broadcast variable would imply sending the data around for every UDF.
### Execution Plan
The execution plan does not differ at all, since it does not provide information on broadcast variables.
```
result.explain()
```
## 2.3 Pandas UDFs
Since we already learnt that Pandas UDFs are executed more efficiently than normal UDFs, we want to provide a better implementation using Pandas. Of course Pandas UDFs can also access broadcast variables.
```
from pyspark.sql.functions import pandas_udf, PandasUDFType
@pandas_udf('string', PandasUDFType.SCALAR)
def lookup_country(usaf, wban):
# Create helper function
def lookup(key):
# Perform lookup by accessing the Python map
return bc_stations.value.get(key)
# Create key from both incoming Pandas series
usaf_wban = usaf + wban
# Perform lookup
return usaf_wban.apply(lookup)
```
### Replace JOIN by Pandas UDF
Again, we replace the original `JOIN` by the Pandas UDF.
```
result = weather.withColumn('country', lookup_country(weather["usaf"], weather["wban"]))
result.limit(10).toPandas()
```
### Execution Plan
Again, let's inspect the execution plan.
```
result.explain(True)
```
| true |
code
| 0.334973 | null | null | null | null |
|
# Sudoku
This tutorial includes everything you need to set up decision optimization engines, build constraint programming models.
When you finish this tutorial, you'll have a foundational knowledge of _Prescriptive Analytics_.
>This notebook is part of the **[Prescriptive Analytics for Python](https://rawgit.com/IBMDecisionOptimization/docplex-doc/master/docs/index.html)**
>It requires a **local installation of CPLEX Optimizers**.
Table of contents:
- [Describe the business problem](#Describe-the-business-problem)
* [How decision optimization (prescriptive analytics) can help](#How--decision-optimization-can-help)
* [Use decision optimization](#Use-decision-optimization)
* [Step 1: Download the library](#Step-1:-Download-the-library)
* [Step 2: Model the Data](#Step-2:-Model-the-data)
* [Step 3: Set up the prescriptive model](#Step-3:-Set-up-the-prescriptive-model)
* [Define the decision variables](#Define-the-decision-variables)
* [Express the business constraints](#Express-the-business-constraints)
* [Express the objective](#Express-the-objective)
* [Solve with Decision Optimization solve service](#Solve-with-Decision-Optimization-solve-service)
* [Step 4: Investigate the solution and run an example analysis](#Step-4:-Investigate-the-solution-and-then-run-an-example-analysis)
* [Summary](#Summary)
****
### Describe the business problem
* Sudoku is a logic-based, combinatorial number-placement puzzle.
* The objective is to fill a 9x9 grid with digits so that each column, each row,
and each of the nine 3x3 sub-grids that compose the grid contains all of the digits from 1 to 9.
* The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a unique solution.
#### References
* See https://en.wikipedia.org/wiki/Sudoku for details
*****
## How decision optimization can help
* Prescriptive analytics technology recommends actions based on desired outcomes, taking into account specific scenarios, resources, and knowledge of past and current events. This insight can help your organization make better decisions and have greater control of business outcomes.
* Prescriptive analytics is the next step on the path to insight-based actions. It creates value through synergy with predictive analytics, which analyzes data to predict future outcomes.
* Prescriptive analytics takes that insight to the next level by suggesting the optimal way to handle that future situation. Organizations that can act fast in dynamic conditions and make superior decisions in uncertain environments gain a strong competitive advantage.
<br/>
+ For example:
+ Automate complex decisions and trade-offs to better manage limited resources.
+ Take advantage of a future opportunity or mitigate a future risk.
+ Proactively update recommendations based on changing events.
+ Meet operational goals, increase customer loyalty, prevent threats and fraud, and optimize business processes.
## Use decision optimization
### Step 1: Download the library
Run the following code to install Decision Optimization CPLEX Modeling library. The *DOcplex* library contains the two modeling packages, Mathematical Programming and Constraint Programming, referred to earlier.
```
import sys
try:
import docplex.cp
except:
if hasattr(sys, 'real_prefix'):
#we are in a virtual env.
!pip install docplex
else:
!pip install --user docplex
```
Note that the more global package <i>docplex</i> contains another subpackage <i>docplex.mp</i> that is dedicated to Mathematical Programming, another branch of optimization.
```
from docplex.cp.model import *
from sys import stdout
```
### Step 2: Model the data
#### Grid range
```
GRNG = range(9)
```
#### Different problems
_zero means cell to be filled with appropriate value_
```
SUDOKU_PROBLEM_1 = ( (0, 0, 0, 0, 9, 0, 1, 0, 0),
(2, 8, 0, 0, 0, 5, 0, 0, 0),
(7, 0, 0, 0, 0, 6, 4, 0, 0),
(8, 0, 5, 0, 0, 3, 0, 0, 6),
(0, 0, 1, 0, 0, 4, 0, 0, 0),
(0, 7, 0, 2, 0, 0, 0, 0, 0),
(3, 0, 0, 0, 0, 1, 0, 8, 0),
(0, 0, 0, 0, 0, 0, 0, 5, 0),
(0, 9, 0, 0, 0, 0, 0, 7, 0),
)
SUDOKU_PROBLEM_2 = ( (0, 7, 0, 0, 0, 0, 0, 4, 9),
(0, 0, 0, 4, 0, 0, 0, 0, 0),
(4, 0, 3, 5, 0, 7, 0, 0, 8),
(0, 0, 7, 2, 5, 0, 4, 0, 0),
(0, 0, 0, 0, 0, 0, 8, 0, 0),
(0, 0, 4, 0, 3, 0, 5, 9, 2),
(6, 1, 8, 0, 0, 0, 0, 0, 5),
(0, 9, 0, 1, 0, 0, 0, 3, 0),
(0, 0, 5, 0, 0, 0, 0, 0, 7),
)
SUDOKU_PROBLEM_3 = ( (0, 0, 0, 0, 0, 6, 0, 0, 0),
(0, 5, 9, 0, 0, 0, 0, 0, 8),
(2, 0, 0, 0, 0, 8, 0, 0, 0),
(0, 4, 5, 0, 0, 0, 0, 0, 0),
(0, 0, 3, 0, 0, 0, 0, 0, 0),
(0, 0, 6, 0, 0, 3, 0, 5, 4),
(0, 0, 0, 3, 2, 5, 0, 0, 6),
(0, 0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0, 0)
)
try:
import numpy as np
import matplotlib.pyplot as plt
VISU_ENABLED = True
except ImportError:
VISU_ENABLED = False
def print_grid(grid):
""" Print Sudoku grid """
for l in GRNG:
if (l > 0) and (l % 3 == 0):
stdout.write('\n')
for c in GRNG:
v = grid[l][c]
stdout.write(' ' if (c % 3 == 0) else ' ')
stdout.write(str(v) if v > 0 else '.')
stdout.write('\n')
def draw_grid(values):
%matplotlib inline
fig, ax = plt.subplots(figsize =(4,4))
min_val, max_val = 0, 9
R = range(0,9)
for l in R:
for c in R:
v = values[c][l]
s = " "
if v > 0:
s = str(v)
ax.text(l+0.5,8.5-c, s, va='center', ha='center')
ax.set_xlim(min_val, max_val)
ax.set_ylim(min_val, max_val)
ax.set_xticks(np.arange(max_val))
ax.set_yticks(np.arange(max_val))
ax.grid()
plt.show()
def display_grid(grid, name):
stdout.write(name)
stdout.write(":\n")
if VISU_ENABLED:
draw_grid(grid)
else:
print_grid(grid)
display_grid(SUDOKU_PROBLEM_1, "PROBLEM 1")
display_grid(SUDOKU_PROBLEM_2, "PROBLEM 2")
display_grid(SUDOKU_PROBLEM_3, "PROBLEM 3")
```
#### Choose your preferred problem (SUDOKU_PROBLEM_1 or SUDOKU_PROBLEM_2 or SUDOKU_PROBLEM_3)
If you change the problem, ensure to re-run all cells below this one.
```
problem = SUDOKU_PROBLEM_3
```
### Step 3: Set up the prescriptive model
```
mdl = CpoModel(name="Sudoku")
```
#### Define the decision variables
```
grid = [[integer_var(min=1, max=9, name="C" + str(l) + str(c)) for l in GRNG] for c in GRNG]
```
#### Express the business constraints
Add alldiff constraints for lines
```
for l in GRNG:
mdl.add(all_diff([grid[l][c] for c in GRNG]))
```
Add alldiff constraints for columns
```
for c in GRNG:
mdl.add(all_diff([grid[l][c] for l in GRNG]))
```
Add alldiff constraints for sub-squares
```
ssrng = range(0, 9, 3)
for sl in ssrng:
for sc in ssrng:
mdl.add(all_diff([grid[l][c] for l in range(sl, sl + 3) for c in range(sc, sc + 3)]))
```
Initialize known cells
```
for l in GRNG:
for c in GRNG:
v = problem[l][c]
if v > 0:
grid[l][c].set_domain((v, v))
```
#### Solve with Decision Optimization solve service
```
print("\nSolving model....")
msol = mdl.solve(TimeLimit=10)
```
### Step 4: Investigate the solution and then run an example analysis
```
display_grid(problem, "Initial problem")
if msol:
sol = [[msol[grid[l][c]] for c in GRNG] for l in GRNG]
stdout.write("Solve time: " + str(msol.get_solve_time()) + "\n")
display_grid(sol, "Solution")
else:
stdout.write("No solution found\n")
```
## Summary
You learned how to set up and use the IBM Decision Optimization CPLEX Modeling for Python to formulate and solve a Constraint Programming model.
#### References
* [CPLEX Modeling for Python documentation](https://rawgit.com/IBMDecisionOptimization/docplex-doc/master/docs/index.html)
* [Decision Optimization on Cloud](https://developer.ibm.com/docloud/)
* Need help with DOcplex or to report a bug? Please go [here](https://developer.ibm.com/answers/smartspace/docloud)
* Contact us at [email protected]
Copyright © 2017, 2018 IBM. IPLA licensed Sample Materials.
| true |
code
| 0.236274 | null | null | null | null |
|
## Dragon Real Estate - Price Predictor
```
import pandas as pd
housing = pd.read_csv("data.csv")
housing.head()
housing.info()
housing['CHAS'].value_counts()
housing.describe()
%matplotlib inline
# # For plotting histogram
# import matplotlib.pyplot as plt
# housing.hist(bins=50, figsize=(20, 15))
```
## Train-Test Splitting
```
# For learning purpose
import numpy as np
def split_train_test(data, test_ratio):
np.random.seed(42)
shuffled = np.random.permutation(len(data))
print(shuffled)
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled[:test_set_size]
train_indices = shuffled[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
# train_set, test_set = split_train_test(housing, 0.2)
# print(f"Rows in train set: {len(train_set)}\nRows in test set: {len(test_set)}\n")
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
print(f"Rows in train set: {len(train_set)}\nRows in test set: {len(test_set)}\n")
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing['CHAS']):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
strat_test_set['CHAS'].value_counts()
strat_train_set['CHAS'].value_counts()
# 95/7
# 376/28
housing = strat_train_set.copy()
```
## Looking for Correlations
```
corr_matrix = housing.corr()
corr_matrix['MEDV'].sort_values(ascending=False)
# from pandas.plotting import scatter_matrix
# attributes = ["MEDV", "RM", "ZN", "LSTAT"]
# scatter_matrix(housing[attributes], figsize = (12,8))
housing.plot(kind="scatter", x="RM", y="MEDV", alpha=0.8)
```
## Trying out Attribute combinations
```
housing["TAXRM"] = housing['TAX']/housing['RM']
housing.head()
corr_matrix = housing.corr()
corr_matrix['MEDV'].sort_values(ascending=False)
housing.plot(kind="scatter", x="TAXRM", y="MEDV", alpha=0.8)
housing = strat_train_set.drop("MEDV", axis=1)
housing_labels = strat_train_set["MEDV"].copy()
```
## Missing Attributes
```
# To take care of missing attributes, you have three options:
# 1. Get rid of the missing data points
# 2. Get rid of the whole attribute
# 3. Set the value to some value(0, mean or median)
a = housing.dropna(subset=["RM"]) #Option 1
a.shape
# Note that the original housing dataframe will remain unchanged
housing.drop("RM", axis=1).shape # Option 2
# Note that there is no RM column and also note that the original housing dataframe will remain unchanged
median = housing["RM"].median() # Compute median for Option 3
housing["RM"].fillna(median) # Option 3
# Note that the original housing dataframe will remain unchanged
housing.shape
housing.describe() # before we started filling missing attributes
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
imputer.fit(housing)
imputer.statistics_
X = imputer.transform(housing)
housing_tr = pd.DataFrame(X, columns=housing.columns)
housing_tr.describe()
```
## Scikit-learn Design
Primarily, three types of objects
1. Estimators - It estimates some parameter based on a dataset. Eg. imputer. It has a fit method and transform method. Fit method - Fits the dataset and calculates internal parameters
2. Transformers - transform method takes input and returns output based on the learnings from fit(). It also has a convenience function called fit_transform() which fits and then transforms.
3. Predictors - LinearRegression model is an example of predictor. fit() and predict() are two common functions. It also gives score() function which will evaluate the predictions.
## Feature Scaling
Primarily, two types of feature scaling methods:
1. Min-max scaling (Normalization)
(value - min)/(max - min)
Sklearn provides a class called MinMaxScaler for this
2. Standardization
(value - mean)/std
Sklearn provides a class called StandardScaler for this
## Creating a Pipeline
```
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
my_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
# ..... add as many as you want in your pipeline
('std_scaler', StandardScaler()),
])
housing_num_tr = my_pipeline.fit_transform(housing)
housing_num_tr.shape
```
## Selecting a desired model for Dragon Real Estates
```
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
# model = LinearRegression()
# model = DecisionTreeRegressor()
model = RandomForestRegressor()
model.fit(housing_num_tr, housing_labels)
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
prepared_data = my_pipeline.transform(some_data)
model.predict(prepared_data)
list(some_labels)
```
## Evaluating the model
```
from sklearn.metrics import mean_squared_error
housing_predictions = model.predict(housing_num_tr)
mse = mean_squared_error(housing_labels, housing_predictions)
rmse = np.sqrt(mse)
rmse
```
## Using better evaluation technique - Cross Validation
```
# 1 2 3 4 5 6 7 8 9 10
from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, housing_num_tr, housing_labels, scoring="neg_mean_squared_error", cv=10)
rmse_scores = np.sqrt(-scores)
rmse_scores
def print_scores(scores):
print("Scores:", scores)
print("Mean: ", scores.mean())
print("Standard deviation: ", scores.std())
print_scores(rmse_scores)
```
Quiz: Convert this notebook into a python file and run the pipeline using Visual Studio Code
## Saving the model
```
from joblib import dump, load
dump(model, 'Dragon.joblib')
```
## Testing the model on test data
```
X_test = strat_test_set.drop("MEDV", axis=1)
Y_test = strat_test_set["MEDV"].copy()
X_test_prepared = my_pipeline.transform(X_test)
final_predictions = model.predict(X_test_prepared)
final_mse = mean_squared_error(Y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
# print(final_predictions, list(Y_test))
final_rmse
prepared_data[0]
```
## Using the model
```
from joblib import dump, load
import numpy as np
model = load('Dragon.joblib')
features = np.array([[-5.43942006, 4.12628155, -1.6165014, -0.67288841, -1.42262747,
-11.44443979304, -49.31238772, 7.61111401, -26.0016879 , -0.5778192 ,
-0.97491834, 0.41164221, -66.86091034]])
model.predict(features)
```
| true |
code
| 0.489564 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/christianadriano/PCA_AquacultureSystem/blob/master/PCA_KMeans_All_Piscicultura.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import pandas as pd #tables for data wrangling
import numpy as np #basic statistical methods
import io #for uploading data
#Manual option
from google.colab import files
uploaded = files.upload() #choose file dados_relativizados_centralizados_piscicultura.csv
#Upload data from cvs file
df = pd.read_csv(io.StringIO(uploaded['dados_relativizados_centralizados_piscicultura.csv'].decode('utf-8')))
#print(df)
column_names = df.columns
#Select fatores Ambientais
feature_names = [name for name in column_names if name.startswith("E")]
#feature_names = list(df.columns["A2_DA":"A4_EUC"])
#print(feature_names)
list_names = ['fazenda'] + feature_names
df_cultivo = df[list_names]
df_cultivo.head()
#Look at correlations
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
corr = df_cultivo.corr()
# using a styled panda's dataframe from https://stackoverflow.com/a/42323184/1215012
cmap = 'coolwarm'
corr.style.background_gradient(cmap, axis=1)\
.set_properties(**{'max-width': '80px', 'font-size': '10pt'})\
.set_precision(2)\
#smaller chart
sns.heatmap(corr, xticklabels=corr.columns, yticklabels=corr.columns, cmap='coolwarm')
#check which ones are statiscally significant
from scipy.stats import pearsonr
import pandas as pd
def calculate_pvalues(df):
df = df.dropna()._get_numeric_data()
dfcols = pd.DataFrame(columns=df.columns)
pvalues = dfcols.transpose().join(dfcols, how='outer')
for r in df.columns:
for c in df.columns:
pvalues[r][c] = round(pearsonr(df[r], df[c])[1], 4)
return pvalues
p_values = calculate_pvalues(df_cultivo)
#Plot p-values
def highlight_significant(val):
'''
highlight in blue only the statistically significant cells
'''
color = 'blue' if val < 0.05 else 'grey'
return 'color: %s' % color
p_values.style.applymap(highlight_significant)
#Smaller plot of p-values
import matplotlib.pyplot as plt
from matplotlib import colors
import numpy as np
np.random.seed(101)
zvals = np.random.rand(100, 100) * 10
# make a color map of fixed colors
cmap_discrete = colors.ListedColormap(['lightblue', 'white'])
bounds=[0,0.05,1]
norm_binary = colors.BoundaryNorm(bounds, cmap_discrete.N)
# tell imshow about color map so that only set colors are used
img = plt.imshow(zvals, interpolation='nearest', origin='lower',
cmap=cmap_discrete, norm=norm_binary)
sns.heatmap(p_values, xticklabels=p_values.columns, yticklabels=p_values.columns, cmap=cmap_discrete, norm=norm_binary)
```
**PCA**
Now we do the PCA
```
#Normalize the data to have MEAN==0
from sklearn.preprocessing import StandardScaler
x = df_cultivo.iloc[:,1:].values
x = StandardScaler().fit_transform(x) # normalizing the features
#print(x)
#Run PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents
, columns = ['principal component 1', 'principal component 2'])
finalDf = pd.concat([principalDf, df_cultivo[['fazenda']]], axis = 1)
#Visualize results of PCA in Two Dimensions
import matplotlib.pyplot as plt
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_title('2 component PCA', fontsize = 20)
targets = df_cultivo['fazenda'].to_numpy()
print(targets)
for target in targets:
indicesToKeep = finalDf['fazenda'] == target
x = finalDf.loc[indicesToKeep, 'principal component 1']
y = finalDf.loc[indicesToKeep, 'principal component 2']
ax.scatter(x,y,s = 100)
ax.annotate(target, (x+0.1,y))
#for name in targets:
ax.legend(targets, loc='top right')
ax.grid()
variance_list =pca.explained_variance_ratio_
print("variance explained by each component:", variance_list)
print("total variance explained:", sum(variance_list))
#principal components for each indicador
#print(principalComponents)
#print(targets)
df_clustering = pd.DataFrame({'fazenda': targets, 'pc1':list(principalComponents[:,0]), 'pc2': list(principalComponents[:,1])}, columns=['fazenda', 'pc1','pc2'])
#df_clustering
#Find clusters
from sklearn.cluster import KMeans
#4 clusters
model = KMeans(4)
model.fit(df_clustering.iloc[:,1:3])
#print(model.cluster_centers_)
#Plot clusters
plt.scatter(df_clustering.iloc[:,1],df_clustering.iloc[:,2], c=model.labels_.astype(float));
plt.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1], s=50, marker="x", color="grey"); # Show the
#To which cluster each point belongs?
df1= df_clustering.assign(cluster=pd.Series(model.labels_).values)
df1.sort_values(by='cluster')
#5 clusters
model = KMeans(5)
model.fit(df_clustering.iloc[:,1:3])
#print(model.cluster_centers_)
#Plot clusters
plt.scatter(df_clustering.iloc[:,1],df_clustering.iloc[:,2], c=model.labels_.astype(float));
plt.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1], s=50, marker="x", color="grey"); # Show the
```
In my view, we have two large clusters and three outliers, as the graph above shows.
```
#To which cluster each point belongs?
df1= df_clustering.assign(cluster=pd.Series(model.labels_).values)
df1.sort_values(by='cluster')
#6 clusters
model = KMeans(6)
model.fit(df_clustering.iloc[:,1:3])
#print(model.cluster_centers_)
#Plot clusters
plt.scatter(df_clustering.iloc[:,1],df_clustering.iloc[:,2], c=model.labels_.astype(float));
plt.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1], s=50, marker="x", color="grey"); # Show the
#To which cluster each point belongs?
df1= df_clustering.assign(cluster=pd.Series(model.labels_).values)
df1.sort_values(by='cluster')
```
Now we analyze 3 Principal Components
```
#Normalize the data to have MEAN==0
from sklearn.preprocessing import StandardScaler
x = df_cultivo.iloc[:,1:].values
x = StandardScaler().fit_transform(x) # normalizing the features
#print(x)
#Run PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents
, columns = ['principal component 1', 'principal component 2','principal component 3'])
finalDf = pd.concat([principalDf, df_cultivo[['fazenda']]], axis = 1)
variance_list =pca.explained_variance_ratio_
print("variance explained by each component:", variance_list)
print("total variance explained:", sum(variance_list))
```
Now we search for clusters for 3 principal components
```
#Find clusters
from sklearn.cluster import KMeans
#4 clusters
model = KMeans(4)
model.fit(df_clustering.iloc[:,1:4])
#print(model.cluster_centers_)
#principal components for each indicador
#print(principalComponents)
#print(targets)
df_clustering = pd.DataFrame({'fazenda': targets, 'pc1':list(principalComponents[:,0]),
'pc2': list(principalComponents[:,1]),'pc3': list(principalComponents[:,2])},
columns=['fazenda', 'pc1','pc2','pc3'])
#df_clustering
#4 clusters
from sklearn.cluster import KMeans
model = KMeans(4)
model.fit(df_clustering.iloc[:,1:4])
#print(model.cluster_centers_)
#Plot clusters
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_zlabel('Principal Component 3', fontsize = 15)
ax.set_title('3-components PCA', fontsize = 20)
targets = df_cultivo['fazenda'].to_numpy()
for target in targets:
indicesToKeep = finalDf['fazenda'] == target
x = finalDf.loc[indicesToKeep, 'principal component 1']
y = finalDf.loc[indicesToKeep, 'principal component 2']
z = finalDf.loc[indicesToKeep, 'principal component 3']
ax.scatter(x,y,z,s = 100)
ax.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1],model.cluster_centers_[:,2], s=150, marker='x', color="black"); # Show the
ax.legend(targets)
ax.grid()
```
Now we search for clusters for the 3 principal components
```
#To which cluster each point belongs?
df1= df_clustering.assign(cluster=pd.Series(model.labels_).values)
df1.sort_values(by='cluster')
```
Comparing k-means of PC12 with PC123, we see that the cluster membership changes completely.
```
#5 clusters
from sklearn.cluster import KMeans
model = KMeans(5)
model.fit(df_clustering.iloc[:,1:4])
#print(model.cluster_centers_)
#Plot clusters
#plt.scatter(df_clustering.iloc[:,1],df_clustering.iloc[:,2], c=model.labels_.astype(float));
#plt.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1], s=50, color="red"); # Show the
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_zlabel('Principal Component 3', fontsize = 15)
ax.set_title('3-components PCA', fontsize = 20)
targets = df_cultivo['fazenda'].to_numpy()
for target in targets:
indicesToKeep = finalDf['fazenda'] == target
x = finalDf.loc[indicesToKeep, 'principal component 1']
y = finalDf.loc[indicesToKeep, 'principal component 2']
z = finalDf.loc[indicesToKeep, 'principal component 3']
ax.scatter(x,y,z,s = 100)
#ax.annotate(target, (x,y))
ax.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1],model.cluster_centers_[:,2], s=150, marker='x', color="black"); # Show the
#for name in targets:
ax.legend(targets)
ax.grid()
#To which cluster each point belongs?
df1= df_clustering.assign(cluster=pd.Series(model.labels_).values)
df1.sort_values(by='cluster')
#6 clusters
from sklearn.cluster import KMeans
model = KMeans(6)
model.fit(df_clustering.iloc[:,1:4])
#print(model.cluster_centers_)
#Plot clusters
#plt.scatter(df_clustering.iloc[:,1],df_clustering.iloc[:,2], c=model.labels_.astype(float));
#plt.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1], s=50, color="red"); # Show the
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_zlabel('Principal Component 3', fontsize = 15)
ax.set_title('3-components PCA', fontsize = 20)
targets = df_cultivo['fazenda'].to_numpy()
for target in targets:
indicesToKeep = finalDf['fazenda'] == target
x = finalDf.loc[indicesToKeep, 'principal component 1']
y = finalDf.loc[indicesToKeep, 'principal component 2']
z = finalDf.loc[indicesToKeep, 'principal component 3']
ax.scatter(x,y,z,s = 100)
#ax.annotate(target, (x,y))
ax.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1],model.cluster_centers_[:,2], s=150, marker='x', color="black"); # Show the
#for name in targets:
ax.legend(targets)
ax.grid()
#To which cluster each point belongs?
df1= df_clustering.assign(cluster=pd.Series(model.labels_).values)
df1.sort_values(by='cluster')
```
| true |
code
| 0.51129 | null | null | null | null |
|
Python programmers will often suggest that there many ways the language can be used to solve a particular
problem. But that some are more appropriate than others. The best solutions are celebrated as Idiomatic
Python and there are lots of great examples of this on StackOverflow and other websites.
A sort of sub-language within Python, Pandas has its own set of idioms. We've alluded to some of these
already, such as using vectorization whenever possible, and not using iterative loops if you don't need to.
Several developers and users within the Panda's community have used the term __pandorable__ for these
idioms. I think it's a great term. So, I wanted to share with you a couple of key features of how you can
make your code pandorable.
```
# Let's start by bringing in our data processing libraries
import pandas as pd
import numpy as np
# And we'll bring in some timing functionality too, from the timeit module
import timeit
# And lets look at some census data from the US
df = pd.read_csv('datasets/census.csv')
df.head()
# The first of the pandas idioms I would like to talk about is called method chaining. The general idea behind
# method chaining is that every method on an object returns a reference to that object. The beauty of this is
# that you can condense many different operations on a DataFrame, for instance, into one line or at least one
# statement of code.
# Here's the pandorable way to write code with method chaining. In this code I'm going to pull out the state
# and city names as a multiple index, and I'm going to do so only for data which has a summary level of 50,
# which in this dataset is county-level data. I'll rename a column too, just to make it a bit more readable.
(df.where(df['SUMLEV']==50)
.dropna()
.set_index(['STNAME','CTYNAME'])
.rename(columns={'ESTIMATESBASE2010': 'Estimates Base 2010'}))
# Lets walk through this. First, we use the where() function on the dataframe and pass in a boolean mask which
# is only true for those rows where the SUMLEV is equal to 50. This indicates in our source data that the data
# is summarized at the county level. With the result of the where() function evaluated, we drop missing
# values. Remember that .where() doesn't drop missing values by default. Then we set an index on the result of
# that. In this case I've set it to the state name followed by the county name. Finally. I rename a column to
# make it more readable. Note that instead of writing this all on one line, as I could have done, I began the
# statement with a parenthesis, which tells python I'm going to span the statement over multiple lines for
# readability.
# Here's a more traditional, non-pandorable way, of writing this. There's nothing wrong with this code in the
# functional sense, you might even be able to understand it better as a new person to the language. It's just
# not as pandorable as the first example.
# First create a new dataframe from the original
df = df[df['SUMLEV']==50] # I'll use the overloaded indexing operator [] which drops nans
# Update the dataframe to have a new index, we use inplace=True to do this in place
df.set_index(['STNAME','CTYNAME'], inplace=True)
# Set the column names
df.rename(columns={'ESTIMATESBASE2010': 'Estimates Base 2010'})
# Now, the key with any good idiom is to understand when it isn't helping you. In this case, you can actually
# time both methods and see which one runs faster
# We can put the approach into a function and pass the function into the timeit function to count the time the
# parameter number allows us to choose how many times we want to run the function. Here we will just set it to
# 10
# Lets write a wrapper for our first function
def first_approach():
global df
# And we'll just paste our code right here
return (df.where(df['SUMLEV']==50)
.dropna()
.set_index(['STNAME','CTYNAME'])
.rename(columns={'ESTIMATESBASE2010': 'Estimates Base 2010'}))
# Read in our dataset anew
df = pd.read_csv('datasets/census.csv')
# And now lets run it
timeit.timeit(first_approach, number=10)
# Now let's test the second approach. As you may notice, we use our global variable df in the function.
# However, changing a global variable inside a function will modify the variable even in a global scope and we
# do not want that to happen in this case. Therefore, for selecting summary levels of 50 only, I create a new
# dataframe for those records
# Let's run this for once and see how fast it is
def second_approach():
global df
new_df = df[df['SUMLEV']==50]
new_df.set_index(['STNAME','CTYNAME'], inplace=True)
return new_df.rename(columns={'ESTIMATESBASE2010': 'Estimates Base 2010'})
# Read in our dataset anew
df = pd.read_csv('datasets/census.csv')
# And now lets run it
timeit.timeit(second_approach, number=10)
# As you can see, the second approach is much faster! So, this is a particular example of a classic time
# readability trade off.
# You'll see lots of examples on stack overflow and in documentation of people using method chaining in their
# pandas. And so, I think being able to read and understand the syntax is really worth your time. But keep in
# mind that following what appears to be stylistic idioms might have performance issues that you need to
# consider as well.
# Here's another pandas idiom. Python has a wonderful function called map, which is sort of a basis for
# functional programming in the language. When you want to use map in Python, you pass it some function you
# want called, and some iterable, like a list, that you want the function to be applied to. The results are
# that the function is called against each item in the list, and there's a resulting list of all of the
# evaluations of that function.
# Pandas has a similar function called applymap. In applymap, you provide some function which should operate
# on each cell of a DataFrame, and the return set is itself a DataFrame. Now I think applymap is fine, but I
# actually rarely use it. Instead, I find myself often wanting to map across all of the rows in a DataFrame.
# And pandas has a function that I use heavily there, called apply. Let's look at an example.
# Let's take a look at our census DataFrame. In this DataFrame, we have five columns for population estimates,
# with each column corresponding with one year of estimates. It's quite reasonable to want to create some new
# columns for minimum or maximum values, and the apply function is an easy way to do this.
# First, we need to write a function which takes in a particular row of data, finds a minimum and maximum
# values, and returns a new row of data nd returns a new row of data. We'll call this function min_max, this
# is pretty straight forward. We can create some small slice of a row by projecting the population columns.
# Then use the NumPy min and max functions, and create a new series with a label values represent the new
# values we want to apply.
def min_max(row):
data = row[['POPESTIMATE2010',
'POPESTIMATE2011',
'POPESTIMATE2012',
'POPESTIMATE2013',
'POPESTIMATE2014',
'POPESTIMATE2015']]
return pd.Series({'min': np.min(data), 'max': np.max(data)})
# Then we just need to call apply on the DataFrame.
# Apply takes the function and the axis on which to operate as parameters. Now, we have to be a bit careful,
# we've talked about axis zero being the rows of the DataFrame in the past. But this parameter is really the
# parameter of the index to use. So, to apply across all rows, which is applying on all columns, you pass axis
# equal to 'columns'.
df.apply(min_max, axis='columns').head()
# Of course there's no need to limit yourself to returning a new series object. If you're doing this as part
# of data cleaning your likely to find yourself wanting to add new data to the existing DataFrame. In that
# case you just take the row values and add in new columns indicating the max and minimum scores. This is a
# regular part of my workflow when bringing in data and building summary or descriptive statistics, and is
# often used heavily with the merging of DataFrames.
# Here's an example where we have a revised version of the function min_max Instead of returning a separate
# series to display the min and max we add two new columns in the original dataframe to store min and max
def min_max(row):
data = row[['POPESTIMATE2010',
'POPESTIMATE2011',
'POPESTIMATE2012',
'POPESTIMATE2013',
'POPESTIMATE2014',
'POPESTIMATE2015']]
# Create a new entry for max
row['max'] = np.max(data)
# Create a new entry for min
row['min'] = np.min(data)
return row
# Now just apply the function across the dataframe
df.apply(min_max, axis='columns')
# Apply is an extremely important tool in your toolkit. The reason I introduced apply here is because you
# rarely see it used with large function definitions, like we did. Instead, you typically see it used with
# lambdas. To get the most of the discussions you'll see online, you're going to need to know how to at least
# read lambdas.
# Here's You can imagine how you might chain several apply calls with lambdas together to create a readable
# yet succinct data manipulation script. One line example of how you might calculate the max of the columns
# using the apply function.
rows = ['POPESTIMATE2010', 'POPESTIMATE2011', 'POPESTIMATE2012', 'POPESTIMATE2013','POPESTIMATE2014',
'POPESTIMATE2015']
# Now we'll just apply this across the dataframe with a lambda
df.apply(lambda x: np.max(x[rows]), axis=1).head()
# If you don't remember lambdas just pause the video for a moment and look up the syntax. A lambda is just an
# unnamed function in python, in this case it takes a single parameter, x, and returns a single value, in this
# case the maximum over all columns associated with row x.
# The beauty of the apply function is that it allows flexibility in doing whatever manipulation that you
# desire, as the function you pass into apply can be any customized however you want. Let's say we want to
# divide the states into four categories: Northeast, Midwest, South, and West We can write a customized
# function that returns the region based on the state the state regions information is obtained from Wikipedia
def get_state_region(x):
northeast = ['Connecticut', 'Maine', 'Massachusetts', 'New Hampshire',
'Rhode Island','Vermont','New York','New Jersey','Pennsylvania']
midwest = ['Illinois','Indiana','Michigan','Ohio','Wisconsin','Iowa',
'Kansas','Minnesota','Missouri','Nebraska','North Dakota',
'South Dakota']
south = ['Delaware','Florida','Georgia','Maryland','North Carolina',
'South Carolina','Virginia','District of Columbia','West Virginia',
'Alabama','Kentucky','Mississippi','Tennessee','Arkansas',
'Louisiana','Oklahoma','Texas']
west = ['Arizona','Colorado','Idaho','Montana','Nevada','New Mexico','Utah',
'Wyoming','Alaska','California','Hawaii','Oregon','Washington']
if x in northeast:
return "Northeast"
elif x in midwest:
return "Midwest"
elif x in south:
return "South"
else:
return "West"
# Now we have the customized function, let's say we want to create a new column called Region, which shows the
# state's region, we can use the customized function and the apply function to do so. The customized function
# is supposed to work on the state name column STNAME. So we will set the apply function on the state name
# column and pass the customized function into the apply function
df['state_region'] = df['STNAME'].apply(lambda x: get_state_region(x))
# Now let's see the results
df[['STNAME','state_region']].head()
```
So there are a couple of Pandas idioms. But I think there's many more, and I haven't talked about them here.
So here's an unofficial assignment for you. Go look at some of the top ranked questions on pandas on Stack
Overflow, and look at how some of the more experienced authors, answer those questions. Do you see any
interesting patterns? Feel free to share them with myself and others in the class.
| true |
code
| 0.561155 | null | null | null | null |
|
<center>
<img src="../../img/ods_stickers.jpg">
## Открытый курс по машинному обучению
<center>Автор материала: Ефремова Дина (@ldinka).
# <center>Исследование возможностей BigARTM</center>
## <center>Тематическое моделирование с помощью BigARTM</center>
#### Интро
BigARTM — библиотека, предназначенная для тематической категоризации текстов; делает разбиение на темы без «учителя».
Я собираюсь использовать эту библиотеку для собственных нужд в будущем, но так как она не предназначена для обучения с учителем, решила, что для начала ее стоит протестировать на какой-нибудь уже размеченной выборке. Для этих целей был использован датасет "20 news groups".
Идея экперимента такова:
- делим выборку на обучающую и тестовую;
- обучаем модель на обучающей выборке;
- «подгоняем» выделенные темы под действительные;
- смотрим, насколько хорошо прошло разбиение;
- тестируем модель на тестовой выборке.
#### Поехали!
**Внимание!** Данный проект был реализован с помощью Python 3.6 и BigARTM 0.9.0. Методы, рассмотренные здесь, могут отличаться от методов в других версиях библиотеки.
<img src="../../img/bigartm_logo.png"/>
### <font color="lightgrey">Не</font>множко теории
У нас есть словарь терминов $W = \{w \in W\}$, который представляет из себя мешок слов, биграмм или n-грамм;
Есть коллекция документов $D = \{d \in D\}$, где $d \subset W$;
Есть известное множество тем $T = \{t \in T\}$;
$n_{dw}$ — сколько раз термин $w$ встретился в документе $d$;
$n_{d}$ — длина документа $d$.
Мы считаем, что существует матрица $\Phi$ распределения терминов $w$ в темах $t$: (фи) $\Phi = (\phi_{wt})$
и матрица распределения тем $t$ в документах $d$: (тета) $\Theta = (\theta_{td})$,
переумножение которых дает нам тематическую модель, или, другими словами, представление наблюдаемого условного распределения $p(w|d)$ терминов $w$ в документах $d$ коллекции $D$:
<center>$\large p(w|d) = \Phi \Theta$</center>
<center>$$\large p(w|d) = \sum_{t \in T} \phi_{wt} \theta_{td}$$</center>
где $\phi_{wt} = p(w|t)$ — вероятности терминов $w$ в каждой теме $t$
и $\theta_{td} = p(t|d)$ — вероятности тем $t$ в каждом документе $d$.
<img src="../../img/phi_theta.png"/>
Нам известны наблюдаемые частоты терминов в документах, это:
<center>$ \large \hat{p}(w|d) = \frac {n_{dw}} {n_{d}} $</center>
Таким образом, наша задача тематического моделирования становится задачей стохастического матричного разложения матрицы $\hat{p}(w|d)$ на стохастические матрицы $\Phi$ и $\Theta$.
Напомню, что матрица является стохастической, если каждый ее столбец представляет дискретное распределение вероятностей, сумма значений каждого столбца равна 1.
Воспользовавшись принципом максимального правдоподобия, т. е. максимизируя логарифм правдоподобия, мы получим:
<center>$
\begin{cases}
\sum_{d \in D} \sum_{w \in d} n_{dw} \ln \sum_{t \in T} \phi_{wt} \theta_{td} \rightarrow \max\limits_{\Phi,\Theta};\\
\sum_{w \in W} \phi_{wt} = 1, \qquad \phi_{wt}\geq0;\\
\sum_{t \in T} \theta_{td} = 1, \quad\quad\;\; \theta_{td}\geq0.
\end{cases}
$</center>
Чтобы из множества решений выбрать наиболее подходящее, введем критерий регуляризации $R(\Phi, \Theta)$:
<center>$
\begin{cases}
\sum_{d \in D} \sum_{w \in d} n_{dw} \ln \sum_{t \in T} \phi_{wt} \theta_{td} + R(\Phi, \Theta) \rightarrow \max\limits_{\Phi,\Theta};\\
\sum_{w \in W} \phi_{wt} = 1, \qquad \phi_{wt}\geq0;\\
\sum_{t \in T} \theta_{td} = 1, \quad\quad\;\; \theta_{td}\geq0.
\end{cases}
$</center>
Два наиболее известных частных случая этой системы уравнений:
- **PLSA**, вероятностный латентный семантический анализ, когда $R(\Phi, \Theta) = 0$
- **LDA**, латентное размещение Дирихле:
$$R(\Phi, \Theta) = \sum_{t,w} (\beta_{w} - 1) \ln \phi_{wt} + \sum_{d,t} (\alpha_{t} - 1) \ln \theta_{td} $$
где $\beta_{w} > 0$, $\alpha_{t} > 0$ — параметры регуляризатора.
Однако оказывается запас неединственности решения настолько большой, что на модель можно накладывать сразу несколько ограничений, такой подход называется **ARTM**, или аддитивной регуляризацией тематических моделей:
<center>$
\begin{cases}
\sum_{d,w} n_{dw} \ln \sum_{t} \phi_{wt} \theta_{td} + \sum_{i=1}^k \tau_{i} R_{i}(\Phi, \Theta) \rightarrow \max\limits_{\Phi,\Theta};\\
\sum_{w \in W} \phi_{wt} = 1, \qquad \phi_{wt}\geq0;\\
\sum_{t \in T} \theta_{td} = 1, \quad\quad\;\; \theta_{td}\geq0.
\end{cases}
$</center>
где $\tau_{i}$ — коэффициенты регуляризации.
Теперь давайте познакомимся с библиотекой BigARTM и разберем еще некоторые аспекты тематического моделирования на ходу.
Если Вас очень сильно заинтересовала теоретическая часть категоризации текстов и тематического моделирования, рекомендую посмотреть видеолекции из курса Яндекса на Coursera «Поиск структуры в данных» четвертой недели: <a href="https://www.coursera.org/learn/unsupervised-learning/home/week/4">Тематическое моделирование</a>.
### BigARTM
#### Установка
Естественно, для начала работы с библиотекой ее надо установить. Вот несколько видео, которые рассказывают, как это сделать в зависимости от вашей операционной системы:
- <a href="https://www.coursera.org/learn/unsupervised-learning/lecture/qmsFm/ustanovka-bigartm-v-windows">Установка BigARTM в Windows</a>
- <a href="https://www.coursera.org/learn/unsupervised-learning/lecture/zPyO0/ustanovka-bigartm-v-linux-mint">Установка BigARTM в Linux</a>
- <a href="https://www.coursera.org/learn/unsupervised-learning/lecture/nuIhL/ustanovka-bigartm-v-mac-os-x">Установка BigARTM в Mac OS X</a>
Либо можно воспользоваться инструкцией с официального сайта, которая, скорее всего, будет гораздо актуальнее: <a href="https://bigartm.readthedocs.io/en/stable/installation/index.html">здесь</a>. Там же указано, как можно установить BigARTM в качестве <a href="https://bigartm.readthedocs.io/en/stable/installation/docker.html">Docker-контейнера</a>.
#### Использование BigARTM
```
import artm
import re
import numpy as np
import seaborn as sns; sns.set()
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.preprocessing import normalize
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib import pyplot as plt
%matplotlib inline
artm.version()
```
Скачаем датасет ***the 20 news groups*** с заранее известным количеством категорий новостей:
```
from sklearn.datasets import fetch_20newsgroups
newsgroups = fetch_20newsgroups('../../data/news_data')
newsgroups['target_names']
```
Приведем данные к формату *Vowpal Wabbit*. Так как BigARTM не рассчитан на обучение с учителем, то мы поступим следующим образом:
- обучим модель на всем корпусе текстов;
- выделим ключевые слова тем и по ним определим, к какой теме они скорее всего относятся;
- сравним наши полученные результаты разбиения с истинными значенями.
```
TEXT_FIELD = "text"
def to_vw_format(document, label=None):
return str(label or '0') + ' |' + TEXT_FIELD + ' ' + ' '.join(re.findall('\w{3,}', document.lower())) + '\n'
all_documents = newsgroups['data']
all_targets = newsgroups['target']
len(newsgroups['target'])
train_documents, test_documents, train_labels, test_labels = \
train_test_split(all_documents, all_targets, random_state=7)
with open('../../data/news_data/20news_train_mult.vw', 'w') as vw_train_data:
for text, target in zip(train_documents, train_labels):
vw_train_data.write(to_vw_format(text, target))
with open('../../data/news_data/20news_test_mult.vw', 'w') as vw_test_data:
for text in test_documents:
vw_test_data.write(to_vw_format(text))
```
Загрузим данные в необходимый для BigARTM формат:
```
batch_vectorizer = artm.BatchVectorizer(data_path="../../data/news_data/20news_train_mult.vw",
data_format="vowpal_wabbit",
target_folder="news_batches")
```
Данные в BigARTM загружаются порционно, укажем в
- *data_path* путь к обучающей выборке,
- *data_format* — формат наших данных, может быть:
* *bow_n_wd* — это вектор $n_{wd}$ в виду массива *numpy.ndarray*, также необходимо передать соответствующий словарь терминов, где ключ — это индекс вектора *numpy.ndarray* $n_{wd}$, а значение — соответствующий токен.
```python
batch_vectorizer = artm.BatchVectorizer(data_format='bow_n_wd',
n_wd=n_wd,
vocabulary=vocabulary)
```
* *vowpal_wabbit* — формат Vowpal Wabbit;
* *bow_uci* — UCI формат (например, с *vocab.my_collection.txt* и *docword.my_collection.txt* файлами):
```python
batch_vectorizer = artm.BatchVectorizer(data_path='',
data_format='bow_uci',
collection_name='my_collection',
target_folder='my_collection_batches')
```
* *batches* — данные, уже сконверченные в батчи с помощью BigARTM;
- *target_folder* — путь для сохранения батчей.
Пока это все параметры, что нам нужны для загрузки наших данных.
После того, как BigARTM создал батчи из данных, можно использовать их для загрузки:
```
batch_vectorizer = artm.BatchVectorizer(data_path="news_batches", data_format='batches')
```
Инициируем модель с известным нам количеством тем. Количество тем — это гиперпараметр, поэтому если он заранее нам неизвестен, то его необходимо настраивать, т. е. брать такое количество тем, при котором разбиение кажется наиболее удачным.
**Важно!** У нас 20 предметных тем, однако некоторые из них довольно узкоспециализированны и смежны, как например 'comp.os.ms-windows.misc' и 'comp.windows.x', или 'comp.sys.ibm.pc.hardware' и 'comp.sys.mac.hardware', тогда как другие размыты и всеобъемлющи: talk.politics.misc' и 'talk.religion.misc'.
Скорее всего, нам не удастся в чистом виде выделить все 20 тем — некоторые из них окажутся слитными, а другие наоборот раздробятся на более мелкие. Поэтому мы попробуем построить 40 «предметных» тем и одну фоновую. Чем больше вы будем строить категорий, тем лучше мы сможем подстроиться под данные, однако это довольно трудоемкое занятие сидеть потом и распределять в получившиеся темы по реальным категориям (<strike>я правда очень-очень задолбалась!</strike>).
Зачем нужны фоновые темы? Дело в том, что наличие общей лексики в темах приводит к плохой ее интерпретируемости. Выделив общую лексику в отдельную тему, мы сильно снизим ее количество в предметных темах, таким образом оставив там лексическое ядро, т. е. ключевые слова, которые данную тему характеризуют. Также этим преобразованием мы снизим коррелированность тем, они станут более независимыми и различимыми.
```
T = 41
model_artm = artm.ARTM(num_topics=T,
topic_names=[str(i) for i in range(T)],
class_ids={TEXT_FIELD:1},
num_document_passes=1,
reuse_theta=True,
cache_theta=True,
seed=4)
```
Передаем в модель следующие параметры:
- *num_topics* — количество тем;
- *topic_names* — названия тем;
- *class_ids* — название модальности и ее вес. Дело в том, что кроме самих текстов, в данных может содержаться такая информация, как автор, изображения, ссылки на другие документы и т. д., по которым также можно обучать модель;
- *num_document_passes* — количество проходов при обучении модели;
- *reuse_theta* — переиспользовать ли матрицу $\Theta$ с предыдущей итерации;
- *cache_theta* — сохранить ли матрицу $\Theta$ в модели, чтобы в дальнейшем ее использовать.
Далее необходимо создать словарь; передадим ему какое-нибудь название, которое будем использовать в будущем для работы с этим словарем.
```
DICTIONARY_NAME = 'dictionary'
dictionary = artm.Dictionary(DICTIONARY_NAME)
dictionary.gather(batch_vectorizer.data_path)
```
Инициализируем модель с тем именем словаря, что мы передали выше, можно зафиксировать *random seed* для вопроизводимости результатов:
```
np.random.seed(1)
model_artm.initialize(DICTIONARY_NAME)
```
Добавим к модели несколько метрик:
- перплексию (*PerplexityScore*), чтобы индентифицировать сходимость модели
* Перплексия — это известная в вычислительной лингвистике мера качества модели языка. Можно сказать, что это мера неопределенности или различности слов в тексте.
- специальный *score* ключевых слов (*TopTokensScore*), чтобы в дальнейшем мы могли идентифицировать по ним наши тематики;
- разреженность матрицы $\Phi$ (*SparsityPhiScore*);
- разреженность матрицы $\Theta$ (*SparsityThetaScore*).
```
model_artm.scores.add(artm.PerplexityScore(name='perplexity_score',
dictionary=DICTIONARY_NAME))
model_artm.scores.add(artm.SparsityPhiScore(name='sparsity_phi_score', class_id="text"))
model_artm.scores.add(artm.SparsityThetaScore(name='sparsity_theta_score'))
model_artm.scores.add(artm.TopTokensScore(name="top_words", num_tokens=15, class_id=TEXT_FIELD))
```
Следующая операция *fit_offline* займет некоторое время, мы будем обучать модель в режиме *offline* в 40 проходов. Количество проходов влияет на сходимость модели: чем их больше, тем лучше сходится модель.
```
%%time
model_artm.fit_offline(batch_vectorizer=batch_vectorizer, num_collection_passes=40)
```
Построим график сходимости модели и увидим, что модель сходится довольно быстро:
```
plt.plot(model_artm.score_tracker["perplexity_score"].value);
```
Выведем значения разреженности матриц:
```
print('Phi', model_artm.score_tracker["sparsity_phi_score"].last_value)
print('Theta', model_artm.score_tracker["sparsity_theta_score"].last_value)
```
После того, как модель сошлась, добавим к ней регуляризаторы. Для начала сглаживающий регуляризатор — это *SmoothSparsePhiRegularizer* с большим положительным коэффициентом $\tau$, который нужно применить только к фоновой теме, чтобы выделить в нее как можно больше общей лексики. Пусть тема с последним индексом будет фоновой, передадим в *topic_names* этот индекс:
```
model_artm.regularizers.add(artm.SmoothSparsePhiRegularizer(name='SparsePhi',
tau=1e5,
dictionary=dictionary,
class_ids=TEXT_FIELD,
topic_names=str(T-1)))
```
Дообучим модель, сделав 20 проходов по ней с новым регуляризатором:
```
%%time
model_artm.fit_offline(batch_vectorizer=batch_vectorizer, num_collection_passes=20)
```
Выведем значения разреженности матриц, заметим, что значение для $\Theta$ немного увеличилось:
```
print('Phi', model_artm.score_tracker["sparsity_phi_score"].last_value)
print('Theta', model_artm.score_tracker["sparsity_theta_score"].last_value)
```
Теперь добавим к модели разреживающий регуляризатор, это тот же *SmoothSparsePhiRegularizer* резуляризатор, только с отрицательным значением $\tau$ и примененный ко всем предметным темам:
```
model_artm.regularizers.add(artm.SmoothSparsePhiRegularizer(name='SparsePhi2',
tau=-5e5,
dictionary=dictionary,
class_ids=TEXT_FIELD,
topic_names=[str(i) for i in range(T-1)]),
overwrite=True)
%%time
model_artm.fit_offline(batch_vectorizer=batch_vectorizer, num_collection_passes=20)
```
Видим, что значения разреженности увеличились еще больше:
```
print(model_artm.score_tracker["sparsity_phi_score"].last_value)
print(model_artm.score_tracker["sparsity_theta_score"].last_value)
```
Посмотрим, сколько категорий-строк матрицы $\Theta$ после регуляризации осталось, т. е. не занулилось/выродилось. И это одна категория:
```
len(model_artm.score_tracker["top_words"].last_tokens.keys())
```
Теперь выведем ключевые слова тем, чтобы определить, каким образом прошло разбиение, и сделать соответствие с нашим начальным списком тем:
```
for topic_name in model_artm.score_tracker["top_words"].last_tokens.keys():
tokens = model_artm.score_tracker["top_words"].last_tokens
res_str = topic_name + ': ' + ', '.join(tokens[topic_name])
print(res_str)
```
Далее мы будем подгонять разбиение под действительные темы с помощью *confusion matrix*.
```
target_dict = {
'alt.atheism': 0,
'comp.graphics': 1,
'comp.os.ms-windows.misc': 2,
'comp.sys.ibm.pc.hardware': 3,
'comp.sys.mac.hardware': 4,
'comp.windows.x': 5,
'misc.forsale': 6,
'rec.autos': 7,
'rec.motorcycles': 8,
'rec.sport.baseball': 9,
'rec.sport.hockey': 10,
'sci.crypt': 11,
'sci.electronics': 12,
'sci.med': 13,
'sci.space': 14,
'soc.religion.christian': 15,
'talk.politics.guns': 16,
'talk.politics.mideast': 17,
'talk.politics.misc': 18,
'talk.religion.misc': 19
}
mixed = [
'comp.sys.ibm.pc.hardware',
'talk.politics.mideast',
'sci.electronics',
'rec.sport.hockey',
'sci.med',
'rec.motorcycles',
'comp.graphics',
'rec.sport.hockey',
'talk.politics.mideast',
'talk.religion.misc',
'rec.autos',
'comp.graphics',
'sci.space',
'soc.religion.christian',
'comp.os.ms-windows.misc',
'sci.crypt',
'comp.windows.x',
'misc.forsale',
'sci.space',
'sci.crypt',
'talk.religion.misc',
'alt.atheism',
'comp.os.ms-windows.misc',
'alt.atheism',
'sci.med',
'comp.os.ms-windows.misc',
'soc.religion.christian',
'talk.politics.guns',
'rec.autos',
'rec.autos',
'talk.politics.mideast',
'rec.sport.baseball',
'talk.religion.misc',
'talk.politics.misc',
'rec.sport.hockey',
'comp.sys.mac.hardware',
'misc.forsale',
'sci.space',
'talk.politics.guns',
'rec.autos',
'-'
]
```
Построим небольшой отчет о правильности нашего разбиения:
```
theta_train = model_artm.get_theta()
model_labels = []
keys = np.sort([int(i) for i in theta_train.keys()])
for i in keys:
max_val = 0
max_idx = 0
for j in theta_train[i].keys():
if j == str(T-1):
continue
if theta_train[i][j] > max_val:
max_val = theta_train[i][j]
max_idx = j
topic = mixed[int(max_idx)]
if topic == '-':
print(i, '-')
label = target_dict[topic]
model_labels.append(label)
print(classification_report(train_labels, model_labels))
print(classification_report(train_labels, model_labels))
mat = confusion_matrix(train_labels, model_labels)
sns.heatmap(mat.T, annot=True, fmt='d', cbar=False)
plt.xlabel('True label')
plt.ylabel('Predicted label');
accuracy_score(train_labels, model_labels)
```
Нам удалось добиться 80% *accuracy*. По матрице ответов мы видим, что для модели темы *comp.sys.ibm.pc.hardware* и *comp.sys.mac.hardware* практически не различимы (<strike>честно говоря, для меня тоже</strike>), в остальном все более или менее прилично.
Проверим модель на тестовой выборке:
```
batch_vectorizer_test = artm.BatchVectorizer(data_path="../../data/news_data/20news_test_mult.vw",
data_format="vowpal_wabbit",
target_folder="news_batches_test")
theta_test = model_artm.transform(batch_vectorizer_test)
test_score = []
for i in range(len(theta_test.keys())):
max_val = 0
max_idx = 0
for j in theta_test[i].keys():
if j == str(T-1):
continue
if theta_test[i][j] > max_val:
max_val = theta_test[i][j]
max_idx = j
topic = mixed[int(max_idx)]
label = target_dict[topic]
test_score.append(label)
print(classification_report(test_labels, test_score))
mat = confusion_matrix(test_labels, test_score)
sns.heatmap(mat.T, annot=True, fmt='d', cbar=False)
plt.xlabel('True label')
plt.ylabel('Predicted label');
accuracy_score(test_labels, test_score)
```
Итого почти 77%, незначительно хуже, чем на обучающей.
**Вывод:** безумно много времени пришлось потратить на подгонку категорий к реальным темам, но в итоге я осталась довольна результатом. Такие смежные темы, как *alt.atheism*/*soc.religion.christian*/*talk.religion.misc* или *talk.politics.guns*/*talk.politics.mideast*/*talk.politics.misc* разделились вполне неплохо. Думаю, что я все-таки попробую использовать BigARTM в будущем для своих <strike>корыстных</strike> целей.
| true |
code
| 0.417212 | null | null | null | null |
|
```
# -*- coding: utf-8 -*-
# This work is part of the Core Imaging Library (CIL) developed by CCPi
# (Collaborative Computational Project in Tomographic Imaging), with
# substantial contributions by UKRI-STFC and University of Manchester.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# Copyright 2019 UKRI-STFC, The University of Manchester
# Authored by: Evangelos Papoutsellis (UKRI-STFC)
```
<h1><center>Primal Dual Hybrid Gradient Algorithm </center></h1>
In this demo, we learn how to use the **Primal Dual Hybrid Algorithm (PDHG)** introduced by [Chambolle & Pock](https://hal.archives-ouvertes.fr/hal-00490826/document) for Tomography Reconstruction. We will solve the following minimisation problem under three different regularisation terms, i.e.,
* $\|\cdot\|_{1}$ or
* Tikhonov regularisation or
* with $L=\nabla$ and Total variation:
<a id='all_reg'></a>
$$\begin{equation}
u^{*} =\underset{u}{\operatorname{argmin}} \frac{1}{2} \| \mathcal{A} u - g\|^{2} +
\underbrace{
\begin{cases}
\alpha\,\|u\|_{1}, & \\[10pt]
\alpha\,\|\nabla u\|_{2}^{2}, & \\[10pt]
\alpha\,\mathrm{TV}(u) + \mathbb{I}_{\{u\geq 0\}}(u).
\end{cases}}_{Regularisers}
\tag{1}
\end{equation}$$
where,
1. $g$ is the Acqusisition data obtained from the detector.
1. $\mathcal{A}$ is the projection operator ( _Radon transform_ ) that maps from an image-space to an acquisition space, i.e., $\mathcal{A} : \mathbb{X} \rightarrow \mathbb{Y}, $ where $\mathbb{X}$ is an __ImageGeometry__ and $\mathbb{Y}$ is an __AcquisitionGeometry__.
1. $\alpha$: regularising parameter that measures the trade-off between the fidelity and the regulariser terms.
1. The total variation (isotropic) is defined as $$\mathrm{TV}(u) = \|\nabla u \|_{2,1} = \sum \sqrt{ (\partial_{y}u)^{2} + (\partial_{x}u)^{2} }$$
1. $\mathbb{I}_{\{u\geq 0\}}(u) : =
\begin{cases}
0, & \mbox{ if } u\geq 0\\
\infty , & \mbox{ otherwise}
\,
\end{cases}
$, $\quad$ a non-negativity constraint for the minimiser $u$.
<h2><center><u> Learning objectives </u></center></h2>
- Load the data using the CIL reader: `TXRMDataReader`.
- Preprocess the data using the CIL processors: `Binner`, `TransmissionAbsorptionConverter`.
- Run FBP and SIRT reconstructions.
- Setup PDHG for 3 different regularisers: $L^{1}$, Tikhonov and Total variation.
<!---
1. Brief intro for non-smooth minimisation problems using PDHG algorithm.
1. Setup and run PDHG with (__non-smooth__) $L^{1}$ norm regulariser. __(No BlockFramework)__
1. Use __BlockFunction__ and __Block Framework__ to setup PDHG for Tikhonov and TV reconstructions.
1. Run Total variation reconstruction with different regularising parameters and compared with FBP and SIRT reconstructions.
At the end of this demo, we will be able to reproduce all the reconstructions presented in the figure below. One can observe that the __Tikhonov regularisation__ with $L = \nabla$ was able to remove the noise but could not preserve the edges. However, this can be achieved with the the total variation reconstruction.
<img src="CIL-Demos/Notebooks/images/recon_all_tomo.jpeg" width="1500"/>
--->
<!-- <h2><center><u> Prerequisites </u></center></h2>
- AcquisitionData, AcquisitionGeometry, AstraProjectorSimple.
- BlockOperator, Gradient.
- FBP, SIRT, CGLS, Tikhonov. -->
We first import all the necessary libraries for this notebook.
<!---
In order to use the PDHG algorithm for the problem above, we need to express our minimisation problem into the following form:
<a id='PDHG_form'></a>
$$\min_{u} \mathcal{F}(K u) + \mathcal{G}(u)$$
where we assume that:
1. $\mathcal{F}$, $\mathcal{G}$ are __convex__ functionals
- $\mathcal{F}: Y \rightarrow \mathbb{R}$
- $\mathcal{G}: X \rightarrow \mathbb{R}$
2. $K$ is a continuous linear operator acting from a space X to another space Y :
$$K : X \rightarrow Y \quad $$
with operator norm defined as $$\| K \| = \max\{ \|K x\|_{Y} : \|x\|_{X}\leq 1 \}.$$
**Note**: The Gradient operator has $\|\nabla\| = \sqrt{8} $ and for the projection operator we use the [Power Method](https://en.wikipedia.org/wiki/Power_iteration) to approximate the greatest eigenvalue of $K$.
--->
```
# Import libraries
from cil.framework import BlockDataContainer
from cil.optimisation.functions import L2NormSquared, L1Norm, BlockFunction, MixedL21Norm, IndicatorBox, TotalVariation
from cil.optimisation.operators import GradientOperator, BlockOperator
from cil.optimisation.algorithms import PDHG, SIRT
from cil.plugins.astra.operators import ProjectionOperator
from cil.plugins.astra.processors import FBP
from cil.plugins.ccpi_regularisation.functions import FGP_TV
from cil.utilities.display import show2D, show_geometry
from cil.utilities.jupyter import islicer
from cil.io import TXRMDataReader
from cil.processors import Binner, TransmissionAbsorptionConverter, Slicer
import matplotlib.pyplot as plt
import numpy as np
import os
```
# Data information
In this demo, we use the **Walnut** found in [Jørgensen_et_all](https://zenodo.org/record/4822516#.YLXyAJMzZp8). In total, there are 6 individual micro Computed Tomography datasets in the native Zeiss TXRM/TXM format. The six datasets were acquired at the 3D Imaging Center at Technical University of Denmark in 2014 (HDTomo3D in 2016) as part of the ERC-funded project High-Definition Tomography (HDTomo) headed by Prof. Per Christian Hansen.
# Load walnut data
```
reader = TXRMDataReader()
pathname = os.path.abspath("/mnt/materials/SIRF/Fully3D/CIL/Walnut/valnut_2014-03-21_643_28/tomo-A")
data_name = "valnut_tomo-A.txrm"
filename = os.path.join(pathname,data_name )
reader.set_up(file_name=filename, angle_unit='radian')
data3D = reader.read()
# reorder data to match default order for Astra/Tigre operator
data3D.reorder('astra')
# Get Image and Acquisition geometries
ag3D = data3D.geometry
ig3D = ag3D.get_ImageGeometry()
```
## Acquisition and Image geometry information
```
print(ag3D)
print(ig3D)
```
# Show Acquisition geometry and full 3D sinogram.
```
show_geometry(ag3D)
show2D(data3D, slice_list = [('vertical',512), ('angle',800), ('horizontal',512)], cmap="inferno", num_cols=3, size=(15,15))
```
# Slice through projections
```
islicer(data3D, direction=1, cmap="inferno")
```
## For demonstration purposes, we extract the central slice and select only 160 angles from the total 1601 angles.
1. We use the `Slicer` processor with step size of 10.
1. We use the `Binner` processor to crop and bin the acquisition data in order to reduce the field of view.
1. We use the `TransmissionAbsorptionConverter` to convert from transmission measurements to absorption based on the Beer-Lambert law.
**Note:** To avoid circular artifacts in the reconstruction space, we subtract the mean value of a background Region of interest (ROI), i.e., ROI that does not contain the walnut.
```
# Extract vertical slice
data2D = data3D.subset(vertical='centre')
# Select every 10 angles
sliced_data = Slicer(roi={'angle':(0,1601,10)})(data2D)
# Reduce background regions
binned_data = Binner(roi={'horizontal':(120,-120,2)})(sliced_data)
# Create absorption data
absorption_data = TransmissionAbsorptionConverter()(binned_data)
# Remove circular artifacts
absorption_data -= np.mean(absorption_data.as_array()[80:100,0:30])
# Get Image and Acquisition geometries for one slice
ag2D = absorption_data.geometry
ag2D.set_angles(ag2D.angles, initial_angle=0.2, angle_unit='radian')
ig2D = ag2D.get_ImageGeometry()
print(" Acquisition Geometry 2D: {} with labels {}".format(ag2D.shape, ag2D.dimension_labels))
print(" Image Geometry 2D: {} with labels {}".format(ig2D.shape, ig2D.dimension_labels))
```
## Define Projection Operator
We can define our projection operator using our __astra__ __plugin__ that wraps the Astra-Toolbox library.
```
A = ProjectionOperator(ig2D, ag2D, device = "gpu")
```
## FBP and SIRT reconstuctions
Now, let's perform simple reconstructions using the **Filtered Back Projection (FBP)** and **Simultaneous Iterative Reconstruction Technique [SIRT](../appendix.ipynb/#SIRT) .**
Recall, for FBP we type
```python
fbp_recon = FBP(ig, ag, device = 'gpu')(absorption_data)
```
For SIRT, we type
```python
x_init = ig.allocate()
sirt = SIRT(initial = x_init, operator = A, data=absorption_data,
max_iteration = 50, update_objective_interval=10)
sirt.run(verbose=1)
sirt_recon = sirt.solution
```
**Note**: In SIRT, a non-negative constraint can be used with
```python
constraint=IndicatorBox(lower=0)
```
## Exercise 1: Run FBP and SIRT reconstructions
Use the code blocks described above and run FBP (`fbp_recon`) and SIRT (`sirt_recon`) reconstructions.
**Note**: To display the results, use
```python
show2D([fbp_recon,sirt_recon], title = ['FBP reconstruction','SIRT reconstruction'], cmap = 'inferno')
```
```
# Setup and run the FBP algorithm
fbp_recon = FBP(..., ..., device = 'gpu')(absorption_data)
# Setup and run the SIRT algorithm, with non-negative constraint
x_init = ig2D.allocate()
sirt = SIRT(initial = x_init,
operator = ...,
data= ...,
constraint = ...,
max_iteration = 300,
update_objective_interval=100)
sirt.run(verbose=1)
sirt_recon = sirt.solution
# Show reconstructions
show2D([fbp_recon,sirt_recon],
title = ['FBP reconstruction','SIRT reconstruction'],
cmap = 'inferno', fix_range=(0,0.05))
```
## Exercise 1: Solution
```
# Setup and run the FBP algorithm
fbp_recon = FBP(ig2D, ag2D, device = 'gpu')(absorption_data)
# Setup and run the SIRT algorithm, with non-negative constraint
x_init = ig2D.allocate()
sirt = SIRT(initial = x_init,
operator = A ,
data = absorption_data,
constraint = IndicatorBox(lower=0),
max_iteration = 300,
update_objective_interval=100)
sirt.run(verbose=1)
sirt_recon = sirt.solution
# Show reconstructions
show2D([fbp_recon,sirt_recon],
title = ['FBP reconstruction','SIRT reconstruction'],
cmap = 'inferno', fix_range=(0,0.05))
```
<h2><center> Why PDHG? </center></h2>
In the previous notebook, we presented the __Tikhonov regularisation__ for tomography reconstruction, i.e.,
<a id='Tikhonov'></a>
$$\begin{equation}
u^{*} =\underset{u}{\operatorname{argmin}} \frac{1}{2} \| \mathcal{A} u - g\|^{2} + \alpha\|L u\|^{2}_{2}
\tag{Tikhonov}
\end{equation}$$
where we can use either the `GradientOperator` ($L = \nabla) $ or the `IdentityOperator` ($L = \mathbb{I}$). Due to the $\|\cdot\|^{2}_{2}$ terms, one can observe that the above objective function is differentiable. As shown in the previous notebook, we can use the standard `GradientDescent` algorithm namely
```python
f1 = LeastSquares(A, absorption_data)
D = GradientOperator(ig2D)
f2 = OperatorCompositionFunction(L2NormSquared(),D)
f = f1 + alpha_tikhonov*f2
gd = GD(x_init=ig2D.allocate(), objective_function=f, step_size=None,
max_iteration=1000, update_objective_interval = 10)
gd.run(100, verbose=1)
```
However, this is not always the case. Consider for example an $L^{1}$ norm for the fidelity, i.e., $\|\mathcal{A} u - g\|_{1}$ or an $L^{1}$ norm of the regulariser i.e., $\|u\|_{1}$ or a non-negativity constraint $\mathbb{I}_{\{u>0\}}(u)$. An alternative is to use **Proximal Gradient Methods**, discused in the previous notebook, e.g., the `FISTA` algorithm, where we require one of the functions to be differentiable and the other to have a __simple__ proximal method, i.e., "easy to solve". For more information, we refer to [Parikh_Boyd](https://web.stanford.edu/~boyd/papers/pdf/prox_algs.pdf#page=30).
Using the __PDHG algorithm__, we can solve minimisation problems where the objective is not differentiable, and the only required assumption is convexity with __simple__ proximal problems.
<h2><center> $L^{1}$ regularisation </center></h2>
Let $L=$`IdentityOperator` in [Tikhonov regularisation](#Tikhonov) and replace the
$$\alpha^{2}\|L u\|^{2}_{2}\quad\mbox{ with }\quad \alpha\|u\|_{1}, $$
which results to a non-differentiable objective function. Hence, we have
<a id='Lasso'></a>
$$\begin{equation}
u^{*} =\underset{u}{\operatorname{argmin}} \frac{1}{2} \| \mathcal{A} u - g\|^{2} + \alpha\|u\|_{1}
\tag{$L^{2}-L^{1}$}
\end{equation}$$
<h2><center> How to setup and run PDHG? </center></h2>
In order to use the PDHG algorithm for the problem above, we need to express our minimisation problem into the following form:
<a id='PDHG_form'></a>
$$\begin{equation}
\min_{u\in\mathbb{X}} \mathcal{F}(K u) + \mathcal{G}(u)
\label{PDHG_form}
\tag{2}
\end{equation}$$
where we assume that:
1. $\mathcal{F}$, $\mathcal{G}$ are __convex__ functionals:
- $\mathcal{F}: \mathbb{Y} \rightarrow \mathbb{R}$
- $\mathcal{G}: \mathbb{X} \rightarrow \mathbb{R}$
1. $K$ is a continuous linear operator acting from a space $\mathbb{X}$ to another space $\mathbb{Y}$ :
$$K : \mathbb{X} \rightarrow \mathbb{Y} \quad $$
with operator norm defined as $$\| K \| = \max\{ \|K x\|_{\mathbb{Y}} : \|x\|_{\mathbb{X}}\leq 1 \}.$$
We can write the problem [($L^{2}-L^{1})$](#Lasso) into [(2)](#PDHG_form), if we let
1. $K = \mathcal{A} \quad \Longleftrightarrow \quad $ `K = A`
1. $\mathcal{F}: Y \rightarrow \mathbb{R}, \mbox{ with } \mathcal{F}(z) := \frac{1}{2}\| z - g \|^{2}, \quad \Longleftrightarrow \quad$ ` F = 0.5 * L2NormSquared(absorption_data)`
1. $\mathcal{G}: X \rightarrow \mathbb{R}, \mbox{ with } \mathcal{G}(z) := \alpha\|z\|_{1}, \quad \Longleftrightarrow \quad$ ` G = alpha * L1Norm()`
Hence, we can verify that with the above setting we have that [($L^{2}-L^{1})$](#Lasso)$\Rightarrow$[(2)](#PDHG_form) for $x=u$, $$\underset{u}{\operatorname{argmin}} \frac{1}{2}\|\mathcal{A} u - g\|^{2}_{2} + \alpha\|u\|_{1} =
\underset{u}{\operatorname{argmin}} \mathcal{F}(\mathcal{A}u) + \mathcal{G}(u) = \underset{x}{\operatorname{argmin}} \mathcal{F}(Kx) + \mathcal{G}(x) $$
The algorithm is described in the [Appendix](../appendix.ipynb/#PDHG) and for every iteration, we solve two (proximal-type) subproblems, i.e., __primal & dual problems__ where
$\mbox{prox}_{\tau \mathcal{G}}(x)$ and $\mbox{prox}_{\sigma \mathcal{F^{*}}}(x)$ are the **proximal operators** of $\mathcal{G}$ and $\mathcal{F}^{*}$ (convex conjugate of $\mathcal{F}$), i.e.,
$$\begin{equation}
\mbox{prox}_{\lambda \mathcal{F}}(x) = \underset{z}{\operatorname{argmin}} \frac{1}{2}\|z - x \|^{2} + \lambda
\mathcal{F}(z) \end{equation}
$$
One application of the proximal operator is similar to a gradient step but is defined for convex and not necessarily differentiable functions.
To setup and run PDHG in CIL:
```python
pdhg = PDHG(f = F, g = G, operator = K,
max_iterations = 500, update_objective_interval = 100)
pdhg.run(verbose=1)
```
**Note:** To monitor convergence, we use `pdhg.run(verbose=1)` that prints the objective value of the primal problem, or `pdhg.run(verbose=2)` that prints the objective value of the primal and dual problems, as well as the primal dual gap. Nothing is printed with `verbose=0`.
<a id='sigma_tau'></a>
### Define operator $K$, functions $\mathcal{F}$ and $\mathcal{G}$
```
K = A
F = 0.5 * L2NormSquared(b=absorption_data)
alpha = 0.01
G = alpha * L1Norm()
```
### Setup and run PDHG
```
# Setup and run PDHG
pdhg_l1 = PDHG(f = F, g = G, operator = K,
max_iteration = 500,
update_objective_interval = 100)
pdhg_l1.run(verbose=1)
# Show reconstuction and ground truth
show2D([pdhg_l1.solution,fbp_recon], fix_range=(0,0.05), title = ['L1 regularisation', 'FBP'], cmap = 'inferno')
# Plot middle line profile
plt.figure(figsize=(30,8))
plt.rcParams.update({'font.size': 15})
plt.rcParams.update({'lines.linewidth': 5})
plt.plot(fbp_recon.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'FBP')
plt.plot(pdhg_l1.solution.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'L1 regularisation')
plt.legend()
plt.title('Middle Line Profiles')
plt.show()
```
<h2><center> PDHG for Total Variation Regularisation </center></h2>
Now, we continue with the setup of the PDHG algorithm using the Total variation regulariser appeared in [(1)](#all_reg).
Similarly, to the [($L^{2}-L^{1}$)](#Lasso) problem, we need to express [($L^{2}-TV$)](#all_reg) in the general form of [PDHG](#PDHG_form). This can be done using two different formulations:
1. Explicit formulation: All the subproblems in the PDHG algorithm have a closed form solution.
1. Implicit formulation: One of the subproblems in the PDHG algorithm is not solved explicitly but an inner solver is used.
---
<h2><center> ($L^{2}-TV$) with Explicit PDHG </center></h2>
For the setup of the **($L^{2}-TV$) Explicit PDHG**, we let
$$\begin{align}
& f_{1}: \mathbb{Y} \rightarrow \mathbb{R}, \quad f_{1}(z_{1}) = \alpha\,\|z_{1}\|_{2,1}, \mbox{ ( the TV term ) }\\
& f_{2}: \mathbb{X} \rightarrow \mathbb{R}, \quad f_{2}(z_{2}) = \frac{1}{2}\|z_{2} - g\|_{2}^{2}, \mbox{ ( the data-fitting term ). }
\end{align}$$
```python
f1 = alpha * MixedL21Norm()
f2 = 0.5 * L2NormSquared(b=absorption_data)
```
For $z = (z_{1}, z_{2})\in \mathbb{Y}\times \mathbb{X}$, we define a separable function, e.g., [BlockFunction,](../appendix.ipynb/#BlockFunction)
$$\mathcal{F}(z) : = \mathcal{F}(z_{1},z_{2}) = f_{1}(z_{1}) + f_{2}(z_{2})$$
```python
F = BlockFunction(f1, f2)
```
In order to obtain an element $z = (z_{1}, z_{2})\in \mathbb{Y}\times \mathbb{X}$, we need to define a `BlockOperator` $K$, using the two operators involved in [$L^{2}-TV$](#TomoTV), i.e., the `GradientOperator` $\nabla$ and the `ProjectionOperator` $\mathcal{A}$.
$$ \mathcal{K} =
\begin{bmatrix}
\nabla\\
\mathcal{A}
\end{bmatrix}
$$
```python
Grad = GradientOperator(ig)
K = BlockOperator(Grad, A)
```
Finally, we enforce a non-negativity constraint by letting $\mathcal{G} = \mathbb{I}_{\{u>0\}}(u)$ $\Longleftrightarrow$ `G = IndicatorBox(lower=0)`
Again, we can verify that with the above setting we can express our problem into [(2)](#PDHG_form), for $x=u$
$$
\begin{align}
\underset{u}{\operatorname{argmin}}\alpha\|\nabla u\|_{2,1} + \frac{1}{2}\|\mathcal{A} u - g\|^{2}_{2} + \mathbb{I}_{\{u>0\}}(u) = \underset{u}{\operatorname{argmin}} f_{1}(\nabla u) + f_{2}(\mathcal{A}u) + \mathbb{I}_{\{u>0\}}(u) \\ = \underset{u}{\operatorname{argmin}} F(
\begin{bmatrix}
\nabla \\
\mathcal{A}
\end{bmatrix}u) + \mathbb{I}_{\{u>0\}}(u) =
\underset{u}{\operatorname{argmin}} \mathcal{F}(Ku) + \mathcal{G}(u) = \underset{x}{\operatorname{argmin}} \mathcal{F}(Kx) + \mathcal{G}(x)
\end{align}
$$
```
# Define BlockFunction F
alpha_tv = 0.0003
f1 = alpha_tv * MixedL21Norm()
f2 = 0.5 * L2NormSquared(b=absorption_data)
F = BlockFunction(f1, f2)
# Define BlockOperator K
Grad = GradientOperator(ig2D)
K = BlockOperator(Grad, A)
# Define Function G
G = IndicatorBox(lower=0)
# Setup and run PDHG
pdhg_tv_explicit = PDHG(f = F, g = G, operator = K,
max_iteration = 1000,
update_objective_interval = 200)
pdhg_tv_explicit.run(verbose=1)
# Show reconstuction and ground truth
show2D([pdhg_tv_explicit.solution,fbp_recon], fix_range=(0,0.055), title = ['TV regularisation','FBP'], cmap = 'inferno')
# Plot middle line profile
plt.figure(figsize=(30,8))
plt.rcParams.update({'font.size': 15})
plt.rcParams.update({'lines.linewidth': 5})
plt.plot(fbp_recon.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'FBP')
plt.plot(pdhg_tv_explicit.solution .subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'TV regularisation')
plt.legend()
plt.title('Middle Line Profiles')
plt.show()
```
## Speed of PDHG convergence
The PDHG algorithm converges when $\sigma\tau\|K\|^{2}<1$, where the variable $\sigma$, $\tau$ are called the _primal and dual stepsizes_. When we setup the PDHG algorithm, the default values of $\sigma$ and $\tau$ are used:
- $\sigma=1.0$
- $\tau = \frac{1.0}{\sigma\|K\|^{2}}$,
and are not passed as arguments in the setup of PDHG. However, **the speed of the algorithm depends heavily on the choice of these stepsizes.** For the following, we encourage you to use different values, such as:
- $\sigma=\frac{1}{\|K\|}$
- $\tau =\frac{1}{\|K\|}$
where $\|K\|$ is the operator norm of $K$.
```python
normK = K.norm()
sigma = 1./normK
tau = 1./normK
PDHG(f = F, g = G, operator = K, sigma=sigma, tau=tau,
max_iteration = 2000,
update_objective_interval = 500)
```
The operator norm is computed using the [Power Method](https://en.wikipedia.org/wiki/Power_iteration) to approximate the greatest eigenvalue of $K$.
## Exercise 2: Setup and run PDHG algorithm for Tikhonov regularisation
Use exactly the same code as above and replace:
$$f_{1}(z_{1}) = \alpha\,\|z_{1}\|_{2,1} \mbox{ with } f_{1}(z_{1}) = \alpha\,\|z_{1}\|_{2}^{2}.$$
```
# Define BlockFunction F
alpha_tikhonov = 0.05
f1 = ...
F = BlockFunction(f1, f2)
# Setup and run PDHG
pdhg_tikhonov_explicit = PDHG(f = F, g = G, operator = K,
max_iteration = 500,
update_objective_interval = 100)
pdhg_tikhonov_explicit.run(verbose=1)
```
## Exercise 2: Solution
```
# Define BlockFunction F
alpha_tikhonov = 0.05
f1 = alpha_tikhonov * L2NormSquared()
F = BlockFunction(f1, f2)
# Setup and run PDHG
pdhg_tikhonov_explicit = PDHG(f = F, g = G, operator = K,
max_iteration = 1000,
update_objective_interval = 200)
pdhg_tikhonov_explicit.run(verbose=1)
# Show reconstuction and ground truth
show2D([pdhg_tikhonov_explicit.solution,fbp_recon], fix_range=(0,0.055), title = ['Tikhonov regularisation','FBP'], cmap = 'inferno')
# Plot middle line profile
plt.figure(figsize=(30,8))
plt.rcParams.update({'font.size': 15})
plt.rcParams.update({'lines.linewidth': 5})
plt.plot(fbp_recon.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'FBP')
plt.plot(pdhg_tikhonov_explicit.solution .subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'Tikhonov regularisation')
plt.legend()
plt.title('Middle Line Profiles')
plt.show()
```
---
<h2><center> ($L^{2}-TV$) with Implicit PDHG </center></h2>
In the implicit PDHG, one of the proximal subproblems, i.e., $\mathrm{prox}_{\tau\mathcal{F}^{*}}$ or $\mathrm{prox}_{\sigma\mathcal{G}}$ are not solved exactly and an iterative solver is used. For the setup of the **Implicit PDHG**, we let
$$\begin{align}
& \mathcal{F}: \mathbb{Y} \rightarrow \mathbb{R}, \quad \mathcal{F}(z_{1}) = \frac{1}{2}\|z_{1} - g\|_{2}^{2}\\
& \mathcal{G}: \mathbb{X} \rightarrow \mathbb{R}, \quad \mathcal{G}(z_{2}) = \alpha\, \mathrm{TV}(z_{2}) = \|\nabla z_{2}\|_{2,1}
\end{align}$$
For the function $\mathcal{G}$, we can use the `TotalVariation` `Function` class from `CIL`. Alternatively, we can use the `FGP_TV` `Function` class from our `cil.plugins.ccpi_regularisation` that wraps regularisation routines from the [CCPi-Regularisation Toolkit](https://github.com/vais-ral/CCPi-Regularisation-Toolkit). For these functions, the `proximal` method implements an iterative solver, namely the **Fast Gradient Projection (FGP)** algorithm that solves the **dual** problem of
$$\begin{equation}
\mathrm{prox}_{\tau G}(u) = \underset{z}{\operatorname{argmin}} \frac{1}{2} \| u - z\|^{2} + \tau\,\alpha\,\mathrm{TV}(z) + \mathbb{I}_{\{z>0\}}(z),
\end{equation}
$$
for every PDHG iteration. Hence, we need to specify the number of iterations for the FGP algorithm. In addition, we can enforce a non-negativity constraint using `lower=0.0`. For the `FGP_TV` class, we can either use `device=cpu` or `device=gpu` to speed up this inner solver.
```python
G = alpha * FGP_TV(max_iteration=100, nonnegativity = True, device = 'gpu')
G = alpha * TotalVariation(max_iteration=100, lower=0.)
```
## Exercise 3: Setup and run implicit PDHG algorithm with the Total variation regulariser
- Using the TotalVariation class, from CIL. This solves the TV denoising problem (using the FGP algorithm) in CPU.
- Using the FGP_TV class from the CCPi regularisation plugin.
**Note:** In the FGP_TV implementation no pixel size information is included when in the forward and backward of the finite difference operator. Hence, we need to divide our regularisation parameter by the pixel size, e.g., $$\frac{\alpha}{\mathrm{ig2D.voxel\_size\_y}}$$
## $(L^{2}-TV)$ Implicit PDHG: using FGP_TV
```
F = 0.5 * L2NormSquared(b=absorption_data)
G = (alpha_tv/ig2D.voxel_size_y) * ...
K = A
# Setup and run PDHG
pdhg_tv_implicit_regtk = PDHG(f = F, g = G, operator = K,
max_iteration = 1000,
update_objective_interval = 200)
pdhg_tv_implicit_regtk.run(verbose=1)
```
## Exercise 3: Solution
```
F = 0.5 * L2NormSquared(b=absorption_data)
G = (alpha_tv/ig2D.voxel_size_y) * FGP_TV(max_iteration=100, device='gpu')
K = A
# Setup and run PDHG
pdhg_tv_implicit_regtk = PDHG(f = F, g = G, operator = K,
max_iteration = 1000,
update_objective_interval = 200)
pdhg_tv_implicit_regtk.run(verbose=1)
# Show reconstuction and ground truth
show2D([pdhg_tv_implicit_regtk.solution,pdhg_tv_explicit.solution,
(pdhg_tv_explicit.solution-pdhg_tv_implicit_regtk.solution).abs()],
fix_range=[(0,0.055),(0,0.055),(0,1e-3)],
title = ['TV (Implicit CCPi-RegTk)','TV (Explicit)', 'Absolute Difference'],
cmap = 'inferno', num_cols=3)
# Plot middle line profile
plt.figure(figsize=(30,8))
plt.rcParams.update({'font.size': 15})
plt.rcParams.update({'lines.linewidth': 5})
plt.plot(pdhg_tv_explicit.solution.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'TV (explicit)')
plt.plot(pdhg_tv_implicit_regtk.solution.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'TV (implicit)')
plt.legend()
plt.title('Middle Line Profiles')
plt.show()
```
In the above comparison between explicit and implicit TV reconstructions, we observe some differences in the reconstructions and in the middle line profiles. This is due to a) the number of iterations and b) $\sigma, \tau$ values used in both the explicit and implicit setup of the PDHG algorithm. You can try more iterations with different values of $\sigma$ and $\tau$ for both cases in order to be sure that converge to the same solution.
For example, you can use:
* max_iteration = 2000
* $\sigma=\tau=\frac{1}{\|K\|}$
## $(L^{2}-TV)$ Implicit PDHG: using TotalVariation
```
G = alpha_tv * TotalVariation(max_iteration=100, lower=0.)
# Setup and run PDHG
pdhg_tv_implicit_cil = PDHG(f = F, g = G, operator = K,
max_iteration = 500,
update_objective_interval = 100)
pdhg_tv_implicit_cil.run(verbose=1)
# Show reconstuction and ground truth
show2D([pdhg_tv_implicit_regtk.solution,
pdhg_tv_implicit_cil.solution,
(pdhg_tv_implicit_cil.solution-pdhg_tv_implicit_regtk.solution).abs()],
fix_range=[(0,0.055),(0,0.055),(0,1e-3)], num_cols=3,
title = ['TV (CIL)','TV (CCPI-RegTk)', 'Absolute Difference'],
cmap = 'inferno')
# Plot middle line profile
plt.figure(figsize=(30,8))
plt.rcParams.update({'font.size': 15})
plt.rcParams.update({'lines.linewidth': 5})
plt.plot(pdhg_tv_implicit_regtk.solution.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'TV (CCPi-RegTk)')
plt.plot(pdhg_tv_implicit_cil.solution.subset(horizontal_y = int(ig2D.voxel_num_y/2)).as_array(), label = 'TV (CIL)')
plt.legend()
plt.title('Middle Line Profiles')
plt.show()
```
# FBP reconstruction with all the projection angles.
```
binned_data3D = Binner(roi={'horizontal':(120,-120,2)})(data3D)
absorption_data3D = TransmissionAbsorptionConverter()(binned_data3D.subset(vertical=512))
absorption_data3D -= np.mean(absorption_data3D.as_array()[80:100,0:30])
ag3D = absorption_data3D.geometry
ag3D.set_angles(ag3D.angles, initial_angle=0.2, angle_unit='radian')
ig3D = ag3D.get_ImageGeometry()
fbp_recon3D = FBP(ig3D, ag3D)(absorption_data3D)
```
# Show all reconstructions
- FBP (1601 projections)
- FBP (160 projections)
- SIRT (160 projections)
- $L^{1}$ regularisation (160 projections)
- Tikhonov regularisation (160 projections)
- Total variation regularisation (160 projections)
```
show2D([fbp_recon3D,
fbp_recon,
sirt_recon,
pdhg_l1.solution,
pdhg_tikhonov_explicit.solution,
pdhg_tv_explicit.solution],
title=['FBP 1601 projections', 'FBP', 'SIRT','$L^{1}$','Tikhonov','TV'],
cmap="inferno",num_cols=3, size=(25,20), fix_range=(0,0.05))
```
## Zoom ROIs
```
show2D([fbp_recon3D.as_array()[175:225,150:250],
fbp_recon.as_array()[175:225,150:250],
sirt_recon.as_array()[175:225,150:250],
pdhg_l1.solution.as_array()[175:225,150:250],
pdhg_tikhonov_explicit.solution.as_array()[175:225,150:250],
pdhg_tv_implicit_regtk.solution.as_array()[175:225,150:250]],
title=['FBP 1601 projections', 'FBP', 'SIRT','$L^{1}$','Tikhonov','TV'],
cmap="inferno",num_cols=3, size=(25,20), fix_range=(0,0.05))
```
<h1><center>Conclusions</center></h1>
In the PDHG algorithm, the step-sizes $\sigma, \tau$ play a significant role in terms of the convergence speed. In the above problems, we used the default values:
* $\sigma = 1.0$, $\tau = \frac{1.0}{\sigma\|K\|^{2}}$
and we encourage you to try different values provided that $\sigma\tau\|K\|^{2}<1$ is satisfied. Certainly, these values are not the optimal ones and there are sevelar accelaration methods in the literature to tune these parameters appropriately, see for instance [Chambolle_Pock2010](https://hal.archives-ouvertes.fr/hal-00490826/document), [Chambolle_Pock2011](https://ieeexplore.ieee.org/document/6126441), [Goldstein et al](https://arxiv.org/pdf/1305.0546.pdf), [Malitsky_Pock](https://arxiv.org/pdf/1608.08883.pdf).
In the following notebook, we are going to present a stochastic version of PDHG, namely **SPDHG** introduced in [Chambolle et al](https://arxiv.org/pdf/1706.04957.pdf) which is extremely useful to reconstruct large datasets, e.g., 3D walnut data. The idea behind SPDHG is to split our initial dataset into smaller chunks and apply forward and backward operations to these randomly selected subsets of the data. SPDHG has been used for different imaging applications and produces significant computational improvements
over the PDHG algorithm, see [Ehrhardt et al](https://arxiv.org/abs/1808.07150) and [Papoutsellis et al](https://arxiv.org/pdf/2102.06126.pdf).
| true |
code
| 0.639342 | null | null | null | null |
|
# Isolated skyrmion in confined helimagnetic nanostructure
**Authors**: Marijan Beg, Marc-Antonio Bisotti, Weiwei Wang, Ryan Pepper, David Cortes-Ortuno
**Date**: 26 June 2016 (Updated 24 Jan 2019)
This notebook can be downloaded from the github repository, found [here](https://github.com/computationalmodelling/fidimag/blob/master/doc/ipynb/isolated_skyrmion.ipynb).
## Problem specification
A thin film disk sample with thickness $t=10 \,\text{nm}$ and diameter $d=100 \,\text{nm}$ is simulated. The material is FeGe with material parameters [1]:
- exchange energy constant $A = 8.78 \times 10^{-12} \,\text{J/m}$,
- magnetisation saturation $M_\text{s} = 3.84 \times 10^{5} \,\text{A/m}$, and
- Dzyaloshinskii-Moriya energy constant $D = 1.58 \times 10^{-3} \,\text{J/m}^{2}$.
It is expected that when the system is initialised in the uniform out-of-plane direction $\mathbf{m}_\text{init} = (0, 0, 1)$, it relaxes to the isolated Skyrmion (Sk) state (See Supplementary Information in Ref. 1). (Note that LLG dynamics is important, which means that artificially disable the precession term in LLG may lead to other states).
## Simulation using the LLG equation
```
from fidimag.micro import Sim
from fidimag.common import CuboidMesh
from fidimag.micro import UniformExchange, Demag, DMI
from fidimag.common import plot
import time
%matplotlib inline
```
The cuboidal thin film mesh which contains the disk is created:
```
d = 100 # diameter (nm)
t = 10 # thickness (nm)
# Mesh discretisation.
dx = dy = 2.5 # nm
dz = 2
mesh = CuboidMesh(nx=int(d/dx), ny=int(d/dy), nz=int(t/dz), dx=dx, dy=dy, dz=dz, unit_length=1e-9)
```
Since the disk geometry is simulated, it is required to set the saturation magnetisation to zero in the regions of the mesh outside the disk. In order to do that, the following function is created:
```
def Ms_function(Ms):
def wrapped_function(pos):
x, y, z = pos[0], pos[1], pos[2]
r = ((x-d/2.)**2 + (y-d/2.)**2)**0.5 # distance from the centre
if r <= d/2:
# Mesh point is inside the disk.
return Ms
else:
# Mesh point is outside the disk.
return 0
return wrapped_function
```
To reduce the relaxation time, we define a state using a python function.
```
def init_m(pos):
x,y,z = pos
x0, y0 = d/2., d/2.
r = ((x-x0)**2 + (y-y0)**2)**0.5
if r<10:
return (0,0, 1)
elif r<30:
return (0,0, -1)
elif r<60:
return (0, 0, 1)
else:
return (0, 0, -1)
```
Having the magnetisation saturation function, the simulation object can be created:
```
# FeGe material paremeters.
Ms = 3.84e5 # saturation magnetisation (A/m)
A = 8.78e-12 # exchange energy constant (J/m)
D = 1.58e-3 # Dzyaloshinkii-Moriya energy constant (J/m**2)
alpha = 1 # Gilbert damping
gamma = 2.211e5 # gyromagnetic ration (m/As)
# Create simulation object.
sim = Sim(mesh)
# sim = Sim(mesh, driver='steepest_descent')
sim.Ms = Ms_function(Ms)
sim.driver.alpha = alpha
sim.driver.gamma = gamma
# Add energies.
sim.add(UniformExchange(A=A))
sim.add(DMI(D=D))
sim.add(Demag())
# Since the magnetisation dynamics is not important in this stage,
# the precession term in LLG equation can be set to artificially zero.
# sim.driver.do_precession = False
# Initialise the system.
sim.set_m(init_m)
```
This is the initial configuration used before relaxation:
```
plot(sim, component='all', z=0.0, cmap='RdBu')
```
Now the system is relaxed to find a metastable state of the system:
```
# Relax the system to its equilibrium.
start = time.time()
sim.driver.relax(dt=1e-13, stopping_dmdt=0.1, max_steps=10000,
save_m_steps=None, save_vtk_steps=None, printing=False)
end = time.time()
#NBVAL_IGNORE_OUTPUT
print('Timing: ', end - start)
sim.save_vtk()
```
The magnetisation components of obtained equilibrium configuration can be plotted in the following way:
We plot the magnetisation at the bottom of the sample:
```
plot(sim, component='all', z=0.0, cmap='RdBu')
```
and at the top of the sample:
```
plot(sim, component='all', z=10.0, cmap='RdBu')
```
and we plot the xy spin angle through the middle of the sample:
```
plot(sim, component='angle', z=5.0, cmap='hsv')
```
## Simulation using Steepest Descent
An alternative method for the minimisation of the energy is using a SteepestDescent method:
```
# Create simulation object.
sim = Sim(mesh, driver='steepest_descent')
sim.Ms = Ms_function(Ms)
sim.driver.gamma = gamma
# Add energies.
sim.add(UniformExchange(A=A))
sim.add(DMI(D=D))
sim.add(Demag())
# The maximum timestep:
sim.driver.tmax = 1
# Initialise the system.
sim.set_m(init_m)
```
In this case the driver has a `minimise` method
```
start = time.time()
sim.driver.minimise(max_steps=10000, stopping_dm=0.5e-4, initial_t_step=1e-2)
end = time.time()
#NBVAL_IGNORE_OUTPUT
print('Timing: ', end - start)
```
And the final state is equivalent to the one found with the LLG technique
```
plot(sim, component='all', z=0.0, cmap='RdBu')
```
## References
[1] Beg, M. et al. Ground state search, hysteretic behaviour, and reversal mechanism of skyrmionic textures in confined helimagnetic nanostructures. *Sci. Rep.* **5**, 17137 (2015).
| true |
code
| 0.526891 | null | null | null | null |
|
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
```
## 1. 加载并可视化数据
```
path = 'LogiReg_data.txt'
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
pdData.head()
pdData.shape
positive = pdData[pdData['Admitted'] == 1]
negative = pdData[pdData['Admitted'] == 0]
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
```
## 2. Sigmoid函数
$$
g(z) = \frac{1}{1+e^{-z}}
$$
```
def sigmoid(z):
return 1 / (1 + np.exp(-z))
nums = np.arange(-10, 10, step=1)
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(nums, sigmoid(nums), 'r')
```
## 3. 建立Model
$$
\begin{array}{ccc}
\begin{pmatrix}\theta_{0} & \theta_{1} & \theta_{2}\end{pmatrix} & \times & \begin{pmatrix}1\\
x_{1}\\
x_{2}
\end{pmatrix}\end{array}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}
$$
```
def model(X, theta):
return sigmoid(np.dot(X, theta.T))
# 在第0列插入1
pdData.insert(0, 'Ones', 1)
# 获取<training data, y>
orig_data = pdData.values
cols = orig_data.shape[1]
X = orig_data[:, 0:cols-1]
y = orig_data[:, cols-1:cols]
# 初始化参数
theta = np.zeros([1, 3])
X[:5]
y[:5]
theta
```
## 4. 建立Loss Function
将对数似然函数去负号
$$
D(h_\theta(x), y) = -y\log(h_\theta(x)) - (1-y)\log(1-h_\theta(x))
$$
求平均损失
$$
J(\theta)=\frac{1}{n}\sum_{i=1}^{n} D(h_\theta(x_i), y_i)
$$
```
def cost(X, y, theta):
left = np.multiply(-y, np.log(model(X, theta)))
right = np.multiply(1 - y, np.log(1 - model(X, theta)))
return np.sum(left - right) / (len(X))
cost(X, y, theta)
```
## 5. 计算梯度
$$
\frac{\partial J}{\partial \theta_j}=-\frac{1}{m}\sum_{i=1}^n (y_i - h_\theta (x_i))x_{ij}
$$
```
def gradient(X, y, theta):
grad = np.zeros(theta.shape)
error = (model(X, theta) - y).ravel()
# 对于每一个参数,取出相关列的数据进行更新
for j in range(len(theta.ravel())):
term = np.multiply(error, X[:, j])
grad[0, j] = np.sum(term) / len(X)
return grad
```
## 6. 梯度下降
```
import time
import numpy.random
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
def stopCriterion(dtype, value, threshold):
if dtype == STOP_ITER:
return value > threshold
elif dtype == STOP_COST:
return abs(value[-1] - value[-2]) < threshold
elif dtype == STOP_GRAD:
return np.linalg.norm(value) < threshold
def shuffleData(data):
# 洗牌操作
np.random.shuffle(data)
cols = data.shape[1]
X = data[:, 0:cols-1]
y = data[:, cols-1:]
return X, y
def descent(data, theta, batchSize, stopType, thresh, alpha):
i = 0
k = 0
init_time = time.time()
X, y = shuffleData(data)
grad = np.zeros(theta.shape)
costs = [cost(X, y, theta)]
while True:
grad = gradient(X[k: k+batchSize], y[k: k+batchSize], theta)
k += batchSize
if k >= n:
k = 0
X, y = shuffleData(data)
theta = theta - alpha*grad
costs.append(cost(X, y, theta))
i += 1
if stopType == STOP_ITER:
value = i
elif stopType == STOP_COST:
value = costs
elif stopType == STOP_GRAD:
value = grad
if stopCriterion(stopType, value, thresh):
break
return theta, i-1, costs, grad, time.time()-init_time
def runExpe(data, theta, batchSize, stopType, thresh, alpha):
theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)
name = "Original" if (data[:,1]>2).sum() > 1 else "Scaled"
name += " data - learning rate: {} - ".format(alpha)
if batchSize == n:
strDescType = "Gradient"
elif batchSize == 1:
strDescType = "Stochastic"
else:
strDescType = "Mini-batch ({})".format(batchSize)
name += strDescType + " descent - Stop: "
if stopType == STOP_ITER:
strStop = "{} iterations".format(thresh)
elif stopType == STOP_COST:
strStop = "costs change < {}".format(thresh)
else:
strStop = "gradient norm < {}".format(thresh)
name += strStop
print ("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(
name, theta, iter, costs[-1], dur))
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(np.arange(len(costs)), costs, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title(name.upper() + ' - Error vs. Iteration')
return theta
```
## 7. 不同的停止策略
### 设定迭代次数
```
#选择的梯度下降方法是基于所有样本的
n=100
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)
```
### 根据损失值停止
```
runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)
```
### 根据梯度变化停止
```
runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)
```
## 8. 不同的梯度下降方法
### Stochastic descent
```
runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001)
# 降低学习率
runExpe(orig_data, theta, 1, STOP_ITER, thresh=15000, alpha=0.000002)
```
结论: 速度快,但稳定性差,需要很小的学习率
### Mini-batch descent
```
runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001)
from sklearn import preprocessing as pp
# 对数据进行标准化 将数据按其属性(按列进行)减去其均值,然后除以其方差。最后得到的结果是,对每个属性/每列来说所有数据都聚集在0附近,方差值为1
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])
runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)
```
结论: 原始数据为0.61,而预处理后0.38。数据做预处理非常重要
```
runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001)
theta = runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002/5, alpha=0.001)
runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002*2, alpha=0.001)
```
## 9. 测试精度
```
def predict(X, theta):
return [1 if x >= 0.5 else 0 for x in model(X, theta)]
scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))
```
| true |
code
| 0.564219 | null | null | null | null |
|
# VIME: Self/Semi Supervised Learning for Tabular Data
# Setup
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import umap
from sklearn.metrics import (average_precision_score, mean_squared_error,
roc_auc_score)
from sklearn.model_selection import train_test_split
from tqdm import tqdm
from vime import VIME, VIME_Self
from vime_data import (
labelled_loss_fn, mask_generator_tf,
pretext_generator_tf, semi_supervised_generator,
to_vime_dataset, unlabelled_loss_fn
)
%matplotlib inline
%load_ext autoreload
%autoreload 2
plt.rcParams["figure.figsize"] = (20,10)
```
# Data
The example data is taken from [Kaggle](https://www.kaggle.com/c/ieee-fraud-detection) but it's already pre-processed and ready to be used. You can checkout the pre-processing notebook in the same folder to get some understanding about what transformations were done to the features.
```
train = pd.read_csv("fraud_train_preprocessed.csv")
test = pd.read_csv("fraud_test_preprocessed.csv")
# Drop nan columns as they are not useful for reconstruction error
nan_columns = [f for f in train.columns if 'nan' in f]
train = train.drop(nan_columns, axis=1)
test = test.drop(nan_columns, axis=1)
# Also, using only numerical columns because NNs have issue with one-hot encoding
num_cols = train.columns[:-125]
# Validation size is 10%
val_size = int(train.shape[0] * 0.1)
X_train = train.iloc[:-val_size, :]
X_val = train.iloc[-val_size:, :]
# Labelled 1% of data, everything else is unlabelled
X_train_labelled = train.sample(frac=0.01)
y_train_labelled = X_train_labelled.pop('isFraud')
X_val_labelled = X_val.sample(frac=0.01)
y_val_labelled = X_val_labelled.pop('isFraud')
X_train_unlabelled = X_train.loc[~X_train.index.isin(X_train_labelled.index), :].drop('isFraud', axis=1)
X_val_unlabelled = X_val.loc[~X_val.index.isin(X_val_labelled.index), :].drop('isFraud', axis=1)
X_train_labelled = X_train_labelled[num_cols]
X_val_labelled = X_val_labelled[num_cols]
X_train_unlabelled = X_train_unlabelled[num_cols]
X_val_unlabelled = X_val_unlabelled[num_cols]
X_val_labelled.shape, X_train_labelled.shape
print("Labelled Fraudsters", y_train_labelled.sum())
print(
"Labelled Proportion:",
np.round(X_train_labelled.shape[0] / (X_train_unlabelled.shape[0] + X_train_labelled.shape[0]), 5)
)
```
The following model will be trained with these hyperparameters:
```
vime_params = {
'alpha': 4,
'beta': 10,
'k': 5,
'p_m': 0.36
}
```
## Self-Supervised Learning
### Data Prep
The model needs 1 input - corrupted X, and 2 outputs - mask and original X.
```
batch_size = 1024
# Datasets
train_ds, train_m = to_vime_dataset(X_train_unlabelled, vime_params['p_m'], batch_size=batch_size, shuffle=True)
val_ds, val_m = to_vime_dataset(X_val_unlabelled, vime_params['p_m'], batch_size=batch_size)
num_features = X_train_unlabelled.shape[1]
print('Proportion Corrupted:', np.round(train_m.numpy().mean(), 2))
# Training
vime_s = VIME_Self(num_features)
vime_s.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
loss={
'mask': 'binary_crossentropy',
'feature': 'mean_squared_error'},
loss_weights={'mask':1, 'feature': vime_params['alpha']}
)
cbs = [tf.keras.callbacks.EarlyStopping(
monitor="val_loss", patience=10, restore_best_weights=True
)]
vime_s.fit(
train_ds,
validation_data=val_ds,
epochs=1000,
callbacks=cbs
)
vime_s.save('./vime_self')
vime_s = tf.keras.models.load_model('./vime_self')
```
### Evaluation
All the evaluation will be done on the validation set
```
val_self_preds = vime_s.predict(val_ds)
```
To evaluate the mask reconstruction ability we can simply check the ROC AUC score for mask predictions across all the features.
```
feature_aucs = []
for i in tqdm(range(X_val_unlabelled.shape[1])):
roc = roc_auc_score(val_m.numpy()[:, i], val_self_preds['mask'][:, i])
feature_aucs.append(roc)
self_metrics = pd.DataFrame({"metric": 'mask_auc',
"metric_values": feature_aucs})
```
Now, we can evaluate the feature reconstruction ability using RMSE and correlation coefficients
```
feature_corrs = []
for i in tqdm(range(X_val_unlabelled.shape[1])):
c = np.corrcoef(X_val_unlabelled.values[:, i], val_self_preds['feature'][:, i])[0, 1]
feature_corrs.append(c)
self_metrics = pd.concat([
self_metrics,
pd.DataFrame({"metric": 'feature_correlation',
"metric_values": feature_corrs})
])
```
From the plot and table above, we can see that the model has learned to reconstruct most of the features. Half of the features are reconstructed with relatively strong correlation with original data. Only a handful of features are not properly reconstructed. Let's check the RMSE across all the features
```
rmses = []
for i in tqdm(range(X_val_unlabelled.shape[1])):
mse = mean_squared_error(X_val_unlabelled.values[:, i], val_self_preds['feature'][:, i])
rmses.append(np.sqrt(mse))
self_metrics = pd.concat([
self_metrics,
pd.DataFrame({"metric": 'RMSE',
"metric_values": rmses})
])
sns.boxplot(x=self_metrics['metric'], y=self_metrics['metric_values'])
plt.title("Self-Supervised VIME Evaluation")
```
RMSE distribution further indicates that mjority of the features are well-reconstructed.
Another way to evaluate the self-supervised model is to look at the embeddings. Since the whole point of corrupting the dataset is to learn to generate robust embeddings, we can assume that if a sample was corrupted 5 times, all 5 embeddings should be relatively close to each other in the vector space. Let's check this hypothesis by corrupting 10 different samples 5 times and projecting their embeddings to 2-dimensional space using UMAP.
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Input, Dense, Dropout
def generate_k_corrupted(x, k, p_m):
x_u_list = []
for i in range(k):
mask = mask_generator_tf(p_m, x)
_, x_corr = pretext_generator_tf(mask, tf.constant(x, dtype=tf.float32))
x_u_list.append(x_corr)
# Prepare input with shape (n, k, d)
x_u_corrupted = np.zeros((x.shape[0], k, x.shape[1]))
for i in range(x.shape[0]):
for j in range(k):
x_u_corrupted[i, j, :] = x_u_list[j][i, :]
return x_u_corrupted
vime_s = tf.keras.models.load_model('./vime_self')
# Sequential model to produce embeddings
encoding_model = Sequential(
[
Input(num_features),
vime_s.encoder
]
)
dense_model = Sequential(
[
Input(num_features),
Dense(num_features, activation="relu"),
]
)
# Create corrupted sample
samples = X_val_unlabelled.sample(10)
sample_corrupted = generate_k_corrupted(
x=samples,
k=5,
p_m=0.4
)
val_encoding = encoding_model.predict(sample_corrupted, batch_size=batch_size)
random_encoding = dense_model.predict(sample_corrupted, batch_size=batch_size)
fig, axs = plt.subplots(1, 2)
# Project corrupted samples
u = umap.UMAP(n_neighbors=5, min_dist=0.8)
corrupted_umap = u.fit_transform(val_encoding.reshape(-1, val_encoding.shape[2]))
sample_ids = np.array([np.repeat(i, 5) for i in range(10)]).ravel()
sns.scatterplot(corrupted_umap[:, 0], corrupted_umap[:, 1], hue=sample_ids, palette="tab10", ax=axs[0])
axs[0].set_title('VIME Embeddings of Corrupted Samples')
plt.legend(title='Sample ID')
# Project corrupted samples
u = umap.UMAP(n_neighbors=5, min_dist=0.8)
corrupted_umap = u.fit_transform(random_encoding.reshape(-1, random_encoding.shape[2]))
sample_ids = np.array([np.repeat(i, 5) for i in range(10)]).ravel()
sns.scatterplot(corrupted_umap[:, 0], corrupted_umap[:, 1], hue=sample_ids, palette="tab10", ax=axs[1])
axs[1].set_title('Not-trained Embeddings of Corrupted Samples')
plt.legend(title='Sample ID')
plt.show()
```
As you can see, the embeddings indeed put the same samples closer to each other, even though some of their values were corrupted. According to the authors, this means that the model has learned useful information about the feature correlations which can be helpful in the downstream tasks. Now, we can use this encoder in the next semi-supervised part.
## Semi-Supervised Learning
```
semi_batch_size = 512
num_features = X_train_unlabelled.shape[1]
```
Since we have different number of labelled and unlabelled examples we need to use generators. They will shuffle and select appropriate number of rows for each training iteration.
```
def train_semi_generator():
return semi_supervised_generator(
X_train_labelled.values,
X_train_unlabelled.values,
y_train_labelled.values,
bs=semi_batch_size
)
def val_semi_generator():
return semi_supervised_generator(
X_val_labelled.values,
X_val_unlabelled.values,
y_val_labelled.values,
bs=semi_batch_size
)
semi_train_dataset = tf.data.Dataset.from_generator(
train_semi_generator,
output_signature=(
tf.TensorSpec(shape=(semi_batch_size, num_features), dtype=tf.float32),
tf.TensorSpec(shape=(semi_batch_size), dtype=tf.float32),
tf.TensorSpec(shape=(semi_batch_size, num_features), dtype=tf.float32)
)
)
semi_val_dataset = tf.data.Dataset.from_generator(
val_semi_generator,
output_signature=(
tf.TensorSpec(shape=(semi_batch_size, num_features), dtype=tf.float32),
tf.TensorSpec(shape=(semi_batch_size), dtype=tf.float32),
tf.TensorSpec(shape=(semi_batch_size, num_features), dtype=tf.float32)
)
)
```
## Self Supervised VIME
```
def train_vime_semi(encoder, train_dataset, val_dataset, train_params, vime_params):
# Model
vime = VIME(encoder)
# Training parameters
iterations = train_params['iterations']
optimizer = tf.keras.optimizers.Adam(train_params['learning_rate'])
early_stop = train_params['early_stop']
# Set metrics to track
best_loss = 1e10
no_improve = 0
# Begining training loop
for it in range(iterations):
# Grab a batch for iteration
it_train = iter(train_dataset)
X_l, y_l, X_u = next(it_train)
# Generate unlabelled batch with k corrupted examples per sample
X_u_corrupted = generate_k_corrupted(X_u, vime_params['k'], vime_params['p_m'])
with tf.GradientTape() as tape:
# Predict labelled & unlabelled
labelled_preds = vime(X_l)
unlabelled_preds = vime(X_u_corrupted)
# Calculate losses
labelled_loss = labelled_loss_fn(y_l, labelled_preds)
unlabelled_loss = unlabelled_loss_fn(unlabelled_preds)
# Total loss
semi_supervised_loss = unlabelled_loss + vime_params['beta'] * labelled_loss
if it % 10 == 0:
val_iter_losses = []
print(f"\nMetrics for Iteration {it}")
for i in range(5):
# Grab a batch
it_val = iter(val_dataset)
X_l_val, y_l_val, X_u_val = next(it_val)
# Generate unlabelled batch with k corrupted examples per sample
X_u_corrupted = generate_k_corrupted(X_u_val, vime_params['k'], vime_params['p_m'])
# Predict labelled & unlabelled
labelled_preds_val = vime(X_l_val)
unlabelled_preds_val = vime(X_u_corrupted)
# Calculate losses
labelled_loss_val = labelled_loss_fn(y_l_val, labelled_preds_val)
unlabelled_loss_val = unlabelled_loss_fn(unlabelled_preds_val)
semi_supervised_loss_val = unlabelled_loss_val + vime_params['beta'] * labelled_loss_val
val_iter_losses.append(semi_supervised_loss_val)
# Average loss over 5 validation iterations
semi_supervised_loss_val = np.mean(val_iter_losses)
print(f"Train Loss {np.round(semi_supervised_loss, 5)}, Val Loss {np.round(semi_supervised_loss_val, 5)}")
# Update metrics if val_loss is better
if semi_supervised_loss_val < best_loss:
best_loss = semi_supervised_loss_val
no_improve = 0
vime.save('./vime')
else:
no_improve += 1
print(f"Validation loss not improved {no_improve} times")
# Early stopping
if no_improve == early_stop:
break
# Update weights
grads = tape.gradient(semi_supervised_loss, vime.trainable_weights)
optimizer.apply_gradients(zip(grads, vime.trainable_weights))
vime = tf.keras.models.load_model('./vime')
return vime
train_params = {
'num_features': num_features,
'iterations': 1000,
'early_stop': 20,
'learning_rate': 0.001
}
vime_self = tf.keras.models.load_model('./vime_self')
vime_semi = train_vime_semi(
encoder = vime_self.encoder,
train_dataset = semi_train_dataset,
val_dataset = semi_val_dataset,
train_params = train_params,
vime_params = vime_params
)
test_ds = tf.data.Dataset.from_tensor_slices(test[num_cols]).batch(batch_size)
vime_tuned_preds = vime_semi.predict(test_ds)
pr = average_precision_score(test['isFraud'], vime_tuned_preds)
print(pr)
```
## Evaluation
Re-training the model 10 times to get distribution of PR AUC scores.
```
vime_prs = []
test_ds = tf.data.Dataset.from_tensor_slices(test[num_cols]).batch(batch_size)
for i in range(10):
train_params = {
'num_features': num_features,
'iterations': 1000,
'early_stop': 10,
'learning_rate': 0.001
}
vime_self = tf.keras.models.load_model('./vime_self')
vime_self.encoder.trainable = False
vime_semi = train_vime_semi(
encoder = vime_self.encoder,
train_dataset = semi_train_dataset,
val_dataset = semi_val_dataset,
train_params = train_params,
vime_params = vime_params
)
# fine-tune
vime_semi = tf.keras.models.load_model('./vime')
vime_semi.encoder.trainable
vime_tuned_preds = vime_semi.predict(test_ds)
pr = average_precision_score(test['isFraud'], vime_tuned_preds)
vime_prs.append(pr)
print('VIME Train', i, "PR AUC:", pr)
```
### Compare with MLP and RF
```
mlp_prs = []
for i in range(10):
base_mlp = Sequential([
Input(shape=num_features),
Dense(num_features),
Dense(128),
Dropout(0.2),
Dense(128),
Dropout(0.2),
Dense(1, activation='sigmoid')
])
base_mlp.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.0001),
loss='binary_crossentropy'
)
# Early stopping based on validation loss
cbs = [tf.keras.callbacks.EarlyStopping(
monitor="val_loss", patience=20, restore_best_weights=True
)]
base_mlp.fit(
x=X_train_labelled.values,
y=y_train_labelled,
validation_data=(X_val_labelled.values, y_val_labelled),
epochs=1000,
callbacks=cbs
)
base_mlp_preds = base_mlp.predict(test_ds)
mlp_prs.append(average_precision_score(test['isFraud'], base_mlp_preds))
from lightgbm import LGBMClassifier
train_tree_X = pd.concat([X_train_labelled, X_val_labelled])
train_tree_y = pd.concat([y_train_labelled, y_val_labelled])
rf_prs = []
for i in tqdm(range(10)):
rf = RandomForestClassifier(max_depth=4)
rf.fit(train_tree_X.values, train_tree_y)
rf_preds = rf.predict_proba(test[X_train_labelled.columns])
rf_prs.append(average_precision_score(test['isFraud'], rf_preds[:, 1]))
metrics_df = pd.DataFrame({"MLP": mlp_prs,
"VIME": vime_prs,
"RF": rf_prs})
metrics_df.boxplot()
plt.ylabel("PR AUC")
plt.show()
metrics_df.describe()
```
| true |
code
| 0.678007 | null | null | null | null |
|
# Model understanding and interpretability
In this colab, we will
- Will learn how to interpret model results and reason about the features
- Visualize the model results
```
import time
# We will use some np and pandas for dealing with input data.
import numpy as np
import pandas as pd
# And of course, we need tensorflow.
import tensorflow as tf
from matplotlib import pyplot as plt
from IPython.display import clear_output
tf.__version__
```
Below we demonstrate both *local* and *global* model interpretability for gradient boosted trees.
Local interpretability refers to an understanding of a model’s predictions at the individual example level, while global interpretability refers to an understanding of the model as a whole.
For local interpretability, we show how to create and visualize per-instance contributions using the technique outlined in [Palczewska et al](https://arxiv.org/pdf/1312.1121.pdf) and by Saabas in [Interpreting Random Forests](http://blog.datadive.net/interpreting-random-forests/) (this method is also available in scikit-learn for Random Forests in the [`treeinterpreter`](https://github.com/andosa/treeinterpreter) package). To distinguish this from feature importances, we refer to these values as directional feature contributions (DFCs).
For global interpretability we show how to retrieve and visualize gain-based feature importances, [permutation feature importances](https://www.stat.berkeley.edu/~breiman/randomforest2001.pdf) and also show aggregated DFCs.
# Setup
## Load dataset
We will be using the titanic dataset, where the goal is to predict passenger survival given characteristiscs such as gender, age, class, etc.
```
tf.logging.set_verbosity(tf.logging.ERROR)
tf.set_random_seed(123)
# Load dataset.
dftrain = pd.read_csv('https://storage.googleapis.com/tf-datasets/titanic/train.csv')
dfeval = pd.read_csv('https://storage.googleapis.com/tf-datasets/titanic/eval.csv')
y_train = dftrain.pop('survived')
y_eval = dfeval.pop('survived')
# Feature columns.
fcol = tf.feature_column
CATEGORICAL_COLUMNS = ['sex', 'n_siblings_spouses', 'parch', 'class', 'deck',
'embark_town', 'alone']
NUMERIC_COLUMNS = ['age', 'fare']
def one_hot_cat_column(feature_name, vocab):
return fcol.indicator_column(
fcol.categorical_column_with_vocabulary_list(feature_name,
vocab))
fc = []
for feature_name in CATEGORICAL_COLUMNS:
# Need to one-hot encode categorical features.
vocabulary = dftrain[feature_name].unique()
fc.append(one_hot_cat_column(feature_name, vocabulary))
for feature_name in NUMERIC_COLUMNS:
fc.append(fcol.numeric_column(feature_name,
dtype=tf.float32))
# Input functions.
def make_input_fn(X, y, n_epochs=None):
def input_fn():
dataset = tf.data.Dataset.from_tensor_slices((X.to_dict(orient='list'), y))
# For training, cycle thru dataset as many times as need (n_epochs=None).
dataset = (dataset
.repeat(n_epochs)
.batch(len(y))) # Use entire dataset since this is such a small dataset.
return dataset
return input_fn
# Training and evaluation input functions.
train_input_fn = make_input_fn(dftrain, y_train)
eval_input_fn = make_input_fn(dfeval, y_eval, n_epochs=1)
```
# Interpret model
## Local interpretability
Output directional feature contributions (DFCs) to explain individual predictions, using the approach outlined in [Palczewska et al](https://arxiv.org/pdf/1312.1121.pdf) and by Saabas in [Interpreting Random Forests](http://blog.datadive.net/interpreting-random-forests/). The DFCs are generated with:
`pred_dicts = list(est.experimental_predict_with_explanations(pred_input_fn))`
```
params = {
'n_trees': 50,
'max_depth': 3,
'n_batches_per_layer': 1,
# You must enable center_bias = True to get DFCs. This will force the model to
# make an initial prediction before using any features (e.g. use the mean of
# the training labels for regression or log odds for classification when
# using cross entropy loss).
'center_bias': True
}
est = tf.estimator.BoostedTreesClassifier(fc, **params)
# Train model.
est.train(train_input_fn)
# Evaluation.
results = est.evaluate(eval_input_fn)
clear_output()
pd.Series(results).to_frame()
```
## Local interpretability
Next you will output the directional feature contributions (DFCs) to explain individual predictions using the approach outlined in [Palczewska et al](https://arxiv.org/pdf/1312.1121.pdf) and by Saabas in [Interpreting Random Forests](http://blog.datadive.net/interpreting-random-forests/) (this method is also available in scikit-learn for Random Forests in the [`treeinterpreter`](https://github.com/andosa/treeinterpreter) package). The DFCs are generated with:
`pred_dicts = list(est.experimental_predict_with_explanations(pred_input_fn))`
(Note: The method is named experimental as we may modify the API before dropping the experimental prefix.)
```
import matplotlib.pyplot as plt
import seaborn as sns
sns_colors = sns.color_palette('colorblind')
pred_dicts = list(est.experimental_predict_with_explanations(eval_input_fn))
def clean_feature_names(df):
"""Boilerplate code to cleans up feature names -- this is unneed in TF 2.0"""
df.columns = [v.split(':')[0].split('_indi')[0] for v in df.columns.tolist()]
df = df.T.groupby(level=0).sum().T
return df
# Create DFC Pandas dataframe.
labels = y_eval.values
probs = pd.Series([pred['probabilities'][1] for pred in pred_dicts])
df_dfc = pd.DataFrame([pred['dfc'] for pred in pred_dicts])
df_dfc.columns = est._names_for_feature_id
df_dfc = clean_feature_names(df_dfc)
df_dfc.describe()
# Sum of DFCs + bias == probabality.
bias = pred_dicts[0]['bias']
dfc_prob = df_dfc.sum(axis=1) + bias
np.testing.assert_almost_equal(dfc_prob.values,
probs.values)
```
Plot results
```
import seaborn as sns # Make plotting nicer.
sns_colors = sns.color_palette('colorblind')
def plot_dfcs(example_id):
label, prob = labels[ID], probs[ID]
example = df_dfc.iloc[ID] # Choose ith example from evaluation set.
TOP_N = 8 # View top 8 features.
sorted_ix = example.abs().sort_values()[-TOP_N:].index
ax = example[sorted_ix].plot(kind='barh', color='g', figsize=(10,5))
ax.grid(False, axis='y')
plt.title('Feature contributions for example {}\n pred: {:1.2f}; label: {}'.format(ID, prob, label))
plt.xlabel('Contribution to predicted probability')
ID = 102
plot_dfcs(ID)
```
**??? ** How would you explain the above plot in plain english?
### Prettier plotting
Color codes based on directionality and adds feature values on figure. Please do not worry about the details of the plotting code :)
```
def plot_example_pretty(example):
"""Boilerplate code for better plotting :)"""
def _get_color(value):
"""To make positive DFCs plot green, negative DFCs plot red."""
green, red = sns.color_palette()[2:4]
if value >= 0: return green
return red
def _add_feature_values(feature_values, ax):
"""Display feature's values on left of plot."""
x_coord = ax.get_xlim()[0]
OFFSET = 0.15
for y_coord, (feat_name, feat_val) in enumerate(feature_values.items()):
t = plt.text(x_coord, y_coord - OFFSET, '{}'.format(feat_val), size=12)
t.set_bbox(dict(facecolor='white', alpha=0.5))
from matplotlib.font_manager import FontProperties
font = FontProperties()
font.set_weight('bold')
t = plt.text(x_coord, y_coord + 1 - OFFSET, 'feature\nvalue',
fontproperties=font, size=12)
TOP_N = 8 # View top 8 features.
sorted_ix = example.abs().sort_values()[-TOP_N:].index # Sort by magnitude.
example = example[sorted_ix]
colors = example.map(_get_color).tolist()
ax = example.to_frame().plot(kind='barh',
color=[colors],
legend=None,
alpha=0.75,
figsize=(10,6))
ax.grid(False, axis='y')
ax.set_yticklabels(ax.get_yticklabels(), size=14)
_add_feature_values(dfeval.iloc[ID].loc[sorted_ix], ax)
ax.set_title('Feature contributions for example {}\n pred: {:1.2f}; label: {}'.format(ID, probs[ID], labels[ID]))
ax.set_xlabel('Contribution to predicted probability', size=14)
plt.show()
return ax
# Plot results.
ID = 102
example = df_dfc.iloc[ID] # Choose ith example from evaluation set.
ax = plot_example_pretty(example)
```
## Global feature importances
1. Gain-based feature importances using `est.experimental_feature_importances`
2. Aggregate DFCs using `est.experimental_predict_with_explanations`
3. Permutation importances
Gain-based feature importances measure the loss change when splitting on a particular feature, while permutation feature importances are computed by evaluating model performance on the evaluation set by shuffling each feature one-by-one and attributing the change in model performance to the shuffled feature.
In general, permutation feature importance are preferred to gain-based feature importance, though both methods can be unreliable in situations where potential predictor variables vary in their scale of measurement or their number of categories and when features are correlated ([source](https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-9-307)). Check out [this article](http://explained.ai/rf-importance/index.html) for an in-depth overview and great discussion on different feature importance types.
## 1. Gain-based feature importances
```
features, importances = est.experimental_feature_importances(normalize=True)
df_imp = pd.DataFrame(importances, columns=['importances'], index=features)
# For plotting purposes. This is not needed in TF 2.0.
df_imp = clean_feature_names(df_imp.T).T.sort_values('importances', ascending=False)
# Visualize importances.
N = 8
ax = df_imp.iloc[0:N][::-1]\
.plot(kind='barh',
color=sns_colors[0],
title='Gain feature importances',
figsize=(10, 6))
ax.grid(False, axis='y')
plt.tight_layout()
```
**???** What does the x axis represent? -- A. It represents relative importance. Specifically, the average reduction in loss that occurs when a split occurs on that feature.
**???** Can we completely trust these results and the magnitudes? -- A. The results can be misleading because variables are correlated.
### 2. Average absolute DFCs
We can also average the absolute values of DFCs to understand impact at a global level.
```
# Plot.
dfc_mean = df_dfc.abs().mean()
sorted_ix = dfc_mean.abs().sort_values()[-8:].index # Average and sort by absolute.
ax = dfc_mean[sorted_ix].plot(kind='barh',
color=sns_colors[1],
title='Mean |directional feature contributions|',
figsize=(10, 6))
ax.grid(False, axis='y')
```
We can also see how DFCs vary as a feature value varies.
```
age = pd.Series(df_dfc.age.values, index=dfeval.age.values).sort_index()
sns.jointplot(age.index.values, age.values);
```
# Visualizing the model's prediction surface
Lets first simulate/create training data using the following formula:
$z=x* e^{-x^2 - y^2}$
Where $z$ is the dependent variable we are trying to predict and $x$ and $y$ are the features.
```
from numpy.random import uniform, seed
from matplotlib.mlab import griddata
# Create fake data
seed(0)
npts = 5000
x = uniform(-2, 2, npts)
y = uniform(-2, 2, npts)
z = x*np.exp(-x**2 - y**2)
# Prep data for training.
df = pd.DataFrame({'x': x, 'y': y, 'z': z})
xi = np.linspace(-2.0, 2.0, 200),
yi = np.linspace(-2.1, 2.1, 210),
xi,yi = np.meshgrid(xi, yi)
df_predict = pd.DataFrame({
'x' : xi.flatten(),
'y' : yi.flatten(),
})
predict_shape = xi.shape
def plot_contour(x, y, z, **kwargs):
# Grid the data.
plt.figure(figsize=(10, 8))
# Contour the gridded data, plotting dots at the nonuniform data points.
CS = plt.contour(x, y, z, 15, linewidths=0.5, colors='k')
CS = plt.contourf(x, y, z, 15,
vmax=abs(zi).max(), vmin=-abs(zi).max(), cmap='RdBu_r')
plt.colorbar() # Draw colorbar.
# Plot data points.
plt.xlim(-2, 2)
plt.ylim(-2, 2)
```
We can visualize our function:
```
zi = griddata(x, y, z, xi, yi, interp='linear')
plot_contour(xi, yi, zi)
plt.scatter(df.x, df.y, marker='.')
plt.title('Contour on training data')
plt.show()
def predict(est):
"""Predictions from a given estimator."""
predict_input_fn = lambda: tf.data.Dataset.from_tensors(dict(df_predict))
preds = np.array([p['predictions'][0] for p in est.predict(predict_input_fn)])
return preds.reshape(predict_shape)
```
First let's try to fit a linear model to the data.
```
fc = [tf.feature_column.numeric_column('x'),
tf.feature_column.numeric_column('y')]
train_input_fn = make_input_fn(df, df.z)
est = tf.estimator.LinearRegressor(fc)
est.train(train_input_fn, max_steps=500);
plot_contour(xi, yi, predict(est))
```
Not very good at all...
**???** Why is the linear model not performing well for this problem? Can you think of how to improve it just using a linear model?
Next let's try to fit a GBDT model to it and try to understand what the model does
```
for n_trees in [1,2,3,10,30,50,100,200]:
est = tf.estimator.BoostedTreesRegressor(fc,
n_batches_per_layer=1,
max_depth=4,
n_trees=n_trees)
est.train(train_input_fn)
plot_contour(xi, yi, predict(est))
plt.text(-1.8, 2.1, '# trees: {}'.format(n_trees), color='w', backgroundcolor='black', size=20)
```
Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.666849 | null | null | null | null |
|
#**Exploratory Data Analysis**
### Setting Up Environment
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.style as style
import seaborn as sns
from scipy.stats import pointbiserialr
from scipy.stats import pearsonr
from scipy.stats import chi2_contingency
from sklearn.impute import SimpleImputer
plt.rcParams["figure.figsize"] = (15,8)
application_data_raw = pd.read_csv('application_data.csv', encoding = 'unicode_escape')
application_data_raw.info()
#application_data_raw.describe()
df = application_data_raw.copy()
```
### Data Cleaning
```
# drop the customer id column
df = df.drop(columns=['SK_ID_CURR'])
# remove invalid values in gender column
df['CODE_GENDER'] = df['CODE_GENDER'].replace("XNA", None)
# drop columns filled >25% with null values
num_missing_values = df.isnull().sum()
nulldf = round(num_missing_values/len(df)*100, 2)
cols_to_keep = nulldf[nulldf<=0.25].index.to_list()
df = df.loc[:, cols_to_keep] # 61 of 121 attributes were removed due to null values.
# impute remaining columns with null values
num_missing_values = df.isnull().sum()
missing_cols = num_missing_values[num_missing_values>0].index.tolist()
for col in missing_cols:
imp_mean = SimpleImputer(strategy='most_frequent')
imp_mean.fit(df[[col]])
df[col] = imp_mean.transform(df[[col]]).ravel()
df.info()
```
### Data Preprocessing
```
continuous_vars = ['CNT_CHILDREN', 'AMT_INCOME_TOTAL', 'AMT_CREDIT', 'AMT_ANNUITY', 'AMT_GOODS_PRICE', 'REGION_POPULATION_RELATIVE',
'DAYS_REGISTRATION', 'DAYS_ID_PUBLISH', 'CNT_FAM_MEMBERS', 'REGION_RATING_CLIENT', 'REGION_RATING_CLIENT_W_CITY',
'HOUR_APPR_PROCESS_START', 'EXT_SOURCE_2', 'DAYS_LAST_PHONE_CHANGE', 'YEARS_BIRTH', 'YEARS_EMPLOYED']
#categorical_variables = df.select_dtypes(include=["category"]).columns.tolist()
#len(categorical_variables)
categorical_vars = ['NAME_CONTRACT_TYPE', 'CODE_GENDER', 'FLAG_OWN_CAR', 'FLAG_OWN_REALTY', 'NAME_INCOME_TYPE','NAME_EDUCATION_TYPE',
'NAME_FAMILY_STATUS', 'NAME_HOUSING_TYPE', 'FLAG_MOBIL', 'FLAG_EMP_PHONE', 'FLAG_WORK_PHONE', 'FLAG_CONT_MOBILE', 'FLAG_PHONE',
'FLAG_EMAIL', 'WEEKDAY_APPR_PROCESS_START', 'REG_REGION_NOT_LIVE_REGION','REG_REGION_NOT_WORK_REGION',
'LIVE_REGION_NOT_WORK_REGION', 'REG_CITY_NOT_LIVE_CITY', 'REG_CITY_NOT_WORK_CITY', 'LIVE_CITY_NOT_WORK_CITY',
'ORGANIZATION_TYPE', 'FLAG_DOCUMENT_2', 'FLAG_DOCUMENT_3', 'FLAG_DOCUMENT_4', 'FLAG_DOCUMENT_5', 'FLAG_DOCUMENT_6',
'FLAG_DOCUMENT_7', 'FLAG_DOCUMENT_8', 'FLAG_DOCUMENT_9', 'FLAG_DOCUMENT_10', 'FLAG_DOCUMENT_11', 'FLAG_DOCUMENT_12',
'FLAG_DOCUMENT_13', 'FLAG_DOCUMENT_14', 'FLAG_DOCUMENT_15', 'FLAG_DOCUMENT_16', 'FLAG_DOCUMENT_17', 'FLAG_DOCUMENT_18',
'FLAG_DOCUMENT_19', 'FLAG_DOCUMENT_20', 'FLAG_DOCUMENT_21']
# plot to see distribution of categorical variables
n_cols = 4
fig, axes = plt.subplots(nrows=int(np.ceil(len(categorical_vars)/n_cols)),
ncols=n_cols,
figsize=(15,45))
for i in range(len(categorical_vars)):
var = categorical_vars[i]
dist = df[var].value_counts()
labels = dist.index
counts = dist.values
ax = axes.flatten()[i]
ax.bar(labels, counts)
ax.tick_params(axis='x', labelrotation = 90)
ax.title.set_text(var)
plt.tight_layout()
plt.show()
# This gives us an idea about which features may already be more useful
# Remove all FLAG_DOCUMENT features except for FLAG_DOCUMENT_3 as most did not submit, insignificant on model
vars_to_drop = []
vars_to_drop = ["FLAG_DOCUMENT_2"]
vars_to_drop += ["FLAG_DOCUMENT_{}".format(i) for i in range(4,22)]
# Unit conversions
df['AMT_INCOME_TOTAL'] = df['AMT_INCOME_TOTAL']/100000 # yearly income to be expressed in hundred thousands
df['YEARS_BIRTH'] = round((df['DAYS_BIRTH']*-1)/365).astype('int64') # days of birth changed to years of birth
df['YEARS_EMPLOYED'] = round((df['DAYS_EMPLOYED']*-1)/365).astype('int64') # days employed change to years employed
df.loc[df['YEARS_EMPLOYED']<0, 'YEARS_EMPLOYED'] = 0
df = df.drop(columns=['DAYS_BIRTH', 'DAYS_EMPLOYED'])
# Encoding categorical variables
def encode_cat(df, var_list):
for var in var_list:
df[var] = df[var].astype('category')
d = dict(zip(df[var], df[var].cat.codes))
df[var] = df[var].map(d)
print(var+" Category Codes")
print(d)
return df
already_coded = ['FLAG_MOBIL', 'FLAG_EMP_PHONE', 'FLAG_WORK_PHONE', 'FLAG_CONT_MOBILE', 'FLAG_PHONE', 'FLAG_EMAIL', 'REG_REGION_NOT_LIVE_REGION',
'REG_REGION_NOT_WORK_REGION', 'LIVE_REGION_NOT_WORK_REGION', 'REG_CITY_NOT_LIVE_CITY', 'REG_CITY_NOT_WORK_CITY',
'LIVE_CITY_NOT_WORK_CITY', 'FLAG_DOCUMENT_2', 'FLAG_DOCUMENT_3', 'FLAG_DOCUMENT_4', 'FLAG_DOCUMENT_5', 'FLAG_DOCUMENT_6',
'FLAG_DOCUMENT_7', 'FLAG_DOCUMENT_8', 'FLAG_DOCUMENT_9', 'FLAG_DOCUMENT_10', 'FLAG_DOCUMENT_11', 'FLAG_DOCUMENT_12',
'FLAG_DOCUMENT_13', 'FLAG_DOCUMENT_14', 'FLAG_DOCUMENT_15', 'FLAG_DOCUMENT_16', 'FLAG_DOCUMENT_17', 'FLAG_DOCUMENT_18',
'FLAG_DOCUMENT_19', 'FLAG_DOCUMENT_20', 'FLAG_DOCUMENT_21']
vars_to_encode = ['NAME_CONTRACT_TYPE', 'CODE_GENDER', 'FLAG_OWN_CAR', 'FLAG_OWN_REALTY', 'NAME_INCOME_TYPE','NAME_EDUCATION_TYPE',
'NAME_FAMILY_STATUS', 'NAME_HOUSING_TYPE', 'WEEKDAY_APPR_PROCESS_START', 'ORGANIZATION_TYPE']
for var in already_coded:
df[var] = df[var].astype('category')
df = encode_cat(df, vars_to_encode)
# removing rows with all 0
df = df[df.T.any()]
df.describe()
```
### Checking for correlations between variables
```
X = df.iloc[:, 1:]
# getting correlation matrix of continuous and categorical variables
cont = ['TARGET'] + continuous_vars
cat = ['TARGET'] + categorical_vars
cont_df = df.loc[:, cont]
cat_df = df.loc[:, cat]
cont_corr = cont_df.corr()
cat_corr = cat_df.corr()
plt.figure(figsize=(10,10));
sns.heatmap(cont_corr,
xticklabels = cont_corr.columns,
yticklabels = cont_corr.columns,
cmap="PiYG",
linewidth = 1);
# Find Point biserial correlation
for cat_var in categorical_vars:
for cont_var in continuous_vars:
data_cat = df[cat_var].to_numpy()
data_cont = df[cont_var].to_numpy()
corr, p_val = pointbiserialr(x=data_cat, y=data_cont)
if np.abs(corr) >= 0.8:
print(f'Categorical variable: {cat_var}, Continuous variable: {cont_var}, correlation: {corr}')
# Find Pearson correlation
total_len = len(continuous_vars)
for idx1 in range(total_len-1):
for idx2 in range(idx1+1, total_len):
cont_var1 = continuous_vars[idx1]
cont_var2 = continuous_vars[idx2]
data_cont1 = X[cont_var1].to_numpy()
data_cont2 = X[cont_var2].to_numpy()
corr, p_val = pearsonr(x=data_cont1, y=data_cont2)
if np.abs(corr) >= 0.8:
print(f' Continuous var 1: {cont_var1}, Continuous var 2: {cont_var2}, correlation: {corr}')
sns.scatterplot(data=X, x='CNT_CHILDREN',y='CNT_FAM_MEMBERS');
# Find Cramer's V correlation
total_len = len(categorical_vars)
for idx1 in range(total_len-1):
for idx2 in range(idx1+1, total_len):
cat_var1 = categorical_vars[idx1]
cat_var2 = categorical_vars[idx2]
c_matrix = pd.crosstab(X[cat_var1], X[cat_var2])
""" calculate Cramers V statistic for categorial-categorial association.
uses correction from Bergsma and Wicher,
Journal of the Korean Statistical Society 42 (2013): 323-328
"""
chi2 = chi2_contingency(c_matrix)[0]
n = c_matrix.sum().sum()
phi2 = chi2/n
r,k = c_matrix.shape
phi2corr = max(0, phi2-((k-1)*(r-1))/(n-1))
rcorr = r-((r-1)**2)/(n-1)
kcorr = k-((k-1)**2)/(n-1)
corr = np.sqrt(phi2corr/min((kcorr-1),(rcorr-1)))
if corr >= 0.8:
print(f'categorical variable 1 {cat_var1}, categorical variable 2: {cat_var2}, correlation: {corr}')
corr, p_val = pearsonr(x=df['REGION_RATING_CLIENT_W_CITY'], y=df['REGION_RATING_CLIENT'])
print(corr)
# High collinearity of 0.95 between variables suggests that one of it should be removed, we shall remove the REGION_RATING_CLIENT_W_CITY.
# Drop highly correlated variables
vars_to_drop += ['CNT_FAM_MEMBERS', 'REG_REGION_NOT_WORK_REGION', 'REG_CITY_NOT_WORK_CITY', 'AMT_GOODS_PRICE', 'REGION_RATING_CLIENT_W_CITY']
features_to_keep = [x for x in df.columns if x not in vars_to_drop]
features_to_keep
new_df = df.loc[:, features_to_keep]
new_df
# Checking correlation of X continuous columns vs TARGET column
plt.figure(figsize=(10,10))
df_corr = new_df.corr()
ax = sns.heatmap(df_corr,
xticklabels=df_corr.columns,
yticklabels=df_corr.columns,
annot = True,
cmap ="RdYlGn")
# No particular feature found to be significantly correlated with the target
# REGION_RATING_CLIENT and REGION_POPULATION_RELATIVE have multicollinearity
features_to_keep.remove('REGION_POPULATION_RELATIVE')
features_to_keep
# These are our final list of features
```
###Plots
```
ax1 = sns.boxplot(y='AMT_CREDIT', x= 'TARGET', data=new_df)
ax1.set_title("Target by amount credit of the loan", fontsize=20);
```
The amount credit of an individual does not seem to have a siginifcant effect on whether a person finds it difficult to pay. But they are crucial for our business reccomendations so we keep them.
```
ax2 = sns.barplot(x='CNT_CHILDREN', y= 'TARGET', data=new_df)
ax2.set_title("Target by number of children", fontsize=20);
```
From these plots, we can see that number of children has quite a significant effect on whether one defaults or not, with an increasing number of children proving more difficulty to return the loan.
```
ax3 = sns.barplot(x='NAME_FAMILY_STATUS', y= 'TARGET', data=new_df);
ax3.set_title("Target by family status", fontsize=20);
plt.xticks(np.arange(6), ['Civil marriage', 'Married', 'Separated', 'Single / not married',
'Unknown', 'Widow'], rotation=20);
```
Widows have the lowest likelihood of finding it difficult to pay, a possible target for our reccomendation strategy.
```
new_df['YEARS_BIRTH_CAT'] = pd.cut(df.YEARS_BIRTH, bins= [21, 25, 35, 45, 55, 69], labels= ["25 and below", "26-35", "36-45", "46-55", "Above 55"])
ax4 = sns.barplot(x='YEARS_BIRTH_CAT', y= 'TARGET', data=new_df);
ax4.set_title("Target by age", fontsize=20);
```
Analysis of age groups on ability to pay shows clear trend that the older you are, the better able you are to pay your loans. We will use this to craft our reccomendations.
```
ax5 = sns.barplot(y='TARGET', x= 'NAME_INCOME_TYPE', data=new_df);
ax5.set_title("Target by income type", fontsize=20);
plt.xticks(np.arange(0, 8),['Businessman', 'Commercial associate', 'Maternity leave', 'Pensioner',
'State servant', 'Student', 'Unemployed', 'Working'], rotation=20);
ax6 = sns.barplot(x='NAME_EDUCATION_TYPE', y= 'TARGET', data=new_df);
ax6.set_title("Target by education type", fontsize=20);
plt.xticks(np.arange(5), ['Academic Degree', 'Higher education', 'Incomplete higher', 'Lower secondary', 'Secondary / secondary special'], rotation=20);
ax7 = sns.barplot(x='ORGANIZATION_TYPE', y= 'TARGET', data=new_df);
ax7.set_title("Target by organization type", fontsize=20);
plt.xticks(np.arange(58), ['Unknown','Advertising','Agriculture', 'Bank', 'Business Entity Type 1', 'Business Entity Type 2',
'Business Entity Type 3', 'Cleaning', 'Construction', 'Culture', 'Electricity', 'Emergency', 'Government', 'Hotel', 'Housing', 'Industry: type 1', 'Industry: type 10', 'Industry: type 11', 'Industry: type 12', 'Industry: type 13', 'Industry: type 2', 'Industry: type 3', 'Industry: type 4', 'Industry: type 5', 'Industry: type 6', 'Industry: type 7', 'Industry: type 8', 'Industry: type 9', 'Insurance', 'Kindergarten', 'Legal Services', 'Medicine', 'Military', 'Mobile', 'Other', 'Police', 'Postal', 'Realtor', 'Religion', 'Restaurant', 'School', 'Security', 'Security Ministries', 'Self-employed', 'Services', 'Telecom', 'Trade: type 1', 'Trade: type 2', 'Trade: type 3', 'Trade: type 4', 'Trade: type 5', 'Trade: type 6', 'Trade: type 7', 'Transport: type 1', 'Transport: type 2', 'Transport: type 3', 'Transport: type 4','University'], rotation=90);
ax8 = sns.barplot(x='NAME_CONTRACT_TYPE', y= 'TARGET', data=new_df);
ax8.set_title("Target by contract type", fontsize=20);
plt.xticks(np.arange(2), ['Cash Loan', 'Revolving Loan']);
```
People who get revolving loans are more likely to pay back their loans than cash loans, perhaps due to the revolving loans being of a lower amount, and also its higher interest rate and recurring nature.
```
ax9 = sns.barplot(x='CODE_GENDER', y= 'TARGET', data=new_df);
ax9.set_title("Target by gender", fontsize=20);
plt.xticks(np.arange(2), ['Female', 'Male']);
```
Males find it harder to pay back their loans than females in general.
```
# Splitting Credit into bins of 10k
new_df['Credit_Category'] = pd.cut(new_df.AMT_CREDIT, bins= [0, 100000, 200000, 300000, 400000, 500000, 600000, 700000, 800000, 900000, 1000000, 4.050000e+06], labels= ["0-100k", "100-200k", "200-300k", "300-400k", "400-500k", "500-600k", "600-700k", "700-800k", "800-900k","900-1 million", "Above 1 million"])
setorder= new_df.groupby('Credit_Category')['TARGET'].mean().sort_values(ascending=False)
ax10 = sns.barplot(x='Credit_Category', y= 'TARGET', data=new_df, order = setorder.index);
ax10.set_title("Target by Credit Category", fontsize=20);
plt.show()
#No. of people who default
print(new_df.loc[new_df["TARGET"]==0, 'Credit_Category',].value_counts().sort_index())
#No. of people who repayed
print(new_df.loc[new_df["TARGET"]==1, 'Credit_Category',].value_counts().sort_index())
new_df['Credit_Category'].value_counts().sort_index()
# This will be useful for our first recommendation
#temp = new_df["Credit_Category"].value_counts()
#df1 = pd.DataFrame({"Credit_Category": temp.index,'Number of contracts': temp.values})
## Calculate the percentage of target=1 per category value
#cat_perc = new_df[["Credit_Category", 'TARGET']].groupby(["Credit_Category"],as_index=False).mean()
#cat_perc["TARGET"] = cat_perc["TARGET"]*100
#cat_perc.sort_values(by='TARGET', ascending=False, inplace=True)
#fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12,6))
#s = sns.countplot(ax=ax1,
# x = "Credit_Category",
# data=new_df,
# hue ="TARGET",
# order=cat_perc["Credit_Category"],
# palette=['g','r'])
#ax1.set_title("Credit Category", fontdict={'fontsize' : 10, 'fontweight' : 3, 'color' : 'Blue'})
#ax1.legend(['Repayer','Defaulter'])
## If the plot is not readable, use the log scale.
##if ylog:
## ax1.set_yscale('log')
## ax1.set_ylabel("Count (log)",fontdict={'fontsize' : 10, 'fontweight' : 3, 'color' : 'Blue'})
#s.set_xticklabels(s.get_xticklabels(),rotation=90)
#s = sns.barplot(ax=ax2, x = "Credit_Category", y='TARGET', order=cat_perc["Credit_Category"], data=cat_perc, palette='Set2')
#s.set_xticklabels(s.get_xticklabels(),rotation=90)
#plt.ylabel('Percent of Defaulters [%]', fontsize=10)
#plt.tick_params(axis='both', which='major', labelsize=10)
#ax2.set_title("Credit Category" + " Defaulter %", fontdict={'fontsize' : 15, 'fontweight' : 5, 'color' : 'Blue'})
#plt.show();
new_df.info()
```
| true |
code
| 0.470493 | null | null | null | null |
|
# Introduction to Python
> Defining Functions with Python
Kuo, Yao-Jen
## TL; DR
> In this lecture, we will talk about defining functions with Python.
## Encapsulations
## What is encapsulation?
> Encapsulation refers to one of two related but distinct notions, and sometimes to the combination thereof:
> 1. A language mechanism for restricting direct access to some of the object's components.
> 2. A language construct that facilitates the bundling of data with the methods (or other functions) operating on that data.
Source: <https://en.wikipedia.org/wiki/Encapsulation_(computer_programming)>
## Why encapsulation?
As our codes piled up, we need a mechanism making them:
- more structured
- more reusable
- more scalable
## Python provides several tools for programmers organizing their codes
- Functions
- Classes
- Modules
- Libraries
## How do we decide which tool to adopt?
Simply put, that depends on **scale** and project spec.
## These components are mixed and matched with great flexibility
- A couple lines of code assembles a function
- A couple of functions assembles a class
- A couple of classes assembles a module
- A couple of modules assembles a library
- A couple of libraries assembles a larger library
## Codes, assemble!

Source: <https://giphy.com/>
## Functions
## What is a function
> A function is a named sequence of statements that performs a computation, either mathematical, symbolic, or graphical. When we define a function, we specify the name and the sequence of statements. Later, we can call the function by name.
## Besides built-in functions or library-powered functions, we sometimes need to self-define our own functions
- `def` the name of our function
- `return` the output of our function
```python
def function_name(INPUTS, ARGUMENTS, ...):
"""
docstring: print documentation when help() is called
"""
# sequence of statements
return OUTPUTS
```
## The principle of designing of a function is about mapping the relationship of inputs and outputs
- The one-on-one relationship
- The many-on-one relationship
- The one-on-many relationship
- The many-on-many releationship
## The one-on-one relationship
Using scalar as input and output.
```
def absolute(x):
"""
Return the absolute value of the x.
"""
if x >= 0:
return x
else:
return -x
```
## Once the function is defined, call as if it is a built-in function
```
help(absolute)
print(absolute(-5566))
print(absolute(5566))
print(absolute(0))
```
## The many-on-one relationship relationship
- Using scalars or structures for fixed inputs
- Using `*args` or `**kwargs` for flexible inputs
## Using scalars for fixed inputs
```
def product(x, y):
"""
Return the product values of x and y.
"""
return x*y
print(product(5, 6))
```
## Using structures for fixed inputs
```
def product(x):
"""
x: an iterable.
Return the product values of x.
"""
prod = 1
for i in x:
prod *= i
return prod
print(product([5, 5, 6, 6]))
```
## Using `*args` for flexible inputs
- As in flexible arguments
- Getting flexible `*args` as a `tuple`
```
def plain_return(*args):
"""
Return args.
"""
return args
print(plain_return(5, 5, 6, 6))
```
## Using `**kwargs` for flexible inputs
- AS in keyword arguments
- Getting flexible `**kwargs` as a `dict`
```
def plain_return(**kwargs):
"""
Retrun kwargs.
"""
return kwargs
print(plain_return(TW='Taiwan', JP='Japan', CN='China', KR='South Korea'))
```
## The one-on-many relationship
- Using default `tuple` with comma
- Using preferred data structure
## Using default `tuple` with comma
```
def as_integer_ratio(x):
"""
Return x as integer ratio.
"""
x_str = str(x)
int_part = int(x_str.split(".")[0])
decimal_part = x_str.split(".")[1]
n_decimal = len(decimal_part)
denominator = 10**(n_decimal)
numerator = int(decimal_part)
while numerator % 2 == 0 and denominator % 2 == 0:
denominator /= 2
numerator /= 2
while numerator % 5 == 0 and denominator % 5 == 0:
denominator /= 5
numerator /= 5
final_numerator = int(int_part*denominator + numerator)
final_denominator = int(denominator)
return final_numerator, final_denominator
print(as_integer_ratio(3.14))
print(as_integer_ratio(0.56))
```
## Using preferred data structure
```
def as_integer_ratio(x):
"""
Return x as integer ratio.
"""
x_str = str(x)
int_part = int(x_str.split(".")[0])
decimal_part = x_str.split(".")[1]
n_decimal = len(decimal_part)
denominator = 10**(n_decimal)
numerator = int(decimal_part)
while numerator % 2 == 0 and denominator % 2 == 0:
denominator /= 2
numerator /= 2
while numerator % 5 == 0 and denominator % 5 == 0:
denominator /= 5
numerator /= 5
final_numerator = int(int_part*denominator + numerator)
final_denominator = int(denominator)
integer_ratio = {
'numerator': final_numerator,
'denominator': final_denominator
}
return integer_ratio
print(as_integer_ratio(3.14))
print(as_integer_ratio(0.56))
```
## The many-on-many relationship
A mix-and-match of one-on-many and many-on-one relationship.
## Handling errors
## Coding mistakes are common, they happen all the time

Source: Google Search
## How does a function designer handle errors?
Python mistakes come in three basic flavors:
- Syntax errors
- Runtime errors
- Semantic errors
## Syntax errors
Errors where the code is not valid Python (generally easy to fix).
```
# Python does not need curly braces to create a code block
for (i in range(10)) {print(i)}
```
## Runtime errors
Errors where syntactically valid code fails to execute, perhaps due to invalid user input (sometimes easy to fix)
- `NameError`
- `TypeError`
- `ZeroDivisionError`
- `IndexError`
- ...etc.
```
print('5566'[4])
```
## Semantic errors
Errors in logic: code executes without a problem, but the result is not what you expect (often very difficult to identify and fix)
```
def product(x):
"""
x: an iterable.
Return the product values of x.
"""
prod = 0 # set
for i in x:
prod *= i
return prod
print(product([5, 5, 6, 6])) # expecting 900
```
## Using `try` and `except` to catch exceptions
```python
try:
# sequence of statements if everything is fine
except TYPE_OF_ERROR:
# sequence of statements if something goes wrong
```
```
try:
exec("""for (i in range(10)) {print(i)}""")
except SyntaxError:
print("Encountering a SyntaxError.")
try:
print('5566'[4])
except IndexError:
print("Encountering a IndexError.")
try:
print(5566 / 0)
except ZeroDivisionError:
print("Encountering a ZeroDivisionError.")
# it is optional to specify the type of error
try:
print(5566 / 0)
except:
print("Encountering a whatever error.")
```
## Scope
## When it comes to defining functions, it is vital to understand the scope of a variable
## What is scope?
> In computer programming, the scope of a name binding, an association of a name to an entity, such as a variable, is the region of a computer program where the binding is valid.
Source: <https://en.wikipedia.org/wiki/Scope_(computer_science)>
## Simply put, now we have a self-defined function, so the programming environment is now split into 2:
- Global
- Local
## A variable declared within the indented block of a function is a local variable, it is only valid inside the `def` block
```
def check_odd_even(x):
mod = x % 2 # local variable, declared inside def block
if mod == 0:
return '{} is a even number.'.format(x)
else:
return '{} is a odd number.'.format(x)
print(check_odd_even(0))
print(x)
print(mod)
```
## A variable declared outside of the indented block of a function is a glocal variable, it is valid everywhere
```
x = 0
mod = x % 2
def check_odd_even():
if mod == 0:
return '{} is a even number.'.format(x)
else:
return '{} is a odd number.'.format(x)
print(check_odd_even())
print(x)
print(mod)
```
## Although global variable looks quite convenient, it is HIGHLY recommended NOT using global variable directly in a indented function block.
| true |
code
| 0.552359 | null | null | null | null |
|
<br><br><font color="gray">DOING COMPUTATIONAL SOCIAL SCIENCE<br>MODULE 10 <strong>PROBLEM SETS</strong></font>
# <font color="#49699E" size=40>MODULE 10 </font>
# What You Need to Know Before Getting Started
- **Every notebook assignment has an accompanying quiz**. Your work in each notebook assignment will serve as the basis for your quiz answers.
- **You can consult any resources you want when completing these exercises and problems**. Just as it is in the "real world:" if you can't figure out how to do something, look it up. My recommendation is that you check the relevant parts of the assigned reading or search for inspiration on [https://stackoverflow.com](https://stackoverflow.com).
- **Each problem is worth 1 point**. All problems are equally weighted.
- **The information you need for each problem set is provided in the blue and green cells.** General instructions / the problem set preamble are in the blue cells, and instructions for specific problems are in the green cells. **You have to execute all of the code in the problem set, but you are only responsible for entering code into the code cells that immediately follow a green cell**. You will also recognize those cells because they will be incomplete. You need to replace each blank `▰▰#▰▰` with the code that will make the cell execute properly (where # is a sequentially-increasing integer, one for each blank).
- Most modules will contain at least one question that requires you to load data from disk; **it is up to you to locate the data, place it in an appropriate directory on your local machine, and replace any instances of the `PATH_TO_DATA` variable with a path to the directory containing the relevant data**.
- **The comments in the problem cells contain clues indicating what the following line of code is supposed to do.** Use these comments as a guide when filling in the blanks.
- **You can ask for help**. If you run into problems, you can reach out to John ([email protected]) or Pierson ([email protected]) for help. You can ask a friend for help if you like, regardless of whether they are enrolled in the course.
Finally, remember that you do not need to "master" this content before moving on to other course materials, as what is introduced here is reinforced throughout the rest of the course. You will have plenty of time to practice and cement your new knowledge and skills.
<div class='alert alert-block alert-danger'>As you complete this assignment, you may encounter variables that can be assigned a wide variety of different names. Rather than forcing you to employ a particular convention, we leave the naming of these variables up to you. During the quiz, submit an answer of 'USER_DEFINED' (without the quotation marks) to fill in any blank that you assigned an arbitrary name to. In most circumstances, this will occur due to the presence of a local iterator in a for-loop.</b></div>
## Package Imports
```
import pandas as pd
import numpy as np
from numpy.random import seed as np_seed
import graphviz
from graphviz import Source
from pyprojroot import here
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
from sklearn import preprocessing
from sklearn.model_selection import train_test_split, cross_val_score, ShuffleSplit
from sklearn.linear_model import LinearRegression, Ridge, Lasso, LogisticRegression
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier, GradientBoostingClassifier
from sklearn.preprocessing import LabelEncoder, LabelBinarizer
from sklearn.neighbors import KNeighborsClassifier
from sklearn.feature_extraction.text import TfidfVectorizer
import tensorflow as tf
from tensorflow import keras
from tensorflow.random import set_seed
import spacy
from time import time
set_seed(42)
np_seed(42)
```
## Defaults
```
x_columns = [
# Religion and Morale
'v54', # Religious services? - 1=More than Once Per Week, 7=Never
'v149', # Do you justify: claiming state benefits? - 1=Never, 10=Always
'v150', # Do you justify: cheating on tax? - 1=Never, 10=Always
'v151', # Do you justify: taking soft drugs? - 1=Never, 10=Always
'v152', # Do you justify: taking a bribe? - 1=Never, 10=Always
'v153', # Do you justify: homosexuality? - 1=Never, 10=Always
'v154', # Do you justify: abortion? - 1=Never, 10=Always
'v155', # Do you justify: divorce? - 1=Never, 10=Always
'v156', # Do you justify: euthanasia? - 1=Never, 10=Always
'v157', # Do you justify: suicide? - 1=Never, 10=Always
'v158', # Do you justify: having casual sex? - 1=Never, 10=Always
'v159', # Do you justify: public transit fare evasion? - 1=Never, 10=Always
'v160', # Do you justify: prostitution? - 1=Never, 10=Always
'v161', # Do you justify: artificial insemination? - 1=Never, 10=Always
'v162', # Do you justify: political violence? - 1=Never, 10=Always
'v163', # Do you justify: death penalty? - 1=Never, 10=Always
# Politics and Society
'v97', # Interested in Politics? - 1=Interested, 4=Not Interested
'v121', # How much confidence in Parliament? - 1=High, 4=Low
'v126', # How much confidence in Health Care System? - 1=High, 4=Low
'v142', # Importance of Democracy - 1=Unimportant, 10=Important
'v143', # Democracy in own country - 1=Undemocratic, 10=Democratic
'v145', # Political System: Strong Leader - 1=Good, 4=Bad
# 'v208', # How often follow politics on TV? - 1=Daily, 5=Never
# 'v211', # How often follow politics on Social Media? - 1=Daily, 5=Never
# National Identity
'v170', # How proud are you of being a citizen? - 1=Proud, 4=Not Proud
'v184', # Immigrants: impact on development of country - 1=Bad, 5=Good
'v185', # Immigrants: take away jobs from Nation - 1=Take, 10=Do Not Take
'v198', # European Union Enlargement - 1=Should Go Further, 10=Too Far Already
]
y_columns = [
# Overview
'country',
# Socio-demographics
'v226', # Year of Birth by respondent
'v261_ppp', # Household Monthly Net Income, PPP-Corrected
]
```
## Problem 1:
<div class="alert alert-block alert-info">
In this assignment, we're going to continue our exploration of the European Values Survey dataset. By wielding the considerable power of Artificial Neural Networks, we'll aim to create a model capable of predicting an individual survey respondent's country of residence. As with all machine/deep learning projects, our first task will involve loading and preparing the data.
</div>
<div class="alert alert-block alert-success">
Load the EVS dataset and use it to create a feature matrix (using all columns from x_columns) and (with the assistance of Scikit Learn's LabelBinarizer) a target array (representing each respondent's country of residence).
</div>
```
# Load EVS Dataset
df = pd.read_csv(PATH_TO_DATA/"evs_module_08.csv")
# Create Feature Matrix (using all columns from x_columns)
X = df[x_columns]
# Initialize LabelBinarizer
country_encoder = ▰▰1▰▰()
# Fit the LabelBinarizer instance to the data's 'country' column and store transformed array as target
y = country_encoder.▰▰2▰▰(np.array(▰▰3▰▰))
```
## Problem 2:
<div class="alert alert-block alert-info">
As part of your work in the previous module, you were introduced to the concept of the train-validate-test split. Up until now, we had made extensive use of Scikit Learn's preprocessing and cross-validation suites in order to easily get the most out of our data. Since we're using TensorFlow for our Artificial Neural Networks, we're going to have to change course a little: we can still use the <code>train_test_split</code> function, but we must now use it twice: the first iteration will produce our test set and a 'temporary' dataset; the second iteration will split the 'temporary' data into training and validation sets. Throughout this process, we must take pains to ensure that each of the data splits are shuffled and stratified.
</div>
<div class="alert alert-block alert-success">
Create shuffled, stratified splits for testing (10% of original dataset), validation (10% of data remaining from test split), and training (90% of data remaining from test split) sets. Submit the number of observations in the <code>X_valid</code> set, as an integer.
</div>
```
# Split into temporary and test sets
X_t, X_test, y_t, y_test = ▰▰1▰▰(
▰▰2▰▰,
▰▰3▰▰,
test_size = ▰▰4▰▰,
shuffle = ▰▰5▰▰,
stratify = y,
random_state = 42
)
# Split into training and validation sets
X_train, X_valid, y_train, y_valid = train_test_split(
▰▰6▰▰,
▰▰7▰▰,
test_size = ▰▰8▰▰,
shuffle = ▰▰9▰▰,
stratify = ▰▰10▰▰,
random_state = 42,
)
len(X_valid)
```
## Problem 3:
<div class="alert alert-block alert-info">
As you work with Keras and Tensorflow, you'll rapidly discover that both packages are very picky about the 'shape' of the data you're using. What's more, you can't always rely on them to correctly infer your data's shape. As such, it's usually a good idea to store the two most important shapes -- number of variables in the feature matrix and number of unique categories in the target -- as explicit, named variables; doing so will save you the trouble of trying to retrieve them later (or as part of your model specification, which can get messy). We'll start with the number of variables in the feature matrix.
</div>
<div class="alert alert-block alert-success">
Store the number of variables in the feature matrix, as an integer, in the <code>num_vars</code> variable. Submit the resulting number as an integer.
</div>
```
# The code we've provided here is just a suggestion; feel free to use any approach you like
num_vars = np.▰▰1▰▰(▰▰2▰▰).▰▰3▰▰[1]
print(num_vars)
```
## Problem 4:
<div class="alert alert-block alert-info">
Now, for the number of categories (a.k.a. labels) in the target.
</div>
<div class="alert alert-block alert-success">
Store the number of categories in the target, as an integer, in the <code>num_vars</code> variable. Submit the resulting number as an integer.
</div>
```
# The code we've provided here is just a suggestion; feel free to use any approach you like
num_labels = ▰▰1▰▰.▰▰2▰▰[1]
print(num_labels)
```
## Problem 5:
<div class="alert alert-block alert-info">
Everything is now ready for us to begin building an Artifical Neural Network! Aside from specifying that the ANN must be built using Keras's <code>Sequential</code> API, we're going to give you the freedom to tackle the creation of your ANN in whichever manner you like. Feel free to use the 'add' method to build each layer one at a time, or pass all of the layers to your model at instantiation as a list, or any other approach you may be familiar with. Kindly ensure that your model matches the specifications below <b>exactly</b>!
</div>
<div class="alert alert-block alert-success">
Using Keras's <code>Sequential</code> API, create a new ANN. Your ANN should have the following layers, in this order:
<ol>
<li> Input layer with one argument: number of variables in the feature matrix
<li> Dense layer with 400 neurons and the "relu" activation function
<li> Dense layer with 10 neurons and the "relu" activation function
<li> Dense layer with neurons equal to the number of labels in the target and the "softmax" activation function
</ol>
Submit the number of hidden layers in your model.
</div>
```
# Create your ANN!
nn_model = keras.models.Sequential()
```
## Problem 6:
<div class="alert alert-block alert-info">
Even though we've specified all of the layers in our model, it isn't yet ready to go. We must first 'compile' the model, during which time we'll specify a number of high-level arguments. Just as in the textbook, we'll go with a fairly standard set of arguments: we'll use Stochastic Gradient Descent as our optimizer, and our only metric will be Accuracy (an imperfect but indispensably simple measure). It'll be up to you to figure out what loss function we should use: you might have to go digging in the textbook to find it!
</div>
<div class="alert alert-block alert-success">
Compile the model according to the specifications outlined in the blue text above. Submit the name of the loss function <b>exactly</b> as it appears in your code (you should only need to include a single underscore -- no other punctuation, numbers, or special characters).
</div>
```
nn_model.▰▰1▰▰(
loss=keras.losses.▰▰2▰▰,
optimizer=▰▰3▰▰,
metrics=[▰▰4▰▰]
)
```
## Problem 7:
<div class="alert alert-block alert-info">
Everything is prepared. All that remains is to train the model!
</div>
<div class="alert alert-block alert-success">
Train your neural network for 100 epochs. Be sure to include the validation data variables.
</div>
```
np_seed(42)
tf.random.set_seed(42)
history = nn_model.▰▰1▰▰(▰▰2▰▰, ▰▰3▰▰, epochs=▰▰4▰▰, validation_data = (▰▰5▰▰, ▰▰6▰▰))
```
## Problem 8:
<div class="alert alert-block alert-info">
For some Neural Networks, 100 epochs is more than ample time to reach a best solution. For others, 100 epochs isn't enough time for the learning process to even get underway. One good method for assessing the progress of your model at a glance involves visualizing how your loss scores and metric(s) -- for both your training and validation sets) -- changed during training.
</div>
<div class="alert alert-block alert-success">
After 100 epochs of training, is the model still appreciably improving? (If it is still improving, you shouldn't see much evidence of overfitting). Submit your answer as a boolean value (True = still improving, False = not still improving).
</div>
```
pd.DataFrame(history.history).plot(figsize = (8, 8))
plt.grid(True)
plt.show()
```
## Problem 9:
<div class="alert alert-block alert-info">
Regardless of whether this model is done or not, it's time to dig into what our model has done. Here, we'll continue re-tracing the steps taken in the textbook, producing a (considerably more involved) confusion matrix, visualizing it as a heatmap, and peering into our model's soul. The first step in this process involves creating the confusion matrix.
</div>
<div class="alert alert-block alert-success">
Using the held-back test data, create a confusion matrix.
</div>
```
y_pred = np.argmax(nn_model.predict(▰▰1▰▰), axis=1)
y_true = np.argmax(▰▰2▰▰, axis=1)
conf_mat = tf.math.confusion_matrix(▰▰3▰▰, ▰▰4▰▰)
```
## Problem 10:
<div class="alert alert-block alert-info">
Finally, we're ready to visualize the matrix we created above. Rather than asking you to recreate the baroque visualization code, we're going to skip straight to interpretation.
</div>
<div class="alert alert-block alert-success">
Plot the confusion matrix heatmap and examine it. Based on what you know about the dataset, should the sum of the values in a column (representing the number of observations from a country) be the same for each country? If so, submit the integer that each column adds up to. If not, submit 0.
</div>
```
sns.set(rc={'figure.figsize':(12,12)})
plt.figure()
sns.heatmap(
np.array(conf_mat).T,
xticklabels=country_encoder.classes_,
yticklabels=country_encoder.classes_,
square=True,
annot=True,
fmt='g',
)
plt.xlabel("Observed")
plt.ylabel("Predicted")
plt.show()
```
## Problem 11:
<div class="alert alert-block alert-success">
Based on what you know about the dataset, should the sum of the values in a row (representing the number of observations your model <b>predicted</b> as being from a country) be the same for each country? If so, submit the integer that each row adds up to. If not, submit 0.
</div>
```
```
## Problem 12:
<div class="alert alert-block alert-success">
If your model was built and run to the specifications outlined in the assignment, your results should include at least three countries whose observations the model struggled to identify (fewer than 7 accurate predictions each). Submit the name of one such country.<br><br>As a result of the randomness inherent to these models, it is possible that your interpretation will be correct, but will be graded as incorrect. If you feel that your interpretation was erroneously graded, please email a screenshot of your confusion matrix heatmap to Pierson along with an explanation of how you arrived at the answer you did.
</div>
```
```
| true |
code
| 0.686974 | null | null | null | null |
|
# GLM: Robust Regression with Outlier Detection
**A minimal reproducable example of Robust Regression with Outlier Detection using Hogg 2010 Signal vs Noise method.**
+ This is a complementary approach to the Student-T robust regression as illustrated in Thomas Wiecki's notebook in the [PyMC3 documentation](http://pymc-devs.github.io/pymc3/GLM-robust/), that approach is also compared here.
+ This model returns a robust estimate of linear coefficients and an indication of which datapoints (if any) are outliers.
+ The likelihood evaluation is essentially a copy of eqn 17 in "Data analysis recipes: Fitting a model to data" - [Hogg 2010](http://arxiv.org/abs/1008.4686).
+ The model is adapted specifically from Jake Vanderplas' [implementation](http://www.astroml.org/book_figures/chapter8/fig_outlier_rejection.html) (3rd model tested).
+ The dataset is tiny and hardcoded into this Notebook. It contains errors in both the x and y, but we will deal here with only errors in y.
**Note:**
+ Python 3.4 project using latest available [PyMC3](https://github.com/pymc-devs/pymc3)
+ Developed using [ContinuumIO Anaconda](https://www.continuum.io/downloads) distribution on a Macbook Pro 3GHz i7, 16GB RAM, OSX 10.10.5.
+ During development I've found that 3 data points are always indicated as outliers, but the remaining ordering of datapoints by decreasing outlier-hood is slightly unstable between runs: the posterior surface appears to have a small number of solutions with similar probability.
+ Finally, if runs become unstable or Theano throws weird errors, try clearing the cache `$> theano-cache clear` and rerunning the notebook.
**Package Requirements (shown as a conda-env YAML):**
```
$> less conda_env_pymc3_examples.yml
name: pymc3_examples
channels:
- defaults
dependencies:
- python=3.4
- ipython
- ipython-notebook
- ipython-qtconsole
- numpy
- scipy
- matplotlib
- pandas
- seaborn
- patsy
- pip
$> conda env create --file conda_env_pymc3_examples.yml
$> source activate pymc3_examples
$> pip install --process-dependency-links git+https://github.com/pymc-devs/pymc3
```
## Setup
```
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import optimize
import pymc3 as pm
import theano as thno
import theano.tensor as T
# configure some basic options
sns.set(style="darkgrid", palette="muted")
pd.set_option('display.notebook_repr_html', True)
plt.rcParams['figure.figsize'] = 12, 8
np.random.seed(0)
```
### Load and Prepare Data
We'll use the Hogg 2010 data available at https://github.com/astroML/astroML/blob/master/astroML/datasets/hogg2010test.py
It's a very small dataset so for convenience, it's hardcoded below
```
#### cut & pasted directly from the fetch_hogg2010test() function
## identical to the original dataset as hardcoded in the Hogg 2010 paper
dfhogg = pd.DataFrame(np.array([[1, 201, 592, 61, 9, -0.84],
[2, 244, 401, 25, 4, 0.31],
[3, 47, 583, 38, 11, 0.64],
[4, 287, 402, 15, 7, -0.27],
[5, 203, 495, 21, 5, -0.33],
[6, 58, 173, 15, 9, 0.67],
[7, 210, 479, 27, 4, -0.02],
[8, 202, 504, 14, 4, -0.05],
[9, 198, 510, 30, 11, -0.84],
[10, 158, 416, 16, 7, -0.69],
[11, 165, 393, 14, 5, 0.30],
[12, 201, 442, 25, 5, -0.46],
[13, 157, 317, 52, 5, -0.03],
[14, 131, 311, 16, 6, 0.50],
[15, 166, 400, 34, 6, 0.73],
[16, 160, 337, 31, 5, -0.52],
[17, 186, 423, 42, 9, 0.90],
[18, 125, 334, 26, 8, 0.40],
[19, 218, 533, 16, 6, -0.78],
[20, 146, 344, 22, 5, -0.56]]),
columns=['id','x','y','sigma_y','sigma_x','rho_xy'])
## for convenience zero-base the 'id' and use as index
dfhogg['id'] = dfhogg['id'] - 1
dfhogg.set_index('id', inplace=True)
## standardize (mean center and divide by 1 sd)
dfhoggs = (dfhogg[['x','y']] - dfhogg[['x','y']].mean(0)) / dfhogg[['x','y']].std(0)
dfhoggs['sigma_y'] = dfhogg['sigma_y'] / dfhogg['y'].std(0)
dfhoggs['sigma_x'] = dfhogg['sigma_x'] / dfhogg['x'].std(0)
## create xlims ylims for plotting
xlims = (dfhoggs['x'].min() - np.ptp(dfhoggs['x'])/5
,dfhoggs['x'].max() + np.ptp(dfhoggs['x'])/5)
ylims = (dfhoggs['y'].min() - np.ptp(dfhoggs['y'])/5
,dfhoggs['y'].max() + np.ptp(dfhoggs['y'])/5)
## scatterplot the standardized data
g = sns.FacetGrid(dfhoggs, size=8)
_ = g.map(plt.errorbar, 'x', 'y', 'sigma_y', 'sigma_x', marker="o", ls='')
_ = g.axes[0][0].set_ylim(ylims)
_ = g.axes[0][0].set_xlim(xlims)
plt.subplots_adjust(top=0.92)
_ = g.fig.suptitle('Scatterplot of Hogg 2010 dataset after standardization', fontsize=16)
```
**Observe**:
+ Even judging just by eye, you can see these datapoints mostly fall on / around a straight line with positive gradient
+ It looks like a few of the datapoints may be outliers from such a line
## Create Conventional OLS Model
The *linear model* is really simple and conventional:
$$\bf{y} = \beta^{T} \bf{X} + \bf{\sigma}$$
where:
$\beta$ = coefs = $\{1, \beta_{j \in X_{j}}\}$
$\sigma$ = the measured error in $y$ in the dataset `sigma_y`
### Define model
**NOTE:**
+ We're using a simple linear OLS model with Normally distributed priors so that it behaves like a ridge regression
```
with pm.Model() as mdl_ols:
## Define weakly informative Normal priors to give Ridge regression
b0 = pm.Normal('b0_intercept', mu=0, sd=100)
b1 = pm.Normal('b1_slope', mu=0, sd=100)
## Define linear model
yest = b0 + b1 * dfhoggs['x']
## Use y error from dataset, convert into theano variable
sigma_y = thno.shared(np.asarray(dfhoggs['sigma_y'],
dtype=thno.config.floatX), name='sigma_y')
## Define Normal likelihood
likelihood = pm.Normal('likelihood', mu=yest, sd=sigma_y, observed=dfhoggs['y'])
```
### Sample
```
with mdl_ols:
## take samples
traces_ols = pm.sample(2000, tune=1000)
```
### View Traces
**NOTE**: I'll 'burn' the traces to only retain the final 1000 samples
```
_ = pm.traceplot(traces_ols[-1000:], figsize=(12,len(traces_ols.varnames)*1.5),
lines={k: v['mean'] for k, v in pm.df_summary(traces_ols[-1000:]).iterrows()})
```
**NOTE:** We'll illustrate this OLS fit and compare to the datapoints in the final plot
---
---
## Create Robust Model: Student-T Method
I've added this brief section in order to directly compare the Student-T based method exampled in Thomas Wiecki's notebook in the [PyMC3 documentation](http://pymc-devs.github.io/pymc3/GLM-robust/)
Instead of using a Normal distribution for the likelihood, we use a Student-T, which has fatter tails. In theory this allows outliers to have a smaller mean square error in the likelihood, and thus have less influence on the regression estimation. This method does not produce inlier / outlier flags but is simpler and faster to run than the Signal Vs Noise model below, so a comparison seems worthwhile.
**Note:** we'll constrain the Student-T 'degrees of freedom' parameter `nu` to be an integer, but otherwise leave it as just another stochastic to be inferred: no need for prior knowledge.
### Define Model
```
with pm.Model() as mdl_studentt:
## Define weakly informative Normal priors to give Ridge regression
b0 = pm.Normal('b0_intercept', mu=0, sd=100)
b1 = pm.Normal('b1_slope', mu=0, sd=100)
## Define linear model
yest = b0 + b1 * dfhoggs['x']
## Use y error from dataset, convert into theano variable
sigma_y = thno.shared(np.asarray(dfhoggs['sigma_y'],
dtype=thno.config.floatX), name='sigma_y')
## define prior for Student T degrees of freedom
nu = pm.Uniform('nu', lower=1, upper=100)
## Define Student T likelihood
likelihood = pm.StudentT('likelihood', mu=yest, sd=sigma_y, nu=nu,
observed=dfhoggs['y'])
```
### Sample
```
with mdl_studentt:
## take samples
traces_studentt = pm.sample(2000, tune=1000)
```
#### View Traces
```
_ = pm.traceplot(traces_studentt[-1000:],
figsize=(12,len(traces_studentt.varnames)*1.5),
lines={k: v['mean'] for k, v in pm.df_summary(traces_studentt[-1000:]).iterrows()})
```
**Observe:**
+ Both parameters `b0` and `b1` show quite a skew to the right, possibly this is the action of a few samples regressing closer to the OLS estimate which is towards the left
+ The `nu` parameter seems very happy to stick at `nu = 1`, indicating that a fat-tailed Student-T likelihood has a better fit than a thin-tailed (Normal-like) Student-T likelihood.
+ The inference sampling also ran very quickly, almost as quickly as the conventional OLS
**NOTE:** We'll illustrate this Student-T fit and compare to the datapoints in the final plot
---
---
## Create Robust Model with Outliers: Hogg Method
Please read the paper (Hogg 2010) and Jake Vanderplas' code for more complete information about the modelling technique.
The general idea is to create a 'mixture' model whereby datapoints can be described by either the linear model (inliers) or a modified linear model with different mean and larger variance (outliers).
The likelihood is evaluated over a mixture of two likelihoods, one for 'inliers', one for 'outliers'. A Bernouilli distribution is used to randomly assign datapoints in N to either the inlier or outlier groups, and we sample the model as usual to infer robust model parameters and inlier / outlier flags:
$$
\mathcal{logL} = \sum_{i}^{i=N} log \left[ \frac{(1 - B_{i})}{\sqrt{2 \pi \sigma_{in}^{2}}} exp \left( - \frac{(x_{i} - \mu_{in})^{2}}{2\sigma_{in}^{2}} \right) \right] + \sum_{i}^{i=N} log \left[ \frac{B_{i}}{\sqrt{2 \pi (\sigma_{in}^{2} + \sigma_{out}^{2})}} exp \left( - \frac{(x_{i}- \mu_{out})^{2}}{2(\sigma_{in}^{2} + \sigma_{out}^{2})} \right) \right]
$$
where:
$\bf{B}$ is Bernoulli-distibuted $B_{i} \in [0_{(inlier)},1_{(outlier)}]$
### Define model
```
def logp_signoise(yobs, is_outlier, yest_in, sigma_y_in, yest_out, sigma_y_out):
'''
Define custom loglikelihood for inliers vs outliers.
NOTE: in this particular case we don't need to use theano's @as_op
decorator because (as stated by Twiecki in conversation) that's only
required if the likelihood cannot be expressed as a theano expression.
We also now get the gradient computation for free.
'''
# likelihood for inliers
pdfs_in = T.exp(-(yobs - yest_in + 1e-4)**2 / (2 * sigma_y_in**2))
pdfs_in /= T.sqrt(2 * np.pi * sigma_y_in**2)
logL_in = T.sum(T.log(pdfs_in) * (1 - is_outlier))
# likelihood for outliers
pdfs_out = T.exp(-(yobs - yest_out + 1e-4)**2 / (2 * (sigma_y_in**2 + sigma_y_out**2)))
pdfs_out /= T.sqrt(2 * np.pi * (sigma_y_in**2 + sigma_y_out**2))
logL_out = T.sum(T.log(pdfs_out) * is_outlier)
return logL_in + logL_out
with pm.Model() as mdl_signoise:
## Define weakly informative Normal priors to give Ridge regression
b0 = pm.Normal('b0_intercept', mu=0, sd=10, testval=pm.floatX(0.1))
b1 = pm.Normal('b1_slope', mu=0, sd=10, testval=pm.floatX(1.))
## Define linear model
yest_in = b0 + b1 * dfhoggs['x']
## Define weakly informative priors for the mean and variance of outliers
yest_out = pm.Normal('yest_out', mu=0, sd=100, testval=pm.floatX(1.))
sigma_y_out = pm.HalfNormal('sigma_y_out', sd=100, testval=pm.floatX(1.))
## Define Bernoulli inlier / outlier flags according to a hyperprior
## fraction of outliers, itself constrained to [0,.5] for symmetry
frac_outliers = pm.Uniform('frac_outliers', lower=0., upper=.5)
is_outlier = pm.Bernoulli('is_outlier', p=frac_outliers, shape=dfhoggs.shape[0],
testval=np.random.rand(dfhoggs.shape[0]) < 0.2)
## Extract observed y and sigma_y from dataset, encode as theano objects
yobs = thno.shared(np.asarray(dfhoggs['y'], dtype=thno.config.floatX), name='yobs')
sigma_y_in = thno.shared(np.asarray(dfhoggs['sigma_y'], dtype=thno.config.floatX),
name='sigma_y_in')
## Use custom likelihood using DensityDist
likelihood = pm.DensityDist('likelihood', logp_signoise,
observed={'yobs': yobs, 'is_outlier': is_outlier,
'yest_in': yest_in, 'sigma_y_in': sigma_y_in,
'yest_out': yest_out, 'sigma_y_out': sigma_y_out})
```
### Sample
```
with mdl_signoise:
## two-step sampling to create Bernoulli inlier/outlier flags
step1 = pm.Metropolis([frac_outliers, yest_out, sigma_y_out, b0, b1])
step2 = pm.step_methods.BinaryGibbsMetropolis([is_outlier])
## take samples
traces_signoise = pm.sample(20000, step=[step1, step2], tune=10000, progressbar=True)
```
### View Traces
```
traces_signoise[-10000:]['b0_intercept']
_ = pm.traceplot(traces_signoise[-10000:], figsize=(12,len(traces_signoise.varnames)*1.5),
lines={k: v['mean'] for k, v in pm.df_summary(traces_signoise[-1000:]).iterrows()})
```
**NOTE:**
+ During development I've found that 3 datapoints id=[1,2,3] are always indicated as outliers, but the remaining ordering of datapoints by decreasing outlier-hood is unstable between runs: the posterior surface appears to have a small number of solutions with very similar probability.
+ The NUTS sampler seems to work okay, and indeed it's a nice opportunity to demonstrate a custom likelihood which is possible to express as a theano function (thus allowing a gradient-based sampler like NUTS). However, with a more complicated dataset, I would spend time understanding this instability and potentially prefer using more samples under Metropolis-Hastings.
---
---
## Declare Outliers and Compare Plots
### View ranges for inliers / outlier predictions
At each step of the traces, each datapoint may be either an inlier or outlier. We hope that the datapoints spend an unequal time being one state or the other, so let's take a look at the simple count of states for each of the 20 datapoints.
```
outlier_melt = pd.melt(pd.DataFrame(traces_signoise['is_outlier', -1000:],
columns=['[{}]'.format(int(d)) for d in dfhoggs.index]),
var_name='datapoint_id', value_name='is_outlier')
ax0 = sns.pointplot(y='datapoint_id', x='is_outlier', data=outlier_melt,
kind='point', join=False, ci=None, size=4, aspect=2)
_ = ax0.vlines([0,1], 0, 19, ['b','r'], '--')
_ = ax0.set_xlim((-0.1,1.1))
_ = ax0.set_xticks(np.arange(0, 1.1, 0.1))
_ = ax0.set_xticklabels(['{:.0%}'.format(t) for t in np.arange(0,1.1,0.1)])
_ = ax0.yaxis.grid(True, linestyle='-', which='major', color='w', alpha=0.4)
_ = ax0.set_title('Prop. of the trace where datapoint is an outlier')
_ = ax0.set_xlabel('Prop. of the trace where is_outlier == 1')
```
**Observe**:
+ The plot above shows the number of samples in the traces in which each datapoint is marked as an outlier, expressed as a percentage.
+ In particular, 3 points [1, 2, 3] spend >=95% of their time as outliers
+ Contrastingly, points at the other end of the plot close to 0% are our strongest inliers.
+ For comparison, the mean posterior value of `frac_outliers` is ~0.35, corresponding to roughly 7 of the 20 datapoints. You can see these 7 datapoints in the plot above, all those with a value >50% or thereabouts.
+ However, only 3 of these points are outliers >=95% of the time.
+ See note above regarding instability between runs.
The 95% cutoff we choose is subjective and arbitrary, but I prefer it for now, so let's declare these 3 to be outliers and see how it looks compared to Jake Vanderplas' outliers, which were declared in a slightly different way as points with means above 0.68.
### Declare outliers
**Note:**
+ I will declare outliers to be datapoints that have value == 1 at the 5-percentile cutoff, i.e. in the percentiles from 5 up to 100, their values are 1.
+ Try for yourself altering cutoff to larger values, which leads to an objective ranking of outlier-hood.
```
cutoff = 5
dfhoggs['outlier'] = np.percentile(traces_signoise[-1000:]['is_outlier'],cutoff, axis=0)
dfhoggs['outlier'].value_counts()
```
### Posterior Prediction Plots for OLS vs StudentT vs SignalNoise
```
g = sns.FacetGrid(dfhoggs, size=8, hue='outlier', hue_order=[True,False],
palette='Set1', legend_out=False)
lm = lambda x, samp: samp['b0_intercept'] + samp['b1_slope'] * x
pm.plot_posterior_predictive_glm(traces_ols[-1000:],
eval=np.linspace(-3, 3, 10), lm=lm, samples=200, color='#22CC00', alpha=.2)
pm.plot_posterior_predictive_glm(traces_studentt[-1000:], lm=lm,
eval=np.linspace(-3, 3, 10), samples=200, color='#FFA500', alpha=.5)
pm.plot_posterior_predictive_glm(traces_signoise[-1000:], lm=lm,
eval=np.linspace(-3, 3, 10), samples=200, color='#357EC7', alpha=.3)
_ = g.map(plt.errorbar, 'x', 'y', 'sigma_y', 'sigma_x', marker="o", ls='').add_legend()
_ = g.axes[0][0].annotate('OLS Fit: Green\nStudent-T Fit: Orange\nSignal Vs Noise Fit: Blue',
size='x-large', xy=(1,0), xycoords='axes fraction',
xytext=(-160,10), textcoords='offset points')
_ = g.axes[0][0].set_ylim(ylims)
_ = g.axes[0][0].set_xlim(xlims)
```
**Observe**:
+ The posterior preditive fit for:
+ the **OLS model** is shown in **Green** and as expected, it doesn't appear to fit the majority of our datapoints very well, skewed by outliers
+ the **Robust Student-T model** is shown in **Orange** and does appear to fit the 'main axis' of datapoints quite well, ignoring outliers
+ the **Robust Signal vs Noise model** is shown in **Blue** and also appears to fit the 'main axis' of datapoints rather well, ignoring outliers.
+ We see that the **Robust Signal vs Noise model** also yields specific estimates of _which_ datapoints are outliers:
+ 17 'inlier' datapoints, in **Blue** and
+ 3 'outlier' datapoints shown in **Red**.
+ From a simple visual inspection, the classification seems fair, and agrees with Jake Vanderplas' findings.
+ Overall, it seems that:
+ the **Signal vs Noise model** behaves as promised, yielding a robust regression estimate and explicit labelling of inliers / outliers, but
+ the **Signal vs Noise model** is quite complex and whilst the regression seems robust and stable, the actual inlier / outlier labelling seems slightly unstable
+ if you simply want a robust regression without inlier / outlier labelling, the **Student-T model** may be a good compromise, offering a simple model, quick sampling, and a very similar estimate.
---
Example originally contributed by Jonathan Sedar 2015-12-21 [github.com/jonsedar](https://github.com/jonsedar)
| true |
code
| 0.696978 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.