prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# ELG Signal-to-Noise Calculations
This notebook provides a standardized calculation of the DESI emission-line galaxy (ELG) signal-to-noise (SNR) figure of merit, for tracking changes to simulation inputs and models. See the accompanying technical note [DESI-3977](https://desi.lbl.gov/DocDB/cgi-bin/private/ShowDocument?docid=3977) for details.
```
%pylab inline
import astropy.table
import astropy.cosmology
import astropy.io.fits as fits
import astropy.units as u
```
Parts of this notebook assume that the [desimodel package](https://github.com/desihub/desimodel) is installed (both its git and svn components) and its `data/` directory is accessible via the `$DESIMODEL` environment variable:
```
import os.path
assert 'DESIMODEL' in os.environ
assert os.path.exists(os.path.join(os.getenv('DESIMODEL'), 'data', 'spectra', 'spec-sky.dat'))
```
Document relevant version numbers:
```
import desimodel
import specsim
print(f'Using desimodel {desimodel.__version__}, specsim {specsim.__version__}')
```
## ELG Spectrum
All peaks are assumed to have the same log-normal rest lineshape specified by a velocity dispersion $\sigma_v$, total flux $F_0$ and central wavelength $\lambda_0$ as:
$$
f(\lambda; F_0, \lambda_0) = \frac{F_0}{\sqrt{2\pi}\,\lambda\,\sigma_{\log}}\, \exp\left[
-\frac{1}{2}\left( \frac{\log_{10}\lambda - \log_{10}\lambda_0}{\sigma_{\log}}\right)^2\right]\; ,
$$
where
$$
\sigma_{\log} \equiv \frac{\sigma_v}{c \log 10} \; .
$$
We use the pretabulated spectrum in `$DESIMODEL/data/spectra/spec-elg-o2flux-8e-17-average-line-ratios.dat` described in Section 2.3 of DESI-867-v1,
which consists of only the following emission lines:
- \[OII](3727A) and \[OII](3730A)
- H-beta
- \[OIII](4960A) and \[OIII](5008A)
- H-alpha
Note that H-alpha is never observable for $z > 0.5$, as is always the case for DESI ELG targets.
Continuum is omitted since we are primarily interested in how well the \[OII] doublet can be identified and measured.
All lines are assumed to have the same velocity dispersion of 70 km/s.
```
elg_spec = astropy.table.Table.read(
os.path.join(os.environ['DESIMODEL'], 'data', 'spectra', 'spec-elg-o2flux-8e-17-average-line-ratios.dat'),
format='ascii')
elg_wlen0 = elg_spec['col1'].data
elg_flux0 = 1e-17 * elg_spec['col2'].data
```
## DESI ELG Sample
Look up the expected redshift distribution of DESI ELG targets from `$DESIMODEL/data/targets/nz_elg.dat`. Note that the [OII] doublet falls off the spectrograph around z = 1.63.
```
def get_elg_nz():
# Read the nz file from $DESIMODEL.
full_name = os.path.join(os.environ['DESIMODEL'], 'data', 'targets', 'nz_elg.dat')
table = astropy.table.Table.read(full_name, format='ascii')
# Extract the n(z) histogram into numpy arrays.
z_lo, z_hi = table['col1'], table['col2']
assert np.all(z_hi[:-1] == z_lo[1:])
z_edge = np.hstack((z_lo, [z_hi[-1]]))
nz = table['col3']
# Trim to bins where n(z) > 0.
non_zero = np.where(nz > 0)[0]
lo, hi = non_zero[0], non_zero[-1] + 1
nz = nz[lo: hi]
z_edge = z_edge[lo: hi + 1]
return nz, z_edge
elg_nz, elg_z_edge = get_elg_nz()
```
Calculate n(z) weights corresponding to an array of ELG redshifts:
```
def get_nz_weight(z):
"""Calculate n(z) weights corresponding to input z values.
"""
nz = np.zeros_like(z)
idx = np.digitize(z, elg_z_edge)
sel = (idx > 0) & (idx <= len(elg_nz))
nz[sel] = elg_nz[idx[sel] - 1]
return nz
```
Sample random redshifts from n(z):
```
def generate_elg_z(n=100, seed=123):
cdf = np.cumsum(elg_nz)
cdf = np.hstack(([0], cdf / cdf[-1]))
gen = np.random.RandomState(seed)
return np.interp(gen.rand(n), cdf, elg_z_edge)
z=generate_elg_z(n=20000)
plt.hist(z, bins=elg_z_edge, histtype='stepfilled')
plt.xlim(elg_z_edge[0], elg_z_edge[-1])
print(f'Mean ELG redshift is {np.mean(z):.3f}')
```
Define a background cosmology for the angular-diameter distance used to scale galaxy angular sizes:
```
LCDM = astropy.cosmology.Planck15
```
Generate random ELG profiles for each target. The mean half-light radius is 0.45" and scales with redshift.
```
def generate_elg_profiles(z, seed=123, verbose=False):
"""ELG profiles are assumed to be disk (Sersic n=1) only.
"""
gen = np.random.RandomState(seed)
nsrc = len(z)
source_fraction = np.zeros((nsrc, 2))
source_half_light_radius = np.zeros((nsrc, 2))
source_minor_major_axis_ratio = np.zeros((nsrc, 2))
source_position_angle = 360. * gen.normal(size=(nsrc, 2))
# Precompute cosmology scale factors.
angscale = (
LCDM.angular_diameter_distance(1.0) /
LCDM.angular_diameter_distance(z)).to(1).value
if verbose:
print(f'mean n(z) DA(1.0)/DA(z) = {np.mean(angscale):.3f}')
# Disk only with random size and ellipticity.
source_fraction[:, 0] = 1.
source_half_light_radius[:, 0] = 0.427 * np.exp(0.25 * gen.normal(size=nsrc)) * angscale
source_minor_major_axis_ratio[:, 0] = np.minimum(0.99, 0.50 * np.exp(0.15 * gen.normal(size=nsrc)))
if verbose:
print(f'mean HLR = {np.mean(source_half_light_radius[:, 0]):.3f}"')
return dict(
source_fraction=source_fraction,
source_half_light_radius=source_half_light_radius,
source_minor_major_axis_ratio=source_minor_major_axis_ratio,
source_position_angle=source_position_angle)
```
Diagnostic plot showing the assumed ELG population (Figure 1 of DESI-3977):
```
def plot_elg_profiles(save=None):
z = generate_elg_z(50000)
sources = generate_elg_profiles(z, verbose=True)
fig, ax = plt.subplots(2, 2, figsize=(8, 6))
ax = ax.flatten()
ax[0].hist(sources['source_minor_major_axis_ratio'][:, 0], range=(0,1), bins=25)
ax[0].set_xlabel('ELG minor/major axis ratio')
ax[0].set_xlim(0, 1)
ax[1].hist(z, bins=np.arange(0.6, 1.8, 0.1))
ax[1].set_xlim(0.6, 1.7)
ax[1].set_xlabel('ELG redshift')
ax[2].hist(sources['source_half_light_radius'][:, 0], bins=25)
ax[2].set_xlabel('ELG half-light radius [arcsec]')
ax[2].set_xlim(0.1, 1.1)
ax[3].scatter(z, sources['source_half_light_radius'][:, 0], s=0.5, alpha=0.5)
ax[3].set_xlabel('ELG redshift')
ax[3].set_ylabel('ELG half-light radius [arcsec]')
ax[3].set_xlim(0.6, 1.7)
ax[3].set_ylim(0.1, 1.1)
plt.tight_layout()
if save:
plt.savefig(save)
plot_elg_profiles(save='elg-sample.png')
```
## Simulated SNR
Given an initialized simulator object, step through different redshifts and calculate the SNR recorded by all fibers for a fixed ELG spectrum. Save the results to a FITS file that can be used by `plot_elg_snr()`.
```
def calculate_elg_snr(simulator, save, description,
z1=0.6, z2=1.65, dz=0.002, zref=1.20,
seed=123, wlen=elg_wlen0, flux=elg_flux0):
"""Calculate the ELG [OII] SNR as a function of redshift.
Parameters
----------
simulator : specsim.simulator.Simulator
Instance of an initialized Simulator object to use. Each fiber will
be simulated independently to study variations across the focal plane.
save : str
Filename to use for saving FITS results.
description : str
Short description for the saved file header, also used for plots later.
z1 : float
Minimum ELG redshift to calculate.
z2 : float
Maximum ELG redshift to calculate.
dz : float
Spacing of equally spaced grid to cover [z1, z2]. z2 will be increased
by up to dz if necessary.
zref : float
Reference redshift used to save signal, noise and fiberloss. Must be
on the grid specified by (z1, z2, dz).
seed : int or None
Random seed used to generate fiber positions and galaxy profiles.
wlen : array
1D array of N rest wavelengths in Angstroms.
flux : array
1D array of N corresponding rest fluxes in erg / (s cm2 Angstrom).
"""
zooms = (3715., 3742.), (4850., 4875.), (4950., 5020.)
gen = np.random.RandomState(seed=seed)
# Generate random focal plane (x,y) positions for each fiber in mm units.
nfibers = simulator.num_fibers
focal_r = np.sqrt(gen.uniform(size=nfibers)) * simulator.instrument.field_radius
phi = 2 * np.pi * gen.uniform(size=nfibers)
xy = (np.vstack([np.cos(phi), np.sin(phi)]) * focal_r).T
# Build the grid of redshifts to simulate.
nz = int(np.ceil((z2 - z1) / dz)) + 1
z2 = z1 + (nz - 1) * dz
z_grid = np.linspace(z1, z2, nz)
iref = np.argmin(np.abs(z_grid - zref))
assert np.abs(zref - z_grid[iref]) < 1e-5, 'zref not in z_grid'
snr2 = np.zeros((4, nz, simulator.num_fibers))
# Initialize the results.
hdus = fits.HDUList()
hdus.append(fits.PrimaryHDU(
header=fits.Header({'SEED': seed, 'NFIBERS': nfibers, 'DESCRIBE': description})))
# Zero-pad the input spectrum if necessary.
wlo = 0.99 * desi.simulated['wavelength'][0] / (1 + z2)
if wlen[0] > wlo:
wlen = np.hstack([[wlo], wlen])
flux = np.hstack([[0.], flux])
# Simulate the specified rest-frame flux.
simulator.source.update_in(
'ELG [OII] doublet', 'elg',
wlen * u.Angstrom, flux * u.erg/(u.s * u.cm**2 * u.Angstrom), z_in=0.)
# Simulate each redshift.
for i, z in enumerate(z_grid):
# Redshift the ELG spectrum.
simulator.source.update_out(z_out=z)
source_flux = np.tile(simulator.source.flux_out, [nfibers, 1])
# Generate source profiles for each target at this redshift. Since the seed is
# fixed, only the redshift scaling of the HLR will change.
sources = generate_elg_profiles(np.full(nfibers, z), seed=seed)
# Simulate each source.
simulator.simulate(source_fluxes=source_flux, focal_positions=xy, **sources)
# Calculate the quadrature sum of SNR in each camera, by fiber.
for output in simulator.camera_output:
rest_wlen = output['wavelength'] / (1 + z)
# Loop over emission lines.
for j, (lo, hi) in enumerate(zooms):
sel = (rest_wlen >= lo) & (rest_wlen < hi)
if not np.any(sel):
continue
# Sum SNR2 over pixels.
pixel_snr2 = output['num_source_electrons'][sel] ** 2 / output['variance_electrons'][sel]
snr2[j, i] += pixel_snr2.sum(axis=0)
if i == iref:
# Save the fiberloss fraction and total variance tabulated on the simulation grid.
table = astropy.table.Table(meta={'ZREF': zref})
sim = simulator.simulated
table['WLEN'] = sim['wavelength'].data
table['FLUX'] = sim['source_flux'].data
table['FIBERLOSS'] = sim['fiberloss'].data
table['NSRC'] = sim['num_source_electrons_b'] + sim['num_source_electrons_r'] + sim['num_source_electrons_z']
table['SKYVAR'] = sim['num_sky_electrons_b'] + sim['num_sky_electrons_r'] + sim['num_sky_electrons_z']
table['NOISEVAR'] = (
sim['read_noise_electrons_b'] ** 2 + sim['read_noise_electrons_r'] ** 2 + sim['read_noise_electrons_z'] ** 2 +
sim['num_dark_electrons_b'] + sim['num_dark_electrons_r'] + sim['num_dark_electrons_z'])
hdus.append(fits.table_to_hdu(table))
hdus[-1].name = 'REF'
# Calculate the n(z) weighted mean SNR for [OII], using the median over fibers at each redshift.
snr_oii = np.median(np.sqrt(snr2[0]), axis=-1)
wgt = get_nz_weight(z_grid)
snr_oii_eff = np.sum(snr_oii * wgt) / np.sum(wgt)
print(f'n(z)-weighted effective [OII] SNR = {snr_oii_eff:.3f}')
# Save the SNR vs redshift arrays for each emission line.
table = astropy.table.Table(meta={'SNREFF': snr_oii_eff})
table['Z'] = z_grid
table['ZWGT'] = wgt
table['SNR_OII'] = np.sqrt(snr2[0])
table['SNR_HBETA'] = np.sqrt(snr2[1])
table['SNR_OIII'] = np.sqrt(snr2[2])
hdus.append(fits.table_to_hdu(table))
hdus[-1].name = 'SNR'
hdus.writeto(save, overwrite=True)
```
Calculate flux limits in bins of redshift, to compare with SRD L3.1.3:
```
def get_flux_limits(z, snr, nominal_flux=8., nominal_snr=7., ax=None):
fluxlim = np.zeros_like(snr)
nonzero = snr > 0
fluxlim[nonzero] = nominal_flux * (nominal_snr / snr[nonzero])
bins = np.linspace(0.6, 1.6, 6)
nlim = len(bins) - 1
medians = np.empty(nlim)
for i in range(nlim):
sel = (z >= bins[i]) & (z < bins[i + 1])
medians[i] = np.median(fluxlim[sel])
if ax is not None:
zmid = 0.5 * (bins[1:] + bins[:-1])
dz = 0.5 * (bins[1] - bins[0])
ax.errorbar(zmid, medians, xerr=dz, color='b', fmt='o', zorder=10, capsize=3)
return fluxlim, medians
```
Plot a summary of the results saved by `calculate_elg_snr()`. Shaded bands show the 5-95 percentile range, with the median drawn as a solid curve. The fiberloss in the lower plot is calculated at the redshift `zref` specified in `calculate_elg_snr()` (since the ELG size distribution is redshift dependent).
```
def plot_elg_snr(name, save=True):
"""Plot a summary of results saved by calculate_elg_snr().
Parameters
----------
name : str
Name of the FITS file saved by calculate_elg_snr().
"""
hdus = fits.open(name)
hdr = hdus[0].header
nfibers = hdr['NFIBERS']
description = hdr['DESCRIBE']
fig, axes = plt.subplots(2, 1, figsize=(8, 6))
plt.suptitle(description, fontsize=14)
snr_table = astropy.table.Table.read(hdus['SNR'])
snr_oii_eff = snr_table.meta['SNREFF']
ref_table = astropy.table.Table.read(hdus['REF'])
zref = ref_table.meta['ZREF']
ax = axes[0]
color = 'rgb'
labels = '[OII]', 'H$\\beta$', '[OIII]'
z_grid = snr_table['Z'].data
for i, tag in enumerate(('SNR_OII', 'SNR_HBETA', 'SNR_OIII')):
snr = snr_table[tag].data
snr_q = np.percentile(snr, (5, 50, 95), axis=-1)
ax.fill_between(z_grid, snr_q[0], snr_q[2], color=color[i], alpha=0.25, lw=0)
ax.plot(z_grid, snr_q[1], c=color[i], ls='-', label=labels[i])
ax.plot([], [], 'k:', label='n(z)')
ax.legend(ncol=4)
ax.set_xlabel('ELG redshift')
ax.set_ylabel(f'Total signal-to-noise ratio')
ax.axhline(7, c='k', ls='--')
rhs = ax.twinx()
rhs.plot(z_grid, snr_table['ZWGT'], 'k:')
rhs.set_yticks([])
ax.set_xlim(z_grid[0], z_grid[-1])
ax.set_ylim(0, 12)
rhs.set_ylim(0, None)
ax.text(0.02, 0.03, f'n(z)-wgtd [OII] SNR={snr_oii_eff:.3f}',
fontsize=12, transform=ax.transAxes)
# Calculate the median [OII] flux limits.
_, fluxlim = get_flux_limits(z_grid, np.median(snr_table['SNR_OII'], axis=-1))
# Print latex-format results for DESI-3977 Table 2.
print(f'&{snr_oii_eff:7.3f}', end='')
for m in fluxlim:
print(f' &{m:5.1f}', end='')
print(' \\\\')
ax = axes[1]
wlen = ref_table['WLEN'].data
dwlen = wlen[1] - wlen[0]
sky_q = np.percentile(ref_table['SKYVAR'].data, (5, 50, 95), axis=-1)
sky_q[sky_q > 0] = 1 / sky_q[sky_q > 0]
ax.fill_between(wlen, sky_q[0], sky_q[2], color='b', alpha=0.5, lw=0)
ax.plot([], [], 'b-', label='sky ivar')
ax.plot(wlen, sky_q[1], 'b.', ms=0.25, alpha=0.5)
noise_q = np.percentile(ref_table['NOISEVAR'].data, (5, 50, 95), axis=-1)
noise_q[noise_q > 0] = 1 / noise_q[noise_q > 0]
ax.fill_between(wlen, noise_q[0], noise_q[2], color='r', alpha=0.25, lw=0)
ax.plot(wlen, noise_q[1], c='r', ls='-', label='noise ivar')
floss_q = np.percentile(ref_table['FIBERLOSS'].data, (5, 50, 95), axis=-1)
ax.plot([], [], 'k-', label='fiberloss')
rhs = ax.twinx()
rhs.fill_between(wlen, floss_q[0], floss_q[2], color='k', alpha=0.25, lw=0)
rhs.plot(wlen, floss_q[1], 'k-')
rhs.set_ylim(0.2, 0.6)
rhs.yaxis.set_major_locator(matplotlib.ticker.MultipleLocator(0.1))
rhs.set_ylabel('Fiberloss')
ax.set_xlabel('Wavelength [A]')
ax.set_ylabel(f'Inverse Variance / {dwlen:.1f}A')
ax.set_xlim(wlen[0], wlen[-1])
ax.set_ylim(0, 0.25)
ax.legend(ncol=3)
plt.subplots_adjust(wspace=0.1, top=0.95, bottom=0.08, left=0.10, right=0.92)
if save:
base, _ = os.path.splitext(name)
plot_name = base + '.png'
plt.savefig(plot_name)
print(f'Saved {plot_name}')
```
## Examples
Demonstrate this calculation for the baseline DESI configuration with 100 fibers:
```
import specsim.simulator
desi = specsim.simulator.Simulator('desi', num_fibers=100)
```
**NOTE: the next cell takes about 15 minutes to run.**
```
%time calculate_elg_snr(desi, save='desimodel-0.9.6.fits', description='desimodel 0.9.6')
```
Plot the results (Figure 2 of DESI-3977):
```
plot_elg_snr('desimodel-0.9.6.fits')
```
Check that the results with GalSim are compatible with those using the (default) fastsim mode of fiberloss calculations:
```
desi.instrument.fiberloss_method = 'galsim'
```
**NOTE: the next cell takes about 30 minutes to run.**
```
%time calculate_elg_snr(desi, save='desimodel-0.9.6-galsim.fits', description='desimodel 0.9.6 (galsim)')
plot_elg_snr('desimodel-0.9.6-galsim.fits')
```
This comparison shows that the "fastsim" fiberloss fractions are about 1% (absolute) higher than "galsim", leading to a slight increase in signal and therefore SNR. The reason for this increase is that "fastsim" assumes a fixed minor / major axis ratio of 0.7 while our ELG population has a distribution of ratios with a median of 0.5. The weighted [OII] SNR values are 6.764 (fastsim) and 6.572 (galsim), which agree at the few percent level.
We use GalSim fiberloss calculations consistently in Figure 2 and Table 2 of DESI-3977.
### CDR Comparison
Compare with the CDR forecasts based on desimodel 0.3.1 and documented in DESI-867, using data from this [FITS file](https://desi.lbl.gov/svn/docs/technotes/spectro/elg-snr/trunk/data/elg_snr2_desimodel-0-3-1.fits):
```
desi867 = astropy.table.Table.read('elg_snr2_desimodel-0-3-1.fits', hdu=1)
```
Check that we can reproduce the figures from DESI-867:
```
def desi_867_fig1():
z = desi867['Z']
snr_all = np.sqrt(desi867['SNR2'])
snr_oii = np.sqrt(desi867['SNR2_OII'])
fig = plt.figure(figsize=(6, 5))
plt.plot(z, snr_all, 'k-', lw=1, label='all lines')
plt.plot(z, snr_oii, 'r-', lw=1, label='[OII] only')
plt.legend(fontsize='large')
plt.axhline(7, c='b', ls='--')
plt.ylim(0, 22)
plt.xlim(z[0], z[-1])
plt.xticks([0.5, 1.0, 1.5])
plt.xlabel('Redshift')
plt.ylabel('S/N')
desi_867_fig1()
def desi_867_fig2():
z = desi867['Z']
snr_all = np.sqrt(desi867['SNR2'])
snr_oii = np.sqrt(desi867['SNR2_OII'])
flux_limit_all, _ = get_flux_limits(z, snr_all)
flux_limit_oii, medians = get_flux_limits(z, snr_oii)
fig = plt.figure(figsize=(6, 5))
plt.plot(z, flux_limit_all, 'k-', lw=1, label='all lines')
plt.plot(z, flux_limit_oii, 'r-', lw=1, label='[OII] only')
plt.legend(loc='upper right', fontsize='large')
_, _ = get_flux_limits(z, snr_oii, ax=plt.gca())
plt.ylim(0, 40)
plt.xlim(z[0], z[-1])
plt.xticks([0.5, 1.0, 1.5])
plt.xlabel('Redshift')
plt.ylabel('[OII] Flux limit ($10^{-17}$ ergs cm$^{-2}$ s$^{-1}$)')
desi_867_fig2()
```
Print a summary for Table 2 of DESI-3977:
```
def cdr_summary():
z = desi867['Z']
snr_oii = np.sqrt(desi867['SNR2_OII'])
wgt = get_nz_weight(z)
snreff = np.sum(wgt * snr_oii) / wgt.sum()
_, medians = get_flux_limits(z, snr_oii)
print(f'0.3.1 (CDR) & {snreff:6.3f}', end='')
for m in medians:
print(f' &{m:5.1f}', end='')
print(' \\\\')
cdr_summary()
```
| true |
code
| 0.665112 | null | null | null | null |
|
```
"""
You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.
Instructions for setting up Colab are as follows:
1. Open a new Python 3 notebook.
2. Import this notebook from GitHub (File -> Upload Notebook -> "GITHUB" tab -> copy/paste GitHub URL)
3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select "GPU" for hardware accelerator)
4. Run this cell to set up dependencies.
"""
# If you're using Google Colab and not running locally, run this cell
# install NeMo
BRANCH = 'v1.0.0b3'
!python -m pip install git+https://github.com/NVIDIA/NeMo.git@$BRANCH#egg=nemo_toolkit[nlp]
# If you're not using Colab, you might need to upgrade jupyter notebook to avoid the following error:
# 'ImportError: IProgress not found. Please update jupyter and ipywidgets.'
! pip install ipywidgets
! jupyter nbextension enable --py widgetsnbextension
# Please restart the kernel after running this cell
from nemo.collections import nlp as nemo_nlp
from nemo.utils.exp_manager import exp_manager
import os
import wget
import torch
import pytorch_lightning as pl
from omegaconf import OmegaConf
```
In this tutorial, we are going to describe how to finetune a BERT-like model based on [BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding](https://arxiv.org/abs/1810.04805) on [GLUE: A Multi-Task Benchmark and Analysis Platform for Natural Language Understanding](https://openreview.net/pdf?id=rJ4km2R5t7).
# GLUE tasks
GLUE Benchmark includes 9 natural language understanding tasks:
## Single-Sentence Tasks
* CoLA - [The Corpus of Linguistic Acceptability](https://arxiv.org/abs/1805.12471) is a set of English sentences from published linguistics literature. The task is to predict whether a given sentence is grammatically correct or not.
* SST-2 - [The Stanford Sentiment Treebank](https://nlp.stanford.edu/~socherr/EMNLP2013_RNTN.pdf) consists of sentences from movie reviews and human annotations of their sentiment. The task is to predict the sentiment of a given sentence: positive or negative.
## Similarity and Paraphrase tasks
* MRPC - [The Microsoft Research Paraphrase Corpus](https://www.aclweb.org/anthology/I05-5002.pdf) is a corpus of sentence pairs automatically extracted from online news sources, with human annotations for whether the sentences in the pair are semantically equivalent.
* QQP - [The Quora Question Pairs](https://www.quora.com/q/quoradata/First-Quora-Dataset-Release-Question-Pairs) dataset is a collection of question pairs from the community question-answering website Quora. The task is to determine whether a pair of questions are semantically equivalent.
* STS-B - [The Semantic Textual Similarity Benchmark](https://arxiv.org/abs/1708.00055) is a collection of sentence pairs drawn from news headlines, video, and image captions, and natural language inference data. The task is to determine how similar two sentences are.
## Inference Tasks
* MNLI - [The Multi-Genre Natural Language Inference Corpus](https://cims.nyu.edu/~sbowman/multinli/multinli_0.9.pdf) is a crowdsourced collection of sentence pairs with textual entailment annotations. Given a premise sentence and a hypothesis sentence, the task is to predict whether the premise entails the hypothesis (entailment), contradicts the hypothesis (contradiction), or neither (neutral). The task has the matched (in-domain) and mismatched (cross-domain) sections.
* QNLI - [The Stanford Question Answering Dataset](https://nlp.stanford.edu/pubs/rajpurkar2016squad.pdf) is a question-answering dataset consisting of question-paragraph pairs, where one of the sentences in the paragraph (drawn from Wikipedia) contains the answer to the corresponding question. The task is to determine whether the context sentence contains the answer to the question.
* RTE The Recognizing Textual Entailment (RTE) datasets come from a series of annual [textual entailment challenges](https://aclweb.org/aclwiki/Recognizing_Textual_Entailment). The task is to determine whether the second sentence is the entailment of the first one or not.
* WNLI - The Winograd Schema Challenge is a reading comprehension task in which a system must read a sentence with a pronoun and select the referent of that pronoun from a list of choices (Hector Levesque, Ernest Davis, and Leora Morgenstern. The winograd schema challenge. In Thirteenth International Conference on the Principles of Knowledge Representation and Reasoning. 2012).
All tasks are classification tasks, except for the STS-B task which is a regression task. All classification tasks are 2-class problems, except for the MNLI task which has 3-classes.
More details about GLUE benchmark could be found [here](https://gluebenchmark.com/).
# Datasets
**To proceed further, you need to download the GLUE data.** For example, you can download [this script](https://gist.githubusercontent.com/W4ngatang/60c2bdb54d156a41194446737ce03e2e/raw/17b8dd0d724281ed7c3b2aeeda662b92809aadd5/download_glue_data.py) using `wget` and then execute it by running:
`python download_glue_data.py`
use `--tasks TASK` if datasets for only selected GLUE tasks are needed
After running the above commands, you will have a folder `glue_data` with data folders for every GLUE task. For example, data for MRPC task would be under glue_data/MRPC.
This tutorial and [examples/nlp/glue_benchmark/glue_benchmark.py](https://github.com/NVIDIA/NeMo/blob/main/examples/nlp/glue_benchmark/glue_benchmark.py) work with all GLUE tasks without any modifications. For this tutorial, we are going to use MRPC task.
```
# supported task names: ["cola", "sst-2", "mrpc", "sts-b", "qqp", "mnli", "qnli", "rte", "wnli"]
TASK = 'mrpc'
DATA_DIR = 'glue_data/MRPC'
WORK_DIR = "WORK_DIR"
MODEL_CONFIG = 'glue_benchmark_config.yaml'
! ls -l $DATA_DIR
```
For each task, there are 3 files: `train.tsv, dev.tsv, and test.tsv`. Note, MNLI has 2 dev sets: matched and mismatched, evaluation on both dev sets will be done automatically.
```
# let's take a look at the training data
! head -n 5 {DATA_DIR}/train.tsv
```
# Model configuration
Now, let's take a closer look at the model's configuration and learn to train the model.
GLUE model is comprised of the pretrained [BERT](https://arxiv.org/pdf/1810.04805.pdf) model followed by a Sequence Regression module (for STS-B task) or Sequence classifier module (for the rest of the tasks).
The model is defined in a config file which declares multiple important sections. They are:
- **model**: All arguments that are related to the Model - language model, a classifier, optimizer and schedulers, datasets and any other related information
- **trainer**: Any argument to be passed to PyTorch Lightning
```
# download the model's configuration file
config_dir = WORK_DIR + '/configs/'
os.makedirs(config_dir, exist_ok=True)
if not os.path.exists(config_dir + MODEL_CONFIG):
print('Downloading config file...')
wget.download('https://raw.githubusercontent.com/NVIDIA/NeMo/v1.0.0b2/examples/nlp/glue_benchmark/' + MODEL_CONFIG, config_dir)
else:
print ('config file is already exists')
# this line will print the entire config of the model
config_path = f'{WORK_DIR}/configs/{MODEL_CONFIG}'
print(config_path)
config = OmegaConf.load(config_path)
print(OmegaConf.to_yaml(config))
```
# Model Training
## Setting up Data within the config
Among other things, the config file contains dictionaries called **dataset**, **train_ds** and **validation_ds**. These are configurations used to setup the Dataset and DataLoaders of the corresponding config.
We assume that both training and evaluation files are located in the same directory, and use the default names mentioned during the data download step.
So, to start model training, we simply need to specify `model.dataset.data_dir`, like we are going to do below.
Also notice that some config lines, including `model.dataset.data_dir`, have `???` in place of paths, this means that values for these fields are required to be specified by the user.
Let's now add the data directory path, task name and output directory for saving predictions to the config.
```
config.model.task_name = TASK
config.model.output_dir = WORK_DIR
config.model.dataset.data_dir = DATA_DIR
```
## Building the PyTorch Lightning Trainer
NeMo models are primarily PyTorch Lightning modules - and therefore are entirely compatible with the PyTorch Lightning ecosystem.
Let's first instantiate a Trainer object
```
print("Trainer config - \n")
print(OmegaConf.to_yaml(config.trainer))
# lets modify some trainer configs
# checks if we have GPU available and uses it
cuda = 1 if torch.cuda.is_available() else 0
config.trainer.gpus = cuda
config.trainer.precision = 16 if torch.cuda.is_available() else 32
# for mixed precision training, uncomment the line below (precision should be set to 16 and amp_level to O1):
# config.trainer.amp_level = O1
# remove distributed training flags
config.trainer.accelerator = None
# setup max number of steps to reduce training time for demonstration purposes of this tutorial
config.trainer.max_steps = 128
trainer = pl.Trainer(**config.trainer)
```
## Setting up a NeMo Experiment
NeMo has an experiment manager that handles logging and checkpointing for us, so let's use it:
```
exp_dir = exp_manager(trainer, config.get("exp_manager", None))
# the exp_dir provides a path to the current experiment for easy access
exp_dir = str(exp_dir)
exp_dir
```
Before initializing the model, we might want to modify some of the model configs. For example, we might want to modify the pretrained BERT model and use [Megatron-LM BERT](https://arxiv.org/abs/1909.08053) or [AlBERT model](https://arxiv.org/abs/1909.11942):
```
# get the list of supported BERT-like models, for the complete list of HugginFace models, see https://huggingface.co/models
print(nemo_nlp.modules.get_pretrained_lm_models_list(include_external=True))
# specify BERT-like model, you want to use, for example, "megatron-bert-345m-uncased" or 'bert-base-uncased'
PRETRAINED_BERT_MODEL = "albert-base-v1"
# add the specified above model parameters to the config
config.model.language_model.pretrained_model_name = PRETRAINED_BERT_MODEL
```
Now, we are ready to initialize our model. During the model initialization call, the dataset and data loaders we'll be prepared for training and evaluation.
Also, the pretrained BERT model will be downloaded, note it can take up to a few minutes depending on the size of the chosen BERT model.
```
model = nemo_nlp.models.GLUEModel(cfg=config.model, trainer=trainer)
```
## Monitoring training progress
Optionally, you can create a Tensorboard visualization to monitor training progress.
```
try:
from google import colab
COLAB_ENV = True
except (ImportError, ModuleNotFoundError):
COLAB_ENV = False
# Load the TensorBoard notebook extension
if COLAB_ENV:
%load_ext tensorboard
%tensorboard --logdir {exp_dir}
else:
print("To use tensorboard, please use this notebook in a Google Colab environment.")
```
Note, it’s recommended to finetune the model on each task separately. Also, based on [GLUE Benchmark FAQ#12](https://gluebenchmark.com/faq), there are might be some differences in dev/test distributions for QQP task and in train/dev for WNLI task.
```
# start model training
trainer.fit(model)
```
## Training Script
If you have NeMo installed locally, you can also train the model with [examples/nlp/glue_benchmark/glue_benchmark.py](https://github.com/NVIDIA/NeMo/blob/main/examples/nlp/glue_benchmark/glue_benchmark.py).
To run training script, use:
`python glue_benchmark.py \
model.dataset.data_dir=PATH_TO_DATA_DIR \
model.task_name=TASK`
Average results after 3 runs:
| Task | Metric | ALBERT-large | ALBERT-xlarge | Megatron-345m | BERT base paper | BERT large paper |
|-------|--------------------------|--------------|---------------|---------------|-----------------|------------------|
| CoLA | Matthew's correlation | 54.94 | 61.72 | 64.56 | 52.1 | 60.5 |
| SST-2 | Accuracy | 92.74 | 91.86 | 95.87 | 93.5 | 94.9 |
| MRPC | F1/Accuracy | 92.05/88.97 | 91.87/88.61 | 92.36/89.46 | 88.9/- | 89.3/- |
| STS-B | Person/Spearman corr. | 90.41/90.21 | 90.07/90.10 | 91.51/91.61 | -/85.8 | -/86.5 |
| QQP | F1/Accuracy | 88.26/91.26 | 88.80/91.65 | 89.18/91.91 | 71.2/- | 72.1/- |
| MNLI | Matched /Mismatched acc. | 86.69/86.81 | 88.66/88.73 | 89.86/89.81 | 84.6/83.4 | 86.7/85.9 |
| QNLI | Accuracy | 92.68 | 93.66 | 94.33 | 90.5 | 92.7 |
| RTE | Accuracy | 80.87 | 82.86 | 83.39 | 66.4 | 70.1 |
WNLI task was excluded from the experiments due to the problematic WNLI set.
The dev sets were used for evaluation for ALBERT and Megatron models, and the test sets results for [the BERT paper](https://arxiv.org/abs/1810.04805).
Hyperparameters used to get the results from the above table, could be found in the table below. Some tasks could be further finetuned to improve performance numbers, the tables are for a baseline reference only.
Each cell in the table represents the following parameters:
Number of GPUs used/ Batch Size/ Learning Rate/ Number of Epochs. For not specified parameters, please refer to the default parameters in the training script.
| Task | ALBERT-large | ALBERT-xlarge | Megatron-345m |
|-------|--------------|---------------|---------------|
| CoLA | 1 / 32 / 1e-5 / 3 | 1 / 32 / 1e-5 / 10 | 4 / 16 / 2e-5 / 12 |
| SST-2 | 4 / 16 / 2e-5 / 5 | 4 / 16 / 2e-5 /12 | 4 / 16 / 2e-5 / 12 |
| MRPC | 1 / 32 / 1e-5 / 5 | 1 / 16 / 2e-5 / 5 | 1 / 16 / 2e-5 / 10 |
| STS-B | 1 / 16 / 2e-5 / 5 | 1 / 16 / 4e-5 / 12 | 4 / 16 / 3e-5 / 12 |
| QQP | 1 / 16 / 2e-5 / 5 | 4 / 16 / 1e-5 / 12 | 4 / 16 / 1e-5 / 12 |
| MNLI | 4 / 64 / 1e-5 / 5 | 4 / 32 / 1e-5 / 5 | 4 / 32 / 1e-5 / 5 |
| QNLI | 4 / 16 / 1e-5 / 5 | 4 / 16 / 1e-5 / 5 | 4 / 16 / 2e-5 / 5 |
| RTE | 1 / 16 / 1e-5 / 5 | 1 / 16 / 1e-5 / 12 | 4 / 16 / 3e-5 / 12 |
| true |
code
| 0.626324 | null | null | null | null |
|
# 深度学习工具 PyTorch 简介
在此 notebook 中,你将了解 [PyTorch](http://pytorch.org/),一款用于构建和训练神经网络的框架。PyTorch 在很多方面都和 Numpy 数组很像。毕竟,这些 Numpy 数组也是张量。PyTorch 会将这些张量当做输入并使我们能够轻松地将张量移到 GPU 中,以便在训练神经网络时加快处理速度。它还提供了一个自动计算梯度的模块(用于反向传播),以及另一个专门用于构建神经网络的模块。总之,与 TensorFlow 和其他框架相比,PyTorch 与 Python 和 Numpy/Scipy 堆栈更协调。
## 神经网络
深度学习以人工神经网络为基础。人工神经网络大致产生于上世纪 50 年代末。神经网络由多个像神经元一样的单个部分组成,这些部分通常称为单元或直接叫做“神经元”。每个单元都具有一定数量的加权输入。我们对这些加权输入求和,然后将结果传递给激活函数,以获得单元的输出。
<img src="assets/simple_neuron.png" width=400px>
数学公式如下所示:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
对于向量来说,为两个向量的点积/内积:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## 张量
实际上神经网络计算只是对*张量*进行一系列线性代数运算,张量是矩阵的泛化形式。向量是一维张量,矩阵是二维张量,包含 3 个索引的数组是三维张量(例如 RGB 彩色图像)。神经网络的基本数据结构是张量,PyTorch(以及几乎所有其他深度学习框架)都是以张量为基础。
<img src="assets/tensor_examples.svg" width=600px>
这些是基本知识,我们现在来看 PyTorch 如何构建简单的神经网络。
```
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
```
我在上面生成了一些数据,我们可以使用该数据获取这个简单网络的输出。这些暂时只是随机数据,之后我们将使用正常数据。我们来看看:
`features = torch.randn((1, 5))` 创建一个形状为 `(1, 5)` 的张量,其中有 1 行和 5 列,包含根据正态分布(均值为 0,标准偏差为 1)随机分布的值。
`weights = torch.randn_like(features)` 创建另一个形状和 `features` 一样的张量,同样包含来自正态分布的值。
最后,`bias = torch.randn((1, 1))` 根据正态分布创建一个值。
和 Numpy 数组一样,PyTorch 张量可以相加、相乘、相减。行为都很类似。但是 PyTorch 张量具有一些优势,例如 GPU 加速,稍后我们会讲解。请计算这个简单单层网络的输出。
> **练习**:计算网络的输出:输入特征为 `features`,权重为 `weights`,偏差为 `bias`。和 Numpy 类似,PyTorch 也有一个对张量求和的 [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) 函数和 `.sum()` 方法。请使用上面定义的函数 `activation` 作为激活函数。
```
## Calculate the output of this network using the weights and bias tensors
```
你可以在同一运算里使用矩阵乘法进行乘法和加法运算。推荐使用矩阵乘法,因为在 GPU 上使用现代库和高效计算资源使矩阵乘法更高效。
如何对特征和权重进行矩阵乘法运算?我们可以使用 [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) 或 [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul),后者更复杂,并支持广播。如果不对`features` 和 `weights` 进行处理,就会报错:
```
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
在任何框架中构建神经网络时,我们都会频繁遇到这种情况。原因是我们的张量不是进行矩阵乘法的正确形状。注意,对于矩阵乘法,第一个张量里的列数必须等于第二个张量里的行数。`features` 和 `weights` 具有相同的形状,即 `(1, 5)`。意味着我们需要更改 `weights` 的形状,以便进行矩阵乘法运算。
**注意:**要查看张量 `tensor` 的形状,请使用 `tensor.shape`。以后也会经常用到。
现在我们有以下几个选择:[`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape)、[`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_) 和 [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view)。
* `weights.reshape(a, b)` 有时候将返回一个新的张量,数据和 `weights` 的一样,大小为 `(a, b)`;有时候返回克隆版,将数据复制到内存的另一个部分。
* `weights.resize_(a, b)` 返回形状不同的相同张量。但是,如果新形状的元素数量比原始张量的少,则会从张量里删除某些元素(但是不会从内存中删除)。如果新形状的元素比原始张量的多,则新元素在内存里未初始化。注意,方法末尾的下划线表示这个方法是**原地**运算。要详细了解如何在 PyTorch 中进行原地运算,请参阅[此论坛话题](https://discuss.pytorch.org/t/what-is-in-place-operation/16244)。
* `weights.view(a, b)` 将返回一个张量,数据和 `weights` 的一样,大小为 `(a, b)`。
我通常使用 `.view()`,但这三个方法对此示例来说都可行。现在,我们可以通过 `weights.view(5, 1)` 变形 `weights`,使其具有 5 行和 1 列。
> **练习**:请使用矩阵乘法计算网络的输出
```
## Calculate the output of this network using matrix multiplication
```
### 堆叠
这就是计算单个神经元的输出的方式。当你将单个单元堆叠为层,并将层堆叠为神经元网络后,你就会发现这个算法的强大之处。一个神经元层的输出变成下一层的输入。对于多个输入单元和输出单元,我们现在需要将权重表示为矩阵。
<img src='assets/multilayer_diagram_weights.png' width=450px>
底部显示的第一个层级是输入,称为**输入层**。中间层称为**隐藏层**,最后一层(右侧)是**输出层**。我们可以再次使用矩阵从数学角度来描述这个网络,然后使用矩阵乘法将每个单元线性组合到一起。例如,可以这样计算隐藏层($h_1$ 和 $h_2$):
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
我们可以将隐藏层当做输出单元的输入,从而得出这个小网络的输出,简单表示为:
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **练习:**使用权重 `W1` 和 `W2` 以及偏差 `B1` 和 `B2` 计算此多层网络的输出。
```
## Your solution here
```
如果计算正确,输出应该为 `tensor([[ 0.3171]])`。
隐藏层数量是网络的参数,通常称为**超参数**,以便与权重和偏差参数区分开。稍后当我们讨论如何训练网络时会提到,层级越多,网络越能够从数据中学习规律并作出准确的预测。
## Numpy 和 Torch 相互转换
加分题!PyTorch 可以实现 Numpy 数组和 Torch 张量之间的转换。Numpy 数组转换为张量数据,可以用 `torch.from_numpy()`。张量数据转换为 Numpy 数组,可以用 `.numpy()` 。
```
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
```
Numpy 数组与 Torch 张量之间共享内存,因此如果你原地更改一个对象的值,另一个对象的值也会更改。
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
```
```python
# Numpy array matches new values from Tensor
a
```
| true |
code
| 0.642432 | null | null | null | null |
|
# 🔢 Vectorizing Guide
Firstly, we must import what we need from Relevance AI
```
from relevanceai import Client
from relevanceai.utils.datasets import (
get_iris_dataset,
get_palmer_penguins_dataset,
get_online_ecommerce_dataset,
)
client = Client()
```
## Example 1
For this first example we going to work with a purely numeric dataset. The Iris dataset contains 4 numeric features and another text column with the label
```
iris_documents = get_iris_dataset()
dataset = client.Dataset("iris")
dataset.insert_documents(iris_documents, create_id=True)
```
Here we can see the dataset schema, pre-vectorization
```
dataset.schema
```
Vectorizing is as simple specifying `create_feature_vector=True`
While species is a text feature, we do not need to vectorize this. Besides, smart typechecking recognises this field as a text field we would not usually vectorize.
`create_feature_vector=True` is what creates our "document" vectors. This concatenates all numeric/vector fields in a single "document" vector. This new vector_field is always called `f"_dim{n_dims}_feature_vector_"`, with n_dims being the size of the concatenated vector.
Furthermore, for nuermic stability accross algorithms, sklearn's StandardScaler is applied to the concatenated vector field. If the concatenated size of a vector field is >512 dims, PCA is automatically applied.
```
dataset.vectorize(create_feature_vector=True)
```
### or
```
dataset.vectorize(fields=["numeric"], create_feature_vector=True)
```
You can see below that the dataset schema has been altered accordingly
```
dataset.schema
```
## Example 2
For this second example we going to work with a mixed numeric and text dataset. The Palmer Penguins dataset contains several numeric features and another text column called "Comments"
```
penguins_documents = get_palmer_penguins_dataset()
dataset.insert_documents(penguins_documents, create_id=True)
```
We must install the default Encoders for text vectorizing from vectorhub
```
!pip install vectorhub[encoders-text-tfhub-windows] # If you are on windows
!pip install vectorhub[encoders-text-tfhub] # other
```
No arguments automatically detects what text and image fieds are presetn in your dataset. Since this is a new function, its typechecking could be faulty. If need be, specifiy the data types in the same format as the schema with `_text_` denoting text_fields and `_image_` denoting image fields.
```
dataset.vectorize()
```
### or
```
dataset.vectorize(fields=["Comments"], create_feature_vector=True)
```
| true |
code
| 0.709271 | null | null | null | null |
|
# Milestone2 Document
## Feedback
- Introduction: A nice introduction!
- Background -0.5: It would be hard for users to understand automatic differentiation, computational graph, and evaluation trace if you don't give the corresponding illustrations in the Background section
**Revision: provided a concrete example of evaluation trace and computational graph**
- How to use -0.5: didn't show how the users can get the package from online. Is AutodiffCST the name of a python file or the package? Please give different names to avoid confusion.
**Revision: added instructions for installation, and change the python file name to AD.py**
- Implementation: Using a tree as the core data structure sounds new. It would be better if you could explain it with more details.
**Revision: Changed core data structure to AD object, and updated the implementation part accordingly.**
## Section 1: Introduction
This package autodiffCST implements automatic differentiation. It can be used to automatically differentiate functions via forward mode and reverse mode, depending on the user's choice. It also provides an option of performing second order differentiation.
Differentiation, namely, the process of finding the derivatives of functions, is very prevalent in various areas of science and engineering. It can often be used to find the extrema of functions with single or multiple variables. With the advance of technology, more complicated functions and larger dataset are developed. The difficulty of performing differentiation has greatly increased and we are more dependent on computers to take derivates. Nowadays, we have three major ways of performing differentiation: symbolic, numerical and automatic (algorithmic) differentiation. We will focus on automatic differentiation for the rest of this document.
## Section 2: Background
### 2.1 An Overview of Auto Differentiation
Automatic differentiation (AD) uses algorithms to efficiently and accurately evaluating derivatives of numeric functions. It has the advantage of avoiding symbolic manipulation of functions while reaching an accuracy close to machine precision. Application of automatic differentiation includes but is not limited to astronomy, dynamic systems, numerical analysis research, optimization in finance and engineering.
The idea behind AD is to break down a function into a sequence of elementary operations and functions that have easily attained derivatives, and then sequencially apply the chain rule to evaluate the derivatives of these operations to compute the derivative of the whole function.
The two main methods of performing automatic differentiation are forward mode and reverse mode. Some other AD algorithms implement a combination of forward mode and reverse mode, but this package will implement them seperately.
To better understand automatic differentiation, it is uncessary to get familar with some key concepts that are used in the algorithms of AD. We will use the rest of this section to briefly introduce them.
### 2.2 Elementary operations and functions
The algorithm of automatic differentiation breaks down functions into elementary arithmetic operations and elementary functions. Elementary arithmetic operations include addition, subtraction, multiplication, division and raising power (we can also consider taking roots of a number as raising it to powers less than $1$). Elementary functions include exponential, logrithmatic, and trigonometry. All of these operations and functions mentioned here have derivates that are easy to compute, so we use them as elementary steps in the evaluation trace of AD.
### 2.3 The Chain Rule
The chain rule can be used to calculate the derivate of nested functions, such in the form of $u(v(t))$. For this function, the derivative of $u$ with respect to $t$ is $$\dfrac{\partial u}{\partial t} = \dfrac{\partial u}{\partial v}\dfrac{\partial v}{\partial t}.$$
A more general form of chain rule applies when a function $h$ has several arguments, or when its argument is a vector. Suppose we have $h = h(y(t))$ where $y \in R^n$ and $t \in R^m $. Here, $h$ is the combination of $n$ functions, each of which has $m$ variables. Using the chain rule, the derivative of $h$ with respect to $t$, now called the gradient of $h$, is
$$ \nabla_{t}h = \sum_{i=1}^{n}{\frac{\partial h}{\partial y_{i}}\nabla y_{i}\left(t\right)}.$$
The chain rule enables us to break down complicated and nested functions into layers and operations. Our automatic differentiation algrithm sequencially sues chain rule to compute the derivative of funtions.
### 2.4 Evaluation Trace and Computational Graph
These two concepts are the core of our automatic differentiation algorithm. Since they are so important and can be created at the same time, creating them would be the first thing to do when a function is inputted into the algorithm.
The evaluation trace tracks each layer of operations while evaluate the input function and its derivative. At each step the evaluation trace holds the traces, elementary operations, numerical values, elementary derivatives and partial derivatives.
The computational graph is a graphical visualization of the evaluation trace. It holds the traces and elementary operations of the steps, connecting them via arrows pointing from input to output for each step. The computational graph helps us to better understand the structure of the function and its evaluation trace. Forward mode performs the operations from the start to the end of the graph or evaluation trace. Reverse mode performs the operations backwards, while applying the chain rule at each time determining the derivate of the trace.
Here, we provide an example of a evaluation trace and a computational graph of the function $f(x,y)=exp(−(sin(x)−cos(y))^2)$, with derivatives evaluated at $f(π/2,π/3)$.
Evaluation trace:
|Trace|Elementary Function| Current Value |Elementary Function Derivative| $\nabla_x$ | $\nabla_y$ |
| :---: | :-----------: | :-------: | :-------------: | :----------: | :-----------: |
| $x_{1}$ | $x_{1}$ | $\frac{\pi}{2}$ | $\dot{x}_{1}$ | $1$ | $0$ |
| $y_{1}$ | $y_{1}$ | $\frac{\pi}{3}$ | $\dot{y}_{1}$ | $0$ | $1$ |
| $v_{1}$ | $sin(x_{1})$ | $1$ | $cos(x_{1})\dot{x}_{1}$ | $0$ | $0$ |
| $v_{2}$ | $cos(y_{1})$ | $0.5$ | $-sin(y_{1})\dot{y}_{1}$| $0$ | $-0.866$ |
| $v_{3}$ | $v_{1}-v_{2}$ | $0.5$ | $\dot{v}_{1}-\dot{v}_{2}$| $0$ | $0.866$ |
| $v_{4}$ | $v_{3}^2$ | $0.25$ | $2v_{3}\dot{v}_{3}$ | $0$ | $0.866$ |
| $v_{5}$ | $-v_{4}$ | $-0.25$| $-\dot{v}_{4}$ | $0$ | $-0.866$ |
| $v_{6}$ | $exp(v_{5})$ | $0.779$| $exp(v_{5})\dot{v}_{5}$ | $0$ | $-0.6746$ |
| $f$ | $v_{6}$ | $0.779$| $\dot{v}_{6}$ | $0$ | $-0.6746$ |
Computational graph:

## Section 3: How to Use AutodiffCST
**Installation**
Our package is for Python 3 only. To install AutodiffCST, you need to have pip3 installed first. If you don't, please install pip3 following these instructions https://pip.pypa.io/en/stable/installing/.
Then, you could install this package by running
```pip3 install AutodiffCST``` from the command line.
An alternative is to clone our repository by running ```git clone https://github.com/auto-differentiaters-in-CST/cs107-FinalProject.git``` from the command line and then ```cd <AD directory>```(directory name will be determined later), ```pip install -r requirements.txt```.
**User Guide**
After installation, users could import this package by ```from AutodiffCST import AD``` and ```from autodiffcst import admath```. These two packages would allow the users to do differentiation on functions with most mathematic operations.
Then, they could simply initiate the AD object by giving the point where they wish to differentiate. Moreover, they could also try other supplementary features as in the code demo provided below.
``` python
# import modules
import numpy as np
from AutodiffCST import AD as ad
from autodiffcst import admath as admath
# base case: initialize AD object with scalar values
x = ad(5, tag = "x") # initialize AD object called "x" with the value 5
y = ad(3, tag = "y") # initialize AD object called "y" with the value 3
f = x*y + 1 # build a function with AD objects, the function will also be an AD object
print(f) # print 9.0
dfdx = f1.diff(direction = "x") # returns the derivative with respect to x
print(dfdx) # print 3
jacobian = ad.jacobian(f1) # returns a gradient vector of f
print(jacobian) # print [5,3]
f2 = x + admath.sin(y) # build a function with AD objects
print(f2) # print AD(value: 5.141120008059867, derivatives: {'x': 1, 'y': -0.9899924966004454})
dfdy = f2.diff(direction= = "y") # returns the derivative with respect to x
print(dfdy) # print -0.9899924966004454
jacobian2 = ad.jacobian(f2) # returns a gradient vector of f
print(jacobian2) # print [1, -0.9899924966004454]
# These are the most important features for our forward AD. Would add more later ...
```
## Section 4: Software Organization
The home directory of our software package would be structured as follows.
- LICENSE
- README.md
- requirements.txt
- docs/
* quickstart_tutotial.md
* model_documentation.md
* testing_guidelines.md
* concepts_explanation.md
* references.md
- setup.py
- autodiffcst/
* \_\_init\_\_.py
* AD.py
* admath.py
- tests/
* test_core.py
* test_extension.py
- TravisCI.yml
- CodeCov.yml
Specificly speaking, the README file would contain a general package description and the necessary information for users to navigate in the subdirectories. Besides, we would place our documentation, testing guidelines, a simple tutorial and relative references in the doc directory. Moreover, to package our model with PyPI, we need to include setup.py and a src directory, where stores the source code about our model. Furthermore, we would put a collection of test cases in tests directory. Last but not least, we would include TravisCI.yml and CodeCov.yml in our home directory for integrated test.
In this package, we plan to use the following public modules.
- Modules for mathmatical calculation:
* Numpy: we would use it for matrix operations, and basic math functions and values, such as sin, cos, \pi, e, etc.
- Modules for testing:
* pydoc
* doctest
* Pytest
- Other modules:
* sys
* setuptools: we would use is for publishing our model with PyPI.
To distribute our package, we would use PyPI so that users could easily install the package with *pip install*.
After installing the package, users can use ```from AutodiffCST import AD``` and ```from autodiffcst import admath``` to import the package. These two modules are where the core of this package resides:
* AD: defines the AD object class that we use to perform automatic differentiation and overwrites basic math operation dunder methods for AD. Also provides two core functions to perform on AD: diff() and jacobian().
* admath: defines functions that perform elementary math operations on AD, which include those that cannot be performed by overwriting dunder methods, such as logarithm and trigonometry.
To better organize our software, we plan to use PyScaffold and Sphinx. The former could help us setting up the project while the latter would polish our documentation.
## Section 5: Implementation
Our main data structure is the AD object, which has the attributes of a value, a derivative and a tag. In terms of the classes, our main class is the AD object, and we would probably have several heritaged class for our extensions.
In the AD class, we would have the following methods:
- a constructor
``` python
def __init__(self, val, tags, der=1, mode = "forward"):
self.val = val
if (isinstance(tags, list)) and (isinstance(ders,dict)):
self.tags = tags
self.ders = ders
else:
self.tags = [tags]
self.ders = {tags: ders}
self.mode = mode
```
- overloaded dunder methods as follows:
``` python
__add__
__sub__
__pow__
__mul__
__mod__
__div__
__iadd__
```
  and more basic operations according to https://www.python-course.eu/python3_magic_methods.php
- a diff method, which takes in a direction, and returns the derivative of the function.
``` python
def diff(self, dir = x):
if isinstance(dir, AD):
return self.der[dir]
else:
return 0
```
- a gradient method, which takes in a vector of directions, and returns a vector of the partial derivatives at each direction.
- a jacobian method, which takes in a vector of AD functions and a vector of directions, and returns the jacobian matrix.
In our implementation, we would use some external dependencies such as Numpy and Math. To deal with elementary functions, we would allow users to enter functions that can be recognized by Python, factor a input function to a series of basic operations/functions (such as sin, sqrt, log, and exp) and use if-statements to check functions and return their symbolic derivatives. These operations are handled in admath.py. The functions in admath takes an AD object as input and performs the corresponding operations on the AD objects by updating their values and derivatives.
# Future Features
1. Differentiate a list of functions. Our package now can deal with one function with multiple varaibles. In the future we plan to take a list of functions as input and output its Jacobian accordingly. Using Numpy array as the data structure to keep the Jacobian would be ideal, so we will need to change the implementation of our current jacobian method.
2. Higher order derivatives. A starting point would be allowing second order derivatives taken on our AD objects and returning the correct Jacobian matrix accordingly. Note that this cannot be achieved by simply applying diff() to an AD object twices, since the Jacobian matrix would be different and the datatype would be different. We would need to store the values of the second derivatives of our AD object at each elementary steps in the evaluation trace. Then we would need another function to return the second derivatives (possibly named second_diff()), which functions similarly to diff(), but returns the second derivatives of the AD object. The jacobian() function will also be modified accordingly. It will include an optional input (possibly initialized as second_order = False for defult and second_order = True for second derivatives), which signals that the function will return the Jacobian containing the second order derivatives of the AD object.
Backup extensions:
3. Backward Mode. Right now our mode for doing automatic differetiation is defaulted to forward mode, because we have not implemented backward mode yet. We would need new functions that use the AD object class to implement backward mode. To keep track of the traces, we need to create a trace table, possibly using Numpy array, in the function that runs backward mode.
4. Newton's method. We would like to use our AD package to solve meaningful problems. One way to achieve this is to use it in an implementation of Newton's method. This will be a script that imports our AD package to calculate the derivatives in Newton's method.
# Building Timeline
- Nov.4: Finish M2A and M2B
- Nov.7: Finish basics dunder methods for one variable
- Nov.14: Finish Test Suite
- Nov.19: Submit M2
| true |
code
| 0.825695 | null | null | null | null |
|
# Live Twitter Sentiments for Cryptocurrencies
Plot the evolution in time of the tweets sentiment for a cryptocurrency. We will use the *tweepy*'s streaming to see the live evolution of the Twitter sentiments for the cryptocurrencies.
* *Inputs*: currency keywords to seach in Twitter, number of tweets to analyse the sentiement, plot update interval in seconds (default = 1.0 seconds).
* *Output*: Plot with sentiment analysis and the mean in time for a specific cryptocurrency.
* *Note*: The free Twitter plan lets you download *100 Tweets per search*, and you can search Tweets from the previous seven days. *Please check the limits of getting tweets per day or month before to use this script!*
### Requirements
* *Language*: Python 3.*
* *Dependencies*: tweepy = retrieve tweets using APIs; json = handling the API results, textblob = text operations and sentiment analysis, re = text processing, matplotlib = plots, numpy = numerical calculations, IPython = interactive plots into notebooks
* *Other tools*: Textblog Corpora for text processing: *python -m textblob.download_corpora*
## How to use
Complete your twitter API credential and your crypto keywords, number of tweets and run the entire notebook.
## Step 1: Import the python dependencies
```
import time, json, re
from tweepy import Stream
from tweepy import OAuthHandler
from tweepy.streaming import StreamListener
from textblob import TextBlob
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
%matplotlib inline
```
## Step 2: Define your data
You need to define the keywords, number of tweets, the update interval, and your twitter API keys. Your can define the key here or read them from a JSON file.
```
# YOUR preference (to complete)
keywords = ["Bitcoin", 'BTC'] # a set of keywords for a crypto
noTweets = 10 # number of tweets/connections
secUpdate = 1.0 # update interval in seconds
# YOUR Twitter API information (to complete)
# if you have a local file with your info, ommit these lines
CONSUMER_KEY = 'YOUR DATA'
CONSUMER_SECRET = 'YOUR DATA'
ACCESS_TOKEN = 'YOUR DATA'
ACCESS_SECRET = 'YOUR DATA'
# Setting a JSON of your credentials (to complete)
creds = {"CONSUMER_KEY": CONSUMER_KEY, "CONSUMER_SECRET": CONSUMER_SECRET,
"ACCESS_TOKEN": ACCESS_TOKEN, "ACCESS_SECRET": ACCESS_SECRET}
# If you didnt define above, load credentials from json file
# (overwrite creds with data from file if available)
try:
print('-> Reading Twitter API credentials from file ... ')
with open("twitter_credentials.json", "r") as file:
creds = json.load(file)
print('Done!')
except:
print('! There is no twitter API credential file! Using the information you defined above!')
```
## Step 3: Define a custom class for Twitter streaming
We will use some variables as globals in order to input parameters from the main code (currency keywords to seach in Twitter, number of tweets to analyse the sentiement, plot refresh time) and to fill list with tweets sentiment, times of the sentiment analysis and means of the sentiments at a specific time. These list will be used to interactivelly plot the evolution of the sentiment and the mean of sentiments.
```
class listener(StreamListener):
def on_data(self,data):
global initime # to calculate the time of analysis
global inidatetime # to print the initial datetime
global count # counting the tweets
global t # list with the time of sentiment analysis
global sent # list with sentiments at moments t
global sentMeans # list of sentiment means at different time
global keywords # external - list with keywords for a crypto
global noTweets # external - number of tweets to get with your twitter API
global secUpdate # external - number of seconds to update the plot
# update the list for analysis time
currTime = int(time.time()-initime)
t.append(currTime)
# get the tweet data
all_data=json.loads(data)
# encode to unicode for different types of characters
tweet=all_data["text"].encode("utf-8")
# remove URLs from tweets
tweet = re.sub(r"http\S+", "", str(tweet))
# remove strange characters from the tweet
tweet=" ".join(re.findall("[a-zA-Z]+", str(tweet)))
# strip the spaces from the tweet
blob=TextBlob(tweet.strip())
# count the tweets
count=count+1
# update the list for sentiments and the means at different time
sent.append(blob.sentiment.polarity)
sentMeans.append(np.mean(sent))
# Plotting sentiment analysis in time for a cryptocurrency
# clear the plot
clear_output(wait=True)
# set axis, labels
plt.xlabel('Time')
plt.ylabel('Twitter sentiment')
# set grid
plt.grid()
# print the current mean of sentiments
print('Live Twitter sentiment analysis for cryptocurrencies')
print('**********************************************************************')
print('From: '+str(inidatetime)+' To: '+str(time.ctime()))
print('Sentiment Mean for '+str(keywords)+': '+str(np.mean(sent)))
# plot sentiments and means in time
plt.plot(t,sent, t,sentMeans)
# add legend
plt.legend(['Sentiment', 'Sentiment Mean'],loc='center left', bbox_to_anchor=(1, 0.5))
# plotting
plt.show()
# wait for update
plt.pause(secUpdate) # wait 1 sec!
# if we have the number of tweets, end the script
if count==noTweets:
return False
else:
return True
def on_error(self,status):
print(status)
```
## Step 4: Run the Twitter stream for sentiment analysis
Initialize all the variables and use the tweets stream for sentiment analysis plotting:
```
# Define external variables to be used inside the streaming class
t = [0] # list with time
sent = [0] # list with tweets sentiment in time
sentMeans = [0] # list with means of sentiment in time
count=0 # curent number of tweet
initime=time.time() # to calculate the time
inidatetime = time.ctime() # initial date time in readable format
# setup the twitter screaming
auth=OAuthHandler(creds['CONSUMER_KEY'],creds['CONSUMER_SECRET'])
auth.set_access_token(creds['ACCESS_TOKEN'],creds['ACCESS_SECRET'])
# start the stream with tweets using your keyworks
twitterStream = Stream(auth, listener(count))
twitterStream.filter(track=keywords)
```
### Hint
You can use this notebook for any twitter search, not limited to the cryptocurrencies!
Hf!
2018@muntisa
| true |
code
| 0.413773 | null | null | null | null |
|
### AD470 - Module 7 Introduction to Deep LearningProgramming Assignment
#### Andrew Boyer
#### Brandan Owens
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.io
from sklearn.preprocessing import StandardScaler
import tensorflow
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.model_selection import train_test_split
```
#### Q.1(a) Use pandas to read in the dataset “Churn_Modelling.csv”
```
churn_df = pd.read_csv("../dataFiles/Churn_Modelling.csv")
churn_df.columns
```
#### (b) Create the following bar plots.
```
sns.countplot(data = churn_df, x = 'Exited' )
sns.countplot(data = churn_df , x = 'Geography', hue = 'Exited')
sns.barplot(data=churn_df , x= 'Geography', y= 'Balance')
```
#### (c) From the dataframe, find the percentage of people who exited, and the percentage of people who did not exit.
```
churn_df['Exited'].value_counts()/churn_df['Exited'].count()*100
```
#### (d) Check for any missing values in the dataframe.
```
churn_df.isnull().values.any()
```
#### (e) Define X and y
```
X = churn_df.drop(['RowNumber', 'CustomerId', 'Surname', 'Exited'], axis=1)
y = churn_df['Exited']
```
#### (f) Get dummies for all categorical variables of X, remember to set drop_first = True.
```
X = pd.get_dummies(X, drop_first = True)
X
```
#### (g) Split the dataset into training set and test set. test_size=0.2, random_state=0
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
#### (h) Use the following codes to do the feature scaling on the training and test sets. (Standardize all numerical variables by subtracting the means and dividing each variable by its standard deviation.)
```
sc_x = StandardScaler()
X_train = pd.DataFrame(sc_x.fit_transform(X_train), columns=X.columns.values)
X_test = pd.DataFrame(sc_x.transform(X_test), columns=X.columns.values)
```
#### (i) Build a 4-layer neural network.
```
#model = keras.Sequential([
# layers.Dense(6, activation='relu', input_shape=[11]),
# layers.Dense(12, activation='relu'),
# layers.Dense(24, activation='relu'),
# layers.Dense(1, activation='sigmoid'),
#])
model = Sequential()
model.add(Dense(6, input_shape=(11,), activation='relu'))
model.add(Dense(12, activation='relu'))
model.add(Dense(24, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.summary()
```
#### (j) Compile the neural network.
```
model.compile(optimizer='adam',
loss = 'binary_crossentropy',
metrics=['accuracy'])
#model.summary()
#x_partial_train = X_train[:100]
#y_partial_train = y_train[:100]
#x_val = X_train[100:]
#y_val = y_train[100:]
```
#### (k) Fit the model on training set. Set the batch_size =10, run for 100 epochs.
```
history = model.fit(
X_train, y_train,
validation_data=(X_test,y_test),
epochs=100,
batch_size =10,
)
```
#### (l) Evaluate the model on test set.
```
test_loss, test_acc = model.evaluate(X_test, y_test, verbose=2)
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training Loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation Loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
plt.plot(epochs, acc, 'bo', label='Training Accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
#### (m) Finally, predict the probability of y = Exited on the test set.
```
prediction = model.predict(X_test)
print(prediction)
new_pred = (prediction > 0.6)
true_count = np.count_nonzero(new_pred)
print(true_count/new_pred.size)
print("% of employees that have a 60% or greater chance of leaving the company")
```
#### Q.2 (a) Download the file 'natural_images.zip', and extra the files.
```
import zipfile
local_zip = "../dataFiles/natural_images.zip"
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('natural_images')
```
#### (b) Use os.listdir to create a list of labels.
```
os.listdir("natural_images")
```
#### (c) Display the first 5 images of each class.
```
from IPython.display import Image, display
display(Image( image file))
```
#### (d) Create the following barplot.
#### (e) Use cv2.imread() to convert images into numpy array (X). Then, use cv2.resize(), so that each image has the size (32,32) Create an array which contains the label of each image (Y).
#### (f) Print the shape of images (X) and shape of labels (Y).
#### (g) Standardize X by dividing X by 255.
#### (h) Use LabelEncoder() to encode Y. Use to_categorical() covert Y into categorical numpy array.
#### (i) Split the data into training set and test set. test_size = 0.33, random_state = 46.
#### (j) But a CNN model- first layer is Conv2D, filters =32, kernel_size = (5,5), activation = relu.- second layer is MaxPool2D, pool_size = (2,2)- third layer is Conv2D, filters =64, kernel_size = (3,3), activation = relu.- fourth layer is MaxPool2D, pool_size = (2,2)- fifth layer to flatten the tensors.- sixth layer is Dense, output shape = 256, activation = relu.- seventh layer is Dense, output shape = 8, activation = softmax.
#### (k) Compile the modelloss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']
#### (l) fit the model, epochs = 25, validation_split = 0.2
#### (m)Plot the change in loss score on training set and validation set over epochs.
#### (n) Plot the change in accuracy on training set and validation set over epochs.
#### (o) Retrain the model using the entire training set and set epochs = 5. Evaluate the model on the test set.
| true |
code
| 0.683353 | null | null | null | null |
|
## UCI SMS Spam Collection Dataset
* **Input**: sms textual content. **Target**: ham or spam
* **data representation**: each sms is repesented with a **fixed-length vector of word indexes**. A word index lookup is generated from the vocabulary list.
* **words embedding**: A word embedding (dense vector) is learnt for each word. That is, each sms is presented as a matrix of (document-word-count, word-embedding-size)
* **convolution layer**: Apply filter(s) to the word-embedding matrix, before input to the fully-connected NN
* **train-data.tsv, valid-datat.tsv**, and **vocab_list.tsv** are prepared and saved in 'data/sms-spam'
```
import tensorflow as tf
from tensorflow import data
from datetime import datetime
import multiprocessing
import shutil
print(tf.__version__)
MODEL_NAME = 'sms-class-model-01'
TRAIN_DATA_FILES_PATTERN = 'data/sms-spam/train-*.tsv'
VALID_DATA_FILES_PATTERN = 'data/sms-spam/valid-*.tsv'
VOCAB_LIST_FILE = 'data/sms-spam/vocab_list.tsv'
N_WORDS_FILE = 'data/sms-spam/n_words.tsv'
RESUME_TRAINING = False
MULTI_THREADING = True
```
## 1. Define Dataset Metadata
```
MAX_DOCUMENT_LENGTH = 100
PAD_WORD = '#=KS=#'
HEADER = ['class', 'sms']
HEADER_DEFAULTS = [['NA'], ['NA']]
TEXT_FEATURE_NAME = 'sms'
TARGET_NAME = 'class'
WEIGHT_COLUNM_NAME = 'weight'
TARGET_LABELS = ['spam', 'ham']
with open(N_WORDS_FILE) as file:
N_WORDS = int(file.read())+2
print(N_WORDS)
```
## 2. Define Data Input Function
### a. TSV parsing logic
```
def parse_tsv_row(tsv_row):
columns = tf.decode_csv(tsv_row, record_defaults=HEADER_DEFAULTS, field_delim='\t')
features = dict(zip(HEADER, columns))
target = features.pop(TARGET_NAME)
# giving more weight to "spam" records are the are only 13% of the training set
features[WEIGHT_COLUNM_NAME] = tf.cond( tf.equal(target,'spam'), lambda: 6.6, lambda: 1.0 )
return features, target
```
### b. Data pipeline input function
```
def parse_label_column(label_string_tensor):
table = tf.contrib.lookup.index_table_from_tensor(tf.constant(TARGET_LABELS))
return table.lookup(label_string_tensor)
def input_fn(files_name_pattern, mode=tf.estimator.ModeKeys.EVAL,
skip_header_lines=0,
num_epochs=1,
batch_size=200):
shuffle = True if mode == tf.estimator.ModeKeys.TRAIN else False
num_threads = multiprocessing.cpu_count() if MULTI_THREADING else 1
buffer_size = 2 * batch_size + 1
print("")
print("* data input_fn:")
print("================")
print("Input file(s): {}".format(files_name_pattern))
print("Batch size: {}".format(batch_size))
print("Epoch Count: {}".format(num_epochs))
print("Mode: {}".format(mode))
print("Thread Count: {}".format(num_threads))
print("Shuffle: {}".format(shuffle))
print("================")
print("")
file_names = tf.matching_files(files_name_pattern)
dataset = data.TextLineDataset(filenames=file_names)
dataset = dataset.skip(skip_header_lines)
if shuffle:
dataset = dataset.shuffle(buffer_size)
dataset = dataset.map(lambda tsv_row: parse_tsv_row(tsv_row),
num_parallel_calls=num_threads)
dataset = dataset.batch(batch_size)
dataset = dataset.repeat(num_epochs)
dataset = dataset.prefetch(buffer_size)
iterator = dataset.make_one_shot_iterator()
features, target = iterator.get_next()
return features, parse_label_column(target)
```
## 3. Define Model Function
```
def process_text(text_feature):
# Load vocabolary lookup table to map word => word_id
vocab_table = tf.contrib.lookup.index_table_from_file(vocabulary_file=VOCAB_LIST_FILE,
num_oov_buckets=1, default_value=-1)
# Get text feature
smss = text_feature
# Split text to words -> this will produce sparse tensor with variable-lengthes (word count) entries
words = tf.string_split(smss)
# Convert sparse tensor to dense tensor by padding each entry to match the longest in the batch
dense_words = tf.sparse_tensor_to_dense(words, default_value=PAD_WORD)
# Convert word to word_ids via the vocab lookup table
word_ids = vocab_table.lookup(dense_words)
# Create a word_ids padding
padding = tf.constant([[0,0],[0,MAX_DOCUMENT_LENGTH]])
# Pad all the word_ids entries to the maximum document length
word_ids_padded = tf.pad(word_ids, padding)
word_id_vector = tf.slice(word_ids_padded, [0,0], [-1, MAX_DOCUMENT_LENGTH])
# Return the final word_id_vector
return word_id_vector
def model_fn(features, labels, mode, params):
hidden_units = params.hidden_units
output_layer_size = len(TARGET_LABELS)
embedding_size = params.embedding_size
window_size = params.window_size
stride = int(window_size/2)
filters = params.filters
# word_id_vector
word_id_vector = process_text(features[TEXT_FEATURE_NAME])
# print("word_id_vector: {}".format(word_id_vector)) # (?, MAX_DOCUMENT_LENGTH)
# layer to take each word_id and convert it into vector (embeddings)
word_embeddings = tf.contrib.layers.embed_sequence(word_id_vector, vocab_size=N_WORDS,
embed_dim=embedding_size)
#print("word_embeddings: {}".format(word_embeddings)) # (?, MAX_DOCUMENT_LENGTH, embbeding_size)
# convolution
words_conv = tf.layers.conv1d(word_embeddings, filters=filters, kernel_size=window_size,
strides=stride, padding='SAME', activation=tf.nn.relu)
#print("words_conv: {}".format(words_conv)) # (?, MAX_DOCUMENT_LENGTH/stride, filters)
words_conv_shape = words_conv.get_shape()
dim = words_conv_shape[1] * words_conv_shape[2]
input_layer = tf.reshape(words_conv,[-1, dim])
#print("input_layer: {}".format(input_layer)) # (?, (MAX_DOCUMENT_LENGTH/stride)*filters)
if hidden_units is not None:
# Create a fully-connected layer-stack based on the hidden_units in the params
hidden_layers = tf.contrib.layers.stack(inputs=input_layer,
layer=tf.contrib.layers.fully_connected,
stack_args= hidden_units,
activation_fn=tf.nn.relu)
# print("hidden_layers: {}".format(hidden_layers)) # (?, last-hidden-layer-size)
else:
hidden_layers = input_layer
# Connect the output layer (logits) to the hidden layer (no activation fn)
logits = tf.layers.dense(inputs=hidden_layers,
units=output_layer_size,
activation=None)
# print("logits: {}".format(logits)) # (?, output_layer_size)
# Provide an estimator spec for `ModeKeys.PREDICT`.
if mode == tf.estimator.ModeKeys.PREDICT:
probabilities = tf.nn.softmax(logits)
predicted_indices = tf.argmax(probabilities, 1)
# Convert predicted_indices back into strings
predictions = {
'class': tf.gather(TARGET_LABELS, predicted_indices),
'probabilities': probabilities
}
export_outputs = {
'prediction': tf.estimator.export.PredictOutput(predictions)
}
# Provide an estimator spec for `ModeKeys.PREDICT` modes.
return tf.estimator.EstimatorSpec(mode,
predictions=predictions,
export_outputs=export_outputs)
# weights
weights = features[WEIGHT_COLUNM_NAME]
# Calculate loss using softmax cross entropy
loss = tf.losses.sparse_softmax_cross_entropy(
logits=logits, labels=labels,
weights=weights
)
tf.summary.scalar('loss', loss)
if mode == tf.estimator.ModeKeys.TRAIN:
# Create Optimiser
optimizer = tf.train.AdamOptimizer(params.learning_rate)
# Create training operation
train_op = optimizer.minimize(
loss=loss, global_step=tf.train.get_global_step())
# Provide an estimator spec for `ModeKeys.TRAIN` modes.
return tf.estimator.EstimatorSpec(mode=mode,
loss=loss,
train_op=train_op)
if mode == tf.estimator.ModeKeys.EVAL:
probabilities = tf.nn.softmax(logits)
predicted_indices = tf.argmax(probabilities, 1)
# Return accuracy and area under ROC curve metrics
labels_one_hot = tf.one_hot(
labels,
depth=len(TARGET_LABELS),
on_value=True,
off_value=False,
dtype=tf.bool
)
eval_metric_ops = {
'accuracy': tf.metrics.accuracy(labels, predicted_indices, weights=weights),
'auroc': tf.metrics.auc(labels_one_hot, probabilities, weights=weights)
}
# Provide an estimator spec for `ModeKeys.EVAL` modes.
return tf.estimator.EstimatorSpec(mode,
loss=loss,
eval_metric_ops=eval_metric_ops)
def create_estimator(run_config, hparams):
estimator = tf.estimator.Estimator(model_fn=model_fn,
params=hparams,
config=run_config)
print("")
print("Estimator Type: {}".format(type(estimator)))
print("")
return estimator
```
## 4. Run Experiment
### a. Set HParam and RunConfig
```
TRAIN_SIZE = 4179
NUM_EPOCHS = 10
BATCH_SIZE = 250
EVAL_AFTER_SEC = 60
TOTAL_STEPS = int((TRAIN_SIZE/BATCH_SIZE)*NUM_EPOCHS)
hparams = tf.contrib.training.HParams(
num_epochs = NUM_EPOCHS,
batch_size = BATCH_SIZE,
embedding_size = 3,
window_size = 3,
filters = 2,
hidden_units=None, #[8],
max_steps = TOTAL_STEPS,
learning_rate = 0.01
)
model_dir = 'trained_models/{}'.format(MODEL_NAME)
run_config = tf.estimator.RunConfig(
log_step_count_steps=5000,
tf_random_seed=19830610,
model_dir=model_dir
)
print(hparams)
print("Model Directory:", run_config.model_dir)
print("")
print("Dataset Size:", TRAIN_SIZE)
print("Batch Size:", BATCH_SIZE)
print("Steps per Epoch:",TRAIN_SIZE/BATCH_SIZE)
print("Total Steps:", TOTAL_STEPS)
print("That is 1 evaluation step after each",EVAL_AFTER_SEC,"training seconds")
```
### b. Define serving function
```
def serving_input_fn():
receiver_tensor = {
'sms': tf.placeholder(tf.string, [None]),
}
features = {
key: tensor
for key, tensor in receiver_tensor.items()
}
return tf.estimator.export.ServingInputReceiver(
features, receiver_tensor)
```
### c. Define TrainSpec and EvaluSpec
```
train_spec = tf.estimator.TrainSpec(
input_fn = lambda: input_fn(
TRAIN_DATA_FILES_PATTERN,
mode = tf.estimator.ModeKeys.TRAIN,
num_epochs=hparams.num_epochs,
batch_size=hparams.batch_size
),
max_steps=hparams.max_steps,
hooks=None
)
eval_spec = tf.estimator.EvalSpec(
input_fn = lambda: input_fn(
VALID_DATA_FILES_PATTERN,
mode=tf.estimator.ModeKeys.EVAL,
batch_size=hparams.batch_size
),
exporters=[tf.estimator.LatestExporter(
name="predict", # the name of the folder in which the model will be exported to under export
serving_input_receiver_fn=serving_input_fn,
exports_to_keep=1,
as_text=True)],
steps=None,
throttle_secs = EVAL_AFTER_SEC
)
```
### d. Run Experiment via train_and_evaluate
```
if not RESUME_TRAINING:
print("Removing previous artifacts...")
shutil.rmtree(model_dir, ignore_errors=True)
else:
print("Resuming training...")
tf.logging.set_verbosity(tf.logging.INFO)
time_start = datetime.utcnow()
print("Experiment started at {}".format(time_start.strftime("%H:%M:%S")))
print(".......................................")
estimator = create_estimator(run_config, hparams)
tf.estimator.train_and_evaluate(
estimator=estimator,
train_spec=train_spec,
eval_spec=eval_spec
)
time_end = datetime.utcnow()
print(".......................................")
print("Experiment finished at {}".format(time_end.strftime("%H:%M:%S")))
print("")
time_elapsed = time_end - time_start
print("Experiment elapsed time: {} seconds".format(time_elapsed.total_seconds()))
```
## 5. Evaluate the Model
```
TRAIN_SIZE = 4179
TEST_SIZE = 1393
train_input_fn = lambda: input_fn(files_name_pattern= TRAIN_DATA_FILES_PATTERN,
mode= tf.estimator.ModeKeys.EVAL,
batch_size= TRAIN_SIZE)
test_input_fn = lambda: input_fn(files_name_pattern= VALID_DATA_FILES_PATTERN,
mode= tf.estimator.ModeKeys.EVAL,
batch_size= TEST_SIZE)
estimator = create_estimator(run_config, hparams)
train_results = estimator.evaluate(input_fn=train_input_fn, steps=1)
print()
print("######################################################################################")
print("# Train Measures: {}".format(train_results))
print("######################################################################################")
test_results = estimator.evaluate(input_fn=test_input_fn, steps=1)
print()
print("######################################################################################")
print("# Test Measures: {}".format(test_results))
print("######################################################################################")
```
## 6. Predict Using Serving Function
```
import os
export_dir = model_dir +"/export/predict/"
saved_model_dir = export_dir + "/" + os.listdir(path=export_dir)[-1]
print(saved_model_dir)
print("")
predictor_fn = tf.contrib.predictor.from_saved_model(
export_dir = saved_model_dir,
signature_def_key="prediction"
)
output = predictor_fn(
{
'sms':[
'ok, I will be with you in 5 min. see you then',
'win 1000 cash free of charge promo hot deal sexy',
'hot girls sexy tonight call girls waiting call chat'
]
}
)
print(output)
```
| true |
code
| 0.578091 | null | null | null | null |
|
```
# Copyright 2021 Google LLC
# Use of this source code is governed by an MIT-style
# license that can be found in the LICENSE file or at
# https://opensource.org/licenses/MIT.
# Notebook authors: Kevin P. Murphy ([email protected])
# and Mahmoud Soliman ([email protected])
# This notebook reproduces figures for chapter 15 from the book
# "Probabilistic Machine Learning: An Introduction"
# by Kevin Murphy (MIT Press, 2021).
# Book pdf is available from http://probml.ai
```
<a href="https://opensource.org/licenses/MIT" target="_parent"><img src="https://img.shields.io/github/license/probml/pyprobml"/></a>
<a href="https://colab.research.google.com/github/probml/pml-book/blob/main/pml1/figure_notebooks/chapter15_neural_networks_for_sequences_figures.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Figure 15.1:<a name='15.1'></a> <a name='rnn'></a>
Recurrent neural network (RNN) for generating a variable length output sequence $\mathbf y _ 1:T $ given an optional fixed length input vector $\mathbf x $.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.1.png" width="256"/>
## Figure 15.2:<a name='15.2'></a> <a name='rnnTimeMachine'></a>
Example output of length 500 generated from a character level RNN when given the prefix ``the''. We use greedy decoding, in which the most likely character at each step is computed, and then fed back into the model. The model is trained on the book \em The Time Machine by H. G. Wells.
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/master/notebooks-d2l/rnn_torch.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
## Figure 15.3:<a name='15.3'></a> <a name='imageCaptioning'></a>
Illustration of a CNN-RNN model for image captioning. The pink boxes labeled ``LSTM'' refer to a specific kind of RNN that we discuss in \cref sec:LSTM . The pink boxes labeled $W_ \text emb $ refer to embedding matrices for the (sampled) one-hot tokens, so that the input to the model is a real-valued vector. From https://bit.ly/2FKnqHm . Used with kind permission of Yunjey Choi.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.3.pdf" width="256"/>
## Figure 15.4:<a name='15.4'></a> <a name='rnnBiPool'></a>
(a) RNN for sequence classification. (b) Bi-directional RNN for sequence classification.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.4_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.4_B.png" width="256"/>
## Figure 15.5:<a name='15.5'></a> <a name='biRNN'></a>
(a) RNN for transforming a sequence to another, aligned sequence. (b) Bi-directional RNN for the same task.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.5_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.5_B.png" width="256"/>
## Figure 15.6:<a name='15.6'></a> <a name='deepRNN'></a>
Illustration of a deep RNN. Adapted from Figure 9.3.1 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.6.png" width="256"/>
## Figure 15.7:<a name='15.7'></a> <a name='seq2seq'></a>
Encoder-decoder RNN architecture for mapping sequence $\mathbf x _ 1:T $ to sequence $\mathbf y _ 1:T' $.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.7.png" width="256"/>
## Figure 15.8:<a name='15.8'></a> <a name='NMT'></a>
(a) Illustration of a seq2seq model for translating English to French. The - character represents the end of a sentence. From Figure 2.4 of <a href='#Luong2016thesis'>[Luo16]</a> . Used with kind permission of Minh-Thang Luong. (b) Illustration of greedy decoding. The most likely French word at each step is highlighted in green, and then fed in as input to the next step of the decoder. From Figure 2.5 of <a href='#Luong2016thesis'>[Luo16]</a> . Used with kind permission of Minh-Thang Luong.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.8_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.8_B.png" width="256"/>
## Figure 15.9:<a name='15.9'></a> <a name='BPTT'></a>
An RNN unrolled (vertically) for 3 time steps, with the target output sequence and loss node shown explicitly. From Figure 8.7.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.9.png" width="256"/>
## Figure 15.10:<a name='15.10'></a> <a name='GRU'></a>
Illustration of a GRU. Adapted from Figure 9.1.3 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.10.png" width="256"/>
## Figure 15.11:<a name='15.11'></a> <a name='LSTM'></a>
Illustration of an LSTM. Adapted from Figure 9.2.4 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.11.png" width="256"/>
## Figure 15.12:<a name='15.12'></a> <a name='stsProb'></a>
Conditional probabilities of generating each token at each step for two different sequences. From Figures 9.8.1--9.8.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.12_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.12_B.png" width="256"/>
## Figure 15.13:<a name='15.13'></a> <a name='beamSearch'></a>
Illustration of beam search using a beam of size $K=2$. The vocabulary is $\mathcal Y = \ A,B,C,D,E\ $, with size $V=5$. We assume the top 2 symbols at step 1 are A,C. At step 2, we evaluate $p(y_1=A,y_2=y)$ and $p(y_1=C,y_2=y)$ for each $y \in \mathcal Y $. This takes $O(K V)$ time. We then pick the top 2 partial paths, which are $(y_1=A,y_2=B)$ and $(y_1=C,y_2=E)$, and continue in the obvious way. Adapted from Figure 9.8.3 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.13.png" width="256"/>
## Figure 15.14:<a name='15.14'></a> <a name='textCNN'></a>
Illustration of the TextCNN model for binary sentiment classification. Adapted from Figure 15.3.5 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.14.png" width="256"/>
## Figure 15.15:<a name='15.15'></a> <a name='wavenet'></a>
Illustration of the wavenet model using dilated (atrous) convolutions, with dilation factors of 1, 2, 4 and 8. From Figure 3 of <a href='#wavenet'>[Aar+16]</a> . Used with kind permission of Aaron van den Oord.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.15.png" width="256"/>
## Figure 15.16:<a name='15.16'></a> <a name='attention'></a>
Attention computes a weighted average of a set of values, where the weights are derived by comparing the query vector to a set of keys. From Figure 10.3.1 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.16.pdf" width="256"/>
## Figure 15.17:<a name='15.17'></a> <a name='attenRegression'></a>
Kernel regression in 1d. (a) Kernel weight matrix. (b) Resulting predictions on a dense grid of test points.
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/master/notebooks/kernel_regression_attention.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.17_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.17_B.png" width="256"/>
## Figure 15.18:<a name='15.18'></a> <a name='seq2seqAttn'></a>
Illustration of seq2seq with attention for English to French translation. Used with kind permission of Minh-Thang Luong.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.18.png" width="256"/>
## Figure 15.19:<a name='15.19'></a> <a name='translationHeatmap'></a>
Illustration of the attention heatmaps generated while translating two sentences from Spanish to English. (a) Input is ``hace mucho frio aqui.'', output is ``it is very cold here.''. (b) Input is ``¿todavia estan en casa?'', output is ``are you still at home?''. Note that when generating the output token ``home'', the model should attend to the input token ``casa'', but in fact it seems to attend to the input token ``?''.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.19_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.19_B.png" width="256"/>
## Figure 15.20:<a name='15.20'></a> <a name='EHR'></a>
Example of an electronic health record. In this example, 24h after admission to the hospital, the RNN classifier predicts the risk of death as 19.9\%; the patient ultimately died 10 days after admission. The ``relevant'' keywords from the input clinical notes are shown in red, as identified by an attention mechanism. From Figure 3 of <a href='#Rajkomar2018'>[Alv+18]</a> . Used with kind permission of Alvin Rakomar.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.20.png" width="256"/>
## Figure 15.21:<a name='15.21'></a> <a name='SNLI'></a>
Illustration of sentence pair entailment classification using an MLP with attention to align the premise (``I do need sleep'') with the hypothesis (``I am tired''). White squares denote active attention weights, blue squares are inactive. (We are assuming hard 0/1 attention for simplicity.) From Figure 15.5.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.21.png" width="256"/>
## Figure 15.22:<a name='15.22'></a> <a name='showAttendTell'></a>
Image captioning using attention. (a) Soft attention. Generates ``a woman is throwing a frisbee in a park''. (b) Hard attention. Generates ``a man and a woman playing frisbee in a field''. From Figure 6 of <a href='#showAttendTell'>[Kel+15]</a> . Used with kind permission of Kelvin Xu.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.22_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.22_B.png" width="256"/>
## Figure 15.23:<a name='15.23'></a> <a name='transformerTranslation'></a>
Illustration of how encoder self-attention for the word ``it'' differs depending on the input context. From https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html . Used with kind permission of Jakob Uszkoreit.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.23.png" width="256"/>
## Figure 15.24:<a name='15.24'></a> <a name='multiHeadAttn'></a>
Multi-head attention. Adapted from Figure 9.3.3 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.24.png" width="256"/>
## Figure 15.25:<a name='15.25'></a> <a name='positionalEncodingSinusoids'></a>
(a) Positional encoding matrix for a sequence of length $n=60$ and an embedding dimension of size $d=32$. (b) Basis functions for columsn 6 to 9.
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/master/notebooks-d2l/positional_encoding.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.25_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.25_B.png" width="256"/>
## Figure 15.26:<a name='15.26'></a> <a name='transformer'></a>
The transformer. From <a href='#Weng2018attention'>[Lil18]</a> . Used with kind permission of Lilian Weng. Adapted from Figures 1--2 of <a href='#Vaswani2017'>[Ash+17]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.26.png" width="256"/>
## Figure 15.27:<a name='15.27'></a> <a name='attentionBakeoff'></a>
Comparison of (1d) CNNs, RNNs and self-attention models. From Figure 10.6.1 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.27.png" width="256"/>
## Figure 15.28:<a name='15.28'></a> <a name='VIT'></a>
The Vision Transformer (ViT) model. This treats an image as a set of input patches. The input is prepended with the special CLASS embedding vector (denoted by *) in location 0. The class label for the image is derived by applying softmax to the final ouput encoding at location 0. From Figure 1 of <a href='#ViT'>[Ale+21]</a> . Used with kind permission of Alexey Dosovitskiy
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.28.png" width="256"/>
## Figure 15.29:<a name='15.29'></a> <a name='transformers_taxonomy'></a>
Venn diagram presenting the taxonomy of different efficient transformer architectures. From <a href='#Tay2020transformers'>[Yi+20]</a> . Used with kind permission of Yi Tay.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.29.pdf" width="256"/>
## Figure 15.30:<a name='15.30'></a> <a name='rand_for_fast_atten'></a>
Attention matrix $\mathbf A $ rewritten as a product of two lower rank matrices $\mathbf Q ^ \prime $ and $(\mathbf K ^ \prime )^ \mkern -1.5mu\mathsf T $ with random feature maps $\boldsymbol \phi (\mathbf q _i) \in \mathbb R ^M$ and $\boldsymbol \phi (\mathbf v _k) \in \mathbb R ^M$ for the corresponding queries/keys stored in the rows/columns. Used with kind permission of Krzysztof Choromanski.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.30.png" width="256"/>
## Figure 15.31:<a name='15.31'></a> <a name='fatten'></a>
Decomposition of the attention matrix $\mathbf A $ can be leveraged to improve attention computations via matrix associativity property. To compute $\mathbf AV $, we first calculate $\mathbf G =(\mathbf k ^ \prime )^ \mkern -1.5mu\mathsf T \mathbf V $ and then $\mathbf q ^ \prime \mathbf G $, resulting in linear in $N$ space and time complexity. Used with kind permission of Krzysztof Choromanski.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.31.png" width="256"/>
## Figure 15.32:<a name='15.32'></a> <a name='elmo'></a>
Illustration of ELMo bidrectional language model. Here $y_t=x_ t+1 $ when acting as the target for the forwards LSTM, and $y_t = x_ t-1 $ for the backwards LSTM. (We add \text \em bos \xspace and \text \em eos \xspace sentinels to handle the edge cases.) From <a href='#Weng2019LM'>[Lil19]</a> . Used with kind permission of Lilian Weng.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.32.png" width="256"/>
## Figure 15.33:<a name='15.33'></a> <a name='GPT'></a>
Illustration of (a) BERT and (b) GPT. $E_t$ is the embedding vector for the input token at location $t$, and $T_t$ is the output target to be predicted. From Figure 3 of <a href='#bert'>[Jac+19]</a> . Used with kind permission of Ming-Wei Chang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.33_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.33_B.png" width="256"/>
## Figure 15.34:<a name='15.34'></a> <a name='bertEmbedding'></a>
Illustration of how a pair of input sequences, denoted A and B, are encoded before feeding to BERT. From Figure 14.8.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.34.png" width="256"/>
## Figure 15.35:<a name='15.35'></a> <a name='bert-tasks'></a>
Illustration of how BERT can be used for different kinds of supervised NLP tasks. (a) Single sentence classification (e.g., sentiment analysis); (b) Sentence-pair classification (e.g., textual entailment); (d) Single sentence tagging (e.g., shallow parsing); (d) Question answering. From Figure 4 of <a href='#bert'>[Jac+19]</a> . Used with kind permission of Ming-Wei Chang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_B.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_C.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_D.png" width="256"/>
## Figure 15.36:<a name='15.36'></a> <a name='T5'></a>
Illustration of how the T5 model (``Text-to-text Transfer Transformer'') can be used to perform multiple NLP tasks, such as translating English to German; determining if a sentence is linguistic valid or not ( \bf CoLA stands for ``Corpus of Linguistic Acceptability''); determining the degree of semantic similarity ( \bf STSB stands for ``Semantic Textual Similarity Benchmark''); and abstractive summarization. From Figure 1 of <a href='#T5'>[Col+19]</a> . Used with kind permission of Colin Raffel.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.36.png" width="256"/>
## References:
<a name='wavenet'>[Aar+16]</a> V. Aaron, D. Sander, Z. Heiga, S. Karen, V. Oriol, G. Alex, K. Nal, S. Andrew and K. Koray. "WaveNet: A Generative Model for Raw Audio". abs/1609.03499 (2016). arXiv: 1609.03499
<a name='ViT'>[Ale+21]</a> D. Alexey, B. Lucas, K. A. Dirk, Z. Xiaohua, U. T. Mostafa, M. Matthias, H. G. Sylvain, U. Jakob and H. Neil. "An Image is Worth 16x16 Words: Transformers for ImageRecognition at Scale". (2021).
<a name='Rajkomar2018'>[Alv+18]</a> R. Alvin, O. Eyal, C. Kai, D. A. Nissan, H. Michaela, L. PeterJ, L. LiuXiaobing, M. Jake, S. Mimi, S. Patrik, Y. Hector, Z. Kun, Z. Yi, F. Gerardo, D. GavinE, I. Jamie, L. Quoc, L. K. Alexander, T. Justin, W. De, W. James, W. Jimbo, L. Dana, V. L, C. Katherine, P. Michael, M. MadabushiSrinivasan, S. NigamH, B. AtulJ, H. D, C. Claire, C. GregS and D. Jeffrey. "Scalable and accurate deep learning with electronic healthrecords". In: NPJ Digit Med (2018).
<a name='Vaswani2017'>[Ash+17]</a> V. Ashish, S. Noam, P. Niki, U. Jakob, J. Llion, G. AidanN, K. KaiserLukasz and P. Illia. "Attention Is All You Need". (2017).
<a name='T5'>[Col+19]</a> R. Colin, S. Noam, R. Adam, L. LeeKatherine, N. Sharan, M. Michael, Z. ZhouYanqi, L. Wei and L. PeterJ. "Exploring the Limits of Transfer Learning with a UnifiedText-to-Text Transformer". abs/1910.10683 (2019). arXiv: 1910.10683
<a name='bert'>[Jac+19]</a> D. Jacob, C. Ming-Wei, L. Kenton and T. ToutanovaKristina. "BERT: Pre-training of Deep Bidirectional Transformers forLanguage Understanding". (2019).
<a name='showAttendTell'>[Kel+15]</a> X. Kelvin, B. JimmyLei, K. Ryan, C. K. Aaron, S. Ruslan, Z. S and B. Yoshua. "Show, Attend and Tell: Neural Image Caption Generation withVisual Attention". (2015).
<a name='Weng2018attention'>[Lil18]</a> W. Lilian "Attention? Attention!". In: lilianweng.github.io/lil-log (2018).
<a name='Weng2019LM'>[Lil19]</a> W. Lilian "Generalized Language Models". In: lilianweng.github.io/lil-log (2019).
<a name='Luong2016thesis'>[Luo16]</a> M. Luong "Neural machine translation". (2016).
<a name='Tay2020transformers'>[Yi+20]</a> T. Yi, D. Mostafa, B. Dara and M. MetzlerDonald. "Efficient Transformers: A Survey". abs/2009.06732 (2020). arXiv: 2009.06732
<a name='dive'>[Zha+20]</a> A. Zhang, Z. Lipton, M. Li and A. Smola. "Dive into deep learning". (2020).
| true |
code
| 0.540681 | null | null | null | null |
|
## Series
```
import pandas as pd
import numpy as np
import random
first_series = pd.Series([1,2,3, np.nan ,"hello"])
first_series
series = pd.Series([1,2,3, np.nan ,"hello"], index = ['A','B','C','Unknown','String'])
series
#indexing the Series with custom values
dict = {"Python": "Fun", "C++": "Outdated","Coding":"Hmm.."}
series = pd.Series(dict)
series
# Dict to pandas Series
series[['Coding','Python']]
series.index
series.values
series.describe()
#Series is a mutable data structures and you can easily change any item’s value:
series['Coding'] = 'Awesome'
series
# add new values:
series['Java'] = 'Okay'
series
# If it is necessary to apply any mathematical operation to Series items, you may done it like below:
num_series = pd.Series([1,2,3,4,5,6,None])
num_series_changed = num_series/2
num_series_changed
# NULL/NaN checking can be performed with isnull() and notnull().
print(series.isnull())
print(num_series.notnull())
print(num_series_changed.notnull())
```
## DataFrames
```
data = {'year': [1990, 1994, 1998, 2002, 2006, 2010, 2014],
'winner': ['Germany', 'Brazil', 'France', 'Brazil','Italy', 'Spain', 'Germany'],
'runner-up': ['Argentina', 'Italy', 'Brazil','Germany', 'France', 'Netherlands', 'Argentina'],
'final score': ['1-0', '0-0 (pen)', '3-0', '2-0', '1-1 (pen)', '1-0', '1-0'] }
world_cup = pd.DataFrame(data, columns=['year', 'winner', 'runner-up', 'final score'])
world_cup
# Another way to set a DataFrame is the using of Python list of dictionaries:
data_2 = [{'year': 1990, 'winner': 'Germany', 'runner-up': 'Argentina', 'final score': '1-0'},
{'year': 1994, 'winner': 'Brazil', 'runner-up': 'Italy', 'final score': '0-0 (pen)'},
{'year': 1998, 'winner': 'France', 'runner-up': 'Brazil', 'final score': '3-0'},
{'year': 2002, 'winner': 'Brazil', 'runner-up': 'Germany', 'final score': '2-0'},
{'year': 2006, 'winner': 'Italy','runner-up': 'France', 'final score': '1-1 (pen)'},
{'year': 2010, 'winner': 'Spain', 'runner-up': 'Netherlands', 'final score': '1-0'},
{'year': 2014, 'winner': 'Germany', 'runner-up': 'Argentina', 'final score': '1-0'}
]
world_cup = pd.DataFrame(data_2)
world_cup
print("First 2 Rows: ",end="\n\n")
print (world_cup.head(2),end="\n\n")
print ("Last 2 Rows : ",end="\n\n")
print (world_cup.tail(2),end="\n\n")
print("Using slicing : ",end="\n\n")
print (world_cup[2:4])
```
### CSV
#### Reading:
`df = pd.read_csv("path\to\the\csv\file\for\reading")`
#### Writing:
`df.to_csv("path\to\the\folder\where\you\want\save\csv\file")`
### TXT file(s)
(txt file can be read as a CSV file with other separator (delimiter); we suppose below that columns are separated by tabulation):
#### Reading:
`df = pd.read_csv("path\to\the\txt\file\for\reading", sep='\t')`
#### Writing:
`df.to_csv("path\to\the\folder\where\you\want\save\txt\file", sep='\t')`
### JSON files
(an open-standard format that uses human-readable text to transmit data objects consisting of attribute–value pairs. It is the most common data format used for asynchronous browser/server communication. By its view it is very similar to Python dictionary)
#### Reading:
`df = pd.read_json("path\to\the\json\file\for\reading", sep='\t')`
#### Writing:
`df.to_json("path\to\the\folder\where\you\want\save\json\file", sep='\t')`
```
# To write world_cup Dataframe to a CSV File
world_cup.to_csv("worldcup.csv")
# To save CSV file without index use index=False attribute
print("File Written!",end="\n\n")
#To check if it was written
import os
print(os.path.exists('worldcup.csv'))
# reading from it in a new dataframe df
df = pd.read_csv('worldcup.csv')
print(df.head())
# We can also load the data without index as :
df = pd.read_csv('worldcup.csv',index_col=0)
print(df)
movies=pd.read_csv("data/movies.csv",encoding = "ISO-8859-1")
# encoding is added only for this specific dataset because it gave error with utf-8
movies['release_date'] = movies['release_date'].map(pd.to_datetime)
print(movies.head(20))
#print(movies.describe())
movies_rating = movies['rating']
# Here we are showing only one column, i.e. a Series
print ('type:', type(movies_rating))
movies_rating.head()
# Filtering data
# Let's display only women
movies_user_female = movies[movies['gender']=='F']
print(movies_user_female.head())
#to see all the different values possible for a given column
occupation_list = movies['occupation']
print(occupation_list)
```
### Work with indexes and MultiIndex option
```
import random
indexes = [random.randrange(0,100) for i in range(5)]
data = [{i:random.randint(0,10) for i in 'ABCDE'} for i in range(5)]
df = pd.DataFrame(data, index=[1,2,3,4,5])
df
movies_user_gender_male = movies[movies['gender']=='M']
movies_user_gender_male_dup = movies_user_gender_male.drop_duplicates(keep=False)
print(movies_user_gender_male.head())
# From this we can clearly see age has missing value and that from 100,000 the data reduced to 74260,
# due to filtering and removing duplicates
#gender = female and age between 30 and 40
gender_required = ['F']
filtered_df = movies[((movies['gender'] == 'F') & (movies['age'] > 30) & (movies['age'] <40))]
filtered_df
```
#### Note
In the above fragment you HAVE TO ADD parantheses to each and every argument that is being compared else you will get an error.
As you can see after filtering result tables (i.e. DataFrames) have non-ordered indexes. To fix this trouble you may write the following:
```
filtered_df = filtered_df.reset_index()
filtered_df.head(10)
# set 'user_id' 'movie_id' as index
filtered_df_new = filtered_df.set_index(['user_id','movie_id'])
filtered_df_new.head(10)
# Note that set_index takes only a list as an argument to it.
# if you remove the [] then only the first argument is set as the index.
# By default, `set_index()` returns a new DataFrame.
# so you’ll have to specify if you’d like the changes to occur in place.
# Here we used filtered_df_new to get the new dataframe and now see the type of filtererd_df_new
print(type(filtered_df_new.index))
```
Notice here that we now have a new sort of 'index' which is `MultiIndex`, which contains information about indexing of DataFrame and allows manipulating with this data.
```
filtered_df_new.index.names
# Gives you the names of the two index values we set as a FrozenList
```
Method `get_level_values()` allows to get all values for the corresponding index level.
`get_level_values(0)` corresponds to 'user_id' and `get_level_values(1)` corresponds to 'movie_id'
```
print(filtered_df_new.index.get_level_values(0))
print(filtered_df_new.index.get_level_values(1))
```
### Selection by label and position
Object selection in pandas is now supported by three types of multi-axis indexing.
* `.loc` works on labels in the index;
* `.iloc` works on the positions in the index (so it only takes integers);
The sequence of the following examples demonstrates how we can manipulate with DataFrame’s rows.
At first let’s get the first row of movies:
```
movies.loc[0]
movies.loc[1:3]
```
If you want to return specific columns then you have to specify them as a separate argument of .loc
```
movies.loc[1:3 , 'movie_title']
movies.loc[1:5 , ['movie_title','age','gender']]
# If more than one column is to be selected then you have to give the second argument of .loc as a list
# movies.iloc[1:5 , ['movie_title','age','gender']]
# Gives error as iloc only uses integer values
movies.iloc[0]
movies.iloc[1:5]
# movies.select(lambda x: x%2==0).head() is the same as :
movies.loc[movies.index.map(lambda x: x%2==0)].head()
# .select() has been deprecated for now and will be completely removed in future updates so use .loc
```
## Working with Missing Data
Pandas primarily uses the value np.nan to represent missing data (in table missed/empty value are marked by NaN). It is by default not included in computations. Missing data creates many issues at mathematical or computational tasks with DataFrames and Series and it’s important to know how fight with these values.
```
ages = movies['age']
sum(ages)
```
This is because there are so many cases where Age isn't given and hence takes on the value of np.nan.
We can use `fillna()`a very effecient pandas method for filling missing values
```
ages = movies['age'].fillna(0)
sum(ages)
```
This fills all the values with 0 and calculates the sum.
To remain only rows with non-null values you can use method `dropna()`
```
ages = movies['age'].dropna()
sum(ages)
movies_nonnull = movies.dropna()
movies_nonnull.head(20)
#14th value was dropped because it had a missing value in a column
movies_notnull = movies.dropna(how='all',subset=['age','occupation'])
#Drops all nan values from movies belonging to age and occupation
movies_notnull.info()
#Notice how age and occupation now have nearly 6000 lesser values
```
Thus, if `how='all'`, we get DataFrame, where all values in both columns from subset are NaN.
If `how='any'`, we get DataFrame, where at least one contains NaN.
```
movies.describe()
```
At first, let’s find all unique dates in `‘release_date’` column of `movies` and then select only dates in range lower than 1995.
```
movies['release_date'] = movies['release_date'].map(pd.to_datetime)
# We map it to_datetime as pandas has a set way to deal with dates and then we can effectively work with dates.
unique_dates = movies['release_date'].drop_duplicates().dropna()
# Drops duplicates and nan values
unique_dates
# find dates with year lower/equal than 1995
unique_dates_1 = filter(lambda x: x.year <= 1995, unique_dates)
# filter() takes two arguments. First one should return only boolean values and the second one is the variable over which ititerates over.
# This basically takes unique_dates and uses the lambda function (here, it returns bool values) and filters True cases.
unique_dates_1
```
Here we have used `drop_duplicates()` method to select only `unique` Series values. Then we can filter `movies` with respect to `release_date` condition. Each `datetime` Python object possesses with attributes `year`, `month`, `day`, etc. allowing to extract values of year, month, day, etc. from the date. We call the new DataFrame as `old_movies`.
```
old_movies = movies[movies['release_date'].isin(unique_dates_1)]
old_movies.head()
```
Now we may filter DataFrame `old_movies` by `age` and `rating`. Lets’ drop `timestamp`, `zip_code`
```
# get all users with age less than 25 that rated old movies higher than 3
old_movies_watch = old_movies[(old_movies['age']<25) & (old_movies['rating']>3)]
# Drop timestamp and zip_code
old_movies_watch = old_movies_watch.drop(['timestamp', 'zip_code'],axis=1)
old_movies_watch.head()
```
`Pandas` has support for accelerating certain types of binary numerical and boolean operations using the `numexpr `library (it uses smart chunking, caching, and multiple cores) and the `bottleneck` libraries (is a set of specialized cython routines that are especially fast when dealing with arrays that have NaNs). It allows one to increase pandas functionality a lot. This advantage is shown for some boolean and calculation operations. To count the time elapsed on operation performing we will use the decorator
```
# this function counts the time for a particular operation
def timer(func):
from datetime import datetime
def wrapper(*args):
start = datetime.now()
func(*args)
end = datetime.now()
return 'elapsed time = {' + str(end - start)+'}'
return wrapper
import random
n = 100
# generate rangon datasets
df_1 = pd.DataFrame({'col :'+str(i):[random.randint(-100,100) for j in range(n)]for i in range(n)})
# here we pass a dictionary to the DataFrame() constructor.
# The key is "col : i" where i can take random values and the value for those keys is i.
df_2 = pd.DataFrame({'col :'+str(i):[random.randint(-100,100) for j in range(n)] for i in range(n)})
@timer
def direct_comparison(df_1, df_2):
bool_df = pd.DataFrame({'col_{}'.format(i): [True for j in range(n)] for i in range(n)})
for i in range(len(df_1.index)):
for j in range(len(df_1.loc[i])):
if df_1.loc[i, df_1.columns[j]] >= df_2.loc[i, df_2.columns[j]]:
bool_df.loc[i,bool_df.columns[j]] = False
return bool_df
@timer
def pandas_comparison(df_1, df_2):
return df_1 < df_2
print ('direct_comparison:', (direct_comparison(df_1, df_2)))
print ('pandas_comparison:', (pandas_comparison(df_1, df_2)))
```
As you can see, the difference in speed is too noticeable.
Besides, pandas possesses methods `eq` (equal), `ne` (not equal), `lt` (less then), `gt` (greater than), `le` (less or equal) and `ge` (greater or equal) for simplifying boolean comparison
## Matrix Addition
```
df = pd.DataFrame({'A':[1,2,3],'B':[-2,-3,-4],"C":[7,8,9]})
dfa = pd.DataFrame({'A':[1,2,3],'D':[6,7,8],"C":[12,12,12]})
dfc = df + dfa
dfc
df.le(dfa)
```
You can also apply the reductions: `empty`, `any()`, `all()`, and `bool()` to provide a way to summarize a boolean result:
```
(df<0).all()
# here horyzontal direction for comparison is taking into account and we check all row’s items
(df < 0).all(axis=1)
# here vertical direction for comparison is taking into
# account and we check if just one column’s item satisfies the condition
(df < 0).any()
# here we check if all DataFrame's items satisfy the condition
(df < 0).any().any()
# here we check if DataFrame no one element
df.empty
```
### Descriptive Statistics
|Function|Description|
|--|-------------------------------|
|abs|absolute value|
|count|number of non-null observations|
|cumsum|cumulative sum (a sequence of partial sums of a given sequence)|
|sum|sum of values|
|mean|mean of values|
|mad|mean absolute deviation|
|median|arithmetic median of values|
|min|minimum value|
|max|maximum value|
|mode|mode|
|prod|product of values|
|std|unbiased standard deviation|
|var|unbiased variance|
```
print("Sum : ", movies['age'].sum())
print(df)
print("Mean : ")
print(df.mean())
print("\nMean of all Mean Values: ")
print(df.mean().mean())
print("\nMedian: ")
print(df.median())
print("\nStandard Deviation: ")
print(df.std())
print("\nVariance: ")
print(df.var())
print("\nMax: ")
print(df.max())
```
## Function Applications
When you need to make some transformations with some column’s or row’s elements, then method `map` will be helpful (it works like pure Python function `map()` ). But there is also possibility to apply some function to each DataFrame element (not to a column or a row) – method `apply(map)` aids in this case.
```
movies.loc[:, (movies.dtypes == np.int64) | (movies.dtypes == np.float64)].apply(np.mean)
# This calculates the mean of all the columns present in movies
# to print mean of all row values in movies :
movies.loc[:,(movies.dtypes==np.int64) | (movies.dtypes==np.float64)].apply(np.mean, axis = 1)
```
### Remember
The attribute axis define the horizontal `(axis=1)` or vertical direction for calculations `(axis=0)`
### Groupby with Dictionary
```
import numpy as np
import pandas as pd
d = {'id':[1,2,3],
'Column 1.1':[14,15,16],
'Column 1.2':[10,10,10],
'Column 1.3':[1,4,5],
'Column 2.1':[1,2,3],
'Column 2.2':[10,10,10],
}
df = pd.DataFrame(d)
df
groupby_dict = {'Column 1.1':'Column 1','Column 1.2':'Column 1','Column 1.3':'Column 1','Column 2.1':'Column 2','Column 2.2':'Column 2'}
df = df.set_index('id')
df=df.groupby(groupby_dict,axis=1).min()
df
import numpy as np
import pandas as pd
dict = {
"ID":[1,2,3],
"Movies":["The Godfather","Fight Club","Casablanca"],
"Week_1_Viewers":[30,30,40],
"Week_2_Viewers":[60,40,80],
"Week_3_Viewers":[40,20,20]
};
df = pd.DataFrame(dict);
df
mapping = {"Week_1_Viewers":"Total_Viewers",
"Week_2_Viewers":"Total_Viewers",
"Week_3_Viewers":"Total_Viewers",
"Movies":"Movies"
}
df = df.set_index('ID')
df=df.groupby(mapping,axis=1).sum()
df
```
### Breaking up a String into columns using regex
```
dict = {'movie_data':['The Godfather 1972 9.2',
'Bird Box 2018 6.8',
'Fight Club 1999 8.8']
}
df = pd.DataFrame(dict)
df
df['Name'] = df['movie_data'].str.extract('(\w*\s\w*)', expand=True)
df['Year'] = df['movie_data'].str.extract('(\d\d\d\d)', expand=True)
df['Rating'] = df['movie_data'].str.extract('(\d\.\d)', expand=True)
df
import re
movie_data = ["Name:The Godfather Year: 1972 Rating: 9.2",
"Name:Bird Box Year: 2018 Rating: 6.8",
"Name:Fight Club Year: 1999 Rating: 8.8"]
movies={"Name":[],
"Year":[],
"Rating":[]}
for item in movie_data:
name_field = re.search("Name:.*",item)
if name_field is not None:
name = re.search('\w*\s\w*',name_field.group())
else:
name = None
movies["Name"].append(name.group())
year_field = re.search("Year: .*",item)
if year_field is not None:
year = re.search('\s\d\d\d\d',year_field.group())
else:
year = None
movies["Year"].append(year.group().strip())
rating_field = re.search("Rating: .*",item)
if rating_field is not None:
rating = re.search('\s\d.\d',rating_field.group())
else:
rating - None
movies["Rating"].append(rating.group().strip())
movies
df = pd.DataFrame(movies)
df
```
### Ranking Rows in Pandas
```
import pandas as pd
movies = {'Name': ['The Godfather', 'Bird Box', 'Fight Club'],
'Year': ['1972', '2018', '1999'],
'Rating': ['9.2', '6.8', '8.8']}
df = pd.DataFrame(movies)
df
df['Rating_Rank'] = df['Rating'].rank(ascending=1)
df
df =df.set_index('Rating_Rank')
df
df.sort_index()
# Example 2
import pandas as pd
student_details = {'Name':['Raj','Raj','Raj','Aravind','Aravind','Aravind','John','John','John','Arjun','Arjun','Arjun'],
'Subject':['Maths','Physics','Chemistry','Maths','Physics','Chemistry','Maths','Physics','Chemistry','Maths','Physics','Chemistry'],
'Marks':[80,90,75,60,40,60,80,55,100,90,75,70]
}
df = pd.DataFrame(student_details)
df
df['Mark_Rank'] = df['Marks'].rank(ascending=0)
df = df.set_index('Mark_Rank')
df
df = df.sort_index()
df
```
| true |
code
| 0.306657 | null | null | null | null |
|
# 使用PyNative进行神经网络的训练调试体验
[](https://gitee.com/mindspore/docs/blob/master/docs/notebook/mindspore_debugging_in_pynative_mode.ipynb)
## 概述
在神经网络训练过程中,数据是否按照自己设计的神经网络运行,是使用者非常关心的事情,如何去查看数据是怎样经过神经网络,并产生变化的呢?这时候需要AI框架提供一个功能,方便使用者将计算图中的每一步变化拆开成单个算子或者深层网络拆分成多个单层来调试观察,了解分析数据在经过算子或者计算层后的变化情况,MindSpore在设计之初就提供了这样的功能模式--`PyNative_MODE`,与此对应的是`GRAPH_MODE`,他们的特点分别如下:
- PyNative模式:也称动态图模式,将神经网络中的各个算子逐一下发执行,方便用户编写和调试神经网络模型。
- Graph模式:也称静态图模式或者图模式,将神经网络模型编译成一整张图,然后下发执行。该模式利用图优化等技术提高运行性能,同时有助于规模部署和跨平台运行。
默认情况下,MindSpore处于Graph模式,可以通过`context.set_context(mode=context.PYNATIVE_MODE)`切换为PyNative模式;同样地,MindSpore处于PyNative模式时,可以通过`context.set_context(mode=context.GRAPH_MODE)`切换为Graph模式。
<br/>本次体验我们将使用一张手写数字图片跑完单次训练,在PyNative模式下,将数据在训练中经过每层神经网络的变化情况打印出来,并计算对应的loss值以及梯度值`grads`,整体流程如下:
1. 环境准备,设置PyNative模式。
2. 数据集准备,并取用单张图片数据。
3. 构建神经网络并设置每层断点打印数据。
4. 构建梯度计算函数。
5. 执行神经网络训练,查看网络各参数梯度。
> 本文档适用于GPU和Ascend环境。
## 环境准备
使用`context.set_context`将模式设置成`PYNATIVE_MODE`。
```
from mindspore import context
context.set_context(mode=context.PYNATIVE_MODE, device_target="GPU")
```
## 数据准备
### 数据集的下载
以下示例代码将数据集下载并解压到指定位置。
```
import os
import requests
requests.packages.urllib3.disable_warnings()
def download_dataset(dataset_url, path):
filename = dataset_url.split("/")[-1]
save_path = os.path.join(path, filename)
if os.path.exists(save_path):
return
if not os.path.exists(path):
os.makedirs(path)
res = requests.get(dataset_url, stream=True, verify=False)
with open(save_path, "wb") as f:
for chunk in res.iter_content(chunk_size=512):
if chunk:
f.write(chunk)
print("The {} file is downloaded and saved in the path {} after processing".format(os.path.basename(dataset_url), path))
train_path = "datasets/MNIST_Data/train"
test_path = "datasets/MNIST_Data/test"
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/train-labels-idx1-ubyte", train_path)
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/train-images-idx3-ubyte", train_path)
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/t10k-labels-idx1-ubyte", test_path)
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/t10k-images-idx3-ubyte", test_path)
```
下载的数据集文件的目录结构如下:
```text
./datasets/MNIST_Data
├── test
│ ├── t10k-images-idx3-ubyte
│ └── t10k-labels-idx1-ubyte
└── train
├── train-images-idx3-ubyte
└── train-labels-idx1-ubyte
```
### 数据集的增强操作
下载下来后的数据集,需要通过`mindspore.dataset`处理成适用于MindSpore框架的数据,再使用一系列框架中提供的工具进行数据增强操作来适应LeNet网络的数据处理需求。
```
import mindspore.dataset.vision.c_transforms as CV
import mindspore.dataset.transforms.c_transforms as C
from mindspore.dataset.vision import Inter
from mindspore import dtype as mstype
import mindspore.dataset as ds
import numpy as np
def create_dataset(data_path, batch_size=32, repeat_size=1,
num_parallel_workers=1):
""" create dataset for train or test
Args:
data_path (str): Data path
batch_size (int): The number of data records in each group
repeat_size (int): The number of replicated data records
num_parallel_workers (int): The number of parallel workers
"""
# define dataset
mnist_ds = ds.MnistDataset(data_path)
# define some parameters needed for data enhancement and rough justification
resize_height, resize_width = 32, 32
rescale = 1.0 / 255.0
shift = 0.0
rescale_nml = 1 / 0.3081
shift_nml = -1 * 0.1307 / 0.3081
# according to the parameters, generate the corresponding data enhancement method
resize_op = CV.Resize((resize_height, resize_width), interpolation=Inter.LINEAR)
rescale_nml_op = CV.Rescale(rescale_nml, shift_nml)
rescale_op = CV.Rescale(rescale, shift)
hwc2chw_op = CV.HWC2CHW()
type_cast_op = C.TypeCast(mstype.int32)
# using map method to apply operations to a dataset
mnist_ds = mnist_ds.map(operations=type_cast_op, input_columns="label", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=resize_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=rescale_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=rescale_nml_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=hwc2chw_op, input_columns="image", num_parallel_workers=num_parallel_workers)
# process the generated dataset
buffer_size = 10000
mnist_ds = mnist_ds.shuffle(buffer_size=buffer_size)
mnist_ds = mnist_ds.batch(batch_size, drop_remainder=True)
mnist_ds = mnist_ds.repeat(repeat_size)
return mnist_ds
```
### 数据图片的提取
本次体验我们只需要一张图片进行训练体验,所以随机选取`batch`中的第一张图片`image`和下标`label`。
```
from mindspore import Tensor
import matplotlib.pyplot as plt
train_data_path = "./datasets/MNIST_Data/train/"
ms_dataset = create_dataset(train_data_path)
dict_data = ms_dataset.create_dict_iterator()
data = next(dict_data)
images = data["image"].asnumpy()
labels = data["label"].asnumpy()
print(images.shape)
count = 1
for i in images:
plt.subplot(4, 8, count)
plt.imshow(np.squeeze(i))
plt.title('num:%s'%labels[count-1])
plt.xticks([])
count += 1
plt.axis("off")
plt.show()
```
当前batch的image数据如上图,后面的体验将提取第一张图片进行训练操作。
### 定义图像显示函数
定义一个图像显示函数`image_show`,插入LeNet5的前面4层神经网络中抽取图像数据并显示。
```
def image_show(x):
count = 1
x = x.asnumpy()
number = x.shape[1]
sqrt_number = int(np.sqrt(number))
for i in x[0]:
plt.subplot(sqrt_number, int(number/sqrt_number), count)
plt.imshow(i)
count += 1
plt.show()
```
## 构建神经网络LeNet5
在`construct`中使用`image_show`,查看每层网络后的图片变化。
> 这里只抽取了图片显示,想要查看具体的数值,可以按照自己的需要进行`print(x)`。
```
import mindspore.nn as nn
import mindspore.ops as ops
from mindspore import dtype as mstype
from mindspore.common.initializer import Normal
class LeNet5(nn.Cell):
"""Lenet network structure."""
# define the operator required
def __init__(self, num_class=10, num_channel=1):
super(LeNet5, self).__init__()
self.conv1 = nn.Conv2d(num_channel, 6, 5, pad_mode='valid')
self.conv2 = nn.Conv2d(6, 16, 5, pad_mode='valid')
self.fc1 = nn.Dense(16 * 5 * 5, 120, weight_init=Normal(0.02))
self.fc2 = nn.Dense(120, 84, weight_init=Normal(0.02))
self.fc3 = nn.Dense(84, num_class, weight_init=Normal(0.02))
self.relu = nn.ReLU()
self.max_pool2d = nn.MaxPool2d(kernel_size=2, stride=2)
self.flatten = nn.Flatten()
self.switch = 1
def construct(self, x):
x = self.conv1(x)
if self.switch > 0:
print("The first layer: convolution layer")
image_show(x)
x = self.relu(x)
x = self.max_pool2d(x)
if self.switch > 0:
print("The second layer: pool layer")
image_show(x)
x = self.conv2(x)
if self.switch > 0:
print("The third layer: convolution layer")
image_show(x)
x = self.relu(x)
x = self.max_pool2d(x)
if self.switch > 0:
print("The fourth layer: pool layer")
image_show(x)
x = self.flatten(x)
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
self.switch -= 1
return x
network = LeNet5()
print("layer conv1:", network.conv1)
print("*"*40)
print("layer fc1:", network.fc1)
```
## 构建计算梯度函数GradWrap
构建梯度下降求值函数,该函数可计算网络中所有权重的梯度。
```
from mindspore import Tensor, ParameterTuple
class GradWrap(nn.Cell):
""" GradWrap definition """
def __init__(self, network):
super(GradWrap, self).__init__(auto_prefix=False)
self.network = network
self.weights = ParameterTuple(filter(lambda x: x.requires_grad, network.get_parameters()))
def construct(self, x, label):
weights = self.weights
return ops.GradOperation(get_by_list=True)(self.network, weights)(x, label)
```
## 执行训练函数
可以从网络中查看当前`batch`中第一张图片`image`的数据在神经网络中的变化,经过神经网络后,计算出其loss值,再根据loss值求参数的偏导即神经网络的梯度值,最后将梯度和loss进行优化。
- image:为当前batch的第一张图片。
- output:表示图片数据经过当前网络训练后生成的值,其张量为(1,10)。
```
from mindspore.nn import WithLossCell, Momentum
net = LeNet5()
optimizer = Momentum(filter(lambda x: x.requires_grad, net.get_parameters()), 0.1, 0.9)
criterion = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')
net_with_criterion = WithLossCell(net, criterion)
train_network = GradWrap(net_with_criterion)
train_network.set_train()
image = images[0][0]
image = image.reshape((1, 1, 32, 32))
plt.imshow(np.squeeze(image))
plt.show()
input_data = Tensor(np.array(image).astype(np.float32))
label = Tensor(np.array([labels[0]]).astype(np.int32))
output = net(Tensor(input_data))
```
将第一层卷积层、第二层池化层、第三层卷积层和第四层池化层的图像特征打印出来后,直观地看到随着深度的增加,图像特征几乎无法用肉眼识别,但是机器可以用这些特征进行学习和识别,后续的全连接层为二维数组,无法图像显示,但可以打印出数据查看,由于数据量过大此处就不打印了,用户可以根据需求选择打印。
### 求loss值和梯度值,并进行优化
先求得loss值,后再根据loss值求梯度(偏导函数值),使用优化器`optimizer`进行优化。
- `loss_output`:即为loss值。
- `grads`:即网络中每层权重的梯度。
- `net_params`:即网络中每层权重的名称,用户可执行`print(net_params)`自行打印。
- `success`:优化参数。
```
loss_output = criterion(output, label)
grads = train_network(input_data, label)
net_params = net.trainable_params()
for i, grad in enumerate(grads):
print("{}:".format(net_params[i].name), grad.shape)
success = optimizer(grads)
loss = loss_output.asnumpy()
print("Loss_value:", loss)
```
具体每层权重的参数有多少,从打印出来的梯度张量能够看到,对应的梯度值用户可以自行选择打印。
## 总结
本次体验我们将MindSpore的数据增强后,使用了`create_dict_iterator`转化成字典,再单独取出来;使用PyNative模式将神经网络分层单独调试,提取并观察数据;用`WithLossCell`在PyNative模式下计算loss值;构造梯度函数`GradWrap`将神经网络中各个权重的梯度计算出来,以上就是本次的全部体验内容。
| true |
code
| 0.728845 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/RachitBansal/AppliancePower_TimeSeries/blob/master/ARIMA_Ukdale.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive',force_remount=True)
from sklearn.externals import joblib
import numpy as np
import matplotlib.pyplot as plt
eq = input("Enter equipment: ")
train_x = np.load(file='./drive/My Drive/ukdale_'+eq+'_x.npy')
train_y = np.load(file='./drive/My Drive/ukdale_'+eq+'_y.npy')
test_y = np.load(file='./drive/My Drive/ukdale_'+eq+'_ty.npy')
test_x = np.load(file='./drive/My Drive/ukdale_'+eq+'_tx.npy')
from pandas import datetime
import pandas as pd
# series = joblib.load("hour_resampled_data.pkl")
# sample = series
# sample = np.array(sample)
# sample = sample[3000:4500,1:2]
# series = np.array(series)
# series = series[:3000,1:2]
# print(series.shape)
# series = pd.DataFrame(series)
# #series.drop(axis = "index")
# print(series.head())
# equipment = int(input('equipment: '))
series = test_x[:3000, 0]
plt.plot(series)
plt.show()
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
# series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
autocorrelation_plot(series)
pyplot.show()
from pandas import datetime
from pandas import DataFrame
from statsmodels.tsa.arima_model import ARIMA
from matplotlib import pyplot
import numpy as np
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
# series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# fit model
series = np.array(series)
model = ARIMA(series, order=(5,1,0))
model_fit = model.fit(disp=0)
print(model_fit.summary())
# plot residual errors
residuals = DataFrame(model_fit.resid)
residuals.plot()
pyplot.show()
residuals.plot(kind='kde')
pyplot.show()
print(residuals.describe())
from pandas import datetime
from matplotlib import pyplot
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error,mean_absolute_error
# equipment = 3
len(list(train_x[0].reshape(-1)))
history = list(train_x[0].reshape(-1))
for i in range(train_x.shape[0] - 1):
history.append(train_x[i+1][-1])
plt.plot(history)
history = list(train_x[0].reshape(-1))
for i in range(1000):
history.append(train_x[-1000+i][-1])
# history.append(x for x in test_x[0].reshape(-1))
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
history = list(test_x[0].reshape(-1))
predictions = []
# history = [x for x in test_x[i].reshape(-1) for i in range(1000)]
for t in range(1000):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test_y[t][0][0]
history.append(obs)
if(t%50==0):
print('predicted=%f, expected=%f' % (yhat, obs))
predictions = np.array(predictions)
print(predictions.shape)
print(test_y.shape)
error = mean_squared_error(test_y[:1000].reshape(-1), predictions)
print('Test MSE: %.3f' % error)
print("RMSE : %.3f"%(np.sqrt(error)))
print("MAE : %.3f"%(mean_absolute_error(test_y[:1000].reshape(-1),predictions)))
# plot
pyplot.plot(test_y[:1000].reshape(-1))
pyplot.plot(predictions)
np.save(arr = np.array(predictions), file = './drive/My Drive/arima_ukdale_preds_1000_eq'+eq+'.npy')
import time
t1 = time.time()
times = []
for t in range(50):
model = ARIMA(history[t], order=(5,1,0))
model_fit = model.fit(disp=0)
t1 = time.time()
output = model_fit.forecast()
t2 = time.time()
times.append(t2-t1)
print(times)
print(sum(times))
def mean_abs_pct_error(actual_values, forecast_values):
err=0
actual_values = pd.DataFrame(actual_values)
forecast_values = pd.DataFrame(forecast_values)
for i in range(len(forecast_values)):
err += np.abs(actual_values.values[i] - forecast_values.values[i])/actual_values.values[i]
return err[0] * 100/len(forecast_values)
mean_abs_pct_error(test,predictions)
```
| true |
code
| 0.503662 | null | null | null | null |
|
# Hyperparameter Optimization [xgboost](https://github.com/dmlc/xgboost)
What the options there're for tuning?
* [GridSearch](http://scikit-learn.org/stable/modules/grid_search.html)
* [RandomizedSearch](http://scikit-learn.org/stable/modules/generated/sklearn.grid_search.RandomizedSearchCV.html)
All right!
Xgboost has about 20 params:
1. base_score
2. **colsample_bylevel**
3. **colsample_bytree**
4. **gamma**
5. **learning_rate**
6. **max_delta_step**
7. **max_depth**
8. **min_child_weight**
9. missing
10. **n_estimators**
11. nthread
12. **objective**
13. **reg_alpha**
14. **reg_lambda**
15. **scale_pos_weight**
16. **seed**
17. silent
18. **subsample**
Let's for tuning will be use 12 of them them with 5-10 possible values, so... there're 12^5 - 12^10 possible cases.
If you will check one case in 10s, for **12^5** you need **30 days** for **12^10** about **20K** years :).
This is too long.. but there's a thid option - **Bayesan optimisation**.
```
import pandas as pd
import xgboost as xgb
import numpy as np
import seaborn as sns
from hyperopt import hp
from hyperopt import hp, fmin, tpe, STATUS_OK, Trials
%matplotlib inline
train = pd.read_csv('bike.csv')
train['datetime'] = pd.to_datetime( train['datetime'] )
train['day'] = train['datetime'].map(lambda x: x.day)
```
## Modeling
```
def assing_test_samples(data, last_training_day=0.3, seed=1):
days = data.day.unique()
np.random.seed(seed)
np.random.shuffle(days)
test_days = days[: int(len(days) * 0.3)]
data['is_test'] = data.day.isin(test_days)
def select_features(data):
columns = data.columns[ (data.dtypes == np.int64) | (data.dtypes == np.float64) | (data.dtypes == np.bool) ].values
return [feat for feat in columns if feat not in ['count', 'casual', 'registered'] and 'log' not in feat ]
def get_X_y(data, target_variable):
features = select_features(data)
X = data[features].values
y = data[target_variable].values
return X,y
def train_test_split(train, target_variable):
df_train = train[train.is_test == False]
df_test = train[train.is_test == True]
X_train, y_train = get_X_y(df_train, target_variable)
X_test, y_test = get_X_y(df_test, target_variable)
return X_train, X_test, y_train, y_test
def fit_and_predict(train, model, target_variable):
X_train, X_test, y_train, y_test = train_test_split(train, target_variable)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
return (y_test, y_pred)
def post_pred(y_pred):
y_pred[y_pred < 0] = 0
return y_pred
def rmsle(y_true, y_pred, y_pred_only_positive=True):
if y_pred_only_positive: y_pred = post_pred(y_pred)
diff = np.log(y_pred+1) - np.log(y_true+1)
mean_error = np.square(diff).mean()
return np.sqrt(mean_error)
assing_test_samples(train)
def etl_datetime(df):
df['year'] = df['datetime'].map(lambda x: x.year)
df['month'] = df['datetime'].map(lambda x: x.month)
df['hour'] = df['datetime'].map(lambda x: x.hour)
df['minute'] = df['datetime'].map(lambda x: x.minute)
df['dayofweek'] = df['datetime'].map(lambda x: x.dayofweek)
df['weekend'] = df['datetime'].map(lambda x: x.dayofweek in [5,6])
etl_datetime(train)
train['{0}_log'.format('count')] = train['count'].map(lambda x: np.log2(x) )
for name in ['registered', 'casual']:
train['{0}_log'.format(name)] = train[name].map(lambda x: np.log2(x+1) )
```
## Tuning hyperparmeters using Bayesian optimization algorithms
```
def objective(space):
model = xgb.XGBRegressor(
max_depth = space['max_depth'],
n_estimators = int(space['n_estimators']),
subsample = space['subsample'],
colsample_bytree = space['colsample_bytree'],
learning_rate = space['learning_rate'],
reg_alpha = space['reg_alpha']
)
X_train, X_test, y_train, y_test = train_test_split(train, 'count')
eval_set = [( X_train, y_train), ( X_test, y_test)]
(_, registered_pred) = fit_and_predict(train, model, 'registered_log')
(_, casual_pred) = fit_and_predict(train, model, 'casual_log')
y_test = train[train.is_test == True]['count']
y_pred = (np.exp2(registered_pred) - 1) + (np.exp2(casual_pred) -1)
score = rmsle(y_test, y_pred)
print "SCORE:", score
return{'loss':score, 'status': STATUS_OK }
space ={
'max_depth': hp.quniform("x_max_depth", 2, 20, 1),
'n_estimators': hp.quniform("n_estimators", 100, 1000, 1),
'subsample': hp.uniform ('x_subsample', 0.8, 1),
'colsample_bytree': hp.uniform ('x_colsample_bytree', 0.1, 1),
'learning_rate': hp.uniform ('x_learning_rate', 0.01, 0.1),
'reg_alpha': hp.uniform ('x_reg_alpha', 0.1, 1)
}
trials = Trials()
best = fmin(fn=objective,
space=space,
algo=tpe.suggest,
max_evals=15,
trials=trials)
print(best)
```
## Links
1. http://hyperopt.github.io/hyperopt/
2. https://districtdatalabs.silvrback.com/parameter-tuning-with-hyperopt
3. http://fastml.com/optimizing-hyperparams-with-hyperopt/
4. https://github.com/Far0n/xgbfi
| true |
code
| 0.306138 | null | null | null | null |
|
# A Char-RNN Implementation in Tensorflow
*This notebook is slightly modified from https://colab.research.google.com/drive/13Vr3PrDg7cc4OZ3W2-grLSVSf0RJYWzb, with the following changes:*
* Main parameters defined at the start instead of middle
* Run all works, because of the added upload_custom_data parameter
* Training time specified in minutes instead of steps, for time-constrained classroom use
---
CharRNN was a well known generative text model (character level LSTM) created by Andrej Karpathy. It allowed easy training and generation of arbitrary text with many hilarious results:
* Music: abc notation
<https://highnoongmt.wordpress.com/2015/05/22/lisls-stis-recurrent-neural-networks-for-folk-music-generation/>,
* Irish folk music
<https://soundcloud.com/seaandsailor/sets/char-rnn-composes-irish-folk-music>-
* Obama speeches
<https://medium.com/@samim/obama-rnn-machine-generated-political-speeches-c8abd18a2ea0>-
* Eminem lyrics
<https://soundcloud.com/mrchrisjohnson/recurrent-neural-shady>- (NSFW ;-))
* Research awards
<http://karpathy.github.io/2015/05/21/rnn-effectiveness/#comment-2073825449>-
* TED Talks
<https://medium.com/@samim/ted-rnn-machine-generated-ted-talks-3dd682b894c0>-
* Movie Titles <http://www.cs.toronto.edu/~graves/handwriting.html>
This notebook contains a reimplementation in Tensorflow. It will let you input a file containing the text you want your generator to mimic, train your model, see the results, and save it for future use.
To get started, start running the cells in order, following the instructions at each step. You will need a sizable text file (try at least 1 MB of text) when prompted to upload one. For exploration you can also use the provided text corpus taken from Shakespeare's works.
The training cell saves a checkpoint every 30 seconds, so you can check the output of your network and not lose any progress.
## Outline
This notebook will guide you through the following steps. Roughly speaking, these will be our steps:
* Upload some data
* Set some training parameters (you can just use the defaults for now)
* Define our Model, training loss function, and data input manager
* Train on a cloud GPU
* Save out model and use it to generate some new text.
Design of the RNN is inspired by [this github project](https://github.com/sherjilozair/char-rnn-tensorflow) which was based on Andrej Karpathy's [char-rnn](https://github.com/karpathy/char-rnn). If you'd like to learn more, Andrej's [blog post](http://karpathy.github.io/2015/05/21/rnn-effectiveness/) is a great place to start.
### Imports and Values Needed to Run this Code
```
%tensorflow_version 1.x
from __future__ import absolute_import, print_function, division
from google.colab import files
from collections import Counter, defaultdict
from copy import deepcopy
from IPython.display import clear_output
from random import randint
import json
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
CHECKPOINT_DIR = './checkpoints/' #Checkpoints are temporarily kept here.
TEXT_ENCODING = 'utf-8'
```
### Let's define our training parameters.
Feel free to leave these untouched at their default values and just run this cell as is. Later, you can come back here and experiment wth these.
These parameters are just for training. Further down at the inference step, we'll define parameters for the text-generation step.
```
#The most common parameters to change
upload_custom_data = False #if false, use the default Shakespeare data
training_time_minutes = 2 #change this depending on how much time you have
#Neural network and optimization default parameters that usually work ok
num_layers = 2
state_size = 256
batch_size = 64
sequence_length = 256
steps_per_epoch = 500
learning_rate = 0.002
learning_rate_decay = 0.95
gradient_clipping = 5.0
```
### Get the training data.
We can either download the works of Shakespeare to train on or upload our own plain text file that we will be training on.
```
if not upload_custom_data:
shakespeare_url = "https://ocw.mit.edu/ans7870/6/6.006/s08/lecturenotes/files/t8.shakespeare.txt"
import urllib
file_contents = urllib.urlopen(shakespeare_url).read()
file_name = "shakespeare"
file_contents = file_contents[10501:] # Skip headers and start at content
print("An excerpt: \n", file_contents[:664])
if upload_custom_data:
uploaded = files.upload()
if type(uploaded) is not dict: uploaded = uploaded.files ## Deal with filedit versions
file_bytes = uploaded[uploaded.keys()[0]]
utf8_string = file_bytes.decode(TEXT_ENCODING)
file_contents = utf8_string if files else ''
file_name = uploaded.keys()[0]
print("An excerpt: \n", file_contents[:664])
```
## Set up the recurrent LSTM network
Before we can do anything, we have to define what our neural network looks like. This next cell creates a class which will contain the tensorflow graph and training parameters that make up the network.
```
class RNN(object):
"""Represents a Recurrent Neural Network using LSTM cells.
Attributes:
num_layers: The integer number of hidden layers in the RNN.
state_size: The size of the state in each LSTM cell.
num_classes: Number of output classes. (E.g. 256 for Extended ASCII).
batch_size: The number of training sequences to process per step.
sequence_length: The number of chars in a training sequence.
batch_index: Index within the dataset to start the next batch at.
on_gpu_sequences: Generates the training inputs for a single batch.
on_gpu_targets: Generates the training labels for a single batch.
input_symbol: Placeholder for a single label for use during inference.
temperature: Used when sampling outputs. A higher temperature will yield
more variance; a lower one will produce the most likely outputs. Value
should be between 0 and 1.
initial_state: The LSTM State Tuple to initialize the network with. This
will need to be set to the new_state computed by the network each cycle.
logits: Unnormalized probability distribution for the next predicted
label, for each timestep in each sequence.
output_labels: A [batch_size, 1] int32 tensor containing a predicted
label for each sequence in a batch. Only generated in infer mode.
"""
def __init__(self,
rnn_num_layers=1,
rnn_state_size=128,
num_classes=256,
rnn_batch_size=1,
rnn_sequence_length=1):
self.num_layers = rnn_num_layers
self.state_size = rnn_state_size
self.num_classes = num_classes
self.batch_size = rnn_batch_size
self.sequence_length = rnn_sequence_length
self.batch_shape = (self.batch_size, self.sequence_length)
print("Built LSTM: ",
self.num_layers ,self.state_size ,self.num_classes ,
self.batch_size ,self.sequence_length ,self.batch_shape)
def build_training_model(self, dropout_rate, data_to_load):
"""Sets up an RNN model for running a training job.
Args:
dropout_rate: The rate at which weights may be forgotten during training.
data_to_load: A numpy array of containing the training data, with each
element in data_to_load being an integer representing a label. For
example, for Extended ASCII, values may be 0 through 255.
Raises:
ValueError: If mode is data_to_load is None.
"""
if data_to_load is None:
raise ValueError('To continue, you must upload training data.')
inputs = self._set_up_training_inputs(data_to_load)
self._build_rnn(inputs, dropout_rate)
def build_inference_model(self):
"""Sets up an RNN model for generating a sequence element by element.
"""
self.input_symbol = tf.placeholder(shape=[1, 1], dtype=tf.int32)
self.temperature = tf.placeholder(shape=(), dtype=tf.float32,
name='temperature')
self.num_options = tf.placeholder(shape=(), dtype=tf.int32,
name='num_options')
self._build_rnn(self.input_symbol, 0.0)
self.temperature_modified_logits = tf.squeeze(
self.logits, 0) / self.temperature
#for beam search
self.normalized_probs = tf.nn.softmax(self.logits)
self.output_labels = tf.multinomial(self.temperature_modified_logits,
self.num_options)
def _set_up_training_inputs(self, data):
self.batch_index = tf.placeholder(shape=(), dtype=tf.int32)
batch_input_length = self.batch_size * self.sequence_length
input_window = tf.slice(tf.constant(data, dtype=tf.int32),
[self.batch_index],
[batch_input_length + 1])
self.on_gpu_sequences = tf.reshape(
tf.slice(input_window, [0], [batch_input_length]), self.batch_shape)
self.on_gpu_targets = tf.reshape(
tf.slice(input_window, [1], [batch_input_length]), self.batch_shape)
return self.on_gpu_sequences
def _build_rnn(self, inputs, dropout_rate):
"""Generates an RNN model using the passed functions.
Args:
inputs: int32 Tensor with shape [batch_size, sequence_length] containing
input labels.
dropout_rate: A floating point value determining the chance that a weight
is forgotten during evaluation.
"""
# Alias some commonly used functions
dropout_wrapper = tf.contrib.rnn.DropoutWrapper
lstm_cell = tf.contrib.rnn.LSTMCell
multi_rnn_cell = tf.contrib.rnn.MultiRNNCell
self._cell = multi_rnn_cell(
[dropout_wrapper(lstm_cell(self.state_size), 1.0, 1.0 - dropout_rate)
for _ in range(self.num_layers)])
self.initial_state = self._cell.zero_state(self.batch_size, tf.float32)
embedding = tf.get_variable('embedding',
[self.num_classes, self.state_size])
embedding_input = tf.nn.embedding_lookup(embedding, inputs)
output, self.new_state = tf.nn.dynamic_rnn(self._cell, embedding_input,
initial_state=self.initial_state)
self.logits = tf.contrib.layers.fully_connected(output, self.num_classes,
activation_fn=None)
```
###Define your loss function
Loss is a measure of how well the neural network is modeling the data distribution.
Pass in your logits and the targets you're training against. In this case, target_weights is a set of multipliers that will put higher emphasis on certain outputs. In this notebook, we'll give all outputs equal importance.
```
def get_loss(logits, targets, target_weights):
with tf.name_scope('loss'):
return tf.contrib.seq2seq.sequence_loss(
logits,
targets,
target_weights,
average_across_timesteps=True)
```
### Define your optimizer
This tells Tensorflow how to reduce the loss. We will use the popular [ADAM algorithm](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer)
```
def get_optimizer(loss, initial_learning_rate, gradient_clipping, global_step,
decay_steps, decay_rate):
with tf.name_scope('optimizer'):
computed_learning_rate = tf.train.exponential_decay(
initial_learning_rate,
global_step,
decay_steps,
decay_rate,
staircase=True)
optimizer = tf.train.AdamOptimizer(computed_learning_rate)
trained_vars = tf.trainable_variables()
gradients, _ = tf.clip_by_global_norm(
tf.gradients(loss, trained_vars),
gradient_clipping)
training_op = optimizer.apply_gradients(
zip(gradients, trained_vars),
global_step=global_step)
return training_op, computed_learning_rate
```
### This class will let us view the progress of our training as it progresses.
```
class LossPlotter(object):
def __init__(self, history_length):
self.global_steps = []
self.losses = []
self.averaged_loss_x = []
self.averaged_loss_y = []
self.history_length = history_length
def draw_plots(self):
self._update_averages(self.global_steps, self.losses,
self.averaged_loss_x, self.averaged_loss_y)
plt.title('Average Loss Over Time')
plt.xlabel('Global Step')
plt.ylabel('Loss')
plt.plot(self.averaged_loss_x, self.averaged_loss_y, label='Loss/Time (Avg)')
plt.plot()
plt.plot(self.global_steps, self.losses,
label='Loss/Time (Last %d)' % self.history_length,
alpha=.1, color='r')
plt.plot()
plt.legend()
plt.show()
plt.title('Loss for the last 100 Steps')
plt.xlabel('Global Step')
plt.ylabel('Loss')
plt.plot(self.global_steps, self.losses,
label='Loss/Time (Last %d)' % self.history_length, color='r')
plt.plot()
plt.legend()
plt.show()
# The notebook will be slowed down at the end of training if we plot the
# entire history of raw data. Plot only the last 100 steps of raw data,
# and the average of each 100 batches. Don't keep unused data.
self.global_steps = []
self.losses = []
self.learning_rates = []
def log_step(self, global_step, loss):
self.global_steps.append(global_step)
self.losses.append(loss)
def _update_averages(self, x_list, y_list,
averaged_data_x, averaged_data_y):
averaged_data_x.append(x_list[-1])
averaged_data_y.append(sum(y_list) / self.history_length)
```
## Now, we're going to start training our model.
This could take a while, so you might want to grab a coffee. Every 30 seconds of training, we're going to save a checkpoint to make sure we don't lose our progress. To monitor the progress of your training, feel free to stop the training every once in a while and run the inference cell to generate text with your model!
First, we will need to turn the plain text file into arrays of tokens (and, later, back). To do this we will use this token mapper helper class:
```
import string
class TokenMapper(object):
def __init__(self):
self.token_mapping = {}
self.reverse_token_mapping = {}
def buildFromData(self, utf8_string, limit=0.00004):
print("Build token dictionary.")
total_num = len(utf8_string)
sorted_tokens = sorted(Counter(utf8_string.decode('utf8')).items(),
key=lambda x: -x[1])
# Filter tokens: Only allow printable characters (not control chars) and
# limit to ones that are resonably common, i.e. skip strange esoteric
# characters in order to reduce the dictionary size.
filtered_tokens = filter(lambda t: t[0] in string.printable or
float(t[1])/total_num > limit, sorted_tokens)
tokens, counts = zip(*filtered_tokens)
self.token_mapping = dict(zip(tokens, range(len(tokens))))
for c in string.printable:
if c not in self.token_mapping:
print("Skipped token for: ", c)
self.reverse_token_mapping = {
val: key for key, val in self.token_mapping.items()}
print("Created dictionary: %d tokens"%len(self.token_mapping))
def mapchar(self, char):
if char in self.token_mapping:
return self.token_mapping[char]
else:
return self.token_mapping[' ']
def mapstring(self, utf8_string):
return [self.mapchar(c) for c in utf8_string]
def maptoken(self, token):
return self.reverse_token_mapping[token]
def maptokens(self, int_array):
return ''.join([self.reverse_token_mapping[c] for c in int_array])
def size(self):
return len(self.token_mapping)
def alphabet(self):
return ''.join([k for k,v in sorted(self.token_mapping.items(),key=itemgetter(1))])
def print(self):
for k,v in sorted(self.token_mapping.items(),key=itemgetter(1)): print(k, v)
def save(self, path):
with open(path, 'wb') as json_file:
json.dump(self.token_mapping, json_file)
def restore(self, path):
with open(path, 'r') as json_file:
self.token_mapping = {}
self.token_mapping.update(json.load(json_file))
self.reverse_token_mapping = {val: key for key, val in self.token_mapping.items()}
```
Now convert the raw input into a list of tokens.
```
# Clean the checkpoint directory and make a fresh one
!rm -rf {CHECKPOINT_DIR}
!mkdir {CHECKPOINT_DIR}
!ls -lt
chars_in_batch = (sequence_length * batch_size)
file_len = len(file_contents)
unique_sequential_batches = file_len // chars_in_batch
mapper = TokenMapper()
mapper.buildFromData(file_contents)
mapper.save(''.join([CHECKPOINT_DIR, 'token_mapping.json']))
input_values = mapper.mapstring(file_contents)
```
###First, we'll build our neural network and add our training operations to the Tensorflow graph.
If you're continuing training after testing your generator, run the next three cells.
```
tf.reset_default_graph()
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
print('Constructing model...')
model = RNN(
rnn_num_layers=num_layers,
rnn_state_size=state_size,
num_classes=mapper.size(),
rnn_batch_size=batch_size,
rnn_sequence_length=sequence_length)
model.build_training_model(0.05, np.asarray(input_values))
print('Constructed model successfully.')
print('Setting up training session...')
neutral_target_weights = tf.constant(
np.ones(model.batch_shape),
tf.float32
)
loss = get_loss(model.logits, model.on_gpu_targets, neutral_target_weights)
global_step = tf.get_variable('global_step', shape=(), trainable=False,
dtype=tf.int32)
training_step, computed_learning_rate = get_optimizer(
loss,
learning_rate,
gradient_clipping,
global_step,
steps_per_epoch,
learning_rate_decay
)
```
The supervisor will manage the training flow and checkpointing.
```
# Create a supervisor that will checkpoint the model in the CHECKPOINT_DIR
sv = tf.train.Supervisor(
logdir=CHECKPOINT_DIR,
global_step=global_step,
save_model_secs=30)
print('Training session ready.')
```
###This next cell will begin the training cycle.
First, we will attempt to pick up training where we left off, if a previous checkpoint exists, then continue the training process.
```
from datetime import datetime
start_time = datetime.now()
with sv.managed_session(config=config) as sess:
print('Training supervisor successfully initialized all variables.')
if not file_len:
raise ValueError('To continue, you must upload training data.')
elif file_len < chars_in_batch:
raise ValueError('To continue, you must upload a larger set of data.')
plotter = LossPlotter(100)
step_number = sess.run(global_step)
zero_state = sess.run([model.initial_state])
max_batch_index = (unique_sequential_batches - 1) * chars_in_batch
while not sv.should_stop() and (datetime.now()-start_time).seconds/60 < training_time_minutes:
feed_dict = {
model.batch_index: randint(0, max_batch_index),
model.initial_state: zero_state
}
[_, _, training_loss, step_number, current_learning_rate, _] = sess.run(
[model.on_gpu_sequences,
model.on_gpu_targets,
loss,
global_step,
computed_learning_rate,
training_step],
feed_dict)
plotter.log_step(step_number, training_loss)
if step_number % 100 == 0:
clear_output(True)
plotter.draw_plots()
print('Latest checkpoint is: %s' %
tf.train.latest_checkpoint(CHECKPOINT_DIR))
print('Learning Rate is: %f' %
current_learning_rate)
if step_number % 10 == 0:
print('global step %d, loss=%f' % (step_number, training_loss))
clear_output(True)
print('Training completed in HH:MM:SS = ', datetime.now()-start_time)
print('Latest checkpoint is: %s' %
tf.train.latest_checkpoint(CHECKPOINT_DIR))
```
## Now, we're going to generate some text!
Here, we'll use the **Beam Search** algorithm to generate some text with our trained model. Beam Search picks N possible next options from each of the current options at every step. This way, if the generator picks an item leading to a bad decision down the line, it can toss the bad result out and keep going with a more likely one.
```
class BeamSearchCandidate(object):
"""Represents a node within the search space during Beam Search.
Attributes:
state: The resulting RNN state after the given sequence has been generated.
sequence: The sequence of selections leading to this node.
probability: The probability of the sequence occurring, computed as the sum
of the probabilty of each character in the sequence at its respective
step.
"""
def __init__(self, init_state, sequence, probability):
self.state = init_state
self.sequence = sequence
self.probability = probability
def search_from(self, tf_sess, rnn_model, temperature, num_options):
"""Expands the num_options most likely next elements in the sequence.
Args:
tf_sess: The Tensorflow session containing the rnn_model.
rnn_model: The RNN to use to generate the next element in the sequence.
temperature: Modifies the probabilities of each character, placing
more emphasis on higher probabilities as the value approaches 0.
num_options: How many potential next options to expand from this one.
Returns: A list of BeamSearchCandidate objects descended from this node.
"""
expanded_set = []
feed = {rnn_model.input_symbol: np.array([[self.sequence[-1]]]),
rnn_model.initial_state: self.state,
rnn_model.temperature: temperature,
rnn_model.num_options: num_options}
[predictions, probabilities, new_state] = tf_sess.run(
[rnn_model.output_labels,
rnn_model.normalized_probs,
rnn_model.new_state], feed)
# Get the indices of the num_beams next picks
picks = [predictions[0][x] for x in range(len(predictions[0]))]
for new_char in picks:
new_seq = deepcopy(self.sequence)
new_seq.append(new_char)
expanded_set.append(
BeamSearchCandidate(new_state, new_seq,
probabilities[0][0][new_char] + self.probability))
return expanded_set
def __eq__(self, other):
return self.sequence == other.sequence
def __ne__(self, other):
return not self.__eq__(other)
def __hash__(self):
return hash(self.sequence())
def beam_search_generate_sequence(tf_sess, rnn_model, primer, temperature=0.85,
termination_condition=None, num_beams=5):
"""Implements a sequence generator using Beam Search.
Args:
tf_sess: The Tensorflow session containing the rnn_model.
rnn_model: The RNN to use to generate the next element in the sequence.
temperature: Controls how 'Creative' the generated sequence is. Values
close to 0 tend to generate the most likely sequence, while values
closer to 1 generate more original sequences. Acceptable values are
within (0, 1].
termination_condition: A function taking one parameter, a list of
integers, that returns True when a condition is met that signals to the
RNN to return what it has generated so far.
num_beams: The number of possible sequences to keep at each step of the
generation process.
Returns: A list of at most num_beams BeamSearchCandidate objects.
"""
candidates = []
rnn_current_state = sess.run([rnn_model.initial_state])
#Initialize the state for the primer
for primer_val in primer[:-1]:
feed = {rnn_model.input_symbol: np.array([[primer_val]]),
rnn_model.initial_state: rnn_current_state
}
[rnn_current_state] = tf_sess.run([rnn_model.new_state], feed)
candidates.append(BeamSearchCandidate(rnn_current_state, primer, num_beams))
while True not in [termination_condition(x.sequence) for x in candidates]:
new_candidates = []
for candidate in candidates:
expanded_candidates = candidate.search_from(
tf_sess, rnn_model, temperature, num_beams)
for new in expanded_candidates:
if new not in new_candidates:
#do not reevaluate duplicates
new_candidates.append(new)
candidates = sorted(new_candidates,
key=lambda x: x.probability, reverse=True)[:num_beams]
return [c for c in candidates if termination_condition(c.sequence)]
```
Input something to start your generated text with, and set how characters long you want the text to be.
"Creativity" refers to how much emphasis your neural network puts on matching a pattern. If you notice looping in the output, try raising this value. If your output seems too random, try lowering it a bit.
If the results don't look too great in general, run the three training cells again for a bit longer. The lower your loss, the more closely your generated text will match the training data.
```
tf.reset_default_graph()
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
sess = tf.InteractiveSession(config=config)
model = RNN(
rnn_num_layers=num_layers,
rnn_state_size=state_size,
num_classes=mapper.size(),
rnn_batch_size=1,
rnn_sequence_length=1)
model.build_inference_model()
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver(tf.global_variables())
ckpt = tf.train.latest_checkpoint(CHECKPOINT_DIR)
saver.restore(sess, ckpt)
def gen(start_with, pred, creativity):
int_array = mapper.mapstring(start_with)
candidates = beam_search_generate_sequence(
sess, model, int_array, temperature=creativity,
termination_condition=pred,
num_beams=1)
gentext = mapper.maptokens(candidates[0].sequence)
return gentext
def lengthlimit(n):
return lambda text: len(text)>n
def sentences(n):
return lambda text: mapper.maptokens(text).count(".")>=n
def paragraph():
return lambda text: mapper.maptokens(text).count("\n")>0
length_of_generated_text = 2000
creativity = 0.85 # Should be greater than 0 but less than 1
print(gen(" ANTONIO: Who is it ?", lengthlimit(length_of_generated_text), creativity))
```
## Let's save a copy of our trained RNN so we can do all kinds of cool things with it later.
```
save_model_to_drive = False ## Set this to true to save directly to Google Drive.
def save_model_hyperparameters(path):
with open(path, 'w') as json_file:
model_params = {
'num_layers': model.num_layers,
'state_size': model.state_size,
'num_classes': model.num_classes
}
json.dump(model_params, json_file)
def save_to_drive(title, content):
# Install the PyDrive wrapper & import libraries.
!pip install -U -q PyDrive
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
# Authenticate and create the PyDrive client.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
newfile = drive.CreateFile({'title': title})
newfile.SetContentFile(content)
newfile.Upload()
print('Uploaded file with ID %s as %s'% (newfile.get('id'),
archive_name))
archive_name = ''.join([file_name,'_seedbank_char-rnn.zip'])
latest_model = tf.train.latest_checkpoint(CHECKPOINT_DIR).split('/')[2]
checkpoints_archive_path = ''.join(['./exports/',archive_name])
if not latest_model:
raise ValueError('You must train a model before you can export one.')
%system mkdir exports
%rm -f {checkpoints_archive_path}
mapper.save(''.join([CHECKPOINT_DIR, 'token_mapping.json']))
save_model_hyperparameters(''.join([CHECKPOINT_DIR, 'model_attributes.json']))
%system zip '{checkpoints_archive_path}' -@ '{CHECKPOINT_DIR}checkpoint' \
'{CHECKPOINT_DIR}token_mapping.json' \
'{CHECKPOINT_DIR}model_attributes.json' \
'{CHECKPOINT_DIR}{latest_model}.'*
if save_model_to_drive:
save_to_drive(archive_name, checkpoints_archive_path)
else:
files.download(checkpoints_archive_path)
```
| true |
code
| 0.730596 | null | null | null | null |
|
(tune-mnist-keras)=
# Using Keras & TensorFlow with Tune
```{image} /images/tf_keras_logo.jpeg
:align: center
:alt: Keras & TensorFlow Logo
:height: 120px
:target: https://keras.io
```
```{contents}
:backlinks: none
:local: true
```
## Example
```
import argparse
import os
from filelock import FileLock
from tensorflow.keras.datasets import mnist
import ray
from ray import tune
from ray.tune.schedulers import AsyncHyperBandScheduler
from ray.tune.integration.keras import TuneReportCallback
def train_mnist(config):
# https://github.com/tensorflow/tensorflow/issues/32159
import tensorflow as tf
batch_size = 128
num_classes = 10
epochs = 12
with FileLock(os.path.expanduser("~/.data.lock")):
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
model = tf.keras.models.Sequential(
[
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(config["hidden"], activation="relu"),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(num_classes, activation="softmax"),
]
)
model.compile(
loss="sparse_categorical_crossentropy",
optimizer=tf.keras.optimizers.SGD(lr=config["lr"], momentum=config["momentum"]),
metrics=["accuracy"],
)
model.fit(
x_train,
y_train,
batch_size=batch_size,
epochs=epochs,
verbose=0,
validation_data=(x_test, y_test),
callbacks=[TuneReportCallback({"mean_accuracy": "accuracy"})],
)
def tune_mnist(num_training_iterations):
sched = AsyncHyperBandScheduler(
time_attr="training_iteration", max_t=400, grace_period=20
)
analysis = tune.run(
train_mnist,
name="exp",
scheduler=sched,
metric="mean_accuracy",
mode="max",
stop={"mean_accuracy": 0.99, "training_iteration": num_training_iterations},
num_samples=10,
resources_per_trial={"cpu": 2, "gpu": 0},
config={
"threads": 2,
"lr": tune.uniform(0.001, 0.1),
"momentum": tune.uniform(0.1, 0.9),
"hidden": tune.randint(32, 512),
},
)
print("Best hyperparameters found were: ", analysis.best_config)
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument(
"--smoke-test", action="store_true", help="Finish quickly for testing"
)
parser.add_argument(
"--server-address",
type=str,
default=None,
required=False,
help="The address of server to connect to if using " "Ray Client.",
)
args, _ = parser.parse_known_args()
if args.smoke_test:
ray.init(num_cpus=4)
elif args.server_address:
ray.init(f"ray://{args.server_address}")
tune_mnist(num_training_iterations=5 if args.smoke_test else 300)
```
## More Keras and TensorFlow Examples
- {doc}`/tune/examples/includes/pbt_memnn_example`: Example of training a Memory NN on bAbI with Keras using PBT.
- {doc}`/tune/examples/includes/tf_mnist_example`: Converts the Advanced TF2.0 MNIST example to use Tune
with the Trainable. This uses `tf.function`.
Original code from tensorflow: https://www.tensorflow.org/tutorials/quickstart/advanced
- {doc}`/tune/examples/includes/pbt_tune_cifar10_with_keras`:
A contributed example of tuning a Keras model on CIFAR10 with the PopulationBasedTraining scheduler.
| true |
code
| 0.7731 | null | null | null | null |
|
#### Implementation of Distributional paper for 1-dimensional games, such as Cartpole.
- https://arxiv.org/abs/1707.06887
<br>
Please note: The 2 dimensional image state requires a lot of memory capacity (~50GB) due to the buffer size of 1,000,000 as in DQN paper.
So, one might want to train an agent with a smaller size (this may cause a lower performance).
#### Please NOTE,
The code lines different from Vanila DQN are annotated with '*/*/*/'.
So, by searching '*/*/*/', you can find these lines.
```
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import gym
import numpy as np
import time
import os
import cv2
import matplotlib.pyplot as plt
from IPython.display import clear_output
class QNetwork(nn.Module):
def __init__(self, input_dim, action_dim, rand_seed=False,
conv_channel_1=32, conv_channel_2=64, conv_channel_3=128,
kernel_1=3, kernel_2=3, kernel_3=3,
stride_1=2, stride_2=2, stride_3=1, n_atoms=51):
super(QNetwork, self).__init__()
self.action_dim = action_dim
self.n_atoms = n_atoms
self.Conv1 = nn.Conv2d(input_dim[0], conv_channel_1, (kernel_1,kernel_1), stride=stride_1)
self.Conv2 = nn.Conv2d(conv_channel_1, conv_channel_2, (kernel_2,kernel_2), stride=stride_2)
self.Conv3 = nn.Conv2d(conv_channel_2, conv_channel_3, (kernel_3,kernel_3), stride=stride_3)
def calculate_conv2d_size(size, kernel_size, stride):
return (size - (kernel_size - 1) - 1) // stride + 1
w, h = input_dim[1], input_dim[2]
convw = calculate_conv2d_size(calculate_conv2d_size(calculate_conv2d_size(w,kernel_1,stride_1),
kernel_2,stride_2),
kernel_3,stride_3)
convh = calculate_conv2d_size(calculate_conv2d_size(calculate_conv2d_size(h,kernel_1,stride_1),
kernel_2,stride_2),
kernel_3,stride_3)
linear_input_size = convw * convh * conv_channel_3
# */*/*/
self.fc1 = nn.Linear(linear_input_size, 512)
self.fc2 = nn.Linear(512, action_dim*n_atoms)
self.relu = nn.ReLU()
# */*/*/
def forward(self, x):
x = self.relu(self.Conv1(x))
x = self.relu(self.Conv2(x))
x = self.relu(self.Conv3(x))
x = x.reshape(x.shape[0], -1)
# */*/*/
Q = self.fc2(self.relu(self.fc1(x))).view(-1, self.action_dim, self.n_atoms)
return F.softmax(Q, dim=2) # Shape: (batch_size, action_dim, n_atoms)
# */*/*/
if __name__ == '__main__':
state_size = (4, 84, 84)
action_size = 10
net = QNetwork(state_size, action_size,
conv_channel_1=32, conv_channel_2=64, conv_channel_3=64)
test = torch.randn(size=(64, 4, 84, 84))
print(net)
print("Network output: ", net(test).shape)
class ReplayBuffer:
""" Experience Replay Buffer in DQN paper """
def __init__(self,
buffer_size: ('int: total size of the Replay Buffer'),
input_dim: ('tuple: a dimension of input data. Ex) (3, 84, 84)'),
batch_size: ('int: a batch size when updating')):
# To check if input image has 3 channels
assert len(input_dim)==3, "The state dimension should be 3-dim! (CHxWxH). Please check if input_dim is right"
self.batch_size = batch_size
self.buffer_size = buffer_size
self.save_count, self.current_size = 0, 0
# One can choose either np.zeros or np.ones.
# The reason using np.ones here is for checking the total memory occupancy of the buffer.
self.state_buffer = np.ones((buffer_size, input_dim[0], input_dim[1], input_dim[2]),
dtype=np.uint8) # data type is np.int8 for saving the memory
self.action_buffer = np.ones(buffer_size, dtype=np.uint8)
self.reward_buffer = np.ones(buffer_size, dtype=np.float32)
self.next_state_buffer = np.ones((buffer_size, input_dim[0], input_dim[1], input_dim[2]),
dtype=np.uint8)
self.done_buffer = np.ones(buffer_size, dtype=np.uint8)
def __len__(self):
return self.current_size
def store(self,
state: np.ndarray,
action: int,
reward: float,
next_state: np.ndarray,
done: int):
self.state_buffer[self.save_count] = state
self.action_buffer[self.save_count] = action
self.reward_buffer[self.save_count] = reward
self.next_state_buffer[self.save_count] = next_state
self.done_buffer[self.save_count] = done
# self.save_count is an index when storing transitions into the replay buffer
self.save_count = (self.save_count + 1) % self.buffer_size
# self.current_size is an indication for how many transitions is stored
self.current_size = min(self.current_size+1, self.buffer_size)
def batch_load(self):
# Selecting samples randomly with a size of self.batch_size
indices = np.random.randint(self.current_size, size=self.batch_size)
return dict(
states=self.state_buffer[indices],
actions=self.action_buffer[indices],
rewards=self.reward_buffer[indices],
next_states=self.next_state_buffer[indices],
dones=self.done_buffer[indices])
class Agent:
def __init__(self,
env: 'Environment',
input_frame: ('int: The number of channels of input image'),
input_dim: ('int: The width and height of pre-processed input image'),
training_frames: ('int: The total number of training frames'),
skipped_frame: ('int: The number of skipped frames in the environment'),
eps_decay: ('float: Epsilon Decay_rate'),
gamma: ('float: Discount Factor'),
update_freq: ('int: Behavior Network Update Frequency'),
target_update_freq: ('int: Target Network Update Frequency'),
update_type: ('str: Update type for target network. Hard or Soft')='hard',
soft_update_tau: ('float: Soft update ratio')=None,
batch_size: ('int: Update batch size')=32,
buffer_size: ('int: Replay buffer size')=1000000,
update_start_buffer_size: ('int: Update starting buffer size')=50000,
learning_rate: ('float: Learning rate')=0.0004,
eps_min: ('float: Epsilon Min')=0.1,
eps_max: ('float: Epsilon Max')=1.0,
device_num: ('int: GPU device number')=0,
rand_seed: ('int: Random seed')=None,
plot_option: ('str: Plotting option')=False,
model_path: ('str: Model saving path')='./',
trained_model_path: ('str: Trained model path')='',
# */*/*/
n_atoms: ('int: The number of atoms')=51,
Vmax: ('int: The maximum Q value')=10,
Vmin: ('int: The minimum Q value')=-10):
# */*/*/
self.action_dim = env.action_space.n
self.device = torch.device(f'cuda:{device_num}' if torch.cuda.is_available() else 'cpu')
self.model_path = model_path
self.env = env
self.input_frames = input_frame
self.input_dim = input_dim
self.training_frames = training_frames
self.skipped_frame = skipped_frame
self.epsilon = eps_max
self.eps_decay = eps_decay
self.eps_min = eps_min
self.gamma = gamma
self.update_freq = update_freq
self.target_update_freq = target_update_freq
self.update_cnt = 0
self.update_type = update_type
self.tau = soft_update_tau
self.batch_size = batch_size
self.buffer_size = buffer_size
self.update_start = update_start_buffer_size
self.seed = rand_seed
self.plot_option = plot_option
# */*/*/
self.n_atoms = n_atoms
self.Vmin = Vmin
self.Vmax = Vmax
self.dz = (Vmax - Vmin) / (n_atoms - 1)
self.support = torch.linspace(Vmin, Vmax, n_atoms).to(self.device)
self.expanded_support = self.support.expand((batch_size, self.action_dim, n_atoms)).to(self.device)
self.q_behave = QNetwork((self.input_frames, self.input_dim, self.input_dim), self.action_dim, n_atoms=self.n_atoms).to(self.device)
self.q_target = QNetwork((self.input_frames, self.input_dim, self.input_dim), self.action_dim, n_atoms=self.n_atoms).to(self.device)
# */*/*/
if trained_model_path: # load a trained model if existing
self.q_behave.load_state_dict(torch.load(trained_model_path))
print("Trained model is loaded successfully.")
# Initialize target network parameters with behavior network parameters
self.q_target.load_state_dict(self.q_behave.state_dict())
self.q_target.eval()
self.optimizer = optim.Adam(self.q_behave.parameters(), lr=learning_rate)
self.memory = ReplayBuffer(self.buffer_size, (self.input_frames, self.input_dim, self.input_dim), self.batch_size)
def select_action(self, state: 'Must be pre-processed in the same way as updating current Q network. See def _compute_loss'):
if np.random.random() < self.epsilon:
return np.zeros(self.action_dim), self.env.action_space.sample()
else:
# if normalization is applied to the image such as devision by 255, MUST be expressed 'state/255' below.
with torch.no_grad():
state = torch.FloatTensor(state).to(self.device).unsqueeze(0)/255
# */*/*/
Qs = self.q_behave(state)*self.expanded_support[0]
Expected_Qs = Qs.sum(2)
# */*/*/
action = Expected_Qs.argmax(1)
# return Q-values and action (Q-values are not required for implementing algorithms. This is just for checking Q-values for each state. Not must-needed)
return Expected_Qs.detach().cpu().numpy()[0], action.detach().item()
def processing_resize_and_gray(self, frame):
''' Convert images to gray scale and resize '''
frame = cv2.cvtColor(frame, cv2.COLOR_RGB2GRAY)
frame = cv2.resize(frame, dsize=(self.input_dim, self.input_dim)).reshape(self.input_dim, self.input_dim).astype(np.uint8)
return frame
def get_init_state(self):
''' return an initial state with a dimension of (self.input_frames, self.input_dim, self.input_dim) '''
init_state = np.zeros((self.input_frames, self.input_dim, self.input_dim))
init_frame = self.env.reset()
init_state[0] = self.processing_resize_and_gray(init_frame)
for i in range(1, self.input_frames):
action = self.env.action_space.sample()
for j in range(self.skipped_frame-1):
state, _, _, _ = self.env.step(action)
state, _, _, _ = self.env.step(action)
init_state[i] = self.processing_resize_and_gray(state)
return init_state
def get_state(self, state, action, skipped_frame=0):
''' return reward, next_state, done '''
next_state = np.zeros((self.input_frames, self.input_dim, self.input_dim))
for i in range(len(state)-1):
next_state[i] = state[i+1]
rewards = 0
dones = 0
for _ in range(skipped_frame-1):
state, reward, done, _ = self.env.step(action)
rewards += reward # reward accumulates for the case that rewards occur while skipping
dones += int(done)
state, reward, done, _ = self.env.step(action)
next_state[-1] = self.processing_resize_and_gray(state)
rewards += reward
dones += int(done)
return rewards, next_state, dones
def store(self, state, action, reward, next_state, done):
self.memory.store(state, action, reward, next_state, done)
def update_behavior_q_net(self):
# update behavior q network with a batch
batch = self.memory.batch_load()
loss = self._compute_loss(batch)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return loss.item()
def target_soft_update(self):
''' target network is updated with Soft Update. tau is a hyperparameter for the updating ratio betweeen target and behavior network '''
for target_param, current_param in zip(self.q_target.parameters(), self.q_behave.parameters()):
target_param.data.copy_(self.tau*current_param.data + (1.0-self.tau)*target_param.data)
def target_hard_update(self):
''' target network is updated with Hard Update '''
self.update_cnt = (self.update_cnt+1) % self.target_update_freq
if self.update_cnt==0:
self.q_target.load_state_dict(self.q_behave.state_dict())
def train(self):
tic = time.time()
losses = []
scores = []
epsilons = []
avg_scores = [[-10000]] # As an initial score, set an arbitrary score of an episode.
score = 0
print("Storing initial buffer..")
state = self.get_init_state()
for frame_idx in range(1, self.update_start+1):
# Store transitions into the buffer until the number of 'self.update_start' transitions is stored
_, action = self.select_action(state)
reward, next_state, done = self.get_state(state, action, skipped_frame=self.skipped_frame)
self.store(state, action, reward, next_state, done)
state = next_state
if done: state = self.get_init_state()
print("Done. Start learning..")
history_store = []
for frame_idx in range(1, self.training_frames+1):
Qs, action = self.select_action(state)
reward, next_state, done = self.get_state(state, action, skipped_frame=self.skipped_frame)
self.store(state, action, reward, next_state, done)
history_store.append([state, Qs, action, reward, next_state, done]) # history_store is for checking an episode later. Not must-needed.
if (frame_idx % self.update_freq) == 0:
loss = self.update_behavior_q_net()
score += reward
losses.append(loss)
if self.update_type=='hard': self.target_hard_update()
elif self.update_type=='soft': self.target_soft_update()
if done:
# For saving and plotting when an episode is done.
scores.append(score)
if np.mean(scores[-10:]) > max(avg_scores):
torch.save(self.q_behave.state_dict(), self.model_path+'{}_Score:{}.pt'.format(frame_idx, np.mean(scores[-10:])))
training_time = round((time.time()-tic)/3600, 1)
np.save(self.model_path+'{}_history_Score_{}_{}hrs.npy'.format(frame_idx, score, training_time), np.array(history_store))
print(" | Model saved. Recent scores: {}, Training time: {}hrs".format(scores[-10:], training_time), ' /'.join(os.getcwd().split('/')[-3:]))
avg_scores.append(np.mean(scores[-10:]))
if self.plot_option=='inline':
scores.append(score)
epsilons.append(self.epsilon)
self._plot(frame_idx, scores, losses, epsilons)
else:
print(score, end='\r')
score=0
state = self.get_init_state()
history_store = []
else: state = next_state
self._epsilon_step()
print("Total training time: {}(hrs)".format((time.time()-tic)/3600))
def _epsilon_step(self):
''' Controlling epsilon decay. Here is the same as DQN paper, linearly decaying rate. '''
self.epsilon = max(self.epsilon-self.eps_decay, 0.1)
def _compute_loss(self, batch: "Dictionary (S, A, R', S', Dones)"):
''' Compute loss. If normalization is used, it must be applied to both 'state' and 'next_state'. ex) state/255 '''
states = torch.FloatTensor(batch['states']).to(self.device) / 255
next_states = torch.FloatTensor(batch['next_states']).to(self.device) / 255
actions = torch.LongTensor(batch['actions']).to(self.device)
rewards = torch.FloatTensor(batch['rewards'].reshape(-1, 1)).to(self.device)
dones = torch.FloatTensor(batch['dones'].reshape(-1, 1)).to(self.device)
# */*/*/
log_behave_Q_dist = self.q_behave(states)[range(self.batch_size), actions].log()
with torch.no_grad():
# Computing projected distribution for a categorical loss
behave_next_Q_dist = self.q_behave(next_states)
next_actions = torch.sum(behave_next_Q_dist*self.expanded_support, 2).argmax(1)
target_next_Q_dist = self.q_target(next_states)[range(self.batch_size), next_actions] # Double DQN.
Tz = rewards + self.gamma*(1 - dones)*self.expanded_support[:,0]
Tz.clamp_(self.Vmin, self.Vmax)
b = (Tz - self.Vmin) / self.dz
l = b.floor().long()
u = b.ceil().long()
l[(l==u) & (u>0)] -= 1 # avoiding the case when floor index and ceil index have the same values
u[(u==0) & (l==0)] += 1 # (because it causes target_next_Q_dist's value to be counted as zero)
batch_init_indices = torch.linspace(0, (self.batch_size-1)*self.n_atoms, self.batch_size).long().unsqueeze(1).expand(self.batch_size, self.n_atoms).to(self.device)
proj_dist = torch.zeros(self.batch_size, self.n_atoms).to(self.device)
proj_dist.view(-1).index_add_(0, (l+batch_init_indices).view(-1), (target_next_Q_dist*(u-b)).view(-1))
proj_dist.view(-1).index_add_(0, (u+batch_init_indices).view(-1), (target_next_Q_dist*(b-l)).view(-1))
# Compute KL divergence between two distributions
loss = torch.sum(-proj_dist*log_behave_Q_dist, 1).mean()
# */*/*/
return loss
def _plot(self, frame_idx, scores, losses, epsilons):
clear_output(True)
plt.figure(figsize=(20, 5), facecolor='w')
plt.subplot(131)
plt.title('frame %s. score: %s' % (frame_idx, np.mean(scores[-10:])))
plt.plot(scores)
plt.subplot(132)
plt.title('loss')
plt.plot(losses)
plt.subplot(133)
plt.title('epsilons')
plt.plot(epsilons)
plt.show()
```
#### Configurations


```
env_list = {
0: "CartPole-v0",
1: "CartPole-v2",
2: "LunarLander-v2",
3: "Breakout-v4",
4: "BreakoutDeterministic-v4",
5: "BreakoutNoFrameskip-v4",
6: "BoxingDeterministic-v4",
7: "PongDeterministic-v4",
}
env_name = env_list[6]
env = gym.make(env_name)
# Same input size as in DQN paper.
input_dim = 84
input_frame = 4
print("env_name", env_name)
print(env.unwrapped.get_action_meanings(), env.action_space.n)
# starting to update Q-network until ReplayBuffer is filled with the number of samples = update_start_buffer_size
update_start_buffer_size = 10000
# total training frames
training_frames = 10000000
# epsilon for exploration
eps_max = 1.0
eps_min = 0.1
eps_decay = 1/1000000
# gamma (used decaying future rewards)
gamma = 0.99
# size of ReplayBuffer
buffer_size = int(1e6) # this is the same size of the paper
# buffer_size = int(1.5e5) # if don't have an enough memory capacity, lower the value like this. But this may cause a bad training performance.
# update batch size
batch_size = 32
learning_rate = 0.0001 # In the paper, they use RMSProp and learning rate 0.00025. In this notebook, the Adam is used with lr=0.0001.
# updating Q-network with 'soft' or 'hard' updating method
update_freq = 4
update_type = 'hard'
soft_update_tau = 0.002
# target network update frequency (applied when it takes 'hard' update).
# 10000 means the target network is updated once while the behavior network is updated 10000 times.
target_update_freq = 10000
# assign skipped_frame to be 0
# because the word 'Deterministic' in the name 'BoxingDeterministic' means it automatically skips 4 frames in the game.
# assign skipped_frame to be 0 when selecting games such as "BreakoutNoFrameskip".
skipped_frame = 0
# cuda device
device_num = 0
# choose plotting option.
# 'inline' - plots status in jupyter notebook
# 'False' - it prints only reward of the episode
plot_options = {1: 'inline', 2: False}
plot_option = plot_options[2]
# */*/*/
n_atoms = 51
Vmax = 10
Vmin = -10
# */*/*/
# The path for saving a trained model.
rand_seed = None
rand_name = ('').join(map(str, np.random.randint(10, size=(3,))))
folder_name = os.getcwd().split('/')[-1]
model_name = 'Test'
model_save_path = f'./model_save/{model_name}/'
if not os.path.exists('./model_save/'):
os.mkdir('./model_save/')
if not os.path.exists(model_save_path):
os.mkdir(model_save_path)
print("model_save_path:", model_save_path)
trained_model_path = ''
agent = Agent(
env,
input_frame,
input_dim,
training_frames,
skipped_frame,
eps_decay,
gamma,
update_freq,
target_update_freq,
update_type,
soft_update_tau,
batch_size,
buffer_size,
update_start_buffer_size,
learning_rate,
eps_min,
eps_max,
device_num,
rand_seed,
plot_option,
model_save_path,
trained_model_path,
n_atoms,
Vmax,
Vmin
)
agent.train()
```
#### An example of results
Storing initial buffer..
Done. Start learning..
| Model saved. Recent scores: [1.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [1.0, -1.0, 2.0, -2.0, 5.0, 2.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [2.0, -2.0, 5.0, 2.0, 0.0, 0.0, -2.0, 3.0, 2.0, 6.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [3.0, 3.0, -2.0, -4.0, 6.0, -1.0, -5.0, 4.0, 6.0, 7.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [4.0, 6.0, 7.0, -4.0, -2.0, -6.0, 1.0, 3.0, 4.0, 6.0], Training time: 0.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, 7.0, -4.0, -2.0, -6.0, 1.0, 3.0, 4.0, 6.0, 9.0], Training time: 0.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [7.0, 1.0, 6.0, 5.0, 5.0, 0.0, -2.0, -1.0, 2.0, 5.0], Training time: 0.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [-4.0, 10.0, 9.0, -10.0, 9.0, -2.0, -5.0, 6.0, 7.0, 11.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [10.0, 9.0, -10.0, 9.0, -2.0, -5.0, 6.0, 7.0, 11.0, 1.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, 1.0, 8.0, -1.0, 2.0, 3.0, 1.0, 7.0, 6.0, 14.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [7.0, 6.0, 14.0, 1.0, 3.0, -1.0, 8.0, 4.0, -4.0, 14.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, 14.0, 1.0, 3.0, -1.0, 8.0, 4.0, -4.0, 14.0, 9.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, -4.0, -2.0, 27.0, 1.0, 4.0, 5.0, 1.0, 13.0, 10.0], Training time: 0.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 1.0, 4.0, 5.0, 1.0, 13.0, 10.0, 1.0, 1.0, 16.0], Training time: 0.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [1.0, 10.0, 13.0, 19.0, 1.0, 6.0, 4.0, 8.0, 12.0, 13.0], Training time: 1.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [10.0, 13.0, 19.0, 1.0, 6.0, 4.0, 8.0, 12.0, 13.0, 10.0], Training time: 1.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [5.0, 3.0, 7.0, 18.0, -1.0, 13.0, 9.0, 10.0, 29.0, 8.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [3.0, 7.0, 18.0, -1.0, 13.0, 9.0, 10.0, 29.0, 8.0, 18.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [7.0, 18.0, -1.0, 13.0, 9.0, 10.0, 29.0, 8.0, 18.0, 8.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [13.0, 9.0, 10.0, 29.0, 8.0, 18.0, 8.0, -1.0, 16.0, 27.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [16.0, 27.0, 8.0, 11.0, 2.0, 19.0, 13.0, 19.0, 12.0, 15.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [14.0, 11.0, 9.0, 11.0, 20.0, 16.0, 7.0, 13.0, 13.0, 37.0], Training time: 1.4hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [18.0, 7.0, 19.0, 15.0, 5.0, 9.0, 18.0, 29.0, 18.0, 18.0], Training time: 1.6hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [15.0, 11.0, 9.0, 33.0, 5.0, 30.0, 12.0, 17.0, 23.0, 15.0], Training time: 1.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [14.0, 22.0, 6.0, 13.0, 16.0, 15.0, 24.0, 28.0, 8.0, 29.0], Training time: 1.9hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [22.0, 6.0, 13.0, 16.0, 15.0, 24.0, 28.0, 8.0, 29.0, 18.0], Training time: 1.9hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [20.0, 16.0, 31.0, 23.0, 24.0, 18.0, 8.0, 15.0, 12.0, 14.0], Training time: 2.5hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 5.0, 27.0, 2.0, 11.0, 19.0, 17.0, 20.0, 23.0, 31.0], Training time: 2.5hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [19.0, 20.0, 20.0, 18.0, 10.0, 37.0, 12.0, 9.0, 25.0, 15.0], Training time: 2.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 8.0, 34.0, 22.0, 17.0, 2.0, 31.0, 13.0, 7.0, 25.0], Training time: 2.8hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [14.0, 18.0, 27.0, 21.0, 22.0, 9.0, -2.0, 28.0, 30.0, 26.0], Training time: 2.8hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [17.0, 23.0, 9.0, 40.0, 9.0, 26.0, 10.0, 26.0, 10.0, 29.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [23.0, 9.0, 40.0, 9.0, 26.0, 10.0, 26.0, 10.0, 29.0, 19.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [11.0, 23.0, 17.0, 13.0, 19.0, 37.0, 21.0, 26.0, 20.0, 16.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [23.0, 17.0, 13.0, 19.0, 37.0, 21.0, 26.0, 20.0, 16.0, 25.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [8.0, 25.0, 19.0, 10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [25.0, 19.0, 10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [19.0, 10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0, 26.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0, 26.0, 33.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0, 26.0, 33.0, 12.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [39.0, 22.0, 35.0, 37.0, 26.0, 33.0, 12.0, 6.0, 26.0, 39.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| true |
code
| 0.831537 | null | null | null | null |
|
<img align="right" src="images/tf-small.png" width="128"/>
<img align="right" src="images/phblogo.png" width="128"/>
<img align="right" src="images/dans.png"/>
---
Start with [convert](https://nbviewer.jupyter.org/github/annotation/banks/blob/master/programs/convert.ipynb)
---
# Getting data from online repos
We show the various automatic ways by which you can get data that is out there on GitHub to your computer.
The work horse is the function `checkoutRepo()` in `tf.applib.repo`.
Text-Fabric uses this function for all operations where data flows from GitHub to your computer.
There are quite some options, and here we explain all the `checkout` options, i.e. the selection of
data from the history.
See also the [documentation](https://annotation.github.io/text-fabric/tf/advanced/repo.html).
```
%load_ext autoreload
%autoreload 2
```
## Leading example
We use markdown display from IPython purely for presentation.
It is not needed to run `checkoutRepo()`.
```
from tf.advanced.helpers import dm
from tf.advanced.repo import checkoutRepo
```
We work with our tiny example TF app: `banks`.
```
ORG = "annotation"
REPO = "banks"
MAIN = "tf"
MOD = "sim/tf"
```
`MAIN`points to the main data, `MOD` points to a module of data: the similarity feature.
## Presenting the results
The function `do()` just formats the results of a `checkoutRepo()` run.
The result of such a run, after the progress messages, is a tuple.
For the explanation of the tuple, read the [docs](https://annotation.github.io/text-fabric/tf/advanced/repo.html).
```
def do(task):
md = f"""
commit | release | local | base | subdir
--- | --- | --- | --- | ---
`{task[0]}` | `{task[1]}` | `{task[2]}` | `{task[3]}` | `{task[4]}`
"""
dm(md)
```
## All the checkout options
We discuss the meaning and effects of the values you can pass to the `checkout` option.
### `clone`
> Look whether the appropriate folder exists under your `~/github` directory.
This is merely a check whether your data exists in the expected location.
* No online checks take place.
* No data is moved or copied.
**NB**: you cannot select releases and commits in your *local* GitHub clone.
The data will be used as it is found on your file system.
**When to use**
> If you are developing new feature data.
When you develop your data in a repository, your development is private as long as you
do not push to GitHub.
You can test your data, even without locally committing your data.
But, if you are ready to share your data, everything is in place, and you only
have to commit and push, and pass the location on github to others, like
```
myorg/myrepo/subfolder
```
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="clone"))
```
We show what happens if you do not have a local github clone in `~/github`.
```
%%sh
mv ~/github/annotation/banks/tf ~/github/annotation/banks/tfxxx
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="clone"))
```
Note that no attempt is made to retrieve online data.
```
%%sh
mv ~/github/annotation/banks/tfxxx ~/github/annotation/banks/tf
```
### `local`
> Look whether the appropriate folder exists under your `~/text-fabric-data` directory.
This is merely a check whether your data exists in the expected location.
* No online checks take place.
* No data is moved or copied.
**When to use**
> If you are using data created and shared by others, and if the data
is already on your system.
You can be sure that no updates are downloaded, and that everything works the same as the last time
you ran your program.
If you do not already have the data, you have to pass `latest` or `hot` or `''` which will be discussed below.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="local"))
```
You see this data because earlier I have downloaded release `v2.0`, which is a tag for
the commit with hash `9713e71c18fd296cf1860d6411312f9127710ba7`.
If you do not have any corresponding data in your `~/text-fabric-data`, you get this:
```
%%sh
mv ~/text-fabric-data/annotation/banks/tf ~/text-fabric-data/annotation/banks/tfxxx
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="local"))
%%sh
mv ~/text-fabric-data/annotation/banks/tfxxx ~/text-fabric-data/annotation/banks/tf
```
### `''` (default)
This is about when you omit the `checkout` parameter, or pass `''` to it.
The destination for local data is your `~/text-fabric-data` folder.
If you have already a local copy of the data, that will be used.
If not:
> Note that if your local data is outdated, no new data will be downloaded.
You need `latest` or `hot` for that.
But what is the latest online copy? In this case we mean:
* the latest *release*, and from that release an appropriate attached zip file
* but if there is no such zip file, we take the files from the corresponding commit
* but if there is no release at all, we take the files from the *latest commit*.
**When to use**
> If you need data created/shared by other people and you want to be sure that you always have the
same copy that you initially downloaded.
* If the data provider makes releases after important modifications, you will get those.
* If the data provider is experimenting after the latest release, and commits them to GitHub,
you do not get those.
However, with `hot`, you `can` get the latest commit, to be discussed below.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout=""))
```
Note that no data has been downloaded, because it has detected that there is already local data on your computer.
If you do not have any checkout of this data on your computer, the data will be downloaded.
```
%%sh
rm -rf ~/text-fabric-data/annotation/banks/tf
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout=""))
```
#### Note about versions and releases
The **version** of the data is not necessarily the same concept as the **release** of it.
It is possible to keep the versions and the releases strictly parallel,
but in text conversion workflows it can be handy to make a distinction between them,
e.g. as follows:
> the version is a property of the input data
> the release is a property of the output data
When you create data from sources using conversion algorithms,
you want to increase the version if you get new input data, e.g. as a result of corrections
made by the author.
But if you modify your conversion algorithm, while still running it on the same input data,
you may release the new output data as a **new release** of the **same version**.
Likewise, when the input data stays the same, but you have corrected typos in the metadata,
you can make a **new release** of the **same version** of the data.
The conversion delivers the features under a specific version,
and Text-Fabric supports those versions: users of TF can select the version they work with.
Releases are made in the version control system (git and GitHub).
The part of Text-Fabric that auto-downloads data is aware of releases.
But once the data has been downloaded in place, there is no machinery in Text-Fabric to handle
different releases.
Yet the release tag and commit hash are passed on to the point where it comes to recording
the provenance of the data.
#### Download a different version
We download version `0.1` of the data.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout=""))
```
Several observations:
* we obtained the older version from the *latest* release, which is still release `v2.0`
* the download looks different from when we downloaded version `0.2`;
this is because the data producer has zipped the `0.2` data and has attached it to release `v2.0`,
but he forgot, or deliberately refused, to attach version `0.1` to that release;
so it has been retrieved directly from the files in the corresponding commit, which is
`9713e71c18fd296cf1860d6411312f9127710ba7`.
For the verification, an online check is needed. The verification consists of checking the release tag and/or commit hash.
If there is no online connection, you get this:
```
%%sh
networksetup -setairportpower en0 off
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout="latest"))
```
or if you do not have local data:
```
%%sh
mv ~/text-fabric-data/annotation/banks/tf/0.1 ~/text-fabric-data/annotation/banks/tf/0.1xxx
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout="latest"))
%%sh
mv ~/text-fabric-data/annotation/banks/tf/0.1xxx ~/text-fabric-data/annotation/banks/tf/0.1
%%sh
networksetup -setairportpower en0 on
```
### `latest`
> The latest online release will be identified,
and if you do not have that copy locally, it will be downloaded.
**When to use**
> If you need data created/shared by other people and you want to be sure that you always have the
latest *stable* version of that data, unreleased data is not good enough.
One of the difference with `checkout=''` is that if there are no releases, you will not get data.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="latest"))
```
There is no sim/tf data in any release commit, so if we look it up, it should fail.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MOD, version="0.2", checkout="latest"))
```
But with `checkout=''` it will only be found if you do not have local data already:
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MOD, version="0.2", checkout=""))
```
In that case there is only one way: `hot`:
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MOD, version="0.2", checkout="hot"))
```
### `hot`
> The latest online commit will be identified,
and if you do not have that copy locally, it will be downloaded.
**When to use**
> If you need data created/shared by other people and you want to be sure that you always have the
latest version of that data, whether released or not.
The difference with `checkout=''` is that if there are releases,
you will now get data that may be newer than the latest release.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="hot"))
```
Observe that data has been downloaded, and that we have now data corresponding to a different commit hash,
and not corresponding to a release.
If we now ask for the latest *stable* data, the data will be downloaded anew.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="latest"))
```
### `v1.0` a specific release
> Look for a specific online release to get data from.
**When to use**
> When you want to replicate something, and need data from an earlier point in the history.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout="v1.0"))
```
We might try to get version `0.2` from this release.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="v1.0"))
```
At that early point in the history there is not yet a version `0.2` of the data.
### `a81746c` a specific commit
> Look for a specific online commit to get data from.
**When to use**
> When you want to replicate something, and need data from an earlier point in the history, and there is no
release for that commit.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.1",
checkout="a81746c5f9627637db4dae04c2d5348bda9e511a",
)
)
```
## *source* and *dest*: an alternative for `~/github` and `~/text-fabric-data`
Everything so far uses the hard-wired `~/github` and `~/text-fabric-data` directories.
But you can change that:
* pass *source* as a replacement for `~/github`.
* pass *dest* as a replacement for `~/text-fabric-data`.
**When to use**
> if you do not want to interfere with the `~/text-fabric-data` directory.
Text-Fabric manages the `~/text-fabric-data` directory,
and if you are experimenting outside Text-Fabric
you may not want to touch its data directory.
> if you want to clone data into your `~/github` directory.
Normally, TF uses your `~/github` directory as a source of information,
and never writes into it.
But if you explicitly pass `dest=~/github`, things change: downloads will
arrive under `~/github`. Use this with care.
> if you work with cloned data outside your `~/github` directory,
you can let the system look in *source* instead of `~/github`.
We customize source and destination directories:
* we put them both under `~/Downloads`
* we give them different names
```
MY_GH = "~/Downloads/repoclones"
MY_TFD = "~/Downloads/textbase"
```
Download a fresh copy of the data to `~/Downloads/textbase` instead.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.2",
checkout="",
source=MY_GH,
dest=MY_TFD,
)
)
```
Lookup the same data locally.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.2",
checkout="",
source=MY_GH,
dest=MY_TFD,
)
)
```
We copy the local github data to the custom location:
```
%%sh
mkdir -p ~/Downloads/repoclones/annotation
cp -R ~/github/annotation/banks ~/Downloads/repoclones/annotation/banks
```
Lookup the data in this alternative directory.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.2",
checkout="clone",
source=MY_GH,
dest=MY_TFD,
)
)
```
Note that the directory trees under the customised *source* and *dest* locations have exactly the same shape as before.
## Conclusion
With the help of `checkoutRepo()` you will be able to make local copies of online data in an organized way.
This will help you when
* you use other people's data
* develop your own data
* share and publish your data
* go back in history.
---
All chapters:
* [use](use.ipynb)
* [share](share.ipynb)
* [app](app.ipynb)
* *repo*
* [compose](compose.ipynb)
---
| true |
code
| 0.429639 | null | null | null | null |
|
# Facial Keypoint Detection
This project will be all about defining and training a convolutional neural network to perform facial keypoint detection, and using computer vision techniques to transform images of faces. The first step in any challenge like this will be to load and visualize the data you'll be working with.
Let's take a look at some examples of images and corresponding facial keypoints.
<img src='images/key_pts_example.png' width=50% height=50%/>
Facial keypoints (also called facial landmarks) are the small magenta dots shown on each of the faces in the image above. In each training and test image, there is a single face and **68 keypoints, with coordinates (x, y), for that face**. These keypoints mark important areas of the face: the eyes, corners of the mouth, the nose, etc. These keypoints are relevant for a variety of tasks, such as face filters, emotion recognition, pose recognition, and so on. Here they are, numbered, and you can see that specific ranges of points match different portions of the face.
<img src='images/landmarks_numbered.jpg' width=30% height=30%/>
---
## Load and Visualize Data
The first step in working with any dataset is to become familiar with your data; you'll need to load in the images of faces and their keypoints and visualize them! This set of image data has been extracted from the [YouTube Faces Dataset](https://www.cs.tau.ac.il/~wolf/ytfaces/), which includes videos of people in YouTube videos. These videos have been fed through some processing steps and turned into sets of image frames containing one face and the associated keypoints.
#### Training and Testing Data
This facial keypoints dataset consists of 5770 color images. All of these images are separated into either a training or a test set of data.
* 3462 of these images are training images, for you to use as you create a model to predict keypoints.
* 2308 are test images, which will be used to test the accuracy of your model.
The information about the images and keypoints in this dataset are summarized in CSV files, which we can read in using `pandas`. Let's read the training CSV and get the annotations in an (N, 2) array where N is the number of keypoints and 2 is the dimension of the keypoint coordinates (x, y).
---
```
# import the required libraries
import glob
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import cv2
key_pts_frame = pd.read_csv('data/training_frames_keypoints.csv')
n = 0
image_name = key_pts_frame.iloc[n, 0]
key_pts = key_pts_frame.iloc[n, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
print('Image name: ', image_name)
print('Landmarks shape: ', key_pts.shape)
print('First 4 key pts: {}'.format(key_pts[:4]))
# print out some stats about the data
print('Number of images: ', key_pts_frame.shape[0])
```
## Look at some images
Below, is a function `show_keypoints` that takes in an image and keypoints and displays them. As you look at this data, **note that these images are not all of the same size**, and neither are the faces! To eventually train a neural network on these images, we'll need to standardize their shape.
```
def show_keypoints(image, key_pts):
"""Show image with keypoints"""
plt.imshow(image)
plt.scatter(key_pts[:, 0], key_pts[:, 1], s=20, marker='.', c='m')
# Display a few different types of images by changing the index n
# select an image by index in our data frame
n = 0
image_name = key_pts_frame.iloc[n, 0]
key_pts = key_pts_frame.iloc[n, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
plt.figure(figsize=(5, 5))
image_show = mpimg.imread(os.path.join('data/training/', image_name));
show_keypoints(image_show, key_pts)
plt.show()
print("image shape: ", image_show.shape)
```
## Dataset class and Transformations
To prepare our data for training, we'll be using PyTorch's Dataset class. Much of this this code is a modified version of what can be found in the [PyTorch data loading tutorial](http://pytorch.org/tutorials/beginner/data_loading_tutorial.html).
#### Dataset class
``torch.utils.data.Dataset`` is an abstract class representing a
dataset. This class will allow us to load batches of image/keypoint data, and uniformly apply transformations to our data, such as rescaling and normalizing images for training a neural network.
Your custom dataset should inherit ``Dataset`` and override the following
methods:
- ``__len__`` so that ``len(dataset)`` returns the size of the dataset.
- ``__getitem__`` to support the indexing such that ``dataset[i]`` can
be used to get the i-th sample of image/keypoint data.
Let's create a dataset class for our face keypoints dataset. We will
read the CSV file in ``__init__`` but leave the reading of images to
``__getitem__``. This is memory efficient because all the images are not
stored in the memory at once but read as required.
A sample of our dataset will be a dictionary
``{'image': image, 'keypoints': key_pts}``. Our dataset will take an
optional argument ``transform`` so that any required processing can be
applied on the sample. We will see the usefulness of ``transform`` in the
next section.
```
from torch.utils.data import Dataset, DataLoader
class FacialKeypointsDataset(Dataset):
"""Face Landmarks dataset."""
def __init__(self, csv_file, root_dir, transform=None):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.key_pts_frame = pd.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.key_pts_frame)
def __getitem__(self, idx):
image_name = os.path.join(self.root_dir,
self.key_pts_frame.iloc[idx, 0])
image = mpimg.imread(image_name)
# if image has an alpha color channel, get rid of it
if(image.shape[2] == 4):
image = image[:,:,0:3]
key_pts = self.key_pts_frame.iloc[idx, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
sample = {'image': image, 'keypoints': key_pts}
if self.transform:
sample = self.transform(sample)
return sample
```
Now that we've defined this class, let's instantiate the dataset and display some images.
```
# Construct the dataset
face_dataset = FacialKeypointsDataset(csv_file='data/training_frames_keypoints.csv',
root_dir='data/training/')
# print some stats about the dataset
print('Length of dataset: ', len(face_dataset))
# Display a few of the images from the dataset
num_to_display = 3
for i in range(num_to_display):
# define the size of images
fig = plt.figure(figsize=(20,10))
# randomly select a sample
rand_i = np.random.randint(0, len(face_dataset))
sample = face_dataset[rand_i]
# print the shape of the image and keypoints
print(i, sample['image'].shape, sample['keypoints'].shape)
ax = plt.subplot(1, num_to_display, i + 1)
ax.set_title('Sample #{}'.format(i))
# Using the same display function, defined earlier
show_keypoints(sample['image'], sample['keypoints'])
```
## Transforms
Now, the images above are not of the same size, and neural networks often expect images that are standardized; a fixed size, with a normalized range for color ranges and coordinates, and (for PyTorch) converted from numpy lists and arrays to Tensors.
Therefore, we will need to write some pre-processing code.
Let's create four transforms:
- ``Normalize``: to convert a color image to grayscale values with a range of [0,1] and normalize the keypoints to be in a range of about [-1, 1]
- ``Rescale``: to rescale an image to a desired size.
- ``RandomCrop``: to crop an image randomly.
- ``ToTensor``: to convert numpy images to torch images.
We will write them as callable classes instead of simple functions so
that parameters of the transform need not be passed everytime it's
called. For this, we just need to implement ``__call__`` method and
(if we require parameters to be passed in), the ``__init__`` method.
We can then use a transform like this:
tx = Transform(params)
transformed_sample = tx(sample)
Observe below how these transforms are generally applied to both the image and its keypoints.
```
import torch
from torchvision import transforms, utils
# tranforms
class Normalize(object):
"""Convert a color image to grayscale and normalize the color range to [0,1]."""
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
image_copy = np.copy(image)
key_pts_copy = np.copy(key_pts)
# convert image to grayscale
image_copy = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
# scale color range from [0, 255] to [0, 1]
image_copy= image_copy/255.0
# scale keypoints to be centered around 0 with a range of [-1, 1]
# mean = 100, sqrt = 50, so, pts should be (pts - 100)/50
key_pts_copy = (key_pts_copy - 100)/50.0
return {'image': image_copy, 'keypoints': key_pts_copy}
class Rescale(object):
"""Rescale the image in a sample to a given size.
Args:
output_size (tuple or int): Desired output size. If tuple, output is
matched to output_size. If int, smaller of image edges is matched
to output_size keeping aspect ratio the same.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
self.output_size = output_size
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
h, w = image.shape[:2]
if isinstance(self.output_size, int):
if h > w:
new_h, new_w = self.output_size * h / w, self.output_size
else:
new_h, new_w = self.output_size, self.output_size * w / h
else:
new_h, new_w = self.output_size
new_h, new_w = int(new_h), int(new_w)
img = cv2.resize(image, (new_w, new_h))
# scale the pts, too
key_pts = key_pts * [new_w / w, new_h / h]
return {'image': img, 'keypoints': key_pts}
class RandomCrop(object):
"""Crop randomly the image in a sample.
Args:
output_size (tuple or int): Desired output size. If int, square crop
is made.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
if isinstance(output_size, int):
self.output_size = (output_size, output_size)
else:
assert len(output_size) == 2
self.output_size = output_size
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
h, w = image.shape[:2]
new_h, new_w = self.output_size
top = np.random.randint(0, h - new_h)
left = np.random.randint(0, w - new_w)
image = image[top: top + new_h,
left: left + new_w]
key_pts = key_pts - [left, top]
return {'image': image, 'keypoints': key_pts}
class ToTensor(object):
"""Convert ndarrays in sample to Tensors."""
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
# if image has no grayscale color channel, add one
if(len(image.shape) == 2):
# add that third color dim
image = image.reshape(image.shape[0], image.shape[1], 1)
# swap color axis because
# numpy image: H x W x C
# torch image: C X H X W
image = image.transpose((2, 0, 1))
return {'image': torch.from_numpy(image),
'keypoints': torch.from_numpy(key_pts)}
```
## Test out the transforms
Let's test these transforms out to make sure they behave as expected. As you look at each transform, note that, in this case, **order does matter**. For example, you cannot crop a image using a value smaller than the original image (and the orginal images vary in size!), but, if you first rescale the original image, you can then crop it to any size smaller than the rescaled size.
```
# test out some of these transforms
rescale = Rescale(100)
crop = RandomCrop(50)
composed = transforms.Compose([Rescale(250),
RandomCrop(224)])
# apply the transforms to a sample image
test_num = 500
sample = face_dataset[test_num]
fig = plt.figure()
for i, tx in enumerate([rescale, crop, composed]):
transformed_sample = tx(sample)
ax = plt.subplot(1, 3, i + 1)
plt.tight_layout()
ax.set_title(type(tx).__name__)
show_keypoints(transformed_sample['image'], transformed_sample['keypoints'])
plt.show()
```
## Create the transformed dataset
Apply the transforms in order to get grayscale images of the same shape. Verify that your transform works by printing out the shape of the resulting data (printing out a few examples should show you a consistent tensor size).
```
# define the data tranform
# order matters! i.e. rescaling should come before a smaller crop
data_transform = transforms.Compose([Rescale(250),
RandomCrop(224),
Normalize(),
ToTensor()])
# create the transformed dataset
transformed_dataset = FacialKeypointsDataset(csv_file='data/training_frames_keypoints.csv',
root_dir='data/training/',
transform=data_transform)
# print some stats about the transformed data
print('Number of images: ', len(transformed_dataset))
# make sure the sample tensors are the expected size
for i in range(5):
sample = transformed_dataset[i]
print(i, sample['image'].size(), sample['keypoints'].size())
```
## Data Iteration and Batching
Right now, we are iterating over this data using a ``for`` loop, but we are missing out on a lot of PyTorch's dataset capabilities, specifically the abilities to:
- Batch the data
- Shuffle the data
- Load the data in parallel using ``multiprocessing`` workers.
``torch.utils.data.DataLoader`` is an iterator which provides all these
features, and we'll see this in use in the *next* notebook, Notebook 2, when we load data in batches to train a neural network!
---
## Ready to Train!
Now that you've seen how to load and transform our data, you're ready to build a neural network to train on this data.
In the next notebook, you'll be tasked with creating a CNN for facial keypoint detection.
| true |
code
| 0.731844 | null | null | null | null |
|
# Simple Use Cases
Simulus is a discrete-event simulator in Python. This document is to demonstrate how to run simulus via a few examples. This is not a tutorial. For that, use [Simulus Tutorial](simulus-tutorial.ipynb). All the examples shown in this guide can be found under the `examples/demos` directory in the simulus source-code distribution.
It's really simple to install simulus. Assuming you have installed pip, you can simply do the following to install simulus:
```
pip install simulus
```
If you don't have administrative privilege to install packages on your machine, you can install it in the per-user managed location using:
```
pip install --user simulus
```
If all are fine at this point, you can simply import the module 'simulus' to start using the simulator.
```
import simulus
```
### Use Case #1: Direct Event Scheduling
One can schedule functions to be executed at designated simulation time. The functions in this case are called event handlers (using the discrete-event simulation terminology).
```
# %load "../examples/demos/case-1.py"
import simulus
# An event handler is a user-defined function; in this case, we take
# one positional argument 'sim', and place all keyworded arguments in
# the dictionary 'params'
def myfunc(sim, **params):
print(str(sim.now) + ": myfunc() runs with params=" + str(params))
# schedule the next event 10 seconds from now
sim.sched(myfunc, sim, **params, offset=10)
# create an anonymous simulator
sim1 = simulus.simulator()
# schedule the first event at 10 seconds
sim1.sched(myfunc, sim1, until=10, msg="hello world", value=100)
# advance simulation until 100 seconds
sim1.run(until=100)
print("simulator.run() ends at " + str(sim1.now))
# we can advance simulation for another 50 seconds
sim1.run(offset=50)
print("simulator.run() ends at " + str(sim1.now))
```
### Use Case #2: Simulation Process
A simulation process is an independent thread of execution. A process can be blocked and therefore advances its simulation time either by sleeping for some duration of time or by being blocked from synchronization primitives (such as semaphores).
```
# %load "../examples/demos/case-2.py"
import simulus
# A process for simulus is a python function with two parameters:
# the first parameter is the simulator, and the second parameter is
# the dictionary containing user-defined parameters for the process
def myproc(sim, intv, id):
print(str(sim.now) + ": myproc(%d) runs with intv=%r" % (id, intv))
while True:
# suspend the process for some time
sim.sleep(intv)
print(str(sim.now) + ": myproc(%d) resumes execution" % id)
# create an anonymous simulator
sim2 = simulus.simulator()
# start a process 100 seconds from now
sim2.process(myproc, sim2, 10, 0, offset=100)
# start another process 5 seconds from now
sim2.process(myproc, sim2, 20, 1, offset=5)
# advance simulation until 200 seconds
sim2.run(until=200)
print("simulator.run() ends at " + str(sim2.now))
sim2.run(offset=50)
print("simulator.run() ends at " + str(sim2.now))
```
### Use Case #3: Process Synchronization with Semaphores
We illustrate the use of semaphore in the context of a classic producer-consumer problem. We are simulating a single-server queue (M/M/1) here.
```
# %load "../examples/demos/case-3.py"
import simulus
from random import seed, expovariate
from statistics import mean, median, stdev
# make it repeatable
seed(12345)
# configuration of the single server queue: the mean inter-arrival
# time, and the mean service time
cfg = {"mean_iat":1, "mean_svc":0.8}
# keep the time of job arrivals, starting services, and departures
arrivals = []
starts = []
finishes = []
# the producer process waits for some random time from an
# exponential distribution, and increments the semaphore
# to represent a new item being produced, and then repeats
def producer(sim, mean_iat, sem):
while True:
iat = expovariate(1.0/mean_iat)
sim.sleep(iat)
#print("%g: job arrives (iat=%g)" % (sim.now, iat))
arrivals.append(sim.now)
sem.signal()
# the consumer process waits for the semaphore (it decrements
# the value and blocks if the value is non-positive), waits for
# some random time from another exponential distribution, and
# then repeats
def consumer(sim, mean_svc, sem):
while True:
sem.wait()
#print("%g: job starts service" % sim.now)
starts.append(sim.now)
svc = expovariate(1.0/mean_svc)
sim.sleep(svc)
#print("%g: job departs (svc=%g)" % (sim.now, svc))
finishes.append(sim.now)
# create an anonymous simulator
sim3 = simulus.simulator()
# create a semaphore with initial value of zero
sem = sim3.semaphore(0)
# start the producer and consumer processes
sim3.process(producer, sim3, cfg['mean_iat'], sem)
sim3.process(consumer, sim3, cfg['mean_svc'], sem)
# advance simulation until 100 seconds
sim3.run(until=1000)
print("simulator.run() ends at " + str(sim3.now))
# calculate and output statistics
print(f'Results: jobs=arrivals:{len(arrivals)}, starts:{len(starts)}, finishes:{len(finishes)}')
waits = [start - arrival for arrival, start in zip(arrivals, starts)]
totals = [finish - arrival for arrival, finish in zip(arrivals, finishes)]
print(f'Wait Time: mean={mean(waits):.1f}, stdev={stdev(waits):.1f}, median={median(waits):.1f}. max={max(waits):.1f}')
print(f'Total Time: mean={mean(totals):.1f}, stdev={stdev(totals):.1f}, median={median(totals):.1f}. max={max(totals):.1f}')
my_lambda = 1.0/cfg['mean_iat'] # mean arrival rate
my_mu = 1.0/cfg['mean_svc'] # mean service rate
my_rho = my_lambda/my_mu # server utilization
my_lq = my_rho*my_rho/(1-my_rho) # number in queue
my_wq = my_lq/my_lambda # wait in queue
my_w = my_wq+1/my_mu # wait in system
print(f'Theoretical Results: mean wait time = {my_wq:.1f}, mean total time = {my_w:.1f}')
```
### Use Case #4: Dynamic Processes
We continue with the previous example. At the time, rathar than using semaphores, we can achieve exactly the same results by dynamically creating processes.
```
# %load "../examples/demos/case-4.py"
import simulus
from random import seed, expovariate
from statistics import mean, median, stdev
# make it repeatable
seed(12345)
# configuration of the single server queue: the mean inter-arrival
# time, and the mean service time
cfg = {"mean_iat":1, "mean_svc":0.8}
# keep the time of job arrivals, starting services, and departures
arrivals = []
starts = []
finishes = []
# we keep the account of the number of jobs in the system (those who
# have arrived but not yet departed); this is used to indicate whether
# there's a consumer process currently running; the value is more than
# 1, we don't need to create a new consumer process
jobs_in_system = 0
# the producer process waits for some random time from an exponential
# distribution to represent a new item being produced, creates a
# consumer process when necessary to represent the item being
# consumed, and then repeats
def producer(sim, mean_iat, mean_svc):
global jobs_in_system
while True:
iat = expovariate(1.0/mean_iat)
sim.sleep(iat)
#print("%g: job arrives (iat=%g)" % (sim.now, iat))
arrivals.append(sim.now)
jobs_in_system += 1
if jobs_in_system <= 1:
sim.process(consumer, sim, mean_svc)
# the consumer process waits for the semaphore (it decrements
# the value and blocks if the value is non-positive), waits for
# some random time from another exponential distribution, and
# then repeats
def consumer(sim, mean_svc):
global jobs_in_system
while jobs_in_system > 0:
#print("%g: job starts service" % sim.now)
starts.append(sim.now)
svc = expovariate(1.0/mean_svc)
sim.sleep(svc)
#print("%g: job departs (svc=%g)" % (sim.now, svc))
finishes.append(sim.now)
jobs_in_system -= 1
# create an anonymous simulator
sim3 = simulus.simulator()
# start the producer process only
sim3.process(producer, sim3, cfg['mean_iat'], cfg['mean_svc'])
# advance simulation until 100 seconds
sim3.run(until=1000)
print("simulator.run() ends at " + str(sim3.now))
# calculate and output statistics
print(f'Results: jobs=arrival:{len(arrivals)}, starts:{len(starts)}, finishes:{len(finishes)}')
waits = [start - arrival for arrival, start in zip(arrivals, starts)]
totals = [finish - arrival for arrival, finish in zip(arrivals, finishes)]
print(f'Wait Time: mean={mean(waits):.1f}, stdev={stdev(waits):.1f}, median={median(waits):.1f}. max={max(waits):.1f}')
print(f'Total Time: mean={mean(totals):.1f}, stdev={stdev(totals):.1f}, median={median(totals):.1f}. max={max(totals):.1f}')
my_lambda = 1.0/cfg['mean_iat'] # mean arrival rate
my_mu = 1.0/cfg['mean_svc'] # mean service rate
my_rho = my_lambda/my_mu # server utilization
my_lq = my_rho*my_rho/(1-my_rho) # number in queue
my_wq = my_lq/my_lambda # wait in queue
my_w = my_wq+1/my_mu # wait in system
print(f'Theoretical Results: mean wait time = {my_wq:.1f}, mean total time = {my_w:.1f}')
```
| true |
code
| 0.315782 | null | null | null | null |
|
<div class="alert alert-block alert-info">
<font size="6"><b><center> Section 2</font></center>
<br>
<font size="6"><b><center> Fully-Connected, Feed-Forward Neural Network Examples </font></center>
</div>
# Example 1: A feedforward network with one hidden layer using torch.nn and simulated data
In developing (and training) a feedforward neural network, the developer needs to make many decisions, many of which are required when developing more complicated neural networks, such as CNN and RNN:
- the depth of the network (i.e. number of layer)
- the width of the network (i.e. number of hidden units per layer)
- the type of nonlinear activation function applied in each hidden layer
- the type of activation function applied in the output layer
- the loss function
- the optimization algorithms
- the regularization technique (*which we will consider in Section 3*)
- number of epoch and batch size
Our first example uses simulated data, which has the advantage that we define our own data generating mechanism and can observe how a neural network can approximate the mechanism.
----
## Simulate and Visualize Data
Let's first consider an example with one explanatory variable.
<br><br>
The output is related to the input using the following function
$$y_i = 3x_{i,1} + x^2 exp(x_{i,1}) + \epsilon_i$$
where $\epsilon$ is an independently and identically distributed (i.i.d.) random variable and $i = 1,2,\dots,n$ is an index of examples (or observations)
```
# In the following example, n=100
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
n = 100 # number of examples (or observations)
# Generate a set of n random numbers from a standard normal distribution
epsilon = np.random.randn(n)
# Generate a set of n random numbers from a uniform[0,1] distribution
x1 = np.random.uniform(0,1,n)
# Create the data generating mechanism
y = 3*x1 + np.power(x1,2)*np.exp(x1) + epsilon
stats.describe(y)
stats.describe(x1)
fig = plt.figure(figsize=(12,8))
plt.subplot(2, 2, 1)
sns.set()
#ax = sns.distplot(x1)
plt.hist(x1)
plt.subplot(2, 2, 2)
plt.scatter(x1, y)
```
**Note: Before training, `numpy array` needs to be converted to `PyTorch's tensors`**
```
type(x1)
print(x1.shape)
print(y.shape)
# convert numpy array to tensor in shape of input size
import torch
x1 = torch.from_numpy(x1.reshape(-1,1)).float()
y = torch.from_numpy(y.reshape(-1,1)).float()
print(x1.shape)
print(y.shape)
```
## Create a network: First Attempt
* Specify a network
* Define a loss function and choose an optimization algorithm
* Train the network
Our first network is a linear regression model
### Create a linear regression model
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class LinearNet(nn.Module):
def __init__(self):
super(LinearNet, self).__init__()
self.linearlayer1 = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = self.linearlayer1(x)
return y_pred
linearNet = LinearNet()
print(linearNet)
```
### Define Loss Function and Optimization Algorithm
```
# Define Optimizer and Loss Function
optimizer = torch.optim.SGD(linearNet.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
```
### Model training and print losses
```
X = Variable(x1)
y_data = Variable(y)
for epoch in range(500):
y_pred = linearNet(X)
loss = torch.sqrt(loss_func(y_pred, y_data))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Plot the prediction and print out the loss
if epoch in [0,99,299,399,499]:
print(epoch)
plt.cla()
plt.scatter(x1.data.numpy(), y.data.numpy())
#plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=2)
plt.scatter(x1.data.numpy(), y_pred.data.numpy())
plt.text(0.7, -1, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 14, 'color': 'red'})
plt.pause(0.1)
plt.show()
```
## Create a Network: 2nd Attempt
### Define a Feed-forward network with 1 hidden layer
**Let's insert a computational graph here**
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class ffNet(nn.Module):
def __init__(self):
super(ffNet, self).__init__()
self.linearCombo1 = torch.nn.Linear(1, 4) # z1 = W1*x1 + b1
self.linearCombo2 = torch.nn.Linear(4, 1) # z2 = W2*h1 + b2
self.relu = torch.nn.ReLU()
def forward(self, x):
h1 = self.relu(self.linearCombo1(x)) # the ReLU (non-linear activation function) is applied to the linear combination of the weights and input (x1)
y_pred = self.linearCombo2(h1)
return y_pred
ffnet = ffNet()
print(ffnet)
```
### Define loss function and optimization algorithm
```
# Define Optimizer and Loss Function
optimizer = torch.optim.SGD(ffnet.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
```
### Model Training
```
X = Variable(x1)
y_data = Variable(y)
for epoch in range(500):
y_pred = ffnet(X)
loss = loss_func(y_pred, y_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch in [0,99,299,399,499]:
print(epoch)
plt.cla()
plt.scatter(x1.data.numpy(), y.data.numpy())
plt.scatter(x1.data.numpy(), y_pred.data.numpy())
#plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=2)
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
plt.pause(0.1)
plt.show()
```
## Create a Network: 3rd Attempt
### Define a Feed-forward network with 2 hidden layers
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class ffNet(nn.Module):
def __init__(self):
super(ffNet, self).__init__()
self.linearlayer1 = torch.nn.Linear(1, 8)
self.linearlayer2 = torch.nn.Linear(8, 4)
self.linearlayer3 = torch.nn.Linear(4, 1)
self.relu = torch.nn.ReLU()
def forward(self, x):
out1 = self.relu(self.linearlayer1(x))
out2 = self.relu(self.linearlayer2(out1))
y_pred = self.linearlayer3(out2)
return y_pred
ffnet2 = ffNet()
print(ffnet2)
```
### Define loss function and optimization algorithm
```
# Define Optimizer and Loss Function
optimizer = torch.optim.SGD(ffnet2.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
```
### Model Training
```
X = Variable(x1)
y_data = Variable(y)
for epoch in range(500):
y_pred = ffnet2(X)
loss = loss_func(y_pred, y_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch in [0,99,299,399,499,999]:
print(epoch)
plt.cla()
plt.scatter(x1.data.numpy(), y.data.numpy())
#plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r', lw=1)
plt.scatter(x1.data.numpy(), y_pred.data.numpy())
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
plt.pause(0.1)
plt.show()
```
# Lab 2
**Review modeling attempt 1 - 3 and design a network to improve the existing results.**
| true |
code
| 0.875681 | null | null | null | null |
|
## 10.4 딥러닝 기반 Q-Learning을 이용하는 강화학습
- 관련 패키지 불러오기
```
# 기본 패키지
import numpy as np
import random
from collections import deque
import matplotlib.pyplot as plt
# 강화학습 환경 패키지
import gym
# 인공지능 패키지: 텐서플로, 케라스
# 호환성을 위해 텐스플로에 포함된 케라스를 불러옴
import tensorflow as tf # v2.4.1 at 7/25/2021
from tensorflow import keras # v2.4.0 at 7/25/2021
from tensorflow.keras import Model, Input
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
```
- Q 함수를 위한 뉴럴넷 구성하기
```
def create_q_model(num_states, num_actions):
inputs = Input(shape=(num_states,))
layer = Dense(32, activation="relu")(inputs)
layer = Dense(16, activation="relu")(layer)
action = Dense(num_actions, activation="linear")(layer)
return Model(inputs=inputs, outputs=action)
model = create_q_model(4,2)
model.summary()
```
- Q함수 뉴럴넷의 학습에 필요한 코드 작성
```
def get_env_model(id='MountainCar-v0'):
env = gym.make(id)
num_states = env.observation_space.shape[0]
num_actions = env.action_space.n
model = create_q_model(num_states, num_actions)
return env, model
def train(model, env):
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
states = np.zeros((10,state_size), dtype=np.float32)
with tf.GradientTape() as tape:
predicts = model(states)
env, model = get_env_model()
train(model, env)
print('Simple processing used in training is completed!')
env_cartpole = gym.make('CartPole-v1')
print('CartPole-v1: ', env_cartpole.observation_space.shape, env_cartpole.action_space.n)
env_mountaincar = gym.make('MountainCar-v0')
print('MountainCar-v0: ', env_mountaincar.observation_space.shape, env_mountaincar.action_space.n)
class World_00:
def __init__(self):
self.get_env_model()
def get_env_model(self):
self.env = gym.make('MountainCar-v0')
self.num_states = env.observation_space.shape[0]
self.num_actions = env.action_space.n
self.model = create_q_model(self.num_states, self.num_actions)
# print(self.model.summary())
def train(self):
states = np.zeros((10,self.num_states), dtype=np.float32)
with tf.GradientTape() as tape:
predicts = self.model(states)
new_world = World_00()
new_world.train()
print('Simple processing used in training is completed!')
def env_test_model_memory(memory, env, model, n_episodes=1000,
flag_render=False):
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
s_array = np.array(s).reshape((1,-1))
Qsa = model.predict(s_array)[0]
a = np.argmax(Qsa)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
print('Notice that the max score is set to 500.0 in CartPole-v1')
def list_rotate(l):
return list(zip(*l))
class World_01(World_00):
def __init__(self):
World_00.__init__(self)
self.memory = deque(maxlen=2000)
self.N_batch = 64
self.t_model = create_q_model(self.num_states, self.num_actions)
self.discount_factor = 0.99
self.learning_rate = 0.001
self.optimizer = Adam(lr=self.learning_rate)
def trial(self, flag_render=False):
env_test_model_memory(self.memory, self.env,
self.model, n_episodes=10, flag_render=flag_render)
print(len(self.memory))
def train_memory(self):
if len(self.memory) >= self.N_batch:
memory_batch = random.sample(self.memory, self.N_batch)
s_l,a_l,r_l,next_s_l,done_l = [np.array(x) for x in list_rotate(memory_batch)]
model_w = self.model.trainable_variables
with tf.GradientTape() as tape:
Qsa_pred_l = self.model(s_l.astype(np.float32))
a_l_onehot = tf.one_hot(a_l, self.num_actions)
Qs_a_pred_l = tf.reduce_sum(a_l_onehot * Qsa_pred_l,
axis=1)
Qsa_tpred_l = self.t_model(next_s_l.astype(np.float32))
Qsa_tpred_l = tf.stop_gradient(Qsa_tpred_l)
max_Q_next_s_a_l = np.amax(Qsa_tpred_l, axis=-1)
Qs_a_l = r_l + (1 - done_l) * self.discount_factor * max_Q_next_s_a_l
loss = tf.reduce_mean(tf.square(Qs_a_l - Qs_a_pred_l))
grads = tape.gradient(loss, model_w)
self.optimizer.apply_gradients(zip(grads, model_w))
new_world = World_01()
new_world.trial()
new_world.train_memory()
new_world.env.close()
print('Completed!')
class World_02(World_01):
def __init__(self):
World_01.__init__(self)
self.epsilon = 0.2
def update_t_model(self):
self.t_model.set_weights(self.model.get_weights())
def best_action(self, s):
if random.random() <= self.epsilon:
return random.randrange(self.num_actions)
else:
s_array = np.array(s).reshape((1,-1))
Qsa = self.model.predict(s_array)[0]
return np.argmax(Qsa)
def trials(self, n_episodes=100, flag_render=False):
memory = self.memory
env = self.env
model = self.model
score_l = []
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
a = self.best_action(s)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
# self.train_memory()
s = next_s
self.train_memory()
self.update_t_model()
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
score_l.append(score)
return score_l
new_world = World_02()
score_l = new_world.trials(n_episodes=50)
new_world.env.close()
np.save('score_l.npy', score_l)
```
---
### 전체코드 (분할 버전)
```
l = [[1,2],[3,4],[5,6]]
list(zip(*l))
# 기본 패키지
import numpy as np
import random
from collections import deque
import matplotlib.pyplot as plt
# 강화학습 환경 패키지
import gym
# 인공지능 패키지: 텐서플로, 케라스
# 호환성을 위해 텐스플로에 포함된 케라스를 불러옴
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import Model, Input
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
def create_q_model(num_states, num_actions):
inputs = Input(shape=(num_states,))
layer = Dense(32, activation="relu")(inputs)
layer = Dense(16, activation="relu")(layer)
action = Dense(num_actions, activation="linear")(layer)
return Model(inputs=inputs, outputs=action)
def list_rotate(l):
return list(zip(*l))
class WorldFull():
def __init__(self):
self.get_env_model() #?
self.memory = deque(maxlen=2000)
self.N_batch = 64
self.t_model = create_q_model(self.num_states, self.num_actions)
self.discount_factor = 0.99
self.learning_rate = 0.001
self.optimizer = Adam(lr=self.learning_rate)
self.epsilon = 0.2
def get_env_model(self):
self.env = gym.make('CartPole-v1')
self.num_states = self.env.observation_space.shape[0]
self.num_actions = self.env.action_space.n
self.model = create_q_model(self.num_states, self.num_actions)
def update_t_model(self):
self.t_model.set_weights(self.model.get_weights())
def best_action(self, s):
if random.random() <= self.epsilon:
return random.randrange(self.num_actions)
else:
s_array = np.array(s).reshape((1,-1))
Qsa = self.model.predict(s_array)[0]
return np.argmax(Qsa)
def train_memory(self):
if len(self.memory) >= self.N_batch:
memory_batch = random.sample(self.memory, self.N_batch)
s_l,a_l,r_l,next_s_l,done_l = [np.array(x) for x in list_rotate(memory_batch)]
model_w = self.model.trainable_variables
with tf.GradientTape() as tape:
Qsa_pred_l = self.model(s_l.astype(np.float32))
a_l_onehot = tf.one_hot(a_l, self.num_actions)
Qs_a_pred_l = tf.reduce_sum(a_l_onehot * Qsa_pred_l,
axis=1)
Qsa_tpred_l = self.t_model(next_s_l.astype(np.float32))
Qsa_tpred_l = tf.stop_gradient(Qsa_tpred_l)
max_Q_next_s_a_l = np.amax(Qsa_tpred_l, axis=-1)
Qs_a_l = r_l + (1 - done_l) * self.discount_factor * max_Q_next_s_a_l
loss = tf.reduce_mean(tf.square(Qs_a_l - Qs_a_pred_l))
grads = tape.gradient(loss, model_w)
self.optimizer.apply_gradients(zip(grads, model_w))
def trials(self, n_episodes=100, flag_render=False):
memory = self.memory
env = self.env
model = self.model
score_l = []
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
a = self.best_action(s)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
# self.train_memory()
s = next_s
self.train_memory()
self.update_t_model()
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
score_l.append(score)
return score_l
new_world = WorldFull()
score_l = new_world.trials(n_episodes=100)
new_world.env.close()
np.save('score_l.npy', score_l)
print('Job completed!')
plt.plot(score_l)
plt.title("Deep Q-Learning for Cartpole")
plt.xlabel("Episode")
plt.ylabel("Score")
plt.plot(score_l)
plt.title("Deep Q-Learning for Cartpole")
plt.xlabel("Episode")
plt.ylabel("Score")
```
---
### 전체코드
```
"""
ENV: MoutainCar
- 2nd hidden layer: 16 --> 32
"""
# 기본 패키지
import numpy as np
import random
from collections import deque
import matplotlib.pyplot as plt
# 강화학습 환경 패키지
import gym
# 인공지능 패키지: 텐서플로, 케라스
# 호환성을 위해 텐스플로에 포함된 케라스를 불러옴
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import Model, Input
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
def create_q_model(num_states, num_actions):
inputs = Input(shape=(num_states,))
layer = Dense(32, activation="relu")(inputs)
layer = Dense(32, activation="relu")(layer)
action = Dense(num_actions, activation="linear")(layer)
return Model(inputs=inputs, outputs=action)
def list_rotate(l):
return list(zip(*l))
class WorldFull():
def __init__(self):
self.get_env_model() #?
self.memory = deque(maxlen=2000)
self.N_batch = 64
self.t_model = create_q_model(self.num_states, self.num_actions)
self.discount_factor = 0.99
self.learning_rate = 0.001
self.optimizer = Adam(lr=self.learning_rate)
self.epsilon = 0.05
def get_env_model(self):
self.env = gym.make('MountainCar-v0')
self.num_states = self.env.observation_space.shape[0]
self.num_actions = self.env.action_space.n
self.model = create_q_model(self.num_states, self.num_actions)
def update_t_model(self):
self.t_model.set_weights(self.model.get_weights())
def best_action(self, s):
if random.random() <= self.epsilon:
return random.randrange(self.num_actions)
else:
s_array = np.array(s).reshape((1,-1))
Qsa = self.model.predict(s_array)[0]
return np.argmax(Qsa)
def train_memory(self):
if len(self.memory) >= self.N_batch:
memory_batch = random.sample(self.memory, self.N_batch)
s_l,a_l,r_l,next_s_l,done_l = [np.array(x) for x in list_rotate(memory_batch)]
model_w = self.model.trainable_variables
with tf.GradientTape() as tape:
Qsa_pred_l = self.model(s_l.astype(np.float32))
a_l_onehot = tf.one_hot(a_l, self.num_actions)
Qs_a_pred_l = tf.reduce_sum(a_l_onehot * Qsa_pred_l,
axis=1)
Qsa_tpred_l = self.t_model(next_s_l.astype(np.float32))
Qsa_tpred_l = tf.stop_gradient(Qsa_tpred_l)
max_Q_next_s_a_l = np.amax(Qsa_tpred_l, axis=-1)
Qs_a_l = r_l + (1 - done_l) * self.discount_factor * max_Q_next_s_a_l
loss = tf.reduce_mean(tf.square(Qs_a_l - Qs_a_pred_l))
grads = tape.gradient(loss, model_w)
self.optimizer.apply_gradients(zip(grads, model_w))
def trials(self, n_episodes=100, flag_render=False):
memory = self.memory
env = self.env
model = self.model
score_l = []
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
a = self.best_action(s)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
# self.train_memory()
s = next_s
self.train_memory()
self.update_t_model()
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
score_l.append(score)
return score_l
new_world = WorldFull()
score_l = new_world.trials(n_episodes=100)
new_world.env.close()
np.save('score_l.npy', score_l)
print('Job completed!')
plt.plot(score_l)
plt.title("Deep Q-Learning for Cartpole")
plt.xlabel("Episode")
plt.ylabel("Score")
```
| true |
code
| 0.581065 | null | null | null | null |
|
# **Swin Transformer: Hierarchical Vision Transformer using Shifted Windows**
**Swin Transformer (ICCV 2021 best paper award (Marr Prize))**
**Authors {v-zeliu1,v-yutlin,yuecao,hanhu,v-yixwe,zhez,stevelin,bainguo}@microsoft.com**
**Official Github**: https://github.com/microsoft/Swin-Transformer
---
**Edited By Su Hyung Choi - [Computer Vision Paper Reviews]**
**[Github: @JonyChoi]** https://github.com/jonychoi/Computer-Vision-Paper-Reviews
Edited Jan 4 2022
---
## **About Swin Transformer**
```
# --------------------------------------------------------
# Swin Transformer
# Copyright (c) 2021 Microsoft
# Licensed under The MIT License [see LICENSE for details]
# Written by Ze Liu
# --------------------------------------------------------
import torch
import torch.nn as nn
import torch.utils.checkpoint as checkpoint
from timm.models.layers import DropPath, to_2tuple, trunc_normal_
class Mlp(nn.Module):
def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
super().__init__()
out_features = out_features or in_features
hidden_features = hidden_features or in_features
self.fc1 = nn.Linear(in_features, hidden_features)
self.act = act_layer()
self.fc2 = nn.Linear(hidden_features, out_features)
self.drop = nn.Dropout(drop)
def forward(self, x):
x = self.fc1(x)
x = self.act(x)
x = self.drop(x)
x = self.fc2(x)
x = self.drop(x)
return x
def window_partition(x, window_size):
"""
Args:
x: (B, H, W, C)
window_size (int): window size
Returns:
windows: (num_windows*B, window_size, window_size, C)
"""
B, H, W, C = x.shape
x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
return windows
def window_reverse(windows, window_size, H, W):
"""
Args:
windows: (num_windows*B, window_size, window_size, C)
window_size (int): Window size
H (int): Height of image
W (int): Width of image
Returns:
x: (B, H, W, C)
"""
B = int(windows.shape[0] / (H * W / window_size / window_size))
x = windows.view(B, H // window_size, W // window_size, window_size, window_size, -1)
x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
return x
class WindowAttention(nn.Module):
r""" Window based multi-head self attention (W-MSA) module with relative position bias.
It supports both of shifted and non-shifted window.
Args:
dim (int): Number of input channels.
window_size (tuple[int]): The height and width of the window.
num_heads (int): Number of attention heads.
qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set
attn_drop (float, optional): Dropout ratio of attention weight. Default: 0.0
proj_drop (float, optional): Dropout ratio of output. Default: 0.0
"""
def __init__(self, dim, window_size, num_heads, qkv_bias=True, qk_scale=None, attn_drop=0., proj_drop=0.):
super().__init__()
self.dim = dim
self.window_size = window_size # Wh, Ww
self.num_heads = num_heads
head_dim = dim // num_heads
self.scale = qk_scale or head_dim ** -0.5
# define a parameter table of relative position bias
self.relative_position_bias_table = nn.Parameter(
torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)) # 2*Wh-1 * 2*Ww-1, nH
# get pair-wise relative position index for each token inside the window
coords_h = torch.arange(self.window_size[0])
coords_w = torch.arange(self.window_size[1])
coords = torch.stack(torch.meshgrid([coords_h, coords_w])) # 2, Wh, Ww
coords_flatten = torch.flatten(coords, 1) # 2, Wh*Ww
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :] # 2, Wh*Ww, Wh*Ww
relative_coords = relative_coords.permute(1, 2, 0).contiguous() # Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1 # shift to start from 0
relative_coords[:, :, 1] += self.window_size[1] - 1
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1) # Wh*Ww, Wh*Ww
self.register_buffer("relative_position_index", relative_position_index)
self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
self.attn_drop = nn.Dropout(attn_drop)
self.proj = nn.Linear(dim, dim)
self.proj_drop = nn.Dropout(proj_drop)
trunc_normal_(self.relative_position_bias_table, std=.02)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x, mask=None):
"""
Args:
x: input features with shape of (num_windows*B, N, C)
mask: (0/-inf) mask with shape of (num_windows, Wh*Ww, Wh*Ww) or None
"""
B_, N, C = x.shape
qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
q, k, v = qkv[0], qkv[1], qkv[2] # make torchscript happy (cannot use tensor as tuple)
q = q * self.scale
attn = (q @ k.transpose(-2, -1))
relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1) # Wh*Ww,Wh*Ww,nH
relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous() # nH, Wh*Ww, Wh*Ww
attn = attn + relative_position_bias.unsqueeze(0)
if mask is not None:
nW = mask.shape[0]
attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
attn = attn.view(-1, self.num_heads, N, N)
attn = self.softmax(attn)
else:
attn = self.softmax(attn)
attn = self.attn_drop(attn)
x = (attn @ v).transpose(1, 2).reshape(B_, N, C)
x = self.proj(x)
x = self.proj_drop(x)
return x
def extra_repr(self) -> str:
return f'dim={self.dim}, window_size={self.window_size}, num_heads={self.num_heads}'
def flops(self, N):
# calculate flops for 1 window with token length of N
flops = 0
# qkv = self.qkv(x)
flops += N * self.dim * 3 * self.dim
# attn = (q @ k.transpose(-2, -1))
flops += self.num_heads * N * (self.dim // self.num_heads) * N
# x = (attn @ v)
flops += self.num_heads * N * N * (self.dim // self.num_heads)
# x = self.proj(x)
flops += N * self.dim * self.dim
return flops
class SwinTransformerBlock(nn.Module):
r""" Swin Transformer Block.
Args:
dim (int): Number of input channels.
input_resolution (tuple[int]): Input resulotion.
num_heads (int): Number of attention heads.
window_size (int): Window size.
shift_size (int): Shift size for SW-MSA.
mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set.
drop (float, optional): Dropout rate. Default: 0.0
attn_drop (float, optional): Attention dropout rate. Default: 0.0
drop_path (float, optional): Stochastic depth rate. Default: 0.0
act_layer (nn.Module, optional): Activation layer. Default: nn.GELU
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
"""
def __init__(self, dim, input_resolution, num_heads, window_size=7, shift_size=0,
mlp_ratio=4., qkv_bias=True, qk_scale=None, drop=0., attn_drop=0., drop_path=0.,
act_layer=nn.GELU, norm_layer=nn.LayerNorm):
super().__init__()
self.dim = dim
self.input_resolution = input_resolution
self.num_heads = num_heads
self.window_size = window_size
self.shift_size = shift_size
self.mlp_ratio = mlp_ratio
if min(self.input_resolution) <= self.window_size:
# if window size is larger than input resolution, we don't partition windows
self.shift_size = 0
self.window_size = min(self.input_resolution)
assert 0 <= self.shift_size < self.window_size, "shift_size must in 0-window_size"
self.norm1 = norm_layer(dim)
self.attn = WindowAttention(
dim, window_size=to_2tuple(self.window_size), num_heads=num_heads,
qkv_bias=qkv_bias, qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()
self.norm2 = norm_layer(dim)
mlp_hidden_dim = int(dim * mlp_ratio)
self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop)
if self.shift_size > 0:
# calculate attention mask for SW-MSA
H, W = self.input_resolution
img_mask = torch.zeros((1, H, W, 1)) # 1 H W 1
h_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
for w in w_slices:
img_mask[:, h, w, :] = cnt
cnt += 1
mask_windows = window_partition(img_mask, self.window_size) # nW, window_size, window_size, 1
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
else:
attn_mask = None
self.register_buffer("attn_mask", attn_mask)
def forward(self, x):
H, W = self.input_resolution
B, L, C = x.shape
assert L == H * W, "input feature has wrong size"
shortcut = x
x = self.norm1(x)
x = x.view(B, H, W, C)
# cyclic shift
if self.shift_size > 0:
shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
else:
shifted_x = x
# partition windows
x_windows = window_partition(shifted_x, self.window_size) # nW*B, window_size, window_size, C
x_windows = x_windows.view(-1, self.window_size * self.window_size, C) # nW*B, window_size*window_size, C
# W-MSA/SW-MSA
attn_windows = self.attn(x_windows, mask=self.attn_mask) # nW*B, window_size*window_size, C
# merge windows
attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)
shifted_x = window_reverse(attn_windows, self.window_size, H, W) # B H' W' C
# reverse cyclic shift
if self.shift_size > 0:
x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
else:
x = shifted_x
x = x.view(B, H * W, C)
# FFN
x = shortcut + self.drop_path(x)
x = x + self.drop_path(self.mlp(self.norm2(x)))
return x
def extra_repr(self) -> str:
return f"dim={self.dim}, input_resolution={self.input_resolution}, num_heads={self.num_heads}, " \
f"window_size={self.window_size}, shift_size={self.shift_size}, mlp_ratio={self.mlp_ratio}"
def flops(self):
flops = 0
H, W = self.input_resolution
# norm1
flops += self.dim * H * W
# W-MSA/SW-MSA
nW = H * W / self.window_size / self.window_size
flops += nW * self.attn.flops(self.window_size * self.window_size)
# mlp
flops += 2 * H * W * self.dim * self.dim * self.mlp_ratio
# norm2
flops += self.dim * H * W
return flops
class PatchMerging(nn.Module):
r""" Patch Merging Layer.
Args:
input_resolution (tuple[int]): Resolution of input feature.
dim (int): Number of input channels.
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
"""
def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
super().__init__()
self.input_resolution = input_resolution
self.dim = dim
self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
self.norm = norm_layer(4 * dim)
def forward(self, x):
"""
x: B, H*W, C
"""
H, W = self.input_resolution
B, L, C = x.shape
assert L == H * W, "input feature has wrong size"
assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."
x = x.view(B, H, W, C)
x0 = x[:, 0::2, 0::2, :] # B H/2 W/2 C
x1 = x[:, 1::2, 0::2, :] # B H/2 W/2 C
x2 = x[:, 0::2, 1::2, :] # B H/2 W/2 C
x3 = x[:, 1::2, 1::2, :] # B H/2 W/2 C
x = torch.cat([x0, x1, x2, x3], -1) # B H/2 W/2 4*C
x = x.view(B, -1, 4 * C) # B H/2*W/2 4*C
x = self.norm(x)
x = self.reduction(x)
return x
def extra_repr(self) -> str:
return f"input_resolution={self.input_resolution}, dim={self.dim}"
def flops(self):
H, W = self.input_resolution
flops = H * W * self.dim
flops += (H // 2) * (W // 2) * 4 * self.dim * 2 * self.dim
return flops
class BasicLayer(nn.Module):
""" A basic Swin Transformer layer for one stage.
Args:
dim (int): Number of input channels.
input_resolution (tuple[int]): Input resolution.
depth (int): Number of blocks.
num_heads (int): Number of attention heads.
window_size (int): Local window size.
mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set.
drop (float, optional): Dropout rate. Default: 0.0
attn_drop (float, optional): Attention dropout rate. Default: 0.0
drop_path (float | tuple[float], optional): Stochastic depth rate. Default: 0.0
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
downsample (nn.Module | None, optional): Downsample layer at the end of the layer. Default: None
use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False.
"""
def __init__(self, dim, input_resolution, depth, num_heads, window_size,
mlp_ratio=4., qkv_bias=True, qk_scale=None, drop=0., attn_drop=0.,
drop_path=0., norm_layer=nn.LayerNorm, downsample=None, use_checkpoint=False):
super().__init__()
self.dim = dim
self.input_resolution = input_resolution
self.depth = depth
self.use_checkpoint = use_checkpoint
# build blocks
self.blocks = nn.ModuleList([
SwinTransformerBlock(dim=dim, input_resolution=input_resolution,
num_heads=num_heads, window_size=window_size,
shift_size=0 if (i % 2 == 0) else window_size // 2,
mlp_ratio=mlp_ratio,
qkv_bias=qkv_bias, qk_scale=qk_scale,
drop=drop, attn_drop=attn_drop,
drop_path=drop_path[i] if isinstance(drop_path, list) else drop_path,
norm_layer=norm_layer)
for i in range(depth)])
# patch merging layer
if downsample is not None:
self.downsample = downsample(input_resolution, dim=dim, norm_layer=norm_layer)
else:
self.downsample = None
def forward(self, x):
for blk in self.blocks:
if self.use_checkpoint:
x = checkpoint.checkpoint(blk, x)
else:
x = blk(x)
if self.downsample is not None:
x = self.downsample(x)
return x
def extra_repr(self) -> str:
return f"dim={self.dim}, input_resolution={self.input_resolution}, depth={self.depth}"
def flops(self):
flops = 0
for blk in self.blocks:
flops += blk.flops()
if self.downsample is not None:
flops += self.downsample.flops()
return flops
class PatchEmbed(nn.Module):
r""" Image to Patch Embedding
Args:
img_size (int): Image size. Default: 224.
patch_size (int): Patch token size. Default: 4.
in_chans (int): Number of input image channels. Default: 3.
embed_dim (int): Number of linear projection output channels. Default: 96.
norm_layer (nn.Module, optional): Normalization layer. Default: None
"""
def __init__(self, img_size=224, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
super().__init__()
img_size = to_2tuple(img_size)
patch_size = to_2tuple(patch_size)
patches_resolution = [img_size[0] // patch_size[0], img_size[1] // patch_size[1]]
self.img_size = img_size
self.patch_size = patch_size
self.patches_resolution = patches_resolution
self.num_patches = patches_resolution[0] * patches_resolution[1]
self.in_chans = in_chans
self.embed_dim = embed_dim
self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
if norm_layer is not None:
self.norm = norm_layer(embed_dim)
else:
self.norm = None
def forward(self, x):
B, C, H, W = x.shape
# FIXME look at relaxing size constraints
assert H == self.img_size[0] and W == self.img_size[1], \
f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."
x = self.proj(x).flatten(2).transpose(1, 2) # B Ph*Pw C
if self.norm is not None:
x = self.norm(x)
return x
def flops(self):
Ho, Wo = self.patches_resolution
flops = Ho * Wo * self.embed_dim * self.in_chans * (self.patch_size[0] * self.patch_size[1])
if self.norm is not None:
flops += Ho * Wo * self.embed_dim
return flops
class SwinTransformer(nn.Module):
r""" Swin Transformer
A PyTorch impl of : `Swin Transformer: Hierarchical Vision Transformer using Shifted Windows` -
https://arxiv.org/pdf/2103.14030
Args:
img_size (int | tuple(int)): Input image size. Default 224
patch_size (int | tuple(int)): Patch size. Default: 4
in_chans (int): Number of input image channels. Default: 3
num_classes (int): Number of classes for classification head. Default: 1000
embed_dim (int): Patch embedding dimension. Default: 96
depths (tuple(int)): Depth of each Swin Transformer layer.
num_heads (tuple(int)): Number of attention heads in different layers.
window_size (int): Window size. Default: 7
mlp_ratio (float): Ratio of mlp hidden dim to embedding dim. Default: 4
qkv_bias (bool): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float): Override default qk scale of head_dim ** -0.5 if set. Default: None
drop_rate (float): Dropout rate. Default: 0
attn_drop_rate (float): Attention dropout rate. Default: 0
drop_path_rate (float): Stochastic depth rate. Default: 0.1
norm_layer (nn.Module): Normalization layer. Default: nn.LayerNorm.
ape (bool): If True, add absolute position embedding to the patch embedding. Default: False
patch_norm (bool): If True, add normalization after patch embedding. Default: True
use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False
"""
def __init__(self, img_size=224, patch_size=4, in_chans=3, num_classes=1000,
embed_dim=96, depths=[2, 2, 6, 2], num_heads=[3, 6, 12, 24],
window_size=7, mlp_ratio=4., qkv_bias=True, qk_scale=None,
drop_rate=0., attn_drop_rate=0., drop_path_rate=0.1,
norm_layer=nn.LayerNorm, ape=False, patch_norm=True,
use_checkpoint=False, **kwargs):
super().__init__()
self.num_classes = num_classes
self.num_layers = len(depths)
self.embed_dim = embed_dim
self.ape = ape
self.patch_norm = patch_norm
self.num_features = int(embed_dim * 2 ** (self.num_layers - 1))
self.mlp_ratio = mlp_ratio
# split image into non-overlapping patches
self.patch_embed = PatchEmbed(
img_size=img_size, patch_size=patch_size, in_chans=in_chans, embed_dim=embed_dim,
norm_layer=norm_layer if self.patch_norm else None)
num_patches = self.patch_embed.num_patches
patches_resolution = self.patch_embed.patches_resolution
self.patches_resolution = patches_resolution
# absolute position embedding
if self.ape:
self.absolute_pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dim))
trunc_normal_(self.absolute_pos_embed, std=.02)
self.pos_drop = nn.Dropout(p=drop_rate)
# stochastic depth
dpr = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))] # stochastic depth decay rule
# build layers
self.layers = nn.ModuleList()
for i_layer in range(self.num_layers):
layer = BasicLayer(dim=int(embed_dim * 2 ** i_layer),
input_resolution=(patches_resolution[0] // (2 ** i_layer),
patches_resolution[1] // (2 ** i_layer)),
depth=depths[i_layer],
num_heads=num_heads[i_layer],
window_size=window_size,
mlp_ratio=self.mlp_ratio,
qkv_bias=qkv_bias, qk_scale=qk_scale,
drop=drop_rate, attn_drop=attn_drop_rate,
drop_path=dpr[sum(depths[:i_layer]):sum(depths[:i_layer + 1])],
norm_layer=norm_layer,
downsample=PatchMerging if (i_layer < self.num_layers - 1) else None,
use_checkpoint=use_checkpoint)
self.layers.append(layer)
self.norm = norm_layer(self.num_features)
self.avgpool = nn.AdaptiveAvgPool1d(1)
self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()
self.apply(self._init_weights)
def _init_weights(self, m):
if isinstance(m, nn.Linear):
trunc_normal_(m.weight, std=.02)
if isinstance(m, nn.Linear) and m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.LayerNorm):
nn.init.constant_(m.bias, 0)
nn.init.constant_(m.weight, 1.0)
@torch.jit.ignore
def no_weight_decay(self):
return {'absolute_pos_embed'}
@torch.jit.ignore
def no_weight_decay_keywords(self):
return {'relative_position_bias_table'}
def forward_features(self, x):
x = self.patch_embed(x)
if self.ape:
x = x + self.absolute_pos_embed
x = self.pos_drop(x)
for layer in self.layers:
x = layer(x)
x = self.norm(x) # B L C
x = self.avgpool(x.transpose(1, 2)) # B C 1
x = torch.flatten(x, 1)
return x
def forward(self, x):
x = self.forward_features(x)
x = self.head(x)
return x
def flops(self):
flops = 0
flops += self.patch_embed.flops()
for i, layer in enumerate(self.layers):
flops += layer.flops()
flops += self.num_features * self.patches_resolution[0] * self.patches_resolution[1] // (2 ** self.num_layers)
flops += self.num_features * self.num_classes
return flops
```
| true |
code
| 0.842992 | null | null | null | null |
|
# Validation
This notebook contains examples of some of the simulations that have been used to validate Disimpy's functionality by comparing the simulated signals to analytical solutions and signals generated by other simulators. Here, we simulate free diffusion and restricted diffusion inside cylinders and spheres.
```
# Import the required packages and modules
import os
import pickle
import numpy as np
import matplotlib.pyplot as plt
from disimpy import gradients, simulations, substrates, utils
from disimpy.gradients import GAMMA
# Define the simulation parameters
n_walkers = int(1e6) # Number of random walkers
n_t = int(1e3) # Number of time points
diffusivity = 2e-9 # In SI units (m^2/s)
```
## Free diffusion
In the case of free diffusion, the analytical expression for the signal is $S = S_0 \exp(-bD)$, where $S_0$ is the signal without diffusion-weighting, $b$ is the b-value, and $D$ is the diffusivity.
```
# Create a Stejskal-Tanner gradient array with ∆ = 40 ms and δ = 30 ms
T = 70e-3
gradient = np.zeros((1, 700, 3))
gradient[0, 1:300, 0] = 1
gradient[0, -300:-1, 0] = -1
bs = np.linspace(1, 3e9, 100)
gradient = np.concatenate([gradient for _ in bs], axis=0)
dt = T / (gradient.shape[1] - 1)
gradient, dt = gradients.interpolate_gradient(gradient, dt, n_t)
gradient = gradients.set_b(gradient, dt, bs)
# Show the waveform of the measurement with the highest b-value
fig, ax = plt.subplots(1, figsize=(7, 4))
for i in range(3):
ax.plot(np.linspace(0, T, n_t), gradient[-1, :, i])
ax.legend(['G$_x$', 'G$_y$', 'G$_z$'])
ax.set_xlabel('Time (s)')
ax.set_ylabel('Gradient magnitude (T/m)')
plt.show()
# Run the simulation
substrate = substrates.free()
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, substrate)
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.plot(bs, np.exp(-bs * diffusivity), color='tab:orange')
ax.scatter(bs, signals / n_walkers, s=10, marker='o')
ax.legend(['Analytical signal', 'Simulated signal'])
ax.set_xlabel('b (ms/μm$^2$)')
ax.set_ylabel('S/S$_0$')
ax.set_yscale('log')
plt.show()
```
## Restricted diffusion and comparison to MISST
Here, diffusion inside cylinders and spheres is simulated and the signals are compared to those calculated with [MISST](http://mig.cs.ucl.ac.uk/index.php?n=Tutorial.MISST) that uses matrix operators to calculate the time evolution of the diffusion signal inside simple geometries. The cylinder is simulated using a triangular mesh and the sphere as an analytically defined surface.
```
# Load and show the cylinder mesh used in the simulations
mesh_path = os.path.join(
os.path.dirname(simulations.__file__), 'tests', 'cylinder_mesh_closed.pkl')
with open(mesh_path, 'rb') as f:
example_mesh = pickle.load(f)
faces = example_mesh['faces']
vertices = example_mesh['vertices']
cylinder_substrate = substrates.mesh(
vertices, faces, periodic=True, init_pos='intra')
utils.show_mesh(cylinder_substrate)
# Run the simulation
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, cylinder_substrate)
# Load MISST signals
tests_dir = os.path.join(os.path.dirname(gradients.__file__), 'tests')
misst_signals = np.loadtxt(os.path.join(tests_dir,
'misst_cylinder_signal_smalldelta_30ms_bigdelta_40ms_radius_5um.txt'))
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.scatter(bs, signals / n_walkers, s=10, marker='o')
ax.scatter(bs, misst_signals, s=10, marker='.')
ax.set_xlabel('b (ms/μm$^2$)')
ax.set_ylabel('S/S$_0$')
ax.legend(['Disimpy', 'MISST'])
ax.set_title('Diffusion in a cylinder')
ax.set_yscale('log')
plt.show()
# Run the simulation
sphere_substrate = substrates.sphere(5e-6)
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, sphere_substrate)
# Load MISST signals
tests_dir = os.path.join(os.path.dirname(gradients.__file__), 'tests')
misst_signals = np.loadtxt(os.path.join(tests_dir,
'misst_sphere_signal_smalldelta_30ms_bigdelta_40ms_radius_5um.txt'))
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.scatter(bs, signals / n_walkers, s=10, marker='o')
ax.scatter(bs, misst_signals, s=10, marker='.')
ax.set_xlabel('b (ms/μm$^2$)')
ax.set_ylabel('S/S$_0$')
ax.legend(['Disimpy', 'MISST'])
ax.set_title('Diffusion in a sphere')
ax.set_yscale('log')
plt.show()
```
## Signal diffraction pattern
In the case of restricted diffusion in a cylinder perpendicular to the direction of the diffusion encoding gradient with short pulses and long diffusion time, the signal minimum occurs at $0.61 · 2 · \pi/r$, where $r$ is the cylinder radius. Details are provided by [Avram et al](https://doi.org/10.1002/nbm.1277), for example.
```
# Create a Stejskal-Tanner gradient array with ∆ = 0.5 s and δ = 0.1 ms
T = 501e-3
gradient = np.zeros((1, n_t, 3))
gradient[0, 1:2, 0] = 1
gradient[0, -2:-1, 0] = -1
dt = T / (gradient.shape[1] - 1)
bs = np.linspace(1, 1e11, 250)
gradient = np.concatenate([gradient for _ in bs], axis=0)
gradient = gradients.set_b(gradient, dt, bs)
q = gradients.calc_q(gradient, dt)
qs = np.max(np.linalg.norm(q, axis=2), axis=1)
# Show the waveform of the measurement with the highest b-value
fig, ax = plt.subplots(1, figsize=(7, 4))
for i in range(3):
ax.plot(np.linspace(0, T, n_t), gradient[-1, :, i])
ax.legend(['G$_x$', 'G$_y$', 'G$_z$'])
ax.set_xlabel('Time (s)')
ax.set_ylabel('Gradient magnitude (T/m)')
plt.show()
# Run the simulation
radius = 10e-6
substrate = substrates.cylinder(
radius=radius, orientation=np.array([0., 0., 1.]))
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, substrate)
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.scatter(1e-6 * qs, signals / n_walkers, s=10, marker='o')
minimum = 1e-6 * .61 * 2 * np.pi / radius
ax.plot([minimum, minimum], [0, 1], ls='--', lw=2, color='tab:orange')
ax.legend(['Analytical minimum', 'Simulated signal'])
ax.set_xlabel('q (μm$^{-1}$)')
ax.set_ylabel('S/S$_0$')
ax.set_yscale('log')
ax.set_ylim([1e-4, 1])
ax.set_xlim([0, max(1e-6 * qs)])
plt.show()
```
| true |
code
| 0.775435 | null | null | null | null |
|
## Basic core
This module contains all the basic functions we need in other modules of the fastai library (split with [`torch_core`](/torch_core.html#torch_core) that contains the ones requiring pytorch). Its documentation can easily be skipped at a first read, unless you want to know what a given function does.
```
from fastai.gen_doc.nbdoc import *
from fastai.core import *
```
## Global constants
`default_cpus = min(16, num_cpus())` <div style="text-align: right"><a href="https://github.com/fastai/fastai/blob/master/fastai/core.py#L45">[source]</a></div>
## Check functions
```
show_doc(has_arg)
```
Examples for two [`fastai.core`](/core.html#core) functions. Docstring shown before calling [`has_arg`](/core.html#has_arg) for reference
```
has_arg(download_url,'url')
has_arg(index_row,'x')
has_arg(index_row,'a')
show_doc(ifnone)
param,alt_param = None,5
ifnone(param,alt_param)
param,alt_param = None,[1,2,3]
ifnone(param,alt_param)
show_doc(is1d)
two_d_array = np.arange(12).reshape(6,2)
print( two_d_array )
print( is1d(two_d_array) )
is1d(two_d_array.flatten())
show_doc(is_listy)
```
Check if `x` is a `Collection`. `Tuple` or `List` qualify
```
some_data = [1,2,3]
is_listy(some_data)
some_data = (1,2,3)
is_listy(some_data)
some_data = 1024
print( is_listy(some_data) )
print( is_listy( [some_data] ) )
some_data = dict([('a',1),('b',2),('c',3)])
print( some_data )
print( some_data.keys() )
print( is_listy(some_data) )
print( is_listy(some_data.keys()) )
print( is_listy(list(some_data.keys())) )
show_doc(is_tuple)
```
Check if `x` is a `tuple`.
```
print( is_tuple( [1,2,3] ) )
print( is_tuple( (1,2,3) ) )
```
## Collection related functions
```
show_doc(arange_of)
arange_of([5,6,7])
type(arange_of([5,6,7]))
show_doc(array)
array([1,2,3])
```
Note that after we call the generator, we do not reset. So the [`array`](/core.html#array) call has 5 less entries than it would if we ran from the start of the generator.
```
def data_gen():
i = 100.01
while i<200:
yield i
i += 1.
ex_data_gen = data_gen()
for _ in range(5):
print(next(ex_data_gen))
array(ex_data_gen)
ex_data_gen_int = data_gen()
array(ex_data_gen_int,dtype=int) #Cast output to int array
show_doc(arrays_split)
data_a = np.arange(15)
data_b = np.arange(15)[::-1]
mask_a = (data_a > 10)
print(data_a)
print(data_b)
print(mask_a)
arrays_split(mask_a,data_a)
np.vstack([data_a,data_b]).transpose().shape
arrays_split(mask_a,np.vstack([data_a,data_b]).transpose()) #must match on dimension 0
show_doc(chunks)
```
You can transform a `Collection` into an `Iterable` of 'n' sized chunks by calling [`chunks`](/core.html#chunks):
```
data = [0,1,2,3,4,5,6,7,8,9]
for chunk in chunks(data, 2):
print(chunk)
for chunk in chunks(data, 3):
print(chunk)
show_doc(df_names_to_idx)
ex_df = pd.DataFrame.from_dict({"a":[1,1,1],"b":[2,2,2]})
print(ex_df)
df_names_to_idx('b',ex_df)
show_doc(extract_kwargs)
key_word_args = {"a":2,"some_list":[1,2,3],"param":'mean'}
key_word_args
(extracted_val,remainder) = extract_kwargs(['param'],key_word_args)
print( extracted_val,remainder )
show_doc(idx_dict)
idx_dict(['a','b','c'])
show_doc(index_row)
data = [0,1,2,3,4,5,6,7,8,9]
index_row(data,4)
index_row(pd.Series(data),7)
data_df = pd.DataFrame([data[::-1],data]).transpose()
data_df
index_row(data_df,7)
show_doc(listify)
to_match = np.arange(12)
listify('a',to_match)
listify('a',5)
listify(77.1,3)
listify( (1,2,3) )
listify((1,2,3),('a','b','c'))
show_doc(random_split)
```
Splitting is done here with `random.uniform()` so you may not get the exact split percentage for small data sets
```
data = np.arange(20).reshape(10,2)
data.tolist()
random_split(0.20,data.tolist())
random_split(0.20,pd.DataFrame(data))
show_doc(range_of)
range_of([5,4,3])
range_of(np.arange(10)[::-1])
show_doc(series2cat)
data_df = pd.DataFrame.from_dict({"a":[1,1,1,2,2,2],"b":['f','e','f','g','g','g']})
data_df
data_df['b']
series2cat(data_df,'b')
data_df['b']
series2cat(data_df,'a')
data_df['a']
show_doc(split_kwargs_by_func)
key_word_args = {'url':'http://fast.ai','dest':'./','new_var':[1,2,3],'testvalue':42}
split_kwargs_by_func(key_word_args,download_url)
show_doc(to_int)
to_int(3.1415)
data = [1.2,3.4,7.25]
to_int(data)
show_doc(uniqueify)
uniqueify( pd.Series(data=['a','a','b','b','f','g']) )
```
## Files management and downloads
```
show_doc(download_url)
show_doc(find_classes)
show_doc(join_path)
show_doc(join_paths)
show_doc(loadtxt_str)
show_doc(save_texts)
```
## Multiprocessing
```
show_doc(num_cpus)
show_doc(parallel)
show_doc(partition)
show_doc(partition_by_cores)
```
## Data block API
```
show_doc(ItemBase, title_level=3)
```
All items used in fastai should subclass this. Must have a [`data`](/tabular.data.html#tabular.data) field that will be used when collating in mini-batches.
```
show_doc(ItemBase.apply_tfms)
show_doc(ItemBase.show)
```
The default behavior is to set the string representation of this object as title of `ax`.
```
show_doc(Category, title_level=3)
```
Create a [`Category`](/core.html#Category) with an `obj` of index [`data`](/tabular.data.html#tabular.data) in a certain classes list.
```
show_doc(EmptyLabel, title_level=3)
show_doc(MultiCategory, title_level=3)
```
Create a [`MultiCategory`](/core.html#MultiCategory) with an `obj` that is a collection of labels. [`data`](/tabular.data.html#tabular.data) corresponds to the one-hot encoded labels and `raw` is a list of associated string.
```
show_doc(FloatItem)
```
## Others
```
show_doc(camel2snake)
camel2snake('DeviceDataLoader')
show_doc(even_mults)
```
In linear scales each element is equidistant from its neighbors:
```
# from 1 to 10 in 5 steps
t = np.linspace(1, 10, 5)
t
for i in range(len(t) - 1):
print(t[i+1] - t[i])
```
In logarithmic scales, each element is a multiple of the previous entry:
```
t = even_mults(1, 10, 5)
t
# notice how each number is a multiple of its predecessor
for i in range(len(t) - 1):
print(t[i+1] / t[i])
show_doc(func_args)
func_args(download_url)
```
Additionally, [`func_args`](/core.html#func_args) can be used with functions that do not belong to the fastai library
```
func_args(np.linspace)
show_doc(noop)
```
Return `x`.
```
# object is returned as-is
noop([1,2,3])
show_doc(one_hot)
```
One-hot encoding is a standard machine learning technique. Assume we are dealing with a 10-class classification problem and we are supplied a list of labels:
```
y = [1, 4, 4, 5, 7, 9, 2, 4, 0]
jekyll_note("""y is zero-indexed, therefore its first element (1) belongs to class 2, its second element (4) to class 5 and so on.""")
len(y)
```
y can equivalently be expressed as a matrix of 9 rows and 10 columns, where each row represents one element of the original y.
```
for label in y:
print(one_hot(label, 10))
show_doc(show_some)
# select 3 elements from a list
some_data = show_some([10, 20, 30, 40, 50], 3)
some_data
type(some_data)
# the separator can be changed
some_data = show_some([10, 20, 30, 40, 50], 3, sep = '---')
some_data
some_data[:-3]
```
[`show_some`](/core.html#show_some) can take as input any class with \_\_len\_\_ and \_\_getitem\_\_
```
class Any(object):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self,i):
return self.data[i]
some_other_data = Any('nice')
show_some(some_other_data, 2)
show_doc(subplots)
show_doc(text2html_table)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
```
show_doc(is_dict)
```
| true |
code
| 0.200753 | null | null | null | null |
|
# Stochastic Volatility model
## Imports & Settings
```
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
import seaborn as sns
import pymc3 as pm
from pymc3.distributions.timeseries import GaussianRandomWalk
sns.set_style('whitegrid')
# model_path = Path('models')
```
## Model assumptions
Asset prices have time-varying volatility (variance of day over day `returns`). In some periods, returns are highly variable, while in others very stable. Stochastic volatility models model this with a latent volatility variable, modeled as a stochastic process. The following model is similar to the one described in the No-U-Turn Sampler paper, Hoffman (2011) p21.
$$\begin{align*}
\sigma &\sim \text{Exponential}(50)\\
\nu &\sim \text{Exponential}(.1)\\
s_i &\sim \text{Normal}(s_{i-1}, \sigma^{-2})\\
\log(r_i) &\sim t(\nu, 0, \exp(-2 s_i))
\end{align*}$$
Here, $r$ is the daily return series and $s$ is the latent log volatility process.
## Get Return Data
First we load some daily returns of the S&P 500.
```
prices = pd.read_hdf('../data/assets.h5', key='sp500/stooq').loc['2000':, 'close']
log_returns = np.log(prices).diff().dropna()
ax = log_returns.plot(figsize=(15, 4),
title='S&P 500 | Daily Log Returns',
rot=0)
ax.yaxis.set_major_formatter(FuncFormatter(lambda y, _: '{:.0%}'.format(y)))
sns.despine()
plt.tight_layout();
```
As you can see, the volatility seems to change over time quite a bit while clustering around certain time-periods, most notably the 2009 financial crash.
## Specify Model in PyMC3
Specifying the model in `PyMC3` mirrors its statistical specification.
```
with pm.Model() as model:
step_size = pm.Exponential('sigma', 50.)
s = GaussianRandomWalk('s', sd=step_size,
shape=len(log_returns))
nu = pm.Exponential('nu', .1)
r = pm.StudentT('r', nu=nu,
lam=pm.math.exp(-2*s),
observed=log_returns)
pm.model_to_graphviz(model)
```
## Fit Model
For this model, the full maximum a posteriori (MAP) point is degenerate and has infinite density. NUTS, however, gives the correct posterior.
```
with model:
trace = pm.sample(tune=2000,
draws=5000,
chains=4,
cores=1,
target_accept=.9)
```
Optionally, persist result as pickle:
```
# with open('model_vol.pkl', 'wb') as buff:
# pickle.dump({'model': model, 'trace': trace}, buff)
```
## Evaluate results
### Trace Plot
```
pm.traceplot(trace, varnames=['sigma', 'nu']);
```
Looking at the returns over time and overlaying the estimated standard deviation we can see how the model tracks the volatility over time.
### In-Sample Predictions
```
pm.trace_to_dataframe(trace).info()
fig, ax = plt.subplots(figsize=(15, 5))
log_returns.plot(ax=ax, lw=.5, xlim=('2000', '2020'), rot=0,
title='In-Sample Fit of Stochastic Volatility Model')
ax.plot(log_returns.index, np.exp(trace[s]).T, 'r', alpha=.03, lw=.5);
ax.set(xlabel='Time', ylabel='Returns')
ax.legend(['S&P 500 (log returns)', 'Stochastic Volatility Model'])
ax.yaxis.set_major_formatter(FuncFormatter(lambda y, _: '{:.0%}'.format(y)))
sns.despine()
fig.tight_layout();
```
| true |
code
| 0.698432 | null | null | null | null |
|
# Метод сопряжённых градиентов (Conjugate gradient method): гадкий утёнок
## На прошлом занятии...
1. Методы спуска
2. Направление убывания
3. Градиентный метод
4. Правила выбора шага
5. Теоремы сходимости
6. Эксперименты
## Система линейных уравнений vs. задача безусловной минимизации
Рассмотрим задачу
$$
\min_{x \in \mathbb{R}^n} \frac{1}{2}x^{\top}Ax - b^{\top}x,
$$
где $A \in \mathbb{S}^n_{++}$.
Из необходимого условия экстремума имеем
$$
Ax^* = b
$$
Также обозначим $f'(x_k) = Ax_k - b = r_k$
## Как решить систему $Ax = b$?
- Прямые методы основаны на матричных разложениях:
- Плотная матрица $A$: для размерностей не больше нескольких тысяч
- Разреженная (sparse) матрица $A$: для размерностей порядка $10^4 - 10^5$
- Итерационные методы: хороши во многих случаях, единственный подход для задач с размерностью $ > 10^6$
## Немного истории...
M. Hestenes и E. Stiefel предложили *метод сопряжённых градиентов* для решения систем линейных уравнений в 1952 году как **прямой** метод.
Также долгое время считалось, что метод представляет только теоретический интерес поскольку
- метод сопряжённых градиентов не работает на логарифмической линейке
- метод сопряжённых градиентов имеет небольшое преимущество перед исключением Гаусса при вычислениях на калькуляторе
- для вычислений на "human computers" слишком много обменов данными
<img src="./human_computer.jpeg">
Метод сопряжённых градиентов необходимо рассматривать как **итерационный метод**, то есть останавливаться до точной сходимости!
Подробнее [здесь](https://www.siam.org/meetings/la09/talks/oleary.pdf)
## Метод сопряжённых направлений
В градиентном спуске направления убывания - анти-градиенты, но для функций с плохо обусловленным гессианом сходимость **медленная**.
**Идея:** двигаться вдоль направлений, которые гарантируют сходимость за $n$ шагов.
**Определение.** Множество ненулевых векторов $\{p_0, \ldots, p_l\}$ называется *сопряжённым* относительно матрицы $A \in \mathbb{S}^n_{++}$, если
$$
p^{\top}_iAp_j = 0, \qquad i \neq j
$$
**Утверждение.** Для любой $x_0 \in \mathbb{R}^n$ последовательность $\{x_k\}$, генерируемая методом сопряжённых направлений, сходится к решению системы $Ax = b$ максимум за $n$ шагов.
```python
def ConjugateDirections(x0, A, b, p):
x = x0
r = A.dot(x) - b
for i in range(len(p)):
alpha = - (r.dot(p[i])) / (p[i].dot(A.dot(p[i])))
x = x + alpha * p[i]
r = A.dot(x) - b
return x
```
### Примеры сопряжённых направлений
- Собственные векторы матрицы $A$
- Для любого набора из $n$ векторов можно провести аналог ортогонализации Грама-Шмидта и получить сопряжённые направления
**Вопрос:** что такое ортогонализация Грама-Шмидта? :)
### Геометрическая интерпретация (Mathematics Stack Exchange)
<center><img src="./cg.png" ></center>
## Метод сопряжённых градиентов
**Идея:** новое направление $p_k$ ищется в виде $p_k = -r_k + \beta_k p_{k-1}$, где $\beta_k$ выбирается, исходя из требования сопряжённости $p_k$ и $p_{k-1}$:
$$
\beta_k = \dfrac{p^{\top}_{k-1}Ar_k}{p^{\top}_{k-1}Ap_{k-1}}
$$
Таким образом, для получения следующего сопряжённого направления $p_k$ необходимо хранить только сопряжённое направление $p_{k-1}$ и остаток $r_k$ с предыдущей итерации.
**Вопрос:** как находить размер шага $\alpha_k$?
## Сопряжённость сопряжённых градиентов
**Теорема**
Пусть после $k$ итераций $x_k \neq x^*$. Тогда
- $\langle r_k, r_i \rangle = 0, \; i = 1, \ldots k - 1$
- $\mathtt{span}(r_0, \ldots, r_k) = \mathtt{span}(r_0, Ar_0, \ldots, A^kr_0)$
- $\mathtt{span}(p_0, \ldots, p_k) = \mathtt{span}(r_0, Ar_0, \ldots, A^kr_0)$
- $p_k^{\top}Ap_i = 0$, $i = 1,\ldots,k-1$
### Теоремы сходимости
**Теорема 1.** Если матрица $A$ имеет только $r$ различных собственных значений, то метод сопряжённых градиентов cойдётся за $r$ итераций.
**Теорема 2.** Имеет место следующая оценка сходимости
$$
\| x_{k} - x^* \|_A \leq 2\left( \dfrac{\sqrt{\kappa(A)} - 1}{\sqrt{\kappa(A)} + 1} \right)^k \|x_0 - x^*\|_A,
$$
где $\|x\|_A = x^{\top}Ax$ и $\kappa(A) = \frac{\lambda_1(A)}{\lambda_n(A)}$ - число обусловленности матрицы $A$, $\lambda_1(A) \geq ... \geq \lambda_n(A)$ - собственные значения матрицы $A$
**Замечание:** сравните коэффициент геометрической прогрессии с аналогом в градиентном спуске.
### Интерпретации метода сопряжённых градиентов
- Градиентный спуск в пространстве $y = Sx$, где $S = [p_0, \ldots, p_n]$, в котором матрица $A$ становится диагональной (или единичной в случае ортонормированности сопряжённых направлений)
- Поиск оптимального решения в [Крыловском подпространстве](https://stanford.edu/class/ee364b/lectures/conj_grad_slides.pdf) $\mathcal{K}_k(A) = \{b, Ab, A^2b, \ldots A^{k-1}b\}$
$$
x_k = \arg\min_{x \in \mathcal{K}_k} f(x)
$$
- Однако естественный базис Крыловского пространства неортогональный и, более того, **плохо обусловлен**.
**Упражнение** Проверьте численно, насколько быстро растёт обусловленность матрицы из векторов $\{b, Ab, ... \}$
- Поэтому его необходимо ортогонализовать, что и происходит в методе сопряжённых градиентов
### Основное свойство
$$
A^{-1}b \in \mathcal{K}_n(A)
$$
Доказательство
- Теорема Гамильтона-Кэли: $p(A) = 0$, где $p(\lambda) = \det(A - \lambda I)$
- $p(A)b = A^nb + a_1A^{n-1}b + \ldots + a_{n-1}Ab + a_n b = 0$
- $A^{-1}p(A)b = A^{n-1}b + a_1A^{n-2}b + \ldots + a_{n-1}b + a_nA^{-1}b = 0$
- $A^{-1}b = -\frac{1}{a_n}(A^{n-1}b + a_1A^{n-2}b + \ldots + a_{n-1}b)$
### Сходимость по функции и по аргументу
- Решение: $x^* = A^{-1}b$
- Минимум функции:
$$
f^* = \frac{1}{2}b^{\top}A^{-\top}AA^{-1}b - b^{\top}A^{-1}b = -\frac{1}{2}b^{\top}A^{-1}b = -\frac{1}{2}\|x^*\|^2_A
$$
- Оценка сходимости по функции:
$$
f(x) - f^* = \frac{1}{2}x^{\top}Ax - b^{\top}x + \frac{1}{2}\|x^*\|_A^2 =\frac{1}{2}\|x\|_A^2 - x^{\top}Ax^* + \frac{1}{2}\|x^*\|_A^2 = \frac{1}{2}\|x - x^*\|_A^2
$$
### Доказательство сходимости
- $x_k$ лежит в $\mathcal{K}_k$
- $x_k = \sum\limits_{i=1}^k c_i A^{i-1}b = p(A)b$, где $p(x)$ некоторый полином степени не выше $k-1$
- $x_k$ минимизирует $f$ на $\mathcal{K}_k$, отсюда
$$
2(f_k - f^*) = \inf_{x \in \mathcal{K}_k} \|x - x^* \|^2_A = \inf_{\mathrm{deg}(p) < k} \|(p(A) - A^{-1})b\|^2_A
$$
- Спектральное разложение $A = U\Lambda U^*$ даёт
$$
2(f_k - f^*) = \inf_{\mathrm{deg}(p) < k} \|(p(\Lambda) - \Lambda^{-1})d\|^2_{\Lambda} = \inf_{\mathrm{deg}(p) < k} \sum_{i=1}^n\frac{d_i^2 (\lambda_ip(\lambda_i) - 1)^2}{\lambda_i} = \inf_{\mathrm{deg}(q) \leq k, q(0) = 1} \sum_{i=1}^n\frac{d_i^2 q(\lambda_i)^2}{\lambda_i}
$$
- Сведём задачу к поиску некоторого многочлена
$$
f_k - f^* \leq \left(\sum_{i=1}^n \frac{d_i^2}{2\lambda_i}\right) \inf_{\mathrm{deg}(q) \leq k, q(0) = 1}\left(\max_{i=1,\ldots,n} q(\lambda_i)^2 \right) = \frac{1}{2}\|x^*\|^2_A \inf_{\mathrm{deg}(q) \leq k, q(0) = 1}\left(\max_{i=1,\ldots,n} q(\lambda_i)^2 \right)
$$
- Пусть $A$ имеет $m$ различных собственных значений, тогда для
$$
r(y) = \frac{(-1)^m}{\lambda_1 \cdot \ldots \cdot \lambda_m}(y - \lambda_i)\cdot \ldots \cdot (y - \lambda_m)
$$
выполнено $\mathrm{deg}(r) = m$ и $r(0) = 1$
- Значение для оптимального полинома степени не выше $k$ оценим сверху значением для полинома $r$ степени $m$
$$
0 \leq f_k - f^* \leq \frac{1}{2}\|x^*\|_A^2 \max_{i=1,\ldots,m} r(\lambda_i) = 0
$$
- Метод сопряжённых градиентов сошёлся за $m$ итераций
### Улучшенная версия метода сопряжённых градиентов
На практике используются следующие формулы для шага $\alpha_k$ и коэффициента $\beta_{k}$:
$$
\alpha_k = \dfrac{r^{\top}_k r_k}{p^{\top}_{k}Ap_{k}} \qquad \beta_k = \dfrac{r^{\top}_k r_k}{r^{\top}_{k-1} r_{k-1}}
$$
**Вопрос:** чем они лучше базовой версии?
### Псевдокод метода сопряжённых градиентов
```python
def ConjugateGradientQuadratic(x0, A, b, eps):
r = A.dot(x0) - b
p = -r
while np.linalg.norm(r) > eps:
alpha = r.dot(r) / p.dot(A.dot(p))
x = x + alpha * p
r_next = r + alpha * A.dot(p)
beta = r_next.dot(r_next) / r.dot(r)
p = -r_next + beta * p
r = r_next
return x
```
## Метод сопряжённых градиентов для неквадратичной функции
**Идея:** использовать градиенты $f'(x_k)$ неквадратичной функции вместо остатков $r_k$ и линейный поиск шага $\alpha_k$ вместо аналитического вычисления. Получим метод Флетчера-Ривса.
```python
def ConjugateGradientFR(f, gradf, x0, eps):
x = x0
grad = gradf(x)
p = -grad
while np.linalg.norm(gradf(x)) > eps:
alpha = StepSearch(x, f, gradf, **kwargs)
x = x + alpha * p
grad_next = gradf(x)
beta = grad_next.dot(grad_next) / grad.dot(grad)
p = -grad_next + beta * p
grad = grad_next
if restart_condition:
p = -gradf(x)
return x
```
### Теорема сходимости
**Теорема.** Пусть
- множество уровней $\mathcal{L}$ ограничено
- существует $\gamma > 0$: $\| f'(x) \|_2 \leq \gamma$ для $x \in \mathcal{L}$
Тогда
$$
\lim_{j \to \infty} \| f'(x_{k_j}) \|_2 = 0
$$
### Перезапуск (restart)
1. Для ускорения метода сопряжённых градиентов используют технику перезапусков: удаление ранее накопленной истории и перезапуск метода с текущей точки, как будто это точка $x_0$
2. Существуют разные условия, сигнализирующие о том, что надо делать перезапуск, например
- $k = n$
- $\dfrac{|\langle f'(x_k), f'(x_{k-1}) \rangle |}{\| f'(x_k) \|_2^2} \geq \nu \approx 0.1$
3. Можно показать (см. Nocedal, Wright Numerical Optimization, Ch. 5, p. 125), что запуск метода Флетчера-Ривза без использования перезапусков на некоторых итерациях может приводить к крайне медленной сходимости!
4. Метод Полака-Рибьера и его модификации лишены подобного недостатка.
### Комментарии
- Замечательная методичка "An Introduction to the Conjugate Gradient Method Without the Agonizing Pain" размещена [тут](https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf)
- Помимо метода Флетчера-Ривса существуют другие способы вычисления $\beta_k$: метод Полака-Рибьера, метод Хестенса-Штифеля...
- Для метода сопряжённых градиентов требуется 4 вектора: каких?
- Самой дорогой операцией является умножение матрицы на вектор
## Эксперименты
### Квадратичная целевая функция
```
import numpy as np
n = 100
# Random
A = np.random.randn(n, n)
A = A.T.dot(A)
# Clustered eigenvalues
# A = np.diagflat([np.ones(n//4), 10 * np.ones(n//4), 100*np.ones(n//4), 1000* np.ones(n//4)])
# U = np.random.rand(n, n)
# Q, _ = np.linalg.qr(U)
# A = Q.dot(A).dot(Q.T)
# A = (A + A.T) * 0.5
print("A is normal matrix: ||AA* - A*A|| =", np.linalg.norm(A.dot(A.T) - A.T.dot(A)))
b = np.random.randn(n)
# Hilbert matrix
# A = np.array([[1.0 / (i+j - 1) for i in range(1, n+1)] for j in range(1, n+1)]) + 1e-3 * np.eye(n)
# b = np.ones(n)
f = lambda x: 0.5 * x.dot(A.dot(x)) - b.dot(x)
grad_f = lambda x: A.dot(x) - b
x0 = np.zeros(n)
```
#### Распределение собственных значений
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.rc("text", usetex=True)
plt.rc("font", family='serif')
import seaborn as sns
sns.set_context("talk")
eigs = np.linalg.eigvalsh(A)
cond_A = np.linalg.cond(A)
print((np.sqrt(cond_A) - 1) / (np.sqrt(cond_A) + 1))
print((cond_A - 1) / (cond_A + 1))
plt.semilogy(np.unique(eigs))
plt.ylabel("Eigenvalues", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
```
#### Правильный ответ
```
import scipy.optimize as scopt
def callback(x, array):
array.append(x)
scopt_cg_array = []
scopt_cg_callback = lambda x: callback(x, scopt_cg_array)
x = scopt.minimize(f, x0, method="CG", jac=grad_f, callback=scopt_cg_callback)
x = x.x
print("||f'(x*)|| =", np.linalg.norm(A.dot(x) - b))
print("f* =", f(x))
```
#### Реализация метода сопряжённых градиентов
```
def ConjugateGradientQuadratic(x0, A, b, tol=1e-8, callback=None):
x = x0
r = A.dot(x0) - b
p = -r
while np.linalg.norm(r) > tol:
alpha = r.dot(r) / p.dot(A.dot(p))
x = x + alpha * p
if callback is not None:
callback(x)
r_next = r + alpha * A.dot(p)
beta = r_next.dot(r_next) / r.dot(r)
p = -r_next + beta * p
r = r_next
return x
import liboptpy.unconstr_solvers as methods
import liboptpy.step_size as ss
print("\t CG quadratic")
cg_quad = methods.fo.ConjugateGradientQuad(A, b)
x_cg = cg_quad.solve(x0, max_iter=1000, tol=1e-7, disp=True)
print("\t Gradient Descent")
gd = methods.fo.GradientDescent(f, grad_f, ss.ExactLineSearch4Quad(A, b))
x_gd = gd.solve(x0, tol=1e-7, disp=True)
print("Condition number of A =", abs(max(eigs)) / abs(min(eigs)))
```
#### График сходимости
```
plt.figure(figsize=(8,6))
plt.semilogy([np.linalg.norm(grad_f(x)) for x in cg_quad.get_convergence()], label=r"$\|f'(x_k)\|^{CG}_2$", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in scopt_cg_array[:5000]], label=r"$\|f'(x_k)\|^{CG_{PR}}_2$", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in gd.get_convergence()], label=r"$\|f'(x_k)\|^{G}_2$", linewidth=2)
plt.legend(loc="best", fontsize=20)
plt.xlabel(r"Iteration number, $k$", fontsize=20)
plt.ylabel("Convergence rate", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
print([np.linalg.norm(grad_f(x)) for x in cg_quad.get_convergence()])
plt.figure(figsize=(8,6))
plt.plot([f(x) for x in cg_quad.get_convergence()], label=r"$f(x^{CG}_k)$", linewidth=2)
plt.plot([f(x) for x in scopt_cg_array], label=r"$f(x^{CG_{PR}}_k)$", linewidth=2)
plt.plot([f(x) for x in gd.get_convergence()], label=r"$f(x^{G}_k)$", linewidth=2)
plt.legend(loc="best", fontsize=20)
plt.xlabel(r"Iteration number, $k$", fontsize=20)
plt.ylabel("Function value", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
```
### Неквадратичная функция
```
import numpy as np
import sklearn.datasets as skldata
import scipy.special as scspec
n = 300
m = 1000
X, y = skldata.make_classification(n_classes=2, n_features=n, n_samples=m, n_informative=n//3)
C = 1
def f(w):
return np.linalg.norm(w)**2 / 2 + C * np.mean(np.logaddexp(np.zeros(X.shape[0]), -y * X.dot(w)))
def grad_f(w):
denom = scspec.expit(-y * X.dot(w))
return w - C * X.T.dot(y * denom) / X.shape[0]
# f = lambda x: -np.sum(np.log(1 - A.T.dot(x))) - np.sum(np.log(1 - x*x))
# grad_f = lambda x: np.sum(A.dot(np.diagflat(1 / (1 - A.T.dot(x)))), axis=1) + 2 * x / (1 - np.power(x, 2))
x0 = np.zeros(n)
print("Initial function value = {}".format(f(x0)))
print("Initial gradient norm = {}".format(np.linalg.norm(grad_f(x0))))
```
#### Реализация метода Флетчера-Ривса
```
def ConjugateGradientFR(f, gradf, x0, num_iter=100, tol=1e-8, callback=None, restart=False):
x = x0
grad = gradf(x)
p = -grad
it = 0
while np.linalg.norm(gradf(x)) > tol and it < num_iter:
alpha = utils.backtracking(x, p, method="Wolfe", beta1=0.1, beta2=0.4, rho=0.5, f=f, grad_f=gradf)
if alpha < 1e-18:
break
x = x + alpha * p
if callback is not None:
callback(x)
grad_next = gradf(x)
beta = grad_next.dot(grad_next) / grad.dot(grad)
p = -grad_next + beta * p
grad = grad_next.copy()
it += 1
if restart and it % restart == 0:
grad = gradf(x)
p = -grad
return x
```
#### График сходимости
```
import scipy.optimize as scopt
import liboptpy.restarts as restarts
n_restart = 60
tol = 1e-5
max_iter = 600
scopt_cg_array = []
scopt_cg_callback = lambda x: callback(x, scopt_cg_array)
x = scopt.minimize(f, x0, tol=tol, method="CG", jac=grad_f, callback=scopt_cg_callback, options={"maxiter": max_iter})
x = x.x
print("\t CG by Polak-Rebiere")
print("Norm of garient = {}".format(np.linalg.norm(grad_f(x))))
print("Function value = {}".format(f(x)))
print("\t CG by Fletcher-Reeves")
cg_fr = methods.fo.ConjugateGradientFR(f, grad_f, ss.Backtracking("Wolfe", rho=0.9, beta1=0.1, beta2=0.4, init_alpha=1.))
x = cg_fr.solve(x0, tol=tol, max_iter=max_iter, disp=True)
print("\t CG by Fletcher-Reeves with restart n")
cg_fr_rest = methods.fo.ConjugateGradientFR(f, grad_f, ss.Backtracking("Wolfe", rho=0.9, beta1=0.1, beta2=0.4,
init_alpha=1.), restarts.Restart(n // n_restart))
x = cg_fr_rest.solve(x0, tol=tol, max_iter=max_iter, disp=True)
print("\t Gradient Descent")
gd = methods.fo.GradientDescent(f, grad_f, ss.Backtracking("Wolfe", rho=0.9, beta1=0.1, beta2=0.4, init_alpha=1.))
x = gd.solve(x0, max_iter=max_iter, tol=tol, disp=True)
plt.figure(figsize=(8, 6))
plt.semilogy([np.linalg.norm(grad_f(x)) for x in cg_fr.get_convergence()], label=r"$\|f'(x_k)\|^{CG_{FR}}_2$ no restart", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in cg_fr_rest.get_convergence()], label=r"$\|f'(x_k)\|^{CG_{FR}}_2$ restart", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in scopt_cg_array], label=r"$\|f'(x_k)\|^{CG_{PR}}_2$", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in gd.get_convergence()], label=r"$\|f'(x_k)\|^{G}_2$", linewidth=2)
plt.legend(loc="best", fontsize=16)
plt.xlabel(r"Iteration number, $k$", fontsize=20)
plt.ylabel("Convergence rate", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
```
#### Время выполнения
```
%timeit scopt.minimize(f, x0, method="CG", tol=tol, jac=grad_f, options={"maxiter": max_iter})
%timeit cg_fr.solve(x0, tol=tol, max_iter=max_iter)
%timeit cg_fr_rest.solve(x0, tol=tol, max_iter=max_iter)
%timeit gd.solve(x0, tol=tol, max_iter=max_iter)
```
## Резюме
1. Сопряжённые направления
2. Метод сопряжённых градиентов
3. Сходимость
4. Эксперименты
| true |
code
| 0.5047 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plotly.com/python/getting-started/) by downloading the client and [reading the primer](https://plotly.com/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plotly.com/python/getting-started/#initialization-for-online-plotting) or [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plotly.com/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Version Check
Note: Ternary Plots are available in version 1.9.10+
Run pip install plotly --upgrade to update your Plotly version
```
import plotly
plotly.__version__
```
### Basic Ternary Plot with Markers
```
import plotly.plotly as py
import plotly.graph_objs as go
rawData = [
{'journalist':75,'developer':25,'designer':0,'label':'point 1'},
{'journalist':70,'developer':10,'designer':20,'label':'point 2'},
{'journalist':75,'developer':20,'designer':5,'label':'point 3'},
{'journalist':5,'developer':60,'designer':35,'label':'point 4'},
{'journalist':10,'developer':80,'designer':10,'label':'point 5'},
{'journalist':10,'developer':90,'designer':0,'label':'point 6'},
{'journalist':20,'developer':70,'designer':10,'label':'point 7'},
{'journalist':10,'developer':20,'designer':70,'label':'point 8'},
{'journalist':15,'developer':5,'designer':80,'label':'point 9'},
{'journalist':10,'developer':10,'designer':80,'label':'point 10'},
{'journalist':20,'developer':10,'designer':70,'label':'point 11'},
];
def makeAxis(title, tickangle):
return {
'title': title,
'titlefont': { 'size': 20 },
'tickangle': tickangle,
'tickfont': { 'size': 15 },
'tickcolor': 'rgba(0,0,0,0)',
'ticklen': 5,
'showline': True,
'showgrid': True
}
data = [{
'type': 'scatterternary',
'mode': 'markers',
'a': [i for i in map(lambda x: x['journalist'], rawData)],
'b': [i for i in map(lambda x: x['developer'], rawData)],
'c': [i for i in map(lambda x: x['designer'], rawData)],
'text': [i for i in map(lambda x: x['label'], rawData)],
'marker': {
'symbol': 100,
'color': '#DB7365',
'size': 14,
'line': { 'width': 2 }
},
}]
layout = {
'ternary': {
'sum': 100,
'aaxis': makeAxis('Journalist', 0),
'baxis': makeAxis('<br>Developer', 45),
'caxis': makeAxis('<br>Designer', -45)
},
'annotations': [{
'showarrow': False,
'text': 'Simple Ternary Plot with Markers',
'x': 0.5,
'y': 1.3,
'font': { 'size': 15 }
}]
}
fig = {'data': data, 'layout': layout}
py.iplot(fig, validate=False)
```
#### Reference
See https://plotly.com/python/reference/#scatterternary for more information and chart attribute options!
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'ternary.ipynb', 'python/ternary-plots/', 'Python Ternary Plots | plotly',
'How to make Ternary plots in Python with Plotly.',
name = 'Ternary Plots',
thumbnail='thumbnail/ternary.jpg', language='python',
page_type='example_index', has_thumbnail='true', display_as='scientific', order=9,
ipynb= '~notebook_demo/39')
```
| true |
code
| 0.447943 | null | null | null | null |
|
# CPSC 330 hw7
```
import numpy as np
import pandas as pd
### BEGIN SOLUTION
from sklearn.impute import SimpleImputer
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OrdinalEncoder, OneHotEncoder
from sklearn.linear_model import Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
from sklearn.metrics import r2_score
### END SOLUTION
```
## Instructions
rubric={points:5}
Follow the [homework submission instructions](https://github.students.cs.ubc.ca/cpsc330-2019w-t2/home/blob/master/docs/homework_instructions.md).
## Exercise 1: time series prediction
In this exercise we'll be looking at a [dataset of avocado prices](https://www.kaggle.com/neuromusic/avocado-prices). You should start by downloading the dataset. As usual, please do not commit it to your repos.
```
df = pd.read_csv("avocado.csv", parse_dates=["Date"], index_col=0)
df.head()
df.shape
df["Date"].min()
df["Date"].max()
```
It looks like the data ranges from the start of 2015 to March 2018 (~2 years ago), for a total of 3.25 years or so. Let's split the data so that we have a 6 months of test data.
```
split_date = '20170925'
df_train = df[df["Date"] <= split_date]
df_test = df[df["Date"] > split_date]
assert len(df_train) + len(df_test) == len(df)
```
#### 1(a)
rubric={points:3}
In the Rain is Australia dataset from Lecture 16, we had different measurements for each Location. What about this dataset: for which categorical feature(s), if any, do we have separate measurements? Justify your answer by referencing the dataset.
### BEGIN SOLUTION
```
df.sort_values(by="Date").head()
```
From the above, we definitely see measurements on the same day at different regresion. Let's now group by region.
```
df.sort_values(by=["region", "Date"]).head()
```
From the above we see that, even in Albany, we have two measurements on the same date. This seems to be due to the type of avocado.
```
df.sort_values(by=["region", "type", "Date"]).head()
```
Great, now we have a sequence of dates with a single row per date. So, the answer is that we have a separate timeseries for each combination of `region` and `type`.
### END SOLUTION
#### 1(b)
rubric={points:3}
In the Rain in Australia dataset, the measurements were generally equally spaced but with some exceptions. How about with this dataset? Justify your answer by referencing the dataset.
### BEGIN SOLUTION
I think it's not unreasonable to do this on `df` rather than `df_train`, but either way is fine.
```
for name, group in df.groupby(['region', 'type']):
print("%-40s %s" % (name, group["Date"].sort_values().diff().min()))
for name, group in df.groupby(['region', 'type']):
print("%-40s %s" % (name, group["Date"].sort_values().diff().max()))
```
It looks almost perfect - just organic avocados in WestTexNewMexico seems to be missing a couple measurements.
```
name
group["Date"].sort_values().diff().value_counts()
```
So, in one case there's a 2-week jump, and in one cast there's a 3-week jump.
```
group["Date"].sort_values().reset_index(drop=True).diff().sort_values()
```
We can see the anomalies occur at index 48 and 127. (Note: I had to `reset_index` because the index was not unique to each row.)
```
group["Date"].sort_values().reset_index(drop=True)[45:50]
```
We can spot the first anomaly: a 2-week jump from Nov 29, 2015 to Dec 13, 2015.
```
group["Date"].sort_values().reset_index(drop=True)[125:130]
```
And we can spot the second anomaly: a 3-week jump from June 11, 2017 to July 2, 2017.
### END SOLUTION
#### 1(c)
rubric={points:1}
In the Rain is Australia dataset, each location was a different place in Australia. For this dataset, look at the names of the regions. Do you think the regions are also all distinct, or are there overlapping regions? Justify your answer by referencing the data.
### BEGIN SOLUTION
```
df["region"].unique()
```
There seems to be a hierarchical structure here: `TotalUS` is split into bigger regions like `West`, `Southeast`, `Northeast`, `Midsouth`; and `California` is split into cities like `Sacramento`, `SanDiego`, `LosAngeles`. It's a bit hard to figure out what's going on.
```
df.query("region == 'TotalUS' and type == 'conventional' and Date == '20150104'")["Total Volume"].values[0]
df.query("region != 'TotalUS' and type == 'conventional' and Date == '20150104'")["Total Volume"].sum()
```
Since the individual regions sum up to more than the total US, it seems that some of the other regions are double-counted, which is consistent with a hierarchical structure. For example, Los Angeles is probalby double counted because it's within `LosAngeles` but also within `California`. What a mess!
### END SOLUTION
We will use the entire dataset despite any location-based weirdness uncovered in the previous part.
We will be trying to forecast the avocado price, which is the `AveragePrice` column. The function below is adapted from Lecture 16, with some improvements.
```
def create_lag_feature(df, orig_feature, lag, groupby, new_feature_name=None, clip=False):
"""
Creates a new feature that's a lagged version of an existing one.
NOTE: assumes df is already sorted by the time columns and has unique indices.
Parameters
----------
df : pandas.core.frame.DataFrame
The dataset.
orig_feature : str
The column name of the feature we're copying
lag : int
The lag; negative lag means values from the past, positive lag means values from the future
groupby : list
Column(s) to group by in case df contains multiple time series
new_feature_name : str
Override the default name of the newly created column
clip : bool
If True, remove rows with a NaN values for the new feature
Returns
-------
pandas.core.frame.DataFrame
A new dataframe with the additional column added.
"""
if new_feature_name is None:
if lag < 0:
new_feature_name = "%s_lag%d" % (orig_feature, -lag)
else:
new_feature_name = "%s_ahead%d" % (orig_feature, lag)
new_df = df.assign(**{new_feature_name : np.nan})
for name, group in new_df.groupby(groupby):
if lag < 0: # take values from the past
new_df.loc[group.index[-lag:],new_feature_name] = group.iloc[:lag][orig_feature].values
else: # take values from the future
new_df.loc[group.index[:-lag], new_feature_name] = group.iloc[lag:][orig_feature].values
if clip:
new_df = new_df.dropna(subset=[new_feature_name])
return new_df
```
We first sort our dataframe properly:
```
df_sort = df.sort_values(by=["region", "type", "Date"]).reset_index(drop=True)
df_sort
```
We then call `create_lag_feature`. This creates a new column in the dataset `AveragePriceNextWeek`, which is the following week's `AveragePrice`. We have set `clip=True` which means it will remove rows where the target would be missing.
```
df_hastarget = create_lag_feature(df_sort, "AveragePrice", +1, ["region", "type"], "AveragePriceNextWeek", clip=True)
df_hastarget
```
I will now split the data:
```
df_train = df_hastarget[df_hastarget["Date"] <= split_date]
df_test = df_hastarget[df_hastarget["Date"] > split_date]
```
#### 1(d)
rubric={points:1}
Why was it reasonable for me to do this operation _before_ splitting the data, despite the fact that this usually constitutes a violation of the Golden Rule?
### BEGIN SOLUTION
Because we were only looking at the dates and creating the future feature. The difference is that the very last time point in our training set now contains the average price from the first time point in our test set. This is a realistic scenario if we wre actually using this model to forecast, so it's not a major concern.
### END SOLUTION
#### 1(e)
rubric={points:1}
Next we will want to build some models to forecast the average avocado price a week in advance. Before we start with any ML, let's try a baseline: just predicting the previous week's `AveragePrice`. What $R^2$ do you get with this approach?
### BEGIN SOLUTION
```
r2_score(df_train["AveragePriceNextWeek"], df_train["AveragePrice"])
r2_score(df_test["AveragePriceNextWeek"], df_test["AveragePrice"])
```
Interesting that this is a less effective prediction strategy in the later part of the dataset. I guess that means the price was fluctuating more in late 2017 / early 2018?
### END SOLUTION
#### 1(f)
rubric={points:10}
Build some models to forecast the average avocado price. Experiment with a few approachs for encoding the date. Justify the decisions you make. Which approach worked best? Report your test score and briefly discuss your results.
Benchmark: you should be able to achieve $R^2$ of at least 0.79 on the test set. I got to 0.80, but not beyond that. Let me know if you do better!
Note: because we only have 2 splits here, we need to be a bit wary of overfitting on the test set. Try not to test on it a ridiculous number of times. If you are interested in some proper ways of dealing with this, see for example sklearn's [TimeSeriesSplit](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.TimeSeriesSplit.html), which is like cross-validation for time series data.
### BEGIN SOLUTION
```
df_train.head()
(df_train.loc[:, "Small Bags": "XLarge Bags"].sum(axis=1) - df_train["Total Bags"]).abs().max()
```
It seems that `Total Bags` is (approximately) the sum of the other 3 bag features, so I will drop `Total Bags`.
```
(df_train.loc[:, "4046": "4770"].sum(axis=1) - df_train["Total Volume"]).abs().max()
```
It seems that `Total Volume` is _not_ the sum of the 3 avocado types, so I will keep all 4 columns.
```
df_train.info()
```
It seems there are no null values, so I will not do any imputation.
Will plot a single time series for exploration purposes:
```
df_train.query("region == 'TotalUS'").set_index("Date").groupby("type")["AveragePrice"].plot(legend=True);
df_train.query("region == 'TotalUS' and type == 'conventional'").plot(x="Date", y="Total Volume");
```
We see some seasonality in the total volume, but not much in the average price - interesting.
I will not scale the `AveragePrice` because I am not scaling `AveragePriceNextWeek` either, and it may be helpful to keep them the same. Alternatively, it may have been effective to predict the _change_ in price instead of next's week's price.
```
numeric_features = ["Total Volume", "4046", "4225", "4770", "Small Bags", "Large Bags", "XLarge Bags", "year"]
categorical_features = ["type", "region"]
keep_features = ["AveragePrice"]
drop_features = ["Date", "Total Bags"]
target_feature = "AveragePriceNextWeek"
```
Next, I grab the `preprocess_features` function from Lecture 16, with a minor modification to allow un-transformed features via `keep_features`:
```
def preprocess_features(df_train, df_test,
numeric_features,
categorical_features,
keep_features,
drop_features,
target_feature):
all_features = numeric_features + categorical_features + keep_features + drop_features + [target_feature]
if set(df_train.columns) != set(all_features):
print("Missing columns", set(df_train.columns) - set(all_features))
print("Extra columns", set(all_features) - set(df_train.columns))
raise Exception("Columns do not match")
# Put the columns in the order we want
df_train = df_train[all_features]
df_test = df_test[all_features]
numeric_transformer = Pipeline([
('imputer', SimpleImputer(strategy='median')),
('scaler', StandardScaler())
])
categorical_transformer = Pipeline([
('imputer', SimpleImputer(strategy='most_frequent')),
('onehot', OneHotEncoder(sparse=False, drop='first'))
])
preprocessor = ColumnTransformer([
('numeric', numeric_transformer, numeric_features),
('categorical', categorical_transformer, categorical_features)
], remainder='passthrough')
preprocessor.fit(df_train);
if len(categorical_features) > 0:
ohe = preprocessor.named_transformers_['categorical'].named_steps['onehot']
ohe_feature_names = list(ohe.get_feature_names(categorical_features))
new_columns = numeric_features + ohe_feature_names + keep_features + drop_features + [target_feature]
else:
new_columns = all_features
X_train_enc = pd.DataFrame(preprocessor.transform(df_train), index=df_train.index, columns=new_columns)
X_test_enc = pd.DataFrame(preprocessor.transform(df_test), index=df_test.index, columns=new_columns)
X_train_enc = X_train_enc.drop(columns=drop_features + [target_feature])
X_test_enc = X_test_enc.drop( columns=drop_features + [target_feature])
y_train = df_train[target_feature]
y_test = df_test[ target_feature]
return X_train_enc, y_train, X_test_enc, y_test
df_train_enc, y_train, df_test_enc, y_test = preprocess_features(df_train, df_test,
numeric_features,
categorical_features,
keep_features,
drop_features,
target_feature)
df_train_enc.head()
lr = Ridge()
lr.fit(df_train_enc, y_train);
lr.score(df_train_enc, y_train)
lr.score(df_test_enc, y_test)
lr_coef = pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_enc.columns, columns=["Coef"])
lr_coef.sort_values(by="Coef", ascending=False)
```
This is not a very impressive showing. We're doing almost the same as the baseline.
Let's see if encoding the date helps at all. We'll try to OHE the month.
```
df_train_month = df_train.assign(Month=df_train["Date"].apply(lambda x: x.month))
df_test_month = df_test.assign( Month=df_test[ "Date"].apply(lambda x: x.month))
df_train_month_enc, y_train, df_test_month_enc, y_test = preprocess_features(df_train_month, df_test_month,
numeric_features,
categorical_features + ["Month"],
keep_features,
drop_features,
target_feature)
df_train_month_enc.head()
lr = Ridge()
lr.fit(df_train_month_enc, y_train);
lr.score(df_train_month_enc, y_train)
lr.score(df_test_month_enc, y_test)
```
A tiny bit better.
```
pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_month_enc.columns, columns=["Coef"]).sort_values(by="Coef", ascending=False)
```
Let's add some lag features. I'm arbitrarily deciding on 4 lags for `AveragePrice` (the most important feature).
```
def add_lags(df):
df = create_lag_feature(df, "AveragePrice", -1, ["region", "type"])
df = create_lag_feature(df, "AveragePrice", -2, ["region", "type"])
df = create_lag_feature(df, "AveragePrice", -3, ["region", "type"])
df = create_lag_feature(df, "AveragePrice", -4, ["region", "type"])
return df
df_train_month_lag = add_lags(df_train_month)
df_test_month_lag = add_lags(df_test_month)
df_train_month_lag
df_train_month_lag_enc, y_train, df_test_month_lag_enc, y_test = preprocess_features(df_train_month_lag, df_test_month_lag,
numeric_features + ["AveragePrice_lag1", "AveragePrice_lag2", "AveragePrice_lag3", "AveragePrice_lag4"],
categorical_features + ["Month"],
keep_features,
drop_features,
target_feature)
lr = Ridge()
lr.fit(df_train_month_lag_enc, y_train);
lr.score(df_train_month_lag_enc, y_train)
lr.score(df_test_month_lag_enc, y_test)
```
This did not seem to help.
```
pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_month_lag_enc.columns, columns=["Coef"]).sort_values(by="Coef", ascending=False)
```
We can also try a random forest:
```
rf = RandomForestRegressor()
rf.fit(df_train_month_lag_enc, y_train);
rf.score(df_train_month_lag_enc, y_train)
rf.score(df_test_month_lag_enc, y_test)
```
For the random forest it may be helpful to model the difference between today and tomorrow. The linear model does not care about this because it just corresponds to changing the coefficient corresponding to `AveragePrice` by 1, but for the random forest it may help:
```
rf = RandomForestRegressor()
rf.fit(df_train_month_lag_enc, y_train - df_train_month_lag_enc["AveragePrice"]);
r2_score(y_train, rf.predict(df_train_month_lag_enc) + df_train_month_lag_enc["AveragePrice"])
r2_score(y_test, rf.predict(df_test_month_lag_enc) + df_test_month_lag_enc["AveragePrice"])
```
This massively overfits when we do this shifting. Let's try a simpler model...
```
rf = RandomForestRegressor(max_depth=8)
rf.fit(df_train_month_lag_enc, y_train - df_train_month_lag_enc["AveragePrice"]);
r2_score(y_train, rf.predict(df_train_month_lag_enc) + df_train_month_lag_enc["AveragePrice"])
r2_score(y_test, rf.predict(df_test_month_lag_enc) + df_test_month_lag_enc["AveragePrice"])
```
Doesn't realy help.
Also, we can just confirm that this shifting has no effect on the linear model (well, a small effect because it's `Ridge` instead of `LinearRegression`, but small):
```
lr = Ridge()
lr.fit(df_train_month_lag_enc, y_train - df_train_month_lag_enc["AveragePrice"]);
r2_score(y_train, lr.predict(df_train_month_lag_enc) + df_train_month_lag_enc["AveragePrice"])
r2_score(y_test, lr.predict(df_test_month_lag_enc) + df_test_month_lag_enc["AveragePrice"])
```
Indeed, this is essentially the same score we had before.
Overall, adding the month helped, but adding the lagged price was surprisingly unhelpful. Perhaps lagged version of other features would have been better, or other representations of the time of year, or dealing with the regions and avocado types a bit more carefully.
### END SOLUTION
#### 1(g)
rubric={points:3}
We talked a little bit about _seasonality_, which is the idea of a periodic component to the time series. For example, in Lecture 16 we attempted to capture this by encoding the month. Something we didn't discuss is _trends_, which are long-term variations in the quantity of interest. Aside from the effects of climate change, the amount of rain in Australia is likely to vary during the year but less likely to have long-term trends over the years. Avocado prices, on the other hand, could easily exhibit trends: for example avocados may just cost more in 2020 than they did in 2015.
Briefly discuss in ~1 paragraph: to what extent, if any, was your model above able to account for seasonality? What about trends?
### BEGIN SOLUTION
I tried to take seasonality into account by having the month as an OHE variable. As far as trends are concerned, the year is also a numeric variable in the model, so it could learn that the price in 2017 is higher than in 2015, say. However, there are very few years in the training set (2015, 16, 17), so that is not a lot of data to learn from. Perhaps including the number of months since the start of the dataset, or something like that, would enable the model to do a bit better with trends. Nonetheless, extrapolating is very hard so we can't necessarily trust our models' handing of trend.
```
pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_month_lag_enc.columns, columns=["Coef"]).loc["year"]
```
It seems that our linear model learned a small positive trend for the year. It would be cool to use SHAP and see what the random forest is doing.
### END SOLUTION
## Exercise 2: very short answer questions
Each question is worth 2 points.
#### 2(a)
rubric={points:4}
The following questions pertain to Lecture 16 on time series data:
1. Sometimes a time series has missing time points or, worse, time points that are unequally spaced in general. Give an example of a real world situation where the time series data would have unequally spaced time points.
2. In class we discussed two approaches to using temporal information: encoding the date as one or more features, and creating lagged versions of features. Which of these (one/other/both/neither) two approaches would struggle with unequally spaced time points? Briefly justify your answer.
### BEGIN SOLUTION
1. Many many examples: credit card transactions, log files, basically any situation where the frequency of the measurements could not be chosen by the person taking the measurements.
2. Encoding the date as, e.g. OHE month works just fine with unequally spaced points. However, the lag features are more problematic, because the "previous" measurement will be a different length of time away in each case.
### END SOLUTION
#### 2(b)
rubric={points:10}
The following questions pertain to Lecture 17 on survival analysis. We'll consider the use case of customer churn analysis.
1. What is the problem with simply labeling customers are "churned" or "not churned" and using standard supervised learning techniques, as we did in hw4?
2. Consider customer A who just joined last week vs. customer B who has been with the service for a year. Who do you expect will leave the service first: probably customer A, probably customer B, or we don't have enough information to answer? (This is a bit tricky - it's OK if you don't know the answer, but try to argue your case.)
3. One of the true/false questions from class was: "If a customer is censored after 5 months with the service, then all customers are censored after 5 months (i.e. no values of `tenure` above 5)." What is the answer if all customers joined the service at the same time? Briefly explain.
4. One of the true/false questions from class was: "If a customer is censored after 5 months with the service, then all customers are censored after 5 months (i.e. no values of `tenure` above 5)." What is the answer if customers did not necessarily join the service at the same time? Briefly explain.
5. If a customer's survival function is almost flat during a certain period, how do we interpret that?
### BEGIN SOLUTION
1. The "not churned" are censored - we don't know if they will churn shortly or in a long time. These people have the same label and our model will be impacted negatively.
2. Not enough information - it depends! Imagine a subscription service where you have to pay a starter fee after a month and then pay a huge fee after a year. Well, customer B just paid that huge fee and will probably stay a while, whereas customer A may leave before paying the huge fee, so customer A will probably leave first. But imagine a service where people are more and more likely to leave every day, e.g. a movie service with only 100 movies, so you can run out easily. In that case customer B will probably leave first.
3. True. If all started at the same time, and a customer is censored after 5 months, that means they all started 5 months ago and are all censored after 5 months.
4. False. That particular customer started 5 months ago, but you may have another customer who started much longer ago.
5. The customer is very unlikely to leave during that period.
### END SOLUTION
#### 2(c)
rubric={points:10}
The following questions pertain to Lecture 18 on clustering.
1. What's the main difference between unsupervised and supervised learning?
2. When choosing $k$ in $k$-means, why not just choose the $k$ that leads to the smallest inertia (sum of squared distances within clusters)?
3. You decide to use clustering for _outlier detection_; that is, to detect instances that are very atypical compared to all the rest. How might you do this with $k$-means?
4. You decide to use clustering for _outlier detection_; that is, to detect instances that are very atypical compared to all the rest. How might you do this with DBSCAN?
5. For hierarchical clustering, we briefly discussed a few different methods for merging clusters: single linkage, average linkage, etc. Why do we have this added complication here - can't we just minimize distance like we did with $k$-means?
### BEGIN SOLUTION
1. Supervised has target values ($y$), unsupervised does not.
2. Because inertia decreases with $k$, so you'd just choose $k=n$, which is not interesting.
3. Look for examples that are very far away from their cluster mean.
4. Look for examples that were not assigned to any cluster.
5. With $k$-means we had to find the distance between a point and a cluster mean. Here, we need to find the distance between two clusters, and, importantly, we have no cluster means. So it's ambiguous how to definite distance between two clusters.
### END SOLUTION
| true |
code
| 0.646209 | null | null | null | null |
|
# Gated PixelCNN receptive fields
Hi everybody!
In this notebook, we will analyse the Gated PixelCNN's block receptive field. Diferent of the original PixelCNN, we expect that the blocks of the Gated PixelCNN do not create blind spots that limit the information flow of the previous pixel in order to model the density probability function.
Let's start!
First, we define the masked convolutions involved in the Gated PixelCNN as presented in the post.
*Note: Here we are using float64 to get more precise values of the gradients and avoid false values.
```
import random as rn
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import FixedLocator
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow import nn
from tensorflow.keras import initializers
from tensorflow.keras.utils import Progbar
tf.keras.backend.set_floatx('float64')
class MaskedConv2D(keras.layers.Layer):
"""Convolutional layers with masks extended to work with Gated PixelCNN.
Convolutional layers with simple implementation of masks type A and B for
autoregressive models. Extended version to work with the verticala and horizontal
stacks from the Gated PixelCNN model.
Arguments:
mask_type: one of `"V"`, `"A"` or `"B".`
filters: Integer, the dimensionality of the output space (i.e. the number of output
filters in the convolution).
kernel_size: An integer or tuple/list of 2 integers, specifying the height and width
of the 2D convolution window.
Can be a single integer to specify the same value for all spatial dimensions.
strides: An integer or tuple/list of 2 integers, specifying the strides of the
convolution along the height and width.
Can be a single integer to specify the same value for all spatial dimensions.
Specifying any stride value != 1 is incompatible with specifying any
`dilation_rate` value != 1.
padding: one of `"valid"` or `"same"` (case-insensitive).
kernel_initializer: Initializer for the `kernel` weights matrix.
bias_initializer: Initializer for the bias vector.
"""
def __init__(self,
mask_type,
filters,
kernel_size,
strides=1,
padding='same',
kernel_initializer='glorot_uniform',
bias_initializer='zeros'):
super(MaskedConv2D, self).__init__()
assert mask_type in {'A', 'B', 'V'}
self.mask_type = mask_type
self.filters = filters
if isinstance(kernel_size, int):
kernel_size = (kernel_size, kernel_size)
self.kernel_size = kernel_size
self.strides = strides
self.padding = padding.upper()
self.kernel_initializer = initializers.get(kernel_initializer)
self.bias_initializer = initializers.get(bias_initializer)
def build(self, input_shape):
kernel_h, kernel_w = self.kernel_size
self.kernel = self.add_weight('kernel',
shape=(kernel_h,
kernel_w,
int(input_shape[-1]),
self.filters),
initializer=self.kernel_initializer,
trainable=True)
self.bias = self.add_weight('bias',
shape=(self.filters,),
initializer=self.bias_initializer,
trainable=True)
mask = np.ones(self.kernel.shape, dtype=np.float64)
# Get centre of the filter for even or odd dimensions
if kernel_h % 2 != 0:
center_h = kernel_h // 2
else:
center_h = (kernel_h - 1) // 2
if kernel_w % 2 != 0:
center_w = kernel_w // 2
else:
center_w = (kernel_w - 1) // 2
if self.mask_type == 'V':
mask[center_h + 1:, :, :, :] = 0.
else:
mask[:center_h, :, :] = 0.
mask[center_h, center_w + (self.mask_type == 'B'):, :, :] = 0.
mask[center_h + 1:, :, :] = 0.
self.mask = tf.constant(mask, dtype=tf.float64, name='mask')
def call(self, input):
masked_kernel = tf.math.multiply(self.mask, self.kernel)
x = nn.conv2d(input,
masked_kernel,
strides=[1, self.strides, self.strides, 1],
padding=self.padding)
x = nn.bias_add(x, self.bias)
return x
```
Then, we define th eblock implementation.
```
class GatedBlock(tf.keras.Model):
""" Gated block that compose Gated PixelCNN."""
def __init__(self, mask_type, filters, kernel_size):
super(GatedBlock, self).__init__(name='')
self.mask_type = mask_type
self.vertical_conv = MaskedConv2D(mask_type='V',
filters=2 * filters,
kernel_size=kernel_size)
self.horizontal_conv = MaskedConv2D(mask_type=mask_type,
filters=2 * filters,
kernel_size=(1, kernel_size))
self.padding = keras.layers.ZeroPadding2D(padding=((1, 0), 0))
self.cropping = keras.layers.Cropping2D(cropping=((0, 1), 0))
self.v_to_h_conv = keras.layers.Conv2D(filters=2 * filters, kernel_size=1)
self.horizontal_output = keras.layers.Conv2D(filters=filters, kernel_size=1)
def _gate(self, x):
tanh_preactivation, sigmoid_preactivation = tf.split(x, 2, axis=-1)
return tf.nn.tanh(tanh_preactivation) * tf.nn.sigmoid(sigmoid_preactivation)
def call(self, input_tensor):
v = input_tensor[0]
h = input_tensor[1]
vertical_preactivation = self.vertical_conv(v)
# Shifting vertical stack feature map down before feed into horizontal stack to
# ensure causality
v_to_h = self.padding(vertical_preactivation)
v_to_h = self.cropping(v_to_h)
v_to_h = self.v_to_h_conv(v_to_h)
horizontal_preactivation = self.horizontal_conv(h)
v_out = self._gate(vertical_preactivation)
horizontal_preactivation = horizontal_preactivation + v_to_h
h_activated = self._gate(horizontal_preactivation)
h_activated = self.horizontal_output(h_activated)
if self.mask_type == 'A':
h_out = h_activated
elif self.mask_type == 'B':
h_out = h + h_activated
return v_out, h_out
```
In order to analyse grow the receptive field grows along the layers, we will start analysing 1 block.
```
height = 10
width = 10
n_channel = 1
data = tf.random.normal((1, height, width, n_channel))
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
model = tf.keras.Model(inputs=inputs, outputs=h)
def plot_receptive_field(model, data):
with tf.GradientTape() as tape:
tape.watch(data)
prediction = model(data)
loss = prediction[:,5,5,0]
gradients = tape.gradient(loss, data)
gradients = np.abs(gradients.numpy().squeeze())
gradients = (gradients > 0).astype('float64')
gradients[5, 5] = 0.5
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
plt.xticks(np.arange(0, 10, step=1))
plt.yticks(np.arange(0, 10, step=1))
ax.xaxis.set_minor_locator(FixedLocator(np.arange(0.5, 10.5, step=1)))
ax.yaxis.set_minor_locator(FixedLocator(np.arange(0.5, 10.5, step=1)))
plt.grid(which="minor")
plt.imshow(gradients, vmin=0, vmax=1)
plt.show()
plot_receptive_field(model, data)
```
Excellent! Like we expected the block considered all the previous blocks in the same row of the analyssed pixel, and the two rows over it.
Note that this receptive field is different from the original PixelCNN. In the original PixelCNN only one row over the analysed pixel influenced in its prediction (when using one masked convolution). In the Gated PixelCNN, the authors used a vertical stack with effective area of 2x3 per vertical convolution. This is not a problem, since the considered pixels still being the ones in past positions. We believe the main coice for this format is to implement an efficient way to apply the masked convolutions without using masking (which we will discuss in future posts).
For the next step, we wll verify a model with 2, 3, 4, and 5 layers
```
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
```
As you can notice, the Gated PixelCNN does not create blind spots when adding more and more layers.
| true |
code
| 0.810441 | null | null | null | null |
|
<img src='https://certificate.tpq.io/quantsdev_banner_color.png' width="250px" align="right">
# Reinforcement Learning
© Dr Yves J Hilpisch | The Python Quants GmbH
[quants@dev Discord Server](https://discord.gg/uJPtp9Awaj) | [@quants_dev](https://twitter.com/quants_dev) | <a href="mailto:[email protected]">[email protected]</a>
<img src="https://hilpisch.com/aiif_cover_shadow.png" width="300px" align="left">
## Imports
```
import os
import math
import random
import numpy as np
import pandas as pd
from pylab import plt, mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
np.set_printoptions(precision=4, suppress=True)
os.environ['PYTHONHASHSEED'] = '0'
%config InlineBackend.figure_format = 'svg'
import warnings as w
w.simplefilter('ignore')
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '4'
import tensorflow as tf
from tensorflow import keras
from keras.layers import Dense, Dropout
from keras.models import Sequential
from sklearn.metrics import accuracy_score
from tensorflow.python.framework.ops import disable_eager_execution
disable_eager_execution()
def set_seeds(seed=100):
random.seed(seed)
np.random.seed(seed)
tf.random.set_seed(seed)
env.seed(seed)
env.action_space.seed(100)
```
## Improved Finance Environment
```
class observation_space:
def __init__(self, n):
self.shape = (n,)
class action_space:
def __init__(self, n):
self.n = n
def seed(self, seed):
pass
def sample(self):
return random.randint(0, self.n - 1)
class Finance:
url = 'http://hilpisch.com/aiif_eikon_eod_data.csv'
def __init__(self, symbol, features, window, lags,
leverage=1, min_performance=0.85,
start=0, end=None, mu=None, std=None):
self.symbol = symbol
self.features = features
self.n_features = len(features)
self.window = window
self.lags = lags
self.leverage = leverage
self.min_performance = min_performance
self.start = start
self.end = end
self.mu = mu
self.std = std
self.observation_space = observation_space(self.lags)
self.action_space = action_space(2)
self._get_data()
self._prepare_data()
def _get_data(self):
self.raw = pd.read_csv(self.url, index_col=0,
parse_dates=True).dropna()
def _prepare_data(self):
self.data = pd.DataFrame(self.raw[self.symbol])
self.data = self.data.iloc[self.start:]
self.data['r'] = np.log(self.data / self.data.shift(1))
self.data.dropna(inplace=True)
self.data['s'] = self.data[self.symbol].rolling(
self.window).mean()
self.data['m'] = self.data['r'].rolling(self.window).mean()
self.data['v'] = self.data['r'].rolling(self.window).std()
self.data.dropna(inplace=True)
if self.mu is None:
self.mu = self.data.mean()
self.std = self.data.std()
self.data_ = (self.data - self.mu) / self.std
self.data_['d'] = np.where(self.data['r'] > 0, 1, 0)
self.data_['d'] = self.data_['d'].astype(int)
if self.end is not None:
self.data = self.data.iloc[:self.end - self.start]
self.data_ = self.data_.iloc[:self.end - self.start]
def _get_state(self):
return self.data_[self.features].iloc[self.bar -
self.lags:self.bar]
def seed(self, seed):
random.seed(seed)
np.random.seed(seed)
def reset(self):
self.treward = 0
self.accuracy = 0
self.performance = 1
self.bar = self.lags
state = self.data_[self.features].iloc[self.bar-
self.lags:self.bar]
return state.values
def step(self, action):
correct = action == self.data_['d'].iloc[self.bar]
ret = self.data['r'].iloc[self.bar] * self.leverage
reward_1 = 1 if correct else 0
reward_2 = abs(ret) if correct else -abs(ret)
self.treward += reward_1
self.bar += 1
self.accuracy = self.treward / (self.bar - self.lags)
self.performance *= math.exp(reward_2)
if self.bar >= len(self.data):
done = True
elif reward_1 == 1:
done = False
elif (self.performance < self.min_performance and
self.bar > self.lags + 15):
done = True
else:
done = False
state = self._get_state()
info = {}
return state.values, reward_1 + reward_2 * 252, done, info
env = Finance('EUR=', ['EUR=', 'r', 'v'], window=10, lags=5)
a = env.action_space.sample()
a
env.reset()
env.step(a)
```
## Improved Financial QL Agent
```
from collections import deque
class FQLAgent:
def __init__(self, hidden_units, learning_rate, learn_env, valid_env, dropout=True):
self.learn_env = learn_env
self.valid_env = valid_env
self.dropout = dropout
self.epsilon = 1.0
self.epsilon_min = 0.1
self.epsilon_decay = 0.98
self.learning_rate = learning_rate
self.gamma = 0.95
self.batch_size = 128
self.max_treward = 0
self.trewards = list()
self.averages = list()
self.performances = list()
self.aperformances = list()
self.vperformances = list()
self.memory = deque(maxlen=2000)
self.model = self._build_model(hidden_units, learning_rate)
def _build_model(self, hu, lr):
model = Sequential()
model.add(Dense(hu, input_shape=(
self.learn_env.lags, self.learn_env.n_features),
activation='relu'))
if self.dropout:
model.add(Dropout(0.3, seed=100))
model.add(Dense(hu, activation='relu'))
if self.dropout:
model.add(Dropout(0.3, seed=100))
model.add(Dense(2, activation='linear'))
model.compile(
loss='mse',
optimizer=keras.optimizers.RMSprop(learning_rate=lr)
)
return model
def act(self, state):
if random.random() <= self.epsilon:
return self.learn_env.action_space.sample()
action = self.model.predict(state)[0, 0]
return np.argmax(action)
def replay(self):
batch = random.sample(self.memory, self.batch_size)
for state, action, reward, next_state, done in batch:
if not done:
reward += self.gamma * np.amax(
self.model.predict(next_state)[0, 0])
target = self.model.predict(state)
target[0, 0, action] = reward
self.model.fit(state, target, epochs=1,
verbose=False)
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decay
def learn(self, episodes):
for e in range(1, episodes + 1):
state = self.learn_env.reset()
state = np.reshape(state, [1, self.learn_env.lags,
self.learn_env.n_features])
for _ in range(10000):
action = self.act(state)
next_state, reward, done, info = \
self.learn_env.step(action)
next_state = np.reshape(next_state,
[1, self.learn_env.lags,
self.learn_env.n_features])
self.memory.append([state, action, reward,
next_state, done])
state = next_state
if done:
treward = _ + 1
self.trewards.append(treward)
av = sum(self.trewards[-25:]) / 25
perf = self.learn_env.performance
self.averages.append(av)
self.performances.append(perf)
self.aperformances.append(
sum(self.performances[-25:]) / 25)
self.max_treward = max(self.max_treward, treward)
templ = 'episode: {:2d}/{} | treward: {:4d} | '
templ += 'perf: {:5.3f} | av: {:5.1f} | max: {:4d}'
print(templ.format(e, episodes, treward, perf,
av, self.max_treward), end='\r')
break
self.validate(e, episodes)
if len(self.memory) > self.batch_size:
self.replay()
print()
def validate(self, e, episodes):
state = self.valid_env.reset()
state = np.reshape(state, [1, self.valid_env.lags,
self.valid_env.n_features])
for _ in range(10000):
action = np.argmax(self.model.predict(state)[0, 0])
next_state, reward, done, info = self.valid_env.step(action)
state = np.reshape(next_state, [1, self.valid_env.lags,
self.valid_env.n_features])
if done:
treward = _ + 1
perf = self.valid_env.performance
self.vperformances.append(perf)
if e % 20 == 0:
templ = 71 * '='
templ += '\nepisode: {:2d}/{} | VALIDATION | '
templ += 'treward: {:4d} | perf: {:5.3f} | '
templ += 'eps: {:.2f}\n'
templ += 71 * '='
print(templ.format(e, episodes, treward,
perf, self.epsilon))
break
symbol = 'EUR='
features = ['r', 's', 'm', 'v']
a = 0
b = 2000
c = 500
learn_env = Finance(symbol, features, window=10, lags=6,
leverage=1, min_performance=0.85,
start=a, end=a + b, mu=None, std=None)
learn_env.data.info()
valid_env = Finance(symbol, features, window=learn_env.window,
lags=learn_env.lags, leverage=learn_env.leverage,
min_performance=learn_env.min_performance,
start=a + b, end=a + b + c,
mu=learn_env.mu, std=learn_env.std)
valid_env.data.info()
set_seeds(100)
agent = FQLAgent(48, 0.0001, learn_env, valid_env, True)
episodes = 61
%time agent.learn(episodes)
agent.epsilon
plt.figure(figsize=(10, 6))
x = range(1, len(agent.averages) + 1)
y = np.polyval(np.polyfit(x, agent.averages, deg=3), x)
plt.plot(agent.averages, label='moving average')
plt.plot(x, y, 'r--', label='regression')
plt.xlabel('episodes')
plt.ylabel('total reward')
plt.legend();
plt.figure(figsize=(10, 6))
x = range(1, len(agent.performances) + 1)
y = np.polyval(np.polyfit(x, agent.performances, deg=3), x)
y_ = np.polyval(np.polyfit(x, agent.vperformances, deg=3), x)
plt.plot(agent.performances[:], label='training')
plt.plot(agent.vperformances[:], label='validation')
plt.plot(x, y, 'r--', label='regression (train)')
plt.plot(x, y_, 'r-.', label='regression (valid)')
plt.xlabel('episodes')
plt.ylabel('gross performance')
plt.legend();
```
<img src="https://certificate.tpq.io/quantsdev_banner_color.png" alt="quants@dev" width="35%" align="right" border="0"><br>
[quants@dev Discord Server](https://discord.gg/uJPtp9Awaj) | [@quants_dev](https://twitter.com/quants_dev) | <a href="mailto:[email protected]">[email protected]</a>
| true |
code
| 0.632616 | null | null | null | null |
|
# The importance of constraints
Constraints determine which potential adversarial examples are valid inputs to the model. When determining the efficacy of an attack, constraints are everything. After all, an attack that looks very powerful may just be generating nonsense. Or, perhaps more nefariously, an attack may generate a real-looking example that changes the original label of the input. That's why you should always clearly define the *constraints* your adversarial examples must meet.
[](https://colab.research.google.com/github/QData/TextAttack/blob/master/docs/2notebook/2_Constraints.ipynb)
[](https://github.com/QData/TextAttack/blob/master/docs/2notebook/2_Constraints.ipynb)
### Classes of constraints
TextAttack evaluates constraints using methods from three groups:
- **Overlap constraints** determine if a perturbation is valid based on character-level analysis. For example, some attacks are constrained by edit distance: a perturbation is only valid if it perturbs some small number of characters (or fewer).
- **Grammaticality constraints** filter inputs based on syntactical information. For example, an attack may require that adversarial perturbations do not introduce grammatical errors.
- **Semantic constraints** try to ensure that the perturbation is semantically similar to the original input. For example, we may design a constraint that uses a sentence encoder to encode the original and perturbed inputs, and enforce that the sentence encodings be within some fixed distance of one another. (This is what happens in subclasses of `textattack.constraints.semantics.sentence_encoders`.)
### A new constraint
To add our own constraint, we need to create a subclass of `textattack.constraints.Constraint`. We can implement one of two functions, either `_check_constraint` or `_check_constraint_many`:
- `_check_constraint` determines whether candidate `TokenizedText` `transformed_text`, transformed from `current_text`, fulfills a desired constraint. It returns either `True` or `False`.
- `_check_constraint_many` determines whether each of a list of candidates `transformed_texts` fulfill the constraint relative to `current_text`. This is here in case your constraint can be vectorized. If not, just implement `_check_constraint`, and `_check_constraint` will be executed for each `(transformed_text, current_text)` pair.
### A custom constraint
For fun, we're going to see what happens when we constrain an attack to only allow perturbations that substitute out a named entity for another. In linguistics, a **named entity** is a proper noun, the name of a person, organization, location, product, etc. Named Entity Recognition is a popular NLP task (and one that state-of-the-art models can perform quite well).
### NLTK and Named Entity Recognition
**NLTK**, the Natural Language Toolkit, is a Python package that helps developers write programs that process natural language. NLTK comes with predefined algorithms for lots of linguistic tasks– including Named Entity Recognition.
First, we're going to write a constraint class. In the `_check_constraints` method, we're going to use NLTK to find the named entities in both `current_text` and `transformed_text`. We will only return `True` (that is, our constraint is met) if `transformed_text` has substituted one named entity in `current_text` for another.
Let's import NLTK and download the required modules:
```
import nltk
nltk.download('punkt') # The NLTK tokenizer
nltk.download('maxent_ne_chunker') # NLTK named-entity chunker
nltk.download('words') # NLTK list of words
```
### NLTK NER Example
Here's an example of using NLTK to find the named entities in a sentence:
```
sentence = ('In 2017, star quarterback Tom Brady led the Patriots to the Super Bowl, '
'but lost to the Philadelphia Eagles.')
# 1. Tokenize using the NLTK tokenizer.
tokens = nltk.word_tokenize(sentence)
# 2. Tag parts of speech using the NLTK part-of-speech tagger.
tagged = nltk.pos_tag(tokens)
# 3. Extract entities from tagged sentence.
entities = nltk.chunk.ne_chunk(tagged)
print(entities)
```
It looks like `nltk.chunk.ne_chunk` gives us an `nltk.tree.Tree` object where named entities are also `nltk.tree.Tree` objects within that tree. We can take this a step further and grab the named entities from the tree of entities:
```
# 4. Filter entities to just named entities.
named_entities = [entity for entity in entities if isinstance(entity, nltk.tree.Tree)]
print(named_entities)
```
### Caching with `@functools.lru_cache`
A little-known feature of Python 3 is `functools.lru_cache`, a decorator that allows users to easily cache the results of a function in an LRU cache. We're going to be using the NLTK library quite a bit to tokenize, parse, and detect named entities in sentences. These sentences might repeat themselves. As such, we'll use this decorator to cache named entities so that we don't have to perform this expensive computation multiple times.
### Putting it all together: getting a list of Named Entity Labels from a sentence
Now that we know how to tokenize, parse, and detect named entities using NLTK, let's put it all together into a single helper function. Later, when we implement our constraint, we can query this function to easily get the entity labels from a sentence. We can even use `@functools.lru_cache` to try and speed this process up.
```
import functools
@functools.lru_cache(maxsize=2**14)
def get_entities(sentence):
tokens = nltk.word_tokenize(sentence)
tagged = nltk.pos_tag(tokens)
# Setting `binary=True` makes NLTK return all of the named
# entities tagged as NNP instead of detailed tags like
#'Organization', 'Geo-Political Entity', etc.
entities = nltk.chunk.ne_chunk(tagged, binary=True)
return entities.leaves()
```
And let's test our function to make sure it works:
```
sentence = 'Jack Black starred in the 2003 film classic "School of Rock".'
get_entities(sentence)
```
We flattened the tree of entities, so the return format is a list of `(word, entity type)` tuples. For non-entities, the `entity_type` is just the part of speech of the word. `'NNP'` is the indicator of a named entity (a proper noun, according to NLTK). Looks like we identified three named entities here: 'Jack' and 'Black', 'School', and 'Rock'. as a 'GPE'. (Seems that the labeler thinks Rock is the name of a place, a city or something.) Whatever technique NLTK uses for named entity recognition may be a bit rough, but it did a pretty decent job here!
### Creating our NamedEntityConstraint
Now that we know how to detect named entities using NLTK, let's create our custom constraint.
```
from textattack.constraints import Constraint
class NamedEntityConstraint(Constraint):
""" A constraint that ensures `transformed_text` only substitutes named entities from `current_text` with other named entities.
"""
def _check_constraint(self, transformed_text, current_text):
transformed_entities = get_entities(transformed_text.text)
current_entities = get_entities(current_text.text)
# If there aren't named entities, let's return False (the attack
# will eventually fail).
if len(current_entities) == 0:
return False
if len(current_entities) != len(transformed_entities):
# If the two sentences have a different number of entities, then
# they definitely don't have the same labels. In this case, the
# constraint is violated, and we return False.
return False
else:
# Here we compare all of the words, in order, to make sure that they match.
# If we find two words that don't match, this means a word was swapped
# between `current_text` and `transformed_text`. That word must be a named entity to fulfill our
# constraint.
current_word_label = None
transformed_word_label = None
for (word_1, label_1), (word_2, label_2) in zip(current_entities, transformed_entities):
if word_1 != word_2:
# Finally, make sure that words swapped between `x` and `x_adv` are named entities. If
# they're not, then we also return False.
if (label_1 not in ['NNP', 'NE']) or (label_2 not in ['NNP', 'NE']):
return False
# If we get here, all of the labels match up. Return True!
return True
```
### Testing our constraint
We need to create an attack and a dataset to test our constraint on. We went over all of this in the transformations tutorial, so let's gloss over this part for now.
```
# Import the model
import transformers
from textattack.models.tokenizers import AutoTokenizer
from textattack.models.wrappers import HuggingFaceModelWrapper
model = transformers.AutoModelForSequenceClassification.from_pretrained("textattack/albert-base-v2-yelp-polarity")
tokenizer = AutoTokenizer("textattack/albert-base-v2-yelp-polarity")
model_wrapper = HuggingFaceModelWrapper(model, tokenizer)
# Create the goal function using the model
from textattack.goal_functions import UntargetedClassification
goal_function = UntargetedClassification(model_wrapper)
# Import the dataset
from textattack.datasets import HuggingFaceDataset
dataset = HuggingFaceDataset("yelp_polarity", None, "test")
from textattack.transformations import WordSwapEmbedding
from textattack.search_methods import GreedySearch
from textattack.shared import Attack
from textattack.constraints.pre_transformation import RepeatModification, StopwordModification
# We're going to the `WordSwapEmbedding` transformation. Using the default settings, this
# will try substituting words with their neighbors in the counter-fitted embedding space.
transformation = WordSwapEmbedding(max_candidates=15)
# We'll use the greedy search method again
search_method = GreedySearch()
# Our constraints will be the same as Tutorial 1, plus the named entity constraint
constraints = [RepeatModification(),
StopwordModification(),
NamedEntityConstraint(False)]
# Now, let's make the attack using these parameters.
attack = Attack(goal_function, constraints, transformation, search_method)
print(attack)
```
Now, let's use our attack. We're going to attack samples until we achieve 5 successes. (There's a lot to check here, and since we're using a greedy search over all potential word swap positions, each sample will take a few minutes. This will take a few hours to run on a single core.)
```
from textattack.loggers import CSVLogger # tracks a dataframe for us.
from textattack.attack_results import SuccessfulAttackResult
results_iterable = attack.attack_dataset(dataset)
logger = CSVLogger(color_method='html')
num_successes = 0
while num_successes < 5:
result = next(results_iterable)
if isinstance(result, SuccessfulAttackResult):
logger.log_attack_result(result)
num_successes += 1
print(f'{num_successes} of 5 successes complete.')
```
Now let's visualize our 5 successes in color:
```
import pandas as pd
pd.options.display.max_colwidth = 480 # increase column width so we can actually read the examples
from IPython.core.display import display, HTML
display(HTML(logger.df[['original_text', 'perturbed_text']].to_html(escape=False)))
```
### Conclusion
Our constraint seems to have done its job: it filtered out attacks that did not swap out a named entity for another, according to the NLTK named entity detector. However, we can see some problems inherent in the detector: it often thinks the first word of a given sentence is a named entity, probably due to capitalization.
We did manage to produce some nice adversarial examples! "Sigh" beacame "Inahles" and the prediction shifted from negative to positive.
| true |
code
| 0.653652 | null | null | null | null |
|
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-59152712-8');
</script>
# `GiRaFFE_NRPy`: Main Driver
## Author: Patrick Nelson
<a id='intro'></a>
**Notebook Status:** <font color=Red><b> Validation in progress </b></font>
**Validation Notes:** This code assembles the various parts needed for GRFFE evolution in order.
### NRPy+ Source Code for this module:
* [GiRaFFE_NRPy/GiRaFFE_NRPy_Main_Driver.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_Main_Driver.py)
### Other critical files (in alphabetical order):
* [GiRaFFE_NRPy/Afield_flux.py](../../edit/in_progress/GiRaFFE_NRPy/Afield_flux.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Afield_flux.ipynb) Generates the expressions to find the flux term of the induction equation.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-A2B.ipynb) Generates the driver to compute the magnetic field from the vector potential/
* [GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-BCs.ipynb) Generates the code to apply boundary conditions to the vector potential, scalar potential, and three-velocity.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_C2P_P2C.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_C2P_P2C.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-C2P_P2C.ipynb) Generates the conservative-to-primitive and primitive-to-conservative solvers.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_Metric_Face_Values.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_Metric_Face_Values.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Metric_Face_Values.ipynb) Generates code to interpolate metric gridfunctions to cell faces.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_PPM.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_PPM.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-PPM.ipynb) Genearates code to reconstruct primitive variables on cell faces.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_Source_Terms.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_Source_Terms.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Source_Terms.ipynb) Genearates code to compute the $\tilde{S}_i$ source term.
* [GiRaFFE_NRPy/Stilde_flux.py](../../edit/in_progress/GiRaFFE_NRPy/Stilde_flux.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Stilde_flux.ipynb) Generates the expressions to find the flux term of the Poynting flux evolution equation.
* [../GRFFE/equations.py](../../edit/GRFFE/equations.py) [\[**tutorial**\]](../Tutorial-GRFFE_Equations-Cartesian.ipynb) Generates code necessary to compute the source terms.
* [../GRHD/equations.py](../../edit/GRHD/equations.py) [\[**tutorial**\]](../Tutorial-GRHD_Equations-Cartesian.ipynb) Generates code necessary to compute the source terms.
## Introduction:
Having written all the various algorithms that will go into evolving the GRFFE equations forward through time, we are ready to write a start-to-finish module to do so. However, to help keep things more organized, we will first create a dedicated module to assemble the various functions we need to run, in order, to perform the evolution. This will reduce the length of the standalone C code, improving that notebook's readability.
<a id='prelim'></a>
# Table of Contents
$$\label{prelim}$$
During a given RK substep, we will perform the following steps in this order, based on the order used in the original `GiRaFFE`:
0. [Step 0](#prelim): Preliminaries
1. [Step 1](#rhs): Calculate the right-hand sides
1. [Step 1.a](#parenthetical): Calculate the portion of the gauge terms for $A_k$, $(\alpha \Phi - \beta^j A_j)$ and $\Phi$, $(\alpha\sqrt{\gamma}A^j - \beta^j [\sqrt{\gamma} \Phi])$ *inside* the parentheses to be finite-differenced.
* **GRFFE/equations.py**, **GRHD/equations.py**
1. [Step 1.b](#source): Calculate the source terms of $\partial_t A_i$, $\partial_t \tilde{S}_i$, and $\partial_t [\sqrt{\gamma} \Phi]$ right-hand sides
* **GRFFE/equations.py**, **GRHD/equations.py**, **GiRaFFE_NRPy/GiRaFFE_NRPy_Source_Terms**
1. [Step 1.c](#flux): Calculate the Flux terms
* In each direction:
* Interpolate the metric gridfunctions to cell faces
* **GiRaFFE_NRPy/GiRaFFE_NRPy_Metric_Face_Values.py**
* Reconstruct primitives $\bar{v}^i$ and $B^i$ on cell faces with the piecewise-parabolic method
* **GiRaFFE_NRPy/GiRaFFE_NRPy_PPM.py**
* Compute the fluxes of $\tilde{S}_i$ and $A_i$ and add the appropriate combinations to the evolution equation right-hand sides
* **GiRaFFE_NRPy/Stilde_flux.py**, **GiRaFFE_NRPy/Afield_flux.py**
1. [Step 2](#poststep): Recover the primitive variables and apply boundary conditions (post-step)
1. [Step 2.a](#potential_bc): Apply boundary conditions to $A_i$ and $\sqrt{\gamma} \Phi$
* **GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py**
1. [Step 2.b](#a2b): Compute $B^i$ from $A_i$
* **GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py**
1. [Step 2.c](#c2p): Run the Conservative-to-Primitive solver
* This applies fixes to $\tilde{S}_i$, then computes $\bar{v}^i$. A current sheet prescription is then applied to $\bar{v}^i$, and $\tilde{S}_i$ is recomputed to be consistent.
* **GiRaFFE_NRPy/GiRaFFE_NRPy_C2P_P2C.py**
1. [Step 2.d](#velocity_bc): Apply outflow boundary conditions to $\bar{v}^i$
* **GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py**
1. [Step 3](#write_out): Write out the C code function
1. [Step 3](#code_validation): Self-Validation against `GiRaFFE_NRPy_Main_Drive.py`
1. [Step 5](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
<a id='prelim'></a>
# Step 0: Preliminaries \[Back to [top](#toc)\]
$$\label{prelim}$$
We begin by importing the NRPy+ core functionality. We also import the Levi-Civita symbol, the GRHD module, and the GRFFE module.
```
# Step 0: Add NRPy's directory to the path
# https://stackoverflow.com/questions/16780014/import-file-from-parent-directory
import os,sys
nrpy_dir_path = os.path.join("..")
if nrpy_dir_path not in sys.path:
sys.path.append(nrpy_dir_path)
from outputC import * # NRPy+: Core C code output module
import finite_difference as fin # NRPy+: Finite difference C code generation module
import NRPy_param_funcs as par # NRPy+: Parameter interface
import grid as gri # NRPy+: Functions having to do with numerical grids
import loop as lp # NRPy+: Generate C code loops
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import reference_metric as rfm # NRPy+: Reference metric support
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
thismodule = "GiRaFFE_NRPy_Main_Driver"
par.set_parval_from_str("grid::GridFuncMemAccess","ETK")
par.set_parval_from_str("finite_difference::FD_CENTDERIVS_ORDER",2)
out_dir = os.path.join("GiRaFFE_standalone_Ccodes")
cmd.mkdir(out_dir)
CoordSystem = "Cartesian"
par.set_parval_from_str("reference_metric::CoordSystem",CoordSystem)
rfm.reference_metric() # Create ReU, ReDD needed for rescaling B-L initial data, generating BSSN RHSs, etc.
# Default Kreiss-Oliger dissipation strength
default_KO_strength = 0.1
diss_strength = par.Cparameters("REAL", thismodule, "diss_strength", default_KO_strength)
outCparams = "outCverbose=False,CSE_sorting=none"
```
<a id='rhs'></a>
# Step 1: Calculate the right-hand sides \[Back to [top](#toc)\]
$$\label{rhs}$$
<a id='parenthetical'></a>
In the method of lines using Runge-Kutta methods, each timestep involves several "RK substeps" during which we will run the same set of function calls. These can be divided into two groups: one in which the RHSs themselves are calculated, and a second in which boundary conditions are applied and auxiliary variables updated (the post-step). Here, we focus on that first group.
## Step 1.a: Calculate the portion of the gauge terms for $A_k$, $(\alpha \Phi - \beta^j A_j)$ and $\Phi$, $(\alpha\sqrt{\gamma}A^j - \beta^j [\sqrt{\gamma} \Phi])$ *inside* the parentheses to be finite-differenced. \[Back to [top](#toc)\]
$$\label{parenthetical}$$
The source terms of our evolution equations consist of two terms that are derivatives of some parenthetical quantity. We can save some effort and execution time (at the cost of memory needed) by computing these parentheticals, storing them, and then finite-differencing that stored variable. For more information, see the notebook for the [implementation](Tutorial-GiRaFFE_NRPy-Source_Terms.ipynb) and the [validation](Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-Source_Terms.ipynb), as well as [Tutorial-GRFFE_Equations-Cartesian](../Tutorial-GRFFE_Equations-Cartesian.ipynb) and [Tutorial-GRHD_Equations-Cartesian](../Tutorial-GRHD_Equations-Cartesian.ipynb) for the terms themselves.
```
import GRHD.equations as GRHD # NRPy+: Generate general relativistic hydrodynamics equations
import GRFFE.equations as GRFFE # NRPy+: Generate general relativisitic force-free electrodynamics equations
gammaDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gammaDD","sym01",DIM=3)
betaU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","betaU",DIM=3)
alpha = gri.register_gridfunctions("AUXEVOL","alpha")
AD = ixp.register_gridfunctions_for_single_rank1("EVOL","AD")
BU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","BU")
ValenciavU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","ValenciavU")
psi6Phi = gri.register_gridfunctions("EVOL","psi6Phi")
StildeD = ixp.register_gridfunctions_for_single_rank1("EVOL","StildeD")
PhievolParenU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","PhievolParenU",DIM=3)
AevolParen = gri.register_gridfunctions("AUXEVOL","AevolParen")
GRHD.compute_sqrtgammaDET(gammaDD)
GRFFE.compute_AD_source_term_parenthetical_for_FD(GRHD.sqrtgammaDET,betaU,alpha,psi6Phi,AD)
GRFFE.compute_psi6Phi_rhs_parenthetical(gammaDD,GRHD.sqrtgammaDET,betaU,alpha,AD,psi6Phi)
parens_to_print = [\
lhrh(lhs=gri.gfaccess("auxevol_gfs","AevolParen"),rhs=GRFFE.AevolParen),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","PhievolParenU0"),rhs=GRFFE.PhievolParenU[0]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","PhievolParenU1"),rhs=GRFFE.PhievolParenU[1]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","PhievolParenU2"),rhs=GRFFE.PhievolParenU[2]),\
]
subdir = "RHSs"
cmd.mkdir(os.path.join(out_dir, subdir))
desc = "Calculate quantities to be finite-differenced for the GRFFE RHSs"
name = "calculate_parentheticals_for_RHSs"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *restrict params,const REAL *restrict in_gfs,REAL *restrict auxevol_gfs",
body = fin.FD_outputC("returnstring",parens_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="AllPoints",
rel_path_for_Cparams=os.path.join("../"))
```
<a id='source'></a>
## Step 1.b: Calculate the source terms of $\partial_t A_i$, $\partial_t \tilde{S}_i$, and $\partial_t [\sqrt{\gamma} \Phi]$ right-hand sides \[Back to [top](#toc)\]
$$\label{source}$$
With the parentheticals stored in memory from the previous step, we can now now calculate the terms on the RHS of $A_i$ and $[\sqrt{\gamma} \Phi]$ that involve the derivatives of those terms. We also compute the other term in the RHS of $[\sqrt{\gamma} \Phi]$, which is a straightforward damping term.
```
xi_damping = par.Cparameters("REAL",thismodule,"xi_damping",0.1)
GRFFE.compute_psi6Phi_rhs_damping_term(alpha,psi6Phi,xi_damping)
AevolParen_dD = ixp.declarerank1("AevolParen_dD",DIM=3)
PhievolParenU_dD = ixp.declarerank2("PhievolParenU_dD","nosym",DIM=3)
A_rhsD = ixp.zerorank1()
psi6Phi_rhs = GRFFE.psi6Phi_damping
for i in range(3):
A_rhsD[i] += -AevolParen_dD[i]
psi6Phi_rhs += -PhievolParenU_dD[i][i]
# Add Kreiss-Oliger dissipation to the GRFFE RHSs:
# psi6Phi_dKOD = ixp.declarerank1("psi6Phi_dKOD")
# AD_dKOD = ixp.declarerank2("AD_dKOD","nosym")
# for i in range(3):
# psi6Phi_rhs += diss_strength*psi6Phi_dKOD[i]*rfm.ReU[i] # ReU[i] = 1/scalefactor_orthog_funcform[i]
# for j in range(3):
# A_rhsD[j] += diss_strength*AD_dKOD[j][i]*rfm.ReU[i] # ReU[i] = 1/scalefactor_orthog_funcform[i]
RHSs_to_print = [\
lhrh(lhs=gri.gfaccess("rhs_gfs","AD0"),rhs=A_rhsD[0]),\
lhrh(lhs=gri.gfaccess("rhs_gfs","AD1"),rhs=A_rhsD[1]),\
lhrh(lhs=gri.gfaccess("rhs_gfs","AD2"),rhs=A_rhsD[2]),\
lhrh(lhs=gri.gfaccess("rhs_gfs","psi6Phi"),rhs=psi6Phi_rhs),\
]
desc = "Calculate AD gauge term and psi6Phi RHSs"
name = "calculate_AD_gauge_psi6Phi_RHSs"
source_Ccode = outCfunction(
outfile = "returnstring", desc=desc, name=name,
params ="const paramstruct *params,const REAL *in_gfs,const REAL *auxevol_gfs,REAL *rhs_gfs",
body = fin.FD_outputC("returnstring",RHSs_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="InteriorPoints",
rel_path_for_Cparams=os.path.join("../")).replace("= NGHOSTS","= NGHOSTS_A2B").replace("NGHOSTS+Nxx0","Nxx_plus_2NGHOSTS0-NGHOSTS_A2B").replace("NGHOSTS+Nxx1","Nxx_plus_2NGHOSTS1-NGHOSTS_A2B").replace("NGHOSTS+Nxx2","Nxx_plus_2NGHOSTS2-NGHOSTS_A2B")
# Note the above .replace() functions. These serve to expand the loop range into the ghostzones, since
# the second-order FD needs fewer than some other algorithms we use do.
with open(os.path.join(out_dir,subdir,name+".h"),"w") as file:
file.write(source_Ccode)
```
We also need to compute the source term of the $\tilde{S}_i$ evolution equation. This term involves derivatives of the four metric, so we can save some effort here by taking advantage of the interpolations done of the metric gridfunctions to the cell faces, which will allow us to take a finite-difference derivative with the accuracy of a higher order and the computational cost of a lower order. However, it will require some more complicated coding, detailed in [Tutorial-GiRaFFE_NRPy-Source_Terms](Tutorial-GiRaFFE_NRPy-Source_Terms.ipynb)
```
import GiRaFFE_NRPy.GiRaFFE_NRPy_Source_Terms as source
# Declare this symbol:
sqrt4pi = par.Cparameters("REAL",thismodule,"sqrt4pi","sqrt(4.0*M_PI)")
source.write_out_functions_for_StildeD_source_term(os.path.join(out_dir,subdir),outCparams,gammaDD,betaU,alpha,
ValenciavU,BU,sqrt4pi)
```
<a id='flux'></a>
## Step 1.c: Calculate the Flux terms \[Back to [top](#toc)\]
$$\label{flux}$$
Now, we will compute the flux terms of $\partial_t A_i$ and $\partial_t \tilde{S}_i$. To do so, we will first need to interpolate the metric gridfunctions to cell faces and to reconstruct the primitives on the cell faces using the code detailed in [Tutorial-GiRaFFE_NRPy-Metric_Face_Values](Tutorial-GiRaFFE_NRPy-Metric_Face_Values.ipynb) and in [Tutorial-GiRaFFE_NRPy-PPM](Tutorial-GiRaFFE_NRPy-PPM.ipynb).
```
subdir = "FCVAL"
cmd.mkdir(os.path.join(out_dir, subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_Metric_Face_Values as FCVAL
FCVAL.GiRaFFE_NRPy_FCVAL(os.path.join(out_dir,subdir))
subdir = "PPM"
cmd.mkdir(os.path.join(out_dir, subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_PPM as PPM
PPM.GiRaFFE_NRPy_PPM(os.path.join(out_dir,subdir))
```
Here, we will write the function to compute the electric field contribution to the induction equation RHS. This is coded with documentation in [Tutorial-GiRaFFE_NRPy-Afield_flux](Tutorial-GiRaFFE_NRPy-Afield_flux.ipynb). The electric field in the $i^{\rm th}$ direction, it will contribute to the $j^{\rm th}$ and $k^{\rm th}$ component of the electric field. That is, in Cartesian coordinates, the component $x$ of the electric field will be the average of the values computed on the cell faces in the $\pm y$- and $\pm z$-directions, and so forth for the other components. This ultimately results in the six functions we create below.
```
import GiRaFFE_NRPy.Afield_flux as Af
# We will pass values of the gridfunction on the cell faces into the function. This requires us
# to declare them as C parameters in NRPy+. We will denote this with the _face infix/suffix.
alpha_face = gri.register_gridfunctions("AUXEVOL","alpha_face")
gamma_faceDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gamma_faceDD","sym01")
beta_faceU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","beta_faceU")
# We'll need some more gridfunctions, now, to represent the reconstructions of BU and ValenciavU
# on the right and left faces
Valenciav_rU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","Valenciav_rU",DIM=3)
B_rU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","B_rU",DIM=3)
Valenciav_lU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","Valenciav_lU",DIM=3)
B_lU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","B_lU",DIM=3)
subdir = "RHSs"
Af.generate_Afield_flux_function_files(out_dir,subdir,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU,True)
```
We must do something similar here, albeit a bit simpler. For instance, the $x$ component of $\partial_t \tilde{S}_i$ will be a finite difference of the flux throught the faces in the $\pm x$ direction; for further detail, see [Tutorial-GiRaFFE_NRPy-Stilde_flux](Tutorial-GiRaFFE_NRPy-Stilde_flux.ipynb).
```
import GiRaFFE_NRPy.Stilde_flux as Sf
subdir = "RHSs"
Sf.generate_C_code_for_Stilde_flux(os.path.join(out_dir,subdir), True, alpha_face,gamma_faceDD,beta_faceU,
Valenciav_rU,B_rU,Valenciav_lU,B_lU,sqrt4pi)
```
<a id='poststep'></a>
# Step 2: Recover the primitive variables and apply boundary conditions \[Back to [top](#toc)\]
$$\label{poststep}$$
With the RHSs computed, we can now recover the primitive variables, which are the Valencia three-velocity $\bar{v}^i$ and the magnetic field $B^i$. We can also apply boundary conditions to the vector potential and velocity. By doing this at each RK substep, we can help ensure the accuracy of the following substeps.
<a id='potential_bc'></a>
## Step 2.a: Apply boundary conditions to $A_i$ and $\sqrt{\gamma} \Phi$ \[Back to [top](#toc)\]
$$\label{potential_bc}$$
First, we will apply boundary conditions to the vector potential, $A_i$, and the scalar potential $\sqrt{\gamma} \Phi$. The file we generate here contains both functions we need for BCs, as documented in [Tutorial-GiRaFFE_NRPy-BCs](Tutorial-GiRaFFE_NRPy-BCs.ipynb).
```
subdir = "boundary_conditions"
cmd.mkdir(os.path.join(out_dir,subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_BCs as BC
BC.GiRaFFE_NRPy_BCs(os.path.join(out_dir,subdir))
```
<a id='a2b'></a>
## Step 2.b: Compute $B^i$ from $A_i$ \[Back to [top](#toc)\]
$$\label{a2b}$$
Now, we will calculate the magnetic field as the curl of the vector potential at all points in our domain; this requires care to be taken in the ghost zones, which is detailed in [Tutorial-GiRaFFE_NRPy-A2B](Tutorial-GiRaFFE_NRPy-A2B.ipynb).
```
subdir = "A2B"
cmd.mkdir(os.path.join(out_dir,subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_A2B as A2B
A2B.GiRaFFE_NRPy_A2B(os.path.join(out_dir,subdir),gammaDD,AD,BU)
```
<a id='c2p'></a>
## Step 2.c: Run the Conservative-to-Primitive solver \[Back to [top](#toc)\]
$$\label{c2p}$$
With these functions, we apply fixes to the Poynting flux, and use that to update the three-velocity. Then, we apply our current sheet prescription to the velocity, and recompute the Poynting flux to agree with the now-fixed velocity. More detail can be found in [Tutorial-GiRaFFE_NRPy-C2P_P2C](Tutorial-GiRaFFE_NRPy-C2P_P2C.ipynb).
```
import GiRaFFE_NRPy.GiRaFFE_NRPy_C2P_P2C as C2P_P2C
C2P_P2C.GiRaFFE_NRPy_C2P(StildeD,BU,gammaDD,betaU,alpha)
values_to_print = [\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD0"),rhs=C2P_P2C.outStildeD[0]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD1"),rhs=C2P_P2C.outStildeD[1]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD2"),rhs=C2P_P2C.outStildeD[2]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","ValenciavU0"),rhs=C2P_P2C.ValenciavU[0]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","ValenciavU1"),rhs=C2P_P2C.ValenciavU[1]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","ValenciavU2"),rhs=C2P_P2C.ValenciavU[2])\
]
subdir = "C2P"
cmd.mkdir(os.path.join(out_dir,subdir))
desc = "Apply fixes to \tilde{S}_i and recompute the velocity to match with current sheet prescription."
name = "GiRaFFE_NRPy_cons_to_prims"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *params,REAL *xx[3],REAL *auxevol_gfs,REAL *in_gfs",
body = fin.FD_outputC("returnstring",values_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="AllPoints,Read_xxs",
rel_path_for_Cparams=os.path.join("../"))
# TINYDOUBLE = par.Cparameters("REAL",thismodule,"TINYDOUBLE",1e-100)
C2P_P2C.GiRaFFE_NRPy_P2C(gammaDD,betaU,alpha, ValenciavU,BU, sqrt4pi)
values_to_print = [\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD0"),rhs=C2P_P2C.StildeD[0]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD1"),rhs=C2P_P2C.StildeD[1]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD2"),rhs=C2P_P2C.StildeD[2]),\
]
desc = "Recompute StildeD after current sheet fix to Valencia 3-velocity to ensure consistency between conservative & primitive variables."
name = "GiRaFFE_NRPy_prims_to_cons"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *params,REAL *auxevol_gfs,REAL *in_gfs",
body = fin.FD_outputC("returnstring",values_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="AllPoints",
rel_path_for_Cparams=os.path.join("../"))
```
<a id='velocity_bc'></a>
## Step 2.d: Apply outflow boundary conditions to $\bar{v}^i$ \[Back to [top](#toc)\]
$$\label{velocity_bc}$$
Now, we can apply outflow boundary conditions to the Valencia three-velocity. This specific type of boundary condition helps avoid numerical error "flowing" into our grid.
This function has already been generated [above](#potential_bc).
<a id='write_out'></a>
# Step 3: Write out the C code function \[Back to [top](#toc)\]
$$\label{write_out}$$
Now, we have generated all the functions we will need for the `GiRaFFE` evolution. So, we will now assemble our evolution driver. This file will first `#include` all of the files we just generated for easy access. Then, we will write a function that calls these functions in the correct order, iterating over the flux directions as necessary.
```
%%writefile $out_dir/GiRaFFE_NRPy_Main_Driver.h
// Structure to track ghostzones for PPM:
typedef struct __gf_and_gz_struct__ {
REAL *gf;
int gz_lo[4],gz_hi[4];
} gf_and_gz_struct;
// Some additional constants needed for PPM:
const int VX=0,VY=1,VZ=2,BX=3,BY=4,BZ=5;
const int NUM_RECONSTRUCT_GFS = 6;
// Include ALL functions needed for evolution
#include "RHSs/calculate_parentheticals_for_RHSs.h"
#include "RHSs/calculate_AD_gauge_psi6Phi_RHSs.h"
#include "PPM/reconstruct_set_of_prims_PPM_GRFFE_NRPy.c"
#include "FCVAL/interpolate_metric_gfs_to_cell_faces.h"
#include "RHSs/calculate_StildeD0_source_term.h"
#include "RHSs/calculate_StildeD1_source_term.h"
#include "RHSs/calculate_StildeD2_source_term.h"
#include "../calculate_E_field_flat_all_in_one.h"
#include "RHSs/calculate_Stilde_flux_D0.h"
#include "RHSs/calculate_Stilde_flux_D1.h"
#include "RHSs/calculate_Stilde_flux_D2.h"
#include "boundary_conditions/GiRaFFE_boundary_conditions.h"
#include "A2B/driver_AtoB.h"
#include "C2P/GiRaFFE_NRPy_cons_to_prims.h"
#include "C2P/GiRaFFE_NRPy_prims_to_cons.h"
void override_BU_with_old_GiRaFFE(const paramstruct *restrict params,REAL *restrict auxevol_gfs,const int n) {
#include "set_Cparameters.h"
char filename[100];
sprintf(filename,"BU0_override-%08d.bin",n);
FILE *out2D = fopen(filename, "rb");
fread(auxevol_gfs+BU0GF*Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,
sizeof(double),Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,out2D);
fclose(out2D);
sprintf(filename,"BU1_override-%08d.bin",n);
out2D = fopen(filename, "rb");
fread(auxevol_gfs+BU1GF*Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,
sizeof(double),Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,out2D);
fclose(out2D);
sprintf(filename,"BU2_override-%08d.bin",n);
out2D = fopen(filename, "rb");
fread(auxevol_gfs+BU2GF*Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,
sizeof(double),Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,out2D);
fclose(out2D);
}
void GiRaFFE_NRPy_RHSs(const paramstruct *restrict params,REAL *restrict auxevol_gfs,const REAL *restrict in_gfs,REAL *restrict rhs_gfs) {
#include "set_Cparameters.h"
// First thing's first: initialize the RHSs to zero!
#pragma omp parallel for
for(int ii=0;ii<Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2*NUM_EVOL_GFS;ii++) {
rhs_gfs[ii] = 0.0;
}
// Next calculate the easier source terms that don't require flux directions
// This will also reset the RHSs for each gf at each new timestep.
calculate_parentheticals_for_RHSs(params,in_gfs,auxevol_gfs);
calculate_AD_gauge_psi6Phi_RHSs(params,in_gfs,auxevol_gfs,rhs_gfs);
// Now, we set up a bunch of structs of pointers to properly guide the PPM algorithm.
// They also count the number of ghostzones available.
gf_and_gz_struct in_prims[NUM_RECONSTRUCT_GFS], out_prims_r[NUM_RECONSTRUCT_GFS], out_prims_l[NUM_RECONSTRUCT_GFS];
int which_prims_to_reconstruct[NUM_RECONSTRUCT_GFS],num_prims_to_reconstruct;
const int Nxxp2NG012 = Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2;
REAL *temporary = auxevol_gfs + Nxxp2NG012*AEVOLPARENGF; //We're not using this anymore
// This sets pointers to the portion of auxevol_gfs containing the relevant gridfunction.
int ww=0;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAVU0GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_RU0GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_LU0GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAVU1GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_RU1GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_LU1GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAVU2GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_RU2GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_LU2GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*BU0GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*B_RU0GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*B_LU0GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*BU1GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*B_RU1GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*B_LU1GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*BU2GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*B_RU2GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*B_LU2GF;
ww++;
// Prims are defined AT ALL GRIDPOINTS, so we set the # of ghostzones to zero:
for(int i=0;i<NUM_RECONSTRUCT_GFS;i++) for(int j=1;j<=3;j++) { in_prims[i].gz_lo[j]=0; in_prims[i].gz_hi[j]=0; }
// Left/right variables are not yet defined, yet we set the # of gz's to zero by default:
for(int i=0;i<NUM_RECONSTRUCT_GFS;i++) for(int j=1;j<=3;j++) { out_prims_r[i].gz_lo[j]=0; out_prims_r[i].gz_hi[j]=0; }
for(int i=0;i<NUM_RECONSTRUCT_GFS;i++) for(int j=1;j<=3;j++) { out_prims_l[i].gz_lo[j]=0; out_prims_l[i].gz_hi[j]=0; }
ww=0;
which_prims_to_reconstruct[ww]=VX; ww++;
which_prims_to_reconstruct[ww]=VY; ww++;
which_prims_to_reconstruct[ww]=VZ; ww++;
which_prims_to_reconstruct[ww]=BX; ww++;
which_prims_to_reconstruct[ww]=BY; ww++;
which_prims_to_reconstruct[ww]=BZ; ww++;
num_prims_to_reconstruct=ww;
// In each direction, perform the PPM reconstruction procedure.
// Then, add the fluxes to the RHS as appropriate.
for(int flux_dirn=0;flux_dirn<3;flux_dirn++) {
// In each direction, interpolate the metric gfs (gamma,beta,alpha) to cell faces.
interpolate_metric_gfs_to_cell_faces(params,auxevol_gfs,flux_dirn+1);
// Then, reconstruct the primitive variables on the cell faces.
// This function is housed in the file: "reconstruct_set_of_prims_PPM_GRFFE_NRPy.c"
reconstruct_set_of_prims_PPM_GRFFE_NRPy(params, auxevol_gfs, flux_dirn+1, num_prims_to_reconstruct,
which_prims_to_reconstruct, in_prims, out_prims_r, out_prims_l, temporary);
// For example, if flux_dirn==0, then at gamma_faceDD00(i,j,k) represents gamma_{xx}
// at (i-1/2,j,k), Valenciav_lU0(i,j,k) is the x-component of the velocity at (i-1/2-epsilon,j,k),
// and Valenciav_rU0(i,j,k) is the x-component of the velocity at (i-1/2+epsilon,j,k).
if(flux_dirn==0) {
// Next, we calculate the source term for StildeD. Again, this also resets the rhs_gfs array at
// each new timestep.
calculate_StildeD0_source_term(params,auxevol_gfs,rhs_gfs);
// Now, compute the electric field on each face of a cell and add it to the RHSs as appropriate
//calculate_E_field_D0_right(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D0_left(params,auxevol_gfs,rhs_gfs);
// Finally, we calculate the flux of StildeD and add the appropriate finite-differences
// to the RHSs.
calculate_Stilde_flux_D0(params,auxevol_gfs,rhs_gfs);
}
else if(flux_dirn==1) {
calculate_StildeD1_source_term(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D1_right(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D1_left(params,auxevol_gfs,rhs_gfs);
calculate_Stilde_flux_D1(params,auxevol_gfs,rhs_gfs);
}
else {
calculate_StildeD2_source_term(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D2_right(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D2_left(params,auxevol_gfs,rhs_gfs);
calculate_Stilde_flux_D2(params,auxevol_gfs,rhs_gfs);
}
for(int count=0;count<=1;count++) {
// This function is written to be general, using notation that matches the forward permutation added to AD2,
// i.e., [F_HLL^x(B^y)]_z corresponding to flux_dirn=0, count=1.
// The SIGN parameter is necessary because
// -E_z(x_i,y_j,z_k) = 0.25 ( [F_HLL^x(B^y)]_z(i+1/2,j,k)+[F_HLL^x(B^y)]_z(i-1/2,j,k)
// -[F_HLL^y(B^x)]_z(i,j+1/2,k)-[F_HLL^y(B^x)]_z(i,j-1/2,k) )
// Note the negative signs on the reversed permutation terms!
// By cyclically permuting with flux_dirn, we
// get contributions to the other components, and by incrementing count, we get the backward permutations:
// Let's suppose flux_dirn = 0. Then we will need to update Ay (count=0) and Az (count=1):
// flux_dirn=count=0 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (0+1+0)%3=AD1GF <- Updating Ay!
// (flux_dirn)%3 = (0)%3 = 0 Vx
// (flux_dirn-count+2)%3 = (0-0+2)%3 = 2 Vz . Inputs Vx, Vz -> SIGN = -1 ; 2.0*((REAL)count)-1.0=-1 check!
// flux_dirn=0,count=1 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (0+1+1)%3=AD2GF <- Updating Az!
// (flux_dirn)%3 = (0)%3 = 0 Vx
// (flux_dirn-count+2)%3 = (0-1+2)%3 = 1 Vy . Inputs Vx, Vy -> SIGN = +1 ; 2.0*((REAL)count)-1.0=2-1=+1 check!
// Let's suppose flux_dirn = 1. Then we will need to update Az (count=0) and Ax (count=1):
// flux_dirn=1,count=0 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (1+1+0)%3=AD2GF <- Updating Az!
// (flux_dirn)%3 = (1)%3 = 1 Vy
// (flux_dirn-count+2)%3 = (1-0+2)%3 = 0 Vx . Inputs Vy, Vx -> SIGN = -1 ; 2.0*((REAL)count)-1.0=-1 check!
// flux_dirn=count=1 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (1+1+1)%3=AD0GF <- Updating Ax!
// (flux_dirn)%3 = (1)%3 = 1 Vy
// (flux_dirn-count+2)%3 = (1-1+2)%3 = 2 Vz . Inputs Vy, Vz -> SIGN = +1 ; 2.0*((REAL)count)-1.0=2-1=+1 check!
// Let's suppose flux_dirn = 2. Then we will need to update Ax (count=0) and Ay (count=1):
// flux_dirn=2,count=0 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (2+1+0)%3=AD0GF <- Updating Ax!
// (flux_dirn)%3 = (2)%3 = 2 Vz
// (flux_dirn-count+2)%3 = (2-0+2)%3 = 1 Vy . Inputs Vz, Vy -> SIGN = -1 ; 2.0*((REAL)count)-1.0=-1 check!
// flux_dirn=2,count=1 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (2+1+1)%3=AD1GF <- Updating Ay!
// (flux_dirn)%3 = (2)%3 = 2 Vz
// (flux_dirn-count+2)%3 = (2-1+2)%3 = 0 Vx . Inputs Vz, Vx -> SIGN = +1 ; 2.0*((REAL)count)-1.0=2-1=+1 check!
calculate_E_field_flat_all_in_one(params,
&auxevol_gfs[IDX4ptS(VALENCIAV_RU0GF+(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(VALENCIAV_RU0GF+(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(VALENCIAV_LU0GF+(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(VALENCIAV_LU0GF+(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_RU0GF +(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(B_RU0GF +(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_LU0GF +(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(B_LU0GF +(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_RU0GF +(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_LU0GF +(flux_dirn-count+2)%3, 0)],
&rhs_gfs[IDX4ptS(AD0GF+(flux_dirn+1+count)%3,0)], 2.0*((REAL)count)-1.0, flux_dirn);
}
}
}
void GiRaFFE_NRPy_post_step(const paramstruct *restrict params,REAL *xx[3],REAL *restrict auxevol_gfs,REAL *restrict evol_gfs,const int n) {
// First, apply BCs to AD and psi6Phi. Then calculate BU from AD
apply_bcs_potential(params,evol_gfs);
driver_A_to_B(params,evol_gfs,auxevol_gfs);
//override_BU_with_old_GiRaFFE(params,auxevol_gfs,n);
// Apply fixes to StildeD, then recompute the velocity at the new timestep.
// Apply the current sheet prescription to the velocities
GiRaFFE_NRPy_cons_to_prims(params,xx,auxevol_gfs,evol_gfs);
// Then, recompute StildeD to be consistent with the new velocities
//GiRaFFE_NRPy_prims_to_cons(params,auxevol_gfs,evol_gfs);
// Finally, apply outflow boundary conditions to the velocities.
apply_bcs_velocity(params,auxevol_gfs);
}
```
<a id='code_validation'></a>
# Step 4: Self-Validation against `GiRaFFE_NRPy_Main_Drive.py` \[Back to [top](#toc)\]
$$\label{code_validation}$$
To validate the code in this tutorial we check for agreement between the files
1. that were generated in this tutorial and
1. those that are generated in the module `GiRaFFE_NRPy_Main_Driver.py`
```
gri.glb_gridfcs_list = []
# Define the directory that we wish to validate against:
valdir = os.path.join("GiRaFFE_validation_Ccodes")
cmd.mkdir(valdir)
import GiRaFFE_NRPy.GiRaFFE_NRPy_Main_Driver as md
md.GiRaFFE_NRPy_Main_Driver_generate_all(valdir)
```
With both sets of codes generated, we can now compare them against each other.
```
import difflib
import sys
print("Printing difference between original C code and this code...")
# Open the files to compare
files = ["GiRaFFE_NRPy_Main_Driver.h",
"RHSs/calculate_parentheticals_for_RHSs.h",
"RHSs/calculate_AD_gauge_psi6Phi_RHSs.h",
"PPM/reconstruct_set_of_prims_PPM_GRFFE_NRPy.c",
"PPM/loop_defines_reconstruction_NRPy.h",
"FCVAL/interpolate_metric_gfs_to_cell_faces.h",
"RHSs/calculate_StildeD0_source_term.h",
"RHSs/calculate_StildeD1_source_term.h",
"RHSs/calculate_StildeD2_source_term.h",
"RHSs/calculate_E_field_D0_right.h",
"RHSs/calculate_E_field_D0_left.h",
"RHSs/calculate_E_field_D1_right.h",
"RHSs/calculate_E_field_D1_left.h",
"RHSs/calculate_E_field_D2_right.h",
"RHSs/calculate_E_field_D2_left.h",
"RHSs/calculate_Stilde_flux_D0.h",
"RHSs/calculate_Stilde_flux_D1.h",
"RHSs/calculate_Stilde_flux_D2.h",
"boundary_conditions/GiRaFFE_boundary_conditions.h",
"A2B/driver_AtoB.h",
"C2P/GiRaFFE_NRPy_cons_to_prims.h",
"C2P/GiRaFFE_NRPy_prims_to_cons.h"]
for file in files:
print("Checking file " + file)
with open(os.path.join(valdir,file)) as file1, open(os.path.join(out_dir,file)) as file2:
# Read the lines of each file
file1_lines = file1.readlines()
file2_lines = file2.readlines()
num_diffs = 0
for line in difflib.unified_diff(file1_lines, file2_lines, fromfile=os.path.join(valdir,file), tofile=os.path.join(out_dir,file)):
sys.stdout.writelines(line)
num_diffs = num_diffs + 1
if num_diffs == 0:
print("No difference. TEST PASSED!")
else:
print("ERROR: Disagreement found with .py file. See differences above.")
sys.exit(1)
```
<a id='latex_pdf_output'></a>
# Step 4: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-GiRaFFE_NRPy_Main_Driver](TTutorial-GiRaFFE_NRPy_Main_Driver.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-GiRaFFE_NRPy_Main_Driver")
```
| true |
code
| 0.370937 | null | null | null | null |
|
Sascha Spors,
Professorship Signal Theory and Digital Signal Processing,
Institute of Communications Engineering (INT),
Faculty of Computer Science and Electrical Engineering (IEF),
University of Rostock, Germany
# Tutorial Digital Signal Processing
**Correlation**,
Winter Semester 2021/22 (Course #24505)
- lecture: https://github.com/spatialaudio/digital-signal-processing-lecture
- tutorial: https://github.com/spatialaudio/digital-signal-processing-exercises
Feel free to contact lecturer [email protected]
WIP...
```
# most common used packages for DSP, have a look into other scipy submodules
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from scipy import signal
def my_xcorr2(x, y, scaleopt='none'):
N = len(x)
M = len(y)
kappa = np.arange(0, N+M-1) - (M-1)
ccf = signal.correlate(x, y, mode='full', method='auto')
if N == M:
if scaleopt == 'none' or scaleopt == 'raw':
ccf /= 1
elif scaleopt == 'biased' or scaleopt == 'bias':
ccf /= N
elif scaleopt == 'unbiased' or scaleopt == 'unbias':
ccf /= (N - np.abs(kappa))
elif scaleopt == 'coeff' or scaleopt == 'normalized':
ccf /= np.sqrt(np.sum(x**2) * np.sum(y**2))
else:
print('scaleopt unknown: we leave output unnormalized')
return kappa, ccf
if True: # test my_xcorr with simple example
x = np.array([0, 1, 0, 0, 0])
y = np.array([1, 0, 0])
# plot my_xcorr2(x, y) vs. my_xcorr2(y, x)
plt.figure(figsize=(9, 2))
plt.subplot(1, 2, 1)
kappa_xy, ccf_xy = my_xcorr2(x, y)
plt.stem(kappa_xy, ccf_xy, basefmt='C0:', use_line_collection=True)
plt.xlabel(r'$\kappa$')
plt.ylabel(r'$\varphi_{xy}[\kappa]$')
plt.title('cross correlation between x and y')
plt.grid(True)
plt.subplot(1, 2, 2)
kappa_yx, ccf_yx = my_xcorr2(y, x)
plt.stem(kappa_yx, ccf_yx, basefmt='C0:', use_line_collection=True)
plt.xlabel(r'$\kappa$')
plt.ylabel(r'$\varphi_{yx}[\kappa]$')
plt.title('cross correlation between y and x')
plt.grid(True)
```
## Normalization schemes for cross correlation of finite length signals
check cross correlation
- of a cosine and a sine signal
- of a normal pdf process that exhibits some repetition
```
case_str = 'cos_sin'
case_str = 'normal_pdf'
if case_str == 'cos_sin':
Nt = 200 # number of samples for a full period
x = np.cos(2*np.pi/Nt * 1 * np.arange(0, Nt)) * 2
y = np.sin(2*np.pi/Nt * 1 * np.arange(0, Nt)) * 2
elif case_str == 'normal_pdf':
Nt = 20000
loc, scale = 2, np.sqrt(2) # mu, sigma
x = scale * np.random.randn(Nt) + loc
y = np.roll(x,-7500) # process similarity for offset of 7500 samples
plt.figure(figsize=(8,6))
plt.subplot(2,2,1)
kappa, ccf = my_xcorr2(x, y, scaleopt='none')
plt.plot(kappa, ccf)
plt.ylabel(r'$\varphi_{xy}[\kappa]$')
plt.title('raw CCF(x,y)')
plt.grid(True)
plt.subplot(2,2,2)
kappa, ccf = my_xcorr2(x, y, scaleopt='biased')
plt.plot(kappa, ccf)
plt.title('biased CCF(x,y)')
plt.grid(True)
plt.subplot(2,2,3)
kappa, ccf = my_xcorr2(x, y, scaleopt='unbiased')
plt.plot(kappa, ccf)
plt.xlabel(r'$\kappa$')
plt.ylabel(r'$\varphi_{xy}[\kappa]$')
plt.title('unbiased CCF(x,y)')
plt.grid(True)
plt.subplot(2,2,4)
kappa, ccf = my_xcorr2(x, y, scaleopt='coeff')
plt.plot(kappa, ccf)
plt.xlabel(r'$\kappa$')
plt.title('normalized CCF(x,y)')
plt.grid(True)
# check that the unbiased estimate of the CCF represents the theoretical
# result best in comparison to the other normalization schemes, at least
# for the chosen examples
```
# **Copyright**
The notebooks are provided as [Open Educational Resources](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebooks for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Frank Schultz, Digital Signal Processing - A Tutorial Featuring Computational Examples* with the URL https://github.com/spatialaudio/digital-signal-processing-exercises
| true |
code
| 0.437884 | null | null | null | null |
|

<h2 align='center'>Data Literacy through Sports Analytics</h2>
<h3 align='center'>Southern Alberta Teachers' Convention 2021</h3>
<h3 align='center'>Tina Leard (Cybera)<br>
Michael Lamoureux (University of Calgary)</h3><br>
<h4 align='center'> Slides at: https://tinyurl.com/callysto-data </h4>

<center><img src='./images/ccby.png' alt="CC BY logo" width='300' /></center>
<p><center><a href='https://creativecommons.org/licenses/by/4.0/' target='_blank'>CC BY</a>:<br>
This license allows reusers to distribute, remix, adapt, and build upon the material in any medium or format,<br>
so long as attribution is given to the creator.
</center></p>
```
import numpy as np
import pandas as pd
from pandas import read_csv
import plotly.graph_objects as go
import plotly.express as px
from plotly import subplots
from plotly.offline import download_plotlyjs, plot,iplot
import cufflinks as cf
cf.go_offline()
from IPython.display import YouTubeVideo
from ipysheet import sheet, cell, cell_range
%matplotlib inline
```
# Overview
- Data literacy via sports
- The learning progression
- Examples of learning and data analysis
- Professional soccer
- Ice hockey
- Field hockey
- Python, Jupyter, and Callysto
<center><img src='./images/data_literacy.png' alt='data literacy' width='85%' /></center>
#### Content and context
(Alberta Education, 2000, 2007, updated 2016, 2017)
## Example: professional soccer event data
```
df_soccer = pd.read_csv("https://raw.githubusercontent.com/metrica-sports/sample-data/master/data/Sample_Game_1/Sample_Game_1_RawEventsData.csv"); df_soccer
```
**Home team passes, second half**
```
df_soccer.loc[lambda df: (df['Team'] == 'Home') & (df['Period'] == 2) & (df['Type'] == 'PASS'), :] \
.iplot(kind="scatter",x = "Start X", y = "Start Y", mode = "markers")
```
## Bridging expert to novice
## Data visualization learning progression
<img src='./images/creating_scaffolding.png' alt='scaffolding' width='95%' />
## Data visualization learning progression
<img src='./images/creating_adapting.png' alt='adapting' width='95%' />
Communicating mathemtical reasoning (Alberta Education, 2007, updated 2016)
## Data gathering learning progression
<br>
<center><img src='./images/data_gathering.png' alt='data gathering' width='85%' /></center>
<br><br><br>Source: <a href='http://oceansofdata.org/sites/oceansofdata.org/files/pervasive-and-persistent-understandings-01-14.pdf' target='_blank'>Pervasive and Persistent Understandings about Data</a>, Kastens (2014)
## Authentic learning approach
- Learning design based on interdisciplinary<br>
connections and real-world examples
- Industry-aligned data science analysis process
- Python, an all-purpose programming language
- Jupyter notebook, a free industry-standard tool for data scientists
- CallystoHub, free cloud computing
## Athlete development
### U15 training to train
- Promotes tactical strategies for in-game decision making, reading the situation and inferring
- Focuses on the team and the process
- Situates personal goals within a team approach
### U18 training to compete
- Emphasizes individual technical and position-specific training
## Youth sports analytics
Online communication,<br>
sometimes through shared video analysis spaces
Video replay during games and training
Post–game video analysis, limitted statistics
## Learning design and flexibility
<br>
<img src='./images/flexibility.png' alt='adapting' width='90%' />
## Two data examples
1. Import a csv file and use a Python spreadsheet<br>to create shot maps (ice hockey)
2. Gather data from video to analyze and make decisions (field hockey)
## Data example 1:
## Using IIHF World Junior Championship data to create graphs and a shot map
## Defining ice hockey net zones:<br> What factors can lead to scoring?
<!--USA Hockey Goaltender Basics https://www.usahockeygoaltending.com/page/show/890039-stance-->
||
|-|-|
|<img src='./images/hockey_net_zones.png' width='100%'/>|<img src='https://cdn.hockeycanada.ca/hockey-canada/Team-Canada/Men/Under-18/2014-15/2014-15_goalie_camp.jpg?q=60' />|
||<a href='https://www.hockeycanada.ca/en-ca/news/34-goaltenders-invited-to-2014-poe-camp' target='_blank'>Image source: Hockey Canada</a>|
```
%%html
<h2>Data source IIHF: Shot charts</h2><br>
<iframe width="1200" height="600" src="https://www.iihf.com/pdf/503/ihm503a13_77a_3_0" frameborder="0" ></iframe>
```
## Tally chart
<img src='./images/hockey_tally.png' alt='tally chart' width='85%' />
## Generating a csv file
Zone,Austria,Canada,Czech_Republic,Finland,Germany,Russia,Switzerland,Slovakia,Sweden,USA,Total<br>
one,0,7,0,3,2,0,0,0,3,3,18<br>
two,0,1,1,0,1,0,0,0,0,0,3<br>
three,0,5,0,2,2,4,1,0,3,6,23<br>
four,0,4,3,2,1,1,0,1,0,3,15<br>
five,0,1,0,2,1,0,0,0,0,0,4<br>
six,1,1,2,4,0,2,0,1,0,2,13<br>
seven,0,6,0,1,3,3,1,1,0,9,24<br>
eight,0,5,1,2,2,3,1,2,3,2,21<br>
nine,0,3,3,0,2,3,2,0,5,0,18<br>
## Exploring scoring on net zones
```
hockey_goals_df = pd.read_csv('./data/hockey_goals.csv')
hockey_goals_df.head(9)
```
### What do measures of central tendency<br>tell us about the total goals per net zone?
```
hockey_goals_df['Total'].sum()
hockey_goals_df['Total'].min()
hockey_goals_df['Total'].max()
scatter_hockey_goals_df = px.scatter(hockey_goals_df,x="Zone",y="Total",title="Total goals per net zone")
scatter_hockey_goals_df.show()
hockey_goals_df['Total'].mean()
hockey_goals_df['Total'].median()
hockey_goals_df['Total'].mode()
```
### Which net zones score above the median?
```
hockey_goals_df = hockey_goals_df.sort_values('Total', ascending=False)
hockey_goals_df
bar_hockey_goals_df = px.bar(hockey_goals_df,
x="Zone", y="Total")
bar_hockey_goals_df.update_layout(title_text='Total goals by net zone')
```
### What connections exist between<br>goalie position and scoring?
```
hockey_goals_df = pd.read_csv('./data/hockey_goals.csv')
hockey_goals_df.Total
spread_sheet_hockey_net = sheet(rows=3, columns=3)
my_cells_net = cell_range([[18,3,23],[15,4,13],[24,21,18]],row_start=0,col_start=0,numeric_format="int")
figure_hockey_net = go.Figure(data=go.Heatmap(
z =list(reversed(my_cells_net.value)),
type = 'heatmap',
colorscale = 'greys',opacity = 1.0))
axis_template = dict(range = [0,5], autorange = True,
showgrid = False, zeroline = False,
showticklabels = False,
ticks = '' )
figure_hockey_net.update_layout(margin = dict(t=50,r=200,b=200,l=200),
xaxis = axis_template,
yaxis = axis_template,
showlegend = False,
width = 800, height = 500, title="Ice hockey net zones",
autosize = True )
# Add image in the background
nLanes = 3
nZones = 3
figure_hockey_net.add_layout_image(
dict(
source="images/hockey_net.png",
xref="x",
yref="y",
x=-0.5,
y=-.5 + nLanes, #this adjusts the placement of the image
sizex=nZones,
sizey=nLanes,
sizing="fill",
opacity=1.0,
layer="above")
)
# changes in my_cells should trigger this function
def calculate(change):
figure_hockey_net.update_traces(z=list(reversed(my_cells_net.value)))
my_cells_net.observe(calculate, 'value')
spread_sheet_hockey_net
139
figure_hockey_net.update() # Click the keys "Shift-return" to update the figure
```
## Data example 2:
## Analyzing youth field hockey data to make decisions
<center><img src='./images/learning_cycle1.png' alt="Learning design and context" width='90%' /></center>
#### Learning design and context notes
The context is physical education, and the content is statistics. Within physical education, in-game skills, fair play, teamwork, and goal setting are integrated. Those outcomes can be applied to in-game decision making. The goal setting can also be part of the communication resulting from the data analysis. When considering in-game decision making, we can define an action as the result of a decision. Decision making is part of a learning cycle that incorporates a technological feedback loop.
(Field Hokcey Alberta, 2020; Field Hockey Canada, 2020; Alberta Education, 2000)
<center><img src='./images/learning_cycle5.png' alt="Learning cycle" width='90%' /></center>
#### Learning cycle notes
The real situation occurs on the field where a decision is made and an action is executed. Then, the athlete forms a mental representation, processing occurs, and a real model is formed. The real model is integrated into the computational model, which results in a technological feedback, then a connection is made back into game play.
(Butler & Winne, 1995; Cleary & Zimmerman, 2001; Hadwin et al., 2017; Leard & Hadwin, 2001)
<center><img src='./images/computational_thinking.png' alt="Computationl thinking" width='90%' /></center>
<a href="https://app.lucidchart.com/documents/view/8e3186f7-bdfe-46af-9c7f-9c426b80d083">Connecting data literacy and sports</a>
#### Computational modelling and data literacy notes
The definition of computational thinking can vary.
Computational thinking is math reasoning combined with critical thinking plus the power of computers. We can use computers to do work more efficiently for us, like compute thousands of lines of data.
Under that definition of computational thinking, we can apply computational thinking strategies. The foundational process is decomposing to look for patterns. We can use computer programming to design algorithms to look for patterns. With these algorithms, we can infer through abstractions.
The abstractions can be in the form of computational models: data visualizations (including graphs from the curriculum), data analyses, and simulations of probability models. The data visualizations can extend beyond the curriculum to support math reasoning.
(Berikan & Özdemir, 2019; Gadanidis, 2020; Guadalupe & Gómez-Blancarte, 2019; Leard & Hadwin, 2001)
<center><img src='./images/analysis_process.png' alt="Data science analysis process" width='90%' /></center>
#### Data science analysis process notes
This data science analysis process was modified from how expert data scientists analyze data and aligned to several provincial curricula.
There are six steps:
1. Understand the problem. What questions are we trying to answer?
2. Gather the data. Find the data sources, with the extension of big data sets.
3. Organize the data so we can explore it, usually in the form of a table.
4. Explore the data to create computational models. Usually, there is more than one model. Look for evidence to answer our questions.
5. Interpret the data through inferences. Explain how the evidence answers our questions.
6. Communicate the results. In the context of sports analytics, the communication might be within a team to decide tactical strategies for game play.
(Alberta Education, 2007, updated 2016; Ferri, 2006; Leard & Hadwin, 2001; Manitoba Education and Training, 2020; Ontario Ministry of Education, 2020)
<center><img src='./images/collective.png' alt="Collective decision making" width='90%' /></center>
#### Learning cycle notes
How the individual makes decisions within the collective responsibilities and actions of the team can be considered. In-game decision making involves in-game communication with team members, with each athlete referring to their own real model.
While in-game decision making will always produce a real model, athletes also need to decide when it is appropriate to connect the real model to the computational model and integrate that connection back into game play.
(BC Ministry of Education, 2020; Hadwin et al., 2017; Leard & Hadwin, 2001)
<center><img src='./images/models.png' alt="Models" width='90%' /></center>
#### Real model and computational model notes
How the individual makes decisions within the collective responsibilities and actions of the team can be considered. In-game decision making involves in-game communication with team members, with each athlete referring to their own real model.
While in-game decision making will always produce a real model, athletes also need to decide when it is appropriate to connect the real model to the computational model and integrate that connection back into game play.
(Field Hockey Canada, 2020)
<center><img src='./images/data_literacy_sports.png' alt="Connecting data literacy and sports" width='90%' /></center>
<center><img src='./images/field_hockey_game.png' alt="Field hockey" width='90%' /></center>
<center><img src='./images/understand1.png' alt="Understand actions" width='90%' /></center>
(Field Hockey Alberta, 2020; Field Hockey Canada, 2020)
<center><img src='./images/actions.png' alt="Understand viewpoints" width='90%' /></center>
```
print ('Passes received')
YouTubeVideo('mIwiiJO7Rk4?start=2893&end=2915', width='600', height='355')
```
<center><img src='./images/gather4.png' alt="Gather" width='90%' /></center>
<center><img src='./images/collection_passing.png' alt="Passing" width='90%' /></center>
## 3. Organize
```
possession_time_df = read_csv('data/field_hockey_possession_time.csv')
possession_time_df.head(8)
```
## 4. Explore
How does ball possession affect outcomes?
```
bar_possession_time_df = px.bar(possession_time_df,x="Possession Time (seconds)",y="Quarter",title="Possession per quarter<br>Home 2 shots on net (Q3); Away 1 shot on net (Q1)",color="Team")
bar_possession_time_df.update_layout(autosize=False, width=600, height=400)
lanes_home_passes_df = read_csv('data/field_hockey_lanes_home_passes.csv')
lanes_home_passes_df.head()
circle_lanes_home_passes_df = px.pie(lanes_home_passes_df,values="Count",names="Action",title="Passes received, intercepted, and missed for Home team")
circle_lanes_home_passes_df.show()
bar_lanes_home_passes_df = px.bar(lanes_home_passes_df,
x="Quarter", y="Count", color="Action", title="Passes per quarter for Home team")
bar_lanes_home_passes_df.update_layout(barmode='stack', xaxis={'categoryorder':'array', 'categoryarray':['first','second','third','fourth']})
```
## 4. Explore passes received
What stays the same and what changes?
```
lanes_home_passes_received_df = lanes_home_passes_df[lanes_home_passes_df['Action']=='pass received']
lanes_home_passes_received_df.head()
bar_lanes_home_passes_received_df = px.bar(lanes_home_passes_received_df,
x="Quarter", y="Count", color="Lane", text="Lane", title="Passes received in lanes per quarter for Home team")
bar_lanes_home_passes_received_df.update_layout(barmode='stack', xaxis={'categoryorder':'array', 'categoryarray':['first','second','third','fourth']})
df_passes_home = pd.read_csv('data/field_hockey_home_passes.csv'); df_passes_home
df_temp_1 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'first') ];
df_temp_2 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'second') ];
df_temp_3 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'third') ];
df_temp_4 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'fourth') ];
#import plotly.tools as tls
fig_all = subplots.make_subplots(rows=1, cols=4)
fig_1 = df_temp_1.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_2 = df_temp_2.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_3 = df_temp_3.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_4 = df_temp_4.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_all.append_trace(fig_1['data'][0], 1, 1)
fig_all.append_trace(fig_2['data'][0], 1, 2)
fig_all.append_trace(fig_3['data'][0], 1, 3)
fig_all.append_trace(fig_4['data'][0], 1, 4)
fig_all.update_xaxes(showticklabels = False, linecolor='black')
fig_all.update_yaxes(showticklabels = False, linecolor='black')
iplot(fig_all)
```
#### Passes in left outside lane of the opponent's net
|||||
|---|---|---|---|
|**Q1: 29%** (14/49)|**Q2: 41%** (13/32)|**Q3: 38%** (16/42)|**Q4: 28%** (8/29)|
```
df_passes_home.loc[lambda df: (df['Lane'] == 1) &(df['Phase of Play'] == 'attack') &(df['Quarter']== 'first') ].sum()
14/49
```
## 5. Interpret<br> How can the data exploration inform decision making?
> - Considering the role of passing versus carrying the ball
> - Keeping the ball out of the zone near the net
> - Attacking on the outer lanes, especially toward the left side of the opponent's net
# The technology in this talk
- **Jupyter** notebooks, **Python** programming, **Pandas** for data
- Free to teachers and students
- **Callysto.ca** project (CanCode, Cybera, PIMS)
- This slideshow **IS** a Jupyter notebook! (take a tour)
## Callysto resources
- <a href="https://www.callysto.ca/starter-kit/">Callysto starter kit</a> Getting started
- <a href="https://courses.callysto.ca">courses.callysto.ca</a> Online courses
- <a href="https://www.callysto.ca/weekly-data-visualization/">Weekly data visualizations</a> Quick activities
<center><a href='https://www.callysto.ca/learning-modules/'><img src='./images/learning_modules.png' target='_blank' alt="Callysto learning modules" width='90%' /></a></center>
<center>All free, all open source, aimed at teachers and students</center>
<p><center>Contact us at <a href="mailto:[email protected]">[email protected]</a><br>
for in-class workshops, virtual hackathons...<br>
<a href="https://twitter.com/callysto_canada">@callysto_canada</a><br>
<a href="https://callysto.ca">callysto.ca</a><br>
<a href="https://www.youtube.com/channel/UCPdq1SYKA42EZBvUlNQUAng">YouTube</a>
</center></p>
## Thank you for your attention!
<center><img src='./images/callysto_logo.png' alt="Callysto logo" width='80%' /></center>
<center><img src='./images/callysto_partners2.png' alt='Callysto partners' width='80%' /></center>
### References
Alberta Education. (2000). *Physical education* [Program of Studies]. https://education.alberta.ca/media/160191/phys2000.pdf
Alberta Education. (2007, updated 2016). *Mathematics kindergarten to grade 9* [Program of Studies]. https://education.alberta.ca/media/3115252/2016_k_to_9_math_pos.pdf
Alberta Education. (2017). *Career and Ttechnology foundations* [Program of Studies]. https://education.alberta.ca/media/3795641/ctf-program-of-studies-jan-4-2019.pdf
BC Ministry of Education. (2020). *BC's digital literacy framework*. https://www2.gov.bc.ca/assets/gov/education/kindergarten-to-grade-12/teach/teaching-tools/digital-literacy-framework.pdf
Berikan, B., & Özdemir, S. (2019). Investigating “problem-solving with datasets” as an implementation of computational thinking: A literature review. *Journal of Educational Computing Research, 58*(2), 502–534. https://doi.org/10.1177/0735633119845694
Butler, D. L., & Winne, P. H. (1995). Feedback and self-regulated learning: A theoretical synthesis. *Review of Educational Research, 65*(3), 245–281. https://doi.org/10.3102/00346543065003245
Cleary, T. J., & Zimmerman, B. J. (2001). Self-regulation differences during athletic practice by experts, non-experts, and novices. *I Journal of Applied Sport Psychology, 13*(2), 185–206. https://doi.org/10.1080/104132001753149883
Ferri, R. B. (2006). Theoretical and empirical differentiations of phases in the modelling process. *ZDM, 38*(2), 86–95. https://doi.org/10.1007/bf02655883
Field Hockey Alberta (2020). *Tactical Seminars*. http://www.fieldhockey.ab.ca/content/tactical-seminars
Field Hockey Canada (2020). *Ahead of the Game*. http://www.fieldhockey.ca/ahead-of-the-game-field-hockey-canada-webinar-series/
Gadanidis, G. (2020, September 2). *Shifting from computational thinking to computational modelling in math education* [Online plenary talk]. Changing the Culture 2020, Pacific Institute for the Mathematical Sciences.
Guadalupe, T. & Gómez-Blancarte, A. (2019). Assessment of informal and formal inferential reasoning: A critical research review. *Statistics Education Research Journal, 18*, 8-25. https://www.researchgate.net/publication/335057564_ASSESSMENT_OF_INFORMAL_AND_FORMAL_INFERENTIAL_REASONING_A_CRITICAL_RESEARCH_REVIEW
Hadwin, A., Järvelä, S., & Miller, M. (2017). Self-Regulation, Co-Regulation, and Shared Regulation in Collaborative Learning Environments. *Handbook of Self-Regulation of Learning and Performance*, 83–106. https://doi.org/10.4324/9781315697048-6
Kastens, K. (2014). *Pervasive and Persistent Understandings about Data*. Oceans of Data Institute. http://oceansofdata.org/sites/oceansofdata.org/files/pervasive-and-persistent-understandings-01-14.pdf
Leard, T., & Hadwin, A. F. (2001, May). *Analyzing logfile data to produce navigation profiles of studying as self-regulated learning* [Paper presentaion]. Canadian Society for the Study of Education, Quebec City, Quebec, Canada.
Manitoba Education and Training (2020). *Literacy with ICT across the curriculum: A model for 21st century learning from K-12*. https://www.edu.gov.mb.ca/k12/tech/lict/index.html
Ontario Ministry of Education. (2020). *The Ontario curriculum grades 1‐8: Mathematics* [Program of Studies]. https://www.dcp.edu.gov.on.ca/en/curriculum/elementary-mathematics
| true |
code
| 0.49469 | null | null | null | null |
|
# Prepare Superresolution Training Data with eo-learn
There are many examples and resources for training superresolution networks on (satellite) imagery:
- [MDL4EO](https://mdl4eo.irstea.fr/2019/03/29/enhancement-of-sentinel-2-images-at-1-5m/)
- [ElementAI HighRes-Net](https://github.com/ElementAI/HighRes-net)
- [Fast.ai superresolution](https://github.com/fastai/course-v3/blob/master/nbs/dl1/lesson7-superres.ipynb)
We'll show you how to use `eo-learn` to prepare data for these tasks (and an example of training the network with `fastai`)
First you'll need to download the [Spacenet Challenge: Paris Data](https://spacenetchallenge.github.io/AOI_Lists/AOI_3_Paris.html). We're using this to get high resolution image chips.
```
from os import path as op
from glob import glob
import datetime
from eolearn.io import ImportFromTiff, SentinelHubInputTask
from eolearn.core import FeatureType, LinearWorkflow, EOTask
from sentinelhub import BBox, CRS, DataSource
from PIL import Image
import numpy as np
from tqdm import tqdm
spacenet_images = glob('AOI_3_Paris_Train/RGB-PanSharpen/*.tif')
# Import the Spacenet chips into EOPatches, as a feature called "spacenet"
input_task = ImportFromTiff((FeatureType.DATA_TIMELESS, 'spacenet'))
# Add Sentinel 2 L2A to our EOPatches covering the same area
time_interval = ('2017-02-28', '2017-04-01') # roughly matching the spacenet dates
add_l2a = SentinelHubInputTask(
data_source=DataSource.SENTINEL2_L2A,
bands=['B04','B03','B02'],
bands_feature=(FeatureType.DATA, 'TRUE-COLOR-S2-L2A'),
additional_data=[(FeatureType.MASK, 'dataMask', 'IS_VALID'), (FeatureType.DATA, 'SCL')],
maxcc=.1,
time_difference=datetime.timedelta(hours=2),
max_threads=3,
resolution=(10,10)
)
# Save the Spacenet and Sentinel images in separate folders. Resize our images when saving
BIG_SIZE = (256, 256)
SMALL_SIZE = (64, 64)
INPUT_FOLDER = 'input'
TARGET_FOLDER = 'target'
class CustomSave(EOTask):
def execute(self, eopatch, image_name=None):
# if we don't have enough data, don't save
spacenet_array = eopatch.data_timeless['spacenet']
data_pct = (np.count_nonzero(spacenet_array) / spacenet_array.size)
if data_pct < 0.9:
return eopatch
# resize images, rescale to 8bit
sentinel_array = eopatch.data[layer][0]
sentinel_array_8bit = (sentinel_array * 255.).astype(np.uint8)
sentinel_img = Image.fromarray(sentinel_array_8bit).resize(SMALL_SIZE, resample=Image.BILINEAR)
sentinel_img.save(op.join(INPUT_FOLDER, f'{image_name}.png'))
spacenet_array_8bit = ((spacenet_array - np.min(spacenet_array, axis=(0, 1))) / (np.max(spacenet_array, axis=(0, 1)) - np.min(spacenet_array, axis=(0, 1))) * 255).astype(np.uint8)
spacenet_image = Image.fromarray(spacenet_array_8bit).resize(BIG_SIZE, resample=Image.BILINEAR)
spacenet_image.save(op.join(TARGET_FOLDER, f'{image_name}.png'))
return eopatch
custom_save = CustomSave()
# Create this as a EOWorkflow to run over all the images
prepare_data = LinearWorkflow(
input_task,
add_l2a,
custom_save
)
# Execute the workflow
pbar = tqdm(total=len(spacenet_images))
for image in spacenet_images:
image_name = op.splitext(op.basename(image))[0].replace('RGB-PanSharpen_AOI_3_Paris_', '')
workflow_input = {
input_task: dict(filename=image),
add_l1c: dict(time_interval=time_interval),
custom_save: dict(image_name=image_name)
}
prepare_data.execute(workflow_input)
pbar.update(1)
```
| true |
code
| 0.474266 | null | null | null | null |
|
# Train DynUNet on Decathlon datasets
This tutorial shows how to train 3D segmentation tasks on all the 10 decathlon datasets with `DynUNet`.
Refer to papers:
`Automated Design of Deep Learning Methods for Biomedical Image Segmentation <https://arxiv.org/abs/1904.08128>`
`nnU-Net: Self-adapting Framework for U-Net-Based Medical Image Segmentation <https://arxiv.org/abs/1809.10486>`
[](https://colab.research.google.com/github/Project-MONAI/tutorials/blob/master/modules/dynunet_tutorial.ipynb)
## Setup environment
```
%pip install -q "monai[itk, ignite, tqdm]"
%pip install -q matplotlib
%matplotlib inline
```
## Setup imports
```
# Copyright 2020 MONAI Consortium
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import os
import logging
import ignite
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import numpy as np
from monai.apps import DecathlonDataset
from monai.config import print_config
from monai.data import DataLoader
from monai.engines import SupervisedTrainer
from monai.handlers import MeanDice, StatsHandler
from monai.inferers import SimpleInferer
from monai.losses import DiceLoss
from monai.networks.nets import DynUNet
from monai.transforms import (
AsDiscreted,
Compose,
LoadNiftid,
AddChanneld,
CropForegroundd,
Spacingd,
Orientationd,
SpatialPadd,
NormalizeIntensityd,
RandCropByPosNegLabeld,
RandZoomd,
CastToTyped,
RandGaussianNoised,
RandGaussianSmoothd,
RandScaleIntensityd,
RandFlipd,
ToTensord,
)
print_config()
```
## Select Decathlon task
The Decathlon dataset contains 10 tasks, this dynUNet tutorial can support all of them.
Just need to select task ID and other parameters will be automatically selected.
(Tested task 04 locally, epoch time is 8 secs on V100 GPU and best metrics is 0.8828 at epoch: 70)
```
task_id = "04"
task_name = {
"01": "Task01_BrainTumour",
"02": "Task02_Heart",
"03": "Task03_Liver",
"04": "Task04_Hippocampus",
"05": "Task05_Prostate",
"06": "Task06_Lung",
"07": "Task07_Pancreas",
"08": "Task08_HepaticVessel",
"09": "Task09_Spleen",
"10": "Task10_Colon",
}
patch_size = {
"01": [128, 128, 128],
"02": [160, 192, 80],
"03": [128, 128, 128],
"04": [40, 56, 40],
"05": [320, 256, 20],
"06": [192, 160, 80],
"07": [224, 224, 40],
"08": [192, 192, 64],
"09": [192, 160, 64],
"10": [192, 160, 56],
}
spacing = {
"01": [1.0, 1.0, 1.0],
"02": [1.25, 1.25, 1.37],
"03": [0.77, 0.77, 1],
"04": [1.0, 1.0, 1.0],
"05": [0.62, 0.62, 3.6],
"06": [0.79, 0.79, 1.24],
"07": [0.8, 0.8, 2.5],
"08": [0.8, 0.8, 1.5],
"09": [0.79, 0.79, 1.6],
"10": [0.78, 0.78, 3],
}
```
## Setup data directory
You can specify a directory with the `MONAI_DATA_DIRECTORY` environment variable.
This allows you to save results and reuse downloads.
If not specified a temporary directory will be used.
```
directory = os.environ.get("MONAI_DATA_DIRECTORY")
root_dir = tempfile.mkdtemp() if directory is None else directory
print(root_dir)
```
## Define train and validation transforms
```
train_transform = Compose(
[
LoadNiftid(keys=["image", "label"]),
AddChanneld(keys=["image", "label"]),
CropForegroundd(keys=["image", "label"], source_key="image"),
Spacingd(
keys=["image", "label"],
pixdim=spacing[task_id],
mode=("bilinear", "nearest"),
),
Orientationd(keys=["image", "label"], axcodes="RAS"),
SpatialPadd(keys=["image", "label"], spatial_size=patch_size[task_id]),
NormalizeIntensityd(keys=["image"], nonzero=False, channel_wise=True),
RandCropByPosNegLabeld(
keys=["image", "label"],
label_key="label",
spatial_size=patch_size[task_id],
pos=1,
neg=1,
num_samples=1,
image_key="image",
image_threshold=0,
),
RandZoomd(
keys=["image", "label"],
min_zoom=0.9,
max_zoom=1.2,
mode=("trilinear", "nearest"),
align_corners=(True, None),
prob=0.16,
),
CastToTyped(keys=["image", "label"], dtype=(np.float32, np.uint8)),
RandGaussianNoised(keys=["image"], std=0.01, prob=0.15),
RandGaussianSmoothd(
keys=["image"],
sigma_x=(0.5, 1.15),
sigma_y=(0.5, 1.15),
sigma_z=(0.5, 1.15),
prob=0.15,
),
RandScaleIntensityd(keys=["image"], factors=0.3, prob=0.15),
RandFlipd(["image", "label"], spatial_axis=[0, 1, 2], prob=0.5),
ToTensord(keys=["image", "label"]),
]
)
val_transform = Compose(
[
LoadNiftid(keys=["image", "label"]),
AddChanneld(keys=["image", "label"]),
CropForegroundd(keys=["image", "label"], source_key="image"),
Spacingd(
keys=["image", "label"],
pixdim=spacing[task_id],
mode=("bilinear", "nearest"),
),
Orientationd(keys=["image", "label"], axcodes="RAS"),
SpatialPadd(keys=["image", "label"], spatial_size=patch_size[task_id]),
NormalizeIntensityd(keys=["image"], nonzero=False, channel_wise=True),
CastToTyped(keys=["image", "label"], dtype=(np.float32, np.uint8)),
ToTensord(keys=["image", "label"]),
]
)
```
## Load data by MONAI DecathlonDataset
```
train_ds = DecathlonDataset(
root_dir=root_dir,
task=task_name[task_id],
transform=train_transform,
section="training",
download=False,
num_workers=4,
)
train_loader = DataLoader(train_ds, batch_size=2, shuffle=True, num_workers=1)
val_ds = DecathlonDataset(
root_dir=root_dir,
task=task_name[task_id],
transform=val_transform,
section="validation",
download=False,
num_workers=4,
)
val_loader = DataLoader(val_ds, batch_size=1, shuffle=False, num_workers=1)
```
## Visualize batch of data to check images and labels
```
for i in range(2):
image, label = val_ds[i]["image"], val_ds[i]["label"]
plt.figure("check", (12, 8))
plt.subplot(1, 2, 1)
plt.title("image")
plt.imshow(image[0, :, :, 10].detach().cpu(), cmap="gray")
plt.subplot(1, 2, 2)
plt.title("label")
plt.imshow(label[0, :, :, 10].detach().cpu())
plt.show()
```
## Customize loss function
Here we combine Dice loss and Cross Entropy loss.
```
class CrossEntropyLoss(nn.Module):
def __init__(self):
super().__init__()
self.loss = nn.CrossEntropyLoss()
def forward(self, y_pred, y_true):
# CrossEntropyLoss target needs to have shape (B, D, H, W)
# Target from pipeline has shape (B, 1, D, H, W)
y_true = torch.squeeze(y_true, dim=1).long()
return self.loss(y_pred, y_true)
class DiceCELoss(nn.Module):
def __init__(self):
super().__init__()
self.dice = DiceLoss(to_onehot_y=True, softmax=True)
self.cross_entropy = CrossEntropyLoss()
def forward(self, y_pred, y_true):
dice = self.dice(y_pred, y_true)
cross_entropy = self.cross_entropy(y_pred, y_true)
return dice + cross_entropy
```
## Initialize training components
```
device = torch.device("cuda:0")
loss = DiceCELoss()
learning_rate = 0.01
max_epochs = 200
sizes, spacings = patch_size[task_id], spacing[task_id]
properties = val_ds.get_properties(keys=["labels", "modality"])
n_class, in_channels = len(properties["labels"]), len(properties["modality"])
best_dice, best_epoch = (n_class - 1) * [0], (n_class - 1) * [0]
strides, kernels = [], []
while True:
spacing_ratio = [sp / min(spacings) for sp in spacings]
stride = [2 if ratio <= 2 and size >= 8 else 1 for (ratio, size) in zip(spacing_ratio, sizes)]
kernel = [3 if ratio <= 2 else 1 for ratio in spacing_ratio]
if all(s == 1 for s in stride):
break
sizes = [i / j for i, j in zip(sizes, stride)]
spacings = [i * j for i, j in zip(spacings, stride)]
kernels.append(kernel)
strides.append(stride)
strides.insert(0, len(spacings) * [1])
kernels.append(len(spacings) * [3])
net = DynUNet(
spatial_dims=3,
in_channels=in_channels,
out_channels=n_class,
kernel_size=kernels,
strides=strides,
upsample_kernel_size=strides[1:],
norm_name="instance",
deep_supervision=True,
deep_supr_num=2,
res_block=False,
).to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate, momentum=0.95)
scheduler = torch.optim.lr_scheduler.LambdaLR(
optimizer, lr_lambda=lambda epoch: (1 - epoch / max_epochs) ** 0.9
)
```
## MONAI evaluator
Here we customized the forward computation, so need to define `_iteration` function.
```
from monai.engines import SupervisedEvaluator
from monai.handlers import StatsHandler, CheckpointSaver, MeanDice
from monai.inferers import SlidingWindowInferer
val_handlers = [
StatsHandler(output_transform=lambda x: None),
CheckpointSaver(save_dir="./runs/", save_dict={"net": net}, save_key_metric=True),
]
val_post_transform = Compose(
[AsDiscreted(keys=("pred", "label"), argmax=(True, False), to_onehot=True, n_classes=n_class)]
)
# Define customized evaluator
class DynUNetEvaluator(SupervisedEvaluator):
def _iteration(self, engine, batchdata):
inputs, targets = self.prepare_batch(batchdata)
inputs, targets = inputs.to(engine.state.device), targets.to(engine.state.device)
flip_inputs = torch.flip(inputs, dims=(2, 3, 4))
def _compute_pred():
pred = self.inferer(inputs, self.network)
flip_pred = torch.flip(self.inferer(flip_inputs, self.network), dims=(2, 3, 4))
return (pred + flip_pred) / 2
# execute forward computation
self.network.eval()
with torch.no_grad():
if self.amp:
with torch.cuda.amp.autocast():
predictions = _compute_pred()
else:
predictions = _compute_pred()
return {"image": inputs, "label": targets, "pred": predictions}
evaluator = DynUNetEvaluator(
device=device,
val_data_loader=val_loader,
network=net,
inferer=SlidingWindowInferer(roi_size=patch_size[task_id], sw_batch_size=4, overlap=0.5),
post_transform=val_post_transform,
key_val_metric={
"val_mean_dice": MeanDice(
include_background=False,
output_transform=lambda x: (x["pred"], x["label"]),
)
},
val_handlers=val_handlers,
amp=True,
)
```
## MONAI trainer
Here we customized loss computation progress, so need to define `_iteration` function.
```
from torch.nn.functional import interpolate
from monai.engines import SupervisedTrainer
from monai.inferers import SimpleInferer
from monai.handlers import LrScheduleHandler, ValidationHandler, StatsHandler
train_handlers = [
LrScheduleHandler(lr_scheduler=scheduler, print_lr=True),
ValidationHandler(validator=evaluator, interval=2, epoch_level=True),
StatsHandler(tag_name="train_loss", output_transform=lambda x: x["loss"]),
]
# define customized trainer
class DynUNetTrainer(SupervisedTrainer):
def _iteration(self, engine, batchdata):
inputs, targets = self.prepare_batch(batchdata)
inputs, targets = inputs.to(engine.state.device), targets.to(engine.state.device)
def _compute_loss(preds, label):
labels = [label] + [interpolate(label, pred.shape[2:]) for pred in preds[1:]]
return sum([0.5 ** i * self.loss_function(p, l) for i, (p, l) in enumerate(zip(preds, labels))])
self.network.train()
self.optimizer.zero_grad()
if self.amp and self.scaler is not None:
with torch.cuda.amp.autocast():
predictions = self.inferer(inputs, self.network)
loss = _compute_loss(predictions, targets)
self.scaler.scale(loss).backward()
self.scaler.step(self.optimizer)
self.scaler.update()
else:
predictions = self.inferer(inputs, self.network)
loss = _compute_loss(predictions, targets).mean()
loss.backward()
self.optimizer.step()
return {"image": inputs, "label": targets, "pred": predictions, "loss": loss.item()}
trainer = DynUNetTrainer(
device=device,
max_epochs=max_epochs,
train_data_loader=train_loader,
network=net,
optimizer=optimizer,
loss_function=loss,
inferer=SimpleInferer(),
post_transform=None,
key_train_metric=None,
train_handlers=train_handlers,
amp=True,
)
```
## Execute training with workflows
```
import logging
import sys
logging.basicConfig(stream=sys.stdout, level=logging.INFO)
trainer.run()
```
## Cleanup data directory
Remove directory if a temporary was used.
```
if directory is None:
shutil.rmtree(root_dir)
```
| true |
code
| 0.715747 | null | null | null | null |
|
<img align="center" style="max-width: 1000px" src="banner.png">
<img align="right" style="max-width: 200px; height: auto" src="hsg_logo.png">
## Lab 02 - "Artificial Neural Networks"
Machine Learning, University of St. Gallen, Spring Term 2022
The lab environment of the "Coding and Artificial Intelligence" IEMBA course at the University of St. Gallen (HSG) is based on Jupyter Notebooks (https://jupyter.org), which allow to perform a variety of statistical evaluations and data analyses.
In this lab, we will learn how to implement, train, and apply our first **Artificial Neural Network (ANN)** using a Python library named `PyTorch`. The `PyTorch` library is an open-source machine learning library for Python, used for a variety of applications such as image classification and natural language processing. We will use the implemented neural network to learn to again classify images of fashion articles from the **Fashion-MNIST** dataset.
The figure below illustrates a high-level view of the machine learning process we aim to establish in this lab:
<img align="center" style="max-width: 700px" src="classification.png">
As always, pls. don't hesitate to ask all your questions either during the lab, post them in our CANVAS (StudyNet) forum (https://learning.unisg.ch), or send us an email (using the course email).
## 1. Lab Objectives:
After today's lab, you should be able to:
> 1. Understand the basic concepts, intuitions and major building blocks of **Artificial Neural Networks (ANNs)**.
> 2. Know how to use Python's **PyTorch library** to train and evaluate neural network based models.
> 3. Understand how to apply neural networks to **classify images** of handwritten digits.
> 4. Know how to **interpret the detection results** of the network as well as its **reconstruction loss**.
Before we start let's watch a motivational video:
```
from IPython.display import YouTubeVideo
# Official Intro | GTC 2017 | I AM AI"
# YouTubeVideo('SUNPrR4o5ZA', width=800, height=400)
```
## 2. Setup of the Jupyter Notebook Environment
Similar to the previous labs, we need to import a couple of Python libraries that allow for data analysis and data visualization. We will mostly use the `PyTorch`, `Numpy`, `Scikit-Learn`, `Matplotlib` and the `Seaborn` and a few utility libraries throughout this lab:
```
# import standard python libraries
import os, urllib, io
from datetime import datetime
import numpy as np
```
Import the Python machine / deep learning libraries:
```
# import the PyTorch deep learning libary
import torch, torchvision
import torch.nn.functional as F
from torch import nn, optim
```
Import the sklearn classification metrics:
```
# import sklearn classification evaluation library
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
```
Import Python plotting libraries:
```
# import matplotlib, seaborn, and PIL data visualization libary
import matplotlib.pyplot as plt
import seaborn as sns
from PIL import Image
```
Enable notebook matplotlib inline plotting:
```
%matplotlib inline
```
Import `Google's GDrive` connector and mount your `GDrive` directories:
```
# import the Google Colab GDrive connector
from google.colab import drive
# mount GDrive inside the Colab notebook
drive.mount('/content/drive')
```
Create a structure of `Colab` Notebook sub-directories inside of `GDrive` to to store the data and the trained neural network models:
```
# create Colab Notebooks directory
notebook_directory = '/content/drive/MyDrive/Colab Notebooks'
if not os.path.exists(notebook_directory): os.makedirs(notebook_directory)
# create data sub-directory inside the Colab Notebooks directory
data_directory = '/content/drive/MyDrive/Colab Notebooks/data_fmnist'
if not os.path.exists(data_directory): os.makedirs(data_directory)
# create models sub-directory inside the Colab Notebooks directory
models_directory = '/content/drive/MyDrive/Colab Notebooks/models_fmnist'
if not os.path.exists(models_directory): os.makedirs(models_directory)
```
Set a random `seed` value to obtain reproducable results:
```
# init deterministic seed
seed_value = 1234
np.random.seed(seed_value) # set numpy seed
torch.manual_seed(seed_value) # set pytorch seed CPU
```
Google Colab provides the use of free GPUs for running notebooks. However, if you just execute this notebook as is, it will use your device's CPU. To run the lab on a GPU, got to `Runtime` > `Change runtime type` and set the Runtime type to `GPU` in the drop-down. Running this lab on a CPU is fine, but you will find that GPU computing is faster. *CUDA* indicates that the lab is being run on GPU.
Enable GPU computing by setting the device flag and init a CUDA seed:
```
# set cpu or gpu enabled device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu').type
# init deterministic GPU seed
torch.cuda.manual_seed(seed_value)
# log type of device enabled
print('[LOG] notebook with {} computation enabled'.format(str(device)))
```
Let's determine if we have access to a GPU provided by e.g. `Google's Colab` environment:
```
!nvidia-smi
```
## 3. Dataset Download and Data Assessment
The **Fashion-MNIST database** is a large database of Zalando articles that is commonly used for training various image processing systems. The database is widely used for training and testing in the field of machine learning. Let's have a brief look into a couple of sample images contained in the dataset:
<img align="center" style="max-width: 700px; height: 300px" src="FashionMNIST.png">
Source: https://www.kaggle.com/c/insar-fashion-mnist-challenge
Further details on the dataset can be obtained via Zalando research's [github page](https://github.com/zalandoresearch/fashion-mnist).
The **Fashion-MNIST database** is an image dataset of Zalando's article images, consisting of in total 70,000 images.
The dataset is divided into a set of **60,000 training examples** and a set of **10,000 evaluation examples**. Each example is a **28x28 grayscale image**, associated with a **label from 10 classes**. Zalando created this dataset with the intention of providing a replacement for the popular **MNIST** handwritten digits dataset. It is a useful addition as it is a bit more complex, but still very easy to use. It shares the same image size and train/test split structure as MNIST, and can therefore be used as a drop-in replacement. It requires minimal efforts on preprocessing and formatting the distinct images.
Let's download, transform and inspect the training images of the dataset. Therefore, let's first define the directory in which we aim to store the training data:
```
train_path = data_directory + '/train_fmnist'
```
Now, let's download the training data accordingly:
```
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
# download and transform training images
fashion_mnist_train_data = torchvision.datasets.FashionMNIST(root=train_path, train=True, transform=transf, download=True)
```
Verify the number of training images downloaded:
```
# determine the number of training data images
len(fashion_mnist_train_data)
```
Furthermore, let's inspect a couple of the downloaded training images:
```
# select and set a (random) image id
image_id = 3000
# retrieve image exhibiting the image id
fashion_mnist_train_data[image_id]
```
Ok, that doesn't seem right :). Let's now seperate the image from its label information:
```
fashion_mnist_train_image, fashion_mnist_train_label = fashion_mnist_train_data[image_id]
```
We can verify the label that our selected image has:
```
fashion_mnist_train_label
```
Ok, we know that the numerical label is 6. Each image is associated with a label from 0 to 9, and this number represents one of the fashion items. So what does 6 mean? Is 6 a bag? A pullover? The order of the classes can be found on Zalando research's [github page](https://github.com/zalandoresearch/fashion-mnist). We need to map each numerical label to its fashion item, which will be useful throughout the lab:
```
fashion_classes = {0: 'T-shirt/top',
1: 'Trouser',
2: 'Pullover',
3: 'Dress',
4: 'Coat',
5: 'Sandal',
6: 'Shirt',
7: 'Sneaker',
8: 'Bag',
9: 'Ankle boot'}
```
So, we can determine the fashion item that the label represents:
```
fashion_classes[fashion_mnist_train_label]
```
Great, let's now visually inspect our sample image:
```
# define tensor to image transformation
trans = torchvision.transforms.ToPILImage()
# set image plot title
plt.title('Example: {}, Label: {}'.format(str(image_id), fashion_classes[fashion_mnist_train_label]))
# plot mnist handwritten digit sample
plt.imshow(trans(fashion_mnist_train_image), cmap='gray')
```
Fantastic, right? Let's now define the directory in which we aim to store the evaluation data:
```
eval_path = data_directory + '/eval_fmnist'
```
And download the evaluation data accordingly:
```
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
# download and transform training images
fashion_mnist_eval_data = torchvision.datasets.FashionMNIST(root=eval_path, train=False, transform=transf, download=True)
```
Let's also verify the number of evaluation images downloaded:
```
# determine the number of evaluation data images
len(fashion_mnist_eval_data)
```
## 4. Neural Network Implementation
In this section we, will implement the architecture of the **neural network** we aim to utilize to learn a model that is capable to classify the 28x28 pixel FashionMNIST images of fashion items. However, before we start the implementation let's briefly revisit the process to be established. The following cartoon provides a birds-eye view:
<img align="center" style="max-width: 1000px" src="https://github.com/HSG-AIML/LabGSERM/blob/main/lab_04/process.png?raw=1">
### 4.1 Implementation of the Neural Network Architecture
The neural network, which we name **'FashionMNISTNet'** consists of three **fully-connected layers** (including an “input layer” and two hidden layers). Furthermore, the **FashionMNISTNet** should encompass the following number of neurons per layer: 100 (layer 1), 50 (layer 2) and 10 (layer 3). Meaning the first layer consists of 100 neurons, the second layer of 50 neurons and third layer of 10 neurons (the number of digit classes we aim to classify.
We will now start implementing the network architecture as a separate Python class. Implementing the network architectures as a **separate class** in Python is good practice in deep learning projects. It will allow us to create and train several instances of the same neural network architecture. This provides us, for example, the opportunity to evaluate different initializations of the network parameters or train models using distinct datasets.
```
# implement the MNISTNet network architecture
class FashionMNISTNet(nn.Module):
# define the class constructor
def __init__(self):
# call super class constructor
super(FashionMNISTNet, self).__init__()
# specify fully-connected (fc) layer 1 - in 28*28, out 100
self.linear1 = nn.Linear(28*28, 100, bias=True) # the linearity W*x+b
self.relu1 = nn.ReLU(inplace=True) # the non-linearity
# specify fc layer 2 - in 100, out 50
self.linear2 = nn.Linear(100, 50, bias=True) # the linearity W*x+b
self.relu2 = nn.ReLU(inplace=True) # the non-linarity
# specify fc layer 3 - in 50, out 10
self.linear3 = nn.Linear(50, 10) # the linearity W*x+b
# add a softmax to the last layer
self.logsoftmax = nn.LogSoftmax(dim=1) # the softmax
# define network forward pass
def forward(self, images):
# reshape image pixels
x = images.view(-1, 28*28)
# define fc layer 1 forward pass
x = self.relu1(self.linear1(x))
# define fc layer 2 forward pass
x = self.relu2(self.linear2(x))
# define layer 3 forward pass
x = self.logsoftmax(self.linear3(x))
# return forward pass result
return x
```
You may have noticed, when reviewing the implementation above, that we applied an additional operator, referred to as **'Softmax'** to the third layer of our neural network.
The **softmax function**, also known as the normalized exponential function, is a function that takes as input a vector of K real numbers, and normalizes it into a probability distribution consisting of K probabilities.
That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after application of the softmax, each component will be in the interval $(0,1)$, and the components will add up to 1, so that they can be interpreted as probabilities. In general, the softmax function $\sigma :\mathbb {R} ^{K}\to \mathbb {R} ^{K}$ is defined by the formula:
<center> $\sigma (\mathbf {z} )_{i}=\ln ({e^{z_{i}} / \sum _{j=1}^{K}e^{z_{j}}})$ </center>
for $i = 1, …, K$ and ${\mathbf {z}}=(z_{1},\ldots ,z_{K})\in \mathbb {R} ^{K}$ (Source: https://en.wikipedia.org/wiki/Softmax_function ).
Let's have a look at the simplified three-class example below. The scores of the distinct predicted classes $c_i$ are computed from the forward propagation of the network. We then take the softmax and obtain the probabilities as shown:
<img align="center" style="max-width: 800px" src="https://github.com/HSG-AIML/LabGSERM/blob/main/lab_04/softmax.png?raw=1">
The output of the softmax describes the probability (or if you may, the confidence) of the neural network that a particular sample belongs to a certain class. Thus, for the first example above, the neural network assigns a confidence of 0.49 that it is a 'three', 0.49 that it is a 'four', and 0.03 that it is an 'eight'. The same goes for each of the samples above.
Now, that we have implemented our first neural network we are ready to instantiate a network model to be trained:
```
model = FashionMNISTNet()
```
Let's push the initialized `FashionMNISTNet` model to the computing `device` that is enabled:
```
model = model.to(device)
```
Let's double check if our model was deployed to the GPU if available:
```
!nvidia-smi
```
Once the model is initialized, we can visualize the model structure and review the implemented network architecture by execution of the following cell:
```
# print the initialized architectures
print('[LOG] FashionMNISTNet architecture:\n\n{}\n'.format(model))
```
Looks like intended? Brilliant! Finally, let's have a look into the number of model parameters that we aim to train in the next steps of the notebook:
```
# init the number of model parameters
num_params = 0
# iterate over the distinct parameters
for param in model.parameters():
# collect number of parameters
num_params += param.numel()
# print the number of model paramters
print('[LOG] Number of to be trained FashionMNISTNet model parameters: {}.'.format(num_params))
```
Ok, our "simple" FashionMNISTNet model already encompasses an impressive number 84'060 model parameters to be trained.
### 4.2 Specification of the Neural Network Loss Function
Now that we have implemented the **FashionMNISTNet** we are ready to train the network. However, prior to starting the training, we need to define an appropriate loss function. Remember, we aim to train our model to learn a set of model parameters $\theta$ that minimize the classification error of the true class $c^{i}$ of a given handwritten digit image $x^{i}$ and its predicted class $\hat{c}^{i} = f_\theta(x^{i})$ as faithfully as possible.
Thereby, the training objective is to learn a set of optimal model parameters $\theta^*$ that optimize $\arg\min_{\theta} \|C - f_\theta(X)\|$ over all training images in the FashionMNIST dataset. To achieve this optimization objective, one typically minimizes a loss function $\mathcal{L_{\theta}}$ as part of the network training. In this lab we use the **'Negative Log Likelihood (NLL)'** loss, defined by:
<center> $\mathcal{L}^{NLL}_{\theta} (c_i, \hat c_i) = - \frac{1}{N} \sum_{i=1}^N \log (\hat{c}_i) $, </center>
for a set of $n$-FashionMNIST images $x^{i}$, $i=1,...,n$ and their respective predicted class labels $\hat{c}^{i}$. This is summed for all the correct classes.
Let's have a look at a brief example:
<img align="center" style="max-width: 900px" src="./loss.png">
As we see in the example, we first compute class predictions for each class. We normalize the predictions with a softmax over all classes, so that we end up with 'probabilities' (that's what comes out of the NN).
To compute the loss, we pick the predicted probability of the true class $\hat{c}_i$ and take the log of it. As the probabilities are on [0,1], the log of them are on [-$\infty$,0]. To maximize the probability of the true class $\hat{c}_i$, we have to maximize $log(\hat{c}_i)$. Due to the softmax, the predicted probabilties of all classes $c_i$ sum to 1: $\sum_i c_i = 1$. Therefore, by maximizing the probability of the true class $\hat{c}_i$, we minimize the probabilities of all the other (wrong) classes.
In ML, it has become common to minimize an 'error' or 'loss' term. Therfore, we sum over the log-likelihoods and take the negative of it. Small values (close to $0$) here translate to high values in true class probability.
During training the **NLL** loss will penalize models that result in a high classification error between the predicted class labels $\hat{c}^{i}$ and their respective true class label $c^{i}$. Luckily, an implementation of the NLL loss is already available in PyTorch! It can be instantiated "off-the-shelf" via the execution of the following PyTorch command:
```
# define the optimization criterion / loss function
nll_loss = nn.NLLLoss()
```
Let's also push the initialized `nll_loss` computation to the computing `device` that is enabled:
```
nll_loss = nll_loss.to(device)
```
## 5. Neural Network Model Training
In this section, we will train our neural network model (as implemented in the section above) using the transformed images of fashion items. More specifically, we will have a detailed look into the distinct training steps as well as how to monitor the training progress.
### 5.1. Preparing the Network Training
So far, we have pre-processed the dataset, implemented the ANN and defined the classification error. Let's now start to train a corresponding model for **20 epochs** and a **mini-batch size of 128** FashionMNIST images per batch. This implies that the whole dataset will be fed to the ANN 20 times in chunks of 128 images yielding to **469 mini-batches** (60.000 images / 128 images per mini-batch) per epoch.
```
# specify the training parameters
num_epochs = 20 # number of training epochs
mini_batch_size = 128 # size of the mini-batches
```
Based on the loss magnitude of a certain mini-batch PyTorch automatically computes the gradients. But even better, based on the gradient, the library also helps us in the optimization and update of the network parameters $\theta$.
We will use the **Stochastic Gradient Descent (SGD) optimization** and set the learning-rate $l = 0.001$. Each mini-batch step the optimizer will update the model parameters $\theta$ values according to the degree of classification error (the MSE loss).
```
# define learning rate and optimization strategy
learning_rate = 0.001
optimizer = optim.SGD(params=model.parameters(), lr=learning_rate)
```
Now that we have successfully implemented and defined the three ANN building blocks let's take some time to review the `FashionMNISTNet` model definition as well as the `loss`. Please, read the above code and comments carefully and don't hesitate to let us know any questions you might have.
Furthermore, lets specify and instantiate a corresponding PyTorch data loader that feeds the image tensors to our neural network:
```
fashion_mnist_train_dataloader = torch.utils.data.DataLoader(fashion_mnist_train_data, batch_size=mini_batch_size, shuffle=True)
```
### 5.2. Running the Network Training
Finally, we start training the model. The detailed training procedure for each mini-batch is performed as follows:
>1. do a forward pass through the FashionMNISTNet network,
>2. compute the negative log likelihood classification error $\mathcal{L}^{NLL}_{\theta}(c^{i};\hat{c}^{i})$,
>3. do a backward pass through the FashionMNISTNet network, and
>4. update the parameters of the network $f_\theta(\cdot)$.
To ensure learning while training our ANN model, we will monitor whether the loss decreases with progressing training. Therefore, we obtain and evaluate the classification performance of the entire training dataset after each training epoch. Based on this evaluation, we can conclude on the training progress and whether the loss is converging (indicating that the model might not improve any further).
The following elements of the network training code below should be given particular attention:
>- `loss.backward()` computes the gradients based on the magnitude of the reconstruction loss,
>- `optimizer.step()` updates the network parameters based on the gradient.
```
# init collection of training epoch losses
train_epoch_losses = []
# set the model in training mode
model.train()
# train the MNISTNet model
for epoch in range(num_epochs):
# init collection of mini-batch losses
train_mini_batch_losses = []
# iterate over all-mini batches
for i, (images, labels) in enumerate(fashion_mnist_train_dataloader):
# push mini-batch data to computation device
images = images.to(device)
labels = labels.to(device)
# run forward pass through the network
output = model(images)
# reset graph gradients
model.zero_grad()
# determine classification loss
loss = nll_loss(output, labels)
# run backward pass
loss.backward()
# update network paramaters
optimizer.step()
# collect mini-batch reconstruction loss
train_mini_batch_losses.append(loss.data.item())
# determine mean min-batch loss of epoch
train_epoch_loss = np.mean(train_mini_batch_losses)
# print epoch loss
now = datetime.utcnow().strftime("%Y%m%d-%H:%M:%S")
print('[LOG {}] epoch: {} train-loss: {}'.format(str(now), str(epoch), str(train_epoch_loss)))
# set filename of actual model
model_name = 'fashion_mnist_model_epoch_{}.pth'.format(str(epoch))
# save current model to GDrive models directory
torch.save(model.state_dict(), os.path.join(models_directory, model_name))
# determine mean min-batch loss of epoch
train_epoch_losses.append(train_epoch_loss)
```
Upon successfull training let's visualize and inspect the training loss per epoch:
```
# prepare plot
fig = plt.figure()
ax = fig.add_subplot(111)
# add grid
ax.grid(linestyle='dotted')
# plot the training epochs vs. the epochs' classification error
ax.plot(np.array(range(1, len(train_epoch_losses)+1)), train_epoch_losses, label='epoch loss (blue)')
# add axis legends
ax.set_xlabel("[training epoch $e_i$]", fontsize=10)
ax.set_ylabel("[Classification Error $\mathcal{L}^{NLL}$]", fontsize=10)
# set plot legend
plt.legend(loc="upper right", numpoints=1, fancybox=True)
# add plot title
plt.title('Training Epochs $e_i$ vs. Classification Error $L^{NLL}$', fontsize=10);
```
Ok, fantastic. The training error is nicely going down. We could train the network a couple more epochs until the error converges. But let's stay with the 20 training epochs for now and continue with evaluating our trained model.
## 6. Neural Network Model Evaluation
Before evaluating our model let's load the best performing model. Remember, that we stored a snapshot of the model after each training epoch to our local model directory. We will now load the last snapshot saved.
```
### load state_dict from some url
# # restore pre-trained model snapshot
# best_model_name = 'https://raw.githubusercontent.com/HSG-AIML-Teaching/ML2022-Lab/main/lab_02/models/fashion_mnist_model_epoch_19.pth'
# # read stored model from the remote location
# model_bytes = urllib.request.urlopen(best_model_name)
# # load model tensor from io.BytesIO object
# model_buffer = io.BytesIO(model_bytes.read())
# # init pre-trained model class
# best_model = FashionMNISTNet()
# # load pre-trained models
# best_model.load_state_dict(torch.load(model_buffer, map_location=torch.device('cpu')))
## load state_dict from local path
# restore pre-trained model snapshot
best_model_name = models_directory +'/fashion_mnist_model_epoch_19.pth'
# load state_dict from path
state_dict_best = torch.load(best_model_name)
# init pre-trained model class
best_model = FashionMNISTNet()
# load pre-trained state_dict to model
best_model.load_state_dict(state_dict_best)
```
Let's inspect if the model was loaded successfully:
```
# set model in evaluation mode
best_model.eval()
```
To evaluate our trained model, we need to feed the FashionMNIST images reserved for evaluation (the images that we didn't use as part of the training process) through the model. Therefore, let's again define a corresponding PyTorch data loader that feeds the image tensors to our neural network:
```
fashion_mnist_eval_dataloader = torch.utils.data.DataLoader(fashion_mnist_eval_data, batch_size=10000, shuffle=True)
```
We will now evaluate the trained model using the same mini-batch approach as we did throughout the network training and derive the mean negative log-likelihood loss of the mini-batches:
```
# init collection of mini-batch losses
eval_mini_batch_losses = []
# iterate over all-mini batches
for i, (images, labels) in enumerate(fashion_mnist_eval_dataloader):
# run forward pass through the network
output = best_model(images)
# determine classification loss
loss = nll_loss(output, labels)
# collect mini-batch reconstruction loss
eval_mini_batch_losses.append(loss.data.item())
# determine mean min-batch loss of epoch
eval_loss = np.mean(eval_mini_batch_losses)
# print epoch loss
now = datetime.utcnow().strftime("%Y%m%d-%H:%M:%S")
print('[LOG {}] eval-loss: {}'.format(str(now), str(eval_loss)))
```
Ok, great. The evaluation loss looks in-line with our training loss. Let's now inspect a few sample predictions to get an impression of the model quality. Therefore, we will again pick a random image of our evaluation dataset and retrieve its PyTorch tensor as well as the corresponding label:
```
# set (random) image id
image_id = 2000
# retrieve image exhibiting the image id
fashion_mnist_eval_image, fashion_mnist_eval_label = fashion_mnist_eval_data[image_id]
```
Let's now inspect the true class of the image we selected:
```
fashion_classes[fashion_mnist_eval_label]
```
Ok, the randomly selected image should contain a bag. Let's inspect the image accordingly:
```
# define tensor to image transformation
trans = torchvision.transforms.ToPILImage()
# set image plot title
plt.title('Example: {}, Label: {}'.format(str(image_id), fashion_classes[fashion_mnist_eval_label]))
# plot mnist handwritten digit sample
plt.imshow(trans(fashion_mnist_eval_image), cmap='gray')
```
Let's compare the true label with the prediction of our model:
```
best_model(fashion_mnist_eval_image)
```
We can even determine the likelihood of the most probable class:
```
most_probable = torch.argmax(best_model(fashion_mnist_eval_image), dim=1).item()
print('Most probable class: {}'.format(most_probable))
print('This class represents the following fashion article: {}'.format(fashion_classes[most_probable]))
```
Let's now obtain the predictions for all the fashion item images of the evaluation data:
```
predictions = torch.argmax(best_model(fashion_mnist_eval_data.data.float()), dim=1)
```
Furthermore, let's obtain the overall classifcation accuracy:
```
metrics.accuracy_score(fashion_mnist_eval_data.targets, predictions.detach())
```
Let's also inspect the confusion matrix to determine major sources of misclassification:
```
# determine classification matrix of the predicted and target classes
mat = confusion_matrix(fashion_mnist_eval_data.targets, predictions.detach())
# initialize the plot and define size
plt.figure(figsize=(8, 8))
# plot corresponding confusion matrix
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, cmap='YlOrRd_r', xticklabels=fashion_classes.values(), yticklabels=fashion_classes.values())
plt.tick_params(axis='both', which='major', labelsize=8, labelbottom = False, bottom=False, top = False, left = False, labeltop=True)
# set plot title
plt.title('Fashion MNIST classification matrix')
# set axis labels
plt.xlabel('[true label]')
plt.ylabel('[predicted label]');
```
Ok, we can easily see that our current model confuses sandals with either sneakers or ankle boots. However, the inverse does not really hold. The model sometimes confuses sneakers with ankle boots, and only very rarely with sandals. The same holds ankle boots. Our model also has issues distinguishing shirts from coats (and, to a lesser degree, from T-shirts and pullovers).
These mistakes are not very surprising, as these items exhibit a high similarity.
## 7. Lab Summary:
In this lab, a step by step introduction into the **design, implementation, training and evaluation** of neural networks to classify images of fashion items is presented. The code and exercises presented in this lab may serves as a starting point for developing more complex, more deep and tailored **neural networks**.
| true |
code
| 0.814975 | null | null | null | null |
|
# SVR with Scale & Quantile Transformer
This Code template is for regression analysis using the SVR Regressor where rescaling method used is Scale and feature transformation is done via Quantile Transformer.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import QuantileTransformer, scale
from sklearn.svm import SVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training.
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=123)
```
###Data Rescaling
####Scale
It is a step of Data Pre Processing which is applied to independent variables or features of data. It basically helps to normalise the data within a particular range. Sometimes, it also helps in speeding up the calculations in an algorithm.
```
x_train =scale(x_train)
x_test = scale(x_test)
```
### Quantile Transformer
This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is therefore a robust preprocessing scheme.
Transform features using quantiles information.
####Epsilon-Support Vector Regression.
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
A Support Vector Machine is a discriminative classifier formally defined by a separating hyperplane. In other terms, for a given known/labelled data points, the SVM outputs an appropriate hyperplane that classifies the inputted new cases based on the hyperplane. In 2-Dimensional space, this hyperplane is a line separating a plane into two segments where each class or group occupied on either side.
Here we will use SVR, the svr implementation is based on libsvm. The fit time scales at least quadratically with the number of samples and maybe impractical beyond tens of thousands of samples.
#### Parameters:
**kernel: {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}, default=’rbf’** ->
Specifies the kernel type to be used in the algorithm. It must be one of ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ or a callable. If none is given, ‘rbf’ will be used. If a callable is given it is used to precompute the kernel matrix.
**degree: int, default=3** ->
Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.
**gamma: {‘scale’, ‘auto’} or float, default=’scale’** ->
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
**coef0: float, default=0.0** ->
Independent term in kernel function. It is only significant in ‘poly’ and ‘sigmoid’.
**tol: float, default=1e-3** ->
Tolerance for stopping criterion.
**C: float, default=1.0** ->
Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2 penalty.
**epsilon: float, default=0.1** ->
Epsilon in the epsilon-SVR model. It specifies the epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance epsilon from the actual value.
**shrinking: bool, default=True** ->
Whether to use the shrinking heuristic. See the User Guide.
**cache_size: float, default=200** ->
Specify the size of the kernel cache (in MB).
**verbose: bool, default=False** ->
Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in libsvm that, if enabled, may not work properly in a multithreaded context.
**max_iter: int, default=-1** ->
Hard limit on iterations within solver, or -1 for no limit.
```
model=make_pipeline(QuantileTransformer(), SVR(kernel='poly', degree=13))
model.fit(x_train, y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
score: The score function returns the coefficient of determination R2 of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
n=len(x_test) if len(x_test)<20 else 20
plt.figure(figsize=(14,10))
plt.plot(range(n),y_test[0:n], color = "green")
plt.plot(range(n),model.predict(x_test[0:n]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Ayush Gupta , Github: [Profile](https://github.com/guptayush179)
| true |
code
| 0.503784 | null | null | null | null |
|
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
from datetime import datetime
import numpy as np
import pandas as pd
import datetime as dt
```
# Reflect Tables into SQLAlchemy ORM
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, MetaData, Table, Column, ForeignKey, Integer, String, Float, DateTime, inspect, distinct, desc, and_
# Create Database Connection
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
Base.metadata.create_all(engine)
# reflect an existing database into a new model
Base=automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# save refernece to the table
Measurement = Base.classes.measurement
Station = Base.classes.station
session = Session(engine)
# We can view all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(bind=engine)
inspector = inspect(engine)
columns = inspector.get_columns('measurement')
for c in columns:
print(c['name'], c["type"])
engine.execute('SELECT * FROM measurement LIMIT 5').fetchall()
columns = inspector.get_columns('station')
for c in columns:
print(c['name'], c["type"])
engine.execute('SELECT * FROM station LIMIT 5').fetchall()
```
# Exploratory Climate Analysis
```
# Design a query to retrieve the last 12 months of precipitation data and plot the results
# Calculate the date 1 year ago from the last data point in the database
end_date, = session.query(Measurement.date).order_by(Measurement.date.desc()).first()
begin_date=dt.datetime.strptime(end_date, '%Y-%m-%d')-dt.timedelta(days=365)
end_date = dt.datetime.strptime(end_date, '%Y-%m-%d')
print(end_date,begin_date)
# Perform a query to retrieve the data and precipitation scores
# data = session.query(Measurement.id,Measurement.station,Measurement.date, Measurement.prcp, Measurement.tobs)\
# .filter(and_(Measurement.date>=begin_date, Measurement.date<=end_date)).all()
data = session.query(Measurement.id,Measurement.station,Measurement.date, Measurement.prcp, Measurement.tobs)\
.filter(Measurement.date>=begin_date).filter(Measurement.date<=end_date).all()
# Save the query results as a Pandas DataFrame and set the index to the date column
# Sort the dataframe by date
prcp_data = pd.DataFrame(data).set_index('date').sort_values(by='date', ascending=False)
# Use Pandas Plotting with Matplotlib to plot the data
prcp_data
# Use Pandas to calcualte the summary statistics for the precipitation data
prcp_data["prcp"].agg(["mean","median", "sum", "count", "max", "min", "std", "var"])
# Design a query to show how many stations are available in this dataset.
stations_lastyr = prcp_data.station.nunique()
stations, = session.query(func.count(distinct(Measurement.station))).order_by
(f'There are {stations_lastyr} unique weather stations with measurments taken in the last year of data. There are {stations} unique weather stations in the entire dataset.')
# What are the most active stations? (i.e. what stations have the most rows)?
# List the stations and the counts in descending order.
active_all = session.query(Measurement.station, func.count(Measurement.station)).group_by(Measurement.station) \
.order_by(desc(func.count(Measurement.station))).all()
active = prcp_data["station"].value_counts() #Returns descending by default
active = pd.DataFrame(active)
# prcp_data["station"].value_counts(normalize=True) #returns percentages of whole instead of count!
print('This is the dataset filtered for the last year of data.')
active
print('This is the whole dataset.')
active_all = [[ i for i, j in active_all ],
[ j for i, j in active_all ]]
active_all
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature of the most active station?
most_active = active.index[0]
active_agg = prcp_data.loc[prcp_data["station"] == most_active]
active_agg["tobs"].agg(["mean", "max", "min"])
most_active_all =
# Choose the station with the highest number of temperature observations.
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
```
## Bonus Challenge Assignment
```
# This function called `calc_temps` will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
# function usage example
print(calc_temps('2012-02-28', '2012-03-05'))
# Use your previous function `calc_temps` to calculate the tmin, tavg, and tmax
# for your trip using the previous year's data for those same dates.
# Plot the results from your previous query as a bar chart.
# Use "Trip Avg Temp" as your Title
# Use the average temperature for the y value
# Use the peak-to-peak (tmax-tmin) value as the y error bar (yerr)
# Calculate the total amount of rainfall per weather station for your trip dates using the previous year's matching dates.
# Sort this in descending order by precipitation amount and list the station, name, latitude, longitude, and elevation
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("01-01")
# calculate the daily normals for your trip
# push each tuple of calculations into a list called `normals`
# Set the start and end date of the trip
# Use the start and end date to create a range of dates
# Stip off the year and save a list of %m-%d strings
# Loop through the list of %m-%d strings and calculate the normals for each date
# Load the previous query results into a Pandas DataFrame and add the `trip_dates` range as the `date` index
# Plot the daily normals as an area plot with `stacked=False`
# class Measurement_two(Base):
# __tablename__= "measurement"
# id = Column(Integer, primary_key=True)
# station = Column(String(200))
# date = Column(DateTime)
# prcp = Column(Float)
# tobs = Column(Float)
# class Station_two(Base):
# __tablename__= "station"
# id = Column(Integer, primary_key=True)
# station = Column(String(200))
# name = Column(String(200))
# latitude = Column(Float)
# longitude = Column(Float)
# elevation = Column(Float)
```
| true |
code
| 0.677714 | null | null | null | null |
|
# Hidden Markov Models
### Problem Statement
The following problem is from the Udacity course on Artificial Intelligence (Thrun and Norvig), chapter 11 (HMMs and filters). It involves a simple scenario where a person's current emotional state is determined by the weather on that particular day. The task is to find the underlying hidden sequence of states (in this case, the weather), given only a set of observations (moods) and information about state/observation changes.
```
#import required libraries
import numpy as np
import warnings
from pprint import pprint
```
$P(\;Rainy\;) = P(R_{0}) = 0.5$ (initial probabilites)
$P(\;Sunny\;) = P(S_{0}) = 0.5$
The chances of weather changing are given as follows:
For rainy weather, $P(S_{tomorrow}|R_{today}) = 0.4$, and $P(R_{tomorrow}|R_{today}) = 0.6$
For sunny weather, $P(R_{tomorrow}|S_{today}) = 0.2$, therefore $P(S_{tomorrow}| S_{today}) = 0.8$
For the purpose of formulating an HMM, we call the above ***Transition Probabilities.***
The corresponding mood changes, given the weather are :
$P(H|R) = 0.4$, therefore $P(G|R) = 0.6$
$P(H|S) = 0.9$, and $P(G|S) = 0.1$
We call these ***Emission Probabilities***
```
S = np.array([0, 1]) # 0 Rainy, 1 Sunny
S_names = ('Rainy', 'Sunny')
pi = np.array([0.5, 0.5]) # Initial Probabilities
O = np.array(['Happy', 'Grumpy']) # Set of observations
A = np.array([[0.6, 0.4], [0.2, 0.8]]) # {R:{R, S}, S:{R, S}} Transition Matrix
B = np.array([[0.4, 0.6], [0.9, 0.1]]) # {R: {H, G}, S: {H, G}} Emission Matrix
Y = np.array([0, 0, 1]) # 0 Happy, 1 Grumpy -- Observation sequence
```
### Hidden Markov Models
[HMMs](https://en.wikipedia.org/wiki/Hidden_Markov_model) are a class of probabilistic graphical models that can predict the sequence of states, given a sequence of observations that are dependent on those states, and when the states themselves are unobservable. HMMs have seen widespread success in a variety of applications, from Speech processing and Robotics to DNA Sequencing. An HMM operates according to a set of assumptions, which are :
1. ** Markov Assumption **
Current state is dependent on only the previous state.
2. ** Stationarity Assumption **
Transition probabilities are independent of time of transition.
3. ** Independence Assumption **
Each observation depends solely on the current underlying state (which in turn depends on the previous one), and is independent of other observations.
An HMM is a **Generative model**, in that it attempts to find the probability of a set of observations being produced or *generated* by a class. The parameters that we pass to the HMM class, defined below, are:
*O* = a set of observations
*S* = a set of states
*A* = transition probabilities, represented as a matrix
*B* = emission probabilities, represented as a matrix
*pi* = initial state probabilties
*Y* = sequence observed
### Viterbi Algorithm
The Viterbi algorithm is a Dynamic Programming algorithm for decoding the observation sequence to uncover the most probable state sequence. Given the required parameters, it starts from the initial state and uses the transition/emission information to calculate probabilities of subsequent states. Information from the previous step is passed along to the next, similar to a belief propagation mechanism (such as one used in the Forward-Backward algorithm explained later).
We store the results of each step in a table or matrix of size $k * t$, where k is the number of possible states, and t is the length of the observation sequence. The idea here is to find the path through possible states that has the maximum probability. Since initially we do not have a transition from state to state, we multiply the initial probabilities (from pi) and $P(\;observation\;|\;state\;)$ (from emission matrix B).
Eg. For the first day, we have the observation as Happy, so :
$P(R_{1}) = P(R_{0}) * P(H|R_{1}) = 0.5 * 0.4 = 0.2$
$P(S_{1}) = P(S_{0}) * P(H|S_{1}) \;= 0.5 * 0.9 = 0.45$
We log both these results in the table, since we are starting from an initial state. For the following observations, however, each state has only its maximum probability of moving to the next state logged.
#### On Day 2 : (observation - Happy) :
If current state = Rainy:
$P(R_{1}) * P(R_{2}|R_{1}) = 0.20 * 0.6 = 0.12$ (given Rainy was previous state)
$P(S_{1}) * P(R_{2}|S_{1}) = 0.45 * 0.2 = 0.09$ (Given Sunny was previous state)
Since $0.12>0.09$, We choose $P(R_{2}|H)$ as the most probable transition from $R_{1}$, and update the table with
$P(R_{2}|H) = P(R_{1}) * P(R_{2}|R_{1}) * P(H|R_{2}) = 0.12 * 0.4 = 0.048$
If current state = Sunny:
$P(R_{1}) * P(S_{2}|R_{1}) = 0.20 * 0.4 = 0.08$ (given Rainy was previous state)
$P(S_{1}) * P(S_{2}|S_{1}) = 0.45 * 0.8 = 0.36$ (given Sunny was previous state)
Here too, we choose $P(S_{2}|H)$ as the most probable transition from $S_{1}$, and add it to the table.
$P(S_{2}|H) = P(S_{1}) * P(S_{2}|S_{1}) * P(H|S_{2}) = 0.36 * 0.9 = 0.324$
#### On Day 3: (observation - Grumpy) :
If current state = Rainy:
$P(R_{2}) * P(R_{3}|R_{2}) = 0.048 * 0.6 = 0.0288$ (given Rainy was previous state)
$P(S_{2}) * P(R_{3}|S_{2}) = 0.324 * 0.2 = 0.0648$ (given Sunny was previous state)
As $0.0648>0.0288$, We choose $P(R_{3}|G)$ as the most probable transition from $R_{2}$, and update the table with
$P(R_{3}|G) = P(R_{2}) * P(R_{3}|R_{2}) * P(G|R_{3}) = 0.0648 * 0.6 = 0.03888$
If current state = Sunny:
$P(R_{2}) * P(S_{3}|R_{2}) = 0.048 * 0.4 = 0.0192$ (given Rainy was previous state)
$P(S_{2}) * P(S_{3}|S_{2}) = 0.324 * 0.8 = 0.2592$ (given Sunny was previous state)
Here too, we choose $P(S_{3}|G)$ as the most probable transition from $S_{1}$, and add it to the table.
$P(S_{3}|G) = P(S_{2}) * P(S_{3}|S_{2}) * P(G|S_{3}) = 0.2592 * 0.1 = 0.02592$
Since now the table is completely filled, we work in reverse from probability of the last observation and its inferred state (in this case, $0.0388$ i.e Rainy) finding which state had the maximum probability upto that point. In this way, we find the most probable sequence of states corresponding to our observations!
```
class HMM:
def __init__(self, observations, states, start_probs, trans_probs, emm_probs, obs_sequence):
self.O = observations
self.S = states
self.state_names = None
self.pi = start_probs
self.A = trans_probs
self.B = emm_probs
self.Y = obs_sequence
self.k = np.array(self.S).shape[0]
self.t = self.Y.shape[0]
self.table_1 = np.zeros((self.k, self.t))
self.output_sequence = np.zeros((self.t,))
self.fwds = None
self.bwds = None
self.smoothened = None
def viterbi(self):
# loop through states, but only for first observation
print "Day 1 : Observation was", self.Y[0], "i.e", self.O[self.Y[0]]
for i in range(self.k):
self.table_1[i, 0] = self.pi[i] * self.B[i, self.Y[0]]
print "Probability of state", i, "-->", self.table_1[i, 0]
print "-------------------------------------------"
print "========================================="
# loop through second to last observation
for i in range(1, self.t):
print "Day", i + 1, ": Observation was", self.Y[i], "i.e", self.O[self.Y[i]]
for j in range(self.k): # loop through states
print "If current state", j, "i.e", self.state_names[j]
max_t1_A = 0.0
for d in range(self.k): # loop through states*states
print "probability of the previous state i.e", d, "-->", self.table_1[d, i - 1]
val = self.table_1[d, i - 1] * self.A[d, j]
print "State", d, "to State", j, "-->", self.A[d, j]
print self.table_1[d, i - 1], "*", self.A[d, j], "=", val
if val > max_t1_A:
max_t1_A = val
else:
continue
self.table_1[j, i] = max_t1_A
tmp = self.table_1[j, i]
self.table_1[j, i] = self.table_1[j, i] * self.B[j, self.Y[i]]
print "Probability of next state given previous state, transition and observation :"
print tmp, "*", self.B[j, self.Y[i]], "=", self.table_1[j, i]
print "-------------------------------------------"
print "==========================================="
print ""
# work backwards from the last day, comparing probabilities
# from observations and transitions up to that day.
for i in range(self.t - 1, -1, -1):
max_at_i = 0.0
max_j = 0.0
for j in range(self.k):
if self.table_1[j][i] > max_at_i:
max_at_i = self.table_1[j][i]
max_j = j
else:
continue
self.output_sequence[i] = j
print "State", self.state_names[int(self.output_sequence[i])], "was most likely on day", i+1
print ""
return self.output_sequence
def get_obs(self, obs_val, emm_prob):
ob_mat = np.zeros((self.k, self.k))
for i in self.S:
for j in self.S:
if i == j:
ob_mat[i, j] = emm_prob[i, obs_val]
return ob_mat
def get_diagonal(self, mat_A, mat_B):
x = np.transpose(mat_A).shape[1]
mat_C = np.dot(mat_A, np.transpose(mat_B))
mat_D = np.zeros((self.k, 1))
for i in range(x):
for j in range(x):
if i == j:
mat_D[i][0] = mat_C[i][j]
return mat_D
def forward_backward(self):
self.m = self.O.shape[0]
# print self.m
obs_mats = [None for i in range(self.t)]
for i in range(self.t):
obs_mats[i] = self.get_obs(self.Y[i], self.B)
print "Observation matrices :"
pprint(obs_mats)
print ""
# forward probability calculation
f = [[] for i in range(self.t + 1)]
f[0] = self.pi.reshape(self.k, 1)
csum = 0.0
for j in f[0]:
csum += j
for j in range(f[0].shape[0]):
f[0][j] = f[0][j] / csum
for i in range(1, self.t + 1):
# print "obs", obs_mats[i-1]
# print "prev f", f[i-1]
f[i] = np.dot(np.dot(obs_mats[i - 1], self.A),
f[i - 1]).reshape(self.k, 1)
# scaling done here
csum = 0.0
for j in f[i]:
csum += j
for j in range(f[i].shape[0]):
f[i][j] = f[i][j] / csum
# print "new f", f[i]
f = np.array(f)
print "Forward probabilities :"
pprint(f)
print ""
# backward probability calculation
b = [[] for i in range(self.t + 1)]
b[-1] = np.array([[1.0] for i in range(self.k)])
for i in range(self.t - 1, -1, -1):
b[i] = np.dot(np.dot(self.A, obs_mats[i]),
b[i + 1]).reshape(self.k, 1)
# scaling done here
csum = 0.0
for j in b[i]:
csum += j
for j in range(b[i].shape[0]):
b[i][j] = b[i][j] / csum
b = np.array(b)
print "Backward probabilities :"
pprint(b)
print ""
# smoothed values
smooth = [[] for i in range(self.t + 1)]
for i in range(self.t + 1):
smooth[i] = self.get_diagonal(f[i], b[i])
csum = 0.0
for j in smooth[i]:
csum += j
for j in range(smooth[i].shape[0]):
smooth[i][j] = smooth[i][j] / csum
smooth = np.array(smooth)
print "Smoothed probabilities :"
pprint(smooth)
self.fwds = f
self.bwds = b
self.smoothened = smooth
for i in range(1, smooth.shape[0]):
max_prob = max(smooth[i].tolist())
print "Day", i, "probability was max for state", smooth[i].tolist().index(max_prob), "-->", max_prob[0]
self.output_sequence[i - 1] = smooth[i].tolist().index(max_prob)
return self.output_sequence
weather_hmm = HMM(O, S, pi, A, B, Y)
weather_hmm.state_names = S_names
obs_states = [O[i] for i in Y]
print "Observations :"
print obs_states, "\n"
with warnings.catch_warnings():
warnings.simplefilter("ignore")
print "Using Viterbi Algorithm:\n"
op1 = weather_hmm.viterbi()
print "Table of state probabilities :"
for i in weather_hmm.table_1:
print "----------------------------"
print "|",
for j in i:
print "{0:.4f} |".format(j),
print ""
print "----------------------------\n"
op_states1 = [S_names[int(i)] for i in op1]
print op_states1
```
### Forward-Backward Algorithm
Explanation : **TO-DO**
```
#reset output sequence values to zero
weather_hmm.output_sequence = np.zeros((weather_hmm.t,))
print "Using Forward-Backward Algorithm:"
op2 = weather_hmm.forward_backward()
op_states2 = [S_names[int(i)] for i in op2]
print op_states2
```
| true |
code
| 0.479077 | null | null | null | null |
|
## Finding entity classes in embeddings
In this notebook we're going to use embeddings to find entity classes and how they correlate with other things
```
%matplotlib inline
from sklearn import svm
from keras.utils import get_file
import os
import gensim
import numpy as np
import random
import requests
import geopandas as gpd
from IPython.core.pylabtools import figsize
figsize(12, 8)
import pycountry
import csv
```
as before, let's load up the model
```
MODEL = 'GoogleNews-vectors-negative300.bin'
path = get_file(MODEL + '.gz', 'https://s3.amazonaws.com/dl4j-distribution/%s.gz' % MODEL)
unzipped = os.path.join('generated', MODEL)
if not os.path.isfile(unzipped):
with open(unzipped, 'wb') as fout:
zcat = subprocess.Popen(['zcat'],
stdin=open(path),
stdout=fout
)
zcat.wait()
```
Most similar to a bunch of countries are some other countries!
```
model = gensim.models.KeyedVectors.load_word2vec_format(unzipped, binary=True)
model.most_similar(positive=['Germany'])
model.most_similar(positive=['Annita_Kirsten'])
```
No we'll create a training set with countries and non countries and get a support vector machine to learn the difference.
```
countries = list(csv.DictReader(open('data/countries.csv')))
countries[:10]
positive = [x['name'] for x in random.sample(countries, 40)]
negative = random.sample(model.vocab.keys(), 5000)
negative[:4]
labelled = [(p, 1) for p in positive] + [(n, 0) for n in negative]
random.shuffle(labelled)
X = np.asarray([model[w] for w, l in labelled])
y = np.asarray([l for w, l in labelled])
X.shape, y.shape
TRAINING_FRACTION = 0.3
cut_off = int(TRAINING_FRACTION * len(labelled))
clf = svm.SVC(kernel='linear')
clf.fit(X[:cut_off], y[:cut_off])
```
We did alright, 99.9% precision:
```
res = clf.predict(X[cut_off:])
missed = [country for (pred, truth, country) in
zip(res, y[cut_off:], labelled[cut_off:]) if pred != truth]
100 - 100 * float(len(missed)) / len(res), missed
all_predictions = clf.predict(model.syn0)
res = []
for word, pred in zip(model.index2word, all_predictions):
if pred:
res.append(word)
if len(res) == 150:
break
random.sample(res, 10)
country_to_idx = {country['name']: idx for idx, country in enumerate(countries)}
country_vecs = np.asarray([model[c['name']] for c in countries])
country_vecs.shape
```
Quick sanity check to see what is similar to Canada:
```
dists = np.dot(country_vecs, country_vecs[country_to_idx['Canada']])
for idx in reversed(np.argsort(dists)[-10:]):
print(countries[idx]['name'], dists[idx])
```
Ranking countries for a specific term:
```
def rank_countries(term, topn=10, field='name'):
if not term in model:
return []
vec = model[term]
dists = np.dot(country_vecs, vec)
return [(countries[idx][field], float(dists[idx]))
for idx in reversed(np.argsort(dists)[-topn:])]
rank_countries('cricket')
```
Now let's visualize this on a world map:
```
world = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))
world.head()
```
We can now plot some maps!
```
def map_term(term):
d = {k.upper(): v for k, v in rank_countries(term, topn=0, field='cc3')}
world[term] = world['iso_a3'].map(d)
world[term] /= world[term].max()
world.dropna().plot(term, cmap='OrRd')
map_term('coffee')
map_term('cricket')
map_term('China')
```
| true |
code
| 0.456773 | null | null | null | null |
|
# Cross Validation
Splitting our datasetes into train/test sets allows us to test our model on unseen examples. However, it might be the case that we got a lucky (or unlucky) split that doesn't represent the model's actual performance. To solve this problem, we'll use a technique called cross-validation, where we use the entire dataset for training and for testing and evaluate the model accordingly.
There are several ways of performing cross-validation, and there are several corresponding iterators defined in scikit-learn. Each defines a `split` method, which will generate arrays of indices from the data set, each array indicating the instances to go into the training or testing set.
```
import pandas as pd
import numpy as np
from sklearn import datasets, svm, metrics, model_selection
x, y = datasets.load_breast_cancer(return_X_y=True)
# Define a function to split our dataset into train/test splits using indices
def kfold_train_test_split(x, y, train_indices, test_indices):
return x[train_indices], x[test_indices], y[train_indices], y[test_indices]
```
### `KFold`
`KFold` is arguably the simplest. It partitions the data into $k$ folds. It does not attempt to keep the proportions of classes.
```
k_fold = model_selection.KFold(n_splits=10) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in k_fold.split(x):
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
### `StratifiedKFold`
`StratifiedKFold` ensures that the proportion of classes are preserved in each training/testing set.
```
stratified_k_fold = model_selection.StratifiedKFold(n_splits=10) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in stratified_k_fold.split(x, y): # y is needed here for stratification, similar to stratify = y.
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
### `ShuffleSplit`
`ShuffleSplit` will generate indepedent pairs of randomly shuffled training and testing sets.
```
shuffle_k_fold = model_selection.ShuffleSplit(n_splits=10, random_state=42) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in shuffle_k_fold.split(x):
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
### `StratifiedShuffleSplit`
`StratifiedShuffleSplit` will generate indepedent pairs of shuffled training and testing sets. Here, however, it will ensure the training and test sets are stratified.
```
stratified_shuffled_k_fold = model_selection.StratifiedShuffleSplit(n_splits=10) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in stratified_shuffled_k_fold.split(x, y): # y is needed here for stratification, similar to stratify = y.
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
| true |
code
| 0.574275 | null | null | null | null |
|
### Simple Residual model in Keras
This notebook is simply for testing a resnet-50 inspired model built in Keras on a numerical signs dataset.
```
import keras
import numpy as np
import matplotlib.pyplot as plt
from keras import layers
from keras.layers import Input, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D,ZeroPadding1D, Conv1D, Add
from keras.layers import MaxPooling2D, Dropout, AveragePooling2D
from keras.models import Model
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle
import warnings
warnings.filterwarnings('ignore')
# Using a signs dataset, with images of numerical signs from 0-9
X = np.load("../data/sign-digits/X.npy")
y = np.load("../data/sign-digits/y.npy")
X.shape = (2062, 64, 64, 1)
X = shuffle(X,random_state=0)
y = shuffle(y,random_state=0)
print(X.shape)
print(y.shape)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.1)
print(X_train.shape)
print(X_test.shape)
# Block corresponding with no change in size
def identity(X, f, filters):
"""
filters: filters for each of the conv2D
f: size of filter to use in mid block
"""
F1,F2,F3 = filters
X_earlier = X
# Block 1
X = Conv2D(F1, kernel_size=(1,1), strides=(1,1),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 2
X = Conv2D(F2, kernel_size=(f,f), strides=(1,1),padding="same",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 3
X = Conv2D(F3, kernel_size=(1,1), strides=(1,1),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Add()([X,X_earlier]) # Add earlier activation
X = Activation("relu")(X)
return X
# Block corresponding with a change in size
def conv_resid(X, f, filters,s):
"""
filters: filters for each of the conv2D
s: stride size to resize the output
"""
F1,F2,F3 = filters
X_earlier = X
# Block 1
X = Conv2D(F1, kernel_size=(1,1), strides=(s,s),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 2
X = Conv2D(F2, kernel_size=(f,f), strides=(1,1),padding="same",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 3
X = Conv2D(F3, kernel_size=(1,1), strides=(1,1),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
# Resize earlier activation (X_earlier)
X_earlier = Conv2D(F3, kernel_size=(1,1), strides=(s,s),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X_earlier)
X_earlier = BatchNormalization(axis=3)(X_earlier)
# Add earlier activation
X = Add()([X,X_earlier])
X = Activation("relu")(X)
return X
# The Input shape for this model will be 64x64x1
def model(input_shape):
X_input = Input(input_shape)
X = ZeroPadding2D(padding=(3,3))(X_input)
X = Conv2D(64,kernel_size=(7,7),padding="valid",kernel_initializer=keras.initializers.glorot_uniform())(X)
X = BatchNormalization(axis=3)(X)
X = Activation(("relu"))(X)
X = MaxPooling2D((3,3),strides=(2,2))(X)
# indentity block 1
X = conv_resid(X, 3, [64,64,256], 1)
X = identity(X, 3, [64,64,256])
X = identity(X, 3, [64,64,256])
# Identity block 2
X = conv_resid(X, 3, [128,128,512], 2)
X = identity(X, 3, [128,128,512])
X = identity(X, 3, [128,128,512])
X = identity(X, 3, [128,128,512])
# Identity block 3
X = conv_resid(X, 3, [256, 256, 1024], 2)
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
# Identity block 4
X = conv_resid(X, 3, [512, 512, 2048], 2)
X = identity(X, 3, [512, 512, 2048])
X = identity(X, 3, [512, 512, 2048])
X = AveragePooling2D((2,2), name="avg_pool")(X)
# Flatten final layer
X = Flatten()(X)
X = Dense(10, activation="softmax",name="dense02",kernel_initializer = keras.initializers.glorot_normal())(X)
model = Model(inputs=X_input, outputs=X, name="resnet")
return model
resid_classi = model(X_train[0].shape)
resid_classi.compile(optimizer="adam", loss="categorical_crossentropy", metrics=['accuracy'])
resid_classi.fit(X_train, y_train,epochs=10,batch_size=10, validation_data=[X_test,y_test])
```
| true |
code
| 0.780986 | null | null | null | null |
|
# How do I create my own dataset?
So Caffe2 uses a binary DB format to store the data that we would like to train models on. A Caffe2 DB is a glorified name of a key-value storage where the keys are usually randomized so that the batches are approximately i.i.d. The values are the real stuff here: they contain the serialized strings of the specific data formats that you would like your training algorithm to ingest. So, the stored DB would look (semantically) like this:
key1 value1
key2 value2
key3 value3
...
To a DB, it treats the keys and values as strings, but you probably want structured contents. One way to do this is to use a TensorProtos protocol buffer: it essentially wraps Tensors, aka multi-dimensional arrays, together with the tensor data type and shape information. Then, one can use the TensorProtosDBInput operator to load the data into an SGD training fashion.
Here, we will show you one example of how to create your own dataset. To this end, we will use the UCI Iris dataset - which was a very popular classical dataset for classifying Iris flowers. It contains 4 real-valued features representing the dimensions of the flower, and classifies things into 3 types of Iris flowers. The dataset can be downloaded [here](https://archive.ics.uci.edu/ml/datasets/Iris).
```
# First let's import a few things needed.
%matplotlib inline
import urllib2 # for downloading the dataset from the web.
import numpy as np
from matplotlib import pyplot
from StringIO import StringIO
from caffe2.python import core, utils, workspace
from caffe2.proto import caffe2_pb2
f = urllib2.urlopen('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data')
raw_data = f.read()
print('Raw data looks like this:')
print(raw_data[:100] + '...')
# load the features to a feature matrix.
features = np.loadtxt(StringIO(raw_data), dtype=np.float32, delimiter=',', usecols=(0, 1, 2, 3))
# load the labels to a feature matrix
label_converter = lambda s : {'Iris-setosa':0, 'Iris-versicolor':1, 'Iris-virginica':2}[s]
labels = np.loadtxt(StringIO(raw_data), dtype=np.int, delimiter=',', usecols=(4,), converters={4: label_converter})
```
Before we do training, one thing that is often beneficial is to separate the dataset into training and testing. In this case, let's randomly shuffle the data, use the first 100 data points to do training, and the remaining 50 to do testing. For more sophisticated approaches, you can use e.g. cross validation to separate your dataset into multiple training and testing splits. Read more about cross validation [here](http://scikit-learn.org/stable/modules/cross_validation.html).
```
random_index = np.random.permutation(150)
features = features[random_index]
labels = labels[random_index]
train_features = features[:100]
train_labels = labels[:100]
test_features = features[100:]
test_labels = labels[100:]
# Let's plot the first two features together with the label.
# Remember, while we are plotting the testing feature distribution
# here too, you might not be supposed to do so in real research,
# because one should not peek into the testing data.
legend = ['rx', 'b+', 'go']
pyplot.title("Training data distribution, feature 0 and 1")
for i in range(3):
pyplot.plot(train_features[train_labels==i, 0], train_features[train_labels==i, 1], legend[i])
pyplot.figure()
pyplot.title("Testing data distribution, feature 0 and 1")
for i in range(3):
pyplot.plot(test_features[test_labels==i, 0], test_features[test_labels==i, 1], legend[i])
```
Now, as promised, let's put things into a Caffe2 DB. In this DB, what would happen is that we will use "train_xxx" as the key, and use a TensorProtos object to store two tensors for each data point: one as the feature and one as the label. We will use Caffe2 python's DB interface to do so.
```
# First, let's see how one can construct a TensorProtos protocol buffer from numpy arrays.
feature_and_label = caffe2_pb2.TensorProtos()
feature_and_label.protos.extend([
utils.NumpyArrayToCaffe2Tensor(features[0]),
utils.NumpyArrayToCaffe2Tensor(labels[0])])
print('This is what the tensor proto looks like for a feature and its label:')
print(str(feature_and_label))
print('This is the compact string that gets written into the db:')
print(feature_and_label.SerializeToString())
# Now, actually write the db.
def write_db(db_type, db_name, features, labels):
db = core.C.create_db(db_type, db_name, core.C.Mode.write)
transaction = db.new_transaction()
for i in range(features.shape[0]):
feature_and_label = caffe2_pb2.TensorProtos()
feature_and_label.protos.extend([
utils.NumpyArrayToCaffe2Tensor(features[i]),
utils.NumpyArrayToCaffe2Tensor(labels[i])])
transaction.put(
'train_%03d'.format(i),
feature_and_label.SerializeToString())
# Close the transaction, and then close the db.
del transaction
del db
write_db("minidb", "iris_train.minidb", train_features, train_labels)
write_db("minidb", "iris_test.minidb", test_features, test_labels)
```
Now, let's create a very simple network that only consists of one single TensorProtosDBInput operator, to showcase how we load data from the DB that we created. For training, you might want to do something more complex: creating a network, train it, get the model, and run the prediction service. To this end you can look at the MNIST tutorial for details.
```
net_proto = core.Net("example_reader")
dbreader = net_proto.CreateDB([], "dbreader", db="iris_train.minidb", db_type="minidb")
net_proto.TensorProtosDBInput([dbreader], ["X", "Y"], batch_size=16)
print("The net looks like this:")
print(str(net_proto.Proto()))
workspace.CreateNet(net_proto)
# Let's run it to get batches of features.
workspace.RunNet(net_proto.Proto().name)
print("The first batch of feature is:")
print(workspace.FetchBlob("X"))
print("The first batch of label is:")
print(workspace.FetchBlob("Y"))
# Let's run again.
workspace.RunNet(net_proto.Proto().name)
print("The second batch of feature is:")
print(workspace.FetchBlob("X"))
print("The second batch of label is:")
print(workspace.FetchBlob("Y"))
```
| true |
code
| 0.53777 | null | null | null | null |
|
# Gases: Perfect and Semiperfect Models
In this Notebook we will use `PerfectIdealGas` and `SemiperfectIdealGas` classes from **pyTurb**, to access the thermodynamic properties with a Perfect Ideal Gas or a Semiperfect Ideal Gas approach. Both classes acquire the thermodynamic properties of different species from the *NASA Glenn coefficients* in `thermo_properties.py`.
Note that `PerfectIdealGas` and `SemiperfectIdealGas` classes are two different approaches for an *Ideal Gas*.
The `gas_models` functions and classes can be found in the following folders:
- pyturb
- gas_models
- thermo_prop
- PerfectIdealGas
- SemiperfectIdealGas
- GasMixture
```python
from pyturb.gas_models import ThermoProperties
from pyturb.gas_models import PerfectIdealGas
from pyturb.gas_models import SemiperfectIdealGas
from pyturb.gas_models import GasMixture
```
For an example about how to declae and use a Gas Mixture in **pyTurb**, go the "Gas Mixtures.ipynb" Notebook.
### Ideal Gas
While an Ideal Gas is characterized by a compressibility factor of 1:
$$Z=1=\frac{pv}{R_gT}$$
Which means that the *Ideal Gas Equation of State* is available: ($pv=R_gT$). It also means that the Mayer Equation is applicable: $R_g=c_p-c_v$.
### Perfect and Semiperfect approaches
A Perfect Gas or a Semiperfect Ideal Gas approach means:
- If the gas is perfect: $c_v, c_p, \gamma_g \equiv constant$
- If the gas is Semiperfect: $c_v(T), c_p(T), \gamma_g(T) \equiv f(T)$
By definition, the model used in `ThermoProperties` provide a 7 coefficients polynomial for the heat capacity at constant pressure ($c_p$):
$$ \frac{c_p}{R_g} = a_1T^{-2}+a_2T^{-1} + a_3 + a_4T + a_5T^2 a_6T^3 + a_7T^4$$
With the $c_p$, the Mayer Equation (valid for $Z=1$) and the heat capacity ratio we can obtain $c_v \left(T\right)$ and $\gamma \left(T\right)$:
$$ R_g =c_p\left(T\right)-c_v \left(T\right) $$
$$\gamma_g\left(T\right) = \frac{c_p\left(T\right)}{c_v\left(T\right)}$$
> In practice, the `PerfectIdealGas` object is a `SemiperfectIdealGas` where the temperature is set to $25ºC$.
### Perfect and Semiperfect content
Both `PerfectIdealGas` and `SemiPerfectIdealGas` classes have the following content:
- **Gas properties:** Ru, Rg, Mg, cp, cp_molar, cv, cv_molar, gamma
- **Gas enthalpies, moles and mass:** h0, h0_molar, mg, Ng
- **Chemical properties:** gas_species, thermo_prop
### Other dependencies:
We will import `numpy` and `pyplot` as well, to make some graphical examples.
---
### Check Gas Species availability:
```
from pyturb.gas_models import ThermoProperties
tp = ThermoProperties()
print(tp.species_list[850:875])
tp.is_available('Air')
```
---
### Import Perfect and Semiperfect Ideal Gas classes:
Examples with Air:
```
from pyturb.gas_models import PerfectIdealGas
from pyturb.gas_models import SemiperfectIdealGas
# Air as perfect gas:
perfect_air = PerfectIdealGas('Air')
# Air as semiperfect gas:
semiperfect_air = SemiperfectIdealGas('Air')
```
---
##### To retrieve the thermodynamic properties you can `print` the `thermo_prop` from the gas:
Including:
- Chemical formula
- Heat of formation
- Molecular mass
- cp coefficients
```
print(perfect_air.thermo_prop)
```
---
You can get the thermodynamic properties directly from the gas object. Note that all units are International System of Units (SI):
```
print(perfect_air.Rg)
print(perfect_air.Mg)
print(perfect_air.cp())
print(perfect_air.cp_molar())
print(perfect_air.cv())
print(perfect_air.cv_molar())
print(perfect_air.gamma())
```
---
##### Use the docstrings for more info about the content of a PerfectIdealGas or a SemiperfectIdealGas:
```
perfect_air?
```
---
##### Compare both models:
Note that *Perfect Ideal Air*, with constant $c_p$, $c_v$ and $\gamma$, yields the same properties than a semiperfect gas model at 25ºC (reference temperature):
```
T = 288.15 #K
cp_perf = perfect_air.cp()
cp_sp = semiperfect_air.cp(T)
print('At T={0:8.2f}K, cp_perfect={1:8.2f}J/kg/K'.format(T, cp_perf))
print('At T={0:8.2f}K, cp_semipft={1:8.2f}J/kg/K'.format(T, cp_sp))
T = 1500 #K
cp_perf = perfect_air.cp()
cp_sp = semiperfect_air.cp(T)
print('At T={0:8.2f}K, cp_perfect={1:8.2f}J/kg/K'.format(T, cp_perf))
print('At T={0:8.2f}K, cp_semipft={1:8.2f}J/kg/K'.format(T, cp_sp))
```
---
##### $c_p$, $c_v$ and $\gamma$ versus temperature:
```
import numpy as np
from matplotlib import pyplot as plt
T = np.linspace(200, 2000, 50)
cp = np.zeros_like(T)
cv = np.zeros_like(T)
gamma = np.zeros_like(T)
for ii, temperature in enumerate(T):
cp[ii] = semiperfect_air.cp(temperature)
cv[ii] = semiperfect_air.cv(temperature)
gamma[ii] = semiperfect_air.gamma(temperature)
fig, (ax1, ax2) = plt.subplots(2)
fig.suptitle('Air properties')
ax1.plot(T, cp)
ax1.plot(T, cv)
ax2.plot(T, gamma)
ax1.set(xlabel="Temperature [K]", ylabel="cp, cv [J/kg/K]")
ax2.set(xlabel="Temperature [K]", ylabel="gamma [-]")
ax1.grid()
ax2.grid()
plt.show()
```
| true |
code
| 0.707 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/lionelsamrat10/machine-learning-a-to-z/blob/main/Deep%20Learning/Convolutional%20Neural%20Networks%20(CNN)/convolutional_neural_network_samrat_with_10_epochs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Convolutional Neural Network
### Importing the libraries
```
import tensorflow as tf
from keras.preprocessing.image import ImageDataGenerator
import numpy as np
tf.__version__
```
## Part 1 - Data Preprocessing
### Preprocessing the Training set
```
# Transforming the Image
# Rescale applies Feature Scaling to each pixels in our images
# We are doing this to avoid Overfitting
train_datagen = ImageDataGenerator(rescale = 1./255,
shear_range = 0.2,
zoom_range = 0.2,
horizontal_flip = True)
# Only 32 images will run in one batch
training_set = train_datagen.flow_from_directory('dataset/training_set',
target_size = (64, 64),
batch_size = 32,
class_mode = 'binary')
```
### Preprocessing the Test set
```
test_datagen = ImageDataGenerator(rescale = 1./255)
test_set = test_datagen.flow_from_directory('dataset/test_set',
target_size = (64, 64),
batch_size = 32,
class_mode = 'binary')
```
## Part 2 - Building the CNN
### Initialising the CNN
```
cnn = tf.keras.models.Sequential();
```
### Step 1 - Convolution
```
cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_size=3, activation='relu', input_shape=[64, 64, 3]))
# Kernel Size is same as the number of rows in the Feature Detector
# The images are resized as 64px X 64px and 3 denotes 3D R, G, B
```
### Step 2 - Pooling
```
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2))
```
### Adding a second convolutional layer
```
cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_size=3, activation='relu'))
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2))
```
### Step 3 - Flattening
```
cnn.add(tf.keras.layers.Flatten()) #Flattens the 2D array into an 1D array
```
### Step 4 - Full Connection
```
cnn.add(tf.keras.layers.Dense(units=128, activation='relu')) # Units mean the number of neurons in the hidden layer
```
### Step 5 - Output Layer
```
cnn.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
```
## Part 3 - Training the CNN
### Compiling the CNN
```
cnn.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
```
### Training the CNN on the Training set and evaluating it on the Test set
```
cnn.fit(x = training_set, validation_data = test_set, epochs = 10)
```
## Part 4 - Making a single prediction
```
from keras.preprocessing import image
test_image = image.load_img('dataset/single_prediction/cat_or_dog_1.jpg', target_size = (64, 64)) # Creates a PIL image
test_image = image.img_to_array(test_image) # Converts the PIL image to a NumPy Array
test_image = np.expand_dims(test_image, axis = 0) # Cobtain the image into a Batch
result = cnn.predict(test_image)
training_set.class_indices
if result[0][0] == 1:
prediction = 'dog'
else:
prediction = 'cat'
print(prediction) # cat_or_dog_1.jpg originally is an image of a dog
```
| true |
code
| 0.747501 | null | null | null | null |
|
... ***CURRENTLY UNDER DEVELOPMENT*** ...
## Simulate Monthly Mean Sea Level using a multivariate-linear regression model based on the annual SST PCs
inputs required:
* WaterLevel historical data from a tide gauge at the study site
* Historical and simulated Annual PCs (*from Notebook 01*)
in this notebook:
* Obtain monthly mean sea level anomalies (MMSLA) from the tidal gauge record
* Perform linear regression between MMSLA and annual PCs
* Obtain predicted timeseries of MMSLA based on simulated timeseries of annual PCs
### Workflow:
<div>
<img src="resources/nb01_02.png" width="300px">
</div>
Monthly sea level variability is typically due to processes occurring at longer timescales than the daily weather. Slowly varying seasonality and anomalies due to ENSO are retained in the climate emulator via the principle components (APC) used to develop the AWT. A multivariate regression model containing a mean plus annual and seasonal cycles at 12-month and 6-month periods for each APC covariate was fit to the MMSLA. This simple model explains ~75% of the variance without any specific information regarding local conditions (i.e., local anomalies due to coastal shelf dynamics, or local SSTAs) and slightly underpredicts extreme monthly sea level anomalies by ~10 cm. While this component of the approach is a subject of ongoing research, the regression model produces an additional ~0.35 m of regional SWL variability about mean sea level, which was deemed sufficient for the purposes of demonstrating the development of the stochastic climate emulator.
```
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# basic import
import os
import os.path as op
from collections import OrderedDict
# python libs
import numpy as np
from numpy.random import multivariate_normal
import xarray as xr
from scipy.stats import linregress
from scipy.optimize import least_squares, curve_fit
from datetime import datetime, timedelta
# DEV: override installed teslakit
import sys
sys.path.insert(0, op.join(os.path.abspath(''), '..', '..', '..'))
# teslakit
from teslakit.database import Database
from teslakit.tides import Calculate_MMSL
from teslakit.statistical import runmean
from teslakit.util.time_operations import date2yearfrac as d2yf
from teslakit.plotting.tides import Plot_Tide_SLR, Plot_Tide_RUNM, Plot_Tide_MMSL, \
Plot_Validate_MMSL_tseries, Plot_Validate_MMSL_scatter, Plot_MMSL_Prediction, \
Plot_MMSL_Histogram
```
## Database and Site parameters
```
# --------------------------------------
# Teslakit database
p_data = r'/media/administrador/HD/Dropbox/Guam/teslakit/data'
db = Database(p_data)
# set site
db.SetSite('GUAM')
# --------------------------------------
# load data and set parameters
WL_split = db.Load_TIDE_hist_astro() # water level historical data (tide gauge)
WL = WL_split.WaterLevels
SST_KMA = db.Load_SST_KMA() # SST Anual Weather Types PCs
SST_PCs_sim_m = db.Load_SST_PCs_sim_m() # simulated SST PCs (monthly)
# parameters for mmsl calculation
mmsl_year_ini = 1947
mmsl_year_end = 2018
```
## Monthly Mean Sea Level
```
# --------------------------------------
# Calculate SLR using linear regression
time = WL.time.values[:]
wl = WL.values[:] * 1000 # (m to mm)
lr_time = np.array(range(len(time))) # for linregress
mask = ~np.isnan(wl) # remove nans with mask
slope, intercept, r_value, p_value, std_err = linregress(lr_time[mask], wl[mask])
slr = intercept + slope * lr_time
# Plot tide with SLR
Plot_Tide_SLR(time, wl, slr);
# --------------------------------------
# remove SLR and runmean from tide
tide_noslr = wl - slr
# calculate tide running mean
time_window = 365*24*3
runm = runmean(tide_noslr, time_window, 'mean')
# remove running mean
tide_noslr_norunm = tide_noslr - runm
# store data
TNSR = xr.DataArray(tide_noslr_norunm, dims=('time'), coords={'time':time})
# Plot tide without SLR and runm
Plot_Tide_RUNM(time, tide_noslr, runm);
# --------------------------------------
# calculate Monthly Mean Sea Level (mmsl)
MMSL = Calculate_MMSL(TNSR, mmsl_year_ini, mmsl_year_end)
# fill nans with interpolated values
p_nan = np.isnan(MMSL.mmsl)
MMSL.mmsl[p_nan]= np.interp(MMSL.time[p_nan], MMSL.time[~p_nan], MMSL.mmsl[~p_nan])
mmsl_time = MMSL.time.values[:]
mmsl_vals = MMSL.mmsl.values[:]
# Plot tide and mmsl
Plot_Tide_MMSL(TNSR.time, TNSR.values, mmsl_time, mmsl_vals);
# store historical mmsl
db.Save_TIDE_hist_mmsl(MMSL)
```
## Monthly Mean Sea Level - Principal Components
The annual PCs are passed to a monthly resolution
```
# --------------------------------------
# SST Anual Weather Types PCs
PCs = np.array(SST_KMA.PCs.values)
PC1, PC2, PC3 = PCs[:,0], PCs[:,1], PCs[:,2]
PCs_years = [int(str(t).split('-')[0]) for t in SST_KMA.time.values[:]]
# MMSL PCs calculations: cut and pad it to monthly resolution
ntrs_m_mean = np.array([])
ntrs_time = []
MMSL_PC1 = np.array([])
MMSL_PC2 = np.array([])
MMSL_PC3 = np.array([])
for c, y in enumerate(PCs_years):
pos = np.where(
(mmsl_time >= np.datetime64('{0}-06-01'.format(y))) &
(mmsl_time <= np.datetime64('{0}-05-29'.format(y+1)))
)
if pos[0].size:
ntrs_m_mean = np.concatenate((ntrs_m_mean, mmsl_vals[pos]),axis=0)
# TODO check for 0s and nans in ntrs_m_mean?
ntrs_time.append(mmsl_time[pos])
MMSL_PC1 = np.concatenate((MMSL_PC1, np.ones(pos[0].size)*PC1[c]),axis=0)
MMSL_PC2 = np.concatenate((MMSL_PC2, np.ones(pos[0].size)*PC2[c]),axis=0)
MMSL_PC3 = np.concatenate((MMSL_PC3, np.ones(pos[0].size)*PC3[c]),axis=0)
ntrs_time = np.concatenate(ntrs_time)
# Parse time to year fraction for linear-regression seasonality
frac_year = np.array([d2yf(x) for x in ntrs_time])
```
## Monthly Mean Sea Level - Multivariate-linear Regression Model
```
# --------------------------------------
# Fit linear regression model
def modelfun(data, *x):
pc1, pc2, pc3, t = data
return x[0] + x[1]*pc1 + x[2]*pc2 + x[3]*pc3 + \
np.array([x[4] + x[5]*pc1 + x[6]*pc2 + x[7]*pc3]).flatten() * np.cos(2*np.pi*t) + \
np.array([x[8] + x[9]*pc1 + x[10]*pc2 + x[11]*pc3]).flatten() * np.sin(2*np.pi*t) + \
np.array([x[12] + x[13]*pc1 + x[14]*pc2 + x[15]*pc3]).flatten() * np.cos(4*np.pi*t) + \
np.array([x[16] + x[17]*pc1 + x[18]*pc2 + x[19]*pc3]).flatten() * np.sin(4*np.pi*t)
# use non-linear least squares to fit our model
split = 160 # train / validation split index
x0 = np.ones(20)
sigma = np.ones(split)
# select data for scipy.optimize.curve_fit
x_train = ([MMSL_PC1[:split], MMSL_PC2[:split], MMSL_PC3[:split], frac_year[:split]])
y_train = ntrs_m_mean[:split]
res_lsq, res_cov = curve_fit(modelfun, x_train, y_train, x0, sigma)
# print optimal parameters and covariance
#print('optimal parameters (minimized sum of squares residual)\n{0}\n'.format(res_lsq))
#print('optimal parameters covariance\n{0}\n'.format(res_cov))
```
## Train and test model
```
# Check model at fitting period
yp_train = modelfun(x_train, *res_lsq)
Plot_Validate_MMSL_tseries(ntrs_time[:split], ntrs_m_mean[:split], yp_train);
Plot_Validate_MMSL_scatter(ntrs_m_mean[:split], yp_train);
# Check model at validation period
x_val = ([MMSL_PC1[split:], MMSL_PC2[split:], MMSL_PC3[split:], frac_year[split:]])
yp_val = modelfun(x_val, *res_lsq)
Plot_Validate_MMSL_tseries(ntrs_time[split:], ntrs_m_mean[split:], yp_val);
Plot_Validate_MMSL_scatter(ntrs_m_mean[split:], yp_val);
# Parameter sampling (generate sample of params based on covariance matrix)
n_sims = 10
theta_gen = res_lsq
theta_sim = multivariate_normal(theta_gen, res_cov, n_sims)
# Check model at validation period
yp_valp = np.ndarray((n_sims, len(ntrs_time[split:]))) * np.nan
for i in range(n_sims):
yp_valp[i, :] = modelfun(x_val, *theta_sim[i,:])
# 95% percentile
yp_val_quant = np.percentile(yp_valp, [2.275, 97.275], axis=0)
Plot_Validate_MMSL_tseries(ntrs_time[split:], ntrs_m_mean[split:], yp_val, mmsl_pred_quantiles=yp_val_quant);
# Fit model using entire dataset
sigma = np.ones(len(frac_year))
x_fit = ([MMSL_PC1, MMSL_PC2, MMSL_PC3, frac_year])
y_fit = ntrs_m_mean
res_lsq, res_cov = curve_fit(modelfun, x_fit, y_fit, x0, sigma)
# obtain model output
yp = modelfun(x_fit, *res_lsq)
# Generate 1000 simulations of the parameters
n_sims = 1000
theta_gen = res_lsq
param_sim = multivariate_normal(theta_gen, res_cov, n_sims)
# Check model
yp_p = np.ndarray((n_sims, len(ntrs_time))) * np.nan
for i in range(n_sims):
yp_p[i, :] = modelfun(x_fit, *param_sim[i,:])
# 95% percentile
yp_quant = np.percentile(yp_p, [2.275, 97.275], axis=0)
Plot_Validate_MMSL_tseries(ntrs_time, ntrs_m_mean, yp, mmsl_pred_quantiles=yp_quant);
# Save model parameters to use in climate change
model_coefs = xr.Dataset({'sim_params' : (('n_sims','n_params'), param_sim)})
db.Save_TIDE_mmsl_params(model_coefs)
```
## Monthly Mean Sea Level - Prediction
```
# --------------------------------------
# Predict 1000 years using simulated PCs (monthly time resolution)
# get simulation time as year fractions
PCs_sim_time = SST_PCs_sim_m.time.values[:]
frac_year_sim = np.array([d2yf(x) for x in PCs_sim_time])
# solve each PCs simulation
y_sim_n = np.ndarray((len(SST_PCs_sim_m.n_sim), len(frac_year_sim))) * np.nan
for s in SST_PCs_sim_m.n_sim:
PCs_s_m = SST_PCs_sim_m.sel(n_sim=s)
MMSL_PC1_sim = PCs_s_m.PC1.values[:]
MMSL_PC2_sim = PCs_s_m.PC2.values[:]
MMSL_PC3_sim = PCs_s_m.PC3.values[:]
# use linear-regression model
x_sim = ([MMSL_PC1_sim, MMSL_PC2_sim, MMSL_PC3_sim, frac_year_sim])
y_sim_n[s, :] = modelfun(x_sim, *param_sim[s,:])
# join output and store it
MMSL_sim = xr.Dataset(
{
'mmsl' : (('n_sim','time'), y_sim_n / 1000), # mm to m
},
{'time' : PCs_sim_time}
)
print(MMSL_sim)
db.Save_TIDE_sim_mmsl(MMSL_sim)
# Plot mmsl simulation
plot_sim = 0
y_sim = MMSL_sim.sel(n_sim=plot_sim).mmsl.values[:] * 1000 # m to mm
t_sim = MMSL_sim.sel(n_sim=plot_sim).time.values[:]
# Plot mmsl prediction
Plot_MMSL_Prediction(t_sim, y_sim);
# compare model histograms
Plot_MMSL_Histogram(ntrs_m_mean, y_sim);
# compare model histograms for all simulations
y_sim = MMSL_sim.mmsl.values[:].flatten() * 1000 # m to mm
Plot_MMSL_Histogram(ntrs_m_mean, y_sim);
```
| true |
code
| 0.311786 | null | null | null | null |
|
# Exact GP Regression with Multiple GPUs and Kernel Partitioning
In this notebook, we'll demonstrate training exact GPs on large datasets using two key features from the paper https://arxiv.org/abs/1903.08114:
1. The ability to distribute the kernel matrix across multiple GPUs, for additional parallelism.
2. Partitioning the kernel into chunks computed on-the-fly when performing each MVM to reduce memory usage.
We'll be using the `protein` dataset, which has about 37000 training examples. The techniques in this notebook can be applied to much larger datasets, but the training time required will depend on the computational resources you have available: both the number of GPUs available and the amount of memory they have (which determines the partition size) have a significant effect on training time.
```
import math
import torch
import gpytorch
import sys
from matplotlib import pyplot as plt
sys.path.append('../')
from LBFGS import FullBatchLBFGS
%matplotlib inline
%load_ext autoreload
%autoreload 2
```
## Downloading Data
We will be using the Protein UCI dataset which contains a total of 40000+ data points. The next cell will download this dataset from a Google drive and load it.
```
import os
import urllib.request
from scipy.io import loadmat
dataset = 'protein'
if not os.path.isfile(f'{dataset}.mat'):
print(f'Downloading \'{dataset}\' UCI dataset...')
urllib.request.urlretrieve('https://drive.google.com/uc?export=download&id=1nRb8e7qooozXkNghC5eQS0JeywSXGX2S',
f'{dataset}.mat')
data = torch.Tensor(loadmat(f'{dataset}.mat')['data'])
```
## Normalization and train/test Splits
In the next cell, we split the data 80/20 as train and test, and do some basic z-score feature normalization.
```
import numpy as np
N = data.shape[0]
# make train/val/test
n_train = int(0.8 * N)
train_x, train_y = data[:n_train, :-1], data[:n_train, -1]
test_x, test_y = data[n_train:, :-1], data[n_train:, -1]
# normalize features
mean = train_x.mean(dim=-2, keepdim=True)
std = train_x.std(dim=-2, keepdim=True) + 1e-6 # prevent dividing by 0
train_x = (train_x - mean) / std
test_x = (test_x - mean) / std
# normalize labels
mean, std = train_y.mean(),train_y.std()
train_y = (train_y - mean) / std
test_y = (test_y - mean) / std
# make continguous
train_x, train_y = train_x.contiguous(), train_y.contiguous()
test_x, test_y = test_x.contiguous(), test_y.contiguous()
output_device = torch.device('cuda:0')
train_x, train_y = train_x.to(output_device), train_y.to(output_device)
test_x, test_y = test_x.to(output_device), test_y.to(output_device)
```
## How many GPUs do you want to use?
In the next cell, specify the `n_devices` variable to be the number of GPUs you'd like to use. By default, we will use all devices available to us.
```
n_devices = torch.cuda.device_count()
print('Planning to run on {} GPUs.'.format(n_devices))
```
## GP Model + Training Code
In the next cell we define our GP model and training code. For this notebook, the only thing different from the Simple GP tutorials is the use of the `MultiDeviceKernel` to wrap the base covariance module. This allows for the use of multiple GPUs behind the scenes.
```
class ExactGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood, n_devices):
super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
base_covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
self.covar_module = gpytorch.kernels.MultiDeviceKernel(
base_covar_module, device_ids=range(n_devices),
output_device=output_device
)
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
def train(train_x,
train_y,
n_devices,
output_device,
checkpoint_size,
preconditioner_size,
n_training_iter,
):
likelihood = gpytorch.likelihoods.GaussianLikelihood().to(output_device)
model = ExactGPModel(train_x, train_y, likelihood, n_devices).to(output_device)
model.train()
likelihood.train()
optimizer = FullBatchLBFGS(model.parameters(), lr=0.1)
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
with gpytorch.beta_features.checkpoint_kernel(checkpoint_size), \
gpytorch.settings.max_preconditioner_size(preconditioner_size):
def closure():
optimizer.zero_grad()
output = model(train_x)
loss = -mll(output, train_y)
return loss
loss = closure()
loss.backward()
for i in range(n_training_iter):
options = {'closure': closure, 'current_loss': loss, 'max_ls': 10}
loss, _, _, _, _, _, _, fail = optimizer.step(options)
print('Iter %d/%d - Loss: %.3f lengthscale: %.3f noise: %.3f' % (
i + 1, n_training_iter, loss.item(),
model.covar_module.module.base_kernel.lengthscale.item(),
model.likelihood.noise.item()
))
if fail:
print('Convergence reached!')
break
print(f"Finished training on {train_x.size(0)} data points using {n_devices} GPUs.")
return model, likelihood
```
## Automatically determining GPU Settings
In the next cell, we automatically determine a roughly reasonable partition or *checkpoint* size that will allow us to train without using more memory than the GPUs available have. Not that this is a coarse estimate of the largest possible checkpoint size, and may be off by as much as a factor of 2. A smarter search here could make up to a 2x performance improvement.
```
import gc
def find_best_gpu_setting(train_x,
train_y,
n_devices,
output_device,
preconditioner_size
):
N = train_x.size(0)
# Find the optimum partition/checkpoint size by decreasing in powers of 2
# Start with no partitioning (size = 0)
settings = [0] + [int(n) for n in np.ceil(N / 2**np.arange(1, np.floor(np.log2(N))))]
for checkpoint_size in settings:
print('Number of devices: {} -- Kernel partition size: {}'.format(n_devices, checkpoint_size))
try:
# Try a full forward and backward pass with this setting to check memory usage
_, _ = train(train_x, train_y,
n_devices=n_devices, output_device=output_device,
checkpoint_size=checkpoint_size,
preconditioner_size=preconditioner_size, n_training_iter=1)
# when successful, break out of for-loop and jump to finally block
break
except RuntimeError as e:
print('RuntimeError: {}'.format(e))
except AttributeError as e:
print('AttributeError: {}'.format(e))
finally:
# handle CUDA OOM error
gc.collect()
torch.cuda.empty_cache()
return checkpoint_size
# Set a large enough preconditioner size to reduce the number of CG iterations run
preconditioner_size = 100
checkpoint_size = find_best_gpu_setting(train_x, train_y,
n_devices=n_devices,
output_device=output_device,
preconditioner_size=preconditioner_size)
```
# Training
```
model, likelihood = train(train_x, train_y,
n_devices=n_devices, output_device=output_device,
checkpoint_size=checkpoint_size,
preconditioner_size=preconditioner_size,
n_training_iter=20)
```
# Testing: Computing test time caches
```
# Get into evaluation (predictive posterior) mode
model.eval()
likelihood.eval()
with torch.no_grad(), gpytorch.settings.fast_pred_var():
latent_pred = model(test_x)
```
# Testing: Computing predictions
```
with torch.no_grad(), gpytorch.settings.fast_pred_var():
%time latent_pred = model(test_x)
test_rmse = torch.sqrt(torch.mean(torch.pow(latent_pred.mean - test_y, 2)))
print(f"Test RMSE: {test_rmse.item()}")
```
| true |
code
| 0.607925 | null | null | null | null |
|
## Purpose: Try different models-- Part5.
### Penalized_SVM.
```
# import dependencies.
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.svm import SVC
```
#### STEP1: Read in dataset. Remove data from 2016-2019.
- data from 2016-2018 will be used to bs test the model.
- data from 2019 will be used to predict the winners of the 2019 WS.
```
# read in the data.
team_data = pd.read_csv("../../Resources/clean_data_1905.csv")
del team_data["Unnamed: 0"]
team_data.head()
# remove data from 2016 through 2019.
team_data_new = team_data.loc[team_data["year"] < 2016]
team_data_new.head()
target = team_data_new["winners"]
features = team_data_new.drop({"team", "year", "winners"}, axis=1)
feature_columns = list(features.columns)
print (target.shape)
print (features.shape)
print (feature_columns)
```
#### STEP2: Split and scale the data.
```
# split data.
X_train, X_test, y_train, y_test = train_test_split(features, target, random_state=42)
# scale data.
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.fit_transform(X_test)
```
#### STEP3: Try the SVC model.
```
# generate the model.
model = SVC(kernel="rbf",
class_weight="balanced",
probability=True)
# fit the model.
model.fit(X_train_scaled, y_train)
# predict.
prediction = model.predict(X_test_scaled)
print ((classification_report(y_test, prediction, target_names=["0", "1"])))
```
#### STEP4: Predict the winner 2016-2018.
```
def predict_the_winner(model, year, team_data, X_train):
'''
INPUT:
-X_train = scaled X train data.
-model = the saved model.
-team_data = complete dataframe with all data.
-year = the year want to look at.
OUTPUT:
-printed prediction.
DESCRIPTION:
-data from year of interest is isolated.
-the data are scaled.
-the prediction is made.
-print out the resulting probability and the name of the team.
'''
# grab the data.
team_data = team_data.loc[team_data["year"] == year].reset_index()
# set features (no team, year, winners).
# set target (winners).
features = team_data[feature_columns]
# scale.
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
features = scaler.fit_transform(features)
# fit the model.
probabilities = model.predict_proba(features)
# convert predictions to datafram.e
WS_predictions = pd.DataFrame(probabilities[:,1])
# Sort the DataFrame (descending)
WS_predictions = WS_predictions.sort_values(0, ascending=False)
WS_predictions['Probability'] = WS_predictions[0]
# Print 50 highest probability HoF inductees from still eligible players
for i, row in WS_predictions.head(50).iterrows():
prob = ' '.join(('WS Probability =', str(row['Probability'])))
print('')
print(prob)
print(team_data.iloc[i,1:27]["team"])
# predict for 2018.
predict_the_winner(model, 2018, team_data, X_train_scaled)
# predict for 2017.
predict_the_winner(model, 2017, team_data, X_train_scaled)
```
Ok. This didn't work. Let's try this penalized model with a grid search.
```
def grid_search_svc(X_train, X_test, y_train, y_test):
'''
INPUT:
-X_train = scaled X train data.
-X_test = scaled X test data.
-y_train = y train data.
-y_test = y test data.
OUTPUT:
-classification report (has F1 score, precision and recall).
-grid = saved model for prediction.
DESCRIPTION:
-the scaled and split data is put through a grid search with svc.
-the model is trained.
-a prediction is made.
-print out the classification report and give the model.
'''
# set up svc model.
model = SVC(kernel="rbf",
class_weight="balanced",
probability=True)
# create gridsearch estimator.
param_grid = {"C": [0.0001, 0.001, 0.01, 0.1, 1, 10, 100],
"gamma": [0.0001, 0.001, 0.01, 0.1]}
grid = GridSearchCV(model, param_grid, verbose=3)
# fit the model.
grid.fit(X_train, y_train)
# predict.
prediction = grid.predict(X_test)
# print out the basic information about the grid search.
print (grid.best_params_)
print (grid.best_score_)
print (grid.best_estimator_)
grid = grid.best_estimator_
predictions = grid.predict(X_test)
print (classification_report(y_test, prediction, target_names=["0", "1"]))
return grid
model_grid = grid_search_svc(X_train, X_test, y_train, y_test)
```
Nope. This is terrible. Lots of no.
| true |
code
| 0.644113 | null | null | null | null |
|
### 当涉及圆形子数组时,有两种情况。
1、情况1:没有交叉边界的最大子数组总和
2、情况2:具有交叉边界的最大子数组总和
写下一些小写的案例,并考虑案例2的一般模式。
记住为输入数组中的所有元素都为负数做一个角点案例句柄。
<img src='https://assets.leetcode.com/users/brianchiang_tw/image_1589539736.png'>
```
class Solution:
def maxSubarraySumCircular(self, A) -> int:
array_sum = 0
local_min_sum, global_min_sum = 0, float('inf')
local_max_sum, global_max_sum = 0, float('-inf')
for num in A:
local_min_sum = min(local_min_sum + num, num)
global_min_sum = min(global_min_sum, local_min_sum)
local_max_sum = max(local_max_sum + num, num)
global_max_sum = max(global_max_sum, local_max_sum)
array_sum += num
if global_max_sum > 0:
return max(array_sum - global_min_sum, global_max_sum)
return global_max_sum
class Solution:
def maxSubarraySumCircular(self, A) -> int:
min_sum = min_glo_sum = max_sum = max_glo_sum = A[0]
for a in A[1:]:
min_sum = min(a, a + min_sum)
min_glo_sum = min(min_sum, min_glo_sum)
max_sum = max(a, a + max_sum)
max_glo_sum = max(max_sum, max_glo_sum)
if sum(A) == min_glo_sum:
return max_glo_sum
return max(max_glo_sum, sum(A) - min_glo_sum)
class Solution:
def maxSubarraySumCircular(self, A) -> int:
array_sum = 0
local_min_sum, global_min_sum = 0, float('inf')
local_max_sum, global_max_sum = 0, float('-inf')
for number in A:
local_min_sum = min( local_min_sum + number, number )
global_min_sum = min( global_min_sum, local_min_sum )
local_max_sum = max( local_max_sum + number, number )
global_max_sum = max( global_max_sum, local_max_sum )
array_sum += number
# global_max_sum denotes the maximum subarray sum without crossing boundary
# arry_sum - global_min_sum denotes the maximum subarray sum with crossing boundary
if global_max_sum > 0:
return max( array_sum - global_min_sum, global_max_sum )
else:
# corner case handle for all number are negative
return global_max_sum
solution = Solution()
solution.maxSubarraySumCircular([3,1,3,2,6])
# 时间复杂度较高
class Solution:
def maxSubarraySumCircular(self, A) -> int:
res = -float('inf')
for i in range(len(A)):
temp_sum = A[i]
temp_max = A[i]
for j in range(i+1, len(A) * 2):
j %= len(A)
if j == i:
break
temp_sum += A[j]
temp_max = max(temp_max, temp_sum)
res = max(temp_max, res, A[i])
return res
from collections import Counter
# 时间复杂度较高
class Solution:
def maxSubarraySumCircular(self, A) -> int:
h = Counter(A)
solution = Solution()
solution.maxSubarraySumCircular([3,1,3,2,6])
```
| true |
code
| 0.785401 | null | null | null | null |
|
# PyTorch Basics
```
import torch
import numpy as np
torch.manual_seed(1234)
```
## Tensors
* Scalar is a single number.
* Vector is an array of numbers.
* Matrix is a 2-D array of numbers.
* Tensors are N-D arrays of numbers.
#### Creating Tensors
You can create tensors by specifying the shape as arguments. Here is a tensor with 5 rows and 3 columns
```
def describe(x):
print("Type: {}".format(x.type()))
print("Shape/size: {}".format(x.shape))
print("Values: \n{}".format(x))
describe(torch.Tensor(2, 3))
describe(torch.randn(2, 3))
```
It's common in prototyping to create a tensor with random numbers of a specific shape.
```
x = torch.rand(2, 3)
describe(x)
```
You can also initialize tensors of ones or zeros.
```
describe(torch.zeros(2, 3))
x = torch.ones(2, 3)
describe(x)
x.fill_(5)
describe(x)
```
Tensors can be initialized and then filled in place.
Note: operations that end in an underscore (`_`) are in place operations.
```
x = torch.Tensor(3,4).fill_(5)
print(x.type())
print(x.shape)
print(x)
```
Tensors can be initialized from a list of lists
```
x = torch.Tensor([[1, 2,],
[2, 4,]])
describe(x)
```
Tensors can be initialized from numpy matrices
```
npy = np.random.rand(2, 3)
describe(torch.from_numpy(npy))
print(npy.dtype)
```
#### Tensor Types
The FloatTensor has been the default tensor that we have been creating all along
```
import torch
x = torch.arange(6).view(2, 3)
describe(x)
x = torch.FloatTensor([[1, 2, 3],
[4, 5, 6]])
describe(x)
x = x.long()
describe(x)
x = torch.tensor([[1, 2, 3],
[4, 5, 6]], dtype=torch.int64)
describe(x)
x = x.float()
describe(x)
x = torch.randn(2, 3)
describe(x)
describe(torch.add(x, x))
describe(x + x)
x = torch.arange(6)
describe(x)
x = x.view(2, 3)
describe(x)
describe(torch.sum(x, dim=0))
describe(torch.sum(x, dim=1))
describe(torch.transpose(x, 0, 1))
import torch
x = torch.arange(6).view(2, 3)
describe(x)
describe(x[:1, :2])
describe(x[0, 1])
indices = torch.LongTensor([0, 2])
describe(torch.index_select(x, dim=1, index=indices))
indices = torch.LongTensor([0, 0])
describe(torch.index_select(x, dim=0, index=indices))
row_indices = torch.arange(2).long()
col_indices = torch.LongTensor([0, 1])
describe(x[row_indices, col_indices])
```
Long Tensors are used for indexing operations and mirror the `int64` numpy type
```
x = torch.LongTensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
describe(x)
print(x.dtype)
print(x.numpy().dtype)
```
You can convert a FloatTensor to a LongTensor
```
x = torch.FloatTensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
x = x.long()
describe(x)
```
### Special Tensor initializations
We can create a vector of incremental numbers
```
x = torch.arange(0, 10)
print(x)
```
Sometimes it's useful to have an integer-based arange for indexing
```
x = torch.arange(0, 10).long()
print(x)
```
## Operations
Using the tensors to do linear algebra is a foundation of modern Deep Learning practices
Reshaping allows you to move the numbers in a tensor around. One can be sure that the order is preserved. In PyTorch, reshaping is called `view`
```
x = torch.arange(0, 20)
print(x.view(1, 20))
print(x.view(2, 10))
print(x.view(4, 5))
print(x.view(5, 4))
print(x.view(10, 2))
print(x.view(20, 1))
```
We can use view to add size-1 dimensions, which can be useful for combining with other tensors. This is called broadcasting.
```
x = torch.arange(12).view(3, 4)
y = torch.arange(4).view(1, 4)
z = torch.arange(3).view(3, 1)
print(x)
print(y)
print(z)
print(x + y)
print(x + z)
```
Unsqueeze and squeeze will add and remove 1-dimensions.
```
x = torch.arange(12).view(3, 4)
print(x.shape)
x = x.unsqueeze(dim=1)
print(x.shape)
x = x.squeeze()
print(x.shape)
```
all of the standard mathematics operations apply (such as `add` below)
```
x = torch.rand(3,4)
print("x: \n", x)
print("--")
print("torch.add(x, x): \n", torch.add(x, x))
print("--")
print("x+x: \n", x + x)
```
The convention of `_` indicating in-place operations continues:
```
x = torch.arange(12).reshape(3, 4)
print(x)
print(x.add_(x))
```
There are many operations for which reduce a dimension. Such as sum:
```
x = torch.arange(12).reshape(3, 4)
print("x: \n", x)
print("---")
print("Summing across rows (dim=0): \n", x.sum(dim=0))
print("---")
print("Summing across columns (dim=1): \n", x.sum(dim=1))
```
#### Indexing, Slicing, Joining and Mutating
```
x = torch.arange(6).view(2, 3)
print("x: \n", x)
print("---")
print("x[:2, :2]: \n", x[:2, :2])
print("---")
print("x[0][1]: \n", x[0][1])
print("---")
print("Setting [0][1] to be 8")
x[0][1] = 8
print(x)
```
We can select a subset of a tensor using the `index_select`
```
x = torch.arange(9).view(3,3)
print(x)
print("---")
indices = torch.LongTensor([0, 2])
print(torch.index_select(x, dim=0, index=indices))
print("---")
indices = torch.LongTensor([0, 2])
print(torch.index_select(x, dim=1, index=indices))
```
We can also use numpy-style advanced indexing:
```
x = torch.arange(9).view(3,3)
indices = torch.LongTensor([0, 2])
print(x[indices])
print("---")
print(x[indices, :])
print("---")
print(x[:, indices])
```
We can combine tensors by concatenating them. First, concatenating on the rows
```
x = torch.arange(6).view(2,3)
describe(x)
describe(torch.cat([x, x], dim=0))
describe(torch.cat([x, x], dim=1))
describe(torch.stack([x, x]))
```
We can concentate along the first dimension.. the columns.
```
x = torch.arange(9).view(3,3)
print(x)
print("---")
new_x = torch.cat([x, x, x], dim=1)
print(new_x.shape)
print(new_x)
```
We can also concatenate on a new 0th dimension to "stack" the tensors:
```
x = torch.arange(9).view(3,3)
print(x)
print("---")
new_x = torch.stack([x, x, x])
print(new_x.shape)
print(new_x)
```
#### Linear Algebra Tensor Functions
Transposing allows you to switch the dimensions to be on different axis. So we can make it so all the rows are columsn and vice versa.
```
x = torch.arange(0, 12).view(3,4)
print("x: \n", x)
print("---")
print("x.tranpose(1, 0): \n", x.transpose(1, 0))
```
A three dimensional tensor would represent a batch of sequences, where each sequence item has a feature vector. It is common to switch the batch and sequence dimensions so that we can more easily index the sequence in a sequence model.
Note: Transpose will only let you swap 2 axes. Permute (in the next cell) allows for multiple
```
batch_size = 3
seq_size = 4
feature_size = 5
x = torch.arange(batch_size * seq_size * feature_size).view(batch_size, seq_size, feature_size)
print("x.shape: \n", x.shape)
print("x: \n", x)
print("-----")
print("x.transpose(1, 0).shape: \n", x.transpose(1, 0).shape)
print("x.transpose(1, 0): \n", x.transpose(1, 0))
```
Permute is a more general version of tranpose:
```
batch_size = 3
seq_size = 4
feature_size = 5
x = torch.arange(batch_size * seq_size * feature_size).view(batch_size, seq_size, feature_size)
print("x.shape: \n", x.shape)
print("x: \n", x)
print("-----")
print("x.permute(1, 0, 2).shape: \n", x.permute(1, 0, 2).shape)
print("x.permute(1, 0, 2): \n", x.permute(1, 0, 2))
```
Matrix multiplication is `mm`:
```
torch.randn(2, 3, requires_grad=True)
x1 = torch.arange(6).view(2, 3).float()
describe(x1)
x2 = torch.ones(3, 2)
x2[:, 1] += 1
describe(x2)
describe(torch.mm(x1, x2))
x = torch.arange(0, 12).view(3,4).float()
print(x)
x2 = torch.ones(4, 2)
x2[:, 1] += 1
print(x2)
print(x.mm(x2))
```
See the [PyTorch Math Operations Documentation](https://pytorch.org/docs/stable/torch.html#math-operations) for more!
## Computing Gradients
```
x = torch.tensor([[2.0, 3.0]], requires_grad=True)
z = 3 * x
print(z)
```
In this small snippet, you can see the gradient computations at work. We create a tensor and multiply it by 3. Then, we create a scalar output using `sum()`. A Scalar output is needed as the the loss variable. Then, called backward on the loss means it computes its rate of change with respect to the inputs. Since the scalar was created with sum, each position in z and x are independent with respect to the loss scalar.
The rate of change of x with respect to the output is just the constant 3 that we multiplied x by.
```
x = torch.tensor([[2.0, 3.0]], requires_grad=True)
print("x: \n", x)
print("---")
z = 3 * x
print("z = 3*x: \n", z)
print("---")
loss = z.sum()
print("loss = z.sum(): \n", loss)
print("---")
loss.backward()
print("after loss.backward(), x.grad: \n", x.grad)
```
### Example: Computing a conditional gradient
$$ \text{ Find the gradient of f(x) at x=1 } $$
$$ {} $$
$$ f(x)=\left\{
\begin{array}{ll}
sin(x) \text{ if } x>0 \\
cos(x) \text{ otherwise } \\
\end{array}
\right.$$
```
def f(x):
if (x.data > 0).all():
return torch.sin(x)
else:
return torch.cos(x)
x = torch.tensor([1.0], requires_grad=True)
y = f(x)
y.backward()
print(x.grad)
```
We could apply this to a larger vector too, but we need to make sure the output is a scalar:
```
x = torch.tensor([1.0, 0.5], requires_grad=True)
y = f(x)
# this is meant to break!
y.backward()
print(x.grad)
```
Making the output a scalar:
```
x = torch.tensor([1.0, 0.5], requires_grad=True)
y = f(x)
y.sum().backward()
print(x.grad)
```
but there was an issue.. this isn't right for this edge case:
```
x = torch.tensor([1.0, -1], requires_grad=True)
y = f(x)
y.sum().backward()
print(x.grad)
x = torch.tensor([-0.5, -1], requires_grad=True)
y = f(x)
y.sum().backward()
print(x.grad)
```
This is because we aren't doing the boolean computation and subsequent application of cos and sin on an elementwise basis. So, to solve this, it is common to use masking:
```
def f2(x):
mask = torch.gt(x, 0).float()
return mask * torch.sin(x) + (1 - mask) * torch.cos(x)
x = torch.tensor([1.0, -1], requires_grad=True)
y = f2(x)
y.sum().backward()
print(x.grad)
def describe_grad(x):
if x.grad is None:
print("No gradient information")
else:
print("Gradient: \n{}".format(x.grad))
print("Gradient Function: {}".format(x.grad_fn))
import torch
x = torch.ones(2, 2, requires_grad=True)
describe(x)
describe_grad(x)
print("--------")
y = (x + 2) * (x + 5) + 3
describe(y)
z = y.mean()
describe(z)
describe_grad(x)
print("--------")
z.backward(create_graph=True, retain_graph=True)
describe_grad(x)
print("--------")
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
y.grad_fn
```
### CUDA Tensors
PyTorch's operations can seamlessly be used on the GPU or on the CPU. There are a couple basic operations for interacting in this way.
```
print(torch.cuda.is_available())
x = torch.rand(3,3)
describe(x)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
x = torch.rand(3, 3).to(device)
describe(x)
print(x.device)
cpu_device = torch.device("cpu")
# this will break!
y = torch.rand(3, 3)
x + y
y = y.to(cpu_device)
x = x.to(cpu_device)
x + y
if torch.cuda.is_available(): # only is GPU is available
a = torch.rand(3,3).to(device='cuda:0') # CUDA Tensor
print(a)
b = torch.rand(3,3).cuda()
print(b)
print(a + b)
a = a.cpu() # Error expected
print(a + b)
```
### Exercises
Some of these exercises require operations not covered in the notebook. You will have to look at [the documentation](https://pytorch.org/docs/) (on purpose!)
(Answers are at the bottom)
#### Exercise 1
Create a 2D tensor and then add a dimension of size 1 inserted at the 0th axis.
#### Exercise 2
Remove the extra dimension you just added to the previous tensor.
#### Exercise 3
Create a random tensor of shape 5x3 in the interval [3, 7)
#### Exercise 4
Create a tensor with values from a normal distribution (mean=0, std=1).
#### Exercise 5
Retrieve the indexes of all the non zero elements in the tensor torch.Tensor([1, 1, 1, 0, 1]).
#### Exercise 6
Create a random tensor of size (3,1) and then horizonally stack 4 copies together.
#### Exercise 7
Return the batch matrix-matrix product of two 3 dimensional matrices (a=torch.rand(3,4,5), b=torch.rand(3,5,4)).
#### Exercise 8
Return the batch matrix-matrix product of a 3D matrix and a 2D matrix (a=torch.rand(3,4,5), b=torch.rand(5,4)).
Answers below
Answers still below.. Keep Going
#### Exercise 1
Create a 2D tensor and then add a dimension of size 1 inserted at the 0th axis.
```
a = torch.rand(3,3)
a = a.unsqueeze(0)
print(a)
print(a.shape)
```
#### Exercise 2
Remove the extra dimension you just added to the previous tensor.
```
a = a.squeeze(0)
print(a.shape)
```
#### Exercise 3
Create a random tensor of shape 5x3 in the interval [3, 7)
```
3 + torch.rand(5, 3) * 4
```
#### Exercise 4
Create a tensor with values from a normal distribution (mean=0, std=1).
```
a = torch.rand(3,3)
a.normal_(mean=0, std=1)
```
#### Exercise 5
Retrieve the indexes of all the non zero elements in the tensor torch.Tensor([1, 1, 1, 0, 1]).
```
a = torch.Tensor([1, 1, 1, 0, 1])
torch.nonzero(a)
```
#### Exercise 6
Create a random tensor of size (3,1) and then horizonally stack 4 copies together.
```
a = torch.rand(3,1)
a.expand(3,4)
```
#### Exercise 7
Return the batch matrix-matrix product of two 3 dimensional matrices (a=torch.rand(3,4,5), b=torch.rand(3,5,4)).
```
a = torch.rand(3,4,5)
b = torch.rand(3,5,4)
torch.bmm(a, b)
```
#### Exercise 8
Return the batch matrix-matrix product of a 3D matrix and a 2D matrix (a=torch.rand(3,4,5), b=torch.rand(5,4)).
```
a = torch.rand(3,4,5)
b = torch.rand(5,4)
torch.bmm(a, b.unsqueeze(0).expand(a.size(0), *b.size()))
```
### END
| true |
code
| 0.500977 | null | null | null | null |
|
# Support Vector Machines
Let's create the same fake income / age clustered data that we used for our K-Means clustering example:
```
import numpy as np
#Create fake income/age clusters for N people in k clusters
def createClusteredData(N, k):
np.random.seed(1234)
pointsPerCluster = float(N)/k
X = []
y = []
for i in range (k):
incomeCentroid = np.random.uniform(20000.0, 200000.0)
ageCentroid = np.random.uniform(20.0, 70.0)
for j in range(int(pointsPerCluster)):
X.append([np.random.normal(incomeCentroid, 10000.0), np.random.normal(ageCentroid, 2.0)])
y.append(i)
X = np.array(X)
y = np.array(y)
return X, y
%matplotlib inline
from pylab import *
from sklearn.preprocessing import MinMaxScaler
(X, y) = createClusteredData(100, 5)
plt.figure(figsize=(8, 6))
plt.scatter(X[:,0], X[:,1], c=y.astype(np.float))
plt.show()
scaling = MinMaxScaler(feature_range=(-1,1)).fit(X)
X = scaling.transform(X)
plt.figure(figsize=(8, 6))
plt.scatter(X[:,0], X[:,1], c=y.astype(np.float))
plt.show()
```
Now we'll use linear SVC to partition our graph into clusters:
```
from sklearn import svm, datasets
C = 1.0
svc = svm.SVC(kernel='linear', C=C).fit(X, y)
```
By setting up a dense mesh of points in the grid and classifying all of them, we can render the regions of each cluster as distinct colors:
```
def plotPredictions(clf):
# Create a dense grid of points to sample
xx, yy = np.meshgrid(np.arange(-1, 1, .001),
np.arange(-1, 1, .001))
# Convert to Numpy arrays
npx = xx.ravel()
npy = yy.ravel()
# Convert to a list of 2D (income, age) points
samplePoints = np.c_[npx, npy]
# Generate predicted labels (cluster numbers) for each point
Z = clf.predict(samplePoints)
plt.figure(figsize=(8, 6))
Z = Z.reshape(xx.shape) #Reshape results to match xx dimension
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8) # Draw the contour
plt.scatter(X[:,0], X[:,1], c=y.astype(np.float)) # Draw the points
plt.show()
plotPredictions(svc)
```
Or just use predict for a given point:
```
print(svc.predict(scaling.transform([[200000, 40]])))
print(svc.predict(scaling.transform([[50000, 65]])))
```
## Activity
"Linear" is one of many kernels scikit-learn supports on SVC. Look up the documentation for scikit-learn online to find out what the other possible kernel options are. Do any of them work well for this data set?
| true |
code
| 0.533337 | null | null | null | null |
|
# Getting Started
In this tutorial, you will know how to
- use the models in **ConvLab-2** to build a dialog agent.
- build a simulator to chat with the agent and evaluate the performance.
- try different module combinations.
- use analysis tool to diagnose your system.
Let's get started!
## Environment setup
Run the command below to install ConvLab-2. Then restart the notebook and skip this commend.
```
# first install ConvLab-2 and restart the notebook
! git clone https://github.com/thu-coai/ConvLab-2.git && cd ConvLab-2 && pip install -e .
# installing en_core_web_sm for spacy to resolve error in BERTNLU
!python -m spacy download en_core_web_sm
```
## build an agent
We use the models adapted on [Multiwoz](https://www.aclweb.org/anthology/D18-1547) dataset to build our agent. This pipeline agent consists of NLU, DST, Policy and NLG modules.
First, import some models:
```
# common import: convlab2.$module.$model.$dataset
from convlab2.nlu.jointBERT.multiwoz import BERTNLU
from convlab2.nlu.milu.multiwoz import MILU
from convlab2.dst.rule.multiwoz import RuleDST
from convlab2.policy.rule.multiwoz import RulePolicy
from convlab2.nlg.template.multiwoz import TemplateNLG
from convlab2.dialog_agent import PipelineAgent, BiSession
from convlab2.evaluator.multiwoz_eval import MultiWozEvaluator
from pprint import pprint
import random
import numpy as np
import torch
```
Then, create the models and build an agent:
```
# go to README.md of each model for more information
# BERT nlu
sys_nlu = BERTNLU()
# simple rule DST
sys_dst = RuleDST()
# rule policy
sys_policy = RulePolicy()
# template NLG
sys_nlg = TemplateNLG(is_user=False)
# assemble
sys_agent = PipelineAgent(sys_nlu, sys_dst, sys_policy, sys_nlg, name='sys')
```
That's all! Let's chat with the agent using its response function:
```
sys_agent.response("I want to find a moderate hotel")
sys_agent.response("Which type of hotel is it ?")
sys_agent.response("OK , where is its address ?")
sys_agent.response("Thank you !")
sys_agent.response("Try to find me a Chinese restaurant in south area .")
sys_agent.response("Which kind of food it provides ?")
sys_agent.response("Book a table for 5 , this Sunday .")
```
## Build a simulator to chat with the agent and evaluate
In many one-to-one task-oriented dialog system, a simulator is essential to train an RL agent. In our framework, we doesn't distinguish user or system. All speakers are **agents**. The simulator is also an agent, with specific policy inside for accomplishing the user goal.
We use `Agenda` policy for the simulator, this policy requires dialog act input, which means we should set DST argument of `PipelineAgent` to None. Then the `PipelineAgent` will pass dialog act to policy directly. Refer to `PipelineAgent` doc for more details.
```
# MILU
user_nlu = MILU()
# not use dst
user_dst = None
# rule policy
user_policy = RulePolicy(character='usr')
# template NLG
user_nlg = TemplateNLG(is_user=True)
# assemble
user_agent = PipelineAgent(user_nlu, user_dst, user_policy, user_nlg, name='user')
```
Now we have a simulator and an agent. we will use an existed simple one-to-one conversation controller BiSession, you can also define your own Session class for your special need.
We add `MultiWozEvaluator` to evaluate the performance. It uses the parsed dialog act input and policy output dialog act to calculate **inform f1**, **book rate**, and whether the task is **success**.
```
evaluator = MultiWozEvaluator()
sess = BiSession(sys_agent=sys_agent, user_agent=user_agent, kb_query=None, evaluator=evaluator)
```
Let's make this two agents chat! The key is `next_turn` method of `BiSession` class.
```
def set_seed(r_seed):
random.seed(r_seed)
np.random.seed(r_seed)
torch.manual_seed(r_seed)
set_seed(20200131)
sys_response = ''
sess.init_session()
print('init goal:')
pprint(sess.evaluator.goal)
print('-'*50)
for i in range(20):
sys_response, user_response, session_over, reward = sess.next_turn(sys_response)
print('user:', user_response)
print('sys:', sys_response)
print()
if session_over is True:
break
print('task success:', sess.evaluator.task_success())
print('book rate:', sess.evaluator.book_rate())
print('inform precision/recall/f1:', sess.evaluator.inform_F1())
print('-'*50)
print('final goal:')
pprint(sess.evaluator.goal)
print('='*100)
```
## Try different module combinations
The combination modes of pipeline agent modules are flexible. We support joint models such as TRADE, SUMBT for word-DST and MDRG, HDSA, LaRL for word-Policy, once the input and output are matched with previous and next module. We also support End2End models such as Sequicity.
Available models:
- NLU: BERTNLU, MILU, SVMNLU
- DST: RuleDST
- Word-DST: SUMBT, TRADE (set `sys_nlu` to `None`)
- Policy: RulePolicy, Imitation, REINFORCE, PPO, GDPL
- Word-Policy: MDRG, HDSA, LaRL (set `sys_nlg` to `None`)
- NLG: Template, SCLSTM
- End2End: Sequicity, DAMD, RNN_rollout (directly used as `sys_agent`)
- Simulator policy: Agenda, VHUS (for `user_policy`)
```
# available NLU models
from convlab2.nlu.svm.multiwoz import SVMNLU
from convlab2.nlu.jointBERT.multiwoz import BERTNLU
from convlab2.nlu.milu.multiwoz import MILU
# available DST models
from convlab2.dst.rule.multiwoz import RuleDST
from convlab2.dst.sumbt.multiwoz import SUMBT
from convlab2.dst.trade.multiwoz import TRADE
# available Policy models
from convlab2.policy.rule.multiwoz import RulePolicy
from convlab2.policy.ppo.multiwoz import PPOPolicy
from convlab2.policy.pg.multiwoz import PGPolicy
from convlab2.policy.mle.multiwoz import MLEPolicy
from convlab2.policy.gdpl.multiwoz import GDPLPolicy
from convlab2.policy.vhus.multiwoz import UserPolicyVHUS
from convlab2.policy.mdrg.multiwoz import MDRGWordPolicy
from convlab2.policy.hdsa.multiwoz import HDSA
from convlab2.policy.larl.multiwoz import LaRL
# available NLG models
from convlab2.nlg.template.multiwoz import TemplateNLG
from convlab2.nlg.sclstm.multiwoz import SCLSTM
# available E2E models
from convlab2.e2e.sequicity.multiwoz import Sequicity
from convlab2.e2e.damd.multiwoz import Damd
```
NLU+RuleDST or Word-DST:
```
# NLU+RuleDST:
sys_nlu = BERTNLU()
# sys_nlu = MILU()
# sys_nlu = SVMNLU()
sys_dst = RuleDST()
# or Word-DST:
# sys_nlu = None
# sys_dst = SUMBT()
# sys_dst = TRADE()
```
Policy+NLG or Word-Policy:
```
# Policy+NLG:
sys_policy = RulePolicy()
# sys_policy = PPOPolicy()
# sys_policy = PGPolicy()
# sys_policy = MLEPolicy()
# sys_policy = GDPLPolicy()
sys_nlg = TemplateNLG(is_user=False)
# sys_nlg = SCLSTM(is_user=False)
# or Word-Policy:
# sys_policy = LaRL()
# sys_policy = HDSA()
# sys_policy = MDRGWordPolicy()
# sys_nlg = None
```
Assemble the Pipeline system agent:
```
sys_agent = PipelineAgent(sys_nlu, sys_dst, sys_policy, sys_nlg, 'sys')
```
Or Directly use an end-to-end model:
```
# sys_agent = Sequicity()
# sys_agent = Damd()
```
Config an user agent similarly:
```
user_nlu = BERTNLU()
# user_nlu = MILU()
# user_nlu = SVMNLU()
user_dst = None
user_policy = RulePolicy(character='usr')
# user_policy = UserPolicyVHUS(load_from_zip=True)
user_nlg = TemplateNLG(is_user=True)
# user_nlg = SCLSTM(is_user=True)
user_agent = PipelineAgent(user_nlu, user_dst, user_policy, user_nlg, name='user')
```
## Use analysis tool to diagnose the system
We provide an analysis tool presents rich statistics and summarizes common mistakes from simulated dialogues, which facilitates error analysis and
system improvement. The analyzer will generate an HTML report which contains
rich statistics of simulated dialogues. For more information, please refer to `convlab2/util/analysis_tool`.
```
from convlab2.util.analysis_tool.analyzer import Analyzer
# if sys_nlu!=None, set use_nlu=True to collect more information
analyzer = Analyzer(user_agent=user_agent, dataset='multiwoz')
set_seed(20200131)
analyzer.comprehensive_analyze(sys_agent=sys_agent, model_name='sys_agent', total_dialog=100)
```
To compare several models:
```
set_seed(20200131)
analyzer.compare_models(agent_list=[sys_agent1, sys_agent2], model_name=['sys_agent1', 'sys_agent2'], total_dialog=100)
```
| true |
code
| 0.388705 | null | null | null | null |
|
# Jetsoncar Rosey V2
Tensorflow 2.0, all in notebook, optimized with RT
```
import tensorflow as tf
print(tf.__version__)
tf.config.experimental.list_physical_devices('GPU') # If device does not show and using conda env with tensorflow-gpu then try restarting computer
# verify the image data directory
import os
data_directory = "/media/michael/BigMemory/datasets/jetsoncar/training_data/data/dataset"
os.listdir(data_directory)[:10]
import matplotlib.pyplot as plt
img = plt.imread(os.path.join(data_directory + "/color_images", os.listdir(data_directory + "/color_images")[0]))
print(img.shape)
plt.imshow(img)
```
## Create the datagenerator and augmentation framework
```
# Include the custom utils.py and perform tests
import importlib
utils = importlib.import_module('utils')
import numpy as np
print(utils.INPUT_SHAPE)
img = utils.load_image(os.path.join(data_directory, 'color_images'),os.listdir(data_directory + "/color_images")[0])
print(img.shape)
fig = plt.figure(figsize=(20,20))
fig.add_subplot(1, 3, 1)
plt.imshow(img)
img, _ = utils.preprocess_data(last_color_image=img)
print(img.shape)
fig.add_subplot(1, 3, 2)
plt.imshow(np.squeeze(img))
plt.show()
# Load the steering angles and image paths from labels.csv
import csv, random
import seaborn as sns
# these will be 2D arrays where each row represents a dataset
x = [] # images
y = [] # steering
z = [] # speed
with open(os.path.join(data_directory, "tags.csv")) as csvfile:
reader = csv.DictReader(csvfile)
for row in reader:
# print(row['Time_stamp'] + ".jpg", row['Steering_angle'])
if not float(row['raw_speed']) == 0:
x.append(row['time_stamp'] + ".jpg",) # get image path
y.append(float(row['raw_steering']),) # get steering value
z.append(float(row['raw_speed']))
print("Number of data samples is " + str(len(y)))
data = list(zip(x,y))
random.shuffle(data)
x,y = zip(*data)
# plot of steering angle distribution without correction
sns.distplot(y)
# plot of speed distribution
sns.distplot(z)
# Split the training data
validation_split = 0.2
train_x = x[0:int(len(x)*(1.0-validation_split))]
train_y = y[0:int(len(y)*(1.0-validation_split))]
print("Training data shape: " + str(len(train_x)))
test_x = x[int(len(x)*(1.0-validation_split)):]
test_y = y[int(len(y)*(1.0-validation_split)):]
print("Validation data shape: " + str(len(test_x)) + "\n")
# Define and test batch generator
def batch_generator(data_dir, image_paths, steering_angles, batch_size, is_training):
"""
Generate training image give image paths and associated steering angles
"""
images = np.empty([batch_size, utils.IMAGE_HEIGHT, utils.IMAGE_WIDTH, utils.IMAGE_CHANNELS], dtype=np.float32)
steers = np.empty(batch_size)
while True:
i = 0
for index in np.random.permutation(len(image_paths)):
img = image_paths[index]
steering_angle = steering_angles[index]
# argumentation
if is_training and np.random.rand() < 0.8:
image, steering_angle = utils.augument(data_dir, os.path.join("color_images",img), steering_angle)
else:
image, _ = utils.preprocess_data(utils.load_image(data_dir, os.path.join("color_images",img)))
# add the image and steering angle to the batch
images[i] = image
steers[i] = steering_angle
i += 1
if i == batch_size:
break
yield images, steers
train_generator = batch_generator(data_directory, train_x, train_y, 32, True)
validation_generator = batch_generator(data_directory, test_x, test_y, 32, False)
train_image = next(train_generator) # returns tuple with steering and throttle
print(train_image[0].shape)
print(train_image[1][0])
plt.imshow(train_image[0][0])
```
## Define the model and start training
```
model = tf.keras.models.Sequential([
tf.keras.Input((utils.IMAGE_HEIGHT, utils.IMAGE_WIDTH, utils.IMAGE_CHANNELS)),
tf.keras.layers.Conv2D(32, (11,11), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(32, (7,7), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(64, (5,5), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(64, (3,3), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(32, (3,3), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,3)),
tf.keras.layers.Conv2D(16, (3,3), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,3)),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(1, activation='linear')
])
model.summary()
model.compile(loss='mean_squared_error', optimizer='adam')
import datetime
log_dir="logs/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir)
print("To view tensorboard please run `tensorboard --logdir logs/fit` in the code directory from the terminal with deeplearning env active")
checkpoint = tf.keras.callbacks.ModelCheckpoint('rosey_v2.{epoch:03d}-{val_loss:.2f}.h5', # filepath = working directory/
monitor='val_loss',
verbose=0,
save_best_only=True,
mode='auto')
model.fit_generator(train_generator,
steps_per_epoch=100,
epochs=20,
validation_data=validation_generator,
validation_steps=1,
callbacks=[tensorboard_callback, checkpoint])
# Test the model
image, steering = next(train_generator)
print(steering)
print(model.predict(image))
print("")
image, steering = next(validation_generator)
print(steering)
print(model.predict(image))
```
## Save the model as tensor RT and export to Jetson format
```
# Load the model that you would like converted to RT
model_path = 'model.h5'
export_path = "/home/michael/Desktop/model"
import shutil
if not os.path.isdir(export_path):
os.mkdir(export_path)
else:
response = input("Do you want to delete existing export_path directory? y/n")
if response == 'y':
shutil.rmtree(export_path)
os.mkdir(export_path)
loaded_model = tf.keras.models.load_model(model_path)
shutil.copy("./utils.py", os.path.join(export_path, "utils.py"))
shutil.copy("./__init__.py", os.path.join(export_path, "__init__.py"))
shutil.copy("./notes.txt", os.path.join(export_path, "notes.txt"))
shutil.copy("./config.yaml", os.path.join(export_path, "config.yaml"))
# Save as tf saved_model (faster than h5)
tf.saved_model.save(loaded_model, export_path)
from tensorflow.python.compiler.tensorrt import trt_convert as trt
conversion_params = trt.DEFAULT_TRT_CONVERSION_PARAMS
conversion_params = conversion_params._replace(max_workspace_size_bytes=(1 << 32))
conversion_params = conversion_params._replace(precision_mode="INT8")
conversion_params = conversion_params._replace(maximum_cached_engines=100)
conversion_params = conversion_params._replace(use_calibration=True)
def my_calibration_input_fn():
for i in range(20):
image, _ = utils.preprocess_data(utils.load_image(data_directory, os.path.join("color_images",x[i])))
yield image.astype(np.float32),
converter = tf.experimental.tensorrt.Converter(input_saved_model_dir=export_path,conversion_params=conversion_params)
gen = my_calibration_input_fn()
converter.convert(calibration_input_fn=my_calibration_input_fn)
converter.build(my_calibration_input_fn)
if not os.path.isdir(os.path.join(export_path, "rt")):
os.mkdir(os.path.join(export_path, "rt"))
converter.save(os.path.join(export_path, "rt"))
# Test normal saved model
saved_model = tf.saved_model.load(export_path) # normal saved model
image, _ = next(validation_generator)
import time
output = saved_model(image.astype(np.float32)) # load once to get more accurate representation of speed
start = time.time()
output = saved_model(image.astype(np.float32))
stop = time.time()
print("inference time: " + str(stop - start))
print("Output: %.20f"%output[8,0])
# Test TRT optimized saved model
saved_model = tf.saved_model.load(os.path.join(export_path, "rt")) # normal saved model
image, _ = next(validation_generator)
import time
output = saved_model(image) # load once to get more accurate representation of speed
start = time.time()
output = saved_model(image)
stop = time.time()
print("inference time: " + str(stop - start))
print("Output: %.20f"%output[8,0])
# Run many samples through and save distribution
validation_generator = batch_generator(data_directory, test_x, test_y, 32, False)
test = []
for i in range(50):
img, _ = next(validation_generator)
test.append(saved_model(img.astype(np.float32))[0][0])
print(str(i), end="\r")
sns.distplot(test)
```
| true |
code
| 0.689933 | null | null | null | null |
|
# Transfer learning & fine-tuning
**Author:** [fchollet](https://twitter.com/fchollet)<br>
**Date created:** 2020/04/15<br>
**Last modified:** 2020/05/12<br>
**Description:** Complete guide to transfer learning & fine-tuning in Keras.
## Setup
```
import numpy as np
import tensorflow as tf
from tensorflow import keras
```
## Introduction
**Transfer learning** consists of taking features learned on one problem, and
leveraging them on a new, similar problem. For instance, features from a model that has
learned to identify racoons may be useful to kick-start a model meant to identify
tanukis.
Transfer learning is usually done for tasks where your dataset has too little data to
train a full-scale model from scratch.
The most common incarnation of transfer learning in the context of deep learning is the
following workflow:
1. Take layers from a previously trained model.
2. Freeze them, so as to avoid destroying any of the information they contain during
future training rounds.
3. Add some new, trainable layers on top of the frozen layers. They will learn to turn
the old features into predictions on a new dataset.
4. Train the new layers on your dataset.
A last, optional step, is **fine-tuning**, which consists of unfreezing the entire
model you obtained above (or part of it), and re-training it on the new data with a
very low learning rate. This can potentially achieve meaningful improvements, by
incrementally adapting the pretrained features to the new data.
First, we will go over the Keras `trainable` API in detail, which underlies most
transfer learning & fine-tuning workflows.
Then, we'll demonstrate the typical workflow by taking a model pretrained on the
ImageNet dataset, and retraining it on the Kaggle "cats vs dogs" classification
dataset.
This is adapted from
[Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python)
and the 2016 blog post
["building powerful image classification models using very little
data"](https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html).
## Freezing layers: understanding the `trainable` attribute
Layers & models have three weight attributes:
- `weights` is the list of all weights variables of the layer.
- `trainable_weights` is the list of those that are meant to be updated (via gradient
descent) to minimize the loss during training.
- `non_trainable_weights` is the list of those that aren't meant to be trained.
Typically they are updated by the model during the forward pass.
**Example: the `Dense` layer has 2 trainable weights (kernel & bias)**
```
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
```
In general, all weights are trainable weights. The only built-in layer that has
non-trainable weights is the `BatchNormalization` layer. It uses non-trainable weights
to keep track of the mean and variance of its inputs during training.
To learn how to use non-trainable weights in your own custom layers, see the
[guide to writing new layers from scratch](https://keras.io/guides/making_new_layers_and_models_via_subclassing/).
**Example: the `BatchNormalization` layer has 2 trainable weights and 2 non-trainable
weights**
```
layer = keras.layers.BatchNormalization()
layer.build((None, 4)) # Create the weights
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
```
Layers & models also feature a boolean attribute `trainable`. Its value can be changed.
Setting `layer.trainable` to `False` moves all the layer's weights from trainable to
non-trainable. This is called "freezing" the layer: the state of a frozen layer won't
be updated during training (either when training with `fit()` or when training with
any custom loop that relies on `trainable_weights` to apply gradient updates).
**Example: setting `trainable` to `False`**
```
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
layer.trainable = False # Freeze the layer
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
```
When a trainable weight becomes non-trainable, its value is no longer updated during
training.
```
# Make a model with 2 layers
layer1 = keras.layers.Dense(3, activation="relu")
layer2 = keras.layers.Dense(3, activation="sigmoid")
model = keras.Sequential([keras.Input(shape=(3,)), layer1, layer2])
# Freeze the first layer
layer1.trainable = False
# Keep a copy of the weights of layer1 for later reference
initial_layer1_weights_values = layer1.get_weights()
# Train the model
model.compile(optimizer="adam", loss="mse")
model.fit(np.random.random((2, 3)), np.random.random((2, 3)))
# Check that the weights of layer1 have not changed during training
final_layer1_weights_values = layer1.get_weights()
np.testing.assert_allclose(
initial_layer1_weights_values[0], final_layer1_weights_values[0]
)
np.testing.assert_allclose(
initial_layer1_weights_values[1], final_layer1_weights_values[1]
)
```
Do not confuse the `layer.trainable` attribute with the argument `training` in
`layer.__call__()` (which controls whether the layer should run its forward pass in
inference mode or training mode). For more information, see the
[Keras FAQ](
https://keras.io/getting_started/faq/#whats-the-difference-between-the-training-argument-in-call-and-the-trainable-attribute).
## Recursive setting of the `trainable` attribute
If you set `trainable = False` on a model or on any layer that has sublayers,
all children layers become non-trainable as well.
**Example:**
```
inner_model = keras.Sequential(
[
keras.Input(shape=(3,)),
keras.layers.Dense(3, activation="relu"),
keras.layers.Dense(3, activation="relu"),
]
)
model = keras.Sequential(
[keras.Input(shape=(3,)), inner_model, keras.layers.Dense(3, activation="sigmoid"),]
)
model.trainable = False # Freeze the outer model
assert inner_model.trainable == False # All layers in `model` are now frozen
assert inner_model.layers[0].trainable == False # `trainable` is propagated recursively
```
## The typical transfer-learning workflow
This leads us to how a typical transfer learning workflow can be implemented in Keras:
1. Instantiate a base model and load pre-trained weights into it.
2. Freeze all layers in the base model by setting `trainable = False`.
3. Create a new model on top of the output of one (or several) layers from the base
model.
4. Train your new model on your new dataset.
Note that an alternative, more lightweight workflow could also be:
1. Instantiate a base model and load pre-trained weights into it.
2. Run your new dataset through it and record the output of one (or several) layers
from the base model. This is called **feature extraction**.
3. Use that output as input data for a new, smaller model.
A key advantage of that second workflow is that you only run the base model once on
your data, rather than once per epoch of training. So it's a lot faster & cheaper.
An issue with that second workflow, though, is that it doesn't allow you to dynamically
modify the input data of your new model during training, which is required when doing
data augmentation, for instance. Transfer learning is typically used for tasks when
your new dataset has too little data to train a full-scale model from scratch, and in
such scenarios data augmentation is very important. So in what follows, we will focus
on the first workflow.
Here's what the first workflow looks like in Keras:
First, instantiate a base model with pre-trained weights.
```python
base_model = keras.applications.Xception(
weights='imagenet', # Load weights pre-trained on ImageNet.
input_shape=(150, 150, 3),
include_top=False) # Do not include the ImageNet classifier at the top.
```
Then, freeze the base model.
```python
base_model.trainable = False
```
Create a new model on top.
```python
inputs = keras.Input(shape=(150, 150, 3))
# We make sure that the base_model is running in inference mode here,
# by passing `training=False`. This is important for fine-tuning, as you will
# learn in a few paragraphs.
x = base_model(inputs, training=False)
# Convert features of shape `base_model.output_shape[1:]` to vectors
x = keras.layers.GlobalAveragePooling2D()(x)
# A Dense classifier with a single unit (binary classification)
outputs = keras.layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
```
Train the model on new data.
```python
model.compile(optimizer=keras.optimizers.Adam(),
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()])
model.fit(new_dataset, epochs=20, callbacks=..., validation_data=...)
```
## Fine-tuning
Once your model has converged on the new data, you can try to unfreeze all or part of
the base model and retrain the whole model end-to-end with a very low learning rate.
This is an optional last step that can potentially give you incremental improvements.
It could also potentially lead to quick overfitting -- keep that in mind.
It is critical to only do this step *after* the model with frozen layers has been
trained to convergence. If you mix randomly-initialized trainable layers with
trainable layers that hold pre-trained features, the randomly-initialized layers will
cause very large gradient updates during training, which will destroy your pre-trained
features.
It's also critical to use a very low learning rate at this stage, because
you are training a much larger model than in the first round of training, on a dataset
that is typically very small.
As a result, you are at risk of overfitting very quickly if you apply large weight
updates. Here, you only want to readapt the pretrained weights in an incremental way.
This is how to implement fine-tuning of the whole base model:
```python
# Unfreeze the base model
base_model.trainable = True
# It's important to recompile your model after you make any changes
# to the `trainable` attribute of any inner layer, so that your changes
# are take into account
model.compile(optimizer=keras.optimizers.Adam(1e-5), # Very low learning rate
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()])
# Train end-to-end. Be careful to stop before you overfit!
model.fit(new_dataset, epochs=10, callbacks=..., validation_data=...)
```
**Important note about `compile()` and `trainable`**
Calling `compile()` on a model is meant to "freeze" the behavior of that model. This
implies that the `trainable`
attribute values at the time the model is compiled should be preserved throughout the
lifetime of that model,
until `compile` is called again. Hence, if you change any `trainable` value, make sure
to call `compile()` again on your
model for your changes to be taken into account.
**Important notes about `BatchNormalization` layer**
Many image models contain `BatchNormalization` layers. That layer is a special case on
every imaginable count. Here are a few things to keep in mind.
- `BatchNormalization` contains 2 non-trainable weights that get updated during
training. These are the variables tracking the mean and variance of the inputs.
- When you set `bn_layer.trainable = False`, the `BatchNormalization` layer will
run in inference mode, and will not update its mean & variance statistics. This is not
the case for other layers in general, as
[weight trainability & inference/training modes are two orthogonal concepts](
https://keras.io/getting_started/faq/#whats-the-difference-between-the-training-argument-in-call-and-the-trainable-attribute).
But the two are tied in the case of the `BatchNormalization` layer.
- When you unfreeze a model that contains `BatchNormalization` layers in order to do
fine-tuning, you should keep the `BatchNormalization` layers in inference mode by
passing `training=False` when calling the base model.
Otherwise the updates applied to the non-trainable weights will suddenly destroy
what the model has learned.
You'll see this pattern in action in the end-to-end example at the end of this guide.
## Transfer learning & fine-tuning with a custom training loop
If instead of `fit()`, you are using your own low-level training loop, the workflow
stays essentially the same. You should be careful to only take into account the list
`model.trainable_weights` when applying gradient updates:
```python
# Create base model
base_model = keras.applications.Xception(
weights='imagenet',
input_shape=(150, 150, 3),
include_top=False)
# Freeze base model
base_model.trainable = False
# Create new model on top.
inputs = keras.Input(shape=(150, 150, 3))
x = base_model(inputs, training=False)
x = keras.layers.GlobalAveragePooling2D()(x)
outputs = keras.layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
loss_fn = keras.losses.BinaryCrossentropy(from_logits=True)
optimizer = keras.optimizers.Adam()
# Iterate over the batches of a dataset.
for inputs, targets in new_dataset:
# Open a GradientTape.
with tf.GradientTape() as tape:
# Forward pass.
predictions = model(inputs)
# Compute the loss value for this batch.
loss_value = loss_fn(targets, predictions)
# Get gradients of loss wrt the *trainable* weights.
gradients = tape.gradient(loss_value, model.trainable_weights)
# Update the weights of the model.
optimizer.apply_gradients(zip(gradients, model.trainable_weights))
```
Likewise for fine-tuning.
## An end-to-end example: fine-tuning an image classification model on a cats vs. dogs dataset
To solidify these concepts, let's walk you through a concrete end-to-end transfer
learning & fine-tuning example. We will load the Xception model, pre-trained on
ImageNet, and use it on the Kaggle "cats vs. dogs" classification dataset.
### Getting the data
First, let's fetch the cats vs. dogs dataset using TFDS. If you have your own dataset,
you'll probably want to use the utility
`tf.keras.preprocessing.image_dataset_from_directory` to generate similar labeled
dataset objects from a set of images on disk filed into class-specific folders.
Transfer learning is most useful when working with very small datasets. To keep our
dataset small, we will use 40% of the original training data (25,000 images) for
training, 10% for validation, and 10% for testing.
```
import tensorflow_datasets as tfds
tfds.disable_progress_bar()
train_ds, validation_ds, test_ds = tfds.load(
"cats_vs_dogs",
# Reserve 10% for validation and 10% for test
split=["train[:40%]", "train[40%:50%]", "train[50%:60%]"],
as_supervised=True, # Include labels
)
print("Number of training samples: %d" % tf.data.experimental.cardinality(train_ds))
print(
"Number of validation samples: %d" % tf.data.experimental.cardinality(validation_ds)
)
print("Number of test samples: %d" % tf.data.experimental.cardinality(test_ds))
```
These are the first 9 images in the training dataset -- as you can see, they're all
different sizes.
```
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 10))
for i, (image, label) in enumerate(train_ds.take(9)):
ax = plt.subplot(3, 3, i + 1)
plt.imshow(image)
plt.title(int(label))
plt.axis("off")
```
We can also see that label 1 is "dog" and label 0 is "cat".
### Standardizing the data
Our raw images have a variety of sizes. In addition, each pixel consists of 3 integer
values between 0 and 255 (RGB level values). This isn't a great fit for feeding a
neural network. We need to do 2 things:
- Standardize to a fixed image size. We pick 150x150.
- Normalize pixel values between -1 and 1. We'll do this using a `Normalization` layer as
part of the model itself.
In general, it's a good practice to develop models that take raw data as input, as
opposed to models that take already-preprocessed data. The reason being that, if your
model expects preprocessed data, any time you export your model to use it elsewhere
(in a web browser, in a mobile app), you'll need to reimplement the exact same
preprocessing pipeline. This gets very tricky very quickly. So we should do the least
possible amount of preprocessing before hitting the model.
Here, we'll do image resizing in the data pipeline (because a deep neural network can
only process contiguous batches of data), and we'll do the input value scaling as part
of the model, when we create it.
Let's resize images to 150x150:
```
size = (150, 150)
train_ds = train_ds.map(lambda x, y: (tf.image.resize(x, size), y))
validation_ds = validation_ds.map(lambda x, y: (tf.image.resize(x, size), y))
test_ds = test_ds.map(lambda x, y: (tf.image.resize(x, size), y))
```
Besides, let's batch the data and use caching & prefetching to optimize loading speed.
```
batch_size = 32
train_ds = train_ds.cache().batch(batch_size).prefetch(buffer_size=10)
validation_ds = validation_ds.cache().batch(batch_size).prefetch(buffer_size=10)
test_ds = test_ds.cache().batch(batch_size).prefetch(buffer_size=10)
```
### Using random data augmentation
When you don't have a large image dataset, it's a good practice to artificially
introduce sample diversity by applying random yet realistic transformations to
the training images, such as random horizontal flipping or small random rotations. This
helps expose the model to different aspects of the training data while slowing down
overfitting.
```
from tensorflow import keras
from tensorflow.keras import layers
data_augmentation = keras.Sequential(
[layers.RandomFlip("horizontal"), layers.RandomRotation(0.1),]
)
```
Let's visualize what the first image of the first batch looks like after various random
transformations:
```
import numpy as np
for images, labels in train_ds.take(1):
plt.figure(figsize=(10, 10))
first_image = images[0]
for i in range(9):
ax = plt.subplot(3, 3, i + 1)
augmented_image = data_augmentation(
tf.expand_dims(first_image, 0), training=True
)
plt.imshow(augmented_image[0].numpy().astype("int32"))
plt.title(int(labels[0]))
plt.axis("off")
```
## Build a model
Now let's built a model that follows the blueprint we've explained earlier.
Note that:
- We add a `Rescaling` layer to scale input values (initially in the `[0, 255]`
range) to the `[-1, 1]` range.
- We add a `Dropout` layer before the classification layer, for regularization.
- We make sure to pass `training=False` when calling the base model, so that
it runs in inference mode, so that batchnorm statistics don't get updated
even after we unfreeze the base model for fine-tuning.
```
base_model = keras.applications.Xception(
weights="imagenet", # Load weights pre-trained on ImageNet.
input_shape=(150, 150, 3),
include_top=False,
) # Do not include the ImageNet classifier at the top.
# Freeze the base_model
base_model.trainable = False
# Create new model on top
inputs = keras.Input(shape=(150, 150, 3))
x = data_augmentation(inputs) # Apply random data augmentation
# Pre-trained Xception weights requires that input be scaled
# from (0, 255) to a range of (-1., +1.), the rescaling layer
# outputs: `(inputs * scale) + offset`
scale_layer = keras.layers.Rescaling(scale=1 / 127.5, offset=-1)
x = scale_layer(x)
# The base model contains batchnorm layers. We want to keep them in inference mode
# when we unfreeze the base model for fine-tuning, so we make sure that the
# base_model is running in inference mode here.
x = base_model(x, training=False)
x = keras.layers.GlobalAveragePooling2D()(x)
x = keras.layers.Dropout(0.2)(x) # Regularize with dropout
outputs = keras.layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
model.summary()
```
## Train the top layer
```
model.compile(
optimizer=keras.optimizers.Adam(),
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()],
)
epochs = 20
model.fit(train_ds, epochs=epochs, validation_data=validation_ds)
```
## Do a round of fine-tuning of the entire model
Finally, let's unfreeze the base model and train the entire model end-to-end with a low
learning rate.
Importantly, although the base model becomes trainable, it is still running in
inference mode since we passed `training=False` when calling it when we built the
model. This means that the batch normalization layers inside won't update their batch
statistics. If they did, they would wreck havoc on the representations learned by the
model so far.
```
# Unfreeze the base_model. Note that it keeps running in inference mode
# since we passed `training=False` when calling it. This means that
# the batchnorm layers will not update their batch statistics.
# This prevents the batchnorm layers from undoing all the training
# we've done so far.
base_model.trainable = True
model.summary()
model.compile(
optimizer=keras.optimizers.Adam(1e-5), # Low learning rate
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()],
)
epochs = 10
model.fit(train_ds, epochs=epochs, validation_data=validation_ds)
```
After 10 epochs, fine-tuning gains us a nice improvement here.
| true |
code
| 0.796925 | null | null | null | null |
|
# Direct optimal control of a pendulum
We want to control an inverted pendulum and stabilize it in the upright position. The equations in Hamiltonian form describing an inverted pendulum with a torsional spring are as following:
$$\begin{equation}
\begin{bmatrix} \dot{q}\\ \dot{p}\\ \end{bmatrix} =
\begin{bmatrix}
0& 1/m \\
-k& -\beta/m\\
\end{bmatrix}
\begin{bmatrix} q\\ p\\ \end{bmatrix} -
\begin{bmatrix}
0\\
mgl \sin{q}\\
\end{bmatrix}+
\begin{bmatrix}
0\\
1\\
\end{bmatrix} u
\end{equation}$$
```
import sys; sys.path.append(2*'../') # go n dirs back
import matplotlib.pyplot as plt
import torch
from torchdyn.numerics.odeint import odeint
from torchcontrol.systems.classic_control import Pendulum
from torchcontrol.cost import IntegralCost
from torchcontrol.controllers import *
%load_ext autoreload
%autoreload 2
# Change device according to your configuration
device = torch.device('cuda:0') if torch.cuda.is_available() else torch.device('cpu') # feel free to change :)
device = torch.device('cpu') # override
```
## Optimal control problem
In order to control the pendulum, we have to define a proper _integral cost function_ which will be our loss to be minimized during training. In a general form, it can be defined as:
$$\begin{equation}
\min_{u_\theta} J = (x(t_f) - x^\star)^\top\mathbf{P} (x(t_f) - x^\star)) + \int_{t_0}^{t_f} \left[ (x(t) - x^\star)^\top \mathbf{Q} (x(t) - x^\star) + (u_\theta(t) - u^\star)^\top \mathbf{R} (u_\theta(t) - u^\star) \right] dt
\end{equation}$$
where $ x $ is the state and $u_\theta$ is the controller; $x^\star$ and $u^\star$ are the desired position and zero-cost controller; matrices $\mathbf{P},~\mathbf{Q}, ~ \mathbf{R}$ are weights for tweaking the performance.
```
# Declaring the cost function
x_star = torch.Tensor([0, 0]).to(device)
u_star = 0.
cost = IntegralCost(x_star=x_star, u_star=u_star, P=0, Q=1, R=0)
```
## Initial conditions
Now we can see how the system behaves with no control input in time. Let's declare some initial variables:
```
from math import pi as π
# Time span
dt = 0.05 # step size
t0, tf = 0, 3 # initial and final time
steps = int((tf - t0)/dt) + 1
t_span = torch.linspace(t0, tf, steps).to(device)
# Initial distribution
x_0 = π # limit of the state distribution (in rads and rads/second)
init_dist = torch.distributions.Uniform(torch.Tensor([-x_0, -x_0]), torch.Tensor([x_0, x_0]))
```
## Box-constrained controller
We want to give a limited control input. We consider the box-constrained neural controller (parameters $\theta$ of $u_\theta$ belong to a feed-forward neural network):
```
?? BoxConstrainedController
# Controller
output_scaling = torch.Tensor([-5, 5]).to(device) # controller limits
u = BoxConstrainedController(2, 1, constrained=True, output_scaling=output_scaling).to(device)
# Initialize pendulum with given controller
pendulum = Pendulum(u, solver='euler')
```
## Optimization loop
Here we run the optimization: in particular, we use stochastic gradient descent with `Adam` to optimize the parameters
```
from tqdm import trange
# Hyperparameters
lr = 1e-3
epochs = 300
bs = 1024
opt = torch.optim.Adam(u.parameters(), lr=lr)
# Training loop
losses=[]
with trange(0, epochs, desc="Epochs") as eps:
for epoch in eps:
x0 = init_dist.sample((bs,)).to(device)
trajectory = pendulum(x0, t_span)
loss = cost(trajectory); losses.append(loss.detach().cpu().item())
loss.backward(); opt.step(); opt.zero_grad()
eps.set_postfix(loss=(loss.detach().cpu().item()))
fig, ax = plt.subplots(1, 1, figsize=(8,4))
ax.plot(losses)
ax.set_title('Losses')
ax.set_xlabel('Epochs')
ax.set_yscale('log')
```
## Plot results
```
# Change the solver to 'dopri5' (adaptive step size, more accurate than Euler)
pendulum.solver = 'dopri5'
# Forward propagate some trajectories
x0 = init_dist.sample((100,)).to(device)*0.8
# Prolong time span
dt = 0.05 # step size
t0, tf = 0, 5 # initial and final time
steps = int((tf - t0)/dt) + 1
t_span = torch.linspace(t0, tf, steps).to(device)
traj = pendulum(x0, t_span)
def plot_pendulum_trajs():
fig, axs = plt.subplots(1, 2, figsize=(12,4))
for i in range(len(x0)):
axs[0].plot(t_span.cpu(), traj[:,i,0].detach().cpu(), 'tab:red', alpha=.3)
axs[1].plot(t_span.cpu(), traj[:,i,1].detach().cpu(), 'tab:blue', alpha=.3)
axs[0].set_xlabel(r'Time [s]'); axs[1].set_xlabel(r'Time [s]')
axs[0].set_ylabel(r'p'); axs[1].set_ylabel(r'q')
axs[0].set_title(r'Positions'); axs[1].set_title(r'Momenta')
plot_pendulum_trajs()
# Plot learned vector field and trajectories in phase space
n_grid = 50
graph_lim = π
def plot_phase_space():
fig, ax = plt.subplots(1, 1, figsize=(6,6))
x = torch.linspace(-graph_lim, graph_lim, n_grid).to(device)
Q, P = torch.meshgrid(x, x) ; z = torch.cat([Q.reshape(-1, 1), P.reshape(-1, 1)], 1)
f = pendulum.dynamics(0, z).detach().cpu()
Fq, Fp = f[:,0].reshape(n_grid, n_grid), f[:,1].reshape(n_grid, n_grid)
val = pendulum.u(0, z).detach().cpu()
U = val.reshape(n_grid, n_grid)
ax.streamplot(Q.T.detach().cpu().numpy(), P.T.detach().cpu().numpy(),
Fq.T.detach().cpu().numpy(), Fp.T.detach().cpu().numpy(), color='black', density=0.6, linewidth=0.5)
ax.set_xlim([-graph_lim, graph_lim]) ; ax.set_ylim([-graph_lim, graph_lim])
traj = pendulum(x0, t_span).detach().cpu()
for j in range(traj.shape[1]):
ax.plot(traj[:,j,0], traj[:,j,1], color='tab:purple', alpha=.4)
ax.set_title('Phase Space')
ax.set_xlabel(r'p')
ax.set_ylabel(r'q')
plot_phase_space()
```
Nice! The controller manages to stabilize the pendulum in our desired $x^\star$ 🎉
| true |
code
| 0.651715 | null | null | null | null |
|
```
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from IPython.display import display
```
## Exercise 1
You've just been hired at a real estate investment firm and they would like you to build a model for pricing houses. You are given a dataset that contains data for house prices and a few features like number of bedrooms, size in square feet and age of the house. Let's see if you can build a model that is able to predict the price. In this exercise we extend what we have learned about linear regression to a dataset with more than one feature. Here are the steps to complete it:
1. Load the dataset ../data/housing-data.csv
- plot the histograms for each feature
- create 2 variables called X and y: X shall be a matrix with 3 columns (sqft,bdrms,age) and y shall be a vector with 1 column (price)
- create a linear regression model in Keras with the appropriate number of inputs and output
- split the data into train and test with a 20% test size
- train the model on the training set and check its accuracy on training and test set
- how's your model doing? Is the loss growing smaller?
- try to improve your model with these experiments:
- normalize the input features with one of the rescaling techniques mentioned above
- use a different value for the learning rate of your model
- use a different optimizer
- once you're satisfied with training, check the R2score on the test set
```
df = pd.read_csv('housing-data.csv')
display(df.info())
display(df.head())
display(df.describe().round(2))
# plot the histograms for each feature
plt.figure(figsize=(15, 5))
for i, feature in enumerate(df.columns):
plt.subplot(1, 4, i+1)
df[feature].plot(kind='hist', title=feature)
plt.xlabel(feature)
```
#### Feature Engineering
```
df['sqft1000'] = df['sqft']/1000.0
df['age10'] = df['age']/10.0
df['price100k'] = df['price']/1e5
display(df.describe().round(2))
```
#### Train/Test split
```
X = df[['sqft1000', 'bdrms', 'age10']].values
y = df['price100k'].values
display(X.shape)
display(y.shape)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2)
```
#### model
```
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam, SGD
model = Sequential()
model.add(Dense(1, input_shape=(3,)))
model.compile(Adam(lr=0.1), 'mean_squared_error')
model.summary()
# Train
history = model.fit(
X_train, y_train,
epochs=40, verbose=0)
historydf = pd.DataFrame(history.history, index=history.epoch)
historydf.plot();
```
#### Evaluate
```
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
from sklearn.metrics import mean_squared_error as mse
print("The Mean Squared Error on the Train set is:\t{:0.5f}".format(mse(y_train, y_train_pred)))
print("The Mean Squared Error on the Test set is:\t{:0.5f}".format(mse(y_test, y_test_pred)))
from sklearn.metrics import r2_score
print("The R2 score on the Train set is:\t{:0.3f}".format(r2_score(y_train, y_train_pred)))
print("The R2 score on the Test set is:\t{:0.3f}".format(r2_score(y_test, y_test_pred)))
```
## Exercise 2
Your boss was extremely happy with your work on the housing price prediction model and decided to entrust you with a more challenging task. They've seen a lot of people leave the company recently and they would like to understand why that's happening. They have collected historical data on employees and they would like you to build a model that is able to predict which employee will leave next. The would like a model that is better than random guessing. They also prefer false negatives than false positives, in this first phase. Fields in the dataset include:
- Employee satisfaction level
- Last evaluation
- Number of projects
- Average monthly hours
- Time spent at the company
- Whether they have had a work accident
- Whether they have had a promotion in the last 5 years
- Department
- Salary
- Whether the employee has left
Your goal is to predict the binary outcome variable `left` using the rest of the data. Since the outcome is binary, this is a classification problem. Here are some things you may want to try out:
1. load the dataset at ../data/HR_comma_sep.csv, inspect it with `.head()`, `.info()` and `.describe()`.
- Establish a benchmark: what would be your accuracy score if you predicted everyone stay?
- Check if any feature needs rescaling. You may plot a histogram of the feature to decide which rescaling method is more appropriate.
- convert the categorical features into binary dummy columns. You will then have to combine them with the numerical features using `pd.concat`.
- do the usual train/test split with a 20% test size
- play around with learning rate and optimizer
- check the confusion matrix, precision and recall
- check if you still get the same results if you use a 5-Fold cross validation on all the data
- Is the model good enough for your boss?
As you will see in this exercise, the a logistic regression model is not good enough to help your boss. In the next chapter we will learn how to go beyond linear models.
This dataset comes from https://www.kaggle.com/ludobenistant/hr-analytics/ and is released under [CC BY-SA 4.0 License](https://creativecommons.org/licenses/by-sa/4.0/).
```
df = pd.read_csv('HR_comma_sep.csv')
display(df.info())
display(df.head())
display(df.describe().round(2))
display(df['left'].value_counts())
```
#### Baseline model
Establish a benchmark: what would be your accuracy score if you predicted everyone stay?
```
df.left.value_counts() / len(df)
```
--> Predict all 0 accuracy = 76.19%
--> Accuracy must >> 76%
#### Feature Engineering
```
df['average_montly_hours_100'] = df['average_montly_hours']/100.0
cat_features = pd.get_dummies(df[['sales', 'salary']])
```
#### Train/Test split
```
display(df.columns)
display(cat_features.columns)
X = pd.concat([df[['satisfaction_level', 'last_evaluation', 'number_project',
'time_spend_company', 'Work_accident',
'promotion_last_5years', 'average_montly_hours_100']],
cat_features], axis=1).values
y = df['left'].values
display(X.shape)
display(y.shape)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2)
```
#### Model
```
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam, SGD
model = Sequential()
model.add(Dense(1, input_shape=(20,), activation='sigmoid'))
model.compile(Adam(lr=0.5), 'binary_crossentropy', metrics=['accuracy'])
model.summary()
# Train
history = model.fit(
X_train, y_train,
epochs=40, verbose=0)
historydf = pd.DataFrame(history.history, index=history.epoch)
historydf.plot();
```
#### Evaluate
```
y_test_pred = model.predict_classes(X_test)
# Confusion matrix
from sklearn.metrics import confusion_matrix
def pretty_confusion_matrix(y_true, y_pred, labels=["False", "True"]):
cm = confusion_matrix(y_true, y_pred)
pred_labels = ['Predicted '+ l for l in labels]
df = pd.DataFrame(cm, index=labels, columns=pred_labels)
return df
pretty_confusion_matrix(y_test, y_test_pred, labels=['Stay', 'Leave'])
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print("The test Accuracy score is {:0.3f}".format(accuracy_score(y_test, y_test_pred)))
print("The test Precision score is {:0.3f}".format(precision_score(y_test, y_test_pred)))
print("The test Recall score is {:0.3f}".format(recall_score(y_test, y_test_pred)))
print("The test F1 score is {:0.3f}".format(f1_score(y_test, y_test_pred)))
# Report
from sklearn.metrics import classification_report
print(classification_report(y_test, y_test_pred))
```
--> the model is not good enough since it performs no better than the benchmark.
#### Cross Validation Trainning
```
from keras.wrappers.scikit_learn import KerasClassifier
def build_logistic_regression_model():
model = Sequential()
model.add(Dense(1, input_dim=20, activation='sigmoid'))
model.compile(Adam(lr=0.5), 'binary_crossentropy', metrics=['accuracy'])
return model
model = KerasClassifier(
build_fn=build_logistic_regression_model,
epochs=25, verbose=0)
from sklearn.model_selection import KFold, cross_val_score
scores = cross_val_score(
model,
X, y,
cv=KFold(5, shuffle=True))
display(scores)
print("The cross validation accuracy is {:0.4f} ± {:0.4f}".format(scores.mean(), scores.std()))
```
--> the model is not good enough since it performs no better than the benchmark.
| true |
code
| 0.722392 | null | null | null | null |
|
# Knowledge Graph Triplet
Generate MS text -> EN Knowledge Graph Triplet.
<div class="alert alert-info">
This tutorial is available as an IPython notebook at [Malaya/example/knowledge-graph-triplet](https://github.com/huseinzol05/Malaya/tree/master/example/knowledge-graph-triplet).
</div>
<div class="alert alert-warning">
This module only trained on standard language structure, so it is not save to use it for local language structure.
</div>
```
%%time
import malaya
```
### List available Transformer model
```
malaya.knowledge_graph.available_transformer()
```
### Load Transformer model
```python
def transformer(model: str = 'base', quantized: bool = False, **kwargs):
"""
Load transformer to generate knowledge graphs in triplet format from texts,
MS text -> EN triplet format.
Parameters
----------
model : str, optional (default='base')
Model architecture supported. Allowed values:
* ``'base'`` - Transformer BASE parameters.
* ``'large'`` - Transformer LARGE parameters.
quantized : bool, optional (default=False)
if True, will load 8-bit quantized model.
Quantized model not necessary faster, totally depends on the machine.
Returns
-------
result: malaya.model.tf.KnowledgeGraph class
"""
```
```
model = malaya.knowledge_graph.transformer()
```
### Load Quantized model
To load 8-bit quantized model, simply pass `quantized = True`, default is `False`.
We can expect slightly accuracy drop from quantized model, and not necessary faster than normal 32-bit float model, totally depends on machine.
```
quantized_model = malaya.knowledge_graph.transformer(quantized = True)
string1 = "Yang Berhormat Dato Sri Haji Mohammad Najib bin Tun Haji Abdul Razak ialah ahli politik Malaysia dan merupakan bekas Perdana Menteri Malaysia ke-6 yang mana beliau menjawat jawatan dari 3 April 2009 hingga 9 Mei 2018. Beliau juga pernah berkhidmat sebagai bekas Menteri Kewangan dan merupakan Ahli Parlimen Pekan Pahang"
string2 = "Pahang ialah negeri yang ketiga terbesar di Malaysia Terletak di lembangan Sungai Pahang yang amat luas negeri Pahang bersempadan dengan Kelantan di utara Perak Selangor serta Negeri Sembilan di barat Johor di selatan dan Terengganu dan Laut China Selatan di timur."
```
These models heavily trained on neutral texts, if you give political or news texts, the results returned not really good.
#### Predict using greedy decoder
```python
def greedy_decoder(self, strings: List[str], get_networkx: bool = True):
"""
Generate triples knowledge graph using greedy decoder.
Example, "Joseph Enanga juga bermain untuk Union Douala." -> "Joseph Enanga member of sports team Union Douala"
Parameters
----------
strings : List[str]
get_networkx: bool, optional (default=True)
If True, will generate networkx.MultiDiGraph.
Returns
-------
result: List[Dict]
"""
```
```
r = model.greedy_decoder([string1, string2])
r[0]
import matplotlib.pyplot as plt
import networkx as nx
g = r[0]['G']
plt.figure(figsize=(6, 6))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
g = r[1]['G']
plt.figure(figsize=(6, 6))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
```
#### Predict using beam decoder
```python
def beam_decoder(self, strings: List[str], get_networkx: bool = True):
"""
Generate triples knowledge graph using beam decoder.
Example, "Joseph Enanga juga bermain untuk Union Douala." -> "Joseph Enanga member of sports team Union Douala"
Parameters
----------
strings : List[str]
get_networkx: bool, optional (default=True)
If True, will generate networkx.MultiDiGraph.
Returns
-------
result: List[Dict]
"""
```
```
r = model.beam_decoder([string1, string2])
g = r[0]['G']
plt.figure(figsize=(6, 6))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
# https://ms.wikipedia.org/wiki/Malaysia
string = """
Malaysia secara rasminya Persekutuan Malaysia ialah sebuah negara raja berperlembagaan persekutuan di Asia Tenggara yang terdiri daripada tiga belas negeri dan tiga wilayah persekutuan, yang menduduki bumi berkeluasan 330,803 kilometer persegi (127,720 bt2). Malaysia terbahagi kepada dua kawasan yang mengapit Laut China Selatan, iaitu Semenanjung Malaysia dan Borneo Malaysia (juga Malaysia Barat dan Timur). Malaysia berkongsi sempadan darat dengan Thailand, Indonesia, dan Brunei dan juga sempadan laut dengan Singapura dan Filipina. Ibu negara Malaysia ialah Kuala Lumpur, manakala Putrajaya merupakan pusat kerajaan persekutuan. Pada tahun 2009, Malaysia diduduki oleh 28 juta penduduk dan pada tahun 2017 dianggarkan telah mencecah lebih 30 juta orang yang menduduki di Malaysia.
Malaysia berakar-umbikan Kerajaan-kerajaan Melayu yang wujud di wilayahnya dan menjadi taklukan Empayar British sejak abad ke-18. Wilayah British pertama di sini dikenali sebagai Negeri-Negeri Selat. Semenanjung Malaysia yang ketika itu dikenali sebagai Tanah Melayu atau Malaya, mula-mula disatukan di bawah komanwel pada tahun 1946, sebelum menjadi Persekutuan Tanah Melayu pada tahun 1948. Pada tahun 1957 Semenanjung Malaysia mencapai Kemerdekaan dan bebas daripada penjajah dan sekali gus menjadi catatan sejarah terpenting bagi Malaysia. Pada tahun 1963, Tanah Melayu bersatu bersama dengan negara Sabah, Sarawak, dan Singapura bagi membentuk Malaysia. Pada tahun 1965, Singapura keluar dari persekutuan untuk menjadi negara kota yang bebas. Semenjak itu, Malaysia menikmati antara ekonomi yang terbaik di Asia, dengan purata pertumbuhan keluaran dalam negara kasarnya (KDNK) kira-kira 6.5% selama 50 tahun pertama kemerdekaannya.
Ekonomi negara yang selama ini dijana oleh sumber alamnya kini juga berkembang dalam sektor-sektor ukur tanah, sains, kejuruteraan, pendidikan, pelancongan, perkapalan, perdagangan dan perubatan.
Ketua negara Malaysia ialah Yang di-Pertuan Agong, iaitu raja elektif yang terpilih dan diundi dari kalangan sembilan raja negeri Melayu. Ketua kerajaannya pula ialah Perdana Menteri. Sistem kerajaan Malaysia banyak berdasarkan sistem parlimen Westminster, dan sistem perundangannya juga berasaskan undang-undang am Inggeris.
Malaysia terletak berdekatan dengan khatulistiwa dan beriklim tropika, serta mempunyai kepelbagaian flora dan fauna, sehingga diiktiraf menjadi salah satu daripada 17 negara megadiversiti. Di Malaysia terletaknya Tanjung Piai, titik paling selatan di seluruh tanah besar Eurasia. Malaysia ialah sebuah negara perintis Persatuan Negara-Negara Asia Tenggara dan Pertubuhan Persidangan Islam, dan juga anggota Kerjasama Ekonomi Asia-Pasifik, Negara-Negara Komanwel, dan Pergerakan Negara-Negara Berkecuali.
"""
def simple_cleaning(string):
return ''.join([s for s in string if s not in ',.\'";'])
string = malaya.text.function.split_into_sentences(string)
string = [simple_cleaning(s) for s in string if len(s) > 50]
string
r = model.greedy_decoder(string)
g = r[0]['G']
for i in range(1, len(r), 1):
g.update(r[i]['G'])
plt.figure(figsize=(17, 17))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
```
| true |
code
| 0.667229 | null | null | null | null |
|
# Access and mosaic Planet NICFI monthly basemaps
> A guide for accessing monthly Planet NICFI basemaps, selecting data by a defined AOI and mosaicing to produce a single image.
You will need a configuration file named `planet_api.cfg` (simple text file with `.cfg` extension will do) to run this notebook. It should be located in your `My Drive` folder.
The contents of the file should reflect the template below, swapping in the API access key that you should have receieved once you signed up for and subscribed to the Planet NICFI program. Please visit https://www.planet.com/nicfi/ to sign up if you have not already.
```
[credentials]
api_key = xxxxxxxxxxxxxxxxx
```
## Setup Notebook
```{admonition} **Version control**
Colab updates without warning to users, which can cause notebooks to break. Therefore, we are pinning library versions.
```
```
!pip install -q rasterio==1.2.10
!pip install -q geopandas==0.10.2
!pip install -q shapely==1.8.0
!pip install -q radiant_mlhub # for dataset access, see: https://mlhub.earth/
# import required libraries
import os, glob, functools, fnmatch, requests, io, shutil, tarfile, json
from pathlib import Path
from zipfile import ZipFile
from itertools import product
from configparser import ConfigParser
import urllib.request
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['axes.grid'] = False
mpl.rcParams['figure.figsize'] = (12,12)
import rasterio
from rasterio.merge import merge
from rasterio.plot import show
import geopandas as gpd
from folium import Map, GeoJson, Figure
from shapely.geometry import box
from IPython.display import clear_output
from radiant_mlhub import Dataset, client, get_session, Collection
# configure Radiant Earth MLHub access
!mlhub configure
# set your root directory and tiled data folders
if 'google.colab' in str(get_ipython()):
# mount google drive
from google.colab import drive
drive.mount('/content/gdrive')
root_dir = '/content/gdrive/My Drive/tf-eo-devseed/'
workshop_dir = '/content/gdrive/My Drive/tf-eo-devseed-workshop'
dirs = [root_dir, workshop_dir]
for d in dirs:
if not os.path.exists(d):
os.makedirs(d)
print('Running on Colab')
else:
root_dir = os.path.abspath("./data/tf-eo-devseed")
workshop_dir = os.path.abspath('./tf-eo-devseed-workshop')
print(f'Not running on Colab, data needs to be downloaded locally at {os.path.abspath(root_dir)}')
# Go to root folder
%cd $root_dir
```
```{admonition} **GCS note!**
We won't be using Google Cloud Storage to download data, but here is a code snippet to show how to practically do so with the a placeholder "aoi" vector file. This code works if you have access to the a project on GCP.
```
```python
#authenticate Google Cloud Storage
from google.colab import auth
auth.authenticate_user()
print("Authenticated Google Gloud access.")
# Imports the Google Cloud client library
from google.cloud import storage
# Instantiates a client
project = 'tf-eo-training-project'
storage_client = storage.Client(project=project)
# The name for the new bucket
bucket_name = "dev-seed-workshop"
data_dir = os.path.join(workshop_dir,'data/')
gcs_to_local_dir = os.path.join(data_dir,'gcs/')
prefix = 'data/'
local_dir = os.path.join(gcs_to_local_dir, prefix)
dirs = [data_dir, gcs_to_local_dir, local_dir]
for dir in dirs:
if not os.path.exists(dir):
os.makedirs(dir)
bucket_name = "dev-seed-workshop"
bucket = storage_client.get_bucket(bucket_name)
blobs = bucket.list_blobs(prefix=prefix) # Get list of files
for blob in blobs:
print(blob)
filename = blob.name.replace('/', '_')
filename_split = os.path.splitext(filename)
filename_zero, fileext = filename_split
basename = os.path.basename(filename_zero)
filename = 'aoi'
blob.download_to_filename(os.path.join(local_dir, "%s%s" % (basename, fileext))) # Download
print(blob, "%s%s" % (basename, fileext))
```
### Get search parameters
- Read the AOI from a [Radiant Earth MLHub dataset](https://mlhub.earth/data/ref_african_crops_kenya_01) that overlaps with NICFI coverage into a Geopandas dataframe.
- Get AOI bounds and centroid.
- Authenticate with Planet NICFI API key.
- Choose mosaic based on month/year of interest.
```
collections = [
'ref_african_crops_kenya_01_labels'
]
def download(collection_id):
print(f'Downloading {collection_id}...')
collection = Collection.fetch(collection_id)
path = collection.download('.')
tar = tarfile.open(path, "r:gz")
tar.extractall()
tar.close()
os.remove(path)
def resolve_path(base, path):
return Path(os.path.join(base, path)).resolve()
def load_df(collection_id):
collection = json.load(open(f'{collection_id}/collection.json', 'r'))
rows = []
item_links = []
for link in collection['links']:
if link['rel'] != 'item':
continue
item_links.append(link['href'])
for item_link in item_links:
item_path = f'{collection_id}/{item_link}'
current_path = os.path.dirname(item_path)
item = json.load(open(item_path, 'r'))
tile_id = item['id'].split('_')[-1]
for asset_key, asset in item['assets'].items():
rows.append([
tile_id,
None,
None,
asset_key,
str(resolve_path(current_path, asset['href']))
])
for link in item['links']:
if link['rel'] != 'source':
continue
link_path = resolve_path(current_path, link['href'])
source_path = os.path.dirname(link_path)
try:
source_item = json.load(open(link_path, 'r'))
except FileNotFoundError:
continue
datetime = source_item['properties']['datetime']
satellite_platform = source_item['collection'].split('_')[-1]
for asset_key, asset in source_item['assets'].items():
rows.append([
tile_id,
datetime,
satellite_platform,
asset_key,
str(resolve_path(source_path, asset['href']))
])
return pd.DataFrame(rows, columns=['tile_id', 'datetime', 'satellite_platform', 'asset', 'file_path'])
for c in collections:
download(c)
# Load the shapefile into a geopandas dataframe (for more info see: https://geopandas.org/en/stable/)
gdf = gpd.read_file(os.path.join(root_dir, 'ref_african_crops_kenya_01_labels/ref_african_crops_kenya_01_labels_00/labels.geojson'))
gdf = gdf.to_crs("EPSG:4326")
# Get AOI bounds
bbox_aoi = gdf.geometry.total_bounds
# Get AOI centroid for plotting with folium
centroid_aoi = [box(*bbox_aoi).centroid.x, box(*bbox_aoi).centroid.y]
# authenticate with Planet NICFI API KEY
config = ConfigParser()
configFilePath = '/content/gdrive/My Drive/planet_api.cfg'
with open(configFilePath) as f:
config.read_file(f)
API_KEY = config.get('credentials', 'api_key')
PLANET_API_KEY = API_KEY # <= insert API key here
#setup Planet base URL
API_URL = "https://api.planet.com/basemaps/v1/mosaics"
#setup session
session = requests.Session()
#authenticate
session.auth = (PLANET_API_KEY, "") #<= change to match variable for API Key if needed
```
```{important}
In the following cell, the **name__is** parameter is the basemap name. It is only differentiable by the time range in the name.
E.g. `planet_medres_normalized_analytic_2021-06_mosaic` is for June, 2021.
```
```
#set params for search using name of mosaic
parameters = {
"name__is" :"planet_medres_normalized_analytic_2021-06_mosaic" # <= customized to month/year of interest
}
#make get request to access mosaic from basemaps API
res = session.get(API_URL, params = parameters)
#response status code
print(res.status_code)
#print metadata for mosaic
mosaic = res.json()
#print("mosaic metadata (this will expose your API key so be careful about if/where you uncomment this line): ", json.dumps(mosaic, indent=2))
#get id
mosaic_id = mosaic['mosaics'][0]['id']
#get bbox for entire mosaic
mosaic_bbox = mosaic['mosaics'][0]['bbox']
print("mosaic_bbox: ", mosaic_bbox)
print("bbox_aoi: ", bbox_aoi)
#converting bbox to string for search params
string_bbox = ','.join(map(str, bbox_aoi))
print('Mosaic id: ', mosaic_id)
```
#### Plot the gridded AOI.
```
m = Map(tiles="Stamen Terrain",
control_scale=True,
location = [centroid_aoi[1], centroid_aoi[0]],
zoom_start = 10,
max_zoom = 20,
min_zoom =6,
width = '100%',
height = '100%',
zoom_control=False )
GeoJson(gdf).add_to(m)
Figure(width=500, height=300).add_child(m)
```
### Request the quad tiles fitting the search parameters
```
#search for mosaic quad using AOI
search_parameters = {
'bbox': string_bbox,
'minimal': True
}
#accessing quads using metadata from mosaic
quads_url = "{}/{}/quads".format(API_URL, mosaic_id)
res = session.get(quads_url, params=search_parameters, stream=True)
print(res.status_code)
quads = res.json()
quads = res.json()
items = quads['items']
#printing an example of quad metadata
#print("quad tiles metadata (this will expose your API key so be careful about if/where you uncomment this line): ", json.dumps(items[0], indent=2))
```
#### Plot the requested quad tiles.
```
for item, i in zip(items, range(len(items))):
quad_box = item["bbox"]
GeoJson(box(*quad_box)).add_to(m)
Figure(width=500, height=300).add_child(m)
# Set directory for downloading the quad tiles to
nicfi_dir = os.path.join(root_dir,'062021_basemap_nicfi_aoi/')
quads_dir = os.path.join(nicfi_dir,'quads/')
dirs = [nicfi_dir, quads_dir]
for dir in dirs:
if not os.path.exists(dir):
os.makedirs(dir)
#iterate over quad download links and saving to folder by id
for i in items:
link = i['_links']['download']
name = i['id']
name = name + '.tiff'
DIR = quads_dir
filename = os.path.join(DIR, name)
#print(filename)
#checks if file already exists before s
if not os.path.isfile(filename):
urllib.request.urlretrieve(link, filename)
```
### Mosaic the quad tiles
```
# File and folder paths
out_mosaic = os.path.join(nicfi_dir,'062021_basemap_nicfi_aoi_Mosaic.tif')
# Make a search criteria to select the quad tile files
search_criteria = "*.tiff"
q = os.path.join(nicfi_dir,'quads', search_criteria)
print(q)
# Get all of the quad tiles
quad_files = glob.glob(q)
quad_files
src_files_to_mosaic = []
for f in quad_files:
src = rasterio.open(f)
src_files_to_mosaic.append(src)
# Create the mosaic
mosaic, out_trans = merge(src_files_to_mosaic)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": mosaic.shape[1],
"width": mosaic.shape[2],
"transform": out_trans
}
)
# Write the mosaic to raster file
with rasterio.open(out_mosaic, "w", **out_meta) as dest:
dest.write(mosaic)
# Write true color (RGB).
rgb_out_mosaic = os.path.join(nicfi_dir,'062021_basemap_nicfi_aoi_rgb_Mosaic.tif')
out_meta.update({"count": 3})
print(out_meta)
rgb = np.dstack([mosaic[2], mosaic[1], mosaic[0]])
rgb = rgb.transpose(2,0,1)
with rasterio.open(rgb_out_mosaic, "w", **out_meta) as dest:
dest.write(rgb)
```
#### Plot the mosaic
```
src = rasterio.open(rgb_out_mosaic)
show(src)
```
| true |
code
| 0.517632 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Array/spectral_unmixing.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Array/spectral_unmixing.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Array/spectral_unmixing.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Array/spectral_unmixing.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# Array-based spectral unmixing.
# Create a mosaic of Landsat 5 images from June through September, 2007.
allBandMosaic = ee.ImageCollection('LANDSAT/LT05/C01/T1') \
.filterDate('2007-06-01', '2007-09-30') \
.select('B[0-7]') \
.median()
# Create some representative endmembers computed previously by sampling
# the Landsat 5 mosaic.
urbanEndmember = [88, 42, 48, 38, 86, 115, 59]
vegEndmember = [50, 21, 20, 35, 50, 110, 23]
waterEndmember = [51, 20, 14, 9, 7, 116, 4]
# Compute the 3x7 pseudo inverse.
endmembers = ee.Array([urbanEndmember, vegEndmember, waterEndmember])
inverse = ee.Image(endmembers.matrixPseudoInverse().transpose())
# Convert the bands to a 2D 7x1 array. The toArray() call concatenates
# pixels from each band along the default axis 0 into a 1D vector per
# pixel, and the toArray(1) call concatenates each band (in this case
# just the one band of 1D vectors) along axis 1, forming a 2D array.
inputValues = allBandMosaic.toArray().toArray(1)
# Matrix multiply the pseudo inverse of the endmembers by the pixels to
# get a 3x1 set of endmembers fractions from 0 to 1.
unmixed = inverse.matrixMultiply(inputValues)
# Create and show a colored image of the endmember fractions. Since we know
# the result has size 3x1, project down to 1D vectors at each pixel (since the
# second axis is pointless now), and then flatten back to a regular scalar
# image.
colored = unmixed \
.arrayProject([0]) \
.arrayFlatten([['urban', 'veg', 'water']])
Map.setCenter(-98.4, 19, 11)
# Load a hillshade to use as a backdrop.
Map.addLayer(ee.Algorithms.Terrain(ee.Image('CGIAR/SRTM90_V4')).select('hillshade'))
Map.addLayer(colored, {'min': 0, 'max': 1},
'Unmixed (red=urban, green=veg, blue=water)')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| true |
code
| 0.655722 | null | null | null | null |
|
<div align="right"><a href="https://github.com/lucasliano/Medidas1">Link Github</a></div>
<img src="logo.jpg" width="400"></img>
<div align="center">
<h1>Resúmen Teórico de Medidas Electrónicas 1</h1>
<h2>Incertidumbre</h2>
<h3>Liaño, Lucas</h3>
</div>
# Contenidos
- **Introducción**
- **Marco Teórico**
- Conceptos Básicos Metrología
- ¿Qué es la incertidumbre?
- Modelo matemático de una medición ($Y$)
- Evaluación incertidumbre Tipo A
- Evaluación incertidumbre Tipo B
- Incertidumbre Conjunta
- Grado de Confianza
- Caso de análisis: $u_{i}(x_{i}) \gg u_{j}(X_{i})$
- Caso de análisis: $u_{i}(x_{i}) \ll u_{j}(X_{i})$
- Correlación
- **Experimentación**
- Caso General
- Caso Incertidumbre tipo A dominante
- Caso Incertidumbre tipo B dominante
- Ejemplo Correlación
- **Bibliografía**
***
# Introducción
El objetivo del presente documento es de resumir, al mismo tiempo que simular, los contenidos teóricos correspondientes a la unidad N°1 de la materia medidas 1. Para ello, utilizaremos los recursos disponibles en el drive de la materia.
<div class="alert alert-success">
<strong>Link:</strong> <a href="https://drive.google.com/folderview?id=1p1eVB4UoS0C-5gyienup-XiewKsTpcNc">https://drive.google.com/folderview?id=1p1eVB4UoS0C-5gyienup-XiewKsTpcNc</a>
</div>
***
# Marco Teórico
## Conceptos Básicos Metrología
La de medición de una magnitud física, atributo de un cuerpo mensurable, consiste en el proceso mediante el cual se da a conocer el valor de dicha magnitud. A lo largo de la historia se han desarrollado diversos modelos de medición, todos ellos consisten en la comparación de la magnitud contra un patrón.
A su vez, a medida que se fueron confeccionando mejores métodos de medición, se empezó a tener en consideración el error en la medida. Este error consiste en una indicación cuantitativa de la calidad del resultado. Valor que demuestra la confiabilidad del proceso.
Actualmente, definimos al **resultado de una medición** como al conjunto de valores de una magnitud, atribuidos a un mensurando. Se puede definir a partir de una función distribución densidad de probabilidad (también denomidada _pdf_, de la sígla inglesa _probability density function_). El resultado de una medición está caracterizado por la media de la muestra, la incertidumbre y el grado de confianza de la medida.
Denominaremos **incertidumbre de una medición** al parámetro asociado con el resultado de la medición que caracteríza la dispersión de los valores atribuidos a un mensurando. Mientras que el **error de medida** será la diferencia entre el valor medido con un valor de referencia. [[1]](http://depa.fquim.unam.mx/amyd/archivero/CALCULODEINCERTIDUMBRESDR.JAVIERMIRANDA_26197.pdf)
#### Tipos de errores
Existen dos tipos:
> **Error sistemático:** Componente del error que en repetidas mediciones permanece constante.
> **Error aleatorio:** Componente del error que en repetidas mediciones varía de manera impredecible.
***
## ¿Qué es la incertidumbre?
Como bien definimos anteriormente, la incertidumbre es un parámetro que caracteríza la dispersión de los valores atribuidos a un mensurando. Esto significa que, considerando al resultado de la medición como una función distribución densidad de probabilidad, la incertidumbre representa el desvío estándar de la misma. Se suele denominar **incertidumbre estándar** a dicha expresión de la incertidumbre.
#### Componentes de la incertidumbre
> **Tipo A:** Componente de la incertidumbre descripta únicamente a partir del estudio estadístico de las muestras.
> **Tipo B:** Componente de la incertidumbre descripta a partir de las hojas de datos previstas por los fabricantes de los instrumentos de medición, junto con datos de calibración.
En las próximas secciones se describe en detalle como son los test efectuados para determinar cada una de las componentes. [[2]](https://es.wikipedia.org/wiki/Propagaci%C3%B3n_de_errores)
***
## Modelo matemático de una medición ($Y$)
Supongamos una magnitud a mensurar ($Y$), la cual se va a estimar de forma indirecta a partir de una relación fundamental con otras $N$ magnitudes mensurables, de manera que se cumple:
\begin{equation}
Y = f(x_{1},x_{2},...,x_{N})
\end{equation}
Como definimos previamente, las variables $x_{i}$ son funciones distribución densidad de probabilidad por ser resultados de mediciones. Cada una de estas mediciones viene determinada, idealmente, por el valor de su media ($\mu_{X_{i}}$), su desvío estándar ($\sigma_{x_{i}}$) y el grado de confianza de la medición. Dado que en la vida real no es posible conseguir una estimación lo suficientemente buena de estos parámetros, se utilizarán sus estimadores en su lugar.
Por tanto, si se tomaron $M$ muestras de cada una de estas variables, podemos utilizar la **media poblacional ($\bar{Y}$)** como estimador de la media ($\mu_{Y}$) de la distribución densidad de probabilidad de la medición como:
\begin{equation}
\hat{Y} = \bar{Y} = \frac{1}{M} \sum_{k=0}^{M} f_{k}(x_{1},x_{2},...,x_{N}) = f(\bar{X_{1}},\bar{X_{2}},...,\bar{X_{N}})
\end{equation}
<div class="alert alert-danger">
<strong>Verificar que esto este bien.</strong> Sospecho que no porque estamos suponiendo que podes aplicar linealidad adentro de la función. Estoy leyendo el ejemplo del calculo de resistencia y hacemos "resistencia= (media_V/media_I)" en la línea 39 del documento compartido en el canal general de Slack.
</div>
Asimismo, para determinar el otro parámetro fundamental de la medición (la incertidumbre) utilizaremos como estimador a la **incertidumbre combinada ($u_{c}$)** definida a partir de la siguiente ecuación,
\begin{equation}
u_{c}^{2}(Y) = \sum_{i=1}^{N} (\dfrac{\partial f}{\partial x_{i}})^{2} \cdot u_{c}^{2}(x_{i}) + 2 \sum_{i=1}^{N-1} \sum_{j = i+1}^{N} \dfrac{\partial f}{\partial x_{i}} \dfrac{\partial f}{\partial x_{j}} u(x_{i},x_{j})
\end{equation}
donde $u(x_{i},x_{j})$ es la expresión de la covariancia entre las pdf de las $x_{i}$.
Esta expresión, para permitir el uso de funciones $f_{k}$ no lineales, es la aproximación por serie de Taylor de primer orden de la expresión original para funciones que cumplen linealidad. [[2]](https://es.wikipedia.org/wiki/Propagaci%C3%B3n_de_errores)
A su vez, a partir de la **ley de propagación de incertidumbres**, podemos decir que para la determinación de una variable unitaria mediante medición directa es posible reducir la expresión anterior a la siguiente:
\begin{equation}
u_{c}^{2}(x_{i}) = u_{i}^{2}(x_{i}) + u_{j}^{2}(x_{i})
\end{equation}
donde denominaremos $u_{i}(x_{i})$ a la incertidumbre tipo A, y $u_{j}(x_{i})$ a la incertidumbre tipo B.
***
## Evaluación incertidumbre Tipo A
La incertidumbre tipo A, recordando que se trata de una medida de dispersión y al ser tipo A se relaciona con la estadística de las muestras, se puede estimar con el desvío estándar experimental de la media ($S(\bar{X_{i}})$). Para ello hace falta recordar algunos conceptos de estadística.
Suponiendo que se toman $N$ muestras:
> **Estimador media poblacional:**
>> $\hat{x_{i}}=\bar{X_{i}}=\dfrac{1}{N} \sum_{k=1}^{N}x_{i,k}$
> **Grados de libertad:**
>> $\nu = N-1$
> **Varianza experimental de las observaciones:**
>> $\hat{\sigma^{2}(X_{i})}=S^{2}(X_{i})=\dfrac{1}{\nu} \sum_{k=1}^{N}(X_{i,k} - \bar{X_{i}})^{2}$
> **Varianza experimental de la media:**
>> $\hat{\sigma^{2}(\bar{X_{i}})}=S^{2}(\bar{X_{i}})=\dfrac{S^{2}(x_{i})}{N}$
<div class="alert alert-success">
<strong>Por ende, la componente de la incertidumbre tipo A nos queda:</strong>
\begin{equation}
u_{i}(x_{i}) = \sqrt{S^{2}(\bar{X_{i}})}
\end{equation}
</div>
<div class="alert alert-info">
<strong>Nota:</strong> Para calcular el std con un divisor de $\nu = N-1$ es necesario modificar un argumento en la función de python. El comando correctamente utilizado es: 'myVars.std(ddof=1)'.
</div>
***
## Evaluación incertidumbre Tipo B
La incertidumbre tipo B viene determinada por la información que proveen los fabricantes de los instrumentos de medición, asi como también por los datos resultantes por la calibración de los mismos.
En estos instrumentos de medición la incertidumbre viene descripta en forma de distribuciones densidad de probabilidad, no en forma estadística. Para ello utilizamos los siguientes estadísticos que caracterízan a las variables aleatorias, en caso de que su dominio fuera continuo:
> **Esperanza:**
>> $E(x)=\int x.f(x)dx$
> **Varianza:**
>> $V(x)=\int x^{2}.f(x)dx$
<div class="alert alert-success">
<strong>Por tanto, si la incertidumbre es un parámetro de dispersión, la misma vendrá descripta por la expresión:</strong>
\begin{equation}
u_{j}(x_{i}) = \sqrt{V(x)}
\end{equation}
</div>
Por simplicidad a la hora de trabajar, a continuación se presenta una tabla con los valores típicos del desvío estándar para el caso de distintas distribuciones. Se demuestra el caso de distribución uniforme.

Suponiendo que la distribución esta centrada en $\bar{X_{i}}$, nos quedaría que $a = \bar{X_{i}} - \Delta X$ y $b = \bar{X_{i}} - \Delta X$.
Por tanto si la expresión de la varianza es $V(x_{i}) = \frac{(b-a)^{2}}{12}$, finalmente quedaría:
\begin{equation}
V(x_{i}) = \frac{(b-a)^{2}}{12} = \frac{(2 \Delta X)^{2}}{12} = \frac{4 \Delta X^{2}}{12} = \frac{\Delta X^{2}}{3}
\end{equation}
\begin{equation}
\sigma_{x_{i}} = \frac{\Delta X}{\sqrt{3}}
\end{equation}
Finalmente la tabla queda,
| Distribution | $u_{j}(x_{i}) = \sigma_{x_{i}}$|
| :----: | :----: |
| Uniforme | $\frac{\Delta X}{\sqrt{3}}$ |
| Normal | $\Delta X $ |
| Normal ($K=2$) | $\frac{\Delta X}{2} $ |
| Triangular | $\frac{\Delta X}{\sqrt{6}}$ |
| U | $\frac{\Delta X}{\sqrt{2}}$ |
<div class="alert alert-danger">
<strong>Verificar que esto este bien.</strong> Me genera dudas el término $\Delta X$. Esto no creo que deba ser así porque en el caso de la distribución normal $\sigma_{x_{i}} = \sigma$. No creo que deba aparecer ningun error absoluto ahí.
</div>
***
## Incertidumbre Conjunta
Como definimos anteriormente, la incertidumbre conjunta queda definida como:
\begin{equation}
u_{c}^{2}(x_{i}) = u_{i}^{2}(x_{i}) + u_{j}^{2}(x_{i})
\end{equation}
#### ¿Qué función distribución densidad de probabilidad tiene $u_{c}$?
Si se conocen $x_{1},x_{2},...,x_{N}$ y $Y$ es una combinación lineal de $x_{i}$ (o en su defecto una aproximación lineal, como en el caso del polinomio de taylor de primer grado de la función), podemos conocer la función distribución densidad de probabilidad a partir de la convolución de las $x_{i}$, al igual que se hace para SLIT. [[3]](https://es.wikipedia.org/wiki/Convoluci%C3%B3n)
Dado que habitualmente no se conoce con precisión la función distribución densidad de probabilidad de $u_{i}(x_{i})$, se suele utilizar el **teorema central del límite** para conocer $u_{c}(x_{i})$. El mismo plantea que cuantas más funciones $x_{i}$ con función distribución densidad de probabilidad deconocida sumemos, más va a tender su resultado a una distribución normal.
***
## Grado de Confianza
Finalmente, el último parámetro que nos interesa conocer para determinar el resultado de la medición es el grado de confianza.
> **Grado de confianza:** Es la probabilidad de que al evaluar nuevamente la media poblacional ($\bar{y}$) nos encontremos con un valor dentro del intervalo $[\bar{Y} - K.\sigma_{Y}(\bar{Y}) \le \mu_{Y} \le \bar{Y} - K.\sigma_{Y}(\bar{Y})]$ para el caso de una distribución que cumpla el teorema central del límite, donde $K$ es el factor de cobertura.
Otra forma de verlo es:

donde el grado de confianza viene representado por $(1-\alpha)$. Recomiendo ver el ejemplo [[4]](https://es.wikipedia.org/wiki/Intervalo_de_confianza#Ejemplo_pr%C3%A1ctico) en caso de no entender lo que representa.
De esta forma, el factor de cobertura ($K$) nos permite modificar el grado de confianza. Agrandar $K$ aumentará el área bajo la curva de la gaussiana, lo que representará un mayor grado de confianza.
Se definirá **incertidumbre expandida** a $U(x_{i}) = K \cdot u_{c}(x_{i})$ si $u_{c}(x_{i})$ es la incertidumbre que nos proveé un grado de confianza de aproximadamente $ 68\% $.
Para una función que distribuye como normal podemos estimar el grado de confianza mediante la siguiente tabla,
| Factor de cobertura | Grado de confianza|
| :----: | :----: |
| $K=1$ | $68.26\% $ |
| $K=2$ | $95.44\% $ |
| $K=3$ | $99.74\% $ |
#### ¿Qué sucede si $u_{c}$ no distribuye normalmente?
En este caso también se podrá utilizar la ecuación $U(x_{i}) = K \cdot u_{c}(x_{i})$, pero el método mediante el cual obtendremos a $K$ será distinto.
***
## Caso de análisis: $u_{i}(x_{i}) \gg u_{j}(X_{i})$
Cuando sucede que la incertidumbre que proveé la evaluación tipo A es muy significativa frente a la tipo B, esto querrá decir que no tenemos suficientes grados de libertad para que $u_{c}(x_{i})$ se aproxime a una gaussiana. En otras palabras, la muestra obtenida no es significativa.
En estos casos vamos a suponer que $u_{c}(x_{i})$ distribuye como t-Student. La distribución t-Student surge justamente del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño.
Como la distribución de t-Student tiene como parámetro los grados de libertad efectivos, debemos calcularlos. Para ello utilizaremos la fórmula de Welch-Satterthwaite:
\begin{equation}
\nu_{eff} = \dfrac{u_{c}^{4}(y)}{\sum_{i=1}^{N} \dfrac{ c_{i}^{4} u^{4}(x_{i})} {\nu_{i}} }
\end{equation}
donde $c_i = \dfrac{\partial f}{\partial x_{i}}$ y $u_{i}(x_{i})$ es la incertidumbre tipo A.

Para obtener el factor de cobertura que nos asegure un factor de cobertura del $95/%$ debemos recurrir a la tabla del t-Student. Para ello existe una función dentro del módulo _scipy.stats_ que nos integra la función hasta lograr un área del $95.4%$.
A continuación presentamos la función que utilizaremos con dicho fin,
~~~
def get_factor_Tstudent(V_eff, porcentaje_confianza_objetivo=95.4):
"""
Funcion de calculo de factor de expansión por T-student
input:
V_eff: Grados de libertad (float)
porcentaje_confianza_objetivo: porcentaje_confianza_objetivo (float)
returns:
Factor de expansión (float)
"""
return np.abs( -(stats.t.ppf((1.0+(porcentaje_confianza_objetivo/100))/2.0,V_eff)) )
~~~
***
## Caso de análisis: $u_{i}(x_{i}) \ll u_{j}(X_{i})~$
Para el caso en el que la incertidumbre del muestreo es muy inferior a la incertidumbre tipo B, nos encontramos frente al caso de incertidumbre B dominante. Esta situación es equivalente a tener la convolución entre una delta de dirac con una función de distribución cualquiera.

Como observamos en la imagen, la función distribución densidad de probabilidad resultate se asemeja más a la distribución uniforme del tipo B. En este caso para encontrar el factor de cobertura utilizaremos otra tabla distinta. En esta tabla el parámetro de entrada es el cociente $\dfrac{u_{i}}{u_{j}}$.
A continuación presentamos la función que utilizaremos con dicho fin,
~~~
def tabla_B(arg):
tabla_tipoB = np.array([
[0.0, 1.65],
[0.1, 1.66],
[0.15, 1.68],
[0.20, 1.70],
[0.25, 1.72],
[0.30, 1.75],
[0.35, 1.77],
[0.40, 1.79],
[0.45, 1.82],
[0.50, 1.84],
[0.55, 1.85],
[0.60, 1.87],
[0.65, 1.89],
[0.70, 1.90],
[0.75, 1.91],
[0.80, 1.92],
[0.85, 1.93],
[0.90, 1.94],
[0.95, 1.95],
[1.00, 1.95],
[1.10, 1.96],
[1.20, 1.97],
[1.40, 1.98],
[1.80, 1.99],
[1.90, 1.99]])
if arg >= 2.0:
K = 2.0
else:
pos_min = np.argmin(np.abs(tabla_tipoB[:,0]-arg))
K = tabla_tipoB[pos_min,1]
return K
~~~
***
## Correlación
Finalmente nos encontramos con el caso mas general. En esta situación las variables se encuentran correlacionadas, por lo que la expresión de $u_{c}(Y)$ debe utilizarse en su totalidad.
Por simplicidad de computo vamos a definir al coeficiente correlación como,
\begin{equation}
r(q,w) = \dfrac{ u(q,w) }{ u(q)u(w) }
\end{equation}
De esta forma podemos expresar a $u_{c}$ como:
\begin{equation}
u_{c}^{2}(Y) = \sum_{i=1}^{N} (\dfrac{\partial f}{\partial x_{i}})^{2} \cdot u_{c}^{2}(x_{i}) + 2 \sum_{i=1}^{N-1} \sum_{j = i+1}^{N} \dfrac{\partial f}{\partial x_{i}} \dfrac{\partial f}{\partial x_{j}} r(x_{i},x_{j})u(x_{i})u(x_{j})
\end{equation}
Esta expresión debe utilizarse cada vez que $r(x_{i},x_{j}) \ne 0$.
# Experimentación
**Comenzamos inicializando los módulos necesarios**
```
# módulos genericos
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from scipy import signal
# Módulos para Jupyter (mejores graficos!)
import warnings
warnings.filterwarnings('ignore')
plt.rcParams['figure.figsize'] = [12, 4]
plt.rcParams['figure.dpi'] = 150 # 200 e.g. is really fine, but slower
from pandas import DataFrame
from IPython.display import HTML
```
**Definimos las funciones previamente mencionadas**
```
# Tabla para el caso A dominante
def get_factor_Tstudent(V_eff, porcentaje_confianza_objetivo=95.4):
"""
Funcion de calculo de factor de expansión por T-student
input:
V_eff: Grados de libertad (float)
porcentaje_confianza_objetivo: porcentaje_confianza_objetivo (float)
returns: .libertad efectivosdenoted
Factor de expansión (float)
"""
return np.abs( -(stats.t.ppf((1.0+(porcentaje_confianza_objetivo/100))/2.0,V_eff)) )
# Tabla para el caso B dominante
def tabla_B(arg):
tabla_tipoB = np.array([
[0.0, 1.65],
[0.1, 1.66],
[0.15, 1.68],
[0.20, 1.70],
[0.25, 1.72],
[0.30, 1.75],
[0.35, 1.77],
[0.40, 1.79],
[0.45, 1.82],
[0.50, 1.84],
[0.55, 1.85],
[0.60, 1.87],
[0.65, 1.89],
[0.70, 1.90],
[0.75, 1.91],
[0.80, 1.92],
[0.85, 1.93],
[0.90, 1.94],
[0.95, 1.95],
[1.00, 1.95],
[1.10, 1.96],
[1.20, 1.97],
[1.40, 1.98],
[1.80, 1.99],
[1.90, 1.99]])
if arg >= 2.0:
K = 2.0
else:
pos_min = np.argmin(np.abs(tabla_tipoB[:,0]-arg))
K = tabla_tipoB[pos_min,1]
return K
```
## Caso general
**Definimos las constantes necesarias**
```
# Constantes del instrumento
CONST_ERROR_PORCENTUAL = 0.5 # Error porcentual del instrumento de medición
CONST_ERROR_CUENTA = 3 # Error en cuentas del instrumento de medición
CONST_DECIMALES = 2 # Cantidad de decimales que representa el instrumento
# Constantes del muestro
N = 10 # Cantidad de muestras tomadas
# Señal a muestrear idealizada
mu = 100 # Valor medio de la distribución normal de la población ideal
std = 2 # Desvío estándar de la distribución normal de la población ideal
# Muestreo mi señal ideal (Normal)
muestra = np.random.randn(N) * std + mu
```
**Ahora solamente genero un gráfico que compare el histograma con la distribución normal de fondo**
```
num_bins = 50
fig, ax = plt.subplots()
# the histogram of the 1.1data
n, bins, patches = ax.hist(muestra, num_bins, density=True)
# add a 'best fit' line
y = ((1 / (np.sqrt(2 * np.pi) * std)) *
np.exp(-0.5 * (1 / std * (bins - mu))**2))
ax.plot(bins, y, '--')
ax.set_xlabel('Smarts')
ax.set_ylabel('Probability density')
ax.set_title('Histogram of IQ: $\mu=$'+ str(mu) + ', $\sigma=$' + str(std))
# Tweak spacing to prevent clipping of ylabel
fig.tight_layout()
plt.show()
media = np.round(muestra.mean(), CONST_DECIMALES) # Redondeamos los decimales a los valores que puede ver el tester
desvio = muestra.std(ddof=1)
print("Mean:",media )
print("STD:" ,desvio)
```
**Calculamos el desvío estándar experimental de la media como:**
\begin{equation}
u_{i}(x_{i}) = \sqrt{S^{2}(\bar{X_{i}})}
\end{equation}
```
#Incertidumbre Tipo A
ui = desvio/np.sqrt(N)
ui
```
**Calculamos el error porcentual total del dispositivo de medición como:**
\begin{equation}
e_{\%T} = e_{\%} + \dfrac{e_{cuenta}\cdot 100\%}{\bar{X_{i}}(10^{cte_{Decimales}})}
\end{equation}
```
#Incertidumbre Tipo B
ERROR_PORCENTUAL_CUENTA = (CONST_ERROR_CUENTA*100)/(media * (10**CONST_DECIMALES ))
ERROR_PORCENTUAL_TOTAL = CONST_ERROR_PORCENTUAL + ERROR_PORCENTUAL_CUENTA
ERROR_PORCENTUAL_CUENTA
```
**Por tanto el error absoluto se representa como:**
\begin{equation}
\Delta X = e_{\%T} \dfrac{\bar{X_{i}}}{100\%}
\end{equation}
```
deltaX = ERROR_PORCENTUAL_TOTAL * media/100
deltaX
```
**Finalmente la incertidumbre tipo B queda:**
\begin{equation}
u_{j}(x_{i}) = \sqrt{Var(x_{i})} = \dfrac{\Delta X}{\sqrt{3}}
\end{equation}
donde recordamos que, al suponer una distribución uniforme en el dispositivo de medición, la varianza nos queda $Var(X_{uniforme}) = \dfrac {(b-a)^{2}}{12}$.
```
uj = deltaX / np.sqrt(3)
uj
```
**Calculamos la incertidumbre conjunta**
Como este es el caso de una medición directa de una sola variable, la expresión apropiada es:
\begin{equation}
u_{c}^{2}(x_{i}) = u_{i}^{2}(x_{i}) + u_{j}^{2}(x_{i})
\end{equation}
```
#incertidumbre combinada
uc = np.sqrt(ui**2 + uj**2)
uc
```
**Ahora debemos evaluar frente a que caso nos encontramos**
En primera instancia evaluamos que componente de la incertidumbre es mayoritaria y en que proporción.
Entonces tenemos tres situaciones posibles:
1. **Caso B dominante** $\Rightarrow \dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \lt 1 \Rightarrow$ Se utiliza la tabla de B dominante.
1. **Caso Normal** $\Rightarrow \dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \gt 1$ y $V_{eff} \gt 30 \Rightarrow$ Se toma $K=2$.
1. **Caso A dominante** $\Rightarrow \dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \gt 1$ y $V_{eff} \lt 30 \Rightarrow$ Se utiliza t-Student con los grados de libertad efectivos.
```
def evaluacion(uc,ui,uj,N):
cte_prop = ui/uj
print("Constante de proporcionalidad", cte_prop)
if cte_prop > 1:
# Calculo los grados de libertad efectivos
veff = int ((uc**4)/((ui**4)/(N-1)))
print("Grados efectivos: ", veff)
if veff > 30:
# Caso Normal
k = 2
else:
# Caso t-Student
k = get_factor_Tstudent(veff)
else:
# Caso B Dominante
k = tabla_B(cte_prop)
print("Constante de expansión: ",k)
return k
```
<div class="alert alert-warning">
<strong>Nota:</strong> La contribución de $u_{j}(x_{i})$ no se tiene en cuenta dado que, al ser una distribución continua, tiene infinitos grados de libertad.
\begin{equation}
\nu_{eff} = \dfrac{u_{c}^{4}(y)}{\sum_{i=1}^{N} \dfrac{ c_{i}^{4} u^{4}(x_{i})} {\nu_{i}} }
\end{equation}
</div>
```
k = evaluacion(uc,ui,uj,N)
```
**Análisis y presentación del resultado**
Como el cociente $\dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \gt 2$, entonces suponemos que nos encontramos frente al caso de distribución normal o distribución t-Student. Para ello utilizamos el criterio de los grados de libertad efectivos.
En este caso los grado de libertad efectivos $V_{eff} \gt 30$, por lo que suponemos distribución normal.
Finalmente presentamos el resultado con 1 dígito significativo.
```
U = uc*k
print("Resultado de la medición: (",np.round(media,1),"+-",np.round(U,1),")V con un grado de confianza del 95%")
```
# Bibliografía
_Nota: Las citas **no** respetan el formato APA._
1. [Evaluación de la Incertidumbre en Datos Experimentales, Javier Miranda Martín del Campo](http://depa.fquim.unam.mx/amyd/archivero/CALCULODEINCERTIDUMBRESDR.JAVIERMIRANDA_26197.pdf)
1. [Propagación de erroes, Wikipedia](https://es.wikipedia.org/wiki/Propagaci%C3%B3n_de_errores)
1. [Convolución, Wikipedia](https://es.wikipedia.org/wiki/Convoluci%C3%B3n)
1. [Intervalo de Confianza, Wikipedia](https://es.wikipedia.org/wiki/Intervalo_de_confianza#Ejemplo_pr%C3%A1ctico)
| true |
code
| 0.427337 | null | null | null | null |
|
### Introduction
This is a `View` Notebook to show an `IntSlider` widget either in an interactive Notebook or in a `Voila` Dashboard mode that will then print the [Fibonnaci sequence](https://en.wikipedia.org/wiki/Fibonacci_number) answer for that number. It will also show how long it takes each handler to calculate the number, which should demonstrate what kind of overhead is involved with `refactored code`, `PythonModel`, and `KernelModel`.
```
import ipywidgets as widgets
grid = widgets.GridspecLayout(4, 3)
# top row
input_label = widgets.Label("User Input")
user_input = widgets.IntText(value=1, description='Fibonnaci n:')
grid[0, 0] = input_label
grid[0, 1:] = user_input
# refactored code row
label1 = widgets.Label('Refactored code')
output1 = widgets.Text(disabled=True, description='Result:')
debug1 = widgets.Text(disabled=True, description='Debug:')
grid[1, 0] = label1
grid[1, 1] = output1
grid[1, 2] = debug1
# PythonModel row
label2 = widgets.Label('PythonModel')
output2 = widgets.Text(disabled=True, description='Result:')
debug2 = widgets.Text(disabled=True, description='Debug:')
grid[2, 0] = label2
grid[2, 1] = output2
grid[2, 2] = debug2
# KernelModel row
label3 = widgets.Label('KernelModel')
output3 = widgets.Text(disabled=True, description='Result:')
debug3 = widgets.Text(disabled=True, description='Debug:')
grid[3, 0] = label3
grid[3, 1] = output3
grid[3, 2] = debug3
grid
import time
### Refactored code handler
def fibonacci_generator():
"A generator that yields the last number in the sequence plus the number before that"
a, b = 0, 1
while True:
yield a
tmp_value = b
b = a + b
a = tmp_value
def handler1(ev):
start = time.time()
gen = fibonacci_generator()
n = user_input.value
for i in range(n+1):
answer = next(gen)
output1.value = str(answer)
debug1.value = 'took %.4f seconds' % (time.time() - start)
user_input.observe(handler1, names='value')
### Create PythonModel and KernelModel objects
import notebook_restified
pm = notebook_restified.PythonModel('model.ipynb')
km = notebook_restified.KernelModel('model.ipynb')
### PythonModel handler
def handler2(ev):
start = time.time()
params = {'n' : user_input.value}
result = pm.execute(params)
output2.value = str(result)
debug2.value = 'took %.4f seconds' % (time.time() - start)
user_input.observe(handler2, names='value')
### KernelModel handler
def handler3(ev):
start = time.time()
params = {'n' : user_input.value}
result = km.execute(params)
output3.value = str(result)
debug3.value = 'took %.4f seconds' % (time.time() - start)
user_input.observe(handler3, names='value')
```
| true |
code
| 0.278232 | null | null | null | null |
|
# Time-energy fit
3ML allows the possibility to model a time-varying source by explicitly fitting the time-dependent part of the model. Let's see this with an example.
First we import what we need:
```
from threeML import *
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
%matplotlib inline
jtplot.style(context="talk", fscale=1, ticks=True, grid=False)
plt.style.use("mike")
```
## Generating the datasets
Then we generate a simulated dataset for a source with a cutoff powerlaw spectrum with a constant photon index and cutoff but with a normalization that changes with time following a powerlaw:
```
def generate_one(K, ax):
# Let's generate some data with y = Powerlaw(x)
gen_function = Cutoff_powerlaw()
gen_function.K = K
# Generate a dataset using the power law, and a
# constant 30% error
x = np.logspace(0, 2, 50)
xyl_generator = XYLike.from_function(
"sim_data", function=gen_function, x=x, yerr=0.3 * gen_function(x)
)
y = xyl_generator.y
y_err = xyl_generator.yerr
ax.loglog(x, gen_function(x))
return x, y, y_err
```
These are the times at which the simulated spectra have been observed
```
time_tags = np.array([1.0, 2.0, 5.0, 10.0])
```
This describes the time-varying normalization. If everything works as it should, we should recover from the fit a normalization of 0.23 and a index of -1.2 for the time law.
```
normalizations = 0.23 * time_tags ** (-3.5)
```
Now that we have a simple function to create the datasets, let's build them.
```
fig, ax = plt.subplots()
datasets = [generate_one(k, ax) for k in normalizations]
ax.set_xlabel("Energy")
ax.set_ylabel("Flux")
```
## Setup the model
Now set up the fit and fit it. First we need to tell 3ML that we are going to fit using an independent variable (time in this case). We init it to 1.0 and set the unit to seconds.
```
time = IndependentVariable("time", 1.0, u.s)
```
Then we load the data that we have generated, tagging them with their time of observation.
```
plugins = []
for i, dataset in enumerate(datasets):
x, y, y_err = dataset
xyl = XYLike("data%i" % i, x, y, y_err)
# This is the important part: we need to tag the instance of the
# plugin so that 3ML will know that this instance corresponds to the
# given tag (a time coordinate in this case). If instead of giving
# one time coordinate we give two time coordinates, then 3ML will
# take the average of the model between the two time coordinates
# (computed as the integral of the model between t1 and t2 divided
# by t2-t1)
xyl.tag = (time, time_tags[i])
# To access the tag we have just set we can use:
independent_variable, start, end = xyl.tag
# NOTE: xyl.tag will return 3 things: the independent variable, the start and the
# end. If like in this case you do not specify an end when assigning the tag, end
# will be None
plugins.append(xyl)
```
Generate the datalist as usual
```
data = DataList(*plugins)
```
Now let's generate the spectral model, in this case a point source with a cutoff powerlaw spectrum.
```
spectrum = Cutoff_powerlaw()
src = PointSource("test", ra=0.0, dec=0.0, spectral_shape=spectrum)
model = Model(src)
```
Now we need to tell 3ML that we are going to use the time coordinate to specify a time dependence for some of the parameters of the model.
```
model.add_independent_variable(time)
```
Now let's specify the time-dependence (a powerlaw) for the normalization of the powerlaw spectrum.
```
time_po = Powerlaw()
time_po.K.bounds = (0.01, 1000)
```
Link the normalization of the cutoff powerlaw spectrum with time through the time law we have just generated.
```
model.link(spectrum.K, time, time_po)
model
```
## Performing the fit
```
jl = JointLikelihood(model, data)
best_fit_parameters, likelihood_values = jl.fit()
for p in plugins:
p.plot(x_scale='log', y_scale='log');
```
| true |
code
| 0.759164 | null | null | null | null |
|
<a name="top"></a>
<div style="width:1000 px">
<div style="float:right; width:98 px; height:98px;">
<img src="https://raw.githubusercontent.com/Unidata/MetPy/master/metpy/plots/_static/unidata_150x150.png" alt="Unidata Logo" style="height: 98px;">
</div>
<h1>Hodographs</h1>
<h3>Unidata Python Workshop</h3>
<div style="clear:both"></div>
</div>
<hr style="height:2px;">
<div style="float:right; width:250 px"><img src="https://unidata.github.io/MetPy/latest/_images/sphx_glr_Advanced_Sounding_001.png" alt="Example Skew-T" style="height: 500px;"></div>
### Questions
1. What is a hodograph?
1. How can MetPy plot hodographs?
1. How can the style of the hodographs be modified to encode other information?
### Objectives
1. <a href="#upperairdata">Obtain upper air data</a>
1. <a href="#simpleplot">Make a simple hodograph</a>
1. <a href="#annotate">Annotate the hodograph with wind vectors</a>
1. <a href="#continuous">Color the plot (continuous)</a>
1. <a href="#segmented">Color the plot (segmented)</a>
<a name="upperairdata"></a>
## Obtain upper air data
Just as we learned in the siphon basics and upper air and skew-T notebook, we need to obtain upperair data to plot. We are going to stick with September 10, 2017 at 00Z for Key West, Fl. If you need a review on obtaining upper air data, please review those lessons.
```
from datetime import datetime
from metpy.units import pandas_dataframe_to_unit_arrays
from siphon.simplewebservice.wyoming import WyomingUpperAir
df = WyomingUpperAir.request_data(datetime(1998, 10, 4, 0), 'OUN')
data = pandas_dataframe_to_unit_arrays(df)
```
<a href="#top">Top</a>
<hr style="height:2px;">
<a name="simpleplot"></a>
## Make a Simple Hodograph
The hodograph is a plot of the wind shear in the sounding. It is constructed by drawing the winds as vectors from the origin and connecting the heads of those vectors. MetPy makes this simple!
```
import matplotlib.pyplot as plt
from metpy.plots import Hodograph
%matplotlib inline
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
h = Hodograph(ax, component_range=60.)
h.add_grid(increment=20)
h.plot(data['u_wind'], data['v_wind'], color='tab:red')
```
It's relatively common to not want or need to display the entire sounding on a hodograph. Let's limit these data to the lowest 10km and plot it again.
```
import metpy.calc as mpcalc
from metpy.units import units
_, u_trimmed, v_trimmed, speed_trimmed, height_trimmed = mpcalc.get_layer(data['pressure'], data['u_wind'],
data['v_wind'], data['speed'], data['height'],
heights=data['height'], depth=10 * units.km)
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot(u_trimmed, v_trimmed, color='tab:red')
```
<a name="annotate"></a>
## Annotate the hodograph with wind vectors
It may be useful when introducing hodographs to actually show the wind vectors on the plot. The `wind_vectors` method does exactly this. It is often necessary to decimate the wind vectors for the plot to be intelligible.
```
h.wind_vectors(u_trimmed[::3], v_trimmed[::3])
fig
```
We can also set the limits to be asymmetric to beter utilize the plot space.
```
ax.set_xlim(-10, 30)
ax.set_ylim(-10, 20)
fig
```
<a name="continuous"></a>
## Color the plot (continuous)
We can color the line on the hodograph by another variable as well. In the simplest case it will be "continuously" colored, changing with the value of the variable such as windspeed.
```
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot_colormapped(u_trimmed, v_trimmed, speed_trimmed)
from metpy.plots import colortables
import numpy as np
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
norm, cmap = colortables.get_with_range('Carbone42', np.min(speed_trimmed), np.max(speed_trimmed))
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot_colormapped(u_trimmed, v_trimmed, speed_trimmed, cmap=cmap, norm=norm)
```
<a name="segmented"></a>
## Color the plot (segmented)
It may be useful when introducing hodographs to actually show the wind vectors on the plot. The `wind_vectors` method does exactly this. It is often necessary to decimate the wind vectors for the plot to be intelligible.
We can also color the hodograph based on another variable - either continuously or in a segmented way. Here we'll color the hodograph by height above ground level.
```
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
boundaries = np.array([0, 1, 3, 5, 8]) * units.km
colors = ['tab:red', 'tab:green', 'tab:blue', 'tab:olive']
# Since we want to do things in terms of AGL, we need to make AGL heights
agl = height_trimmed - height_trimmed[0]
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot_colormapped(u_trimmed, v_trimmed, agl, bounds=boundaries, colors=colors)
```
<a href="#top">Top</a>
<hr style="height:2px;">
| true |
code
| 0.64579 | null | null | null | null |
|
```
import holoviews as hv
hv.extension('bokeh')
hv.opts.defaults(hv.opts.Curve(width=500),
hv.opts.Image(width=500, colorbar=True, cmap='Viridis'))
import numpy as np
import scipy.signal
import scipy.fft
from IPython.display import Audio
```
# Diseño de sistemas y filtros IIR
Un filtro FIR de buena calidad puede requerir una gran cantidad de coeficientes
Es posible implementar filtros más eficientes usando **recursividad**. Esta es la base de los filtros de respuesta al impulso infinita o IIR que veremos en esta lección
## Definición de un sistema IIR
Generalizando el sistema FIR para incluir versiones pasadas de la salida y asumiendo $a[0] = 1$ llegamos a
$$
\begin{align}
y[n] &= b[0] x[n] + b[1] x[n-1] + b[2] x[n-2] + \ldots + b[L] x[n-L] \nonumber \\
& - a[1] y[n-1] - a[2] y[n-2] - \ldots - a[M] y[n-M] \nonumber \\
&= \sum_{l=0}^{L} b[l] x[n-l] - \sum_{m=1}^{M} a[m] y[n-m] \nonumber \\
\sum_{m=0}^{M} a[m] y[n-m] &= \sum_{l=0}^{L} b[l] x[n-l] \nonumber \\
(a * y)[n] &= (b * x)[n], \nonumber
\end{align}
$$
es decir dos convoluciones discretas que definen una **ecuación de diferencias**
Este tipo de sistema se conoce como
- sistema *infinite impulse response* (IIR)
- sistema *auto-regresive moving average* (ARMA)
- autoregresivo de orden M: incluye valores pasados de la salida
- media movil de orden L+1: pondera el valor presente y pasados de la entrada
Podemos ver el sistema IIR como una generalización del sistema FIR. El caso particular del sistema FIR se recupera si
$a[m] = 0$ para $m=[1, \ldots, M]$
### Respuesta en frecuencia del sistema IIR
Aplicando la transformada de Fourier convertimos las convoluciones en multiplicaciones y encontramos la respuesta en frecuencia como
$$
\begin{align}
\text{DFT}_N[(a * y)[n]] &= \text{DFT}_N[(b * x)[n]] \nonumber \\
A[k] Y[k] &= B[k] X[k] \nonumber \\
H[k] = \frac{Y[k]}{X[k]} &= \frac{B[k]}{A[k]} = \frac{ \sum_{l=0}^L b[l]e^{-j \frac{2\pi}{N} nl} }{ \sum_{m=0}^M a[m]e^{-j \frac{2\pi}{N} mk}} \nonumber
\end{align}
$$
que existe siempre que $A[k] \neq 0$.
La respuesta en frecuencia también suele expresarse como
$$
H[k] = K \frac{ \prod_{l=1}^L (e^{j \frac{2\pi}{N} k}- \beta[l]) }{ \prod_{m=1}^M (e^{j \frac{2\pi}{N} k}- \alpha[m])}
$$
donde
- $K$ se llama **ganancia**
- las raices del polinomio del numerador $\alpha$ se llaman conjuntamente **ceros**
- las raices del polinomio del denominador $\beta$ se llaman conjuntamente **polos**
### Ejemplo de respuesta al impulso de un sistema IIR
Consideremos el siguiente sistema IIR
$$
\begin{align}
y[n] &= (1-\gamma) x[n] + \gamma y[n-1] \nonumber \\
y[n] - \gamma y[n-1] &= (1-\gamma) x[n] \nonumber
\end{align}
$$
Los coeficientes del sistema son
$a[0] = 1$, $a[1] = -\gamma$ y $b[0] = (1-\gamma)$
Es decir que es AR de orden 1 y MA de orden 1
¿Cúal es su respuesta al impulso? Asumiendo $y[n]=0, n<0$, tenemos que
$$
\begin{matrix}
n & \delta[n] & y[n] \\
-2 & 0 & 0 \\
-1 & 0 & 0 \\
0 & 1 & (1-\gamma) \\
1 & 0 & \gamma(1-\gamma) \\
2 & 0 & \gamma^2(1-\gamma) \\
3 & 0 & \gamma^3(1-\gamma) \\
4 & 0 & \gamma^4(1-\gamma) \\
\end{matrix}
$$
¿Cómo cambia la respuesta al impulso con distintos valores de $\gamma$? ¿Qué pasa si $\gamma \geq 1$?
Respondamos estas preguntas visualizando la respuesta al impulso de este sistema con la función `scipy.signal.dimpulse`
```
# Valores de gamma que probaremos:
gamma = [-1.5, -1, -0.5, 0.5, 1., 1.5]
p = []
for g in gamma:
t, y = scipy.signal.dimpulse(([1-g, 0], [1,-g], 1), x0=0, n=30)
p.append(hv.Curve((t, y[0][:, 0]), label=f"gamma={g}"))
hv.Layout(p).cols(3).opts(hv.opts.Curve(width=250, height=200, axiswise=True))
```
De las figuras podemos ver que:
- Para $\gamma < 0$ (primera fila) los coeficientes del sistema son alternantes en signo
- Para $|\gamma| < 1$ los coeficientes del sistema tienden a cero
- Para $|\gamma| > 1$ los coeficientes del sistema divergen y tienen a infinito
:::{warning}
A diferencia de un sistema FIR, el sistema IIR puede tener configuraciones inestables en que los coeficientes crecen o decrecen infinitamente
:::
Por otro lado consideremos el sistema anterior y asumamos que $|\gamma|<1$, desenrollando tenemos que
$$
\begin{align}
y[0] &= (1-\gamma) x[0] \nonumber \\
y[1] &= (1-\gamma) (x[1] + \gamma x[0]) \nonumber \\
y[2] &= (1-\gamma) (x[2] + \gamma x[1] + \gamma^2 x[0]) \nonumber \\
y[3] &= (1-\gamma) (x[3] + \gamma x[2] + \gamma^2 x[1] + \gamma^3 x[0]) \nonumber \\
y[4] &= (1-\gamma) (x[4] + \gamma x[3] + \gamma^2 x[2] + \gamma^3 x[1] + \gamma^4 x[0]) \nonumber \\
y[5] &= \ldots \nonumber
\end{align}
$$
:::{note}
Con un sistema IIR de pocos coeficientes podemos representar un sistema FIR considerablemente más grande
:::
En el ejemplo anterior, si escogemos $\gamma$ tal que $\gamma^{20 }\approx 0$ entonces aproximamos un sistema FIR de orden 20 con tan sólo 3 coeficientes
### Ejemplo de respuesta en frecuencia de un sistema IIR
Para el sistema del ejemplo anterior su respuesta en frecuencia es
$$
\begin{align}
Y[k] &= (1-\gamma) X[k] + \gamma Y[k] e^{-j \frac{2\pi}{N} k} \nonumber \\
H[k] = \frac{Y[k]}{X[k]} &= \frac{1-\gamma}{1 - \gamma e^{-j \frac{2\pi}{N} k} } \nonumber
\end{align}
$$
que en notación de polos y ceros se escribe como
$$
H[k] = (1-\gamma)\frac{e^{j \frac{2\pi}{N} k} - 0}{e^{j \frac{2\pi}{N} k} - \gamma }
$$
es decir que tiene un cero en $0$, un polo en $\gamma$ y una ganancia de $(1-\gamma)$
Para entender mejor este sistema estudiemos la magnitud de $|H[k]|$ para $\gamma < 1$
$$
\begin{align}
| H[k]| &= \frac{|1-\gamma|}{|1 - \gamma e^{-j \frac{2\pi}{N} k}|} \nonumber \\
&= \frac{1-\gamma}{\sqrt{1 - 2\gamma \cos(\frac{2\pi}{N} k) + \gamma^2}} \nonumber
\end{align}
$$
¿Cómo se ve $|H[k]|$? ¿Qué función cumple este sistema?
```
k = np.arange(-24, 25)/50
Hk = lambda gamma, k : (1-gamma)/np.sqrt(1 - 2*gamma*np.cos(2.0*np.pi*k) + gamma**2)
p = []
for gamma in [0.25, 0.5, 0.75]:
p.append(hv.Curve((k, Hk(gamma, k)), 'Frecuencia', 'Respuesta', label=f'gamma={gamma}'))
hv.Overlay(p)
```
:::{note}
Este sistema atenua las frecuencias altas, es decir que actua como un filtro pasa bajos
:::
## Diseño de filtros IIR simples
Los filtros IIR más simples son los de un polo y un cero, es decir filtros de primer orden
$$
H[k] = \frac{b[0] + b[1] e^{-j \frac{2\pi}{N} k}}{1 + a[1] e^{-j \frac{2\pi}{N} k}} = K\frac{e^{j \frac{2\pi}{N} k} - \beta}{e^{j \frac{2\pi}{N} k} - \alpha }
$$
donde podemos reconocer
- $b[0]=K$
- $\beta = - b[1] \cdot K$
- $\alpha=-a[1]$
Definimos la frecuencia de corte $f_c$ como aquella frecuencia en la que el filtro alcanza una atenuación de 0.7 (-3 dB). Haciendo la equivalencia con el ejemplo anterior tenemos que $\gamma = e^{-2\pi f_c}$
### Receta para un filtro pasa bajo IIR con frecuencia de corte $f_c$
Asignamos
- $b[0] = 1 - e^{-2\pi f_c}$
- $b[1] = 0$
- $a[1] = -e^{-2\pi f_c}$
Lo que resulta en la siguiente respuesta en frecuencia
$$
H[k] = \frac{1-e^{-2\pi f_c}}{1 - e^{-2\pi f_c} e^{-j \frac{2\pi}{N} k}} = (1-e^{-2\pi f_c}) \frac{(e^{j \frac{2\pi}{N} k}- 0)}{(e^{j \frac{2\pi}{N} k} - e^{-2\pi f_c} )}
$$
Es decir un cero en $0$, un polo en $e^{-2\pi f_c}$ y ganancia $1-e^{-2\pi f_c}$
### Receta para un filtro pasa alto IIR con frecuencia de corte $f_c$
Asignamos
- $b[0] = (1 + e^{-2\pi f_c})/2$
- $b[1] = -(1 + e^{-2\pi f_c})/2$
- $a[1] = -e^{-2\pi f_c}$
Lo que resulta en la siguiente respuesta en frecuencia
$$
H[k] = \frac{1+e^{-2\pi f_c}}{2} \frac{(e^{j \frac{2\pi}{N} k} - 1)}{(e^{j \frac{2\pi}{N} k} - e^{-2\pi f_c})}
$$
Es decir un cero en $1$, un polo en $e^{-2\pi f_c}$ y ganancia $\frac{1+e^{-2\pi f_c}}{2}$
### Aplicar un filtro a una señal con scipy
Para filtrar una señal unidimensional con un filtro IIR (sin variar la fase de la señal) podemos utilizar la función
```python
scipy.signal.filtfilt(b, # Coeficientes del numerador
a, # Coeficientes del denominador
x, # Señal a filtrar
...
)
```
Los siguientes ejemplos muestran un señal de tipo pulso rectangular filtrada con sistemas IIR de primer orden pasa bajo y pasa-alto diseñados con las recetas mostradas anteriormente
```
n = np.arange(0, 500)
x = 0.5 + 0.5*scipy.signal.square((n)/(2.*np.pi*5), duty=0.3)
def iir_low_pass(signal, fc):
gamma = np.exp(-2*np.pi*(fc))
b, a = [(1-gamma), 0], [1, -gamma]
return scipy.signal.filtfilt(b, a, signal)
y = {}
for fc in [0.05, 0.02, 0.01]:
y[fc] = iir_low_pass(x, fc)
px = hv.Curve((n, x))
py = []
for fc, y_ in y.items():
py.append(hv.Curve((n, y_), label=f'fc={fc}'))
hv.Layout([px, hv.Overlay(py)]).cols(1).opts(hv.opts.Curve(height=200))
def iir_high_pass(signal, fc):
gamma = np.exp(-2*np.pi*(fc))
b, a = [(1+gamma)/2, -(1+gamma)/2], [1, -gamma]
return scipy.signal.filtfilt(b, a, signal)
y = {}
for fc in [0.01, 0.02, 0.05]:
y[fc] = iir_high_pass(x, fc)
px = hv.Curve((n, x))
py = []
for fc, y_ in y.items():
py.append(hv.Curve((n, y_), label=f'fc={fc}'))
hv.Layout([px, hv.Overlay(py)]).cols(1).opts(hv.opts.Curve(height=200))
```
:::{note}
El filtro pasa-bajos suaviza los cambios de los pulsos rectangulares. El filtro pasa-altos elimina las zonas constantes y resalta los cambios de la señal.
:::
## Diseño de filtros IIR de segundo orden
Los filtros IIR de segundo orden o **biquad** tienen dos polos y dos ceros.
Su respuesta en frecuencia es
$$
H[k] = \frac{b[0] + b[1] W_N^k + b[2] W_N^{2k}}{1 + a[1] W_N^k + a[2] W_N^{2k}} = K \frac{(W_N^{-k} - \beta_1) (W_N^{-k} - \beta_2)}{(W_N^{-k} - \alpha_1)(W_N^{-k} - \alpha_2)},
$$
donde $W_N = e^{-j \frac{2 \pi}{N}}$ y la relación entreo coeficientes y polos/ceros es:
$$
b[0] = K, \quad b[1] = -K (\beta_1 + \beta_2), \quad b[2]= K \beta_1\beta_2
$$
$$
a[1] = - (\alpha_1 + \alpha_2), \quad a[2]=\alpha_1 \alpha_2
$$
Con arquitecturas de segundo orden se pueden crear filtros pasabanda y rechaza banda
## Diseño de filtros IIR de orden mayor
Para crear los coeficientes de filtro IIR de orden mayor podemos usar la función
```python
scipy.signal.iirfilter(N, # Orden del filtro
Wn, # Frecuencias de corte (normalizadas en [0,1])
fs, # Frecuencia de muestreo
btype='bandpass', # Tipo de filtro: 'bandpass', 'lowpass', 'highpass', 'bandstop'
ftype='butter', # Familia del filtro: 'butter', 'ellip', 'cheby1', 'cheby2', 'bessel'
output='ba', # Retornar coeficientes
...
)
```
El filtro Butterworth es óptimo en el sentido de tener la banda de paso lo más plana posible.
Otros filtros se diseñaron con otras consideraciones.
Los filtros IIR digitales están basados en los filtros IIR analógicos.
Observe como al aumentar el orden el filtro pasabajo IIR comienza a cortar de forma más abrupta
```
Hk = {}
for order in [1, 2, 5, 20]:
b, a = scipy.signal.iirfilter(N=order, Wn=0.2, fs=1,
ftype='butter', btype='lowpass', output='ba')
freq, response = scipy.signal.freqz(b, a, fs=1)
Hk[order] = np.abs(response)
p = []
for order, response in Hk.items():
p.append(hv.Curve((freq, response), 'Frecuencia', 'Respuesta', label=f'orden={order}'))
hv.Overlay(p)
```
## Comparación de la respuesta en frecuencia de filtros FIR e IIR del orden equivalente
Comparemos la respuesta en frecuencia de un filtro IIR y otro FIR ambos pasa-bajo con 20 coeficientes
```
Fs = 1
fc = 0.25
h = scipy.signal.firwin(numtaps=20, cutoff=fc, pass_zero=True, window='hann', fs=Fs)
b, a = scipy.signal.iirfilter(N=9, Wn=fc, fs=Fs, ftype='butter', btype='lowpass')
display(len(h), len(b)+len(a))
freq_fir, response_fir = scipy.signal.freqz(h, 1, fs=Fs)
freq_iir, response_iir = scipy.signal.freqz(b, a, fs=Fs)
p1 = hv.Curve((freq_fir, np.abs(response_fir)), 'Frecuencia', 'Respuesta', label='FIR')
p2 = hv.Curve((freq_iir, np.abs(response_iir)), 'Frecuencia', 'Respuesta', label='IIR')
hv.Overlay([p1, p2])*hv.VLine(fc).opts(color='k', alpha=0.5)
```
La linea negra marca la ubicación de la frecuencia de corte
:::{note}
El filtro IIR es mucho más abrupto, es decir filtra mejor, que el filtro FIR equivalente
:::
Una desventaja del filtro IIR es que por definición introduce una desfase no constante en la señal de salida
```
freq_fir, delay_fir = scipy.signal.group_delay(system=(h, 1), fs=Fs)
freq_iir, delay_iir = scipy.signal.group_delay(system=(b, a), fs=Fs)
p1 = hv.Curve((freq_fir, delay_fir), 'Frecuencia', 'Desfase', label='FIR')
p2 = hv.Curve((freq_iir, delay_iir), 'Frecuencia', 'Desfase', label='IIR')
hv.Overlay([p1, p2])*hv.VLine(fc).opts(color='k', alpha=0.5)
```
¿Cómo se ve una señal filtrada donde se preserva la fase versus una donde no se preserva la fase?
Consideremos la señal rectangular anterior y apliquemos un filtro pasa-bajo IIR de orden 1
Esta vez compararemos el filtro con la función `scipy.signal.lfilter` y la función `scipy.signal.filtfilt`. La primera no preserva la fase mientras que la segunda si lo hace
```
Fs = 1
fc = 0.01
n = np.arange(0, 500)
x = 0.5 + 0.5*scipy.signal.square((n)/(2.*np.pi*5), duty=0.3)
b, a = scipy.signal.iirfilter(N=1, Wn=fc, fs=Fs, ftype='butter', btype='lowpass')
# No se preserva la fase
y_lfilter = scipy.signal.lfilter(b, a, x)
# Se preserva la fase
y_filtfilt = scipy.signal.filtfilt(b, a, x)
px = hv.Curve((n, x), 'Tiempo', 'Entrada')
py = []
py.append(hv.Curve((n, y_filtfilt), 'Tiempo', 'Salida', label=f'Fase constante'))
py.append(hv.Curve((n, y_lfilter), 'Tiempo', 'Salida', label=f'Fase no constante'))
hv.Layout([px, hv.Overlay(py)]).cols(1).opts(hv.opts.Curve(height=200))
```
:::{note}
En el caso donde no se preserva la fase podemos notar que la señal de salida está desplazada con respecto a la original. Además los cambios tienen una transición asimétrica
:::
La función `scipy.signal.filtfilt` "arregla" el problema del desfase filtrando la señal dos veces. La primera vez se filtra hacia adelante en el tiempo y la segunda vez hacia atrás. Por ende no se puede aplicar en un escenario de tipo *streaming* donde los datos van llegando de forma causal.
En una aplicación causal donde se necesite preservar la fase debemos usar un filtro FIR.
## Apéndice: Efectos de audio con filtros IIR
El siguiente ejemplo muestra como implementar el conocido filtro <a href="https://en.wikipedia.org/wiki/Wah-wah_(music)">Wah-wah</a> usando un sistema IIR
Este es un filtro pasabanda modulado con ancho de pasada fijo $f_b$ [Hz] y una frecuencia central variable $f_c$ [Hz], donde La frecuencia central se modula con una onda lenta
Se modela como el siguiente sistema **IIR**
$$
H[k] = \frac{(1+c)W_N^{2k} -(1+c) }{W_N^{2k} + d(1-c)W_N^k -c}
$$
donde
$$
d=-\cos(2\pi f_c/f_s)
$$
y
$$
c = \frac{\tan(\pi f_b/f_s) -1}{\tan(2\pi f_b /f_s)+1}
$$
Veamos como modifica este filtro una señal de audio
```
import librosa
data, fs = librosa.load("../../data/DPSAU.ogg")
Audio(data, rate=fs)
data_wah = []
zi = np.zeros(shape=(2,))
# Parámetros fijos del filtro
fb, Nw = 200, 5
c = (np.tan(np.pi*fb/fs) - 1.)/(np.tan(2*np.pi*fb/fs) +1)
# Filtramos una ventana de la señal moviendo lentamente fc
for k in range(len(data)//Nw):
# Cálculo de la frecuencia central
fc = 500 + 2000*(np.cos(2.0*np.pi*k*30./fs) +1)/2
d = -np.cos(2*np.pi*fc/fs)
# Coeficientes del filtro
b, a = [(1+c), 0, -(1+c)], [1, d*(1-c), -c]
# Filtramos, usando el filtrado anterior como borde (zi)
data2, zi = scipy.signal.lfilter(b, a, data[k*Nw:(k+1)*Nw], zi=zi)
# Guardamos
data_wah.append(data2)
Audio(np.hstack(data_wah), rate=int(fs))
```
Si quieres profundizar en el tema de los filtros IIR aplicados a efectos de audio recomiendo: https://www.ee.columbia.edu/~ronw/adst-spring2010/lectures/lecture2.pdf
| true |
code
| 0.252453 | null | null | null | null |
|
# The Schrödinger equation
#### Let's have some serious fun!
We'll look at the solutions of the Schrödinger equation for a harmonic potential.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import numpy as np
import math
from math import pi as Pi
import matplotlib.pyplot as plt
from scipy import (inf, integrate)
import seaborn as sns
sns.set()
```
### Prelude: Hermite's Polynomials
Hermite's Polynomials are a subset of polynomials that will help us construct solutions of the Schrödinger equation.
#### Modelling polynomials
Some object-oriented Python programming with polynomials. We represent an arbitrary polynomial
$$
P(x) = \sum_{n=0}^{N} p_n \cdot x^n
$$
unambiguously by its coefficients $p_n$, i.e. an array of real numbers of length $N+1$. Apart from the algebraic operators we also define the multiplication with x as ```mulx()``` and the differentiation as ```d_dx()```.
```
class Polynomial():
"""
A class representing a polynomial by its coefficients
"""
def __init__(self, array=[0]):
self.p = np.array(array)
def mulx(self):
return Polynomial(np.insert(self.p, 0, 0))
def d_dx(self):
return Polynomial([i*self.p[i] for i in range(1, len(self.p))])
def __eq__(self, other):
return np.equal(self.p, other.p).all()
def __rmul__(self, number):
return Polynomial(number * self.p)
def __sub__(self, other):
l=max(len(self.p), len(other.p))
return Polynomial(Polynomial.pad(self.p,l) - Polynomial.pad(other.p,l))
def __add__(self, other):
l=max(len(self.p), len(other.p))
return Polynomial(Polynomial.pad(self.p,l) + Polynomial.pad(other.p,l))
def __call__(self, x):
return np.sum([self.p[i] * x**i for i in range(len(self.p))], axis=0)
@staticmethod
def pad(array, l):
if len(array) == l:
return array
if len(array) > l:
raise ValueError("can't pad to lower dimension")
return np.append(array, np.zeros(l-len(array)))
@staticmethod
def mono_repr(c, i):
if c==0:
return ''
if i==0:
return str(int(c))
elif i==1:
return "{}x".format(int(c))
else:
if c==1:
return "x^{}".format(i)
else:
return "{}x^{}".format(int(c),i)
def __repr__(self):
return " + ".join(
np.flipud([Polynomial.mono_repr(self.p[i],i)
for i in range(len(self.p)) if self.p[i] != 0] ))
```
#### The Hermite Polynomial generator
Now, Hermite's polynomials are a special subset of all polynomials, defined e.g. by a recursion relation:
From [Wikipedia](https://en.wikipedia.org/wiki/Hermite_polynomials) (if not good memories), we know that
$$
H_n(x) = (2x-\frac{d}{dx})^n \cdot 1
$$
generates the *physicist's* Hermite polynomials. We define our python generator in a recursive fashion returning Polynomial instances
$$
H_n(x) = (2x-\frac{d}{dx}) \cdot H_{n-1}
$$
```
def H(n):
if n<0:
raise ValueError("Not defined for negativ n")
if n==0:
return Polynomial([1])
p = H(n-1)
return 2 * p.mulx() - p.d_dx()
```
Note that we can evaluate the polynomial at any (even complex) x.
```
H_3 = H(3)
H_3, H_3(1), H_3(1+2j)
```
The Hermite polynomials have the special properties:
$$
x \cdot H_\nu(x) = \frac{1}{2} H_{\nu+1}(x) + \nu \cdot H_{\nu-1}(x)
$$
$$
\frac{d}{dx}H_\nu(x) = 2 \nu \cdot H_{\nu-1}(x)
$$
which we can verify using our implementation for the first 10 polynomials ($\nu = {1..9}$):
```
[H(nu).mulx() == .5 * H(nu+1) + nu*H(nu-1) for nu in range(1,10)]
[H(nu).d_dx() == 2 * nu * H(nu - 1) for nu in range(1,10)]
```
---
### The time-dependent Schrödinger equation
$$
i\hbar \frac{\partial \Psi(x,t)}{\partial t} =
\mathcal{H}\Psi(x,t) =
E\Psi(x,t)
$$
This is the Schrödinger equation. Now, with the time-independent Hamilton operator $\mathcal{H}$ for a particle with mass m and the harmonic potential given by $ V(x)=\frac{1}{2}m\omega^2 x^2$ looks like
$$
\mathcal{H} = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + \frac{1}{2}m\omega^2 x^2
$$
we can separate the variables $x$ and $t$ like so:
$$
\Psi(x, t) = \psi(x) \cdot \varphi(t)
$$
and solve both
$$
i\hbar \frac{\partial \varphi(t)}{\partial t} = E \cdot \varphi(t)
$$
and
$$
[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + \frac{1}{2}m\omega^2 x^2] \cdot \psi(x) = E \psi(x)
$$
separately.
A neat trick to get rid of the physical constants is rescaling:
$$\xi = \frac{m \omega}{\hbar} \cdot x$$
with which you can easily check by yourself that the Schrödinger equation becomes:
$$
[ -\frac{\partial^2}{\partial \xi^2} + \xi^2 - \frac{2E}{\hbar \omega}] \cdot \psi(\xi) = 0
$$
where we postulate the boundary conditions for a constrained particle as
$$
\psi(-\infty) = \psi(\infty) = 0
$$
The so-called stationary solutions of the equation in $x$ form an ortho-normal eigenbasis of the Hilbert space of bounded functions $\psi_{\nu}(\xi)$ with eigenvalues $E_{\nu}=\hbar \omega (\nu + \frac{1}{2})$. And although we're not interested in the boring (yawn!) stationary solutions, we'll use this eigenbasis to construct an analytical function that obeys the time-dependent Schrödinger equation.
With the above eigenvalues we finally arrive at the following concise representation of the time-independent Schrödinger equation.
$$
[ -\frac{\partial^2}{\partial \xi^2} + \xi^2 - (2\nu+1)] \cdot \psi(\xi) = 0
$$
### Functions as eigenvectors
The solutions of this equation span a vector space, a so-called Hilbert space. That means we can define addition, multiplication by a number and even an inner product on these functions. When we look at functions as vectors in a Hilbert space, then the Schrödinger equation can as well be considered an eigenvalue problem. We'll provide the solutions without proof.
The eigenfunctions are composed of the Hermite polynomials and a gaussian:
$$
\psi_\nu(\xi) = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}} \cdot H_\nu(\xi) \cdot
e^{-\frac{\xi^2}{2}}
$$
$$
\varphi_\nu(t) = e^{-i (\nu+\frac{1}{2}) t}
$$
Thus arriving at the full solution of the time-dependent Schrödinger equation as
$$
\psi_\nu(\xi, t) = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}} \cdot H_\nu(\xi) \cdot
e^{-\frac{\xi^2}{2}-i(\nu+\frac{1}{2}) t}
$$
These solutions are called stationary because they rotate in the complex plane keeping their shape. That means that for every x the value of $\psi_\nu(x)$ rotates in the complex plane with exactly the same *frequency* as any other. Please note that we have clandestinely scaled the time t such that it *swallowed* the physical constants. For our purpose, namely visualizing the non-stationary solutions of the Schrödinger equation, this does not make a difference.
---
Defining the normalization factor $A_\nu$ as
$$
A_\nu = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}}
$$
we visualize these stationary solutions such that we get an idea what they look like:
```
def A(nu):
return 1/math.sqrt(2**nu * math.factorial(nu) * math.sqrt(math.pi))
def psi(nu):
def _psi(x):
return A(nu) * H(nu)(x) * np.exp(-x*x/2)
return _psi
N_points=200
x_ = np.linspace(-6, 6, N_points)
plt.plot(x_, psi(0)(x_))
plt.plot(x_, psi(1)(x_))
plt.plot(x_, psi(2)(x_))
plt.plot(x_, psi(3)(x_));
```
---
#### Ortho-normal basis
Let's verify that our $\psi_\nu(\xi)$ form an ortho-normal basis with the inner product $\langle \psi_\mu | \psi_\nu \rangle$, $\mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ defined by
$$
\int_{-\infty}^{\infty} \bar{\psi}_\nu(\xi) \cdot \psi_\mu(\xi) d\xi= \delta^{\mu\nu}
$$
$\bar{\psi}_\nu(\xi)$ being the complex conjugate of $\psi_\nu(\xi)$
```
[[round(integrate.quad(lambda x: psi(mu)(x)*psi(nu)(x), -inf, +inf)[0], 6) for mu in range(5)] for nu in range(5)]
```
You can see that all inner products of two basis functions are zero, apart from the product with itself, which is what the *Kronecker* delta $\delta^{\mu \nu}$ demands.
---
### The fun part: coherent solutions
Now, let's have some fun. As we have just verified, the eigenstates of the Schrödinger equation form an ortho-normal basis of the Hilbert space of functions in one dimension. We expect that one can approximate any other bounded function as a linear combination of the first $N$ eigenfunctions. We'll do that for the following shifted gaussian. Note that is is centered around $x=-3$, so it's not equal to the first basis function.
```
x0=-3
fun=lambda x: psi(0)(x-x0)
#sns.set_style("ticks", {"xtick.major.size": 2, "ytick.major.size": .1})
sns.set()
plt.plot(x_, fun(x_));
```
We compute it's coordinates in the Schrödinger eigenbases simply by projecting it to the first $N$ eigenfunctions like this
```
N = 15
coords = [integrate.quad(lambda x: psi(mu)(x)*fun(x), -inf, +inf)[0] for mu in range(N)]
coords
```
Calling those coordinates $c_\nu$, we compute
$$
\psi_0(x-x_0) \approx \big[\sum_{\nu=0}^9 c_\nu \cdot A_\nu H_\nu(x)\big] \cdot e^{-\frac{-x^2}{2}}
$$
```
pol = Polynomial([0])
for nu in range(N):
pol = pol + coords[nu] * A(nu) * H(nu)
projection = lambda x: pol(x) * np.exp(-x*x/2)
plt.plot(x_, projection(x_));
```
What you see is that the 15-dimensional projection of our shifted function into the Schrödinger eigenbasis is a formidable approximation.
It's actually much more than an approximation. You can interpret this function as the wave function of a particle resting (the momentum is zero) at $x=x_0$. Remember there's still the harmonic potential. Thus, in the limit of classical mechanics, we would expect that our particle will slowly accelerate to the right until it *feels* the potential there. Then it would reflect and move all the way back. Lacking friction, we indeed expect that this oscillation continues until eternity.
---
#### Let the clock tick...
Because now we have this function as a linear combination of Schrödinger solutions, we can switch on time and see ourselves. Under the influence of the time-dependent Schrödinger equation, the the fifteen eigenvectors each rotate at their own frequency determined by the eigenvalue $2\nu+1$
The time-dependent solutions
$$
\psi_\nu(\xi, t) = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}} \cdot H_\nu(\xi) \cdot
e^{-\frac{\xi^2}{2}-i(\nu+\frac{1}{2}) t}
$$
Note that now this function is complex-valued!
```
def psit(nu):
def _psi(x, t):
return A(nu) * H(nu)(x) * np.exp(-x*x/2) * np.exp(-1j*(nu+.5)*t)
return _psi
psit(3)(1, .3)
```
---
#### 3-D data
To appreciate the dynamics of a wave function in time we display both the real part and the imaginary part of the complex value of $\psi$.
- The figure's y-axis is our space coordinate $x$
- its z-axis spans the real part of the wave function
- and its x-axis spans the wave function's imaginary part
```
import mpl_toolkits.mplot3d.axes3d as p3
```
We display $\psi_2(x, t) $ at $t=0.5$
```
x_ = np.linspace(-6,6, N_points)
f = psit(2)(x_, 0.5)
r_f = [c.real for c in f]
i_f = [c.imag for c in f]
fig=plt.figure(figsize=(12,8))
ax = fig.gca(projection='3d')
ax.view_init(30, -15)
ax.set_xlim(-1, 1)
ax.set_zlim(-1, 1)
ax.set_xlabel('Imag')
ax.set_ylabel('X')
ax.set_zlabel('Real')
ax.plot(i_f, x_, r_f)
plt.show()
```
As you can see, the function is tilted in the complex plan due to the complex phase $e^{-\frac{5}{2}it}$
---
#### Time-dependent wave functions
Here, we'll create an analytical time-dependent wave function from our set of coordinates in Hilbert space that represent the resting particle at $x_0=-3$
```
def WF(sc):
return lambda x,t: sum([sc[nu] * np.exp(-1j*(nu+.5)*t) * A(nu) * H(nu)(x) * np.exp(-x*x/2)
# ============================== ==================================
# ^ ^
# time dependent coefficient Basis function
for nu in range(len(sc))])
particle = WF(coords)
particle(-3, 0) # a particle resting at x=-3 at time t=0
```
### Animating a Schrödinger particle!
```
%autosave 3600
N_frames=100
N_Points=200
XL, XR = -6, 6
def snapshot(N, f, t):
x = np.linspace(XL,XR, N)
f=f(x, t)
r_f = np.array([c.real for c in f])
i_f = np.array([c.imag for c in f])
return np.array([i_f, x, r_f])
def update(num, n_points, n_frames, wave_function, line):
data= snapshot(n_points, wave_function, num*4.0/n_frames*math.pi)
line.set_data(data[0], data[1])
line.set_3d_properties(data[2])
return line
```
Recording the animation will take a couple of seconds. Be patient. It's worth waiting for!
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
fig=plt.figure(figsize=(12,8))
ax = p3.Axes3D(fig)
initial_data = snapshot(N_points, particle, 0.0)
line = ax.plot(initial_data[0], initial_data[1], initial_data[2])[0]
ax.set_xlim(-1, 1)
ax.set_zlim(-1, 1)
ax.set_ylim(XL, XR)
ax.set_xlabel('Imag')
ax.set_ylabel('X')
ax.set_zlabel('Real')
ax.set_title('Schroedinger particle in action!')
ax.view_init(10, -10)
line_ani = animation.FuncAnimation(
fig, update, N_frames,
fargs=(N_Points, N_frames, particle, line),
interval=200, blit=False)
jshtml = line_ani.to_jshtml()
#Uncomment and run this cell the see the movie. The cell will be so large that the notebook refuses to save. Thus I always comment it out before saving.
#HTML(data=jshtml)
# Uncomment to save your file and serve it elsewhere
#with open("Schroedinger.html", "w") as file:
# file.write(jshtml)
```
---
### Measuring location and momentum
Measurements in the real world are represented by computing expectation values of the operator associated with the given observable.
#### Angle notation
In the following, we denote eigenfunctions of the Schrödinger equation in angle notation
$$
|\nu \rangle \equiv \psi_\nu(x,t)
$$
In our unit-free notation, and introducing a more concise notation for the partial derivative, the momentum operator $\hat{p}$ is defined by
$$
\hat{p} = -i \partial_x
$$
Operators in our Hilbert space will be written in *hat* notation. You have seen $\hat{p}$ already. The Hamilton operator becomes:
$$
\hat{H} = \hat{p}^2 + \hat{x}^2
$$
Note that we're back to using $x$, but what we really mean is the unit-less $\xi$.
The Schrödinger equation in its eigenbasis looks like
$$
\hat{H} |\nu\rangle = 2(\nu+1)|\nu\rangle
$$
The inner product of any two wave functions (not necessarily basisvectors) as defined by the integral over the product of both functions has a neat short notation:
$$
\langle \psi_1 | \psi_2 \rangle
\equiv
\int_{-\infty}^{\infty} \bar{\psi_1}(\xi) \cdot \psi_2(\xi) d\xi
$$
The expectation value of an observable represented by an Operator like e.g. $\hat{p}$, given a particular wave function $\psi$ is defined by
$$
\langle \psi | \hat{p} | \psi \rangle
\equiv
\int_{-\infty}^{\infty} \bar{\psi}(\xi) \cdot (-i\partial_x) \psi(\xi) d\xi
$$
---
#### Dirac's ladder operators
Let us introduce the two *ladder* operators $a$ and $a^\dagger$ as
$$
a \equiv \frac{1}{\sqrt 2} (\hat{x} + i\hat{p})
$$
$$
a^\dagger \equiv \frac{1}{\sqrt 2} (\hat{x} - i\hat{p})
$$
using which we can express $\hat{p}$ and $\hat{x}$ like so:
$$
\hat{p} = \frac{i}{\sqrt 2}(a^\dagger - a)
$$
$$
\hat{x} = \frac{1}{\sqrt 2}(a^\dagger + a)
$$
Then you can convince yourself easily using the properties of the Hermite polynomials:
$$
x \cdot H_\nu(x) = \frac{1}{2} H_{\nu+1}(x) + \nu \cdot H_{\nu-1}(x)
$$
$$
\frac{d}{dx}H_\nu(x) = 2 \nu \cdot H_{\nu-1}(x)
$$
and our solutions of the Schrödinger equations
$$
\psi_\nu(x) = A_\nu \cdot H_\nu(x) \cdot
e^{-\frac{x^2}{2}}
$$
that
$$ a|\nu\rangle = \sqrt{\nu} |\nu-1 \rangle $$
and
$$ a^\dagger|\nu\rangle = \sqrt{\nu+1} |\nu+1 \rangle $$
It should be obvious by now why these operators are called *ladder* operators. They map each basis vector on the next resp. previous basis vector. And this neat property leads to a surprisingly simple method of applying $\hat{p}$ or $\hat{x}$ to arbitrary wave functions.
---
#### Matrix representation
We can compute a matrix representation easily by projecting the the result of every
$a|\nu\rangle$ resp. $a^\dagger|\nu\rangle$ onto every eigenvector.
$$
\langle \mu|a|\nu\rangle = \sqrt{\nu}\cdot\langle \mu | \nu-1\rangle = \sqrt{\nu} \cdot \delta^{\mu,\nu-1}
$$
and
$$
\langle \mu|a^\dagger|\nu\rangle = \sqrt{\nu+1}\cdot\langle \mu | \nu+1\rangle = \sqrt{\nu+1} \cdot \delta^{\mu,\nu+1}
$$
In this matrix representation, the ladder operators populate the positions right above or below the diagonal, respectively.
$$
a = \left[
\begin{array}{c c c c c c}
0 & 1 & 0 & 0 & 0 & 0 & \dots \\
0 & 0 & \sqrt{2} & 0 & 0 & 0 & \dots\\
0 & 0 & 0 & \sqrt{3} & 0 & 0 & \dots\\
0 & 0 & 0 & 0 & \sqrt{4} & 0 & \dots\\
0 & 0 & 0 & 0 & 0 & \sqrt{5} & \dots\\
0 & 0 & 0 & 0 & 0 & 0 & \dots \\
\dots
\end{array}
\right]
$$
$$
a^\dagger =
\left[
\begin{array}{c c c c c c}
0 & 0 & 0 & 0 & 0 & 0 & \dots\\
1 & 0 & 0 & 0 & 0 & 0 & \dots\\
0 & \sqrt{2} & 0 & 0 & 0 & 0 & \dots\\
0 & 0 & \sqrt{3} & 0 & 0 & 0 & \dots\\
0 & 0 & 0 & \sqrt{4} & 0 & 0 & \dots\\
0 & 0 & 0 & 0 & \sqrt{5} & 0 & \dots\\
\dots
\end{array}
\right]
$$
which leads to
$$
\hat{p} = \frac{1}{\sqrt{2}} \cdot \left[
\begin{array}{c c c c c c}
0 & 1 & 0 & 0 & 0 & 0 & \dots\\
i & 0 & \sqrt{2} & 0 & 0 & 0 & \dots\\
0 & i\sqrt{2} & 0 & \sqrt{3} & 0 & 0 & \dots\\
0 & 0 & i\sqrt{3} & 0 & \sqrt{4} & 0 & \dots\\
0 & 0 & 0 & i\sqrt{4} & 0 & \sqrt{5} & \dots\\
0 & 0 & 0 & 0 & i\sqrt{5} & 0 & \dots\\
\dots
\end{array}
\right]
$$
$$
\hat{x} = \frac{1}{\sqrt{2}} \cdot \left[
\begin{array}{c c c c c c}
0 & i & 0 & 0 & 0 & 0 & \dots\\
1 & 0 & i\sqrt{2} & 0 & 0 & 0 & \dots\\
0 & \sqrt{2} & 0 & i\sqrt{3} & 0 & 0 & \dots\\
0 & 0 & \sqrt{3} & 0 & i\sqrt{4} & 0 & \dots\\
0 & 0 & 0 & \sqrt{4} & 0 & i\sqrt{5} & \dots\\
0 & 0 & 0 & 0 & \sqrt{5} & 0 & \dots\\
\dots
\end{array}
\right]
$$
---
With these matrices we can do all our calculations just like highschool algebra! Let's verify that
$$ a|2\rangle = \sqrt{2} \cdot |1\rangle $$
and
$$ a^\dagger |2\rangle = \sqrt{3} \cdot |3\rangle $$
```
N=4 # just so that displaying the matrices doesn't clutter the notebook
```
The ladder operators as numpy arrays:
```
a=np.array([[math.sqrt(nu) if mu==nu-1 else 0.0 for nu in range(N)] for mu in range(N)])
a
a_d=np.array([[math.sqrt(nu+1) if mu==nu+1 else 0.0 for nu in range(N)] for mu in range(N)])
a_d
nu2 = np.array([0, 0, 1, 0])
np.matmul(a, nu2), np.matmul(a_d, nu2)
```
Convinced?
---
#### Expectation values
We can do even more exciting stuff with these matrices. Remember our initial wave function from the movie? It was a gaussian located a x=-3, and I claimed that it was at rest. It's about time to prove both.
The expectation value of the location $x$ is defined by
$$
\langle \psi | \hat{x} | \psi \rangle
\equiv
\int_{-\infty}^{\infty} \bar{\psi}(x) \cdot x \cdot \psi(x) dx
$$
```
# Using the 15-dimensional coordinates of our initial wave function in the Hilbert space spun by the
# solutions of the Schrödinger equation with harmonic potential
c = coords
N = len(coords)
a=np.array([[math.sqrt(nu) if mu==nu-1 else 0.0 for nu in range(N)] for mu in range(N)])
a_d=np.array([[math.sqrt(nu+1) if mu==nu+1 else 0.0 for nu in range(N)] for mu in range(N)])
```
Below we calculate
$$
\langle \psi | \hat{x} | \psi \rangle =
\frac{1}{\sqrt{2}} \cdot (\langle \psi | \hat{a} \psi \rangle + \langle \psi | \hat{a}^\dagger \psi \rangle)
= \frac{1}{\sqrt{2}} \cdot (\psi^T \cdot \mathbb{M} \cdot \psi + \psi^T \cdot \mathbb{M}^\dagger \cdot \psi)
$$
where $\psi^T$ is the transposed vector and $\mathbb{M}, \mathbb{M}^\dagger$ are the matrix representations of the ladder operators $a, a^\dagger$.
```
psi=np.array(coords)
1/math.sqrt(2) * (np.matmul(np.matmul(psi.T, a), psi) + np.matmul(np.matmul(psi.T, a_d), psi))
# Transposing is just for visual clarity.
# Actually, Python would understand the matmul operation correctly, anyway.
```
Convinced? That's almost exactly what we expected.
Btw. we could have been smarter by computing the $\hat{x}$ operator first and then compute the expectation value of it: Let's do that also for $\hat{p}$
$\hat{p} = \frac{i}{\sqrt 2}(a^\dagger - a)$ ;
$\hat{x} = \frac{1}{\sqrt 2}(a^\dagger + a)$:
```
p_hat = 1j/math.sqrt(2) * ( a_d - a )
x_hat = 1/math.sqrt(2) * ( a_d + a )
```
$\langle \psi | \hat{p} | \psi \rangle$:
```
np.matmul(np.matmul(psi.T, p_hat), psi)
```
That's almost zero. C'mon, now you are convinced, right?
---
#### Observing location and momentum over time
```
def psi_t(sc, t):
return np.array([sc[nu] * np.exp(-1j*(nu+.5)*t) for nu in range(N)])
psi_07 = psi_t(psi, 0.7)
psi_07
```
Please note that for complex coefficients we must compute $\langle \psi | $ as the complex conjugate of $| \psi \rangle$
```
np.matmul(np.matmul(np.conj(psi_07).T, p_hat), psi_07)
def p_exp (sc, t):
psit = psi_t(sc, t)
return np.matmul(np.matmul(np.conj(psit).T, p_hat), psit).real
p_exp(psi, .7)
def x_exp (sc, t):
psit = psi_t(sc, t)
return np.matmul(np.matmul(np.conj(psit).T, x_hat), psit).real
x_exp(psi, np.array(0.7))
t_ = np.linspace(0, 2*math.pi, 100)
xt_ = [x_exp(psi, t) for t in t_]
pt_ = [p_exp(psi, t) for t in t_]
plt.plot(xt_, pt_);
```
Just like in classical mechanics, the expectation values of location and momentum form an elipse (in our case even a perfect circle) in the phase space spun by values of $p$ and $x$.
| true |
code
| 0.757486 | null | null | null | null |
|
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.decomposition import PCA
```
### Generate a dataset
```
xy = np.random.multivariate_normal([0,0], [[10,7],[7,10]],1000)
plt.plot(xy[:,0],xy[:,1],"o")
plt.show()
```
### Create a Principle Component Analysis (PCA) object
What is `n_components`?
```
pca = PCA(n_components=2)
```
`num_components` is the number of axes on which you spread the data out. You can only have as many components as you have axes (2 in this case).
### Fit the axes
What does the following code do?
```
xy_pca = pca.fit(xy)
```
Does the PCA, finding the primary axes of variation.
```
plt.plot(xy[:,0],xy[:,1],"o")
scalar = xy_pca.explained_variance_[0]
plt.plot([0,xy_pca.components_[0,0]*scalar/2],[0,xy_pca.components_[0,1]*scalar/2],color="red")
plt.plot([0,-xy_pca.components_[0,0]*scalar/2],[0,-xy_pca.components_[0,1]*scalar/2],color="red")
scalar = xy_pca.explained_variance_[1]
plt.plot([0,xy_pca.components_[1,0]*scalar/2],[0,xy_pca.components_[1,1]*scalar/2],color="yellow")
plt.plot([0,-xy_pca.components_[1,0]*scalar/2],[0,-xy_pca.components_[1,1]*scalar/2],color="yellow")
```
### What does the following do?
```
xy_trans = xy_pca.transform(xy)
```
Transforms `x` and `y` onto the PCA axes.
```
fig, ax = plt.subplots(1,2,figsize=(10,5))
ax[0].plot(xy[:,0],xy[:,1],"o")
ax[0].set_xlabel("x")
ax[0].set_ylabel("y")
ax[0].set_xlim((-15,15)); ax[0].set_ylim((-15,15))
ax[1].plot(xy_trans[:,0],xy_trans[:,1],"o")
ax[1].set_xlabel("PCA1")
ax[1].set_ylabel("PCA2")
ax[1].set_xlim((-15,15)); ax[1].set_ylim((-15,15))
plt.show()
```
### What does the following do?
```
print("Variation explained:")
print("First component: {:.3f}".format(xy_pca.explained_variance_ratio_[0]))
print("Second component: {:.3f}".format(xy_pca.explained_variance_ratio_[1]))
```
Describes how much variation each PCA axis captures.
Informally: if you only included the first component in a predictive model, the $R^{2}$ between you prediction and reality would be 0.85.
### Some helper code, which takes an xy_pair and does all of the steps above.
```
def pca_wrapper(xy_pairs):
"""
Take an array of x/y data and perform a principle component analysis.
"""
fig, ax = plt.subplots(1,2,figsize=(10,5))
ax[0].plot(xy_pairs[:,0],xy_pairs[:,1],"o")
ax[0].set_xlim((-18,18))
ax[0].set_ylim((-18,18))
ax[0].set_title("raw x,y data")
ax[0].set_xlabel("x")
ax[0].set_ylabel("y")
# Perform the PCA fit
pca = PCA(n_components=2)
z = pca.fit(xy_pairs)
# Transforom the data onto the new PCA axes
new_xy_pairs = z.transform(xy_pairs)
# Plot the PCA data
ax[1].plot(new_xy_pairs[:,0],new_xy_pairs[:,1],"o")
ax[1].set_title("PCA transformed data")
ax[1].set_xlim((-18,18))
ax[1].set_ylim((-18,18))
ax[1].set_xlabel("PCA1")
ax[1].set_ylabel("PCA2")
print("Variation explained:")
print("First component: {:.3f}".format(pca.explained_variance_ratio_[0]))
print("Second component: {:.3f}".format(pca.explained_variance_ratio_[1]))
```
### How does fraction variation relate to skew in the data?
```
d1 = np.random.multivariate_normal([0,0], [[10,1],[1,10]],1000)
pca_wrapper(d1)
d2 = np.random.multivariate_normal([0,0], [[10,5],[5,10]],1000)
pca_wrapper(d2)
d3 = np.random.multivariate_normal([0,0], [[10,9],[9,10]],1000)
pca_wrapper(d3)
```
The stronger the covariation between parameters, the more readily the PCA can reduce dimensionality.
### Using PCA to try to classify things
### The "Iris" dataset
<img style="margin:auto" align="center" src="https://www.math.umd.edu/~petersd/666/html/iris_with_labels.jpg" />
+ Three species of iris
+ Four properties measured for many representatives from each species
+ Properties are: sepal length, sepal width, petal length, petal width
### Load in the data
```
iris = datasets.load_iris()
obs = iris.data
species = iris.target
mean = obs.mean(axis=0)
std = obs.std(axis=0)
obs = (obs - mean)/std
```
The mean, standard deviation business normalizes the data so the values are all on the same scale.
```
def plot_slice(obs_r,axis_i,axis_j):
"""
Define a helper function.
"""
plt.plot(obs_r[species == 0,axis_i],obs_r[species == 0,axis_j],"o",color='navy')
plt.plot(obs_r[species == 1,axis_i],obs_r[species == 1,axis_j],"o",color='turquoise')
plt.plot(obs_r[species == 2,axis_i],obs_r[species == 2,axis_j],"o",color='darkorange')
plt.xlabel(axis_i)
plt.ylabel(axis_j)
plt.show()
```
### Species separate on some axes, but not all axes
```
plot_slice(obs,axis_i=0,axis_j=1)
```
### Do PCA
```
pca = PCA(n_components=4)
obs_pca = pca.fit(obs)
obs_trans = obs_pca.transform(obs)
```
### What is different about PCA axes?
```
plot_slice(obs_trans,axis_i=0,axis_j=1)
```
All of that separating power is jammed into the first axis.
### Quantify this with explained varience ratio:
```
for r in obs_pca.explained_variance_ratio_:
print("{:.3f}".format(r))
```
### Summary
+ PCA is a way to spread data out on "natural" axes
+ Clusters in PCA space can be used to classify things
+ Axes may be hard to interpret directly
| true |
code
| 0.694426 | null | null | null | null |
|
# Counterfactual explanations with ordinally encoded categorical variables
This example notebook illustrates how to obtain [counterfactual explanations](https://docs.seldon.io/projects/alibi/en/latest/methods/CFProto.html) for instances with a mixture of ordinally encoded categorical and numerical variables. A more elaborate notebook highlighting additional functionality can be found [here](./cfproto_cat_adult_ohe.ipynb). We generate counterfactuals for instances in the *adult* dataset where we predict whether a person's income is above or below $50k.
```
import tensorflow as tf
tf.get_logger().setLevel(40) # suppress deprecation messages
tf.compat.v1.disable_v2_behavior() # disable TF2 behaviour as alibi code still relies on TF1 constructs
from tensorflow.keras.layers import Dense, Input, Embedding, Concatenate, Reshape, Dropout, Lambda
from tensorflow.keras.models import Model
from tensorflow.keras.utils import to_categorical
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import os
from sklearn.preprocessing import OneHotEncoder
from time import time
from alibi.datasets import fetch_adult
from alibi.explainers import CounterfactualProto
print('TF version: ', tf.__version__)
print('Eager execution enabled: ', tf.executing_eagerly()) # False
```
## Load adult dataset
The `fetch_adult` function returns a `Bunch` object containing the features, the targets, the feature names and a mapping of the categories in each categorical variable.
```
adult = fetch_adult()
data = adult.data
target = adult.target
feature_names = adult.feature_names
category_map_tmp = adult.category_map
target_names = adult.target_names
```
Define shuffled training and test set:
```
def set_seed(s=0):
np.random.seed(s)
tf.random.set_seed(s)
set_seed()
data_perm = np.random.permutation(np.c_[data, target])
X = data_perm[:,:-1]
y = data_perm[:,-1]
idx = 30000
y_train, y_test = y[:idx], y[idx+1:]
```
Reorganize data so categorical features come first:
```
X = np.c_[X[:, 1:8], X[:, 11], X[:, 0], X[:, 8:11]]
```
Adjust `feature_names` and `category_map` as well:
```
feature_names = feature_names[1:8] + feature_names[11:12] + feature_names[0:1] + feature_names[8:11]
print(feature_names)
category_map = {}
for i, (_, v) in enumerate(category_map_tmp.items()):
category_map[i] = v
```
Create a dictionary with as keys the categorical columns and values the number of categories for each variable in the dataset. This dictionary will later be used in the counterfactual explanation.
```
cat_vars_ord = {}
n_categories = len(list(category_map.keys()))
for i in range(n_categories):
cat_vars_ord[i] = len(np.unique(X[:, i]))
print(cat_vars_ord)
```
## Preprocess data
Scale numerical features between -1 and 1:
```
X_num = X[:, -4:].astype(np.float32, copy=False)
xmin, xmax = X_num.min(axis=0), X_num.max(axis=0)
rng = (-1., 1.)
X_num_scaled = (X_num - xmin) / (xmax - xmin) * (rng[1] - rng[0]) + rng[0]
X_num_scaled_train = X_num_scaled[:idx, :]
X_num_scaled_test = X_num_scaled[idx+1:, :]
```
Combine numerical and categorical data:
```
X = np.c_[X[:, :-4], X_num_scaled].astype(np.float32, copy=False)
X_train, X_test = X[:idx, :], X[idx+1:, :]
print(X_train.shape, X_test.shape)
```
## Train a neural net
The neural net will use entity embeddings for the categorical variables.
```
def nn_ord():
x_in = Input(shape=(12,))
layers_in = []
# embedding layers
for i, (_, v) in enumerate(cat_vars_ord.items()):
emb_in = Lambda(lambda x: x[:, i:i+1])(x_in)
emb_dim = int(max(min(np.ceil(.5 * v), 50), 2))
emb_layer = Embedding(input_dim=v+1, output_dim=emb_dim, input_length=1)(emb_in)
emb_layer = Reshape(target_shape=(emb_dim,))(emb_layer)
layers_in.append(emb_layer)
# numerical layers
num_in = Lambda(lambda x: x[:, -4:])(x_in)
num_layer = Dense(16)(num_in)
layers_in.append(num_layer)
# combine
x = Concatenate()(layers_in)
x = Dense(60, activation='relu')(x)
x = Dropout(.2)(x)
x = Dense(60, activation='relu')(x)
x = Dropout(.2)(x)
x = Dense(60, activation='relu')(x)
x = Dropout(.2)(x)
x_out = Dense(2, activation='softmax')(x)
nn = Model(inputs=x_in, outputs=x_out)
nn.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
return nn
set_seed()
nn = nn_ord()
nn.summary()
nn.fit(X_train, to_categorical(y_train), batch_size=128, epochs=30, verbose=0)
```
## Generate counterfactual
Original instance:
```
X = X_test[0].reshape((1,) + X_test[0].shape)
```
Initialize counterfactual parameters:
```
shape = X.shape
beta = .01
c_init = 1.
c_steps = 5
max_iterations = 500
rng = (-1., 1.) # scale features between -1 and 1
rng_shape = (1,) + data.shape[1:]
feature_range = ((np.ones(rng_shape) * rng[0]).astype(np.float32),
(np.ones(rng_shape) * rng[1]).astype(np.float32))
```
Initialize explainer. Since the `Embedding` layers in `tf.keras` do not let gradients propagate through, we will only make use of the model's predict function, treat it as a black box and perform numerical gradient calculations.
```
set_seed()
# define predict function
predict_fn = lambda x: nn.predict(x)
cf = CounterfactualProto(predict_fn,
shape,
beta=beta,
cat_vars=cat_vars_ord,
max_iterations=max_iterations,
feature_range=feature_range,
c_init=c_init,
c_steps=c_steps,
eps=(.01, .01) # perturbation size for numerical gradients
)
```
Fit explainer. Please check the [documentation](https://docs.seldon.io/projects/alibi/en/latest/methods/CFProto.html) for more info about the optional arguments.
```
cf.fit(X_train, d_type='abdm', disc_perc=[25, 50, 75]);
```
Explain instance:
```
set_seed()
explanation = cf.explain(X)
```
Helper function to more clearly describe explanations:
```
def describe_instance(X, explanation, eps=1e-2):
print('Original instance: {} -- proba: {}'.format(target_names[explanation.orig_class],
explanation.orig_proba[0]))
print('Counterfactual instance: {} -- proba: {}'.format(target_names[explanation.cf['class']],
explanation.cf['proba'][0]))
print('\nCounterfactual perturbations...')
print('\nCategorical:')
X_orig_ord = X
X_cf_ord = explanation.cf['X']
delta_cat = {}
for i, (_, v) in enumerate(category_map.items()):
cat_orig = v[int(X_orig_ord[0, i])]
cat_cf = v[int(X_cf_ord[0, i])]
if cat_orig != cat_cf:
delta_cat[feature_names[i]] = [cat_orig, cat_cf]
if delta_cat:
for k, v in delta_cat.items():
print('{}: {} --> {}'.format(k, v[0], v[1]))
print('\nNumerical:')
delta_num = X_cf_ord[0, -4:] - X_orig_ord[0, -4:]
n_keys = len(list(cat_vars_ord.keys()))
for i in range(delta_num.shape[0]):
if np.abs(delta_num[i]) > eps:
print('{}: {:.2f} --> {:.2f}'.format(feature_names[i+n_keys],
X_orig_ord[0,i+n_keys],
X_cf_ord[0,i+n_keys]))
describe_instance(X, explanation)
```
The person's incomce is predicted to be above $50k by increasing his or her capital gain.
| true |
code
| 0.476275 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/arjunparmar/VIRTUON/blob/main/Harshit/SwapNet_Experimentation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
## Imports
import os
import sys
import random
import numpy as np
import cv2
import matplotlib.pyplot as plt
from glob import glob
import tensorflow
from tensorflow import keras
from tensorflow.python.keras import backend as K
from tensorflow.python.keras.preprocessing import image
from tensorflow.python.keras.preprocessing.image import ImageDataGenerator
from tensorflow.python.keras.layers import concatenate, Concatenate
## Seeding
seed = 2019
random.seed = seed
np.random.seed = seed
tensorflow.seed = seed
def load_image(img_path, show=False):
img = cv2.imread(img_path)
img = cv2.resize(img, (128,128))
img_tensor = image.img_to_array(img) # (height, width, channels)
#|img_tensor = np.expand_dims(img_tensor, axis=0) # (1, height, width, channels), add a dimension because the model expects this shape: (batch_size, height, width, channels) # imshow expects values in the range [0, 1]
return img_tensor
!mkdir seg_train
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/seg_train/* /content/seg_train/
!mkdir seg_test
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/seg_test/* /content/seg_test/
!mkdir pos_train
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/pose_train/* /content/pos_train/
!mkdir pos_test
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/pose_test/* /content/pos_test/
x = []
y = []
def get_image(path):
data =[]
for subdir, dirs, files in os.walk(path):
for f in files:
path = os.path.join(subdir, f)
img = load_image(path)
# print(img.shape)
data.append(img)
return data
x_1 = get_image(r'/content/pos_train') #BS
x_2 = get_image(r'/content/seg_train') #CS
y = get_image(r'/content/seg_train')
x_1 = np.asarray(x_1)
x_2 = np.asarray(x_2)
y = np.asarray(y)
print(x_1.shape)
print(x_2.shape)
print(y.shape)
def down_block(x, filters, kernel_size=(3, 3), padding="same", strides=1):
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(x)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
p = keras.layers.MaxPool2D((2, 2), (2, 2))(c)
return c, p
def up_block(x, skip, filters, kernel_size=(3, 3), padding="same", strides=1):
us = keras.layers.UpSampling2D((2, 2))(x)
concat = keras.layers.Concatenate()([us, skip])
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(concat)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
return c
def bottleneck(x, filters, kernel_size=(3, 3), padding="same", strides=1):
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(x)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
return c
def res_block(u3):
c1 = keras.layers.Conv2D(64, kernel_size= (3,3), padding="same", strides=1, activation="relu")(u3)
c2 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c1)
c3 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c2)
c3 = keras.layers.Concatenate()([u3, c3])
c4 = keras.layers.Conv2D(64, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c3)
c5 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c4)
c6 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c5)
c6 = keras.layers.Concatenate()([u3, c3, c6])
c7 = keras.layers.Conv2D(64, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c6)
c8 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c7)
c9 = keras.layers.Conv2D(16, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c8)
return c9
K.clear_session()
def UNet():
f = [16, 32, 64, 128, 256]
inputs1 = keras.layers.Input((128,128, 3))
inputs2 = keras.layers.Input((128,128, 3))
p0 = inputs1
c1, p1 = down_block(p0, f[0]) #128 -> 64
c2, p2 = down_block(p1, f[1]) #64 -> 32
c3, p3 = down_block(p2, f[2]) #32 -> 16
bn1 = bottleneck(p3, f[3])
print(bn1.shape)
inputs2 = keras.layers.Input((128,128, 3))
np0 = inputs2
nc1, np1 = down_block(np0, f[0]) #128 -> 64
nc2, np2 = down_block(np1, f[1]) #64 -> 32
nc3, np3 = down_block(np2, f[2]) #32 -> 16
bn2 = bottleneck(np3, f[3])
print(bn2.shape)
bn = keras.layers.Concatenate()([bn1, bn2])
print(bn.shape)
u1 = up_block(bn, nc3, f[2]) #16 -> 32
u2 = up_block(u1, nc2, f[1]) #32 -> 64
u3 = up_block(u2, nc1, f[0]) #64 -> 128
print(u3.shape)
#apply resblocks
res = res_block(u3)
outputs = keras.layers.Conv2D(3, (1, 1), padding="same", activation="sigmoid")(res)
model = keras.models.Model([inputs1, inputs2], outputs)
return model
model = UNet()
model.compile(optimizer="adam", loss="categorical_crossentropy", metrics=["acc"])
model.summary()
#Data augmentation to generate new data from the given data at the time of each batch
# construct the training image generator for data augmentation
batch_size = 32
aug = ImageDataGenerator(rotation_range=20)
# train the network
model.fit_generator(aug.flow([x_1, x_2], y, batch_size=batch_size), steps_per_epoch=len(x_1) // batch_size, epochs=100)
def plot(img):
plt.imshow(img)
plt.axis('off')
plt.show()
p1 = r'/content/pos_test/0.jpg'
img1= cv2.imread(p1)
plot(img1)
p2 = r'/content/seg_test/0.jpg'
img2= cv2.imread(p2)
plot(img2)
img1 = load_image(p1)
img2 = load_image(p2)
print(img1.shape)
print(img2.shape)
img1 = np.expand_dims(img1, axis = 0)
img2 = np.expand_dims(img2, axis = 0)
result = model.predict([img1, img2])
# result = np.resize(result, (128,128,3))
result.shape
result = np.squeeze(result)
plt.imshow(result)
```
| true |
code
| 0.614278 | null | null | null | null |
|
<table style="float:left; border:none">
<tr style="border:none">
<td style="border:none">
<a href="https://bokeh.org/">
<img
src="assets/bokeh-transparent.png"
style="width:50px"
>
</a>
</td>
<td style="border:none">
<h1>Bokeh Tutorial</h1>
</td>
</tr>
</table>
<div style="float:right;"><h2>08. Graph and Network Plots</h2></div>
This chapter will cover how to plot network node/link graphs in Bokeh using NetworkX. For information on creating graph renderers from a low level, see [Visualizing Network Graphs](https://docs.bokeh.org/en/latest/docs/user_guide/graph.html)
```
from bokeh.io import show, output_notebook
from bokeh.plotting import figure
output_notebook()
```
## Plotting from NetworkX
The easiest way to plot network graphs with Bokeh is to use the `from_networkx` function. This function accepts any NetworkX graph and returns a Bokeh `GraphRenderer` that can be added to a plot. The `GraphRenderer` has `node_renderer` and `edge_renderer` properties that contain the Bokeh renderers that draw the nodes and edges, respectively.
The example below shows a Bokeh plot of `nx.desargues_graph()`, setting some of the node and edge properties.
```
import networkx as nx
from bokeh.models import Range1d, Plot
from bokeh.plotting import from_networkx
G = nx.desargues_graph()
# We could use figure here but don't want all the axes and titles
plot = Plot(x_range=Range1d(-2, 2), y_range=Range1d(-2, 2))
# Create a Bokeh graph from the NetworkX input using nx.spring_layout
graph = from_networkx(G, nx.spring_layout, scale=1.8, center=(0,0))
plot.renderers.append(graph)
# Set some of the default node glyph (Circle) properties
graph.node_renderer.glyph.update(size=20, fill_color="orange")
# Set some edge properties too
graph.edge_renderer.glyph.line_dash = [2,2]
show(plot)
# Exercise: try a different NetworkX layout, and set some properies on `graph.edge_renderer.glyph`
# and `graph.node_renderer.glyph`
```
## Adding Extra Data Columns.
The `node_renderer` and `edge_renderer` properties of the graph renderer each have a `data_source` that is a standard `ColumnDataSource` that you can add new data to, e.g. to drive a hover tool, or to specify colors for the renderer. The example below demonstates both.
```
from bokeh.models import HoverTool
from bokeh.palettes import Category20_20
G = nx.desargues_graph() # always 20 nodes
# We could use figure here but don't want all the axes and titles
plot = Plot(x_range=Range1d(-2, 2), y_range=Range1d(-2, 2))
# Create a Bokeh graph from the NetworkX input using nx.spring_layout
graph = from_networkx(G, nx.spring_layout, scale=1.8, center=(0,0))
plot.renderers.append(graph)
# Add some new columns to the node renderer data source
graph.node_renderer.data_source.data['index'] = list(range(len(G)))
graph.node_renderer.data_source.data['colors'] = Category20_20
graph.node_renderer.glyph.update(size=20, fill_color="colors")
plot.add_tools(HoverTool(tooltips="index: @index"))
show(plot)
# Exercise: Add your own columns for other node or edge properties e.g. fill_alpha or line_color,
# or to show other fields in a tooltoip
```
## Inspection and Selection Policies
Bokeh graph renderers have `inspection_policy` and `selection_policy` properties. These can be used to control how hover inspections highlight the graph, or how selection tools make selections. These properties may be set to any of the inpection policies in `bokeh.graphs`. For instance, if a user hovers over a node, you may wish to highlight all the associated edges as well. This can be accomplished by setting the inspection policy:
graph.inspection_policy = NodesAndLinkedEdges()
as the example below demonstrates.
```
from bokeh.models.graphs import NodesAndLinkedEdges
from bokeh.models import Circle, HoverTool, MultiLine
G = nx.gnm_random_graph(15, 30)
# We could use figure here but don't want all the axes and titles
plot = Plot(x_range=Range1d(-2, 2), y_range=Range1d(-2 ,2))
# Create a Bokeh graph from the NetworkX input using nx.spring_layout
graph = from_networkx(G, nx.spring_layout, scale=1.8, center=(0,0))
plot.renderers.append(graph)
# Blue circles for nodes, and light grey lines for edges
graph.node_renderer.glyph = Circle(size=25, fill_color='#2b83ba')
graph.edge_renderer.glyph = MultiLine(line_color="#cccccc", line_alpha=0.8, line_width=2)
# green hover for both nodes and edges
graph.node_renderer.hover_glyph = Circle(size=25, fill_color='#abdda4')
graph.edge_renderer.hover_glyph = MultiLine(line_color='#abdda4', line_width=4)
# When we hover over nodes, highlight adjecent edges too
graph.inspection_policy = NodesAndLinkedEdges()
plot.add_tools(HoverTool(tooltips=None))
show(plot)
# Exercise: try a different inspection (or selection) policy like NodesOnly or EdgesAndLinkedNodes
```
# Next Section
Click on this link to go to the next notebook: [09 - Geographic Plots](09%20-%20Geographic%20Plots.ipynb).
To go back to the overview, click [here](00%20-%20Introduction%20and%20Setup.ipynb).
| true |
code
| 0.654398 | null | null | null | null |
|
# Overlap matrices
This notebook will look at different ways of plotting overlap matrices and making them visually appealing.
One way to guarantee right color choices for color blind poeple is using this tool: https://davidmathlogic.com/colorblind
```
%pylab inline
import pandas as pd
import seaborn as sbn
sbn.set_style("ticks")
sbn.set_context("notebook", font_scale = 1.5)
data = np.loadtxt('raw_matrices_review.dat')
good = (data[:9][:])
bad = data[-9:][:]
ugly = data[9:18][:]
# Your Standard plot
fig =figsize(8,8)
ax = sbn.heatmap(bad,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=sbn.light_palette((210, 90, 60), input="husl") )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
# Changing the colour map
from matplotlib import colors
from matplotlib.colors import LogNorm
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#117733','#88CCEE', '#FBE8EB'])
bounds=[0.0, 0.025, 0.1, 0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[0.2, 0.4, 0.6, 0.8 ,1.0])
#ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=0, linecolor='white', annot_kws={"size": 14},square=True,robust=True,cmap='bone_r', vmin=0, vmax=1 )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
for _, spine in ax.spines.items():
spine.set_visible(True)
show_annot_array = ugly >= 0.0001
for text, show_annot in zip(ax.texts, (element for row in show_annot_array for element in row)):
text.set_visible(show_annot)
# Changing the colour map
from matplotlib import colors
from matplotlib.colors import LogNorm
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#117733','#88CCEE', '#FBE8EB'])
bounds=[0.0, 0.025, 0.1, 0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[0.2, 0.4, 0.6, 0.8 ,1.0])
#ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax = sbn.heatmap(good,annot=True, fmt='.2f', linewidths=0, linecolor='black', annot_kws={"size": 14},square=True,robust=True,cmap='bone_r',vmin=0, vmax=1 )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
for _, spine in ax.spines.items():
spine.set_visible(True)
show_annot_array = good >= 0.001
for text, show_annot in zip(ax.texts, (element for row in show_annot_array for element in row)):
text.set_visible(show_annot)
# Changing the colour map
from matplotlib import colors
from matplotlib.colors import LogNorm
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#117733','#88CCEE', '#FBE8EB'])
bounds=[0.0, 0.025, 0.1, 0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[0.2, 0.4, 0.6, 0.8 ,1.0])
#ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax = sbn.heatmap(bad,annot=True, fmt='.2f', linewidths=0, linecolor='black', annot_kws={"size": 14},square=True,robust=True,cmap='bone_r',vmin=0, vmax=1 )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
for _, spine in ax.spines.items():
spine.set_visible(True)
show_annot_array = bad >= 0.01
for text, show_annot in zip(ax.texts, (element for row in show_annot_array for element in row)):
text.set_visible(show_annot)
# Changing the colour map
from matplotlib import colors
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
bounds=[0.0, 0.025, 0.1, 0.3,0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[.025, .1, .3,0.8])
ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
bounds=[0.0, 0.025, 0.1, 0.3,0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[.025, .1, .3,0.8])
ax = sbn.heatmap(bad,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm, cbar_kws=cbar_kws )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
bounds=[0.0, 0.025, 0.1, 0.3,0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[.025, .1, .3,0.8])
ax = sbn.heatmap(good,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True, cmap=cmap, norm=norm,vmin=0,vmax=1,cbar_kws=cbar_kws )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
cbar_kws={'ticks': '[0.0, 0.2, 0.4, 0.6, 0.8, 1.0]'}
# Playing with pandas and getting more exotic
df = pd.DataFrame(bad, columns=["1","2","3","4","5","6","7","8","9"])
#https://towardsdatascience.com/better-heatmaps-and-correlation-matrix-plots-in-python-41445d0f2bec
def heatmap(x, y, x1,y1, **kwargs):
if 'color' in kwargs:
color = kwargs['color']
else:
color = [1]*len(x)
if 'palette' in kwargs:
palette = kwargs['palette']
n_colors = len(palette)
else:
n_colors = 256 # Use 256 colors for the diverging color palette
palette = sbn.color_palette("Blues", n_colors)
if 'color_range' in kwargs:
color_min, color_max = kwargs['color_range']
else:
color_min, color_max = min(color), max(color) # Range of values that will be mapped to the palette, i.e. min and max possible correlation
def value_to_color(val):
if color_min == color_max:
return palette[-1]
else:
val_position = float((val - color_min)) / (color_max - color_min) # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
ind = int(val_position * (n_colors - 1)) # target index in the color palette
return palette[ind]
if 'size' in kwargs:
size = kwargs['size']
else:
size = [1]*len(x)
if 'size_range' in kwargs:
size_min, size_max = kwargs['size_range'][0], kwargs['size_range'][1]
else:
size_min, size_max = min(size), max(size)
size_scale = kwargs.get('size_scale', 500)
def value_to_size(val):
if size_min == size_max:
return 1 * size_scale
else:
val_position = (val - size_min) * 0.99 / (size_max - size_min) + 0.01 # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
return val_position * size_scale
if 'x_order' in kwargs:
x_names = [t for t in kwargs['x_order']]
else:
x_names = [t for t in sorted(set([v for v in x]))]
x_to_num = {p[1]:p[0] for p in enumerate(x_names)}
if 'y_order' in kwargs:
y_names = [t for t in kwargs['y_order']]
else:
y_names = [t for t in sorted(set([v for v in y]))]
y_to_num = {p[1]:p[0] for p in enumerate(y_names)}
plot_grid = plt.GridSpec(1, 15, hspace=0.2, wspace=0.1) # Setup a 1x10 grid
ax = plt.subplot(plot_grid[:,:-1]) # Use the left 14/15ths of the grid for the main plot
marker = kwargs.get('marker', 's')
kwargs_pass_on = {k:v for k,v in kwargs.items() if k not in [
'color', 'palette', 'color_range', 'size', 'size_range', 'size_scale', 'marker', 'x_order', 'y_order'
]}
print(x_names)
print(y_names)
print('here------------')
ax.scatter(
x=x1,
y=y1,
marker=marker,
s=[value_to_size(v) for v in size],
c=[value_to_color(v) for v in color],
**kwargs_pass_on
)
ax.set_xticks([v for k,v in x_to_num.items()])
ax.set_xticklabels([k for k in x_to_num], rotation=45, horizontalalignment='right')
ax.set_yticks([v for k,v in y_to_num.items()])
ax.set_yticklabels([k for k in y_to_num])
ax.grid(False, 'major')
ax.grid(True, 'minor')
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
ax.set_xlim([-0.5, max([v for v in x_to_num.values()]) + 0.5])
ax.set_ylim([-0.5, max([v for v in y_to_num.values()]) + 0.5])
ax.set_facecolor('#F1F1F1')
# Add color legend on the right side of the plot
if color_min < color_max:
ax = plt.subplot(plot_grid[:,-1]) # Use the rightmost column of the plot
col_x = [0]*len(palette) # Fixed x coordinate for the bars
bar_y=np.linspace(color_min, color_max, n_colors) # y coordinates for each of the n_colors bars
bar_height = bar_y[1] - bar_y[0]
ax.barh(
y=bar_y,
width=[5]*len(palette), # Make bars 5 units wide
left=col_x, # Make bars start at 0
height=bar_height,
color=palette,
linewidth=0
)
ax.set_xlim(1, 2) # Bars are going from 0 to 5, so lets crop the plot somewhere in the middle
ax.grid(False) # Hide grid
ax.set_facecolor('white') # Make background white
ax.set_xticks([]) # Remove horizontal ticks
ax.set_yticks(np.linspace(min(bar_y), max(bar_y), 3)) # Show vertical ticks for min, middle and max
ax.yaxis.tick_right() # Show vertical ticks on the right
def corrplot(data, size_scale=500, marker='s'):
corr = pd.melt(data.reset_index(), id_vars='index')
print(corr)
corr.columns = ['index', 'variable', 'value']
x_names = [t for t in sorted(set([v for v in corr['index']]))]
x_to_num = {p[1]:p[0] for p in enumerate(x_names)}
x=[x_to_num[v] for v in corr['index']]
y_names = [t for t in sorted(set([v for v in corr['index']]))]
y_to_num = {p[1]:p[0] for p in enumerate(y_names)}
y=[y_to_num[v] for v in corr['index']]
heatmap(
corr['index'], corr['value'],x1,y1,
color=corr['value'], color_range=[0, 1],
palette=sbn.diverging_palette(20, 220, n=256),
size=corr['value'].abs(), size_range=[0,1],
marker=marker,
x_order=data.columns,
y_order=data.columns[::-1],
size_scale=size_scale
)
corrplot(df)
corr = pd.melt(df.reset_index(), id_vars='index')
print(corr)
x_names = [t for t in sorted(set([v for v in corr['index']]))]
x_to_num = {p[1]:p[0] for p in enumerate(x_names)}
x1=[x_to_num[v] for v in corr['index']]
y_names = [t for t in sorted(set([v for v in corr['variable']]))]
y_to_num = {p[1]:p[0] for p in enumerate(y_names)}
y1=[y_to_num[v] for v in corr['variable']]
def value_to_size(val):
if size_min == size_max:
return 1 * size_scale
else:
val_position = (val - size_min) * 0.99 / (size_max - size_min) + 0.01 # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
return val_position * size_scale
value_names = [t for t in sorted(set([v for v in corr['value']]))]
value = []
for v in corr['value']:
value.append(v)
for v in corr['value']:
print (v)
n_colors = 256 # Use 256 colors for the diverging color palette
palette = sbn.cubehelix_palette(n_colors)
mapping = linspace(0,1,256)
c_index = np.digitize(value, mapping)
plot_colors =[]
for i in c_index:
plot_colors.append(palette[i])
s =np.array(value)*4000
fig = figsize(10,10)
plot_grid = plt.GridSpec(1, 15, hspace=0.2, wspace=0.1) # Setup a 1x10 grid
ax = plt.subplot(plot_grid[:,:-1]) # Use the left 14/15ths of the grid for the main plot
ax.scatter(x1,y1,marker='s',s=s,c=plot_colors)
sbn.despine()
ax.grid(False, 'major')
ax.grid(True, 'minor', color='white')
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
ax.set_xlim([-0.5, max([v for v in x_to_num.values()]) + 0.5])
ax.set_ylim([-0.5, max([v for v in y_to_num.values()]) + 0.5])
ax.set_facecolor((0,0,0))
plt.gca().invert_yaxis()
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
xlabel(r'$\lambda$ index')
ylabel(r'$\lambda$ index')
def value_to_size(val, vlaue):
size_scale = 500
size = [1]*len(value)
size_min, size_max = min(size), max(size)
if size_min == size_max:
return 1 * size_scale
else:
val_position = (val - size_min) * 0.99 / (size_max - size_min) + 0.01 # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
return val_position * size_scale
heatmap2
value_to_size(value[5], value)
from biokit.viz import corrplot
c = corrplot.Corrplot(df)
c.plot()
def plot(index, columns):
values = "bad_status"
vmax = 0.10
cellsize_vmax = 10000
g_ratio = df.pivot_table(index=index, columns=columns, values=values, aggfunc="mean")
g_size = df.pivot_table(index=index, columns=columns, values=values, aggfunc="size")
annot = np.vectorize(lambda x: "" if np.isnan(x) else "{:.1f}%".format(x * 100))(g_ratio)
# adjust visual balance
figsize = (g_ratio.shape[1] * 0.8, g_ratio.shape[0] * 0.8)
cbar_width = 0.05 * 6.0 / figsize[0]
f, ax = plt.subplots(1, 1, figsize=figsize)
cbar_ax = f.add_axes([.91, 0.1, cbar_width, 0.8])
heatmap2(g_ratio, ax=ax, cbar_ax=cbar_ax,
vmax=vmax, cmap="PuRd", annot=annot, fmt="s", annot_kws={"fontsize":"small"},
cellsize=g_size, cellsize_vmax=cellsize_vmax,
square=True, ax_kws={"title": "{} x {}".format(index, columns)})
plt.show()
"""
This script is created by modifying seaborn matrix.py
in https://github.com/mwaskom/seaborn, by Michael L. Waskom
"""
from __future__ import division
import itertools
import matplotlib as mpl
from matplotlib.collections import LineCollection
import matplotlib.pyplot as plt
from matplotlib import gridspec
import matplotlib.patheffects as patheffects
import numpy as np
import pandas as pd
from scipy.cluster import hierarchy
import seaborn as sns
from seaborn import cm
from seaborn.axisgrid import Grid
from seaborn.utils import (despine, axis_ticklabels_overlap, relative_luminance, to_utf8)
from seaborn.external.six import string_types
def _index_to_label(index):
"""Convert a pandas index or multiindex to an axis label."""
if isinstance(index, pd.MultiIndex):
return "-".join(map(to_utf8, index.names))
else:
return index.name
def _index_to_ticklabels(index):
"""Convert a pandas index or multiindex into ticklabels."""
if isinstance(index, pd.MultiIndex):
return ["-".join(map(to_utf8, i)) for i in index.values]
else:
return index.values
def _matrix_mask(data, mask):
"""Ensure that data and mask are compatabile and add missing values.
Values will be plotted for cells where ``mask`` is ``False``.
``data`` is expected to be a DataFrame; ``mask`` can be an array or
a DataFrame.
"""
if mask is None:
mask = np.zeros(data.shape, np.bool)
if isinstance(mask, np.ndarray):
# For array masks, ensure that shape matches data then convert
if mask.shape != data.shape:
raise ValueError("Mask must have the same shape as data.")
mask = pd.DataFrame(mask,
index=data.index,
columns=data.columns,
dtype=np.bool)
elif isinstance(mask, pd.DataFrame):
# For DataFrame masks, ensure that semantic labels match data
if not mask.index.equals(data.index) \
and mask.columns.equals(data.columns):
err = "Mask must have the same index and columns as data."
raise ValueError(err)
# Add any cells with missing data to the mask
# This works around an issue where `plt.pcolormesh` doesn't represent
# missing data properly
mask = mask | pd.isnull(data)
return mask
class _HeatMapper2(object):
"""Draw a heatmap plot of a matrix with nice labels and colormaps."""
def __init__(self, data, vmin, vmax, cmap, center, robust, annot, fmt,
annot_kws, cellsize, cellsize_vmax,
cbar, cbar_kws,
xticklabels=True, yticklabels=True, mask=None, ax_kws=None, rect_kws=None):
"""Initialize the plotting object."""
# We always want to have a DataFrame with semantic information
# and an ndarray to pass to matplotlib
if isinstance(data, pd.DataFrame):
plot_data = data.values
else:
plot_data = np.asarray(data)
data = pd.DataFrame(plot_data)
# Validate the mask and convet to DataFrame
mask = _matrix_mask(data, mask)
plot_data = np.ma.masked_where(np.asarray(mask), plot_data)
# Get good names for the rows and columns
xtickevery = 1
if isinstance(xticklabels, int):
xtickevery = xticklabels
xticklabels = _index_to_ticklabels(data.columns)
elif xticklabels is True:
xticklabels = _index_to_ticklabels(data.columns)
elif xticklabels is False:
xticklabels = []
ytickevery = 1
if isinstance(yticklabels, int):
ytickevery = yticklabels
yticklabels = _index_to_ticklabels(data.index)
elif yticklabels is True:
yticklabels = _index_to_ticklabels(data.index)
elif yticklabels is False:
yticklabels = []
# Get the positions and used label for the ticks
nx, ny = data.T.shape
if not len(xticklabels):
self.xticks = []
self.xticklabels = []
elif isinstance(xticklabels, string_types) and xticklabels == "auto":
self.xticks = "auto"
self.xticklabels = _index_to_ticklabels(data.columns)
else:
self.xticks, self.xticklabels = self._skip_ticks(xticklabels,
xtickevery)
if not len(yticklabels):
self.yticks = []
self.yticklabels = []
elif isinstance(yticklabels, string_types) and yticklabels == "auto":
self.yticks = "auto"
self.yticklabels = _index_to_ticklabels(data.index)
else:
self.yticks, self.yticklabels = self._skip_ticks(yticklabels,
ytickevery)
# Get good names for the axis labels
xlabel = _index_to_label(data.columns)
ylabel = _index_to_label(data.index)
self.xlabel = xlabel if xlabel is not None else ""
self.ylabel = ylabel if ylabel is not None else ""
# Determine good default values for the colormapping
self._determine_cmap_params(plot_data, vmin, vmax,
cmap, center, robust)
# Determine good default values for cell size
self._determine_cellsize_params(plot_data, cellsize, cellsize_vmax)
# Sort out the annotations
if annot is None:
annot = False
annot_data = None
elif isinstance(annot, bool):
if annot:
annot_data = plot_data
else:
annot_data = None
else:
try:
annot_data = annot.values
except AttributeError:
annot_data = annot
if annot.shape != plot_data.shape:
raise ValueError('Data supplied to "annot" must be the same '
'shape as the data to plot.')
annot = True
# Save other attributes to the object
self.data = data
self.plot_data = plot_data
self.annot = annot
self.annot_data = annot_data
self.fmt = fmt
self.annot_kws = {} if annot_kws is None else annot_kws
#self.annot_kws.setdefault('color', "black")
self.annot_kws.setdefault('ha', "center")
self.annot_kws.setdefault('va', "center")
self.cbar = cbar
self.cbar_kws = {} if cbar_kws is None else cbar_kws
self.cbar_kws.setdefault('ticks', mpl.ticker.MaxNLocator(6))
self.ax_kws = {} if ax_kws is None else ax_kws
self.rect_kws = {} if rect_kws is None else rect_kws
# self.rect_kws.setdefault('edgecolor', "black")
def _determine_cmap_params(self, plot_data, vmin, vmax,
cmap, center, robust):
"""Use some heuristics to set good defaults for colorbar and range."""
calc_data = plot_data.data[~np.isnan(plot_data.data)]
if vmin is None:
vmin = np.percentile(calc_data, 2) if robust else calc_data.min()
if vmax is None:
vmax = np.percentile(calc_data, 98) if robust else calc_data.max()
self.vmin, self.vmax = vmin, vmax
# Choose default colormaps if not provided
if cmap is None:
if center is None:
self.cmap = cm.rocket
else:
self.cmap = cm.icefire
elif isinstance(cmap, string_types):
self.cmap = mpl.cm.get_cmap(cmap)
elif isinstance(cmap, list):
self.cmap = mpl.colors.ListedColormap(cmap)
else:
self.cmap = cmap
# Recenter a divergent colormap
if center is not None:
vrange = max(vmax - center, center - vmin)
normlize = mpl.colors.Normalize(center - vrange, center + vrange)
cmin, cmax = normlize([vmin, vmax])
cc = np.linspace(cmin, cmax, 256)
self.cmap = mpl.colors.ListedColormap(self.cmap(cc))
def _determine_cellsize_params(self, plot_data, cellsize, cellsize_vmax):
if cellsize is None:
self.cellsize = np.ones(plot_data.shape)
self.cellsize_vmax = 1.0
else:
if isinstance(cellsize, pd.DataFrame):
cellsize = cellsize.values
self.cellsize = cellsize
if cellsize_vmax is None:
cellsize_vmax = cellsize.max()
self.cellsize_vmax = cellsize_vmax
def _skip_ticks(self, labels, tickevery):
"""Return ticks and labels at evenly spaced intervals."""
n = len(labels)
if tickevery == 0:
ticks, labels = [], []
elif tickevery == 1:
ticks, labels = np.arange(n) + .5, labels
else:
start, end, step = 0, n, tickevery
ticks = np.arange(start, end, step) + .5
labels = labels[start:end:step]
return ticks, labels
def _auto_ticks(self, ax, labels, axis):
"""Determine ticks and ticklabels that minimize overlap."""
transform = ax.figure.dpi_scale_trans.inverted()
bbox = ax.get_window_extent().transformed(transform)
size = [bbox.width, bbox.height][axis]
axis = [ax.xaxis, ax.yaxis][axis]
tick, = axis.set_ticks([0])
fontsize = tick.label.get_size()
max_ticks = int(size // (fontsize / 72))
if max_ticks < 1:
return [], []
tick_every = len(labels) // max_ticks + 1
tick_every = 1 if tick_every == 0 else tick_every
ticks, labels = self._skip_ticks(labels, tick_every)
return ticks, labels
def plot(self, ax, cax):
"""Draw the heatmap on the provided Axes."""
# Remove all the Axes spines
#despine(ax=ax, left=True, bottom=True)
# Draw the heatmap and annotate
height, width = self.plot_data.shape
xpos, ypos = np.meshgrid(np.arange(width) + .5, np.arange(height) + .5)
data = self.plot_data.data
cellsize = self.cellsize
mask = self.plot_data.mask
if not isinstance(mask, np.ndarray) and not mask:
mask = np.zeros(self.plot_data.shape, np.bool)
annot_data = self.annot_data
if not self.annot:
annot_data = np.zeros(self.plot_data.shape)
# Draw rectangles instead of using pcolormesh
# Might be slower than original heatmap
for x, y, m, val, s, an_val in zip(xpos.flat, ypos.flat, mask.flat, data.flat, cellsize.flat, annot_data.flat):
if not m:
vv = (val - self.vmin) / (self.vmax - self.vmin)
size = np.clip(s / self.cellsize_vmax, 0.1, 1.0)
color = self.cmap(vv)
rect = plt.Rectangle([x - size / 2, y - size / 2], size, size, facecolor=color, **self.rect_kws)
ax.add_patch(rect)
if self.annot:
annotation = ("{:" + self.fmt + "}").format(an_val)
text = ax.text(x, y, annotation, **self.annot_kws)
print(text)
# add edge to text
text_luminance = relative_luminance(text.get_color())
text_edge_color = ".15" if text_luminance > .408 else "w"
text.set_path_effects([mpl.patheffects.withStroke(linewidth=1, foreground=text_edge_color)])
# Set the axis limits
ax.set(xlim=(0, self.data.shape[1]), ylim=(0, self.data.shape[0]))
# Set other attributes
ax.set(**self.ax_kws)
if self.cbar:
norm = mpl.colors.Normalize(vmin=self.vmin, vmax=self.vmax)
scalar_mappable = mpl.cm.ScalarMappable(cmap=self.cmap, norm=norm)
scalar_mappable.set_array(self.plot_data.data)
cb = ax.figure.colorbar(scalar_mappable, cax, ax, **self.cbar_kws)
cb.outline.set_linewidth(0)
# if kws.get('rasterized', False):
# cb.solids.set_rasterized(True)
# Add row and column labels
if isinstance(self.xticks, string_types) and self.xticks == "auto":
xticks, xticklabels = self._auto_ticks(ax, self.xticklabels, 0)
else:
xticks, xticklabels = self.xticks, self.xticklabels
if isinstance(self.yticks, string_types) and self.yticks == "auto":
yticks, yticklabels = self._auto_ticks(ax, self.yticklabels, 1)
else:
yticks, yticklabels = self.yticks, self.yticklabels
ax.set(xticks=xticks, yticks=yticks)
xtl = ax.set_xticklabels(xticklabels)
ytl = ax.set_yticklabels(yticklabels, rotation="vertical")
# Possibly rotate them if they overlap
ax.figure.draw(ax.figure.canvas.get_renderer())
if axis_ticklabels_overlap(xtl):
plt.setp(xtl, rotation="vertical")
if axis_ticklabels_overlap(ytl):
plt.setp(ytl, rotation="horizontal")
# Add the axis labels
ax.set(xlabel=self.xlabel, ylabel=self.ylabel)
# Invert the y axis to show the plot in matrix form
ax.invert_yaxis()
def heatmap2(data, vmin=None, vmax=None, cmap=None, center=None, robust=False,
annot=None, fmt=".2g", annot_kws=None,
cellsize=None, cellsize_vmax=None,
cbar=True, cbar_kws=None, cbar_ax=None,
square=False, xticklabels="auto", yticklabels="auto",
mask=None, ax=None, ax_kws=None, rect_kws=None):
# Initialize the plotter object
plotter = _HeatMapper2(data, vmin, vmax, cmap, center, robust,
annot, fmt, annot_kws,
cellsize, cellsize_vmax,
cbar, cbar_kws, xticklabels,
yticklabels, mask, ax_kws, rect_kws)
# Draw the plot and return the Axes
if ax is None:
ax = plt.gca()
if square:
ax.set_aspect("equal")
# delete grid
ax.grid(False)
plotter.plot(ax, cbar_ax)
return ax
fig =figsize(10,10)
ax = heatmap2(good,annot=True, fmt='.2f',cellsize=np.array(value),cellsize_vmax=1, annot_kws={"size": 13},square=True,robust=True,cmap='PiYG' )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
ax.grid(False, 'major')
ax.grid(True, 'minor', color='black', alpha=0.3)
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
fig =figsize(8,8)
ax = sbn.heatmap(good,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},cmap=sbn.light_palette((210, 90, 60), input="husl") )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
sbn.despine()
ax.grid(False, 'major')
ax.grid(True, 'minor', color='white')
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
text = ax.text(x, y, annotation, **self.annot_kws)
# add edge to text
text_luminance = relative_luminance(text.get_color())
text_edge_color = ".15" if text_luminance > .408 else "w"
text.set_path_effects([mpl.patheffects.withStroke(linewidth=1, foreground=text_edge_color)])
ax.text()
```
| true |
code
| 0.481271 | null | null | null | null |
|
# 5. Statistical Packages in Python for Mathematicians
Statisticians use the following packages in Python:
- Data creation: `random`
- Data analysis/manipulation: `pandas`, `scikit-learn`
- Statistical functions: `scipy.stats`
- Statistical data visualization: `matplotlib`, `seaborn`
- Statistical data exploration: `statsmodels`
## Table of Contents
- Random
- Scipy Statistics
- Seaborn
- Statistical Models
- Python vs. R
Next week? Choose among:
- Machine Learning 2/Deep Learning: `scikit-learn`, `keras`, `tensorflow`
- SAGE
- Other: ___________?
## 5.1 Random
The `random` package implements pseudo-random number generators for various distributions.
```
import random
```
The documentation is available here: https://docs.python.org/3/library/random.html.
```
help(random)
```
Almost all module functions depend on the basic function `random()`, which generates a random float uniformly in the semi-open range `[0.0, 1.0)`. Python uses the Mersenne Twister as the core generator. It produces 53-bit precision floats and has a period of `2**19937-1`. The underlying implementation in C is both fast and threadsafe. The Mersenne Twister is one of the most extensively tested random number generators in existence. However, being completely deterministic, it is not suitable for all purposes, and is completely unsuitable for cryptographic purposes.
```
random.uniform(0,1)
```
For integers, there is uniform selection from a range. For sequences, there is uniform selection of a random element. Let's play a simple game.
```
number = random.choice(range(1,11))
choice = 0
while number != choice:
choice = int(input('Choose a number between 1 and 10 (inclusive): '))
print('Congratulations, you have guessed the right number!')
```
If we used the following line, the number above would be equal to `3`:
```
random.seed(2) # initialize the random number generator
```
We can also use NumPy's random sampling package `numpy.random` (https://docs.scipy.org/doc/numpy-1.15.0/reference/routines.random.html):
```
import numpy as np
np.random.uniform(0,1)
# dir(np.random)
```
With this package, we could immediately create samples drawn from a specific distribution:
```
sample = np.random.normal(0,1,100000)
# sample
import matplotlib.pyplot as plt
plt.hist(sample, bins=50, density=True)
plt.show()
```
## 5.2 Scipy Statistics
This module contains a large number of probability distributions.
```
import scipy.stats
help(scipy.stats)
```
Let's plot some probability density functions of the Gaussian distribution:
```
from scipy.stats import norm
x = np.linspace(-5,5,num=200)
fig = plt.figure(figsize=(12,6))
for mu, s in zip([0.5, 0.5, 0.5], [0.2, 0.5, 0.8]):
plt.plot(x, norm.pdf(x,mu,s), lw=2,
label="$\mu={0:.1f}, s={1:.1f}$".format(mu, s))
plt.fill_between(x, norm.pdf(x, mu, s), alpha = .4)
plt.xlim([-5,5])
plt.legend(loc=0)
plt.ylabel("pdf at $x$")
plt.xlabel("$x$")
plt.show()
```
Let's create an interactive plot of the Gamma distribution:
```
%%capture
from ipywidgets import interactive
from scipy.stats import gamma
x = np.arange(0, 40, 0.005)
shape, scale = 5, 0.5
fig, ax = plt.subplots()
y = gamma.pdf(x, shape, scale=scale)
line = ax.plot(x, y)
ax.set_ylim((0,0.5))
def gamma_update(shape, scale):
y = gamma.pdf(x, shape, scale=scale)
line[0].set_ydata(y)
fig.canvas.draw()
display(fig)
interactive(gamma_update, shape=(0.1, 10.0), scale=(0.3, 3.0))
```
## 5.3 Seaborn
Seaborn is a Python data visualization library based on `matplotlib`. It is the equivalent to `R`'s package `ggplot2` and provides a high-level interface for drawing attractive and informative statistical graphics.
```
import seaborn as sns
```
We will create some basic `seaborn` plots. A gallery is alvailable here: http://seaborn.pydata.org/examples/index.html.
A scatterplot of a bivariate normal distribution:
```
import pandas as pd
mean, cov = [0, 1], [(1, .5), (.5, 1)]
data = np.random.multivariate_normal(mean, cov, 500)
df = pd.DataFrame(data, columns=["x", "y"])
sns.jointplot(x="x", y="y", data=df)
```
A scatterplot matrix:
```
df
df = sns.load_dataset("iris")
sns.pairplot(df, hue="species")
tips = sns.load_dataset("tips")
tips
```
A linear model plot:
```
sns.lmplot(x="total_bill", y="tip", data=tips, hue="smoker")
```
## 5.4 Statistical Models
Statsmodels is a Python package that allows users to explore data, estimate statistical models, and perform statistical tests. An extensive list of descriptive statistics, statistical tests, plotting functions, and result statistics are available for different types of data and each estimator. It complements SciPy's stats module.
```
import numpy as np
import statsmodels.api as sm
```
The user guide can be found here: https://www.statsmodels.org/stable/user-guide.html.
Let's explore our `iris` dataset again:
```
df
```
We would like to know whether the `sepal_length` depends on the explanatory variable `species`. Let's create a boxplot:
```
sns.boxplot(x="species", y="sepal_length", data=df)
```
It seems like this is indeed the case. However, we need to perform some statistical test to conclude this. Let's do some ANOVA (see syllabus Statistical Models, M. de Gunst):
```
lm = sm.OLS.from_formula('sepal_length ~ species', data=df)
fitted_model = lm.fit()
print(sm.stats.anova_lm(fitted_model))
```
We conclude that `species` is a significant explanatory variable for `sepal_length`. We can find the coefficients using the following code:
```
print(fitted_model.summary())
```
Now let's explore a dataset from `statsmodels`:
```
spector_data = sm.datasets.spector.load_pandas().data
spector_data
```
We will again do some ANOVA:
```
m = sm.OLS.from_formula('GRADE ~ GPA + TUCE', spector_data)
print(m.df_model, m.df_resid)
print(m.endog_names, m.exog_names)
res = m.fit()
# res.summary()
print(res.summary())
```
From this table, we conclude that `GPA` is a significant factor but `TUCE` is not. We can extract the coefficients of our fitted model as follows:
```
res.params # parameters
```
Given the values `GPA` and `TUCE`, we can get a predicted value for `GRADE`:
```
m.predict(res.params, [1, 4.0, 25])
```
We predict `GRADE = 1`.
We can also perform some _Fisher tests_ to check whether the explanatory variables are significant:
```
a = res.f_test("GPA = 0")
a.summary()
b = res.f_test("GPA = TUCE = 0")
b.summary()
```
Now let's take the full model:
```
spector_data
m = sm.OLS.from_formula('GRADE ~ GPA + TUCE + PSI', spector_data)
res1 = m.fit()
print(res1.summary())
```
As we can see, `PSI` is an important explanatory variable! We compare our models using the information criteria, or by performing some other tests:
```
res1.compare_f_test(res) # res1 better
res1.compare_lm_test(res)
res1.compare_lr_test(res)
help(sm)
```
We can also use a generalized linear model using the `sm.GLM` function or do some time series analysis using the `sm.tsa` subpackage. The investigation of this is left to the entusiastic reader. An introduction video can be found here:
```
from IPython.display import YouTubeVideo
YouTubeVideo('o7Ux5jKEbcw', width=533, height=300)
```
## 5.5 Python vs. R
There’s a lot of recurrent discussion on the right tool to use for statistics and machine learning. `R` and `Python` are often considered alternatives: they are both good for statistics and machine learning tasks. But which one is the fastest? For a benchmark, it is relatively hard to make it fair: the speed of execution may well depend on the code, or the speed of the different libraries used. We decide to do classification on the Iris dataset. It is a relatively easy Machine Learning project, which seems to make for a fair comparison. We use the commonly used libraries in both `R` and `Python`. The following steps are executed:
1. Read a csv file with the iris data.
2. Randomly split the data in 80% training data and 20% test data.
3. Fit a number of models (logistic regression, linear discriminant analysis, k-nearest neighbors, and support vector machines) on the training data using built-in grid-search and cross-validation methods
4. Evaluate each of those best models on the test data and select the best model
We get the following results:
```
# %load resources/python_vs_R.py
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import GridSearchCV, KFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn import svm
def main():
names = ["sepal_length", "sepal_width", "petal_length", "petal_width", "Name"]
iris_data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data", names = names)
train, test = train_test_split(iris_data, test_size=0.2)
X_train = train.drop('Name', axis=1)
y_train = train['Name']
X_test = test.drop('Name', axis=1)
y_test = test['Name']
# logistic regression
lr = LogisticRegression(solver='lbfgs', multi_class='auto', max_iter=1000)
lr.fit(X_train, y_train)
# linear discriminant analysis
lda = LinearDiscriminantAnalysis()
lda.fit(X_train,y_train)
# KNN (k-nearest neighbours)
parameters = {'n_neighbors': range(1,11)}
knn = GridSearchCV(KNeighborsClassifier(), parameters, scoring = 'accuracy', cv = KFold(n_splits=5))
knn.fit(X_train,y_train)
# SVM
parameters = {'C': range(1,11)}
svc = GridSearchCV(svm.SVC(kernel = 'linear'), parameters, scoring = 'accuracy', cv = KFold(n_splits=5))
svc.fit(X_train,y_train)
# evaluate
lr_test_acc = lr.score(X_test,y_test)
lda_test_acc = lda.score(X_test,y_test)
knn_test_acc = knn.best_estimator_.score(X_test,y_test)
svc_test_acc= svc.best_estimator_.score(X_test,y_test)
# print(lr_test_acc, lda_test_acc, knn_test_acc, svc_test_acc)
from datetime import datetime as dt
now = dt.now()
for i in range(5):
main()
print(dt.now() - now)
```
It seems that the `Python` code runs a little bit faster. However, when we make the model more complex, or use multiprocessing, the difference is even higher! If speed matters, using `Python` is the best alternative.
### 🔴 *Next Week:*
```
np.random.choice(['Machine learning 2','Something else'], p=[0.99,0.01])
```
| true |
code
| 0.568236 | null | null | null | null |
|
# Analysis for the floor control detection (FCD) model and competitor models
This notebook analyses the predictions of the FCD model and the competitor models discussed in the paper and show how they are compared over a few performance measurements. It also includes some stats about the dataset and the annotated floor properties, and an optimised FCD model for highest accuracy.
```
import itertools
import pathlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pyjags
from scipy import optimize as soptimize
import predict_fcd
import utils.annotated_floor
import utils.iteration
import utils.mcmc_plot
import utils.path
%load_ext autoreload
%autoreload 2
plt.style.use('ggplot')
plt.rcParams.update({'axes.titlesize': 'large'})
np.random.seed(1234)
FEATURES_DIR = pathlib.Path('features')
PREDICTIONS_DIR = pathlib.Path('predictions')
ANALYSIS_SAMPLE_RATE = 10
SAMPLE_RATE = {
'fcd': 50,
'optimised_fcd': 50,
'lstm': 20,
'partial_lstm': 20,
'vad': 50,
'random': ANALYSIS_SAMPLE_RATE,
}
MODELS = list(SAMPLE_RATE.keys())
DEFAULT_FCD_PARAMS = (0.35, 0.1)
OPTIMISED_FCD_PARAMS = (1.78924915, 1.06722576) # Overriden by lengthy optimisation below
CHAINS = 4
ITERATIONS = 10_000
```
# Utilities
Utility functions and generator functions that are used throughout the code and use the constants declared above. More utilities are imported from the `util` package. These are considered more generic.
### General utilities
```
def array_to_series(x, name, sample_rate):
'''
Convert a numpy array to a pandas series
with time index.
'''
x = x[::sample_rate // ANALYSIS_SAMPLE_RATE]
return pd.Series(
x,
index=np.arange(len(x)) / ANALYSIS_SAMPLE_RATE,
name=name,
)
def utterances_to_floor(utterances_df):
'''
Calculate the floor timeseries from a dataframe
of utterances (every row has start_time, end_time,
and participant).
'''
return array_to_series(
list(
utils.annotated_floor.gen(
utterances_df,
sample_rate=ANALYSIS_SAMPLE_RATE,
)
),
name='floor',
sample_rate=ANALYSIS_SAMPLE_RATE,
)
```
### Random model utilities
```
def _generate_random_model_intervals(average_floor_duration):
floor_holder = np.random.randint(2)
previous_timestamp = 0
while True:
samples = np.random.exponential(average_floor_duration, 100)
timestamps = samples.cumsum() + previous_timestamp
for timestamp in timestamps:
yield {
'start_time': previous_timestamp,
'end_time': timestamp,
'participant': floor_holder,
}
floor_holder = (floor_holder * -1) + 1
previous_timestamp = timestamp
def calculate_random_model(average_floor_duration, part_duration):
'''
Calculate a random floor array with turns duration distributin
exponentially with `average_floor_duration` as mean.
'''
gen = _generate_random_model_intervals(average_floor_duration)
gen = itertools.takewhile(lambda i: i['start_time'] < part_duration, gen)
return list(
utils.iteration.intervals_to_values_gen(
gen,
sample_rate=ANALYSIS_SAMPLE_RATE,
key='participant',
)
)
```
### Dataset stats utilities
```
def dataset_stats_gen():
'''
Calculate basic stats about the annotated floor.
'''
for part in utils.path.session_parts_gen(train_set=True, test_set=True):
utterances_df = pd.read_csv(FEATURES_DIR / 'utterances' / f'{part}.csv')
floor_intervals = list(utils.annotated_floor.utterances_to_floor_intervals_gen(utterances_df))
floor = utterances_to_floor(utterances_df)
yield {
'competition_for_floor': np.isnan(floor).mean(),
'average_floor_duration': np.mean([i['end_time'] - i['start_time'] for i in floor_intervals]),
'average_part_duration': utterances_df['end_time'].max(),
}
```
### Performance measurment generator functions
```
def accuracy(model, floor):
'''
Every 10 seconds, if defined floor (no competition nor silence)
yields 1 if the model and the floor agrees, 0 otherwise. 10 seconds
jumps are used to make sure the samples are independent.
'''
jump = 10 * ANALYSIS_SAMPLE_RATE
both = pd.concat([model, floor], axis=1)[::jump].dropna()
yield from (both.iloc[:, 0] == both.iloc[:, 1]).astype(int)
def backchannels(model, utterances_df):
'''
For each backchannel yield 1 if the model report a floor
for the partner, 0 otherwise.
'''
backchannels = utterances_df[utterances_df['backchannel']]
for _, bc in backchannels.iterrows():
bc_timestamp = bc['start_time']
prediction_at_bc = model[bc_timestamp:].values[0]
if prediction_at_bc:
yield int(prediction_at_bc != bc['participant'])
def _floor_holder_changes(array):
array = array[~np.isnan(array)]
items = utils.iteration.dedup(array)
return len(list(items)) - 1 # number of changes is number of values minus 1
def stability(model, floor):
'''
Ratio of actual floor changes vs. predicted floor changes.
'''
annotated_floor_changes = _floor_holder_changes(floor)
model_floor_changes = _floor_holder_changes(model)
yield annotated_floor_changes / model_floor_changes
def lag(model, floor):
'''
Yield positive lags in seconds.
'''
model_change = pd.Series(dict(utils.iteration.dedup(model.dropna().iteritems(), key=lambda x: x[1])))
floor_change = pd.Series(dict(utils.iteration.dedup(floor.dropna().iteritems(), key=lambda x: x[1])))
visited_timestamps = set()
for timestamp, prediction in model_change.iteritems():
previous_floors = floor_change[:timestamp]
if not previous_floors.empty:
current_floor_timestamp = previous_floors.index[-1]
current_floor_value = previous_floors.values[-1]
if (current_floor_value == prediction and current_floor_timestamp not in visited_timestamps):
yield (timestamp - current_floor_timestamp)
visited_timestamps.add(current_floor_timestamp)
```
### Models' performance (stats) collection utilities
```
def _part_models_stats_gen(part, average_floor_duration):
utterances_df = pd.read_csv(FEATURES_DIR / 'utterances' / f'{part}.csv')
floor = utterances_to_floor(utterances_df)
rms = np.load(FEATURES_DIR / 'FCD' / f'{part}.npy')
models = {
'fcd': np.load(PREDICTIONS_DIR / 'FCD' / f'{part}.npy'),
'optimised_fcd': list(predict_fcd.gen_from_rms(rms, *OPTIMISED_FCD_PARAMS)),
'lstm': np.load(PREDICTIONS_DIR / 'LSTM' / f'full-{part}.npy'),
'partial_lstm': np.load(PREDICTIONS_DIR / 'LSTM' / f'partial-{part}.npy'),
'vad': np.load(PREDICTIONS_DIR / 'VAD' / f'{part}.npy'),
'random': calculate_random_model(
average_floor_duration,
part_duration=floor.index[-1],
),
}
models_df = pd.concat(
[array_to_series(x, name=n, sample_rate=SAMPLE_RATE[n]) for n, x in models.items()],
axis=1,
)
measurement_functions_and_args = {
backchannels: utterances_df,
**{f: floor for f in [accuracy, stability, lag]},
}
for model in models:
for f, arg in measurement_functions_and_args.items():
for value in f(models_df[model], arg):
yield {
'part': part,
'model': model,
'measurement': f.__name__,
'value': value,
}
def models_stats_gen(average_floor_duration):
'''
Calculate the performance measure for each model accross the
test-set.
'''
for part in utils.path.session_parts_gen(train_set=False, test_set=True):
yield from _part_models_stats_gen(part, average_floor_duration)
```
### Bayesian analysis utilities
```
def gamma_template(mode, sd):
'''
Return a string template with shape and rate from mode and sd.
'''
rate = f'({mode} + sqrt({mode} ^ 2 + 4 * {sd} ^ 2)) / (2 * {sd} ^ 2)'
shape = f'1 + {mode} * {rate}'
return f'{shape}, {rate}'
def beta_template(mode, k):
'''
Return a string template with a and b from mode and concentration.
'''
a = f'{mode} * ({k} - 2) + 1'
b = f'(1 - {mode}) * ({k} - 2) + 1'
return f'{a}, {b}'
def run_model(code, data):
'''
Create and sample a JAGS model.
'''
model = pyjags.Model(code=code, data=data, chains=CHAINS)
return model.sample(ITERATIONS, vars=['mode'])
def mode_comparison(trace, models, diag_xlim, comp_xlim):
utils.mcmc_plot.param_comparison(
trace,
'mode',
comparison=[MODELS.index(m) for m in models],
names=models,
diag_xlim=diag_xlim,
comp_xlim=comp_xlim,
)
def compare_two(models, traces, xlim):
_, axes = plt.subplots(ncols=len(traces), figsize=(8, 2))
for ax, (measurement, trace) in zip(axes, traces.items()):
m1, m2 = [MODELS.index(m) for m in models]
ax.set(title=measurement)
ax.axvline(0, linestyle='--', c='grey')
utils.mcmc_plot.dist(
trace['mode'][m1].reshape(-1) - trace['mode'][m2].reshape(-1),
histplot_kwargs={'binrange': xlim},
ax=ax,
)
def _hdi_as_dict(model, samples):
return {
'model': model,
'hdi_start': np.percentile(samples, 2.5),
'hdi_end': np.percentile(samples, 97.5),
}
def hdi_summary(models, trace):
for m in models:
samples = trace['mode'][MODELS.index(m)].reshape(-1)
yield _hdi_as_dict(m, samples)
for m1, m2 in itertools.combinations(models, 2):
samples_m1 = trace['mode'][MODELS.index(m1)].reshape(-1)
samples_m2 = trace['mode'][MODELS.index(m2)].reshape(-1)
diff = samples_m1 - samples_m2
yield _hdi_as_dict(f'{m1} - {m2}', diff)
```
# Analysis starts here!
## Dataset stats
```
dataset_stats_df = pd.DataFrame(dataset_stats_gen())
dataset_stats_df.describe()
# Keep the average floor duration for later, for the random model
average_floor_duration = dataset_stats_df['average_floor_duration'].mean()
```
## Optimising FCD parameters for accuracy
This is done on the train set.
```
optimisation_data = []
for part in utils.path.session_parts_gen(train_set=True, test_set=False):
utterances_df = pd.read_csv(FEATURES_DIR / 'utterances' / f'{part}.csv')
floor = utterances_to_floor(utterances_df)
rms = np.load(FEATURES_DIR / 'FCD' / f'{part}.npy')
optimisation_data.append((rms, floor))
def get_negative_accuracy_from_model(params):
accuracies = []
for rms, floor in optimisation_data:
fcd_gen = predict_fcd.gen_from_rms(rms, *params)
fcd = array_to_series(list(fcd_gen), name='fcd', sample_rate=SAMPLE_RATE['fcd'])
accuracies.append(np.mean(list(accuracy(fcd, floor))))
return -np.mean(accuracies)
```
**Note!** This cell takes a while to run. It is commented out as the entire notebook can be executed without it. The default optimised parameters (declared at the top of the notebook) are used in that case.
```
# %%time
# res = soptimize.basinhopping(
# get_negative_accuracy_from_model,
# DEFAULT_FCD_PARAMS,
# seed=1234,
# )
# OPTIMISED_FCD_PARAMS = res.x
# res
```
**Example of the output of the cell above for reference**
```
CPU times: user 1h 7min 23s, sys: 24.2 s, total: 1h 7min 47s
Wall time: 1h 7min 40s
fun: -0.890908193538182
lowest_optimization_result: fun: -0.890908193538182
hess_inv: array([[1, 0],
[0, 1]])
jac: array([0., 0.])
message: 'Optimization terminated successfully.'
nfev: 3
nit: 0
njev: 1
status: 0
success: True
x: array([1.78924915, 1.06722576])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 303
nit: 100
njev: 101
x: array([1.78924915, 1.06722576])
```
## The average of the models' performance on each measurement
```
models_stats_df = pd.DataFrame(models_stats_gen(average_floor_duration))
models_stats_df['model'] = pd.Categorical(
models_stats_df['model'],
categories=MODELS,
ordered=True,
)
for c in ['part', 'measurement']:
models_stats_df[c] = models_stats_df[c].astype('category')
(
models_stats_df
# Average within parts
.groupby(['model', 'measurement', 'part'])
.mean()
# Average accross parts
.reset_index()
.pivot_table(index='model', columns='measurement', values='value')
)
```
## Bayesian analysis of differences between the models
Here we estimate the mode of the accuracy, backchannels classification, stability, and lag, for each model. The Bayesian method provides a direct way to estimate the differences between the modes.
```
group_by_measurement = models_stats_df.groupby('measurement')
```
### Accuracy
```
hierarchical_beta_code = f"""
model {{
for (m in 1:n_models) {{
for (p in 1:n_parts) {{
correct[m, p] ~ dbin(part_mode[m, p], attempts[m, p])
part_mode[m, p] ~ dbeta({beta_template('mode[m]', 'concentration[m]')})
}}
mode[m] ~ dunif(0, 1)
concentration[m] = concentration_minus_two[m] + 2
concentration_minus_two[m] ~ dgamma({gamma_template(20, 20)})
}}
}}
"""
_df = group_by_measurement.get_group('accuracy')
accuracy_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'correct': _df.pivot_table(index='model', columns='part', values='value', aggfunc='sum'),
'attempts': _df.pivot_table(index='model', columns='part', values='value', aggfunc='count'),
}
accuracy_trace = run_model(code=hierarchical_beta_code, data=accuracy_data)
mode_comparison(accuracy_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 1), comp_xlim=(-0.6, 0.6))
```
### Backchannels categorisation
```
_df = group_by_measurement.get_group('backchannels')
bc_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'correct': _df.pivot_table(index='model', columns='part', values='value', aggfunc='sum'),
'attempts': _df.pivot_table(index='model', columns='part', values='value', aggfunc='count'),
}
bc_trace = run_model(code=hierarchical_beta_code, data=bc_data)
mode_comparison(bc_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 1), comp_xlim=(-0.6, 0.6))
```
### Stability
```
stability_code = f"""
model {{
for (m in 1:n_models) {{
for (p in 1:n_parts) {{
stability[m, p] ~ dgamma({gamma_template('mode[m]', 'sd[m]')})
}}
mode[m] ~ dgamma({gamma_template(1, 1)})
sd[m] ~ dgamma({gamma_template(1, 1)})
}}
}}
"""
_df = group_by_measurement.get_group('stability')
stability_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'stability': _df.pivot(index='model', columns='part', values='value'),
}
stability_trace = run_model(code=stability_code, data=stability_data)
mode_comparison(stability_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 1.25), comp_xlim=(-1.2, 1.2))
```
### Lag
```
lag_code = f"""
model {{
for (i in 1:n_lags) {{
lag[i] ~ dexp(1 / part_mean[models[i], part[i]])
}}
for (i in 1:n_models) {{
for (j in 1:n_parts) {{
part_mean[i, j] ~ dgamma({gamma_template('mode[i]', 'sd[i]')})
}}
mode[i] ~ dgamma({gamma_template(0.5, 1)})
sd[i] ~ dgamma({gamma_template(1, 1)})
}}
}}
"""
_df = group_by_measurement.get_group('lag')
lag_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'n_lags': len(_df),
'lag': _df['value'],
'models': _df['model'].cat.codes + 1,
'part': _df['part'].cat.codes + 1,
}
lag_trace = run_model(code=lag_code, data=lag_data)
mode_comparison(lag_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 2.1), comp_xlim=(-2.2, 2.2))
```
### FCD with default params vs. optimised FCD
```
traces = {
'accuracy': accuracy_trace,
'backchannels': bc_trace,
'stability': stability_trace,
'lag': lag_trace,
}
compare_two(['fcd', 'optimised_fcd'], traces, xlim=(-0.75, 0.75))
```
### LSTM vs. partial-LSTM
```
compare_two(['lstm', 'partial_lstm'], traces, xlim=(-0.75, 0.75))
```
### Optimised FCD vs. LSTM
This is marely to see if the lag of the optimised FCD is better.
```
compare_two(['optimised_fcd', 'lstm'], traces, xlim=(-0.75, 0.75))
```
### HDIs summary
```
models = ['fcd', 'lstm', 'random']
comp_values = [0.5, 0.5, 1, average_floor_duration / 2]
fig, axes = plt.subplots(nrows=len(traces), figsize=(8, 8), sharex=True)
for ax, (measurement, trace), comp_value in zip(axes, traces.items(), comp_values):
yticks = {}
ax.axvline(0, linestyle='--', c='grey')
if comp_value:
ax.axvline(comp_value, linestyle='dotted', c='grey')
for i, row in enumerate(hdi_summary(models, trace)):
ax.plot((row['hdi_start'], row['hdi_end']), (-i, -i), linewidth=4, c='k')
for tail, alignment in zip(['hdi_start', 'hdi_end'], ['right', 'left']):
s = format(row[tail], '.2f').replace('-0', '-').lstrip('0')
ax.text(row[tail], -i + 0.1, s, horizontalalignment=alignment)
yticks[-i] = row['model']
ax.set(title=measurement)
ax.set_yticks(list(yticks.keys()))
ax.set_yticklabels(list(yticks.values()))
fig.tight_layout()
fig.savefig('graphics/hdis.svg')
```
| true |
code
| 0.636155 | null | null | null | null |
|
# 3D Object Detection Evaluation Tutorial
Welcome to the 3D object detection evaluation tutorial! We'll walk through the steps to submit your detections to the competition server.
```
from av2.evaluation.detection.eval import evaluate
from av2.evaluation.detection.utils import DetectionCfg
from pathlib import Path
from av2.utils.io import read_feather, read_all_annotations
```
### Constructing the evaluation configuration
The `DetectionCfg` class stores the configuration for the 3D object detection challenge.
- During evaluation, we remove _all_ cuboids which are not within the region-of-interest (ROI) which spatially is a 5 meter dilation of the drivable area isocontour.
- **NOTE**: If you would like to _locally_ enable this behavior, you **must** pass in the directory to sensor dataset (to build the raster maps from the included vector maps).
```
dataset_dir = Path.home() / "data" / "datasets" / "av2" / "sensor" # Path to your AV2 sensor dataset directory.
competition_cfg = DetectionCfg(dataset_dir=dataset_dir) # Defaults to competition parameters.
split = "val"
gts = read_all_annotations(dataset_dir=dataset_dir, split=split) # Contains all annotations in a particular split.
display(gts)
```
## Preparing detections for submission.
The evaluation expects the following 14 fields within a `pandas.DataFrame`:
- `tx_m`: x-component of the object translation in the egovehicle reference frame.
- `ty_m`: y-component of the object translation in the egovehicle reference frame.
- `tz_m`: z-component of the object translation in the egovehicle reference frame.
- `length_m`: Object extent along the x-axis in meters.
- `width_m`: Object extent along the y-axis in meters.
- `height_m`: Object extent along the z-axis in meters.
- `qw`: Real quaternion coefficient.
- `qx`: First quaternion coefficient.
- `qy`: Second quaternion coefficient.
- `qz`: Third quaternion coefficient.
- `score`: Object confidence.
- `log_id`: Log id associated with the detection.
- `timestamp_ns`: Timestamp associated with the detection.
- `category`: Object category.
Additional details can be found in [SUBMISSION_FORMAT.md](../src/av2/evaluation/detection/SUBMISSION_FORMAT.md).
```
# If you've already aggregated your detections into one file.
dts_path = Path("detections.feather")
dts = read_feather(dts_path)
dts, gts, metrics = evaluate(dts, gts, cfg=competition_cfg) # Evaluate instances.
display(metrics)
```
Finally, if you would like to submit to the evaluation server, you just need to export your detections into a `.feather` file. This can be done by:
```python
dts.to_feather("detections.feather")
```
| true |
code
| 0.711481 | null | null | null | null |
|
# Quantum Cryptography: Quantum Key Distribution
***
### Contributors:
A.J. Rasmusson, Richard Barney
Have you ever wanted to send a super secret message to a friend? Then you need a key to encrypt your message, and your friend needs the same key to decrypt your message. But, how do you send a super secret key to your friend without your eavesdropping enemies finding out what it is? Businesses and governments face this problem every day. People are always innovating new ways to intercept personal data or other sensitive information. Ideally, we'd like to find a way to share information that cannot be intercepted. [Quantum key distribution](https://en.wikipedia.org/wiki/Quantum_key_distribution) (QKD) was created as a solution to this problem. In this tutorial, you'll learn about and implement a version of the [BB84 QKD protocol](https://en.wikipedia.org/wiki/BB84), developed by Bennet and Brassard, to generate a secure, [one-time pad](https://en.wikipedia.org/wiki/One-time_pad) encryption key.
Quantum key distribution is all about making the right information publicly known at the right times (and keeping the secret information secret). This tutorial will take you through a quantum key distribution between you (Alice) and your friend Bob. After you get a feel for the ropes by sending your first encrypted message to Bob, we'll introduce Eve--your eavesdropping enemy. You'll learn how to detect Eve's presence and thus prevent her from intercepting your super secret key and decrypting your messages.
```
#import all the packages
# Checking the version of PYTHON
import sys
if sys.version_info < (3,5):
raise Exception('Please use Python version 3.5 or greater.')
#append to system path so qiskit and Qconfig can be found from home directory
sys.path.append('../qiskit-sdk-py/')
# Import the QuantumProgram and configuration
from qiskit import QuantumProgram
#import Qconfig
#other useful packages
import math
```
## Part 1: Encrypting and Decrypting a Message
### Pick Your Super Secret Message
The super secret message you want to send must be the same or less than the length of the super secret key.
If the key is shorter than the message, you will be forced to use parts of the key more than once. This may allow your lurking enemies to pick up a pattern in your encrypted message and possibly decrypt it. (As you'll see later on, we need to start out with a key at least double the number of characters used in your message. For now, don't worry about those details, pick your message! For this tutorial, we picked the initial key to be 3x greater--just to be safe.) Enter your message on the line below which reads "mes = ".
```
#Super secret message
mes = 'hello world'
print('Your super secret message: ',mes)
#initial size of key
n = len(mes)*3
#break up message into smaller parts if length > 10
nlist = []
for i in range(int(n/10)):
nlist.append(10)
if n%10 != 0:
nlist.append(n%10)
print('Initial key length: ',n)
```
### The Big Picture
Now that you (Alice) have the key, here's the big question: how are we going to get your key to Bob without eavesdroppers intercepting it? Quantum key distribution! Here are the steps and big picture (the effects of eavesdropping will be discussed later on):
1. You (Alice) generate a random string--the key you wish to give to Bob.
2. You (Alice) convert your string bits into corresponding qubits.
3. You (Alice) send those qubits to Bob, BUT! you randomly rotate some into a superposition. This effectively turns your key into random noise. (This is good because your lurking enemies might measure your qubits.)
4. Bob receives yours qubits AND randomly rotates some qubits in the opposite direction before measuring.
5. Alice and Bob publicly share which qubits they rotated. When they both did the same thing (either both did nothing or both rotated), they know the original key bit value made it to Bob! (Overall, you can see that only some of the bits from Alice's original key should make it.)
6. Alice and Bob create their keys. Alice modifies her original key by keeping only the bits that she knows made it to Bob. Bob does the same.
Alice and Bob now have matching keys! They can now use this key to encrypt and decrypt their messages.
<img src='QKDnoEve.png'>
Here we see Alice sending the initial key to Bob. She sends her qubits and rotates them based on her rotation string. Bob rotates the incoming qubits based on his rotation string and measures the qubits.
### Step 1: Alice Generates a Random Key
You and your friend need a super secret key so you can encrypt your message and your friend can decrypt it. Let's make a key--a pure random key.
To make a purely random string, we'll use quantum superposition. A qubit in the xy-plane of the [Bloch sphere](https://quantumexperience.ng.bluemix.net/qx/tutorial?sectionId=beginners-guide&page=004-The_Weird_and_Wonderful_World_of_the_Qubit~2F001-The_Weird_and_Wonderful_World_of_the_Qubit) is in a 50-50 [superposition](https://quantumexperience.ng.bluemix.net/qx/tutorial?sectionId=beginners-guide&page=005-Single-Qubit_Gates~2F002-Creating_superposition); 50% of the time it'll be measured as 0, and 50% of the time it'll be measured as 1. We have Alice prepare several qubits like this and measure them to generate a purely random string of 1s and 0s.
```
# Make random strings of length string_length
def randomStringGen(string_length):
#output variables used to access quantum computer results at the end of the function
output_list = []
output = ''
#start up your quantum program
qp = QuantumProgram()
backend = 'local_qasm_simulator'
circuits = ['rs']
#run circuit in batches of 10 qubits for fastest results. The results
#from each run will be appended and then clipped down to the right n size.
n = string_length
temp_n = 10
temp_output = ''
for i in range(math.ceil(n/temp_n)):
#initialize quantum registers for circuit
q = qp.create_quantum_register('q',temp_n)
c = qp.create_classical_register('c',temp_n)
rs = qp.create_circuit('rs',[q],[c])
#create temp_n number of qubits all in superpositions
for i in range(temp_n):
rs.h(q[i]) #the .h gate is the Hadamard gate that makes superpositions
rs.measure(q[i],c[i])
#execute circuit and extract 0s and 1s from key
result = qp.execute(circuits, backend, shots=1)
counts = result.get_counts('rs')
result_key = list(result.get_counts('rs').keys())
temp_output = result_key[0]
output += temp_output
#return output clipped to size of desired string length
return output[:n]
key = randomStringGen(n)
print('Initial key: ',key)
```
### Steps 2-4: Send Alice's Qubits to Bob
Alice turns her key bits into corresponding qubit states. If a bit is a 0 she will prepare a qubit on the negative z axis. If the bit is a 1 she will prepare a qubit on the positive z axis. Next, if Alice has a 1 in her rotate string, she rotates her key qubit with a [Hadamard](https://quantumexperience.ng.bluemix.net/qx/tutorial?sectionId=beginners-guide&page=005-Single-Qubit_Gates~2F002-Creating_superposition) gate. She then sends the qubit to Bob. If Bob has a 1 in his rotate string, he rotates the incoming qubit in the opposite direction with a Hadamard gate. Bob then measures the state of the qubit and records the result. The quantum circuit below executes each of these steps.
```
#generate random rotation strings for Alice and Bob
Alice_rotate = randomStringGen(n)
Bob_rotate = randomStringGen(n)
print("Alice's rotation string:",Alice_rotate)
print("Bob's rotation string: ",Bob_rotate)
#start up your quantum program
backend = 'local_qasm_simulator'
shots = 1
circuits = ['send_over']
Bob_result = ''
for ind,l in enumerate(nlist):
#define temp variables used in breaking up quantum program if message length > 10
if l < 10:
key_temp = key[10*ind:10*ind+l]
Ar_temp = Alice_rotate[10*ind:10*ind+l]
Br_temp = Bob_rotate[10*ind:10*ind+l]
else:
key_temp = key[l*ind:l*(ind+1)]
Ar_temp = Alice_rotate[l*ind:l*(ind+1)]
Br_temp = Bob_rotate[l*ind:l*(ind+1)]
#start up the rest of your quantum program
qp2 = QuantumProgram()
q = qp2.create_quantum_register('q',l)
c = qp2.create_classical_register('c',l)
send_over = qp2.create_circuit('send_over',[q],[c])
#prepare qubits based on key; add Hadamard gates based on Alice's and Bob's
#rotation strings
for i,j,k,n in zip(key_temp,Ar_temp,Br_temp,range(0,len(key_temp))):
i = int(i)
j = int(j)
k = int(k)
if i > 0:
send_over.x(q[n])
#Look at Alice's rotation string
if j > 0:
send_over.h(q[n])
#Look at Bob's rotation string
if k > 0:
send_over.h(q[n])
send_over.measure(q[n],c[n])
#execute quantum circuit
result_so = qp2.execute(circuits, backend, shots=shots)
counts_so = result_so.get_counts('send_over')
result_key_so = list(result_so.get_counts('send_over').keys())
Bob_result += result_key_so[0][::-1]
print("Bob's results: ", Bob_result)
```
### Steps 5-6: Compare Rotation Strings and Make Keys
Alice and Bob can now generate a secret quantum encryption key. First, they publicly share their rotation strings. If a bit in Alice's rotation string is the same as the corresponding bit in Bob's they know that Bob's result is the same as what Alice sent. They keep these bits to form the new key. (Alice based on her original key and Bob based on his measured results).
```
def makeKey(rotation1,rotation2,results):
key = ''
count = 0
for i,j in zip(rotation1,rotation2):
if i == j:
key += results[count]
count += 1
return key
Akey = makeKey(Bob_rotate,Alice_rotate,key)
Bkey = makeKey(Bob_rotate,Alice_rotate,Bob_result)
print("Alice's key:",Akey)
print("Bob's key: ",Bkey)
```
### Pause
We see that using only the public knowledge of Bob's and Alice's rotation strings, Alice and Bob can create the same identical key based on Alice's initial random key and Bob's results. Wow!! :D
<strong>If Alice's and Bob's key length is less than the message</strong>, the encryption is compromised. If this is the case for you, rerun all the cells above and see if you get a longer key. (We set the initial key length to 3x the message length to avoid this, but it's still possible.)
### Encrypt (and decrypt) using quantum key
We can now use our super secret key to encrypt and decrypt messages!! (of length less than the key). Note: the below "encryption" method is not powerful and should not be used for anything you want secure; it's just for fun. In real life, the super secret key you made and shared with Bob would be used in a much more sophisticated encryption algorithm.
```
#make key same length has message
shortened_Akey = Akey[:len(mes)]
encoded_m=''
#encrypt message mes using encryption key final_key
for m,k in zip(mes,shortened_Akey):
encoded_c = chr(ord(m) + 2*ord(k) % 256)
encoded_m += encoded_c
print('encoded message: ',encoded_m)
#make key same length has message
shortened_Bkey = Bkey[:len(mes)]
#decrypt message mes using encryption key final_key
result = ''
for m,k in zip(encoded_m,shortened_Bkey):
encoded_c = chr(ord(m) - 2*ord(k) % 256)
result += encoded_c
print('recovered message:',result)
```
# Part 2: Eve the Eavesdropper
What if someone is eavesdropping on Alice and Bob's line of communication? This process of random string making and rotations using quantum mechanics is only useful if it's robust against eavesdroppers.
Eve is your lurking enemy. She eavesdrops by intercepting your transmission to Bob. To be sneaky, Eve must send on the intercepted transmission--otherwise Bob will never receive anything and know that something is wrong!
Let's explain further why Eve can be detected. If Eve intercepts a qubit from Alice, she will not know if Alice rotated its state or not. Eve can only measure a 0 or 1. And she can't measure the qubit and then send the same qubit on, because her measurement will destroy the quantum state. Consequently, Eve doesn't know when or when not to rotate to recreate Alice's original qubit. She may as well send on qubits that have not been rotated, hoping to get the rotation right 50% of the time. After she sends these qubits to Bob, Alice and Bob can compare select parts of their keys to see if they have discrepancies in places they should not.
The scheme goes as follows:
1. Alice sends her qubit transmission Bob--but Eve measures the results
2. To avoid suspicion, Eve prepares qubits corresponding to the bits she measured and sends them to Bob.
3. Bob and Alice make their keys like normal
4. Alice and Bob randomly select the same parts of their keys to share publicly
5. If the selected part of the keys don't match, they know Eve was eavesdropping
6. If the selected part of the keys DO match, they can be confident Eve wasn't eavesdropping
7. They throw away the part of the key they made public and encrypt and decrypt super secret messages with the portion of the key they have left.
<img src="QKD.png">
Here we see Alice sending her qubits, rotationing them based on her rotation string, and Eve intercepting the transmittion. Eve then sending her results onto Bob who--like normal--rotates and measures the qubits.
### Step 1: Eve intercepts Alice's transmission
The code below has Alice sending her qubits and Eve intercepting them. It then displays the results of Eve's measurements.
```
#start up your quantum program
backend = 'local_qasm_simulator'
shots = 1
circuits = ['Eve']
Eve_result = ''
for ind,l in enumerate(nlist):
#define temp variables used in breaking up quantum program if message length > 10
if l < 10:
key_temp = key[10*ind:10*ind+l]
Ar_temp = Alice_rotate[10*ind:10*ind+l]
else:
key_temp = key[l*ind:l*(ind+1)]
Ar_temp = Alice_rotate[l*ind:l*(ind+1)]
#start up the rest of your quantum program
qp3 = QuantumProgram()
q = qp3.create_quantum_register('q',l)
c = qp3.create_classical_register('c',l)
Eve = qp3.create_circuit('Eve',[q],[c])
#prepare qubits based on key; add Hadamard gates based on Alice's and Bob's
#rotation strings
for i,j,n in zip(key_temp,Ar_temp,range(0,len(key_temp))):
i = int(i)
j = int(j)
if i > 0:
Eve.x(q[n])
if j > 0:
Eve.h(q[n])
Eve.measure(q[n],c[n])
#execute
result_eve = qp3.execute(circuits, backend, shots=shots)
counts_eve = result_eve.get_counts('Eve')
result_key_eve = list(result_eve.get_counts('Eve').keys())
Eve_result += result_key_eve[0][::-1]
print("Eve's results: ", Eve_result)
```
### Step 2: Eve deceives Bob
Eve sends her measured qubits on to Bob to deceive him! Since she doesn't know which of the qubits she measured were in a superposition or not, she doesn't even know whether to send the exact values she measured or opposite values. In the end, sending on the exact values is just as good a deception as mixing them up again.
```
#start up your quantum program
backend = 'local_qasm_simulator'
shots = 1
circuits = ['Eve2']
Bob_badresult = ''
for ind,l in enumerate(nlist):
#define temp variables used in breaking up quantum program if message length > 10
if l < 10:
key_temp = key[10*ind:10*ind+l]
Eve_temp = Eve_result[10*ind:10*ind+l]
Br_temp = Bob_rotate[10*ind:10*ind+l]
else:
key_temp = key[l*ind:l*(ind+1)]
Eve_temp = Eve_result[l*ind:l*(ind+1)]
Br_temp = Bob_rotate[l*ind:l*(ind+1)]
#start up the rest of your quantum program
qp4 = QuantumProgram()
q = qp4.create_quantum_register('q',l)
c = qp4.create_classical_register('c',l)
Eve2 = qp4.create_circuit('Eve2',[q],[c])
#prepare qubits
for i,j,n in zip(Eve_temp,Br_temp,range(0,len(key_temp))):
i = int(i)
j = int(j)
if i > 0:
Eve2.x(q[n])
if j > 0:
Eve2.h(q[n])
Eve2.measure(q[n],c[n])
#execute
result_eve = qp4.execute(circuits, backend, shots=shots)
counts_eve = result_eve.get_counts('Eve2')
result_key_eve = list(result_eve.get_counts('Eve2').keys())
Bob_badresult += result_key_eve[0][::-1]
print("Bob's previous results (w/o Eve):",Bob_result)
print("Bob's results from Eve:\t\t ",Bob_badresult)
```
### Step 4: Spot Check
Alice and Bob know Eve is lurking out there. They decide to pick a few random values from their individual keys and compare with each other. This requires making these subsections of their keys public (so the other can see them). If any of the values in their keys are different, they know Eve's eavesdropping messed up the superposition Alice originally created! If they find all the values are identical, they can be reasonably confident that Eve wasn't eavesdropping. Of course, making some random key values known to the public will require them to remove those values from their keys because those parts are no longer super secret. Also, Alice and Bob need to make sure they are sharing corresponding values from their respective keys.
Let's make a check key. If the randomly generated check key is a one, Alice and Bob will compare that part of their keys with each other (aka make publicly known).
```
#make keys for Alice and Bob
Akey = makeKey(Bob_rotate,Alice_rotate,key)
Bkey = makeKey(Bob_rotate,Alice_rotate,Bob_badresult)
print("Alice's key: ",Akey)
print("Bob's key: ",Bkey)
check_key = randomStringGen(len(Akey))
print('spots to check:',check_key)
```
### Steps 5-7: Compare strings and detect Eve
Alice and Bob compare the subsections of their keys. If they notice any discrepancy, they know that Eve was trying to intercept their message. They create new keys by throwing away the parts they shared publicly. It's possible that by throwing these parts away, they will not have a key long enough to encrypt the message and they will have to try again.
```
#find which values in rotation string were used to make the key
Alice_keyrotate = makeKey(Bob_rotate,Alice_rotate,Alice_rotate)
Bob_keyrotate = makeKey(Bob_rotate,Alice_rotate,Bob_rotate)
# Detect Eve's interference
#extract a subset of Alice's key
sub_Akey = ''
sub_Arotate = ''
count = 0
for i,j in zip(Alice_rotate,Akey):
if int(check_key[count]) == 1:
sub_Akey += Akey[count]
sub_Arotate += Alice_keyrotate[count]
count += 1
#extract a subset of Bob's key
sub_Bkey = ''
sub_Brotate = ''
count = 0
for i,j in zip(Bob_rotate,Bkey):
if int(check_key[count]) == 1:
sub_Bkey += Bkey[count]
sub_Brotate += Bob_keyrotate[count]
count += 1
print("subset of Alice's key:",sub_Akey)
print("subset of Bob's key: ",sub_Bkey)
#compare Alice and Bob's key subsets
secure = True
for i,j in zip(sub_Akey,sub_Bkey):
if i == j:
secure = True
else:
secure = False
break;
if not secure:
print('Eve detected!')
else:
print('Eve escaped detection!')
#sub_Akey and sub_Bkey are public knowledge now, so we remove them from Akey and Bkey
if secure:
new_Akey = ''
new_Bkey = ''
for index,i in enumerate(check_key):
if int(i) == 0:
new_Akey += Akey[index]
new_Bkey += Bkey[index]
print('new A and B keys: ',new_Akey,new_Bkey)
if(len(mes)>len(new_Akey)):
print('Your new key is not long enough.')
```
# Probability of Detecting Eve
The longer the key, the more likely you will detect Eve. In fact, the [probability](hhttps://en.wikipedia.org/wiki/Quantum_key_distribution#Intercept_and_resend) goes up as a function of $1 - (3/4)^n$ where n is the number of bits Alice and Bob compare in their spot check. So, the longer the key, the more bits you can use to compare and the more likely you will detect Eve.
```
#!!! you may need to execute this cell twice in order to see the output due to an problem with matplotlib
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0., 30.0)
y = 1-(3/4)**x
plt.plot(y)
plt.title('Probablity of detecting Eve')
plt.xlabel('# of key bits compared')
plt.ylabel('Probablity of detecting Eve')
plt.show()
```
| true |
code
| 0.248968 | null | null | null | null |
|
_ELMED219-2021_. Alexander S. Lundervold, 10.01.2021.
# Natural language processing and machine learning: a small case-study
This is a quick example of some techniques and ideas from natural language processing (NLP) and some modern approaches to NLP based on _deep learning_.
> Note: we'll take a close look at what deep learning is in tomorrow's lecture and lab.
> Note: If you want to run this notebook on your own computer, ask Alexander for assistance. The software requirements are different from the other ELMED219 notebooks (and also slightly more tricky to install, depending on your setup).
# Setup
We'll use the [spacy library]() for NLP and the [fastai]() library for deep learning.
```
import spacy
from fastai.text.all import *
from pprint import pprint as pp
```
# Load data
We use a data set collected in the work of Wakamiya et.al, _Tweet Classification Toward Twitter-Based Disease Surveillance: New Data, Methods, and Evaluations_, 2019: https://www.jmir.org/2019/2/e12783/

The data us supposed to represent tweets that discusses one or more of eight symptoms.
From the original paper:
<img src="assets/medweb_examples.png">
We'll only look at the English language tweets:
```
df = pd.read_csv('data/medweb/medwebdata.csv')
df.head()
pp(df['Tweet'][10])
```
From this text the goal is to determine whether the person is talking about one or more of the eight symptoms or conditions listed above:
```
list(df.columns[2:-2])
```
> **BUT:** How can a computer read??
<img src="http://2.bp.blogspot.com/_--uVHetkUIQ/TDae5jGna8I/AAAAAAAAAK0/sBSpLudWmcw/s1600/reading.gif">
# Prepare the data
For a computer, everything is numbers. We have to convert the text to a series of numbers, and then feed those to the computer.
This can be done in two widely used steps in natural language processing: **tokenization** and **numericalization**:
## Tokenization
In tokenization the text is split into single words, called tokens. A simple way to achieve this is to split according to spaces in the text. But then we, among other things, lose punctuation, and also the fact that some words are contractions of multiple words (for example _isn't_ and _don't_).
<img src="https://spacy.io/tokenization-57e618bd79d933c4ccd308b5739062d6.svg">
Here are some result after tokenization:
```
data_lm = TextDataLoaders.from_df(df, text_col='Tweet', is_lm=True, valid_pct=0.1)
data_lm.show_batch(max_n=2)
```
Tokens starting with "xx" are special. `xxbos` means the beginning of the text, `xxmaj` means that the following word is capitalized, `xxup` means that the following word is in all caps, and so on.
The tokens `xxunk` replaces words that are rare in the text corpus. We keep only words that appear at least twice (with a set maximum number of different words, 60.000 in our case). This is called our **vocabulary**.
## Numericalization
We convert tokens to numbers by making a list of all the tokens that have been used and assign them to numbers.
The above text is replaced by numbers, as in this example
```
data_lm.train_ds[0][0]
```
> **We are now in a position where the computer can compute on the text.**
# "Classical" versus deep learning-based NLP
```
#import sys
#!{sys.executable} -m spacy download en
nlp = spacy.load('en')
```
### Sentence Boundary Detection: splitting into sentences
Example sentence:
> _"Patient presents for initial evaluation of cough. Cough is reported to have developed acutely and has been present for 4 days. Symptom severity is moderate. Will return next week."_
```
sentence = "Patient presents for initial evaluation of cough. Cough is reported to have developed acutely and has been present for 4 days. Symptom severity is moderate. Will return next week."
doc = nlp(sentence)
for sent in doc.sents:
print(sent)
```
### Named Entity Recognition
```
for ent in doc.ents:
print(ent.text, ent.label_)
from spacy import displacy
displacy.render(doc, style='ent', jupyter=True)
```
### Dependency parsing
```
displacy.render(doc, style='dep', jupyter=True, options={'distance': 90})
```
> There's a lot more to natural language processing, of course! Have a look at [spaCy 101: Everything you need to know](https://spacy.io/usage/spacy-101) for some examples.
In general, data preparation and feature engineering is a huge and difficult undertaking when using machine learning to analyse text.
However, in what's called _deep learning_ (discussed in detail tomorrow) most of this work is done by the computer! That's because deep learning does feature extraction _and_ prediction in the same model.
This results in much less work and, often, _in much better models_!
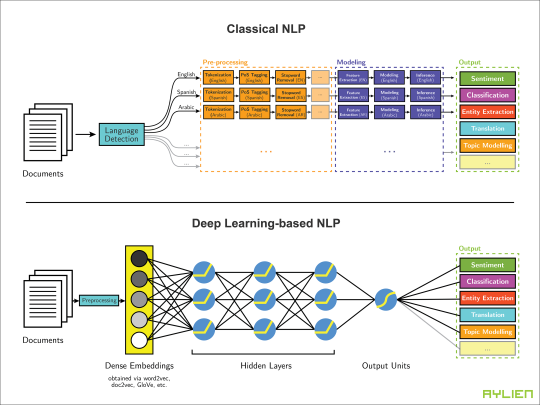
# Deep learning language model
We now come to a relatively new and very powerful idea for deep learning and NLP. An idea that created a small revolution in NLP a couple of years ago ([1](https://blog.openai.com/language-unsupervised/), [2](http://ruder.io/nlp-imagenet/))
We want to create a system that can classify text into one or more categories. This is a difficult problem as the computer must somehow implicitly learn to "read".
Idea: why not _first_ teach the computer to "read" and _then_ let it loose on the classification task?
We can teach the computer to "understand" language by training it to predict the next word of a sentence, using as much training data we can get hold of. This is called ***language modelling*** in NLP.
This is a difficult task: to guess the next word of a sentence one has to know a lot about language, and also a lot about the world.
> What word fits here? _"The light turned green and Per crossed the ___"_
Luckily, obtaining large amounts of training data for language models is simple: any text can be used. The labels are simply the next word of a subpart of the text.
We can for example use Wikipedia. After the model performs alright at predicting the next word of Wikipedia text, we can fine-tune it on text that's closer to the classification task we're after.
> This is often called ***transfer learning***.
We can use the tweet text to fine-tune a model that's already been pretrained on Wikipedia:
```
data_lm = TextDataLoaders.from_df(df, text_col='Tweet', is_lm=True, valid_pct=0.1)
data_lm.show_batch(max_n=3)
learn = language_model_learner(data_lm, AWD_LSTM, pretrained=True,
metrics=[accuracy, Perplexity()], wd=0.1).to_fp16()
```
Let's start training:
```
learn.fit_one_cycle(1, 1e-2)
learn.unfreeze()
learn.fit_one_cycle(10, 1e-3)
```
...and save the parts of the model that we can reuse for classification later:
```
learn.save_encoder('medweb_finetuned')
```
## Test the language model
We can test the language model by having it guess the next given number of words on a starting text:
```
def make_text(seed_text, nb_words):
"""
Use the trained language model to produce text.
Input:
seed_text: some text to get the model started
nb_words: number of words to produce
"""
pred = learn.predict(seed_text, nb_words, temperature=0.75)
pp(pred)
make_text("I'm not feeling too good as my", 10)
make_text("No, that's a", 40)
```
Now we have something that seems to produce text that resembles the text to be classified.
> **Note:** It's interesting to see that the model can come up with text that makes some sense (mostly thanks to training on Wikipedia), and that the text resembles the medical tweets (thanks to the fine-tuning).
> **Note** also that an accuracy of 30-40% when predicting the next word of a sentence is pretty impressive, as the number of possibilities is very large (equal to the size of the vocabulary).
> **Also note** that this is not the task we care about: it's a pretext task before the tweet classification.
# Classifier
```
medweb = DataBlock(blocks=(TextBlock.from_df(text_cols='Tweet', seq_len=12, vocab=data_lm.vocab), MultiCategoryBlock),
get_x = ColReader(cols='text'),
get_y = ColReader(cols='labels', label_delim=";"),
splitter = ColSplitter(col='is_test'))
data = medweb.dataloaders(df, bs=8)
```
Now our task is to predict the possible classes the tweets can be assigned to:
```
data.show_batch()
learn_clf = text_classifier_learner(data, AWD_LSTM, seq_len=16, pretrained=True,
drop_mult=0.5, metrics=accuracy_multi).to_fp16()
learn_clf = learn_clf.load_encoder('medweb_finetuned')
learn_clf.fine_tune(12, base_lr=1e-2)
```
## Is it a good classifier?
We can test it out on some example text:
```
learn_clf.predict("I'm feeling really bad. My head hurts. My nose is runny. I've felt like this for days.")
```
It seems to produce reasonable results. _But remember that this is a very small data set._ One cannot expect very great things when asking the model to make predictions on text outside the small material it has been trained on. This illustrates the need for "big data" in deep learning.
### How does it compare to other approaches?
From the [original article](https://www.jmir.org/2019/2/e12783/) that presented the data set:
<img src="assets/medweb_results.png">
# End notes
* This of course only skratches the surface of NLP and deep learning applied to NLP. The goal was to "lift the curtain" and show some of the ideas behind modern text analysis software.
* If you're interested in digging into deep learning for NLP you should check out `fastai` (used above) and also `Hugging Face`: https://huggingface.co.
| true |
code
| 0.385114 | null | null | null | null |
|
```
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from ml.data import create_lineal_data
from ml.visualization import decision_boundary
%matplotlib inline
```
# Función de coste y gradiente
## Generación de datos
### Entrenamiento
```
np.random.seed(0) # Para hacer más determinística la generación de datos
samples_per_class = 5
Xa = np.c_[create_lineal_data(0.75, 0.9, spread=0.2, data_size=samples_per_class)]
Xb = np.c_[create_lineal_data(0.5, 0.75, spread=0.2, data_size=samples_per_class)]
X_train = np.r_[Xa, Xb]
y_train = np.r_[np.zeros(samples_per_class), np.ones(samples_per_class)]
cmap_dots = ListedColormap(['tomato', 'dodgerblue'])
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cmap_dots, edgecolors='k')
plt.show()
```
### Validación
```
np.random.seed(0) # Para hacer más determinística la generación de datos
samples_per_class = 25
Xa = np.c_[create_lineal_data(0.75, 0.9, spread=0.2, data_size=samples_per_class)]
Xb = np.c_[create_lineal_data(0.5, 0.75, spread=0.2, data_size=samples_per_class)]
X_val = np.r_[Xa, Xb]
y_val = np.r_[np.zeros(samples_per_class), np.ones(samples_per_class)]
cmap_dots = ListedColormap(['tomato', 'dodgerblue'])
plt.scatter(X_val[:, 0], X_val[:, 1], c=y_val, cmap=cmap_dots, edgecolors='k')
plt.show()
```
## Regresión Logística
### Función de coste y gradiente
```
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def logloss(w, x, y):
m = y.shape[0]
y_hat = sigmoid(x.dot(w))
cost1 = np.log(y_hat).dot(y)
cost2 = np.log(1 - y_hat).dot(1 - y)
J = -(cost1 + cost2)
return J
def logloss_gradient(w, x, y):
m = y.shape[0]
y_hat = sigmoid(x.dot(w))
gradient = np.dot(x.T, y_hat - y)
return gradient
```
### Algoritmo de optimización (descenso por la gradiente)
```
def gradient_descent(w, x_train, y_train, x_val, y_va, cost_function,
cost_function_gradient, alpha=0.01, max_iter=1000):
train_costs = np.zeros(max_iter)
val_costs = np.zeros(max_iter)
for iteration in range(max_iter):
train_costs[iteration] = cost_function(w, x_train, y_train)
val_costs[iteration] = cost_function(w, x_val, y_val)
gradient = cost_function_gradient(w, x_train, y_train)
w = w - alpha * gradient
return w, train_costs, val_costs
# Agregar el vector de bias a los ejemplos (bias trick)
X_b_train = np.c_[np.ones(X_train.shape[0]), X_train]
X_b_val = np.c_[np.ones(X_val.shape[0]), X_val]
w0 = np.zeros(X_b_train.shape[1]) # Initial weights
w, train_costs, val_costs = gradient_descent(w0, X_b_train, y_train, X_b_val, y_val,
logloss, logloss_gradient, max_iter=20000)
```
### Exactitud (entrenamiento vs validación)
```
y_pred = (X_b_train.dot(w) >= 0.5).astype(np.int) # Obtenemos las predicciones (como 0 o 1)
accuracy = (y_train == y_pred).astype(np.int).sum() / y_train.shape[0] # Calcular la exactitud
print("Exactitud del algoritmo para conjunto de entrenamiento: %.2f" % accuracy)
y_pred = (X_b_val.dot(w) >= 0.5).astype(np.int) # Obtenemos las predicciones (como 0 o 1)
accuracy = (y_val == y_pred).astype(np.int).sum() / y_val.shape[0] # Calcular la exactitud
print("Exactitud del algoritmo para conjunto de validación: %.2f" % accuracy)
```
### Curva de aprendizaje (entrenamiento vs validación)
```
plt.plot(train_costs, label="Datos de entrenamiento")
plt.plot(val_costs, label="Datos de validación")
plt.xlabel("Iteraciones")
plt.ylabel("Costo")
plt.title("Curva de aprendizaje")
plt.legend()
plt.show()
```
### Frontera de decisión
```
xx, yy, Z = decision_boundary(np.r_[X_train, X_val], w)
cmap_back = ListedColormap(['lightcoral', 'skyblue'])
cmap_dots = ['tomato', 'dodgerblue', 'red', 'darkslateblue']
plt.figure(figsize=(6, 5), dpi= 80, facecolor='w', edgecolor='k')
plt.pcolormesh(xx, yy, Z, cmap=cmap_back)
for i in (0, 1):
plt.scatter(X_train[y_train==i, 0], X_train[y_train==i, 1],
color=cmap_dots[i], label='Entrenamiento clase %d' % i,
edgecolor='k', s=20)
plt.scatter(X_val[y_val==i, 0], X_val[y_val==i, 1],
color=cmap_dots[i+2], label='Validación clase %d' % i,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.legend()
plt.show()
```
| true |
code
| 0.620277 | null | null | null | null |
|
# Notebook served by Voilà
#### Notebook copied from https://github.com/ChakriCherukuri/mlviz
<h2>Gradient Descent</h2>
* Given a the multi-variable function $\large {F(x)}$ differentiable in a neighborhood of a point $\large a$
* $\large F(x)$ decreases fastest if one goes from $\large a$ in the direction of the negative gradient of $\large F$ at $\large a$, $\large -\nabla{F(a)}$
<h3>Gradient Descent Algorithm:</h3>
* Choose a starting point, $\large x_0$
* Choose the sequence $\large x_0, x_1, x_2, ...$ such that
$ \large x_{n+1} = x_n - \eta \nabla(F(x_n) $
So convergence of the gradient descent depends on the starting point $\large x_0$ and the learning rate $\large \eta$
```
from time import sleep
import numpy as np
from ipywidgets import *
import bqplot.pyplot as plt
from bqplot import Toolbar
f = lambda x: np.exp(-x) * np.sin(5 * x)
df = lambda x: -np.exp(-x) * np.sin(5 * x) + 5 * np.cos(5 *x) * np.exp(-x)
x = np.linspace(0.5, 2.5, 500)
y = f(x)
def update_sol_path(x, y):
with sol_path.hold_sync():
sol_path.x = x
sol_path.y = y
with sol_points.hold_sync():
sol_points.x = x
sol_points.y = y
def gradient_descent(x0, f, df, eta=.1, tol=1e-6, num_iters=10):
x = [x0]
i = 0
while i < num_iters:
x_prev = x[-1]
grad = df(x_prev)
x_curr = x_prev - eta * grad
x.append(x_curr)
sol_lbl.value = sol_lbl_tmpl.format(x_curr)
sleep(.5)
update_sol_path(x, [f(i) for i in x])
if np.abs(x_curr - x_prev) < tol:
break
i += 1
txt_layout = Layout(width='150px')
x0_box = FloatText(description='x0', layout=txt_layout, value=2.4)
eta_box = FloatText(description='Learning Rate',
style={'description_width':'initial'},
layout=txt_layout, value=.1)
go_btn = Button(description='GO', button_style='success', layout=Layout(width='50px'))
reset_btn = Button(description='Reset', button_style='success', layout=Layout(width='100px'))
sol_lbl_tmpl = 'x = {:.4f}'
sol_lbl = Label()
# sol_lbl.layout.width = '300px'
# plot of curve and solution
fig_layout = Layout(width='720px', height='500px')
fig = plt.figure(layout=fig_layout, title='Gradient Descent', display_toolbar=True)
fig.pyplot = Toolbar(figure=fig)
curve = plt.plot(x, y, colors=['dodgerblue'], stroke_width=2)
sol_path = plt.plot([], [], colors=['#ccc'], opacities=[.7])
sol_points = plt.plot([], [], 'mo', default_size=20)
def optimize():
f.marks = [curve]
gradient_descent(x0_box.value, f, df, eta=eta_box.value)
def reset():
curve.scales['x'].min = .4
curve.scales['x'].max = 2.5
curve.scales['y'].min = -.5
curve.scales['y'].max = .4
sol_path.x = sol_path.y = []
sol_points.x = sol_points.y = []
sol_lbl.value = ''
go_btn.on_click(lambda btn: optimize())
reset_btn.on_click(lambda btn: reset())
final_fig = VBox([fig, fig.pyplot],
layout=Layout(overflow_x='hidden'))
HBox([final_fig, VBox([x0_box, eta_box, go_btn, reset_btn, sol_lbl])])
```
| true |
code
| 0.412027 | null | null | null | null |
|
# Exp 101 analysis
See `./informercial/Makefile` for experimental
details.
```
import os
import numpy as np
from IPython.display import Image
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set_style('ticks')
matplotlib.rcParams.update({'font.size': 16})
matplotlib.rc('axes', titlesize=16)
from infomercial.exp import meta_bandit
from infomercial.exp import epsilon_bandit
from infomercial.exp import beta_bandit
from infomercial.exp import softbeta_bandit
from infomercial.local_gym import bandit
from infomercial.exp.meta_bandit import load_checkpoint
import gym
def plot_meta(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_E = result["scores_E"]
scores_R = result["scores_R"]
values_R = result["values_R"]
values_E = result["values_E"]
ties = result["ties"]
policies = result["policies"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
plt.plot(episodes, np.repeat(best, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# Policy
policies = np.asarray(policies)
episodes = np.asarray(episodes)
plt.subplot(grid[1, 0])
m = policies == 0
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_E$", color="purple")
m = policies == 1
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_R$", color="grey")
plt.ylim(-.1, 1+.1)
plt.ylabel("Controlling\npolicy")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# score
plt.subplot(grid[2, 0])
plt.scatter(episodes, scores_E, color="purple", alpha=0.4, s=2, label="E")
plt.plot(episodes, scores_E, color="purple", alpha=0.4)
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.plot(episodes, scores_R, color="grey", alpha=0.4)
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[3, 0])
plt.scatter(episodes, values_E, color="purple", alpha=0.4, s=2, label="$Q_E$")
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Ties
plt.subplot(grid[4, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Ties
plt.subplot(grid[5, 0])
plt.scatter(episodes, ties, color="black", alpha=.5, s=2, label="$\pi_{tie}$ : 1\n $\pi_\pi$ : 0")
plt.ylim(-.1, 1+.1)
plt.ylabel("Ties index")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_epsilon(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_R = result["scores_R"]
values_R = result["values_R"]
epsilons = result["epsilons"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
for b in best:
plt.plot(episodes, np.repeat(b, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# score
plt.subplot(grid[1, 0])
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[2, 0])
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# best
plt.subplot(grid[3, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Decay
plt.subplot(grid[4, 0])
plt.scatter(episodes, epsilons, color="black", alpha=.5, s=2)
plt.ylabel("$\epsilon_R$")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_critic(critic_name, env_name, result):
# -
env = gym.make(env_name)
best = env.best
# Data
critic = result[critic_name]
arms = list(critic.keys())
values = list(critic.values())
# Plotz
fig = plt.figure(figsize=(8, 3))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0])
plt.scatter(arms, values, color="black", alpha=.5, s=30)
plt.plot([best]*10, np.linspace(min(values), max(values), 10), color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Arm")
```
# Load and process data
```
data_path ="/Users/qualia/Code/infomercial/data/"
exp_name = "exp97"
sorted_params = load_checkpoint(os.path.join(data_path, f"{exp_name}_sorted.pkl"))
# print(sorted_params.keys())
best_params = sorted_params[0]
sorted_params
```
# Performance
of best parameters
```
env_name = 'BanditTwoHigh10-v0'
num_episodes = 1000
# Run w/ best params
result = epsilon_bandit(
env_name=env_name,
num_episodes=num_episodes,
lr_R=best_params["lr_R"],
epsilon=best_params["epsilon"],
seed_value=2,
)
print(best_params)
plot_epsilon(env_name, result=result)
plot_critic('critic_R', env_name, result)
```
# Sensitivity
to parameter choices
```
total_Rs = []
eps = []
lrs_R = []
lrs_E = []
trials = list(sorted_params.keys())
for t in trials:
total_Rs.append(sorted_params[t]['total_R'])
lrs_R.append(sorted_params[t]['lr_R'])
eps.append(sorted_params[t]['epsilon'])
# Init plot
fig = plt.figure(figsize=(5, 18))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Do plots:
# Arm
plt.subplot(grid[0, 0])
plt.scatter(trials, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("total R")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.scatter(trials, lrs_R, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("lr_R")
_ = sns.despine()
plt.subplot(grid[2, 0])
plt.scatter(lrs_R, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("lrs_R")
plt.ylabel("total_Rs")
_ = sns.despine()
plt.subplot(grid[3, 0])
plt.scatter(eps, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("epsilon")
plt.ylabel("total_Rs")
_ = sns.despine()
```
# Parameter correlations
```
from scipy.stats import spearmanr
spearmanr(eps, lrs_R)
spearmanr(eps, total_Rs)
spearmanr(lrs_R, total_Rs)
```
# Distributions
of parameters
```
# Init plot
fig = plt.figure(figsize=(5, 6))
grid = plt.GridSpec(3, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(eps, color="black")
plt.xlabel("epsilon")
plt.ylabel("Count")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.hist(lrs_R, color="black")
plt.xlabel("lr_R")
plt.ylabel("Count")
_ = sns.despine()
```
of total reward
```
# Init plot
fig = plt.figure(figsize=(5, 2))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(total_Rs, color="black", bins=50)
plt.xlabel("Total reward")
plt.ylabel("Count")
# plt.xlim(0, 10)
_ = sns.despine()
```
| true |
code
| 0.658857 | null | null | null | null |
|
# Análisis de la Movilidad en Bogotá
¿Cuáles son las rutas más críticas de movilidad y sus características en la ciudad de Bogotá?
Se toman los datos de la plataforma:
https://datos.movilidadbogota.gov.co
```
import pandas as pd
import os
os.chdir('../data_raw')
data_file_list = !ls
data_file_list
data_file_list[len(data_file_list)-1]
```
La adquisición de datos será de 4 meses del año 2019 con el propósito de optimizar espacio de almacenamiento y cargas de procesamiento.
```
''' Función df_builder
Recibe como parámetro de entrada una lista de archivos CSV,
hace la lectura y concatena los dataframes, siendo esta concatenación el retorno.
Los datos en los archivos CSV deben tener la misma estructura.
'''
def df_builder(data_list):
n_files = len(data_list) - 1
df_full = pd.read_csv(data_list[n_files])
for i in range(n_files):
df_i = pd.read_csv(data_list[i])
df_full = pd.concat([df_full, df_i])
return df_full
df_mov = df_builder(data_file_list)
df_mov.shape
df_mov.describe
df_mov.dtypes
## Limpieza de datos
# Verificación que todos los registros correspondan con el año de estudio: 2019
df_mov['AÑO'].value_counts()
```
Dentro de los datasets obtenidos se encuentran datos de otros años.
Vamos a eliminar los registros del año 2020.
```
df_mov.shape # Tamaño original
## Borrar los renglones cuando el AÑO es igual que 2020
df_mov = df_mov.loc[df_mov['AÑO'] == 2019]
df_mov['AÑO'].value_counts() # Verificación
df_mov.shape # Tamaño final del dataframe
```
### Columnas sin datos
Vamos a verificar las columnas que no tienen datos (Nan), posterior las eliminamos para tener un dataset más limpio.
```
df_mov['CODIGO'].value_counts()
df_mov['COEF_BRT'].value_counts()
df_mov['COEF_MIXTO'].value_counts()
df_mov['VEL_MEDIA_BRT'].value_counts()
df_mov['VEL_MEDIA_MIXTO'].value_counts()
df_mov['VEL_MEDIA_PONDERADA'].value_counts()
df_mov['VEL_PONDERADA'].value_counts()
## Borrar las columnas
df_mov = df_mov.drop(labels=['CODIGO', 'COEF_BRT', 'COEF_MIXTO', 'VEL_MEDIA_BRT',
'VEL_MEDIA_MIXTO', 'VEL_MEDIA_PONDERADA', 'VEL_PONDERADA'], axis=1)
df_mov.describe
df_mov.columns
df_mov.to_csv('../notebook/data/data_Mov_Bogota_2019.csv', index=None)
```
## Análisis Unidimensional de las Variables
```
## Conteo de la ocurrencia de una variable y un valor
# Conteo de la movilidad en cada mes
df_mov_sorted = df_mov.sort_values('MES')
df_mov_sorted['MES'].hist(bins=15, xrot=45, grid=True)
##plt.xticks(rotation=45)
df_mov['DIA_SEMANA'].value_counts(normalize=True)
df_mov['NAME_FROM'].value_counts()
df_mov['NAME_TO'].value_counts()
df_mov
```
## Análisis Multidimensional de las Variables
Velocidad promedio versus la trayectoria realizada.
La trayectoria se va a definir como la concatenación entre NAME_FROM y NAME_TO.
```
df_mov['TRAYEC'] = df_mov['NAME_FROM'] + ' - ' +df_mov['NAME_TO']
df_mov['TRAYEC'].value_counts()
```
Mediana de la velocidad promedio en cada trayecto. VEL_PROMEDIO que es más común en cada trayecto:
```
medianVel_Tray = df_mov.groupby('TRAYEC').median()['VEL_PROMEDIO']
medianVel_Tray
```
## Análisis de Texto
```
import nltk
from nltk.corpus import stopwords
print(stopwords.words('spanish'))
list_lite_NAME_TO = df_mov['NAME_TO'].value_counts().sort_values(ascending=False).index[0:10]
list_lite_NAME_TO
df_mov_filter_lite_NAME_TO = df_mov[df_mov['NAME_TO'].isin(list_lite_NAME_TO)]
df_mov_filter_lite_NAME_TO
textos_destino = ''
for row in df_mov_filter_lite_NAME_TO['NAME_TO']:
textos_destino = textos_destino + ' ' + row
## to check the ModuleNotFoundError: No module named 'wordcloud'
## install:
## /anaconda3/bin/python -m pip install wordcloud
import sys
print(sys.executable)
from wordcloud import WordCloud
import matplotlib.pyplot as plt
wc = WordCloud(background_color= 'white')
wc.generate(textos_destino)
plt.axis("off")
plt.imshow(wc, interpolation='bilinear')
plt.show()
```
| true |
code
| 0.418608 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/jonkrohn/ML-foundations/blob/master/notebooks/2-linear-algebra-ii.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Linear Algebra II: Matrix Operations
This topic, *Linear Algebra II: Matrix Operations*, builds on the basics of linear algebra. It is essential because these intermediate-level manipulations of tensors lie at the heart of most machine learning approaches and are especially predominant in deep learning.
Through the measured exposition of theory paired with interactive examples, you’ll develop an understanding of how linear algebra is used to solve for unknown values in high-dimensional spaces as well as to reduce the dimensionality of complex spaces. The content covered in this topic is itself foundational for several other topics in the *Machine Learning Foundations* series, especially *Probability & Information Theory* and *Optimization*.
Over the course of studying this topic, you'll:
* Develop a geometric intuition of what’s going on beneath the hood of machine learning algorithms, including those used for deep learning.
* Be able to more intimately grasp the details of machine learning papers as well as all of the other subjects that underlie ML, including calculus, statistics, and optimization algorithms.
* Reduce the dimensionalty of complex spaces down to their most informative elements with techniques such as eigendecomposition, singular value decomposition, and principal components analysis.
**Note that this Jupyter notebook is not intended to stand alone. It is the companion code to a lecture or to videos from Jon Krohn's [Machine Learning Foundations](https://github.com/jonkrohn/ML-foundations) series, which offer detail on the following:**
*Review of Matrix Properties*
* Modern Linear Algebra Applications
* Tensors, Vectors, and Norms
* Matrix Multiplication
* Matrix Inversion
* Identity, Diagonal and Orthogonal Matrices
*Segment 2: Eigendecomposition*
* Eigenvectors
* Eigenvalues
* Matrix Determinants
* Matrix Decomposition
* Applications of Eigendecomposition
*Segment 3: Matrix Operations for Machine Learning*
* Singular Value Decomposition (SVD)
* The Moore-Penrose Pseudoinverse
* The Trace Operator
* Principal Component Analysis (PCA): A Simple Machine Learning Algorithm
* Resources for Further Study of Linear Algebra
## Segment 1: Review of Tensor Properties
```
import numpy as np
import torch
```
### Vector Transposition
```
x = np.array([25, 2, 5])
x
x.shape
x = np.array([[25, 2, 5]])
x
x.shape
x.T
x.T.shape
x_p = torch.tensor([25, 2, 5])
x_p
x_p.T
x_p.view(3, 1) # "view" because we're changing output but not the way x is stored in memory
```
**Return to slides here.**
## $L^2$ Norm
```
x
(25**2 + 2**2 + 5**2)**(1/2)
np.linalg.norm(x)
```
So, if units in this 3-dimensional vector space are meters, then the vector $x$ has a length of 25.6m
```
# the following line of code will fail because torch.norm() requires input to be float not integer
# torch.norm(p)
torch.norm(torch.tensor([25, 2, 5.]))
```
**Return to slides here.**
### Matrices
```
X = np.array([[25, 2], [5, 26], [3, 7]])
X
X.shape
X_p = torch.tensor([[25, 2], [5, 26], [3, 7]])
X_p
X_p.shape
```
**Return to slides here.**
### Matrix Transposition
```
X
X.T
X_p.T
```
**Return to slides here.**
### Matrix Multiplication
Scalars are applied to each element of matrix:
```
X*3
X*3+3
X_p*3
X_p*3+3
```
Using the multiplication operator on two tensors of the same size in PyTorch (or Numpy or TensorFlow) applies element-wise operations. This is the **Hadamard product** (denoted by the $\odot$ operator, e.g., $A \odot B$) *not* **matrix multiplication**:
```
A = np.array([[3, 4], [5, 6], [7, 8]])
A
X
X * A
A_p = torch.tensor([[3, 4], [5, 6], [7, 8]])
A_p
X_p * A_p
```
Matrix multiplication with a vector:
```
b = np.array([1, 2])
b
np.dot(A, b) # even though technically dot products is between 2 vectors
b_p = torch.tensor([1, 2])
b_p
torch.matmul(A_p, b_p)
```
Matrix multiplication with two matrices:
```
B = np.array([[1, 9], [2, 0]])
B
np.dot(A, B) # note first column is same as Xb
B_p = torch.tensor([[1, 9], [2, 0]])
B_p
torch.matmul(A_p, B_p)
```
### Matrix Inversion
```
X = np.array([[4, 2], [-5, -3]])
X
Xinv = np.linalg.inv(X)
Xinv
y = np.array([4, -7])
y
w = np.dot(Xinv, y)
w
```
Show that $y = Xw$:
```
np.dot(X, w)
X_p = torch.tensor([[4, 2], [-5, -3.]]) # note that torch.inverse() requires floats
X_p
Xinv_p = torch.inverse(X_p)
Xinv_p
y_p = torch.tensor([4, -7.])
y_p
w_p = torch.matmul(Xinv_p, y_p)
w_p
torch.matmul(X_p, w_p)
```
**Return to slides here.**
## Segment 2: Eigendecomposition
### Eigenvectors and Eigenvalues
Let's say we have a vector $v$:
```
v = np.array([3, 1])
v
```
Let's plot $v$ using Hadrien Jean's handy `plotVectors` function (from [this notebook](https://github.com/hadrienj/deepLearningBook-Notes/blob/master/2.7%20Eigendecomposition/2.7%20Eigendecomposition.ipynb) under [MIT license](https://github.com/hadrienj/deepLearningBook-Notes/blob/master/LICENSE)).
```
import matplotlib.pyplot as plt
def plotVectors(vecs, cols, alpha=1):
"""
Plot set of vectors.
Parameters
----------
vecs : array-like
Coordinates of the vectors to plot. Each vectors is in an array. For
instance: [[1, 3], [2, 2]] can be used to plot 2 vectors.
cols : array-like
Colors of the vectors. For instance: ['red', 'blue'] will display the
first vector in red and the second in blue.
alpha : float
Opacity of vectors
Returns:
fig : instance of matplotlib.figure.Figure
The figure of the vectors
"""
plt.figure()
plt.axvline(x=0, color='#A9A9A9', zorder=0)
plt.axhline(y=0, color='#A9A9A9', zorder=0)
for i in range(len(vecs)):
x = np.concatenate([[0,0],vecs[i]])
plt.quiver([x[0]],
[x[1]],
[x[2]],
[x[3]],
angles='xy', scale_units='xy', scale=1, color=cols[i],
alpha=alpha)
plotVectors([v], cols=['lightblue'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
```
"Applying" a matrix to a vector (i.e., performing matrix-vector multiplication) can linearly transform the vector, e.g, rotate it or rescale it.
The identity matrix, introduced earlier, is the exception that proves the rule: Applying an identity matrix does not transform the vector:
```
I = np.array([[1, 0], [0, 1]])
I
Iv = np.dot(I, v)
Iv
v == Iv
plotVectors([Iv], cols=['blue'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
```
In contrast, let's see what happens when we apply (some non-identity matrix) $A$ to the vector $v$:
```
A = np.array([[-1, 4], [2, -2]])
A
Av = np.dot(A, v)
Av
plotVectors([v, Av], ['lightblue', 'blue'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
# a second example:
v2 = np.array([2, 1])
plotVectors([v2, np.dot(A, v2)], ['lightgreen', 'green'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
```
We can concatenate several vectors together into a matrix (say, $V$), where each column is a separate vector. Then, whatever linear transformations we apply to $V$ will be independently applied to each column (vector):
```
v
# recall that we need to convert array to 2D to transpose into column, e.g.:
np.matrix(v).T
v3 = np.array([-3, -1]) # mirror image of x over both axes
v4 = np.array([-1, 1])
V = np.concatenate((np.matrix(v).T,
np.matrix(v2).T,
np.matrix(v3).T,
np.matrix(v4).T),
axis=1)
V
IV = np.dot(I, V)
IV
AV = np.dot(A, V)
AV
# function to convert column of matrix to 1D vector:
def vectorfy(mtrx, clmn):
return np.array(mtrx[:,clmn]).reshape(-1)
vectorfy(V, 0)
vectorfy(V, 0) == v
plotVectors([vectorfy(V, 0), vectorfy(V, 1), vectorfy(V, 2), vectorfy(V, 3),
vectorfy(AV, 0), vectorfy(AV, 1), vectorfy(AV, 2), vectorfy(AV, 3)],
['lightblue', 'lightgreen', 'lightgray', 'orange',
'blue', 'green', 'gray', 'red'])
_ = plt.xlim(-4, 6)
_ = plt.ylim(-5, 5)
```
Now that we can appreciate linear transformation of vectors by matrices, let's move on to working with eigenvectors and eigenvalues.
An **eigenvector** (*eigen* is German for "typical"; we could translate *eigenvector* to "characteristic vector") is a special vector $v$ such that when it is transformed by some matrix (let's say $A$), the product $Av$ has the exact same direction as $v$.
An **eigenvalue** is a scalar (traditionally represented as $\lambda$) that simply scales the eigenvector $v$ such that the following equation is satisfied:
$Av = \lambda v$
Easiest way to understand this is to work through an example:
```
A
```
Eigenvectors and eigenvalues can be derived algebraically (e.g., with the [QR algorithm](https://en.wikipedia.org/wiki/QR_algorithm), which was independent developed in the 1950s by both [Vera Kublanovskaya](https://en.wikipedia.org/wiki/Vera_Kublanovskaya) and John Francis), however this is outside scope of today's class. We'll cheat with NumPy `eig()` method, which returns a tuple of:
* a vector of eigenvalues
* a matrix of eigenvectors
```
lambdas, V = np.linalg.eig(A)
```
The matrix contains as many eigenvectors as there are columns of A:
```
V # each column is a separate eigenvector v
```
With a corresponding eigenvalue for each eigenvector:
```
lambdas
```
Let's confirm that $Av = \lambda v$ for the first eigenvector:
```
v = V[:,0]
v
lambduh = lambdas[0] # note that "lambda" is reserved term in Python
lambduh
Av = np.dot(A, v)
Av
lambduh * v
plotVectors([Av, v], ['blue', 'lightblue'])
_ = plt.xlim(-1, 2)
_ = plt.ylim(-1, 2)
```
And again for the second eigenvector of A:
```
v2 = V[:,1]
v2
lambda2 = lambdas[1]
lambda2
Av2 = np.dot(A, v2)
Av2
lambda2 * v2
plotVectors([Av, v, Av2, v2],
['blue', 'lightblue', 'green', 'lightgreen'])
_ = plt.xlim(-1, 4)
_ = plt.ylim(-3, 2)
```
Using the PyTorch `eig()` method, we can do exactly the same:
```
A
A_p = torch.tensor([[-1, 4], [2, -2.]]) # must be float for PyTorch eig()
A_p
eigens = torch.eig(A_p, eigenvectors=True)
eigens
v_p = eigens.eigenvectors[:,0]
v_p
lambda_p = eigens.eigenvalues[0][0]
lambda_p
Av_p = torch.matmul(A_p, v_p)
Av_p
lambda_p * v_p
v2_p = eigens.eigenvectors[:,1]
v2_p
lambda2_p = eigens.eigenvalues[1][0]
lambda2_p
Av2_p = torch.matmul(A_p, v2_p)
Av2_p
lambda2_p * v2_p
plotVectors([Av_p.numpy(), v_p.numpy(), Av2_p.numpy(), v2_p.numpy()],
['blue', 'lightblue', 'green', 'lightgreen'])
_ = plt.xlim(-1, 4)
_ = plt.ylim(-3, 2)
```
### Eigenvectors in >2 Dimensions
While plotting gets trickier in higher-dimensional spaces, we can nevertheless find and use eigenvectors with more than two dimensions. Here's a 3D example (there are three dimensions handled over three rows):
```
X
lambdas_X, V_X = np.linalg.eig(X)
V_X # one eigenvector per column of X
lambdas_X # a corresponding eigenvalue for each eigenvector
```
Confirm $Xv = \lambda v$ for an example vector:
```
v_X = V_X[:,0]
v_X
lambda_X = lambdas_X[0]
lambda_X
np.dot(X, v_X) # matrix multiplication
lambda_X * v_X
```
**Exercises**:
1. Use PyTorch to confirm $Xv = \lambda v$ for the first eigenvector of $X$.
2. Confirm $Xv = \lambda v$ for the remaining eigenvectors of $X$ (you can use NumPy or PyTorch, whichever you prefer).
**Return to slides here.**
### 2x2 Matrix Determinants
```
X
np.linalg.det(X)
```
**Return to slides here.**
```
N = np.array([[-4, 1], [-8, 2]])
N
np.linalg.det(N)
# Uncommenting the following line results in a "singular matrix" error
# Ninv = np.linalg.inv(N)
N = torch.tensor([[-4, 1], [-8, 2.]]) # must use float not int
torch.det(N)
```
**Return to slides here.**
### Generalizing Determinants
```
X = np.array([[1, 2, 4], [2, -1, 3], [0, 5, 1]])
X
np.linalg.det(X)
```
### Determinants & Eigenvalues
```
lambdas, V = np.linalg.eig(X)
lambdas
np.product(lambdas)
```
**Return to slides here.**
```
np.abs(np.product(lambdas))
B = np.array([[1, 0], [0, 1]])
B
plotVectors([vectorfy(B, 0), vectorfy(B, 1)],
['lightblue', 'lightgreen'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
N
np.linalg.det(N)
NB = np.dot(N, B)
NB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(NB, 0), vectorfy(NB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-6, 6)
_ = plt.ylim(-9, 3)
I
np.linalg.det(I)
IB = np.dot(I, B)
IB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(IB, 0), vectorfy(IB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
J = np.array([[-0.5, 0], [0, 2]])
J
np.linalg.det(J)
np.abs(np.linalg.det(J))
JB = np.dot(J, B)
JB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(JB, 0), vectorfy(JB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
doubleI = I*2
np.linalg.det(doubleI)
doubleIB = np.dot(doubleI, B)
doubleIB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(doubleIB, 0), vectorfy(doubleIB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
```
**Return to slides here.**
### Eigendecomposition
The **eigendecomposition** of some matrix $A$ is
$A = V \Lambda V^{-1}$
Where:
* As in examples above, $V$ is the concatenation of all the eigenvectors of $A$
* $\Lambda$ (upper-case $\lambda$) is the diagonal matrix diag($\lambda$). Note that the convention is to arrange the lambda values in descending order; as a result, the first eigenvector (and its associated eigenvector) may be a primary characteristic of the matrix $A$.
```
# This was used earlier as a matrix X; it has nice clean integer eigenvalues...
A = np.array([[4, 2], [-5, -3]])
A
lambdas, V = np.linalg.eig(A)
V
Vinv = np.linalg.inv(V)
Vinv
Lambda = np.diag(lambdas)
Lambda
```
Confirm that $A = V \Lambda V^{-1}$:
```
np.dot(V, np.dot(Lambda, Vinv))
```
Eigendecomposition is not possible with all matrices. And in some cases where it is possible, the eigendecomposition involves complex numbers instead of straightforward real numbers.
In machine learning, however, we are typically working with real symmetric matrices, which can be conveniently and efficiently decomposed into real-only eigenvectors and real-only eigenvalues. If $A$ is a real symmetric matrix then...
$A = Q \Lambda Q^T$
...where $Q$ is analogous to $V$ from the previous equation except that it's special because it's an orthogonal matrix.
```
A = np.array([[2, 1], [1, 2]])
A
lambdas, Q = np.linalg.eig(A)
lambdas
Lambda = np.diag(lambdas)
Lambda
Q
```
Recalling that $Q^TQ = QQ^T = I$, can demonstrate that $Q$ is an orthogonal matrix:
```
np.dot(Q.T, Q)
np.dot(Q, Q.T)
```
Let's confirm $A = Q \Lambda Q^T$:
```
np.dot(Q, np.dot(Lambda, Q.T))
```
**Exercises**:
1. Use PyTorch to decompose the matrix $P$ (below) into its components $V$, $\Lambda$, and $V^{-1}$. Confirm that $P = V \Lambda V^{-1}$.
2. Use PyTorch to decompose the symmetric matrix $S$ (below) into its components $Q$, $\Lambda$, and $Q^T$. Confirm that $S = Q \Lambda Q^T$.
```
P = torch.tensor([[25, 2, -5], [3, -2, 1], [5, 7, 4.]])
P
S = torch.tensor([[25, 2, -5], [2, -2, 1], [-5, 1, 4.]])
S
```
**Return to slides here.**
## Segment 3: Matrix Operations for ML
### Singular Value Decomposition (SVD)
As on slides, SVD of matrix $A$ is:
$A = UDV^T$
Where:
* $U$ is an orthogonal $m \times m$ matrix; its columns are the **left-singular vectors** of $A$.
* $V$ is an orthogonal $n \times n$ matrix; its columns are the **right-singular vectors** of $A$.
* $D$ is a diagonal $m \times n$ matrix; elements along its diagonal are the **singular values** of $A$.
```
A = np.array([[-1, 2], [3, -2], [5, 7]])
A
U, d, VT = np.linalg.svd(A) # V is already transposed
U
VT
d
np.diag(d)
D = np.concatenate((np.diag(d), [[0, 0]]), axis=0)
D
np.dot(U, np.dot(D, VT))
```
SVD and eigendecomposition are closely related to each other:
* Left-singular vectors of $A$ = eigenvectors of $AA^T$.
* Right-singular vectors of $A$ = eigenvectors of $A^TA$.
* Non-zero singular values of $A$ = square roots of eigenvectors of $AA^T$ = square roots of eigenvectors of $A^TA$
**Exercise**: Using the matrix `P` from the preceding PyTorch exercises, demonstrate that these three SVD-eigendecomposition equations are true.
### Image Compression via SVD
The section features code adapted from [Frank Cleary's](https://gist.github.com/frankcleary/4d2bd178708503b556b0).
```
import time
from PIL import Image
```
Fetch photo of Oboe, a terrier, with the book *Deep Learning Illustrated*:
```
! wget https://raw.githubusercontent.com/jonkrohn/DLTFpT/master/notebooks/oboe-with-book.jpg
img = Image.open('oboe-with-book.jpg')
plt.imshow(img)
```
Convert image to grayscale so that we don't have to deal with the complexity of multiple color channels:
```
imggray = img.convert('LA')
plt.imshow(imggray)
```
Convert data into numpy matrix, which doesn't impact image data:
```
imgmat = np.array(list(imggray.getdata(band=0)), float)
imgmat.shape = (imggray.size[1], imggray.size[0])
imgmat = np.matrix(imgmat)
plt.imshow(imgmat, cmap='gray')
```
Calculate SVD of the image:
```
U, sigma, V = np.linalg.svd(imgmat)
```
As eigenvalues are arranged in descending order in diag($\lambda$) so to are singular values, by convention, arranged in descending order in $D$ (or, in this code, diag($\sigma$)). Thus, the first left-singular vector of $U$ and first right-singular vector of $V$ may represent the most prominent feature of the image:
```
reconstimg = np.matrix(U[:, :1]) * np.diag(sigma[:1]) * np.matrix(V[:1, :])
plt.imshow(reconstimg, cmap='gray')
```
Additional singular vectors improve the image quality:
```
for i in [2, 4, 8, 16, 32, 64]:
reconstimg = np.matrix(U[:, :i]) * np.diag(sigma[:i]) * np.matrix(V[:i, :])
plt.imshow(reconstimg, cmap='gray')
title = "n = %s" % i
plt.title(title)
plt.show()
```
With 64 singular vectors, the image is reconstructed quite well, however the data footprint is much smaller than the original image:
```
imgmat.shape
full_representation = 4032*3024
full_representation
svd64_rep = 64*4032 + 64 + 64*3024
svd64_rep
svd64_rep/full_representation
```
Specifically, the image represented as 64 singular vectors is 3.7% of the size of the original!
**Return to slides here.**
### The Moore-Penrose Pseudoinverse
Let's calculate the pseudoinverse $A^+$ of some matrix $A$ using the formula from the slides:
$A^+ = VD^+U^T$
```
A
```
As shown earlier, the NumPy SVD method returns $U$, $d$, and $V^T$:
```
U, d, VT = np.linalg.svd(A)
U
VT
d
```
To create $D^+$, we first invert the non-zero values of $d$:
```
D = np.diag(d)
D
1/8.669
1/4.104
```
...and then we would take the tranpose of the resulting matrix.
Because $D$ is a diagonal matrix, this can, however, be done in a single step by inverting $D$:
```
Dinv = np.linalg.inv(D)
Dinv
```
The final $D^+$ matrix needs to have a shape that can undergo matrix multiplication in the $A^+ = VD^+U^T$ equation. These dimensions can be obtained from $A$:
```
A.shape[0]
A.shape[1]
Dplus = np.zeros((3, 2)).T
Dplus
Dplus[:2, :2] = Dinv
Dplus
```
Now we have everything we need to calculate $A^+$ with $VD^+U^T$:
```
np.dot(VT.T, np.dot(Dplus, U.T))
```
Working out this derivation is helpful for understanding how Moore-Penrose pseudoinverses work, but unsurprisingly NumPy is loaded with an existing method `pinv()`:
```
np.linalg.pinv(A)
```
**Exercise**
Use the `torch.svd()` method to calculate the pseudoinverse of `A_p`, confirming that your result matches the output of `torch.pinverse(A_p)`:
```
A_p = torch.tensor([[-1, 2], [3, -2], [5, 7.]])
A_p
torch.pinverse(A_p)
```
**Return to slides here.**
For regression problems, we typically have many more cases ($n$, or rows of $X$) than features to predict ($m$, or columns of $X$). Let's solve a miniature example of such an overdetermined situation.
We have eight data points ($n$ = 8):
```
x1 = [0, 1, 2, 3, 4, 5, 6, 7.]
y = [1.86, 1.31, .62, .33, .09, -.67, -1.23, -1.37]
fig, ax = plt.subplots()
_ = ax.scatter(x1, y)
```
Although it appears there is only one predictor ($x_1$), we need a second one (let's call it $x_0$) in order to allow for a $y$-intercept (therefore, $m$ = 2). Without this second variable, the line we fit to the plot would need to pass through the origin (0, 0). The $y$-intercept is constant across all the points so we can set it equal to `1` across the board:
```
x0 = np.ones(8)
x0
```
Concatenate $x_0$ and $x_1$ into a matrix $X$:
```
X = np.concatenate((np.matrix(x0).T, np.matrix(x1).T), axis=1)
X
```
From the slides, we know that we can compute the weights $w$ using the pseudoinverse of $w = X^+y$:
```
w = np.dot(np.linalg.pinv(X), y)
w
```
The first weight corresponds to the $y$-intercept of the line, which is typically denoted as $b$:
```
b = np.asarray(w).reshape(-1)[0]
b
```
While the second weight corresponds to the slope of the line, which is typically denoted as $m$:
```
m = np.asarray(w).reshape(-1)[1]
m
```
With the weights we can plot the line to confirm it fits the points:
```
fig, ax = plt.subplots()
ax.scatter(x1, y)
x_min, x_max = ax.get_xlim()
y_min, y_max = b, b + m*(x_max-x_min)
ax.plot([x_min, x_max], [y_min, y_max])
_ = ax.set_xlim([x_min, x_max])
```
### The Trace Operator
Denoted as Tr($A$). Simply the sum of the diagonal elements of a matrix: $$\sum_i A_{i,i}$$
```
A = np.array([[25, 2], [5, 4]])
A
25 + 4
np.trace(A)
```
The trace operator has a number of useful properties that come in handy while rearranging linear algebra equations, e.g.:
* Tr($A$) = Tr($A^T$)
* Assuming the matrix shapes line up: Tr(ABC) = Tr(CAB) = Tr(BCA)
In particular, the trace operator can provide a convenient way to calculate a matrix's Frobenius norm: $$||A||_F = \sqrt{\mathrm{Tr}(AA^\mathrm{T})}$$
**Exercise**
Using the matrix `A_p`:
1. Identify the PyTorch trace method and the trace of the matrix.
2. Further, use the PyTorch Frobenius norm method (for the left-hand side of the equation) and the trace method (for the right-hand side of the equation) to demonstrate that $||A||_F = \sqrt{\mathrm{Tr}(AA^\mathrm{T})}$
```
A_p
```
**Return to slides here.**
### Principal Component Analysis
This PCA example code is adapted from [here](https://jupyter.brynmawr.edu/services/public/dblank/CS371%20Cognitive%20Science/2016-Fall/PCA.ipynb).
```
from sklearn import datasets
iris = datasets.load_iris()
iris.data.shape
iris.get("feature_names")
iris.data[0:6,:]
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X = pca.fit_transform(iris.data)
X.shape
X[0:6,:]
plt.scatter(X[:, 0], X[:, 1])
iris.target.shape
iris.target[0:6]
unique_elements, counts_elements = np.unique(iris.target, return_counts=True)
np.asarray((unique_elements, counts_elements))
list(iris.target_names)
plt.scatter(X[:, 0], X[:, 1], c=iris.target)
```
**Return to slides here.**
| true |
code
| 0.686948 | null | null | null | null |
|

## Classification
Classification - predicting the discrete class ($y$) of an object from a vector of input features ($\vec x$).
Models used in this notebook include: Logistic Regression, Support Vector Machines, KNN
**Author List**: Kevin Li
**Original Sources**: http://scikit-learn.org, http://archive.ics.uci.edu/ml/datasets/Iris
**License**: Feel free to do whatever you want to with this code
## Iris Dataset
```
from sklearn import datasets
# import some data to play with
iris = datasets.load_iris()
X = iris.data
Y = iris.target
# type(iris)
print("feature vector shape=", X.shape)
print("class shape=", Y.shape)
print(iris.target_names, type(iris.target_names))
print(iris.feature_names, type(iris.feature_names))
print type (X)
print X[0:5]
print type (Y)
print Y[0:5]
print "---"
print(iris.DESCR)
# specifies that figures should be shown inline, directly in the notebook.
%pylab inline
# Learn more about thhis visualization package at http://seaborn.pydata.org/
# http://seaborn.pydata.org/tutorial/axis_grids.html
# http://seaborn.pydata.org/tutorial/aesthetics.html#aesthetics-tutorial
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="white")
df = sns.load_dataset("iris")
print "df is a ", type(df)
g = sns.PairGrid(df, diag_sharey=False,hue="species")
g.map_lower(sns.kdeplot, cmap="Blues_d")
g.map_upper(plt.scatter)
g.map_diag(sns.kdeplot, lw=3)
# sns.load_dataset?
sns.load_dataset
```
- Logistic Regression: `linear_model.LogisticRegression`
- KNN Classification: `neighbors.KNeighborsClassifier`
- LDA / QDA: `lda.LDA` / `lda.QDA`
- Naive Bayes: `naive_bayes.GaussianNB`
- Support Vector Machines: `svm.SVC`
- Classification Trees: `tree.DecisionTreeClassifier`
- Random Forest: `ensemble.RandomForestClassifier`
- Multi-class & multi-label Classification is supported: `multiclass.OneVsRest` `multiclass.OneVsOne`
- Boosting & Ensemble Learning: xgboost, cart
## Logistic Regression
A standard logistic sigmoid function
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/8/88/Logistic-curve.svg/320px-Logistic-curve.svg.png" width="50%">
```
%matplotlib inline
import numpy as np
from sklearn import linear_model, datasets
# set_context
sns.set_context("talk")
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, 1:3] # we only take the first two features.
Y = iris.target
h = .02 # step size in the mesh
# https://en.wikipedia.org/wiki/Logistic_regression
logreg = linear_model.LogisticRegression(C=1e5)
# we create an instance of Neighbours Classifier and fit the data.
logreg.fit(X, Y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
# numpy.ravel: Return a contiguous flattened array.
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=get_cmap("Spectral"))
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
#plt.xlim(xx.min(), xx.max())
#plt.ylim(yy.min(), yy.max())
#plt.xticks(())
#plt.yticks(())
plt.show()
```
## Support Vector Machines (Bell Labs, 1992)
<img src="http://docs.opencv.org/2.4/_images/optimal-hyperplane.png" width="50%">
```
# adapted from http://scikit-learn.org/0.13/auto_examples/svm/plot_iris.html#example-svm-plot-iris-py
%matplotlib inline
import numpy as np
from sklearn import svm, datasets
sns.set_context("talk")
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, 1:3] # we only take the first two features. We could
# avoid this ugly slicing by using a two-dim dataset
Y = iris.target
h = 0.02 # step size in the mesh
# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0 # SVM regularization parameter
svc = svm.SVC(kernel='linear', C=C).fit(X, Y)
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C).fit(X, Y)
poly_svc = svm.SVC(kernel='poly', degree=3, C=C).fit(X, Y)
lin_svc = svm.LinearSVC(C=C).fit(X, Y)
# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# title for the plots
titles = ['SVC with linear kernel',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel',
'LinearSVC (linear kernel)']
clfs = [svc, rbf_svc, poly_svc, lin_svc]
f,axs = plt.subplots(2,2)
for i, clf in enumerate(clfs):
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, m_max]x[y_min, y_max].
ax = axs[i//2][i % 2]
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z,cmap=get_cmap("Spectral"))
ax.axis('off')
# Plot also the training points
ax.scatter(X[:, 0], X[:, 1], c=Y,cmap=get_cmap("Spectral"))
ax.set_title(titles[i])
```
## Beyond Linear SVM
```
# SVM with polynomial kernel visualization
from IPython.display import YouTubeVideo
YouTubeVideo("3liCbRZPrZA")
```
## kNearestNeighbors (kNN)
```
# %load http://scikit-learn.org/stable/_downloads/plot_classification.py
"""
================================
Nearest Neighbors Classification
================================
Sample usage of Nearest Neighbors classification.
It will plot the decision boundaries for each class.
"""
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
n_neighbors = 15
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features. We could
# avoid this ugly slicing by using a two-dim dataset
y = iris.target
h = .02 # step size in the mesh
# Create color maps
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
for weights in ['uniform', 'distance']:
# we create an instance of Neighbours Classifier and fit the data.
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(X, y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, weights = '%s')"
% (n_neighbors, weights))
plt.show()
```
##### Back to the Iris Data Set
```
iris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target
indices = np.random.permutation(len(iris_X))
iris_X_train = iris_X[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_X_test = iris_X[indices[-10:]]
iris_y_test = iris_y[indices[-10:]]
# Create and fit a nearest-neighbor classifier
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(iris_X_train, iris_y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=15, p=2,
weights='uniform')
print("predicted:", knn.predict(iris_X_test))
print("actual :", iris_y_test)
```
| true |
code
| 0.656631 | null | null | null | null |
|
# Day 9 - Finding the sum, again, with a running series
* https://adventofcode.com/2020/day/9
This looks to be a variant of the [day 1, part 1 puzzle](./Day%2001.ipynb); finding the sum of two numbers in a set. Only now, we have to make sure we know what number to remove as we progres! This calls for a _sliding window_ iterator really, where we view the whole series through a slit X entries wide as it moves along the inputs.
As this puzzle is easier with a set of numbers, I create a sliding window of size `preamble + 2`, so we have access to the value to be removed and the value to be checked, at the same time; to achieve this, I created a window function that takes an *offset*, where you can take `offset` fewer items at the start, then have the window grow until it reaches the desired size:
```
from collections import deque
from itertools import islice
from typing import Iterable, Iterator, TypeVar
T = TypeVar("T")
def window(iterable: Iterable[T], n: int = 2, offset: int = 0) -> Iterator[deque[T]]:
it = iter(iterable)
queue = deque(islice(it, n - offset), maxlen=n)
yield queue
append = queue.append
for elem in it:
append(elem)
yield queue
def next_invalid(numbers: Iterable[int], preamble: int = 25) -> int:
it = window(numbers, preamble + 2, 2)
pool = set(next(it))
for win in it:
to_check = win[-1]
if len(win) == preamble + 2:
# remove the value now outside of our preamble window
pool.remove(win[0])
# validate the value can be created from a sum
for a in pool:
b = to_check - a
if b == a:
continue
if b in pool:
# number validated
break
else:
# no valid sum found
return to_check
pool.add(to_check)
test = [int(v) for v in """\
35
20
15
25
47
40
62
55
65
95
102
117
150
182
127
219
299
277
309
576
""".split()]
assert next_invalid(test, 5) == 127
import aocd
number_stream = [int(v) for v in aocd.get_data(day=9, year=2020).split()]
print("Part 1:", next_invalid(number_stream))
```
## Part 2
To solve the second part, you need a _dynamic_ window size over the input stream, and a running total. When the running total equals the value from part 1, we can then take the min and max values from the window.
- While the running total is too low, grow the window one stap and add the extra value to the total
- If the running total is too high, remove a value at the back of the window from the running total, and shrink that side of the window by one step.
With the Python `deque` (double-ended queue) already used in part one, this is a trivial task to achieve:
```
def find_weakness(numbers: Iterable[int], preamble: int = 25) -> int:
invalid = next_invalid(numbers, preamble)
it = iter(numbers)
total = next(it)
window = deque([total])
while total != invalid and window:
if total < invalid:
window.append(next(it))
total += window[-1]
else:
total -= window.popleft()
if not window:
raise ValueError("Could not find a weakness")
return min(window) + max(window)
assert find_weakness(test, 5) == 62
print("Part 2:", find_weakness(number_stream))
```
| true |
code
| 0.544983 | null | null | null | null |
|
# Campus SEIR Modeling
## Campus infection data
The following data consists of new infections reported since August 3, 2020, from diagnostic testing administered by the Wellness Center and University Health Services at the University of Notre Dame. The data is publically available on the [Notre Dame Covid-19 Dashboard](https://here.nd.edu/our-approach/dashboard/).
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
from datetime import timedelta
data = [
["2020-08-03", 0],
["2020-08-04", 0],
["2020-08-05", 0],
["2020-08-06", 1],
["2020-08-07", 0],
["2020-08-08", 1],
["2020-08-09", 2],
["2020-08-10", 4],
["2020-08-11", 4],
["2020-08-12", 7],
["2020-08-13", 10],
["2020-08-14", 14],
["2020-08-15", 3],
["2020-08-16", 15],
["2020-08-17", 80],
]
df = pd.DataFrame(data, columns=["date", "new cases"])
df["date"] = pd.to_datetime(df["date"])
fig, ax = plt.subplots(figsize=(8,4))
ax.bar(df["date"], df["new cases"], width=0.6)
ax.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.MO))
ax.xaxis.set_major_formatter(mdates.DateFormatter("%b %d"))
plt.title("Reported New Infections")
plt.grid()
```
## Fitting an SEIR model to campus data
Because of the limited amount of data available at the time this notebook was prepared, the model fitting has been limited to an SEIR model for infectious disease in a homogeneous population. In an SEIR model, the progression of an epidemic can be modeled by the rate processes shown in the following diagram.
$$\text{Susceptible}
\xrightarrow {\frac{\beta S I}{N}}
\text{Exposed}
\xrightarrow{\alpha E}
\text{Infectious}
\xrightarrow{\gamma I}
\text{Recovered} $$
which yeild the following model for the population of the four compartments
$$\begin{align*}
\frac{dS}{dt} &= -\beta S \frac{I}{N} \\
\frac{dE}{dt} &= \beta S \frac{I}{N} - \alpha E \\
\frac{dI}{dt} &= \alpha E - \gamma I \\
\frac{dR}{dt} &= \gamma I \\
\end{align*}$$
The recovery rate is given by $\gamma = 1/t_{recovery}$ where the average recovery time $t_{recovery}$ is estimated as 8 days.
| Parameter | Description | Estimated Value | Source |
| :-- | :-- | :-- | :-- |
| $N$ | campus population | 15,000 | estimate |
| $\alpha$ | 1/average latency period | 1/(3.0 d) |
| $\gamma$ | 1/average recovery period | 1/(8.0 d) | literature |
| $\beta$ | infection rate constant | tbd | fitted to data |
| $I_0$ | initial infectives on Aug 3, 2020 | tbd | fitted to data
| $R_0$ | reproduction number | ${\beta}/{\gamma}$ |
```
N = 15000 # estimated campus population
gamma = 1/8.0 # recovery rate = 1 / average recovery time in days
alpha = 1/3.0
def model(t, y, beta):
S, E, I, R = y
dSdt = -beta*S*I/N
dEdt = beta*S*I/N - alpha*E
dIdt = alpha*E - gamma*I
dRdt = gamma*I
return np.array([dSdt, dEdt, dIdt, dRdt])
def solve_model(t, params):
beta, I_initial = params
IC = [N - I_initial, I_initial, 0.0, 0.0]
soln = solve_ivp(lambda t, y: model(t, y, beta), np.array([t[0], t[-1]]),
IC, t_eval=t, atol=1e-6, rtol=1e-9)
S, E, I, R = soln.y
U = beta*S*I/N
return S, E, I, R, U
def residuals(df, params):
S, E, I, R, U = solve_model(df.index, params)
return np.linalg.norm(df["new cases"] - U)
def fit_model(df, params_est=[0.5, 0.5]):
return minimize(lambda params: residuals(df, params), params_est, method="Nelder-Mead").x
def plot_data(df):
plt.plot(df.index, np.array(df["new cases"]), "r.", ms=20, label="data")
plt.xlabel("days")
plt.title("new cases")
plt.legend()
def plot_model(t, params):
print("R0 =", round(beta/gamma, 1))
S, E, I, R, U = solve_model(t, params)
plt.plot(t, U, lw=3, label="model")
plt.xlabel("days")
plt.title("new cases")
plt.legend()
plot_data(df)
beta, I_initial = fit_model(df)
plot_model(df.index, [beta, I_initial])
```
## Fitted parameter values
```
from tabulate import tabulate
parameter_table = [
["N", 15000],
["I0", I_initial],
["beta", beta],
["gamma", gamma],
["R0", beta/gamma]
]
print(tabulate(parameter_table, headers=["Parameter", "Value"]))
```
## Short term predictions of newly confirmed cases
Using the fitted parameters, the following code presents a short term projection of newly diagnosed infections. Roughly speaking, the model projects a 50% increase per day in newly diagnosed cases as a result of testing sympotomatic individuals.
The number of infected but asympotomatic individuals is unknown at this time, but can be expected to be a 2x multiple of this projection.
```
# prediction horizon (days ahead)
H = 1
# retrospective lag
K = 6
fig, ax = plt.subplots(1, 1, figsize=(12, 4))
for k in range(0, K+1):
# use data up to k days ago
if k > 0:
beta, I_initial = fit_model(df[:-k])
P = max(df[:-k].index) + H
c = 'b'
a = 0.25
else:
beta, I_initial = fit_model(df)
P = max(df.index) + H
c = 'r'
a = 1.0
# simulation
t = np.linspace(0, P, P+1)
S, E, I, R, U = solve_model(t, [beta, I_initial])
# plotting
dates = [df["date"][0] + timedelta(days=t) for t in t]
ax.plot(dates, U, c, lw=3, alpha=a)
ax.plot(df["date"], df["new cases"], "r.", ms=25, label="new infections (data)")
ax.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.MO))
ax.xaxis.set_major_formatter(mdates.DateFormatter("%b %d"))
ax.grid(True)
ax.set_title(f"{H} day-ahead predictions of confirmed new cases");
```
| true |
code
| 0.601652 | null | null | null | null |
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
<!--NAVIGATION-->
< [Keyboard Shortcuts in the IPython Shell](01.02-Shell-Keyboard-Shortcuts.ipynb) | [Contents](Index.ipynb) | [Input and Output History](01.04-Input-Output-History.ipynb) >
# IPython Magic Commands
The previous two sections showed how IPython lets you use and explore Python efficiently and interactively.
Here we'll begin discussing some of the enhancements that IPython adds on top of the normal Python syntax.
These are known in IPython as *magic commands*, and are prefixed by the ``%`` character.
These magic commands are designed to succinctly solve various common problems in standard data analysis.
Magic commands come in two flavors: *line magics*, which are denoted by a single ``%`` prefix and operate on a single line of input, and *cell magics*, which are denoted by a double ``%%`` prefix and operate on multiple lines of input.
We'll demonstrate and discuss a few brief examples here, and come back to more focused discussion of several useful magic commands later in the chapter.
## Pasting Code Blocks: ``%paste`` and ``%cpaste``
When working in the IPython interpreter, one common gotcha is that pasting multi-line code blocks can lead to unexpected errors, especially when indentation and interpreter markers are involved.
A common case is that you find some example code on a website and want to paste it into your interpreter.
Consider the following simple function:
``` python
>>> def donothing(x):
... return x
```
The code is formatted as it would appear in the Python interpreter, and if you copy and paste this directly into IPython you get an error:
```ipython
In [2]: >>> def donothing(x):
...: ... return x
...:
File "<ipython-input-20-5a66c8964687>", line 2
... return x
^
SyntaxError: invalid syntax
```
In the direct paste, the interpreter is confused by the additional prompt characters.
But never fear–IPython's ``%paste`` magic function is designed to handle this exact type of multi-line, marked-up input:
```ipython
In [3]: %paste
>>> def donothing(x):
... return x
## -- End pasted text --
```
The ``%paste`` command both enters and executes the code, so now the function is ready to be used:
```ipython
In [4]: donothing(10)
Out[4]: 10
```
A command with a similar intent is ``%cpaste``, which opens up an interactive multiline prompt in which you can paste one or more chunks of code to be executed in a batch:
```ipython
In [5]: %cpaste
Pasting code; enter '--' alone on the line to stop or use Ctrl-D.
:>>> def donothing(x):
:... return x
:--
```
These magic commands, like others we'll see, make available functionality that would be difficult or impossible in a standard Python interpreter.
## Running External Code: ``%run``
As you begin developing more extensive code, you will likely find yourself working in both IPython for interactive exploration, as well as a text editor to store code that you want to reuse.
Rather than running this code in a new window, it can be convenient to run it within your IPython session.
This can be done with the ``%run`` magic.
For example, imagine you've created a ``myscript.py`` file with the following contents:
```python
#-------------------------------------
# file: myscript.py
def square(x):
"""square a number"""
return x ** 2
for N in range(1, 4):
print(N, "squared is", square(N))
```
You can execute this from your IPython session as follows:
```ipython
In [6]: %run myscript.py
1 squared is 1
2 squared is 4
3 squared is 9
```
Note also that after you've run this script, any functions defined within it are available for use in your IPython session:
```ipython
In [7]: square(5)
Out[7]: 25
```
There are several options to fine-tune how your code is run; you can see the documentation in the normal way, by typing **``%run?``** in the IPython interpreter.
## Timing Code Execution: ``%timeit``
Another example of a useful magic function is ``%timeit``, which will automatically determine the execution time of the single-line Python statement that follows it.
For example, we may want to check the performance of a list comprehension:
```ipython
In [8]: %timeit L = [n ** 2 for n in range(1000)]
1000 loops, best of 3: 325 µs per loop
```
The benefit of ``%timeit`` is that for short commands it will automatically perform multiple runs in order to attain more robust results.
For multi line statements, adding a second ``%`` sign will turn this into a cell magic that can handle multiple lines of input.
For example, here's the equivalent construction with a ``for``-loop:
```ipython
In [9]: %%timeit
...: L = []
...: for n in range(1000):
...: L.append(n ** 2)
...:
1000 loops, best of 3: 373 µs per loop
```
We can immediately see that list comprehensions are about 10% faster than the equivalent ``for``-loop construction in this case.
We'll explore ``%timeit`` and other approaches to timing and profiling code in [Profiling and Timing Code](01.07-Timing-and-Profiling.ipynb).
## Help on Magic Functions: ``?``, ``%magic``, and ``%lsmagic``
Like normal Python functions, IPython magic functions have docstrings, and this useful
documentation can be accessed in the standard manner.
So, for example, to read the documentation of the ``%timeit`` magic simply type this:
```ipython
In [10]: %timeit?
```
Documentation for other functions can be accessed similarly.
To access a general description of available magic functions, including some examples, you can type this:
```ipython
In [11]: %magic
```
For a quick and simple list of all available magic functions, type this:
```ipython
In [12]: %lsmagic
```
Finally, I'll mention that it is quite straightforward to define your own magic functions if you wish.
We won't discuss it here, but if you are interested, see the references listed in [More IPython Resources](01.08-More-IPython-Resources.ipynb).
<!--NAVIGATION-->
< [Keyboard Shortcuts in the IPython Shell](01.02-Shell-Keyboard-Shortcuts.ipynb) | [Contents](Index.ipynb) | [Input and Output History](01.04-Input-Output-History.ipynb) >
| true |
code
| 0.493164 | null | null | null | null |
|

# Ejemplo de simulación numérica
```
import numpy as np
from scipy.integrate import odeint
from matplotlib import rc
import matplotlib.pyplot as plt
%matplotlib inline
rc("text", usetex=True)
rc("font", size=18)
rc("figure", figsize=(6,4))
rc("axes", grid=True)
```
## Problema físico

Definimos un SR con el origen en el orificio donde el hilo atravieza el plano, la coordenada $\hat{z}$ apuntando hacia abajo. Con esto sacamos, de la segunda ley de Newton para las particulas:
$$
\begin{align}
\text{Masa 1)}\quad&\vec{F}_1 = m_1 \vec{a}_1 \\
&-T \hat{r} = m_1 \vec{a}_1 \\
&-T \hat{r} = m_1 \left\{ \left(\ddot{r} - r \dot{\theta}^2\right) \hat{r} + \left(r\ddot{\theta} + 2\dot{r}\dot{\theta}\right)\hat{\theta} \right\} \\
&\begin{cases}
\hat{r})\ - T = m_1\left( \ddot{r} - r\, \dot{\theta}^2\right)\\
\hat{\theta})\ 0 = m_1 \left(r \ddot{\theta} + 2 \dot{r}\dot{\theta}\right)\\
\end{cases}\\
\\
\text{Masa 2)}\quad&\vec{F}_2 = m_2 \vec{a}_2 \\
&-T \hat{z} + m_2 g \hat{z} = m_2 \ddot{z} \hat{z} \\
\implies & \boxed{T = m_2 \left( g - \ddot{z} \right)}\\
\end{align}
$$
Ahora reemplazando este resultado para la tension (que es igual en ambas expresiones) y entendiendo que $\ddot{z} = -\ddot{r}$ pues la soga es ideal y de largo constante, podemos rescribir las ecuaciones obtenidas para la masa 1 como:
$$
\begin{cases}
\hat{r})\quad - m_2 \left( g + \ddot{r} \right) = m_1\left( \ddot{r} - r\, \dot{\theta}^2\right)\\
\\
\hat{\theta})\quad 0 = m_1 \left(r \ddot{\theta} + 2 \dot{r}\dot{\theta}\right)
\end{cases}
\implies
\begin{cases}
\hat{r})\quad \ddot{r} = \dfrac{- m_2 g + m_1 r \dot{\theta}^2}{m_1 + m_2}\\
\\
\hat{\theta})\quad \ddot{\theta} = -2 \dfrac{\dot{r}\dot{\theta}}{r}\\
\end{cases}
$$
La gracia de estos métodos es lograr encontrar una expresión de la forma $y'(x) = f(x,t)$ donde x será la solución buscada, aca como estamos en un sistema de segundo orden en dos variables diferentes ($r$ y $\theta$) sabemos que nuestra solución va a tener que involucrar 4 componentes. Es como en el oscilador armónico, que uno tiene que definir posicion y velocidad inicial para poder conocer el sistema, solo que aca tenemos dos para $r$ y dos para $\theta$.
Se puede ver entonces que vamos a necesitar una solucion del tipo:
$$\mathbf{X} = \begin{pmatrix} r \\ \dot{r}\\ \theta \\ \dot{\theta} \end{pmatrix} $$
Y entonces
$$
\dot{\mathbf{X}} =
\begin{pmatrix} \dot{r} \\ \ddot{r}\\ \dot{\theta} \\ \ddot{\theta} \end{pmatrix} =
\begin{pmatrix} \dot{r} \\ \dfrac{-m_2 g + m_1 r \dot{\theta}^2}{m_1 + m_2} \\ \dot{\theta} \\ -2 \dfrac{\dot{r}\dot{\theta}}{r} \end{pmatrix} =
\mathbf{f}(\mathbf{X}, t)
$$
---
Si alguno quiere, tambien se puede escribir la evolucion del sistema de una forma piola, que no es otra cosa que una querida expansión de Taylor a orden lineal.
$$
\begin{align}
r(t+dt) &= r(t) + \dot{r}(t)\cdot dt \\
\dot{r}(t+dt) &= \dot{r}(t) + \ddot{r}(t)\cdot dt \\
\theta(t+dt) &= \theta(t) + \dot{\theta}(t)\cdot dt \\
\dot{\theta}(t+dt) &= \dot{\theta}(t) + \ddot{\theta}(t)\cdot dt
\end{align}
\implies
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}(t + dt) =
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}(t) +
\begin{pmatrix}
\dot{r}\\
\ddot{r}\\
\dot{\theta}\\
\ddot{\theta}
\end{pmatrix}(t) \cdot dt
$$
Aca tenemos que recordar que la compu no puede hacer cosas continuas, porque son infinitas cuentas, entones si o si hay que discretizar el tiempo y el paso temporal!
$$
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}_{i+1} =
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}_i +
\begin{pmatrix}
\dot{r}\\
\ddot{r}\\
\dot{\theta}\\
\ddot{\theta}
\end{pmatrix}_i \cdot dt
$$
Si entonces decido llamar a este vector columna $\mathbf{X}$, el sistema queda escrito como:
$$
\mathbf{X}_{i+1} = \mathbf{X}_i + \dot{\mathbf{X}}_i\ dt
$$
Donde sale denuevo que $\dot{\mathbf{X}}$ es lo que está escrito arriba.
Es decir que para encontrar cualquier valor, solo hace falta saber el vector anterior y la derivada, pero las derivadas ya las tenemos (es todo el trabajo que hicimos de fisica antes)!!
---
---
De cualquier forma que lo piensen, ojala hayan entendido que entonces con tener las condiciones iniciales y las ecuaciones diferenciales ya podemos resolver (tambien llamado *integrar*) el sistema.
```
# Constantes del problema:
M1 = 3
M2 = 3
g = 9.81
# Condiciones iniciales del problema:
r0 = 2
r_punto0 = 0
tita0 = 0
tita_punto0 = 1
C1 = (M2*g)/(M1+M2) # Defino constantes utiles
C2 = (M1)/(M1+M2)
cond_iniciales = [r0, r_punto0, tita0, tita_punto0]
def derivada(X, t, c1, c2): # esto sería la f del caso { x' = f(x,t) }
r, r_punto, tita, tita_punto = X
deriv = [0, 0, 0, 0] # es como el vector columna de arriba pero en filado
deriv[0] = r_punto # derivada de r
deriv[1] = -c1 + c2*r*(tita_punto)**2 # r dos puntos
deriv[2] = tita_punto # derivada de tita
deriv[3] = -2*r_punto*tita_punto/r
return deriv
def resuelvo_sistema(m1, m2, tmax = 20):
t0 = 0
c1 = (m2*g)/(m1+m2) # Defino constantes utiles
c2 = (m1)/(m1+m2)
t = np.arange(t0, tmax, 0.001)
# aca podemos definirnos nuestro propio algoritmo de integracion
# o bien usar el que viene a armado de scipy.
# Ojo que no es perfecto eh, a veces es mejor escribirlo uno
out = odeint(derivada, cond_iniciales, t, args = (c1, c2,))
return [t, out.T]
t, (r, rp, tita, titap) = resuelvo_sistema(M1, M2, tmax=10)
plt.figure()
plt.plot(t, r/r0, 'r')
plt.ylabel(r"$r / r_0$")
plt.xlabel(r"tiempo")
# plt.savefig("directorio/r_vs_t.pdf", dpi=300)
plt.figure()
plt.plot(t, tita-tita0, 'b')
plt.ylabel(r"$\theta - \theta_0$")
plt.xlabel(r"tiempo")
# plt.savefig("directorio/tita_vs_t.pdf", dpi=300)
plt.figure()
plt.plot(r*np.cos(tita-tita0)/r0, r*np.sin(tita-tita0)/r0, 'g')
plt.ylabel(r"$r/r_0\ \sin\left(\theta - \theta_0\right)$")
plt.xlabel(r"$r/r_0\ \cos\left(\theta - \theta_0\right)$")
# plt.savefig("directorio/trayectoria.pdf", dpi=300)
```
Todo muy lindo!!
Cómo podemos verificar si esto está andando ok igual? Porque hasta acá solo sabemos que dio razonable, pero el ojímetro no es una medida cuantitativa.
Una opción para ver que el algoritmo ande bien (y que no hay errores numéricos, y que elegimos un integrador apropiado **ojo con esto eh... te estoy mirando a vos, Runge-Kutta**), es ver si se conserva la energía.
Les recuerdo que la energía cinética del sistema es $K = \frac{1}{2} m_1 \left|\vec{v}_1 \right|^2 + \frac{1}{2} m_2 \left|\vec{v}_2 \right|^2$, cuidado con cómo se escribe cada velocidad, y que la energía potencial del sistema únicamente depende de la altura de la pelotita colgante.
Hace falta conocer la longitud $L$ de la cuerda para ver si se conserva la energía mecánica total? (Spoiler: No. Pero piensen por qué)
Les queda como ejercicio a ustedes verificar eso, y también pueden experimentar con distintos metodos de integración a ver qué pasa con cada uno, abajo les dejamos una ayudita para que prueben.
```
from scipy.integrate import solve_ivp
def resuelvo_sistema(m1, m2, tmax = 20, metodo='RK45'):
t0 = 0
c1 = (m2*g)/(m1+m2) # Defino constantes utiles
c2 = (m1)/(m1+m2)
t = np.arange(t0, tmax, 0.001)
# acá hago uso de las lambda functions, solamente para usar
# la misma funcion que definimos antes. Pero como ahora
# voy a usar otra funcion de integracion (no odeint)
# que pide otra forma de definir la funcion, en vez de pedir
# f(x,t) esta te pide f(t, x), entonces nada, hay que dar vuelta
# parametros y nada mas...
deriv_bis = lambda t, x: derivada(x, t, c1, c2)
out = solve_ivp(fun=deriv_bis, t_span=(t0, tmax), y0=cond_iniciales,\
method=metodo, t_eval=t)
return out
# Aca armo dos arrays con los metodos posibles y otro con colores
all_metodos = ['RK45', 'RK23', 'Radau', 'BDF', 'LSODA']
all_colores = ['r', 'b', 'm', 'g', 'c']
# Aca les dejo la forma piola de loopear sobre dos arrays a la par
for met, col in zip(all_metodos, all_colores):
result = resuelvo_sistema(M1, M2, tmax=30, metodo=met)
t = result.t
r, rp, tita, titap = result.y
plt.plot(t, r/r0, col, label=met)
plt.xlabel("tiempo")
plt.ylabel(r"$r / r_0$")
plt.legend(loc=3)
```
Ven cómo los distintos métodos van modificando más y más la curva de $r(t)$ a medida que van pasando los pasos de integración. Tarea para ustedes es correr el mismo código con la conservación de energía.
Cuál es mejor, por qué y cómo saberlo son preguntas que deberán hacerse e investigar si en algún momento trabajan con esto.
Por ejemplo, pueden buscar en Wikipedia "Symplectic Integrator" y ver qué onda.
### Les dejamos también abajo la simulación de la trayectoria de la pelotita
```
from matplotlib import animation
%matplotlib notebook
result = resuelvo_sistema(M1, M2, tmax=30, metodo='Radau')
t = result.t
r, rp, tita, titap = result.y
fig, ax = plt.subplots()
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.plot(r*np.cos(tita)/r0, r*np.sin(tita)/r0, 'm', lw=0.2)
line, = ax.plot([], [], 'ko', ms=5)
N_SKIP = 50
N_FRAMES = int(len(r)/N_SKIP)
def animate(frame_no):
i = frame_no*N_SKIP
r_i = r[i]/r0
tita_i = tita[i]
line.set_data(r_i*np.cos(tita_i), r_i*np.sin(tita_i))
return line,
anim = animation.FuncAnimation(fig, animate, frames=N_FRAMES,
interval=50, blit=False)
```
Recuerden que esta animación no va a parar eh, sabemos que verla te deja en una especie de trance místico, pero recuerden pararla cuando haya transcurrido suficiente tiempo
# Animación Interactiva
Usando `ipywidgets` podemos agregar sliders a la animación, para modificar el valor de las masitas
```
from ipywidgets import interactive, interact, FloatProgress
from IPython.display import clear_output, display
%matplotlib inline
@interact(m1=(0,5,0.5), m2=(0,5,0.5), tmax=(0.01,20,0.5)) #Permite cambiar el parámetro de la ecuación
def resuelvo_sistema(m1, m2, tmax = 20):
t0 = 0
c1 = (m2*g)/(m1+m2) # Defino constantes utiles
c2 = (m1)/(m1+m2)
t = np.arange(t0, tmax, 0.05)
# out = odeint(derivada, cond_iniciales, t, args = (c1, c2,))
r, rp, tita, titap = odeint(derivada, cond_iniciales, t, args=(c1, c2,)).T
plt.xlim((-1,1))
plt.ylim((-1,1))
plt.plot(r*np.cos(tita)/r0, r*np.sin(tita)/r0,'b-')
# plt.xlabel("tiempo")
# plt.ylabel(r"$r / r_0$")
# plt.show()
```
| true |
code
| 0.527864 | null | null | null | null |
|
# 4 データ前処理
## 4.1 欠損データへの対処
```
from IPython.core.display import display
import pandas as pd
from io import StringIO
csv_data = '''A,B,C,D
1.0,2.0,3.0,4.0
5.0,6.0,,8.0
10.0,11.0,12.0,'''
df = pd.read_csv(StringIO(csv_data))
df
# 各特徴量の欠測値をカウント
df.isnull().sum()
df.values
```
### 4.1.1 欠測値を持つサンプル/特徴量を取り除く
```
# 欠測値を含む行を削除
df.dropna()
# 欠測値を含む列を削除
df.dropna(axis=1)
# すべての列がNaNである行だけを削除
df.dropna(how='all')
# 非NaN値が4つ未満の行を削除
df.dropna(thresh=4)
# 特定の列にNaNが含まれている行だけを削除
df.dropna(subset=['C'])
```
### 4.1.2 欠測値を補完する
```
from sklearn.preprocessing import Imputer
# 欠測値補完のインスタンスを生成(平均値補完)
# median: 中央値、most_frequent: 最頻値
imr = Imputer(missing_values='NaN', strategy='mean', axis=0)
# データを適合
imr = imr.fit(df)
# 補完を実行
imputed_data = imr.transform(df.values)
imputed_data
```
## 4.2 カテゴリデータの処理
```
import pandas as pd
# サンプルデータを生成
df = pd.DataFrame([
['green', 'M', 10.1, 'class1'],
['red', 'L', 13.5, 'class2'],
['blue', 'XL', 15.3, 'class1'],
])
# 列名を設定
df.columns = ['color', 'size', 'price', 'classlabel']
df
```
### 4.2.1 順序特徴量のマッピング
```
# Tシャツのサイズと整数を対応させるディクショナリを生成
size_mapping = {'XL': 3, 'L': 2, 'M': 1}
# Tシャツのサイズを整数に変換
df['size'] = df['size'].map(size_mapping)
df
# Tシャツのサイズを文字列に戻す辞書
inv_size_mapping = {v: k for k, v in size_mapping.items()}
inv_size_mapping
```
### 4.2.2 クラスラベルのエンコーディング
```
import numpy as np
# クラスラベルと整数を対応させる辞書
class_mapping = {label: i for i, label in enumerate(np.unique(df['classlabel']))}
class_mapping
# クラスラベルを整数に変換
df['classlabel'] = df['classlabel'].map(class_mapping)
df
inv_class_mapping = {v: k for k, v in class_mapping.items()}
# 整数からクラスラベルに変換
df['classlabel'] = df['classlabel'].map(inv_class_mapping)
df
from sklearn.preprocessing import LabelEncoder
class_le = LabelEncoder()
y = class_le.fit_transform(df['classlabel'].values)
y
class_le.inverse_transform(y)
```
### 4.2.3 名義特徴量での one-hot エンコーディング
```
# Tシャツの色、サイズ、価格を抽出
X = df[['color', 'size', 'price']].values
color_le = LabelEncoder()
X[:, 0] = color_le.fit_transform(X[:, 0])
X
from sklearn.preprocessing import OneHotEncoder
# one-hot エンコーダの生成
ohe = OneHotEncoder(categorical_features=[0])
# one-hot エンコーディングを実行
ohe.fit_transform(X).toarray()
# one-hot エンコーディングを実行
pd.get_dummies(df[['price', 'color', 'size']])
```
## 4.3 データセットをトレーニングデータセットとテストデータセットに分割する
```
# http://archive.ics.uci.edu/ml/datasets/Wine
df_wine = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
display(df_wine.head())
# 列名を設定
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline']
display(df_wine.head())
print('Class labels', np.unique(df_wine['Class label']))
from sklearn.cross_validation import train_test_split
# 特徴量とクラスラベルを別々に抽出
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
# 全体の30%をテストデータにする
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
```
## 4.4 特徴量の尺度を揃える
```
from sklearn.preprocessing import MinMaxScaler
# min-max スケーリングのインスタンスを生成
mms = MinMaxScaler()
# トレーニングデータをスケーリング
X_train_norm = mms.fit_transform(X_train)
# テストデータをスケーリング
X_test_norm = mms.transform(X_test)
X_train, X_train_norm
from sklearn.preprocessing import StandardScaler
# 標準化のインスタンスを生成
stdsc = StandardScaler()
X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.transform(X_test)
X_train_std
```
## 4.5 有益な特徴量の選択
### 4.5.1 L1 正則化による疎な解
```
from sklearn.linear_model import LogisticRegression
# L1正則化ロジスティック回帰のインスタンスを生成
LogisticRegression(penalty='l1')
# L1正則化ロジスティック回帰のインスタンスを生成(逆正則化パラメータ C=0.1)
lr = LogisticRegression(penalty='l1', C=0.1)
lr.fit(X_train_std, y_train)
print('Training accuracy:', lr.score(X_train_std, y_train))
print('Test accuracy:', lr.score(X_test_std, y_test))
# 切片の表示
lr.intercept_
# 重み係数の表示
lr.coef_
import matplotlib.pyplot as plt
fig = plt.figure()
ax = plt.subplot(111)
colors = ['blue', 'green', 'red', 'cyan', 'magenta', 'yellow', 'black',
'pink', 'lightgreen', 'lightblue', 'gray', 'indigo', 'orange']
# 空のリストを生成(重み係数、逆正則化パラメータ
weights, params = [], []
# 逆正則化パラメータの値ごとに処理
for c in np.arange(-4, 6):
# print(c) # -4~5
lr = LogisticRegression(penalty='l1', C=10 ** c, random_state=0)
lr.fit(X_train_std, y_train)
weights.append(lr.coef_[1])
params.append(10 ** c)
# 重み係数をNumPy配列に変換
weights = np.array(weights)
# 各重み係数をプロット
# print(weights.shape[1]) # -> 13
for column, color in zip(range(weights.shape[1]), colors):
plt.plot(params, weights[:, column], label=df_wine.columns[column + 1], color=color)
# y=0 に黒い破線を引く
plt.axhline(0, color='black', linestyle='--', linewidth=3)
plt.xlim([10 ** (-5), 10 ** 5])
# 軸のラベルの設定
plt.ylabel('weight coefficient')
plt.xlabel('C')
# 横軸を対数スケールに設定
plt.xscale('log')
plt.legend(loc='upper left')
ax.legend(loc='upper center', bbox_to_anchor=(1.38, 1.03), ncol=1, fancybox=True)
plt.show()
```
### 4.5.2 逐次特徴選択アルゴリズム
```
from sklearn.base import clone
from itertools import combinations
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
class SBS():
"""
逐次後退選択(sequencial backward selection)を実行するクラス
"""
def __init__(self, estimator, k_features, scoring=accuracy_score,
test_size=0.25, random_state=1):
self.scoring = scoring # 特徴量を評価する指標
self.estimator = clone(estimator) # 推定器
self.k_features = k_features # 選択する特徴量の個数
self.test_size = test_size # テストデータの悪愛
self.random_state = random_state # 乱数種を固定する random_state
def fit(self, X, y):
# トレーニングデータとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=self.test_size,
random_state=self.random_state)
#print(len(X_train), len(X_test), len(y_train), len(y_test))
# 全ての特徴量の個数、列インデックス
dim = X_train.shape[1]
self.indices_ = tuple(range(dim))
self.subsets_ = [self.indices_]
#print(self.indices_)
# 全ての特徴量を用いてスコアを算出
score = self._calc_score(X_train, y_train, X_test, y_test, self.indices_)
# スコアを格納
self.scores_ = [score]
# 指定した特徴量の個数になるまで処理を反復
while dim > self.k_features:
# 空のリストの生成(スコア、列インデックス)
scores = []
subsets = []
# 特徴量の部分集合を表す列インデックスの組み合わせ毎に処理を反復
for p in combinations(self.indices_, r=dim - 1):
# スコアを算出して格納
score = self._calc_score(X_train, y_train, X_test, y_test, p)
scores.append(score)
# 特徴量の部分集合を表す列インデックスのリストを格納
subsets.append(p)
# 最良のスコアのインデックスを抽出
best = np.argmax(scores)
# 最良のスコアとなる列インデックスを抽出して格納
self.indices_ = subsets[best]
self.subsets_.append(self.indices_)
# 特徴量の個数を1つだけ減らして次のステップへ
dim -= 1
# スコアを格納
self.scores_.append(scores[best])
# 最後に格納したスコア
self.k_score_ = self.scores_[-1]
return self
def transform(self, X):
# 抽出した特徴量を返す
return X[:, self.indices_]
def _calc_score(self, X_train, y_train, X_test, y_test, indices):
# 指定された列番号 indices の特徴量を抽出してモデルに適合
self.estimator.fit(X_train[:, indices], y_train)
# テストデータを用いてクラスラベルを予測
y_pred = self.estimator.predict(X_test[:, indices])
# 真のクラスラベルと予測値を用いてスコアを算出
score = self.scoring(y_test, y_pred)
return score
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
knn = KNeighborsClassifier(n_neighbors=2)
sbs = SBS(knn, k_features=1)
sbs.fit(X_train_std, y_train)
# 近傍点の個数のリスト
k_feat = [len(k) for k in sbs.subsets_]
display(k_feat)
# 横軸を近傍店の個数、縦軸をスコアとした折れ線グラフのプロット
plt.plot(k_feat, sbs.scores_, marker='o')
plt.ylim([0.7, 1.1])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.show()
k5 = list(sbs.subsets_[8])
print(k5)
print(df_wine.columns[1:][k5])
# 13個全ての特徴量を用いてモデルに適合
knn.fit(X_train_std, y_train)
# トレーニングの正解率を出力
print('Training accuracy:', knn.score(X_train_std, y_train))
# テストの正解率を出力
print('Test accuracy:', knn.score(X_test_std, y_test))
# 5個の特徴量を用いてモデルに適合
knn.fit(X_train_std[:, k5], y_train)
# トレーニングの正解率を出力
print('Training accuracy:', knn.score(X_train_std[:, k5], y_train))
# テストの正解率を出力
print('Test accuracy:', knn.score(X_test_std[:, k5], y_test))
```
## 4.6 ランダムフォレストで特徴量の重要度にアクセスする
```
from sklearn.ensemble import RandomForestClassifier
# Wine データセットの特徴量の名所
feat_labels = df_wine.columns[1:]
# ランダムフォレストオブジェクトの生成
# (木の個数=10,000、すべての怖を用いて並列計算を実行
forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1)
# モデルに適合
forest.fit(X_train, y_train)
# 特徴量の重要度を抽出
importances = forest.feature_importances_
# 重要度の降順で特徴量のインデックスを抽出
indices = np.argsort(importances)[::-1]
# 重要度の降順で特徴量の名称、重要度を表示
for f in range(X_train.shape[1]):
print("{:2d}) {:<30} {:f}".format(f + 1, feat_labels[indices[f]], importances[indices[f]]))
plt.title('Feature Importances')
plt.bar(range(X_train.shape[1]), importances[indices], color='lightblue', align='center')
plt.xticks(range(X_train.shape[1]), feat_labels[indices], rotation=90)
plt.xlim([-1, X_train.shape[1]])
plt.tight_layout()
plt.show()
from sklearn.feature_selection import SelectFromModel
# 特徴選択オブジェクトの生成(重要度のしきい値を0.15に設定)
sfm = SelectFromModel(forest, prefit=True, threshold=0.15)
# 特徴量を抽出
X_selected = sfm.transform(X_train)
X_selected.shape
for f in range(X_selected.shape[1]):
print("{:2d}) {:<30} {:f}".format(f + 1, feat_labels[indices[f]], importances[indices[f]]))
```
| true |
code
| 0.353512 | null | null | null | null |
|
# CLX Asset Classification (Supervised)
## Authors
- Eli Fajardo (NVIDIA)
- Görkem Batmaz (NVIDIA)
- Bhargav Suryadevara (NVIDIA)
## Table of Contents
* Introduction
* Dataset
* Reading in the datasets
* Training and inference
* References
# Introduction
In this notebook, we will show how to predict the function of a server with Windows Event Logs using cudf, cuml and pytorch. The machines are labeled as DC, SQL, WEB, DHCP, MAIL and SAP. The dependent variable will be the type of the machine. The features are selected from Windows Event Logs which is in a tabular format. This is a first step to learn the behaviours of certain types of machines in data-centres by classifying them probabilistically. It could help to detect unusual behaviour in a data-centre. For example, some compromised computers might be acting as web/database servers but with their original tag.
This work could be expanded by using different log types or different events from the machines as features to improve accuracy. Various labels can be selected to cover different types of machines or data-centres.
## Library imports
```
from clx.analytics.asset_classification import AssetClassification
import cudf
from cuml.preprocessing import train_test_split
from cuml.preprocessing import LabelEncoder
import torch
from sklearn.metrics import accuracy_score, f1_score, confusion_matrix
import pandas as pd
from os import path
import s3fs
```
## Initialize variables
10000 is chosen as the batch size to optimise the performance for this dataset. It can be changed depending on the data loading mechanism or the setup used.
EPOCH should also be adjusted depending on convergence for a specific dataset.
label_col indicates the total number of features used plus the dependent variable. Feature names are listed below.
```
batch_size = 10000
label_col = '19'
epochs = 15
ac = AssetClassification()
```
## Read the dataset into a GPU dataframe with `cudf.read_csv()`
The original data had many other fields. Many of them were either static or mostly blank. After filtering those, there were 18 meaningful columns left. In this notebook we use a fake continuous feature to show the inclusion of continuous features too. When you are using raw data the cell below need to be uncommented
```
# win_events_gdf = cudf.read_csv("raw_features_and_labels.csv")
```
```
win_events_gdf.dtypes
eventcode int64
keywords object
privileges object
message object
sourcename object
taskcategory object
account_for_which_logon_failed_account_domain object
detailed_authentication_information_authentication_package object
detailed_authentication_information_key_length float64
detailed_authentication_information_logon_process object
detailed_authentication_information_package_name_ntlm_only object
logon_type float64
network_information_workstation_name object
new_logon_security_id object
impersonation_level object
network_information_protocol float64
network_information_direction object
filter_information_layer_name object
cont1 int64
label object
dtype: object
```
### Define categorical and continuous feature columns.
```
cat_cols = [
"eventcode",
"keywords",
"privileges",
"message",
"sourcename",
"taskcategory",
"account_for_which_logon_failed_account_domain",
"detailed_authentication_information_authentication_package",
"detailed_authentication_information_key_length",
"detailed_authentication_information_logon_process",
"detailed_authentication_information_package_name_ntlm_only",
"logon_type",
"network_information_workstation_name",
"new_logon_security_id",
"impersonation_level",
"network_information_protocol",
"network_information_direction",
"filter_information_layer_name",
"label"
]
cont_cols = [
"cont1"
]
```
The following are functions used to preprocess categorical and continuous feature columns. This can very depending on what best fits your application and data.
```
def categorize_columns(cat_gdf):
for col in cat_gdf.columns:
cat_gdf[col] = cat_gdf[col].astype('str')
cat_gdf[col] = cat_gdf[col].fillna("NA")
cat_gdf[col] = LabelEncoder().fit_transform(cat_gdf[col])
cat_gdf[col] = cat_gdf[col].astype('int16')
return cat_gdf
def normalize_conts(cont_gdf):
means, stds = (cont_gdf.mean(0), cont_gdf.std(ddof=0))
cont_gdf = (cont_gdf - means) / stds
return cont_gdf
```
Preprocessing steps below are not executed in this notebook, because we release already preprocessed data.
```
#win_events_gdf[cat_cols] = categorize_columns(win_events_gdf[cat_cols])
#win_events_gdf[cont_cols] = normalize_conts(win_events_gdf[cont_cols])
```
Read Windows Event data already preprocessed by above steps
```
S3_BASE_PATH = "rapidsai-data/cyber/clx"
WINEVT_PREPROC_CSV = "win_events_features_preproc.csv"
# Download Zeek conn log
if not path.exists(WINEVT_PREPROC_CSV):
fs = s3fs.S3FileSystem(anon=True)
fs.get(S3_BASE_PATH + "/" + WINEVT_PREPROC_CSV, WINEVT_PREPROC_CSV)
win_events_gdf = cudf.read_csv("win_events_features_preproc.csv")
win_events_gdf.head()
```
### Split the dataset into training and test sets using cuML `train_test_split` function
Column 19 contains the ground truth about each machine's function that the logs come from. i.e. DC, SQL, WEB, DHCP, MAIL and SAP. Hence it will be used as a label.
```
X_train, X_test, Y_train, Y_test = train_test_split(win_events_gdf, "label", train_size=0.9)
X_train["label"] = Y_train
X_train.head()
Y_train.unique()
```
### Print Labels
Making sure the test set contains all labels
```
Y_test.unique()
```
## Training
Asset Classification training uses the fastai tabular model. More details can be found at https://github.com/fastai/fastai/blob/master/fastai/tabular/models.py#L6
Feature columns will be embedded so that they can be used as categorical values. The limit can be changed depending on the accuracy of the dataset.
Adam is the optimizer used in the training process; it is popular because it produces good results in various tasks. In its paper, computing the first and the second moment estimates and updating the parameters are summarized as follows
$$\alpha_{t}=\alpha \cdot \sqrt{1-\beta_{2}^{t}} /\left(1-\beta_{1}^{t}\right)$$
More detailson Adam can be found at https://arxiv.org/pdf/1412.6980.pdf
We have found that the way we partition the dataframes with a 10000 batch size gives us the optimum data loading capability. The **batch_size** argument can be adjusted for different sizes of datasets.
```
cat_cols.remove("label")
ac.train_model(X_train, cat_cols, cont_cols, "label", batch_size, epochs, lr=0.01, wd=0.0)
```
## Evaluation
```
pred_results = ac.predict(X_test, cat_cols, cont_cols).to_array()
true_results = Y_test.to_array()
f1_score_ = f1_score(pred_results, true_results, average='micro')
print('micro F1 score: %s'%(f1_score_))
torch.cuda.empty_cache()
labels = ["DC","DHCP","MAIL","SAP","SQL","WEB"]
a = confusion_matrix(true_results, pred_results)
pd.DataFrame(a, index=labels, columns=labels)
```
The confusion matrix shows that some machines' function can be predicted really well, whereas some of them need more tuning or more features. This work can be improved and expanded to cover individual data-centres to create a realistic map of the network using ML by not just relying on the naming conventions. It could also help to detect more prominent scale anomalies like multiple machines, not acting per their tag.
## References:
* https://github.com/fastai/fastai/blob/master/fastai/tabular/models.py#L6
* https://jovian.ml/aakashns/04-feedforward-nn
* https://www.kaggle.com/dienhoa/reverse-tabular-module-of-fast-ai-v1
* https://github.com/fastai/fastai/blob/master/fastai/layers.py#L44
| true |
code
| 0.541954 | null | null | null | null |
|

# Chapter 8: Basic Data Wrangling With Pandas
<h2>Chapter Outline<span class="tocSkip"></span></h2>
<hr>
<div class="toc"><ul class="toc-item"><li><span><a href="#1.-DataFrame-Characteristics" data-toc-modified-id="1.-DataFrame-Characteristics-2">1. DataFrame Characteristics</a></span></li><li><span><a href="#2.-Basic-DataFrame-Manipulations" data-toc-modified-id="2.-Basic-DataFrame-Manipulations-3">2. Basic DataFrame Manipulations</a></span></li><li><span><a href="#3.-DataFrame-Reshaping" data-toc-modified-id="3.-DataFrame-Reshaping-4">3. DataFrame Reshaping</a></span></li><li><span><a href="#4.-Working-with-Multiple-DataFrames" data-toc-modified-id="4.-Working-with-Multiple-DataFrames-5">4. Working with Multiple DataFrames</a></span></li><li><span><a href="#5.-More-DataFrame-Operations" data-toc-modified-id="5.-More-DataFrame-Operations-6">5. More DataFrame Operations</a></span></li></ul></div>
## Chapter Learning Objectives
<hr>
- Inspect a dataframe with `df.head()`, `df.tail()`, `df.info()`, `df.describe()`.
- Obtain dataframe summaries with `df.info()` and `df.describe()`.
- Manipulate how a dataframe displays in Jupyter by modifying Pandas configuration options such as `pd.set_option("display.max_rows", n)`.
- Rename columns of a dataframe using the `df.rename()` function or by accessing the `df.columns` attribute.
- Modify the index name and index values of a dataframe using `.set_index()`, `.reset_index()` , `df.index.name`, `.index`.
- Use `df.melt()` and `df.pivot()` to reshape dataframes, specifically to make tidy dataframes.
- Combine dataframes using `df.merge()` and `pd.concat()` and know when to use these different methods.
- Apply functions to a dataframe `df.apply()` and `df.applymap()`
- Perform grouping and aggregating operations using `df.groupby()` and `df.agg()`.
- Perform aggregating methods on grouped or ungrouped objects such as finding the minimum, maximum and sum of values in a dataframe using `df.agg()`.
- Remove or fill missing values in a dataframe with `df.dropna()` and `df.fillna()`.
## 1. DataFrame Characteristics
<hr>
Last chapter we looked at how we can create dataframes. Let's now look at some helpful ways we can view our dataframe.
```
import numpy as np
import pandas as pd
```
### Head/Tail
The `.head()` and `.tail()` methods allow you to view the top/bottom *n* (default 5) rows of a dataframe. Let's load in the cycling data set from last chapter and try them out:
```
df = pd.read_csv('data/cycling_data.csv')
df.head()
```
The default return value is 5 rows, but we can pass in any number we like. For example, let's take a look at the top 10 rows:
```
df.head(10)
```
Or the bottom 5 rows:
```
df.tail()
```
### DataFrame Summaries
Three very helpful attributes/functions for getting high-level summaries of your dataframe are:
- `.shape`
- `.info()`
- `.describe()`
`.shape` is just like the ndarray attribute we've seen previously. It gives the shape (rows, cols) of your dataframe:
```
df.shape
```
`.info()` prints information about the dataframe itself, such as dtypes, memory usages, non-null values, etc:
```
df.info()
```
`.describe()` provides summary statistics of the values within a dataframe:
```
df.describe()
```
By default, `.describe()` only print summaries of numeric features. We can force it to give summaries on all features using the argument `include='all'` (although they may not make sense!):
```
df.describe(include='all')
```
### Displaying DataFrames
Displaying your dataframes effectively can be an important part of your workflow. If a dataframe has more than 60 rows, Pandas will only display the first 5 and last 5 rows:
```
pd.DataFrame(np.random.rand(100))
```
For dataframes of less than 60 rows, Pandas will print the whole dataframe:
```
df
```
I find the 60 row threshold to be a little too much, I prefer something more like 20. You can change the setting using `pd.set_option("display.max_rows", 20)` so that anything with more than 20 rows will be summarised by the first and last 5 rows as before:
```
pd.set_option("display.max_rows", 20)
df
```
There are also other display options you can change, such as how many columns are shown, how numbers are formatted, etc. See the [official documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/options.html#options-and-settings) for more.
One display option I will point out is that Pandas allows you to style your tables, for example by highlighting negative values, or adding conditional colour maps to your dataframe. Below I'll style values based on their value ranging from negative (purple) to postive (yellow) but you can see the [styling documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/style.html#Styling) for more examples.
```
test = pd.DataFrame(np.random.randn(5, 5),
index = [f"row_{_}" for _ in range(5)],
columns = [f"feature_{_}" for _ in range(5)])
test.style.background_gradient(cmap='plasma')
```
### Views vs Copies
In previous chapters we've discussed views ("looking" at a part of an existing object) and copies (making a new copy of the object in memory). These things get a little abstract with Pandas and "...it’s very hard to predict whether it will return a view or a copy" (that's a quote straight [from a dedicated section in the Pandas documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy)).
Basically, it depends on the operation you are trying to perform, your dataframe's structure and the memory layout of the underlying array. But don't worry, let me tell you all you need to know. Firstly, the most common warning you'll encounter in Pandas is the `SettingWithCopy`, Pandas raises it as a warning that you might not be doing what you think you're doing. Let's see an example. You may recall there is one outlier `Time` in our dataframe:
```
df[df['Time'] > 4000]
```
Imagine we wanted to change this to `2000`. You'd probably do the following:
```
df[df['Time'] > 4000]['Time'] = 2000
```
Ah, there's that warning. Did our dataframe get changed?
```
df[df['Time'] > 4000]
```
No it didn't, even though you probably thought it did. What happened above is that `df[df['Time'] > 4000]` was executed first and returned a copy of the dataframe, we can confirm by using `id()`:
```
print(f"The id of the original dataframe is: {id(df)}")
print(f" The id of the indexed dataframe is: {id(df[df['Time'] > 4000])}")
```
We then tried to set a value on this new object by appending `['Time'] = 2000`. Pandas is warning us that we are doing that operation on a copy of the original dataframe, which is probably not what we want. To fix this, you need to index in a single go, using `.loc[]` for example:
```
df.loc[df['Time'] > 4000, 'Time'] = 2000
```
No error this time! And let's confirm the change:
```
df[df['Time'] > 4000]
```
The second thing you need to know is that if you're ever in doubt about whether something is a view or a copy, you can just use the `.copy()` method to force a copy of a dataframe. Just like this:
```
df2 = df[df['Time'] > 4000].copy()
```
That way, your guaranteed a copy that you can modify as you wish.
## 2. Basic DataFrame Manipulations
<hr>
### Renaming Columns
We can rename columns two ways:
1. Using `.rename()` (to selectively change column names)
2. By setting the `.columns` attribute (to change all column names at once)
```
df
```
Let's give it a go:
```
df.rename(columns={"Date": "Datetime",
"Comments": "Notes"})
df
```
Wait? What happened? Nothing changed? In the code above we did actually rename columns of our dataframe but we didn't modify the dataframe inplace, we made a copy of it. There are generally two options for making permanent dataframe changes:
- 1. Use the argument `inplace=True`, e.g., `df.rename(..., inplace=True)`, available in most functions/methods
- 2. Re-assign, e.g., `df = df.rename(...)`
The Pandas team recommends **Method 2 (re-assign)**, for a [few reasons](https://www.youtube.com/watch?v=hK6o_TDXXN8&t=700) (mostly to do with how memory is allocated under the hood).
```
df = df.rename(columns={"Date": "Datetime",
"Comments": "Notes"})
df
```
If you wish to change all of the columns of a dataframe, you can do so by setting the `.columns` attribute:
```
df.columns = [f"Column {_}" for _ in range(1, 7)]
df
```
### Changing the Index
You can change the index labels of a dataframe in 3 main ways:
1. `.set_index()` to make one of the columns of the dataframe the index
2. Directly modify `df.index.name` to change the index name
3. `.reset_index()` to move the current index as a column and to reset the index with integer labels starting from 0
4. Directly modify the `.index()` attribute
```
df
```
Below I will set the index as `Column 1` and rename the index to "New Index":
```
df = df.set_index("Column 1")
df.index.name = "New Index"
df
```
I can send the index back to a column and have a default integer index using `.reset_index()`:
```
df = df.reset_index()
df
```
Like with column names, we can also modify the index directly, but I can't remember ever doing this, usually I'll use `.set_index()`:
```
df.index
df.index = range(100, 133, 1)
df
```
### Adding/Removing Columns
There are two main ways to add/remove columns of a dataframe:
1. Use `[]` to add columns
2. Use `.drop()` to drop columns
Let's re-read in a fresh copy of the cycling dataset.
```
df = pd.read_csv('data/cycling_data.csv')
df
```
We can add a new column to a dataframe by simply using `[]` with a new column name and value(s):
```
df['Rider'] = 'Tom Beuzen'
df['Avg Speed'] = df['Distance'] * 1000 / df['Time'] # avg. speed in m/s
df
df = df.drop(columns=['Rider', 'Avg Speed'])
df
```
### Adding/Removing Rows
You won't often be adding rows to a dataframe manually (you'll usually add rows through concatenating/joining - that's coming up next). You can add/remove rows of a dataframe in two ways:
1. Use `.append()` to add rows
2. Use `.drop()` to drop rows
```
df
```
Let's add a new row to the bottom of this dataframe:
```
another_row = pd.DataFrame([["12 Oct 2019, 00:10:57", "Morning Ride", "Ride",
2331, 12.67, "Washed and oiled bike last night"]],
columns = df.columns,
index = [33])
df = df.append(another_row)
df
```
We can drop all rows above index 30 using `.drop()`:
```
df.drop(index=range(30, 34))
```
## 3. DataFrame Reshaping
<hr>
[Tidy data](https://vita.had.co.nz/papers/tidy-data.pdf) is about "linking the structure of a dataset with its semantics (its meaning)". It is defined by:
1. Each variable forms a column
2. Each observation forms a row
3. Each type of observational unit forms a table
Often you'll need to reshape a dataframe to make it tidy (or for some other purpose).

Source: [r4ds](https://r4ds.had.co.nz/tidy-data.html#fig:tidy-structure)
### Melt and Pivot
Pandas `.melt()`, `.pivot()` and `.pivot_table()` can help reshape dataframes
- `.melt()`: make wide data long.
- `.pivot()`: make long data width.
- `.pivot_table()`: same as `.pivot()` but can handle multiple indexes.

Source: [Garrick Aden-Buie's GitHub](https://github.com/gadenbuie/tidyexplain#spread-and-gather)
The below data shows how many courses different instructors taught across different years. If the question you want to answer is something like: "Does the number of courses taught vary depending on year?" then the below would probably not be considered tidy because there are multiple observations of courses taught in a year per row (i.e., there is data for 2018, 2019 and 2020 in a single row):
```
df = pd.DataFrame({"Name": ["Tom", "Mike", "Tiffany", "Varada", "Joel"],
"2018": [1, 3, 4, 5, 3],
"2019": [2, 4, 3, 2, 1],
"2020": [5, 2, 4, 4, 3]})
df
```
Let's make it tidy with `.melt()`. `.melt()` takes a few arguments, most important is the `id_vars` which indicated which column should be the "identifier".
```
df_melt = df.melt(id_vars="Name",
var_name="Year",
value_name="Courses")
df_melt
```
The `value_vars` argument allows us to select which specific variables we want to "melt" (if you don't specify `value_vars`, all non-identifier columns will be used). For example, below I'm omitting the `2018` column:
```
df.melt(id_vars="Name",
value_vars=["2019", "2020"],
var_name="Year",
value_name="Courses")
```
Sometimes, you want to make long data wide, which we can do with `.pivot()`. When using `.pivot()` we need to specify the `index` to pivot on, and the `columns` that will be used to make the new columns of the wider dataframe:
```
df_pivot = df_melt.pivot(index="Name",
columns="Year",
values="Courses")
df_pivot
```
You'll notice that Pandas set our specified `index` as the index of the new dataframe and preserved the label of the columns. We can easily remove these names and reset the index to make our dataframe look like it originally did:
```
df_pivot = df_pivot.reset_index()
df_pivot.columns.name = None
df_pivot
```
`.pivot()` will often get you what you want, but it won't work if you want to:
- Use multiple indexes (next chapter), or
- Have duplicate index/column labels
In these cases you'll have to use `.pivot_table()`. I won't focus on it too much here because I'd rather you learn about `pivot()` first.
```
df = pd.DataFrame({"Name": ["Tom", "Tom", "Mike", "Mike"],
"Department": ["CS", "STATS", "CS", "STATS"],
"2018": [1, 2, 3, 1],
"2019": [2, 3, 4, 2],
"2020": [5, 1, 2, 2]}).melt(id_vars=["Name", "Department"], var_name="Year", value_name="Courses")
df
```
In the above case, we have duplicates in `Name`, so `pivot()` won't work. It will throw us a `ValueError: Index contains duplicate entries, cannot reshape`:
```
df.pivot(index="Name",
columns="Year",
values="Courses")
```
In such a case, we'd use `.pivot_table()`. It will apply an aggregation function to our duplicates, in this case, we'll `sum()` them up:
```
df.pivot_table(index="Name", columns='Year', values='Courses', aggfunc='sum')
```
If we wanted to keep the numbers per department, we could specify both `Name` and `Department` as multiple indexes:
```
df.pivot_table(index=["Name", "Department"], columns='Year', values='Courses')
```
The result above is a mutlti-index or "hierarchically indexed" dataframe (more on those next chapter). If you ever have a need to use it, you can read more about `pivot_table()` in the [documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/reshaping.html#pivot-tables).
## 4. Working with Multiple DataFrames
<hr>
Often you'll work with multiple dataframes that you want to stick together or merge. `df.merge()` and `df.concat()` are all you need to know for combining dataframes. The Pandas [documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/merging.html) is very helpful for these functions, but they are pretty easy to grasp.
```{note}
The example joins shown in this section are inspired by [Chapter 15](https://stat545.com/join-cheatsheet.html) of Jenny Bryan's STAT 545 materials.
```
### Sticking DataFrames Together with `pd.concat()`
You can use `pd.concat()` to stick dataframes together:
- Vertically: if they have the same **columns**, OR
- Horizontally: if they have the same **rows**
```
df1 = pd.DataFrame({'A': [1, 3, 5],
'B': [2, 4, 6]})
df2 = pd.DataFrame({'A': [7, 9, 11],
'B': [8, 10, 12]})
df1
df2
pd.concat((df1, df2), axis=0) # axis=0 specifies a vertical stick, i.e., on the columns
```
Notice that the indexes were simply joined together? This may or may not be what you want. To reset the index, you can specify the argument `ignore_index=True`:
```
pd.concat((df1, df2), axis=0, ignore_index=True)
```
Use `axis=1` to stick together horizontally:
```
pd.concat((df1, df2), axis=1, ignore_index=True)
```
You are not limited to just two dataframes, you can concatenate as many as you want:
```
pd.concat((df1, df2, df1, df2), axis=0, ignore_index=True)
```
### Joining DataFrames with `pd.merge()`
`pd.merge()` gives you the ability to "join" dataframes using different rules (just like with SQL if you're familiar with it). You can use `df.merge()` to join dataframes based on shared `key` columns. Methods include:
- "inner join"
- "outer join"
- "left join"
- "right join"
See this great [cheat sheet](https://pandas.pydata.org/pandas-docs/stable/getting_started/comparison/comparison_with_sql.html#compare-with-sql-join) and [these great animations](https://github.com/gadenbuie/tidyexplain) for more insights.
```
df1 = pd.DataFrame({"name": ['Magneto', 'Storm', 'Mystique', 'Batman', 'Joker', 'Catwoman', 'Hellboy'],
'alignment': ['bad', 'good', 'bad', 'good', 'bad', 'bad', 'good'],
'gender': ['male', 'female', 'female', 'male', 'male', 'female', 'male'],
'publisher': ['Marvel', 'Marvel', 'Marvel', 'DC', 'DC', 'DC', 'Dark Horse Comics']})
df2 = pd.DataFrame({'publisher': ['DC', 'Marvel', 'Image'],
'year_founded': [1934, 1939, 1992]})
```

An "inner" join will return all rows of `df1` where matching values for "publisher" are found in `df2`:
```
pd.merge(df1, df2, how="inner", on="publisher")
```

An "outer" join will return all rows of `df1` and `df2`, placing NaNs where information is unavailable:
```
pd.merge(df1, df2, how="outer", on="publisher")
```

Return all rows from `df1` and all columns of `df1` and `df2`, populated where matches occur:
```
pd.merge(df1, df2, how="left", on="publisher")
```

```
pd.merge(df1, df2, how="right", on="publisher")
```
There are many ways to specify the `key` to join dataframes on, you can join on index values, different, column names, etc. Another helpful argument is the `indicator` argument which will add a column to the result telling you where matches were found in the dataframes:
```
pd.merge(df1, df2, how="outer", on="publisher", indicator=True)
```
By the way, you can use `pd.concat()` to do a simple "inner" or "outer" join on multiple datadrames at once. It's less flexible than merge, but can be useful sometimes.
## 5. More DataFrame Operations
<hr>
### Applying Custom Functions
There will be times when you want to apply a function that is not built-in to Pandas. For this, we also have methods:
- `df.apply()`, applies a function column-wise or row-wise across a dataframe (the function must be able to accept/return an array)
- `df.applymap()`, applies a function element-wise (for functions that accept/return single values at a time)
- `series.apply()`/`series.map()`, same as above but for Pandas series
For example, say you want to use a numpy function on a column in your dataframe:
```
df = pd.read_csv('data/cycling_data.csv')
df[['Time', 'Distance']].apply(np.sin)
```
Or you may want to apply your own custom function:
```
def seconds_to_hours(x):
return x / 3600
df[['Time']].apply(seconds_to_hours)
```
This may have been better as a lambda function...
```
df[['Time']].apply(lambda x: x / 3600)
```
You can even use functions that require additional arguments. Just specify the arguments in `.apply()`:
```
def convert_seconds(x, to="hours"):
if to == "hours":
return x / 3600
elif to == "minutes":
return x / 60
df[['Time']].apply(convert_seconds, to="minutes")
```
Some functions only accept/return a scalar:
```
int(3.141)
float([3.141, 10.345])
```
For these, we need `.applymap()`:
```
df[['Time']].applymap(int)
```
However, there are often "vectorized" versions of common functions like this already available, which are much faster. In the case above, we can use `.astype()` to change the dtype of a whole column quickly:
```
time_applymap = %timeit -q -o -r 3 df[['Time']].applymap(float)
time_builtin = %timeit -q -o -r 3 df[['Time']].astype(float)
print(f"'astype' is {time_applymap.average / time_builtin.average:.2f} faster than 'applymap'!")
```
### Grouping
Often we are interested in examining specific groups in our data. `df.groupby()` allows us to group our data based on a variable(s).
```
df = pd.read_csv('data/cycling_data.csv')
df
```
Let's group this dataframe on the column `Name`:
```
dfg = df.groupby(by='Name')
dfg
```
What is a `DataFrameGroupBy` object? It contains information about the groups of the dataframe:

The groupby object is really just a dictionary of index-mappings, which we could look at if we wanted to:
```
dfg.groups
```
We can also access a group using the `.get_group()` method:
```
dfg.get_group('Afternoon Ride')
```
The usual thing to do however, is to apply aggregate functions to the groupby object:

```
dfg.mean()
```
We can apply multiple functions using `.aggregate()`:
```
dfg.aggregate(['mean', 'sum', 'count'])
```
And even apply different functions to different columns:
```
def num_range(x):
return x.max() - x.min()
dfg.aggregate({"Time": ['max', 'min', 'mean', num_range],
"Distance": ['sum']})
```
By the way, you can use aggregate for non-grouped dataframes too. This is pretty much what `df.describe` does under-the-hood:
```
df.agg(['mean', 'min', 'count', num_range])
```
### Dealing with Missing Values
Missing values are typically denoted with `NaN`. We can use `df.isnull()` to find missing values in a dataframe. It returns a boolean for each element in the dataframe:
```
df.isnull()
```
But it's usually more helpful to get this information by row or by column using the `.any()` or `.info()` method:
```
df.info()
df[df.isnull().any(axis=1)]
```
When you have missing values, we usually either drop them or impute them.You can drop missing values with `df.dropna()`:
```
df.dropna()
```
Or you can impute ("fill") them using `.fillna()`. This method has various options for filling, you can use a fixed value, the mean of the column, the previous non-nan value, etc:
```
df = pd.DataFrame([[np.nan, 2, np.nan, 0],
[3, 4, np.nan, 1],
[np.nan, np.nan, np.nan, 5],
[np.nan, 3, np.nan, 4]],
columns=list('ABCD'))
df
df.fillna(0) # fill with 0
df.fillna(df.mean()) # fill with the mean
df.fillna(method='bfill') # backward (upwards) fill from non-nan values
df.fillna(method='ffill') # forward (downward) fill from non-nan values
```
Finally, sometimes I use visualizations to help identify (patterns in) missing values. One thing I often do is print a heatmap of my dataframe to get a feel for where my missing values are. If you want to run this code, you may need to install `seaborn`:
```sh
conda install seaborn
```
```
import seaborn as sns
sns.set(rc={'figure.figsize':(7, 7)})
df
sns.heatmap(df.isnull(), cmap='viridis', cbar=False);
# Generate a larger synthetic dataset for demonstration
np.random.seed(2020)
npx = np.zeros((100,20))
mask = np.random.choice([True, False], npx.shape, p=[.1, .9])
npx[mask] = np.nan
sns.heatmap(pd.DataFrame(npx).isnull(), cmap='viridis', cbar=False);
```
| true |
code
| 0.531088 | null | null | null | null |
|
```
#hide
from qbism import *
```
# Tutorial
> "Chauncey Wright, a nearly forgotten philosopher of real merit, taught me when young that I must not say necessary about the universe, that we don’t know whether anything is necessary or not. So I describe myself as a bettabilitarian. I believe that we can bet on the behavior of the universe in its contact with us." (Oliver Wendell Holmes, Jr.)
QBism, as I understand it, consists of two interlocking components, one part philosophical and one part mathematical. We'll deal with the mathematical part first.
## The Math
A Von Neumann measurement consists in a choice of observable represented by a Hermitian operator $H$. Such an operator will have real eigenvalues and orthogonal eigenvectors. For example, $H$ could be the energy operator. Then the eigenvectors would represent possible energy states, and the eigenvalues would represent possible values of the energy. According to textbook quantum mechanics, which state the system ends up in after a measurement will in general be random, and quantum mechanics allows you to calculate the probabilities.
A Hermitian observable provides what is known as a "projection valued measure." Suppose our system were represented by a density matrix $\rho$. We could form the projectors $P_{i} = \mid v_{i} \rangle \langle v_{i} \mid$, where $\mid v_{i} \rangle$ is the $i^{th}$ eigenvector. Then the probability for the $i^{th}$ outcome would be given by $Pr(i) = tr(P_{i}\rho)$, and the state after measurement would be given by $\frac{P_{i} \rho P_{i}}{tr(P_{i}\rho)}$. Moreover, the expectation value of the observable $\langle H \rangle$ would be given by $tr(H\rho)$, and it amounts to a sum over the eigenvalues weighted by the corresponding probabilities.
```
import numpy as np
import qutip as qt
d = 2
rho = qt.rand_dm(d)
H = qt.rand_herm(d)
L, V = H.eigenstates()
P = [v*v.dag() for v in V]
p = [(proj*rho).tr() for proj in P]
print("probabilities: %s" % p)
print("expectation value: %.3f" % (H*rho).tr())
print("expectation value again: %.3f" % (sum([L[i]*p[i] for i in range(d)])))
```
<hr>
But there is a more general notion of measurement: a POVM (a positive operator valued measure). A POVM consists in a set of positive semidefinite operators that sum to the identity, i.e., a set $\{E_{i}\}$ such that $\sum_{i} E_{i} = I$. Positive semidefinite just means that the eigenvalues must be non-negative, so that $\langle \psi \mid E \mid \psi \rangle$ is always positive or zero for any $\mid \psi \rangle$. Indeed, keep in mind that density matrices are defined by Hermitian, positive semi-definite operators with trace $1$.
For a POVM, each *operator* corresponds to a possible outcome of the experiment, and whereas for a Von Neumann measurement, assuming no degeneracies, there would be $d$ possible outcomes, corresponding to the dimension of the Hilbert space, there can be *any* number of outcomes to a POVM measurement, as long as all the associated operators sum to the identity. The probability of an outcome, however, is similarly given by $Pr(i) = tr(E_{i}\rho)$.
If we write each $E_{i}$ as a product of so-called Kraus operators $E_{i} = A_{i}^{\dagger}A_{i}$, then the state after measurement will be: $\frac{A_{i}\rho A_{i}^{\dagger}}{tr(E_{i}\rho)}$. The Kraus operators, however, aren't uniquely defined by the POVM, and so the state after measurement will depend on its implementation: to implement POVM's, you couple your system to an auxilliary system and make a standard measurement on the latter. We'll show how to do that in a little bit!
In the case we'll be considering, however, the $\{E_{i}\}$ will be rank-1, and so the state after measurement will be $\frac{\Pi_{i}\rho \Pi_{i}}{tr(\Pi_{i}\rho)}$ as before, where $\Pi_{i}$ are normalized projectors associated to each element of the POVM (details to follow).
(For a reference, recall that spin coherent states form an "overcomplete" basis, or frame, for spin states of a given $j$ value. This can be viewed as a POVM. In this case, the POVM would have an infinite number of elements, one for each point on the sphere: and the integral over the sphere gives $1$.)
<hr>
A very special kind of POVM is a so-called SIC-POVM: a symmetric informationally complete positive operator valued measure. They've been conjectured to exist in all dimensions, and numerical evidence suggests this is indeed the case. For a given Hilbert space of dimension $d$, a SIC is a set of $d^2$ rank-one projection operators $\Pi_{i} = \mid \psi_{i} \rangle \langle \psi_{i} \mid$ such that:
$$tr(\Pi_{k}\Pi_{l}) = \frac{d\delta_{k,l} + 1}{d+1} $$
Such a set of projectors will be linearly independent, and if you rescale they to $\frac{1}{d}\Pi_{i}$, they form a POVM: $\sum_{i} \frac{1}{d} \Pi_{i} = I$.
The key point is that for any quantum state $\rho$, a SIC specifies a measurement *for which the probabilities of outcomes $p(i)$ specify $\rho$ itself*. Normally, say, in the case of a qubit, we'd have to measure the separate expectation values $(\langle X \rangle, \langle Y \rangle, \langle Z \rangle)$ to nail down the state: in other words, we'd have to repeat many times three *different* measurements. But for a SIC-POVM, the probabilities on each of the elements of the POVM fully determine the state: we're talking here about a *single* type of measurement.
<hr>
Thanks to Chris Fuchs & Co., we have a repository of SIC-POVM's in a variety of dimensions. One can download them [here](http://www.physics.umb.edu/Research/QBism/solutions.html). You'll get a zip of text files, one for each dimension: and in each text file will be a single complex vector: the "fiducial" vector. From this vector, the SIC can be derived.
In order to do this, we first define (with Sylvester) the unitary clock and shift matrices for a given dimension $d$:
$$
X = \begin{pmatrix}
0 & 0 & 0 & \cdots & 0 & 1\\
1 & 0 & 0 & \cdots & 0 & 0\\
0 & 1 & 0 & \cdots & 0 & 0\\
0 & 0 & 1 & \cdots & 0 & 0\\
\vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\
0 & 0 & 0 & \cdots & 1 & 0\\
\end{pmatrix}
$$
$$
Z = \begin{pmatrix}
1 & 0 & 0 & \cdots & 0\\
0 & \omega & 0 & \cdots & 0\\
0 & 0 & \omega^2 & \cdots & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
0 & 0 & 0 & \cdots & \omega^{d-1}
\end{pmatrix}
$$
Where $\omega = e^{\frac{2\pi i}{d}}$.
Note that when $d=2$, this amounts to Pauli $X$ and $Z$.
```
def shift(d):
return sum([qt.basis(d, i+1)*qt.basis(d, i).dag()\
if i != d-1 else qt.basis(d, 0)*qt.basis(d, i).dag()\
for i in range(d) for j in range(d)])/d
def clock(d):
w = np.exp(2*np.pi*1j/d)
return qt.Qobj(np.diag([w**i for i in range(d)]))
```
We can then define displacement operators:
$$D_{a,b} = (-e^{\frac{i\pi}{d}})^{ab}X^{b}Z^{a} $$
For $a, b$ each from $0$ to $d$.
```
def displace(d, a, b):
Z, X = clock(d), shift(d)
return (-np.exp(1j*np.pi/d))**(a*b)*X**b*Z**a
def displacement_operators(d):
return dict([((a, b), displace(d, a, b)) for b in range(d) for a in range(d)])
```
Finally, if we act on the fiducial vector with each of the displacement operators, we obtain the $d^2$ pure states, whose projectors, weighted by $\frac{1}{d}$, form the SIC-POVM.
```
def sic_states(d):
fiducial = load_fiducial(d)
return [D*fiducial for index, D in displacement_operators(d).items()]
```
Cf. `load_fiducial`.
By the way, this construction works because these SIC-POVM's are covariant under the Weyl-Heisenberg group. This means is that if you apply one of those displacement operators to all the SIC states, you get the same set of SIC states back! They just switch places among themselves. (It's also worth considering the action of elements of the "Clifford group", since these operators leave the Weyl-Heisenberg group invariant or, in other words, "normalize" it.)
```
sic = sic_states(2)
D = displacement_operators(2)
print(sic)
print()
print([D[(1,1)]*state for state in sic])
```
As far as anyone knows, the construction seems to work for SIC's in all dimensions. It's worth noting, however, the exceptional case of $d=8$, where there is *also another* SIC-POVM covariant under the tensor product of three copies of the Pauli group ($d=2$). Cf. `hoggar_fiducial`.
We can test that a given SIC has the property:
$$tr(\Pi_{k}\Pi_{l}) = \frac{d\delta_{k,l} + 1}{d+1} $$
```
def test_sic_states(states):
d = int(np.sqrt(len(states)))
for i, s in enumerate(states):
for j, t in enumerate(states):
should_be = 1 if i == j else 1/(d+1)
print("(%d, %d): %.4f | should be: %.4f" % (i, j, np.abs(s.overlap(t)**2), should_be))
states = sic_states(2)
test_sic_states(states)
```
In the case of a two dimensional Hilbert space, the SIC-POVM states will form a regular tetrahedron in the Bloch sphere:
```
pts = np.array([[qt.expect(qt.sigmax(), state),\
qt.expect(qt.sigmay(), state),\
qt.expect(qt.sigmaz(), state)] for state in states])
sphere = qt.Bloch()
sphere.point_size = [300]
sphere.add_points(pts.T)
sphere.add_vectors(pts)
sphere.make_sphere()
```
In general, in higher dimensions, the study of SIC's is a very interesting geometry problem involving the study of "maximal sets of complex equiangular lines," which has implications in various domains of mathematics.
```
def sic_povm(d):
return [(1/d)*state*state.dag() for state in sic_states(d)]
d = 2
ref_povm = sic_povm(d)
print("elements sum to identity? %s" % np.allclose(sum(ref_povm), qt.identity(d)))
```
Given a density matrix $\rho$, we can expand it in terms of the SIC-POVM elements via $tr(E_{i}\rho)$:
```
def dm_probs(dm, ref_povm):
return np.array([(e*dm).tr() for e in ref_povm]).real
rho = qt.rand_dm(d)
p = dm_probs(rho, ref_povm)
print("probabilities: %s" % p)
print("sum to 1? %s" % np.isclose(sum(p), 1))
```
From these probabilities, we can uniquely reconstruct the density matrix via:
$$ \rho = \sum_{i} ((d+1)p(i) - \frac{1}{d})\Pi_{i} $$
Where $\Pi_{i}$ are the projectors onto the SIC states: $E_{i} = \frac{1}{d}\Pi_{i}$.
Or given the fact that $\sum_{i} \frac{1}{d} \Pi_{i} = I$:
$$\rho = (d+1) \sum_{i} p(i)\Pi_{i} - I $$
```
def probs_dm_sic(p, ref_povm):
d = int(np.sqrt(len(p)))
return sum([((d+1)*p[i] - 1/d)*(e/e.tr()) for i, e in enumerate(ref_povm)])
def probs_dm_sic2(p, ref_povm):
d = int(np.sqrt(len(p)))
return (d+1)*sum([p[i]*e/e.tr() for i, e in enumerate(ref_povm)]) - qt.identity(d)
rho2 = probs_dm_sic(p, ref_povm)
rho3 = probs_dm_sic2(p, ref_povm)
print("recovered? %s" % (np.allclose(rho, rho2, rtol=1e-02, atol=1e-04) and np.allclose(rho, rho3, rtol=1e-02, atol=1e-04)))
```
<hr>
Now suppose we have the following situation. We first make a SIC-POVM measurement, and then we make a standard Von Neumann (PVM) measurement on a given system. Following the vivid imagery of Fuchs, we'll refer to the SIC-POVM as being "up in the sky" and the Von Neumann measurement as being "down on the ground".
So given our state $\rho$, above we've calculated the probabilities $p(i)$ for each outcome of the POVM. Now we'd like to assign probabilities for the outcomes of the Von Neumann measurement. What we need are the conditional probabilities $r(j|i)$, the probability of Von Neumann outcome $j$ given that the SIC-POVM returned $i$. Then:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
This is just standard probability theory: the law of total probability. The probability for an outcome $j$ of the Von Neumann measurement is the sum over all the conditional probabilities for $j$, given some outcome $i$ of the SIC-POVM, multiplied by the probability that $i$ occured.
The standard way of thinking about this would be that after the SIC-POVM measurement:
$\rho^{\prime} = \sum_{i} p(i)\Pi_{i}$
In other words, after the first measurement, $\rho$ becomes a mixture of outcome states weighted by the probabilities of them occuring. In this simple case, where we aren't considering a subsystem of larger system, and we're sticking with SIC-POVM's whose elements, we recall, are rank-1, we can just use the projectors $\Pi_{i}$ for the SIC-POVM outcome states. Then the probabilities for the Von Neumann measurement are:
$s(j) = tr(\tilde{\Pi}_{j}\rho^{\prime})$
Where $\tilde{\Pi}_{j}$ is the projector for the $j^{th}$ Von Neumann outcome.
```
von_neumann = qt.rand_herm(d)
vn_projectors = [v*v.dag() for v in von_neumann.eigenstates()[1]]
vn_rho = sum([prob*ref_povm[i]/ref_povm[i].tr() for i, prob in enumerate(p)])
vn_s = np.array([(proj*vn_rho).tr() for proj in vn_projectors]).real
print("vn probabilities after sic: %s" % vn_s)
```
Alternatively, however, we could form conditional probabilities directly:
$r(j|i) = tr(\tilde{\Pi}_{j}\Pi_{i})$
Where $\Pi_{i}$ is the projector for the $i^{th}$ POVM outcome (in the sky), and $\tilde{\Pi}_{j}$ is the projector for the $j^{th}$ Von Neumann outcome (on the ground).
Then we can use the formula:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
```
def vn_conditional_probs(von_neumann, ref_povm):
d = von_neumann.shape[0]
vn_projectors = [v*v.dag() for v in von_neumann.eigenstates()[1]]
return np.array([[(vn_projectors[j]*(e/e.tr())).tr() for i, e in enumerate(ref_povm)] for j in range(d)]).real
def vn_posterior(dm, von_neumann, ref_povm):
d = dm.shape[0]
p = dm_probs(rho, ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
return np.array([sum([p[i]*r[j][i] for i in range(d**2)]) for j in range(d)])
print("vn probabilities after sic: %s" % vn_posterior(rho, von_neumann, ref_povm))
```
Indeed, $r(j|i)$ is a valid conditional probability matrix: its columns all sum to 1.
```
np.sum(vn_conditional_probs(von_neumann, ref_povm), axis=0)
```
Incidentally, there's no need to confine ourselves to the case of Von Neumann measurements. Suppose the "measurement on the ground" is given by another POVM. In fact, we can get one by just rotating our SIC-POVM by some random unitary. We'll obtain another SIC-POVM $\{F_{j}\}$.
In this case, we'd form $\rho^{\prime} = \sum_{i} p(i)\Pi_{i}$ just as before, and then take $s(j) = tr(F_{j}\rho^{\prime})$.
```
U = qt.rand_unitary(d)
ground_povm = [U*e*U.dag() for e in ref_povm]
povm_rho = sum([prob*ref_povm[i]/ref_povm[i].tr() for i, prob in enumerate(p)])
povm_s = np.array([(e*povm_rho).tr() for e in ground_povm]).real
print("povm probabilities after sic: %s" % povm_s)
```
And alternatively, we could work with the conditional probabilities:
$r(j|i) = tr(F_{j}\Pi_{i})$
And then apply:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
Where now $j$ will range from $0$ to $d^2$.
```
def povm_conditional_probs(povm, ref_povm):
d = int(np.sqrt(len(ref_povm)))
return np.array([[(a*(b/b.tr())).tr() for i, b in enumerate(ref_povm)] for j, a in enumerate(povm)]).real
def povm_posterior(dm, povm, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = povm_conditional_probs(povm, ref_povm)
return np.array([sum([p[i]*r[j][i] for i in range(d**2)]) for j in range(d**2)])
print("povm probabilities after sic: %s" % povm_posterior(rho, ground_povm, ref_povm))
```
<hr>
Okay, now we get to the punch line. Let's consider the case of the Von Neumann measurement. Suppose we *didn't* make the SIC-POVM measurement first. What would the probabilities be? Well, we all know:
$q(j) = tr(\tilde{\Pi}_{i}\rho)$
```
vn_p = np.array([(proj*rho).tr() for proj in vn_projectors]).real
print("vn probabilities (no sic in the sky): %s" % vn_p)
```
Now it turns out that we can get these same probabilities in a different way:
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - 1$
```
def vn_born(dm, von_neumann, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
return np.array([(d+1)*sum([p[i]*r[j][i] for i in range(d**2)]) - 1 for j in range(d)]).real
print("vn probabilities (no sic in the sky): %s" % vn_born(rho, von_neumann, ref_povm))
```
In other words, we can express the usual quantum probabilities in the case that we go directly to the Von Neumann measurement in a way that looks *ridiculously* close to our formula from before, involving probabilities for the SIC-POVM outcomes and conditional probabilities for Von Neumann outcomes given SIC-POVM outcomes! We sum over *hypothetical* outcomes of the SIC-POVM, multiplying the probability of each outcome, given our state $\rho$, by the conditional probability for the Von Neumann measurement giving the $j^{th}$ outcome, given that the SIC-POVM outcome was $i$. Except the formula is somewhat deformed by the the $(d+1)$ and the $-1$.
Clearly, this is equivalent to the usual Born Rule: but it's expressed *entirely* in terms of probabilities and conditional probabilities. It makes sense, in the end, that you can do this, given that the probabilities for the SIC-POVM measurement completely nail down the state. The upshot is that we can just work with the probabilities instead! Indeed, we could just pick some SIC-POVM to be our "reference apparatus", and describe any quantum state we're ever interested in terms of probabilities with reference to it, and any measurement in terms of conditional probabilities.
Operationally, what *is* difference between:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
and
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - 1$
The difference is precisely *whether the SIC-POVM measurement has actually been performed*. If it has, then we lose quantum coherence. If it hasn't, we maintain it. In other words, the difference between classical and quantum is summed up in the minor difference between these two formulas.
In slogan form, due to Asher Peres, "unperformed measurements have no results." We'll get to the philosophy of this later, but the point is that classically speaking, we should be able to use the law of total probability *whether or not we actually do the measurement in the sky*: but quantum mechanically, if we don't actually do the measurement, we can't. But we have something just as good: the Born Rule.
<hr>
If we want to consider a more general measurement "on the ground," in particular, another SIC-POVM measurement, then our formula becomes:
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - \frac{1}{d}[\sum_{i}^{d^2} r(j|i) ]$
Where now $i$ ranges to $d^2$.
```
print("povm probabilities (no sic in the sky): %s" % dm_probs(rho, ground_povm))
def povm_born(dm, povm, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = povm_conditional_probs(povm, ref_povm)
return np.array([(d+1)*sum([p[i]*r[j][i] for i in range(d**2)]) - (1/d)*sum([r[j][i] for i in range(d**2)]) for j in range(d**2)]).real
print("povm probabilities (no sic in the sky): %s" % povm_born(rho, ground_povm, ref_povm))
```
We can write these rules in much more compact matrix form.
Define $\Phi = (d+1)I_{d^2} - \frac{1}{d}J_{d^2}$
Where $I_{d^2}$ is the $d^2 \times d^2$ identity, and $J_{d^2}$ is the $d^2 \times d^2$ matrix all full of $1$'s.
If $R$ is the matrix of conditional probabilities, and $p$ is the vector of probabilities for the reference POVM in the sky, then the vector of values for $q(i)$ is:
$\vec{q} = R \Phi p$
```
def vn_born_matrix(dm, von_neumann, ref_povm):
d = rho.shape[0]
p = dm_probs(dm, ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
phi = (d+1)*np.eye(d**2) - (1/d)*np.ones((d**2,d**2))
return r @ phi @ p
print("vn probabilities (no sic in the sky): %s" % vn_born_matrix(rho, von_neumann, ref_povm))
def povm_born_matrix(dm, povm, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = povm_conditional_probs(povm, ref_povm)
phi = (d+1)*np.eye(d**2) - (1/d)*np.ones((d**2,d**2))
return r @ phi @ p
print("povm probabilities (no sic in the sky): %s" % povm_born_matrix(rho, ground_povm, ref_povm))
```
And for that matter, we can calculate the "classical" probabilities from before in the same vectorized way: we just leave out $\Phi$!
```
print("vn probabilities after sic: %s" % (vn_conditional_probs(von_neumann, ref_povm) @ dm_probs(rho, ref_povm)))
print("povm probabilities after sic: %s" % (povm_conditional_probs(ground_povm, ref_povm) @ dm_probs(rho, ref_povm)))
```
In fact, this this is how qbist operators are implemented in this library behind the scenes. It allows one to easily handle the general case of IC-POVM's (informationally complete POVM's) which aren't SIC's: in that case, the matrix $\Phi$ will be different. Cf. `povm_phi`.
<hr>
Let's consider time evolution in this picture. We evolve our $\rho$ by some unitary:
$\rho_{t} = U \rho U^{\dagger}$
Naturally, we can calculate the new probabilities with reference to our SIC-POVM:
```
U = qt.rand_unitary(d)
rhot = U*rho*U.dag()
pt = dm_probs(rhot, ref_povm)
print("time evolved probabilities: %s" % pt)
```
But we could also express this in terms of conditional probabilities:
$u(j|i) = \frac{1}{d}tr(\Pi_{j}U\Pi_{i}U^{\dagger})$
As:
$p_{t}(j) = \sum_{i}^{d^2} ((d+1)p(i) - \frac{1}{d})u(j|i)$
```
def temporal_conditional_probs(U, ref_povm):
d = U.shape[0]
return np.array([[(1/d)*((a/a.tr())*U*(b/b.tr())*U.dag()).tr() for i, b in enumerate(ref_povm)] for j, a in enumerate(ref_povm)]).real
u = temporal_conditional_probs(U, ref_povm)
pt2 = np.array([sum([((d+1)*p[i] - 1/d)*u[j][i] for i in range(d**2)]) for j in range(d**2)]).real
print("time evolved probabilities: %s" % pt2)
```
We can compare this to the standard rule for stochastic evolution:
$p_{t}(j) = \sum_{i} p(i)u(j|i)$
We can see how the expression is deformed in exactly the same way. Indeed $u(j|i)$ is a doubly stochastic matrix: its rows and colums all sum to 1. And we can describe the time evolution of the quantum system in terms of it.
```
print(np.sum(u, axis=0))
print(np.sum(u, axis=1))
```
For more on the subleties of time evolution, consider the notes on `conditional_probs`.
<hr>
You can express the inner product between states in terms of SIC-POVM probability vectors via:
$tr(\rho \sigma) = d(d+1)[\vec{p} \cdot \vec{s}] - 1$
```
d = 3
ref_povm = sic_povm(d)
rho = qt.rand_dm(d)
sigma = qt.rand_dm(d)
p = dm_probs(rho, ref_povm)
s = dm_probs(sigma, ref_povm)
def quantum_inner_product_sic(p, s):
d = int(np.sqrt(len(p)))
return d*(d+1)*np.dot(p, s) - 1
print("inner product of rho and sigma: %.3f" % (rho*sigma).tr().real)
print("inner product of rho and sigma: %.3f" % quantum_inner_product_sic(p, s))
```
This brings up an important point.
You might wonder: Suppose we have a SIC-POVM with $d^2$ elements which provides $d^2$ probabilities which completely nail down the quantum state, given as a $d \times d$ density matrix. But what if we just start off with any old random vector of $d^2$ probabilities? Will we always get a valid density matrix? In other words, we've seen how we can start with quantum states, and then proceed to do quantum mechanics entirely in terms of probabilities and conditional probabilities. But now we're considering going in reverse. Does *any* assignment of probabilities to SIC-POVM outcomes specify a valid quantum state?
Well: any probability assignment will give us a $\rho$ which is Hermitian and has trace 1, which is great--BUT: this $\rho$ may not be positive-semidefinite (which is a requirement for density matrices). Like: if you assigned any old probabilites to the SIC-POVM outcomes, and then constructed a correponding $\rho$, it might end up having negative eigenvalues. Since the eigenvalues of $\rho$ are supposed to be probabilities (positive, summing to 1, etc), this is a problem.
In fact, you can't even have probability vectors that are too sharply peaked at any one value!
```
d = 3
povm = sic_povm(d)
vec = np.zeros(d**2)
vec[np.random.randint(d**2)] = 1
print("probs: %s" % vec)
print(probs_dm(vec, povm))
```
Note the negative entries. Furthermore, even if we start off in a SIC-POVM state, that doesn't mean we'll get that state with certainty after the measurement--indeed, unlike with projective measurements, repeated measurements don't always give the same results.
```
d = 3
povm = sic_povm(d)
print(dm_probs(povm[0]/povm[0].tr(), povm))
```
Above we see the probabilities for SIC-POVM outcomes given that we start off in the first SIC-POVM state. We see that indeed, the first SIC-POVM state has the highest probability, but all the other elements have non-zero probability (and for SIC's this is the same probability: not true for general IC-POVM's).
Indeed, it's a theorem that no such probability vector can have an element which exceeds $\frac{1}{d}$, and that the number of $0$ entries is bounded above by $\frac{d(d-1)}{2}$.
So we need another constraint. In other words, the quantum state space is a *proper subset* of the probability simplex over $d^2$ outcomes. There's some very interesting work exploring the geometric aspects of this constraint.
For example, insofar as pure states are those Hermitian matrices satisfying $tr(\rho^2) = tr(\rho^3) = 1$, we can evidently finagle this into two conditions:
$\sum_{i}^{d^2} p(i)^2 = \frac{2}{d(d+1)}$
and
$\sum_{i,j,k} c_{i, j, k}p(i)p(j)p(k) = \frac{d+7}{(d+1)^3}$
Where $c_{i, j, k} = \Re{[tr(\Pi_{i}\Pi_{j}\Pi_{k})]}$, which is a real-valued, completely symmetric three index tensor. The quantum state space is the <a href="https://en.wikipedia.org/wiki/Convex_hull">convex hull</a> of probability distributions satisfying these two equations.
On this same note, considering our expression for the inner product, since we know that the inner product between two quantum states $\rho$ and $\sigma$ is bounded between $0$ and $1$, we must have:
$\frac{1}{d(d+1)} \leq \vec{p} \cdot \vec{s} \leq \frac{2}{d(d+1)}$
The upper bound corresponds to our first condition. Call two vectors $\vec{p}$ and $\vec{s}$ "consistent" if their inner product obeys both inequalities. If we have a subset of the probability simplex for which every pair of vectors satisfies the inequalities, call it a "germ." If adding one more vector to a germ makes the set inconsistent, call the germ "maximal." And finally, call a maximal germ a "qplex." The space of quantum states in the SIC representation form a qplex, but not all qplexes correspond to quantum state spaces. The geometry of the qplexes are explored in <a href="https://arxiv.org/abs/1612.03234">Introducing the Qplex: A Novel Arena for Quantum Theory</a>. The conclusion?
"\[Turning\] to the problem of identifying the “missing assumption” which will serve to pick out quantum state space uniquely from the set of all qplexes... Of course, as is usual in such cases, there is more than one possibility. We identify one such assumption: the requirement that the symmetry group contain a subgroup isomorphic to the projective unitary group. This is a useful result because it means that we have a complete characterization of quantum state space in probabilistic terms. It also has an important corollary: That SIC existence in dimension d is equivalent to the existence of a certain kind of subgroup of the real orthogonal group in dimension $d^2 − 1$."
<hr>
Here's one final thing, for flavor. Having specified a SIC-POVM with $n$ elements and then an additional measurement (Von Neumann or POVM), we can construct the matrix $r(j|i)$.
```
d = 2
ref_povm = sic_povm(d)
von_neumann = qt.rand_herm(d)
n = len(ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
r
```
We can then consider its rows, and extract a set of vectors $s_{j}$, each of which sums to 1:
$r(j|i) = n\gamma_{j} s_{j}(i)$
```
s = np.array([row/sum(row) for row in r])
gammas = [sum(row)/n for row in r]
np.array([n*gammas[i]*row for i, row in enumerate(s)])
```
We'll call these vectors $s_{j}$ "measurement vectors."
Suppose we're completely indifferent to the outcomes of the POVM in the sky. We could represent this by: $p(i) = \frac{1}{n}$. In other words, equal probability for each outcome.
The probabilities for outcomes to the later Von Neumann measurement would be:
$q(j) = \frac{1}{n}\sum_{i}r(j|i)$
```
p = [1/n for i in range(n)]
vn_probs = np.array([sum([p[i]*r[j][i] for i in range(n)]) for j in range(d)])
vn_probs
```
We could describe this by assigning to $\rho$ the maximally mixed state.
```
max_mixed = qt.identity(d)/d
vn_born(max_mixed, von_neumann, ref_povm)
```
But we could also rewrite $q(j)$ as:
$q(j) = \frac{1}{n} \sum_{i} n\gamma_{j} s_{j}(i) = \gamma_{j} \sum_{i} s_{j}(i)$
And since the $s_{j}(i)$ sum to 1:
$q(j) = \gamma_{j}$
```
np.array([gammas[j]*sum([s[j][i] for i in range(n)]) for j in range(d)])
gammas
```
Thus you can interpret the $\gamma_{j}$'s as: the probabilities of obtaining the $j^{th}$ outcome on the ground when you're completely indifferent to the potential outcomes in the sky.
Now let's rewrite:
$r(j|i) = n\gamma_{j} s_{j}(i)$
as
$s_{j}(i) = \frac{\frac{1}{n}r(j|i)}{\gamma_{j}}$
We know that $\gamma_{j}$ is the probability of obtaining $j$ on the ground, given complete ignorance about the potential outcomes of the sky experiment. We also know that $\frac{1}{n}$ is the probability assigned to each outcome of the sky experiment from complete indifference.
So write $Pr_{CI}(i)= \frac{1}{n}$ and $Pr_{CI}(j) = \gamma_{i}$, where $CI$ stands for complete ignorance/indifference. And we could apply the same notation: $Pr_{CI}(j|i) = r(j|i)$:
$s_{j}(i) = \frac{Pr_{CI}(i)Pr_{CI}(j|i)}{Pr_{CI}(j)}$
But this is just the Baysian formula for inverting conditional probabilities:
$Pr_{CI}(i|j) = \frac{Pr_{CI}(i)Pr_{CI}(j|i)}{Pr_{CI}(j)}$
In a similar vein:
<img src="img/fuchs.png">
<hr>
## Interlude: Implementing POVM's
It's worth mentioning how POVM's are actually implemented in practice. Here's the simplest way of thinking about it. Suppose we have a system with Hilbert space dimension $d$, and we have a POVM with $n$ elements. (In the case of our SIC-POVM's, we'd have $d^2$ elements.) We then adjoin an auxilliary system with Hilbert space dimension $n$: as many dimensions as POVM elements. So now we're working with $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$.
Let's define projectors onto the basis states of the auxilliary system: $\Xi_{i} = I_{d} \otimes \mid i \rangle \langle i \mid$. If we denote the elements of the POVM by $\{ E_{i} \}$, then we can construct an isometry:
$V = \sum_{i}^{n} \sqrt{E_{i}} \otimes \mid i \rangle$
Such that any element of the POVM can be written:
$E_{i} = V^{\dagger}\Xi_{i}V $
```
d = 3
my_povm = sic_povm(d)
n = len(my_povm)
aux_projectors = [qt.tensor(qt.identity(d), qt.basis(n, i)*qt.basis(n, i).dag()) for i in range(n)]
V = sum([qt.tensor(my_povm[i].sqrtm(), qt.basis(n, i)) for i in range(n)])
povm_elements = [V.dag()*aux_projectors[i]*V for i in range(n)]
print("recovered povm elements? %s" % np.all([np.allclose(my_povm[i], povm_elements[i]) for i in range(n)]))
```
So this isometry $V$ takes us from $\mathcal{H}_{d}$ to $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$.
We can extend this to a unitary $U$ (that takes $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$ to $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$) using the QR decomposition. In essence, we use the Gram-Schmidt procedure to fill out the rectangular matrix to a square matrix with extra orthogonal columns. (And then we have to rearrange the columns so that the columns of $V$ appear every $n^{th}$ column, in order to take into account the tensor product structure.)
```
Q, R = np.linalg.qr(V, mode="complete")
for i in range(d):
Q.T[[i,n*i]] = Q.T[[n*i,i]]
Q[:,n*i] = V[:,i].T
U = qt.Qobj(Q)
U.dims = [[d, n],[d, n]]
```
We can check our work. It should be the case that:
$V = U(I_{d} \otimes \mid 0 \rangle)$
```
print("recovered V?: %s" % np.allclose(V, U*qt.tensor(qt.identity(d), qt.basis(n, 0))))
```
Now for the finale. We know how to calculate the probabilities for each of the POVM outcomes. It's just:
$Pr(i) = tr(E_{i}\rho)$
To actually implement this, we start off with our auxilliary system in the $\mid 0 \rangle$ state, so that the overall density matrix is: $\rho \otimes \mid 0 \rangle \langle 0 \mid$. We then evolve the system and the auxilliary with our unitary $U$:
$$U [\rho \otimes \mid 0 \rangle \langle 0 \mid] U^{\dagger} $$
Finally, we perform a standard Von Neumann measurement on the auxilliary system (whose outcomes correspond to the basis states we've been using). Recalling that we defined the projectors onto the auxilliary basis states as $\Xi_{i} = I_{d} \otimes \mid i \rangle \langle i \mid$, we can then write probabilities for each outcome:
$Pr(i) = tr(\Xi_{i} U [\rho \otimes \mid 0 \rangle \langle 0 \mid] U^{\dagger} )$
These are the same probabilities as above.
```
rho = qt.rand_dm(d)
povm_probs = np.array([(my_povm[i]*rho).tr() for i in range(n)]).real
system_aux_probs = np.array([(aux_projectors[i]*\
U*qt.tensor(rho, qt.basis(n,0)*qt.basis(n,0).dag())*U.dag()).tr()\
for i in range(n)]).real
print("povm probs:\n%s" % povm_probs)
print("system and aux probs:\n%s" % system_aux_probs)
```
Moreover, we can see that the states after measurement correspond to the SIC-POVM projectors:
```
states = [(aux_projectors[i]*(U*qt.tensor(rho, qt.basis(n,0)*qt.basis(n,0).dag())*U.dag())).ptrace(0) for i in range(n)]
print(states[0].unit())
print(d*my_povm[0])
```
Indeed, whether you buy the philosophy that we're about to go into, SIC-POVM's have deep practical value in terms of quantum tomography and quantum information theory generally.
Cf. `implement_povm`.
<hr>
## The Philosophy
So in some sense the difference between classical and quantum is summed up in the difference between these two formulas:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
and
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - 1$
In the first case, I make a SIC-POVM measurement in the sky, and then make a Von Neumann measurement on the ground. I can calculate the probabilities for the outcomes of the latter measurement using the law of total probability. Given the probabilities for the sky outcomes, and the conditional probabilities that relate ground outcomes to sky outcomes, I can calculate the probabilities for ground outcomes. Classically speaking, and this is the crucial point, I could use the first formula *whether or not I actually did the sky measurement*.
In other words, insofar as classically we've identified the relevant "degrees of freedom," and the assignment of sky probabilities uniquely characterizes the state, then it's a matter of mathematical convenience if we express $s(j)$ as a sum over those degrees of freedom $\sum_{i}^{d^2} p(i)r(j|i)$: by the nature of the formula, by the law of total probability, all the $i$'s drop out, and we're left with the value for $j$. We could actually perform the sky measurement or not: either way, we'd use the same formula to calculate the ground probabilities.
This is precisely what changes with quantum mechanics: it makes a difference *whether you actually do the sky measurement or not*. If you do, then you use the classical formula. If you don't, then you use the quantum formula.
One way of interpreting the moral of this is that, to quote Asher Peres again, "Unperformed measurements have no results." In contrast, classically, you *can* always regard unperformed measurements as having results: indeed, classical objectivity consists in, as it were, everything wearing its outcomes on its sleeve. In other words, outcomes aren't a special category: one can just speak of the properties of things. And this is just another way of saying you can use the law of total probability whether or not you actually do an intermediate measurement. But this is exactly what you can't rely on in quantum mechanics.
But remarkably, all you need to do to update your probability calculus is to use the quantum formula, which is ultimately the Born Rule in disguise. In other words, in a world where unperformed measurements have no results, when we consider different kinds of sequences of measurements, we need a (minor) addition to probability theory so that our probability assignments are coherent/consistent/no one can make a buck off of us.
Moreover, Blake Stacey makes the nice point, considering the realtionship between SIC-POVM's and Von Neumann measurements:
"Two orthogonal quantum states are perfectly distinguishable with respect to some experiment, yet in terms of the reference \[SIC-POVM\] measurement, they are inevitably overlapping probability distributions. The idea that any two valid probability distributions for the reference measurement must overlap, and that the minimal overlap in fact corresponds to distinguishability with respect to some other test, expresses the fact that quantum probability is not about hidden variables" (Stacey 2020).
<hr>
de Finetti famously advocated a subjectivist, personalist view of classical probability theory, and he and his theorems have proved to be an inspiration for QBists like Christopher Fuchs and others. In this view, probabilities don't "exist" out in the world: they are mathematical representations of personal beliefs which you are free to update in the face of new evidence. There isn't ever "one objective probability distribution" for things: rather, there's a constant personal process of convergence towards better beliefs. If you don't want to make bad bets, there are some basic consistency criteria that your probabilities have to satisfy. And that's what probability theory as such amounts to. The rest is just "priors."
"Statisticians for years had been speaking of how statistical sampling can reveal the 'unknown probability distribution'. But from de Finetti’s point of view, this makes as little sense as the unknown quantum state made for us. What de Finetti’s representation theorem established was that all this talk of an unknown probability was just that, talk. Instead, one could show that there was a way of thinking of the resultant of statistical sampling purely in terms of a transition from prior subjective probabilities (for the sampler himself) to posterior subjective probabilities (for the sampler himself). That is, every bit of statistical sampling from beginning to end wasn’t about revealing a true state of affairs (the “unknown probability”), but about the statistician’s own states of information about a set of “exchangeable” trials, full stop. The quantum de Finetti theorem does the same sort of thing, but for quantum states" (Fuchs 2018).
Indeed, QBists advocate a similar epistemic interpretation of the quantum state. The quantum state does not represent a quantum system. It represents *your beliefs about that quantum system*. In other words, interpretations that assign ontological roles to quantum states miss the mark. Quantum states are just packages of probabilities, indeed, probabilities personal to you. (In this sense, one can see a close relation to relational interpretations of quantum mechanics, where the quantum state is always defined not objectively, but to one system relative to another system.) Similarly, all the superstructure of quantum mechanics, operators, time evolution, etc-- are all just a matter of making subjective probabilities consistent with each other, given the *objective fact* that you should use the quantum formula when you haven't done an intermediate measurement, and the classical formula if you have. (And one should also mention that the formulas above imply that the *dimension* of the Hilbert space is, in fact, objective.)
On the other hand, QBists also hold that the very outcomes of measurements themselves are subjective--not in the sense of being vacuously open to intepretation, but in the sense that they are *experiences*; and it is precisely these subjective experiences that are being gambled upon. In other words, quantum mechanics is not a theory of the objective physical world as such, but is instead a first person theory by which one may predict the future consequences of one's own actions in experience.
This is how they deal with the dilemma of Wigner's friend. Fuchs: "...for the QBist, the real world, the one both agents are embedded in—with its objects and events—is taken for granted. What is not taken for granted is each agent's access to the parts of it he has not touched. Wigner holds two thoughts in his head: a) that his friend interacted with a quantum system, eliciting some consequences of the interaction for himself, and b) after the specified time, for any of Wigner's own future interactions with his friend or the system or both, he ought to gamble upon their consequences according to $U(\rho \otimes \mid \psi \rangle \langle \psi \mid) U^{\dagger}$. One statement refers to the friend's potential experiences, and one refers to Wigner's own. So long as it is explicit that $U(\rho \otimes \mid \psi \rangle \langle \psi \mid) U^{\dagger}$ refers to the latter--i.e., how Wigner should gamble upon the things that might happen to him--making no statement whatsoever about the former, there is no conflict. The world is filled with all the same things it was before quantum theory came along, like each of our experiences, that rock and that tree, and all the other things under the sun; it is just that quantum theory provides a calculus for gambling on each agent's experiences--it doesn't give anything other than that. It certainly doesn't give one agent the ability to conceptually pierce the other agent's personal experience. It is true that with enough effort Wigner \[could apply the reverse unitary, disentangling the friend and the spin\], causing him to predict that his friend will have amnesia to any future questions on his old measurement results. But we always knew Wigner could do that--a mallet to the head would have been good enough" (Fuchs, Stacey 2019).
Most assuredly, this is not a solipsistic theory: indeed, the actual results of measurement are precisely not within one's control. The way they imagine it is that whenever you set up an experiment, you divide the world into subject and object: the subject has the autonomy to set up the experiment, and the object has the autonomy to respond to the experiment. But the act of measurement itself is a kind of creation, a mutual experience which transcends the very distinction between subject and object itself, a linkage between oneself and the other. "QBism says that when an agent reaches out and touches a quantum system—when he performs a quantum measurement—this process gives rise to birth in a nearly literal sense" (Fuchs, Stacey 2019).
The only conflict here is with a notion that the only valid physical theories are those that attempt to directly represent the universe "in its totality as a pre-existing static system; an unchanging, monistic something that just *is*." Moreover, a theory like QBism clears a space for "real particularity and 'interiority' in the world." For Wigner, considering his friend and the system, with his back turned, "that phenomenon has an inside, a vitality that he takes no part in until he again interacts with one or both relevant pieces of it."
Often in the interpretation of quantum mechanics, one tries to achieve objectivity by focusing on the big bulky apparatuses we use and the "objective" record of outcomes left behind by these machines. The QBists take a different track: Bohr himself considers the analogy of a blind man seeing with a stick. He's not actively, rationally thinking about the stick and how it's skittering off this or that: rather, for him, it becomes an extension of his body: he *sees with the stick*. And thus one can understand Fuchs's three tenants of QBism:
1. Quantum Theory Is Normative, Not Descriptive
2. My Probabilities Cannot Tell Nature What To Do
3. A Measuring Device Is Literally an Extension of the Agent
<hr>
<img width=600 src="img/qbism_assumptions1.png">
<img width=600 src="img/qbism_assumptions2.png">
<hr>
Indeed, one might wonder about entanglement in this picture. In line with the discussion of Wigner's friend, we can interpret entanglement and the use of tensor product itself as relating to the objective fact that we require a way of representing correlations while being completely agnostic about what is correlated insofar as we haven't yet reached out and "touched" the thing.
Moreover, in this sense, one can look at QBism as a completely "local" theory. An experimenter has one half of an entangled pair of spins, and makes a measurement, and has an experience. In the textbook way of thinking it, this causes the state of the other spin to immedietely collapse. QBism takes a different approach. They say: quantum theory allows the experimenter to predict that if they go over and measure the other spin in the same direction, they will have another experience, of the answers of the two particles being correlated. But just because quantum theory licenses the experimenter to assign a probability 1 for the latter outcome after they do the first measurement doesn't mean that the latter particle *really is now $\uparrow$, say, as a property*. If the experimenter never actually goes to check out the other particle, it's yet another unperformed measurement: and it has no outcome yet. To paraphrase William James, if it isn't experienced, it isn't real. And in order to "cash out" on entanglement, one actually has to traverse the distance between the two particles and compare the results.
With regard to quantum teleportation, in this view, it's not about getting "things" from one place to another, but about making one's information cease referring to this part of the universe and start referring instead to another part of the universe, without referring to anything else in between. "The only nontrivial thing transferred in the process of teleportation is *reference*" (Fuchs, Stacey 2019).
<hr>
One of the things that makes QBism so interesting is its attempt to give nature as much latitude as possible. Usually in science, we're mentally trying to constraint nature, applying concepts, laws, systems, to it, etc. QBism instead proposes that we live in a unfinished world, whose creation is ongoing and ceaseless, and that this profound openendedness is the real meaning behind "quantum indeterminism." In itself, the universe is not governed by immutable laws and initial conditions fixed from the beginning: instead, new situations are coming into being all the time. Of course, regularities arise by evolution, the laws of large numbers, symmetries and so forth. But they take seriously John Wheeler's idea of the "participatory universe," that we and everything else are constantly engaged bringing the universe into being, together.
Wheeler writes:
"How did the universe come into being? Is that some strange, far-off process beyond hope of analysis? Or is the mechanism that comes into play one which all the time shows itself? Of all the signs that testify to 'quantum phenomenon' as being the elementary act and building block of existence, none is more striking than its utter absence of internal structure and its untouchability. For a process of creation that can and does operate anywhere, that is more basic than particles or fields or spacetime geometry themselves, a process that reveals and yet hides itself, what could one have dreamed up out of pure imagination more magic and more fitting than this?"
"'Law without law': It is difficult to see what else than that can be the “plan” for physics. It is preposterous to think of the laws of physics as installed by a Swiss watchmaker to endure from everlasting to everlasting when we know that the universe began with a big bang. The laws must have come into being. Therefore they could not have been always a hundred percent accurate. That means that they are derivative, not primary. Also derivative, also not primary is the statistical law of distribution of the molecules of a dilute gas between two intersecting portions of a total volume. This law is always violated and yet always upheld. The individual molecules laugh at it; yet as they laugh they find themselves obeying it. ... Are the laws of physics of a similar statistical character? And if so, statistics of what? Of billions and billions of acts of observer-participancy which individually defy all law? . . . \[Might\] the entirety of existence, rather than \[be\] built on particles or fields or multidimensional geometry, \[be\] built on billions upon billions of elementary quantum phenomena, those elementary acts of observer-participancy?"
<img src="img/wheeler.png">
<hr>
In such world, to quote William James, "Theories thus become instruments, not answers to enigmas, in which we can rest. We don’t lie back upon them, we move forward, and, on occasion, make nature over again by their aid." Moreover, in relegating quantum states to the observers who use them for predictions, one clears some ontological space for the quantum systems themselves to be "made of" who knows what qualitative, experiential stuff.
"\[QBism\] means that reality differs from one agent to another. This is not as strange as it may sound. What is real for an agent rests entirely on what that agent experiences, and different agents have different experiences. An agent-dependent reality is constrained by the fact that different agents can communicate their experience to each other, limited only by the extent that personal experience can be expressed in ordinary language. Bob’s verbal representation of his own experience can enter Alice’s, and vice-versa. In this way a common body of reality can be constructed, limited only by the inability of language to represent the full flavor — the “qualia” — of personal experience" (Fuchs, Mermin, Schack 2013).
Indeed, the QBists reach back in time and draw on the work of the old American pragmatists: James, John Dewey, Charles Sanders Peirce, and others. It's interesting to read their works particularly as many of them date from the pre-quantum era, so that even in the very face of classical physics, they were advocating a radically indeterministic, experience-first view of the world.
For example, James writes:
"Chance] is a purely negative and relative term, giving us no information about that of which it is predicated, except that it happens to be disconnected with something else—not controlled, secured, or necessitated by other things in advance of its own actual presence... What I say is that it tells us nothing about what a thing may be in itself to call it “chance.” ... All you mean by calling it “chance” is that this is not guaranteed, that it may also fall out otherwise. For the system of other things has no positive hold on the chance-thing. Its origin is in a certain fashion negative: it escapes, and says, Hands off! coming, when it comes, as a free gift, or not at all."
"This negativeness, however, and this opacity of the chance-thing when thus considered ab extra, or from the point of view of previous things or distant things, do not preclude its having any amount of positiveness and luminosity from within, and at its own place and moment. All that its chance-character asserts about it is that there is something in it really of its own, something that is not the unconditional property of the whole. If the whole wants this property, the whole must wait till it can get it, if it be a matter of chance. That the universe may actually be a sort of joint-stock society of this sort, in which the sharers have both limited liabilities and limited powers, is of course a simple and conceivable notion."
<hr>
"Why may not the world be a sort of republican banquet of this sort, where all the qualities of being respect one another’s personal sacredness, yet sit at the common table of space and time?
To me this view seems deeply probable. Things cohere, but the act of cohesion itself implies but few conditions, and leaves the rest of their qualifications indeterminate. As the first three notes of a tune comport many endings, all melodious, but the tune is not named till a particular ending has actually come,—so the parts actually known of the universe may comport many ideally possible complements. But as the facts are not the complements, so the knowledge of the one is not the knowledge of the other in anything but the few necessary elements of which all must partake in order to be together at all. Why, if one act of knowledge could from one point take in the total perspective, with all mere possibilities abolished, should there ever have been anything more than that act? Why duplicate it by the tedious unrolling, inch by inch, of the foredone reality? No answer seems possible. On the other hand, if we stipulate only a partial community of partially independent powers, we see perfectly why no one part controls the whole view, but each detail must come and be actually given, before, in any special sense, it can be said to be determined at all. This is the moral view, the view that gives to other powers the same freedom it would have itself."
<hr>
"Does our act then create the world’s salvation so far as it makes room for itself, so far as it leaps into the gap? Does it create, not the whole world’s salvation of course, but just so much of this as itself covers of the world’s extent? Here I take the bull by the horns, and in spite of the whole crew of rationalists and monists, of whatever brand they be, I ask why not? Our acts, our turning-places, where we seem to ourselves to make ourselves and grow, are the parts of the world to which we are closest, the parts of which our knowledge is the most intimate and complete. Why should we not take them at their facevalue? Why may they not be the actual turning-places and growing-places which they seem to be, of the world—why not the workshop of being, where we catch fact in the making, so that nowhere may the world grow in any other kind of way than this?"
"Irrational! we are told. How can new being come in local spots and patches which add themselves or stay away at random, independently of the rest? There must be a reason for our acts, and where in the last resort can any reason be looked for save in the material pressure or the logical compulsion of the total nature of the world? There can be but one real agent of growth, or seeming growth, anywhere, and that agent is the integral world itself. It may grow all-over, if growth there be, but that single parts should grow per se is irrational."
"But if one talks of rationality—and of reasons for things, and insists that they can’t just come in spots, what kind of a reason can there ultimately be why anything should come at all?"
<hr>
"What does determinism profess? It professes that those parts of the universe already laid down absolutely appoint and decree what the other parts shall be. The future has no ambiguous possibilities hidden in its womb; the part we call the present is compatible with only one totality. Any other future complement than the one fixed from eternity is impossible. The whole is in each and every part, and welds it with the rest into an absolute unity, an iron block, in which there can be no equivocation or shadow of turning."
"Indeterminism, on the contrary, says that the parts have a certain amount of loose play on one another, so that the laying down of one of them does not necessarily determine what the others shall be. It admits that possibilities may be in excess of actualities, and that things not yet revealed to our knowledge may really in themselves be ambiguous. Of two alternative futures which we conceive, both may now be really possible; and the one become impossible only at the very moment when the other excludes it by becoming real itself. Indeterminism thus denies the world to be one unbending unit of fact. It says there is a certain ultimate pluralism in it."
<hr>
"The import of the difference between pragmatism and rationalism is now in sight throughout its whole extent. The essential contrast is that for rationalism reality is ready-made and complete from all eternity, while for pragmatism it is still in the making, and awaits part of its complexion from the future. On the one side the universe is absolutely secure, on the other it is still pursuing its adventures..."
"The humanist view of 'reality,' as something resisting, yet malleable, which controls our thinking as an energy that must be taken 'account' of incessantly is evidently a difficult one to introduce to novices...
The alternative between pragmatism and rationalism, in the shape in which we now have it before us, is no longer a question in the theory of knowledge, it concerns the structure of the universe itself."
"On the pragmatist side we have only one edition of the universe, unfinished, growing in all sorts of places, especially in the places where thinking beings are at work. On the rationalist side we have a universe in many editions, one real one, the infinite folio, or ́edition de luxe, eternally complete; and then the various finite editions, full of false readings, distorted and mutilated each in its own way."
<hr>
And yet, we know that quantum mechanics presents many faces, Bohmian deterministic faces, the many faces of Many Worlds, and so forth. It's beautiful, in a way: there's something for everybody. One is reminded of another passage from James:
"The history of philosophy is to a great extent that of a certain clash of human temperaments. Undignified as such a treatment may seem to some of my colleagues, I shall have to take account of this clash and explain a good many of the divergencies of philosophies by it. Of whatever temperament a professional philosopher is, he tries, when philosophizing, to sink the fact of his temperament. Temperament is no conventionally recognized reason, so he urges impersonal reasons only for his conclusions. Yet his temperament really gives him a stronger bias than any of his more strictly objective premises. It loads the evidence for him one way or the other ... just as this fact or that principle would. He trusts his temperament. Wanting a universe that suits it, he believes in any representation of the universe that does suit it."
"Why does Clifford fearlessly proclaim his belief in the conscious-automaton theory, although the ‘proofs’ before him are the same which make Mr. Lewes reject it? Why does he believe in primordial units of ‘mind-stuff’ on evidence which would seem quite worthless to Professor Bain? Simply because, like every human being of the slightest mental originality, he is peculiarly sensitive to evidence that bears in some one direction. It is utterly hopeless to try to exorcise such sensitiveness by calling it the disturbing subjective factor, and branding it as the root of all evil. ‘Subjective’ be it called! and ‘disturbing’ to those whom it foils! But if it helps those who, as Cicero says, “vim naturae magis sentiunt” \[feel the force of nature more\], it is good and not evil. Pretend what we may, the whole man within us is at work when we form our philosophical opinions. Intellect, will, taste, and passion co-operate just as they do in practical affairs...\[I\]n the forum \[one\] can make no claim, on the bare ground of his temperament, to superior discernment or authority. There arises thus a certain insincerity in our philosophic discussions: the potentest of all our premises is never mentioned. I am sure it would contribute to clearness if in these lectures we should break this rule and mention it, and I accordingly feel free to do so."
Indeed, for James, the value of a philosophy lies not so much in its proofs, but in the total vision that it expresses. As I say, perhaps the universe itself has something for everyone, whatever their temperament.
<hr>
As a final word, it seems to me that QBism has taught us something genuinely new about quantum theory and its relationship to probability theory. On the other hand, it also pretends to be a theory of "experience": and yet, I'm not sure that I've learned anything new about experience. If QBism is to really prove itself, it will have to make novel predictions not just on the quantum side, but also on the side of our everyday perceptions.
"The burning question for the QBist is how to model in Hilbert-space terms the common sorts of measurements we perform just by opening our eyes, cupping our ears, and extending our fingers" (Fuchs, Stacey 2019).
## Bibliography
<a href="https://arxiv.org/abs/1612.07308">QBism: Quantum Theory as a Hero’s Handbook</a>
<a href="https://arxiv.org/abs/1612.03234">Introducing the Qplex: A Novel Arena for Quantum Theory</a>
<a href="https://arxiv.org/abs/1311.5253">An Introduction to QBism with an Application to the Locality of Quantum Mechanics</a>
<a href="https://arxiv.org/abs/1003.5209">QBism, the Perimeter of Quantum Bayesianism</a>
<a href="https://arxiv.org/abs/1301.3274">Quantum-Bayesian Coherence: The No-Nonsense Version</a>
<a href="https://arxiv.org/abs/1401.7254">Some Negative Remarks on Operational Approaches to Quantum Theory</a>
<a href="https://arxiv.org/abs/1405.2390">My Struggles with the Block Universe</a>
<a href="https://arxiv.org/abs/1412.4209">Quantum Measurement and the Paulian Idea</a>
<a href="https://arxiv.org/abs/quant-ph/0105039">Notes on a Paulian Idea</a>
<a href="https://arxiv.org/abs/1601.04360">On Participatory Realism</a>
<a href="https://arxiv.org/abs/0906.1968">Delirium Quantum</a>
<a href="https://arxiv.org/abs/1703.07901">The SIC Question: History and State of Play</a>
<a href="https://arxiv.org/abs/1705.03483">Notwithstanding Bohr, the Reasons for QBism</a>
<a href="https://arxiv.org/abs/2012.14397">The Born Rule as Dutch-Book Coherence (and only a little more)</a>
<a href="https://arxiv.org/abs/quant-ph/0205039">Quantum Mechanics as Quantum Information (and only a little more)</a>
<a href="https://arxiv.org/abs/1907.02432">Quantum Theory as Symmetry Broken by Vitality</a>
https://en.wikipedia.org/wiki/POVM
https://en.wikipedia.org/wiki/SIC-POVM
<a href="refs/wheeler_law_without_law.pdf">Law without Law</a>
<a href="http://www.gutenberg.org/ebooks/11984">A Pluralistic Universe</a>
<a href="http://www.gutenberg.org/ebooks/32547">Essays in Radical Empiricism</a>
| true |
code
| 0.375706 | null | null | null | null |
|
# 5장
```
import matplotlib
matplotlib.rc('font', family="NanumBarunGothicOTF")
%matplotlib inline
```
# 5.2 아이리스 데이터셋
```
import pandas as pd
from matplotlib import pyplot as plt
import sklearn.datasets
def get_iris_df():
ds = sklearn.datasets.load_iris()
df = pd.DataFrame(ds['data'], columns=ds['feature_names'])
code_species_map = dict(zip(
range(3), ds['target_names']))
df['species'] = [code_species_map[c] for c in ds['target']]
return df
df = get_iris_df()
df_iris = df
```
# 5.3 원형 차트
```
sums_by_species = df.groupby('species').sum()
var = 'sepal width (cm)'
sums_by_species[var].plot(kind='pie', fontsize=20)
plt.ylabel(var, horizontalalignment='left')
plt.title('꽃받침 너비로 분류한 붓꽃', fontsize=25)
# plt.savefig('iris_pie_for_one_variable.png')
# plt.close()
sums_by_species = df.groupby('species').sum()
sums_by_species.plot(kind='pie', subplots=True,
layout=(2,2), legend=False)
plt.title('종에 따른 전체 측정값Total Measurements, by Species')
# plt.savefig('iris_pie_for_each_variable.png')
# plt.close()
```
# 5.4 막대그래프
```
sums_by_species = df.groupby('species').sum()
var = 'sepal width (cm)'
sums_by_species[var].plot(kind='bar', fontsize=15, rot=30)
plt.title('꽃받침 너비(cm)로 분류한 붓꽃', fontsize=20)
# plt.savefig('iris_bar_for_one_variable.png')
# plt.close()
sums_by_species = df.groupby('species').sum()
sums_by_species.plot(
kind='bar', subplots=True, fontsize=12)
plt.suptitle('종에 따른 전체 측정값')
# plt.savefig('iris_bar_for_each_variable.png')
# plt.close()
```
# 5.5 히스토그램
```
df.plot(kind='hist', subplots=True, layout=(2,2))
plt.suptitle('붓꽃 히스토그램', fontsize=20)
# plt.show()
for spec in df['species'].unique():
forspec = df[df['species']==spec]
forspec['petal length (cm)'].plot(kind='hist', alpha=0.4, label=spec)
plt.legend(loc='upper right')
plt.suptitle('종에 따른 꽃잎 길이')
# plt.savefig('iris_hist_by_spec.png')
```
# 5.6 평균, 표준편차, 중간값, 백분위
```
col = df['petal length (cm)']
average = col.mean()
std = col.std()
median = col.quantile(0.5)
percentile25 = col.quantile(0.25)
percentile75 = col.quantile(0.75)
print(average, std, median, percentile25, percentile75)
```
### 아웃라이어 걸러내기
```
col = df['petal length (cm)']
perc25 = col.quantile(0.25)
perc75 = col.quantile(0.75)
clean_avg = col[(col>perc25)&(col<perc75)].mean()
print(clean_avg)
```
# 5.7 상자그림
```
col = 'sepal length (cm)'
df['ind'] = pd.Series(df.index).apply(lambda i: i% 50)
df.pivot('ind','species')[col].plot(kind='box')
# plt.show()
```
# 5.8 산포도
```
df.plot(kind="scatter",
x="sepal length (cm)", y="sepal width (cm)")
plt.title("Length vs Width")
# plt.show()
colors = ["r", "g", "b"]
markers= [".", "*", "^"]
fig, ax = plt.subplots(1, 1)
for i, spec in enumerate(df['species'].unique() ):
ddf = df[df['species']==spec]
ddf.plot(kind="scatter",
x="sepal width (cm)", y="sepal length (cm)",
alpha=0.5, s=10*(i+1), ax=ax,
color=colors[i], marker=markers[i], label=spec)
plt.legend()
plt.show()
import pandas as pd
import sklearn.datasets as ds
import matplotlib.pyplot as plt
# 팬다스 데이터프레임 생성
bs = ds.load_boston()
df = pd.DataFrame(bs.data, columns=bs.feature_names)
df['MEDV'] = bs.target
# 일반적인 산포도
df.plot(x='CRIM',y='MEDV',kind='scatter')
plt.title('일반축에 나타낸 범죄 발생률')
# plt.show()
```
## 로그를 적용
```
df.plot(x='CRIM',y='MEDV',kind='scatter',logx=True)
plt.title('Crime rate on logarithmic axis')
plt.show()
```
# 5.10 산포 행렬
```
from pandas.tools.plotting import scatter_matrix
scatter_matrix(df_iris)
plt.show()
```
# 5.11 히트맵
```
df_iris.plot(kind="hexbin", x="sepal width (cm)", y="sepal length (cm)")
plt.show()
```
# 5.12 상관관계
```
df["sepal width (cm)"].corr(df["sepal length (cm)"]) # Pearson corr
df["sepal width (cm)"].corr(df["sepal length (cm)"], method="pearson")
df["sepal width (cm)"].corr(df["sepal length (cm)"], method="spearman")
df["sepal width (cm)"].corr(df["sepal length (cm)"], method="spearman")
```
# 5.12 시계열 데이터
```
# $ pip install statsmodels
import statsmodels.api as sm
dta = sm.datasets.co2.load_pandas().data
dta.plot()
plt.title("이산화탄소 농도")
plt.ylabel("PPM")
plt.show()
```
## 구글 주가 불러오는 코드는 야후 API가 작동하지 않아서 생략합니다.
| true |
code
| 0.6195 | null | null | null | null |
|
In this notebook you can define your own configuration and run the model based on your custom configuration.
## Dataset
`dataset_name` is the name of the dataset which will be used in the model. In case of using KITTI, `dataset_path` shows the path to `data_paths` directory that contains every image and its pair path, and for Cityscape it is the path to the directory that contains `leftImg8bit` and `rightImg8bit` folders. The `resize` value selects the width, and the height dimensions that each image will be resized to.
```
dataset_name: 'KITTI'
dataset_path = '.'
resize = [128, 256]
```
## Model
`baseline_model` selects the compression model. The accepted models for this parameter are bmshj18 for [Variational image compression with a scale hyperprior](https://arxiv.org/abs/1802.01436) and bls17 for [End-to-end Optimized Image Compression](https://arxiv.org/abs/1611.01704). If `use_side_info` is set as `True`, then the baseline model is modified using our proposed method for using side information for compressing.
If `load_weight` is `True`, then in model initialization, the weight saved in `weight_path` is loaded to the model. You can also specify the experiment name in `experiment_name`.
```
baseline_model = 'bls17' # can be bmshj18 for Variational image compression with a scale hyperprior by Ballé, et al.
# or bls17 for End-to-end Optimized Image Compression by Ballé, et al.
use_side_info = True # if True then the modified version of baseline model for distributed compression is used.
num_filters = 192 # number of filters used in the baseline model network
cuda = True
load_weight = False
weight_path = './pretrained_weights/ours+balle17_MS-SSIM_lambda3e-05.pt' # weight path for loading the weight
# note that we provide some pretrained weights, accessible from the anonymous link provided in README.md
```
## Training
For training set `train` to be `True`. `lambda` shows the lambda value in the rate-distortion equation and `alpha` and `beta` correspond to the handles on the reconstruction of the correlated image and amount of common information extracted from the decoder-only side information, respectively. `distortion_loss` selects the distortion evaluating method. Its accepted values are MS-SSIM for the ms-ssim method or MSE for mean squared error.
`verbose_period: 50` indicates that every 50 epochs print the results of the validation dataset.
```
train = True
epochs = 50000
train_batch_size = 1
lr = 0.0001
lmbda = 0.00003 # the lambda value in rate-distortion equation
alpha = 1
beta = 1
distortion_loss = 'MS-SSIM' # can be MS-SSIM or MSE. selects the method by which the distortion is calculated during training
verbose_period = 50 # non-positive value indicates no verbose
```
## Weights and Results parameters
If you wish to save the model weights after training set `save_weights` `True`. `save_output_path` shows the directory path where the model weights are saved.
For the weights, in `save_output_path` a `weight` folder will be created, and the weights will be saved there with the name according to `experiment_name`.
```
save_weights = True
save_output_path = './outputs' # path where results and weights will be saved
experiment_name = 'bls17_with_side_info_MS-SSIM_lambda:3e-05'
```
## Test
If you wish to test the model and save the results set `test` to `True`. If `save_image` is set to `True` then a `results` folder will be created, and the reconstructed images will be saved in `save_output_path/results` during testing, with the results named according to `experiment_name`.
```
test = True
save_image = True
```
## Inference
In order to (only) carry out inference, please open `configs/config.yaml` and change the relevant lines as follows:
```
resize = [128, 256] # we used this crop size for our inference
dataset_path = '.'
train = False
load_weight = True
test = True
save_output_path = './inference'
save_image = True
```
Download the desired weights and put them in `pretrained_weights` folder and put the dataset folder in the root .
Based on the weight you chose, specify the weight name, and the experiment name in `configs/config.yaml`:
```
weight_path: './pretrained_weights/...' # load a specified pre-trained weight
experiment_name: '...' # a handle for the saved results of the inference
```
Also, change `baseline_model` and `use_side_info` parameters in `configs/config.yaml` accordingly.
For example, for the `balle2017+ours` weights, these parameters should be:
```
baseline_model: 'bls17'
use_side_info: True
```
After running the code using the commands in below section, the results will be saved in `inference` folder.
## Saving Custom Configuration
By running this piece of code you can save your configuration as a yaml file file in the configs folder. You can set your configuration file name by changing `config_name` variable.
```
import yaml
config = {
"dataset_name": dataset_name,
"dataset_path": dataset_path,
"resize": resize,
"baseline_model": baseline_model,
"use_side_info": use_side_info,
"num_filters": num_filters,
"cuda": cuda,
"load_weight": load_weight,
"weight_path": weight_path,
"experiment_name": experiment_name,
"train": train,
"epochs": epochs,
"train_batch_size": train_batch_size,
"lr": lr,
"lambda": lmbda,
"distortion_loss": distortion_loss,
"verbose_period": verbose_period,
"save_weights": save_weights,
"save_output_path": save_output_path,
"test": test,
"save_image": save_image
}
config_name = "CUSTOM_CONFIG_FILE_NAME.yaml"
with open('configs/' + config_name) + config_name, 'w') as outfile:
yaml.dump(config, outfile, default_flow_style=None, sort_keys=False)
```
## Running the Model
```
!python main.py --config=configs/$config_name
```
| true |
code
| 0.656741 | null | null | null | null |
|
[0: NumPy and the ndarray](gridded_data_tutorial_0.ipynb) | **1: Introduction to xarray** | [2: Daymet data access](gridded_data_tutorial_2.ipynb) | [3: Investigating SWE at Mt. Rainier with Daymet](gridded_data_tutorial_3.ipynb)
# Notebook 1: Introduction to xarray
Waterhackweek 2020 | Steven Pestana ([email protected])
**By the end of this notebook you will be able to:**
* Create xarray DataArrays and Datasets
* Index and slice DataArrays and Datasets
* Make plots using xarray objects
* Export xarray Datasets as NetCDF or CSV files
---
#### What do we mean by "gridded data"?
Broadly speaking, this can mean any data with a corresponding location in one or more dimensions. Typically, our dimensions represent points on the Earth's surface in two or three dimensions (latitude, longitude, and elevation), and often include time as an additional dimension. You may also hear the term "raster" data, which also means data points on some grid. These multi-dimensional datasets can be thought of as 2-D images, stacks of 2-D images, or data "cubes" in 3 or more dimensions.
Examples of gridded data:
* Satellite images of Earth's surface, where each pixel represents reflection or emission at some wavelength
* Climate model output, where the model is evaluated at discrete nodes or grid cells
Examples of raster/gridded data formats that combine multi-dimensional data along with metadata in a single file:
* [NetCDF](https://www.unidata.ucar.edu/software/netcdf/docs/) (Network Common Data Form) for model data, satellite imagery, and more
* [GeoTIFF](https://trac.osgeo.org/geotiff/) for georeferenced raster imagery (satellite images, digital elevation models, maps, and more)
* [HDF-EOS](https://earthdata.nasa.gov/esdis/eso/standards-and-references/hdf-eos5) (Hierarchical Data Format - Earth Observing Systems)
* [GRIB](https://en.wikipedia.org/wiki/GRIB) (GRIdded Binary) for meteorological data
**How can we easily work with these types of data in python?**
Some python packages for working with gridded data:
* [rasterio](https://rasterio.readthedocs.io/en/latest/)
* [xarray](https://xarray.pydata.org/en/stable/)
* [rioxarray](https://corteva.github.io/rioxarray/stable/)
* [cartopy](https://scitools.org.uk/cartopy/docs/latest/)
**Today we'll be using xarray!**
---
# xarray
The [xarray](https://xarray.pydata.org/) library allows us to read, manipulate, and create **labeled** multi-dimensional arrays and datasets, such as [NetCDF](https://www.unidata.ucar.edu/software/netcdf/) files.
In the image below, we can imagine having two "data cubes" (3-dimensional data arrays) of temperature and precipitation values, each of which corresponds to a particular x and y spatial coordinate, and t time step.
<img src="https://xarray.pydata.org/en/stable/_images/dataset-diagram.png" width=700>
Let's import xarray and start to explore its features...
```
# import the package, and give it the alias "xr"
import xarray as xr
# we will also be using numpy and pandas, import both of these
import numpy as np
import pandas as pd
# for plotting, import matplotlib.pyplot
import matplotlib.pyplot as plt
# tell jupyter to display plots "inline" in the notebook
%matplotlib inline
```
---
# DataArrays
Similar to the `numpy.ndarray` object, the `xarray.DataArray` is a multi-dimensional array, with the addition of labeled dimensions, coordinates, and other metadata. A [DataArray](https://xarray.pydata.org/en/stable/generated/xarray.DataArray.html) contains the following:
* `values` which store the actual data values in a `numpy.ndarray`
* `dims` are the names for each dimension of the `values` array
* `coords` are arrays of labels for each point
* `attrs` is a [dictionary](https://docs.python.org/3/tutorial/datastructures.html#dictionaries) that can contain additional metadata
**Let's create some fake air temperature data to see how these different parts work together to form a DataArray.**
Our goal here is to have 100 years of annual maximum air temperature data for a 10 by 10 grid in a DataArray. (Our data will have a shape of 100 x 10 x 10)
I'm going to use a numpy function to generate some random numbers that are [normally distributed](https://numpy.org/devdocs/reference/random/generated/numpy.random.normal.html) (`np.random.normal()`).
```
# randomly generated annual maximum air temperature data for a 10 by 10 grid
# choose a mean and standard deviation for our random data
mean = 20
standard_deviation = 5
# specify that we want to generate 100 x 10 x 10 random samples
samples = (100, 10, 10)
# generate the random samples
air_temperature_max = np.random.normal(mean, standard_deviation, samples)
# look at this ndarray we just made
air_temperature_max
# look at the shape of this ndarray
air_temperature_max.shape
```
`air_temperature` will be the `values` within the DataArray. It is a three-dimensional array, and we've given it a shape of 100x10x10.
The three dimensions will need names (`dims`) and labels (`coords`)
**Make the `coords` that will be our 100 years**
```
# Make a sequence of 100 years to be our time dimension
years = pd.date_range('1920', periods=100, freq ='1Y')
```
**Make the `coords` that will be our longitudes and latitudes**
```
# Make a sequence of linearly spaced longitude and latitude values
lon = np.linspace(-119, -110, 10)
lat = np.linspace(30, 39, 10)
```
**Make the `dims` names**
```
# We can call our dimensions time, lat, and lon corresponding to the dimensions with lengths 100 (years) and 10 (lat and lon) respectively
dimensions = ['time', 'lat', 'lon']
```
**Finally we can create a metadata dictionary which will be included in the DataArray**
```
metadata = {'units': 'C',
'description': 'maximum annual air temperature'}
```
**Now that we have all the individual components of an xarray DataArray, we can create it**
```
tair_max = xr.DataArray(air_temperature_max,
coords=[years, lat, lon],
dims=dimensions,
name='tair_max',
attrs=metadata)
```
**Inspect the DataArray we just created**
```
tair_max
# Get the DataArray dimensions (labels for coordinates)
tair_max.dims
# Get the DataArray coordinates
tair_max.coords
# Look at our attributes
tair_max.attrs
# Take a look at the data values
tair_max.values
```
---
## DataArray indexing/slicing methods
DataArrays can be [indexed or sliced](https://xarray.pydata.org/en/stable/indexing.html) much like ndarrays, but with the addition of using labels.
| Dimension lookup | Index lookup | DataArray syntax |
| --- | --- | --- |
| positional | by integer | `da[:,0]` |
| positional | by label | `da.loc[:,'east_watershed']` |
| by name | by integer | `da.isel(watershed=0)` |
| by name | by label | `da.sel(watershed='east_watershed')` |
Let's select by name and by label, air temperature for just one year, and plot it. (Conveniently, x-array will add axes labels and a title by default.)
```
tair_max.sel(time='2019').plot()
```
Similarly we can select by longitude and latitude to plot a timeseries. (We made this easy on ourselves here by choosing whole number integers for our longitude and latitude)
```
tair_max.sel(lat=34, lon=-114).plot()
```
Now let's select a shorter time range using a `slice()` to plot data for this location.
```
tair_max.sel(lat=34, lon=-114, time=slice('2000','2020')).plot()
```
And if we try to plot the whole DataArray, xarray gives us a histogram!
```
tair_max.plot()
```
---
# Datasets
Similar to the `pandas.dataframe`, the `xarray.Dataset` contains one or more labeled `xarray.DataArray` objects.
We can create a [Dataset](https://xarray.pydata.org/en/stable/data-structures.html#dataset) with our simulated data here.
**First, create a two more DataArrays with annual miminum air temperatures, and annual cumulative precipitation**
```
# randomly generated annual minimum air temperature data for a 10 by 10 grid
air_temperature_min = np.random.normal(-10, 10, (100, 10, 10))
# randomly generated annualcumulative precipitation data for a 10 by 10 grid
cumulative_precip = np.random.normal(100, 25, (100, 10, 10))
```
Make the DataArrays (note that we're using the same `coords` and `dims` as our first maximum air temperature DataArray)
```
tair_min = xr.DataArray(air_temperature_min,
coords=[years, lat, lon],
dims=dimensions,
name='tair_min',
attrs={'units':'C',
'description': 'minimum annual air temperature'})
precip = xr.DataArray(cumulative_precip,
coords=[years, lat, lon],
dims=dimensions,
name='cumulative_precip',
attrs={'units':'cm',
'description': 'annual cumulative precipitation'})
```
**Now merge our two DataArrays and create a Dataset.**
```
my_data = xr.merge([tair_max, tair_min, precip])
# inspect the Dataset
my_data
```
## Dataset indexing/slicing methods
Datasets can also be [indexed or sliced](https://xarray.pydata.org/en/stable/indexing.html) using the `.isel()` or `.sel()` methods.
| Dimension lookup | Index lookup | Dataset syntax |
| --- | --- | --- |
| positional | by integer | *n/a* |
| positional | by label | *n/a* |
| by name | by integer | `ds.isel(location=0)` |
| by name | by label | `ds.sel(location='stream_gage_1')` |
**Select with `.sel()` temperatures and precipitation for just one grid cell**
```
# by name, by label
my_data.sel(lon='-114', lat='35')
```
**Select with `.isel()` temperatures and precipitation for just one year**
```
# by name, by integer
my_data.isel(time=0)
```
---
## Make some plots:
Using our indexing/slicing methods, create some plots showing 1) a timseries of all three variables at a single point, then 2) plot some maps of each variable for two points in time.
```
# 1) create a timeseries for the two temperature variables for a single location
# create a figure with 2 rows and 1 column of subplots
fig, ax = plt.subplots(nrows=2, ncols=1, figsize=(10,7), tight_layout=True)
# pick a longitude and latitude in our dataset
my_lon=-114
my_lat=35
# first subplot
# Plot tair_max
my_data.sel(lon=my_lon, lat=my_lat).tair_max.plot(ax=ax[0], color='r', linestyle='-', label='Tair_max')
# Plot tair_min
my_data.sel(lon=my_lon, lat=my_lat).tair_min.plot(ax=ax[0], color='b', linestyle='--', label='Tair_max')
# Add a title
ax[0].set_title('Annual maximum and minimum air temperatures at {}, {}'.format(my_lon,my_lat))
# Add a legend
ax[0].legend(loc='lower left')
# second subplot
# Plot precip
my_data.sel(lon=my_lon, lat=my_lat).cumulative_precip.plot(ax=ax[1], color='black', linestyle='-', label='Cumulative Precip.')
# Add a title
ax[1].set_title('Annualcumulative precipitation at {}, {}'.format(my_lon,my_lat))
# Add a legend
ax[1].legend(loc='lower left')
# Save the figure
plt.savefig('my_data_plot_timeseries.jpg')
# 2) plot maps of temperature and precipitation for two years
# create a figure with 2 rows and 3 columns of subplots
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(15,7), tight_layout=True)
# The two years we want to plot
year1 = '1980'
year2 = '2019'
# Plot tair_max for the year 1980
my_data.sel(time=year1).tair_max.plot(ax=ax[0,0], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[0,0].set_title('Tair_max {}'.format(year1));
# Plot tair_max for the year 1980
my_data.sel(time=year1).tair_min.plot(ax=ax[0,1], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[0,1].set_title('Tair_min {}'.format(year1));
# Plot tair_max for the year 1980
my_data.sel(time=year1).cumulative_precip.plot(ax=ax[0,2], cmap='Blues')
# set a title for this subplot
ax[0,2].set_title('Precip {}'.format(year1));
# Plot tair_max for the year 2019
my_data.sel(time=year2).tair_max.plot(ax=ax[1,0], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[1,0].set_title('Tair_max {}'.format(year2));
# Plot tair_max for the year 2019
my_data.sel(time=year2).tair_min.plot(ax=ax[1,1], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[1,1].set_title('Tair_min {}'.format(year2));
# Plot tair_max for the year 2019
my_data.sel(time=year2).cumulative_precip.plot(ax=ax[1,2], cmap='Blues')
# set a title for this subplot
ax[1,2].set_title('Precip {}'.format(year2));
# save the figure as a jpg image
plt.savefig('my_data_plot_rasters.jpg')
```
---
## Save our data to a file:
**As a NetCDF file:**
```
my_data.to_netcdf('my_data.nc')
```
**We can also convert a Dataset or DataArray to a pandas dataframe**
```
my_data.to_dataframe()
```
**Via a pandas dataframe, save our data to a csv file**
```
my_data.to_dataframe().to_csv('my_data.csv')
```
| true |
code
| 0.658747 | null | null | null | null |
|
```
# reload packages
%load_ext autoreload
%autoreload 2
```
### Choose GPU (this may not be needed on your computer)
```
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=''
```
### load packages
```
from tfumap.umap import tfUMAP
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
import umap
import pandas as pd
```
### Load dataset
```
from sklearn.datasets import make_moons
X_train, Y_train = make_moons(1000, random_state=0, noise=0.1)
X_test, Y_test = make_moons(1000, random_state=1, noise=0.1)
X_valid, Y_valid = make_moons(1000, random_state=2, noise=0.1)
def norm(x):
return (x - np.min(x)) / (np.max(x) - np.min(x))
X_train = norm(X_train)
X_valid = norm(X_valid)
X_test = norm(X_test)
X_train_flat = X_train
X_test_flat = X_test
plt.scatter(X_test[:,0], X_test[:,1], c=Y_test)
```
### Create model and train
### define networks
```
dims = (2)
n_components = 2
from tfumap.vae import VAE, Sampling
encoder_inputs = tf.keras.Input(shape=dims)
x = tf.keras.layers.Flatten()(encoder_inputs)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
z_mean = tf.keras.layers.Dense(n_components, name="z_mean")(x)
z_log_var = tf.keras.layers.Dense(n_components, name="z_log_var")(x)
z = Sampling()([z_mean, z_log_var])
encoder = tf.keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")
encoder.summary()
latent_inputs = tf.keras.Input(shape=(n_components,))
x = tf.keras.layers.Dense(units=100, activation="relu")(latent_inputs)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
decoder_outputs = tf.keras.layers.Dense(units=2, activation="sigmoid")(x)
decoder = tf.keras.Model(latent_inputs, decoder_outputs, name="decoder")
decoder.summary()
```
### Create model and train
```
X_train.shape
vae = VAE(encoder, decoder)
vae.compile(optimizer=tf.keras.optimizers.Adam())
vae.fit(X_train, epochs=500, batch_size=128)
z = vae.encoder.predict(X_train)[0]
```
### Plot model output
```
fig, ax = plt.subplots( figsize=(8, 8))
sc = ax.scatter(
z[:, 0],
z[:, 1],
c=Y_train.astype(int)[:len(z)].flatten(),
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow embedding", fontsize=20)
plt.colorbar(sc, ax=ax);
z_recon = decoder.predict(z)
fig, ax = plt.subplots()
ax.scatter(z_recon[:,0], z_recon[:,1], s = 1, c = z_recon[:,0], alpha = 1)
ax.axis('equal')
```
### Save output
```
from tfumap.paths import ensure_dir, MODEL_DIR
dataset = 'moons'
output_dir = MODEL_DIR/'projections'/ dataset / 'vae'
ensure_dir(output_dir)
encoder.save(output_dir / 'encoder')
decoder.save(output_dir / 'encoder')
#loss_df.to_pickle(output_dir / 'loss_df.pickle')
np.save(output_dir / 'z.npy', z)
```
| true |
code
| 0.723132 | null | null | null | null |
|
# Benchmark NumPyro in large dataset
This notebook uses `numpyro` and replicates experiments in references [1] which evaluates the performance of NUTS on various frameworks. The benchmark is run with CUDA 10.1 on a NVIDIA RTX 2070.
```
import time
import numpy as np
import jax.numpy as jnp
from jax import random
import numpyro
import numpyro.distributions as dist
from numpyro.examples.datasets import COVTYPE, load_dataset
from numpyro.infer import HMC, MCMC, NUTS
assert numpyro.__version__.startswith('0.3.0')
# NB: replace gpu by cpu to run this notebook in cpu
numpyro.set_platform("gpu")
```
We do preprocessing steps as in [source code](https://github.com/google-research/google-research/blob/master/simple_probabilistic_programming/no_u_turn_sampler/logistic_regression.py) of reference [1]:
```
_, fetch = load_dataset(COVTYPE, shuffle=False)
features, labels = fetch()
# normalize features and add intercept
features = (features - features.mean(0)) / features.std(0)
features = jnp.hstack([features, jnp.ones((features.shape[0], 1))])
# make binary feature
_, counts = np.unique(labels, return_counts=True)
specific_category = jnp.argmax(counts)
labels = (labels == specific_category)
N, dim = features.shape
print("Data shape:", features.shape)
print("Label distribution: {} has label 1, {} has label 0"
.format(labels.sum(), N - labels.sum()))
```
Now, we construct the model:
```
def model(data, labels):
coefs = numpyro.sample('coefs', dist.Normal(jnp.zeros(dim), jnp.ones(dim)))
logits = jnp.dot(data, coefs)
return numpyro.sample('obs', dist.Bernoulli(logits=logits), obs=labels)
```
## Benchmark HMC
```
step_size = jnp.sqrt(0.5 / N)
kernel = HMC(model, step_size=step_size, trajectory_length=(10 * step_size), adapt_step_size=False)
mcmc = MCMC(kernel, num_warmup=500, num_samples=500, progress_bar=False)
mcmc.warmup(random.PRNGKey(2019), features, labels, extra_fields=('num_steps',))
mcmc.get_extra_fields()['num_steps'].sum().copy()
tic = time.time()
mcmc.run(random.PRNGKey(2020), features, labels, extra_fields=['num_steps'])
num_leapfrogs = mcmc.get_extra_fields()['num_steps'].sum().copy()
toc = time.time()
print("number of leapfrog steps:", num_leapfrogs)
print("avg. time for each step :", (toc - tic) / num_leapfrogs)
mcmc.print_summary()
```
In CPU, we get `avg. time for each step : 0.02782863507270813`.
## Benchmark NUTS
```
mcmc = MCMC(NUTS(model), num_warmup=50, num_samples=50, progress_bar=False)
mcmc.warmup(random.PRNGKey(2019), features, labels, extra_fields=('num_steps',))
mcmc.get_extra_fields()['num_steps'].sum().copy()
tic = time.time()
mcmc.run(random.PRNGKey(2020), features, labels, extra_fields=['num_steps'])
num_leapfrogs = mcmc.get_extra_fields()['num_steps'].sum().copy()
toc = time.time()
print("number of leapfrog steps:", num_leapfrogs)
print("avg. time for each step :", (toc - tic) / num_leapfrogs)
mcmc.print_summary()
```
In CPU, we get `avg. time for each step : 0.028006251705287415`.
## Compare to other frameworks
| | HMC | NUTS |
| ------------- |----------:|----------:|
| Edward2 (CPU) | | 56.1 ms |
| Edward2 (GPU) | | 9.4 ms |
| Pyro (CPU) | 35.4 ms | 35.3 ms |
| Pyro (GPU) | 3.5 ms | 4.2 ms |
| NumPyro (CPU) | 27.8 ms | 28.0 ms |
| NumPyro (GPU) | 1.6 ms | 2.2 ms |
Note that in some situtation, HMC is slower than NUTS. The reason is the number of leapfrog steps in each HMC trajectory is fixed to $10$, while it is not fixed in NUTS.
**Some takeaways:**
+ The overhead of iterative NUTS is pretty small. So most of computation time is indeed spent for evaluating potential function and its gradient.
+ GPU outperforms CPU by a large margin. The data is large, so evaluating potential function in GPU is clearly faster than doing so in CPU.
## References
1. `Simple, Distributed, and Accelerated Probabilistic Programming,` [arxiv](https://arxiv.org/abs/1811.02091)<br>
Dustin Tran, Matthew D. Hoffman, Dave Moore, Christopher Suter, Srinivas Vasudevan, Alexey Radul, Matthew Johnson, Rif A. Saurous
| true |
code
| 0.460046 | null | null | null | null |
|
# Chapter 1 - Softmax from First Principles
## Language barriers between humans and autonomous systems
If our goal is to help humans and autnomous systems communicate, we need to speak in a common language. Just as humans have verbal and written languages to communicate ideas, so have we developed mathematical languages to communicate information. Probability is one of those languages and, thankfully for us, autonomous systems are pretty good at describing probabilities, even if humans aren't. This document shows one technique for translating a human language (English) into a language known by autonomous systems (probability).
Our translator is something called the **SoftMax classifier**, which is one type of probability distribution that takes discrete labels and translates them to probabilities. We'll show you the details on how to create a softmax model, but let's get to the punchline first: we can decompose elements of human language to represent a partitioning of arbitrary state spaces.
Say, for instance, we'd like to specify the location of an object in two dimensional cartesian coordinates. Our state space is all combinations of *x* and *y*, and we'd like to translate human language into some probability that our target is at a given combination of *x* and *y*. One common tactic humans use to communicate position is range (near, far, next to, etc.) and bearing (North, South, SouthEast, etc.). This already completely partitions our *xy* space: if something is north, it's not south; if it's east, it's not west; and so on.
A softmax model that translates range and bearing into probability in a state space is shown below:
<img src="https://raw.githubusercontent.com/COHRINT/cops_and_robots/master/notebooks/softmax/img/softmax_range_bearing.png" alt="Softmax range and bearing" width=500px>
Assuming that *next to* doesn't require a range, we see seventeen different word combinations we can use to describe something's position: two ranges (*nearby* and *far*) for each cardinal and intercardinal direction (eight total), and then one extra label for *next to*. This completely partitions our entire state space $\mathbb{R}^2$.
This range and bearing language is, by its nature, inexact. If I say, "That boat is far north.", you don't have a deterministic notion of exactly where the boat is -- but you have a good sense of where it is, and where it is not. We can represent that sense probabilistically, such that the probability of a target existing at a location described by a range and bearing label is nonzero over the entire state space, but that probability is very small if not in the area most associated with that label.
What do we get from this probabilistic interpretation of the state space? We get a two-way translation between humans and autonomous systems to describe anything we'd like. If our state space is one-dimensional relative velocity (i.e. the derivative of range without bearing), I can say, "She's moving really fast!", to give the autonomous system a probability distribution over my target's velocity with an expected value of, say, 4 m/s. Alternatively, if my autnomous system knows my target's moving at 0.04352 m/s, it can tell me, "Your target is moving slowly." Our labeled partitioning of the state space (that is, our classifier) is the mechanism that translates for us.
## Softmax model construction
The [SoftMax function](http://en.wikipedia.org/wiki/Softmax_function) goes by many names: normalized exponential, multinomial logistic function, log-linear model, sigmoidal function. We use the SoftMax function to develop a classification model for our state space:
$$
\begin{equation}
P(L=i \vert \mathbf{x}) = \frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}}
\end{equation}
$$
Where $L = i$ is our random variable of class labels instantiated as class $i$, $\mathbf{x}$ is our state vector, $\mathbf{w}_i$ is a vector of parameters (or weights) associated with our class $i$, $b_i$ is a bias term for class $i$, and $M$ is the total number of classes.
The terms *label* and *class* require some distinction: a label is a set of words associated with a class (i.e. *far northwest*) whereas a class is a probability distribution over the entire state space. They are sometimes used interchangeably, and the specific meaning should be clear from context.
Several key factors come out of the SoftMax equation:
- The probabilities of all classes for any given point $\mathbf{x}$ sum to 1.
- The probability any single class for any given point $\mathbf{x}$ is bounded by 0 and 1.
- The space can be partitioned into an arbitrary number of classes (with some restrictions about those classes - more on this later).
- The probability of one class for a given point $\mathbf{x}$ is determined by that class' weighted exponential sum of the state vector *relative* to the weighted exponential sums of *all* classes.
- Since the probability of a class is conditioned on $\mathbf{x}$, we can apply estimators such as [Maximum Likelihood](http://en.wikipedia.org/wiki/Maximum_likelihood) to learn SoftMax models.
- $P(L=i \vert \mathbf{x})$ is convex in $\mathbf{w_i}$ for any $\mathbf{x}$.
Let's try to get some intuition about this setup. For a two-dimensional case with state $\mathbf{x} = \begin{bmatrix}x & y\end{bmatrix}^T$, each class $i$ has weights $\mathbf{w}_i = \begin{bmatrix}w_{i,x} & w_{i,y}\end{bmatrix}^T$. Along with the constant bias term $b_i$, we have one weighted linear function of $x$ and one weighted linear function of $y$. Each class's probability is normalized with respect to the sum of all other classes, so the weights can be seen as a relative scaling of one class over another in any given state. The bias weight increases a class's probability in all cases, the $x$ weight increases the class's probability for greater values of $x$ (and positive weights), and the $y$ weight, naturally, increases the class's probability for greater values of $y$ (and positive weights).
We can get fancy with our state space, having states of the form $\mathbf{x} = \begin{bmatrix}x & y & x^2 & y^2 & 2xy\end{bmatrix}^T$, but we'll build up to states like that. Let's look at some simpler concepts first.
## Class boundaries
For any two classes, we can take the ratio of their probabilities to determine the **odds** of one class instead of the other:
$$
L(i,j) =\frac{P(L=i \vert \mathbf{x})}{P(L=j \vert \mathbf{x})} =
\frac{\frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{\sum_{k=i}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}}}{\frac{e^{\mathbf{w}_j^T \mathbf{x} + b_{j}}}{\sum_{k=i}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}}} = \frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{e^{\mathbf{w}_j^T\mathbf{x} + b_j}}
$$
When $L(i,j)=1$, the two classes have equal probability. This doesn't give us a whole lot of insight until we take the **log-odds** (the logarithm of the odds):
$$
\begin{align}
L_{log}(i,j) &=
\log{\frac{P(L=i \vert \mathbf{x})}{P(L=j \vert \mathbf{x})}}
= \log{\frac{e^{\mathbf{w}_i^T \mathbf{x} + b_j}}{e^{\mathbf{w}_j^T\mathbf{x} + b_j}}}
= (\mathbf{w}_i^T\mathbf{x} + b_i)- (\mathbf{w}_j^T\mathbf{x} + b_j) \\
&= (\mathbf{w}_i - \mathbf{w}_j)^T\mathbf{x} + (b_i - b_j)
\end{align}
$$
When $L_{log}(i,j) = \log{L(i,j)} = \log{1} = 0$, we have equal probability between the two classes, and we've also stumbled upon the equation for an n-dimensional affine hyperplane dividing the two classes:
$$
\begin{align}
0 &= (\mathbf{w}_i - \mathbf{w}_j)^T\mathbf{x} + (b_i - b_j) \\
&= (w_{i,x_1} - w_{j,x_1})x_1 + (w_{i,x_2} - w_{j,x_2})x_2 + \dots + (w_{i,x_n} - w_{j,x_n})x_n + (b_i - b_j)
\end{align}
$$
This follows from the general definition of an <a href="http://en.wikipedia.org/wiki/Plane_(geometry)#Point-normal_form_and_general_form_of_the_equation_of_a_plane">Affine Hyperplane</a> (that is, an n-dimensional flat plane):
$$
a_1x_1 + a_2x_2 + \dots + a_nx_n + b = 0
$$
Where $a_1 = w_{i,x_1} - w_{j,x_1}$, $a_2 = w_{i,x_2} - w_{j,x_2}$, and so on. This gives us a general formula for the division of class boundaries -- that is, we can specify the class boundaries directly, rather than specifying the weights leading to those class boundaries.
### Example
Let's take a step back and look at an example. Suppose I'm playing Pac-Man, and I want to warn our eponymous hero of a ghost approaching him. Let's restrict my language to the four intercardinal directions: NE, SE, SW and NW. My state space is $\mathbf{x} = \begin{bmatrix}x & y\end{bmatrix}^T$ (one term for each cartesian direction in $\mathbb{R}^2$).
<img src="https://raw.githubusercontent.com/COHRINT/cops_and_robots/master/notebooks/softmax/img/pacman.png" alt="Pacman with intercardinal bearings" width="500px">
In this simple problem, we can expect our weights to be something along the lines of:
$$
\begin{align}
\mathbf{w}_{SW} &= \begin{bmatrix}-1 & -1 \end{bmatrix}^T \\
\mathbf{w}_{NW} &= \begin{bmatrix}-1 & 1 \end{bmatrix}^T \\
\mathbf{w}_{SE} &= \begin{bmatrix}1 & -1 \end{bmatrix}^T \\
\mathbf{w}_{NE} &= \begin{bmatrix}1 & 1 \end{bmatrix}^T \\
\end{align}
$$
If we run these weights in our SoftMax model, we get the following results:
```
# See source at: https://github.com/COHRINT/cops_and_robots/blob/master/src/cops_and_robots/robo_tools/fusion/softmax.py
import numpy as np
from cops_and_robots.robo_tools.fusion.softmax import SoftMax
%matplotlib inline
labels = ['SW', 'NW', 'SE',' NE']
weights = np.array([[-1, -1],
[-1, 1],
[1, -1],
[1, 1],
])
pacman = SoftMax(weights, class_labels=labels)
pacman.plot(title='Unshifted Pac-Man Bearing Model')
```
Which is along the right path, but needs to be shifted down to Pac-Man's location. Say Pac-Man is approximately one quarter of the map south from the center point, we can bias our model accordingly (assuming a $10m \times 10m$ space):
$$
\begin{align}
b_{SW} &= -2.5\\
b_{NW} &= 2.5\\
b_{SE} &= -2.5\\
b_{NE} &= 2.5\\
\end{align}
$$
```
biases = np.array([-2.5, 2.5, -2.5, 2.5,])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Y-Shifted Pac-Man Bearing Model')
```
Looking good! Note that we'd get the same answer had we used the following weights:
$$
\begin{align}
b_{SW} &= -5\\
b_{NW} &= 0\\
b_{SE} &= -5\\
b_{NE} &= 0\\
\end{align}
$$
Because the class boundaries and probability distributions are defined by the *relative differences*.
But this simply shifts the weights in the $y$ direction. How do we go about shifting weights in any state dimension?
Remember that our biases will essentially scale an entire class, so, what we did was scale up the two classes that have a positive scaling for negative $y$ values. If we want to place the center of the four classes in the top-left, for instance, we'll want to bias the NW class less than the other classes.
Let's think of what happens if we use another coordinate system:
$$
\mathbf{x}' = \mathbf{x} + \mathbf{b}
$$
Where $\mathbf{x}'$ is our new state vector and $\mathbf{b}$ are offsets to each state in our original coordinate frame (assume the new coordinate system is unbiased). For example, something like:
$$
\mathbf{x}' = \begin{bmatrix}x & y\end{bmatrix}^T + \begin{bmatrix}2 & -3\end{bmatrix}^T = \begin{bmatrix}x + 2 & y -3\end{bmatrix}^T
$$
Can we represent this shift simply by adjusting our biases, instead of having to redefine our state vector? Assuming we're just shifting the distributions, the probabilities, and thus, the hyperplanes, will simply be shifted as well, so we have:
$$
0 = (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x}' = (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x} + (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{b}
$$
Which retains our original state and shifts only our biases. If we distribute the offset $\mathbf{b}$, we can define each class's bias term:
$$
\begin{align}
b_i - b_j &= (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{b} \\
&= \mathbf{w}_i^T \mathbf{b} - \mathbf{w}_j^T \mathbf{b}
\end{align}
$$
Our bias for each class $i$ in our original coordinate frame is simply $\mathbf{w}_i^T \mathbf{b}$.
Let's try this out with $\mathbf{b} = \begin{bmatrix}2 & -3\end{bmatrix}^T$ (remembering that this will push the shifted origin negatively along the x-axis and positively along the y-axis):
$$
\begin{align}
b_{SW} &= \begin{bmatrix}-1 & -1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} = 1\\
b_{NW} &= \begin{bmatrix}-1 & 1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} =-5 \\
b_{SE} &= \begin{bmatrix}1 & -1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} = 5\\
b_{NE} &= \begin{bmatrix}1 & 1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} = -1 \\
\end{align}
$$
```
biases = np.array([1, -5, 5, -1,])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Shifted Pac-Man Bearing Model')
```
One other thing we can illustrate with this example: how would the SoftMax model change if we multiplied all our weights and biases by 10?
We get:
```
weights = np.array([[-10, -10],
[-10, 10],
[10, -10],
[10, 10],
])
biases = np.array([10, -50, 50, -10,])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Steep Pac-Man Bearing Model')
```
Why does this increase in slope happen? Let's investigate.
## SoftMax slope for linear states
The [gradient](http://en.wikipedia.org/wiki/Gradient) of $P(L=i \vert \mathbf{x})$ will give us a function for the slope of our SoftMax model of class $i$. For a linear state space, such as our go-to $\mathbf{x} = \begin{bmatrix}x & y\end{bmatrix}$, our gradient is defined as:
$$
\nabla P(L=i \vert \mathbf{x}) = \nabla \frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}} =
\frac{\partial}{\partial x} \frac{e^{\mathbf{w}_i^T \mathbf{x}}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x}}} \mathbf{\hat{i}} +
\frac{\partial}{\partial y} \frac{e^{\mathbf{w}_i^T \mathbf{x}}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x}}} \mathbf{\hat{j}}
$$
Where $\mathbf{\hat{i}}$ and $\mathbf{\hat{j}}$ are unit vectors in the $x$ and $y$ dimensions, respectively. Given the structure of our equation, the form of either partial derivative will be the same as the other, so let's look at the partial with respect to $x$, using some abused notation:
$$
\begin{align}
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x} &= \frac{d P(L = i \vert x)} {dx} =
\frac{\partial}{\partial x} \frac{e^{w_{i,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}} \\
&= \frac{w_{i,x}e^{w_{i,x}x}\sum_{k=1}^M e^{w_{k,x}x} - e^{w_{i,x}x}(\sum_{k=1}^M w_{k,x}e^{w_{k,x}x})}{(\sum_{k=1}^M e^{w_{k,x}x})^2} \\
&= \frac{w_{i,x}e^{w_{i,x}x}\sum_{k=1}^M e^{w_{k,x}x}}{(\sum_{k=1}^M e^{w_{k,x}x})^2} -
\frac{e^{w_{i,x}x}(\sum_{k=1}^M w_{k,x}e^{w_{k,x}x})}{(\sum_{k=1}^M e^{w_{k,x}x})^2}\\
&= w_{i,x} \left( \frac{e^{w_{i,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\right) -
\left( \frac{e^{w_{i,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\right)\frac{\sum_{k=1}^M w_{k,x}e^{w_{k,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\\
& = P(L = i \vert x) \left(w_{i,x} - \frac{\sum_{k=1}^M w_{k,x}e^{w_{k,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\right) \\
& = P(L = i \vert x) \left(w_{i,x} - \sum_{k=1}^M w_{k,x}P(L = k \vert x) \right) \\
\end{align}
$$
Where line 2 was found using the quotient rule. This is still hard to interpret, so let's break it down into multiple cases:
If $P(L = i \vert x) \approx 1$, the remaining probabilities are near zero, thus reducing the impact of their weights, leaving:
$$
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x}
\approx P(L = i \vert x) \left(w_{i,x} - w_{i,x}P(L = i \vert x) \right)
= 0
$$
This makes sense: a dominating probability will be flat.
If $P(L = i \vert x) \approx 0$, we get:
$$
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x}
\approx 0 \left(w_{i,x} - w_{i,x}P(L = i \vert x) \right)
= 0
$$
This also makes sense: a diminished probability will be flat.
We can expect the greatest slope of a [logistic function](http://en.wikipedia.org/wiki/Logistic_function) (which is simply a univariate SoftMax function) to appear at its midpoint $P(L = i \vert x) = 0.5$. Our maximum slope, then, is:
$$
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x}
= 0.5 \left(w_{i,x} - \sum_{k=1}^M w_{k,x}P(L = k \vert x) \right) \\
= 0.5 \left(w_{i,x} - \sum^M _{\substack{k = 1, \\ k \neq i}} w_{k,x}P(L = k \vert x) - 0.5w_{i,x}\right) \\
= 0.25w_{i,x} - 0.5\sum^M _{\substack{k = 1, \\ k \neq i}} w_{k,x}P(L = k \vert x) \\
$$
NOTE: This section feels really rough, and possibly unnecessary. I need to work on it some more.
## Rotations
Just as we were able to shift our SoftMax distributions to a new coordinate origin, we can apply a [rotation](http://en.wikipedia.org/wiki/Rotation_matrix) to our weights and biases. Let's once again update our weights and biases through a new, rotated, coordinate scheme:
$$
R(\theta)\mathbf{x}' = R(\theta)(\mathbf{x} + \mathbf{b})
$$
As before, we examine the case at the linear hyperplane boundaries:
$$
0 = (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x}' = (\mathbf{w}_i - \mathbf{w}_j)^T R(\theta)\mathbf{x} + (\mathbf{w}_i - \mathbf{w}_j)^T R(\theta) \mathbf{b}
$$
Our weights are already defined, so we simply need to multiply them by $R(\theta)$ to find our rotated weights. Let's find our biases:
$$
\begin{align}
b_i - b_j &= (\mathbf{w}_i - \mathbf{w}_j)^T R(\theta) \mathbf{b} \\
&= \mathbf{w}_i^T R(\theta) \mathbf{b} - \mathbf{w}_j^T R(\theta) \mathbf{b}
\end{align}
$$
So, under rotation, $b_i = \mathbf{w}_i^T R(\theta) \mathbf{b}$.
Let's try this with a two-dimensional rotation matrix using $\theta = \frac{\pi}{4} rad$ and $\mathbf{b} = \begin{bmatrix}2 & -3\end{bmatrix}^T$:
$$
\begin{align}
b_{SW} &= \begin{bmatrix}-1 & -1 \end{bmatrix}
\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = -2\sqrt{2} \\
b_{NW} &= \begin{bmatrix}-1 & 1 \end{bmatrix}
\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = -3\sqrt{2} \\
b_{SE} &= \begin{bmatrix}1 & -1 \end{bmatrix}
\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = 3\sqrt{2} \\
b_{NE} &= \begin{bmatrix}1 & 1 \end{bmatrix}\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = 2\sqrt{2} \\
\end{align}
$$
```
# Define rotation matrix
theta = np.pi/4
R = np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
# Rotate weights
weights = np.array([[-1, -1],
[-1, 1],
[1, -1],
[1, 1],
])
weights = np.dot(weights,R)
# Apply rotated biases
biases = np.array([-2 * np.sqrt(2),
-3 * np.sqrt(2),
3 * np.sqrt(2),
2 * np.sqrt(2),])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Rotated and Shifted Pac-Man Bearing Model')
```
##Summary
That should be a basic introduction to the SoftMax model. We've only barely scraped the surface of why you might want to use SoftMax models as a tool for aspects of HRI.
Let's move on to [Chapter 2](02_from_normals.ipynb) where we examine a more practical way of constructing SoftMax distributions.
```
from IPython.core.display import HTML
# Borrowed style from Probabilistic Programming and Bayesian Methods for Hackers
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
| true |
code
| 0.627894 | null | null | null | null |
|
---
_You are currently looking at **version 1.1** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-text-mining/resources/d9pwm) course resource._
---
# Assignment 1
In this assignment, you'll be working with messy medical data and using regex to extract relevant infromation from the data.
Each line of the `dates.txt` file corresponds to a medical note. Each note has a date that needs to be extracted, but each date is encoded in one of many formats.
The goal of this assignment is to correctly identify all of the different date variants encoded in this dataset and to properly normalize and sort the dates.
Here is a list of some of the variants you might encounter in this dataset:
* 04/20/2009; 04/20/09; 4/20/09; 4/3/09
* Mar-20-2009; Mar 20, 2009; March 20, 2009; Mar. 20, 2009; Mar 20 2009;
* 20 Mar 2009; 20 March 2009; 20 Mar. 2009; 20 March, 2009
* Mar 20th, 2009; Mar 21st, 2009; Mar 22nd, 2009
* Feb 2009; Sep 2009; Oct 2010
* 6/2008; 12/2009
* 2009; 2010
Once you have extracted these date patterns from the text, the next step is to sort them in ascending chronological order accoring to the following rules:
* Assume all dates in xx/xx/xx format are mm/dd/yy
* Assume all dates where year is encoded in only two digits are years from the 1900's (e.g. 1/5/89 is January 5th, 1989)
* If the day is missing (e.g. 9/2009), assume it is the first day of the month (e.g. September 1, 2009).
* If the month is missing (e.g. 2010), assume it is the first of January of that year (e.g. January 1, 2010).
* Watch out for potential typos as this is a raw, real-life derived dataset.
With these rules in mind, find the correct date in each note and return a pandas Series in chronological order of the original Series' indices.
For example if the original series was this:
0 1999
1 2010
2 1978
3 2015
4 1985
Your function should return this:
0 2
1 4
2 0
3 1
4 3
Your score will be calculated using [Kendall's tau](https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient), a correlation measure for ordinal data.
*This function should return a Series of length 500 and dtype int.*
```
# Load the data
# Reference: https://necromuralist.github.io/data_science/posts/extracting-dates-from-medical-data/
import pandas
doc = []
with open('dates.txt') as file:
for line in file:
doc.append(line)
data = pandas.Series(doc)
data.head(10)
data.describe()
# 4 The Grammar
# 4.1 Cardinality
ZERO_OR_MORE = '*'
ONE_OR_MORE = "+"
ZERO_OR_ONE = '?'
EXACTLY_TWO = "{2}"
ONE_OR_TWO = "{1,2}"
EXACTLY_ONE = '{1}'
# 4.2 Groups and Classes
GROUP = r"({})"
NAMED = r"(?P<{}>{})"
CLASS = "[{}]"
NEGATIVE_LOOKAHEAD = "(?!{})"
NEGATIVE_LOOKBEHIND = "(?<!{})"
POSITIVE_LOOKAHEAD = "(?={})"
POSITIVE_LOOKBEHIND = "(?<={})"
ESCAPE = "\{}"
# 4.3 Numbers
DIGIT = r"\d"
ONE_DIGIT = DIGIT + EXACTLY_ONE
ONE_OR_TWO_DIGITS = DIGIT + ONE_OR_TWO
NON_DIGIT = NEGATIVE_LOOKAHEAD.format(DIGIT)
TWO_DIGITS = DIGIT + EXACTLY_TWO
THREE_DIGITS = DIGIT + "{3}"
EXACTLY_TWO_DIGITS = DIGIT + EXACTLY_TWO + NON_DIGIT
FOUR_DIGITS = DIGIT + r"{4}" + NON_DIGIT
# 4.4 String Literals
SLASH = r"/"
OR = r'|'
LOWER_CASE = "a-z"
SPACE = "\s"
DOT = "."
DASH = "-"
COMMA = ","
PUNCTUATION = CLASS.format(DOT + COMMA + DASH)
EMPTY_STRING = ""
# 4.5 Dates
# These are parts to build up the date-expressions.
MONTH_SUFFIX = (CLASS.format(LOWER_CASE) + ZERO_OR_MORE
+ CLASS.format(SPACE + DOT + COMMA + DASH) + ONE_OR_TWO)
MONTH_PREFIXES = "Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec".split()
MONTHS = [month + MONTH_SUFFIX for month in MONTH_PREFIXES]
MONTHS = GROUP.format(OR.join(MONTHS))
DAY_SUFFIX = CLASS.format(DASH + COMMA + SPACE) + ONE_OR_TWO
DAYS = ONE_OR_TWO_DIGITS + DAY_SUFFIX
YEAR = FOUR_DIGITS
# This is for dates like Mar 21st, 2009, those with suffixes on the days.
CONTRACTED = (ONE_OR_TWO_DIGITS
+ LOWER_CASE
+ EXACTLY_TWO
)
CONTRACTION = NAMED.format("contraction",
MONTHS
+ CONTRACTED
+ DAY_SUFFIX
+ YEAR)
# This is for dates that have no days in them, like May 2009.
NO_DAY_BEHIND = NEGATIVE_LOOKBEHIND.format(DIGIT + SPACE)
NO_DAY = NAMED.format("no_day", NO_DAY_BEHIND + MONTHS + YEAR)
# This is for the most common form (that I use) - May 21, 2017.
WORDS = NAMED.format("words", MONTHS + DAYS + YEAR)
BACKWARDS = NAMED.format("backwards", ONE_OR_TWO_DIGITS + SPACE + MONTHS + YEAR)
slashed = SLASH.join([ONE_OR_TWO_DIGITS,
ONE_OR_TWO_DIGITS,
EXACTLY_TWO_DIGITS])
dashed = DASH.join([ONE_OR_TWO_DIGITS,
ONE_OR_TWO_DIGITS,
EXACTLY_TWO_DIGITS])
TWENTIETH_CENTURY = NAMED.format("twentieth",
OR.join([slashed, dashed]))
NUMERIC = NAMED.format("numeric",
SLASH.join([ONE_OR_TWO_DIGITS,
ONE_OR_TWO_DIGITS,
FOUR_DIGITS]))
NO_PRECEDING_SLASH = NEGATIVE_LOOKBEHIND.format(SLASH)
NO_PRECEDING_SLASH_DIGIT = NEGATIVE_LOOKBEHIND.format(CLASS.format(SLASH + DIGIT))
NO_ONE_DAY = (NO_PRECEDING_SLASH_DIGIT
+ ONE_DIGIT
+ SLASH
+ FOUR_DIGITS)
NO_TWO_DAYS = (NO_PRECEDING_SLASH
+ TWO_DIGITS
+ SLASH
+ FOUR_DIGITS)
NO_DAY_NUMERIC = NAMED.format("no_day_numeric",
NO_ONE_DAY
+ OR
+ NO_TWO_DAYS
)
CENTURY = GROUP.format('19' + OR + "20") + TWO_DIGITS
DIGIT_SLASH = DIGIT + SLASH
DIGIT_DASH = DIGIT + DASH
DIGIT_SPACE = DIGIT + SPACE
LETTER_SPACE = CLASS.format(LOWER_CASE) + SPACE
COMMA_SPACE = COMMA + SPACE
YEAR_PREFIX = NEGATIVE_LOOKBEHIND.format(OR.join([
DIGIT_SLASH,
DIGIT_DASH,
DIGIT_SPACE,
LETTER_SPACE,
COMMA_SPACE,
]))
YEAR_ONLY = NAMED.format("year_only",
YEAR_PREFIX + CENTURY
)
IN_PREFIX = POSITIVE_LOOKBEHIND.format(CLASS.format('iI') + 'n' + SPACE) + CENTURY
SINCE_PREFIX = POSITIVE_LOOKBEHIND.format(CLASS.format("Ss") + 'ince' + SPACE) + CENTURY
AGE = POSITIVE_LOOKBEHIND.format("Age" + SPACE + TWO_DIGITS + COMMA + SPACE) + CENTURY
AGE_COMMA = POSITIVE_LOOKBEHIND.format("Age" + COMMA + SPACE + TWO_DIGITS + COMMA + SPACE) + CENTURY
OTHERS = ['delivery', "quit", "attempt", "nephrectomy", THREE_DIGITS]
OTHERS = [POSITIVE_LOOKBEHIND.format(label + SPACE) + CENTURY for label in OTHERS]
OTHERS = OR.join(OTHERS)
LEFTOVERS_PREFIX = OR.join([IN_PREFIX, SINCE_PREFIX, AGE, AGE_COMMA]) + OR + OTHERS
LEFTOVERS = NAMED.format("leftovers", LEFTOVERS_PREFIX)
DATE = NAMED.format("date", OR.join([NUMERIC,
TWENTIETH_CENTURY,
WORDS,
BACKWARDS,
CONTRACTION,
NO_DAY,
NO_DAY_NUMERIC,
YEAR_ONLY,
LEFTOVERS]))
def twentieth_century(date):
"""adds a 19 to the year
Args:
date (re.Regex): Extracted date
"""
month, day, year = date.group(1).split(SLASH)
year = "19{}".format(year)
return SLASH.join([month, day, year])
def take_two(line):
match = re.search(TWENTIETH_CENTURY, line)
if match:
return twentieth_century(match)
return line
def extract_and_count(expression, data, name):
"""extract all matches and report the count
Args:
expression (str): regular expression to match
data (pandas.Series): data with dates to extratc
name (str): name of the group for the expression
Returns:
tuple (pandas.Series, int): extracted dates, count
"""
extracted = data.str.extractall(expression)[name]
count = len(extracted)
print("'{}' matched {} rows".format(name, count))
return extracted, count
numeric, numeric_count = extract_and_count(NUMERIC, data, 'numeric')
# 'numeric' matched 25 rows
twentieth, twentieth_count = extract_and_count(TWENTIETH_CENTURY, data, 'twentieth')
# 'twentieth' matched 100 rows
words, words_count = extract_and_count(WORDS, data, 'words')
# 'words' matched 34 rows
backwards, backwards_count = extract_and_count(BACKWARDS, data, 'backwards')
# 'backwards' matched 69 rows
contraction_data, contraction = extract_and_count(CONTRACTION, data, 'contraction')
# 'contraction' matched 0 rows
no_day, no_day_count = extract_and_count(NO_DAY, data, 'no_day')
# 'no_day' matched 115 rows
no_day_numeric, no_day_numeric_count = extract_and_count(NO_DAY_NUMERIC, data,
"no_day_numeric")
# 'no_day_numeric' matched 112 rows
year_only, year_only_count = extract_and_count(YEAR_ONLY, data, "year_only")
# 'year_only' matched 15 rows
leftovers, leftovers_count = extract_and_count(LEFTOVERS, data, "leftovers")
# 'leftovers' matched 30 rows
found = data.str.extractall(DATE)
total_found = len(found.date)
print("Total Found: {}".format(total_found))
print("Remaining: {}".format(len(data) - total_found))
print("Discrepancy: {}".format(total_found - (numeric_count
+ twentieth_count
+ words_count
+ backwards_count
+ contraction
+ no_day_count
+ no_day_numeric_count
+ year_only_count
+ leftovers_count)))
# Total Found: 500
# Remaining: 0
# Discrepancy: 0
missing = [label for label in data.index if label not in found.index.levels[0]]
try:
print(missing[0], data.loc[missing[0]])
except IndexError:
print("all rows matched")
# all rows matched
def clean(source, expression, replacement, sample=5):
"""applies the replacement to the source
as a side-effect shows sample rows before and after
Args:
source (pandas.Series): source of the strings
expression (str): regular expression to match what to replace
replacement: function or expression to replace the matching expression
sample (int): number of randomly chosen examples to show
Returns:
pandas.Series: the source with the replacement applied to it
"""
print("Random Sample Before:")
print(source.sample(sample))
cleaned = source.str.replace(expression, replacement)
print("\nRandom Sample After:")
print(cleaned.sample(sample))
print("\nCount of cleaned: {}".format(len(cleaned)))
assert len(source) == len(cleaned)
return cleaned
def clean_punctuation(source, sample=5):
"""removes punctuation
Args:
source (pandas.Series): data to clean
sample (int): size of sample to show
Returns:
pandas.Series: source with punctuation removed
"""
print("Cleaning Punctuation")
if any(source.str.contains(PUNCTUATION)):
source = clean(source, PUNCTUATION, EMPTY_STRING)
return source
LONG_TO_SHORT = dict(January="Jan",
February="Feb",
March="Mar",
April="Apr",
May="May",
June="Jun",
July="Jul",
August="Aug",
September="Sep",
October="Oct",
November="Nov",
December="Dec")
# it turns out there are spelling errors in the data so this has to be fuzzy
LONG_TO_SHORT_EXPRESSION = OR.join([GROUP.format(month)
+ CLASS.format(LOWER_CASE)
+ ZERO_OR_MORE
for month in LONG_TO_SHORT.values()])
def long_month_to_short(match):
"""convert long month to short
Args:
match (re.Match): object matching a long month
Returns:
str: shortened version of the month
"""
return match.group(match.lastindex)
def convert_long_months_to_short(source, sample=5):
"""convert long month names to short
Args:
source (pandas.Series): data with months
sample (int): size of sample to show
Returns:
pandas.Series: data with short months
"""
return clean(source,
LONG_TO_SHORT_EXPRESSION,
long_month_to_short)
def add_month_date(match):
"""adds 01/01 to years
Args:
match (re.Match): object that only matched a 4-digit year
Returns:
str: 01/01/YYYY
"""
return "01/01/" + match.group()
def add_january_one(source):
"""adds /01/01/ to year-only dates
Args:
source (pandas.Series): data with the dates
Returns:
pandas.Series: years in source with /01/01/ added
"""
return clean(source, YEAR_ONLY, add_month_date)
two_digit_expression = GROUP.format(ONE_OR_TWO_DIGITS) + POSITIVE_LOOKAHEAD.format(SLASH)
def two_digits(match):
"""add a leading zero if needed
Args:
match (re.Match): match with one or two digits
Returns:
str: the matched string with leading zero if needed
"""
# for some reason the string-formatting raises an error if it's a string
# so cast it to an int
return "{:02}".format(int(match.group()))
def clean_two_digits(source, sample=5):
"""makes sure source has two-digits
Args:
source (pandas.Series): data with digit followed by slash
sample (int): number of samples to show
Returns:
pandas.Series: source with digits coerced to two digits
"""
return clean(source, two_digit_expression, two_digits, sample)
def clean_two_digits_isolated(source, sample=5):
"""cleans two digits that are standalone
Args:
source (pandas.Series): source of the data
sample (int): number of samples to show
Returns:
pandas.Series: converted data
"""
return clean(source, ONE_OR_TWO_DIGITS, two_digits, sample)
digits = ("{:02}".format(month) for month in range(1, 13))
MONTH_TO_DIGITS = dict(zip(MONTH_PREFIXES, digits))
SHORT_MONTHS_EXPRESSION = OR.join((GROUP.format(month) for month in MONTH_TO_DIGITS))
def month_to_digits(match):
"""converts short month to digits
Args:
match (re.Match): object with short-month
Returns:
str: month as two-digit number (e.g. Jan -> 01)
"""
return MONTH_TO_DIGITS[match.group()]
def convert_short_month_to_digits(source, sample=5):
"""converts three-letter months to two-digits
Args:
source (pandas.Series): data with three-letter months
sample (int): number of samples to show
Returns:
pandas.Series: source with short-months coverted to digits
"""
return clean(source,
SHORT_MONTHS_EXPRESSION,
month_to_digits,
sample)
def clean_months(source, sample=5):
"""clean up months (which start as words)
Args:
source (pandas.Series): source of the months
sample (int): number of random samples to show
"""
cleaned = clean_punctuation(source)
print("Converting long months to short")
cleaned = clean(cleaned,
LONG_TO_SHORT_EXPRESSION,
long_month_to_short, sample)
print("Converting short months to digits")
cleaned = clean(cleaned,
SHORT_MONTHS_EXPRESSION,
month_to_digits, sample)
return cleaned
def frame_to_series(frame, index_source, samples=5):
"""re-combines data-frame into a series
Args:
frame (pandas.DataFrame): frame with month, day, year columns
index_source (pandas.series): source to copy index from
samples (index): number of random entries to print when done
Returns:
pandas.Series: series with dates as month/day/year
"""
combined = frame.month + SLASH + frame.day + SLASH + frame.year
combined.index = index_source.index
print(combined.sample(samples))
return combined
year_only_cleaned = add_january_one(year_only)
# Random Sample Before:
# match
# 472 0 2010
# 495 0 1979
# 497 0 2008
# 481 0 1974
# 486 0 1973
# Name: year_only, dtype: object
# Random Sample After:
# match
# 495 0 01/01/1979
# 470 0 01/01/1983
# 462 0 01/01/1988
# 481 0 01/01/1974
# 480 0 01/01/2013
# Name: year_only, dtype: object
# Count of cleaned: 15
leftovers_cleaned = add_january_one(leftovers)
# Random Sample Before:
# match
# 487 0 1992
# 477 0 1994
# 498 0 2005
# 488 0 1977
# 484 0 2004
# Name: leftovers, dtype: object
# Random Sample After:
# match
# 464 0 01/01/2016
# 455 0 01/01/1984
# 465 0 01/01/1976
# 475 0 01/01/2015
# 498 0 01/01/2005
# Name: leftovers, dtype: object
# Count of cleaned: 30
cleaned = pandas.concat([year_only_cleaned, leftovers_cleaned])
print(len(cleaned))
no_day_numeric_cleaned = clean_two_digits(no_day_numeric)
no_day_numeric_cleaned = clean(no_day_numeric_cleaned,
SLASH,
lambda m: "/01/")
original = len(cleaned)
cleaned = pandas.concat([cleaned, no_day_numeric_cleaned])
assert len(cleaned) == no_day_numeric_count + original
print(len(cleaned))
no_day_cleaned = clean_months(no_day)
no_day_cleaned = clean(no_day_cleaned,
SPACE + ONE_OR_MORE,
lambda match: "/01/")
original = len(cleaned)
cleaned = pandas.concat([cleaned, no_day_cleaned])
print(len(cleaned))
assert len(cleaned) == no_day_count + original
frame = pandas.DataFrame(backwards.str.split().tolist(),
columns="day month year".split())
frame.head()
frame.day = clean_two_digits(frame.day)
frame.month = clean_months(frame.month)
backwards_cleaned = frame_to_series(frame, backwards)
original = len(cleaned)
cleaned = pandas.concat([cleaned, backwards_cleaned])
assert len(cleaned) == original + backwards_count
print(len(cleaned))
frame = pandas.DataFrame(words.str.split().tolist(), columns="month day year".split())
print(frame.head())
frame.month = clean_months(frame.month)
frame.day = clean_punctuation(frame.day)
frame.head()
words_cleaned = frame_to_series(frame, words)
original = len(cleaned)
cleaned = pandas.concat([cleaned, words_cleaned])
assert len(cleaned) == original + words_count
print(len(cleaned))
print(twentieth.iloc[21])
twentieth_cleaned = twentieth.str.replace(DASH, SLASH)
print(cleaned.iloc[21])
frame = pandas.DataFrame(twentieth_cleaned.str.split(SLASH).tolist(),
columns=["month", "day", "year"])
print(frame.head())
frame.month = clean_two_digits_isolated(frame.month)
frame.day = clean_two_digits_isolated(frame.day)
frame.head()
frame.year = clean(frame.year, TWO_DIGITS, lambda match: "19" + match.group())
twentieth_cleaned = frame_to_series(frame, twentieth)
original = len(cleaned)
cleaned = pandas.concat([cleaned, twentieth_cleaned])
assert len(cleaned) == original + twentieth_count
print(numeric.head())
has_dashes = numeric.str.contains(DASH)
print(numeric[has_dashes])
frame = pandas.DataFrame(numeric.str.split(SLASH).tolist(),
columns="month day year".split())
print(frame.head())
frame.month = clean_two_digits_isolated(frame.month)
frame.day = clean_two_digits_isolated(frame.day)
numeric_cleaned = frame_to_series(frame, numeric)
original = len(cleaned)
cleaned = pandas.concat([cleaned, numeric_cleaned])
assert len(cleaned) == original + numeric_count
print(len(cleaned))
cleaned = pandas.concat([numeric_cleaned,
twentieth_cleaned,
words_cleaned,
backwards_cleaned,
no_day_cleaned,
no_day_numeric_cleaned,
year_only_cleaned,
leftovers_cleaned,
])
print(len(cleaned))
print(cleaned.head())
assert len(cleaned) == len(data)
print(cleaned.head())
datetimes = pandas.to_datetime(cleaned, format="%m/%d/%Y")
print(datetimes.head())
sorted_dates = datetimes.sort_values()
print(sorted_dates.head())
print(sorted_dates.tail())
answer = pandas.Series(sorted_dates.index.labels[0])
print(answer.head())
def date_sorter():
return answer
```
| true |
code
| 0.567817 | null | null | null | null |
|
```
%matplotlib inline
```
Training a Classifier
=====================
This is it. You have seen how to define neural networks, compute loss and make
updates to the weights of the network.
Now you might be thinking,
What about data?
----------------
Generally, when you have to deal with image, text, audio or video data,
you can use standard python packages that load data into a numpy array.
Then you can convert this array into a ``torch.*Tensor``.
- For images, packages such as Pillow, OpenCV are useful
- For audio, packages such as scipy and librosa
- For text, either raw Python or Cython based loading, or NLTK and
SpaCy are useful
Specifically for vision, we have created a package called
``torchvision``, that has data loaders for common datasets such as
Imagenet, CIFAR10, MNIST, etc. and data transformers for images, viz.,
``torchvision.datasets`` and ``torch.utils.data.DataLoader``.
This provides a huge convenience and avoids writing boilerplate code.
For this tutorial, we will use the CIFAR10 dataset.
It has the classes: ‘airplane’, ‘automobile’, ‘bird’, ‘cat’, ‘deer’,
‘dog’, ‘frog’, ‘horse’, ‘ship’, ‘truck’. The images in CIFAR-10 are of
size 3x32x32, i.e. 3-channel color images of 32x32 pixels in size.
.. figure:: /_static/img/cifar10.png
:alt: cifar10
cifar10
Training an image classifier
----------------------------
We will do the following steps in order:
1. Load and normalizing the CIFAR10 training and test datasets using
``torchvision``
2. Define a Convolution Neural Network
3. Define a loss function
4. Train the network on the training data
5. Test the network on the test data
1. Loading and normalizing CIFAR10
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Using ``torchvision``, it’s extremely easy to load CIFAR10.
```
import torch
import torchvision
import torchvision.transforms as transforms
```
The output of torchvision datasets are PILImage images of range [0, 1].
We transform them to Tensors of normalized range [-1, 1].
```
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
```
Let us show some of the training images, for fun.
```
import matplotlib.pyplot as plt
import numpy as np
# functions to show an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
2. Define a Convolution Neural Network
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Copy the neural network from the Neural Networks section before and modify it to
take 3-channel images (instead of 1-channel images as it was defined).
```
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
```
3. Define a Loss function and optimizer
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Let's use a Classification Cross-Entropy loss and SGD with momentum.
```
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
```
4. Train the network
^^^^^^^^^^^^^^^^^^^^
This is when things start to get interesting.
We simply have to loop over our data iterator, and feed the inputs to the
network and optimize.
```
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
```
5. Test the network on the test data
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
We have trained the network for 2 passes over the training dataset.
But we need to check if the network has learnt anything at all.
We will check this by predicting the class label that the neural network
outputs, and checking it against the ground-truth. If the prediction is
correct, we add the sample to the list of correct predictions.
Okay, first step. Let us display an image from the test set to get familiar.
```
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
Okay, now let us see what the neural network thinks these examples above are:
```
outputs = net(images)
```
The outputs are energies for the 10 classes.
Higher the energy for a class, the more the network
thinks that the image is of the particular class.
So, let's get the index of the highest energy:
```
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
for j in range(4)))
```
The results seem pretty good.
Let us look at how the network performs on the whole dataset.
```
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
```
That looks waaay better than chance, which is 10% accuracy (randomly picking
a class out of 10 classes).
Seems like the network learnt something.
Hmmm, what are the classes that performed well, and the classes that did
not perform well:
```
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %2d %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))
```
Okay, so what next?
How do we run these neural networks on the GPU?
Training on GPU
----------------
Just like how you transfer a Tensor on to the GPU, you transfer the neural
net onto the GPU.
Let's first define our device as the first visible cuda device if we have
CUDA available:
```
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# Assume that we are on a CUDA machine, then this should print a CUDA device:
print(device)
net.to(device)
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs
inputs, labels = data
inputs, labels = inputs.to(device), labels.to(device)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs).to(device)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
```
The rest of this section assumes that `device` is a CUDA device.
Then these methods will recursively go over all modules and convert their
parameters and buffers to CUDA tensors:
.. code:: python
net.to(device)
Remember that you will have to send the inputs and targets at every step
to the GPU too:
.. code:: python
inputs, labels = inputs.to(device), labels.to(device)
Why dont I notice MASSIVE speedup compared to CPU? Because your network
is realllly small.
**Exercise:** Try increasing the width of your network (argument 2 of
the first ``nn.Conv2d``, and argument 1 of the second ``nn.Conv2d`` –
they need to be the same number), see what kind of speedup you get.
**Goals achieved**:
- Understanding PyTorch's Tensor library and neural networks at a high level.
- Train a small neural network to classify images
Training on multiple GPUs
-------------------------
If you want to see even more MASSIVE speedup using all of your GPUs,
please check out :doc:`data_parallel_tutorial`.
Where do I go next?
-------------------
- :doc:`Train neural nets to play video games </intermediate/reinforcement_q_learning>`
- `Train a state-of-the-art ResNet network on imagenet`_
- `Train a face generator using Generative Adversarial Networks`_
- `Train a word-level language model using Recurrent LSTM networks`_
- `More examples`_
- `More tutorials`_
- `Discuss PyTorch on the Forums`_
- `Chat with other users on Slack`_
| true |
code
| 0.768581 | null | null | null | null |
|
# Collaboration and Competition
---
In this notebook, you will learn how to use the Unity ML-Agents environment for the third project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893) program.
### 1. Start the Environment
We begin by importing the necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
from unityagents import UnityEnvironment
import numpy as np
import copy
from collections import namedtuple, deque
import random
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
%matplotlib inline
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Tennis.app"`
- **Windows** (x86): `"path/to/Tennis_Windows_x86/Tennis.exe"`
- **Windows** (x86_64): `"path/to/Tennis_Windows_x86_64/Tennis.exe"`
- **Linux** (x86): `"path/to/Tennis_Linux/Tennis.x86"`
- **Linux** (x86_64): `"path/to/Tennis_Linux/Tennis.x86_64"`
- **Linux** (x86, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86"`
- **Linux** (x86_64, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86_64"`
For instance, if you are using a Mac, then you downloaded `Tennis.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Tennis.app")
```
```
env = UnityEnvironment(file_name="Tennis_Linux_NoVis/Tennis.x86_64")
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
In this environment, two agents control rackets to bounce a ball over a net. If an agent hits the ball over the net, it receives a reward of +0.1. If an agent lets a ball hit the ground or hits the ball out of bounds, it receives a reward of -0.01. Thus, the goal of each agent is to keep the ball in play.
The observation space consists of 8 variables corresponding to the position and velocity of the ball and racket. Two continuous actions are available, corresponding to movement toward (or away from) the net, and jumping.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
```
### 3. Take Random Actions in the Environment
In the next code cell, you will learn how to use the Python API to control the agents and receive feedback from the environment.
Once this cell is executed, you will watch the agents' performance, if they select actions at random with each time step. A window should pop up that allows you to observe the agents.
Of course, as part of the project, you'll have to change the code so that the agents are able to use their experiences to gradually choose better actions when interacting with the environment!
```
for i in range(1, 6): # play game for 5 episodes
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
states = env_info.vector_observations # get the current state (for each agent)
scores = np.zeros(num_agents) # initialize the score (for each agent)
while True:
actions = np.random.randn(num_agents, action_size) # select an action (for each agent)
actions = np.clip(actions, -1, 1) # all actions between -1 and 1
env_info = env.step(actions)[brain_name] # send all actions to tne environment
next_states = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
scores += env_info.rewards # update the score (for each agent)
states = next_states # roll over states to next time step
if np.any(dones): # exit loop if episode finished
break
print('Score (max over agents) from episode {}: {}'.format(i, np.max(scores)))
```
When finished, you can close the environment.
```
# env.close()
```
### 4. It's Your Turn!
Now it's your turn to train your own agent to solve the environment! When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
### 5. My Multi DDPG
```
from ddpg.multi_ddpg_agent import Agent
agent_0 = Agent(state_size, action_size, num_agents=1, random_seed=0)
agent_1 = Agent(state_size, action_size, num_agents=1, random_seed=0)
def get_actions(states, add_noise):
'''gets actions for each agent and then combines them into one array'''
action_0 = agent_0.act(states, add_noise) # agent 0 chooses an action
action_1 = agent_1.act(states, add_noise) # agent 1 chooses an action
return np.concatenate((action_0, action_1), axis=0).flatten()
SOLVED_SCORE = 0.5
CONSEC_EPISODES = 100
PRINT_EVERY = 10
ADD_NOISE = True
def run_multi_ddpg(n_episodes=2000, max_t=1000, train_mode=True):
"""Multi-Agent Deep Deterministic Policy Gradient (MADDPG)
Params
======
n_episodes (int) : maximum number of training episodes
max_t (int) : maximum number of timesteps per episode
train_mode (bool) : if 'True' set environment to training mode
"""
scores_window = deque(maxlen=CONSEC_EPISODES)
scores_all = []
moving_average = []
best_score = -np.inf
best_episode = 0
already_solved = False
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=train_mode)[brain_name] # reset the environment
states = np.reshape(env_info.vector_observations, (1,48)) # get states and combine them
agent_0.reset()
agent_1.reset()
scores = np.zeros(num_agents)
while True:
actions = get_actions(states, ADD_NOISE) # choose agent actions and combine them
env_info = env.step(actions)[brain_name] # send both agents' actions together to the environment
next_states = np.reshape(env_info.vector_observations, (1, 48)) # combine the agent next states
rewards = env_info.rewards # get reward
done = env_info.local_done # see if episode finished
agent_0.step(states, actions, rewards[0], next_states, done, 0) # agent 1 learns
agent_1.step(states, actions, rewards[1], next_states, done, 1) # agent 2 learns
scores += np.max(rewards) # update the score for each agent
states = next_states # roll over states to next time step
if np.any(done): # exit loop if episode finished
break
ep_best_score = np.max(scores)
scores_window.append(ep_best_score)
scores_all.append(ep_best_score)
moving_average.append(np.mean(scores_window))
# save best score
if ep_best_score > best_score:
best_score = ep_best_score
best_episode = i_episode
# print results
if i_episode % PRINT_EVERY == 0:
print(f'Episodes {i_episode}\tMax Reward: {np.max(scores_all[-PRINT_EVERY:]):.3f}\tMoving Average: {moving_average[-1]:.3f}')
# determine if environment is solved and keep best performing models
if moving_average[-1] >= SOLVED_SCORE:
if not already_solved:
print(f'Solved in {i_episode-CONSEC_EPISODES} episodes! \
\n<-- Moving Average: {moving_average[-1]:.3f} over past {CONSEC_EPISODES} episodes')
already_solved = True
torch.save(agent_0.actor_local.state_dict(), 'checkpoint_actor_0.pth')
torch.save(agent_0.critic_local.state_dict(), 'checkpoint_critic_0.pth')
torch.save(agent_1.actor_local.state_dict(), 'checkpoint_actor_1.pth')
torch.save(agent_1.critic_local.state_dict(), 'checkpoint_critic_1.pth')
elif ep_best_score >= best_score:
print(f'Best episode {i_episode}\tMax Reward: {ep_best_score:.3f}\tMoving Average: {moving_average[-1]:.3f}')
torch.save(agent_0.actor_local.state_dict(), 'checkpoint_actor_0.pth')
torch.save(agent_0.critic_local.state_dict(), 'checkpoint_critic_0.pth')
torch.save(agent_1.actor_local.state_dict(), 'checkpoint_actor_1.pth')
torch.save(agent_1.critic_local.state_dict(), 'checkpoint_critic_1.pth')
elif (i_episode-best_episode) >= 200:
# stop training if model stops converging
print('Done')
break
else:
continue
return scores_all, moving_average
scores, avgs = run_multi_ddpg()
plt.plot(np.arange(1, len(scores)+1), scores, label='Score')
plt.plot(np.arange(len(scores)), avgs, c='r', label='100 Average')
plt.legend(loc=0)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.title('Udacity Project3 Solution by Bongsang')
plt.savefig('result.png')
plt.show()
env.close()
```
| true |
code
| 0.567397 | null | null | null | null |
|
# K-Nearest Neighbours
Let’s build a K-Nearest Neighbours model from scratch.
First, we will define some generic `KNN` object. In the constructor, we pass three parameters:
- The number of neighbours being used to make predictions
- The distance measure we want to use
- Whether or not we want to use weighted distances
```
import sys
sys.path.append("D:/source/skratch/source")
from collections import Counter
import numpy as np
from utils.distances import euclidean
class KNN:
def __init__(self, k, distance=euclidean, weighted=False):
self.k = k
self.weighted = weighted # Whether or not to use weighted distances
self.distance = distance
```
Now we will define the fit function, which is the function which describes how to train a model. For a K-Nearest Neighbours model, the training is rather simplistic. Indeed, all there needs to be done is to store the training instances as the model’s parameters.
```
def fit(self, X, y):
self.X_ = X
self.y_ = y
return self
```
Similarly, we can build an update function which will update the state of the model as more data points are provided for training. Training a model by feeding it data in a stream-like fashion is often referred to as online learning. Not all models allow for computationally efficient online learning, but K-Nearest Neighbours does.
```
def update(self, X, y):
self.X_ = np.concatenate((self.X_, X))
self.y_ = np.concatenate((self.y_, y))
return self
```
In order to make predictions, we also need to create a predict function. For a K-Nearest Neighbours model, a prediction is made in two steps:
- Find the K-nearest neighbours by computing their distances to the data point we want to predict
- Given these neighbours and their distances, compute the predicted output
```
def predict(self, X):
predictions = []
for x in X:
neighbours, distances = self._get_neighbours(x)
prediction = self._vote(neighbours, distances)
predictions.append(prediction)
return np.array(predictions)
```
Retrieving the neighbours can be done by calculating all pairwise distances between the data point and the data stored inside the state of the model. Once these distances are known, the K instances that have the shortest distance to the example are returned.
```
def _get_neighbours(self, x):
distances = np.array([self._distance(x, x_) for x_ in self.X_])
indices = np.argsort(distances)[:self.k]
return self.y_[indices], distances[indices]
```
In case we would like to use weighted distances, we need to compute the weights. By default, these weights are all set to 1 to make all instances equal. To weigh the instances, neighbours that are closer are typically favoured by given them a weight equal to 1 divided by their distance.
>If neighbours have distance 0, since we can’t divide by zero, their weight is set to 1, and all other weights are set to 0. This is also how scikit-learn deals with this problem according to their source code.
```
def _get_weights(self, distances):
weights = np.ones_like(distances, dtype=float)
if self.weighted:
if any(distances == 0):
weights[distances != 0] = 0
else:
weights /= distances
return weights
```
The only function that we have yet to define is the vote function that is called in the predict function. Depending on the implementation of that function, K-Nearest Neighbours can be used for regression, classification, or even as a meta-learner.
## KNN for Regression
In order to use K-Nearest Neighbour for regression, the vote function is defined as the average of the neighbours. In case weighting is used, the vote function returns the weighted average, favouring closer instances.
```
class KNN_Regressor(KNN):
def _vote(self, targets, distances):
weights = self._get_weights(distances)
return np.sum(weights * targets) / np.sum(weights)
```
## KNN for Classification
In the classification case, the vote function uses a majority voting scheme. If weighting is used, each neighbour has a different impact on the prediction.
```
class KNN_Classifier(KNN):
def _vote(self, classes, distances):
weights = self._get_weights(distances)
prediction = None
max_weighted_frequency = 0
for c in classes:
weighted_frequency = np.sum(weights[classes == c])
if weighted_frequency > max_weighted_frequency:
prediction = c
max_weighted_frequency = weighted_frequency
return prediction
```
| true |
code
| 0.531939 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.