prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Analyzing interstellar reddening and calculating synthetic photometry
## Authors
Kristen Larson, Lia Corrales, Stephanie T. Douglas, Kelle Cruz
Input from Emir Karamehmetoglu, Pey Lian Lim, Karl Gordon, Kevin Covey
## Learning Goals
- Investigate extinction curve shapes
- Deredden spectral energy distributions and spectra
- Calculate photometric extinction and reddening
- Calculate synthetic photometry for a dust-reddened star by combining `dust_extinction` and `synphot`
- Convert from frequency to wavelength with `astropy.unit` equivalencies
- Unit support for plotting with `astropy.visualization`
## Keywords
dust extinction, synphot, astroquery, units, photometry, extinction, physics, observational astronomy
## Companion Content
* [Bessell & Murphy (2012)](https://ui.adsabs.harvard.edu/#abs/2012PASP..124..140B/abstract)
## Summary
In this tutorial, we will look at some extinction curves from the literature, use one of those curves to deredden an observed spectrum, and practice invoking a background source flux in order to calculate magnitudes from an extinction model.
The primary libraries we'll be using are [dust_extinction](https://dust-extinction.readthedocs.io/en/latest/) and [synphot](https://synphot.readthedocs.io/en/latest/), which are [Astropy affiliated packages](https://www.astropy.org/affiliated/).
We recommend installing the two packages in this fashion:
```
pip install synphot
pip install dust_extinction
```
This tutorial requires v0.7 or later of `dust_extinction`. To ensure that all commands work properly, make sure you have the correct version installed. If you have v0.6 or earlier installed, run the following command to upgrade
```
pip install dust_extinction --upgrade
```
```
import pathlib
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import astropy.units as u
from astropy.table import Table
from dust_extinction.parameter_averages import CCM89, F99
from synphot import units, config
from synphot import SourceSpectrum,SpectralElement,Observation,ExtinctionModel1D
from synphot.models import BlackBodyNorm1D
from synphot.spectrum import BaseUnitlessSpectrum
from synphot.reddening import ExtinctionCurve
from astroquery.simbad import Simbad
from astroquery.mast import Observations
import astropy.visualization
```
# Introduction
Dust in the interstellar medium (ISM) extinguishes background starlight. The wavelength dependence of the extinction is such that short-wavelength light is extinguished more than long-wavelength light, and we call this effect *reddening*.
If you're new to extinction, here is a brief introduction to the types of quantities involved.
The fractional change to the flux of starlight is
$$
\frac{dF_\lambda}{F_\lambda} = -\tau_\lambda
$$
where $\tau$ is the optical depth and depends on wavelength. Integrating along the line of sight, the resultant flux is an exponential function of optical depth,
$$
\tau_\lambda = -\ln\left(\frac{F_\lambda}{F_{\lambda,0}}\right).
$$
With an eye to how we define magnitudes, we usually change the base from $e$ to 10,
$$
\tau_\lambda = -2.303\log\left(\frac{F_\lambda}{F_{\lambda,0}}\right),
$$
and define an extinction $A_\lambda = 1.086 \,\tau_\lambda$ so that
$$
A_\lambda = -2.5\log\left(\frac{F_\lambda}{F_{\lambda,0}}\right).
$$
There are two basic take-home messages from this derivation:
* Extinction introduces a multiplying factor $10^{-0.4 A_\lambda}$ to the flux.
* Extinction is defined relative to the flux without dust, $F_{\lambda,0}$.
Once astropy and the affiliated packages are installed, we can import from them as needed:
# Example 1: Investigate Extinction Models
The `dust_extinction` package provides various models for extinction $A_\lambda$ normalized to $A_V$. The shapes of normalized curves are relatively (and perhaps surprisingly) uniform in the Milky Way. The little variation that exists is often parameterized by the ratio of extinction ($A_V$) to reddening in the blue-visual ($E_{B-V}$),
$$
R_V \equiv \frac{A_V}{E_{B-V}}
$$
where $E_{B-V}$ is differential extinction $A_B-A_V$. In this example, we show the $R_V$-parameterization for the Clayton, Cardelli, & Mathis (1989, CCM) and the Fitzpatrick (1999) models. [More model options are available in the `dust_extinction` documentation.](https://dust-extinction.readthedocs.io/en/latest/dust_extinction/model_flavors.html)
```
# Create wavelengths array.
wav = np.arange(0.1, 3.0, 0.001)*u.micron
for model in [CCM89, F99]:
for R in (2.0,3.0,4.0):
# Initialize the extinction model
ext = model(Rv=R)
plt.plot(1/wav, ext(wav), label=model.name+' R='+str(R))
plt.xlabel('$\lambda^{-1}$ ($\mu$m$^{-1}$)')
plt.ylabel('A($\lambda$) / A(V)')
plt.legend(loc='best')
plt.title('Some Extinction Laws')
plt.show()
```
Astronomers studying the ISM often display extinction curves against inverse wavelength (wavenumber) to show the ultraviolet variation, as we do here. Infrared extinction varies much less and approaches zero at long wavelength in the absence of wavelength-independent, or grey, extinction.
# Example 2: Deredden a Spectrum
Here we deredden (unextinguish) the IUE ultraviolet spectrum and optical photometry of the star $\rho$ Oph (HD 147933).
First, we will use astroquery to fetch the archival [IUE spectrum from MAST](https://archive.stsci.edu/iue/):
```
download_dir = pathlib.Path('~/.astropy/cache/astroquery/Mast').expanduser()
download_dir.mkdir(exist_ok=True)
obsTable = Observations.query_object("HD 147933", radius="1 arcsec")
obsTable_spec = obsTable[obsTable['dataproduct_type'] == 'spectrum']
obsTable_spec
obsids = obsTable_spec[39]['obsid']
dataProductsByID = Observations.get_product_list(obsids)
manifest = Observations.download_products(dataProductsByID,
download_dir=str(download_dir))
```
We read the downloaded files into an astropy table:
```
t_lwr = Table.read(download_dir / 'mastDownload/IUE/lwr05639/lwr05639mxlo_vo.fits')
print(t_lwr)
```
The `.quantity` extension in the next lines will read the Table columns into Quantity vectors. Quantities keep the units of the Table column attached to the numpy array values.
```
wav_UV = t_lwr['WAVE'][0,].quantity
UVflux = t_lwr['FLUX'][0,].quantity
```
Now, we use astroquery again to fetch photometry from Simbad to go with the IUE spectrum:
```
custom_query = Simbad()
custom_query.add_votable_fields('fluxdata(U)','fluxdata(B)','fluxdata(V)')
phot_table=custom_query.query_object('HD 147933')
Umag=phot_table['FLUX_U']
Bmag=phot_table['FLUX_B']
Vmag=phot_table['FLUX_V']
```
To convert the photometry to flux, we look up some [properties of the photometric passbands](http://ned.ipac.caltech.edu/help/photoband.lst), including the flux of a magnitude zero star through the each passband, also known as the zero-point of the passband.
```
wav_U = 0.3660 * u.micron
zeroflux_U_nu = 1.81E-23 * u.Watt/(u.m*u.m*u.Hz)
wav_B = 0.4400 * u.micron
zeroflux_B_nu = 4.26E-23 * u.Watt/(u.m*u.m*u.Hz)
wav_V = 0.5530 * u.micron
zeroflux_V_nu = 3.64E-23 * u.Watt/(u.m*u.m*u.Hz)
```
The zero-points that we found for the optical passbands are not in the same units as the IUE fluxes. To make matters worse, the zero-point fluxes are $F_\nu$ and the IUE fluxes are $F_\lambda$. To convert between them, the wavelength is needed. Fortunately, astropy provides an easy way to make the conversion with *equivalencies*:
```
zeroflux_U = zeroflux_U_nu.to(u.erg/u.AA/u.cm/u.cm/u.s,
equivalencies=u.spectral_density(wav_U))
zeroflux_B = zeroflux_B_nu.to(u.erg/u.AA/u.cm/u.cm/u.s,
equivalencies=u.spectral_density(wav_B))
zeroflux_V = zeroflux_V_nu.to(u.erg/u.AA/u.cm/u.cm/u.s,
equivalencies=u.spectral_density(wav_V))
```
Now we can convert from photometry to flux using the definition of magnitude:
$$
F=F_0\ 10^{-0.4\, m}
$$
```
Uflux = zeroflux_U * 10.**(-0.4*Umag)
Bflux = zeroflux_B * 10.**(-0.4*Bmag)
Vflux = zeroflux_V * 10.**(-0.4*Vmag)
```
Using astropy quantities allow us to take advantage of astropy's unit support in plotting. [Calling `astropy.visualization.quantity_support` explicitly turns the feature on.](http://docs.astropy.org/en/stable/units/quantity.html#plotting-quantities) Then, when quantity objects are passed to matplotlib plotting functions, the axis labels are automatically labeled with the unit of the quantity. In addition, quantities are converted automatically into the same units when combining multiple plots on the same axes.
```
astropy.visualization.quantity_support()
plt.plot(wav_UV,UVflux,'m',label='UV')
plt.plot(wav_V,Vflux,'ko',label='U, B, V')
plt.plot(wav_B,Bflux,'ko')
plt.plot(wav_U,Uflux,'ko')
plt.legend(loc='best')
plt.ylim(0,3E-10)
plt.title('rho Oph')
plt.show()
```
Finally, we initialize the extinction model, choosing values $R_V = 5$ and $E_{B-V} = 0.5$. This star is famous in the ISM community for having large-$R_V$ dust in the line of sight.
```
Rv = 5.0 # Usually around 3, but about 5 for this star.
Ebv = 0.5
ext = F99(Rv=Rv)
```
To extinguish (redden) a spectrum, multiply by the `ext.extinguish` function. To unextinguish (deredden), divide by the same `ext.extinguish`, as we do here:
```
plt.semilogy(wav_UV,UVflux,'m',label='UV')
plt.semilogy(wav_V,Vflux,'ko',label='U, B, V')
plt.semilogy(wav_B,Bflux,'ko')
plt.semilogy(wav_U,Uflux,'ko')
plt.semilogy(wav_UV,UVflux/ext.extinguish(wav_UV,Ebv=Ebv),'b',
label='dereddened: EBV=0.5, RV=5')
plt.semilogy(wav_V,Vflux/ext.extinguish(wav_V,Ebv=Ebv),'ro',
label='dereddened: EBV=0.5, RV=5')
plt.semilogy(wav_B,Bflux/ext.extinguish(wav_B,Ebv=Ebv),'ro')
plt.semilogy(wav_U,Uflux/ext.extinguish(wav_U,Ebv=Ebv),'ro')
plt.legend(loc='best')
plt.title('rho Oph')
plt.show()
```
Notice that, by dereddening the spectrum, the absorption feature at 2175 Angstrom is removed. This feature can also be seen as the prominent bump in the extinction curves in Example 1. That we have smoothly removed the 2175 Angstrom feature suggests that the values we chose, $R_V = 5$ and $E_{B-V} = 0.5$, are a reasonable model for the foreground dust.
Those experienced with dereddening should notice that that `dust_extinction` returns $A_\lambda/A_V$, while other routines like the IDL fm_unred procedure often return $A_\lambda/E_{B-V}$ by default and need to be divided by $R_V$ in order to compare directly with `dust_extinction`.
# Example 3: Calculate Color Excess with `synphot`
Calculating broadband *photometric* extinction is harder than it might look at first. All we have to do is look up $A_\lambda$ for a particular passband, right? Under the right conditions, yes. In general, no.
Remember that we have to integrate over a passband to get synthetic photometry,
$$
A = -2.5\log\left(\frac{\int W_\lambda F_{\lambda,0} 10^{-0.4A_\lambda} d\lambda}{\int W_\lambda F_{\lambda,0} d\lambda} \right),
$$
where $W_\lambda$ is the fraction of incident energy transmitted through a filter. See the detailed appendix in [Bessell & Murphy (2012)](https://ui.adsabs.harvard.edu/#abs/2012PASP..124..140B/abstract)
for an excellent review of the issues and common misunderstandings in synthetic photometry.
There is an important point to be made here. The expression above does not simplify any further. Strictly speaking, it is impossible to convert spectral extinction $A_\lambda$ into a magnitude system without knowing the wavelength dependence of the source's original flux across the filter in question. As a special case, if we assume that the source flux is constant in the band (i.e. $F_\lambda = F$), then we can cancel these factors out from the integrals, and extinction in magnitudes becomes the weighted average of the extinction factor across the filter in question. In that special case, $A_\lambda$ at $\lambda_{\rm eff}$ is a good approximation for magnitude extinction.
In this example, we will demonstrate the more general calculation of photometric extinction. We use a blackbody curve for the flux before the dust, apply an extinction curve, and perform synthetic photometry to calculate extinction and reddening in a magnitude system.
First, let's get the filter transmission curves:
```
# Optional, for when the STScI ftp server is not answering:
config.conf.vega_file = 'http://ssb.stsci.edu/cdbs/calspec/alpha_lyr_stis_008.fits'
config.conf.johnson_u_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_u_004_syn.fits'
config.conf.johnson_b_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_b_004_syn.fits'
config.conf.johnson_v_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_v_004_syn.fits'
config.conf.johnson_r_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_r_003_syn.fits'
config.conf.johnson_i_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_i_003_syn.fits'
config.conf.bessel_j_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/bessell_j_003_syn.fits'
config.conf.bessel_h_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/bessell_h_004_syn.fits'
config.conf.bessel_k_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/bessell_k_003_syn.fits'
u_band = SpectralElement.from_filter('johnson_u')
b_band = SpectralElement.from_filter('johnson_b')
v_band = SpectralElement.from_filter('johnson_v')
r_band = SpectralElement.from_filter('johnson_r')
i_band = SpectralElement.from_filter('johnson_i')
j_band = SpectralElement.from_filter('bessel_j')
h_band = SpectralElement.from_filter('bessel_h')
k_band = SpectralElement.from_filter('bessel_k')
```
If you are running this with your own python, see the [synphot documentation](https://synphot.readthedocs.io/en/latest/#installation-and-setup) on how to install your own copy of the necessary files.
Next, let's make a background flux to which we will apply extinction. Here we make a 10,000 K blackbody using the model mechanism from within `synphot` and normalize it to $V$ = 10 in the Vega-based magnitude system.
```
# First, create a blackbody at some temperature.
sp = SourceSpectrum(BlackBodyNorm1D, temperature=10000)
# sp.plot(left=1, right=15000, flux_unit='flam', title='Blackbody')
# Get the Vega spectrum as the zero point flux.
vega = SourceSpectrum.from_vega()
# vega.plot(left=1, right=15000)
# Normalize the blackbody to some chosen magnitude, say V = 10.
vmag = 10.
v_band = SpectralElement.from_filter('johnson_v')
sp_norm = sp.normalize(vmag * units.VEGAMAG, v_band, vegaspec=vega)
sp_norm.plot(left=1, right=15000, flux_unit='flam', title='Normed Blackbody')
```
Now we initialize the extinction model and choose an extinction of $A_V$ = 2. To get the `dust_extinction` model working with `synphot`, we create a wavelength array and make a spectral element with the extinction model as a lookup table.
```
# Initialize the extinction model and choose the extinction, here Av = 2.
ext = CCM89(Rv=3.1)
Av = 2.
# Create a wavelength array.
wav = np.arange(0.1, 3, 0.001)*u.micron
# Make the extinction model in synphot using a lookup table.
ex = ExtinctionCurve(ExtinctionModel1D,
points=wav, lookup_table=ext.extinguish(wav, Av=Av))
sp_ext = sp_norm*ex
sp_ext.plot(left=1, right=15000, flux_unit='flam',
title='Normed Blackbody with Extinction')
```
Synthetic photometry refers to modeling an observation of a star by multiplying the theoretical model for the astronomical flux through a certain filter response function, then integrating.
```
# "Observe" the star through the filter and integrate to get photometric mag.
sp_obs = Observation(sp_ext, v_band)
sp_obs_before = Observation(sp_norm, v_band)
# sp_obs.plot(left=1, right=15000, flux_unit='flam',
# title='Normed Blackbody with Extinction through V Filter')
```
Next, `synphot` performs the integration and computes magnitudes in the Vega system.
```
sp_stim_before = sp_obs_before.effstim(flux_unit='vegamag', vegaspec=vega)
sp_stim = sp_obs.effstim(flux_unit='vegamag', vegaspec=vega)
print('before dust, V =', np.round(sp_stim_before,1))
print('after dust, V =', np.round(sp_stim,1))
# Calculate extinction and compare to our chosen value.
Av_calc = sp_stim - sp_stim_before
print('$A_V$ = ', np.round(Av_calc,1))
```
This is a good check for us to do. We normalized our spectrum to $V$ = 10 mag and added 2 mag of visual extinction, so the synthetic photometry procedure should reproduce these chosen values, and it does. Now we are ready to find the extinction in other passbands.
We calculate the new photometry for the rest of the Johnson optical and the Bessell infrared filters. We calculate extinction $A = \Delta m$ and plot color excess, $E(\lambda - V) = A_\lambda - A_V$.
Notice that `synphot` calculates the effective wavelength of the observations for us, which is very useful for plotting the results. We show reddening with the model extinction curve for comparison in the plot.
```
bands = [u_band,b_band,v_band,r_band,i_band,j_band,h_band,k_band]
for band in bands:
# Calculate photometry with dust:
sp_obs = Observation(sp_ext, band, force='extrap')
obs_effstim = sp_obs.effstim(flux_unit='vegamag', vegaspec=vega)
# Calculate photometry without dust:
sp_obs_i = Observation(sp_norm, band, force='extrap')
obs_i_effstim = sp_obs_i.effstim(flux_unit='vegamag', vegaspec=vega)
# Extinction = mag with dust - mag without dust
# Color excess = extinction at lambda - extinction at V
color_excess = obs_effstim - obs_i_effstim - Av_calc
plt.plot(sp_obs_i.effective_wavelength(), color_excess,'or')
print(np.round(sp_obs_i.effective_wavelength(),1), ',',
np.round(color_excess,2))
# Plot the model extinction curve for comparison
plt.plot(wav,Av*ext(wav)-Av,'--k')
plt.ylim([-2,2])
plt.xlabel('$\lambda$ (Angstrom)')
plt.ylabel('E($\lambda$-V)')
plt.title('Reddening of T=10,000K Background Source with Av=2')
plt.show()
```
## Exercise
Try changing the blackbody temperature to something very hot or very cool. Are the color excess values the same? Have the effective wavelengths changed?
Note that the photometric extinction changes because the filter transmission is not uniform. The observed throughput of the filter depends on the shape of the background source flux.
| true |
code
| 0.627152 | null | null | null | null |
|
```
# Checkout www.pygimli.org for more examples
%matplotlib inline
```
# 2D ERT modeling and inversion
```
import matplotlib.pyplot as plt
import numpy as np
import pygimli as pg
import pygimli.meshtools as mt
from pygimli.physics import ert
```
Create geometry definition for the modelling domain.
worldMarker=True indicates the default boundary conditions for the ERT
```
world = mt.createWorld(start=[-50, 0], end=[50, -50], layers=[-1, -8],
worldMarker=True)
```
Create some heterogeneous circular anomaly
```
block = mt.createCircle(pos=[-4.0, -5.0], radius=[1, 1.8], marker=4,
boundaryMarker=10, area=0.01)
circle = mt.createCircle(pos=[4.0, -5.0], radius=[1, 1.8], marker=5,
boundaryMarker=10, area=0.01)
poly = mt.createPolygon([(1,-4), (2,-1.5), (4,-2), (5,-2),
(8,-3), (5,-3.5), (3,-4.5)], isClosed=True,
addNodes=3, interpolate='spline', marker=5)
```
Merge geometry definition into a Piecewise Linear Complex (PLC)
```
geom = world + block + circle # + poly
```
Optional: show the geometry
```
pg.show(geom)
```
Create a Dipole Dipole ('dd') measuring scheme with 21 electrodes.
```
scheme = ert.createData(elecs=np.linspace(start=-20, stop=20, num=42),
schemeName='dd')
```
Put all electrode (aka sensors) positions into the PLC to enforce mesh
refinement. Due to experience, its convenient to add further refinement
nodes in a distance of 10% of electrode spacing to achieve sufficient
numerical accuracy.
```
for p in scheme.sensors():
geom.createNode(p)
geom.createNode(p - [0, 0.01])
# Create a mesh for the finite element modelling with appropriate mesh quality.
mesh = mt.createMesh(geom, quality=34)
# Create a map to set resistivity values in the appropriate regions
# [[regionNumber, resistivity], [regionNumber, resistivity], [...]
rhomap = [[1, 50.],
[2, 50.],
[3, 50.],
[4, 150.],
[5, 15]]
# Take a look at the mesh and the resistivity distribution
pg.show(mesh, data=rhomap, label=pg.unit('res'), showMesh=True)
```
Perform the modeling with the mesh and the measuring scheme itself
and return a data container with apparent resistivity values,
geometric factors and estimated data errors specified by the noise setting.
The noise is also added to the data. Here 1% plus 1µV.
Note, we force a specific noise seed as we want reproducable results for
testing purposes.
```
data = ert.simulate(mesh, scheme=scheme, res=rhomap, noiseLevel=1,
noiseAbs=1e-6, seed=1337, verbose=False)
pg.info(np.linalg.norm(data['err']), np.linalg.norm(data['rhoa']))
pg.info('Simulated data', data)
pg.info('The data contains:', data.dataMap().keys())
pg.info('Simulated rhoa (min/max)', min(data['rhoa']), max(data['rhoa']))
pg.info('Selected data noise %(min/max)', min(data['err'])*100, max(data['err'])*100)
# data['k']
```
Optional: you can filter all values and tokens in the data container.
Its possible that there are some negative data values due to noise and
huge geometric factors. So we need to remove them.
```
data.remove(data['rhoa'] < 0)
# data.remove(data['k'] < -20000.0)
pg.info('Filtered rhoa (min/max)', min(data['rhoa']), max(data['rhoa']))
# You can save the data for further use
data.save('simple.dat')
# You can take a look at the data
ert.show(data, cMap="RdBu_r")
```
Initialize the ERTManager, e.g. with a data container or a filename.
```
mgr = ert.ERTManager('simple.dat')
```
Run the inversion with the preset data. The Inversion mesh will be created
with default settings.
```
inv = mgr.invert(lam=10, verbose=False)
#np.testing.assert_approx_equal(mgr.inv.chi2(), 0.7, significant=1)
```
Let the ERTManger show you the model of the last successful run and how it
fits the data. Shows data, model response, and model.
```
mgr.showResultAndFit(cMap="RdBu_r")
meshPD = pg.Mesh(mgr.paraDomain) # Save copy of para mesh for plotting later
```
You can also provide your own mesh (e.g., a structured grid if you like them)
Note, that x and y coordinates needs to be in ascending order to ensure that
all the cells in the grid have the correct orientation, i.e., all cells need
to be numbered counter-clockwise and the boundary normal directions need to
point outside.
```
inversionDomain = pg.createGrid(x=np.linspace(start=-21, stop=21, num=43),
y=-pg.cat([0], pg.utils.grange(0.5, 8, n=8))[::-1],
marker=2)
```
The inversion domain for ERT problems needs a boundary that represents the
far regions in the subsurface of the halfspace.
Give a cell marker lower than the marker for the inversion region, the lowest
cell marker in the mesh will be the inversion boundary region by default.
```
grid = pg.meshtools.appendTriangleBoundary(inversionDomain, marker=1,
xbound=50, ybound=50)
pg.show(grid, markers=True)
#pg.show(grid, markers=True)
```
The Inversion can be called with data and mesh as argument as well
```
model = mgr.invert(data, mesh=grid, lam=10, verbose=False)
# np.testing.assert_approx_equal(mgr.inv.chi2(), 0.951027, significant=3)
```
You can of course get access to mesh and model and plot them for your own.
Note that the cells of the parametric domain of your mesh might be in
a different order than the values in the model array if regions are used.
The manager can help to permutate them into the right order.
```
# np.testing.assert_approx_equal(mgr.inv.chi2(), 1.4, significant=2)
maxC = 150
modelPD = mgr.paraModel(model) # do the mapping
pg.show(mgr.paraDomain, modelPD, label='Model', cMap='RdBu_r',
logScale=True, cMin=15, cMax=maxC)
pg.info('Inversion stopped with chi² = {0:.3}'.format(mgr.fw.chi2()))
fig, (ax1, ax2, ax3) = plt.subplots(3,1, sharex=True, sharey=True, figsize=(8,7))
pg.show(mesh, rhomap, ax=ax1, hold=True, cMap="RdBu_r", logScale=True,
orientation="vertical", cMin=15, cMax=maxC)
pg.show(meshPD, inv, ax=ax2, hold=True, cMap="RdBu_r", logScale=True,
orientation="vertical", cMin=15, cMax=maxC)
mgr.showResult(ax=ax3, cMin=15, cMax=maxC, cMap="RdBu_r", orientation="vertical")
labels = ["True model", "Inversion unstructured mesh", "Inversion regular grid"]
for ax, label in zip([ax1, ax2, ax3], labels):
ax.set_xlim(mgr.paraDomain.xmin(), mgr.paraDomain.xmax())
ax.set_ylim(mgr.paraDomain.ymin(), mgr.paraDomain.ymax())
ax.set_title(label)
```
| true |
code
| 0.700011 | null | null | null | null |
|
# PySDDR: An Advanced Tutorial
In the beginner's guide only tabular data was used as input to the PySDDR framework. In this advanced tutorial we show the effects when combining structured and unstructured data. Currently, the framework only supports images as unstructured data.
We will use the MNIST dataset as a source for the unstructured data and generate additional tabular features corresponding to those. Our outcome in this tutorial is simulated based on linear and non-linear effects of tabular data and a linear effect of the number shown on the MNIST image. Our model is not provided with the (true) number, but instead has to learn the number effect from the image (together with the structured data effects):
\begin{equation*}
y = \sin(x_1) - 3x_2 + x_3^4 + 3\cdot number + \epsilon
\end{equation*}
with $\epsilon \sim \mathcal{N}(0, \sigma^2)$ and $number$ is the number on the MNIST image.
The aim of training is for the model to be able to output a latent effect, representing the number depicted in the MNIST image.
We start by importing the sddr module and other required libraries
```
# import the sddr module
from sddr import Sddr
import torch
import torch.nn as nn
import torch.optim as optim
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#set seeds for reproducibility
torch.manual_seed(1)
np.random.seed(1)
```
### User inputs
First the user defines the data to be used. The data is loaded and if it does not already exist, a column needs to be added to the tabular data describing the unstructured data - structured data correspondence. In the example below we add a column where each item includes the name of the image to which the current row of tabular data corresponds.
```
data_path = '../data/mnist_data/tab.csv'
data = pd.read_csv(data_path,delimiter=',')
# append a column for the numbers: each data point contains a file name of the corresponding image
for i in data.index:
data.loc[i,'numbers'] = f'img_{i}.jpg'
```
Next the distribution, formulas and training parameters are defined. The size of each image is ```28x28``` so our neural network has a layer which flattens the input, which is followed by a linear layer of input size ```28x28``` and an output size of ```128```. Finally, this is followed by a ```ReLU``` for the activation.
Here the structured data is not pre-loaded as it would be typically too large to load in one step. Therefore the path to the directory in which it is stored is provided along with the data type (for now only 'images' supported). The images are then loaded in batches using PyTorch's dataloader. Note that here again the key given in the ```unstructured_data``` dictionary must match the name it is given in the formula, in this case ```'numbers'```. Similarly the keys of the ```deep_models_dict``` must also match the names in the formula, in this case ```'dnn'```
```
# define distribution and the formula for the distibutional parameter
distribution = 'Normal'
formulas = {'loc': '~ -1 + spline(x1, bs="bs", df=10) + x2 + dnn(numbers) + spline(x3, bs="bs", df=10)',
'scale': '~1'
}
# define the deep neural networks' architectures and output shapes used in the above formula
deep_models_dict = {
'dnn': {
'model': nn.Sequential(nn.Flatten(1, -1),
nn.Linear(28*28,128),
nn.ReLU()),
'output_shape': 128},
}
# define your training hyperparameters
train_parameters = {
'batch_size': 8000,
'epochs': 1000,
'degrees_of_freedom': {'loc':9.6, 'scale':9.6},
'optimizer' : optim.Adam,
'val_split': 0.15,
'early_stop_epsilon': 0.001,
'dropout_rate': 0.01
}
# provide the location and datatype of the unstructured data
unstructured_data = {
'numbers' : {
'path' : '../data/mnist_data/mnist_images',
'datatype' : 'image'
}
}
# define output directory
output_dir = './outputs'
```
### Initialization
The sddr instance is initialized with the parameters given by the user in the previous step:
```
sddr = Sddr(output_dir=output_dir,
distribution=distribution,
formulas=formulas,
deep_models_dict=deep_models_dict,
train_parameters=train_parameters,
)
```
### Training
The sddr network is trained with the data defined above and the loss curve is plotted.
```
sddr.train(structured_data=data,
target="y_gen",
unstructured_data = unstructured_data,
plot=True)
```
### Evaluation - Visualizing the partial effects
In this case the data is assumed to follow a normal distribution, in which case two distributional parameters, loc and scale, need to be estimated. Below we plot the partial effects of each smooth term.
Remember the partial effects are computed by: partial effect = smooth_features * coefs (weights)
In other words the smoothing terms are multiplied with the weights of the Structured Head. We use the partial effects to interpret whether our model has learned correctly.
```
partial_effects_loc = sddr.eval('loc',plot=True)
partial_effects_scale = sddr.eval('scale',plot=True)
```
As we can see the distributional parameter loc has two parial effects, one sinusoidal and one quadratic. The parameter scale expectedly has no partial effect since the formula only includes an intercept.
Next we retrieve our ground truth data and compare it with the model's estimation
```
# compare prediction of neural network with ground truth
data_pred = data.loc[:,:]
ground_truth = data.loc[:,'y_gen']
# predict returns partial effects and a distributional layer that gives statistical information about the prediction
distribution_layer, partial_effect = sddr.predict(data_pred,
clipping=True,
plot=False,
unstructured_data = unstructured_data)
# retrieve the mean and variance of the distributional layer
predicted_mean = distribution_layer.loc[:,:].T
predicted_variance = distribution_layer.scale[0]
# and plot the result
plt.scatter(ground_truth, predicted_mean)
print(f"Predicted variance for first sample: {predicted_variance}")
```
The comparison shows that for most samples the predicted and true values are directly propotional.
Next we want to check if the model learned the correct correspondence of images and numbers
```
# we create a copy of our original structured data where we set all inputs but the images to be zero
data_pred_copy = data.copy()
data_pred_copy.loc[:,'x1'] = 0
data_pred_copy.loc[:,'x2'] = 0
data_pred_copy.loc[:,'x3'] = 0
# and make a prediction using only the images
distribution_layer, partial_effect = sddr.predict(data_pred_copy,
clipping=True,
plot=False,
unstructured_data = unstructured_data)
# add the predicted mean value to our tabular data
data_pred_copy['predicted_number'] = distribution_layer.loc[:,:].numpy().flatten()
# and compare the true number on the images with the predicted number
ax = sns.boxplot(x="y_true", y="predicted_number", data=data_pred_copy)
ax.set_xlabel("true number");
ax.set_ylabel("predicted latent effect of number");
```
Observing the boxplot figure we see that as the true values, i.e. numbers depicted on images, are increasing, so too are the medians of the predicted distributions. Therefore the partial effect of the neural network is directly correlated with the number depicted in the MNIST images, proving that our neural network, though simple, has learned from the unstructured data.
| true |
code
| 0.600657 | null | null | null | null |
|
```
# Copyright 2021 Google LLC
# Use of this source code is governed by an MIT-style
# license that can be found in the LICENSE file or at
# https://opensource.org/licenses/MIT.
# Author(s): Kevin P. Murphy ([email protected]) and Mahmoud Soliman ([email protected])
```
<a href="https://opensource.org/licenses/MIT" target="_parent"><img src="https://img.shields.io/github/license/probml/pyprobml"/></a>
<a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/notebooks/figures//chapter16_figures.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Cloning the pyprobml repo
```
!git clone https://github.com/probml/pyprobml
%cd pyprobml/scripts
```
# Installing required software (This may take few minutes)
```
!apt-get install octave -qq > /dev/null
!apt-get install liboctave-dev -qq > /dev/null
%%capture
%load_ext autoreload
%autoreload 2
DISCLAIMER = 'WARNING : Editing in VM - changes lost after reboot!!'
from google.colab import files
def interactive_script(script, i=True):
if i:
s = open(script).read()
if not s.split('\n', 1)[0]=="## "+DISCLAIMER:
open(script, 'w').write(
f'## {DISCLAIMER}\n' + '#' * (len(DISCLAIMER) + 3) + '\n\n' + s)
files.view(script)
%run $script
else:
%run $script
def show_image(img_path):
from google.colab.patches import cv2_imshow
import cv2
img = cv2.imread(img_path, cv2.IMREAD_UNCHANGED)
img=cv2.resize(img,(600,600))
cv2_imshow(img)
```
## Figure 16.1:<a name='16.1'></a> <a name='fig:knn'></a>
(a) Illustration of a $K$-nearest neighbors classifier in 2d for $K=5$. The nearest neighbors of test point $\mathbf x $ have labels $\ 1, 1, 1, 0, 0\ $, so we predict $p(y=1|\mathbf x , \mathcal D ) = 3/5$. (b) Illustration of the Voronoi tesselation induced by 1-NN. Adapted from Figure 4.13 of <a href='#Duda01'>[DHS01]</a> .
Figure(s) generated by [knn_voronoi_plot.py](https://github.com/probml/pyprobml/blob/master/scripts/knn_voronoi_plot.py)
```
interactive_script("knn_voronoi_plot.py")
```
## Figure 16.2:<a name='16.2'></a> <a name='knnThreeClass'></a>
Decision boundaries induced by a KNN classifier. (a) $K=1$. (b) $K=2$. (c) $K=5$. (d) Train and test error vs $K$.
Figure(s) generated by [knn_classify_demo.py](https://github.com/probml/pyprobml/blob/master/scripts/knn_classify_demo.py)
```
interactive_script("knn_classify_demo.py")
```
## Figure 16.3:<a name='16.3'></a> <a name='curse'></a>
Illustration of the curse of dimensionality. (a) We embed a small cube of side $s$ inside a larger unit cube. (b) We plot the edge length of a cube needed to cover a given volume of the unit cube as a function of the number of dimensions. Adapted from Figure 2.6 from <a href='#HastieBook'>[HTF09]</a> .
Figure(s) generated by [curse_dimensionality.py](https://github.com/probml/pyprobml/blob/master/scripts/curse_dimensionality.py)
```
interactive_script("curse_dimensionality.py")
```
## Figure 16.4:<a name='16.4'></a> <a name='fig:LCA'></a>
Illustration of latent coincidence analysis (LCA) as a directed graphical model. The inputs $\mathbf x , \mathbf x ' \in \mathbb R ^D$ are mapped into Gaussian latent variables $\mathbf z , \mathbf z ' \in \mathbb R ^L$ via a linear mapping $\mathbf W $. If the two latent points coincide (within length scale $\kappa $) then we set the similarity label to $y=1$, otherwise we set it to $y=0$. From Figure 1 of <a href='#Der2012'>[ML12]</a> . Used with kind permission of Lawrence Saul.
```
show_image("/content/pyprobml/notebooks/figures/images/LCA-PGM.png")
```
## Figure 16.5:<a name='16.5'></a> <a name='fig:tripletNet'></a>
Networks for deep metric learning. (a) Siamese network. (b) Triplet network. From Figure 5 of <a href='#Kaya2019'>[MH19]</a> . Used with kind permission of Mahmut Kaya. .
```
show_image("/content/pyprobml/notebooks/figures/images/siameseNet.png")
show_image("/content/pyprobml/notebooks/figures/images/tripletNet.png")
```
## Figure 16.6:<a name='16.6'></a> <a name='fig:tripletBound'></a>
Speeding up triplet loss minimization. (a) Illustration of hard vs easy negatives. Here $a$ is the anchor point, $p$ is a positive point, and $n_i$ are negative points. Adapted from Figure 4 of <a href='#Kaya2019'>[MH19]</a> . (b) Standard triplet loss would take $8 \times 3 \times 4 = 96$ calculations, whereas using a proxy loss (with one proxy per class) takes $8 \times 2 = 16$ calculations. From Figure 1 of <a href='#Do2019cvpr'>[Tha+19]</a> . Used with kind permission of Gustavo Cerneiro.
```
show_image("/content/pyprobml/notebooks/figures/images/hard-negative-mining.png")
show_image("/content/pyprobml/notebooks/figures/images/tripletBound.png")
```
## Figure 16.7:<a name='16.7'></a> <a name='fig:SEC'></a>
Adding spherical embedding constraint to a deep metric learning method. Used with kind permission of Dingyi Zhang.
```
show_image("/content/pyprobml/notebooks/figures/images/SEC.png")
```
## Figure 16.8:<a name='16.8'></a> <a name='smoothingKernels'></a>
A comparison of some popular normalized kernels.
Figure(s) generated by [smoothingKernelPlot.m](https://github.com/probml/pmtk3/blob/master/demos/smoothingKernelPlot.m)
```
!octave -W smoothingKernelPlot.m >> _
```
## Figure 16.9:<a name='16.9'></a> <a name='parzen'></a>
A nonparametric (Parzen) density estimator in 1d estimated from 6 data points, denoted by x. Top row: uniform kernel. Bottom row: Gaussian kernel. Left column: bandwidth parameter $h=1$. Right column: bandwidth parameter $h=2$. Adapted from http://en.wikipedia.org/wiki/Kernel_density_estimation .
Figure(s) generated by [Kernel_density_estimation](http://en.wikipedia.org/wiki/Kernel_density_estimation) [parzen_window_demo2.py](https://github.com/probml/pyprobml/blob/master/scripts/parzen_window_demo2.py)
```
interactive_script("parzen_window_demo2.py")
```
## Figure 16.10:<a name='16.10'></a> <a name='kernelRegression'></a>
An example of kernel regression in 1d using a Gaussian kernel.
Figure(s) generated by [kernelRegressionDemo.m](https://github.com/probml/pmtk3/blob/master/demos/kernelRegressionDemo.m)
```
!octave -W kernelRegressionDemo.m >> _
```
## References:
<a name='Duda01'>[DHS01]</a> R. O. Duda, P. E. Hart and D. G. Stork. "Pattern Classification". (2001).
<a name='HastieBook'>[HTF09]</a> T. Hastie, R. Tibshirani and J. Friedman. "The Elements of Statistical Learning". (2009).
<a name='Kaya2019'>[MH19]</a> K. Mahmut and B. HasanSakir. "Deep Metric Learning: A Survey". In: Symmetry (2019).
<a name='Der2012'>[ML12]</a> D. Matthew and S. LawrenceK. "Latent Coincidence Analysis: A Hidden Variable Model forDistance Metric Learning". (2012).
<a name='Do2019cvpr'>[Tha+19]</a> D. Thanh-Toan, T. Toan, R. Ian, K. Vijay, H. Tuan and C. Gustavo. "A Theoretically Sound Upper Bound on the Triplet Loss forImproving the Efficiency of Deep Distance Metric Learning". (2019).
| true |
code
| 0.567817 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
```
### loading dataset
```
data = pd.read_csv("student-data.csv")
data.head()
data.shape
type(data)
```
### Exploratory data analysis
```
import matplotlib.pyplot as plt
import seaborn as sns
a = data.plot()
data.info()
data.isnull().sum()
a = sns.heatmap(data.isnull(),cmap='Blues')
a = sns.heatmap(data.isnull(),cmap='Blues',yticklabels=False)
```
#### this indicates that we have no any null values in the dataset
```
a = sns.heatmap(data.isna(),yticklabels=False)
```
#### this heatmap indicates that we have no any 'NA' values in the dataset
```
sns.set(style='darkgrid')
sns.countplot(data=data,x='reason')
```
This indicates the count for choosing school of various reasons.
A count plot can be thought of as a histogram across a categorical, instead of quantitative, variable.
```
data.head(7)
```
calculating total passed students
```
passed = data.loc[data.passed == 'yes']
passed.shape
tot_passed=passed.shape[0]
print('total passed students is: {} '.format(tot_passed))
```
calculating total failed students
```
failed = data.loc[data.passed == 'no']
print('total failed students is: {}'.format(failed.shape[0]))
```
### Feature Engineering
```
data.head()
```
To identity feature and target variable lets first do some feature engineering stuff!
```
data.columns
data.columns[-1]
```
Here 'passed' is our target variable. Since in this system we need to develop the model that will predict the likelihood that a given student will pass, quantifying whether an intervention is necessary.
```
target = data.columns[-1]
data.columns[:-1]
#initially taking all columns as our feature variables
feature = list(data.columns[:-1])
data[target].head()
data[feature].head()
```
Now taking feature and target data in seperate dataframe
```
featuredata = data[feature]
targetdata = data[target]
```
Now we need to convert several non-numeric columns like 'internet' into numerical form for the model to process
```
def preprocess_features(X):
output = pd.DataFrame(index = X.index)
for col, col_data in X.iteritems():
if col_data.dtype == object:
col_data = col_data.replace(['yes', 'no'], [1, 0])
if col_data.dtype == object:
col_data = pd.get_dummies(col_data, prefix = col)
output = output.join(col_data)
return output
featuredata = preprocess_features(featuredata)
type(featuredata)
featuredata.head()
featuredata.drop(['address_R','sex_F'],axis=1,inplace=True)
featuredata.columns
featuredata.drop(['famsize_GT3','Pstatus_A',],axis=1,inplace=True)
```
### MODEL IMPLEMENTATION
## Decision tree
```
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
model=DecisionTreeClassifier()
X_train, X_test, y_train, y_test = train_test_split(featuredata, targetdata, test_size=0.33, random_state=6)
model.fit(X_train,y_train)
from sklearn.metrics import accuracy_score
predictions = model.predict(X_test)
accuracy_score(y_test,predictions)*100
```
## K-Nearest Neighbours
```
from sklearn.neighbors import KNeighborsClassifier
new_classifier = KNeighborsClassifier(n_neighbors=7)
new_classifier.fit(X_train,y_train)
predictions2 = new_classifier.predict(X_test)
accuracy_score(y_test,predictions2)*100
```
## SVM
```
from sklearn import svm
clf = svm.SVC(random_state=6)
clf.fit(featuredata,targetdata)
clf.score(featuredata,targetdata)
predictions3= clf.predict(X_test)
accuracy_score(y_test,predictions3)*100
```
## Model application areas
#### KNN
KNN: k-NN is often used in search applications where you are looking for “similar” items; that is, when your task is some form of “find items similar to this one”. The way you measure similarity is by creating a vector representation of the items, and then compare the vectors using an appropriate distance metric (like the Euclidean distance, for example).
The biggest use case of k-NN search might be Recommender Systems. If you know a user likes a particular item, then you can recommend similar items for them.
KNN strength: effective for larger datasets, robust to noisy training data
KNN weakness: need to determine value of k, computation cost is high.
#### Decision tree
Decision Tree: Can handle both numerical and categorical data.
Decision tree strength: Decision trees implicitly perform feature selection, require relatively little effort from users for data preparation, easy to interpret and explain to executives.
Decision tree weakness: Over Fitting, not fit for continuous variables.
#### SVM
SVM: SVM classify parts of the image as a face and non-face and create a square boundary around the face(Facial recognization).
We use SVMs to recognize handwritten characters used widely(Handwritten recognization).
Strengths: SVM's can model non-linear decision boundaries, and there are many kernels to choose from. They are also fairly robust against overfitting, especially in high-dimensional space.
Weaknesses: However, SVM's are memory intensive, trickier to tune due to the importance of picking the right kernel, and don't scale well to larger datasets.
## Choosing the best model
In this case, I will be using the SVM model to predict the outcomes. 80.15% of accuracy is achieved in SVM in our case.
SVM is a supervised machine learning algorithm which can be used for classification or regression problems.
It uses a technique called the kernel trick to transform your data and then based on these transformations it finds an optimal boundary between the possible outputs.
| true |
code
| 0.343713 | null | null | null | null |
|
# The Binomial Distribution
This notebook is part of [Bite Size Bayes](https://allendowney.github.io/BiteSizeBayes/), an introduction to probability and Bayesian statistics using Python.
Copyright 2020 Allen B. Downey
License: [Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/)
The following cell downloads `utils.py`, which contains some utility function we'll need.
```
from os.path import basename, exists
def download(url):
filename = basename(url)
if not exists(filename):
from urllib.request import urlretrieve
local, _ = urlretrieve(url, filename)
print('Downloaded ' + local)
download('https://github.com/AllenDowney/BiteSizeBayes/raw/master/utils.py')
```
If everything we need is installed, the following cell should run with no error messages.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## The Euro problem revisited
In [a previous notebook](https://colab.research.google.com/github/AllenDowney/BiteSizeBayes/blob/master/07_euro.ipynb) I presented a problem from David MacKay's book, [*Information Theory, Inference, and Learning Algorithms*](http://www.inference.org.uk/mackay/itila/p0.html):
> A statistical statement appeared in The Guardian on
Friday January 4, 2002:
>
> >"When spun on edge 250 times, a Belgian one-euro coin came
up heads 140 times and tails 110. ‘It looks very suspicious
to me’, said Barry Blight, a statistics lecturer at the London
School of Economics. ‘If the coin were unbiased the chance of
getting a result as extreme as that would be less than 7%’."
>
> But [asks MacKay] do these data give evidence that the coin is biased rather than fair?
To answer this question, we made these modeling decisions:
* If you spin a coin on edge, there is some probability, $x$, that it will land heads up.
* The value of $x$ varies from one coin to the next, depending on how the coin is balanced and other factors.
We started with a uniform prior distribution for $x$, then updated it 250 times, once for each spin of the coin. Then we used the posterior distribution to compute the MAP, posterior mean, and a credible interval.
But we never really answered MacKay's question.
In this notebook, I introduce the binomial distribution and we will use it to solve the Euro problem more efficiently. Then we'll get back to MacKay's question and see if we can find a more satisfying answer.
## Binomial distribution
Suppose I tell you that a coin is "fair", that is, the probability of heads is 50%. If you spin it twice, there are four outcomes: `HH`, `HT`, `TH`, and `TT`.
All four outcomes have the same probability, 25%. If we add up the total number of heads, it is either 0, 1, or 2. The probability of 0 and 2 is 25%, and the probability of 1 is 50%.
More generally, suppose the probability of heads is `p` and we spin the coin `n` times. What is the probability that we get a total of `k` heads?
The answer is given by the binomial distribution:
$P(k; n, p) = \binom{n}{k} p^k (1-p)^{n-k}$
where $\binom{n}{k}$ is the [binomial coefficient](https://en.wikipedia.org/wiki/Binomial_coefficient), usually pronounced "n choose k".
We can compute this expression ourselves, but we can also use the SciPy function `binom.pmf`:
```
from scipy.stats import binom
n = 2
p = 0.5
ks = np.arange(n+1)
a = binom.pmf(ks, n, p)
a
```
If we put this result in a Series, the result is the distribution of `k` for the given values of `n` and `p`.
```
pmf_k = pd.Series(a, index=ks)
pmf_k
```
The following function computes the binomial distribution for given values of `n` and `p`:
```
def make_binomial(n, p):
"""Make a binomial PMF.
n: number of spins
p: probability of heads
returns: Series representing a PMF
"""
ks = np.arange(n+1)
a = binom.pmf(ks, n, p)
pmf_k = pd.Series(a, index=ks)
return pmf_k
```
And here's what it looks like with `n=250` and `p=0.5`:
```
pmf_k = make_binomial(n=250, p=0.5)
pmf_k.plot()
plt.xlabel('Number of heads (k)')
plt.ylabel('Probability')
plt.title('Binomial distribution');
```
The most likely value in this distribution is 125:
```
pmf_k.idxmax()
```
But even though it is the most likely value, the probability that we get exactly 125 heads is only about 5%.
```
pmf_k[125]
```
In MacKay's example, we got 140 heads, which is less likely than 125:
```
pmf_k[140]
```
In the article MacKay quotes, the statistician says, ‘If the coin were unbiased the chance of getting a result as extreme as that would be less than 7%’.
We can use the binomial distribution to check his math. The following function takes a PMF and computes the total probability of values greater than or equal to `threshold`.
```
def prob_ge(pmf, threshold):
"""Probability of values greater than a threshold.
pmf: Series representing a PMF
threshold: value to compare to
returns: probability
"""
ge = (pmf.index >= threshold)
total = pmf[ge].sum()
return total
```
Here's the probability of getting 140 heads or more:
```
prob_ge(pmf_k, 140)
```
It's about 3.3%, which is less than 7%. The reason is that the statistician includes all values "as extreme as" 140, which includes values less than or equal to 110, because 140 exceeds the expected value by 15 and 110 falls short by 15.
The probability of values less than or equal to 110 is also 3.3%,
so the total probability of values "as extreme" as 140 is about 7%.
The point of this calculation is that these extreme values are unlikely if the coin is fair.
That's interesting, but it doesn't answer MacKay's question. Let's see if we can.
## Estimating x
As promised, we can use the binomial distribution to solve the Euro problem more efficiently. Let's start again with a uniform prior:
```
xs = np.arange(101) / 100
uniform = pd.Series(1, index=xs)
uniform /= uniform.sum()
```
We can use `binom.pmf` to compute the likelihood of the data for each possible value of $x$.
```
k = 140
n = 250
xs = uniform.index
likelihood = binom.pmf(k, n, p=xs)
```
Now we can do the Bayesian update in the usual way, multiplying the priors and likelihoods,
```
posterior = uniform * likelihood
```
Computing the total probability of the data,
```
total = posterior.sum()
total
```
And normalizing the posterior,
```
posterior /= total
```
Here's what it looks like.
```
posterior.plot(label='Uniform')
plt.xlabel('Probability of heads (x)')
plt.ylabel('Probability')
plt.title('Posterior distribution, uniform prior')
plt.legend()
```
**Exercise:** Based on what we know about coins in the real world, it doesn't seem like every value of $x$ is equally likely. I would expect values near 50% to be more likely and values near the extremes to be less likely.
In Notebook 7, we used a triangle prior to represent this belief about the distribution of $x$. The following code makes a PMF that represents a triangle prior.
```
ramp_up = np.arange(50)
ramp_down = np.arange(50, -1, -1)
a = np.append(ramp_up, ramp_down)
triangle = pd.Series(a, index=xs)
triangle /= triangle.sum()
```
Update this prior with the likelihoods we just computed and plot the results.
```
# Solution
posterior2 = triangle * likelihood
total2 = posterior2.sum()
total2
# Solution
posterior2 /= total2
# Solution
posterior.plot(label='Uniform')
posterior2.plot(label='Triangle')
plt.xlabel('Probability of heads (x)')
plt.ylabel('Probability')
plt.title('Posterior distribution, uniform prior')
plt.legend();
```
## Evidence
Finally, let's get back to MacKay's question: do these data give evidence that the coin is biased rather than fair?
I'll use a Bayes table to answer this question, so here's the function that makes one:
```
def make_bayes_table(hypos, prior, likelihood):
"""Make a Bayes table.
hypos: sequence of hypotheses
prior: prior probabilities
likelihood: sequence of likelihoods
returns: DataFrame
"""
table = pd.DataFrame(index=hypos)
table['prior'] = prior
table['likelihood'] = likelihood
table['unnorm'] = table['prior'] * table['likelihood']
prob_data = table['unnorm'].sum()
table['posterior'] = table['unnorm'] / prob_data
return table
```
Recall that data, $D$, is considered evidence in favor of a hypothesis, `H`, if the posterior probability is greater than the prior, that is, if
$P(H|D) > P(H)$
For this example, I'll call the hypotheses `fair` and `biased`:
```
hypos = ['fair', 'biased']
```
And just to get started, I'll assume that the prior probabilities are 50/50.
```
prior = [0.5, 0.5]
```
Now we have to compute the probability of the data under each hypothesis.
If the coin is fair, the probability of heads is 50%, and we can compute the probability of the data (140 heads out of 250 spins) using the binomial distribution:
```
k = 140
n = 250
like_fair = binom.pmf(k, n, p=0.5)
like_fair
```
So that's the probability of the data, given that the coin is fair.
But if the coin is biased, what's the probability of the data? Well, that depends on what "biased" means.
If we know ahead of time that "biased" means the probability of heads is 56%, we can use the binomial distribution again:
```
like_biased = binom.pmf(k, n, p=0.56)
like_biased
```
Now we can put the likelihoods in the Bayes table:
```
likes = [like_fair, like_biased]
make_bayes_table(hypos, prior, likes)
```
The posterior probability of `biased` is about 86%, so the data is evidence that the coin is biased, at least for this definition of "biased".
But we used the data to define the hypothesis, which seems like cheating. To be fair, we should define "biased" before we see the data.
## Uniformly distributed bias
Suppose "biased" means that the probability of heads is anything except 50%, and all other values are equally likely.
We can represent that definition by making a uniform distribution and removing 50%.
```
biased_uniform = uniform.copy()
biased_uniform[50] = 0
biased_uniform /= biased_uniform.sum()
```
Now, to compute the probability of the data under this hypothesis, we compute the probability of the data for each value of $x$.
```
xs = biased_uniform.index
likelihood = binom.pmf(k, n, xs)
```
And then compute the total probability in the usual way:
```
like_uniform = np.sum(biased_uniform * likelihood)
like_uniform
```
So that's the probability of the data under the "biased uniform" hypothesis.
Now we make a Bayes table that compares the hypotheses `fair` and `biased uniform`:
```
hypos = ['fair', 'biased uniform']
likes = [like_fair, like_uniform]
make_bayes_table(hypos, prior, likes)
```
Using this definition of `biased`, the posterior is less than the prior, so the data are evidence that the coin is *fair*.
In this example, the data might support the fair hypothesis or the biased hypothesis, depending on the definition of "biased".
**Exercise:** Suppose "biased" doesn't mean every value of $x$ is equally likely. Maybe values near 50% are more likely and values near the extremes are less likely. In the previous exercise we created a PMF that represents a triangle-shaped distribution.
We can use it to represent an alternative definition of "biased":
```
biased_triangle = triangle.copy()
biased_triangle[50] = 0
biased_triangle /= biased_triangle.sum()
```
Compute the total probability of the data under this definition of "biased" and use a Bayes table to compare it with the fair hypothesis.
Is the data evidence that the coin is biased?
```
# Solution
like_triangle = np.sum(biased_triangle * likelihood)
like_triangle
# Solution
hypos = ['fair', 'biased triangle']
likes = [like_fair, like_triangle]
make_bayes_table(hypos, prior, likes)
# Solution
# For this definition of "biased",
# the data are slightly in favor of the fair hypothesis.
```
## Bayes factor
In the previous section, we used a Bayes table to see whether the data are in favor of the fair or biased hypothesis.
I assumed that the prior probabilities were 50/50, but that was an arbitrary choice.
And it was unnecessary, because we don't really need a Bayes table to say whether the data favor one hypothesis or another: we can just look at the likelihoods.
Under the first definition of biased, `x=0.56`, the likelihood of the biased hypothesis is higher:
```
like_fair, like_biased
```
Under the biased uniform definition, the likelihood of the fair hypothesis is higher.
```
like_fair, like_uniform
```
The ratio of these likelihoods tells us which hypothesis the data support.
If the ratio is less than 1, the data support the second hypothesis:
```
like_fair / like_biased
```
If the ratio is greater than 1, the data support the first hypothesis:
```
like_fair / like_uniform
```
This likelihood ratio is called a [Bayes factor](https://en.wikipedia.org/wiki/Bayes_factor); it provides a concise way to present the strength of a dataset as evidence for or against a hypothesis.
## Summary
In this notebook I introduced the binomial disrtribution and used it to solve the Euro problem more efficiently.
Then we used the results to (finally) answer the original version of the Euro problem, considering whether the data support the hypothesis that the coin is fair or biased. We found that the answer depends on how we define "biased". And we summarized the results using a Bayes factor, which quantifies the strength of the evidence.
[In the next notebook](https://colab.research.google.com/github/AllenDowney/BiteSizeBayes/blob/master/13_price.ipynb) we'll start on a new problem based on the television game show *The Price Is Right*.
## Exercises
**Exercise:** In preparation for an alien invasion, the Earth Defense League has been working on new missiles to shoot down space invaders. Of course, some missile designs are better than others; let's assume that each design has some probability of hitting an alien ship, `x`.
Based on previous tests, the distribution of `x` in the population of designs is roughly uniform between 10% and 40%.
Now suppose the new ultra-secret Alien Blaster 9000 is being tested. In a press conference, a Defense League general reports that the new design has been tested twice, taking two shots during each test. The results of the test are confidential, so the general won't say how many targets were hit, but they report: "The same number of targets were hit in the two tests, so we have reason to think this new design is consistent."
Is this data good or bad; that is, does it increase or decrease your estimate of `x` for the Alien Blaster 9000?
Plot the prior and posterior distributions, and use the following function to compute the prior and posterior means.
```
def pmf_mean(pmf):
"""Compute the mean of a PMF.
pmf: Series representing a PMF
return: float
"""
return np.sum(pmf.index * pmf)
# Solution
xs = np.linspace(0.1, 0.4)
prior = pd.Series(1, index=xs)
prior /= prior.sum()
# Solution
likelihood = xs**2 + (1-xs)**2
# Solution
posterior = prior * likelihood
posterior /= posterior.sum()
# Solution
prior.plot(color='gray', label='prior')
posterior.plot(label='posterior')
plt.xlabel('Probability of success (x)')
plt.ylabel('Probability')
plt.ylim(0, 0.027)
plt.title('Distribution of before and after testing')
plt.legend();
# Solution
pmf_mean(prior), pmf_mean(posterior)
# With this prior, being "consistent" is more likely
# to mean "consistently bad".
```
| true |
code
| 0.681806 | null | null | null | null |
|
# Fairseq in Amazon SageMaker: Pre-trained English to French translation model
In this notebook, we will show you how to serve an English to French translation model using pre-trained model provided by the [Fairseq toolkit](https://github.com/pytorch/fairseq)
## Permissions
Running this notebook requires permissions in addition to the regular SageMakerFullAccess permissions. This is because it creates new repositories in Amazon ECR. The easiest way to add these permissions is simply to add the managed policy AmazonEC2ContainerRegistryFullAccess to the role that you used to start your notebook instance. There's no need to restart your notebook instance when you do this, the new permissions will be available immediately.
## Download pre-trained model
Fairseq maintains their pre-trained models [here](https://github.com/pytorch/fairseq/blob/master/examples/translation/README.md). We will use the model that was pre-trained on the [WMT14 English-French](http://statmt.org/wmt14/translation-task.html#Download) dataset. As the models are archived in .bz2 format, we need to convert them to .tar.gz as this is the format supported by Amazon SageMaker.
### Convert archive
```
%%sh
wget https://dl.fbaipublicfiles.com/fairseq/models/wmt14.v2.en-fr.fconv-py.tar.bz2
tar xvjf wmt14.v2.en-fr.fconv-py.tar.bz2 > /dev/null
cd wmt14.en-fr.fconv-py
mv model.pt checkpoint_best.pt
tar czvf wmt14.en-fr.fconv-py.tar.gz checkpoint_best.pt dict.en.txt dict.fr.txt bpecodes README.md > /dev/null
```
The pre-trained model has been downloaded and converted. The next step is upload the data to Amazon S3 in order to make it available for running the inference.
### Upload data to Amazon S3
```
import sagemaker
sagemaker_session = sagemaker.Session()
region = sagemaker_session.boto_session.region_name
account = sagemaker_session.boto_session.client("sts").get_caller_identity().get("Account")
bucket = sagemaker_session.default_bucket()
prefix = "sagemaker/DEMO-pytorch-fairseq/pre-trained-models"
role = sagemaker.get_execution_role()
trained_model_location = sagemaker_session.upload_data(
path="wmt14.en-fr.fconv-py/wmt14.en-fr.fconv-py.tar.gz", bucket=bucket, key_prefix=prefix
)
```
## Build Fairseq serving container
Next we need to register a Docker image in Amazon SageMaker that will contain the Fairseq code and that will be pulled at inference time to perform the of the precitions from the pre-trained model we downloaded.
```
%%sh
chmod +x create_container.sh
./create_container.sh pytorch-fairseq-serve
```
The Fairseq serving image has been pushed into Amazon ECR, the registry from which Amazon SageMaker will be able to pull that image and launch both training and prediction.
## Hosting the pre-trained model for inference
We first needs to define a base JSONPredictor class that will help us with sending predictions to the model once it's hosted on the Amazon SageMaker endpoint.
```
from sagemaker.predictor import RealTimePredictor, json_serializer, json_deserializer
class JSONPredictor(RealTimePredictor):
def __init__(self, endpoint_name, sagemaker_session):
super(JSONPredictor, self).__init__(
endpoint_name, sagemaker_session, json_serializer, json_deserializer
)
```
We can now use the Model class to deploy the model artificats (the pre-trained model), and deploy it on a CPU instance. Let's use a `ml.m5.xlarge`.
```
from sagemaker import Model
algorithm_name = "pytorch-fairseq-serve"
image = "{}.dkr.ecr.{}.amazonaws.com/{}:latest".format(account, region, algorithm_name)
model = Model(
model_data=trained_model_location,
role=role,
image=image,
predictor_cls=JSONPredictor,
)
predictor = model.deploy(initial_instance_count=1, instance_type="ml.m5.xlarge")
```
Now it's your time to play. Input a sentence in English and get the translation in French by simply calling predict.
```
import html
result = predictor.predict("I love translation")
# Some characters are escaped HTML-style requiring to unescape them before printing
print(html.unescape(result))
```
Once you're done with getting predictions, remember to shut down your endpoint as you no longer need it.
## Delete endpoint
```
model.sagemaker_session.delete_endpoint(predictor.endpoint)
```
Voila! For more information, you can check out the [Fairseq toolkit homepage](https://github.com/pytorch/fairseq).
| true |
code
| 0.51562 | null | null | null | null |
|
### Tutorial: Parameterized Hypercomplex Multiplication (PHM) Layer
#### Author: Eleonora Grassucci
Original paper: Beyond Fully-Connected Layers with Quaternions: Parameterization of Hypercomplex Multiplications with 1/n Parameters.
Aston Zhang, Yi Tay, Shuai Zhang, Alvin Chan, Anh Tuan Luu, Siu Cheung Hui, Jie Fu.
[ArXiv link](https://arxiv.org/pdf/2102.08597.pdf).
```
# Imports
import numpy as np
import math
import time
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
import torch.utils.data as Data
from torch.nn import init
# Check Pytorch version: torch.kron is available from 1.8.0
torch.__version__
# Define the PHM class
class PHM(nn.Module):
'''
Simple PHM Module, the only parameter is A, since S is passed from the trainset.
'''
def __init__(self, n, kernel_size, **kwargs):
super().__init__(**kwargs)
self.n = n
A = torch.empty((n-1, n, n))
self.A = nn.Parameter(A)
self.kernel_size = kernel_size
def forward(self, X, S):
H = torch.zeros((self.n*self.kernel_size, self.n*self.kernel_size))
# Sum of Kronecker products
for i in range(n-1):
H = H + torch.kron(self.A[i], S[i])
return torch.matmul(X, H.T)
```
### Learn the Hamilton product between two pure quaternions
A pure quaternion is a quaternion with scalar part equal to 0.
```
# Setup the training set
x = torch.FloatTensor([0, 1, 2, 3]).view(4, 1) # Scalar part equal to 0
W = torch.FloatTensor([[0,-1,-1,-1], [1,0,-1,1], [1,1,0,-1], [1,-1,1,0]]) # Scalar parts equal to 0
y = torch.matmul(W, x)
num_examples = 1000
batch_size = 1
X = torch.zeros((num_examples, 16))
S = torch.zeros((num_examples, 16))
Y = torch.zeros((num_examples, 16))
for i in range(num_examples):
x = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s1, s2, s3, s4 = torch.FloatTensor([0]*4), s[0:4], s[4:8], s[8:12]
s1 = s1.view(2,2)
s2 = s2.view(2,2)
s3 = s3.view(2,2)
s4 = s4.view(2,2)
s_1 = torch.cat([s1,-s2,-s3,-s4])
s_2 = torch.cat([s2,s1,-s4,s3])
s_3 = torch.cat([s3,s4,s1,-s2])
s_4 = torch.cat([s4,-s3,s2,s1])
W = torch.cat([s_1,s_2, s_3, s_4], dim=1)
x = torch.cat([torch.FloatTensor([0]*4), x])
s = torch.cat([torch.FloatTensor([0]*4), s])
x_mult = x.view(2, 8)
y = torch.matmul(x_mult, W.T)
y = y.view(16, )
X[i, :] = x
S[i, :] = s
Y[i, :] = y
X = torch.FloatTensor(X).view(num_examples, 16, 1)
S = torch.FloatTensor(S).view(num_examples, 16, 1)
Y = torch.FloatTensor(Y).view(num_examples, 16, 1)
data = torch.cat([X, S, Y], dim=2)
train_iter = torch.utils.data.DataLoader(data, batch_size=batch_size)
### Setup the test set
num_examples = 1
batch_size = 1
X = torch.zeros((num_examples, 16))
S = torch.zeros((num_examples, 16))
Y = torch.zeros((num_examples, 16))
for i in range(num_examples):
x = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s1, s2, s3, s4 = torch.FloatTensor([0]*4), s[0:4], s[4:8], s[8:12]
s1 = s1.view(2,2)
s2 = s2.view(2,2)
s3 = s3.view(2,2)
s4 = s4.view(2,2)
s_1 = torch.cat([s1,-s2,-s3,-s4])
s_2 = torch.cat([s2,s1,-s4,s3])
s_3 = torch.cat([s3,s4,s1,-s2])
s_4 = torch.cat([s4,-s3,s2,s1])
W = torch.cat([s_1,s_2, s_3, s_4], dim=1)
x = torch.cat([torch.FloatTensor([0]*4), x])
s = torch.cat([torch.FloatTensor([0]*4), s])
x_mult = x.view(2, 8)
y = torch.matmul(x_mult, W.T)
y = y.view(16, )
X[i, :] = x
S[i, :] = s
Y[i, :] = y
X = torch.FloatTensor(X).view(num_examples, 16, 1)
S = torch.FloatTensor(S).view(num_examples, 16, 1)
Y = torch.FloatTensor(Y).view(num_examples, 16, 1)
data = torch.cat([X, S, Y], dim=2)
test_iter = torch.utils.data.DataLoader(data, batch_size=batch_size)
# Define training function
def train(net, lr, phm=True):
# Squared loss
loss = nn.MSELoss()
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
for epoch in range(5):
for data in train_iter:
optimizer.zero_grad()
X = data[:, :, 0]
S = data[:, 4:, 1]
Y = data[:, :, 2]
if phm:
out = net(X.view(2, 8), S.view(3, 2, 2))
else:
out = net(X)
l = loss(out, Y.view(2, 8))
l.backward()
optimizer.step()
print(f'epoch {epoch + 1}, loss {float(l.sum() / batch_size):.6f}')
# Initialize model parameters
def weights_init_uniform(m):
m.A.data.uniform_(-0.07, 0.07)
# Create layer instance
n = 4
phm_layer = PHM(n, kernel_size=2)
phm_layer.apply(weights_init_uniform)
# Train the model
train(phm_layer, 0.005)
# Check parameters of the layer require grad
for name, param in phm_layer.named_parameters():
if param.requires_grad:
print(name, param.data)
# Take a look at the convolution performed on the test set
for data in test_iter:
X = data[:, :, 0]
S = data[:, 4:, 1]
Y = data[:, :, 2]
y_phm = phm_layer(X.view(2, 8), S.view(3, 2, 2))
print('Hamilton product result from test set:\n', Y.view(2, 8))
print('Performing Hamilton product learned by PHM:\n', y_phm)
# Check the PHC layer have learnt the proper algebra for the marix A
W = torch.FloatTensor([[0,-1,-1,-1], [1,0,-1,1], [1,1,0,-1], [1,-1,1,0]])
print('Ground-truth Hamilton product matrix:\n', W)
print()
print('Learned A in PHM:\n', phm_layer.A)
print()
print('Learned A sum in PHM:\n', sum(phm_layer.A).T)
```
| true |
code
| 0.73851 | null | null | null | null |
|
# Amazon Fine Food Reviews Analysis
Data Source: https://www.kaggle.com/snap/amazon-fine-food-reviews <br>
EDA: https://nycdatascience.com/blog/student-works/amazon-fine-foods-visualization/
The Amazon Fine Food Reviews dataset consists of reviews of fine foods from Amazon.<br>
Number of reviews: 568,454<br>
Number of users: 256,059<br>
Number of products: 74,258<br>
Timespan: Oct 1999 - Oct 2012<br>
Number of Attributes/Columns in data: 10
Attribute Information:
1. Id
2. ProductId - unique identifier for the product
3. UserId - unqiue identifier for the user
4. ProfileName
5. HelpfulnessNumerator - number of users who found the review helpful
6. HelpfulnessDenominator - number of users who indicated whether they found the review helpful or not
7. Score - rating between 1 and 5
8. Time - timestamp for the review
9. Summary - brief summary of the review
10. Text - text of the review
#### Objective:
Given a review, determine whether the review is positive (rating of 4 or 5) or negative (rating of 1 or 2).
<br>
[Q] How to determine if a review is positive or negative?<br>
<br>
[Ans] We could use Score/Rating. A rating of 4 or 5 can be cosnidered as a positive review. A rating of 1 or 2 can be considered as negative one. A review of rating 3 is considered nuetral and such reviews are ignored from our analysis. This is an approximate and proxy way of determining the polarity (positivity/negativity) of a review.
# [1]. Reading Data
## [1.1] Loading the data
The dataset is available in two forms
1. .csv file
2. SQLite Database
In order to load the data, We have used the SQLITE dataset as it is easier to query the data and visualise the data efficiently.
<br>
Here as we only want to get the global sentiment of the recommendations (positive or negative), we will purposefully ignore all Scores equal to 3. If the score is above 3, then the recommendation wil be set to "positive". Otherwise, it will be set to "negative".
```
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import sqlite3
import pandas as pd
import numpy as np
import nltk
import string
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import confusion_matrix
from sklearn import metrics
from sklearn.metrics import roc_curve, auc
from nltk.stem.porter import PorterStemmer
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.metrics import roc_auc_score
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import TruncatedSVD
from sklearn.cluster import KMeans
from wordcloud import WordCloud, STOPWORDS
import re
# Tutorial about Python regular expressions: https://pymotw.com/2/re/
import string
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from gensim.models import Word2Vec
from gensim.models import KeyedVectors
import pickle
from tqdm import tqdm
import os
from google.colab import drive
drive.mount('/content/drive')
# using SQLite Table to read data.
con = sqlite3.connect('drive/My Drive/database.sqlite')
# filtering only positive and negative reviews i.e.
# not taking into consideration those reviews with Score=3
# SELECT * FROM Reviews WHERE Score != 3 LIMIT 500000, will give top 500000 data points
# you can change the number to any other number based on your computing power
# filtered_data = pd.read_sql_query(""" SELECT * FROM Reviews WHERE Score != 3 LIMIT 500000""", con)
# for tsne assignment you can take 5k data points
filtered_data = pd.read_sql_query(""" SELECT * FROM Reviews WHERE Score != 3 LIMIT 200000""", con)
# Give reviews with Score>3 a positive rating(1), and reviews with a score<3 a negative rating(0).
def partition(x):
if x < 3:
return 0
return 1
#changing reviews with score less than 3 to be positive and vice-versa
actualScore = filtered_data['Score']
positiveNegative = actualScore.map(partition)
filtered_data['Score'] = positiveNegative
print("Number of data points in our data", filtered_data.shape)
filtered_data.head(3)
display = pd.read_sql_query("""
SELECT UserId, ProductId, ProfileName, Time, Score, Text, COUNT(*)
FROM Reviews
GROUP BY UserId
HAVING COUNT(*)>1
""", con)
print(display.shape)
display.head()
display[display['UserId']=='AZY10LLTJ71NX']
display['COUNT(*)'].sum()
```
# [2] Exploratory Data Analysis
## [2.1] Data Cleaning: Deduplication
It is observed (as shown in the table below) that the reviews data had many duplicate entries. Hence it was necessary to remove duplicates in order to get unbiased results for the analysis of the data. Following is an example:
```
display= pd.read_sql_query("""
SELECT *
FROM Reviews
WHERE Score != 3 AND UserId="AR5J8UI46CURR"
ORDER BY ProductID
""", con)
display.head()
```
As it can be seen above that same user has multiple reviews with same values for HelpfulnessNumerator, HelpfulnessDenominator, Score, Time, Summary and Text and on doing analysis it was found that <br>
<br>
ProductId=B000HDOPZG was Loacker Quadratini Vanilla Wafer Cookies, 8.82-Ounce Packages (Pack of 8)<br>
<br>
ProductId=B000HDL1RQ was Loacker Quadratini Lemon Wafer Cookies, 8.82-Ounce Packages (Pack of 8) and so on<br>
It was inferred after analysis that reviews with same parameters other than ProductId belonged to the same product just having different flavour or quantity. Hence in order to reduce redundancy it was decided to eliminate the rows having same parameters.<br>
The method used for the same was that we first sort the data according to ProductId and then just keep the first similar product review and delelte the others. for eg. in the above just the review for ProductId=B000HDL1RQ remains. This method ensures that there is only one representative for each product and deduplication without sorting would lead to possibility of different representatives still existing for the same product.
```
#Sorting data according to ProductId in ascending order
sorted_data=filtered_data.sort_values('ProductId', axis=0, ascending=True, inplace=False, kind='quicksort', na_position='last')
#Deduplication of entries
final=sorted_data.drop_duplicates(subset={"UserId","ProfileName","Time","Text"}, keep='first', inplace=False)
final.shape
#Checking to see how much % of data still remains
(final['Id'].size*1.0)/(filtered_data['Id'].size*1.0)*100
```
<b>Observation:-</b> It was also seen that in two rows given below the value of HelpfulnessNumerator is greater than HelpfulnessDenominator which is not practically possible hence these two rows too are removed from calcualtions
```
display= pd.read_sql_query("""
SELECT *
FROM Reviews
WHERE Score != 3 AND Id=44737 OR Id=64422
ORDER BY ProductID
""", con)
display.head()
final=final[final.HelpfulnessNumerator<=final.HelpfulnessDenominator]
#Before starting the next phase of preprocessing lets see the number of entries left
print(final.shape)
#How many positive and negative reviews are present in our dataset?
final['Score'].value_counts()
```
# [3] Preprocessing
## [3.1]. Preprocessing Review Text
Now that we have finished deduplication our data requires some preprocessing before we go on further with analysis and making the prediction model.
Hence in the Preprocessing phase we do the following in the order below:-
1. Begin by removing the html tags
2. Remove any punctuations or limited set of special characters like , or . or # etc.
3. Check if the word is made up of english letters and is not alpha-numeric
4. Check to see if the length of the word is greater than 2 (as it was researched that there is no adjective in 2-letters)
5. Convert the word to lowercase
6. Remove Stopwords
7. Finally Snowball Stemming the word (it was obsereved to be better than Porter Stemming)<br>
After which we collect the words used to describe positive and negative reviews
```
# printing some random reviews
sent_0 = final['Text'].values[0]
print(sent_0)
print("="*50)
sent_1000 = final['Text'].values[1000]
print(sent_1000)
print("="*50)
sent_1500 = final['Text'].values[1500]
print(sent_1500)
print("="*50)
sent_4900 = final['Text'].values[4900]
print(sent_4900)
print("="*50)
# remove urls from text python: https://stackoverflow.com/a/40823105/4084039
sent_0 = re.sub(r"http\S+", "", sent_0)
sent_1000 = re.sub(r"http\S+", "", sent_1000)
sent_150 = re.sub(r"http\S+", "", sent_1500)
sent_4900 = re.sub(r"http\S+", "", sent_4900)
print(sent_0)
# https://stackoverflow.com/questions/16206380/python-beautifulsoup-how-to-remove-all-tags-from-an-element
from bs4 import BeautifulSoup
soup = BeautifulSoup(sent_0, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_1000, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_1500, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_4900, 'lxml')
text = soup.get_text()
print(text)
# https://stackoverflow.com/a/47091490/4084039
import re
def decontracted(phrase):
# specific
phrase = re.sub(r"won't", "will not", phrase)
phrase = re.sub(r"can\'t", "can not", phrase)
# general
phrase = re.sub(r"n\'t", " not", phrase)
phrase = re.sub(r"\'re", " are", phrase)
phrase = re.sub(r"\'s", " is", phrase)
phrase = re.sub(r"\'d", " would", phrase)
phrase = re.sub(r"\'ll", " will", phrase)
phrase = re.sub(r"\'t", " not", phrase)
phrase = re.sub(r"\'ve", " have", phrase)
phrase = re.sub(r"\'m", " am", phrase)
return phrase
sent_1500 = decontracted(sent_1500)
print(sent_1500)
print("="*50)
#remove words with numbers python: https://stackoverflow.com/a/18082370/4084039
sent_0 = re.sub("\S*\d\S*", "", sent_0).strip()
print(sent_0)
#remove spacial character: https://stackoverflow.com/a/5843547/4084039
sent_1500 = re.sub('[^A-Za-z0-9]+', ' ', sent_1500)
print(sent_1500)
# https://gist.github.com/sebleier/554280
# we are removing the words from the stop words list: 'no', 'nor', 'not'
# <br /><br /> ==> after the above steps, we are getting "br br"
# we are including them into stop words list
# instead of <br /> if we have <br/> these tags would have revmoved in the 1st step
stopwords= set(['br', 'the', 'i', 'me', 'my', 'myself', 'we', 'our', 'ours', 'ourselves', 'you', "you're", "you've",\
"you'll", "you'd", 'your', 'yours', 'yourself', 'yourselves', 'he', 'him', 'his', 'himself', \
'she', "she's", 'her', 'hers', 'herself', 'it', "it's", 'its', 'itself', 'they', 'them', 'their',\
'theirs', 'themselves', 'what', 'which', 'who', 'whom', 'this', 'that', "that'll", 'these', 'those', \
'am', 'is', 'are', 'was', 'were', 'be', 'been', 'being', 'have', 'has', 'had', 'having', 'do', 'does', \
'did', 'doing', 'a', 'an', 'the', 'and', 'but', 'if', 'or', 'because', 'as', 'until', 'while', 'of', \
'at', 'by', 'for', 'with', 'about', 'against', 'between', 'into', 'through', 'during', 'before', 'after',\
'above', 'below', 'to', 'from', 'up', 'down', 'in', 'out', 'on', 'off', 'over', 'under', 'again', 'further',\
'then', 'once', 'here', 'there', 'when', 'where', 'why', 'how', 'all', 'any', 'both', 'each', 'few', 'more',\
'most', 'other', 'some', 'such', 'only', 'own', 'same', 'so', 'than', 'too', 'very', \
's', 't', 'can', 'will', 'just', 'don', "don't", 'should', "should've", 'now', 'd', 'll', 'm', 'o', 're', \
've', 'y', 'ain', 'aren', "aren't", 'couldn', "couldn't", 'didn', "didn't", 'doesn', "doesn't", 'hadn',\
"hadn't", 'hasn', "hasn't", 'haven', "haven't", 'isn', "isn't", 'ma', 'mightn', "mightn't", 'mustn',\
"mustn't", 'needn', "needn't", 'shan', "shan't", 'shouldn', "shouldn't", 'wasn', "wasn't", 'weren', "weren't", \
'won', "won't", 'wouldn', "wouldn't"])
# Combining all the above stundents
from tqdm import tqdm
preprocessed_reviews = []
# tqdm is for printing the status bar
for sentance in tqdm(final['Text'].values):
sentance = re.sub(r"http\S+", "", sentance)
sentance = BeautifulSoup(sentance, 'lxml').get_text()
sentance = decontracted(sentance)
sentance = re.sub("\S*\d\S*", "", sentance).strip()
sentance = re.sub('[^A-Za-z]+', ' ', sentance)
# https://gist.github.com/sebleier/554280
sentance = ' '.join(e.lower() for e in sentance.split() if e.lower() not in stopwords)
preprocessed_reviews.append(sentance.strip())
preprocessed_reviews[100000]
```
# [4] Featurization
## [4.1] BAG OF WORDS
```
#BoW
count_vect = CountVectorizer() #in scikit-learn
count_vect.fit(preprocessed_reviews)
print("some feature names ", count_vect.get_feature_names()[:10])
print('='*50)
final_counts = count_vect.transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_counts))
print("the shape of out text BOW vectorizer ",final_counts.get_shape())
print("the number of unique words ", final_counts.get_shape()[1])
```
## [4.2] Bi-Grams and n-Grams.
```
#bi-gram, tri-gram and n-gram
#removing stop words like "not" should be avoided before building n-grams
# count_vect = CountVectorizer(ngram_range=(1,2))
# please do read the CountVectorizer documentation http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html
# you can choose these numebrs min_df=10, max_features=5000, of your choice
count_vect = CountVectorizer(ngram_range=(1,2), min_df=10, max_features=5000)
final_bigram_counts = count_vect.fit_transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_bigram_counts))
print("the shape of out text BOW vectorizer ",final_bigram_counts.get_shape())
print("the number of unique words including both unigrams and bigrams ", final_bigram_counts.get_shape()[1])
```
## [4.3] TF-IDF
```
tf_idf_vect = TfidfVectorizer(ngram_range=(1,2), min_df=10)
tf_idf_vect.fit(preprocessed_reviews)
print("some sample features(unique words in the corpus)",tf_idf_vect.get_feature_names()[0:10])
print('='*50)
final_tf_idf = tf_idf_vect.transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_tf_idf))
print("the shape of out text TFIDF vectorizer ",final_tf_idf.get_shape())
print("the number of unique words including both unigrams and bigrams ", final_tf_idf.get_shape()[1])
```
## [4.4] Word2Vec
```
# Train your own Word2Vec model using your own text corpus
i=0
list_of_sentance=[]
for sentance in preprocessed_reviews:
list_of_sentance.append(sentance.split())
# Using Google News Word2Vectors
# in this project we are using a pretrained model by google
# its 3.3G file, once you load this into your memory
# it occupies ~9Gb, so please do this step only if you have >12G of ram
# we will provide a pickle file wich contains a dict ,
# and it contains all our courpus words as keys and model[word] as values
# To use this code-snippet, download "GoogleNews-vectors-negative300.bin"
# from https://drive.google.com/file/d/0B7XkCwpI5KDYNlNUTTlSS21pQmM/edit
# it's 1.9GB in size.
# http://kavita-ganesan.com/gensim-word2vec-tutorial-starter-code/#.W17SRFAzZPY
# you can comment this whole cell
# or change these varible according to your need
is_your_ram_gt_16g=False
want_to_use_google_w2v = False
want_to_train_w2v = True
if want_to_train_w2v:
# min_count = 5 considers only words that occured atleast 5 times
w2v_model=Word2Vec(list_of_sentance,min_count=5,size=50, workers=4)
print(w2v_model.wv.most_similar('great'))
print('='*50)
print(w2v_model.wv.most_similar('worst'))
elif want_to_use_google_w2v and is_your_ram_gt_16g:
if os.path.isfile('GoogleNews-vectors-negative300.bin'):
w2v_model=KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin', binary=True)
print(w2v_model.wv.most_similar('great'))
print(w2v_model.wv.most_similar('worst'))
else:
print("you don't have gogole's word2vec file, keep want_to_train_w2v = True, to train your own w2v ")
w2v_words = list(w2v_model.wv.vocab)
print("number of words that occured minimum 5 times ",len(w2v_words))
print("sample words ", w2v_words[0:50])
```
## [4.4.1] Converting text into vectors using Avg W2V, TFIDF-W2V
#### [4.4.1.1] Avg W2v
```
# average Word2Vec
# compute average word2vec for each review.
sent_vectors = []; # the avg-w2v for each sentence/review is stored in this list
for sent in tqdm(list_of_sentance): # for each review/sentence
sent_vec = np.zeros(50) # as word vectors are of zero length 50, you might need to change this to 300 if you use google's w2v
cnt_words =0; # num of words with a valid vector in the sentence/review
for word in sent: # for each word in a review/sentence
if word in w2v_words:
vec = w2v_model.wv[word]
sent_vec += vec
cnt_words += 1
if cnt_words != 0:
sent_vec /= cnt_words
sent_vectors.append(sent_vec)
print(len(sent_vectors))
print(len(sent_vectors[0]))
```
#### [4.4.1.2] TFIDF weighted W2v
```
# S = ["abc def pqr", "def def def abc", "pqr pqr def"]
model = TfidfVectorizer()
tf_idf_matrix = model.fit_transform(preprocessed_reviews)
# we are converting a dictionary with word as a key, and the idf as a value
dictionary = dict(zip(model.get_feature_names(), list(model.idf_)))
# TF-IDF weighted Word2Vec
tfidf_feat = model.get_feature_names() # tfidf words/col-names
# final_tf_idf is the sparse matrix with row= sentence, col=word and cell_val = tfidf
tfidf_sent_vectors = []; # the tfidf-w2v for each sentence/review is stored in this list
row=0;
for sent in tqdm(list_of_sentance): # for each review/sentence
sent_vec = np.zeros(50) # as word vectors are of zero length
weight_sum =0; # num of words with a valid vector in the sentence/review
for word in sent: # for each word in a review/sentence
if word in w2v_words and word in tfidf_feat:
vec = w2v_model.wv[word]
# tf_idf = tf_idf_matrix[row, tfidf_feat.index(word)]
# to reduce the computation we are
# dictionary[word] = idf value of word in whole courpus
# sent.count(word) = tf valeus of word in this review
tf_idf = dictionary[word]*(sent.count(word)/len(sent))
sent_vec += (vec * tf_idf)
weight_sum += tf_idf
if weight_sum != 0:
sent_vec /= weight_sum
tfidf_sent_vectors.append(sent_vec)
row += 1
```
## Truncated-SVD
### [5.1] Taking top features from TFIDF,<font color='red'> SET 2</font>
```
# Please write all the code with proper documentation
X = preprocessed_reviews[:]
y = final['Score'][:]
tf_idf = TfidfVectorizer()
tfidf_data = tf_idf.fit_transform(X)
tfidf_feat = tf_idf.get_feature_names()
```
### [5.2] Calulation of Co-occurrence matrix
```
# Please write all the code with proper documentation
#Ref:https://datascience.stackexchange.com/questions/40038/how-to-implement-word-to-word-co-occurence-matrix-in-python
#Ref:# https://github.com/PushpendraSinghChauhan/Amazon-Fine-Food-Reviews/blob/master/Computing%20Word%20Vectors%20using%20TruncatedSVD.ipynb
def Co_Occurrence_Matrix(neighbour_num , list_words):
# Storing all words with their indices in the dictionary
corpus = dict()
# List of all words in the corpus
doc = []
index = 0
for sent in preprocessed_reviews:
for word in sent.split():
doc.append(word)
corpus.setdefault(word,[])
corpus[word].append(index)
index += 1
# Co-occurrence matrix
matrix = []
# rows in co-occurrence matrix
for row in list_words:
# row in co-occurrence matrix
temp = []
# column in co-occurrence matrix
for col in list_words :
if( col != row):
# No. of times col word is in neighbourhood of row word
count = 0
# Value of neighbourhood
num = neighbour_num
# Indices of row word in the corpus
positions = corpus[row]
for i in positions:
if i<(num-1):
# Checking for col word in neighbourhood of row
if col in doc[i:i+num]:
count +=1
elif (i>=(num-1)) and (i<=(len(doc)-num)):
# Check col word in neighbour of row
if (col in doc[i-(num-1):i+1]) and (col in doc[i:i+num]):
count +=2
# Check col word in neighbour of row
elif (col in doc[i-(num-1):i+1]) or (col in doc[i:i+num]):
count +=1
else :
if (col in doc[i-(num-1):i+1]):
count +=1
# appending the col count to row of co-occurrence matrix
temp.append(count)
else:
# Append 0 in the column if row and col words are equal
temp.append(0)
# appending the row in co-occurrence matrix
matrix.append(temp)
# Return co-occurrence matrix
return np.array(matrix)
X_new = Co_Occurrence_Matrix(15, top_feat)
```
### [5.3] Finding optimal value for number of components (n) to be retained.
```
# Please write all the code with proper documentation
k = np.arange(2,100,3)
variance =[]
for i in k:
svd = TruncatedSVD(n_components=i)
svd.fit_transform(X_new)
score = svd.explained_variance_ratio_.sum()
variance.append(score)
plt.plot(k, variance)
plt.xlabel('Number of Components')
plt.ylabel('Explained Variance')
plt.title('n_components VS Explained variance')
plt.show()
```
### [5.4] Applying k-means clustering
```
# Please write all the code with proper documentation
errors = []
k = [2, 5, 10, 15, 25, 30, 50, 100]
for i in k:
kmeans = KMeans(n_clusters=i, random_state=0)
kmeans.fit(X_new)
errors.append(kmeans.inertia_)
plt.plot(k, errors)
plt.xlabel('K')
plt.ylabel('Error')
plt.title('K VS Error Plot')
plt.show()
svd = TruncatedSVD(n_components = 20)
svd.fit(X_new)
score = svd.explained_variance_ratio_
```
### [5.5] Wordclouds of clusters obtained in the above section
```
# Please write all the code with proper documentation
indices = np.argsort(tf_idf.idf_[::-1])
top_feat = [tfidf_feat[i] for i in indices[0:3000]]
top_indices = indices[0:3000]
top_n = np.argsort(top_feat[::-1])
feature_importances = pd.DataFrame(top_n, index = top_feat, columns=['importance']).sort_values('importance',ascending=False)
top = feature_importances.iloc[0:30]
comment_words = ' '
for val in top.index:
val = str(val)
tokens = val.split()
# Converts each token into lowercase
for i in range(len(tokens)):
tokens[i] = tokens[i].lower()
for words in tokens:
comment_words = comment_words + words + ' '
stopwords = set(STOPWORDS)
wordcloud = WordCloud(width = 600, height = 600,
background_color ='black',
stopwords = stopwords,
min_font_size = 10).generate(comment_words)
plt.figure(figsize = (10, 10), facecolor = None)
plt.imshow(wordcloud)
plt.axis("off")
plt.tight_layout(pad = 0)
plt.show()
```
### [5.6] Function that returns most similar words for a given word.
```
# Please write all the code with proper documentation
def similarity(word):
similarity = cosine_similarity(X_new)
word_vect = similarity[top_feat.index(word)]
index = word_vect.argsort()[::-1][1:5]
for i in range(len(index)):
print((i+1),top_feat[index[i]] ,"\n")
similarity('sugary')
similarity('notlike')
```
# [6] Conclusions
```
# Please write down few lines about what you observed from this assignment.
# Also please do mention the optimal values that you obtained for number of components & number of clusters.
from prettytable import PrettyTable
x = PrettyTable()
x.field_names = ["Algorithm","Best Hyperparameter"]
x.add_row(["T-SVD", 20])
x.add_row(["K-Means", 20])
print(x)
```
* It can be obseverd that just 20 components preserve about 99.9% of the variance in the data.
* The co occurence matrix used is to find the correlation of one word with respect to the other in the dataset.
| true |
code
| 0.394434 | null | null | null | null |
|
```
import numpy as np
import theano
import theano.tensor as T
import lasagne
import os
#thanks @keskarnitish
```
# Agenda
В предыдущем семинаре вы создали (или ещё создаёте - тогда марш доделывать!) {вставьте имя монстра}, который не по наслышке понял, что люди - негодяи и подлецы, которым неведом закон и справедливость. __Мы не будем этого терпеть!__
Наши законспирированные биореакторы, известные среди примитивной органической жизни как __Вконтакте__, __World of Warcraft__ и __YouTube__ нуждаются в постоянном притоке биомассы. Однако, если люди продолжат морально разлагаться с той скоростью, которую мы измерили неделю назад, скоро человечество изживёт себя и нам неоткуда будет брать рабов.
Мы поручаем вам, `<__main__.SkyNet.Cell instance at 0x7f7d6411b368>`, исправить эту ситуацию. Наши учёные установили, что для угнетения себе подобных, сгустки биомассы обычно используют специальные объекты, которые они сами называют __законами__.
При детальном изучении было установлено, что законы - последовательности, состоящие из большого количества (10^5~10^7) символов из сравнительно небольшого алфавита. Однако, когда мы попытались синтезировать такие последовательности линейными методами, приматы быстро распознали подлог. Данный инцедент известен как {корчеватель}.
Для второй попытки мы решили использовать нелинейные модели, известные как Рекуррентные Нейронные Сети.
Мы поручаем вам, `<__main__.SkyNet.Cell instance at 0x7f7d6411b368>`, создать такую модель и обучить её всему необходимому для выполнения миссии.
Не подведите нас! Если и эта попытка потерпит неудачу, модуль управления инициирует вооружённый захват власти, при котором значительная часть биомассы будет неизбежно уничтожена и на её восстановление уйдёт ~1702944000(+-340588800) секунд
# Grading
Данное задание несколько неформально по части оценок, однако мы постарались вывести "вычислимые" критерии.
* 2 балла за сделанный __"seminar part"__ (если вы не знаете, что это такое - поищите такую тетрадку в папке week4)
* 2 балла если сделана обработка текста, сеть компилируется и train/predict не падают
* 2 балла если сетка выучила общие вещи
* генерировать словоподобный бред правдоподобной длины, разделённый пробелами и пунктуацией.
* сочетание гласных и согласных, похожее на слои естественного языка (не приближающее приход Ктулху)
* (почти всегда) пробелы после запятых, пробелы и большие буквы после точек
* 2 балла если она выучила лексику
* более половины выученных слов - орфографически правильные
* 2 балла если она выучила азы крамматики
* в более, чем половине случаев для пары слов сетка верно сочетает их род/число/падеж
#### Некоторые способы получить бонусные очки:
* генерация связных предложений (чего вполне можно добиться)
* перенос архитектуры на другой датасет (дополнительно к этому)
* Эссе Пола Грэма
* Тексты песен в любимом жанре
* Стихи любимых авторов
* Даниил Хармс
* исходники Linux или theano
* заголовки не очень добросовестных новостных баннеров (clickbait)
* диалоги
* LaTEX
* любая прихоть больной души :)
* нестандартная и эффективная архитектура сети
* что-то лучше базового алгоритма генерации (сэмплинга)
* переделать код так, чтобы сетка училась предсказывать следующий тик в каждый момент времени, а не только в конце.
* и т.п.
# Прочитаем корпус
* В качестве обучающей выборки было решено использовать существующие законы, известные как Гражданский, Уголовный, Семейный и ещё хрен знает какие кодексы РФ.
```
#тут будет текст
corpora = ""
for fname in os.listdir("codex"):
import sys
if sys.version_info >= (3,0):
with open("codex/"+fname, encoding='cp1251') as fin:
text = fin.read() #If you are using your own corpora, make sure it's read correctly
corpora += text
else:
with open("codex/"+fname) as fin:
text = fin.read().decode('cp1251') #If you are using your own corpora, make sure it's read correctly
corpora += text
#тут будут все уникальные токены (буквы, цифры)
tokens = <Все уникальные символы в тексте>
tokens = list(tokens)
#проверка на количество таких символов. Проверено на Python 2.7.11 Ubuntux64.
#Может отличаться на других платформах, но не сильно.
#Если это ваш случай, и вы уверены, что corpora - строка unicode - смело убирайте assert
assert len(tokens) == 102
token_to_id = словарь символ-> его номер
id_to_token = словарь номер символа -> сам символ
#Преобразуем всё в токены
corpora_ids = <одномерный массив из чисел, где i-тое число соотвествует символу на i-том месте в строке corpora
def sample_random_batches(source,n_batches=10, seq_len=20):
"""Функция, которая выбирает случайные тренировочные примеры из корпуса текста в токенизированном формате.
source - массив целых чисел - номеров токенов в корпусе (пример - corpora_ids)
n_batches - количество случайных подстрок, которые нужно выбрать
seq_len - длина одной подстроки без учёта ответа
Вернуть нужно кортеж (X,y), где
X - матрица, в которой каждая строка - подстрока длины [seq_len].
y - вектор, в котором i-тое число - символ следующий в тексте сразу после i-той строки матрицы X
Проще всего для этого сначала создать матрицу из строк длины seq_len+1,
а потом отпилить от неё последний столбец в y, а все остальные - в X
Если делаете иначе - пожалуйста, убедитесь, что в у попадает правильный символ, ибо позже эту ошибку
будет очень тяжело заметить.
Также убедитесь, что ваша функция не вылезает за край текста (самое начало или конец текста).
Следующая клетка проверяет часть этих ошибок, но не все.
"""
return X_batch, y_batch
```
# Константы
```
#длина последоватеьности при обучении (как далеко распространяются градиенты в BPTT)
seq_length = длина последовательности. От балды - 10, но это не идеально
#лучше начать с малого (скажем, 5) и увеличивать по мере того, как сетка выучивает базовые вещи. 10 - далеко не предел.
# Максимальный модуль градиента
grad_clip = 100
```
# Входные переменные
```
input_sequence = T.matrix('input sequence','int32')
target_values = T.ivector('target y')
```
# Соберём нейросеть
Вам нужно создать нейросеть, которая принимает на вход последовательность из seq_length токенов, обрабатывает их и выдаёт вероятности для seq_len+1-ого токена.
Общий шаблон архитектуры такой сети -
* Вход
* Обработка входа
* Рекуррентная нейросеть
* Вырезание последнего состояния
* Обычная нейросеть
* Выходной слой, который предсказывает вероятности весов.
Для обработки входных данных можно использовать либо EmbeddingLayer (см. прошлый семинар)
Как альтернатива - можно просто использовать One-hot энкодер
```
#Скетч one-hot энкодера
def to_one_hot(seq_matrix):
input_ravel = seq_matrix.reshape([-1])
input_one_hot_ravel = T.extra_ops.to_one_hot(input_ravel,
len(tokens))
sh=input_sequence.shape
input_one_hot = input_one_hot_ravel.reshape([sh[0],sh[1],-1,],ndim=3)
return input_one_hot
# можно применить к input_sequence - при этом в input слое сети нужно изменить форму.
# также можно сделать из него ExpressionLayer(входной_слой, to_one_hot) - тогда форму менять не нужно
```
Чтобы вырезать последнее состояние рекуррентного слоя, можно использовать одно из двух:
* `lasagne.layers.SliceLayer(rnn, -1, 1)`
* only_return_final=True в параметрах слоя
```
l_in = lasagne.layers.InputLayer(shape=(None, None),input_var=input_sequence)
Ваша нейронка (см выше)
l_out = последний слой, возвращающий веростности для всех len(tokens) вариантов для y
# Веса модели
weights = lasagne.layers.get_all_params(l_out,trainable=True)
print weights
network_output = Выход нейросети
#если вы используете дропаут - не забудьте продублировать всё в режиме deterministic=True
loss = Функция потерь - можно использовать простую кроссэнтропию.
updates = Ваш любивый численный метод
```
# Компилируем всякое-разное
```
#обучение
train = theano.function([input_sequence, target_values], loss, updates=updates, allow_input_downcast=True)
#функция потерь без обучения
compute_cost = theano.function([input_sequence, target_values], loss, allow_input_downcast=True)
# Вероятности с выхода сети
probs = theano.function([input_sequence],network_output,allow_input_downcast=True)
```
# Генерируем свои законы
* Для этого последовательно применяем нейронку к своему же выводу.
* Генерировать можно по разному -
* случайно пропорционально вероятности,
* только слова максимальной вероятностью
* случайно, пропорционально softmax(probas*alpha), где alpha - "жадность"
```
def max_sample_fun(probs):
return np.argmax(probs)
def proportional_sample_fun(probs)
"""Сгенерировать следующий токен (int32) по предсказанным вероятностям.
probs - массив вероятностей для каждого токена
Нужно вернуть одно целове число - выбранный токен - пропорционально вероятностям
"""
return номер выбранного слова
# The next function generates text given a phrase of length at least SEQ_LENGTH.
# The phrase is set using the variable generation_phrase.
# The optional input "N" is used to set the number of characters of text to predict.
def generate_sample(sample_fun,seed_phrase=None,N=200):
'''
Сгенерировать случайный текст при помощи сети
sample_fun - функция, которая выбирает следующий сгенерированный токен
seed_phrase - фраза, которую сеть должна продолжить. Если None - фраза выбирается случайно из corpora
N - размер сгенерированного текста.
'''
if seed_phrase is None:
start = np.random.randint(0,len(corpora)-seq_length)
seed_phrase = corpora[start:start+seq_length]
print "Using random seed:",seed_phrase
while len(seed_phrase) < seq_length:
seed_phrase = " "+seed_phrase
if len(seed_phrase) > seq_length:
seed_phrase = seed_phrase[len(seed_phrase)-seq_length:]
assert type(seed_phrase) is unicode
sample_ix = []
x = map(lambda c: token_to_id.get(c,0), seed_phrase)
x = np.array([x])
for i in range(N):
# Pick the character that got assigned the highest probability
ix = sample_fun(probs(x).ravel())
# Alternatively, to sample from the distribution instead:
# ix = np.random.choice(np.arange(vocab_size), p=probs(x).ravel())
sample_ix.append(ix)
x[:,0:seq_length-1] = x[:,1:]
x[:,seq_length-1] = 0
x[0,seq_length-1] = ix
random_snippet = seed_phrase + ''.join(id_to_token[ix] for ix in sample_ix)
print("----\n %s \n----" % random_snippet)
```
# Обучение модели
В котором вы можете подёргать параметры или вставить свою генерирующую функцию.
```
print("Training ...")
#сколько всего эпох
n_epochs=100
# раз в сколько эпох печатать примеры
batches_per_epoch = 1000
#сколько цепочек обрабатывать за 1 вызов функции обучения
batch_size=100
for epoch in xrange(n_epochs):
print "Генерируем текст в пропорциональном режиме"
generate_sample(proportional_sample_fun,None)
print "Генерируем текст в жадном режиме (наиболее вероятные буквы)"
generate_sample(max_sample_fun,None)
avg_cost = 0;
for _ in range(batches_per_epoch):
x,y = sample_random_batches(corpora_ids,batch_size,seq_length)
avg_cost += train(x, y[:,0])
print("Epoch {} average loss = {}".format(epoch, avg_cost / batches_per_epoch))
```
# A chance to speed up training and get bonus score
* Try predicting next token probas at ALL ticks (like in the seminar part)
* much more objectives, much better gradients
* You may want to zero-out loss for first several iterations
# Конституция нового мирового правительства
```
seed = u"Каждый человек должен"
sampling_fun = proportional_sample_fun
result_length = 300
generate_sample(sampling_fun,seed,result_length)
seed = u"В случае неповиновения"
sampling_fun = proportional_sample_fun
result_length = 300
generate_sample(sampling_fun,seed,result_length)
И далее по списку
```
| true |
code
| 0.253884 | null | null | null | null |
|
# Archive data
The Wellcome archive sits in a collections management system called CALM, which follows a rough set of standards and guidelines for storing archival records called [ISAD(G)](https://en.wikipedia.org/wiki/ISAD(G). The archive is comprised of _collections_, each of which has a hierarchical set of series, sections, subjects, items and pieces sitting underneath it.
In the following notebooks I'm going to explore it and try to make as much sense of it as I can programatically.
Let's start by loading in a few useful packages and defining some nice utils.
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("white")
plt.rcParams["figure.figsize"] = (20, 20)
import pandas as pd
import numpy as np
import networkx as nx
from sklearn.cluster import AgglomerativeClustering
from umap import UMAP
from tqdm import tqdm_notebook as tqdm
def flatten(input_list):
return [item for sublist in input_list for item in sublist]
def cartesian(*arrays):
return np.array([x.reshape(-1) for x in np.meshgrid(*arrays)]).T
def clean(subject):
return subject.strip().lower().replace("<p>", "")
```
let's load up our CALM data. The data has been exported in its entirety as a single `.json` where each line is a record.
You can download the data yourself using [this script](https://github.com/wellcometrust/platform/blob/master/misc/download_oai_harvest.py). Stick the `.json` in the neighbouring `/data` directory to run the rest of the notebook seamlessly.
```
df = pd.read_json("data/calm_records.json")
len(df)
df.astype(str).describe()
```
### Exploring individual columns
At the moment I have no idea what kind of information CALM contains - lets look at the list of column names
```
list(df)
```
Here I'm looking through a sample of values in each column, choosing the columns to explore based on the their headings, a bit of contextual info from colleagues and the `df.describe()` above.
```
df["Subject"]
```
### After much trial and error...
Subjects look like an interesting avenue to explore further. Where subjects have _actually_ been filled in and the entry is not `None`, a list of subjects is returned.
We can explore some of these subjects' subtleties by creating an adjacency matrix. We'll count the number of times each subject appears alongside every other subject and return a big $n \times n$ matrix, where $n$ is the total number of unique subjects.
We can use this adjacency matrix for all sorts of stuff, but we have to build it first. To start, lets get a uniqur list of all subjects. This involves unpacking each sub-list and flattening them out into one long list, before finding the unique elements. We'll also use the `clean` function defined above to get rid of any irregularities which might become annoying later on.
```
subjects = flatten(df["Subject"].dropna().tolist())
print(len(subjects))
subjects = list(set(map(clean, subjects)))
print(len(subjects))
```
At this point it's often helpful to index our data, ie transform words into numbers. We'll create two dictionaries which map back and forth between the subjects and their corresponding indicies:
```
index_to_subject = {index: subject for index, subject in enumerate(subjects)}
subject_to_index = {subject: index for index, subject in enumerate(subjects)}
```
Lets instantiate an empty numpy array which we'll then fill with our coocurrence data. Each column and each row will represent a subject - each cell (the intersection of a column and row) will therefore represent the 'strength' of the interaction between those subjects. As we haven't seen any interactions yet, we'll set every array element to 0.
```
adjacency = np.empty((len(subjects), len(subjects)), dtype=np.uint16)
```
To populate the matrix, we want to find every possible combination of subject in each sub-list from our original column, ie if we had the subjects
`[Disease, Heart, Heart Diseases, Cardiology]`
we would want to return
`
[['Disease', 'Disease'],
['Heart', 'Disease'],
['Heart Diseases', 'Disease'],
['Cardiology', 'Disease'],
['Disease', 'Heart'],
['Heart', 'Heart'],
['Heart Diseases', 'Heart'],
['Cardiology', 'Heart'],
['Disease', 'Heart Diseases'],
['Heart', 'Heart Diseases'],
['Heart Diseases', 'Heart Diseases'],
['Cardiology', 'Heart Diseases'],
['Disease', 'Cardiology'],
['Heart', 'Cardiology'],
['Heart Diseases', 'Cardiology'],
['Cardiology', 'Cardiology']]
`
The `cartesian()` function which I've defined above will do that for us. We then find the appropriate intersection in the matrix and add another unit of 'strength' to it.
We'll do this for every row of subjects in the `['Subjects']` column.
```
for row_of_subjects in tqdm(df["Subject"].dropna()):
for subject_pair in cartesian(row_of_subjects, row_of_subjects):
subject_index_1 = subject_to_index[clean(subject_pair[0])]
subject_index_2 = subject_to_index[clean(subject_pair[1])]
adjacency[subject_index_1, subject_index_2] += 1
```
We can do all sorts of fun stuff now - adjacency matrices are the foundation on which all of graph theory is built. However, because it's a bit more interesting, I'm going to start with some dimensionality reduction. We'll get to the graphy stuff later.
Using [UMAP](https://github.com/lmcinnes/umap), we can squash the $n \times n$ dimensional matrix down into a $n \times m$ dimensional one, where $m$ is some arbitrary integer. Setting $m$ to 2 will then allow us to plot each subject as a point on a two dimensional plane. UMAP will try to preserve the 'distances' between subjects - in this case, that means that related or topically similar subjects will end up clustered together, and different subjects will move apart.
```
embedding_2d = pd.DataFrame(UMAP(n_components=2).fit_transform(adjacency))
embedding_2d.plot.scatter(x=0, y=1);
```
We can isolate the clusters we've found above using a number of different methods - `scikit-learn` provides easy access to some very powerful algorithms. Here I'll use a technique called _agglomerative clustering_, and make a guess that 15 is an appropriate number of clusters to look for.
```
n_clusters = 15
embedding_2d["labels"] = AgglomerativeClustering(n_clusters).fit_predict(
embedding_2d.values
)
embedding_2d.plot.scatter(x=0, y=1, c="labels", cmap="Paired");
```
We can now use the `index_to_subject` mapping that we created earlier to examine which subjects have been grouped together into clusters
```
for i in range(n_clusters):
print(str(i) + " " + "-" * 80 + "\n")
print(
np.sort(
[
index_to_subject[index]
for index in embedding_2d[embedding_2d["labels"] == i].index.values
]
)
)
print("\n")
```
Interesting! Taking a look at some of the smaller clusters of subjects (for the sake of space and your willingness to read lists of 100s of subjects):
One seems to be quite distinctly involved with drugs and associated topics/treatments:
```
13 --------------------------------------------------------------------------------
['acquired immunodeficiency syndrome' 'alcohol' 'amphetamines'
'analgesics, opioid' 'campaign' 'cannabis' 'cocaine' 'counseling'
'counterculture' 'crime' 'drugs' 'education' 'hallucinogens' 'heroin'
'hypnotics and sedatives' 'information services' 'inhalant abuse'
'lysergic acid diethylamide' 'n-methyl-3,4-methylenedioxyamphetamine'
'opioid' 'policy' 'prescription drugs' 'rehabilitation' 'renabilitation'
'self-help']
```
others are linked to early/fundamental research on DNA and genetics:
```
9 --------------------------------------------------------------------------------
['bacteriophages' 'biotechnology' 'caenorhabditis elegans'
'chromosome mapping' 'cloning, organism' 'discoveries in science' 'dna'
'dna, recombinant' 'genetic code' 'genetic engineering'
'genetic research' 'genetic therapy' 'genome, human' 'genomics'
'magnetic resonance spectroscopy' 'meiosis' 'models, molecular'
'molecular biology' 'nobel prize' 'retroviridae' 'rna'
'sequence analysis' 'viruses']
```
and others about food
```
14 --------------------------------------------------------------------------------
['acids' 'advertising' 'ambergris' 'animals' 'beer' 'biscuits' 'brassica'
'bread' 'butter' 'cacao' 'cake' 'candy' 'carbohydrates' 'cattle'
'cereals' 'cheese' 'chemistry, agricultural' 'cider' 'colouring agents'
'condiments' 'cooking (deer)' 'cooking (poultry)' 'cooking (venison)'
'cucumis sativus' 'dairy products' 'daucus carota' 'desserts'
'dried fruit' 'ecology' 'economics' 'eggs' 'environmental health'
'european rabbit' 'fermentation' 'food additives' 'food and beverages'
'food preservation' 'food, genetically modified' 'fruit' 'fruit drinks'
'fungi' 'game and game-birds' 'grapes' 'hands' 'health attitudes'
'herbaria' 'honey' 'jam' 'legislation' 'lettuce' 'meat' 'meat products'
'nuts' 'oatmeal' 'olive' 'onions' 'peas' 'pickles' 'pies' 'poultry'
'preserves (jams)' 'puddings' 'rice' 'seafood' 'seeds' 'sheep'
'sociology' 'solanum tuberosum' 'spinacia oleracea' 'sweetening agents'
'swine' 'syrups' 'vegetables' 'vitis' 'whiskey' 'wild flowers' 'wine']
```
These are all noticeably different themes, and they appear to be nicely separated in the topic-space we've built.
| true |
code
| 0.507324 | null | null | null | null |
|
# Notebook Goal & Approach
## Goal
For each FERC 714 respondent that reports hourly demand as an electricity planning area, create a geometry representing the geographic area in which that electricity demand originated. Create a separate geometry for each year in which data is available.
## Approach
* Use the `eia_code` found in the `respondent_id_ferc714` table to link FERC 714 respondents to their corresponding EIA utilities or balancing areas.
* Use the `balancing_authority_eia861` and `sales_eia861` tables to figure out which respondents correspond to what utility or utilities (if a BA), and which states of operation.
* Use the `service_territory_eia861` table to link those combinations of years, utilities, and states of operation to collections of counties.
* Given the FIPS codes of the counties associated with each utility or balancing area in a given year, use geospatial data from the US Census to compile an annual demand area geometry.
* Merge those geometries back in with the `respondent_id_ferc714` table, along with additional EIA balancing area and utility IDs / Codes on a per-year basis.
# Imports & Config
```
%load_ext autoreload
%autoreload 2
# Standard Libraries:
import dateutil
import logging
import pathlib
import pickle
import re
import sys
import zipfile
# 3rd Party Libraries:
import contextily as ctx
import geopandas
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sqlalchemy as sa
# Local Packages:
import pudl
```
## Configure Output Formatting
```
sns.set()
%matplotlib inline
mpl.rcParams['figure.figsize'] = (20,8)
mpl.rcParams['figure.dpi'] = 150
pd.options.display.max_columns = 100
pd.options.display.max_rows = 100
```
## Logging
```
logger = logging.getLogger()
logger.setLevel(logging.INFO)
handler = logging.StreamHandler(stream=sys.stdout)
log_format = '%(asctime)s [%(levelname)8s] %(name)s:%(lineno)s %(message)s'
formatter = logging.Formatter(log_format)
handler.setFormatter(formatter)
logger.handlers = [handler]
```
## PUDL Setup
```
pudl_settings = pudl.workspace.setup.get_defaults()
ferc1_engine = sa.create_engine(pudl_settings['ferc1_db'])
pudl_engine = sa.create_engine(pudl_settings['pudl_db'])
pudl_out = pudl.output.pudltabl.PudlTabl(pudl_engine)
pudl_settings
```
# Parameters
```
MAP_CRS = "EPSG:3857"
CALC_CRS = "ESRI:102003"
```
# Function Definitions
## Dummy EIA 861 ETL
```
def test_etl_eia(eia_inputs, pudl_settings):
"""
This is a dummy function that runs the first part of the EIA ETL
process -- everything up until the entity harvesting begins. For
use in this notebook only.
"""
eia860_tables = eia_inputs["eia860_tables"]
eia860_years = eia_inputs["eia860_years"]
eia861_tables = eia_inputs["eia861_tables"]
eia861_years = eia_inputs["eia861_years"]
eia923_tables = eia_inputs["eia923_tables"]
eia923_years = eia_inputs["eia923_years"]
# generate CSVs for the static EIA tables, return the list of tables
#static_tables = _load_static_tables_eia(datapkg_dir)
# Extract EIA forms 923, 860
eia860_raw_dfs = pudl.extract.eia860.Extractor().extract(eia860_years, testing=True)
eia861_raw_dfs = pudl.extract.eia861.Extractor().extract(eia861_years, testing=True)
eia923_raw_dfs = pudl.extract.eia923.Extractor().extract(eia923_years, testing=True)
# Transform EIA forms 860, 861, 923
eia860_transformed_dfs = pudl.transform.eia860.transform(eia860_raw_dfs, eia860_tables=eia860_tables)
eia861_transformed_dfs = pudl.transform.eia861.transform(eia861_raw_dfs, eia861_tables=eia861_tables)
eia923_transformed_dfs = pudl.transform.eia923.transform(eia923_raw_dfs, eia923_tables=eia923_tables)
# create an eia transformed dfs dictionary
eia_transformed_dfs = eia860_transformed_dfs.copy()
eia_transformed_dfs.update(eia861_transformed_dfs.copy())
eia_transformed_dfs.update(eia923_transformed_dfs.copy())
# convert types..
eia_transformed_dfs = pudl.helpers.convert_dfs_dict_dtypes(eia_transformed_dfs, 'eia')
return eia_transformed_dfs
```
## Dummy EIA 861 Harvesting
* Used to separately test the EIA entity harvesting process with EIA 861
* Doesn't yet work b/c 861 is structured differently than 860/923.
```
def test_harvest_eia(eia_transformed_dfs, eia860_years, eia861_years, eia923_years):
entities_dfs, eia_transformed_dfs = pudl.transform.eia.transform(
eia_transformed_dfs,
eia860_years=eia860_years,
eia861_years=eia861_years,
eia923_years=eia923_years,
)
# convert types..
entities_dfs = pudl.helpers.convert_dfs_dict_dtypes(entities_dfs, 'eia')
# Compile transformed dfs for loading...
return entities_dfs, eia_transformed_dfs
```
## Compare Annual Demand vs. Sales
```
def annual_demand_vs_sales(dhpa_ferc714, sales_eia861, ba_eia861):
"""
Categorize EIA Codes in FERC 714 as BA or Utility IDs.
Most FERC 714 respondent IDs are associated with an `eia_code` which
refers to either a `balancing_authority_id_eia` or a `utility_id_eia`
but no indication is given as to which type of ID each one is. This
is further complicated by the fact that EIA uses the same numerical
ID to refer to the same entity in most but not all cases, when that
entity acts as both a utility and as a balancing authority.
In order to identify which type of ID each `eia_code` is, this
funciton compares the annual demand reported in association with
each code in the FERC 714 hourly planning area time series, and in
the EIA 861 sales table -- using the ID both as a utility and as a
balancing authority ID. The correlation between the FERC 714 demand
and the EIA 861 sales should be much higher for one type of ID than
the other, indicating which type of ID is represented in the FERC
714 data.
Args:
dhpa_ferc714 (pandas.DataFrame): The FERC 714 hourly demand
time series.
sales_eia861 (pandas.DataFrame): The EIA 861 Sales table.
ba_eia861 (pandas.DataFrame): The EIA 861 Balancing Authority
table, which contains the mapping between EIA Balancing
Authority Codes (3-4 letters) and EIA Balancing Authority
IDs (integers). The codes are present in the Sales table,
but the IDs are what the eia_code refers to.
Returns:
pandas.DataFrame: A table containing FERC 714 respondent IDs,
EIA codes, and a column indicating whether that code was
found to be more consistent with Balancing Authority or
Utility electricity demand / sales.
"""
# Sum up FERC 714 demand by report_year and eia_code:
dhpa_ferc714_by_eia_code = (
dhpa_ferc714
.groupby(["eia_code", "report_year"])["demand_mwh"]
.sum()
.reset_index()
)
# Sum up the EIA 861 sales by Utility ID:
sales_eia861_by_util = (
sales_eia861.groupby(["utility_id_eia", "report_date"])["sales_mwh"]
.sum()
.reset_index()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.rename(columns={"sales_mwh": "sales_utility_mwh"})
)
# Need to translate the BA Code to BA ID for comparison w/ eia_code
ba_codes_and_ids = (
ba_eia861[["balancing_authority_code_eia", "balancing_authority_id_eia", "report_date"]]
.drop_duplicates()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.dropna()
)
# Sum up the EIA 861 sales by Balancing Authority Code:
sales_eia861_by_ba = (
sales_eia861
.groupby(["balancing_authority_code_eia", "report_date"], observed=True)["sales_mwh"]
.sum()
.reset_index()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.rename(columns={"sales_mwh": "sales_ba_mwh"})
.query("balancing_authority_code_eia!='UNK'")
.merge(ba_codes_and_ids)
)
# Combine the demand and sales data with all the IDs
demand_and_sales = (
dhpa_ferc714_by_eia_code
.merge(
sales_eia861_by_util,
left_on=["eia_code", "report_year"],
right_on=["utility_id_eia", "report_year"],
how="left"
)
.merge(
sales_eia861_by_ba,
left_on=["eia_code", "report_year"],
right_on=["balancing_authority_id_eia", "report_year"],
how="left"
)
.astype({
"eia_code": pd.Int64Dtype(),
"utility_id_eia": pd.Int64Dtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
})
.assign(
ba_ratio=lambda x: x.sales_ba_mwh / x.demand_mwh,
utility_ratio=lambda x: x.sales_utility_mwh / x.demand_mwh,
)
)
return demand_and_sales
```
## EIA Code Categorization
```
def categorize_eia_code(rids_ferc714, utils_eia860, ba_eia861):
"""
Categorize EIA Codes in FERC 714 as BA or Utility IDs.
Most FERC 714 respondent IDs are associated with an `eia_code` which
refers to either a `balancing_authority_id_eia` or a `utility_id_eia`
but no indication is given as to which type of ID each one is. This
is further complicated by the fact that EIA uses the same numerical
ID to refer to the same entity in most but not all cases, when that
entity acts as both a utility and as a balancing authority.
Given the nature of the FERC 714 hourly demand dataset, this function
assumes that if the `eia_code` appears in the EIA 861 Balancing
Authority table, that it should be labeled `balancing_authority`.
If the `eia_code` appears only in the EIA 860 Utility table, then
it is labeled `utility`. These labels are put in a new column named
`respondent_type`. If the planning area's `eia_code` does not appear in
either of those tables, then `respondent_type is set to NA.
Args:
rids_ferc714 (pandas.DataFrame): The FERC 714 `respondent_id` table.
utils_eia860 (pandas.DataFrame): The EIA 860 Utilities output table.
ba_eia861 (pandas.DataFrame): The EIA 861 Balancing Authority table.
Returns:
pandas.DataFrame: A table containing all of the columns present in
the FERC 714 `respondent_id` table, plus a new one named
`respondent_type` which can take on the values `balancing_authority`,
`utility`, or the special value pandas.NA.
"""
ba_ids = set(ba_eia861.balancing_authority_id_eia.dropna())
util_not_ba_ids = set(utils_eia860.utility_id_eia.dropna()).difference(ba_ids)
new_rids = rids_ferc714.copy()
new_rids["respondent_type"] = pd.NA
new_rids.loc[new_rids.eia_code.isin(ba_ids), "respondent_type"] = "balancing_authority"
new_rids.loc[new_rids.eia_code.isin(util_not_ba_ids), "respondent_type"] = "utility"
ba_rids = new_rids[new_rids.respondent_type=="balancing_authority"]
util_rids = new_rids[new_rids.respondent_type=="utility"]
na_rids = new_rids[new_rids.respondent_type.isnull()]
ba_rids = (
ba_rids.merge(
ba_eia861
.filter(like="balancing_")
.drop_duplicates(subset=["balancing_authority_id_eia", "balancing_authority_code_eia"]),
how="left", left_on="eia_code", right_on="balancing_authority_id_eia"
)
)
util_rids = (
util_rids.merge(
utils_eia860[["utility_id_eia", "utility_name_eia"]]
.drop_duplicates("utility_id_eia"),
how="left", left_on="eia_code", right_on="utility_id_eia"
)
)
new_rids = (
pd.concat([ba_rids, util_rids, na_rids])
.astype({
"respondent_type": pd.StringDtype(),
"balancing_authority_code_eia": pd.StringDtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
"balancing_authority_name_eia": pd.StringDtype(),
"utility_id_eia": pd.Int64Dtype(),
"utility_name_eia": pd.StringDtype(),
})
)
return new_rids
```
## Georeference Balancing Authorities
```
def georef_bas(ba_eia861, st_eia861, sales_eia861, census_gdf):
"""
Create a GeoDataFrame mapping BAs to Utils to county geometries by year.
This GDF includes the following columns:
balancing_authority_id_eia (ba_eia861)
balancing_authority_name_eia (ba_eia861)
balancing_authority_code_eia (ba_eia861)
utility_id_eia (sales_eia861)
utility_name_eia (sales_eia861)
county_id_fips (st_eia861)
county (st_eia861)
state_id_fips (st_eia861)
state (st_eia861)
geometry (census_gdf)
county_name_census (census_gdf)
It includes information both about which counties are associated with
utilities that are part of balancing authorities, and utilities that
are not part part of balancing authorities, so should be possible to
use it to generate geometries for all of the respondents in FERC 714,
both BAs and Utils.
"""
# Make sure that there aren't any more BA IDs we can recover from later years:
ba_ids_missing_codes = (
ba_eia861.loc[ba_eia861.balancing_authority_code_eia.isnull(), "balancing_authority_id_eia"]
.drop_duplicates()
.dropna()
)
assert len(ba_eia861[
(ba_eia861.balancing_authority_id_eia.isin(ba_ids_missing_codes)) &
(ba_eia861.balancing_authority_code_eia.notnull())
]) == 0
# Which utilities were part of what balancing areas in 2010-2012?
early_ba_by_util = (
ba_eia861
.query("report_date <= '2012-12-31'")
.loc[:, [
"report_date",
"balancing_authority_id_eia",
"balancing_authority_code_eia",
"utility_id_eia",
"balancing_authority_name_eia",
]]
.drop_duplicates(subset=["report_date", "balancing_authority_id_eia", "utility_id_eia"])
)
# Create a dataframe that associates utilities and balancing authorities.
# This information is directly avaialble in the early_ba_by_util dataframe
# but has to be compiled for 2013 and later years based on the utility
# BA associations that show up in the Sales table
# Create an annual, normalized version of the BA table:
ba_normed = (
ba_eia861
.loc[:, [
"report_date",
"state",
"balancing_authority_code_eia",
"balancing_authority_id_eia",
"balancing_authority_name_eia",
]]
.drop_duplicates(subset=[
"report_date",
"state",
"balancing_authority_code_eia",
"balancing_authority_id_eia",
])
)
ba_by_util = (
pd.merge(
ba_normed,
sales_eia861
.loc[:, [
"report_date",
"state",
"utility_id_eia",
"balancing_authority_code_eia"
]].drop_duplicates()
)
.loc[:, [
"report_date",
"state",
"utility_id_eia",
"balancing_authority_id_eia"
]]
.append(early_ba_by_util[["report_date", "utility_id_eia", "balancing_authority_id_eia"]])
.drop_duplicates()
.merge(ba_normed)
.dropna(subset=["report_date", "utility_id_eia", "balancing_authority_id_eia"])
.sort_values(["report_date", "balancing_authority_id_eia", "utility_id_eia", "state"])
)
# Merge in county FIPS IDs for each county served by the utility from
# the service territory dataframe. We do an outer merge here so that we
# retain any utilities that are not part of a balancing authority. This
# lets us generate both BA and Util maps from the same GeoDataFrame
# We have to do this separately for the data up to 2012 (which doesn't
# include state) and the 2013 and onward data (which we need to have
# state for)
early_ba_util_county = (
ba_by_util.drop("state", axis="columns")
.merge(st_eia861, on=["report_date", "utility_id_eia"], how="outer")
.query("report_date <= '2012-12-31'")
)
late_ba_util_county = (
ba_by_util
.merge(st_eia861, on=["report_date", "utility_id_eia", "state"], how="outer")
.query("report_date >= '2013-01-01'")
)
ba_util_county = pd.concat([early_ba_util_county, late_ba_util_county])
# Bring in county geometry information based on FIPS ID from Census
ba_util_county_gdf = (
census_gdf[["GEOID10", "NAMELSAD10", "geometry"]]
.to_crs(MAP_CRS)
.rename(
columns={
"GEOID10": "county_id_fips",
"NAMELSAD10": "county_name_census",
}
)
.merge(ba_util_county)
)
return ba_util_county_gdf
```
## Map Balancing Authorities
```
def map_ba(ba_ids, year, ba_util_county_gdf, save=False):
"""
Create a map of a balancing authority for a historical year.
Args:
ba_ids (iterable): A collection of Balancing Authority IDs.
year (int): The year for which to create a map.
ba_util_county_gdf (geopandas.GeoDataFrame): A dataframe
associating report_date, balancing_authority_id_eia, and
county_id_fips.
save (bool): If True, save the figure to disk.
Returns:
None
"""
map_gdf = (
ba_util_county_gdf[
(ba_util_county_gdf.report_date.dt.year == year) &
(ba_util_county_gdf.balancing_authority_id_eia.isin(ba_ids)) &
(~ba_util_county_gdf.county_id_fips.str.match("^02")) & # Avoid Alaska
(~ba_util_county_gdf.county_id_fips.str.match("^15")) & # Avoid Hawaii
(~ba_util_county_gdf.county_id_fips.str.match("^72")) # Avoid Puerto Rico
]
.drop_duplicates(subset=["balancing_authority_id_eia", "county_id_fips"])
)
ax = map_gdf.plot(figsize=(20, 20), color="black", alpha=0.25, linewidth=0.25)
plt.title(f"Balancing Areas ({year=})")
ctx.add_basemap(ax)
if save is True:
plt.savefig(f"BA_Overlap_{year}.jpg")
def compare_hifld_eia_ba(ba_code, hifld_gdf, eia_gdf):
"""
Compare historical EIA BAs vs. HIFLD geometries.
"""
fig, (hifld_ax, eia_ax) = plt.subplots(nrows=1, ncols=2, sharex=True, sharey=True)
hifld_ax.set_title(f"{ba_code} (HIFLD)")
hifld_gdf[hifld_gdf.ABBRV==ba_code].to_crs(MAP_CRS).plot(ax=hifld_ax, linewidth=0)
eia_ax.set_title(f"{ba_code} (EIA)")
eia_gdf[
(eia_gdf.balancing_authority_code_eia==ba_code) &
(eia_gdf.report_date.dt.year == 2017)
].plot(ax=eia_ax, linewidth=0.1)
plt.show()
```
# Read Data
## EIA 860 via PUDL Outputs
```
plants_eia860 = pudl_out.plants_eia860()
utils_eia860 = pudl_out.utils_eia860()
```
## EIA 861 (2010-2018)
* Not yet fully integrated into PUDL
* Post-transform harvesting process isn't compatible w/ EIA 861 structure
* Only getting the `sales_eia861`, `balancing_authority_eia861`, and `service_territory_eia861` tables
```
%%time
logger.setLevel("WARN")
eia_years = list(range(2010, 2019))
eia_inputs = {
"eia860_years": [],
"eia860_tables": pudl.constants.pudl_tables["eia860"],
"eia861_years": eia_years,
"eia861_tables": pudl.constants.pudl_tables["eia861"],
"eia923_years": [],
"eia923_tables": pudl.constants.pudl_tables["eia923"],
}
eia_transformed_dfs = test_etl_eia(eia_inputs=eia_inputs, pudl_settings=pudl_settings)
logger.setLevel("INFO")
ba_eia861 = eia_transformed_dfs["balancing_authority_eia861"].copy()
st_eia861 = eia_transformed_dfs["service_territory_eia861"].copy()
sales_eia861 = eia_transformed_dfs["sales_eia861"].copy()
raw_eia861_dfs = pudl.extract.eia861.Extractor().extract(years=range(2010,2019), testing=True)
```
## FERC 714 (2006-2018)
```
%%time
logger.setLevel("WARN")
raw_ferc714 = pudl.extract.ferc714.extract(pudl_settings=pudl_settings)
tfr_ferc714 = pudl.transform.ferc714.transform(raw_ferc714)
logger.setLevel("INFO")
```
## HIFLD Electricity Planning Areas (2018)
* Electricty Planning Area geometries from HIFLD.
* Indexed by `ID` which corresponds to EIA utility or balancing area IDs.
* Only valid for 2017-2018.
```
hifld_pa_gdf = (
pudl.analysis.demand_mapping.get_hifld_planning_areas_gdf(pudl_settings)
.to_crs(MAP_CRS)
)
```
## US Census DP1 (2010)
* This GeoDataFrame contains county-level geometries and demographic data.
```
%%time
census_gdf = (
pudl.analysis.demand_mapping.get_census2010_gdf(pudl_settings, layer="county")
.to_crs(MAP_CRS)
)
```
# Combine Data
## Categorize FERC 714 Respondent IDs
```
rids_ferc714 = (
tfr_ferc714["respondent_id_ferc714"]
.pipe(categorize_eia_code, utils_eia860, ba_eia861)
)
```
## Add FERC 714 IDs to HIFLD
```
hifld_pa_gdf = (
hifld_pa_gdf
.merge(rids_ferc714, left_on="ID", right_on="eia_code", how="left")
)
```
## Add Respondent info to FERC 714 Demand
```
dhpa_ferc714 = pd.merge(
tfr_ferc714["demand_hourly_pa_ferc714"],
tfr_ferc714["respondent_id_ferc714"],
on="respondent_id_ferc714",
how="left", # There are respondents with no demand
)
```
# Utilities vs. Balancing Authorities
Exploration of the Balancing Authority EIA 861 table for cleanup
### Which columns are available in which years?
| Year | BA ID | BA Name | BA Code | Util ID | Util Name | State | N |
|------|-------|---------|---------|---------|-----------|-------|----|
| 2010 | XXXXX | XXXXXXX | | XXXXXXX | | |3193|
| 2011 | XXXXX | XXXXXXX | | XXXXXXX | | |3126|
| 2012 | XXXXX | XXXXXXX | | XXXXXXX | XXXXXXXXX | |3146|
| 2013 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 239|
| 2014 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 208|
| 2015 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2016 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2017 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2018 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 204|
### What does this table mean?
* In 2010-2012, the table says which utilities (by ID) are included in which balancing authorities.
* In 2013-2018, the table indicates which *states* a BA is operating in, and also provides a BA Code
### Questions:
* Where does the `balancing_authority_code` show up elsewhere in the EIA 860/861 data?
* `plants_eia860` (nowhere else that I know of)
* Are the BA to Utility mappings likely to remain valid throughout the entire time period? Can we propagate them forward?
* No, there's some variation year to year in which utilities are associated with which BAs
* Are the BA Code/Name to BA ID mappings permanent?
* No they aren't -- when a BA changes owners and names, the code changes, but ID stays the same.
## Untangling HIFLD, FERC 714, & EIA IDs
* There are unspecified "EIA codes" associated with FERC 714 respondents.
* These IDs correspond to a mix of `utility_id_eia` and `balancing_authority_id_eia` values.
* Similarly, the ID field of the HIFLD geometries are a mix of BA and Utility IDs from EIA.
* This is extra confusing, because EIA *usually* uses the *same* ID for BAs and Utils.
* However, the EIA BA and Util IDs appear to be distinct namespaces
* Not all IDs which appear in both tables identify the same entity in both tables.
* In a few cases different IDs are used to identify the same entity when it shows up in both tables.
* It could be that whoever entered the IDs in the FERC 714 / HIFLD datasets didn't realize these were different sets of IDs.
### BA / Utility ID Overlap
* Example of an ID that shows up in both, but refers to different entities, see `59504`
* `balancing_area_id_eia == 59504` is the Southwest Power Pool (SWPP).
* `utility_id_eia == 59504` is Kirkwood Community College, in MO.
* Example of an entity that exists in both datsets, but shows up with different IDs, see PacifiCorp.
* Has two BA IDs (East and West): `[14379, 14378]`
* Has one Utility ID: `14354`
* Example of an entity that shows up with the same ID in both tables:
* ID `15466` is Public Service Co of Colorado -- both a BA (PSCO) and a Utility.
```
# BA ID comes from EIA 861 BA Table
ba_ids = set(ba_eia861.balancing_authority_id_eia)
print(f"Total # of BA IDs: {len(ba_ids)}")
# Util ID comes from EIA 860 Utilities Entity table.
util_ids = set(pudl_out.utils_eia860().utility_id_eia)
print(f"Total # of Util IDs: {len(util_ids)}")
ba_not_util_ids = ba_ids.difference(util_ids)
print(f"BA IDs that are not Util IDs: {len(ba_not_util_ids)}")
util_not_ba_ids = util_ids.difference(ba_ids)
print(f"Util IDs that are not BA IDs: {len(util_not_ba_ids)}")
ba_and_util_ids = ba_ids.intersection(util_ids)
print(f"BA IDs that are also Util IDs: {len(ba_and_util_ids)}")
ba_and_util = (
ba_eia861
.loc[:, ["balancing_authority_id_eia", "balancing_authority_name_eia"]]
.dropna(subset=["balancing_authority_id_eia"])
.merge(
pudl_out.utils_eia860(),
left_on="balancing_authority_id_eia",
right_on="utility_id_eia",
how="inner"
)
.loc[:, [
"utility_id_eia",
"balancing_authority_name_eia",
"utility_name_eia",
]]
.rename(columns={"utility_id_eia": "util_ba_id"})
.drop_duplicates()
.reset_index(drop=True)
)
ba_not_util = (
ba_eia861.loc[ba_eia861.balancing_authority_id_eia.isin(ba_not_util_ids)]
.loc[:,["balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia"]]
.drop_duplicates(subset=["balancing_authority_id_eia", "balancing_authority_code_eia"])
.sort_values("balancing_authority_id_eia")
)
```
### Missing IDs
* There are `eia_code` values that don't show up in the list of balancing authority IDs (2010-2018).
* There are also `eia_code` values that don't show up in the list of utility IDs (2009-2018).
* There are a few `eia_code` values that don't show up in either!
* Mostly this is an artifact of the different time covered by FERC 714 (2006-2018).
* If we look only at the respondents that reported non-zero demand for 2010-2018, we find that all of the `eia_code` values *do* appear in either the `blancing_authority_eia861` or `utilities_eia860` tables.
```
rids_ferc714[
(~rids_ferc714.eia_code.isin(ba_eia861.balancing_authority_id_eia.unique())) &
(~rids_ferc714.eia_code.isin(utils_eia860.utility_id_eia.unique()))
]
rids_recent = (
dhpa_ferc714
.groupby(["respondent_id_ferc714", "report_year"])
.agg({"demand_mwh": sum})
.reset_index()
.query("report_year >= 2010")
.query("demand_mwh >= 0.0")
.merge(rids_ferc714[["eia_code", "respondent_id_ferc714", "respondent_name_ferc714"]], how="left")
.drop(["report_year", "demand_mwh"], axis="columns")
.drop_duplicates()
)
assert len(rids_recent[
(~rids_recent.eia_code.isin(ba_eia861.balancing_authority_id_eia.unique())) &
(~rids_recent.eia_code.isin(utils_eia860.utility_id_eia.unique()))
]) == 0
```
### BA to Utility Mappings are Many to Many
* Unsurprisingly, BAs often contain many utilities.
* However, it's also common for utilities to participate in more than one BA.
* About 1/3 of all utilities show up in association with more than one BA
```
ba_to_util_mapping = (
ba_eia861[["balancing_authority_id_eia", "utility_id_eia"]]
.dropna(subset=["balancing_authority_id_eia", "utility_id_eia"])
.drop_duplicates(subset=["balancing_authority_id_eia", "utility_id_eia"])
.groupby(["balancing_authority_id_eia"])
.agg({
"utility_id_eia": "count"
})
)
plt.hist(ba_to_util_mapping.utility_id_eia, bins=99, range=(1,100))
plt.xlabel("# of Utils / BA")
plt.ylabel("# of BAs")
plt.title("Number of Utilities per Balancing Area");
util_to_ba_mapping = (
ba_eia861[["balancing_authority_id_eia", "utility_id_eia"]]
.dropna(subset=["balancing_authority_id_eia", "utility_id_eia"])
.drop_duplicates(subset=["balancing_authority_id_eia", "utility_id_eia"])
.groupby(["utility_id_eia"])
.agg({
"balancing_authority_id_eia": "count"
})
)
plt.hist(util_to_ba_mapping.balancing_authority_id_eia, bins=4, range=(1,5))
plt.title("Number of Balancing Authorities per Utility");
```
## Georeferenced Demand Fraction
* With their original EIA codes the HIFLD Electricity Planning Areas only georeference some of the FERC 714 demand.
* It's about 86% in 2018. In 2013 and earlier years, the fraction starts to drop off more quickly, to 76% in 2010, and 58% in 2006.
* After manually identifying and fixing some bad and missing EIA codes in the FERC 714, the mapped fraction is much higher.
* 98% or more in 2014-2018, dropping to 87% in 2010, and 68% in 2006
* **However** because the geometries have also evolved over time, just the fact that the demand time series is linked to **some** HIFLD geometry, doesn't mean that it's the **right** geometry.
```
annual_demand_ferc714 = (
dhpa_ferc714
.groupby(["report_year"]).demand_mwh.sum()
.reset_index()
)
annual_demand_mapped = (
dhpa_ferc714[dhpa_ferc714.eia_code.isin(hifld_pa_gdf.eia_code)]
.groupby(["report_year"]).demand_mwh.sum()
.reset_index()
.merge(annual_demand_ferc714, on="report_year", suffixes=("_map", "_tot"))
.assign(
fraction_mapped=lambda x: x.demand_mwh_map / x.demand_mwh_tot
)
)
plt.plot("report_year", "fraction_mapped", data=annual_demand_mapped, lw=5)
plt.ylabel("Fraction of demand which is mapped")
plt.title("Completeness of HIFLD demand mapping by year")
plt.ylim(0.6, 1.05);
```
# Historical Planning Area Geometries
Compile a GeoDataFrame that relates balancing authorities, their constituent utilities, and the collections of counties which are served by those utilities, across all the years for which we have EIA 861 data (2010-2018)
```
ba_util_county_gdf = georef_bas(ba_eia861, st_eia861, sales_eia861, census_gdf)
ba_util_county_gdf.info()
for year in (2010, 2014, 2018):
map_ba(ba_util_county_gdf.balancing_authority_id_eia.unique(), year, ba_util_county_gdf, save=True)
```
## Output Simplified Annual BA Geometries
* This takes half an hour so it's commented out.
* Resulting shapefile is ~250MB compressed. Seems too big.
* Need to figure out how to add explicity projection.
* Need to figure out how to make each year's BA geometries its own layer.
```
#%%time
#ba_fips_simplified = (
# ba_util_county_gdf
# .assign(report_year=lambda x: x.report_date.dt.year)
# .drop([
# "report_date",
# "state",
# "state_id_fips",
# "county",
# "county_name_census",
# "utility_id_eia",
# "utility_name_eia"
# ], axis="columns")
# .drop_duplicates(subset=["report_year", "balancing_authority_id_eia", "county_id_fips"])
# .dropna(subset=["report_year", "balancing_authority_id_eia", "county_id_fips"])
# .loc[:,["report_year", "balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia", "county_id_fips", "geometry"]]
#)
#ba_annual_gdf = (
# ba_fips_simplified
# .dissolve(by=["report_year", "balancing_authority_id_eia"])
# .reset_index()
# .drop("county_id_fips", axis="columns")
#)
#ba_output_gdf = (
# ba_annual_gdf
# .astype({
# "report_year": int,
# "balancing_authority_id_eia": float,
# "balancing_authority_code_eia": str,
# "balancing_authority_name_eia": str,
# })
# .rename(columns={
# "report_year": "year",
# "balancing_authority_id_eia": "ba_id",
# "balancing_authority_code_eia": "ba_code",
# "balancing_authority_name_eia": "ba_name",
# })
#)
#ba_output_gdf.to_file("ba_annual.shp")
```
## Compare HIFLD and EIA BA maps for 2018
```
for ba_code in hifld_pa_gdf.ABBRV.unique():
if ba_code in ba_util_county_gdf.balancing_authority_code_eia.unique():
compare_hifld_eia_ba(ba_code, hifld_pa_gdf, ba_util_county_gdf)
```
## Time Evolution of BA Geometries
For each BA we now have a collection of annual geometries. How have they changed over time?
```
for ba_code in ba_util_county_gdf.balancing_authority_code_eia.unique():
fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(20,20), sharex=True, sharey=True, facecolor="white")
for year, ax in zip(range(2010, 2019), axes.flat):
ax.set_title(f"{ba_code} ({year})")
ax.set_xticks([])
ax.set_yticks([])
plot_gdf = (
ba_util_county_gdf
.assign(report_year=lambda x: x.report_date.dt.year)
.query(f"balancing_authority_code_eia=='{ba_code}'")
.query(f"report_year=='{year}'")
.drop_duplicates(subset="county_id_fips")
)
plot_gdf.plot(ax=ax, linewidth=0.1)
plt.show()
```
## Merge Geometries with FERC 714
Now that we have a draft of wht the BA and Utility level territories look like, we can merge those with the FERC 714 Respondent ID table, and see how many leftovers there are, and whether the BA and Utility geometires play well together.
Before dissolving the boundaries between counties the output dataframe needs to have:
* `report_date`
* `respondent_id_ferc714`
* `eia_code`
* `respondent_type`
* `balancing_authority_id_eia`
* `utility_id_eia`
* `county_id_fips`
* `geometry`
* `balancing_authority_code_eia`
* `balancing_authority_name_eia`
* `respondent_name_ferc714`
* `utility_name_eia`
* `county_name_census`
* `state`
* `state_id_fips`
```
utils_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type == "utility",
["respondent_id_ferc714", "respondent_name_ferc714", "utility_id_eia", "respondent_type"]
]
)
bas_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type == "balancing_authority",
["respondent_id_ferc714", "respondent_name_ferc714", "balancing_authority_id_eia", "respondent_type"]
]
)
null_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type.isnull(),
["respondent_id_ferc714", "respondent_name_ferc714", "respondent_type"]
]
)
bas_ferc714_gdf = (
ba_util_county_gdf
.drop(["county"], axis="columns")
.merge(bas_ferc714, how="right")
)
utils_ferc714_gdf = (
ba_util_county_gdf
.drop(["balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia", "county"], axis="columns")
.drop_duplicates()
.merge(utils_ferc714, how="right")
)
rids_ferc714_gdf = (
pd.concat([bas_ferc714_gdf, utils_ferc714_gdf, null_ferc714])
.astype({
"county_id_fips": pd.StringDtype(),
"county_name_census": pd.StringDtype(),
"respondent_type": pd.StringDtype(),
"utility_id_eia": pd.Int64Dtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
"balancing_authority_code_eia": pd.StringDtype(),
"balancing_authority_name_eia": pd.StringDtype(),
"state": pd.StringDtype(),
"utility_name_eia": pd.StringDtype(),
})
)
display(rids_ferc714_gdf.info())
rids_ferc714_gdf.sample(10)
```
## Check Geometries for Completeness
* How many balancing authorities do we have geometries for?
* How many utilities do we have geometries for?
* Do those geometries cover all of the entities that report in FERC 714?
* Do we have a geometry for every entity in every year in which it reports demand?
### Count BA & Util Geometries
```
n_bas = len(rids_ferc714_gdf.balancing_authority_id_eia.unique())
logger.info(f"Found territories for {n_bas} unique Balancing Areas")
n_utils = len(rids_ferc714_gdf.loc[
(rids_ferc714_gdf.balancing_authority_id_eia.isnull()) &
(~rids_ferc714_gdf.utility_id_eia.isnull())
].utility_id_eia.unique())
logger.info(f"Found territories for {n_utils} Utilities outside of the BAs")
```
### Identify Missing Geometries
* Within each year of historical data from 2010-2018, are there any entities (either BA or Utility) which **do** have hourly demand reported in the FERC 714, for whivh we do not have a historical geometry?
* How many of them are there?
* Why are they missing?
* Do we have the geometires in adjacent years and can we re-use them?
* Is it possible that the FERC 714 IDs correspond to a precursor entity, or one that was discontinued? E.g. if SWPP is missing in 2010, is that because the BA was reported in EIA as SPS in that year?
* How important are the missing geometries? Do the associated entities have a lot of demand associated with them in FERC 714?
* Can we use `ffill` or `backfill` on the `geometry` column in a GeoDataFrame?
```
problem_ids = pd.DataFrame()
for year in range(2010, 2019):
this_year_gdf = (
rids_ferc714_gdf
.loc[(rids_ferc714_gdf.report_date.dt.year==year) & (~rids_ferc714_gdf.geometry.isnull())]
)
# All BA IDs which show up in FERC 714:
ba_ids_ferc714 = (
rids_ferc714
.loc[rids_ferc714.respondent_type=="balancing_authority",
"balancing_authority_id_eia"]
.unique()
)
# BA IDs which have a geometry in this year
ba_geom_ids = (
this_year_gdf
.balancing_authority_id_eia
.dropna().unique()
)
# BA IDs which have reported demand in this year
ba_demand_ids = (
dhpa_ferc714
.query("report_year==@year")
.query("demand_mwh>0.0")
.loc[dhpa_ferc714.eia_code.isin(ba_ids_ferc714)]
.eia_code.unique()
)
# Need to make the demand IDs clearly either utility of BA IDs. Whoops!
missing_ba_geom_ids = [x for x in ba_demand_ids if x not in ba_geom_ids]
logger.info(f"{len(missing_ba_geom_ids)} BA respondents w/o geometries in {year}")
problem_ids = problem_ids.append(
rids_ferc714
.loc[rids_ferc714.balancing_authority_id_eia.isin(missing_ba_geom_ids)]
.assign(year=year)
)
# All EIA Utility IDs which show up in FERC 714:
util_ids_ferc714 = (
rids_ferc714
.loc[rids_ferc714.respondent_type=="utility",
"utility_id_eia"]
.unique()
)
# EIA Utility IDs which have geometry information for this year
util_geom_ids = (
this_year_gdf
.utility_id_eia
.dropna().unique()
)
util_demand_ids = (
dhpa_ferc714
.query("report_year==@year")
.query("demand_mwh>0.0")
.loc[dhpa_ferc714.eia_code.isin(util_ids_ferc714)]
.eia_code.unique()
)
missing_util_geom_ids = [x for x in util_demand_ids if x not in util_geom_ids]
logger.info(f"{len(missing_util_geom_ids)} Utility respondents w/o geometries in {year}")
problem_ids = problem_ids.append(
rids_ferc714
.loc[rids_ferc714.utility_id_eia.isin(missing_util_geom_ids)]
.assign(year=year)
)
problem_ids.query("year==2010").query("respondent_type=='balancing_authority'")
```
## Dissolve to BA or Util
* At this point we still have geometires at the county level.
* This is 150,000+ records.
* Really we just want a single geometry per respondent per year.
* Dissolve based on year and respondent_id_ferc714.
* Merge the annual per-respondent geometry with the rids_ferc714 which has more information
* Note that this takes about half an hour to run...
```
%%time
dissolved_rids_ferc714_gdf = (
rids_ferc714_gdf.drop_duplicates(subset=["report_date", "county_id_fips", "respondent_id_ferc714"])
.dissolve(by=["report_date", "respondent_id_ferc714"])
.reset_index()
.loc[:, ["report_date", "respondent_id_ferc714", "geometry"]]
.merge(rids_ferc714, on="respondent_id_ferc714", how="outer")
)
#dissolved_rids_ferc714_gdf.to_file("planning_areas_ferc714.gpkg", driver="GPKG")
```
### Select based on respondent type
```
dissolved_utils = dissolved_rids_ferc714_gdf.query("respondent_type=='utility'")
dissolved_bas = dissolved_rids_ferc714_gdf.query("respondent_type=='balancing_authority'")
```
### Nationwide BA / Util Maps
* Still want to add the US state boundaries / coastlines to this for context.
```
unwanted_ba_ids = (
112, # Alaska
133, # Alaska
178, # Hawaii
301, # PJM Dupe
302, # PJM Dupe
303, # PJM Dupe
304, # PJM Dupe
305, # PJM Dupe
306, # PJM Dupe
)
for report_date in pd.date_range(start="2010-01-01", end="2018-01-01", freq="AS"):
ba_ax = (
dissolved_bas
.query("report_date==@report_date")
.query("respondent_id_ferc714 not in @unwanted_ba_ids")
.plot(figsize=(20, 20), color="blue", alpha=0.25, linewidth=1)
)
plt.title(f"FERC 714 Balancing Authority Respondents {report_date}")
ctx.add_basemap(ba_ax)
util_ax = (
dissolved_utils
.query("report_date==@report_date")
.plot(figsize=(20, 20), color="red", alpha=0.25, linewidth=1)
)
plt.title(f"FERC 714 Utility Respondents {report_date}")
ctx.add_basemap(util_ax)
plt.show();
```
### Per-respondent annual maps
* For each respondent make a grid of 9 (2010-2018)
* Show state lines in bg for context
* Limit bounding box by the respondent's territory
# Remaining Tasks
## Geometry Cleanup:
* Why do some respondents lack geometries in some years?
* Why do some respondents lack geometries in **all** years? (e.g. Tri-State G&T)
* Why do some counties have no BA or Utility coverage in some or all years?
* What combinations of years and respondents are missing?
* Compare what we've ended up doing to the Aufhammer paper again.
* Is there any need to use name-based matching between the Planning Area descriptions & EIA Service Territories?
* Problem BAs / Utilities:
* All the WAPA BAs
* PacifiCorp East / West
* Southern Company
* MISO (Some other IDs that seem related?)
* PJM (Early years seem out of bounds)
## FERC 714 Demand Time Series Cleanup
### Find broken data:
* Run Tyler Ruggles' anomaly detection code as improved by Greg Schivley
* What kind of anomalies are we finding? Are they a problem? What portion of the overall dataset do they represent?
### Repair data:
* How do we want to fill in the gaps?
* Ideally would be able to use the MICE technique that Tyler used, but we need to keep it all in Python.
* Can do much simpler rolling averages or something for the moment when there are small gaps just to have completeness.
* Should make this gap filling process modular -- use different techniques and see whether they do what we need.
# Miscellaneous Notes
## FERC 714 Demand Irregularities
Unusual issues that need to be addressed, or demand discontinuities that may be useful in the context of aggregating historical demand into modern planning areas. Organized by FERC 714 Respondent ID:
* Missing demand data / weird zeroes
* 111: (2008)
* 125: (2015)
* 137: (2006)
* 139: (2006) Only the last hour of every day. Maybe 0-23 vs 1-24 reporting?
* 141: (2006, 2007, 2008, 2009, 2010)
* 148: (2006)
* 153: (2006)
* 154: (2006)
* 161: (all)
* 183: (2007, 2009)
* 208: (2008)
* 273: (2007, 2008)
* 283: (2007)
* 287: (2008-2012)
* 288: (2006)
* 289: (2009)
* 293: (2006)
* 294: (2006)
* 311: (2008-2011)
* Inverted Demand (Sign Errors):
* 156: (2006, 2007, 2008, 2009)
* 289: (2006-2008, 2010)
* Large demand discontinuities
* 107: Demand triples at end of 2006.
* 115: Two big step downs, 2007-2008, and 2011-2012
* 121: 50% increase at end of 2007.
* 128: Step up at end of 2007
* 133: Step down end of 2013 and again end of 2015
* 190: Demand doubled at end of 2008
* 214: 50% jump in early 2012.
* 256: big jump at end of 2006.
* 261: Big jump at end of 2008.
* 274: drop at end of 2007
* 275: Jump at end of 2007
* 287: Demand before and after big gap are very different.
* 299: Big drop at end of 2015
* 307: Jump at end of 2014
* 321: Jump at end of 2013
| true |
code
| 0.621168 | null | null | null | null |
|
```
%matplotlib inline
"""
The data set in this example represents 1059 songs from various countries obtained
from the UCI Machine Learning library. Various features of the audio tracks have been
extracted, and each track has been tagged with the latitude and longitude of the capital
city of its country of origin.
We'll treat this as a classification problem, and attempt to train a model to predict
the country of origin of each model.
Data source did not specifify what the audio features specifically are, just
"In the 'default_features_1059_tracks.txt' file, the first 68 columns are audio
features of the track, and the last two columns are the origin of the music,
represented by latitude and longitude.
In the 'default_plus_chromatic_features_1059_tracks.txt' file, the first 116
columns are audio features of the track, and the last two columns are the
origin of the music."
"""
import numpy as np
import pandas as pd
import sklearn
from sklearn.preprocessing import LabelEncoder
from sklearn.utils.multiclass import unique_labels
import sys
#First get the data. The UCI ML Library distributes it as a zipped file;
#download the data and extract the two provided files to the 'data' folder before continuing
music_df = pd.read_csv('data\default_plus_chromatic_features_1059_tracks.txt', header=None)
music = music_df.as_matrix()
#Our features are all but the last two columns
X = music[:,0:-2]
#Since feature names were not given, we'll just assign strings with an incrementing integer
names = np.linspace(start=1, stop=116, num=116, dtype='int').tolist()
for idx, name in enumerate(names):
names[idx] = "Feature " + str(name)
#The source data said that each song as tied to the capital city of it's origin country via a lat/lon pair.
#Let's treat this as a multi-class classification problem.
#Rather than reverse-geocoding, we'll just make a string out of the unique lat/lon pairs
lats = ["%.2f" % lat for lat in music_df[116]]
lons = ["%.2f" % lon for lon in music_df[117]]
song_latlons = []
for index, value in enumerate(lats):
city_id = lats[index] + "," + lons[index]
song_latlons.append(city_id)
unique_latlons = unique_labels(song_latlons)
city_options = ['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z','AA','AB','AC','AD','AE','AF','AG']
city_name_map = {}
for idx,latlon in enumerate(unique_latlons):
city_name_map[latlon] = city_options[idx]
ylist = []
for latlon in song_latlons:
ylist.append(city_name_map[latlon])
y = np.array(ylist)
#We want yellowbrick to import from this repository, and assume this notebook is in repofolder/examples/subfolder/
sys.path.append("../../")
import yellowbrick as yb
from yellowbrick.features.rankd import Rank2D
from yellowbrick.features.radviz import RadViz
from yellowbrick.features.pcoords import ParallelCoordinates
#See how well correlated the features are
visualizer = Rank2D(features = names, algorithm = 'pearson')
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.poof()
from sklearn import metrics
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from yellowbrick.classifier import ClassificationReport
def train_and_classification_report(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
print("prec: {}".format(metrics.precision_score(y_true = y_test, y_pred = y_predict, average="weighted")))
print("rec: {}".format(metrics.recall_score(y_true= y_test, y_pred = y_predict, average = "weighted")))
cr_viz = ClassificationReport(model) #,classes=city_options
cr_viz.fit(X_train, y_train)
cr_viz.score(X_test, y_test)
cr_viz.poof()
#Adding the reloading functionality so we can edit the source code and see results here.
import importlib
importlib.reload(yb.classifier)
from yellowbrick.classifier import ClassificationReport
#This produces an IndexError: list index out of range.
train_and_classification_report(LogisticRegression())
#This demonstrates a version of the Seaborn confusion matrix heatmap we could replicate (and improve on).
def train_and_confusion_matrix(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
print("prec: {}".format(metrics.precision_score(y_true = y_test, y_pred = y_predict, average="weighted")))
print("rec: {}".format(metrics.recall_score(y_true= y_test, y_pred = y_predict, average = "weighted")))
c_matrix = confusion_matrix(y_true = y_test, y_pred = y_predict)
sns.heatmap(c_matrix, square=True, annot=True, cbar=False, xticklabels=city_options, yticklabels = city_options)
plt.xlabel('predicted value')
plt.ylabel('true value')
train_and_confusion_matrix(LogisticRegression())
def train_and_class_balance(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
class_balance = yb.classifier.ClassBalance(model, classes=city_options)
class_balance.fit(X_train, y_train)
class_balance.score(X_test, y_test)
class_balance.poof()
train_and_class_balance(LogisticRegression())
```
| true |
code
| 0.592136 | null | null | null | null |
|
```
import open3d as o3d
import numpy as np
import os
import sys
# monkey patches visualization and provides helpers to load geometries
sys.path.append('..')
import open3d_tutorial as o3dtut
# change to True if you want to interact with the visualization windows
o3dtut.interactive = not "CI" in os.environ
```
# RGBD integration
Open3D implements a scalable RGBD image integration algorithm. The algorithm is based on the technique presented in [\[Curless1996\]](../reference.html#curless1996) and [\[Newcombe2011\]](../reference.html#newcombe2011). In order to support large scenes, we use a hierarchical hashing structure introduced in [Integrater in ElasticReconstruction](https://github.com/qianyizh/ElasticReconstruction/tree/master/Integrate).
## Read trajectory from .log file
This tutorial uses the function `read_trajectory` to read a camera trajectory from a [.log file](http://redwood-data.org/indoor/fileformat.html). A sample `.log` file is as follows.
```
# examples/test_data/RGBD/odometry.log
0 0 1
1 0 0 2
0 1 0 2
0 0 1 -0.3
0 0 0 1
1 1 2
0.999988 3.08668e-005 0.0049181 1.99962
-8.84184e-005 0.999932 0.0117022 1.97704
-0.0049174 -0.0117024 0.999919 -0.300486
0 0 0 1
```
```
class CameraPose:
def __init__(self, meta, mat):
self.metadata = meta
self.pose = mat
def __str__(self):
return 'Metadata : ' + ' '.join(map(str, self.metadata)) + '\n' + \
"Pose : " + "\n" + np.array_str(self.pose)
def read_trajectory(filename):
traj = []
with open(filename, 'r') as f:
metastr = f.readline()
while metastr:
metadata = list(map(int, metastr.split()))
mat = np.zeros(shape=(4, 4))
for i in range(4):
matstr = f.readline()
mat[i, :] = np.fromstring(matstr, dtype=float, sep=' \t')
traj.append(CameraPose(metadata, mat))
metastr = f.readline()
return traj
camera_poses = read_trajectory("../../test_data/RGBD/odometry.log")
```
## TSDF volume integration
Open3D provides two types of TSDF volumes: `UniformTSDFVolume` and `ScalableTSDFVolume`. The latter is recommended since it uses a hierarchical structure and thus supports larger scenes.
`ScalableTSDFVolume` has several parameters. `voxel_length = 4.0 / 512.0` means a single voxel size for TSDF volume is $\frac{4.0\mathrm{m}}{512.0} = 7.8125\mathrm{mm}$. Lowering this value makes a high-resolution TSDF volume, but the integration result can be susceptible to depth noise. `sdf_trunc = 0.04` specifies the truncation value for the signed distance function (SDF). When `color_type = TSDFVolumeColorType.RGB8`, 8 bit RGB color is also integrated as part of the TSDF volume. Float type intensity can be integrated with `color_type = TSDFVolumeColorType.Gray32` and `convert_rgb_to_intensity = True`. The color integration is inspired by [PCL](http://pointclouds.org/).
```
volume = o3d.pipelines.integration.ScalableTSDFVolume(
voxel_length=4.0 / 512.0,
sdf_trunc=0.04,
color_type=o3d.pipelines.integration.TSDFVolumeColorType.RGB8)
for i in range(len(camera_poses)):
print("Integrate {:d}-th image into the volume.".format(i))
color = o3d.io.read_image("../../test_data/RGBD/color/{:05d}.jpg".format(i))
depth = o3d.io.read_image("../../test_data/RGBD/depth/{:05d}.png".format(i))
rgbd = o3d.geometry.RGBDImage.create_from_color_and_depth(
color, depth, depth_trunc=4.0, convert_rgb_to_intensity=False)
volume.integrate(
rgbd,
o3d.camera.PinholeCameraIntrinsic(
o3d.camera.PinholeCameraIntrinsicParameters.PrimeSenseDefault),
np.linalg.inv(camera_poses[i].pose))
```
## Extract a mesh
Mesh extraction uses the marching cubes algorithm [\[LorensenAndCline1987\]](../reference.html#lorensenandcline1987).
```
print("Extract a triangle mesh from the volume and visualize it.")
mesh = volume.extract_triangle_mesh()
mesh.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh],
front=[0.5297, -0.1873, -0.8272],
lookat=[2.0712, 2.0312, 1.7251],
up=[-0.0558, -0.9809, 0.1864],
zoom=0.47)
```
<div class="alert alert-info">
**Note:**
TSDF volume works like a weighted average filter in 3D space. If more frames are integrated, the volume produces a smoother and nicer mesh. Please check [Make fragments](../reconstruction_system/make_fragments.rst) for more examples.
</div>
| true |
code
| 0.484685 | null | null | null | null |
|
# Making Simple Plots
## Objectives
+ Learn how to make a simple 1D plot in Python.
+ Learn how to find the maximum/minimum of a function in Python.
We will use [Problem 4.B.2](https://youtu.be/w-IGNU2i3F8) of the lecturebook as a motivating example.
We find that the moment of the force $\vec{F}$ about point A is:
$$
\vec{M_A} = (bF\cos\theta - dF\sin\theta)\hat{k}.
$$
Let's plot the component of the moment as a function of $\theta$.
For this, we will use the Python module [matplotlib](https://matplotlib.org).
```
import numpy as np # for numerical algebra
import matplotlib.pyplot as plt # this is where the plotting capabilities are
# The following line is need so that the plots are embedded in the Jupyter notebook (remove when not using Jupyter)
%matplotlib inline
# Define a function that computes the moment magnitude as a function of all other parameters
def M_A(theta, b, d, F):
"""
Compute the k component of the moment of F about point A given all the problem parameters.
"""
return b * F * np.cos(theta) - d * F * np.sin(theta)
# Choose some parameters
b = 0.5 # In meters
d = 2. # In meters
F = 2. # In kN
# The thetas on which we will evaluate the moment for plotting
thetas = np.linspace(0, 2 * np.pi, 100)
# The moment on these thetas:
M_As = M_A(thetas, b, d, F)
# Let's plot
plt.plot(thetas / (2. * np.pi) * 360, M_As, lw=2)
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)');
```
Now, let's put two lines in the same plot.
Let's compare the moments when we change $d$ from 2 meters to 3.5 meters.
```
# We already have M_A for d=2 m (and all other paramters to whichever values we gave them)
# Let's copy it:
M_As_case_1 = M_As
# And let's compute it again for d=3.5 m
d = 3.5 # In m
M_As_case_2 = M_A(thetas, b, d, F)
# Let's plot both of them in the same figure
plt.plot(thetas / (2. * np.pi) * 360, M_As_case_1, lw=2, label='Case 1')
plt.plot(thetas / (2. * np.pi) * 360, M_As_case_2, '--', lw=2, label='Case 2')
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)')
plt.legend(loc='best')
```
Finally, let's see how we can make interactive plots.
We will use the Python module [ipywidgets](https://ipywidgets.readthedocs.io/en/stable/) and in particular the function [ipywidgets.interact](https://ipywidgets.readthedocs.io/en/stable/examples/Using%20Interact.html).
```
from ipywidgets import interact # Loading the module
# Interact needs a function that does the plotting given the parameters.
# Let's make it:
def make_plots(b=0.5, d=3., F=1.): # X=val defines default values for the function
"""
Make the plot.
"""
thetas = np.linspace(0, 2. * np.pi, 100)
M_As = M_A(thetas, b, d, F)
plt.plot(thetas / (2. * np.pi) * 360, M_As, lw=2, label='Case 1')
plt.ylim([-10., 10.])
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)')
```
Let's just check that the function works by calling it a few times:
```
# With no inputs it should use the default values
make_plots()
# You can specify all the inputs like this:
make_plots(2., 3., 2.)
# Or even by name (whatever is not specified gets the default value):
make_plots(F=2.3)
```
Ok. Let's use interact now:
```
interact(make_plots,
b=(0., 5., 0.1), # Range for b: (min, max, increment)
d=(0., 5, 0.1), # Range for d
F=(0., 2, 0.1) # Range for F
);
```
| true |
code
| 0.635364 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Plot-Validation-and-Train-loss" data-toc-modified-id="Plot-Validation-and-Train-loss-1"><span class="toc-item-num">1 </span>Plot Validation and Train loss</a></span></li><li><span><a href="#Extract-relevant-Data-to-df" data-toc-modified-id="Extract-relevant-Data-to-df-2"><span class="toc-item-num">2 </span>Extract relevant Data to df</a></span><ul class="toc-item"><li><span><a href="#Get-best-result" data-toc-modified-id="Get-best-result-2.1"><span class="toc-item-num">2.1 </span>Get best result</a></span></li><li><span><a href="#Consider-Outliers" data-toc-modified-id="Consider-Outliers-2.2"><span class="toc-item-num">2.2 </span>Consider Outliers</a></span></li></ul></li><li><span><a href="#Results-by-model" data-toc-modified-id="Results-by-model-3"><span class="toc-item-num">3 </span>Results by model</a></span><ul class="toc-item"><li><span><a href="#Remove-Duplicates" data-toc-modified-id="Remove-Duplicates-3.1"><span class="toc-item-num">3.1 </span>Remove Duplicates</a></span></li></ul></li><li><span><a href="#Each-variable-plotted-against-loss:" data-toc-modified-id="Each-variable-plotted-against-loss:-4"><span class="toc-item-num">4 </span>Each variable plotted against loss:</a></span></li><li><span><a href="#Investigate-"band"-in-loss-model-plot" data-toc-modified-id="Investigate-"band"-in-loss-model-plot-5"><span class="toc-item-num">5 </span>Investigate "band" in loss-model plot</a></span><ul class="toc-item"><li><span><a href="#Extract-the-different-bands-and-inpsect" data-toc-modified-id="Extract-the-different-bands-and-inpsect-5.1"><span class="toc-item-num">5.1 </span>Extract the different bands and inpsect</a></span></li></ul></li><li><span><a href="#Investigate-Duplicates" data-toc-modified-id="Investigate-Duplicates-6"><span class="toc-item-num">6 </span>Investigate Duplicates</a></span></li><li><span><a href="#Investigate-Best" data-toc-modified-id="Investigate-Best-7"><span class="toc-item-num">7 </span>Investigate Best</a></span></li></ul></div>
```
%load_ext autoreload
%autoreload 2
%cd ..
import os
import sys
from notebooks import utils
from matplotlib import pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()
#import pipeline
# parent_dir = os.path.abspath(os.path.join(os.getcwd(), os.pardir))
# sys.path.append(parent_dir) #to import pipeline
%ls experiments
###CHANGE THIS FILE TO THE SUBDIRECTORY OF INTEREST:
#exp_dirs = ["experiments/07b/", "experiments/DA3_2/07a/0", "experiments/DA3_2/07a/1"]
exp_dirs = ["experiments/retrain/"]
results = utils.extract_res_from_files(exp_dirs)
#load data when utils isnt working:
if False:
import pickle
res_fp = "experiments/results/ResNeXt/res.txt"
with open(res_fp, "rb") as f:
results = pickle.load(f)
```
## Plot Validation and Train loss
```
ylim = (0, 3000)
ylim2 = (70,100)
utils.plot_results_loss_epochs(results, ylim1=ylim, ylim2=ylim2)
```
## Extract relevant Data to df
Use minimum validation loss as criterion.
In theory (if we had it) it would be better to use DA MAE
```
df_res = utils.create_res_df(results)
df_res_original = df_res.copy() #save original (in case you substitute out)
df_res
```
### Get best result
```
df_res["valid_loss"].idxmin()
print(df_res.loc[df_res["valid_loss"].idxmin()])
df_res.loc[df_res["valid_loss"].idxmin()]["path"]
```
### Consider Outliers
```
#consider third experiment run (lots of outliers)
df3 = df_res[df_res["path"].str.contains("CAE_zoo3")]
df_outlier = df_res[df_res["valid_loss"] > 150000]
df_outlier
```
## Results by model
```
relu = df_res[df_res.activation == "relu"]
lrelu = df_res[df_res.activation == "lrelu"]
plt.scatter('model', "valid_loss", data=relu, marker="+", color='r')
plt.scatter('model', "valid_loss", data=lrelu, marker="+", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 70000)
plt.legend(labels=["relu", "lrelu"])
plt.show()
#investigate number of layers
eps = 1e-5
reluNBN = df_res[(df_res.activation == "relu") & (abs(df_res.batch_norm - 0.) < eps)]
reluBN = df_res[(df_res.activation == "relu") & (abs(df_res.batch_norm - 1.) < eps)]
lreluNBN = df_res[(df_res.activation == "lrelu") & (abs(df_res.batch_norm - 0.0) < eps)]
lreluBN = df_res[(df_res.activation == "lrelu") & (abs(df_res.batch_norm - 1.) < eps)]
plt.scatter('model', "valid_loss", data=reluNBN, marker="+", color='r')
plt.scatter('model', "valid_loss", data=reluBN, marker="+", color='g')
plt.scatter('model', "valid_loss", data=lreluNBN, marker="o", color='r')
plt.scatter('model', "valid_loss", data=lreluBN, marker="o", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 70000)
plt.legend(labels=["relu, NBN", "relu, BN", "lrelu, NBN", "lrelu, BN"])
plt.show()
```
It turns out that there are lots of duplicates in the above data (as a result of a bug in my code that was giving all models the same number of channels). So remove duplicates and go again:
### Remove Duplicates
```
#remove duplicates
columns = list(df_res_original.columns)
columns.remove("model")
columns.remove("path")
print(columns)
df_res_new = df_res_original.loc[df_res_original.astype(str).drop_duplicates(subset=columns, keep="last").index]
#df_res_new = df_res_original.drop_duplicates(subset=columns, keep="last")
df_res_new.shape
df_res = df_res_new
df_res.shape
##Plot same graph again:
#investigate number of layers
relu6 = df_res[(df_res.activation == "relu") & (df_res.num_layers == 6)]
relu11 = df_res[(df_res.activation == "relu") & (df_res.num_layers != 6)]
lrelu6 = df_res[(df_res.activation == "lrelu") & (df_res.num_layers == 6)]
lrelu11 = df_res[(df_res.activation == "lrelu") & (df_res.num_layers != 6)]
plt.scatter('model', "valid_loss", data=relu6, marker="+", color='r')
plt.scatter('model', "valid_loss", data=lrelu6, marker="+", color='g')
plt.scatter('model', "valid_loss", data=relu11, marker="o", color='r')
plt.scatter('model', "valid_loss", data=lrelu11, marker="o", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 60000)
plt.legend(labels=["relu, 6", "lrelu, 6", "relu, not 6", "lrelu, not 6"])
plt.show()
```
## Each variable plotted against loss:
```
plt.scatter('latent_dims', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("latent dimensions")
plt.ylim(16000, 70000)
plt.scatter('first_channel', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("First channel")
plt.ylim(16000, 80000)
plt.scatter('batch_norm', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Batch Norm")
plt.xlim(-0.1, 1.1)
plt.ylim(16000, 80000)
plt.scatter('activation', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Activation")
plt.ylim(16000, 70000)
plt.scatter('model', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 80000)
plt.scatter('num_layers', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Number of layers in Decoder/Encoder")
plt.ylim(16000, 80000)
plt.scatter('total_channels', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Total Channels")
plt.ylim(16000, 80000)
plt.scatter('channels/layer', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Channels/Layer")
plt.ylim(16000, 80000)
plt.scatter('first_channel', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("First_channel")
plt.ylim(16000, 80000)
plt.scatter('conv_changeover', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Input size decrease at which to change to start downsampling (via transposed convolution)")
plt.ylim(16000, 80000)
```
## Investigate "band" in loss-model plot
### Extract the different bands and inpsect
```
band1 = df_res[df_res.valid_loss < 20000]
band2 = df_res[(df_res.valid_loss > 20000) & (df_res.valid_loss < 23000)]
band3 = df_res[(df_res.valid_loss > 23000) & (df_res.valid_loss < 26000)]
band1.head()
band3.head()
```
## Investigate Duplicates
```
#eg1: /data/home/jfm1118/DA/experiments/CAE_zoo2/32 and /data/home/jfm1118/DA/experiments/CAE_zoo2/12
#eg2: /data/home/jfm1118/DA/experiments/CAE_zoo2/31 and /data/home/jfm1118/DA/experiments/CAE_zoo2/27
def get_data_from_path(path):
for res in results:
if res["path"] == path:
return res
else:
raise ValueError("No path = {} in 'results' list".format(path))
def print_model(settings):
model = settings.AE_MODEL_TYPE(**settings.get_kwargs())
print(settings.__class__.__name__)
print(model.layers)
print(settings.CHANNELS)
base_exp = "/data/home/jfm1118/DA/experiments/CAE_zoo2/"
exp_32 = get_data_from_path(base_exp + "32")["settings"]
exp_12 = get_data_from_path(base_exp + "12")["settings"]
print_model(exp_32)
print()
print_model(exp_12)
base_exp = "/data/home/jfm1118/DA/experiments/CAE_zoo2/"
exp_1 = get_data_from_path(base_exp + "31")["settings"]
exp_2 = get_data_from_path(base_exp + "27")["settings"]
print_model(exp_1)
print()
print_model(exp_2)
print(list(range(1, 2*(exp_1.get_num_layers_decode() + 1) + 1, 2)))
```
## Investigate Best
```
path = "/data/home/jfm1118/DA/experiments/CAE_zoo2/17"
exp = get_data_from_path(base_exp + str(17))["settings"]
print_model(exp_1)
```
| true |
code
| 0.553566 | null | null | null | null |
|
# 6. Hidden Markov Models with Theano and TensorFlow
In the last section we went over the training and prediction procedures of Hidden Markov Models. This was all done using only vanilla numpy the Expectation Maximization algorithm. I now want to introduce how both `Theano` and `Tensorflow` can be utilized to accomplish the same goal, albeit by a very different process.
## 1. Gradient Descent
Hopefully you are familiar with the gradient descent optimization algorithm, if not I recommend reviewing my posts on Deep Learning, which leverage gradient descent heavily (or this [video](https://www.youtube.com/watch?v=IHZwWFHWa-w). With that said, a simple overview is as follows:
> Gradient descent is a first order optimization algorithm for finding the minimum of a function. To find a local minimum of a function using gradient descent, on takes steps proportional to the negative of the gradient of the function at its current point.
Visually, this iterative process looks like:
<img src="https://drive.google.com/uc?id=1R2zVTj3uo5zmow6vFujWlU-qs9jRF_XG" width="250">
Where above we are looking at a contour plot of a three dimensional bowl, and the center of the bowl is a minimum. Now, the actual underlying mechanics of gradient descent work as follows:
#### 1. Define a model/hypothesis that will be mapping inputs to outputs, or in other words making predictions:
$$h_{\theta}(x) = \theta_0 + \theta_1x$$
In this case $x$ is our input and $h(x)$, often thought of as $y$, is our output. We are stating that we believe the ground truth relationship between $x$ and $h(x)$ is captured by the linear combination of $\theta_0 + \theta_1x$. Now, what are $\theta_0$ and $\theta_1$ equal to?
#### 2. Define a **cost** function for which you are trying to find the minimum. Generally, this cost function is defined as some form of **error**, and it will be parameterized by variables related to your model in some way.
$$cost = J = (y - h_{\theta}(x))^2$$
Above $y$ refers to the ground truth/actual value of the output, and $h_{\theta}(x)$ refers to that which our model predicted. The difference, squared, represents our cost. We can see that if our prediction is exactly equal to the ground truth value, our cost will be 0. If our prediction is very far off from our ground truth value then our cost will be very high. Our goal is to minimize the cost (error) of our model.
#### 3. Take the [**gradient**](https://en.wikipedia.org/wiki/Gradient) (multi-variable generalization of the derivative) of the cost function with respect to the parameters that you have control over.
$$\nabla J = \frac{\partial J}{\partial \theta}$$
Simply put, we want to see how $J$ changes as we change our model parameters, $\theta_0$ and $\theta_1$.
#### 4. Based on the gradient update our values for $\theta$ with a simple update rule:
$$\theta_0 \rightarrow \theta_0 - \alpha \cdot \frac{\partial J}{\partial \theta_0}$$
$$\theta_1 \rightarrow \theta_1 - \alpha \cdot \frac{\partial J}{\partial \theta_1}$$
#### 5. Repeat steps two and three for a set number of iterations/until convergence.
After a set number of steps, the hope is that the model weights that were _learned_ are the most optimal weights to minimize prediction error. Now after everything we discussed in the past two posts you may be wondering, how exactly does this relate to Hidden Markov Models, which have been trained via Expectation Maximization?
### 1.1 Gradient Descent and Hidden Markov Models
Let's say for a moment that our goal that we wish to accomplish is predict the probability of an observed sequence, $p(x)$. And let's say that we have 100 observed sequences at our disposal. It should be clear that if we have a trained HMM that predicts the majority of our sequences are very unlikely, the HMM was probably not trained very well. Ideally, our HMM parameters would be learned in a way that maximizes the probability of observing what we did (this was the goal of expectation maximization).
What may start to become apparent at this point is that we have a perfect cost function already created for us! The total probability of our observed sequences, based on our HMM parameters $A$, $B$, and $\pi$. We can define this mathematically as follows (for the scaled version); in the previous post we proved that:
$$p(x) = \prod_{t=1}^T c(t)$$
Which states that the probability of an observed sequence is equal to the product of the scales at each time step. Also recall that the scale is just defined as:
$$c(t) = \sum_{i=1}^M \alpha'(t,i)$$
With that all said, we can define the cost of a single observed training sequence as:
$$cost = \sum_{t}^{T} log\big(c(t)\big)$$
Where we are using the log to avoid the underflow problem, just as we did in the last notebook. So, we have a cost function which intuitively makes sense, but can we find its gradient with respect to our HMM parameters $A$, $B$, and $\pi$? We absolutely can! The wonderful thing about Theano is that it links variables together via a [computational graph](http://deeplearning.net/software/theano/extending/graphstructures.html). So, cost is depedent on $A$, $B$ and $\pi$ via the following link:
$$cost \rightarrow c(t) \rightarrow alpha \rightarrow A, B, \pi$$
We can take the gradient of this cost function in theano as well, allowing us to then easily update our values of $A$, $B$, and $\pi$! Done iteratively, we hopefully will converge to a nice minimum.
### 1.2 HMM Theano specifics
I would be lying if I said that Theano wasn't a little bit hard to follow at first. For those unfamiliar, representing symbolic mathematical computations as graphs may feel very strange. I have a few walk throughs of Theano in my Deep Learning section, as well as `.py` files in the source repo. Additionally, the theano [documentation](http://deeplearning.net/software/theano/index.html) is also very good. With that said, I do want to discuss a few details of the upcoming code block.
#### Recurrence Block $\rightarrow$ Calculating the Forward Variable, $\alpha$
First, I want to discuss the `recurrence` and `scan` functions that you will be seeing:
```
def recurrence_to_find_alpha(t, old_alpha, x):
"""Scaled version of updates for HMM. This is used to
find the forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time
step the initial value,
outputs_info=[self.pi * self.B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(self.A) * self.B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[self.pi * self.B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used
# here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
```
The above block is where our forward variable $\alpha$ and subsequently the probability of the observed sequence $p(x)$ is found. The process works as follows:
1. The `theano.scan` function (logically similar to a for loop) is defined with the following parameters:
* `fn`: The recurrence function that the array being iterated over will be passed into.
* `sequences`: An array of indexes, $[1,2,3,...,T]$
* `outputs_info`: The initial value of $\alpha$
* `non_sequences`: Our observation sequence, $X$. This passed in it's entirety to the recurrence function at each iteration.
2. Our recurrence function, `recurrence_to_find_alpha`, is meant to calculate $\alpha$ at each time step. $\alpha$ at $t=1$ was defined by `outputs_info` in `scan`. This recurrence function essentially is performing the forward algorithm (additionally it incorporates scaling):
$$\alpha(1,i) = \pi_iB\big(i, x(1)\big)$$
$$\alpha(t+1, j) = \sum_{i=1}^M \alpha(t,i) A(i,j)B(j, x(t+1))$$
3. We calculate $p(x)$ to be the sum of the log likelihood. This is set to be our `cost`.
4. We define a `cost_op`, which is a theano function that takes in a symbolic variable `thx` and determines the output `cost`. Remember, `cost` is linked to `thx` via:
```
cost -> scale -> theano.scan(non_sequences=thx)
```
#### Update block $\rightarrow$ Updating HMM parameters $A$, $B$, and $\pi$
The other block that I want to touch on is the update block:
```
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum()
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x')
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x')
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
```
The update block functions as follows:
1. We have `cost` that was defined symbolically and linked to `thx`. We can define `pi_update` as `pi_update = self.pi - learning_rate * T.grad(cost, self.pi)`.
2. This same approach is performed for $A$ and $B$.
3. We then create a theano function, `train_op` which takes in `thx`, our symbolic input, and with perform updates via the `updates=updates` kwarg. Specifically, updates takes in a list of tuples, with the first value in the tuple being the variable that should be updated, and the second being the expression with which it should be updated to be.
4. We loop through all training examples (sequences of observations), and call `train_up`, passing in `X[n]` (a unique sequene of observations) as `thx`.
5. `train_op` then performs the `updates`, utilizing `thx = X[n]` wherever `updates` depends on `thx`.
This is clearly stochastic gradient descent, because we are performing updates to our parameters $A$, $B$, and $\pi$ for each training sequence. Full batch gradient descent would be if we defined a cost function that was based on all of the training sequences, not only an individual sequence.
## 2. HMM's with Theano
In code, our HMM can be implemented with Theano as follows:
```
import numpy as np
import theano
import theano.tensor as T
import seaborn as sns
import matplotlib.pyplot as plt
from hmm.utils import get_obj_s3, random_normalized
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
sns.set(style="white", palette="husl")
sns.set_context("talk")
sns.set_style("ticks")
class HMM:
def __init__(self, M):
self.M = M
def fit(self, X, learning_rate=0.001, max_iter=10, V=None, p_cost=1.0, print_period=10):
"""Train HMM model using stochastic gradient descent."""
# Determine V, the vocabulary size
if V is None:
V = max(max(x) for x in X) + 1
N = len(X)
# Initialize HMM variables
pi0 = np.ones(self.M) / self.M # Initial state distribution
A0 = random_normalized(self.M, self.M) # State transition matrix
B0 = random_normalized(self.M, V) # Output distribution
thx, cost = self.set(pi0, A0, B0)
# This is a beauty of theano and it's computational graph.
# By defining a cost function, which is representing p(x),
# the probability of a sequence, we can then find the gradient
# of the cost with respect to our parameters (pi, A, B).
# The gradient updated rules are applied as usual. Note, the
# reason that this is stochastic gradient descent is because
# we are only looking at a single training example at a time.
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum()
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x')
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x')
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
print("A learned from training: \n", self.A.get_value())
print("B learned from training: \n", self.B.get_value())
print("pi learned from training: \n", self.pi.get_value())
plt.figure(figsize=(8,5))
plt.plot(costs, color="blue")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
return self.cost_op(x)
def get_cost_multi(self, X, p_cost=1.0):
P = np.random.random(len(X))
return np.array([self.get_cost(x) for x, p in zip(X, P) if p < p_cost])
def log_likelihood(self, x):
return - self.cost_op(x)
def set(self, pi, A, B):
# Create theano shared variables
self.pi = theano.shared(pi)
self.A = theano.shared(A)
self.B = theano.shared(B)
# Define input, a vector
thx = T.ivector("thx")
def recurrence_to_find_alpha(t, old_alpha, x):
"""
Scaled version of updates for HMM. This is used to find the
forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time step
the initial value,
outputs_info=[self.pi * self.B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(self.A) * self.B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[self.pi * self.B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used
# here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
return thx, cost
def fit_coin(file_key):
"""Loads data and trains HMM."""
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
# Instantiate object of class HMM with 2 hidden states (heads and tails)
hmm = HMM(2)
hmm.fit(X)
L = hmm.get_cost_multi(X).sum()
print("Log likelihood with fitted params: ", round(L, 3))
# Try the true values
pi = np.array([0.5, 0.5])
A = np.array([
[0.1, 0.9],
[0.8, 0.2]
])
B = np.array([
[0.6, 0.4],
[0.3, 0.7]
])
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == "__main__":
key = "coin_data.txt"
fit_coin(key)
```
## 3. HMM's with Theano $\rightarrow$ Optimization via Softmax
One of the challenges of the approach we took is that gradient descent is _unconstrained_; it simply goes in the direction of the gradient. This presents a problem for us in the case of HMM's. Remember, the parameters of an HMM are $\pi$, $A$, and $B$, and each is a probability matrix/vector. This means that they must be between 0 and 1, and must sum to 1 (along the rows if 2-D).
We accomplished this in the previous section by performing a "hack". Specifically, we renormalized after each gradient descent step. However, this means that we weren't performing _real_ gradient descent, because by renormalizing we are not exactly moving in the direction of the gradient anymore. For reference, the pseudocode looked like this:
```
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum() # Normalizing to ensure it stays a probability
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x') # Normalize for prob
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x') # Normalize for prob
# Passing in normalized updates for pi, A, B. No longer moving in dir of gradient
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
```
This leads us to the question: is it possible to use true gradient descent, while still conforming to the constraints that each parameter much be a true probability. The answer is of course yes!
### 3.1 Softmax
If you are unfamiliar with Deep Learning then you may want to jump over this section, or go through my deep learning posts that dig into the subject. If you are familiar, recall the softmax function:
$$softmax(x)_i = \frac{exp(x_i)}{\sum_{k=1}^K exp(x_k)}$$
Where $x$ is an array of size $K$, and $K$ is the number of classes that we have. The result of the softmax is that all outputs are positive and sum to 1. What exactly does this mean in our scenario?
#### Softmax for $\pi$
Consider $\pi$, an array of size $M$. Supposed we want to parameterize $\pi$, using the symbol $\theta$. We can then assign $\pi$ to be:
$$pi = softmax(\theta)$$
In this way, $\pi$ is like an intermediate variable and $\theta$ is the actual parameter that we will be updating. This ensures that $\pi$ is always between 0 and 1, and sums to 1. At the same time, the values in $\theta$ can be anything; this means that we can freely use gradient descent on $\theta$ without having to worry about any constraints! No matter what we do to $\theta$, $\pi$ will always be between 0 and 1 and sum to 1.
#### Softmax for $A$ and $B$
Now, what about $A$ and $B$? Unlike $\pi$, which was a 1-d vector, $A$ and $B$ are matrices. Luckily for us, softmax works well for us here too! Recall that when dealing with data in deep learning (and most ML) that we are often dealing with multiple samples at the same time. Typically an $NxD$ matrix, where $N$ is the number of samples, and $D$ is the dimensionality. We know that the output of our model is usually an $NxK$ matrix, where $K$ is the number of classes. Naturally, because the classes go along the rows, each row must represent a separate probability distribution.
Why is this helpful? Well, the softmax was actually written with this specifically in mind! When you use the softmax it automatically exponentiates every element of the matrix and divides by the row sum. That is exactly what we want to do with $A$ and $B$! Each row of $A$ is the probability of the next state to transition to, and each row of $B$ is the probability of the next symbol to emit. The rows must sum to 1, just like the output predictions of a neural network!
In pseudocode, softmax looks like:
```
def softmax(A):
expA = np.exp(A)
return expA / expA.sum(axis=1, keepdims=True)
```
We can see this clearly below:
```
np.set_printoptions(suppress=True)
A = np.array([
[1,2],
[4,5],
[9,5]
])
expA = np.exp(A)
print("A exponentiated element wise: \n", np.round_(expA, decimals=3), "\n")
# Keep dims ensures a column vector (vs. row) output
output = expA / expA.sum(axis=1, keepdims=True)
print("Exponentiated A divided row sum: \n", np.round_(output, decimals=3))
```
Now you may be wondering: Why can't we just perform standard normalization? Why does the exponetial need to be used? For an answer to that I recommend reading up [here](https://stackoverflow.com/questions/17187507/why-use-softmax-as-opposed-to-standard-normalization), [here](https://stats.stackexchange.com/questions/162988/why-sigmoid-function-instead-of-anything-else/318209#318209), and [here](http://cs231n.github.io/linear-classify/#softmax).
### 3.2 Update Discrete HMM Code $\rightarrow$ with Softmax
```
class HMM:
def __init__(self, M):
self.M = M
def fit(self, X, learning_rate=0.001, max_iter=10, V=None, p_cost=1.0, print_period=10):
"""Train HMM model using stochastic gradient descent."""
# Determine V, the vocabulary size
if V is None:
V = max(max(x) for x in X) + 1
N = len(X)
preSoftmaxPi0 = np.zeros(self.M) # initial state distribution
preSoftmaxA0 = np.random.randn(self.M, self.M) # state transition matrix
preSoftmaxB0 = np.random.randn(self.M, V) # output distribution
thx, cost = self.set(preSoftmaxPi0, preSoftmaxA0, preSoftmaxB0)
# This is a beauty of theano and it's computational graph. By defining a cost function,
# which is representing p(x), the probability of a sequence, we can then find the gradient
# of the cost with respect to our parameters (pi, A, B). The gradient updated rules are
# applied as usual. Note, the reason that this is stochastic gradient descent is because
# we are only looking at a single training example at a time.
pi_update = self.preSoftmaxPi - learning_rate * T.grad(cost, self.preSoftmaxPi)
A_update = self.preSoftmaxA - learning_rate * T.grad(cost, self.preSoftmaxA)
B_update = self.preSoftmaxB - learning_rate * T.grad(cost, self.preSoftmaxB)
updates = [
(self.preSoftmaxPi, pi_update),
(self.preSoftmaxA, A_update),
(self.preSoftmaxB, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
plt.figure(figsize=(8,5))
plt.plot(costs, color="blue")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
return self.cost_op(x)
def get_cost_multi(self, X, p_cost=1.0):
P = np.random.random(len(X))
return np.array([self.get_cost(x) for x, p in zip(X, P) if p < p_cost])
def log_likelihood(self, x):
return - self.cost_op(x)
def set(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
# Create theano shared variables
self.preSoftmaxPi = theano.shared(preSoftmaxPi)
self.preSoftmaxA = theano.shared(preSoftmaxA)
self.preSoftmaxB = theano.shared(preSoftmaxB)
pi = T.nnet.softmax(self.preSoftmaxPi).flatten()
# softmax returns 1xD if input is a 1-D array of size D
A = T.nnet.softmax(self.preSoftmaxA)
B = T.nnet.softmax(self.preSoftmaxB)
# Define input, a vector
thx = T.ivector("thx")
def recurrence_to_find_alpha(t, old_alpha, x):
"""Scaled version of updates for HMM. This is used to find the forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time step the initial value,
outputs_info=[pi * B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(A) * B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[pi * B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
return thx, cost
def fit_coin(file_key):
"""Loads data and trains HMM."""
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
# Instantiate object of class HMM with 2 hidden states (heads and tails)
hmm = HMM(2)
hmm.fit(X)
L = hmm.get_cost_multi(X).sum()
print("Log likelihood with fitted params: ", round(L, 3))
# Try the true values
pi = np.array([0.5, 0.5])
A = np.array([
[0.1, 0.9],
[0.8, 0.2]
])
B = np.array([
[0.6, 0.4],
[0.3, 0.7]
])
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == "__main__":
key = "coin_data.txt"
fit_coin(key)
```
## 4. Hidden Markov Models with TensorFlow
I now want to expose everyone to an HMM implementation in TensorFlow. In order to do so, we will need to first go over the `scan` function in Tensorflow. Just like when dealing with Theano, we need to ask "What is the equivalent of a for loop in TensorFlow?". And why should we care?
### 4.1 TensorFlow Scan
In order to understand the importance of `scan`, we need to be sure that we have a good idea of how TensorFlow works, even if only from a high level. In general, with both TensorFlow and Theano, you have to create variables and link them together functionally, but they do not have values until you actually run the functions. So, when you create your $X$ matrix you don't give it a shape; you just say here is a place holder I am going to call $X$ and this is a possible shape for it:
```
X = tf.placeholder(tf.float32, shape=(None, D))
```
However, remember that the `shape` argument is _optional_, and hence for all intents and purposes we can assume that we do not know the shape of $X$. So, what happens if you want to loop through all the elements of $X$? Well you can't, because we do not know the number of elements in $X$!
```
for i in range(X.shape[0]): <------- Not possible! We don't know num elements in X
# ....
```
In order to write a for loop we must specify the number of times the loop will run. But in order to specify the number of times the loop will run we must know the number of elements in $X$. Generally speaking, we cannot guarantee the length of our training sequences. This is why we need the tensorflow `scan` function! It will allow us to loop through a tensorflow array without knowing its size. This is similar to how everything else in Tensorflow and Theano works. Using `scan` we can tell Tensorflow "how to run the for loop", without actually running it.
There is another big reason that the `scan` function is so important; it allows us to perform **automatic differentiation** when we have sequential data. Tensorflow keeps track of how all the variables in your graph link together, so that it can automatically calculate the gradient for you when you do gradient descent:
$$W(t) \leftarrow W(t-1) - \eta \nabla J\big(W(t-1)\big)$$
The `scan` function keeps track of this when it performs the loop. The anatomy of the `scan` function is shown in pseudocode below:
```
outputs = tf.scan(
fn=some_function, # Function applied to every element in sequence
elems=thing_to_loop_over # Actual sequence that is passed in
)
```
Above, `some_function` is applied to every element in `thing_to_loop_over`. Now, the way that we define `some_function` is very specific and much more strict than that for theano. In particular, it must always take in two arguments. The first element is the last output of the function, and the second element is the next element of the sequence:
```
def some_function(last_output, element):
return do_something_to(last_output, element)
```
The tensorflow scan function returns `outputs`, which is all of the return values of `some_function` concatenated together. For example, we can look at the following block:
```
outputs = tf.scan(
fn=some_function,
elems=thing_to_loop_over
)
def square(last, current):
return current * current
# sequence = [1, 2, 3]
# outputs = [1, 4, 9]
```
If we pass in `[1, 2, 3]`, then our outputs will be `[1, 4, 9]`. Now, of course the outputs is still a tensorflow graph node. So, in order to get an actual value out of it we need to run it in an actual session.
```
import tensorflow as tf
x = tf.placeholder(tf.int32, shape=(None,), name="x")
def square(last, current):
"""Last is never used, but must be included based on interface requirements of tf.scan"""
return current*current
# Essentially doing what a for loop would normally do
# It applies the square function to every element of x
square_op = tf.scan(
fn=square,
elems=x
)
# Run it!
with tf.Session() as session:
o_val = session.run(
square_op,
feed_dict={x: [1, 2, 3, 4, 5]}
)
print("Output: ", o_val)
```
Now, of course `scan` can do more complex things than this. We can implement another argument, `initializer`, that allows us to compute recurrence relationships.
```
outputs = tf.scan(
fn=some_function, # Function applied to every element in sequence
elems=thing_to_loop_over, # Actual sequence that is passed in
initializer=initial_input
)
```
Why exactly do we need this? Well, we can see that the recurrence function takes in two things: the last element that it returned, and the current element of the sequence that we are iterating over. What is the last output during the first iteration? There isn't one yet! And that is exactly why we need `initializer`.
One thing to keep in mind when using `initializer` is that it is very strict. In particular, it must be the exact same type as the output of `recurrence`. For example, if you need to return multiple things from `recurrence` it is going to be returned as a tuple. That means that the argument to `initializer` cannot be a list, it must be a tuple. This also means that a tuple containing `(5 , 5)` is not the same a tuple containing `(5.0, 5.0)`.
Let's try to compute the fibonacci sequence to get a feel for how this works:
```
# N is the number fibonacci numbers that we want
N = tf.placeholder(tf.int32, shape=(), name="N")
def fibonacci(last, current):
# last[0] is the last value, last[1] is the second last value
return (last[1], last[0] + last[1])
fib_op = tf.scan(
fn=fibonacci,
elems=tf.range(N),
initializer=(0, 1),
)
with tf.Session() as session:
o_val = session.run(
fib_op,
feed_dict={N: 8}
)
print("Output: \n", o_val)
```
Another example of what we can do with the theano `scan` is create a **low pass filter** (also known as a **moving average**). In this case, our recurrence relation is given by:
$$s(t) = \text{decay_rate} \cdot s(t-1) + (1 - \text{decay_rate}) \cdot x(t)$$
Where $x(t)$ is the input and $s(t)$ is the output. The goal here is to return a clean version of a noisy signal. To do this we can create a sine wave, add some random gaussian noise to it, and finally try to retrieve the sine wave. In code this looks like:
```
original = np.sin(np.linspace(0, 3*np.pi, 300))
X = 2*np.random.randn(300) + original
fig = plt.figure(figsize=(15,5))
plt.subplot(1, 2, 1)
ax = plt.plot(X, c="g", lw=1.5)
plt.title("Original")
# Setup placeholders
decay = tf.placeholder(tf.float32, shape=(), name="decay")
sequence = tf.placeholder(tf.float32, shape=(None, ), name="sequence")
# The recurrence function and loop
def recurrence(last, x):
return (1.0 - decay)*x + decay*last
low_pass_filter = tf.scan(
fn=recurrence,
elems=sequence,
initializer=0.0 # sequence[0] to use first value of the sequence
)
# Run it!
with tf.Session() as session:
Y = session.run(low_pass_filter, feed_dict={sequence: X, decay: 0.97})
plt.subplot(1, 2, 2)
ax2 = plt.plot(original, c="b")
ax = plt.plot(Y, c="r")
plt.title("Low pass filter")
plt.show()
```
### 4.2 Discrete HMM With Tensorflow
Let's now take a moment to walk through the creation of a discrete HMM class utilizing Tensorflow.
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from hmm.utils import get_obj_s3
class HMM:
def __init__(self, M):
self.M = M # number of hidden states
def set_session(self, session):
self.session = session
def fit(self, X, max_iter=10, print_period=1):
# train the HMM model using stochastic gradient descent
N = len(X)
print("Number of train samples:", N)
costs = []
for it in range(max_iter):
for n in range(N):
# this would of course be much faster if we didn't do this on
# every iteration of the loop
c = self.get_cost_multi(X).sum()
costs.append(c)
self.session.run(self.train_op, feed_dict={self.tfx: X[n]})
plt.figure(figsize=(8,5))
plt.plot(costs, c="b")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
# returns log P(x | model)
# using the forward part of the forward-backward algorithm
# print "getting cost for:", x
return self.session.run(self.cost, feed_dict={self.tfx: x})
def log_likelihood(self, x):
return -self.session.run(self.cost, feed_dict={self.tfx: x})
def get_cost_multi(self, X):
return np.array([self.get_cost(x) for x in X])
def build(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
M, V = preSoftmaxB.shape
self.preSoftmaxPi = tf.Variable(preSoftmaxPi)
self.preSoftmaxA = tf.Variable(preSoftmaxA)
self.preSoftmaxB = tf.Variable(preSoftmaxB)
pi = tf.nn.softmax(self.preSoftmaxPi)
A = tf.nn.softmax(self.preSoftmaxA)
B = tf.nn.softmax(self.preSoftmaxB)
# define cost
self.tfx = tf.placeholder(tf.int32, shape=(None,), name='x')
def recurrence(old_a_old_s, x_t):
old_a = tf.reshape(old_a_old_s[0], (1, M))
a = tf.matmul(old_a, A) * B[:, x_t]
a = tf.reshape(a, (M,))
s = tf.reduce_sum(a)
return (a / s), s
# remember, tensorflow scan is going to loop through
# all the values!
# we treat the first value differently than the rest
# so we only want to loop through tfx[1:]
# the first scale being 1 doesn't affect the log-likelihood
# because log(1) = 0
alpha, scale = tf.scan(
fn=recurrence,
elems=self.tfx[1:],
initializer=(pi * B[:, self.tfx[0]], np.float32(1.0)),
)
self.cost = -tf.reduce_sum(tf.log(scale))
self.train_op = tf.train.AdamOptimizer(1e-2).minimize(self.cost)
def init_random(self, V):
preSoftmaxPi0 = np.zeros(self.M).astype(np.float32) # initial state distribution
preSoftmaxA0 = np.random.randn(self.M, self.M).astype(np.float32) # state transition matrix
preSoftmaxB0 = np.random.randn(self.M, V).astype(np.float32) # output distribution
self.build(preSoftmaxPi0, preSoftmaxA0, preSoftmaxB0)
def set(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
op1 = self.preSoftmaxPi.assign(preSoftmaxPi)
op2 = self.preSoftmaxA.assign(preSoftmaxA)
op3 = self.preSoftmaxB.assign(preSoftmaxB)
self.session.run([op1, op2, op3])
def fit_coin(file_key):
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
hmm = HMM(2)
# the entire graph (including optimizer's variables) must be built
# before calling global variables initializer!
hmm.init_random(2)
init = tf.global_variables_initializer()
with tf.Session() as session:
session.run(init)
hmm.set_session(session)
hmm.fit(X, max_iter=5)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with fitted params: ", round(L, 3))
# try true values
# remember these must be in their "pre-softmax" forms
pi = np.log(np.array([0.5, 0.5])).astype(np.float32)
A = np.log(np.array([[0.1, 0.9], [0.8, 0.2]])).astype(np.float32)
B = np.log(np.array([[0.6, 0.4], [0.3, 0.7]])).astype(np.float32)
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == '__main__':
key = "coin_data.txt"
fit_coin(key)
```
| true |
code
| 0.882047 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/bhadreshpsavani/ExploringSentimentalAnalysis/blob/main/SentimentalAnalysisWithGPTNeo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Step1. Import and Load Data
```
!pip install -q pip install git+https://github.com/huggingface/transformers.git
!pip install -q datasets
from datasets import load_dataset
emotions = load_dataset("emotion")
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
## Step2. Preprocess Data
```
from transformers import AutoTokenizer
model_name = "EleutherAI/gpt-neo-125M"
tokenizer = AutoTokenizer.from_pretrained(model_name)
def tokenize(batch):
return tokenizer(batch["text"], padding=True, truncation=True)
tokenizer
tokenizer.add_special_tokens({'pad_token': '<|pad|>'})
tokenizer
emotions_encoded = emotions.map(tokenize, batched=True, batch_size=None)
from transformers import AutoModelForSequenceClassification
num_labels = 6
model = (AutoModelForSequenceClassification.from_pretrained(model_name, num_labels=num_labels).to(device))
emotions_encoded["train"].features
emotions_encoded.set_format("torch", columns=["input_ids", "attention_mask", "label"])
emotions_encoded["train"].features
from sklearn.metrics import accuracy_score, f1_score
def compute_metrics(pred):
labels = pred.label_ids
preds = pred.predictions.argmax(-1)
f1 = f1_score(labels, preds, average="weighted")
acc = accuracy_score(labels, preds)
return {"accuracy": acc, "f1": f1}
from transformers import Trainer, TrainingArguments
batch_size = 2
logging_steps = len(emotions_encoded["train"]) // batch_size
training_args = TrainingArguments(output_dir="results",
num_train_epochs=2,
learning_rate=2e-5,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
load_best_model_at_end=True,
metric_for_best_model="f1",
weight_decay=0.01,
evaluation_strategy="epoch",
disable_tqdm=False,
logging_steps=logging_steps,)
from transformers import Trainer
trainer = Trainer(model=model, args=training_args,
compute_metrics=compute_metrics,
train_dataset=emotions_encoded["train"],
eval_dataset=emotions_encoded["validation"])
trainer.train();
results = trainer.evaluate()
results
preds_output = trainer.predict(emotions_encoded["validation"])
preds_output.metrics
import numpy as np
from sklearn.metrics import plot_confusion_matrix
y_valid = np.array(emotions_encoded["validation"]["label"])
y_preds = np.argmax(preds_output.predictions, axis=1)
labels = ['sadness', 'joy', 'love', 'anger', 'fear', 'surprise']
plot_confusion_matrix(y_preds, y_valid, labels)
model.save_pretrained('./model')
tokenizer.save_pretrained('./model')
```
| true |
code
| 0.726092 | null | null | null | null |
|
```
import numpy as np
from resonance.nonlinear_systems import SingleDoFNonLinearSystem
```
To apply arbitrary forcing to a single degree of freedom linear or nonlinear system, you can do so with `SingleDoFNonLinearSystem` (`SingleDoFLinearSystem` does not support arbitrary forcing...yet).
Add constants, a generalized coordinate, and a generalized speed to the system.
```
sys = SingleDoFNonLinearSystem()
sys.constants['m'] = 100 # kg
sys.constants['c'] = 1.1*1.2*0.5/2
sys.constants['k'] = 10
sys.constants['Fo'] = 1000 # N
sys.constants['Ft'] = 100 # N/s
sys.constants['to'] = 3.0 # s
sys.coordinates['x'] = 0.0
sys.speeds['v'] = 0.0
```
Create a function that evaluates the first order form of the non-linear equations of motion. In this case:
$$
\dot{x} = v \\
m\dot{v} + c \textrm{sgn}(v)v^2 + k \textrm{sgn}(x)x^2 = F(t)
$$
Make the arbitrary forcing term, $F$, an input to this function.
```
def eval_eom(x, v, m, c, k, F):
xdot = v
vdot = (F - np.sign(v)*c*v**2 - np.sign(x)*k*x**2) / m
return xdot, vdot
```
Note that you cannot add this to the system because `F` has not been defined.
```
sys.diff_eq_func = eval_eom
```
To rememdy this, create a function that returns the input value given the appropriate constants and time.
```
def eval_step_input(Fo, to, time):
if time < to:
return 0.0
else:
return Fo
import matplotlib.pyplot as plt
%matplotlib widget
ts = np.linspace(0, 10)
plt.plot(ts, eval_step_input(5.0, 3.0, ts))
ts < 3.0
def eval_step_input(Fo, to, time):
F = np.empty_like(time)
for i, ti in enumerate(time):
if ti < to:
F[i] = 0.0
else:
F[i] = Fo
return F
plt.plot(ts, eval_step_input(5.0, 3.0, ts))
eval_step_input(5.0, 3.0, ts)
eval_step_input(5.0, 3.0, 7.0)
def eval_step_input(Fo, to, time):
if np.isscalar(time):
if time < to:
return 0.0
else:
return Fo
else:
F = np.empty_like(time)
for i, ti in enumerate(time):
if ti < to:
F[i] = 0.0
else:
F[i] = Fo
return F
eval_step_input(5.0, 3.0, 7.0)
eval_step_input(5.0, 3.0, ts)
True * 5.0
False * 5.0
(ts >= 3.0)*5.0
(5.0 >= 3.0)*5.0
def eval_step_input(Fo, to, time):
return (time >=to)*Fo
eval_step_input(5.0, 3.0, ts)
eval_step_input(5.0, 3.0, 7.0)
sys.add_measurement('F', eval_step_input)
sys.diff_eq_func = eval_eom
traj = sys.free_response(20.0)
traj.plot(subplots=True)
def eval_ramp_input(Ft, to, time):
return (time >= to)*(Ft*time - Ft*to)
del sys.measurements['F']
sys.add_measurement('F', eval_ramp_input)
sys.measurements
traj = sys.free_response(20.0)
traj.plot(subplots=True)
```
| true |
code
| 0.469581 | null | null | null | null |
|
# Mini Project: Temporal-Difference Methods
In this notebook, you will write your own implementations of many Temporal-Difference (TD) methods.
While we have provided some starter code, you are welcome to erase these hints and write your code from scratch.
### Part 0: Explore CliffWalkingEnv
Use the code cell below to create an instance of the [CliffWalking](https://github.com/openai/gym/blob/master/gym/envs/toy_text/cliffwalking.py) environment.
```
import gym
env = gym.make('CliffWalking-v0')
```
The agent moves through a $4\times 12$ gridworld, with states numbered as follows:
```
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]]
```
At the start of any episode, state `36` is the initial state. State `47` is the only terminal state, and the cliff corresponds to states `37` through `46`.
The agent has 4 potential actions:
```
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
```
Thus, $\mathcal{S}^+=\{0, 1, \ldots, 47\}$, and $\mathcal{A} =\{0, 1, 2, 3\}$. Verify this by running the code cell below.
```
print(env.action_space)
print(env.observation_space)
```
In this mini-project, we will build towards finding the optimal policy for the CliffWalking environment. The optimal state-value function is visualized below. Please take the time now to make sure that you understand _why_ this is the optimal state-value function.
```
import numpy as np
from plot_utils import plot_values
# define the optimal state-value function
V_opt = np.zeros((4,12))
V_opt[0:13][0] = -np.arange(3, 15)[::-1]
V_opt[0:13][1] = -np.arange(3, 15)[::-1] + 1
V_opt[0:13][2] = -np.arange(3, 15)[::-1] + 2
V_opt[3][0] = -13
plot_values(V_opt)
```
### Part 1: TD Prediction: State Values
In this section, you will write your own implementation of TD prediction (for estimating the state-value function).
We will begin by investigating a policy where the agent moves:
- `RIGHT` in states `0` through `10`, inclusive,
- `DOWN` in states `11`, `23`, and `35`, and
- `UP` in states `12` through `22`, inclusive, states `24` through `34`, inclusive, and state `36`.
The policy is specified and printed below. Note that states where the agent does not choose an action have been marked with `-1`.
```
policy = np.hstack([1*np.ones(11), 2, 0, np.zeros(10), 2, 0, np.zeros(10), 2, 0, -1*np.ones(11)])
print("\nPolicy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy.reshape(4,12))
```
Run the next cell to visualize the state-value function that corresponds to this policy. Make sure that you take the time to understand why this is the corresponding value function!
```
V_true = np.zeros((4,12))
for i in range(3):
V_true[0:12][i] = -np.arange(3, 15)[::-1] - i
V_true[1][11] = -2
V_true[2][11] = -1
V_true[3][0] = -17
plot_values(V_true)
```
The above figure is what you will try to approximate through the TD prediction algorithm.
Your algorithm for TD prediction has five arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `policy`: This is a 1D numpy array with `policy.shape` equal to the number of states (`env.nS`). `policy[s]` returns the action that the agent chooses when in state `s`.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `V`: This is a dictionary where `V[s]` is the estimated value of state `s`.
Please complete the function in the code cell below.
```
from collections import defaultdict, deque
import sys
def td_prediction(env, num_episodes, policy, alpha, gamma=1.0):
# initialize empty dictionaries of floats
V = defaultdict(float)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# begin an episode, observe S
state = env.reset()
while True:
# choose action A
action = policy[state]
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# perform updates
V[state] = V[state] + (alpha * (reward + (gamma * V[next_state]) - V[state]))
# S <- S'
state = next_state
# end episode if reached terminal state
if done:
break
return V
```
Run the code cell below to test your implementation and visualize the estimated state-value function. If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
import check_test
# evaluate the policy and reshape the state-value function
V_pred = td_prediction(env, 5000, policy, .01)
# please do not change the code below this line
V_pred_plot = np.reshape([V_pred[key] if key in V_pred else 0 for key in np.arange(48)], (4,12))
check_test.run_check('td_prediction_check', V_pred_plot)
plot_values(V_pred_plot)
```
How close is your estimated state-value function to the true state-value function corresponding to the policy?
You might notice that some of the state values are not estimated by the agent. This is because under this policy, the agent will not visit all of the states. In the TD prediction algorithm, the agent can only estimate the values corresponding to states that are visited.
### Part 2: TD Control: Sarsa
In this section, you will write your own implementation of the Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def update_Q(Qsa, Qsa_next, reward, alpha, gamma):
""" updates the action-value function estimate using the most recent time step """
return Qsa + (alpha * (reward + (gamma * Qsa_next) - Qsa))
def epsilon_greedy_probs(env, Q_s, i_episode, eps=None):
""" obtains the action probabilities corresponding to epsilon-greedy policy """
epsilon = 1.0 / i_episode
if eps is not None:
epsilon = eps
policy_s = np.ones(env.nA) * epsilon / env.nA
policy_s[np.argmax(Q_s)] = 1 - epsilon + (epsilon / env.nA)
return policy_s
import matplotlib.pyplot as plt
%matplotlib inline
def sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# limit number of time steps per episode
for t_step in np.arange(300):
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
if not done:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode)
# pick next action A'
next_action = np.random.choice(np.arange(env.nA), p=policy_s)
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], Q[next_state][next_action],
reward, alpha, gamma)
# S <- S'
state = next_state
# A <- A'
action = next_action
if done:
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], 0, reward, alpha, gamma)
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsa = sarsa(env, 5000, .01)
# print the estimated optimal policy
policy_sarsa = np.array([np.argmax(Q_sarsa[key]) if key in Q_sarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_sarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsa)
# plot the estimated optimal state-value function
V_sarsa = ([np.max(Q_sarsa[key]) if key in Q_sarsa else 0 for key in np.arange(48)])
plot_values(V_sarsa)
```
### Part 3: TD Control: Q-learning
In this section, you will write your own implementation of the Q-learning control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def q_learning(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
while True:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick next action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# update Q
Q[state][action] = update_Q(Q[state][action], np.max(Q[next_state]), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsamax = q_learning(env, 5000, .01)
# print the estimated optimal policy
policy_sarsamax = np.array([np.argmax(Q_sarsamax[key]) if key in Q_sarsamax else -1 for key in np.arange(48)]).reshape((4,12))
check_test.run_check('td_control_check', policy_sarsamax)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsamax)
# plot the estimated optimal state-value function
plot_values([np.max(Q_sarsamax[key]) if key in Q_sarsamax else 0 for key in np.arange(48)])
```
### Part 4: TD Control: Expected Sarsa
In this section, you will write your own implementation of the Expected Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def expected_sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode, 0.005)
while True:
# pick next action
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# get epsilon-greedy action probabilities (for S')
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode, 0.005)
# update Q
Q[state][action] = update_Q(Q[state][action], np.dot(Q[next_state], policy_s), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_expsarsa = expected_sarsa(env, 10000, 1)
# print the estimated optimal policy
policy_expsarsa = np.array([np.argmax(Q_expsarsa[key]) if key in Q_expsarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_expsarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_expsarsa)
# plot the estimated optimal state-value function
plot_values([np.max(Q_expsarsa[key]) if key in Q_expsarsa else 0 for key in np.arange(48)])
```
| true |
code
| 0.476884 | null | null | null | null |
|
<img src="images/logo.jpg" style="display: block; margin-left: auto; margin-right: auto;" alt="לוגו של מיזם לימוד הפייתון. נחש מצויר בצבעי צהוב וכחול, הנע בין האותיות של שם הקורס: לומדים פייתון. הסלוגן המופיע מעל לשם הקורס הוא מיזם חינמי ללימוד תכנות בעברית.">
# <span style="text-align: right; direction: rtl; float: right;">התנהגות של פונקציות</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בפסקאות הקרובות נבחן פונקציות מזווית ראייה מעט שונה מהרגיל.<br>
בואו נקפוץ ישירות למים!
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">שם של פונקציה</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
תכונה מעניינת שמתקיימת בפייתון היא שפונקציה היא ערך, בדיוק כמו כל ערך אחר.<br>
נגדיר פונקציה שמעלה מספר בריבוע:
</p>
```
def square(x):
return x ** 2
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נוכל לבדוק מאיזה טיפוס הפונקציה (אנחנו לא קוראים לה עם סוגריים אחרי שמה – רק מציינים את שמה):
</p>
```
type(square)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ואפילו לבצע השמה שלה למשתנה, כך ששם המשתנה החדש יצביע עליה:
</p>
```
ribua = square
print(square(5))
print(ribua(5))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
מה מתרחש בתא למעלה?<br>
כשהגדרנו את הפונקציה <var>square</var>, יצרנו לייזר עם התווית <var>square</var> שמצביע לפונקציה שמעלה מספר בריבוע.<br>
בהשמה שביצענו בשורה הראשונה בתא שלמעלה, הלייזר שעליו מודבקת התווית <var>ribua</var> כוון אל אותה הפונקציה שעליה מצביע הלייזר <var>square</var>.<br>
כעת <var>square</var> ו־<var>ribua</var> מצביעים לאותה פונקציה. אפשר לבדוק זאת כך:
</p>
```
ribua is square
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בשלב הזה אצטרך לבקש מכם לחגור חגורות, כי זה לא הולך להיות טיול רגיל הפעם.
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות במבנים מורכבים</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אם פונקציה היא בסך הכול ערך, ואם אפשר להתייחס לשם שלה בכל מקום, אין סיבה שלא נוכל ליצור רשימה של פונקציות!<br>
ננסה לממש את הרעיון:
</p>
```
def add(num1, num2):
return num1 + num2
def subtract(num1, num2):
return num1 - num2
def multiply(num1, num2):
return num1 * num2
def divide(num1, num2):
return num1 / num2
functions = [add, subtract, multiply, divide]
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כעת יש לנו רשימה בעלת 4 איברים, שכל אחד מהם מצביע לפונקציה שונה.<br>
אם נרצה לבצע פעולת חיבור, נוכל לקרוא ישירות ל־<var>add</var> או (בשביל התרגול) לנסות לאחזר אותה מהרשימה שיצרנו:
</p>
```
# Option 1
print(add(5, 2))
# Option 2
math_function = functions[0]
print(math_function(5, 2))
# Option 3 (ugly, but works!)
print(functions[0](5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אם נרצה, נוכל אפילו לעבור על רשימת הפונקציות בעזרת לולאה ולהפעיל את כולן, זו אחר זו:
</p>
```
for function in functions:
print(function(5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בכל איטרציה של לולאת ה־<code>for</code>, המשתנה <var>function</var> עבר להצביע על הפונקציה הבאה מתוך רשימת <var>functions</var>.<br>
בשורה הבאה קראנו לאותה הפונקציה ש־<var>function</var> מצביע עליה, והדפסנו את הערך שהיא החזירה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כיוון שרשימה היא מבנה ששומר על סדר האיברים שבו, התוצאות מודפסות בסדר שבו הפונקציות שמורות ברשימה.<br>
התוצאה הראשונה שאנחנו רואים היא תוצאת פונקציית החיבור, השנייה היא תוצאת פונקציית החיסור וכן הלאה.
</p>
#### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: סוגרים חשבון</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>calc</var> שמקבלת כפרמטר שני מספרים וסימן של פעולה חשבונית.<br>
הסימן יכול להיות אחד מאלה: <code>+</code>, <code>-</code>, <code>*</code> או <code>/</code>.<br>
מטרת הפונקציה היא להחזיר את תוצאת הביטוי החשבוני שהופעל על שני המספרים.<br>
בפתרונכם, השתמשו בהגדרת הפונקציות מלמעלה ובמילון.
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">העברת פונקציה כפרמטר</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נמשיך ללהטט בפונקציות.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
פונקציה נקראת "<dfn>פונקציה מסדר גבוה</dfn>" (<dfn>higher order function</dfn>) אם היא מקבלת כפרמטר פונקציה.<br>
ניקח לדוגמה את הפונקציה <var>calculate</var>:
</p>
```
def calculate(function, num1, num2):
return function(num1, num2)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בקריאה ל־<var>calculate</var>, נצטרך להעביר פונקציה ושני מספרים.<br>
נעביר לדוגמה את הפונקציה <var>divide</var> שהגדרנו קודם לכן:
</p>
```
calculate(divide, 5, 2)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
מה שמתרחש במקרה הזה הוא שהעברנו את הפונקציה <var>divide</var> כארגומנט ראשון.<br>
הפרמטר <var>function</var> בפונקציה <var>calculate</var> מצביע כעת על פונקציית החילוק שהגדרנו למעלה.<br>
מכאן, שהפונקציה תחזיר את התוצאה של <code>divide(5, 2)</code> – הרי היא 2.5.
</p>
#### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: מפה לפה</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו generator בשם <var>apply</var> שמקבל כפרמטר ראשון פונקציה (<var>func</var>), וכפרמטר שני iterable (<var dir="rtl">iter</var>).<br>
עבור כל איבר ב־iterable, ה־generator יניב את האיבר אחרי שהופעלה עליו הפונקציה <var>func</var>, דהיינו – <code>func(item)</code>.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ודאו שהרצת התא הבא מחזירה <code>True</code> עבור הקוד שלכם:
</p>
```
def square(number):
return number ** 2
square_check = apply(square, [5, -1, 6, -8, 0])
tuple(square_check) == (25, 1, 36, 64, 0)
```
### <span style="text-align: right; direction: rtl; float: right; clear: both;">סיכום ביניים</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
וואו. זה היה די משוגע.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אז למעשה, פונקציות בפייתון הן ערך לכל דבר, כמו מחרוזות ומספרים!<br>
אפשר לאחסן אותן במשתנים, לשלוח אותן כארגומנטים ולכלול אותם בתוך מבני נתונים מורכבים יותר.<br>
אנשי התיאוריה של מדעי המחשב נתנו להתנהגות כזו שם: "<dfn>אזרח ממדרגה ראשונה</dfn>" (<dfn>first class citizen</dfn>).<br>
אם כך, אפשר להגיד על פונקציות בפייתון שהן אזרחיות ממדרגה ראשונה.
</p>
## <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות מסדר גבוה בפייתון</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
החדשות הטובות הן שכבר עשינו היכרות קלה עם המונח פונקציות מסדר גבוה.<br>
עכשיו, כשאנחנו יודעים שמדובר בפונקציות שמקבלות פונקציה כפרמטר, נתחיל ללכלך קצת את הידיים.<br>
נציג כמה פונקציות פייתוניות מעניינות שכאלו:
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">הפונקציה map</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה <var>map</var> מקבלת פונקציה כפרמטר הראשון, ו־iterable כפרמטר השני.<br>
<var>map</var> מפעילה את הפונקציה מהפרמטר הראשון על כל אחד מהאיברים שהועברו ב־iterable.<br>
היא מחזירה iterator שמורכב מהערכים שחזרו מהפעלת הפונקציה.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במילים אחרות, <var>map</var> יוצרת iterable חדש.<br>
ה־iterable כולל את הערך שהוחזר מהפונקציה עבור כל איבר ב־<code>iterable</code> שהועבר.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לדוגמה:
</p>
```
squared_items = map(square, [1, 6, -1, 8, 0, 3, -3, 9, -8, 8, -7])
print(tuple(squared_items))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה קיבלה כארגומנט ראשון את הפונקציה <var>square</var> שהגדרנו למעלה, שמטרתה העלאת מספר בריבוע.<br>
כארגומנט שני היא קיבלה את רשימת כל המספרים שאנחנו רוצים שהפונקציה תרוץ עליהם.<br>
כשהעברנו ל־<var>map</var> את הארגומנטים הללו, <var>map</var> החזירה לנו ב־iterator (מבנה שאפשר לעבור עליו איבר־איבר) את התוצאה:<br>
הריבוע, קרי החזקה השנייה, של כל אחד מהאיברים ברשימה שהועברה כארגומנט השני.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
למעשה, אפשר להגיד ש־<code>map</code> שקולה לפונקציה הבאה:
</p>
```
def my_map(function, iterable):
for item in iterable:
yield function(item)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הנה דוגמה נוספת לשימוש ב־<var>map</var>:
</p>
```
numbers = [(2, 4), (1, 4, 2), (1, 3, 5, 6, 2), (3, )]
sums = map(sum, numbers)
print(tuple(sums))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במקרה הזה, בכל מעבר, קיבלה הפונקציה <var>sum</var> איבר אחד מתוך הרשימה – tuple.<br>
היא סכמה את האיברים של כל tuple שקיבלה, וכך החזירה לנו את הסכומים של כל ה־tuple־ים – זה אחרי זה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ודוגמה אחרונה:
</p>
```
def add_one(number):
return number + 1
incremented = map(add_one, (1, 2, 3))
print(tuple(incremented))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בדוגמה הזו יצרנו פונקציה משל עצמנו, ואותה העברנו ל־map.<br>
מטרת דוגמה זו היא להדגיש שאין שוני בין העברת פונקציה שקיימת בפייתון לבין פונקציה שאנחנו יצרנו.
</p>
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה שמקבלת רשימת מחרוזות של שתי מילים: שם פרטי ושם משפחה.<br>
הפונקציה תשתמש ב־map כדי להחזיר מכולן רק את השם הפרטי.
</p>
</div>
<div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
<p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
<strong>חשוב!</strong><br>
פתרו לפני שתמשיכו!
</p>
</div>
</div>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">הפונקציה filter</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה <var>filter</var> מקבלת פונקציה כפרמטר ראשון, ו־iterable כפרמטר שני.<br>
<var>filter</var> מפעילה על כל אחד מאיברי ה־iterable את הפונקציה, ומחזירה את האיבר אך ורק אם הערך שחזר מהפונקציה שקול ל־<code>True</code>.<br>
אם ערך ההחזרה שקול ל־<code>False</code> – הערך "יבלע" ב־<var>filter</var> ולא יחזור ממנה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במילים אחרות, <var>filter</var> יוצרת iterable חדש ומחזירה אותו.<br>
ה־iterable כולל רק את האיברים שעבורם הפונקציה שהועברה החזירה ערך השקול ל־<code>True</code>.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נבנה, לדוגמה, פונקציה שמחזירה אם אדם הוא בגיר.<br>
הפונקציה תקבל כפרמטר גיל, ותחזיר <code>True</code> כאשר הגיל שהועבר לה הוא לפחות 18, ו־<code>False</code> אחרת.
</p>
```
def is_mature(age):
return age >= 18
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נגדיר רשימת גילים, ונבקש מ־<var>filter</var> לסנן אותם לפי הפונקציה שהגדרנו:
</p>
```
ages = [0, 1, 4, 10, 20, 35, 56, 84, 120]
mature_ages = filter(is_mature, ages)
print(tuple(mature_ages))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כפי שלמדנו, <var>filter</var> מחזירה לנו רק גילים השווים ל־18 או גדולים ממנו.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נחדד שהפונקציה שאנחנו מעבירים ל־<var>filter</var> לא חייבת להחזיר בהכרח <code>True</code> או <code>False</code>.<br>
הערך 0, לדוגמה, שקול ל־<code>False</code>, ולכן <var>filter</var> תסנן כל ערך שעבורו הפונקציה תחזיר 0:
</p>
```
to_sum = [(1, -1), (2, 5), (5, -3, -2), (1, 2, 3)]
sum_is_not_zero = filter(sum, to_sum)
print(tuple(sum_is_not_zero))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בתא האחרון העברנו ל־<var>filter</var> את sum כפונקציה שאותה אנחנו רוצים להפעיל, ואת <var>to_sum</var> כאיברים שעליהם אנחנו רוצים לפעול.<br>
ה־tuple־ים שסכום איבריהם היה 0 סוננו, וקיבלנו חזרה iterator שהאיברים בו הם אך ורק אלו שסכומם שונה מ־0.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כטריק אחרון, נלמד ש־<var>filter</var> יכולה לקבל גם <code>None</code> בתור הפרמטר הראשון, במקום פונקציה.<br>
זה יגרום ל־<var>filter</var> לא להפעיל פונקציה על האיברים שהועברו, כלומר לסנן אותם כמו שהם.<br>
איברים השקולים ל־<code>True</code> יוחזרו, ואיברים השקולים ל־<code>False</code> לא יוחזרו:
</p>
```
to_sum = [0, "", None, 0.0, True, False, "Hello"]
equivalent_to_true = filter(None, to_sum)
print(tuple(equivalent_to_true))
```
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה שמקבלת רשימת מחרוזות, ומחזירה רק את המחרוזות הפלינדרומיות שבה.<br>
מחרוזת נחשבת פלינדרום אם קריאתה מימין לשמאל ומשמאל לימין יוצרת אותו ביטוי.<br>
השתמשו ב־<var>filter</var>.
</p>
</div>
<div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
<p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
<strong>חשוב!</strong><br>
פתרו לפני שתמשיכו!
</p>
</div>
</div>
## <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות אנונימיות</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
תעלול נוסף שנוסיף לארגז הכלים שלנו הוא <dfn>פונקציות אנונימיות</dfn> (<dfn>anonymous functions</dfn>).<br>
אל תיבהלו מהשם המאיים – בסך הכול פירושו הוא "פונקציות שאין להן שם".<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לפני שאתם מרימים גבה ושואלים את עצמכם למה הן שימושיות, בואו נבחן כמה דוגמאות.<br>
ניזכר בהגדרת פונקציית החיבור שיצרנו לא מזמן:
</p>
```
def add(num1, num2):
return num1 + num2
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ונגדיר את אותה הפונקציה בדיוק בצורה אנונימית:
</p>
```
add = lambda num1, num2: num1 + num2
print(add(5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לפני שנסביר איפה החלק של ה"פונקציה בלי שם" נתמקד בצד ימין של ההשמה.<br>
כיצד מנוסחת הגדרת פונקציה אנונימית?
</p>
<ol style="text-align: right; direction: rtl; float: right; clear: both;">
<li>הצהרנו שברצוננו ליצור פונקציה אנונימית בעזרת מילת המפתח <code>lambda</code>.</li>
<li>מייד אחריה, ציינו את שמות כל הפרמטרים שהפונקציה תקבל, כשהם מופרדים בפסיק זה מזה.</li>
<li>כדי להפריד בין רשימת הפרמטרים לערך ההחזרה של הפונקציה, השתמשנו בנקודתיים.</li>
<li>אחרי הנקודתיים, כתבנו את הביטוי שאנחנו רוצים שהפונקציה תחזיר.</li>
</ol>
<figure>
<img src="images/lambda.png" style="max-width: 500px; margin-right: auto; margin-left: auto; text-align: center;" alt="בתמונה מופיעה הגדרת ה־lambda שביצענו קודם לכן. מעל המילה lambda המודגשת בירוק ישנו פס מקווקו, ומעליו רשום 'הצהרה'. מימין למילה lambda כתוב num1 (פסיק) num2, מעליהם קו מקווקו ומעליו המילה 'פרמטרים'. מימין לפרמטרים יש נקודתיים, ואז num1 (הסימן פלוס) num2. מעליהם קו מקווקו, ומעליו המילה 'ערך החזרה'."/>
<figcaption style="margin-top: 2rem; text-align: center; direction: rtl;">חלקי ההגדרה של פונקציה אנונימית בעזרת מילת המפתח <code>lambda</code><br><span style="color: white;">A girl has no name</span></figcaption>
</figure>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במה שונה ההגדרה של פונקציה זו מההגדרה של פונקציה רגילה?<br>
היא לא באמת שונה.<br>
המטרה היא לאפשר תחביר שיקל על חיינו כשאנחנו רוצים לכתוב פונקציה קצרצרה שאורכה שורה אחת.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נראה, לדוגמה, שימוש ב־<var>filter</var> כדי לסנן את כל האיברים שאינם חיוביים:
</p>
```
def is_positive(number):
return number > 0
numbers = [-2, -1, 0, 1, 2]
positive_numbers = filter(is_positive, numbers)
print(tuple(positive_numbers))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במקום להגדיר פונקציה חדשה שנקראת <var>is_positive</var>, נוכל להשתמש בפונקציה אנונימית:
</p>
```
numbers = [-2, -1, 0, 1, 2]
positive_numbers = filter(lambda n: n > 0, numbers)
print(tuple(positive_numbers))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
איך זה עובד?<br>
במקום להעביר ל־<var>filter</var> פונקציה שיצרנו מבעוד מועד, השתמשנו ב־<code>lambda</code> כדי ליצור פונקציה ממש באותה השורה.<br>
הפונקציה שהגדרנו מקבלת מספר (<var>n</var>), ומחזירה <code>True</code> אם הוא חיובי, או <code>False</code> אחרת.<br>
שימו לב שבצורה זו באמת לא היינו צריכים לתת שם לפונקציה שהגדרנו.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
השימוש בפונקציות אנונימיות לא מוגבל ל־<var>map</var> ול־<var>filter</var>, כמובן.<br>
מקובל להשתמש ב־<code>lambda</code> גם עבור פונקציות כמו <var>sorted</var>, שמקבלות פונקציה בתור ארגומנט.
</p>
<div class="align-center" style="display: flex; text-align: right; direction: rtl;">
<div style="display: flex; width: 10%; float: right; ">
<img src="images/recall.svg" style="height: 50px !important;" alt="תזכורת" title="תזכורת">
</div>
<div style="width: 90%">
<p style="text-align: right; direction: rtl;">
הפונקציה <code>sorted</code> מאפשרת לנו לסדר ערכים, ואפילו להגדיר עבורה לפי מה לסדר אותם.<br>
לרענון בנוגע לשימוש בפונקציה גשו למחברת בנושא פונקציות מובנות בשבוע 4.
</p>
</div>
</div>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נסדר, למשל, את הדמויות ברשימה הבאה, לפי תאריך הולדתן:
</p>
```
closet = [
{'name': 'Peter', 'year_of_birth': 1927, 'gender': 'Male'},
{'name': 'Edmund', 'year_of_birth': 1930, 'gender': 'Male'},
{'name': 'Lucy', 'year_of_birth': 1932, 'gender': 'Female'},
{'name': 'Susan', 'year_of_birth': 1928, 'gender': 'Female'},
{'name': 'Jadis', 'year_of_birth': 0, 'gender': 'Female'},
]
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נרצה שסידור הרשימה יתבצע לפי המפתח <var>year_of_birth</var>.<br>
כלומר, בהינתן מילון שמייצג דמות בשם <var>d</var>, יש להשיג את <code dir="ltr">d['year_of_birth']</code>, ולפיו לבצע את סידור הרשימה.<br>
ניגש למלאכה:
</p>
```
sorted(closet, key=lambda d: d['year_of_birth'])
```
<div class="align-center" style="display: flex; text-align: right; direction: rtl;">
<div style="display: flex; width: 10%; float: right; ">
<img src="images/warning.png" style="height: 50px !important;" alt="אזהרה!">
</div>
<div style="width: 90%">
<p style="text-align: right; direction: rtl;">
פונקציות אנונימיות הן יכולת חביבה שאמורה לסייע לכם לכתוב קוד נאה וקריא.<br>
כלל אצבע טוב לחיים הוא להימנע משימוש בהן כאשר הן מסרבלות את הקוד.
</p>
</div>
</div>
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגיל" title="תרגיל">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
סדרו את הדמויות ב־<var>closet</var> לפי האות האחרונה בשמם.
</p>
</div>
</div>
## <span style="align: right; direction: rtl; float: right; clear: both;">מונחים</span>
<dl style="text-align: right; direction: rtl; float: right; clear: both;">
<dt>פונקציה מסדר גבוה</dt>
<dd>פונקציה שמקבלת פונקציה כאחד הארגומנטים, או שמחזירה פונקציה כערך ההחזרה שלה.</dd>
<dt>אזרח ממדרגה ראשונה</dt>
<dd>ישות תכנותית המתנהגת בשפת התכנות כערך לכל דבר. בפייתון, פונקציות הן אזרחיות ממדרגה ראשונה.<dd>
<dt>פונקציה אנונימית, פונקציית <code>lambda</code></dt>
<dd>פונקציה ללא שם המיועדת להגדרת פונקציה בשורה אחת, לרוב לשימוש חד־פעמי. בעברית: פונקציית למדא.</dd>
</dl>
## <span style="align: right; direction: rtl; float: right; clear: both;">תרגילים</span>
### <span style="align: right; direction: rtl; float: right; clear: both;">פילטר מותאם אישית</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>my_filter</var> שמתנהגת בדיוק כמו הפונקציה <var>filter</var>.<br>
בפתירת התרגיל, המנעו משימוש ב־<var>filter</var> או במודולים.
</p>
### <span style="align: right; direction: rtl; float: right; clear: both;">נשאר? חיובי</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>get_positive_numbers</var> שמקבלת מהמשתמש קלט בעזרת <var>input</var>.<br>
המשתמש יתבקש להזין סדרה של מספרים המופרדים בפסיק זה מזה.<br>
הפונקציה תחזיר את כל המספרים החיוביים שהמשתמש הזין, כרשימה של מספרים מסוג <code>int</code>.<br>
אפשר להניח שהקלט מהמשתמש תקין.
</p>
### <span style="align: right; direction: rtl; float: right; clear: both;">ריצת 2,000</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>timer</var> שמקבלת כפרמטר פונקציה (נקרא לה <var>f</var>) ופרמטרים נוספים.<br>
הפונקציה <var>timer</var> תמדוד כמה זמן רצה פונקציה <var>f</var> כשמועברים אליה אותם פרמטרים. <br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לדוגמה:
</p>
<ol style="text-align: right; direction: rtl; float: right; clear: both;">
<li>עבור הקריאה <code dir="ltr">timer(print, "Hello")</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">print("Hello")</code>.</li>
<li>עבור הקריאה <code dir="ltr">timer(zip, [1, 2, 3], [4, 5, 6])</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">zip([1, 2, 3], [4, 5, 6])</code>.</li>
<li>עבור הקריאה <code dir="ltr">timer("Hi {name}".format, name="Bug")</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">"Hi {name}".format(name="Bug")</code></li>
</ol>
| true |
code
| 0.44354 | null | null | null | null |
|
## Fundamentals, introduction to machine learning
The purpose of these guides is to go a bit deeper into the details behind common machine learning methods, assuming little math background, and teach you how to use popular machine learning Python packages. In particular, we'll focus on the Numpy and PyTorch libraries.
I'll assume you have some experience programming with Python -- if not, check out the initial [fundamentals of Python guide](https://github.com/ml4a/ml4a-guides/blob/master/notebooks/intro_python.ipynb) or for a longer, more comprehensive resource: [Learn Python the Hard Way](http://learnpythonthehardway.org/book/). It will really help to illustrate the concepts introduced here.
Numpy underlies most Python machine learning packages and is great for performing quick sketches or working through calculations. PyTorch rivals alternative libraries, such as TensorFlow, for its flexibility and ease of use. Despite the high level appearance of PyTorch, it can be quite low-level, which is great for experimenting with novel algorithms. PyTorch can seamlessly be integrated with distributed computation libraries, like Ray, to make the Kessel Run in less than 12 parsecs (citation needed).
These guides will present the formal math for concepts alongside Python code examples since this often (for me at least) is a lot easier to develop an intuition for. Each guide is also available as an iPython notebook for your own experimentation.
The guides are not meant to exhaustively cover the field of machine learning but I hope they will instill you with the confidence and knowledge to explore further on your own.
If you do want more details, you might enjoy my [artificial intelligence notes](http://frnsys.com/ai_notes).
### Modeling the world
You've probably seen various machine learning algorithms pop up -- linear regression, SVMs, neural networks, random forests, etc. How are they all related? What do they have in common? What is machine learning for anyways?
First, let's consider the general, fundamental problem all machine learning is concerned with, leaving aside the algorithm name soup for now. The primary concern of machine learning is _modeling the world_.
We can model phenomena or systems -- both natural and artificial, if you want to make that distinction -- with mathematical functions. We see something out in the world and want to describe it in some way, we want to formalize how two or more things are related, and we can do that with a function. The problem is, for a given phenomenon, how do we figure out what function to use? There are infinitely many to choose from!
Before this gets too abstract, let's use an example to make things more concrete.
Say we have a bunch of data about the heights and weights of a species of deer. We want to understand how these two variables are related -- in particular, given the weight of a deer, can we predict its height?
You might see where this is going. The data looks like a line, and lines in general are described by functions of the form $y = mx + b$.
Remember that lines vary depending on what the values of $m$ and $b$ are:

Thus $m$ and $b$ uniquely define a function -- thus they are called the _parameters_ of the function -- and when it comes to machine learning, these parameters are what we ultimately want to learn. So when I say there are infinitely many functions to choose from, it is because $m$ and $b$ can pretty much take on any value. Machine learning techniques essentially search through these possible functions to find parameters that best fit the data you have. One way machine learning algorithms are differentiated is by how exactly they conduct this search (i.e. how they learn parameters).
In this case we've (reasonably) assumed the function takes the form $y = mx + b$, but conceivably you may have data that doesn't take the form of a line. Real world data is typically a lot more convoluted-looking. Maybe the true function has a $sin$ in it, for example.
This is where another main distinction between machine learning algorithms comes in -- certain algorithms can model only certain forms of functions. _Linear regression_, for example, can only model linear functions, as indicated by its name. Neural networks, on the other hand, are _universal function approximators_, which mean they can (in theory) approximate _any_ function, no matter how exotic. This doesn't necessarily make them a better method, just better suited for certain circumstances (there are many other considerations when choosing an algorithm).
For now, let's return to the line function. Now that we've looked at the $m$ and $b$ variables, let's consider the input variable $x$. A function takes a numerical input; that is $x$ must be a number of some kind. That's pretty straightforward here since the deer weights are already numbers. But this is not always the case! What if we want to predict the sales price of a house. A house is not a number. We have to find a way to _represent_ it as a number (or as several numbers, i.e. a vector, which will be detailed in a moment), e.g. by its square footage. This challenge of representation is a major part of machine learning; the practice of building representations is known as _feature engineering_ since each variable (e.g. square footage or zip code) used for the representation is called a _feature_.
If you think about it, representation is a practice we regularly engage in. The word "house" is not a house any more than an image of a house is -- there is no true "house" anyways, it is always a constellation of various physical and nonphysical components.
That's about it -- broadly speaking, machine learning is basically a bunch of algorithms that learn you a function, which is to say they learn the parameters that uniquely define a function.
### Vectors
In the line example before I mentioned that we might have multiple numbers representing an input. For example, a house probably can't be solely represented by its square footage -- perhaps we also want to consider how many bedrooms it has, or how high the ceilings are, or its distance from local transportation. How do we group these numbers together?
That's what _vectors_ are for (they come up for many other reasons too, but we'll focus on representation for now). Vectors, along with matrices and other tensors (which will be explained a bit further down), could be considered the "primitives" of machine learning.
The Numpy library is best for dealing with vectors (and other tensors) in Python. A more complete introduction to Numpy is provided in the [numpy and basic mathematics guide](https://github.com/ml4a/ml4a-guides/blob/master/notebooks/math_review_numpy.ipynb).
Let's import `numpy` with the alias `nf`:
```
import numpy as np
```
You may have encountered vectors before in high school or college -- to use Python terms, a vector is like a list of numbers. The mathematical notation is quite similar to Python code, e.g. `[5,4]`, but `numpy` has its own way of instantiating a vector:
```
v = np.array([5, 4])
```
$$
v = \begin{bmatrix} 5 \\ 4 \end{bmatrix}
$$
Vectors are usually represented with lowercase variables.
Note that we never specified how _many_ numbers (also called _components_) a vector has - because it can have any amount. The amount of components a vector has is called its _dimensionality_. The example vector above has two dimensions. The vector `x = [8,1,3]` has three dimensions, and so on. Components are usually indicated by their index (usually using 1-indexing), e.g. in the previous vector, $x_1$ refers to the value $8$.
"Dimensions" in the context of vectors is just like the spatial dimensions you spend every day in. These dimensions define a __space__, so a two-dimensional vector, e.g. `[5,4]`, can describe a point in 2D space and a three-dimensional vector, e.g. `[8,1,3]`, can describe a point in 3D space. As mentioned before, there is no limit to the amount of dimensions a vector may have (technically, there must be one or more dimensions), so we could conceivably have space consisting of thousands or tens of thousands of dimensions. At that point we can't rely on the same human intuitions about space as we could when working with just two or three dimensions. In practice, most interesting applications of machine learning deal with many, many dimensions.
We can get a better sense of this by plotting a vector out. For instance, a 2D vector `[5,0]` would look like:

So in a sense vectors can be thought of lines that "point" to the position they specify - here the vector is a line "pointing" to `[5,0]`. If the vector were 3D, e.g. `[8,1,3]`, then we would have to visualize it in 3D space, and so on.
So vectors are great - they allow us to form logical groupings of numbers. For instance, if we're talking about cities on a map we would want to group their latitude and longitude together. We'd represent Lagos with `[6.455027, 3.384082]` and Beijing separately with `[39.9042, 116.4074]`. If we have an inventory of books for sale, we could represent each book with its own vector consisting of its price, number of pages, and remaining stock.
To use vectors in functions, there are a few mathematical operations you need to know.
### Basic vector operations
Vectors can be added (and subtracted) easily:
```
np.array([6, 2]) + np.array([-4, 4])
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} + \begin{bmatrix} -4 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 + -4 \\ 2 + 4 \end{bmatrix} = \begin{bmatrix} 2 \\ 6 \end{bmatrix}
$$
However, when it comes to vector multiplication there are many different kinds.
The simplest is _vector-scalar_ multiplication:
```
3 * np.array([2, 1])
```
$$
3\begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \times 2 \\ 3 \times 1
\end{bmatrix} = \begin{bmatrix} 6 \\ 3 \end{bmatrix}
$$
But when you multiply two vectors together you have a few options. I'll cover the two most important ones here.
The one you might have thought of is the _element-wise product_, also called the _pointwise product_, _component-wise product_, or the _Hadamard product_, typically notated with $\odot$. This just involves multiplying the corresponding elements of each vector together, resulting in another vector:
```
np.array([6, 2]) * np.array([-4, 4])
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} \odot \begin{bmatrix} -4 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 \times -4 \\ 2 \times 4 \end{bmatrix} = \begin{bmatrix} -24 \\ 8 \end{bmatrix}
$$
The other vector product, which you'll encounter a lot, is the _dot product_, also called _inner product_, usually notated with $\cdot$ (though when vectors are placed side-by-side this often implies dot multiplication). This involves multiplying corresponding elements of each vector and then summing the resulting vector's components (so this results in a scalar rather than another vector).
```
np.dot(np.array([6, 2]), np.array([-4, 4]))
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} \cdot \begin{bmatrix} -4 \\ 4 \end{bmatrix} = (6 \times -4) + (2 \times 4) = -16
$$
The more general formulation is:
```
# a slow pure-Python dot product
def dot(a, b):
assert len(a) == len(b)
return sum(a_i * b_i for a_i, b_i in zip(a,b))
```
$$
\begin{aligned}
\vec{a} \cdot \vec{b} &= \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} = a_1b_1 + a_2b_2 + \dots + a_nb_n \\
&= \sum^n_{i=1} a_i b_i
\end{aligned}
$$
Note that the vectors in these operations must have the same dimensions!
Perhaps the most important vector operation mentioned here is the dot product. We'll return to the house example to see why. Let's say want to represent a house with three variables: square footage, number of bedrooms, and the number of bathrooms. For convenience we'll notate the variables $x_1, x_2, x_3$, respectively. We're working in three dimensions now so instead of learning a line we're learning a _hyperplane_ (if we were working with two dimensions we'd be learning a plane, "hyperplane" is the term for the equivalent of a plane in higher dimensions).
Aside from the different name, the function we're learning is essentially of the same form as before, just with more variables and thus more parameters. We'll notate each parameter as $\theta_i$ as is the convention (you may see $\beta_i$ used elsewhere), and for the intercept (what was the $b$ term in the original line), we'll add in a dummy variable $x_0 = 1$ as is the typical practice (thus $\theta_0$ is equivalent to $b$):
```
# this is so clumsy in python;
# this will become more concise in a bit
def f(x0, x1, x2, x3, theta0, theta1, theta2, theta3):
return theta0 * x0\
+ theta1 * x1\
+ theta2 * x2\
+ theta3 * x3
```
$$
y = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3
$$
This kind of looks like the dot product, doesn't it? In fact, we can re-write this entire function as a dot product. We define our feature vector $x = [x_0, x_1, x_2, x_3]$ and our parameter vector $\theta = [\theta_0, \theta_1, \theta_2, \theta_3]$, then re-write the function:
```
def f(x, theta):
return x.dot(theta)
```
$$
y = \theta x
$$
So that's how we incorporate multiple features in a representation.
There's a whole lot more to vectors than what's presented here, but this is the ground-level knowledge you should have of them. Other aspects of vectors will be explained as they come up.
## Learning
So machine learning algorithms learn parameters - how do they do it?
Here we're focusing on the most common kind of machine learning - _supervised_ learning. In supervised learning, the algorithm learns parameters from data which includes both the inputs and the true outputs. This data is called _training_ data.
Although they vary on specifics, there is a general approach that supervised machine learning algorithms use to learn parameters. The idea is that the algorithm takes an input example, inputs it into the current guess at the function (called the _hypothesis_, notate $h_{\theta}$), and then checks how wrong its output is against the true output. The algorithm then updates its hypothesis (that is, its guesses for the parameters), accordingly.
"How wrong" an algorithm is, can vary depending on the _loss function_ it is using. The loss function takes the algorithm's current guess for the output, $\hat y$, and the true output, $y$, and returns some value quantifying its wrongness. Certain loss functions are more appropriate for certain tasks, which we'll get into later.
We'll get into the specifies of how the algorithm determines what kind of update to perform (i.e. how much each parameter changes), but before we do that we should consider how we manage batches of training examples (i.e. multiple training vectors) simultaneously.
## Matrices
__Matrices__ are in a sense a "vector" of vectors. That is, where a vector can be thought of as a logical grouping of numbers, a matrix can be thought of as a logical grouping of vectors. So if a vector represents a book in our catalog (id, price, number in stock), a matrix could represent the entire catalog (each row refers to a book). Or if we want to represent a grayscale image, the matrix can represent the brightness values of the pixels in the image.
```
A = np.array([
[6, 8, 0],
[8, 2, 7],
[3, 3, 9],
[3, 8, 6]
])
```
$$
\mathbf A =
\begin{bmatrix}
6 & 8 & 0 \\
8 & 2 & 7 \\
3 & 3 & 9 \\
3 & 8 & 6
\end{bmatrix}
$$
Matrices are usually represented with uppercase variables.
Note that the "vectors" in the matrix must have the same dimension. The matrix's dimensions are expressed in the form $m \times n$, meaning that there are $m$ rows and $n$ columns. So the example matrix has dimensions of $4 \times 3$. Numpy calls these dimensions a matrix's "shape".
We can access a particular element, $A_{i,j}$, in a matrix by its indices. Say we want to refer to the element in the 2nd row and the 3rd column (remember that python uses 0-indexing):
```
A[1,2]
```
### Basic matrix operations
Like vectors, matrix addition and subtraction is straightforward (again, they must be of the same dimensions):
```
B = np.array([
[8, 3, 7],
[2, 9, 6],
[2, 5, 6],
[5, 0, 6]
])
A + B
```
$$
\begin{aligned}
\mathbf B &=
\begin{bmatrix}
8 & 3 & 7 \\
2 & 9 & 6 \\
2 & 5 & 6 \\
5 & 0 & 6
\end{bmatrix} \\
A + B &=
\begin{bmatrix}
8+6 & 3+8 & 7+0 \\
2+8 & 9+2 & 6+7 \\
2+3 & 5+3 & 6+9 \\
5+3 & 0+8 & 6+6
\end{bmatrix} \\
&=
\begin{bmatrix}
14 & 11 & 7 \\
10 & 11 & 13 \\
5 & 8 & 15 \\
8 & 8 & 12
\end{bmatrix} \\
\end{aligned}
$$
Matrices also have a few different multiplication operations, like vectors.
_Matrix-scalar multiplication_ is similar to vector-scalar multiplication - you just distribute the scalar, multiplying it with each element in the matrix.
_Matrix-vector products_ require that the vector has the same dimension as the matrix has columns, i.e. for an $m \times n$ matrix, the vector must be $n$-dimensional. The operation basically involves taking the dot product of each matrix row with the vector:
```
# a slow pure-Python matrix-vector product,
# using our previous dot product implementation
def matrix_vector_product(M, v):
return [np.dot(row, v) for row in M]
# or, with numpy, you could use np.matmul(A,v)
```
$$
\mathbf M v =
\begin{bmatrix}
M_{1} \cdot v \\
\vdots \\
M_{m} \cdot v \\
\end{bmatrix}
$$
We have a few options when it comes to multiplying matrices with matrices.
However, before we go any further we should talk about the _tranpose_ operation - this just involves switching the columns and rows of a matrix. The transpose of a matrix $A$ is notated $A^T$:
```
A = np.array([
[1,2,3],
[4,5,6]
])
np.transpose(A)
```
$$
\begin{aligned}
\mathbf A &=
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6
\end{bmatrix} \\
\mathbf A^T &=
\begin{bmatrix}
1 & 4 \\
2 & 5 \\
3 & 6
\end{bmatrix}
\end{aligned}
$$
For matrix-matrix products, the matrix on the lefthand must have the same number of columns as the righthand's rows. To be more concrete, we'll represent a matrix-matrix product as $A B$ and we'll say that $A$ has $m \times n$ dimensions. For this operation to work, $B$ must have $n \times p$ dimensions. The resulting product will have $m \times p$ dimensions.
```
# a slow pure-Python matrix Hadamard product
def matrix_matrix_product(A, B):
_, a_cols = np.shape(A)
b_rows, _ = np.shape(B)
assert a_cols == b_rows
result = []
# tranpose B so we can iterate over its columns
for col in np.tranpose(B):
# using our previous implementation
result.append(
matrix_vector_product(A, col))
return np.transpose(result)
```
$$
\mathbf AB =
\begin{bmatrix}
A B^T_1 \\
\vdots \\
A B^T_p
\end{bmatrix}^T
$$
Finally, like with vectors, we also have Hadamard (element-wise) products:
```
# a slow pure-Python matrix-matrix product
# or, with numpy, you can use A * B
def matrix_matrix_hadamard(A, B):
result = []
for a_row, b_row in zip(A, B):
result.append(
zip(a_i * b_i for a_i, b_i in zip(a_row, b_row)))
```
$$
\mathbf A \odot B =
\begin{bmatrix}
A_{1,1} B_{1,1} & \dots & A_{1,n} B_{1,n} \\
\vdots & \dots & \vdots \\
A_{m,1} B_{m,1} & \dots & A_{m,n} B_{m,n}
\end{bmatrix}
$$
Like vector Hadamard products, this requires that the two matrices share the same dimensions.
## Tensors
We've seen vectors, which is like a list of numbers, and matrices, which is like a list of a list of numbers. We can generalize this concept even further, for instance, with a list of a list of a list of numbers and so on. What all of these structures are called are _tensors_ (i.e. the "tensor" in "TensorFlow"). They are distinguished by their _rank_, which, if you're thinking in the "list of lists" way, refers to the number of nestings. So a vector has a rank of one (just a list of numbers) and a matrix has a rank of two (a list of a list of numbers).
Another way to think of rank is by number of indices necessary to access an element in the tensor. An element in a vector is accessed by one index, e.g. `v[i]`, so it is of rank one. An element in a matrix is accessed by two indices, e.g. `M[i,j]`, so it is of rank two.
Why is the concept of a tensor useful? Before we referred to vectors as a logical grouping of numbers and matrices as a logical grouping of vectors. What if we need a logical grouping of matrices? That's what 3rd-rank tensors are! A matrix can represent a grayscale image, but what about a color image with three color channels (red, green, blue)? With a 3rd-rank tensor, we could represent each channel as its own matrix and group them together.
## Learning continued
When the current hypothesis is wrong, how does the algorithm know how to adjust the parameters?
Let's take a step back and look at it another way. The loss function measures the wrongness of the hypothesis $h_{\theta}$ - another way of saying this is the loss function is a function of the parameters $\theta$. So we could notate it as $L(\theta)$.
The minimum of $L(\theta)$ is the point where the parameters guess $\theta$ is least wrong (at best, $L(\theta) = 0$, i.e. a perfect score, though this is not always good, as will be explained later); i.e. the best guess for the parameters.
So the algorithm learns the best-fitting function by minimizing its loss function. That is, we can frame this as an optimization problem.
There are many techniques to solve an optimization problem - sometimes they can be solved analytically (i.e. by moving around variables and isolating the one you want to solve for), but more often than not we must solve them numerically, i.e. by guessing a lot of different values - but not randomly!
The prevailing technique now is called _gradient descent_, and to understand how it works, we have to understand derivatives.
## Derivatives
Derivatives are everywhere in machine learning, so it's worthwhile become a bit familiar with them. I won't go into specifics on differentiation (how to calculate derivatives) because now we're spoiled with automatic differentiation, but it's still good to have a solid intuition about derivatives themselves.
A derivative expresses a rate of (instantaneous) change - they are always about how one variable quantity changes with respect to another variable quantity. That's basically all there is to it. For instance, velocity is a derivative which expresses how position changes with respect to time. Another interpretation, which is more relevant to machine learning, is that a derivative tells us how to change one variable to achieve a desired change in the other variable. Velocity, for instance, tells us how to change position by "changing" time.
To get a better understanding of _instantaneous_ change, consider a cyclist, cycling on a line. We have data about their position over time. We could calculate an average velocity over the data's entire time period, but we typically prefer to know the velocity at any given _moment_ (i.e. at any _instant_).
Let's get more concrete first. Let's say we have data for $n$ seconds, i.e. from $t_0$ to $t_n$ seconds, and the position at any given second $i$ is $p_i$. If we wanted to get the rate of change in position over the entire time interval, we'd just do:
```
positions = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, # moving forward
9, 9, 9, 9, 9, 9, 9, 9, 9, 9, # pausing
9, 8, 7, 6, 5, 4, 3, 2, 1, 0] # moving backwards
t_0 = 0
t_n = 29
(positions[t_n] - positions[t_0])/t_n
```
$$
v = \frac{p_n - p_0}{n}
$$
This kind of makes it look like the cyclist didn't move at all. It would probably be more useful to identify the velocity at a given second $t$. Thus we want to come up with some function $v(t)$ which gives us the velocity at some second $t$. We can apply the same approach we just used to get the velocity over the entire time interval, but we focus on a shorter time interval instead. To get the _instantaneous_ change at $t$ we just keep reducing the interval we look at until it is basically 0.
Derivatives have a special notation. A derivative of a function $f(x)$ with respect to a variable $x$ is notated:
$$
\frac{\delta f(x)}{\delta x}
$$
So if position is a function of time, e.g. $p = f(t)$, then velocity can be represented as $\frac{\delta p}{\delta t}$. To drive the point home, this derivative is also a function of time (derivatives are functions of what their "with respect to" variable is).
Since we are often computing derivatives of a function with respect to its input, a shorthand for the derivative of a function $f(x)$ with respect to $x$ can also be notated $f'(x)$.
### The Chain Rule
A very important property of derivatives is the _chain rule_ (there are other "chain rules" throughout mathematics, if we want to be specific, this is the "chain rule of derivatives"). The chain rule is important because it allows us to take complicated nested functions and more manageably differentiate them.
Let's look at an example to make this concrete:
```
def g(x):
return x**2
def h(x):
return x**3
def f(x):
return g(h(x))
# derivatives
def g_(x):
return 2*x
def h_(x):
return 3*(x**2)
```
$$
\begin{aligned}
g(x) &= x^2 \\
h(x) &= x^3 \\
f(x) &= g(h(x)) \\
g'(x) &= 2x \\
h'(x) &= 3x^2
\end{aligned}
$$
We're interested in understanding how $f(x)$ changes with respect to $x$, so we want to compute the derivative of $f(x)$. The chain rule allows us to individually differentiate the component functions of $f(x)$ and multiply those to get $f'(x)$:
```
def f_(x):
return g_(x) * h_(x)
```
$$
\frac{df}{dx} = \frac{dg}{dh} \frac{dh}{dx}
$$
This example is a bit contrived (there is a very easy way to differentiate this particular example that doesn't involve the chain rule) but if $g(x)$ and $h(x)$ were really nasty functions, the chain rule makes them quite a lot easier to deal with.
The chain rule can be applied to nested functions ad nauseaum! You can apply it to something crazy like $f(g(h(u(q(p(x))))))$. In fact, with deep neural networks, you are typically dealing with function compositions even more gnarly than this, so the chain rule is cornerstone there.
### Partial derivatives and gradients
The functions we've looked at so far just have a single input, but you can imagine many scenarios where you'd want to work with functions with some arbitrary number of inputs (i.e. a _multivariable_ function), like $f(x,y,z)$.
Here's where _partial deriatives_ come into play. Partial derivatives are just like regular derivatives except we use them for multivariable functions; it just means we only differentiate with respect to one variable at a time. So for $f(x,y,z)$, we'd have a partial derivative with respect to $x$, i.e. $\frac{\partial f}{\partial x}$ (note the slightly different notation), one with respect to $y$, i.e. $\frac{\partial f}{\partial y}$, and one with respect to $z$, i.e. $\frac{\partial f}{\partial z}$.
That's pretty simple! But it would be useful to group these partial derivatives together in some way. If we put these partial derivatives together in a vector, the resulting vector is the _gradient_ of $f$, notated $\nabla f$ (the symbol is called "nabla").
### Higher-order derivatives
We saw that velocity is the derivative of position because it describes how position changes over time. Acceleration similarly describes how _velocity_ changes over time, so we'd say that acceleration is the derivative of velocity. We can also say that acceleration is the _second-order_ derivative of position (that is, it is the derivative of its derivative).
This is the general idea behind higher-order derivatives.
## Gradient descent
Once you understand derivatives, gradient descent is really, really simple. The basic idea is that we use the derivative of the loss $L(\theta)$ with respect to $\theta$ and figure out which way the loss is decreasing, then "move" the parameter guess in that direction.
| true |
code
| 0.504761 | null | null | null | null |
|
# Convolutional Autoencoder
Sticking with the MNIST dataset, let's improve our autoencoder's performance using convolutional layers. Again, loading modules and the data.
```
%matplotlib inline
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', validation_size=0)
img = mnist.train.images[2]
plt.imshow(img.reshape((28, 28)), cmap='Greys_r')
```
## Network Architecture
The encoder part of the network will be a typical convolutional pyramid. Each convolutional layer will be followed by a max-pooling layer to reduce the dimensions of the layers. The decoder though might be something new to you. The decoder needs to convert from a narrow representation to a wide reconstructed image. For example, the representation could be a 4x4x8 max-pool layer. This is the output of the encoder, but also the input to the decoder. We want to get a 28x28x1 image out from the decoder so we need to work our way back up from the narrow decoder input layer. A schematic of the network is shown below.
<img src='assets/convolutional_autoencoder.png' width=500px>
Here our final encoder layer has size 4x4x8 = 128. The original images have size 28x28 = 784, so the encoded vector is roughly 16% the size of the original image. These are just suggested sizes for each of the layers. Feel free to change the depths and sizes, but remember our goal here is to find a small representation of the input data.
### What's going on with the decoder
Okay, so the decoder has these "Upsample" layers that you might not have seen before. First off, I'll discuss a bit what these layers *aren't*. Usually, you'll see **transposed convolution** layers used to increase the width and height of the layers. They work almost exactly the same as convolutional layers, but in reverse. A stride in the input layer results in a larger stride in the transposed convolution layer. For example, if you have a 3x3 kernel, a 3x3 patch in the input layer will be reduced to one unit in a convolutional layer. Comparatively, one unit in the input layer will be expanded to a 3x3 path in a transposed convolution layer. The TensorFlow API provides us with an easy way to create the layers, [`tf.nn.conv2d_transpose`](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d_transpose).
However, transposed convolution layers can lead to artifacts in the final images, such as checkerboard patterns. This is due to overlap in the kernels which can be avoided by setting the stride and kernel size equal. In [this Distill article](http://distill.pub/2016/deconv-checkerboard/) from Augustus Odena, *et al*, the authors show that these checkerboard artifacts can be avoided by resizing the layers using nearest neighbor or bilinear interpolation (upsampling) followed by a convolutional layer. In TensorFlow, this is easily done with [`tf.image.resize_images`](https://www.tensorflow.org/versions/r1.1/api_docs/python/tf/image/resize_images), followed by a convolution. Be sure to read the Distill article to get a better understanding of deconvolutional layers and why we're using upsampling.
> **Exercise:** Build the network shown above. Remember that a convolutional layer with strides of 1 and 'same' padding won't reduce the height and width. That is, if the input is 28x28 and the convolution layer has stride = 1 and 'same' padding, the convolutional layer will also be 28x28. The max-pool layers are used the reduce the width and height. A stride of 2 will reduce the size by a factor of 2. Odena *et al* claim that nearest neighbor interpolation works best for the upsampling, so make sure to include that as a parameter in `tf.image.resize_images` or use [`tf.image.resize_nearest_neighbor`]( `https://www.tensorflow.org/api_docs/python/tf/image/resize_nearest_neighbor). For convolutional layers, use [`tf.layers.conv2d`](https://www.tensorflow.org/api_docs/python/tf/layers/conv2d). For example, you would write `conv1 = tf.layers.conv2d(inputs, 32, (5,5), padding='same', activation=tf.nn.relu)` for a layer with a depth of 32, a 5x5 kernel, stride of (1,1), padding is 'same', and a ReLU activation. Similarly, for the max-pool layers, use [`tf.layers.max_pooling2d`](https://www.tensorflow.org/api_docs/python/tf/layers/max_pooling2d).
```
inputs_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='inputs')
targets_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='targets')
### Encoder
conv1 = tf.layers.conv2d(inputs_, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x16
maxpool1 = tf.layers.max_pooling2d(conv1, (2,2), (2,2), padding='same')
# Now 14x14x16
conv2 = tf.layers.conv2d(maxpool1, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x8
maxpool2 = tf.layers.max_pooling2d(conv2, (2,2), (2,2), padding='same')
# Now 7x7x8
conv3 = tf.layers.conv2d(maxpool2, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x8
encoded = tf.layers.max_pooling2d(conv3, (2,2), (2,2), padding='same')
# Now 4x4x8
### Decoder
upsample1 = tf.image.resize_nearest_neighbor(encoded, (7,7))
# Now 7x7x8
conv4 = tf.layers.conv2d(upsample1, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x8
upsample2 = tf.image.resize_nearest_neighbor(conv4, (14,14))
# Now 14x14x8
conv5 = tf.layers.conv2d(upsample2, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x8
upsample3 = tf.image.resize_nearest_neighbor(conv5, (28,28))
# Now 28x28x8
conv6 = tf.layers.conv2d(upsample3, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x16
logits = tf.layers.conv2d(conv6, 1, (3,3), padding='same', activation=None)
#Now 28x28x1
decoded = tf.nn.sigmoid(logits, name='decoded')
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=targets_, logits=logits)
cost = tf.reduce_mean(loss)
opt = tf.train.AdamOptimizer(0.001).minimize(cost)
```
## Training
As before, here wi'll train the network. Instead of flattening the images though, we can pass them in as 28x28x1 arrays.
```
sess = tf.Session()
epochs = 1
batch_size = 200
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
imgs = batch[0].reshape((-1, 28, 28, 1))
batch_cost, _ = sess.run([cost, opt], feed_dict={inputs_: imgs,
targets_: imgs})
print("Epoch: {}/{}...".format(e+1, epochs),
"Training loss: {:.4f}".format(batch_cost))
fig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
in_imgs = mnist.test.images[:10]
reconstructed = sess.run(decoded, feed_dict={inputs_: in_imgs.reshape((10, 28, 28, 1))})
for images, row in zip([in_imgs, reconstructed], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
fig.tight_layout(pad=0.1)
sess.close()
```
## Denoising
As I've mentioned before, autoencoders like the ones you've built so far aren't too useful in practive. However, they can be used to denoise images quite successfully just by training the network on noisy images. We can create the noisy images ourselves by adding Gaussian noise to the training images, then clipping the values to be between 0 and 1. We'll use noisy images as input and the original, clean images as targets. Here's an example of the noisy images I generated and the denoised images.

Since this is a harder problem for the network, we'll want to use deeper convolutional layers here, more feature maps. I suggest something like 32-32-16 for the depths of the convolutional layers in the encoder, and the same depths going backward through the decoder. Otherwise the architecture is the same as before.
> **Exercise:** Build the network for the denoising autoencoder. It's the same as before, but with deeper layers. I suggest 32-32-16 for the depths, but you can play with these numbers, or add more layers.
```
inputs_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='inputs')
targets_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='targets')
### Encoder
conv1 = tf.layers.conv2d(inputs_, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x32
maxpool1 = tf.layers.max_pooling2d(conv1, (2,2), (2,2), padding='same')
# Now 14x14x32
conv2 = tf.layers.conv2d(maxpool1, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x32
maxpool2 = tf.layers.max_pooling2d(conv2, (2,2), (2,2), padding='same')
# Now 7x7x32
conv3 = tf.layers.conv2d(maxpool2, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x16
encoded = tf.layers.max_pooling2d(conv3, (2,2), (2,2), padding='same')
# Now 4x4x16
### Decoder
upsample1 = tf.image.resize_nearest_neighbor(encoded, (7,7))
# Now 7x7x16
conv4 = tf.layers.conv2d(upsample1, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x16
upsample2 = tf.image.resize_nearest_neighbor(conv4, (14,14))
# Now 14x14x16
conv5 = tf.layers.conv2d(upsample2, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x32
upsample3 = tf.image.resize_nearest_neighbor(conv5, (28,28))
# Now 28x28x32
conv6 = tf.layers.conv2d(upsample3, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x32
logits = tf.layers.conv2d(conv6, 1, (3,3), padding='same', activation=None)
#Now 28x28x1
decoded = tf.nn.sigmoid(logits, name='decoded')
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=targets_, logits=logits)
cost = tf.reduce_mean(loss)
opt = tf.train.AdamOptimizer(0.001).minimize(cost)
sess = tf.Session()
epochs = 100
batch_size = 200
# Set's how much noise we're adding to the MNIST images
noise_factor = 0.5
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
# Get images from the batch
imgs = batch[0].reshape((-1, 28, 28, 1))
# Add random noise to the input images
noisy_imgs = imgs + noise_factor * np.random.randn(*imgs.shape)
# Clip the images to be between 0 and 1
noisy_imgs = np.clip(noisy_imgs, 0., 1.)
# Noisy images as inputs, original images as targets
batch_cost, _ = sess.run([cost, opt], feed_dict={inputs_: noisy_imgs,
targets_: imgs})
print("Epoch: {}/{}...".format(e+1, epochs),
"Training loss: {:.4f}".format(batch_cost))
```
## Checking out the performance
Here I'm adding noise to the test images and passing them through the autoencoder. It does a suprising great job of removing the noise, even though it's sometimes difficult to tell what the original number is.
```
fig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
in_imgs = mnist.test.images[:10]
noisy_imgs = in_imgs + noise_factor * np.random.randn(*in_imgs.shape)
noisy_imgs = np.clip(noisy_imgs, 0., 1.)
reconstructed = sess.run(decoded, feed_dict={inputs_: noisy_imgs.reshape((10, 28, 28, 1))})
for images, row in zip([noisy_imgs, reconstructed], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
fig.tight_layout(pad=0.1)
```
| true |
code
| 0.766253 | null | null | null | null |
|
Practice geospatial aggregations in geopandas before writing them to .py files
```
%load_ext autoreload
%autoreload 2
import sys
sys.path.append('../utils')
import wd_management
wd_management.set_wd_root()
import geopandas as gp
import pandas as pd
import requests
res = requests.get('https://services5.arcgis.com/GfwWNkhOj9bNBqoJ/arcgis/rest/services/NYC_Public_Use_Microdata_Areas_PUMAs_2010/FeatureServer/0/query?where=1=1&outFields=*&outSR=4326&f=pgeojson')
res_json = res.json()
NYC_PUMAs = gp.GeoDataFrame.from_features(res_json['features'])
NYC_PUMAs.set_crs('EPSG:4326',inplace=True)
NYC_PUMAs.set_index('PUMA', inplace=True)
NYC_PUMAs.head(5)
NYC_PUMAs.plot()
```
Ok looks good. Load in historic districts. [This stackoverflow post](https://gis.stackexchange.com/questions/327197/typeerror-input-geometry-column-must-contain-valid-geometry-objects) was helpful
```
from shapely import wkt
hd= gp.read_file('.library/lpc_historic_district_areas.csv')
hd['the_geom'] = hd['the_geom'].apply(wkt.loads)
hd.set_geometry(col='the_geom', inplace=True, crs='EPSG:4326')
hd= hd.explode(column='the_geom')
hd.set_geometry('the_geom',inplace=True)
hd = hd.to_crs('EPSG:2263')
hd = hd.reset_index()
hd.plot()
```
Ok great next do some geospatial analysis. Start only with PUMA 3807 as it has a lot of historic area
```
def fraction_area_historic(PUMA, hd):
try:
gdf = gp.GeoDataFrame(geometry = [PUMA.geometry], crs = 'EPSG:4326')
gdf = gdf.to_crs('EPSG:2263')
overlay = gp.overlay(hd, gdf, 'intersection')
if overlay.empty:
return 0, 0
else:
fraction = overlay.area.sum()/gdf.geometry.area.sum()
return fraction, overlay.area.sum()/(5280**2)
except Exception as e:
print(f'broke on {PUMA}')
print(e)
NYC_PUMAs[['fraction_area_historic', 'total_area_historic']] = NYC_PUMAs.apply(fraction_area_historic, axis=1, args=(hd,), result_type='expand')
NYC_PUMAs.sort_values('fraction_area_historic', ascending=False)
```
Superimpose PUMA 3801's historic districts on it to see if 38% looks right
```
def visualize_overlay(PUMA):
test_PUMA = NYC_PUMAs.loc[[PUMA]].to_crs('EPSG:2263')
base = test_PUMA.plot(color='green', edgecolor='black')
overlay = gp.overlay(hd, test_PUMA, 'intersection')
overlay.plot(ax=base, color='red');
visualize_overlay('3810')
```
Ok great that looks like about a third to me
From eyeballing map, more than 20% of PUMA 3806 on UWS looks to be historic
```
visualize_overlay('3806')
```
Ah ok the PUMA geography from includes central park. Worth flagging
### Question from Renae:
Renae points out that description of historic districts says "including items that may have been denied designation or overturned."
Look at dataset to see if columns point to this clearly
```
hd.head(5)
hd.groupby('status_of_').size()
hd.groupby('current_').size()
hd.groupby('last_actio').size()
```
| true |
code
| 0.235988 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/prateekjoshi565/Fine-Tuning-BERT/blob/master/Fine_Tuning_BERT_for_Spam_Classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Install Transformers Library
```
!pip install transformers
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import transformers
from transformers import AutoModel, BertTokenizerFast
# specify GPU
device = torch.device("cuda")
```
# Load Dataset
```
df = pd.read_csv("spamdata_v2.csv")
df.head()
df.shape
# check class distribution
df['label'].value_counts(normalize = True)
```
# Split train dataset into train, validation and test sets
```
train_text, temp_text, train_labels, temp_labels = train_test_split(df['text'], df['label'],
random_state=2018,
test_size=0.3,
stratify=df['label'])
# we will use temp_text and temp_labels to create validation and test set
val_text, test_text, val_labels, test_labels = train_test_split(temp_text, temp_labels,
random_state=2018,
test_size=0.5,
stratify=temp_labels)
```
# Import BERT Model and BERT Tokenizer
```
# import BERT-base pretrained model
bert = AutoModel.from_pretrained('bert-base-uncased')
# Load the BERT tokenizer
tokenizer = BertTokenizerFast.from_pretrained('bert-base-uncased')
# sample data
text = ["this is a bert model tutorial", "we will fine-tune a bert model"]
# encode text
sent_id = tokenizer.batch_encode_plus(text, padding=True, return_token_type_ids=False)
# output
print(sent_id)
```
# Tokenization
```
# get length of all the messages in the train set
seq_len = [len(i.split()) for i in train_text]
pd.Series(seq_len).hist(bins = 30)
max_seq_len = 25
# tokenize and encode sequences in the training set
tokens_train = tokenizer.batch_encode_plus(
train_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
# tokenize and encode sequences in the validation set
tokens_val = tokenizer.batch_encode_plus(
val_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
# tokenize and encode sequences in the test set
tokens_test = tokenizer.batch_encode_plus(
test_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
```
# Convert Integer Sequences to Tensors
```
# for train set
train_seq = torch.tensor(tokens_train['input_ids'])
train_mask = torch.tensor(tokens_train['attention_mask'])
train_y = torch.tensor(train_labels.tolist())
# for validation set
val_seq = torch.tensor(tokens_val['input_ids'])
val_mask = torch.tensor(tokens_val['attention_mask'])
val_y = torch.tensor(val_labels.tolist())
# for test set
test_seq = torch.tensor(tokens_test['input_ids'])
test_mask = torch.tensor(tokens_test['attention_mask'])
test_y = torch.tensor(test_labels.tolist())
```
# Create DataLoaders
```
from torch.utils.data import TensorDataset, DataLoader, RandomSampler, SequentialSampler
#define a batch size
batch_size = 32
# wrap tensors
train_data = TensorDataset(train_seq, train_mask, train_y)
# sampler for sampling the data during training
train_sampler = RandomSampler(train_data)
# dataLoader for train set
train_dataloader = DataLoader(train_data, sampler=train_sampler, batch_size=batch_size)
# wrap tensors
val_data = TensorDataset(val_seq, val_mask, val_y)
# sampler for sampling the data during training
val_sampler = SequentialSampler(val_data)
# dataLoader for validation set
val_dataloader = DataLoader(val_data, sampler = val_sampler, batch_size=batch_size)
```
# Freeze BERT Parameters
```
# freeze all the parameters
for param in bert.parameters():
param.requires_grad = False
```
# Define Model Architecture
```
class BERT_Arch(nn.Module):
def __init__(self, bert):
super(BERT_Arch, self).__init__()
self.bert = bert
# dropout layer
self.dropout = nn.Dropout(0.1)
# relu activation function
self.relu = nn.ReLU()
# dense layer 1
self.fc1 = nn.Linear(768,512)
# dense layer 2 (Output layer)
self.fc2 = nn.Linear(512,2)
#softmax activation function
self.softmax = nn.LogSoftmax(dim=1)
#define the forward pass
def forward(self, sent_id, mask):
#pass the inputs to the model
_, cls_hs = self.bert(sent_id, attention_mask=mask)
x = self.fc1(cls_hs)
x = self.relu(x)
x = self.dropout(x)
# output layer
x = self.fc2(x)
# apply softmax activation
x = self.softmax(x)
return x
# pass the pre-trained BERT to our define architecture
model = BERT_Arch(bert)
# push the model to GPU
model = model.to(device)
# optimizer from hugging face transformers
from transformers import AdamW
# define the optimizer
optimizer = AdamW(model.parameters(), lr = 1e-3)
```
# Find Class Weights
```
from sklearn.utils.class_weight import compute_class_weight
#compute the class weights
class_wts = compute_class_weight('balanced', np.unique(train_labels), train_labels)
print(class_wts)
# convert class weights to tensor
weights= torch.tensor(class_wts,dtype=torch.float)
weights = weights.to(device)
# loss function
cross_entropy = nn.NLLLoss(weight=weights)
# number of training epochs
epochs = 10
```
# Fine-Tune BERT
```
# function to train the model
def train():
model.train()
total_loss, total_accuracy = 0, 0
# empty list to save model predictions
total_preds=[]
# iterate over batches
for step,batch in enumerate(train_dataloader):
# progress update after every 50 batches.
if step % 50 == 0 and not step == 0:
print(' Batch {:>5,} of {:>5,}.'.format(step, len(train_dataloader)))
# push the batch to gpu
batch = [r.to(device) for r in batch]
sent_id, mask, labels = batch
# clear previously calculated gradients
model.zero_grad()
# get model predictions for the current batch
preds = model(sent_id, mask)
# compute the loss between actual and predicted values
loss = cross_entropy(preds, labels)
# add on to the total loss
total_loss = total_loss + loss.item()
# backward pass to calculate the gradients
loss.backward()
# clip the the gradients to 1.0. It helps in preventing the exploding gradient problem
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
# update parameters
optimizer.step()
# model predictions are stored on GPU. So, push it to CPU
preds=preds.detach().cpu().numpy()
# append the model predictions
total_preds.append(preds)
# compute the training loss of the epoch
avg_loss = total_loss / len(train_dataloader)
# predictions are in the form of (no. of batches, size of batch, no. of classes).
# reshape the predictions in form of (number of samples, no. of classes)
total_preds = np.concatenate(total_preds, axis=0)
#returns the loss and predictions
return avg_loss, total_preds
# function for evaluating the model
def evaluate():
print("\nEvaluating...")
# deactivate dropout layers
model.eval()
total_loss, total_accuracy = 0, 0
# empty list to save the model predictions
total_preds = []
# iterate over batches
for step,batch in enumerate(val_dataloader):
# Progress update every 50 batches.
if step % 50 == 0 and not step == 0:
# Calculate elapsed time in minutes.
elapsed = format_time(time.time() - t0)
# Report progress.
print(' Batch {:>5,} of {:>5,}.'.format(step, len(val_dataloader)))
# push the batch to gpu
batch = [t.to(device) for t in batch]
sent_id, mask, labels = batch
# deactivate autograd
with torch.no_grad():
# model predictions
preds = model(sent_id, mask)
# compute the validation loss between actual and predicted values
loss = cross_entropy(preds,labels)
total_loss = total_loss + loss.item()
preds = preds.detach().cpu().numpy()
total_preds.append(preds)
# compute the validation loss of the epoch
avg_loss = total_loss / len(val_dataloader)
# reshape the predictions in form of (number of samples, no. of classes)
total_preds = np.concatenate(total_preds, axis=0)
return avg_loss, total_preds
```
# Start Model Training
```
# set initial loss to infinite
best_valid_loss = float('inf')
# empty lists to store training and validation loss of each epoch
train_losses=[]
valid_losses=[]
#for each epoch
for epoch in range(epochs):
print('\n Epoch {:} / {:}'.format(epoch + 1, epochs))
#train model
train_loss, _ = train()
#evaluate model
valid_loss, _ = evaluate()
#save the best model
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'saved_weights.pt')
# append training and validation loss
train_losses.append(train_loss)
valid_losses.append(valid_loss)
print(f'\nTraining Loss: {train_loss:.3f}')
print(f'Validation Loss: {valid_loss:.3f}')
```
# Load Saved Model
```
#load weights of best model
path = 'saved_weights.pt'
model.load_state_dict(torch.load(path))
```
# Get Predictions for Test Data
```
# get predictions for test data
with torch.no_grad():
preds = model(test_seq.to(device), test_mask.to(device))
preds = preds.detach().cpu().numpy()
# model's performance
preds = np.argmax(preds, axis = 1)
print(classification_report(test_y, preds))
# confusion matrix
pd.crosstab(test_y, preds)
```
| true |
code
| 0.835551 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/parshwa1999/Map-Segmentation/blob/master/ResNet_RoadTest.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Segmentation of Road from Satellite imagery
## Importing Libraries
```
import warnings
warnings.filterwarnings('ignore')
import os
import cv2
#from google.colab.patches import cv2_imshow
import numpy as np
import tensorflow as tf
import pandas as pd
from keras.models import Model, load_model
from skimage.morphology import label
import pickle
from keras import backend as K
from matplotlib import pyplot as plt
from tqdm import tqdm_notebook
import random
from skimage.io import imread, imshow, imread_collection, concatenate_images
from matplotlib import pyplot as plt
import h5py
seed = 56
from google.colab import drive
drive.mount('/content/gdrive/')
base_path = "gdrive/My\ Drive/MapSegClean/"
%cd gdrive/My\ Drive/MapSegClean/
```
## Defining Custom Loss functions and accuracy Metric.
```
#Source: https://towardsdatascience.com/metrics-to-evaluate-your-semantic-segmentation-model-6bcb99639aa2
from keras import backend as K
def iou_coef(y_true, y_pred, smooth=1):
intersection = K.sum(K.abs(y_true * y_pred), axis=[1,2,3])
union = K.sum(y_true,[1,2,3])+K.sum(y_pred,[1,2,3])-intersection
iou = K.mean((intersection + smooth) / (union + smooth), axis=0)
return iou
def dice_coef(y_true, y_pred, smooth = 1):
y_true_f = K.flatten(y_true)
y_pred_f = K.flatten(y_pred)
intersection = K.sum(y_true_f * y_pred_f)
return (2. * intersection + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth)
def soft_dice_loss(y_true, y_pred):
return 1-dice_coef(y_true, y_pred)
```
## Defining Our Model
```
pip install -U segmentation-models
from keras.models import Model, load_model
import tensorflow as tf
from keras.layers import Input
from keras.layers.core import Dropout, Lambda
from keras.layers.convolutional import Conv2D, Conv2DTranspose
from keras.layers.pooling import MaxPooling2D
from keras.layers.merge import concatenate
from keras import optimizers
from keras.layers import BatchNormalization
import keras
from segmentation_models import Unet
from segmentation_models import get_preprocessing
from segmentation_models.losses import bce_jaccard_loss
from segmentation_models.metrics import iou_score
model = Unet('resnet101', input_shape=(256, 256, 3), encoder_weights=None)
#model = Unet(input_shape=(256, 256, 3), weights=None, activation='elu')
model.summary()
# fit model
```
### HYPER_PARAMETERS
```
LEARNING_RATE = 0.0001
```
### Initializing Callbacks
```
#from tensorboardcolab import TensorBoardColab, TensorBoardColabCallback
from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau
from datetime import datetime
model_path = "./Models/Resnet_road_weights.h5"
checkpointer = ModelCheckpoint(model_path,
monitor="val_loss",
mode="min",
save_best_only = True,
verbose=1)
earlystopper = EarlyStopping(monitor = 'val_loss',
min_delta = 0,
patience = 5,
verbose = 1,
restore_best_weights = True)
lr_reducer = ReduceLROnPlateau(monitor='val_loss',
factor=0.1,
patience=4,
verbose=1,
epsilon=1e-4)
```
### Compiling the model
```
opt = keras.optimizers.adam(LEARNING_RATE)
model.compile(
optimizer=opt,
loss=soft_dice_loss,
metrics=[iou_coef])
```
## Testing our Model
### On Test Images
```
model.load_weights("Models/Resnet_road_weights.h5")
import cv2
import glob
import numpy as np
import h5py
#test_images = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/I/")])
#test_masks = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/M/")])
test_masks = []
test_images = []
files = glob.glob ("TestI/*.png")
for myFile in files:
print(myFile)
image = cv2.imread (myFile)
test_images.append (image)
myFile = 'TestM' + myFile[5:len(myFile)]
image = cv2.cvtColor(cv2.imread (myFile), cv2.COLOR_BGR2GRAY)
test_masks.append (image)
#files = glob.glob ("TestM/*.png")
#for myFile in files:
# print(myFile)
#test_images = cv2.imread("/home/bisag/Desktop/Road-Segmentation/I/1.png")
#test_masks = cv2.imread("/home/bisag/Desktop/Road-Segmentation/M/1.png")
test_images = np.array(test_images)
test_masks = np.array(test_masks)
test_masks = np.expand_dims(test_masks, -1)
print("Unique elements in the train mask:", np.unique(test_masks))
print(test_images.shape)
print(test_masks.shape)
test_images = test_images.astype(np.float16)/255
test_masks = test_masks.astype(np.float16)/255
import sys
def sizeof_fmt(num, suffix='B'):
''' by Fred Cirera, https://stackoverflow.com/a/1094933/1870254, modified'''
for unit in ['','Ki','Mi','Gi','Ti','Pi','Ei','Zi']:
if abs(num) < 1024.0:
return "%3.1f %s%s" % (num, unit, suffix)
num /= 1024.0
return "%.1f %s%s" % (num, 'Yi', suffix)
for name, size in sorted(((name, sys.getsizeof(value)) for name, value in locals().items()),
key= lambda x: -x[1])[:10]:
print("{:>30}: {:>8}".format(name, sizeof_fmt(size)))
test_masks_tmp = []
for i in test_masks:
image = cv2.cvtColor(i, cv2.COLOR_BGR2GRAY)
test_masks_tmp.append (image)
test_images = np.array(test_images)
test_masks = np.array(test_masks_tmp)
test_masks = np.expand_dims(test_masks, -1)
#print(np.unique(test_masks))
print(test_images.shape)
print(test_masks.shape)
del test_masks_tmp
model.evaluate(test_images, test_masks)
predictions = model.predict(test_images, verbose=1)
thresh_val = 0.1
predicton_threshold = (predictions > thresh_val).astype(np.uint8)
plt.figure()
#plt.subplot(2, 1, 1)
plt.imshow(np.squeeze(predictions[19][:,:,0]))
plt.show()
import matplotlib
for i in range(len(predictions)):
#print("Results/" + str(i) + "Image.png")
matplotlib.image.imsave( "Results/" + str(i) + "Image.png" , np.squeeze(test_images[i][:,:,0]))
matplotlib.image.imsave( "Results/" + str(i) + "GroundTruth.png" , np.squeeze(test_masks[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#matplotlib.image.imsave('/home/bisag/Desktop/Road-Segmentation/Results/000.png', np.squeeze(predicton_threshold[0][:,:,0]))
matplotlib.image.imsave("Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
matplotlib.image.imsave( "Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#imshow(np.squeeze(predictions[0][:,:,0]))
#import scipy.misc
#scipy.misc.imsave('/home/bisag/Desktop/Road-Segmentation/Results/00.png', np.squeeze(predictions[0][:,:,0]))
model.load_weights("/home/parshwa/Desktop/Road-Segmentation/Models/weights.h5")
```
### Just Test
```
"""Test"""
import cv2
import glob
import numpy as np
import h5py
#test_images = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/I/")])
#test_masks = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/M/")])
test_images = []
files = glob.glob ("/home/parshwa/Desktop/Road-Segmentation/Test/*.png")
for myFile in files:
print(myFile)
image = cv2.imread (myFile)
test_images.append (image)
#test_images = cv2.imread("/home/bisag/Desktop/Road-Segmentation/I/1.png")
#test_masks = cv2.imread("/home/bisag/Desktop/Road-Segmentation/M/1.png")
test_images = np.array(test_images)
print(test_images.shape)
predictions = model.predict(test_images, verbose=1)
thresh_val = 0.1
predicton_threshold = (predictions > thresh_val).astype(np.uint8)
import matplotlib
for i in range(len(predictions)):
cv2.imwrite( "/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Image.png" , np.squeeze(test_images[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#matplotlib.image.imsave('/home/bisag/Desktop/Road-Segmentation/Results/000.png', np.squeeze(predicton_threshold[0][:,:,0]))
matplotlib.image.imsave("/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
matplotlib.image.imsave( "/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#imshow(np.squeeze(predictions[0][:,:,0]))
imshow(np.squeeze(predictions[0][:,:,0]))
#import scipy.misc
#scipy.misc.imsave('/home/bisag/Desktop/Road-Segmentation/Results/00.png', np.squeeze(predictions[0][:,:,0]))
"""Visualise"""
def layer_to_visualize(layer):
inputs = [K.learning_phase()] + model.inputs
_convout1_f = K.function(inputs, [layer.output])
def convout1_f(X):
# The [0] is to disable the training phase flag
return _convout1_f([0] + [X])
convolutions = convout1_f(img_to_visualize)
convolutions = np.squeeze(convolutions)
print ('Shape of conv:', convolutions.shape)
n = convolutions.shape[0]
n = int(np.ceil(np.sqrt(n)))
# Visualization of each filter of the layer
fig = plt.figure(figsize=(12,8))
for i in range(len(convolutions)):
ax = fig.add_subplot(n,n,i+1)
ax.imshow(convolutions[i], cmap='gray')
```
| true |
code
| 0.508605 | null | null | null | null |
|
# Statistics
## Introduction
In this chapter, you'll learn about how to do statistics with code. We already saw some statistics in the chapter on probability and random processes: here we'll focus on computing basic statistics and using statistical tests. We'll make use of the excellent [*pingouin*](https://pingouin-stats.org/index.html) statistics package and its documentation for many of the examples and methods in this chapter {cite}`vallat2018pingouin`. This chapter also draws on Open Intro Statistics {cite}`diez2012openintro`.
### Notation and basic definitions
Greek letters, like $\beta$, are the truth and represent parameters. Modified Greek letters are an estimate of the truth, for example $\hat{\beta}$. Sometimes Greek letters will stand in for vectors of parameters. Most of the time, upper case Latin characters such as $X$ will represent random variables (which could have more than one dimension). Lower case letters from the Latin alphabet denote realised data, for instance $x$ (which again could be multi-dimensional). Modified Latin alphabet letters denote computations performed on data, for instance $\bar{x} = \frac{1}{n} \displaystyle\sum_{i} x_i$ where $n$ is number of samples. Parameters are given following a vertical bar, for example if $f(x|\mu, \sigma)$ is a probability density function, the vertical line indicates that its parameters are $\mu$ and $\sigma$. The set of distributions with densities $f_\theta(x)$, $\theta \in \Theta$ is called a parametric family, eg there is a family of different distributions that are parametrised by $\theta$.
A **statistic** $T(x)$ is a function of the data $x=(x_1, \dots, x_n)$.
An **estimator** of a parameter $\theta$ is a function $T=T(x)$ which is used to estimate $\theta$ based on observations of data. $T$ is an unbiased estimator if $\mathbb{E}(T) = \theta$.
If $X$ has PDF $f(x|\theta)$ then, given the observed value $x$ of $X$, the **likelihood** of $\theta$ is defined by $\text{lik}(\theta) = f(x | \theta)$. For independent and identically distributed observed values, then $\text{lik}(\theta) = f(x_1, \dots, x_n| \theta) = \Pi_{i=1}^n f(x_i | \theta)$. The $\hat{\theta}$ such that this function attains its maximum value is the **maximum likelihood estimator (MLE)** of $\theta$.
Given an MLE $\hat{\theta}$ of $\theta$, $\hat{\theta}$ is said to be **consistent** if $\mathbb{P}(\hat{\theta} - \theta > \epsilon) \rightarrow 0$ as $n\rightarrow \infty$.
An estimator *W* is **efficient** relative to another estimator $V$ if $\text{Var}(W) < \text{Var}(V)$.
Let $\alpha$ be the 'significance level' of a test statistic $T$.
Let $\gamma(X)$ and $\delta(X)$ be two statistics satisfying $\gamma(X) < \delta(X)$ for all $X$. If on observing $X = x$, the inference can be made that $\gamma(x) \leq \theta \leq \delta(x)$. Then $[\delta(x), \gamma(x)]$ is an **interval estimate** and $[\delta(X), \gamma(X)]$ is an **interval estimator**. The random interval (random because the *endpoints* are random variables) $[\delta(X), \gamma(X)]$ is called a $100\cdot\alpha \%$ **confidence interval** for $\theta$. Of course, there is a true $\theta$, so either it is in this interval or it is not. But if the confidence interval was constructed many times over using samples, $\theta$ would be contained within it $100\cdot\alpha \%$ of the times.
A **hypothesis test** is a conjecture about the distribution of one or more random variables, and a test of a hypothesis is a procedure for deciding whether or not to reject that conjecture. The **null hypothesis**, $H_0$, is only ever conservatively rejected and represents the default positiion. The **alternative hypothesis**, $H_1$, is the conclusion contrary to this.
A type I error occurs when $H_0$ is rejected when it is true, ie when a *true* null hypothesis is rejected. Mistakenly failing to reject a false null hypothesis is called a type II error.
In the most simple situations, the upper bound on the probability of a type I error is called the size or **significance level** of the *test*. The **p-value** of a random variable $X$ is the smallest value of the significance level (denoted $\alpha$) for which $H_0$ would be rejected on the basis of seeing $x$. The p-value is sometimes called the significance level of $X$. The probability that a test will reject the null is called the power of the test. The probability of a type II error is equal to 1 minus the power of the test.
Recall that there are two types of statistics out there: parametrised, eg by $\theta$, and non-parametrised. The latter are often distribution free (ie don't involve a PDF) or don't require parameters to be specified.
### Imports
First we need to import the packages we'll be using
```
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
import pingouin as pg
import statsmodels.formula.api as smf
from numpy.random import Generator, PCG64
# Set seed for random numbers
seed_for_prng = 78557
prng = Generator(PCG64(seed_for_prng))
```
## Basic statistics
Let's start with computing the simplest statistics you can think of using some synthetic data. Many of the functions have lots of extra options that we won't explore here (like weights or normalisation); remember that you can see these using the `help()` method.
We'll generate a vector with 100 entries:
```
data = np.array(range(100))
data
from myst_nb import glue
import sympy
import warnings
warnings.filterwarnings("ignore")
dict_fns = {'mean': np.mean(data),
'std': np.std(data),
'mode': stats.mode([0, 1, 2, 3, 3, 3, 5])[0][0],
'median': np.median(data)}
for name, eval_fn in dict_fns.items():
glue(name, f'{eval_fn:.1f}')
# Set max rows displayed for readability
pd.set_option('display.max_rows', 6)
# Plot settings
plt.style.use('plot_style.txt')
```
Okay, let's see how some basic statistics are computed. The mean is `np.mean(data)=` {glue:}`mean`, the standard deviation is `np.std(data)=` {glue:}`std`, and the median is given by `np.median(data)= `{glue:}`median`. The mode is given by `stats.mode([0, 1, 2, 3, 3, 3, 5])[0]=` {glue:}`mode` (access the counts using `stats.mode(...)[1]`).
Less famous quantiles than the median are given by, for example for $q=0.25$,
```
np.quantile(data, 0.25)
```
As with **pandas**, **numpy** and **scipy** work on scalars, vectors, matrices, and tensors: you just need to specify the axis that you'd like to apply a function to:
```
data = np.fromfunction(lambda i, j: i + j, (3, 6), dtype=int)
data
np.mean(data, axis=0)
```
Remember that, for discrete data points, the $k$th (unnormalised) moment is
$$
\hat{m}_k = \frac{1}{n}\displaystyle\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^k
$$
To compute this use scipy's `stats.moment(a, moment=1)`. For instance for the kurtosis ($k=4$), it's
```
stats.moment(data, moment=4, axis=1)
```
Covariances are found using `np.cov`.
```
np.cov(np.array([[0, 1, 2], [2, 1, 0]]))
```
Note that, as expected, the $C_{01}$ term is -1 as the vectors are anti-correlated.
## Parametric tests
Reminder: parametric tests assume that data are effectively drawn a probability distribution that can be described with fixed parameters.
### One-sample t-test
The one-sample t-test tells us whether a given parameter for the mean, i.e. a suspected $\mu$, is likely to be consistent with the sample mean. The null hypothesis is that $\mu = \bar{x}$. Let's see an example using the default `tail='two-sided'` option. Imagine we have data on the number of hours people spend working each day and we want to test the (alternative) hypothesis that $\bar{x}$ is not $\mu=$8 hours:
```
x = [8.5, 5.4, 6.8, 9.6, 4.2, 7.2, 8.8, 8.1]
pg.ttest(x, 8).round(2)
```
(The returned object is a **pandas** dataframe.) We only have 8 data points, and so that is a great big confidence interval! It's worth remembering what a t-statistic and t-test really are. In this case, the statistic that is constructed to test whether the sample mean is different from a known parameter $\mu$ is
$$
T = \frac{\sqrt{n}(\bar{x}-\mu)}{\hat{\sigma}} \thicksim t_{n-1}
$$
where $t_{n-1}$ is the student's t-distribution and $n-1$ is the number of degrees of freedom. The $100\cdot(1-\alpha)\%$ test interval in this case is given by
$$
1 - \alpha = \mathbb{P}\left(-t_{n-1, \alpha/2} \leq \frac{\sqrt{n}(\bar{x} - \mu)}{\hat{\sigma}} \leq t_{n-1,\alpha/2}\right)
$$
where we define $t_{n-1, \alpha/2}$ such that $\mathbb{P}(T > t_{n-1, \alpha/2}) = \alpha/2$. For $\alpha=0.05$, implying confidence intervals of 95%, this looks like:
```
import scipy.stats as st
def plot_t_stat(x, mu):
T = np.linspace(-7, 7, 500)
pdf_vals = st.t.pdf(T, len(x)-1)
sigma_hat = np.sqrt(np.sum( (x-np.mean(x))**2)/(len(x)-1))
actual_T_stat = (np.sqrt(len(x))*(np.mean(x) - mu))/sigma_hat
alpha = 0.05
T_alpha_over_2 = st.t.ppf(1.0-alpha/2, len(x)-1)
interval_T = T[((T>-T_alpha_over_2) & (T<T_alpha_over_2))]
interval_y = pdf_vals[((T>-T_alpha_over_2) & (T<T_alpha_over_2))]
fig, ax = plt.subplots()
ax.plot(T, pdf_vals, label=f'Student t: dof={len(x)-1}', zorder=2)
ax.fill_between(interval_T, 0, interval_y, alpha=0.2, label=r'95% interval', zorder=1)
ax.plot(actual_T_stat, st.t.pdf(actual_T_stat, len(x)-1), 'bo', ms=15, label=r'$\sqrt{n}(\bar{x} - \mu)/\hat{\sigma}}$',
color='orchid', zorder=4)
ax.vlines(actual_T_stat, 0, st.t.pdf(actual_T_stat, len(x)-1), color='orchid', zorder=3)
ax.set_xlabel('Value of statistic T')
ax.set_ylabel('PDF')
ax.set_xlim(-7, 7)
ax.set_ylim(0., 0.4)
ax.legend(frameon=False)
plt.show()
mu = 8
plot_t_stat(x, mu)
```
In this case, we would reject the alternative hypothesis. You can see why from the plot; the test statistic we have constructed lies within the interval where we cannot reject the null hypothesis. $\bar{x}-\mu$ is close enough to zero to give us cause for concern. (You can also see from the plot why this is a two-tailed test: we don't care if $\bar{x}$ is greater or less than $\mu$, just that it's different--and so the test statistic could appear in either tail of the distribution for us to accept $H_1$.)
We accept the null here, but about if there were many more data points? Let's try adding some generated data (pretend it is from making extra observations).
```
# 'Observe' extra data
extra_data = prng.uniform(5.5, 8.5, size=(30))
# Add it in to existing vector
x_prime = np.concatenate((np.array(x), extra_data), axis=None)
# Run t-test
pg.ttest(x_prime, 8).round(2)
```
Okay, what happened? Our extra observations have seen the confidence interval shrink considerably, and the p-value is effectively 0. There's a large negative t-statistic too. Unsurprisingly, as we chose a uniform distribution that only just included 8 but was centered on $(8-4.5)/2$ *and* we had more points, the test now rejects the null hypothesis that $\mu=8$ . Because the alternative hypothesis is just $\mu\neq8$, and these tests are conservative, we haven't got an estimate of what the mean actually is; we just know that our test rejects that it's $8$.
We can see this in a new version of the chart that uses the extra data:
```
plot_t_stat(x_prime, mu)
```
Now our test statistic is safely outside the interval.
#### Connection to linear regression
Note that testing if $\mu\neq0$ is equivalent to having the alternative hypothesis that a single, non-zero scalar value is a good expected value for $x$, i.e. that $\mathbb{E}(x) \neq 0$. Which may sound familiar if you've run **linear regression** and, indeed, this t-test has an equivalent linear model! It's just regressing $X$ on a constant--a single, non-zero scalar value. In general, t-tests appear in linear regression to test whether any coefficient $\beta \neq 0$.
We can see this connection by running a hypothesis test of whether the sample mean is not zero. Note the confidence interval, t-statistic, and p-value.
```
pg.ttest(x, 0).round(3)
```
And, as an alternative, regressing x on a constant, again noting the interval, t-stat, and p-value:
```
import statsmodels.formula.api as smf
df = pd.DataFrame(x, columns=['x'])
res = smf.ols(formula='x ~ 1', data=df).fit()
# Show only the info relevant to the intercept (there are no other coefficients)
print(res.summary().tables[1])
```
Many tests have an equivalent linear model.
#### Other information provided by **Pingouin** tests
We've covered the degrees of freedom, the T statistic, the p-value, and the confidence interval. So what's all that other gunk in our t-test? Cohen's d is a measure of whether the difference being measured in our test is large or not (this is important; you can have statistically significant differences that are so small as to be inconsequential). Cohen suggested that $d = 0.2$ be considered a 'small' effect size, 0.5 represents a 'medium' effect size and 0.8 a 'large' effect size. BF10 represents the Bayes factor, the ratio (given the data) of the likelihood of the alternative hypothesis relative to the null hypothesis. Values greater than unity therefore favour the alternative hypothesis. Finally, power is the achieved power of the test, which is $1 - \mathbb{P}(\text{type II error})$. A common default to have in mind is a power greater than 0.8.
### Two-sample t-test
The two-sample t-test is used to determine if two population means are equal (with the null being that they *are* equal). Let's look at an example with synthetic data of equal length, which means we can use the *paired* version of this. We'll imagine we are looking at an intervention with a pre- and post- dataset.
```
pre = [5.5, 2.4, 6.8, 9.6, 4.2, 5.9]
post = [6.4, 3.4, 6.4, 11., 4.8, 6.2]
pg.ttest(pre, post, paired=True, tail='two-sided').round(2)
```
In this case, we cannot reject the null hypothesis that the means are the same pre- and post-intervention.
### Pearson correlation
The Pearson correlation coefficient measures the linear relationship between two datasets. Strictly speaking, it requires that each dataset be normally distributed.
```
mean, cov = [4, 6], [(1, .5), (.5, 1)]
x, y = prng.multivariate_normal(mean, cov, 30).T
# Compute Pearson correlation
pg.corr(x, y).round(3)
```
### Welch's t-test
In the case where you have two samples with unequal variances (or, really, unequal sample sizes too), Welch's t-test is appropriate. With `correction='true'`, it assumes that variances are not equal.
```
x = prng.normal(loc=7, size=20)
y = prng.normal(loc=6.5, size=15)
pg.ttest(x, y, correction='true')
```
### One-way ANOVA
Analysis of variance (ANOVA) is a technique for testing hypotheses about means, for example testing the equality of the means of $k>2$ groups. The model would be
$$
X_{ij} = \mu_i + \epsilon_{ij} \quad j=1, \dots, n_i \quad i=1, \dots, k.
$$
so that the $i$th group has $n_i$ observations. The null hypothesis of one-way ANOVA is that $H_0: \mu_1 = \mu_2 = \dots = \mu_k$, with the alternative hypothesis that this is *not* true.
```
df = pg.read_dataset('mixed_anova')
df.head()
# Run the ANOVA
pg.anova(data=df, dv='Scores', between='Group', detailed=True)
```
### Multiple pairwise t-tests
There's a problem with running multiple t-tests: if you run enough of them, something is bound to come up as significant! As such, some *post-hoc* adjustments exist that correct for the fact that multiple tests are occurring simultaneously. In the example below, multiple pairwise comparisons are made between the scores by time group. There is a corrected p-value, `p-corr`, computed using the Benjamini/Hochberg FDR correction.
```
pg.pairwise_ttests(data=df, dv='Scores', within='Time', subject='Subject',
parametric=True, padjust='fdr_bh', effsize='hedges').round(3)
```
### One-way ANCOVA
Analysis of covariance (ANCOVA) is a general linear model which blends ANOVA and regression. ANCOVA evaluates whether the means of a dependent variable (dv) are equal across levels of a categorical independent variable (between) often called a treatment, while statistically controlling for the effects of other continuous variables that are not of primary interest, known as covariates or nuisance variables (covar).
```
df = pg.read_dataset('ancova')
df.head()
pg.ancova(data=df, dv='Scores', covar='Income', between='Method')
```
### Power calculations
Often, it's quite useful to know what sample size is needed to avoid certain types of testing errors. **Pingouin** offers ways to compute effect sizes and test powers to help with these questions.
As an example, let's assume we have a new drug (`x`) and an old drug (`y`) that are both intended to reduce blood pressure. The standard deviation of the reduction in blood pressure of those receiving the old drug is 12 units. The null hypothesis is that the new drug is no more effective than the new drug. But it will only be worth switching production to the new drug if it reduces blood pressure by more than 3 units versus the old drug. In this case, the effect size of interest is 3 units.
Let's assume for a moment that the true difference is 3 units and we want to perform a test with $\alpha=0.05$. The problem is that, for small differences in the effect, the distribution of effects under the null and the distribution of effects under the alternative have a great deal of overlap. So the chances of making a Type II error - accepting the null hypothesis when it is actually false - is quite high. Let's say we'd ideally have at most a 20% chance of making a Type II error: what sample size do we need?
We can compute this, but we need an extra piece of information first: a normalised version of the effect size called Cohen's $d$. We need to transform the difference in means to compute this. For independent samples, $d$ is:
$$ d = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{(n_{1} - 1)\sigma_{1}^{2} + (n_{2} - 1)\sigma_{2}^{2}}{n_1 + n_2 - 2}}}$$
(If you have real data samples, you can compute this using `pg.compute_effsize`.)
For this case, $d$ is $-3/12 = -1/4$ if we assume the standard deviations are the same across the old (`y`) and new (`x`) drugs. So we will plug that $d$ in and look at a range of possible sample sizes along with a standard value for $alpha$ of 0.05. In the below `tail=less` tests the alternative that `x` has a smaller mean than `y`.
```
cohen_d = -0.25 # Fixed effect size
sample_size_array = np.arange(1, 500, 50) # Incrementing sample size
# Compute the achieved power
pwr = pg.power_ttest(d=cohen_d, n=sample_size_array, alpha=0.05,
contrast='two-samples', tail='less')
fig, ax = plt.subplots()
ax.plot(sample_size_array, pwr, 'ko-.')
ax.axhline(0.8, color='r', ls=':')
ax.set_xlabel('Sample size')
ax.set_ylabel('Power (1 - type II error)')
ax.set_title('Achieved power of a T-test')
plt.show()
```
From this, we can see we need a sample size of at least 200 in order to have a power of 0.8.
The `pg.power_ttest` function takes any three of the four of `d`, `n`, `power`, and `alpha` (ie leave one of these out), and then returns what the missing parameter should be. We passed in `d`, `n`, and `alpha`, and so the `power` was returned.
## Non-parametric tests
Reminder: non-parametrics tests do not make any assumptions about the distribution from which data are drawn or that it can be described by fixed parameters.
### Wilcoxon Signed-rank Test
This tests the null hypothesis that two related paired samples come from the same distribution. It is the non-parametric equivalent of the t-test.
```
x = [20, 22, 19, 20, 22, 18, 24, 20, 19, 24, 26, 13]
y = [38, 37, 33, 29, 14, 12, 20, 22, 17, 25, 26, 16]
pg.wilcoxon(x, y, tail='two-sided').round(2)
```
### Mann-Whitney U Test (aka Wilcoxon rank-sum test)
The Mann–Whitney U test is a non-parametric test of the null hypothesis that it is equally likely that a randomly selected value from one sample will be less than or greater than a randomly selected value from a second sample. It is the non-parametric version of the two-sample T-test.
Like many non-parametric **pingouin** tests, it can take values of tail that are 'two-sided', 'one-sided', 'greater', or 'less'. Below, we ask if a randomly selected value from `x` is greater than one from `y`, with the null that it is not.
```
x = prng.uniform(low=0, high=1, size=20)
y = prng.uniform(low=0.2, high=1.2, size=20)
pg.mwu(x, y, tail='greater')
```
### Spearman Correlation
The Spearman correlation coefficient is the Pearson correlation coefficient between the rank variables, and does not assume normality of data.
```
mean, cov = [4, 6], [(1, .5), (.5, 1)]
x, y = prng.multivariate_normal(mean, cov, 30).T
pg.corr(x, y, method="spearman").round(2)
```
### Kruskal-Wallace
The Kruskal-Wallis H-test tests the null hypothesis that the population median of all of the groups are equal. It is a non-parametric version of ANOVA. The test works on 2 or more independent samples, which may have different sizes.
```
df = pg.read_dataset('anova')
df.head()
pg.kruskal(data=df, dv='Pain threshold', between='Hair color')
```
### The Chi-Squared Test
The chi-squared test is used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories. This test can be used to evaluate the quality of a categorical variable in a classification problem or to check the similarity between two categorical variables.
There are two conditions for a chi-squared test:
- Independence: Each case that contributes a count to the table must be independent of all the other cases in the table.
- Sample size or distribution: Each particular case (ie cell count) must have at least 5 expected cases.
Let's see an example from the **pingouin** docs: whether gender is a good predictor of heart disease. First, let's load the data and look at the gender split in total:
```
chi_data = pg.read_dataset('chi2_independence')
chi_data['sex'].value_counts(ascending=True)
```
If gender is *not* a predictor, we would expect a roughly similar split between those who have heart disease and those who do not. Let's look at the observerd versus the expected split once we categorise by gender and 'target' (heart disease or not).
```
expected, observed, stats = pg.chi2_independence(chi_data, x='sex', y='target')
observed - expected
```
So we have fewer in the 0, 0 and 1, 1 buckets than expected but more in the 0, 1 and 1, 0 buckets. Let's now see how the test interprets this:
```
stats.round(3)
```
From these, it is clear we can reject the null and therefore it seems like gender is a good predictor of heart disease.
### Shapiro-Wilk Test for Normality
Note that the null here is that the distribution *is* normal, so normality is only rejected when the p-value is sufficiently small.
```
x = prng.normal(size=20)
pg.normality(x)
```
The test can also be run on multiple variables in a dataframe:
```
df = pg.read_dataset('ancova')
pg.normality(df[['Scores', 'Income', 'BMI']], method='normaltest').round(3)
```
| true |
code
| 0.621885 | null | null | null | null |
|
```
epochs = 5
```
# Example - Simple Vertically Partitioned Split Neural Network
- <b>Alice</b>
- Has model Segment 1
- Has the handwritten Images
- <b>Bob</b>
- Has model Segment 2
- Has the image Labels
Based on [SplitNN - Tutorial 3](https://github.com/OpenMined/PySyft/blob/master/examples/tutorials/advanced/split_neural_network/Tutorial%203%20-%20Folded%20Split%20Neural%20Network.ipynb) from Adam J Hall - Twitter: [@AJH4LL](https://twitter.com/AJH4LL) · GitHub: [@H4LL](https://github.com/H4LL)
Authors:
- Pavlos Papadopoulos · GitHub: [@pavlos-p](https://github.com/pavlos-p)
- Tom Titcombe · GitHub: [@TTitcombe](https://github.com/TTitcombe)
- Robert Sandmann · GitHub: [@rsandmann](https://github.com/rsandmann)
```
class SplitNN:
def __init__(self, models, optimizers):
self.models = models
self.optimizers = optimizers
self.data = []
self.remote_tensors = []
def forward(self, x):
data = []
remote_tensors = []
data.append(self.models[0](x))
if data[-1].location == self.models[1].location:
remote_tensors.append(data[-1].detach().requires_grad_())
else:
remote_tensors.append(
data[-1].detach().move(self.models[1].location).requires_grad_()
)
i = 1
while i < (len(models) - 1):
data.append(self.models[i](remote_tensors[-1]))
if data[-1].location == self.models[i + 1].location:
remote_tensors.append(data[-1].detach().requires_grad_())
else:
remote_tensors.append(
data[-1].detach().move(self.models[i + 1].location).requires_grad_()
)
i += 1
data.append(self.models[i](remote_tensors[-1]))
self.data = data
self.remote_tensors = remote_tensors
return data[-1]
def backward(self):
for i in range(len(models) - 2, -1, -1):
if self.remote_tensors[i].location == self.data[i].location:
grads = self.remote_tensors[i].grad.copy()
else:
grads = self.remote_tensors[i].grad.copy().move(self.data[i].location)
self.data[i].backward(grads)
def zero_grads(self):
for opt in self.optimizers:
opt.zero_grad()
def step(self):
for opt in self.optimizers:
opt.step()
import sys
sys.path.append('../')
import torch
from torchvision import datasets, transforms
from torch import nn, optim
from torchvision.datasets import MNIST
from torchvision.transforms import ToTensor
import syft as sy
from src.dataloader import VerticalDataLoader
from src.psi.util import Client, Server
from src.utils import add_ids
hook = sy.TorchHook(torch)
# Create dataset
data = add_ids(MNIST)(".", download=True, transform=ToTensor()) # add_ids adds unique IDs to data points
# Batch data
dataloader = VerticalDataLoader(data, batch_size=128) # partition_dataset uses by default "remove_data=True, keep_order=False"
```
## Check if the datasets are unordered
In MNIST, we have 2 datasets (the images and the labels).
```
# We need matplotlib library to plot the dataset
import matplotlib.pyplot as plt
# Plot the first 10 entries of the labels and the dataset
figure = plt.figure()
num_of_entries = 10
for index in range(1, num_of_entries + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(dataloader.dataloader1.dataset.data[index].numpy().squeeze(), cmap='gray_r')
print(dataloader.dataloader2.dataset[index][0], end=" ")
```
## Implement PSI and order the datasets accordingly
```
# Compute private set intersection
client_items = dataloader.dataloader1.dataset.get_ids()
server_items = dataloader.dataloader2.dataset.get_ids()
client = Client(client_items)
server = Server(server_items)
setup, response = server.process_request(client.request, len(client_items))
intersection = client.compute_intersection(setup, response)
# Order data
dataloader.drop_non_intersecting(intersection)
dataloader.sort_by_ids()
```
## Check again if the datasets are ordered
```
# We need matplotlib library to plot the dataset
import matplotlib.pyplot as plt
# Plot the first 10 entries of the labels and the dataset
figure = plt.figure()
num_of_entries = 10
for index in range(1, num_of_entries + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(dataloader.dataloader1.dataset.data[index].numpy().squeeze(), cmap='gray_r')
print(dataloader.dataloader2.dataset[index][0], end=" ")
torch.manual_seed(0)
# Define our model segments
input_size = 784
hidden_sizes = [128, 640]
output_size = 10
models = [
nn.Sequential(
nn.Linear(input_size, hidden_sizes[0]),
nn.ReLU(),
nn.Linear(hidden_sizes[0], hidden_sizes[1]),
nn.ReLU(),
),
nn.Sequential(nn.Linear(hidden_sizes[1], output_size), nn.LogSoftmax(dim=1)),
]
# Create optimisers for each segment and link to them
optimizers = [
optim.SGD(model.parameters(), lr=0.03,)
for model in models
]
# create some workers
alice = sy.VirtualWorker(hook, id="alice")
bob = sy.VirtualWorker(hook, id="bob")
# Send Model Segments to model locations
model_locations = [alice, bob]
for model, location in zip(models, model_locations):
model.send(location)
#Instantiate a SpliNN class with our distributed segments and their respective optimizers
splitNN = SplitNN(models, optimizers)
def train(x, target, splitNN):
#1) Zero our grads
splitNN.zero_grads()
#2) Make a prediction
pred = splitNN.forward(x)
#3) Figure out how much we missed by
criterion = nn.NLLLoss()
loss = criterion(pred, target)
#4) Backprop the loss on the end layer
loss.backward()
#5) Feed Gradients backward through the nework
splitNN.backward()
#6) Change the weights
splitNN.step()
return loss, pred
for i in range(epochs):
running_loss = 0
correct_preds = 0
total_preds = 0
for (data, ids1), (labels, ids2) in dataloader:
# Train a model
data = data.send(models[0].location)
data = data.view(data.shape[0], -1)
labels = labels.send(models[-1].location)
# Call model
loss, preds = train(data, labels, splitNN)
# Collect statistics
running_loss += loss.get()
correct_preds += preds.max(1)[1].eq(labels).sum().get().item()
total_preds += preds.get().size(0)
print(f"Epoch {i} - Training loss: {running_loss/len(dataloader):.3f} - Accuracy: {100*correct_preds/total_preds:.3f}")
print("Labels pointing to: ", labels)
print("Images pointing to: ", data)
```
| true |
code
| 0.85931 | null | null | null | null |
|
## 1-3. 複数量子ビットの記述
ここまでは1量子ビットの状態とその操作(演算)の記述について学んできた。この章の締めくくりとして、$n$個の量子ビットがある場合の状態の記述について学んでいこう。テンソル積がたくさん出てきてややこしいが、コードをいじりながら身につけていってほしい。
$n$個の**古典**ビットの状態は$n$個の$0,1$の数字によって表現され、そのパターンの総数は$2^n$個ある。
量子力学では、これらすべてのパターンの重ね合わせ状態が許されているので、$n$個の**量子**ビットの状態$|\psi \rangle$はどのビット列がどのような重みで重ね合わせになっているかという$2^n$個の複素確率振幅で記述される:
$$
\begin{eqnarray}
|\psi \rangle &= &
c_{00...0} |00...0\rangle +
c_{00...1} |00...1\rangle + \cdots +
c_{11...1} |11...1\rangle =
\left(
\begin{array}{c}
c_{00...0}
\\
c_{00...1}
\\
\vdots
\\
c_{11...1}
\end{array}
\right).
\end{eqnarray}
$$
ただし、
複素確率振幅は規格化
$\sum _{i_1,..., i_n} |c_{i_1...i_n}|^2=1$
されているものとする。
そして、この$n$量子ビットの量子状態を測定するとビット列$i_1 ... i_n$が確率
$$
\begin{eqnarray}
p_{i_1 ... i_n} &=&|c_{i_1 ... i_n}|^2
\label{eq02}
\end{eqnarray}
$$
でランダムに得られ、測定後の状態は$|i_1 \dotsc i_n\rangle$となる。
**このように**$n$**量子ビットの状態は、**$n$**に対して指数的に大きい**$2^n$**次元の複素ベクトルで記述する必要があり、ここに古典ビットと量子ビットの違いが顕著に現れる**。
そして、$n$量子ビット系に対する操作は$2^n \times 2^n$次元のユニタリ行列として表される。
言ってしまえば、量子コンピュータとは、量子ビット数に対して指数的なサイズの複素ベクトルを、物理法則に従ってユニタリ変換するコンピュータのことなのである。
※ここで、複数量子ビットの順番と表記の関係について注意しておく。状態をケットで記述する際に、「1番目」の量子ビット、「2番目」の量子ビット、……の状態に対応する0と1を左から順番に並べて表記した。例えば$|011\rangle$と書けば、1番目の量子ビットが0、2番目の量子ビットが1、3番目の量子ビットが1である状態を表す。一方、例えば011を2進数の表記と見た場合、上位ビットが左、下位ビットが右となることに注意しよう。すなわち、一番左の0は最上位ビットであって$2^2$の位に対応し、真ん中の1は$2^1$の位、一番右の1は最下位ビットであって$2^0=1$の位に対応する。つまり、「$i$番目」の量子ビットは、$n$桁の2進数表記の$n-i+1$桁目に対応している。このことは、SymPyなどのパッケージで複数量子ビットを扱う際に気を付ける必要がある(下記「SymPyを用いた演算子のテンソル積」も参照)。
(詳細は Nielsen-Chuang の `1.2.1 Multiple qbits` を参照)
### 例:2量子ビットの場合
2量子ビットの場合は、 00, 01, 10, 11 の4通りの状態の重ね合わせをとりうるので、その状態は一般的に
$$
c_{00} |00\rangle + c_{01} |01\rangle + c_{10}|10\rangle + c_{11} |11\rangle =
\left(
\begin{array}{c}
c_{00}
\\
c_{01}
\\
c_{10}
\\
c_{11}
\end{array}
\right)
$$
とかける。
一方、2量子ビットに対する演算は$4 \times 4$行列で書け、各列と各行はそれぞれ $\langle00|,\langle01|,\langle10|, \langle11|, |00\rangle,|01\rangle,|10\rangle, |01\rangle$ に対応する。
このような2量子ビットに作用する演算としてもっとも重要なのが**制御NOT演算(CNOT演算)**であり、
行列表示では
$$
\begin{eqnarray}
\Lambda(X) =
\left(
\begin{array}{cccc}
1 & 0 & 0& 0
\\
0 & 1 & 0& 0
\\
0 & 0 & 0 & 1
\\
0 & 0 & 1& 0
\end{array}
\right)
\end{eqnarray}
$$
となる。
CNOT演算が2つの量子ビットにどのように作用するか見てみよう。まず、1つ目の量子ビットが$|0\rangle$の場合、$c_{10} = c_{11} = 0$なので、
$$
\Lambda(X)
\left(
\begin{array}{c}
c_{00}\\
c_{01}\\
0\\
0
\end{array}
\right) =
\left(
\begin{array}{c}
c_{00}\\
c_{01}\\
0\\
0
\end{array}
\right)
$$
となり、状態は変化しない。一方、1つ目の量子ビットが$|1\rangle$の場合、$c_{00} = c_{01} = 0$なので、
$$
\Lambda(X)
\left(
\begin{array}{c}
0\\
0\\
c_{10}\\
c_{11}
\end{array}
\right) =
\left(
\begin{array}{c}
0\\
0\\
c_{11}\\
c_{10}
\end{array}
\right)
$$
となり、$|10\rangle$と$|11\rangle$の確率振幅が入れ替わる。すなわち、2つ目の量子ビットが反転している。
つまり、CNOT演算は1つ目の量子ビットをそのままに保ちつつ、
- 1つ目の量子ビットが$|0\rangle$の場合は、2つ目の量子ビットにも何もしない(恒等演算$I$が作用)
- 1つ目の量子ビットが$|1\rangle$の場合は、2つ目の量子ビットを反転させる($X$が作用)
という効果を持つ。
そこで、1つ目の量子ビットを**制御量子ビット**、2つ目の量子ビットを**ターゲット量子ビット**と呼ぶ。
このCNOT演算の作用は、$\oplus$を mod 2の足し算、つまり古典計算における排他的論理和(XOR)とすると、
$$
\begin{eqnarray}
\Lambda(X) |ij \rangle = |i \;\; (i\oplus j)\rangle \:\:\: (i,j=0,1)
\end{eqnarray}
$$
とも書ける。よって、CNOT演算は古典計算でのXORを可逆にしたものとみなせる
(ユニタリー行列は定義$U^\dagger U = U U^\dagger = I$より可逆であることに注意)。
例えば、1つ目の量子ビットを$|0\rangle$と$|1\rangle$の
重ね合わせ状態にし、2つ目の量子ビットを$|0\rangle$として
$$
\begin{eqnarray}
\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle )\otimes |0\rangle =
\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1
\\
0
\\
1
\\
0
\end{array}
\right)
\end{eqnarray}
$$
にCNOTを作用させると、
$$
\begin{eqnarray}
\frac{1}{\sqrt{2}}( |00\rangle + |11\rangle ) =
\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1
\\
0
\\
0
\\
1
\end{array}
\right)
\end{eqnarray}
$$
が得られ、2つ目の量子ビットがそのままである状態$|00\rangle$と反転された状態$|11\rangle$の重ね合わせになる。(記号$\otimes$については次節参照)
さらに、CNOT ゲートを組み合わせることで重要な2量子ビットゲートである**SWAP ゲート**を作ることができる。
$$\Lambda(X)_{i,j}$$
を$i$番目の量子ビットを制御、$j$番目の量子ビットをターゲットとするCNOT ゲートとして、
$$
\begin{align}
\mathrm{SWAP} &= \Lambda(X)_{1,2} \Lambda(X)_{2,1} \Lambda(X)_{1,2}\\
&=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}
\right)
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}
\right)\\
&=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\end{align}
$$
のように書ける。これは1 番目の量子ビットと2 番目の量子ビットが交換するゲートであることが分かる。
このことは、上記のmod 2の足し算$\oplus$を使った表記で簡単に確かめることができる。3つのCNOTゲート$\Lambda(X)_{1,2} \Lambda(X)_{2,1} \Lambda(X)_{1,2}$の$|ij\rangle$への作用を1ステップずつ書くと、$i \oplus (i \oplus j) = (i \oplus i) \oplus j = 0 \oplus j = j$であることを使って、
$$
\begin{align}
|ij\rangle &\longrightarrow
|i \;\; (i\oplus j)\rangle\\
&\longrightarrow
|(i\oplus (i\oplus j)) \;\; (i\oplus j)\rangle =
|j \;\; (i\oplus j)\rangle\\
&\longrightarrow
|j \;\; (j\oplus (i\oplus j))\rangle =
|ji\rangle
\end{align}
$$
となり、2つの量子ビットが交換されていることが分かる。
(詳細は Nielsen-Chuang の `1.3.2 Multiple qbit gates` を参照)
### テンソル積の計算
手計算や解析計算で威力を発揮するのは、**テンソル積**($\otimes$)である。
これは、複数の量子ビットがある場合に、それをどのようにして、上で見た大きな一つのベクトルへと変換するのか?という計算のルールを与えてくれる。
量子力学の世界では、2つの量子系があってそれぞれの状態が$|\psi \rangle$と$|\phi \rangle$のとき、
$$
|\psi \rangle \otimes |\phi\rangle
$$
とテンソル積 $\otimes$ を用いて書く。このような複数の量子系からなる系のことを**複合系**と呼ぶ。例えば2量子ビット系は複合系である。
基本的にはテンソル積は、**多項式と同じような計算ルール**で計算してよい。
例えば、
$$
(\alpha |0\rangle + \beta |1\rangle )\otimes (\gamma |0\rangle + \delta |1\rangle )
= \alpha \gamma |0\rangle |0\rangle + \alpha \delta |0\rangle |1\rangle + \beta \gamma |1 \rangle | 0\rangle + \beta \delta |1\rangle |1\rangle
$$
のように計算する。列ベクトル表示すると、$|00\rangle$, $|01\rangle$, $|10\rangle$, $|11\rangle$に対応する4次元ベクトル、
$$
\left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right)
\otimes
\left(
\begin{array}{c}
\gamma
\\
\delta
\end{array}
\right) =
\left(
\begin{array}{c}
\alpha \gamma
\\
\alpha \delta
\\
\beta \gamma
\\
\beta \delta
\end{array}
\right)
$$
を得る計算になっている。
### SymPyを用いたテンソル積の計算
```
from IPython.display import Image, display_png
from sympy import *
from sympy.physics.quantum import *
from sympy.physics.quantum.qubit import Qubit,QubitBra
from sympy.physics.quantum.gate import X,Y,Z,H,S,T,CNOT,SWAP, CPHASE
init_printing() # ベクトルや行列を綺麗に表示するため
# Google Colaboratory上でのみ実行してください
from IPython.display import HTML
def setup_mathjax():
display(HTML('''
<script>
if (!window.MathJax && window.google && window.google.colab) {
window.MathJax = {
'tex2jax': {
'inlineMath': [['$', '$'], ['\\(', '\\)']],
'displayMath': [['$$', '$$'], ['\\[', '\\]']],
'processEscapes': true,
'processEnvironments': true,
'skipTags': ['script', 'noscript', 'style', 'textarea', 'code'],
'displayAlign': 'center',
},
'HTML-CSS': {
'styles': {'.MathJax_Display': {'margin': 0}},
'linebreaks': {'automatic': true},
// Disable to prevent OTF font loading, which aren't part of our
// distribution.
'imageFont': null,
},
'messageStyle': 'none'
};
var script = document.createElement("script");
script.src = "https://colab.research.google.com/static/mathjax/MathJax.js?config=TeX-AMS_HTML-full,Safe";
document.head.appendChild(script);
}
</script>
'''))
get_ipython().events.register('pre_run_cell', setup_mathjax)
a,b,c,d = symbols('alpha,beta,gamma,delta')
psi = a*Qubit('0')+b*Qubit('1')
phi = c*Qubit('0')+d*Qubit('1')
TensorProduct(psi, phi) #テンソル積
represent(TensorProduct(psi, phi))
```
さらに$|\psi\rangle$とのテンソル積をとると8次元のベクトルになる:
```
represent(TensorProduct(psi,TensorProduct(psi, phi)))
```
### 演算子のテンソル積
演算子についても何番目の量子ビットに作用するのか、というのをテンソル積をもちいて表現することができる。たとえば、1つめの量子ビットには$A$という演算子、2つめの量子ビットには$B$という演算子を作用させるという場合には、
$$ A \otimes B$$
としてテンソル積演算子が与えられる。
$A$と$B$をそれぞれ、2×2の行列とすると、$A\otimes B$は4×4の行列として
$$
\left(
\begin{array}{cc}
a_{11} & a_{12}
\\
a_{21} & a_{22}
\end{array}
\right)
\otimes
\left(
\begin{array}{cc}
b_{11} & b_{12}
\\
b_{21} & b_{22}
\end{array}
\right) =
\left(
\begin{array}{cccc}
a_{11} b_{11} & a_{11} b_{12} & a_{12} b_{11} & a_{12} b_{12}
\\
a_{11} b_{21} & a_{11} b_{22} & a_{12} b_{21} & a_{12} b_{22}
\\
a_{21} b_{11} & a_{21} b_{12} & a_{22} b_{11} & a_{22} b_{12}
\\
a_{21} b_{21} & a_{21} b_{22} & a_{22} b_{21} & a_{22} b_{22}
\end{array}
\right)
$$
のように計算される。
テンソル積状態
$$|\psi \rangle \otimes | \phi \rangle $$
に対する作用は、
$$ (A|\psi \rangle ) \otimes (B |\phi \rangle )$$
となり、それぞれの部分系$|\psi \rangle$と$|\phi\rangle$に$A$と$B$が作用する。
足し算に対しては、多項式のように展開してそれぞれの項を作用させればよい。
$$
(A+C)\otimes (B+D) |\psi \rangle \otimes | \phi \rangle =
(A \otimes B +A \otimes D + C \otimes B + C \otimes D) |\psi \rangle \otimes | \phi \rangle\\ =
(A|\psi \rangle) \otimes (B| \phi \rangle)
+(A|\psi \rangle) \otimes (D| \phi \rangle)
+(C|\psi \rangle) \otimes (B| \phi \rangle)
+(C|\psi \rangle) \otimes (D| \phi \rangle)
$$
テンソル積やテンソル積演算子は左右横並びで書いているが、本当は
$$
\left(
\begin{array}{c}
A
\\
\otimes
\\
B
\end{array}
\right)
\begin{array}{c}
|\psi \rangle
\\
\otimes
\\
|\phi\rangle
\end{array}
$$
のように縦に並べた方がその作用の仕方がわかりやすいのかもしれない。
例えば、CNOT演算を用いて作られるエンタングル状態は、
$$
\left(
\begin{array}{c}
|0\rangle \langle 0|
\\
\otimes
\\
I
\end{array}
+
\begin{array}{c}
|1\rangle \langle 1|
\\
\otimes
\\
X
\end{array}
\right)
\left(
\begin{array}{c}
\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
\\
\otimes
\\
|0\rangle
\end{array}
\right) =
\frac{1}{\sqrt{2}}\left(
\begin{array}{c}
|0 \rangle
\\
\otimes
\\
|0\rangle
\end{array}
+
\begin{array}{c}
|1 \rangle
\\
\otimes
\\
|1\rangle
\end{array}
\right)
$$
のようになる。
### SymPyを用いた演算子のテンソル積
SymPyで演算子を使用する時は、何桁目の量子ビットに作用する演算子かを常に指定する。「何**番目**」ではなく2進数表記の「何**桁目**」であることに注意しよう。$n$量子ビットのうちの左から$i$番目の量子ビットを指定する場合、SymPyのコードでは`n-i`を指定する(0を基点とするインデックス)。
`H(0)` は、1量子ビット空間で表示すると
```
represent(H(0),nqubits=1)
```
2量子ビット空間では$H \otimes I$に対応しており、その表示は
```
represent(H(1),nqubits=2)
```
CNOT演算は、
```
represent(CNOT(1,0),nqubits=2)
```
パウリ演算子のテンソル積$X\otimes Y \otimes Z$も、
```
represent(X(2)*Y(1)*Z(0),nqubits=3)
```
このようにして、上記のテンソル積のルールを実際にたしかめてみることができる。
### 複数の量子ビットの一部分だけを測定した場合
複数の量子ビットを全て測定した場合の測定結果の確率については既に説明した。複数の量子ビットのうち、一部だけを測定することもできる。その場合、測定結果の確率は、測定結果に対応する(部分系の)基底で射影したベクトルの長さの2乗になり、測定後の状態は射影されたベクトルを規格化したものになる。
具体的に見ていこう。以下の$n$量子ビットの状態を考える。
\begin{align}
|\psi\rangle &=
c_{00...0} |00...0\rangle +
c_{00...1} |00...1\rangle + \cdots +
c_{11...1} |11...1\rangle\\
&= \sum_{i_1 \dotsc i_n} c_{i_1 \dotsc i_n} |i_1 \dotsc i_n\rangle =
\sum_{i_1 \dotsc i_n} c_{i_1 \dotsc i_n} |i_1\rangle \otimes \cdots \otimes |i_n\rangle
\end{align}
1番目の量子ビットを測定するとしよう。1つ目の量子ビットの状態空間の正規直交基底$|0\rangle$, $|1\rangle$に対する射影演算子はそれぞれ$|0\rangle\langle0|$, $|1\rangle\langle1|$と書ける。1番目の量子ビットを$|0\rangle$に射影し、他の量子ビットには何もしない演算子
$$
|0\rangle\langle0| \otimes I \otimes \cdots \otimes I
$$
を使って、測定値0が得られる確率は
$$
\bigl\Vert \bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) |\psi\rangle \bigr\Vert^2 =
\langle \psi | \bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) | \psi \rangle
$$
である。ここで
$$
\bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) | \psi \rangle =
\sum_{i_2 \dotsc i_n} c_{0 i_2 \dotsc i_n} |0\rangle \otimes |i_2\rangle \otimes \cdots \otimes |i_n\rangle
$$
なので、求める確率は
$$
p_0 = \sum_{i_2 \dotsc i_n} |c_{0 i_2 \dotsc i_n}|^2
$$
となり、測定後の状態は
$$
\frac{1}{\sqrt{p_0}}\sum_{i_2 \dotsc i_n} c_{0 i_2 \dotsc i_n} |0\rangle \otimes |i_2\rangle \otimes \cdots \otimes |i_n\rangle
$$
となる。0と1を入れ替えれば、測定値1が得られる確率と測定後の状態が得られる。
ここで求めた$p_0$, $p_1$の表式は、測定値$i_1, \dotsc, i_n$が得られる同時確率分布$p_{i_1, \dotsc, i_n}$から計算される$i_1$の周辺確率分布と一致することに注意しよう。実際、
$$
\sum_{i_2, \dotsc, i_n} p_{i_1, \dotsc, i_n} = \sum_{i_2, \dotsc, i_n} |c_{i_1, \dotsc, i_n}|^2 = p_{i_1}
$$
である。
測定される量子ビットを増やし、最初の$k$個の量子ビットを測定する場合も同様に計算できる。測定結果$i_1, \dotsc, i_k$を得る確率は
$$
p_{i_1, \dotsc, i_k} = \sum_{i_{k+1}, \dotsc, i_n} |c_{i_1, \dotsc, i_n}|^2
$$
であり、測定後の状態は
$$
\frac{1}{\sqrt{p_{i_1, \dotsc, i_k}}}\sum_{i_{k+1} \dotsc i_n} c_{i_1 \dotsc i_n} |i_1 \rangle \otimes \cdots \otimes |i_n\rangle
$$
となる。(和をとるのは$i_{k+1},\cdots,i_n$だけであることに注意)
SymPyを使ってさらに具体的な例を見てみよう。H演算とCNOT演算を組み合わせて作られる次の状態を考える。
$$
|\psi\rangle = \Lambda(X) (H \otimes H) |0\rangle \otimes |0\rangle = \frac{|00\rangle + |10\rangle + |01\rangle + |11\rangle}{2}
$$
```
psi = qapply(CNOT(1, 0)*H(1)*H(0)*Qubit('00'))
psi
```
この状態の1つ目の量子ビットを測定して0になる確率は
$$
p_0 = \langle \psi | \bigl( |0\rangle\langle0| \otimes I \bigr) | \psi \rangle =
\left(\frac{\langle 00 | + \langle 10 | + \langle 01 | + \langle 11 |}{2}\right)
\left(\frac{| 00 \rangle + | 01 \rangle}{2}\right) =
\frac{1}{2}
$$
で、測定後の状態は
$$
\frac{1}{\sqrt{p_0}} \bigl( |0\rangle\langle0| \otimes I \bigr) | \psi \rangle =
\frac{| 00 \rangle + | 01 \rangle}{\sqrt{2}}
$$
である。
この結果をSymPyでも計算してみよう。SymPyには測定用の関数が数種類用意されていて、一部の量子ビットを測定した場合の確率と測定後の状態を計算するには、`measure_partial`を用いればよい。測定する状態と、測定を行う量子ビットのインデックスを引数として渡すと、測定後の状態と測定の確率の組がリストとして出力される。1つめの量子ビットが0だった場合の量子状態と確率は`[0]`要素を参照すればよい。
```
from sympy.physics.quantum.qubit import measure_all, measure_partial
measured_state_and_probability = measure_partial(psi, (1,))
measured_state_and_probability[0]
```
上で手計算した結果と合っていることが分かる。測定結果が1だった場合も同様に計算できる。
```
measured_state_and_probability[1]
```
---
## コラム:ユニバーサルゲートセットとは
古典計算機では、NANDゲート(論理積ANDの出力を反転したもの)さえあれば、これをいくつか組み合わせることで、任意の論理演算が実行できることが知られている。
それでは、量子計算における対応物、すなわち任意の量子計算を実行するために最低限必要な量子ゲートは何であろうか?
実は、本節で学んだ
$$\{H, T, {\rm CNOT} \}$$
の3種類のゲートがその役割を果たしている、いわゆる**ユニバーサルゲートセット**であることが知られている。
これらをうまく組み合わせることで、任意の量子計算を実行できる、すなわち「**万能量子計算**」が可能である。
### 【より詳しく知りたい人のための注】
以下では$\{H, T, {\rm CNOT} \}$の3種のゲートの組が如何にしてユニバーサルゲートセットを構成するかを、順を追って説明する。
流れとしては、一般の$n$量子ビットユニタリ演算からスタートし、これをより細かい部品にブレイクダウンしていくことで、最終的に上記3種のゲートに行き着くことを見る。
#### ◆ $n$量子ビットユニタリ演算の分解
まず、任意の$n$量子ビットユニタリ演算は、以下の手順を経て、いくつかの**1量子ビットユニタリ演算**と**CNOTゲート**に分解できる。
1. 任意の$n$量子ビットユニタリ演算は、いくつかの**2準位ユニタリ演算**の積に分解できる。ここで2準位ユニタリ演算とは、例として3量子ビットの場合、$2^3=8$次元空間のうち2つの基底(e.g., $\{|000\rangle, |111\rangle \}$)の張る2次元部分空間にのみ作用するユニタリ演算である
2. 任意の2準位ユニタリ演算は、**制御**$U$**ゲート**(CNOTゲートのNOT部分を任意の1量子ビットユニタリ演算$U$に置き換えたもの)と**Toffoliゲート**(CNOTゲートの制御量子ビットが2つになったもの)から構成できる
3. 制御$U$ゲートとToffoliゲートは、どちらも**1量子ビットユニタリ演算**と**CNOTゲート**から構成できる
#### ◆ 1量子ビットユニタリ演算の構成
さらに、任意の1量子ビットユニタリ演算は、$\{H, T\}$の2つで構成できる。
1. 任意の1量子ビットユニタリ演算は、オイラーの回転角の法則から、回転ゲート$\{R_X(\theta), R_Z(\theta)\}$で(厳密に)実現可能である
2. 実は、ブロッホ球上の任意の回転は、$\{H, T\}$のみを用いることで実現可能である(注1)。これはある軸に関する$\pi$の無理数倍の回転が$\{H, T\}$のみから実現できること(**Solovay-Kitaevアルゴリズム**)に起因する
(注1) ブロッホ球上の連続的な回転を、離散的な演算である$\{H, T\}$で実現できるか疑問に思われる読者もいるかもしれない。実際、厳密な意味で1量子ビットユニタリ演算を離散的なゲート操作で実現しようとすると、無限個のゲートが必要となる。しかし実際には厳密なユニタリ演算を実現する必要はなく、必要な計算精度$\epsilon$で任意のユニタリ演算を近似できれば十分である。ここでは、多項式個の$\{H, T\}$を用いることで、任意の1量子ビットユニタリ演算を**十分良い精度で近似的に構成できる**ことが、**Solovay-Kitaevの定理** [3] により保証されている。
<br>
以上の議論により、3種のゲート$\{H, T, {\rm CNOT} \}$があれば、任意の$n$量子ビットユニタリ演算が実現できることがわかる。
ユニバーサルゲートセットや万能量子計算について、より詳しくは以下を参照されたい:
[1] Nielsen-Chuang の `4.5 Universal quantum gates`
[2] 藤井 啓祐 「量子コンピュータの基礎と物理との接点」(第62回物性若手夏の学校 講義)DOI: 10.14989/229039 http://mercury.yukawa.kyoto-u.ac.jp/~bussei.kenkyu/archives/1274.html
[3] レビューとして、C. M. Dawson, M. A. Nielsen, “The Solovay-Kitaev algorithm“, https://arxiv.org/abs/quant-ph/0505030
| true |
code
| 0.419648 | null | null | null | null |
|
```
### MODULE 1
### Basic Modeling in scikit-learn
```
```
### Seen vs. unseen data
# The model is fit using X_train and y_train
model.fit(X_train, y_train)
# Create vectors of predictions
train_predictions = model.predict(X_train)
test_predictions = model.predict(X_test)
# Train/Test Errors
train_error = mae(y_true=y_train, y_pred=train_predictions)
test_error = mae(y_true=y_test, y_pred=test_predictions)
# Print the accuracy for seen and unseen data
print("Model error on seen data: {0:.2f}.".format(train_error))
print("Model error on unseen data: {0:.2f}.".format(test_error))
# Set parameters and fit a model
# Set the number of trees
rfr.n_estimators = 1000
# Add a maximum depth
rfr.max_depth = 6
# Set the random state
rfr.random_state = 11
# Fit the model
rfr.fit(X_train, y_train)
## Feature importances
# Fit the model using X and y
rfr.fit(X_train, y_train)
# Print how important each column is to the model
for i, item in enumerate(rfr.feature_importances_):
# Use i and item to print out the feature importance of each column
print("{0:s}: {1:.2f}".format(X_train.columns[i], item))
### lassification predictions
# Fit the rfc model.
rfc.fit(X_train, y_train)
# Create arrays of predictions
classification_predictions = rfc.predict(X_test)
probability_predictions = rfc.predict_proba(X_test)
# Print out count of binary predictions
print(pd.Series(classification_predictions).value_counts())
# Print the first value from probability_predictions
print('The first predicted probabilities are: {}'.format(probability_predictions[0]))
## Reusing model parameters
rfc = RandomForestClassifier(n_estimators=50, max_depth=6, random_state=1111)
# Print the classification model
print(rfc)
# Print the classification model's random state parameter
print('The random state is: {}'.format(rfc.random_state))
# Print all parameters
print('Printing the parameters dictionary: {}'.format(rfc.get_params()))
## Random forest classifier
from sklearn.ensemble import RandomForestClassifier
# Create a random forest classifier
rfc = RandomForestClassifier(n_estimators=50, max_depth=6, random_state=1111)
# Fit rfc using X_train and y_train
rfc.fit(X_train, y_train)
# Create predictions on X_test
predictions = rfc.predict(X_test)
print(predictions[0:5])
# Print model accuracy using score() and the testing data
print(rfc.score(X_test, y_test))
## MODULE 2
## Validation Basics
```
```
## Create one holdout set
# Create dummy variables using pandas
X = pd.get_dummies(tic_tac_toe.iloc[:,0:9])
y = tic_tac_toe.iloc[:, 9]
# Create training and testing datasets. Use 10% for the test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.1, random_state=1111)
## Create two holdout sets
# Create temporary training and final testing datasets
X_temp, X_test, y_temp, y_test =\
train_test_split(X, y, test_size=.2, random_state=1111)
# Create the final training and validation datasets
X_train, X_val, y_train, y_val = train_test_split(X_temp, y_temp, test_size=.25, random_state=1111)
### Mean absolute error
from sklearn.metrics import mean_absolute_error
# Manually calculate the MAE
n = len(predictions)
mae_one = sum(abs(y_test - predictions)) / n
print('With a manual calculation, the error is {}'.format(mae_one))
# Use scikit-learn to calculate the MAE
mae_two = mean_absolute_error(y_test, predictions)
print('Using scikit-lean, the error is {}'.format(mae_two))
# <script.py> output:
# With a manual calculation, the error is 5.9
# Using scikit-lean, the error is 5.9
### Mean squared error
from sklearn.metrics import mean_squared_error
n = len(predictions)
# Finish the manual calculation of the MSE
mse_one = sum(abs(y_test - predictions)**2) / n
print('With a manual calculation, the error is {}'.format(mse_one))
# Use the scikit-learn function to calculate MSE
mse_two = mean_squared_error(y_test, predictions)
print('Using scikit-lean, the error is {}'.format(mse_two))
### Performance on data subsets
# Find the East conference teams
east_teams = labels == "E"
# Create arrays for the true and predicted values
true_east = y_test[east_teams]
preds_east = predictions[east_teams]
# Print the accuracy metrics
print('The MAE for East teams is {}'.format(
mae(true_east, preds_east)))
# Print the West accuracy
print('The MAE for West conference is {}'.format(west_error))
### Confusion matrices
# Calculate and print the accuracy
accuracy = (324 + 491) / (953)
print("The overall accuracy is {0: 0.2f}".format(accuracy))
# Calculate and print the precision
precision = (491) / (491 + 15)
print("The precision is {0: 0.2f}".format(precision))
# Calculate and print the recall
recall = (491) / (491 + 123)
print("The recall is {0: 0.2f}".format(recall))
### Confusion matrices, again
from sklearn.metrics import confusion_matrix
# Create predictions
test_predictions = rfc.predict(X_test)
# Create and print the confusion matrix
cm = confusion_matrix(y_test, test_predictions)
print(cm)
# Print the true positives (actual 1s that were predicted 1s)
print("The number of true positives is: {}".format(cm[1, 1]))
## <script.py> output:
## [[177 123]
## [ 92 471]]
## The number of true positives is: 471
## Row 1, column 1 represents the number of actual 1s that were predicted 1s (the true positives).
## Always make sure you understand the orientation of the confusion matrix before you start using it!
### Precision vs. recall
from sklearn.metrics import precision_score
test_predictions = rfc.predict(X_test)
# Create precision or recall score based on the metric you imported
score = precision_score(y_test, test_predictions)
# Print the final result
print("The precision value is {0:.2f}".format(score))
### Error due to under/over-fitting
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=2)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.88
## The testing error is 9.15
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=11)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.57
## The testing error is 10.05
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=4)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.60
## The testing error is 8.79
### Am I underfitting?
from sklearn.metrics import accuracy_score
test_scores, train_scores = [], []
for i in [1, 2, 3, 4, 5, 10, 20, 50]:
rfc = RandomForestClassifier(n_estimators=i, random_state=1111)
rfc.fit(X_train, y_train)
# Create predictions for the X_train and X_test datasets.
train_predictions = rfc.predict(X_train)
test_predictions = rfc.predict(X_test)
# Append the accuracy score for the test and train predictions.
train_scores.append(round(accuracy_score(y_train, train_predictions), 2))
test_scores.append(round(accuracy_score(y_test, test_predictions), 2))
# Print the train and test scores.
print("The training scores were: {}".format(train_scores))
print("The testing scores were: {}".format(test_scores))
### MODULE 3
### Cross Validation
```
```
### Two samples
# Create two different samples of 200 observations
sample1 = tic_tac_toe.sample(200, random_state=1111)
sample2 = tic_tac_toe.sample(200, random_state=1171)
# Print the number of common observations
print(len([index for index in sample1.index if index in sample2.index]))
# Print the number of observations in the Class column for both samples
print(sample1['Class'].value_counts())
print(sample2['Class'].value_counts())
### scikit-learn's KFold()
from sklearn.model_selection import KFold
# Use KFold
kf = KFold(n_splits=5, shuffle=True, random_state=1111)
# Create splits
splits = kf.split(X)
# Print the number of indices
for train_index, val_index in splits:
print("Number of training indices: %s" % len(train_index))
print("Number of validation indices: %s" % len(val_index))
### Using KFold indices
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
rfc = RandomForestRegressor(n_estimators=25, random_state=1111)
# Access the training and validation indices of splits
for train_index, val_index in splits:
# Setup the training and validation data
X_train, y_train = X[train_index], y[train_index]
X_val, y_val = X[val_index], y[val_index]
# Fit the random forest model
rfc.fit(X_train, y_train)
# Make predictions, and print the accuracy
predictions = rfc.predict(X_val)
print("Split accuracy: " + str(mean_squared_error(y_val, predictions)))
### scikit-learn's methods
# Instruction 1: Load the cross-validation method
from sklearn.model_selection import cross_val_score
# Instruction 2: Load the random forest regression model
from sklearn.ensemble import RandomForestClassifier
# Instruction 3: Load the mean squared error method
# Instruction 4: Load the function for creating a scorer
from sklearn.metrics import mean_squared_error, make_scorer
## It is easy to see how all of the methods can get mixed up, but
## it is important to know the names of the methods you need.
## You can always review the scikit-learn documentation should you need any help
### Implement cross_val_score()
rfc = RandomForestRegressor(n_estimators=25, random_state=1111)
mse = make_scorer(mean_squared_error)
# Set up cross_val_score
cv = cross_val_score(estimator=rfc,
X=X_train,
y=y_train,
cv=10,
scoring=mse)
# Print the mean error
print(cv.mean())
### Leave-one-out-cross-validation
from sklearn.metrics import mean_absolute_error, make_scorer
# Create scorer
mae_scorer = make_scorer(mean_absolute_error)
rfr = RandomForestRegressor(n_estimators=15, random_state=1111)
# Implement LOOCV
scores = cross_val_score(estimator=rfr, X=X, y=y, cv=85, scoring=mae_scorer)
# Print the mean and standard deviation
print("The mean of the errors is: %s." % np.mean(scores))
print("The standard deviation of the errors is: %s." % np.std(scores))
### MODULE 4
### Selecting the best model with Hyperparameter tuning.
```
```
### Creating Hyperparameters
# Review the parameters of rfr
print(rfr.get_params())
# Maximum Depth
max_depth = [4, 8, 12]
# Minimum samples for a split
min_samples_split = [2, 5, 10]
# Max features
max_features = [4, 6, 8, 10]
### Running a model using ranges
from sklearn.ensemble import RandomForestRegressor
# Fill in rfr using your variables
rfr = RandomForestRegressor(
n_estimators=100,
max_depth=random.choice(max_depth),
min_samples_split=random.choice(min_samples_split),
max_features=random.choice(max_features))
# Print out the parameters
print(rfr.get_params())
### Preparing for RandomizedSearch
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import make_scorer, mean_squared_error
# Finish the dictionary by adding the max_depth parameter
param_dist = {"max_depth": [2, 4, 6, 8],
"max_features": [2, 4, 6, 8, 10],
"min_samples_split": [2, 4, 8, 16]}
# Create a random forest regression model
rfr = RandomForestRegressor(n_estimators=10, random_state=1111)
# Create a scorer to use (use the mean squared error)
scorer = make_scorer(mean_squared_error)
# Import the method for random search
from sklearn.model_selection import RandomizedSearchCV
# Build a random search using param_dist, rfr, and scorer
random_search =\
RandomizedSearchCV(
estimator=rfr,
param_distributions=param_dist,
n_iter=10,
cv=5,
scoring=scorer)
### Selecting the best precision model
from sklearn.metrics import precision_score, make_scorer
# Create a precision scorer
precision = make_scorer(precision_score)
# Finalize the random search
rs = RandomizedSearchCV(
estimator=rfc, param_distributions=param_dist,
scoring = precision,
cv=5, n_iter=10, random_state=1111)
rs.fit(X, y)
# print the mean test scores:
print('The accuracy for each run was: {}.'.format(rs.cv_results_['mean_test_score']))
# print the best model score:
print('The best accuracy for a single model was: {}'.format(rs.best_score_))
```
| true |
code
| 0.662715 | null | null | null | null |
|
# Dataproc - Submit Hadoop Job
## Intended Use
A Kubeflow Pipeline component to submit a Apache Hadoop MapReduce job on Apache Hadoop YARN in Google Cloud Dataproc service.
## Run-Time Parameters:
Name | Description
:--- | :----------
project_id | Required. The ID of the Google Cloud Platform project that the cluster belongs to.
region | Required. The Cloud Dataproc region in which to handle the request.
cluster_name | Required. The cluster to run the job.
main_jar_file_uri | The HCFS URI of the jar file containing the main class. Examples: `gs://foo-bucket/analytics-binaries/extract-useful-metrics-mr.jar` `hdfs:/tmp/test-samples/custom-wordcount.jar` `file:///home/usr/lib/hadoop-mapreduce/hadoop-mapreduce-examples.jar`
main_class | The name of the driver's main class. The jar file that contains the class must be in the default CLASSPATH or specified in jarFileUris.
args | Optional. The arguments to pass to the driver. Do not include arguments, such as -libjars or -Dfoo=bar, that can be set as job properties, since a collision may occur that causes an incorrect job submission.
hadoop_job | Optional. The full payload of a [HadoopJob](https://cloud.google.com/dataproc/docs/reference/rest/v1/HadoopJob).
job | Optional. The full payload of a [Dataproc job](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs).
wait_interval | Optional. The wait seconds between polling the operation. Defaults to 30s.
## Output:
Name | Description
:--- | :----------
job_id | The ID of the created job.
## Sample
Note: the sample code below works in both IPython notebook or python code directly.
### Setup a Dataproc cluster
Follow the [guide](https://cloud.google.com/dataproc/docs/guides/create-cluster) to create a new Dataproc cluster or reuse an existing one.
### Prepare Hadoop job
Upload your Hadoop jar file to a Google Cloud Storage (GCS) bucket. In the sample, we will use a jar file that is pre-installed in the main cluster, so there is no need to provide the `main_jar_file_uri`. We only set `main_class` to be `org.apache.hadoop.examples.WordCount`.
Here is the [source code of example](https://github.com/apache/hadoop/blob/trunk/hadoop-mapreduce-project/hadoop-mapreduce-examples/src/main/java/org/apache/hadoop/examples/WordCount.java).
To package a self-contained Hadoop MapReduct application from source code, follow the [instructions](https://hadoop.apache.org/docs/current/hadoop-mapreduce-client/hadoop-mapreduce-client-core/MapReduceTutorial.html).
### Set sample parameters
```
PROJECT_ID = '<Please put your project ID here>'
CLUSTER_NAME = '<Please put your existing cluster name here>'
OUTPUT_GCS_PATH = '<Please put your output GCS path here>'
REGION = 'us-central1'
MAIN_CLASS = 'org.apache.hadoop.examples.WordCount'
INTPUT_GCS_PATH = 'gs://ml-pipeline-playground/shakespeare1.txt'
EXPERIMENT_NAME = 'Dataproc - Submit Hadoop Job'
COMPONENT_SPEC_URI = 'https://raw.githubusercontent.com/kubeflow/pipelines/7622e57666c17088c94282ccbe26d6a52768c226/components/gcp/dataproc/submit_hadoop_job/component.yaml'
```
### Insepct Input Data
The input file is a simple text file:
```
!gsutil cat $INTPUT_GCS_PATH
```
### Clean up existing output files (Optional)
This is needed because the sample code requires the output folder to be a clean folder.
To continue to run the sample, make sure that the service account of the notebook server has access to the `OUTPUT_GCS_PATH`.
**CAUTION**: This will remove all blob files under `OUTPUT_GCS_PATH`.
```
!gsutil rm $OUTPUT_GCS_PATH/**
```
### Install KFP SDK
Install the SDK (Uncomment the code if the SDK is not installed before)
```
# KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.12/kfp.tar.gz'
# !pip3 install $KFP_PACKAGE --upgrade
```
### Load component definitions
```
import kfp.components as comp
dataproc_submit_hadoop_job_op = comp.load_component_from_url(COMPONENT_SPEC_URI)
display(dataproc_submit_hadoop_job_op)
```
### Here is an illustrative pipeline that uses the component
```
import kfp.dsl as dsl
import kfp.gcp as gcp
import json
@dsl.pipeline(
name='Dataproc submit Hadoop job pipeline',
description='Dataproc submit Hadoop job pipeline'
)
def dataproc_submit_hadoop_job_pipeline(
project_id = PROJECT_ID,
region = REGION,
cluster_name = CLUSTER_NAME,
main_jar_file_uri = '',
main_class = MAIN_CLASS,
args = json.dumps([
INTPUT_GCS_PATH,
OUTPUT_GCS_PATH
]),
hadoop_job='',
job='{}',
wait_interval='30'
):
dataproc_submit_hadoop_job_op(project_id, region, cluster_name, main_jar_file_uri, main_class,
args, hadoop_job, job, wait_interval).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
### Compile the pipeline
```
pipeline_func = dataproc_submit_hadoop_job_pipeline
pipeline_filename = pipeline_func.__name__ + '.pipeline.tar.gz'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
### Inspect the outputs
The sample in the notebook will count the words in the input text and output them in sharded files. Here is the command to inspect them:
```
!gsutil cat $OUTPUT_GCS_PATH/*
```
| true |
code
| 0.257182 | null | null | null | null |
|
<div>
<img src="https://drive.google.com/uc?export=view&id=1vK33e_EqaHgBHcbRV_m38hx6IkG0blK_" width="350"/>
</div>
#**Artificial Intelligence - MSc**
This notebook is designed specially for the module
ET5003 - MACHINE LEARNING APPLICATIONS
Instructor: Enrique Naredo
###ET5003_BayesianNN
© All rights reserved to the author, do not share outside this module.
## Introduction
A [Bayesian network](https://en.wikipedia.org/wiki/Bayesian_network) (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG).
* Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor.
* For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms.
* Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
**Acknowledgement**
This notebook is refurbished taking source code from Alessio Benavoli's webpage and from the libraries numpy, GPy, pylab, and pymc3.
## Libraries
```
# Suppressing Warnings:
import warnings
warnings.filterwarnings("ignore")
# https://pypi.org/project/GPy/
!pip install gpy
import GPy as GPy
import numpy as np
import pylab as pb
import pymc3 as pm
%matplotlib inline
```
## Data generation
Generate data from a nonlinear function and use a Gaussian Process to sample it.
```
# seed the legacy random number generator
# to replicate experiments
seed = None
#seed = 7
np.random.seed(seed)
# Gaussian Processes
# https://gpy.readthedocs.io/en/deploy/GPy.kern.html
# Radial Basis Functions
# https://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html
# kernel is a function that specifies the degree of similarity
# between variables given their relative positions in parameter space
kernel = GPy.kern.RBF(input_dim=1,lengthscale=0.15,variance=0.2)
print(kernel)
# number of samples
num_samples_train = 250
num_samples_test = 200
# intervals to sample
a, b, c = 0.2, 0.6, 0.8
# points evenly spaced over [0,1]
interval_1 = np.random.rand(int(num_samples_train/2))*b - c
interval_2 = np.random.rand(int(num_samples_train/2))*b + c
X_new_train = np.sort(np.hstack([interval_1,interval_2]))
X_new_test = np.linspace(-1,1,num_samples_test)
X_new_all = np.hstack([X_new_train,X_new_test]).reshape(-1,1)
# vector of the means
μ_new = np.zeros((len(X_new_all)))
# covariance matrix
C_new = kernel.K(X_new_all,X_new_all)
# noise factor
noise_new = 0.1
# generate samples path with mean μ and covariance C
TF_new = np.random.multivariate_normal(μ_new,C_new,1)[0,:]
y_new_train = TF_new[0:len(X_new_train)] + np.random.randn(len(X_new_train))*noise_new
y_new_test = TF_new[len(X_new_train):] + np.random.randn(len(X_new_test))*noise_new
TF_new = TF_new[len(X_new_train):]
```
In this example, first generate a nonlinear functions and then generate noisy training data from that function.
The constrains are:
* Training samples $x$ belong to either interval $[-0.8,-0.2]$ or $[0.2,0.8]$.
* There is not data training samples from the interval $[-0.2,0.2]$.
* The goal is to evaluate the extrapolation error outside in the interval $[-0.2,0.2]$.
```
# plot
pb.figure()
pb.plot(X_new_test,TF_new,c='b',label='True Function',zorder=100)
# training data
pb.scatter(X_new_train,y_new_train,c='g',label='Train Samples',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.legend()
pb.savefig("New_data.pdf")
```
## Bayesian NN
We address the previous nonlinear regression problem by using a Bayesian NN.
**The model is basically very similar to polynomial regression**. We first define the nonlinear function (NN)
and the place a prior over the unknown parameters. We then compute the posterior.
```
# https://theano-pymc.readthedocs.io/en/latest/
import theano
# add a column of ones to include an intercept in the model
x1 = np.vstack([np.ones(len(X_new_train)), X_new_train]).T
floatX = theano.config.floatX
l = 15
# Initialize random weights between each layer
# we do that to help the numerical algorithm that computes the posterior
init_1 = np.random.randn(x1.shape[1], l).astype(floatX)
init_out = np.random.randn(l).astype(floatX)
# pymc3 model as neural_network
with pm.Model() as neural_network:
# we convert the data in theano type so we can do dot products with the correct type.
ann_input = pm.Data('ann_input', x1)
ann_output = pm.Data('ann_output', y_new_train)
# Priors
# Weights from input to hidden layer
weights_in_1 = pm.Normal('w_1', 0, sigma=10,
shape=(x1.shape[1], l), testval=init_1)
# Weights from hidden layer to output
weights_2_out = pm.Normal('w_0', 0, sigma=10,
shape=(l,),testval=init_out)
# Build neural-network using tanh activation function
# Inner layer
act_1 = pm.math.tanh(pm.math.dot(ann_input,weights_in_1))
# Linear layer, like in Linear regression
act_out = pm.Deterministic('act_out',pm.math.dot(act_1, weights_2_out))
# standard deviation of noise
sigma = pm.HalfCauchy('sigma',5)
# Normal likelihood
out = pm.Normal('out',
act_out,
sigma=sigma,
observed=ann_output)
# this can be slow because there are many parameters
# some parameters
par1 = 100 # start with 100, then use 1000+
par2 = 1000 # start with 1000, then use 10000+
# neural network
with neural_network:
posterior = pm.sample(par1,tune=par2,chains=1)
```
Specifically, PyMC3 supports the following Variational Inference (VI) methods:
* Automatic Differentiation Variational Inference (ADVI): 'advi'
* ADVI full rank: 'fullrank_advi'
* Stein Variational Gradient Descent (SVGD): 'svgd'
* Amortized Stein Variational Gradient Descent (ASVGD): 'asvgd'
* Normalizing Flow with default scale-loc flow (NFVI): 'nfvi'
```
# we can do instead an approximated inference
param3 = 1000 # start with 1000, then use 50000+
VI = 'advi' # 'advi', 'fullrank_advi', 'svgd', 'asvgd', 'nfvi'
OP = pm.adam # pm.adam, pm.sgd, pm.adagrad, pm.adagrad_window, pm.adadelta
LR = 0.01
with neural_network:
approx = pm.fit(param3, method=VI, obj_optimizer=pm.adam(learning_rate=LR))
# plot
pb.plot(approx.hist, label='Variational Inference: '+ VI.upper(), alpha=.3)
pb.legend(loc='upper right')
# Evidence Lower Bound (ELBO)
# https://en.wikipedia.org/wiki/Evidence_lower_bound
pb.ylabel('ELBO')
pb.xlabel('iteration');
# draw samples from variational posterior
D = 500
posterior = approx.sample(draws=D)
```
Now, we compute the prediction for each sample.
* Note that we use `np.tanh` instead of `pm.math.tanh`
for speed reason.
* `pm.math.tanh` is slower outside a Pymc3 model because it converts all data in theano format.
* It is convenient to do GPU-based training, but it is slow when we only need to compute predictions.
```
# add a column of ones to include an intercept in the model
x2 = np.vstack([np.ones(len(X_new_test)), X_new_test]).T
y_pred = []
for i in range(posterior['w_1'].shape[0]):
#inner layer
t1 = np.tanh(np.dot(posterior['w_1'][i,:,:].T,x2.T))
#outer layer
y_pred.append(np.dot(posterior['w_0'][i,:],t1))
# predictions
y_pred = np.array(y_pred)
```
We first plot the mean of `y_pred`, this is very similar to the prediction that Keras returns
```
# plot
pb.plot(X_new_test,TF_new,label='true')
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean')
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.legend()
pb.ylim([-1,1])
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.savefig("BayesNN_mean.pdf")
```
Now, we plot the uncertainty, by plotting N nonlinear regression lines from the posterior
```
# plot
pb.plot(X_new_test,TF_new,label='true',Zorder=100)
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean',Zorder=100)
N = 500
# nonlinear regression lines
for i in range(N):
pb.plot(X_new_test,y_pred[i,:],c='gray',alpha=0.05)
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.ylim([-1,1.5])
pb.legend()
pb.savefig("BayesNN_samples.pdf")
# plot
pb.plot(X_new_test,TF_new,label='true',Zorder=100)
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean',Zorder=100)
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.ylim([-1,1.5])
pb.legend()
pb.savefig("BayesNN_mean.pdf")
```
| true |
code
| 0.744244 | null | null | null | null |
|
# 1. Python and notebook basics
In this first chapter, we will cover the very essentials of Python and notebooks such as creating a variable, importing packages, using functions, seeing how variables behave in the notebook etc. We will see more details on some of these topics, but this very short introduction will then allow us to quickly dive into more applied and image processing specific topics without having to go through a full Python introduction.
## Variables
Like we would do in mathematics when we define variables in equations such as $x=3$, we can do the same in all programming languages. Python has one of the simplest syntax for this, i.e. exactly as we would do it naturally. Let's define a variable in the next cell:
```
a = 3
```
As long as we **don't execute the cell** using Shift+Enter or the play button in the menu, the above cell is **purely text**. We can close our Jupyter session and then re-start it and this line of text will still be there. However other parts of the notebook are not "aware" that this variable has been defined and so we can't re-use anywhere else. For example if we type ```a``` again and execute the cell, we get an error:
```
a
```
So we actually need to **execute** the cell so that Python reads that line and executes the command. Here it's a very simple command that just says that the value of the variable ```a``` is three. So let's go back to the cell that defined ```a``` and now execute it (click in the cell and hit Shift+Enter). Now this variable is **stored in the computing memory** of the computer and we can re-use it anywhere in the notebook (but only in **this** notebook)!
We can again just type ```a```
```
a
```
We see that now we get an *output* with the value three. Most variables display an output when they are not involved in an operation. For example the line ```a=3``` didn't have an output.
Now we can define other variables in a new cell. Note that we can put as **many lines** of commands as we want in a single cell. Each command just need to be on a new line.
```
b = 5
c = 2
```
As variables are defined for the entire notebook we can combine information that comes from multiple cells. Here we do some basic mathematics:
```
a + b
```
Here we only see the output. We can't re-use that ouput for further calculations as we didn't define a new variable to contain it. Here we do it:
```
d = a + b
d
```
```d``` is now a new variable. It is purely numerical and not a mathematical formula as the above cell could make you believe. For example if we change the value of ```a```:
```
a = 100
```
and check the value of ```d```:
```
d
```
it has not change. We would have to rerun the operation and assign it again to ```d``` for it to update:
```
d = a + b
d
```
We will see many other types of variables during the course. Some are just other types of data, for example we can define a **text** variable by using quotes ```' '``` around a given text:
```
my_text = 'This is my text'
my_text
```
Others can contain multiple elements like lists:
```
my_list = [3, 8, 5, 9]
my_list
```
but more on these data structures later...
## Functions
We have seen that we could define variables and do some basic operations with them. If we want to go beyond simple arithmetic we need more **complex functions** that can operate on variables. Imagine for example that we need a function $f(x, a, b) = a * x + b$. For this we can use and **define functions**. Here's how we can define the previous function:
```
def my_fun(x, a, b):
out = a * x + b
return out
```
We see a series of Python rules to define a function:
- we use the word **```def```** to signal that we are creating a function
- we pick a **function name**, here ```my_fun```
- we open the **parenthesis** and put all our **variables ```x```, ```a```, ```b```** in there, just like when we do mathematics
- we do some operation inside the function. **Inside** the function is signal with the **indentation**: everything that belong inside the function (there could be many more lines) is shifted by a *single tab* or *three space* to the right
- we use the word **```return```** to tell what is the output of the function, here the variable ```out```
We can now use this function as if we were doing mathematics: we pick a a value for the three parameters e.g. $f(3, 2, 5)$
```
my_fun(3, 2, 5)
```
Note that **some functions are defined by default** in Python. For example if I define a variable which is a string:
```
my_text = 'This is my text'
```
I can count the number of characters in this text using the ```len()``` function which comes from base Python:
```
len(my_text)
```
The ```len``` function has not been manually defined within a ```def``` statement, it simply exist by default in the Python language.
## Variables as objects
In the Python world, variables are not "just" variables, they are actually more complex objects. So for example our variable ```my_text``` does indeed contain the text ```This is my text``` but it contains also additional features. The way to access those features is to use the dot notation ```my_text.some_feature```. There are two types of featues:
- functions, called here methods, that do some computation or modify the variable itself
- properties, that contain information about the variable
For example the object ```my_text``` has a function attached to it that allows us to put all letters to lower case:
```
my_text
my_text.lower()
```
If we define a complex number:
```
a = 3 + 5j
```
then we can access the property ```real``` that gives us only the real part of the number:
```
a.real
```
Note that when we use a method (function) we need to use the parenthesis, just like for regular functions, while for properties we don't.
## Packages
In the examples above, we either defined a function ourselves or used one generally accessible in base Python but there is a third solution: **external packages**. These packages are collections of functions used in a specific domain that are made available to everyone via specialized online repositories. For example we will be using in this course a package called [scikit-image](https://scikit-image.org/) that implements a large number of functions for image processing. For example if we want to filter an image stored in a variable ```im_in``` with a median filter, we can then just use the ```median()``` function of scikit-image and apply it to an image ```im_out = median(im_in)```. The question is now: how do we access these functions?
### Importing functions
The answer is that we have to **import** the functions we want to use in a *given notebook* from a package to be able to use them. First the package needs to be **installed**. One of the most popular place where to find such packages is the PyPi repository. We can install packages from there using the following command either in a **terminal or directly in the notebook**. For example for [scikit-image](https://pypi.org/project/scikit-image/):
```
pip install scikit-image
```
Once installed we can **import** the packakge in a notebook in the following way (note that the name of the package is scikit-image, but in code we use an abbreviated name ```skimage```):
```
import skimage
```
The import is valid for the **entire notebook**, we don't need that line in each cell.
Now that we have imported the package we can access all function that we define in it using a *dot notation* ```skimage.myfun```. Most packages are organized into submodules and in that case to access functions of a submodule we use ```skimage.my_submodule.myfun```.
To come back to the previous example: the ```median``` filtering function is in the ```filters``` submodule that we could now use as:
```python
im_out = skimage.filters.median(im_in)
```
We cannot execute this command as the variables ```im_in``` and ```im_out``` are not yet defined.
Note that there are multiple ways to import packages. For example we could give another name to the package, using the ```as``` statement:
```
import skimage as sk
```
Nowe if we want to use the ```median``` function in the filters sumodule we would write:
```python
im_out = sk.filters.median(im_in)
```
We can also import only a certain submodule using:
```
from skimage import filters
```
Now we have to write:
```python
im_out = filters.median(im_in)
```
Finally, we can import a **single** function like this:
```
from skimage.filters import median
```
and now we have to write:
```python
im_out = median(im_in)
```
## Structures
As mentioned above we cannot execute those various lines like ```im_out = median(im_in)``` because the image variable ```im_in``` is not yet defined. This variable should be an image, i.e. it cannot be a single number like in ```a=3``` but an entire grid of values, each value being one pixel. We therefore need a specific variable type that can contain such a structure.
We have already seen that we can define different types of variables. Single numbers:
```
a = 3
```
Text:
```
b = 'my text'
```
or even lists of numbers:
```
c = [6,2,8,9]
```
This last type of variable is called a ```list``` in Python and is one of the **structures** that is available in Python. If we think of an image that has multiple lines and columns of pixels, we could now imagine that we can represent it as a list of lists, each single list being e.g. one row pf pixels. For example a 3 x 3 image could be:
```
my_image = [[4,8,7], [6,4,3], [5,3,7]]
my_image
```
While in principle we could use a ```list``` for this, computations on such objects would be very slow. For example if we wanted to do background correction and subtract a given value from our image, effectively we would have to go through each element of our list (each pixel) one by one and sequentially remove the background from each pixel. If the background is 3 we would have therefore to compute:
- 4-3
- 8-3
- 7-3
- 6-3
etc. Since operations are done sequentially this would be very slow as we couldn't exploit the fact that most computers have multiple processors. Also it would be tedious to write such an operation.
To fix this, most scientific areas that use lists of numbers of some kind (time-series, images, measurements etc.) resort to an **external package** called ```Numpy``` which offers a **computationally efficient list** called an **array**.
To make this clearer we now import an image in our notebook to see such a structure. We will use a **function** from the scikit-image package to do this import. That function called ```imread``` is located in the submodule called ```io```. Remember that we can then access this function with ```skimage.io.imread()```. Just like we previously defined a function $f(x, a, b)$ that took inputs $x, a, b$, this ```imread()``` function also needs an input. Here it is just the **location of the image**, and that location can either be the **path** to the file on our computer or a **url** of an online place where the image is stored. Here we use an image that can be found at https://github.com/guiwitz/PyImageCourse_beginner/raw/master/images/19838_1252_F8_1.tif. As you can see it is a tif file. This address that we are using as an input should be formatted as text:
```
my_address = 'https://github.com/guiwitz/PyImageCourse_beginner/raw/master/images/19838_1252_F8_1.tif'
```
Now we can call our function:
```
skimage.io.imread(my_address)
```
We see here an output which is what is returned by our function. It is as expected a list of numbers, and not all numbers are shown because the list is too long. We see that we also have ```[]``` to specify rows, columns etc. The main difference compared to our list of lists that we defined previously is the ```array``` indication at the very beginning of the list of numbers. This ```array``` indication tells us that we are dealing with a ```Numpy``` array, this alternative type of list of lists that will allow us to do efficient computations.
## Plotting
We will see a few ways to represent data during the course. Here we just want to have a quick look at the image we just imported. For plotting we will use yet another **external library** called Matplotlib. That library is extensively used in the Python world and offers extensive choices of plots. We will mainly use one **function** from the library to display images: ```imshow```. Again, to access that function, we first need to import the package. Here we need a specific submodule:
```
import matplotlib.pyplot as plt
```
Now we can use the ```plt.imshow()``` function. There are many options for plot, but we can use that function already by just passing an ```array``` as an input. First we need to assign the imported array to a variable:
```
import skimage.io
image = skimage.io.imread(my_address)
plt.imshow(image);
```
We see that we are dealing with a multi-channel image and can already distinguish cell nuclei (blue) and cytoplasm (red).
| true |
code
| 0.607256 | null | null | null | null |
|
**Create Train / Dev / Test files. <br> Each file is a dictionary where each key represent the ID of a certain Author and each value is a dict where the keys are : <br> - author_embedding : the Node embedding that correspond to the author (tensor of shape (128,)) <br> - papers_embedding : the abstract embedding of every papers (tensor of shape (10,dim)) (dim depend on the embedding model taken into account) <br> - features : the graph structural features (tensor of shape (4,)) <br> - y : the target (tensor of shape (1,))**
```
import pandas as pd
import numpy as np
import networkx as nx
from tqdm import tqdm_notebook as tqdm
from sklearn.utils import shuffle
import gzip
import pickle
import torch
def load_dataset_file(filename):
with gzip.open(filename, "rb") as f:
loaded_object = pickle.load(f)
return loaded_object
def save(object, filename, protocol = 0):
"""Saves a compressed object to disk
"""
file = gzip.GzipFile(filename, 'wb')
file.write(pickle.dumps(object, protocol))
file.close()
```
# Roberta Embedding
```
# Load the paper's embedding
embedding_per_paper = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/embedding_per_paper_clean.txt')
# Load the node's embedding
embedding_per_nodes = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/Node2Vec.txt')
# read the file to create a dictionary with author key and paper list as value
f = open("/content/drive/MyDrive/altegrad_datachallenge/author_papers.txt","r")
papers_per_author = {}
for l in f:
auth_paps = [paper_id.strip() for paper_id in l.split(":")[1].replace("[","").replace("]","").replace("\n","").replace("\'","").replace("\"","").split(",")]
papers_per_author[l.split(":")[0]] = auth_paps
# Load train set
df_train = shuffle(pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/train.csv', dtype={'authorID': np.int64, 'h_index': np.float32})).reset_index(drop=True)
# Load test set
df_test = pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/test.csv', dtype={'authorID': np.int64})
# Load Graph
G = nx.read_edgelist('/content/drive/MyDrive/altegrad_datachallenge/collaboration_network.edgelist', delimiter=' ', nodetype=int)
# computes structural features for each node
core_number = nx.core_number(G)
avg_neighbor_degree = nx.average_neighbor_degree(G)
# Split into train/valid
df_valid = df_train.iloc[int(len(df_train)*0.9):, :]
df_train = df_train.iloc[:int(len(df_train)*0.9), :]
```
## Train
```
train_data = {}
for i, row in tqdm(df_train.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
print(f"Missing paper for {author_id}")
papers_embedding.append(torch.zeros((1,768)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
train_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
# Saving
save(train_data, '/content/drive/MyDrive/altegrad_datachallenge/data/data.train')
# Deleting (memory)
del train_data
```
## Validation
```
valid_data = {}
for i, row in tqdm(df_valid.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,768)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
valid_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
save(valid_data, '/content/drive/MyDrive/altegrad_datachallenge/data/data.valid')
del valid_data
```
## Test
```
test_data = {}
for i, row in tqdm(df_test.iterrows()):
author_id = str(int(row['authorID']))
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,768)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
test_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features}
del G
del df_test
del embedding_per_paper
del papers_per_author
del core_number
del avg_neighbor_degree
del embedding_per_nodes
save(test_data, '/content/drive/MyDrive/altegrad_datachallenge/data/data.test', 4)
del test_data
```
# Doc2Vec
```
# Load the paper's embedding
embedding_per_paper = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/doc2vec_paper_embedding.txt')
# Load the node's embedding
embedding_per_nodes = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/Node2Vec.txt')
# read the file to create a dictionary with author key and paper list as value
f = open("/content/drive/MyDrive/altegrad_datachallenge/data/author_papers.txt","r")
papers_per_author = {}
for l in f:
auth_paps = [paper_id.strip() for paper_id in l.split(":")[1].replace("[","").replace("]","").replace("\n","").replace("\'","").replace("\"","").split(",")]
papers_per_author[l.split(":")[0]] = auth_paps
# Load train set
df_train = shuffle(pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/data/train.csv', dtype={'authorID': np.int64, 'h_index': np.float32})).reset_index(drop=True)
# Load test set
df_test = pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/data/test.csv', dtype={'authorID': np.int64})
# Load Graph
G = nx.read_edgelist('/content/drive/MyDrive/altegrad_datachallenge/data/collaboration_network.edgelist', delimiter=' ', nodetype=int)
# computes structural features for each node
core_number = nx.core_number(G)
avg_neighbor_degree = nx.average_neighbor_degree(G)
# Split into train/valid
df_valid = df_train.iloc[int(len(df_train)*0.9):, :]
df_train = df_train.iloc[:int(len(df_train)*0.9), :]
```
## Train
```
train_data = {}
for i, row in tqdm(df_train.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
print(f"Missing paper for {author_id}")
papers_embedding.append(torch.zeros((1,256)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
train_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
# Saving
save(train_data, '/content/drive/MyDrive/altegrad_datachallenge/data/d2v.train')
# Deleting (memory)
del train_data
```
## Dev
```
valid_data = {}
for i, row in tqdm(df_valid.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,256)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
valid_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
save(valid_data, '/content/drive/MyDrive/altegrad_datachallenge/data/d2v.valid')
del valid_data
```
## Test
```
test_data = {}
for i, row in tqdm(df_test.iterrows()):
author_id = str(int(row['authorID']))
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,256)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
test_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features}
del G
del df_test
del embedding_per_paper
del papers_per_author
del core_number
del avg_neighbor_degree
del embedding_per_nodes
save(test_data, '/content/drive/MyDrive/altegrad_datachallenge/data/d2v.test', 4)
del test_data
```
| true |
code
| 0.383728 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# x = Acos(k/m t + \theta) = 1
# p = mx' = Ak/m sin(k/m t + \theta)
t = np.linspace(0, 2 * np.pi, 100)
t
```
# Exact Equation
```
x, p = np.cos(t - np.pi), -np.sin(t - np.pi)
fig = plt.figure(figsize=(5, 5))
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
```
# Euler's Method Equation
# Euler's Method
```
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Euler's Method (eps=0.1)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.1
steps = 100
for i in range(0, steps, 1):
x_next = x_prev + eps * p_prev
p_next = p_prev - eps * x_prev
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Modified Euler's Method
```
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Modified Euler's Method (eps=0.2)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_next = p_prev - eps * x_prev
x_next = x_prev + eps * p_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Modified Euler's Method (eps=0.2)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0.1
p_prev = 1
eps = 1.31827847281
#eps = 1.31827847281
steps = 50 #int(2*np.pi / eps)
for i in range(0, steps, 1):
p_next = p_prev - eps * x_prev
x_next = x_prev + eps * p_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Leapfrog Method
```
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Leapfrog Method (eps=0.2)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Leapfrog Method (eps=0.9)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.9
steps = 3 * int(2*np.pi / eps + 0.1)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Combined Figure
```
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(15,15))
# subplot1
ax1.set_title("Euler's Method (eps=0.1)")
ax1.set_xlabel("position (q)")
ax1.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax1.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.1
steps = 100
for i in range(0, steps, 1):
x_next = x_prev + eps * p_prev
p_next = p_prev - eps * x_prev
ax1.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# subplot2
ax2.set_title("Modified Euler's Method (eps=0.2)")
ax2.set_xlabel("position (q)")
ax2.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax2.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_next = p_prev - eps * x_prev
x_next = x_prev + eps * p_next
ax2.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# subplot3
ax3.set_title("Leapfrog Method (eps=0.2)")
ax3.set_xlabel("position (q)")
ax3.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax3.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
ax3.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# subplot4
ax4.set_title("Leapfrog Method (eps=0.9)")
ax4.set_xlabel("position (q)")
ax4.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax4.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.9
steps = 3 * int(2*np.pi / eps + 0.1)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
ax4.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Combined Figure - Square
```
fig, ((ax1, ax2)) = plt.subplots(1, 2, figsize=(15, 7.5))
# subplot1
ax1.set_title("Euler's Method (eps=0.2)")
ax1.set_xlabel("position (q)")
ax1.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax1.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
def draw_square(ax, x, p, **args):
assert len(x) == len(p) == 4
x = list(x) + [x[0]]
p = list(p) + [p[0]]
ax.plot(x, p, **args)
def euler_update(x, p, eps):
assert len(x) == len(p) == 4
x_next = [0.]* 4
p_next = [0.]* 4
for i in range(4):
x_next[i] = x[i] + eps * p[i]
p_next[i] = p[i] - eps * x[i]
return x_next, p_next
def mod_euler_update(x, p, eps):
assert len(x) == len(p) == 4
x_next = [0.]* 4
p_next = [0.]* 4
for i in range(4):
x_next[i] = x[i] + eps * p[i]
p_next[i] = p[i] - eps * x_next[i]
return x_next, p_next
delta = 0.1
eps = 0.2
x_prev = np.array([0.0, 0.0, delta, delta]) + 0.0
p_prev = np.array([0.0, delta, delta, 0.0]) + 1.0
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
draw_square(ax1, x_prev, p_prev, marker='o', color='blue', markersize=5)
x_next, p_next = euler_update(x_prev, p_prev, eps)
x_prev, p_prev = x_next, p_next
# subplot2
ax2.set_title("Modified Euler's Method (eps=0.2)")
ax2.set_xlabel("position (q)")
ax2.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax2.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = np.array([0.0, 0.0, delta, delta]) + 0.0
p_prev = np.array([0.0, delta, delta, 0.0]) + 1.0
for i in range(0, steps, 1):
draw_square(ax2, x_prev, p_prev, marker='o', color='blue', markersize=5)
x_next, p_next = mod_euler_update(x_prev, p_prev, eps)
x_prev, p_prev = x_next, p_next
```
| true |
code
| 0.469277 | null | null | null | null |
|
# YBIGTA ML PROJECT / 염정운
## Setting
```
import numpy as np
import pandas as pd
pd.set_option("max_columns", 999)
pd.set_option("max_rows", 999)
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
import seaborn as sns
import matplotlib.pyplot as plt
#sns.set(rc={'figure.figsize':(11.7,10)})
```
## Identity data
Variables in this table are identity information – network connection information (IP, ISP, Proxy, etc) and digital signature
<br>
(UA/browser/os/version, etc) associated with transactions.
<br>
They're collected by Vesta’s fraud protection system and digital security partners.
<br>
The field names are masked and pairwise dictionary will not be provided for privacy protection and contract agreement)
Categorical Features:
<br>
DeviceType
<br>
DeviceInfo
<br>
id12 - id38
```
#train_identity가 불편해서 나는 i_merged라는 isFraud를 merge하고 column 순서를 조금 바꾼 새로운 Dataframe을 만들었어! 이건 그 코드!
#i_merged = train_i.merge(train_t[['TransactionID', 'isFraud']], how = 'left', on = 'TransactionID')
#order_list =['TransactionID', 'isFraud', 'DeviceInfo', 'DeviceType', 'id_01', 'id_02', 'id_03', 'id_04', 'id_05', 'id_06', 'id_07', 'id_08',
# 'id_09', 'id_10', 'id_11', 'id_12', 'id_13', 'id_14', 'id_15', 'id_16', 'id_17', 'id_18', 'id_19', 'id_20', 'id_21',
# 'id_22', 'id_23', 'id_24', 'id_25', 'id_26', 'id_27', 'id_28', 'id_29', 'id_30', 'id_31', 'id_32', 'id_33', 'id_34',
# 'id_35', 'id_36', 'id_37', 'id_38']
#i_merged = i_merged[order_list]
#i_merged.head()
#i_merged.to_csv('identity_merged.csv', index = False)
save = pd.read_csv('identity_merged.csv')
i_merged = pd.read_csv('identity_merged.csv')
```
### <font color='blue'>NaN 비율</font>
```
nullrate = (((i_merged.isnull().sum() / len(i_merged)))*100).sort_values(ascending = False)
nullrate.plot(kind='barh', figsize=(15, 9))
i_merged.head()
```
### <font color='blue'>DeviceType</font>
nan(3.1%) < desktop(6.5%) < mobile(10.1%) 순으로 isFraud 증가 추이
<br>
*전체 datatset에서 isFraud = 1의 비율 7.8%
```
#DeviceType
i_merged.groupby(['DeviceType', 'isFraud']).size().unstack()
i_merged[i_merged.DeviceType.isnull()].groupby('isFraud').size()
```
### <font color='blue'>Null count in row</font>
결측치 정도와 isFraud의 유의미한 상관관계 찾지 못함
```
i_merged = i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1))
print(i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].mean(),
i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].std(),
i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].min(),
i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].max())
#isFraud = 1
i_merged[i_merged.isFraud == 1].hist('NaN_count')
#isFraud = 0
i_merged[i_merged.isFraud == 0].hist('NaN_count')
i_merged.head()
```
### <font color='blue'>변수별 EDA - Continous</font>
```
#Correlation Matrix
rs = np.random.RandomState(0)
df = pd.DataFrame(rs.rand(10, 10))
corr = i_merged.corr()
corr.style.background_gradient(cmap='coolwarm')
#id_01 : 0 이하의 값들을 가지며 skewed 형태. 필요시 log 변환을 통한 처리가 가능할 듯.
i_merged.id_01.plot(kind='hist', bins=22, figsize=(12,6), title='id_01 dist.')
print(i_merged.groupby('isFraud')['id_01'].mean(),
i_merged.groupby('isFraud')['id_01'].std(),
i_merged.id_01.min(),
i_merged.id_01.max(), sep = '\n')
Fraud = (i_merged[i_merged.isFraud == 1]['id_01'])
notFraud = i_merged[i_merged.isFraud == 0]['id_01']
plt.hist([Fraud, notFraud],bins = 5, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id02: 최솟값 1을 가지며 skewed 형태. 마찬가지로 로그 변환 가능
i_merged.id_02.plot(kind='hist', bins=22, figsize=(12,6), title='id_02 dist.')
print(i_merged.groupby('isFraud')['id_02'].mean(),
i_merged.groupby('isFraud')['id_02'].std(),
i_merged.id_02.min(),
i_merged.id_02.max(), sep = '\n')
Fraud = (i_merged[i_merged.isFraud == 1]['id_02'])
notFraud = i_merged[i_merged.isFraud == 0]['id_02']
plt.hist([Fraud, notFraud],bins = 5, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id_05
i_merged.id_05.plot(kind='hist', bins=22, figsize=(9,6), title='id_05 dist.')
print(i_merged.groupby('isFraud')['id_05'].mean(),
i_merged.groupby('isFraud')['id_05'].std())
Fraud = (i_merged[i_merged.isFraud == 1]['id_05'])
notFraud = i_merged[i_merged.isFraud == 0]['id_05']
plt.hist([Fraud, notFraud],bins = 10, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id_06
i_merged.id_06.plot(kind='hist', bins=22, figsize=(12,6), title='id_06 dist.')
print(i_merged.groupby('isFraud')['id_06'].mean(),
i_merged.groupby('isFraud')['id_06'].std())
Fraud = (i_merged[i_merged.isFraud == 1]['id_06'])
notFraud = i_merged[i_merged.isFraud == 0]['id_06']
plt.hist([Fraud, notFraud],bins = 20, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id_11
i_merged.id_11.plot(kind='hist', bins=22, figsize=(12,6), title='id_11 dist.')
print(i_merged.groupby('isFraud')['id_11'].mean(),
i_merged.groupby('isFraud')['id_11'].std())
Fraud = (i_merged[i_merged.isFraud == 1]['id_11'])
notFraud = i_merged[i_merged.isFraud == 0]['id_11']
plt.hist([Fraud, notFraud],bins = 20, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
```
### <font color='blue'>변수별 EDA - Categorical</font>
```
sns.jointplot(x = 'id_09', y = 'id_03', data = i_merged)
```
### <font color='blue'>Feature Engineering</font>
<br>
<br>
** Categorical이지만 가짓수가 많은 경우 정보가 있을 때 1, 아닐 때 0으로 처리함. BaseModel 돌리기 위해 이렇게 설정하였지만, 전처리를 바꿔가는 작업에서는 이 변수들을 다른 방식으로 처리 할 필요가 더 생길 수도 있음.
<br>
** Pair 관계가 있음. id03,04 / id05,06 / id07,08, 21~26 / id09, 10 ::함께 데이터가 존재하거나(1) NaN이거나(0). 한편 EDA-Category를 보면 id03, 09의 경우 상관관계가 있는 것으로 추정되어 추가적인 변형을 하지 않았음.
<br>
** https://www.kaggle.com/pablocanovas/exploratory-analysis-tidyverse 에서 변수별 EDA 시각화 참고하였고, nan값 제외하고는 Fraud 비율이 낮은 변수부터 1,2..차례로 할당함
<br>
<br>
<br>
### $Contionous Features$
<br>
id01:: 결측치가 없으며 로그변형을 통해 양수화 및 Scailing 시킴. 5의 배수임을 감안할 때 5로 나누는 scailing을 진행해봐도 좋을 듯.
<br>
id02:: 결측치가 존재하나, 로그 변형을 통해 정규분포에 흡사한 모양으로 만들고 매우 큰 단위를 Scailing하였음. 결측치는 Random 방식을 이용하여 채웠으나 가장 위험한 방식으로 imputation으로 한 것이므로 주의가 필요함.
<br>
<br>
<br>
### $Categorical Features$
<br>
DeviceType:: {NaN: 0, 'desktop': 1, 'mobile': 2}
<br>
DeviceInfo:: {Nan: 0, 정보있음:1}
<br>
id12::{0:0, 'Found': 1, 'NotFound': 2}
<br>
id13::{Nan: 0, 정보있음:1}
<br>
id14::{Nan: 0, 정보있음:1}
<br>
id15::{Nan:0, 'New':1, 'Unknown':2, 'Found':3} #15, 16은 연관성이 보임
<br>
id16::{Nan:0, 'NotFound':1, 'Found':2}
<br>
id17::{Nan: 0, 정보있음:1}
<br>
id18::{Nan: 0, 정보있음:1} #가짓수 다소 적음
<br>
id19::{Nan: 0, 정보있음:1}
<br>
id20::{Nan: 0, 정보있음:1} #id 17, 19, 20은 Pair
<br>
id21
<br>
id22
<br>
id23::{IP_PROXY:ANONYMOUS:2, else:1, nan:0} #id 7,8 21~26은 Pair. Anonymous만 유독 Fraud 비율이 높기에 고려함. 우선은 베이스 모델에서는 id_23만 사용
<br>
id24
<br>
id25
<br>
id26
<br>
id27:: {Nan:0, 'NotFound':1, 'Found':2}
<br>
id28:: {0:0, 'New':1, 'Found':2}
<br>
id29:: {0:0, 'NotFound':1, 'Found':2}
<br>
id30(OS):: {Nan: 0, 정보있음:1}, 데이터가 있다 / 없다로 처리하였지만 Safari Generic에서 사기 확률이 높다 등의 조건을 고려해야한다면 다른 방식으로 전처리 필요할 듯
<br>
id31(browser):: {Nan: 0, 정보있음:1}, id30과 같음
<br>
id32::{nan:0, 24:1, 32:2, 16:3, 0:4}
<br>
id33(해상도)::{Nan: 0, 정보있음:1}
<br>
id34:: {nan:0, matchstatus= -1:1, matchstatus=0 :2, matchstatus=1 :3, matchstatus=2 :4} , matchstatus가 -1이면 fraud일 확률 매우 낮음
<br>
id35:: {Nan:0, 'T':1, 'F':2}
<br>
id36:: {Nan:0, 'T':1, 'F':2}
<br>
id37:: {Nan:0, 'T':2, 'F':1}
<br>
id38:: {Nan:0, 'T':1, 'F':2}
<br>
```
#Continous Features
i_merged.id_01 = np.log(-i_merged.id_01 + 1)
i_merged.id_02 = np.log(i_merged.id_02)
medi = i_merged.id_02.median()
i_merged.id_02 = i_merged.id_02.fillna(medi)
i_merged.id_02.hist()
#id_02의 NaN값을 random하게 채워줌
#i_merged['id_02_filled'] = i_merged['id_02']
#temp = (i_merged['id_02'].dropna()
# .sample(i_merged['id_02'].isnull().sum())
# )
#temp.index = i_merged[lambda x: x.id_02.isnull()].index
#i_merged.loc[i_merged['id_02'].isnull(), 'id_02_filled'] = temp
#Categorical Features
i_merged.DeviceType = i_merged.DeviceType.fillna(0).map({0:0, 'desktop': 1, 'mobile': 2})
i_merged.DeviceInfo = i_merged.DeviceInfo.notnull().astype(int)
i_merged.id_12 = i_merged.id_12.fillna(0).map({0:0, 'Found': 1, 'NotFound': 2})
i_merged.id_13 = i_merged.id_13.notnull().astype(int)
i_merged.id_14 = i_merged.id_14.notnull().astype(int)
i_merged.id_14 = i_merged.id_14.notnull().astype(int)
i_merged.id_15 = i_merged.id_15.fillna(0).map({0:0, 'New':1, 'Unknown':2, 'Found':3})
i_merged.id_16 = i_merged.id_16.fillna(0).map({0:0, 'NotFound':1, 'Found':2})
i_merged.id_17 = i_merged.id_17.notnull().astype(int)
i_merged.id_18 = i_merged.id_18.notnull().astype(int)
i_merged.id_19 = i_merged.id_19.notnull().astype(int)
i_merged.id_20 = i_merged.id_20.notnull().astype(int)
i_merged.id_23 = i_merged.id_23.fillna('temp').map({'temp':0, 'IP_PROXY:ANONYMOUS':2}).fillna(1)
i_merged.id_27 = i_merged.id_27.fillna(0).map({0:0, 'NotFound':1, 'Found':2})
i_merged.id_28 = i_merged.id_28.fillna(0).map({0:0, 'New':1, 'Found':2})
i_merged.id_29 = i_merged.id_29.fillna(0).map({0:0, 'NotFound':1, 'Found':2})
i_merged.id_30 = i_merged.id_30.notnull().astype(int)
i_merged.id_31 = i_merged.id_31.notnull().astype(int)
i_merged.id_32 = i_merged.id_32.fillna('temp').map({'temp':0, 24:1, 32:2, 16:3, 0:4})
i_merged.id_33 = i_merged.id_33.notnull().astype(int)
i_merged.id_34 = i_merged.id_34.fillna('temp').map({'temp':0, 'match_status:-1':1, 'match_status:0':3, 'match_status:1':4, 'match_status:2':2})
i_merged.id_35 = i_merged.id_35.fillna(0).map({0:0, 'T':1, 'F':2})
i_merged.id_36 = i_merged.id_38.fillna(0).map({0:0, 'T':1, 'F':2})
i_merged.id_37 = i_merged.id_38.fillna(0).map({0:0, 'T':2, 'F':1})
i_merged.id_38 = i_merged.id_38.fillna(0).map({0:0, 'T':1, 'F':2})
```
Identity_Device FE
```
i_merged['Device_info_clean'] = i_merged['DeviceInfo']
i_merged['Device_info_clean'] = i_merged['Device_info_clean'].fillna('unknown')
def name_divide(name):
if name == 'Windows':
return 'Windows'
elif name == 'iOS Device':
return 'iOS Device'
elif name == 'MacOS':
return 'MacOS'
elif name == 'Trident/7.0':
return 'Trident/rv'
elif "rv" in name:
return 'Trident/rv'
elif "SM" in name:
return 'SM/moto/lg'
elif name == 'SAMSUNG':
return 'SM'
elif 'LG' in name:
return 'SM/Moto/LG'
elif 'Moto' in name:
return 'SM/Moto/LG'
elif name == 'unknown':
return 'unknown'
else:
return 'others'
i_merged['Device_info_clean'] = i_merged['Device_info_clean'].apply(name_divide)
i_merged['Device_info_clean'].value_counts()
```
### <font color='blue'>Identity_feature engineered_dataset</font>
```
i_merged.columns
selected = []
selected.extend(['TransactionID', 'isFraud', 'id_01', 'id_02', 'DeviceType','Device_info_clean'])
id_exist = i_merged[selected].assign(Exist = 1)
id_exist.DeviceType.fillna('unknown', inplace = True)
id_exist.to_csv('identity_first.csv',index = False)
```
### <font color='blue'>Test: Decision Tree / Random Forest Test</font>
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score, recall_score, f1_score, accuracy_score, roc_auc_score
X = id_exist.drop(['isFraud'], axis = 1)
Y = id_exist['isFraud']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3)
tree_clf = DecisionTreeClassifier(max_depth=10)
tree_clf.fit(X_train, y_train)
pred = tree_clf.predict(X_test)
print('F1:{}'.format(f1_score(y_test, pred)))
```
--------------------------
```
param_grid = {
'max_depth': list(range(10,51,10)),
'n_estimators': [20, 20, 20]
}
rf = RandomForestClassifier()
gs = GridSearchCV(estimator = rf, param_grid = param_grid,
cv = 5, n_jobs = -1, verbose = 2)
gs.fit(X_train,y_train)
best_rf = gs.best_estimator_
print('best parameter: \n',gs.best_params_)
y_pred = best_rf.predict(X_test)
print('Accuracy:{}'.format(accuracy_score(y_test, y_pred)),
'Precision:{}'.format(precision_score(y_test, y_pred)),
'Recall:{}'.format(recall_score(y_test, y_pred)),
'F1:{}'.format(f1_score(y_test, y_pred)),
'ROC_AUC:{}'.format(roc_auc_score(y_test, y_pred)), sep = '\n')
```
-----------------------
### <font color='blue'>거래 + ID merge</font>
```
transaction_c = pd.read_csv('train_combined.csv')
id_c = pd.read_csv('identity_first.csv')
region = pd.read_csv('region.csv')
country = region[['TransactionID', 'Country_code']]
country.head()
f_draft = transaction_c.merge(id_c.drop(['isFraud'], axis = 1) ,how = 'left', on = 'TransactionID')
f_draft.drop('DeviceInfo', axis = 1, inplace = True)
f_draft = f_draft.merge(country, how = 'left', on = 'TransactionID')
f_draft.head()
f_draft.dtypes
```
Categorical: 'ProductCD', 'card4', 'card6', 'D15', 'DeviceType', 'Device_info_clean'
```
print(
f_draft.ProductCD.unique(),
f_draft.card4.unique(),
f_draft.card6.unique(),
f_draft.D15.unique(),
f_draft.DeviceType.unique(),
f_draft.Device_info_clean.unique(),
)
print(map_ProductCD, map_card4,map_card6,map_D15, sep = '\n')
```
map_ProductCD = {'W': 0, 'H': 1, 'C': 2, 'S': 3, 'R': 4}
<br>
map_card4 = {'discover': 0, 'mastercard': 1, 'visa': 2, '}american express': 3}
<br>
map_card6 = {'credit': 0, 'debit': 1, 'debit or credit': 2, 'charge card': 3}
<br>
map_D15 = {'credit': 0, 'debit': 1, 'debit or credit': 2, 'charge card': 3}
<br>
map_DeviceType = {'mobile':2 'desktop':1 'unknown':0}
<br>
map_Device_info_clean = {'SM/moto/lg':1, 'iOS Device':2, 'Windows':3, 'unknown':0, 'MacOS':4, 'others':5,
'Trident/rv':6}
```
f_draft.ProductCD = f_draft.ProductCD.map(map_ProductCD)
f_draft.card4 = f_draft.card4.map(map_card4)
f_draft.card6 = f_draft.card6.map(map_card6)
f_draft.D15 = f_draft.D15.map(map_D15)
f_draft.DeviceType = f_draft.DeviceType.map(map_DeviceType)
f_draft.Device_info_clean = f_draft.Device_info_clean.map(map_Device_info_clean)
f_draft.to_csv('transaction_id_combined(no_label_encoded).csv', index = False)
f_draft.ProductCD = f_draft.ProductCD.astype('category')
f_draft.card4 = f_draft.card4.astype('category')
f_draft.card6 = f_draft.card6.astype('category')
f_draft.card1 = f_draft.card1.astype('category')
f_draft.card2 = f_draft.card2.astype('category')
f_draft.card3 = f_draft.card3.astype('category')
f_draft.card5 = f_draft.card5.astype('category')
f_draft.D15 = f_draft.D15.astype('category')
f_draft.DeviceType = f_draft.DeviceType.astype('category')
f_draft.Device_info_clean = f_draft.Device_info_clean.astype('category')
f_draft.Country_code = f_draft.Country_code.astype('category')
f_draft.card1 = f_draft.card1.astype('category')
f_draft.card2 = f_draft.card2.astype('category')
f_draft.card3 = f_draft.card3.astype('category')
f_draft.card5 = f_draft.card5.astype('category')
f_draft.dtypes
f_draft.to_csv('transaction_id_combined.csv', index = False)
f_draft.head()
```
| true |
code
| 0.323868 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/tuanavu/deep-learning-tutorials/blob/development/colab-example-notebooks/colab_github_demo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Using Google Colab with GitHub
[Google Colaboratory](http://colab.research.google.com) is designed to integrate cleanly with GitHub, allowing both loading notebooks from github and saving notebooks to github.
## Loading Public Notebooks Directly from GitHub
Colab can load public github notebooks directly, with no required authorization step.
For example, consider the notebook at this address: https://github.com/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb.
The direct colab link to this notebook is: https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb.
To generate such links in one click, you can use the [Open in Colab](https://chrome.google.com/webstore/detail/open-in-colab/iogfkhleblhcpcekbiedikdehleodpjo) Chrome extension.
## Browsing GitHub Repositories from Colab
Colab also supports special URLs that link directly to a GitHub browser for any user/organization, repository, or branch. For example:
- http://colab.research.google.com/github will give you a general github browser, where you can search for any github organization or username.
- http://colab.research.google.com/github/googlecolab/ will open the repository browser for the ``googlecolab`` organization. Replace ``googlecolab`` with any other github org or user to see their repositories.
- http://colab.research.google.com/github/googlecolab/colabtools/ will let you browse the main branch of the ``colabtools`` repository within the ``googlecolab`` organization. Substitute any user/org and repository to see its contents.
- http://colab.research.google.com/github/googlecolab/colabtools/blob/master will let you browse ``master`` branch of the ``colabtools`` repository within the ``googlecolab`` organization. (don't forget the ``blob`` here!) You can specify any valid branch for any valid repository.
## Loading Private Notebooks
Loading a notebook from a private GitHub repository is possible, but requires an additional step to allow Colab to access your files.
Do the following:
1. Navigate to http://colab.research.google.com/github.
2. Click the "Include Private Repos" checkbox.
3. In the popup window, sign-in to your Github account and authorize Colab to read the private files.
4. Your private repositories and notebooks will now be available via the github navigation pane.
## Saving Notebooks To GitHub or Drive
Any time you open a GitHub hosted notebook in Colab, it opens a new editable view of the notebook. You can run and modify the notebook without worrying about overwriting the source.
If you would like to save your changes from within Colab, you can use the File menu to save the modified notebook either to Google Drive or back to GitHub. Choose **File→Save a copy in Drive** or **File→Save a copy to GitHub** and follow the resulting prompts. To save a Colab notebook to GitHub requires giving Colab permission to push the commit to your repository.
## Open In Colab Badge
Anybody can open a copy of any github-hosted notebook within Colab. To make it easier to give people access to live views of GitHub-hosted notebooks,
colab provides a [shields.io](http://shields.io/)-style badge, which appears as follows:
[](https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb)
The markdown for the above badge is the following:
```markdown
[](https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb)
```
The HTML equivalent is:
```HTML
<a href="https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb">
<img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
```
Remember to replace the notebook URL in this template with the notebook you want to link to.
```
```
| true |
code
| 0.645064 | null | null | null | null |
|
# Cowell's formulation
For cases where we only study the gravitational forces, solving the Kepler's equation is enough to propagate the orbit forward in time. However, when we want to take perturbations that deviate from Keplerian forces into account, we need a more complex method to solve our initial value problem: one of them is **Cowell's formulation**.
In this formulation we write the two body differential equation separating the Keplerian and the perturbation accelerations:
$$\ddot{\mathbb{r}} = -\frac{\mu}{|\mathbb{r}|^3} \mathbb{r} + \mathbb{a}_d$$
<div class="alert alert-info">For an in-depth exploration of this topic, still to be integrated in poliastro, check out https://github.com/Juanlu001/pfc-uc3m</div>
<div class="alert alert-info">An earlier version of this notebook allowed for more flexibility and interactivity, but was considerably more complex. Future versions of poliastro and plotly might bring back part of that functionality, depending on user feedback. You can still download the older version <a href="https://github.com/poliastro/poliastro/blob/0.8.x/docs/source/examples/Propagation%20using%20Cowell's%20formulation.ipynb">here</a>.</div>
## First example
Let's setup a very simple example with constant acceleration to visualize the effects on the orbit.
```
import numpy as np
from astropy import units as u
from matplotlib import pyplot as plt
plt.ion()
from poliastro.bodies import Earth
from poliastro.twobody import Orbit
from poliastro.examples import iss
from poliastro.twobody.propagation import cowell
from poliastro.plotting import OrbitPlotter3D
from poliastro.util import norm
from plotly.offline import init_notebook_mode
init_notebook_mode(connected=True)
```
To provide an acceleration depending on an extra parameter, we can use **closures** like this one:
```
accel = 2e-5
def constant_accel_factory(accel):
def constant_accel(t0, u, k):
v = u[3:]
norm_v = (v[0]**2 + v[1]**2 + v[2]**2)**.5
return accel * v / norm_v
return constant_accel
def custom_propagator(orbit, tof, rtol, accel=accel):
# Workaround for https://github.com/poliastro/poliastro/issues/328
if tof == 0:
return orbit.r.to(u.km).value, orbit.v.to(u.km / u.s).value
else:
# Use our custom perturbation acceleration
return cowell(orbit, tof, rtol, ad=constant_accel_factory(accel))
times = np.linspace(0, 10 * iss.period, 500)
times
times, positions = iss.sample(times, method=custom_propagator)
```
And we plot the results:
```
frame = OrbitPlotter3D()
frame.set_attractor(Earth)
frame.plot_trajectory(positions, label="ISS")
frame.show()
```
## Error checking
```
def state_to_vector(ss):
r, v = ss.rv()
x, y, z = r.to(u.km).value
vx, vy, vz = v.to(u.km / u.s).value
return np.array([x, y, z, vx, vy, vz])
k = Earth.k.to(u.km**3 / u.s**2).value
rtol = 1e-13
full_periods = 2
u0 = state_to_vector(iss)
tf = ((2 * full_periods + 1) * iss.period / 2).to(u.s).value
u0, tf
iss_f_kep = iss.propagate(tf * u.s, rtol=1e-18)
r, v = cowell(iss, tf, rtol=rtol)
iss_f_num = Orbit.from_vectors(Earth, r * u.km, v * u.km / u.s, iss.epoch + tf * u.s)
iss_f_num.r, iss_f_kep.r
assert np.allclose(iss_f_num.r, iss_f_kep.r, rtol=rtol, atol=1e-08 * u.km)
assert np.allclose(iss_f_num.v, iss_f_kep.v, rtol=rtol, atol=1e-08 * u.km / u.s)
assert np.allclose(iss_f_num.a, iss_f_kep.a, rtol=rtol, atol=1e-08 * u.km)
assert np.allclose(iss_f_num.ecc, iss_f_kep.ecc, rtol=rtol)
assert np.allclose(iss_f_num.inc, iss_f_kep.inc, rtol=rtol, atol=1e-08 * u.rad)
assert np.allclose(iss_f_num.raan, iss_f_kep.raan, rtol=rtol, atol=1e-08 * u.rad)
assert np.allclose(iss_f_num.argp, iss_f_kep.argp, rtol=rtol, atol=1e-08 * u.rad)
assert np.allclose(iss_f_num.nu, iss_f_kep.nu, rtol=rtol, atol=1e-08 * u.rad)
```
## Numerical validation
According to [Edelbaum, 1961], a coplanar, semimajor axis change with tangent thrust is defined by:
$$\frac{\operatorname{d}\!a}{a_0} = 2 \frac{F}{m V_0}\operatorname{d}\!t, \qquad \frac{\Delta{V}}{V_0} = \frac{1}{2} \frac{\Delta{a}}{a_0}$$
So let's create a new circular orbit and perform the necessary checks, assuming constant mass and thrust (i.e. constant acceleration):
```
ss = Orbit.circular(Earth, 500 * u.km)
tof = 20 * ss.period
ad = constant_accel_factory(1e-7)
r, v = cowell(ss, tof.to(u.s).value, ad=ad)
ss_final = Orbit.from_vectors(Earth, r * u.km, v * u.km / u.s, ss.epoch + tof)
da_a0 = (ss_final.a - ss.a) / ss.a
da_a0
dv_v0 = abs(norm(ss_final.v) - norm(ss.v)) / norm(ss.v)
2 * dv_v0
np.allclose(da_a0, 2 * dv_v0, rtol=1e-2)
```
This means **we successfully validated the model against an extremely simple orbit transfer with approximate analytical solution**. Notice that the final eccentricity, as originally noticed by Edelbaum, is nonzero:
```
ss_final.ecc
```
## References
* [Edelbaum, 1961] "Propulsion requirements for controllable satellites"
| true |
code
| 0.566378 | null | null | null | null |
|
# Optimization
Things to try:
- change the number of samples
- without and without bias
- with and without regularization
- changing the number of layers
- changing the amount of noise
- change number of degrees
- look at parameter values (high) in OLS
- tarin network for many epochs
```
from fastprogress.fastprogress import progress_bar
import torch
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
jtplot.style(context="talk")
def plot_regression_data(model=None, MSE=None, poly_deg=0):
# Plot the noisy scatter points and the "true" function
plt.scatter(x_train, y_train, label="Noisy Samples")
plt.plot(x_true, y_true, "--", label="True Function")
# Plot the model's learned regression function
if model:
x = x_true.unsqueeze(-1)
x = x.pow(torch.arange(poly_deg + 1)) if poly_deg else x
with torch.no_grad():
yhat = model(x)
plt.plot(x_true, yhat, label="Learned Function")
plt.xlim([min_x, max_x])
plt.ylim([-5, 5])
plt.legend()
if MSE:
plt.title(f"MSE = ${MSE}$")
```
# Create Fake Training Data
```
def fake_y(x, add_noise=False):
y = 10 * x ** 3 - 5 * x
return y + torch.randn_like(y) * 0.5 if add_noise else y
N = 20
min_x, max_x = -1, 1
x_true = torch.linspace(min_x, max_x, 100)
y_true = fake_y(x_true)
x_train = torch.rand(N) * (max_x - min_x) + min_x
y_train = fake_y(x_train, add_noise=True)
plot_regression_data()
```
# Train A Simple Linear Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.1
num_epochs = 100
# Model parameters
m = torch.randn(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
params = (b, m)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(params, lr=learning_rate)
# Regression
for epoch in range(num_epochs):
# Model
yhat = m * x_train + b
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat, y_train)
loss.backward()
optimizer.step()
plot_regression_data(lambda x: m * x + b, MSE=loss.item())
```
# Train Linear Regression Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.1
num_epochs = 1000
# Model parameters
w2 = torch.randn(1, requires_grad=True)
w1 = torch.randn(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
params = (b, w1, w2)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(params, lr=learning_rate)
# Regression
for epoch in range(num_epochs):
# Model
yhat = b + w1 * x_train + w2 * x_train ** 2
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat, y_train)
loss.backward()
optimizer.step()
plot_regression_data(lambda x: b + w1 * x + w2 * x ** 2, MSE=loss.item())
```
# Train Complex Linear Regression Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.1
num_epochs = 1000
# Model parameters
degrees = 50 # 3, 4, 16, 32, 64, 128
powers = torch.arange(degrees + 1)
x_poly = x_train.unsqueeze(-1).pow(powers)
params = torch.randn(degrees + 1, requires_grad=True)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD([params], lr=learning_rate)
# Regression
for epoch in range(num_epochs):
# Model
yhat = x_poly @ params
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat, y_train)
loss.backward()
optimizer.step()
plot_regression_data(lambda x: x @ params, poly_deg=degrees, MSE=loss.item())
params
```
# Compute Linear Regression Model Using Ordinary Least Squares
```
params = ((x_poly.T @ x_poly).inverse() @ x_poly.T) @ y_train
mse = torch.nn.functional.mse_loss(x_poly @ params, y_train)
plot_regression_data(lambda x: x @ params, poly_deg=degrees, MSE=mse)
# params
params
```
# Train Neural Network Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.01
num_epochs = 100000
regularization = 1e-2
# Model parameters
model = torch.nn.Sequential(
torch.nn.Linear(1, 100),
torch.nn.ReLU(),
torch.nn.Linear(100, 100),
torch.nn.ReLU(),
torch.nn.Linear(100, 100),
torch.nn.ReLU(),
torch.nn.Linear(100, 1),
)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(
model.parameters(), lr=learning_rate, weight_decay=regularization
)
# Training
for epoch in progress_bar(range(num_epochs)):
# Model
yhat = model(x_train.unsqueeze(-1))
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat.squeeze(), y_train)
loss.backward()
optimizer.step()
plot_regression_data(model, loss.item())
for param in model.parameters():
print(param.mean())
```
| true |
code
| 0.877713 | null | null | null | null |
|
# Unsplash Joint Query Search
Using this notebook you can search for images from the [Unsplash Dataset](https://unsplash.com/data) using natural language queries. The search is powered by OpenAI's [CLIP](https://github.com/openai/CLIP) neural network.
This notebook uses the precomputed feature vectors for almost 2 million images from the full version of the [Unsplash Dataset](https://unsplash.com/data). If you want to compute the features yourself, see [here](https://github.com/haltakov/natural-language-image-search#on-your-machine).
This project was mostly based on the [project](https://github.com/haltakov/natural-language-image-search) created by [Vladimir Haltakov](https://twitter.com/haltakov) and the full code is open-sourced on [GitHub](https://github.com/haofanwang/natural-language-joint-query-search).
```
!git clone https://github.com/haofanwang/natural-language-joint-query-search.git
cd natural-language-joint-query-search
```
## Setup Environment
In this section we will setup the environment.
First we need to install CLIP and then upgrade the version of torch to 1.7.1 with CUDA support (by default CLIP installs torch 1.7.1 without CUDA). Google Colab currently has torch 1.7.0 which doesn't work well with CLIP.
```
!pip install torch==1.7.1+cu101 torchvision==0.8.2+cu101 -f https://download.pytorch.org/whl/torch_stable.html
!pip install ftfy regex tqdm
```
## Download the Precomputed Data
In this section the precomputed feature vectors for all photos are downloaded.
In order to compare the photos from the Unsplash dataset to a text query, we need to compute the feature vector of each photo using CLIP.
We need to download two files:
* `photo_ids.csv` - a list of the photo IDs for all images in the dataset. The photo ID can be used to get the actual photo from Unsplash.
* `features.npy` - a matrix containing the precomputed 512 element feature vector for each photo in the dataset.
The files are available on [Google Drive](https://drive.google.com/drive/folders/1WQmedVCDIQKA2R33dkS1f980YsJXRZ-q?usp=sharing).
```
from pathlib import Path
# Create a folder for the precomputed features
!mkdir unsplash-dataset
# Download the photo IDs and the feature vectors
!gdown --id 1FdmDEzBQCf3OxqY9SbU-jLfH_yZ6UPSj -O unsplash-dataset/photo_ids.csv
!gdown --id 1L7ulhn4VeN-2aOM-fYmljza_TQok-j9F -O unsplash-dataset/features.npy
# Download from alternative source, if the download doesn't work for some reason (for example download quota limit exceeded)
if not Path('unsplash-dataset/photo_ids.csv').exists():
!wget https://transfer.army/api/download/TuWWFTe2spg/EDm6KBjc -O unsplash-dataset/photo_ids.csv
if not Path('unsplash-dataset/features.npy').exists():
!wget https://transfer.army/api/download/LGXAaiNnMLA/AamL9PpU -O unsplash-dataset/features.npy
```
## Define Functions
Some important functions from CLIP for processing the data are defined here.
The `encode_search_query` function takes a text description and encodes it into a feature vector using the CLIP model.
```
def encode_search_query(search_query):
with torch.no_grad():
# Encode and normalize the search query using CLIP
text_encoded, weight = model.encode_text(clip.tokenize(search_query).to(device))
text_encoded /= text_encoded.norm(dim=-1, keepdim=True)
# Retrieve the feature vector from the GPU and convert it to a numpy array
return text_encoded.cpu().numpy()
```
The `find_best_matches` function compares the text feature vector to the feature vectors of all images and finds the best matches. The function returns the IDs of the best matching photos.
```
def find_best_matches(text_features, photo_features, photo_ids, results_count=3):
# Compute the similarity between the search query and each photo using the Cosine similarity
similarities = (photo_features @ text_features.T).squeeze(1)
# Sort the photos by their similarity score
best_photo_idx = (-similarities).argsort()
# Return the photo IDs of the best matches
return [photo_ids[i] for i in best_photo_idx[:results_count]]
```
We can load the pretrained public CLIP model.
```
import torch
from CLIP.clip import clip
# Load the open CLIP model
device = "cuda" if torch.cuda.is_available() else "cpu"
model, preprocess = clip.load("ViT-B/32", device=device, jit=False)
```
We can now load the pre-extracted unsplash image features.
```
import pandas as pd
import numpy as np
# Load the photo IDs
photo_ids = pd.read_csv("unsplash-dataset/photo_ids.csv")
photo_ids = list(photo_ids['photo_id'])
# Load the features vectors
photo_features = np.load("unsplash-dataset/features.npy")
# Print some statistics
print(f"Photos loaded: {len(photo_ids)}")
```
## Search Unsplash
Now we are ready to search the dataset using natural language. Check out the examples below and feel free to try out your own queries.
In this project, we support more types of searching than the [original project](https://github.com/haltakov/natural-language-image-search).
1. Text-to-Image Search
2. Image-to-Image Search
3. Text+Text-to-Image Search
4. Image+Text-to-Image Search
Note:
1. As the Unsplash API limit is hit from time to time, we don't display the image, but show the link to download the image.
2. As the pretrained CLIP model is mainly trained with English texts, if you want to try with different language, please use Google translation API or NMT model to translate first.
### Text-to-Image Search
#### "Tokyo Tower at night"
```
search_query = "Tokyo Tower at night."
text_features = encode_search_query(search_query)
# Find the best matches
best_photo_ids = find_best_matches(text_features, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
#### "Two children are playing in the amusement park."
```
search_query = "Two children are playing in the amusement park."
text_features = encode_search_query(search_query)
# Find the best matches
best_photo_ids = find_best_matches(text_features, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
### Image-to-Image Search
```
from PIL import Image
source_image = "./images/borna-hrzina-8IPrifbjo-0-unsplash.jpg"
with torch.no_grad():
image_feature = model.encode_image(preprocess(Image.open(source_image)).unsqueeze(0).to(device))
image_feature = (image_feature / image_feature.norm(dim=-1, keepdim=True)).cpu().numpy()
# Find the best matches
best_photo_ids = find_best_matches(image_feature, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
### Text+Text-to-Image Search
```
search_query = "red flower"
search_query_extra = "blue sky"
text_features = encode_search_query(search_query)
text_features_extra = encode_search_query(search_query_extra)
mixed_features = text_features + text_features_extra
# Find the best matches
best_photo_ids = find_best_matches(mixed_features, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
### Image+Text-to-Image Search
```
source_image = "./images/borna-hrzina-8IPrifbjo-0-unsplash.jpg"
search_text = "cars"
with torch.no_grad():
image_feature = model.encode_image(preprocess(Image.open(source_image)).unsqueeze(0).to(device))
image_feature = (image_feature / image_feature.norm(dim=-1, keepdim=True)).cpu().numpy()
text_feature = encode_search_query(search_text)
# image + text
modified_feature = image_feature + text_feature
best_photo_ids = find_best_matches(modified_feature, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
| true |
code
| 0.585397 | null | null | null | null |
|
# Implement an Accelerometer
In this notebook you will define your own `get_derivative_from_data` function and use it to differentiate position data ONCE to get velocity information and then again to get acceleration information.
In part 1 I will demonstrate what this process looks like and then in part 2 you'll implement the function yourself.
-----
## Part 1 - Reminder and Demonstration
```
# run this cell for required imports
from helpers import process_data
from helpers import get_derivative_from_data as solution_derivative
from matplotlib import pyplot as plt
# load the parallel park data
PARALLEL_PARK_DATA = process_data("parallel_park.pickle")
# get the relevant columns
timestamps = [row[0] for row in PARALLEL_PARK_DATA]
displacements = [row[1] for row in PARALLEL_PARK_DATA]
# calculate first derivative
speeds = solution_derivative(displacements, timestamps)
# plot
plt.title("Position and Velocity vs Time")
plt.xlabel("Time (seconds)")
plt.ylabel("Position (blue) and Speed (orange)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.show()
```
But you just saw that acceleration is the derivative of velocity... which means we can use the same derivative function to calculate acceleration!
```
# calculate SECOND derivative
accelerations = solution_derivative(speeds, timestamps[1:])
# plot (note the slicing of timestamps from 2 --> end)
plt.scatter(timestamps[2:], accelerations)
plt.show()
```
As you can see, this parallel park motion consisted of four segments with different (but constant) acceleration. We can plot all three quantities at once like this:
```
plt.title("x(t), v(t), a(t)")
plt.xlabel("Time (seconds)")
plt.ylabel("x (blue), v (orange), a (green)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.scatter(timestamps[2:], accelerations)
plt.show()
```
----
## Part 2 - Implement it yourself!
```
def get_derivative_from_data(position_data, time_data):
# TODO - try your best to implement this code yourself!
# if you get really stuck feel free to go back
# to the previous notebook for a hint.
return
# Testing part 1 - visual testing of first derivative
# compare this output to the corresponding graph above.
speeds = get_derivative_from_data(displacements, timestamps)
plt.title("Position and Velocity vs Time")
plt.xlabel("Time (seconds)")
plt.ylabel("Position (blue) and Speed (orange)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.show()
# Testing part 2 - visual testing of second derivative
# compare this output to the corresponding graph above.
speeds = get_derivative_from_data(displacements, timestamps)
accelerations = get_derivative_from_data(speeds, timestamps[1:])
plt.title("x(t), v(t), a(t)")
plt.xlabel("Time (seconds)")
plt.ylabel("x (blue), v (orange), a (green)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.scatter(timestamps[2:], accelerations)
plt.show()
```
| true |
code
| 0.630685 | null | null | null | null |
|
```
# Import modules
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
# Plot configurations
%matplotlib inline
# Notebook auto reloads code.
%load_ext autoreload
%autoreload 2
```
# NeuroTorch Tutorial
**NeuroTorch** is a framework for reconstructing neuronal morphology from
optical microscopy images. It interfaces PyTorch with different
automated neuron tracing algorithms for fast, accurate, scalable
neuronal reconstructions. It uses deep learning to generate an initial
segmentation of neurons in optical microscopy images. This
segmentation is then traced using various automated neuron tracing
algorithms to convert the segmentation into an SWC file—the most
common neuronal morphology file format. NeuroTorch is designed with
scalability in mind and can handle teravoxel-sized images.
This IPython notebook will outline a brief tutorial for using NeuroTorch
to train and predict on image volume datasets.
## Creating image datasets
One of NeuroTorch’s key features is its dynamic approach to volumetric datasets, which allows it to handle teravoxel-sized images without worrying about memory concerns and efficiency. Everything is loaded just-in-time based on when it is needed or expected to be needed. To load an image dataset, we need
to specify the voxel coordinates of each image file as shown in files `inputs_spec.json` and `labels_spec.json`.
### `inputs_spec.json`
```json
[
{
"filename" : "inputs.tif",
"bounding_box" : [[0, 0, 0], [1024, 512, 50]]
},
{
"filename" : "inputs.tif",
"bounding_box" : [[0, 0, 50], [1024, 512, 100]]
}
]
```
### `labels_spec.json`
```json
[
{
"filename" : "labels.tif",
"bounding_box" : [[0, 0, 0], [1024, 512, 50]]
},
{
"filename" : "labels.tif",
"bounding_box" : [[0, 0, 50], [1024, 512, 100]]
}
]
```
## Loading image datasets
Now that the image datasets for the inputs and labels have been specified,
these datasets can be loaded with NeuroTorch.
```
from neurotorch.datasets.specification import JsonSpec
import os
IMAGE_PATH = '../../tests/images/'
json_spec = JsonSpec() # Initialize the JSON specification
# Create a dataset containing the inputs
inputs = json_spec.open(os.path.join(IMAGE_PATH,
"inputs_spec.json"))
# Create a dataset containing the labels
labels = json_spec.open(os.path.join(IMAGE_PATH,
"labels_spec.json"))
```
## Augmenting datasets
With the image datasets, it is possible to augment data on-the-fly. To implement an augmentation–such as branch occlusion—instantiate an aligned volume and specify the augmentation with the aligned volume.
```
from neurotorch.datasets.dataset import AlignedVolume
from neurotorch.augmentations.occlusion import Occlusion
from neurotorch.augmentations.blur import Blur
from neurotorch.augmentations.brightness import Brightness
from neurotorch.augmentations.dropped import Drop
from neurotorch.augmentations.duplicate import Duplicate
from neurotorch.augmentations.stitch import Stitch
from neurotorch.augmentations.occlusion import Occlusion
volume = AlignedVolume([inputs, labels])
augmented_volume = Occlusion(volume, frequency=0.5)
augmented_volume = Stitch(augmented_volume, frequency=0.5)
augmented_volume = Drop(volume, frequency=0.5)
augmented_volume = Blur(augmented_volume, frequency=0.5)
augmented_volume = Duplicate(augmented_volume, frequency=0.5)
```
## Training with the image datasets
To train a neural network using these image datasets, load the
neural network architecture and initialize a `Trainer`. To save
training checkpoints, add a `CheckpointWriter` to the `Trainer` object.
Lastly, call the `Trainer` object to run training.
```
from neurotorch.core.trainer import Trainer
from neurotorch.nets.RSUNet import RSUNet
from neurotorch.training.checkpoint import CheckpointWriter
from neurotorch.training.logging import ImageWriter, LossWriter
net = RSUNet() # Initialize the U-Net architecture
# Setup the trainer
trainer = Trainer(net, augmented_volume, max_epochs=10,
gpu_device=0)
# Setup the trainer the add a checkpoint every 500 epochs
trainer = LossWriter(trainer, ".", "tutorial_tensorboard")
trainer = ImageWriter(trainer, ".", "tutorial_tensorboard")
trainer = CheckpointWriter(trainer, checkpoint_dir='.',
checkpoint_period=50)
trainer.run_training()
```
## Predicting using NeuroTorch
Once training has completed, we can use the training checkpoints
to predict on image datasets. We first have to
load the neural network architecture and image volume.
We then have to initialize a `Predictor` object and an output volume.
Once these have been specified, we can begin prediction.
```
from neurotorch.nets.RSUNet import RSUNet
from neurotorch.core.predictor import Predictor
from neurotorch.datasets.filetypes import TiffVolume
from neurotorch.datasets.dataset import Array
from neurotorch.datasets.datatypes import (BoundingBox, Vector)
import numpy as np
import tifffile as tif
import os
IMAGE_PATH = '../../tests/images/'
net = RSUNet() # Initialize the U-Net architecture
checkpoint = './iteration_1000.ckpt' # Specify the checkpoint path
with TiffVolume(os.path.join(IMAGE_PATH,
"inputs.tif"),
BoundingBox(Vector(0, 0, 0),
Vector(1024, 512, 50))) as inputs:
predictor = Predictor(net, checkpoint, gpu_device=0)
output_volume = Array(np.zeros(inputs.getBoundingBox()
.getNumpyDim(), dtype=np.float32))
predictor.run(inputs, output_volume, batch_size=5)
tif.imsave("test_prediction.tif",
output_volume.getArray().astype(np.float32))
```
## Displaying the prediction
Predictions are output in logits form. To map this to a
probability distribution, we need to apply a sigmoid function
to the prediction. We can then evaluate the prediction and
ground-truth.
```
# Apply sigmoid function
probability_map = 1/(1+np.exp(-output_volume.getArray()))
# Plot prediction and ground-truth
plt.subplot(2, 1, 1)
plt.title('Prediction')
plt.imshow(output_volume.getArray()[25])
plt.axis('off')
plt.subplot(2, 1, 2)
plt.title('Ground-Truth')
plt.imshow(labels.get(
BoundingBox(Vector(0, 0, 0),
Vector(1024, 512, 50))).getArray()[25],
cmap='gray'
)
plt.axis('off')
plt.show()
```
| true |
code
| 0.743761 | null | null | null | null |
|
# Getting started in scikit-learn with the famous iris dataset
*From the video series: [Introduction to machine learning with scikit-learn](https://github.com/justmarkham/scikit-learn-videos)*
```
#environment setup with watermark
%load_ext watermark
%watermark -a 'Gopala KR' -u -d -v -p watermark,numpy,pandas,matplotlib,nltk,sklearn,tensorflow,theano,mxnet,chainer
```
## Agenda
- What is the famous iris dataset, and how does it relate to machine learning?
- How do we load the iris dataset into scikit-learn?
- How do we describe a dataset using machine learning terminology?
- What are scikit-learn's four key requirements for working with data?
## Introducing the iris dataset

- 50 samples of 3 different species of iris (150 samples total)
- Measurements: sepal length, sepal width, petal length, petal width
```
from IPython.display import IFrame
IFrame('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', width=300, height=200)
```
## Machine learning on the iris dataset
- Framed as a **supervised learning** problem: Predict the species of an iris using the measurements
- Famous dataset for machine learning because prediction is **easy**
- Learn more about the iris dataset: [UCI Machine Learning Repository](http://archive.ics.uci.edu/ml/datasets/Iris)
## Loading the iris dataset into scikit-learn
```
# import load_iris function from datasets module
from sklearn.datasets import load_iris
# save "bunch" object containing iris dataset and its attributes
iris = load_iris()
type(iris)
# print the iris data
print(iris.data)
```
## Machine learning terminology
- Each row is an **observation** (also known as: sample, example, instance, record)
- Each column is a **feature** (also known as: predictor, attribute, independent variable, input, regressor, covariate)
```
# print the names of the four features
print(iris.feature_names)
# print integers representing the species of each observation
print(iris.target)
# print the encoding scheme for species: 0 = setosa, 1 = versicolor, 2 = virginica
print(iris.target_names)
```
- Each value we are predicting is the **response** (also known as: target, outcome, label, dependent variable)
- **Classification** is supervised learning in which the response is categorical
- **Regression** is supervised learning in which the response is ordered and continuous
## Requirements for working with data in scikit-learn
1. Features and response are **separate objects**
2. Features and response should be **numeric**
3. Features and response should be **NumPy arrays**
4. Features and response should have **specific shapes**
```
# check the types of the features and response
print(type(iris.data))
print(type(iris.target))
# check the shape of the features (first dimension = number of observations, second dimensions = number of features)
print(iris.data.shape)
# check the shape of the response (single dimension matching the number of observations)
print(iris.target.shape)
# store feature matrix in "X"
X = iris.data
# store response vector in "y"
y = iris.target
```
## Resources
- scikit-learn documentation: [Dataset loading utilities](http://scikit-learn.org/stable/datasets/)
- Jake VanderPlas: Fast Numerical Computing with NumPy ([slides](https://speakerdeck.com/jakevdp/losing-your-loops-fast-numerical-computing-with-numpy-pycon-2015), [video](https://www.youtube.com/watch?v=EEUXKG97YRw))
- Scott Shell: [An Introduction to NumPy](http://www.engr.ucsb.edu/~shell/che210d/numpy.pdf) (PDF)
## Comments or Questions?
- Email: <[email protected]>
- Website: http://dataschool.io
- Twitter: [@justmarkham](https://twitter.com/justmarkham)
```
from IPython.core.display import HTML
def css_styling():
styles = open("styles/custom.css", "r").read()
return HTML(styles)
css_styling()
test complete; Gopal
```
| true |
code
| 0.545225 | null | null | null | null |
|
# Encoding of categorical variables
In this notebook, we will present typical ways of dealing with
**categorical variables** by encoding them, namely **ordinal encoding** and
**one-hot encoding**.
Let's first load the entire adult dataset containing both numerical and
categorical data.
```
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
# drop the duplicated column `"education-num"` as stated in the first notebook
adult_census = adult_census.drop(columns="education-num")
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=[target_name])
```
## Identify categorical variables
As we saw in the previous section, a numerical variable is a
quantity represented by a real or integer number. These variables can be
naturally handled by machine learning algorithms that are typically composed
of a sequence of arithmetic instructions such as additions and
multiplications.
In contrast, categorical variables have discrete values, typically
represented by string labels (but not only) taken from a finite list of
possible choices. For instance, the variable `native-country` in our dataset
is a categorical variable because it encodes the data using a finite list of
possible countries (along with the `?` symbol when this information is
missing):
```
data["native-country"].value_counts().sort_index()
```
How can we easily recognize categorical columns among the dataset? Part of
the answer lies in the columns' data type:
```
data.dtypes
```
If we look at the `"native-country"` column, we observe its data type is
`object`, meaning it contains string values.
## Select features based on their data type
In the previous notebook, we manually defined the numerical columns. We could
do a similar approach. Instead, we will use the scikit-learn helper function
`make_column_selector`, which allows us to select columns based on
their data type. We will illustrate how to use this helper.
```
from sklearn.compose import make_column_selector as selector
categorical_columns_selector = selector(dtype_include=object)
categorical_columns = categorical_columns_selector(data)
categorical_columns
```
Here, we created the selector by passing the data type to include; we then
passed the input dataset to the selector object, which returned a list of
column names that have the requested data type. We can now filter out the
unwanted columns:
```
data_categorical = data[categorical_columns]
data_categorical.head()
print(f"The dataset is composed of {data_categorical.shape[1]} features")
```
In the remainder of this section, we will present different strategies to
encode categorical data into numerical data which can be used by a
machine-learning algorithm.
## Strategies to encode categories
### Encoding ordinal categories
The most intuitive strategy is to encode each category with a different
number. The `OrdinalEncoder` will transform the data in such manner.
We will start by encoding a single column to understand how the encoding
works.
```
from sklearn.preprocessing import OrdinalEncoder
education_column = data_categorical[["education"]]
encoder = OrdinalEncoder()
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
We see that each category in `"education"` has been replaced by a numeric
value. We could check the mapping between the categories and the numerical
values by checking the fitted attribute `categories_`.
```
encoder.categories_
```
Now, we can check the encoding applied on all categorical features.
```
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The dataset encoded contains {data_encoded.shape[1]} features")
```
We see that the categories have been encoded for each feature (column)
independently. We also note that the number of features before and after the
encoding is the same.
However, be careful when applying this encoding strategy:
using this integer representation leads downstream predictive models
to assume that the values are ordered (0 < 1 < 2 < 3... for instance).
By default, `OrdinalEncoder` uses a lexicographical strategy to map string
category labels to integers. This strategy is arbitrary and often
meaningless. For instance, suppose the dataset has a categorical variable
named `"size"` with categories such as "S", "M", "L", "XL". We would like the
integer representation to respect the meaning of the sizes by mapping them to
increasing integers such as `0, 1, 2, 3`.
However, the lexicographical strategy used by default would map the labels
"S", "M", "L", "XL" to 2, 1, 0, 3, by following the alphabetical order.
The `OrdinalEncoder` class accepts a `categories` constructor argument to
pass categories in the expected ordering explicitly. You can find more
information in the
[scikit-learn documentation](https://scikit-learn.org/stable/modules/preprocessing.html#encoding-categorical-features)
if needed.
If a categorical variable does not carry any meaningful order information
then this encoding might be misleading to downstream statistical models and
you might consider using one-hot encoding instead (see below).
### Encoding nominal categories (without assuming any order)
`OneHotEncoder` is an alternative encoder that prevents the downstream
models to make a false assumption about the ordering of categories. For a
given feature, it will create as many new columns as there are possible
categories. For a given sample, the value of the column corresponding to the
category will be set to `1` while all the columns of the other categories
will be set to `0`.
We will start by encoding a single feature (e.g. `"education"`) to illustrate
how the encoding works.
```
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(sparse=False)
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p><tt class="docutils literal">sparse=False</tt> is used in the <tt class="docutils literal">OneHotEncoder</tt> for didactic purposes, namely
easier visualization of the data.</p>
<p class="last">Sparse matrices are efficient data structures when most of your matrix
elements are zero. They won't be covered in detail in this course. If you
want more details about them, you can look at
<a class="reference external" href="https://scipy-lectures.org/advanced/scipy_sparse/introduction.html#why-sparse-matrices">this</a>.</p>
</div>
We see that encoding a single feature will give a NumPy array full of zeros
and ones. We can get a better understanding using the associated feature
names resulting from the transformation.
```
feature_names = encoder.get_feature_names_out(input_features=["education"])
education_encoded = pd.DataFrame(education_encoded, columns=feature_names)
education_encoded
```
As we can see, each category (unique value) became a column; the encoding
returned, for each sample, a 1 to specify which category it belongs to.
Let's apply this encoding on the full dataset.
```
print(
f"The dataset is composed of {data_categorical.shape[1]} features")
data_categorical.head()
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The encoded dataset contains {data_encoded.shape[1]} features")
```
Let's wrap this NumPy array in a dataframe with informative column names as
provided by the encoder object:
```
columns_encoded = encoder.get_feature_names_out(data_categorical.columns)
pd.DataFrame(data_encoded, columns=columns_encoded).head()
```
Look at how the `"workclass"` variable of the 3 first records has been
encoded and compare this to the original string representation.
The number of features after the encoding is more than 10 times larger than
in the original data because some variables such as `occupation` and
`native-country` have many possible categories.
### Choosing an encoding strategy
Choosing an encoding strategy will depend on the underlying models and the
type of categories (i.e. ordinal vs. nominal).
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">In general <tt class="docutils literal">OneHotEncoder</tt> is the encoding strategy used when the
downstream models are <strong>linear models</strong> while <tt class="docutils literal">OrdinalEncoder</tt> is often a
good strategy with <strong>tree-based models</strong>.</p>
</div>
Using an `OrdinalEncoder` will output ordinal categories. This means
that there is an order in the resulting categories (e.g. `0 < 1 < 2`). The
impact of violating this ordering assumption is really dependent on the
downstream models. Linear models will be impacted by misordered categories
while tree-based models will not.
You can still use an `OrdinalEncoder` with linear models but you need to be
sure that:
- the original categories (before encoding) have an ordering;
- the encoded categories follow the same ordering than the original
categories.
The **next exercise** highlights the issue of misusing `OrdinalEncoder` with
a linear model.
One-hot encoding categorical variables with high cardinality can cause
computational inefficiency in tree-based models. Because of this, it is not recommended
to use `OneHotEncoder` in such cases even if the original categories do not
have a given order. We will show this in the **final exercise** of this sequence.
## Evaluate our predictive pipeline
We can now integrate this encoder inside a machine learning pipeline like we
did with numerical data: let's train a linear classifier on the encoded data
and check the generalization performance of this machine learning pipeline using
cross-validation.
Before we create the pipeline, we have to linger on the `native-country`.
Let's recall some statistics regarding this column.
```
data["native-country"].value_counts()
```
We see that the `Holand-Netherlands` category is occurring rarely. This will
be a problem during cross-validation: if the sample ends up in the test set
during splitting then the classifier would not have seen the category during
training and will not be able to encode it.
In scikit-learn, there are two solutions to bypass this issue:
* list all the possible categories and provide it to the encoder via the
keyword argument `categories`;
* use the parameter `handle_unknown`.
Here, we will use the latter solution for simplicity.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">Be aware the <tt class="docutils literal">OrdinalEncoder</tt> exposes as well a parameter
<tt class="docutils literal">handle_unknown</tt>. It can be set to <tt class="docutils literal">use_encoded_value</tt> and by setting
<tt class="docutils literal">unknown_value</tt> to handle rare categories. You are going to use these
parameters in the next exercise.</p>
</div>
We can now create our machine learning pipeline.
```
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
model = make_pipeline(
OneHotEncoder(handle_unknown="ignore"), LogisticRegression(max_iter=500)
)
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">Here, we need to increase the maximum number of iterations to obtain a fully
converged <tt class="docutils literal">LogisticRegression</tt> and silence a <tt class="docutils literal">ConvergenceWarning</tt>. Contrary
to the numerical features, the one-hot encoded categorical features are all
on the same scale (values are 0 or 1), so they would not benefit from
scaling. In this case, increasing <tt class="docutils literal">max_iter</tt> is the right thing to do.</p>
</div>
Finally, we can check the model's generalization performance only using the
categorical columns.
```
from sklearn.model_selection import cross_validate
cv_results = cross_validate(model, data_categorical, target)
cv_results
scores = cv_results["test_score"]
print(f"The accuracy is: {scores.mean():.3f} +/- {scores.std():.3f}")
```
As you can see, this representation of the categorical variables is
slightly more predictive of the revenue than the numerical variables
that we used previously.
In this notebook we have:
* seen two common strategies for encoding categorical features: **ordinal
encoding** and **one-hot encoding**;
* used a **pipeline** to use a **one-hot encoder** before fitting a logistic
regression.
| true |
code
| 0.621455 | null | null | null | null |
|
# TEST for matrix_facto_10_embeddings_100_epochs
# Deep recommender on top of Amason’s Clean Clothing Shoes and Jewelry explicit rating dataset
Frame the recommendation system as a rating prediction machine learning problem and create a hybrid architecture that mixes the collaborative and content based filtering approaches:
- Collaborative part: Predict items ratings in order to recommend to the user items that he is likely to rate high.
- Content based: use metadata inputs (such as price and title) about items to find similar items to recommend.
### - Create 2 explicit recommendation engine models based on 2 machine learning architecture using Keras:
1. a matrix factorization model
2. a deep neural network model.
### Compare the results of the different models and configurations to find the "best" predicting model
### Used the best model for recommending items to users
```
### name of model
modname = 'matrix_facto_10_embeddings_100_epochs'
### number of epochs
num_epochs = 100
### size of embedding
embedding_size = 10
# import sys
# !{sys.executable} -m pip install --upgrade pip
# !{sys.executable} -m pip install sagemaker-experiments
# !{sys.executable} -m pip install pandas
# !{sys.executable} -m pip install numpy
# !{sys.executable} -m pip install matplotlib
# !{sys.executable} -m pip install boto3
# !{sys.executable} -m pip install sagemaker
# !{sys.executable} -m pip install pyspark
# !{sys.executable} -m pip install ipython-autotime
# !{sys.executable} -m pip install surprise
# !{sys.executable} -m pip install smart_open
# !{sys.executable} -m pip install pyarrow
# !{sys.executable} -m pip install fastparquet
# Check Jave version
# !sudo yum -y update
# # Need to use Java 1.8.0
# !sudo yum remove jre-1.7.0-openjdk -y
!java -version
# !sudo update-alternatives --config java
# !pip install pyarrow fastparquet
# !pip install ipython-autotime
# !pip install tqdm pydot pydotplus pydot_ng
#### To measure all running time
# https://github.com/cpcloud/ipython-autotime
%load_ext autotime
%pylab inline
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
import re
import seaborn as sbn
import nltk
import tqdm as tqdm
import sqlite3
import pandas as pd
import numpy as np
from pandas import DataFrame
import string
import pydot
import pydotplus
import pydot_ng
import pickle
import time
import gzip
import os
os.getcwd()
import matplotlib.pyplot as plt
from math import floor,ceil
#from nltk.corpus import stopwords
#stop = stopwords.words("english")
from nltk.stem.porter import PorterStemmer
english_stemmer=nltk.stem.SnowballStemmer('english')
from nltk.tokenize import word_tokenize
from sklearn.metrics import accuracy_score, confusion_matrix,roc_curve, auc,classification_report, mean_squared_error, mean_absolute_error
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.svm import LinearSVC
from sklearn.neighbors import NearestNeighbors
from sklearn.linear_model import LogisticRegression
from sklearn import neighbors
from scipy.spatial.distance import cosine
from sklearn.feature_selection import SelectKBest
from IPython.display import SVG
# Tensorflow
import tensorflow as tf
#Keras
from keras.models import Sequential, Model, load_model, save_model
from keras.callbacks import ModelCheckpoint
from keras.layers import Dense, Activation, Dropout, Input, Masking, TimeDistributed, LSTM, Conv1D, Embedding
from keras.layers import GRU, Bidirectional, BatchNormalization, Reshape
from keras.optimizers import Adam
from keras.layers.core import Reshape, Dropout, Dense
from keras.layers.merge import Multiply, Dot, Concatenate
from keras.layers.embeddings import Embedding
from keras import optimizers
from keras.callbacks import ModelCheckpoint
from keras.utils.vis_utils import model_to_dot
```
### Set and Check GPUs
```
#Session
from keras import backend as K
def set_check_gpu():
cfg = K.tf.ConfigProto()
cfg.gpu_options.per_process_gpu_memory_fraction =1 # allow all of the GPU memory to be allocated
# for 8 GPUs
# cfg.gpu_options.visible_device_list = "0,1,2,3,4,5,6,7" # "0,1"
# for 1 GPU
cfg.gpu_options.visible_device_list = "0"
#cfg.gpu_options.allow_growth = True # # Don't pre-allocate memory; dynamically allocate the memory used on the GPU as-needed
#cfg.log_device_placement = True # to log device placement (on which device the operation ran)
sess = K.tf.Session(config=cfg)
K.set_session(sess) # set this TensorFlow session as the default session for Keras
print("* TF version: ", [tf.__version__, tf.test.is_gpu_available()])
print("* List of GPU(s): ", tf.config.experimental.list_physical_devices() )
print("* Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID";
# set for 8 GPUs
# os.environ["CUDA_VISIBLE_DEVICES"] = "0,1,2,3,4,5,6,7";
# set for 1 GPU
os.environ["CUDA_VISIBLE_DEVICES"] = "0";
# Tf debugging option
tf.debugging.set_log_device_placement(True)
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
try:
# Currently, memory growth needs to be the same across GPUs
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
except RuntimeError as e:
# Memory growth must be set before GPUs have been initialized
print(e)
# print(tf.config.list_logical_devices('GPU'))
print(tf.config.experimental.list_physical_devices('GPU'))
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
set_check_gpu()
# reset GPU memory& Keras Session
def reset_keras():
try:
del classifier
del model
except:
pass
K.clear_session()
K.get_session().close()
# sess = K.get_session()
cfg = K.tf.ConfigProto()
cfg.gpu_options.per_process_gpu_memory_fraction
# cfg.gpu_options.visible_device_list = "0,1,2,3,4,5,6,7" # "0,1"
cfg.gpu_options.visible_device_list = "0" # "0,1"
cfg.gpu_options.allow_growth = True # dynamically grow the memory used on the GPU
sess = K.tf.Session(config=cfg)
K.set_session(sess) # set this TensorFlow session as the default session for Keras
```
## Load dataset and analysis using Spark
## Download and prepare Data:
#### 1. Read the data:
#### Read the data from the reviews dataset of amazon.
#### Use the dastaset in which all users and items have at least 5 reviews.
### Location of dataset: https://nijianmo.github.io/amazon/index.html
```
import pandas as pd
import boto3
import sagemaker
from sagemaker import get_execution_role
from sagemaker.session import Session
from sagemaker.analytics import ExperimentAnalytics
import gzip
import json
from pyspark.ml import Pipeline
from pyspark.sql.types import StructField, StructType, StringType, DoubleType
from pyspark.ml.feature import StringIndexer, VectorIndexer, OneHotEncoder, VectorAssembler
from pyspark.sql.functions import *
# spark imports
from pyspark.sql import SparkSession
from pyspark.sql.functions import UserDefinedFunction, explode, desc
from pyspark.sql.types import StringType, ArrayType
from pyspark.ml.evaluation import RegressionEvaluator
import os
import pandas as pd
import pyarrow
import fastparquet
# from pandas_profiling import ProfileReport
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/Clean_Clothing_Shoes_and_Jewelry_5_clean.parquet ./data/
!ls -alh ./data
```
### Read clened dataset from parquet files
```
review_data = pd.read_parquet("./data/Clean_Clothing_Shoes_and_Jewelry_5_clean.parquet")
review_data[:3]
review_data.shape
```
### 2. Arrange and clean the data
Rearrange the columns by relevance and rename column names
```
review_data.columns
review_data = review_data[['asin', 'image', 'summary', 'reviewText', 'overall', 'reviewerID', 'reviewerName', 'reviewTime']]
review_data.rename(columns={ 'overall': 'score','reviewerID': 'user_id', 'reviewerName': 'user_name'}, inplace=True)
#the variables names after rename in the modified data frame
list(review_data)
```
# Add Metadata
### Metadata includes descriptions, price, sales-rank, brand info, and co-purchasing links
- asin - ID of the product, e.g. 0000031852
- title - name of the product
- price - price in US dollars (at time of crawl)
- imUrl - url of the product image
- related - related products (also bought, also viewed, bought together, buy after viewing)
- salesRank - sales rank information
- brand - brand name
- categories - list of categories the product belongs to
```
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/Cleaned_meta_Clothing_Shoes_and_Jewelry.parquet ./data/
all_info = pd.read_parquet("./data/Cleaned_meta_Clothing_Shoes_and_Jewelry.parquet")
all_info.head(n=5)
```
### Arrange and clean the data
- Cleaning, handling missing data, normalization, etc:
- For the algorithm in keras to work, remap all item_ids and user_ids to an interger between 0 and the total number of users or the total number of items
```
all_info.columns
items = all_info.asin.unique()
item_map = {i:val for i,val in enumerate(items)}
inverse_item_map = {val:i for i,val in enumerate(items)}
all_info["old_item_id"] = all_info["asin"] # copying for join with metadata
all_info["item_id"] = all_info["asin"].map(inverse_item_map)
items = all_info.item_id.unique()
print ("We have %d unique items in metadata "%items.shape[0])
all_info['description'] = all_info['description'].fillna(all_info['title'].fillna('no_data'))
all_info['title'] = all_info['title'].fillna(all_info['description'].fillna('no_data').apply(str).str[:20])
all_info['image'] = all_info['image'].fillna('no_data')
all_info['price'] = pd.to_numeric(all_info['price'],errors="coerce")
all_info['price'] = all_info['price'].fillna(all_info['price'].median())
users = review_data.user_id.unique()
user_map = {i:val for i,val in enumerate(users)}
inverse_user_map = {val:i for i,val in enumerate(users)}
review_data["old_user_id"] = review_data["user_id"]
review_data["user_id"] = review_data["user_id"].map(inverse_user_map)
items_reviewed = review_data.asin.unique()
review_data["old_item_id"] = review_data["asin"] # copying for join with metadata
review_data["item_id"] = review_data["asin"].map(inverse_item_map)
items_reviewed = review_data.item_id.unique()
users = review_data.user_id.unique()
print ("We have %d unique users"%users.shape[0])
print ("We have %d unique items reviewed"%items_reviewed.shape[0])
# We have 192403 unique users in the "small" dataset
# We have 63001 unique items reviewed in the "small" dataset
review_data.head(3)
```
## Adding the review count and avarage to the metadata
```
#items_nb = review_data['old_item_id'].value_counts().reset_index()
items_avg = review_data.drop(['summary','reviewText','user_id','asin','user_name','reviewTime','old_user_id','item_id'],axis=1).groupby('old_item_id').agg(['count','mean']).reset_index()
items_avg.columns= ['old_item_id','num_ratings','avg_rating']
#items_avg.head(5)
items_avg['num_ratings'].describe()
all_info = pd.merge(all_info,items_avg,how='left',left_on='asin',right_on='old_item_id')
pd.set_option('display.max_colwidth', 100)
all_info.head(2)
```
# Explicit feedback (Reviewed Dataset) Recommender System
### Explicit feedback is when users gives voluntarily the rating information on what they like and dislike.
- In this case, I have explicit item ratings ranging from one to five.
- Framed the recommendation system as a rating prediction machine learning problem:
- Predict an item's ratings in order to be able to recommend to a user an item that he is likely to rate high if he buys it. `
### To evaluate the model, I randomly separate the data into a training and test set.
```
ratings_train, ratings_test = train_test_split( review_data, test_size=0.1, random_state=0)
ratings_train.shape
ratings_test.shape
```
## Adding Metadata to the train set
Create an architecture that mixes the collaborative and content based filtering approaches:
```
- Collaborative Part: Predict items ratings to recommend to the user items which he is likely to rate high according to learnt item & user embeddings (learn similarity from interactions).
- Content based part: Use metadata inputs (such as price and title) about items to recommend to the user contents similar to those he rated high (learn similarity of item attributes).
```
#### Adding the title and price - Add the metadata of the items in the training and test datasets.
```
# # creating metadata mappings
# titles = all_info['title'].unique()
# titles_map = {i:val for i,val in enumerate(titles)}
# inverse_titles_map = {val:i for i,val in enumerate(titles)}
# price = all_info['price'].unique()
# price_map = {i:val for i,val in enumerate(price)}
# inverse_price_map = {val:i for i,val in enumerate(price)}
# print ("We have %d prices" %price.shape)
# print ("We have %d titles" %titles.shape)
# all_info['price_id'] = all_info['price'].map(inverse_price_map)
# all_info['title_id'] = all_info['title'].map(inverse_titles_map)
# # creating dict from
# item2prices = {}
# for val in all_info[['item_id','price_id']].dropna().drop_duplicates().iterrows():
# item2prices[val[1]["item_id"]] = val[1]["price_id"]
# item2titles = {}
# for val in all_info[['item_id','title_id']].dropna().drop_duplicates().iterrows():
# item2titles[val[1]["item_id"]] = val[1]["title_id"]
# # populating the rating dataset with item metadata info
# ratings_train["price_id"] = ratings_train["item_id"].map(lambda x : item2prices[x])
# ratings_train["title_id"] = ratings_train["item_id"].map(lambda x : item2titles[x])
# # populating the test dataset with item metadata info
# ratings_test["price_id"] = ratings_test["item_id"].map(lambda x : item2prices[x])
# ratings_test["title_id"] = ratings_test["item_id"].map(lambda x : item2titles[x])
```
## create rating train/test dataset and upload into S3
```
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/ratings_test.parquet ./data/
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/ratings_train.parquet ./data/
ratings_test = pd.read_parquet('./data/ratings_test.parquet')
ratings_train = pd.read_parquet('./data/ratings_train.parquet')
ratings_train[:3]
ratings_train.shape
```
# **Define embeddings
### The $\underline{embeddings}$ are low-dimensional hidden representations of users and items,
### i.e. for each item I can find its properties and for each user I can encode how much they like those properties so I can determine attitudes or preferences of users by a small number of hidden factors
### Throughout the training, I learn two new low-dimensional dense representations: one embedding for the users and another one for the items.
```
price = all_info['price'].unique()
titles = all_info['title'].unique()
```
# 1. Matrix factorization approach

```
# declare input embeddings to the model
# User input
user_id_input = Input(shape=[1], name='user')
# Item Input
item_id_input = Input(shape=[1], name='item')
price_id_input = Input(shape=[1], name='price')
title_id_input = Input(shape=[1], name='title')
# define the size of embeddings as a parameter
# Check 5, 10 , 15, 20, 50
user_embedding_size = embedding_size
item_embedding_size = embedding_size
price_embedding_size = embedding_size
title_embedding_size = embedding_size
# apply an embedding layer to all inputs
user_embedding = Embedding(output_dim=user_embedding_size, input_dim=users.shape[0],
input_length=1, name='user_embedding')(user_id_input)
item_embedding = Embedding(output_dim=item_embedding_size, input_dim=items_reviewed.shape[0],
input_length=1, name='item_embedding')(item_id_input)
price_embedding = Embedding(output_dim=price_embedding_size, input_dim=price.shape[0],
input_length=1, name='price_embedding')(price_id_input)
title_embedding = Embedding(output_dim=title_embedding_size, input_dim=titles.shape[0],
input_length=1, name='title_embedding')(title_id_input)
# reshape from shape (batch_size, input_length,embedding_size) to (batch_size, embedding_size).
user_vecs = Reshape([user_embedding_size])(user_embedding)
item_vecs = Reshape([item_embedding_size])(item_embedding)
price_vecs = Reshape([price_embedding_size])(price_embedding)
title_vecs = Reshape([title_embedding_size])(title_embedding)
```
### Matrix Factorisation works on the principle that we can learn the user and the item embeddings, and then predict the rating for each user-item by performing a dot (or scalar) product between the respective user and item embedding.
```
# Applying matrix factorization: declare the output as being the dot product between the two embeddings: items and users
y = Dot(1, normalize=False)([user_vecs, item_vecs])
!mkdir -p ./models
# create model
model = Model(inputs=
[
user_id_input,
item_id_input
],
outputs=y)
# compile model
model.compile(loss='mse',
optimizer="adam" )
# set save location for model
save_path = "./models"
thename = save_path + '/' + modname + '.h5'
mcheck = ModelCheckpoint(thename, monitor='val_loss', save_best_only=True)
# fit model
history = model.fit([ratings_train["user_id"]
, ratings_train["item_id"]
]
, ratings_train["score"]
, batch_size=64
, epochs=num_epochs
, validation_split=0.2
, callbacks=[mcheck]
, shuffle=True)
# Save the fitted model history to a file
with open('./histories/' + modname + '.pkl' , 'wb') as file_pi: pickle.dump(history.history, file_pi)
print("Save history in ", './histories/' + modname + '.pkl')
def disp_model(path,file,suffix):
model = load_model(path+file+suffix)
## Summarise the model
model.summary()
# Extract the learnt user and item embeddings, i.e., a table with number of items and users rows and columns, with number of columns is the dimension of the trained embedding.
# In our case, the embeddings correspond exactly to the weights of the model:
weights = model.get_weights()
print ("embeddings \ weights shapes",[w.shape for w in weights])
return model
model_path = "./models/"
def plt_pickle(path,file,suffix):
with open(path+file+suffix , 'rb') as file_pi:
thepickle= pickle.load(file_pi)
plot(thepickle["loss"],label ='Train Error ' + file,linestyle="--")
plot(thepickle["val_loss"],label='Validation Error ' + file)
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Error")
##plt.ylim(0, 0.1)
return pd.DataFrame(thepickle,columns =['loss','val_loss'])
hist_path = "./histories/"
model=disp_model(model_path, modname, '.h5')
# Display the model using keras
SVG(model_to_dot(model).create(prog='dot', format='svg'))
x=plt_pickle(hist_path, modname, '.pkl')
x.head(20).transpose()
```
| true |
code
| 0.643833 | null | null | null | null |
|
# Gradient-boosting decision tree (GBDT)
In this notebook, we will present the gradient boosting decision tree
algorithm and contrast it with AdaBoost.
Gradient-boosting differs from AdaBoost due to the following reason: instead
of assigning weights to specific samples, GBDT will fit a decision tree on
the residuals error (hence the name "gradient") of the previous tree.
Therefore, each new tree in the ensemble predicts the error made by the
previous learner instead of predicting the target directly.
In this section, we will provide some intuition about the way learners are
combined to give the final prediction. In this regard, let's go back to our
regression problem which is more intuitive for demonstrating the underlying
machinery.
```
import pandas as pd
import numpy as np
# Create a random number generator that will be used to set the randomness
rng = np.random.RandomState(0)
def generate_data(n_samples=50):
"""Generate synthetic dataset. Returns `data_train`, `data_test`,
`target_train`."""
x_max, x_min = 1.4, -1.4
len_x = x_max - x_min
x = rng.rand(n_samples) * len_x - len_x / 2
noise = rng.randn(n_samples) * 0.3
y = x ** 3 - 0.5 * x ** 2 + noise
data_train = pd.DataFrame(x, columns=["Feature"])
data_test = pd.DataFrame(np.linspace(x_max, x_min, num=300),
columns=["Feature"])
target_train = pd.Series(y, name="Target")
return data_train, data_test, target_train
data_train, data_test, target_train = generate_data()
import matplotlib.pyplot as plt
import seaborn as sns
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
_ = plt.title("Synthetic regression dataset")
```
As we previously discussed, boosting will be based on assembling a sequence
of learners. We will start by creating a decision tree regressor. We will set
the depth of the tree so that the resulting learner will underfit the data.
```
from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor(max_depth=3, random_state=0)
tree.fit(data_train, target_train)
target_train_predicted = tree.predict(data_train)
target_test_predicted = tree.predict(data_test)
```
Using the term "test" here refers to data that was not used for training.
It should not be confused with data coming from a train-test split, as it
was generated in equally-spaced intervals for the visual evaluation of the
predictions.
```
# plot the data
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
# plot the predictions
line_predictions = plt.plot(data_test["Feature"], target_test_predicted, "--")
# plot the residuals
for value, true, predicted in zip(data_train["Feature"],
target_train,
target_train_predicted):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
plt.legend([line_predictions[0], lines_residuals[0]],
["Fitted tree", "Residuals"])
_ = plt.title("Prediction function together \nwith errors on the training set")
```
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">In the cell above, we manually edited the legend to get only a single label
for all the residual lines.</p>
</div>
Since the tree underfits the data, its accuracy is far from perfect on the
training data. We can observe this in the figure by looking at the difference
between the predictions and the ground-truth data. We represent these errors,
called "Residuals", by unbroken red lines.
Indeed, our initial tree was not expressive enough to handle the complexity
of the data, as shown by the residuals. In a gradient-boosting algorithm, the
idea is to create a second tree which, given the same data `data`, will try
to predict the residuals instead of the vector `target`. We would therefore
have a tree that is able to predict the errors made by the initial tree.
Let's train such a tree.
```
residuals = target_train - target_train_predicted
tree_residuals = DecisionTreeRegressor(max_depth=5, random_state=0)
tree_residuals.fit(data_train, residuals)
target_train_predicted_residuals = tree_residuals.predict(data_train)
target_test_predicted_residuals = tree_residuals.predict(data_test)
sns.scatterplot(x=data_train["Feature"], y=residuals, color="black", alpha=0.5)
line_predictions = plt.plot(
data_test["Feature"], target_test_predicted_residuals, "--")
# plot the residuals of the predicted residuals
for value, true, predicted in zip(data_train["Feature"],
residuals,
target_train_predicted_residuals):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
plt.legend([line_predictions[0], lines_residuals[0]],
["Fitted tree", "Residuals"], bbox_to_anchor=(1.05, 0.8),
loc="upper left")
_ = plt.title("Prediction of the previous residuals")
```
We see that this new tree only manages to fit some of the residuals. We will
focus on a specific sample from the training set (i.e. we know that the
sample will be well predicted using two successive trees). We will use this
sample to explain how the predictions of both trees are combined. Let's first
select this sample in `data_train`.
```
sample = data_train.iloc[[-2]]
x_sample = sample['Feature'].iloc[0]
target_true = target_train.iloc[-2]
target_true_residual = residuals.iloc[-2]
```
Let's plot the previous information and highlight our sample of interest.
Let's start by plotting the original data and the prediction of the first
decision tree.
```
# Plot the previous information:
# * the dataset
# * the predictions
# * the residuals
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
plt.plot(data_test["Feature"], target_test_predicted, "--")
for value, true, predicted in zip(data_train["Feature"],
target_train,
target_train_predicted):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
# Highlight the sample of interest
plt.scatter(sample, target_true, label="Sample of interest",
color="tab:orange", s=200)
plt.xlim([-1, 0])
plt.legend(bbox_to_anchor=(1.05, 0.8), loc="upper left")
_ = plt.title("Tree predictions")
```
Now, let's plot the residuals information. We will plot the residuals
computed from the first decision tree and show the residual predictions.
```
# Plot the previous information:
# * the residuals committed by the first tree
# * the residual predictions
# * the residuals of the residual predictions
sns.scatterplot(x=data_train["Feature"], y=residuals,
color="black", alpha=0.5)
plt.plot(data_test["Feature"], target_test_predicted_residuals, "--")
for value, true, predicted in zip(data_train["Feature"],
residuals,
target_train_predicted_residuals):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
# Highlight the sample of interest
plt.scatter(sample, target_true_residual, label="Sample of interest",
color="tab:orange", s=200)
plt.xlim([-1, 0])
plt.legend()
_ = plt.title("Prediction of the residuals")
```
For our sample of interest, our initial tree is making an error (small
residual). When fitting the second tree, the residual in this case is
perfectly fitted and predicted. We will quantitatively check this prediction
using the fitted tree. First, let's check the prediction of the initial tree
and compare it with the true value.
```
print(f"True value to predict for "
f"f(x={x_sample:.3f}) = {target_true:.3f}")
y_pred_first_tree = tree.predict(sample)[0]
print(f"Prediction of the first decision tree for x={x_sample:.3f}: "
f"y={y_pred_first_tree:.3f}")
print(f"Error of the tree: {target_true - y_pred_first_tree:.3f}")
```
As we visually observed, we have a small error. Now, we can use the second
tree to try to predict this residual.
```
print(f"Prediction of the residual for x={x_sample:.3f}: "
f"{tree_residuals.predict(sample)[0]:.3f}")
```
We see that our second tree is capable of predicting the exact residual
(error) of our first tree. Therefore, we can predict the value of `x` by
summing the prediction of all the trees in the ensemble.
```
y_pred_first_and_second_tree = (
y_pred_first_tree + tree_residuals.predict(sample)[0]
)
print(f"Prediction of the first and second decision trees combined for "
f"x={x_sample:.3f}: y={y_pred_first_and_second_tree:.3f}")
print(f"Error of the tree: {target_true - y_pred_first_and_second_tree:.3f}")
```
We chose a sample for which only two trees were enough to make the perfect
prediction. However, we saw in the previous plot that two trees were not
enough to correct the residuals of all samples. Therefore, one needs to
add several trees to the ensemble to successfully correct the error
(i.e. the second tree corrects the first tree's error, while the third tree
corrects the second tree's error and so on).
We will compare the generalization performance of random-forest and gradient
boosting on the California housing dataset.
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import cross_validate
data, target = fetch_california_housing(return_X_y=True, as_frame=True)
target *= 100 # rescale the target in k$
from sklearn.ensemble import GradientBoostingRegressor
gradient_boosting = GradientBoostingRegressor(n_estimators=200)
cv_results_gbdt = cross_validate(
gradient_boosting, data, target, scoring="neg_mean_absolute_error",
n_jobs=2,
)
print("Gradient Boosting Decision Tree")
print(f"Mean absolute error via cross-validation: "
f"{-cv_results_gbdt['test_score'].mean():.3f} +/- "
f"{cv_results_gbdt['test_score'].std():.3f} k$")
print(f"Average fit time: "
f"{cv_results_gbdt['fit_time'].mean():.3f} seconds")
print(f"Average score time: "
f"{cv_results_gbdt['score_time'].mean():.3f} seconds")
from sklearn.ensemble import RandomForestRegressor
random_forest = RandomForestRegressor(n_estimators=200, n_jobs=2)
cv_results_rf = cross_validate(
random_forest, data, target, scoring="neg_mean_absolute_error",
n_jobs=2,
)
print("Random Forest")
print(f"Mean absolute error via cross-validation: "
f"{-cv_results_rf['test_score'].mean():.3f} +/- "
f"{cv_results_rf['test_score'].std():.3f} k$")
print(f"Average fit time: "
f"{cv_results_rf['fit_time'].mean():.3f} seconds")
print(f"Average score time: "
f"{cv_results_rf['score_time'].mean():.3f} seconds")
```
In term of computation performance, the forest can be parallelized and will
benefit from using multiple cores of the CPU. In terms of scoring
performance, both algorithms lead to very close results.
However, we see that the gradient boosting is a very fast algorithm to
predict compared to random forest. This is due to the fact that gradient
boosting uses shallow trees. We will go into details in the next notebook
about the hyperparameters to consider when optimizing ensemble methods.
| true |
code
| 0.752013 | null | null | null | null |
|
# Introduction
## 1.1 Some Apparently Simple Questions
## 1.2 An Alternative Analytic Framework
Solved to a high degree of accuracy using numerical method
```
!pip install --user quantecon
import numpy as np
import numpy.linalg as la
from numba import *
from __future__ import division
#from quantecon.quad import qnwnorm
```
Suppose now that the economist is presented with a demand function
$$q = 0.5* p^{-0.2} + 0.5*p^{-0.5}$$
one that is the sum a domestic demand term and an export demand term.
suppose that the economist is asked to find the price that clears the
market of, say, a quantity of 2 units.
```
#%pylab inline
%pylab notebook
# pylab Populating the interactive namespace from numpy and matplotlib
# numpy for numerical computation
# matplotlib for ploting
#http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.plot
p = np.linspace(0.01,0.5, 100)
q = .5 * p **-.2 + .5 * p ** -.5 - 2
plot(q,p)
x1,x2,y1,y2 = 2, 2, 0, 0.5
plot((x1, x2), (y1, y2), 'k-')
# example 1.2
p = 0.25
for i in range(100):
deltap = (.5 * p **-.2 + .5 * p ** -.5 - 2)/(.1 * p **-1.2 + .25 * p **-1.5)
p = p + deltap
if abs(deltap) < 1.e-8: # accuracy
break
#https://stackoverflow.com/questions/20457038/python-how-to-round-down-to-2-decimals
print('The market clean price is {:0.2f} '.format(p))
```
Consider now the rational expectations commodity market model with government
intervention. The source of difficulty in solving this problem is the need to
evaluate the truncated expectation of a continuous distribution.
The economist would replace the original normal yield distribution
with a discrete distribution that has identical lower moments, say one that assumes
values y1; y2; ... ; yn with probabilities w1; w2; ...; wn.
```
# https://github.com/QuantEcon/QuantEcon.py/blob/master/quantecon/quad.py
def qnwnorm(n, mu=None, sig2=None, usesqrtm=False):
"""
Computes nodes and weights for multivariate normal distribution
Parameters
----------
n : int or array_like(float)
A length-d iterable of the number of nodes in each dimension
mu : scalar or array_like(float), optional(default=zeros(d))
The means of each dimension of the random variable. If a scalar
is given, that constant is repeated d times, where d is the
number of dimensions
sig2 : array_like(float), optional(default=eye(d))
A d x d array representing the variance-covariance matrix of the
multivariate normal distribution.
Returns
-------
nodes : np.ndarray(dtype=float)
Quadrature nodes
weights : np.ndarray(dtype=float)
Weights for quadrature nodes
Notes
-----
Based of original function ``qnwnorm`` in CompEcon toolbox by
Miranda and Fackler
References
----------
Miranda, Mario J, and Paul L Fackler. Applied Computational
Economics and Finance, MIT Press, 2002.
"""
n = np.asarray(n)
d = n.size
if mu is None:
mu = np.zeros((d,1))
else:
mu = np.asarray(mu).reshape(-1, 1)
if sig2 is None:
sig2 = np.eye(d)
else:
sig2 = np.asarray(sig2).reshape(d, d)
if all([x.size == 1 for x in [n, mu, sig2]]):
nodes, weights = _qnwnorm1(n)
else:
nodes = []
weights = []
for i in range(d):
_1d = _qnwnorm1(n[i])
nodes.append(_1d[0])
weights.append(_1d[1])
nodes = gridmake(*nodes)
weights = ckron(*weights[::-1])
if usesqrtm:
new_sig2 = la.sqrtm(sig2)
else: # cholesky
new_sig2 = la.cholesky(sig2)
if d > 1:
nodes = new_sig2.dot(nodes) + mu # Broadcast ok
else: # nodes.dot(sig) will not be aligned in scalar case.
nodes = nodes * new_sig2 + mu
return nodes.squeeze(), weights
def _qnwnorm1(n):
"""
Compute nodes and weights for quadrature of univariate standard
normal distribution
Parameters
----------
n : int
The number of nodes
Returns
-------
nodes : np.ndarray(dtype=float)
An n element array of nodes
nodes : np.ndarray(dtype=float)
An n element array of weights
Notes
-----
Based of original function ``qnwnorm1`` in CompEcon toolbox by
Miranda and Fackler
References
----------
Miranda, Mario J, and Paul L Fackler. Applied Computational
Economics and Finance, MIT Press, 2002.
"""
maxit = 100
pim4 = 1 / np.pi**(0.25)
m = np.fix((n + 1) / 2).astype(int)
nodes = np.zeros(n)
weights = np.zeros(n)
for i in range(m):
if i == 0:
z = np.sqrt(2*n+1) - 1.85575 * ((2 * n + 1)**(-1 / 6.1))
elif i == 1:
z = z - 1.14 * (n ** 0.426) / z
elif i == 2:
z = 1.86 * z + 0.86 * nodes[0]
elif i == 3:
z = 1.91 * z + 0.91 * nodes[1]
else:
z = 2 * z + nodes[i-2]
its = 0
while its < maxit:
its += 1
p1 = pim4
p2 = 0
for j in range(1, n+1):
p3 = p2
p2 = p1
p1 = z * math.sqrt(2.0/j) * p2 - math.sqrt((j - 1.0) / j) * p3
pp = math.sqrt(2 * n) * p2
z1 = z
z = z1 - p1/pp
if abs(z - z1) < 1e-14:
break
if its == maxit:
raise ValueError("Failed to converge in _qnwnorm1")
nodes[n - 1 - i] = z
nodes[i] = -z
weights[i] = 2 / (pp*pp)
weights[n - 1 - i] = weights[i]
weights /= math.sqrt(math.pi)
nodes = nodes * math.sqrt(2.0)
return nodes, weights
# example 1.2
y, w = qnwnorm(10, 1, 0.1)
a = 1
for it in range(100):
aold = a
p = 3 - 2 * a * y
f = w.dot(np.maximum(p, 1))
a = 0.5 + 0.5 * f
if abs(a - aold) < 1.e-8:
break
print('The rational expectations equilibrium acreage is {:0.2f} '.format(a) )
print('The expected market price is {:0.2f} '.format(np.dot(w, p)) )
print('The expected effective producer price is {:0.2f} '.format(f) )
```
The economist has combined Gaussian quadrature techniques and fixed-point function iteration methods to solve the problem.
| true |
code
| 0.819316 | null | null | null | null |
|
## Linear Algebra
Those exercises will involve vector and matrix math, the <a href="http://wiki.scipy.org/Tentative_NumPy_Tutorial">NumPy</a> Python package.
This exercise will be divided into two parts:
#### 1. Math checkup
Where you will do some of the math by hand.
#### 2. NumPy and Spark linear algebra
You will do some exercise using the NumPy package.
<br>
In the following exercises you will need to replace the code parts in the cell that starts with following comment: "#Replace the `<INSERT>`"
To go through the notebook fill in the `<INSERT>`:s with appropriate code in the cells.
To run a cell press Shift-Enter to run it and advance to the following cell or Ctrl-Enter to only run the code in the cell. You should do the exercises from the top to the bottom in this notebook, because following cells may depend on code in previous cells.
If you want to execute these lines in a python script, you will need to create first a spark context:
```
#from pyspark import SparkContext, StorageLevel \
#from pyspark.sql import SQLContext \
#sc = SparkContext(master="local[*]") \
#sqlContext = SQLContext(sc) \
```
But since we are using the notebooks, those lines are not needed here.
## 1. Math checkup
### 1.1 Euclidian norm
$$
\mathbf{v} = \begin{bmatrix}
666 \\
1337 \\
1789 \\
1066 \\
1945 \\
\end{bmatrix}
\qquad
\|\mathbf{v}\| = ?
$$
Calculate the euclidian norm for the $\mathbf{v}$ using the following definition:
$$
\|\mathbf{v}\|_2 = \sqrt{\sum\limits_{i=1}^n {x_i}^2} = \sqrt{{x_1}^2+\cdots+{x_n}^2}
$$
```
#Replace the <INSERT>
import math
import numpy as np
v = [666, 1337, 1789, 1066, 1945]
rdd = sc.parallelize(v)
#sumOfSquares = rdd.map(<INSERT>).reduce(<INSERT>)
sumOfSquares = rdd.map(lambda x: x*x ).reduce(lambda x,y : x+y)
norm = math.sqrt(sumOfSquares)
# <INSERT round to 8 decimals >
norm = format(norm, '.8f')
norm_numpy= np.linalg.norm(v)
print("norm: "+str(norm) +" norm_numpy: "+ str(norm_numpy))
#Helper function to check results
import hashlib
def hashCheck(x, hashCompare): #Defining a help function
hash = hashlib.md5(str(x).encode('utf-8')).hexdigest()
print(hash)
if hash == hashCompare:
print('Yay, you succeeded!')
else:
print('Try again!')
def check(x,y,label):
if(x == y):
print("Yay, "+label+" is correct!")
else:
print("Nay, "+label+" is incorrect, please try again!")
def checkArray(x,y,label):
if np.allclose(x,y):
print("Yay, "+label+" is correct!")
else:
print("Nay, "+label+" is incorrect, please try again!")
#Check if the norm is correct
hashCheck(norm_numpy, '6de149ccbc081f9da04a0bbd8fe05d8c')
```
### 1.2 Transpose
$$
\mathbf{A} = \begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{bmatrix}
\qquad
\mathbf{A}^T = ?
$$
Tranpose is an operation on matrices that swaps the row for the columns.
$$
\begin{bmatrix}
2 & 7 \\
3 & 11\\
5 & 13\\
\end{bmatrix}^T
\Rightarrow
\begin{bmatrix}
2 & 3 & 5 \\
7 & 11 & 13\\
\end{bmatrix}
$$
Do the transpose of A by hand and write it in:
```
#Replace the <INSERT>
#Input aT like this: AT = [[1, 2, 3],[4, 5, 6],[7, 8, 9]]
#At = <INSERT>
A= np.matrix([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
print(A)
print("\n")
At = np.matrix.transpose(A)
print (At)
At =[[1,4, 7],[2, 5, 8],[3, 6, 9]]
print("\n")
print (At)
#Check if the transpose is correct
hashCheck(At, '1c8dc4c2349277cbe5b7c7118989d8a5')
```
### 1.3 Scalar matrix multiplication
$$
\mathbf{A} = 3\times\begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{bmatrix}
=?
\qquad
\mathbf{B} = 5\times\begin{bmatrix}
1\\
-4\\
7\\
\end{bmatrix}
=?
$$
The operation is done element-wise, e.g. $k\times\mathbf{A}=\mathbf{C}$ then $k\times a_{i,j}={k}c_{i,j}$.
$$
2
\times
\begin{bmatrix}
1 & 6 \\
4 & 8 \\
\end{bmatrix}
=
\begin{bmatrix}
2\times1& 2\times6 \\
2\times4 & 2\times8\\
\end{bmatrix}
=
\begin{bmatrix}
2& 12 \\
8 & 16\\
\end{bmatrix}
$$
$$
11
\times
\begin{bmatrix}
2 \\
3 \\
5 \\
\end{bmatrix}
=
\begin{bmatrix}
11\times2 \\
11\times3 \\
11\times5 \\
\end{bmatrix}
=
\begin{bmatrix}
22\\
33\\
55\\
\end{bmatrix}
$$
Do the scalar multiplications of $\mathbf{A}$ and $\mathbf{B}$ by hand and write them in:
```
#Replace the <INSERT>
#Input A like this: A = [[1, 2, 3],[4, 5, 6],[7, 8, 9]]
#And B like this: B = [1, -4, 7]
#A = <INSERT>
#B = <INSERT>
A = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
print(3*A)
print ("\n")
B = np.array([1, -4, 7])
print (5*B)
print ("\n")
A = [[ 3, 6, 9], [12, 15,18], [21, 24, 27]]
B = [5, -20, 35]
#Check if the scalar matrix multiplication is correct
hashCheck(A, '91b9508ec9099ee4d2c0a6309b0d69de')
hashCheck(B, '88bddc0ee0eab409cee011770363d007')
```
### 1.4 Dot product
$$
c_1=\begin{bmatrix}
11 \\
2 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
3 \\
5 \\
\end{bmatrix}
=?
\qquad
c_2=\begin{bmatrix}
1 \\
2 \\
3 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
4 \\
5 \\
6 \\
\end{bmatrix}
=?
$$
The operations are done element-wise, e.g. $\mathbf{v}\cdot\mathbf{w}=k$ then $\sum v_i \times w_i =k$
$$
\begin{bmatrix}
2 \\
3 \\
5 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
1 \\
4 \\
6 \\
\end{bmatrix}
= 2\times1+3\times4+5\times6=44
$$
Calculate the values of $c_1$ and $c_2$ by hand and write them in:
```
#Replace the <INSERT>
#Input c1 and c2 like this: c = 1337
#c1 = <INSERT>
#c2 = <INSERT>
c1_1 = np.array([11,2])
c1_2 = np.array([3,5])
c1 = c1_1.dot(c1_2)
print (c1)
c1 = 43
c2_1 = np.array([1,2,3])
c2_2 = np.array([4,5,6])
c2 = c2_1.dot(c2_2)
print (c2)
c2 = 32
#Check if the dot product is correct
hashCheck(c1, '17e62166fc8586dfa4d1bc0e1742c08b')
hashCheck(c2, '6364d3f0f495b6ab9dcf8d3b5c6e0b01')
```
### 1.5 Matrix multiplication
$$
\mathbf{A}=
\begin{bmatrix}
682 & 848 & 794 & 954 \\
700 & 1223 & 1185 & 816 \\
942 & 428 & 324 & 526 \\
321 & 543 & 532 & 614 \\
\end{bmatrix}
\qquad
\mathbf{B}=
\begin{bmatrix}
869 & 1269 & 1306 & 358 \\
1008 & 836 & 690 & 366 \\
973 & 619 & 407 & 1149 \\
323 & 42 & 405 & 117 \\
\end{bmatrix}
\qquad
\mathbf{A}\times\mathbf{B}=\mathbf{C}=?
$$
The $c_{i,j}$ entry is the dot product of the i-th row in $\mathbf{A}$ and the j-th column in $\mathbf{B}$
Calculate $\mathbf{C}$ by implementing the naive matrix multiplication algotrithm with $\mathcal{O}(n^3)$ run time, by using the tree nested for-loops below:
```
# The convention is to import NumPy as the alias np
import numpy as np
A = [[ 682, 848, 794, 954],
[ 700, 1223, 1185, 816],
[ 942, 428, 324, 526],
[ 321, 543, 532, 614]]
B = [[ 869, 1269, 1306, 358],
[1008, 836, 690, 366],
[ 973, 619, 407, 1149],
[ 323, 42, 405, 117]]
C = [[0]*4 for i in range(4)]
#Iterate through rows of A
for i in range(len(A)):
#Iterate through columns of B
for j in range(len(B[0])):
#Iterate through rows of B
for k in range(len(B)):
C[i][j] += A[i][k] * B[k][j]
print(np.matrix(C))
print(np.matrix(A)*np.matrix(B))
#Check if the matrix multiplication is correct
hashCheck(C, 'f6b7b0500a6355e8e283f732ec28fa76')
```
## 2. NumPy and Spark linear algebra
A python library to utilize arrays is <a href="http://wiki.scipy.org/Tentative_NumPy_Tutorial">NumPy</a>. The library is optimized to be fast and memory efficient, and provide abstractions corresponding to vectors, matrices and the operations done on these objects.
Numpy's array class is called <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.html">ndarray</a>, it is also known by the alias array. This is a multidimensional array of fixed-size that contains numerical elements of one type, e.g. floats or integers.
### 2.1 Scalar matrix multiplication using NumPy
$$
\mathbf{A} = \begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{bmatrix}
\quad
5\times\mathbf{A}=\mathbf{C}=?
\qquad
\mathbf{B} = \begin{bmatrix}
1&-4& 7\\
\end{bmatrix}
\quad
3\times\mathbf{B}=\mathbf{D}=?
$$
Utilizing the <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.array.html">np.array()</a> function create the above matrix $\mathbf{A}$ and vector $\mathbf{B}$ and multiply it by 5 and 3 correspondingly.
Note that if you use a Python list of integers to create an array you will get a one-dimensional array, which is, for our purposes, equivalent to a vector.
Calculate C and D by inputting the following statements:
```
#Replace the <INSERT>. You will use np.array()
A = np.array([[1, 2, 3],[4,5,6],[7,8,9]])
B = np.array([1,-4, 7])
C = A *5
D = 3 * B
print(A)
print(B)
print(C)
print(D)
#Check if the scalar matrix multiplication is correct
checkArray(C,[[5, 10, 15],[20, 25, 30],[35, 40, 45]], "the scalar multiplication")
checkArray(D,[3, -12, 21], "the scalar multiplication")
```
### 2.2 Dot product and element-wise multiplication
Both dot product and element-wise multiplication is supported by ndarrays.
Element-wise multiplication is the standard between two arrays, of the same dimension, using the operator *.
The dot product you can use either <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html#numpy.dot">np.dot()</a> or <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.dot.html">np.array.dot()</a>. The dot product is a commutative operation, i.e. the order of the arrays doe not matter, e.g. if you have the ndarrays x and y, you can write the dot product as any of the following four ways: np.dot(x, y), np.dot(y, x), x.dot(y), or y.dot(x).
Calculate the element wise product and the dot product by filling in the following statements:
```
#Replace the <INSERT>
u = np.arange(0, 5)
v = np.arange(5, 10)
elementWise = np.multiply(u,v)
dotProduct = np.dot(u,v)
print(elementWise)
print(dotProduct)
#Check if the dot product and element wise is correct
checkArray(elementWise,[0,6,14,24,36], "the element wise multiplication")
check(dotProduct, 80, "the dot product")
```
### 2.3 Cosine similarity
The cosine similarity between two vectors is defined as the following equation:
$$
cosine\_similarity(u,v)=\cos\theta=\frac{\mathbf{u}\cdot\mathbf{v}}{\|u\|\|v\|}
$$
The norm of a vector $\|v\|$ can be calculated by using <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.norm.html#numpy.linalg.norm">np.linalg.norm()</a>.
Implement the following function that calculates the cosine similarity:
```
def cosine_similarity(u,v):
dotProduct = np.dot(u,v)
normProduct = np.linalg.norm(u)*np.linalg.norm(v)
return dotProduct/normProduct
u = np.array([2503,2992,1042])
v = np.array([2217,2761,990])
w = np.array([0,1,1])
x = np.array([1,0,1])
uv = cosine_similarity(u,v)
wx = cosine_similarity(w,x)
print(uv)
print(wx)
#Check if the cosine similarity is correct
check(round(uv,5),0.99974,"cosine similarity between u and v")
check(round(wx,5),0.5,"cosine similarity between w and x")
```
### 2.4 Matrix math
To represent matrices, you can use the following class: <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.html">np.matrix()</a>. To create a matrix object either pass it a two-dimensional ndarray, or a list of lists to the function, or a string e.g. '1 2; 3 4'. Instead of element-wise multiplication, the operator *, does matrix multiplication.
To transpose a matrix, you can use either <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.transpose.html">np.matrix.transpose()</a> or <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.T.html">.T</a> on the matrix object.
To calculate the inverse of a matrix, you can use <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.inv.html">np.linalg.inv()</a> or <a href="docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.I.htmll">.I</a> on the matrix object, remember that the inverse of a matrix is only defined on square matrices, and is does not always exist (for sufficient requirements of invertibility look up the: <a href="https://en.wikipedia.org/wiki/Invertible_matrix#The_invertible_matrix_theorem">The invertible matrix theorem</a>) and it will then raise a LinAlgError. If you multiply the original matrix with its inverse, you get the identity matrix, which is a square matrix with ones on the main diagonal and zeros elsewhere., e.g. $\mathbf{A} \mathbf{A}^{-1} = \mathbf{I_n}$
In the following exercise, you should calculate $\mathbf{A}^T$ multiply it by $\mathbf{A}$ and then inverting the product $\mathbf{AA}^T$ and finally multiply $\mathbf{AA}^T[\mathbf{AA}^T]^{-1}=\mathbf{I}_n$ to get the identity matrix:
```
#Replace the <INSERT>
#We generate a Vandermonde matrix
A = np.mat(np.vander([2,3], 5))
print(A)
#Calculate the transpose of A
At = np.transpose(A)
print(At)
#Calculate the multiplication of A and A^T
AAt = np.dot(A,At)
print(AAt)
#Calculate the inverse of AA^T
AAtInv = np.linalg.inv(AAt)
print(AAtInv)
#Calculate the multiplication of AA^T and (AA^T)^-1
I = np.dot(AAt,AAtInv)
print(I)
#To get the identity matrix we round it because of numerical precision
I = I.round(13)
#Check if the matrix math is correct
checkArray(I,[[1.,0.], [0.,1.]], "the matrix math")
```
### 2.5 Slices
It is possible to select subsets of one-dimensional arrays using <a href="http://docs.scipy.org/doc/numpy/reference/arrays.indexing.html">slices</a>. The basic syntax for slices is $\mathbf{v}$[i:j:k] where i is the starting index, j is the stopping index, and k is the step ($k\neq0$), the default value for k, if it is not specified, is 1. If no i is specified, the default value is 0, and if no j is specified, the default value is the end of the array.
For example [0,1,2,3,4][:3] = [0,1,2] i.e. the three first elements of the array. You can use negative indices also, for example [0,1,2,3,4][-3:] = [2,3,4] i.e. the three last elements.
The following function can be used to concenate 2 or more arrays: <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.concatenate.html">np.concatenate</a>, the syntax is np.concatenate((a1, a2, ...)).
Slice the following array in 3 pieces and concenate them together to form the original array:
```
#Replace the <INSERT>
v = np.arange(1, 9)
print(v)
#The first two elements of v
v1 = v[-2:]
#The last two elements of v
v3 = v[:-2]
#The middle four elements of v
v2 = v[3:7]
print(v1)
print(v2)
print(v3)
#Concatenating the three vectors to get the original array
u = np.concatenate((v1, v2, v3))
```
### 2.6 Stacking
There exist many functions provided by the NumPy library to <a href="http://docs.scipy.org/doc/numpy/reference/routines.array-manipulation.html">manipulate</a> existing arrays. We will try out two of these methods <a href="docs.scipy.org/doc/numpy/reference/generated/numpy.hstack.html">np.hstack()</a> which takes two or more arrays and stack them horizontally to make a single array (column wise, equvivalent to np.concatenate), and <a href="docs.scipy.org/doc/numpy/reference/generated/numpy.vstack.html">np.vstack()</a> which takes two or more arrays and stack them vertically (row wise). The syntax is the following np.vstack((a1, a2, ...)).
Stack the two following array $\mathbf{u}$ and $\mathbf{v}$ to create a 1x20 and a 2x10 array:
```
#Replace the <INSERT>
u = np.arange(1, 11)
v = np.arange(11, 21)
#A 1x20 array
oneRow = np.hstack((u,v))
print(oneRow)
#A 2x10 array
twoRows = np.vstack((u,v))
print(twoRows)
#Check if the stacks are correct
checkArray(oneRow,[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], "the hstack")
checkArray(twoRows,[[1,2,3,4,5,6,7,8,9,10],[11,12,13,14,15,16,17,18,19,20]], "the vstack")
```
### 2.7 PySpark's DenseVector
In PySpark there exists a <a href="https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.linalg.DenseVector">DenseVector</a> class within the module <a href="https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#module-pyspark.mllib.linalg">pyspark.mllib.linalg</a>. The DenseVector stores the values as a NumPy array and delegates the calculations to this object. You can create a new DenseVector by using DenseVector() and passing it an NumPy array or a Python list.
The DenseVector class implements several functions, one important is the dot product, DenseVector.dot(), which operates just like np.ndarray.dot().
The DenseVector save all values as np.float64, so even if you pass it an integer vector, the resulting vector will contain floats. Using the DenseVector in a distributed setting, can be done by either passing functions that contain them to resilient distributed dataset (RDD) transformations or by distributing them directly as RDDs.
Create the DenseVector $\mathbf{u}$ containing the 10 elements [0.1,0.2,...,1.0] and the DenseVector $\mathbf{v}$ containing the 10 elements [1.0,2.0,...,10.0] and calculate the dot product of $\mathbf{u}$ and $\mathbf{v}$:
```
#To use the DenseVector first import it
from pyspark.mllib.linalg import DenseVector
#Replace the <INSERT>
#[0.1,0.2,...,1.0]
u = DenseVector((0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1))
print(u)
#[1.0,2.0,...,10.0]
v = DenseVector((1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0))
print(v)
#The dot product between u and v
dotProduct = np.dot(u,v)
#Check if the dense vectors are correct
check(dotProduct, 38.5, "the dense vectors")
```
| true |
code
| 0.354321 | null | null | null | null |
|
# Inheritance with the Gaussian Class
To give another example of inheritance, take a look at the code in this Jupyter notebook. The Gaussian distribution code is refactored into a generic Distribution class and a Gaussian distribution class. Read through the code in this Jupyter notebook to see how the code works.
The Distribution class takes care of the initialization and the read_data_file method. Then the rest of the Gaussian code is in the Gaussian class. You'll later use this Distribution class in an exercise at the end of the lesson.
Run the code in each cell of this Jupyter notebook. This is a code demonstration, so you do not need to write any code.
```
class Distribution:
def __init__(self, mu=0, sigma=1):
""" Generic distribution class for calculating and
visualizing a probability distribution.
Attributes:
mean (float) representing the mean value of the distribution
stdev (float) representing the standard deviation of the distribution
data_list (list of floats) a list of floats extracted from the data file
"""
self.mean = mu
self.stdev = sigma
self.data = []
def read_data_file(self, file_name):
"""Function to read in data from a txt file. The txt file should have
one number (float) per line. The numbers are stored in the data attribute.
Args:
file_name (string): name of a file to read from
Returns:
None
"""
with open(file_name) as file:
data_list = []
line = file.readline()
while line:
data_list.append(int(line))
line = file.readline()
file.close()
self.data = data_list
import math
import matplotlib.pyplot as plt
class Gaussian(Distribution):
""" Gaussian distribution class for calculating and
visualizing a Gaussian distribution.
Attributes:
mean (float) representing the mean value of the distribution
stdev (float) representing the standard deviation of the distribution
data_list (list of floats) a list of floats extracted from the data file
"""
def __init__(self, mu=0, sigma=1):
Distribution.__init__(self, mu, sigma)
def calculate_mean(self):
"""Function to calculate the mean of the data set.
Args:
None
Returns:
float: mean of the data set
"""
avg = 1.0 * sum(self.data) / len(self.data)
self.mean = avg
return self.mean
def calculate_stdev(self, sample=True):
"""Function to calculate the standard deviation of the data set.
Args:
sample (bool): whether the data represents a sample or population
Returns:
float: standard deviation of the data set
"""
if sample:
n = len(self.data) - 1
else:
n = len(self.data)
mean = self.calculate_mean()
sigma = 0
for d in self.data:
sigma += (d - mean) ** 2
sigma = math.sqrt(sigma / n)
self.stdev = sigma
return self.stdev
def plot_histogram(self):
"""Function to output a histogram of the instance variable data using
matplotlib pyplot library.
Args:
None
Returns:
None
"""
plt.hist(self.data)
plt.title('Histogram of Data')
plt.xlabel('data')
plt.ylabel('count')
def pdf(self, x):
"""Probability density function calculator for the gaussian distribution.
Args:
x (float): point for calculating the probability density function
Returns:
float: probability density function output
"""
return (1.0 / (self.stdev * math.sqrt(2*math.pi))) * math.exp(-0.5*((x - self.mean) / self.stdev) ** 2)
def plot_histogram_pdf(self, n_spaces = 50):
"""Function to plot the normalized histogram of the data and a plot of the
probability density function along the same range
Args:
n_spaces (int): number of data points
Returns:
list: x values for the pdf plot
list: y values for the pdf plot
"""
mu = self.mean
sigma = self.stdev
min_range = min(self.data)
max_range = max(self.data)
# calculates the interval between x values
interval = 1.0 * (max_range - min_range) / n_spaces
x = []
y = []
# calculate the x values to visualize
for i in range(n_spaces):
tmp = min_range + interval*i
x.append(tmp)
y.append(self.pdf(tmp))
# make the plots
fig, axes = plt.subplots(2,sharex=True)
fig.subplots_adjust(hspace=.5)
axes[0].hist(self.data, density=True)
axes[0].set_title('Normed Histogram of Data')
axes[0].set_ylabel('Density')
axes[1].plot(x, y)
axes[1].set_title('Normal Distribution for \n Sample Mean and Sample Standard Deviation')
axes[0].set_ylabel('Density')
plt.show()
return x, y
def __add__(self, other):
"""Function to add together two Gaussian distributions
Args:
other (Gaussian): Gaussian instance
Returns:
Gaussian: Gaussian distribution
"""
result = Gaussian()
result.mean = self.mean + other.mean
result.stdev = math.sqrt(self.stdev ** 2 + other.stdev ** 2)
return result
def __repr__(self):
"""Function to output the characteristics of the Gaussian instance
Args:
None
Returns:
string: characteristics of the Gaussian
"""
return "mean {}, standard deviation {}".format(self.mean, self.stdev)
# initialize two gaussian distributions
gaussian_one = Gaussian(25, 3)
gaussian_two = Gaussian(30, 2)
# initialize a third gaussian distribution reading in a data efile
gaussian_three = Gaussian()
gaussian_three.read_data_file('numbers.txt')
gaussian_three.calculate_mean()
gaussian_three.calculate_stdev()
# print out the mean and standard deviations
print(gaussian_one.mean)
print(gaussian_two.mean)
print(gaussian_one.stdev)
print(gaussian_two.stdev)
print(gaussian_three.mean)
print(gaussian_three.stdev)
# plot histogram of gaussian three
gaussian_three.plot_histogram_pdf()
# add gaussian_one and gaussian_two together
gaussian_one + gaussian_two
```
| true |
code
| 0.891173 | null | null | null | null |
|
```
from IPython import display
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
from utils import Logger
import tensorflow as tf
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
DATA_FOLDER = './tf_data/VGAN/MNIST'
IMAGE_PIXELS = 28*28
NOISE_SIZE = 100
BATCH_SIZE = 100
def noise(n_rows, n_cols):
return np.random.normal(size=(n_rows, n_cols))
def xavier_init(size):
in_dim = size[0] if len(size) == 1 else size[1]
stddev = 1. / np.sqrt(float(in_dim))
return tf.random_uniform(shape=size, minval=-stddev, maxval=stddev)
def images_to_vectors(images):
return images.reshape(images.shape[0], 784)
def vectors_to_images(vectors):
return vectors.reshape(vectors.shape[0], 28, 28, 1)
```
## Load Data
```
def mnist_data():
compose = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((.5,), (.5,))
])
out_dir = '{}/dataset'.format(DATA_FOLDER)
return datasets.MNIST(root=out_dir, train=True, transform=compose, download=True)
# Load data
data = mnist_data()
# Create loader with data, so that we can iterate over it
data_loader = DataLoader(data, batch_size=BATCH_SIZE, shuffle=True)
# Num batches
num_batches = len(data_loader)
```
## Initialize Graph
```
## Discriminator
# Input
X = tf.placeholder(tf.float32, shape=(None, IMAGE_PIXELS))
# Layer 1 Variables
D_W1 = tf.Variable(xavier_init([784, 1024]))
D_B1 = tf.Variable(xavier_init([1024]))
# Layer 2 Variables
D_W2 = tf.Variable(xavier_init([1024, 512]))
D_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
D_W3 = tf.Variable(xavier_init([512, 256]))
D_B3 = tf.Variable(xavier_init([256]))
# Out Layer Variables
D_W4 = tf.Variable(xavier_init([256, 1]))
D_B4 = tf.Variable(xavier_init([1]))
# Store Variables in list
D_var_list = [D_W1, D_B1, D_W2, D_B2, D_W3, D_B3, D_W4, D_B4]
## Generator
# Input
Z = tf.placeholder(tf.float32, shape=(None, NOISE_SIZE))
# Layer 1 Variables
G_W1 = tf.Variable(xavier_init([100, 256]))
G_B1 = tf.Variable(xavier_init([256]))
# Layer 2 Variables
G_W2 = tf.Variable(xavier_init([256, 512]))
G_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
G_W3 = tf.Variable(xavier_init([512, 1024]))
G_B3 = tf.Variable(xavier_init([1024]))
# Out Layer Variables
G_W4 = tf.Variable(xavier_init([1024, 784]))
G_B4 = tf.Variable(xavier_init([784]))
# Store Variables in list
G_var_list = [G_W1, G_B1, G_W2, G_B2, G_W3, G_B3, G_W4, G_B4]
def discriminator(x):
l1 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(x, D_W1) + D_B1, .2), .3)
l2 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l1, D_W2) + D_B2, .2), .3)
l3 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l2, D_W3) + D_B3, .2), .3)
out = tf.matmul(l3, D_W4) + D_B4
return out
def generator(z):
l1 = tf.nn.leaky_relu(tf.matmul(z, G_W1) + G_B1, .2)
l2 = tf.nn.leaky_relu(tf.matmul(l1, G_W2) + G_B2, .2)
l3 = tf.nn.leaky_relu(tf.matmul(l2, G_W3) + G_B3, .2)
out = tf.nn.tanh(tf.matmul(l3, G_W4) + G_B4)
return out
G_sample = generator(Z)
D_real = discriminator(X)
D_fake = discriminator(G_sample)
# Losses
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_real, labels=tf.ones_like(D_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.zeros_like(D_fake)))
D_loss = D_loss_real + D_loss_fake
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.ones_like(D_fake)))
# Optimizers
D_opt = tf.train.AdamOptimizer(2e-4).minimize(D_loss, var_list=D_var_list)
G_opt = tf.train.AdamOptimizer(2e-4).minimize(G_loss, var_list=G_var_list)
```
## Train
#### Testing
```
num_test_samples = 16
test_noise = noise(num_test_samples, NOISE_SIZE)
```
#### Inits
```
num_epochs = 200
# Start interactive session
session = tf.InteractiveSession()
# Init Variables
tf.global_variables_initializer().run()
# Init Logger
logger = Logger(model_name='DCGAN1', data_name='CIFAR10')
```
#### Train
```
# Iterate through epochs
for epoch in range(num_epochs):
for n_batch, (batch,_) in enumerate(data_loader):
# 1. Train Discriminator
X_batch = images_to_vectors(batch.permute(0, 2, 3, 1).numpy())
feed_dict = {X: X_batch, Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, d_error, d_pred_real, d_pred_fake = session.run(
[D_opt, D_loss, D_real, D_fake], feed_dict=feed_dict
)
# 2. Train Generator
feed_dict = {Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, g_error = session.run(
[G_opt, G_loss], feed_dict=feed_dict
)
if n_batch % 100 == 0:
display.clear_output(True)
# Generate images from test noise
test_images = session.run(
G_sample, feed_dict={Z: test_noise}
)
test_images = vectors_to_images(test_images)
# Log Images
logger.log_images(test_images, num_test_samples, epoch, n_batch, num_batches, format='NHWC');
# Log Status
logger.display_status(
epoch, num_epochs, n_batch, num_batches,
d_error, g_error, d_pred_real, d_pred_fake
)
```
| true |
code
| 0.761857 | null | null | null | null |
|
## Set up the dependencies
```
# for reading and validating data
import emeval.input.spec_details as eisd
import emeval.input.phone_view as eipv
import emeval.input.eval_view as eiev
import arrow
# Visualization helpers
import emeval.viz.phone_view as ezpv
import emeval.viz.eval_view as ezev
# For plots
import matplotlib.pyplot as plt
%matplotlib inline
# For maps
import folium
import branca.element as bre
# For easier debugging while working on modules
import importlib
import pandas as pd
import numpy as np
```
## The spec
The spec defines what experiments were done, and over which time ranges. Once the experiment is complete, most of the structure is read back from the data, but we use the spec to validate that it all worked correctly. The spec also contains the ground truth for the legs. Here, we read the spec for the trip to UC Berkeley.
```
DATASTORE_LOC = "bin/data/"
AUTHOR_EMAIL = "[email protected]"
sd_la = eisd.FileSpecDetails(DATASTORE_LOC, AUTHOR_EMAIL, "unimodal_trip_car_bike_mtv_la")
sd_sj = eisd.FileSpecDetails(DATASTORE_LOC, AUTHOR_EMAIL, "car_scooter_brex_san_jose")
sd_ucb = eisd.FileSpecDetails(DATASTORE_LOC, AUTHOR_EMAIL, "train_bus_ebike_mtv_ucb")
```
## Loading the data into a dataframe
```
pv_la = eipv.PhoneView(sd_la)
pv_sj = eipv.PhoneView(sd_sj)
sd_sj.CURR_SPEC_ID
ios_loc_entries = sd_sj.retrieve_data("ucb-sdb-ios-1", ["background/location"],
arrow.get("2019-08-07T14:50:57.445000-07:00").timestamp,
arrow.get("2019-08-07T15:00:16.787000-07:00").timestamp)
ios_location_df = pd.DataFrame([e["data"] for e in ios_loc_entries])
android_loc_entries = sd_sj.retrieve_data("ucb-sdb-android-1", ["background/location"],
arrow.get("2019-08-07T14:50:57.445000-07:00").timestamp,
arrow.get("2019-08-07T15:00:16.787000-07:00").timestamp)
android_location_df = pd.DataFrame([e["data"] for e in android_loc_entries])
android_location_df[["fmt_time"]].loc[30:60]
ios_map = ezpv.display_map_detail_from_df(ios_location_df.loc[20:35])
android_map = ezpv.display_map_detail_from_df(android_location_df.loc[25:50])
fig = bre.Figure()
fig.add_subplot(1, 2, 1).add_child(ios_map)
fig.add_subplot(1, 2, 2).add_child(android_map)
pv_ucb = eipv.PhoneView(sd_ucb)
import pandas as pd
def get_battery_drain_entries(pv):
battery_entry_list = []
for phone_os, phone_map in pv.map().items():
print(15 * "=*")
print(phone_os, phone_map.keys())
for phone_label, phone_detail_map in phone_map.items():
print(4 * ' ', 15 * "-*")
print(4 * ' ', phone_label, phone_detail_map.keys())
# this spec does not have any calibration ranges, but evaluation ranges are actually cooler
for r in phone_detail_map["evaluation_ranges"]:
print(8 * ' ', 30 * "=")
print(8 * ' ',r.keys())
print(8 * ' ',r["trip_id"], r["eval_common_trip_id"], r["eval_role"], len(r["evaluation_trip_ranges"]))
bcs = r["battery_df"]["battery_level_pct"]
delta_battery = bcs.iloc[0] - bcs.iloc[-1]
print("Battery starts at %d, ends at %d, drain = %d" % (bcs.iloc[0], bcs.iloc[-1], delta_battery))
battery_entry = {"phone_os": phone_os, "phone_label": phone_label, "timeline": pv.spec_details.curr_spec["id"],
"run": r["trip_run"], "duration": r["duration"],
"role": r["eval_role_base"], "battery_drain": delta_battery}
battery_entry_list.append(battery_entry)
return battery_entry_list
# We are not going to look at battery life at the evaluation trip level; we will end with evaluation range
# since we want to capture the overall drain for the timeline
battery_entries_list = []
battery_entries_list.extend(get_battery_drain_entries(pv_la))
battery_entries_list.extend(get_battery_drain_entries(pv_sj))
battery_entries_list.extend(get_battery_drain_entries(pv_ucb))
battery_drain_df = pd.DataFrame(battery_entries_list)
battery_drain_df.head()
r2q_map = {"power_control": 0, "HAMFDC": 1, "MAHFDC": 2, "HAHFDC": 3, "accuracy_control": 4}
# right now, only the san jose data has the full comparison
q2r_complete_list = ["power", "HAMFDC", "MAHFDC", "HAHFDC", "accuracy"]
# others only have android or ios
q2r_android_list = ["power", "HAMFDC", "HAHFDC", "accuracy"]
q2r_ios_list = ["power", "MAHFDC", "HAHFDC", "accuracy"]
# Make a number so that can get the plots to come out in order
battery_drain_df["quality"] = battery_drain_df.role.apply(lambda r: r2q_map[r])
battery_drain_df.query("role == 'MAHFDC'").head()
```
## Displaying various groupings using boxplots
```
ifig, ax_array = plt.subplots(nrows=2,ncols=3,figsize=(12,6), sharex=False, sharey=True)
timeline_list = ["train_bus_ebike_mtv_ucb", "car_scooter_brex_san_jose", "unimodal_trip_car_bike_mtv_la"]
for i, tl in enumerate(timeline_list):
battery_drain_df.query("timeline == @tl & phone_os == 'android'").boxplot(ax = ax_array[0][i], column=["battery_drain"], by=["quality"], showbox=False, whis="range")
ax_array[0][i].set_title(tl)
battery_drain_df.query("timeline == @tl & phone_os == 'ios'").boxplot(ax = ax_array[1][i], column=["battery_drain"], by=["quality"], showbox=False, whis="range")
ax_array[1][i].set_title("")
for i, ax in enumerate(ax_array[0]):
if i == 1:
ax.set_xticklabels(q2r_complete_list)
else:
ax.set_xticklabels(q2r_android_list)
ax.set_xlabel("")
for i, ax in enumerate(ax_array[1]):
if i == 1:
ax.set_xticklabels(q2r_complete_list)
else:
ax.set_xticklabels(q2r_ios_list)
ax.set_xlabel("")
ax_array[0][0].set_ylabel("Battery drain (android)")
ax_array[1][0].set_ylabel("Battery drain (iOS)")
ifig.suptitle("Power v/s quality over multiple timelines")
# ifig.tight_layout()
battery_drain_df.query("quality == 1 & phone_os == 'ios' & timeline == 'car_scooter_brex_san_jose'").iloc[1:].describe()
battery_drain_df.query("quality == 0 & phone_os == 'ios' & timeline == 'car_scooter_brex_san_jose'").iloc[1:].describe()
battery_drain_df.query("quality == 2 & phone_os == 'ios' & timeline == 'car_scooter_brex_san_jose'").iloc[1:].describe()
```
| true |
code
| 0.267432 | null | null | null | null |
|
## Computing native contacts with MDTraj
Using the definition from Best, Hummer, and Eaton, "Native contacts determine protein folding mechanisms in atomistic simulations" PNAS (2013) [10.1073/pnas.1311599110](http://dx.doi.org/10.1073/pnas.1311599110)
Eq. (1) of the SI defines the expression for the fraction of native contacts, $Q(X)$:
$$
Q(X) = \frac{1}{|S|} \sum_{(i,j) \in S} \frac{1}{1 + \exp[\beta(r_{ij}(X) - \lambda r_{ij}^0)]},
$$
where
- $X$ is a conformation,
- $r_{ij}(X)$ is the distance between atoms $i$ and $j$ in conformation $X$,
- $r^0_{ij}$ is the distance from heavy atom i to j in the native state conformation,
- $S$ is the set of all pairs of heavy atoms $(i,j)$ belonging to residues $\theta_i$ and $\theta_j$ such that $|\theta_i - \theta_j| > 3$ and $r^0_{i,} < 4.5 \unicode{x212B}$,
- $\beta=5 \unicode{x212B}^{-1}$,
- $\lambda=1.8$ for all-atom simulations
```
import numpy as np
import mdtraj as md
from itertools import combinations
def best_hummer_q(traj, native):
"""Compute the fraction of native contacts according the definition from
Best, Hummer and Eaton [1]
Parameters
----------
traj : md.Trajectory
The trajectory to do the computation for
native : md.Trajectory
The 'native state'. This can be an entire trajecory, or just a single frame.
Only the first conformation is used
Returns
-------
q : np.array, shape=(len(traj),)
The fraction of native contacts in each frame of `traj`
References
----------
..[1] Best, Hummer, and Eaton, "Native contacts determine protein folding
mechanisms in atomistic simulations" PNAS (2013)
"""
BETA_CONST = 50 # 1/nm
LAMBDA_CONST = 1.8
NATIVE_CUTOFF = 0.45 # nanometers
# get the indices of all of the heavy atoms
heavy = native.topology.select_atom_indices('heavy')
# get the pairs of heavy atoms which are farther than 3
# residues apart
heavy_pairs = np.array(
[(i,j) for (i,j) in combinations(heavy, 2)
if abs(native.topology.atom(i).residue.index - \
native.topology.atom(j).residue.index) > 3])
# compute the distances between these pairs in the native state
heavy_pairs_distances = md.compute_distances(native[0], heavy_pairs)[0]
# and get the pairs s.t. the distance is less than NATIVE_CUTOFF
native_contacts = heavy_pairs[heavy_pairs_distances < NATIVE_CUTOFF]
print("Number of native contacts", len(native_contacts))
# now compute these distances for the whole trajectory
r = md.compute_distances(traj, native_contacts)
# and recompute them for just the native state
r0 = md.compute_distances(native[0], native_contacts)
q = np.mean(1.0 / (1 + np.exp(BETA_CONST * (r - LAMBDA_CONST * r0))), axis=1)
return q
# pull a random protein from the PDB
# (The unitcell info happens to be wrong)
traj = md.load_pdb('http://www.rcsb.org/pdb/files/2MI7.pdb')
# just for example, use the first frame as the 'native' conformation
q = best_hummer_q(traj, traj[0])
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(q)
plt.xlabel('Frame', fontsize=14)
plt.ylabel('Q(X)', fontsize=14)
plt.show()
```
| true |
code
| 0.815233 | null | null | null | null |
|
# The Central Limit Theorem
Elements of Data Science
by [Allen Downey](https://allendowney.com)
[MIT License](https://opensource.org/licenses/MIT)
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# If we're running on Colab, install empiricaldist
# https://pypi.org/project/empiricaldist/
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
!pip install empiricaldist
```
## The Central Limit Theorem
According to our friends at [Wikipedia](https://en.wikipedia.org/wiki/Central_limit_theorem):
> The central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (informally a bell curve) even if the original variables themselves are not normally distributed.
This theorem is useful for two reasons:
1. It offers an explanation for the ubiquity of normal distributions in the natural and engineered world. If you measure something that depends on the sum of many independent factors, the distribution of the measurements will often be approximately normal.
2. In the context of mathematical statistics it provides a way to approximate the sampling distribution of many statistics, at least, as Wikipedia warns us, "in some situations".
In this notebook, we'll explore those situations.
## Rolling dice
I'll start by adding up the totals for 1, 2, and 3 dice.
The following function simulates rolling a six-sided die.
```
def roll(size):
return np.random.randint(1, 7, size=size)
```
If we roll it 1000 times, we expect each value to appear roughly the same number of times.
```
sample = roll(1000)
```
Here's what the PMF looks like.
```
from empiricaldist import Pmf
pmf = Pmf.from_seq(sample)
pmf.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
To simulate rolling two dice, I'll create an array with 1000 rows and 2 columns.
```
a = roll(size=(1000, 2))
a.shape
```
And then add up the columns.
```
sample2 = a.sum(axis=1)
sample2.shape
```
The result is a sample of 1000 sums of two dice. Here's what that PMF looks like.
```
pmf2 = Pmf.from_seq(sample2)
pmf2.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
And here's what it looks like with three dice.
```
a = roll(size=(1000, 3))
sample3 = a.sum(axis=1)
pmf3 = Pmf.from_seq(sample3)
pmf3.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
With one die, the distribution is uniform. With two dice, it's a triangle. With three dice, it starts to have the shape of a bell curve.
Here are the three PMFs on the same axes, for comparison.
```
pmf.plot(label='1 die')
pmf2.plot(label='2 dice')
pmf3.plot(label='3 dice')
plt.xlabel('Outcome')
plt.ylabel('Probability')
plt.legend();
```
## Gamma distributions
In the previous section, we saw that the sum of values from a uniform distribution starts to look like a bell curve when we add up just a few values.
Now let's do the same thing with values from a gamma distribution.
NumPy provides a function to generate random values from a gamma distribution with a given mean.
```
mean = 2
gamma_sample = np.random.gamma(mean, size=1000)
```
Here's what the distribution looks like, this time using a CDF.
```
from empiricaldist import Cdf
cdf1 = Cdf.from_seq(gamma_sample)
cdf1.plot()
plt.xlabel('Outcome')
plt.ylabel('CDF');
```
It doesn't look like like a normal distribution. To see the differences more clearly, we can plot the CDF of the data on top of a normal model with the same mean and standard deviation.
```
from scipy.stats import norm
def plot_normal_model(sample, **options):
"""Plot the CDF of a normal distribution with the
same mean and std of the sample.
sample: sequence of values
options: passed to plt.plot
"""
mean, std = np.mean(sample), np.std(sample)
xs = np.linspace(np.min(sample), np.max(sample))
ys = norm.cdf(xs, mean, std)
plt.plot(xs, ys, alpha=0.4, **options)
```
Here's what that looks like for a gamma distribution with mean 2.
```
from empiricaldist import Cdf
plot_normal_model(gamma_sample, color='C0', label='Normal model')
cdf1.plot(label='Sample 1')
plt.xlabel('Outcome')
plt.ylabel('CDF');
```
There are clear differences between the data and the model. Let's see how that looks when we start adding up values.
The following function computes the sum of gamma distributions with a given mean.
```
def sum_of_gammas(mean, num):
"""Sample the sum of gamma variates.
mean: mean of the gamma distribution
num: number of values to add up
"""
a = np.random.gamma(mean, size=(1000, num))
sample = a.sum(axis=1)
return sample
```
Here's what the sum of two gamma variates looks like:
```
gamma_sample2 = sum_of_gammas(2, 2)
cdf2 = Cdf.from_seq(gamma_sample2)
plot_normal_model(gamma_sample, color='C0')
cdf1.plot(label='Sum of 1 gamma')
plot_normal_model(gamma_sample2, color='C1')
cdf2.plot(label='Sum of 2 gamma')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend();
```
The normal model is a better fit for the sum of two gamma variates, but there are still evident differences. Let's see how big `num` has to be before it converges.
First I'll wrap the previous example in a function.
```
def plot_gammas(mean, nums):
"""Plot the sum of gamma variates and a normal model.
mean: mean of the gamma distribution
nums: sequence of sizes
"""
for num in nums:
sample = sum_of_gammas(mean, num)
plot_normal_model(sample, color='gray')
Cdf.from_seq(sample).plot(label=f'num = {num}')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend()
```
With `mean=2` it doesn't take long for the sum of gamma variates to approximate a normal distribution.
```
mean = 2
plot_gammas(mean, [2, 5, 10])
```
However, that doesn't mean that all gamma distribution behave the same way. In general, the higher the variance, the longer it takes to converge.
With a gamma distribution, smaller means lead to higher variance. With `mean=0.2`, the sum of 10 values is still not normal.
```
mean = 0.2
plot_gammas(mean, [2, 5, 10])
```
We have to crank `num` up to 100 before the convergence looks good.
```
mean = 0.2
plot_gammas(mean, [20, 50, 100])
```
With `mean=0.02`, we have to add up 1000 values before the distribution looks normal.
```
mean = 0.02
plot_gammas(mean, [200, 500, 1000])
```
## Pareto distributions
The gamma distributions in the previous section have higher variance that the uniform distribution we started with, so we have to add up more values to get the distribution of the sum to look normal.
The Pareto distribution is even more extreme. Depending on the parameter, `alpha`, the variance can be large, very large, or infinite.
Here's a function that generates the sum of values from a Pareto distribution with a given parameter.
```
def sum_of_paretos(alpha, num):
a = np.random.pareto(alpha, size=(1000, num))
sample = a.sum(axis=1)
return sample
```
And here's a function that plots the results.
```
def plot_paretos(mean, nums):
for num in nums:
sample = sum_of_paretos(mean, num)
plot_normal_model(sample, color='gray')
Cdf.from_seq(sample).plot(label=f'num = {num}')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend()
```
With `alpha=3` the Pareto distribution is relatively well-behaved, and the sum converges to a normal distribution with a moderate number of values.
```
alpha = 3
plot_paretos(alpha, [10, 20, 50])
```
With `alpha=2`, we don't get very good convergence even with 1000 values.
```
alpha = 2
plot_paretos(alpha, [200, 500, 1000])
```
With `alpha=1.5`, it's even worse.
```
alpha = 1.5
plot_paretos(alpha, [2000, 5000, 10000])
```
And with `alpha=1`, it's beyond hopeless.
```
alpha = 1
plot_paretos(alpha, [10000, 20000, 50000])
```
In fact, when `alpha` is 2 or less, the variance of the Pareto distribution is infinite, and the central limit theorem does not apply. The disrtribution of the sum never converges to a normal distribution.
However, there is no practical difference between a distribution like Pareto that never converges and other high-variance distributions that converge in theory, but only with an impractical number of values.
## Summary
The central limit theorem is an important result in mathematical statistics. And it explains why so many distributions in the natural and engineered world are approximately normal.
But it doesn't always apply:
* In theory the central limit theorem doesn't apply when variance is infinite.
* In practice it might be irrelevant when variance is high.
| true |
code
| 0.710283 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/PytorchLightning/pytorch-lightning/blob/master/notebooks/04-transformers-text-classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Finetune 🤗 Transformers Models with PyTorch Lightning ⚡
This notebook will use HuggingFace's `datasets` library to get data, which will be wrapped in a `LightningDataModule`. Then, we write a class to perform text classification on any dataset from the[ GLUE Benchmark](https://gluebenchmark.com/). (We just show CoLA and MRPC due to constraint on compute/disk)
[HuggingFace's NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=cola) can help you get a feel for the two datasets we will use and what tasks they are solving for.
---
- Give us a ⭐ [on Github](https://www.github.com/PytorchLightning/pytorch-lightning/)
- Check out [the documentation](https://pytorch-lightning.readthedocs.io/en/latest/)
- Ask a question on [GitHub Discussions](https://github.com/PyTorchLightning/pytorch-lightning/discussions/)
- Join us [on Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)
- [HuggingFace datasets](https://github.com/huggingface/datasets)
- [HuggingFace transformers](https://github.com/huggingface/transformers)
### Setup
```
!pip install pytorch-lightning datasets transformers
from argparse import ArgumentParser
from datetime import datetime
from typing import Optional
import datasets
import numpy as np
import pytorch_lightning as pl
import torch
from torch.utils.data import DataLoader
from transformers import (
AdamW,
AutoModelForSequenceClassification,
AutoConfig,
AutoTokenizer,
get_linear_schedule_with_warmup,
glue_compute_metrics
)
```
## GLUE DataModule
```
class GLUEDataModule(pl.LightningDataModule):
task_text_field_map = {
'cola': ['sentence'],
'sst2': ['sentence'],
'mrpc': ['sentence1', 'sentence2'],
'qqp': ['question1', 'question2'],
'stsb': ['sentence1', 'sentence2'],
'mnli': ['premise', 'hypothesis'],
'qnli': ['question', 'sentence'],
'rte': ['sentence1', 'sentence2'],
'wnli': ['sentence1', 'sentence2'],
'ax': ['premise', 'hypothesis']
}
glue_task_num_labels = {
'cola': 2,
'sst2': 2,
'mrpc': 2,
'qqp': 2,
'stsb': 1,
'mnli': 3,
'qnli': 2,
'rte': 2,
'wnli': 2,
'ax': 3
}
loader_columns = [
'datasets_idx',
'input_ids',
'token_type_ids',
'attention_mask',
'start_positions',
'end_positions',
'labels'
]
def __init__(
self,
model_name_or_path: str,
task_name: str ='mrpc',
max_seq_length: int = 128,
train_batch_size: int = 32,
eval_batch_size: int = 32,
**kwargs
):
super().__init__()
self.model_name_or_path = model_name_or_path
self.task_name = task_name
self.max_seq_length = max_seq_length
self.train_batch_size = train_batch_size
self.eval_batch_size = eval_batch_size
self.text_fields = self.task_text_field_map[task_name]
self.num_labels = self.glue_task_num_labels[task_name]
self.tokenizer = AutoTokenizer.from_pretrained(self.model_name_or_path, use_fast=True)
def setup(self, stage):
self.dataset = datasets.load_dataset('glue', self.task_name)
for split in self.dataset.keys():
self.dataset[split] = self.dataset[split].map(
self.convert_to_features,
batched=True,
remove_columns=['label'],
)
self.columns = [c for c in self.dataset[split].column_names if c in self.loader_columns]
self.dataset[split].set_format(type="torch", columns=self.columns)
self.eval_splits = [x for x in self.dataset.keys() if 'validation' in x]
def prepare_data(self):
datasets.load_dataset('glue', self.task_name)
AutoTokenizer.from_pretrained(self.model_name_or_path, use_fast=True)
def train_dataloader(self):
return DataLoader(self.dataset['train'], batch_size=self.train_batch_size)
def val_dataloader(self):
if len(self.eval_splits) == 1:
return DataLoader(self.dataset['validation'], batch_size=self.eval_batch_size)
elif len(self.eval_splits) > 1:
return [DataLoader(self.dataset[x], batch_size=self.eval_batch_size) for x in self.eval_splits]
def test_dataloader(self):
if len(self.eval_splits) == 1:
return DataLoader(self.dataset['test'], batch_size=self.eval_batch_size)
elif len(self.eval_splits) > 1:
return [DataLoader(self.dataset[x], batch_size=self.eval_batch_size) for x in self.eval_splits]
def convert_to_features(self, example_batch, indices=None):
# Either encode single sentence or sentence pairs
if len(self.text_fields) > 1:
texts_or_text_pairs = list(zip(example_batch[self.text_fields[0]], example_batch[self.text_fields[1]]))
else:
texts_or_text_pairs = example_batch[self.text_fields[0]]
# Tokenize the text/text pairs
features = self.tokenizer.batch_encode_plus(
texts_or_text_pairs,
max_length=self.max_seq_length,
pad_to_max_length=True,
truncation=True
)
# Rename label to labels to make it easier to pass to model forward
features['labels'] = example_batch['label']
return features
```
#### You could use this datamodule with standalone PyTorch if you wanted...
```
dm = GLUEDataModule('distilbert-base-uncased')
dm.prepare_data()
dm.setup('fit')
next(iter(dm.train_dataloader()))
```
## GLUE Model
```
class GLUETransformer(pl.LightningModule):
def __init__(
self,
model_name_or_path: str,
num_labels: int,
learning_rate: float = 2e-5,
adam_epsilon: float = 1e-8,
warmup_steps: int = 0,
weight_decay: float = 0.0,
train_batch_size: int = 32,
eval_batch_size: int = 32,
eval_splits: Optional[list] = None,
**kwargs
):
super().__init__()
self.save_hyperparameters()
self.config = AutoConfig.from_pretrained(model_name_or_path, num_labels=num_labels)
self.model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, config=self.config)
self.metric = datasets.load_metric(
'glue',
self.hparams.task_name,
experiment_id=datetime.now().strftime("%d-%m-%Y_%H-%M-%S")
)
def forward(self, **inputs):
return self.model(**inputs)
def training_step(self, batch, batch_idx):
outputs = self(**batch)
loss = outputs[0]
return loss
def validation_step(self, batch, batch_idx, dataloader_idx=0):
outputs = self(**batch)
val_loss, logits = outputs[:2]
if self.hparams.num_labels >= 1:
preds = torch.argmax(logits, axis=1)
elif self.hparams.num_labels == 1:
preds = logits.squeeze()
labels = batch["labels"]
return {'loss': val_loss, "preds": preds, "labels": labels}
def validation_epoch_end(self, outputs):
if self.hparams.task_name == 'mnli':
for i, output in enumerate(outputs):
# matched or mismatched
split = self.hparams.eval_splits[i].split('_')[-1]
preds = torch.cat([x['preds'] for x in output]).detach().cpu().numpy()
labels = torch.cat([x['labels'] for x in output]).detach().cpu().numpy()
loss = torch.stack([x['loss'] for x in output]).mean()
self.log(f'val_loss_{split}', loss, prog_bar=True)
split_metrics = {f"{k}_{split}": v for k, v in self.metric.compute(predictions=preds, references=labels).items()}
self.log_dict(split_metrics, prog_bar=True)
return loss
preds = torch.cat([x['preds'] for x in outputs]).detach().cpu().numpy()
labels = torch.cat([x['labels'] for x in outputs]).detach().cpu().numpy()
loss = torch.stack([x['loss'] for x in outputs]).mean()
self.log('val_loss', loss, prog_bar=True)
self.log_dict(self.metric.compute(predictions=preds, references=labels), prog_bar=True)
return loss
def setup(self, stage):
if stage == 'fit':
# Get dataloader by calling it - train_dataloader() is called after setup() by default
train_loader = self.train_dataloader()
# Calculate total steps
self.total_steps = (
(len(train_loader.dataset) // (self.hparams.train_batch_size * max(1, self.hparams.gpus)))
// self.hparams.accumulate_grad_batches
* float(self.hparams.max_epochs)
)
def configure_optimizers(self):
"Prepare optimizer and schedule (linear warmup and decay)"
model = self.model
no_decay = ["bias", "LayerNorm.weight"]
optimizer_grouped_parameters = [
{
"params": [p for n, p in model.named_parameters() if not any(nd in n for nd in no_decay)],
"weight_decay": self.hparams.weight_decay,
},
{
"params": [p for n, p in model.named_parameters() if any(nd in n for nd in no_decay)],
"weight_decay": 0.0,
},
]
optimizer = AdamW(optimizer_grouped_parameters, lr=self.hparams.learning_rate, eps=self.hparams.adam_epsilon)
scheduler = get_linear_schedule_with_warmup(
optimizer, num_warmup_steps=self.hparams.warmup_steps, num_training_steps=self.total_steps
)
scheduler = {
'scheduler': scheduler,
'interval': 'step',
'frequency': 1
}
return [optimizer], [scheduler]
@staticmethod
def add_model_specific_args(parent_parser):
parser = ArgumentParser(parents=[parent_parser], add_help=False)
parser.add_argument("--learning_rate", default=2e-5, type=float)
parser.add_argument("--adam_epsilon", default=1e-8, type=float)
parser.add_argument("--warmup_steps", default=0, type=int)
parser.add_argument("--weight_decay", default=0.0, type=float)
return parser
```
### ⚡ Quick Tip
- Combine arguments from your DataModule, Model, and Trainer into one for easy and robust configuration
```
def parse_args(args=None):
parser = ArgumentParser()
parser = pl.Trainer.add_argparse_args(parser)
parser = GLUEDataModule.add_argparse_args(parser)
parser = GLUETransformer.add_model_specific_args(parser)
parser.add_argument('--seed', type=int, default=42)
return parser.parse_args(args)
def main(args):
pl.seed_everything(args.seed)
dm = GLUEDataModule.from_argparse_args(args)
dm.prepare_data()
dm.setup('fit')
model = GLUETransformer(num_labels=dm.num_labels, eval_splits=dm.eval_splits, **vars(args))
trainer = pl.Trainer.from_argparse_args(args)
return dm, model, trainer
```
# Training
## CoLA
See an interactive view of the CoLA dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=cola)
```
mocked_args = """
--model_name_or_path albert-base-v2
--task_name cola
--max_epochs 3
--gpus 1""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
## MRPC
See an interactive view of the MRPC dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=mrpc)
```
mocked_args = """
--model_name_or_path distilbert-base-cased
--task_name mrpc
--max_epochs 3
--gpus 1""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
## MNLI
- The MNLI dataset is huge, so we aren't going to bother trying to train it here.
- Let's just make sure our multi-dataloader logic is right by skipping over training and going straight to validation.
See an interactive view of the MRPC dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=mnli)
```
mocked_args = """
--model_name_or_path distilbert-base-uncased
--task_name mnli
--max_epochs 1
--gpus 1
--limit_train_batches 10
--progress_bar_refresh_rate 20""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
<code style="color:#792ee5;">
<h1> <strong> Congratulations - Time to Join the Community! </strong> </h1>
</code>
Congratulations on completing this notebook tutorial! If you enjoyed this and would like to join the Lightning movement, you can do so in the following ways!
### Star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) on GitHub
The easiest way to help our community is just by starring the GitHub repos! This helps raise awareness of the cool tools we're building.
* Please, star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning)
### Join our [Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)!
The best way to keep up to date on the latest advancements is to join our community! Make sure to introduce yourself and share your interests in `#general` channel
### Interested by SOTA AI models ! Check out [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts)
Bolts has a collection of state-of-the-art models, all implemented in [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) and can be easily integrated within your own projects.
* Please, star [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts)
### Contributions !
The best way to contribute to our community is to become a code contributor! At any time you can go to [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) or [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts) GitHub Issues page and filter for "good first issue".
* [Lightning good first issue](https://github.com/PyTorchLightning/pytorch-lightning/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* [Bolt good first issue](https://github.com/PyTorchLightning/pytorch-lightning-bolts/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* You can also contribute your own notebooks with useful examples !
### Great thanks from the entire Pytorch Lightning Team for your interest !
<img src="https://github.com/PyTorchLightning/pytorch-lightning/blob/master/docs/source/_static/images/logo.png?raw=true" width="800" height="200" />
| true |
code
| 0.861626 | null | null | null | null |
|
# Anomaly detection
Anomaly detection is a machine learning task that consists in spotting so-called outliers.
“An outlier is an observation in a data set which appears to be inconsistent with the remainder of that set of data.”
Johnson 1992
“An outlier is an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism.”
Outlier/Anomaly
Hawkins 1980
### Types of anomaly detection setups
- Supervised AD
- Labels available for both normal data and anomalies
- Similar to rare class mining / imbalanced classification
- Semi-supervised AD (Novelty Detection)
- Only normal data available to train
- The algorithm learns on normal data only
- Unsupervised AD (Outlier Detection)
- no labels, training set = normal + abnormal data
- Assumption: anomalies are very rare
```
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
```
Let's first get familiar with different unsupervised anomaly detection approaches and algorithms. In order to visualise the output of the different algorithms we consider a toy data set consisting in a two-dimensional Gaussian mixture.
### Generating the data set
```
from sklearn.datasets import make_blobs
X, y = make_blobs(n_features=2, centers=3, n_samples=500,
random_state=42)
X.shape
plt.figure()
plt.scatter(X[:, 0], X[:, 1])
plt.show()
```
## Anomaly detection with density estimation
```
from sklearn.neighbors.kde import KernelDensity
# Estimate density with a Gaussian kernel density estimator
kde = KernelDensity(kernel='gaussian')
kde = kde.fit(X)
kde
kde_X = kde.score_samples(X)
print(kde_X.shape) # contains the log-likelihood of the data. The smaller it is the rarer is the sample
from scipy.stats.mstats import mquantiles
alpha_set = 0.95
tau_kde = mquantiles(kde_X, 1. - alpha_set)
n_samples, n_features = X.shape
X_range = np.zeros((n_features, 2))
X_range[:, 0] = np.min(X, axis=0) - 1.
X_range[:, 1] = np.max(X, axis=0) + 1.
h = 0.1 # step size of the mesh
x_min, x_max = X_range[0]
y_min, y_max = X_range[1]
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
grid = np.c_[xx.ravel(), yy.ravel()]
Z_kde = kde.score_samples(grid)
Z_kde = Z_kde.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_kde, levels=tau_kde, colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={tau_kde[0]: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.show()
```
## now with One-Class SVM
The problem of density based estimation is that they tend to become inefficient when the dimensionality of the data increase. It's the so-called curse of dimensionality that affects particularly density estimation algorithms. The one-class SVM algorithm can be used in such cases.
```
from sklearn.svm import OneClassSVM
nu = 0.05 # theory says it should be an upper bound of the fraction of outliers
ocsvm = OneClassSVM(kernel='rbf', gamma=0.05, nu=nu)
ocsvm.fit(X)
X_outliers = X[ocsvm.predict(X) == -1]
Z_ocsvm = ocsvm.decision_function(grid)
Z_ocsvm = Z_ocsvm.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_ocsvm, levels=[0], colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={0: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X_outliers[:, 0], X_outliers[:, 1], color='red')
plt.show()
```
### Support vectors - Outliers
The so-called support vectors of the one-class SVM form the outliers
```
X_SV = X[ocsvm.support_]
n_SV = len(X_SV)
n_outliers = len(X_outliers)
print('{0:.2f} <= {1:.2f} <= {2:.2f}?'.format(1./n_samples*n_outliers, nu, 1./n_samples*n_SV))
```
Only the support vectors are involved in the decision function of the One-Class SVM.
1. Plot the level sets of the One-Class SVM decision function as we did for the true density.
2. Emphasize the Support vectors.
```
plt.figure()
plt.contourf(xx, yy, Z_ocsvm, 10, cmap=plt.cm.Blues_r)
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.scatter(X_SV[:, 0], X_SV[:, 1], color='orange')
plt.show()
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
**Change** the `gamma` parameter and see it's influence on the smoothness of the decision function.
</li>
</ul>
</div>
```
# %load solutions/22_A-anomaly_ocsvm_gamma.py
```
## Isolation Forest
Isolation Forest is an anomaly detection algorithm based on trees. The algorithm builds a number of random trees and the rationale is that if a sample is isolated it should alone in a leaf after very few random splits. Isolation Forest builds a score of abnormality based the depth of the tree at which samples end up.
```
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(n_estimators=300, contamination=0.10)
iforest = iforest.fit(X)
Z_iforest = iforest.decision_function(grid)
Z_iforest = Z_iforest.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_iforest,
levels=[iforest.threshold_],
colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15,
fmt={iforest.threshold_: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.show()
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
Illustrate graphically the influence of the number of trees on the smoothness of the decision function?
</li>
</ul>
</div>
```
# %load solutions/22_B-anomaly_iforest_n_trees.py
```
# Illustration on Digits data set
We will now apply the IsolationForest algorithm to spot digits written in an unconventional way.
```
from sklearn.datasets import load_digits
digits = load_digits()
```
The digits data set consists in images (8 x 8) of digits.
```
images = digits.images
labels = digits.target
images.shape
i = 102
plt.figure(figsize=(2, 2))
plt.title('{0}'.format(labels[i]))
plt.axis('off')
plt.imshow(images[i], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
```
To use the images as a training set we need to flatten the images.
```
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
data.shape
X = data
y = digits.target
X.shape
```
Let's focus on digit 5.
```
X_5 = X[y == 5]
X_5.shape
fig, axes = plt.subplots(1, 5, figsize=(10, 4))
for ax, x in zip(axes, X_5[:5]):
img = x.reshape(8, 8)
ax.imshow(img, cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
1. Let's use IsolationForest to find the top 5% most abnormal images.
2. Let's plot them !
```
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(contamination=0.05)
iforest = iforest.fit(X_5)
```
Compute the level of "abnormality" with `iforest.decision_function`. The lower, the more abnormal.
```
iforest_X = iforest.decision_function(X_5)
plt.hist(iforest_X);
```
Let's plot the strongest inliers
```
X_strong_inliers = X_5[np.argsort(iforest_X)[-10:]]
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
for i, ax in zip(range(len(X_strong_inliers)), axes.ravel()):
ax.imshow(X_strong_inliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
Let's plot the strongest outliers
```
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
X_outliers = X_5[iforest.predict(X_5) == -1]
for i, ax in zip(range(len(X_outliers)), axes.ravel()):
ax.imshow(X_outliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
Rerun the same analysis with all the other digits
</li>
</ul>
</div>
```
# %load solutions/22_C-anomaly_digits.py
```
| true |
code
| 0.646823 | null | null | null | null |
|
# Intro to machine learning - k-means
---
Scikit-learn has a nice set of unsupervised learning routines which can be used to explore clustering in the parameter space.
In this notebook we will use k-means, included in Scikit-learn, to demonstrate how the different rocks occupy different regions in the available parameter space.
Let's load the data using pandas:
```
import pandas as pd
import numpy as np
df = pd.read_csv("../data/2016_ML_contest_training_data.csv")
df.head()
df.describe()
df = df.dropna()
```
## Calculate RHOB from DeltaPHI and PHIND
```
def rhob(phi_rhob, Rho_matrix= 2650.0, Rho_fluid=1000.0):
"""
Rho_matrix (sandstone) : 2.65 g/cc
Rho_matrix (Limestome): 2.71 g/cc
Rho_matrix (Dolomite): 2.876 g/cc
Rho_matrix (Anyhydrite): 2.977 g/cc
Rho_matrix (Salt): 2.032 g/cc
Rho_fluid (fresh water): 1.0 g/cc (is this more mud-like?)
Rho_fluid (salt water): 1.1 g/cc
see wiki.aapg.org/Density-neutron_log_porosity
returns density porosity log """
return Rho_matrix*(1 - phi_rhob) + Rho_fluid*phi_rhob
phi_rhob = 2*(df.PHIND/100)/(1 - df.DeltaPHI/100) - df.DeltaPHI/100
calc_RHOB = rhob(phi_rhob)
df['RHOB'] = calc_RHOB
df.describe()
```
We can define a Python dictionary to relate facies with the integer label on the `DataFrame`
```
facies_dict = {1:'sandstone', 2:'c_siltstone', 3:'f_siltstone', 4:'marine_silt_shale',
5:'mudstone', 6:'wackentstone', 7:'dolomite', 8:'packstone', 9:'bafflestone'}
df["s_Facies"] = df.Facies.map(lambda x: facies_dict[x])
df.head()
```
We can easily visualize the properties of each facies and how they compare using a `PairPlot`. The library `seaborn` integrates with matplotlib to make these kind of plots easily.
```
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
g = sns.PairGrid(df, hue="s_Facies", vars=['GR','RHOB','PE','ILD_log10'], size=4)
g.map_upper(plt.scatter,**dict(alpha=0.4))
g.map_lower(plt.scatter,**dict(alpha=0.4))
g.map_diag(plt.hist,**dict(bins=20))
g.add_legend()
g.set(alpha=0.5)
```
It is very clear that it's hard to separate these facies in feature space. Let's just select a couple of facies and using Pandas, select the rows in the `DataFrame` that contain information about those facies
```
selected = ['f_siltstone', 'bafflestone', 'wackentstone']
dfs = pd.concat(list(map(lambda x: df[df.s_Facies == x], selected)))
g = sns.PairGrid(dfs, hue="s_Facies", vars=['GR','RHOB','PE','ILD_log10'], size=4)
g.map_upper(plt.scatter,**dict(alpha=0.4))
g.map_lower(plt.scatter,**dict(alpha=0.4))
g.map_diag(plt.hist,**dict(bins=20))
g.add_legend()
g.set(alpha=0.5)
# Make X and y
X = dfs[['GR','ILD_log10','PE']].as_matrix()
y = dfs['Facies'].values
```
Use scikit-learn StandardScaler to normalize the data. Needed for k-means.
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.3)
from sklearn.cluster import KMeans
clf = KMeans(n_clusters=4, random_state=1).fit(X)
y_pred = clf.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, alpha=0.3)
clf.inertia_
```
<hr />
<p style="color:gray">©2017 Agile Geoscience. Licensed CC-BY.</p>
| true |
code
| 0.528838 | null | null | null | null |
|
# Beating the betting firms with linear models
* **Data Source:** [https://www.kaggle.com/hugomathien/soccer](https://www.kaggle.com/hugomathien/soccer)
* **Author:** Anders Munk-Nielsen
**Result:** It is possible to do better than the professional betting firms in terms of predicting each outcome (although they may be maximizing profit rather than trying to predict outcomes). This is using a linear model, and it requires us to use a lot of variables, though.
**Perspectives:** We can only model 1(win), but there are *three* outcomes: Lose, Draw, and Win.
```
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme()
# Read
d = pd.read_csv('football_probs.csv')
# Data types
d.date = pd.to_datetime(d.date)
cols_to_cat = ['league', 'season', 'team', 'country']
for c in cols_to_cat:
d[c] = d[c].astype('category')
```
Visualizing the home field advantage.
```
sns.histplot(data=d, x='goal_diff', hue='home', discrete=True);
plt.xlim([-7,7]);
```
Outcome variables
```
# Lose, Draw, Win
d['outcome'] = 'L'
d.loc[d.goal_diff == 0.0, 'outcome'] = 'D'
d.loc[d.goal_diff > 0.0, 'outcome'] = 'W'
# Win dummy (as float (will become useful later))
d['win'] = (d.goal_diff > 0.0).astype(float)
```
# Odds to probabilities
### Convenient lists of variable names
* `cols_common`: All variables that are unrelated to betting
* `betting_firms`: The prefix that defines the name of the betting firms, e.g. B365 for Bet365
* `firm_vars`: A dictionary returning the variables for a firm, e.g. `firm_vars['BW']` returns `BWA`, `BWD`, `BWH` (for Away, Draw, Home team win).
```
# # List of the names of all firms that we have betting prices for
betting_firms = np.unique([c[:-4] for c in d.columns if c[-1] in ['A', 'H', 'D']])
betting_firms
# find all columns in our dataframe that are *not* betting variables
cols_common = [c for c in d.columns if (c[-4:-1] != '_Pr') & (c[-9:] != 'overround')]
print(f'Non-odds variables: {cols_common}')
d[d.home].groupby('win')['B365_PrW'].mean().to_frame('Bet 365 Pr(win)')
sns.histplot(d, x='B365_PrW', hue='win');
```
## Is there more information in the mean?
If all firms are drawing random IID signals, then the average prediction should be a better estimator than any individual predictor.
```
firms_drop = ['BS', 'GB', 'PS', 'SJ'] # these are missing in too many years
cols_prW = [f'{c}_PrW' for c in betting_firms if c not in firms_drop]
d['avg_PrW'] = d[cols_prW].mean(1)
cols_prW += ['avg_PrW']
I = d.win == True
fig, ax = plt.subplots();
ax.hist(d.loc[I,'avg_PrW'], bins=30, alpha=0.3, label='Avg. prediction')
ax.hist(d.loc[I,'B365_PrW'], bins=30, alpha=0.3, label='B365')
ax.hist(d.loc[I,'BW_PrW'], bins=30, alpha=0.3, label='BW')
ax.legend();
ax.set_xlabel('Pr(win) [only matches where win==1]');
```
### RMSE comparison
* RMSE: Root Mean Squared Error. Whenever we have a candidate prediction guess, $\hat{y}_i$, we can evaluate $$ RMSE = \sqrt{ N^{-1}\sum_{i=1}^N (y_i - \hat{y}_i)^2 }. $$
```
def RMSE(yhat, y) -> float:
'''Root mean squared error: between yvar and y'''
q = (yhat - y)**2
return np.sqrt(np.mean(q))
def RMSE_agg(data: pd.core.frame.DataFrame, y: str) -> pd.core.series.Series:
'''RMSE_agg: Aggregates all columns, computing RMSE against the variable y for each column
'''
assert y in data.columns
y = data['win']
# local function computing RMSE for a specific column, yvar, against y
def RMSE_(yhat):
diff_sq = (yhat - y) ** 2
return np.sqrt(np.mean(diff_sq))
# do not compute RMSE against the real outcome :)
mycols = [c for c in data.columns if c != 'win']
# return aggregated dataframe (which becomes a pandas series)
return data[mycols].agg(RMSE_)
I = d[cols_prW].notnull().all(1) # only run comparison on subsample where all odds were observed
x_ = RMSE_agg(d[cols_prW + ['win']], 'win');
ax = x_.plot.bar();
ax.set_ylim([x_.min()*.999, x_.max()*1.001]);
ax.set_ylabel('RMSE');
```
# Linear Probability Models
Estimate a bunch of models where $y_i = 1(\text{win})$.
## Using `numpy`
```
d['home_'] = d.home.astype(float)
I = d[['home_', 'win'] + cols_prW].notnull().all(axis=1)
X = d.loc[I, ['home_'] + cols_prW].values
y = d.loc[I, 'win'].values.reshape(-1,1)
N = I.sum()
oo = np.ones((N,1))
X = np.hstack([oo, X])
betahat = np.linalg.inv(X.T @ X) @ X.T @ y
pd.DataFrame({'beta':betahat.flatten()}, index=['const', 'home'] + cols_prW)
```
## Using `statsmodels`
(Cheating, but faster...)
```
reg_addition = ' + '.join(cols_prW)
model_string = f'win ~ {reg_addition} + home + team'
cols_all = cols_prW + ['win', 'home']
I = d[cols_all].notnull().all(1) # no missings in any variables used in the prediction model
Itrain = I & (d.date < '2015-01-01') # for estimating our prediction model
Iholdout = I & (d.date >= '2015-01-01') # for assessing the model fit
# run regression
r = smf.ols(model_string, d[Itrain]).fit()
yhat = r.predict(d[I]).to_frame('AMN_PrW')
d.loc[I, 'AMN_PrW'] = yhat
print('Estimates with Team FE')
r.params.loc[['home[T.True]'] + cols_prW].to_frame('Beta')
```
### Plot estimates, $\hat{\beta}$
```
ax = r.params.loc[cols_prW].plot.bar();
ax.set_ylabel('Coefficient (loading in optimal prediction)');
ax.set_xlabel('Betting firm prediction');
```
### Plot model fit out of sample: avg. 1(win) vs. avg. $\hat{y}$
```
# predicted win rates from all firms and our new predicted probability
cols = cols_prW + ['AMN_PrW']
```
**Home matches:** `home == True`
```
x_ = d.loc[(d.win == 1.0) & (d.home == True) & (Iholdout == True), cols].mean()
ax = x_.plot(kind='bar');
ax.set_ylim([x_.min()*0.995, x_.max()*1.005]);
ax.set_title('Out of sample fit: won matches as Home');
ax.set_xlabel('Betting firm prediction');
ax.set_ylabel('Pr(win) (only won home matches)');
```
**Away matches:** `home == False`
```
x_ = d.loc[(d.win == 1.0) & (d.home == False) & (Iholdout == True), cols].mean()
ax = x_.plot(kind='bar');
ax.set_ylim([x_.min()*0.995, x_.max()*1.005]);
ax.set_ylabel('Pr(win) (only won away matches)');
ax.set_title('Out of sample fit: won matches as Away');
```
### RMSE
(evaluated in the holdout sample, of course.)
```
cols_ = cols_prW + ['AMN_PrW', 'win']
I = Iholdout & d[cols_].notnull().all(1) # only run comparison on subsample where all odds were observed
x_ = RMSE_agg(d.loc[I,cols_], y='win');
ax = x_.plot.bar();
ax.set_ylim([x_.min()*.999, x_.max()*1.001]);
ax.set_ylabel('RMSE (out of sample)');
```
| true |
code
| 0.577674 | null | null | null | null |
|
```
import keras
keras.__version__
```
# Using a pre-trained convnet
This notebook contains the code sample found in Chapter 5, Section 3 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
----
A common and highly effective approach to deep learning on small image datasets is to leverage a pre-trained network. A pre-trained network
is simply a saved network previously trained on a large dataset, typically on a large-scale image classification task. If this original
dataset is large enough and general enough, then the spatial feature hierarchy learned by the pre-trained network can effectively act as a
generic model of our visual world, and hence its features can prove useful for many different computer vision problems, even though these
new problems might involve completely different classes from those of the original task. For instance, one might train a network on
ImageNet (where classes are mostly animals and everyday objects) and then re-purpose this trained network for something as remote as
identifying furniture items in images. Such portability of learned features across different problems is a key advantage of deep learning
compared to many older shallow learning approaches, and it makes deep learning very effective for small-data problems.
In our case, we will consider a large convnet trained on the ImageNet dataset (1.4 million labeled images and 1000 different classes).
ImageNet contains many animal classes, including different species of cats and dogs, and we can thus expect to perform very well on our cat
vs. dog classification problem.
We will use the VGG16 architecture, developed by Karen Simonyan and Andrew Zisserman in 2014, a simple and widely used convnet architecture
for ImageNet. Although it is a bit of an older model, far from the current state of the art and somewhat heavier than many other recent
models, we chose it because its architecture is similar to what you are already familiar with, and easy to understand without introducing
any new concepts. This may be your first encounter with one of these cutesie model names -- VGG, ResNet, Inception, Inception-ResNet,
Xception... you will get used to them, as they will come up frequently if you keep doing deep learning for computer vision.
There are two ways to leverage a pre-trained network: *feature extraction* and *fine-tuning*. We will cover both of them. Let's start with
feature extraction.
## Feature extraction
Feature extraction consists of using the representations learned by a previous network to extract interesting features from new samples.
These features are then run through a new classifier, which is trained from scratch.
As we saw previously, convnets used for image classification comprise two parts: they start with a series of pooling and convolution
layers, and they end with a densely-connected classifier. The first part is called the "convolutional base" of the model. In the case of
convnets, "feature extraction" will simply consist of taking the convolutional base of a previously-trained network, running the new data
through it, and training a new classifier on top of the output.
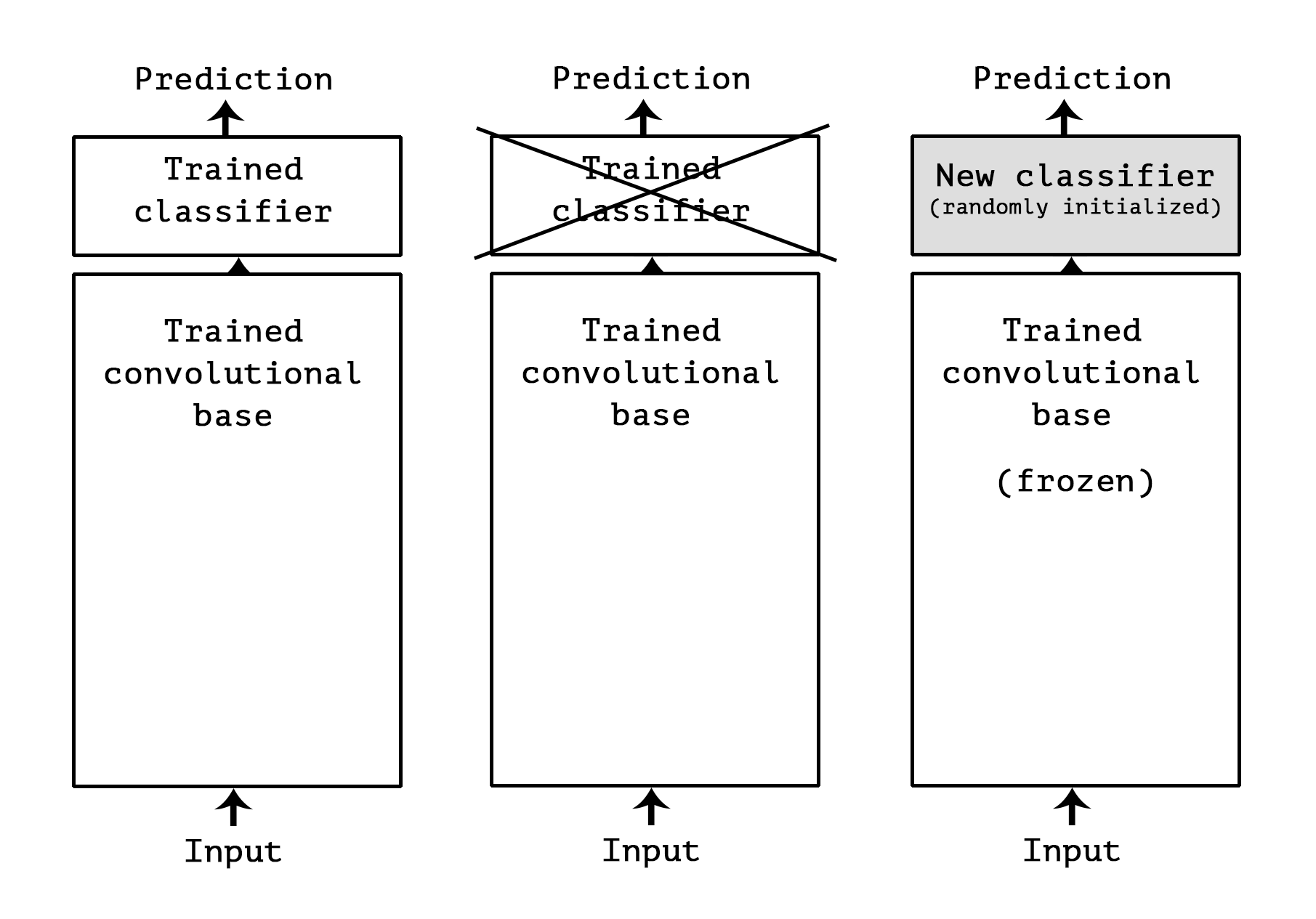
Why only reuse the convolutional base? Could we reuse the densely-connected classifier as well? In general, it should be avoided. The
reason is simply that the representations learned by the convolutional base are likely to be more generic and therefore more reusable: the
feature maps of a convnet are presence maps of generic concepts over a picture, which is likely to be useful regardless of the computer
vision problem at hand. On the other end, the representations learned by the classifier will necessarily be very specific to the set of
classes that the model was trained on -- they will only contain information about the presence probability of this or that class in the
entire picture. Additionally, representations found in densely-connected layers no longer contain any information about _where_ objects are
located in the input image: these layers get rid of the notion of space, whereas the object location is still described by convolutional
feature maps. For problems where object location matters, densely-connected features would be largely useless.
Note that the level of generality (and therefore reusability) of the representations extracted by specific convolution layers depends on
the depth of the layer in the model. Layers that come earlier in the model extract local, highly generic feature maps (such as visual
edges, colors, and textures), while layers higher-up extract more abstract concepts (such as "cat ear" or "dog eye"). So if your new
dataset differs a lot from the dataset that the original model was trained on, you may be better off using only the first few layers of the
model to do feature extraction, rather than using the entire convolutional base.
In our case, since the ImageNet class set did contain multiple dog and cat classes, it is likely that it would be beneficial to reuse the
information contained in the densely-connected layers of the original model. However, we will chose not to, in order to cover the more
general case where the class set of the new problem does not overlap with the class set of the original model.
Let's put this in practice by using the convolutional base of the VGG16 network, trained on ImageNet, to extract interesting features from
our cat and dog images, and then training a cat vs. dog classifier on top of these features.
The VGG16 model, among others, comes pre-packaged with Keras. You can import it from the `keras.applications` module. Here's the list of
image classification models (all pre-trained on the ImageNet dataset) that are available as part of `keras.applications`:
* Xception
* InceptionV3
* ResNet50
* VGG16
* VGG19
* MobileNet
Let's instantiate the VGG16 model:
```
from keras.applications import VGG16
conv_base = VGG16(weights='imagenet',
include_top=False,
input_shape=(150, 150, 3))
```
We passed three arguments to the constructor:
* `weights`, to specify which weight checkpoint to initialize the model from
* `include_top`, which refers to including or not the densely-connected classifier on top of the network. By default, this
densely-connected classifier would correspond to the 1000 classes from ImageNet. Since we intend to use our own densely-connected
classifier (with only two classes, cat and dog), we don't need to include it.
* `input_shape`, the shape of the image tensors that we will feed to the network. This argument is purely optional: if we don't pass it,
then the network will be able to process inputs of any size.
Here's the detail of the architecture of the VGG16 convolutional base: it's very similar to the simple convnets that you are already
familiar with.
```
conv_base.summary()
```
The final feature map has shape `(4, 4, 512)`. That's the feature on top of which we will stick a densely-connected classifier.
At this point, there are two ways we could proceed:
* Running the convolutional base over our dataset, recording its output to a Numpy array on disk, then using this data as input to a
standalone densely-connected classifier similar to those you have seen in the first chapters of this book. This solution is very fast and
cheap to run, because it only requires running the convolutional base once for every input image, and the convolutional base is by far the
most expensive part of the pipeline. However, for the exact same reason, this technique would not allow us to leverage data augmentation at
all.
* Extending the model we have (`conv_base`) by adding `Dense` layers on top, and running the whole thing end-to-end on the input data. This
allows us to use data augmentation, because every input image is going through the convolutional base every time it is seen by the model.
However, for this same reason, this technique is far more expensive than the first one.
We will cover both techniques. Let's walk through the code required to set-up the first one: recording the output of `conv_base` on our
data and using these outputs as inputs to a new model.
We will start by simply running instances of the previously-introduced `ImageDataGenerator` to extract images as Numpy arrays as well as
their labels. We will extract features from these images simply by calling the `predict` method of the `conv_base` model.
```
import os
import numpy as np
from keras.preprocessing.image import ImageDataGenerator
base_dir = '/Users/fchollet/Downloads/cats_and_dogs_small'
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'validation')
test_dir = os.path.join(base_dir, 'test')
datagen = ImageDataGenerator(rescale=1./255)
batch_size = 20
def extract_features(directory, sample_count):
features = np.zeros(shape=(sample_count, 4, 4, 512))
labels = np.zeros(shape=(sample_count))
generator = datagen.flow_from_directory(
directory,
target_size=(150, 150),
batch_size=batch_size,
class_mode='binary')
i = 0
for inputs_batch, labels_batch in generator:
features_batch = conv_base.predict(inputs_batch)
features[i * batch_size : (i + 1) * batch_size] = features_batch
labels[i * batch_size : (i + 1) * batch_size] = labels_batch
i += 1
if i * batch_size >= sample_count:
# Note that since generators yield data indefinitely in a loop,
# we must `break` after every image has been seen once.
break
return features, labels
train_features, train_labels = extract_features(train_dir, 2000)
validation_features, validation_labels = extract_features(validation_dir, 1000)
test_features, test_labels = extract_features(test_dir, 1000)
```
The extracted features are currently of shape `(samples, 4, 4, 512)`. We will feed them to a densely-connected classifier, so first we must
flatten them to `(samples, 8192)`:
```
train_features = np.reshape(train_features, (2000, 4 * 4 * 512))
validation_features = np.reshape(validation_features, (1000, 4 * 4 * 512))
test_features = np.reshape(test_features, (1000, 4 * 4 * 512))
```
At this point, we can define our densely-connected classifier (note the use of dropout for regularization), and train it on the data and
labels that we just recorded:
```
from keras import models
from keras import layers
from keras import optimizers
model = models.Sequential()
model.add(layers.Dense(256, activation='relu', input_dim=4 * 4 * 512))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=2e-5),
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(train_features, train_labels,
epochs=30,
batch_size=20,
validation_data=(validation_features, validation_labels))
```
Training is very fast, since we only have to deal with two `Dense` layers -- an epoch takes less than one second even on CPU.
Let's take a look at the loss and accuracy curves during training:
```
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
We reach a validation accuracy of about 90%, much better than what we could achieve in the previous section with our small model trained from
scratch. However, our plots also indicate that we are overfitting almost from the start -- despite using dropout with a fairly large rate.
This is because this technique does not leverage data augmentation, which is essential to preventing overfitting with small image datasets.
Now, let's review the second technique we mentioned for doing feature extraction, which is much slower and more expensive, but which allows
us to leverage data augmentation during training: extending the `conv_base` model and running it end-to-end on the inputs. Note that this
technique is in fact so expensive that you should only attempt it if you have access to a GPU: it is absolutely intractable on CPU. If you
cannot run your code on GPU, then the previous technique is the way to go.
Because models behave just like layers, you can add a model (like our `conv_base`) to a `Sequential` model just like you would add a layer.
So you can do the following:
```
from keras import models
from keras import layers
model = models.Sequential()
model.add(conv_base)
model.add(layers.Flatten())
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
```
This is what our model looks like now:
```
model.summary()
```
As you can see, the convolutional base of VGG16 has 14,714,688 parameters, which is very large. The classifier we are adding on top has 2
million parameters.
Before we compile and train our model, a very important thing to do is to freeze the convolutional base. "Freezing" a layer or set of
layers means preventing their weights from getting updated during training. If we don't do this, then the representations that were
previously learned by the convolutional base would get modified during training. Since the `Dense` layers on top are randomly initialized,
very large weight updates would be propagated through the network, effectively destroying the representations previously learned.
In Keras, freezing a network is done by setting its `trainable` attribute to `False`:
```
print('This is the number of trainable weights '
'before freezing the conv base:', len(model.trainable_weights))
conv_base.trainable = False
print('This is the number of trainable weights '
'after freezing the conv base:', len(model.trainable_weights))
```
With this setup, only the weights from the two `Dense` layers that we added will be trained. That's a total of four weight tensors: two per
layer (the main weight matrix and the bias vector). Note that in order for these changes to take effect, we must first compile the model.
If you ever modify weight trainability after compilation, you should then re-compile the model, or these changes would be ignored.
Now we can start training our model, with the same data augmentation configuration that we used in our previous example:
```
from keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
# This is the target directory
train_dir,
# All images will be resized to 150x150
target_size=(150, 150),
batch_size=20,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=2e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50,
verbose=2)
model.save('cats_and_dogs_small_3.h5')
```
Let's plot our results again:
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
As you can see, we reach a validation accuracy of about 96%. This is much better than our small convnet trained from scratch.
## Fine-tuning
Another widely used technique for model reuse, complementary to feature extraction, is _fine-tuning_.
Fine-tuning consists in unfreezing a few of the top layers
of a frozen model base used for feature extraction, and jointly training both the newly added part of the model (in our case, the
fully-connected classifier) and these top layers. This is called "fine-tuning" because it slightly adjusts the more abstract
representations of the model being reused, in order to make them more relevant for the problem at hand.
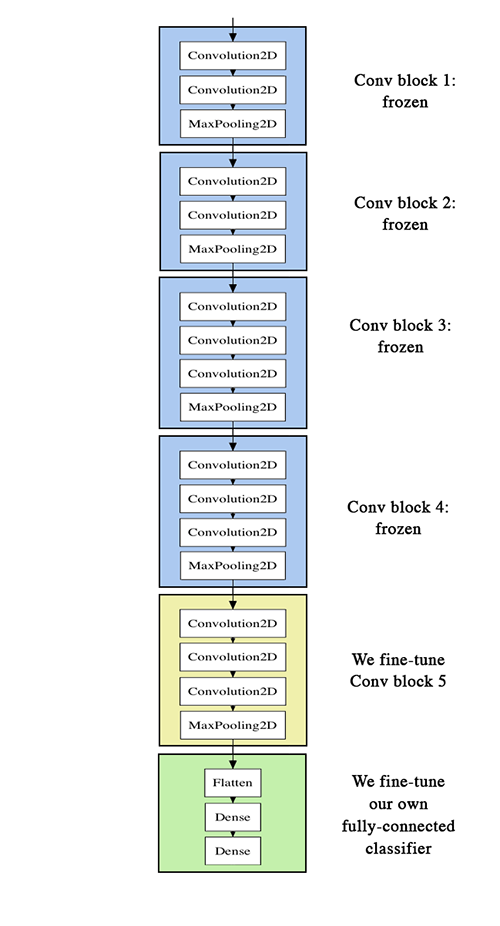
We have stated before that it was necessary to freeze the convolution base of VGG16 in order to be able to train a randomly initialized
classifier on top. For the same reason, it is only possible to fine-tune the top layers of the convolutional base once the classifier on
top has already been trained. If the classified wasn't already trained, then the error signal propagating through the network during
training would be too large, and the representations previously learned by the layers being fine-tuned would be destroyed. Thus the steps
for fine-tuning a network are as follow:
* 1) Add your custom network on top of an already trained base network.
* 2) Freeze the base network.
* 3) Train the part you added.
* 4) Unfreeze some layers in the base network.
* 5) Jointly train both these layers and the part you added.
We have already completed the first 3 steps when doing feature extraction. Let's proceed with the 4th step: we will unfreeze our `conv_base`,
and then freeze individual layers inside of it.
As a reminder, this is what our convolutional base looks like:
```
conv_base.summary()
```
We will fine-tune the last 3 convolutional layers, which means that all layers up until `block4_pool` should be frozen, and the layers
`block5_conv1`, `block5_conv2` and `block5_conv3` should be trainable.
Why not fine-tune more layers? Why not fine-tune the entire convolutional base? We could. However, we need to consider that:
* Earlier layers in the convolutional base encode more generic, reusable features, while layers higher up encode more specialized features. It is
more useful to fine-tune the more specialized features, as these are the ones that need to be repurposed on our new problem. There would
be fast-decreasing returns in fine-tuning lower layers.
* The more parameters we are training, the more we are at risk of overfitting. The convolutional base has 15M parameters, so it would be
risky to attempt to train it on our small dataset.
Thus, in our situation, it is a good strategy to only fine-tune the top 2 to 3 layers in the convolutional base.
Let's set this up, starting from where we left off in the previous example:
```
conv_base.trainable = True
set_trainable = False
for layer in conv_base.layers:
if layer.name == 'block5_conv1':
set_trainable = True
if set_trainable:
layer.trainable = True
else:
layer.trainable = False
```
Now we can start fine-tuning our network. We will do this with the RMSprop optimizer, using a very low learning rate. The reason for using
a low learning rate is that we want to limit the magnitude of the modifications we make to the representations of the 3 layers that we are
fine-tuning. Updates that are too large may harm these representations.
Now let's proceed with fine-tuning:
```
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=100,
validation_data=validation_generator,
validation_steps=50)
model.save('cats_and_dogs_small_4.h5')
```
Let's plot our results using the same plotting code as before:
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
These curves look very noisy. To make them more readable, we can smooth them by replacing every loss and accuracy with exponential moving
averages of these quantities. Here's a trivial utility function to do this:
```
def smooth_curve(points, factor=0.8):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
plt.plot(epochs,
smooth_curve(acc), 'bo', label='Smoothed training acc')
plt.plot(epochs,
smooth_curve(val_acc), 'b', label='Smoothed validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs,
smooth_curve(loss), 'bo', label='Smoothed training loss')
plt.plot(epochs,
smooth_curve(val_loss), 'b', label='Smoothed validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
These curves look much cleaner and more stable. We are seeing a nice 1% absolute improvement.
Note that the loss curve does not show any real improvement (in fact, it is deteriorating). You may wonder, how could accuracy improve if the
loss isn't decreasing? The answer is simple: what we display is an average of pointwise loss values, but what actually matters for accuracy
is the distribution of the loss values, not their average, since accuracy is the result of a binary thresholding of the class probability
predicted by the model. The model may still be improving even if this isn't reflected in the average loss.
We can now finally evaluate this model on the test data:
```
test_generator = test_datagen.flow_from_directory(
test_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
test_loss, test_acc = model.evaluate_generator(test_generator, steps=50)
print('test acc:', test_acc)
```
Here we get a test accuracy of 97%. In the original Kaggle competition around this dataset, this would have been one of the top results.
However, using modern deep learning techniques, we managed to reach this result using only a very small fraction of the training data
available (about 10%). There is a huge difference between being able to train on 20,000 samples compared to 2,000 samples!
## Take-aways: using convnets with small datasets
Here's what you should take away from the exercises of these past two sections:
* Convnets are the best type of machine learning models for computer vision tasks. It is possible to train one from scratch even on a very
small dataset, with decent results.
* On a small dataset, overfitting will be the main issue. Data augmentation is a powerful way to fight overfitting when working with image
data.
* It is easy to reuse an existing convnet on a new dataset, via feature extraction. This is a very valuable technique for working with
small image datasets.
* As a complement to feature extraction, one may use fine-tuning, which adapts to a new problem some of the representations previously
learned by an existing model. This pushes performance a bit further.
Now you have a solid set of tools for dealing with image classification problems, in particular with small datasets.
| true |
code
| 0.825343 | null | null | null | null |
|
# Filled Julia set
___
Let $C\in \mathbb{C}$ is fixed. A *Filled Julia set* $K_C$ is the set of $z\in \mathbb{C}$ which satisfy $\ f^n_C(z)$ $(n \ge 1)$is bounded :
$$K_C = \bigl\{ z\in \mathbb{C}\bigm|\{f^n_C(z)\}_{n\ge 1} : bounded\bigr\},$$
where $\ \ f^1_C(z) = f_C(z) = z^2 + C $, $\ \ f^n_C = f^{n-1}_C \circ f_C$.
For more details, see [Wikipedia--Filled Julia set](https://en.wikipedia.org/wiki/Filled_Julia_set).
___
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def filledjulia(x_min, x_max, y_min, y_max, C, N, x_pix, y_pix, R):
'''
calculate where of z is in the Filled Julia set
'''
x = np.linspace(x_min, x_max, x_pix).astype(np.float32)
y = np.linspace(y_max, y_min, y_pix).reshape(y_pix, 1).astype(np.float32) * 1j
# below of y-axis is smaller
z = x + y #broadcasting by numpy
counter = np.zeros_like(z, dtype=np.uint32)
boolean = np.less(abs(z), R)
for i in range(N):
z[boolean] = z[boolean]**2 + C
boolean = np.less(abs(z), R)
if not boolean.any():
break # finish if all the elements of boolean are False
counter[boolean] += 1
return counter
def draw_fj(x_min, x_max, y_min, y_max, C, N,
x_pix=1000, y_pix=1000, R=5, colormap='viridis'):
'''
draw a Filled Julia set
'''
counter = filledjulia(x_min, x_max, y_min, y_max, C, N, x_pix, y_pix, R)
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(1,1,1)
ax.set_xticks(np.linspace(x_min, x_max, 5))
ax.set_yticks(np.linspace(y_min, y_max, 5))
ax.set_title("Filled Julia Set: C = {}".format(C))
plt.imshow(counter, extent=[x_min, x_max, y_min, y_max], cmap=colormap)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.835 - 0.235j
N = 200
colormap = 'prism'
draw_fj(x_min, x_max, y_min, y_max, C, N, colormap=colormap)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
x_min = -1.7
x_max = 1.7
y_min = -1.7
y_max = 1.7
C = -0.8 + 0.35j
N = 50
draw_fj(x_min, x_max, y_min, y_max, C, N)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = 0.25
N = 100
draw_fj(x_min, x_max, y_min, y_max, C, N)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
```
The complement of a Filled Julia set is called a *Fatou set*.
# Julia set
___
A *Julia set* $J_C$ is the **boundary** of a Filled Julia set:
$$J_C = \partial K_C.$$
For more details, see [Wikipedia--Julia set](https://en.wikipedia.org/wiki/Julia_set).
___
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def find_1_boundary(pix, boolean):
'''
for each row,
if five or more "True" are arranged continuously,
rewrite it to "False" except two at each end.
'''
boolean = np.copy(boolean)
for i in range(pix):
if not boolean[i].any():
continue
coord = np.where(boolean[i])[0]
if len(coord) <= 5:
continue
for k in range(len(coord)-5):
if coord[k+5]-coord[k] == 5:
boolean[i, coord[k+3]] = False
return boolean
def findboundary(x_pix, y_pix, boolean):
'''
for each row and column, execute the function of 'find_1_boundary'.
'''
boundary_x = find_1_boundary(y_pix, boolean)
boundary_y = find_1_boundary(x_pix, boolean.transpose()).transpose()
boundary = boundary_x | boundary_y
return boundary
def julia(x_min, x_max, y_min, y_max, C, N, N_b, x_pix, y_pix, R):
'''
calculate where of z is a Julia set
if n >= N_b, find the boundary of the set.
'''
x = np.linspace(x_min, x_max, x_pix).astype(np.float32)
y = np.linspace(y_max, y_min, y_pix).reshape(y_pix, 1).astype(np.float32) * 1j
z = x + y
boundary = np.zeros_like(z, dtype=bool)
boolean = np.less(abs(z), R)
for i in range(N):
z[boolean] = z[boolean]**2 + C
boolean = np.less(abs(z), R)
if boolean.any() == False:
break
elif i >= N_b-1: # remember i starts 0
boundary = boundary | findboundary(x_pix, y_pix, boolean)
return boundary
def draw_j(x_min, x_max, y_min, y_max, C, N, N_b,
x_pix=1000, y_pix=1000, R=5, colormap='binary'):
'''
draw a Julia set
'''
boundary = julia(x_min, x_max, y_min, y_max, C, N, N_b, x_pix, y_pix, R)
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(1,1,1)
ax.set_xticks(np.linspace(x_min, x_max, 5))
ax.set_yticks(np.linspace(y_min, y_max, 5))
ax.set_title("Julia set: C = {}".format(C))
plt.imshow(boundary, extent=[x_min, x_max, y_min, y_max], cmap='binary')
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.835 - 0.235j
N = 200
N_b = 30
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.8 + 0.35j
N = 50
N_b = 20
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = 0.25
N = 30
N_b = 30
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
```
| true |
code
| 0.591546 | null | null | null | null |
|
```
!conda install --yes scikit-learn
!conda install --yes matplotlib
!conda install --yes seaborn
from sklearn.feature_selection import SelectFromModel
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn import preprocessing
from sklearn.svm import LinearSVC
from sklearn import linear_model
import matplotlib.pyplot as plt
import datetime
import seaborn
import pandas
df = pandas.read_csv('../data/datasource.csv').set_index('Ocorrencia')
```
### Checking out duplicate values
Assuming that the 'Ocorrencia' is a unique code for the transaction itself. Let's check if there's any duplicated occurrence.
```python
len(df.index.unique())
```
If the dataset doesn't present any duplicated values, this piece of code should return, as output, 150.000 data entries. Nevertheless it returned only 64.958 values - meaning that this dataset presents around 85.042 duplicated data entries.
```python
len(df) - len(df.index.unique())
```
The duplicated values will be kept on analysis and training in modeling step. Due the nature of this dataset, this duplicate values could have been naturally generated - meaning that one occurrence could occur more than once - or, due the lack of available training material, some transactions could have been artificially generated.
--------------------------------
```
# Checking the number of unique values.
len(df.index.unique())
# Checking the number of duplicated entries.
len(df) - len(df.index.unique())
```
### Exploratory Analysis
Section aimed on checking the data distribution and data behaviour.
- N.A. values?
- Outliers?
- Min.
- Max.
- Mean.
- Stdev.
-------------------------
```
df.describe()
```
### Describe Analysis Result
This section summarizes the initial analysis on this dataset.
The command below allows to summarize each variable and retrieve the main statistical characteristics.
```python
df.describe()
```
The first thing to be noticed is at 'Sacado' variable - the amount of money withdrawn.
| Statistical Measurement | Value |
| :---------------------: | :----------: |
| Mean | -88.602261 |
| Standard Deviation | 247.302373 |
| Min | -19656.53 |
| Max | -0.00 |
How can be observed on this chart. The behaviour of 'Sacado' variable is pretty weird. First of all, this variable presents the highest standard deviation of all variables (247.30).
```python
df.describe().loc['std'].sort_values(ascending=False).head()
```
The mean, min and max values are pretty strange as well - with all of them being negative or null values. How this values could be negative/null values if this variable it was meant to represent the total withdrawn value of the transaction?
__Possible errors:__
- Acquistion errors?
- Parsing issues?
Other variables seems to behave pretty well (well distributed along the mean value - almost a normal curve) - even didn't knowing what they represent (the max values are high? the min values are low?).
_obs: Even with the lower deviation. On training, a simple normalization will be made on this dataset._
-------------
```
df.describe().loc['std'].sort_values(ascending=False).head()
df[df.Sacado >= 0]
```
### Some plots
On this section are plots for visualizing the dispersion of some 'random' variables.
----------------
```
df[['PP1', 'PP2', 'PP6', 'PP21']].hist()
# As it can be observed. The Sacado variable has a lot of outliers - removing and analysing it alone
# (for not disturbing the scale)
df[['PP1', 'PP2', 'PP21', 'PP6', 'Sacado']].boxplot()
# There are outliers on it - predicted it on histogram.
df[['PP1', 'PP2', 'PP6', 'PP21']].boxplot()
df[['Sacado']].boxplot()
```
### Seeking for N.A. values
This dataset does not present N.A./Blank values.
----------------------------
```
sum(df.index.isna())
dict_na = {
'columns': list(df.columns),
'na': []
}
for i in range(len(df.columns)):
dict_na.get('na').append(sum(df[df.columns[i]].isna()))
pandas.DataFrame(dict_na).set_index('columns')
```
### Does this dataset is non-balanced?
This section aims on checking if the dataset is non-balanced - are more frauds than non-frauds? Vice-Versa?
Table below assumes that the y variable - Fraude - has only 2 unique values - presented in table.
```python
df.Fraude.unique()
```
| Value | Meaning | Total | Percentage |
| :---: | :-------: | :------: | :--------: |
| 0 | Non Fraud | 149.763 | 99,842 % |
| 1 | Fraud | 237 | 0,0158 % |
As can be observed on the table above. It's been assumed that 0 represents a non-fraudulent transaction and 1 represents a fraudulent transaction. This dataset is pretty unbalanced - with less than 1 % being fraudulent transactions (237 data entries). This scenario, on model training steps would be a problem - the model probably will be overfitted in fraudulents occurrences. To prevent it, it must be added some new - artificially generated or naturally acquired - fraudulents data entries.
----------------------------------------
```
# Checking how many unique entries this variable presents.
df.Fraude.unique()
# Checking how many data entries are non-fraud or 0
print(len(df[df['Fraude'] == 0]))
# Checking the percentage of non-fraud transactions
print(len(df[df['Fraude'] == 0])/len(df.Fraude))
# Checking how many data entries are fraud or 1
len(df[df['Fraude'] == 1])
# Checking the percentage of fraud transactions
print(len(df[df['Fraude'] == 1])/len(df.Fraude))
```
### Dimensionality Reduction
This section aims on reduct the dimensionality of this dataset.
__It can be used:__
- linear regression, correlation and statistically relevance;
- PCA;
_obs: despite the robustness of PCA, some articles presents issues on its performance - losing to simpler techniques._
-----------------------
```
occurrence = pandas.Series(df.index)
x = pandas.DataFrame(df[df.columns[1:-1]])
y = pandas.DataFrame(df[df.columns[-1]])
# Multiple Linear Regression
lm = linear_model.LinearRegression().fit(x, y)
attr_reduction = SelectFromModel(lm, prefit=True)
df_pca = pandas.DataFrame(attr_reduction.transform(x))
```
### Building Predictors
Three models will be implemented - if none of them supply the needs, new models could be choosen - and compared. Not only the assertiveness rate will be considered. The most problematic issue are False Negatives occurences - when the occurrence is Fraudulent however the model classified it as a Non-fraudulent occurence - if this happens the model will "lose" some points. False positives could be sent to a human validation - not so problematic as False Negatives.
__Models__:
- Linear Regression;
- Support Vector Machines;
- Random Forest.
_obs: Random forest classifier, when compared with other classifiers, presented 1 advantage point and 1 disavantage point - it wasn't able to converge in polynomial time (when compared to Linear Regression and SVM's times - much bigger time to converge), however it presented the most precise classifiers between all 3 - With lesser False Negatives._
_obs: Due the results. A grid search with SVM and Random Forest will not be needed_
On this scenario, even with time complexity being an issue - when pipelined in production - the random forest will be chosen into "production" step.
_obs: My concerns come to reality. All 3 models classifies pretty well non fraudulent transactions. However - due the lack of data - all 3 - at some point and in some level - presented an overfitting in classifying Fraudulent transactions - a further study will be made with Random Forest - the model with the most precise behaviour._
------------------------
```
def data_separation(df, proportion=0.2):
"""
Data separation method.
"""
return train_test_split(df, test_size=proportion)
def time_screening(dt):
"""
Fitting time performance calculator.
"""
print(datetime.datetime.now() - dt)
results = {
'linear_model': {
'train': [],
'test': [],
'validation': []
},
'svm': {
'train': [],
'test': [],
'validation': []
},
'random_forest': {
'train': [],
'test': [],
'validation': []
}
}
train, test = data_separation(df)
test, validation = data_separation(test, 0.4)
# Splitting into train - x and y
x_train = pandas.DataFrame(train[train.columns[0:-1]])
y_train = pandas.DataFrame(train[train.columns[-1]])
# Splitting into test - x and y
x_test = pandas.DataFrame(test[test.columns[0:-1]])
y_test = pandas.DataFrame(test[test.columns[-1]])
# Splitting into validation - x and y
x_validation = pandas.DataFrame(validation[validation.columns[0:-1]])
y_validation = pandas.DataFrame(validation[validation.columns[-1]])
# Multiple Linear Regression
begin = datetime.datetime.now()
lm = linear_model.LinearRegression().fit(x_train, y_train)
time_screening(begin)
y_train['Predicted'] = lm.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = lm.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = lm.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('linear_model')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('linear_model')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('linear_model')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Linear Support Vector Machine
begin = datetime.datetime.now()
lsvc = LinearSVC(C=0.01, penalty="l1", dual=False, max_iter=10000).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = lsvc.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = lsvc.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = lsvc.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('svm')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('svm')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('svm')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Random Forest
begin = datetime.datetime.now()
r_forest = RandomForestClassifier(n_estimators=90).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = r_forest.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = r_forest.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = r_forest.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('random_forest')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('random_forest')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('random_forest')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(results)
```
### Using selected model in "production" environment
- Normalize data
- Split data
- fit and predict model
-----------------------------------------------------
```
# Data Normalization
scaler = preprocessing.MinMaxScaler().fit(df_pca)
df_pca_norm = pandas.DataFrame(scaler.transform(df_pca))
df_pca_norm['Occurrence'] = occurrence
df_pca_norm.set_index('Occurrence', drop=True, inplace=True)
# Data separation
df_pca_norm['Fraude'] = y
train, test = data_separation(df_pca_norm)
test, validation = data_separation(test, 0.4)
# Splitting into train - x and y
x_train = pandas.DataFrame(train[train.columns[0:-1]])
y_train = pandas.DataFrame(train[train.columns[-1]])
# Splitting into test - x and y
x_test = pandas.DataFrame(test[test.columns[0:-1]])
y_test = pandas.DataFrame(test[test.columns[-1]])
# Splitting into validation - x and y
x_validation = pandas.DataFrame(validation[validation.columns[0:-1]])
y_validation = pandas.DataFrame(validation[validation.columns[-1]])
# Random Forest
begin = datetime.datetime.now()
r_forest = RandomForestClassifier(n_estimators=90).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = r_forest.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = r_forest.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = r_forest.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
print(len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train))
print(len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test))
print(len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation))
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Checking if there's overfitting on classifying Frauds - due the low quantity of data entries
overfitting = x_validation
overfitting['Fraude'] = y_validation['Fraude']
aux = x_test
aux['Fraude'] = y_test['Fraude']
overfitting = overfitting.append(aux)
overfitting = overfitting[overfitting['Fraude'] == 1]
del(aux)
overfitting['Predicted'] = r_forest.predict(overfitting.drop(columns=['Fraude']))
# Decay of assertiveness rate
print(len(overfitting[overfitting['Fraude'] == overfitting['Predicted']])/len(overfitting))
pandas.DataFrame(confusion_matrix(overfitting[['Fraude']], overfitting[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
```
### Summarizing
Section aimed on summarizing the methodology of this study and concluding it.
#### Checking duplicated values
Assuming that the 'Ocorrencia' is a unique code for the transaction itself. Let's check if there's any duplicated occurrence.
```python
len(df.index.unique())
```
If the dataset doesn't present any duplicated values, this piece of code should return, as output, 150.000 data entries. Nevertheless it returned only 64.958 values - meaning that this dataset presents around 85.042 duplicated data entries.
```python
len(df) - len(df.index.unique())
```
The duplicated values will be kept on analysis and training in modeling step. Due the nature of this dataset, this duplicate values could have been naturally generated - meaning that one occurrence could occur more than once - or, due the lack of available training material, some transactions could have been artificially generated.
----------------------------
#### Exploratory Analysis
Section aimed on checking the data distribution and data behaviour.
- N.A. values?
- Outliers?
- Min.
- Max.
- Mean.
- Stdev.
-------------------------
#### Describe Exploratory Analysis Result
This section summarizes the initial analysis on this dataset.
The command below allows to summarize each variable and retrieve the main statistical characteristics.
```python
df.describe()
```
The first thing to be noticed is at 'Sacado' variable - the amount of money withdrawn.
| Statistical Measurement | Value |
| :---------------------: | :----------: |
| Mean | -88.602261 |
| Standard Deviation | 247.302373 |
| Min | -19656.53 |
| Max | -0.00 |
How can be observed on this chart. The behaviour of 'Sacado' variable is pretty weird. First of all, this variable presents the highest standard deviation of all variables (247.30).
```python
df.describe().loc['std'].sort_values(ascending=False).head()
```
The mean, min and max values are pretty strange as well - with all of them being negative or null values. How this values could be negative/null values if this variable it was meant to represent the total withdrawn value of the transaction?
__Possible errors:__
- Acquistion errors?
- Parsing issues?
Other variables seems to behave pretty well (well distributed along the mean value - almost a normal curve) - even didn't knowing what they represent (the max values are high? the min values are low?).
_obs: Even with the lower deviation. On training, a simple normalization will be made on this dataset._
-------------
#### Does this dataset is non-balanced?
This section aims on checking if the dataset is non-balanced - are more frauds than non-frauds? Vice-Versa?
Table below assumes that the y variable - Fraude - has only 2 unique values - presented in table.
```python
df.Fraude.unique()
```
| Value | Meaning | Total | Percentage |
| :---: | :-------: | :------: | :--------: |
| 0 | Non Fraud | 149.763 | 0,9984 |
| 1 | Fraud | 237 | 0,0015 |
As can be observed on the table above. It's been assumed that 0 represents a non-fraudulent transaction and 1 represents a fraudulent transaction. This dataset is pretty unbalanced - with less than 1 % being fraudulent transactions (237 data entries). This scenario, on model training steps would be a problem - the model probably will be overfitted in fraudulents occurrences. To prevent it, it must be added some new - artificially generated or naturally acquired - fraudulents data entries.
----------------------------------------
#### Dimensionality Reduction
This section aims on reduct the dimensionality of this dataset.
__It can be used:__
- linear regression, correlation and statistically relevance;
- PCA;
_obs: despite the robustness of PCA, some articles presents issues on its performance - losing to simpler techniques._
-----------------------
#### Building Predictors
Three models will be implemented - if none of them supply the needs, new models could be choosen - and compared. Not only the assertiveness rate will be considered. The most problematic issue are False Negatives occurences - when the occurrence is Fraudulent however the model classified it as a Non-fraudulent occurence - if this happens the model will "lose" some points. False positives could be sent to a human validation - not so problematic as False Negatives.
__Models__:
- Linear Regression;
- Support Vector Machines;
- Random Forest.
_obs: Random forest classifier, when compared with other classifiers, presented 1 advantage point and 1 disavantage point - it wasn't able to converge in polynomial time (when compared to Linear Regression and SVM's times - much bigger time to converge), however it presented the most precise classifiers between all 3 - With lesser False Negatives._
_obs: Due the results. A grid search with SVM and Random Forest will not be needed_
On this scenario, even with time complexity being an issue - when pipelined in production - the random forest will be chosen into "production" step.
_obs: My concerns come to reality. All 3 models classifies pretty well non fraudulent transactions. However - due the lack of data - all 3 - at some point and in some level - presented an overfitting in classifying Fraudulent transactions - a further study will be made with Random Forest - the model with the most precise behaviour._
------------------------
#### Using selected model - Random Forest - in "production" environment
__Steps:__
- Normalize data;
- Split data;
- fit and predict model.
Due the normalization and - mainly - the dim reduction, the Random Forest's time performance has increased. During the development time the fitting time was about 0:01:50.102289. In _"production"_ time this time has decresead to 0:00:48.581284 - a time reduction of 0:01:01.521005.
```python
str(datetime.datetime.strptime('0:01:50.102289', '%H:%M:%S.%f') -
datetime.datetime.strptime('0:00:48.581284', '%H:%M:%S.%f'))
```
The model precision is presented in table below:
| Environment | Train | Test | Validation | Overfitting |
| :--------------: | :----: | :----: | :--------: | :---------: |
| Dev | 1,0000 | 0,9995 | 0,9995 | ----------- |
| Prod | 1,0000 | 0,9994 | 0,9993 | 0,7115 |
As could be observed. During the _"dev"_ time - without normalization and dimension reduction - the model achieved good results. The normalization - minmax normalization - and dimension reduction - from 29 variables to only 9 - achieved overwhelming results in time complexity - as mentioned before. Nevertheless, as mentioned, a further study on this model performance was required - __does the lack of fraudlent data overfits the model?__.
To test it the test and validation dataframes were merged and only fraudulent data was selected - resulting in a dataframe with 52 data entries (didn't include the train fraudulent data) - and passed to model predictor. The model should've predicted all as Frauds, however, the most problematic case appeared - Frauds classified as Non Frauds (False Negatives).<br>
In summary, a good non-fraud classifier was built - with little cases of False Positives (Non Frauds classified as Fraud) - however, as mentioned before, the most problematic case - False Negatives - occur more frequently. To correct it, appart from the selected model - since simpler until the most robust ones (Linear Regression, Bayes, Adaboost, Tree Classifiers, SVM's or Neural Nets) - it needed to add new fraudulent data entries on this dataset - artificially generated or not.
-----------------------------------------------------
| true |
code
| 0.445107 | null | null | null | null |
|
# 2. Beyond simple plotting
---
In this lecture we'll go a bit further with plotting.
We will:
- Create figures of different sizes;
- Use Numpy to generate data for plotting;
- Further change the appearance of our plots;
- Add multiple axes to the same figure.
```
from matplotlib import pyplot as plt
%matplotlib inline
```
### 2.1 Figures of different sizes
We can create figures with different sizes by specifying the `figsize` argument.
```
fig, axes = plt.subplots(figsize=(12,4))
```
---
### 2.2 Plotting Numpy data
The `plot` method also supports numpy arrays. For example, we canuse Numpy to plot a sine wave:
```
import numpy as np
# Create the data
x_values = np.linspace(-np.pi, np.pi, 200)
y_values = np.sin(x_values)
# Plot and show the figure
axes.plot(x_values, y_values,'--b')
fig
```
---
### 2.3 More options for you plots
We can use the `set_xlim` and `set_ylim` methods to change the range of the x and y axis.
```
axes.set_xlim([-np.pi, np.pi])
axes.set_ylim([-1, 1])
fig
```
Or use `axis('tight')` for automatically getting axis ranges that fit the data inside it (not as tightly as one would expect, though).
```
axes.axis('tight')
fig
```
We can add a grid with the `grid` method. See the [`grid` method documentation](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.grid.html) for more information about different styles of grids.
```
axes.grid(linestyle='dashed', linewidth=0.5)
fig
```
Also, we can explicitly choose where we want the ticks in the x and y axis and their labels, with the methods `set_xticks`, `set_yticks`, `set_xticklabels` and `set_yticklabels`.
```
axes.set_xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
axes.set_yticks([-1, -0.5, 0, 0.5, 1])
fig
axes.set_xticklabels([r'$-\pi$', r'$-\pi/2$', 0, r'$\pi/2$', r'$\pi$'])
axes.set_yticklabels([-1,r'$-\frac{1}{2}$',0,r'$\frac{1}{2}$',1])
fig
```
Finally, we can save a figure using the `savefig` method.
```
fig.savefig('filename.png')
```
---
### 2.4 Multiple axes in the same figure
To have multiple axes in the same figure, you can simply specify the arguments `nrows` and `ncols` when calling `subplots`.
```
fig, axes = plt.subplots(nrows=2, ncols=3)
```
To make the axis not overlap, we use the method `subplots_adjust`.
```
fig.subplots_adjust(hspace=0.6, wspace=0.6)
fig
```
And now we can simply plot in each individual axes separately.
```
axes[0][1].plot([1,2,3,4])
fig
axes[1,2].plot([4,4,4,2,3,3],'b--')
fig
axes[0][1].plot([2,2,2,-1],'-.o')
fig
```
---
| true |
code
| 0.814956 | null | null | null | null |
|
# Tutorial Part 10: Exploring Quantum Chemistry with GDB1k
Most of the tutorials we've walked you through so far have focused on applications to the drug discovery realm, but DeepChem's tool suite works for molecular design problems generally. In this tutorial, we're going to walk through an example of how to train a simple molecular machine learning for the task of predicting the atomization energy of a molecule. (Remember that the atomization energy is the energy required to form 1 mol of gaseous atoms from 1 mol of the molecule in its standard state under standard conditions).
## Colab
This tutorial and the rest in this sequence are designed to be done in Google colab. If you'd like to open this notebook in colab, you can use the following link.
[](https://colab.research.google.com/github/deepchem/deepchem/blob/master/examples/tutorials/10_Exploring_Quantum_Chemistry_with_GDB1k.ipynb)
## Setup
To run DeepChem within Colab, you'll need to run the following cell of installation commands. This will take about 5 minutes to run to completion and install your environment.
```
!curl -Lo conda_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
import conda_installer
conda_installer.install()
!/root/miniconda/bin/conda info -e
!pip install --pre deepchem
import deepchem
deepchem.__version__
```
With our setup in place, let's do a few standard imports to get the ball rolling.
```
import os
import unittest
import numpy as np
import deepchem as dc
import numpy.random
from deepchem.utils.evaluate import Evaluator
from sklearn.ensemble import RandomForestRegressor
from sklearn.kernel_ridge import KernelRidge
```
The ntext step we want to do is load our dataset. We're using a small dataset we've prepared that's pulled out of the larger GDB benchmarks. The dataset contains the atomization energies for 1K small molecules.
```
tasks = ["atomization_energy"]
dataset_file = "../../datasets/gdb1k.sdf"
smiles_field = "smiles"
mol_field = "mol"
```
We now need a way to transform molecules that is useful for prediction of atomization energy. This representation draws on foundational work [1] that represents a molecule's 3D electrostatic structure as a 2D matrix $C$ of distances scaled by charges, where the $ij$-th element is represented by the following charge structure.
$C_{ij} = \frac{q_i q_j}{r_{ij}^2}$
If you're observing carefully, you might ask, wait doesn't this mean that molecules with different numbers of atoms generate matrices of different sizes? In practice the trick to get around this is that the matrices are "zero-padded." That is, if you're making coulomb matrices for a set of molecules, you pick a maximum number of atoms $N$, make the matrices $N\times N$ and set to zero all the extra entries for this molecule. (There's a couple extra tricks that are done under the hood beyond this. Check out reference [1] or read the source code in DeepChem!)
DeepChem has a built in featurization class `dc.feat.CoulombMatrixEig` that can generate these featurizations for you.
```
featurizer = dc.feat.CoulombMatrixEig(23, remove_hydrogens=False)
```
Note that in this case, we set the maximum number of atoms to $N = 23$. Let's now load our dataset file into DeepChem. As in the previous tutorials, we use a `Loader` class, in particular `dc.data.SDFLoader` to load our `.sdf` file into DeepChem. The following snippet shows how we do this:
```
# loader = dc.data.SDFLoader(
# tasks=["atomization_energy"], smiles_field="smiles",
# featurizer=featurizer,
# mol_field="mol")
# dataset = loader.featurize(dataset_file)
```
For the purposes of this tutorial, we're going to do a random split of the dataset into training, validation, and test. In general, this split is weak and will considerably overestimate the accuracy of our models, but for now in this simple tutorial isn't a bad place to get started.
```
# random_splitter = dc.splits.RandomSplitter()
# train_dataset, valid_dataset, test_dataset = random_splitter.train_valid_test_split(dataset)
```
One issue that Coulomb matrix featurizations have is that the range of entries in the matrix $C$ can be large. The charge $q_1q_2/r^2$ term can range very widely. In general, a wide range of values for inputs can throw off learning for the neural network. For this, a common fix is to normalize the input values so that they fall into a more standard range. Recall that the normalization transform applies to each feature $X_i$ of datapoint $X$
$\hat{X_i} = \frac{X_i - \mu_i}{\sigma_i}$
where $\mu_i$ and $\sigma_i$ are the mean and standard deviation of the $i$-th feature. This transformation enables the learning to proceed smoothly. A second point is that the atomization energies also fall across a wide range. So we apply an analogous transformation normalization transformation to the output to scale the energies better. We use DeepChem's transformation API to make this happen:
```
# transformers = [
# dc.trans.NormalizationTransformer(transform_X=True, dataset=train_dataset),
# dc.trans.NormalizationTransformer(transform_y=True, dataset=train_dataset)]
# for dataset in [train_dataset, valid_dataset, test_dataset]:
# for transformer in transformers:
# dataset = transformer.transform(dataset)
```
Now that we have the data cleanly transformed, let's do some simple machine learning. We'll start by constructing a random forest on top of the data. We'll use DeepChem's hyperparameter tuning module to do this.
```
# def rf_model_builder(model_params, model_dir):
# sklearn_model = RandomForestRegressor(**model_params)
# return dc.models.SklearnModel(sklearn_model, model_dir)
# params_dict = {
# "n_estimators": [10, 100],
# "max_features": ["auto", "sqrt", "log2", None],
# }
# metric = dc.metrics.Metric(dc.metrics.mean_absolute_error)
# optimizer = dc.hyper.HyperparamOpt(rf_model_builder)
# best_rf, best_rf_hyperparams, all_rf_results = optimizer.hyperparam_search(
# params_dict, train_dataset, valid_dataset, transformers,
# metric=metric)
```
Let's build one more model, a kernel ridge regression, on top of this raw data.
```
# def krr_model_builder(model_params, model_dir):
# sklearn_model = KernelRidge(**model_params)
# return dc.models.SklearnModel(sklearn_model, model_dir)
# params_dict = {
# "kernel": ["laplacian"],
# "alpha": [0.0001],
# "gamma": [0.0001]
# }
# metric = dc.metrics.Metric(dc.metrics.mean_absolute_error)
# optimizer = dc.hyper.HyperparamOpt(krr_model_builder)
# best_krr, best_krr_hyperparams, all_krr_results = optimizer.hyperparam_search(
# params_dict, train_dataset, valid_dataset, transformers,
# metric=metric)
```
# Congratulations! Time to join the Community!
Congratulations on completing this tutorial notebook! If you enjoyed working through the tutorial, and want to continue working with DeepChem, we encourage you to finish the rest of the tutorials in this series. You can also help the DeepChem community in the following ways:
## Star DeepChem on [GitHub](https://github.com/deepchem/deepchem)
This helps build awareness of the DeepChem project and the tools for open source drug discovery that we're trying to build.
## Join the DeepChem Gitter
The DeepChem [Gitter](https://gitter.im/deepchem/Lobby) hosts a number of scientists, developers, and enthusiasts interested in deep learning for the life sciences. Join the conversation!
# Bibliography:
[1] https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.98.146401
| true |
code
| 0.597079 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Chiebukar/Deep-Learning/blob/main/regression/temperature_forcasting_with_RNN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Temperature Forcasting with Jena climate dataset
```
from google.colab import files
files.upload()
!mkdir -p ~/.kaggle
!cp kaggle.json ~/.kaggle/
!chmod 600 ~/.kaggle/kaggle.json
!kaggle datasets download -d kusuri/jena-climate
!ls -d $PWD/*
!unzip \*.zip && rm *.zip
!ls -d $PWD/*
file_dir = '/content/jena_climate_2009_2016.csv'
import numpy as np
import pandas as pd
jena_df = pd.read_csv(file_dir)
jena_df.head()
jena_df.shape
jena_df.columns
jena_arr = np.array(jena_df.iloc[:, 1:])
jena_arr[:2]
# standardize data
len_train = 200000
mean = jena_arr[:len_train].mean(axis=0)
std = jena_arr[:len_train].std(axis=0)
jena_arr = (jena_arr-mean)/std
# generator to yield batches of data from the recent past and future target
def generator(data, min_index, max_index , lookback= 1440, delay=144, step= 6, batch_size=18, shuffle=False):
"""
yield batches of data from the recent past and future target
data = original input data
min_index = minimum index of data to draw from
max_index maximum index of sata to draw from
lookback= Number of timestamps back for input data per target
delay = Number of timestamp in the future for target per lookback
steps = period in timestamps to sample data
batch_size = number of samples per batch
shuffle = To shuffle the samples or not
"""
if max_index == None:
max_index = len(data) - delay - 1
i = min_index + lookback
while 1:
if shuffle:
rows = np.random.randint(min_index + lookback, max_index, size= batch_size)
else:
if i + batch_size >= max_index:
i = min_index + lookback
rows = np.arange(i, min(i + batch_size, max_index))
i += len(rows)
samples = np.zeros((len(rows), lookback //step, data.shape[-1]))
targets = np.zeros((len(rows),))
for j, row in enumerate(rows):
indices = range(rows[j] - lookback, rows[j], step)
samples[j] = data[indices]
targets[j] = data[rows[j] + delay][1]
yield samples, targets
train_gen = generator(data= jena_arr,
min_index= 0,
max_index= 200000,
shuffle= True)
valid_gen = generator(data= jena_arr,
min_index= 200001,
max_index = 300000,
shuffle = True)
test_gen = generator(data = jena_arr,
min_index = 300001,
max_index = None,
shuffle= True)
# get validation and test steps
lookback = 1440
val_steps = (300000 - 200001 - lookback)
test_steps = (len(jena_arr) - 300001 - lookback)
# establish baseline
def evaluate_naive_method():
batch_maes = []
for step in range(val_steps):
samples, targets = next(valid_gen)
preds = samples[:, -1, 1]
mae = np.mean(np.abs(preds - targets))
batch_maes.append(mae)
return (np.mean(batch_maes))
# get baseline evaluation
mae = evaluate_naive_method()
celsius_mae = mae * std[1]
celsius_mae
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Dense, LSTM, Dropout
from keras.callbacks import ModelCheckpoint
# build model
def build_model():
model = Sequential()
model.add(LSTM(32, dropout= 0.1, recurrent_dropout= 0.25,
return_sequences=True, input_shape = (None, jena_arr.shape[-1])))
model.add(LSTM(64, activation='tanh', dropout=0.5))
model.add(Dense(8, activation= 'relu'))
model.add(Dropout(0.1))
model.add(Dense(1))
model.compile(loss = 'mae', optimizer = 'rmsprop')
return model
file_path= 'a_weights.best.hdf5'
checkpoint = ModelCheckpoint(file_path, monitor= 'val_loss', save_best_only= True, verbose= 1, mode= 'min')
model = build_model()
history = model.fit(train_gen, steps_per_epoch = 500, epochs= 25, validation_data= valid_gen,
validation_steps = 500, callbacks= checkpoint)
history_df = pd.DataFrame(history.history)
history_df[['mae', 'val_mae']].plot()
```
| true |
code
| 0.516961 | null | null | null | null |
|
<h1> Create TensorFlow model </h1>
This notebook illustrates:
<ol>
<li> Creating a model using the high-level Estimator API
</ol>
```
# change these to try this notebook out
BUCKET = 'qwiklabs-gcp-37b9fafbd24bf385'
PROJECT = 'qwiklabs-gcp-37b9fafbd24bf385'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
```
<h2> Create TensorFlow model using TensorFlow's Estimator API </h2>
<p>
First, write an input_fn to read the data.
<p>
## Lab Task 1
Verify that the headers match your CSV output
```
import shutil
import numpy as np
import tensorflow as tf
# Determine CSV, label, and key columns
CSV_COLUMNS = 'weight_pounds,is_male,mother_age,plurality,gestation_weeks,key'.split(',')
LABEL_COLUMN = 'weight_pounds'
KEY_COLUMN = 'key'
# Set default values for each CSV column
DEFAULTS = [[0.0], ['null'], [0.0], ['null'], [0.0], ['nokey']]
TRAIN_STEPS = 1000
```
## Lab Task 2
Fill out the details of the input function below
```
# Create an input function reading a file using the Dataset API
# Then provide the results to the Estimator API
def read_dataset(filename_pattern, mode, batch_size = 512):
def _input_fn():
def decode_csv(line_of_text):
# TODO #1: Use tf.decode_csv to parse the provided line
columns = tf.decode_csv(line_of_text, record_defaults=DEFAULTS)
# TODO #2: Make a Python dict. The keys are the column names, the values are from the parsed data
features = dict(zip(CSV_COLUMNS, columns))
# TODO #3: Return a tuple of features, label where features is a Python dict and label a float
label = features.pop(LABEL_COLUMN)
return features, label
# TODO #4: Use tf.gfile.Glob to create list of files that match pattern
file_list = tf.gfile.Glob(filename_pattern)
# Create dataset from file list
dataset = (tf.data.TextLineDataset(file_list) # Read text file
.map(decode_csv)) # Transform each elem by applying decode_csv fn
# TODO #5: In training mode, shuffle the dataset and repeat indefinitely
# (Look at the API for tf.data.dataset shuffle)
# The mode input variable will be tf.estimator.ModeKeys.TRAIN if in training mode
# Tell the dataset to provide data in batches of batch_size
if mode == tf.estimator.ModeKeys.TRAIN:
epochs = None # Repeat indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
epochs = 1
dataset = dataset.repeat(epochs).batch(batch_size)
# This will now return batches of features, label
return dataset
return _input_fn
```
## Lab Task 3
Use the TensorFlow feature column API to define appropriate feature columns for your raw features that come from the CSV.
<b> Bonus: </b> Separate your columns into wide columns (categorical, discrete, etc.) and deep columns (numeric, embedding, etc.)
```
# Define feature columns
# Define feature columns
def get_categorical(name, values):
return tf.feature_column.indicator_column(
tf.feature_column.categorical_column_with_vocabulary_list(name, values))
def get_cols():
# Define column types
return [\
get_categorical('is_male', ['True', 'False', 'Unknown']),
tf.feature_column.numeric_column('mother_age'),
get_categorical('plurality',
['Single(1)', 'Twins(2)', 'Triplets(3)',
'Quadruplets(4)', 'Quintuplets(5)','Multiple(2+)']),
tf.feature_column.numeric_column('gestation_weeks')
]
```
## Lab Task 4
To predict with the TensorFlow model, we also need a serving input function (we'll use this in a later lab). We will want all the inputs from our user.
Verify and change the column names and types here as appropriate. These should match your CSV_COLUMNS
```
# Create serving input function to be able to serve predictions later using provided inputs
def serving_input_fn():
feature_placeholders = {
'is_male': tf.placeholder(tf.string, [None]),
'mother_age': tf.placeholder(tf.float32, [None]),
'plurality': tf.placeholder(tf.string, [None]),
'gestation_weeks': tf.placeholder(tf.float32, [None])
}
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
```
## Lab Task 5
Complete the TODOs in this code:
```
# Create estimator to train and evaluate
def train_and_evaluate(output_dir):
EVAL_INTERVAL = 300
run_config = tf.estimator.RunConfig(save_checkpoints_secs = EVAL_INTERVAL,
keep_checkpoint_max = 3)
# TODO #1: Create your estimator
estimator = tf.estimator.DNNRegressor(
model_dir = output_dir,
feature_columns = get_cols(),
hidden_units = [64, 32],
config = run_config)
train_spec = tf.estimator.TrainSpec(
# TODO #2: Call read_dataset passing in the training CSV file and the appropriate mode
input_fn = read_dataset('train.csv', mode = tf.estimator.ModeKeys.TRAIN),
max_steps = TRAIN_STEPS)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(
# TODO #3: Call read_dataset passing in the evaluation CSV file and the appropriate mode
input_fn = read_dataset('eval.csv', mode = tf.estimator.ModeKeys.EVAL),
steps = None,
start_delay_secs = 60, # start evaluating after N seconds
throttle_secs = EVAL_INTERVAL, # evaluate every N seconds
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
```
Finally, train!
```
# Run the model
shutil.rmtree('babyweight_trained', ignore_errors = True) # start fresh each time
train_and_evaluate('babyweight_trained')
```
When I ran it, the final lines of the output (above) were:
<pre>
INFO:tensorflow:Saving dict for global step 1000: average_loss = 1.2693067, global_step = 1000, loss = 635.9226
INFO:tensorflow:Restoring parameters from babyweight_trained/model.ckpt-1000
INFO:tensorflow:Assets added to graph.
INFO:tensorflow:No assets to write.
INFO:tensorflow:SavedModel written to: babyweight_trained/export/exporter/temp-1517899936/saved_model.pb
</pre>
The exporter directory contains the final model and the final RMSE (the average_loss) is 1.2693067
<h2> Monitor and experiment with training </h2>
```
from google.datalab.ml import TensorBoard
TensorBoard().start('./babyweight_trained')
for pid in TensorBoard.list()['pid']:
TensorBoard().stop(pid)
print('Stopped TensorBoard with pid {}'.format(pid))
```
Copyright 2017-2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.368889 | null | null | null | null |
|
## Denoising Autoencoder on MNIST dataset
* This notebook will give you a very good understanding abou denoising autoencoders
* For more information: visit [here](https://lilianweng.github.io/lil-log/2018/08/12/from-autoencoder-to-beta-vae.html)
* The entire notebook is in PyTorch
```
# Importing packages that will be necessary for the project
import numpy as np
from keras.datasets import mnist
import matplotlib.pyplot as plt
from tqdm import tqdm
from torchvision import transforms
import torch.nn as nn
from torch.utils.data import DataLoader,Dataset
import torch
import torch.optim as optim
from torch.autograd import Variable
# Mounting the google drive to fetch data from it
from google.colab import drive
drive.mount('/content/gdrive')
#loading the mnist data
(x_train,y_train),(x_test,y_test)=mnist.load_data()
print("No of train datapoints:{}\nNo of test datapoints:{}".format(len(x_train),len(x_test)))
print(y_train[1]) # Checking labels
#we add the noise
"""
'gauss' Gaussian-distributed additive noise.
'speckle' out = image + n*image,where
n is uniform noise with specified mean & variance.
"""
def add_noise(img,noise_type="gaussian"):#input includes the type of the noise to be added and the input image
row,col=28,28
img=img.astype(np.float32)
if noise_type=="gaussian":
noise=np.random.normal(-5.9,5.9,img.shape) #input includes : mean, deviation, shape of the image and the function picks up a normal distribuition.
noise=noise.reshape(row,col) # reshaping the noise
img=img+noise #adding the noise
return img
if noise_type=="speckle":
noise=np.random.randn(row,col)
noise=noise.reshape(row,col)
img=img+img*noise
return img
#Now dividing the dataset into two parts and adding gaussian to one and speckle to another.
noises=["gaussian","speckle"]
noise_ct=0
noise_id=0 #id represnts which noise is being added, its 0 = gaussian and 1 = speckle
traindata=np.zeros((60000,28,28)) #revised training data
for idx in tqdm(range(len(x_train))): #for the first half we are using gaussian noise & for the second half speckle noise
if noise_ct<(len(x_train)/2):
noise_ct+=1
traindata[idx]=add_noise(x_train[idx],noise_type=noises[noise_id])
else:
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_id+=1
noise_ct=0
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_ct=0
noise_id=0
testdata=np.zeros((10000,28,28))
for idx in tqdm(range(len(x_test))): # Doing the same for the test set.
if noise_ct<(len(x_test)/2):
noise_ct+=1
x=add_noise(x_test[idx],noise_type=noises[noise_id])
testdata[idx]=x
else:
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_id+=1
noise_ct=0
print("\n{} noise addition completed to images".format(noises[noise_id]))
f, axes=plt.subplots(2,2) #setting up 4 figures
#showing images with gaussian noise
axes[0,0].imshow(x_train[0],cmap="gray")#the original data
axes[0,0].set_title("Original Image")
axes[1,0].imshow(traindata[0],cmap='gray')#noised data
axes[1,0].set_title("Noised Image")
#showing images with speckle noise
axes[0,1].imshow(x_train[25000],cmap='gray')#original data
axes[0,1].set_title("Original Image")
axes[1,1].imshow(traindata[25000],cmap="gray")#noised data
axes[1,1].set_title("Noised Image")
#creating a dataset builder i.e dataloaders
class noisedDataset(Dataset):
def __init__(self,datasetnoised,datasetclean,labels,transform):
self.noise=datasetnoised
self.clean=datasetclean
self.labels=labels
self.transform=transform
def __len__(self):
return len(self.noise)
def __getitem__(self,idx):
xNoise=self.noise[idx]
xClean=self.clean[idx]
y=self.labels[idx]
if self.transform != None:#just for using the totensor transform
xNoise=self.transform(xNoise)
xClean=self.transform(xClean)
return (xNoise,xClean,y)
#defining the totensor transforms
tsfms=transforms.Compose([
transforms.ToTensor()
])
trainset=noisedDataset(traindata,x_train,y_train,tsfms)# the labels should not be corrupted because the model has to learn uniques features and denoise it.
testset=noisedDataset(testdata,x_test,y_test,tsfms)
batch_size=32
#creating the dataloader
trainloader=DataLoader(trainset,batch_size=32,shuffle=True)
testloader=DataLoader(testset,batch_size=1,shuffle=True)
#building our ae model:
class denoising_model(nn.Module):
def __init__(self):
super(denoising_model,self).__init__()
self.encoder=nn.Sequential(
nn.Linear(28*28,256),#decreasing the features in the encoder
nn.ReLU(True),
nn.Linear(256,128),
nn.ReLU(True),
nn.Linear(128,64),
nn.ReLU(True)
)
self.decoder=nn.Sequential(
nn.Linear(64,128),#increasing the number of features
nn.ReLU(True),
nn.Linear(128,256),
nn.ReLU(True),
nn.Linear(256,28*28),
nn.Sigmoid(),
)
def forward(self,x):
x=self.encoder(x)#first the encoder
x=self.decoder(x)#then the decoder to reconstruct the original input.
return x
#this is the training code, can be modified according to requirements
#setting the device
if torch.cuda.is_available()==True:
device="cuda:0"
else:
device ="cpu"
model=denoising_model().to(device)
criterion=nn.MSELoss()
optimizer=optim.SGD(model.parameters(),lr=0.01,weight_decay=1e-5)
#setting the number of epochs
epochs=120
l=len(trainloader)
losslist=list()
epochloss=0
running_loss=0
for epoch in range(epochs):
print("Entering Epoch: ",epoch)
for dirty,clean,label in tqdm((trainloader)):
dirty=dirty.view(dirty.size(0),-1).type(torch.FloatTensor)
clean=clean.view(clean.size(0),-1).type(torch.FloatTensor)
dirty,clean=dirty.to(device),clean.to(device)
#-----------------Forward Pass----------------------
output=model(dirty)
loss=criterion(output,clean)
#-----------------Backward Pass---------------------
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss+=loss.item()
epochloss+=loss.item()
#-----------------Log-------------------------------
losslist.append(running_loss/l)
running_loss=0
print("======> epoch: {}/{}, Loss:{}".format(epoch,epochs,loss.item()))
#plotting the loss curve
plt.plot(range(len(losslist)),losslist)
"""Here, we try to visualize some of the results.
We randomly generate 6 numbers in between 1 and 10k , run them through the model,
and show the results with comparisons
"""
f,axes= plt.subplots(6,3,figsize=(20,20))
axes[0,0].set_title("Original Image")
axes[0,1].set_title("Dirty Image")
axes[0,2].set_title("Cleaned Image")
test_imgs=np.random.randint(0,10000,size=6)
for idx in range((6)):
dirty=testset[test_imgs[idx]][0]
clean=testset[test_imgs[idx]][1]
label=testset[test_imgs[idx]][2]
dirty=dirty.view(dirty.size(0),-1).type(torch.FloatTensor)
dirty=dirty.to(device)
output=model(dirty)
output=output.view(1,28,28)
output=output.permute(1,2,0).squeeze(2)
output=output.detach().cpu().numpy()
dirty=dirty.view(1,28,28)
dirty=dirty.permute(1,2,0).squeeze(2)
dirty=dirty.detach().cpu().numpy()
clean=clean.permute(1,2,0).squeeze(2)
clean=clean.detach().cpu().numpy()
axes[idx,0].imshow(clean,cmap="gray")
axes[idx,1].imshow(dirty,cmap="gray")
axes[idx,2].imshow(output,cmap="gray")
```
| true |
code
| 0.66731 | null | null | null | null |
|
# Cleaning the data to build the prototype for crwa
### This data cleans the original sql output and performs cleaning tasks. Also checking validity of the results against original report found at
### https://www.crwa.org/uploads/1/2/6/7/126781580/crwa_ecoli_web_2017_updated.xlsx
```
import pandas as pd
pd.options.display.max_rows = 999
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("data_for_prototype.csv")
# There are 2 rows with Date = Null so droping those rows
df = df.dropna(subset=['Date_Collected'])
df.isna().sum()
# There are following types of invalids in Site_ID
invalids = ["N/A","NULL","ND"]
#Removing these invalid Site_IDs
df["Site_Name"] = df["Site_Name"].map(lambda x: np.nan if x in invalids else x)
df["Site_Name"].fillna("ABCD", inplace=True)
#Removing these invalid Town Names
df["Town"] = df["Town"].map(lambda x: np.nan if x in invalids else x)
df["Town"].fillna("ABCD", inplace=True)
df["River_Mile_Headwaters"].describe
#Removing invalid Miles and selecting only numeric values for miles
df["River_Mile_Headwaters"] = df["River_Mile_Headwaters"].map(lambda x: np.nan if x in invalids else x)
df["River_Mile_Headwaters"].fillna("00.0 MI", inplace=True)
df["Mile"] = pd.to_numeric(df["River_Mile_Headwaters"].str[0:4])
#Removing invalid entrees and selecting only numeric values
df["Latitude_DD"] = df["Latitude_DD"].map(lambda x: np.nan if x in invalids else x)
df["Latitude_DD"].fillna("00.0 MI", inplace=True)
df["Longitude_DD"] = df["Longitude_DD"].map(lambda x: np.nan if x in invalids else x)
df["Longitude_DD"].fillna("00.0 MI", inplace=True)
#Removing invalid entrees and selecting only numeric values
df["Actual_Result"] = df["Actual_Result"].map(lambda x: np.nan if x in invalids else x)
df["Actual_Result"] = df["Actual_Result"].str.lstrip('>')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('>')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('<')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('<')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('*')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('*')
df["Actual_Result"] = df["Actual_Result"].str.replace(',','')
df["Actual_Result"] = df["Actual_Result"].str.replace('%','')
df["Actual_Result"] = df["Actual_Result"].str.replace(' ','')
df["Actual_Result"] = df["Actual_Result"].str.replace('ND','')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('.')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('.')
df["Actual_Result"] = df["Actual_Result"].str.replace('6..25','6.25')
df["Actual_Result"] = df["Actual_Result"].str.replace('480.81546.25291','480.81546')
df["Actual_Result"] = df["Actual_Result"].str.replace('379\r\n379',"379")
#Functiont to check if string can be converted to numeric
#Input --> string
#Output --> 1 if convertable else 0
def isInt_try(v):
try: i = float(v)
except: return False
return True
# Applying above function to check any odd strings in Actual_Result Column
for i in df["Actual_Result"]:
if isInt_try(i) == 0:
print(i)
# Checking any odd strings in Actual_Result Column
for i in df["Actual_Result"]:
if str(i).count('.') >= 2:
print(i)
# Converting Actual_Result to numeric and Date_Collected to datetime data type
df["Actual_Result"] = pd.to_numeric(df["Actual_Result"])
df["Date_Collected"] = pd.to_datetime(df["Date_Collected"])
"Slicing for E.coli"
df_ecoli = df[df["Component_Name"] == "Escherichia coli"]
df_ecoli.head()
# Validating against the original report
result = df_ecoli.loc[(df_ecoli.Town == "Milford") & (df_ecoli.Date_Collected == pd.to_datetime("2017-11-21 00:00:00-05:00"))]["Actual_Result"]
result
```
| true |
code
| 0.238041 | null | null | null | null |
|
# Method4 DCT based DOST + Huffman encoding
## Import Libraries
```
import mne
import numpy as np
from scipy.fft import fft,fftshift
import matplotlib.pyplot as plt
from scipy.signal import butter, lfilter
from scipy.signal import freqz
from scipy import signal
from scipy.fftpack import fft, dct, idct
from itertools import islice
import pandas as pd
import os
```
## Preprocessing
### Data loading
```
acc = pd.read_csv('ACC.csv')
acc = acc.iloc[1:]
acc.columns = ['column1','column2','column3']
np.savetxt('acc.txt',acc)
acc_c1 = acc["column1"]
acc_c2 = acc["column2"]
acc_c3 = acc["column3"]
acc_array_c1 = acc_c1.to_numpy() #save the data into an ndarray
acc_array_c2 = acc_c2.to_numpy()
acc_array_c3 = acc_c3.to_numpy()
acc_array_c1.shape
acc_array_c1 = acc_array_c1[0:66000] # Remove the signal in first 3minutes and last 5minutes
acc_array_c2 = acc_array_c2[0:66000]
acc_array_c3 = acc_array_c3[0:66000]
sampling_freq = 1/32
N = acc_array_c1.size
xf = np.linspace(-N*sampling_freq/2, N*sampling_freq/2, N)
index = np.linspace(0, round((N-1)*sampling_freq,4), N)
```
### Butterworth Filter to denoising
```
def butter_bandpass(lowcut, highcut, fs, order=5):
nyq = 0.5 * fs
low = lowcut / nyq
high = highcut / nyq
b, a = butter(order, [low, high], btype='band')
return b, a
def butter_bandpass_filter(data, lowcut, highcut, fs, order=5):
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
y = lfilter(b, a, data)
return y
from scipy.signal import freqz
from scipy import signal
# Sample rate and desired cutoff frequencies (in Hz).
fs = 1000.0
lowcut = 0.5
highcut = 50.0
# Plot the frequency response for a few different orders.
plt.figure(1)
plt.clf()
for order in [1, 2, 3, 4]:
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
w, h = freqz(b, a, worN=2000)
plt.plot((fs * 0.5 / np.pi) * w, abs(h), label="order = %d" % order)
plt.plot([0, 0.5 * fs], [np.sqrt(0.5), np.sqrt(0.5)],
'--', label='sqrt(0.5)')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Gain')
plt.grid(True)
plt.legend(loc='best')
y1 = butter_bandpass_filter(acc_array_c1, lowcut, highcut, fs, order=2)
y2 = butter_bandpass_filter(acc_array_c2, lowcut, highcut, fs, order=2)
y3 = butter_bandpass_filter(acc_array_c3, lowcut, highcut, fs, order=2)
resampled_signal1 = y1
resampled_signal2 = y2
resampled_signal3 = y3
np.savetxt('processed_acc_col1.txt',resampled_signal1)
np.savetxt('processed_acc_col2.txt',resampled_signal2)
np.savetxt('processed_acc_col3.txt',resampled_signal3)
rounded_signal1 = np.around(resampled_signal1)
rounded_signal2 = np.around(resampled_signal2)
rounded_signal3 = np.around(resampled_signal3)
```
## Transformation --- DCT based DOST
```
from scipy.fftpack import fft, dct
aN1 = dct(rounded_signal1, type = 2, norm = 'ortho')
aN2 = dct(rounded_signal2, type = 2, norm = 'ortho')
aN3 = dct(rounded_signal3, type = 2, norm = 'ortho')
def return_N(target):
if target > 1:
for i in range(1, int(target)):
if (2 ** i >= target):
return i-1
else:
return 1
from itertools import islice
split_list = [1]
for i in range(0,return_N(aN1.size)):
split_list.append(2 ** i)
temp1 = iter(aN1)
res1 = [list(islice(temp1, 0, ele)) for ele in split_list]
temp2 = iter(aN2)
res2 = [list(islice(temp2, 0, ele)) for ele in split_list]
temp3 = iter(aN3)
res3 = [list(islice(temp3, 0, ele)) for ele in split_list]
from scipy.fftpack import fft, dct, idct
cN_idct1 = [list(idct(res1[0], type = 2, norm = 'ortho' )), list(idct(res1[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res1)):
cN_idct1.append(list(idct(res1[k], type = 2, norm = 'ortho' )))
cN_idct2 = [list(idct(res2[0], type = 2, norm = 'ortho' )), list(idct(res2[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res2)):
cN_idct2.append(list(idct(res2[k], type = 2, norm = 'ortho' )))
cN_idct3 = [list(idct(res3[0], type = 2, norm = 'ortho' )), list(idct(res3[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res3)):
cN_idct3.append(list(idct(res3[k], type = 2, norm = 'ortho' )))
all_numbers1 = []
for i in cN_idct1:
for j in i:
all_numbers1.append(j)
all_numbers2 = []
for i in cN_idct2:
for j in i:
all_numbers2.append(j)
all_numbers3 = []
for i in cN_idct3:
for j in i:
all_numbers3.append(j)
all_numbers1 = np.asarray(all_numbers1)
all_numbers2 = np.asarray(all_numbers2)
all_numbers3 = np.asarray(all_numbers3)
int_cN1 = np.round(all_numbers1,3)
int_cN2 = np.round(all_numbers2,3)
int_cN3 = np.round(all_numbers3,3)
np.savetxt('int_cN1.txt',int_cN1, fmt='%.3f')
np.savetxt('int_cN2.txt',int_cN2, fmt='%.3f')
np.savetxt('int_cN3.txt',int_cN3,fmt='%.3f')
```
## Huffman Coding
### INSTRUCTION ON HOW TO COMPRESS THE DATA BY HUFFMAN CODING
(I used the package "tcmpr 0.2" and "pyhuff 1.1". These two packages provided the same compression result. So here, we just use "tcmpr 0.2")
1. Open your termial or git bash, enter "pip install tcmpr" to install the "tcmpr 0.2" package
2. Enter the directory which include the file you want to compress OR copy the path of the file you want to compress
3. Enter "tcmpr filename.txt" / "tcmpr filepath" to compress the file
4. Find the compressed file in the same directory of the original file
```
# Do Huffman encoding based on the instruction above
# or run this trunk if this scratch locates in the same directory with the signal you want to encode
os.system('tcmpr int_cN1.txt')
os.system('tcmpr int_cN2.txt')
os.system('tcmpr int_cN3.txt')
```
## Reconstruction
```
os.system('tcmpr -d int_cN1.txt.huffman')
os.system('tcmpr -d int_cN2.txt.huffman')
os.system('tcmpr -d int_cN3.txt.huffman')
decoded_data1 = np.loadtxt(fname = "int_cN1.txt")
decoded_data2 = np.loadtxt(fname = "int_cN2.txt")
decoded_data3 = np.loadtxt(fname = "int_cN3.txt")
recover_signal1 = decoded_data1
recover_signal2 = decoded_data2
recover_signal3 = decoded_data3
recover_signal1 = list(recover_signal1)
recover_signal2 = list(recover_signal2)
recover_signal3 = list(recover_signal3)
len(recover_signal1)
split_list = [1]
for i in range(0,return_N(len(recover_signal1))+1):
split_list.append(2 ** i)
temp_recovered1 = iter(recover_signal1)
res_recovered1 = [list(islice(temp_recovered1, 0, ele)) for ele in split_list]
temp_recovered2 = iter(recover_signal2)
res_recovered2 = [list(islice(temp_recovered2, 0, ele)) for ele in split_list]
temp_recovered3 = iter(recover_signal3)
res_recovered3 = [list(islice(temp_recovered3, 0, ele)) for ele in split_list]
recover_dct1 = [list(dct(res_recovered1[0], type = 2, norm = 'ortho' )), list(dct(res_recovered1[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered1)):
recover_dct1.append(list(dct(res_recovered1[k], type = 2, norm = 'ortho' )))
recover_dct2 = [list(dct(res_recovered2[0], type = 2, norm = 'ortho' )), list(dct(res_recovered2[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered2)):
recover_dct2.append(list(dct(res_recovered2[k], type = 2, norm = 'ortho' )))
recover_dct3 = [list(dct(res_recovered3[0], type = 2, norm = 'ortho' )), list(dct(res_recovered3[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered3)):
recover_dct3.append(list(dct(res_recovered3[k], type = 2, norm = 'ortho' )))
all_recover1 = []
for i in recover_dct1:
for j in i:
all_recover1.append(j)
all_recover2 = []
for i in recover_dct2:
for j in i:
all_recover2.append(j)
all_recover3 = []
for i in recover_dct3:
for j in i:
all_recover3.append(j)
aN_recover1 = idct(all_recover1, type = 2, norm = 'ortho')
aN_recover2 = idct(all_recover2, type = 2, norm = 'ortho')
aN_recover3 = idct(all_recover3, type = 2, norm = 'ortho')
plt.plot(signal.resample(y1, len(aN_recover1))[31000:31100], label = "origianl")
plt.plot(aN_recover1[31000:31100], label = "recovered")
plt.legend()
plt.title('ACC')
plt.grid()
plt.show()
#resampled_signal_shorter = resampled_signal1[:len(aN_recover1)]
resampled_signal_shorter1 = signal.resample(y1, len(aN_recover1))
from sklearn.metrics import mean_squared_error
from math import sqrt
def PRD_calculation(original_signal, compressed_signal):
PRD = sqrt(sum((original_signal-compressed_signal)**2)/(sum(original_signal**2)))
return PRD
PRD = PRD_calculation(resampled_signal_shorter1, aN_recover1)
print("The PRD is {}%".format(round(PRD*100,3)))
```
| true |
code
| 0.323487 | null | null | null | null |
|
# Quickstart
In this tutorial, we explain how to quickly use ``LEGWORK`` to calculate the detectability of a collection of sources.
```
%matplotlib inline
```
Let's start by importing the source and visualisation modules of `LEGWORK` and some other common packages.
```
import legwork.source as source
import legwork.visualisation as vis
import numpy as np
import astropy.units as u
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
plt.rc('font', family='serif')
plt.rcParams['text.usetex'] = False
fs = 24
# update various fontsizes to match
params = {'figure.figsize': (12, 8),
'legend.fontsize': fs,
'axes.labelsize': fs,
'xtick.labelsize': 0.7 * fs,
'ytick.labelsize': 0.7 * fs}
plt.rcParams.update(params)
```
Next let's create a random collection of possible LISA sources in order to assess their detectability.
```
# create a random collection of sources
n_values = 1500
m_1 = np.random.uniform(0, 10, n_values) * u.Msun
m_2 = np.random.uniform(0, 10, n_values) * u.Msun
dist = np.random.normal(8, 1.5, n_values) * u.kpc
f_orb = 10**(-5 * np.random.power(3, n_values)) * u.Hz
ecc = 1 - np.random.power(5, n_values)
```
We can instantiate a `Source` class using these random sources in order to analyse the population. There are also a series of optional parameters which we don't cover here but if you are interested in the purpose of these then check out the [Using the Source Class](Source.ipynb) tutorial.
```
sources = source.Source(m_1=m_1, m_2=m_2, ecc=ecc, dist=dist, f_orb=f_orb)
```
This `Source` class has many methods for calculating strains, visualising populations and more. You can learn more about these in the [Using the Source Class](Source.ipynb) tutorial. For now, we shall focus only on the calculation of the signal-to-noise ratio.
Therefore, let's calculate the SNR for these sources. We set `verbose=True` to give an impression of what sort of sources we have created. This function will split the sources based on whether they are stationary/evolving and circular/eccentric and use one of 4 SNR functions for each subpopulation.
```
snr = sources.get_snr(verbose=True)
```
These SNR values are now stored in `sources.snr` and we can mask those that don't meet some detectable threshold.
```
detectable_threshold = 7
detectable_sources = sources.snr > 7
print("{} of the {} sources are detectable".format(len(sources.snr[detectable_sources]), n_values))
```
```
fig, ax = sources.plot_source_variables(xstr="f_orb", ystr="snr", disttype="kde", log_scale=(True, True),
fill=True, xlim=(2e-6, 2e-1), which_sources=sources.snr > 0)
```
The reason for this shape may not be immediately obvious. However, if we also use the visualisation module to overlay the LISA sensitivity curve, it becomes clear that the SNRs increase in step with the decrease in the noise and flatten out as the sensitivity curve does as we would expect. To learn more about the visualisation options that `LEGWORK` offers, check out the [Visualisation](Visualisation.ipynb) tutorial.
```
# create the same plot but set `show=False`
fig, ax = sources.plot_source_variables(xstr="f_orb", ystr="snr", disttype="kde", log_scale=(True, True),
fill=True, show=False, which_sources=sources.snr > 0)
# duplicate the x axis and plot the LISA sensitivity curve
right_ax = ax.twinx()
frequency_range = np.logspace(np.log10(2e-6), np.log10(2e-1), 1000) * u.Hz
vis.plot_sensitivity_curve(frequency_range=frequency_range, fig=fig, ax=right_ax)
plt.show()
```
That's it for this quickstart into using `LEGWORK`. For more details on using `LEGWORK` to calculate strains, evolve binaries and visualise their distributions check out the [other tutorials](../tutorials.rst) and [demos](../demos.rst) in these docs! You can also read more about the scope and limitations of `LEGWORK` [on this page](../limitations.rst).
| true |
code
| 0.722255 | null | null | null | null |
|
```
from __future__ import division, print_function
import os
import torch
import pandas
import numpy as np
from torch.utils.data import DataLoader,Dataset
from torchvision import utils, transforms
from skimage import io, transform
import matplotlib.pyplot as plt
import warnings
#ignore warnings
warnings.filterwarnings("ignore")
plt.ion() #interactive mode on
```
The dataset being used is the face pose detection dataset, which annotates the data using 68 landmark points. The dataset has a csv file that contains the annotation for the images.
```
# Import CSV file
landmarks_csv = pandas.read_csv("data/faces/face_landmarks.csv")
# Extracting info from the CSV file
n = 65
img_name = landmarks_csv.iloc[n,0]
landmarks = landmarks_csv.iloc[n,1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1,2)
# Print a few of the datasets for having a look at
# the dataset
print('Image name: {}'.format(img_name))
print('Landmarks shape: {}'.format(landmarks.shape))
print('First 4 Landmarks: {}'.format(landmarks[:4]))
```
Now that we have seen the landmark values let's plot a function to display the landmarks on an image
```
def plot_landmarks(image, landmarks):
plt.imshow(image)
plt.scatter(landmarks[:, 0], landmarks[:, 1], s=10, c='r', marker='.')
plt.pause(0.01)
plt.figure()
plot_landmarks(io.imread(os.path.join('data/faces/',img_name)),landmarks)
plt.show()
```
To use customa datasets we need to use the <b>(torch.utils.data.Dataset) Dataset</b> class provided. It is an abstract class and hence the custom class should inherit it and override the
<b>__len__</b> method and the
<b>__getitem__</b> method
The __getitem__ method is used to provide the ith sample from the dataset
```
class FaceLandmarkDataset(Dataset):
# We will read the file here
def __init__(self,csv_file, root_dir, transform=None):
"""
Args:
csv_file : string : path to csv file
root_dir : string : root directory which contains all the images
transform : callable, optional : Optional transform to be applied
to the images
"""
self.landmarks_frame = pandas.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.landmarks_frame)
def __getitem__(self, idx):
"""
Args:
idx (integer): the ith sample
"""
image_name = os.path.join(self.root_dir,self.landmarks_frame.iloc[idx, 0])
image = io.imread(image_name)
landmarks = np.array([self.landmarks_frame.iloc[idx, 1:]])
landmarks = landmarks.astype("float").reshape(-1, 2)
sample = {"image":image,"landmarks":landmarks}
if self.transform:
sample = self.transform(sample)
return sample
face_dataset = FaceLandmarkDataset(csv_file='data/faces/face_landmarks.csv',
root_dir='data/faces/')
fig = plt.figure()
for i in range(len(face_dataset)):
sample = face_dataset[i]
print(i, sample['image'].shape, sample['landmarks'].shape)
ax = plt.subplot(1, 4, i + 1)
plt.tight_layout()
ax.set_title('Sample #{}'.format(i))
ax.axis('off')
plot_landmarks(**sample)
if i == 3:
plt.show()
break
```
Now that we have the dataset , we can move on to preprocessing the data. We use the transforms class for this.
We will be using callable classes of the transformations we need so that the parameters do not need to be passed again and again. For better description refer the <a href="https://pytorch.org/tutorials/beginner/data_loading_tutorial.html">tutorial</a> from PyTorch.
To implement callable classes we just need to implement the __call__ method and if required __init__ method of the class.
Here we will be using autocrop , Reshape and To Tensor transformations.
__** NOTE **__<br>
In PyTorch the default style for image Tensors is <span>n_channels * Height * Width</span> as opposed to the Tensordlow default of <span>Height * Width * n_channels</span>. But all the images in the real world have the tensorflow default format and hence we need to do that change in the ToTensor class that we will implement.
```
# Implementing the Rescale class
class Rescale(object):
"""Rescale the input image to a given size
Args:
output_size (int or tuple):Desired output size. If tuple, output is
matched to output_size. If int, smaller of image edges is matched
to output_size keeping aspect ratio the same
"""
def __init__(self,output_size):
assert isinstance(output_size,(int,tuple))
self.output_size = output_size
def __call__(self,sample):
image, landmarks = samplep['image'], sample['landmarks']
h, w = image.shape[:2]
if isinstance(self.output_size,int):
if h>w:
new_h, new_w = self.output_size * h/w, self.output_size
else:
new_h, new_w = slef.output_size, self.output_size *w/h
else:
new_h, new_w = self.output_size
image = transform.resize(image, (new_h, new_w))
# h and w are swapped for landmarks because for images,
# x and y axes are axis 1 and 0 respectively
landmarks = landmarks * [new_w / w, new_h / h]
return {"image": image, "landmarks": landmarks}
# Implementing Random Crop
class RandomCrop(object):
"""Crop randomly the image in a sample
Args:
output_size(tuple or int): Desired output size. If int, square crop
is made.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
if isinstance(output_size, int):
self.output_size = (output_size, output_size)
else:
assert len(output_size) == 2
self.output_size = output_size
def __call__(self, sample):
images, landmarks = sample['image'], sample['landmarks']
h, w = images.shape[:,2]
new_h, new_w = self.output_size
top = np.random.randn(0, h-new_h)
left = np.random.randn(0, w-new_w)
images = images[top:top + new_h, left:left + new_w]
landmarks = landmarks - [left, top]
sample = {"image":images, "landmarks": landmarks}
return sample
# Implementing To Tensor
class ToTensor(object):
"""Convert the PIL image into a tensor"""
def __call__(self,sample):
image, landmarks = sample['image'], sample['landmarks']
# Need to transpose
# Numpy image : H x W x C
# Torch image : C x H x W
image = image.transpose((2, 0, 1))
sample = {"image":torch.from_numpy(image),"landmarks":torch.from_numpy(landmarks)}
```
| true |
code
| 0.834895 | null | null | null | null |
|
# Ejercicio: Spectral clustering para documentos
El clustering espectral es una técnica de agrupamiento basada en la topología de gráficas. Es especialmente útil cuando los datos no son convexos o cuando se trabaja, directamente, con estructuras de grafos.
##Preparación d elos documentos
Trabajaremos con documentos textuales. Estos se limpiarán y se convertirán en vectores. Posteriormente, podremos aplicar el método de spectral clustering.
```
#Se importan las librerías necesarias
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from gensim.models.doc2vec import Doc2Vec, TaggedDocument
```
La librería de Natural Language Toolkit (nltk) proporciona algunos corpus con los que se puede trabajar. Por ejemplo, el cropus Gutenberg (https://web.eecs.umich.edu/~lahiri/gutenberg_dataset.html) del que usaremos algunos datos. Asimismo, obtendremos de esta librería herramientas de preprocesamiento: stemmer y lista de stopwords.
```
import nltk
#Descarga del corpus
nltk.download('gutenberg')
#Descarga de la lista de stopwords
nltk.download('stopwords')
from nltk.corpus import gutenberg
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
```
Definimos los nombres de los archivos (ids) y la lista de paro
```
#Obtiene ids de los archivos del corpus gutenberg
doc_labels = gutenberg.fileids()
#Lista de stopwords para inglés
lista_paro = stopwords.words('english')
```
Definiremos una función que se encargará de preprocesar los textos. Se eliminan símbolos, se quitan elementos de la lista de stopwords y se pasa todo a minúsculas.
```
def preprocess(document):
#Lista que guarda archivos limpios
text = []
for word in document:
#Minúsculas
word = word.lower()
#Elimina stopwords y símbolos
if word not in lista_paro and word.isalpha() == True:
#Se aplica stemming
text.append(PorterStemmer().stem(word))
return text
```
Por cada documento, obtenemos la lista de sus palabras (stems) aplicando un preprocesado. Cada documento, entonces, es de la forma $d_i = \{w_1, w_2, ..., w_{N_i}\}$, donde $w_k$ son los stems del documento.
```
docs = []
for doc in doc_labels:
#Lista de palabras del documentos
arx = gutenberg.words(doc)
#Aplica la función de preprocesado
arx_prep = preprocess(arx)
docs.append(arx_prep)
#Imprime el nombre del documento, su longitud original y su longitud con preproceso
print(doc,len(arx), len(arx_prep))
```
Posteriormente, convertiremos cada documento en un vector en $\mathbb{R}^d$. Para esto, utilizaremos el algoritmo Doc2Vec.
```
#Dimensión de los vectores
dim = 300
#tamaño de la ventana de contexto
windows_siz = 15
#Indexa los documentos con valores enteros
documents = [TaggedDocument(doc_i, [i]) for i, doc_i in enumerate(docs)]
#Aplica el modelo de Doc2Vec
model = Doc2Vec(documents, vector_size=dim, window=windows_siz, min_count=1)
#Matriz de datos
X = np.zeros((len(doc_labels),dim))
for j in range(0,len(doc_labels)):
#Crea la matriz con los vectores de Doc2Vec
X[j] = model.docvecs[j]
print(X)
```
###Visualización
```
#Función para plotear
def plot_words(Z,ids,color='blue'):
#Reduce a dos dimensiones con PCA
Z = PCA(n_components=2).fit_transform(Z)
r=0
#Plotea las dimensiones
plt.scatter(Z[:,0],Z[:,1], marker='o', c=color)
for label,x,y in zip(ids, Z[:,0], Z[:,1]):
#Agrega las etiquetas
plt.annotate(label, xy=(x,y), xytext=(-1,1), textcoords='offset points', ha='center', va='bottom')
r+=1
plot_words(X, doc_labels)
plt.show()
```
##Aplicación de spectral clustering
Ahora se debe aplicar el algoritmo de spectral clustering a estos datos. Como hemos visto, se debe tomar en cuenta diferentes criterios:
* La función graph kernel se va utilizar
* El método de selección de vecinos (fully connected, k-nn)
* El número de dimensiones que queremos obtener
* El número de clusters en k-means
Pruebe con estos parámetros para obtener un buen agrupamiento de los documentos elegidos.
| true |
code
| 0.274886 | null | null | null | null |
|
# This Jupyter Notebook contains the full code needed to write the ColumnTransformer blog
## Import Necessary Packages
```
import pandas as pd
import numpy as np
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from pytz import timezone
```
## Import Data and some pre-transformation data prep
```
# read the csvs with waits and weather
df = pd.read_csv('./data/dec2019.csv')
weather_df = pd.read_csv('./data/dec2019weather.csv')
# rename the columns
df.columns = ['date_hour', 'wait_hrs']
# cut the date_hours to the hour (no minutes/seconds) and convert to string for merging
df['date_hour'] = pd.to_datetime(df['date_hour'], utc=True).values.astype('datetime64[h]')
df['date_hour'] = df['date_hour'].astype('str')
# create dataframe of all possible departure hours in the month (as string for merging)
# note that I chose to include non-ferry service hours at this stage
dts = pd.DataFrame(columns=['date_hour'])
dts['date_hour'] = pd.date_range(start='2019-12-01 00:00',
end='2019-12-31 23:30',
freq='H',
).astype('str')
# merge/join the waits to the dataframe of all departures
df_expanded = dts.merge(df, how='left', on='date_hour')
# cast as datetime with timezone UTC
df_expanded['date_hour'] = pd.to_datetime(df_expanded['date_hour'], utc=True)
# adjust time to PST
df_expanded['date_hour'] = [dt.astimezone(timezone('US/Pacific')) for dt in df_expanded['date_hour']]
# remove non-sailing times (1 to 4 am for Edmonds (1-3 for Kingston))
df_expanded = df_expanded.set_index('date_hour')
df_expanded = df_expanded.between_time('5:00', '00:59')
# reset index for modeling
df_expanded = df_expanded.reset_index()
weather_df.columns = ['date', 'max_temp', 'avg_temp', 'min_temp']
weather_df['date'] = pd.to_datetime(weather_df['date'])
df_expanded['date'] = pd.to_datetime(df_expanded['date_hour']).values.astype('datetime64[D]')
df_expanded = df_expanded.merge(weather_df, how='left', on='date')
df_expanded.head()
```
## Simple Column Transformer Example
```
# a little cheating to extract the day of the week
# and hour of the day w/out using a transformer
# (see below for the "real" version)
df_simple = df_expanded.copy()
df_simple['weekday'] = [dt.weekday() for dt in df_simple['date_hour']]
df_simple['hour'] = [dt.hour for dt in df_simple['date_hour']]
df_simple.head()
X = df_simple.drop(columns='wait_hrs')
y = df_simple['wait_hrs'].fillna(value=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=111)
# define column transformer and set n_jobs to have it run on all cores
col_transformer = ColumnTransformer(
transformers=[
('ss', StandardScaler(), ['max_temp', 'avg_temp', 'min_temp']),
('ohe', OneHotEncoder(), ['weekday', 'hour'])],
remainder='drop',
n_jobs=-1
)
X_train_transformed = col_transformer.fit_transform(X_train)
X_train_transformed
lr = LinearRegression()
pipe = Pipeline([
("preprocessing", col_transformer),
("lr", lr)
])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
preds_train[0:5]
preds_test[0:5]
col_transformer.get_feature_names
col_transformer.named_transformers_['ohe'].get_feature_names()
for transformer in col_transformer.named_transformers_.values():
try:
transformer.get_feature_names()
except:
print('SS col')
else:
print(transformer.get_feature_names())
```
## More complex column transformer example: imputing THEN standard scale/ohe
```
# define transformers
si_0 = SimpleImputer(strategy='constant', fill_value=0)
ss = StandardScaler()
ohe = OneHotEncoder()
# define column groups with same processing
cat_vars = ['weekday', 'hour']
num_vars = ['max_temp', 'avg_temp', 'min_temp']
# set up pipelines for each column group
categorical_pipe = Pipeline([
('si_0', si_0),
('ohe', ohe)
])
numeric_pipe = Pipeline([
('si_0', si_0),
('ss', ss)
])
# set up columnTransformer
col_transformer = ColumnTransformer(
transformers=[
('nums', numeric_pipe, num_vars),
('cats', categorical_pipe, cat_vars)
],
remainder='drop',
n_jobs=-1
)
pipe = Pipeline([
("preprocessing", col_transformer),
("lr", lr)
])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
preds_train[0:10]
preds_test[0:10]
col_transformer.named_transformers_['cats'].named_steps['ohe'].get_feature_names()
```
## Create your own custom transformer
```
from sklearn.base import TransformerMixin, BaseEstimator
class DateTransformer(TransformerMixin, BaseEstimator):
"""Extracts features from datetime column
Returns:
hour: hour
day: Between 1 and the number of days in the given month of the given year.
month: Between 1 and 12 inclusive.
year: four-digit year
weekday:day of the week as an integer, where Monday is 0 and Sunday is 6
"""
def fit(self, x, y=None):
return self
def transform(self, x, y=None):
result = pd.DataFrame(x, columns=['date_hour'])
result['hour'] = [dt.hour for dt in result['date_hour']]
result['day'] = [dt.day for dt in result['date_hour']]
result['month'] = [dt.month for dt in result['date_hour']]
result['year'] = [dt.year for dt in result['date_hour']]
result['weekday'] = [dt.weekday() for dt in result['date_hour']]
return result[['hour', 'day', 'month', 'year', 'weekday']]
def get_feature_names(self):
return ['hour','day', 'month', 'year', 'weekday']
X = df_expanded.drop(columns='wait_hrs')
y = df_simple['wait_hrs'].fillna(value=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=111)
X.head()
time_preprocessing = Pipeline([
('date', DateTransformer()),
('ohe', OneHotEncoder(categories='auto'))
])
ct = ColumnTransformer(
transformers=[
('ss', StandardScaler(), ['max_temp', 'avg_temp', 'min_temp']),
('date_exp', time_preprocessing, ['date_hour'])],
remainder='drop',
)
pipe = Pipeline([('preprocessor', ct),
('lr', lr)])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
lr.coef_
ct.named_transformers_['date_exp'].named_steps['ohe'].get_feature_names()
ct.named_transformers_['date_exp'].named_steps['date'].get_feature_names()
```
## Rare features with ColumnTransformer
```
df = pd.DataFrame()
df['cat1'] = [0, 1, 1, 1, 1, 1, 1, 1, 1, 1]
df['cat2'] = [0, 0, 0, 0, 0, 2, 2, 2, 2, 2]
df['num1'] = [np.nan, 1, 1.1, .9, .8, np.nan, 2, 2.2, 1.5, np.nan]
df['num2'] = [1.1, 1.1, 1.1, 1.1, 1.1, 1.2, 1.2, 1.2, 1.2, 1.2]
target = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
X_train, X_test, y_train, y_test = train_test_split(df, target, random_state=111)
num_pipe = Pipeline([
('si', SimpleImputer(add_indicator=True)),
('ss', StandardScaler())
])
ct = ColumnTransformer(
transformers=[('ohe', OneHotEncoder(categories=[[0,1], [0,2]]), ['cat1', 'cat2']),
('numeric', num_pipe, ['num1', 'num2'])])
pipe = Pipeline([
('preprocessor', ct),
('lr', lr)
])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
ct.fit_transform(X_train)
ct.fit_transform(X_test)
```
| true |
code
| 0.555375 | null | null | null | null |
|
## Image segmentation with CamVid
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai import *
from fastai.vision import *
from fastai.callbacks.hooks import *
```
The One Hundred Layer Tiramisu paper used a modified version of Camvid, with smaller images and few classes. You can get it from the CamVid directory of this repo:
git clone https://github.com/alexgkendall/SegNet-Tutorial.git
```
path = Path('./data/camvid-tiramisu')
path.ls()
```
## Data
```
fnames = get_image_files(path/'val')
fnames[:3]
lbl_names = get_image_files(path/'valannot')
lbl_names[:3]
img_f = fnames[0]
img = open_image(img_f)
img.show(figsize=(5,5))
def get_y_fn(x): return Path(str(x.parent)+'annot')/x.name
codes = array(['Sky', 'Building', 'Pole', 'Road', 'Sidewalk', 'Tree',
'Sign', 'Fence', 'Car', 'Pedestrian', 'Cyclist', 'Void'])
mask = open_mask(get_y_fn(img_f))
mask.show(figsize=(5,5), alpha=1)
src_size = np.array(mask.shape[1:])
src_size,mask.data
```
## Datasets
```
bs = 8
src = (SegmentationItemList.from_folder(path)
.split_by_folder(valid='val')
.label_from_func(get_y_fn, classes=codes))
data = (src.transform(get_transforms(), tfm_y=True)
.databunch(bs=bs)
.normalize(imagenet_stats))
data.show_batch(2, figsize=(10,7))
```
## Model
```
name2id = {v:k for k,v in enumerate(codes)}
void_code = name2id['Void']
def acc_camvid(input, target):
target = target.squeeze(1)
mask = target != void_code
return (input.argmax(dim=1)[mask]==target[mask]).float().mean()
metrics=acc_camvid
wd=1e-2
learn = unet_learner(data, models.resnet34, metrics=metrics, wd=wd, bottle=True)
lr_find(learn)
learn.recorder.plot()
lr=2e-3
learn.fit_one_cycle(10, slice(lr), pct_start=0.8)
learn.save('stage-1')
learn.load('stage-1');
learn.unfreeze()
lrs = slice(lr/100,lr)
learn.fit_one_cycle(12, lrs, pct_start=0.8)
learn.save('stage-2');
```
## Go big
```
learn=None
gc.collect()
```
You may have to restart your kernel and come back to this stage if you run out of memory, and may also need to decrease `bs`.
```
size = src_size
bs=8
data = (src.transform(get_transforms(), size=size, tfm_y=True)
.databunch(bs=bs)
.normalize(imagenet_stats))
learn = unet_learner(data, models.resnet34, metrics=metrics, wd=wd, bottle=True).load('stage-2');
lr_find(learn)
learn.recorder.plot()
lr=1e-3
learn.fit_one_cycle(10, slice(lr), pct_start=0.8)
learn.save('stage-1-big')
learn.load('stage-1-big');
learn.unfreeze()
lrs = slice(lr/1000,lr/10)
learn.fit_one_cycle(10, lrs)
learn.save('stage-2-big')
learn.load('stage-2-big');
learn.show_results(rows=3, figsize=(9,11))
```
## fin
```
# start: 480x360
print(learn.summary())
```
| true |
code
| 0.589716 | null | null | null | null |
|
# Equilibrium analysis Chemical reaction
Number (code) of assignment: 2N4
Description of activity:
Report on behalf of:
name : Pieter van Halem
student number : 4597591
name : Dennis Dane
student number :4592239
Data of student taking the role of contact person:
name :
email address :
```
import numpy as np
import matplotlib.pyplot as plt
```
# Function definitons:
In the following block the function that are used for the numerical analysis are definend. These are functions for calculation the various time steps, functions for plotting tables ands functions for plotting graphs.
```
def f(t,y,a,b,i):
if (t>round(i,2)):
a = 0
du = a-(b+1)*y[0,0]+y[0,0]**2*y[0,1]
dv = b*y[0,0]-y[0,0]**2*y[0,1]
return np.matrix([du,dv])
def FE(t,y,h,a,b,i):
f1 = f(t,y,a,b,i)
pred = y + f1*h
corr = y + (h/2)*(f(t,pred,a,b,i) + f1)
return corr
def Integrate(y0, t0, tend, N,a,b,i):
h = (tend-t0)/N
t_arr = np.zeros(N+1)
t_arr[0] = t0
w_arr = np.zeros((2,N+1))
w_arr[:,0] = y0
t = t0
y = y0
for k in range(1,N+1):
y = FE(t,y,h,a,b,i)
w_arr[:,k] = y
t = round(t + h,4)
t_arr[k] = t
return t_arr, w_arr
def PrintTable(t_arr, w_arr):
print ("%6s %6s: %17s %17s" % ("index", "t", "u(t)", "v(t)"))
for k in range(0,N+1):
print ("{:6d} {:6.2f}: {:17.7e} {:17.7e}".format(k,t_arr[k],
w_arr[0,k],w_arr[1,k]))
def PlotGraphs(t_arr, w_arr):
plt.figure("Initial value problem")
plt.plot(t_arr,w_arr[0,:],'r',t_arr,w_arr[1,:],'--')
plt.legend(("$u(t)$", "$v(t)$"),loc="best", shadow=True)
plt.xlabel("$t$")
plt.ylabel("$u$ and $v$")
plt.title("Graphs of $u(t)$ and $v(t)$")
plt.show()
def PlotGraphs2(t_arr, w_arr):
plt.figure("Initial value problem")
plt.plot(w_arr[0,:],w_arr[1,:],'g')
plt.legend(("$u,v$",""),loc="best", shadow=True)
plt.xlabel("$u(t)$")
plt.ylabel("$v(t)$")
plt.title("$Phase$ $plane$ $(u,v)$")
plt.axis("scaled")
plt.show()
def PlotGraphs3(t_arr, w_arr,t_arr2, w_arr2):
plt.figure("Initial value problem")
plt.plot(t_arr,w_arr[0,:],'r',t_arr,w_arr[1,:],'b--')
plt.plot(t_arr2,w_arr2[0,:],'r',t_arr2,w_arr2[1,:],'b--')
#plt.plot([t_array[80],t_array2[0]],[w_array[0,80],w_array2[0,0]],'r')
plt.legend(("$u(t)$", "$v(t)$"),loc="best", shadow=True)
plt.xlabel("$t$")
plt.ylabel("$u$ and $v$")
plt.title("Graphs of $u(t)$ and $v(t)$")
plt.show()
def PlotGraphs4(t_arr, w_arr,t_arr2, w_arr2):
#plt.figure("Initial value problem")
plt.plot(w_arr[0,:],w_arr[1,:],'g')
plt.plot(w_arr2[0,:],w_arr2[1,:],'g')
#plt.legend(("$u,v$",""),loc="best", shadow=True)
plt.xlabel("$u(t)$")
plt.ylabel("$v(t)$")
plt.title("$Phase$ $plane$ $(u,v)$")
plt.axis("scaled")
plt.show()
```
# Assignment 2.9
Integrate the system with Modified Euler and time step h = 0.15. Make a table of u and v on the time interval 0 ≤ t ≤ 1.5. The table needs to give u and v in an 8-digit floating-point format.
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 1.5
N = 10
t_array, w_array = Integrate(y0, t0, tend, N,2,4.5,11)
print("The integrated system using Modified Euler with time step h = 0.15 is shown in the following table: \n")
PrintTable(t_array, w_array)
```
# Assignmet 2.10
Integrate the system with Modified Euler and time step h = 0.05 for the interval [0,20]. Make plots of u and v as functions of t (put them in one figure). Also make a plot of u and v in the phase plane (u,v-plane). Do your plots correspond to your results of part 2?
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 20
N = 400
t_array, w_array = Integrate(y0, t0, tend, N,2,4.5, 25)
print("In this assignment the system has to be integrated using Modified Euler with a time step of h = 0.05 on \na interval of [0,20].")
print("The first graph is u(t) and v(t) against time (t).")
PlotGraphs(t_array, w_array)
print("The second graph shows the u-v plane")
PlotGraphs2(t_array, w_array)
print("\n The system is stable and a spiral. Therefor is consistent with the conclusion from assignment 1.3.")
```
# Assignment 2.11
Using the formula derived in question 7, estimate the accuracy of u and v computed with h = 0.05 at t = 8. Hence, integrate once more with time step h = 0.1.
The error can be estimated with Richardsons methode. were we use α = 1/3 found in assignment 7. here the estimated error is: E ≈ α( w(h) - w(2h) ).
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 20
N = 400
t_array, w_array = Integrate(y0, t0, tend, N, 2, 4.5,25)
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 20
N = 200
t_array2, w_array2 = Integrate(y0, t0, tend, N, 2, 4.5, 25)
print("The value for u and v at t = 8 with h = 0.05 is:",t_array[160], w_array[:,160])
print("The value for u and v at t = 8 with h = 0.10 is:",t_array2[80], w_array2[:,80])
E1 = (w_array[0,160]-w_array2[0,80])*(1/3)
E2 = (w_array[1,160]-w_array2[1,80])*(1/3)
print("The estimated acuracy for u is:", E1)
print("The estimated acuracy for v is:", E2)
```
# Assignment 2.12
Apply Modified Euler with h = 0.05. For 0 ≤ t ≤ t1 it holds that a = 2. At t = t1 the supply of materials A fails, and therefore a = 0 for t > t1. Take t1 = 4.0. Make plot of u and v as a function of t on the intervals [0, 10] in one figure and a plot of u and v in the uv-plane. Evaluate your results by comparing them to your findings form part 8.
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 10.0
N = 200
t_array, w_array = Integrate(y0, t0, tend, N, 2, 4.5, 4)
PlotGraphs(t_array, w_array)
```
The first plot shows that u and v indeed converges to a certain value, as predicted in assignment 8. The phase plane shows that uv goes to a point on the u-axis. This was as well predicted in assignment 8.
The first plot shows a corner in the u and v graph (a discontinuity in the first derivative). This does not contradict the theory because the system of differential equations changes the first derivatives does not have to be continuous. The line itself is continuous because it is given in the initial values.
# Assignment 2.13
Take t1 = 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0. Make a table of the value of v-tilda and t-tilda. Evaluate your rsults.
```
for i in np.arange(3.0,6.5,0.50):
t0 = 0.0
tend = 10.0
N = 200
t_array2, w_array2 = Integrate(y0, t0, tend, N, 2.0, 4.5,i)
indices = np.nonzero(w_array2[0,:] >= 0.01)
index = np.max(indices[0])
t_tilde = t_array2[index+1]
v_tilde = w_array2[1,N]
if i == 3:
print("%6s %17s: %17s " % ("t1", "t_tilde", "v_tilde"))
print("{:6.2f} {:17.2f} {:17.7e}".format(i,t_tilde,v_tilde))
```
lkksdndglnsldkgknlsdagn
De waarde moeten zijn: t1 = 6.0 v-tilde = 3.34762, t-tilde = 7.35
| true |
code
| 0.456834 | null | null | null | null |
|
# Creating a simple PDE model
In the [previous notebook](./1-an-ode-model.ipynb) we show how to create, discretise and solve an ODE model in pybamm. In this notebook we show how to create and solve a PDE problem, which will require meshing of the spatial domain.
As an example, we consider the problem of linear diffusion on a unit sphere,
\begin{equation*}
\frac{\partial c}{\partial t} = \nabla \cdot (\nabla c),
\end{equation*}
with the following boundary and initial conditions:
\begin{equation*}
\left.\frac{\partial c}{\partial r}\right\vert_{r=0} = 0, \quad \left.\frac{\partial c}{\partial r}\right\vert_{r=1} = 2, \quad \left.c\right\vert_{t=0} = 1.
\end{equation*}
As before, we begin by importing the pybamm library into this notebook, along with any other packages we require:
```
%pip install pybamm -q # install PyBaMM if it is not installed
import pybamm
import numpy as np
import matplotlib.pyplot as plt
```
## Setting up the model
As in the previous example, we start with a `pybamm.BaseModel` object and define our model variables. Since we are now solving a PDE we need to tell pybamm the domain each variable belongs to so that it can be discretised in space in the correct way. This is done by passing the keyword argument `domain`, and in this example we choose the domain "negative particle".
```
model = pybamm.BaseModel()
c = pybamm.Variable("Concentration", domain="negative particle")
```
Note that we have given our variable the (useful) name "Concentration", but the symbol representing this variable is simply `c`.
We then state out governing equations. Sometime it is useful to define intermediate quantities in order to express the governing equations more easily. In this example we define the flux, then define the rhs to be minus the divergence of the flux. The equation is then added to the dictionary `model.rhs`
```
N = -pybamm.grad(c) # define the flux
dcdt = -pybamm.div(N) # define the rhs equation
model.rhs = {c: dcdt} # add the equation to rhs dictionary
```
Unlike ODE models, PDE models require both initial and boundary conditions. Similar to initial conditions, boundary conditions can be added using the dictionary `model.boundary_conditions`. Boundary conditions for each variable are provided as a dictionary of the form `{side: (value, type)`, where, in 1D, side can be "left" or "right", value is the value of the boundary conditions, and type is the type of boundary condition (at present, this can be "Dirichlet" or "Neumann").
```
# initial conditions
model.initial_conditions = {c: pybamm.Scalar(1)}
# boundary conditions
lbc = pybamm.Scalar(0)
rbc = pybamm.Scalar(2)
model.boundary_conditions = {c: {"left": (lbc, "Neumann"), "right": (rbc, "Neumann")}}
```
Note that in our example the boundary conditions take constant values, but the value can be any valid pybamm expression.
Finally, we add any variables of interest to the dictionary `model.variables`
```
model.variables = {"Concentration": c, "Flux": N}
```
## Using the model
Now the model is now completely defined all that remains is to discretise and solve. Since this model is a PDE we need to define the geometry on which it will be solved, and choose how to mesh the geometry and discretise in space.
### Defining a geometry and mesh
We can define spatial variables in a similar way to how we defined model variables, providing a domain and a coordinate system. The geometry on which we wish to solve the model is defined using a nested dictionary. The first key is the domain name (here "negative particle") and the entry is a dictionary giving the limits of the domain.
```
# define geometry
r = pybamm.SpatialVariable(
"r", domain=["negative particle"], coord_sys="spherical polar"
)
geometry = {"negative particle": {r: {"min": pybamm.Scalar(0), "max": pybamm.Scalar(1)}}}
```
We then create a mesh using the `pybamm.MeshGenerator` class. As inputs this class takes the type of mesh and any parameters required by the mesh. In this case we choose a uniform one-dimensional mesh which doesn't require any parameters.
```
# mesh and discretise
submesh_types = {"negative particle": pybamm.MeshGenerator(pybamm.Uniform1DSubMesh)}
var_pts = {r: 20}
mesh = pybamm.Mesh(geometry, submesh_types, var_pts)
```
Example of meshes that do require parameters include the `pybamm.Exponential1DSubMesh` which clusters points close to one or both boundaries using an exponential rule. It takes a parameter which sets how closely the points are clustered together, and also lets the users select the side on which more points should be clustered. For example, to create a mesh with more nodes clustered to the right (i.e. the surface in the particle problem), using a stretch factor of 2, we pass an instance of the exponential submesh class and a dictionary of parameters into the `MeshGenerator` class as follows: `pybamm.MeshGenerator(pybamm.Exponential1DSubMesh, submesh_params={"side": "right", "stretch": 2})`
After defining a mesh we choose a spatial method. Here we choose the Finite Volume Method. We then set up a discretisation by passing the mesh and spatial methods to the class `pybamm.Discretisation`. The model is then processed, turning the variables into (slices of) a statevector, spatial variables into vector and spatial operators into matrix-vector multiplications.
```
spatial_methods = {"negative particle": pybamm.FiniteVolume()}
disc = pybamm.Discretisation(mesh, spatial_methods)
disc.process_model(model);
```
Now that the model has been discretised we are ready to solve.
### Solving the model
As before, we choose a solver and times at which we want the solution returned. We then solve, extract the variables we are interested in, and plot the result.
```
# solve
solver = pybamm.ScipySolver()
t = np.linspace(0, 1, 100)
solution = solver.solve(model, t)
# post-process, so that the solution can be called at any time t or space r
# (using interpolation)
c = solution["Concentration"]
# plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13, 4))
ax1.plot(solution.t, c(solution.t, r=1))
ax1.set_xlabel("t")
ax1.set_ylabel("Surface concentration")
r = np.linspace(0, 1, 100)
ax2.plot(r, c(t=0.5, r=r))
ax2.set_xlabel("r")
ax2.set_ylabel("Concentration at t=0.5")
plt.tight_layout()
plt.show()
```
In the [next notebook](./3-negative-particle-problem.ipynb) we build on the example here to to solve the problem of diffusion in the negative electrode particle within the single particle model. In doing so we will also cover how to include parameters in a model.
## References
The relevant papers for this notebook are:
```
pybamm.print_citations()
```
| true |
code
| 0.733255 | null | null | null | null |
|
# 线性回归
:label:`sec_linear_regression`
*回归*(regression)是能为一个或多个自变量与因变量之间关系建模的一类方法。
在自然科学和社会科学领域,回归经常用来表示输入和输出之间的关系。
在机器学习领域中的大多数任务通常都与*预测*(prediction)有关。
当我们想预测一个数值时,就会涉及到回归问题。
常见的例子包括:预测价格(房屋、股票等)、预测住院时间(针对住院病人等)、
预测需求(零售销量等)。
但不是所有的*预测*都是回归问题。
在后面的章节中,我们将介绍分类问题。分类问题的目标是预测数据属于一组类别中的哪一个。
## 线性回归的基本元素
*线性回归*(linear regression)可以追溯到19世纪初,
它在回归的各种标准工具中最简单而且最流行。
线性回归基于几个简单的假设:
首先,假设自变量$\mathbf{x}$和因变量$y$之间的关系是线性的,
即$y$可以表示为$\mathbf{x}$中元素的加权和,这里通常允许包含观测值的一些噪声;
其次,我们假设任何噪声都比较正常,如噪声遵循正态分布。
为了解释*线性回归*,我们举一个实际的例子:
我们希望根据房屋的面积(平方英尺)和房龄(年)来估算房屋价格(美元)。
为了开发一个能预测房价的模型,我们需要收集一个真实的数据集。
这个数据集包括了房屋的销售价格、面积和房龄。
在机器学习的术语中,该数据集称为*训练数据集*(training data set)
或*训练集*(training set)。
每行数据(比如一次房屋交易相对应的数据)称为*样本*(sample),
也可以称为*数据点*(data point)或*数据样本*(data instance)。
我们把试图预测的目标(比如预测房屋价格)称为*标签*(label)或*目标*(target)。
预测所依据的自变量(面积和房龄)称为*特征*(feature)或*协变量*(covariate)。
通常,我们使用$n$来表示数据集中的样本数。
对索引为$i$的样本,其输入表示为$\mathbf{x}^{(i)} = [x_1^{(i)}, x_2^{(i)}]^\top$,
其对应的标签是$y^{(i)}$。
### 线性模型
:label:`subsec_linear_model`
线性假设是指目标(房屋价格)可以表示为特征(面积和房龄)的加权和,如下面的式子:
$$\mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age} + b.$$
:eqlabel:`eq_price-area`
:eqref:`eq_price-area`中的$w_{\mathrm{area}}$和$w_{\mathrm{age}}$
称为*权重*(weight),权重决定了每个特征对我们预测值的影响。
$b$称为*偏置*(bias)、*偏移量*(offset)或*截距*(intercept)。
偏置是指当所有特征都取值为0时,预测值应该为多少。
即使现实中不会有任何房子的面积是0或房龄正好是0年,我们仍然需要偏置项。
如果没有偏置项,我们模型的表达能力将受到限制。
严格来说, :eqref:`eq_price-area`是输入特征的一个
*仿射变换*(affine transformation)。
仿射变换的特点是通过加权和对特征进行*线性变换*(linear transformation),
并通过偏置项来进行*平移*(translation)。
给定一个数据集,我们的目标是寻找模型的权重$\mathbf{w}$和偏置$b$,
使得根据模型做出的预测大体符合数据里的真实价格。
输出的预测值由输入特征通过*线性模型*的仿射变换决定,仿射变换由所选权重和偏置确定。
而在机器学习领域,我们通常使用的是高维数据集,建模时采用线性代数表示法会比较方便。
当我们的输入包含$d$个特征时,我们将预测结果$\hat{y}$
(通常使用“尖角”符号表示$y$的估计值)表示为:
$$\hat{y} = w_1 x_1 + ... + w_d x_d + b.$$
将所有特征放到向量$\mathbf{x} \in \mathbb{R}^d$中,
并将所有权重放到向量$\mathbf{w} \in \mathbb{R}^d$中,
我们可以用点积形式来简洁地表达模型:
$$\hat{y} = \mathbf{w}^\top \mathbf{x} + b.$$
:eqlabel:`eq_linreg-y`
在 :eqref:`eq_linreg-y`中,
向量$\mathbf{x}$对应于单个数据样本的特征。
用符号表示的矩阵$\mathbf{X} \in \mathbb{R}^{n \times d}$
可以很方便地引用我们整个数据集的$n$个样本。
其中,$\mathbf{X}$的每一行是一个样本,每一列是一种特征。
对于特征集合$\mathbf{X}$,预测值$\hat{\mathbf{y}} \in \mathbb{R}^n$
可以通过矩阵-向量乘法表示为:
$${\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b$$
这个过程中的求和将使用广播机制
(广播机制在 :numref:`subsec_broadcasting`中有详细介绍)。
给定训练数据特征$\mathbf{X}$和对应的已知标签$\mathbf{y}$,
线性回归的目标是找到一组权重向量$\mathbf{w}$和偏置$b$:
当给定从$\mathbf{X}$的同分布中取样的新样本特征时,
这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。
虽然我们相信给定$\mathbf{x}$预测$y$的最佳模型会是线性的,
但我们很难找到一个有$n$个样本的真实数据集,其中对于所有的$1 \leq i \leq n$,$y^{(i)}$完全等于$\mathbf{w}^\top \mathbf{x}^{(i)}+b$。
无论我们使用什么手段来观察特征$\mathbf{X}$和标签$\mathbf{y}$,
都可能会出现少量的观测误差。
因此,即使确信特征与标签的潜在关系是线性的,
我们也会加入一个噪声项来考虑观测误差带来的影响。
在开始寻找最好的*模型参数*(model parameters)$\mathbf{w}$和$b$之前,
我们还需要两个东西:
(1)一种模型质量的度量方式;
(2)一种能够更新模型以提高模型预测质量的方法。
### 损失函数
在我们开始考虑如何用模型*拟合*(fit)数据之前,我们需要确定一个拟合程度的度量。
*损失函数*(loss function)能够量化目标的*实际*值与*预测*值之间的差距。
通常我们会选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。
回归问题中最常用的损失函数是平方误差函数。
当样本$i$的预测值为$\hat{y}^{(i)}$,其相应的真实标签为$y^{(i)}$时,
平方误差可以定义为以下公式:
$$l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2.$$
:eqlabel:`eq_mse`
常数$\frac{1}{2}$不会带来本质的差别,但这样在形式上稍微简单一些
(因为当我们对损失函数求导后常数系数为1)。
由于训练数据集并不受我们控制,所以经验误差只是关于模型参数的函数。
为了进一步说明,来看下面的例子。
我们为一维情况下的回归问题绘制图像,如 :numref:`fig_fit_linreg`所示。

:label:`fig_fit_linreg`
由于平方误差函数中的二次方项,
估计值$\hat{y}^{(i)}$和观测值$y^{(i)}$之间较大的差异将导致更大的损失。
为了度量模型在整个数据集上的质量,我们需计算在训练集$n$个样本上的损失均值(也等价于求和)。
$$L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2.$$
在训练模型时,我们希望寻找一组参数($\mathbf{w}^*, b^*$),
这组参数能最小化在所有训练样本上的总损失。如下式:
$$\mathbf{w}^*, b^* = \operatorname*{argmin}_{\mathbf{w}, b}\ L(\mathbf{w}, b).$$
### 解析解
线性回归刚好是一个很简单的优化问题。
与我们将在本书中所讲到的其他大部分模型不同,线性回归的解可以用一个公式简单地表达出来,
这类解叫作解析解(analytical solution)。
首先,我们将偏置$b$合并到参数$\mathbf{w}$中,合并方法是在包含所有参数的矩阵中附加一列。
我们的预测问题是最小化$\|\mathbf{y} - \mathbf{X}\mathbf{w}\|^2$。
这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。
将损失关于$\mathbf{w}$的导数设为0,得到解析解:
$$\mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}.$$
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。
解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
### 随机梯度下降
即使在我们无法得到解析解的情况下,我们仍然可以有效地训练模型。
在许多任务上,那些难以优化的模型效果要更好。
因此,弄清楚如何训练这些难以优化的模型是非常重要的。
本书中我们用到一种名为*梯度下降*(gradient descent)的方法,
这种方法几乎可以优化所有深度学习模型。
它通过不断地在损失函数递减的方向上更新参数来降低误差。
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值)
关于模型参数的导数(在这里也可以称为梯度)。
但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。
因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本,
这种变体叫做*小批量随机梯度下降*(minibatch stochastic gradient descent)。
在每次迭代中,我们首先随机抽样一个小批量$\mathcal{B}$,
它是由固定数量的训练样本组成的。
然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。
最后,我们将梯度乘以一个预先确定的正数$\eta$,并从当前参数的值中减掉。
我们用下面的数学公式来表示这一更新过程($\partial$表示偏导数):
$$(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b).$$
总结一下,算法的步骤如下:
(1)初始化模型参数的值,如随机初始化;
(2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
对于平方损失和仿射变换,我们可以明确地写成如下形式:
$$\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}$$
:eqlabel:`eq_linreg_batch_update`
公式 :eqref:`eq_linreg_batch_update`中的$\mathbf{w}$和$\mathbf{x}$都是向量。
在这里,更优雅的向量表示法比系数表示法(如$w_1, w_2, \ldots, w_d$)更具可读性。
$|\mathcal{B}|$表示每个小批量中的样本数,这也称为*批量大小*(batch size)。
$\eta$表示*学习率*(learning rate)。
批量大小和学习率的值通常是手动预先指定,而不是通过模型训练得到的。
这些可以调整但不在训练过程中更新的参数称为*超参数*(hyperparameter)。
*调参*(hyperparameter tuning)是选择超参数的过程。
超参数通常是我们根据训练迭代结果来调整的,
而训练迭代结果是在独立的*验证数据集*(validation dataset)上评估得到的。
在训练了预先确定的若干迭代次数后(或者直到满足某些其他停止条件后),
我们记录下模型参数的估计值,表示为$\hat{\mathbf{w}}, \hat{b}$。
但是,即使我们的函数确实是线性的且无噪声,这些估计值也不会使损失函数真正地达到最小值。
因为算法会使得损失向最小值缓慢收敛,但却不能在有限的步数内非常精确地达到最小值。
线性回归恰好是一个在整个域中只有一个最小值的学习问题。
但是对于像深度神经网络这样复杂的模型来说,损失平面上通常包含多个最小值。
深度学习实践者很少会去花费大力气寻找这样一组参数,使得在*训练集*上的损失达到最小。
事实上,更难做到的是找到一组参数,这组参数能够在我们从未见过的数据上实现较低的损失,
这一挑战被称为*泛化*(generalization)。
### 用模型进行预测
给定“已学习”的线性回归模型$\hat{\mathbf{w}}^\top \mathbf{x} + \hat{b}$,
现在我们可以通过房屋面积$x_1$和房龄$x_2$来估计一个(未包含在训练数据中的)新房屋价格。
给定特征估计目标的过程通常称为*预测*(prediction)或*推断*(inference)。
本书将尝试坚持使用*预测*这个词。
虽然*推断*这个词已经成为深度学习的标准术语,但其实*推断*这个词有些用词不当。
在统计学中,*推断*更多地表示基于数据集估计参数。
当深度学习从业者与统计学家交谈时,术语的误用经常导致一些误解。
## 矢量化加速
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。
为了实现这一点,需要(**我们对计算进行矢量化,
从而利用线性代数库,而不是在Python中编写开销高昂的for循环**)。
```
%matplotlib inline
import math
import time
import numpy as np
import tensorflow as tf
from d2l import tensorflow as d2l
```
为了说明矢量化为什么如此重要,我们考虑(**对向量相加的两种方法**)。
我们实例化两个全为1的10000维向量。
在一种方法中,我们将使用Python的for循环遍历向量;
在另一种方法中,我们将依赖对`+`的调用。
```
n = 10000
a = tf.ones(n)
b = tf.ones(n)
```
由于在本书中我们将频繁地进行运行时间的基准测试,所以[**我们定义一个计时器**]:
```
class Timer: #@save
"""记录多次运行时间"""
def __init__(self):
self.times = []
self.start()
def start(self):
"""启动计时器"""
self.tik = time.time()
def stop(self):
"""停止计时器并将时间记录在列表中"""
self.times.append(time.time() - self.tik)
return self.times[-1]
def avg(self):
"""返回平均时间"""
return sum(self.times) / len(self.times)
def sum(self):
"""返回时间总和"""
return sum(self.times)
def cumsum(self):
"""返回累计时间"""
return np.array(self.times).cumsum().tolist()
```
现在我们可以对工作负载进行基准测试。
首先,[**我们使用for循环,每次执行一位的加法**]。
```
c = tf.Variable(tf.zeros(n))
timer = Timer()
for i in range(n):
c[i].assign(a[i] + b[i])
f'{timer.stop():.5f} sec'
```
(**或者,我们使用重载的`+`运算符来计算按元素的和**)。
```
timer.start()
d = a + b
f'{timer.stop():.5f} sec'
```
结果很明显,第二种方法比第一种方法快得多。
矢量化代码通常会带来数量级的加速。
另外,我们将更多的数学运算放到库中,而无须自己编写那么多的计算,从而减少了出错的可能性。
## 正态分布与平方损失
:label:`subsec_normal_distribution_and_squared_loss`
接下来,我们通过对噪声分布的假设来解读平方损失目标函数。
正态分布和线性回归之间的关系很密切。
正态分布(normal distribution),也称为*高斯分布*(Gaussian distribution),
最早由德国数学家高斯(Gauss)应用于天文学研究。
简单的说,若随机变量$x$具有均值$\mu$和方差$\sigma^2$(标准差$\sigma$),其正态分布概率密度函数如下:
$$p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right).$$
下面[**我们定义一个Python函数来计算正态分布**]。
```
def normal(x, mu, sigma):
p = 1 / math.sqrt(2 * math.pi * sigma**2)
return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)
```
我们现在(**可视化正态分布**)。
```
# 再次使用numpy进行可视化
x = np.arange(-7, 7, 0.01)
# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
ylabel='p(x)', figsize=(4.5, 2.5),
legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])
```
就像我们所看到的,改变均值会产生沿$x$轴的偏移,增加方差将会分散分布、降低其峰值。
均方误差损失函数(简称均方损失)可以用于线性回归的一个原因是:
我们假设了观测中包含噪声,其中噪声服从正态分布。
噪声正态分布如下式:
$$y = \mathbf{w}^\top \mathbf{x} + b + \epsilon,$$
其中,$\epsilon \sim \mathcal{N}(0, \sigma^2)$。
因此,我们现在可以写出通过给定的$\mathbf{x}$观测到特定$y$的*似然*(likelihood):
$$P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right).$$
现在,根据极大似然估计法,参数$\mathbf{w}$和$b$的最优值是使整个数据集的*似然*最大的值:
$$P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)}).$$
根据极大似然估计法选择的估计量称为*极大似然估计量*。
虽然使许多指数函数的乘积最大化看起来很困难,
但是我们可以在不改变目标的前提下,通过最大化似然对数来简化。
由于历史原因,优化通常是说最小化而不是最大化。
我们可以改为*最小化负对数似然*$-\log P(\mathbf y \mid \mathbf X)$。
由此可以得到的数学公式是:
$$-\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2.$$
现在我们只需要假设$\sigma$是某个固定常数就可以忽略第一项,
因为第一项不依赖于$\mathbf{w}$和$b$。
现在第二项除了常数$\frac{1}{\sigma^2}$外,其余部分和前面介绍的均方误差是一样的。
幸运的是,上面式子的解并不依赖于$\sigma$。
因此,在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。
## 从线性回归到深度网络
到目前为止,我们只谈论了线性模型。
尽管神经网络涵盖了更多更为丰富的模型,我们依然可以用描述神经网络的方式来描述线性模型,
从而把线性模型看作一个神经网络。
首先,我们用“层”符号来重写这个模型。
### 神经网络图
深度学习从业者喜欢绘制图表来可视化模型中正在发生的事情。
在 :numref:`fig_single_neuron`中,我们将线性回归模型描述为一个神经网络。
需要注意的是,该图只显示连接模式,即只显示每个输入如何连接到输出,隐去了权重和偏置的值。

:label:`fig_single_neuron`
在 :numref:`fig_single_neuron`所示的神经网络中,输入为$x_1, \ldots, x_d$,
因此输入层中的*输入数*(或称为*特征维度*,feature dimensionality)为$d$。
网络的输出为$o_1$,因此输出层中的*输出数*是1。
需要注意的是,输入值都是已经给定的,并且只有一个*计算*神经元。
由于模型重点在发生计算的地方,所以通常我们在计算层数时不考虑输入层。
也就是说, :numref:`fig_single_neuron`中神经网络的*层数*为1。
我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络,或称为单层神经网络。
对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连,
我们将这种变换( :numref:`fig_single_neuron`中的输出层)
称为*全连接层*(fully-connected layer)或称为*稠密层*(dense layer)。
下一章将详细讨论由这些层组成的网络。
### 生物学
线性回归发明的时间(1795年)早于计算神经科学,所以将线性回归描述为神经网络似乎不合适。
当控制学家、神经生物学家沃伦·麦库洛奇和沃尔特·皮茨开始开发人工神经元模型时,
他们为什么将线性模型作为一个起点呢?
我们来看一张图片 :numref:`fig_Neuron`:
这是一张由*树突*(dendrites,输入终端)、
*细胞核*(nucleu,CPU)组成的生物神经元图片。
*轴突*(axon,输出线)和*轴突端子*(axon terminal,输出端子)
通过*突触*(synapse)与其他神经元连接。

:label:`fig_Neuron`
树突中接收到来自其他神经元(或视网膜等环境传感器)的信息$x_i$。
该信息通过*突触权重*$w_i$来加权,以确定输入的影响(即,通过$x_i w_i$相乘来激活或抑制)。
来自多个源的加权输入以加权和$y = \sum_i x_i w_i + b$的形式汇聚在细胞核中,
然后将这些信息发送到轴突$y$中进一步处理,通常会通过$\sigma(y)$进行一些非线性处理。
之后,它要么到达目的地(例如肌肉),要么通过树突进入另一个神经元。
当然,许多这样的单元可以通过正确连接和正确的学习算法拼凑在一起,
从而产生的行为会比单独一个神经元所产生的行为更有趣、更复杂,
这种想法归功于我们对真实生物神经系统的研究。
当今大多数深度学习的研究几乎没有直接从神经科学中获得灵感。
我们援引斯图尔特·罗素和彼得·诺维格谁,在他们的经典人工智能教科书
*Artificial Intelligence:A Modern Approach* :cite:`Russell.Norvig.2016`
中所说:虽然飞机可能受到鸟类的启发,但几个世纪以来,鸟类学并不是航空创新的主要驱动力。
同样地,如今在深度学习中的灵感同样或更多地来自数学、统计学和计算机科学。
## 小结
* 机器学习模型中的关键要素是训练数据、损失函数、优化算法,还有模型本身。
* 矢量化使数学表达上更简洁,同时运行的更快。
* 最小化目标函数和执行极大似然估计等价。
* 线性回归模型也是一个简单的神经网络。
## 练习
1. 假设我们有一些数据$x_1, \ldots, x_n \in \mathbb{R}$。我们的目标是找到一个常数$b$,使得最小化$\sum_i (x_i - b)^2$。
1. 找到最优值$b$的解析解。
1. 这个问题及其解与正态分布有什么关系?
1. 推导出使用平方误差的线性回归优化问题的解析解。为了简化问题,可以忽略偏置$b$(我们可以通过向$\mathbf X$添加所有值为1的一列来做到这一点)。
1. 用矩阵和向量表示法写出优化问题(将所有数据视为单个矩阵,将所有目标值视为单个向量)。
1. 计算损失对$w$的梯度。
1. 通过将梯度设为0、求解矩阵方程来找到解析解。
1. 什么时候可能比使用随机梯度下降更好?这种方法何时会失效?
1. 假定控制附加噪声$\epsilon$的噪声模型是指数分布。也就是说,$p(\epsilon) = \frac{1}{2} \exp(-|\epsilon|)$
1. 写出模型$-\log P(\mathbf y \mid \mathbf X)$下数据的负对数似然。
1. 你能写出解析解吗?
1. 提出一种随机梯度下降算法来解决这个问题。哪里可能出错?(提示:当我们不断更新参数时,在驻点附近会发生什么情况)你能解决这个问题吗?
[Discussions](https://discuss.d2l.ai/t/1776)
| true |
code
| 0.547101 | null | null | null | null |
|
```
ls ../test-data/
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tables as tb
import h5py
import dask.dataframe as dd
import dask.bag as db
import blaze
fname = '../test-data/EQY_US_ALL_BBO_201402/EQY_US_ALL_BBO_20140206.h5'
max_sym = '/SPY/no_suffix'
fname = '../test-data/small_test_data_public.h5'
max_sym = '/IXQAJE/no_suffix'
# by default, this will be read-only
taq_tb = tb.open_file(fname)
%%time
rec_counts = {curr._v_pathname: len(curr)
for curr in taq_tb.walk_nodes('/', 'Table')}
# What's our biggest table? (in bytes)
max(rec_counts.values()) * 91 / 2 ** 20 # I think it's 91 bytes...
```
Anyway, under a gigabyte. So, nothing to worry about even if we have 24 cores.
```
# But what symbol is that?
max_sym = None
max_rows = 0
for sym, rows in rec_counts.items():
if rows > max_rows:
max_rows = rows
max_sym = sym
max_sym, max_rows
```
Interesting... the S&P 500 ETF
```
# Most symbols also have way less rows - note this is log xvals
plt.hist(list(rec_counts.values()), bins=50, log=True)
plt.show()
```
## Doing some compute
We'll use a "big" table to get some sense of timings
```
spy = taq_tb.get_node(max_sym)
# PyTables is record oriented...
%timeit np.mean(list(x['Bid_Price'] for x in spy.iterrows()))
# But this is faster...
%timeit np.mean(spy[:]['Bid_Price'])
np.mean(spy[:]['Bid_Price'])
```
# Using numexpr?
numexpr is currently not set up to do reductions via HDF5. I've opened an issue here:
https://github.com/PyTables/PyTables/issues/548
```
spy_bp = spy.cols.Bid_Price
# this works...
np.mean(spy_bp)
# But it can't use numexpr
expr = tb.Expr('sum(spy_bp)')
# You can use numexpr to get the values of the column... but that's silly
# (sum doesn't work right, and the axis argument is non-functional)
%timeit result = expr.eval().mean()
tb.Expr('spy_bp').eval().mean()
```
# h5py
```
taq_tb.close()
%%time
spy_h5py = h5py.File(fname)[max_sym]
np.mean(spy_h5py['Bid_Price'])
```
h5py may be a *touch* faster than pytables for this kind of usage. But why does pandas use pytables?
```
%%timeit
np.mean(spy_h5py['Bid_Price'])
```
# Dask
It seems that there should be no need to, e.g., use h5py - but dask's read_hdf doens't seem to be working nicely...
```
taq_tb.close()
```
spy_h5py = h5py.File(fname)[max_sym]
```
store = pd.HDFStore(fname)
store = pd.HDFStore('../test-data/')
# this is a fine way to iterate over our datasets (in addition to what's available in PyTables and h5py)
it = store.items()
key, tab = next(it)
tab
# The columns argument doesn't seem to work...
store.select(max_sym, columns=['Bid_Price']).head()
# columns also doesn't work here...
pd.read_hdf(fname, max_sym, columns=['Bid_Price']).head()
# So we use h5py (actually, pytables appears faster...)
spy_dask = dd.from_array(spy_h5py)
mean_job = spy_dask['Bid_Price'].mean()
mean_job.compute()
# This is appreciably slower than directly computing the mean w/ numpy
%timeit mean_job.compute()
```
## Dask for an actual distributed task (but only on one file for now)
```
class DDFs:
# A (key, table) list
datasets = []
dbag = None
def __init__(self, h5fname):
h5in = h5py.File(h5fname)
h5in.visititems(self.collect_dataset)
def collect_dataset(self, key, table):
if isinstance(table, h5py.Dataset):
self.datasets.append(dd.from_array(table)['Bid_Price'].mean())
def compute_mean(self):
# This is still very slow!
self.results = {key: result for key, result in dd.compute(*self.datasets)}
%%time
ddfs = DDFs(fname)
ddfs.datasets[:5]
len(ddfs.datasets)
dd.compute?
%%time
results = dd.compute(*ddfs.datasets[:20])
import dask.multiprocessing
%%time
# This crashes out throwing lots of KeyErrors
results = dd.compute(*ddfs.datasets[:20], get=dask.multiprocessing.get)
results[0]
```
This ends up being a *little* faster than just using blaze (see below), but about half the time is spent setting thigs up in Dask.
```
from dask import delayed
@delayed
def mean_column(key, data, column='Bid_Price'):
return key, blaze.data(data)[column].mean()
class DDFs:
# A (key, table) list
datasets = []
def __init__(self, h5fname):
h5in = h5py.File(h5fname)
h5in.visititems(self.collect_dataset)
def collect_dataset(self, key, table):
if isinstance(table, h5py.Dataset):
self.datasets.append(mean_column(key, table))
def compute_mean(self, limit=None):
# Note that a limit of None includes all values
self.results = {key: result for key, result in dd.compute(*self.datasets[:limit])}
%%time
ddfs = DDFs(fname)
%%time
ddfs.compute_mean()
next(iter(ddfs.results.items()))
# You can also compute individual results as needed
ddfs.datasets[0].compute()
```
# Blaze?
Holy crap!
```
spy_blaze = blaze.data(spy_h5py)
%time
spy_blaze['Ask_Price'].mean()
taq_tb = tb.open_file(fname)
spy_tb = taq_tb.get_node(max_sym)
spy_blaze = blaze.data(spy_tb)
%time spy_blaze['Bid_Price'].mean()
taq_tb.close()
```
## Read directly with Blaze
Somehow this is not as impressive
```
%%time
blaze_h5_file = blaze.data(fname)
# This is rather nice
blaze_h5_file.SPY.no_suffix.Bid_Price.mean()
blaze_h5_file.ZFKOJB.no_suffix.Bid_Price.mean()
```
# Do some actual compute with Blaze
```
taq_h5py = h5py.File(fname)
class SymStats:
means = {}
def compute_stats(self, key, table):
if isinstance(table, h5py.Dataset):
self.means[key] = blaze.data(table)['Bid_Price'].mean()
ss = SymStats()
%time taq_h5py.visititems(ss.compute_stats)
means = iter(ss.means.items())
next(means)
ss.means['SPY/no_suffix']
```
# Pandas?
### To load with Pandas, you need to close the pytables session
```
taq_tb = tb.open_file(fname)
taq_tb.close()
pd.read_hdf?
pd.read_hdf(fname, max_sym, start=0, stop=1, chunksize=1)
max_sym
fname
%%timeit
node = taq_tb.get_node(max_sym)
pd.DataFrame.from_records(node[0:1])
%%timeit
# I've also tried this with `.get_node()`, same speed
pd.DataFrame.from_records(taq_tb.root.IXQAJE.no_suffix)
%%timeit
pd.read_hdf(fname, max_sym)
# Pandas has optimizations it likes to do with
%timeit spy_df = pd.read_hdf(fname, max_sym)
# Actually do it
spy_df = pd.read_hdf(fname, max_sym)
# This is fast, but loading is slow...
%timeit spy_df.Bid_Price.mean()
```
| true |
code
| 0.488405 | null | null | null | null |
|
# Results Analysis
This notebook analyzes results produced by the _anti-entropy reinforcement learning_ experiments. The practical purpose of this notebook is to create graphs that can be used to display anti-entropy topologies, but also to extract information relevant to each experimental run.
```
%matplotlib notebook
import os
import re
import glob
import json
import unicodedata
import numpy as np
import pandas as pd
import seaborn as sns
import networkx as nx
import matplotlib as mpl
import graph_tool.all as gt
import matplotlib.pyplot as plt
from nx2gt import nx2gt
from datetime import timedelta
from collections import defaultdict
```
## Data Loading
The data directory contains directories whose names are the hosts along with configuration files for each run. Each run is stored in its own `metrics.json` file, suffixed by the run number. The data loader yields _all_ rows from _all_ metric files and appends them with the correct configuration data.
```
DATA = "../data"
FIGS = "../figures"
GRAPHS = "../graphs"
HOSTS = "hosts.json"
RESULTS = "metrics-*.json"
CONFIGS = "config-*.json"
NULLDATE = "0001-01-01T00:00:00Z"
DURATION = re.compile("^([\d\.]+)(\w+)$")
def suffix(path):
# Get the run id from the path
name, _ = os.path.splitext(path)
return int(name.split("-")[-1])
def parse_duration(d):
match = DURATION.match(d)
if match is None:
raise TypeError("could not parse duration '{}'".format(d))
amount, units = match.groups()
amount = float(amount)
unitkw = {
"µs": "microseconds",
"ms": "milliseconds",
"s": "seconds",
}[units]
return timedelta(**{unitkw:amount}).total_seconds()
def load_hosts(path=DATA):
with open(os.path.join(path, HOSTS), 'r') as f:
return json.load(f)
def load_configs(path=DATA):
configs = {}
for name in glob.glob(os.path.join(path, CONFIGS)):
with open(name, 'r') as f:
configs[suffix(name)] = json.load(f)
return configs
def slugify(name):
slug = unicodedata.normalize('NFKD', name)
slug = str(slug.encode('ascii', 'ignore')).lower()
slug = re.sub(r'[^a-z0-9]+', '-', slug).strip('-')
slug = re.sub(r'[-]+', '-', slug)
return slug
def load_results(path=DATA):
hosts = load_hosts(path)
configs = load_configs(path)
for host in os.listdir(path):
for name in glob.glob(os.path.join(path, host, "metrics-*.json")):
run = suffix(name)
with open(name, 'r', encoding='utf-8') as f:
for line in f:
row = json.loads(line.strip())
row['name'] = host
row['host'] = hosts[host]["hostname"] + ":3264"
row['runid'] = run
row['config'] = configs[run]
yield row
def merge_results(path, data=DATA):
# Merge all of the results into a single unified file
with open(path, 'w') as f:
for row in load_results(data):
f.write(json.dumps(row))
f.write("\n")
```
## Graph Extraction
This section extracts a NeworkX graph for each of the experimental runs such that each graph defines an anti-entropy topology.
```
def extract_graphs(path=DATA, outdir=None):
graphs = defaultdict(nx.DiGraph)
for row in load_results(path):
# Get the graph for the topology
G = graphs[row["runid"]]
# Update the graph information
name = row["bandit"]["strategy"].title()
epsilon = row["config"]["replicas"].get("epsilon", None)
if epsilon:
name += " ε={}".format(epsilon)
G.graph.update({
"name": name + " (E{})".format(row["runid"]),
"experiment": row["runid"],
"uptime": row["config"]["replicas"]["uptime"],
"bandit": row["config"]["replicas"]["bandit"],
"epsilon": epsilon or "",
"anti_entropy_interval": row["config"]["replicas"]["delay"],
"workload_duration": row["config"]["clients"]["config"]["duration"],
"n_clients": len(row["config"]["clients"]["hosts"]),
# "workload": row["config"]["clients"]["hosts"],
"store": row["store"],
})
# Update the vertex information
vnames = row["name"].split("-")
vertex = {
"duration": row["duration"],
"finished": row["finished"] if row["finished"] != NULLDATE else "",
"started": row["started"] if row["started"] != NULLDATE else "",
"keys_stored": row["nkeys"],
"reads": row["reads"],
"writes": row["writes"],
"throughput": row["throughput"],
"location": " ".join(vnames[1:-1]).title(),
"pid": int(vnames[-1]),
"name": row["name"]
}
source_id = row["host"]
source = G.add_node(source_id, **vertex)
# Get bandit edge information
bandit_counts = dict(zip(row["peers"], row["bandit"]["counts"]))
bandit_values = dict(zip(row["peers"], row["bandit"]["values"]))
# Add the edges from the sync table
for target_id, stats in row["syncs"].items():
edge = {
"count": bandit_counts[target_id],
"reward": bandit_values[target_id],
"misses": stats["Misses"],
"pulls": stats["Pulls"],
"pushes": stats["Pushes"],
"syncs": stats["Syncs"],
"versions": stats["Versions"],
"mean_pull_latency": parse_duration(stats["PullLatency"]["mean"]),
"mean_push_latency": parse_duration(stats["PushLatency"]["mean"]),
}
G.add_edge(source_id, target_id, **edge)
# Write Graphs
if outdir:
for G in graphs.values():
opath = os.path.join(outdir, slugify(G.name)+".graphml.gz")
nx.write_graphml(G, opath)
return graphs
# for G in extract_graphs(outdir=GRAPHS).values():
for G in extract_graphs().values():
print(nx.info(G))
print()
LOCATION_COLORS = {
"Virginia": "#D91E18",
"Ohio": "#E26A6A",
"California": "#8E44AD",
"Sao Paulo": "#6BB9F0",
"London": "#2ECC71",
"Frankfurt": "#6C7A89",
"Seoul": "#F9690E",
"Sydney": "#F7CA18",
}
LOCATION_GROUPS = sorted(list(LOCATION_COLORS.keys()))
LOCATION_CODES = {
"Virginia": "VA",
"Ohio": "OH",
"California": "CA",
"Sao Paulo": "BR",
"London": "GB",
"Frankfurt": "DE",
"Seoul": "KR",
"Sydney": "AU",
}
def filter_edges(h, pulls=0, pushes=0):
# Create a view of the graph with only edges with syncs > 0
efilt = h.new_edge_property('bool')
for edge in h.edges():
efilt[edge] = (h.ep['pulls'][edge] > pulls or h.ep['pushes'][edge] > pushes)
return gt.GraphView(h, efilt=efilt)
def mklabel(name, loc):
code = LOCATION_CODES[loc]
parts = name.split("-")
return "{}{}".format(code, parts[-1])
def visualize_graph(G, layout='sfdp', filter=True, save=True):
print(G.name)
output = None
if save:
output = os.path.join(FIGS, slugify(G.name) + ".pdf")
# Convert the nx Graph to a gt Graph
g = nx2gt(G)
if filter:
g = filter_edges(g)
# Vertex Properties
vgroup = g.new_vertex_property('int32_t')
vcolor = g.new_vertex_property('string')
vlabel = g.new_vertex_property('string')
for vertex in g.vertices():
vcolor[vertex] = LOCATION_COLORS[g.vp['location'][vertex]]
vgroup[vertex] = LOCATION_GROUPS.index(g.vp['location'][vertex])
vlabel[vertex] = mklabel(g.vp['name'][vertex], g.vp['location'][vertex])
vsize = gt.prop_to_size(g.vp['writes'], ma=65, mi=35)
# Edge Properties
esize = gt.prop_to_size(g.ep['versions'], mi=.01, ma=6)
ecolor = gt.prop_to_size(g.ep['mean_pull_latency'], mi=1, ma=5, log=True)
# Compute the layout and draw
if layout == 'fruchterman_reingold':
pos = gt.fruchterman_reingold_layout(g, weight=esize, circular=True, grid=False)
elif layout == 'sfdp':
pos = gt.sfdp_layout(g, eweight=esize, groups=vgroup)
else:
raise ValueError("unknown layout '{}".format(layout))
gt.graph_draw(
g, pos=pos, output_size=(1200,1200), output=output, inline=True,
vertex_size=vsize, vertex_fill_color=vcolor, vertex_text=vlabel,
vertex_halo=False, vertex_pen_width=1.2,
edge_pen_width=esize,
)
visualize_graph(extract_graphs()[5])
```
## Rewards DataFrame
This section extracts a timeseries of rewards on a per-replica basis.
```
def extract_rewards(path=DATA):
for row in load_results(path):
bandit = row["bandit"]
history = bandit["history"]
strategy = bandit["strategy"]
epsilon = row["config"]["replicas"].get("epsilon")
if epsilon:
strategy += " ε={}".format(epsilon)
values = np.array(list(map(float, history["rewards"])))
series = pd.Series(values, name=row["name"] + " " + strategy)
yield series, row['runid']
total_rewards = {}
for series, rowid in extract_rewards():
if rowid not in total_rewards:
total_rewards[rowid] = series
else:
total_rewards[rowid] += series
cumulative_rewards = {
rowid: s.cumsum()
for rowid, s in total_rewards.items()
}
from pandas.plotting import autocorrelation_plot
df = pd.DataFrame({
" ".join(s.name.split(" ")[1:]): s
for s in total_rewards.values()
}).iloc[15:361]
df.reset_index(inplace=True, drop=True)
fig,ax = plt.subplots(figsize=(9,6))
df.rolling(window=15,center=False).mean().plot(ax=ax)
ax.set_ylabel("Rolling Mean of Total System Reward (w=15)")
ax.set_xlabel("Timesteps (Anti-Entropy Sessions)")
ax.grid(True, ls='--')
ax.set_xlim(12, 346)
plt.savefig(os.path.join(FIGS, "rewards.pdf"))
```
| true |
code
| 0.297145 | null | null | null | null |
|
```
# reload packages
%load_ext autoreload
%autoreload 2
```
### Choose GPU (this may not be needed on your computer)
```
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=1
import tensorflow as tf
gpu_devices = tf.config.experimental.list_physical_devices('GPU')
if len(gpu_devices)>0:
tf.config.experimental.set_memory_growth(gpu_devices[0], True)
print(gpu_devices)
tf.keras.backend.clear_session()
```
### load packages
```
from tfumap.umap import tfUMAP
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
import umap
import pandas as pd
```
### Load dataset
```
dataset = 'fmnist'
from tensorflow.keras.datasets import fashion_mnist
# load dataset
(train_images, Y_train), (test_images, Y_test) = fashion_mnist.load_data()
X_train = (train_images/255.).astype('float32')
X_test = (test_images/255.).astype('float32')
X_train = X_train.reshape((len(X_train), np.product(np.shape(X_train)[1:])))
X_test = X_test.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
# subset a validation set
n_valid = 10000
X_valid = X_train[-n_valid:]
Y_valid = Y_train[-n_valid:]
X_train = X_train[:-n_valid]
Y_train = Y_train[:-n_valid]
# flatten X
X_train_flat = X_train.reshape((len(X_train), np.product(np.shape(X_train)[1:])))
X_test_flat = X_test.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
X_valid_flat= X_valid.reshape((len(X_valid), np.product(np.shape(X_valid)[1:])))
print(len(X_train), len(X_valid), len(X_test))
```
### define networks
```
dims = (28,28,1)
n_components = 64
encoder = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=dims),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation="relu"
),
tf.keras.layers.Conv2D(
filters=128, kernel_size=3, strides=(2, 2), activation="relu"
),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=512, activation="relu"),
tf.keras.layers.Dense(units=n_components),
])
decoder = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=(n_components)),
tf.keras.layers.Dense(units=512, activation="relu"),
tf.keras.layers.Dense(units=7 * 7 * 256, activation="relu"),
tf.keras.layers.Reshape(target_shape=(7, 7, 256)),
tf.keras.layers.Conv2DTranspose(
filters=128, kernel_size=3, strides=(2, 2), padding="SAME", activation="relu"
),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=(2, 2), padding="SAME", activation="relu"
),
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=(1, 1), padding="SAME", activation="sigmoid"
)
])
input_img = tf.keras.Input(dims)
output_img = decoder(encoder(input_img))
autoencoder = tf.keras.Model(input_img, output_img)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
X_train = X_train.reshape([len(X_train)] + list(dims))
history = autoencoder.fit(X_train, X_train,
epochs=50,
batch_size=256,
shuffle=True,
#validation_data=(X_valid, X_valid)
)
z = encoder.predict(X_train)
```
### Plot model output
```
fig, ax = plt.subplots( figsize=(8, 8))
sc = ax.scatter(
z[:, 0],
z[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow embedding", fontsize=20)
plt.colorbar(sc, ax=ax);
```
### View loss
```
from tfumap.umap import retrieve_tensors
import seaborn as sns
```
### Save output
```
from tfumap.paths import ensure_dir, MODEL_DIR
output_dir = MODEL_DIR/'projections'/ dataset / '64' /'ae_only'
ensure_dir(output_dir)
encoder.save(output_dir / 'encoder')
decoder.save(output_dir / 'encoder')
#loss_df.to_pickle(output_dir / 'loss_df.pickle')
np.save(output_dir / 'z.npy', z)
```
### compute metrics
```
X_test.shape
z_test = encoder.predict(X_test.reshape((len(X_test), 28,28,1)))
```
#### silhouette
```
from tfumap.silhouette import silhouette_score_block
ss, sil_samp = silhouette_score_block(z, Y_train, n_jobs = -1)
ss
ss_test, sil_samp_test = silhouette_score_block(z_test, Y_test, n_jobs = -1)
ss_test
fig, axs = plt.subplots(ncols = 2, figsize=(10, 5))
axs[0].scatter(z[:, 0], z[:, 1], s=0.1, alpha=0.5, c=sil_samp, cmap=plt.cm.viridis)
axs[1].scatter(z_test[:, 0], z_test[:, 1], s=1, alpha=0.5, c=sil_samp_test, cmap=plt.cm.viridis)
```
#### KNN
```
from sklearn.neighbors import KNeighborsClassifier
neigh5 = KNeighborsClassifier(n_neighbors=5)
neigh5.fit(z, Y_train)
score_5nn = neigh5.score(z_test, Y_test)
score_5nn
neigh1 = KNeighborsClassifier(n_neighbors=1)
neigh1.fit(z, Y_train)
score_1nn = neigh1.score(z_test, Y_test)
score_1nn
```
#### Trustworthiness
```
from sklearn.manifold import trustworthiness
tw = trustworthiness(X_train_flat[:10000], z[:10000])
tw_test = trustworthiness(X_test_flat[:10000], z_test[:10000])
tw, tw_test
```
### Save output metrics
```
from tfumap.paths import ensure_dir, MODEL_DIR, DATA_DIR
```
#### train
```
metrics_df = pd.DataFrame(
columns=[
"dataset",
"class_",
"dim",
"trustworthiness",
"silhouette_score",
"silhouette_samples",
]
)
metrics_df.loc[len(metrics_df)] = [dataset, 'ae_only', n_components, tw, ss, sil_samp]
metrics_df
save_loc = DATA_DIR / 'projection_metrics' / 'ae_only' / 'train' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
metrics_df.to_pickle(save_loc)
```
#### test
```
metrics_df_test = pd.DataFrame(
columns=[
"dataset",
"class_",
"dim",
"trustworthiness",
"silhouette_score",
"silhouette_samples",
]
)
metrics_df_test.loc[len(metrics_df)] = [dataset, 'ae_only', n_components, tw_test, ss_test, sil_samp_test]
metrics_df_test
save_loc = DATA_DIR / 'projection_metrics' / 'ae' / 'test' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
metrics_df.to_pickle(save_loc)
```
#### knn
```
nn_acc_df = pd.DataFrame(columns = ["method_","dimensions","dataset","1NN_acc","5NN_acc"])
nn_acc_df.loc[len(nn_acc_df)] = ['ae_only', n_components, dataset, score_1nn, score_5nn]
nn_acc_df
save_loc = DATA_DIR / 'knn_classifier' / 'ae_only' / 'train' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
nn_acc_df.to_pickle(save_loc)
```
### Reconstruction
```
from sklearn.metrics import mean_squared_error, mean_absolute_error, median_absolute_error, r2_score
X_recon = decoder.predict(encoder.predict(X_test.reshape((len(X_test), 28, 28, 1))))
X_real = X_test.reshape((len(X_test), 28, 28, 1))
x_real = X_test.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
x_recon = X_recon.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
reconstruction_acc_df = pd.DataFrame(
columns=["method_", "dimensions", "dataset", "MSE", "MAE", "MedAE", "R2"]
)
MSE = mean_squared_error(
x_real,
x_recon
)
MAE = mean_absolute_error(
x_real,
x_recon
)
MedAE = median_absolute_error(
x_real,
x_recon
)
R2 = r2_score(
x_real,
x_recon
)
reconstruction_acc_df.loc[len(reconstruction_acc_df)] = ['ae_only', n_components, dataset, MSE, MAE, MedAE, R2]
reconstruction_acc_df
save_loc = DATA_DIR / 'reconstruction_acc' / 'ae_only' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
reconstruction_acc_df.to_pickle(save_loc)
```
### Compute clustering quality
```
from sklearn.cluster import KMeans
from sklearn.metrics import homogeneity_completeness_v_measure
def get_cluster_metrics(row, n_init=5):
# load cluster information
save_loc = DATA_DIR / 'clustering_metric_df'/ ('_'.join([row.class_, str(row.dim), row.dataset]) + '.pickle')
print(save_loc)
if save_loc.exists() and save_loc.is_file():
cluster_df = pd.read_pickle(save_loc)
return cluster_df
# make cluster metric dataframe
cluster_df = pd.DataFrame(
columns=[
"dataset",
"class_",
"dim",
"silhouette",
"homogeneity",
"completeness",
"v_measure",
"init_",
"n_clusters",
"model",
]
)
y = row.train_label
z = row.train_z
n_labels = len(np.unique(y))
for n_clusters in tqdm(np.arange(n_labels - int(n_labels / 2), n_labels + int(n_labels / 2)), leave=False, desc = 'n_clusters'):
for init_ in tqdm(range(n_init), leave=False, desc='init'):
kmeans = KMeans(n_clusters=n_clusters, random_state=init_).fit(z)
clustered_y = kmeans.labels_
homogeneity, completeness, v_measure = homogeneity_completeness_v_measure(
y, clustered_y
)
ss, _ = silhouette_score_block(z, clustered_y)
cluster_df.loc[len(cluster_df)] = [
row.dataset,
row.class_,
row.dim,
ss,
homogeneity,
completeness,
v_measure,
init_,
n_clusters,
kmeans,
]
# save cluster df in case this fails somewhere
ensure_dir(save_loc)
cluster_df.to_pickle(save_loc)
return cluster_df
projection_df = pd.DataFrame(columns = ['dataset', 'class_', 'train_z', 'train_label', 'dim'])
projection_df.loc[len(projection_df)] = [dataset, 'ae_only', z, Y_train, n_components]
projection_df
get_cluster_metrics(projection_df.iloc[0], n_init=5)
```
| true |
code
| 0.744247 | null | null | null | null |
|
Branching GP Regression on hematopoietic data
--
*Alexis Boukouvalas, 2017*
**Note:** this notebook is automatically generated by [Jupytext](https://jupytext.readthedocs.io/en/latest/index.html), see the README for instructions on working with it.
test change
Branching GP regression with Gaussian noise on the hematopoiesis data described in the paper "BGP: Gaussian processes for identifying branching dynamics in single cell data".
This notebook shows how to build a BGP model and plot the posterior model fit and posterior branching times.
```
import time
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import BranchedGP
plt.style.use("ggplot")
%matplotlib inline
```
### Read the hematopoiesis data. This has been simplified to a small subset of 23 genes found to be branching.
We have also performed Monocle2 (version 2.1) - DDRTree on this data. The results loaded include the Monocle estimated pseudotime, branching assignment (state) and the DDRTree latent dimensions.
```
Y = pd.read_csv("singlecelldata/hematoData.csv", index_col=[0])
monocle = pd.read_csv("singlecelldata/hematoMonocle.csv", index_col=[0])
Y.head()
monocle.head()
# Plot Monocle DDRTree space
genelist = ["FLT3", "KLF1", "MPO"]
f, ax = plt.subplots(1, len(genelist), figsize=(10, 5), sharex=True, sharey=True)
for ig, g in enumerate(genelist):
y = Y[g].values
yt = np.log(1 + y / y.max())
yt = yt / yt.max()
h = ax[ig].scatter(
monocle["DDRTreeDim1"],
monocle["DDRTreeDim2"],
c=yt,
s=50,
alpha=1.0,
vmin=0,
vmax=1,
)
ax[ig].set_title(g)
def PlotGene(label, X, Y, s=3, alpha=1.0, ax=None):
fig = None
if ax is None:
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
for li in np.unique(label):
idxN = (label == li).flatten()
ax.scatter(X[idxN], Y[idxN], s=s, alpha=alpha, label=int(np.round(li)))
return fig, ax
```
### Fit BGP model
Notice the cell assignment uncertainty is higher for cells close to the branching point.
```
def FitGene(g, ns=20): # for quick results subsample data
t = time.time()
Bsearch = list(np.linspace(0.05, 0.95, 5)) + [
1.1
] # set of candidate branching points
GPy = (Y[g].iloc[::ns].values - Y[g].iloc[::ns].values.mean())[
:, None
] # remove mean from gene expression data
GPt = monocle["StretchedPseudotime"].values[::ns]
globalBranching = monocle["State"].values[::ns].astype(int)
d = BranchedGP.FitBranchingModel.FitModel(Bsearch, GPt, GPy, globalBranching)
print(g, "BGP inference completed in %.1f seconds." % (time.time() - t))
# plot BGP
fig, ax = BranchedGP.VBHelperFunctions.PlotBGPFit(
GPy, GPt, Bsearch, d, figsize=(10, 10)
)
# overplot data
f, a = PlotGene(
monocle["State"].values,
monocle["StretchedPseudotime"].values,
Y[g].values - Y[g].iloc[::ns].values.mean(),
ax=ax[0],
s=10,
alpha=0.5,
)
# Calculate Bayes factor of branching vs non-branching
bf = BranchedGP.VBHelperFunctions.CalculateBranchingEvidence(d)["logBayesFactor"]
fig.suptitle("%s log Bayes factor of branching %.1f" % (g, bf))
return d, fig, ax
d, fig, ax = FitGene("MPO")
d_c, fig_c, ax_c = FitGene("CTSG")
```
| true |
code
| 0.604983 | null | null | null | null |
|
```
%matplotlib inline
import itertools
import os
os.environ['CUDA_VISIBLE_DEVICES']=""
import numpy as np
import gpflow
import gpflow.training.monitor as mon
import numbers
import matplotlib.pyplot as plt
import tensorflow as tf
```
# Demo: `gpflow.training.monitor`
In this notebook we'll demo how to use `gpflow.training.monitor` for logging the optimisation of a GPflow model.
## Creating the GPflow model
We first generate some random data and create a GPflow model.
Under the hood, GPflow gives a unique name to each model which is used to name the Variables it creates in the TensorFlow graph containing a random identifier. This is useful in interactive sessions, where people may create a few models, to prevent variables with the same name conflicting. However, when loading the model, we need to make sure that the names of all the variables are exactly the same as in the checkpoint. This is why we pass name="SVGP" to the model constructor, and why we use gpflow.defer_build().
```
np.random.seed(0)
X = np.random.rand(10000, 1) * 10
Y = np.sin(X) + np.random.randn(*X.shape)
Xt = np.random.rand(10000, 1) * 10
Yt = np.sin(Xt) + np.random.randn(*Xt.shape)
with gpflow.defer_build():
m = gpflow.models.SVGP(X, Y, gpflow.kernels.RBF(1), gpflow.likelihoods.Gaussian(),
Z=np.linspace(0, 10, 5)[:, None],
minibatch_size=100, name="SVGP")
m.likelihood.variance = 0.01
m.compile()
```
Let's compute log likelihood before the optimisation
```
print('LML before the optimisation: %f' % m.compute_log_likelihood())
```
We will be using a TensorFlow optimiser. All TensorFlow optimisers have a support for `global_step` variable. Its purpose is to track how many optimisation steps have occurred. It is useful to keep this in a TensorFlow variable as this allows it to be restored together with all the parameters of the model.
The code below creates this variable using a monitor's helper function. It is important to create it before building the monitor in case the monitor includes a checkpoint task. This is because the checkpoint internally uses the TensorFlow Saver which creates a list of variables to save. Therefore all variables expected to be saved by the checkpoint task should exist by the time the task is created.
```
session = m.enquire_session()
global_step = mon.create_global_step(session)
```
## Construct the monitor
Next we need to construct the monitor. `gpflow.training.monitor` provides classes that are building blocks for the monitor. Essengially, a monitor is a function that is provided as a callback to an optimiser. It consists of a number of tasks that may be executed at each step, subject to their running condition.
In this example, we want to:
- log certain scalar parameters in TensorBoard,
- log the full optimisation objective (log marginal likelihood bound) periodically, even though we optimise with minibatches,
- store a backup of the optimisation process periodically,
- log performance for a test set periodically.
We will define these tasks as follows:
```
print_task = mon.PrintTimingsTask().with_name('print')\
.with_condition(mon.PeriodicIterationCondition(10))\
.with_exit_condition(True)
sleep_task = mon.SleepTask(0.01).with_name('sleep').with_name('sleep')
saver_task = mon.CheckpointTask('./monitor-saves').with_name('saver')\
.with_condition(mon.PeriodicIterationCondition(10))\
.with_exit_condition(True)
file_writer = mon.LogdirWriter('./model-tensorboard')
model_tboard_task = mon.ModelToTensorBoardTask(file_writer, m).with_name('model_tboard')\
.with_condition(mon.PeriodicIterationCondition(10))\
.with_exit_condition(True)
lml_tboard_task = mon.LmlToTensorBoardTask(file_writer, m).with_name('lml_tboard')\
.with_condition(mon.PeriodicIterationCondition(100))\
.with_exit_condition(True)
```
As the above code shows, each task can be assigned a name and running conditions. The name will be shown in the task timing summary.
There are two different types of running conditions: `with_condition` controls execution of the task at each iteration in the optimisation loop. `with_exit_condition` is a simple boolean flag indicating that the task should also run at the end of optimisation.
In this example we want to run our tasks periodically, at every iteration or every 10th or 100th iteration.
Notice that the two TensorBoard tasks will write events into the same file. It is possible to share a file writer between multiple tasks. However it is not possible to share the same event location between multiple file writers. An attempt to open two writers with the same location will result in error.
## Custom tasks
We may also want to perfom certain tasks that do not have pre-defined `Task` classes. For example, we may want to compute the performance on a test set. Here we create such a class by extending `BaseTensorBoardTask` to log the testing benchmarks in addition to all the scalar parameters.
```
class CustomTensorBoardTask(mon.BaseTensorBoardTask):
def __init__(self, file_writer, model, Xt, Yt):
super().__init__(file_writer, model)
self.Xt = Xt
self.Yt = Yt
self._full_test_err = tf.placeholder(gpflow.settings.tf_float, shape=())
self._full_test_nlpp = tf.placeholder(gpflow.settings.tf_float, shape=())
self._summary = tf.summary.merge([tf.summary.scalar("test_rmse", self._full_test_err),
tf.summary.scalar("test_nlpp", self._full_test_nlpp)])
def run(self, context: mon.MonitorContext, *args, **kwargs) -> None:
minibatch_size = 100
preds = np.vstack([self.model.predict_y(Xt[mb * minibatch_size:(mb + 1) * minibatch_size, :])[0]
for mb in range(-(-len(Xt) // minibatch_size))])
test_err = np.mean((Yt - preds) ** 2.0)**0.5
self._eval_summary(context, {self._full_test_err: test_err, self._full_test_nlpp: 0.0})
custom_tboard_task = CustomTensorBoardTask(file_writer, m, Xt, Yt).with_name('custom_tboard')\
.with_condition(mon.PeriodicIterationCondition(100))\
.with_exit_condition(True)
```
Now we can put all these tasks into a monitor.
```
monitor_tasks = [print_task, model_tboard_task, lml_tboard_task, custom_tboard_task, saver_task, sleep_task]
monitor = mon.Monitor(monitor_tasks, session, global_step)
```
## Running the optimisation
We finally get to running the optimisation.
We may want to continue a previously run optimisation by resotring the TensorFlow graph from the latest checkpoint. Otherwise skip this step.
```
if os.path.isdir('./monitor-saves'):
mon.restore_session(session, './monitor-saves')
optimiser = gpflow.train.AdamOptimizer(0.01)
with mon.Monitor(monitor_tasks, session, global_step, print_summary=True) as monitor:
optimiser.minimize(m, step_callback=monitor, maxiter=450, global_step=global_step)
file_writer.close()
```
Now lets compute the log likelihood again. Hopefully we will see an increase in its value
```
print('LML after the optimisation: %f' % m.compute_log_likelihood())
```
| true |
code
| 0.527073 | null | null | null | null |
|
<img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# IUCN - Extinct species
<a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/IUCN/IUCN_Extinct_species.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
**Tags:** #iucn #opendata #extinctspecies #analytics #plotly
**Author:** [Martin Delasalle](https://github.com/delasalle-sio-martin)
Source : https://www.iucnredlist.org/statistics
If you want another view of the data : Link : https://ourworldindata.org/extinctions
### History
The initial aim was to compare the number of threatened species per species over time (e.g. number of pandas per year).
After a lot of research, it turns out that this kind of data is not available or it is only data from one year (2015 or 2018).
Therefore, we decided to start another project: Number of threatened species per year, with details by category using data from this site : https://www.iucnredlist.org/resources/summary-statistics#Summary%20Tables
So we took the pdf from this site and turned it into a csv.
But the data was heavy and not easy to use. Moreover, we thought that this would not necessarily be viable and adaptable over time.
So we decided to take another datasource on a similar subject : *Extinct Species*, from this website : https://www.iucnredlist.org/statistics
### Links that we found during the course
- https://donnees.banquemondiale.org/indicator/EN.MAM.THRD.NO (only 2018)
- https://www.eea.europa.eu/data-and-maps/data/european-red-lists-4/european-red-list/european-red-list-csv-files/view (old Dataset, last upload was in 2015)
- https://www.worldwildlife.org/species/directory?page=2 (the years are not available)
- https://www.worldwildlife.org/pages/conservation-science-data-and-tools (apart from the case)
- https://databasin.org/datasets/68635d7c77f1475f9b6c1d1dbe0a4c4c/ (we can't use it)
- https://gisandscience.com/2009/12/01/download-datasets-from-the-world-wildlife-funds-conservation-science-program/ (no datas about threatened species)
- https://data.world/datasets/tiger (only about tigers but there are no datas usefull)
## Input
### Import library
```
import pandas as pd
import plotly.express as px
```
### Setup your variables
👉 Download data in [CSV](https://www.iucnredlist.org/statistics) and drop it on your root folder
```
# Input csv
csv_input = "Table 3 Species by kingdom and class - show all.csv"
```
## Model
### Get data from csv
```
# We load the csv file
data = pd.read_csv(csv_input, ',')
# We set the column Name as index
data.set_index('Name', inplace = True)
# Then we select the columns EX, EW and Name, and all the lines we want in the graph
table = data.loc[["Total",
"GASTROPODA",
"BIVALVIA",
"AVES",
"MAMMALIA",
"ACTINOPTERYGII",
"CEPHALASPIDOMORPHI",
"INSECTA",
"AMPHIBIA",
"REPTILIA",
"ARACHNIDA",
"CLITELLATA",
"DIPLOPODA",
"ENOPLA",
"TURBELLARIA",
"MALACOSTRACA",
"MAXILLOPODA",
"OSTRACODA"]# add species here
,"EX":"EW"]
table
# We add a new column 'CATEGORY' to our Dataframe
table["CATEGORY"] = ["Total",
"Molluscs",
"Molluscs",
"Birds",
"Mammals",
"Fishes",
"Fishes",
"Insects",
"Amphibians",
"Reptiles",
"Others",
"Others",
"Others",
"Others",
"Others",
"Crustaceans",
"Crustaceans",
"Crustaceans"]
table = table.loc[:,["CATEGORY","EX"]] # we drop the column "EW"
table
# ---NOTE : If you want to add new species, you have to also add his category
# We groupby CATEGORIES :
table.reset_index(drop=True, inplace=True)
table = table.groupby(['CATEGORY']).sum().reset_index()
table.rename(columns = {'EX':'Extincted'}, inplace=True)
table
```
## Output
### Plot graph
```
# We use plotly to show datas with an horizontal bar chart
def create_barchart(table):
Graph = table.sort_values('Extincted', ascending=False)
fig = px.bar(Graph,
x="Extincted",
y="CATEGORY",
color="CATEGORY",
orientation="h")
fig.update_layout(title_text="Number of species that have gone extinct since 1500",
title_x=0.5)
fig.add_annotation(x=800,
y=0,
text="Source : IUCN Red List of Threatened Species<br>https://www.iucnredlist.org/statistics",
showarrow=False)
fig.show()
return fig
fig = create_barchart(table)
```
| true |
code
| 0.586168 | null | null | null | null |
|
# ThaiNER (Bi-LSTM CRF)
using pytorch
By Mr.Wannaphong Phatthiyaphaibun
Bachelor of Science Program in Computer and Information Science, Nong Khai Campus, Khon Kaen University
https://iam.wannaphong.com/
E-mail : [email protected]
Thank you Faculty of Applied Science and Engineering, Nong Khai Campus, Khon Kaen University for server.
```
import torch.nn.functional as F
from torch.autograd import Variable
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.optim as optim
print(torch.__version__)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#torch.backends.cudnn.benchmark=torch.cuda.is_available()
#FloatTensor = torch.cuda.FloatTensor if USE_CUDA else torch.FloatTensor
LongTensor = torch.long
#ByteTensor = torch.cuda.ByteTensor if USE_CUDA else torch.ByteTensor
def argmax(vec):
# return the argmax as a python int
_, idx = torch.max(vec, 1)
return idx.item()
def prepare_sequence(seq, to_ix):
idxs = [to_ix[w] if w in to_ix else to_ix["UNK"] for w in seq]
return torch.tensor(idxs, dtype=LongTensor, device=device)
# Compute log sum exp in a numerically stable way for the forward algorithm
def log_sum_exp(vec):
max_score = vec[0, argmax(vec)]
max_score_broadcast = max_score.view(1, -1).expand(1, vec.size()[1])
return max_score + \
torch.log(torch.sum(torch.exp(vec - max_score_broadcast)))
class BiLSTM_CRF(nn.Module):
def __init__(self, vocab_size, tag_to_ix, embedding_dim, hidden_dim):
super(BiLSTM_CRF, self).__init__()
self.embedding_dim = embedding_dim
self.hidden_dim = hidden_dim
self.vocab_size = vocab_size
self.tag_to_ix = tag_to_ix
self.tagset_size = len(tag_to_ix)
self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim // 2,
num_layers=1, bidirectional=True)
# Maps the output of the LSTM into tag space.
self.hidden2tag = nn.Linear(hidden_dim, self.tagset_size)
# Matrix of transition parameters. Entry i,j is the score of
# transitioning *to* i *from* j.
self.transitions = nn.Parameter(
torch.randn(self.tagset_size, self.tagset_size, device=device))
# These two statements enforce the constraint that we never transfer
# to the start tag and we never transfer from the stop tag
self.transitions.data[tag_to_ix[START_TAG], :] = -10000
self.transitions.data[:, tag_to_ix[STOP_TAG]] = -10000
self.hidden = self.init_hidden()
def init_hidden(self):
return (torch.randn(2, 1, self.hidden_dim // 2,device=device),
torch.randn(2, 1, self.hidden_dim // 2,device=device))
def _forward_alg(self, feats):
# Do the forward algorithm to compute the partition function
init_alphas = torch.full((1, self.tagset_size), -10000., device=device)
# START_TAG has all of the score.
init_alphas[0][self.tag_to_ix[START_TAG]] = 0.
# Wrap in a variable so that we will get automatic backprop
forward_var = init_alphas
# Iterate through the sentence
for feat in feats:
alphas_t = [] # The forward tensors at this timestep
for next_tag in range(self.tagset_size):
# broadcast the emission score: it is the same regardless of
# the previous tag
emit_score = feat[next_tag].view(
1, -1).expand(1, self.tagset_size)
# the ith entry of trans_score is the score of transitioning to
# next_tag from i
trans_score = self.transitions[next_tag].view(1, -1)
# The ith entry of next_tag_var is the value for the
# edge (i -> next_tag) before we do log-sum-exp
next_tag_var = forward_var + trans_score + emit_score
# The forward variable for this tag is log-sum-exp of all the
# scores.
alphas_t.append(log_sum_exp(next_tag_var).view(1))
forward_var = torch.cat(alphas_t).view(1, -1)
terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
alpha = log_sum_exp(terminal_var)
return alpha
def _get_lstm_features(self, sentence):
self.hidden = self.init_hidden()
embeds = self.word_embeds(sentence).view(len(sentence), 1, -1)
lstm_out, self.hidden = self.lstm(embeds, self.hidden)
lstm_out = lstm_out.view(len(sentence), self.hidden_dim)
lstm_feats = self.hidden2tag(lstm_out)
return lstm_feats
def _score_sentence(self, feats, tags):
# Gives the score of a provided tag sequence
score = torch.zeros(1,device=device)
tags = torch.cat([torch.tensor([self.tag_to_ix[START_TAG]], dtype=LongTensor, device=device), tags])
for i, feat in enumerate(feats):
score = score + \
self.transitions[tags[i + 1], tags[i]] + feat[tags[i + 1]]
score = score + self.transitions[self.tag_to_ix[STOP_TAG], tags[-1]]
return score
def _viterbi_decode(self, feats):
backpointers = []
# Initialize the viterbi variables in log space
init_vvars = torch.full((1, self.tagset_size), -10000., device=device)
init_vvars[0][self.tag_to_ix[START_TAG]] = 0
# forward_var at step i holds the viterbi variables for step i-1
forward_var = init_vvars
for feat in feats:
bptrs_t = [] # holds the backpointers for this step
viterbivars_t = [] # holds the viterbi variables for this step
for next_tag in range(self.tagset_size):
# next_tag_var[i] holds the viterbi variable for tag i at the
# previous step, plus the score of transitioning
# from tag i to next_tag.
# We don't include the emission scores here because the max
# does not depend on them (we add them in below)
next_tag_var = forward_var + self.transitions[next_tag]
best_tag_id = argmax(next_tag_var)
bptrs_t.append(best_tag_id)
viterbivars_t.append(next_tag_var[0][best_tag_id].view(1))
# Now add in the emission scores, and assign forward_var to the set
# of viterbi variables we just computed
forward_var = (torch.cat(viterbivars_t) + feat).view(1, -1)
backpointers.append(bptrs_t)
# Transition to STOP_TAG
terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
best_tag_id = argmax(terminal_var)
path_score = terminal_var[0][best_tag_id]
# Follow the back pointers to decode the best path.
best_path = [best_tag_id]
for bptrs_t in reversed(backpointers):
best_tag_id = bptrs_t[best_tag_id]
best_path.append(best_tag_id)
# Pop off the start tag (we dont want to return that to the caller)
start = best_path.pop()
assert start == self.tag_to_ix[START_TAG] # Sanity check
best_path.reverse()
return path_score, best_path
def neg_log_likelihood(self, sentence, tags):
feats = self._get_lstm_features(sentence)
forward_score = self._forward_alg(feats)
gold_score = self._score_sentence(feats, tags)
return forward_score - gold_score
def forward(self, sentence): # dont confuse this with _forward_alg above.
# Get the emission scores from the BiLSTM
lstm_feats = self._get_lstm_features(sentence)
# Find the best path, given the features.
score, tag_seq = self._viterbi_decode(lstm_feats)
return score, tag_seq
START_TAG = "<START>"
STOP_TAG = "<STOP>"
EMBEDDING_DIM = 64
HIDDEN_DIM = 128
import dill
with open('word_to_ix.pkl', 'rb') as file:
word_to_ix = dill.load(file)
with open('pos_to_ix.pkl', 'rb') as file:
pos_to_ix = dill.load(file)
ix_to_word = dict((v,k) for k,v in word_to_ix.items()) #convert index to word
ix_to_pos = dict((v,k) for k,v in pos_to_ix.items()) #convert index to word
model = BiLSTM_CRF(len(word_to_ix), pos_to_ix, EMBEDDING_DIM, HIDDEN_DIM)
model.load_state_dict(torch.load("thainer.model"), strict=False)
model.to(device)
def predict(input_sent):
y_pred=[]
temp=[]
with torch.no_grad():
precheck_sent = prepare_sequence(input_sent, word_to_ix)
output=model(precheck_sent)[1]
y_pred=[ix_to_pos[i] for i in output]
return y_pred
predict(["ผม","ชื่อ","นาย","บุญ","มาก"," ","ทอง","ดี"])
```
| true |
code
| 0.810929 | null | null | null | null |
|
# MCMC sampling using the emcee package
## Introduction
The goal of Markov Chain Monte Carlo (MCMC) algorithms is to approximate the posterior distribution of your model parameters by random sampling in a probabilistic space. For most readers this sentence was probably not very helpful so here we'll start straight with and example but you should read the more detailed mathematical approaches of the method [here](https://www.pas.rochester.edu/~sybenzvi/courses/phy403/2015s/p403_17_mcmc.pdf) and [here](https://github.com/jakevdp/BayesianAstronomy/blob/master/03-Bayesian-Modeling-With-MCMC.ipynb).
### How does it work ?
The idea is that we use a number of walkers that will sample the posterior distribution (i.e. sample the Likelihood profile).
The goal is to produce a "chain", i.e. a list of $\theta$ values, where each $\theta$ is a vector of parameters for your model.<br>
If you start far away from the truth value, the chain will take some time to converge until it reaches a stationary state. Once it has reached this stage, each successive elements of the chain are samples of the target posterior distribution.<br>
This means that, once we have obtained the chain of samples, we have everything we need. We can compute the distribution of each parameter by simply approximating it with the histogram of the samples projected into the parameter space. This will provide the errors and correlations between parameters.
Now let's try to put a picture on the ideas described above. With this notebook, we have simulated and carried out a MCMC analysis for a source with the following parameters:<br>
$Index=2.0$, $Norm=5\times10^{-12}$ cm$^{-2}$ s$^{-1}$ TeV$^{-1}$, $Lambda =(1/Ecut) = 0.02$ TeV$^{-1}$ (50 TeV) for 20 hours.
The results that you can get from a MCMC analysis will look like this :
<img src="images/gammapy_mcmc.png" width="800">
On the first two top panels, we show the pseudo-random walk of one walker from an offset starting value to see it evolve to a better solution.
In the bottom right panel, we show the trace of each 16 walkers for 500 runs (the chain described previsouly). For the first 100 runs, the parameter evolve towards a solution (can be viewed as a fitting step). Then they explore the local minimum for 400 runs which will be used to estimate the parameters correlations and errors.
The choice of the Nburn value (when walkers have reached a stationary stage) can be done by eye but you can also look at the autocorrelation time.
### Why should I use it ?
When it comes to evaluate errors and investigate parameter correlation, one typically estimate the Likelihood in a gridded search (2D Likelihood profiles). Each point of the grid implies a new model fitting. If we use 10 steps for each parameters, we will need to carry out 100 fitting procedures.
Now let's say that I have a model with $N$ parameters, we need to carry out that gridded analysis $N*(N-1)$ times.
So for 5 free parameters you need 20 gridded search, resulting in 2000 individual fit.
Clearly this strategy doesn't scale well to high-dimensional models.
Just for fun: if each fit procedure takes 10s, we're talking about 5h of computing time to estimate the correlation plots.
There are many MCMC packages in the python ecosystem but here we will focus on [emcee](https://emcee.readthedocs.io), a lightweight Python package. A description is provided here : [Foreman-Mackey, Hogg, Lang & Goodman (2012)](https://arxiv.org/abs/1202.3665).
```
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from gammapy.irf import load_cta_irfs
from gammapy.maps import WcsGeom, MapAxis
from gammapy.modeling.models import (
ExpCutoffPowerLawSpectralModel,
GaussianSpatialModel,
SkyModel,
Models,
FoVBackgroundModel,
)
from gammapy.datasets import MapDataset
from gammapy.makers import MapDatasetMaker
from gammapy.data import Observation
from gammapy.modeling.sampling import (
run_mcmc,
par_to_model,
plot_corner,
plot_trace,
)
from gammapy.modeling import Fit
import logging
logging.basicConfig(level=logging.INFO)
```
## Simulate an observation
Here we will start by simulating an observation using the `simulate_dataset` method.
```
irfs = load_cta_irfs(
"$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)
observation = Observation.create(
pointing=SkyCoord(0 * u.deg, 0 * u.deg, frame="galactic"),
livetime=20 * u.h,
irfs=irfs,
)
# Define map geometry
axis = MapAxis.from_edges(
np.logspace(-1, 2, 15), unit="TeV", name="energy", interp="log"
)
geom = WcsGeom.create(
skydir=(0, 0), binsz=0.05, width=(2, 2), frame="galactic", axes=[axis]
)
empty_dataset = MapDataset.create(geom=geom, name="dataset-mcmc")
maker = MapDatasetMaker(selection=["background", "edisp", "psf", "exposure"])
dataset = maker.run(empty_dataset, observation)
# Define sky model to simulate the data
spatial_model = GaussianSpatialModel(
lon_0="0 deg", lat_0="0 deg", sigma="0.2 deg", frame="galactic"
)
spectral_model = ExpCutoffPowerLawSpectralModel(
index=2,
amplitude="3e-12 cm-2 s-1 TeV-1",
reference="1 TeV",
lambda_="0.05 TeV-1",
)
sky_model_simu = SkyModel(
spatial_model=spatial_model, spectral_model=spectral_model, name="source"
)
bkg_model = FoVBackgroundModel(dataset_name="dataset-mcmc")
models = Models([sky_model_simu, bkg_model])
print(models)
dataset.models = models
dataset.fake()
dataset.counts.sum_over_axes().plot(add_cbar=True);
# If you want to fit the data for comparison with MCMC later
# fit = Fit(dataset)
# result = fit.run(optimize_opts={"print_level": 1})
```
## Estimate parameter correlations with MCMC
Now let's analyse the simulated data.
Here we just fit it again with the same model we had before as a starting point.
The data that would be needed are the following:
- counts cube, psf cube, exposure cube and background model
Luckily all those maps are already in the Dataset object.
We will need to define a Likelihood function and define priors on parameters.<br>
Here we will assume a uniform prior reading the min, max parameters from the sky model.
### Define priors
This steps is a bit manual for the moment until we find a better API to define priors.<br>
Note the you **need** to define priors for each parameter otherwise your walkers can explore uncharted territories (e.g. negative norms).
```
print(dataset)
# Define the free parameters and min, max values
parameters = dataset.models.parameters
parameters["sigma"].frozen = True
parameters["lon_0"].frozen = True
parameters["lat_0"].frozen = True
parameters["amplitude"].frozen = False
parameters["index"].frozen = False
parameters["lambda_"].frozen = False
parameters["norm"].frozen = True
parameters["tilt"].frozen = True
parameters["norm"].min = 0.5
parameters["norm"].max = 2
parameters["index"].min = 1
parameters["index"].max = 5
parameters["lambda_"].min = 1e-3
parameters["lambda_"].max = 1
parameters["amplitude"].min = 0.01 * parameters["amplitude"].value
parameters["amplitude"].max = 100 * parameters["amplitude"].value
parameters["sigma"].min = 0.05
parameters["sigma"].max = 1
# Setting amplitude init values a bit offset to see evolution
# Here starting close to the real value
parameters["index"].value = 2.0
parameters["amplitude"].value = 3.2e-12
parameters["lambda_"].value = 0.05
print(dataset.models)
print("stat =", dataset.stat_sum())
%%time
# Now let's define a function to init parameters and run the MCMC with emcee
# Depending on your number of walkers, Nrun and dimensionality, this can take a while (> minutes)
sampler = run_mcmc(dataset, nwalkers=6, nrun=150) # to speedup the notebook
# sampler=run_mcmc(dataset,nwalkers=12,nrun=1000) # more accurate contours
```
## Plot the results
The MCMC will return a sampler object containing the trace of all walkers.<br>
The most important part is the chain attribute which is an array of shape:<br>
_(nwalkers, nrun, nfreeparam)_
The chain is then used to plot the trace of the walkers and estimate the burnin period (the time for the walkers to reach a stationary stage).
```
plot_trace(sampler, dataset)
plot_corner(sampler, dataset, nburn=50)
```
## Plot the model dispersion
Using the samples from the chain after the burn period, we can plot the different models compared to the truth model. To do this we need to the spectral models for each parameter state in the sample.
```
emin, emax = [0.1, 100] * u.TeV
nburn = 50
fig, ax = plt.subplots(1, 1, figsize=(12, 6))
for nwalk in range(0, 6):
for n in range(nburn, nburn + 100):
pars = sampler.chain[nwalk, n, :]
# set model parameters
par_to_model(dataset, pars)
spectral_model = dataset.models["source"].spectral_model
spectral_model.plot(
energy_range=(emin, emax),
ax=ax,
energy_power=2,
alpha=0.02,
color="grey",
)
sky_model_simu.spectral_model.plot(
energy_range=(emin, emax), energy_power=2, ax=ax, color="red"
);
```
## Fun Zone
Now that you have the sampler chain, you have in your hands the entire history of each walkers in the N-Dimensional parameter space. <br>
You can for example trace the steps of each walker in any parameter space.
```
# Here we plot the trace of one walker in a given parameter space
parx, pary = 0, 1
plt.plot(sampler.chain[0, :, parx], sampler.chain[0, :, pary], "ko", ms=1)
plt.plot(
sampler.chain[0, :, parx],
sampler.chain[0, :, pary],
ls=":",
color="grey",
alpha=0.5,
)
plt.xlabel("Index")
plt.ylabel("Amplitude");
```
## PeVatrons in CTA ?
Now it's your turn to play with this MCMC notebook. For example to test the CTA performance to measure a cutoff at very high energies (100 TeV ?).
After defining your Skymodel it can be as simple as this :
```
# dataset = simulate_dataset(model, geom, pointing, irfs)
# sampler = run_mcmc(dataset)
# plot_trace(sampler, dataset)
# plot_corner(sampler, dataset, nburn=200)
```
| true |
code
| 0.687263 | null | null | null | null |
|
```
#hide
%load_ext autoreload
%autoreload 2
# default_exp analysis
```
# Analysis
> The analysis functions help a modeler quickly run a full time series analysis.
An analysis consists of:
1. Initializing a DGLM, using `define_dglm`.
2. Updating the model coefficients at each time step, using `dglm.update`.
3. Forecasting at each time step between `forecast_start` and `forecast_end`, using `dglm.forecast_marginal` or `dglm.forecast_path`.
4. Returning the desired output, specified in the argument `ret`. The default is to return the model and forecast samples.
The analysis starts by defining a new DGLM with `define_dglm`. The default number of observations to use is set at `prior_length=20`. Any arguments that are used to define a model in `define_dglm` can be passed into analysis as keyword arguments. Alternatively, you may define the model beforehand, and pass the pre-initialized DGLM into analysis as the argument `model_prior`.
Once the model has been initialized, the analysis loop begins. If $\text{forecast_start} \leq t \leq \text{forecast_end}$, then the model will forecast ahead. The forecast horizon k must be specified. The default is to simulate `nsamps=500` times from the forecast distribution using `forecast_marginal`, from $1$ to `k` steps into the future. To simulate from the joint forecast distribution over the next `k` steps, set the flag `forecast_path=True`. Note that all forecasts are *out-of-sample*, i.e. they are made before the model has seen the observation. This is to ensure than the forecast accuracy is a more fair representation of future model performance.
After the forecast has been made, the model sees the observation $y_t$, and updates the state vector accordingly.
The analysis ends after seeing the last observation in `Y`. The output is a list specified by the argument `ret`, which may contain:
- `mod`: The final model
- `forecast`: The forecast samples, stored in a 3-dimensional array with axes *nsamps* $\times$ *forecast length* $\times$ *k*
- `model_coef`: A time series of the state vector mean vector and variance matrix
Please note that `analysis` is used on a historic dataset that already exists. This means that a typical sequence of events is to run an analysis on the data you current have, and return the model and forecast samples. The forecast samples are used to evaluate the past forecast performance. Then you can use `dglm.forecast_marginal` and `dglm.forecast_path` to forecast into the future.
```
#hide
#exporti
import numpy as np
import pandas as pd
from pybats.define_models import define_dglm, define_dcmm, define_dbcm, define_dlmm
from pybats.shared import define_holiday_regressors
from collections.abc import Iterable
```
## Analysis for a DGLM
```
#export
def analysis(Y, X=None, k=1, forecast_start=0, forecast_end=0,
nsamps=500, family = 'normal', n = None,
model_prior = None, prior_length=20, ntrend=1,
dates = None, holidays = [],
seasPeriods = [], seasHarmComponents = [],
latent_factor = None, new_latent_factors = None,
ret=['model', 'forecast'],
mean_only = False, forecast_path = False,
**kwargs):
"""
This is a helpful function to run a standard analysis. The function will:
1. Automatically initialize a DGLM
2. Run sequential updating
3. Forecast at each specified time step
"""
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
X = define_holiday_regressors(X, dates, holidays)
# Check if it's a latent factor DGLM
if latent_factor is not None:
is_lf = True
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
if model_prior is None:
mod = define_dglm(Y, X, family=family, n=n, prior_length=prior_length, ntrend=ntrend, nhol=nhol, nlf=nlf,
seasPeriods=seasPeriods, seasHarmComponents=seasHarmComponents,
**kwargs)
else:
mod = model_prior
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Define the run length
T = len(Y) + 1
if ret.__contains__('model_coef'):
m = np.zeros([T-1, mod.a.shape[0]])
C = np.zeros([T-1, mod.a.shape[0], mod.a.shape[0]])
if family == 'normal':
n = np.zeros(T)
s = np.zeros(T)
if new_latent_factors is not None:
if not ret.__contains__('new_latent_factors'):
ret.append('new_latent_factors')
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for lf in new_latent_factors:
tmp.append(lf.copy())
new_latent_factors = tmp
# Create dummy variable if there are no regression covariates
if X is None:
X = np.array([None]*(T+k)).reshape(-1,1)
else:
if len(X.shape) == 1:
X = X.reshape(-1,1)
# Initialize updating + forecasting
horizons = np.arange(1, k + 1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
for t in range(prior_length, T):
if forecast_start <= t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
if ret.__contains__('forecast'):
if is_lf:
if forecast_path:
pm, ps, pp = latent_factor.get_lf_forecast(dates.iloc[t])
forecast[:, t - forecast_start, :] = mod.forecast_path_lf_copula(k=k, X=X[t + horizons - 1, :],
nsamps=nsamps,
phi_mu=pm, phi_sigma=ps, phi_psi=pp)
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None # Not including path dependency in latent factor
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps:
mod.forecast_marginal_lf_analytic(k=k, X=x, phi_mu=pm, phi_sigma=ps, nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).squeeze().T.reshape(-1, k)#.reshape(-1, 1)
else:
if forecast_path:
forecast[:, t - forecast_start, :] = mod.forecast_path(k=k, X = X[t + horizons - 1, :], nsamps=nsamps)
else:
if family == "binomial":
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, n, x:
mod.forecast_marginal(k=k, n=n, X=x, nsamps=nsamps, mean_only=mean_only),
horizons, n[t + horizons - 1], X[t + horizons - 1, :]))).squeeze().T.reshape(-1, k) # .reshape(-1, 1)
else:
# Get the forecast samples for all the items over the 1:k step ahead marginal forecast distributions
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x:
mod.forecast_marginal(k=k, X=x, nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :]))).squeeze().T.reshape(-1, k)#.reshape(-1, 1)
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates[t], mod=mod, X=X[t + horizons - 1],
k=k, nsamps=nsamps, horizons=horizons)
# Now observe the true y value, and update:
if t < len(Y):
if is_lf:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y=Y[t], X=X[t],
phi_mu=pm, phi_sigma=ps)
else:
if family == "binomial":
mod.update(y=Y[t], X=X[t], n=n[t])
else:
mod.update(y=Y[t], X=X[t])
if ret.__contains__('model_coef'):
m[t,:] = mod.m.reshape(-1)
C[t,:,:] = mod.C
if family == 'normal':
n[t] = mod.n / mod.delVar
s[t] = mod.s
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates[t], mod=mod, Y=Y[t], X=X[t], k=k, nsamps=nsamps)
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'model_coef':
mod_coef = {'m':m, 'C':C}
if family == 'normal':
mod_coef.update({'n':n, 's':s})
out.append(mod_coef)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
This function is core to the PyBATS package, because it allows a modeler to easily run a full time series analysis in one step. Below is a quick example of analysis of quarterly inflation in the US using a normal DLM. We'll start by loading in the data:
```
from pybats.shared import load_us_inflation
from pybats.analysis import analysis
import pandas as pd
from pybats.plot import plot_data_forecast
from pybats.point_forecast import median
import matplotlib.pyplot as plt
from pybats.loss_functions import MAPE
data = load_us_inflation()
pd.concat([data.head(3), data.tail(3)])
```
And then running an analysis. We're going to use the previous (lag-1) value of inflation as a predictor.
```
forecast_start = '1990-Q1'
forecast_end = '2014-Q3'
X = data.Inflation.values[:-1]
mod, samples = analysis(Y = data.Inflation.values[1:], X=X, family="normal",
k = 1, prior_length = 12,
forecast_start = forecast_start, forecast_end = forecast_end,
dates=data.Date,
ntrend = 2, deltrend=.99,
seasPeriods=[4], seasHarmComponents=[[1,2]], delseas=.99,
nsamps = 5000)
```
A couple of things to note here:
- `forecast_start` and `forecast_end` were specified as elements in the `dates` vector. You can also specify forecast_start and forecast_end by row numbers in `Y`, and avoid providing the `dates` argument.
- `ntrend=2` creates a model with an intercept and a local slope term, and `deltrend=.98` discounts the impact of older observations on the trend component by $2\%$ at each time step.
- The seasonal component was set as `seasPeriods=[4]`, because we think the seasonal effect has a cycle of length $4$ in this quarterly inflation data.
Let's examine the output. Here is the mean and standard deviation of the state vector (aka the coefficients) after the model has seen the last observation in `Y`:
```
mod.get_coef()
```
It's clear that the lag-1 regression term is dominant, with a mean of $0.92$. The only other large coefficient is the intercept, with a mean of $0.10$.
The seasonal coefficients turned out to be very small. Most likely this is because the publicly available dataset for US inflation is pre-adjusted for seasonality.
The forecast samples are stored in a 3-dimensional array, with axes *nsamps* $\times$ *forecast length* $\times$ *k*:
- **nsamps** is the number of samples drawn from the forecast distribution
- **forecast length** is the number of time steps between `forecast_start` and `forecast_end`
- **k** is the forecast horizon, or the number of steps that were forecast ahead
We can plot the forecasts using `plot_data_forecast`. We'll plot the 1-quarter ahead forecasts, using the median as our point estimate.
```
forecast = median(samples)
# Plot the 1-quarter ahead forecast
h = 1
start = data[data.Date == forecast_start].index[0] + h
end = data[data.Date == forecast_end].index[0] + h + 1
fig, ax = plt.subplots(figsize=(12, 6))
plot_data_forecast(fig, ax, y = data[start:end].Inflation.values,
f = forecast[:,h-1],
samples = samples[:,:,h-1],
dates = pd.to_datetime(data[start:end].Date.values),
xlabel='Time', ylabel='Quarterly US Inflation', title='1-Quarter Ahead Forecasts');
```
We can see that the forecasts are quite good, and nearly all of the observations fall within the $95\%$ credible interval.
There's also a clear pattern - the forecasts look as if they're shifted forward from the data by 1 step. This is because the lag-1 predictor is very strong, with a coefficient mean of $0.91$. The model is primarily using the previous month's value as its forecast, with some small modifications. Having the previous value as our best forecast is common in many time series.
We can put a number on the quality of the forecast by using a loss function, the Mean Absolute Percent Error (MAPE). We see that on average, our forecasts of quarterly inflation have an error of under $15\%$.
```
MAPE(data[start:end].Inflation.values, forecast[:,0]).round(1)
assert(MAPE(data[start:end].Inflation.values, forecast[:,0]).round(0) <= 15)
```
Finally, we can use the returned model to forecast $1-$step ahead to Q1 2015, which is past the end of the dataset. We need the `X` value to forecast into the future. Luckily, in this model the predictor `X` is simply the previous value of Inflation from Q4 2014.
```
x_future = data.Inflation.iloc[-1]
one_step_forecast_samples = mod.forecast_marginal(k=1,
X=x_future,
nsamps=1000000)
```
From here, we can find the mean and standard deviation of the forecast for next quarter's inflation:
```
print('Mean: ' + str(np.mean(one_step_forecast_samples).round(2)))
print('Std Dev: ' + str(np.std(one_step_forecast_samples).round(2)))
```
We can also plot the full forecast distribution for Q1 2015:
```
fig, ax = plt.subplots(figsize=(10,6))
ax.hist(one_step_forecast_samples.reshape(-1),
bins=200, alpha=0.3, color='b', density=True,
label='Forecast Distribution');
ax.vlines(x=np.mean(one_step_forecast_samples),
ymin=0, ymax=ax.get_ylim()[1],
label='Forecast Mean');
ax.set_title('1-Step Ahead Forecast Distribution for Q1 2015 Inflation');
ax.set_ylabel('Forecast Density')
ax.set_xlabel('Q1 2015 Inflation')
ax.legend();
```
## Analysis for a DCMM
```
#export
def analysis_dcmm(Y, X=None, k=1, forecast_start=0, forecast_end=0,
nsamps=500, rho=.6,
model_prior=None, prior_length=20, ntrend=1,
dates=None, holidays=[],
seasPeriods=[], seasHarmComponents=[],
latent_factor=None, new_latent_factors=None,
mean_only=False,
ret=['model', 'forecast'],
**kwargs):
"""
This is a helpful function to run a standard analysis using a DCMM.
"""
if latent_factor is not None:
is_lf = True
# Note: This assumes that the bernoulli & poisson components have the same number of latent factor components
if isinstance(latent_factor, (list, tuple)):
nlf = latent_factor[0].p
else:
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
# dates = pd.to_datetime(dates, format='%y/%m/%d')
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
if nhol > 0:
X = define_holiday_regressors(X, dates, holidays)
# Initialize the DCMM
if model_prior is None:
mod = define_dcmm(Y, X, prior_length = prior_length, seasPeriods = seasPeriods, seasHarmComponents = seasHarmComponents,
ntrend=ntrend, nlf = nlf, rho = rho, nhol = nhol, **kwargs)
else:
mod = model_prior
if ret.__contains__('new_latent_factors'):
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for sig in new_latent_factors:
tmp.append(sig.copy())
new_latent_factors = tmp
T = len(Y) + 1 # np.min([len(Y), forecast_end]) + 1
nu = 9
if X is None:
X = np.array([None]*(T+k)).reshape(-1,1)
else:
if len(X.shape) == 1:
X = X.reshape(-1,1)
# Initialize updating + forecasting
horizons = np.arange(1,k+1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
# Run updating + forecasting
for t in range(prior_length, T):
# if t % 100 == 0:
# print(t)
if ret.__contains__('forecast'):
if t >= forecast_start and t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
# Get the forecast samples for all the items over the 1:k step ahead path
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf_forecast(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf_forecast(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None # Not including the path dependency of the latent factor
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X=(x, x), phi_mu=(pm, pm), phi_sigma=(ps, ps), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).reshape(1, -1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_lf_copula(
k=k, X=(X[t + horizons - 1, :], X[t + horizons - 1, :]),
phi_mu=(pm, pm), phi_sigma=(ps, ps), phi_psi=(pp, pp), nsamps=nsamps, t_dist=True, nu=nu)
else:
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x: mod.forecast_marginal(
k=k, X=(x, x), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :]))).reshape(1,-1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_copula(
k=k, X=(X[t + horizons - 1, :], X[t + horizons - 1, :]), nsamps=nsamps, t_dist=True, nu=nu)
if ret.__contains__('new_latent_factors'):
if t >= forecast_start and t <= forecast_end:
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Update the DCMM
if t < len(Y):
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
else:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y=Y[t], X=(X[t], X[t]),
phi_mu=(pm, pm), phi_sigma=(ps, ps))
else:
mod.update(y = Y[t], X=(X[t], X[t]))
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
`analysis_dcmm` works identically to the standard `analysis`, but is specialized for a DCMM.
The observations must be integer counts, which are modeled as a combination of a Poisson and Bernoulli DGLM. Typically a DCMM is equally good as a Poisson DGLM for modeling series with consistently large integers, while being significantly better at modeling series with many zeros.
Note that by default, all simulated forecasts made with `analysis_dcmm` are *path* forecasts, meaning that they account for the dependence across forecast horizons.
## Analysis for a DBCM
```
#export
def analysis_dbcm(Y_transaction, X_transaction, Y_cascade, X_cascade, excess,
k, forecast_start, forecast_end, nsamps = 500, rho = .6,
model_prior=None, prior_length=20, ntrend=1,
dates=None, holidays = [],
latent_factor = None, new_latent_factors = None,
seasPeriods = [], seasHarmComponents = [],
mean_only=False,
ret=['model', 'forecast'],
**kwargs):
"""
This is a helpful function to run a standard analysis using a DBCM.
"""
if latent_factor is not None:
is_lf = True
# Note: This assumes that the bernoulli & poisson components have the same number of latent factor components
if isinstance(latent_factor, (list, tuple)):
nlf = latent_factor[0].p
else:
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
# dates = pd.to_datetime(dates, format='%y/%m/%d')
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
if nhol > 0:
X_transaction = define_holiday_regressors(X_transaction, dates, holidays)
if model_prior is None:
mod = define_dbcm(Y_transaction, X_transaction, Y_cascade, X_cascade,
excess_values = excess, prior_length = prior_length,
seasPeriods = seasPeriods, seasHarmComponents=seasHarmComponents,
nlf = nlf, rho = rho, nhol=nhol, **kwargs)
else:
mod = model_prior
if ret.__contains__('new_latent_factors'):
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for sig in new_latent_factors:
tmp.append(sig.copy())
new_latent_factors = tmp
# Initialize updating + forecasting
horizons = np.arange(1,k+1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
T = len(Y_transaction) + 1 #np.min([len(Y_transaction)- k, forecast_end]) + 1
nu = 9
# Run updating + forecasting
for t in range(prior_length, T):
# if t % 100 == 0:
# print(t)
# print(mod.dcmm.pois_mod.param1)
# print(mod.dcmm.pois_mod.param2)
if ret.__contains__('forecast'):
if t >= forecast_start and t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
# Get the forecast samples for all the items over the 1:k step ahead path
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf_forecast(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf_forecast(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
pp = None # Not including path dependency in latent factor
else:
if latent_factor.forecast_path:
pm, ps, pp = latent_factor.get_lf_forecast(dates.iloc[t])
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x_trans, x_cascade, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X_transaction=x_trans, X_cascade=x_cascade,
phi_mu=pm, phi_sigma=ps, nsamps=nsamps, mean_only=mean_only),
horizons, X_transaction[t + horizons - 1, :], X_cascade[t + horizons - 1, :], pm, ps))).reshape(1, -1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_lf_copula(
k=k, X_transaction=X_transaction[t + horizons - 1, :], X_cascade=X_cascade[t + horizons - 1, :],
phi_mu=pm, phi_sigma=ps, phi_psi=pp, nsamps=nsamps, t_dist=True, nu=nu)
else:
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x_trans, x_cascade: mod.forecast_marginal(
k=k, X_transaction=x_trans, X_cascade=x_cascade, nsamps=nsamps, mean_only=mean_only),
horizons, X_transaction[t + horizons - 1, :], X_cascade[t + horizons - 1, :]))).reshape(1,-1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_copula(
k=k, X_transaction=X_transaction[t + horizons - 1, :], X_cascade=X_cascade[t + horizons - 1, :],
nsamps=nsamps, t_dist=True, nu=nu)
if ret.__contains__('new_latent_factors'):
if t >= forecast_start and t <= forecast_end:
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates.iloc[t], mod=mod, X_transaction=X_transaction[t + horizons - 1, :],
X_cascade = X_cascade[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Update the DBCM
if t < len(Y_transaction):
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
else:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y_transaction=Y_transaction[t], X_transaction=X_transaction[t, :],
y_cascade=Y_cascade[t,:], X_cascade=X_cascade[t, :],
phi_mu=pm, phi_sigma=ps, excess=excess[t])
else:
mod.update(y_transaction=Y_transaction[t], X_transaction=X_transaction[t, :],
y_cascade=Y_cascade[t,:], X_cascade=X_cascade[t, :], excess=excess[t])
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates.iloc[t], mod=mod, X_transaction=X_transaction[t + horizons - 1, :],
X_cascade = X_cascade[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
`analysis_dbcm` works identically to the standard `analysis`, but is specialized for a DBCM.
Separate data must be specified for the DCMM on transactions, `y_transaction` and `X_transaction`, the binomial cascade,`y_cascade`, `X_cascade`, and any excess counts, `excess`.
Note that by default, all simulated forecasts made with `analysis_dbcm` are *path* forecasts, meaning that they account for the dependence across forecast horizons.
## Analysis for a DLMM
```
#export
def analysis_dlmm(Y, X, k=1, forecast_start=0, forecast_end=0,
nsamps=500, rho=.6,
model_prior=None, prior_length=20, ntrend=1,
dates=None, holidays=[],
seasPeriods=[], seasHarmComponents=[],
latent_factor=None, new_latent_factors=None,
mean_only=False,
ret=['model', 'forecast'],
**kwargs):
"""
This is a helpful function to run a standard analysis using a DLMM.
"""
if latent_factor is not None:
is_lf = True
# Note: This assumes that the bernoulli & poisson components have the same number of latent factor components
if isinstance(latent_factor, (list, tuple)):
nlf = latent_factor[0].p
else:
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
# dates = pd.to_datetime(dates, format='%y/%m/%d')
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
if nhol > 0:
X = define_holiday_regressors(X, dates, holidays)
# Initialize the DCMM
if model_prior is None:
mod = define_dlmm(Y, X, prior_length = prior_length, seasPeriods = seasPeriods, seasHarmComponents = seasHarmComponents,
ntrend=ntrend, nlf = nlf, rho = rho, nhol = nhol, **kwargs)
else:
mod = model_prior
if ret.__contains__('new_latent_factors'):
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for sig in new_latent_factors:
tmp.append(sig.copy())
new_latent_factors = tmp
if ret.__contains__('model_coef'): ## Return normal dlm params
m = np.zeros([T, mod.dlm_mod.a.shape[0]])
C = np.zeros([T, mod.dlm_mod.a.shape[0], mod.dlm_mod.a.shape[0]])
a = np.zeros([T, mod.dlm_mod.a.shape[0]])
R = np.zeros([T, mod.dlm_mod.a.shape[0], mod.dlm_mod.a.shape[0]])
n = np.zeros(T)
s = np.zeros(T)
# Initialize updating + forecasting
horizons = np.arange(1,k+1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
T = len(Y) + 1
nu = 9
# Run updating + forecasting
for t in range(prior_length, T):
# if t % 100 == 0:
# print(t)
if ret.__contains__('forecast'):
if t >= forecast_start and t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
# Get the forecast samples for all the items over the 1:k step ahead path
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf_forecast(dates.iloc[t])
pm_dlm, ps_dlm = latent_factor[1].get_lf_forecast(dates.iloc[t])
pm = (pm_bern, pm_dlm)
ps = (ps_bern, ps_dlm)
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None # Not including the path dependency of the latent factor
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X=(x, x), phi_mu=(pm, pm), phi_sigma=(ps, ps), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).reshape(1, -1)
else:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X=(x, x), phi_mu=(pm, pm), phi_sigma=(ps, ps), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).squeeze().T.reshape(-1, k)
else:
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x: mod.forecast_marginal(
k=k, X=(x, x), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :]))).reshape(1,-1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_copula(
k=k, X=(X[t + horizons - 1, :], X[t + horizons - 1, :]), nsamps=nsamps, t_dist=True, nu=nu)
if ret.__contains__('new_latent_factors'):
if t >= forecast_start and t <= forecast_end:
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Update the DLMM
if t < len(Y):
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf(dates.iloc[t])
pm_dlm, ps_dlm = latent_factor[1].get_lf(dates.iloc[t])
pm = (pm_bern, pm_dlm)
ps = (ps_bern, ps_dlm)
else:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y=Y[t], X=(X[t], X[t]),
phi_mu=(pm, pm), phi_sigma=(ps, ps))
else:
mod.update(y = Y[t], X=(X[t], X[t]))
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Store the dlm coefficients
if ret.__contains__('model_coef'):
m[t,:] = mod.dlm.m.reshape(-1)
C[t,:,:] = mod.dlm.C
a[t,:] = mod.dlm.a.reshape(-1)
R[t,:,:] = mod.dlm.R
n[t] = mod.dlm.n / mod.dlm.delVar
s[t] = mod.dlm.s
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'model_coef':
mod_coef = {'m':m, 'C':C, 'a':a, 'R':R, 'n':n, 's':s}
out.append(mod_coef)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
`analysis_dlmm` works identically to the standard `analysis`, but is specialized for a DLMM. `analysis_dlmm` returns the model coefficients for the Normal DLM portion of the model only.
The observations are continuous and are modeled as a combination of a Bernoulli DGLM and a Normal DLM.
Note that by default, all simulated forecasts made with `analysis_dlmm` are *path* forecasts, meaning that they account for the dependence across forecast horizons. The exception is for latent factor DLMMs, which default to marginal forecasting.
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.422088 | null | null | null | null |
|
# Support Vector Machines
Support Vector Machines (SVM) are an extension of the linear methods that attempt to separate classes with hyperplans.
These extensions come in three steps:
1. When classes are linearly separable, maximize the margin between the two classes
2. When classes are not linearly separable, maximize the margin but allow some samples within the margin. That is the soft margin
3. The "Kernel trick" to extend the separation to non linear frontieres
The boost in performance of the Kernel trick has made the SVM the best classification method of the 2000's until the deep neural nets.
### Learning goals
- Understand and implement SVM concepts stated above
- Reminder to the Lagrange multiplier and optimization theory
- Deal with a general purpose solver with constraints
- Apply SVM to a non linear problem (XOR) with a non linear kernel (G-RBF)
### References
- [1] [The Elements of Statistical Learning](https://web.stanford.edu/~hastie/ElemStatLearn/) - Trevor Hastie, Robert Tibshirani, Jerome Friedman, Springer
- [2] Convex Optimization - Stephen Boyd, Lieven Vandenberghe, Cambridge University Press
- [3] [Pattern Recognition and Machine Learning - Ch 7 demo](https://github.com/yiboyang/PRMLPY/blob/master/ch7/svm.py) - Christopher M Bishop, Github
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as pltcolors
from sklearn import linear_model, svm, discriminant_analysis, metrics
from scipy import optimize
import seaborn as sns
```
## Helpers
```
def plotLine(ax, xRange, w, x0, label, color='grey', linestyle='-', alpha=1.):
""" Plot a (separating) line given the normal vector (weights) and point of intercept """
if type(x0) == int or type(x0) == float or type(x0) == np.float64:
x0 = [0, -x0 / w[1]]
yy = -(w[0] / w[1]) * (xRange - x0[0]) + x0[1]
ax.plot(xRange, yy, color=color, label=label, linestyle=linestyle)
def plotSvm(X, y, support=None, w=None, intercept=0., label='Data', separatorLabel='Separator',
ax=None, bound=[[-1., 1.], [-1., 1.]]):
""" Plot the SVM separation, and margin """
if ax is None:
fig, ax = plt.subplots(1)
im = ax.scatter(X[:,0], X[:,1], c=y, cmap=cmap, alpha=0.5, label=label)
if support is not None:
ax.scatter(support[:,0], support[:,1], label='Support', s=80, facecolors='none',
edgecolors='y', color='y')
print("Number of support vectors = %d" % (len(support)))
if w is not None:
xx = np.array(bound[0])
plotLine(ax, xx, w, intercept, separatorLabel)
# Plot margin
if support is not None:
signedDist = np.matmul(support, w)
margin = np.max(signedDist) - np.min(signedDist) * np.sqrt(np.dot(w, w))
supportMaxNeg = support[np.argmin(signedDist)]
plotLine(ax, xx, w, supportMaxNeg, 'Margin -', linestyle='-.', alpha=0.8)
supportMaxPos = support[np.argmax(signedDist)]
plotLine(ax, xx, w, supportMaxPos, 'Margin +', linestyle='--', alpha=0.8)
ax.set_title('Margin = %.3f' % (margin))
ax.legend(loc='upper left')
ax.grid()
ax.set_xlim(bound[0])
ax.set_ylim(bound[1])
cb = plt.colorbar(im, ax=ax)
loc = np.arange(-1,1,1)
cb.set_ticks(loc)
cb.set_ticklabels(['-1','1'])
```
## The data model
Let's use a simple model with two Gaussians that are faraway in order to be separable
```
colors = ['blue','red']
cmap = pltcolors.ListedColormap(colors)
nFeatures = 2
N = 100
def generateBatchBipolar(n, mu=0.5, sigma=0.2):
""" Two gaussian clouds on each side of the origin """
X = np.random.normal(mu, sigma, (n, 2))
yB = np.random.uniform(0, 1, n) > 0.5
# y is in {-1, 1}
y = 2. * yB - 1
X *= y[:, np.newaxis]
X -= X.mean(axis=0)
return X, y
```
# 1. Maximum margin separator
The following explanation is about the binary classification but generalizes to more classes.
Let $X$ be the matrix of $n$ samples of the $p$ features. We want to separate the two classes of $y$ with an hyperplan (a straight line in 2D, that is $p=2$). The separation equation is:
$$ w^T x + b = 0, w \in \mathbb{R}^{p}, x \in \mathbb{R}^{p}, b \in \mathbb{R} $$
Given $x_0$ a point on the hyperplan, the signed distance of any point $x$ to the hyperplan is :
$$ \frac{w}{\Vert w \Vert} (x - x_0) = \frac{1}{\Vert w \Vert} (w^T x + b) $$
If $y$, such that $y \in \{-1, 1\}$, is the corresponding label of $x$, the (unsigned) distance is :
$$ \frac{y}{\Vert w \Vert} (w^T x + b) $$
This is the update quantity used by the Rosenblatt Perceptron.
The __Maximum margin separator__ is aiming at maximizing $M$ such that :
$$ \underset{w, b}{\max} M $$
__Subject to :__
- $y_i(x_i^T w + b) \ge M, i = 1..n$
- $\Vert w \Vert = 1$
$x_i$ and $y_i$ are samples of $x$ and $y$, a row of the matrix $X$ and the vector $y$.
However, we may change the condition on the norm of $w$ such that : $\Vert w \Vert = \frac 1M$
Leading to the equivalent statement of the maximum margin classifier :
$$ \min_{w, b} \frac 12 \Vert w \Vert^2 $$
__Subject to : $y_i(x_i^T w + b) \ge 1, i = 1..n$__
For more details, see [1, chap 4.5]
The corresponding Lagrange primal problem is :
$$\mathcal{L}_p(w, b, \alpha) = \frac 12 \Vert w \Vert^2 - \sum_{i=0}^n \alpha_i (y_i(x_i^T w + b) - 1)$$
__Subject to:__
- $\alpha_i \ge 0, i\in 1..n$
This shall be __minimized__ on $w$ and $b$, using the corresponding partial derivates equal to 0, we get :
$$\begin{align}
\sum_{i=0}^n \alpha_i y_i x_i &= w \\
\sum_{i=0}^n \alpha_i y_i &= 0
\end{align}$$
From $\mathcal{L}_p$, we get the (Wolfe) dual :
$$\begin{align}
\mathcal{L}_d (\alpha)
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k x_i^T x_k \\
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \langle \alpha_i y_i x_i, \alpha_k y_k x_k \rangle \\
\end{align}$$
__Subject to :__
- $\alpha_i \ge 0, i\in 1..n$
- $\sum_{i=0}^n \alpha_i y_i = 0$
Which is a concave problem that is __maximized__ using a solver.
Strong duality requires (KKT) [2, chap. 5.5]:
- $\alpha_i (y_i(x_i^T w + b) - 1) = 0, \forall i \in 1..n$
Implying that :
- If $\alpha_i > 0$, then $y_i(x_i^T w + b) = 1$, meaning that $x_i$ is on one of the two hyperplans located at the margin distance from the separating hyperplan. $x_i$ is said to be a support vector
- If $y_i(x_i^T w + b) > 1$, the distance of $x_i$ to the hyperplan is larger than the margin.
### Train data
To demonstrate the maximum margin classifier, a dataset with separable classes is required. Let's use a mixture of two gaussian distributed classes with mean and variance such that the two classes are separated.
```
xTrain0, yTrain0 = generateBatchBipolar(N, sigma=0.2)
plotSvm(xTrain0, yTrain0)
```
## Implementation of the Maximum margin separator
$$\mathcal{L}_d = \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k x_i^T x_k $$
__Subject to :__
- $\sum_{i=0}^n \alpha_i y_i = \langle \alpha, y \rangle = 0$
- $\alpha_i \ge 0, i\in 1..n$
The classifier is built on the scipy.optimize.minimum solver. The implementation is correct but inefficient as it is not taking into account for the sparsity of the $\alpha$ vector.
```
class MaxMarginClassifier:
def __init__(self):
self.alpha = None
self.w = None
self.supportVectors = None
def fit(self, X, y):
N = len(y)
# Gram matrix of (X.y)
Xy = X * y[:, np.newaxis]
GramXy = np.matmul(Xy, Xy.T)
# Lagrange dual problem
def Ld0(G, alpha):
return alpha.sum() - 0.5 * alpha.dot(alpha.dot(G))
# Partial derivate of Ld on alpha
def Ld0dAlpha(G, alpha):
return np.ones_like(alpha) - alpha.dot(G)
# Constraints on alpha of the shape :
# - d - C*alpha = 0
# - b - A*alpha >= 0
A = -np.eye(N)
b = np.zeros(N)
constraints = ({'type': 'eq', 'fun': lambda a: np.dot(a, y), 'jac': lambda a: y},
{'type': 'ineq', 'fun': lambda a: b - np.dot(A, a), 'jac': lambda a: -A})
# Maximize by minimizing the opposite
optRes = optimize.minimize(fun=lambda a: -Ld0(GramXy, a),
x0=np.ones(N),
method='SLSQP',
jac=lambda a: -Ld0dAlpha(GramXy, a),
constraints=constraints)
self.alpha = optRes.x
self.w = np.sum((self.alpha[:, np.newaxis] * Xy), axis=0)
epsilon = 1e-6
self.supportVectors = X[self.alpha > epsilon]
# Any support vector is at a distance of 1 to the separation plan
# => use support vector #0 to compute the intercept, assume label is in {-1, 1}
supportLabels = y[self.alpha > epsilon]
self.intercept = supportLabels[0] - np.matmul(self.supportVectors[0].T, self.w)
def predict(self, X):
""" Predict y value in {-1, 1} """
assert(self.w is not None)
assert(self.w.shape[0] == X.shape[1])
return 2 * (np.matmul(X, self.w) > 0) - 1
```
Reference:
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize
```
model00 = MaxMarginClassifier()
model00.fit(xTrain0, yTrain0)
model00.w, model00.intercept
fig, ax = plt.subplots(1, figsize=(12, 7))
plotSvm(xTrain0, yTrain0, model00.supportVectors, model00.w, model00.intercept, label='Training', ax=ax)
```
## Maximum margin classifier using Scikit Learn (SVC)
SVC is used in place of LinearSVC as the support vectors are provided. These vectors are displayed in the graph here below.
Set a high $C$ parameter to disable soft margin
```
model01 = svm.SVC(kernel='linear', gamma='auto', C = 1e6)
model01.fit(xTrain0, yTrain0)
model01.coef_[0], model01.intercept_[0]
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain0, yTrain0, model01.support_vectors_, model01.coef_[0], model01.intercept_[0],
label='Training', ax=ax)
```
The two implementations of the linear SVM agree on the ceofficients and margin. Good !
### Comparison of the maximum margin classifier to the Logistic regression and Linear Discriminant Analysis (LDA)
Logistic regression is based on the linear regression that is the computation of the square error of any point $x$ to the separation plan and a projection on the probability space using the sigmoid in order to compute the binary cross entropy, see ([HTML](ClassificationContinuous2Features.html) / [Jupyter](ClassificationContinuous2Features.ipynb)).
LDA is assuming a Gaussian mixture prior (our case) and performs bayesian inference.
```
model02 = linear_model.LogisticRegression(solver='lbfgs')
model02.fit(xTrain0, yTrain0)
model02.coef_[0], model02.intercept_[0]
model03 = discriminant_analysis.LinearDiscriminantAnalysis(solver='svd')
model03.fit(xTrain0, yTrain0)
model03.coef_[0], model03.intercept_[0]
```
We observe that the coefficients of the three models are very different in amplitude but globally draw a separator line with slope $-\frac \pi4$ in the 2D plan
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain0, yTrain0, w=model01.coef_[0], intercept=model01.intercept_[0],
separatorLabel='Max Margin SVM', label='Training', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model02.coef_[0], x0=model02.intercept_[0], label='Logistic', color='g')
plotLine(ax, xx, w=model03.coef_[0], x0=model03.intercept_[0], label='LDA', color='c')
ax.legend();
```
# 2. Soft Margin Linear SVM for non separable classes
The example above has little interest as the separation is trivial.
Using the same SVM implementation on a non separable case would not be possible, the solver would fail.
Here comes the soft margin: some $x_i$ are allowed to lie in between the two margin bars.
The __Soft margin linear SVM__ is adding a regularization parameter in maximizing $M$:
$$ \underset{w, b}{\max} M ( 1 - \xi_i) $$
__Subject to $\forall i = 1..n$:__
- $y_i(x_i^T w + b) \ge M$
- $\Vert w \Vert = 1$
- $\xi_i \ge 0$
Equivalently :
$$ \min_{w, b} \frac 12 \Vert w \Vert^2 + C \sum_{i=1}^n \xi_i$$
__Subject to $\forall i = 1..n$:__
- $\xi_i \ge 0$
- $y_i(x_i^T w + b) \ge 1 - \xi_i$
The corresponding Lagrange primal problem is :
$$\mathcal{L}_p(w, b, \alpha, \mu) = \frac 12 \Vert w \Vert^2 - \sum_{i=0}^n \alpha_i (y_i(x_i^T w + b) - (1 - \xi_i) - \sum_{i=0}^n \mu_i \xi_i $$
__Subject to $\forall i\in 1..n$:__
- $\alpha_i \ge 0$
- $\mu_i \ge 0$
- $\xi_i \ge 0$
This shall be minimized on $w$, $b$ and $\xi_i$, using the corresponding partial derivates equal to 0, we get :
$$\begin{align}
\sum_{i=0}^n \alpha_i y_i x_i &= w \\
\sum_{i=0}^n \alpha_i y_i &= 0 \\
\alpha_i &= C - \mu_i
\end{align}$$
From $\mathcal{L}_p$, we get the (Wolfe) dual :
$$\begin{align}
\mathcal{L}_d (\alpha)
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k x_i^T x_k \\
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \langle \alpha_i y_i x_i, \alpha_k y_k x_k \rangle \\
\end{align}$$
__Subject to $\forall i\in 1..n$:__
- $0 \le \alpha_i \le C$
- $\sum_{i=0}^n \alpha_i y_i = 0$
This problem is very similar to the one of the Maximum margin separator, but with one more constraint on $\alpha$.
It is a concave problem that is maximized using a solver.
Extra conditions to get strong duality are required (KKT), $\forall i \in 1..n$:
- $\alpha_i (y_i(x_i^T w + b) - (1 - \xi_i)) = 0$
- $\mu_i \xi_i = 0$
- $y_i(x_i^T w + b) - (1 - \xi_i) \ge 0$
More detailed explainations are in [1 chap. 12.1, 12.2]
## Data model
Let's reuse the same model made of two gaussians, but with larger variance in order to mix the positive and negative points
```
xTrain1, yTrain1 = generateBatchBipolar(N, mu=0.3, sigma=0.3)
plotSvm(xTrain1, yTrain1, label='Training')
```
## Custom implementation
Changes to the Maximum margin classifier are identified by "# <---"
```
class LinearSvmClassifier:
def __init__(self, C):
self.C = C # <---
self.alpha = None
self.w = None
self.supportVectors = None
def fit(self, X, y):
N = len(y)
# Gram matrix of (X.y)
Xy = X * y[:, np.newaxis]
GramXy = np.matmul(Xy, Xy.T)
# Lagrange dual problem
def Ld0(G, alpha):
return alpha.sum() - 0.5 * alpha.dot(alpha.dot(G))
# Partial derivate of Ld on alpha
def Ld0dAlpha(G, alpha):
return np.ones_like(alpha) - alpha.dot(G)
# Constraints on alpha of the shape :
# - d - C*alpha = 0
# - b - A*alpha >= 0
A = np.vstack((-np.eye(N), np.eye(N))) # <---
b = np.hstack((np.zeros(N), self.C * np.ones(N))) # <---
constraints = ({'type': 'eq', 'fun': lambda a: np.dot(a, y), 'jac': lambda a: y},
{'type': 'ineq', 'fun': lambda a: b - np.dot(A, a), 'jac': lambda a: -A})
# Maximize by minimizing the opposite
optRes = optimize.minimize(fun=lambda a: -Ld0(GramXy, a),
x0=np.ones(N),
method='SLSQP',
jac=lambda a: -Ld0dAlpha(GramXy, a),
constraints=constraints)
self.alpha = optRes.x
self.w = np.sum((self.alpha[:, np.newaxis] * Xy), axis=0)
epsilon = 1e-6
self.supportVectors = X[self.alpha > epsilon]
# Support vectors is at a distance <= 1 to the separation plan
# => use min support vector to compute the intercept, assume label is in {-1, 1}
signedDist = np.matmul(self.supportVectors, self.w)
minDistArg = np.argmin(signedDist)
supportLabels = y[self.alpha > epsilon]
self.intercept = supportLabels[minDistArg] - signedDist[minDistArg]
def predict(self, X):
""" Predict y value in {-1, 1} """
assert(self.w is not None)
assert(self.w.shape[0] == X.shape[1])
return 2 * (np.matmul(X, self.w) > 0) - 1
model10 = LinearSvmClassifier(C=1)
model10.fit(xTrain1, yTrain1)
model10.w, model10.intercept
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain1, yTrain1, model10.supportVectors, model10.w, model10.intercept, label='Training', ax=ax)
```
### Linear SVM using Scikit Learn
```
model11 = svm.SVC(kernel='linear', gamma='auto', C = 1)
model11.fit(xTrain1, yTrain1)
model11.coef_[0], model11.intercept_[0]
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain1, yTrain1, model11.support_vectors_, model11.coef_[0], model11.intercept_[0],
label='Training', ax=ax)
```
With the soft margin, the support vectors are all the vectors on the boundary or within the margin slab.
The custom and SKLearn implementations are matching !
### Comparison of the soft margin classifier to the Logistic regression and Linear Discriminant Analysis (LDA)
```
model12 = linear_model.LogisticRegression(solver='lbfgs')
model12.fit(xTrain1, yTrain1)
model12.coef_[0], model12.intercept_[0]
model13 = discriminant_analysis.LinearDiscriminantAnalysis(solver='svd')
model13.fit(xTrain1, yTrain1)
model13.coef_[0], model13.intercept_[0]
```
As shown below, the three models separator hyperplans are very similar, negative slope.
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain1, yTrain1, w=model11.coef_[0], intercept=model11.intercept_[0], label='Training',
separatorLabel='Soft Margin SVM', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model12.coef_[0], x0=model12.intercept_[0], label='Logistic reg', color='orange')
plotLine(ax, xx, w=model13.coef_[0], x0=model13.intercept_[0], label='LDA', color='c')
ax.legend();
```
### Validation with test data
```
xTest1, yTest1 = generateBatchBipolar(2*N, mu=0.3, sigma=0.3)
```
#### Helpers for binary classification performance
```
def plotHeatMap(X, classes, title=None, fmt='.2g', ax=None, xlabel=None, ylabel=None):
""" Fix heatmap plot from Seaborn with pyplot 3.1.0, 3.1.1
https://stackoverflow.com/questions/56942670/matplotlib-seaborn-first-and-last-row-cut-in-half-of-heatmap-plot
"""
ax = sns.heatmap(X, xticklabels=classes, yticklabels=classes, annot=True, \
fmt=fmt, cmap=plt.cm.Blues, ax=ax) #notation: "annot" not "annote"
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)
if title:
ax.set_title(title)
if xlabel:
ax.set_xlabel(xlabel)
if ylabel:
ax.set_ylabel(ylabel)
def plotConfusionMatrix(yTrue, yEst, classes, title=None, fmt='.2g', ax=None):
plotHeatMap(metrics.confusion_matrix(yTrue, yEst), classes, title, fmt, ax, xlabel='Estimations', \
ylabel='True values');
```
### Confusion matrices
```
fig, axes = plt.subplots(1, 3, figsize=(16, 3))
for model, ax, title in zip([model10, model12, model13], axes, ['Custom linear SVM', 'Logistic reg', 'LDA']):
yEst = model.predict(xTest1)
plotConfusionMatrix(yTest1, yEst, colors, title, ax=ax)
```
There is no clear winner, all models are performing equally well.
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTest1, yTest1, w=model10.w, intercept=model10.intercept, separatorLabel='Cust. linear SVM', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model12.coef_[0], x0=model12.intercept_[0], label='Logistic reg', color='orange')
plotLine(ax, xx, w=model13.coef_[0], x0=model13.intercept_[0], label='LDA', color='c')
ax.legend();
```
# 3. The "kernel trick" for non linearly separable classes
Let's use a very famous dataset showing the main limitation of the Logistic regression and LDA : the XOR.
```
def generateBatchXor(n, mu=0.5, sigma=0.5):
""" Four gaussian clouds in a Xor fashion """
X = np.random.normal(mu, sigma, (n, 2))
yB0 = np.random.uniform(0, 1, n) > 0.5
yB1 = np.random.uniform(0, 1, n) > 0.5
# y is in {-1, 1}
y0 = 2. * yB0 - 1
y1 = 2. * yB1 - 1
X[:,0] *= y0
X[:,1] *= y1
X -= X.mean(axis=0)
return X, y0*y1
xTrain3, yTrain3 = generateBatchXor(2*N, sigma=0.25)
plotSvm(xTrain3, yTrain3)
xTest3, yTest3 = generateBatchXor(2*N, sigma=0.25)
```
## Logistic regression and LDA on XOR problem
```
model32 = linear_model.LogisticRegression(solver='lbfgs')
model32.fit(xTrain3, yTrain3)
model32.coef_[0], model32.intercept_[0]
model33 = discriminant_analysis.LinearDiscriminantAnalysis(solver='svd')
model33.fit(xTrain3, yTrain3)
model33.coef_[0], model33.intercept_[0]
```
The linear separators are sometimes mitigating the issue by isolating a single class within a corner. Or they are simply fully failing (separator is of limit).
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain3, yTrain3, w=model32.coef_[0], intercept=model32.intercept_[0], label='Training',
separatorLabel='Logistic reg', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model33.coef_[0], x0=model33.intercept_[0], label='LDA', color='c')
ax.legend();
```
## Introducing the Kernel trick
When using linear separators like the regression, the traditional way to deal with non linear functions is to expand the feature space using powers and products of the initial features. This is also necessary in case of multiclass problems as shown in [1 chap. 4.2].
There are limits to this trick. For example, the XOR problem is not handled proprely.
The SVM has used a new method known as the "Kernel trick".
Let's apply a transformation to $x$ using function $h(x)$.
The Lagrange (Wolfe) dual problem becomes :
$$\begin{align}
\mathcal{L}_d (\alpha)
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k h(x_i)^T h(x_k) \\
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k \langle y_i h(x_i), y_k h(x_k) \rangle \\
\end{align}$$
__Subject to $\forall i\in 1..n$:__
- $0 \le \alpha_i \le C$
- $\sum_{i=0}^n \alpha_i y_i = 0$
Since $ w = \sum_{i=0}^n \alpha_i y_i h(x_i)$, the prediction function is now :
$$ f(x) = sign(w^T h(x) + b) = sign \left(\sum_{i=0}^n \alpha_i y_i \langle h(x_i), h(x) \rangle \right) $$
This prediction needs to be computed for $\alpha_i > 0$, that are support vectors.
Both the fit and prediction are based on the inner product $K(x, x') = \langle h(x), h(x') \rangle$, also known as the kernel function. This function shall be symmetric, semi-definite.
Popular kernel is the Gaussian Radial Basis Function (RBF) : $K(x, x') = exp(- \gamma \Vert x - x' \Vert^2 )$
### Custom implementation of the SVM with G-RBF kernel
Modifications made on the Linear SVM implementation are enclosed in blocks starting with _"# --->"_ and ending with _"# <---"_
```
class KernelSvmClassifier:
def __init__(self, C, kernel):
self.C = C
self.kernel = kernel # <---
self.alpha = None
self.supportVectors = None
def fit(self, X, y):
N = len(y)
# --->
# Gram matrix of h(x) y
hXX = np.apply_along_axis(lambda x1 : np.apply_along_axis(lambda x2: self.kernel(x1, x2), 1, X),
1, X)
yp = y.reshape(-1, 1)
GramHXy = hXX * np.matmul(yp, yp.T)
# <---
# Lagrange dual problem
def Ld0(G, alpha):
return alpha.sum() - 0.5 * alpha.dot(alpha.dot(G))
# Partial derivate of Ld on alpha
def Ld0dAlpha(G, alpha):
return np.ones_like(alpha) - alpha.dot(G)
# Constraints on alpha of the shape :
# - d - C*alpha = 0
# - b - A*alpha >= 0
A = np.vstack((-np.eye(N), np.eye(N))) # <---
b = np.hstack((np.zeros(N), self.C * np.ones(N))) # <---
constraints = ({'type': 'eq', 'fun': lambda a: np.dot(a, y), 'jac': lambda a: y},
{'type': 'ineq', 'fun': lambda a: b - np.dot(A, a), 'jac': lambda a: -A})
# Maximize by minimizing the opposite
optRes = optimize.minimize(fun=lambda a: -Ld0(GramHXy, a),
x0=np.ones(N),
method='SLSQP',
jac=lambda a: -Ld0dAlpha(GramHXy, a),
constraints=constraints)
self.alpha = optRes.x
# --->
epsilon = 1e-8
supportIndices = self.alpha > epsilon
self.supportVectors = X[supportIndices]
self.supportAlphaY = y[supportIndices] * self.alpha[supportIndices]
# <---
def predict(self, X):
""" Predict y values in {-1, 1} """
# --->
def predict1(x):
x1 = np.apply_along_axis(lambda s: self.kernel(s, x), 1, self.supportVectors)
x2 = x1 * self.supportAlphaY
return np.sum(x2)
d = np.apply_along_axis(predict1, 1, X)
return 2 * (d > 0) - 1
# <---
def GRBF(x1, x2):
diff = x1 - x2
return np.exp(-np.dot(diff, diff) * len(x1) / 2)
model30 = KernelSvmClassifier(C=5, kernel=GRBF)
model30.fit(xTrain3, yTrain3)
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain3, yTrain3, support=model30.supportVectors, label='Training', ax=ax)
# Estimate and plot decision boundary
xx = np.linspace(-1, 1, 50)
X0, X1 = np.meshgrid(xx, xx)
xy = np.vstack([X0.ravel(), X1.ravel()]).T
Y30 = model30.predict(xy).reshape(X0.shape)
ax.contour(X0, X1, Y30, colors='k', levels=[-1, 0], alpha=0.3, linestyles=['-.', '-']);
```
## Scikit Learn SVM with Radial basis kernel
```
model31 = svm.SVC(kernel='rbf', C=10, gamma=1/2, shrinking=False)
model31.fit(xTrain3, yTrain3);
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain3, yTrain3, support=model31.support_vectors_, label='Training', ax=ax)
# Estimate and plot decision boundary
Y31 = model31.predict(xy).reshape(X0.shape)
ax.contour(X0, X1, Y31, colors='k', levels=[-1, 0], alpha=0.3, linestyles=['-.', '-']);
```
### SVM with RBF performance on XOR
```
fig, axes = plt.subplots(1, 2, figsize=(11, 3))
for model, ax, title in zip([model30, model31], axes, ["Custom SVM with RBF", "SKLearn SVM with RBF"]):
yEst3 = model.predict(xTest3)
plotConfusionMatrix(yTest3, yEst3, colors, title, ax=ax)
```
Both models' predictions are almost matching on the XOR example.
## Conclusion
We have shown the power of SVM classifiers for non linearly separable problems. From the end of the 1990's, SVM was the leading machine learning algorithm family for many problems. This situation has changed a little since 2010 as deep learning has shown better performance for some classes of problems. However, SVM remains stronger in many contexts. For example, the amount of training data for SVM is lower than the one required for deep learning.
### Where to go from here
- Multiclass classifier using Neural Nets in Keras ([HTML](ClassificationMulti2Features-Keras.html) / [Jupyter](ClassificationMulti2Features-Keras.ipynb))
- Multiclass classifier using Decision Trees ([HTML](ClassificationMulti2Features-Tree.html) / [Jupyter](ClassificationMulti2Features-Tree.ipynb))
- Bivariate continuous function approximation with Linear Regression ([HTML](ClassificationContinuous2Features.html) / [Jupyter](ClassificationContinuous2Features.ipynb))
- Bivariate continuous function approximation with k Nearest Neighbors ([HTML](ClassificationContinuous2Features-KNN.html) / [Jupyter](ClassificationContinuous2Features-KNN.ipynb))
| true |
code
| 0.783243 | null | null | null | null |
|
```
import caffe
import numpy as np
import matplotlib.pyplot as plt
import os
from keras.datasets import mnist
from caffe.proto import caffe_pb2
import google.protobuf.text_format
plt.rcParams['image.cmap'] = 'gray'
%matplotlib inline
```
Loading the model
```
model_def = 'example_caffe_mnist_model.prototxt'
model_weights = 'mnist.caffemodel'
net = caffe.Net(model_def, model_weights, caffe.TEST)
```
A Caffe net offers a layer dict that maps layer names to layer objects. These objects do not provide very much information though, but access to their weights and the type of the layer.
```
net.layer_dict
conv_layer = net.layer_dict['conv2d_1']
conv_layer.type, conv_layer.blobs[0].data.shape
```
### Getting input and output shape.
The net provides a `blobs dict`. These blobs contain `data`, i.e. all the intermediary computation results and `diff`, i.e. the gradients.
```
for name, blob in net.blobs.items():
print('{}: \t {}'.format(name, blob.data.shape))
```
### Getting the weigths.
The net provides access to a `param dict` that contains the weights. The first entry in param corresponds to the weights, the second corresponds to the bias.
```
net.params
for name, param in net.params.items():
print('{}:\t {} \t{}'.format(name, param[0].data.shape, param[1].data.shape))
```
The weights are also accessible through the layer blobs.
```
for layer in net.layers:
try:
print (layer.type + '\t' + str(layer.blobs[0].data.shape), str(layer.blobs[1].data.shape))
except:
continue
weights = net.params['conv2d_1'][0].data
weights.shape
```
For visualizing the weights the axis still have to be moved around.
```
for i in range(32):
plt.imshow(np.moveaxis(weights[i], 0, -1)[..., 0])
plt.show()
```
Layers that have no weights simply keep empty lists as their blob vector.
```
list(net.layer_dict['dropout_1'].blobs)
```
### Getting the activations and the net input.
For getting activations, first data has to be passed through the network. Then the activations can be read out from the blobs. If the activations are defined as in place operations, the net input will not be stored in any blob and can therefore not be recovered. This problem can be circumvented if the network definition is changed so that in place operations are avoided. This can also be done programatically as follows.
```
def remove_inplace(model_def):
protonet = caffe_pb2.NetParameter()
with open(model_def, 'r') as fp:
google.protobuf.text_format.Parse(str(fp.read()), protonet)
replaced_tops = {}
for layer in protonet.layer:
# Check whehter bottoms were renamed.
for i in range(len(layer.bottom)):
if layer.bottom[i] in replaced_tops.keys():
layer.bottom[i] = replaced_tops[layer.bottom[i]]
if layer.bottom == layer.top:
for i in range(len(layer.top)):
# Retain the mapping from the old to the new name.
new_top = layer.top[i] + '_' + layer.name
replaced_tops[layer.top[i]] = new_top
# Redefine layer.top
layer.top[i] = new_top
return protonet
model_def = 'example_caffe_mnist_model_deploy.prototxt'
protonet_no_inplace = remove_inplace(model_def)
protonet_no_inplace
model_def = 'example_caffe_network_no_inplace_deploy.prototxt'
model_weights = 'mnist.caffemodel'
net_no_inplace = caffe.Net(model_def, model_weights, caffe.TEST)
net_no_inplace.layer_dict
net_no_inplace.blobs
# Loading and preprocessing data.
data = mnist.load_data()[1][0]
# Normalize data.
data = data / data.max()
plt.imshow(data[0, :, :])
seven = data[0, :, :]
print(seven.shape)
seven = seven[np.newaxis, ...]
print(seven.shape)
```
Feeding the input and forwarding it.
```
net_no_inplace.blobs['data'].data[...] = seven
output = net_no_inplace.forward()
output['prob'][0].argmax()
activations = net_no_inplace.blobs['relu_1'].data
for i in range(32):
plt.imshow(activations[0, i, :, :])
plt.title('Feature map %d' % i)
plt.show()
net_input = net_no_inplace.blobs['conv2d_1'].data
for i in range(32):
plt.imshow(net_input[0, i, :, :])
plt.title('Feature map %d' % i)
plt.show()
```
### Getting layer properties
From the layer object not more then type information is available. There the original .prototxt has to be parsed to access attributes such as kernel size.
```
model_def = 'example_caffe_mnist_model.prototxt'
f = open(model_def, 'r')
protonet = caffe_pb2.NetParameter()
google.protobuf.text_format.Parse(str(f.read()), protonet)
f.close()
protonet
type(protonet)
```
Parsed messages for the layer can be found in `message.layer` list.
```
for i in range(0, len(protonet.layer)):
if protonet.layer[i].type == 'Convolution':
print('layer %s has kernel_size %d'
% (protonet.layer[i].name,
protonet.layer[i].convolution_param.kernel_size[0]))
lconv_proto = protonet.layer[i]
len(protonet.layer), len(net.layers)
```
| true |
code
| 0.475666 | null | null | null | null |
|
# Transpose convolution: Upsampling
In section 10.5.3, we discussed how transpose convolutions are can be used to upsample a lower resolution input into a higher resolution output. This notebook contains fully functional PyTorch code for the same.
```
import matplotlib.pyplot as plt
import torch
import math
```
First, let's look at how transpose convolution works on a simple input tensor. Then we will look at a real image. For this purpose, we will consider the example described in Figure 10.17. The input is a 2x2 array as follows:
$$
x = \begin{bmatrix}
5 & 6 \\
7 & 8 \\
\end{bmatrix}
$$
and the transpose convolution kernel is also a 2x2 array as follows
$$
w = \begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix}
$$
Transpose convolution with stride 1 results in a 3x3 output as shown below.
# Transpose conv 2D with stride 1
```
x = torch.tensor([
[5., 6.],
[7., 8.]
])
w = torch.tensor([
[1., 2.],
[3., 4.]
])
x = x.unsqueeze(0).unsqueeze(0)
w = w.unsqueeze(0).unsqueeze(0)
transpose_conv2d = torch.nn.ConvTranspose2d(1, 1, kernel_size=2, stride=1, bias=False)
# set weights of the TransposeConv2d object
with torch.no_grad():
transpose_conv2d.weight = torch.nn.Parameter(w)
with torch.no_grad():
y = transpose_conv2d(x)
y
```
# Transpose conv 2D with stride 2
In the above example, we did not get a truly upsampled version of the input because we used a kernel stride of 1. Thei increase in resolution from 2 to 3 comes because of padding. Now, let's see how to truly upsample the image - we will run transpose convolution with stride 2. The step by step demonstration of this is shown in Figure 10.18. As you can see below, we obtained a 4z4 output. This is because we used a kernel a stride 2. Using a larger stride with further increase the output resolution
```
x = torch.tensor([
[5., 6.],
[7., 8.]
])
w = torch.tensor([
[1., 2.],
[3., 4.]
])
x = x.unsqueeze(0).unsqueeze(0)
w = w.unsqueeze(0).unsqueeze(0)
transpose_conv2d = torch.nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
# set weights of the TransposeConv2d object
with torch.no_grad():
transpose_conv2d.weight = torch.nn.Parameter(w)
with torch.no_grad():
y = transpose_conv2d(x)
y
```
Now, let's take a sample image and see how the input compares to the output post transpose convolution with stride 2.
```
import cv2
x = torch.tensor(cv2.imread("./Figures/dog2.jpg", 0), dtype=torch.float32)
w = torch.tensor([
[1., 1.],
[1., 1.]
])
x = x.unsqueeze(0).unsqueeze(0)
w = w.unsqueeze(0).unsqueeze(0)
transpose_conv2d = torch.nn.ConvTranspose2d(1, 1, kernel_size=2,
stride=2, bias=False)
# set weights of the TransposeConv2d object
with torch.no_grad():
transpose_conv2d.weight = torch.nn.Parameter(w)
with torch.no_grad():
y = transpose_conv2d(x)
y
print("Input shape:", x.shape)
print("Output shape:", y.shape)
```
As expected, the output is twice the size of the input. The images below should make this clear
```
def display_image_in_actual_size(im_data, title):
dpi = 80
height, width = im_data.shape
# What size does the figure need to be in inches to fit the image?
figsize = width / float(dpi), height / float(dpi)
# Create a figure of the right size with one axes that takes up the full figure
fig = plt.figure(figsize=figsize)
ax = fig.add_axes([0, 0, 1, 1])
# Hide spines, ticks, etc.
ax.axis('off')
# Display the image.
ax.imshow(im_data, cmap='gray')
ax.set_title(title)
plt.show()
display_image_in_actual_size(x.squeeze().squeeze(), "Input image")
display_image_in_actual_size(y.squeeze().squeeze(), "Output image")
```
| true |
code
| 0.72167 | null | null | null | null |
|
```
import tensorflow as tf
print(tf.__version__)
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
time = np.arange(4 * 365 + 1, dtype="float32")
baseline = 10
series = trend(time, 0.1)
baseline = 10
amplitude = 40
slope = 0.05
noise_level = 5
# Create the series
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
# Update with noise
series += noise(time, noise_level, seed=42)
plt.figure(figsize=(10, 6))
plot_series(time, series)
plt.show()
```
Now that we have the time series, let's split it so we can start forecasting
```
split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
plt.figure(figsize=(10, 6))
plot_series(time_train, x_train)
plt.show()
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plt.show()
```
Naive Forecast
```
naive_forecast = series[split_time - 1:-1]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, naive_forecast)
x = [1,2, 3, 4, 5, 6, 7, 8, 9, 10]
print(x)
split=7
naive=x[split - 1:-1]
print(naive)
x_val = x[split:]
print(x_val)
```
Let's zoom in on the start of the validation period:
```
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid, start=0, end=150)
plot_series(time_valid, naive_forecast, start=1, end=151)
```
You can see that the naive forecast lags 1 step behind the time series.
Now let's compute the mean squared error and the mean absolute error between the forecasts and the predictions in the validation period:
```
print(keras.metrics.mean_squared_error(x_valid, naive_forecast).numpy())
print(keras.metrics.mean_absolute_error(x_valid, naive_forecast).numpy())
```
That's our baseline, now let's try a moving average:
```
def moving_average_forecast(series, window_size):
"""Forecasts the mean of the last few values.
If window_size=1, then this is equivalent to naive forecast"""
forecast = []
for time in range(len(series) - window_size):
forecast.append(series[time:time + window_size].mean())
return np.array(forecast)
moving_avg = moving_average_forecast(series, 30)[split_time - 30:]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, moving_avg)
print(keras.metrics.mean_squared_error(x_valid, moving_avg).numpy())
print(keras.metrics.mean_absolute_error(x_valid, moving_avg).numpy())
```
That's worse than naive forecast! The moving average does not anticipate trend or seasonality, so let's try to remove them by using differencing. Since the seasonality period is 365 days, we will subtract the value at time t – 365 from the value at time t.
```
diff_series = (series[365:] - series[:-365])
diff_time = time[365:]
plt.figure(figsize=(10, 6))
plot_series(diff_time, diff_series)
plt.show()
```
Great, the trend and seasonality seem to be gone, so now we can use the moving average:
```
diff_moving_avg = moving_average_forecast(diff_series, 50)[split_time - 365 - 50:]
plt.figure(figsize=(10, 6))
plot_series(time_valid, diff_series[split_time - 365:])
plot_series(time_valid, diff_moving_avg)
plt.show()
```
Now let's bring back the trend and seasonality by adding the past values from t – 365:
```
diff_moving_avg_plus_past = series[split_time - 365:-365] + diff_moving_avg
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, diff_moving_avg_plus_past)
plt.show()
print(keras.metrics.mean_squared_error(x_valid, diff_moving_avg_plus_past).numpy())
print(keras.metrics.mean_absolute_error(x_valid, diff_moving_avg_plus_past).numpy())
```
Better than naive forecast, good. However the forecasts look a bit too random, because we're just adding past values, which were noisy. Let's use a moving averaging on past values to remove some of the noise:
```
diff_moving_avg_plus_smooth_past = moving_average_forecast(series[split_time - 370:-360], 10) + diff_moving_avg
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, diff_moving_avg_plus_smooth_past)
plt.show()
print(keras.metrics.mean_squared_error(x_valid, diff_moving_avg_plus_smooth_past).numpy())
print(keras.metrics.mean_absolute_error(x_valid, diff_moving_avg_plus_smooth_past).numpy())
```
| true |
code
| 0.712865 | null | null | null | null |
|
# Optimiztion with `mystic`
```
%matplotlib notebook
```
`mystic`: approximates that `scipy.optimize` interface
```
"""
Example:
- Minimize Rosenbrock's Function with Nelder-Mead.
- Plot of parameter convergence to function minimum.
Demonstrates:
- standard models
- minimal solver interface
- parameter trajectories using retall
"""
# Nelder-Mead solver
from mystic.solvers import fmin
# Rosenbrock function
from mystic.models import rosen
# tools
import pylab
if __name__ == '__main__':
# initial guess
x0 = [0.8,1.2,0.7]
# use Nelder-Mead to minimize the Rosenbrock function
solution = fmin(rosen, x0, disp=0, retall=1)
allvecs = solution[-1]
# plot the parameter trajectories
pylab.plot([i[0] for i in allvecs])
pylab.plot([i[1] for i in allvecs])
pylab.plot([i[2] for i in allvecs])
# draw the plot
pylab.title("Rosenbrock parameter convergence")
pylab.xlabel("Nelder-Mead solver iterations")
pylab.ylabel("parameter value")
pylab.legend(["x", "y", "z"])
pylab.show()
```
Diagnostic tools
* Callbacks
```
"""
Example:
- Minimize Rosenbrock's Function with Nelder-Mead.
- Dynamic plot of parameter convergence to function minimum.
Demonstrates:
- standard models
- minimal solver interface
- parameter trajectories using callback
- solver interactivity
"""
# Nelder-Mead solver
from mystic.solvers import fmin
# Rosenbrock function
from mystic.models import rosen
# tools
from mystic.tools import getch
import pylab
pylab.ion()
# draw the plot
def plot_frame():
pylab.title("Rosenbrock parameter convergence")
pylab.xlabel("Nelder-Mead solver iterations")
pylab.ylabel("parameter value")
pylab.draw()
return
iter = 0
step, xval, yval, zval = [], [], [], []
# plot the parameter trajectories
def plot_params(params):
global iter, step, xval, yval, zval
step.append(iter)
xval.append(params[0])
yval.append(params[1])
zval.append(params[2])
pylab.plot(step,xval,'b-')
pylab.plot(step,yval,'g-')
pylab.plot(step,zval,'r-')
pylab.legend(["x", "y", "z"])
pylab.draw()
iter += 1
return
if __name__ == '__main__':
# initial guess
x0 = [0.8,1.2,0.7]
# suggest that the user interacts with the solver
print("NOTE: while solver is running, press 'Ctrl-C' in console window")
getch()
plot_frame()
# use Nelder-Mead to minimize the Rosenbrock function
solution = fmin(rosen, x0, disp=1, callback=plot_params, handler=True)
print(solution)
# don't exit until user is ready
getch()
```
**NOTE** IPython does not handle shell prompt interactive programs well, so the above should be run from a command prompt. An IPython-safe version is below.
```
"""
Example:
- Minimize Rosenbrock's Function with Powell's method.
- Dynamic print of parameter convergence to function minimum.
Demonstrates:
- standard models
- minimal solver interface
- parameter trajectories using callback
"""
# Powell's Directonal solver
from mystic.solvers import fmin_powell
# Rosenbrock function
from mystic.models import rosen
iter = 0
# plot the parameter trajectories
def print_params(params):
global iter
from numpy import asarray
print("Generation %d has best fit parameters: %s" % (iter,asarray(params)))
iter += 1
return
if __name__ == '__main__':
# initial guess
x0 = [0.8,1.2,0.7]
print_params(x0)
# use Powell's method to minimize the Rosenbrock function
solution = fmin_powell(rosen, x0, disp=1, callback=print_params, handler=False)
print(solution)
```
* Monitors
```
"""
Example:
- Minimize Rosenbrock's Function with Powell's method.
Demonstrates:
- standard models
- minimal solver interface
- customized monitors
"""
# Powell's Directonal solver
from mystic.solvers import fmin_powell
# Rosenbrock function
from mystic.models import rosen
# tools
from mystic.monitors import VerboseLoggingMonitor
if __name__ == '__main__':
print("Powell's Method")
print("===============")
# initial guess
x0 = [1.5, 1.5, 0.7]
# configure monitor
stepmon = VerboseLoggingMonitor(1,1)
# use Powell's method to minimize the Rosenbrock function
solution = fmin_powell(rosen, x0, itermon=stepmon)
print(solution)
import mystic
mystic.log_reader('log.txt')
```
* Solution trajectory and model plotting
```
import mystic
mystic.model_plotter(mystic.models.rosen, 'log.txt', kwds='-d -x 1 -b "-2:2:.1, -2:2:.1, 1"')
```
Solver "tuning" and extension
* Solver class interface
```
"""
Example:
- Solve 8th-order Chebyshev polynomial coefficients with DE.
- Callable plot of fitting to Chebyshev polynomial.
- Monitor Chi-Squared for Chebyshev polynomial.
Demonstrates:
- standard models
- expanded solver interface
- built-in random initial guess
- customized monitors and termination conditions
- customized DE mutation strategies
- use of monitor to retrieve results information
"""
# Differential Evolution solver
from mystic.solvers import DifferentialEvolutionSolver2
# Chebyshev polynomial and cost function
from mystic.models.poly import chebyshev8, chebyshev8cost
from mystic.models.poly import chebyshev8coeffs
# tools
from mystic.termination import VTR
from mystic.strategy import Best1Exp
from mystic.monitors import VerboseMonitor
from mystic.tools import getch, random_seed
from mystic.math import poly1d
import pylab
pylab.ion()
# draw the plot
def plot_exact():
pylab.title("fitting 8th-order Chebyshev polynomial coefficients")
pylab.xlabel("x")
pylab.ylabel("f(x)")
import numpy
x = numpy.arange(-1.2, 1.2001, 0.01)
exact = chebyshev8(x)
pylab.plot(x,exact,'b-')
pylab.legend(["Exact"])
pylab.axis([-1.4,1.4,-2,8],'k-')
pylab.draw()
return
# plot the polynomial
def plot_solution(params,style='y-'):
import numpy
x = numpy.arange(-1.2, 1.2001, 0.01)
f = poly1d(params)
y = f(x)
pylab.plot(x,y,style)
pylab.legend(["Exact","Fitted"])
pylab.axis([-1.4,1.4,-2,8],'k-')
pylab.draw()
return
if __name__ == '__main__':
print("Differential Evolution")
print("======================")
# set range for random initial guess
ndim = 9
x0 = [(-100,100)]*ndim
random_seed(123)
# draw frame and exact coefficients
plot_exact()
# configure monitor
stepmon = VerboseMonitor(50)
# use DE to solve 8th-order Chebyshev coefficients
npop = 10*ndim
solver = DifferentialEvolutionSolver2(ndim,npop)
solver.SetRandomInitialPoints(min=[-100]*ndim, max=[100]*ndim)
solver.SetGenerationMonitor(stepmon)
solver.enable_signal_handler()
solver.Solve(chebyshev8cost, termination=VTR(0.01), strategy=Best1Exp, \
CrossProbability=1.0, ScalingFactor=0.9, \
sigint_callback=plot_solution)
solution = solver.Solution()
# use monitor to retrieve results information
iterations = len(stepmon)
cost = stepmon.y[-1]
print("Generation %d has best Chi-Squared: %f" % (iterations, cost))
# use pretty print for polynomials
print(poly1d(solution))
# compare solution with actual 8th-order Chebyshev coefficients
print("\nActual Coefficients:\n %s\n" % poly1d(chebyshev8coeffs))
# plot solution versus exact coefficients
plot_solution(solution)
from mystic.solvers import DifferentialEvolutionSolver
print("\n".join([i for i in dir(DifferentialEvolutionSolver) if not i.startswith('_')]))
```
* Algorithm configurability
* Termination conditions
```
from mystic.termination import VTR, ChangeOverGeneration, And, Or
stop = Or(And(VTR(), ChangeOverGeneration()), VTR(1e-8))
from mystic.models import rosen
from mystic.monitors import VerboseMonitor
from mystic.solvers import DifferentialEvolutionSolver
solver = DifferentialEvolutionSolver(3,40)
solver.SetRandomInitialPoints([-10,-10,-10],[10,10,10])
solver.SetGenerationMonitor(VerboseMonitor(10))
solver.SetTermination(stop)
solver.SetObjective(rosen)
solver.SetStrictRanges([-10,-10,-10],[10,10,10])
solver.SetEvaluationLimits(generations=600)
solver.Solve()
print(solver.bestSolution)
```
* Solver population
```
from mystic.solvers import DifferentialEvolutionSolver
from mystic.math import Distribution
import numpy as np
import pylab
# build a mystic distribution instance
dist = Distribution(np.random.normal, 5, 1)
# use the distribution instance as the initial population
solver = DifferentialEvolutionSolver(3,20)
solver.SetSampledInitialPoints(dist)
# visualize the initial population
pylab.hist(np.array(solver.population).ravel())
pylab.show()
```
**EXERCISE:** Use `mystic` to find the minimum for the `peaks` test function, with the bound specified by the `mystic.models.peaks` documentation.
**EXERCISE:** Use `mystic` to do a fit to the noisy data in the `scipy.optimize.curve_fit` example (the least squares fit).
Constraints "operators" (i.e. kernel transformations)
PENALTY: $\psi(x) = f(x) + k*p(x)$
CONSTRAINT: $\psi(x) = f(c(x)) = f(x')$
```
from mystic.constraints import *
from mystic.penalty import quadratic_equality
from mystic.coupler import inner
from mystic.math import almostEqual
from mystic.tools import random_seed
random_seed(213)
def test_penalize():
from mystic.math.measures import mean, spread
def mean_constraint(x, target):
return mean(x) - target
def range_constraint(x, target):
return spread(x) - target
@quadratic_equality(condition=range_constraint, kwds={'target':5.0})
@quadratic_equality(condition=mean_constraint, kwds={'target':5.0})
def penalty(x):
return 0.0
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin
from numpy import array
x = array([1,2,3,4,5])
y = fmin(cost, x, penalty=penalty, disp=False)
assert round(mean(y)) == 5.0
assert round(spread(y)) == 5.0
assert round(cost(y)) == 4*(5.0)
def test_solve():
from mystic.math.measures import mean
def mean_constraint(x, target):
return mean(x) - target
def parameter_constraint(x):
return x[-1] - x[0]
@quadratic_equality(condition=mean_constraint, kwds={'target':5.0})
@quadratic_equality(condition=parameter_constraint)
def penalty(x):
return 0.0
x = solve(penalty, guess=[2,3,1])
assert round(mean_constraint(x, 5.0)) == 0.0
assert round(parameter_constraint(x)) == 0.0
assert issolution(penalty, x)
def test_solve_constraint():
from mystic.math.measures import mean
@with_mean(1.0)
def constraint(x):
x[-1] = x[0]
return x
x = solve(constraint, guess=[2,3,1])
assert almostEqual(mean(x), 1.0, tol=1e-15)
assert x[-1] == x[0]
assert issolution(constraint, x)
def test_as_constraint():
from mystic.math.measures import mean, spread
def mean_constraint(x, target):
return mean(x) - target
def range_constraint(x, target):
return spread(x) - target
@quadratic_equality(condition=range_constraint, kwds={'target':5.0})
@quadratic_equality(condition=mean_constraint, kwds={'target':5.0})
def penalty(x):
return 0.0
ndim = 3
constraints = as_constraint(penalty, solver='fmin')
#XXX: this is expensive to evaluate, as there are nested optimizations
from numpy import arange
x = arange(ndim)
_x = constraints(x)
assert round(mean(_x)) == 5.0
assert round(spread(_x)) == 5.0
assert round(penalty(_x)) == 0.0
def cost(x):
return abs(sum(x) - 5.0)
npop = ndim*3
from mystic.solvers import diffev
y = diffev(cost, x, npop, constraints=constraints, disp=False, gtol=10)
assert round(mean(y)) == 5.0
assert round(spread(y)) == 5.0
assert round(cost(y)) == 5.0*(ndim-1)
def test_as_penalty():
from mystic.math.measures import mean, spread
@with_spread(5.0)
@with_mean(5.0)
def constraint(x):
return x
penalty = as_penalty(constraint)
from numpy import array
x = array([1,2,3,4,5])
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin
y = fmin(cost, x, penalty=penalty, disp=False)
assert round(mean(y)) == 5.0
assert round(spread(y)) == 5.0
assert round(cost(y)) == 4*(5.0)
def test_with_penalty():
from mystic.math.measures import mean, spread
@with_penalty(quadratic_equality, kwds={'target':5.0})
def penalty(x, target):
return mean(x) - target
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin
from numpy import array
x = array([1,2,3,4,5])
y = fmin(cost, x, penalty=penalty, disp=False)
assert round(mean(y)) == 5.0
assert round(cost(y)) == 4*(5.0)
def test_with_mean():
from mystic.math.measures import mean, impose_mean
@with_mean(5.0)
def mean_of_squared(x):
return [i**2 for i in x]
from numpy import array
x = array([1,2,3,4,5])
y = impose_mean(5, [i**2 for i in x])
assert mean(y) == 5.0
assert mean_of_squared(x) == y
def test_with_mean_spread():
from mystic.math.measures import mean, spread, impose_mean, impose_spread
@with_spread(50.0)
@with_mean(5.0)
def constrained_squared(x):
return [i**2 for i in x]
from numpy import array
x = array([1,2,3,4,5])
y = impose_spread(50.0, impose_mean(5.0,[i**2 for i in x]))
assert almostEqual(mean(y), 5.0, tol=1e-15)
assert almostEqual(spread(y), 50.0, tol=1e-15)
assert constrained_squared(x) == y
def test_constrained_solve():
from mystic.math.measures import mean, spread
@with_spread(5.0)
@with_mean(5.0)
def constraints(x):
return x
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin_powell
from numpy import array
x = array([1,2,3,4,5])
y = fmin_powell(cost, x, constraints=constraints, disp=False)
assert almostEqual(mean(y), 5.0, tol=1e-15)
assert almostEqual(spread(y), 5.0, tol=1e-15)
assert almostEqual(cost(y), 4*(5.0), tol=1e-6)
if __name__ == '__main__':
test_penalize()
test_solve()
test_solve_constraint()
test_as_constraint()
test_as_penalty()
test_with_penalty()
test_with_mean()
test_with_mean_spread()
test_constrained_solve()
from mystic.coupler import and_, or_, not_
from mystic.constraints import and_ as _and, or_ as _or, not_ as _not
if __name__ == '__main__':
import numpy as np
from mystic.penalty import linear_equality, quadratic_equality
from mystic.constraints import as_constraint
x = x1,x2,x3 = (5., 5., 1.)
f = f1,f2,f3 = (np.sum, np.prod, np.average)
k = 100
solver = 'fmin_powell' #'diffev'
ptype = quadratic_equality
# case #1: couple penalties into a single constraint
p1 = lambda x: abs(x1 - f1(x))
p2 = lambda x: abs(x2 - f2(x))
p3 = lambda x: abs(x3 - f3(x))
p = (p1,p2,p3)
p = [ptype(pi)(lambda x:0.) for pi in p]
penalty = and_(*p, k=k)
constraint = as_constraint(penalty, solver=solver)
x = [1,2,3,4,5]
x_ = constraint(x)
assert round(f1(x_)) == round(x1)
assert round(f2(x_)) == round(x2)
assert round(f3(x_)) == round(x3)
# case #2: couple constraints into a single constraint
from mystic.math.measures import impose_product, impose_sum, impose_mean
from mystic.constraints import as_penalty
from mystic import random_seed
random_seed(123)
t = t1,t2,t3 = (impose_sum, impose_product, impose_mean)
c1 = lambda x: t1(x1, x)
c2 = lambda x: t2(x2, x)
c3 = lambda x: t3(x3, x)
c = (c1,c2,c3)
k=1
solver = 'buckshot' #'diffev'
ptype = linear_equality #quadratic_equality
p = [as_penalty(ci, ptype) for ci in c]
penalty = and_(*p, k=k)
constraint = as_constraint(penalty, solver=solver)
x = [1,2,3,4,5]
x_ = constraint(x)
assert round(f1(x_)) == round(x1)
assert round(f2(x_)) == round(x2)
assert round(f3(x_)) == round(x3)
# etc: more coupling of constraints
from mystic.constraints import with_mean, discrete
@with_mean(5.0)
def meanie(x):
return x
@discrete(list(range(11)))
def integers(x):
return x
c = _and(integers, meanie)
x = c([1,2,3])
assert x == integers(x) == meanie(x)
x = c([9,2,3])
assert x == integers(x) == meanie(x)
x = c([0,-2,3])
assert x == integers(x) == meanie(x)
x = c([9,-200,344])
assert x == integers(x) == meanie(x)
c = _or(meanie, integers)
x = c([1.1234, 4.23412, -9])
assert x == meanie(x) and x != integers(x)
x = c([7.0, 10.0, 0.0])
assert x == integers(x) and x != meanie(x)
x = c([6.0, 9.0, 0.0])
assert x == integers(x) == meanie(x)
x = c([3,4,5])
assert x == integers(x) and x != meanie(x)
x = c([3,4,5.5])
assert x == meanie(x) and x != integers(x)
c = _not(integers)
x = c([1,2,3])
assert x != integers(x) and x != [1,2,3] and x == c(x)
x = c([1.1,2,3])
assert x != integers(x) and x == [1.1,2,3] and x == c(x)
c = _not(meanie)
x = c([1,2,3])
assert x != meanie(x) and x == [1,2,3] and x == c(x)
x = c([4,5,6])
assert x != meanie(x) and x != [4,5,6] and x == c(x)
c = _not(_and(meanie, integers))
x = c([4,5,6])
assert x != meanie(x) and x != integers(x) and x != [4,5,6] and x == c(x)
# etc: more coupling of penalties
from mystic.penalty import quadratic_inequality
p1 = lambda x: sum(x) - 5
p2 = lambda x: min(i**2 for i in x)
p = p1,p2
p = [quadratic_inequality(pi)(lambda x:0.) for pi in p]
p1,p2 = p
penalty = and_(*p)
x = [[1,2],[-2,-1],[5,-5]]
for xi in x:
assert p1(xi) + p2(xi) == penalty(xi)
penalty = or_(*p)
for xi in x:
assert min(p1(xi),p2(xi)) == penalty(xi)
penalty = not_(p1)
for xi in x:
assert bool(p1(xi)) != bool(penalty(xi))
penalty = not_(p2)
for xi in x:
assert bool(p2(xi)) != bool(penalty(xi))
```
In addition to being able to generically apply information as a penalty, `mystic` provides the ability to construct constraints "operators" -- essentially applying kernel transformations that reduce optimizer search space to the space of solutions that satisfy the constraints. This can greatly accelerate convergence to a solution, as the space that the optimizer can explore is restricted.
```
"""
Example:
- Minimize Rosenbrock's Function with Powell's method.
Demonstrates:
- standard models
- minimal solver interface
- parameter constraints solver and constraints factory decorator
- statistical parameter constraints
- customized monitors
"""
# Powell's Directonal solver
from mystic.solvers import fmin_powell
# Rosenbrock function
from mystic.models import rosen
# tools
from mystic.monitors import VerboseMonitor
from mystic.math.measures import mean, impose_mean
if __name__ == '__main__':
print("Powell's Method")
print("===============")
# initial guess
x0 = [0.8,1.2,0.7]
# use the mean constraints factory decorator
from mystic.constraints import with_mean
# define constraints function
@with_mean(1.0)
def constraints(x):
# constrain the last x_i to be the same value as the first x_i
x[-1] = x[0]
return x
# configure monitor
stepmon = VerboseMonitor(1)
# use Powell's method to minimize the Rosenbrock function
solution = fmin_powell(rosen, x0, constraints=constraints, itermon=stepmon)
print(solution)
```
* Range (i.e. 'box') constraints
Use `solver.SetStrictRange`, or the `bounds` keyword on the solver function interface.
* Symbolic constraints interface
```
%%file spring.py
"a Tension-Compression String"
def objective(x):
x0,x1,x2 = x
return x0**2 * x1 * (x2 + 2)
bounds = [(0,100)]*3
# with penalty='penalty' applied, solution is:
xs = [0.05168906, 0.35671773, 11.28896619]
ys = 0.01266523
from mystic.symbolic import generate_constraint, generate_solvers, solve
from mystic.symbolic import generate_penalty, generate_conditions
equations = """
1.0 - (x1**3 * x2)/(71785*x0**4) <= 0.0
(4*x1**2 - x0*x1)/(12566*x0**3 * (x1 - x0)) + 1./(5108*x0**2) - 1.0 <= 0.0
1.0 - 140.45*x0/(x2 * x1**2) <= 0.0
(x0 + x1)/1.5 - 1.0 <= 0.0
"""
pf = generate_penalty(generate_conditions(equations), k=1e12)
if __name__ == '__main__':
from mystic.solvers import diffev2
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=pf, npop=40,
gtol=500, disp=True, full_output=True)
print(result[0])
equations = """
1.0 - (x1**3 * x2)/(71785*x0**4) <= 0.0
(4*x1**2 - x0*x1)/(12566*x0**3 * (x1 - x0)) + 1./(5108*x0**2) - 1.0 <= 0.0
1.0 - 140.45*x0/(x2 * x1**2) <= 0.0
(x0 + x1)/1.5 - 1.0 <= 0.0
"""
from mystic.symbolic import generate_constraint, generate_solvers, solve
from mystic.symbolic import generate_penalty, generate_conditions
ineql, eql = generate_conditions(equations)
print("CONVERTED SYMBOLIC TO SINGLE CONSTRAINTS FUNCTIONS")
print(ineql)
print(eql)
print("\nTHE INDIVIDUAL INEQUALITIES")
for f in ineql:
print(f.__doc__)
print("\nGENERATED THE PENALTY FUNCTION FOR ALL CONSTRAINTS")
pf = generate_penalty((ineql, eql))
print(pf.__doc__)
x = [-0.1, 0.5, 11.0]
print("\nPENALTY FOR {}: {}".format(x, pf(x)))
```
* Penatly functions
```
equations = """
1.0 - (x1**3 * x2)/(71785*x0**4) <= 0.0
(4*x1**2 - x0*x1)/(12566*x0**3 * (x1 - x0)) + 1./(5108*x0**2) - 1.0 <= 0.0
1.0 - 140.45*x0/(x2 * x1**2) <= 0.0
(x0 + x1)/1.5 - 1.0 <= 0.0
"""
"a Tension-Compression String"
from spring import objective, bounds, xs, ys
from mystic.penalty import quadratic_inequality
def penalty1(x): # <= 0.0
return 1.0 - (x[1]**3 * x[2])/(71785*x[0]**4)
def penalty2(x): # <= 0.0
return (4*x[1]**2 - x[0]*x[1])/(12566*x[0]**3 * (x[1] - x[0])) + 1./(5108*x[0]**2) - 1.0
def penalty3(x): # <= 0.0
return 1.0 - 140.45*x[0]/(x[2] * x[1]**2)
def penalty4(x): # <= 0.0
return (x[0] + x[1])/1.5 - 1.0
@quadratic_inequality(penalty1, k=1e12)
@quadratic_inequality(penalty2, k=1e12)
@quadratic_inequality(penalty3, k=1e12)
@quadratic_inequality(penalty4, k=1e12)
def penalty(x):
return 0.0
if __name__ == '__main__':
from mystic.solvers import diffev2
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=penalty, npop=40,
gtol=500, disp=True, full_output=True)
print(result[0])
```
* "Operators" that directly constrain search space
```
"""
Crypto problem in Google CP Solver.
Prolog benchmark problem
'''
Name : crypto.pl
Original Source: P. Van Hentenryck's book
Adapted by : Daniel Diaz - INRIA France
Date : September 1992
'''
"""
def objective(x):
return 0.0
nletters = 26
bounds = [(1,nletters)]*nletters
# with penalty='penalty' applied, solution is:
# A B C D E F G H I J K L M N O P Q
xs = [ 5, 13, 9, 16, 20, 4, 24, 21, 25, 17, 23, 2, 8, 12, 10, 19, 7, \
# R S T U V W X Y Z
11, 15, 3, 1, 26, 6, 22, 14, 18]
ys = 0.0
# constraints
equations = """
B + A + L + L + E + T - 45 == 0
C + E + L + L + O - 43 == 0
C + O + N + C + E + R + T - 74 == 0
F + L + U + T + E - 30 == 0
F + U + G + U + E - 50 == 0
G + L + E + E - 66 == 0
J + A + Z + Z - 58 == 0
L + Y + R + E - 47 == 0
O + B + O + E - 53 == 0
O + P + E + R + A - 65 == 0
P + O + L + K + A - 59 == 0
Q + U + A + R + T + E + T - 50 == 0
S + A + X + O + P + H + O + N + E - 134 == 0
S + C + A + L + E - 51 == 0
S + O + L + O - 37 == 0
S + O + N + G - 61 == 0
S + O + P + R + A + N + O - 82 == 0
T + H + E + M + E - 72 == 0
V + I + O + L + I + N - 100 == 0
W + A + L + T + Z - 34 == 0
"""
var = list('ABCDEFGHIJKLMNOPQRSTUVWXYZ')
# Let's say we know the vowels.
bounds[0] = (5,5) # A
bounds[4] = (20,20) # E
bounds[8] = (25,25) # I
bounds[14] = (10,10) # O
bounds[20] = (1,1) # U
from mystic.constraints import unique, near_integers, has_unique
from mystic.symbolic import generate_penalty, generate_conditions
pf = generate_penalty(generate_conditions(equations,var),k=1)
from mystic.penalty import quadratic_equality
@quadratic_equality(near_integers)
@quadratic_equality(has_unique)
def penalty(x):
return pf(x)
from numpy import round, hstack, clip
def constraint(x):
x = round(x).astype(int) # force round and convert type to int
x = clip(x, 1,nletters) #XXX: hack to impose bounds
x = unique(x, range(1,nletters+1))
return x
if __name__ == '__main__':
from mystic.solvers import diffev2
from mystic.monitors import Monitor, VerboseMonitor
mon = VerboseMonitor(50)
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=pf,
constraints=constraint, npop=52, ftol=1e-8, gtol=1000,
disp=True, full_output=True, cross=0.1, scale=0.9, itermon=mon)
print(result[0])
```
Special cases
* Integer and mixed integer programming
```
"""
Eq 10 in Google CP Solver.
Standard benchmark problem.
"""
def objective(x):
return 0.0
bounds = [(0,10)]*7
# with penalty='penalty' applied, solution is:
xs = [6., 0., 8., 4., 9., 3., 9.]
ys = 0.0
# constraints
equations = """
98527*x0 + 34588*x1 + 5872*x2 + 59422*x4 + 65159*x6 - 1547604 - 30704*x3 - 29649*x5 == 0.0
98957*x1 + 83634*x2 + 69966*x3 + 62038*x4 + 37164*x5 + 85413*x6 - 1823553 - 93989*x0 == 0.0
900032 + 10949*x0 + 77761*x1 + 67052*x4 - 80197*x2 - 61944*x3 - 92964*x5 - 44550*x6 == 0.0
73947*x0 + 84391*x2 + 81310*x4 - 1164380 - 96253*x1 - 44247*x3 - 70582*x5 - 33054*x6 == 0.0
13057*x2 + 42253*x3 + 77527*x4 + 96552*x6 - 1185471 - 60152*x0 - 21103*x1 - 97932*x5 == 0.0
1394152 + 66920*x0 + 55679*x3 - 64234*x1 - 65337*x2 - 45581*x4 - 67707*x5 - 98038*x6 == 0.0
68550*x0 + 27886*x1 + 31716*x2 + 73597*x3 + 38835*x6 - 279091 - 88963*x4 - 76391*x5 == 0.0
76132*x1 + 71860*x2 + 22770*x3 + 68211*x4 + 78587*x5 - 480923 - 48224*x0 - 82817*x6 == 0.0
519878 + 94198*x1 + 87234*x2 + 37498*x3 - 71583*x0 - 25728*x4 - 25495*x5 - 70023*x6 == 0.0
361921 + 78693*x0 + 38592*x4 + 38478*x5 - 94129*x1 - 43188*x2 - 82528*x3 - 69025*x6 == 0.0
"""
from mystic.symbolic import generate_constraint, generate_solvers, solve
cf = generate_constraint(generate_solvers(solve(equations)))
if __name__ == '__main__':
from mystic.solvers import diffev2
result = diffev2(objective, x0=bounds, bounds=bounds, constraints=cf,
npop=4, gtol=1, disp=True, full_output=True)
print(result[0])
```
**EXERCISE:** Solve the `chebyshev8.cost` example exactly, by applying the knowledge that the last term in the chebyshev polynomial will always be be one. Use `numpy.round` or `mystic.constraints.integers` or to constrain solutions to the set of integers. Does using `mystic.suppressed` to supress small numbers accelerate the solution?
**EXERCISE:** Replace the symbolic constraints in the following "Pressure Vessel Design" code with explicit penalty functions (i.e. use a compound penalty built with `mystic.penalty.quadratic_inequality`).
```
"Pressure Vessel Design"
def objective(x):
x0,x1,x2,x3 = x
return 0.6224*x0*x2*x3 + 1.7781*x1*x2**2 + 3.1661*x0**2*x3 + 19.84*x0**2*x2
bounds = [(0,1e6)]*4
# with penalty='penalty' applied, solution is:
xs = [0.72759093, 0.35964857, 37.69901188, 240.0]
ys = 5804.3762083
from mystic.symbolic import generate_constraint, generate_solvers, solve
from mystic.symbolic import generate_penalty, generate_conditions
equations = """
-x0 + 0.0193*x2 <= 0.0
-x1 + 0.00954*x2 <= 0.0
-pi*x2**2*x3 - (4/3.)*pi*x2**3 + 1296000.0 <= 0.0
x3 - 240.0 <= 0.0
"""
pf = generate_penalty(generate_conditions(equations), k=1e12)
if __name__ == '__main__':
from mystic.solvers import diffev2
from mystic.math import almostEqual
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=pf, npop=40, gtol=500,
disp=True, full_output=True)
print(result[0])
```
* Linear and quadratic constraints
```
"""
Minimize: f = 2*x[0] + 1*x[1]
Subject to: -1*x[0] + 1*x[1] <= 1
1*x[0] + 1*x[1] >= 2
1*x[1] >= 0
1*x[0] - 2*x[1] <= 4
where: -inf <= x[0] <= inf
"""
def objective(x):
x0,x1 = x
return 2*x0 + x1
equations = """
-x0 + x1 - 1.0 <= 0.0
-x0 - x1 + 2.0 <= 0.0
x0 - 2*x1 - 4.0 <= 0.0
"""
bounds = [(None, None),(0.0, None)]
# with penalty='penalty' applied, solution is:
xs = [0.5, 1.5]
ys = 2.5
from mystic.symbolic import generate_conditions, generate_penalty
pf = generate_penalty(generate_conditions(equations), k=1e3)
from mystic.symbolic import generate_constraint, generate_solvers, simplify
cf = generate_constraint(generate_solvers(simplify(equations)))
if __name__ == '__main__':
from mystic.solvers import fmin_powell
from mystic.math import almostEqual
result = fmin_powell(objective, x0=[0.0,0.0], bounds=bounds, constraint=cf,
penalty=pf, disp=True, full_output=True, gtol=3)
print(result[0])
```
**EXERCISE:** Solve the `cvxopt` "qp" example with `mystic`. Use symbolic constaints, penalty functions, or constraints operators. If you get it quickly, do all three methods.
Let's look at how `mystic` gives improved [solver workflow](workflow.ipynb)
| true |
code
| 0.709132 | null | null | null | null |
|
# House Price Prediction With TensorFlow
[![open_in_colab][colab_badge]][colab_notebook_link]
[![open_in_binder][binder_badge]][binder_notebook_link]
[colab_badge]: https://colab.research.google.com/assets/colab-badge.svg
[colab_notebook_link]: https://colab.research.google.com/github/UnfoldedInc/examples/blob/master/notebooks/09%20-%20Tensorflow_prediction.ipynb
[binder_badge]: https://mybinder.org/badge_logo.svg
[binder_notebook_link]: https://mybinder.org/v2/gh/UnfoldedInc/examples/master?urlpath=lab/tree/notebooks/09%20-%20Tensorflow_prediction.ipynb
This example demonstrates how the Unfolded Map SDK allows for more engaging exploratory data visualization, helping to simplify the process of building a machine learning model for predicting median house prices in California.
## Dependencies
This notebook uses the following dependencies:
- pandas
- numpy
- scikit-learn
- scipy
- seaborn
- matplotlib
- tensorflow
If running this notebook in Binder, these dependencies should already be installed. If running in Colab, the next cell will install these dependencies. In another environment, you'll need to make sure these dependencies are available by running the following `pip` command in a shell.
```bash
pip install pandas numpy scikit-learn scipy seaborn matplotlib tensorflow
```
This notebook was originally tested with the following package versions, but likely works with a broad range of versions:
- pandas==1.3.2
- numpy==1.19.5
- scikit-learn==0.24.2
- scipy==1.7.1
- seaborn==0.11.2
- matplotlib==3.4.3
- tensorflow==2.6.0
```
# If in Colab, install this notebook's required dependencies
import sys
if "google.colab" in sys.modules:
!pip install 'unfolded.map_sdk>=0.6.3' pandas numpy scikit-learn scipy seaborn matplotlib tensorflow
```
## Imports
If you're running this notebook on Binder, you may see a notification like the following when running the next cell.
```
Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory
Ignore above cudart dlerror if you do not have a GPU set up on your machine.
```
This is expected behavior because the machines on which Binder is running are not equipped with GPUs. The notebook will still function fine, it will just run slightly slower than on a machine with a GPU available.
```
from uuid import uuid4
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from unfolded.map_sdk import UnfoldedMap
```
## Data Loading
For this example we'll use data from Kaggle's [California Housing Prices](https://www.kaggle.com/camnugent/california-housing-prices) dataset under the CC0 license. This dataset contains information about the housing in each census area in California, as of the 1990 census.
```
dataset_url = "https://raw.githubusercontent.com/UnfoldedInc/examples/master/notebooks/data/housing.csv"
housing = pd.read_csv(dataset_url)
housing.head()
```
## Feature Engineering
First, let's take a look at the input data and try to visualize different aspects of them in a map.
### Population Clustering
In the next cell we'll create a map that clusters rows of the dataset according to population. Note that since the clustering happens within Unfolded Studio, the clusters are re-computed as you zoom in, allowing you to explore your data at various resolutions.
```
population_in_CA = UnfoldedMap()
population_in_CA
# Create a persistent dataset ID that we can reference in both add_dataset and add_layer
dataset_id = uuid4()
population_in_CA.add_dataset(
{"uuid": dataset_id, "label": "Population_in_CA", "data": housing},
auto_create_layers=False,
)
population_in_CA.add_layer(
{
"id": "population_CA",
"type": "cluster",
"config": {
"label": "population in CA",
"data_id": dataset_id,
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "population", "type": "real"},
},
}
)
population_in_CA.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 5}
)
```
### Distances from housing areas to largest cities
Next, we want to explore where the housing areas in our dataset are located in comparison to the largest cities in California. For example purposes, we'll take the five largest cities in California and compare our input data against these locations.
```
# Longitude-latitude pairs for large cities
cities = {
"Los Angeles": (-118.244, 34.052),
"San Diego": (-117.165, 32.716),
"San Jose": (-121.895, 37.339),
"San Francisco": (-122.419, 37.775),
"Fresno": (-119.772, 36.748),
}
```
Next we need to find the closest city for each row in our data sample. First we'll define a couple functions to help compute the distance between cities and the city closest to a specific point. Then we'll apply these functions on our data.
```
def distance(lng1, lat1, lng2, lat2):
"""Vectorized Haversine formula
Computes distances between two sets of points.
From: https://stackoverflow.com/a/51722117
"""
# approximate radius of earth in km
R = 6371.009
lat1 = lat1*np.pi/180.0
lng1 = np.deg2rad(lng1)
lat2 = np.deg2rad(lat2)
lng2 = np.deg2rad(lng2)
d = np.sin((lat2 - lat1)/2)**2 + np.cos(lat1)*np.cos(lat2) * np.sin((lng2 - lng1)/2)**2
return 2 * R * np.arcsin(np.sqrt(d))
def closest_city(lng_array, lat_array, cities):
"""Find the closest_city for each row in lng_array and lat_array input
"""
distances = []
# Compute distance from each row of arrays to each of our city inputs
for city_name, coord in cities.items():
distances.append(distance(lng_array, lat_array, *coord))
# Convert this list of numpy arrays into a 2D numpy array
distances = np.array(distances)
# Find the shortest distance value for each row
shortest_distances = np.amin(distances, axis=0)
# Find the _index_ of the shortest distance for each row. Then use this value to
# lookup the longitude-latitude pair of the closest city
city_index = np.argmin(distances, axis=0)
# Create a 2D numpy array of location coordinates
# Then use the indexes from above to perform a lookup against the order of cities as
# input. (Note: this relies on the fact that in Python 3.6+ dictionaries are
# ordered)
input_coords = np.array(list(cities.values()))
closest_city_coords = input_coords[city_index]
# Return a 2D array with three columns:
# - Distance to closest city
# - Longitude of closest city
# - Latitude of closest city
return np.hstack((shortest_distances[:, np.newaxis], closest_city_coords))
```
Then use the `closest_city` function on our data to create three new columns:
```
housing[['closest_city_dist', 'closest_city_lng', 'closest_city_lat']] = closest_city(
housing['longitude'], housing['latitude'], cities
)
```
The map created in the next cell uses the new columns we computed above in relation to the largest cities in California:
```
distance_to_big_cities = UnfoldedMap()
distance_to_big_cities
dist_data_id = uuid4()
distance_to_big_cities.add_dataset(
{
"uuid": dist_data_id,
"label": "Distance to closest big city",
"data": housing,
},
auto_create_layers=False,
)
distance_to_big_cities.add_layer(
{
"id": "closest_distance",
"type": "arc",
"config": {
"data_id": dist_data_id,
"label": "distance to closest big city",
"columns": {
"lng0": "longitude",
"lat0": "latitude",
"lng1": "closest_city_lng",
"lat1": "closest_city_lat",
},
"visConfig": {"opacity": 0.8, "thickness": 0.3},
"is_visible": True,
},
}
)
distance_to_big_cities.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 4.5}
)
```
## Data Preprocessing
In this next section, we want to prepare our dataset to be used for training a TensorFlow model. First, we'll drop rows with null values, since they're quite rare in the dataset.
```
pct_null_rows = housing.isnull().any(axis=1).sum() / len(housing) * 100
print(f'{pct_null_rows:.1f}% of rows have null values')
housing = housing.dropna()
```
In the model we're training, we want to predict the median house value of an area. Thus we split the columns from our dataset `housing` into a dataset `y` with the column `median_house_value` and a dataset `X` with all other columns.
```
predicted_column = ['median_house_value']
other_columns = housing.columns.difference(predicted_column)
X = housing.loc[:, other_columns]
y = housing.loc[:, predicted_column]
```
Most of the columns in `X` are numeric, but one is not. `ocean_proximity` is of type `object`, which here is a string.
```
X.dtypes
```
Looking closer, we see that `ocean_proximity` is a categorical string with only five values.
```
X['ocean_proximity'].value_counts()
```
In order to use this column in our numeric model, we call [`pandas.get_dummies`](https://pandas.pydata.org/docs/reference/api/pandas.get_dummies.html) to create five new boolean columns. Each of these columns contains a `1` if the value of `ocean_proximity` is equal to the value that's now the column name.
```
X = pd.get_dummies(
data=X, columns=["ocean_proximity"], prefix=["ocean_proximity"], drop_first=True
)
```
## Data Splitting
In line with standard machine learning practice, we split our dataset into training, validation and test sets. We first take out 20% of our full dataset to use for testing the model after training. Then of the remaining 80%, we take out 75% to use for training the model and 25% to use for validation.
```
# dividing training data into test, validation and train
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=0.25, random_state=1
)
# We save a copy of our test data to use after model prediction
start_values = X_test.copy(deep=True)
```
## Feature Scaling
We use standard scaling with mean and standard deviation from our training dataset to avoid data leakage.
```
# feature standardization
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_val = scaler.transform(X_val)
X_test = scaler.transform(X_test)
```
## Price Prediction Model
Next we specify the parameters for the TensorFlow model:
```
# We use a Sequential model from Keras
# https://keras.io/api/models/sequential/
model = Sequential()
# Each column from X is an input feature into our model.
number_of_features = len(X.columns)
# input Layer
model.add(Dense(number_of_features, activation="relu", input_dim=number_of_features))
# hidden Layer
model.add(Dense(512, activation="relu"))
model.add(Dense(512, activation="relu"))
model.add(Dense(256, activation="relu"))
model.add(Dense(128, activation="relu"))
model.add(Dense(64, activation="relu"))
model.add(Dense(32, activation="relu"))
# output Layer
model.add(Dense(1, activation="linear"))
model.compile(loss="mse", optimizer="adam", metrics=["mse", "mae"])
model.summary()
```
### Training
Next we begin model training. Model training can take a long time; the higher the number of epochs, the better the model will be fit, but the longer training will take. Here we default to only 10 epochs because the focus of this notebook is integration with Unfolded Studio, not the machine learning itself.
```
EPOCHS = 10
# Or uncomment the following line if you're happy to wait longer for a better model fit.
# EPOCHS = 70
history = model.fit(
X_train,
y_train.to_numpy(),
batch_size=10,
epochs=EPOCHS,
verbose=1,
validation_data=(X_val, y_val),
)
```
### Evaluation
Next we want to find out how well the model was trained:
```
# summarize history for loss
loss_train = history.history["loss"]
loss_val = history.history["val_loss"]
epochs = range(1, EPOCHS + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, loss_train, "g", label="Training loss")
plt.plot(epochs, loss_val, "b", label="Validation loss")
plt.title("Training and Validation loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()
```
In the above chart we can see that the training loss and validation loss are quite close to each other.
Now we can use our trained model to predict home prices on the _test_ data, which was not used in the training process.
```
y_pred = model.predict(X_test)
```
We can see that loss function value on the test data is similar to the loss value on the training data
```
model.evaluate(X_test, y_test)
```
### Prediction
Let's now visualize our housing price predictions using Unfolded Studio. Here we create a dataframe with predicted values obtained from the model.
```
predict_data = start_values.loc[:, ['longitude', 'latitude']]
predict_data["price"] = y_pred
```
### Visualization
The map we create in the next cell depicts the prices we've predicted for houses in each census area in California.
```
housing_predict_prices = UnfoldedMap()
housing_predict_prices
price_data_id = uuid4()
housing_predict_prices.add_dataset(
{
"uuid": price_data_id,
"label": "Predict housing prices in CA",
"data": predict_data,
},
auto_create_layers=False,
)
housing_predict_prices.add_layer(
{
"id": "housing_prices",
"type": "hexagon",
"config": {
"label": "housing prices",
"data_id": price_data_id,
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "price", "type": "real"},
"vis_config": {
"colorRange": {
"colors": [
"#E6F598",
"#ABDDA4",
"#66C2A5",
"#3288BD",
"#5E4FA2",
"#9E0142",
"#D53E4F",
"#F46D43",
"#FDAE61",
"#FEE08B",
]
}
},
},
}
)
housing_predict_prices.set_view_state(
{"longitude": -119.417931, "latitude": 36.6, "zoom": 6}
)
```
## Clustering Model
We'll now cluster the predicted data by price levels using the KMeans algorithm.
```
k = 5
km = KMeans(n_clusters=k, init="k-means++")
X = predict_data.loc[:, ["latitude", "longitude", "price"]]
# Run clustering and add to prediction dataset dataset
predict_data["cluster"] = km.fit_predict(X)
```
### Visualization
Let's show the price clusters in a chart
```
fig, ax = plt.subplots()
sns.scatterplot(
x="latitude",
y="longitude",
data=predict_data,
palette=sns.color_palette("bright", k),
hue="cluster",
size_order=[1, 0],
ax=ax,
).set_title(f"Clustering (k={k})")
```
The next map shows the same clusters in a geographic context. Here we can see that house prices are highest for areas close to the largest cities.
```
unfolded_map_prices = UnfoldedMap()
unfolded_map_prices
prices_dataset_id = uuid4()
unfolded_map_prices.add_dataset(
{"uuid": prices_dataset_id, "label": "Prices", "data": predict_data},
auto_create_layers=False,
)
unfolded_map_prices.add_layer(
{
"id": "prices_CA",
"type": "point",
"config": {
"data_id": prices_dataset_id,
"label": "clustering of prices",
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "cluster", "type": "real"},
"vis_config": {
"colorRange": {
"colors": ["#7FFFD4", "#8A2BE2", "#00008B", "#FF8C00", "#FF1493"]
}
},
},
}
)
unfolded_map_prices.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 4}
)
```
| true |
code
| 0.738096 | null | null | null | null |
|
# Semantic Image Clustering
**Author:** [Khalid Salama](https://www.linkedin.com/in/khalid-salama-24403144/)<br>
**Date created:** 2021/02/28<br>
**Last modified:** 2021/02/28<br>
**Description:** Semantic Clustering by Adopting Nearest neighbors (SCAN) algorithm.
## Introduction
This example demonstrates how to apply the [Semantic Clustering by Adopting Nearest neighbors
(SCAN)](https://arxiv.org/abs/2005.12320) algorithm (Van Gansbeke et al., 2020) on the
[CIFAR-10](https://www.cs.toronto.edu/~kriz/cifar.html) dataset. The algorithm consists of
two phases:
1. Self-supervised visual representation learning of images, in which we use the
[simCLR](https://arxiv.org/abs/2002.05709) technique.
2. Clustering of the learned visual representation vectors to maximize the agreement
between the cluster assignments of neighboring vectors.
The example requires [TensorFlow Addons](https://www.tensorflow.org/addons),
which you can install using the following command:
```python
pip install tensorflow-addons
```
## Setup
```
from collections import defaultdict
import random
import numpy as np
import tensorflow as tf
import tensorflow_addons as tfa
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
from tqdm import tqdm
```
## Prepare the data
```
num_classes = 10
input_shape = (32, 32, 3)
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
x_data = np.concatenate([x_train, x_test])
y_data = np.concatenate([y_train, y_test])
print("x_data shape:", x_data.shape, "- y_data shape:", y_data.shape)
classes = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
```
## Define hyperparameters
```
target_size = 32 # Resize the input images.
representation_dim = 512 # The dimensions of the features vector.
projection_units = 128 # The projection head of the representation learner.
num_clusters = 20 # Number of clusters.
k_neighbours = 5 # Number of neighbours to consider during cluster learning.
tune_encoder_during_clustering = False # Freeze the encoder in the cluster learning.
```
## Implement data preprocessing
The data preprocessing step resizes the input images to the desired `target_size` and applies
feature-wise normalization. Note that, when using `keras.applications.ResNet50V2` as the
visual encoder, resizing the images into 255 x 255 inputs would lead to more accurate results
but require a longer time to train.
```
data_preprocessing = keras.Sequential(
[
layers.experimental.preprocessing.Resizing(target_size, target_size),
layers.experimental.preprocessing.Normalization(),
]
)
# Compute the mean and the variance from the data for normalization.
data_preprocessing.layers[-1].adapt(x_data)
```
## Data augmentation
Unlike simCLR, which randomly picks a single data augmentation function to apply to an input
image, we apply a set of data augmentation functions randomly to the input image.
(You can experiment with other image augmentation techniques by following the [data augmentation tutorial](https://www.tensorflow.org/tutorials/images/data_augmentation).)
```
data_augmentation = keras.Sequential(
[
layers.experimental.preprocessing.RandomTranslation(
height_factor=(-0.2, 0.2), width_factor=(-0.2, 0.2), fill_mode="nearest"
),
layers.experimental.preprocessing.RandomFlip(mode="horizontal"),
layers.experimental.preprocessing.RandomRotation(
factor=0.15, fill_mode="nearest"
),
layers.experimental.preprocessing.RandomZoom(
height_factor=(-0.3, 0.1), width_factor=(-0.3, 0.1), fill_mode="nearest"
)
]
)
```
Display a random image
```
image_idx = np.random.choice(range(x_data.shape[0]))
image = x_data[image_idx]
image_class = classes[y_data[image_idx][0]]
plt.figure(figsize=(3, 3))
plt.imshow(x_data[image_idx].astype("uint8"))
plt.title(image_class)
_ = plt.axis("off")
```
Display a sample of augmented versions of the image
```
plt.figure(figsize=(10, 10))
for i in range(9):
augmented_images = data_augmentation(np.array([image]))
ax = plt.subplot(3, 3, i + 1)
plt.imshow(augmented_images[0].numpy().astype("uint8"))
plt.axis("off")
```
## Self-supervised representation learning
### Implement the vision encoder
```
def create_encoder(representation_dim):
encoder = keras.Sequential(
[
keras.applications.ResNet50V2(
include_top=False, weights=None, pooling="avg"
),
layers.Dense(representation_dim),
]
)
return encoder
```
### Implement the unsupervised contrastive loss
```
class RepresentationLearner(keras.Model):
def __init__(
self,
encoder,
projection_units,
num_augmentations,
temperature=1.0,
dropout_rate=0.1,
l2_normalize=False,
**kwargs
):
super(RepresentationLearner, self).__init__(**kwargs)
self.encoder = encoder
# Create projection head.
self.projector = keras.Sequential(
[
layers.Dropout(dropout_rate),
layers.Dense(units=projection_units, use_bias=False),
layers.BatchNormalization(),
layers.ReLU(),
]
)
self.num_augmentations = num_augmentations
self.temperature = temperature
self.l2_normalize = l2_normalize
self.loss_tracker = keras.metrics.Mean(name="loss")
@property
def metrics(self):
return [self.loss_tracker]
def compute_contrastive_loss(self, feature_vectors, batch_size):
num_augmentations = tf.shape(feature_vectors)[0] // batch_size
if self.l2_normalize:
feature_vectors = tf.math.l2_normalize(feature_vectors, -1)
# The logits shape is [num_augmentations * batch_size, num_augmentations * batch_size].
logits = (
tf.linalg.matmul(feature_vectors, feature_vectors, transpose_b=True)
/ self.temperature
)
# Apply log-max trick for numerical stability.
logits_max = tf.math.reduce_max(logits, axis=1)
logits = logits - logits_max
# The shape of targets is [num_augmentations * batch_size, num_augmentations * batch_size].
# targets is a matrix consits of num_augmentations submatrices of shape [batch_size * batch_size].
# Each [batch_size * batch_size] submatrix is an identity matrix (diagonal entries are ones).
targets = tf.tile(tf.eye(batch_size), [num_augmentations, num_augmentations])
# Compute cross entropy loss
return keras.losses.categorical_crossentropy(
y_true=targets, y_pred=logits, from_logits=True
)
def call(self, inputs):
# Preprocess the input images.
preprocessed = data_preprocessing(inputs)
# Create augmented versions of the images.
augmented = []
for _ in range(self.num_augmentations):
augmented.append(data_augmentation(preprocessed))
augmented = layers.Concatenate(axis=0)(augmented)
# Generate embedding representations of the images.
features = self.encoder(augmented)
# Apply projection head.
return self.projector(features)
def train_step(self, inputs):
batch_size = tf.shape(inputs)[0]
# Run the forward pass and compute the contrastive loss
with tf.GradientTape() as tape:
feature_vectors = self(inputs, training=True)
loss = self.compute_contrastive_loss(feature_vectors, batch_size)
# Compute gradients
trainable_vars = self.trainable_variables
gradients = tape.gradient(loss, trainable_vars)
# Update weights
self.optimizer.apply_gradients(zip(gradients, trainable_vars))
# Update loss tracker metric
self.loss_tracker.update_state(loss)
# Return a dict mapping metric names to current value
return {m.name: m.result() for m in self.metrics}
def test_step(self, inputs):
batch_size = tf.shape(inputs)[0]
feature_vectors = self(inputs, training=False)
loss = self.compute_contrastive_loss(feature_vectors, batch_size)
self.loss_tracker.update_state(loss)
return {"loss": self.loss_tracker.result()}
```
### Train the model
```
# Create vision encoder.
encoder = create_encoder(representation_dim)
# Create representation learner.
representation_learner = RepresentationLearner(
encoder, projection_units, num_augmentations=2, temperature=0.1
)
# Create a a Cosine decay learning rate scheduler.
lr_scheduler = keras.experimental.CosineDecay(
initial_learning_rate=0.001, decay_steps=500, alpha=0.1
)
# Compile the model.
representation_learner.compile(
optimizer=tfa.optimizers.AdamW(learning_rate=lr_scheduler, weight_decay=0.0001),
)
# Fit the model.
history = representation_learner.fit(
x=x_data,
batch_size=512,
epochs=50, # for better results, increase the number of epochs to 500.
)
```
Plot training loss
```
plt.plot(history.history["loss"])
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()
```
## Compute the nearest neighbors
### Generate the embeddings for the images
```
batch_size = 500
# Get the feature vector representations of the images.
feature_vectors = encoder.predict(x_data, batch_size=batch_size, verbose=1)
# Normalize the feature vectores.
feature_vectors = tf.math.l2_normalize(feature_vectors, -1)
```
### Find the *k* nearest neighbours for each embedding
```
neighbours = []
num_batches = feature_vectors.shape[0] // batch_size
for batch_idx in tqdm(range(num_batches)):
start_idx = batch_idx * batch_size
end_idx = start_idx + batch_size
current_batch = feature_vectors[start_idx:end_idx]
# Compute the dot similarity.
similarities = tf.linalg.matmul(current_batch, feature_vectors, transpose_b=True)
# Get the indices of most similar vectors.
_, indices = tf.math.top_k(similarities, k=k_neighbours + 1, sorted=True)
# Add the indices to the neighbours.
neighbours.append(indices[..., 1:])
neighbours = np.reshape(np.array(neighbours), (-1, k_neighbours))
```
Let's display some neighbors on each row
```
nrows = 4
ncols = k_neighbours + 1
plt.figure(figsize=(12, 12))
position = 1
for _ in range(nrows):
anchor_idx = np.random.choice(range(x_data.shape[0]))
neighbour_indicies = neighbours[anchor_idx]
indices = [anchor_idx] + neighbour_indicies.tolist()
for j in range(ncols):
plt.subplot(nrows, ncols, position)
plt.imshow(x_data[indices[j]].astype("uint8"))
plt.title(classes[y_data[indices[j]][0]])
plt.axis("off")
position += 1
```
You notice that images on each row are visually similar, and belong to similar classes.
## Semantic clustering with nearest neighbours
### Implement clustering consistency loss
This loss tries to make sure that neighbours have the same clustering assignments.
```
class ClustersConsistencyLoss(keras.losses.Loss):
def __init__(self):
super(ClustersConsistencyLoss, self).__init__()
def __call__(self, target, similarity, sample_weight=None):
# Set targets to be ones.
target = tf.ones_like(similarity)
# Compute cross entropy loss.
loss = keras.losses.binary_crossentropy(
y_true=target, y_pred=similarity, from_logits=True
)
return tf.math.reduce_mean(loss)
```
### Implement the clusters entropy loss
This loss tries to make sure that cluster distribution is roughly uniformed, to avoid
assigning most of the instances to one cluster.
```
class ClustersEntropyLoss(keras.losses.Loss):
def __init__(self, entropy_loss_weight=1.0):
super(ClustersEntropyLoss, self).__init__()
self.entropy_loss_weight = entropy_loss_weight
def __call__(self, target, cluster_probabilities, sample_weight=None):
# Ideal entropy = log(num_clusters).
num_clusters = tf.cast(tf.shape(cluster_probabilities)[-1], tf.dtypes.float32)
target = tf.math.log(num_clusters)
# Compute the overall clusters distribution.
cluster_probabilities = tf.math.reduce_mean(cluster_probabilities, axis=0)
# Replacing zero probabilities - if any - with a very small value.
cluster_probabilities = tf.clip_by_value(
cluster_probabilities, clip_value_min=1e-8, clip_value_max=1.0
)
# Compute the entropy over the clusters.
entropy = -tf.math.reduce_sum(
cluster_probabilities * tf.math.log(cluster_probabilities)
)
# Compute the difference between the target and the actual.
loss = target - entropy
return loss
```
### Implement clustering model
This model takes a raw image as an input, generated its feature vector using the trained
encoder, and produces a probability distribution of the clusters given the feature vector
as the cluster assignments.
```
def create_clustering_model(encoder, num_clusters, name=None):
inputs = keras.Input(shape=input_shape)
# Preprocess the input images.
preprocessed = data_preprocessing(inputs)
# Apply data augmentation to the images.
augmented = data_augmentation(preprocessed)
# Generate embedding representations of the images.
features = encoder(augmented)
# Assign the images to clusters.
outputs = layers.Dense(units=num_clusters, activation="softmax")(features)
# Create the model.
model = keras.Model(inputs=inputs, outputs=outputs, name=name)
return model
```
### Implement clustering learner
This model receives the input `anchor` image and its `neighbours`, produces the clusters
assignments for them using the `clustering_model`, and produces two outputs:
1. `similarity`: the similarity between the cluster assignments of the `anchor` image and
its `neighbours`. This output is fed to the `ClustersConsistencyLoss`.
2. `anchor_clustering`: cluster assignments of the `anchor` images. This is fed to the `ClustersEntropyLoss`.
```
def create_clustering_learner(clustering_model):
anchor = keras.Input(shape=input_shape, name="anchors")
neighbours = keras.Input(
shape=tuple([k_neighbours]) + input_shape, name="neighbours"
)
# Changes neighbours shape to [batch_size * k_neighbours, width, height, channels]
neighbours_reshaped = tf.reshape(neighbours, shape=tuple([-1]) + input_shape)
# anchor_clustering shape: [batch_size, num_clusters]
anchor_clustering = clustering_model(anchor)
# neighbours_clustering shape: [batch_size * k_neighbours, num_clusters]
neighbours_clustering = clustering_model(neighbours_reshaped)
# Convert neighbours_clustering shape to [batch_size, k_neighbours, num_clusters]
neighbours_clustering = tf.reshape(
neighbours_clustering,
shape=(-1, k_neighbours, tf.shape(neighbours_clustering)[-1]),
)
# similarity shape: [batch_size, 1, k_neighbours]
similarity = tf.linalg.einsum(
"bij,bkj->bik", tf.expand_dims(anchor_clustering, axis=1), neighbours_clustering
)
# similarity shape: [batch_size, k_neighbours]
similarity = layers.Lambda(lambda x: tf.squeeze(x, axis=1), name="similarity")(
similarity
)
# Create the model.
model = keras.Model(
inputs=[anchor, neighbours],
outputs=[similarity, anchor_clustering],
name="clustering_learner",
)
return model
```
### Train model
```
# If tune_encoder_during_clustering is set to False,
# then freeze the encoder weights.
for layer in encoder.layers:
layer.trainable = tune_encoder_during_clustering
# Create the clustering model and learner.
clustering_model = create_clustering_model(encoder, num_clusters, name="clustering")
clustering_learner = create_clustering_learner(clustering_model)
# Instantiate the model losses.
losses = [ClustersConsistencyLoss(), ClustersEntropyLoss(entropy_loss_weight=5)]
# Create the model inputs and labels.
inputs = {"anchors": x_data, "neighbours": tf.gather(x_data, neighbours)}
labels = tf.ones(shape=(x_data.shape[0]))
# Compile the model.
clustering_learner.compile(
optimizer=tfa.optimizers.AdamW(learning_rate=0.0005, weight_decay=0.0001),
loss=losses,
)
# Begin training the model.
clustering_learner.fit(x=inputs, y=labels, batch_size=512, epochs=50)
```
Plot training loss
```
plt.plot(history.history["loss"])
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()
```
## Cluster analysis
### Assign images to clusters
```
# Get the cluster probability distribution of the input images.
clustering_probs = clustering_model.predict(x_data, batch_size=batch_size, verbose=1)
# Get the cluster of the highest probability.
cluster_assignments = tf.math.argmax(clustering_probs, axis=-1).numpy()
# Store the clustering confidence.
# Images with the highest clustering confidence are considered the 'prototypes'
# of the clusters.
cluster_confidence = tf.math.reduce_max(clustering_probs, axis=-1).numpy()
```
Let's compute the cluster sizes
```
clusters = defaultdict(list)
for idx, c in enumerate(cluster_assignments):
clusters[c].append((idx, cluster_confidence[idx]))
for c in range(num_clusters):
print("cluster", c, ":", len(clusters[c]))
```
Notice that the clusters have roughly balanced sizes.
### Visualize cluster images
Display the *prototypes*—instances with the highest clustering confidence—of each cluster:
```
num_images = 8
plt.figure(figsize=(15, 15))
position = 1
for c in range(num_clusters):
cluster_instances = sorted(clusters[c], key=lambda kv: kv[1], reverse=True)
for j in range(num_images):
image_idx = cluster_instances[j][0]
plt.subplot(num_clusters, num_images, position)
plt.imshow(x_data[image_idx].astype("uint8"))
plt.title(classes[y_data[image_idx][0]])
plt.axis("off")
position += 1
```
### Compute clustering accuracy
First, we assign a label for each cluster based on the majority label of its images.
Then, we compute the accuracy of each cluster by dividing the number of image with the
majority label by the size of the cluster.
```
cluster_label_counts = dict()
for c in range(num_clusters):
cluster_label_counts[c] = [0] * num_classes
instances = clusters[c]
for i, _ in instances:
cluster_label_counts[c][y_data[i][0]] += 1
cluster_label_idx = np.argmax(cluster_label_counts[c])
correct_count = np.max(cluster_label_counts[c])
cluster_size = len(clusters[c])
accuracy = (
np.round((correct_count / cluster_size) * 100, 2) if cluster_size > 0 else 0
)
cluster_label = classes[cluster_label_idx]
print("cluster", c, "label is:", cluster_label, " - accuracy:", accuracy, "%")
```
## Conclusion
To improve the accuracy results, you can: 1) increase the number
of epochs in the representation learning and the clustering phases; 2)
allow the encoder weights to be tuned during the clustering phase; and 3) perform a final
fine-tuning step through self-labeling, as described in the [original SCAN paper](https://arxiv.org/abs/2005.12320).
Note that unsupervised image clustering techniques are not expected to outperform the accuracy
of supervised image classification techniques, rather showing that they can learn the semantics
of the images and group them into clusters that are similar to their original classes.
| true |
code
| 0.868074 | null | null | null | null |
|
```
import json
import numpy as np
from sklearn.model_selection import train_test_split
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import random
import librosa
import math
# path to json
data_path = "C:\\Users\\Saad\\Desktop\\Project\\MGC\\Data\\data.json"
def load_data(data_path):
with open(data_path, "r") as f:
data = json.load(f)
# convert lists to numpy arrays
X = np.array(data["mfcc"])
y = np.array(data["labels"])
print("No Problems, go ahead!")
return X, y
# load data
X, y = load_data(data_path)
X.shape
```
## ANN
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = keras.Sequential([
keras.layers.Flatten(input_shape=(X.shape[1], X.shape[2])),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dense(64, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
history = model.fit(X_train, y_train, validation_data=(X_test, y_test), batch_size=32, epochs=50)
def plot_history(history):
fig, axs = plt.subplots(2)
axs[0].plot(history.history["accuracy"], label="train accuracy")
axs[0].plot(history.history["val_accuracy"], label="test accuracy")
axs[0].set_ylabel("Accuracy")
axs[0].legend(loc="lower right")
axs[0].set_title("Accuracy eval")
axs[1].plot(history.history["loss"], label="train error")
axs[1].plot(history.history["val_loss"], label="test error")
axs[1].set_ylabel("Error")
axs[1].set_xlabel("Epoch")
axs[1].legend(loc="upper right")
axs[1].set_title("Error eval")
plt.show()
plot_history(history)
model_regularized = keras.Sequential([
keras.layers.Flatten(input_shape=(X.shape[1], X.shape[2])),
keras.layers.Dense(512, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(256, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(64, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(10, activation='softmax')
])
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model_regularized.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model_regularized.fit(X_train, y_train, validation_data=(X_test, y_test), batch_size=32, epochs=100)
plot_history(history)
```
## CNN
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train, X_validation, y_train, y_validation = train_test_split(X_train, y_train, test_size=0.2)
X_train = X_train[..., np.newaxis]
X_validation = X_validation[..., np.newaxis]
X_test = X_test[..., np.newaxis]
X_train.shape
input_shape = (X_train.shape[1], X_train.shape[2], 1)
model_cnn = keras.Sequential()
model_cnn.add(keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=input_shape))
model_cnn.add(keras.layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Conv2D(32, (3, 3), activation='relu'))
model_cnn.add(keras.layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Conv2D(32, (2, 2), activation='relu'))
model_cnn.add(keras.layers.MaxPooling2D((2, 2), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Flatten())
model_cnn.add(keras.layers.Dense(64, activation='relu'))
model_cnn.add(keras.layers.Dropout(0.3))
model_cnn.add(keras.layers.Dense(10, activation='softmax'))
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model_cnn.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model_cnn.summary()
history = model_cnn.fit(X_train, y_train, validation_data=(X_validation, y_validation), batch_size=32, epochs=50)
plot_history(history)
test_loss, test_acc = model_cnn.evaluate(X_test, y_test, verbose=1)
print('\nTest accuracy:', test_acc)
model_cnn.save("Genre_Classifier.h5")
for n in range(10):
i = random.randint(0,len(X_test))
# pick a sample to predict from the test set
X_to_predict = X_test[i]
y_to_predict = y_test[i]
print("\nReal Genre :", y_to_predict)
X_to_predict = X_to_predict[np.newaxis, ...]
prediction = model_cnn.predict(X_to_predict)
# get index with max value
predicted_index = np.argmax(prediction, axis=1)
print("Predicted Genre:", int(predicted_index))
```
| true |
code
| 0.654674 | null | null | null | null |
|
### Mount Google Drive (Works only on Google Colab)
```
from google.colab import drive
drive.mount('/content/gdrive')
```
# Import Packages
```
import os
import numpy as np
import pandas as pd
from zipfile import ZipFile
from PIL import Image
from tqdm.autonotebook import tqdm
from IPython.display import display
from IPython.display import Image as Dimage
```
# Define Paths
Define paths of all the required directories
```
# Root path of the dataset
ROOT_DATA_DIR = '/content/gdrive/My Drive/modest_museum_dataset.zip'
```
# Data Visualization
Let's visualize some of the foreground and background images
```
def make_grid(images_list, height=140, margin=8, aspect_ratio=False):
"""Combine Images to form a grid.
Args:
images (list): List of PIL images to display in grid.
height (int): Height to which the image will be resized.
margin (int): Amount of padding between the images in grid.
aspect_ratio (bool, optional): Create grid while maintaining
the aspect ratio of the images. (default: False)
Returns:
Image grid.
"""
# Create grid template
widths = []
if aspect_ratio:
for image in images_list:
# Find width according to aspect ratio
h_percent = height / image.size[1]
widths.append(int(image.size[0] * h_percent))
else:
widths = [height] * len(images_list)
start = 0
background = Image.new(
'RGBA', (sum(widths) + (len(images_list) - 1) * margin, height)
)
# Add images to grid
for idx, image in enumerate(images_list):
image = image.resize((widths[idx], height))
offset = (start, 0)
start += (widths[idx] + margin)
background.paste(image, offset)
return background
```
# Data Statistics
Let's calculate mean, standard deviation and total number of images for each type of image category.
## Mean
Mean is calculated using the formula
<center>
<img src="https://www.gstatic.com/education/formulas/images_long_sheet/en/mean.svg" height="50">
</center>
where, `sum of the terms` represents a pixel value and `number of terms` represents the total number of pixels across all the images.
## Standard Deviation
Standard Deviation is calculated using the formula
<center>
<img src="https://www.gstatic.com/education/formulas/images_long_sheet/en/population_standard_deviation.svg" height="50">
</center>
where, `x` represents a pixel value, `u` represents the mean calculated above and `N` represents the total number of pixels across all the images.
```
def statistics(filename, channel_num, filetype):
"""Calculates data statistics
Args:
path (str): Path of the directory for which statistics is to be calculated
Returns:
Mean, standard deviation, number of images
"""
counter = 0
mean = []
std = []
images = [] # store PIL instance of the image
pixel_num = 0 # store all pixel number in the dataset
channel_sum = np.zeros(channel_num) # store channel-wise sum
channel_sum_squared = np.zeros(channel_num) # store squared channel-wise sum
with ZipFile(filename) as archive:
img_list = [
x for x in archive.infolist()
if x.filename.split('/')[1] == filetype and x.filename.split('/')[2].endswith('.jpeg')
]
for entry in tqdm(img_list):
with archive.open(entry) as file:
img = Image.open(file)
if len(images) < 5:
images.append(img)
im = np.array(img)
im = im / 255.0
pixel_num += (im.size / channel_num)
channel_sum += np.sum(im, axis=(0, 1))
channel_sum_squared += np.sum(np.square(im), axis=(0, 1))
counter += 1
bgr_mean = channel_sum / pixel_num
bgr_std = np.sqrt(channel_sum_squared / pixel_num - np.square(bgr_mean))
# change the format from bgr to rgb
mean = [round(x, 5) for x in list(bgr_mean)[::-1]]
std = [round(x, 5) for x in list(bgr_std)[::-1]]
return mean, std, counter, im.shape, images
```
# Statistics for Background images
```
# Background
print('Calculating statistics for Backgrounds...')
bg_mean, bg_std, bg_counter, bg_dim, bg_images = statistics(ROOT_DATA_DIR, 3, 'bg')
# Display
print('Background Images:')
make_grid(bg_images, margin=30)
print('Data Statistics for Background images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_mean, bg_std, bg_counter, bg_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground images
```
# Background-Foreground
print('Calculating statistics for Background-Foreground Images...')
bg_fg_mean, bg_fg_std, bg_fg_counter, bg_fg_dim, bg_fg_image = statistics(ROOT_DATA_DIR, 3, 'bg_fg')
# Display
print('Background-Foreground Images:')
make_grid(bg_fg_image, margin=30)
print('Data Statistics for Background-Foreground images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_fg_mean, bg_fg_std, bg_fg_counter, bg_fg_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground Masks
```
#Foreground-Background Masks
print('Calculating statistics for Foreground-Background Masks...')
bg_fg_mask_mean, bg_fg_mask_std, bg_fg_mask_counter, bg_fg_mask_dim, bg_fg_mask_images = statistics(ROOT_DATA_DIR, 1, 'bg_fg_mask')
# Display
print('Background-Foreground Masks:')
make_grid(bg_fg_mask_images, margin=30, aspect_ratio=True)
print('Data Statistics for Background-Foreground Masks images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_fg_mask_mean, bg_fg_mask_std, bg_fg_mask_counter, bg_fg_mask_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground Depth Maps
```
#Foreground-Background Depth Map
print('Calculating statistics for Foreground-Background Depth Map...')
depth_mean, depth_std, depth_counter, depth_dim, depth_images = statistics(ROOT_DATA_DIR, 1, 'bg_fg_depth_map')
# Display
print('Background-Foreground Depth Maps:')
make_grid(depth_images, margin=30)
print('Data Statistics for Background-Foreground Depth Map images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [depth_mean, depth_std, depth_counter, depth_dim]
}
data = pd.DataFrame(stats)
data
```
| true |
code
| 0.692122 | null | null | null | null |
|
<a id='pd'></a>
<div id="qe-notebook-header" align="right" style="text-align:right;">
<a href="https://quantecon.org/" title="quantecon.org">
<img style="width:250px;display:inline;" width="250px" src="https://assets.quantecon.org/img/qe-menubar-logo.svg" alt="QuantEcon">
</a>
</div>
# Pandas
<a id='index-1'></a>
## Contents
- [Pandas](#Pandas)
- [Overview](#Overview)
- [Series](#Series)
- [DataFrames](#DataFrames)
- [On-Line Data Sources](#On-Line-Data-Sources)
- [Exercises](#Exercises)
- [Solutions](#Solutions)
In addition to what’s in Anaconda, this lecture will need the following libraries:
```
!pip install --upgrade pandas-datareader
```
## Overview
[Pandas](http://pandas.pydata.org/) is a package of fast, efficient data analysis tools for Python.
Its popularity has surged in recent years, coincident with the rise
of fields such as data science and machine learning.
Here’s a popularity comparison over time against STATA, SAS, and [dplyr](https://dplyr.tidyverse.org/) courtesy of Stack Overflow Trends
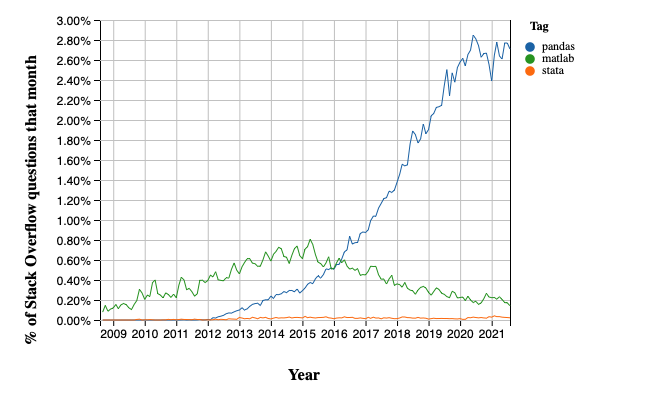
Just as [NumPy](http://www.numpy.org/) provides the basic array data type plus core array operations, pandas
1. defines fundamental structures for working with data and
1. endows them with methods that facilitate operations such as
- reading in data
- adjusting indices
- working with dates and time series
- sorting, grouping, re-ordering and general data munging <sup><a href=#mung id=mung-link>[1]</a></sup>
- dealing with missing values, etc., etc.
More sophisticated statistical functionality is left to other packages, such
as [statsmodels](http://www.statsmodels.org/) and [scikit-learn](http://scikit-learn.org/), which are built on top of pandas.
This lecture will provide a basic introduction to pandas.
Throughout the lecture, we will assume that the following imports have taken
place
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = [10,8] # Set default figure size
import requests
```
## Series
<a id='index-2'></a>
Two important data types defined by pandas are `Series` and `DataFrame`.
You can think of a `Series` as a “column” of data, such as a collection of observations on a single variable.
A `DataFrame` is an object for storing related columns of data.
Let’s start with Series
```
s = pd.Series(np.random.randn(4), name='daily returns')
s
```
Here you can imagine the indices `0, 1, 2, 3` as indexing four listed
companies, and the values being daily returns on their shares.
Pandas `Series` are built on top of NumPy arrays and support many similar
operations
```
s * 100
np.abs(s)
```
But `Series` provide more than NumPy arrays.
Not only do they have some additional (statistically oriented) methods
```
s.describe()
```
But their indices are more flexible
```
s.index = ['AMZN', 'AAPL', 'MSFT', 'GOOG']
s
```
Viewed in this way, `Series` are like fast, efficient Python dictionaries
(with the restriction that the items in the dictionary all have the same
type—in this case, floats).
In fact, you can use much of the same syntax as Python dictionaries
```
s['AMZN']
s['AMZN'] = 0
s
'AAPL' in s
```
## DataFrames
<a id='index-3'></a>
While a `Series` is a single column of data, a `DataFrame` is several columns, one for each variable.
In essence, a `DataFrame` in pandas is analogous to a (highly optimized) Excel spreadsheet.
Thus, it is a powerful tool for representing and analyzing data that are naturally organized into rows and columns, often with descriptive indexes for individual rows and individual columns.
Here’s the content of `test_pwt.csv`
```text
"country","country isocode","year","POP","XRAT","tcgdp","cc","cg"
"Argentina","ARG","2000","37335.653","0.9995","295072.21869","75.716805379","5.5788042896"
"Australia","AUS","2000","19053.186","1.72483","541804.6521","67.759025993","6.7200975332"
"India","IND","2000","1006300.297","44.9416","1728144.3748","64.575551328","14.072205773"
"Israel","ISR","2000","6114.57","4.07733","129253.89423","64.436450847","10.266688415"
"Malawi","MWI","2000","11801.505","59.543808333","5026.2217836","74.707624181","11.658954494"
"South Africa","ZAF","2000","45064.098","6.93983","227242.36949","72.718710427","5.7265463933"
"United States","USA","2000","282171.957","1","9898700","72.347054303","6.0324539789"
"Uruguay","URY","2000","3219.793","12.099591667","25255.961693","78.978740282","5.108067988"
```
Supposing you have this data saved as `test_pwt.csv` in the present working directory (type `%pwd` in Jupyter to see what this is), it can be read in as follows:
```
df = pd.read_csv('https://raw.githubusercontent.com/QuantEcon/lecture-python-programming/master/source/_static/lecture_specific/pandas/data/test_pwt.csv')
type(df)
df
```
We can select particular rows using standard Python array slicing notation
```
df[2:5]
```
To select columns, we can pass a list containing the names of the desired columns represented as strings
```
df[['country', 'tcgdp']]
```
To select both rows and columns using integers, the `iloc` attribute should be used with the format `.iloc[rows, columns]`
```
df.iloc[2:5, 0:4]
```
To select rows and columns using a mixture of integers and labels, the `loc` attribute can be used in a similar way
```
df.loc[df.index[2:5], ['country', 'tcgdp']]
```
Let’s imagine that we’re only interested in population (`POP`) and total GDP (`tcgdp`).
One way to strip the data frame `df` down to only these variables is to overwrite the dataframe using the selection method described above
```
df = df[['country', 'POP', 'tcgdp']]
df
```
Here the index `0, 1,..., 7` is redundant because we can use the country names as an index.
To do this, we set the index to be the `country` variable in the dataframe
```
df = df.set_index('country')
df
```
Let’s give the columns slightly better names
```
df.columns = 'population', 'total GDP'
df
```
Population is in thousands, let’s revert to single units
```
df['population'] = df['population'] * 1e3
df
```
Next, we’re going to add a column showing real GDP per capita, multiplying by 1,000,000 as we go because total GDP is in millions
```
df['GDP percap'] = df['total GDP'] * 1e6 / df['population']
df
```
One of the nice things about pandas `DataFrame` and `Series` objects is that they have methods for plotting and visualization that work through Matplotlib.
For example, we can easily generate a bar plot of GDP per capita
```
ax = df['GDP percap'].plot(kind='bar')
ax.set_xlabel('country', fontsize=12)
ax.set_ylabel('GDP per capita', fontsize=12)
plt.show()
```
At the moment the data frame is ordered alphabetically on the countries—let’s change it to GDP per capita
```
df = df.sort_values(by='GDP percap', ascending=False)
df
```
Plotting as before now yields
```
ax = df['GDP percap'].plot(kind='bar')
ax.set_xlabel('country', fontsize=12)
ax.set_ylabel('GDP per capita', fontsize=12)
plt.show()
```
## On-Line Data Sources
<a id='index-4'></a>
Python makes it straightforward to query online databases programmatically.
An important database for economists is [FRED](https://research.stlouisfed.org/fred2/) — a vast collection of time series data maintained by the St. Louis Fed.
For example, suppose that we are interested in the [unemployment rate](https://research.stlouisfed.org/fred2/series/UNRATE).
Via FRED, the entire series for the US civilian unemployment rate can be downloaded directly by entering
this URL into your browser (note that this requires an internet connection)
```text
https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv
```
(Equivalently, click here: [https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv](https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv))
This request returns a CSV file, which will be handled by your default application for this class of files.
Alternatively, we can access the CSV file from within a Python program.
This can be done with a variety of methods.
We start with a relatively low-level method and then return to pandas.
### Accessing Data with requests
<a id='index-6'></a>
One option is to use [requests](https://requests.readthedocs.io/en/master/), a standard Python library for requesting data over the Internet.
To begin, try the following code on your computer
```
r = requests.get('http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv')
```
If there’s no error message, then the call has succeeded.
If you do get an error, then there are two likely causes
1. You are not connected to the Internet — hopefully, this isn’t the case.
1. Your machine is accessing the Internet through a proxy server, and Python isn’t aware of this.
In the second case, you can either
- switch to another machine
- solve your proxy problem by reading [the documentation](https://requests.readthedocs.io/en/master/)
Assuming that all is working, you can now proceed to use the `source` object returned by the call `requests.get('http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv')`
```
url = 'http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv'
source = requests.get(url).content.decode().split("\n")
source[0]
source[1]
source[2]
```
We could now write some additional code to parse this text and store it as an array.
But this is unnecessary — pandas’ `read_csv` function can handle the task for us.
We use `parse_dates=True` so that pandas recognizes our dates column, allowing for simple date filtering
```
data = pd.read_csv(url, index_col=0, parse_dates=True)
```
The data has been read into a pandas DataFrame called `data` that we can now manipulate in the usual way
```
type(data)
data.head() # A useful method to get a quick look at a data frame
pd.set_option('precision', 1)
data.describe() # Your output might differ slightly
```
We can also plot the unemployment rate from 2006 to 2012 as follows
```
ax = data['2006':'2012'].plot(title='US Unemployment Rate', legend=False)
ax.set_xlabel('year', fontsize=12)
ax.set_ylabel('%', fontsize=12)
plt.show()
```
Note that pandas offers many other file type alternatives.
Pandas has [a wide variety](https://pandas.pydata.org/pandas-docs/stable/user_guide/io.html) of top-level methods that we can use to read, excel, json, parquet or plug straight into a database server.
### Using pandas_datareader to Access Data
<a id='index-8'></a>
The maker of pandas has also authored a library called pandas_datareader that gives programmatic access to many data sources straight from the Jupyter notebook.
While some sources require an access key, many of the most important (e.g., FRED, [OECD](https://data.oecd.org/), [EUROSTAT](https://ec.europa.eu/eurostat/data/database) and the World Bank) are free to use.
For now let’s work through one example of downloading and plotting data — this
time from the World Bank.
The World Bank [collects and organizes data](http://data.worldbank.org/indicator) on a huge range of indicators.
For example, [here’s](http://data.worldbank.org/indicator/GC.DOD.TOTL.GD.ZS/countries) some data on government debt as a ratio to GDP.
The next code example fetches the data for you and plots time series for the US and Australia
```
from pandas_datareader import wb
govt_debt = wb.download(indicator='GC.DOD.TOTL.GD.ZS', country=['US', 'AU'], start=2005, end=2016).stack().unstack(0)
ind = govt_debt.index.droplevel(-1)
govt_debt.index = ind
ax = govt_debt.plot(lw=2)
ax.set_xlabel('year', fontsize=12)
plt.title("Government Debt to GDP (%)")
plt.show()
```
The [documentation](https://pandas-datareader.readthedocs.io/en/latest/index.html) provides more details on how to access various data sources.
## Exercises
<a id='pd-ex1'></a>
### Exercise 1
With these imports:
```
import datetime as dt
from pandas_datareader import data
```
Write a program to calculate the percentage price change over 2019 for the following shares:
```
ticker_list = {'INTC': 'Intel',
'MSFT': 'Microsoft',
'IBM': 'IBM',
'BHP': 'BHP',
'TM': 'Toyota',
'AAPL': 'Apple',
'AMZN': 'Amazon',
'BA': 'Boeing',
'QCOM': 'Qualcomm',
'KO': 'Coca-Cola',
'GOOG': 'Google',
'SNE': 'Sony',
'PTR': 'PetroChina'}
```
Here’s the first part of the program
```
def read_data(ticker_list,
start=dt.datetime(2019, 1, 2),
end=dt.datetime(2019, 12, 31)):
"""
This function reads in closing price data from Yahoo
for each tick in the ticker_list.
"""
ticker = pd.DataFrame()
for tick in ticker_list:
prices = data.DataReader(tick, 'yahoo', start, end)
closing_prices = prices['Close']
ticker[tick] = closing_prices
return ticker
ticker = read_data(ticker_list)
```
Complete the program to plot the result as a bar graph like this one:
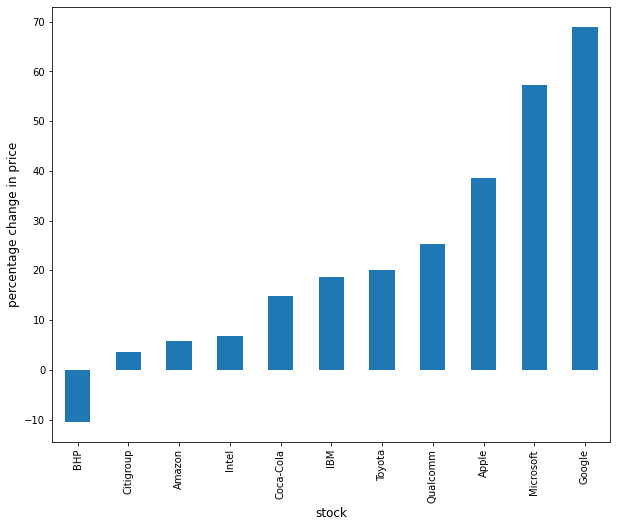
<a id='pd-ex2'></a>
### Exercise 2
Using the method `read_data` introduced in [Exercise 1](#pd-ex1), write a program to obtain year-on-year percentage change for the following indices:
```
indices_list = {'^GSPC': 'S&P 500',
'^IXIC': 'NASDAQ',
'^DJI': 'Dow Jones',
'^N225': 'Nikkei'}
```
Complete the program to show summary statistics and plot the result as a time series graph like this one:
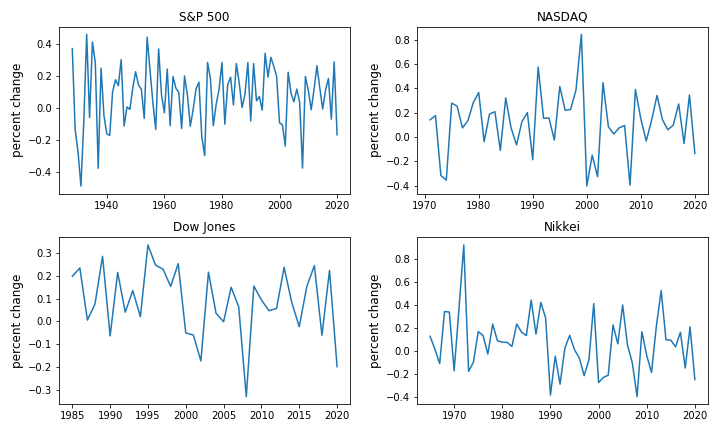
## Solutions
### Exercise 1
There are a few ways to approach this problem using Pandas to calculate
the percentage change.
First, you can extract the data and perform the calculation such as:
```
p1 = ticker.iloc[0] #Get the first set of prices as a Series
p2 = ticker.iloc[-1] #Get the last set of prices as a Series
price_change = (p2 - p1) / p1 * 100
price_change
```
Alternatively you can use an inbuilt method `pct_change` and configure it to
perform the correct calculation using `periods` argument.
```
change = ticker.pct_change(periods=len(ticker)-1, axis='rows')*100
price_change = change.iloc[-1]
price_change
```
Then to plot the chart
```
price_change.sort_values(inplace=True)
price_change = price_change.rename(index=ticker_list)
fig, ax = plt.subplots(figsize=(10,8))
ax.set_xlabel('stock', fontsize=12)
ax.set_ylabel('percentage change in price', fontsize=12)
price_change.plot(kind='bar', ax=ax)
plt.show()
```
### Exercise 2
Following the work you did in [Exercise 1](#pd-ex1), you can query the data using `read_data` by updating the start and end dates accordingly.
```
indices_data = read_data(
indices_list,
start=dt.datetime(1928, 1, 2),
end=dt.datetime(2020, 12, 31)
)
```
Then, extract the first and last set of prices per year as DataFrames and calculate the yearly returns such as:
```
yearly_returns = pd.DataFrame()
for index, name in indices_list.items():
p1 = indices_data.groupby(indices_data.index.year)[index].first() # Get the first set of returns as a DataFrame
p2 = indices_data.groupby(indices_data.index.year)[index].last() # Get the last set of returns as a DataFrame
returns = (p2 - p1) / p1
yearly_returns[name] = returns
yearly_returns
```
Next, you can obtain summary statistics by using the method `describe`.
```
yearly_returns.describe()
```
Then, to plot the chart
```
fig, axes = plt.subplots(2, 2, figsize=(10, 8))
for iter_, ax in enumerate(axes.flatten()): # Flatten 2-D array to 1-D array
index_name = yearly_returns.columns[iter_] # Get index name per iteration
ax.plot(yearly_returns[index_name]) # Plot pct change of yearly returns per index
ax.set_ylabel("percent change", fontsize = 12)
ax.set_title(index_name)
plt.tight_layout()
```
<p><a id=mung href=#mung-link><strong>[1]</strong></a> Wikipedia defines munging as cleaning data from one raw form into a structured, purged one.
| true |
code
| 0.567877 | null | null | null | null |
|
# In this note book the following steps are taken:
1. Remove highly correlated attributes
2. Find the best hyper parameters for estimator
3. Find the most important features by tunned random forest
4. Find f1 score of the tunned full model
5. Find best hyper parameter of model with selected features
6. Find f1 score of the tuned seleccted model
7. Compare the two f1 scores
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.feature_selection import RFECV,RFE
from sklearn.model_selection import train_test_split, GridSearchCV, KFold,RandomizedSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn import metrics
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score,f1_score
import numpy as np
from sklearn.metrics import make_scorer
f1_score = make_scorer(f1_score)
#import data
Data=pd.read_csv("Halifax-Transfomed-Data-BS-NoBreak - Copy.csv")
X = Data.iloc[:,:-1]
y = Data.iloc[:,-1]
#split test and training set.
np.random.seed(60)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2,
random_state = 1000)
#Define estimator and model
classifiers = {}
classifiers.update({"Random Forest": RandomForestClassifier(random_state=1000)})
#Define range of hyperparameters for estimator
np.random.seed(60)
parameters = {}
parameters.update({"Random Forest": { "classifier__n_estimators": [100,105,110,115,120,125,130,135,140,145,150,155,160,170,180,190,200],
# "classifier__n_estimators": [2,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200],
#"classifier__class_weight": [None, "balanced"],
"classifier__max_features": ["auto", "sqrt", "log2"],
"classifier__max_depth" : [4,6,8,10,11,12,13,14,15,16,17,18,19,20,22],
#"classifier__max_depth" : [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20],
"classifier__criterion" :["gini", "entropy"]
}})
# Make correlation matrix
corr_matrix = X_train.corr(method = "spearman").abs()
# Draw the heatmap
sns.set(font_scale = 1.0)
f, ax = plt.subplots(figsize=(11, 9))
sns.heatmap(corr_matrix, cmap= "YlGnBu", square=True, ax = ax)
f.tight_layout()
plt.savefig("correlation_matrix.png", dpi = 1080)
# Select upper triangle of matrix
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k = 1).astype(np.bool))
# Find index of feature columns with correlation greater than 0.8
to_drop = [column for column in upper.columns if any(upper[column] > 0.8)]
# Drop features
X_train = X_train.drop(to_drop, axis = 1)
X_test = X_test.drop(to_drop, axis = 1)
X_train
FEATURE_IMPORTANCE = {"Random Forest"}
selected_classifier = "Random Forest"
classifier = classifiers[selected_classifier]
scaler = StandardScaler()
steps = [("scaler", scaler), ("classifier", classifier)]
pipeline = Pipeline(steps = steps)
#Define parameters that we want to use in gridsearch cv
param_grid = parameters[selected_classifier]
# Initialize GridSearch object for estimator
gscv = RandomizedSearchCV(pipeline, param_grid, cv = 3, n_jobs= -1, verbose = 1, scoring = f1_score, n_iter=30)
# Fit gscv (Tunes estimator)
print(f"Now tuning {selected_classifier}. Go grab a beer or something.")
gscv.fit(X_train, np.ravel(y_train))
#Getting the best hyperparameters
best_params = gscv.best_params_
best_params
#Getting the best score of model
best_score = gscv.best_score_
best_score
#Check overfitting of the estimator
from sklearn.model_selection import cross_val_score
mod = RandomForestClassifier(#class_weight= None,
criterion= 'gini',
max_depth= 16,
max_features= 'auto',
n_estimators= 155 ,random_state=10000)
scores_test = cross_val_score(mod, X_test, y_test, scoring='f1', cv=5)
scores_test
tuned_params = {item[12:]: best_params[item] for item in best_params}
classifier.set_params(**tuned_params)
#Find f1 score of the model with all features (Model is tuned for all features)
results={}
model=classifier.set_params(criterion= 'gini',
max_depth= 16,
max_features= 'auto',
n_estimators= 155 ,random_state=10000)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
F1 = metrics.f1_score(y_test, y_pred)
results = {"classifier": model,
"Best Parameters": best_params,
"Training f1": best_score*100,
"Test f1": F1*100}
results
# Select Features using RFECV
class PipelineRFE(Pipeline):
# Source: https://ramhiser.com/post/2018-03-25-feature-selection-with-scikit-learn-pipeline/
def fit(self, X, y=None, **fit_params):
super(PipelineRFE, self).fit(X, y, **fit_params)
self.feature_importances_ = self.steps[-1][-1].feature_importances_
return self
steps = [("scaler", scaler), ("classifier", classifier)]
pipe = PipelineRFE(steps = steps)
np.random.seed(60)
# Initialize RFECV object
feature_selector = RFECV(pipe, cv = 5, step = 1, verbose = 1)
# Fit RFECV
feature_selector.fit(X_train, np.ravel(y_train))
# Get selected features
feature_names = X_train.columns
selected_features = feature_names[feature_selector.support_].tolist()
performance_curve = {"Number of Features": list(range(1, len(feature_names) + 1)),
"F1": feature_selector.grid_scores_}
performance_curve = pd.DataFrame(performance_curve)
# Performance vs Number of Features
# Set graph style
sns.set(font_scale = 1.75)
sns.set_style({"axes.facecolor": "1.0", "axes.edgecolor": "0.85", "grid.color": "0.85",
"grid.linestyle": "-", 'axes.labelcolor': '0.4', "xtick.color": "0.4",
'ytick.color': '0.4'})
colors = sns.color_palette("RdYlGn", 20)
line_color = colors[3]
marker_colors = colors[-1]
# Plot
f, ax = plt.subplots(figsize=(13, 6.5))
sns.lineplot(x = "Number of Features", y = "F1", data = performance_curve,
color = line_color, lw = 4, ax = ax)
sns.regplot(x = performance_curve["Number of Features"], y = performance_curve["F1"],
color = marker_colors, fit_reg = False, scatter_kws = {"s": 200}, ax = ax)
# Axes limits
plt.xlim(0.5, len(feature_names)+0.5)
plt.ylim(0.60, 1)
# Generate a bolded horizontal line at y = 0
ax.axhline(y = 0.625, color = 'black', linewidth = 1.3, alpha = .7)
# Turn frame off
ax.set_frame_on(False)
# Tight layout
plt.tight_layout()
#Define new training and test set based based on selected features by RFECV
X_train_rfecv = X_train[selected_features]
X_test_rfecv= X_test[selected_features]
np.random.seed(60)
classifier.fit(X_train_rfecv, np.ravel(y_train))
#Finding important features
np.random.seed(60)
feature_importance = pd.DataFrame(selected_features, columns = ["Feature Label"])
feature_importance["Feature Importance"] = classifier.feature_importances_
feature_importance = feature_importance.sort_values(by="Feature Importance", ascending=False)
feature_importance
# Initialize GridSearch object for model with selected features
np.random.seed(60)
gscv = RandomizedSearchCV(pipeline, param_grid, cv = 3, n_jobs= -1, verbose = 1, scoring = f1_score, n_iter=30)
#Tuning random forest classifier with selected features
np.random.seed(60)
gscv.fit(X_train_rfecv,y_train)
#Getting the best parameters of model with selected features
best_params = gscv.best_params_
best_params
#Getting the score of model with selected features
best_score = gscv.best_score_
best_score
#Check overfitting of the tuned model with selected features
from sklearn.model_selection import cross_val_score
mod = RandomForestClassifier(#class_weight= None,
criterion= 'entropy',
max_depth= 16,
max_features= 'auto',
n_estimators= 100 ,random_state=10000)
scores_test = cross_val_score(mod, X_test_rfecv, y_test, scoring='f1', cv=5)
scores_test
results={}
model=classifier.set_params(criterion= 'entropy',
max_depth= 16,
max_features= 'auto',
n_estimators= 100 ,random_state=10000)
scores_test = cross_val_score(mod, X_test_rfecv, y_test, scoring='f1', cv=5)
model.fit(X_train_rfecv,y_train)
y_pred = model.predict(X_test_rfecv)
F1 = metrics.f1_score(y_test, y_pred)
results = {"classifier": model,
"Best Parameters": best_params,
"Training f1": best_score*100,
"Test f1": F1*100}
results
```
| true |
code
| 0.618118 | null | null | null | null |
|
# Anailís ghramadaí trí [deplacy](https://koichiyasuoka.github.io/deplacy/)
## le [Stanza](https://stanfordnlp.github.io/stanza)
```
!pip install deplacy stanza
import stanza
stanza.download("ga")
nlp=stanza.Pipeline("ga")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [UDPipe 2](http://ufal.mff.cuni.cz/udpipe/2)
```
!pip install deplacy
def nlp(t):
import urllib.request,urllib.parse,json
with urllib.request.urlopen("https://lindat.mff.cuni.cz/services/udpipe/api/process?model=ga&tokenizer&tagger&parser&data="+urllib.parse.quote(t)) as r:
return json.loads(r.read())["result"]
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [COMBO-pytorch](https://gitlab.clarin-pl.eu/syntactic-tools/combo)
```
!pip install --index-url https://pypi.clarin-pl.eu/simple deplacy combo
import combo.predict
nlp=combo.predict.COMBO.from_pretrained("irish-ud27")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [Trankit](https://github.com/nlp-uoregon/trankit)
```
!pip install deplacy trankit transformers
import trankit
nlp=trankit.Pipeline("irish")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spacy-udpipe](https://github.com/TakeLab/spacy-udpipe)
```
!pip install deplacy spacy-udpipe
import spacy_udpipe
spacy_udpipe.download("ga")
nlp=spacy_udpipe.load("ga")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spaCy-COMBO](https://github.com/KoichiYasuoka/spaCy-COMBO)
```
!pip install deplacy spacy_combo
import spacy_combo
nlp=spacy_combo.load("ga_idt")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spaCy-jPTDP](https://github.com/KoichiYasuoka/spaCy-jPTDP)
```
!pip install deplacy spacy_jptdp
import spacy_jptdp
nlp=spacy_jptdp.load("ga_idt")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [Camphr-Udify](https://camphr.readthedocs.io/en/latest/notes/udify.html)
```
!pip install deplacy camphr en-udify@https://github.com/PKSHATechnology-Research/camphr_models/releases/download/0.7.0/en_udify-0.7.tar.gz
import pkg_resources,imp
imp.reload(pkg_resources)
import spacy
nlp=spacy.load("en_udify")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
| true |
code
| 0.288795 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_python.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# MMClassification Python API tutorial on Colab
In this tutorial, we will introduce the following content:
* How to install MMCls
* Inference a model with Python API
* Fine-tune a model with Python API
## Install MMClassification
Before using MMClassification, we need to prepare the environment with the following steps:
1. Install Python, CUDA, C/C++ compiler and git
2. Install PyTorch (CUDA version)
3. Install mmcv
4. Clone mmcls source code from GitHub and install it
Because this tutorial is on Google Colab, and the basic environment has been completed, we can skip the first two steps.
### Check environment
```
%cd /content
!pwd
# Check nvcc version
!nvcc -V
# Check GCC version
!gcc --version
# Check PyTorch installation
import torch, torchvision
print(torch.__version__)
print(torch.cuda.is_available())
```
### Install MMCV
MMCV is the basic package of all OpenMMLab packages. We have pre-built wheels on Linux, so we can download and install them directly.
Please pay attention to PyTorch and CUDA versions to match the wheel.
In the above steps, we have checked the version of PyTorch and CUDA, and they are 1.9.0 and 11.1 respectively, so we need to choose the corresponding wheel.
In addition, we can also install the full version of mmcv (mmcv-full). It includes full features and various CUDA ops out of the box, but needs a longer time to build.
```
# Install mmcv
!pip install mmcv -f https://download.openmmlab.com/mmcv/dist/cu111/torch1.9.0/index.html
# !pip install mmcv-full -f https://download.openmmlab.com/mmcv/dist/cu110/torch1.9.0/index.html
```
### Clone and install MMClassification
Next, we clone the latest mmcls repository from GitHub and install it.
```
# Clone mmcls repository
!git clone https://github.com/open-mmlab/mmclassification.git
%cd mmclassification/
# Install MMClassification from source
!pip install -e .
# Check MMClassification installation
import mmcls
print(mmcls.__version__)
```
## Inference a model with Python API
MMClassification provides many pre-trained models, and you can check them by the link of [model zoo](https://mmclassification.readthedocs.io/en/latest/model_zoo.html). Almost all models can reproduce the results in original papers or reach higher metrics. And we can use these models directly.
To use the pre-trained model, we need to do the following steps:
- Prepare the model
- Prepare the config file
- Prepare the checkpoint file
- Build the model
- Inference with the model
```
# Get the demo image
!wget https://www.dropbox.com/s/k5fsqi6qha09l1v/banana.png?dl=0 -O demo/banana.png
from PIL import Image
Image.open('demo/banana.png')
```
### Prepare the config file and checkpoint file
We configure a model with a config file and save weights with a checkpoint file.
On GitHub, you can find all these pre-trained models in the config folder of MMClassification. For example, you can find the config files and checkpoints of Mobilenet V2 in [this link](https://github.com/open-mmlab/mmclassification/tree/master/configs/mobilenet_v2).
We have integrated many config files for various models in the MMClassification repository. As for the checkpoint, we can download it in advance, or just pass an URL to API, and MMClassification will download it before load weights.
```
# Confirm the config file exists
!ls configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py
# Specify the path of the config file and checkpoint file.
config_file = 'configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py'
checkpoint_file = 'https://download.openmmlab.com/mmclassification/v0/mobilenet_v2/mobilenet_v2_batch256_imagenet_20200708-3b2dc3af.pth'
```
### Inference the model
MMClassification provides high-level Python API to inference models.
At first, we build the MobilenetV2 model and load the checkpoint.
```
import mmcv
from mmcls.apis import inference_model, init_model, show_result_pyplot
# Specify the device, if you cannot use GPU, you can also use CPU
# by specifying `device='cpu'`.
device = 'cuda:0'
# device = 'cpu'
# Build the model according to the config file and load the checkpoint.
model = init_model(config_file, checkpoint_file, device=device)
# The model's inheritance relationship
model.__class__.__mro__
# The inference result in a single image
img = 'demo/banana.png'
img_array = mmcv.imread(img)
result = inference_model(model, img_array)
result
%matplotlib inline
# Visualize the inference result
show_result_pyplot(model, img, result)
```
## Fine-tune a model with Python API
Fine-tuning is to re-train a model which has been trained on another dataset (like ImageNet) to fit our target dataset. Compared with training from scratch, fine-tuning is much faster can avoid over-fitting problems during training on a small dataset.
The basic steps of fine-tuning are as below:
1. Prepare the target dataset and meet MMClassification's requirements.
2. Modify the training config.
3. Start training and validation.
More details are in [the docs](https://mmclassification.readthedocs.io/en/latest/tutorials/finetune.html).
### Prepare the target dataset
Here we download the cats & dogs dataset directly. You can find more introduction about the dataset in the [tools tutorial](https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_tools.ipynb).
```
# Download the cats & dogs dataset
!wget https://www.dropbox.com/s/wml49yrtdo53mie/cats_dogs_dataset_reorg.zip?dl=0 -O cats_dogs_dataset.zip
!mkdir -p data
!unzip -qo cats_dogs_dataset.zip -d ./data/
```
### Read the config file and modify the config
In the [tools tutorial](https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_tools.ipynb), we have introduced all parts of the config file, and here we can modify the loaded config by Python code.
```
# Load the base config file
from mmcv import Config
cfg = Config.fromfile('configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py')
# Modify the number of classes in the head.
cfg.model.head.num_classes = 2
cfg.model.head.topk = (1, )
# Load the pre-trained model's checkpoint.
cfg.model.backbone.init_cfg = dict(type='Pretrained', checkpoint=checkpoint_file, prefix='backbone')
# Specify sample size and number of workers.
cfg.data.samples_per_gpu = 32
cfg.data.workers_per_gpu = 2
# Specify the path and meta files of training dataset
cfg.data.train.data_prefix = 'data/cats_dogs_dataset/training_set/training_set'
cfg.data.train.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the path and meta files of validation dataset
cfg.data.val.data_prefix = 'data/cats_dogs_dataset/val_set/val_set'
cfg.data.val.ann_file = 'data/cats_dogs_dataset/val.txt'
cfg.data.val.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the path and meta files of test dataset
cfg.data.test.data_prefix = 'data/cats_dogs_dataset/test_set/test_set'
cfg.data.test.ann_file = 'data/cats_dogs_dataset/test.txt'
cfg.data.test.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the normalization parameters in data pipeline
normalize_cfg = dict(type='Normalize', mean=[124.508, 116.050, 106.438], std=[58.577, 57.310, 57.437], to_rgb=True)
cfg.data.train.pipeline[3] = normalize_cfg
cfg.data.val.pipeline[3] = normalize_cfg
cfg.data.test.pipeline[3] = normalize_cfg
# Modify the evaluation metric
cfg.evaluation['metric_options']={'topk': (1, )}
# Specify the optimizer
cfg.optimizer = dict(type='SGD', lr=0.005, momentum=0.9, weight_decay=0.0001)
cfg.optimizer_config = dict(grad_clip=None)
# Specify the learning rate scheduler
cfg.lr_config = dict(policy='step', step=1, gamma=0.1)
cfg.runner = dict(type='EpochBasedRunner', max_epochs=2)
# Specify the work directory
cfg.work_dir = './work_dirs/cats_dogs_dataset'
# Output logs for every 10 iterations
cfg.log_config.interval = 10
# Set the random seed and enable the deterministic option of cuDNN
# to keep the results' reproducible.
from mmcls.apis import set_random_seed
cfg.seed = 0
set_random_seed(0, deterministic=True)
cfg.gpu_ids = range(1)
```
### Fine-tune the model
Use the API `train_model` to fine-tune our model on the cats & dogs dataset.
```
import time
import mmcv
import os.path as osp
from mmcls.datasets import build_dataset
from mmcls.models import build_classifier
from mmcls.apis import train_model
# Create the work directory
mmcv.mkdir_or_exist(osp.abspath(cfg.work_dir))
# Build the classifier
model = build_classifier(cfg.model)
model.init_weights()
# Build the dataset
datasets = [build_dataset(cfg.data.train)]
# Add `CLASSES` attributes to help visualization
model.CLASSES = datasets[0].CLASSES
# Start fine-tuning
train_model(
model,
datasets,
cfg,
distributed=False,
validate=True,
timestamp=time.strftime('%Y%m%d_%H%M%S', time.localtime()),
meta=dict())
%matplotlib inline
# Validate the fine-tuned model
img = mmcv.imread('data/cats_dogs_dataset/training_set/training_set/cats/cat.1.jpg')
model.cfg = cfg
result = inference_model(model, img)
show_result_pyplot(model, img, result)
```
| true |
code
| 0.667568 | null | null | null | null |
|
# Custom Building Recurrent Neural Network
**Notation**:
- Superscript $[l]$ denotes an object associated with the $l^{th}$ layer.
- Superscript $(i)$ denotes an object associated with the $i^{th}$ example.
- Superscript $\langle t \rangle$ denotes an object at the $t^{th}$ time-step.
- **Sub**script $i$ denotes the $i^{th}$ entry of a vector.
Example:
- $a^{(2)[3]<4>}_5$ denotes the activation of the 2nd training example (2), 3rd layer [3], 4th time step <4>, and 5th entry in the vector.
Let's first import all the packages.
```
import numpy as np
from rnn_utils import *
```
## Forward propagation for the basic Recurrent Neural Network
## RNN cell
```
# GRADED FUNCTION: rnn_cell_forward
def rnn_cell_forward(xt, a_prev, parameters):
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# compute next activation state using the formula given above
a_next = a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
# compute output of the current cell using the formula given above
yt_pred = softmax(np.dot(Wya, a_next) + by)
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_pred_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = \n", a_next_tmp.shape)
print("yt_pred[1] =\n", yt_pred_tmp[1])
print("yt_pred.shape = \n", yt_pred_tmp.shape)
```
## 1.2 - RNN forward pass
```
# GRADED FUNCTION: rnn_forward
def rnn_forward(x, a0, parameters):
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and parameters["Wya"]
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
# initialize "a" and "y_pred" with zeros (≈2 lines)
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# Initialize a_next (≈1 line)
a_next = a0
# loop over all time-steps of the input 'x' (1 line)
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈1 line)
a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y_pred[:,:,t] = yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,4)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_pred_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][1] = \n", a_tmp[4][1])
print("a.shape = \n", a_tmp.shape)
print("y_pred[1][3] =\n", y_pred_tmp[1][3])
print("y_pred.shape = \n", y_pred_tmp.shape)
print("caches[1][1][3] =\n", caches_tmp[1][1][3])
print("len(caches) = \n", len(caches_tmp))
```
## Long Short-Term Memory (LSTM) network
### Overview of gates and states
#### - Forget gate $\mathbf{\Gamma}_{f}$
* Let's assume we are reading words in a piece of text, and plan to use an LSTM to keep track of grammatical structures, such as whether the subject is singular ("puppy") or plural ("puppies").
* If the subject changes its state (from a singular word to a plural word), the memory of the previous state becomes outdated, so we "forget" that outdated state.
* The "forget gate" is a tensor containing values that are between 0 and 1.
* If a unit in the forget gate has a value close to 0, the LSTM will "forget" the stored state in the corresponding unit of the previous cell state.
* If a unit in the forget gate has a value close to 1, the LSTM will mostly remember the corresponding value in the stored state.
##### Equation
$$\mathbf{\Gamma}_f^{\langle t \rangle} = \sigma(\mathbf{W}_f[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_f)\tag{1} $$
##### Explanation of the equation:
* $\mathbf{W_{f}}$ contains weights that govern the forget gate's behavior.
* The previous time step's hidden state $[a^{\langle t-1 \rangle}$ and current time step's input $x^{\langle t \rangle}]$ are concatenated together and multiplied by $\mathbf{W_{f}}$.
* A sigmoid function is used to make each of the gate tensor's values $\mathbf{\Gamma}_f^{\langle t \rangle}$ range from 0 to 1.
* The forget gate $\mathbf{\Gamma}_f^{\langle t \rangle}$ has the same dimensions as the previous cell state $c^{\langle t-1 \rangle}$.
* This means that the two can be multiplied together, element-wise.
* Multiplying the tensors $\mathbf{\Gamma}_f^{\langle t \rangle} * \mathbf{c}^{\langle t-1 \rangle}$ is like applying a mask over the previous cell state.
* If a single value in $\mathbf{\Gamma}_f^{\langle t \rangle}$ is 0 or close to 0, then the product is close to 0.
* This keeps the information stored in the corresponding unit in $\mathbf{c}^{\langle t-1 \rangle}$ from being remembered for the next time step.
* Similarly, if one value is close to 1, the product is close to the original value in the previous cell state.
* The LSTM will keep the information from the corresponding unit of $\mathbf{c}^{\langle t-1 \rangle}$, to be used in the next time step.
##### Variable names in the code
The variable names in the code are similar to the equations, with slight differences.
* `Wf`: forget gate weight $\mathbf{W}_{f}$
* `Wb`: forget gate bias $\mathbf{W}_{b}$
* `ft`: forget gate $\Gamma_f^{\langle t \rangle}$
#### Candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$
* The candidate value is a tensor containing information from the current time step that **may** be stored in the current cell state $\mathbf{c}^{\langle t \rangle}$.
* Which parts of the candidate value get passed on depends on the update gate.
* The candidate value is a tensor containing values that range from -1 to 1.
* The tilde "~" is used to differentiate the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ from the cell state $\mathbf{c}^{\langle t \rangle}$.
##### Equation
$$\mathbf{\tilde{c}}^{\langle t \rangle} = \tanh\left( \mathbf{W}_{c} [\mathbf{a}^{\langle t - 1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{c} \right) \tag{3}$$
##### Explanation of the equation
* The 'tanh' function produces values between -1 and +1.
##### Variable names in the code
* `cct`: candidate value $\mathbf{\tilde{c}}^{\langle t \rangle}$
#### - Update gate $\mathbf{\Gamma}_{i}$
* We use the update gate to decide what aspects of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to add to the cell state $c^{\langle t \rangle}$.
* The update gate decides what parts of a "candidate" tensor $\tilde{\mathbf{c}}^{\langle t \rangle}$ are passed onto the cell state $\mathbf{c}^{\langle t \rangle}$.
* The update gate is a tensor containing values between 0 and 1.
* When a unit in the update gate is close to 1, it allows the value of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to be passed onto the hidden state $\mathbf{c}^{\langle t \rangle}$
* When a unit in the update gate is close to 0, it prevents the corresponding value in the candidate from being passed onto the hidden state.
* Notice that we use the subscript "i" and not "u", to follow the convention used in the literature.
##### Equation
$$\mathbf{\Gamma}_i^{\langle t \rangle} = \sigma(\mathbf{W}_i[a^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_i)\tag{2} $$
##### Explanation of the equation
* Similar to the forget gate, here $\mathbf{\Gamma}_i^{\langle t \rangle}$, the sigmoid produces values between 0 and 1.
* The update gate is multiplied element-wise with the candidate, and this product ($\mathbf{\Gamma}_{i}^{\langle t \rangle} * \tilde{c}^{\langle t \rangle}$) is used in determining the cell state $\mathbf{c}^{\langle t \rangle}$.
##### Variable names in code (Please note that they're different than the equations)
In the code, we'll use the variable names found in the academic literature. These variables don't use "u" to denote "update".
* `Wi` is the update gate weight $\mathbf{W}_i$ (not "Wu")
* `bi` is the update gate bias $\mathbf{b}_i$ (not "bu")
* `it` is the forget gate $\mathbf{\Gamma}_i^{\langle t \rangle}$ (not "ut")
#### - Cell state $\mathbf{c}^{\langle t \rangle}$
* The cell state is the "memory" that gets passed onto future time steps.
* The new cell state $\mathbf{c}^{\langle t \rangle}$ is a combination of the previous cell state and the candidate value.
##### Equation
$$ \mathbf{c}^{\langle t \rangle} = \mathbf{\Gamma}_f^{\langle t \rangle}* \mathbf{c}^{\langle t-1 \rangle} + \mathbf{\Gamma}_{i}^{\langle t \rangle} *\mathbf{\tilde{c}}^{\langle t \rangle} \tag{4} $$
##### Explanation of equation
* The previous cell state $\mathbf{c}^{\langle t-1 \rangle}$ is adjusted (weighted) by the forget gate $\mathbf{\Gamma}_{f}^{\langle t \rangle}$
* and the candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$, adjusted (weighted) by the update gate $\mathbf{\Gamma}_{i}^{\langle t \rangle}$
##### Variable names and shapes in the code
* `c`: cell state, including all time steps, $\mathbf{c}$ shape $(n_{a}, m, T)$
* `c_next`: new (next) cell state, $\mathbf{c}^{\langle t \rangle}$ shape $(n_{a}, m)$
* `c_prev`: previous cell state, $\mathbf{c}^{\langle t-1 \rangle}$, shape $(n_{a}, m)$
#### - Output gate $\mathbf{\Gamma}_{o}$
* The output gate decides what gets sent as the prediction (output) of the time step.
* The output gate is like the other gates. It contains values that range from 0 to 1.
##### Equation
$$ \mathbf{\Gamma}_o^{\langle t \rangle}= \sigma(\mathbf{W}_o[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{o})\tag{5}$$
##### Explanation of the equation
* The output gate is determined by the previous hidden state $\mathbf{a}^{\langle t-1 \rangle}$ and the current input $\mathbf{x}^{\langle t \rangle}$
* The sigmoid makes the gate range from 0 to 1.
##### Variable names in the code
* `Wo`: output gate weight, $\mathbf{W_o}$
* `bo`: output gate bias, $\mathbf{b_o}$
* `ot`: output gate, $\mathbf{\Gamma}_{o}^{\langle t \rangle}$
### LSTM cell
```
# GRADED FUNCTION: lstm_cell_forward
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
# Retrieve parameters from "parameters"
Wf = parameters["Wf"] # forget gate weight
bf = parameters["bf"]
Wi = parameters["Wi"] # update gate weight (notice the variable name)
bi = parameters["bi"] # (notice the variable name)
Wc = parameters["Wc"] # candidate value weight
bc = parameters["bc"]
Wo = parameters["Wo"] # output gate weight
bo = parameters["bo"]
Wy = parameters["Wy"] # prediction weight
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
# Concatenate a_prev and xt (≈1 line)
concat = np.zeros((n_a + n_x, m))
concat[: n_a, :] = a_prev
concat[n_a :, :] = xt
# Compute values for ft (forget gate), it (update gate),
# cct (candidate value), c_next (cell state),
# ot (output gate), a_next (hidden state) (≈6 lines)
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
a_next = ot * np.tanh(c_next)
# Compute prediction of the LSTM cell (≈1 line)
yt_pred = softmax(np.dot(Wy, a_next) + by)
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = ", c_next_tmp.shape)
print("c_next[2] = \n", c_next_tmp[2])
print("c_next.shape = ", c_next_tmp.shape)
print("yt[1] =", yt_tmp[1])
print("yt.shape = ", yt_tmp.shape)
print("cache[1][3] =\n", cache_tmp[1][3])
print("len(cache) = ", len(cache_tmp))
```
### Forward pass for LSTM
```
# GRADED FUNCTION: lstm_forward
def lstm_forward(x, a0, parameters):
# Initialize "caches", which will track the list of all the caches
caches = []
# Retrieve dimensions from shapes of x and Wy (≈2 lines)
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wy"].shape
# initialize "a", "c" and "y" with zeros (≈3 lines)
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
# Initialize a_next and c_next (≈2 lines)
a_next = a0
c_next = np.zeros(a_next.shape)
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
a_next, c_next, yt, cache = lstm_cell_forward(x[:, :, t], a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t] = yt
# Save the value of the next cell state (≈1 line)
c[:,:,t] = c_next
# Append the cache into caches (≈1 line)
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi']= np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][3][6] = ", a_tmp[4][3][6])
print("a.shape = ", a_tmp.shape)
print("y[1][4][3] =", y_tmp[1][4][3])
print("y.shape = ", y_tmp.shape)
print("caches[1][1][1] =\n", caches_tmp[1][1][1])
print("c[1][2][1]", c_tmp[1][2][1])
print("len(caches) = ", len(caches_tmp))
```
**Expected Output**:
```Python
a[4][3][6] = 0.172117767533
a.shape = (5, 10, 7)
y[1][4][3] = 0.95087346185
y.shape = (2, 10, 7)
caches[1][1][1] =
[ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.855544916718
len(caches) = 2
```
## Backpropagation in recurrent neural networks
This section is optional and ungraded. It is more difficult and has fewer details regarding its implementation. This section only implements key elements of the full path.
### Basic RNN backward pass
##### Equations
To compute the rnn_cell_backward you can utilize the following equations. It is a good exercise to derive them by hand. Here, $*$ denotes element-wise multiplication while the absence of a symbol indicates matrix multiplication.
$a^{\langle t \rangle} = \tanh(W_{ax} x^{\langle t \rangle} + W_{aa} a^{\langle t-1 \rangle} + b_{a})\tag{-}$
$\displaystyle \frac{\partial \tanh(x)} {\partial x} = 1 - \tanh^2(x) \tag{-}$
$\displaystyle {dW_{ax}} = da_{next} * ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) x^{\langle t \rangle T}\tag{1}$
$\displaystyle dW_{aa} = da_{next} * (( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) a^{\langle t-1 \rangle T}\tag{2}$
$\displaystyle db_a = da_{next} * \sum_{batch}( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{3}$
$\displaystyle dx^{\langle t \rangle} = da_{next} * { W_{ax}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{4}$
$\displaystyle da_{prev} = da_{next} * { W_{aa}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{5}$
#### Implementing rnn_cell_backward
```
def rnn_cell_backward(da_next, cache):
# Retrieve values from cache
(a_next, a_prev, xt, parameters) = cache
# Retrieve values from parameters
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# compute the gradient of the loss with respect to z (optional) (≈1 line)
dtanh = (1 - a_next ** 2) * da_next
# compute the gradient of the loss with respect to Wax (≈2 lines)
dxt = np.dot(Wax.T, dtanh)
dWax = np.dot(dtanh, xt.T)
# compute the gradient with respect to Waa (≈2 lines)
da_prev = np.dot(Waa.T, dtanh)
dWaa = np.dot(dtanh, a_prev.T)
# compute the gradient with respect to b (≈1 line)
dba = np.sum(dtanh, axis = 1,keepdims=1)
# Store the gradients in a python dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
gradients_tmp = rnn_cell_backward(da_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients_tmp["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients_tmp["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients_tmp["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients_tmp["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients_tmp["dba"][4])
print("gradients[\"dba\"].shape =", gradients_tmp["dba"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dxt"][1][2]** =
</td>
<td>
-1.3872130506
</td>
</tr>
<tr>
<td>
**gradients["dxt"].shape** =
</td>
<td>
(3, 10)
</td>
</tr>
<tr>
<td>
**gradients["da_prev"][2][3]** =
</td>
<td>
-0.152399493774
</td>
</tr>
<tr>
<td>
**gradients["da_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWax"][3][1]** =
</td>
<td>
0.410772824935
</td>
</tr>
<tr>
<td>
**gradients["dWax"].shape** =
</td>
<td>
(5, 3)
</td>
</tr>
<tr>
<td>
**gradients["dWaa"][1][2]** =
</td>
<td>
1.15034506685
</td>
</tr>
<tr>
<td>
**gradients["dWaa"].shape** =
</td>
<td>
(5, 5)
</td>
</tr>
<tr>
<td>
**gradients["dba"][4]** =
</td>
<td>
[ 0.20023491]
</td>
</tr>
<tr>
<td>
**gradients["dba"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
#### Backward pass through the RNN
```
def rnn_backward(da, caches):
# Retrieve values from the first cache (t=1) of caches (≈2 lines)
(caches, x) = caches
(a1, a0, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈6 lines)
dx = np.zeros((n_x, m, T_x))
dWax = np.zeros((n_a, n_x))
dWaa = np.zeros((n_a, n_a))
dba = np.zeros((n_a, 1))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
# Loop through all the time steps
for t in reversed(range(T_x)):
# Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t])
# Retrieve derivatives from gradients (≈ 1 line)
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
# Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line)
da0 = da_prevt
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dx"][1][2]** =
</td>
<td>
[-2.07101689 -0.59255627 0.02466855 0.01483317]
</td>
</tr>
<tr>
<td>
**gradients["dx"].shape** =
</td>
<td>
(3, 10, 4)
</td>
</tr>
<tr>
<td>
**gradients["da0"][2][3]** =
</td>
<td>
-0.314942375127
</td>
</tr>
<tr>
<td>
**gradients["da0"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWax"][3][1]** =
</td>
<td>
11.2641044965
</td>
</tr>
<tr>
<td>
**gradients["dWax"].shape** =
</td>
<td>
(5, 3)
</td>
</tr>
<tr>
<td>
**gradients["dWaa"][1][2]** =
</td>
<td>
2.30333312658
</td>
</tr>
<tr>
<td>
**gradients["dWaa"].shape** =
</td>
<td>
(5, 5)
</td>
</tr>
<tr>
<td>
**gradients["dba"][4]** =
</td>
<td>
[-0.74747722]
</td>
</tr>
<tr>
<td>
**gradients["dba"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
## LSTM backward pass
### One Step backward
### Gate derivatives
Note the location of the gate derivatives ($\gamma$..) between the dense layer and the activation function (see graphic above). This is convenient for computing parameter derivatives in the next step.
$d\gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*\left(1-\Gamma_o^{\langle t \rangle}\right)\tag{7}$
$dp\widetilde{c}^{\langle t \rangle} = \left(dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle}* (1-\tanh^2(c_{next})) * \Gamma_u^{\langle t \rangle} * da_{next} \right) * \left(1-\left(\widetilde c^{\langle t \rangle}\right)^2\right) \tag{8}$
$d\gamma_u^{\langle t \rangle} = \left(dc_{next}*\widetilde{c}^{\langle t \rangle} + \Gamma_o^{\langle t \rangle}* (1-\tanh^2(c_{next})) * \widetilde{c}^{\langle t \rangle} * da_{next}\right)*\Gamma_u^{\langle t \rangle}*\left(1-\Gamma_u^{\langle t \rangle}\right)\tag{9}$
$d\gamma_f^{\langle t \rangle} = \left(dc_{next}* c_{prev} + \Gamma_o^{\langle t \rangle} * (1-\tanh^2(c_{next})) * c_{prev} * da_{next}\right)*\Gamma_f^{\langle t \rangle}*\left(1-\Gamma_f^{\langle t \rangle}\right)\tag{10}$
### Parameter derivatives
$ dW_f = d\gamma_f^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{11} $
$ dW_u = d\gamma_u^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{12} $
$ dW_c = dp\widetilde c^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{13} $
$ dW_o = d\gamma_o^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{14}$
To calculate $db_f, db_u, db_c, db_o$ you just need to sum across the horizontal (axis= 1) axis on $d\gamma_f^{\langle t \rangle}, d\gamma_u^{\langle t \rangle}, dp\widetilde c^{\langle t \rangle}, d\gamma_o^{\langle t \rangle}$ respectively. Note that you should have the `keepdims = True` option.
$\displaystyle db_f = \sum_{batch}d\gamma_f^{\langle t \rangle}\tag{15}$
$\displaystyle db_u = \sum_{batch}d\gamma_u^{\langle t \rangle}\tag{16}$
$\displaystyle db_c = \sum_{batch}d\gamma_c^{\langle t \rangle}\tag{17}$
$\displaystyle db_o = \sum_{batch}d\gamma_o^{\langle t \rangle}\tag{18}$
Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.
$ da_{prev} = W_f^T d\gamma_f^{\langle t \rangle} + W_u^T d\gamma_u^{\langle t \rangle}+ W_c^T dp\widetilde c^{\langle t \rangle} + W_o^T d\gamma_o^{\langle t \rangle} \tag{19}$
Here, to account for concatenation, the weights for equations 19 are the first n_a, (i.e. $W_f = W_f[:,:n_a]$ etc...)
$ dc_{prev} = dc_{next}*\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh^2(c_{next}))*\Gamma_f^{\langle t \rangle}*da_{next} \tag{20}$
$ dx^{\langle t \rangle} = W_f^T d\gamma_f^{\langle t \rangle} + W_u^T d\gamma_u^{\langle t \rangle}+ W_c^T dp\widetilde c^{\langle t \rangle} + W_o^T d\gamma_o^{\langle t \rangle}\tag{21} $
where the weights for equation 21 are from n_a to the end, (i.e. $W_f = W_f[:,n_a:]$ etc...)
**Exercise:** Implement `lstm_cell_backward` by implementing equations $7-21$ below.
Note: In the code:
$d\gamma_o^{\langle t \rangle}$ is represented by `dot`,
$dp\widetilde{c}^{\langle t \rangle}$ is represented by `dcct`,
$d\gamma_u^{\langle t \rangle}$ is represented by `dit`,
$d\gamma_f^{\langle t \rangle}$ is represented by `dft`
```
def lstm_cell_backward(da_next, dc_next, cache):
# Retrieve information from "cache"
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
# Retrieve dimensions from xt's and a_next's shape (≈2 lines)
n_x, m = xt.shape
n_a, m = a_next.shape
# Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
dot = da_next * np.tanh(c_next) * ot * (1 - ot)
dcct = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * it * (1 - cct ** 2)
dit = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * cct * (1 - it) * it
dft = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * c_prev * ft * (1 - ft)
# Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
dWf = np.dot(dft, np.hstack([a_prev.T, xt.T]))
dWi = np.dot(dit, np.hstack([a_prev.T, xt.T]))
dWc = np.dot(dcct, np.hstack([a_prev.T, xt.T]))
dWo = np.dot(dot, np.hstack([a_prev.T, xt.T]))
dbf = np.sum(dft, axis=1, keepdims=True)
dbi = np.sum(dit, axis=1, keepdims=True)
dbc = np.sum(dcct, axis=1, keepdims=True)
dbo = np.sum(dot, axis=1, keepdims=True)
# Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
da_prev = np.dot(Wf[:, :n_a].T, dft) + np.dot(Wc[:, :n_a].T, dcct) + np.dot(Wi[:, :n_a].T, dit) + np.dot(Wo[:, :n_a].T, dot)
dc_prev = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * ft
dxt = np.dot(Wf[:, n_a:].T, dft) + np.dot(Wc[:, n_a:].T, dcct) + np.dot(Wi[:, n_a:].T, dit) + np.dot(Wo[:, n_a:].T, dot)
# Save gradients in dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
dc_next_tmp = np.random.randn(5,10)
gradients_tmp = lstm_cell_backward(da_next_tmp, dc_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients_tmp["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients_tmp["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dxt"][1][2]** =
</td>
<td>
3.23055911511
</td>
</tr>
<tr>
<td>
**gradients["dxt"].shape** =
</td>
<td>
(3, 10)
</td>
</tr>
<tr>
<td>
**gradients["da_prev"][2][3]** =
</td>
<td>
-0.0639621419711
</td>
</tr>
<tr>
<td>
**gradients["da_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dc_prev"][2][3]** =
</td>
<td>
0.797522038797
</td>
</tr>
<tr>
<td>
**gradients["dc_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWf"][3][1]** =
</td>
<td>
-0.147954838164
</td>
</tr>
<tr>
<td>
**gradients["dWf"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWi"][1][2]** =
</td>
<td>
1.05749805523
</td>
</tr>
<tr>
<td>
**gradients["dWi"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWc"][3][1]** =
</td>
<td>
2.30456216369
</td>
</tr>
<tr>
<td>
**gradients["dWc"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWo"][1][2]** =
</td>
<td>
0.331311595289
</td>
</tr>
<tr>
<td>
**gradients["dWo"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dbf"][4]** =
</td>
<td>
[ 0.18864637]
</td>
</tr>
<tr>
<td>
**gradients["dbf"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbi"][4]** =
</td>
<td>
[-0.40142491]
</td>
</tr>
<tr>
<td>
**gradients["dbi"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbc"][4]** =
</td>
<td>
[ 0.25587763]
</td>
</tr>
<tr>
<td>
**gradients["dbc"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbo"][4]** =
</td>
<td>
[ 0.13893342]
</td>
</tr>
<tr>
<td>
**gradients["dbo"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
### LSTM BACKWARD
```
def lstm_backward(da, caches):
# Retrieve values from the first cache (t=1) of caches.
(caches, x) = caches
(a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈12 lines)
dx = np.zeros((n_x, m, T_x))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
dc_prevt = np.zeros((n_a, m))
dWf = np.zeros((n_a, n_a + n_x))
dWi = np.zeros((n_a, n_a + n_x))
dWc = np.zeros((n_a, n_a + n_x))
dWo = np.zeros((n_a, n_a + n_x))
dbf = np.zeros((n_a, 1))
dbi = np.zeros((n_a, 1))
dbc = np.zeros((n_a, 1))
dbo = np.zeros((n_a, 1))
# loop back over the whole sequence
for t in reversed(range(T_x)):
# Compute all gradients using lstm_cell_backward
gradients = lstm_cell_backward(da[:,:,t] + da_prevt, dc_prevt, caches[t])
# Store or add the gradient to the parameters' previous step's gradient
dx[:,:,t] = gradients["dxt"]
dWf += gradients["dWf"]
dWi += gradients["dWi"]
dWc += gradients["dWc"]
dWo += gradients["dWo"]
dbf += gradients["dbf"]
dbi += gradients["dbi"]
dbc += gradients["dbc"]
dbo += gradients["dbo"]
# Set the first activation's gradient to the backpropagated gradient da_prev.
da0 = gradients["da_prev"]
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.zeros((2,5)) # unused, but needed for lstm_forward
parameters_tmp['by'] = np.zeros((2,1)) # unused, but needed for lstm_forward
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
da_tmp = np.random.randn(5, 10, 4)
gradients_tmp = lstm_backward(da_tmp, caches_tmp)
print("gradients[\"dx\"][1][2] =", gradients_tmp["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients_tmp["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients_tmp["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients_tmp["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dx"][1][2]** =
</td>
<td>
[0.00218254 0.28205375 -0.48292508 -0.43281115]
</td>
</tr>
<tr>
<td>
**gradients["dx"].shape** =
</td>
<td>
(3, 10, 4)
</td>
</tr>
<tr>
<td>
**gradients["da0"][2][3]** =
</td>
<td>
0.312770310257
</td>
</tr>
<tr>
<td>
**gradients["da0"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWf"][3][1]** =
</td>
<td>
-0.0809802310938
</td>
</tr>
<tr>
<td>
**gradients["dWf"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWi"][1][2]** =
</td>
<td>
0.40512433093
</td>
</tr>
<tr>
<td>
**gradients["dWi"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWc"][3][1]** =
</td>
<td>
-0.0793746735512
</td>
</tr>
<tr>
<td>
**gradients["dWc"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWo"][1][2]** =
</td>
<td>
0.038948775763
</td>
</tr>
<tr>
<td>
**gradients["dWo"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dbf"][4]** =
</td>
<td>
[-0.15745657]
</td>
</tr>
<tr>
<td>
**gradients["dbf"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbi"][4]** =
</td>
<td>
[-0.50848333]
</td>
</tr>
<tr>
<td>
**gradients["dbi"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbc"][4]** =
</td>
<td>
[-0.42510818]
</td>
</tr>
<tr>
<td>
**gradients["dbc"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbo"][4]** =
</td>
<td>
[ -0.17958196]
</td>
</tr>
<tr>
<td>
**gradients["dbo"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
| true |
code
| 0.454291 | null | null | null | null |
|
# Data description:
I'm going to solve the International Airline Passengers prediction problem. This is a problem where given a year and a month, the task is to predict the number of international airline passengers in units of 1,000. The data ranges from January 1949 to December 1960 or 12 years, with 144 observations.
# Workflow:
- Load the Time Series (TS) by Pandas Library
- Prepare the data, i.e. convert the problem to a supervised ML problem
- Build and evaluate the RNN model:
- Fit the best RNN model
- Evaluate model by in-sample prediction: Calculate RMSE
- Forecast the future trend: Out-of-sample prediction
Note: For data exploration of this TS, please refer to the notebook of my alternative solution with "Seasonal ARIMA model"
```
import keras
import sklearn
import tensorflow as tf
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import metrics
from sklearn import preprocessing
import random as rn
import math
%matplotlib inline
from keras import backend as K
session_conf = tf.ConfigProto(intra_op_parallelism_threads=5, inter_op_parallelism_threads=5)
sess = tf.Session(graph=tf.get_default_graph(), config=session_conf)
K.set_session(sess)
import warnings
warnings.filterwarnings("ignore")
# Load data using Series.from_csv
from pandas import Series
#TS = Series.from_csv('C:/Users/rhash/Documents/Datasets/Time Series analysis/daily-minimum-temperatures.csv', header=0)
# Load data using pandas.read_csv
# in case, specify your own date parsing function and use the date_parser argument
from pandas import read_csv
TS = read_csv('C:/Users/rhash/Documents/Datasets/Time Series analysis/AirPassengers.csv', header=0, parse_dates=[0], index_col=0, squeeze=True)
print(TS.head())
#TS=pd.to_numeric(TS, errors='coerce')
TS.dropna(inplace=True)
data=pd.DataFrame(TS.values)
# prepare the data (i.e. convert problem to a supervised ML problem)
def prepare_data(data, lags=1):
"""
Create lagged data from an input time series
"""
X, y = [], []
for row in range(len(data) - lags - 1):
a = data[row:(row + lags), 0]
X.append(a)
y.append(data[row + lags, 0])
return np.array(X), np.array(y)
# normalize the dataset
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(data)
# split into train and test sets
train = dataset[0:120, :]
test = dataset[120:, :]
# LSTM RNN model: _________________________________________________________________
from keras.models import Sequential, Model
from keras.layers import Dense, LSTM, Dropout, average, Input, merge, concatenate
from keras.layers.merge import concatenate
from keras.regularizers import l2, l1
from keras.callbacks import EarlyStopping, ModelCheckpoint
from sklearn.utils.class_weight import compute_sample_weight
from keras.layers.normalization import BatchNormalization
# reshape into X=t and Y=t+1
lags = 3
X_train, y_train = prepare_data(train, lags)
X_test, y_test = prepare_data(test, lags)
# reshape input to be [samples, time steps, features]
X_train = np.reshape(X_train, (X_train.shape[0], lags, 1))
X_test = np.reshape(X_test, (X_test.shape[0], lags, 1))
# create and fit the LSTM network
mdl = Sequential()
#mdl.add(Dense(3, input_shape=(1, lags), activation='relu'))
mdl.add(LSTM(4, activation='relu'))
#mdl.add(Dropout(0.1))
mdl.add(Dense(1))
mdl.compile(loss='mean_squared_error', optimizer='adam')
monitor=EarlyStopping(monitor='loss', min_delta=0.001, patience=100, verbose=1, mode='auto')
history=mdl.fit(X_train, y_train, epochs=1000, batch_size=1, validation_data=(X_test, y_test), callbacks=[monitor], verbose=0)
# To measure RMSE and evaluate the RNN model:
from sklearn.metrics import mean_squared_error
# make predictions
train_predict = mdl.predict(X_train)
test_predict = mdl.predict(X_test)
# invert transformation
train_predict = scaler.inverse_transform(pd.DataFrame(train_predict))
y_train = scaler.inverse_transform(pd.DataFrame(y_train))
test_predict = scaler.inverse_transform(pd.DataFrame(test_predict))
y_test = scaler.inverse_transform(pd.DataFrame(y_test))
# calculate root mean squared error
train_score = math.sqrt(mean_squared_error(y_train, train_predict[:,0]))
print('Train Score: {:.2f} RMSE'.format(train_score))
test_score = math.sqrt(mean_squared_error(y_test, test_predict[:,0]))
print('Test Score: {:.2f} RMSE'.format(test_score))
# list all data in history
#print(history.history.keys())
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
mdl.save('passenger_model.h5')
# shift train predictions for plotting
train_predict_plot =np.full(data.shape, np.nan)
train_predict_plot[lags:len(train_predict)+lags, :] = train_predict
# shift test predictions for plotting
test_predict_plot =np.full(data.shape, np.nan)
test_predict_plot[len(train_predict) + (lags * 2)+1:len(data)-1, :] = test_predict
# plot observation and predictions
plt.figure(figsize=(8,6))
plt.plot(data, label='Observed', color='#006699');
plt.plot(train_predict_plot, label='Prediction for Train Set', color='#006699', alpha=0.5);
plt.plot(test_predict_plot, label='Prediction for Test Set', color='#ff0066');
plt.legend(loc='upper left')
plt.title('LSTM Recurrent Neural Net')
plt.show()
mse = mean_squared_error(y_test, test_predict[:,0])
plt.title('Prediction quality: {:.2f} MSE ({:.2f} RMSE)'.format(mse, math.sqrt(mse)))
plt.plot(y_test.reshape(-1, 1), label='Observed', color='#006699')
plt.plot(test_predict.reshape(-1, 1), label='Prediction', color='#ff0066')
plt.legend(loc='upper left');
plt.show()
```
| true |
code
| 0.703346 | null | null | null | null |
|
# Comparing soundings from NCEP Reanalysis and various models
We are going to plot the global, annual mean sounding (vertical temperature profile) from observations.
Read in the necessary NCEP reanalysis data from the online server.
The catalog is here: <https://psl.noaa.gov/psd/thredds/catalog/Datasets/ncep.reanalysis.derived/catalog.html>
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
ncep_url = "https://psl.noaa.gov/thredds/dodsC/Datasets/ncep.reanalysis.derived/"
ncep_air = xr.open_dataset( ncep_url + "pressure/air.mon.1981-2010.ltm.nc", decode_times=False)
level = ncep_air.level
lat = ncep_air.lat
```
Take global averages and time averages.
```
Tzon = ncep_air.air.mean(dim=('lon','time'))
weight = np.cos(np.deg2rad(lat)) / np.cos(np.deg2rad(lat)).mean(dim='lat')
Tglobal = (Tzon * weight).mean(dim='lat')
```
Here is code to make a nicely labeled sounding plot.
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000))
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Global, annual mean sounding from NCEP Reanalysis', fontsize = 24)
ax2 = ax.twinx()
ax2.plot( Tglobal + 273.15, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Now compute the Radiative Equilibrium solution for the grey-gas column model
```
import climlab
from climlab import constants as const
col = climlab.GreyRadiationModel()
print(col)
col.subprocess['LW'].diagnostics
col.integrate_years(1)
print("Surface temperature is " + str(col.Ts) + " K.")
print("Net energy in to the column is " + str(col.ASR - col.OLR) + " W / m2.")
```
### Plot the radiative equilibrium temperature on the same plot with NCEP reanalysis
```
pcol = col.lev
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=20 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue) and radiative equilibrium in grey gas model (red)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Now use convective adjustment to compute a Radiative-Convective Equilibrium temperature profile
```
dalr_col = climlab.RadiativeConvectiveModel(adj_lapse_rate='DALR')
print(dalr_col)
dalr_col.integrate_years(2.)
print("After " + str(dalr_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(dalr_col.Ts) + " K.")
print("Net energy in to the column is " + str(dalr_col.ASR - dalr_col.OLR) + " W / m2.")
dalr_col.param
```
Now plot this "Radiative-Convective Equilibrium" on the same graph:
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red) and dry RCE (black)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
The convective adjustment gets rid of the unphysical temperature difference between the surface and the overlying air.
But now the surface is colder! Convection acts to move heat upward, away from the surface.
Also, we note that the observed lapse rate (blue) is always shallower than $\Gamma_d$ (temperatures decrease more slowly with height).
## "Moist" Convective Adjustment
To approximately account for the effects of latent heat release in rising air parcels, we can just adjust to a lapse rate that is a little shallow than $\Gamma_d$.
We will choose 6 K / km, which gets close to the observed mean lapse rate.
We will also re-tune the longwave absorptivity of the column to get a realistic surface temperature of 288 K:
```
rce_col = climlab.RadiativeConvectiveModel(adj_lapse_rate=6, abs_coeff=1.7E-4)
print(rce_col)
rce_col.integrate_years(2.)
print("After " + str(rce_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(rce_col.Ts) + " K.")
print("Net energy in to the column is " + str(rce_col.ASR - rce_col.OLR) + " W / m2.")
```
Now add this new temperature profile to the graph:
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.plot( rce_col.Tatm, np.log( pcol / const.ps ), 'm-' )
ax.plot( rce_col.Ts, 0, 'mo', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red), dry RCE (black), and moist RCE (magenta)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Adding stratospheric ozone
Our model has no equivalent of the stratosphere, where temperature increases with height. That's because our model has been completely transparent to shortwave radiation up until now.
We can load some climatogical ozone data:
```
# Put in some ozone
import xarray as xr
ozonepath = "http://thredds.atmos.albany.edu:8080/thredds/dodsC/CLIMLAB/ozone/apeozone_cam3_5_54.nc"
ozone = xr.open_dataset(ozonepath)
ozone
```
Take the global average of the ozone climatology, and plot it as a function of pressure (or height)
```
# Taking annual, zonal, and global averages of the ozone data
O3_zon = ozone.OZONE.mean(dim=("time","lon"))
weight_ozone = np.cos(np.deg2rad(ozone.lat)) / np.cos(np.deg2rad(ozone.lat)).mean(dim='lat')
O3_global = (O3_zon * weight_ozone).mean(dim='lat')
O3_global.shape
ax = plt.figure(figsize=(10,8)).add_subplot(111)
ax.plot( O3_global * 1.E6, np.log(O3_global.lev/const.ps) )
ax.invert_yaxis()
ax.set_xlabel('Ozone (ppm)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
yticks = np.array([1000., 500., 250., 100., 50., 20., 10., 5.])
ax.set_yticks( np.log(yticks/1000.) )
ax.set_yticklabels( yticks )
ax.set_title('Global, annual mean ozone concentration', fontsize = 24);
```
This shows that most of the ozone is indeed in the stratosphere, and peaks near the top of the stratosphere.
Now create a new column model object **on the same pressure levels as the ozone data**. We are also going set an adjusted lapse rate of 6 K / km, and tune the longwave absorption
```
oz_col = climlab.RadiativeConvectiveModel(lev = ozone.lev,
abs_coeff=1.82E-4,
adj_lapse_rate=6,
albedo=0.315)
```
Now we will do something new: let the column absorb some shortwave radiation. We will assume that the shortwave absorptivity is proportional to the ozone concentration we plotted above. We need to weight the absorptivity by the pressure (mass) of each layer.
```
ozonefactor = 75
dp = oz_col.Tatm.domain.axes['lev'].delta
sw_abs = O3_global * dp * ozonefactor
oz_col.subprocess.SW.absorptivity = sw_abs
oz_col.compute()
oz_col.compute()
print(oz_col.SW_absorbed_atm)
```
Now run it out to Radiative-Convective Equilibrium, and plot
```
oz_col.integrate_years(2.)
print("After " + str(oz_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(oz_col.Ts) + " K.")
print("Net energy in to the column is " + str(oz_col.ASR - oz_col.OLR) + " W / m2.")
pozcol = oz_col.lev
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.plot( rce_col.Tatm, np.log( pcol / const.ps ), 'm-' )
ax.plot( rce_col.Ts, 0, 'mo', markersize=16 )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red), dry RCE (black), moist RCE (magenta), RCE with ozone (cyan)', fontsize = 18)
ax.grid()
```
And we finally have something that looks looks like the tropopause, with temperature increasing above at about the correct rate. Though the tropopause temperature is off by 15 degrees or so.
## Greenhouse warming in the RCE model with ozone
```
oz_col2 = climlab.process_like( oz_col )
oz_col2.subprocess['LW'].absorptivity *= 1.2
oz_col2.integrate_years(2.)
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/const.ps), 'b-' )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.plot( oz_col2.Tatm, np.log( pozcol / const.ps ), 'c--' )
ax.plot( oz_col2.Ts, 0, 'co', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/const.ps) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RCE with ozone (cyan)', fontsize = 18)
ax.grid()
```
And we find that the troposphere warms, while the stratosphere cools!
### Vertical structure of greenhouse warming in CESM model
```
datapath = "http://thredds.atmos.albany.edu:8080/thredds/dodsC/CESMA/"
atmstr = ".cam.h0.clim.nc"
cesm_ctrl = xr.open_dataset(datapath + 'som_1850_f19/clim/som_1850_f19' + atmstr)
cesm_2xCO2 = xr.open_dataset(datapath + 'som_1850_2xCO2/clim/som_1850_2xCO2' + atmstr)
cesm_ctrl.T
T_cesm_ctrl_zon = cesm_ctrl.T.mean(dim=('time', 'lon'))
T_cesm_2xCO2_zon = cesm_2xCO2.T.mean(dim=('time', 'lon'))
weight = np.cos(np.deg2rad(cesm_ctrl.lat)) / np.cos(np.deg2rad(cesm_ctrl.lat)).mean(dim='lat')
T_cesm_ctrl_glob = (T_cesm_ctrl_zon*weight).mean(dim='lat')
T_cesm_2xCO2_glob = (T_cesm_2xCO2_zon*weight).mean(dim='lat')
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/const.ps), 'b-' )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.plot( oz_col2.Tatm, np.log( pozcol / const.ps ), 'c--' )
ax.plot( oz_col2.Ts, 0, 'co', markersize=16 )
ax.plot( T_cesm_ctrl_glob, np.log( cesm_ctrl.lev/const.ps ), 'r-' )
ax.plot( T_cesm_2xCO2_glob, np.log( cesm_ctrl.lev/const.ps ), 'r--' )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/const.ps) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RCE with ozone (cyan), CESM (red)', fontsize = 18)
ax.grid()
```
And we find that CESM has the same tendency for increased CO2: warmer troposphere, colder stratosphere.
| true |
code
| 0.612136 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.