prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# US Treasury Interest Rates / Yield Curve Data
---
A look at the US Treasury yield curve, according to interest rates published by the US Treasury.
```
import pandas as pd
import altair as alt
import numpy as np
url = 'https://www.treasury.gov/resource-center/data-chart-center/interest-rates/pages/TextView.aspx?data=yieldYear&year={year}'
def fetchRates(year):
df = pd.read_html(url.format(year=year), skiprows=0, attrs={ "class": "t-chart" })[0]
df['Date'] = pd.to_datetime(df.Date)
return df.set_index('Date').resample('1m').last().reset_index()
fetchTsRates = lambda years: pd.concat(map(fetchRates, years))
#fetchRates(2019).head()
```
## How do the interest rates look for the past 4 years (by instrument)?
```
years = range(2016, 2022)
fields = ['Date', '3 mo', '1 yr', '2 yr', '7 yr', '10 yr']
dfm = fetchTsRates(years)[fields].melt(id_vars='Date', var_name='Maturity')
alt.Chart(dfm).mark_line().encode(
alt.X('Date:T', axis=alt.Axis(title='')),
alt.Y('value:Q',
axis=alt.Axis(title='Interest Rate [%]'),
scale=alt.Scale(domain=[np.floor(dfm['value'].apply(float).min()), np.ceil(dfm['value'].apply(float).max())])),
alt.Color('Maturity:N', sort=fields[1:]),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='U.S. Treasury Yields from {y1} to {y2}'.format(y1=min(years), y2=max(years)),
height=450,
width=700,
background='white'
)
```
### Same chart as above, just a different mix of instruments
```
years = range(2016, 2022)
fields = ['Date', '6 mo', '2 yr', '3 yr', '10 yr', '30 yr']
dfm = fetchTsRates(years)[fields].melt(id_vars='Date', var_name='Maturity')
c = alt.Chart(dfm).mark_line().encode(
alt.X('Date:T', axis=alt.Axis(title='')),
alt.Y('value:Q',
axis=alt.Axis(title='Interest Rate [%]'),
scale=alt.Scale(domain=[np.floor(dfm['value'].apply(float).min()), np.ceil(dfm['value'].apply(float).max())])),
alt.Color('Maturity:N', sort=fields[1:]),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='U.S. Treasury Yields from {y1} to {y2}'.format(y1=min(years), y2=max(years)),
height=450,
width=700,
background='white'
)
c.save('us-treasury-rates.png')
c.display()
```
## How did that chart look for the 4 years before 2008?
```
years = range(2004, 2010)
fields = ['Date', '6 mo', '2 yr', '3 yr', '10 yr', '30 yr']
dfm2 = fetchTsRates(years)[fields].melt(id_vars='Date', var_name='Maturity')
alt.Chart(dfm2).mark_line().encode(
alt.X('Date:T', axis=alt.Axis(title='', format='%b %Y')),
alt.Y('value:Q',
axis=alt.Axis(title='Interest Rate [%]'),
scale=alt.Scale(domain=[np.floor(dfm2['value'].apply(float).min()), np.ceil(dfm2['value'].apply(float).max())])),
alt.Color('Maturity:N', sort=fields[1:]),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='U.S. Treasury Yields from {y1} to {y2}'.format(y1=min(years), y2=max(years)),
height=450,
width=700,
background='white'
)
year = 2019
alt.Chart(fetchRates(year).melt(id_vars='Date', var_name='Maturity')).mark_line().encode(
alt.X('Date:T', axis=alt.Axis(title='')),
alt.Y('value:Q', axis=alt.Axis(title='Interest Rate [%]'), scale=alt.Scale(zero=False)),
alt.Color('Maturity:N',
sort=['1 mo', '2 mo', '3 mo', '6 mo', '1 yr', '2 yr', '3 yr', '5 yr', '7 yr', '10 yr', '20 yr', '30 yr']),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='U.S. Treasury Yields for {year}'.format(year=year),
height=450,
width=700
).interactive()
year = 2007
alt.Chart(fetchRates(year).melt(id_vars='Date', var_name='Maturity')).mark_line().encode(
alt.X('Date:T', axis=alt.Axis(title='')),
alt.Y('value:Q', axis=alt.Axis(title='Interest Rate [%]'), scale=alt.Scale(zero=False)),
alt.Color('Maturity:N',
sort=['1 mo', '2 mo', '3 mo', '6 mo', '1 yr', '2 yr', '3 yr', '5 yr', '7 yr', '10 yr', '20 yr', '30 yr']),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='U.S. Treasury Yields for {year}'.format(year=year),
height=450,
width=700
).interactive()
year = 1996
alt.Chart(fetchRates(year).melt(id_vars='Date', var_name='Maturity')).mark_line().encode(
alt.X('Date:T', axis=alt.Axis(title='')),
alt.Y('value:Q', axis=alt.Axis(title='Interest Rate [%]'), scale=alt.Scale(zero=False)),
alt.Color('Maturity:N'),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='U.S. Treasury Yields for {year}'.format(year=year),
height=450,
width=700
).interactive()
```
## Visualizing the "yield curve" of US Treasuries
```
years = range(2004, 2009)
instruments = {
0.25: '3 Month T-bill',
0.5: '6 Month T-bill',
2: '2 Year Note',
10: '10 Year Note',
30: '30 Year Bond'
}
fieldsToYears = {'3 mo': 0.25, '6 mo': 0.5, '2 yr': 2, '10 yr': 10, '30 yr': 30}
fields = [i for i in fieldsToYears.keys()]
dfm2 = fetchTsRates(years)[fields + ['Date']].melt(id_vars='Date', var_name='Maturity')
dfm2["Year"] = dfm2.Date.apply(lambda v: v.year)
alt.Chart(dfm2.groupby(["Maturity", "Year"]).agg({ "value": "mean" }).reset_index()).mark_line().encode(
alt.X('Maturity:O', axis=alt.Axis(title='Maturity', labelAngle=0), sort=fields),
alt.Y('value:Q', axis=alt.Axis(title='Interest Rate [%]')),
alt.Color('Year:N'),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='U.S. Treasury Yield comparison [{y1} to {y2}]'.format(y1=min(years), y2=max(years)),
height=450,
width=700
)
years = range(2016, 2022)
instruments = {
0.25: '3 Month T-bill',
0.5: '6 Month T-bill',
2: '2 Year Note',
10: '10 Year Note',
30: '30 Year Bond'
}
fieldsToYears = {'3 mo': 0.25, '6 mo': 0.5, '2 yr': 2, '10 yr': 10, '30 yr': 30}
fields = [i for i in fieldsToYears.keys()]
dfm2 = fetchTsRates(years)[fields + ['Date']].melt(id_vars='Date', var_name='Maturity')
dfm2["Year"] = dfm2.Date.apply(lambda v: v.year)
alt.Chart(dfm2.groupby(["Maturity", "Year"]).agg({ "value": "mean" }).reset_index()).mark_line().encode(
alt.X('Maturity:O', axis=alt.Axis(title='Maturity', labelAngle=0), sort=fields),
alt.Y('value:Q', axis=alt.Axis(title='Interest Rate [%]')),
alt.Color('Year:N'),
tooltip=[alt.Tooltip('Date:T', format='%b %Y'), alt.Tooltip('Maturity:N'), alt.Tooltip('value:Q')]
).properties(
title='Yearly Average U.S. Treasury Yield comparison [{y1} to {y2}]'.format(y1=min(years), y2=max(years)),
height=450,
width=700
)
```
| true |
code
| 0.416797 | null | null | null | null |
|
# Exercices
With each exercice will teach you one aspect of deep learning. The process of machine learning can be decompose in 7 steps :
* Data preparation
* Model definition
* Model training
* Model evaluation
* Hyperparameter tuning
* Prediction
## 3 - Model training
- 3.1 Metrics : evaluate model
- 3.2 Loss function (mean square error, cross entropy)
- 3.3 Optimizer function (stochastic gradient descent)
- 3.4 Batch size, epoch number
### Load dataset
```
import torchvision.datasets as dset
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
data_path = './data'
#trans = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (1.0,))])
trans = transforms.Compose([transforms.Resize((32, 32)), transforms.ToTensor()])
# if not exist, download mnist dataset
train_set = dset.MNIST(root=data_path, train=True, transform=trans, download=True)
test_set = dset.MNIST(root=data_path, train=False, transform=trans, download=True)
batch = 4
data_train_loader = DataLoader(train_set, batch_size=batch, shuffle=True, num_workers=8)
data_test_loader = DataLoader(test_set, batch_size=batch, num_workers=8)
classes = ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9')
```
### Define the network architecture
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel, 6 output channels, 5x5 square convolution
# kernel
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square you can only specify a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # all dimensions except the batch dimension
num_features = 1
for s in size:
num_features *= s
return num_features
leNet = Net()
print(leNet)
```
### Define loss criterion and optimizer
```
import torch.optim as optim
criterion = nn.MSELoss()
optimizer = optim.SGD(leNet.parameters(), lr=0.01)
```
### Training loop
```
for epoch in range(3): # loop over the dataset multiple times
leNet.train()
running_loss = 0.0
for i, (images, labels) in enumerate(data_train_loader):
optimizer.zero_grad()
output = leNet(images)
# align vectors labels <=> outputs
label_vect = torch.zeros(4, 10, dtype=torch.float)
for j in range(0, len(labels)):
label_vect[j, labels[j]] = 1.0
loss = criterion(output, label_vect)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
print('[{:d}] loss: {:.5f}'.format(epoch + 1, running_loss / (batch*len(data_train_loader))))
print('Finished Training')
```
### Test the model
```
import matplotlib.pyplot as plt
import numpy as np
def imshow(images, labels):
npimg = images.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.title("Ground Truth: {}".format(labels))
import torchvision
dataiter = iter(data_test_loader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images), labels)
outputs = leNet(images)
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]] for j in range(4)))
```
### Saving leNet
```
torch.save({
'epoch': 1,
'model_state_dict': leNet.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': loss,
}, 'checkpoint-MKTD-pytorch-3.last')
```
| true |
code
| 0.844922 | null | null | null | null |
|
# Real World Example:
### AI, Machine Learning & Data Science
---
# What is the Value for your Business?
- By seeing acutal examples you'll be empowered to ask the right questions (and get fair help from consultants, startups, or data analytics companies)
- This will help you make the correct decisions for your business
# Demystify
This is a real world example of how you'd solve a Machine Learning prediciton problem.
**Common Machine Learning Use Cases in Companies:**
- Discover churn risk of customers
- Predict optimal price levels (investments / retail)
- Predict future revenues
- Build recommendation systems
- Customer value scoring
- Fraud detection
- Customer insights (characteristics)
- Predict sentiment of text / client feedback
- Object detecton in images
- etc etc...
## Why Python?
Python is general purpose and can do Software development, Web development, AI. Python has experienced incredible growth over the last couple of years.
<img src='https://zgab33vy595fw5zq-zippykid.netdna-ssl.com/wp-content/uploads/2017/09/growth_major_languages-1-1400x1200.png' width=400px></img>
Source: https://stackoverflow.blog/2017/09/06/incredible-growth-python/
# Everything is free!
The best software today is open source and it's also enterprise-ready. Anyone can download and use them for free (even for business purposes).
**Examples of great, free AI libraries:**
* Anaconda
* Google's TensorFlow
* Scikit-learn
* Pandas
* Keras
* Matplotlib
* SQL
* Spark
* Numpy
## State-of-the-Art algorithms
No matter what algorithm you want to use (Linear Regression, Random Forests, Neural Networks, or Deep Learning), **all of the latest methods are implemented optimized for Python**.
## Big Data
Python code can run on any computer. Therefore, you can scale your computations and utilize for example cloud resources to run big data jobs.
**Great tools for Big Data:**
- Spark
- Databricks
- Hadoop / MapReduce
- Kafka
- Amazon EC2
- Amazon S3
# Note on data collection
- Collect all the data you can! (storage is cheap)
---
----
# Real world example of AI: Titanic Analysis
Titanic notebook is open source. All of our material is online. Anyone can developt sophisticated AI programs and solutions.
___
## The difficult part is never to implement the algorithm
The hard part of a machine learning problem is to get data into the right format so you can solve the problem. We'll illustrate this below.
___

# __Titanic Survivor Analysis__
**Sources:**
* **Training + explanations**: https://www.kaggle.com/c/titanic
___
___
# Understanding the connections between passanger information and survival rate
The sinking of the RMS Titanic is one of the most infamous shipwrecks in history. On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 passengers and crew. This sensational tragedy shocked the international community and led to better safety regulations for ships.
One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others.
### **Our task is to train a machine learning model on a data set consisting of 891 samples of people who were onboard of the Titanic. And then, be able to predict if the passengers survived or not.**
# Import packages
```
# No warnings
import warnings
warnings.filterwarnings('ignore') # Filter out warnings
# data analysis and wrangling
import pandas as pd
import numpy as np
# visualization
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
# machine learning
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB # Gaussian Naive Bays
from sklearn.linear_model import Perceptron
from sklearn.tree import DecisionTreeClassifier
import xgboost as xgb
from plot_distribution import plot_distribution
plt.rcParams['figure.figsize'] = (9, 5)
```
### Load Data
```
df = pd.read_csv('data/train.csv')
```
<a id='sec3'></a>
___
## Part 2: Exploring the Data
**Data descriptions**
<img src="data/Titanic_Variable.png">
```
# preview the data
df.head(3)
# General data statistics
df.describe()
```
### Histograms
```
df.hist(figsize=(13,10));
# Balanced data set?
y_numbers = df['Survived'].map({0:'Deceased',1:'Survived'}).value_counts()
y_numbers
# Imbalanced data set, our classifiers have to outperform 62 % accuracy
y_numbers[1] / y_numbers[0]
```
> #### __Interesting Fact:__
> Third Class passengers were the first to board, with First and Second Class passengers following up to an hour before departure.
> Third Class passengers were inspected for ailments and physical impairments that might lead to their being refused entry to the United States, while First Class passengers were personally greeted by Captain Smith.
```
# Analysis of survival rate for the socioeconmic classes?
df[['Pclass', 'Survived']].groupby(['Pclass'], as_index=True) \
.mean().sort_values(by='Survived', ascending=False)
```
___
> #### __Brief Remarks Regarding the Data__
> * `PassengerId` is a random number (incrementing index) and thus does not contain any valuable information.
> * `Survived, Passenger Class, Age, Siblings Spouses, Parents Children` and `Fare` are numerical values (no need to transform them) -- but, we might want to group them (i.e. create categorical variables).
> * `Sex, Embarked` are categorical features that we need to map to integer values. `Name, Ticket` and `Cabin` might also contain valuable information.
___
```
df.head(1)
```
### Dropping Unnecessary data
__Note:__ It is important to remove variables that convey information already captured by some other variable. Doing so removes the correlation, while also diminishing potential overfit.
```
# Drop columns 'Ticket', 'Cabin', 'Fare' need to do it
# for both test and training
df = df.drop(['PassengerId','Ticket', 'Cabin','Fare'], axis=1)
```
<a id='sec4'></a>
____
## Part 3: Transforming the data
### 3.1 _The Title of the person can be used to predict survival_
```
# List example titles in Name column
df.Name
# Create column called Title
df['Title'] = df['Name'].str.extract(' ([A-Za-z]+)\.', expand=False)
# Double check that our titles makes sense (by comparing to sex)
pd.crosstab(df['Title'], df['Sex'])
# Map rare titles to one group
df['Title'] = df['Title'].\
replace(['Lady', 'Countess','Capt', 'Col', 'Don', 'Dr',\
'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
df['Title'] = df['Title'].replace('Mlle', 'Miss') #Mademoiselle
df['Title'] = df['Title'].replace('Ms', 'Miss')
df['Title'] = df['Title'].replace('Mme', 'Mrs') #Madame
# We now have more logical (contemporary) titles, and fewer groups
# See if we can get some insights
df[['Title', 'Survived']].groupby(['Title']).mean()
# We can plot the survival chance for each title
sns.countplot(x='Survived', hue="Title", data=df, order=[1,0])
plt.xticks(range(2),['Survived','Deceased']);
# Title dummy mapping: Map titles to binary dummy columns
binary_encoded = pd.get_dummies(df.Title)
df[binary_encoded.columns] = binary_encoded
# Remove unique variables for analysis (Title is generally bound to Name, so it's also dropped)
df = df.drop(['Name', 'Title'], axis=1)
df.head()
```
### Map Gender column to binary (male = 0, female = 1) categories
```
# convert categorical variable to numeric
df['Sex'] = df['Sex']. \
map( {'female': 1, 'male': 0} ).astype(int)
df.head()
```
### Handle missing values for age
```
df.Age = df.Age.fillna(df.Age.median())
```
### Split age into bands and look at survival rates
```
# Age bands
df['AgeBand'] = pd.cut(df['Age'], 5)
df[['AgeBand', 'Survived']].groupby(['AgeBand'], as_index=False)\
.mean().sort_values(by='AgeBand', ascending=True)
```
### Suvival probability against age
```
# Plot the relative survival rate distributions against Age of passangers
# subsetted by the gender
plot_distribution( df , var = 'Age' , target = 'Survived' ,\
row = 'Sex' )
# Recall: {'male': 0, 'female': 1}
# Change Age column to
# map Age ranges (AgeBands) to ordinal integer numbers
df.loc[ df['Age'] <= 16, 'Age'] = 0
df.loc[(df['Age'] > 16) & (df['Age'] <= 32), 'Age'] = 1
df.loc[(df['Age'] > 32) & (df['Age'] <= 48), 'Age'] = 2
df.loc[(df['Age'] > 48) & (df['Age'] <= 64), 'Age'] = 3
df.loc[ df['Age'] > 64, 'Age']=4
df = df.drop(['AgeBand'], axis=1)
df.head()
# Note we could just run
# df['Age'] = pd.cut(df['Age'], 5,labels=[0,1,2,3,4])
```
### Travel Party Size
How did the number of people the person traveled with impact the chance of survival?
```
# SibSp = Number of Sibling / Spouses
# Parch = Parents / Children
df['FamilySize'] = df['SibSp'] + df['Parch'] + 1
# Survival chance against FamilySize
df[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=True) \
.mean().sort_values(by='Survived', ascending=False)
# Plot it, 1 is survived
sns.countplot(x='Survived', hue="FamilySize", data=df, order=[1,0]);
# Create binary variable if the person was alone or not
df['IsAlone'] = 0
df.loc[df['FamilySize'] == 1, 'IsAlone'] = 1
df[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=True).mean()
# We will only use the binary IsAlone feature for further analysis
df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1, inplace=True)
df.head()
```
# Feature construction
```
# We can also create new features based on intuitive combinations
# Here is an example when we say that the age times socioclass is a determinant factor
df['Age*Class'] = df.Age.values * df.Pclass.values
df.loc[:, ['Age*Class', 'Age', 'Pclass']].head()
```
## Port the person embarked from
Let's see how that influences chance of survival
<img src= "data/images/titanic_voyage_map.png">
>___
```
# Fill NaN 'Embarked' Values in the dfs
freq_port = df['Embarked'].dropna().mode()[0]
df['Embarked'] = df['Embarked'].fillna(freq_port)
# Plot it, 1 is survived
sns.countplot(x='Survived', hue="Embarked", data=df, order=[1,0]);
df[['Embarked', 'Survived']].groupby(['Embarked'], as_index=True) \
.mean().sort_values(by='Survived', ascending=False)
# Create categorical dummy variables for Embarked values
binary_encoded = pd.get_dummies(df.Embarked)
df[binary_encoded.columns] = binary_encoded
df.drop('Embarked', axis=1, inplace=True)
df.head()
```
### Finished -- Preprocessing Complete!
```
# All features are approximately on the same scale
# no need for feature engineering / normalization
df.head(7)
```
### Sanity Check: View the correlation between features
```
# Uncorrelated features are generally more powerful predictors
colormap = plt.cm.viridis
plt.figure(figsize=(12,12))
plt.title('Pearson Correlation of Features', y=1.05, size=15)
sns.heatmap(df.corr().round(2)\
,linewidths=0.1,vmax=1.0, square=True, cmap=colormap, \
linecolor='white', annot=True);
```
<a id='sec5'></a>
___
### Machine Learning, Prediction and Artifical Intelligence
Now we will use Machine Learning algorithms in order to predict if the person survived.
**We will choose the best model from:**
1. Logistic Regression
2. K-Nearest Neighbors (KNN)
3. Support Vector Machines (SVM)
4. Perceptron
5. XGBoost
6. Random Forest
7. Neural Network (Deep Learning)
### Setup Training and Validation Sets
```
X = df.drop("Survived", axis=1) # Training & Validation data
Y = df["Survived"] # Response / Target Variable
print(X.shape, Y.shape)
# Split training set so that we validate on 20% of the data
# Note that our algorithms will never have seen the validation
np.random.seed(1337) # set random seed for reproducibility
from sklearn.model_selection import train_test_split
X_train, X_val, Y_train, Y_val = \
train_test_split(X, Y, test_size=0.2)
print('Training Samples:', X_train.shape, Y_train.shape)
print('Validation Samples:', X_val.shape, Y_val.shape)
```
___
> ## General ML workflow
> 1. Create Model Object
> 2. Train the Model
> 3. Predict on _unseen_ data
> 4. Evaluate accuracy.
___
## Compare Different Prediciton Models
### 1. Logistic Regression
```
logreg = LogisticRegression() # create
logreg.fit(X_train, Y_train) # train
acc_log_2 = logreg.score(X_val, Y_val) # predict & evaluate
print('Logistic Regression accuracy:',\
str(round(acc_log_2*100,2)),'%')
```
### 2. K-Nearest Neighbour
```
knn = KNeighborsClassifier(n_neighbors = 5) # instantiate
knn.fit(X_train, Y_train) # fit
acc_knn = knn.score(X_val, Y_val) # predict + evaluate
print('K-Nearest Neighbors labeling accuracy:', str(round(acc_knn*100,2)),'%')
```
### 3. Support Vector Machine
```
# Support Vector Machines Classifier (non-linear kernel)
svc = SVC() # instantiate
svc.fit(X_train, Y_train) # fit
acc_svc = svc.score(X_val, Y_val) # predict + evaluate
print('Support Vector Machines labeling accuracy:', str(round(acc_svc*100,2)),'%')
```
### 4. Perceptron
```
perceptron = Perceptron() # instantiate
perceptron.fit(X_train, Y_train) # fit
acc_perceptron = perceptron.score(X_val, Y_val) # predict + evalaute
print('Perceptron labeling accuracy:', str(round(acc_perceptron*100,2)),'%')
```
### 5. Gradient Boosting
```
# XGBoost, same API as scikit-learn
gradboost = xgb.XGBClassifier(n_estimators=1000) # instantiate
gradboost.fit(X_train, Y_train) # fit
acc_xgboost = gradboost.score(X_val, Y_val) # predict + evalute
print('XGBoost labeling accuracy:', str(round(acc_xgboost*100,2)),'%')
```
### 6. Random Forest
```
# Random Forest
random_forest = RandomForestClassifier(n_estimators=500) # instantiate
random_forest.fit(X_train, Y_train) # fit
acc_rf = random_forest.score(X_val, Y_val) # predict + evaluate
print('Random Forest labeling accuracy:', str(round(acc_rf*100,2)),'%')
```
### 7. Neural Networks (Deep Learning)
```
from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add( Dense(units=300, activation='relu', input_shape=(13,) ))
model.add( Dense(units=100, activation='relu'))
model.add( Dense(units=50, activation='relu'))
model.add( Dense(units=1, activation='sigmoid') )
model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
model.fit(X_train, Y_train, epochs = 50, batch_size= 50)
# # Evaluate the model Accuracy on test set
print('Neural Network accuracy:',str(round(model.evaluate(X_val, Y_val, batch_size=50,verbose=False)[1]*100,2)),'%')
```
### Importance scores in the random forest model
```
# Look at importnace of features for random forest
def plot_model_var_imp( model , X , y ):
imp = pd.DataFrame(
model.feature_importances_ ,
columns = [ 'Importance' ] ,
index = X.columns
)
imp = imp.sort_values( [ 'Importance' ] , ascending = True )
imp[ : 10 ].plot( kind = 'barh' )
print ('Training accuracy Random Forest:',model.score( X , y ))
plot_model_var_imp(random_forest, X_train, Y_train)
```
<a id='sec6'></a>
___
## Appendix I:
#### Why are our models maxing out at around 80%?
#### __John Jacob Astor__
<img src= "data/images/john-jacob-astor.jpg">
John Jacob Astor perished in the disaster even though our model predicted he would survive. Astor was the wealthiest person on the Titanic -- his ticket fare was valued at over 35,000 USD in 2016 -- it seems likely that he would have been among of the approximatelly 35 percent of men in first class to survive. However, this was not the case: although his pregnant wife survived, John Jacob Astor’s body was recovered a week later, along with a gold watch, a diamond ring with three stones, and no less than 92,481 USD (2016 value) in cash.
<br >
#### __Olaus Jorgensen Abelseth__
<img src= "data/images/olaus-jorgensen-abelseth.jpg">
Avelseth was a 25-year-old Norwegian sailor, a man in 3rd class, and not expected to survive by classifier. However, once the ship sank, he survived by swimming for 20 minutes in the frigid North Atlantic water before joining other survivors on a waterlogged collapsible boat.
Abelseth got married three years later, settled down as a farmer in North Dakota, had 4 kids, and died in 1980 at the age of 94.
<br >
### __Key Takeaway__
As engineers and business professionals we are trained to answer the question 'what could we do to improve on an 80 percent average'. These data points represent real people. Each time our model was wrong we should be glad -- in such misclasifications we will likely find incredible stories of human nature and courage triumphing over extremely difficult odds.
__It is important to never lose sight of the human element when analyzing data that deals with people.__
<a id='sec7'></a>
___
## Appendix II: Resources and references to material we won't cover in detail
> * **Gradient Boosting:** http://blog.kaggle.com/2017/01/23/a-kaggle-master-explains-gradient-boosting/
> * **Jupyter Notebook (tutorial):** https://www.datacamp.com/community/tutorials/tutorial-jupyter-notebook
> * **K-Nearest Neighbors (KNN):** https://towardsdatascience.com/introduction-to-k-nearest-neighbors-3b534bb11d26
> * **Logistic Regression:** https://towardsdatascience.com/5-reasons-logistic-regression-should-be-the-first-thing-you-learn-when-become-a-data-scientist-fcaae46605c4
> * **Naive Bayes:** http://scikit-learn.org/stable/modules/naive_bayes.html
> * **Perceptron:** http://aass.oru.se/~lilien/ml/seminars/2007_02_01b-Janecek-Perceptron.pdf
> * **Random Forest:** https://medium.com/@williamkoehrsen/random-forest-simple-explanation-377895a60d2d
> * **Support Vector Machines (SVM):** https://towardsdatascience.com/https-medium-com-pupalerushikesh-svm-f4b42800e989
<br>
___
___

| true |
code
| 0.599895 | null | null | null | null |
|
## Neural Networks in PyMC3 estimated with Variational Inference
(c) 2016 by Thomas Wiecki
## Current trends in Machine Learning
There are currently three big trends in machine learning: **Probabilistic Programming**, **Deep Learning** and "**Big Data**". Inside of PP, a lot of innovation is in making things scale using **Variational Inference**. In this blog post, I will show how to use **Variational Inference** in [PyMC3](http://pymc-devs.github.io/pymc3/) to fit a simple Bayesian Neural Network. I will also discuss how bridging Probabilistic Programming and Deep Learning can open up very interesting avenues to explore in future research.
### Probabilistic Programming at scale
**Probabilistic Programming** allows very flexible creation of custom probabilistic models and is mainly concerned with **insight** and learning from your data. The approach is inherently **Bayesian** so we can specify **priors** to inform and constrain our models and get uncertainty estimation in form of a **posterior** distribution. Using [MCMC sampling algorithms](http://twiecki.github.io/blog/2015/11/10/mcmc-sampling/) we can draw samples from this posterior to very flexibly estimate these models. [PyMC3](http://pymc-devs.github.io/pymc3/) and [Stan](http://mc-stan.org/) are the current state-of-the-art tools to consruct and estimate these models. One major drawback of sampling, however, is that it's often very slow, especially for high-dimensional models. That's why more recently, **variational inference** algorithms have been developed that are almost as flexible as MCMC but much faster. Instead of drawing samples from the posterior, these algorithms instead fit a distribution (e.g. normal) to the posterior turning a sampling problem into and optimization problem. [ADVI](http://arxiv.org/abs/1506.03431) -- Automatic Differentation Variational Inference -- is implemented in [PyMC3](http://pymc-devs.github.io/pymc3/) and [Stan](http://mc-stan.org/), as well as a new package called [Edward](https://github.com/blei-lab/edward/) which is mainly concerned with Variational Inference.
Unfortunately, when it comes traditional ML problems like classification or (non-linear) regression, Probabilistic Programming often plays second fiddle (in terms of accuracy and scalability) to more algorithmic approaches like [ensemble learning](https://en.wikipedia.org/wiki/Ensemble_learning) (e.g. [random forests](https://en.wikipedia.org/wiki/Random_forest) or [gradient boosted regression trees](https://en.wikipedia.org/wiki/Boosting_(machine_learning)).
### Deep Learning
Now in its third renaissance, deep learning has been making headlines repeatadly by dominating almost any object recognition benchmark, [kicking ass at Atari games](https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf), and [beating the world-champion Lee Sedol at Go](http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html). From a statistical point, Neural Networks are extremely good non-linear function approximators and representation learners. While mostly known for classification, they have been extended to unsupervised learning with [AutoEncoders](https://arxiv.org/abs/1312.6114) and in all sorts of other interesting ways (e.g. [Recurrent Networks](https://en.wikipedia.org/wiki/Recurrent_neural_network), or [MDNs](http://cbonnett.github.io/MDN_EDWARD_KERAS_TF.html) to estimate multimodal distributions). Why do they work so well? No one really knows as the statistical properties are still not fully understood.
A large part of the innoviation in deep learning is the ability to train these extremely complex models. This rests on several pillars:
* Speed: facilitating the GPU allowed for much faster processing.
* Software: frameworks like [Theano](http://deeplearning.net/software/theano/) and [TensorFlow](https://www.tensorflow.org/) allow flexible creation of abstract models that can then be optimized and compiled to CPU or GPU.
* Learning algorithms: training on sub-sets of the data -- stochastic gradient descent -- allows us to train these models on massive amounts of data. Techniques like drop-out avoid overfitting.
* Architectural: A lot of innovation comes from changing the input layers, like for convolutional neural nets, or the output layers, like for [MDNs](http://cbonnett.github.io/MDN_EDWARD_KERAS_TF.html).
### Bridging Deep Learning and Probabilistic Programming
On one hand we Probabilistic Programming which allows us to build rather small and focused models in a very principled and well-understood way to gain insight into our data; on the other hand we have deep learning which uses many heuristics to train huge and highly complex models that are amazing at prediction. Recent innovations in variational inference allow probabilistic programming to scale model complexity as well as data size. We are thus at the cusp of being able to combine these two approaches to hopefully unlock new innovations in Machine Learning. For more motivation, see also [Dustin Tran's](https://twitter.com/dustinvtran) recent [blog post](http://dustintran.com/blog/a-quick-update-edward-and-some-motivations/).
While this would allow Probabilistic Programming to be applied to a much wider set of interesting problems, I believe this bridging also holds great promise for innovations in Deep Learning. Some ideas are:
* **Uncertainty in predictions**: As we will see below, the Bayesian Neural Network informs us about the uncertainty in its predictions. I think uncertainty is an underappreciated concept in Machine Learning as it's clearly important for real-world applications. But it could also be useful in training. For example, we could train the model specifically on samples it is most uncertain about.
* **Uncertainty in representations**: We also get uncertainty estimates of our weights which could inform us about the stability of the learned representations of the network.
* **Regularization with priors**: Weights are often L2-regularized to avoid overfitting, this very naturally becomes a Gaussian prior for the weight coefficients. We could, however, imagine all kinds of other priors, like spike-and-slab to enforce sparsity (this would be more like using the L1-norm).
* **Transfer learning with informed priors**: If we wanted to train a network on a new object recognition data set, we could bootstrap the learning by placing informed priors centered around weights retrieved from other pre-trained networks, like [GoogLeNet](https://arxiv.org/abs/1409.4842).
* **Hierarchical Neural Networks**: A very powerful approach in Probabilistic Programming is hierarchical modeling that allows pooling of things that were learned on sub-groups to the overall population (see my tutorial on [Hierarchical Linear Regression in PyMC3](http://twiecki.github.io/blog/2014/03/17/bayesian-glms-3/)). Applied to Neural Networks, in hierarchical data sets, we could train individual neural nets to specialize on sub-groups while still being informed about representations of the overall population. For example, imagine a network trained to classify car models from pictures of cars. We could train a hierarchical neural network where a sub-neural network is trained to tell apart models from only a single manufacturer. The intuition being that all cars from a certain manufactures share certain similarities so it would make sense to train individual networks that specialize on brands. However, due to the individual networks being connected at a higher layer, they would still share information with the other specialized sub-networks about features that are useful to all brands. Interestingly, different layers of the network could be informed by various levels of the hierarchy -- e.g. early layers that extract visual lines could be identical in all sub-networks while the higher-order representations would be different. The hierarchical model would learn all that from the data.
* **Other hybrid architectures**: We can more freely build all kinds of neural networks. For example, Bayesian non-parametrics could be used to flexibly adjust the size and shape of the hidden layers to optimally scale the network architecture to the problem at hand during training. Currently, this requires costly hyper-parameter optimization and a lot of tribal knowledge.
## Bayesian Neural Networks in PyMC3
### Generating data
First, lets generate some toy data -- a simple binary classification problem that's not linearly separable.
```
%matplotlib inline
import pymc3 as pm
import theano.tensor as T
import theano
import sklearn
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('white')
from sklearn import datasets
from sklearn.preprocessing import scale
from sklearn.cross_validation import train_test_split
from sklearn.datasets import make_moons
X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000)
X = scale(X)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5)
fig, ax = plt.subplots()
ax.scatter(X[Y==0, 0], X[Y==0, 1], label='Class 0')
ax.scatter(X[Y==1, 0], X[Y==1, 1], color='r', label='Class 1')
sns.despine(); ax.legend()
ax.set(xlabel='X', ylabel='Y', title='Toy binary classification data set');
```
### Model specification
A neural network is quite simple. The basic unit is a [perceptron](https://en.wikipedia.org/wiki/Perceptron) which is nothing more than [logistic regression](http://pymc-devs.github.io/pymc3/notebooks/posterior_predictive.html#Prediction). We use many of these in parallel and then stack them up to get hidden layers. Here we will use 2 hidden layers with 5 neurons each which is sufficient for such a simple problem.
```
# Trick: Turn inputs and outputs into shared variables.
# It's still the same thing, but we can later change the values of the shared variable
# (to switch in the test-data later) and pymc3 will just use the new data.
# Kind-of like a pointer we can redirect.
# For more info, see: http://deeplearning.net/software/theano/library/compile/shared.html
ann_input = theano.shared(X_train)
ann_output = theano.shared(Y_train)
n_hidden = 5
# Initialize random weights between each layer
init_1 = np.random.randn(X.shape[1], n_hidden)
init_2 = np.random.randn(n_hidden, n_hidden)
init_out = np.random.randn(n_hidden)
with pm.Model() as neural_network:
# Weights from input to hidden layer
weights_in_1 = pm.Normal('w_in_1', 0, sd=1,
shape=(X.shape[1], n_hidden),
testval=init_1)
# Weights from 1st to 2nd layer
weights_1_2 = pm.Normal('w_1_2', 0, sd=1,
shape=(n_hidden, n_hidden),
testval=init_2)
# Weights from hidden layer to output
weights_2_out = pm.Normal('w_2_out', 0, sd=1,
shape=(n_hidden,),
testval=init_out)
# Build neural-network using tanh activation function
act_1 = T.tanh(T.dot(ann_input,
weights_in_1))
act_2 = T.tanh(T.dot(act_1,
weights_1_2))
act_out = T.nnet.sigmoid(T.dot(act_2,
weights_2_out))
# Binary classification -> Bernoulli likelihood
out = pm.Bernoulli('out',
act_out,
observed=ann_output)
```
That's not so bad. The `Normal` priors help regularize the weights. Usually we would add a constant `b` to the inputs but I omitted it here to keep the code cleaner.
### Variational Inference: Scaling model complexity
We could now just run a MCMC sampler like [`NUTS`](http://pymc-devs.github.io/pymc3/api.html#nuts) which works pretty well in this case but as I already mentioned, this will become very slow as we scale our model up to deeper architectures with more layers.
Instead, we will use the brand-new [ADVI](http://pymc-devs.github.io/pymc3/api.html#advi) variational inference algorithm which was recently added to `PyMC3`. This is much faster and will scale better. Note, that this is a mean-field approximation so we ignore correlations in the posterior.
```
%%time
with neural_network:
# Run ADVI which returns posterior means, standard deviations, and the evidence lower bound (ELBO)
v_params = pm.variational.advi(n=50000)
```
< 40 seconds on my older laptop. That's pretty good considering that NUTS is having a really hard time. Further below we make this even faster. To make it really fly, we probably want to run the Neural Network on the GPU.
As samples are more convenient to work with, we can very quickly draw samples from the variational posterior using `sample_vp()` (this is just sampling from Normal distributions, so not at all the same like MCMC):
```
with neural_network:
trace = pm.variational.sample_vp(v_params, draws=5000)
```
Plotting the objective function (ELBO) we can see that the optimization slowly improves the fit over time.
```
plt.plot(v_params.elbo_vals)
plt.ylabel('ELBO')
plt.xlabel('iteration')
```
Now that we trained our model, lets predict on the hold-out set using a posterior predictive check (PPC). We use [`sample_ppc()`](http://pymc-devs.github.io/pymc3/api.html#pymc3.sampling.sample_ppc) to generate new data (in this case class predictions) from the posterior (sampled from the variational estimation).
```
# Replace shared variables with testing set
ann_input.set_value(X_test)
ann_output.set_value(Y_test)
# Creater posterior predictive samples
ppc = pm.sample_ppc(trace, model=neural_network, samples=500)
# Use probability of > 0.5 to assume prediction of class 1
pred = ppc['out'].mean(axis=0) > 0.5
fig, ax = plt.subplots()
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1])
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
sns.despine()
ax.set(title='Predicted labels in testing set', xlabel='X', ylabel='Y');
plt.savefig("nn-0.png",dpi=400)
print('Accuracy = {}%'.format((Y_test == pred).mean() * 100))
```
Hey, our neural network did all right!
## Lets look at what the classifier has learned
For this, we evaluate the class probability predictions on a grid over the whole input space.
```
grid = np.mgrid[-3:3:100j,-3:3:100j]
grid_2d = grid.reshape(2, -1).T
X, Y = grid
dummy_out = np.ones(grid.shape[1], dtype=np.int8)
ann_input.set_value(grid_2d)
ann_output.set_value(dummy_out)
# Creater posterior predictive samples
ppc = pm.sample_ppc(trace, model=neural_network, samples=500)
```
### Probability surface
```
cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True)
fig, ax = plt.subplots(figsize=(10, 6))
contour = ax.contourf(X, Y, ppc['out'].mean(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1])
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Posterior predictive mean probability of class label = 0');
plt.savefig("nn-1.png",dpi=400)
```
### Uncertainty in predicted value
So far, everything I showed we could have done with a non-Bayesian Neural Network. The mean of the posterior predictive for each class-label should be identical to maximum likelihood predicted values. However, we can also look at the standard deviation of the posterior predictive to get a sense for the uncertainty in our predictions. Here is what that looks like:
```
cmap = sns.cubehelix_palette(light=1, as_cmap=True)
fig, ax = plt.subplots(figsize=(10, 6))
contour = ax.contourf(X, Y, ppc['out'].std(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1])
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Uncertainty (posterior predictive standard deviation)');
plt.savefig("nn-2.png",dpi=400)
```
We can see that very close to the decision boundary, our uncertainty as to which label to predict is highest. You can imagine that associating predictions with uncertainty is a critical property for many applications like health care. To further maximize accuracy, we might want to train the model primarily on samples from that high-uncertainty region.
## Mini-batch ADVI: Scaling data size
So far, we have trained our model on all data at once. Obviously this won't scale to something like ImageNet. Moreover, training on mini-batches of data (stochastic gradient descent) avoids local minima and can lead to faster convergence.
Fortunately, ADVI can be run on mini-batches as well. It just requires some setting up:
```
from six.moves import zip
# Set back to original data to retrain
ann_input.set_value(X_train)
ann_output.set_value(Y_train)
# Tensors and RV that will be using mini-batches
minibatch_tensors = [ann_input, ann_output]
minibatch_RVs = [out]
# Generator that returns mini-batches in each iteration
def create_minibatch(data):
rng = np.random.RandomState(0)
while True:
# Return random data samples of set size 100 each iteration
ixs = rng.randint(len(data), size=50)
yield data[ixs]
minibatches = zip(
create_minibatch(X_train),
create_minibatch(Y_train),
)
total_size = len(Y_train)
```
While the above might look a bit daunting, I really like the design. Especially the fact that you define a generator allows for great flexibility. In principle, we could just pool from a database there and not have to keep all the data in RAM.
Lets pass those to `advi_minibatch()`:
```
%%time
with neural_network:
# Run advi_minibatch
v_params = pm.variational.advi_minibatch(
n=50000, minibatch_tensors=minibatch_tensors,
minibatch_RVs=minibatch_RVs, minibatches=minibatches,
total_size=total_size, learning_rate=1e-2, epsilon=1.0
)
with neural_network:
trace = pm.variational.sample_vp(v_params, draws=5000)
plt.plot(v_params.elbo_vals)
plt.ylabel('ELBO')
plt.xlabel('iteration')
sns.despine()
```
As you can see, mini-batch ADVI's running time is much lower. It also seems to converge faster.
For fun, we can also look at the trace. The point is that we also get uncertainty of our Neural Network weights.
```
pm.traceplot(trace);
```
## Summary
Hopefully this blog post demonstrated a very powerful new inference algorithm available in [PyMC3](http://pymc-devs.github.io/pymc3/): [ADVI](http://pymc-devs.github.io/pymc3/api.html#advi). I also think bridging the gap between Probabilistic Programming and Deep Learning can open up many new avenues for innovation in this space, as discussed above. Specifically, a hierarchical neural network sounds pretty bad-ass. These are really exciting times.
## Next steps
[`Theano`](http://deeplearning.net/software/theano/), which is used by `PyMC3` as its computational backend, was mainly developed for estimating neural networks and there are great libraries like [`Lasagne`](https://github.com/Lasagne/Lasagne) that build on top of `Theano` to make construction of the most common neural network architectures easy. Ideally, we wouldn't have to build the models by hand as I did above, but use the convenient syntax of `Lasagne` to construct the architecture, define our priors, and run ADVI.
While we haven't successfully run `PyMC3` on the GPU yet, it should be fairly straight forward (this is what `Theano` does after all) and further reduce the running time significantly. If you know some `Theano`, this would be a great area for contributions!
You might also argue that the above network isn't really deep, but note that we could easily extend it to have more layers, including convolutional ones to train on more challenging data sets.
I also presented some of this work at PyData London, view the video below:
<iframe width="560" height="315" src="https://www.youtube.com/embed/LlzVlqVzeD8" frameborder="0" allowfullscreen></iframe>
Finally, you can download this NB [here](https://github.com/twiecki/WhileMyMCMCGentlySamples/blob/master/content/downloads/notebooks/bayesian_neural_network.ipynb). Leave a comment below, and [follow me on twitter](https://twitter.com/twiecki).
## Acknowledgements
[Taku Yoshioka](https://github.com/taku-y) did a lot of work on ADVI in PyMC3, including the mini-batch implementation as well as the sampling from the variational posterior. I'd also like to the thank the Stan guys (specifically Alp Kucukelbir and Daniel Lee) for deriving ADVI and teaching us about it. Thanks also to Chris Fonnesbeck, Andrew Campbell, Taku Yoshioka, and Peadar Coyle for useful comments on an earlier draft.
| true |
code
| 0.710729 | null | null | null | null |
|
# 1.1 Getting started
## Prerequisites
### Installation
This tutorial requires **signac**, so make sure to install the package before starting.
The easiest way to do so is using conda:
```$ conda config --add channels conda-forge```
```$ conda install signac```
or pip:
```pip install signac --user```
Please refer to the [documentation](https://docs.signac.io/en/latest/installation.html#installation) for detailed instructions on how to install signac.
After successful installation, the following cell should execute without error:
```
import signac
```
We start by removing all data which might be left-over from previous executions of this tutorial.
```
%rm -rf projects/tutorial/workspace
```
## A minimal example
For this tutorial we want to compute the volume of an ideal gas as a function of its pressure and thermal energy using the ideal gas equation
$p V = N kT$, where
$N$ refers to the system size, $p$ to the pressure, $kT$ to the thermal energy and $V$ is the volume of the system.
```
def V_idg(N, kT, p):
return N * kT / p
```
We can execute the complete study in just a few lines of code.
First, we initialize the project directory and get a project handle:
```
import signac
project = signac.init_project(name="TutorialProject", root="projects/tutorial")
```
We iterate over the variable of interest *p* and construct a complete state point *sp* which contains all the meta data associated with our data.
In this simple example the meta data is very compact, but in principle the state point may be highly complex.
Next, we obtain a *job* handle and store the result of the calculation within the *job document*.
The *job document* is a persistent dictionary for storage of simple key-value pairs.
Here, we exploit that the state point dictionary *sp* can easily be passed into the `V_idg()` function using the [keyword expansion syntax](https://docs.python.org/dev/tutorial/controlflow.html#keyword-arguments) (`**sp`).
```
for p in 0.1, 1.0, 10.0:
sp = {"p": p, "kT": 1.0, "N": 1000}
job = project.open_job(sp)
job.document["V"] = V_idg(**sp)
```
We can then examine our results by iterating over the data space:
```
for job in project:
print(job.sp.p, job.document["V"])
```
That's it.
...
Ok, there's more...
Let's have a closer look at the individual components.
## The Basics
The **signac** data management framework assists the user in managing the data space of individual *projects*.
All data related to one or multiple projects is stored in a *workspace*, which by default is a directory called `workspace` within the project's root directory.
```
print(project.root_directory())
print(project.workspace())
```
The core idea is to tightly couple state points, unique sets of parameters, with their associated data.
In general, the parameter space needs to contain all parameters that will affect our data.
For the ideal gas that is a 3-dimensional space spanned by the thermal energy *kT*, the pressure *p* and the system size *N*.
These are the **input parameters** for our calculations, while the calculated volume *V* is the **output data**.
In terms of **signac** this relationship is represented by an instance of `Job`.
We use the `open_job()` method to get a *job handle* for a specific set of input parameters.
```
job = project.open_job({"p": 1.0, "kT": 1.0, "N": 1000})
```
The *job* handle tightly couples our input parameters (*p*, *kT*, *N*) with the storage location of the output data.
You can inspect both the input parameters and the storage location explicitly:
```
print(job.statepoint())
print(job.workspace())
```
For convenience, a job's *state point* may also be accessed via the short-hand `sp` attribute.
For example, to access the pressure value `p` we can use either of the two following expressions:
```
print(job.statepoint()["p"])
print(job.sp.p)
```
Each *job* has a **unique id** representing the state point.
This means opening a job with the exact same input parameters is guaranteed to have the **exact same id**.
```
job2 = project.open_job({"kT": 1.0, "N": 1000, "p": 1.0})
print(job.id, job2.id)
```
The *job id* is used to uniquely identify data associated with a specific state point.
Think of the *job* as a container that is used to store all data associated with the state point.
For example, it should be safe to assume that all files that are stored within the job's workspace directory are tightly coupled to the job's statepoint.
```
print(job.workspace())
```
Let's store the volume calculated for each state point in a file called `V.txt` within the job's workspace.
```
import os
fn_out = os.path.join(job.workspace(), "V.txt")
with open(fn_out, "w") as file:
V = V_idg(**job.statepoint())
file.write(str(V) + "\n")
```
Because this is such a common pattern, **signac** signac allows you to short-cut this with the `job.fn()` method.
```
with open(job.fn("V.txt"), "w") as file:
V = V_idg(**job.statepoint())
file.write(str(V) + "\n")
```
Sometimes it is easier to temporarily switch the *current working directory* while storing data for a specific job.
For this purpose, we can use the `Job` object as [context manager](https://docs.python.org/3/reference/compound_stmts.html#with).
This means that we switch into the workspace directory associated with the job after entering, and switch back into the original working directory after exiting.
```
with job:
with open("V.txt", "w") as file:
file.write(str(V) + "\n")
```
Another alternative to store light-weight data is the *job document* as shown in the minimal example.
The *job document* is a persistent JSON storage file for simple key-value pairs.
```
job.document["V"] = V_idg(**job.statepoint())
print(job.statepoint(), job.document)
```
Since we are usually interested in more than one state point, the standard operation is to iterate over all variable(s) of interest, construct the full state point, get the associated job handle, and then either just initialize the job or perform the full operation.
```
for pressure in 0.1, 1.0, 10.0:
statepoint = {"p": pressure, "kT": 1.0, "N": 1000}
job = project.open_job(statepoint)
job.document["V"] = V_idg(**job.statepoint())
```
Let's verify our result by inspecting the data.
```
for job in project:
print(job.statepoint(), job.document)
```
Those are the basics for using **signac** for data management.
The [next section](signac_102_Exploring_Data.ipynb) demonstrates how to explore an existing data space.
| true |
code
| 0.713194 | null | null | null | null |
|
```
"""
A randomly connected network learning a sequence
This example contains a reservoir network of 500 neurons.
400 neurons are excitatory and 100 neurons are inhibitory.
The weights are initialized randomly, based on a log-normal distribution.
The network activity is stimulated with three different inputs (A, B, C).
The inputs are given in i a row (A -> B -> C -> A -> ...)
The experiment is defined in 'pelenet/experiments/sequence.py' file.
A log file, parameters, and plot figures are stored in the 'log' folder for every run of the simulation.
NOTE: The main README file contains some more information about the structure of pelenet
"""
# Load pelenet modules
from pelenet.utils import Utils
from pelenet.experiments.sequence import SequenceExperiment
# Official modules
import numpy as np
import matplotlib.pyplot as plt
# Overwrite default parameters (pelenet/parameters/ and pelenet/experiments/sequence.py)
parameters = {
# Experiment
'seed': 1, # Random seed
'trials': 10, # Number of trials
'stepsPerTrial': 60, # Number of simulation steps for every trial
# Neurons
'refractoryDelay': 2, # Refactory period
'voltageTau': 100, # Voltage time constant
'currentTau': 5, # Current time constant
'thresholdMant': 1200, # Spiking threshold for membrane potential
# Network
'reservoirExSize': 400, # Number of excitatory neurons
'reservoirConnPerNeuron': 35, # Number of connections per neuron
'isLearningRule': True, # Apply a learning rule
'learningRule': '2^-2*x1*y0 - 2^-2*y1*x0 + 2^-4*x1*y1*y0 - 2^-3*y0*w*w', # Defines the learning rule
# Input
'inputIsSequence': True, # Activates sequence input
'inputSequenceSize': 3, # Number of input clusters in sequence
'inputSteps': 20, # Number of steps the trace input should drive the network
'inputGenSpikeProb': 0.8, # Probability of spike for the generator
'inputNumTargetNeurons': 40, # Number of neurons activated by the input
# Probes
'isExSpikeProbe': True, # Probe excitatory spikes
'isInSpikeProbe': True, # Probe inhibitory spikes
'isWeightProbe': True # Probe weight matrix at the end of the simulation
}
# Initilizes the experiment, also initializes the log
# Creating a new object results in a new log entry in the 'log' folder
# The name is optional, it is extended to the folder in the log directory
exp = SequenceExperiment(name='random-network-sequence-learning', parameters=parameters)
# Instantiate the utils singleton
utils = Utils.instance()
# Build the network, in this function the weight matrix, inputs, probes, etc. are defined and created
exp.build()
# Run the network simulation, afterwards the probes are postprocessed to nice arrays
exp.run()
# Weight matrix before learning (randomly initialized)
exp.net.plot.initialExWeightMatrix()
# Plot distribution of weights
exp.net.plot.initialExWeightDistribution(figsize=(12,3))
# Plot spike trains of the excitatory (red) and inhibitory (blue) neurons
exp.net.plot.reservoirSpikeTrain(figsize=(12,6), to=600)
# Weight matrix after learning
exp.net.plot.trainedExWeightMatrix()
# Sorted weight matrix after learning
supportMask = utils.getSupportWeightsMask(exp.net.trainedWeightsExex)
exp.net.plot.weightsSortedBySupport(supportMask)
```
| true |
code
| 0.879432 | null | null | null | null |
|
# Google form analysis visualizations
## Table of Contents
['Google form analysis' functions checks](#funcchecks)
['Google form analysis' functions tinkering](#functinkering)
```
%run "../Functions/1. Google form analysis.ipynb"
```
## 'Google form analysis' functions checks
<a id=funcchecks />
## 'Google form analysis' functions tinkering
<a id=functinkering />
```
binarizedAnswers = plotBasicStats(getSurveysOfBiologists(gform), 'non biologists', includeUndefined = True)
gform.loc[:, [localplayerguidkey, 'Temporality']].groupby('Temporality').count()
#sample = gform.copy()
samples = [
[gform.copy(), 'complete set'],
[gform[gform['Language'] == 'en'], 'English'],
[gform[gform['Language'] == 'fr'], 'French'],
[gform[gform['What is your gender?'] == 'Female'], 'female'],
[gform[gform['What is your gender?'] == 'Male'], 'male'],
[getSurveysOfUsersWhoAnsweredBoth(gform), 'answered both'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'en']), 'answered both, en'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'fr']), 'answered both, fr'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['What is your gender?'] == 'Female']), 'answered both, female'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['What is your gender?'] == 'Male']), 'answered both, male'],
]
_progress = FloatProgress(min=0, max=len(samples))
display(_progress)
includeAll = False
includeBefore = True
includeAfter = True
includeUndefined = False
includeProgress = True
includeRelativeProgress = False
for sample, title in samples:
## basic stats:
### mean score
### median score
### std
## sample can be: all, those who answered both before and after,
## those who played between date1 and date2, ...
#def plotBasicStats(sample, title, includeAll, includeBefore, includeAfter, includeUndefined, includeProgress, includeRelativeProgress):
stepsPerInclude = 2
includeCount = np.sum([includeAll, includeBefore, includeAfter, includeUndefined, includeProgress])
stepsCount = stepsPerInclude*includeCount + 3
#print("stepsPerInclude=" + str(stepsPerInclude))
#print("includeCount=" + str(includeCount))
#print("stepsCount=" + str(stepsCount))
__progress = FloatProgress(min=0, max=stepsCount)
display(__progress)
sampleBefore = sample[sample['Temporality'] == 'before']
sampleAfter = sample[sample['Temporality'] == 'after']
sampleUndefined = sample[sample['Temporality'] == 'undefined']
#uniqueBefore = sampleBefore[localplayerguidkey]
#uniqueAfter =
#uniqueUndefined =
scientificQuestions = correctAnswers.copy()
allQuestions = correctAnswers + demographicAnswers
categories = ['all', 'before', 'after', 'undefined', 'progress', 'rel. progress']
data = {}
sciBinarized = pd.DataFrame()
allBinarized = pd.DataFrame()
scoresAll = pd.DataFrame()
sciBinarizedBefore = pd.DataFrame()
allBinarizedBefore = pd.DataFrame()
scoresBefore = pd.DataFrame()
sciBinarizedAfter = pd.DataFrame()
allBinarizedAfter = pd.DataFrame()
scoresAfter = pd.DataFrame()
sciBinarizedUndefined = pd.DataFrame()
allBinarizedUndefined = pd.DataFrame()
scoresUndefined = pd.DataFrame()
scoresProgress = pd.DataFrame()
## basic stats:
### mean score
### median score
### std
if includeAll:
sciBinarized = getAllBinarized( _source = scientificQuestions, _form = sample)
__progress.value += 1
allBinarized = getAllBinarized( _source = allQuestions, _form = sample)
__progress.value += 1
scoresAll = pd.Series(np.dot(sciBinarized, np.ones(sciBinarized.shape[1])))
data[categories[0]] = createStatSet(scoresAll, sample[localplayerguidkey])
if includeBefore or includeProgress:
sciBinarizedBefore = getAllBinarized( _source = scientificQuestions, _form = sampleBefore)
__progress.value += 1
allBinarizedBefore = getAllBinarized( _source = allQuestions, _form = sampleBefore)
__progress.value += 1
scoresBefore = pd.Series(np.dot(sciBinarizedBefore, np.ones(sciBinarizedBefore.shape[1])))
temporaryStatSetBefore = createStatSet(scoresBefore, sampleBefore[localplayerguidkey])
if includeBefore:
data[categories[1]] = temporaryStatSetBefore
if includeAfter or includeProgress:
sciBinarizedAfter = getAllBinarized( _source = scientificQuestions, _form = sampleAfter)
__progress.value += 1
allBinarizedAfter = getAllBinarized( _source = allQuestions, _form = sampleAfter)
__progress.value += 1
scoresAfter = pd.Series(np.dot(sciBinarizedAfter, np.ones(sciBinarizedAfter.shape[1])))
temporaryStatSetAfter = createStatSet(scoresAfter, sampleAfter[localplayerguidkey])
if includeAfter:
data[categories[2]] = temporaryStatSetAfter
if includeUndefined:
sciBinarizedUndefined = getAllBinarized( _source = scientificQuestions, _form = sampleUndefined)
__progress.value += 1
allBinarizedUndefined = getAllBinarized( _source = allQuestions, _form = sampleUndefined)
__progress.value += 1
scoresUndefined = pd.Series(np.dot(sciBinarizedUndefined, np.ones(sciBinarizedUndefined.shape[1])))
data[categories[3]] = createStatSet(scoresUndefined, sampleUndefined[localplayerguidkey])
if includeProgress:
data[categories[4]] = {
'count' : min(temporaryStatSetAfter['count'], temporaryStatSetBefore['count']),
'unique' : min(temporaryStatSetAfter['unique'], temporaryStatSetBefore['unique']),
'median' : temporaryStatSetAfter['median']-temporaryStatSetBefore['median'],
'mean' : temporaryStatSetAfter['mean']-temporaryStatSetBefore['mean'],
'std' : temporaryStatSetAfter['std']-temporaryStatSetBefore['std'],
}
__progress.value += 2
result = pd.DataFrame(data)
__progress.value += 1
print(title)
print(result)
if (includeBefore and includeAfter) or includeProgress:
if (len(scoresBefore) > 2 and len(scoresAfter) > 2):
ttest = ttest_ind(scoresBefore, scoresAfter)
print("t test: statistic=" + repr(ttest.statistic) + " pvalue=" + repr(ttest.pvalue))
print()
## percentage correct
### percentage correct - max 5 columns
percentagePerQuestionAll = pd.DataFrame()
percentagePerQuestionBefore = pd.DataFrame()
percentagePerQuestionAfter = pd.DataFrame()
percentagePerQuestionUndefined = pd.DataFrame()
percentagePerQuestionProgress = pd.DataFrame()
tables = []
if includeAll:
percentagePerQuestionAll = getPercentagePerQuestion(allBinarized)
tables.append([percentagePerQuestionAll, categories[0]])
if includeBefore or includeProgress:
percentagePerQuestionBefore = getPercentagePerQuestion(allBinarizedBefore)
if includeBefore:
tables.append([percentagePerQuestionBefore, categories[1]])
if includeAfter or includeProgress:
percentagePerQuestionAfter = getPercentagePerQuestion(allBinarizedAfter)
if includeAfter:
tables.append([percentagePerQuestionAfter, categories[2]])
if includeUndefined:
percentagePerQuestionUndefined = getPercentagePerQuestion(allBinarizedUndefined)
tables.append([percentagePerQuestionUndefined, categories[3]])
if includeProgress or includeRelativeProgress:
percentagePerQuestionProgress = percentagePerQuestionAfter - percentagePerQuestionBefore
if includeProgress:
tables.append([percentagePerQuestionProgress, categories[4]])
if includeRelativeProgress:
# use temporaryStatSetAfter['count'], temporaryStatSetBefore['count']?
percentagePerQuestionProgress2 = percentagePerQuestionProgress.copy()
for index in range(0,len(percentagePerQuestionProgress.index)):
if (0 == percentagePerQuestionBefore.iloc[index,0]):
percentagePerQuestionProgress2.iloc[index,0] = 0
else:
percentagePerQuestionProgress2.iloc[index,0] = \
percentagePerQuestionProgress.iloc[index,0]/percentagePerQuestionBefore.iloc[index,0]
tables.append([percentagePerQuestionProgress2, categories[5]])
__progress.value += 1
graphTitle = '% correct: '
toConcat = []
for table,category in tables:
concat = (len(table.values) > 0)
for elt in table.iloc[:,0].values:
if np.isnan(elt):
concat = False
break
if(concat):
graphTitle = graphTitle + category + ' '
toConcat.append(table)
if (len(toConcat) > 0):
percentagePerQuestionConcatenated = pd.concat(
toConcat
, axis=1)
if(len(title) > 0):
graphTitle = graphTitle + ' - ' + title
_fig = plt.figure(figsize=(20,20))
_ax1 = plt.subplot(111)
_ax1.set_title(graphTitle)
sns.heatmap(percentagePerQuestionConcatenated.round().astype(int),ax=_ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d')
__progress.value += 1
### percentage cross correct
### percentage cross correct, conditionnally
if(__progress.value != stepsCount):
print("__progress.value=" + str(__progress.value) + " != stepsCount=" + str(stepsCount))
_progress.value += 1
if(_progress.value != len(samples)):
print("__progress.value=" + str(__progress.value) + " != len(samples)=" + str(len(samples)))
# sciBinarized, sciBinarizedBefore, sciBinarizedAfter, sciBinarizedUndefined, \
# allBinarized, allBinarizedBefore, allBinarizedAfter, allBinarizedUndefined
ttest = ttest_ind(scoresBefore, scoresAfter)
type(scoresBefore), len(scoresBefore),\
type(scoresAfter), len(scoresAfter),\
ttest
type(tables)
sciBinarized = getAllBinarized( _source = scientificQuestions, _form = sample)
series = pd.Series(np.dot(sciBinarized, np.ones(sciBinarized.shape[1])))
#ids = pd.Series()
ids = sample[localplayerguidkey]
#def createStatSet(series, ids):
if(0 == len(ids)):
ids = series.index
result = {
'count' : len(ids),
'unique' : len(ids.unique()),
'median' : series.median(),
'mean' : series.mean(),
'std' : series.std()}
result
## percentage correct
### percentage correct - 3 columns
### percentage cross correct
### percentage cross correct, conditionnally
#_binarized = allBinarized
#_binarized = allBinarizedUndefined
_binarized = allBinarizedBefore
#def getPercentagePerQuestion(_binarized):
totalPerQuestionDF = pd.DataFrame(data=np.dot(np.ones(_binarized.shape[0]), _binarized), index=_binarized.columns)
percentagePerQuestion = totalPerQuestionDF*100 / _binarized.shape[0]
percentagePerQuestion
#totalPerQuestion = np.dot(np.ones(allSciBinarized.shape[0]), allSciBinarized)
#totalPerQuestion.shape
totalPerQuestionSci = np.dot(np.ones(sciBinarized.shape[0]), sciBinarized)
totalPerQuestionAll = np.dot(np.ones(allBinarized.shape[0]), allBinarized)
percentagePerQuestionAll = getPercentagePerQuestion(allBinarized)
percentagePerQuestionBefore = getPercentagePerQuestion(allBinarizedBefore)
percentagePerQuestionAfter = getPercentagePerQuestion(allBinarizedAfter)
percentagePerQuestionUndefined = getPercentagePerQuestion(allBinarizedUndefined)
percentagePerQuestionConcatenated = pd.concat(
[
percentagePerQuestionAll,
percentagePerQuestionBefore,
percentagePerQuestionAfter,
percentagePerQuestionUndefined,
]
, axis=1)
_fig = plt.figure(figsize=(20,20))
_ax1 = plt.subplot(111)
_ax1.set_title('percentage correct per question: all, before, after, undefined')
sns.heatmap(percentagePerQuestionConcatenated.round().astype(int),ax=_ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d')
samples = [gform, gform[gform['Language'] == 'en'], gform[gform['Language'] == 'fr'],
getSurveysOfUsersWhoAnsweredBoth(gform),
getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'en']),
getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'fr'])]
for sample in samples:
sciBinarized, sciBinarizedBefore, sciBinarizedAfter, sciBinarizedUndefined, \
allBinarized, allBinarizedBefore, allBinarizedAfter, allBinarizedUndefined = plotBasicStats(sample)
```
### abandoned algorithms
```
#totalPerQuestion = np.dot(np.ones(sciBinarized.shape[0]), sciBinarized)
#totalPerQuestion.shape
totalPerQuestionSci = np.dot(np.ones(sciBinarized.shape[0]), sciBinarized)
totalPerQuestionAll = np.dot(np.ones(allBinarized.shape[0]), allBinarized)
totalPerQuestionDFAll = pd.DataFrame(data=np.dot(np.ones(allBinarized.shape[0]), allBinarized), index=allBinarized.columns)
percentagePerQuestionAll = totalPerQuestionDFAll*100 / allBinarized.shape[0]
#totalPerQuestionDF
#percentagePerQuestion
#before
totalPerQuestionDFBefore = pd.DataFrame(
data=np.dot(np.ones(allBinarizedBefore.shape[0]), allBinarizedBefore), index=allBinarizedBefore.columns
)
percentagePerQuestionBefore = totalPerQuestionDFBefore*100 / allBinarizedBefore.shape[0]
#after
totalPerQuestionDFAfter = pd.DataFrame(
data=np.dot(np.ones(allBinarizedAfter.shape[0]), allBinarizedAfter), index=allBinarizedAfter.columns
)
percentagePerQuestionAfter = totalPerQuestionDFAfter*100 / allBinarizedAfter.shape[0]
_fig = plt.figure(figsize=(20,20))
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax2.get_yaxis().set_visible(False)
ax3.get_yaxis().set_visible(False)
sns.heatmap(percentagePerQuestionAll.round().astype(int),ax=ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionBefore.round().astype(int),ax=ax2,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionAfter.round().astype(int),ax=ax3,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=True)
ax1.set_title('percentage correct per question - all')
ax2.set_title('percentage correct per question - before')
ax3.set_title('percentage correct per question - after')
# Fine-tune figure; make subplots close to each other and hide x ticks for
# all but bottom plot.
_fig.tight_layout()
_fig = plt.figure(figsize=(20,20))
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax2.get_yaxis().set_visible(False)
ax3.get_yaxis().set_visible(False)
sns.heatmap(percentagePerQuestionAll.round().astype(int),ax=ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionBefore.round().astype(int),ax=ax2,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionAfter.round().astype(int),ax=ax3,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=True)
ax1.set_title('percentage correct per question - all')
ax2.set_title('percentage correct per question - before')
ax3.set_title('percentage correct per question - after')
# Fine-tune figure; make subplots close to each other and hide x ticks for
# all but bottom plot.
_fig.tight_layout()
_fig = plt.figure(figsize=(20,20))
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax2.get_yaxis().set_visible(False)
ax3.get_yaxis().set_visible(False)
sns.heatmap(percentagePerQuestionAll.round().astype(int),ax=ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionBefore.round().astype(int),ax=ax2,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionAfter.round().astype(int),ax=ax3,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=True)
ax1.set_title('percentage correct per question - all')
ax2.set_title('percentage correct per question - before')
ax3.set_title('percentage correct per question - after')
# Fine-tune figure; make subplots close to each other and hide x ticks for
# all but bottom plot.
_fig.tight_layout()
percentagePerQuestionConcatenated = pd.concat([
percentagePerQuestionAll,
percentagePerQuestionBefore,
percentagePerQuestionAfter]
, axis=1)
_fig = plt.figure(figsize=(20,20))
_ax1 = plt.subplot(111)
_ax1.set_title('percentage correct per question: all, before, after')
sns.heatmap(percentagePerQuestionConcatenated.round().astype(int),ax=_ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d')
```
### sample getters tinkering
```
##### getRMAfter / Before tinkering
#def getRMAfters(sample):
afters = sample[sample['Temporality'] == 'after']
#def getRMBefores(sample):
befores = sample[sample['Temporality'] == 'before']
QPlayed1 = 'Have you ever played an older version of Hero.Coli before?'
QPlayed2 = 'Have you played the current version of Hero.Coli?'
QPlayed3 = 'Have you played the arcade cabinet version of Hero.Coli?'
QPlayed4 = 'Have you played the Android version of Hero.Coli?'
```
#### set operators
```
# equality tests
#(sample1.columns == sample2.columns).all()
#sample1.columns.duplicated().any() or sample2.columns.duplicated().any()
#pd.concat([sample1, sample2], axis=1).columns.duplicated().any()
```
##### getUnionQuestionnaires tinkering
```
sample1 = befores
sample2 = afters
#def getUnionQuestionnaires(sample1, sample2):
if (not (sample1.columns == sample2.columns).all()):
print("warning: parameter columns are not the same")
result = pd.concat([sample1, sample2]).drop_duplicates()
```
##### getIntersectionQuestionnaires tinkering
```
sample1 = befores[:15]
sample2 = befores[10:]
#def getIntersectionQuestionnaires(sample1, sample2):
if (not (sample1.columns == sample2.columns).all()):
print("warning: parameter columns are not the same")
result = pd.merge(sample1, sample2, how = 'inner').drop_duplicates()
```
##### getIntersectionUsersSurveys tinkering
```
sample1 = befores
sample2 = afters
# get sample1 and sample2 rows where users are common to sample1 and sample2
#def getIntersectionUsersSurveys(sample1, sample2):
result1 = sample1[sample1[localplayerguidkey].isin(sample2[localplayerguidkey])]
result2 = sample2[sample2[localplayerguidkey].isin(sample1[localplayerguidkey])]
result = getUnionQuestionnaires(result1,result2)
len(sample1), len(sample2), len(result)
```
##### getGFormBefores tinkering
```
sample = gform
# returns users who declared that they have never played the game, whatever platform
# previousPlayPositives is defined in '../Static data/English localization.ipynb'
#def getGFormBefores(sample):
befores = sample[
~sample[QPlayed1].isin(previousPlayPositives)
& ~sample[QPlayed2].isin(previousPlayPositives)
& ~sample[QPlayed3].isin(previousPlayPositives)
& ~sample[QPlayed4].isin(previousPlayPositives)
]
len(befores)
```
##### getGFormAfters tinkering
```
sample = gform
# returns users who declared that they have already played the game, whatever platform
# previousPlayPositives is defined in '../Static data/English localization.ipynb'
#def getGFormAfters(sample):
afters = sample[
sample[QPlayed1].isin(previousPlayPositives)
| sample[QPlayed2].isin(previousPlayPositives)
| sample[QPlayed3].isin(previousPlayPositives)
| sample[QPlayed4].isin(previousPlayPositives)
]
len(afters)
```
##### getGFormTemporality tinkering
```
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[3]
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
sample = gform
answerTemporalities[1]
#while result != 'after':
_GFUserId = getRandomGFormGUID()
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
# returns an element of answerTemporalities
# previousPlayPositives is defined in '../Static data/English localization.ipynb'
#def getGFormRowGFormTemporality(_gformRow):
result = answerTemporalities[2]
if (_gformRow[QPlayed1] in previousPlayPositives)\
or (_gformRow[QPlayed2] in previousPlayPositives)\
or (_gformRow[QPlayed3] in previousPlayPositives)\
or (_gformRow[QPlayed4] in previousPlayPositives):
result = answerTemporalities[1]
else:
result = answerTemporalities[0]
result
```
#### getSurveysOfUsersWhoAnsweredBoth tinkering
```
sample = gform
gfMode = True
rmMode = False
#def getSurveysOfUsersWhoAnsweredBoth(sample, gfMode = True, rmMode = False):
befores = sample
afters = sample
if gfMode:
befores = getGFormBefores(befores)
afters = getGFormAfters(afters)
if rmMode:
befores = getRMBefores(befores)
afters = getRMAfters(afters)
result = getIntersectionUsersSurveys(befores, afters)
((len(getGFormBefores(sample)),\
len(getRMBefores(sample)),\
len(befores)),\
(len(getGFormAfters(sample)),\
len(getRMAfters(sample)),\
len(afters)),\
len(result)),\
\
((getUniqueUserCount(getGFormBefores(sample)),\
getUniqueUserCount(getRMBefores(sample)),\
getUniqueUserCount(befores)),\
(getUniqueUserCount(getGFormAfters(sample)),\
getUniqueUserCount(getRMAfters(sample)),\
getUniqueUserCount(afters)),\
getUniqueUserCount(result))
len(getSurveysOfUsersWhoAnsweredBoth(gform, gfMode = True, rmMode = True)[localplayerguidkey])
```
#### getSurveysThatAnswered tinkering
```
sample = gform
#_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[1]
#sample = gform[gform[localplayerguidkey] == _GFUserId]
hardPolicy = True
questionsAndPositiveAnswers = [[Q6BioEdu, biologyStudyPositives],
[Q8SynBio, yesNoIdontknowPositives],
[Q9BioBricks, yesNoIdontknowPositives]]
#def getSurveysThatAnswered(sample, questionsAndPositiveAnswers, hardPolicy = True):
filterSeries = []
if hardPolicy:
filterSeries = pd.Series(True, sample.index)
for question, positiveAnswers in questionsAndPositiveAnswers:
filterSeries = filterSeries & (sample[question].isin(positiveAnswers))
else:
filterSeries = pd.Series(False, sample.index)
for question, positiveAnswers in questionsAndPositiveAnswers:
filterSeries = filterSeries | (sample[question].isin(positiveAnswers))
result = sample[filterSeries]
```
#### getSurveysOfBiologists tinkering
```
sample = gform
hardPolicy = True
#def getSurveysOfBiologists(sample, hardPolicy = True):
Q6BioEdu = 'How long have you studied biology?' #biologyStudyPositives
#irrelevant QInterest 'Are you interested in biology?' #biologyInterestPositives
Q8SynBio = 'Before playing Hero.Coli, had you ever heard about synthetic biology?' #yesNoIdontknowPositives
Q9BioBricks = 'Before playing Hero.Coli, had you ever heard about BioBricks?' #yesNoIdontknowPositives
questionsAndPositiveAnswers = [[Q6BioEdu, biologyStudyPositives],
[Q8SynBio, yesNoIdontknowPositives],
[Q9BioBricks, yesNoIdontknowPositives]]
result = getSurveysThatAnswered(sample, questionsAndPositiveAnswers, hardPolicy)
print(len(result) > 0)
gform.index
len(result)
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[0]
sample = gform[gform[localplayerguidkey] == _GFUserId]
len(getSurveysOfBiologists(sample)) > 0
```
#### getSurveysOfGamers tinkering
```
sample = gform
hardPolicy = True
#def getSurveysOfGamers(sample, hardPolicy = True):
Q2Interest = 'Are you interested in video games?' #interestPositives
Q3Play = 'Do you play video games?' #frequencyPositives
questionsAndPositiveAnswers = [[Q2Interest, interestPositives], [Q3Play, frequencyPositives]]
result = getSurveysThatAnswered(sample, questionsAndPositiveAnswers, hardPolicy)
len(result)
type(filterSeries)
len(afters[afters[QPlayed1].isin(previousPlayPositives)
| afters[QPlayed2].isin(previousPlayPositives)
| afters[QPlayed3].isin(previousPlayPositives)
| afters[QPlayed4].isin(previousPlayPositives)
]),\
len(afters[afters[QPlayed1].isin(previousPlayPositives)]),\
len(afters[afters[QPlayed2].isin(previousPlayPositives)]),\
len(afters[afters[QPlayed3].isin(previousPlayPositives)]),\
len(afters[afters[QPlayed4].isin(previousPlayPositives)])
```
#### getSurveysWithMatchingAnswers tinkering
```
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[2]
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
sample = gform
sample = gform
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
hardPolicy = False
Q4 = 'How old are you?'
Q5 = 'What is your gender?'
Q2Interest = 'Are you interested in video games?'
Q3Play = 'Do you play video games?'
Q6BioEdu = 'How long have you studied biology?'
Q7BioInterest = 'Are you interested in biology?'
Q8SynBio = 'Before playing Hero.Coli, had you ever heard about synthetic biology?'
Q9BioBricks = 'Before playing Hero.Coli, had you ever heard about BioBricks?'
Q42 = 'Language'
strictList = [Q4, Q5]
extendedList = [Q2Interest, Q3Play, Q6BioEdu, Q8SynBio, Q9BioBricks, Q42]
#def getSurveysWithMatchingAnswers(sample, _gformRow, strictList, extendedList = [], hardPolicy = False):
questions = strictList
if (hardPolicy):
questions += extendedList
questionsAndPositiveAnswers = []
for q in questions:
questionsAndPositiveAnswers.append([q, [_gformRow[q]]])
getSurveysThatAnswered(sample, questionsAndPositiveAnswers, True)
```
#### getMatchingDemographics tinkering
```
sample = gform
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
hardPolicy = True
#def getMatchingDemographics(sample, _gformRow, hardPolicy = False):
# age and gender
Q4 = 'How old are you?'
Q5 = 'What is your gender?'
# interests, hobbies, and knowledge - evaluation may vary after playing
Q2Interest = 'Are you interested in video games?'
Q3Play = 'Do you play video games?'
Q6BioEdu = 'How long have you studied biology?'
Q7BioInterest = 'Are you interested in biology?'
Q8SynBio = 'Before playing Hero.Coli, had you ever heard about synthetic biology?'
Q9BioBricks = 'Before playing Hero.Coli, had you ever heard about BioBricks?'
# language may vary: players may have missed the opportunity to set it, or may want to try and change it
Q42 = 'Language'
getSurveysWithMatchingAnswers(
sample,
_gformRow, [Q4, Q5],
extendedList = [Q2Interest, Q3Play, Q6BioEdu, Q8SynBio, Q9BioBricks, Q42],
hardPolicy = hardPolicy
)
questionsAndPositiveAnswers
```
#### getGFormRowCorrection tinkering
```
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
_source = correctAnswers
#def getGFormRowCorrection( _gformRow, _source = correctAnswers):
result = _gformRow.copy()
if(len(_gformRow) == 0):
print("this gform row is empty")
else:
result = pd.Series(index = _gformRow.index, data = np.full(len(_gformRow), np.nan))
for question in result.index:
_correctAnswers = _source.loc[question]
if(len(_correctAnswers) > 0):
result.loc[question] = False
for _correctAnswer in _correctAnswers:
if str(_gformRow.loc[question]).startswith(str(_correctAnswer)):
result.loc[question] = True
break
result
```
#### getGFormRowScore tinkering
```
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
_source = correctAnswers
#def getGFormRowScore( _gformRow, _source = correctAnswers):
correction = getGFormRowCorrection( _gformRow, _source = _source)
_counts = correction.value_counts()
_thisScore = 0
if(True in _counts):
_thisScore = _counts[True]
_thisScore
```
#### getGFormDataPreview tinkering
```
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[2]
sample = gform
# for per-gform, manual analysis
#def getGFormDataPreview(_GFUserId, sample):
gforms = gform[gform[localplayerguidkey] == _GFUserId]
result = {}
for _ilocIndex in range(0, len(gforms)):
gformsIndex = gforms.index[_ilocIndex]
currentGForm = gforms.iloc[_ilocIndex]
subresult = {}
subresult['date'] = currentGForm['Timestamp']
subresult['temporality RM'] = currentGForm['Temporality']
subresult['temporality GF'] = getGFormRowGFormTemporality(currentGForm)
subresult['score'] = getGFormRowScore(currentGForm)
subresult['genderAge'] = [currentGForm['What is your gender?'], currentGForm['How old are you?']]
# search for other users with similar demographics
matchingDemographics = getMatchingDemographics(sample, currentGForm)
matchingDemographicsIds = []
#print(type(matchingDemographics))
#print(matchingDemographics.index)
for matchesIndex in matchingDemographics.index:
matchingDemographicsIds.append([matchesIndex, matchingDemographics.loc[matchesIndex, localplayerguidkey]])
subresult['demographic matches'] = matchingDemographicsIds
result['survey' + str(_ilocIndex)] = subresult
print(result)
for match in result['survey0']['demographic matches']:
print(match[0])
```
| true |
code
| 0.340348 | null | null | null | null |
|
# Programming Assignment
## Готовим LDA по рецептам
Как вы уже знаете, в тематическом моделировании делается предположение о том, что для определения тематики порядок слов в документе не важен; об этом гласит гипотеза <<мешка слов>>. Сегодня мы будем работать с несколько нестандартной для тематического моделирования коллекцией, которую можно назвать <<мешком ингредиентов>>, потому что на состоит из рецептов блюд разных кухонь. Тематические модели ищут слова, которые часто вместе встречаются в документах, и составляют из них темы. Мы попробуем применить эту идею к рецептам и найти кулинарные <<темы>>. Эта коллекция хороша тем, что не требует предобработки. Кроме того, эта задача достаточно наглядно иллюстрирует принцип работы тематических моделей.
Для выполнения заданий, помимо часто используемых в курсе библиотек, потребуются модули json и gensim. Первый входит в дистрибутив Anaconda, второй можно поставить командой
pip install gensim
или
conda install gensim
Построение модели занимает некоторое время. На ноутбуке с процессором Intel Core i7 и тактовой частотой 2400 МГц на построение одной модели уходит менее 10 минут.
### Загрузка данных
Коллекция дана в json-формате: для каждого рецепта известны его id, кухня ("cuisine") и список ингредиентов, в него входящих. Загрузить данные можно с помощью модуля json (он входит в дистрибутив Anaconda):
```
import json
with open("recipes.json") as f:
recipes = json.load(f)
print recipes[1]
```
### Составление корпуса
```
from gensim import corpora, models
import numpy as np
```
Наша коллекция небольшая и влезает в оперативную память. Gensim может работать с такими данными и не требует их сохранения на диск в специальном формате. Для этого коллекция должна быть представлена в виде списка списков, каждый внутренний список соответствует отдельному документу и состоит из его слов. Пример коллекции из двух документов:
[["hello", "world"], ["programming", "in", "python"]]
Преобразуем наши данные в такой формат, а затем создадим объекты corpus и dictionary, с которыми будет работать модель.
```
texts = [recipe["ingredients"] for recipe in recipes]
dictionary = corpora.Dictionary(texts) # составляем словарь
corpus = [dictionary.doc2bow(text) for text in texts] # составляем корпус документов
corpus[0]
print texts[0]
print corpus[0]
```
У объекта dictionary есть две полезных переменных: dictionary.id2token и dictionary.token2id; эти словари позволяют находить соответствие между ингредиентами и их индексами.
### Обучение модели
Вам может понадобиться [документация](https://radimrehurek.com/gensim/models/ldamodel.html) LDA в gensim.
__Задание 1.__ Обучите модель LDA с 40 темами, установив количество проходов по коллекции 5 и оставив остальные параметры по умолчанию. Затем вызовите метод модели show_topics, указав количество тем 40 и количество токенов 10, и сохраните результат (топы ингредиентов в темах) в отдельную переменную. Если при вызове метода show_topics указать параметр formatted=True, то топы ингредиентов будет удобно выводить на печать, если formatted=False, будет удобно работать со списком программно. Выведите топы на печать, рассмотрите темы, а затем ответьте на вопрос:
Сколько раз ингредиенты "salt", "sugar", "water", "mushrooms", "chicken", "eggs" встретились среди топов-10 всех 40 тем? При ответе __не нужно__ учитывать составные ингредиенты, например, "hot water".
Передайте 6 чисел в функцию save_answers1 и загрузите сгенерированный файл в форму.
У gensim нет возможности фиксировать случайное приближение через параметры метода, но библиотека использует numpy для инициализации матриц. Поэтому, по утверждению автора библиотеки, фиксировать случайное приближение нужно командой, которая написана в следующей ячейке. __Перед строкой кода с построением модели обязательно вставляйте указанную строку фиксации random.seed.__
```
np.random.seed(76543)
# здесь код для построения модели:
ldamodel = models.ldamodel.LdaModel(corpus, id2word=dictionary, num_topics=40, passes=5)
topics = ldamodel.show_topics(num_topics=40, num_words=10, formatted=False)
c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs = 0, 0, 0, 0, 0, 0
for topic in topics:
for word2prob in topic[1]:
word = word2prob[0]
if word == 'salt':
c_salt += 1
elif word == 'sugar':
c_sugar += 1
elif word == 'water':
c_water += 1
elif word == 'mushrooms':
c_mushrooms += 1
elif word == 'chicken':
c_chicken += 1
elif word == 'eggs':
c_eggs += 1
def save_answers1(c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs):
with open("cooking_LDA_pa_task1.txt", "w") as fout:
fout.write(" ".join([str(el) for el in [c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs]]))
save_answers1(c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs)
print c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs
```
### Фильтрация словаря
В топах тем гораздо чаще встречаются первые три рассмотренных ингредиента, чем последние три. При этом наличие в рецепте курицы, яиц и грибов яснее дает понять, что мы будем готовить, чем наличие соли, сахара и воды. Таким образом, даже в рецептах есть слова, часто встречающиеся в текстах и не несущие смысловой нагрузки, и поэтому их не желательно видеть в темах. Наиболее простой прием борьбы с такими фоновыми элементами - фильтрация словаря по частоте. Обычно словарь фильтруют с двух сторон: убирают очень редкие слова (в целях экономии памяти) и очень частые слова (в целях повышения интерпретируемости тем). Мы уберем только частые слова.
```
import copy
dictionary2 = copy.deepcopy(dictionary)
```
__Задание 2.__ У объекта dictionary2 есть переменная dfs - это словарь, ключами которого являются id токена, а элементами - число раз, сколько слово встретилось во всей коллекции. Сохраните в отдельный список ингредиенты, которые встретились в коллекции больше 4000 раз. Вызовите метод словаря filter_tokens, подав в качестве первого аргумента полученный список популярных ингредиентов. Вычислите две величины: dict_size_before и dict_size_after - размер словаря до и после фильтрации.
Затем, используя новый словарь, создайте новый корпус документов, corpus2, по аналогии с тем, как это сделано в начале ноутбука. Вычислите две величины: corpus_size_before и corpus_size_after - суммарное количество ингредиентов в корпусе (иными словами, сумма длин всех документов коллекции) до и после фильтрации.
Передайте величины dict_size_before, dict_size_after, corpus_size_before, corpus_size_after в функцию save_answers2 и загрузите сгенерированный файл в форму.
```
more4000 = [w for w, count in dictionary2.dfs.iteritems() if count > 4000]
dict_size_before = len(dictionary2.items())
dictionary2.filter_tokens(bad_ids=more4000)
dict_size_after = len(dictionary2.items())
def get_corpus_size(corp):
res = 0
for doc in corp:
res += len(doc)
#for w in doc:
# res += w[1]
return res
corpus_size_before = get_corpus_size(corpus)
corpus2 = [dictionary2.doc2bow(text) for text in texts] # составляем корпус документов
corpus_size_after = get_corpus_size(corpus2)
def save_answers2(dict_size_before, dict_size_after, corpus_size_before, corpus_size_after):
with open("cooking_LDA_pa_task2.txt", "w") as fout:
fout.write(" ".join([str(el) for el in [dict_size_before, dict_size_after, corpus_size_before, corpus_size_after]]))
save_answers2(dict_size_before, dict_size_after, corpus_size_before, corpus_size_after)
```
### Сравнение когерентностей
__Задание 3.__ Постройте еще одну модель по корпусу corpus2 и словарю dictioanary2, остальные параметры оставьте такими же, как при первом построении модели. Сохраните новую модель в другую переменную (не перезаписывайте предыдущую модель). Не забудьте про фиксирование seed!
Затем воспользуйтесь методом top_topics модели, чтобы вычислить ее когерентность. Передайте в качестве аргумента соответствующий модели корпус. Метод вернет список кортежей (топ токенов, когерентность), отсортированных по убыванию последней. Вычислите среднюю по всем темам когерентность для каждой из двух моделей и передайте в функцию save_answers3.
```
np.random.seed(76543)
# здесь код для построения модели:
ldamodel2 = models.ldamodel.LdaModel(corpus2, id2word=dictionary2, num_topics=40, passes=5)
coherences = ldamodel.top_topics(corpus)
coherences2 = ldamodel2.top_topics(corpus2)
import numpy as np
list1 = np.array([])
for coh in coherences:
list1 = np.append(list1, coh[1])
list2 = np.array([])
for coh in coherences2:
list2 = np.append(list2, coh[1])
coherence = list1.mean()
coherence2 = list2.mean()
def save_answers3(coherence, coherence2):
with open("cooking_LDA_pa_task3.txt", "w") as fout:
fout.write(" ".join(["%3f"%el for el in [coherence, coherence2]]))
save_answers3(coherence, coherence2)
```
Считается, что когерентность хорошо соотносится с человеческими оценками интерпретируемости тем. Поэтому на больших текстовых коллекциях когерентность обычно повышается, если убрать фоновую лексику. Однако в нашем случае этого не произошло.
### Изучение влияния гиперпараметра alpha
В этом разделе мы будем работать со второй моделью, то есть той, которая построена по сокращенному корпусу.
Пока что мы посмотрели только на матрицу темы-слова, теперь давайте посмотрим на матрицу темы-документы. Выведите темы для нулевого (или любого другого) документа из корпуса, воспользовавшись методом get_document_topics второй модели:
Также выведите содержимое переменной .alpha второй модели:
У вас должно получиться, что документ характеризуется небольшим числом тем. Попробуем поменять гиперпараметр alpha, задающий априорное распределение Дирихле для распределений тем в документах.
__Задание 4.__ Обучите третью модель: используйте сокращенный корпус (corpus2 и dictionary2) и установите параметр __alpha=1__, passes=5. Не забудьте задать количество тем и зафиксировать seed! Выведите темы новой модели для нулевого документа; должно получиться, что распределение над множеством тем практически равномерное. Чтобы убедиться в том, что во второй модели документы описываются гораздо более разреженными распределениями, чем в третьей, посчитайте суммарное количество элементов, __превосходящих 0.01__, в матрицах темы-документы обеих моделей. Другими словами, запросите темы модели для каждого документа с параметром minimum_probability=0.01 и просуммируйте число элементов в получаемых массивах. Передайте две суммы (сначала для модели с alpha по умолчанию, затем для модели в alpha=1) в функцию save_answers4.
```
def save_answers4(count_model2, count_model3):
with open("cooking_LDA_pa_task4.txt", "w") as fout:
fout.write(" ".join([str(el) for el in [count_model2, count_model3]]))
```
Таким образом, гиперпараметр alpha влияет на разреженность распределений тем в документах. Аналогично гиперпараметр eta влияет на разреженность распределений слов в темах.
### LDA как способ понижения размерности
Иногда распределения над темами, найденные с помощью LDA, добавляют в матрицу объекты-признаки как дополнительные, семантические, признаки, и это может улучшить качество решения задачи. Для простоты давайте просто обучим классификатор рецептов на кухни на признаках, полученных из LDA, и измерим точность (accuracy).
__Задание 5.__ Используйте модель, построенную по сокращенной выборке с alpha по умолчанию (вторую модель). Составьте матрицу $\Theta = p(t|d)$ вероятностей тем в документах; вы можете использовать тот же метод get_document_topics, а также вектор правильных ответов y (в том же порядке, в котором рецепты идут в переменной recipes). Создайте объект RandomForestClassifier со 100 деревьями, с помощью функции cross_val_score вычислите среднюю accuracy по трем фолдам (перемешивать данные не нужно) и передайте в функцию save_answers5.
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import cross_val_score
def save_answers5(accuracy):
with open("cooking_LDA_pa_task5.txt", "w") as fout:
fout.write(str(accuracy))
```
Для такого большого количества классов это неплохая точность. Вы можете попроовать обучать RandomForest на исходной матрице частот слов, имеющей значительно большую размерность, и увидеть, что accuracy увеличивается на 10-15%. Таким образом, LDA собрал не всю, но достаточно большую часть информации из выборки, в матрице низкого ранга.
### LDA --- вероятностная модель
Матричное разложение, использующееся в LDA, интерпретируется как следующий процесс генерации документов.
Для документа $d$ длины $n_d$:
1. Из априорного распределения Дирихле с параметром alpha сгенерировать распределение над множеством тем: $\theta_d \sim Dirichlet(\alpha)$
1. Для каждого слова $w = 1, \dots, n_d$:
1. Сгенерировать тему из дискретного распределения $t \sim \theta_{d}$
1. Сгенерировать слово из дискретного распределения $w \sim \phi_{t}$.
Подробнее об этом в [Википедии](https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation).
В контексте нашей задачи получается, что, используя данный генеративный процесс, можно создавать новые рецепты. Вы можете передать в функцию модель и число ингредиентов и сгенерировать рецепт :)
```
def generate_recipe(model, num_ingredients):
theta = np.random.dirichlet(model.alpha)
for i in range(num_ingredients):
t = np.random.choice(np.arange(model.num_topics), p=theta)
topic = model.show_topic(0, topn=model.num_terms)
topic_distr = [x[1] for x in topic]
terms = [x[0] for x in topic]
w = np.random.choice(terms, p=topic_distr)
print w
```
### Интерпретация построенной модели
Вы можете рассмотреть топы ингредиентов каждой темы. Большиснтво тем сами по себе похожи на рецепты; в некоторых собираются продукты одного вида, например, свежие фрукты или разные виды сыра.
Попробуем эмпирически соотнести наши темы с национальными кухнями (cuisine). Построим матрицу A размера темы x кухни, ее элементы $a_{tc}$ - суммы p(t|d) по всем документам d, которые отнесены к кухне c. Нормируем матрицу на частоты рецептов по разным кухням, чтобы избежать дисбаланса между кухнями. Следующая функция получает на вход объект модели, объект корпуса и исходные данные и возвращает нормированную матрицу A. Ее удобно визуализировать с помощью seaborn.
```
import pandas
import seaborn
from matplotlib import pyplot as plt
%matplotlib inline
def compute_topic_cuisine_matrix(model, corpus, recipes):
# составляем вектор целевых признаков
targets = list(set([recipe["cuisine"] for recipe in recipes]))
# составляем матрицу
tc_matrix = pandas.DataFrame(data=np.zeros((model.num_topics, len(targets))), columns=targets)
for recipe, bow in zip(recipes, corpus):
recipe_topic = model.get_document_topics(bow)
for t, prob in recipe_topic:
tc_matrix[recipe["cuisine"]][t] += prob
# нормируем матрицу
target_sums = pandas.DataFrame(data=np.zeros((1, len(targets))), columns=targets)
for recipe in recipes:
target_sums[recipe["cuisine"]] += 1
return pandas.DataFrame(tc_matrix.values/target_sums.values, columns=tc_matrix.columns)
def plot_matrix(tc_matrix):
plt.figure(figsize=(10, 10))
seaborn.heatmap(tc_matrix, square=True)
# Визуализируйте матрицу
```
Чем темнее квадрат в матрице, тем больше связь этой темы с данной кухней. Мы видим, что у нас есть темы, которые связаны с несколькими кухнями. Такие темы показывают набор ингредиентов, которые популярны в кухнях нескольких народов, то есть указывают на схожесть кухонь этих народов. Некоторые темы распределены по всем кухням равномерно, они показывают наборы продуктов, которые часто используются в кулинарии всех стран.
Жаль, что в датасете нет названий рецептов, иначе темы было бы проще интерпретировать...
### Заключение
В этом задании вы построили несколько моделей LDA, посмотрели, на что влияют гиперпараметры модели и как можно использовать построенную модель.
| true |
code
| 0.208501 | null | null | null | null |
|
```
# reload packages
%load_ext autoreload
%autoreload 2
```
### Choose GPU (this may not be needed on your computer)
```
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=''
```
### load packages
```
from tfumap.umap import tfUMAP
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
import umap
import pandas as pd
```
### Load dataset
```
from sklearn.datasets import make_moons
X_train, Y_train = make_moons(1000, random_state=0, noise=0.1)
X_train_flat = X_train
X_test, Y_test = make_moons(1000, random_state=1, noise=0.1)
X_test_flat = X_test
X_valid, Y_valid = make_moons(1000, random_state=2, noise=0.1)
plt.scatter(X_test[:,0], X_test[:,1], c=Y_test)
```
### Create model and train
```
embedder = tfUMAP(direct_embedding=True, verbose=True, negative_sample_rate=5, training_epochs=100)
z = embedder.fit_transform(X_train_flat)
```
### Plot model output
```
fig, ax = plt.subplots( figsize=(8, 8))
sc = ax.scatter(
z[:, 0],
z[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow embedding", fontsize=20)
plt.colorbar(sc, ax=ax);
```
### View loss
```
from tfumap.umap import retrieve_tensors
import seaborn as sns
loss_df = retrieve_tensors(embedder.tensorboard_logdir)
loss_df[:3]
ax = sns.lineplot(x="step", y="val", hue="group", data=loss_df[loss_df.variable=='umap_loss'])
ax.set_xscale('log')
```
### Save output
```
from tfumap.paths import ensure_dir, MODEL_DIR
output_dir = MODEL_DIR/'projections'/ 'moons' / 'direct'
ensure_dir(output_dir)
embedder.save(output_dir)
loss_df.to_pickle(output_dir / 'loss_df.pickle')
np.save(output_dir / 'z.npy', z)
```
### Compare to direct embedding with base UMAP
```
from umap import UMAP
z_umap = UMAP(verbose=True).fit_transform(X_train_flat)
### realign using procrustes
from scipy.spatial import procrustes
z_align, z_umap_align, disparity = procrustes(z, z_umap)
print(disparity)
fig, axs = plt.subplots(ncols=2, figsize=(20, 8))
ax = axs[0]
sc = ax.scatter(
z_align[:, 0],
z_align[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow", fontsize=20)
#plt.colorbar(sc, ax=ax);
ax = axs[1]
sc = ax.scatter(
z_umap_align[:, 0],
z_umap_align[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP with UMAP-learn", fontsize=20)
#plt.colorbar(sc, ax=ax);
```
| true |
code
| 0.680109 | null | null | null | null |
|
# BiDirectional LSTM classifier in keras
#### Load dependencies
```
import keras
from keras.datasets import imdb
from keras.preprocessing.sequence import pad_sequences
from keras.models import Sequential
from keras.layers import Embedding, SpatialDropout1D, Dense, Flatten, Dropout, LSTM
from keras.layers.wrappers import Bidirectional
from keras.callbacks import ModelCheckpoint # new!
import os # new!
from sklearn.metrics import roc_auc_score, roc_curve # new!
import matplotlib.pyplot as plt # new!
%matplotlib inline
# output directory name:
output_dir = 'model_output/bilstm'
# training:
epochs = 6
batch_size = 128
# vector-space embedding:
n_dim = 64
n_unique_words = 10000
max_review_length = 200
pad_type = trunc_type = 'pre'
drop_embed = 0.2
# neural network architecture:
n_lstm = 256
droput_lstm = 0.2
```
#### Load data
For a given data set:
* the Keras text utilities [here](https://keras.io/preprocessing/text/) quickly preprocess natural language and convert it into an index
* the `keras.preprocessing.text.Tokenizer` class may do everything you need in one line:
* tokenize into words or characters
* `num_words`: maximum unique tokens
* filter out punctuation
* lower case
* convert words to an integer index
```
(x_train, y_train), (x_valid, y_valid) = imdb.load_data(num_words=n_unique_words)
```
#### Preprocess data
```
x_train = pad_sequences(x_train, maxlen=max_review_length, padding=pad_type, truncating=trunc_type, value=0)
x_valid = pad_sequences(x_valid, maxlen=max_review_length, padding=pad_type, truncating=trunc_type, value=0)
x_train[:6]
for i in range(6):
print len(x_train[i])
```
#### Design neural network architecture
```
model = Sequential()
model.add(Embedding(n_unique_words, n_dim, input_length=max_review_length))
model.add(SpatialDropout1D(drop_embed))
# model.add(Conv1D(n_conv, k_conv, activation='relu'))
# model.add(Conv1D(n_conv, k_conv, activation='relu'))
# model.add(GlobalMaxPooling1D())
# model.add(Dense(n_dense, activation='relu'))
# model.add(Dropout(dropout))
model.add(Bidirectional(LSTM(n_lstm, dropout=droput_lstm)))
model.add(Dense(1, activation='sigmoid'))
model.summary()
n_dim, n_unique_words, n_dim * n_unique_words
max_review_length, n_dim, n_dim * max_review_length
```
#### Configure Model
```
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
modelcheckpoint = ModelCheckpoint(filepath=output_dir+"/weights.{epoch:02d}.hdf5")
if not os.path.exists(output_dir):
os.makedirs(output_dir)
model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs,
verbose=1, validation_data=(x_valid, y_valid), callbacks=[modelcheckpoint])
```
#### Evaluate
```
model.load_weights(output_dir+"/weights.01.hdf5") # zero-indexed
y_hat = model.predict_proba(x_valid)
len(y_hat)
y_hat[0]
plt.hist(y_hat)
_ = plt.axvline(x=0.5, color='orange')
pct_auc = roc_auc_score(y_valid, y_hat)*100.0
"{:0.2f}".format(pct_auc)
```
| true |
code
| 0.733473 | null | null | null | null |
|
```
from aide_design.play import*
from aide_design import floc_model as floc
from aide_design import cdc_functions as cdc
from aide_design.unit_process_design.prefab import lfom_prefab_functional as lfom
from pytexit import py2tex
import math
```
# 1 L/s Plants in Parallel
# CHANCEUX
## Priya Aggarwal, Sung Min Kim, Felix Yang
AguaClara has been designing and building water treatment plants since 2005 in Honduras, 2013 in India, and 2017 in Nicaragua. It has been providing gravity powered water treatment systems to thousands of people in rural communities. However, there were populations that could not be targeted due to the technology only being scaled up from 6 L/s. For towns and rural areas with populations with smaller needs, AguaClara technologies were out of their reach.
Recently a one liter per second (1 LPS) plant was developed based on traditional AguaClara technology, to bring sustainable water treatment to towns with populations of 300 people per plant.
The first 1 LPS plant fabricated was sent to Cuatro Comunidades in Honduras, where a built in place plant already exists, and is currently operating without the filter attachment, also known as Enclosed Stacked Rapid Sand Filter (EStaRS). EStaRS is the last step in the 1 LPS plant processes before chlorination and completes the 4 step water treatment process: flocculation, sedimentation, filtration, and chlorination.
Having water treatment plants for smaller flow rates would increase AguaClara’s reach and allow it to help more people. Despite being in its initial stages, the demand for this technology is increasing. Three 1 LPS plants were recently ordered for a town that did not have water treatment. However, the implementation of 1 LPS plants is a problem that has not yet been solved.
This project has stemmed from the possibility of implementing AguaClara technologies to be helpful in Puerto Rico’s post hurricane rebuild effort. The goal of this project is to assess whether the portable 1 L/s plant could be a viable option to help rural communities have safe drinking water. The project models multiple 1 L/s plants working in parallel to provide for the community and plans for the future when communities would need to add capacity. For this project, the team has set 6 L/s as the design constraint. We need experience building and deploying 1 LPS plants to determine the economics and ease of operation to compare to those of built in place plants. For example, if we need 12 L/s, it could still be reasonable to use the 1 LPS plants in parallel or select a 16 L/s built in place plant if more than 12 L/s is needed. Because the dividing line between the modular prefabricated 1 LPS plants and the build in place plants is unknown, the team chose 6 L/s because it is the smallest built in place plant capacity.
Our model is based on the following:
* Standardization modular designs for each plant (1 plant has one EStaRs and Flocculator)
* One entrance tank and chemical dosing controller
* Entrance Tank accomodates to 6 L/s flow
* Coagulant/ Chlorine dosing according to flow by operator
* Parallel Layout for convenience
* Extendable shelter walls to add capacity using chain-link fencing
* Manifolds connecting up to 3 plants (accounting for 3 L/s) from the sedimentation tank to the ESTaRS and after filtration for chlorination (using Ts and fernco caps)
* Manifolds to prevent flow to other filters being cut off if filters need to be backwashed and lacks enough flow
* Equal flow to the filters and chlorination from the manifolds
Calculations follow below.
### Chemical Dosing Flow Rates
Below the functions for calculating the flow rate of the coagulant and chlorine based on the target plant flow rate are shown. The Q_Plant and concentrations of PACL and Cl can be set by the engineer and is set to 3 L/s in this sample calculation.
Chlorine would be ideally done at the end of the filtration where flow recombines so that the operator would only have to administer chlorine at one point. However our drafts did not account for that and instead lack piping that unites the top and bottom 1 L/s plants. Only the 6 L/s draft reflects this optimal design for chlorination.
```
#using Q_plant as the target variable, sample values of what a plant conditions might be are included below
Temperature = u.Quantity(20,u.degC)
Desired_PACl_Concentration=3*u.mg/u.L
Desired_Cl_Concentration=3*u.mg/u.L
C_stock_PACl=70*u.gram/u.L
C_stock_Cl=51.4*u.gram/u.L
NuPaCl = cdc.viscosity_kinematic_pacl(C_stock_PACl,Temperature)
RatioError = 0.1
KMinor = 2
Q_Plant= 3*u.L/u.s
def CDC(Q_Plant, DesiredCl_Concentration,C_stock_PACl):
Q_CDC=(Q_Plant*Desired_PACl_Concentration/C_stock_PACl).to(u.mL/u.s)
return (Q_CDC)
def Chlorine_Dosing(Q_Plant,Desired_Cl_Concentration,C_stock_Cl):
Q_Chlorine=(Q_Plant*Desired_Cl_Concentration/C_stock_Cl).to(u.mL/u.s)
return (Q_Chlorine)
print('The flow rate of coagulant is ',CDC(Q_Plant, Desired_PACl_Concentration, C_stock_PACl).to(u.L/u.hour))
print('The flow rate of chlorine is ',Chlorine_Dosing(Q_Plant, Desired_Cl_Concentration, C_stock_Cl).to(u.L/u.hour))
```
### SPACE CONSTRAINTS
In the code below the team is calculating the floor plan area. The X distance and Y distance are the length and width of the floor plan respectively. The dimensions of the sedimentation tank, flocculator, and entrance tank are accounted for in this calculation.
```
#Claculting the Y distance For the Sed Tank
#properties of sedimentation tank
Sed_Tank_Diameter=0.965*u.m
Length_Top_Half=1.546*u.m #See image for clearer understanding
Y_Sed_Top_Half=Length_Top_Half*math.cos(60*u.degrees)
print(Y_Sed_Top_Half)
Y_Sed_Total=Sed_Tank_Diameter+Y_Sed_Top_Half
print(Y_Sed_Total)
```
SED TANK: Based on the calculation above, the space the Sedimentation tank would take on the floor plant is found to be 1.738 m.

This is a picture of the sedimentation tank with dimensions showing the distance jutting out from the sedimentation tank. This distance of 0.773 m is added to the sedimentation tank diameter totalling 1.738 meters.
ESTaRS: The dimensions of the ESTaRS are set and did not need to be calculated. A single manifold can collect water from the sed tanks and send it to the EStaRS. There will be valves on the manifold system installed before the entrance to the ESTaRS to allow for backwashing. These valves can be shut to allow for enough flow to provide backwashing capacity. There will be a manifold connecting flow after filtration to equate the flow for chlorination.
FLOCCULATOR: We want symmetrical piping systems coming out of the flocculator. There is a flocculator for each plant so that available head going into the parallel sedimentation tanks will be the same. We will have an asymmetrical exit lauder system coming out of the sedimentation tanks going into the ESTaRS (diagram).
ENTRANCE TANK: The entrance tank is set to be at the front of the plant. The focus of this project is to calculate the dimensions and design the plant. The entrance tank dimensions should be left to be designed in the future. An estimated dimension was set in the drawing included in this project. There will be a grit chamber included after the entrance tank. The traditional design for rapid mix that is used in AguaClara plants will be included in the entrance tank.
CONTACT CHAMBER: A contact chamber is included after the entrance tank to ensure that the coagulant is mixed with all of the water before it separates into the multiple treatment trains. Like the entrance tank, contact chamber dimensions should be left to be designed in the future. An estimated dimension was set in the drawing included in this project.
WOODEN PLATFORM: The wooden platform is 4m long, 0.8m wide, and is 1.4 meters high allowing for the operator to be able to access the top of the sedimentation tank, flocculator, and ESTaRS. It would be placed in between every sedimentation tank. In the case of only a single sedimentation tank it would go on the right of the tank because the plant expands to the right.
```
#Spacing due to Entrance Tank and contact chamber #estimated values
Space_ET=0.5*u.m
CC_Diameter=0.4*u.m
Space_Between_ET_CC=0.1*u.m
Space_CC_ET=1*u.m
#Spacing due to Manifold between contact chamber and flocculators
Space_CC_Floc=1.116*u.m
#Spacing due to Flocculator
Space_Flocc_Sed=.1*u.m
Space_Flocculator=0.972*u.m
#Spacing due to the Manifold
Space_Manifold=0.40*u.m
#Spacing due to ESTaRS
Space_ESTaRS=0.607*u.m
#Spacing for ESTaRS Manifold to the wall
Space_ESTaRS_Wall=0.962*u.m
```
The Y distance below 3 L/s is set to be as a sum of the total Y distance of the flocculator, sedimentation tank, and ESTaRS. An additional 2 meters of Y distance is added for operator access around the plant. The lengths between the sedimentation tank, flocculator and ESTarS were kept minimal but additional Y distance can be taken off between the sedimentation tank and ESTaRS. This is because the ESTaRS can hide under the sloping half of the sedimentation tank but this orientation would not account for the manifold drawn in the picture.
The total Y distance is calculated below.
```
Y_Length_Top=(Space_CC_ET+Space_CC_Floc+Space_Flocc_Sed
+Space_Flocculator+Y_Sed_Total+Space_Manifold+Space_ESTaRS+
Space_ESTaRS_Wall)
Y_Length_Bottom=Y_Length_Top-0.488*u.m
```
Below are functions that can be used to design a plant based on the desired flow rate
```
def X(Q):
if Q>3*u.L/u.s:
X_Distance_Bottom=X(Q-3*u.L/u.s)
X_Distance_Top=6.9*u.m
return(X_Distance_Top,X_Distance_Bottom)
else:
Q_Plant=Q.to(u.L/u.s)
Extra_Space=2*u.m
X_Distance=(Q_Plant.magnitude-1)*1*u.m+(Q_Plant.magnitude)*.965*u.m+Extra_Space
return(X_Distance.to(u.m))
def Y(Q):
if Q>3*u.L/u.s:
return(Y_Length_Top+Y_Length_Bottom)
else:
return(Y_Length_Top)
print(X(Q_Plant_2).to(u.m))
def Area_Plant(Q):
if Q>3*u.L/u.s:
X_Distance_Bottom=X(Q-3*u.L/u.s)
Area_Bottom=X_Distance_Bottom*Y_Length_Bottom*((Q/u.L*u.s-3))
Area_Top=X(3*u.L/u.s)*Y_Length_Top
Area_Total=Area_Top+Area_Bottom
return(Area_Total)
else:
H_Distance=X(Q_Plant)
Y_Distance=Y_Length_Top
Area_Total=H_Distance*Y_Distance
return(Area.to(u.m**2))
```

This is a layout of a sample plant for three 1 L/s tanks running in parallel. Check bottom of document for additional drafts.
A platform will be in between sedimentation tanks as a way for the operators to have access to the sedimentation tanks. The platform height will be 1.4m to allow the plant operators 0.5m to view the sedimentation tanks just as in the built in place plants. The operator access requirements influence the optimal plant layout because the operators movements and safety have to be considered. The manifold will be built underneath the platform for space efficiency. The image below shows the wooden platform with 4m of length but could be truncated or extended to depending on the situation. The last image shows the platform in between the sedimentation tanks in the 3 L/s sample plant.

Wooden platforms would fill up the space in between sedimentation tanks to allow for operator access to the top of sedimentation tanks, ESTaRS and flocculators.

### Adding Capacity
When adding capacity up to plant flow rates of 3 L/s, vertical distance will be constant so adding capacity will only change the horizontal distance of the plant. We define a set of flocculator, sedimentation tank, and EStARS as a 1 L/s plant.
After the capacity of the plant reaches 3 L/s, additional 1 L/s plants will be added to the bottom half of the building, using a mirrored layout as the top half of the building. The only difference between the spacing is that the additions no longer need another entrance tank so the width of the bottom half of the plant is shorter than the width of the top half. This was done instead of simply increasing the length of the plant each time capacity was added because the length of the pipe between the contact chamber and the farthest flocculator would become increasingly large. This addition of major losses would cause different flow rates between the farther 1LPS plant and the closest one.
The following function will only account for adding 1 L/s plants one at at a time
```
def Additional_Area(Q_Plant,Q_Extra):
if (Q_Plant+Q_Extra>3*u.L/u.s):
X_Distance_Extra=X(Q_Extra)
Y_Distance_Extra=Y_Length_Bottom
Area=(X_Distance_Extra*Y_Distance_Extra).to(u.m**2)
return(Area)
else:
Q=Q_Extra.to(u.L/u.s)
Horizontal=(Q_Extra.magnitude)*.965*u.m+(Q_Extra.magnitude)*1*u.m
Vertical=5.512*u.m
Extra_Area=Vertical*Horizontal
print('Extra length that has to be added is '+ut.sig(Horizontal,4))
return(ut.sig(Extra_Area,2))
```
### ESTaRS
The total surface area required for the ESTaRS filter is simply a product of the area one ESTaRS requires and the flow rate coming into the plant. The surface area required for an ESTaRS was measured in the DeFrees lab. It is approximately a square meter.
```
ESTaRS_SA=1*u.m**2/u.L
def Area_ESTaRS(Q):
Q_Plant=Q.to(u.L/u.s)
Surface_Area_ESTaRS=(ESTaRS_SA.magnitude)*Q_Plant.magnitude
return(Surface_Area_ESTaRS*u.m**2)
print('Surface area required for the ESTaR(s) is',Area_ESTaRS(Q_Plant))
```
### Flocculators
The total surface area required for the ESTaRS filter is simply a product of the area one ESTaRS requires and the flow rate coming into the plant. The surface area required for an ESTaRS was measured in the DeFrees lab. It is approximately a square meter.
```
Flocc_SA=0.972*u.m*0.536*u.m*u.L/u.s
def Area_Flocc(Q):
Q_Plant=Q.to(u.L/u.s)
Surface_Area_Flocc=(Flocc_SA.magnitude)*Q_Plant.magnitude
return(Surface_Area_Flocc*u.m**2)
print('Surface area required for the flocculator(s) is',Area_Flocc(Q_Plant))
```
### Manifold Headloss Calculations
The amount of headloss has to be minimal so that the amount of head availible coming out of the exit launder is enough to drive water fast enough to fluidize the sand bed in ESTaRS. This fluidization is required for backwashing the filter. Since the calculation for 4 inch pipe has a headloss for less than 1mm we conclude that the manifold is economically feasible. Any futher increase in the diameter of the manifold would become increasingly expensive.
```
SDR = 26
SF=1.33
Q_Manifold = 1 * u.L/u.s #max flowrate for a manifold
Q_UpperBound=SF*Q_Manifold
L_pipe = 5*u.m #Length sed tank to it’s ESTaRS
K_minor_bend=0.3
K_minor_branch=1
K_minor_contractions=1
K_minor_total= 2*(K_minor_bend+K_minor_branch+K_minor_contractions) # (two bends, two dividing branch, and two contractions)
# The maximum viscosity will occur at the lowest temperature.
T_crit = u.Quantity(10,u.degC)
nu = pc.viscosity_kinematic(T_crit)
e = 0.1 * u.mm
Manifold_1LPS_ID=4*u.inch
Headloss_Max=10*u.mm
Manifold_Diam=pc.diam_pipe(Q_Manifold,Headloss_Max,L_pipe,nu,e,K_minor_total).to(u.inch)
print(Manifold_Diam.to(u.inch))
print('The minimum pipe inner diameter is '+ ut.sig(Manifold_Diam,2)+'.')
Manifold_ND = pipe.ND_SDR_available(Manifold_Diam,SDR)
print('The nominal diameter of the manifold is '+ut.sig(Manifold_ND,2)+' ('+ut.sig(Manifold_ND.to(u.inch),2)+').')
HLCheck = pc.headloss(Q_UpperBound,Manifold_1LPS_ID,L_pipe,nu,e,K_minor_total)
print('The head loss is',HLCheck.to(u.mm))
```
# Drafts of 1 L/s Plant to 6 L/s Plant

A sample 1 L/s plant. The red t's indicate where the piping system can be expanded to include more 1 L/s systems. Additionally the t would be covered by a fernco cap so that the pipe can be removed when the plant is adding capacity. See cell below for pictures of manifolds with caps.

The sample 2 L/s plant. The red t's indicate where the piping system can be expanded to include more 1 L/s plants. Additionally the t exit that isn't connected to any piping would be covered by a fernco cap so that the pipe can be removed when the plant is adding capacity.

The sample 3 L/s plant. There are now no more t's that can be extended because the manifold was designed for up to 3 1 L/s plants. Further capacities are added on the bottom half of the plant like in the next 3 pictures.

The sample 4 L/s plant. Like in the 1 L/s plant the red t's indicate the start of the 2nd manifold system.

The sample 5 L/s plant. The length (x-direction) is extended by the diameter of a sedimentation tank and one meter like in the top half of the plant. However the width of the bottom half is slightly lower because it can use the already built entrance tank used for the first 3 L/s systems.

The sample 6 L/s plant. The building is now at full capacity with an area of 91.74 m^2. The flow reunites to allow for chlorination to be administered at one point.
# Manifold Drafts

The manifold with 1 L/s. The elbow at the top is connected to the exit launder of the sedimentation tank. The flow goes from the exit launder into the reducer which is not yet connected in the draft to the ESTaRS. The removeable fernco cap that allows for further expansions of the manifold pipe system can be seen in the picture.

The manifold with 2 L/s. Again a fernco cap is used to allow for future expansions up to 3 L/s.

The manifold with 3 L/s. Here there are no fernco caps because the manifold is designed for up to connections with three 1 L/s plants.
| true |
code
| 0.455683 | null | null | null | null |
|
# Task 4: Classification
_All credit for the code examples of this notebook goes to the book "Hands-On Machine Learning with Scikit-Learn & TensorFlow" by A. Geron. Modifications were made and text was added by K. Zoch in preparation for the hands-on sessions._
# Setup
First, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Function to save a figure. This also decides that all output files
# should stored in the subdirectorz 'classification'.
PROJECT_ROOT_DIR = "."
EXERCISE = "classification"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "output", EXERCISE, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
# Preparing the dataset
Define a function to sort the dataset into the 'targets' train and test data. This is needed because we want to use the same 60,000 data points for training, and the sam e10,000 data points for testing on every machine (and the dataset provided through Scikit-Learn is already prepared in this way).
```
def sort_by_target(mnist):
reorder_train = np.array(sorted([(target, i) for i, target in enumerate(mnist.target[:60000])]))[:, 1]
reorder_test = np.array(sorted([(target, i) for i, target in enumerate(mnist.target[60000:])]))[:, 1]
mnist.data[:60000] = mnist.data[reorder_train]
mnist.target[:60000] = mnist.target[reorder_train]
mnist.data[60000:] = mnist.data[reorder_test + 60000]
mnist.target[60000:] = mnist.target[reorder_test + 60000]
```
Now fetch the dataset using the SciKit-Learn function (this might take a moment ...).
```
# We need this try/except for different Scikit-Learn versions.
try:
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, cache=True)
mnist.target = mnist.target.astype(np.int8) # fetch_openml() returns targets as strings
sort_by_target(mnist) # fetch_openml() returns an unsorted dataset
except ImportError:
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')
mnist["data"], mnist["target"]
```
Let's have a look at what the 'data' key contains: it is a numpy array with one row per instance and one column per feature.
```
mnist["data"]
```
And the same for the 'target' key which is an array of labels.
```
mnist["target"]
```
Now, let's first define the more useful `x` and `y` aliases for the data and target keys, and let's have a look at the type of data using the `shape` function: we see 70,000 entries in the data array, with 784 features each. The 784 correspond to 28x28 pixels of an image with brightness values between 0 and 255.
```
X, y = mnist["data"], mnist["target"]
X.shape # get some information about its shape
28*28 # just a little cross-check we're doing the correct arithmetics here ...
X[36000][160:200] # Plot brightness values [160:200] of the random image X[36000].
```
Now let's have a look at one of the images. We just pick a random image and use the `numpy.reshape()` function to reshape it into an array of 28x28 pixels. Then we can plot it with `matplotlib.pyplot.imshow()`:
```
some_digit = X[36000]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap = mpl.cm.binary,
interpolation="nearest")
plt.axis("off")
save_fig("some_digit_plot")
plt.show()
```
Let's quickly define a function to plot one of the digits, we will need it later down the line. It might also be useful to have a function to plot multiple digits in a batch (we will also use this function later). The following two cells will not produce any output.
```
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = mpl.cm.binary,
interpolation="nearest")
plt.axis("off")
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = mpl.cm.binary, **options)
plt.axis("off")
```
Great, now we can plot multiple digits at once. Let's ignore the details of the `np.r_[]` function and the indexing used within it for now and focus on what it does: it takes ten examples of each digit from the data array, which we can then plot with our `plot_digits()` function.
```
plt.figure(figsize=(9,9))
example_images = np.r_[X[:12000:600], X[13000:30600:600], X[30600:60000:590]]
plot_digits(example_images, images_per_row=10)
save_fig("more_digits_plot")
plt.show()
```
Ok, at this point we have a fairly good idea how our data array looks like: we have an array of 70,000 images with 28x28 pixels each. The entries in the array are sorted according to ascending digits, i.e. it starts with images of zeros and ends with images of nines at entry 59,999. Entries `x[60000:]` onwards are meant to be used for testing and again contain images of all digits in ascending order.
Before starting with binary classification, let's quickly confirm that the labels stored in `y` actually make sense. We previously looked at entry `X[36000]` and it looked like a five. Does `y[36000]` say the same?
```
y[36000]
```
Good! As a very last step, let's split train and test and store them separately. Because we also don't want our training to be biased, we should shuffle the entries randomly (i.e. not sort them in ascending order anymore). We can do this with the `np.random.permutation(60000)` function which returns a random permutation of the numbers between zero and 60,000.
```
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
import numpy as np
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
```
# Binary classifier
Before going towards a classifier, which can distinguish _all_ digits, let's start with something simple. Since our random digit `X[36000]` was a five, why not design a classifier that can distinguish fives from other digits? Let's first rewrite our labels from integers to booleans:
```
y_train_5 = (y_train == 5) # an array of booleans which is 'True' whenever y_train is == 5
y_test_5 = (y_test == 5)
y_train_5 # let's look at the array
```
A good model for the classification is the Stochastic Gradient Descent that was introduced in the lecture. Conveniently, Skiki-Learn already has such a classifier implemented, so let's import it and give it our training data `X_train` with the true labels `y_train_5`.
```
from sklearn.linear_model import SGDClassifier
# SDG relies on randomness, but by fixing the `random_state` we can get reproducible results.
# The other values are just to avoid a warning issued by Skikit-Learn ...
sgd_clf = SGDClassifier(random_state=42, max_iter=5, tol=-np.infty)
sgd_clf.fit(X_train, y_train_5)
```
If the training of the classifier was successful, it should be able to predict the label of our example instance `X[36000]` correctly.
```
sgd_clf.predict([some_digit])
```
That's good, but it doesn't really give us an idea about the overall performance of the classifier. One good measure for this introduced in the lecture is the cross-validation score. In k-fold cross-validation, the training data is split into k equal subsets. Then the classifier is trained on k-1 sets and evaluated on set k. It's called cross-validation, because this is done for all k possible (and non-redundant) permutations. In case of a 3-fold, this means we train on subsets 1 and 2 and validated on 3, train on 1 and 3 and validate on 2, and train on 2 and 3 and validate on 1. The _score_ represents the prediction accuracy on the validation fold.
```
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
```
While these numbers seem amazingly good, keep in mind, that only 10% of our training data are images of fives, so even a classifier which always predicts 'not five' would reach an accuracy of about 90% ...
In the following box, maybe you can try to implement the cross validation yourself! The `StratifiedKFold` creates k non-biased subsets of the training data. The input to the `StratifiedKFold.split(X, y)` are the training data `X` (in our case called `X_train`) and the labels (in our case for the five-classifier `y_train_5`). The `sklearn.base.clone` function will help to make a copy of the classifier object.
```
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_indices, test_indices in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf) # make a clone of the classifier
# [...] some code is missing here
X_train_folds = X_train[train_indices]
y_train_folds = y_train_5[train_indices]
clone_clf.fit(X_train_folds, y_train_folds)
X_test_fold = X_train[test_indices]
y_test_fold = y_train_5[test_indices]
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print("Fraction of correct predictions: %s" % (n_correct / len(y_pred)))
```
Let's move on to another performance measure: the confusion matrix. The confusion matrix is a 2x2 matrix and includes the number of true positives, false positives (type-I error), true negatives and false negatives (type-II error). First, let's use another of Scitkit-Learn's functions: `cross_val_predict` takes our classifier, our training data and our true labels, and automatically performs a k-fold cross-validation. It returns an array of the predicted labels.
```
from sklearn.model_selection import cross_val_predict
# Take our SGD classifer and perform a 3-fold cross-validation.
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
# Print some of the predicted labels.
print(y_train_pred)
```
Using cross-validation always gives us a 'clean', i.e. unbiased estimate of our prediction power, because the performance of the classifier is evaluated on data it hadn't seen during training. Now we have our predicted labels in `y_train_pred` and can compare them to the true labels `y_train_5`. So let's create a confusion matrix.
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
```
How do we read this? The rows correspond to the _true_ classes, the columns to the _predicted_ classes. So the 53,272 means that about fifty-three thousand numbers that are 'not five' were predicted as such, while 1307 were predicted to be fives. 4344 true fives were predicted to be fives, but 1077 were not. Sometimes it makes sense to normalise the confusion matrix by rows, so that the values in the cells give an idea how large the _fraction_ of correctly and incorrectly predicted instances is. So let's try this:
```
matrix = confusion_matrix(y_train_5, y_train_pred)
row_sums = matrix.sum(axis=1)
matrix / row_sums[:, np.newaxis]
```
There are other metrics to evaluate the performance of classifiers as we saw in the lecture. One example is the _precision_ which is the rate of true positives among all positives. The precision is a measure how many of our predicted positives are _actually_ positives, i.e. it can be calculated as TP / (TP + FP) (TP = true positives, FP = false positives).
```
from sklearn.metrics import precision_score, recall_score
print(precision_score(y_train_5, y_train_pred))
# Can you reproduce this value by hand? All info should be in the confusion matrix.
tp = matrix[1][1]
fp = matrix[0][1]
precision_by_hand = tp / (tp + fp)
print("By hand: %s" % precision_by_hand)
```
Or in words: 77% of our predicted fives are _actually_ fives, while 23% of the predicted fives are other numbers.
Another metric, which is often used in conjunction with the _precision_, is the _recall_. The recall is a measure of how many of the true positives as predicted as such, i.e. "how many true positives do we identify". It is easy to reach perfect precision if you just make your classifier reject all negatives, but it's impossible to keep a high recall score in that case. Let's look at our classifier's recall:
```
print(recall_score(y_train_5, y_train_pred))
# Again, it should be straight-forward to make this calculation by hand. Can you try?
tp = matrix[1][1]
fn = matrix[1][0]
recall_by_hand = tp / (tp + fn)
print("By hand: %s" % recall_by_hand)
```
In words: only 80% of the fives are correctly predicted to be fives. Doesn't look as great as the 95% prediction rate, does it? A nice combination for precision and recall is their harmonic mean, usually known (and in the lecture introduced as) the _F_1 score_. The harmonic mean (as opposed to the arithmetic mean) is very sensitive low values, so only a good balance between precision and recall will lead to a high F_1 score. Very conveniently, Scikit-Learn comes with an implementation of the score already, but can you also calculate it by hand?
```
from sklearn.metrics import f1_score
print(f1_score(y_train_5, y_train_pred))
# Once more, it is fairly easy to calculate this by hand. Give it a try!
f1_score_by_hand = 2 / (1/precision_by_hand + 1/recall_by_hand)
print("By hand: %s" % f1_score_by_hand)
```
Of course, a balanced precision and recall is not _always_ desirable. Whether you want both to be equally high, depends on the use case. Sometimes, you'd definitely want to classify as many true positives as such, with the tradeoff to have low precision (example: in a test for a virus you want every true positive to know that they might be infected, but you might get a few false positives). In other cases, you might want a high precision with the tradeoff that you don't detect all positives as such (example: it's ok to remove some harmless videos in a video filter, but you don't want harmful content to pass your filter).
## Decision function
When we use the `predict()` function, our classifier gives a boolean prediction. But how is that prediction done? The classifier calculates a score, called 'decision_function' in Scikit-Learn, and any instance above a certain threshold is classified as 'true', any instance below as 'false'. By retrieving the decision function directly, we can look at different tradeoffs between precision and recall.
```
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
method="decision_function")
print(y_scores) # Print scores to get an idea ...
```
This again gives us a numpy array with 60,000 entries, all of which contain a floating point value with the predicted score. Now, as we've seen before, Scikit-Learn provides many functions out-of-the-box to evaluate classifiers. The following `precision_recall_curve` metric gives us tuples of precision, recall and threshold values based on our training data. It takes the true labels, in our case `y_train_5` and the `y_scores` to calculate these. We can then use thes values to plot curves for precision and recall for different threshold values.
```
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
print(precisions)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.xlabel("Threshold", fontsize=16)
plt.legend(loc="upper left", fontsize=16)
plt.ylim([0, 1])
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
save_fig("precision_recall_vs_threshold_plot")
plt.show()
```
Looks good! Bonus question: why is the precision curve bumpier than the recall?
Let's assume we want to optimise our classfier for a precision value of 93%. Can you find a good threshold? The below threshold is just a test value and definitely too low.
```
threshold = -20000
y_train_pred_93 = (y_scores > threshold)
print("precision: %s" % precision_score(y_train_5, y_train_pred_93))
print("recall: %s" % recall_score(y_train_5, y_train_pred_93))
```
Sometimes, plotting precision vs. recall can also be helpful.
```
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
save_fig("precision_vs_recall_plot")
plt.show()
```
# ROC curves
Because it's an extremely common performance measure, we should also have a look at the ROC curve (_receiver operating characteristic_). ROC curves plot true positives vs. false positives, or usually the true positive _rate_ vs. the false positive _rate_. While the first is exactly what we called _recall_ so far, the latter is one minus the _true negative rate_, also called specificity. Let's import the ROC curve from Scikit-Learn, this will give us tuples of FPR, TPR and threshold values again.
```
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
```
Now we can plot them:
```
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([0, 1, 0, 1])
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
save_fig("roc_curve_plot")
plt.show()
```
It is always desirable to have the curve as close to the top left corner as above. As a measure for this, one usually calculates the _area under curve_. What is the AUC value for a random classifier?
```
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
```
# Multiclass classification
So far we have completely ignored the fact that our training data not only includes fives and 'other digits', but in fact ten different input labels (one for each digit). Multiclass classification will allow us to distinguish each of them individually and predict the _most likely class_ for each instance. Scikit-Learn is clever enough to realise, that our label array `y_train` contains ten different classes, so – without explicitly telling us – it runs ten binary classifiers when we call the `fit()` function on the SGD classifier. Each of these binary classifiers trains one class vs. all others ("one-versus-all"). Let's try it out:
```
sgd_clf.fit(X_train, y_train)
```
How does it classify our previous example of something that looked like a five?
```
sgd_clf.predict([some_digit])
```
Great! But what exactly happens under the hood? It actually calculates ten different scores for the ten different binary classifiers and picks the class with the highest score. We can see this by calling the `decision_function()` as we did earlier:
```
some_digit_scores = sgd_clf.decision_function([some_digit])
print(some_digit_scores) # Print us the array content
print("Largest entry: %s" % np.argmax(some_digit_scores)) # Get the index of the largest entry
```
Scikit-Learn even comes with a class to run the one-versus-one approach as well. We can just give it our SGD classifier instance and then call the `fit()` function on it:
```
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(sgd_clf)
ovo_clf.fit(X_train, y_train)
# What does it predict for our random five?
ovo_clf.predict([some_digit])
```
And how many classifiers does this one-versus-one approach need? Can you come up with the formula?
```
print("Number of estimators: %s" % len(ovo_clf.estimators_))
```
Back to the one-versus-all approach – how good are we? For that, we can calculate the cross-validation score once more to get values for the accuracy. Bear in mind that now we are running a _ten-class_ classification!
```
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
```
This is not bad at all, although you could probably spend hours optimising the hyperparameters of this model. How good does the onve-versus-one approach perform? Try it out!
Let's look at some other performance measures for the one-versus-all classifier. A good point to start is the confusing matrix.
```
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train, cv=3)
conf_mx = confusion_matrix(y_train_pred, y_train)
conf_mx
```
Ok, maybe it's better to display this in a plot:
```
def plot_confusion_matrix(matrix):
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111)
plt.xlabel('Predicted class', fontsize=16)
plt.ylabel('True class', fontsize=16)
cax = ax.matshow(matrix)
fig.colorbar(cax)
plot_confusion_matrix(conf_mx)
save_fig("confusion_matrix_plot", tight_layout=False)
plt.show()
```
It's still very hard to see what's going on. So maybe we should (1) normalise the matrix by rows again, (2) "remove" all diagonal entries, because those are not interesting for us for the error analysis.
```
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
np.fill_diagonal(norm_conf_mx, 0)
plot_confusion_matrix(norm_conf_mx)
save_fig("confusion_matrix_errors_plot", tight_layout=False)
plt.show()
```
It seems we're predicting many of the eights wrong. In particular, many of them are predicted to be a five! On the other hand, not many fives are misclassified as eights. Interesting, right? Let's pick out some eights and fives, each of which are either correctly predicted, or predicted as the other class. Maybe looking at the pictures with our "human learning" algorithm will see the problem.
```
cl_a, cl_b = 8, 5 # Define class a and class b for the plot
# Training data from class a, which is predicted as a.
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
# Training data from class a, which is predicted as b.
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
# Training data from class b, which is predicted as a.
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
# Training data from class b, which is predicted as b.
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
save_fig("error_analysis_digits_plot")
plt.show()
```
| true |
code
| 0.644477 | null | null | null | null |
|
# "Build Your First Neural Network with PyTorch"
* article <https://curiousily.com/posts/build-your-first-neural-network-with-pytorch/>
* dataset <https://www.kaggle.com/jsphyg/weather-dataset-rattle-package>
requires `torch 1.4.0`
```
import os
from os.path import dirname
import numpy as np
import pandas as pd
from tqdm import tqdm
import seaborn as sns
from pylab import rcParams
import matplotlib.pyplot as plt
from matplotlib import rc
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
import torch
from torch import nn, optim
import torch.nn.functional as F
%matplotlib inline
sns.set(style='whitegrid', palette='muted', font_scale=1.2)
HAPPY_COLORS_PALETTE = ["#01BEFE", "#FFDD00", "#FF7D00", "#FF006D", "#93D30C", "#8F00FF"]
sns.set_palette(sns.color_palette(HAPPY_COLORS_PALETTE))
rcParams["figure.figsize"] = 12, 8
RANDOM_SEED = 42
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)
df = pd.read_csv(dirname(os.getcwd()) + "/dat/weatherAUS.csv")
df.describe()
df.shape
# data pre-processing
cols = [ "Rainfall", "Humidity3pm", "Pressure9am", "RainToday", "RainTomorrow" ]
df = df[cols]
df.head()
df["RainToday"].replace({"No": 0, "Yes": 1}, inplace = True)
df["RainTomorrow"].replace({"No": 0, "Yes": 1}, inplace = True)
df.head()
# drop missing values
df = df.dropna(how="any")
df.head()
sns.countplot(df.RainTomorrow);
df.RainTomorrow.value_counts() / df.shape[0]
X = df[["Rainfall", "Humidity3pm", "RainToday", "Pressure9am"]]
y = df[["RainTomorrow"]]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=RANDOM_SEED)
X_train = torch.from_numpy(X_train.to_numpy()).float()
X_test = torch.from_numpy(X_test.to_numpy()).float()
y_train = torch.squeeze(torch.from_numpy(y_train.to_numpy()).float())
y_test = torch.squeeze(torch.from_numpy(y_test.to_numpy()).float())
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
class Net (nn.Module):
def __init__ (self, n_features):
super(Net, self).__init__()
self.fc1 = nn.Linear(n_features, 5)
self.fc2 = nn.Linear(5, 3)
self.fc3 = nn.Linear(3, 1)
def forward (self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return torch.sigmoid(self.fc3(x))
net = Net(X_train.shape[1])
# training
criterion = nn.BCELoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)
# weather forecast
def calculate_accuracy (y_true, y_pred):
predicted = y_pred.ge(.5).view(-1)
return (y_true == predicted).sum().float() / len(y_true)
def round_tensor (t, decimal_places=3):
return round(t.item(), decimal_places)
MAX_EPOCH = 5000
for epoch in range(MAX_EPOCH):
y_pred = net(X_train)
y_pred = torch.squeeze(y_pred)
train_loss = criterion(y_pred, y_train)
if epoch % 100 == 0:
train_acc = calculate_accuracy(y_train, y_pred)
y_test_pred = net(X_test)
y_test_pred = torch.squeeze(y_test_pred)
test_loss = criterion(y_test_pred, y_test)
test_acc = calculate_accuracy(y_test, y_test_pred)
print(
f'''epoch {epoch}
Train set - loss: {round_tensor(train_loss)}, accuracy: {round_tensor(train_acc)}
Test set - loss: {round_tensor(test_loss)}, accuracy: {round_tensor(test_acc)}
''')
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
# save the model
MODEL_PATH = "model.pth"
torch.save(net, MODEL_PATH)
# restore model
net = torch.load(MODEL_PATH)
# evaluation
classes = ["No rain", "Raining"]
y_pred = net(X_test)
y_pred = y_pred.ge(.5).view(-1).cpu()
y_test = y_test.cpu()
print(classification_report(y_test, y_pred, target_names=classes))
cm = confusion_matrix(y_test, y_pred)
df_cm = pd.DataFrame(cm, index=classes, columns=classes)
hmap = sns.heatmap(df_cm, annot=True, fmt="d")
hmap.yaxis.set_ticklabels(hmap.yaxis.get_ticklabels(), rotation=0, ha='right')
hmap.xaxis.set_ticklabels(hmap.xaxis.get_ticklabels(), rotation=30, ha='right')
plt.ylabel('True label')
plt.xlabel('Predicted label');
def will_it_rain (rainfall, humidity, rain_today, pressure):
t = torch.as_tensor([rainfall, humidity, rain_today, pressure]).float().cpu()
output = net(t)
print("net(t)", output.item())
return output.ge(0.5).item()
will_it_rain(rainfall=10, humidity=10, rain_today=True, pressure=2)
will_it_rain(rainfall=0, humidity=1, rain_today=False, pressure=100)
```
| true |
code
| 0.764584 | null | null | null | null |
|
## Part 2: Introduction to Feed Forward Networks
### 1. What is a neural network?
#### 1.1 Neurons
A neuron is software that is roughly modeled after the neuons in your brain. In software, we model it with an _affine function_ and an _activation function_.
One type of neuron is the perceptron, which outputs a binary output 0 or 1 given an input [7]:
<img src="perceptron.jpg" width="600" height="480" />
You can add an activation function to the end isntead of simply thresholding values to clip values from 0 to 1. One common activiation function is the logistic function.
<img src="sigmoid_neuron.jpg" width="600" height="480" />
The most common activation function used nowadays is the rectified linear unit, which is simply max(0, z) where z = w * x + b, or the neurons output.
#### 1.2 Hidden layers and multi-layer perceptrons
A multi-layer perceptron (MLP) is quite simply layers on these perceptrons that are wired together. The layers between the input layer and the output layer are known as the hidden layers. The below is a four layer network with two hidden layers [7]:
<img src="hidden_layers.jpg" width="600" height="480" />
### 2. Tensorflow
Tensorflow (https://www.tensorflow.org/install/) is an extremely popular deep learning library built by Google and will be the main library used for of the rest of these notebooks (in the last lesson, we briefly used numpy, a numerical computation library that's useful but does not have deep learning functionality). NOTE: Other popular deep learning libraries include Pytorch and Caffe2. Keras is another popular one, but its API has since been absorbed into Tensorflow. Tensorflow is chosen here because:
* it has the most active community on Github
* it's well supported by Google in terms of core features
* it has Tensorflow serving, which allows you to serve your models online (something we'll see in a future notebook)
* it has Tensorboard for visualization (which we will use in this lesson)
Let's train our first model to get a sense of how powerful Tensorflow can be!
```
# Some initial setup. Borrowed from:
# https://github.com/ageron/handson-ml/blob/master/09_up_and_running_with_tensorflow.ipynb
# Common imports
import numpy as np
import os
import tensorflow as tf
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "tensorflow"
def save_fig(fig_id):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
def stabilize_output():
tf.reset_default_graph()
# needed to avoid the following error: https://github.com/RasaHQ/rasa_core/issues/80
tf.keras.backend.clear_session()
tf.set_random_seed(seed=42)
np.random.seed(seed=42)
print "Done"
```
Below we will train our first model using the example from the Tensorflow tutorial: https://www.tensorflow.org/tutorials/
This will show you the basics of training a model!
```
# The example below is also in https://colab.research.google.com/github/tensorflow/models/blob/master/samples/core/get_started/_index.ipynb
# to ensure relatively stable output across sessions
stabilize_output()
mnist = tf.keras.datasets.mnist
# load data (requires Internet connection)
(x_train, y_train),(x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# build a model
model = tf.keras.models.Sequential([
# flattens the input
tf.keras.layers.Flatten(),
# 1 "hidden" layer with 512 units - more on this in the next notebook
tf.keras.layers.Dense(512, activation=tf.nn.relu),
# example of regularization - dropout is a way of dropping hidden units at a certain factor
# this essentially results in a model averaging across a large set of possible configurations of the hidden layer above
# and results in model that should generalize better
tf.keras.layers.Dropout(0.2),
# 10 because there's possible didigts - 0 to 9
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# train a model (using 5 epochs -> notice the accuracy improving with each epoch)
model.fit(x_train, y_train, epochs=5)
print model.metrics_names # see https://keras.io/models/model/ for the full API
# evaluate model accuracy
model.evaluate(x_test, y_test)
```
You should see something similar to [0.06788356024027743, 0.9806]. The first number is the final loss and the second number is the accuracy.
Congratulations, it means you've trained a classifier that classifies digit images in the MNIST Dataset with __98% accuracy__! We'll break down how the model is optimizing to achieve this accuracy below.
### 3. More Training of Neural Networks in Tensorflow
#### 3.1: Data Preparation
We load the CIFAR-10 dataset using the tf.keras API.
```
# Borrowed from http://cs231n.github.io/assignments2018/assignment2/
def load_cifar10(num_training=49000, num_validation=1000, num_test=10000):
"""
Fetch the CIFAR-10 dataset from the web and perform preprocessing to prepare
it for the two-layer neural net classifier. These are the same steps as
we used for the SVM, but condensed to a single function.
"""
# Load the raw CIFAR-10 dataset and use appropriate data types and shapes
# NOTE: Download will take a few minutes but once downloaded, it should be cached.
cifar10 = tf.keras.datasets.cifar10.load_data()
(X_train, y_train), (X_test, y_test) = cifar10
X_train = np.asarray(X_train, dtype=np.float32)
y_train = np.asarray(y_train, dtype=np.int32).flatten()
X_test = np.asarray(X_test, dtype=np.float32)
y_test = np.asarray(y_test, dtype=np.int32).flatten()
# Subsample the data
mask = range(num_training, num_training + num_validation)
X_val = X_train[mask]
y_val = y_train[mask]
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
# Normalize the data: subtract the mean pixel and divide by std
mean_pixel = X_train.mean(axis=(0, 1, 2), keepdims=True)
std_pixel = X_train.std(axis=(0, 1, 2), keepdims=True)
X_train = (X_train - mean_pixel) / std_pixel
X_val = (X_val - mean_pixel) / std_pixel
X_test = (X_test - mean_pixel) / std_pixel
return X_train, y_train, X_val, y_val, X_test, y_test
# Invoke the above function to get our data.
# N - index of the number of datapoints (minibatch size)
# H - index of the the height of the feature map
# W - index of the width of the feature map
NHW = (0, 1, 2)
X_train, y_train, X_val, y_val, X_test, y_test = load_cifar10()
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape, y_train.dtype)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
```
#### 3.2 Preparation: Dataset object
Borrowed from CS231N [2], we will define a `Dataset` class for iteration to store data and labels.
```
class Dataset(object):
def __init__(self, X, y, batch_size, shuffle=False):
"""
Construct a Dataset object to iterate over data X and labels y
Inputs:
- X: Numpy array of data, of any shape
- y: Numpy array of labels, of any shape but with y.shape[0] == X.shape[0]
- batch_size: Integer giving number of elements per minibatch
- shuffle: (optional) Boolean, whether to shuffle the data on each epoch
"""
assert X.shape[0] == y.shape[0], 'Got different numbers of data and labels'
self.X, self.y = X, y
self.batch_size, self.shuffle = batch_size, shuffle
def __iter__(self):
N, B = self.X.shape[0], self.batch_size
idxs = np.arange(N)
if self.shuffle:
np.random.shuffle(idxs)
return iter((self.X[i:i+B], self.y[i:i+B]) for i in range(0, N, B))
train_dset = Dataset(X_train, y_train, batch_size=64, shuffle=True)
val_dset = Dataset(X_val, y_val, batch_size=64, shuffle=False)
test_dset = Dataset(X_test, y_test, batch_size=64)
print "Done"
# We can iterate through a dataset like this:
for t, (x, y) in enumerate(train_dset):
print(t, x.shape, y.shape)
if t > 5: break
# You can also optionally set GPU to true if you are working on AWS/Google Cloud (more on that later). For now,
# we to false
# Set up some global variables
USE_GPU = False
if USE_GPU:
device = '/device:GPU:0'
else:
device = '/cpu:0'
# Constant to control how often we print when training models
print_every = 100
print('Using device: ', device)
# Borrowed fromcs231n.github.io/assignments2018/assignment2/
# We define a flatten utility function to help us flatten our image data - the 32x32x3
# (or 32 x 32 image size with three channels for RGB) flattens into 3072
def flatten(x):
"""
Input:
- TensorFlow Tensor of shape (N, D1, ..., DM)
Output:
- TensorFlow Tensor of shape (N, D1 * ... * DM)
"""
N = tf.shape(x)[0]
return tf.reshape(x, (N, -1))
def two_layer_fc(x, params):
"""
A fully-connected neural network; the architecture is:
fully-connected layer -> ReLU -> fully connected layer.
Note that we only need to define the forward pass here; TensorFlow will take
care of computing the gradients for us.
The input to the network will be a minibatch of data, of shape
(N, d1, ..., dM) where d1 * ... * dM = D. The hidden layer will have H units,
and the output layer will produce scores for C classes.
Inputs:
- x: A TensorFlow Tensor of shape (N, d1, ..., dM) giving a minibatch of
input data.
- params: A list [w1, w2] of TensorFlow Tensors giving weights for the
network, where w1 has shape (D, H) and w2 has shape (H, C).
Returns:
- scores: A TensorFlow Tensor of shape (N, C) giving classification scores
for the input data x.
"""
w1, w2 = params # Unpack the parameters
x = flatten(x) # Flatten the input; now x has shape (N, D)
h = tf.nn.relu(tf.matmul(x, w1)) # Hidden layer: h has shape (N, H)
scores = tf.matmul(h, w2) # Compute scores of shape (N, C)
return scores
def two_layer_fc_test():
# TensorFlow's default computational graph is essentially a hidden global
# variable. To avoid adding to this default graph when you rerun this cell,
# we clear the default graph before constructing the graph we care about.
tf.reset_default_graph()
hidden_layer_size = 42
# Scoping our computational graph setup code under a tf.device context
# manager lets us tell TensorFlow where we want these Tensors to be
# placed.
with tf.device(device):
# Set up a placehoder for the input of the network, and constant
# zero Tensors for the network weights. Here we declare w1 and w2
# using tf.zeros instead of tf.placeholder as we've seen before - this
# means that the values of w1 and w2 will be stored in the computational
# graph itself and will persist across multiple runs of the graph; in
# particular this means that we don't have to pass values for w1 and w2
# using a feed_dict when we eventually run the graph.
x = tf.placeholder(tf.float32)
w1 = tf.zeros((32 * 32 * 3, hidden_layer_size))
w2 = tf.zeros((hidden_layer_size, 10))
# Call our two_layer_fc function to set up the computational
# graph for the forward pass of the network.
scores = two_layer_fc(x, [w1, w2])
# Use numpy to create some concrete data that we will pass to the
# computational graph for the x placeholder.
x_np = np.zeros((64, 32, 32, 3))
with tf.Session() as sess:
# The calls to tf.zeros above do not actually instantiate the values
# for w1 and w2; the following line tells TensorFlow to instantiate
# the values of all Tensors (like w1 and w2) that live in the graph.
sess.run(tf.global_variables_initializer())
# Here we actually run the graph, using the feed_dict to pass the
# value to bind to the placeholder for x; we ask TensorFlow to compute
# the value of the scores Tensor, which it returns as a numpy array.
scores_np = sess.run(scores, feed_dict={x: x_np})
print scores_np
print(scores_np.shape)
two_layer_fc_test()
# should print a bunch of zeros
# should print {64, 10}
print "Done"
```
#### 3.3 Training
We will now train using the gradient descent algorithm explained in the previous notebook. The check_accuracy function below lets us check the accuracy of our neural network.
As explained in CS231N:
"The `training_step` function has three basic steps:
1. Compute the loss
2. Compute the gradient of the loss with respect to all network weights
3. Make a weight update step using (stochastic) gradient descent.
Note that the step of updating the weights is itself an operation in the computational graph - the calls to `tf.assign_sub` in `training_step` return TensorFlow operations that mutate the weights when they are executed. There is an important bit of subtlety here - when we call `sess.run`, TensorFlow does not execute all operations in the computational graph; it only executes the minimal subset of the graph necessary to compute the outputs that we ask TensorFlow to produce. As a result, naively computing the loss would not cause the weight update operations to execute, since the operations needed to compute the loss do not depend on the output of the weight update. To fix this problem, we insert a **control dependency** into the graph, adding a duplicate `loss` node to the graph that does depend on the outputs of the weight update operations; this is the object that we actually return from the `training_step` function. As a result, asking TensorFlow to evaluate the value of the `loss` returned from `training_step` will also implicitly update the weights of the network using that minibatch of data.
We need to use a few new TensorFlow functions to do all of this:
- For computing the cross-entropy loss we'll use `tf.nn.sparse_softmax_cross_entropy_with_logits`: https://www.tensorflow.org/api_docs/python/tf/nn/sparse_softmax_cross_entropy_with_logits
- For averaging the loss across a minibatch of data we'll use `tf.reduce_mean`:
https://www.tensorflow.org/api_docs/python/tf/reduce_mean
- For computing gradients of the loss with respect to the weights we'll use `tf.gradients`: https://www.tensorflow.org/api_docs/python/tf/gradients
- We'll mutate the weight values stored in a TensorFlow Tensor using `tf.assign_sub`: https://www.tensorflow.org/api_docs/python/tf/assign_sub
- We'll add a control dependency to the graph using `tf.control_dependencies`: https://www.tensorflow.org/api_docs/python/tf/control_dependencies"
```
# Borrowed from cs231n.github.io/assignments2018/assignment2/
def training_step(scores, y, params, learning_rate):
"""
Set up the part of the computational graph which makes a training step.
Inputs:
- scores: TensorFlow Tensor of shape (N, C) giving classification scores for
the model.
- y: TensorFlow Tensor of shape (N,) giving ground-truth labels for scores;
y[i] == c means that c is the correct class for scores[i].
- params: List of TensorFlow Tensors giving the weights of the model
- learning_rate: Python scalar giving the learning rate to use for gradient
descent step.
Returns:
- loss: A TensorFlow Tensor of shape () (scalar) giving the loss for this
batch of data; evaluating the loss also performs a gradient descent step
on params (see above).
"""
# First compute the loss; the first line gives losses for each example in
# the minibatch, and the second averages the losses acros the batch
losses = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=scores)
loss = tf.reduce_mean(losses)
# Compute the gradient of the loss with respect to each parameter of the the
# network. This is a very magical function call: TensorFlow internally
# traverses the computational graph starting at loss backward to each element
# of params, and uses backpropagation to figure out how to compute gradients;
# it then adds new operations to the computational graph which compute the
# requested gradients, and returns a list of TensorFlow Tensors that will
# contain the requested gradients when evaluated.
grad_params = tf.gradients(loss, params)
# Make a gradient descent step on all of the model parameters.
new_weights = []
for w, grad_w in zip(params, grad_params):
new_w = tf.assign_sub(w, learning_rate * grad_w)
new_weights.append(new_w)
# Insert a control dependency so that evaluting the loss causes a weight
# update to happen; see the discussion above.
with tf.control_dependencies(new_weights):
return tf.identity(loss)
# Train using stochastic gradient descent without momentum
def train(model_fn, init_fn, learning_rate):
"""
Train a model on CIFAR-10.
Inputs:
- model_fn: A Python function that performs the forward pass of the model
using TensorFlow; it should have the following signature:
scores = model_fn(x, params) where x is a TensorFlow Tensor giving a
minibatch of image data, params is a list of TensorFlow Tensors holding
the model weights, and scores is a TensorFlow Tensor of shape (N, C)
giving scores for all elements of x.
- init_fn: A Python function that initializes the parameters of the model.
It should have the signature params = init_fn() where params is a list
of TensorFlow Tensors holding the (randomly initialized) weights of the
model.
- learning_rate: Python float giving the learning rate to use for SGD.
"""
# First clear the default graph
tf.reset_default_graph()
is_training = tf.placeholder(tf.bool, name='is_training')
# Set up the computational graph for performing forward and backward passes,
# and weight updates.
with tf.device(device):
# Set up placeholders for the data and labels
x = tf.placeholder(tf.float32, [None, 32, 32, 3])
y = tf.placeholder(tf.int32, [None])
params = init_fn() # Initialize the model parameters
scores = model_fn(x, params) # Forward pass of the model
loss = training_step(scores, y, params, learning_rate)
# Now we actually run the graph many times using the training data
with tf.Session() as sess:
# Initialize variables that will live in the graph
sess.run(tf.global_variables_initializer())
for t, (x_np, y_np) in enumerate(train_dset):
# Run the graph on a batch of training data; recall that asking
# TensorFlow to evaluate loss will cause an SGD step to happen.
feed_dict = {x: x_np, y: y_np}
loss_np = sess.run(loss, feed_dict=feed_dict)
# Periodically print the loss and check accuracy on the val set
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss_np))
check_accuracy(sess, val_dset, x, scores, is_training)
# Helper method for evaluating our model accuracy (note it also runs the computational graph but doesn't update loss)
def check_accuracy(sess, dset, x, scores, is_training=None):
"""
Check accuracy on a classification model.
Inputs:
- sess: A TensorFlow Session that will be used to run the graph
- dset: A Dataset object on which to check accuracy
- x: A TensorFlow placeholder Tensor where input images should be fed
- scores: A TensorFlow Tensor representing the scores output from the
model; this is the Tensor we will ask TensorFlow to evaluate.
Returns: Nothing, but prints the accuracy of the model
"""
num_correct, num_samples = 0, 0
for x_batch, y_batch in dset:
feed_dict = {x: x_batch, is_training: 0}
scores_np = sess.run(scores, feed_dict=feed_dict)
y_pred = scores_np.argmax(axis=1)
num_samples += x_batch.shape[0]
num_correct += (y_pred == y_batch).sum()
acc = float(num_correct) / num_samples
print('Got %d / %d correct (%.2f%%)' % (num_correct, num_samples, 100 * acc))
print "Done"
# Borrowed from cs231n.github.io/assignments2018/assignment2/
# We initialize the weight matrices for our models using a method known as Kaiming's normalization method [8]
def kaiming_normal(shape):
if len(shape) == 2:
fan_in, fan_out = shape[0], shape[1]
elif len(shape) == 4:
fan_in, fan_out = np.prod(shape[:3]), shape[3]
return tf.random_normal(shape) * np.sqrt(2.0 / fan_in)
def two_layer_fc_init():
"""
Initialize the weights of a two-layer network (one hidden layer), for use with the
two_layer_network function defined above.
Inputs: None
Returns: A list of:
- w1: TensorFlow Variable giving the weights for the first layer
- w2: TensorFlow Variable giving the weights for the second layer
"""
# Numer of neurons in hidden layer
hidden_layer_size = 4000
# Now we initialize the weights of our two layer network using tf.Variable
# "A TensorFlow Variable is a Tensor whose value is stored in the graph and persists across runs of the
# computational graph; however unlike constants defined with `tf.zeros` or `tf.random_normal`,
# the values of a Variable can be mutated as the graph runs; these mutations will persist across graph runs.
# Learnable parameters of the network are usually stored in Variables."
w1 = tf.Variable(kaiming_normal((3 * 32 * 32, hidden_layer_size)))
w2 = tf.Variable(kaiming_normal((hidden_layer_size, 10)))
return [w1, w2]
print "Done"
# Now we actually train our model with one *epoch* ! We use a learning rate of 0.01
learning_rate = 1e-2
train(two_layer_fc, two_layer_fc_init, learning_rate)
# You should see an accuracy of >40% with just one epoch (an epoch in this case consists of 700 iterations
# of gradient descent but can be tuned)
```
#### 3.3 Keras
Note in the first cell, we used the tf.keras Sequential API to make a neural network but here we use "barebones" Tensorflow. One of the good (and possibly bad) things about Tensorflow is that there are several ways to create a neural network and train it. Here are some possible ways:
* Barebones tensorflow
* tf.keras Model API
* tf.keras Sequential API
Here is a table of comparison borrowed from [2]:
| API | Flexibility | Convenience |
|---------------|-------------|-------------|
| Barebone | High | Low |
| `tf.keras.Model` | High | Medium |
| `tf.keras.Sequential` | Low | High |
Note that with the tf.keras Model API, you have the options of using the **object-oriented API**, where each layer of the neural network is represented as a Python object (like `tf.layers.Dense`) or the **functional API**, where each layer is a Python function (like `tf.layers.dense`). We will only use the Sequential API and skip the Model API in the cells below because we will simply trade off lots of flexiblity for convenience.
```
# Now we will train the same model using the Sequential API.
# First we set up our training and model initializiation functions
def train_keras(model_init_fn, optimizer_init_fn, num_epochs=1):
"""
Simple training loop for use with models defined using tf.keras. It trains
a model for one epoch on the CIFAR-10 training set and periodically checks
accuracy on the CIFAR-10 validation set.
Inputs:
- model_init_fn: A function that takes no parameters; when called it
constructs the model we want to train: model = model_init_fn()
- optimizer_init_fn: A function which takes no parameters; when called it
constructs the Optimizer object we will use to optimize the model:
optimizer = optimizer_init_fn()
- num_epochs: The number of epochs to train for
Returns: Nothing, but prints progress during trainingn
"""
tf.reset_default_graph()
with tf.device(device):
# Construct the computational graph we will use to train the model. We
# use the model_init_fn to construct the model, declare placeholders for
# the data and labels
x = tf.placeholder(tf.float32, [None, 32, 32, 3])
y = tf.placeholder(tf.int32, [None])
# We need a place holder to explicitly specify if the model is in the training
# phase or not. This is because a number of layers behaves differently in
# training and in testing, e.g., dropout and batch normalization.
# We pass this variable to the computation graph through feed_dict as shown below.
is_training = tf.placeholder(tf.bool, name='is_training')
# Use the model function to build the forward pass.
scores = model_init_fn(x, is_training)
# Compute the loss like we did in Part II
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=scores)
loss = tf.reduce_mean(loss)
# Use the optimizer_fn to construct an Optimizer, then use the optimizer
# to set up the training step. Asking TensorFlow to evaluate the
# train_op returned by optimizer.minimize(loss) will cause us to make a
# single update step using the current minibatch of data.
# Note that we use tf.control_dependencies to force the model to run
# the tf.GraphKeys.UPDATE_OPS at each training step. tf.GraphKeys.UPDATE_OPS
# holds the operators that update the states of the network.
# For example, the tf.layers.batch_normalization function adds the running mean
# and variance update operators to tf.GraphKeys.UPDATE_OPS.
optimizer = optimizer_init_fn()
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops):
train_op = optimizer.minimize(loss)
# Now we can run the computational graph many times to train the model.
# When we call sess.run we ask it to evaluate train_op, which causes the
# model to update.
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
t = 0
for epoch in range(num_epochs):
print('Starting epoch %d' % epoch)
for x_np, y_np in train_dset:
feed_dict = {x: x_np, y: y_np, is_training:1}
loss_np, _ = sess.run([loss, train_op], feed_dict=feed_dict)
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss_np))
check_accuracy(sess, val_dset, x, scores, is_training=is_training)
print()
t += 1
def model_init_fn(inputs, is_training):
input_shape = (32, 32, 3)
hidden_layer_size, num_classes = 4000, 10
initializer = tf.variance_scaling_initializer(scale=2.0)
layers = [
tf.layers.Flatten(input_shape=input_shape),
tf.layers.Dense(hidden_layer_size, activation=tf.nn.relu,
kernel_initializer=initializer),
tf.layers.Dense(num_classes, kernel_initializer=initializer),
]
model = tf.keras.Sequential(layers)
return model(inputs)
def optimizer_init_fn():
return tf.train.GradientDescentOptimizer(learning_rate)
print "Done"
# Now the actual training
learning_rate = 1e-2
train_keras(model_init_fn, optimizer_init_fn)
# Again, you should see accuracy > 40% after one epoch (700 iterations) of gradient descent
```
### 4. Backpropagation
You'll often hear the term "backpropagation" or "backprop," which is a way of updating a neural network. Google has a great demo that walks you through the backpropagation algorithm in detail. I encourage you to check it out!
https://google-developers.appspot.com/machine-learning/crash-course/backprop-scroll/
See also this seminar by Geoffrey Hinton, a premier deep learning researcher, on whether the brain can do back-propagation. It's an interesting lecture with relatively : https://www.youtube.com/watch?v=VIRCybGgHts
### 5. References
<pre>
[1] Fast.ai (http://course.fast.ai/)
[2] CS231N (http://cs231n.github.io/)
[3] CS224D (http://cs224d.stanford.edu/syllabus.html)
[4] Hands on Machine Learning (https://github.com/ageron/handson-ml)
[5] Deep learning with Python Notebooks (https://github.com/fchollet/deep-learning-with-python-notebooks)
[6] Deep learning by Goodfellow et. al (http://www.deeplearningbook.org/)
[7] Neural networks online book (http://neuralnetworksanddeeplearning.com/)
[8] He et al, *Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
*, ICCV 2015, https://arxiv.org/abs/1502.01852
</pre>
| true |
code
| 0.746347 | null | null | null | null |
|
```
import tensorflow as tf
print(tf.__version__)
import tensorflow_datasets as tfds
print(tfds.__version__)
```
# Get dataset
```
SPLIT_WEIGHTS = (8, 1, 1)
splits = tfds.Split.TRAIN.subsplit(weighted=SPLIT_WEIGHTS)
(raw_train, raw_validation, raw_test), metadata = tfds.load('cats_vs_dogs',
split=list(splits),
with_info=True,
as_supervised=True)
print(metadata.features)
import matplotlib.pyplot as plt
%matplotlib inline
get_label_name = metadata.features['label'].int2str
for image, label in raw_train.take(2):
plt.figure()
plt.imshow(image)
plt.title(get_label_name(label))
```
# Prepare input pipelines
```
IMG_SIZE = 160
BATCH_SIZE = 32
SHUFFLE_BUFFER_SIZE = 1000
def normalize_img(image, label):
image = tf.cast(image, tf.float32)
image = (image / 127.5) - 1.0
image = tf.image.resize(image, (IMG_SIZE, IMG_SIZE))
return image, label
ds_train = raw_train.map(normalize_img)
ds_validation = raw_validation.map(normalize_img)
ds_test = raw_test.map(normalize_img)
ds_train = ds_train.shuffle(SHUFFLE_BUFFER_SIZE).batch(BATCH_SIZE)
ds_validation = ds_validation.shuffle(SHUFFLE_BUFFER_SIZE).batch(BATCH_SIZE)
ds_test = ds_test.batch(BATCH_SIZE)
```
# Get pretrained model
```
base_model = tf.keras.applications.MobileNetV2(input_shape=(IMG_SIZE, IMG_SIZE, 3),
include_top=False,
weights='imagenet')
base_model.trainable = False
model = tf.keras.Sequential([
base_model,
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(1)
])
model.summary()
```
# (Optional): Use Tensorflow Hub
```
import tensorflow_hub as hub
print(hub.__version__)
feature_extractor_url = "https://tfhub.dev/google/imagenet/mobilenet_v2_035_160/classification/4"
base_model = hub.KerasLayer(feature_extractor_url, input_shape=(IMG_SIZE, IMG_SIZE, 3), trainable=False)
model = tf.keras.Sequential([
base_model,
tf.keras.layers.Dense(1)
])
model.summary()
```
# Compile model
```
base_learning_rate = 1e-4
model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=base_learning_rate),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
```
# Evaluate random model
```
loss0, accuracy0 = model.evaluate(ds_validation)
```
# Train model
```
initial_epochs = 3
history = model.fit(ds_train,
epochs=initial_epochs,
validation_data=ds_validation)
```
# Fine-tune
```
base_model.trainable = True
base_learning_rate = 1e-5
model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=base_learning_rate),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
model.summary()
fine_tune_epochs = 3
total_epochs = initial_epochs + fine_tune_epochs
history_fine = model.fit(ds_train,
epochs=total_epochs,
initial_epoch=history.epoch[-1],
validation_data=ds_validation)
```
| true |
code
| 0.792835 | null | null | null | null |
|
# Example 3. CNN + DDA
Here, we train the same CNN as in previous notebook but applying the Direct Domain Adaptation method (DDA) to reduce the gap between MNIST and MNIST-M datasets.
-------
This code is modified from [https://github.com/fungtion/DANN_py3](https://github.com/fungtion/DANN_py3).
```
import os
import sys
import tqdm
import random
import numpy as np
from numpy.fft import rfft2, irfft2, fftshift, ifftshift
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.nn as nn
import torch.utils.data
from torchvision import datasets
from torchvision import transforms
from components.data_loader import GetLoader
from components.model import CNNModel
from components.test import test
import components.shared as sd
# os.environ["CUDA_VISIBLE_DEVICES"] = "2"
```
### Init paths
```
# Paths to datasets
source_dataset_name = 'MNIST'
target_dataset_name = 'mnist_m'
source_image_root = os.path.join('dataset', source_dataset_name)
target_image_root = os.path.join('dataset', target_dataset_name)
os.makedirs('./dataset', exist_ok=True)
# Where to save outputs
model_root = './out_ex3_cnn_da'
os.makedirs(model_root, exist_ok=True)
```
### Init training
```
cuda = True
cudnn.benchmark = True
# Hyperparameters
lr = 1e-3
batch_size = 128
image_size = 28
n_epoch = 100
# manual_seed = random.randint(1, 10000)
manual_seed = 222
random.seed(manual_seed)
torch.manual_seed(manual_seed)
print(f'Random seed: {manual_seed}')
```
### Data
```
# Transformations / augmentations
img_transform_source = transforms.Compose([
transforms.Resize(image_size),
transforms.ToTensor(),
transforms.Normalize(mean=(0.1307,), std=(0.3081,)),
transforms.Lambda(lambda x: x.repeat(3, 1, 1)),
])
img_transform_target = transforms.Compose([
transforms.Resize(image_size),
transforms.ToTensor(),
transforms.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5))
])
# Load MNIST dataset
dataset_source = datasets.MNIST(
root='dataset',
train=True,
transform=img_transform_source,
download=True
)
# Load MNIST-M dataset
train_list = os.path.join(target_image_root, 'mnist_m_train_labels.txt')
dataset_target = GetLoader(
data_root=os.path.join(target_image_root, 'mnist_m_train'),
data_list=train_list,
transform=img_transform_target
)
```
# Direct Domain Adaptation (DDA)
## Average auto-correlation
For entire dataset
```
def get_global_acorr_for_loader(loader):
""" The average auto-correlation of all images in the dataset """
global_acorr = np.zeros((3, 28, 15), dtype=np.complex128)
prog_bar = tqdm.tqdm(loader)
for data, _ in prog_bar:
data_f = np.fft.rfft2(data, s=data.shape[-2:], axes=(-2, -1))
# Auto-correlation is multiplication with the conjucate of self
# in frequency domain
global_acorr += data_f * np.conjugate(data_f)
global_acorr /= len(loader)
print(global_acorr.shape)
return np.fft.fftshift(global_acorr)
def route_to(fname):
""" Shortcut for routing to the save folder """
return os.path.join(model_root, fname)
# Compute global acorr if not in the folder, load otherwise
if not 'gacorr_dst_tr.npy' in os.listdir(model_root):
print('Save global acorr')
gacorr_dst_tr = get_global_acorr_for_loader(dataset_target)
gacorr_src_tr = get_global_acorr_for_loader(dataset_source)
np.save(route_to('gacorr_dst_tr.npy'), gacorr_dst_tr)
np.save(route_to('gacorr_src_tr.npy'), gacorr_src_tr)
else:
print('Load global acorr')
gacorr_dst_tr = np.load(route_to('gacorr_dst_tr.npy'))
gacorr_src_tr = np.load(route_to('gacorr_src_tr.npy'))
```
## Average cross-correlation
Pick a random pixel(-s) from each image in the dataset and average
```
# Window size
crop_size = 1
print(f'Use the crop size for xcorr = {crop_size}')
def crop_ref(x, n=1, edge=5):
"""Crop a window from the image
Args:
x(np.ndarray): image [c, h, w]
n(int): window size
edge(int): margin to avoid from edges of the image
"""
if n % 2 == 0: n+=1;
k = int((n - 1) / 2)
nz, nx = x.shape[-2:]
dim1 = np.random.randint(0+k+edge, nz-k-edge)
dim2 = np.random.randint(0+k, nx-k)
out = x[..., dim1-k:dim1+k+1, dim2-k:dim2+k+1]
return out
# crop_ref(np.ones((2, 100, 100)), n=5).shape
def get_global_xcorr_for_loader(loader, crop_size=1):
# Init the placeholder for average
rand_pixel = np.zeros((3, crop_size, crop_size))
# Loop over all images in the dataset
prog_bar = tqdm.tqdm(loader)
for data, _ in prog_bar:
rand_pixel += np.mean(crop_ref(data, crop_size).numpy(), axis=0)
rand_pixel /= len(loader)
# Place the mean pixel into center of an empty image
c, h ,w = data.shape
mid_h, mid_w = int(h // 2), int(w // 2)
embed = np.zeros_like(data)
embed[..., mid_h:mid_h+1, mid_w:mid_w+1] = rand_pixel
global_xcorr = np.fft.rfft2(embed, s=data.shape[-2:], axes=(-2, -1))
return np.fft.fftshift(global_xcorr)
# Compute global xcorr if not in the folder, load otherwise
if not 'gxcorr_dst_tr.npy' in os.listdir(model_root):
# if True:
print('Save global xcorr')
gxcorr_dst_tr = get_global_xcorr_for_loader(dataset_target, crop_size)
gxcorr_src_tr = get_global_xcorr_for_loader(dataset_source, crop_size)
np.save(route_to('gxcorr_dst_tr.npy'), gxcorr_dst_tr)
np.save(route_to('gxcorr_src_tr.npy'), gxcorr_src_tr)
else:
print('Load global xcorr')
gxcorr_dst_tr = np.load(route_to('gxcorr_dst_tr.npy'))
gxcorr_src_tr = np.load(route_to('gxcorr_src_tr.npy'))
```
## Train Loader
```
def flip_channels(x):
"""Reverse polarity of random channels"""
flip_matrix = np.random.choice([-1, 1], 3)[..., np.newaxis, np.newaxis]
return (x * flip_matrix).astype(np.float32)
def shuffle_channels(x):
"""Change order of channels"""
return np.random.permutation(x)
def normalize_channels(x):
"""Map data to [-1,1] range. The scaling after conv(xcorr, acorr) is not
suitable for image processing so this function fixes it"""
cmin = np.min(x, axis=(-2,-1))[..., np.newaxis, np.newaxis]
x -= cmin
cmax = np.max(np.abs(x), axis=(-2,-1))[..., np.newaxis, np.newaxis]
x /= cmax
x *= 2
x -= 1
return x.astype(np.float32)
class DDALoaderTrain(torch.utils.data.Dataset):
def __init__(self, loader1, avg_acorr2, p=0.5, crop_size=1):
super().__init__()
self.loader1 = loader1
self.avg_acorr2 = avg_acorr2
self.p = p
self.crop_size = crop_size
def __len__(self):
return len(self.loader1)
def __getitem__(self, item):
# Get main data (data, label)
data, label = self.loader1.__getitem__(item)
data_fft = fftshift(rfft2(data, s=data.shape[-2:], axes=(-2, -1)))
# Get random pixel from another data from the same dataset
random_index = np.random.randint(0, len(self.loader1))
another_data, _ = self.loader1.__getitem__(random_index)
rand_pixel = crop_ref(another_data, self.crop_size)
# Convert to Fourier domain
c, h ,w = another_data.shape
mid_h, mid_w = int(h // 2), int(w // 2)
embed = np.zeros_like(another_data)
embed[:, mid_h:mid_h+1, mid_w:mid_w+1] = rand_pixel
pixel_fft = np.fft.rfft2(embed, s=another_data.shape[-2:], axes=(-2, -1))
pixel_fft = np.fft.fftshift(pixel_fft)
# Cross-correlate the data sample with the random pixel from the same dataset
xcorr = data_fft * np.conjugate(pixel_fft)
# Convolve the ruslt with the auto-correlation of another dataset
conv = xcorr * self.avg_acorr2
# Reverse Fourier domain and map channels to [-1, 1] range
data_da = fftshift(irfft2(ifftshift(conv), axes=(-2, -1)))
data_da = normalize_channels(data_da)
# Apply data augmentations
if np.random.rand() < self.p:
data_da = flip_channels(data_da)
if np.random.rand() < self.p:
data_da = shuffle_channels(data_da)
# Return a pair of data / label
return data_da.astype(np.float32), label
dataset_source = DDALoaderTrain(dataset_source, gacorr_dst_tr)
dataset_target = DDALoaderTrain(dataset_target, gacorr_src_tr)
dummy_data, dummy_label = dataset_source.__getitem__(0)
print('Image shape: {}\t Label: {}'.format(dummy_data.shape, dummy_label))
```
# Test Loader
```
class DDALoaderTest(torch.utils.data.Dataset):
def __init__(self, loader1, avg_acorr2, avg_xcorr1):
super().__init__()
self.loader1 = loader1
self.avg_acorr2 = avg_acorr2
self.avg_xcorr1 = avg_xcorr1
def __len__(self):
return len(self.loader1)
def __getitem__(self, item):
data, label = self.loader1.__getitem__(item)
data_fft = fftshift(rfft2(data, s=data.shape[-2:], axes=(-2, -1)))
xcorr = data_fft * np.conjugate(self.avg_xcorr1)
conv = xcorr * self.avg_acorr2
data_da = fftshift(irfft2(ifftshift(conv), axes=(-2, -1)))
data_da = normalize_channels(data_da)
return data_da.astype(np.float32), label
```
Re-define the test function so it accounts for the average cross-correlation and auto-correlation from source and target datasets
```
def test(dataset_name, model_root, crop_size=1):
image_root = os.path.join('dataset', dataset_name)
if dataset_name == 'mnist_m':
test_list = os.path.join(image_root, 'mnist_m_test_labels.txt')
dataset = GetLoader(
data_root=os.path.join(image_root, 'mnist_m_test'),
data_list=test_list,
transform=img_transform_target
)
if not 'gxcorr_dst_te.npy' in os.listdir(model_root):
print('Save global acorr and xcorr')
# acorr
gacorr_src_te = get_global_acorr_for_loader(dataset)
np.save(route_to('gacorr_src_te.npy'), gacorr_src_te)
# xcorr
gxcorr_dst_te = get_global_xcorr_for_loader(dataset, crop_size)
np.save(route_to('gxcorr_dst_te.npy'), gxcorr_dst_te)
else:
gacorr_src_te = np.load(route_to('gacorr_src_te.npy'))
gxcorr_dst_te = np.load(route_to('gxcorr_dst_te.npy'))
# Init loader for MNIST-M
dataset = DDALoaderTest(dataset, gacorr_src_te, gxcorr_dst_te)
else:
dataset = datasets.MNIST(
root='dataset',
train=False,
transform=img_transform_source,
)
if not 'gxcorr_src_te.npy' in os.listdir(model_root):
print('Save global acorr and xcorr')
# acorr
gacorr_dst_te = get_global_acorr_for_loader(dataset)
np.save(route_to('gacorr_dst_te.npy'), gacorr_dst_te)
# xcorr
gxcorr_src_te = get_global_xcorr_for_loader(dataset, crop_size)
np.save(route_to('gxcorr_src_te.npy'), gxcorr_src_te)
else:
gacorr_dst_te = np.load(route_to('gacorr_dst_te.npy'))
gxcorr_src_te = np.load(route_to('gxcorr_src_te.npy'))
# Init loader for MNIST
dataset = DDALoaderTest(dataset, gacorr_dst_te, gxcorr_src_te)
dataloader = torch.utils.data.DataLoader(
dataset=dataset,
batch_size=batch_size,
shuffle=False,
num_workers=8
)
""" test """
my_net = torch.load(os.path.join(model_root, 'mnist_mnistm_model_epoch_current.pth'))
my_net = my_net.eval()
if cuda:
my_net = my_net.cuda()
len_dataloader = len(dataloader)
data_target_iter = iter(dataloader)
i = 0
n_total = 0
n_correct = 0
while i < len_dataloader:
# test model using target data
data_target = data_target_iter.next()
t_img, t_label = data_target
_batch_size = len(t_label)
if cuda:
t_img = t_img.cuda()
t_label = t_label.cuda()
class_output, _ = my_net(input_data=t_img, alpha=0)
pred = class_output.data.max(1, keepdim=True)[1]
n_correct += pred.eq(t_label.data.view_as(pred)).cpu().sum()
n_total += _batch_size
i += 1
accu = n_correct.data.numpy() * 1.0 / n_total
return accu
```
# Training
```
dataloader_source = torch.utils.data.DataLoader(
dataset=dataset_source,
batch_size=batch_size,
shuffle=True,
num_workers=8)
dataloader_target = torch.utils.data.DataLoader(
dataset=dataset_target,
batch_size=batch_size,
shuffle=True,
num_workers=8)
class CNNModel(nn.Module):
def __init__(self):
super(CNNModel, self).__init__()
self.feature = nn.Sequential()
self.feature.add_module('f_conv1', nn.Conv2d(3, 64, kernel_size=5))
self.feature.add_module('f_bn1', nn.BatchNorm2d(64))
self.feature.add_module('f_pool1', nn.MaxPool2d(2))
self.feature.add_module('f_relu1', nn.ReLU(True))
self.feature.add_module('f_conv2', nn.Conv2d(64, 50, kernel_size=5))
self.feature.add_module('f_bn2', nn.BatchNorm2d(50))
self.feature.add_module('f_drop1', nn.Dropout2d())
self.feature.add_module('f_pool2', nn.MaxPool2d(2))
self.feature.add_module('f_relu2', nn.ReLU(True))
self.class_classifier = nn.Sequential()
self.class_classifier.add_module('c_fc1', nn.Linear(50 * 4 * 4, 100))
self.class_classifier.add_module('c_bn1', nn.BatchNorm1d(100))
self.class_classifier.add_module('c_relu1', nn.ReLU(True))
self.class_classifier.add_module('c_drop1', nn.Dropout())
self.class_classifier.add_module('c_fc2', nn.Linear(100, 100))
self.class_classifier.add_module('c_bn2', nn.BatchNorm1d(100))
self.class_classifier.add_module('c_relu2', nn.ReLU(True))
self.class_classifier.add_module('c_fc3', nn.Linear(100, 10))
self.class_classifier.add_module('c_softmax', nn.LogSoftmax(dim=1))
def forward(self, input_data, alpha):
input_data = input_data.expand(input_data.data.shape[0], 3, 28, 28)
feature = self.feature(input_data)
feature = feature.view(-1, 50 * 4 * 4)
class_output = self.class_classifier(feature)
return class_output, 0
# load model
my_net = CNNModel()
# setup optimizer
optimizer = optim.Adam(my_net.parameters(), lr=lr)
loss_class = torch.nn.NLLLoss()
if cuda:
my_net = my_net.cuda()
loss_class = loss_class.cuda()
for p in my_net.parameters():
p.requires_grad = True
# Record losses for each epoch (used in compare.ipynb)
losses = {'test': {'acc_bw': [], 'acc_color': []}}
name_losses = 'losses.pkl'
if not name_losses in os.listdir(model_root):
# if True:
# training
best_accu_t = 0.0
for epoch in range(n_epoch):
len_dataloader = min(len(dataloader_source), len(dataloader_target))
data_source_iter = iter(dataloader_source)
data_target_iter = iter(dataloader_target)
for i in range(len_dataloader):
p = float(i + epoch * len_dataloader) / n_epoch / len_dataloader
alpha = 2. / (1. + np.exp(-10 * p)) - 1
# training model using source data
data_source = data_source_iter.next()
s_img, s_label = data_source
my_net.zero_grad()
batch_size = len(s_label)
if cuda:
s_img = s_img.cuda()
s_label = s_label.cuda()
class_output, _ = my_net(input_data=s_img, alpha=alpha)
err_s_label = loss_class(class_output, s_label)
err = err_s_label
err.backward()
optimizer.step()
sys.stdout.write('\r epoch: %d, [iter: %d / all %d], err_s_label: %f' \
% (epoch, i + 1, len_dataloader, err_s_label.data.cpu().numpy()))
sys.stdout.flush()
torch.save(my_net, '{0}/mnist_mnistm_model_epoch_current.pth'.format(model_root))
print('\n')
accu_s = test(source_dataset_name, model_root)
print('Accuracy of the %s dataset: %f' % ('mnist', accu_s))
accu_t = test(target_dataset_name, model_root)
print('Accuracy of the %s dataset: %f\n' % ('mnist_m', accu_t))
losses['test']['acc_bw'].append(accu_s)
losses['test']['acc_color'].append(accu_t)
if accu_t > best_accu_t:
best_accu_s = accu_s
best_accu_t = accu_t
torch.save(my_net, '{0}/mnist_mnistm_model_epoch_best.pth'.format(model_root))
print('============ Summary ============= \n')
print('Accuracy of the %s dataset: %f' % ('mnist', best_accu_s))
print('Accuracy of the %s dataset: %f' % ('mnist_m', best_accu_t))
print('Corresponding model was save in ' + model_root + '/mnist_mnistm_model_epoch_best.pth')
sd.save_dict(os.path.join(model_root, 'losses.pkl'), losses)
else:
path_losses = os.path.join(model_root, name_losses)
print(f'Losses from previous run found!')
losses = sd.load_dict(path_losses)
sd.plot_curves(losses)
print('============ Summary ============= \n')
print('Accuracy of the %s dataset: %f' % ('mnist', max(losses['test']['acc_bw'])))
print('Accuracy of the %s dataset: %f' % ('mnist_m', max(losses['test']['acc_color'])))
print('Corresponding model was saved into ' + model_root + '/mnist_mnistm_model_epoch_best.pth')
```
| true |
code
| 0.623663 | null | null | null | null |
|
## Swow On and Free Scenes
```
from plot_helpers import *
plt.style.use('fivethirtyeight')
casi_data = PixelClassifier(CASI_DATA, CLOUD_MASK, VEGETATION_MASK)
hillshade = RasterFile(HILLSHADE, band_number=1).band_values()
snow_on_diff_data = RasterFile(SNOW_ON_DIFF, band_number=1)
band_values_snow_on_diff = snow_on_diff_data.band_values()
band_values_snow_on_diff_mask = band_values_snow_on_diff.mask.copy()
snow_free_diff_data = RasterFile(SNOW_FREE_DIFF, band_number=1)
band_values_snow_free_diff = snow_free_diff_data.band_values()
band_values_snow_free_diff_mask = band_values_snow_free_diff.mask.copy()
```
## Snow Pixels comparison
```
band_values_snow_free_diff.mask = casi_data.snow_surfaces(band_values_snow_free_diff_mask)
band_values_snow_on_diff.mask = casi_data.snow_surfaces(band_values_snow_on_diff_mask)
ax = box_plot_compare(
[
band_values_snow_free_diff,
band_values_snow_on_diff,
],
[
'SfM Bare Ground\n- Lidar Bare Ground',
'SfM Snow\n- Lidar Snow',
],
)
ax.set_ylabel('$\Delta$ Elevation (m)')
ax.set_ylim([-1, 1]);
color_map = LinearSegmentedColormap.from_list(
'snow_pixels',
['royalblue', 'none'],
N=2
)
plt.figure(figsize=(6,6), dpi=150)
plt.imshow(hillshade, cmap='gray', clim=(1, 255), alpha=0.5)
plt.imshow(
band_values_snow_on_diff.mask,
cmap=color_map,
)
set_axes_style(plt.gca())
plt.xticks([])
plt.yticks([]);
```
## Stable Ground
```
lidar_data = RasterFile(LIDAR_SNOW_DEPTH, band_number=1)
band_values_lidar = lidar_data.band_values()
sfm_data = RasterFile(SFM_SNOW_DEPTH, band_number=1)
band_values_sfm = sfm_data.band_values()
band_values_lidar.mask = casi_data.stable_surfaces(band_values_lidar.mask)
band_values_sfm.mask = casi_data.stable_surfaces(band_values_sfm.mask)
band_values_snow_on_diff.mask = casi_data.stable_surfaces(band_values_snow_on_diff_mask)
band_values_snow_free_diff.mask = casi_data.stable_surfaces(band_values_snow_free_diff_mask)
data_sources = [
band_values_lidar,
band_values_sfm,
band_values_snow_on_diff,
band_values_snow_free_diff,
]
labels=[
'Lidar Snow\n Depth',
'SfM Snow\n Depth',
'Snow On\n Scenes',
'Bare Ground\n Scenes',
]
ax = box_plot_compare(data_sources, labels)
ax.set_ylim([-1.2, 1.2]);
color_map = LinearSegmentedColormap.from_list(
'snow_pixels',
['sienna', 'none'],
N=2
)
plt.figure(figsize=(6,6), dpi=150)
plt.imshow(hillshade, cmap='gray', clim=(1, 255), alpha=0.5)
plt.imshow(
band_values_snow_on_diff.mask,
cmap=color_map,
)
set_axes_style(plt.gca())
plt.xticks([])
plt.yticks([]);
```
| true |
code
| 0.673084 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/desaibhargav/VR/blob/main/notebooks/Semantic_Search.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## **Dependencies**
```
!pip install -U -q sentence-transformers
!git clone https://github.com/desaibhargav/VR.git
```
## **Imports**
```
import pandas as pd
import numpy as np
import torch
import time
from typing import Generator
from sentence_transformers import SentenceTransformer, CrossEncoder, util
from VR.backend.chunker import Chunker
```
## **Dataset**
```
# load scrapped data (using youtube_client.py)
dataset = pd.read_pickle('VR/datasets/youtube_scrapped.pickle')
# split transcripts of videos to smaller blocks or chunks (using chunker.py)
chunked = Chunker(chunk_by='length', expected_threshold=100, min_tolerable_threshold=75).get_chunks(dataset)
# finally, create dataset
dataset_untagged = dataset.join(chunked).drop(columns=['subtitles', 'timestamps'])
df = dataset_untagged.copy().dropna()
print(f"Average length of block: {df.length_of_block.mean()}, Standard Deviation: {df.length_of_block.std()}")
```
## **Semantic Search**
---
The idea is to compute embeddings of the query (entered by user) and use cosine similarity to find the `top_k` most similar blocks.
Blocks are nothing but the entire video transcript (big string) split into fixed length strings (small strings, ~100 words).
---
The reason for such a design choice was threefold, handled by `chunker.py` (refer the repo):
1. First and foremost, some videoes can be very long (over ~40 minutes) which means the transcript for the same is a **massive** string, and we need to avoid hitting the processing length limits of pre-trained models.
2. Secondly, and more importantly, it is always good to maintain the inputs at a length on which the models being used were trained (to stay as close as poossible to the training set for optimum results).
3. But perhaps, most importantly, the purpose for splitting transcripts to blocks is so that the recommendations can be targeted to a snippet within a video. The vision is to recommend many snippets from various videoes highly relevant to the query, rather than entire videoes themselves in which matching snippets have been found (which may sometimes be long and the content may not always be related to the query).
---
```
# request to enable GPU
if not torch.cuda.is_available():
print("Warning: No GPU found. Please add GPU to your notebook")
# load model (to encode the dataset)
bi_encoder = SentenceTransformer('paraphrase-distilroberta-base-v1')
# number of blocks we want to retrieve with the bi-encoder
top_k = 200
# the bi-encoder will retrieve 50 blocks (top_k).
# we use a cross-encoder, to re-rank the results list to improve the quality.
cross_encoder = CrossEncoder('cross-encoder/ms-marco-electra-base')
# encode dataset
corpus_embeddings = bi_encoder.encode(df.block.to_list(), convert_to_tensor=True, show_progress_bar=True)
# send corpus embeddings to GPU
corpus_embeddings = torch.tensor(corpus_embeddings).cuda()
# this function will search the dataset for passages that answer the query
def search(query):
start_time = time.time()
# encode the query using the bi-encoder and find potentially relevant passages
question_embedding = bi_encoder.encode(query, convert_to_tensor=True)
# send query embeddings to GPU
question_embedding = question_embedding.cuda()
# perform sematic search by computing cosine similarity between corpus and query embeddings
# return top_k highest similarity matches
hits = util.semantic_search(question_embedding, corpus_embeddings, top_k=top_k)[0]
# now, score all retrieved passages with the cross_encoder
cross_inp = [[query, df.block.to_list()[hit['corpus_id']]] for hit in hits]
cross_scores = cross_encoder.predict(cross_inp)
# sort results by the cross-encoder scores
for idx in range(len(cross_scores)):
hits[idx]['cross-score'] = cross_scores[idx]
hits = sorted(hits, key=lambda x: x['cross-score'], reverse=True)
end_time = time.time()
# print output of top-5 hits (for iteractive environments only)
print(f"Input query: {query}")
print(f"Results (after {round(end_time - start_time, 2)} seconds):")
for hit in hits[0:10]:
print("\t{:.3f}\t{}".format(hit['cross-score'], df.block.to_list()[hit['corpus_id']].replace("\n", " ")))
```
## **Try some queries!**
```
query = "I feel lost in life. I feel like there is no purpose of living. How should I deal with this?"
search(query)
query = "I just recently became a parent and I am feeling very nervous. What is the best way to bring up a child?"
search(query)
query = "I had a divorce. I feel like a failure. How should I handle this heartbreak?"
search(query)
query = "How to be confident while making big decisions in life?"
search(query)
```
## **Semantic Search x Auxiliary Features**
This section is under active development.
---
This purpose of this section is to explore two primary frontiers:
1. Just semantic search yields satisfactory results, but comes at the cost of compute power. The bottleneck for compute power is the cross-encoder step. This section explores how to reduce the search area, so that semantic search (by the cross-encoder) is performed over a small number blocks, significantly cutting down on the recommendation time.
2. Other than the content itself, several other features such as video statistics (views, likes, dislikes), video titles, video descriptions, video tags present in the dataset can be leveraged to improve the recommendations.
---
```
```
| true |
code
| 0.655694 | null | null | null | null |
|
```
%matplotlib inline
```
Saving and loading models for inference in PyTorch
==================================================
There are two approaches for saving and loading models for inference in
PyTorch. The first is saving and loading the ``state_dict``, and the
second is saving and loading the entire model.
Introduction
------------
Saving the model’s ``state_dict`` with the ``torch.save()`` function
will give you the most flexibility for restoring the model later. This
is the recommended method for saving models, because it is only really
necessary to save the trained model’s learned parameters.
When saving and loading an entire model, you save the entire module
using Python’s
`pickle <https://docs.python.org/3/library/pickle.html>`__ module. Using
this approach yields the most intuitive syntax and involves the least
amount of code. The disadvantage of this approach is that the serialized
data is bound to the specific classes and the exact directory structure
used when the model is saved. The reason for this is because pickle does
not save the model class itself. Rather, it saves a path to the file
containing the class, which is used during load time. Because of this,
your code can break in various ways when used in other projects or after
refactors.
In this recipe, we will explore both ways on how to save and load models
for inference.
Setup
-----
Before we begin, we need to install ``torch`` if it isn’t already
available.
::
pip install torch
Steps
-----
1. Import all necessary libraries for loading our data
2. Define and intialize the neural network
3. Initialize the optimizer
4. Save and load the model via ``state_dict``
5. Save and load the entire model
1. Import necessary libraries for loading our data
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For this recipe, we will use ``torch`` and its subsidiaries ``torch.nn``
and ``torch.optim``.
```
import torch
import torch.nn as nn
import torch.optim as optim
```
2. Define and intialize the neural network
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For sake of example, we will create a neural network for training
images. To learn more see the Defining a Neural Network recipe.
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
print(net)
```
3. Initialize the optimizer
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We will use SGD with momentum.
```
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
```
4. Save and load the model via ``state_dict``
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let’s save and load our model using just ``state_dict``.
```
# Specify a path
PATH = "state_dict_model.pt"
# Save
torch.save(net.state_dict(), PATH)
# Load
model = Net()
model.load_state_dict(torch.load(PATH))
model.eval()
```
A common PyTorch convention is to save models using either a ``.pt`` or
``.pth`` file extension.
Notice that the ``load_state_dict()`` function takes a dictionary
object, NOT a path to a saved object. This means that you must
deserialize the saved state_dict before you pass it to the
``load_state_dict()`` function. For example, you CANNOT load using
``model.load_state_dict(PATH)``.
Remember too, that you must call ``model.eval()`` to set dropout and
batch normalization layers to evaluation mode before running inference.
Failing to do this will yield inconsistent inference results.
5. Save and load entire model
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now let’s try the same thing with the entire model.
```
# Specify a path
PATH = "entire_model.pt"
# Save
torch.save(net, PATH)
# Load
model = torch.load(PATH)
model.eval()
```
Again here, remember that you must call model.eval() to set dropout and
batch normalization layers to evaluation mode before running inference.
Congratulations! You have successfully saved and load models for
inference in PyTorch.
Learn More
----------
Take a look at these other recipes to continue your learning:
- `Saving and loading a general checkpoint in PyTorch <https://pytorch.org/tutorials/recipes/recipes/saving_and_loading_a_general_checkpoint.html>`__
- `Saving and loading multiple models in one file using PyTorch <https://pytorch.org/tutorials/recipes/recipes/saving_multiple_models_in_one_file.html>`__
| true |
code
| 0.772874 | null | null | null | null |
|
# 實驗:實作InceptionV3網路架構
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/taipeitechmmslab/MMSLAB-TF2/blob/master/Lab8.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/taipeitechmmslab/MMSLAB-TF2/blob/master/Lab8.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
### Import必要套件
```
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
```
---
## Keras Applications
### 創建InceptionV3網路架構
- 輸入大小(預設):(299, 299, 3)
- 權重(預設):`imagenet`
- 輸出類別(預設):1000個類別
```
model = tf.keras.applications.InceptionV3(include_top=True, weights='imagenet')
```
透過`model.summary`可以察看網路模型的每一層資訊:
```
model.summary()
```
將網路模型儲存到TensorBoard上:
```
model_tb = tf.keras.callbacks.TensorBoard(log_dir='lab8-logs-inceptionv3-keras')
model_tb.set_model(model)
```
### 資料前處理和輸出解碼
使用別人提供的模型預測,需要注意兩件事情,1)訓練時的資料前處理,2)輸出結果對應到的類別。
Keras很貼心的提供每個模型相對應的資料預處理和輸出解碼的函式。
- preprocess_input:網路架構的影像前處理(注意:每一個模型在訓練時做的資料正規化並不會相同,例如:VGG、ResNet-50輸入影像為0~255的數值,而inception_v3、xception輸入影像為-1~1的數值)。
- decode_predictions:對應網路架構的輸出解碼。
Import資料預處理和輸出解碼的函式:
```
from tensorflow.keras.applications.inception_v3 import preprocess_input
from tensorflow.keras.applications.inception_v3 import decode_predictions
```
### 預測輸出結果
創建影像讀取的函式:讀取影像,並將影像大小縮放大299x299x3的尺寸。
```
def read_img(img_path, resize=(299,299)):
img_string = tf.io.read_file(img_path) # 讀取檔案
img_decode = tf.image.decode_image(img_string) # 將檔案以影像格式來解碼
img_decode = tf.image.resize(img_decode, resize) # 將影像resize到網路輸入大小
# 將影像格式增加到4維(batch, height, width, channels),模型預測要求格式
img_decode = tf.expand_dims(img_decode, axis=0)
return img_decode
```
從資料夾中讀取一張影像(elephant.jpg)作為測試:
```
img_path = 'image/elephant.jpg'
img = read_img(img_path) # 透過剛創建的函式讀取影像
plt.imshow(tf.cast(img, tf.uint8)[0]) # 透過matplotlib顯示圖片需將影像轉為Integers
```
預測結果:
```
img = preprocess_input(img) # 影像前處理
preds = model.predict(img) # 預測圖片
print("Predicted:", decode_predictions(preds, top=3)[0]) # 輸出預測最高的三個類別
```
---
## TensorFlow Hub
Install:
```
pip install tensorflow-hub
```
Search:
https://tfhub.dev/
```
import tensorflow as tf
import tensorflow_hub as hub
```
### 創建Inception V3模型
Model:
https://tfhub.dev/google/tf2-preview/inception_v3/classification/2
num_classes = 1001 classes of the classification from the original training
Image:height x width = 299 x 299 pixels, 3 RGB color values in the range 0~1
labels file: https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt
```
# Inception V3預訓練模型的URL
module_url = "https://tfhub.dev/google/tf2-preview/inception_v3/classification/4"
# 創建一個Sequential Model,網路模型裡面包含了Inception V3網路層
model = tf.keras.Sequential([
# hub.KerasLayer將載入的Inception V3模型封裝成網路層(Keras Layer)
hub.KerasLayer(module_url,
input_shape=(299, 299, 3), # 模型輸入大小
output_shape=(1001, ), # 模型輸出大小
name='Inception_v3') # 網路層名稱
])
model.summary()
```
### 資料前處理和輸出解碼
創建資料前處理函式:
```
def read_img(img_path, resize=(299,299)):
img_string = tf.io.read_file(img_path) # 讀取檔案
img_decode = tf.image.decode_image(img_string) # 將檔案以影像格式來解碼
img_decode = tf.image.resize(img_decode, resize) # 將影像resize到網路輸入大小
img_decode = img_decode / 255.0 # 對影像做正規畫,將數值縮放到0~1之間
# 將影像格式增加到4維(batch, height, width, channels),模型預測要求格式
img_decode = tf.expand_dims(img_decode, axis=0) #
return img_decode
```
創建輸出解碼器:
```
# 下載ImageNet 的標籤檔
labels_path = tf.keras.utils.get_file('ImageNetLabels.txt', 'https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt')
# 讀取標籤檔中的數據
with open(labels_path) as file:
lines = file.read().splitlines()
print(lines) # 顯示讀取的標籤
imagenet_labels = np.array(lines) # 將標籤轉成numpy array做為網路輸出的解碼器
```
### 預測輸出結果
從資料夾中讀取一張影像(elephant.jpg)作為測試:
```
img_path = 'image/elephant.jpg'
img = read_img(img_path) # 透過剛創建的函式讀取影像
plt.imshow(img[0])
```
預測結果:
```
preds = model.predict(img) # 預測圖片
index = np.argmax(preds) # 取得預測結果最大的Index
print("Predicted:", imagenet_labels[index]) # 透過解碼器將輸出轉成標籤
```
顯示最好的三個預測:
```
# 取得預測結果最大的三個indexs
top3_indexs = np.argsort(preds)[0, ::-1][:3]
print("Predicted:", imagenet_labels[top3_indexs]) # 透過解碼器將輸出轉成標籤
```
| true |
code
| 0.500244 | null | null | null | null |
|
```
%matplotlib notebook
import pickle
import numpy as np
import matplotlib.pyplot as plt
from refnx.reflect import SLD, Slab, ReflectModel, MixedReflectModel
from refnx.dataset import ReflectDataset as RD
from refnx.analysis import Objective, CurveFitter, PDF, Parameter, process_chain, load_chain
from FreeformVFP import FreeformVFP
# Version numbers allow you to repeat the analysis on your computer and obtain identical results.
import refnx, scipy
refnx.version.version, np.version.version, scipy.version.version
```
# Load data
Three datasets are included, pNIPAM at 25 °C, 32.5 °C and 40 °C.
pNIPAM is thermoresponsive; the 25 °C is a swollen, diffuse layer, whilst the 40 °C data is a collapsed slab.
```
data = RD("pNIPAM brush in d2o at 25C.dat")
# data = RD("pNIPAM brush in d2o at 32C.dat")
# data = RD("pNIPAM brush in d2o at 40C.dat")
```
# Define materials and slab components
For simplicity some parameters that may normally have been allowed to vary have been set to predetermined optimum values.
```
si = SLD(2.07, 'si')
sio2 = SLD(2.9, 'sio2')
d2o = SLD(6.23 , 'd2o')
polymer = SLD(0.81, 'polymer')
si_l = si(0, 0)
sio2_l = sio2(20, 4.8)
d2o_l = d2o(0, 0)
```
# Create the freeform component
```
NUM_KNOTS = 4
#Polymer layer 1
polymer_0 = polymer(2, 0.5)
# Polymer-Solvent interface (spline)
polymer_vfp = FreeformVFP(adsorbed_amount=120,
vff=[0.6] * NUM_KNOTS,
dzf=[1/(NUM_KNOTS + 1)] * (NUM_KNOTS + 1),
polymer_sld=polymer,
name='freeform vfp',
left_slabs=[polymer_0])
```
# Set parameter bounds
```
sio2.real.setp(vary=True, bounds=(2.8, 3.47))
polymer_0.thick.setp(vary=True, bounds=(2, 20))
polymer_0.vfsolv.setp(vary=True, bounds=(0.1, 0.7))
polymer_vfp.adsorbed_amount.setp(vary=True, bounds=(100, 130))
# We can enforce monotonicity through the bounds we place on the fractional volume fraction changes.
enforce_mono = True
if enforce_mono:
bounds = (0.1, 1)
else:
bounds = (0.1, 1.5)
# Here we set the bounds on the knot locations
for idx in range(NUM_KNOTS):
polymer_vfp.vff[idx].setp(vary=True, bounds=bounds)
polymer_vfp.dzf[idx].setp(vary=True, bounds=(0.05, 1))
polymer_vfp.dzf[-1].setp(vary=True, bounds=(0.05, 1))
polymer_vfp.dzf[0].setp(vary=True, bounds=(0.005, 1))
```
# Create the structure, model, objective
```
structure = si_l | sio2_l | polymer_0 | polymer_vfp | d2o_l
# contracting the slab representation reduces computation time.
structure.contract = 1.5
model = ReflectModel(structure)
model.bkg.setp(vary=True, bounds=(1e-6, 1e-5))
objective = Objective(model, data)
fitter= CurveFitter(objective)
fitter.fit('differential_evolution');
fig, [ax_vfp, ax_sld, ax_refl] = plt.subplots(1, 3, figsize=(10,3), dpi=90)
z = np.linspace(-50, 1750, 2000)
ax_vfp.plot(*polymer_vfp.profile())
ax_sld.plot(*structure.sld_profile(z))
ax_refl.plot(data.x, objective.generative())
ax_refl.errorbar(data.x, data.y, yerr=data.y_err)
ax_refl.set_yscale('log')
fig.tight_layout()
```
| true |
code
| 0.646655 | null | null | null | null |
|
### Forced Alignment with Wav2Vec2
In this notebook we are going to follow [this pytorch tutorial](https://pytorch.org/tutorials/intermediate/forced_alignment_with_torchaudio_tutorial.html) to align script to speech with torchaudio using the CTC segmentation algorithm described in [ CTC-Segmentation of Large Corpora for German End-to-end Speech Recognition](https://arxiv.org/abs/2007.09127)
The process of alignment looks like the following.
1. Estimate the frame-wise label probability from audio waveform
Generate the trellis matrix which represents the probability of labels aligned at time step.
2. Find the most likely path from the trellis matrix.
3. In this example, we use torchaudio’s Wav2Vec2 model for acoustic feature extraction.
### Installation of `tourchaudio`
```
!pip install torchaudio
```
### Imports
```
import os, requests, torch, torchaudio, IPython
from dataclasses import dataclass
import matplotlib.pyplot as plt
SPEECH_URL = 'https://download.pytorch.org/torchaudio/test-assets/Lab41-SRI-VOiCES-src-sp0307-ch127535-sg0042.flac'
SPEECH_FILE = 'speech.flac'
if not os.path.exists(SPEECH_FILE):
with open(SPEECH_FILE, 'wb') as file:
with requests.get(SPEECH_URL) as resp:
resp.raise_for_status()
file.write(resp.content)
```
### Generate frame-wise label probability
The first step is to generate the label class porbability of each aduio frame. We can use a ``Wav2Vec2`` model that is trained for ASR.
``torchaudio`` provides easy access to pretrained models with associated labels.
**Note:** In the subsequent sections, we will compute the probability in log-domain to avoid numerical instability. For this purpose, we normalize the emission with ``log_softmax``.
```
bundle = torchaudio.pipelines.WAV2VEC2_ASR_BASE_960H
model = bundle.get_model()
labels = bundle.get_labels()
with torch.inference_mode():
waveform, _ = torchaudio.load(SPEECH_FILE)
emissions, _ = model(waveform)
emissions = torch.log_softmax(emissions, dim=-1)
emission = emissions[0].cpu().detach()
```
### Visualization
```
print(labels)
plt.imshow(emission.T)
plt.colorbar()
plt.title("Frame-wise class probability")
plt.xlabel("Time")
plt.ylabel("Labels")
plt.show()
```
### Generate alignment probability (trellis)
From the emission matrix, next we generate the trellis which represents
the probability of transcript labels occur at each time frame.
Trellis is 2D matrix with time axis and label axis. The label axis
represents the transcript that we are aligning. In the following, we use
$t$ to denote the index in time axis and $j$ to denote the
index in label axis. $c_j$ represents the label at label index
$j$.
To generate, the probability of time step $t+1$, we look at the
trellis from time step $t$ and emission at time step $t+1$.
There are two path to reach to time step $t+1$ with label
$c_{j+1}$. The first one is the case where the label was
$c_{j+1}$ at $t$ and there was no label change from
$t$ to $t+1$. The other case is where the label was
$c_j$ at $t$ and it transitioned to the next label
$c_{j+1}$ at $t+1$.
The follwoing diagram illustrates this transition.
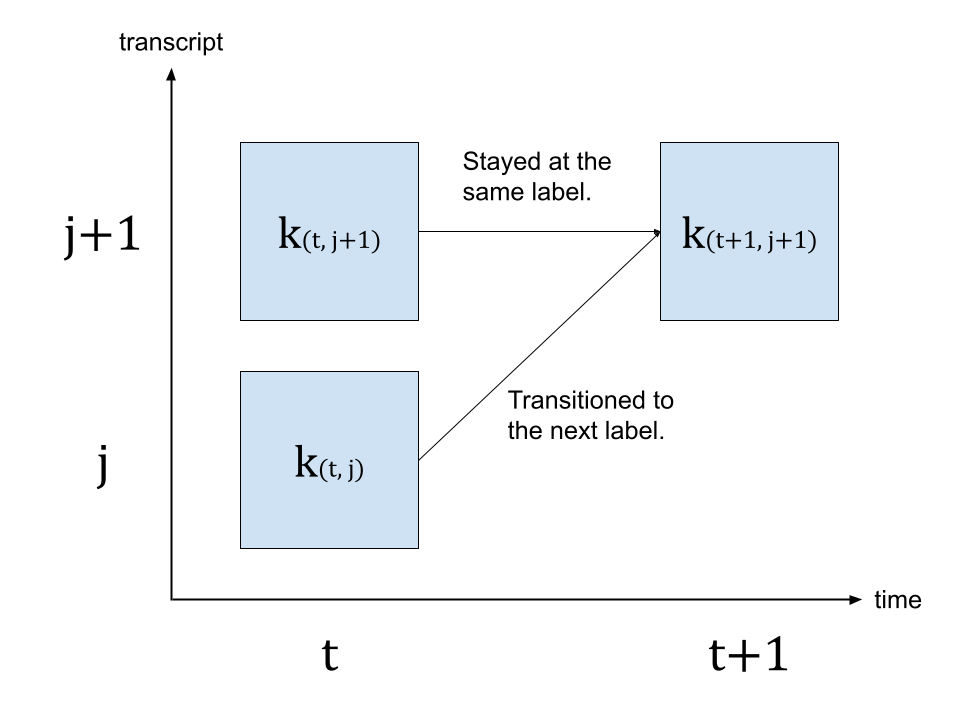
Since we are looking for the most likely transitions, we take the more
likely path for the value of $k_{(t+1, j+1)}$, that is
$ k_{(t+1, j+1)} = max( k_{(t, j)} p(t+1, c_{j+1}), k_{(t, j+1)} p(t+1,
repeat) ) $
where $k$ represents is trellis matrix, and $p(t, c_j)$
represents the probability of label $c_j$ at time step $t$.
$repeat$ represents the blank token from CTC formulation. (For the
detail of CTC algorithm, please refer to the `Sequence Modeling with CTC
[distill.pub] <https://distill.pub/2017/ctc/>`__)
```
transcript = 'I|HAD|THAT|CURIOSITY|BESIDE|ME|AT|THIS|MOMENT'
dictionary = {c: i for i, c in enumerate(labels)}
tokens = [dictionary[c] for c in transcript]
print(list(zip(transcript, tokens)))
def get_trellis(emission, tokens, blank_id=0):
num_frame = emission.size(0)
num_tokens = len(tokens)
# Trellis has extra diemsions for both time axis and tokens.
# The extra dim for tokens represents <SoS> (start-of-sentence)
# The extra dim for time axis is for simplification of the code.
trellis = torch.full((num_frame+1, num_tokens+1), -float('inf'))
trellis[:, 0] = 0
for t in range(num_frame):
trellis[t+1, 1:] = torch.maximum(
# Score for staying at the same token
trellis[t, 1:] + emission[t, blank_id],
# Score for changing to the next token
trellis[t, :-1] + emission[t, tokens],
)
return trellis
trellis = get_trellis(emission, tokens)
trellis
```
### Visualization.
```
plt.imshow(trellis[1:, 1:].T, origin='lower')
plt.annotate("- Inf", (trellis.size(1) / 5, trellis.size(1) / 1.5))
plt.colorbar()
plt.show()
```
>In the above visualization, we can see that there is a trace of high probability crossing the matrix diagonally.
### Find the most likely path (backtracking)
Once the trellis is generated, we will traverse it following the
elements with high probability.
We will start from the last label index with the time step of highest
probability, then, we traverse back in time, picking stay
($c_j \rightarrow c_j$) or transition
($c_j \rightarrow c_{j+1}$), based on the post-transition
probability $k_{t, j} p(t+1, c_{j+1})$ or
$k_{t, j+1} p(t+1, repeat)$.
Transition is done once the label reaches the beginning.
The trellis matrix is used for path-finding, but for the final
probability of each segment, we take the frame-wise probability from
emission matrix.
```
@dataclass
class Point:
token_index: int
time_index: int
score: float
def backtrack(trellis, emission, tokens, blank_id=0):
# Note:
# j and t are indices for trellis, which has extra dimensions
# for time and tokens at the beginning.
# When refering to time frame index `T` in trellis,
# the corresponding index in emission is `T-1`.
# Similarly, when refering to token index `J` in trellis,
# the corresponding index in transcript is `J-1`.
j = trellis.size(1) - 1
t_start = torch.argmax(trellis[:, j]).item()
path = []
for t in range(t_start, 0, -1):
# 1. Figure out if the current position was stay or change
# Note (again):
# `emission[J-1]` is the emission at time frame `J` of trellis dimension.
# Score for token staying the same from time frame J-1 to T.
stayed = trellis[t-1, j] + emission[t-1, blank_id]
# Score for token changing from C-1 at T-1 to J at T.
changed = trellis[t-1, j-1] + emission[t-1, tokens[j-1]]
# 2. Store the path with frame-wise probability.
prob = emission[t-1, tokens[j-1] if changed > stayed else 0].exp().item()
# Return token index and time index in non-trellis coordinate.
path.append(Point(j-1, t-1, prob))
# 3. Update the token
if changed > stayed:
j -= 1
if j == 0:
break
else:
raise ValueError('Failed to align')
return path[::-1]
path = backtrack(trellis, emission, tokens)
print(path)
```
### Visualization
```
def plot_trellis_with_path(trellis, path):
# To plot trellis with path, we take advantage of 'nan' value
trellis_with_path = trellis.clone()
for i, p in enumerate(path):
trellis_with_path[p.time_index, p.token_index] = float('nan')
plt.imshow(trellis_with_path[1:, 1:].T, origin='lower')
plot_trellis_with_path(trellis, path)
plt.title("The path found by backtracking")
plt.show()
```
Looking good. Now this path contains repetations for the same labels, so let’s merge them to make it close to the original transcript.
When merging the multiple path points, we simply take the average probability for the merged segments.
```
# Merge the labels
@dataclass
class Segment:
label: str
start: int
end: int
score: float
def __repr__(self):
return f"{self.label}\t({self.score:4.2f}): [{self.start:5d}, {self.end:5d})"
@property
def length(self):
return self.end - self.start
def merge_repeats(path):
i1, i2 = 0, 0
segments = []
while i1 < len(path):
while i2 < len(path) and path[i1].token_index == path[i2].token_index:
i2 += 1
score = sum(path[k].score for k in range(i1, i2)) / (i2 - i1)
segments.append(Segment(transcript[path[i1].token_index], path[i1].time_index, path[i2-1].time_index + 1, score))
i1 = i2
return segments
segments = merge_repeats(path)
for seg in segments:
print(seg)
```
### Visualization
```
def plot_trellis_with_segments(trellis, segments, transcript):
# To plot trellis with path, we take advantage of 'nan' value
trellis_with_path = trellis.clone()
for i, seg in enumerate(segments):
if seg.label != '|':
trellis_with_path[seg.start+1:seg.end+1, i+1] = float('nan')
plt.figure()
plt.title("Path, label and probability for each label")
ax1 = plt.axes()
ax1.imshow(trellis_with_path.T, origin='lower')
ax1.set_xticks([])
for i, seg in enumerate(segments):
if seg.label != '|':
ax1.annotate(seg.label, (seg.start + .7, i + 0.3))
ax1.annotate(f'{seg.score:.2f}', (seg.start - .3, i + 4.3))
plt.figure()
plt.title("Probability for each label at each time index")
ax2 = plt.axes()
xs, hs = [], []
for p in path:
label = transcript[p.token_index]
if label != '|':
xs.append(p.time_index + 1)
hs.append(p.score)
for seg in segments:
if seg.label != '|':
ax2.axvspan(seg.start+.4, seg.end+.4, color='gray', alpha=0.2)
ax2.annotate(seg.label, (seg.start + .8, -0.07))
ax2.bar(xs, hs, width=0.5)
ax2.axhline(0, color='black')
ax2.set_position(ax1.get_position())
ax2.set_xlim(ax1.get_xlim())
ax2.set_ylim(-0.1, 1.1)
plot_trellis_with_segments(trellis, segments, transcript)
plt.show()
```
Looks good. Now let’s merge the words. The Wav2Vec2 model uses ``'|'`` as the word boundary, so we merge the segments before each occurance of ``'|'``.
```
# Merge words
def merge_words(segments, separator='|'):
words = []
i1, i2 = 0, 0
while i1 < len(segments):
if i2 >= len(segments) or segments[i2].label == separator:
if i1 != i2:
segs = segments[i1:i2]
word = ''.join([seg.label for seg in segs])
score = sum(seg.score * seg.length for seg in segs) / sum(seg.length for seg in segs)
words.append(Segment(word, segments[i1].start, segments[i2-1].end, score))
i1 = i2 + 1
i2 = i1
else:
i2 += 1
return words
word_segments = merge_words(segments)
for word in word_segments:
print(word)
```
### Visualization
```
trellis_with_path = trellis.clone()
for i, seg in enumerate(segments):
if seg.label != '|':
trellis_with_path[seg.start+1:seg.end+1, i+1] = float('nan')
plt.imshow(trellis_with_path[1:, 1:].T, origin='lower')
ax1 = plt.gca()
ax1.set_yticks([])
ax1.set_xticks([])
for word in word_segments:
plt.axvline(word.start - 0.5)
plt.axvline(word.end - 0.5)
for i, seg in enumerate(segments):
if seg.label != '|':
plt.annotate(seg.label, (seg.start, i + 0.3))
plt.annotate(f'{seg.score:.2f}', (seg.start , i + 4), fontsize=8)
plt.show()
# The original waveform
ratio = waveform.size(1) / (trellis.size(0) - 1)
plt.plot(waveform[0])
for word in word_segments:
x0 = ratio * word.start
x1 = ratio * word.end
plt.axvspan(x0, x1, alpha=0.1, color='red')
plt.annotate(f'{word.score:.2f}', (x0, 0.8))
for seg in segments:
if seg.label != '|':
plt.annotate(seg.label, (seg.start * ratio, 0.9))
ax2 = plt.gca()
xticks = ax2.get_xticks()
plt.xticks(xticks, xticks / bundle.sample_rate)
plt.xlabel('time [second]')
ax2.set_position(ax1.get_position())
ax2.set_yticks([])
ax2.set_ylim(-1.0, 1.0)
ax2.set_xlim(0, waveform.size(-1))
plt.show()
# Generate the audio for each segment
print(transcript)
IPython.display.display(IPython.display.Audio(SPEECH_FILE))
for i, word in enumerate(word_segments):
x0 = int(ratio * word.start)
x1 = int(ratio * word.end)
filename = f"{i}_{word.label}.wav"
torchaudio.save(filename, waveform[:, x0:x1], bundle.sample_rate)
print(f"{word.label}: {x0 / bundle.sample_rate:.3f} - {x1 / bundle.sample_rate:.3f}")
IPython.display.display(IPython.display.Audio(filename))
```
| true |
code
| 0.716014 | null | null | null | null |
|
```
import pandas as pd
import random
```
### Read the data
```
movies_df = pd.read_csv('mymovies.csv')
ratings_df = pd.read_csv('myratings.csv')
```
### Select the data
The recommender system should avoid bias, for example, the recommender system should not recommend movie with just 1 rating which is also a 5-star rating. But should recommend movies with more ratings.
Therefore, we only take into account movies with at least 200 ratings and users who have at least rated 50 movies.
```
user_threshold = 50
movie_threshold = 200
filtered_users = ratings_df['user'].value_counts()>=user_threshold
filtered_users = filtered_users[filtered_users].index.tolist()
filtered_movies = ratings_df['item'].value_counts()>=movie_threshold
filtered_movies = filtered_movies[filtered_movies].index.tolist()
filtered_df = ratings_df[(ratings_df['user'].isin(filtered_users)) & (ratings_df['item'].isin(filtered_movies))]
display(filtered_df)
```
### Select a group of n random users
Here we let n = 5, we select 5 random users from the filtered dataset
```
#Select a random group of user
user_ids = filtered_df['user'].unique()
group_users_ids = random.sample(list(user_ids), 5)
group_users_ids
```
### Select rated and unrated movies for the given group
We now can get the rated movies all users in the groups, and from that, we can also get the unrated movies for the whole group of 5
```
selected_group_rating = ratings_df.loc[ratings_df['user'].isin(group_users_ids)]
group_rated_movies_ids = selected_group_rating['item'].unique()
group_unrated_movies_ids = set(movies_df['item']) - set(group_rated_movies_ids)
group_rated_movies_df = movies_df.loc[movies_df['item'].isin(group_rated_movies_ids)]
group_unrated_movies_df = movies_df.loc[movies_df['item'].isin(group_unrated_movies_ids)]
group_rated_movies_df
group_unrated_movies_df
```
### Calculate expected ratings for unrated movies
For each users, we need to calculate the expected ratings for the user's unrated movies. To calculate unrated ratings, we first need to train
an algorithm, here, the SVD algorithm from Surprise is used
```
from surprise import Reader, Dataset, SVD
from surprise.model_selection.validation import cross_validate
```
We perform 5-fold cross validation on the whole ratings dataset to see how well SVD will perform
```
reader = Reader()
data = Dataset.load_from_df(ratings_df[['user', 'item', 'rating']], reader)
svd = SVD()
cross_validate(svd, data, measures=['RMSE', 'MAE'], cv=5, verbose=True)
```
Next, We train the SVD model on the dataset
```
trainset = data.build_full_trainset()
svd = svd.fit(trainset)
def predict(user):
unrated_movies = list(group_unrated_movies_df['item'].unique())
pred = pd.DataFrame()
i = 0
for item in unrated_movies:
pred = pred.append({'user':user,'item': item, 'predicted_rating':svd.predict(user, item)[3]}, ignore_index=True)
return pred
users_rating = []
for user in group_users_ids:
prediction = predict(user)
prediction = prediction.sort_values('predicted_rating')
prediction = prediction.merge(movies_df, on= 'item')
users_rating.append(prediction[['user','item','title','predicted_rating']])
```
The algorithm will iterate through 5 users, for each user, it will calculate the predicted rating for each unrated movie. Then the algorithm combines the predicted ratings of 5 users into one big dataset, to perform aggregation calculation
```
final = pd.concat([df for df in users_rating], ignore_index = True)
final
```
### Additive Strategy
```
additive = final.copy()
additive= additive.groupby(['item','title']).sum()
additive = additive.sort_values(by="predicted_rating", ascending=False).reset_index()
additive
```
### Most Pleasure Strategy
```
most_pleasure = final.copy()
most_pleasure = final.copy()
most_pleasure= most_pleasure.groupby(['item','title']).max()
most_pleasure = most_pleasure.sort_values(by="predicted_rating", ascending=False).reset_index()
most_pleasure
```
### Least Misery Strategy
```
least_misery = final.copy()
least_misery = final.copy()
least_misery= least_misery.groupby(['item','title']).min()
least_misery = least_misery.sort_values(by="predicted_rating", ascending=False).reset_index()
least_misery
def fairness():
titles = []
for uid in group_users_ids:
data = final.loc[final['user'] == uid]
data = data.sort_values(by = 'predicted_rating', ascending = False).reset_index().iloc[0]['title']
titles.append([uid,data])
return titles
tt = fairness()
print(tt)
def gen_rec_and_explain():
most_pleasure = final.copy()
most_pleasure= most_pleasure.groupby(['item','title']).max()
most_pleasure = most_pleasure.sort_values(by="predicted_rating", ascending=False).reset_index()
most_pleasure_movie = most_pleasure.iloc[0:5]['title']
least_misery = final.copy()
least_misery= least_misery.groupby(['item','title']).min()
least_misery = least_misery.sort_values(by="predicted_rating", ascending=False).reset_index()
least_misery_movie = least_misery.iloc[0:5]['title']
additive = final.copy()
additive= additive.groupby(['item','title']).sum()
additive = additive.sort_values(by="predicted_rating", ascending=False).reset_index()
additive_movie = additive.iloc[0:5]['title']
fairnesss = fairness()
print("#FAIR")
for uid, title in fairnesss:
print("The movie {} is the most favorite movie of user {}".format(title, uid))
print("#ADD: ")
print("The movies: {} was recommended to you because they have highest additive rating within your group".format(list(additive_movie)))
print("#LEAST: ")
print("The movies: {} was recommended to you because they are everyones' preferences ".format(list(least_misery_movie)))
print("#MOST: ")
print("The movies: {} was recommended to you because they are the most loved".format(list(most_pleasure_movie)))
gen_rec_and_explain()
import itertools
from lenskit.algorithms import Recommender
from lenskit.algorithms.user_knn import UserUser
user_user = UserUser(15, min_nbrs=3) # Minimum (3) and maximum (15) number of neighbors to consider
recsys = Recommender.adapt(user_user)
recsys.fit(ratings_df)
group_unseen_df = pd.DataFrame(list(itertools.product(group_users_ids, group_unrated_movies_ids)), columns=['user', 'item'])
group_unseen_df['predicted_rating'] = recsys.predict(group_unseen_df)
group_unseen_df = group_unseen_df.loc[group_unseen_df['predicted_rating'].notnull()]
display(group_unseen_df)
group_unseen_df
group_unseen_df.groupby('item').sum()
additive_df = group_unseen_df.groupby('item').sum()
additive_df = additive_df.join(movies_df['title'], on='item')
additive_df = additive_df.sort_values(by="predicted_rating", ascending=False).reset_index()[['item', 'title', 'predicted_rating']]
display(additive_df.head(10))
additive_df = group_unseen_df.groupby('item').sum()
additive_df
movies_df.loc[movies_df['item'] == 177593]
```
| true |
code
| 0.280888 | null | null | null | null |
|
# GLM: Logistic Regression
* This is a reproduction with a few slight alterations of [Bayesian Log Reg](http://jbencook.github.io/portfolio/bayesian_logistic_regression.html) by J. Benjamin Cook
* Author: Peadar Coyle and J. Benjamin Cook
* How likely am I to make more than $50,000 US Dollars?
* Exploration of model selection techniques too - I use WAIC to select the best model.
* The convenience functions are all taken from Jon Sedars work.
* This example also has some explorations of the features so serves as a good example of Exploratory Data Analysis and how that can guide the model creation/ model selection process.
```
%matplotlib inline
import pandas as pd
import numpy as np
import pymc3 as pm
import matplotlib.pyplot as plt
import seaborn
import warnings
warnings.filterwarnings('ignore')
from collections import OrderedDict
from time import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import fmin_powell
from scipy import integrate
import theano as thno
import theano.tensor as T
def run_models(df, upper_order=5):
'''
Convenience function:
Fit a range of pymc3 models of increasing polynomial complexity.
Suggest limit to max order 5 since calculation time is exponential.
'''
models, traces = OrderedDict(), OrderedDict()
for k in range(1,upper_order+1):
nm = 'k{}'.format(k)
fml = create_poly_modelspec(k)
with pm.Model() as models[nm]:
print('\nRunning: {}'.format(nm))
pm.glm.GLM.from_formula(fml, df, family=pm.glm.families.Normal())
traces[nm] = pm.sample(2000, chains=1, init=None, tune=1000)
return models, traces
def plot_traces(traces, retain=1000):
'''
Convenience function:
Plot traces with overlaid means and values
'''
ax = pm.traceplot(traces[-retain:], figsize=(12,len(traces.varnames)*1.5),
lines={k: v['mean'] for k, v in pm.summary(traces[-retain:]).iterrows()})
for i, mn in enumerate(pm.summary(traces[-retain:])['mean']):
ax[i,0].annotate('{:.2f}'.format(mn), xy=(mn,0), xycoords='data'
,xytext=(5,10), textcoords='offset points', rotation=90
,va='bottom', fontsize='large', color='#AA0022')
def create_poly_modelspec(k=1):
'''
Convenience function:
Create a polynomial modelspec string for patsy
'''
return ('income ~ educ + hours + age ' + ' '.join(['+ np.power(age,{})'.format(j)
for j in range(2,k+1)])).strip()
```
The [Adult Data Set](http://archive.ics.uci.edu/ml/datasets/Adult) is commonly used to benchmark machine learning algorithms. The goal is to use demographic features, or variables, to predict whether an individual makes more than \\$50,000 per year. The data set is almost 20 years old, and therefore, not perfect for determining the probability that I will make more than \$50K, but it is a nice, simple dataset that can be used to showcase a few benefits of using Bayesian logistic regression over its frequentist counterpart.
The motivation for myself to reproduce this piece of work was to learn how to use Odd Ratio in Bayesian Regression.
```
data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data", header=None, names=['age', 'workclass', 'fnlwgt',
'education-categorical', 'educ',
'marital-status', 'occupation',
'relationship', 'race', 'sex',
'captial-gain', 'capital-loss',
'hours', 'native-country',
'income'])
data.head(10)
```
## Scrubbing and cleaning
We need to remove any null entries in Income.
And we also want to restrict this study to the United States.
```
data = data[~pd.isnull(data['income'])]
data[data['native-country']==" United-States"]
income = 1 * (data['income'] == " >50K")
age2 = np.square(data['age'])
data = data[['age', 'educ', 'hours']]
data['age2'] = age2
data['income'] = income
income.value_counts()
```
## Exploring the data
Let us get a feel for the parameters.
* We see that age is a tailed distribution. Certainly not Gaussian!
* We don't see much of a correlation between many of the features, with the exception of Age and Age2.
* Hours worked has some interesting behaviour. How would one describe this distribution?
```
g = seaborn.pairplot(data)
# Compute the correlation matrix
corr = data.corr()
# Generate a mask for the upper triangle
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(11, 9))
# Generate a custom diverging colormap
cmap = seaborn.diverging_palette(220, 10, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
seaborn.heatmap(corr, mask=mask, cmap=cmap, vmax=.3,
linewidths=.5, cbar_kws={"shrink": .5}, ax=ax)
```
We see here not many strong correlations. The highest is 0.30 according to this plot. We see a weak-correlation between hours and income
(which is logical), we see a slighty stronger correlation between education and income (which is the kind of question we are answering).
## The model
We will use a simple model, which assumes that the probability of making more than $50K
is a function of age, years of education and hours worked per week. We will use PyMC3
do inference.
In Bayesian statistics, we treat everything as a random variable and we want to know the posterior probability distribution of the parameters
(in this case the regression coefficients)
The posterior is equal to the likelihood $$p(\theta | D) = \frac{p(D|\theta)p(\theta)}{p(D)}$$
Because the denominator is a notoriously difficult integral, $p(D) = \int p(D | \theta) p(\theta) d \theta $ we would prefer to skip computing it. Fortunately, if we draw examples from the parameter space, with probability proportional to the height of the posterior at any given point, we end up with an empirical distribution that converges to the posterior as the number of samples approaches infinity.
What this means in practice is that we only need to worry about the numerator.
Getting back to logistic regression, we need to specify a prior and a likelihood in order to draw samples from the posterior. We could use sociological knowledge about the effects of age and education on income, but instead, let's use the default prior specification for GLM coefficients that PyMC3 gives us, which is $p(θ)=N(0,10^{12}I)$. This is a very vague prior that will let the data speak for themselves.
The likelihood is the product of n Bernoulli trials, $\prod^{n}_{i=1} p_{i}^{y} (1 - p_{i})^{1-y_{i}}$,
where $p_i = \frac{1}{1 + e^{-z_i}}$,
$z_{i} = \beta_{0} + \beta_{1}(age)_{i} + \beta_2(age)^{2}_{i} + \beta_{3}(educ)_{i} + \beta_{4}(hours)_{i}$ and $y_{i} = 1$ if income is greater than 50K and $y_{i} = 0$ otherwise.
With the math out of the way we can get back to the data. Here I use PyMC3 to draw samples from the posterior. The sampling algorithm used is NUTS, which is a form of Hamiltonian Monte Carlo, in which parameteres are tuned automatically. Notice, that we get to borrow the syntax of specifying GLM's from R, very convenient! I use a convenience function from above to plot the trace infromation from the first 1000 parameters.
```
with pm.Model() as logistic_model:
pm.glm.GLM.from_formula('income ~ age + age2 + educ + hours', data, family=pm.glm.families.Binomial())
trace_logistic_model = pm.sample(2000, chains=1, init=None, tune=1000)
plot_traces(trace_logistic_model, retain=1000)
```
## Some results
One of the major benefits that makes Bayesian data analysis worth the extra computational effort in many circumstances is that we can be explicit about our uncertainty. Maximum likelihood returns a number, but how certain can we be that we found the right number? Instead, Bayesian inference returns a distribution over parameter values.
I'll use seaborn to look at the distribution of some of these factors.
```
plt.figure(figsize=(9,7))
trace = trace_logistic_model[1000:]
seaborn.jointplot(trace['age'], trace['educ'], kind="hex", color="#4CB391")
plt.xlabel("beta_age")
plt.ylabel("beta_educ")
plt.show()
```
So how do age and education affect the probability of making more than $$50K?$ To answer this question, we can show how the probability of making more than $50K changes with age for a few different education levels. Here, we assume that the number of hours worked per week is fixed at 50. PyMC3 gives us a convenient way to plot the posterior predictive distribution. We need to give the function a linear model and a set of points to evaluate. We will pass in three different linear models: one with educ == 12 (finished high school), one with educ == 16 (finished undergrad) and one with educ == 19 (three years of grad school).
```
# Linear model with hours == 50 and educ == 12
lm = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] +
samples['age']*x +
samples['age2']*np.square(x) +
samples['educ']*12 +
samples['hours']*50)))
# Linear model with hours == 50 and educ == 16
lm2 = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] +
samples['age']*x +
samples['age2']*np.square(x) +
samples['educ']*16 +
samples['hours']*50)))
# Linear model with hours == 50 and educ == 19
lm3 = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] +
samples['age']*x +
samples['age2']*np.square(x) +
samples['educ']*19 +
samples['hours']*50)))
```
Each curve shows how the probability of earning more than $ 50K$ changes with age. The red curve represents 19 years of education, the green curve represents 16 years of education and the blue curve represents 12 years of education. For all three education levels, the probability of making more than $50K increases with age until approximately age 60, when the probability begins to drop off. Notice that each curve is a little blurry. This is because we are actually plotting 100 different curves for each level of education. Each curve is a draw from our posterior distribution. Because the curves are somewhat translucent, we can interpret dark, narrow portions of a curve as places where we have low uncertainty and light, spread out portions of the curve as places where we have somewhat higher uncertainty about our coefficient values.
```
# Plot the posterior predictive distributions of P(income > $50K) vs. age
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm, samples=100, color="blue", alpha=.15)
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm2, samples=100, color="green", alpha=.15)
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm3, samples=100, color="red", alpha=.15)
import matplotlib.lines as mlines
blue_line = mlines.Line2D(['lm'], [], color='b', label='High School Education')
green_line = mlines.Line2D(['lm2'], [], color='g', label='Bachelors')
red_line = mlines.Line2D(['lm3'], [], color='r', label='Grad School')
plt.legend(handles=[blue_line, green_line, red_line], loc='lower right')
plt.ylabel("P(Income > $50K)")
plt.xlabel("Age")
plt.show()
b = trace['educ']
plt.hist(np.exp(b), bins=20, normed=True)
plt.xlabel("Odds Ratio")
plt.show()
```
Finally, we can find a credible interval (remember kids - credible intervals are Bayesian and confidence intervals are frequentist) for this quantity. This may be the best part about Bayesian statistics: we get to interpret credibility intervals the way we've always wanted to interpret them. We are 95% confident that the odds ratio lies within our interval!
```
lb, ub = np.percentile(b, 2.5), np.percentile(b, 97.5)
print("P(%.3f < O.R. < %.3f) = 0.95" % (np.exp(lb),np.exp(ub)))
```
## Model selection
One question that was immediately asked was what effect does age have on the model, and why should it be $age^2$ versus age? We'll run the model with a few changes to see what effect higher order terms have on this model in terms of WAIC.
```
models_lin, traces_lin = run_models(data, 4)
dfwaic = pd.DataFrame(index=['k1','k2','k3','k4'], columns=['lin'])
dfwaic.index.name = 'model'
for nm in dfwaic.index:
dfwaic.loc[nm, 'lin'] = pm.waic(traces_lin[nm],models_lin[nm])[0]
dfwaic = pd.melt(dfwaic.reset_index(), id_vars=['model'], var_name='poly', value_name='waic')
g = seaborn.factorplot(x='model', y='waic', col='poly', hue='poly', data=dfwaic, kind='bar', size=6)
```
WAIC confirms our decision to use age^2.
| true |
code
| 0.685923 | null | null | null | null |
|
# Exercises
## Playing with the interpreter
Try to execute some simple statements and expressions (one at a time) e.g
```
print("Hello!")
1j**2
1 / 2
1 // 2
5 + 5
10 / 2 + 5
my_tuple = (1, 2, 3)
my_tuple[0] = 1
2.3**4.5
```
Do you understand what is going on in all cases?
Most Python functions and objects can provide documentation via **help** function. Look the documentation of e.g open function with ```help(open)```
Play with tabulator completion, by typing just ```pr``` and pressing then tabulator key. Pressing Shift-tab (after finalising completion) one sees also short documentation about the function or object. This works also on variable names, try e.g.
```
my_extremely_long_variable_name = 5
my <TAB>
```
## Basic syntax
Try to assign the value 6 to the following variable names
````
first-name
family_name
3PO
____variable
inb4tool8
print
in
```
Which of them are valid to assign to?
Extra: why do you think the ones that cause an error are not valid? What's the reason?
You probably noticed that even though ``print`` is a method in the namespace it was still valid to create a variable called ``print``. If you now try to actually print something, you will get an error. For built-in functions (such as print) one can recover with the following code
```
print = __builtin__.print
print("hello")
```
Are the following pieces valid Python code?
** Case 1 **
```
numbers = [4, 5, 6, 9, 11]
sum = 0
for n in numbers:
sum += n
print("Sum is now"), sum
```
** Case 2 **
```
x = 11
test(x)
def test(a):
if a < 0:
print("negative number")
```
## Tuples and lists
1. Create a tuple called ``mytuple``, with the following strings: "sausage", "eggs" and "bacon"
2. check it's type using ``type()``
3. Create than a list called ``mylist`` with the same contents. You use can the normal list definition syntax (``[]``) or coerce it from the tuple with the ``list()`` function.
Attempt to append the string "spam"
to ``mylist`` and ``mytuple`` using ``append``.
List objects have a sort()
function, use that for sorting the list alphabetically (e.g.
mylist.sort() ). What is now the first item of the list?
Next, remove the first item from the list, investigate the contents and remove then last item from the list.
### Slicing
Using ``range()`` create a list that has the numbers from 50 to 0 with a step of -2. Note that in Python 3 ``range()`` returns an *iterator* (we'll discuss iterators more later on), ``list(range(args))`` returns an actual list.
Using slicing syntax, select
* the last 4 items from the list
* the items from index 10 to index 13
* the first 5 items from the list
Read up on the [stride syntax](https://en.wikipedia.org/wiki/Array_slicing#1991:_Python) . Then using it select
* every third value in the list
* the values with an odd-numbered index in the list
### Multidimensional lists
Create a two dimensional list of (x,y) value pairs, i.e.
arbitrary long list whose elements are two element lists.
Are you able to use slicing for extracting only the y values? (Answer is no, but try it in any case)
## Dictionaries
Create a dictionary whose keys are the fruits “pineapple”, “strawberry”, and “banana”. As values use numbers
representing e.g. prices.
Add “orange” to the dictionary and then remove “banana” from the dictionary. Investigate the contents of dictionary and pay attention to the order of key-value pairs.
# Bonus exercises
Create a new “fruits” dictionary where the values are also
dictionaries containing key-value pairs for color and weight,
e.g.
```
fruits['apple'] = {'color':'green', 'weight': 120}
```
Change the color of *apple* from green to red
It is often useful idiom to create empty lists or dictionaries
and add contents little by little.
Create first an empty dictionary for a mid-term grades of
students. Then, add a key-value pairs where the keys are
student names and the values are empty lists.
Finally, add values to the lists and investigate the contents of the
dictionary.
| true |
code
| 0.460956 | null | null | null | null |
|
**_Privacy and Confidentiality Exercises_**
This notebook shows you how to prepare your results for export and what you have to keep in mind in general when you want to export output. You will learn how to prepare files for export so they meet our export requirements.
```
# Load packages
%pylab inline
from __future__ import print_function
import os
import pandas as pd
import numpy as np
import psycopg2
import matplotlib.pyplot as plt
%matplotlib inline
matplotlib.style.use('ggplot')
```
# General Remarks on Disclosure Review
This notebook provides you with information on how to prepare research output for disclosure control. It outlines how to prepare different kind of outputs before submitting an export request and gives you an overview of the information needed for disclosure review.
## Files you can export
In general you can export any kind of file format. However, most research results that researchers typically export are tables, graphs, regression output and aggregated data. Thus, we ask you to export one of these types which implies that every result you would like to export needs to be saved in either .csv, .txt or graph format.
## Jupyter notebooks are only exported to retrieve code
Unfortunately, you can't export results in a jupyter notebook. Doing disclosure reviews on output in jupyter notebooks is too burdensome for us. Jupyter notebooks will only be exported when the output is deleted for the purpose of exporting code. This does not mean that you won't need your jupyter notebooks during the export process.
## Documentation of code is important
During the export process we ask you to provide the code for every output you are asking to export. It is important for ADRF staff to have the code to better understand what you exactly did. Understanding how research results are created is important to understand your research output. Thus, it is important to document every single step of your analysis in your jupyter notebook.
## General rules to keep in mind
A more detailed description of the rules for exporting results can be found on the class website. This is just a quick overview. We recommend that you to go to the class website and read the entire guidelines before you prepare your files for export.
- The disclosure review is based on the underlying observations of your study. Every statistic you want to export should be based on at least 10 individual data points
- Document your code so the reviewer can follow your data work. Assessing re-identification risks highly depends on the context. Thus it is important that you provide context info with your anlysis for the reviewer
- Save the requested output with the corresponding code in you input and output folder. Make sure the code is executable. The code should exactly produce the output you requested
- In case you are exporting powerpoint slides that show project results you have to provide the code which produces the output in the slide
- Please export results only when there are final and you need them for your presentation or final projcet report
# Disclosure Review Walkthrough
We will IL DES data and MO DES to construct our statistics we are interested in, and prepare it in a way so we can submit the output for disclosure review.
```
# get working directory
mypath = (os.getcwd())
print(mypath)
# connect to database
db_name = "appliedda"
hostname = "10.10.2.10"
conn = psycopg2.connect(database=db_name, host = hostname)
```
## pull data
In this example we will use the workers who had a job in both MO and IL at some point over the course of our datasets (2005-2016)
```
# Get data
query = """
SELECT *, il_wage + mo_wage AS earnings
FROM ada_18_uchi.il_mo_overlap_by_qtr
WHERE year = 2011
AND quarter IN (2,3)"""
# Save query in dataframe
df = pd.read_sql( query, con = conn )
# Check dataframe
df.head()
# another way to check dataframe
df.info()
# basic stats of
df.describe()
# let's add an earnings categorization for "low", "mid" and "high" using a simple function
def earn_calc(earn):
if earn < 16500:
return('low')
elif earn < 45000:
return('mid')
else:
return('high')
earn_calc(24000)
df['earn_cat'] = df['earnings'].apply(lambda x: earn_calc(x))
```
We now have loaded the data that we need to generate some basic statistics about our populations we want to compare
```
# Let's look at some first desccriptives by group
grouped = df.groupby('earn_cat')
grouped.describe()
grouped.describe().T
```
Statistics in this table will be released if the statistic is based on at least 10 entities (in this example individuals). We can see that the total number of individuals we observe in each group completely satisfies this (see cell count). However, we also report percentiles, and we report the minimum and maximum value. Especially the minimum and maximum value are most likely representing one individual person.
Thus, during disclosure review these values will be supressed.
```
# Now let's export the statistics. Ideally we want to have a csv file
# We can safe the statistics in a dataframe
export1 = grouped.describe()
# and then print to csv
export1.to_csv('descriptives_by_group.csv')
```
### Reminder: Export of Statistics
You can save any dataframe as a csv file and export this csv file. The only thing you have to keep in mind is that besides the statistic X you are interested in you have to include a variable count of X so we can see on how many observations the statistic is based on. This also applies if you aggregate data. For example if you agregate by benefit type, we need to know how many observations are in each benefit program (because after the aggregation each benefit type will be only one data point).
### Problematic Output
Some subgroups (eg for some of the Illinois datasets dealing with race and gender) will result in cell sizes representing less than 10 people.
Tables with cells representing less than 10 individuals won't be released. In this case, disclosure review would mean to delete all cells with counts of less than 10. In addition, secondary suppression has to take place. The disclosure reviewer has to delete as many cells as needed to make it impossible to recalculate the suppressed values.
### How to do it better
Instead of asking for export of a tables like this, you should prepare your tables in advance that all cell sizes are at least represented by a minimum of 10 observations.
### Reminder: Export of Tables
For tables of any kind you need to provide the underlying counts of the statistics presented in the table. Make sure you provide all counts. If you calculate ratios, for example employment rates you need to provide the count of individuals who are employed and the count of the ones who are not. If you are interested in percentages we still need the underlying counts for disclosure review. Please label the table in a way that we can easily understand what you are plotting.
```
df[['il_flag', 'mo_flag']].describe(percentiles = [.5, .9, .99, .999])
# for this example let's cap the job counts to 5
df['il_flag'] = df['il_flag'].apply(lambda x: x if x < 5 else 5)
df['mo_flag'] = df['mo_flag'].apply(lambda x: x if x < 5 else 5)
# Let's say we are interested in plotting parts of the crosstabulation as a graph, for example benefit type and race
# First we need to calulate the counts
graph = df.groupby(['earn_cat', 'il_flag'])['ssn'].count()
# Note: we need to add the unstack command here because our dataframe has nested indices.
# We need to flatten out the data before plotting the graph
print(graph)
print(graph.unstack())
# Now we can generate the graph
mygraph = graph.unstack().plot(kind='bar')
```
In this graph it is not clearly visible how many observations are in each bar. Thus we either have to provide a corresponding table (as we generated earlier), or we can use the table=True option to add a table of counts to the graph. In addition, we wnat to make sure that all our axes and legend are labeled properly.
```
# Graphical representation including underlying values: the option table=True displays the underlying counts
mygraph = graph.unstack().plot(kind='bar', table=True, figsize=(7,5), fontsize=7)
# Adjust legend and axes
mygraph.legend(["Unknown","1", "2", "3", "4", '5'], loc = 1, ncol= 3, fontsize=9)
mygraph.set_ylabel("Number of Observations", fontsize=9)
# Add table with counts
# We don't need an x axis if we display table
mygraph.axes.get_xaxis().set_visible(False)
# Grab table info
table = mygraph.tables[0]
# Format table and figure
table.set_fontsize(9)
```
> in this example there is a problematic value, we will instead cap to 4 maximum jobs to ensure all cells are more than 10
```
# for this example let's cap the job counts to 5
df['il_flag'] = df['il_flag'].apply(lambda x: x if x < 4 else 4)
df['mo_flag'] = df['mo_flag'].apply(lambda x: x if x < 4 else 4)
# create our new "graph" dataframe to plot with
graph = df.groupby(['earn_cat', 'il_flag'])['ssn'].count()
# confirm we solved the issue
mygraph = graph.unstack().plot(kind='bar', table=True, figsize=(7,5), fontsize=7)
# Adjust legend and axes
mygraph.legend(["Unknown","1", "2", "3", "4", '5'], loc = 1, ncol= 3, fontsize=9)
mygraph.set_ylabel("Number of Observations", fontsize=9)
# Add table with counts
# We don't need an x axis if we display table
mygraph.axes.get_xaxis().set_visible(False)
# Grab table info
table = mygraph.tables[0]
# Format table and figure
table.set_fontsize(9)
# We want to export the graph without the table though
# Because we already generated the crosstab earlier which shows the counts
mygraph = graph.unstack().plot(kind='bar', figsize=(7,5), fontsize=7, rot=0)
# Adjust legend and axes
mygraph.legend(["Unknown","1", "2", "3", "4", '5'], loc = 1, ncol= 3, fontsize=9)
mygraph.set_ylabel("Number of Observations", fontsize=9)
mygraph.set_xlabel("Income category", fontsize=9)
mygraph.annotate('Source: IL & MO DES', xy=(0.7,-0.2), xycoords="axes fraction");
# Now we can export the graph as pdf
# Save plot to file
export2 = mygraph.get_figure()
export2.set_size_inches(15,10, forward=True)
export2.savefig('barchart_jobs_income_category.pdf', bbox_inches='tight', dpi=300)
```
### Reminder: Export of Graphs
It is important that every point which is plotted in a graph is based on at least 10 observations. Thus scatterplots for example cannot be released. In case you are interested in a histogram you have to change the bin size to make sure that every bin contains at least 10 people. In addition to the graph you have to provide the ADRF with the underlying table in a .csv or .txt file. This file should have the same name as the graph so ADRF can directly see which files go together. Alternatively you can include the counts in the graph as shown in the example above.
| true |
code
| 0.672466 | null | null | null | null |
|
# Logistic Regression with Hyperparameter Optimization (scikit-learn)
<a href="https://colab.research.google.com/github/VertaAI/modeldb/blob/master/client/workflows/examples-without-verta/notebooks/sklearn-census.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Imports
```
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings("ignore", category=ConvergenceWarning)
import itertools
import time
import numpy as np
import pandas as pd
from sklearn import model_selection
from sklearn import linear_model
from sklearn import metrics
```
---
## Prepare Data
```
try:
import wget
except ImportError:
!pip install wget # you may need pip3
import wget
train_data_url = "http://s3.amazonaws.com/verta-starter/census-train.csv"
train_data_filename = wget.download(train_data_url)
test_data_url = "http://s3.amazonaws.com/verta-starter/census-test.csv"
test_data_filename = wget.download(test_data_url)
df_train = pd.read_csv("census-train.csv")
X_train = df_train.iloc[:,:-1].values
y_train = df_train.iloc[:, -1]
df_train.head()
```
## Prepare Hyperparameters
```
hyperparam_candidates = {
'C': [1e-4, 1e-1, 1, 10, 1e3],
'solver': ['liblinear', 'lbfgs'],
'max_iter': [15, 28],
}
# total models 20
# create hyperparam combinations
hyperparam_sets = [dict(zip(hyperparam_candidates.keys(), values))
for values
in itertools.product(*hyperparam_candidates.values())]
```
## Run Validation
```
# create validation split
(X_val_train, X_val_test,
y_val_train, y_val_test) = model_selection.train_test_split(X_train, y_train,
test_size=0.2,
shuffle=True)
def run_experiment(hyperparams):
# create and train model
model = linear_model.LogisticRegression(**hyperparams)
model.fit(X_train, y_train)
# calculate and log validation accuracy
val_acc = model.score(X_val_test, y_val_test)
print(hyperparams, end=' ')
print("Validation accuracy: {:.4f}".format(val_acc))
# NOTE: run_experiment() could also be defined in a module, and executed in parallel
for hyperparams in hyperparam_sets:
run_experiment(hyperparams)
```
## Pick the best hyperparameters and train the full data
```
best_hyperparams = {}
model = linear_model.LogisticRegression(multi_class='auto', **best_hyperparams)
model.fit(X_train, y_train)
```
## Calculate Accuracy on Full Training Set
```
train_acc = model.score(X_train, y_train)
print("Training accuracy: {:.4f}".format(train_acc))
```
---
| true |
code
| 0.557424 | null | null | null | null |
|
# Other widget libraries
We would have loved to show you everything the Jupyter Widgets ecosystem has to offer today, but we are blessed to have such an active community of widget creators and unfortunately can't fit all widgets in a single session, no matter how long.
This notebook lists some of the widget libraries we wanted to demo but did not have enough time to include in the session. Enjoy!
# ipyleaflet: Interactive maps
## A Jupyter - LeafletJS bridge
## https://github.com/jupyter-widgets/ipyleaflet
ipyleaflet is a jupyter interactive widget library which provides interactive maps to the Jupyter notebook.
- MIT Licensed
**Installation:**
```bash
conda install -c conda-forge ipyleaflet
```
```
from ipywidgets import Text, HTML, HBox
from ipyleaflet import GeoJSON, WidgetControl, Map
import json
m = Map(center = (43,-100), zoom = 4)
geo_json_data = json.load(open('us-states-density-colored.json'))
geojson = GeoJSON(data=geo_json_data, hover_style={'color': 'black', 'dashArray': '5, 5', 'weight': 2})
m.add_layer(geojson)
html = HTML('''
<h4>US population density</h4>
Hover over a state
''')
html.layout.margin = '0px 20px 20px 20px'
control = WidgetControl(widget=html, position='topright')
m.add_control(control)
def update_html(properties, **kwargs):
html.value = '''
<h4>US population density</h4>
<h2><b>{}</b></h2>
{} people / mi^2
'''.format(properties['name'], properties['density'])
geojson.on_hover(update_html)
m
```
# pythreejs: 3D rendering in the browser
## A Jupyter - threejs bridge
## https://github.com/jupyter-widgets/pythreejs
Pythreejs is a jupyter interactive widget bringing fast WebGL 3d visualization to the Jupyter notebook.
- Originally authored by Jason Grout, currently maintained by Vidar Tonaas Fauske
- BSD Licensed
Pythreejs is *not* a 3d plotting library, it only exposes the threejs scene objects to the Jupyter kernel.
**Installation:**
```bash
conda install -c conda-forge pythreejs
```
```
from pythreejs import *
import numpy as np
from IPython.display import display
from ipywidgets import HTML, Text, Output, VBox
from traitlets import link, dlink
# Generate surface data:
view_width = 600
view_height = 400
nx, ny = (20, 20)
xmax=1
x = np.linspace(-xmax, xmax, nx)
y = np.linspace(-xmax, xmax, ny)
xx, yy = np.meshgrid(x, y)
z = xx ** 2 - yy ** 2
#z[6,1] = float('nan')
# Generate scene objects from data:
surf_g = SurfaceGeometry(z=list(z[::-1].flat),
width=2 * xmax,
height=2 * xmax,
width_segments=nx - 1,
height_segments=ny - 1)
surf = Mesh(geometry=surf_g,
material=MeshLambertMaterial(map=height_texture(z[::-1], 'YlGnBu_r')))
surfgrid = SurfaceGrid(geometry=surf_g, material=LineBasicMaterial(color='black'),
position=[0, 0, 1e-2]) # Avoid overlap by lifting grid slightly
# Set up picking bojects:
hover_point = Mesh(geometry=SphereGeometry(radius=0.05),
material=MeshLambertMaterial(color='green'))
click_picker = Picker(controlling=surf, event='dblclick')
hover_picker = Picker(controlling=surf, event='mousemove')
# Set up scene:
key_light = DirectionalLight(color='white', position=[3, 5, 1], intensity=0.4)
c = PerspectiveCamera(position=[0, 3, 3], up=[0, 0, 1], aspect=view_width / view_height,
children=[key_light])
scene = Scene(children=[surf, c, surfgrid, hover_point, AmbientLight(intensity=0.8)])
renderer = Renderer(camera=c, scene=scene,
width=view_width, height=view_height,
controls=[OrbitControls(controlling=c), click_picker, hover_picker])
# Set up picking responses:
# Add a new marker when double-clicking:
out = Output()
def f(change):
value = change['new']
with out:
print('Clicked on %s' % (value,))
point = Mesh(geometry=SphereGeometry(radius=0.05),
material=MeshLambertMaterial(color='hotpink'),
position=value)
scene.add(point)
click_picker.observe(f, names=['point'])
# Have marker follow picker point:
link((hover_point, 'position'), (hover_picker, 'point'))
# Show picker point coordinates as a label:
h = HTML()
def g(change):
h.value = 'Green point at (%.3f, %.3f, %.3f)' % tuple(change['new'])
h.value += ' Double-click to add marker'
g({'new': hover_point.position})
hover_picker.observe(g, names=['point'])
display(VBox([h, renderer, out]))
```
# bqplot: complex interactive visualizations
## https://github.com/bloomberg/bqplot
## A Jupyter - d3.js bridge
bqplot is a jupyter interactive widget library bringing d3.js visualization to the Jupyter notebook.
- Apache Licensed
bqplot implements the abstractions of Wilkinson’s “The Grammar of Graphics” as interactive Jupyter widgets.
bqplot provides both
- high-level plotting procedures with relevant defaults for common chart types,
- lower-level descriptions of data visualizations meant for complex interactive visualization dashboards and applications involving mouse interactions and user-provided Python callbacks.
**Installation:**
```bash
conda install -c conda-forge bqplot
```
```
import numpy as np
import bqplot as bq
xs = bq.LinearScale()
ys = bq.LinearScale()
x = np.arange(100)
y = np.cumsum(np.random.randn(2, 100), axis=1) #two random walks
line = bq.Lines(x=x, y=y, scales={'x': xs, 'y': ys}, colors=['red', 'green'])
xax = bq.Axis(scale=xs, label='x', grid_lines='solid')
yax = bq.Axis(scale=ys, orientation='vertical', tick_format='0.2f', label='y', grid_lines='solid')
fig = bq.Figure(marks=[line], axes=[xax, yax], animation_duration=1000)
display(fig)
# update data of the line mark
line.y = np.cumsum(np.random.randn(2, 100), axis=1)
```
# ipympl: The Matplotlib Jupyter Widget Backend
## https://github.com/matplotlib/ipympl
Enabling interaction with matplotlib charts in the Jupyter notebook and JupyterLab
- BSD-3-Clause
**Installation:**
```bash
conda install -c conda-forge ipympl
```
Enabling the `widget` backend. This requires ipympl. ipympl can be install via pip or conda.
```
%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import VBox, FloatSlider
```
When using the `widget` backend from ipympl, fig.canvas is a proper Jupyter interactive widget, which can be embedded in Layout classes like HBox and Vbox.
One can bound figure attributes to other widget values.
```
plt.ioff()
plt.clf()
slider = FloatSlider(
value=1.0,
min=0.02,
max=2.0
)
fig1 = plt.figure(1)
x1 = np.linspace(0, 20, 500)
lines = plt.plot(x1, np.sin(slider.value * x1))
def update_lines(change):
lines[0].set_data(x1, np.sin(change.new * x1))
fig1.canvas.draw()
fig1.canvas.flush_events()
slider.observe(update_lines, names='value')
VBox([slider, fig1.canvas])
```
# ipytree: Interactive tree view based on ipywidgets
## https://github.com/QuantStack/ipytree/
ipytree is a jupyter interactive widget library which provides a tree widget to the Jupyter notebook.
- MIT Licensed
**Installation:**
```bash
conda install -c conda-forge ipytree
```
## Create a tree
```
from ipywidgets import Text, link
from ipytree import Tree, Node
tree = Tree()
tree.add_node(Node('node1'))
node2 = Node('node2')
tree.add_node(node2)
tree
node3 = Node('node3', disabled=True)
node4 = Node('node4')
node5 = Node('node5', [Node('1'), Node('2')])
node2.add_node(node3)
node2.add_node(node4)
node2.add_node(node5)
```
| true |
code
| 0.549882 | null | null | null | null |
|
```
from IPython import display
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
from utils import Logger
import tensorflow as tf
import numpy as np
DATA_FOLDER = './tf_data/VGAN/MNIST'
IMAGE_PIXELS = 28*28
NOISE_SIZE = 100
BATCH_SIZE = 100
def noise(n_rows, n_cols):
return np.random.normal(size=(n_rows, n_cols))
def xavier_init(size):
in_dim = size[0] if len(size) == 1 else size[1]
stddev = 1. / np.sqrt(float(in_dim))
return tf.random_uniform(shape=size, minval=-stddev, maxval=stddev)
def images_to_vectors(images):
return images.reshape(images.shape[0], 784)
def vectors_to_images(vectors):
return vectors.reshape(vectors.shape[0], 28, 28, 1)
```
## Load Data
```
def mnist_data():
compose = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((.5, .5, .5), (.5, .5, .5))
])
out_dir = '{}/dataset'.format(DATA_FOLDER)
return datasets.MNIST(root=out_dir, train=True, transform=compose, download=True)
# Load data
data = mnist_data()
# Create loader with data, so that we can iterate over it
data_loader = DataLoader(data, batch_size=BATCH_SIZE, shuffle=True)
# Num batches
num_batches = len(data_loader)
```
## Initialize Graph
```
## Discriminator
# Input
X = tf.placeholder(tf.float32, shape=(None, IMAGE_PIXELS))
# Layer 1 Variables
D_W1 = tf.Variable(xavier_init([784, 1024]))
D_B1 = tf.Variable(xavier_init([1024]))
# Layer 2 Variables
D_W2 = tf.Variable(xavier_init([1024, 512]))
D_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
D_W3 = tf.Variable(xavier_init([512, 256]))
D_B3 = tf.Variable(xavier_init([256]))
# Out Layer Variables
D_W4 = tf.Variable(xavier_init([256, 1]))
D_B4 = tf.Variable(xavier_init([1]))
# Store Variables in list
D_var_list = [D_W1, D_B1, D_W2, D_B2, D_W3, D_B3, D_W4, D_B4]
## Generator
# Input
Z = tf.placeholder(tf.float32, shape=(None, NOISE_SIZE))
# Layer 1 Variables
G_W1 = tf.Variable(xavier_init([100, 256]))
G_B1 = tf.Variable(xavier_init([256]))
# Layer 2 Variables
G_W2 = tf.Variable(xavier_init([256, 512]))
G_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
G_W3 = tf.Variable(xavier_init([512, 1024]))
G_B3 = tf.Variable(xavier_init([1024]))
# Out Layer Variables
G_W4 = tf.Variable(xavier_init([1024, 784]))
G_B4 = tf.Variable(xavier_init([784]))
# Store Variables in list
G_var_list = [G_W1, G_B1, G_W2, G_B2, G_W3, G_B3, G_W4, G_B4]
def discriminator(x):
l1 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(x, D_W1) + D_B1, .2), .3)
l2 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l1, D_W2) + D_B2, .2), .3)
l3 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l2, D_W3) + D_B3, .2), .3)
out = tf.matmul(l3, D_W4) + D_B4
return out
def generator(z):
l1 = tf.nn.leaky_relu(tf.matmul(z, G_W1) + G_B1, .2)
l2 = tf.nn.leaky_relu(tf.matmul(l1, G_W2) + G_B2, .2)
l3 = tf.nn.leaky_relu(tf.matmul(l2, G_W3) + G_B3, .2)
out = tf.nn.tanh(tf.matmul(l3, G_W4) + G_B4)
return out
G_sample = generator(Z)
D_real = discriminator(X)
D_fake = discriminator(G_sample)
# Losses
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_real, labels=tf.ones_like(D_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.zeros_like(D_fake)))
D_loss = D_loss_real + D_loss_fake
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.ones_like(D_fake)))
# Optimizers
D_opt = tf.train.AdamOptimizer(2e-4).minimize(D_loss, var_list=D_var_list)
G_opt = tf.train.AdamOptimizer(2e-4).minimize(G_loss, var_list=G_var_list)
```
## Train
#### Testing
```
num_test_samples = 16
test_noise = noise(num_test_samples, NOISE_SIZE)
```
#### Inits
```
num_epochs = 200
# Start interactive session
session = tf.InteractiveSession()
# Init Variables
tf.global_variables_initializer().run()
# Init Logger
logger = Logger(model_name='DCGAN1', data_name='CIFAR10')
```
#### Train
```
# Iterate through epochs
for epoch in range(num_epochs):
for n_batch, (batch,_) in enumerate(data_loader):
# 1. Train Discriminator
X_batch = images_to_vectors(batch.permute(0, 2, 3, 1).numpy())
feed_dict = {X: X_batch, Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, d_error, d_pred_real, d_pred_fake = session.run(
[D_opt, D_loss, D_real, D_fake], feed_dict=feed_dict
)
# 2. Train Generator
feed_dict = {Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, g_error = session.run(
[G_opt, G_loss], feed_dict=feed_dict
)
if n_batch % 100 == 0:
display.clear_output(True)
# Generate images from test noise
test_images = session.run(
G_sample, feed_dict={Z: test_noise}
)
test_images = vectors_to_images(test_images)
# Log Images
logger.log_images(test_images, num_test_samples, epoch, n_batch, num_batches, format='NHWC');
# Log Status
logger.display_status(
epoch, num_epochs, n_batch, num_batches,
d_error, g_error, d_pred_real, d_pred_fake
)
```
| true |
code
| 0.764117 | null | null | null | null |
|
# Mining the Social Web, 2nd Edition
## Appendix B: OAuth Primer
This IPython Notebook provides an interactive way to follow along with and explore the numbered examples from [_Mining the Social Web (3rd Edition)_](http://bit.ly/Mining-the-Social-Web-3E). The intent behind this notebook is to reinforce the concepts from the sample code in a fun, convenient, and effective way. This notebook assumes that you are reading along with the book and have the context of the discussion as you work through these exercises.
In the somewhat unlikely event that you've somehow stumbled across this notebook outside of its context on GitHub, [you can find the full source code repository here](http://bit.ly/Mining-the-Social-Web-3E).
## Copyright and Licensing
You are free to use or adapt this notebook for any purpose you'd like. However, please respect the [Simplified BSD License](https://github.com/mikhailklassen/Mining-the-Social-Web-3rd-Edition/blob/master/LICENSE) that governs its use.
## Notes
While the chapters in the book opt to simplify the discussion by avoiding a discussion of OAuth and instead opting to use application credentials provided by social web properties for API access, this notebook demonstrates how to implement some OAuth flows for several of the more prominent social web properties. While IPython Notebook is used for consistency and ease of learning, and in some cases, this actually adds a little bit of extra complexity in some cases given the nature of embedding a web server and handling asynchronous callbacks. (Still, the overall code should be straightforward to adapt as needed.)
# Twitter OAuth 1.0a Flow with IPython Notebook
Twitter implements OAuth 1.0A as its standard authentication mechanism, and in order to use it to make requests to Twitter's API, you'll need to go to https://dev.twitter.com/apps and create a sample application. There are three items you'll need to note for an OAuth 1.0A workflow, a consumer key and consumer secret that identify the application as well as the oauth_callback URL that tells Twitter where redirect back to after the user has authorized the application. Note that you will need an ordinary Twitter account in order to login, create an app, and get these credentials. Keep in mind that for development purposes or for accessing your own account's data, you can simply use the oauth token and oauth token secret that are provided in your appliation settings to authenticate as opposed to going through the steps here. The process of obtaining an the oauth token and oauth token secret is fairly straight forward (especially with the help of a good library), but an implementation in IPython Notebook is a bit tricker due to the nature of embedding a web server, capturing information within web server contexts, and handling the various redirects along the way.
You must ensure that your browser is not blocking popups in order for this script to work.
<img src="files/resources/ch01-twitter/images/Twitter-AppCredentials-oauth_callback.png" width="600px">
## Example 1. Twitter OAuth 1.0a Flow
```
import json
from flask import Flask, request
from threading import Timer
from IPython.display import IFrame
from IPython.display import display
from IPython.display import Javascript as JS
import twitter
from twitter.oauth_dance import parse_oauth_tokens
from twitter.oauth import read_token_file, write_token_file
OAUTH_FILE = "/tmp/twitter_oauth"
# XXX: Go to http://twitter.com/apps/new to create an app and get values
# for these credentials that you'll need to provide in place of these
# empty string values that are defined as placeholders.
# See https://dev.twitter.com/docs/auth/oauth for more information
# on Twitter's OAuth implementation and ensure that *oauth_callback*
# is defined in your application settings as shown below if you are
# using Flask in this IPython Notebook
# Define a few variables that will bleed into the lexical scope of a couple of
# functions below
CONSUMER_KEY = ''
CONSUMER_SECRET = ''
oauth_callback = 'http://127.0.0.1:5000/oauth_helper'
# Setup a callback handler for when Twitter redirects back to us after the user authorizes the app
webserver = Flask("TwitterOAuth")
@webserver.route("/oauth_helper")
def oauth_helper():
oauth_verifier = request.args.get('oauth_verifier')
# Pick back up credentials from ipynb_oauth_dance
oauth_token, oauth_token_secret = read_token_file(OAUTH_FILE)
_twitter = twitter.Twitter(
auth=twitter.OAuth(
oauth_token, oauth_token_secret, CONSUMER_KEY, CONSUMER_SECRET),
format='', api_version=None)
oauth_token, oauth_token_secret = parse_oauth_tokens(
_twitter.oauth.access_token(oauth_verifier=oauth_verifier))
# This web server only needs to service one request, so shut it down
shutdown_after_request = request.environ.get('werkzeug.server.shutdown')
shutdown_after_request()
# Write out the final credentials that can be picked up after the blocking
# call to webserver.run() below.
write_token_file(OAUTH_FILE, oauth_token, oauth_token_secret)
return "%s %s written to %s" % (oauth_token, oauth_token_secret, OAUTH_FILE)
# To handle Twitter's OAuth 1.0a implementation, we'll just need to implement a custom
# "oauth dance" and will closely follower the pattern defined in twitter.oauth_dance.
def ipynb_oauth_dance():
_twitter = twitter.Twitter(
auth=twitter.OAuth('', '', CONSUMER_KEY, CONSUMER_SECRET),
format='', api_version=None)
oauth_token, oauth_token_secret = parse_oauth_tokens(
_twitter.oauth.request_token(oauth_callback=oauth_callback))
# Need to write these interim values out to a file to pick up on the callback from Twitter
# that is handled by the web server in /oauth_helper
write_token_file(OAUTH_FILE, oauth_token, oauth_token_secret)
oauth_url = ('http://api.twitter.com/oauth/authorize?oauth_token=' + oauth_token)
# Tap the browser's native capabilities to access the web server through a new window to get
# user authorization
display(JS("window.open('%s')" % oauth_url))
# After the webserver.run() blocking call, start the oauth dance that will ultimately
# cause Twitter to redirect a request back to it. Once that request is serviced, the web
# server will shutdown, and program flow will resume with the OAUTH_FILE containing the
# necessary credentials
Timer(1, lambda: ipynb_oauth_dance()).start()
webserver.run(host='0.0.0.0')
# The values that are read from this file are written out at
# the end of /oauth_helper
oauth_token, oauth_token_secret = read_token_file(OAUTH_FILE)
# These 4 credentials are what is needed to authorize the application
auth = twitter.oauth.OAuth(oauth_token, oauth_token_secret,
CONSUMER_KEY, CONSUMER_SECRET)
twitter_api = twitter.Twitter(auth=auth)
print(twitter_api)
```
# Facebook OAuth 2.0 Flow with IPython Notebook
Facebook implements OAuth 2.0 as its standard authentication mechanism, and this example demonstrates how get an access token for making API requests once you've created an app and gotten a "client id" value that can be used to initiate an OAuth flow. Note that you will need an ordinary Facebook account in order to login, create an app, and get these credentials. You can create an app through the "Developer" section of your account settings as shown below or by navigating directly to https://developers.facebook.com/apps/. During development or debugging cycles, or to just access data in your own account, you may sometimes find it convenient to also reference the access token that's available to you through the Graph API Explorer tool at https://developers.facebook.com/tools/explorer as opposed to using the flow described here. The process of obtaining an access token is fairly straight forward, but an implementation in IPython Notebook is a bit tricker due to the nature of embedding a web server, capturing information within web server contexts, and handling the various redirects along the way.
You must ensure that your browser is not blocking popups in order for this script to work.
<br />
<br />
<img src="files/resources/ch02-facebook/images/fb_create_app.png" width="400px"><br />
Create apps at https://developers.facebook.com/apps/<br />
<br />
<img src="files/resources/ch02-facebook/images/fb_edit_app.png" width="400px"><br />
Clicking on the app in your list to see the app dashboard and access app settings.
## Example 2. Facebook OAuth 2.0 Flow
```
import urllib
from flask import Flask, request
from threading import Timer
from IPython.display import display
from IPython.display import Javascript as JS
# XXX: Get this value from your Facebook application's settings for the OAuth flow
# at https://developers.facebook.com/apps
APP_ID = ''
# This value is where Facebook will redirect. We'll configure an embedded
# web server to be serving requests here
REDIRECT_URI = 'http://localhost:5000/oauth_helper'
# You could customize which extended permissions are being requested for your app
# by adding additional items to the list below. See
# https://developers.facebook.com/docs/reference/login/extended-permissions/
EXTENDED_PERMS = ['user_likes']
# A temporary file to store a code from the web server
OAUTH_FILE = 'resources/ch02-facebook/access_token.txt'
# Configure an emedded web server that accepts one request, parses
# the fragment identifier out of the browser window redirects to another
# handler with the parsed out value in the query string where it can be captured
# and stored to disk. (A webserver cannot capture information in the fragment
# identifier or that work would simply be done in here.)
webserver = Flask("FacebookOAuth")
@webserver.route("/oauth_helper")
def oauth_helper():
return '''<script type="text/javascript">
var at = window.location.hash.substring("access_token=".length+1).split("&")[0];
setTimeout(function() { window.location = "/access_token_capture?access_token=" + at }, 1000 /*ms*/);
</script>'''
# Parses out a query string parameter and stores it to disk. This is required because
# the address space that Flask uses is not shared with IPython Notebook, so there is really
# no other way to share the information than to store it to a file and access it afterward
@webserver.route("/access_token_capture")
def access_token_capture():
access_token = request.args.get('access_token')
f = open(OAUTH_FILE, 'w') # Store the code as a file
f.write(access_token)
f.close()
# It is safe (and convenient) to shut down the web server after this request
shutdown_after_request = request.environ.get('werkzeug.server.shutdown')
shutdown_after_request()
return access_token
# Send an OAuth request to Facebook, handle the redirect, and display the access
# token that's included in the redirect for the user to copy and paste
args = dict(client_id=APP_ID, redirect_uri=REDIRECT_URI,
scope=','.join(EXTENDED_PERMS), type='user_agent', display='popup'
)
oauth_url = 'https://facebook.com/dialog/oauth?' + urllib.parse.urlencode(args)
Timer(1, lambda: display(JS("window.open('%s')" % oauth_url))).start()
webserver.run(host='0.0.0.0')
access_token = open(OAUTH_FILE).read()
print(access_token)
```
# LinkedIn OAuth 2.0 Flow with IPython Notebook
LinkedIn implements OAuth 2.0 as one of its standard authentication mechanism, and "Example 3" demonstrates how to use it to get an access token for making API requests once you've created an app and gotten the "API Key" and "Secret Key" values that are part of the OAuth flow. Note that you will need an ordinary LinkedIn account in order to login, create an app, and get these credentials. You can create an app through the "Developer" section of your account settings as shown below or by navigating directly to https://www.linkedin.com/secure/developer.
You must ensure that your browser is not blocking popups in order for this script to work.
<img src="files/resources/ch04-linkedin/images/LinkedIn-app.png" width="600px">
## Example 3. Using LinkedIn OAuth credentials to receive an access token an authorize an application
Note: You must ensure that your browser is not blocking popups in order for this script to work. LinkedIn's OAuth flow appears to expressly involve opening a new window, and it does not appear that an inline frame can be used as is the case with some other social web properties. You may also find it very convenient to ensure that you are logged into LinkedIn at http://www.linkedin.com/ with this browser before executing this script, because the OAuth flow will prompt you every time you run it if you are not already logged in. If for some reason you cause IPython Notebook to hang, just select "Kernel => Interrupt" from its menu.
```
import os
from threading import Timer
from flask import Flask, request
from linkedin import linkedin # pip install python3-linkedin
from IPython.display import display
from IPython.display import Javascript as JS
# XXX: Get these values from your application's settings for the OAuth flow
CONSUMER_KEY = ''
CONSUMER_SECRET = ''
# This value is where LinkedIn will redirect. We'll configure an embedded
# web server to be serving requests here. Make sure to add this to your
# app settings
REDIRECT_URL = 'http://localhost:5000/oauth_helper'
# A temporary file to store a code from the web server
OAUTH_FILE = 'resources/ch04-linkedin/linkedin.authorization_code'
# These should match those in your app settings
permissions = {'BASIC_PROFILE': 'r_basicprofile',
'EMAIL_ADDRESS': 'r_emailaddress',
'SHARE': 'w_share',
'COMPANY_ADMIN': 'rw_company_admin'}
# Configure an emedded web server that accepts one request, stores a file
# that will need to be accessed outside of the request context, and
# immediately shuts itself down
webserver = Flask("OAuthHelper")
@webserver.route("/oauth_helper")
def oauth_helper():
code = request.args.get('code')
f = open(OAUTH_FILE, 'w') # Store the code as a file
f.write(code)
f.close()
shutdown_after_request = request.environ.get('werkzeug.server.shutdown')
shutdown_after_request()
return """<p>Handled redirect and extracted code <strong>%s</strong>
for authorization</p>""" % (code,)
# Send an OAuth request to LinkedIn, handle the redirect, and display the access
# token that's included in the redirect for the user to copy and paste
auth = linkedin.LinkedInAuthentication(CONSUMER_KEY, CONSUMER_SECRET, REDIRECT_URL,
permissions.values())
# Display popup after a brief delay to ensure that the web server is running and
# can handle the redirect back from LinkedIn
Timer(1, lambda: display(JS("window.open('%s')" % auth.authorization_url))).start()
# Run the server to accept the redirect back from LinkedIn and capture the access
# token. This command blocks, but the web server is configured to shut itself down
# after it serves a request, so after the redirect occurs, program flow will continue
webserver.run(host='0.0.0.0')
# As soon as the request finishes, the web server shuts down and these remaining commands
# are executed, which exchange an authorization code for an access token. This process
# seems to need full automation because the authorization code expires very quickly.
auth.authorization_code = open(OAUTH_FILE).read()
auth.get_access_token()
# Prevent stale tokens from sticking around, which could complicate debugging
os.remove(OAUTH_FILE)
# How you can use the application to access the LinkedIn API...
app = linkedin.LinkedInApplication(auth)
print(app.get_profile())
```
| true |
code
| 0.285198 | null | null | null | null |
|
# Text Generation with Neural Networks
Import necessary packages for preprocessing, model building, etc. We follow the steps described in the theoretical part of this summer school as follows:
0. Define Reseach Goal (already done)
2. Retrieve Data
3. Prepare Data
4. Explore Data
5. Model Data
6. Present and automate Model
```
from keras.callbacks import LambdaCallback
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LSTM
from keras.optimizers import RMSprop
from keras.utils.data_utils import get_file
from keras.models import load_model
from keras import backend as K
import numpy as np
import random
import sys
import io
```
# 1. Retrieve Data
Load your data! You can pick up data from everywhere, such as plain text, HTML, source code, etc.
You can either automatically download with Keras get_file function or download it manually and import it in this notebook.
## Example Data Set
[trump.txt](https://raw.githubusercontent.com/harshilkamdar/trump-tweets/master/trump.txt)
```
#path = get_file('trump.txt', origin='https://raw.githubusercontent.com/harshilkamdar/trump-tweets/master/trump.txt')
text = io.open('resources/shakespeare.txt', encoding='utf-8').read().lower()
print('corpus length:', len(text))
```
# 2. Prepare Data
As described in the theoretical part of this workshop we need to convert our text into a word embedding that can be processed by a (later) defined Neural Network.
## 2.1. Create Classes
The goal after this step is to have a variable which contains the distinct characters of the text. Characters can be letters, digits, punctions, new lines, spaces, etc.
### Example:
Let's assume we have the following text as input: "hallo. "
After the following step, we want to have all distinct characters, i.e.:
``[ "h", "a", "l", "o", ".", " " ] ``
```
chars = sorted(list(set(text)))
print('total chars:', len(chars))
```
## 2.2. Create Training Set
In the following section we need to create our test set based on our text. The idea is to map a sequence of characters to a class. In this case, a class is one of our distinct characters defined in the previous task. This means that a sequence of characters predicts the next character. This is important for the later model to know which characters come after specific sequences. The sequence length can be chosen. So try out different squence length.
### Example:
Our text is still: "hallo. "
Sequence length: 2 (i.e. 2 characters predict the next character)
The result (training set) should be defined as follows:
``
Seuences --> Class
"ha" --> "l"
"al" --> "l"
"ll" --> "o"
"lo" --> "."
"o." --> " "
``
You can read the previous example like this: Squence "ha" predicts the next character " l ", sequence "al" predicts next character " l " and so on.
```
seqlen = 40 # Sequence length parameter
step = 5 # Determines the how many characters the window should be shifted in the text
sequences = [] # List of sequences
char_class = [] # Corresponding class of each sequence
for i in range(0, len(text) - seqlen, step):
sequences.append(text[i: i + seqlen])
char_class.append(text[i + seqlen])
print('#no sequences:', len(sequences))
```
## 2.3. Check your Data
Now that we processed our data, it's time to understand what we have built so far.
```
for idx in range(len(sequences[:10])):
print(sequences[idx], ":" , char_class[idx])
# Print from 1st to 10th character
chars[:10]
# Print from 150th to 160th character :-)
chars[150:160]
```
## 2.4. Vectorization of Training Sequences
The following section describes the desired form of our final training set.
text: "hallo. ".
As defined above we have a couple of sequences mapping to the next appearing character in the text (e.g. "ha" mapping to "l"). But first of all, we transform each sequence to the following one-hot-encoded matrix.
**Example:**
sequence "ha" maps to the following matrix
| | h | a | l | o | . | ' ' |
|-----|-----|-----|-----|-----|-----|-----|
| h | 1 | 0 | 0 | 0 | 0 | 0 |
| a | 0 | 1 | 0 | 0 | 0 | 0 |
next sequence "al" maps to the following matrix
| | h | a | l | o | . | ' ' |
|-----|-----|-----|-----|-----|-----|-----|
| a | 0 | 1 | 0 | 0 | 0 | 0 |
| l | 0 | 0 | 1 | 0 | 0 | 0 |
... And so on
## 2.5. Vectorization of Target Classes
We build our target classes similar to the training set. We need a one hot-encoded vector for each target (which is a character).
**Example:** for target char "l" the vector looks like this
| | h | a | l | o | . | ' ' |
|-----|-----|-----|-----|-----|-----|-----|
| l | 0 | 0 | 1 | 0 | 0 | 0 |
```
# Indexed characters as dictionary
char_indices = dict((c, i) for i, c in enumerate(chars))
# Both matrices will initialized with zeros
training_set = np.zeros((len(sequences), seqlen, len(chars)), dtype=np.bool)
target_char = np.zeros((len(sequences), len(chars)), dtype=np.bool)
for i, sequence in enumerate(sequences):
for t, char in enumerate(sequence):
training_set[i, t, char_indices[char]] = 1
target_char[i, char_indices[char_class[i]]] = 1
```
# 3. Explore Data
```
# Let's check the shape of the training_set
training_set.shape
```
Output: (x, y, z)
x = number of all sequences to test
y = window size to predict the next character
z = number of all appearing characters in text (for one-hot-enconding)
```
# Let's check the shape of the target_char (act as our target classes)
target_char.shape
```
Output: (x, y)
x = number of all sequences to test
y = the mapping of each sequence to the next character
# 4. Model data
Let's get down to business! Create your model.
Try different model configuration (see [keras doc](https://keras.io/models/about-keras-models/#about-keras-models))
```
model = Sequential()
# build the model: a LSTM
model = Sequential()
model.add(LSTM(128, input_shape=(seqlen, len(chars))))
model.add(Dense(len(chars)))
model.add(Activation('softmax'))
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
model.summary()
def getNextCharIdx(preds, temperature=1.0):
# helper function to sample an index from a probability array
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / temperature
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)
# Creation of reverse char index, to get the char for the predicted class
indices_char = dict((i, c) for i, c in enumerate(chars))
def on_epoch_end(epoch, logs):
# Function invoked at end of each epoch. Prints generated text.
print()
print('----- Generating text after Epoch: %d' % epoch)
start_index = random.randint(0, len(text) - seqlen - 1)
for diversity in [1, 0.1, 0.5]:
print('----- diversity:', diversity)
generated = ''
sentence = text[start_index: start_index + seqlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(1000):
x_pred = np.zeros((1, seqlen, len(chars)))
for t, char in enumerate(sentence):
x_pred[0, t, char_indices[char]] = 1.
preds = model.predict(x_pred, verbose=0)[0]
next_index = getNextCharIdx(preds, diversity)
next_char = indices_char[next_index]
generated += next_char
sentence = sentence[1:] + next_char
sys.stdout.write(next_char)
sys.stdout.flush()
print()
print_callback = LambdaCallback(on_epoch_end=on_epoch_end)
```
# 5. Evaluate Model
We are not at the sweet part of the model. Let's fit our model and see what it prints!
```
model.fit(training_set, target_char,
batch_size=128,
epochs=150,
callbacks=[print_callback])
```
# Present and Automate
Having a model trained for hours is a valuable asset! We need now to store the model and use it to solve the problem we wanted to solve with Machine Learning. Keras has a simple function to save a model to the local file system and also a function to load the model again and have it ready for our task!
```
model.save('shakespeareModel.h5')
model = load_model('shakespeareModel.h5')
```
| true |
code
| 0.703931 | null | null | null | null |
|
# ML Scripts
So far, we've done everything inside the Jupyter notebooks but we're going to now move our code into individual python scripts. We will lay out the code that needs to be inside each script but checkout the `API` lesson to see how it all comes together.
<div align="left">
<a href="https://github.com/madewithml/lessons/blob/master/notebooks/03_APIs/02_ML_Scripts/02_PT_ML_Scripts.ipynb" role="button"><img class="notebook-badge-image" src="https://img.shields.io/static/v1?label=&message=View%20On%20GitHub&color=586069&logo=github&labelColor=2f363d"></a>
<a href="https://colab.research.google.com/github/madewithml/lessons/blob/master/notebooks/03_APIs/02_ML_Scripts/02_PT_ML_Scripts.ipynb"><img class="notebook-badge-image" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"></a>
</div>
# data.py
## Load data
```
import numpy as np
import pandas as pd
import random
import urllib
SEED = 1234
DATA_FILE = 'news.csv'
INPUT_FEATURE = 'title'
OUTPUT_FEATURE = 'category'
# Set seed for reproducibility
np.random.seed(SEED)
random.seed(SEED)
# Load data from GitHub to notebook's local drive
url = "https://raw.githubusercontent.com/madewithml/lessons/master/data/news.csv"
response = urllib.request.urlopen(url)
html = response.read()
with open(DATA_FILE, 'wb') as fp:
fp.write(html)
# Load data
df = pd.read_csv(DATA_FILE, header=0)
X = df[INPUT_FEATURE].values
y = df[OUTPUT_FEATURE].values
df.head(5)
```
## Preprocessing
```
import re
LOWER = True
FILTERS = r"[!\"'#$%&()*\+,-./:;<=>?@\\\[\]^_`{|}~]"
def preprocess_texts(texts, lower, filters):
preprocessed_texts = []
for text in texts:
if lower:
text = ' '.join(word.lower() for word in text.split(" "))
text = re.sub(r"([.,!?])", r" \1 ", text)
text = re.sub(filters, r"", text)
text = re.sub(' +', ' ', text) # remove multiple spaces
text = text.strip()
preprocessed_texts.append(text)
return preprocessed_texts
original_text = X[0]
X = np.array(preprocess_texts(X, lower=LOWER, filters=FILTERS))
print (f"{original_text} → {X[0]}")
```
## Split data
```
import collections
from sklearn.model_selection import train_test_split
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
SHUFFLE = True
def train_val_test_split(X, y, val_size, test_size, shuffle):
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=test_size, stratify=y, shuffle=shuffle)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=val_size, stratify=y_train, shuffle=shuffle)
return X_train, X_val, X_test, y_train, y_val, y_test
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
class_counts = dict(collections.Counter(y))
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"{X_train[0]} → {y_train[0]}")
print (f"Classes: {class_counts}")
```
# tokenizers.py
## Tokenizer
```
import json
import re
SEPARATOR = ' ' # word level
class Tokenizer(object):
def __init__(self, separator, pad_token='<PAD>', oov_token='<UNK>',
token_to_index={'<PAD>': 0, '<UNK>': 1}):
self.separator = separator
self.oov_token = oov_token
self.token_to_index = token_to_index
self.index_to_token = {v: k for k, v in self.token_to_index.items()}
def __len__(self):
return len(self.token_to_index)
def __str__(self):
return f"<Tokenizer(num_tokens={len(self)})>"
def fit_on_texts(self, texts):
for text in texts:
for token in text.split(self.separator):
if token not in self.token_to_index:
index = len(self)
self.token_to_index[token] = index
self.index_to_token[index] = token
return self
def texts_to_sequences(self, texts):
sequences = []
for text in texts:
sequence = []
for token in text.split(self.separator):
sequence.append(self.token_to_index.get(
token, self.token_to_index[self.oov_token]))
sequences.append(sequence)
return sequences
def sequences_to_texts(self, sequences):
texts = []
for sequence in sequences:
text = []
for index in sequence:
text.append(self.index_to_token.get(index, self.oov_token))
texts.append(self.separator.join([token for token in text]))
return texts
def save(self, fp):
with open(fp, 'w') as fp:
contents = {
'separator': self.separator,
'oov_token': self.oov_token,
'token_to_index': self.token_to_index
}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
# Input vectorizer
X_tokenizer = Tokenizer(separator=SEPARATOR)
X_tokenizer.fit_on_texts(texts=X_train)
vocab_size = len(X_tokenizer)
print (X_tokenizer)
# Convert text to sequence of tokens
original_text = X_train[0]
X_train = np.array(X_tokenizer.texts_to_sequences(X_train))
X_val = np.array(X_tokenizer.texts_to_sequences(X_val))
X_test = np.array(X_tokenizer.texts_to_sequences(X_test))
preprocessed_text = X_tokenizer.sequences_to_texts([X_train[0]])
print (f"{original_text} \n\t→ {preprocessed_text} \n\t→ {X_train[0]}")
# Save tokenizer
X_tokenizer.save(fp='X_tokenizer.json')
# Load tokenizer
X_tokenizer = Tokenizer.load(fp='X_tokenizer.json')
print (X_tokenizer)
```
## Label Encoder
```
class LabelEncoder(object):
def __init__(self, class_to_index={}):
self.class_to_index = class_to_index
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
def __len__(self):
return len(self.class_to_index)
def __str__(self):
return f"<LabelEncoder(num_classes={len(self)})>"
def fit(self, y_train):
for i, class_ in enumerate(np.unique(y_train)):
self.class_to_index[class_] = i
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
return self
def transform(self, y):
return np.array([self.class_to_index[class_] for class_ in y])
def decode(self, index):
return self.index_to_class.get(index, None)
def save(self, fp):
with open(fp, 'w') as fp:
contents = {
'class_to_index': self.class_to_index
}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
# Output vectorizer
y_tokenizer = LabelEncoder()
# Fit on train data
y_tokenizer = y_tokenizer.fit(y_train)
print (y_tokenizer)
classes = y_tokenizer.classes
print (f"classes: {classes}")
# Convert labels to tokens
class_ = y_train[0]
y_train = y_tokenizer.transform(y_train)
y_val = y_tokenizer.transform(y_val)
y_test = y_tokenizer.transform(y_test)
print (f"{class_} → {y_train[0]}")
# Class weights
counts = np.bincount(y_train)
class_weights = {i: 1.0/count for i, count in enumerate(counts)}
print (f"class counts: {counts},\nclass weights: {class_weights}")
# Save label encoder
y_tokenizer.save(fp='y_tokenizer.json')
# Load label encoder
y_tokenizer = LabelEncoder.load(fp='y_tokenizer.json')
print (y_tokenizer)
```
# datasets.py
```
import math
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
BATCH_SIZE = 128
FILTER_SIZES = [2, 3, 4]
# Set seed for reproducibility
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.cuda.manual_seed_all(SEED) # multi-GPU.
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
USE_CUDA = True
DEVICE = torch.device('cuda' if (torch.cuda.is_available() and USE_CUDA) else 'cpu')
print (DEVICE)
```
## Pad
```
def pad_sequences(X, max_seq_len):
sequences = np.zeros((len(X), max_seq_len))
for i, sequence in enumerate(X):
sequences[i][:len(sequence)] = sequence
return sequences
# Pad sequences
inputs = [[1,2,3], [1,2,3,4], [1,2]]
max_seq_len = max(len(x) for x in inputs)
padded_inputs = pad_sequences(X=inputs, max_seq_len=max_seq_len)
print (padded_inputs.shape)
print (padded_inputs)
```
## Dataset
```
class TextDataset(Dataset):
def __init__(self, X, y, batch_size, max_filter_size):
self.X = X
self.y = y
self.batch_size = batch_size
self.max_filter_size = max_filter_size
def __len__(self):
return len(self.y)
def __str__(self):
return f"<Dataset(N={len(self)}, batch_size={self.batch_size}, num_batches={self.get_num_batches()})>"
def __getitem__(self, index):
X = self.X[index]
y = self.y[index]
return X, y
def get_num_batches(self):
return math.ceil(len(self)/self.batch_size)
def collate_fn(self, batch):
"""Processing on a batch."""
# Get inputs
X = np.array(batch)[:, 0]
y = np.array(batch)[:, 1]
# Pad inputs
max_seq_len = max(self.max_filter_size, max([len(x) for x in X]))
X = pad_sequences(X=X, max_seq_len=max_seq_len)
return X, y
def generate_batches(self, shuffle=False, drop_last=False):
dataloader = DataLoader(dataset=self, batch_size=self.batch_size,
collate_fn=self.collate_fn, shuffle=shuffle,
drop_last=drop_last, pin_memory=True)
for (X, y) in dataloader:
X = torch.LongTensor(X.astype(np.int32))
y = torch.LongTensor(y.astype(np.int32))
yield X, y
# Create datasets
train_set = TextDataset(X=X_train, y=y_train, batch_size=BATCH_SIZE, max_filter_size=max(FILTER_SIZES))
val_set = TextDataset(X=X_val, y=y_val, batch_size=BATCH_SIZE, max_filter_size=max(FILTER_SIZES))
test_set = TextDataset(X=X_test, y=y_test, batch_size=BATCH_SIZE, max_filter_size=max(FILTER_SIZES))
print (train_set)
print (train_set[0])
# Generate batch
batch_X, batch_y = next(iter(test_set.generate_batches()))
print (batch_X.shape)
print (batch_y.shape)
```
# utils.py
## Embeddings
```
from io import BytesIO
from urllib.request import urlopen
from zipfile import ZipFile
EMBEDDING_DIM = 100
def load_glove_embeddings(embeddings_file):
"""Load embeddings from a file."""
embeddings = {}
with open(embeddings_file, "r") as fp:
for index, line in enumerate(fp):
values = line.split()
word = values[0]
embedding = np.asarray(values[1:], dtype='float32')
embeddings[word] = embedding
return embeddings
def make_embeddings_matrix(embeddings, token_to_index, embedding_dim):
"""Create embeddings matrix to use in Embedding layer."""
embedding_matrix = np.zeros((len(token_to_index), embedding_dim))
for word, i in token_to_index.items():
embedding_vector = embeddings.get(word)
if embedding_vector is not None:
embedding_matrix[i] = embedding_vector
return embedding_matrix
# Unzip the file (may take ~3-5 minutes)
resp = urlopen('http://nlp.stanford.edu/data/glove.6B.zip')
zipfile = ZipFile(BytesIO(resp.read()))
zipfile.namelist()
# Write embeddings to file
embeddings_file = 'glove.6B.{0}d.txt'.format(EMBEDDING_DIM)
zipfile.extract(embeddings_file)
!ls
# Create embeddings
embeddings_file = 'glove.6B.{0}d.txt'.format(EMBEDDING_DIM)
glove_embeddings = load_glove_embeddings(embeddings_file=embeddings_file)
embedding_matrix = make_embeddings_matrix(
embeddings=glove_embeddings, token_to_index=X_tokenizer.token_to_index,
embedding_dim=EMBEDDING_DIM)
print (embedding_matrix.shape)
```
# model.py
## Model
```
import torch.nn.functional as F
NUM_FILTERS = 50
HIDDEN_DIM = 128
DROPOUT_P = 0.1
class TextCNN(nn.Module):
def __init__(self, embedding_dim, vocab_size, num_filters, filter_sizes,
hidden_dim, dropout_p, num_classes, pretrained_embeddings=None,
freeze_embeddings=False, padding_idx=0):
super(TextCNN, self).__init__()
# Initialize embeddings
if pretrained_embeddings is None:
self.embeddings = nn.Embedding(
embedding_dim=embedding_dim, num_embeddings=vocab_size,
padding_idx=padding_idx)
else:
pretrained_embeddings = torch.from_numpy(pretrained_embeddings).float()
self.embeddings = nn.Embedding(
embedding_dim=embedding_dim, num_embeddings=vocab_size,
padding_idx=padding_idx, _weight=pretrained_embeddings)
# Freeze embeddings or not
if freeze_embeddings:
self.embeddings.weight.requires_grad = False
# Conv weights
self.filter_sizes = filter_sizes
self.conv = nn.ModuleList(
[nn.Conv1d(in_channels=embedding_dim,
out_channels=num_filters,
kernel_size=f) for f in filter_sizes])
# FC weights
self.dropout = nn.Dropout(dropout_p)
self.fc1 = nn.Linear(num_filters*len(filter_sizes), hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, x_in, channel_first=False):
# Embed
x_in = self.embeddings(x_in)
if not channel_first:
x_in = x_in.transpose(1, 2) # (N, channels, sequence length)
# Conv + pool
z = []
conv_outputs = [] # for interpretability
max_seq_len = x_in.shape[2]
for i, f in enumerate(self.filter_sizes):
# `SAME` padding
padding_left = int((self.conv[i].stride[0]*(max_seq_len-1) - max_seq_len + self.filter_sizes[i])/2)
padding_right = int(math.ceil((self.conv[i].stride[0]*(max_seq_len-1) - max_seq_len + self.filter_sizes[i])/2))
# Conv + pool
_z = self.conv[i](F.pad(x_in, (padding_left, padding_right)))
conv_outputs.append(_z)
_z = F.max_pool1d(_z, _z.size(2)).squeeze(2)
z.append(_z)
# Concat conv outputs
z = torch.cat(z, 1)
# FC layers
z = self.fc1(z)
z = self.dropout(z)
logits = self.fc2(z)
return conv_outputs, logits
# Initialize model
model = TextCNN(embedding_dim=EMBEDDING_DIM,
vocab_size=vocab_size,
num_filters=NUM_FILTERS,
filter_sizes=FILTER_SIZES,
hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P,
num_classes=len(classes),
pretrained_embeddings=embedding_matrix,
freeze_embeddings=False).to(DEVICE)
print (model.named_parameters)
```
# train.py
## Training
```
from pathlib import Path
from torch.optim import Adam
from torch.optim.lr_scheduler import ReduceLROnPlateau
from torch.utils.tensorboard import SummaryWriter
%load_ext tensorboard
LEARNING_RATE = 1e-4
PATIENCE = 3
NUM_EPOCHS = 100
def train_step(model, device, dataset, optimizer):
"""Train step."""
# Set model to train mode
model.train()
train_loss = 0.
correct = 0
# Iterate over train batches
for i, (X, y) in enumerate(dataset.generate_batches()):
# Set device
X, y = X.to(device), y.to(device)
# Reset gradients
optimizer.zero_grad()
# Forward pass
_, logits = model(X)
# Define loss
loss = F.cross_entropy(logits, y)
# Backward pass
loss.backward()
# Update weights
optimizer.step()
# Metrics
y_pred = logits.max(dim=1)[1]
correct += torch.eq(y_pred, y).sum().item()
train_loss += (loss.item() - train_loss) / (i + 1)
train_acc = 100. * correct / len(dataset)
return train_loss, train_acc
def test_step(model, device, dataset):
"""Validation or test step."""
# Set model to eval mode
model.eval()
loss = 0.
correct = 0
y_preds = []
y_targets = []
# Iterate over val batches
with torch.no_grad():
for i, (X, y) in enumerate(dataset.generate_batches()):
# Set device
X, y = X.to(device), y.to(device)
# Forward pass
_, logits = model(X)
# Metrics
loss += F.cross_entropy(logits, y, reduction='sum').item()
y_pred = logits.max(dim=1)[1]
correct += torch.eq(y_pred, y).sum().item()
# Outputs
y_preds.extend(y_pred.cpu().numpy())
y_targets.extend(y.cpu().numpy())
loss /= len(dataset)
accuracy = 100. * correct / len(dataset)
return y_preds, y_targets, loss, accuracy
def train(model, optimizer, scheduler,
train_set, val_set, test_set, writer):
# Epochs
best_val_loss = np.inf
for epoch in range(NUM_EPOCHS):
# Steps
train_loss, train_acc = train_step(model, DEVICE, train_set, optimizer)
_, _, val_loss, val_acc = test_step(model, DEVICE, val_set)
# Metrics
print (f"Epoch: {epoch} | train_loss: {train_loss:.2f}, train_acc: {train_acc:.1f}, val_loss: {val_loss:.2f}, val_acc: {val_acc:.1f}")
writer.add_scalar(tag='training loss', scalar_value=train_loss, global_step=epoch)
writer.add_scalar(tag='training accuracy', scalar_value=train_acc, global_step=epoch)
writer.add_scalar(tag='validation loss', scalar_value=val_loss, global_step=epoch)
writer.add_scalar(tag='validation accuracy', scalar_value=val_acc, global_step=epoch)
# Adjust learning rate
scheduler.step(val_loss)
# Early stopping
if val_loss < best_val_loss:
best_val_loss = val_loss
patience = PATIENCE # reset patience
torch.save(model.state_dict(), MODEL_PATH)
else:
patience -= 1
if not patience: # 0
print ("Stopping early!")
break
# Optimizer
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)
scheduler = ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=3)
# Path to save model
MODEL_NAME = 'TextCNN'
MODEL_PATH = Path(f'models/{MODEL_NAME}.h5')
Path(MODEL_PATH.parent).mkdir(parents=True, exist_ok=True)
# TensorBoard writer
log_dir = f'tensorboard/{MODEL_NAME}'
!rm -rf {log_dir} # remove if it already exists
writer = SummaryWriter(log_dir=log_dir)
# Training
train(model, optimizer, scheduler,
train_set, val_set, test_set, writer)
%tensorboard --logdir {log_dir}
```
## Evaluation
```
import io
import itertools
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_recall_fscore_support
def plot_confusion_matrix(y_pred, y_target, classes, cmap=plt.cm.Blues):
"""Plot a confusion matrix using ground truth and predictions."""
# Confusion matrix
cm = confusion_matrix(y_target, y_pred)
cm_norm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
# Figure
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(cm, cmap=plt.cm.Blues)
fig.colorbar(cax)
# Axis
plt.title("Confusion matrix")
plt.ylabel("True label")
plt.xlabel("Predicted label")
ax.set_xticklabels([''] + classes)
ax.set_yticklabels([''] + classes)
ax.xaxis.set_label_position('bottom')
ax.xaxis.tick_bottom()
# Values
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, f"{cm[i, j]:d} ({cm_norm[i, j]*100:.1f}%)",
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
# Display
plt.show()
def get_performance(y_pred, y_target, classes):
"""Per-class performance metrics. """
performance = {'overall': {}, 'class': {}}
metrics = precision_recall_fscore_support(y_target, y_pred)
# Overall performance
performance['overall']['precision'] = np.mean(metrics[0])
performance['overall']['recall'] = np.mean(metrics[1])
performance['overall']['f1'] = np.mean(metrics[2])
performance['overall']['num_samples'] = np.float64(np.sum(metrics[3]))
# Per-class performance
for i in range(len(classes)):
performance['class'][classes[i]] = {
"precision": metrics[0][i],
"recall": metrics[1][i],
"f1": metrics[2][i],
"num_samples": np.float64(metrics[3][i])
}
return performance
# Test
y_preds, y_targets, test_loss, test_acc = test_step(model, DEVICE, test_set)
print (f"test_loss: {test_loss:.2f}, test_acc: {test_acc:.1f}")
# Class performance
performance = get_performance(y_preds, y_targets, classes)
print (json.dumps(performance, indent=4))
# Confusion matrix
plt.rcParams["figure.figsize"] = (7,7)
plot_confusion_matrix(y_preds, y_targets, classes)
print (classification_report(y_targets, y_preds))
```
# inference.py
## Load model
```
# Load model
model = TextCNN(embedding_dim=EMBEDDING_DIM,
vocab_size=vocab_size,
num_filters=NUM_FILTERS,
filter_sizes=FILTER_SIZES,
hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P,
num_classes=len(classes),
pretrained_embeddings=embedding_matrix,
freeze_embeddings=False).to(DEVICE)
model.load_state_dict(torch.load(MODEL_PATH))
model.eval()
```
## Inference
```
import collections
def get_probability_distribution(y_prob, classes):
results = {}
for i, class_ in enumerate(classes):
results[class_] = np.float64(y_prob[i])
sorted_results = {k: v for k, v in sorted(
results.items(), key=lambda item: item[1], reverse=True)}
return sorted_results
def get_top_n_grams(tokens, conv_outputs, filter_sizes):
# Process conv outputs for each unique filter size
n_grams = {}
for i, filter_size in enumerate(filter_sizes):
# Identify most important n-gram (excluding last token)
popular_indices = collections.Counter([np.argmax(conv_output) \
for conv_output in conv_outputs[filter_size]])
# Get corresponding text
start = popular_indices.most_common(1)[-1][0]
n_gram = " ".join([token for token in tokens[start:start+filter_size]])
n_grams[filter_size] = n_gram
return n_grams
# Inputs
texts = ["The Wimbledon tennis tournament starts next week!",
"The President signed in the new law."]
texts = preprocess_texts(texts, lower=LOWER, filters=FILTERS)
X_infer = np.array(X_tokenizer.texts_to_sequences(texts))
print (f"{texts[0]} \n\t→ {X_tokenizer.sequences_to_texts(X_infer)[0]} \n\t→ {X_infer[0]}")
y_filler = np.array([0]*len(texts))
# Dataset
infer_set = TextDataset(X=X_infer, y=y_filler, batch_size=BATCH_SIZE,
max_filter_size=max(FILTER_SIZES))
# Iterate over infer batches
conv_outputs = collections.defaultdict(list)
y_probs = []
with torch.no_grad():
for i, (X, y) in enumerate(infer_set.generate_batches()):
# Set device
X, y = X.to(DEVICE), y.to(DEVICE)
# Forward pass
conv_outputs_, logits = model(X)
y_prob = F.softmax(logits, dim=1)
# Save probabilities
y_probs.extend(y_prob.cpu().numpy())
for i, filter_size in enumerate(FILTER_SIZES):
conv_outputs[filter_size].extend(conv_outputs_[i].cpu().numpy())
# Results
results = []
for index in range(len(X_infer)):
results.append({
'raw_input': texts[index],
'preprocessed_input': X_tokenizer.sequences_to_texts([X_infer[index]])[0],
'probabilities': get_probability_distribution(y_prob[index], y_tokenizer.classes),
'top_n_grams': get_top_n_grams(
tokens=preprocessed_input.split(' '),
conv_outputs={k:v[index] for k,v in conv_outputs.items()},
filter_sizes=FILTER_SIZES)})
print (json.dumps(results, indent=4))
```
Use inferences to collect information how the model performs on your real world data and use it to improve it over time.
- Use a probability threshold for the top class (ex. If the predicted class is less than 75%, send the inference for review).
- Combine the above with Use probability thresholds for each class (ex. if the predicted class is `Sports` at 85% but that class's precision/recall is low, then send it for review but maybe you don't do this when the predicted class is `Sports` but above 90%.
- If the preprocessed sentence has <UNK> tokens, send the inference for further review.
- When latency is not an issue, use the n-grams to validate the prediction.
Check out the `API` lesson to see how all of this comes together to create an ML service.
---
Share and discover ML projects at <a href="https://madewithml.com/">Made With ML</a>.
<div align="left">
<a class="ai-header-badge" target="_blank" href="https://github.com/madewithml/lessons"><img src="https://img.shields.io/github/stars/madewithml/lessons.svg?style=social&label=Star"></a>
<a class="ai-header-badge" target="_blank" href="https://www.linkedin.com/company/madewithml"><img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a class="ai-header-badge" target="_blank" href="https://twitter.com/madewithml"><img src="https://img.shields.io/twitter/follow/madewithml.svg?label=Follow&style=social"></a>
</div>
| true |
code
| 0.474631 | null | null | null | null |
|
## Content-Based Filtering Using Neural Networks
This notebook relies on files created in the [content_based_preproc.ipynb](./content_based_preproc.ipynb) notebook. Be sure to run the code in there before completing this notebook.
Also, we'll be using the **python3** kernel from here on out so don't forget to change the kernel if it's still Python2.
This lab illustrates:
1. how to build feature columns for a model using tf.feature_column
2. how to create custom evaluation metrics and add them to Tensorboard
3. how to train a model and make predictions with the saved model
Tensorflow Hub should already be installed. You can check that it is by using "pip freeze".
```
%bash
pip freeze | grep tensor
```
If 'tensorflow-hub' isn't one of the outputs above, then you'll need to install it. Uncomment the cell below and execute the commands. After doing the pip install, click **"Reset Session"** on the notebook so that the Python environment picks up the new packages.
```
#%bash
#pip install tensorflow-hub
import os
import tensorflow as tf
import numpy as np
import tensorflow_hub as hub
import shutil
PROJECT = 'cloud-training-demos' # REPLACE WITH YOUR PROJECT ID
BUCKET = 'cloud-training-demos-ml' # REPLACE WITH YOUR BUCKET NAME
REGION = 'us-central1' # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# do not change these
os.environ['PROJECT'] = PROJECT
os.environ['BUCKET'] = BUCKET
os.environ['REGION'] = REGION
os.environ['TFVERSION'] = '1.8'
%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
```
### Build the feature columns for the model.
To start, we'll load the list of categories, authors and article ids we created in the previous **Create Datasets** notebook.
```
categories_list = open("categories.txt").read().splitlines()
authors_list = open("authors.txt").read().splitlines()
content_ids_list = open("content_ids.txt").read().splitlines()
mean_months_since_epoch = 523
```
In the cell below we'll define the feature columns to use in our model. If necessary, remind yourself the [various feature columns](https://www.tensorflow.org/api_docs/python/tf/feature_column) to use.
For the embedded_title_column feature column, use a Tensorflow Hub Module to create an embedding of the article title. Since the articles and titles are in German, you'll want to use a German language embedding module.
Explore the text embedding Tensorflow Hub modules [available here](https://alpha.tfhub.dev/). Filter by setting the language to 'German'. The 50 dimensional embedding should be sufficient for our purposes.
```
embedded_title_column = hub.text_embedding_column(
key="title",
module_spec="https://tfhub.dev/google/nnlm-de-dim50/1",
trainable=False)
content_id_column = tf.feature_column.categorical_column_with_hash_bucket(
key="content_id",
hash_bucket_size= len(content_ids_list) + 1)
embedded_content_column = tf.feature_column.embedding_column(
categorical_column=content_id_column,
dimension=10)
author_column = tf.feature_column.categorical_column_with_hash_bucket(key="author",
hash_bucket_size=len(authors_list) + 1)
embedded_author_column = tf.feature_column.embedding_column(
categorical_column=author_column,
dimension=3)
category_column_categorical = tf.feature_column.categorical_column_with_vocabulary_list(
key="category",
vocabulary_list=categories_list,
num_oov_buckets=1)
category_column = tf.feature_column.indicator_column(category_column_categorical)
months_since_epoch_boundaries = list(range(400,700,20))
months_since_epoch_column = tf.feature_column.numeric_column(
key="months_since_epoch")
months_since_epoch_bucketized = tf.feature_column.bucketized_column(
source_column = months_since_epoch_column,
boundaries = months_since_epoch_boundaries)
crossed_months_since_category_column = tf.feature_column.indicator_column(tf.feature_column.crossed_column(
keys = [category_column_categorical, months_since_epoch_bucketized],
hash_bucket_size = len(months_since_epoch_boundaries) * (len(categories_list) + 1)))
feature_columns = [embedded_content_column,
embedded_author_column,
category_column,
embedded_title_column,
crossed_months_since_category_column]
```
### Create the input function.
Next we'll create the input function for our model. This input function reads the data from the csv files we created in the previous labs.
```
record_defaults = [["Unknown"], ["Unknown"],["Unknown"],["Unknown"],["Unknown"],[mean_months_since_epoch],["Unknown"]]
column_keys = ["visitor_id", "content_id", "category", "title", "author", "months_since_epoch", "next_content_id"]
label_key = "next_content_id"
def read_dataset(filename, mode, batch_size = 512):
def _input_fn():
def decode_csv(value_column):
columns = tf.decode_csv(value_column,record_defaults=record_defaults)
features = dict(zip(column_keys, columns))
label = features.pop(label_key)
return features, label
# Create list of files that match pattern
file_list = tf.gfile.Glob(filename)
# Create dataset from file list
dataset = tf.data.TextLineDataset(file_list).map(decode_csv)
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
num_epochs = 1 # end-of-input after this
dataset = dataset.repeat(num_epochs).batch(batch_size)
return dataset.make_one_shot_iterator().get_next()
return _input_fn
```
### Create the model and train/evaluate
Next, we'll build our model which recommends an article for a visitor to the Kurier.at website. Look through the code below. We use the input_layer feature column to create the dense input layer to our network. This is just a sigle layer network where we can adjust the number of hidden units as a parameter.
Currently, we compute the accuracy between our predicted 'next article' and the actual 'next article' read next by the visitor. We'll also add an additional performance metric of top 10 accuracy to assess our model. To accomplish this, we compute the top 10 accuracy metric, add it to the metrics dictionary below and add it to the tf.summary so that this value is reported to Tensorboard as well.
```
def model_fn(features, labels, mode, params):
net = tf.feature_column.input_layer(features, params['feature_columns'])
for units in params['hidden_units']:
net = tf.layers.dense(net, units=units, activation=tf.nn.relu)
# Compute logits (1 per class).
logits = tf.layers.dense(net, params['n_classes'], activation=None)
predicted_classes = tf.argmax(logits, 1)
from tensorflow.python.lib.io import file_io
with file_io.FileIO('content_ids.txt', mode='r') as ifp:
content = tf.constant([x.rstrip() for x in ifp])
predicted_class_names = tf.gather(content, predicted_classes)
if mode == tf.estimator.ModeKeys.PREDICT:
predictions = {
'class_ids': predicted_classes[:, tf.newaxis],
'class_names' : predicted_class_names[:, tf.newaxis],
'probabilities': tf.nn.softmax(logits),
'logits': logits,
}
return tf.estimator.EstimatorSpec(mode, predictions=predictions)
table = tf.contrib.lookup.index_table_from_file(vocabulary_file="content_ids.txt")
labels = table.lookup(labels)
# Compute loss.
loss = tf.losses.sparse_softmax_cross_entropy(labels=labels, logits=logits)
# Compute evaluation metrics.
accuracy = tf.metrics.accuracy(labels=labels,
predictions=predicted_classes,
name='acc_op')
top_10_accuracy = tf.metrics.mean(tf.nn.in_top_k(predictions=logits,
targets=labels,
k=10))
metrics = {
'accuracy': accuracy,
'top_10_accuracy' : top_10_accuracy}
tf.summary.scalar('accuracy', accuracy[1])
tf.summary.scalar('top_10_accuracy', top_10_accuracy[1])
if mode == tf.estimator.ModeKeys.EVAL:
return tf.estimator.EstimatorSpec(
mode, loss=loss, eval_metric_ops=metrics)
# Create training op.
assert mode == tf.estimator.ModeKeys.TRAIN
optimizer = tf.train.AdagradOptimizer(learning_rate=0.1)
train_op = optimizer.minimize(loss, global_step=tf.train.get_global_step())
return tf.estimator.EstimatorSpec(mode, loss=loss, train_op=train_op)
```
### Train and Evaluate
```
outdir = 'content_based_model_trained'
shutil.rmtree(outdir, ignore_errors = True) # start fresh each time
tf.summary.FileWriterCache.clear() # ensure filewriter cache is clear for TensorBoard events file
estimator = tf.estimator.Estimator(
model_fn=model_fn,
model_dir = outdir,
params={
'feature_columns': feature_columns,
'hidden_units': [200, 100, 50],
'n_classes': len(content_ids_list)
})
train_spec = tf.estimator.TrainSpec(
input_fn = read_dataset("training_set.csv", tf.estimator.ModeKeys.TRAIN),
max_steps = 2000)
eval_spec = tf.estimator.EvalSpec(
input_fn = read_dataset("test_set.csv", tf.estimator.ModeKeys.EVAL),
steps = None,
start_delay_secs = 30,
throttle_secs = 60)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
```
This takes a while to complete but in the end, I get about **30% top 10 accuracy**.
### Make predictions with the trained model.
With the model now trained, we can make predictions by calling the predict method on the estimator. Let's look at how our model predicts on the first five examples of the training set.
To start, we'll create a new file 'first_5.csv' which contains the first five elements of our training set. We'll also save the target values to a file 'first_5_content_ids' so we can compare our results.
```
%%bash
head -5 training_set.csv > first_5.csv
head first_5.csv
awk -F "\"*,\"*" '{print $2}' first_5.csv > first_5_content_ids
```
Recall, to make predictions on the trained model we pass a list of examples through the input function. Complete the code below to make predicitons on the examples contained in the "first_5.csv" file we created above.
```
output = list(estimator.predict(input_fn=read_dataset("first_5.csv", tf.estimator.ModeKeys.PREDICT)))
import numpy as np
recommended_content_ids = [np.asscalar(d["class_names"]).decode('UTF-8') for d in output]
content_ids = open("first_5_content_ids").read().splitlines()
```
Finally, we map the content id back to the article title. Let's compare our model's recommendation for the first example. This can be done in BigQuery. Look through the query below and make sure it is clear what is being returned.
```
import google.datalab.bigquery as bq
recommended_title_sql="""
#standardSQL
SELECT
(SELECT MAX(IF(index=6, value, NULL)) FROM UNNEST(hits.customDimensions)) AS title
FROM `cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
AND (SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) = \"{}\"
LIMIT 1""".format(recommended_content_ids[0])
current_title_sql="""
#standardSQL
SELECT
(SELECT MAX(IF(index=6, value, NULL)) FROM UNNEST(hits.customDimensions)) AS title
FROM `cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
AND (SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) = \"{}\"
LIMIT 1""".format(content_ids[0])
recommended_title = bq.Query(recommended_title_sql).execute().result().to_dataframe()['title'].tolist()[0]
current_title = bq.Query(current_title_sql).execute().result().to_dataframe()['title'].tolist()[0]
print("Current title: {} ".format(current_title))
print("Recommended title: {}".format(recommended_title))
```
### Tensorboard
As usual, we can monitor the performance of our training job using Tensorboard.
```
from google.datalab.ml import TensorBoard
TensorBoard().start('content_based_model_trained')
for pid in TensorBoard.list()['pid']:
TensorBoard().stop(pid)
print("Stopped TensorBoard with pid {}".format(pid))
```
| true |
code
| 0.658637 | null | null | null | null |
|
# Uncertainty Sampling on the Radio Galaxy Zoo
```
import sys
import h5py, numpy, sklearn.neighbors
from astropy.coordinates import SkyCoord
import matplotlib.pyplot as plt
sys.path.insert(1, '..')
import crowdastro.train, crowdastro.test
TRAINING_H5_PATH = '../training.h5'
CROWDASTRO_H5_PATH = '../crowdastro.h5'
NORRIS_DAT_PATH = '../data/norris_2006_atlas_classifications_ra_dec_only.dat'
CLASSIFIER_OUT_PATH = '../classifier.pkl'
ASTRO_TRANSFORMER_OUT_PATH = '../astro_transformer.pkl'
IMAGE_TRANSFORMER_OUT_PATH = '../image_transformer.pkl'
IMAGE_SIZE = 200 * 200
ARCMIN = 1 / 60
N_JOBS = 8
%matplotlib inline
# Load labels.
with h5py.File(TRAINING_H5_PATH, 'r') as training_h5:
crowdsourced_labels = training_h5['labels'].value
with h5py.File(CROWDASTRO_H5_PATH, 'r') as crowdastro_h5:
ir_names = crowdastro_h5['/wise/cdfs/string'].value
ir_positions = crowdastro_h5['/wise/cdfs/numeric'].value[:, :2]
ir_tree = sklearn.neighbors.KDTree(ir_positions)
with open(NORRIS_DAT_PATH, 'r') as norris_dat:
norris_coords = [r.strip().split('|') for r in norris_dat]
norris_labels = numpy.zeros((len(ir_positions)))
for ra, dec in norris_coords:
# Find a neighbour.
skycoord = SkyCoord(ra=ra, dec=dec, unit=('hourangle', 'deg'))
ra = skycoord.ra.degree
dec = skycoord.dec.degree
((dist,),), ((ir,),) = ir_tree.query([(ra, dec)])
if dist < 0.1:
norris_labels[ir] = 1
def softmax(x):
exp = numpy.exp(x - numpy.max(x))
out = exp / exp.sum()
return out
def train_and_test(hidden_atlas_training_indices):
"""
hidden_atlas_training_indices: ATLAS indices to hide.
"""
with h5py.File(TRAINING_H5_PATH, 'r') as training_h5, h5py.File(CROWDASTRO_H5_PATH, 'r') as crowdastro_h5:
n_static = 5 if training_h5.attrs['ir_survey'] == 'wise' else 6
train_indices = training_h5['is_ir_train'].value
atlas_train_indices = training_h5['is_atlas_train'].value
# Remove all IR objects near hidden ATLAS objects.
for atlas_index in hidden_atlas_training_indices:
ir = crowdastro_h5['/atlas/cdfs/numeric'][atlas_index, n_static + IMAGE_SIZE:]
nearby = (ir < ARCMIN).nonzero()[0]
for ir_index in nearby:
train_indices[ir_index] = 0
n_ir = train_indices.sum()
# We can now proceed as usual with training/testing.
outputs = training_h5['labels'].value[train_indices]
n = len(outputs)
astro_inputs = numpy.minimum(
training_h5['features'][train_indices, :n_static], 1500)
image_inputs = training_h5['features'].value[train_indices, n_static:]
astro_transformer = sklearn.pipeline.Pipeline([
('normalise', sklearn.preprocessing.Normalizer()),
('scale', sklearn.preprocessing.StandardScaler()),
])
image_transformer = sklearn.pipeline.Pipeline([
('normalise', sklearn.preprocessing.Normalizer()),
])
features = []
features.append(astro_transformer.fit_transform(astro_inputs))
features.append(image_transformer.fit_transform(image_inputs))
inputs = numpy.hstack(features)
classifier = sklearn.linear_model.LogisticRegression(
class_weight='balanced', n_jobs=N_JOBS)
classifier.fit(inputs, outputs)
# Test the classifier.
test_indices = training_h5['is_atlas_test'].value
numeric_subjects = crowdastro_h5['/atlas/cdfs/numeric'][test_indices, :]
n_norris_agree = 0
n_crowdsourced_agree = 0
n_all_agree = 0
n_either_agree = 0
n_no_host = 0
n_total = 0
for subject in numeric_subjects:
swire = subject[2 + IMAGE_SIZE:]
nearby = swire < ARCMIN
astro_inputs = numpy.minimum(training_h5['features'][nearby, :n_static],
1500)
image_inputs = training_h5['features'][nearby, n_static:]
features = []
features.append(astro_transformer.transform(astro_inputs))
features.append(image_transformer.transform(image_inputs))
inputs = numpy.hstack(features)
crowdsourced_outputs = crowdsourced_labels[nearby]
norris_outputs = norris_labels[nearby]
if sum(crowdsourced_outputs) < 1 or sum(norris_outputs) < 1:
# No hosts!
n_no_host += 1
continue
selection = classifier.predict_proba(inputs)[:, 1].argmax()
n_norris_agree += norris_outputs[selection]
n_crowdsourced_agree += crowdsourced_outputs[selection]
n_all_agree += norris_outputs[selection] * crowdsourced_outputs[selection]
n_either_agree += norris_outputs[selection] or crowdsourced_outputs[selection]
n_total += 1
# Compute the uncertainties of the pool.
pool_indices = training_h5['is_atlas_train'].value
numeric_subjects = crowdastro_h5['/atlas/cdfs/numeric'][pool_indices, :]
uncertainties = []
for subject in numeric_subjects:
swire = subject[2 + IMAGE_SIZE:]
nearby = swire < ARCMIN
astro_inputs = numpy.minimum(training_h5['features'][nearby, :n_static],
1500)
image_inputs = training_h5['features'][nearby, n_static:]
features = []
features.append(astro_transformer.transform(astro_inputs))
features.append(image_transformer.transform(image_inputs))
inputs = numpy.hstack(features)
probs = softmax(classifier.predict_proba(inputs)[:, 1])
entropy = -numpy.sum(numpy.log(probs) * probs)
uncertainties.append(entropy)
return (n_norris_agree / n_total, n_crowdsourced_agree / n_total,
n_all_agree / n_total, n_either_agree / n_total, uncertainties, n_ir)
# Randomly hide 90% of labels.
with h5py.File(TRAINING_H5_PATH, 'r') as training_h5:
atlas_train_indices = training_h5['is_atlas_train'].value
initial_hidden_atlas_training_indices = numpy.arange(atlas_train_indices.sum())
numpy.random.shuffle(initial_hidden_atlas_training_indices)
initial_hidden_atlas_training_indices = initial_hidden_atlas_training_indices[
:9 * len(initial_hidden_atlas_training_indices) // 10]
initial_hidden_atlas_training_indices.sort()
# Testing random label selection.
norris_accuracies_random = []
rgz_accuracies_random = []
all_accuracies_random = []
any_accuracies_random = []
n_ir_random = []
n_batch = 100
n_epochs = 25
numpy.random.seed(0)
hidden_atlas_training_indices = initial_hidden_atlas_training_indices[:]
for epoch in range(n_epochs):
print('Epoch {}/{}'.format(epoch + 1, n_epochs))
# Train, test, and generate uncertainties.
results = train_and_test(hidden_atlas_training_indices)
norris_accuracies_random.append(results[0])
rgz_accuracies_random.append(results[1])
all_accuracies_random.append(results[2])
any_accuracies_random.append(results[3])
n_ir_random.append(results[5])
# Choose n_batch new labels at random.
if len(hidden_atlas_training_indices) < n_batch:
break
else:
numpy.random.shuffle(hidden_atlas_training_indices)
hidden_atlas_training_indices = hidden_atlas_training_indices[:-n_batch]
hidden_atlas_training_indices.sort()
# Testing uncertainty sampling label selection.
norris_accuracies_uncsample = []
rgz_accuracies_uncsample = []
all_accuracies_uncsample = []
any_accuracies_uncsample = []
n_ir_uncsample = []
hidden_atlas_training_indices = initial_hidden_atlas_training_indices[:]
for epoch in range(n_epochs):
print('Epoch {}/{}'.format(epoch + 1, n_epochs))
# Train, test, and generate uncertainties.
results = train_and_test(hidden_atlas_training_indices)
uncertainties = results[4]
norris_accuracies_uncsample.append(results[0])
rgz_accuracies_uncsample.append(results[1])
all_accuracies_uncsample.append(results[2])
any_accuracies_uncsample.append(results[3])
n_ir_uncsample.append(results[5])
# Choose the n_batch most uncertain objects to label.
if len(hidden_atlas_training_indices) < n_batch:
break
else:
hidden_atlas_training_indices = numpy.array(
sorted(hidden_atlas_training_indices, key=lambda z: uncertainties[z]))[:-n_batch]
hidden_atlas_training_indices.sort()
plt.figure(figsize=(15, 10))
plt.subplot(2, 2, 1)
plt.plot(all_accuracies_random, c='pink')
plt.plot(any_accuracies_random, c='darkred')
plt.plot(all_accuracies_uncsample, c='lightgreen')
plt.plot(any_accuracies_uncsample, c='darkgreen')
plt.xlabel('{}-batch epochs'.format(n_batch))
plt.ylabel('Classification accuracy')
plt.legend(['Norris & RGZ (passive)', 'Norris | RGZ (passive)',
'Norris & RGZ (unc)', 'Norris | RGZ (unc)'], loc='lower right')
plt.subplot(2, 2, 2)
plt.plot(norris_accuracies_random, c='red')
plt.plot(norris_accuracies_uncsample, c='green')
plt.legend(['Norris (passive)', 'Norris (unc)'], loc='lower right')
plt.xlabel('{}-batch epochs'.format(n_batch))
plt.ylabel('Classification accuracy')
plt.subplot(2, 2, 3)
plt.plot(rgz_accuracies_random, c='red')
plt.plot(rgz_accuracies_uncsample, c='green')
plt.legend(['RGZ (passive)', 'RGZ (unc)'], loc='lower right')
plt.xlabel('{}-batch epochs'.format(n_batch))
plt.ylabel('Classification accuracy')
plt.subplot(2, 2, 4)
plt.plot(numpy.array(n_ir_random) - numpy.array(n_ir_uncsample))
plt.xlabel('{}-batch epochs'.format(n_batch))
plt.ylabel('Difference in number of IR examples')
plt.show()
```
Conclusion: Uncertainty sampling with entropy doesn't work very well.
| true |
code
| 0.589775 | null | null | null | null |
|
# Assignment 1: Numpy RNN
Implement a RNN and run BPTT
```
from typing import Dict, Tuple
import numpy as np
class RNN(object):
"""Numpy implementation of sequence-to-one recurrent neural network for regression tasks."""
def __init__(self, input_size: int, hidden_size: int, output_size: int):
"""Initialization
Parameters
----------
input_size : int
Number of input features per time step
hidden_size : int
Number of hidden units in the RNN
output_size : int
Number of output units.
"""
super(RNN, self).__init__()
self.input_size = input_size # D in literature
self.hidden_size = hidden_size # I in literature
self.output_size = output_size # K in literature
# create and initialize weights of the network
# as 90% of the usages in the scriptum are W.T, R.T, V.T
init = lambda shape: np.random.uniform(-0.2, 0.2, shape)
self.W = init((hidden_size, input_size)) # I X D
self.R = init((hidden_size, hidden_size)) # I x I
self.bs = np.zeros((hidden_size))
self.V = init((output_size, hidden_size)) # K x I
self.by = np.zeros((output_size))
# place holder to store intermediates for backprop
self.a = None
self.y_hat = None
self.grads = None
self.x = None
def forward(self, x: np.ndarray) -> np.ndarray:
"""Forward pass through the RNN.
Parameters
----------
x : np.ndarray
Input sequence(s) of shape [sequence length, number of features]
Returns
-------
NumPy array containing the network prediction for the input sample.
"""
self.x = x
# as we have no activation function (f(t) is linear)
# a(t) = f(s(t)) = s(t) = W^T . x(t) + R^T . a(t-1) + bs
# = tanh( W^T . x(t) + R^T . a(t-1) + bs )
self.a = np.zeros((self.input_size, self.hidden_size)) # to make accessing t = -1 possible
for t in range(len(x)):
self.a[t] = np.tanh(self.W @ x[t] + self.R @ self.a[t-1] + self.bs)
self.y_hat = self.V @ self.a[t] + self.by
return self.y_hat # sequence-to-1 model, so we only return the last
def forward_fast(self, x: np.ndarray) -> np.ndarray:
""" optimized method without saving to self.a """
a = np.tanh(self.W @ x[0] + self.bs)
for t in range(1, len(x)):
a = np.tanh(self.W @ x[t] + self.R @ a + self.bs)
return self.V @ a + self.by
def backward(self, d_loss: np.ndarray) -> Dict:
"""Calculate the backward pass through the RNN.
Parameters
----------
d_loss : np.ndarray
The gradient of the loss w.r.t the network output in the shape [output_size,]
Returns
-------
Dictionary containing the gradients for each network weight as key-value pair.
"""
# create view, so that we don't have to reshape every time we call it
a = self.a.reshape(self.a.shape[0], 1, self.a.shape[1])
x = self.x.reshape(self.x.shape[0], 1, self.x.shape[1])
# needs to be calculated only once
d_V = d_loss @ a[-1]
d_by = d_loss
# init with 0 and sum it up
d_W = np.zeros_like(self.W)
d_R = np.zeros_like(self.R)
d_bs = np.zeros_like(self.bs)
# instead of using * diag, we use elementwise multiplication
delta = d_loss.T @ self.V * (1 - a[-1] ** 2)
for t in reversed(range(self.input_size)):
d_bs += delta.reshape(self.bs.shape)
d_W += delta.T @ x[t]
if t > 0:
d_R += delta.T @ a[t-1]
# a[t] = tanh(..) -> derivation = 1-tanh² -> reuse already calculated tanh
# calculate delta for the next step at t-1
delta = delta @ self.R * (1 - a[t-1] ** 2)
self.grads = {'W': d_W, 'R': d_R, 'V': d_V, 'bs': d_bs, 'by': d_by}
return self.grads
def update(self, lr: float):
# update weights, aggregation is already done in backward
w = self.get_weights()
for name in w.keys():
w[name] -= lr * self.grads[name]
# reset internal class attributes
self.grads = {}
self.y_hat, self.a = None, None
def get_weights(self) -> Dict:
return {'W': self.W, 'R': self.R, 'V': self.V, 'bs': self.bs, 'by': self.by}
def set_weights(self, weights: Dict):
if not all(name in weights.keys() for name in ['W', 'R', 'V']):
raise ValueError("Missing one of 'W', 'R', 'V' keys in the weight dictionary")
for name, w in weights.items():
self.__dir__["name"] = w
```
<h2 style="color:rgb(0,120,170)">Numerical gradient check</h2>
To validate your implementation, especially the backward pass, use the two-sided gradient approximation given by the equation below.
```
def get_numerical_gradient(model: RNN, x: np.ndarray, eps: float=1e-7) -> Dict:
"""Implementation of the two-sided numerical gradient approximation
Parameters
----------
model : RNN
The RNN model object
x : np.ndarray
Input sequence(s) of shape [sequence length, number of features]
eps : float
The epsilon used for numerical gradient approximation
Returns
-------
A dictionary containing the numerical gradients for each weight of the RNN. Make sure
to name the dictionary keys like the names of the RNN gradients dictionary (e.g.
'd_R' for the weight 'R')
"""
g = {}
# iterate all weight-matrices w and all positions i, and calculate the num. grad.
for name, w in model.get_weights().items():
# initialize weight gradients with zero
wg = np.zeros_like(w)
# this makes a backup copy of original weights
for i, orig in np.ndenumerate(w): # can be 1d or 2d
# caculate for +eps
w[i] += eps
plus = model.forward_fast(x)
# calculate for -eps
w[i] = orig - eps
minus = model.forward_fast(x)
w[i] = orig # reset
# set weight gradient for this weight and this index
wg[i] = np.sum(plus - minus) / (2*eps)
# add calculated weights into return-weights
g[name] = wg
return g
def get_analytical_gradient(model: RNN, x: np.ndarray) -> Dict:
"""Helper function to get the analytical gradient.
Parameters
----------
model : RNN
The RNN model object
x : np.ndarray
Input sequence(s) of shape [sequence length, number of features]
Returns
-------
A dictionary containing the analytical gradients for each weight of the RNN.
"""
loss = model.forward(x)
return model.backward(np.ones((model.output_size, 1)))
def gradient_check(model: RNN, x: np.ndarray, treshold: float = 1e-7):
"""Perform gradient checking.
You don't have to do anything in this function.
Parameters
----------
model : RNN
The RNN model object
x : np.ndarray
Input sequence(s) of shape [sequence length, number of features]
eps : float
The epsilon used for numerical gradient approximation
"""
numerical_grads = get_numerical_gradient(model, x)
analytical_grads = get_analytical_gradient(model, x)
for key, num_grad in numerical_grads.items():
difference = np.linalg.norm(num_grad - analytical_grads[key])
# assert num_grad.shape == analytical_grads[key].shape
if difference < treshold:
print(f"Gradient check for {key} passed (difference {difference:.3e})")
else:
print(f"Gradient check for {key} failed (difference {difference:.3e})")
```
<h2 style="color:rgb(0,120,170)">Compare the time for gradient computation</h2>
Finally, use the code below to investigate the benefit of being able to calculate the exact analytical gradient.
```
print("Gradient check with a single output neuron:")
model = RNN(input_size=5, hidden_size=10, output_size=1)
x = np.random.rand(5, 5)
gradient_check(model, x)
print("\nGradient check with multiple output neurons:")
model = RNN(input_size=5, hidden_size=10, output_size=5)
x = np.random.rand(5, 5)
gradient_check(model, x)
analytical_time = %timeit -o get_analytical_gradient(model, x)
numerical_time = %timeit -o get_numerical_gradient(model, x)
if analytical_time.average < numerical_time.average:
fraction = numerical_time.average / analytical_time.average
print(f"The analytical gradient computation was {fraction:.0f} times faster")
else:
fraction = analytical_time.average / numerical_time.average
print(f"The numerical gradient computation was {fraction:.0f} times faster")
```
| true |
code
| 0.952086 | null | null | null | null |
|
# Predicting Credit Card Default with Neural Networks
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
%matplotlib inline
```
### Back with the credit card default dataset
```
# Loading the dataset
DATA_DIR = '../data'
FILE_NAME = 'credit_card_default.csv'
data_path = os.path.join(DATA_DIR, FILE_NAME)
ccd = pd.read_csv(data_path, index_col="ID")
ccd.rename(columns=lambda x: x.lower(), inplace=True)
ccd.rename(columns={'default payment next month':'default'}, inplace=True)
# getting the groups of features
bill_amt_features = ['bill_amt'+ str(i) for i in range(1,7)]
pay_amt_features = ['pay_amt'+ str(i) for i in range(1,7)]
numerical_features = ['limit_bal','age'] + bill_amt_features + pay_amt_features
# Creating creating binary features
ccd['male'] = (ccd['sex'] == 1).astype('int')
ccd['grad_school'] = (ccd['education'] == 1).astype('int')
ccd['university'] = (ccd['education'] == 2).astype('int')
#ccd['high_school'] = (ccd['education'] == 3).astype('int')
ccd['married'] = (ccd['marriage'] == 1).astype('int')
# simplifying pay features
pay_features= ['pay_' + str(i) for i in range(1,7)]
for x in pay_features:
ccd.loc[ccd[x] <= 0, x] = 0
# simplifying delayed features
delayed_features = ['delayed_' + str(i) for i in range(1,7)]
for pay, delayed in zip(pay_features, delayed_features):
ccd[delayed] = (ccd[pay] > 0).astype(int)
# creating a new feature: months delayed
ccd['months_delayed'] = ccd[delayed_features].sum(axis=1)
```
## Split and standarize the dataset
```
numerical_features = numerical_features + ['months_delayed']
binary_features = ['male','married','grad_school','university']
X = ccd[numerical_features + binary_features]
y = ccd['default'].astype(int)
## Split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=5/30, random_state=101)
## Standarize
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train[numerical_features])
X_train.loc[:, numerical_features] = scaler.transform(X_train[numerical_features])
# Standarize also the testing set
X_test.loc[:, numerical_features] = scaler.transform(X_test[numerical_features])
```
### Building the neural network for classification
```
from keras.models import Sequential
nn_classifier = Sequential()
from keras.layers import Dense
n_input = X_train.shape[1]
n_units_hidden = 64
nn_classifier.add(Dense(units=n_units_hidden, activation='relu', input_shape=(n_input,)))
# add 2nd hidden layer
nn_classifier.add(Dense(units=n_units_hidden, activation='relu'))
# add 3th hidden layer
nn_classifier.add(Dense(units=n_units_hidden, activation='relu'))
# add 4th hidden layer
nn_classifier.add(Dense(units=n_units_hidden, activation='relu'))
# add 5th hidden layer
nn_classifier.add(Dense(units=n_units_hidden, activation='relu'))
# output layer
nn_classifier.add(Dense(1, activation='sigmoid'))
```
### Training the network
```
## compiling step
nn_classifier.compile(loss='binary_crossentropy', optimizer='adam')
nn_classifier.summary()
nn_classifier.save_weights('class_initial_w.h5')
batch_size = 64
n_epochs = 150
nn_classifier.fit(X_train, y_train, epochs=n_epochs, batch_size=batch_size)
```
## Evaluating predictions
```
## Getting the probabilities
y_pred_train_prob = nn_classifier.predict(X_train)
y_pred_test_prob = nn_classifier.predict(X_test)
## Classifications from predictions
y_pred_train = (y_pred_train_prob > 0.5).astype(int)
y_pred_test = (y_pred_test_prob > 0.5).astype(int)
from sklearn.metrics import accuracy_score
train_acc = accuracy_score(y_true=y_train, y_pred=y_pred_train)
test_acc = accuracy_score(y_true=y_test, y_pred=y_pred_test)
print("Train Accuracy: {:0.3f} \nTest Accuracy: {:0.3f}".format(train_acc, test_acc))
```
## Re-training the network with less epochs
```
## load the initial weights
nn_classifier.load_weights('class_initial_w.h5')
batch_size = 64
n_epochs = 50
nn_classifier.compile(loss='binary_crossentropy', optimizer='adam')
nn_classifier.fit(X_train, y_train, epochs=n_epochs, batch_size=batch_size)
## Getting the probabilities
y_pred_train_prob = nn_classifier.predict(X_train)
y_pred_test_prob = nn_classifier.predict(X_test)
## Classifications from predictions
y_pred_train = (y_pred_train_prob > 0.5).astype(int)
y_pred_test = (y_pred_test_prob > 0.5).astype(int)
## Calculating accuracy
train_acc = accuracy_score(y_true=y_train, y_pred=y_pred_train)
test_acc = accuracy_score(y_true=y_test, y_pred=y_pred_test)
print("Train Accuracy: {:0.3f} \nTest Accuracy: {:0.3f}".format(train_acc, test_acc))
```
| true |
code
| 0.614712 | null | null | null | null |
|
## Model one policy variables
This notebook extracts the selected policy variables in the `indicator_list` from IMF and World Bank (wb) data sources, and writes them to a csv file.
```
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
warnings.filterwarnings('ignore')
pd.options.display.float_format = '{:20,.2f}'.format
```
| variable | origin | source |granularity|countries| description | composition |
| --------------------------|-------------------|-------------|-----------|---------|-------------------------------------------------------------|-------------------------------------------------------------------|
| total debt service | - | wb econ | yearly | 217 | Total debt service (% of GNI) | - |
| interest payments | - | wb econ | yearly | 217 | Interest payments on external debt (% of GNI) | - |
| lending interest rate | - | wb econ | yearly | 217 | Lending interest rate (%) | - |
| firms using banks | - | wb econ | yearly | 217 | Firms using banks to finance investment (% of firms) | - |
| bank capital ratio | - | wb econ | yearly | 217 | Bank capital to assets ratio (%) | - |
| tax revenue gdp share | - | wb econ | yearly | 217 | Tax revenue (% of GDP) | - |
| short term debt | - | wb econ | yearly | 217 | Short-term debt (% of total external debt) | - |
| inflation | - | wb econ | yearly | 217 | Inflation, GDP deflator (annual %) | - |
| GDP growth | - | wb econ | yearly | 217 | GDP growth (annual %) | - |
| real interest rate | - | wb econ | yearly | 217 | Real interest rate (%) | - |
| firm market cap | - | wb econ | yearly | 217 | Market capitalization of listed domestic companies (% of GDP) | - |
| GDP per capita growth | - | wb econ | yearly | 217 | GDP per capita growth (annual %) | - |
| GDP | - | wb econ | yearly | 217 | GDP (constant 2010 USD) | - |
| GNI growth | - | wb econ | yearly | 217 | GNI growth (annual %) | - |
| interest payments | - | wb econ | yearly | 217 | Interest payments (% of expense) | - |
| nonperforming bank loans | - | wb econ | yearly | 217 | Bank nonperforming loans to total gross loans (%) | - |
| savings | - | wb econ | yearly | 217 | Gross domestic savings (% of GDP) | - |
| gross savings | - | wb econ | yearly | 217 | Gross savings (% of GNI) | - |
| GNI per capita growth | - | wb econ | yearly | 217 | GNI per capita growth (annual %) | - |
| employee compensation | - | wb econ | yearly | 217 | Compensation of employees (% of expense) | - |
| reserves | - | wb econ | yearly | 217 | Total reserves (% of total external debt) | - |
| broad money | - | wb econ | yearly | 217 | Broad money (% of GDP) | - |
| GNI | - | wb econ | yearly | 217 | GNI (constant 2010 USD) | - |
| government debt | - | wb econ | yearly | 217 | Central government debt, total (% of GDP) | - |
```
indicator_list = ['Total debt service (% of GNI)', 'Interest payments on external debt (% of GNI)',
'Lending interest rate (%)', 'Firms using banks to finance investment (% of firms)',
'Bank capital to assets ratio (%)', 'Tax revenue (% of GDP)', 'Short-term debt (% of total external debt)',
'Inflation, GDP deflator (annual %)', 'GDP growth (annual %)', 'Real interest rate (%)',
'Market capitalization of listed domestic companies (% of GDP)', 'GDP per capita growth (annual %)',
'GDP (constant 2010 US$)', 'GNI growth (annual %)', 'Interest payments (% of expense)',
'Bank nonperforming loans to total gross loans (%)', 'Gross domestic savings (% of GDP)',
'Gross savings (% of GNI)', 'GNI per capita growth (annual %)', 'Compensation of employees (% of expense)',
'Total reserves (% of total external debt)', 'Broad money (% of GDP)', 'GNI (constant 2010 US$)',
'Central government debt, total (% of GDP)']
len(indicator_list)
```
## Load imf monthly data
```
%%bash
wc -l imf/*.csv
time_values = [str('%sM%s' % (y, m)) for m in list(range(1, 13)) for y in list(range(1960, 2018))]
imf_columns = ['Country Name', 'Indicator Name'] + time_values
imf_country_aggregates = ['Euro Area']
def load_imf_monthly(file_name, indicators, imf_columns, country_aggregates):
csv_df = pd.read_csv('data/imf/%s' % file_name).fillna(0)
base_df = csv_df.loc[csv_df['Attribute'] == 'Value'].drop(columns=['Attribute'])
monthly_df = base_df.loc[(base_df['Indicator Name'].isin(indicators))]
imf_df = monthly_df[imf_columns].fillna(0)
df = pd.melt(imf_df, id_vars=['Country Name', 'Indicator Name'], var_name='date', value_name='value')
df['date'] = pd.to_datetime(df['date'], format='%YM%m')
df.columns = ['country', 'indicator', 'date', 'value']
return df.loc[~df['country'].isin(country_aggregates)]
imf_pplt_df = load_imf_monthly('PPLT_11-25-2018 19-25-01-32_timeSeries.csv', indicator_list, imf_columns, imf_country_aggregates)
imf_cpi_df = load_imf_monthly('CPI_11-25-2018 19-14-47-26_timeSeries.csv', indicator_list, imf_columns, imf_country_aggregates)
imf_df = pd.concat([imf_cpi_df, imf_pplt_df], join='outer')
imf_df.size
imf_df.head(15)
len(imf_df['country'].unique())
imf_countries = sorted(list(imf_df['country'].unique()))
```
### Load world bank yearly data
```
%%bash
wc -l world_bank/*.csv
wb_country_aggregates = ['nan', 'Lower middle income', 'Post-demographic dividend', 'High income',
'Pre-demographic dividend', 'East Asia & Pacific (IDA & IBRD countries)',
'Europe & Central Asia (excluding high income)', 'Heavily indebted poor countries (HIPC)',
'Caribbean small states', 'Pacific island small states', 'Middle income',
'Late-demographic dividend', 'OECD members', 'IDA & IBRD total', 'Not classified',
'East Asia & Pacific (excluding high income)',
'Latin America & the Caribbean (IDA & IBRD countries)', 'Low income', 'Low & middle income',
'IDA blend', 'IBRD only', 'Sub-Saharan Africa (excluding high income)',
'Fragile and conflict affected situations', 'Europe & Central Asia (IDA & IBRD countries)',
'Euro area', 'Other small states', 'Europe & Central Asia', 'Arab World',
'Latin America & Caribbean (excluding high income)',
'Sub-Saharan Africa (IDA & IBRD countries)', 'Early-demographic dividend', 'IDA only',
'Small states', 'Middle East & North Africa (excluding high income)', 'East Asia & Pacific',
'South Asia', 'European Union', 'Least developed countries: UN classification',
'Middle East & North Africa (IDA & IBRD countries)', 'Upper middle income',
'South Asia (IDA & IBRD)', 'Central Europe and the Baltics', 'Sub-Saharan Africa',
'Latin America & Caribbean', 'Middle East & North Africa', 'IDA total', 'North America',
'Last Updated: 11/14/2018', 'Data from database: World Development Indicators', 'World']
wb_cols = ['Country Name', 'Series Name'] + [str('%s [YR%s]' % (y, y)) for y in list(range(1960, 2018))]
def load_wb_yearly(file_name, indicators, wb_columns, country_aggregates):
csv_df = pd.read_csv('world_bank/%s' % file_name).fillna(0)
base_df = csv_df.loc[(csv_df['Series Name'].isin(indicators))]
wb_df = base_df[wb_columns].fillna(0)
df = pd.melt(wb_df, id_vars=['Country Name', 'Series Name'], var_name='date', value_name='value')
df['date'] = pd.to_datetime(df['date'].map(lambda x: int(x.split(' ')[0])), format='%Y')
df.columns = ['country', 'indicator', 'date', 'value']
return df.loc[~df['country'].isin(country_aggregates)]
wb_econ_df = load_wb_yearly('ECON.csv', indicator_list, wb_cols, wb_country_aggregates)
wb_hnp_df = load_wb_yearly('HNP.csv', indicator_list, wb_cols, wb_country_aggregates)
wb_pop_df = load_wb_yearly('POP.csv', indicator_list, wb_cols, wb_country_aggregates)
wb_df = pd.concat([wb_econ_df, wb_hnp_df, wb_pop_df], join='outer')
wb_df.size
wb_df.head(15)
len(wb_df['country'].unique())
wb_countries = sorted(list(wb_df['country'].unique()))
```
### Combine the two datasets
```
imf_specific = [country for country in imf_countries if country not in wb_countries]
len(imf_specific)
imf_to_wb_country_map = {
'Afghanistan, Islamic Republic of': 'Afghanistan',
'Armenia, Republic of': 'Armenia',
'Azerbaijan, Republic of': 'Azerbaijan',
'Bahrain, Kingdom of': 'Bahrain',
'China, P.R.: Hong Kong': 'Hong Kong SAR, China',
'China, P.R.: Macao': 'Macao SAR, China',
'China, P.R.: Mainland': 'China',
'Congo, Democratic Republic of': 'Congo, Dem. Rep.',
'Congo, Republic of': 'Congo, Rep.',
'Egypt': 'Egypt, Arab Rep.',
'French Territories: New Caledonia': 'New Caledonia',
'Iran, Islamic Republic of': 'Iran',
'Korea, Republic of': 'Korea, Rep.',
'Kosovo, Republic of': 'Kosovo',
"Lao People's Democratic Republic": 'Lao PDR',
'Serbia, Republic of': 'Serbia',
'Sint Maarten': 'Sint Maarten (Dutch part)',
'Timor-Leste, Dem. Rep. of': 'Timor-Leste',
'Venezuela, Republica Bolivariana de': 'Venezuela, RB',
'Venezuela, República Bolivariana de': 'Venezuela, RB',
'Yemen, Republic of': 'Yemen'
}
imf_df = imf_df.replace({'country': imf_to_wb_country_map})
policy_df = pd.concat([wb_df, imf_df], join='outer')
policy_df.size
policy_df.head(15)
indicators = sorted(list(policy_df['indicator'].unique()))
assert len(indicators) == len(indicator_list), 'The number of retrieved variables (%s) does not match the number of specified variables (%s).\nThe following variables are missing:\n\n %s' % (len(indicators), len(indicator_list), [i for i in indicator_list if i not in indicators])
policy_df.to_csv('model_one/policy.csv', sep=';', index=False)
```
| true |
code
| 0.319662 | null | null | null | null |
|
# Testing `TFNoiseAwareModel`
We'll start by testing the `textRNN` model on a categorical problem from `tutorials/crowdsourcing`. In particular we'll test for (a) basic performance and (b) proper construction / re-construction of the TF computation graph both after (i) repeated notebook calls, and (ii) with `GridSearch` in particular.
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import os
os.environ['SNORKELDB'] = 'sqlite:///{0}{1}crowdsourcing.db'.format(os.getcwd(), os.sep)
from snorkel import SnorkelSession
session = SnorkelSession()
```
### Load candidates and training marginals
```
from snorkel.models import candidate_subclass
from snorkel.contrib.models.text import RawText
Tweet = candidate_subclass('Tweet', ['tweet'], cardinality=5)
train_tweets = session.query(Tweet).filter(Tweet.split == 0).order_by(Tweet.id).all()
len(train_tweets)
from snorkel.annotations import load_marginals
train_marginals = load_marginals(session, train_tweets, split=0)
train_marginals.shape
```
### Train `LogisticRegression`
```
# Simple unigram featurizer
def get_unigram_tweet_features(c):
for w in c.tweet.text.split():
yield w, 1
# Construct feature matrix
from snorkel.annotations import FeatureAnnotator
featurizer = FeatureAnnotator(f=get_unigram_tweet_features)
%time F_train = featurizer.apply(split=0)
F_train
%time F_test = featurizer.apply_existing(split=1)
F_test
from snorkel.learning.tensorflow import LogisticRegression
model = LogisticRegression(cardinality=Tweet.cardinality)
model.train(F_train.todense(), train_marginals)
```
### Train `SparseLogisticRegression`
Note: Testing doesn't currently work with `LogisticRegression` above, but no real reason to use that over this...
```
from snorkel.learning.tensorflow import SparseLogisticRegression
model = SparseLogisticRegression(cardinality=Tweet.cardinality)
model.train(F_train, train_marginals, n_epochs=50, print_freq=10)
import numpy as np
test_labels = np.load('crowdsourcing_test_labels.npy')
acc = model.score(F_test, test_labels)
print(acc)
assert acc > 0.6
# Test with batch size s.t. N % batch_size == 1...
model.score(F_test, test_labels, batch_size=9)
```
### Train basic LSTM
With dev set scoring during execution (note we use test set here to be simple)
```
from snorkel.learning.tensorflow import TextRNN
test_tweets = session.query(Tweet).filter(Tweet.split == 1).order_by(Tweet.id).all()
train_kwargs = {
'dim': 100,
'lr': 0.001,
'n_epochs': 25,
'dropout': 0.2,
'print_freq': 5
}
lstm = TextRNN(seed=123, cardinality=Tweet.cardinality)
lstm.train(train_tweets, train_marginals, X_dev=test_tweets, Y_dev=test_labels, **train_kwargs)
acc = lstm.score(test_tweets, test_labels)
print(acc)
assert acc > 0.60
# Test with batch size s.t. N % batch_size == 1...
lstm.score(test_tweets, test_labels, batch_size=9)
```
### Run `GridSearch`
```
from snorkel.learning.utils import GridSearch
# Searching over learning rate
param_ranges = {'lr': [1e-3, 1e-4], 'dim': [50, 100]}
model_class_params = {'seed' : 123, 'cardinality': Tweet.cardinality}
model_hyperparams = {
'dim': 100,
'n_epochs': 20,
'dropout': 0.1,
'print_freq': 10
}
searcher = GridSearch(TextRNN, param_ranges, train_tweets, train_marginals,
model_class_params=model_class_params,
model_hyperparams=model_hyperparams)
# Use test set here (just for testing)
lstm, run_stats = searcher.fit(test_tweets, test_labels)
acc = lstm.score(test_tweets, test_labels)
print(acc)
assert acc > 0.60
```
### Reload saved model outside of `GridSearch`
```
lstm = TextRNN(seed=123, cardinality=Tweet.cardinality)
lstm.load('TextRNN_best', save_dir='checkpoints/grid_search')
acc = lstm.score(test_tweets, test_labels)
print(acc)
assert acc > 0.60
```
### Reload a model with different structure
```
lstm.load('TextRNN_0', save_dir='checkpoints/grid_search')
acc = lstm.score(test_tweets, test_labels)
print(acc)
assert acc < 0.60
```
# Testing `GenerativeModel`
### Testing `GridSearch` on crowdsourcing data
```
from snorkel.annotations import load_label_matrix
import numpy as np
L_train = load_label_matrix(session, split=0)
train_labels = np.load('crowdsourcing_train_labels.npy')
from snorkel.learning import GenerativeModel
# Searching over learning rate
searcher = GridSearch(GenerativeModel, {'epochs': [0, 10, 30]}, L_train)
# Use training set labels here (just for testing)
gen_model, run_stats = searcher.fit(L_train, train_labels)
acc = gen_model.score(L_train, train_labels)
print(acc)
assert acc > 0.97
```
| true |
code
| 0.55917 | null | null | null | null |
|
```
from scripts.setup_libs import *
```
# [CatBoost](https://github.com/catboost/catboost)
Бустинг от Яндекса для категориальных фичей и много чего еще.
Для начала настоятельно рекомендуется посмотреть видео. Там идет основная теория по CatBoost
```
from IPython.display import YouTubeVideo
YouTubeVideo('UYDwhuyWYSo', width=640, height=360)
```
Резюмируя видео:
Catboost строится на **Obvious Decision Tree** (ODT полное бинарное дерево) - это значит, что на каждом уровне дерева во всех вершинах идет разбиение по одному и тому же признаку. Дерево полное и симметричное. Листов - $2^H$, где $H$ - высота дерева и количество используемых фич.
В Catboost куча фичей для скорости и регуляризации.
Регуляризация (стараемся делать как можно более разные деревья):
* Чтобы базовое дерево было небольшое, обычно берется какая-то часть фич (max_features) например $0.1$ от общего числа. В силу большого количества деревьев в композиции, информация не потеряется.
* При построении дерева можно использовать **бутстреп для выборки**.
* При слитинге в дереве к скору можно добавлять случайную величину.
Скорость:
* Так как мы еще до обучения знаем схему дерева (потому что ODT) - мы знаем количество листьев. Количество разных значений будет равно количеству листьев, поэтому на шаге обучения базового дерева давайте приближать не **полный вектор антиградиентов** (который размера количества фич), а **вектор листов**. В этом случае сильно сокращается время выбора наилучшего сплита на каждом этапе обучения базового дерева.
* Бинаризация численных данных, для ускорения нахождения наилучшего сплита. Слабая - равномерная или медианная. Хорошие **MaxLogSum**, **GreedyLogSum**
* На верхних вершинах дерева делаем только один градиентный шаг, на нижних можно несколько.
* **Ordered boosting**
# [Примеры](https://catboost.ai/docs/concepts/python-usages-examples.html#custom-objective-function) работы с CatBoost
Еще одно очень полезное видео, но теперь уже с практикой.
```
from IPython.display import YouTubeVideo
YouTubeVideo('xl1fwCza9C8', width=640, height=360)
```
## Простой пример
```
train_data = [[1, 4, 5, 6],
[4, 5, 6, 7],
[30, 40, 50, 60]]
eval_data = [[2, 4, 6, 8],
[1, 4, 50, 60]]
train_labels = [10, 20, 30]
# Initialize CatBoostRegressor
model = CatBoostRegressor(iterations=2,
learning_rate=1,
depth=2)
# Fit model
model.fit(train_data, train_labels)
# Get predictions
preds = model.predict(eval_data)
```
## Визуализация
```
rng = np.random.RandomState(31337)
boston = load_boston()
y = boston['target']
X = boston['data']
kf = KFold(n_splits=3, shuffle=True, random_state=rng)
X_train, X_rest, y_train, y_rest = train_test_split(X, y, test_size=0.25)
X_val, X_test, y_val, y_test = train_test_split(X_rest, y_rest, test_size=0.5)
cb = CatBoostRegressor(silent=True, eval_metric="MAE", custom_metric=["MAPE"])
```
Тут включена крутая визуализация, с которой можно поиграться, она не работает в Jupyter Lab, но работает в Jupyter Notebook
```
cb.fit(X_train, y_train, eval_set=[(X_val , y_val ), (X_test, y_test)], plot=True)
```
## Бинаризации float
Выбрать стратегию бинаризации можно установив параметр *feature_border_type*.
- **Uniform**. Границы выбираются равномерно по значениям;
- **Median**. В каждый бин попадает примерно одинаковое число различных значений;
- **UniformAndQuantiles**. Uniform + Median;
- **MaxLogSum, GreedyLogSum**. Максимизируется значение формулы $\sum_{i=1}^K \log(n_i)$, где $K$ - требуемое кол-во бинов, $n_i$ число объектов в этом бакете;
- **MinEntropy**. Аналогично, но максимизируется энтропия: $-\sum_{i=1}^K n_i \log(n_i)$
```
from sklearn.model_selection import GridSearchCV
params = {"feature_border_type": [
"Uniform",
"Median",
"UniformAndQuantiles",
"MaxLogSum",
"GreedyLogSum",
"MinEntropy"
]}
cb = CatBoostRegressor(silent=True)
grid = GridSearchCV(cb, params)
grid.fit(X, y)
for score, strategy in sorted(zip(grid.cv_results_['mean_test_score'],
grid.cv_results_['param_feature_border_type'].data)):
print("MSE: {}, strategy: {}".format(score, strategy))
```
## Feature importance
```
cb = CatBoostRegressor(silent=True)
cb.fit(X_train, y_train)
for value, name in sorted(zip(cb.get_feature_importance(fstr_type="FeatureImportance"),
boston["feature_names"])):
print("{}\t{}".format(name, value))
```
# Categorical features
```
from catboost.datasets import titanic
titanic_df = titanic()
X = titanic_df[0].drop('Survived',axis=1)
y = titanic_df[0].Survived
X.head(5)
is_cat = (X.dtypes != float)
is_cat.to_dict()
is_cat = (X.dtypes != float)
for feature, feat_is_cat in is_cat.to_dict().items():
if feat_is_cat:
X[feature].fillna("NAN", inplace=True)
cat_features_index = np.where(is_cat)[0]
cat_features_index
X.columns
```
Аналогом для класса DMatrix в катбусте служит класс **catboost.Pool**. Помимо прочего, содержит индексы категориальных факторов и описание пар для режима попарного обучения.
[Подробнее](https://tech.yandex.com/catboost/doc/dg/concepts/python-reference_pool-docpage/)
```
from catboost import Pool
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=.85, random_state=1234)
train_pool = Pool(data=X_train,
label=y_train,
cat_features=cat_features_index, # в явном виде передаем категориальные фичи, которыми хотим работать
feature_names=list(X_train.columns)) # названия фич, для удобной визуализации и дебага
test_pool = Pool(data=X_test,
label=y_test,
cat_features=cat_features_index,
feature_names=list(X_test.columns))
from catboost import CatBoostClassifier
from sklearn.metrics import roc_auc_score
model = CatBoostClassifier(eval_metric='Accuracy', use_best_model=True, random_seed=42)
model.fit(train_pool, eval_set=test_pool, metric_period=100)
y_pred = model.predict_proba(X_test)
roc_auc_score(y_test, y_pred[:, 1])
```
На самом деле в Catboost происходит еще много чего интересного при обработке категорий:
- среднее сглаживается некоторым априорным приближением;
- по факту обучается несколько (3) модели на разных перестановках;
- рассматриваются композиции категориальных факторов (max_ctr_complexity);
- в момент применения модели, новые объекты приписываются в конец перестановки по обучающей выборке и, таким образом, статистика для них считается по всем имеющимся данным;
- таргето-независимые счетчики считаются по всем данным.
- для факторов с небольшим числом различных значений производится OneHotEncoding (параметр one_hot_max_size - максимальное значение для OneHotEncoding'а)
# [Категориальные статистики](https://catboost.ai/docs/concepts/algorithm-main-stages_cat-to-numberic.html)
Одно из основных преимуществ катбуста - обработка категориальных факторов.
Такие факторы заменяются на "счетчики": для каждого значения кат.фактора **по таргету** вычисляется некоторая **статистика** этого значения (счетчик, ctr), например, среднее значение таргета по объектам, которые имеют данное значение категориального фактора. Далее категориальный фактор заменяется на подсчитанные для него статистики (каждое значение фактора на свою статистику).
Будем использовать технику кодирования категориальных признаков средним значением целевого признака.
Основная идея – для каждого значения категориального признака посчитать среднее значение целевого признака и заменить категориальный признак на посчитанные средние.
Давайте попробуем сделать следующую операцию:
* Возьмем категориальную фичу (один столбец). Пусть фича принимает $m$ значений: $l_1, \ldots, l_m$
* Заменим значение $l_k$ на $\frac{1}{N_{l_k}}\sum_{i \in l_k}y_i$ - среднее значение целевой переменной для данного значения категориальной фичи.
* Переменной в тесте будут приравниваться все средние значение данных
```
df_train = pd.DataFrame({'float':[1,2,3,4,5],
'animal': ['cat', 'dog', 'cat', 'dog', 'cat'],
'sign': ['rock', 'rock', 'paper', 'paper', 'paper']})
y_train = np.array([0,1,0,1, 0])
df_test = pd.DataFrame({'float':[6,7,8,9],
'animal': ['cat', 'dog', 'cat', 'dog'],
'sign': ['rock', 'rock', 'paper', 'paper']})
import warnings
warnings.filterwarnings("ignore")
def mean_target(df_train, y_train, df_test):
n = len(df_train)
cat_features = df_train.columns[df_train.dtypes == 'object'].tolist()
float_features = df_train.columns[df_train.dtypes != 'object'].tolist()
new_X_train = df_train.copy()
new_X_train['y'] = y_train
new_X_test = df_test.copy()
for col in cat_features:
mean_dict = new_X_train.groupby(col)['y'].mean().to_dict()
new_X_train[col + '_mean'] = df_train[col].map(mean_dict)
new_X_test[col + '_mean'] = df_test[col].map(mean_dict)
return new_X_train, new_X_test
X_train, X_test = mean_target(df_train, y_train, df_test)
X_train
X_test
```
Данный подход лучше чем One-Hot, так как при нем мы можем серьезно вылететь за пределы памяти.
#### Важный момент.
В ходе подсчета статистики мы по сути сильно привязываемся к данным. Из-за чего может произойти сильное **переобучение**.
## Накопительные статистики
Такие манипуляции очень легко могут привести к переобучению, потому что в данные подливается информация о метках объектов, после чего происходит обучение.
Поэтому в катбусте делают **накопительные статистики**
Особенности работы с категориальными факторами:
- объекты перемешиваются в случайном порядке;
- для i-го объекта и j-го признака в перестановке **статистика** (счетчик) вычисляется по всем объектам, идущим **до него** с таким же значением признака
- заменяем все категориальные факторы в выборке и обучаем модель
- Тестовую же выборку просто приравниваем к средним значениям по
```
def late_mean_target(df_train, df_test, y_train):
n = len(df_train)
cat_features = df_train.columns[df_train.dtypes == 'object'].tolist()
num_features = df_train.columns[df_train.dtypes != 'object'].tolist()
new_X_test = df_test.copy()
new_X_train = df_train.copy()
new_X_train['y'] = y_train
new_X_train = new_X_train.sample(frac=1).reset_index() #shuffling
new_X_train['ones'] = np.ones((len(X_train),))
for col in cat_features:
mean_dict = new_X_train.groupby(col)['y'].mean().to_dict()
new_X_test[col + '_mean'] = df_test[col].map(mean_dict) / n
count = new_X_train.groupby([col])['ones'].apply(lambda x: x.cumsum())
cum = new_X_train.groupby([col])['y'].apply(lambda x: x.cumsum())
new_X_train[col + '_mean'] = (cum - new_X_train['y'])/count
return new_X_train, new_X_test
df_train = pd.DataFrame({'float':[1,2,3,4,5],
'animal': ['cat', 'dog', 'cat', 'dog', 'cat'],
'sign': ['rock', 'rock', 'paper', 'paper', 'paper']})
y_train = np.array([0,1,0,1, 0])
df_test = pd.DataFrame({'float':[6,7,8,9],
'animal': ['cat', 'dog', 'cat', 'dog'],
'sign': ['rock', 'rock', 'paper', 'paper']})
X_train, X_test = late_mean_target(df_train, df_test, y_train)
X_train
X_test
```
# Полезные ссылки
* [Tutorial](https://github.com/catboost/tutorials)
* [Github Catboost](https://github.com/catboost/catboost)
* [Статья о Catboost на arxiv](https://arxiv.org/pdf/1706.09516.pdf)
| true |
code
| 0.403185 | null | null | null | null |
|
## Reinforcement Learning Tutorial -1: Q Learning
#### MD Muhaimin Rahman
sezan92[at]gmail[dot]com
Q learning , can be said one of the most famous -and kind of intuitive- of all Reinforcement learning algorithms. In fact ,the recent all algorithms using Deep learning , are based on the Q learning algorithms. So, to work on recent algorithms, one must have a good idea on Q learning.
### Intuition
First , start with an Intuition. Lets assume , you are in a maze

Okay okay! I admit, it is not a maze. just a house with 5 rooms. And I got it from, this [link](http://mnemstudio.org/path-finding-q-learning-tutorial.htm) . Your goal is to get out of this place, no matter where you are. But you dont know - atleast pretend to - how to get there! After wondering about the map, you stumbled upon a mysterious letter with a lot of numbers in the room.

The matrix has 6 columns and 6 rows. What you will have to do , is to go to the room with highest value. Suppose, you are in room number 2. Then , you will have to move to room number 3 . Then you get out! Look at the picture again! You can try with every state, you are guaranteed to get out of the house, using this matrix! .
In the world of RL, every room is called a ```state```, movement from one state to another is called ```action```. Our game has a very ***JARGONISH*** name, ```Markov Decision Process``` . Maybe they invented this name to freak everybody out. But in short, this process means, your action from current state never depends on previous state. Practically such processes are impossible, but it helps to simplify problems
Now the question is , how can we get this ?
- First , initialize the matrix as Zeros

- Then we will apply the Q learning update equation
\begin{equation}
Q(s_t,a) = Q(s_t,a) + \alpha (Q'(s_{t+1},a)-Q(s_t,a))
\end{equation}
Here, $s_t$ is state at time $t$ , $s_{t+1}$ means the next state, $a$ is action , $r$ is reward we get-if we can get - from one state to another state. Q(s_t,a_t) means Q matrix value for state $s_t$ and action $a_t$ , $Q'(s_{t+1},a)$ means target Q value with state $s_{t+1}$ and the ***BEST ACTION*** for next state. Here $\alpha $ is learning rate}
Before we proceed, let me ask you, does this equation ring a bell ? I mean, haven't you seen a similar equation ?
Yeah, you got it , it is similar to Gradient descent Equation. If you dont know Gradient descent equation, I am sorry, you wont be able to get the future tutorials. So I suggest you get the basic and working Idea of Neural Networks and Gradient descent algorithms
Now ,How can we get $Q'(s_{t+1},a)$ ?
Using Bellman Equation
\begin{equation}
Q'(s_{t+1},a) = r+ \gamma max(Q(s_{t+1},a_t))
\end{equation}
It means the target $Q$ value for every state and action is the sum of reward with that state and action, and the maximum $Q$ value of next state multiplied with discount factor $\gamma$
***Where did this equation came from ? ***
Okay chill! let's start from the game again ! So suppose , every room has reward, $R_t,R_{t+1},R_{t+2},R_{t+3},R_{t+4},R_{t+5}$.. So obviously , the value of a state will be the expected cumulative reward
\begin{equation}
Q(s,a) = R_t + R_{t+1} + R_{t+2}+ R_{t+3}+ R_{t+4}+ R_{t+5}
\end{equation}
Suppose, someone comes here, and says, He wants give more weight to sooner rewards than later rewards. What should we do ? We will introduce, discount factor, $\gamma$ , which is $0<\gamma<1$ ..
\begin{equation}
Q(s,a) = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2}+ \gamma^3 R_{t+3}+ \gamma^4 R_{t+4}+ \gamma^5 R_{t+5}
\end{equation}
\begin{equation}
Q(s,a) = R_t + \gamma [R_{t+1} + \gamma R_{t+2}+ \gamma^2 R_{t+3}+ \gamma^3 R_{t+4}+ \gamma^4 R_{t+5}]
\end{equation}
This equation can be rewritten as
\begin{equation}
Q(s_t,a) = R_t+\gamma Q(s_{t+1},a_{t+1})
\end{equation}
Suppose, we have some finite discrete actions in our hand, and each resulting $Q$ values of its own, what we will do ? We will try to take the action of maximum $Q$ value!
\begin{equation}
Q(s_t,a) = R_t+\gamma max(Q(s_{t+1},a))
\end{equation}
### Coding!
Let's start coding!
I will be using ***Open Ai*** gym environment. The Introduction and Installtion of environments are given [here](https://github.com/openai/gym)
```
import gym
import numpy as np
```
Initialization of Environments
I will use the Mountaincar environment by Open AI gym. It is a classic problem invented from 90s. I intend to use this environment for all algorithms .

In this game, your task is to get the car reach that green flag. For every step you will get -1 .So , your job is to reach the goal position with minimum steps. Maximum steps limit is 200.
```
env = gym.make('MountainCar-v0')
s = env.reset() #Reset the car
```
```env.reset()``` gives the initial state. State is the position and velocity of the car in a given time
This game's actions can be 0,1,2 . 0 for left, 1 for doing nothing, 2 for right
```env.step(action)``` returns four arguments
- next state
- reward
- terminal , it means if game is over or not
- info , for now , it is unnecessary
Hyper Parameters
- ```legal_actions``` number of actions
- ```actions``` the actions list
- ```gamma``` discount factor $\gamma$
- ```lr``` learning rate $\alpha$
- ```num_episodes``` number of episodes
- ```epsilon``` epsilon , to choose random actions
- ```epsilon_decay``` epsilon decay rate
```
legal_actions=env.action_space.n
actions = [0,1,2]
gamma =0.99
lr =0.5
num_episodes =30000
epsilon =0.5
epsilon_decay =0.99
```
Codeblock to discretize the state. Because ***Q learning*** doesnt work on continuous state space, we have to convert states into 10 discrete states
```
N_BINS = [10,10]
MIN_VALUES = [0.6,0.07]
MAX_VALUES = [-1.2,-.07]
BINS = [np.linspace(MIN_VALUES[i], MAX_VALUES[i], N_BINS[i]) for i in range(len(N_BINS))]
rList =[]
def discretize(obs):
return tuple([int(np.digitize(obs[i], BINS[i])) for i in range(len(N_BINS))])
```
Q Learning CLass
```
class QL:
def __init__(self,Q,policy,
legal_actions,
actions,
gamma,
lr):
self.Q = Q #Q matrix
self.policy =policy
self.legal_actions=legal_actions
self.actions = actions
self.gamma =gamma
self.lr =lr
def q_value(self,s,a):
"""Gets the Q value for a certain state and action"""
if (s,a) in self.Q:
self.Q[(s,a)]
else:
self.Q[s,a]=0
return self.Q[s,a]
def action(self,s):
"""Gets the action for cetain state"""
if s in self.policy:
return self.policy[s]
else:
self.policy[s] = np.random.randint(0,self.legal_actions)
return self.policy[s]
def learn(self,s,a,s1,r,done):
"""Updates the Q matrix"""
if done== False:
self.Q[(s,a)] =self.q_value(s,a)+ self.lr*(r+self.gamma*max([self.q_value(s1,a1) for a1 in self.actions]) - self.q_value(s,a))
else:
self.Q[(s,a)] =self.q_value(s,a)+ self.lr*(r - self.q_value(s,a))
self.q_values = [self.q_value(s,a1) for a1 in self.actions]
self.policy[s] = self.actions[self.q_values.index(max(self.q_values))]
```
Q Matrix Parameters
- ```Q``` - Q table. We will use dictionary data structure.
- ```policy``` - policy table , it will give us the action for given state
```
Q = {}
policy ={}
legal_actions =3
QL = QL(Q,policy,legal_actions,actions,gamma,lr)
```
Training
### Psuedocode
- get initial state $s_{raw}$
- discretize initial state , $s \gets discretize(s_{raw})$
- set total reward to zero , $r_{total} \gets 0$
- set terminal $d$ to false , $d \gets False$
- for each step
- - choose action based on epsilon greedy policy
- - get next state $s1_{raw} $, reward , $r$, terminal $d$ doing the action
- - $s1 \gets discretize(s1_{raw}) $
- - $r_{total} \gets r_{total}+r$
- - if $d == True $
- - - if $r_{total}<-199$
- - - - then give $r \gets -100$
- - - - Update $Q$ table
- - - - break
- - else
- - - Update $Q$ table
- - - break
- - $s \gets s1$
```
for i in range(num_episodes):
s_raw= env.reset() #initialize
s = discretize(s_raw) #discretize the state
rAll =0 #total reward
d = False
j = 0
for j in range(200):
#epsilon greedy. to choose random actions initially when Q is all zeros
if np.random.random()< epsilon:
a = np.random.randint(0,legal_actions)
epsilon = epsilon*epsilon_decay
else:
a =QL.action(s)
s1_raw,r,d,_ = env.step(a)
rAll=rAll+r
s1 = discretize(s1_raw)
env.render()
if d:
if rAll<-199:
r =-100 #punishment, if the game finishes before reaching the goal , we can give punishment
QL.learn(s,a,s1,r,d)
print("Failed! Reward %d"%rAll)
elif rAll>-199:
print("Passed! Reward %d"%rAll)
break
QL.learn(s,a,s1,r,d)
if j==199:
print("Reward %d after full episode"%(rAll))
s = s1
env.close()
```
| true |
code
| 0.304197 | null | null | null | null |
|
# Marginalized Gaussian Mixture Model
Author: [Austin Rochford](http://austinrochford.com)
```
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
import pymc3 as pm
import seaborn as sns
SEED = 383561
np.random.seed(SEED) # from random.org, for reproducibility
```
Gaussian mixtures are a flexible class of models for data that exhibits subpopulation heterogeneity. A toy example of such a data set is shown below.
```
N = 1000
W = np.array([0.35, 0.4, 0.25])
MU = np.array([0., 2., 5.])
SIGMA = np.array([0.5, 0.5, 1.])
component = np.random.choice(MU.size, size=N, p=W)
x = np.random.normal(MU[component], SIGMA[component], size=N)
fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(x, bins=30, normed=True, lw=0);
```
A natural parameterization of the Gaussian mixture model is as the [latent variable model](https://en.wikipedia.org/wiki/Latent_variable_model)
$$
\begin{align*}
\mu_1, \ldots, \mu_K
& \sim N(0, \sigma^2) \\
\tau_1, \ldots, \tau_K
& \sim \textrm{Gamma}(a, b) \\
\boldsymbol{w}
& \sim \textrm{Dir}(\boldsymbol{\alpha}) \\
z\ |\ \boldsymbol{w}
& \sim \textrm{Cat}(\boldsymbol{w}) \\
x\ |\ z
& \sim N(\mu_z, \tau^{-1}_i).
\end{align*}
$$
An implementation of this parameterization in PyMC3 is available [here](gaussian_mixture_model.ipynb). A drawback of this parameterization is that is posterior relies on sampling the discrete latent variable $z$. This reliance can cause slow mixing and ineffective exploration of the tails of the distribution.
An alternative, equivalent parameterization that addresses these problems is to marginalize over $z$. The marginalized model is
$$
\begin{align*}
\mu_1, \ldots, \mu_K
& \sim N(0, \sigma^2) \\
\tau_1, \ldots, \tau_K
& \sim \textrm{Gamma}(a, b) \\
\boldsymbol{w}
& \sim \textrm{Dir}(\boldsymbol{\alpha}) \\
f(x\ |\ \boldsymbol{w})
& = \sum_{i = 1}^K w_i\ N(x\ |\ \mu_i, \tau^{-1}_i),
\end{align*}
$$
where
$$N(x\ |\ \mu, \sigma^2) = \frac{1}{\sqrt{2 \pi} \sigma} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right)$$
is the probability density function of the normal distribution.
Marginalizing $z$ out of the model generally leads to faster mixing and better exploration of the tails of the posterior distribution. Marginalization over discrete parameters is a common trick in the [Stan](http://mc-stan.org/) community, since Stan does not support sampling from discrete distributions. For further details on marginalization and several worked examples, see the [_Stan User's Guide and Reference Manual_](http://www.uvm.edu/~bbeckage/Teaching/DataAnalysis/Manuals/stan-reference-2.8.0.pdf).
PyMC3 supports marginalized Gaussian mixture models through its `NormalMixture` class. (It also supports marginalized general mixture models through its `Mixture` class.) Below we specify and fit a marginalized Gaussian mixture model to this data in PyMC3.
```
with pm.Model() as model:
w = pm.Dirichlet('w', np.ones_like(W))
mu = pm.Normal('mu', 0., 10., shape=W.size)
tau = pm.Gamma('tau', 1., 1., shape=W.size)
x_obs = pm.NormalMixture('x_obs', w, mu, tau=tau, observed=x)
with model:
trace = pm.sample(5000, n_init=10000, tune=1000, random_seed=SEED)[1000:]
```
We see in the following plot that the posterior distribution on the weights and the component means has captured the true value quite well.
```
pm.traceplot(trace, varnames=['w', 'mu']);
pm.plot_posterior(trace, varnames=['w', 'mu']);
```
We can also sample from the model's posterior predictive distribution, as follows.
```
with model:
ppc_trace = pm.sample_posterior_predictive(trace, 5000, random_seed=SEED)
```
We see that the posterior predictive samples have a distribution quite close to that of the observed data.
```
fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(x, bins=30, normed=True,
histtype='step', lw=2,
label='Observed data');
ax.hist(ppc_trace['x_obs'], bins=30, normed=True,
histtype='step', lw=2,
label='Posterior predictive distribution');
ax.legend(loc=1);
```
| true |
code
| 0.657483 | null | null | null | null |
|
# 基于注意力的神经机器翻译
此笔记本训练一个将波斯语翻译为英语的序列到序列(sequence to sequence,简写为 seq2seq)模型。此例子难度较高,需要对序列到序列模型的知识有一定了解。
训练完此笔记本中的模型后,你将能够输入一个波斯语句子,例如 *"من می دانم."*,并返回其英语翻译 *"I know."*
对于一个简单的例子来说,翻译质量令人满意。但是更有趣的可能是生成的注意力图:它显示在翻译过程中,输入句子的哪些部分受到了模型的注意。
<img src="https://tensorflow.google.cn/images/spanish-english.png" alt="spanish-english attention plot">
请注意:运行这个例子用一个 P100 GPU 需要花大约 10 分钟。
```
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.model_selection import train_test_split
import unicodedata
import re
import numpy as np
import os
import io
import time
```
## 下载和准备数据集
我们将使用 http://www.manythings.org/anki/ 提供的一个语言数据集。这个数据集包含如下格式的语言翻译对:
```
May I borrow this book? ¿Puedo tomar prestado este libro?
```
这个数据集中有很多种语言可供选择。我们将使用英语 - 波斯语数据集。为方便使用,我们在谷歌云上提供了此数据集的一份副本。但是你也可以自己下载副本。下载完数据集后,我们将采取下列步骤准备数据:
1. 给每个句子添加一个 *开始* 和一个 *结束* 标记(token)。
2. 删除特殊字符以清理句子。
3. 创建一个单词索引和一个反向单词索引(即一个从单词映射至 id 的词典和一个从 id 映射至单词的词典)。
4. 将每个句子填充(pad)到最大长度。
```
'''
# 下载文件
path_to_zip = tf.keras.utils.get_file(
'spa-eng.zip', origin='http://storage.googleapis.com/download.tensorflow.org/data/spa-eng.zip',
extract=True)
path_to_file = os.path.dirname(path_to_zip)+"/spa-eng/spa.txt"
'''
path_to_file = "./lan/pes.txt"
# 将 unicode 文件转换为 ascii
def unicode_to_ascii(s):
return ''.join(c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn')
def preprocess_sentence(w):
w = unicode_to_ascii(w.lower().strip())
# 在单词与跟在其后的标点符号之间插入一个空格
# 例如: "he is a boy." => "he is a boy ."
# 参考:https://stackoverflow.com/questions/3645931/python-padding-punctuation-with-white-spaces-keeping-punctuation
w = re.sub(r"([?.!,¿])", r" \1 ", w)
w = re.sub(r'[" "]+', " ", w)
# 除了 (a-z, A-Z, ".", "?", "!", ","),将所有字符替换为空格
w = re.sub(r"[^a-zA-Z?.!,¿]+", " ", w)
w = w.rstrip().strip()
# 给句子加上开始和结束标记
# 以便模型知道何时开始和结束预测
w = '<start> ' + w + ' <end>'
return w
en_sentence = u"May I borrow this book?"
sp_sentence = u"¿Puedo tomar prestado este libro?"
print(preprocess_sentence(en_sentence))
print(preprocess_sentence(sp_sentence).encode('utf-8'))
# 1. 去除重音符号
# 2. 清理句子
# 3. 返回这样格式的单词对:[ENGLISH, SPANISH]
def create_dataset(path, num_examples):
lines = io.open(path, encoding='UTF-8').read().strip().split('\n')
word_pairs = [[preprocess_sentence(w) for w in l.split('\t')] for l in lines[:num_examples]]
return zip(*word_pairs)
en, sp = create_dataset(path_to_file, None)
print(en[-1])
print(sp[-1])
def max_length(tensor):
return max(len(t) for t in tensor)
def tokenize(lang):
lang_tokenizer = tf.keras.preprocessing.text.Tokenizer(
filters='')
lang_tokenizer.fit_on_texts(lang)
tensor = lang_tokenizer.texts_to_sequences(lang)
tensor = tf.keras.preprocessing.sequence.pad_sequences(tensor,
padding='post')
return tensor, lang_tokenizer
def load_dataset(path, num_examples=None):
# 创建清理过的输入输出对
targ_lang, inp_lang = create_dataset(path, num_examples)
input_tensor, inp_lang_tokenizer = tokenize(inp_lang)
target_tensor, targ_lang_tokenizer = tokenize(targ_lang)
return input_tensor, target_tensor, inp_lang_tokenizer, targ_lang_tokenizer
```
### 限制数据集的大小以加快实验速度(可选)
在超过 10 万个句子的完整数据集上训练需要很长时间。为了更快地训练,我们可以将数据集的大小限制为 3 万个句子(当然,翻译质量也会随着数据的减少而降低):
```
# 尝试实验不同大小的数据集
num_examples = 30000
input_tensor, target_tensor, inp_lang, targ_lang = load_dataset(path_to_file, num_examples)
# 计算目标张量的最大长度 (max_length)
max_length_targ, max_length_inp = max_length(target_tensor), max_length(input_tensor)
# 采用 80 - 20 的比例切分训练集和验证集
input_tensor_train, input_tensor_val, target_tensor_train, target_tensor_val = train_test_split(input_tensor, target_tensor, test_size=0.2)
# 显示长度
print(len(input_tensor_train), len(target_tensor_train), len(input_tensor_val), len(target_tensor_val))
def convert(lang, tensor):
for t in tensor:
if t!=0:
print ("%d ----> %s" % (t, lang.index_word[t]))
print ("Input Language; index to word mapping")
convert(inp_lang, input_tensor_train[0])
print ()
print ("Target Language; index to word mapping")
convert(targ_lang, target_tensor_train[0])
```
### 创建一个 tf.data 数据集
```
BUFFER_SIZE = len(input_tensor_train)
BATCH_SIZE = 64
steps_per_epoch = len(input_tensor_train)//BATCH_SIZE
embedding_dim = 256
units = 1024
vocab_inp_size = len(inp_lang.word_index)+1
vocab_tar_size = len(targ_lang.word_index)+1
dataset = tf.data.Dataset.from_tensor_slices((input_tensor_train, target_tensor_train)).shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE, drop_remainder=True)
example_input_batch, example_target_batch = next(iter(dataset))
example_input_batch.shape, example_target_batch.shape
```
## 编写编码器 (encoder) 和解码器 (decoder) 模型
实现一个基于注意力的编码器 - 解码器模型。关于这种模型,你可以阅读 TensorFlow 的 [神经机器翻译 (序列到序列) 教程](https://github.com/tensorflow/nmt)。本示例采用一组更新的 API。此笔记本实现了上述序列到序列教程中的 [注意力方程式](https://github.com/tensorflow/nmt#background-on-the-attention-mechanism)。下图显示了注意力机制为每个输入单词分配一个权重,然后解码器将这个权重用于预测句子中的下一个单词。下图和公式是 [Luong 的论文](https://arxiv.org/abs/1508.04025v5)中注意力机制的一个例子。
<img src="https://tensorflow.google.cn/images/seq2seq/attention_mechanism.jpg" width="500" alt="attention mechanism">
输入经过编码器模型,编码器模型为我们提供形状为 *(批大小,最大长度,隐藏层大小)* 的编码器输出和形状为 *(批大小,隐藏层大小)* 的编码器隐藏层状态。
下面是所实现的方程式:
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_0.jpg" alt="attention equation 0" width="800">
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_1.jpg" alt="attention equation 1" width="800">
本教程的编码器采用 [Bahdanau 注意力](https://arxiv.org/pdf/1409.0473.pdf)。在用简化形式编写之前,让我们先决定符号:
* FC = 完全连接(密集)层
* EO = 编码器输出
* H = 隐藏层状态
* X = 解码器输入
以及伪代码:
* `score = FC(tanh(FC(EO) + FC(H)))`
* `attention weights = softmax(score, axis = 1)`。 Softmax 默认被应用于最后一个轴,但是这里我们想将它应用于 *第一个轴*, 因为分数 (score) 的形状是 *(批大小,最大长度,隐藏层大小)*。最大长度 (`max_length`) 是我们的输入的长度。因为我们想为每个输入分配一个权重,所以 softmax 应该用在这个轴上。
* `context vector = sum(attention weights * EO, axis = 1)`。选择第一个轴的原因同上。
* `embedding output` = 解码器输入 X 通过一个嵌入层。
* `merged vector = concat(embedding output, context vector)`
* 此合并后的向量随后被传送到 GRU
每个步骤中所有向量的形状已在代码的注释中阐明:
```
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, enc_units, batch_sz):
super(Encoder, self).__init__()
self.batch_sz = batch_sz
self.enc_units = enc_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.enc_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
def call(self, x, hidden):
x = self.embedding(x)
output, state = self.gru(x, initial_state = hidden)
return output, state
def initialize_hidden_state(self):
return tf.zeros((self.batch_sz, self.enc_units))
encoder = Encoder(vocab_inp_size, embedding_dim, units, BATCH_SIZE)
# 样本输入
sample_hidden = encoder.initialize_hidden_state()
sample_output, sample_hidden = encoder(example_input_batch, sample_hidden)
print ('Encoder output shape: (batch size, sequence length, units) {}'.format(sample_output.shape))
print ('Encoder Hidden state shape: (batch size, units) {}'.format(sample_hidden.shape))
class BahdanauAttention(tf.keras.layers.Layer):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, query, values):
# 隐藏层的形状 == (批大小,隐藏层大小)
# hidden_with_time_axis 的形状 == (批大小,1,隐藏层大小)
# 这样做是为了执行加法以计算分数
hidden_with_time_axis = tf.expand_dims(query, 1)
# 分数的形状 == (批大小,最大长度,1)
# 我们在最后一个轴上得到 1, 因为我们把分数应用于 self.V
# 在应用 self.V 之前,张量的形状是(批大小,最大长度,单位)
score = self.V(tf.nn.tanh(
self.W1(values) + self.W2(hidden_with_time_axis)))
# 注意力权重 (attention_weights) 的形状 == (批大小,最大长度,1)
attention_weights = tf.nn.softmax(score, axis=1)
# 上下文向量 (context_vector) 求和之后的形状 == (批大小,隐藏层大小)
context_vector = attention_weights * values
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
attention_layer = BahdanauAttention(10)
attention_result, attention_weights = attention_layer(sample_hidden, sample_output)
print("Attention result shape: (batch size, units) {}".format(attention_result.shape))
print("Attention weights shape: (batch_size, sequence_length, 1) {}".format(attention_weights.shape))
class Decoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, dec_units, batch_sz):
super(Decoder, self).__init__()
self.batch_sz = batch_sz
self.dec_units = dec_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.dec_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc = tf.keras.layers.Dense(vocab_size)
# 用于注意力
self.attention = BahdanauAttention(self.dec_units)
def call(self, x, hidden, enc_output):
# 编码器输出 (enc_output) 的形状 == (批大小,最大长度,隐藏层大小)
context_vector, attention_weights = self.attention(hidden, enc_output)
# x 在通过嵌入层后的形状 == (批大小,1,嵌入维度)
x = self.embedding(x)
# x 在拼接 (concatenation) 后的形状 == (批大小,1,嵌入维度 + 隐藏层大小)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# 将合并后的向量传送到 GRU
output, state = self.gru(x)
# 输出的形状 == (批大小 * 1,隐藏层大小)
output = tf.reshape(output, (-1, output.shape[2]))
# 输出的形状 == (批大小,vocab)
x = self.fc(output)
return x, state, attention_weights
decoder = Decoder(vocab_tar_size, embedding_dim, units, BATCH_SIZE)
sample_decoder_output, _, _ = decoder(tf.random.uniform((64, 1)),
sample_hidden, sample_output)
print ('Decoder output shape: (batch_size, vocab size) {}'.format(sample_decoder_output.shape))
```
## 定义优化器和损失函数
```
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
```
## 检查点(基于对象保存)
```
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(optimizer=optimizer,
encoder=encoder,
decoder=decoder)
```
## 训练
1. 将 *输入* 传送至 *编码器*,编码器返回 *编码器输出* 和 *编码器隐藏层状态*。
2. 将编码器输出、编码器隐藏层状态和解码器输入(即 *开始标记*)传送至解码器。
3. 解码器返回 *预测* 和 *解码器隐藏层状态*。
4. 解码器隐藏层状态被传送回模型,预测被用于计算损失。
5. 使用 *教师强制 (teacher forcing)* 决定解码器的下一个输入。
6. *教师强制* 是将 *目标词* 作为 *下一个输入* 传送至解码器的技术。
7. 最后一步是计算梯度,并将其应用于优化器和反向传播。
```
@tf.function
def train_step(inp, targ, enc_hidden):
loss = 0
with tf.GradientTape() as tape:
enc_output, enc_hidden = encoder(inp, enc_hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']] * BATCH_SIZE, 1)
# 教师强制 - 将目标词作为下一个输入
for t in range(1, targ.shape[1]):
# 将编码器输出 (enc_output) 传送至解码器
predictions, dec_hidden, _ = decoder(dec_input, dec_hidden, enc_output)
loss += loss_function(targ[:, t], predictions)
# 使用教师强制
dec_input = tf.expand_dims(targ[:, t], 1)
batch_loss = (loss / int(targ.shape[1]))
variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, variables)
optimizer.apply_gradients(zip(gradients, variables))
return batch_loss
EPOCHS = 10
for epoch in range(EPOCHS):
start = time.time()
enc_hidden = encoder.initialize_hidden_state()
total_loss = 0
for (batch, (inp, targ)) in enumerate(dataset.take(steps_per_epoch)):
batch_loss = train_step(inp, targ, enc_hidden)
total_loss += batch_loss
if batch % 100 == 0:
print('Epoch {} Batch {} Loss {:.4f}'.format(epoch + 1,
batch,
batch_loss.numpy()))
# 每 2 个周期(epoch),保存(检查点)一次模型
if (epoch + 1) % 2 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print('Epoch {} Loss {:.4f}'.format(epoch + 1,
total_loss / steps_per_epoch))
print('Time taken for 1 epoch {} sec\n'.format(time.time() - start))
```
## 翻译
* 评估函数类似于训练循环,不同之处在于在这里我们不使用 *教师强制*。每个时间步的解码器输入是其先前的预测、隐藏层状态和编码器输出。
* 当模型预测 *结束标记* 时停止预测。
* 存储 *每个时间步的注意力权重*。
请注意:对于一个输入,编码器输出仅计算一次。
```
def evaluate(sentence):
attention_plot = np.zeros((max_length_targ, max_length_inp))
sentence = preprocess_sentence(sentence)
inputs = [inp_lang.word_index[i] for i in sentence.split(' ')]
inputs = tf.keras.preprocessing.sequence.pad_sequences([inputs],
maxlen=max_length_inp,
padding='post')
inputs = tf.convert_to_tensor(inputs)
result = ''
hidden = [tf.zeros((1, units))]
enc_out, enc_hidden = encoder(inputs, hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']], 0)
for t in range(max_length_targ):
predictions, dec_hidden, attention_weights = decoder(dec_input,
dec_hidden,
enc_out)
# 存储注意力权重以便后面制图
attention_weights = tf.reshape(attention_weights, (-1, ))
attention_plot[t] = attention_weights.numpy()
predicted_id = tf.argmax(predictions[0]).numpy()
result += targ_lang.index_word[predicted_id] + ' '
if targ_lang.index_word[predicted_id] == '<end>':
return result, sentence, attention_plot
# 预测的 ID 被输送回模型
dec_input = tf.expand_dims([predicted_id], 0)
return result, sentence, attention_plot
# 注意力权重制图函数
def plot_attention(attention, sentence, predicted_sentence):
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)
ax.matshow(attention, cmap='viridis')
fontdict = {'fontsize': 14}
ax.set_xticklabels([''] + sentence, fontdict=fontdict, rotation=90)
ax.set_yticklabels([''] + predicted_sentence, fontdict=fontdict)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
plt.show()
def translate(sentence):
result, sentence, attention_plot = evaluate(sentence)
print('Input: %s' % (sentence))
print('Predicted translation: {}'.format(result))
attention_plot = attention_plot[:len(result.split(' ')), :len(sentence.split(' '))]
plot_attention(attention_plot, sentence.split(' '), result.split(' '))
```
## 恢复最新的检查点并验证
```
# 恢复检查点目录 (checkpoint_dir) 中最新的检查点
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
translate(u'hace mucho frio aqui.')
translate(u'esta es mi vida.')
translate(u'¿todavia estan en casa?')
# 错误的翻译
translate(u'trata de averiguarlo.')
```
| true |
code
| 0.552298 | null | null | null | null |
|
This is from a "Getting Started" competition from Kaggle [Titanic competition](https://www.kaggle.com/c/titanic) to showcase how we can use Auto-ML along with datmo and docker, in order to track our work and make machine learning workflow reprocible and usable. Some part of data analysis is inspired from this [kernel](https://www.kaggle.com/sinakhorami/titanic-best-working-classifier)
This approach can be categorized into following methods,
1. Exploratory Data Analysis (EDA)
2. Data Cleaning
3. Using Auto-ML to figure out the best algorithm and hyperparameter
During the process of EDA and feature engineering, we would be using datmo to create versions of work by creating snapshot.
```
%matplotlib inline
import numpy as np
import pandas as pd
import re as re
train = pd.read_csv('./input/train.csv', header = 0, dtype={'Age': np.float64})
test = pd.read_csv('./input/test.csv' , header = 0, dtype={'Age': np.float64})
full_data = [train, test]
print (train.info())
```
#### 1. Exploratory Data Analysis
###### To understand how each feature has the contribution to Survive
###### a. `Sex`
```
print (train[["Sex", "Survived"]].groupby(['Sex'], as_index=False).mean())
```
###### b. `Pclass`
```
print (train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean())
```
c. `SibSp and Parch`
With the number of siblings/spouse and the number of children/parents we can create new feature called Family Size.
```
for dataset in full_data:
dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1
print (train[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=False).mean())
```
`FamilySize` seems to have a significant effect on our prediction. `Survived` has increased until a `FamilySize` of 4 and has decreased after that. Let's categorize people to check they are alone or not.
```
for dataset in full_data:
dataset['IsAlone'] = 0
dataset.loc[dataset['FamilySize'] == 1, 'IsAlone'] = 1
print (train[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean())
```
d. `Embarked`
we fill the missing values with most occured value `S`
```
for dataset in full_data:
dataset['Embarked'] = dataset['Embarked'].fillna('S')
print (train[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean())
```
e. `Fare`
Fare also has some missing values which will be filled with the median
```
for dataset in full_data:
dataset['Fare'] = dataset['Fare'].fillna(train['Fare'].median())
train['CategoricalFare'] = pd.qcut(train['Fare'], 4)
print (train[['CategoricalFare', 'Survived']].groupby(['CategoricalFare'], as_index=False).mean())
```
It shows the `Fare` has a significant affect on survival, showcasing that people haivng paid higher fares had higher chances of survival
f. `Age`
There are plenty of missing values in this feature. # generate random numbers between (mean - std) and (mean + std). then we categorize age into 5 range.
```
for dataset in full_data:
age_avg = dataset['Age'].mean()
age_std = dataset['Age'].std()
age_null_count = dataset['Age'].isnull().sum()
age_null_random_list = np.random.randint(age_avg - age_std, age_avg + age_std, size=age_null_count)
dataset['Age'][np.isnan(dataset['Age'])] = age_null_random_list
dataset['Age'] = dataset['Age'].astype(int)
train['CategoricalAge'] = pd.cut(train['Age'], 5)
print (train[['CategoricalAge', 'Survived']].groupby(['CategoricalAge'], as_index=False).mean())
```
g. `Name`
Let's the title of people
```
def get_title(name):
title_search = re.search(' ([A-Za-z]+)\.', name)
# If the title exists, extract and return it.
if title_search:
return title_search.group(1)
return ""
for dataset in full_data:
dataset['Title'] = dataset['Name'].apply(get_title)
print("=====Title vs Sex=====")
print(pd.crosstab(train['Title'], train['Sex']))
print("")
print("=====Title vs Survived=====")
print (train[['Title', 'Survived']].groupby(['Title'], as_index=False).mean())
```
Let's categorize it and check the title impact on survival rate convert the rare titles to `Rare`
```
for dataset in full_data:
dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
print (train[['Title', 'Survived']].groupby(['Title'], as_index=False).mean())
import json
config = {"features analyzed": ["Sex", "Pclass", "FamilySize", "IsAlone", "Embarked", "Fare", "Age", "Title"]}
with open('config.json', 'w') as outfile:
json.dump(config, outfile)
```
#### Creating a datmo snapshot to save my work, this helps me save my current work before proceeding onto data cleaning
```bash
home:~/datmo-tutorials/auto-ml$ datmo snapshot create -m "EDA"
Creating a new snapshot
Created snapshot with id: 30803662ab49bb1ef67a5d0861eecf91cff1642f
home:~/datmo-tutorials/auto-ml$ datmo snapshot ls
+---------+-------------+-------------------------------------------+-------+---------+-------+
| id | created at | config | stats | message | label |
+---------+-------------+-------------------------------------------+-------+---------+-------+
| 30803662| 2018-05-15 | {u'features analyzed': [u'Sex', | {} | EDA | None |
| | 23:15:44 | u'Pclass', u'FamilySize', u'IsAlone', | | | |
| | | u'Embarked', u'Fare', u'Age', u'Title']} | | | |
+---------+-------------+-------------------------------------------+-------+---------+-------+
```
#### 2. Data Cleaning
Now let's clean our data and map our features into numerical values.
```
train_copy = train.copy()
test_copy = test.copy()
full_data_copy = [train_copy, test_copy]
for dataset in full_data_copy:
# Mapping Sex
dataset['Sex'] = dataset['Sex'].map( {'female': 0, 'male': 1} ).astype(int)
# Mapping titles
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
# Mapping Embarked
dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
# Mapping Fare
dataset.loc[ dataset['Fare'] <= 7.91, 'Fare'] = 0
dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare'] = 2
dataset.loc[ dataset['Fare'] > 31, 'Fare'] = 3
dataset['Fare'] = dataset['Fare'].astype(int)
# Mapping Age
dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
dataset.loc[ dataset['Age'] > 64, 'Age'] = 4
# Feature Selection
drop_elements = ['PassengerId', 'Name', 'Ticket', 'Cabin', 'SibSp',\
'Parch', 'FamilySize']
train_copy = train_copy.drop(drop_elements, axis = 1)
train_copy = train_copy.drop(['CategoricalAge', 'CategoricalFare'], axis = 1)
test_copy = test_copy.drop(drop_elements, axis = 1)
print (train_copy.head(10))
train_copy = train_copy.values
test_copy = test_copy.values
config = {"selected features": ["Sex", "Pclass", "Age", "Fare", "Embarked", "Fare", "IsAlone", "Title"]}
with open('config.json', 'w') as outfile:
json.dump(config, outfile)
```
#### 3. Using Auto-ML to figure out the best algorithm and hyperparameter
##### Now we have cleaned our data it's time to use auto-ml in order to get the best algorithm for this data

```
from tpot import TPOTClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
X = train_copy[0::, 1::]
y = train_copy[0::, 0]
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.75, test_size=0.25)
tpot = TPOTClassifier(generations=5, population_size=50, verbosity=2)
tpot.fit(X_train, y_train)
print(tpot.score(X_test, y_test))
tpot.export('tpot_titanic_pipeline.py')
stats = {"accuracy": (tpot.score(X_test, y_test))}
with open('stats.json', 'w') as outfile:
json.dump(stats, outfile)
```
### Let's again create a datmo snapshot to save my work, this helps me save my current work before changing my feature selection
```bash
home:~/datmo-tutorials/auto-ml$ datmo snapshot create -m "auto-ml-1"
Creating a new snapshot
Created snapshot with id: adf76fa7d0800cc6eec033d4b00f97536bcb0c20
home:~/datmo-tutorials/auto-ml$ datmo snapshot ls
+---------+-------------+-------------------------------------------+-----------------+---------------+-------+
| id | created at | config | stats | message | label |
+---------+-------------+-------------------------------------------+-----------------+---------------+-------+
| adf76fa7| 2018-05-16 | {u'selected features': [u'Sex', u'Pclass',|{u'accuracy': | auto-ml-1 | None |
| | 01:24:53 | u'Age', u'Fare', u'Embarked', | 0.8206278} | | |
| | | u'Fare', u'IsAlone', u'Title']} | | | |
| 30803662| 2018-05-15 | {u'features analyzed': [u'Sex', | {} | EDA | None |
| | 23:15:44 | u'Pclass', u'FamilySize', u'IsAlone', | | | |
| | | u'Embarked', u'Fare', u'Age', u'Title']} | | | |
+---------+-------------+-------------------------------------------+-----------------+---------------+-------+
```
#### Another feature selection
1. Let's leave `FamilySize` rather than just unsing `IsAlone`
2. Let's use `Fare_Per_Person` insted of binning `Fare`
```
train_copy = train.copy()
test_copy = test.copy()
full_data_copy = [train_copy, test_copy]
for dataset in full_data_copy:
# Mapping Sex
dataset['Sex'] = dataset['Sex'].map( {'female': 0, 'male': 1} ).astype(int)
# Mapping titles
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
# Mapping Embarked
dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
# Mapping Fare
dataset['FarePerPerson']=dataset['Fare']/(dataset['FamilySize']+1)
# Mapping Age
dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
dataset.loc[ dataset['Age'] > 64, 'Age'] = 4
# Feature Selection
drop_elements = ['PassengerId', 'Name', 'Ticket', 'Cabin', 'SibSp',\
'Parch', 'IsAlone', 'Fare']
train_copy = train_copy.drop(drop_elements, axis = 1)
train_copy = train_copy.drop(['CategoricalAge', 'CategoricalFare'], axis = 1)
test_copy = test_copy.drop(drop_elements, axis = 1)
print (train_copy.head(10))
train_copy = train_copy.values
test_copy = test_copy.values
from tpot import TPOTClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
X = train_copy[0::, 1::]
y = train_copy[0::, 0]
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.75, test_size=0.25)
tpot = TPOTClassifier(generations=5, population_size=50, verbosity=2)
tpot.fit(X_train, y_train)
print(tpot.score(X_test, y_test))
tpot.export('tpot_titanic_pipeline.py')
config = {"selected features": ["Sex", "Pclass", "Age", "Fare", "Embarked", "FarePerPerson", "FamilySize", "Title"]}
with open('config.json', 'w') as outfile:
json.dump(config, outfile)
stats = {"accuracy": (tpot.score(X_test, y_test))}
with open('stats.json', 'w') as outfile:
json.dump(stats, outfile)
```
### Let's again create a datmo snapshot to save my final work
```bash
home:~/datmo-tutorials/auto-ml$ datmo snapshot create -m "auto-ml-2"
Creating a new snapshot
Created snapshot with id: 30f8366b7de96d58a7ef8cda266216b01cab4940
home:~/datmo-tutorials/auto-ml$ datmo snapshot ls
+---------+-------------+-------------------------------------------+-----------------+---------------+-------+
| id | created at | config | stats | message | label |
+---------+-------------+-------------------------------------------+-----------------+---------------+-------+
| 30f8366b| 2018-05-16 | {u'selected features': [u'Sex', u'Pclass',|{u'accuracy': | auto-ml-2 | None |
| | 03:04:06 | u'Age', u'Fare', u'Embarked', u'Title', | 0.8206278} | | |
| | | u'FarePerPerson', u'FamilySize']} | | | |
| adf76fa7| 2018-05-16 | {u'selected features': [u'Sex', u'Pclass',|{u'accuracy': | auto-ml-1 | None |
| | 01:24:53 | u'Age', u'Fare', u'Embarked', | 0.8206278} | | |
| | | u'Fare', u'IsAlone', u'Title']} | | | |
| 30803662| 2018-05-15 | {u'features analyzed': [u'Sex', | {} | EDA | None |
| | 23:15:44 | u'Pclass', u'FamilySize', u'IsAlone', | | | |
| | | u'Embarked', u'Fare', u'Age', u'Title']} | | | |
+---------+-------------+-------------------------------------------+-----------------+---------------+-------+
```
#### Let's now move to a different snapshot in order to either get the `experimentation.ipynb`, `submission.csv` or `tpot_titanice_pipeline.py` or any other files in that version
We perform `checkout` command in order to achieve it
```bash
home:~/datmo-tutorials/auto-ml$ # Run this command: datmo snapshot checkout --id <snapshot-id>
home:~/datmo-tutorials/auto-ml$ datmo snapshot checkout --id 30803662
```
| true |
code
| 0.471041 | null | null | null | null |
|
```
%matplotlib inline
from pyvista import set_plot_theme
set_plot_theme('document')
```
Colormap Choices {#colormap_example}
================
Use a Matplotlib, Colorcet, cmocean, or custom colormap when plotting
scalar values.
```
from pyvista import examples
import pyvista as pv
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import numpy as np
```
Any colormap built for `matplotlib`, `colorcet`, or `cmocean` is fully
compatible with PyVista. Colormaps are typically specified by passing
the string name of the colormap to the plotting routine via the `cmap`
argument.
See [Matplotlib\'s complete list of available
colormaps](https://matplotlib.org/tutorials/colors/colormaps.html),
[Colorcet\'s complete
list](https://colorcet.holoviz.org/user_guide/index.html), and
[cmocean\'s complete list](https://matplotlib.org/cmocean/).
Custom Made Colormaps
=====================
To get started using a custom colormap, download some data with scalar
values to plot.
```
mesh = examples.download_st_helens().warp_by_scalar()
# Add scalar array with range (0, 100) that correlates with elevation
mesh['values'] = pv.plotting.normalize(mesh['Elevation']) * 100
```
Build a custom colormap - here we make a colormap with 5 discrete colors
and we specify the ranges where those colors fall:
```
# Define the colors we want to use
blue = np.array([12/256, 238/256, 246/256, 1])
black = np.array([11/256, 11/256, 11/256, 1])
grey = np.array([189/256, 189/256, 189/256, 1])
yellow = np.array([255/256, 247/256, 0/256, 1])
red = np.array([1, 0, 0, 1])
mapping = np.linspace(mesh['values'].min(), mesh['values'].max(), 256)
newcolors = np.empty((256, 4))
newcolors[mapping >= 80] = red
newcolors[mapping < 80] = grey
newcolors[mapping < 55] = yellow
newcolors[mapping < 30] = blue
newcolors[mapping < 1] = black
# Make the colormap from the listed colors
my_colormap = ListedColormap(newcolors)
```
Simply pass the colormap to the plotting routine!
```
mesh.plot(scalars='values', cmap=my_colormap)
```
Or you could make a simple colormap\... any Matplotlib colormap can be
passed to PyVista!
```
boring_cmap = plt.cm.get_cmap("viridis", 5)
mesh.plot(scalars='values', cmap=boring_cmap)
```
You can also pass a list of color strings to the color map. This
approach divides up the colormap into 5 equal parts.
```
mesh.plot(scalars=mesh['values'], cmap=['black', 'blue', 'yellow', 'grey', 'red'])
```
If you still wish to have control of the separation of values, you can
do this by creating a scalar array and passing that to the plotter along
with the the colormap
```
scalars = np.empty(mesh.n_points)
scalars[mesh['values'] >= 80] = 4 # red
scalars[mesh['values'] < 80] = 3 # grey
scalars[mesh['values'] < 55] = 2 # yellow
scalars[mesh['values'] < 30] = 1 # blue
scalars[mesh['values'] < 1] = 0 # black
mesh.plot(scalars=scalars, cmap=['black', 'blue', 'yellow', 'grey', 'red'])
```
Matplotlib vs. Colorcet
=======================
Let\'s compare Colorcet\'s perceptually uniform \"fire\" colormap to
Matplotlib\'s \"hot\" colormap much like the example on the [first page
of Colorcet\'s docs](https://colorcet.holoviz.org/index.html).
The \"hot\" version washes out detail at the high end, as if the image
is overexposed, while \"fire\" makes detail visible throughout the data
range.
Please note that in order to use Colorcet\'s colormaps including
\"fire\", you must have Colorcet installed in your Python environment:
`pip install colorcet`
```
p = pv.Plotter(shape=(2, 2), border=False)
p.subplot(0, 0)
p.add_mesh(mesh, scalars='Elevation', cmap="fire",
lighting=True, scalar_bar_args={'title': "Colorcet Fire"})
p.subplot(0, 1)
p.add_mesh(mesh, scalars='Elevation', cmap="fire",
lighting=False, scalar_bar_args={'title': "Colorcet Fire (No Lighting)"})
p.subplot(1, 0)
p.add_mesh(mesh, scalars='Elevation', cmap="hot",
lighting=True, scalar_bar_args={'title': "Matplotlib Hot"})
p.subplot(1, 1)
p.add_mesh(mesh, scalars='Elevation', cmap="hot",
lighting=False, scalar_bar_args={'title': "Matplotlib Hot (No Lighting)"})
p.show()
```
| true |
code
| 0.671794 | null | null | null | null |
|
# Matplotlib and NumPy crash course
You may install numpy, matplotlib, sklearn and many other usefull package e.g. via Anaconda distribution.
```
import numpy as np
```
## NumPy basics
### Array creation
```
np.array(range(10))
np.ndarray(shape=(5, 4))
np.linspace(0, 1, num=20)
np.arange(0, 20)
np.zeros(shape=(5, 4))
np.ones(shape=(5,4))
```
Possible types of array:
- bool
- various ints
- float, double
- string
```
np.ones(shape=(2, 3), dtype="string")
np.zeros(shape=(2, 3), dtype=bool)
np.savetxt("eye.txt", np.eye(5, 6))
np.loadtxt("eye.txt")
%rm eye.txt
```
## Array operations
```
a = np.linspace(0, 9, num=10)
a + 1
a * a
a - a
print a.max()
print a.min()
np.sum(a)
a = np.random.standard_normal(size=(25, ))
a
b = a.reshape((5, 5))
b
b.T
np.sum(b)
print np.sum(b, axis=1)
print np.sum(b, axis=0)
### Matrix multiplication
np.dot(b, b)
np.vstack([b, b])
```
### Custom functions
```
def plus(x, y):
return x + y
plus_v = np.vectorize(plus)
plus_v(np.arange(10), np.arange(10, 20))
plus_v(np.arange(10), 10)
@np.vectorize
def plus(x, y):
return x + y
plus(np.arange(10), 10)
```
### Performance
```
N = 10000000
a = np.random.standard_normal(size=N)
b = np.random.standard_normal(size=N)
%%time
a + b
ab = zip(range(N), range(N))
%%time
_ = [ a + b for a, b in ab ]
```
### Slices
```
a = np.arange(15)
a = a.reshape((3,5))
a
# Just a copy of the array
a[:]
a[:, 0]
a[1, :]
a[2, :] = (np.arange(5) + 1) * 10
a
a < 10
a[a < 12]
np.where(a < 12)
xs, ys = np.where(a < 20)
a[xs, ys]
```
## Matplotlib
```
import matplotlib.pyplot as plt
# Don't forget this magic expression if want to show plots in notebook
%matplotlib inline
xs = np.arange(100)
ys = np.cumsum(np.random.standard_normal(size=100))
```
### Line plot
```
plt.figure()
plt.plot(xs, ys)
plt.show()
# A little bit of options
plt.figure()
plt.plot(xs, ys, label="1st series", color="green")
plt.plot(xs, ys.max() - ys, label="2nd series", color="red")
plt.legend(loc="upper right")
plt.xlabel("Time, sec")
plt.ylabel("Something")
plt.title("Just two random series")
plt.show()
```
### Bar plot
```
plt.figure()
plt.bar(xs, ys)
plt.show()
plt.figure()
h, bins, patches = plt.hist(ys)
plt.show()
```
### Scatter plot
```
xs1 = np.random.standard_normal(size=100)
ys1 = np.random.standard_normal(size=100)
xs2 = np.random.standard_normal(size=100) + 3
ys2 = np.random.standard_normal(size=100)
plt.scatter(xs1, ys1, label="class1", color="green")
plt.scatter(xs2, ys2, label="class2", color="red")
plt.plot([1.5, 1.5], [-4, 4], linewidth=3)
plt.legend()
```
### Images
```
means=np.array([[-1, 1], [-1, 1]])
stds = np.array([1, 1.1])
@np.vectorize
def normal_density(mx, my, std, x, y):
return np.exp(
-((x - mx) ** 2 + (y - my) ** 2) / 2.0 / std / std
) / std / std
@np.vectorize
def f(x, y):
return np.sum(
normal_density(means[0, :], means[1, :], stds, x, y)
)
mx, my = np.meshgrid(np.linspace(-2, 2, 100), np.linspace(-2, 2, 100))
fs = f(mx, my)
plt.contourf(mx, my, fs, 20, cmap=plt.cm.coolwarm)
plt.colorbar()
plt.contour(mx, my, fs, 20, cmap=plt.cm.coolwarm)
plt.colorbar()
plt.matshow(fs)
plt.colorbar()
plt.imshow(fs)
plt.colorbar()
plt.imshow(np.rot90(fs), extent=[-2, 2, -2, 2])
plt.colorbar()
plt.contour(mx, my, fs, 15, colors="black")
```
# Exercises
- load MNIST dataset
- create arrays of features and labels
- write a procedure to plot digits
- calculate mean, std of images for each class, plot the results
- plot distribution of pixel values: general, for different classes
- *find out which pixel has the most information about label (advanced)*
- *make 3D plots using mplot3d or plotly (advanced)*
| true |
code
| 0.504761 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
from scipy.optimize import minimize
import networkx as nx
from networkx.generators.random_graphs import erdos_renyi_graph
from IPython.display import Image
from qiskit import QuantumCircuit, execute, Aer
from qiskit.tools.visualization import circuit_drawer, plot_histogram
from quantuminspire.credentials import get_authentication
from quantuminspire.api import QuantumInspireAPI
from quantuminspire.qiskit import QI
QI_URL = 'https://api.quantum-inspire.com/'
```
In this notebook you will apply what you have just learned about cqasm and Quantum Inspire. We will consider a simple quantum algorithm, the quantum approximate optimization algorithm (QAOA), for which you will code the circuit in cqasm and send some jobs to real quantum hardware on the Quantum Inspire platform.
## 1. Recap: QAOA and MAXCUT
### Introduction to the Quantum Approximate Optimization Algorithm
$$\newcommand{\ket}[1]{\left|{#1}\right\rangle}$$
$$\newcommand{\bra}[1]{\left\langle{#1}\right|}$$
$$\newcommand{\braket}[2]{\left\langle{#1}\middle|{#2}\right\rangle}$$
Consider some combinatorial optimization problem with objective function $C:x\rightarrow \mathbb{R}$ acting on $n$-bit strings $x\in \{0,1\}^n$, domain $\mathcal{D} \subseteq \{0,1\}^n$, and objective
\begin{align}
\max_{x \in \mathcal{D}} C(x).
\end{align}
In maximization, an approximate optimization algorithm aims to find a string $x'$ that achieves a desired approximation ratio $\alpha$, i.e.
\begin{equation}
\frac{C(x')}{C^*}\geq \alpha,
\end{equation}
where $C^* = \max_{x \in \mathcal{D}} C(x)$.
In QAOA, such combinatorial optimization problems are encoded into a cost Hamiltonian $H_C$, a mixing Hamiltonian $H_M$ and some initial quantum state $\ket{\psi_0}$. The cost Hamiltonian is diagonal in the computational basis by design, and represents $C$ if its eigenvalues satisfy
\begin{align}
H_C \ket{x} = C(x) \ket{x} \text{ for all } x \in \{0,1\}^n.
\end{align}
The mixing Hamiltonian $H_M$ depends on $\mathcal{D}$ and its structure, and is in the unconstrained case (i.e. when $\mathcal{D}=\{0,1\}^n$) usually taken to be the transverse field Hamiltonian $H_M = \sum_{j} X_j$. Constraints (i.e. when $\mathcal{D}\subset \{0,1\}^n$) can be incorporated directly into the mixing Hamiltonian or are added as a penalty function in the cost Hamiltonian. The initial quantum state $\ket{\psi_0}$ is usually taken as the uniform superposition over all possible states in the domain. $\text{QAOA}_p$, parametrized in $\gamma=(\gamma_0,\gamma_1,\dots,\gamma_{p-1}),\beta=(\beta_0,\beta_1,\dots,\beta_{p-1})$, refers to a level-$p$ QAOA circuit that applies $p$ steps of alternating time evolutions of the cost and mixing Hamiltonians on the initial state. At step $k$, the unitaries of the time evolutions are given by
\begin{align}
U_C(\gamma_k) = e^{-i \gamma_k H_C }, \label{eq:UC} \\
U_M(\beta_k) = e^{-i \beta_k H_M }. \label{eq:UM}
\end{align}
So the final state $\ket{\gamma,\beta}$ of $\text{QAOA}_p$ is given by
\begin{align}
\ket{\gamma,\beta} = \prod_{k=0}^{p-1} U_M(\beta_k) U_C(\gamma_k) \ket{\psi_0}.
\end{align}
The expectation value $ F_p(\gamma,\beta)$ of the cost Hamiltonian for state $\ket{\gamma,\beta}$ is given by
\begin{align}
F_p(\gamma,\beta) =
\bra{\gamma,\beta}H_C\ket{\gamma,\beta},
\label{eq:Fp}
\end{align}
and can be statistically estimated by taking samples of $\ket{\gamma,\beta}$. The achieved approximation ratio (in expectation) of $\text{QAOA}_p$ is then
\begin{equation}
\alpha = \frac{F_p(\gamma,\beta)}{C^*}.
\end{equation}
The parameter combinations of $\gamma,\beta$ are usually found through a classical optimization procedure that uses $F_p(\gamma,\beta)$ as a black-box function to be maximized.
### Example application: MAXCUT
MaxCut is an NP-hard optimisation problem that looks for an optimal 'cut' for a graph $G(V,E)$, in the sense that the cut generates a subset of nodes $S \subset V$ that shares the largest amount of edges with its complement $ V\setminus S$. In slightly modified form (omitting the constant), it has the following objective function
\begin{align}
\max_{s} \frac{1}{2} \sum_{
\langle i,j \rangle \in E} 1-s_i s_j,
\end{align}
where the $s_i\in\{-1,1\}$ are the variables and $i,j$ are the edge indices. This function can be easily converted into an Ising cost Hamiltonian, which takes the form
\begin{align}
H_C = \frac{1}{2}\sum_{\langle i,j\rangle \in E} I-Z_i Z_j.
\end{align}
We use the standard mixing Hamiltonian that sums over all nodes:
\begin{align}
H_M = \sum_{v \in V} X_v.
\end{align}
As the initial state $\ket{\Psi_0}$ we take the uniform superposition, given by
\begin{align}
\ket{\psi_0} = \frac{1}{\sqrt{2^{|V|}}}\sum_{x=0}^{2^{|V|}-1} \ket{x}
\end{align}
The goal of this workshop is to guide you through an implemented code that simulates a small quantum computer running the QAOA algorithm applied to the MAXCUT problem. We will use qiskit as well as cqasm as SDK's. For the sake of run time, you will always run the classical optimization part using the qiskit simulator: it would take too long for our purposes to do the actual function evualtions in the classical optimization step on the hardware.
## 2. Some useful functions and intializations
We first define some useful functions to be used later throughout the code.
```
# Just some function to draw graphs
def draw_cc_graph(G,node_color='b',fig_size=4):
plt.figure(figsize=(fig_size,fig_size))
nx.draw(G, G.pos,
node_color= node_color,
with_labels=True,
node_size=1000,font_size=14)
plt.show()
# Define the objective function
def maxcut_obj(x,G):
cut = 0
for i, j in G.edges():
if x[i] != x[j]:
# the edge is cut, negative value in agreement with the optimizer (which is a minimizer)
cut -= 1
return cut
# Brute force method
def brute_force(G):
n = len(G.nodes)
costs = np.zeros(0)
costs=[]
for i in range(2**n):
calc_costs = -1*maxcut_obj(bin(i)[2:].zfill(n),G)
costs.append(calc_costs)
max_costs_bf = max(costs)
index_max = costs.index(max(costs))
max_sol_bf = bin(index_max)[2:].zfill(n)
return max_costs_bf, max_sol_bf,costs
# Generating the distribution resulting from random guessing the solution
def random_guessing_dist(G):
dictio= dict()
n = len(G.nodes())
for i in range(2**n):
key = bin(i)[2:].zfill(n)
dictio[key] = maxcut_obj(bin(i)[2:].zfill(n),G)
RG_energies_dist = defaultdict(int)
for x in dictio:
RG_energies_dist[maxcut_obj(x,G)] += 1
return RG_energies_dist
# Visualize multiple distributions
def plot_E_distributions(E_dists,p,labels):
plt.figure()
x_min = 1000
x_max = - 1000
width = 0.25/len(E_dists)
for index,E_dist in enumerate(E_dists):
pos = width*index-width*len(E_dists)/4
label = labels[index]
X_list,Y_list = zip(*E_dist.items())
X = -np.asarray(X_list)
Y = np.asarray(Y_list)
plt.bar(X + pos, Y/np.sum(Y), color = 'C'+str(index), width = width,label= label+', $p=$'+str(p))
if np.min(X)<x_min:
x_min = np.min(X)
if np.max(X)>x_max:
x_max = np.max(X)
plt.xticks(np.arange(x_min,x_max+1))
plt.legend()
plt.xlabel('Objective function value')
plt.ylabel('Probability')
plt.show()
# Determinet the expected objective function value from the random guessing distribution
def energy_random_guessing(RG_energies_dist):
energy_random_guessing = 0
total_count = 0
for energy in RG_energies_dist.keys():
count = RG_energies_dist[energy]
energy_random_guessing += energy*count
total_count += count
energy_random_guessing = energy_random_guessing/total_count
return energy_random_guessing
```
### Test instances
```
w2 = np.matrix([
[0, 1],
[1, 0]])
G2 = nx.from_numpy_matrix(w2)
positions = nx.circular_layout(G2)
G2.pos=positions
print('G2:')
draw_cc_graph(G2)
w3 = np.matrix([
[0, 1, 1],
[1, 0, 1],
[1, 1, 0]])
G3 = nx.from_numpy_matrix(w3)
positions = nx.circular_layout(G3)
G3.pos=positions
print('G3:')
draw_cc_graph(G3)
```
## 3. Circuit generators
We provide you with an example written in qiskit. You have to write the one for cqasm yourself.
### Qiskit generators
```
class Qiskit(object):
# Cost operator:
def get_cost_operator_circuit(G, gamma):
N = G.number_of_nodes()
qc = QuantumCircuit(N,N)
for i, j in G.edges():
qc.cx(i,j)
qc.rz(2*gamma, j)
qc.cx(i,j)
return qc
# Mixing operator
def get_mixer_operator_circuit(G, beta):
N = G.number_of_nodes()
qc = QuantumCircuit(N,N)
for n in G.nodes():
qc.rx(2*beta, n)
return qc
# Build the circuit:
def get_qaoa_circuit(G, beta, gamma):
assert(len(beta) == len(gamma))
p = len(beta) # number of unitary operations
N = G.number_of_nodes()
qc = QuantumCircuit(N,N)
# first step: apply Hadamards to obtain uniform superposition
qc.h(range(N))
# second step: apply p alternating operators
for i in range(p):
qc.compose(Qiskit.get_cost_operator_circuit(G,gamma[i]),inplace=True)
qc.compose(Qiskit.get_mixer_operator_circuit(G,beta[i]),inplace=True)
# final step: measure the result
qc.barrier(range(N))
qc.measure(range(N), range(N))
return qc
# Show the circuit for the G3 (triangle) graph
p = 1
beta = np.random.rand(p)*2*np.pi
gamma = np.random.rand(p)*2*np.pi
qc = Qiskit.get_qaoa_circuit(G3,beta, gamma)
qc.draw(output='mpl')
```
### cqasm generators
Now it is up to you to apply what we have learned about cqasm to write the script for the cost and mixing operators:
```
class Cqasm(object):
### We give them this part
def get_qasm_header(N_qubits):
"""
Create cQASM header for `N_qubits` qubits and prepare all in |0>-state.
"""
header = f"""
version 1.0
qubits {N_qubits}
prep_z q[0:{N_qubits-1}]
"""
return header
def get_cost_operator(graph, gamma, p=1):
"""
Create cost operator for given angle `gamma`.
"""
layer_list = graph.number_of_edges()*[None]
for n, (i,j) in enumerate(graph.edges()):
layer_list[n] = '\n'.join([f"CNOT q[{i}], q[{j}]",
f"Rz q[{j}], {2*gamma}",
f"CNOT q[{i}], q[{j}]"])
return f".U_gamma_{p}\n" + '\n'.join(layer_list) + '\n'
def get_mixing_operator(graph, beta, p=1):
"""
Create mixing operator for given angle `beta`.
Use parallel application of single qubit gates.
"""
U_beta = "{" + ' | '.join([f"Rx q[{i}], {2*beta}" for i in graph.nodes()]) + "}"
return f".U_beta_{p}\n" + U_beta + '\n'
def get_qaoa_circuit(graph, beta, gamma):
"""
Create full QAOA circuit for given `graph` and angles `beta` and `gamma`.
"""
assert len(beta) == len(gamma)
p = len(beta) # number of layers
N_qubits = graph.number_of_nodes()
circuit_str = Cqasm.get_qasm_header(5) #N_qubits)
# first step: apply Hadamards to obtain uniform superposition
circuit_str += "{" + ' | '.join([f"H q[{i}]" for i in graph.nodes()]) + "}\n\n"
# second step: apply p alternating operators
circuit_str += '\n'.join([Cqasm.get_cost_operator(graph, gamma[i], i+1)
+ Cqasm.get_mixing_operator(graph, beta[i], i+1) for i in range(p)])
# final step: measure the result
circuit_str += "\n"
circuit_str += "measure_all"
return circuit_str
```
## 4. Hybrid-quantum classical optimization
Since QAOA is usually adopted as a hybrid quantum-classical algorithm, we need to construct an outer loop which optimizes the estimated $\bra{\gamma,\beta}H\ket{\gamma,\beta}$.
```
# Black-box function that describes the energy output of the QAOA quantum circuit
def get_black_box_objective(G, p, SDK = 'qiskit', backend = None, shots=2**10):
if SDK == 'cqasm':
if not backend:
backend = 'QX single-node simulator'
backend_type = qi.get_backend_type_by_name(backend)
def f(theta):
# first half is betas, second half is gammas
beta = theta[:p]
gamma = theta[p:]
qc = Cqasm.get_qaoa_circuit(G, beta, gamma)
result = qi.execute_qasm(qc, backend_type=backend_type, number_of_shots=shots)
counts = result['histogram']
# return the energy
return compute_maxcut_energy(counts, G)
if SDK == 'qiskit':
if not backend:
backend = 'qasm_simulator'
backend = Aer.get_backend(backend)
def f(theta):
# first half is betas, second half is gammas
beta = theta[:p]
gamma = theta[p:]
qc = Qiskit.get_qaoa_circuit(G,beta, gamma)
counts = execute(qc, backend,shots=shots).result().get_counts()
# return the energy
return compute_maxcut_energy(counts, G)
else:
return 'error: SDK not found'
return f
# Estimate the expectation value based on the circuit output
def compute_maxcut_energy(counts, G):
energy = 0
total_counts = 0
for meas, meas_count in counts.items():
obj_for_meas = maxcut_obj(meas, G)
energy += obj_for_meas * meas_count
total_counts += meas_count
return energy / total_counts
```
## 5. A simple instance on the quantum inspire platform: 2-qubit case
Let us first consider the most simple MAXCUT instance. We have just two nodes, and an optimal cut with objective value 1 would be to place both nodes in its own set.
```
G=G2
max_costs_bf, max_sol_bf,costs = brute_force(G)
print("brute force method best cut: ",max_costs_bf)
print("best string brute force method:",max_sol_bf)
colors = ['red' if x == '0' else 'b' for x in max_sol_bf]
draw_cc_graph(G,node_color = colors)
```
Using qiskit, the circuit would look the following:
```
# Test and show circuit for some beta,gamma
p = 1
beta = np.random.rand(p)*np.pi
gamma = np.random.rand(p)*2*np.pi
qc = Qiskit.get_qaoa_circuit(G,beta, gamma)
qc.draw(output='mpl')
```
Now let's run our hybrid-quantum algorithm simulation using qiskit:
```
# Parameters that can be changed:
p = 1
lb = np.zeros(2*p)
ub = np.hstack([np.full(p, np.pi), np.full(p, 2*np.pi)])
init_point = np.random.uniform(lb, ub, 2*p)
shots = 2**10
optimiser = 'COBYLA'
max_iter = 100
# Training of the parameters beta and gamma
obj = get_black_box_objective(G,p,SDK='qiskit',shots=shots)
# Lower and upper bounds: beta \in {0, pi}, gamma \in {0, 2*pi}
bounds = [lb,ub]
# Maximum number of iterations: 100
res = minimize(obj, init_point, method=optimiser, bounds = bounds, options={'maxiter':max_iter, 'disp': True})
print(res)
#Determine the approximation ratio:
print('Approximation ratio is',-res['fun']/max_costs_bf)
# Extract the optimal values for beta and gamma and run a new circuit with these parameters
optimal_theta = res['x']
qc = Qiskit.get_qaoa_circuit(G, optimal_theta[:p], optimal_theta[p:])
counts = execute(qc,backend = Aer.get_backend('qasm_simulator'),shots=shots).result().get_counts()
plt.bar(counts.keys(), counts.values())
plt.xlabel('String')
plt.ylabel('Count')
plt.show()
RG_dist = random_guessing_dist(G)
# Measurement distribution
E_dist = defaultdict(int)
for k, v in counts.items():
E_dist[maxcut_obj(k,G)] += v
plot_E_distributions([E_dist,RG_dist],p,['Qiskit','random guessing'])
E_random_guessing = energy_random_guessing(RG_dist)
print('Energy from random guessing is', E_random_guessing)
X_list,Y_list = zip(*E_dist.items())
X = -np.asarray(X_list)
Y = np.asarray(Y_list)
print('Probability of measuring the optimal solution is',Y[np.argmax(X)]/shots)
```
Now that we have obtained some good values for $\beta$ and $\gamma$ through classical simulation, let's see what Starmon-5 would give us.
The figure below shows the topology of Starmon-5. Since q0 is not connected to q1, we have to relabel the nodes. Networkx as such an option, by using 'nx.relabel_nodes(G,{1:2}' we can relabel node 1 as node 2. Since q0 is connected to q2, this does allow us to run our cqasm code on Starmon-5. For qiskit, this step is irrelevant as we have all-to-all connectivity in the simulation.
```
Image(filename='Starmon5.png')
qc_Cqasm = Cqasm.get_qaoa_circuit(nx.relabel_nodes(G, {1: 2}), optimal_theta[:p], optimal_theta[p:])
print(qc_Cqasm)
```
Now we run the Cqasm-circuit on the Starmon-5 Hardware.
```
authentication = get_authentication()
QI.set_authentication(authentication, QI_URL)
qiapi = QuantumInspireAPI(QI_URL, authentication)
result = qiapi.execute_qasm(qc_Cqasm, backend_type=qiapi.get_backend_type('Starmon-5'), number_of_shots=2**10)
counts_QI = result['histogram']
```
Inspecting 'counts_QI', we see that it returns the integer corresponding to the bit string result of the measurement
```
counts_QI
```
Note that we measure more than just the two relevant qubits, since we had the 'measure all' command in the the cqasm code. The distribution over the strings looks the following:
```
counts_bin = {}
for k,v in counts_QI.items():
counts_bin[f'{int(k):05b}'] = v
print(counts_bin)
plt.bar(counts_bin.keys(), counts_bin.values())
plt.xlabel('State')
plt.ylabel('Measurement probability')
plt.xticks(rotation='vertical')
plt.show()
```
Let's create another counts dictionary with only the relevant qubits, which are q0 and q2:
```
counts_bin_red = defaultdict(float)
for string in counts_bin:
q0 = string[-1]
q1 = string[-3]
counts_bin_red[(q0+q1)]+=counts_bin[string]
counts_bin_red
```
We now plot all distributions (qiskit, Starmon-5, and random guessing) in a single plot.
```
#Determine the approximation ratio:
print('Approximation ratio on the hardware is',-compute_maxcut_energy(counts_bin_red,G)/max_costs_bf)
# Random guessing distribution
RG_dist = random_guessing_dist(G)
# Measurement distribution
E_dist_S5 = defaultdict(int)
for k, v in counts_bin_red.items():
E_dist_S5[maxcut_obj(k,G)] += v
plot_E_distributions([E_dist,E_dist_S5,RG_dist],p,['Qiskit','Starmon-5','random guessing'])
X_list,Y_list = zip(*E_dist_S5.items())
X = -np.asarray(X_list)
Y = np.asarray(Y_list)
print('Probability of measuring the optimal solution is',Y[np.argmax(X)])
E_random_guessing = energy_random_guessing(RG_dist)
print('Expected approximation ratio random guessing is', -E_random_guessing/max_costs_bf)
```
## 6. Compilation issues: the triangle graph
For the graph with just two nodes we already had some minor compilation issues, but this was easily fixed by relabeling the nodes. We will now consider an example for which relabeling is simply not good enough to get it mapped to the Starmon-5 toplogy.
```
G=G3
max_costs_bf, max_sol_bf,costs = brute_force(G)
print("brute force method best cut: ",max_costs_bf)
print("best string brute force method:",max_sol_bf)
colors = ['red' if x == '0' else 'b' for x in max_sol_bf]
draw_cc_graph(G,node_color = colors)
```
Due to the topology of Starmon-5 this graph cannot be executed without any SWAPS. Therefore, we ask you to write a new circuit generator that uses SWAPS in order to make the algorithm work with the Starmon-5 topology. Let's also swap back to the original graph configuration, so that we can in the end measure only the qubits that correspond to a node in the graph (this is already written for you)
```
def QAOA_triangle_circuit_cqasm(graph, beta, gamma):
circuit_str = Cqasm.get_qasm_header(5)
circuit_str += "{" + ' | '.join([f"H q[{i}]" for i in graph.nodes()]) + "}\n\n"
def get_triangle_cost_operator(graph, gamma, p):
layer_list = graph.number_of_edges() * [None]
for n, edge in enumerate(graph.edges()):
if 0 in edge and 1 in edge:
layer_list[n] = '\n'.join([f"SWAP q[{edge[0]}], q[2]",
f"CNOT q[2], q[{edge[1]}]",
f"Rz q[{edge[1]}], {2*gamma}",
f"CNOT q[2], q[{edge[1]}]",
f"SWAP q[{edge[0]}], q[2]" ])
else:
layer_list[n] = '\n'.join([f"CNOT q[{edge[0]}], q[{edge[1]}]",
f"Rz q[{edge[1]}], {2*gamma}",
f"CNOT q[{edge[0]}], q[{edge[1]}]"])
return f".U_gamma_{p}\n" + '\n'.join(layer_list) + '\n'
circuit_str += '\n'.join([get_triangle_cost_operator(graph, gamma[i], i+1)
+ Cqasm.get_mixing_operator(graph, beta[i], i+1) for i in range(p)])
circuit_str += "\n"
circuit_str += "{" + ' | '.join([f"measure q[{i}]" for i in graph.nodes()]) + "}\n"
return circuit_str
```
We now run the same procedure as before to obtain good parameter values
```
# Parameters that can be changed:
p = 1
lb = np.zeros(2*p)
ub = np.hstack([np.full(p, np.pi), np.full(p, 2*np.pi)])
init_point = np.random.uniform(lb, ub, 2*p)
shots = 2**10
optimiser = 'COBYLA'
max_iter = 100
# Training of the parameters beta and gamma
obj = get_black_box_objective(G,p,SDK='qiskit',shots=shots)
# Lower and upper bounds: beta \in {0, pi}, gamma \in {0, 2*pi}
bounds = [lb,ub]
# Maximum number of iterations: 100
res = minimize(obj, init_point, method=optimiser, bounds = bounds,options={'maxiter':max_iter, 'disp': True})
print(res)
#Determine the approximation ratio:
print('Approximation ratio is',-res['fun']/max_costs_bf)
# Extract the optimal values for beta and gamma and run a new circuit with these parameters
optimal_theta = res['x']
qc = Qiskit.get_qaoa_circuit(G, optimal_theta[:p], optimal_theta[p:])
counts = execute(qc,backend = Aer.get_backend('qasm_simulator'),shots=shots).result().get_counts()
# Random guessing distribution
RG_dist = random_guessing_dist(G)
# Measurement distribution
E_dist = defaultdict(int)
for k, v in counts.items():
E_dist[maxcut_obj(k,G)] += v
X_list,Y_list = zip(*E_dist.items())
X = -np.asarray(X_list)
Y = np.asarray(Y_list)
print('Probability of measuring the optimal solution is',Y[np.argmax(X)]/shots)
E_random_guessing = energy_random_guessing(RG_dist)
print('Expected approximation ratio random guessing is', -E_random_guessing/max_costs_bf)
plt.bar(counts.keys(), counts.values())
plt.xlabel('String')
plt.ylabel('Count')
plt.show()
```
Let's run it on Starmon-5 again!
```
# Extract the optimal values for beta and gamma and run a new circuit with these parameters
optimal_theta = res['x']
qasm_circuit = QAOA_triangle_circuit_cqasm(G, optimal_theta[:p], optimal_theta[p:])
qiapi = QuantumInspireAPI(QI_URL, authentication)
result = qiapi.execute_qasm(qasm_circuit, backend_type=qiapi.get_backend_type('Starmon-5'), number_of_shots=shots)
counts = result['histogram']
print(qasm_circuit)
print(result)
counts
counts_bin = {}
for k,v in counts.items():
counts_bin[f'{int(k):03b}'] = v
print(counts_bin)
plt.bar(counts_bin.keys(), counts_bin.values())
plt.xlabel('String')
plt.ylabel('Probability')
plt.show()
#Determine the approximation ratio:
print('Approximation ratio on the hardware is',-compute_maxcut_energy(counts_bin,G)/max_costs_bf)
# Random guessing distribution
RG_dist = random_guessing_dist(G)
# Measurement distribution
E_dist_S5 = defaultdict(int)
for k, v in counts_bin.items():
E_dist_S5[maxcut_obj(k,G)] += v
plot_E_distributions([E_dist,E_dist_S5,RG_dist],p,['Qiskit','Starmon-5','random guessing'])
X_list,Y_list = zip(*E_dist_S5.items())
X = -np.asarray(X_list)
Y = np.asarray(Y_list)
print('Probability of measuring the optimal solution is',Y[np.argmax(X)])
E_random_guessing = energy_random_guessing(RG_dist)
print('Expected approximation ratio random guessing is', -E_random_guessing/max_costs_bf)
```
## 7. More advanced questions
Some questions you could look at:
- What is the performance on other graph instances?
- How scalable is this hardware for larger problem sizes?
- How much can the circuit be optimized for certain graph instances?
- Are the errors perfectly random or is there some correlation?
- Are there tricks to find good parameters?
| true |
code
| 0.687879 | null | null | null | null |
|
##### Detection and Location Chain
**Abstract**: This hackathon project represents our effort to combine our existing machine learning and photogrametry efforts and further combine those efforts with both Cloud and Edge based solutions based upon Xilinx FPGA acceleration.
The Trimble team decided that the Xilinx hackathon would provide an excellent oppertunity to take the first steps in combining these technologies and learning how to use the varied Xilinx techologies.
Our initial hope was to use a TensorFlow system to provide the machine learning component of our test based on an AWS Ultrascale instance. That technology was unavailable for the hackathon, so during the event we trained a system based on a more stardard AWS Tensorflow instance and accessed that instance via Pynq networking.
The Team Trimble is composed of
* Roy Godzdanker – Trimble Product Architect for ICT
* Robert Banefield – Trimble Data Machine Learning Specialist
* Vinod Khare – Trimble ICT Photogrammetry
* Ashish Khare – Trimble Geomatics Photogrammetry
* Young-Jin Lee – Trimble ICT Photogrammetry
* Matt Compton - Trimble ICT Design Engineer
_NOTES_:
1. The TensorFlow system is sitting at an AWS instance. This is the slow and simple one for my debug effort. In the spirit of the hackathon, we started in training at the beginning of the night. This implies that it's capabilities were not exceptional at the beginning of the night and it will be better as the newly trained net is swapped in in the morning. Further tests back at the ranch will include testing this chain against some of the other theoretical models. The current net underperforms some previous efforts, further exploration is needed here
2. We also need to explore the TensorFlow element as an edge device. Advances in Xilinx FPGA tools may make that cost competative with a GPU box.
3. Xilinx HLS looks to be able to add needed acceleration functions but this needs further exploration going forward. We explored the idea of overly with python controled DMA, this is very promising
The following are globals used within this project To Change this to different image set, simply change the images indicated and run through the notebook again.
1. Camera data is sent to the system from a remote repository.
2. The Camera Data is sent to the Pynq to being processing.
3. The TensorFlow cloud delivers metadata for the images that were transferred to it back to the Pynq via net transfer
4. The Pynq software uses the photogrammetric OpenCV software chain that we wrote to estimate and calculate geometric position. In addition, images are displayed on the HDMI monitor and LCD display so we can see what is going on and to serve as a debug aid
5. The calculated position of the object is returned.
```
## Imports
import cv2
import json
import matplotlib.pyplot as pyplot
import numpy
import matplotlib.patches as patches
import pynq.overlays.base
import pynq.lib.arduino as arduino
import pynq.lib.video as video
import requests
import scipy
import sys
import PIL
## Config
gAWS_TENSORFLOW_INSTANCE = 'http://34.202.159.80'
gCAMERA0_IMAGE = "/home/xilinx/jupyter_notebooks/trimble-mp/CAM2_image_0032.jpg"
gCAMERA1_IMAGE = "/home/xilinx/jupyter_notebooks/trimble-mp/CAM3_image_0032.jpg"
```
Turn on the HDMI coming off the pink board. This is used in a fashion that is different than their primary test notes and may be difficult to complete during the time period. Specifically, the hdmi out is used without the input
```
base = pynq.overlays.base.BaseOverlay("base.bit")
hdmi_in = base.video.hdmi_in
hdmi_out = base.video.hdmi_out
v = video.VideoMode(1920,1080,24)
hdmi_out.configure(v, video.PIXEL_BGR)
hdmi_out.start()
outframe = hdmi_out.newframe()
```
Using Pillow, pull in the chosen image for Camera 0
```
# Read images
image0BGR = cv2.imread(gCAMERA0_IMAGE)
image1BGR = cv2.imread(gCAMERA1_IMAGE)
image0 = image0BGR[...,::-1]
image1 = image1BGR[...,::-1]
```
Do exactly the same for the second image of the overlapping pair from camera 1
To send one of these to the HDMI, we are going to have to reformat it to fit the provided HDMI display
```
# Show image 0 on HDMI
# Need to resize it first
outframe[:] = cv2.resize(image0BGR, (1920, 1080));
hdmi_out.writeframe(outframe)
```
We will also display Young-Jin to the LCD screen. Why ? Because Young Jin does awesome work and deserves to be famous and also because I can
```
## Show image on LCD
# Open LCD object and clear
lcd = arduino.Arduino_LCD18(base.ARDUINO)
lcd.clear()
# Write image to disk
nw = 160
nl = 128
cv2.imwrite("/home/xilinx/small.jpg", cv2.resize(image0BGR, (nw,nl)))
# Display!
lcd.display("/home/xilinx/small.jpg",x_pos=0,y_pos=127,orientation=3,background=[255,255,255])
```
We now need to classify the images. This runs the remote version of TensorFlow on the image to get the bounding box. The following routine wraps this for simplicity. The spun up AWS TensorFlow instance is expecting to get be
sent a JPEG and will classify and send back the results as JSON.
The IP address of the spun up AWS instance is given by the global gAWS_TENSORFLOW_INSTANCE which is specified at the
beginning of this note book.
```
def RemoteTensorFlowClassify(image_name_string):
f = open(image_name_string,'rb')
r = requests.put(gAWS_TENSORFLOW_INSTANCE, data=f)
return json.loads(r.content.decode())
```
Actually call the defined function on images from camera 1 and camera 2.
```
#Return the object that camera zero sees with the maximum score
cam0_json_return = RemoteTensorFlowClassify(gCAMERA0_IMAGE)
json0 = cam0_json_return["image_detection"]
max = 0.0
out = []
for var in json0['object']:
if (var['score'] > max):
out = var
json0 = out
json0
#Return the object that camera one sees with the maximum score
cam1_json_return = RemoteTensorFlowClassify(gCAMERA1_IMAGE)
json1 = cam1_json_return["image_detection"]
max = 0.0
out = []
for var in json1['object']:
if (var['score'] > max):
out = var
json1 = out
json1
```
The AWS tensorflow reports the bounding boxes for the required object.
```
def DrawRect(the_json,the_image, x1, x2, y1, y2 ):
# Currently offline until the TesnorFlow net is fixed
#x1 = int(the_json["xmin"])
#y1 = int(the_json["ymin"])
#x2 = int(the_json["xmax"])
#y2 = int(the_json["ymax"])
fig, ax = pyplot.subplots(1)
ax.imshow(the_image)
rect = patches.Rectangle((x1,y1), (x2-x1), (y2-y1), linewidth = 1 , edgecolor = 'r', facecolor='none')
ax.add_patch(rect)
pyplot.show()
## Convert to grayscale
grayImage0 = cv2.cvtColor(image0, cv2.COLOR_RGB2GRAY)
grayImage1 = cv2.cvtColor(image1, cv2.COLOR_RGB2GRAY)
def IsInsideROI(pt, the_json, x1, x2, y1, y2):
# x_min = int(the_json["object"]["xmin"])
# y_min = int(the_json["object"]["ymin"])
# x_max = int(the_json["object"]["xmax"])
# y_max = int(the_json["object"]["ymax"])
x_min = x1
y_min = y1
x_max = x2
y_max = y2
if(pt[0]>=x_min and pt[0] <=x_max and pt[1]>=y_min and pt[1]<=y_max):
return True
else:
return False
## Detect keypoints
Brisk = cv2.BRISK_create()
keyPoints0 = Brisk.detect(grayImage0)
keyPoints1 = Brisk.detect(grayImage1)
## Find keypoints inside ROI
roiKeyPoints0 = numpy.asarray([k for k in keyPoints0 if IsInsideROI(k.pt,json0, 955, 1045, 740, 1275 )])
roiKeyPoints1 = numpy.asarray([k for k in keyPoints1 if IsInsideROI(k.pt,json1, 1335, 1465, 910, 1455 )])
## Compute descriptors for keypoitns inside ROI
[keyPoints0, desc0] = Brisk.compute(grayImage0, roiKeyPoints0);
[keyPoints1, desc1] = Brisk.compute(grayImage1, roiKeyPoints1);
## Find matches of ROI keypoints
BF = cv2.BFMatcher()
matches = BF.match(desc0, desc1)
## Extract pixel coordinates from matched keypoints
x_C0 = numpy.asarray([keyPoints0[match.queryIdx].pt for match in matches])
x_C1 = numpy.asarray([keyPoints1[match.trainIdx].pt for match in matches])
```
Full mesh triangularization is off line until we reconsile the camera calibration. There was an issue discovered during the hackathon that needs to be examined in teh lab setup s the code below this will not function until we reconsile the camera calibration config.
```
# Triangulate points
# We need projection matrices for camera 0 and camera 1
f = 8.350589e+000 / 3.45E-3
cx = -3.922872e-002 / 3.45E-3
cy = -1.396717e-004 / 3.45E-3
K_C0 = numpy.transpose(numpy.asarray([[f, 0, 0], [0, f, 0], [cx, cy, 1]]))
k_C0 = numpy.asarray([1.761471e-003, -2.920431e-005, -8.341438e-005, -9.470247e-006, -1.140118e-007])
[R_C0, J] = cv2.Rodrigues(numpy.asarray([1.5315866633, 2.6655790203, -0.0270418317]))
T_C0 = numpy.transpose(numpy.asarray([[152.9307390952, 260.3066944976, 351.7405264829]])) * 1000
f = 8.259861e+000 / 3.45E-3
cx = 8.397453e-002 / 3.45E-3
cy = -2.382030e-002 / 3.45E-3
K_C0 = numpy.transpose(numpy.asarray([[f, 0, 0], [0, f, 0], [cx, cy, 1]]))
K_C1 = numpy.asarray([1.660053e-003, -2.986269e-005, -7.461966e-008, -2.247960e-004, -2.290483e-006])
[R_C1, J] = cv2.Rodrigues(numpy.asarray([1.4200199799, -2.6113619450, -0.1371719827]))
T_C1 = numpy.transpose(numpy.asarray([[146.8718203137, 259.9661037150, 351.5832136366]])) * 1000
P_C0 = numpy.dot(K_C0,numpy.concatenate((R_C0, T_C0), 1))
P_C1 = numpy.dot(K_C1,numpy.concatenate((R_C1, T_C1), 1))
# Compute 3D coordinates of detected points
X_C0 = cv2.convertPointsFromHomogeneous(numpy.transpose(cv2.triangulatePoints(P_C0, P_C1, numpy.transpose(x_C0), numpy.transpose(x_C1))))
```
| true |
code
| 0.400046 | null | null | null | null |
|
## Make your own heatmap based on Strava activities
This notebook shows you how to create your own heatmap based on your Strava activities.
You need to create a Strava API application in order to use their API. Follow the instructions on this page to create your app: <https://medium.com/@annthurium/getting-started-with-the-strava-api-a-tutorial-f3909496cd2d>
After setting up the app, note down the following information (you will need it to run this notebook):
- Client id
- Client secret
**Note:** Strava imposes some request limits (30'000/day, and 600/every 15min).
```
!pip install stravaio folium
import os
import logging
import json
import urllib
import requests
import folium
from stravaio import StravaIO
# Paste your client id and client secret here.
STRAVA_CLIENT_ID = "ENTER-YOUR-CLIENT-ID"
STRAVA_CLIENT_SECRET = "ENTER-YOUR-CLIENT-SECRET"
```
### Authorization with Strava
The cell below creates the proper authorization link using the Stravaio Python library, which is used later to retrieve activities.
It is important to run this cell, just pasting the access_token from your Strava settings will not work, because Stravaio needs to be authorized.
- Run the cell below and click the link that is printed, when prompted click "Authorize" on the website that opens
- After you click "Authorize" you see something like, "This site can't be reached"
- Stay on that page and look at the URL
- The URL will show the authorization code (the bit after "code=" in the URL) and scope you accepted
- Copy the code and paste it below and continue the notebook execution
More detailed info can be found here:
- <https://developers.strava.com/docs/getting-started/>
- <https://developers.strava.com/docs/authentication/>
```
params_oauth = {
"client_id": STRAVA_CLIENT_ID,
"response_type": "code",
"redirect_uri": f"http://localhost:8000/authorization_successful",
"scope": "read,profile:read_all,activity:read",
"state": 'https://github.com/sladkovm/strava-http', # Sladkovm is the author of the Stravaio library
"approval_prompt": "force"
}
values_url = urllib.parse.urlencode(params_oauth)
base_url = 'https://www.strava.com/oauth/authorize'
authorize_url = base_url + '?' + values_url
print(authorize_url)
# Paste the code from the URL here. Afterwards there are no manual steps anymore.
AUTHORIZATION_CODE = "ENTER-YOUR-AUTHORIZATION-CODE"
```
The following cell retrieves an access token using the authorization code. That access token can then be used to retrieve Strava data.
```
payload = {
"client_id": STRAVA_CLIENT_ID,
"client_secret": STRAVA_CLIENT_SECRET,
"grant_type": "authorization_code",
"code": AUTHORIZATION_CODE,
}
response = requests.request(
"POST", "https://www.strava.com/api/v3/oauth/token", data=payload
)
response = json.loads(response.text)
TOKEN = response["access_token"]
!pip install stravaio folium
client = StravaIO(access_token=TOKEN)
athlete = client.get_logged_in_athlete()
activities = client.get_logged_in_athlete_activities(after=20170101)
m = folium.Map(
tiles="cartodbpositron",
location=[59.925, 10.728123],
zoom_start=11.5,
control_scale=True
)
folium.TileLayer("cartodbpositron").add_to(m)
folium.TileLayer("cartodbdark_matter").add_to(m)
folium.LayerControl().add_to(m)
def downsample(l, n):
"""Returns every nth element from list l. Returns the
original list if n is set to 1.
Used to reduce the number of GPS points per activity,
to improve performance of the website.
"""
return l[0::n]
def map_activities(activities, folium_map, opacity=0.5, weight=1):
if len(activities) == 0:
logging.info("No activities found, returning empty folium map.")
return folium_map
counter = 0
for a in activities:
if a.type == "Workout":
continue
streams = client.get_activity_streams(a.id, athlete.id)
try:
points = list(zip(streams.lat, streams.lng))
points = downsample(l=points, n=2)
if a.type == "Run":
folium.PolyLine(
locations=points, color="#ff9933", opacity=opacity, weight=weight
).add_to(folium_map)
elif a.type == "Ride":
folium.PolyLine(
locations=points, color="#0066ff", opacity=opacity, weight=weight
).add_to(folium_map)
elif a.type == "NordicSki":
folium.PolyLine(
locations=points, color="#00ffff", opacity=opacity, weight=weight
).add_to(folium_map)
elif a.type == "AlpineSki":
folium.PolyLine(
locations=points, color="#00ccff", opacity=opacity, weight=weight
).add_to(folium_map)
elif a.type == "Canoeing":
folium.PolyLine(
locations=points, color="#00ff55", opacity=opacity, weight=weight
).add_to(folium_map)
elif a.type == "IceSkate":
folium.PolyLine(
locations=points, color="#f6ff00", opacity=opacity, weight=weight
).add_to(folium_map)
else:
folium.PolyLine(
locations=points, color="#cc00ff", opacity=opacity, weight=weight
).add_to(folium_map)
logging.critical("Mapped activity with id: {}".format(a.id))
except Exception:
logging.error("Could not map activity with id: {}".format(a.id))
return folium_map
m = map_activities(
activities=activities,
folium_map=m,
opacity=0.5,
weight=2
)
m
```
| true |
code
| 0.461563 | null | null | null | null |
|
# <p style="text-align: center;"> Part Two: Scaling & Normalization </p>
```
from IPython.display import HTML
from IPython.display import Image
Image(url= "https://miro.medium.com/max/3316/1*yR54MSI1jjnf2QeGtt57PA.png")
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
The raw code for this IPython notebook is by default hidden for easier reading.
To toggle on/off the raw code, click <a href="javascript:code_toggle()">here</a>.''')
```
# <p style="text-align: center;"> Table of Contents </p>
- ## 1. [Introduction](#Introduction)
- ### 1.1 [Abstract](#abstract)
- ### 1.2 [Importing Libraries](#importing_libraries)
- ## 2. [Data Scaling](#data_scaling)
- ### 2.1 [Standardization](#standardization)
- ### 2.2 [Normalization](#normalization)
- ### 2.3 [The Big Question – Normalize or Standardize?](#the_big_question)
- ### 2.4 [Implementation](#implementation)
- #### 2.4.1 [Original Distributions](#original_distributions)
- #### 2.4.2 [Adding a Feature with Much Larger Values](#larger_values)
- #### 2.4.3 [MinMaxScaler](#min_max_scaler)
- #### 2.4.4 [StandardScaler](#standard_scaler)
- #### 2.4.5 [RobustScaler](#robust_scaler)
- #### 2.4.6 [Normalizer](#normalizer)
- #### 2.4.7 [Combined Plot](#combined_plot)
- ## 3. [Conclusion](#Conclusion)
- ## 4. [Contribution](#Contribution)
- ## 5. [Citation](#Citation)
- ## 6. [License](#License)
# <p style="text-align: center;"> 1.0 Introduction </p> <a id='Introduction'></a>
# 1.1 Abstract <a id='abstract'></a>
Welcome to the Data Cleaning
[Back to top](#Introduction)
# 1.2 Importing Libraries <a id='importing_libraries'></a>
This is the official start to any Data Science or Machine Learning Project. A Python library is a reusable chunk of code that you may want to include in your programs/ projects.
In this step we import a few libraries that are required in our program. Some major libraries that are used are Numpy, Pandas, MatplotLib, Seaborn, Sklearn etc.
[Back to top](#Introduction)
```
# modules we'll use
import pandas as pd
import numpy as np
# for Box-Cox Transformation
from scipy import stats
# for min_max scaling
from sklearn import preprocessing
from mlxtend.preprocessing import minmax_scaling
# plotting modules
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
from astropy.table import Table, Column
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
matplotlib.style.use('ggplot')
np.random.seed(34)
```
# 2.0 Data Scaling <a id='data_scaling'></a>
## Why Should we Use Feature Scaling?
The first question we need to address – why do we need to scale the variables in our dataset? Some machine learning algorithms are sensitive to feature scaling while others are virtually invariant to it.
Machine learning models learn a mapping from input variables to an output variable. As such, the scale and distribution of the data drawn from the domain may be different for each variable. Input variables may have different units (e.g. feet, kilometers, and hours) that, in turn, may mean the variables have different scales.
### Gradient Descent Based Algorithms
Machine learning algorithms like linear regression, logistic regression, neural network, etc. that use gradient descent as an optimization technique require data to be scaled. Take a look at the formula for gradient descent below:

The presence of feature value X in the formula will affect the step size of the gradient descent. The difference in ranges of features will cause different step sizes for each feature. To ensure that the gradient descent moves smoothly towards the minima and that the steps for gradient descent are updated at the same rate for all the features, we scale the data before feeding it to the model.
> Having features on a similar scale can help the gradient descent converge more quickly towards the minima.
### Distance-Based Algorithms
Distance algorithms like KNN, K-means, and SVM are most affected by the range of features. This is because behind the scenes they are using distances between data points to determine their similarity.
For example, let’s say we have data containing high school CGPA scores of students (ranging from 0 to 5) and their future incomes (in thousands Dollars):

Since both the features have different scales, there is a chance that higher weightage is given to features with higher magnitude. This will impact the performance of the machine learning algorithm and obviously, we do not want our algorithm to be biassed towards one feature.
> Therefore, we scale our data before employing a distance based algorithm so that all the features contribute equally to the result.

The effect of scaling is conspicuous when we compare the Euclidean distance between data points for students A and B, and between B and C, before and after scaling as shown below:

Scaling has brought both the features into the picture and the distances are now more comparable than they were before we applied scaling.
### Tree-Based Algorithms
Tree-based algorithms, on the other hand, are fairly insensitive to the scale of the features. Think about it, a decision tree is only splitting a node based on a single feature. The decision tree splits a node on a feature that increases the homogeneity of the node. This split on a feature is not influenced by other features.
So, there is virtually no effect of the remaining features on the split. This is what makes them invariant to the scale of the features!
One of the reasons that it's easy to get confused between scaling and normalization is because the terms are sometimes used interchangeably and, to make it even more confusing, they are very similar! In both cases, you're transforming the values of numeric variables so that the transformed data points have specific helpful properties.
[Back to top](#Introduction)
## 2.1 Standardization <a id='standardization'></a>
**Scaling (Standardization):** Change in the range of your data.
Differences in the scales across input variables may increase the difficulty of the problem being modeled. A model with large weight values is often unstable, meaning that it may suffer from poor performance during learning and sensitivity to input values resulting in higher generalization error.
This means that you're transforming your data so that it fits within a specific scale, like 0-100 or 0-1. You want to scale data when you're using methods based on measures of how far apart data points are, like support vector machines (SVM) or k-nearest neighbors (KNN). With these algorithms, a change of "1" in any numeric feature is given the same importance.
For example, you might be looking at the prices of some products in both Yen and US Dollars. One US Dollar is worth about 100 Yen, but if you don't scale your prices, methods like SVM or KNN will consider a difference in price of 1 Yen as important as a difference of 1 US Dollar! This clearly doesn't fit with our intuitions of the world. With currency, you can convert between currencies. But what about if you're looking at something like height and weight? It's not entirely clear how many pounds should equal one inch (or how many kilograms should equal one meter).
By scaling your variables, you can help compare different variables on equal footing
Standardization is scaling a technique where the values are centered around the mean with a unit standard deviation. This means that the mean of the attribute becomes zero and the resultant distribution has a unit standard deviation.
Here’s the formula for standardization:

- Mu is the mean of the feature values and
- Sigma is the standard deviation of the feature values. Note that in this case, the values are not restricted to a particular range.
[Back to top](#Introduction)
```
# generate 1000 data points randomly drawn from an exponential distribution
original_data = np.random.exponential(size=1000)
# mix-max scale the data between 0 and 1
scaled_data = minmax_scaling(original_data, columns=[0])
# plot both together to compare
fig, ax = plt.subplots(1,2)
sns.distplot(original_data, ax=ax[0])
ax[0].set_title("Original Data")
sns.distplot(scaled_data, ax=ax[1])
ax[1].set_title("Scaled data")
```
## 2.2 Normalization <a id='normalization'></a>
**Normalization:** Change in the shape of the distribution of data.
Normalization scales each input variable separately to the range 0-1, which is the range for floating-point values where we have the most precision. Normalization requires that you know or are able to accurately estimate the minimum and maximum observable values. You may be able to estimate these values from your available data.
Scaling just changes the range of your data. Normalization is a more radical transformation. The point of normalization is to change your observations so that they can be described as a normal distribution.
Normal distribution: Also known as the "bell curve", this is a specific statistical distribution where a roughly equal observations fall above and below the mean, the mean and the median are the same, and there are more observations closer to the mean. The normal distribution is also known as the Gaussian distribution.
In general, you'll normalize your data if you're going to be using a machine learning or statistics technique that assumes your data is normally distributed. Some examples of these include linear discriminant analysis (LDA) and Gaussian naive Bayes. (Pro tip: any method with "Gaussian" in the name probably assumes normality.)
Normalization is a scaling technique in which values are shifted and rescaled so that they end up ranging between 0 and 1. It is also known as Min-Max scaling.
Here’s the formula for normalization:

Here, Xmax and Xmin are the maximum and the minimum values of the feature respectively.
- When the value of X is the minimum value in the column, the numerator will be 0, and hence X’ is 0
- On the other hand, when the value of X is the maximum value in the column, the numerator is equal to the denominator and thus the value of X’ is 1
- If the value of X is between the minimum and the maximum value, then the value of X’ is between 0 and 1
**PS:-** The method we're using to normalize here is called the Box-Cox Transformation.
Now, the big question in your mind must be when should we use normalization and when should we use standardization? Let’s find out!
[Back to top](#Introduction)
```
# normalize the exponential data with boxcox
normalized_data = stats.boxcox(original_data)
# plot both together to compare
fig, ax=plt.subplots(1,2)
sns.distplot(original_data, ax=ax[0])
ax[0].set_title("Original Data")
sns.distplot(normalized_data[0], ax=ax[1])
ax[1].set_title("Normalized data")
```
## 2.3 The Big Question – Normalize or Standardize? <a id='the_big_question'></a>
Normalization vs. standardization is an eternal question among machine learning newcomers. Let me elaborate on the answer in this section.
- Normalization is good to use when you know that the distribution of your data does not follow a Gaussian distribution. This can be useful in algorithms that do not assume any distribution of the data like K-Nearest Neighbors and Neural Networks.
- Standardization, on the other hand, can be helpful in cases where the data follows a Gaussian distribution. However, this does not have to be necessarily true. Also, unlike normalization, standardization does not have a bounding range. So, even if you have outliers in your data, they will not be affected by standardization.
However, at the end of the day, the choice of using normalization or standardization will depend on your problem and the machine learning algorithm you are using. There is no hard and fast rule to tell you when to normalize or standardize your data. You can always start by fitting your model to raw, normalized and standardized data and compare the performance for best results.
It is a good practice to fit the scaler on the training data and then use it to transform the testing data. This would avoid any data leakage during the model testing process. Also, the scaling of target values is generally not required.
[Back to top](#Introduction)
## 2.4 Implementation <a id='implementation'></a>
This is all good in theory, but how do we implement it in real life. The sklearn library has various modules in the preprocessing section which implement these in different ways. The 4, that are most widely used and that we're going to implement here are:-
- **MinMaxScalar:** The MinMaxScaler transforms features by scaling each feature to a given range. This range can be set by specifying the feature_range parameter (default at (0,1)). This scaler works better for cases where the distribution is not Gaussian or the standard deviation is very small. However, it is sensitive to outliers, so if there are outliers in the data, you might want to consider another scaler.
> x_scaled = (x-min(x)) / (max(x)–min(x))
- **StandardScaler:** Sklearn its main scaler, the StandardScaler, uses a strict definition of standardization to standardize data. It purely centers the data by using the following formula, where u is the mean and s is the standard deviation.
> x_scaled = (x — u) / s
- **RobustScalar:** If your data contains many outliers, scaling using the mean and standard deviation of the data is likely to not work very well. In these cases, you can use the RobustScaler. It removes the median and scales the data according to the quantile range. The exact formula of the RobustScaler is not specified by the documentation. By default, the scaler uses the Inter Quartile Range (IQR), which is the range between the 1st quartile and the 3rd quartile. The quantile range can be manually set by specifying the quantile_range parameter when initiating a new instance of the RobustScaler.
- **Normalizer:**
- **‘l1’:** The l1 norm uses the sum of all the values as and thus gives equal penalty to all parameters, enforcing sparsity.
> x_normalized = x / sum(X)
- **‘l2’:** The l2 norm uses the square root of the sum of all the squared values. This creates smoothness and rotational invariance. Some models, like PCA, assume rotational invariance, and so l2 will perform better.
> x_normalized = x / sqrt(sum((i\**2) for i in X))
**`TLDR`**
- Use MinMaxScaler as your default
- Use RobustScaler if you have outliers and can handle a larger range
- Use StandardScaler if you need normalized features
- Use Normalizer sparingly - it normalizes rows, not columns
[Back to top](#Introduction)
### 2.4.1 Original Distributions <a id='original_distributions'></a>
Let's make several types of random distributions. We're doing this because when we deal with real world data, the data is not necessarily in a normal (Gaussian) distribution. Each type of scaling may have a different effect depending on the type of the distribution, thus we take examples of 5 different type of distributions here.
- **Beta:** The Beta distribution is a probability distribution on probabilities.
- **Exponential:** The exponential distribution is a probability distribution which represents the time between events in a Poisson process.
- **Normal (Platykurtic):** The term "platykurtic" refers to a statistical distribution in which the excess kurtosis value is negative. For this reason, a platykurtic distribution will have thinner tails than a normal distribution, resulting in fewer extreme positive or negative events.
- **Normal (Leptokurtic):** Leptokurtic distributions are statistical distributions with kurtosis over three. It is one of three major categories found in kurtosis analysis.
- **Bimodal:** The bimodal distribution has two peaks.
[Back to top](#Introduction)
```
#create columns of various distributions
df = pd.DataFrame({
'beta': np.random.beta(5, 1, 1000) * 60, # beta
'exponential': np.random.exponential(10, 1000), # exponential
'normal_p': np.random.normal(10, 2, 1000), # normal platykurtic
'normal_l': np.random.normal(10, 10, 1000), # normal leptokurtic
})
# make bimodal distribution
first_half = np.random.normal(20, 3, 500)
second_half = np.random.normal(-20, 3, 500)
bimodal = np.concatenate([first_half, second_half])
df['bimodal'] = bimodal
# create list of column names to use later
col_names = list(df.columns)
```
After defining the distributions, lets visualize them
```
# plot original distribution plot
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('Original Distributions')
sns.kdeplot(df['beta'], ax=ax1)
sns.kdeplot(df['exponential'], ax=ax1)
sns.kdeplot(df['normal_p'], ax=ax1)
sns.kdeplot(df['normal_l'], ax=ax1)
sns.kdeplot(df['bimodal'], ax=ax1);
df.describe()
df.plot()
```
As we can clearly see from the statistics and the plots, all values are in the same ball park. But what happens if we disturb this by adding a feature with much larger values.
### 2.4.2 Adding a Feature with Much Larger Values <a id='larger_values'></a>
This feature could be home prices, for example.
[Back to Top](#Introduction)
```
normal_big = np.random.normal(1000000, 10000, (1000,1)) # normal distribution of large values
df['normal_big'] = normal_big
col_names.append('normal_big')
df['normal_big'].plot(kind='kde')
df.normal_big.mean()
```
We've got a normalish distribution with a mean near 1,000,0000. But if we put this on the same plot as the original distributions, you can't even see the earlier columns.
```
# plot original distribution plot with larger value feature
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('Original Distributions')
sns.kdeplot(df['beta'], ax=ax1)
sns.kdeplot(df['exponential'], ax=ax1)
sns.kdeplot(df['normal_p'], ax=ax1)
sns.kdeplot(df['normal_l'], ax=ax1)
sns.kdeplot(df['bimodal'], ax=ax1);
sns.kdeplot(df['normal_big'], ax=ax1);
df.describe()
```
The new, high-value distribution is way to the right. And here's a plot of the values.
```
df.plot()
```
### 2.4.3 MinMaxScaler <a id='min_max_scaler'></a>
MinMaxScaler subtracts the column mean from each value and then divides by the range.
[Back to Top](#Introduction)
```
mm_scaler = preprocessing.MinMaxScaler()
df_mm = mm_scaler.fit_transform(df)
df_mm = pd.DataFrame(df_mm, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After MinMaxScaler')
sns.kdeplot(df_mm['beta'], ax=ax1)
sns.kdeplot(df_mm['exponential'], ax=ax1)
sns.kdeplot(df_mm['normal_p'], ax=ax1)
sns.kdeplot(df_mm['normal_l'], ax=ax1)
sns.kdeplot(df_mm['bimodal'], ax=ax1)
sns.kdeplot(df_mm['normal_big'], ax=ax1);
df_mm.describe()
```
Notice how the shape of each distribution remains the same, but now the values are between 0 and 1. Our feature with much larger values was brought into scale with our other features.
### 2.4.4 StandardScaler <a id='standard_scaler'></a>
StandardScaler is scales each column to have 0 mean and unit variance.
[Back to Top](#Introduction)
```
s_scaler = preprocessing.StandardScaler()
df_s = s_scaler.fit_transform(df)
df_s = pd.DataFrame(df_s, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After StandardScaler')
sns.kdeplot(df_s['beta'], ax=ax1)
sns.kdeplot(df_s['exponential'], ax=ax1)
sns.kdeplot(df_s['normal_p'], ax=ax1)
sns.kdeplot(df_s['normal_l'], ax=ax1)
sns.kdeplot(df_s['bimodal'], ax=ax1)
sns.kdeplot(df_s['normal_big'], ax=ax1);
```
You can see that all features now have 0 mean.
```
df_s.describe()
```
### 2.4.5 RobustScaler <a id='robust_scaler'></a>
RobustScaler subtracts the column median and divides by the interquartile range.
[Back to Top](#Introduction)
```
r_scaler = preprocessing.RobustScaler()
df_r = r_scaler.fit_transform(df)
df_r = pd.DataFrame(df_r, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After RobustScaler')
sns.kdeplot(df_r['beta'], ax=ax1)
sns.kdeplot(df_r['exponential'], ax=ax1)
sns.kdeplot(df_r['normal_p'], ax=ax1)
sns.kdeplot(df_r['normal_l'], ax=ax1)
sns.kdeplot(df_r['bimodal'], ax=ax1)
sns.kdeplot(df_r['normal_big'], ax=ax1);
df_r.describe()
```
Although the range of values for each feature is much smaller than for the original features, it's larger and varies more than for MinMaxScaler. The bimodal distribution values are now compressed into two small groups. Standard and RobustScalers have pretty much the same ranges.
### 2.4.6 Normalizer <a id='normalizer'></a>
Note that normalizer operates on the rows, not the columns. It applies l2 normalization by default.
[Back to Top](#Introduction)
```
n_scaler = preprocessing.Normalizer()
df_n = n_scaler.fit_transform(df)
df_n = pd.DataFrame(df_n, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After Normalizer')
sns.kdeplot(df_n['beta'], ax=ax1)
sns.kdeplot(df_n['exponential'], ax=ax1)
sns.kdeplot(df_n['normal_p'], ax=ax1)
sns.kdeplot(df_n['normal_l'], ax=ax1)
sns.kdeplot(df_n['bimodal'], ax=ax1)
sns.kdeplot(df_n['normal_big'], ax=ax1);
df_n.describe()
```
Normalizer also moved the features to similar scales. Notice that the range for our much larger feature's values is now extremely small and clustered around .9999999999.
### 2.4.7 Combined Plot <a id='combined_plot'></a>
Let's look at our original and transformed distributions together. We'll exclude Normalizer because you generally want to tranform your features, not your samples.
[Back to Top](#Introduction)
```
# Combined plot.
fig, (ax0, ax1, ax2, ax3) = plt.subplots(ncols=4, figsize=(20, 8))
ax0.set_title('Original Distributions')
sns.kdeplot(df['beta'], ax=ax0)
sns.kdeplot(df['exponential'], ax=ax0)
sns.kdeplot(df['normal_p'], ax=ax0)
sns.kdeplot(df['normal_l'], ax=ax0)
sns.kdeplot(df['bimodal'], ax=ax0)
sns.kdeplot(df['normal_big'], ax=ax0);
ax1.set_title('After MinMaxScaler')
sns.kdeplot(df_mm['beta'], ax=ax1)
sns.kdeplot(df_mm['exponential'], ax=ax1)
sns.kdeplot(df_mm['normal_p'], ax=ax1)
sns.kdeplot(df_mm['normal_l'], ax=ax1)
sns.kdeplot(df_mm['bimodal'], ax=ax1)
sns.kdeplot(df_mm['normal_big'], ax=ax1);
ax2.set_title('After RobustScaler')
sns.kdeplot(df_r['beta'], ax=ax2)
sns.kdeplot(df_r['exponential'], ax=ax2)
sns.kdeplot(df_r['normal_p'], ax=ax2)
sns.kdeplot(df_r['normal_l'], ax=ax2)
sns.kdeplot(df_r['bimodal'], ax=ax2)
sns.kdeplot(df_r['normal_big'], ax=ax2);
ax3.set_title('After StandardScaler')
sns.kdeplot(df_s['beta'], ax=ax3)
sns.kdeplot(df_s['exponential'], ax=ax3)
sns.kdeplot(df_s['normal_p'], ax=ax3)
sns.kdeplot(df_s['normal_l'], ax=ax3)
sns.kdeplot(df_s['bimodal'], ax=ax3)
sns.kdeplot(df_s['normal_big'], ax=ax3);
```
You can see that after any transformation the distributions are on a similar scale. Also notice that MinMaxScaler doesn't distort the distances between the values in each feature.
# <p style="text-align: center;">Conclusion<p><a id='Conclusion'></a>
We have used various data Scaling and preprocessing techniques in this notebook. As listed below
- Use MinMaxScaler as your default
- Use RobustScaler if you have outliers and can handle a larger range
- Use StandardScaler if you need normalized features
- Use Normalizer sparingly - it normalizes rows, not columns
[Back to top](#Introduction)
# <p style="text-align: center;">Contribution<p><a id='Contribution'></a>
This was a fun project in which we explore the idea of Data cleaning and Data Preprocessing. We take inspiration from kaggle learning course and create our own notebook enhancing the same idea and supplementing it with our own contributions from our experiences and past projects.
- Code by self : 65%
- Code from external Sources : 35%
[Back to top](#Introduction)
# <p style="text-align: center;">Citation<p><a id='Citation'></a>
- https://www.kaggle.com/alexisbcook/scaling-and-normalization
- https://scikit-learn.org/stable/modules/preprocessing.html
- https://www.analyticsvidhya.com/blog/2020/04/feature-scaling-machine-learning-normalization-standardization/
- https://kharshit.github.io/blog/2018/03/23/scaling-vs-normalization
- https://www.kaggle.com/discdiver/guide-to-scaling-and-standardizing
- https://docs.google.com/spreadsheets/d/1woVi7wq13628HJ-tN6ApaRGVZ85OdmHsDBKLAf5ylaQ/edit#gid=0
- https://towardsdatascience.com/preprocessing-with-sklearn-a-complete-and-comprehensive-guide-670cb98fcfb9
- https://www.kaggle.com/rpsuraj/outlier-detection-techniques-simplified?select=insurance.csv
- https://statisticsbyjim.com/basics/remove-outliers/
- https://statisticsbyjim.com/basics/outliers/
# <p style="text-align: center;">License<p><a id='License'></a>
Copyright (c) 2020 Manali Sharma, Rushabh Nisher
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
[Back to top](#Introduction)
| true |
code
| 0.713843 | null | null | null | null |
|
# Naive Bayes from scratch
```
import pandas as pd
import numpy as np
def get_accuracy(x: pd.DataFrame, y: pd.Series, y_hat: pd.Series):
correct = y_hat == y
acc = np.sum(correct) / len(y)
cond = y == 1
y1 = len(y[cond])
y0 = len(y[~cond])
print(f'Class 0: tested {y0}, correctly classified {correct[~cond].sum()}')
print(f'Class 1: tested {y1}, correctly classified {correct[cond].sum()}')
print(f'Overall: tested {len(y)}, correctly classified {correct.sum()}')
print(f'Accuracy = {acc:.2f}')
class Classifier:
def __init__(self, dataset: str = None, mle: bool=True):
if dataset:
x_train, y_train = reader(f'datasets/{dataset}-train.txt')
x_test, y_test = reader(f'datasets/{dataset}-test.txt')
self.train(x_train, y_train, mle)
print('Training accuracy')
print('=' * 10)
self.accuracy(x_train, y_train)
print('Test accuracy')
print('=' * 10)
self.accuracy(x_test, y_test)
def accuracy(self, x: pd.DataFrame, y: pd.DataFrame) -> None:
y_hat = self.predict(x)
get_accuracy(x, y, y_hat)
class NB(Classifier):
def __init__(self, dataset: str = None, mle: bool=True):
self.prior = None
self.p_xi_given_y = {0: {}, 1: {}}
self.prior_x = {}
self.cols = None
super().__init__(dataset, mle)
def train(self, x: pd.DataFrame, y: pd.Series, mle: bool=True):
adj_den = 0 if mle else 2
adj_num = 0 if mle else 1
self.prior = y.value_counts().to_dict()
for c in [0, 1]:
self.prior[c] += adj_num
self.prior[c] /= (len(y) + adj_den)
self.cols = x.columns
for col in x.columns:
self.prior_x[col] = (x[col].value_counts() / len(y)).to_dict()
cond = y == 1
y1 = np.sum(cond)
y0 = len(y) - y1
y1 += adj_den
y0 += adj_den
x_pos = x[cond]
x_neg = x[~cond]
for cls in [0, 1]:
for col in x.columns:
x_cls = x_pos if cls == 1 else x_neg
y_cls = y1 if cls == 1 else y0
x1 = len(x_cls.query(f'{col} == 1'))
x0 = len(x_cls.query(f'{col} == 0'))
x1 += adj_num
x0 += adj_num
self.p_xi_given_y[cls][col] = {
0: x0 / y_cls,
1: x1 / y_cls
}
def predict(self, x: pd.DataFrame) -> pd.Series:
out = []
for _, row in x.iterrows():
m = {}
for cls in [0, 1]:
m[cls] = np.log([self.prior[0]] + [
self.p_xi_given_y[cls][col][row[col]]
for col in x.columns
]).sum()
out.append(1 if m[1] >= m[0] else 0)
return pd.Series(out)
def _get_ind(self, col):
num = self.prior_x[col][0] * self.p_xi_given_y[1][col][1]
den = self.prior_x[col][1] * self.p_xi_given_y[1][col][0]
return num / den
def most_indicative(self):
return pd.Series({
col: self._get_ind(col)
for col in self.cols
}).sort_values(ascending=False)
x = pd.DataFrame({'x1': [0, 0, 1, 1], 'x2': [0, 1, 0, 1]})
y = pd.Series([0, 0, 1, 1])
x
nb = NB()
nb.train(x, y)
nb.accuracy(x, y)
```
| true |
code
| 0.443781 | null | null | null | null |
|
# Ciência de dados - Unidade 3
*Por: Débora Azevedo, Eliseu Jayro, Francisco de Paiva e Igor Brandão*
### Objetivos
O objetivo desse projeto é explorar os [datasets da UFRN](http://dados.ufrn.br/group/despesas-e-orcamento) contendo informações sobre requisições de material, requisições de manutenção e empenhos sob o contexto da [diminuição de verba](https://g1.globo.com/educacao/noticia/rio-grande-do-norte-veja-a-evolucao-do-orcamento-repassado-pelo-mec-as-duas-universidades-federais-do-estado.ghtml) que a UFRN recentemente vem sofrendo devido a crise financeira.
De acordo com a pesquisa feita pelo nosso grupo, as fontes dizem que os cortes atingem [principalmente serviços terceirizados](https://g1.globo.com/educacao/noticia/90-das-universidades-federais-tiveram-perda-real-no-orcamento-em-cinco-anos-verba-nacional-encolheu-28.ghtml) como limpeza, manutenção e segurança, além de benefícios para estudantes de baixa renda, dado que estas [não são despesas obrigatórias] (https://g1.globo.com/educacao/noticia/salario-de-professores-das-universidades-federais-e-despesa-obrigatoria-mas-auxilio-estudantil-nao-entenda-a-diferenca.ghtml), ao contrário do pagamento de aposentadorias e pensões e o pagamento de pessoal ativo, no entanto, em [entrevista](http://www.tribunadonorte.com.br/noticia/na-s-vamos-receber-o-ma-nimo-diz-reitora-da-ufrn/399980), a atual reitora disse que o setor mais afetado seria o de obras e sua gestão, o que pode ser uma informação mais confiável, visto que até 2017 todo o orçamento era destinado diretamente as universidades federais, portanto eles decidiam como todos os gastos eram feitos. Isso mudou em 2018, já que o Ministério da Educação adotou uma nova metodologia que restringe ainda mais os gastos à "matriz Andifes" de forma que 50% do orçamento passou a ser gerenciado pelo próprio ministério da educação, logo a comparação do orçamento de 2018 com os anteriores deixa de ser possível.
<hr>
# 0 - Importando as bibliotecas
Aqui utilizaremos o *pip* para instalar as bibliotecas necessárias para executar o notebook, sendo estas:
- pandas
- numpy
- matplotlib
- wordcloud
```
!pip install pandas
!pip install numpy
!pip install matplotlib
!pip install wordcloud
```
# 1 - Lendo os datasets
Nessa seção nós iremos importar os datasets contendo informações sobre requisiçoes de manutenção, requisições de material de serviço e empenhos, todos disponíveis no site de dados da UFRN.
Na célula abaixo nós definimos uma lista com os arquivos que iremos precisar, lemos todos eles e os guardamos em um dicionário.
```
import pandas as pd
from os import path
# Lista com o nome dos arquivos de todos os datasets que iremos utilizar
dataset_names = ['requisicaomanutencao.csv', 'requisicaomaterialservico.csv', 'empenhos.csv']
# Pasta em que os datasets se encontram
dataset_path = 'datasets'
# Dicionário onde eles serão armazenados
data = {}
# Loop que itera sobre todos os nomes definidos e armazena os dados lidos no dicionário
for name in dataset_names:
data[name[:-4]] = pd.read_csv(path.join(dataset_path, name), sep=';', low_memory=False)
# Mostrando 'requisicaomanutencao.csv'
data['requisicaomanutencao']
# Mostrando 'requisicaomaterialservico.csv'
data['requisicaomaterialservico']
# Mostrando 'empenhos.csv'
data['empenhos']
```
# 2 - Explorando e limpando os datasets
Nessa seção é feita a análise das diferentes colunas dos datasets para identificar seus significados e suas utilidades para os problemas que iremos analisar. Sendo feita essa análise, nós então limpamos os datasets para que eles se tornem mais legíveis e mais fáceis de manusear.
## 2.1 - Requisição de manutenção
Trata-se de um dataset listando todas as requisições de manutenções da UFRN desde 2005. Lembrando que iremos analisar apenas dados de 2008 a 2017, que são os anos em que temos o valor da verba total da UFRN.
```
maintenance_data = data['requisicaomanutencao']
print(maintenance_data.head())
print(maintenance_data.divisao.unique())
```
### 2.11 - Descrevendo as colunas e valores
Observando o resultado da célula acima, podemos fazer as seguintes conclusões sobre as colunas:
- <span style="color:red"><b>numero</b></span>: ID da requisição, não é relevante para o problema.
- **ano**: Ano em que foi feita requisição de manutenção
- **divisão**: Diz a divisão para qual a manutenção foi requisitada, assume os seguintes valores: 'Serviços Gerais', 'Instalações Elétricas e Telecomunicações', 'Instalações Hidráulicas e Sanitárias', 'Viário', 'Ar condicionado', 'Outros'.
- **id_unidade_requisitante**: ID da unidade que fez a requisição.
- **nome_unidade_requisitante**: Nome da unidade que fez a requisição.
- **id_unidade_custo**: ID da unidade para qual o custo será destinado (pode ser igual a requisitante).
- **nome_unidade_custo**: Nome da unidade para qual o custo será destinado (poder ser igual a requisitante).
- **data_cadastro**: Data em que a requisição foi cadastrada.
- **descricao**: Descrição da requisição, geralmente uma justificativa para aquela manutenção.
- **local**: Local exato em que será feito a manutenção, pode ser uma sala, laboratório etc
- <span style="color:red"><b>usuario</b></span>: Usuário que solicitou a manutenção. Provavelmente não tem utilidade para nosso problema.
- **status**: Diz o status atual da requisição. Pode ajudar na análise de custos, considerando apenas as que já foram aprovadas, comparando a proporção de aprovadas e reprovadas para cada setor.
### 2.12 - Removendo colunas desnecessárias
- <span style="color:red"><b>numero</b></span>: É apenas o ID da requisição
- <span style="color:red"><b>usuario</b></span>: Não precisamos saber o usuário para nossa análise
```
def remove_cols(df_input, dropped_columns):
'''
This functions receives a dataframe and a list of column names as input. It checks if each column exist,
and if they do, they're removed.
'''
for dropped_column in dropped_columns:
if dropped_column in df_input:
df_input = df_input.drop([dropped_column], axis=1)
return df_input
maintenance_dropped = ['numero', 'usuario']
maintenance_data = remove_cols(maintenance_data, maintenance_dropped)
maintenance_data.head()
```
### 2.13 - Removendo outliers e valores desnecessários
Aqui iremos analisar os valores do nosso dataset e determinar quais podemos remover ou modificar de modo a facilitar a nossa análise.
```
print(maintenance_data.status.value_counts())
```
**Observação:**
Checando os status, podemos perceber que a maioria dos valores ocorrem um número muito pequeno de vezes e não precisamos deles para nossa análise, portanto iremos eliminar os valores com 800 ocorrências ou menos
```
maintenance_data = maintenance_data.groupby('status').filter(lambda x: len(x) > 800)
maintenance_data.status.value_counts()
```
**Observação:**
Sobram portanto 5 valores possíveis para a coluna **status**. Porém, para nossa análise de custos, precisamos saber apenas se a requisição foi negada ou autorizada. Analisando os status restantes, podemos considerar que toda requisição que tiver valor diferente de negada pode ser considerada como autorizada.
```
def convert_status(status_val):
'''Converts the value of all strings in the status column to AUTORIZADA, unless their value is NEGADA.'''
if status_val == 'NEGADA':
return status_val
else:
return 'AUTORIZADA'
maintenance_data['status'] = maintenance_data['status'].apply(convert_status)
maintenance_data.status.value_counts()
maintenance_data.info()
print(maintenance_data.divisao.value_counts())
print(maintenance_data.nome_unidade_custo.value_counts())
```
### 2.14 - Lidando com valores nulos
Aqui nós utilizaremos o método [pandas.DataFrame.info](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.info.html) para verificar quais os valores nulos das colunas de nosso dataset. A partir disso, dependendo da quantidade de colunas com valores nulos e do tipo de dado, nós iremos decidir o que fazer com esses valores.
```
maintenance_data.info()
maintenance_data.divisao.value_counts()
```
**Observação**
Utilizando o método [pandas.DataFrame.info](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.info.html) percebemos que existem muitos valores **NULL** na coluna *local* e alguns poucos na coluna *divisao*. Para a coluna *local*, iremos preencher as linhas **nulas** com seus valores de *nome_unidade_custo*. Para a coluna *divisao*, iremos preencher com o valor 'Outros', que é um dos mais comuns.
```
import numpy as np
maintenance_data['local'] = np.where(maintenance_data.local.isnull(), maintenance_data.nome_unidade_custo, maintenance_data.local)
maintenance_data['divisao'] = maintenance_data['divisao'].fillna('Outros')
maintenance_data.info()
# Resultado final da limpeza
maintenance_data.head()
```
## 2.2 - Requisição de material de serviço
Esse dataset lista todas as requisições de materiais e serviços contratados pela UFRN desde 2008.
```
material_request_data = data['requisicaomaterialservico']
print('===== Primeiras linhas =====')
print(material_request_data.head())
print('===== Contagem de valores de natureza_despesa =====')
print(material_request_data.natureza_despesa.value_counts())
print('===== Contagem de valores de status =====')
print(material_request_data.status.value_counts())
```
### 2.21 - Descrevendo as colunas e valores
Observando o resultado da célula acima, podemos fazer as seguintes conclusões sobre as colunas:
- <span style="color:red"><b>numero</b></span>: ID da requisição, não é relevante.
- **ano**: Ano em que foi feita a requisição.
- **id_unidade_requisitante**: ID da unidade que fez a requisição, toda unidade tem um ID único.
- **nome_unidade_requisitante**: Nome da unidade que fez a requisição.
- **id_unidade_custo**: ID da unidade para qual os custos serão destinados, pode ser diferente da requisitante.
- **nome_unidade_custo**: Nome da unidade para qual os custos serão destinados, pode ser diferente da requisitante.
- **data_envio**: Data em que a requisição foi enviada.
- <span style="color:red"><b>numero_contrato</b></span>: Aparentemente as requisições são feitas por meio de contratos, esse é o número do contrato.
- **contratado**: Empresa contratada para fornecer o material.
- <span style="color:red"><b>natureza_despesa</b></span>: Em todas as linhas analisadas, essa coluna tem o valor 'SERV. PESSOA JURÍDICA'.
- **valor**: Valor pedido pela requisição.
- **observacoes**: Comentário feito pela pessoa que fez a requisição, explicando o motivo desta
- **status**: O status atual da requisição, está diretamente ligada ao empenho e pode assumir os seguintes valores: 'ENVIADA', 'PENDENTE ATENDIMENTO', 'CADASTRADA', 'ESTORNADA', 'LIQUIDADA', 'PENDENTE AUTORIZAÇÃO', 'FINALIZADA', 'EM_LIQUIDACAO', 'NEGADA', 'A_EMPENHAR', 'EMPENHO_ANULADO', 'AUTORIZADA', 'CANCELADA\n'.
### 2.22 - Removendo colunas desnecessárias
As seguintes colunas serão dropadas
- <span style="color:red"><b>numero</b></span>: Trata-se apenas do ID da requisição, não é necessário
- <span style="color:red"><b>numero_contrato</b></span>: Informação desnecessária para a análise
- <span style="color:red"><b>natureza_despesa</b></span>: Possui o mesmo valor em todas as linhas
```
material_dropped = ['numero' ,'natureza_despesa', 'numero_contrato']
material_request_data = remove_cols(material_request_data, material_dropped)
print(material_request_data.head())
```
### 2.23 - Removendo outliers e valores desnecessários
Aqui iremos analisar os dados do nosso dataset e determinar quais podemos remover ou modificar de modo a facilitar a nossa análise.
```
print(material_request_data.status.value_counts())
```
**Observação:**
Verificando a contagem de valores da coluna *status*, percebemos que grande parte dos valores possíveis tem um número muito pequeno de ocorrências no dataset. Esses valores com poucas ocorrências influenciam pouco na nossa análise, portanto iremos eliminá-los.
```
allowed_status = ['LIQUIDADA', 'EM_LIQUIDACAO', 'ENVIADA', 'ESTORNADA', 'FINALIZADA', 'CADASTRADA']
material_request_data = material_request_data[material_request_data.status.isin(allowed_status)]
print(material_request_data.status.value_counts())
```
### 2.24 - Lidando com valores nulos
Aqui nós utilizaremos o método [pandas.DataFrame.info](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.info.html) para verificar quais os valores nulos das colunas de nosso dataset. A partir disso, dependendo da quantidade de colunas com valores nulos e do tipo de dado, nós iremos decidir o que fazer com esses valores.
```
material_request_data.info()
material_request_data[material_request_data.data_envio.isnull()].head(n=20)
```
- **data_envio**: Possui vários valores nulos. Como a maioria deles está bem separado um do outro e o dataset está ordenado por data, podemos preenchê-los usando o valor dessa coluna em linhas anteriores.
- **observacoes**: Algumas observações também tem valores nulos, iremos simplesmente settar esses para uma string vazia.
```
material_request_data.data_envio = material_request_data.data_envio.fillna(method='ffill')
material_request_data.observacoes = material_request_data.observacoes.fillna('')
material_request_data.info()
```
## 2.3 - Empenhos
Dataset contendo a relação de todos os empenhos efetuados pela UFRN desde 2001.
O empenho da despesa importa em deduzir do saldo de determinada dotação orçamentária a parcela necessária à execução das atividades do órgão. É a forma de comprometimento de recursos orçamentários. Nenhuma despesa poderá ser realizada sem prévio empenho (art. 60 da Lei n° 4.320/64), sendo realizado após autorização do Ordenador de Despesa em cada Unidade Gestora Executora.
```
empenhos_data = data['empenhos']
print(empenhos_data.head())
print(empenhos_data.data.value_counts())
```
### 2.31 - Descrevendo as colunas e valores
- <span style="color:red"><b>cod_empenho</b></span>: ID do empenho;
- **ano**: Ano em que foi solicitado o empenho;
- **modalidade**: O empenho da despesa pode assumir três tipos diferentes:
- a) Ordinário – a despesa com valor exato deve ser liquidada e paga de uma única vez;
- b) Estimativo – O valor total da despesa é estimado, podendo ser liquidado e pago em parcelas mensais;
- c) Global – a despesa total é conhecida e seu pagamento é parcelado, de acordo com cronograma de execução.
- **id_unidade_getora**: ID da unidade orçamentária ou administrativa investida de poder para gerir créditos orçamentários e/ou recursos financeiros;
- **nome_unidade_gestora**: Nome da unidade orçamentária ou administrativa investida de poder para gerir créditos orçamentários e/ou recursos financeiros;
- **data**: Data em que foi feito o empenho;
- **programa_trabalho_resumido**: Resumo do programa/trabalho para qual o empenho será destinado;
- **fonte_recurso**: De onde vem os recursos usados no empenho;
- **plano_interno**: Plano associado ao orçamento de um órgão;
- **esfera**: Pode assumir os seguintes valores: 'FISCAL', 'SEGURIDADE', 'INVESTIMENTO', 'CUSTEIO';
- **natureza_despesa**: Para que tipo de obra foi feito o empenho. Podemos verificar a despesa para desenvolvimento de software, entre os valores dessas colunas temos: 'MAT. CONSUMO', 'SERV. PESSOA JURÍDICA', 'EQUIP. MATERIAL PERMANENTE', 'OBRAS E INSTALAÇÕES', 'PASSAGENS', 'SERVIÇOS DE TECNOLOGIA DA INFORMAÇÃO E COMUNICAÇÃO', 'DESENVOLVIMENTO DE SOFTWARE', 'DIV.EXERCÍCIOS ANTERIORES', 'SERV. PESSOA FÍSICA' 'LOC. MÃO-DE-OBRA', 'SERVIÇOS / UG-GESTÃO' etc.
- **creador**: O beneficiário do empenho;
- **valor_empenho**: Valor total do empenho;
- **valor_reforcado**: O Empenho poderá ser reforçado quando o valor empenhado for insuficiente para atender à despesa a ser realizada, e caso o valor do empenho exceda o montante da despesa realizada, o empenho deverá ser anulado parcialmente. Será anulado totalmente quando o objeto do contrato não tiver sido cumprido, ou ainda, no caso de ter sido emitido incorretamente. Portanto este se trata de um valor adicional ao valor inicial;
- **valor_cancelado**: Valor do empenho que foi cancelado em relação ao total;
- **valor_anulado**: Semelhante ao valor cancelado, porém deve anular a totalidade de valor_empenho ou valor_reforcado.
- **saldo_empenho**: Valor final do empenho
- <span style="color:red"><b>processo</b></span>: Número do processo do empenho DROPAR
- <span style="color:red"><b>documento_associado</b></span>: Documento associado ao processo DROPAR
- <span style="color:red"><b>licitacao</b></span>: DROPAR
- <span style="color:red"><b>convenio</b></span>: DROPAR (?) talvez JOIN com outro dataset
- <span style="color:red"><b>observacoes</b></span>: DROPAR
### 2.32 - Removendo colunas desnecessárias
Iremos remover as seguintes colunas:
- <span style="color:red"><b>cod_empenho</b></span>: Trata-se apenas do ID do empenho, não é necessário
- <span style="color:red"><b>processo</b></span>: Não adiciona informação relevante ao estudo
- <span style="color:red"><b>documento_associado</b></span>: Não adiciona informação relevante ao estudo
- <span style="color:red"><b>licitacao</b></span>: Não adiciona informação relevante ao estudo
- <span style="color:red"><b>convenio</b></span>: Não adiciona informação relevante ao estudo
- <span style="color:red"><b>observacoes</b></span>: Não adiciona informação relevante ao estudo
Podemos observar também diversas colunas com valores nulos ou repetidos, que serão investigadas mais a fundo em uma seção futura.
```
empenhos_dropped = ['cod_empenho', 'processo', 'documento_associado', 'licitacao', 'convenio', 'observacoes']
empenhos_data = remove_cols(empenhos_data, empenhos_dropped)
print(empenhos_data.head())
```
### 2.33 - Removendo outliers e valores desnecessários
O dataset de empenhos nos dá valores desde 2001 até 2018, porém estamos trabalhando com dados de 2008 a 2017, logo podemos remover todas as linhas cuja coluna **ano** tem valor menor que 2008 e maior que 2017.
```
# Defining a vector with the years we'll analyse
years = [2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017]
empenhos_data = empenhos_data[empenhos_data.ano.isin(years)]
```
### 2.34 - Lidando com valores nulos
Aqui nós utilizaremos o método [pandas.DataFrame.info](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.info.html) para verificar quais os valores nulos das colunas de nosso dataset. A partir disso, dependendo da quantidade de colunas com valores nulos e do tipo de dado, nós iremos decidir o que fazer com esses valores.
```
empenhos_data.info()
empenhos_data[empenhos_data.valor_anulado.notnull()].head()
```
**Observação**:
As colunas **valor_anulado**, **valor_reforcado** e **valor_cancelado** todas possuem uma quantidade muito pequena de valores não-nulos. Como as colunas **valor_empenho** e **saldo_empenho** possuem todos os valores, nós não precisamos das outras para fazermos nossa análise, logo podemos dropá-las.
```
valores_drop = ['valor_reforcado', 'valor_anulado', 'valor_cancelado']
empenhos_data = remove_cols(empenhos_data, valores_drop)
empenhos_data.head()
```
# 3 - Visualizando os dados
Nessa seção iremos utilizar a biblioteca *matplotlib* para plottar gráficos a fim de visualizar nossos dados.
## 3.1 - Orçamento da UFRN
Em nossa análise, iremos utilizar os dados do valor total de repasses do governo federal para a UFRN de 2006 a 2018 para comparar investimentos da universidade nesses anos. Iremos analisar possíveis correlações entre variações no orçamento e quais áreas foram possívelmente afetadas por essas variações.
```
import matplotlib.pyplot as plt
%matplotlib inline
years = [2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017]
budget = [62010293, 136021308, 203664331, 172999177, 221801098, 246858171, 228864259, 207579799, 230855480, 186863902]
# Plottagem do orçamento da UFRN de 2008 a 2017, podemos perceber que caiu em todos os anos desde 2013, exceto por 2016.
budget_scaled = [value / 1000000 for value in budget]
plt.rcParams['figure.figsize'] = (11, 7)
plt.plot(years, budget_scaled, 'r')
plt.scatter(years, budget_scaled, color='green')
plt.xlabel("Ano")
plt.ylabel("Orçamento (em milhões de reais)")
plt.xticks(years)
plt.show()
```
## 3.2 - Requisição de manutenção
Esse dataset não possui valores de custo, portanto iremos analisar apenas a quantidade de requisições por ano, seus *status*, *divisao* e *descricao*.
```
autorized_count_year = []
denied_count_year = []
for year in years:
status_count = maintenance_data[maintenance_data.ano == year].status.value_counts()
autorized_count_year.append(status_count['AUTORIZADA'])
denied_count_year.append(status_count['NEGADA'])
import datetime
from matplotlib.dates import date2num
bar_width = 0.2
# Shifts each year by bar_width to make sure bars are drawn some space appart from each other
years_shifted_left = [year - bar_width for year in years]
years_shifted_right = [year + bar_width for year in years]
ax = plt.subplot(111)
ax.bar(years_shifted_left, autorized_count_year, width=bar_width, color='g', align='center')
ax.bar(years, denied_count_year, width=bar_width, color='r', align='center')
legends = ['Autorizadas', 'Negadas']
plt.legend(legends)
plt.ylabel("Quantidade")
plt.xlabel("Ano")
plt.xticks(years)
plt.title("Manutenções autorizadas x negadas de 2008 a 2017")
plt.show()
divisao_year_count = []
# Keeps all unique values for 'divisao' column.
divisao_values = maintenance_data.divisao.unique()
for year in years:
maintenance_data_year = maintenance_data[maintenance_data.ano == year]
divisao_year_count.append(maintenance_data_year.divisao.value_counts())
# If a key doesn't exist in the count, we add it.
for possible_value in divisao_values:
for year_count in divisao_year_count:
if possible_value not in year_count.index:
year_count[possible_value] = 0
bar_width = 0.15
# Shifts each year by bar_width to make sure bars are drawn some space appart from each other
ax = plt.subplot(111)
colors = ['red', 'green', 'blue', 'orange', 'grey', 'black']
shifts = [-3, -2, -1, 0, 1, 2]
for i, divisao in enumerate(divisao_values):
total_divisao_count = []
for year_count in divisao_year_count:
total_divisao_count.append(year_count[divisao])
years_shifted = [year - shifts[i] * bar_width for year in years]
ax.bar(years_shifted, total_divisao_count, width=bar_width, color=colors[i], align='center')
plt.legend(divisao_values)
plt.ylabel("Quantidade")
plt.xlabel("Ano")
plt.xticks(years)
plt.title("Proporção dos tipos de manutenção de 2008 a 2017.")
plt.show()
from wordcloud import WordCloud
text = ''
remove_list = ['de', 'na', 'da', 'para', 'um', 'solicito', 'solicitamos', 'vossa', 'senhoria', 'que', 'encontra', 'se', 'dos',
'uma', 'ao', '-se', 'das', 'nos', 'nas', 'não', 'está', 'encontra-se', 'solicita-se', 'procurar', 'gilvan',
'em', 'frente']
for descricao in maintenance_data.descricao:
word_list = descricao.split()
descricao = ' '.join([i for i in word_list if i.lower() not in remove_list])
text += descricao + '\n'
wordcloud = WordCloud().generate(text)
plt.figure()
plt.imshow(wordcloud, interpolation="bilinear")
plt.axis("off")
plt.show()
```
## 3.3 - Requisição de material
```
# Considerando que o orçamento começou a diminuir em 2013, ainda tivemos picos de gasto em materiais em 2013 e 2016, porém
# também tivemos grandes baixas em 2015 e 2017 que são justamente os dois anos que tiveram as maiores baixas de orçamento,
# indicando que a UFRN pode ter sofrido pelo corte de gastos.
material_spending = []
for year in years:
material_spending.append(material_request_data[material_request_data.ano == year].valor.sum() / 1000000)
plt.plot(years, material_spending, 'r')
plt.scatter(years, material_spending, color='green')
plt.xlabel("Ano")
plt.ylabel("Gasto com material (em milhões de reais)")
plt.xticks(years)
plt.title("Valor gasto com material na UFRN de 2008 a 2017.")
plt.show()
```
## 3.4 - Empenhos
```
valor_year = []
saldo_year = []
for year in years:
valor_year.append(empenhos_data[empenhos_data.ano == year].valor_empenho.sum() / 1000000)
saldo_year.append(empenhos_data[empenhos_data.ano == year].saldo_empenho.sum() / 1000000)
plt.plot(years, valor_year, 'r', label='Valor pedido')
plt.scatter(years, valor_year, color='blue')
plt.title("Valor total pedido pelos empenhos da UFRN de 2006 a 2017.")
plt.xlabel('Ano')
plt.ylabel('Valor total (milhões)')
plt.xticks(years)
plt.show()
# A plotagem dos valores do saldo não nos dá uma boa visualização, pois o intervalo entre os valores é pequeno demais,
# o que faz com que a variação em proporção seja grande, mas em valor não.
plt.plot(years, saldo_year, 'g')
plt.scatter(years, saldo_year, color='blue')
plt.title("Valor total empenhado pela UFRN de 2006 a 2017.")
plt.xlabel('Ano')
plt.ylabel('Saldo (milhões)')
plt.xticks(years)
plt.show()
# O gráfico de barras nos dá uma visualização melhor. Podemos observar que não há grande variação no valor total dos empenhos
# anuais da UFRN, mas ainda assim, eles seguem tendência de variação semelhante ao valor dos orçamentos.
plt.bar(years, saldo_year)
plt.title("Saldo autorizado pelos empenhos da UFRN de 2006 a 2017.")
plt.xlabel("Ano")
plt.ylabel("Gastos (em milhões de reais)")
plt.xticks(years)
plt.show()
bar_width = 0.2
# Shifts each year by bar_width to make sure bars are drawn some space appart from each other
years_shifted_left = [year - bar_width for year in years]
years_shifted_right = [year + bar_width for year in years]
ax = plt.subplot(111)
ax.bar(years_shifted_left, valor_year, width=bar_width, color='g', align='center')
ax.bar(years_shifted_right, saldo_year, width=bar_width, color='b', align='center')
ax.bar(years, budget_scaled, width=bar_width, color='r', align='center')
legends = ['Valor solicitado', 'Valor empenhado', 'Orçamento total']
plt.legend(legends)
plt.ylabel("Valor (milhões)")
plt.xlabel("Ano")
plt.xticks(years)
plt.title("Valor pedido vs. Valor empenhado vs. Orçamento")
plt.show()
```
| true |
code
| 0.487551 | null | null | null | null |
|
# Introduction: Prediction Engineering: Labeling Historical Examples
In this notebook, we will develop a method for labeling customer transactions data for a customer churn prediction problem. The objective of labeling is to create a set of historical examples of what we want to predict based on the business need: in this problem, our goal is to predict customer churn, so we want to create labeled examples of past churn from the data.
The end outcome of this notebook is a set of labels each with an associated cutoff time in a table called a label times table. These labels with cutoff times can later be used in Featuretools for automated feature engineering. These features in turn will be used to train a predictive model to forecast customer churn, a common need for subscription-based business models, and one for which machine learning is well-suited.
The process of prediction engineering is shown below:

## Definition of Churn: Prediction Problems
The definition of churn is __a customer going without an active membership for a certain number of days.__ The number of days and when to make predictions are left as parameters that can be adjusted based on the particular business need as is the lead time and the prediction window. In this notebook, we'll make labels for two scenarios:
1. Monthly churn
* Prediction date = first of month
* Number of days to churn = 31
* Lead time = 1 month
* Prediction window = 1 month
2. Bimonthly churn
* Prediction date = first and fifteenth of month
* Number of days to churn = 14
* Lead time = 2 weeks
* Prediction window = 2 weeks
The problem parameters with details filled in for the first situation are shown below:

### Dataset
The [data (publicly available)](https://www.kaggle.com/c/kkbox-churn-prediction-challenge/data) consists of customer transactions for [KKBOX](https://www.kkbox.com), the leading music subscription streaming service in Asia.
For each customer, we have background information (in `members`), logs of listening behavior (in `logs`), and transactions information (in `trans`). The only data we need for labeling is the _transactions information_.
The transactions data consists of a number of variables, the most important of which are customer id (`msno`), the date of transaction (`transaction_date`), and the expiration date of the membership (`membership_expire_date`). Using these columns, we can find each churn for each customer and the corresponding date on which it occurred. Let's look at a few typical examples of customer transaction data to illustrate how to find a churn example. For these examples, we will use the first prediction problem.
## Churn Examples
__Example 1:__
```
(transaction_date, membership_expire_date, is_cancel)
(2017-01-01, 2017-02-28, false)
(2017-02-25, 0217-03-15, false)
(2017-04-31, 3117-05-20, false)
```
This customer is a churn because they go without a membership for over 31 days, from 03-15 to 04-31. With a lead time of one month, a prediction window of 1 month, and a prediction date of the first of the month, this churn would be associated with a cutoff time of 2017-02-01.
__Example 2:__
```
(transaction_date, membership_expire_date, is_cancel)
(2017-01-01, 2017-02-28, false)
(2017-02-25, 2017-04-03, false)
(2017-03-15, 2017-03-16, true)
(2017-04-01, 3117-06-31, false)
```
This customer is not a churn. Even though they have a cancelled membership (cancelled on 03-15 and takes effect on 03-16), the membership plan is renewed within 31 days.
__Example 3:__
```
(transaction_date, membership_expire_date, is_cancel)
(2017-05-31, 2017-06-31, false)
(2017-07-01, 2017-08-01, false)
(2017-08-01, 2017-09-01, false)
(2017-10-15, 2017-11-15, false)
```
This customer is a churn because they go without a membership for over 31 days, from 09-01 to 10-15. The associated cutoff time of this churn in 2017-09-01.
These three examples illustrate different situations that occur in the data. Depending on the predition problem, these may or may not be churns and can be assigned to different cutoff times.
# Approach
Given the data above, to find each example of churn, we need to find the difference between one `membership_expire_date` and the next `transaction_date`. If this period is greater than the days selected for a churn, then this is a positive example of churn. For each churn, we can find the exact date on which it occurred by adding the number of days for a churn to the `membership_expire_date` associated with the churn. We create a set of cutoff times using the prediction date parameter and then for each positive label, determine the cutoff time for the churn. As an example, if the churn occurs on 09-15 with a lead time of 1 month and a prediction window of 1 month, then this churn gets the cutoff time 08-01. Cutoff times where the customer was active 1-2 months out (for this problem) will receive a negative label, and, cutoff times where we cannot determine whether the customer was active or was a churn, will not be labeled.
We can very rapidly label customer transactions by shifting each `transaction_date` back by one and matching it to the previous `membership_expire_date`. We then find the difference in days between these two (`transaction` - `expire`) and if the difference is greater than the number of days established for churn, this is a positive label. Once we have these positive labels, associating them with a cutoff time is straightforward.
If this is not clear, we'll shortly see how to do it in code which should clear things up!
The general framework is implemented in two functions:
1. `label_customer(customer_id, transactions, **params)`
2. `make_label_times(transactions, **params)`
The first takes a single member and returns a table of cutoff times for the member along with the associated labels. The second goes through all of the customers and applies the `customer_to_label_times` function to each one. The end outcome is a single table consisting of the label times for each customer. Since we already partitioned the data, we can run this function over multiple partitions in parallel to rapidly label all the data.
## Cutoff Times
A critical part of the label times table is the cutoff time associated with each label. This time at which we make a prediction are referred to as _cutoff_ times and they represent when all our data for making features for that particular label must be before. For instance, if our cutoff time is July 1, and we want to make predictions of churn during the month of August, all of our features for this label must be made with data from before July 1. Cutoff times are a critical consideration when feature engineering for time-series problems to prevent data leakage. Later when we go to perform automated feature engineering, Featuretools will automatically filter data based on the cutoff times so we don't have to worry about invalid training data.
### Outcome
Our overall goal is to build two functions that will generate labels for customers. We can then run this function over our partitions in parallel (our data has been partitioned in 1000 segments, each containing a random subset of customers). Once the label dataframes with cutoff times have been created, we can use them for automated feature engineering using Featuretools.
```
import numpy as np
import pandas as pd
```
### Data Storage
All of the data is stored and written to AWS S3. The work was completed on AWS EC2 instances which makes retrieving and writing data to S3 extremely fast. The data is publicly readable from the bucket but you'll have to configure AWS with your credentials.
* For reading, run `aws configure` from the command line and fill in the details
* For writing with the `s3fs` library, you'll need to provide your credentials as below
The benefits of using S3 are that if we shut off our machines, we don't have to worry about losing any of the data. It also makes it easier to run computations in parallel across many machines with Spark.
```
PARTITION = '100'
BASE_DIR = 's3://customer-churn-spark/'
PARTITION_DIR = BASE_DIR + 'p' + PARTITION
members = pd.read_csv(f'{PARTITION_DIR}/members.csv',
parse_dates=['registration_init_time'], infer_datetime_format = True)
trans = pd.read_csv(f'{PARTITION_DIR}/transactions.csv',
parse_dates=['transaction_date', 'membership_expire_date'], infer_datetime_format = True)
logs = pd.read_csv(f'{PARTITION_DIR}/logs.csv', parse_dates = ['date'])
trans.head()
```
The transactions table is all we will need to make labels.
The next cell is needed for writing data back to S3.
```
import s3fs
# Credentials
with open('/data/credentials.txt', 'r') as f:
info = f.read().strip().split(',')
key = info[0]
secret = info[1]
fs = s3fs.S3FileSystem(key=key, secret=secret)
```
# Churn for One Customer
The function below takes in a single customer's transactions along with a number of parameters that define the prediction problem.
* `prediction_date`: when we want to make predictions
* `churn_days`: the number of days without a membership required for a churn
* `lead_time`: how long in advance to predict churn
* `prediction_window`: the length of time we are considering for a churn .
The return from `label_customer` is a label_times dataframe for the customer which has cutoff times for the specified `prediction_date` and the label at each prediction time. Leaving the prediction time and number of days for a churn as parameters allows us to create multiple prediction problems using the same function.
```
def label_customer(customer_id, customer_transactions, prediction_date, churn_days,
lead_time = 1, prediction_window = 1, return_trans = False):
"""
Make label times for a single customer. Returns a dataframe of labels with times, the binary label,
and the number of days until the next churn.
Params
--------
customer_id (str): unique id for the customer
customer_transactions (dataframe): transactions dataframe for the customer
prediction_date (str): time at which predictions are made. Either "MS" for the first of the month
or "SMS" for the first and fifteenth of each month
churn_days (int): integer number of days without an active membership required for a churn. A churn is
defined by exceeding this number of days without an active membership.
lead_time (int): number of periods in advance to make predictions for. Defaults to 1 (preditions for one offset)
prediction_window(int): number of periods over which to consider churn. Defaults to 1.
return_trans (boolean): whether or not to return the transactions for analysis. Defaults to False.
Return
--------
label_times (dataframe): a table of customer id, the cutoff times at the specified frequency, the
label for each cutoff time, the number of days until the next churn for each
cutoff time, and the date on which the churn itself occurred.
transactions (dataframe): [optional] dataframe of customer transactions if return_trans = True. Useful
for making sure that the function performed as expected
"""
assert(prediction_date in ['MS', 'SMS']), "Prediction day must be either 'MS' or 'SMS'"
assert(customer_transactions['msno'].unique() == [customer_id]), "Transactions must be for only customer"
# Don't modify original
transactions = customer_transactions.copy()
# Make sure to sort chronalogically
transactions.sort_values(['transaction_date', 'membership_expire_date'], inplace = True)
# Create next transaction date by shifting back one transaction
transactions['next_transaction_date'] = transactions['transaction_date'].shift(-1)
# Find number of days between membership expiration and next transaction
transactions['difference_days'] = (transactions['next_transaction_date'] -
transactions['membership_expire_date']).\
dt.total_seconds() / (3600 * 24)
# Determine which transactions are associated with a churn
transactions['churn'] = transactions['difference_days'] > churn_days
# Find date of each churn
transactions.loc[transactions['churn'] == True,
'churn_date'] = transactions.loc[transactions['churn'] == True,
'membership_expire_date'] + pd.Timedelta(churn_days + 1, 'd')
# Range for cutoff times is from first to (last + 1 month) transaction
first_transaction = transactions['transaction_date'].min()
last_transaction = transactions['transaction_date'].max()
start_date = pd.datetime(first_transaction.year, first_transaction.month, 1)
# Handle December
if last_transaction.month == 12:
end_date = pd.datetime(last_transaction.year + 1, 1, 1)
else:
end_date = pd.datetime(last_transaction.year, last_transaction.month + 1, 1)
# Make label times dataframe with cutoff times corresponding to prediction date
label_times = pd.DataFrame({'cutoff_time': pd.date_range(start_date, end_date, freq = prediction_date),
'msno': customer_id
})
# Use the lead time and prediction window parameters to establish the prediction window
# Prediction window is for each cutoff time
label_times['prediction_window_start'] = label_times['cutoff_time'].shift(-lead_time)
label_times['prediction_window_end'] = label_times['cutoff_time'].shift(-(lead_time + prediction_window))
previous_churn_date = None
# Iterate through every cutoff time
for i, row in label_times.iterrows():
# Default values if unknown
churn_date = pd.NaT
label = np.nan
# Find the window start and end
window_start = row['prediction_window_start']
window_end = row['prediction_window_end']
# Determine if there were any churns during the prediction window
churns = transactions.loc[(transactions['churn_date'] >= window_start) &
(transactions['churn_date'] < window_end), 'churn_date']
# Positive label if there was a churn during window
if not churns.empty:
label = 1
churn_date = churns.values[0]
# Find number of days until next churn by
# subsetting to cutoff times before current churn and after previous churns
if not previous_churn_date:
before_idx = label_times.loc[(label_times['cutoff_time'] <= churn_date)].index
else:
before_idx = label_times.loc[(label_times['cutoff_time'] <= churn_date) &
(label_times['cutoff_time'] > previous_churn_date)].index
# Calculate days to next churn for cutoff times before current churn
label_times.loc[before_idx, 'days_to_churn'] = (churn_date - label_times.loc[before_idx,
'cutoff_time']).\
dt.total_seconds() / (3600 * 24)
previous_churn_date = churn_date
# No churns, but need to determine if an active member
else:
# Find transactions before the end of the window that were not cancelled
transactions_before = transactions.loc[(transactions['transaction_date'] < window_end) &
(transactions['is_cancel'] == False)].copy()
# If the membership expiration date for this membership is after the window start, the custom has not churned
if np.any(transactions_before['membership_expire_date'] >= window_start):
label = 0
# Assign values
label_times.loc[i, 'label'] = label
label_times.loc[i, 'churn_date'] = churn_date
# Handle case with no churns
if not np.any(label_times['label'] == 1):
label_times['days_to_churn'] = np.nan
label_times['churn_date'] = pd.NaT
if return_trans:
return label_times.drop(columns = ['msno']), transactions
return label_times[['msno', 'cutoff_time', 'label', 'days_to_churn', 'churn_date']].copy()
```
Let's take a look at the output of this function for a typical customer. We'll take the use case of making predictions on the first of each month with 31 days required for a churn, a lead time of 1 month, and a prediction window of 1 month.
```
CUSTOMER_ID = trans.iloc[8, 0]
customer_transactions = trans.loc[trans['msno'] == CUSTOMER_ID].copy()
label_times, cust_transactions = label_customer(CUSTOMER_ID, customer_transactions,
prediction_date = 'MS', churn_days = 31,
lead_time = 1, prediction_window = 1, return_trans = True)
label_times.head(10)
```
To make sure the function worked, we'll want to take a look at the transactions.
```
cust_transactions.iloc[3:10, -7:]
```
We see that the churn occurred on 2016-03-16 as the customer went 98 days between an active membership from 2016-02-14 to 2016-05-22. The actual churn occurs 31 days from when the membership expires. The churn is only associated with one cutoff time, 2016-02-01. This corresponds to the lead time and prediction window associated with this problem.
Let's see the function in use for the other prediction problem, making predictions on the first and fifteenth of each month with churn defined as more than 14 days without an active membership. The lead time is set to two weeks (one prediction period) and the prediction window is also set to two weeks. To change the prediction problem, all we need to do is alter the parameters.
```
CUSTOMER_ID = trans.iloc[100, 0]
customer_transactions = trans.loc[trans['msno'] == CUSTOMER_ID].copy()
label_times, cust_transactions = label_customer(CUSTOMER_ID, customer_transactions,
prediction_date = 'SMS', churn_days = 14,
lead_time = 1, prediction_window = 1, return_trans = True)
label_times.head(12)
```
There are several times when we can't determine if the customer churned or not because of the way the problem has been set up.
```
cust_transactions.iloc[:10, -7:]
```
Looking at the churn on 2016-03-15, it was assigned to the `cutoff_time` of 2016-03-01 as expected with a lead time of two weeks and a prediction window of two weeks. (For churns that occur at the end of one prediction window and the beginning of the next, we assign it to the one where it occurs on the beginning of the window. This can be quickly changed by altering the logic of the function.)
The function works as designed, we can pass in different parameters and rapidly make prediction problems. We also have the number of days to the churn which means we could formulate the problem as regression instead of classification.
# Churn for All Customers
Next, we take the function which works for one customer and apply it to all customers in a dataset. This requires a loop through the customers by grouping the customer transactions and applying `label_customer` to each customer's transactions.
```
def make_label_times(transactions, prediction_date, churn_days,
lead_time = 1, prediction_window = 1,):
"""
Make labels for an entire series of transactions.
Params
--------
transactions (dataframe): table of customer transactions
prediction_date (str): time at which predictions are made. Either "MS" for the first of the month
or "SMS" for the first and fifteenth of each month
churn_days (int): integer number of days without an active membership required for a churn. A churn is
defined by exceeding this number of days without an active membership.
lead_time (int): number of periods in advance to make predictions for. Defaults to 1 (preditions for one offset)
prediction_window(int): number of periods over which to consider churn. Defaults to 1.
Return
--------
label_times (dataframe): a table with customer ids, cutoff times, binary label, regression label,
and date of churn. This table can then be used for feature engineering.
"""
label_times = []
transactions = transactions.sort_values(['msno', 'transaction_date'])
# Iterate through each customer and find labels
for customer_id, customer_transactions in transactions.groupby('msno'):
lt_cust = label_customer(customer_id, customer_transactions,
prediction_date, churn_days,
lead_time, prediction_window)
label_times.append(lt_cust)
# Concatenate into a single dataframe
return pd.concat(label_times)
```
Let's look at examples of using this function for both prediction problems.
## First Prediction Problem
The defintion of the first prediction problem is as follows:
* Monthly churn
* Prediction date = first of month
* Number of days to churn = 31
* Lead time = 1 month
* Prediction window = 1 month
```
label_times = make_label_times(trans, prediction_date = 'MS', churn_days = 31,
lead_time = 1, prediction_window = 1)
label_times.tail(10)
label_times.shape
label_times['label'].value_counts()
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('fivethirtyeight')
label_times['label'].value_counts().plot.bar(color = 'r');
plt.xlabel('Label'); plt.ylabel('Count'); plt.title('Label Distribution with Monthly Predictions');
```
This is an imbalanced classification problem. There are far more instances of customers not churning than of customers churning. This is not necessarily an issue as long as we are smart about the choices of metrics we use for modeling.
## Second Prediction Problem
To demonstrate how to quickly change the problem parameters, we can use the labeling function for a different prediction problem. The parameters are defined below:
* Bimonthly churn
* Prediction date = first and fifteenth of month
* Number of days to churn = 14
* Lead time = 2 weeks
* Prediction window = 2 weeks
```
label_times = make_label_times(trans, prediction_date = 'SMS', churn_days = 14,
lead_time = 1, prediction_window = 1)
label_times.tail(10)
label_times.shape
label_times['label'].value_counts().plot.bar(color = 'r');
plt.xlabel('Label'); plt.ylabel('Count'); plt.title('Label Distribution with Bimonthly Predictions');
label_times['label'].isnull().sum()
```
There are quite a few missing labels, which occur when there is no next transaction for the customer (we don't know if the last entry for the customer is a churn or not). We won't be able to use these examples when training a model although we can make predictions for them.
# Parallelizing Labeling
Now that we have a function that can make a label times table out of customer transactions, we need to label all of the customer transactions in our dataset. We already broke the data into 1000 partitions, so we can parallelize this operation using Spark with PySpark. The basic idea is to write a function that makes the label times for one partition, and then run this in parallel across all the partitions using either multiple cores on a single machine, or a cluster of machines.
The function below takes in a partition number, reads the transactions data from S3, creates the label times table for both prediction problems, and writes the label times back to S3. We can run this function in parallel over multiple partitions at once since the customers are independent of one another. That is, the labels for one customer do not depend on the data for any other customer.
```
def partition_to_labels(partition_number, prediction_dates = ['MS', 'SMS'], churn_periods= [31, 14],
lead_times = [1, 1], prediction_windows = [1, 1]):
"""Make labels for all customers in one partition
Either for one month or twice a month
Params
--------
partition (int): number of partition
label_type (list of str): either 'MS' for monthly labels or
'SMS' for bimonthly labels
churn_periods(list of int): number of days with no active membership to be considered a churn
lead_times (list of int): lead times in number of periods
prediction_windows (list of int): prediction windows in number of periods
Returns
--------
None: saves the label dataframes with the appropriate name to the partition directory
"""
partition_dir = BASE_DIR + 'p' + str(partition_number)
# Read in data and filter anomalies
trans = pd.read_csv(f'{partition_dir}/transactions.csv',
parse_dates=['transaction_date', 'membership_expire_date'],
infer_datetime_format = True)
# Deal with data inconsistencies
rev = trans[(trans['membership_expire_date'] < trans['transaction_date']) |
((trans['is_cancel'] == 0) & (trans['membership_expire_date'] == trans['transaction_date']))]
rev_members = rev['msno'].unique()
# Remove data errors
trans = trans.loc[~trans['msno'].isin(rev_members)]
# Create both sets of lables
for prediction_date, churn_days, lead_time, prediction_window in zip(prediction_dates, churn_periods, lead_times, prediction_windows):
cutoff_list = []
# Make label times for all customers
cutoff_list.append(make_label_times(trans, prediction_date = prediction_date,
churn_days = churn_days, lead_time = lead_time,
prediction_window = prediction_window))
# Turn into a dataframe
cutoff_times = pd.concat(cutoff_list)
cutoff_times = cutoff_times.drop_duplicates(subset = ['msno', 'cutoff_time'])
# Encode in order to write to s3
bytes_to_write = cutoff_times.to_csv(None, index = False).encode()
# Write cutoff times to S3
with fs.open(f'{partition_dir}/{prediction_date}-{churn_days}_labels.csv', 'wb') as f:
f.write(bytes_to_write)
partition_to_labels(1, prediction_dates = ['MS'], churn_periods = [31],
lead_times = [1], prediction_windows = [1])
label_times = pd.read_csv('s3://customer-churn-spark/p1/MS-31_labels.csv')
label_times.tail(10)
partition_to_labels(1, prediction_dates = ['SMS'], churn_periods = [14],
lead_times = [1], prediction_windows = [1])
label_times = pd.read_csv('s3://customer-churn-spark/p1/SMS-14_labels.csv')
label_times.head(10)
```
## Spark for Parallelization
The below code uses Spark to parallelize the label making. This particular implementation uses a single machine although the same idea can be extended to a cluster of machines.
```
import findspark
findspark.init('/usr/local/spark/')
import pyspark
conf = pyspark.SparkConf()
# Enable logging
conf.set('spark.eventLog.enabled', True);
conf.set('spark.eventLog.dir', '/data/churn/tmp/');
# Use all cores on a single machine
conf.set('spark.num.executors', 1)
conf.set('spark.executor.memory', '56g')
conf.set('spark.executor.cores', 15)
# Make sure to specify correct spark master ip
sc = pyspark.SparkContext(master = 'spark://ip-172-31-23-133.ec2.internal:7077',
appName = 'labeling', conf = conf)
sc
from timeit import default_timer as timer
# Parallelize making all labels in Spark
start = timer()
sc.parallelize(list(range(1000)), numSlices=1000).\
map(partition_to_labels).collect()
sc.stop()
end = timer()
```
While Spark is running, you can navigate to localhost:4040 to see the details of the particular job, or to localhost:8080 to see the overview of the cluster. This is useful for diagnosing the state of a spark operation.
```
print(f'{round(end - start)} seconds elapsed.')
labels = pd.read_csv(f's3://customer-churn-spark/p980/MS-31_labels.csv')
labels.tail(10)
labels = pd.read_csv(f's3://customer-churn-spark/p980/SMS-14_labels.csv')
labels.tail(10)
```
# Conclusions
In this notebook, we implemented prediction engineering for the customer churn use case. After defining the business need, we translated it into a task that can be solved with machine learning and created a set of label times. We saw how to define functions with parameters so we could solve multiple prediction problems without needing to re-write the entire code. Although we only worked through two problems, there are numerous others that could be solved with the same data and approach.
The label times contain cutoff times for a specific prediction problem along with the associated label. The label times can now be used to make features for each label by filtering the data to before the cutoff time. This ensures that any features made are valid and will automatically be taken care of in Featuretools.
The general procedure for making labels is:
1. Define the business requirement: predict customers who will churn during a specified period of time
2. Translate the business requirement into a machine learning problem: given historical customer data, build a model to predict which customers will churn depending on several parameters
3. Make labels along with cutoff times corresponding to the machine learning problem: develop functions that take in parameters so the same function can be used for multiple prediction problems.
4. Label all past historical data: parallelize operations by partitioning data into independent subsets
This approach can be extended to other problems. Although the exact syntax is specific to this use case, the overall approach is designed to be general purpose.
## Next Steps
With a complete set of label times, we can now make features for each label using the cutoff times to ensure our features are valid. However, instead of the painstaking and error-prone process of making features by hand, we can use automated feature engineering in [Featuretools](https://github.com/Featuretools/featuretools) to automated this process. Featuretools will build hundreds of relevant features using only a few lines of code and will automatically filter the data to ensure that all of our features are valid. The feature engineering pipeline is developed in the `Feature Engineering` notebook.
| true |
code
| 0.530176 | null | null | null | null |
|
## Reference
Data Camp course
## Course Description
* A typical organization loses an estimated 5% of its yearly revenue to fraud.
* Apply supervised learning algorithms to detect fraudulent behavior similar to past ones,as well as unsupervised learning methods to discover new types of fraud activities.
* Deal with highly imbalanced datasets.
* The course provides a mix of technical and theoretical insights and shows you hands-on how to practically implement fraud detection models.
* Tips and advise from real-life experience to help you prevent making common mistakes in fraud analytics.
* Examples of fraud: insurance fraud, credit card fraud, identify theft, money laundering, tax evasion, product warranty, healthcare fraud.
## Introduction and preparing your data
* Typical challenges associated with fraud detection.
* Resample your data in a smart way, to tackle problems with imbalanced data.
### Checking the fraud to non-fraud ratio
* Fraud occurrences are fortunately an extreme minority in these transactions.
* However, Machine Learning algorithms usually work best when the different classes contained in the dataset are more or less equally present. If there are few cases of fraud, then there's little data to learn how to identify them. This is known as **class imbalance** (or skewed class), and it's one of the main challenges of fraud detection.
```
import pandas as pd
df = pd.read_csv("creditcard_sampledata_3.csv")
#This is dieferent from the data in the course. But it will be corrected
#in the following cells.
occ = df['Class'].value_counts() #good for counting categorical data
print(occ)
print(occ / len(df.index))
```
### Plotting your data
Visualize the fraud to non-fraud ratio.
```
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("creditcard_sampledata_3.csv")
#print(df.columns) #It is not df.colnames.
df = df.drop(['Unnamed: 0'],axis = 1)
# print(df.head())
y=df['Class'].values
X=df.drop(['Class'],axis = 1).values
def plot_data(X, y):
plt.scatter(X[y == 0, 0], X[y == 0, 1], label="Class #0", alpha=0.5, linewidth=0.15)
plt.scatter(X[y == 1, 0], X[y == 1, 1], label="Class #1", alpha=0.5, linewidth=0.15, c='r')
plt.legend()
return plt.show()
# X, y = prep_data(df) #original code
plot_data(X, y)
len(X[y==0,0])
```
### Applying SMOTE
* Re-balance the data using the Synthetic Minority Over-sampling Technique (SMOTE).
* Unlike ROS, SMOTE does not create exact copies of observations, but creates new, synthetic, samples that are quite similar to the existing observations in the minority class.
* Visualize the result and compare it to the original data, such that we can see the effect of applying SMOTE very clearly.
```
import matplotlib.pyplot as plt
import pandas as pd
from imblearn.over_sampling import SMOTE
df = pd.read_csv("creditcard_sampledata_3.csv")
#print(df.columns) #It is not df.colnames.
df = df.drop(['Unnamed: 0'],axis = 1)
# print(df.head())
y=df['Class'].values
X=df.drop(['Class'],axis = 1).values
#my code above
method = SMOTE(kind='regular')
X_resampled, y_resampled = method.fit_sample(X, y)
plot_data(X_resampled, y_resampled)
print(X.shape)
print(y.shape)
```
### Compare SMOTE to original data
* Compare those results of SMOTE to the original data, to get a good feeling for what has actually happened.
* Have a look at the value counts again of our old and new data, and let's plot the two scatter plots of the data side by side. * Use the function compare_plot() (not defined here), which takes the following arguments: X, y, X_resampled, y_resampled, method=''. The function plots the original data in a scatter plot, along with the resampled side by side.
```
print(pd.value_counts(pd.Series(y)))
print(pd.value_counts(pd.Series(y_resampled)))
compare_plot(X, y, X_resampled, y_resampled, method='SMOTE')
# This fundtion is not defined here. But the result picture is as below
#The compare_plot should be implemented by the subplot defined on dataframe, or by the subplot way summarized elsewhere.
```

### Exploring the traditional way to catch fraud
* Try finding fraud cases in our credit card dataset the "old way". First you'll define threshold values using common statistics, to split fraud and non-fraud. Then, use those thresholds on your features to detect fraud. This is common practice within fraud analytics teams.
* Statistical thresholds are often determined by looking at the mean values of observations.
* Check whether feature means differ between fraud and non-fraud cases. Then, use that information to create common sense thresholds.
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from imblearn.over_sampling import SMOTE
df = pd.read_csv("creditcard_sampledata_3.csv")
#print(df.columns) #It is not df.colnames.
df = df.drop(['Unnamed: 0'],axis = 1)
#print(df.head())
y=df['Class'].values
X=df.drop(['Class'],axis = 1).values
#my code above
# Run a groupby command on our labels and obtain the mean for each feature
df.groupby('Class').mean()
# Implement a rule for stating which cases are flagged as fraud
df['flag_as_fraud'] = np.where(np.logical_and(df['V1'] < -3, df['V3'] < -5), 1, 0)
# Create a crosstab of flagged fraud cases versus the actual fraud cases
print(pd.crosstab(df.Class, df.flag_as_fraud, rownames=['Actual Fraud'], colnames=['Flagged Fraud']))
```
Not bad, with this rule, we detect 22 out of 50 fraud cases, but can't detect the other 28, and get 16 false positives. In the next exercise, we'll see how this measures up to a machine learning model.
### Using ML classification to catch fraud
* Use a simple machine learning model on our credit card data instead.
* Implement a Logistic Regression model.
```
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# Fit a logistic regression model to our data
model = LogisticRegression()
model.fit(X_train, y_train)
# Obtain model predictions
predicted = model.predict(X_test)
# Print the classifcation report and confusion matrix
print('Classification report:\n', classification_report(y_test, predicted))
conf_mat = confusion_matrix(y_true=y_test, y_pred=predicted)
print('Confusion matrix:\n', conf_mat)
```
* We are getting much less false positives, so that's an improvement.
* We're catching a higher percentage of fraud cases, so that is also better than before.
### Logistic regression combined with SMOTE
```
# This is the pipeline module we need for this from imblearn
from imblearn.pipeline import Pipeline
# Define which resampling method and which ML model to use in the pipeline
resampling = SMOTE(kind='borderline2')
model = LogisticRegression()
# Define the pipeline, tell it to combine SMOTE with the Logistic Regression model
pipeline = Pipeline([('SMOTE', resampling), ('Logistic Regression', model)])
```
### Using a pipeline
Treat the pipeline as if it were a single machine learning model. Our data X and y are already defined, and the pipeline is defined in the previous exercise.
```
# Split your data X and y, into a training and a test set and fit the pipeline onto the training data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# Fit your pipeline onto your training set and obtain predictions by fitting the model onto the test data
pipeline.fit(X_train, y_train)
predicted = pipeline.predict(X_test)
# Obtain the results from the classification report and confusion matrix
print('Classifcation report:\n', classification_report(y_test, predicted))
conf_mat = confusion_matrix(y_true=y_test, y_pred=predicted)
print('Confusion matrix:\n', conf_mat)
```
* The SMOTE slightly improves our results. We now manage to find all cases of fraud, but we have a slightly higher number of false positives, albeit only 7 cases.
* Remember, not in all cases does resampling necessarily lead to better results. **When the fraud cases are very spread and scattered over the data, using SMOTE can introduce a bit of bias.** Nearest neighbors aren't necessarily also fraud cases, so the synthetic samples might 'confuse' the model slightly.
* In the next chapters, we'll learn how to also adjust our machine learning models to better detect the minority fraud cases.
## Fraud detection using labelled data
* Flag fraudulent transactions with supervised learning.
* Use classifiers, adjust them and compare them to find the most efficient fraud detection model.
### Natural hit rate
* Explore how prevalent fraud is in the dataset, to understand what the "natural accuracy" is, if we were to predict everything as non-fraud.
* It's is important to understand which level of "accuracy" you need to "beat" in order to get a better prediction than by doing nothing.
* Create a random forest classifier for fraud detection. That will serve as the "baseline" model that you're going to try to improve in the upcoming exercises.
```
import matplotlib.pyplot as plt
import pandas as pd
from imblearn.over_sampling import SMOTE
df = pd.read_csv("creditcard_sampledata_2.csv")
#print(df.columns) #It is not df.colnames.
df = df.drop(['Unnamed: 0'],axis = 1)
# print(df.head())
y=df['Class'].values
X=df.drop(['Class'],axis = 1).values
#extra code above
# Count the total number of observations from the length of y
total_obs = len(y)
# Count the total number of non-fraudulent observations
non_fraud = [i for i in y if i == 0]
count_non_fraud = non_fraud.count(0)
# Calculate the percentage of non fraud observations in the dataset
percentage = (float(count_non_fraud)/float(total_obs)) * 100
# Print the percentage: this is our "natural accuracy" by doing nothing
print(percentage)
```
This tells us that by doing nothing, we would be correct in 95.9% of the cases. So now you understand, that if we get an accuracy of less than this number, our model does not actually add any value in predicting how many cases are correct.
### Random Forest Classifier - part 1
```
print(X.shape)
print(y.shape)
from sklearn.ensemble import RandomForestClassifier
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
model = RandomForestClassifier(random_state=5)
```
### Random Forest Classifier - part 2
See how our Random Forest model performs without doing anything special to it.
```
model.fit(X_train, y_train)
predicted = model.predict(X_test)
from sklearn.metrics import accuracy_score
model.fit(X_train, y_train)
predicted = model.predict(X_test)
print(accuracy_score(y_test, predicted))
```
### Performance metrics for the RF model
* In the previous exercises you obtained an accuracy score for your random forest model. This time, we know accuracy can be misleading in the case of fraud detection.
* With highly imbalanced fraud data, the AUROC curve is a more reliable performance metric, used to compare different classifiers. Moreover, the classification report tells you about the precision and recall of your model, whilst the confusion matrix actually shows how many fraud cases you can predict correctly. So let's get these performance metrics.
* Continue working on the same random forest model from the previous exercise. The model, defined as model = RandomForestClassifier(random_state=5) has been fitted to the training data already, and X_train, y_train, X_test, y_test are available.
```
from sklearn.metrics import classification_report, confusion_matrix, roc_auc_score
predicted = model.predict(X_test)
probs = model.predict_proba(X_test)
# Print the ROC curve, classification report and confusion matrix
print(roc_auc_score(y_test, probs[:,1]))
print(classification_report(y_test, predicted))
print(confusion_matrix(y_test, predicted))
```
You have now obtained more meaningful performance metrics that tell us how well the model performs, given the highly imbalanced data that you're working with. The model predicts 76 cases of fraud, out of which 73 are actual fraud. You have only 3 false positives. This is really good, and as a result you have a very high precision score. You do however, don't catch 18 cases of actual fraud. Recall is therefore not as good as precision. Let's try to improve that in the following exercises.
### Plotting the Precision Recall Curve
* Plot a Precision-Recall curve, to investigate the trade-off between the two in your model. In this curve Precision and Recall are inversely related; as Precision increases, Recall falls and vice-versa. A balance between these two needs to be achieved in your model, otherwise you might end up with many false positives, or not enough actual fraud cases caught. To achieve this and to compare performance, the precision-recall curves come in handy.
* The Random Forest Classifier is available as model, and the predictions as predicted. You can simply obtain the average precision score and the PR curve from the sklearn package. T
* The function plot_pr_curve() plots the results.
```
from sklearn.metrics import average_precision_score
# Calculate average precision and the PR curve
average_precision = average_precision_score(y_test, predicted)
# Calculate average precision and the PR curve
average_precision = average_precision_score(y_test, predicted)
# Obtain precision and recall
precision, recall, _ = precision_recall_curve(y_test, predicted)
# Plot the recall precision tradeoff
plot_pr_curve(recall, precision, average_precision)
#This function is unavailable.
```

### Model adjustments
* A simple way to adjust the random forest model to deal with highly imbalanced fraud data, is to use the **class_weights option **when defining your sklearn model. However, as you will see, it is a bit of a blunt force mechanism and might not work for your very special case.
* Explore the weight = "balanced_subsample" mode the Random Forest model from the earlier exercise.
```
model = RandomForestClassifier(class_weight='balanced_subsample', random_state=5)
model.fit(X_train, y_train)
# Obtain the predicted values and probabilities from the model
predicted = model.predict(X_test)
probs = model.predict_proba(X_test)
print(roc_auc_score(y_test, probs[:,1]))
print(classification_report(y_test, predicted))
print(confusion_matrix(y_test, predicted))
```
* The model results don't improve drastically. We now have 3 less false positives, but now 19 in stead of 18 false negatives, i.e. cases of fraud we are not catching. If we mostly care about catching fraud, and not so much about the false positives, this does actually not improve our model at all, albeit a simple option to try.
* In the next exercises we will see how to more smartly tweak your model to focus on reducing false negatives and catch more fraud.
### Adjusting your Random Forest to fraud detection
* Explore the options for the random forest classifier, as we'll assign weights and tweak the shape of the decision trees in the forest.
* Define weights manually, to be able to off-set that imbalance slightly. In our case we have 300 fraud to 7000 non-fraud cases, so by setting the weight ratio to 1:12, we get to a 1/3 fraud to 2/3 non-fraud ratio, which is good enough for training the model on.
```
# Change the model options
model = RandomForestClassifier(bootstrap=True, class_weight={0:1, 1:12}, criterion='entropy',
max_depth=10,
min_samples_leaf=10,
# Change the number of trees to use
n_estimators=20, n_jobs=-1, random_state=5)
# Run the function get_model_results
# get_model_results(X_train, y_train, X_test, y_test, model)
#This function fits the model to your training data, predicts and obtains performance metrics
#similar to the steps you did in the previous exercises.
```
* By smartly defining more options in the model, you can obtain better predictions. You have effectively reduced the number of false negatives, i.e. you are catching more cases of fraud, whilst keeping the number of false positives low.
* In this exercise you've manually changed the options of the model. There is a smarter way of doing it, by using GridSearchCV, which you'll see in the next exercise!
### GridSearchCV to find optimal parameters
With GridSearchCV you can define which performance metric to score the options on. Since for fraud detection we are mostly interested in catching as many fraud cases as possible, you can optimize your model settings to get the **best possible Recall score.** If you also cared about reducing the number of false positives, you could optimize on F1-score, this gives you that nice Precision-Recall trade-off.
```
from sklearn.model_selection import GridSearchCV
# Define the parameter sets to test
param_grid = {'n_estimators': [1, 30], 'max_features': ['auto', 'log2'], 'max_depth': [4, 8], 'criterion': ['gini', 'entropy']
}
model = RandomForestClassifier(random_state=5)
CV_model = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='recall', n_jobs=-1)
CV_model.fit(X_train, y_train)
CV_model.best_params_
```
### Model results using GridSearchCV
* You discovered that the best parameters for your model are that the split criterion should be set to 'gini', the number of estimators (trees) should be 30, the maximum depth of the model should be 8 and the maximum features should be set to "log2".
* Let's give this a try and see how well our model performs. You can use the get_model_results() function again to save time.
```
# Input the optimal parameters in the model
model = RandomForestClassifier(class_weight={0:1,1:12}, criterion='gini',
max_depth=8, max_features='log2', min_samples_leaf=10, n_estimators=30, n_jobs=-1, random_state=5)
# Get results from your model
# get_model_results(X_train, y_train, X_test, y_test, model)
```
<script.py> output:
precision recall f1-score support
0.0 0.99 1.00 1.00 2099
1.0 0.95 0.84 0.89 91
micro avg 0.99 0.99 0.99 2190
macro avg 0.97 0.92 0.94 2190
weighted avg 0.99 0.99 0.99 2190
[[2095 4]
[ 15 76]]
* The number of false positives has now been slightly reduced even further, which means we are catching more cases of fraud.
* However, you see that the number of false positives actually went up. That is that Precision-Recall trade-off in action.
* To decide which final model is best, you need to take into account how bad it is not to catch fraudsters, versus how many false positives the fraud analytics team can deal with. Ultimately, this final decision should be made by you and the fraud team together.
### Logistic Regression
* Combine three algorithms into one model with the VotingClassifier. This allows us to benefit from the different aspects from all models, and hopefully improve overall performance and detect more fraud. The first model, the Logistic Regression, has a slightly higher recall score than our optimal Random Forest model, but gives a lot more false positives.
* You'll also add a Decision Tree with balanced weights to it. The data is already split into a training and test set, i.e. X_train, y_train, X_test, y_test are available.
* In order to understand how the Voting Classifier can potentially improve your original model, you should check the standalone results of the Logistic Regression model first.
```
# Define the Logistic Regression model with weights
model = LogisticRegression(class_weight={0:1, 1:15}, random_state=5)
# Get the model results
# get_model_results(X_train, y_train, X_test, y_test, model)
```
precision recall f1-score support
0.0 0.99 0.98 0.99 2099
1.0 0.63 0.88 0.73 91
` micro avg 0.97 0.97 0.97 2190
macro avg 0.81 0.93 0.86 2190
weighted avg 0.98 0.97 0.98 2190
`
`
[[2052 47]
[ 11 80]]
`
The Logistic Regression has quite different performance from the Random Forest. More false positives, but also a better Recall. It will therefore will a useful addition to the Random Forest in an ensemble model.
### Voting Classifier
* Combine three machine learning models into one, to improve our Random Forest fraud detection model from before. You'll combine our usual Random Forest model, with the Logistic Regression from the previous exercise, with a simple Decision Tree.
* Use the short cut get_model_results() to see the immediate result of the ensemble model.
```
from sklearn.ensemble import VotingClassifier
from sklearn.tree import DecisionTreeClassifier
# Define the three classifiers to use in the ensemble
clf1 = LogisticRegression(class_weight={0:1, 1:15}, random_state=5)
clf2 = RandomForestClassifier(class_weight={0:1, 1:12}, criterion='gini', max_depth=8, max_features='log2',
min_samples_leaf=10, n_estimators=30, n_jobs=-1, random_state=5)
clf3 = DecisionTreeClassifier(random_state=5, class_weight="balanced")
# Combine the classifiers in the ensemble model
ensemble_model = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('dt', clf3)], voting='hard')
# Get the results
# get_model_results(X_train, y_train, X_test, y_test, ensemble_model)
```
<script.py> output:
precision recall f1-score support
0.0 0.99 1.00 0.99 2099
1.0 0.90 0.86 0.88 91
micro avg 0.99 0.99 0.99 2190
macro avg 0.95 0.93 0.94 2190
weighted avg 0.99 0.99 0.99 2190
[[2090 9]
[ 13 78]]
* By combining the classifiers, you can take the best of multiple models. You've increased the cases of fraud you are catching from 76 to 78, and you only have 5 extra false positives in return.
* If you do care about catching as many fraud cases as you can, whilst keeping the false positives low, this is a pretty good trade-off.
* The Logistic Regression as a standalone was quite bad in terms of false positives, and the Random Forest was worse in terms of false negatives. By combining these together you indeed managed to improve performance.
### Adjust weights within the Voting Classifier
* The Voting Classifier allows you to improve your fraud detection performance, by combining good aspects from multiple models. Now let's try to adjust the weights we give to these models. By increasing or decreasing weights you can play with how much emphasis you give to a particular model relative to the rest. This comes in handy when a certain model has overall better performance than the rest, but you still want to combine aspects of the others to further improve your results.
* The data is already split into a training and test set, and clf1, clf2 and clf3 are available and defined as before, i.e. they are the Logistic Regression, the Random Forest model and the Decision Tree respectively.
```
ensemble_model = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft', weights=[1, 4, 1], flatten_transform=True)
# Get results
# get_model_results(X_train, y_train, X_test, y_test, ensemble_model)
```
<script.py> output:
precision recall f1-score support
0.0 0.99 1.00 1.00 2099
1.0 0.94 0.85 0.89 91
micro avg 0.99 0.99 0.99 2190
macro avg 0.97 0.92 0.94 2190
weighted avg 0.99 0.99 0.99 2190
[[2094 5]
[ 14 77]]
The weight option allows you to play with the individual models to get the best final mix for your fraud detection model. Now that you have finalized fraud detection with supervised learning, let's have a look at how fraud detection can be done when you don't have any labels to train on.
## Fraud detection using unlabelled data
* Use unsupervised learning techniques to detect fraud.
* Segment customers, use K-means clustering and other clustering algorithms to find suspicious occurrences in your data.
### Exploring your data
* Look at bank payment transaction data.
* Distinguish normal from abnormal (thus potentially fraudulent) behavior. As a fraud analyst to understand what is "normal", you need to have a good understanding of the data and its characteristics.
```
import pandas as pd
df = pd.read_csv('banksim.csv')
df = df.drop(['Unnamed: 0'],axis = 1)
print(df.head())
print(df.groupby('category').mean())
```
Even from simple group by, we can find that the majority of fraud is observed in travel, leisure and sports related transactions.
### Customer segmentation
* Check whether there are any obvious patterns for the clients in this data, thus whether you need to segment your data into groups, or whether the data is rather homogenous.
* There is not a lot client information available; However, there is data on **age ** available, so let's see whether there is any significant difference between behavior of age groups.
```
# Group by age groups and get the mean
print(df.groupby('age').mean())
# Group by age groups and get the mean
df.groupby('age').mean()
# Count the values of the observations in each age group
print(df['age'].value_counts())
```
* Does it make sense to divide your data into age segments before running a fraud detection algorithm?
* No, the age groups who are the largest are relatively similar. As you can see the average amount spent as well as fraud occurrence is rather similar across groups. Age group '0' stands out but since there are only 40 cases, it does not make sense to split these out in a separate group and run a separate model on them.
### Using statistics to define normal behavior
* In the previous exercises we saw that fraud is more prevalent in certain transaction categories, but that there is no obvious way to segment our data into for example age groups.
* This time, let's investigate the average amounts spend in normal transactions versus fraud transactions. This gives you an idea of how fraudulent transactions differ structurally from normal transactions.
```
# Create two dataframes with fraud and non-fraud data
df_fraud = df.loc[df.fraud == 1]
df_non_fraud = df.loc[df.fraud == 0]
# Plot histograms of the amounts in fraud and non-fraud data
plt.hist(df_fraud.amount, alpha=0.5, label='fraud')
plt.hist(df_non_fraud.amount, alpha=0.5, label='nonfraud')
plt.legend()
plt.show()
```
* As the number fraud observations is much smaller, it is difficult to see the full distribution.
* Nonetheless, you can see that the fraudulent transactions tend to be on the larger side relative to normal observations.
* This helps us later in detecting fraud from non-fraud. In the next chapter you're going to implement a clustering model to distinguish between normal and abnormal transactions, when the fraud labels are no longer available.
### Scaling the data
For ML algorithms using distance based metrics, it is crucial to always scale your data, as features using different scales will distort your results. K-means uses the Euclidian distance to assess distance to cluster centroids, therefore you first need to scale your data before continuing to implement the algorithm.
```
import pandas as pd
df = pd.read_csv('banksim_adj.csv')
X = df.drop(['Unnamed: 0'],axis = 1).values
y = df['fraud'].values
print(df.head())
#extra code above. The data might not be same as the DataCamp
from sklearn.preprocessing import MinMaxScaler
X = np.array(df).astype(np.float)
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)
```
### K-means clustering
* For fraud detection, K-means clustering is straightforward to implement and relatively powerful in predicting suspicious cases. It is a good algorithm to start with when working on fraud detection problems.
* However, fraud data is oftentimes very large, especially when you are working with transaction data. MiniBatch K-means is an efficient way to implement K-means on a large dataset, which you will use in this exercise.
```
# Import MiniBatchKmeans
from sklearn.cluster import MiniBatchKMeans
kmeans = MiniBatchKMeans(n_clusters=8, random_state=0)
kmeans.fit(X_scaled)
```
### Elbow method
* It is important to get the number of clusters right, especially when you want to **use the outliers of those clusters as fraud predictions**.
* Apply the Elbow method and see what the optimal number of clusters should be based on this method.
```
clustno = range(1, 10)
kmeans = [MiniBatchKMeans(n_clusters=i) for i in clustno]
score = [kmeans[i].fit(X_scaled).score(X_scaled) for i in range(len(kmeans))]
plt.plot(clustno, score)
plt.xlabel('Number of Clusters')
plt.ylabel('Score')
plt.title('Elbow Curve')
plt.show()
```
The optimal number of clusters should probably be at around 3 clusters, as that is where the elbow is in the curve.
### Detecting outliers
* Use the K-means algorithm to predict fraud, and compare those predictions to the actual labels that are saved, to sense check our results.
* The fraudulent transactions are typically flagged as the observations that are furthest aways from the cluster centroid.
* How to determine the cut-off in this exercise.
```
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=0)
kmeans = MiniBatchKMeans(n_clusters=3, random_state=42).fit(X_train)
X_test_clusters = kmeans.predict(X_test)
X_test_clusters_centers = kmeans.cluster_centers_
dist = [np.linalg.norm(x-y) for x, y in zip(X_test, X_test_clusters_centers[X_test_clusters])]
# np.linagl.norm calculate the 'norm' of a vector or a matrix.
# Create fraud predictions based on outliers on clusters
km_y_pred = np.array(dist)
km_y_pred[dist >= np.percentile(dist, 95)] = 1
km_y_pred[dist < np.percentile(dist, 95)] = 0
print(len(X_test))
print(len(X_test_clusters))
print(X_test_clusters)
print('--------------------')
print(X_test_clusters_centers)
print(len(dist))
```
### Checking model results
In the previous exercise you've flagged all observations to be fraud, if they are in the top 5th percentile in distance from the cluster centroid. I.e. these are the very outliers of the three clusters. For this exercise you have the scaled data and labels already split into training and test set, so y_test is available. The predictions from the previous exercise, km_y_pred, are also available. Let's create some performance metrics and see how well you did.
```
# Obtain the ROC score
print(roc_auc_score(y_test, km_y_pred))
#output: 0.8197704982668266
# Obtain the ROC score
print(roc_auc_score(y_test, km_y_pred))
# Create a confusion matrix
km_cm = confusion_matrix(y_test, km_y_pred)
# Plot the confusion matrix in a figure to visualize results
# plot_confusion_matrix(km_cm)
```

Question
If you were to decrease the percentile used as a cutoff point in the previous exercise to 93% instead of 95%, what would that do to your prediction results?
The number of fraud cases caught increases, but false positives also increase.
### DB scan
* Explore using a density based clustering method (DBSCAN) to detect fraud. The advantage of DBSCAN is that you do not need to define the number of clusters beforehand. Also, DBSCAN can handle weirdly shaped data (i.e. non-convex) much better than K-means can.
* This time, you are **not going to take the outliers of the clusters and use that for fraud, but take the smallest clusters in the data and label those as fraud**. You again have the scaled dataset, i.e. X_scaled available.
```
from sklearn.cluster import DBSCAN
# Initialize and fit the DBscan model
db = DBSCAN(eps=0.9, min_samples=10, n_jobs=-1).fit(X_scaled)
# Obtain the predicted labels and calculate number of clusters
pred_labels = db.labels_
n_clusters = len(set(pred_labels)) - (1 if -1 in labels else 0)
# # Print performance metrics for DBscan
# print('Estimated number of clusters: %d' % n_clusters)
# print("Homogeneity: %0.3f" % homogeneity_score(labels, pred_labels))
# print("Silhouette Coefficient: %0.3f" % silhouette_score(X_scaled, pred_labels))
```
output:
`
Estimated number of clusters: 18
Homogeneity: 0.633
Silhouette Coefficient: 0.707
`
The number of clusters is much higher than with K-means. For fraud detection this is for now OK, as we are only interested in the smallest clusters, since those are considered as abnormal. Now let's have a look at those clusters and decide which one to flag as fraud.
### Assessing smallest clusters
* Check the clusters that came out of DBscan, and flag certain clusters as fraud:
* Figure out how big the clusters are, and filter out the smallest. Then take the smallest ones and flag those as fraud.
* Check with the original labels whether this does actually do a good job in detecting fraud.
Available are the DBscan model predictions, so n_clusters is available as well as the cluster labels, which are saved under pred_labels.
```
counts = np.bincount(pred_labels[pred_labels >= 0])
print(counts)
```
output:
[3252 145 2714 55 174 119 122 98 54 15 76 15 43 25
51 47 42 15 25 20 19 10]
```
# Count observations in each cluster number
counts = np.bincount(pred_labels[pred_labels>=0])
# Sort the sample counts of the clusters and take the top 3 smallest clusters
smallest_clusters = np.argsort(counts)[:3]
# Print the results
print("The smallest clusters are clusters:")
print(smallest_clusters)
```
output:
The smallest clusters are clusters:
[21 17 9]
```
# Count observations in each cluster number
counts = np.bincount(pred_labels[pred_labels>=0])
# Sort the sample counts of the clusters and take the top 3 smallest clusters
smallest_clusters = np.argsort(counts)[:3]
# Print the counts of the smallest clusters only
print("Their counts are:")
print(counts[smallest_clusters])
```
<script.py> output:
Their counts are:
[10 15 15]
So now we know which smallest clusters you could flag as fraud. If you were to take more of the smallest clusters, you cast your net wider and catch more fraud, but most likely also more false positives. It is up to the fraud analyst to find the right amount of cases to flag and to investigate. In the next exercise you'll check the results with the actual labels.
### Checking results
In this exercise you're going to check the results of your DBscan fraud detection model. In reality, you often don't have reliable labels and this where a fraud analyst can help you validate the results. He/She can check your results and see whether the cases you flagged are indeed suspicious. You can also check historically known cases of fraud and see whether your model flags them.
In this case, you'll use the fraud labels to check your model results. The predicted cluster numbers are available under pred_labels as well as the original fraud labels labels.
```
# Create a dataframe of the predicted cluster numbers and fraud labels
df = pd.DataFrame({'clusternr':pred_labels,'fraud':labels})
# Create a condition flagging fraud for the smallest clusters
df['predicted_fraud'] = np.where((df['clusternr']==21) | (df['clusternr']==17) | (df['clusternr']==9), 1, 0)
# Run a crosstab on the results
print(pd.crosstab(df.fraud, df.predicted_fraud, rownames=['Actual Fraud'], colnames=['Flagged Fraud']))
```
output:
` Flagged Fraud 0 1
Actual Fraud
0 6973 16
1 176 24
`
How does this compare to the K-means model?
* The good thing is: our of all flagged cases, roughly 2/3 are actually fraud! Since you only take the three smallest clusters, by definition you flag less cases of fraud, so you catch less but also have less false positives. However, you are missing quite a lot of fraud cases.
* Increasing the amount of smallest clusters you flag could improve that, at the cost of more false positives of course.
## Fraud detection using text
Use text data, text mining and topic modeling to detect fraudulent behavior.
### Word search with dataframes
* Work with text data, containing emails from Enron employees.
* Using string operations on dataframes, you can easily sift through messy email data and create flags based on word-hits.
```
import pandas as pd
df = pd.read_csv('enron_emails_clean.csv',index_col = 0)
# Find all cleaned emails that contain 'sell enron stock'
mask = df['clean_content'].str.contains('sell enron stock', na=False)
# Select the data from df that contain the searched for words
print(df.loc[mask])
```
### Using list of terms
* Search on more than one term.
* Create a full "fraud dictionary" of terms that could potentially flag fraudulent clients and/or transactions. Fraud analysts often will have an idea what should be in such a dictionary. In this exercise you're going to flag a multitude of terms, and in the next exercise you'll create a new flag variable out of it. The 'flag' can be used either directly in a machine learning model as a feature, or as an additional filter on top of your machine learning model results.
```
# Create a list of terms to search for
searchfor = ['enron stock', 'sell stock', 'stock bonus', 'sell enron stock']
# Filter cleaned emails on searchfor list and select from df
filtered_emails = df.loc[df['clean_content'].str.contains('|'.join(searchfor), na=False)]
# print(filtered_emails)
```
### Creating a flag
This time you are going to create an actual flag variable that gives a 1 when the emails get a hit on the search terms of interest, and 0 otherwise. This is the last step you need to make in order to actually use the text data content as a feature in a machine learning model, or as an actual flag on top of model results. You can continue working with the dataframe df containing the emails, and the searchfor list is the one defined in the last exercise.
```
import numpy as np
# Create flag variable where the emails match the searchfor terms
df['flag'] = np.where((df['clean_content'].str.contains('|'.join(searchfor)) == True), 1, 0)
# Count the values of the flag variable
count = df['flag'].value_counts()
print(count)
```
You have now managed to search for a list of strings in several lines of text data. These skills come in handy when you want to flag certain words based on what you discovered in your topic model, or when you know beforehand what you want to search for. In the next exercises you're going to learn how to clean text data and to create your own topic model to further look for indications of fraud in your text data.
### Removing stopwords
In the following exercises you're going to clean the Enron emails, in order to be able to use the data in a topic model. Text cleaning can be challenging, so you'll learn some steps to do this well. The dataframe containing the emails df is available. In a first step you need to define the list of stopwords and punctuations that are to be removed in the next exercise from the text data. Let's give it a try.
```
# Import nltk packages and string
from nltk.corpus import stopwords
import string
# Define stopwords to exclude
stop = set(stopwords.words('english'))
# stop.update(("to","cc","subject","http","from","sent", "ect", "u", "fwd", "www", "com"))
# Define punctuations to exclude and lemmatizer
exclude = set(string.punctuation)
```
The following is the stop contents. However, stop = set(stopwords('english')) has problems to run.
{'a',
'about',
'above',
'after',
'again',
'against',
'ain',
'all',
'am',
.
.
.
'y',
'you',
"you'd",
"you'll",
"you're",
"you've",
'your',
'yours',
'yourself',
'yourselves'
}
### Cleaning text data
Now that you've defined the stopwords and punctuations, let's use these to clean our enron emails in the dataframe df further. The lists containing stopwords and punctuations are available under stop and exclude There are a few more steps to take before you have cleaned data, such as "lemmatization" of words, and stemming the verbs. The verbs in the email data are already stemmed, and the lemmatization is already done for you in this exercise.
```
# Import the lemmatizer from nltk
from nltk.stem.wordnet import WordNetLemmatizer
lemma = WordNetLemmatizer()
# Define word cleaning function
def clean(text, stop):
text = text.rstrip()
# Remove stopwords
stop_free = " ".join([word for word in text.lower().split() if ((word not in stop) and (not word.isdigit()))])
# Remove punctuations
punc_free = ''.join(word for word in stop_free if word not in exclude)
# Lemmatize all words
normalized = " ".join(lemma.lemmatize(word) for word in punc_free.split())
return normalized
# Import the lemmatizer from nltk
from nltk.stem.wordnet import WordNetLemmatizer
lemma = WordNetLemmatizer()
# Import the lemmatizer from nltk
from nltk.stem.wordnet import WordNetLemmatizer
lemma = WordNetLemmatizer()
# Define word cleaning function
def clean(text, stop):
text = text.rstrip()
stop_free = " ".join([i for i in text.lower().split() if((i not in stop) and (not i.isdigit()))])
punc_free = ''.join(i for i in stop_free if i not in exclude)
normalized = " ".join(lemma.lemmatize(i) for i in punc_free.split())
return normalized
# Clean the emails in df and print results
text_clean=[]
for text in df['clean_content']:
text_clean.append(clean(text, stop).split())
print(text_clean)
```
Now that you have cleaned your data entirely with the necessary steps, including splitting the text into words, removing stopwords and punctuations, and lemmatizing your words. You are now ready to run a topic model on this data. In the following exercises you're going to explore how to do that.
### Create dictionary and corpus
In order to run an LDA topic model, you first need to define your dictionary and corpus first, as those need to go into the model. You're going to continue working on the cleaned text data that you've done in the previous exercises. That means that text_clean is available for you already to continue working with, and you'll use that to create your dictionary and corpus.
This exercise will take a little longer to execute than usual.
```
# Import the packages
import gensim
from gensim import corpora
# Define the dictionary
dictionary = corpora.Dictionary(text_clean)
# Define the corpus
corpus = [dictionary.doc2bow(text) for text in text_clean]
# Print corpus and dictionary
print(dictionary)
print(corpus)
```
Dictionary(8948 unique tokens: ['conducted', 'read', 'wil', 'daniel', 'piazze']...)
[[(0, 1), (1, 2), (2, 1), (3, 1), (4, 2), (5, 1), (6, 2), (7, 1), (8, 1), (9, 1), (10, 5), (11, 2), (12, 1), (13, 1), (14, 1), (15, 1), (16, 1), (17, 1), (18, 1), (19, 1), (20, 1), (21, 1), (22, 1), (23, 1), (24, 1),....] total length.
Note doc2bow is doc to bag of words.
### LDA model (It is is not linear discriminant analysis)
Now it's time to build the LDA model. Using the dictionary and corpus, you are ready to discover which topics are present in the Enron emails. With a quick print of words assigned to the topics, you can do a first exploration about whether there are any obvious topics that jump out. Be mindful that the topic model is heavy to calculate so it will take a while to run. Let's give it a try!
```
ldamodel = gensim.models.ldamodel.LdaModel(corpus, num_topics=5, id2word=dictionary, passes=5)
# Save the topics and top 5 words
topics = ldamodel.print_topics(num_words=5)
# Print the results
for topic in topics:
print(topic)
```
`(0, '0.024*"enron" + 0.015*"ect" + 0.011*"com" + 0.007*"hou" + 0.005*"company"')
(1, '0.032*"enron" + 0.011*"com" + 0.009*"diabetes" + 0.008*"message" + 0.006*"please"')
(2, '0.031*"enron" + 0.011*"company" + 0.010*"said" + 0.007*"mr" + 0.005*"partnership"')
(3, '0.021*"enron" + 0.012*"employee" + 0.010*"company" + 0.009*"million" + 0.009*"com"')
(4, '0.040*"error" + 0.021*"database" + 0.018*"borland" + 0.018*"engine" + 0.018*"initialize"')
`
You have now successfully created your first topic model on the Enron email data. However, the print of words doesn't really give you enough information to find a topic that might lead you to signs of fraud. You'll therefore need to closely inspect the model results in order to be able to detect anything that can be related to fraud in your data.
Below are visualisation results from the pyLDAvis library available. Have a look at topic 1 and 3 from the LDA model on the Enron email data. Which one would you research further for fraud detection purposes and why?

Topic 1 seems to discuss the employee share option program, and seems to point to internal conversation (with "please, may, know" etc), so this is more likely to be related to the internal accounting fraud and trading stock with insider knowledge. Topic 3 seems to be more related to general news around Enron.
### Finding fraudsters based on topic
In this exercise you're going to link the results from the topic model back to your original data. You now learned that you want to flag everything related to topic 3. As you will see, this is actually not that straightforward. You'll be given the function get_topic_details() which takes the arguments ldamodel and corpus. It retrieves the details of the topics for each line of text. With that function, you can append the results back to your original data. If you want to learn more detail on how to work with the model results, which is beyond the scope of this course, you're highly encouraged to read this article (https://www.machinelearningplus.com/nlp/topic-modeling-gensim-python/).
Available for you are the dictionary and corpus, the text data text_clean as well as your model results ldamodel. Also defined is get_topic_details().
```
# Run get_topic_details function and check the results
print(get_topic_details(ldamodel, corpus))
# Add original text to topic details in a dataframe
contents = pd.DataFrame({'Original text': text_clean})
topic_details = pd.concat([get_topic_details(ldamodel, corpus), contents], axis=1)
topic_details.head()
# Add original text to topic details in a dataframe
contents = pd.DataFrame({'Original text':text_clean})
topic_details = pd.concat([get_topic_details(ldamodel, corpus), contents], axis=1)
# Create flag for text highest associated with topic 3
topic_details['flag'] = np.where((topic_details['Dominant_Topic'] == 3.0), 1, 0)
print(topic_details.head())
```
You have now flagged all data that is highest associated with topic 3, that seems to cover internal conversation about enron stock options. You are a true detective. With these exercises you have demonstrated that text mining and topic modeling can be a powerful tool for fraud detection.
### Summary
* We may apply all types of machine learning algorithms to handle anomaly and fraud detection.
* Supervised learning such as classification algorithms, neural network, etc.
* Unsupervised learning such as clustering algorithms.
* All the linear or nonlinear dimension reduction techniques that can be used directly to handle anomaly detection, or can be combined with other supervised/unsupervised learning algorithm.
* Natural language processing.
* Directly constructing Gaussian distribution (or other contributions) and flag outliers.
* Use network analysis for fraud or anomaly detection.
| true |
code
| 0.535584 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/tensorflow/tpu/blob/master/tools/colab/profiling_tpus_in_colab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
##### Copyright 2018 The TensorFlow Hub Authors.
Copyright 2019-2020 Google LLC
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
# Profiling TPUs in Colab <a href="https://cloud.google.com/tpu/"><img valign="middle" src="https://raw.githubusercontent.com/GoogleCloudPlatform/tensorflow-without-a-phd/master/tensorflow-rl-pong/images/tpu-hexagon.png" width="50"></a>
Adapted from [TPU colab example](https://colab.sandbox.google.com/notebooks/tpu.ipynb).
## Overview
This example works through training a model to classify images of
flowers on Google's lightning-fast Cloud TPUs. Our model takes as input a photo of a flower and returns whether it is a daisy, dandelion, rose, sunflower, or tulip. A key objective of this colab is to show you how to set up and run TensorBoard, the program used for visualizing and analyzing program performance on Cloud TPU.
This notebook is hosted on GitHub. To view it in its original repository, after opening the notebook, select **File > View on GitHub**.
## Instructions
<h3><a href="https://cloud.google.com/tpu/"><img valign="middle" src="https://raw.githubusercontent.com/GoogleCloudPlatform/tensorflow-without-a-phd/master/tensorflow-rl-pong/images/tpu-hexagon.png" width="50"></a> Train on TPU </h3>
* Create a Cloud Storage bucket for your TensorBoard logs at http://console.cloud.google.com/storage. Give yourself Storage Legacy Bucket Owner permission on the bucket.
You will need to provide the bucket name when launching TensorBoard in the **Training** section.
Note: User input is required when launching and viewing TensorBoard, so do not use **Runtime > Run all** to run through the entire colab.
## Authentication for connecting to GCS bucket for logging.
```
import os
IS_COLAB_BACKEND = 'COLAB_GPU' in os.environ # this is always set on Colab, the value is 0 or 1 depending on GPU presence
if IS_COLAB_BACKEND:
from google.colab import auth
# Authenticates the Colab machine and also the TPU using your
# credentials so that they can access your private GCS buckets.
auth.authenticate_user()
```
## Updating tensorboard_plugin_profile
```
!pip install -U pip install -U tensorboard_plugin_profile==2.3.0
```
## Enabling and testing the TPU
First, you'll need to enable TPUs for the notebook:
- Navigate to Edit→Notebook Settings
- select TPU from the Hardware Accelerator drop-down
Next, we'll check that we can connect to the TPU:
```
%tensorflow_version 2.x
import tensorflow as tf
print("Tensorflow version " + tf.__version__)
try:
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection
print('Running on TPU ', tpu.cluster_spec().as_dict()['worker'])
except ValueError:
raise BaseException('ERROR: Not connected to a TPU runtime; please see the previous cell in this notebook for instructions!')
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
tpu_strategy = tf.distribute.experimental.TPUStrategy(tpu)
import re
import numpy as np
from matplotlib import pyplot as plt
```
## Input data
Our input data is stored on Google Cloud Storage. To more fully use the parallelism TPUs offer us, and to avoid bottlenecking on data transfer, we've stored our input data in TFRecord files, 230 images per file.
Below, we make heavy use of `tf.data.experimental.AUTOTUNE` to optimize different parts of input loading.
All of these techniques are a bit overkill for our (small) dataset, but demonstrate best practices for using TPUs.
```
AUTO = tf.data.experimental.AUTOTUNE
IMAGE_SIZE = [331, 331]
batch_size = 16 * tpu_strategy.num_replicas_in_sync
gcs_pattern = 'gs://flowers-public/tfrecords-jpeg-331x331/*.tfrec'
validation_split = 0.19
filenames = tf.io.gfile.glob(gcs_pattern)
split = len(filenames) - int(len(filenames) * validation_split)
train_fns = filenames[:split]
validation_fns = filenames[split:]
def parse_tfrecord(example):
features = {
"image": tf.io.FixedLenFeature([], tf.string), # tf.string means bytestring
"class": tf.io.FixedLenFeature([], tf.int64), # shape [] means scalar
"one_hot_class": tf.io.VarLenFeature(tf.float32),
}
example = tf.io.parse_single_example(example, features)
decoded = tf.image.decode_jpeg(example['image'], channels=3)
normalized = tf.cast(decoded, tf.float32) / 255.0 # convert each 0-255 value to floats in [0, 1] range
image_tensor = tf.reshape(normalized, [*IMAGE_SIZE, 3])
one_hot_class = tf.reshape(tf.sparse.to_dense(example['one_hot_class']), [5])
return image_tensor, one_hot_class
def load_dataset(filenames):
# Read from TFRecords. For optimal performance, we interleave reads from multiple files.
records = tf.data.TFRecordDataset(filenames, num_parallel_reads=AUTO)
return records.map(parse_tfrecord, num_parallel_calls=AUTO)
def get_training_dataset():
dataset = load_dataset(train_fns)
# Create some additional training images by randomly flipping and
# increasing/decreasing the saturation of images in the training set.
def data_augment(image, one_hot_class):
modified = tf.image.random_flip_left_right(image)
modified = tf.image.random_saturation(modified, 0, 2)
return modified, one_hot_class
augmented = dataset.map(data_augment, num_parallel_calls=AUTO)
# Prefetch the next batch while training (autotune prefetch buffer size).
return augmented.repeat().shuffle(2048).batch(batch_size).prefetch(AUTO)
training_dataset = get_training_dataset()
validation_dataset = load_dataset(validation_fns).batch(batch_size).prefetch(AUTO)
```
Let's take a peek at the training dataset we've created:
```
CLASSES = ['daisy', 'dandelion', 'roses', 'sunflowers', 'tulips']
def display_one_flower(image, title, subplot, color):
plt.subplot(subplot)
plt.axis('off')
plt.imshow(image)
plt.title(title, fontsize=16, color=color)
# If model is provided, use it to generate predictions.
def display_nine_flowers(images, titles, title_colors=None):
subplot = 331
plt.figure(figsize=(13,13))
for i in range(9):
color = 'black' if title_colors is None else title_colors[i]
display_one_flower(images[i], titles[i], 331+i, color)
plt.tight_layout()
plt.subplots_adjust(wspace=0.1, hspace=0.1)
plt.show()
def get_dataset_iterator(dataset, n_examples):
return dataset.unbatch().batch(n_examples).as_numpy_iterator()
training_viz_iterator = get_dataset_iterator(training_dataset, 9)
# Re-run this cell to show a new batch of images
images, classes = next(training_viz_iterator)
class_idxs = np.argmax(classes, axis=-1) # transform from one-hot array to class number
labels = [CLASSES[idx] for idx in class_idxs]
display_nine_flowers(images, labels)
```
## Model
To get maxmimum accuracy, we leverage a pretrained image recognition model (here, [Xception](http://openaccess.thecvf.com/content_cvpr_2017/papers/Chollet_Xception_Deep_Learning_CVPR_2017_paper.pdf)). We drop the ImageNet-specific top layers (`include_top=false`), and add a max pooling and a softmax layer to predict our 5 classes.
```
def create_model():
pretrained_model = tf.keras.applications.Xception(input_shape=[*IMAGE_SIZE, 3], include_top=False)
pretrained_model.trainable = True
model = tf.keras.Sequential([
pretrained_model,
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(5, activation='softmax')
])
model.compile(
optimizer='adam',
loss = 'categorical_crossentropy',
metrics=['accuracy']
)
return model
with tpu_strategy.scope(): # creating the model in the TPUStrategy scope means we will train the model on the TPU
model = create_model()
model.summary()
```
## Training
Calculate the number of images in each dataset. Rather than actually load the data to do so (expensive), we rely on hints in the filename. This is used to calculate the number of batches per epoch.
```
def count_data_items(filenames):
# The number of data items is written in the name of the .tfrec files, i.e. flowers00-230.tfrec = 230 data items
n = [int(re.compile(r"-([0-9]*)\.").search(filename).group(1)) for filename in filenames]
return np.sum(n)
n_train = count_data_items(train_fns)
n_valid = count_data_items(validation_fns)
train_steps = count_data_items(train_fns) // batch_size
print("TRAINING IMAGES: ", n_train, ", STEPS PER EPOCH: ", train_steps)
print("VALIDATION IMAGES: ", n_valid)
```
Calculate and show a learning rate schedule. We start with a fairly low rate, as we're using a pre-trained model and don't want to undo all the fine work put into training it.
```
EPOCHS = 12
start_lr = 0.00001
min_lr = 0.00001
max_lr = 0.00005 * tpu_strategy.num_replicas_in_sync
rampup_epochs = 5
sustain_epochs = 0
exp_decay = .8
def lrfn(epoch):
if epoch < rampup_epochs:
return (max_lr - start_lr)/rampup_epochs * epoch + start_lr
elif epoch < rampup_epochs + sustain_epochs:
return max_lr
else:
return (max_lr - min_lr) * exp_decay**(epoch-rampup_epochs-sustain_epochs) + min_lr
lr_callback = tf.keras.callbacks.LearningRateScheduler(lambda epoch: lrfn(epoch), verbose=True)
rang = np.arange(EPOCHS)
y = [lrfn(x) for x in rang]
plt.plot(rang, y)
print('Learning rate per epoch:')
```
Train the model. While the first epoch will be quite a bit slower as we must XLA-compile the execution graph and load the data, later epochs should complete in ~5s.
```
# Load the TensorBoard notebook extension.
%load_ext tensorboard
# Get TPU profiling service address. This address will be needed for capturing
# profile information with TensorBoard in the following steps.
service_addr = tpu.get_master().replace(':8470', ':8466')
print(service_addr)
# Launch TensorBoard.
%tensorboard --logdir=gs://bucket-name # Replace the bucket-name variable with your own gcs bucket
```
The TensorBoard UI is displayed in a browser window. In this colab, perform the following steps to prepare to capture profile information.
1. Click on the dropdown menu box on the top right side and scroll down and click PROFILE. A new window appears that shows: **No profile data was found** at the top.
1. Click on the CAPTURE PROFILE button. A new dialog appears. The top input line shows: **Profile Service URL or TPU name**. Copy and paste the Profile Service URL (the service_addr value shown before launching TensorBoard) into the top input line. While still on the dialog box, start the training with the next step.
1. Click on the next colab cell to start training the model.
1. Watch the output from the training until several epochs have completed. This allows time for the profile data to start being collected. Return to the dialog box and click on the CAPTURE button. If the capture succeeds, the page will auto refresh and redirect you to the profiling results.
```
history = model.fit(training_dataset, validation_data=validation_dataset,
steps_per_epoch=train_steps, epochs=EPOCHS, callbacks=[lr_callback])
final_accuracy = history.history["val_accuracy"][-5:]
print("FINAL ACCURACY MEAN-5: ", np.mean(final_accuracy))
def display_training_curves(training, validation, title, subplot):
ax = plt.subplot(subplot)
ax.plot(training)
ax.plot(validation)
ax.set_title('model '+ title)
ax.set_ylabel(title)
ax.set_xlabel('epoch')
ax.legend(['training', 'validation'])
plt.subplots(figsize=(10,10))
plt.tight_layout()
display_training_curves(history.history['accuracy'], history.history['val_accuracy'], 'accuracy', 211)
display_training_curves(history.history['loss'], history.history['val_loss'], 'loss', 212)
```
Accuracy goes up and loss goes down. Looks good!
## Next steps
More TPU/Keras examples include:
- [Shakespeare in 5 minutes with Cloud TPUs and Keras](https://colab.research.google.com/github/tensorflow/tpu/blob/master/tools/colab/shakespeare_with_tpu_and_keras.ipynb)
- [Fashion MNIST with Keras and TPUs](https://colab.research.google.com/github/tensorflow/tpu/blob/master/tools/colab/fashion_mnist.ipynb)
We'll be sharing more examples of TPU use in Colab over time, so be sure to check back for additional example links, or [follow us on Twitter @GoogleColab](https://twitter.com/googlecolab).
| true |
code
| 0.692668 | null | null | null | null |
|
# Generating percentiles for TensorFlow model input features
The current TensorFlow model uses histogram-like percentile features, which are kind of a continuous version of one-hot features.
For example, if key cutoff points are `[-3, 1, 0, 2, 10]`, we might encode a value `x` as `sigma((x - cutoff) / scale)`. If `sigma` is the sigmoid function, `x = 0.1`, and `scale = 0.1`, then we'd get `[1, 1, 0.73, 0, 0]`, in other words `x` is definitely above the first 2 points, mostly above the third, and below the fourth and fifth. If we increase `scale` to `2.0`, then values are less discrete: `[0.82, 0.63, 0.51, 0.28, 0.01]`.
This notebook generates appropriate cutoff points for these, to reflect most data encountered.
```
# Different options for soft-onehot function.
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(-10, 10, 100)
cutoff = 1.0
sigmoid = lambda x: 1/(1+np.exp(-x))
scale = 2.0
logit = (x - cutoff) / scale
plt.plot(x, sigmoid(logit))
plt.plot(x, np.exp(- logit * logit))
NUM_LCS = 10_000 # key parameter, turn it down if you want this notebook to finish faster.
# Settings determining type of features extracted.
window_size = 10
band_time_diff = 4.0
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from justice.datasets import plasticc_data
source = plasticc_data.PlasticcBcolzSource.get_default()
bcolz_source = plasticc_data.PlasticcBcolzSource.get_default()
meta_table = bcolz_source.get_table('test_set_metadata')
%time all_ids = meta_table['object_id'][:]
%%time
import random
sample_ids = random.Random(828372).sample(list(all_ids), NUM_LCS)
lcs = []
_chunk_sz = 100
for start in range(0, len(sample_ids), _chunk_sz):
lcs.extend(plasticc_data.PlasticcDatasetLC.bcolz_get_lcs_by_obj_ids(
bcolz_source=source,
dataset="test_set",
obj_ids=sample_ids[start:start + _chunk_sz]
))
%%time
from justice.features import band_settings_params
from justice.features import dense_extracted_features
from justice.features import feature_combinators
from justice.features import metadata_features
from justice.features import per_point_dataset
from justice.features import raw_value_features
batch_size = 32
rve = raw_value_features.RawValueExtractor(
window_size=window_size,
band_settings=band_settings_params.BandSettings(lcs[0].expected_bands)
)
mve = metadata_features.MetadataValueExtractor()
data_gen = per_point_dataset.PerPointDatasetGenerator(
extract_fcn=feature_combinators.combine([rve.extract, mve.extract]),
batch_size=batch_size,
)
def input_fn():
return data_gen.make_dataset_lcs(lcs)
def per_band_model_fn(band_features, params):
batch_size = params["batch_size"]
window_size = params["window_size"]
wf = dense_extracted_features.WindowFeatures(
band_features, batch_size=batch_size, window_size=window_size, band_time_diff=band_time_diff)
dflux_dt = wf.dflux_dt(clip_magnitude=None)
init_layer = dense_extracted_features.initial_layer(wf, include_flux_and_time=True)
init_layer_masked = wf.masked(init_layer, value_if_masked=0, expected_extra_dims=[3])
return {
"initial_layer": init_layer_masked,
"in_window": wf.in_window,
}
def model_fn(features, labels, mode, params):
band_settings = band_settings_params.BandSettings.from_params(params)
per_band_data = band_settings.per_band_sub_model_fn(
per_band_model_fn, features, params=params
)
predictions = {
'band_{}.{}'.format(band, name): tensor
for band, tensor_dict in zip(band_settings.bands, per_band_data)
for name, tensor in tensor_dict.items()
}
predictions['time'] = features['time']
predictions['object_id'] = features['object_id']
return tf.estimator.EstimatorSpec(
mode=mode, predictions=predictions, loss=tf.constant(0.0), train_op=tf.no_op()
)
params = {
'batch_size': batch_size,
'window_size': window_size,
'flux_scale_epsilon': 0.5,
'lc_bands': lcs[0].expected_bands,
}
estimator = tf.estimator.Estimator(
model_fn=model_fn,
params=params
)
predictions = list(estimator.predict(input_fn=input_fn, yield_single_examples=True))
print(f"Got {len(predictions)} predictions.")
predictions[4]
def get_values_df(band):
arrays = [x[f"band_{band}.initial_layer"] for x in predictions if x[f"band_{band}.in_window"]]
return pd.DataFrame(np.concatenate(arrays, axis=0), columns=["dflux_dt", "dflux", "dtime"])
df = get_values_df(lcs[0].expected_bands[0])
df.hist('dflux_dt', bins=32)
df.hist('dflux', bins=32)
df.hist('dtime', bins=32)
```
## Really messy code to get a histogram with mostly-unique bins.
Because we want fixed-size arrays for TensorFlow code, we want a set of e.g. 32 unique cutoff points that reflect a good distribution of cutoffs. However its is really messy, because there tend to be strong peaks in the histogram which are repeated frequently.
```
import collections
import scipy.optimize
def _some_duplicates(non_unique, unique, num_desired):
to_duplicate_candidates = non_unique.tolist()
for x in unique:
to_duplicate_candidates.remove(x)
unique = unique.tolist()
while len(unique) < num_desired:
assert len(unique) <= num_desired
to_duplicate = random.choice(to_duplicate_candidates)
unique.insert(unique.index(to_duplicate), to_duplicate)
return unique
def unique_percentiles(array, num_desired):
partition_size = 100.0 / num_desired
epsilon = 0.05 * partition_size
solution = None
optimal_solution = None
def _actual_unique(vals):
nonlocal solution, optimal_solution
if optimal_solution is not None:
return 0 # stop optimization, or at least return quickly
num_points_base, perturb = vals
num_points = int(round(num_desired * num_points_base))
perturb = abs(perturb)
q = np.linspace(0, 100, int(num_points))
rng = np.random.RandomState(int(1e6 * perturb))
noise = rng.normal(loc=0, scale=min(1.0, 10 * perturb) * epsilon, size=q.shape)
noise[0] = 0
noise[-1] = 0
q += noise
non_unique = np.percentile(array, q=q, interpolation='linear')
unique = np.unique(non_unique)
result = abs(num_desired - len(unique))
if num_desired == len(unique):
optimal_solution = unique
elif len(unique) <= num_desired <= len(unique) + 1:
solution = _some_duplicates(non_unique, unique, num_desired)
return (4 if len(unique) > num_desired else 1) * result + perturb
res = scipy.optimize.minimize(
_actual_unique,
x0=[1.0, 0.1],
options={'maxiter': 1000, 'rhobeg': 0.3},
tol=1e-6,
method='COBYLA')
if optimal_solution is None and solution is None:
raise ValueError(f"Could not find deduplicated percentiles!")
return optimal_solution if optimal_solution is not None else solution
desired_num_cutoffs = 32
all_solutions = []
for band in lcs[0].expected_bands:
df = get_values_df(band)
for i, column in enumerate(df.columns):
print(band, column)
percentiles = np.array(unique_percentiles(df[column], desired_num_cutoffs), dtype=np.float32)
median_scale = np.median(percentiles[1:] - percentiles[:-1])
all_solutions.append({
'band': band,
'column_index': i,
'column': column,
'median_scale': float(median_scale),
'cutoffs': percentiles,
})
with_settings = {
'window_size': window_size,
'band_time_diff': band_time_diff,
'desired_num_cutoffs': desired_num_cutoffs,
'solutions': all_solutions
}
```
## Save to nicely-formatted JSON
Writes numpy arrays as strings, then rewrites those strings.
```
import datetime
import json
from justice import path_util
class ArrayPreEncoder(json.JSONEncoder):
def default(self, obj):
if isinstance(obj, np.ndarray):
return "<<<<{}>>>>".format(", ".join(f"{x:.8f}" for x in obj.tolist()))
else:
print(obj)
return json.JSONEncoder.default(self, obj)
def _encode(x):
result = json.dumps(x, indent=2, cls=ArrayPreEncoder).replace('"<<<<', '[').replace('>>>>"', ']')
json.loads(result) # error if not decodable
return result
now = datetime.datetime.now()
path = path_util.data_dir / 'tf_align_model' / 'feature_extraction' / (
f"cutoffs__window_sz-{window_size}__{now.year:04d}-{now.month:02d}-{now.day:02d}.json")
path.parent.mkdir(parents=True, exist_ok=True)
with open(str(path), 'w') as f:
f.write(_encode(with_settings))
```
| true |
code
| 0.62778 | null | null | null | null |
|
# A glimpse into the inner working of a 2 layer Neural network
```
%load_ext autoreload
%autoreload 2
import numpy as np
from numpy import random as nprand
from cs771 import plotData as pd, utils, genSyntheticData as gsd
from keras.models import Sequential
from keras.layers import Dense as dense
from keras import optimizers
d = 2
n = 20
r = 2
tmp1 = gsd.genSphericalData( d, n, [-5, -5], r )
tmp2 = gsd.genSphericalData( d, n, [5, 5], r )
XPos = np.vstack( (tmp1, tmp2) )
yPos = np.ones( (XPos.shape[0],) )
tmp1 = gsd.genSphericalData( d, n, [-5, 5], r )
tmp2 = gsd.genSphericalData( d, n, [5, -5], r )
XNeg = np.vstack( (tmp1, tmp2) )
yNeg = np.zeros( (XNeg.shape[0],) )
X = np.vstack( (XPos, XNeg) )
y = np.concatenate( (yPos, yNeg) )
n = X.shape[0]
idx = nprand.permutation( n )
X = X[idx]
y = y[idx]
mu = np.mean( X, axis = 0 )
sigma = np.std( X, axis = 0 )
X -= mu
X /= sigma
# You may get deprecation warnings about tensorflow when you run
# this cell for the first time. This is okay and not an error
# It seems TF has disabled several functional API in its new version
# and keras routines have not (yet) been upgraded to use them and
# continue to use the old (deprecated) routines hence the warnings
model = Sequential()
model.add( dense( units = 2, activation = "sigmoid", input_dim = 2, use_bias = True ) )
model.add( dense( units = 1, activation = "sigmoid", use_bias = True ) )
# Setting a very large learning rate lr may make the NN temperamental and cause
# it to converge to a local optima. Keras supports "callbacks" which allow the
# user to dynamically lower learning rate if progress has stalled
opt = optimizers.Adam( lr = 0.1, beta_1 = 0.9, beta_2 = 0.999, amsgrad = True )
# Metrics are just for sake of display, not for sake of training
# Set verbose = 1 or 2 to see metrics reported for every epoch of training
# Notice that whereas loss value goes down almost monotonically, the accuracy
# may fluctuate i.e. go down a bit before finally going up again
model.compile( loss = "binary_crossentropy", optimizer = opt, metrics = ["binary_accuracy"] )
history = model.fit( X, y, epochs = 50, batch_size = n//8, verbose = 0 )
fig0, ax0 = pd.getFigList( nrows = 1, ncols = 2, sizex = 5, sizey = 4 )
ax0[0].plot(history.history['loss'])
ax0[1].plot(history.history['binary_accuracy'])
ax0[0].set_xlabel( "Epochs" )
ax0[0].set_ylabel( "Binary Cross Entropy Loss" )
ax0[1].set_xlabel( "Epochs" )
ax0[1].set_ylabel( "Classification Accuracy" )
def ffpredict( X ):
# Our shading code anyway converts predictions to [0,1] scores
return model.predict_classes( X )
fig = pd.getFigure( 10, 10 )
(xlim, ylim) = np.max( np.abs( X ), axis = 0 ) * 1.1
pd.shade2D( ffpredict, fig, mode = "batch", xlim = xlim, ylim = ylim )
pd.plot2D( X[y == 1], fig, color = 'g', marker = '+' )
pd.plot2D( X[y == 0], fig, color = 'r', marker = 'x' )
def sigmoid( a ):
return 1/(1 + np.exp( -a ))
def getHiddenLayerActivations( X ):
return sigmoid( X.dot( w ) + b )
# Our network learns a function of the form (s = sigmoid function)
# s( u.T * s( P.T * x + q ) + v )
# Weights that go to the hidden layer
P = model.layers[0].get_weights()[0]
q = model.layers[0].get_weights()[1]
# Weights that go to the output layer
u = model.layers[1].get_weights()[0]
v = model.layers[1].get_weights()[1]
# Get the post activations of the first hidden layer neuron
# The multiplication with sign(u[0]) is just to make sure
# that the colors turn out nicely in the plots
w = P[:,0] * np.sign( u[0] )
b = q[0] * np.sign( u[0] )
fig2 = pd.getFigure( 10, 10 )
pd.shade2DProb( getHiddenLayerActivations, fig2, mode = "batch", xlim = xlim, ylim = ylim )
pd.plot2D( X[y == 1], fig2, color = 'g', marker = '+' )
pd.plot2D( X[y == 0], fig2, color = 'r', marker = 'x' )
# Get the post activations of the second hidden layer neuron
# The multiplication with sign(u[1]) is yet again just to make
# sure that the colors turn out nicely in the plots
w = P[:,1] * np.sign( u[1] )
b = q[1] * np.sign( u[1] )
fig3 = pd.getFigure( 10, 10 )
pd.shade2DProb( getHiddenLayerActivations, fig3, mode = "batch", xlim = xlim, ylim = ylim )
pd.plot2D( X[y == 1], fig3, color = 'g', marker = '+' )
pd.plot2D( X[y == 0], fig3, color = 'r', marker = 'x' )
# Note that the two nodes in the hidden layer cooperate to learn the classifier
# Neither node can fully classify the red points from the green points on its own
# so they share the burden. Each node takes up the responsibility of isolating
# one red clump from the rest of the data. Together they make a perfect classifier :)
# One can interpret these two nodes as learning two useful features such that the
# learning problem become linearly separable when given these two new features
print( model.layers[0].get_weights() )
print( model.layers[1].get_weights() )
# See the value of the weights below and verify that they indeed are of the form
# that we saw in the toy code (that demonstrated universality of NN)
```
| true |
code
| 0.743811 | null | null | null | null |
|
### - Canonical Correlation Analysis btw Cell painting & L1000
- This notebook focus on calculating the canonical coefficients between the canonical variables of Cell painting and L1000 level-4 profiles after applying PCA on them.
---------------------------------------------
- The aim of CCA is finding the relationship between two lumped variables in a way that the correlation between these twos is maximum. Obviously, there are several linear combinations of variables, but the aim is to pick only those linear functions which best express the correlations between the two variable sets. These linear functions are called the canonical variables, and the correlations between corresponding pairs of canonical variables are called canonical correlations. [CCA read](https://medium.com/analytics-vidhya/what-is-canonical-correlation-analysis-58ef4349c0b0) [cca_tutorial](https://github.com/google/svcca/blob/master/tutorials/001_Introduction.ipynb)
```
from google.colab import drive
drive.mount('/content/drive')
import os, sys
from matplotlib import pyplot as plt
%matplotlib inline
import numpy as np
import pickle
import pandas as pd
import seaborn as sns
import gzip
sns.set_context("talk")
sns.set_style("darkgrid")
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.cross_decomposition import CCA
###know the current directory
os.getcwd()
os.chdir('/content/drive')
# !cat 'My Drive/profiles/cell_painting/cca_core.py'
sys.path.append('My Drive/profiles/cell_painting/')
import cca_core
L1000_cp_dir = 'My Drive/profiles/L1000_cellpainting_comparison/L1000_CP_lvl4_datasets'
df_train = pd.read_csv(os.path.join(L1000_cp_dir, 'train_lvl4_data.csv.gz'),
compression='gzip',low_memory = False)
df_test = pd.read_csv(os.path.join(L1000_cp_dir, 'test_lvl4_data.csv.gz'),
compression='gzip',low_memory = False)
df_targets = pd.read_csv(os.path.join(L1000_cp_dir, 'target_labels.csv'))
metadata_cols = ['replicate_name', 'replicate_id', 'Metadata_broad_sample', 'Metadata_pert_id', 'Metadata_Plate',
'Metadata_Well', 'Metadata_broad_id', 'Metadata_moa', 'sig_id', 'pert_id', 'pert_idose',
'det_plate', 'det_well', 'Metadata_broad_sample', 'pert_iname', 'moa', 'dose']
target_cols = df_targets.columns[1:]
df_train_y = df_train[target_cols].copy()
df_train_x = df_train.drop(target_cols, axis = 1).copy()
df_test_y = df_test[target_cols].copy()
df_test_x = df_test.drop(target_cols, axis = 1).copy()
df_train_x.drop(metadata_cols, axis = 1, inplace = True)
df_test_x.drop(metadata_cols, axis = 1, inplace = True)
cp_cols = df_train_x.columns.tolist()[:696]
L1000_cols = df_train_x.columns.tolist()[696:]
df_train_cp_x = df_train_x.iloc[:, :696].copy()
df_train_L1000_x = df_train_x.iloc[:, 696:].copy()
df_test_cp_x = df_test_x.iloc[:, :696].copy()
df_test_L1000_x = df_test_x.iloc[:, 696:].copy()
df_cp_x = pd.concat([df_train_cp_x, df_test_cp_x])
df_L1000_x = pd.concat([df_train_L1000_x, df_test_L1000_x])
def normalize(df):
'''Normalize using Standardscaler'''
norm_model = StandardScaler()
df_norm = pd.DataFrame(norm_model.fit_transform(df),index = df.index,columns = df.columns)
return df_norm
df_L1000_x = normalize(df_L1000_x)
df_cp_x = normalize(df_cp_x)
# taking the first 300 PCs for CCA and SVCCA
def pca_preprocess(df,n_comp1 = 300,feat_new = ['pca'+ str(i) for i in range(300)]):
pca = PCA(n_components=n_comp1, random_state=42)
df_pca = pd.DataFrame(pca.fit_transform(df),columns=feat_new)
return(df_pca)
df_L1_pc_x = pca_preprocess(df_L1000_x)
df_cp_pc_x = pca_preprocess(df_cp_x)
```
#### - CCA on CP & L1000 train data
```
cca_results = cca_core.get_cca_similarity(df_cp_pc_x.values.T, df_L1_pc_x.values.T, epsilon=1e-10, verbose=False)
plt.figure(figsize=(12,8))
sns.set_context('talk', font_scale = 0.85)
sns.lineplot(x=range(len(cca_results["cca_coef1"])), y=cca_results["cca_coef1"])
plt.title("CCA correlation coefficients between CP and L1000 canonical variables (300) after PCA")
print("Mean Canonical Correlation co-efficient between CP and L1000 canonical variables (300):", np.mean(cca_results["cca_coef1"]))
```
#### - (Singular Vectors)CCA as a method to analyze the correlation between Cell painting & L1000
```
print("Results using SVCCA keeping 300 dims")
# Mean subtract activations
cacts1 = df_cp_pc_x.values.T - np.mean(df_cp_pc_x.values.T, axis=1, keepdims=True)
cacts2 = df_L1_pc_x.values.T - np.mean(df_L1_pc_x.values.T, axis=1, keepdims=True)
# Perform SVD
U1, s1, V1 = np.linalg.svd(cacts1, full_matrices=False)
U2, s2, V2 = np.linalg.svd(cacts2, full_matrices=False)
svacts1 = np.dot(s1[:300]*np.eye(300), V1[:300])
# can also compute as svacts1 = np.dot(U1.T[:20], cacts1)
svacts2 = np.dot(s2[:300]*np.eye(300), V2[:300])
# can also compute as svacts1 = np.dot(U2.T[:20], cacts2)
svcca_results = cca_core.get_cca_similarity(svacts1, svacts2, epsilon=1e-10, verbose=False)
print('mean svcca correlation coefficient:', np.mean(svcca_results["cca_coef1"]))
plt.figure(figsize=(12,8))
sns.set_context('talk', font_scale = 0.85)
plt.plot(svcca_results["cca_coef1"], lw=2.0)
plt.xlabel("Sorted CCA Correlation Coeff Idx")
plt.ylabel("CCA Correlation Coefficient Value")
plt.title("SVCCA correlation coefficients between CP and L1000 canonical variables (300)")
```
### - Using Sklearn CCA package for CCA
```
cca = CCA(n_components=df_cp_pc_x.shape[1])
cp_cca_vars, L1000_cca_vars = cca.fit_transform(df_cp_pc_x, df_L1_pc_x)
canonical_coeffs = np.corrcoef(cp_cca_vars.T, L1000_cca_vars.T).diagonal(offset=df_cp_pc_x.shape[1])
print('mean svcca correlation coefficient:', np.mean(svcca_results["cca_coef1"]))
plt.figure(figsize=(12,8))
sns.set_context('talk', font_scale = 0.85)
plt.plot(canonical_coeffs, lw=2.0)
plt.xlabel("Sorted CCA Correlation Coeff Idx")
plt.ylabel("CCA Correlation Coefficient Value")
plt.title("CCA correlation coefficients between CP and L1000 canonical variables after PCA")
```
#### - Ultimately for further analysis, focus will be on the first few canonical variables of both CP and L1000 that have the highest canonical coefficients.
| true |
code
| 0.586582 | null | null | null | null |
|
# Skip-gram word2vec
In this notebook, I'll lead you through using TensorFlow to implement the word2vec algorithm using the skip-gram architecture. By implementing this, you'll learn about embedding words for use in natural language processing. This will come in handy when dealing with things like machine translation.
## Readings
Here are the resources I used to build this notebook. I suggest reading these either beforehand or while you're working on this material.
* A really good [conceptual overview](http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/) of word2vec from Chris McCormick
* [First word2vec paper](https://arxiv.org/pdf/1301.3781.pdf) from Mikolov et al.
* [NIPS paper](http://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf) with improvements for word2vec also from Mikolov et al.
* An [implementation of word2vec](http://www.thushv.com/natural_language_processing/word2vec-part-1-nlp-with-deep-learning-with-tensorflow-skip-gram/) from Thushan Ganegedara
* TensorFlow [word2vec tutorial](https://www.tensorflow.org/tutorials/word2vec)
## Word embeddings
When you're dealing with words in text, you end up with tens of thousands of classes to predict, one for each word. Trying to one-hot encode these words is massively inefficient, you'll have one element set to 1 and the other 50,000 set to 0. The matrix multiplication going into the first hidden layer will have almost all of the resulting values be zero. This a huge waste of computation.

To solve this problem and greatly increase the efficiency of our networks, we use what are called embeddings. Embeddings are just a fully connected layer like you've seen before. We call this layer the embedding layer and the weights are embedding weights. We skip the multiplication into the embedding layer by instead directly grabbing the hidden layer values from the weight matrix. We can do this because the multiplication of a one-hot encoded vector with a matrix returns the row of the matrix corresponding the index of the "on" input unit.

Instead of doing the matrix multiplication, we use the weight matrix as a lookup table. We encode the words as integers, for example "heart" is encoded as 958, "mind" as 18094. Then to get hidden layer values for "heart", you just take the 958th row of the embedding matrix. This process is called an **embedding lookup** and the number of hidden units is the **embedding dimension**.
<img src='assets/tokenize_lookup.png' width=500>
There is nothing magical going on here. The embedding lookup table is just a weight matrix. The embedding layer is just a hidden layer. The lookup is just a shortcut for the matrix multiplication. The lookup table is trained just like any weight matrix as well.
Embeddings aren't only used for words of course. You can use them for any model where you have a massive number of classes. A particular type of model called **Word2Vec** uses the embedding layer to find vector representations of words that contain semantic meaning.
## Word2Vec
The word2vec algorithm finds much more efficient representations by finding vectors that represent the words. These vectors also contain semantic information about the words. Words that show up in similar contexts, such as "black", "white", and "red" will have vectors near each other. There are two architectures for implementing word2vec, CBOW (Continuous Bag-Of-Words) and Skip-gram.
<img src="assets/word2vec_architectures.png" width="500">
In this implementation, we'll be using the skip-gram architecture because it performs better than CBOW. Here, we pass in a word and try to predict the words surrounding it in the text. In this way, we can train the network to learn representations for words that show up in similar contexts.
First up, importing packages.
```
import time
import numpy as np
import tensorflow as tf
import utils
```
Load the [text8 dataset](http://mattmahoney.net/dc/textdata.html), a file of cleaned up Wikipedia articles from Matt Mahoney. The next cell will download the data set to the `data` folder. Then you can extract it and delete the archive file to save storage space.
```
from urllib.request import urlretrieve
from os.path import isfile, isdir
from tqdm import tqdm
import zipfile
dataset_folder_path = 'data'
dataset_filename = 'text8.zip'
dataset_name = 'Text8 Dataset'
class DLProgress(tqdm):
last_block = 0
def hook(self, block_num=1, block_size=1, total_size=None):
self.total = total_size
self.update((block_num - self.last_block) * block_size)
self.last_block = block_num
if not isfile(dataset_filename):
with DLProgress(unit='B', unit_scale=True, miniters=1, desc=dataset_name) as pbar:
urlretrieve(
'http://mattmahoney.net/dc/text8.zip',
dataset_filename,
pbar.hook)
if not isdir(dataset_folder_path):
with zipfile.ZipFile(dataset_filename) as zip_ref:
zip_ref.extractall(dataset_folder_path)
with open('data/text8') as f:
text = f.read()
```
## Preprocessing
Here I'm fixing up the text to make training easier. This comes from the `utils` module I wrote. The `preprocess` function coverts any punctuation into tokens, so a period is changed to ` <PERIOD> `. In this data set, there aren't any periods, but it will help in other NLP problems. I'm also removing all words that show up five or fewer times in the dataset. This will greatly reduce issues due to noise in the data and improve the quality of the vector representations. If you want to write your own functions for this stuff, go for it.
```
words = utils.preprocess(text)
print(words[:30])
print("Total words: {}".format(len(words)))
print("Unique words: {}".format(len(set(words))))
```
And here I'm creating dictionaries to covert words to integers and backwards, integers to words. The integers are assigned in descending frequency order, so the most frequent word ("the") is given the integer 0 and the next most frequent is 1 and so on. The words are converted to integers and stored in the list `int_words`.
```
vocab_to_int, int_to_vocab = utils.create_lookup_tables(words)
int_words = [vocab_to_int[word] for word in words]
```
## Subsampling
Words that show up often such as "the", "of", and "for" don't provide much context to the nearby words. If we discard some of them, we can remove some of the noise from our data and in return get faster training and better representations. This process is called subsampling by Mikolov. For each word $w_i$ in the training set, we'll discard it with probability given by
$$ P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}} $$
where $t$ is a threshold parameter and $f(w_i)$ is the frequency of word $w_i$ in the total dataset.
I'm going to leave this up to you as an exercise. Check out my solution to see how I did it.
> **Exercise:** Implement subsampling for the words in `int_words`. That is, go through `int_words` and discard each word given the probablility $P(w_i)$ shown above. Note that $P(w_i)$ is that probability that a word is discarded. Assign the subsampled data to `train_words`.
```
from collections import Counter
import random
threshold = 1e-5
threshold = 0.0006849873916398326
word_counts = Counter(int_words)
total_count = len(int_words)
print(total_count)
freqs = {word: count/total_count for word, count in word_counts.items()}
p_drop = {word: 1 - np.sqrt(threshold/freqs[word]) for word in word_counts}
train_words = [word for word in int_words if random.random() < (1 - p_drop[word])]
print(len(train_words))
print(train_words[:10])
```
## Making batches
Now that our data is in good shape, we need to get it into the proper form to pass it into our network. With the skip-gram architecture, for each word in the text, we want to grab all the words in a window around that word, with size $C$.
From [Mikolov et al.](https://arxiv.org/pdf/1301.3781.pdf):
"Since the more distant words are usually less related to the current word than those close to it, we give less weight to the distant words by sampling less from those words in our training examples... If we choose $C = 5$, for each training word we will select randomly a number $R$ in range $< 1; C >$, and then use $R$ words from history and $R$ words from the future of the current word as correct labels."
> **Exercise:** Implement a function `get_target` that receives a list of words, an index, and a window size, then returns a list of words in the window around the index. Make sure to use the algorithm described above, where you chose a random number of words to from the window.
```
def get_target(words, idx, window_size=5):
''' Get a list of words in a window around an index. '''
R = np.random.randint(1, window_size+1)
start = idx - R if (idx - R) > 0 else 0
stop = idx + R
target_words = set(words[start:idx] + words[idx+1:stop+1])
return list(target_words)
```
Here's a function that returns batches for our network. The idea is that it grabs `batch_size` words from a words list. Then for each of those words, it gets the target words in the window. I haven't found a way to pass in a random number of target words and get it to work with the architecture, so I make one row per input-target pair. This is a generator function by the way, helps save memory.
```
def get_batches(words, batch_size, window_size=5):
''' Create a generator of word batches as a tuple (inputs, targets) '''
n_batches = len(words)//batch_size
# only full batches
words = words[:n_batches*batch_size]
for idx in range(0, len(words), batch_size):
x, y = [], []
batch = words[idx:idx+batch_size]
for ii in range(len(batch)):
batch_x = batch[ii]
batch_y = get_target(batch, ii, window_size)
y.extend(batch_y)
x.extend([batch_x]*len(batch_y))
yield x, y
```
## Building the graph
From [Chris McCormick's blog](http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/), we can see the general structure of our network.

The input words are passed in as one-hot encoded vectors. This will go into a hidden layer of linear units, then into a softmax layer. We'll use the softmax layer to make a prediction like normal.
The idea here is to train the hidden layer weight matrix to find efficient representations for our words. We can discard the softmax layer becuase we don't really care about making predictions with this network. We just want the embedding matrix so we can use it in other networks we build from the dataset.
I'm going to have you build the graph in stages now. First off, creating the `inputs` and `labels` placeholders like normal.
> **Exercise:** Assign `inputs` and `labels` using `tf.placeholder`. We're going to be passing in integers, so set the data types to `tf.int32`. The batches we're passing in will have varying sizes, so set the batch sizes to [`None`]. To make things work later, you'll need to set the second dimension of `labels` to `None` or `1`.
```
train_graph = tf.Graph()
with train_graph.as_default():
inputs = tf.placeholder(tf.int32, [None], name='inputs')
labels = tf.placeholder(tf.int32, [None, None], name='labels')
```
## Embedding
The embedding matrix has a size of the number of words by the number of units in the hidden layer. So, if you have 10,000 words and 300 hidden units, the matrix will have size $10,000 \times 300$. Remember that we're using tokenized data for our inputs, usually as integers, where the number of tokens is the number of words in our vocabulary.
> **Exercise:** Tensorflow provides a convenient function [`tf.nn.embedding_lookup`](https://www.tensorflow.org/api_docs/python/tf/nn/embedding_lookup) that does this lookup for us. You pass in the embedding matrix and a tensor of integers, then it returns rows in the matrix corresponding to those integers. Below, set the number of embedding features you'll use (200 is a good start), create the embedding matrix variable, and use `tf.nn.embedding_lookup` to get the embedding tensors. For the embedding matrix, I suggest you initialize it with a uniform random numbers between -1 and 1 using [tf.random_uniform](https://www.tensorflow.org/api_docs/python/tf/random_uniform).
```
n_vocab = len(int_to_vocab)
n_embedding = 200 # Number of embedding features
with train_graph.as_default():
embedding = tf.Variable(tf.random_uniform((n_vocab, n_embedding), -1, 1))
embed = tf.nn.embedding_lookup(embedding, inputs)
```
## Negative sampling
For every example we give the network, we train it using the output from the softmax layer. That means for each input, we're making very small changes to millions of weights even though we only have one true example. This makes training the network very inefficient. We can approximate the loss from the softmax layer by only updating a small subset of all the weights at once. We'll update the weights for the correct label, but only a small number of incorrect labels. This is called ["negative sampling"](http://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf). Tensorflow has a convenient function to do this, [`tf.nn.sampled_softmax_loss`](https://www.tensorflow.org/api_docs/python/tf/nn/sampled_softmax_loss).
> **Exercise:** Below, create weights and biases for the softmax layer. Then, use [`tf.nn.sampled_softmax_loss`](https://www.tensorflow.org/api_docs/python/tf/nn/sampled_softmax_loss) to calculate the loss. Be sure to read the documentation to figure out how it works.
```
# Number of negative labels to sample
n_sampled = 100
with train_graph.as_default():
softmax_w = tf.Variable(tf.truncated_normal((n_vocab, n_embedding), stddev=0.1))
softmax_b = tf.Variable(tf.zeros(n_vocab))
# Calculate the loss using negative sampling
loss = tf.nn.sampled_softmax_loss(softmax_w, softmax_b,
labels, embed,
n_sampled, n_vocab)
cost = tf.reduce_mean(loss)
optimizer = tf.train.AdamOptimizer().minimize(cost)
```
## Validation
This code is from Thushan Ganegedara's implementation. Here we're going to choose a few common words and few uncommon words. Then, we'll print out the closest words to them. It's a nice way to check that our embedding table is grouping together words with similar semantic meanings.
```
with train_graph.as_default():
## From Thushan Ganegedara's implementation
valid_size = 16 # Random set of words to evaluate similarity on.
valid_window = 100
# pick 8 samples from (0,100) and (1000,1100) each ranges. lower id implies more frequent
valid_examples = np.array(random.sample(range(valid_window), valid_size//2))
valid_examples = np.append(valid_examples,
random.sample(range(1000,1000+valid_window), valid_size//2))
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
# We use the cosine distance:
norm = tf.sqrt(tf.reduce_sum(tf.square(embedding), 1, keep_dims=True))
normalized_embedding = embedding / norm
valid_embedding = tf.nn.embedding_lookup(normalized_embedding, valid_dataset)
similarity = tf.matmul(valid_embedding, tf.transpose(normalized_embedding))
# If the checkpoints directory doesn't exist:
!mkdir checkpoints
epochs = 10
batch_size = 1000
window_size = 10
with train_graph.as_default():
saver = tf.train.Saver()
with tf.Session(graph=train_graph) as sess:
iteration = 1
loss = 0
sess.run(tf.global_variables_initializer())
for e in range(1, epochs+1):
batches = get_batches(train_words, batch_size, window_size)
start = time.time()
for x, y in batches:
feed = {inputs: x,
labels: np.array(y)[:, None]}
train_loss, _ = sess.run([cost, optimizer], feed_dict=feed)
loss += train_loss
if iteration % 100 == 0:
end = time.time()
print("Epoch {}/{}".format(e, epochs),
"Iteration: {}".format(iteration),
"Avg. Training loss: {:.4f}".format(loss/100),
"{:.4f} sec/batch".format((end-start)/100))
loss = 0
start = time.time()
if iteration % 1000 == 0:
# note that this is expensive (~20% slowdown if computed every 500 steps)
sim = similarity.eval()
for i in range(valid_size):
valid_word = int_to_vocab[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log = 'Nearest to %s:' % valid_word
for k in range(top_k):
close_word = int_to_vocab[nearest[k]]
log = '%s %s,' % (log, close_word)
print(log)
iteration += 1
save_path = saver.save(sess, "checkpoints/text8.ckpt")
embed_mat = sess.run(normalized_embedding)
```
Restore the trained network if you need to:
```
with train_graph.as_default():
saver = tf.train.Saver()
with tf.Session(graph=train_graph) as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
embed_mat = sess.run(embedding)
```
## Visualizing the word vectors
Below we'll use T-SNE to visualize how our high-dimensional word vectors cluster together. T-SNE is used to project these vectors into two dimensions while preserving local stucture. Check out [this post from Christopher Olah](http://colah.github.io/posts/2014-10-Visualizing-MNIST/) to learn more about T-SNE and other ways to visualize high-dimensional data.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
viz_words = 500
tsne = TSNE()
embed_tsne = tsne.fit_transform(embed_mat[:viz_words, :])
fig, ax = plt.subplots(figsize=(14, 14))
for idx in range(viz_words):
plt.scatter(*embed_tsne[idx, :], color='steelblue')
plt.annotate(int_to_vocab[idx], (embed_tsne[idx, 0], embed_tsne[idx, 1]), alpha=0.7)
```
| true |
code
| 0.531574 | null | null | null | null |
|
# pipegraph User Guide
## Rationale
[scikit-learn](http://scikit-learn.org/stable/) provides a useful set of data preprocessors and machine learning models. The `Pipeline` object can effectively encapsulate a chain of transformers followed by final model. Other functions, like `GridSearchCV` can effectively use `Pipeline` objects to find the set of parameters that provide the best estimator.
### Pipeline + GridSearchCV: an awesome combination
Let's consider a simple example to illustrate the advantages of using `Pipeline` and `GridSearchCV`.
First let's import the libraries we will use and then let's build some artificial data set following a simple polynomial rule
```
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
X = 2*np.random.rand(100,1)-1
y = 40 * X**5 + 3*X*2 + 3*X + 3*np.random.randn(100,1)
```
Once we have some data ready, we instantiate the transformers and a regressor we want to fit:
```
scaler = MinMaxScaler()
polynomial_features = PolynomialFeatures()
linear_model = LinearRegression()
```
We define the steps that form the Pipeline object and then we instantiate such a Pipeline
```
steps = [('scaler', scaler),
('polynomial_features', polynomial_features),
('linear_model', linear_model)]
pipe = Pipeline(steps=steps)
```
Now we can pass this pipeline to `GridSearchCV`. When the `GridSearchCV` object is fitted, the search for the best combination for hyperparameters is performed according to the values provided in the `param_grid` parameter:
```
param_grid = {'polynomial_features__degree': range(1, 11),
'linear_model__fit_intercept': [True, False]}
grid_search_regressor = GridSearchCV(estimator=pipe, param_grid=param_grid, refit=True)
grid_search_regressor.fit(X, y);
```
And now we can check the results of fitting the Pipeline and the values of the hyperparameters:
```
y_pred = grid_search_regressor.predict(X)
plt.scatter(X, y)
plt.scatter(X, y_pred)
plt.show()
coef = grid_search_regressor.best_estimator_.get_params()['linear_model'].coef_
degree = grid_search_regressor.best_estimator_.get_params()['polynomial_features'].degree
print('Information about the parameters of the best estimator: \n degree: {} \n coefficients: {} '.format(degree, coef))
```
### Pipeline weaknesses:
From this example we can learn that `Pipeline` and `GridSearchCV` are very useful tools to consider when attempting to fit models. As far as the needs of the user can be satisfied by a set of transformers followed by a final model, this approach seems to be highly convenient. Additional advantages of such approach are the **parallel computation** and **memoization** capabilities of GridSearchCV.
Unfortunately though, current implementation of scikit-learn's `Pipeline`:
- Does not allow postprocessors after the final model
- Does not allow extracting information about intermediate results
- The X is transformed on every transformer but the following step can not have access to X variable values beyond the previous step
- Only allows single path workflows
### pipegraph goals:
[pipegraph](https://github.com/mcasl/PipeGraph) was programmed in order to allow researchers and practitioners to:
- Use multiple path workflows
- Have access to every variable value produced by any step of the workflow
- Use an arbitraty number of models and transformers in the way the user prefers
- Express the model as a graph consisting of transformers, regressors, classifiers or custom blocks
- Build new custom block in an easy way
- Provide the community some adapters to scikit-learn's objects that may help further developments
## pipegraph main interface: The PipeGraphRegressor and PipeGraphClassifier classes
`pipegraph` provides the user two main classes: `PipeGraphRegressor` and `PipeGraphClassifier`. They both provide a familiar interface to the raw `PipeGraph` class that most users will not need to use. The `PipeGraph` class provides greater versatility allowing an arbitrary number of inputs and outputs and may be the base class for those users facing applications with such special needs. Most users, though, will be happy using just the former two classes provided as main interface to operate the library.
As the names intend to imply, `PipeGraphRegressor` is the class to use for regression models and `PipeGraphClassifier` is intended for classification problems. Indeed, the only difference between these two classes is the default scoring function that has been chosen accordingly to scikit-learn defaults for each case. Apart from that, both classes share the same code. It must be noticed though, that any of these classes can comprise a plethora of different regressors or clasiffiers. It is the final step the one that will define whether we are defining a classification or regression problem.
## From a single path workflow to a graph with multiple paths: Understanding connections
These two classes provide an interface as similar to scikit-learn's `Pipeline` as possible in order to ease their use to those already familiar with scikit-learn. There is a slight but important difference that empowers these two classes: the `PipeGraph` related classes accept extra information about which input variables are needed by each step, thus allowing multiple path workflows.
To clarify the usage of these connections, let's start using `pipegraph` with a simple example that could be otherwise perfectly expressed using a scikit-learn's `Pipeline` as well. In this simple case, the data is transformed using a `MinMaxScaler` transformer and the preprocessed data is fed to a `LinearRegression` model. Figure 1 shows the steps of this PipeGraphRegressor and the connections between them: which input variables each one accepts and their origin, that is, if they are provided by a previous step, like the output of `scaler`, named `predict`, that is used by `linear_model`'s `X` variable; or `y` which is not calculated by any previous block but is passed by the user in the `fit` or `predict` method calls.
<img src="./images/figure_1-a.png" width="400" />
Figure 1. PipeGraph diagram showing the steps and their connections
In this first simple example of `pipegraph` the last step is a regressor, and thus the `PipeGraphRegressor` class is the most adequate class to choose. But other than that, we define the steps as usual for a standard `Pipeline`: as a list of tuples (label, sklearn object). We are not introducing yet any information at all about the connections, in which case the `PipeGraphRegressor` object is built considering that the steps follow a linear workflow in the same way as a standard `Pipeline`.
```
from pipegraph import PipeGraphRegressor
X = 2*np.random.rand(100,1)-1
y = 40 * X**5 + 3*X*2 + 3*X + 3*np.random.randn(100,1)
scaler = MinMaxScaler()
linear_model = LinearRegression()
steps = [('scaler', scaler),
('linear_model', linear_model)]
pgraph = PipeGraphRegressor(steps=steps)
pgraph.fit(X, y)
```
As the printed output shows, the internal links displayed by the `fit_connections` and `predict_connections` parameters are in line with those we saw in Figure 1 and those expected by a single path pipeline. As we did not specify these values, they were created by `PipeGRaphRegressor.__init__()` method as a comodity. We can have a look at these values by directly inspecting the attributes values. As `PipeGraphRegressor` and `PipeGraphClassifier` are wrappers of a `PipeGraph` object stored in the `_pipegraph` attribute, we have to dig a bit deeper to find the `fit_connections`
```
pgraph._pipegraph.fit_connections
```
Figure 2 surely will help understading the syntax used by the connections dictionary. It goes like this:
- The keys of the top level entries of the dictionary must be the same as those of the previously defined steps.
- The values assocciated to these keys define the variables from other steps that are going to be considered as inputs for the current step. They are dictionaries themselves, where:
- The keys of the nested dictionary represent the input variables as named at the current step.
- The values assocciated to these keys define the steps that hold the desired information and the variables as named at that step. This information can be written as:
- A tuple with the label of the step in position 0 followed by the name of the output variable in position 1.
- A string:
- If the string value is one of the labels from the steps, then it is interpreted as tuple, as previously, with the label of the step in position 0 and 'predict' as name of the output variable in position 1.
- Otherwise, it is considered to be a variable from an external source, such as those provided by the user while invoking the ``fit``, ``predict`` or ``fit_predict`` methods.
<img src="./images/figure_1-b.png" width="700" />
Figure 2. Illustration of the connections of the PipeGraph
The choice of name 'predict' for default output variables was made for convenience reasons as it will be illustrated later on. The developers preferred using always the same word for every block even though it might not be a regressor nor a classifier.
Finally, let's get the predicted values from this `PipeGraphRegressor` for illustrative purposes:
```
y_pred = pgraph.predict(X)
plt.scatter(X, y, label='Original Data')
plt.scatter(X, y_pred, label='Predicted Data')
plt.title('Plots of original and predicted data')
plt.legend(loc='best')
plt.grid(True)
plt.xlabel('Index')
plt.ylabel('Value of Data')
plt.show()
```
## `GridSearchCV` compatibility requirements
Both `PipeGraphRegressor`and `PipeGraphClassifier` are compatible with `GridSearchCV` provided the last step can be scored, either:
- by using `PipeGraphRegressor` or `PipeGraphClassifier` default scoring functions,
- by implementing a custom scoring function capable of handling that last step inputs and outputs,
- by using a `NeutralRegressor` or `NeutralClassifier` block as final step.
Those pipegraphs with a last step from scikit-learn's estimators set will work perfectly well using `PipeGraphRegressor` or `PipeGraphClassifier` default scoring functions. The other two alternative cover those cases in which a custom block with non standard inputs is provided. In that case, choosing a neutral regressor or classifier is usually a much simpler approach than writing customs scoring function. `NeutralRegressor` or `NeutralClassifier` are two classes provided for users convenience so that no special scoring function is needed. They just allow the user to pick some variables from other previous steps as `X` and `y` and provide compatibility to use a default scoring function.
### Example using default scoring functions
We will show more complex examples in what follows, but let's first illustrate with a simple example how to use `GrisSearchCV` with the default scoring functions. Figure 3 shows the steps of the model:
- **scaler**: a preprocessing step using a `MinMaxScaler` object,
- **polynomial_features**: a transformer step that generates a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified one,
- **linear_model**: the `LinearRegression` object we want to fit.
<img src="./images/figure_2.png" width="700" />
Figure 3. Using a PipeGraphRegressor object as estimator by GridSearchCV
Firstly, we import the necessary libraries and create some artificial data.
```
from sklearn.preprocessing import PolynomialFeatures
X = 2*np.random.rand(100,1)-1
y = 40 * X**5 + 3*X*2 + 3*X + 3*np.random.randn(100,1)
scaler = MinMaxScaler()
polynomial_features = PolynomialFeatures()
linear_model = LinearRegression()
```
Secondly, we define the steps and a ``param_grid`` dictionary as specified by `GridSearchCV`.
In this case we just want to explore a few possibilities varying the degree of the polynomials and whether to use or not an intercept at the linear model.
```
steps = [('scaler', scaler),
('polynomial_features', polynomial_features),
('linear_model', linear_model)]
param_grid = {'polynomial_features__degree': range(1, 11),
'linear_model__fit_intercept': [True, False]}
```
Now, we use ``PipeGraphRegressor`` as estimator for `GridSearchCV` and perform the ``fit`` and ``predict`` operations. As the last steps, a linear regressor from scikit-learn, already works with the default scoring functions, no extra efforts are needed to make it compatible with `GridSearchCV`.
```
pgraph = PipeGraphRegressor(steps=steps)
grid_search_regressor = GridSearchCV(estimator=pgraph, param_grid=param_grid, refit=True)
grid_search_regressor.fit(X, y)
y_pred = grid_search_regressor.predict(X)
plt.scatter(X, y)
plt.scatter(X, y_pred)
plt.show()
coef = grid_search_regressor.best_estimator_.get_params()['linear_model'].coef_
degree = grid_search_regressor.best_estimator_.get_params()['polynomial_features'].degree
print('Information about the parameters of the best estimator: \n degree: {} \n coefficients: {} '.format(degree, coef))
```
This example showed how to use `GridSearchCV` with `PipeGraphRegressor` in a simple single path workflow with default scoring functions. Let's explore in next section a more complex example.
## Multiple path workflow examples
Untill now, all the examples we showed displayed a single path sequence of steps and thus they could have been equally easily done using sickit-learn standard `Pipeline`. We are going to show now in the following examples multiple path cases in which we illustrate some compatibility constrains that occur and how to deal with them successfully.
### Example: Injecting a varying vector in the sample_weight parameter of LinearRegression
This example illustrates the case in which a varying vector is injected to a linear regression model as ``sample_weight`` in order to evaluate them and obtain the sample_weight that generates the best results.
The steps of this model are shown in Figure 4. To perform such experiment, the following issues appear:
- The shape of the graph is not a single path workflow as those that can be implemented using Pipeline. Thus, we need to use `pipegraph`.
- The model has 3 input variables, `X`, `y`, and `sample_weight`. The `Pipegraph` class can accept an arbitrary number of input variables, but, in order to use scikit-learn's current implementation of GridSearchCV, only `X` and `y` are accepted. We can do the trick but previously concatenating `X` and `sample_weight` into a single pandas DataFrame, for example, in order to comply with GridSearchCV requisites. That implies that the graph must be capable of separating afterwards the augmented `X` into the two components again. The **selector** step is in charge of this splitting. This step features a `ColumnSelector` custom step. This is not a scikit-learn original object but a custom class that allows to split an array into columns. In this case, ``X`` augmented data is column-wise divided as specified in a mapping dictionary. We will talk later on about custom blocks.
- The information provided to the ``sample_weight`` parameter of the LinearRegression step varies on the different scenarios explored by GridSearchCV. In a GridSearchCV with Pipeline, ``sample_weight`` can't vary because it is treated as a ``fit_param`` instead of a variable. Using pipegraph's connections this is no longer a problem.
- As we need a custom transformer to apply the power function to the sample_weight vector, we implement the **custom_power** step featuring a `CustomPower` custom class. Again, we will talk later on about custom blocks.
The three other steps from the model are already known:
- **scaler**: implements `MinMaxScaler` class
- **polynomial_features**: Contains a `PolynomialFeatures` object
- **linear_model**: Contains a `LinearRegression` model
<img src="./images/figure_3.png" width="600" />
Figure 4. A multipath model
Let's import the new components:
```
import pandas as pd
from pipegraph.base import ColumnSelector
from pipegraph.demo_blocks import CustomPower
```
We create an augmented ``X`` in which all data but ``y`` is concatenated. In this case, we concatenate ``X`` and ``sample_weight`` vector.
```
X = pd.DataFrame(dict(X=np.array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]),
sample_weight=np.array([0.01, 0.95, 0.10, 0.95, 0.95, 0.10, 0.10, 0.95, 0.95, 0.95, 0.01])))
y = np.array( [ 10, 4, 20, 16, 25 , -60, 85, 64, 81, 100, 150])
```
Next we define the steps and we use `PipeGraphRegressor` as estimator for `GridSearchCV`.
```
scaler = MinMaxScaler()
polynomial_features = PolynomialFeatures()
linear_model = LinearRegression()
custom_power = CustomPower()
selector = ColumnSelector(mapping={'X': slice(0, 1),
'sample_weight': slice(1,2)})
steps = [('selector', selector),
('custom_power', custom_power),
('scaler', scaler),
('polynomial_features', polynomial_features),
('linear_model', linear_model)]
pgraph = PipeGraphRegressor(steps=steps)
```
Now, we have to define the connections of the model. We could have specified a dictionary containing the connections, but [as suggested by Joel Nothman](https://github.com/scikit-learn-contrib/scikit-learn-contrib/issues/28), scikit-learn users might find more convenient to use a method `inject` like in this example. Let's see `inject`s docstring:
```
import inspect
print(inspect.getdoc(pgraph.inject))
```
`inject` allows to chain different calls to progressively describe all the connections needed in an easy to read manner:
```
(pgraph.inject(sink='selector', sink_var='X', source='_External', source_var='X')
.inject('custom_power', 'X', 'selector', 'sample_weight')
.inject('scaler', 'X', 'selector', 'X')
.inject('polynomial_features', 'X', 'scaler')
.inject('linear_model', 'X', 'polynomial_features')
.inject('linear_model', 'y', source_var='y')
.inject('linear_model', 'sample_weight', 'custom_power'))
```
Then we define ``param_grid`` as expected by `GridSearchCV` to explore several possibilities of varying parameters.
```
param_grid = {'polynomial_features__degree': range(1, 3),
'linear_model__fit_intercept': [True, False],
'custom_power__power': [1, 5, 10, 20, 30]}
grid_search_regressor = GridSearchCV(estimator=pgraph, param_grid=param_grid, refit=True)
grid_search_regressor.fit(X, y)
y_pred = grid_search_regressor.predict(X)
plt.scatter(X.loc[:,'X'], y)
plt.scatter(X.loc[:,'X'], y_pred)
plt.show()
power = grid_search_regressor.best_estimator_.get_params()['custom_power']
print('Power that obtains the best results in the linear model: \n {}'.format(power))
```
This example showed how to solve current limitations of scikit-learn `Pipeline`:
- Displayed a multipath workflow successfully implemented by **pipegraph**
- Showed how to circumvent current limitations of standard `GridSearchCV`, in particular, the restriction on the number of input parameters
- Showed the flexibility of **pipegraph** for specifying the connections in an easy to read manner using the `inject` method
- Demonstrated the capability of injecting previous steps' output into other models parameters, such as it is the case of the sample_weight parameter in the linear regressor.
### Example: Combination of classifiers
A set of classifiers is combined as input to a neural network. Additionally, the scaled inputs are injected as well to
the neural network. The data is firstly transformed by scaling its features.
Steps of the **PipeGraph**:
- **scaler**: A `MinMaxScaler` data preprocessor
- **gaussian_nb**: A `GaussianNB` classifier
- **svc**: A `SVC` classifier
- **concat**: A `Concatenator` custom class that appends the outputs of the `GaussianNB`, `SVC` classifiers, and the scaled inputs.
- **mlp**: A `MLPClassifier` object
<img src="./images/figure_4.png" width="700" />
Figure 5. PipeGraph diagram showing the steps and their connections
```
from pipegraph.base import PipeGraphClassifier, Concatenator
from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
iris = load_iris()
X = iris.data
y = iris.target
scaler = MinMaxScaler()
gaussian_nb = GaussianNB()
svc = SVC()
mlp = MLPClassifier()
concatenator = Concatenator()
steps = [('scaler', scaler),
('gaussian_nb', gaussian_nb),
('svc', svc),
('concat', concatenator),
('mlp', mlp)]
```
In this example we use a `PipeGraphClassifier` because the result is a classification and we want to take advantage of scikit-learn default scoring method for classifiers. Once more, we use the `inject` chain of calls to define the connections.
```
pgraph = PipeGraphClassifier(steps=steps)
(pgraph.inject(sink='scaler', sink_var='X', source='_External', source_var='X')
.inject('gaussian_nb', 'X', 'scaler')
.inject('gaussian_nb', 'y', source_var='y')
.inject('svc', 'X', 'scaler')
.inject('svc', 'y', source_var='y')
.inject('concat', 'X1', 'scaler')
.inject('concat', 'X2', 'gaussian_nb')
.inject('concat', 'X3', 'svc')
.inject('mlp', 'X', 'concat')
.inject('mlp', 'y', source_var='y')
)
param_grid = {'svc__C': [0.1, 0.5, 1.0],
'mlp__hidden_layer_sizes': [(3,), (6,), (9,),],
'mlp__max_iter': [5000, 10000]}
grid_search_classifier = GridSearchCV(estimator=pgraph, param_grid=param_grid, refit=True)
grid_search_classifier.fit(X, y)
y_pred = grid_search_classifier.predict(X)
grid_search_classifier.best_estimator_.get_params()
# Code for plotting the confusion matrix taken from 'Python Data Science Handbook' by Jake VanderPlas
from sklearn.metrics import confusion_matrix
import seaborn as sns; sns.set() # for plot styling
mat = confusion_matrix(y_pred, y)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False)
plt.xlabel('true label')
plt.ylabel('predicted label');
plt.show()
```
This example displayed complex data injections that are successfully managed by **pipegraph**.
### Example: Demultiplexor - multiplexor
An imaginative layout using a classifier to predict the cluster labels and fitting a separate model for each cluster. We will elaborate on this example in the examples that follow introducing variations. AS the Figure shows, the steps of the **PipeGraph** are:
- **scaler**: A :class:`MinMaxScaler` data preprocessor
- **classifier**: A :class:`GaussianMixture` classifier
- **demux**: A custom :class:`Demultiplexer` class in charge of splitting the input arrays accordingly to the selection input vector
- **lm_0**: A :class:`LinearRegression` model
- **lm_1**: A :class:`LinearRegression` model
- **lm_2**: A :class:`LinearRegression` model
- **mux**: A custom :class:`Multiplexer` class in charge of combining different input arrays into a single one accordingly to the selection input vector
<img src="./images/figure_5.png" width="700" />
Figure 6. PipeGraph diagram showing the steps and their connections
```
from pipegraph.base import PipeGraphRegressor, Demultiplexer, Multiplexer
from sklearn.mixture import GaussianMixture
X_first = pd.Series(np.random.rand(100,))
y_first = pd.Series(4 * X_first + 0.5*np.random.randn(100,))
X_second = pd.Series(np.random.rand(100,) + 3)
y_second = pd.Series(-4 * X_second + 0.5*np.random.randn(100,))
X_third = pd.Series(np.random.rand(100,) + 6)
y_third = pd.Series(2 * X_third + 0.5*np.random.randn(100,))
X = pd.concat([X_first, X_second, X_third], axis=0).to_frame()
y = pd.concat([y_first, y_second, y_third], axis=0).to_frame()
scaler = MinMaxScaler()
gaussian_mixture = GaussianMixture(n_components=3)
demux = Demultiplexer()
lm_0 = LinearRegression()
lm_1 = LinearRegression()
lm_2 = LinearRegression()
mux = Multiplexer()
steps = [('scaler', scaler),
('classifier', gaussian_mixture),
('demux', demux),
('lm_0', lm_0),
('lm_1', lm_1),
('lm_2', lm_2),
('mux', mux), ]
```
Instead of using ``inject`` as in previous example, in this one we are going to pass a dictionary describing the connections to PipeGraph constructor
```
connections = { 'scaler': {'X': 'X'},
'classifier': {'X': 'scaler'},
'demux': {'X': 'scaler',
'y': 'y',
'selection': 'classifier'},
'lm_0': {'X': ('demux', 'X_0'),
'y': ('demux', 'y_0')},
'lm_1': {'X': ('demux', 'X_1'),
'y': ('demux', 'y_1')},
'lm_2': {'X': ('demux', 'X_2'),
'y': ('demux', 'y_2')},
'mux': {'0': 'lm_0',
'1': 'lm_1',
'2': 'lm_2',
'selection': 'classifier'}}
pgraph = PipeGraphRegressor(steps=steps, fit_connections=connections)
pgraph.fit(X, y)
y_pred = pgraph.predict(X)
plt.scatter(X, y)
plt.scatter(X, y_pred)
plt.show()
```
### Example: Encapsulating several blocks into a PipeGraph and reusing it
We consider the previous example in which we had the following pipegraph model:
<img src="./images/figure_6.png" width="700" />
We can be interested in using a fragment of the pipegraph, for example, those blocks marked with the circle (the Demultiplexer, the linear model collection, and the Multiplexer), as a single block in another pipegraph:
<img src="./images/figure_7.png" width="500" />
We prepare the data and build a PipeGraph with these steps alone:
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.mixture import GaussianMixture
from sklearn.linear_model import LinearRegression
from pipegraph.base import PipeGraph, PipeGraphRegressor, Demultiplexer, Multiplexer
# Prepare some artificial data
X_first = pd.Series(np.random.rand(100,))
y_first = pd.Series(4 * X_first + 0.5*np.random.randn(100,))
X_second = pd.Series(np.random.rand(100,) + 3)
y_second = pd.Series(-4 * X_second + 0.5*np.random.randn(100,))
X_third = pd.Series(np.random.rand(100,) + 6)
y_third = pd.Series(2 * X_third + 0.5*np.random.randn(100,))
X = pd.concat([X_first, X_second, X_third], axis=0).to_frame()
y = pd.concat([y_first, y_second, y_third], axis=0).to_frame()
# Create a single complex block
demux = Demultiplexer()
lm_0 = LinearRegression()
lm_1 = LinearRegression()
lm_2 = LinearRegression()
mux = Multiplexer()
three_multiplexed_models_steps = [
('demux', demux),
('lm_0', lm_0),
('lm_1', lm_1),
('lm_2', lm_2),
('mux', mux), ]
three_multiplexed_models_connections = {
'demux': {'X': 'X',
'y': 'y',
'selection': 'selection'},
'lm_0': {'X': ('demux', 'X_0'),
'y': ('demux', 'y_0')},
'lm_1': {'X': ('demux', 'X_1'),
'y': ('demux', 'y_1')},
'lm_2': {'X': ('demux', 'X_2'),
'y': ('demux', 'y_2')},
'mux': {'0': 'lm_0',
'1': 'lm_1',
'2': 'lm_2',
'selection': 'selection'}}
three_multiplexed_models = PipeGraph(steps=three_multiplexed_models_steps,
fit_connections=three_multiplexed_models_connections )
```
Now we can treat this PipeGraph as a reusable component and use it as a unitary step in another PipeGraph:
```
scaler = MinMaxScaler()
gaussian_mixture = GaussianMixture(n_components=3)
models = three_multiplexed_models
steps = [('scaler', scaler),
('classifier', gaussian_mixture),
('models', three_multiplexed_models), ]
connections = {'scaler': {'X': 'X'},
'classifier': {'X': 'scaler'},
'models': {'X': 'scaler',
'y': 'y',
'selection': 'classifier'},
}
pgraph = PipeGraphRegressor(steps=steps, fit_connections=connections)
pgraph.fit(X, y)
y_pred = pgraph.predict(X)
plt.scatter(X, y)
plt.scatter(X, y_pred)
plt.show()
```
### Example: Dynamically built component using initialization parameters
Last section showed how the user can choose to encapsulate several blocks into a PipeGraph and use it as a single unit in another PipeGraph. Now we will see how these components can be dynamically built on runtime depending on initialization parameters.
<img src="./images/figure_8.png" width="700" />
We can think of programatically changing the number of regression models inside this component we isolated in the previous example. First we do it by using initialization parameters in a ``PipeGraph`` subclass we called ``pipegraph.base.RegressorsWithParametrizedNumberOfReplicas``:
```
import inspect
from pipegraph.base import RegressorsWithParametrizedNumberOfReplicas
print(inspect.getsource(RegressorsWithParametrizedNumberOfReplicas))
```
As it can be seen from the source code, in this example we are basically interested in using a PipeGraph object whose `__init__` has different parameters than the usual ones. Thus, we subclass PipeGRaph and reimplement the `__init__` method. In doing so, we are capable of working out the structure of the steps and connections before calling the `super().__init__` method that provides the regular `PipeGraph` object.
Using this new component we can build a PipeGraph with as many multiplexed models as given by the `number_of_replicas` parameter:
```
scaler = MinMaxScaler()
gaussian_mixture = GaussianMixture(n_components=3)
models = RegressorsWithParametrizedNumberOfReplicas(number_of_replicas=3,
model_prototype=LinearRegression(),
model_parameters={})
steps = [('scaler', scaler),
('classifier', gaussian_mixture),
('models', models), ]
connections = {'scaler': {'X': 'X'},
'classifier': {'X': 'scaler'},
'models': {'X': 'scaler',
'y': 'y',
'selection': 'classifier'},
}
pgraph = PipeGraphRegressor(steps=steps, fit_connections=connections)
pgraph.fit(X, y)
y_pred = pgraph.predict(X)
plt.scatter(X, y)
plt.scatter(X, y_pred)
plt.show()
```
### Example: Dynamically built component using input signal values during the fit stage
Last example showed how to grow a PipeGraph object programatically during runtime using the `__init__` method. In this example, we are going to show how we can change the internal structure of a PipeGraph object, not during initialization but during fit. Specifically, we will show how the multiplexed model can be dynamically added on runtime depending on input signal values during `fit`.
Now we consider the possibility of using the classifier's output to automatically adjust the number of replicas.
This can be seen as PipeGraph changing its inner topology to adapt its connections and steps to other components
context. This morphing capability opens interesting possibilities to explore indeed.
```
import inspect
from pipegraph.base import RegressorsWithDataDependentNumberOfReplicas
print(inspect.getsource(RegressorsWithDataDependentNumberOfReplicas))
```
Again we subclass from parent `PipeGraph` class and implement a different `__init__`. In this example we won't make use of a `number_of_replicas` parameter, as it will be inferred from data during `fit` and thus we are satisfied by passing only those parameters allowing us to change the regressor models. As it can be seen from the code, the `__init__` method just stores the values provided by the user and it is the `fit` method the one in charge of growing the inner structure of the pipegraph.
Using this new component we can build a simplified PipeGraph:
```
scaler = MinMaxScaler()
gaussian_mixture = GaussianMixture(n_components=3)
models = RegressorsWithDataDependentNumberOfReplicas(model_prototype=LinearRegression(), model_parameters={})
steps = [('scaler', scaler),
('classifier', gaussian_mixture),
('models', models), ]
connections = {'scaler': {'X': 'X'},
'classifier': {'X': 'scaler'},
'models': {'X': 'scaler',
'y': 'y',
'selection': 'classifier'},
}
pgraph = PipeGraphRegressor(steps=steps, fit_connections=connections)
pgraph.fit(X, y)
y_pred = pgraph.predict(X)
plt.scatter(X, y)
plt.scatter(X, y_pred)
plt.show()
```
### Example: GridSearch on dynamically built component using input signal values
Previous example showed how a PipeGraph object can be dynamically built on runtime depending on input signal values during fit. Now, in this example we will show how to use `GridSearchCV` to explore the best combination of hyperparameters.
```
from sklearn.model_selection import train_test_split
from pipegraph.base import NeutralRegressor
# We prepare some data
X_first = pd.Series(np.random.rand(100,))
y_first = pd.Series(4 * X_first + 0.5*np.random.randn(100,))
X_second = pd.Series(np.random.rand(100,) + 3)
y_second = pd.Series(-4 * X_second + 0.5*np.random.randn(100,))
X_third = pd.Series(np.random.rand(100,) + 6)
y_third = pd.Series(2 * X_third + 0.5*np.random.randn(100,))
X = pd.concat([X_first, X_second, X_third], axis=0).to_frame()
y = pd.concat([y_first, y_second, y_third], axis=0).to_frame()
X_train, X_test, y_train, y_test = train_test_split(X, y)
```
To ease the calculation of the score for the GridSearchCV we add a neutral regressor as a last step, capable of
calculating the score using a default scoring function. This is much more convenient than worrying about programming
a custom scoring function for a block with an arbitrary number of inputs.
```
scaler = MinMaxScaler()
gaussian_mixture = GaussianMixture(n_components=3)
models = RegressorsWithDataDependentNumberOfReplicas(model_prototype=LinearRegression(), model_parameters={})
neutral_regressor = NeutralRegressor()
steps = [('scaler', scaler),
('classifier', gaussian_mixture),
('models', models),
('neutral', neutral_regressor)]
connections = {'scaler': {'X': 'X'},
'classifier': {'X': 'scaler'},
'models': {'X': 'scaler',
'y': 'y',
'selection': 'classifier'},
'neutral': {'X': 'models'}
}
pgraph = PipeGraphRegressor(steps=steps, fit_connections=connections)
```
Using GridSearchCV to find the best number of clusters and the best regressors
```
from sklearn.model_selection import GridSearchCV
param_grid = {'classifier__n_components': range(2,10)}
gs = GridSearchCV(estimator=pgraph, param_grid=param_grid, refit=True)
gs.fit(X_train, y_train)
y_pred = gs.predict(X_train)
plt.scatter(X_train, y_train)
plt.scatter(X_train, y_pred)
print("Score:" , gs.score(X_test, y_test))
print("classifier__n_components:", gs.best_estimator_.get_params()['classifier__n_components'])
```
### Example: Alternative solution
Now we consider an alternative solution to the previous example. The solution already shown displayed the potential
of being able to morph the graph during fitting. A simpler approach is considered in this example by reusing
components and combining the classifier with the demultiplexed models.
```
from pipegraph.base import ClassifierAndRegressorsBundle
print(inspect.getsource(ClassifierAndRegressorsBundle))
```
As before, we built a custom block by subclassing PipeGraph and the modifying the `__init__` method to provide the parameters specifically needed for our purposes. Then we chain in the same PipeGraph the classifier, and the already available and known block for creating multiplexed models by providing parameters during `__init__`. It must be noticed that both the classifier and the models share have the same number of clusters and model: the number_of_replicas value provided by the user.
Using this new component we can build a simplified PipeGraph:
```
scaler = MinMaxScaler()
classifier_and_models = ClassifierAndRegressorsBundle(number_of_replicas=6)
neutral_regressor = NeutralRegressor()
steps = [('scaler', scaler),
('bundle', classifier_and_models),
('neutral', neutral_regressor)]
connections = {'scaler': {'X': 'X'},
'bundle': {'X': 'scaler', 'y': 'y'},
'neutral': {'X': 'bundle'}}
pgraph = PipeGraphRegressor(steps=steps, fit_connections=connections)
```
Using GridSearchCV to find the best number of clusters and the best regressors
```
from sklearn.model_selection import GridSearchCV
param_grid = {'bundle__number_of_replicas': range(3,10)}
gs = GridSearchCV(estimator=pgraph, param_grid=param_grid, refit=True)
gs.fit(X_train, y_train)
y_pred = gs.predict(X_train)
plt.scatter(X_train, y_train)
plt.scatter(X_train, y_pred)
print("Score:" , gs.score(X_test, y_test))
print("bundle__number_of_replicas:", gs.best_estimator_.get_params()['bundle__number_of_replicas'])
```
| true |
code
| 0.673836 | null | null | null | null |
|
# 04 - Full waveform inversion with Devito and scipy.optimize.minimize
## Introduction
In this tutorial we show how [Devito](http://www.opesci.org/devito-public) can be used with [scipy.optimize.minimize](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) to solve the FWI gradient based minimization problem described in the previous tutorial.
```python
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
```
> Minimization of scalar function of one or more variables.
>
> In general, the optimization problems are of the form:
>
> minimize f(x) subject to
>
> g_i(x) >= 0, i = 1,...,m
> h_j(x) = 0, j = 1,...,p
> where x is a vector of one or more variables. g_i(x) are the inequality constraints. h_j(x) are the equality constrains.
[scipy.optimize.minimize](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) provides a wide variety of methods for solving minimization problems depending on the context. Here we are going to focus on using L-BFGS via [scipy.optimize.minimize(method=’L-BFGS-B’)](https://docs.scipy.org/doc/scipy/reference/optimize.minimize-lbfgsb.html#optimize-minimize-lbfgsb)
```python
scipy.optimize.minimize(fun, x0, args=(), method='L-BFGS-B', jac=None, bounds=None, tol=None, callback=None, options={'disp': None, 'maxls': 20, 'iprint': -1, 'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000, 'ftol': 2.220446049250313e-09, 'maxcor': 10, 'maxfun': 15000})```
The argument `fun` is a callable function that returns the misfit between the simulated and the observed data. If `jac` is a Boolean and is `True`, `fun` is assumed to return the gradient along with the objective function - as is our case when applying the adjoint-state method.
## Setting up (synthetic) data
We are going to set up the same synthetic test case as for the previous tutorial (refer back for details). The code below is slightly re-engineered to make it suitable for using with scipy.optimize.minimize.
```
#NBVAL_IGNORE_OUTPUT
from examples.seismic import Model, demo_model
import numpy as np
# Define the grid parameters
def get_grid():
shape = (101, 101) # Number of grid point (nx, nz)
spacing = (10., 10.) # Grid spacing in m. The domain size is now 1km by 1km
origin = (0., 0.) # Need origin to define relative source and receiver locations
return shape, spacing, origin
# Define the test phantom; in this case we are using a simple circle
# so we can easily see what is going on.
def get_true_model():
shape, spacing, origin = get_grid()
return demo_model('circle-isotropic', vp=3.0, vp_background=2.5,
origin=origin, shape=shape, spacing=spacing, nbpml=40)
# The initial guess for the subsurface model.
def get_initial_model():
shape, spacing, origin = get_grid()
return demo_model('circle-isotropic', vp=2.5, vp_background=2.5,
origin=origin, shape=shape, spacing=spacing, nbpml=40)
from examples.seismic.acoustic import AcousticWaveSolver
from examples.seismic import RickerSource, Receiver
# Inversion crime alert! Here the worker is creating the 'observed' data
# using the real model. For a real case the worker would be reading
# seismic data from disk.
def get_data(param):
""" Returns source and receiver data for a single shot labeled 'shot_id'.
"""
true_model = get_true_model()
dt = true_model.critical_dt # Time step from model grid spacing
# Set up source data and geometry.
nt = int(1 + (param['tn']-param['t0']) / dt) # Discrete time axis length
src = RickerSource(name='src', grid=true_model.grid, f0=param['f0'],
time=np.linspace(param['t0'], param['tn'], nt))
src.coordinates.data[0, :] = [30, param['shot_id']*1000./(param['nshots']-1)]
# Set up receiver data and geometry.
nreceivers = 101 # Number of receiver locations per shot
rec = Receiver(name='rec', grid=true_model.grid, npoint=nreceivers, ntime=nt)
rec.coordinates.data[:, 1] = np.linspace(0, true_model.domain_size[0], num=nreceivers)
rec.coordinates.data[:, 0] = 980. # 20m from the right end
# Set up solver - using model_in so that we have the same dt,
# otherwise we should use pandas to resample the time series data.
solver = AcousticWaveSolver(true_model, src, rec, space_order=4)
# Generate synthetic receiver data from true model
true_d, _, _ = solver.forward(src=src, m=true_model.m)
return src, true_d, nt, solver
```
## Create operators for gradient based inversion
To perform the inversion we are going to use [scipy.optimize.minimize(method=’L-BFGS-B’)](https://docs.scipy.org/doc/scipy/reference/optimize.minimize-lbfgsb.html#optimize-minimize-lbfgsb).
First we define the functional, ```f```, and gradient, ```g```, operator (i.e. the function ```fun```) for a single shot of data.
```
from devito import Function, clear_cache
# Create FWI gradient kernel for a single shot
def fwi_gradient_i(x, param):
# Need to clear the workers cache.
clear_cache()
# Get the current model and the shot data for this worker.
model0 = get_initial_model()
model0.m.data[:] = x.astype(np.float32).reshape(model0.m.data.shape)
src, rec, nt, solver = get_data(param)
# Create symbols to hold the gradient and the misfit between
# the 'measured' and simulated data.
grad = Function(name="grad", grid=model0.grid)
residual = Receiver(name='rec', grid=model0.grid, ntime=nt, coordinates=rec.coordinates.data)
# Compute simulated data and full forward wavefield u0
d, u0, _ = solver.forward(src=src, m=model0.m, save=True)
# Compute the data misfit (residual) and objective function
residual.data[:] = d.data[:] - rec.data[:]
f = .5*np.linalg.norm(residual.data.flatten())**2
# Compute gradient using the adjoint-state method. Note, this
# backpropagates the data misfit through the model.
solver.gradient(rec=residual, u=u0, m=model0.m, grad=grad)
# return the objective functional and gradient.
return f, np.array(grad.data)
```
Next we define the global functional and gradient function that sums the contributions to f and g for each shot of data.
```
def fwi_gradient(x, param):
# Initialize f and g.
param['shot_id'] = 0
f, g = fwi_gradient_i(x, param)
# Loop through all shots summing f, g.
for i in range(1, param['nshots']):
param['shot_id'] = i
f_i, g_i = fwi_gradient_i(x, param)
f += f_i
g[:] += g_i
# Note the explicit cast; while the forward/adjoint solver only requires float32,
# L-BFGS-B in SciPy expects a flat array in 64-bit floats.
return f, g.flatten().astype(np.float64)
```
## FWI with L-BFGS-B
Equipped with a function to calculate the functional and gradient, we are finally ready to call ```scipy.optimize.minimize```.
```
#NBVAL_SKIP
# Change to the WARNING log level to reduce log output
# as compared to the default DEBUG
from devito import configuration
configuration['log_level'] = 'WARNING'
# Set up a dictionary of inversion parameters.
param = {'t0': 0.,
'tn': 1000., # Simulation lasts 1 second (1000 ms)
'f0': 0.010, # Source peak frequency is 10Hz (0.010 kHz)
'nshots': 9} # Number of shots to create gradient from
# Define bounding box constraints on the solution.
def apply_box_constraint(m):
# Maximum possible 'realistic' velocity is 3.5 km/sec
# Minimum possible 'realistic' velocity is 2 km/sec
return np.clip(m, 1/3.5**2, 1/2**2)
# Many optimization methods in scipy.optimize.minimize accept a callback
# function that can operate on the solution after every iteration. Here
# we use this to apply box constraints and to monitor the true relative
# solution error.
relative_error = []
def fwi_callbacks(x):
# Apply boundary constraint
x.data[:] = apply_box_constraint(x)
# Calculate true relative error
true_x = get_true_model().m.data.flatten()
relative_error.append(np.linalg.norm((x-true_x)/true_x))
# Initialize solution
model0 = get_initial_model()
# Finally, calling the minimizing function. We are limiting the maximum number
# of iterations here to 10 so that it runs quickly for the purpose of the
# tutorial.
from scipy import optimize
result = optimize.minimize(fwi_gradient, model0.m.data.flatten().astype(np.float64),
args=(param, ), method='L-BFGS-B', jac=True,
callback=fwi_callbacks,
options={'maxiter':10, 'disp':True})
# Print out results of optimizer.
print(result)
#NBVAL_SKIP
# Show what the update does to the model
from examples.seismic import plot_image, plot_velocity
model0.m.data[:] = result.x.astype(np.float32).reshape(model0.m.data.shape)
model0.vp = np.sqrt(1. / model0.m.data[40:-40, 40:-40])
plot_velocity(model0)
#NBVAL_SKIP
# Plot percentage error
plot_image(100*np.abs(model0.vp-get_true_model().vp.data)/get_true_model().vp.data, cmap="hot")
```
While we are resolving the circle at the centre of the domain there are also lots of artifacts throughout the domain.
```
#NBVAL_SKIP
import matplotlib.pyplot as plt
# Plot objective function decrease
plt.figure()
plt.loglog(relative_error)
plt.xlabel('Iteration number')
plt.ylabel('True relative error')
plt.title('Convergence')
plt.show()
```
<sup>This notebook is part of the tutorial "Optimised Symbolic Finite Difference Computation with Devito" presented at the Intel® HPC Developer Conference 2017.</sup>
| true |
code
| 0.752419 | null | null | null | null |
|
# End-to-End Machine Learning Project
In this chapter you will work through an example project end to end, pretending to be a recently hired data scientist at a real estate company. Here are the main steps you will go through:
1. Look at the big picture
2. Get the data
3. Discover and visualize the data to gain insights.
4. Prepare the data for Machine learning algorithms.
5. Select a model and train it
6. Fine-tune your model.
7. Present your solution
8. Launch, monitor, and maintain your system.
## Working with Real Data
When you are learning about Machine Leaning, it is best to experimentwith real-world data, not artificial datasets.
Fortunately, there are thousands of open datasets to choose from, ranging across all sorts of domains. Here are a few places you can look to get data:
* Popular open data repositories:
- [UC Irvine Machine Learning Repository](http://archive.ics.uci.edu/ml/)
- [Kaggle](https://www.kaggle.com/datasets) datasets
- Amazon's [AWS](https://registry.opendata.aws/) datasets
* Meta Portals:
- [Data Portals](http://dataportals.org/)
- [OpenDataMonitor](http://opendatamonitor.eu/)
- [Quandl](http://quandl.com)
## Frame the Problem
The problem is that your model' output (a prediction of a district's median housing price) will be fed to another ML system along with many other signals*. This downstream will determine whether it is worth investing in a given area or not. Getting this right is critical, as it directly affects revenue.
```
Other Signals
|
Upstream Components --> (District Data) --> [District Pricing prediction model](your component) --> (District prices) --> [Investment Analaysis] --> Investments
```
### Pipelines
A sequence of data processing components is called a **data pipeline**. Pipelines are very common in Machine Learning systems, since a lot of data needs to manipulated to make sure the machine learning model/algorithms understands the data, as algorithms understand only numbers.
## Download the Data:
You could use your web browser and download the data, but it is preferabble to make a function to do the same.
```
import os
import tarfile
import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
"""
Function to download the housing_data
"""
os.makedirs(housing_path, exist_ok=True)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
import pandas as pd
import numpy as np
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
fetch_housing_data()
housing = load_housing_data()
```
## Take a quick look at the Data Structure
Each row represents one district. There are 10 attributes:
```
longitude, latitude, housing_median_age, total_rooms, total_bedrooms, population, households, median_income, median_house_value, ocean_proximity
```
The `info()` method is useful to give a quick description of the data.
```
housing.head()
housing.info()
housing["ocean_proximity"].value_counts()
housing.describe()
%matplotlib inline
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20, 15))
plt.show();
```
> 🔑 **Note:** The `hist()` method relies on Matplotlib, which in turn relies on a user-specified graphical backend to draw on your screen. The simplest option is to use Jupyter's magic command `%matplotlib inline`. This tells jupyter to set up Matplotlib so that it uses Jupyter's own backend. Note that calling `plot()` is optional as Jupyter does this automatically.
#### There are few things you might notice in these histograms:
1. First the median income attribute does not look like it is expressed in US dollars (USD). The data has been scaled at 15 for higher median incomes and at 0.5 for lower median incomes. The numbers represent roughly tens of thousands of dollars(e.g., 3 actually means about $30,000). Working with oreoricessed attributes is common in Machine learning and it is not necessarily a problem. But you should try to understand how the data was computed.
2. The housing median age and the median house value were also capped.
3. These attributes have very different scales.
4. Many histograms of this dataset are *tail-heavy* i.e., they extend much farther to the right of the median than to the left. This may make it bit harder for Machine Learning Algorithms to unerstand patterns. We will try transfprming these attributes later on to have more bell shaped-distributions.
> ‼️ **Note:** Wait! Before you look at the data any further, you need to create a test set, put it aside and never look at it.
## Create a Test Set
Scikit-learn provides a few functions to split datasets into multiple subsets in various ways:
1. The `train_test_split()` function is the simplest and most used function from scikit-learn for this purpose.
2. For Stratified sampling, `StartifiedShuffleSplit()` would be useful
3. And probably so many more functions...
```
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
train_set.shape, test_set.shape
from sklearn.model_selection import StratifiedShuffleSplit
housing["income_cat"] = pd.cut(housing["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_i, test_i in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_i]
strat_test_set = housing.loc[test_i]
strat_train_set.shape
# Now remove the income_cat attribute so the data is back to its original state
for _ in (strat_train_set, strat_test_set):
_.drop("income_cat", axis=1, inplace=True)
```
## Discover and Visualize the Data to Gain More Insights
So far you have only taken a quick glance at the data to get a general understanding of the kind of data you are manipulating. Now the goal is to go into a lttle more depth.
First, make sure you have put the test set aside and you are only exploring the training data set. In our case the set is quite small, so you can work directly on the full set. Let's create a copy so that you can play woth it without harming the training set:
```
housing = strat_train_set.copy()
```
### Visualizing Geopgraphical Data
Since there is geographical information (latitude and longitude), it is a good idea to create a scatterplot pf all districts to visualize the data.
```
housing.plot(kind="scatter", x="longitude", y="latitude");
# Setting the alpha optin to 0.1 makes it easier to visualize the places where there is a high -density of data points.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1);
```
Now from the above graph, we can clearly see the high-density areas. Our brains are very good at spotting patterns in pictures, but you may need to play around with visualization parameters to make the patterns stand out.
Now let's look at the housing prices. The radius of each circle represents the district's populaiton (option `s`), and the color represents the price (option `c`). We will use a predefined color map (option `cmap`) called `jet`, which ranges from blue (low values) to red (high prices):
```
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10, 7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True)
plt.legend();
```
### Looking for Correlations
Since the dataset is not too large, you can easily compute the *standard correlation coeffecient* (also known as *Pearson's r*) between every pair of attributes using the `corr()` method
```
corr_matrix = housing.corr()
# Now let's look at how much each attribute correlates with the median house value
corr_matrix["median_house_value"].sort_values(ascending=False)
```
#### The Standard Correlation Coeffecient
The correlation coeffecient ranges from -1 to 1. When it is close to 1, it means that there is strong positive correlation. While, when the coeffecient is close to -1, it means there is a strong negative correlation. Finally coeffecients close to 0 mean that there is no linear correlation.
<img src="Fig..png" alt="Standard correlation coeffecients of various Datasets"/>
> 🔑 **Note:** The correlation coeffecient only measures linear correlations ("if x goes up, then y generally goes up/down"). It may completely miss out on nonlinear relationships (e.g., "if x is close to 0, then y generally goes up"). Note how all the plots of the bottom row have a correlation coeffecient equal to 0, despite the fact that that their axes are clearly not independent: these examples are nonlinearly correlated.
Another way to check for correlation between attributes is to use the pandas `scatter_matrix()` function, which plots every numerical attribute against every other numerical attribute.Since there are 11 numerical attributes, you would get 11^2 = 121 plots, which too large to fit inour page. So let's just focus on a few promising attributes that seem most correlated with median housing value:
```
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 12));
# The most promising attribute to predict the median house value is the median income
housing.plot(kind="scatter", x="median_income", y="median_house_value", alpha=.1);
```
This plot reveals a few things:
1. The correlation is indeed very strong as you can see clearly the upward trend, and the points are not too dispersed.
2. The price cap that we noticed earlier is clearly visible as a horizontal line at $500,000. There are a few more less-obvious lines that you may want to remove to prevent your algorithms from learning to reproduce these data quirks.
## Experimenting with Attribute Combinations
Till now, you identified a few data quirks that you may want to clean up before feeding the data to the Machine Learning algorithms, and you found out interesting correlations between attributes.
One last thing you may want to do before preparing the data for Machine learning algorithms, is to try out various attribute combinations.
For Example, the total number of rooms in a district is not very useful if you don't know how many households there are. What you really want is the number of rooms per household... and so on. Let's create these new attributes:
```
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
```
Hey, not bad! The new attributes have some more correlation
## Prepare the Data for Machine Learning Algorithms
It's time to prepare the data for your Machine Learning algorithm. Instead of doing this manually, you should write functions for this purpose, for several good reasons:
- This will allow you to reproduce these transformations easily on any dataset (e.g., the next time you get a fres dataset).
- You will gradually build a library of transformations functions that you can reuse in your future projects.
- You can use these functions in your live system to transform the new data before feeding it to your algorithms.
- This will make it possible for you to easily try various transformations and see what works best.
```
# Let's revert to a clean training set
housing = strat_train_set.drop("median_house_value", axis=1)
housing_labels = strat_train_set["median_house_value"].copy()
```
### Data Cleaning
Most Machine Learning algorithms cannot work with data that have missing features, so let's create a few functions to take care of them. We say earlier that the `total_bedrooms` attribute has some missing values, so let's fix this. You have three options to do so:
1. Get rid of the corresponding districts.
2. Get rid of the whole attribute.
3. Set the values to some value (zero, the mean, the median, the mode, etc.)
You can accomplish these easily using DataFrame's `dropna()`, `drop()`, `fillna()` methods:
```
# housing.dropna(subset=["total_bedrooms"])
# housing.drop("total_bedrooms", axis=1)
# median = housing["total_bedrooms"].median()
# housing["total_bedrooms"].fillna(median, inplace=True)
```
But we'll be using the Scikit-Learning platform.
Scikit-Learn provides a handy class to take care of the missing values: `SimpleImputer`.
```
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
# Since the median can be computed only on numerical attributes, drop the ocean_proximity attribute which is a String
housing_num = housing.drop("ocean_proximity", axis=1)
imputer.fit(housing_num)
X = imputer.transform(housing_num)
# The result is a plain numpy array, converting into a dataframe
housing_tr = pd.DataFrame(X, columns=housing_num.columns, index=housing_num.index)
imputer.statistics_
housing_tr.info()
```
### Handling Text and Categorical Attributes
So far we have only dealt with numerical attributes, but now let's look at text attributes. In this dataset, there is just one: the `ocean_proximity` attribute. Let's look at its value fo first 10 instances:
```
# First 10 instances
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)
housing["ocean_proximity"].value_counts()
# It's not arbitary text. Therefore, it is categorical text.
# One hot encoding the data
from sklearn.preprocessing import OneHotEncoder
cat_enc = OneHotEncoder()
housing_cat_one_hot = cat_enc.fit_transform(housing_cat)
housing_cat_one_hot
housing_cat_one_hot.toarray()
cat_enc.categories_
```
### Custom Trasformers
Although Scikit-Learn provides many useful transformers, you will need to write your own for tasks such as custom cleanup operations or combining specific attributes. You will want your transformer to work seamlessely with Scikit-Learn functionalitites (such as `pipelines`), all you need to do is create a class and implement three methods: `fit()`, `transform()`, and `fit_transform()`.
```
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
class CombinedAttributeAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room=True):
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self
def transform(self, X, y=None):
rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
population_per_household = X[:, population_ix] / X[:, households_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributeAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)
```
### Feature Scaling
One of the most imprtant features you need to apply to your data is *feature scaling*. With a few exceptions, Machine Learning algorithms don't perform well numerical attributes have very different scales. There are two common ways to get all the attributes to have the same scale, namely, *min-max scaling* and *standardization*.
Min-Max Scaling (also known as *Normalization*) is the simplest: the values are shifted to a range of 0-1.
Standardization is using standard deviation.
### Transformation Pipelines
As you can see, there are many data transformation steps that need to be executed in an order. Fortunately, Scikit-Learn provides the `Pipeline` class to help with sequences of transformations. Here is a small pipeline for the numerical attributes:
```
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', CombinedAttributeAdder()),
('std_scaler', StandardScaler())
])
housing_num_tr = num_pipeline.fit_transform(housing_num)
housing
from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing)
```
## Select and Train a Model
At last!😃 You framed the problem, you got your data and explored it, you sampled a training set and a test set, and you wrote transformation pipelines to clean up and prepare your data for Machine learning slgorithms automatically. You are now ready to select and train a Machine Learning Model.💗
### Training Machine Learning Models on the training set and evaluating on the Same
The following experiments will be implemented:
1. Linear Regression Model
2. Decision Tree Regression Model
3. Random Forest Regression Model
```
# 1. Linear Regression model
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
from sklearn.metrics import mean_squared_error
lin_reg_predictions = lin_reg.predict(housing_prepared)
lin_reg_predictions[:10]
lin_reg_results = np.sqrt(mean_squared_error(housing_labels, lin_reg_predictions))
lin_reg_results
# 2. Decision Tree Regression Model
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)
tree_reg_predictions = tree_reg.predict(housing_prepared)
tree_reg_predictions[:10]
tree_reg_results = np.sqrt(mean_squared_error(housing_labels, tree_reg_predictions))
tree_reg_results
# 3. Random Forest Regressor
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
forest_reg_predictions = forest_reg.predict(housing_prepared)
forest_reg_predictions[:10]
forest_reg_results = np.sqrt(mean_squared_error(housing_labels, forest_reg_predictions))
forest_reg_results
```
### Better Evaluation using Cross-Validation
A great feature of Scikit-Learn is its *K-fold cross-validaation* feature. The following code randomy splits the training set into 10 distinct subsets called folds, then it trains and evaluates the Decision Tree model 10 times, picking a different fold for evaluation every time and training other 9 folds. The result is an array containing the 10 evaluation scores.
```
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores)
tree_rmse_scores.mean()
```
> 🔑 **Note:** Scikit-Learn's cross-validation features expect a utility function (grater is better) rather than a cost function (lower is better), so the scoring function is actually the opposite of MSE (i.e., a negative value), which is why the preceding code computes -scores before calculating the square root.
```
# Function to display the scores of any model
from sklearn.model_selection import cross_val_score
def display_scores(model):
scores = cross_val_score(model, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
rmse_scores = np.sqrt(-scores)
print(f"Scores: {rmse_scores}")
print(f"Scores: {rmse_scores.mean()}")
print(f"Standard deviation: {rmse_scores.std()}")
display_scores(lin_reg)
display_scores(tree_reg)
display_scores(forest_reg)
```
| true |
code
| 0.750418 | null | null | null | null |
|
# Reading and writing LAS files
This notebook goes with [the Agile blog post](https://agilescientific.com/blog/2017/10/23/x-lines-of-python-load-curves-from-las) of 23 October.
Set up a `conda` environment with:
conda create -n welly python=3.6 matplotlib=2.0 scipy pandas
You'll need `welly` in your environment:
conda install tqdm # Should happen automatically but doesn't
pip install welly
This will also install the latest versions of `striplog` and `lasio`.
```
import welly
ls ../data/*.LAS
```
### 1. Load the LAS file with `lasio`
```
import lasio
l = lasio.read('../data/P-129.LAS') # Line 1.
```
That's it! But the object itself doesn't tell us much — it's really just a container:
```
l
```
### 2. Look at the WELL section of the header
```
l.header['Well'] # Line 2.
```
### 3. Look at the curve data
The curves are all present one big NumPy array:
```
l.data
```
Or we can go after a single curve object:
```
l.curves.GR # Line 3.
```
And there's a shortcut to its data:
```
l['GR'] # Line 4.
```
...so it's easy to make a plot against depth:
```
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(15,3))
plt.plot(l['DEPT'], l['GR'])
plt.show()
```
### 4. Inspect the curves as a `pandas` dataframe
```
l.df().head() # Line 5.
```
### 5. Load the LAS file with `welly`
```
from welly import Well
w = Well.from_las('../data/P-129.LAS') # Line 6.
```
`welly` Wells know how to display some basics:
```
w
```
And the `Well` object also has `lasio`'s access to a pandas DataFrame:
```
w.df().head()
```
### 6. Look at `welly`'s Curve object
Like the `Well`, a `Curve` object can report a bit about itself:
```
gr = w.data['GR'] # Line 7.
gr
```
One important thing about Curves is that each one knows its own depths — they are stored as a property called `basis`. (It's not actually stored, but computed on demand from the start depth, the sample interval (which must be constant for the whole curve) and the number of samples in the object.)
```
gr.basis
```
### 7. Plot part of a curve
We'll grab the interval from 300 m to 1000 m and plot it.
```
gr.to_basis(start=300, stop=1000).plot() # Line 8.
```
### 8. Smooth a curve
Curve objects are, fundamentally, NumPy arrays. But they have some extra tricks. We've already seen `Curve.plot()`.
Using the `Curve.smooth()` method, we can easily smooth a curve, eg by 15 m (passing `samples=True` would smooth by 15 samples):
```
sm = gr.smooth(window_length=15, samples=False) # Line 9.
sm.plot()
```
### 9. Export a set of curves as a matrix
You can get at all the data through the lasio `l.data` object:
```
print("Data shape: {}".format(w.las.data.shape))
w.las.data
```
But we might want to do some other things, such as specify which curves you want (optionally using aliases like GR1, GRC, NGC, etc for GR), resample the data, or specify a start and stop depth — `welly` can do all this stuff. This method is also wrapped by `Project.data_as_matrix()` which is nice because it ensures that all the wells are exported at the same sample interval.
Here are the curves in this well:
```
w.data.keys()
keys=['CALI', 'DT', 'DTS', 'RHOB', 'SP']
w.plot(tracks=['TVD']+keys)
X, basis = w.data_as_matrix(keys=keys, start=275, stop=1850, step=0.5, return_basis=True)
w.data['CALI'].shape
```
So CALI had 12,718 points in it... since we downsampled to 0.5 m and removed the top and tail, we should have substantially fewer points:
```
X.shape
plt.figure(figsize=(15,3))
plt.plot(X.T[0])
plt.show()
```
### 10+. BONUS: fix the lat, lon
OK, we're definitely going to go over our budget on this one.
Did you notice that the location of the well did not get loaded properly?
```
w.location
```
Let's look at some of the header:
# LAS format log file from PETREL
# Project units are specified as depth units
#==================================================================
~Version information
VERS. 2.0:
WRAP. YES:
#==================================================================
~WELL INFORMATION
#MNEM.UNIT DATA DESCRIPTION
#---- ------ -------------- -----------------------------
STRT .M 1.0668 :START DEPTH
STOP .M 1939.13760 :STOP DEPTH
STEP .M 0.15240 :STEP
NULL . -999.25 :NULL VALUE
COMP . Elmworth Energy Corporation :COMPANY
WELL . Kennetcook #2 :WELL
FLD . Windsor Block :FIELD
LOC . Lat = 45* 12' 34.237" N :LOCATION
PROV . Nova Scotia :PROVINCE
UWI. Long = 63* 45'24.460 W :UNIQUE WELL ID
LIC . P-129 :LICENSE NUMBER
CTRY . CA :COUNTRY (WWW code)
DATE. 10-Oct-2007 :LOG DATE {DD-MMM-YYYY}
SRVC . Schlumberger :SERVICE COMPANY
LATI .DEG :LATITUDE
LONG .DEG :LONGITUDE
GDAT . :GeoDetic Datum
SECT . 45.20 Deg N :Section
RANG . PD 176 :Range
TOWN . 63.75 Deg W :Township
Look at **LOC** and **UWI**. There are two problems:
1. These items are in the wrong place. (Notice **LATI** and **LONG** are empty.)
2. The items are malformed, with lots of extraneous characters.
We can fix this in two steps:
1. Remap the header items to fix the first problem.
2. Parse the items to fix the second one.
We'll define these in reverse because the remapping uses the transforming function.
```
import re
def transform_ll(text):
"""
Parses malformed lat and lon so they load properly.
"""
def callback(match):
d = match.group(1).strip()
m = match.group(2).strip()
s = match.group(3).strip()
c = match.group(4).strip()
if c.lower() in ('w', 's') and d[0] != '-':
d = '-' + d
return ' '.join([d, m, s])
pattern = re.compile(r""".+?([-0-9]+?).? ?([0-9]+?).? ?([\.0-9]+?).? +?([NESW])""", re.I)
text = pattern.sub(callback, text)
return welly.utils.dms2dd([float(i) for i in text.split()])
```
Make sure that works!
```
print(transform_ll("""Lat = 45* 12' 34.237" N"""))
remap = {
'LATI': 'LOC', # Use LOC for the parameter LATI.
'LONG': 'UWI', # Use UWI for the parameter LONG.
'LOC': None, # Use nothing for the parameter SECT.
'SECT': None, # Use nothing for the parameter SECT.
'RANG': None, # Use nothing for the parameter RANG.
'TOWN': None, # Use nothing for the parameter TOWN.
}
funcs = {
'LATI': transform_ll, # Pass LATI through this function before loading.
'LONG': transform_ll, # Pass LONG through it too.
'UWI': lambda x: "No UWI, fix this!"
}
w = Well.from_las('../data/P-129.LAS', remap=remap, funcs=funcs)
w.location.latitude, w.location.longitude
w.uwi
```
Let's just hope the mess is the same mess in every well. (LOL, no-one's that lucky.)
<hr>
**© 2017 [agilescientific.com](https://www.agilescientific.com/) and licensed [CC-BY 4.0](https://creativecommons.org/licenses/by/4.0/)**
| true |
code
| 0.367582 | null | null | null | null |
|
#### Jupyter notebooks
This is a [Jupyter](http://jupyter.org/) notebook using Python. You can install Jupyter locally to edit and interact with this notebook.
# Finite difference methods for transient PDE
## Method of Lines
Our method for solving time-dependent problems will be to discretize in space first, resulting in a system of ordinary differential equations
$$ M \dot u = f(u) $$
where the "mass matrix" $M$ might be diagonal and $f(u)$ represents a spatial discretization that has the form $f(u) = A u$ for linear problems.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
def ode_euler(f, u0, tfinal=1, h=0.1):
u = np.array(u0)
t = 0
thist = [t]
uhist = [u0]
while t < tfinal:
h = min(h, tfinal - t)
u += h * f(t, u)
t += h
thist.append(t)
uhist.append(u.copy())
return np.array(thist), np.array(uhist)
tests = []
class fcos:
def __init__(self, k=5):
self.k = k
def __repr__(self):
return 'fcos(k={:d})'.format(self.k)
def f(self, t, u):
return -self.k * (u - np.cos(t))
def u(self, t, u0):
k2p1 = self.k**2+1
return (u0 - self.k**2/k2p1) * np.exp(-self.k*t) + self.k*(np.sin(t) + self.k*np.cos(t))/k2p1
tests.append(fcos(k=2))
tests.append(fcos(k=10))
u0 = np.array([.2])
plt.figure()
for test in tests:
thist, uhist = ode_euler(test.f, u0, h=.1, tfinal=6)
plt.plot(thist, uhist, '.', label=repr(test)+' Forward Euler')
plt.plot(thist, test.u(thist, u0), label=repr(test)+' exact')
plt.plot(thist, np.cos(thist), label='cos')
plt.legend(loc='upper right');
```
### Midpoint Method
What if instead of evaluating the function at the end of the time step, we evaluated in the middle of the time step using the average of the endpoint values.
$$ \tilde u(h) = u(0) + h f\left(\frac h 2, \frac{\tilde u(h) + u(0)}{2} \right) $$
For the linear problem, this reduces to
$$ \Big(I - \frac h 2 A \Big) u(h) = \Big(I + \frac h 2 A\Big) u(0) .$$
```
def ode_midpoint_linear(A, u0, tfinal=1, h=0.1):
u = u0.copy()
t = 0
thist = [t]
uhist = [u0]
I = np.eye(len(u))
while t < tfinal:
h = min(h, tfinal - t)
u = np.linalg.solve(I - .5*h*A, (I + .5*h*A) @ u)
t += h
thist.append(t)
uhist.append(u.copy())
return np.array(thist), np.array(uhist)
thist, uhist = ode_midpoint_linear(test.A, u0, h=.2, tfinal=15)
plt.figure()
plt.plot(thist, uhist, '*')
plt.plot(thist, test.u(thist, u0))
plt.title('Midpoint');
```
## $\theta$ method
The above methods are all special cases of the $\theta$ method
$$ \tilde u(h) = u(0) + h f\left(\theta h, \theta\tilde u(h) + (1-\theta)u(0) \right) $$
which, for linear problems, is solved as
$$ (I - h \theta A) u(h) = \Big(I + h (1-\theta) A \Big) u(0) . $$
$\theta=0$ is explicit Euler, $\theta=1$ is implicit Euler, and $\theta=1/2$ is the midpoint rule.
The stability function is
$$ R(z) = \frac{1 + (1-\theta)z}{1 - \theta z}. $$
```
for theta in [.2, .5, .8]:
plot_stability(xx, yy, (1 + (1-theta)*zz)/(1 - theta*zz), '$\\theta={:3.1f}$'.format(theta))
```
We will generalize slightly to allow solution of a linear differential algebraic equation
$$ M \dot u = A u + f(t,x) $$
where $M$ is (for now) a diagonal matrix that has zero rows at boundary conditions. With this generalization, the $\theta$ method becomes
$$ (M - h \theta A) u(h) = \Big(M + h (1-\theta) A \Big) u(0) + h f(h\theta, x) . $$
We will assume that $M$ is nonsingular if $\theta=0$.
```
def dae_theta_linear(M, A, u0, rhsfunc, bcs=[], tfinal=1, h=0.1, theta=.5):
u = u0.copy()
t = 0
hist = [(t,u0)]
while t < tfinal:
if tfinal - t < 1.01*h:
h = tfinal - t
tnext = tfinal
else:
tnext = t + h
h = min(h, tfinal - t)
rhs = (M + (1-theta)*h*A) @ u + h*rhsfunc(t+theta*h)
for i, f in bcs:
rhs[i] = theta*h*f(t+theta*h, x[i])
u = np.linalg.solve(M - theta*h*A, rhs)
t = tnext
hist.append((t, u.copy()))
return hist
```
### Stiff decay to cosine
```
test = fcos(k=5000)
u0 = np.array([.2])
hist = dae_theta_linear(np.eye(1), -test.k, u0,
lambda t: test.k*np.cos(t),
h=.1, tfinal=6, theta=.5)
hist = np.array(hist)
plt.plot(hist[:,0], hist[:,1], 'o')
tt = np.linspace(0, 6, 200)
plt.plot(tt, test.u(tt,u0));
```
#### Observations
* $\theta=1$ is robust
* $\theta=1/2$ gets correct long-term behavior, but has oscillations at early times
* $\theta < 1/2$ allows oscillations to grow
### Definition: $A$-stability
A method is $A$-stable if the stability region
$$ \{ z : |R(z)| \le 1 \} $$
contains the entire left half plane $$ \Re[z] \le 0 .$$
This means that the method can take arbitrarily large time steps without becoming unstable (diverging) for any problem that is indeed physically stable.
### Definition: $L$-stability
A time integrator with stability function $R(z)$ is $L$-stable if
$$ \lim_{z\to\infty} R(z) = 0 .$$
For the $\theta$ method, we have
$$ \lim_{z\to \infty} \frac{1 + (1-\theta)z}{1 - \theta z} = \frac{1-\theta}{\theta} . $$
Evidently only $\theta=1$ is $L$-stable.
## Transient PDE
### Diffusion (heat equation)
Let's first consider diffusion of a quantity $u(t,x)$
$$ \dot u(t,x) - u''(t,x) = f(t,x) \qquad t > 0, -1 < x < 1 \\
u(0,x) = g(x) \qquad u(t,-1) = h_L(t) \qquad u'(t,1) = h_R(t) .$$
Let's use a Chebyshev discretization in space.
```
%run fdtools.py # define cosspace, vander_chebyshev, and chebeval
def diffusion_cheb(n, left, right):
"""Solve the diffusion PDE on (-1,1) using n elements with rhsfunc(x) forcing.
The left and right boundary conditions are specified as a pair (deriv, func) where
* deriv=0 for Dirichlet u(x_endpoint) = func(x_endpoint)
* deriv=1 for Neumann u'(x_endpoint) = func(x_endpoint)"""
x = cosspace(-1, 1, n+1) # n+1 points is n "elements"
T = chebeval(x)
L = -T[2]
bcs = []
for i,deriv,func in [(0, *left), (-1, *right)]:
L[i] = T[deriv][i]
bcs.append((i, func))
M = np.eye(n+1)
M[[0,-1]] = 0
return x, M, -L @ np.linalg.inv(T[0]), bcs
x, M, A, bcs = diffusion_cheb(80, (0, lambda t,x: 0*x), (0, lambda t,x: 0*x+.5))
hist = dae_theta_linear(M, A, np.exp(-(x*8)**2), lambda t: 0*x, bcs,
h=.005, theta=.5, tfinal=0.3)
for t, u in hist[::10]:
plt.plot(x, u, label='$t={:4.2f}$'.format(t))
plt.legend(loc='lower left');
```
#### Observations
* Sharp central spike is diffused very quickly.
* Artifacts with $\theta < 1$.
#### Manufactured solution
```
class exact_tanh:
def __init__(self, k=1, x0=0):
self.k = k
self.x0 = x0
def u(self, t, x):
return np.tanh(self.k*(x - t - self.x0))
def u_x(self, t, x):
return self.k * np.cosh(self.k*(x - t - self.x0))**(-2)
def u_t(self, t, x):
return -self.u_x(t, x)
def u_xx(self, t, x):
return -2 * self.k**2 * np.tanh(self.k*(x - t - self.x0)) * np.cosh(self.k*(x - t - self.x0))**(-2)
def heatrhs(self, t, x):
return self.u_t(t,x) - self.u_xx(t,x)
ex = exact_tanh(2, -.3)
x, M, A, bcs = diffusion_cheb(20, (0, ex.u), (1, ex.u_x))
hist = dae_theta_linear(M, A, ex.u(0,x), lambda t: ex.heatrhs(t,x), bcs)
for t, u in hist:
plt.plot(x, u, label='$t={:3.1f}$'.format(t))
plt.legend(loc='lower right');
def mms_error(n):
x, M, A, bcs = diffusion_cheb(n, (0, ex.u), (1, ex.u_x))
hist = dae_theta_linear(M, A, ex.u(0,x),
lambda t: ex.heatrhs(t,x), bcs, h=1/n**2, theta=1)
return np.linalg.norm(hist[-1][1] - ex.u(hist[-1][0], x),
np.inf)
ns = np.logspace(.8, 1.6, 10).astype(int)
errors = [mms_error(n) for n in ns]
plt.loglog(ns, errors, 'o', label='numerical')
for p in range(1,4):
plt.loglog(ns, 1/ns**(p), label='$n^{-%d}$'%p)
plt.xlabel('n')
plt.ylabel('error')
plt.legend(loc='lower left');
```
#### Observations
* Errors are limited by time (not spatial) discretization error. This is a result of using the (spectrally accurate) Chebyshev method in space.
* $\theta=1$ is more accurate than $\theta = 1/2$, despite the latter being second order accurate in time. This is analogous to the stiff relaxation to cosine test.
#### Largest eigenvalues
```
def maxeig(n):
x, M, A, bcs = diffusion_cheb(n, (0, ex.u), (1, ex.u_x))
lam = np.linalg.eigvals(-A)
return max(lam)
plt.loglog(ns, [maxeig(n) for n in ns], 'o', label='cheb')
for p in range(1,5):
plt.loglog(ns, ns**(p), label='$n^{%d}$'%p)
plt.xlabel('n')
plt.ylabel('$\max \sigma(A)$')
plt.legend(loc='lower left');
```
### Finite difference method
```
def maxeig_fd(n):
dx = 2/n
A = 1/dx**2 * (2 * np.eye(n+1) - np.eye(n+1, k=1) - np.eye(n+1, k=-1))
return max(np.linalg.eigvals(A))
plt.loglog(2/ns, [maxeig_fd(n) for n in ns], 'o', label='fd')
for p in range(1,4):
plt.loglog(2/ns, 4*(2/ns)**(-p), label='$4 h^{-%d}$'%p)
plt.xlabel('h')
plt.ylabel('$\max \sigma(A)$')
plt.legend(loc='upper right');
```
#### Question: max explicit Euler time step
Express the maximum stable time step $\Delta t$ using explicit Euler in terms of the grid spacing $\Delta x$.
## Hyperbolic (wave) equations
The simplest hyperbolic equation is linear advection
$$ \dot u(t,x) + c u'(t,x) = f(t,x) $$
where $c$ is the wave speed and $f$ is a source term. In the homogenous ($f = 0$) case, the solution is given by characteristics
$$ u(t,x) = u(0, x - ct) . $$
This PDE also requires boundary conditions, but as a first-order equation, we can only enforce boundary conditions at one boundary. It turns out that this needs to be the _inflow_ boundary, so if $c > 0$, that is the left boundary condition $u(t, -1) = g(t)$. We can solve this system using Chebyshev methods.
```
def advection_cheb(n, c, left=(None,None), right=(None,None)):
"""Discretize the advection PDE on (-1,1) using n elements with rhsfunc(x) forcing.
The left boundary conditions are specified as a pair (deriv, func) where
* deriv=0 for Dirichlet u(x_endpoint) = func(x_endpoint)
* deriv=1 for Neumann u'(x_endpoint) = func(x_endpoint)"""
x = cosspace(-1, 1, n+1) # n+1 points is n "elements"
T = chebeval(x)
A = -c*T[1]
M = np.eye(n+1)
bcs = []
for i,deriv,func in [(0, *left), (-1, *right)]:
if deriv is None: continue
A[i] = T[deriv][i]
M[i] = 0
bcs.append((i, func))
return x, M, A @ np.linalg.inv(T[0]), bcs
x, M, A, bcs = advection_cheb(40, 1, left=(0, lambda t,x: 0*x))
hist = dae_theta_linear(M, A, np.exp(-(x*4)**2), lambda t: 0*x, bcs,
h=.001, theta=1)
for t, u in hist[::len(hist)//10]:
plt.plot(x, u, label='$t={:3.1f}$'.format(t))
plt.legend(loc='lower left')
np.linalg.cond(A)
lam = np.linalg.eigvals(A[:,:])
print(A[0,:5])
plt.plot(lam.real, lam.imag, '.');
```
#### Observations
* $\theta > 1/2$ causes decay in amplitude
* $\theta < 1/2$ causes growth -- unstable
* An undershoot develops behind the traveling wave and increasing resolution doesn't make it go away
* We need an *upwind* boundary condition, otherwise the system is unstable
* Only Dirichlet inflow conditions are appropriate -- Neumann conditions produce a singular matrix
### Finite difference
```
def advection_fd(n, c, stencil=2, bias=0, left=None, right=None):
x = np.linspace(-1, 1, n+1)
A = np.zeros((n+1,n+1))
for i in range(n+1):
sleft = max(0, i - stencil//2 + bias)
sleft = min(sleft, n+1 - stencil)
A[i,sleft:sleft+stencil] = -c*fdstencil(x[i], x[sleft:sleft+stencil])[1]
M = np.eye(n+1)
bcs = []
for i, func in [(0, left), (-1, right)]:
if func is None: continue
A[i] = 0
A[i,i] = 1
M[i] = 0
bcs.append((i, func))
return x, M, A, bcs
x, M, A, bcs = advection_fd(40, c=1, stencil=3, bias=0, left=lambda t,x: 0*x)
hist = dae_theta_linear(M, A, np.exp(-(x*4)**2), lambda t: 0*x, bcs,
h=2/(len(x)-1), theta=.5)
for t, u in hist[::len(hist)//10]:
plt.plot(x, u, label='$t={:3.1f}$'.format(t))
plt.legend(loc='lower left')
print('stencil', A[3,:7])
print('cond', np.linalg.cond(A))
lam = np.linalg.eigvals(A[1:,1:])
plt.plot(lam.real, lam.imag, '.')
#plt.spy(A[:6,:6]);
```
#### Observations
* Centered methods have an undershoot behind the traveling wave
* Upwind biasing of the stencil tends to reduce artifacts, but only `stencil=2` removes undershoots
* Downwind biasing is usually unstable
* With upwinded `stencil=2`, we can use an explicit integrator, but the time step must satisfy
$$ c \Delta t < \Delta x $$
* The upwind methods are in general dissipative -- amplitude is lost even with very accurate time integration
* The higher order upwind methods always produce artifacts for sharp transitions
### Phase analysis
We can apply the advection differencing stencils to the test functions $$ \phi(x, \theta) = e^{i \theta x}$$ and compare to the exact derivative $$ \frac{d \phi}{d x} = i \theta \phi(x, \theta) . $$
```
x = np.arange(-1, 1+1)
s1 = fdstencil(0, x)[1]
print(s1)
theta = np.linspace(0, np.pi)
phi = np.exp(1j*np.outer(x, theta))
plt.plot(theta, np.sin(theta))
plt.plot(theta, np.abs(s1 @ phi), '.')
plt.plot(theta, theta);
```
# Runge-Kutta methods
The methods we have considered thus far can all be expressed as Runge-Kutta methods, which are expressed in terms of $s$ "stage" equations (possibly coupled) and a completion formula. For the ODE
$$ \dot u = f(t, u) $$
the Runge-Kutta method is
$$\begin{split}
Y_i = u(t) + h \sum_j a_{ij} f(t+c_j h, Y_j) \\
u(t+h) = u(t) + h \sum_j b_j f(t+c_j h, Y_j)
\end{split}$$
where $c$ is a vector of *abscissa*, $A$ is a table of coefficients, and $b$ is a vector of completion weights.
These coefficients are typically expressed in a Butcher Table
$$ \left[ \begin{array}{c|c} c & A \\ \hline & b^T \end{array} \right] = \left[ \begin{array}{c|cc}
c_0 & a_{00} & a_{01} \\
c_1 & a_{10} & a_{11} \\
\hline
& b_0 & b_1
\end{array} \right] . $$
We will see that, for consistency, the abscissa $c$ are always the row sums of $A$ and that $\sum_i b_i = 1$.
If the matrix $A$ is strictly lower triangular, then the method is **explicit** (does not require solving equations). We have seen forward Euler
$$ \left[ \begin{array}{c|cc}
0 & 0 \\
\hline
& 1
\end{array} \right] ,$$
backward Euler
$$ \left[ \begin{array}{c|c}
1 & 1 \\
\hline
& 1
\end{array} \right] ,$$
and Midpoint
$$ \left[ \begin{array}{c|c}
\frac 1 2 & \frac 1 2 \\
\hline
& 1
\end{array} \right]. $$
Indeed, the $\theta$ method is
$$ \left[ \begin{array}{c|c}
\theta & \theta \\
\hline
& 1
\end{array} \right] $$
and an alternative "endpoint" variant of $\theta$ (a generalization of the trapezoid rule) is
$$ \left[ \begin{array}{c|cc}
0 & 0 & 0 \\
1 & 1-\theta & \theta \\
\hline
& 1-\theta & \theta
\end{array} \right]. $$
## Stability
To develop an algebraic expression for stability in terms of the Butcher Table, we consider the test equation
$$ \dot u = \lambda u $$
and apply the RK method to yield
$$ \begin{split} Y_i = u(0) + h \sum_j a_{ij} \lambda Y_j \\
u(h) = u(0) + h \sum_j b_j \lambda Y_j \end{split} $$
or, in matrix form,
$$ \begin{split} Y = \mathbb 1 u(0) + h \lambda A Y \\
u(h) = u(0) + h \lambda b^T Y \end{split} $$
where $\mathbb 1$ is a column vector of length $s$ consisting of all ones.
This reduces to
$$ u(h) = \underbrace{\Big( 1 + h\lambda b^T (I - h \lambda A)^{-1} \mathbb 1 \Big)}_{R(h\lambda)} u(0) . $$
```
def Rstability(A, b, z):
s = len(b)
def R(z):
return 1 + z*b.dot(np.linalg.solve(np.eye(s) - z*A, np.ones(s)))
f = np.vectorize(R)
return f(z)
def rk_butcher_theta(theta):
A = np.array([[theta]])
b = np.array([1])
return A, b
def zmeshgrid(xlen=5, ylen=5):
xx = np.linspace(-xlen, xlen, 100)
yy = np.linspace(-ylen, ylen, 100)
x, y = np.meshgrid(xx, yy)
z = x + 1j*y
return x, y, z
def plot_rkstability(A, b, label=''):
from matplotlib import plt, ticker, cm, axis
import np as np
x, y, z = zmeshgrid()
data = np.abs(Rstability(A, b, z))
cs = plt.contourf(x, y, data, np.arange(0, 2, 0.1), cmap=cm.coolwarm)
cbar = plt.colorbar(cs, ticks=np.linspace(0, 2, 5))
plt.axhline(y=0, xmin=-20.0, xmax=20.0, linewidth=1, linestyle='--', color='grey')
plt.axvline(x=0, ymin=-20.0, ymax=20.0, linewidth=1, linestyle='--', color='grey')
cs = plt.contour(x, y, data, np.arange(0, 2, 0.5), colors='k')
plt.clabel(cs, fontsize=6)
for c in cs.collections:
plt.setp(c, linewidth=1)
plt.title('Stability region' + (': ' + label if label else ''))
A, b = rk_butcher_theta(.5)
plot_rkstability(A, b, label='$\\theta$')
def rk_butcher_theta_endpoint(theta):
A = np.array([[0, 0], [1-theta, theta]])
b = np.array([1-theta, theta])
return A, b
A, b = rk_butcher_theta_endpoint(.5)
plot_rkstability(A, b, label='$\\theta$ endpoint')
```
Evidently the endpoint variant of $\theta$ has the same stability function as the original (midpoint) variant that we've been using. These methods are equivalent for linear problems, but different for nonlinear problems.
## Higher order explicit methods: Heun's and RK4
Explicit Euler steps can be combined to create more accurate methods. One such example is Heun's method,
$$ \left[ \begin{array}{c|cc}
0 & 0 & 0 \\
1 & 1 & 0 \\
\hline
& \frac 1 2 & \frac 1 2
\end{array} \right]. $$
Another explicit method is the famous four-stage RK4,
$$ \left[ \begin{array}{c|cccc}
0 & 0 & 0 & 0 & 0 \\
\frac 1 2 & \frac 1 2 & 0 & 0 & 0 \\
\frac 1 2 & 0 & \frac 1 2 & 0 & 0 \\
1 & 0 & 0 & 1 & 0 \\
\hline
& \frac 1 6 & \frac 1 3 & \frac 1 3 & \frac 1 6
\end{array} \right] . $$
```
def rk_butcher_heun():
A = np.array([[0, 0],[1,0]])
b = np.array([.5, .5])
return A, b
A, b = rk_butcher_heun()
plot_rkstability(A, b, label='Heun')
def rk_butcher_4():
A = np.array([[0,0,0,0],[.5,0,0,0],[0,.5,0,0],[0,0,1,0]])
b = np.array([1/6, 1/3, 1/3, 1/6])
return A, b
A, b = rk_butcher_4()
plot_rkstability(A, b, label='RK4')
```
Finally a method with lots of stability along the imaginary axis. Let's try it on some test problems.
```
def ode_rkexplicit(f, u0, butcher=None, tfinal=1, h=.1):
if butcher is None:
A, b = rk_butcher_4()
else:
A, b = butcher
c = np.sum(A, axis=1)
s = len(c)
u = u0.copy()
t = 0
hist = [(t,u0)]
while t < tfinal:
if tfinal - t < 1.01*h:
h = tfinal - t
tnext = tfinal
else:
tnext = t + h
h = min(h, tfinal - t)
fY = np.zeros((len(u0), s))
for i in range(s):
Yi = u.copy()
for j in range(i):
Yi += h * A[i,j] * fY[:,j]
fY[:,i] = f(t + h*c[i], Yi)
u += h * fY @ b
t = tnext
hist.append((t, u.copy()))
return hist
test = linear(np.array([[0, 1],[-1, 0]]))
u0 = np.array([.5, 0])
hist = ode_rkexplicit(test.f, u0, rk_butcher_4(), tfinal=50, h=.8)
times = [t for t,u in hist]
plt.plot(times, [u for t,u in hist], '.')
plt.plot(times, test.u(times, u0));
```
#### Observations
* Solutions look pretty good and we didn't need a solve.
* We needed to evaluate the right hand side $s$ times per step
```
def mms_error(h, rk_butcher):
hist = ode_rkexplicit(test.f, u0, rk_butcher(), tfinal=20, h=h)
times = [t for t,u in hist]
u = np.array([u for t,u in hist])
return np.linalg.norm(u - test.u(times, u0), np.inf)
hs = np.logspace(-1.5, .5, 20)
error_heun = [mms_error(h, rk_butcher_heun) for h in hs]
error_rk4 = [mms_error(h, rk_butcher_4) for h in hs]
plt.loglog(hs, error_heun, 'o', label='Heun')
plt.loglog(hs, error_rk4, 's', label='RK4')
for p in [2,3,4]:
plt.loglog(hs, hs**p, label='$h^%d$'%p)
plt.title('Accuracy')
plt.legend(loc='lower right')
plt.ylabel('Error')
plt.xlabel('$h$');
```
## Work-precision diagrams for comparing methods
Since these methods do not cost the same per step, it is more enlightening to compare them using some measure of cost. For large systems of ODE, such as arise by discretizing a PDE, the cost of time integration is dominated by evaluating the right hand side (discrete spatial operator) on each stage. Measuring CPU time is a more holistic measure of cost, but the results depend on the implementation, computer, and possible operating system interference/variability. Counting right hand side function evaluations is a convenient, reproducible measure of cost.
```
plt.loglog(20*2/hs, error_heun, 'o', label='Heun')
plt.loglog(20*4/hs, error_rk4, 's', label='RK4')
plt.title('Error vs cost')
plt.ylabel('Error')
plt.xlabel('# function evaluations')
plt.legend(loc='upper right');
test = linear(np.array([[0, 1, 0],[-1, 0, 0],[10, 0, -10]]))
print(np.linalg.eigvals(test.A))
u0 = np.array([.5, 0, 0])
hist = ode_rkexplicit(test.f, u0, rk_butcher_4(), tfinal=5, h=.1)
times = [t for t,u in hist]
plt.plot(times, [u for t,u in hist], '.')
plt.plot(times, test.u(times, u0));
hs = np.logspace(-2, -.7, 20)
error_heun = [mms_error(h, rk_butcher_heun) for h in hs]
error_rk4 = [mms_error(h, rk_butcher_4) for h in hs]
plt.loglog(20*2/hs, error_heun, 'o', label='Heun')
plt.loglog(20*4/hs, error_rk4, 's', label='RK4')
plt.title('Error vs cost')
plt.ylabel('Error')
plt.xlabel('# function evaluations')
plt.legend(loc='upper right');
```
Evidently Heun becomes resolved at lower cost than RK4.
## Refinement in space and time
When solving a transient PDE, we should attempt to balance spatial discretization error with temporal discretization error. If we wish to use the same type of method across a range of accuracies, we need to
1. choose spatial and temporal discretizations with the same order of accuracy,
* choose grid/step sizes so the leading error terms are of comparable size, and
* ensure that both spatial and temporal discretizations are stable throughout the refinement range.
Since temporal discretization errors are proportional to the duration, simulations that run for a long time will need to use more accurate time discretizations.
# Runge-Kutta order conditions
We consider the autonomous differential equation
$$ \dot u = f(u) . $$
Higher derivatives of the exact soultion can be computed using the chain rule, e.g.,
\begin{align*}
\ddot u(t) &= f'(u) \dot u = f'(u) f(u) \\
\dddot u(t) &= f''(u) f(u) f(u) + f'(u) f'(u) f(u) . \\
\end{align*}
Note that if $f(u)$ is linear, $f''(u) = 0$.
Meanwhile, the numerical solution is a function of the time step $h$,
$$\begin{split}
Y_i(h) &= u(0) + h \sum_j a_{ij} f(Y_j) \\
U(h) &= u(0) + h \sum_j b_j f(Y_j).
\end{split}$$
We will take the limit $h\to 0$ and equate derivatives of the numerical solution. First we differentiate the stage equations,
\begin{split}
Y_i(0) &= u(0) \\
\dot Y_i(0) &= \sum_j a_{ij} f(Y_j) \\
\ddot Y_i(0) &= 2 \sum_j a_{ij} \dot f(Y_j) \\
&= 2 \sum_j a_{ij} f'(Y_j) \dot Y_j \\
&= 2\sum_{j,k} a_{ij} a_{jk} f'(Y_j) f(Y_k) \\
\dddot Y_i(0) &= 3 \sum_j a_{ij} \ddot f (Y_j) \\
&= 3 \sum_j a_{ij} \Big( \sum_k f''(Y_j) \dot Y_j \dot Y_k + f'(Y_j) \ddot Y_j \Big) \\
&= 3 \sum_{j,k,\ell} a_{ij} a_{jk} \Big( a_{j\ell} f''(Y_j) f(Y_k) f(Y_\ell) + 2 a_{k\ell} f'(Y_j) f'(Y_k) f(Y_\ell) \Big)
\end{split}
where we have used Liebnitz's formula for the $m$th derivative,
$$ (h \phi(h))^{(m)}|_{h=0} = m \phi^{(m-1)}(0) .$$
Similar formulas apply for $\dot U(0)$, $\ddot U(0)$, and $\dddot U(0)$, with $b_j$ in place of $a_{ij}$.
Equating terms $\dot u(0) = \dot U(0)$ yields
$$ \sum_j b_j = 1, $$
equating $\ddot u(0) = \ddot U(0)$ yields
$$ 2 \sum_{j,k} b_j a_{jk} = 1 , $$
and equating $\dddot u(0) = \dddot U(0)$ yields the two equations
\begin{split}
3\sum_{j,k,\ell} b_j a_{jk} a_{j\ell} &= 1 \\
6 \sum_{j,k,\ell} b_j a_{jk} a_{k\ell} &= 1 .
\end{split}
#### Observations
* These are systems of nonlinear equations for the coefficients $a_{ij}$ and $b_j$. There is no guarantee that they have solutions.
* The number of equations grows rapidly as the order increases.
| | $u^{(1)}$ | $u^{(2)}$ | $u^{(3)}$ | $u^{(4)}$ | $u^{(5)}$ | $u^{(6)}$ | $u^{(7)}$ | $u^{(8)}$ | $u^{(9)}$ | $u^{(10)}$ |
| ------------- |-------------| -----| --- |
| # terms | 1 | 1 | 2 | 4 | 9 | 20 | 48 | 115 | 286 | 719 |
| cumulative | 1 | 2 | 4 | 8 | 17 | 37 | 85 | 200 | 486 | 1205 |
* Usually the number of order conditions does not exactly match the number of free parameters, meaning that the remaining parameters can be optimized (usually numerically) for different purposes, such as to minimize the leading error terms or to maximize stability in certain regions of the complex plane. Finding globally optimal solutions can be extremely demanding.
* The arithmetic managing the derivatives gets messy, but can be managed using rooted trees.

#### Theorem (from Hairer, Nørsett, and Wanner)
A Runge-Kutta method is of order $p$ if and only if
$$ \gamma(\mathcal t) \sum_{j} b_j \Phi_j(t) = 1 $$
for all trees $t$ of order $\le p$.
For a linear autonomous equation
$$ \dot u = A u $$
we only need one additional order condition per order of accuracy because $f'' = 0$.
These conditions can also be derived by equating derivatives of the stability function $R(z)$ with the exponential $e^z$.
For a linear non-autonomous equation
$$ \dot u = A(t) u + g(t) $$
or more generally, an autonomous system with quadratic right hand side,
$$ \dot u = B (u \otimes u) + A u + C $$
where $B$ is a rank 3 tensor, we have $f''' = 0$, thus limiting the number of order conditions.
# Embedded error estimation and adaptive control
It is often possible to design Runge-Kutta methods with multiple completion orders, say of order $p$ and $p-1$.
$$\left[ \begin{array}{c|c} c & A \\ \hline & b^T \\ & \tilde b^T \end{array} \right] . $$
The classical RK4 does not come with an embedded method, but most subsequent RK methods do.
The [Bogacki-Shampine method](https://en.wikipedia.org/wiki/Bogacki%E2%80%93Shampine_method) is given by
```
def rk_butcher_bs3():
A = np.array([[0, 0, 0, 0],
[1/2, 0, 0, 0],
[0, 3/4, 0, 0],
[2/9, 1/3, 4/9, 0]])
b = np.array([[2/9, 1/3, 4/9, 0],
[7/24, 1/4, 1/3, 1/8]])
return A, b
A, b = rk_butcher_bs3()
plot_rkstability(A, b[0], label='Bogacki-Shampine 3')
plt.figure()
plot_rkstability(A, b[1], label='Bogacki-Shampine 2')
```
While this method has four stages, it has the "first same as last" (FSAL) property meaning that the fourth stage exactly matches the completion formula, thus the first stage of the next time step. This means it can be implemented using only three function evaluations per time step.
Higher order methods with embedded error estimation include
* [Fehlberg](https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta%E2%80%93Fehlberg_method), a 6-stage, 5th order method for which the 4th order embedded formula has been optimized for accuracy.
* [Dormand-Prince](https://en.wikipedia.org/wiki/Dormand%E2%80%93Prince_method), a 7-stage, 5th order method with the FSAL property, with the 5th order completion formula optimized for accuracy.
```
# We can import and clean these coefficient tables directly from Wikipedia
import pandas
from fractions import Fraction
dframe = pandas.read_html('https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta%E2%80%93Fehlberg_method')[0]
dframe
# Clean up unicode minus sign, NaN, and convert to float
dfloat = dframe.applymap(lambda s: s.replace('−', '-') if isinstance(s, str) else s) \
.fillna(0).applymap(Fraction).astype(float)
dfloat
# Extract the Butcher table
darray = np.array(dfloat)
A = darray[:6,2:]
b = darray[6:,2:]
pandas.DataFrame(A) # Labeled tabular display
plot_rkstability(A, b[0], label='Fehlberg 5')
plt.figure()
plot_rkstability(A, b[1], label='Fehlberg 4')
dframe = pandas.read_html('https://en.wikipedia.org/wiki/Dormand%E2%80%93Prince_method')[0]
dfloat = dframe.applymap(lambda s: s.replace('−', '-') if isinstance(s, str) else s).fillna(0).applymap(Fraction).astype(float)
darray = np.array(dfloat)
A = darray[:7,2:]
b = darray[7:,2:]
pandas.DataFrame(A)
plot_rkstability(A, b[0], label='DP 5')
plt.figure()
plot_rkstability(A, b[1], label='DP 4')
```
## Adaptive control
Given a completion formula $b^T$ of order $p$ and $\tilde b^T$ of order $p-1$, an estimate of the local truncation error (on this step) is given by
$$ e_{\text{loc}}(h) = \lVert h (b - \tilde b)^T f(Y) \rVert \in O(h^p) . $$
Given a tolerance $\epsilon$, we would like to find $h_*$ such that
$$ e_{\text{loc}}(h_*) < \epsilon . $$
If $$e_{\text{loc}}(h) = c h^p$$ for some constant $c$, then
$$ c h_*^p < \epsilon $$
implies
$$ h_* < \left( \frac{\epsilon}{c} \right)^{1/p} . $$
Given the estimate with the current $h$,
$$ c = e_{\text{loc}}(h) / h^p $$
we conclude
$$ \frac{h_*}{h} < \left( \frac{\epsilon}{e_{\text{loc}}(h)} \right)^{1/p} . $$
#### Notes
* Usually a "safety factor" less than 1 is included so the predicted error is less than the threshold to reject a time step.
* We have used an absolute tolerance above. If the values of solution variables vary greatly in time, a relative tolerance $e_{\text{loc}}(h) / \lVert u(t) \rVert$ or a combination thereof is desirable.
* There is a debate about whether one should optimize the rate at which error is accumulated with respect to work (estimate above) or with respect to simulated time (as above, but with error behaving as $O(h^{p-1})$). For problems with a range of time scales at different periods, this is usually done with respect to work.
* Global error control is an active research area.
# Homework 4: Due 2018-12-03 (Monday)
* Implement an explicit Runge-Kutta integrator that takes an initial time step $h_0$ and an error tolerance $\epsilon$.
* You can use the Bogacki-Shampine method or any other method with an embedded error estimate.
* A step should be rejected if the local truncation error exceeds the tolerance.
* Test your method on the nonlinear equation
$$ \begin{bmatrix} \dot u_0 \\ \dot u_1 \end{bmatrix} = \begin{bmatrix} u_1 \\ k (1-u_0^2) u_1 - u_0 \end{bmatrix} $$
for $k=2$, $k=5$, and $k=20$.
* Make a work-precision diagram for your adaptive method and for constant step sizes.
* State your conclusions or ideas (in a README, or Jupyter notebook) about appropriate (efficient, accurate, reliable) methods for this type of problem.
# Implicit Runge-Kutta methods
We have been considering examples of high-order explicit Runge-Kutta methods.
For processes like diffusion, the time step becomes limited (under grid refinement, but usually for practical resolution) by stability rather than accuracy. Implicit methods, especially $A$-stable and $L$-stable methods, allow much larger time steps.
### Diagonally implicit
A Runge-Kutta method is called **diagonally implicit** if the Butcher matrix $A$ is lower triangular, in which case the stages can be solved sequentially. Each stage equation has the form
$$ Y_i - h a_{ii} f(Y_i) = u(0) + h \sum_{j<i} a_{ij} f(Y_j) $$
where all terms in the right hand side are known.
For stiff problems, it is common to multiply though by $\alpha = (h a_{ii})^{-1}$, yielding
$$ \alpha Y_i - f(Y_i) = \alpha u(0) + \sum_{j<i} \frac{a_{ij}}{a_{ii}} f(Y_j) . $$
* It is common for solvers to reuse a linearization associated with $f(Y_i)$.
* It is common to have setup costs associated with the solution of the "shifted" problem.
Methods with constant diagonals, $a_{ii} = a_{jj}$, are often desired to amortize setup costs. These methods are called **singly diagonally implicit**. There are also related methods called Rosenbrock or Roserbrock-W that more aggressively amortize setup costs.
| true |
code
| 0.551815 | null | null | null | null |
|
### An Auto correct system is an application that changes mispelled words into the correct ones.
```
# In this notebook I'll show how to implement an Auto Correct System that its very usefull.
# This auto correct system only search for spelling erros, not contextual errors.
```
*The implementation can be divided into 4 steps:*
[1]. **Identity a mispelled word.**
[2]. **Find strings n Edit Distance away**
[3]. **Filter Candidates** (*as Real Words that are spelled correct*)
[4]. **Calculate Word Probabilities.** (*Choose the most likely cadidate to be the replacement*)
### 1. Identity a mispelled Word
*To identify if a word was mispelled, you can check if the word is in the dictionary / vocabulary.*
```
vocab = ['dean','deer','dear','fries','and','coke', 'congratulations', 'my']
word_test = 'Congratulations my deah'
word_test = word_test.lower()
word_test = word_test.split()
for word in word_test:
if word in vocab:
print(f'The word: {word} is in the vocab')
else:
print(f"The word: {word} isn't in the vocabulary")
```
### 2. Find strings n Edit Distance Away
*Edit is a operation performed on a string to change into another string. Edit distance count the number of these operations*
*So **n Edit Distance** tells you how many operations away one string is from another.*
*For this application we'll use the Levenshtein Distance value's cost, where this edit value are:*
* **Insert** - Operation where you insert a letter, the cost is equal to 1.
* **Delete** - Operation where you delete a letter, the cost is equal to 1.
* **Replace** - Operation where you replace one letter to another, the cost is equal to 2.
* **Switch** - Operation where you swap 2 **adjacent** letters
*Also we'll use the Minimum Edit Distance which is the minimum number of edits needed to transform 1 string into the other, for that we are using n = 2 and the Dynamic Programming algorithm. ( will be explained when it is implemented ) for evaluate our model*
```
# To implement this operations we need to split the word into 2 parts in all possible ways
word = 'dear'
split_word = [[word[:i], word[i:]] for i in range(len(word) + 1)]
for i in split_word:
print(i)
# The delete operation need to delete each possible letter from the original word.
delete_operation = [[L + R[1:]] for L, R in split_word if R ]
for i in delete_operation:
print(i)
# The same way the insert operation need to add each possible letter from the vocab to the original word
letters = 'abcdefghijklmnopqrstuvwxyz'
insert_operation = [L + s + R for L, R in split_word for s in letters]
c = 0
print('the first insert operations: ')
print()
for i in insert_operation:
print(i)
c += 1
if c == 4:
break
c = 0
print('the last insert operations:')
print()
for i in insert_operation:
c += 1
if c > 126:
print(i)
# Switch Operation
switch_operation = [[L[:-1] + R[0] + L[-1] + R[1:]] for L, R in split_word if R and L]
for i in switch_operation:
print(i)
# Replace Operation
letters = 'abcdefghijklmnopqrstuvwxyz'
replace_operation = [L + s + (R[1:] if len(R) > 1 else '') for L, R in split_word if R for s in letters ]
c = 0
print('the first replace operations: ')
print()
for i in replace_operation:
print(i)
c += 1
if c == 4:
break
c = 0
print('the last replace operations:')
print()
for i in replace_operation:
c += 1
if c > 100:
print(i)
# Remember that at the end we need to remove the word it self
replace_operation = set(replace_operation)
replace_operation.discard('dear')
```
### 3. Filter Candidates
*We only want to consider real and correctly spelled words form the candidate lists, so we need to compare to a know dictionary.*
*If the string does not appears in the dict, remove from the candidates, this way resulting in a list of actual words only*
```
vocab = ['dean','deer','dear','fries','and','coke', 'congratulations', 'my']
# for example we can use the replace operations words to filter in our vocab
filtered_words = [word for word in replace_operation if word in vocab]
print(filtered_words)
```
### 4. Calculate the words probabilities
*We need to find the most likely word from the cadidate list, to calculate the probability of a word in the
sentence we need to first calculate the word frequencies, also we want to count the total number of word in the body of texts
or corpus.*
*So we compute the probability that each word will appear if randomly selected from the corpus of words.*
$$P(w_i) = \frac{C(w_i)}{M} \tag{Eq 01}$$
*where*
$C(w_i)$ *is the total number of times $w_i$ appears in the corpus.*
$M$ *is the total number of words in the corpus.*
*For example, the probability of the word 'am' in the sentence **'I am happy because I am learning'** is:*
$$P(am) = \frac{C(w_i)}{M} = \frac {2}{7} \tag{Eq 02}.$$
### Now the we know the four steps of the Auto Correct System, we can start to implement it
```
# import libraries
import re
from collections import Counter
import numpy as np
import pandas as pd
```
*The first thing to do is the data pre processing, for this example we'll use the file called **'shakespeare.txt'** this file can be found in the directory.*
```
def process_data(filename):
"""
Input:
A file_name which is found in the current directory. We just have to read it in.
Output:
words: a list containing all the words in the corpus (text file you read) in lower case.
"""
words = []
with open(filename, 'r') as f:
text = f.read()
words = re.findall(r'\w+', text)
words = [word.lower() for word in words]
return words
words = process_data('shakespeare.txt')
vocab = set(words) # eliminate duplicates
print(f'The vocabulary has {len(vocab)} unique words.')
```
*The second step, we need to count the frequency of every word in the dictionary to later calculate the probabilities*
```
def get_count(word):
'''
Input:
word_l: a set of words representing the corpus.
Output:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
'''
word_count_dict = {}
word_count_dict = Counter(word)
return word_count_dict
word_count_dict = get_count(words)
print(f'There are {len(word_count_dict)} key par values')
print(f"The count for the word 'thee' is {word_count_dict.get('thee',0)}")
```
*Now we must calculate the probability that each word appears using the (eq 01):*
```
def get_probs(word_count_dict):
'''
Input:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
Output:
probs: A dictionary where keys are the words and the values are the probability that a word will occur.
'''
probs = {}
total_words = 0
for word, value in word_count_dict.items():
total_words += value # we add the quantity of each word appears
for word, value in word_count_dict.items():
probs[word] = value / total_words
return probs
probs = get_probs(word_count_dict)
print(f"Length of probs is {len(probs)}")
print(f"P('thee') is {probs['thee']:.4f}")
```
*Now, that we have computed $P(w_i)$ for all the words in the corpus, we'll write the functions such as delete, insert, switch and replace to manipulate strings so that we can edit the erroneous strings and return the right spellings of the words.*
```
def delete_letter(word, verbose = False):
'''
Input:
word: the string/word for which you will generate all possible words
in the vocabulary which have 1 missing character
Output:
delete_l: a list of all possible strings obtained by deleting 1 character from word
'''
delete = []
split_word = []
split_word = [[word[:i], word[i:]] for i in range(len(word))]
delete = [L + R[1:] for L, R in split_word if R]
if verbose: print(f"input word {word}, \nsplit_word = {split_word}, \ndelete_word = {delete}")
return delete
delete_word = delete_letter(word="cans",
verbose=True)
def switch_letter(word, verbose = False):
'''
Input:
word: input string
Output:
switches: a list of all possible strings with one adjacent charater switched
'''
switch = []
split_word = []
split_word = [[word[:i], word[i:]] for i in range(len(word))]
switch = [L[:-1] + R[0] + L[-1] + R[1:] for L, R in split_word if L and R]
if verbose: print(f"Input word = {word} \nsplit = {split_word} \nswitch = {switch}")
return switch
switch_word_l = switch_letter(word="eta",
verbose=True)
def replace_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
replaces: a list of all possible strings where we replaced one letter from the original word.
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
replace = []
split_word = []
split_word = [(word[:i], word[i:]) for i in range(len(word))]
replace = [L + s + (R[1:] if len(R) > 1 else '') for L, R in split_word if R for s in letters ]
# we need to remove the actual word from the list
replace = set(replace)
replace.discard(word)
replace = sorted(list(replace)) # turn the set back into a list and sort it, for easier viewing
if verbose: print(f"Input word = {word} \nsplit = {split_word} \nreplace {replace}")
return replace
replace_l = replace_letter(word='can',
verbose=True)
def insert_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
inserts: a set of all possible strings with one new letter inserted at every offset
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
insert = []
split_word = []
split_word = [(word[:i], word[i:]) for i in range(len(word) + 1 )]
insert = [L + s + R for L, R in split_word for s in letters]
if verbose: print(f"Input word {word} \nsplit = {split_word} \ninsert = {insert}")
return insert
insert = insert_letter('at', True)
print(f"Number of strings output by insert_letter('at') is {len(insert)}")
```
*Now that we have implemented the string manipulations, we'll create two functions that, given a string, will return all the possible single and double edits on that string. These will be `edit_one_letter()` and `edit_two_letters()`.*
```
def edit_one_letter(word, allow_switches = True): # The 'switch' function is a less common edit function,
# so will be selected by an "allow_switches" input argument.
"""
Input:
word: the string/word for which we will generate all possible wordsthat are one edit away.
Output:
edit_one_set: a set of words with one possible edit. Please return a set. and not a list.
"""
edit_one_set = set()
all_word, words = [] , []
words.append(insert_letter(word))
words.append(delete_letter(word))
words.append(replace_letter(word))
if allow_switches == True:
words.append(switch_letter(word))
for i in words:
for each_word in i:
if each_word == word: # we exclude the word it self
continue
all_word.append(each_word)
edit_one_set = set(all_word)
return edit_one_set
tmp_word = "at"
tmp_edit_one_set = edit_one_letter(tmp_word)
# turn this into a list to sort it, in order to view it
tmp_edit_one = sorted(list(tmp_edit_one_set))
print(f"input word: {tmp_word} \nedit_one \n{tmp_edit_one}\n")
print(f"The type of the returned object should be a set {type(tmp_edit_one_set)}")
print(f"Number of outputs from edit_one_letter('at') is {len(edit_one_letter('at'))}")
def edit_two_letters(word, allow_switches = True):
'''
Input:
word: the input string/word
Output:
edit_two_set: a set of strings with all possible two edits
'''
edit_two_set = set()
if allow_switches == True:
first_edit = edit_one_letter(word)
else:
first_edit = edit_one_letter(word, allow_switches = False)
first_edit = set(first_edit)
second_edit = []
final_edit = []
if allow_switches == True:
for each_word in first_edit:
second_edit.append(edit_one_letter(each_word))
for i in second_edit:
for each_word in i:
final_edit.append(each_word)
edit_two_set = set(final_edit)
else:
for each_word in first_edit:
second_edit.append(edit_one_letter(each_word, allow_switches = False))
for i in second_edit:
for each_word in i:
final_edit.append(each_word)
edit_two_set = set(final_edit)
return edit_two_set
tmp_edit_two_set = edit_two_letters("a")
tmp_edit_two_l = sorted(list(tmp_edit_two_set))
print(f"Number of strings with edit distance of two: {len(tmp_edit_two_l)}")
print(f"First 10 strings {tmp_edit_two_l[:10]}")
print(f"Last 10 strings {tmp_edit_two_l[-10:]}")
print(f"The data type of the returned object should be a set {type(tmp_edit_two_set)}")
print(f"Number of strings that are 2 edit distances from 'at' is {len(edit_two_letters('at'))}")
```
*Now we will use the `edit_two_letters` function to get a set of all the possible 2 edits on our word. We will then use those strings to get the most probable word we meant to substitute our word typing suggestion.*
```
def get_corrections(word, probs, vocab, n=2, verbose = False):
'''
Input:
word: a user entered string to check for suggestions
probs: a dictionary that maps each word to its probability in the corpus
vocab: a set containing all the vocabulary
n: number of possible word corrections you want returned in the dictionary
Output:
n_best: a list of tuples with the most probable n corrected words and their probabilities.
'''
suggestions = []
n_best = []
# look if the word exist in the vocab, if doesn't, the edit_one_letter fuction its used, if any of the letter created
# exists in the vocab, take the two letter edit function, if any of this situations are in the vocab, take the input word
suggestions = list((word in vocab) or (edit_one_letter(word).intersection(vocab)) or (edit_two_letter(word).intersection(vocab)) or word)
n_best= [[word, probs[word]] for word in (suggestions)] # make a list with the possible word and probability.
if verbose: print("entered word = ", word, "\nsuggestions = ", set(suggestions))
return n_best
my_word = 'dys'
tmp_corrections = get_corrections(my_word, probs, vocab, 2, verbose=True) # keep verbose=True
for i, word_prob in enumerate(tmp_corrections):
print(f"word {i}: {word_prob[0]}, probability {word_prob[1]:.6f}")
print(f'The highest score for all the candidates is the word {tmp_corrections[np.argmax(word_prob)][0]}')
```
*Now that we have implemented the auto-correct system, how do you evaluate the similarity between two strings? For example: 'waht' and 'what'.*
*Also how do you efficiently find the shortest path to go from the word, 'waht' to the word 'what'?*
*We will implement a dynamic programming system that will tell you the minimum number of edits required to convert a string into another string.*
### Dynamic Programming
*Dynamic Programming breaks a problem down into subproblems which can be combined to form the final solution. Here, given a string source[0..i] and a string target[0..j], we will compute all the combinations of substrings[i, j] and calculate their edit distance. To do this efficiently, we will use a table to maintain the previously computed substrings and use those to calculate larger substrings.*
*You have to create a matrix and update each element in the matrix as follows:*
$$\text{Initialization}$$
\begin{align}
D[0,0] &= 0 \\
D[i,0] &= D[i-1,0] + del\_cost(source[i]) \tag{eq 03}\\
D[0,j] &= D[0,j-1] + ins\_cost(target[j]) \\
\end{align}
*So converting the source word **play** to the target word **stay**, using an insert cost of one, a delete cost of 1, and replace cost of 2 would give you the following table:*
<table style="width:20%">
<tr>
<td> <b> </b> </td>
<td> <b># </b> </td>
<td> <b>s </b> </td>
<td> <b>t </b> </td>
<td> <b>a </b> </td>
<td> <b>y </b> </td>
</tr>
<tr>
<td> <b> # </b></td>
<td> 0</td>
<td> 1</td>
<td> 2</td>
<td> 3</td>
<td> 4</td>
</tr>
<tr>
<td> <b> p </b></td>
<td> 1</td>
<td> 2</td>
<td> 3</td>
<td> 4</td>
<td> 5</td>
</tr>
<tr>
<td> <b> l </b></td>
<td>2</td>
<td>3</td>
<td>4</td>
<td>5</td>
<td>6</td>
</tr>
<tr>
<td> <b> a </b></td>
<td>3</td>
<td>4</td>
<td>5</td>
<td>4</td>
<td>5</td>
</tr>
<tr>
<td> <b> y </b></td>
<td>4</td>
<td>5</td>
<td>6</td>
<td>5</td>
<td>4</td>
</tr>
</table>
*The operations used in this algorithm are 'insert', 'delete', and 'replace'. These correspond to the functions that we defined earlier: insert_letter(), delete_letter() and replace_letter(). switch_letter() is not used here.*
*The diagram below describes how to initialize the table. Each entry in D[i,j] represents the minimum cost of converting string source[0:i] to string target[0:j]. The first column is initialized to represent the cumulative cost of deleting the source characters to convert string "EER" to "". The first row is initialized to represent the cumulative cost of inserting the target characters to convert from "" to "NEAR".*
<div style="width:image width px; font-size:100%; text-align:center;"><img src='EditDistInit4.PNG' alt="alternate text" width="width" height="height" style="width:1000px;height:400px;"/> Figure 1 Initializing Distance Matrix</div>
*Note that the formula for $D[i,j]$ shown in the image is equivalent to:*
\begin{align}
\\
D[i,j] =min
\begin{cases}
D[i-1,j] + del\_cost\\
D[i,j-1] + ins\_cost\\
D[i-1,j-1] + \left\{\begin{matrix}
rep\_cost; & if src[i]\neq tar[j]\\
0 ; & if src[i]=tar[j]
\end{matrix}\right.
\end{cases}
\tag{5}
\end{align}
*The variable `sub_cost` (for substitution cost) is the same as `rep_cost`; replacement cost. We will stick with the term "replace" whenever possible.*
<div style="width:image width px; font-size:100%; text-align:center;"><img src='EditDistExample1.PNG' alt="alternate text" width="width" height="height" style="width:1200px;height:400px;"/> Figure 2 Examples Distance Matrix</div>
```
def min_edit_distance(source, target, ins_cost = 1, del_cost = 1, rep_cost = 2):
'''
Input:
source: a string corresponding to the string you are starting with
target: a string corresponding to the string you want to end with
ins_cost: an integer setting the insert cost
del_cost: an integer setting the delete cost
rep_cost: an integer setting the replace cost
Output:
D: a matrix of len(source)+1 by len(target)+1 containing minimum edit distances
med: the minimum edit distance (med) required to convert the source string to the target
'''
m = len(source)
n = len(target)
# initialize cost matrix with zeros and dimensions (m+1, n+1)
D = np.zeros((m+1, n+1), dtype = int)
# Fill in column 0, from row 1 to row m, both inclusive
for row in range(1, m+1): # Replace None with the proper range
D[row, 0] = D[row -1, 0] + del_cost
# Fill in row 0, for all columns from 1 to n, both inclusive
for column in range(1, n+1):
D[0, column] = D[0, column - 1] + ins_cost
# Loop through row 1 to row m, both inclusive
for row in range(1, m+1):
# Loop through column 1 to column n, both inclusive
for column in range(1, n+1):
# initialize r_cost to the 'replace' cost that is passed into this function
r_cost = rep_cost
# check to see if source character at the previous row
# matches the target haracter at the previous column
if source[row - 1] == target[column - 1]:
# Update the replacement cost to 0 if source and
# target are equal
r_cost = 0
# Update the cost atow, col based on previous entries in the cost matrix
# Refer to the equation calculate for D[i,j] (the mininum of the three calculated)
D[row, column] = min([D[row-1, column] + del_cost, D[row, column-1] + ins_cost, D[row-1, column-1] + r_cost])
# Set the minimum edit distance with the cost found at row m, column n
med = D[m, n]
return D, med
# testing your implementation
source = 'play'
target = 'stay'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list('#' + source)
cols = list('#' + target)
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
# testing your implementation
source = 'eer'
target = 'near'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list(source)
idx.insert(0, '#')
cols = list(target)
cols.insert(0, '#')
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
```
| true |
code
| 0.27762 | null | null | null | null |
|
## Birthday Paradox
In a group of 5 people, how likely is it that everyone has a unique birthday (assuming that nobody was born on February 29th of a leap year)? You may feel it is highly likely because there are $365$ days in a year and loosely speaking, $365$ is "much greater" than $5$. Indeed, as you shall see, this probability is greater than $0.9$. However, in a group of $25$ or more, what is the probability that no two persons have the same birthday? You might be surprised to know that the answer is less than a half. This is known as the "birthday paradox".
In general, for a group of $n$ people, the probability that no two persons share the same birthday can be calculated as:
\begin{align*}
P &= \frac{\text{Number of } n \text{-permutations of birthdays}}{\text{Total number of birthday assignments allowing repeated birthdays}}\\
&= \frac{365!/(365-n)!}{365^n}\\
&= \prod_{k=1}^n \frac{365-k+1}{365}
\end{align*}
Observe that this value decreases with $n$. At $n=23$, this value goes below half. The following cell simulates this event and compares the associated empirical and theoretical probabilities. You can use the slider called "iterations" to vary the number of iterations performed by the code.
```
import itertools
import random
import matplotlib.pyplot as plt
import numpy as np
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
# Range of number of people
PEOPLE = np.arange(1, 26)
# Days in year
DAYS = 365
def prob_unique_birthdays(num_people):
'''
Returns the probability that all birthdays are unique, among a given
number of people with uniformly-distributed birthdays.
'''
return (np.arange(DAYS, DAYS - num_people, -1) / DAYS).prod()
def sample_unique_birthdays(num_people):
'''
Selects a sample of people with uniformly-distributed birthdays, and
returns True if all birthdays are unique (or False otherwise).
'''
bdays = np.random.randint(0, DAYS, size=num_people)
unique_bdays = np.unique(bdays)
return len(bdays) == len(unique_bdays)
def plot_probs(iterations):
'''
Plots a comparison of the probability of a group of people all having
unique birthdays, between the theoretical and empirical probabilities.
'''
sample_prob = [] # Empirical prob. of unique-birthday sample
prob = [] # Theoretical prob. of unique-birthday sample
# Compute data points to plot
np.random.seed(1)
for num_people in PEOPLE:
unique_count = sum(sample_unique_birthdays(num_people)
for i in range(iterations))
sample_prob.append(unique_count / iterations)
prob.append(prob_unique_birthdays(num_people))
# Plot results
plt.plot(PEOPLE, prob, 'k-', linewidth = 3.0, label='Theoretical probability')
plt.plot(PEOPLE, sample_prob, 'bo-', linewidth = 3.0, label='Empirical probability')
plt.gcf().set_size_inches(20, 10)
plt.axhline(0.5, color='red', linewidth = 4.0, label='0.5 threshold')
plt.xlabel('Number of people', fontsize = 18)
plt.ylabel('Probability of unique birthdays', fontsize = 18)
plt.grid()
plt.xticks(fontsize = 18)
plt.yticks(fontsize = 18)
plt.legend(fontsize = 18)
plt.show()
interact(plot_probs,
iterations=widgets.IntSlider(min=50, value = 500, max=5050, step=200),
continuous_update=False, layout='bottom');
```
## Conditional Probability
Oftentimes it is advantageous to infer the probability of certain events conditioned on other events. Say you want to estimate the probability that it will rain on a particular day. There are copious number of factors that affect rain on a particular day, but [certain clouds are good indicators of rains](https://www.nationalgeographic.com/science/earth/earths-atmosphere/clouds/). Then the question is how likely are clouds a precursor to rains? These types of problems are called [statistical classification](https://en.wikipedia.org/wiki/Statistical_classification), and concepts such as conditional probability and Bayes rule play an important role in its solution.
Dice, coins and cards are useful examples which we can use to understand the fundamental concepts of probability. There are even more interesting real world examples where we can apply these principles to. Let us analyze the [student alcohol consumption](https://www.kaggle.com/uciml/student-alcohol-consumption) dataset and see if we can infer any information regarding a student's performance relative to the time they spend studying.
<span style="color:red">NOTE:</span> Before continuing, please download the dataset and add it to the folder where this notebook resides. If necessary, you can also review our Pandas notebook.
```
import pandas as pd
import matplotlib.pyplot as plt
```
The dataset consists of two parts, `student-por.csv` and `student-mat.csv`, represents the students' performance in Portuguese and Math courses, respectively. We will consider the scores in the Portuguese courses, and leave the math courses optionally to you.
```
data_por = pd.read_csv("student-por.csv")
```
Of the dataset's [various attributes](https://www.kaggle.com/uciml/student-alcohol-consumption/home), we will use the following two
- `G3` - final grade related with the course subject, Math or Portuguese (numeric: from 0 to 20, output target)
- `studytime` - weekly study time (numeric: 1 : < 2 hours, 2 : 2 to 5 hours, 3 : 5 to 10 hours, or 4 : > 10 hours)
```
attributes = ["G3","studytime"]
data_por = data_por[attributes]
```
We are interested in the relationship between study-time and grade performance, but to start, let us view each attribute individually.
The probability that a student's study-time falls in an interval can be approximated by
$${P(\text{study interval}) = \frac{\text{Number of students with this study interval}}{Total\ number\ of\ students}}$$
This is an emperical estimate, and in later lectures we will reason why this is a valid assumption.
```
data_temp = data_por["studytime"].value_counts()
P_studytime = pd.DataFrame((data_temp/data_temp.sum()).sort_index())
P_studytime.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_studytime.columns = ["Probability"]
P_studytime.columns.name = "Study Interval"
P_studytime.plot.bar(figsize=(12,9),fontsize=18)
plt.ylabel("Probability",fontsize=16)
plt.xlabel("Study Interval",fontsize=18)
```
Note that the largest number of students studied between two and five hours, and the smallest studied over 10 hours.
Let us call scores of at least 15 "high". The probability of a student getting a high score can be approximated by
$$P(\text{high score}) = \frac{\text{Number of students with high scores}}{\text{Total number of students}}$$
```
data_temp = (data_por["G3"]>=15).value_counts()
P_score15_p = pd.DataFrame(data_temp/data_temp.sum())
P_score15_p.index = ["Low","High"]
P_score15_p.columns = ["Probability"]
P_score15_p.columns.name = "Score"
print(P_score15_p)
P_score15_p.plot.bar(figsize=(10,6),fontsize=16)
plt.xlabel("Score",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
Proceeding to more interesting observations, suppose we want to find the probability of the various study-intervals when the student scored high. By conditional probability, this can be calculated by:
$$P(\text{study interval}\ |\ \text{highscore})=\frac{\text{Number of students with study interval AND highscore}}{\text{Total number of students with highscore}}$$
```
score = 15
data_temp = data_por.loc[data_por["G3"]>=score,"studytime"]
P_T_given_score15= pd.DataFrame((data_temp.value_counts()/data_temp.shape[0]).sort_index())
P_T_given_score15.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_T_given_score15.columns = ["Probability"]
print("Probability of study interval given that the student gets a highscore:")
P_T_given_score15.columns.name="Study Interval"
P_T_given_score15.plot.bar(figsize=(12,9),fontsize=16)
plt.xlabel("Studt interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
The above metric is something we can only calculate after the students have obtained their results. But how about the other way? What if we want to **predict** the probability that a student gets a score greater than 15 given that they studied for a particular period of time . Using the estimated values we can use the **Bayes rule** to calculate this probability.
$$P(\text{student getting a highscore}\ |\ \text{study interval})=\frac{P(\text{study interval}\ |\ \text{the student scored high})P(\text{highscore})}{P(\text{study interval})}$$
```
P_score15_given_T_p = P_T_given_score15 * P_score15_p.loc["High"] / P_studytime
print("Probability of high score given study interval :")
pd.DataFrame(P_score15_given_T_p).plot.bar(figsize=(12,9),fontsize=18).legend(loc="best")
plt.xlabel("Study interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
Do you find the results surprising? Roughly speaking, the longer students study, the more likely they are to score high. However, once they study over 10 hours, their chances of scoring high decline. You may want to check whether the same phenomenon occurs for the math scores too.
## Try it yourself
If interested, you can try the same analysis for the students math scores. For example, you can get the probabilities of the different study intervals.
```
data_math = pd.read_csv("student-mat.csv")
data_temp = data_math["studytime"].value_counts()
P_studytime_m = pd.DataFrame(data_temp/data_temp.sum())
P_studytime_m.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_studytime_m.columns = ["Probability"]
P_studytime_m.columns.name = "Study Interval"
P_studytime_m.plot.bar(figsize=(12,9),fontsize=16)
plt.xlabel("Study Interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
| true |
code
| 0.672332 | null | null | null | null |
|
## Conceptual description
As people interact, they tend to become more alike in their beliefs, attitudes and behaviour. In "The Dissemination of Culture: A Model with Local Convergence and Global Polarization" (1997), Robert Axelrod presents an agent-based model to explain cultural diffusion. Analogous to Schelling's segregation model, the key to this conceptualization is the emergence of polarization from the interaction of individual agents. The basic premise is that the more similar an actor is to a neighbor, the more likely that that actor will adopt one of the neighbor's traits.
In the model below, this is implemented by initializing the model by filling an excel-like grid with agents with random values [0,1] for each of four traits (music, sports, favorite color and drink).
Each step, each agent (in random order) chooses a random neighbor from the 8 neighbors proportionaly to how similar it is to each of its neighbors, and adopts one randomly selected differing trait from this neighbor. Similarity between any two agents is calculated by 1 - euclidian distance over the four traits.
To visualize the model, the four traits are transformed into 'RGBA' (Red-Green-Blue-Alpha) values; i.e. a color and an opacity. The visualizations below show the clusters of homogeneity being formed.
```
import random
import numpy as np
from mesa import Model, Agent
import mesa.time as time
from mesa.time import RandomActivation
from mesa.space import SingleGrid
from mesa.datacollection import DataCollector
class CulturalDiff(Model):
"""
Model class for the Schelling segregation model.
Parameters
----------
height : int
height of grid
width : int
height of grid
seed : int
random seed
Attributes
----------
height : int
width : int
density : float
schedule : RandomActivation instance
grid : SingleGrid instance
"""
def __init__(self, height=20, width=20, seed=None):
__init__(seed=seed)
self.height = height
self.width = width
self.schedule = time.BaseScheduler(self)
self.grid = SingleGrid(width, height, torus=True)
self.datacollector = DataCollector(model_reporters={'diversity':count_nr_cultures})
# Fill grid with agents with random traits
# Note that this implementation does not guarantee some set distribution of traits.
# Therefore, examining the effect of minorities etc is not facilitated.
for cell in self.grid.coord_iter():
agent = CulturalDiffAgent(cell, self)
self.grid.position_agent(agent, cell)
self.schedule.add(agent)
def step(self):
"""
Run one step of the model.
"""
self.datacollector.collect(self)
self.schedule.step
class CulturalDiffAgent(Agent):
"""
Schelling segregation agent
Parameters
----------
pos : tuple of 2 ints
the x,y coordinates in the grid
model : Model instance
"""
def __init__(self, pos, model):
super().__init__(pos, model)
self.pos = pos
self.profile = np.asarray([random.random() for _ in range(4)])
def step(self):
#For each neighbor, calculate the euclidian distance
# similarity is 1 - distance
neighbor_similarity_dict = []
for neighbor in self.model.grid.neighbor_iter(self.pos, moore=True):
neighbor_similarity = 1-np.linalg.norm(self.profile-neighbor.profile)
neighbor_similarity_dict[neighbor] = neighbor_similarity
# Proportional to this similarity, pick a 'random' neighbor to interact with
neighbor_to_interact = self.random.choices(list(neighbor_similarity_dict.keys()),
weights=neighbor_similarity_dict.values())[0]
# Select a trait that differs between the selected neighbor and self and change that trait in self
# we are using some numpy boolean indexing to make this short and easy
not_same_features = self.profile != neighbor_to_interact.profile
if np.any(not_same_features):
index_for_trait = self.random.choice(np.nonzero(not_same_features)[0])
self.profile[index_for_trait] = neighbor_to_interact.profile[index_for_trait]
def count_nr_cultures(model):
cultures = set()
for (cell, x,y) in model.grid.coord_iter():
if cell:
cultures.add(tuple(cell.profile))
return len(cultures)
```
# Visualization
## Static images
Visualization of this model are static images. A visualization after initialization, after 20 steps, after 50 steps, and after 200 steps is presented.
### After initialization
```
model = CulturalDiff(seed=123456789)
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import seaborn as sns
import pandas as pd
def plot_model(model, ax):
grid = np.zeros((model.height, model.width, 4))
for (cell, i, j) in model.grid.coord_iter():
color = [0,0,0,0] #in case not every cell is filled, the default colour is white
if cell is not None:
color = cell.profile
grid[i,j] = color
plt.imshow(grid)
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 20 steps
```
for i in range(20):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 50 steps
```
for i in range(30):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 200 steps
```
for i in range(150):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
| true |
code
| 0.819803 | null | null | null | null |
|
## Imports
```
import numpy as np
import matplotlib.pyplot as plt
%tensorflow_version 2.x
import tensorflow as tf
from tensorflow import keras
from keras.models import Sequential, Model
from keras.layers import Flatten, Dense, LSTM, GRU, SimpleRNN, RepeatVector, Input
from keras import backend as K
from keras.utils.vis_utils import plot_model
import keras.regularizers
import keras.optimizers
```
## Load data
```
!git clone https://github.com/luisferuam/DLFBT-LAB
f = open('DLFBT-LAB/data/el_quijote.txt', 'r')
quijote = f.read()
f.close()
print(len(quijote))
```
## Input/output sequences
```
quijote_x = quijote[:-1]
quijote_y = quijote[1:]
```
## Some utility functions
```
def one_hot_encoding(data):
symbols = np.unique(data)
char_to_ix = {s: i for i, s in enumerate(symbols)}
ix_to_char = {i: s for i, s in enumerate(symbols)}
data_numeric = np.zeros(data.shape)
for s in symbols:
data_numeric[data == s] = char_to_ix[s]
one_hot_values = np.array(list(ix_to_char.keys()))
data_one_hot = 1 * (data_numeric[:, :, None] == one_hot_values[None, None, :])
return data_one_hot, symbols
def prepare_sequences(x, y, wlen):
(n, dim) = x.shape
nchunks = dim//wlen
xseq = np.array(np.split(x, nchunks, axis=1))
xseq = xseq.reshape((n*nchunks, wlen))
yseq = np.array(np.split(y, nchunks, axis=1))
yseq = yseq.reshape((n*nchunks, wlen))
return xseq, yseq
def get_data_from_strings(data_str_x, data_str_y, wlen):
"""
Inputs:
data_str_x: list of input strings
data_str_y: list of output strings
wlen: window length
Returns:
input/output data organized in batches
"""
# The batch size is the number of input/output strings:
batch_size = len(data_str_x)
# Clip all strings at length equal to the largest multiple of wlen that is
# lower than all string lengths:
minlen = len(data_str_x[0])
for c in data_str_x:
if len(c) < minlen:
minlen = len(c)
while minlen % wlen != 0:
minlen -=1
data_str_x = [c[:minlen] for c in data_str_x]
data_str_y = [c[:minlen] for c in data_str_y]
# Transform strings to numpy array:
x = np.array([[c for c in m] for m in data_str_x])
y = np.array([[c for c in m] for m in data_str_y])
# Divide into batches:
xs, ys = prepare_sequences(x, y, wlen)
# Get one-hot encoding:
xs_one_hot, xs_symbols = one_hot_encoding(xs)
ys_one_hot, ys_symbols = one_hot_encoding(ys)
# Get sparse encoding:
xs_sparse = np.argmax(xs_one_hot, axis=2)
ys_sparse = np.argmax(ys_one_hot, axis=2)
# Return:
return xs_one_hot, ys_one_hot, xs_sparse, ys_sparse, xs_symbols, ys_symbols
```
## Batches for training and test
```
batch_size = 32
seq_len = 50
longitud = len(quijote_x) // batch_size
print(longitud)
print(longitud*batch_size)
qx = [quijote_x[i*(batch_size+longitud):(i+1)*(batch_size+longitud)] for i in range(batch_size)]
qy = [quijote_y[i*(batch_size+longitud):(i+1)*(batch_size+longitud)] for i in range(batch_size)]
xs_one_hot, ys_one_hot, xs_sparse, ys_sparse, xs_symbols, ys_symbols = get_data_from_strings(qx, qy, seq_len)
char_to_ix = {s: i for i, s in enumerate(xs_symbols)}
ix_to_char = {i: s for i, s in enumerate(ys_symbols)}
print(xs_symbols)
print(xs_symbols.shape)
print(ys_symbols)
print(ys_symbols.shape)
xs_symbols == ys_symbols
vocab_len = xs_symbols.shape[0]
print(vocab_len)
num_batches = xs_one_hot.shape[0] / batch_size
print(xs_one_hot.shape[0])
print(batch_size)
print(num_batches)
```
## Training/test partition
```
print(xs_one_hot.shape)
print(ys_one_hot.shape)
print(xs_sparse.shape)
print(ys_sparse.shape)
ntrain = int(num_batches*0.75)*batch_size
xs_one_hot_train = xs_one_hot[:ntrain]
ys_one_hot_train = ys_one_hot[:ntrain]
xs_sparse_train = xs_sparse[:ntrain]
ys_sparse_train = ys_sparse[:ntrain]
xs_one_hot_test = xs_one_hot[ntrain:]
ys_one_hot_test = ys_one_hot[ntrain:]
xs_sparse_test = xs_sparse[ntrain:]
ys_sparse_test = ys_sparse[ntrain:]
print(xs_one_hot_train.shape)
print(xs_one_hot_test.shape)
```
## Function to evaluate the model on test data
```
def evaluate_network(model, x, y, batch_size):
mean_loss = []
mean_acc = []
for i in range(0, x.shape[0], batch_size):
batch_data_x = x[i:i+batch_size, :, :]
batch_data_y = y[i:i+batch_size, :, :]
loss, acc = model.test_on_batch(batch_data_x, batch_data_y)
mean_loss.append(loss)
mean_acc.append(acc)
return np.array(mean_loss).mean(), np.array(mean_acc).mean()
```
## Function that copies the weigths from ``source_model`` to ``dest_model``
```
def copia_pesos(source_model, dest_model):
for source_layer, dest_layer in zip(source_model.layers, dest_model.layers):
dest_layer.set_weights(source_layer.get_weights())
```
## Function that samples probabilities from model
```
def categorical(p):
return (p.cumsum(-1) >= np.random.uniform(size=p.shape[:-1])[..., None]).argmax(-1)
```
## Function that generates text
```
def genera_texto(first_char, num_chars):
texto = "" + first_char
next_char = first_char
next_one_hot = np.zeros(vocab_len)
next_one_hot[char_to_ix[next_char]] = 1.
next_one_hot = next_one_hot[None, None, :]
for i in range(num_chars):
probs = model2.predict_on_batch(next_one_hot)
next_ix = categorical(probs.ravel())
next_char = ix_to_char[next_ix]
next_one_hot = np.zeros(vocab_len)
next_one_hot[char_to_ix[next_char]] = 1.
next_one_hot = next_one_hot[None, None, :]
texto += next_char
return texto
```
## Network definition
```
K.clear_session()
nunits = 200
model1 = Sequential()
#model1.add(SimpleRNN(nunits, batch_input_shape=(batch_size, seq_len, vocab_len),
# return_sequences=True, stateful=True, unroll=True))
model1.add(LSTM(nunits, batch_input_shape=(batch_size, seq_len, vocab_len),
return_sequences=True, stateful=True, unroll=True))
model1.add(Dense(vocab_len, activation='softmax'))
model1.summary()
```
## Network that generates text
```
model2 = Sequential()
#model2.add(SimpleRNN(nunits, batch_input_shape=(1, 1, vocab_len),
# return_sequences=True, stateful=True, unroll=True))
model2.add(LSTM(nunits, batch_input_shape=(1, 1, vocab_len),
return_sequences=True, stateful=True, unroll=True))
model2.add(Dense(vocab_len, activation='softmax'))
model2.summary()
```
## Training
```
#learning_rate = 0.5 # Probar entre 0.05 y 5
#clip = 0.005 # Probar entre 0.0005 y 0.05
learning_rate = 0.5
clip = 0.002
#model1.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.SGD(lr=learning_rate, clipvalue=clip), metrics=['accuracy'])
model1.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.Adam(), metrics=['accuracy'])
num_epochs = 500 # Dejar en 100, la red tarda unos 10 minutos
model1_loss = np.zeros(num_epochs)
model1_acc = np.zeros(num_epochs)
model1_loss_test = np.zeros(num_epochs)
model1_acc_test = np.zeros(num_epochs)
for epoch in range(num_epochs):
model1.reset_states()
mean_tr_loss = []
mean_tr_acc = []
for i in range(0, xs_one_hot_train.shape[0], batch_size):
batch_data_x = xs_one_hot_train[i:i+batch_size, :, :]
batch_data_y = ys_one_hot_train[i:i+batch_size, :, :]
tr_loss, tr_acc = model1.train_on_batch(batch_data_x, batch_data_y)
mean_tr_loss.append(tr_loss)
mean_tr_acc.append(tr_acc)
model1_loss[epoch] = np.array(mean_tr_loss).mean()
model1_acc[epoch] = np.array(mean_tr_acc).mean()
model1.reset_states()
model1_loss_test[epoch], model1_acc_test[epoch] = evaluate_network(model1, xs_one_hot_test, ys_one_hot_test, batch_size)
print("\rTraining epoch: %d / %d" % (epoch+1, num_epochs), end="")
print(", loss = %f, acc = %f" % (model1_loss[epoch], model1_acc[epoch]), end="")
print(", test loss = %f, test acc = %f" % (model1_loss_test[epoch], model1_acc_test[epoch]), end="")
# Genero texto:
copia_pesos(model1, model2)
model2.reset_states()
print(" >>> %s" % genera_texto('e', 200)) #, end="")
```
## Plots
```
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(model1_loss, label="train")
plt.plot(model1_loss_test, label="test")
plt.grid(True)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(model1_acc, label="train")
plt.plot(model1_acc_test, label="test")
plt.grid(True)
plt.xlabel('epoch')
plt.ylabel('acc')
plt.title('accuracy')
plt.legend()
plt.show()
model2.reset_states()
print(genera_texto('A', 1000))
```
| true |
code
| 0.618838 | null | null | null | null |
|
# Table of Contents
<p><div class="lev1 toc-item"><a href="#Linear-Regression-problem" data-toc-modified-id="Linear-Regression-problem-1"><span class="toc-item-num">1 </span>Linear Regression problem</a></div><div class="lev1 toc-item"><a href="#Gradient-Descent" data-toc-modified-id="Gradient-Descent-2"><span class="toc-item-num">2 </span>Gradient Descent</a></div><div class="lev1 toc-item"><a href="#Gradient-Descent---Classification" data-toc-modified-id="Gradient-Descent---Classification-3"><span class="toc-item-num">3 </span>Gradient Descent - Classification</a></div><div class="lev1 toc-item"><a href="#Gradient-descent-with-numpy" data-toc-modified-id="Gradient-descent-with-numpy-4"><span class="toc-item-num">4 </span>Gradient descent with numpy</a></div>
```
%matplotlib inline
from fastai.learner import *
```
In this part of the lecture we explain Stochastic Gradient Descent (SGD) which is an **optimization** method commonly used in neural networks. We will illustrate the concepts with concrete examples.
# Linear Regression problem
The goal of linear regression is to fit a line to a set of points.
```
# Here we generate some fake data
def lin(a,b,x): return a*x+b
def gen_fake_data(n, a, b):
x = s = np.random.uniform(0,1,n)
y = lin(a,b,x) + 0.1 * np.random.normal(0,3,n)
return x, y
x, y = gen_fake_data(50, 3., 8.)
plt.scatter(x,y, s=8); plt.xlabel("x"); plt.ylabel("y");
```
You want to find **parameters** (weights) $a$ and $b$ such that you minimize the *error* between the points and the line $a\cdot x + b$. Note that here $a$ and $b$ are unknown. For a regression problem the most common *error function* or *loss function* is the **mean squared error**.
```
def mse(y_hat, y): return ((y_hat - y) ** 2).mean()
```
Suppose we believe $a = 10$ and $b = 5$ then we can compute `y_hat` which is our *prediction* and then compute our error.
```
y_hat = lin(10,5,x)
mse(y_hat, y)
def mse_loss(a, b, x, y): return mse(lin(a,b,x), y)
mse_loss(10, 5, x, y)
```
So far we have specified the *model* (linear regression) and the *evaluation criteria* (or *loss function*). Now we need to handle *optimization*; that is, how do we find the best values for $a$ and $b$? How do we find the best *fitting* linear regression.
# Gradient Descent
For a fixed dataset $x$ and $y$ `mse_loss(a,b)` is a function of $a$ and $b$. We would like to find the values of $a$ and $b$ that minimize that function.
**Gradient descent** is an algorithm that minimizes functions. Given a function defined by a set of parameters, gradient descent starts with an initial set of parameter values and iteratively moves toward a set of parameter values that minimize the function. This iterative minimization is achieved by taking steps in the negative direction of the function gradient.
Here is gradient descent implemented in [PyTorch](http://pytorch.org/).
```
# generate some more data
x, y = gen_fake_data(10000, 3., 8.)
x.shape, y.shape
x,y = V(x),V(y)
# Create random weights a and b, and wrap them in Variables.
a = V(np.random.randn(1), requires_grad=True)
b = V(np.random.randn(1), requires_grad=True)
a,b
learning_rate = 1e-3
for t in range(10000):
# Forward pass: compute predicted y using operations on Variables
loss = mse_loss(a,b,x,y)
if t % 1000 == 0: print(loss.data[0])
# Computes the gradient of loss with respect to all Variables with requires_grad=True.
# After this call a.grad and b.grad will be Variables holding the gradient
# of the loss with respect to a and b respectively
loss.backward()
# Update a and b using gradient descent; a.data and b.data are Tensors,
# a.grad and b.grad are Variables and a.grad.data and b.grad.data are Tensors
a.data -= learning_rate * a.grad.data
b.data -= learning_rate * b.grad.data
# Zero the gradients
a.grad.data.zero_()
b.grad.data.zero_()
```
Nearly all of deep learning is powered by one very important algorithm: **stochastic gradient descent (SGD)**. SGD can be seeing as an approximation of **gradient descent** (GD). In GD you have to run through *all* the samples in your training set to do a single itaration. In SGD you use *only one* or *a subset* of training samples to do the update for a parameter in a particular iteration. The subset use in every iteration is called a **batch** or **minibatch**.
# Gradient Descent - Classification
For a fixed dataset $x$ and $y$ `mse_loss(a,b)` is a function of $a$ and $b$. We would like to find the values of $a$ and $b$ that minimize that function.
**Gradient descent** is an algorithm that minimizes functions. Given a function defined by a set of parameters, gradient descent starts with an initial set of parameter values and iteratively moves toward a set of parameter values that minimize the function. This iterative minimization is achieved by taking steps in the negative direction of the function gradient.
Here is gradient descent implemented in [PyTorch](http://pytorch.org/).
```
def gen_fake_data2(n, a, b):
x = np.random.uniform(0,1,n)
y = lin(a,b,x) + 0.1 * np.random.normal(0,3,n)
return x, np.where(y>10, 1., 0.)
x,y = gen_fake_data2(10000, 3., 8.)
x,y = V(x),V(y)
def nll(y_hat, y):
y_hat = torch.clamp(y_hat, 1e-5, 1-1e-5)
return (y*y_hat.log() + (1.-y)*(1.-y_hat).log()).mean()
a = V(np.random.randn(1), requires_grad=True)
b = V(np.random.randn(1), requires_grad=True)
learning_rate = 1e-2
for t in range(3000):
p = (-lin(a,b,x)).exp()
y_hat = 1./(1.+p)
loss = nll(y_hat, y)
if t % 1000 == 0:
print(np.exp(loss.data[0]), np.mean(to_np(y)==(to_np(y_hat)>0.5)))
# print(y_hat)
loss.backward()
a.data -= learning_rate * a.grad.data
b.data -= learning_rate * b.grad.data
a.grad.data.zero_()
b.grad.data.zero_()
```
Nearly all of deep learning is powered by one very important algorithm: **stochastic gradient descent (SGD)**. SGD can be seeing as an approximation of **gradient descent** (GD). In GD you have to run through *all* the samples in your training set to do a single itaration. In SGD you use *only one* or *a subset* of training samples to do the update for a parameter in a particular iteration. The subset use in every iteration is called a **batch** or **minibatch**.
# Gradient descent with numpy
```
from matplotlib import rcParams, animation, rc
from ipywidgets import interact, interactive, fixed
from ipywidgets.widgets import *
rc('animation', html='html5')
rcParams['figure.figsize'] = 3, 3
x, y = gen_fake_data(50, 3., 8.)
a_guess,b_guess = -1., 1.
mse_loss(y, a_guess, b_guess, x)
lr=0.01
def upd():
global a_guess, b_guess
y_pred = lin(a_guess, b_guess, x)
dydb = 2 * (y_pred - y)
dyda = x*dydb
a_guess -= lr*dyda.mean()
b_guess -= lr*dydb.mean()
fig = plt.figure(dpi=100, figsize=(5, 4))
plt.scatter(x,y)
line, = plt.plot(x,lin(a_guess,b_guess,x))
plt.close()
def animate(i):
line.set_ydata(lin(a_guess,b_guess,x))
for i in range(30): upd()
return line,
ani = animation.FuncAnimation(fig, animate, np.arange(0, 20), interval=100)
ani
```
| true |
code
| 0.701432 | null | null | null | null |
|
# Convolutional Neural Network in Keras
Bulding a Convolutional Neural Network to classify Fashion-MNIST.
#### Set seed for reproducibility
```
import numpy as np
np.random.seed(42)
```
#### Load dependencies
```
import os
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Layer, Activation, Dense, Dropout, Conv2D, MaxPooling2D, Flatten, LeakyReLU, BatchNormalization
from tensorflow.keras.callbacks import TensorBoard, ModelCheckpoint, EarlyStopping
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.models import load_model
from keras_contrib.layers.advanced_activations.sinerelu import SineReLU
from matplotlib import pyplot as plt
%matplotlib inline
```
#### Load data
```
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
```
#### Preprocess data
Flatten and normalise input data.
```
X_train = X_train.reshape(-1, 28, 28, 1)
X_test = X_test.reshape(-1, 28, 28, 1)
X_train = X_train.astype("float32")/255.
X_test = X_test.astype("float32")/255.
# One-hot encoded categories
n_classes = 10
y_train = to_categorical(y_train, n_classes)
y_test = to_categorical(y_test, n_classes)
```
#### Design Neural Network architecture
```
model = Sequential()
model.add(Conv2D(32, 7, padding = 'same', input_shape = (28, 28, 1)))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(32, 7, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.20))
model.add(Conv2D(64, 3, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(64, 3, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.30))
model.add(Conv2D(128, 2, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(128, 2, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.40))
model.add(Flatten())
model.add(Dense(512))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Dropout(0.50))
model.add(Dense(10, activation = "softmax"))
model.summary()
```
#### Callbacks
```
modelCheckpoint = ModelCheckpoint(monitor='val_accuracy', filepath='model_output/weights-cnn-fashion-mnist.hdf5',
save_best_only=True, mode='max')
earlyStopping = EarlyStopping(monitor='val_accuracy', mode='max', patience=5)
if not os.path.exists('model_output'):
os.makedirs('model_output')
tensorboard = TensorBoard("logs/convnet-fashion-mnist")
```
#### Configure model
```
model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
```
#### Train!
```
history = model.fit(X_train, y_train, batch_size = 128, epochs = 20, verbose = 1,
validation_split = 0.1, callbacks=[modelCheckpoint, earlyStopping, tensorboard])
```
#### Test Predictions
```
saved_model = load_model('model_output/weights-cnn-fashion-mnist.hdf5')
predictions = saved_model.predict_classes(X_test, verbose = 2)
print(predictions)
# np.std(history.history['loss'])
```
#### Test Final Accuracy
```
final_loss, final_acc = saved_model.evaluate(X_test, y_test, verbose = 2)
print("Final loss: {0:.4f}, final accuracy: {1:.4f}".format(final_loss, final_acc))
image = X_test[0].reshape(1, 28, 28, 1)
predictions = model.predict_classes(image, verbose = 2)
print(predictions)
plt.imshow(X_test[0].reshape((28, 28)), cmap='gray')
# 0 T-shirt/top
# 1 Trouser
# 2 Pullover
# 3 Dress
# 4 Coat
# 5 Sandal
# 6 Shirt
# 7 Sneaker
# 8 Bag
# 9 Ankle boot
```
| true |
code
| 0.713631 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Automated Machine Learning
**BikeShare Demand Forecasting**
## Contents
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Compute](#Compute)
1. [Data](#Data)
1. [Train](#Train)
1. [Featurization](#Featurization)
1. [Evaluate](#Evaluate)
## Introduction
This notebook demonstrates demand forecasting for a bike-sharing service using AutoML.
AutoML highlights here include built-in holiday featurization, accessing engineered feature names, and working with the `forecast` function. Please also look at the additional forecasting notebooks, which document lagging, rolling windows, forecast quantiles, other ways to use the forecast function, and forecaster deployment.
Make sure you have executed the [configuration notebook](../../../configuration.ipynb) before running this notebook.
Notebook synopsis:
1. Creating an Experiment in an existing Workspace
2. Configuration and local run of AutoML for a time-series model with lag and holiday features
3. Viewing the engineered names for featurized data and featurization summary for all raw features
4. Evaluating the fitted model using a rolling test
## Setup
```
import azureml.core
import pandas as pd
import numpy as np
import logging
from azureml.core import Workspace, Experiment, Dataset
from azureml.train.automl import AutoMLConfig
from datetime import datetime
```
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
```
print("This notebook was created using version 1.17.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
```
As part of the setup you have already created a <b>Workspace</b>. To run AutoML, you also need to create an <b>Experiment</b>. An Experiment corresponds to a prediction problem you are trying to solve, while a Run corresponds to a specific approach to the problem.
```
ws = Workspace.from_config()
# choose a name for the run history container in the workspace
experiment_name = 'automl-bikeshareforecasting'
experiment = Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['SKU'] = ws.sku
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Run History Name'] = experiment_name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Compute
You will need to create a [compute target](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
#### Creation of AmlCompute takes approximately 5 minutes.
If the AmlCompute with that name is already in your workspace this code will skip the creation process.
As with other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. Please read this article on the default limits and how to request more quota.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your cluster.
amlcompute_cluster_name = "bike-cluster"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=4)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
## Data
The [Machine Learning service workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-workspace) is paired with the storage account, which contains the default data store. We will use it to upload the bike share data and create [tabular dataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) for training. A tabular dataset defines a series of lazily-evaluated, immutable operations to load data from the data source into tabular representation.
```
datastore = ws.get_default_datastore()
datastore.upload_files(files = ['./bike-no.csv'], target_path = 'dataset/', overwrite = True,show_progress = True)
```
Let's set up what we know about the dataset.
**Target column** is what we want to forecast.
**Time column** is the time axis along which to predict.
```
target_column_name = 'cnt'
time_column_name = 'date'
dataset = Dataset.Tabular.from_delimited_files(path = [(datastore, 'dataset/bike-no.csv')]).with_timestamp_columns(fine_grain_timestamp=time_column_name)
dataset.take(5).to_pandas_dataframe().reset_index(drop=True)
```
### Split the data
The first split we make is into train and test sets. Note we are splitting on time. Data before 9/1 will be used for training, and data after and including 9/1 will be used for testing.
```
# select data that occurs before a specified date
train = dataset.time_before(datetime(2012, 8, 31), include_boundary=True)
train.to_pandas_dataframe().tail(5).reset_index(drop=True)
test = dataset.time_after(datetime(2012, 9, 1), include_boundary=True)
test.to_pandas_dataframe().head(5).reset_index(drop=True)
```
## Forecasting Parameters
To define forecasting parameters for your experiment training, you can leverage the ForecastingParameters class. The table below details the forecasting parameter we will be passing into our experiment.
|Property|Description|
|-|-|
|**time_column_name**|The name of your time column.|
|**forecast_horizon**|The forecast horizon is how many periods forward you would like to forecast. This integer horizon is in units of the timeseries frequency (e.g. daily, weekly).|
|**country_or_region_for_holidays**|The country/region used to generate holiday features. These should be ISO 3166 two-letter country/region codes (i.e. 'US', 'GB').|
|**target_lags**|The target_lags specifies how far back we will construct the lags of the target variable.|
|**drop_column_names**|Name(s) of columns to drop prior to modeling|
## Train
Instantiate a AutoMLConfig object. This defines the settings and data used to run the experiment.
|Property|Description|
|-|-|
|**task**|forecasting|
|**primary_metric**|This is the metric that you want to optimize.<br> Forecasting supports the following primary metrics <br><i>spearman_correlation</i><br><i>normalized_root_mean_squared_error</i><br><i>r2_score</i><br><i>normalized_mean_absolute_error</i>
|**blocked_models**|Models in blocked_models won't be used by AutoML. All supported models can be found at [here](https://docs.microsoft.com/en-us/python/api/azureml-train-automl-client/azureml.train.automl.constants.supportedmodels.forecasting?view=azure-ml-py).|
|**experiment_timeout_hours**|Experimentation timeout in hours.|
|**training_data**|Input dataset, containing both features and label column.|
|**label_column_name**|The name of the label column.|
|**compute_target**|The remote compute for training.|
|**n_cross_validations**|Number of cross validation splits.|
|**enable_early_stopping**|If early stopping is on, training will stop when the primary metric is no longer improving.|
|**forecasting_parameters**|A class that holds all the forecasting related parameters.|
This notebook uses the blocked_models parameter to exclude some models that take a longer time to train on this dataset. You can choose to remove models from the blocked_models list but you may need to increase the experiment_timeout_hours parameter value to get results.
### Setting forecaster maximum horizon
The forecast horizon is the number of periods into the future that the model should predict. Here, we set the horizon to 14 periods (i.e. 14 days). Notice that this is much shorter than the number of days in the test set; we will need to use a rolling test to evaluate the performance on the whole test set. For more discussion of forecast horizons and guiding principles for setting them, please see the [energy demand notebook](https://github.com/Azure/MachineLearningNotebooks/tree/master/how-to-use-azureml/automated-machine-learning/forecasting-energy-demand).
```
forecast_horizon = 14
```
### Config AutoML
```
from azureml.automl.core.forecasting_parameters import ForecastingParameters
forecasting_parameters = ForecastingParameters(
time_column_name=time_column_name,
forecast_horizon=forecast_horizon,
country_or_region_for_holidays='US', # set country_or_region will trigger holiday featurizer
target_lags='auto', # use heuristic based lag setting
drop_column_names=['casual', 'registered'] # these columns are a breakdown of the total and therefore a leak
)
automl_config = AutoMLConfig(task='forecasting',
primary_metric='normalized_root_mean_squared_error',
blocked_models = ['ExtremeRandomTrees'],
experiment_timeout_hours=0.3,
training_data=train,
label_column_name=target_column_name,
compute_target=compute_target,
enable_early_stopping=True,
n_cross_validations=3,
max_concurrent_iterations=4,
max_cores_per_iteration=-1,
verbosity=logging.INFO,
forecasting_parameters=forecasting_parameters)
```
We will now run the experiment, you can go to Azure ML portal to view the run details.
```
remote_run = experiment.submit(automl_config, show_output=False)
remote_run
remote_run.wait_for_completion()
```
### Retrieve the Best Model
Below we select the best model from all the training iterations using get_output method.
```
best_run, fitted_model = remote_run.get_output()
fitted_model.steps
```
## Featurization
You can access the engineered feature names generated in time-series featurization. Note that a number of named holiday periods are represented. We recommend that you have at least one year of data when using this feature to ensure that all yearly holidays are captured in the training featurization.
```
fitted_model.named_steps['timeseriestransformer'].get_engineered_feature_names()
```
### View the featurization summary
You can also see what featurization steps were performed on different raw features in the user data. For each raw feature in the user data, the following information is displayed:
- Raw feature name
- Number of engineered features formed out of this raw feature
- Type detected
- If feature was dropped
- List of feature transformations for the raw feature
```
# Get the featurization summary as a list of JSON
featurization_summary = fitted_model.named_steps['timeseriestransformer'].get_featurization_summary()
# View the featurization summary as a pandas dataframe
pd.DataFrame.from_records(featurization_summary)
```
## Evaluate
We now use the best fitted model from the AutoML Run to make forecasts for the test set. We will do batch scoring on the test dataset which should have the same schema as training dataset.
The scoring will run on a remote compute. In this example, it will reuse the training compute.
```
test_experiment = Experiment(ws, experiment_name + "_test")
```
### Retrieving forecasts from the model
To run the forecast on the remote compute we will use a helper script: forecasting_script. This script contains the utility methods which will be used by the remote estimator. We copy the script to the project folder to upload it to remote compute.
```
import os
import shutil
script_folder = os.path.join(os.getcwd(), 'forecast')
os.makedirs(script_folder, exist_ok=True)
shutil.copy('forecasting_script.py', script_folder)
```
For brevity, we have created a function called run_forecast that submits the test data to the best model determined during the training run and retrieves forecasts. The test set is longer than the forecast horizon specified at train time, so the forecasting script uses a so-called rolling evaluation to generate predictions over the whole test set. A rolling evaluation iterates the forecaster over the test set, using the actuals in the test set to make lag features as needed.
```
from run_forecast import run_rolling_forecast
remote_run = run_rolling_forecast(test_experiment, compute_target, best_run, test, target_column_name)
remote_run
remote_run.wait_for_completion(show_output=False)
```
### Download the prediction result for metrics calcuation
The test data with predictions are saved in artifact outputs/predictions.csv. You can download it and calculation some error metrics for the forecasts and vizualize the predictions vs. the actuals.
```
remote_run.download_file('outputs/predictions.csv', 'predictions.csv')
df_all = pd.read_csv('predictions.csv')
from azureml.automl.core.shared import constants
from azureml.automl.runtime.shared.score import scoring
from sklearn.metrics import mean_absolute_error, mean_squared_error
from matplotlib import pyplot as plt
# use automl metrics module
scores = scoring.score_regression(
y_test=df_all[target_column_name],
y_pred=df_all['predicted'],
metrics=list(constants.Metric.SCALAR_REGRESSION_SET))
print("[Test data scores]\n")
for key, value in scores.items():
print('{}: {:.3f}'.format(key, value))
# Plot outputs
%matplotlib inline
test_pred = plt.scatter(df_all[target_column_name], df_all['predicted'], color='b')
test_test = plt.scatter(df_all[target_column_name], df_all[target_column_name], color='g')
plt.legend((test_pred, test_test), ('prediction', 'truth'), loc='upper left', fontsize=8)
plt.show()
```
Since we did a rolling evaluation on the test set, we can analyze the predictions by their forecast horizon relative to the rolling origin. The model was initially trained at a forecast horizon of 14, so each prediction from the model is associated with a horizon value from 1 to 14. The horizon values are in a column named, "horizon_origin," in the prediction set. For example, we can calculate some of the error metrics grouped by the horizon:
```
from metrics_helper import MAPE, APE
df_all.groupby('horizon_origin').apply(
lambda df: pd.Series({'MAPE': MAPE(df[target_column_name], df['predicted']),
'RMSE': np.sqrt(mean_squared_error(df[target_column_name], df['predicted'])),
'MAE': mean_absolute_error(df[target_column_name], df['predicted'])}))
```
To drill down more, we can look at the distributions of APE (absolute percentage error) by horizon. From the chart, it is clear that the overall MAPE is being skewed by one particular point where the actual value is of small absolute value.
```
df_all_APE = df_all.assign(APE=APE(df_all[target_column_name], df_all['predicted']))
APEs = [df_all_APE[df_all['horizon_origin'] == h].APE.values for h in range(1, forecast_horizon + 1)]
%matplotlib inline
plt.boxplot(APEs)
plt.yscale('log')
plt.xlabel('horizon')
plt.ylabel('APE (%)')
plt.title('Absolute Percentage Errors by Forecast Horizon')
plt.show()
```
| true |
code
| 0.617282 | null | null | null | null |
|
# Getting Started with BentoML
[BentoML](http://bentoml.ai) is an open-source framework for machine learning **model serving**, aiming to **bridge the gap between Data Science and DevOps**.
Data Scientists can easily package their models trained with any ML framework using BentoMl and reproduce the model for serving in production. BentoML helps with managing packaged models in the BentoML format, and allows DevOps to deploy them as online API serving endpoints or offline batch inference jobs, on any cloud platform.
This getting started guide demonstrates how to use BentoML to serve a sklearn modeld via a REST API server, and then containerize the model server for production deployment.

BentoML requires python 3.6 or above, install dependencies via `pip`:
```
# Install PyPI packages required in this guide, including BentoML
!pip install -q bentoml
!pip install -q 'scikit-learn>=0.23.2' 'pandas>=1.1.1'
```
Before started, let's discuss how BentoML's project structure would look like. For most use-cases, users can follow this minimal scaffold
for deploying with BentoML to avoid any potential errors (example project structure can be found under [guides/quick-start](https://github.com/bentoml/BentoML/tree/master/guides/quick-start)):
bento_deploy/
├── bento_packer.py # responsible for packing BentoService
├── bento_service.py # BentoService definition
├── model.py # DL Model definitions
├── train.py # training scripts
└── requirements.txt
Let's prepare a trained model for serving with BentoML. Train a classifier model on the [Iris data set](https://en.wikipedia.org/wiki/Iris_flower_data_set):
```
from sklearn import svm
from sklearn import datasets
# Load training data
iris = datasets.load_iris()
X, y = iris.data, iris.target
# Model Training
clf = svm.SVC(gamma='scale')
clf.fit(X, y)
```
## Create a Prediction Service with BentoML
Model serving with BentoML comes after a model is trained. The first step is creating a
prediction service class, which defines the models required and the inference APIs which
contains the serving logic. Here is a minimal prediction service created for serving
the iris classifier model trained above:
```
%%writefile bento_service.py
import pandas as pd
from bentoml import env, artifacts, api, BentoService
from bentoml.adapters import DataframeInput
from bentoml.frameworks.sklearn import SklearnModelArtifact
@env(infer_pip_packages=True)
@artifacts([SklearnModelArtifact('model')])
class IrisClassifier(BentoService):
"""
A minimum prediction service exposing a Scikit-learn model
"""
@api(input=DataframeInput(), batch=True)
def predict(self, df: pd.DataFrame):
"""
An inference API named `predict` with Dataframe input adapter, which codifies
how HTTP requests or CSV files are converted to a pandas Dataframe object as the
inference API function input
"""
return self.artifacts.model.predict(df)
```
This code defines a prediction service that packages a scikit-learn model and provides
an inference API that expects a `pandas.Dataframe` object as its input. BentoML also supports other API input
data types including `JsonInput`, `ImageInput`, `FileInput` and
[more](https://docs.bentoml.org/en/latest/api/adapters.html).
In BentoML, **all inference APIs are suppose to accept a list of inputs and return a
list of results**. In the case of `DataframeInput`, each row of the dataframe is mapping
to one prediction request received from the client. BentoML will convert HTTP JSON
requests into :code:`pandas.DataFrame` object before passing it to the user-defined
inference API function.
This design allows BentoML to group API requests into small batches while serving online
traffic. Comparing to a regular flask or FastAPI based model server, this can increases
the overall throughput of the API server by 10-100x depending on the workload.
The following code packages the trained model with the prediction service class
`IrisClassifier` defined above, and then saves the IrisClassifier instance to disk
in the BentoML format for distribution and deployment:
```
# import the IrisClassifier class defined above
from bento_service import IrisClassifier
# Create a iris classifier service instance
iris_classifier_service = IrisClassifier()
# Pack the newly trained model artifact
iris_classifier_service.pack('model', clf)
# Prepare input data for testing the prediction service
import pandas as pd
test_input_df = pd.DataFrame(X).sample(n=5)
test_input_df.to_csv("./test_input.csv", index=False)
test_input_df
# Test the service's inference API python interface
iris_classifier_service.predict(test_input_df)
# Start a dev model server to test out everything
iris_classifier_service.start_dev_server()
import requests
response = requests.post(
"http://127.0.0.1:5000/predict",
json=test_input_df.values.tolist()
)
print(response.text)
# Stop the dev model server
iris_classifier_service.stop_dev_server()
# Save the prediction service to disk for deployment
saved_path = iris_classifier_service.save()
```
BentoML stores all packaged model files under the
`~/bentoml/{service_name}/{service_version}` directory by default.
The BentoML file format contains all the code, files, and configs required to
deploy the model for serving.
## REST API Model Serving
To start a REST API model server with the `IrisClassifier` saved above, use
the `bentoml serve` command:
```
!bentoml serve IrisClassifier:latest
```
If you are running this notebook from Google Colab, you can start the dev server with `--run-with-ngrok` option, to gain acccess to the API endpoint via a public endpoint managed by [ngrok](https://ngrok.com/):
```
!bentoml serve IrisClassifier:latest --run-with-ngrok
```
The `IrisClassifier` model is now served at `localhost:5000`. Use `curl` command to send
a prediction request:
```bash
curl -i \
--header "Content-Type: application/json" \
--request POST \
--data '[[5.1, 3.5, 1.4, 0.2]]' \
localhost:5000/predict
```
Or with `python` and [request library](https://requests.readthedocs.io/):
```python
import requests
response = requests.post("http://127.0.0.1:5000/predict", json=[[5.1, 3.5, 1.4, 0.2]])
print(response.text)
```
Note that BentoML API server automatically converts the Dataframe JSON format into a
`pandas.DataFrame` object before sending it to the user-defined inference API function.
The BentoML API server also provides a simple web UI dashboard.
Go to http://localhost:5000 in the browser and use the Web UI to send
prediction request:

## Containerize model server with Docker
One common way of distributing this model API server for production deployment, is via
Docker containers. And BentoML provides a convenient way to do that.
Note that `docker` is __not available in Google Colab__. You will need to download and run this notebook locally to try out this containerization with docker feature.
If you already have docker configured, simply run the follow command to product a
docker container serving the `IrisClassifier` prediction service created above:
```
!bentoml containerize IrisClassifier:latest -t iris-classifier:v1
```
Start a container with the docker image built in the previous step:
```
!docker run -p 5000:5000 iris-classifier:v1 --workers=2
```
This made it possible to deploy BentoML bundled ML models with platforms such as
[Kubeflow](https://www.kubeflow.org/docs/components/serving/bentoml/),
[Knative](https://knative.dev/community/samples/serving/machinelearning-python-bentoml/),
[Kubernetes](https://docs.bentoml.org/en/latest/deployment/kubernetes.html), which
provides advanced model deployment features such as auto-scaling, A/B testing,
scale-to-zero, canary rollout and multi-armed bandit.
## Load saved BentoService
`bentoml.load` is the API for loading a BentoML packaged model in python:
```
import bentoml
import pandas as pd
bento_svc = bentoml.load(saved_path)
# Test loaded bentoml service:
bento_svc.predict(test_input_df)
```
The BentoML format is pip-installable and can be directly distributed as a
PyPI package for using in python applications:
```
!pip install -q {saved_path}
# The BentoService class name will become packaged name
import IrisClassifier
installed_svc = IrisClassifier.load()
installed_svc.predict(test_input_df)
```
This also allow users to upload their BentoService to pypi.org as public python package
or to their organization's private PyPi index to share with other developers.
`cd {saved_path} & python setup.py sdist upload`
*You will have to configure ".pypirc" file before uploading to pypi index.
You can find more information about distributing python package at:
https://docs.python.org/3.7/distributing/index.html#distributing-index*
# Launch inference job from CLI
BentoML cli supports loading and running a packaged model from CLI. With the `DataframeInput` adapter, the CLI command supports reading input Dataframe data from CLI argument or local `csv` or `json` files:
```
!bentoml run IrisClassifier:latest predict --input '{test_input_df.to_json()}' --quiet
!bentoml run IrisClassifier:latest predict \
--input-file "./test_input.csv" --format "csv" --quiet
# run inference with the docker image built above
!docker run -v $(PWD):/tmp iris-classifier:v1 \
bentoml run /bento predict --input-file "/tmp/test_input.csv" --format "csv" --quiet
```
# Deployment Options
Check out the [BentoML deployment guide](https://docs.bentoml.org/en/latest/deployment/index.html)
to better understand which deployment option is best suited for your use case.
* One-click deployment with BentoML:
- [AWS Lambda](https://docs.bentoml.org/en/latest/deployment/aws_lambda.html)
- [AWS SageMaker](https://docs.bentoml.org/en/latest/deployment/aws_sagemaker.html)
- [AWS EC2](https://docs.bentoml.org/en/latest/deployment/aws_ec2.html)
- [Azure Functions](https://docs.bentoml.org/en/latest/deployment/azure_functions.html)
* Deploy with open-source platforms:
- [Docker](https://docs.bentoml.org/en/latest/deployment/docker.html)
- [Kubernetes](https://docs.bentoml.org/en/latest/deployment/kubernetes.html)
- [Knative](https://docs.bentoml.org/en/latest/deployment/knative.html)
- [Kubeflow](https://docs.bentoml.org/en/latest/deployment/kubeflow.html)
- [KFServing](https://docs.bentoml.org/en/latest/deployment/kfserving.html)
- [Clipper](https://docs.bentoml.org/en/latest/deployment/clipper.html)
* Manual cloud deployment guides:
- [AWS ECS](https://docs.bentoml.org/en/latest/deployment/aws_ecs.html)
- [Google Cloud Run](https://docs.bentoml.org/en/latest/deployment/google_cloud_run.html)
- [Azure container instance](https://docs.bentoml.org/en/latest/deployment/azure_container_instance.html)
- [Heroku](https://docs.bentoml.org/en/latest/deployment/heroku.html)
# Summary
This is what it looks like when using BentoML to serve and deploy a model in the cloud. BentoML also supports [many other Machine Learning frameworks](https://docs.bentoml.org/en/latest/examples.html) besides Scikit-learn. The [BentoML core concepts](https://docs.bentoml.org/en/latest/concepts.html) doc is recommended for anyone looking to get a deeper understanding of BentoML.
Join the [BentoML Slack](https://join.slack.com/t/bentoml/shared_invite/enQtNjcyMTY3MjE4NTgzLTU3ZDc1MWM5MzQxMWQxMzJiNTc1MTJmMzYzMTYwMjQ0OGEwNDFmZDkzYWQxNzgxYWNhNjAxZjk4MzI4OGY1Yjg) to follow the latest development updates and roadmap discussions.
| true |
code
| 0.460592 | null | null | null | null |
|
# Time Complexity Examples
```
def logarithmic_problem(N):
i = N
while i > 1:
# do something
i = i // 2 # move on
%time logarithmic_problem(10000)
def linear_problem(N):
i = N
while i > 1:
# do something
i = i - 1 # move on
%time linear_problem(10000)
def quadratic_problem(N):
i = N
while i > 1:
j = N
while j > 1:
# do something
j = j - 1 # move on
i = i - 1
%time quadratic_problem(10000)
```
# Problem
Given an array(A) of numbers sorted in increasing order, implement a function that returns the index of a target(k) if found in A, and -1 otherwise.
### Brute-force solution: Linear Search
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def linear_search(A, k):
for idx, element in enumerate(A):
if element == k:
return idx
return -1
linear_search(A, 15)
linear_search(A, 100)
```
### Efficient solution: Binary Search
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def binary_search(A, k):
left, right = 0, len(A)-1
while left<=right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
return mid
return -1
binary_search(A, 15)
binary_search(A, 17)
```
### Binary Search common bugs:
#### BUG-1: one-off bug
not handling arrays of size=1
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def binary_search_bug1(A, k):
left, right = 0, len(A)-1
#HERE: < instead of <=
while left<right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
return mid
return -1
binary_search_bug1(A, 35)
binary_search_bug1(A, 30)
binary_search_bug1(A, 15)
binary_search_bug1([15], 15)
```
#### BUG-2: integer overflow
not handling the case where summing two integers can return an integer bigger than what the memory can take
```
# because python3 only imposes limits
# on float, we are going to illustrate
# this issue using floats instead of ints
import sys
right = sys.float_info.max
left = sys.float_info.max - 1000
mid = (right + left) // 2
mid
mid = (right - left)//2 + left
mid
```
## Problem variant1:
#### Search a sorted array for first occurrence of target(k)
Given an array(A) of numbers sorted in increasing order, implement a function that returns the index of the first occurence of a target(k) if found in A, and -1 otherwise.
```
A = [5, 8, 8, 8, 8, 19, 30, 35, 40, 51]
def first_occurence_search(A, k):
left, right, res = 0, len(A)-1, -1
while left<=right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
# update res
res = mid
# keep looking on the left
right = mid-1
return res
binary_search(A, 8)
first_occurence_search(A, 8)
```
## Problem variant2:
#### Search a sorted array for entry equal to its index
Given a sorted array(A) of distinct integers, implement a function that returns the index i if A[i] = i, and -1 otherwise.
```
A = [-3, 0, 2, 5, 7, 9, 18, 35, 40, 51]
def search_entry_equal_to_its_index(A):
left, right = 0, len(A)-1
while left<=right:
mid = (right - left)//2 + left
difference = A[mid] - mid
if difference < 0:
#look on the right
left = mid+1
elif difference > 0:
#look on the left
right = mid-1
else:
return mid
return -1
search_entry_equal_to_its_index(A)
```
| true |
code
| 0.485783 | null | null | null | null |
|
# Differentially Private Covariance
SmartNoise offers three different functionalities within its `covariance` function:
1. Covariance between two vectors
2. Covariance matrix of a matrix
3. Cross-covariance matrix of a pair of matrices, where element $(i,j)$ of the returned matrix is the covariance of column $i$ of the left matrix and column $j$ of the right matrix.
```
# load libraries
import os
import opendp.smartnoise.core as sn
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# establish data information
data_path = os.path.join('.', 'data', 'PUMS_california_demographics_1000', 'data.csv')
var_names = ["age", "sex", "educ", "race", "income", "married"]
data = np.genfromtxt(data_path, delimiter=',', names=True)
```
### Functionality
Below we show the relationship between the three methods by calculating the same covariance in each. We use a much larger $\epsilon$ than would ever be used in practice to show that the methods are consistent with one another.
```
with sn.Analysis() as analysis:
wn_data = sn.Dataset(path = data_path, column_names = var_names)
# get scalar covariance
age_income_cov_scalar = sn.dp_covariance(left = sn.to_float(wn_data['age']),
right = sn.to_float(wn_data['income']),
privacy_usage = {'epsilon': 5000},
left_lower = 0.,
left_upper = 100.,
left_rows = 1000,
right_lower = 0.,
right_upper = 500_000.,
right_rows = 1000)
# get full covariance matrix
age_income_cov_matrix = sn.dp_covariance(data = sn.to_float(wn_data['age', 'income']),
privacy_usage = {'epsilon': 5000},
data_lower = [0., 0.],
data_upper = [100., 500_000],
data_rows = 1000)
# get cross-covariance matrix
cross_covar = sn.dp_covariance(left = sn.to_float(wn_data['age', 'income']),
right = sn.to_float(wn_data['age', 'income']),
privacy_usage = {'epsilon': 5000},
left_lower = [0., 0.],
left_upper = [100., 500_000.],
left_rows = 1_000,
right_lower = [0., 0.],
right_upper = [100., 500_000.],
right_rows = 1000)
# analysis.release()
print('scalar covariance:\n{0}\n'.format(age_income_cov_scalar.value))
print('covariance matrix:\n{0}\n'.format(age_income_cov_matrix.value))
print('cross-covariance matrix:\n{0}'.format(cross_covar.value))
```
### DP Covariance in Practice
We now move to an example with a much smaller $\epsilon$.
```
with sn.Analysis() as analysis:
wn_data = sn.Dataset(path = data_path, column_names = var_names)
# get full covariance matrix
cov = sn.dp_covariance(data = sn.to_float(wn_data['age', 'sex', 'educ', 'income', 'married']),
privacy_usage = {'epsilon': 1.},
data_lower = [0., 0., 1., 0., 0.],
data_upper = [100., 1., 16., 500_000., 1.],
data_rows = 1000)
analysis.release()
# store DP covariance and correlation matrix
dp_cov = cov.value
dp_corr = dp_cov / np.outer(np.sqrt(np.diag(dp_cov)), np.sqrt(np.diag(dp_cov)))
# get non-DP covariance/correlation matrices
age = list(data[:]['age'])
sex = list(data[:]['sex'])
educ = list(data[:]['educ'])
income = list(data[:]['income'])
married = list(data[:]['married'])
non_dp_cov = np.cov([age, sex, educ, income, married])
non_dp_corr = non_dp_cov / np.outer(np.sqrt(np.diag(non_dp_cov)), np.sqrt(np.diag(non_dp_cov)))
print('Non-DP Correlation Matrix:\n{0}\n\n'.format(pd.DataFrame(non_dp_corr)))
print('DP Correlation Matrix:\n{0}'.format(pd.DataFrame(dp_corr)))
fig, (ax_1, ax_2) = plt.subplots(1, 2, figsize = (9, 11))
# generate a mask for the upper triangular matrix
mask = np.triu(np.ones_like(non_dp_corr, dtype = np.bool))
# generate color palette
cmap = sns.diverging_palette(220, 10, as_cmap = True)
# get correlation plots
ax_1.title.set_text('Non-DP Correlation Matrix')
sns.heatmap(non_dp_corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, ax = ax_1)
ax_1.set_xticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_1.set_yticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_2.title.set_text('DP Correlation Matrix')
sns.heatmap(dp_corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, ax = ax_2)
ax_2.set_xticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_2.set_yticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
```
Notice that the differentially private correlation matrix contains values outside of the feasible range for correlations, $[-1, 1]$. This is not uncommon, especially for analyses with small $\epsilon$, and is not necessarily indicative of a problem. In this scenario, we will not use these correlations for anything other than visualization, so we will leave our result as is.
Sometimes, you may get a result that does cause problems for downstream analysis. For example, say your differentially private covariance matrix is not positive semi-definite. There are a number of ways to deal with problems of this type.
1. Relax your original plans: For example, if you want to invert your DP covariance matrix and are unable to do so, you could instead take the pseudoinverse.
2. Manual Post-Processing: Choose some way to change the output such that it is consistent with what you need for later analyses. This changed output is still differentially private (we will use this idea again in the next section). For example, map all negative variances to small positive value.
3. More releases: You could perform the same release again (perhaps with a larger $\epsilon$) and combine your results in some way until you have a release that works for your purposes. Note that additional $\epsilon$ from will be consumed everytime this happens.
### Post-Processing of DP Covariance Matrix: Regression Coefficient
Differentially private outputs are "immune" to post-processing, meaning functions of differentially private releases are also differentially private (provided that the functions are independent of the underlying data in the dataset). This idea provides us with a relatively easy way to generate complex differentially private releases from simpler ones.
Say we wanted to run a linear regression of the form $income = \alpha + \beta \cdot educ$ and want to find an differentially private estimate of the slope, $\hat{\beta}_{DP}$. We know that
$$ \beta = \frac{cov(income, educ)}{var(educ)}, $$
and so
$$ \hat{\beta}_{DP} = \frac{\hat{cov}(income, educ)_{DP}}{ \hat{var}(educ)_{DP} }. $$
We already have differentially private estimates of the necessary covariance and variance, so we can plug them in to find $\hat{\beta}_{DP}$.
```
'''income = alpha + beta * educ'''
# find DP estimate of beta
beta_hat_dp = dp_cov[2,3] / dp_cov[2,2]
beta_hat = non_dp_cov[2,3] / non_dp_cov[2,2]
print('income = alpha + beta * educ')
print('DP coefficient: {0}'.format(beta_hat_dp))
print('Non-DP Coefficient: {0}'.format(beta_hat))
```
This result is implausible, as it would suggest that an extra year of education is associated with, on average, a decrease in annual income of nearly $11,000. It's not uncommon for this to be the case for DP releases constructed as post-processing from other releases, especially when they involve taking ratios.
If you find yourself in such as situation, it is often worth it to spend some extra privacy budget to estimate your quantity of interest using an algorithm optimized for that specific use case.
| true |
code
| 0.627181 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mashyko/object_detection/blob/master/Model_Quickload.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Tutorials Installation:
https://caffe2.ai/docs/tutorials.html
First download the tutorials source.
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/My Drive/
!git clone --recursive https://github.com/caffe2/tutorials caffe2_tutorials
# Model Quickload
This notebook will show you how to quickly load a pretrained SqueezeNet model and test it on images of your choice in four main steps.
1. Load the model
2. Format the input
3. Run the test
4. Process the results
The model used in this tutorial has been pretrained on the full 1000 class ImageNet dataset, and is downloaded from Caffe2's [Model Zoo](https://github.com/caffe2/caffe2/wiki/Model-Zoo). For an all around more in-depth tutorial on using pretrained models check out the [Loading Pretrained Models](https://github.com/caffe2/caffe2/blob/master/caffe2/python/tutorials/Loading_Pretrained_Models.ipynb) tutorial.
Before this script will work, you need to download the model and install it. You can do this by running:
```
sudo python -m caffe2.python.models.download -i squeezenet
```
Or make a folder named `squeezenet`, download each file listed below to it, and place it in the `/caffe2/python/models/` directory:
* [predict_net.pb](https://download.caffe2.ai/models/squeezenet/predict_net.pb)
* [init_net.pb](https://download.caffe2.ai/models/squeezenet/init_net.pb)
Notice, the helper function *parseResults* will translate the integer class label of the top result to an English label by searching through the [inference codes file](inference_codes.txt). If you want to really test the model's capabilities, pick a code from the file, find an image representing that code, and test the model with it!
```
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/My Drive/caffe2_tutorials
!pip3 install torch torchvision
!python -m caffe2.python.models.download -i squeezenet
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import numpy as np
import operator
# load up the caffe2 workspace
from caffe2.python import workspace
# choose your model here (use the downloader first)
from caffe2.python.models import squeezenet as mynet
# helper image processing functions
import helpers
##### Load the Model
# Load the pre-trained model
init_net = mynet.init_net
predict_net = mynet.predict_net
# Initialize the predictor with SqueezeNet's init_net and predict_net
p = workspace.Predictor(init_net, predict_net)
##### Select and format the input image
# use whatever image you want (urls work too)
# img = "https://upload.wikimedia.org/wikipedia/commons/a/ac/Pretzel.jpg"
# img = "images/cat.jpg"
# img = "images/cowboy-hat.jpg"
# img = "images/cell-tower.jpg"
# img = "images/Ducreux.jpg"
# img = "images/pretzel.jpg"
# img = "images/orangutan.jpg"
# img = "images/aircraft-carrier.jpg"
img = "images/flower.jpg"
# average mean to subtract from the image
mean = 128
# the size of images that the model was trained with
input_size = 227
# use the image helper to load the image and convert it to NCHW
img = helpers.loadToNCHW(img, mean, input_size)
##### Run the test
# submit the image to net and get a tensor of results
results = p.run({'data': img})
##### Process the results
# Quick way to get the top-1 prediction result
# Squeeze out the unnecessary axis. This returns a 1-D array of length 1000
preds = np.squeeze(results)
# Get the prediction and the confidence by finding the maximum value and index of maximum value in preds array
curr_pred, curr_conf = max(enumerate(preds), key=operator.itemgetter(1))
print("Top-1 Prediction: {}".format(curr_pred))
print("Top-1 Confidence: {}\n".format(curr_conf))
# Lookup our result from the inference list
response = helpers.parseResults(results)
print(response)
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img=mpimg.imread('images/flower.jpg') #image to array
# show the original image
plt.figure()
plt.imshow(img)
plt.axis('on')
plt.title('Original image = RGB')
plt.show()
```
| true |
code
| 0.685015 | null | null | null | null |
|
<table border="0">
<tr>
<td>
<img src="https://ictd2016.files.wordpress.com/2016/04/microsoft-research-logo-copy.jpg" style="width 30px;" />
</td>
<td>
<img src="https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/MSR-ALICE-HeaderGraphic-1920x720_1-800x550.jpg" style="width 100px;"/></td>
</tr>
</table>
# Dynamic Double Machine Learning: Use Cases and Examples
Dynamic DoubleML is an extension of the Double ML approach for treatments assigned sequentially over time periods. This estimator will account for treatments that can have causal effects on future outcomes. For more details, see [this paper](https://arxiv.org/abs/2002.07285) or the [EconML docummentation](https://econml.azurewebsites.net/).
For example, the Dynamic DoubleML could be useful in estimating the following causal effects:
* the effect of investments on revenue at companies that receive investments at regular intervals ([see more](https://arxiv.org/abs/2103.08390))
* the effect of prices on demand in stores where prices of goods change over time
* the effect of income on health outcomes in people who receive yearly income
The preferred data format is balanced panel data. Each panel corresponds to one entity (e.g. company, store or person) and the different rows in a panel correspond to different time points. Example:
||Company|Year|Features|Investment|Revenue|
|---|---|---|---|---|---|
|1|A|2018|...|\$1,000|\$10,000|
|2|A|2019|...|\$2,000|\$12,000|
|3|A|2020|...|\$3,000|\$15,000|
|4|B|2018|...|\$0|\$5,000|
|5|B|2019|...|\$100|\$10,000|
|6|B|2020|...|\$1,200|\$7,000|
|7|C|2018|...|\$1,000|\$20,000|
|8|C|2019|...|\$1,500|\$25,000|
|9|C|2020|...|\$500|\$15,000|
(Note: when passing the data to the DynamicDML estimator, the "Company" column above corresponds to the `groups` argument at fit time. The "Year" column above should not be passed in as it will be inferred from the "Company" column)
If group memebers do not appear together, it is assumed that the first instance of a group in the dataset corresponds to the first period of that group, the second instance of the group corresponds to the second period, etc. Example:
||Company|Features|Investment|Revenue|
|---|---|---|---|---|
|1|A|...|\$1,000|\$10,000|
|2|B|...|\$0|\$5,000
|3|C|...|\$1,000|\$20,000|
|4|A|...|\$2,000|\$12,000|
|5|B|...|\$100|\$10,000|
|6|C|...|\$1,500|\$25,000|
|7|A|...|\$3,000|\$15,000|
|8|B|...|\$1,200|\$7,000|
|9|C|...|\$500|\$15,000|
In this dataset, 1<sup>st</sup> row corresponds to the first period of group `A`, 4<sup>th</sup> row corresponds to the second period of group `A`, etc.
In this notebook, we show the performance of the DynamicDML on synthetic and observational data.
## Notebook Contents
1. [Example Usage with Average Treatment Effects](#1.-Example-Usage-with-Average-Treatment-Effects)
2. [Example Usage with Heterogeneous Treatment Effects](#2.-Example-Usage-with-Heterogeneous-Treatment-Effects)
```
%load_ext autoreload
%autoreload 2
import econml
# Main imports
from econml.dynamic.dml import DynamicDML
from econml.tests.dgp import DynamicPanelDGP, add_vlines
# Helper imports
import numpy as np
from sklearn.linear_model import Lasso, LassoCV, LogisticRegression, LogisticRegressionCV, MultiTaskLassoCV
import matplotlib.pyplot as plt
%matplotlib inline
```
# 1. Example Usage with Average Treatment Effects
## 1.1 DGP
We consider a data generating process from a markovian treatment model.
In the example bellow, $T_t\rightarrow$ treatment(s) at time $t$, $Y_t\rightarrow$outcome at time $t$, $X_t\rightarrow$ features and controls at time $t$ (the coefficients $e, f$ will pick the features and the controls).
\begin{align}
X_t =& (\pi'X_{t-1} + 1) \cdot A\, T_{t-1} + B X_{t-1} + \epsilon_t\\
T_t =& \gamma\, T_{t-1} + (1-\gamma) \cdot D X_t + \zeta_t\\
Y_t =& (\sigma' X_{t} + 1) \cdot e\, T_{t} + f X_t + \eta_t
\end{align}
with $X_0, T_0 = 0$ and $\epsilon_t, \zeta_t, \eta_t \sim N(0, \sigma^2)$. Moreover, $X_t \in R^{n_x}$, $B[:, 0:s_x] \neq 0$ and $B[:, s_x:-1] = 0$, $\gamma\in [0, 1]$, $D[:, 0:s_x] \neq 0$, $D[:, s_x:-1]=0$, $f[0:s_x]\neq 0$, $f[s_x:-1]=0$. We draw a single time series of samples of length $n\_panels \cdot n\_periods$.
```
# Define DGP parameters
np.random.seed(123)
n_panels = 5000 # number of panels
n_periods = 3 # number of time periods in each panel
n_treatments = 2 # number of treatments in each period
n_x = 100 # number of features + controls
s_x = 10 # number of controls (endogeneous variables)
s_t = 10 # treatment support size
# Generate data
dgp = DynamicPanelDGP(n_periods, n_treatments, n_x).create_instance(
s_x, random_seed=12345)
Y, T, X, W, groups = dgp.observational_data(n_panels, s_t=s_t, random_seed=12345)
true_effect = dgp.true_effect
```
## 1.2 Train Estimator
```
est = DynamicDML(
model_y=LassoCV(cv=3, max_iter=1000),
model_t=MultiTaskLassoCV(cv=3, max_iter=1000),
cv=3)
est.fit(Y, T, X=None, W=W, groups=groups)
# Average treatment effect of all periods on last period for unit treatments
print(f"Average effect of default policy: {est.ate():0.2f}")
# Effect of target policy over baseline policy
# Must specify a treatment for each period
baseline_policy = np.zeros((1, n_periods * n_treatments))
target_policy = np.ones((1, n_periods * n_treatments))
eff = est.effect(T0=baseline_policy, T1=target_policy)
print(f"Effect of target policy over baseline policy: {eff[0]:0.2f}")
# Period treatment effects + interpretation
for i, theta in enumerate(est.intercept_.reshape(-1, n_treatments)):
print(f"Marginal effect of a treatments in period {i+1} on period {n_periods} outcome: {theta}")
# Period treatment effects with confidence intervals
est.summary()
conf_ints = est.intercept__interval(alpha=0.05)
```
## 1.3 Performance Visualization
```
# Some plotting boilerplate code
plt.figure(figsize=(15, 5))
plt.errorbar(np.arange(n_periods*n_treatments)-.04, est.intercept_, yerr=(conf_ints[1] - est.intercept_,
est.intercept_ - conf_ints[0]), fmt='o', label='DynamicDML')
plt.errorbar(np.arange(n_periods*n_treatments), true_effect.flatten(), fmt='o', alpha=.6, label='Ground truth')
for t in np.arange(1, n_periods):
plt.axvline(x=t * n_treatments - .5, linestyle='--', alpha=.4)
plt.xticks([t * n_treatments - .5 + n_treatments/2 for t in range(n_periods)],
["$\\theta_{}$".format(t) for t in range(n_periods)])
plt.gca().set_xlim([-.5, n_periods*n_treatments - .5])
plt.ylabel("Effect")
plt.legend()
plt.show()
```
# 2. Example Usage with Heterogeneous Treatment Effects on Time-Invariant Unit Characteristics
We can also estimate treatment effect heterogeneity with respect to the value of some subset of features $X$ in the initial period. Heterogeneity is currently only supported with respect to such initial state features. This for instance can support heterogeneity with respect to time-invariant unit characteristics. In that case you can simply pass as $X$ a repetition of some unit features that stay constant in all periods. You can also pass time-varying features, and their time varying component will be used as a time-varying control. However, heterogeneity will only be estimated with respect to the initial state.
## 2.1 DGP
```
# Define additional DGP parameters
het_strength = .5
het_inds = np.arange(n_x - n_treatments, n_x)
# Generate data
dgp = DynamicPanelDGP(n_periods, n_treatments, n_x).create_instance(
s_x, hetero_strength=het_strength, hetero_inds=het_inds, random_seed=12)
Y, T, X, W, groups = dgp.observational_data(n_panels, s_t=s_t, random_seed=1)
ate_effect = dgp.true_effect
het_effect = dgp.true_hetero_effect[:, het_inds + 1]
```
## 2.2 Train Estimator
```
est = DynamicDML(
model_y=LassoCV(cv=3),
model_t=MultiTaskLassoCV(cv=3),
cv=3)
est.fit(Y, T, X=X, W=W, groups=groups, inference="auto")
est.summary()
# Average treatment effect for test points
X_test = X[np.arange(0, 25, 3)]
print(f"Average effect of default policy:{est.ate(X=X_test):0.2f}")
# Effect of target policy over baseline policy
# Must specify a treatment for each period
baseline_policy = np.zeros((1, n_periods * n_treatments))
target_policy = np.ones((1, n_periods * n_treatments))
eff = est.effect(X=X_test, T0=baseline_policy, T1=target_policy)
print("Effect of target policy over baseline policy for test set:\n", eff)
# Coefficients: intercept is of shape n_treatments*n_periods
# coef_ is of shape (n_treatments*n_periods, n_hetero_inds).
# first n_treatment rows are from first period, next n_treatment
# from second period, etc.
est.intercept_, est.coef_
# Confidence intervals
conf_ints_intercept = est.intercept__interval(alpha=0.05)
conf_ints_coef = est.coef__interval(alpha=0.05)
```
## 2.3 Performance Visualization
```
# parse true parameters in array of shape (n_treatments*n_periods, 1 + n_hetero_inds)
# first column is the intercept
true_effect_inds = []
for t in range(n_treatments):
true_effect_inds += [t * (1 + n_x)] + (list(t * (1 + n_x) + 1 + het_inds) if len(het_inds)>0 else [])
true_effect_params = dgp.true_hetero_effect[:, true_effect_inds]
true_effect_params = true_effect_params.reshape((n_treatments*n_periods, 1 + het_inds.shape[0]))
# concatenating intercept and coef_
param_hat = np.hstack([est.intercept_.reshape(-1, 1), est.coef_])
lower = np.hstack([conf_ints_intercept[0].reshape(-1, 1), conf_ints_coef[0]])
upper = np.hstack([conf_ints_intercept[1].reshape(-1, 1), conf_ints_coef[1]])
plt.figure(figsize=(15, 5))
plt.errorbar(np.arange(n_periods * (len(het_inds) + 1) * n_treatments),
true_effect_params.flatten(), fmt='*', label='Ground Truth')
plt.errorbar(np.arange(n_periods * (len(het_inds) + 1) * n_treatments),
param_hat.flatten(), yerr=((upper - param_hat).flatten(),
(param_hat - lower).flatten()), fmt='o', label='DynamicDML')
add_vlines(n_periods, n_treatments, het_inds)
plt.legend()
plt.show()
```
| true |
code
| 0.720325 | null | null | null | null |
|
```
# default_exp models.cox
```
# Cox Proportional Hazard
> SA with features apart from time
We model the the instantaneous hazard as the product of two functions, one with the time component, and the other with the feature component.
$$
\begin{aligned}
\lambda(t,x) = \lambda(t)h(x)
\end{aligned}
$$
It is important to have the seperation of these functions to arrive at an analytical solution. This is so that the time component can be integrated out to give the survival function.
$$
\begin{aligned}
\int_0^T \lambda(t,x) dt &= \int_0^T \lambda(t)h(x) dt\\
&= h(x)\int_0^T \lambda(t) dt\\
S(t) &= \exp\left(-h(x)\int_{-\infty}^t \lambda(\tau) d\tau\right)
\end{aligned}
$$
```
# export
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from sklearn.preprocessing import MaxAbsScaler, StandardScaler
from torchlife.losses import hazard_loss
from torchlife.models.ph import PieceWiseHazard
# torch.Tensor.ndim = property(lambda x: x.dim())
# hide
%load_ext autoreload
%autoreload 2
%matplotlib inline
# export
class ProportionalHazard(nn.Module):
"""
Hazard proportional to time and feature component as shown above.
parameters:
- breakpoints: time points where hazard would change
- max_t: maximum point of time to plot to.
- dim: number of input dimensions of x
- h: (optional) number of hidden units (for x only).
"""
def __init__(self, breakpoints:np.array, t_scaler:MaxAbsScaler, x_scaler:StandardScaler,
dim:int, h:tuple=(), **kwargs):
super().__init__()
self.baseλ = PieceWiseHazard(breakpoints, t_scaler)
self.x_scaler = x_scaler
nodes = (dim,) + h + (1,)
self.layers = nn.ModuleList([nn.Linear(a,b, bias=False)
for a,b in zip(nodes[:-1], nodes[1:])])
def forward(self, t, t_section, x):
logλ, Λ = self.baseλ(t, t_section)
for layer in self.layers[:-1]:
x = F.relu(layer(x))
log_hx = self.layers[-1](x)
logλ += log_hx
Λ = torch.exp(log_hx + torch.log(Λ))
return logλ, Λ
def survival_function(self, t:np.array, x:np.array) -> torch.Tensor:
if len(t.shape) == 1:
t = t[:,None]
t = self.baseλ.t_scaler.transform(t)
if len(x.shape) == 1:
x = x[None, :]
if len(x) == 1:
x = np.repeat(x, len(t), axis=0)
x = self.x_scaler.transform(x)
with torch.no_grad():
x = torch.Tensor(x)
# get the times and time sections for survival function
breakpoints = self.baseλ.breakpoints[1:].cpu().numpy()
t_sec_query = np.searchsorted(breakpoints.squeeze(), t.squeeze())
# convert to pytorch tensors
t_query = torch.Tensor(t)
t_sec_query = torch.LongTensor(t_sec_query)
# calculate cumulative hazard according to above
_, Λ = self.forward(t_query, t_sec_query, x)
return torch.exp(-Λ)
def plot_survival_function(self, t:np.array, x:np.array) -> None:
s = self.survival_function(t, x)
# plot
plt.figure(figsize=(12,5))
plt.plot(t, s)
plt.xlabel('Time')
plt.ylabel('Survival Probability')
plt.show()
```
## Fitting Cox Proportional Hazard Model
```
# hide
from torchlife.data import create_db, get_breakpoints
import pandas as pd
# hide
url = "https://raw.githubusercontent.com/CamDavidsonPilon/lifelines/master/lifelines/datasets/rossi.csv"
df = pd.read_csv(url)
df.head()
# hide
df.rename(columns={'week':'t', 'arrest':'e'}, inplace=True)
breakpoints = get_breakpoints(df)
db, t_scaler, x_scaler = create_db(df, breakpoints)
# hide
from fastai.basics import Learner
x_dim = df.shape[1] - 2
model = ProportionalHazard(breakpoints, t_scaler, x_scaler, x_dim, h=(3,3))
learner = Learner(db, model, loss_func=hazard_loss)
# wd = 1e-4
# learner.lr_find()
# learner.recorder.plot()
# hide
epochs = 10
learner.fit(epochs, lr=1)
```
## Plotting hazard functions
```
model.baseλ.plot_hazard()
x = df.drop(['t', 'e'], axis=1).iloc[4]
t = np.arange(df['t'].max())
model.plot_survival_function(t, x)
# hide
from nbdev.export import *
notebook2script()
```
| true |
code
| 0.798285 | null | null | null | null |
|
>This notebook is part of our [Introduction to Machine Learning](http://www.codeheroku.com/course?course_id=1) course at [Code Heroku](http://www.codeheroku.com/).
Hey folks, today we are going to discuss about the application of gradient descent algorithm for solving machine learning problems. Let’s take a brief overview about the the things that we are going to discuss in this article:
- What is gradient descent?
- How gradient descent algorithm can help us solving machine learning problems
- The math behind gradient descent algorithm
- Implementation of gradient descent algorithm in Python
So, without wasting any time, let’s begin :)
# What is gradient descent?
Here’s what Wikipedia says: “Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function.”
Now, you might be thinking “Wait, what does that mean? What do you want to say?”
Don’t worry, we will elaborate everything about gradient descent in this article and all of it will start making sense to you in a moment :)
To understand gradient descent algorithm, let us first understand a real life machine learning problem:
Suppose you have a dataset where you are provided with the number of hours a student studies per day and the percentage of marks scored by the corresponding student. If you plot a 2D graph of this dataset, it will look something like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_1.png">
Now, if someone approaches you and says that a new student has taken admission and you need to predict the score of that student based on the number of hours he studies. How would you do that?
To predict the score of the new student, at first you need to find out a relationship between “Hours studied” and “Score” from the existing dataset. By taking a look over the visual graph plotting, we can see that a linear relationship can be established between these two things. So, by drawing a straight line over the data points in the graph, we can establish the relationship. Let’s see how would it look if we try to draw a straight line over the data points. It would look something like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_2.png">
Great! Now we have the relationship between “Hours Studied” and “Score”. So, now if someone asks us to predict the score of a student who studies 10 hours per day, we can just simply put Hours Studied = 10 data point over the relationship line and predict the value of his score like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_3.png">
From the above picture, we can easily say that the new student who studies 10 hours per day would probably score around 60. Pretty easy, right? By the way, the relationship line that we have drawn is called the “regression” line. And because the relationship we have established is a linear relationship, the line is actually called “linear regression” line. Hence, this machine learning model that we have created is known as linear regression model.
At this point, you might have noticed that all the data points do not lie perfectly over the regression line. So, there might be some difference between the predicted value and the actual value. We call this difference as error(or cost).
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_err.png">
In machine learning world, we always try to build a model with as minimum error as possible. To achieve this, we have to calculate the error of our model in order to best fit the regression line over it. We have different kinds of error like- total error, mean error, mean squared error etc.
Total error: Summation of the absolute difference between predicted and actual value for all the data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_4.png">
Mean error: Total error / number of data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_5.png">
Mean squared error: Summation of the square of absolute difference / number of data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_6.png">
Below is an example of calculating these errors:
<img src="http://www.codeheroku.com/static/blog/images/error_calc.png">
We will use the Mean Squared Error(M.S.E) to calculate the error and determine the best linear regression line(the line with the minimum error value) for our model.
Now the question is, how would you represent a regression line in a computer?
The answer is simple. Remember the equation of a straight line? We can use the same equation in order to represent the regression line in computer. If you can’t recall it, let me quickly remind you, it’s **y = M * x + B**
<img src="http://www.codeheroku.com/static/blog/images/line_repr.png">
Here, M is the slope of the line and B is the Y intercept. Let’s quickly recall about slope and Y intercept.
Slope is the amount by which the line is rising on the Y axis for every block that you go towards right in the X axis. This tells us the direction of the line and the rate by which our line is increasing. Mathematically speaking, this means  for a specified amount of distance on the line.
From the dotted lines in the above picture, we can see that for every 2 blocks in the X axis, the line rises by 1 block in the Y axis.<br>
Hence, slope, M = ½ = 0.5<br>
And it’s a positive value, which indicates that the line is increasing in the upward direction.
Now, let’s come to Y intercept. It is the distance which tells us exactly where the line cuts the Y axis. From the above picture, we can see that the line is cutting Y axis on point (0,1). So, the Y intercept(B) in this case is the distance between (0,0) and (0,1) = 1.
Hence, the straight line on the above picture can be represented through the following equation:
y = 0.5 * x + 1
Now we know how to represent the regression line in a computer. Everything seems good so far. But, the biggest question still remains unanswered- “How would the computer know the right value of M and B for drawing the regression line with the minimum error?”
Exactly that’s why we need the gradient descent algorithm. Gradient descent is a trial and error method, which will iteratively give us different values of M and B to try. In each iteration, we will draw a regression line using these values of M and B and will calculate the error for this model. We will continue until we get the values of M and B such that the error is minimum.
Let’s have a more elaborative view of gradient descent algorithm:
Step 1: Start with random values of M and B
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s1.png">
Step 2: Adjust M and B such that error reduces
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s2.png">
Step 3: Repeat until we get the best values of M and B (until convergence)
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s3.png">
By the way, the application of gradient descent is not limited to regression problems only. It is an optimization algorithm which can be applied to any problem in general.
# The math behind gradient descent
Till now we have understood that we will use gradient descent to minimize the error for our model. But, now let us see exactly how gradient descent finds the best values of M and B for us.
Gradient descent tries to minimize the error. Right?
So, we can say that it tries to minimize the following function(cost function):
<img src="http://www.codeheroku.com/static/blog/images/gd_err_fnc.png">
At first we will take random values of M and B. So, we will get a random error corresponding to these values. Thus, a random point will be plotted on the above graph. At this point, there will be some error. So, our objective will be to reduce this error.
In general, how would you approach towards the minimum value of a function? By finding its derivative. Right? The same thing applies here.
We will obtain the partial derivative of J with respect to M and B. This will give us the direction of the slope of tangent at the given point. We would like to move in the opposite direction of the slope in order to approach towards the minimum value.
<img src="http://www.codeheroku.com/static/blog/images/gd_db_dm_calc.png">
So far, we have only got the direction of the slope and we know we need to move in its opposite direction. But, in each iteration, by how much amount we should move in the opposite direction? This amount is called the learning rate(alpha). Learning rate determines the step size of our movement towards the minimal point.
So, choosing the right learning rate is very important. If the learning rate is too small, it will take more time to converge. On the other hand, if the learning rate is very high, it may overshoot the minimum point and diverge.
<img src="http://www.codeheroku.com/static/blog/images/gd_ch_alpha.png">
To sum up, what we have till now is-
1. A random point is chosen initially by choosing random values of M and B.
2. Direction of the slope of that point is found by finding delta_m and delta_b
3. Since we want to move in the opposite direction of the slope, we will multiply -1 with both delta_m and delta_b.
4. Since delta_m and delta_b gives us only the direction, we need to multiply both of them with the learning rate(alpha) to specify the step size of each iteration.
5. Next, we need to modify the current values of M and B such that the error is reduced.
<img src="http://www.codeheroku.com/static/blog/images/gd_9.png">
6. We need to repeat steps 2 to 5 until we converge at the minimum point.
# Implementation of gradient descent using Python
This was everything about gradient descent algorithm. Now we will implement this algorithm using Python.
Let us first import all required libraries and read the dataset using Pandas library(the csv file can be downloaded from this [link](https://github.com/codeheroku/Introduction-to-Machine-Learning/tree/master/gradient%20descent/starter%20code)):
```
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("student_scores.csv") #Read csv file using Pandas library
```
Next, we need to read the values of X and Y from the dataframe and create a scatter plot of that data.
```
X = df["Hours"] #Read values of X from dataframe
Y = df["Scores"] #Read values of Y from dataframe
plt.plot(X,Y,'o') # 'o' for creating scatter plot
plt.title("Implementing Gradient Descent")
plt.xlabel("Hours Studied")
plt.ylabel("Student Score")
```
After that, we will initially choose m = 0 and b = 0
```
m = 0
b = 0
```
Now, we need to create a function(gradient descent function) which will take the current value of m and b and then give us better values of m and b.
```
def grad_desc(X,Y,m,b):
for point in zip(X,Y):
x = point[0] #value of x of a point
y_actual = point[1] #Actual value of y for that point
y_prediction = m*x + b #Predicted value of y for given x
error = y_prediction - y_actual #Error in the estimation
#Using alpha = 0.0005
delta_m = -1 * (error*x) * 0.0005 #Calculating delta m
delta_b = -1 * (error) * 0.0005 #Calculating delta b
m = m + delta_m #Modifying value of m for reducing error
b = b + delta_b #Modifying value of b for reducing error
return m,b #Returning better values of m and b
```
Notice, in the above code, we are using learning rate(alpha) = 0.0005 . You can try to modify this value and try this example with different learning rates.
Now we will make a function which will help us to plot the regression line on the graph.
```
def plot_regression_line(X,m,b):
regression_x = X.values #list of values of x
regression_y = [] #list of values of y
for x in regression_x:
y = m*x + b #calculating the y_prediction
regression_y.append(y) #adding the predicted value in list of y
plt.plot(regression_x,regression_y) #plot the regression line
plt.pause(1) #pause for 1 second before plotting next line
```
Now, when we will run the grad_desc() function, each time we will get a better result for regression line. Let us create a loop and run the grad_desc() function for 10 times and visualize the results.
```
for i in range(0,10):
m,b = grad_desc(X,Y,m,b) #call grad_desc() to get better m & b
plot_regression_line(X,m,b) #plot regression line with m & b
```
Finally, we need to show the plot by adding the following statement:
```
plt.show()
```
So, the full code for our program is:
```
import pandas as pd
import matplotlib.pyplot as plt
# function for plotting regression line
def plot_regression_line(X,m,b):
regression_x = X.values
regression_y = []
for x in regression_x:
y = m*x + b
regression_y.append(y)
plt.plot(regression_x,regression_y)
plt.pause(1)
df = pd.read_csv("student_scores.csv")
X = df["Hours"]
Y = df["Scores"]
plt.plot(X,Y,'o')
plt.title("Implementing Gradient Descent")
plt.xlabel("Hours Studied")
plt.ylabel("Student Score")
m = 0
b = 0
# gradient descent function
def grad_desc(X,Y,m,b):
for point in zip(X,Y):
x = point[0]
y_actual = point[1]
y_prediction = m*x + b
error = y_prediction - y_actual
delta_m = -1 * (error*x) * 0.0005
delta_b = -1 * (error) * 0.0005
m = m + delta_m
b = b + delta_b
return m,b
for i in range(0,10):
m,b = grad_desc(X,Y,m,b)
plot_regression_line(X,m,b)
plt.show()
```
Now let’s run the above program for different values of learning rate(alpha).
For alpha = 0.0005 , the output will look like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_1.gif">
For alpha = 0.05 , it will look like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_2.gif">
For alpha = 1, it will overshoot the minimum point and diverge like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_3.gif">
The gradient descent algorithm about which we discussed in this article is called stochastic gradient descent. There are also other types of gradient descent algorithms like- batch gradient descent, mini batch gradient descent etc.
>If this article was helpful to you, check out our [Introduction to Machine Learning](http://www.codeheroku.com/course?course_id=1) Course at [Code Heroku](http://www.codeheroku.com/) for a complete guide to Machine Learning.
| true |
code
| 0.616272 | null | null | null | null |
|
**Chapter 10 – Introduction to Artificial Neural Networks with Keras**
_This notebook contains all the sample code and solutions to the exercises in chapter 10._
# Setup
First, let's import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20 and TensorFlow ≥2.0-preview.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# TensorFlow ≥2.0-preview is required
import tensorflow as tf
assert tf.__version__ >= "2.0"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ann"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
```
# Perceptrons
**Note**: we set `max_iter` and `tol` explicitly to avoid warnings about the fact that their default value will change in future versions of Scikit-Learn.
```
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron(max_iter=1000, tol=1e-3, random_state=42)
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])
y_pred
a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]
axes = [0, 5, 0, 2]
x0, x1 = np.meshgrid(
np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")
plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes)
save_fig("perceptron_iris_plot")
plt.show()
```
# Activation functions
```
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def relu(z):
return np.maximum(0, z)
def derivative(f, z, eps=0.000001):
return (f(z + eps) - f(z - eps))/(2 * eps)
z = np.linspace(-5, 5, 200)
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(z, np.sign(z), "r-", linewidth=1, label="Step")
plt.plot(z, sigmoid(z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, np.tanh(z), "b-", linewidth=2, label="Tanh")
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
plt.legend(loc="center right", fontsize=14)
plt.title("Activation functions", fontsize=14)
plt.axis([-5, 5, -1.2, 1.2])
plt.subplot(122)
plt.plot(z, derivative(np.sign, z), "r-", linewidth=1, label="Step")
plt.plot(0, 0, "ro", markersize=5)
plt.plot(0, 0, "rx", markersize=10)
plt.plot(z, derivative(sigmoid, z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=2, label="Tanh")
plt.plot(z, derivative(relu, z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
#plt.legend(loc="center right", fontsize=14)
plt.title("Derivatives", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("activation_functions_plot")
plt.show()
def heaviside(z):
return (z >= 0).astype(z.dtype)
def mlp_xor(x1, x2, activation=heaviside):
return activation(-activation(x1 + x2 - 1.5) + activation(x1 + x2 - 0.5) - 0.5)
x1s = np.linspace(-0.2, 1.2, 100)
x2s = np.linspace(-0.2, 1.2, 100)
x1, x2 = np.meshgrid(x1s, x2s)
z1 = mlp_xor(x1, x2, activation=heaviside)
z2 = mlp_xor(x1, x2, activation=sigmoid)
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.contourf(x1, x2, z1)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: heaviside", fontsize=14)
plt.grid(True)
plt.subplot(122)
plt.contourf(x1, x2, z2)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: sigmoid", fontsize=14)
plt.grid(True)
```
# Building an Image Classifier
First let's import TensorFlow and Keras.
```
import tensorflow as tf
from tensorflow import keras
tf.__version__
keras.__version__
```
Let's start by loading the fashion MNIST dataset. Keras has a number of functions to load popular datasets in `keras.datasets`. The dataset is already split for you between a training set and a test set, but it can be useful to split the training set further to have a validation set:
```
fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()
```
The training set contains 60,000 grayscale images, each 28x28 pixels:
```
X_train_full.shape
```
Each pixel intensity is represented as a byte (0 to 255):
```
X_train_full.dtype
```
Let's split the full training set into a validation set and a (smaller) training set. We also scale the pixel intensities down to the 0-1 range and convert them to floats, by dividing by 255.
```
X_valid, X_train = X_train_full[:5000] / 255., X_train_full[5000:] / 255.
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test / 255.
```
You can plot an image using Matplotlib's `imshow()` function, with a `'binary'`
color map:
```
plt.imshow(X_train[0], cmap="binary")
plt.axis('off')
plt.show()
```
The labels are the class IDs (represented as uint8), from 0 to 9:
```
y_train
```
Here are the corresponding class names:
```
class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
```
So the first image in the training set is a coat:
```
class_names[y_train[0]]
```
The validation set contains 5,000 images, and the test set contains 10,000 images:
```
X_valid.shape
X_test.shape
```
Let's take a look at a sample of the images in the dataset:
```
n_rows = 4
n_cols = 10
plt.figure(figsize=(n_cols * 1.2, n_rows * 1.2))
for row in range(n_rows):
for col in range(n_cols):
index = n_cols * row + col
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(X_train[index], cmap="binary", interpolation="nearest")
plt.axis('off')
plt.title(class_names[y_train[index]], fontsize=12)
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig('fashion_mnist_plot', tight_layout=False)
plt.show()
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.layers
model.summary()
keras.utils.plot_model(model, "my_mnist_model.png", show_shapes=True)
hidden1 = model.layers[1]
hidden1.name
model.get_layer(hidden1.name) is hidden1
weights, biases = hidden1.get_weights()
weights
weights.shape
biases
biases.shape
model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
```
This is equivalent to:
```python
model.compile(loss=keras.losses.sparse_categorical_crossentropy,
optimizer=keras.optimizers.SGD(),
metrics=[keras.metrics.sparse_categorical_accuracy])
```
```
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid))
history.params
print(history.epoch)
history.history.keys()
import pandas as pd
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1)
save_fig("keras_learning_curves_plot")
plt.show()
model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(2)
y_pred = model.predict_classes(X_new)
y_pred
np.array(class_names)[y_pred]
y_new = y_test[:3]
y_new
```
# Regression MLP
Let's load, split and scale the California housing dataset (the original one, not the modified one as in chapter 2):
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
keras.layers.Dense(1)
])
model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_pred = model.predict(X_new)
plt.plot(pd.DataFrame(history.history))
plt.grid(True)
plt.gca().set_ylim(0, 1)
plt.show()
y_pred
```
# Functional API
Not all neural network models are simply sequential. Some may have complex topologies. Some may have multiple inputs and/or multiple outputs. For example, a Wide & Deep neural network (see [paper](https://ai.google/research/pubs/pub45413)) connects all or part of the inputs directly to the output layer.
```
np.random.seed(42)
tf.random.set_seed(42)
input_ = keras.layers.Input(shape=X_train.shape[1:])
hidden1 = keras.layers.Dense(30, activation="relu")(input_)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.models.Model(inputs=[input_], outputs=[output])
model.summary()
model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
y_pred = model.predict(X_new)
```
What if you want to send different subsets of input features through the wide or deep paths? We will send 5 features (features 0 to 4), and 6 through the deep path (features 2 to 7). Note that 3 features will go through both (features 2, 3 and 4).
```
np.random.seed(42)
tf.random.set_seed(42)
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="output")(concat)
model = keras.models.Model(inputs=[input_A, input_B], outputs=[output])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
X_train_A, X_train_B = X_train[:, :5], X_train[:, 2:]
X_valid_A, X_valid_B = X_valid[:, :5], X_valid[:, 2:]
X_test_A, X_test_B = X_test[:, :5], X_test[:, 2:]
X_new_A, X_new_B = X_test_A[:3], X_test_B[:3]
history = model.fit((X_train_A, X_train_B), y_train, epochs=20,
validation_data=((X_valid_A, X_valid_B), y_valid))
mse_test = model.evaluate((X_test_A, X_test_B), y_test)
y_pred = model.predict((X_new_A, X_new_B))
```
Adding an auxiliary output for regularization:
```
np.random.seed(42)
tf.random.set_seed(42)
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="main_output")(concat)
aux_output = keras.layers.Dense(1, name="aux_output")(hidden2)
model = keras.models.Model(inputs=[input_A, input_B],
outputs=[output, aux_output])
model.compile(loss=["mse", "mse"], loss_weights=[0.9, 0.1], optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit([X_train_A, X_train_B], [y_train, y_train], epochs=20,
validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid]))
total_loss, main_loss, aux_loss = model.evaluate(
[X_test_A, X_test_B], [y_test, y_test])
y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B])
```
# The subclassing API
```
class WideAndDeepModel(keras.models.Model):
def __init__(self, units=30, activation="relu", **kwargs):
super().__init__(**kwargs)
self.hidden1 = keras.layers.Dense(units, activation=activation)
self.hidden2 = keras.layers.Dense(units, activation=activation)
self.main_output = keras.layers.Dense(1)
self.aux_output = keras.layers.Dense(1)
def call(self, inputs):
input_A, input_B = inputs
hidden1 = self.hidden1(input_B)
hidden2 = self.hidden2(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
main_output = self.main_output(concat)
aux_output = self.aux_output(hidden2)
return main_output, aux_output
model = WideAndDeepModel(30, activation="relu")
model.compile(loss="mse", loss_weights=[0.9, 0.1], optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit((X_train_A, X_train_B), (y_train, y_train), epochs=10,
validation_data=((X_valid_A, X_valid_B), (y_valid, y_valid)))
total_loss, main_loss, aux_loss = model.evaluate((X_test_A, X_test_B), (y_test, y_test))
y_pred_main, y_pred_aux = model.predict((X_new_A, X_new_B))
model = WideAndDeepModel(30, activation="relu")
```
# Saving and Restoring
```
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
model.save("my_keras_model.h5")
model = keras.models.load_model("my_keras_model.h5")
model.predict(X_new)
model.save_weights("my_keras_weights.ckpt")
model.load_weights("my_keras_weights.ckpt")
```
# Using Callbacks during Training
```
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5", save_best_only=True)
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb])
model = keras.models.load_model("my_keras_model.h5") # rollback to best model
mse_test = model.evaluate(X_test, y_test)
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
early_stopping_cb = keras.callbacks.EarlyStopping(patience=10,
restore_best_weights=True)
history = model.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, early_stopping_cb])
mse_test = model.evaluate(X_test, y_test)
class PrintValTrainRatioCallback(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
print("\nval/train: {:.2f}".format(logs["val_loss"] / logs["loss"]))
val_train_ratio_cb = PrintValTrainRatioCallback()
history = model.fit(X_train, y_train, epochs=1,
validation_data=(X_valid, y_valid),
callbacks=[val_train_ratio_cb])
```
# TensorBoard
```
root_logdir = os.path.join(os.curdir, "my_logs")
def get_run_logdir():
import time
run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S")
return os.path.join(root_logdir, run_id)
run_logdir = get_run_logdir()
run_logdir
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
tensorboard_cb = keras.callbacks.TensorBoard(run_logdir)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, tensorboard_cb])
```
To start the TensorBoard server, one option is to open a terminal, if needed activate the virtualenv where you installed TensorBoard, go to this notebook's directory, then type:
```bash
$ tensorboard --logdir=./my_logs --port=6006
```
You can then open your web browser to [localhost:6006](http://localhost:6006) and use TensorBoard. Once you are done, press Ctrl-C in the terminal window, this will shutdown the TensorBoard server.
Alternatively, you can load TensorBoard's Jupyter extension and run it like this:
```
%load_ext tensorboard
%tensorboard --logdir=./my_logs --port=6006
run_logdir2 = get_run_logdir()
run_logdir2
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=0.05))
tensorboard_cb = keras.callbacks.TensorBoard(run_logdir2)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, tensorboard_cb])
```
Notice how TensorBoard now sees two runs, and you can compare the learning curves.
Check out the other available logging options:
```
help(keras.callbacks.TensorBoard.__init__)
```
# Hyperparameter Tuning
```
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]):
model = keras.models.Sequential()
model.add(keras.layers.InputLayer(input_shape=input_shape))
for layer in range(n_hidden):
model.add(keras.layers.Dense(n_neurons, activation="relu"))
model.add(keras.layers.Dense(1))
optimizer = keras.optimizers.SGD(lr=learning_rate)
model.compile(loss="mse", optimizer=optimizer)
return model
keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model)
keras_reg.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
mse_test = keras_reg.score(X_test, y_test)
y_pred = keras_reg.predict(X_new)
np.random.seed(42)
tf.random.set_seed(42)
from scipy.stats import reciprocal
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
"n_hidden": [0, 1, 2, 3],
"n_neurons": np.arange(1, 100),
"learning_rate": reciprocal(3e-4, 3e-2),
}
rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10, cv=3, verbose=2)
rnd_search_cv.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
rnd_search_cv.best_params_
rnd_search_cv.best_score_
rnd_search_cv.best_estimator_
rnd_search_cv.score(X_test, y_test)
model = rnd_search_cv.best_estimator_.model
model
model.evaluate(X_test, y_test)
```
# Exercise solutions
## 1. to 9.
See appendix A.
## 10.
TODO
| true |
code
| 0.656768 | null | null | null | null |
|
Copyright 2021 DeepMind Technologies Limited
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
https://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
#Generative Art Using Neural Visual Grammars and Dual Encoders
**Chrisantha Fernando, Piotr Mirowski, Dylan Banarse, S. M. Ali Eslami, Jean-Baptiste Alayrac, Simon Osindero**
DeepMind, 2021
##Arnheim 1
###Generate paintings from text prompts.
Whilst there are perhaps only a few scientific methods, there seem to be almost as many artistic methods as there are artists. Artistic processes appear to inhabit the highest order of open-endedness. To begin to understand some of the processes of art making it is helpful to try to automate them even partially.
In this paper, a novel algorithm for producing generative art is described which allows a user to input a text string, and which in a creative response to this string, outputs an image which interprets that string. It does so by evolving images using a hierarchical neural [Lindenmeyer system](https://en.wikipedia.org/wiki/L-system), and evaluating these images along the way using an image text dual encoder trained on billions of images and their associated text from the internet.
In doing so we have access to and control over an instance of an artistic process, allowing analysis of which aspects of the artistic process become the task of the algorithm, and which elements remain the responsibility of the artist.
This colab accompanies the paper [Generative Art Using Neural Visual Grammars and Dual Encoders](https://arxiv.org/abs/2105.00162)
##Instructions
1. Click "Connect" button in the top right corner of this Colab
1. Select Runtime -> Change runtime type -> Hardware accelerator -> GPU
1. Select High-RAM for "Runtime shape" option
1. Navigate to "Get text input"
1. Enter text for IMAGE_NAME
1. Select "Run All" from Runtime menu
# Imports
```
#@title Set CUDA version for PyTorch
import subprocess
CUDA_version = [s for s in subprocess.check_output(["nvcc", "--version"]
).decode("UTF-8").split(", ")
if s.startswith("release")][0].split(" ")[-1]
print("CUDA version:", CUDA_version)
if CUDA_version == "10.0":
torch_version_suffix = "+cu100"
elif CUDA_version == "10.1":
torch_version_suffix = "+cu101"
elif CUDA_version == "10.2":
torch_version_suffix = ""
else:
torch_version_suffix = "+cu110"
! nvidia-smi
#@title Install and import PyTorch and Clip
! pip install torch==1.7.1{torch_version_suffix} torchvision==0.8.2{torch_version_suffix} -f https://download.pytorch.org/whl/torch_stable.html
! pip install git+https://github.com/openai/CLIP.git --no-deps
! pip install ftfy regex
import torch
import torch.nn as nn
import clip
print("Torch version:", torch.__version__)
#@title Install and import ray multiprocessing
! pip install -q -U ray[default]
import ray
#@title Import all other needed libraries
import collections
import copy
import cloudpickle
import time
import numpy as np
import matplotlib.pyplot as plt
import math
from PIL import Image
from PIL import ImageDraw
from skimage import transform
#@title Load CLIP {vertical-output: true}
CLIP_MODEL = "ViT-B/32"
device = torch.device("cuda")
print(f"Downloading CLIP model {CLIP_MODEL}...")
model, _ = clip.load(CLIP_MODEL, device, jit=False)
```
# Neural Visual Grammar
### Drawing primitives
```
def to_homogeneous(p):
r, c = p
return np.stack((r, c, np.ones_like(p[0])), axis=0)
def from_homogeneous(p):
p = p / p.T[:, 2]
return p[0].astype("int32"), p[1].astype("int32")
def apply_scale(scale, lineh):
return np.stack([lineh[0, :] * scale,
lineh[1, :] * scale,
lineh[2, :]])
def apply_translation(translation, lineh, offset_r=0, offset_c=0):
r, c = translation
return np.stack([lineh[0, :] + c + offset_c,
lineh[1, :] + r + offset_r,
lineh[2, :]])
def apply_rotation(translation, rad, lineh):
r, c = translation
cos_rad = np.cos(rad)
sin_rad = np.sin(rad)
return np.stack(
[(lineh[0, :] - c) * cos_rad - (lineh[1, :] - r) * sin_rad + c,
(lineh[0, :] - c) * sin_rad + (lineh[1, :] - r) * cos_rad + r,
lineh[2, :]])
def transform_lines(line_from, line_to, translation, angle, scale,
translation2, angle2, scale2, img_siz2):
"""Transform lines by translation, angle and scale, twice.
Args:
line_from: Line start point.
line_to: Line end point.
translation: 1st translation to line.
angle: 1st angle of rotation for line.
scale: 1st scale for line.
translation2: 2nd translation to line.
angle2: 2nd angle of rotation for line.
scale2: 2nd scale for line.
img_siz2: Offset for 2nd translation.
Returns:
Transformed lines.
"""
if len(line_from.shape) == 1:
line_from = np.expand_dims(line_from, 0)
if len(line_to.shape) == 1:
line_to = np.expand_dims(line_to, 0)
# First transform.
line_from_h = to_homogeneous(line_from.T)
line_to_h = to_homogeneous(line_to.T)
line_from_h = apply_scale(scale, line_from_h)
line_to_h = apply_scale(scale, line_to_h)
translated_line_from = apply_translation(translation, line_from_h)
translated_line_to = apply_translation(translation, line_to_h)
translated_mid_point = (translated_line_from + translated_line_to) / 2.0
translated_mid_point = translated_mid_point[[1, 0]]
line_from_transformed = apply_rotation(translated_mid_point,
np.pi * angle,
translated_line_from)
line_to_transformed = apply_rotation(translated_mid_point,
np.pi * angle,
translated_line_to)
line_from_transformed = np.array(from_homogeneous(line_from_transformed))
line_to_transformed = np.array(from_homogeneous(line_to_transformed))
# Second transform.
line_from_h = to_homogeneous(line_from_transformed)
line_to_h = to_homogeneous(line_to_transformed)
line_from_h = apply_scale(scale2, line_from_h)
line_to_h = apply_scale(scale2, line_to_h)
translated_line_from = apply_translation(
translation2, line_from_h, offset_r=img_siz2, offset_c=img_siz2)
translated_line_to = apply_translation(
translation2, line_to_h, offset_r=img_siz2, offset_c=img_siz2)
translated_mid_point = (translated_line_from + translated_line_to) / 2.0
translated_mid_point = translated_mid_point[[1, 0]]
line_from_transformed = apply_rotation(translated_mid_point,
np.pi * angle2,
translated_line_from)
line_to_transformed = apply_rotation(translated_mid_point,
np.pi * angle2,
translated_line_to)
return np.concatenate([from_homogeneous(line_from_transformed),
from_homogeneous(line_to_transformed)],
axis=1)
```
### Hierarchical stroke painting functions
```
# PaintingCommand
# origin_top: Origin of line defined by top level LSTM
# angle_top: Angle of line defined by top level LSTM
# scale_top: Scale for line defined by top level LSTM
# origin_bottom: Origin of line defined by bottom level LSTM
# angle_bottom: Angle of line defined by bottom level LSTM
# scale_bottom: Scale for line defined by bottom level LSTM
# position_choice: Selects between use of:
# Origin, angle and scale from both LSTM levels
# Origin, angle and scale just from top level LSTM
# Origin, angle and scale just from bottom level LSTM
# transparency: Line transparency determined by bottom level LSTM
PaintingCommand = collections.namedtuple("PaintingCommand",
["origin_top",
"angle_top",
"scale_top",
"origin_bottom",
"angle_bottom",
"scale_bottom",
"position_choice",
"transparency"])
def paint_over_image(img, strokes, painting_commands,
allow_strokes_beyond_image_edges, coeff_size=1):
"""Make marks over an existing image.
Args:
img: Image to draw on.
strokes: Stroke descriptions.
painting_commands: Top-level painting commands with transforms for the i
sets of strokes.
allow_strokes_beyond_image_edges: Allow strokes beyond image boundary.
coeff_size: Determines low res (1) or high res (10) image will be drawn.
Returns:
num_strokes: The number of strokes made.
"""
img_center = 112. * coeff_size
# a, b and c: determines the stroke width distribution (see 'weights' below)
a = 10. * coeff_size
b = 2. * coeff_size
c = 300. * coeff_size
# d: extent that the strokes are allowed to go beyond the edge of the canvas
d = 223 * coeff_size
def _clip_colour(col):
return np.clip((np.round(col * 255. + 128.)).astype(np.int32), 0, 255)
# Loop over all the top level...
t0_over = time.time()
num_strokes = sum(len(s) for s in strokes)
translations = np.zeros((2, num_strokes,), np.float32)
translations2 = np.zeros((2, num_strokes,), np.float32)
angles = np.zeros((num_strokes,), np.float32)
angles2 = np.zeros((num_strokes,), np.float32)
scales = np.zeros((num_strokes,), np.float32)
scales2 = np.zeros((num_strokes,), np.float32)
weights = np.zeros((num_strokes,), np.float32)
lines_from = np.zeros((num_strokes, 2), np.float32)
lines_to = np.zeros((num_strokes, 2), np.float32)
rgbas = np.zeros((num_strokes, 4), np.float32)
k = 0
for i in range(len(strokes)):
# Get the top-level transforms for the i-th bunch of strokes
painting_comand = painting_commands[i]
translation_a = painting_comand.origin_top
angle_a = (painting_comand.angle_top + 1) / 5.0
scale_a = 0.5 + (painting_comand.scale_top + 1) / 3.0
translation_b = painting_comand.origin_bottom
angle_b = (painting_comand.angle_bottom + 1) / 5.0
scale_b = 0.5 + (painting_comand.scale_bottom + 1) / 3.0
position_choice = painting_comand.position_choice
solid_colour = painting_comand.transparency
# Do we use origin, angle and scale from both, top or bottom LSTM levels?
if position_choice > 0.33:
translation = translation_a
angle = angle_a
scale = scale_a
translation2 = translation_b
angle2 = angle_b
scale2 = scale_b
elif position_choice > -0.33:
translation = translation_a
angle = angle_a
scale = scale_a
translation2 = [-img_center, -img_center]
angle2 = 0.
scale2 = 1.
else:
translation = translation_b
angle = angle_b
scale = scale_b
translation2 = [-img_center, -img_center]
angle2 = 0.
scale2 = 1.
# Store top-level transforms
strokes_i = strokes[i]
n_i = len(strokes_i)
angles[k:(k+n_i)] = angle
angles2[k:(k+n_i)] = angle2
scales[k:(k+n_i)] = scale
scales2[k:(k+n_i)] = scale2
translations[0, k:(k+n_i)] = translation[0]
translations[1, k:(k+n_i)] = translation[1]
translations2[0, k:(k+n_i)] = translation2[0]
translations2[1, k:(k+n_i)] = translation2[1]
# ... and the bottom level stroke definitions.
for j in range(n_i):
z_ij = strokes_i[j]
# Store line weight (we will process micro-strokes later)
weights[k] = z_ij[4]
# Store line endpoints
lines_from[k, :] = (z_ij[0], z_ij[1])
lines_to[k, :] = (z_ij[2], z_ij[3])
# Store colour and alpha
rgbas[k, 0] = z_ij[7]
rgbas[k, 1] = z_ij[8]
rgbas[k, 2] = z_ij[9]
if solid_colour > -0.5:
rgbas[k, 3] = 25.5
else:
rgbas[k, 3] = z_ij[11]
k += 1
# Draw all the strokes in a batch as sequence of length 2 * num_strokes
t1_over = time.time()
lines_from *= img_center/2.0
lines_to *= img_center/2.0
rr, cc = transform_lines(lines_from, lines_to, translations, angles, scales,
translations2, angles2, scales2, img_center)
if not allow_strokes_beyond_image_edges:
rrm = np.round(np.clip(rr, 1, d-1)).astype(int)
ccm = np.round(np.clip(cc, 1, d-1)).astype(int)
else:
rrm = np.round(rr).astype(int)
ccm = np.round(cc).astype(int)
# Plot all the strokes
t2_over = time.time()
img_pil = Image.fromarray(img)
canvas = ImageDraw.Draw(img_pil, "RGBA")
rgbas[:, :3] = _clip_colour(rgbas[:, :3])
rgbas[:, 3] = (np.clip(5.0 * np.abs(rgbas[:, 3]), 0, 255)).astype(np.int32)
weights = (np.clip(np.round(weights * b + a), 2, c)).astype(np.int32)
for k in range(num_strokes):
canvas.line((rrm[k], ccm[k], rrm[k+num_strokes], ccm[k+num_strokes]),
fill=tuple(rgbas[k]), width=weights[k])
img[:] = np.asarray(img_pil)[:]
t3_over = time.time()
if VERBOSE_CODE:
print("{:.2f}s to store {} stroke defs, {:.4f}s to "
"compute them, {:.4f}s to plot them".format(
t1_over - t0_over, num_strokes, t2_over - t1_over,
t3_over - t2_over))
return num_strokes
```
### Recurrent Neural Network Layer Generator
```
# DrawingLSTMSpec - parameters defining the LSTM architecture
# input_spec_size: Size if sequence elements
# num_lstms: Number of LSTMs at each layer
# net_lstm_hiddens: Number of hidden LSTM units
# net_mlp_hiddens: Number of hidden units in MLP layer
DrawingLSTMSpec = collections.namedtuple("DrawingLSTMSpec",
["input_spec_size",
"num_lstms",
"net_lstm_hiddens",
"net_mlp_hiddens"])
class MakeGeneratorLstm(nn.Module):
"""Block of parallel LSTMs with MLP output heads."""
def __init__(self, drawing_lstm_spec, output_size):
"""Build drawing LSTM architecture using spec.
Args:
drawing_lstm_spec: DrawingLSTMSpec with architecture parameters
output_size: Number of outputs for the MLP head layer
"""
super(MakeGeneratorLstm, self).__init__()
self._num_lstms = drawing_lstm_spec.num_lstms
self._input_layer = nn.Sequential(
nn.Linear(drawing_lstm_spec.input_spec_size,
drawing_lstm_spec.net_lstm_hiddens),
torch.nn.LeakyReLU(0.2, inplace=True))
lstms = []
heads = []
for _ in range(self._num_lstms):
lstm_layer = nn.LSTM(
input_size=drawing_lstm_spec.net_lstm_hiddens,
hidden_size=drawing_lstm_spec.net_lstm_hiddens,
num_layers=2, batch_first=True, bias=True)
head_layer = nn.Sequential(
nn.Linear(drawing_lstm_spec.net_lstm_hiddens,
drawing_lstm_spec.net_mlp_hiddens),
torch.nn.LeakyReLU(0.2, inplace=True),
nn.Linear(drawing_lstm_spec.net_mlp_hiddens, output_size))
lstms.append(lstm_layer)
heads.append(head_layer)
self._lstms = nn.ModuleList(lstms)
self._heads = nn.ModuleList(heads)
def forward(self, x):
pred = []
x = self._input_layer(x)*10.0
for i in range(self._num_lstms):
y, _ = self._lstms[i](x)
y = self._heads[i](y)
pred.append(y)
return pred
```
### DrawingLSTM - A Drawing Recurrent Neural Network
```
Genotype = collections.namedtuple("Genotype",
["top_lstm",
"bottom_lstm",
"input_sequence",
"initial_img"])
class DrawingLSTM:
"""LSTM for processing input sequences and generating resultant drawings.
Comprised of two LSTM layers.
"""
def __init__(self, drawing_lstm_spec, allow_strokes_beyond_image_edges):
"""Create DrawingLSTM to interpret input sequences and paint an image.
Args:
drawing_lstm_spec: DrawingLSTMSpec with LSTM architecture parameters
allow_strokes_beyond_image_edges: Draw lines outside image boundary
"""
self._input_spec_size = drawing_lstm_spec.input_spec_size
self._num_lstms = drawing_lstm_spec.num_lstms
self._allow_strokes_beyond_image_edges = allow_strokes_beyond_image_edges
with torch.no_grad():
self.top_lstm = MakeGeneratorLstm(drawing_lstm_spec,
self._input_spec_size)
self.bottom_lstm = MakeGeneratorLstm(drawing_lstm_spec, 12)
self._init_all(self.top_lstm, torch.nn.init.normal_, mean=0., std=0.2)
self._init_all(self.bottom_lstm, torch.nn.init.normal_, mean=0., std=0.2)
def _init_all(self, a_model, init_func, *params, **kwargs):
"""Method for initialising model with given init_func, params and kwargs."""
for p in a_model.parameters():
init_func(p, *params, **kwargs)
def _feed_top_lstm(self, input_seq):
"""Feed all input sequences input_seq into the LSTM models."""
x_in = input_seq.reshape((len(input_seq), 1, self._input_spec_size))
x_in = np.tile(x_in, (SEQ_LENGTH, 1))
x_torch = torch.from_numpy(x_in).type(torch.FloatTensor)
y_torch = self.top_lstm(x_torch)
y_torch = [y_torch_k.detach().numpy() for y_torch_k in y_torch]
del x_in
del x_torch
# There are multiple LSTM heads. For each sequence, read out the head and
# length of intermediary output to keep and return intermediary outputs.
readouts_top = np.clip(
np.round(self._num_lstms/2.0 * (1 + input_seq[:, 1])).astype(np.int32),
0, self._num_lstms-1)
lengths_top = np.clip(
np.round(10.0 * (1 + input_seq[:, 0])).astype(np.int32),
0, SEQ_LENGTH) + 1
intermediate_strings = []
for i in range(len(readouts_top)):
y_torch_i = y_torch[readouts_top[i]][i]
intermediate_strings.append(y_torch_i[0:lengths_top[i], :])
return intermediate_strings
def _feed_bottom_lstm(self, intermediate_strings, input_seq, coeff_size=1):
"""Feed all input sequences into the LSTM models.
Args:
intermediate_strings: top level strings
input_seq: input sequences fed to the top LSTM
coeff_size: sets centre origin
Returns:
strokes: Painting strokes.
painting_commands: Top-level painting commands with origin, angle and scale
information, as well as transparency.
"""
img_center = 112. * coeff_size
coeff_origin = 100. * coeff_size
top_lengths = []
for i in range(len(intermediate_strings)):
top_lengths.append(len(intermediate_strings[i]))
y_flat = np.concatenate(intermediate_strings, axis=0)
tiled_y_flat = y_flat.reshape((len(y_flat), 1, self._input_spec_size))
tiled_y_flat = np.tile(tiled_y_flat, (SEQ_LENGTH, 1))
y_torch = torch.from_numpy(tiled_y_flat).type(torch.FloatTensor)
z_torch = self.bottom_lstm(y_torch)
z_torch = [z_torch_k.detach().numpy() for z_torch_k in z_torch]
del tiled_y_flat
del y_torch
# There are multiple LSTM heads. For each sequence, read out the head and
# length of intermediary output to keep and return intermediary outputs.
readouts = np.clip(np.round(
NUM_LSTMS/2.0 * (1 + y_flat[:, 0])).astype(np.int32), 0, NUM_LSTMS-1)
lengths_bottom = np.clip(
np.round(10.0 * (1 + y_flat[:, 1])).astype(np.int32), 0, SEQ_LENGTH) + 1
strokes = []
painting_commands = []
offset = 0
for i in range(len(intermediate_strings)):
origin_top = [(1+input_seq[i, 2]) * img_center,
(1+input_seq[i, 3]) * img_center]
angle_top = input_seq[i, 4]
scale_top = input_seq[i, 5]
for j in range(len(intermediate_strings[i])):
k = j + offset
z_torch_ij = z_torch[readouts[k]][k]
strokes.append(z_torch_ij[0:lengths_bottom[k], :])
y_ij = y_flat[k]
origin_bottom = [y_ij[2] * coeff_origin, y_ij[3] * coeff_origin]
angle_bottom = y_ij[4]
scale_bottom = y_ij[5]
position_choice = y_ij[6]
transparency = y_ij[7]
painting_command = PaintingCommand(
origin_top, angle_top, scale_top, origin_bottom, angle_bottom,
scale_bottom, position_choice, transparency)
painting_commands.append(painting_command)
offset += top_lengths[i]
del y_flat
return strokes, painting_commands
def make_initial_genotype(self, initial_img, sequence_length,
input_spec_size):
"""Make and return initial DNA weights for LSTMs, input sequence, and image.
Args:
initial_img: Image (to be appended to the genotype)
sequence_length: Length of the input sequence (i.e. number of strokes)
input_spec_size: Number of inputs for each element in the input sequences
Returns:
Genotype NamedTuple with fields: [parameters of network 0,
parameters of network 1,
input sequence,
initial_img]
"""
dna_top = []
with torch.no_grad():
for _, params in self.top_lstm.named_parameters():
dna_top.append(params.clone())
param_size = params.numpy().shape
dna_top[-1] = np.random.uniform(
0.1 * DNA_SCALE, 0.3
* DNA_SCALE) * np.random.normal(size=param_size)
dna_bottom = []
with torch.no_grad():
for _, params in self.bottom_lstm.named_parameters():
dna_bottom.append(params.clone())
param_size = params.numpy().shape
dna_bottom[-1] = np.random.uniform(
0.1 * DNA_SCALE, 0.3
* DNA_SCALE) * np.random.normal(size=param_size)
input_sequence = np.random.uniform(
-1, 1, size=(sequence_length, input_spec_size))
return Genotype(dna_top, dna_bottom, input_sequence, initial_img)
def draw(self, img, genotype):
"""Add to the image using the latest genotype and get latest input sequence.
Args:
img: image to add to.
genotype: as created by make_initial_genotype.
Returns:
image with new strokes added.
"""
t0_draw = time.time()
img = img + genotype.initial_img
input_sequence = genotype.input_sequence
# Generate the strokes for drawing in batch mode.
# input_sequence is between 10 and 20 but is evolved, can go to 200.
intermediate_strings = self._feed_top_lstm(input_sequence)
strokes, painting_commands = self._feed_bottom_lstm(
intermediate_strings, input_sequence)
del intermediate_strings
# Now we can go through the output strings producing the strokes.
t1_draw = time.time()
num_strokes = paint_over_image(
img, strokes, painting_commands, self._allow_strokes_beyond_image_edges,
coeff_size=1)
t2_draw = time.time()
if VERBOSE_CODE:
print(
"Draw {:.2f}s (net {:.2f}s plot {:.2f}s {:.1f}ms/strk {}".format(
t2_draw - t0_draw, t1_draw - t0_draw, t2_draw - t1_draw,
(t2_draw - t1_draw) / num_strokes * 1000, num_strokes))
return img
```
## DrawingGenerator
```
class DrawingGenerator:
"""Creates a drawing using a DrawingLSTM."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.primitives = ["c", "r", "l", "b", "p", "j"]
self.pop = []
self.size = image_size
self.fitnesses = np.zeros(1)
self.noise = 2
self.mutation_std = 0.0004
# input_spec_size, num_lstms, net_lstm_hiddens,
# net_mlp_hiddens, output_size, allow_strokes_beyond_image_edges
self.drawing_lstm = DrawingLSTM(drawing_lstm_spec,
allow_strokes_beyond_image_edges)
def make_initial_genotype(self, initial_img, sequence_length, input_spec_size):
"""Use drawing_lstm to create initial genotypye."""
self.genotype = self.drawing_lstm.make_initial_genotype(
initial_img, sequence_length, input_spec_size)
return self.genotype
def _copy_genotype_to_generator(self, genotype):
"""Copy genotype's data into generator's parameters.
Copies the parameters in genotype (genotype.top_lstm[:] and
genotype.bottom_lstm[:]) into the parmaters for the drawing network so it
can be used to evaluate the genotype.
Args:
genotype: as created by make_initial_genotype.
Returns:
None
"""
self.genotype = copy.deepcopy(genotype)
i = 0
with torch.no_grad():
for _, param in self.drawing_lstm.top_lstm.named_parameters():
param.copy_(torch.tensor(self.genotype.top_lstm[i]))
i = i + 1
i = 0
with torch.no_grad():
for _, param in self.drawing_lstm.bottom_lstm.named_parameters():
param.copy_(torch.tensor(self.genotype.bottom_lstm[i]))
i = i + 1
def _interpret_genotype(self, genotype):
img = np.zeros((self.size, self.size, 3), dtype=np.uint8)
img = self.drawing_lstm.draw(img, genotype)
return img
def draw_from_genotype(self, genotype):
"""Copy input sequence and LSTM weights from `genotype`, run and draw."""
self._copy_genotype_to_generator(genotype)
return self._interpret_genotype(self.genotype)
def visualize_genotype(self, genotype):
"""Plot histograms of genotype"s data."""
plt.show()
inp_seq = np.array(genotype.input_sequence).flatten()
plt.title("input seq")
plt.hist(inp_seq)
plt.show()
inp_seq = np.array(genotype.top_lstm).flatten()
plt.title("LSTM top")
plt.hist(inp_seq)
plt.show()
inp_seq = np.array(genotype.bottom_lstm).flatten()
plt.title("LSTM bottom")
plt.hist(inp_seq)
plt.show()
def mutate(self, genotype):
"""Mutates `genotype`. This function is static.
Args:
genotype: genotype structure to mutate parameters of.
Returns:
new_genotype: Mutated copy of supplied genotype.
"""
new_genotype = copy.deepcopy(genotype)
new_input_seq = new_genotype.input_sequence
n = len(new_input_seq)
if np.random.uniform() < 1.0:
# Standard gaussian small mutation of input sequence.
if np.random.uniform() > 0.5:
new_input_seq += (
np.random.uniform(0.001, 0.2) * np.random.normal(
size=new_input_seq.shape))
# Low frequency large mutation of individual parts of the input sequence.
for i in range(n):
if np.random.uniform() < 2.0/n:
for j in range(len(new_input_seq[i])):
if np.random.uniform() < 2.0/len(new_input_seq[i]):
new_input_seq[i][j] = new_input_seq[i][j] + 0.5*np.random.normal()
# Adding and deleting elements from the input sequence.
if np.random.uniform() < 0.01:
if VERBOSE_MUTATION:
print("Mutation: adding")
a = np.random.uniform(-1, 1, size=(1, INPUT_SPEC_SIZE))
pos = np.random.randint(1, len(new_input_seq))
new_input_seq = np.insert(new_input_seq, pos, a, axis=0)
if np.random.uniform() < 0.02:
if VERBOSE_MUTATION:
print("Mutation: deleting")
pos = np.random.randint(1, len(new_input_seq))
new_input_seq = np.delete(new_input_seq, pos, axis=0)
n = len(new_input_seq)
# Swapping two elements in the input sequence.
if np.random.uniform() < 0.01:
element1 = np.random.randint(0, n)
element2 = np.random.randint(0, n)
while element1 == element2:
element2 = np.random.randint(0, n)
temp = copy.deepcopy(new_input_seq[element1])
new_input_seq[element1] = copy.deepcopy(new_input_seq[element2])
new_input_seq[element2] = temp
# Duplicate an element in the input sequence (with some mutation).
if np.random.uniform() < 0.01:
if VERBOSE_MUTATION:
print("Mutation: duplicating")
element1 = np.random.randint(0, n)
element2 = np.random.randint(0, n)
while element1 == element2:
element2 = np.random.randint(0, n)
new_input_seq[element1] = copy.deepcopy(new_input_seq[element2])
noise = 0.05 * np.random.normal(size=new_input_seq[element1].shape)
new_input_seq[element1] += noise
# Ensure that the input sequence is always between -1 and 1
# so that positions make sense.
new_genotype = new_genotype._replace(
input_sequence=np.clip(new_input_seq, -1.0, 1.0))
# Mutates dna of networks.
if np.random.uniform() < 1.0:
for net in range(2):
for layer in range(len(new_genotype[net])):
weights = new_genotype[net][layer]
if np.random.uniform() < 0.5:
noise = 0.00001 * np.random.standard_cauchy(size=weights.shape)
weights += noise
else:
noise = np.random.normal(size=weights.shape)
noise *= np.random.uniform(0.0001, 0.006)
weights += noise
if np.random.uniform() < 0.01:
noise = np.random.normal(size=weights.shape)
noise *= np.random.uniform(0.1, 0.3)
weights = noise
# Ensure weights are between -10 and 10.
weights = np.clip(weights, -1.0, 1.0)
new_genotype[net][layer] = weights
return new_genotype
```
## Evaluator
```
class Evaluator:
"""Evaluator for a drawing."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.drawing_generator = DrawingGenerator(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges)
self.calls = 0
def make_initial_genotype(self, img, sequence_length, input_spec_size):
return self.drawing_generator.make_initial_genotype(img, sequence_length,
input_spec_size)
def evaluate_genotype(self, pickled_genotype, id_num):
"""Evaluate genotype and return genotype's image.
Args:
pickled_genotype: pickled genotype to be evaluated.
id_num: ID number of genotype.
Returns:
dict: drawing and id_num.
"""
genotype = cloudpickle.loads(pickled_genotype)
drawing = self.drawing_generator.draw_from_genotype(genotype)
self.calls += 1
return {"drawing": drawing, "id": id_num}
def mutate(self, genotype):
"""Create a mutated version of genotype."""
return self.drawing_generator.mutate(genotype)
```
# Evolution
## Fitness calculation, tournament, and crossover
```
IMAGE_MEAN = torch.tensor([0.48145466, 0.4578275, 0.40821073]).cuda()
IMAGE_STD = torch.tensor([0.26862954, 0.26130258, 0.27577711]).cuda()
def get_fitness(pictures, use_projective_transform,
projective_transform_coefficient):
"""Run CLIP on a batch of `pictures` and return `fitnesses`.
Args:
pictures: batch if images to evaluate
use_projective_transform: Add transformed versions of the image
projective_transform_coefficient: Degree of transform
Returns:
Similarities between images and the text
"""
# Do we use projective transforms of images before CLIP eval?
t0 = time.time()
pictures_trans = np.swapaxes(np.array(pictures), 1, 3) / 244.0
if use_projective_transform:
for i in range(len(pictures_trans)):
matrix = np.eye(3) + (
projective_transform_coefficient * np.random.normal(size=(3, 3)))
tform = transform.ProjectiveTransform(matrix=matrix)
pictures_trans[i] = transform.warp(pictures_trans[i], tform.inverse)
# Run the CLIP evaluator.
t1 = time.time()
image_input = torch.tensor(np.stack(pictures_trans)).cuda()
image_input -= IMAGE_MEAN[:, None, None]
image_input /= IMAGE_STD[:, None, None]
with torch.no_grad():
image_features = model.encode_image(image_input).float()
t2 = time.time()
similarity = torch.cosine_similarity(
text_features, image_features, dim=1).cpu().numpy()
t3 = time.time()
if VERBOSE_CODE:
print(f"get_fitness init {t1-t0:.4f}s, CLIP {t2-t1:.4f}s, sim {t3-t2:.4f}s")
return similarity
def crossover(dna_winner, dna_loser, crossover_prob):
"""Create new genotype by combining two genotypes.
Randomly replaces parts of the genotype 'dna_winner' with parts of dna_loser
to create a new genotype based mostly on on both 'parents'.
Args:
dna_winner: The high-fitness parent genotype - gets replaced with child.
dna_loser: The lower-fitness parent genotype.
crossover_prob: Probability of crossover between winner and loser.
Returns:
dna_winner: The result of crossover from parents.
"""
# Copy single input signals
for i in range(len(dna_winner[2])):
if i < len(dna_loser[2]):
if np.random.uniform() < crossover_prob:
dna_winner[2][i] = copy.deepcopy(dna_loser[2][i])
# Copy whole modules
for i in range(len(dna_winner[0])):
if i < len(dna_loser[0]):
if np.random.uniform() < crossover_prob:
dna_winner[0][i] = copy.deepcopy(dna_loser[0][i])
# Copy whole modules
for i in range(len(dna_winner[1])):
if i < len(dna_loser[1]):
if np.random.uniform() < crossover_prob:
dna_winner[1][i] = copy.deepcopy(dna_loser[1][i])
return dna_winner
def truncation_selection(population, fitnesses, evaluator, use_crossover,
crossover_prob):
"""Create new population using truncation selection.
Creates a new population by copying across the best 50% genotypes and
filling the rest with (for use_crossover==False) a mutated copy of each
genotype or (for use_crossover==True) with children created through crossover
between each winner and a genotype in the bottom 50%.
Args:
population: list of current population genotypes.
fitnesses: list of evaluated fitnesses.
evaluator: class that evaluates a draw generator.
use_crossover: Whether to use crossover between winner and loser.
crossover_prob: Probability of crossover between winner and loser.
Returns:
new_pop: the new population.
best: genotype.
"""
fitnesses = np.array(-fitnesses)
ordered_fitness_ids = fitnesses.argsort()
best = copy.deepcopy(population[ordered_fitness_ids[0]])
pop_size = len(population)
if not use_crossover:
new_pop = []
for i in range(int(pop_size/2)):
new_pop.append(copy.deepcopy(population[ordered_fitness_ids[i]]))
for i in range(int(pop_size/2)):
new_pop.append(evaluator.mutate(
copy.deepcopy(population[ordered_fitness_ids[i]])))
else:
new_pop = []
for i in range(int(pop_size/2)):
new_pop.append(copy.deepcopy(population[ordered_fitness_ids[i]]))
for i in range(int(pop_size/2)):
new_pop.append(evaluator.mutate(crossover(
copy.deepcopy(population[ordered_fitness_ids[i]]),
population[ordered_fitness_ids[int(pop_size/2) + i]], crossover_prob
)))
return new_pop, best
```
##Remote workers
```
VERBOSE_DURATION = False
@ray.remote
class Worker(object):
"""Takes a pickled dna and evaluates it, returning result."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.evaluator = Evaluator(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges)
def compute(self, dna_pickle, genotype_id):
if VERBOSE_DURATION:
t0 = time.time()
res = self.evaluator.evaluate_genotype(dna_pickle, genotype_id)
if VERBOSE_DURATION:
duration = time.time() - t0
print(f"Worker {genotype_id} evaluated params in {duration:.1f}sec")
return res
def create_workers(num_workers, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
"""Create the workers.
Args:
num_workers: Number of parallel workers for evaluation.
image_size: Length of side of (square) image
drawing_lstm_spec: DrawingLSTMSpec for LSTM network
allow_strokes_beyond_image_edges: Whether to draw outside the edges
Returns:
List of workers.
"""
worker_pool = []
for w_i in range(num_workers):
print("Creating worker", w_i, flush=True)
worker_pool.append(Worker.remote(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges))
return worker_pool
```
##Plotting
```
def plot_training_res(batch_drawings, fitness_history, idx=None):
"""Plot fitnesses and timings.
Args:
batch_drawings: Drawings
fitness_history: History of fitnesses
idx: Index of drawing to show, default is highest fitness
"""
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
if idx is None:
idx = np.argmax(fitness_history[-1])
ax1.plot(fitness_history, ".")
ax1.set_title("Fitnesses")
ax2.imshow(batch_drawings[idx])
ax2.set_title(f"{PROMPT} (fit: {fitness_history[-1][idx]:.3f})")
plt.show()
def plot_samples(batch_drawings, num_samples=16):
"""Plot sample of drawings.
Args:
batch_drawings: Batch of drawings to sample from
num_samples: Number to displa
"""
num_samples = min(len(batch_drawings), num_samples)
num_rows = int(math.floor(np.sqrt(num_samples)))
num_cols = int(math.ceil(num_samples / num_rows))
row_images = []
for c in range(0, num_samples, num_cols):
if c + num_cols <= num_samples:
row_images.append(np.concatenate(batch_drawings[c:(c+num_cols)], axis=1))
composite_image = np.concatenate(row_images, axis=0)
_, ax = plt.subplots(1, 1, figsize=(20, 20))
ax.imshow(composite_image)
ax.set_title(PROMPT)
```
## Population and evolution main loop
```
def make_population(pop_size, evaluator, image_size, input_spec_size,
sequence_length):
"""Make initial population.
Args:
pop_size: number of genotypes in population.
evaluator: An Evaluator class instance for generating initial genotype.
image_size: Size of initial image for genotype to draw on.
input_spec_size: Sequence element size
sequence_length: Initial length of sequences
Returns:
Initialised population.
"""
print(f"Creating initial population of size {pop_size}")
pop = []
for _ in range(pop_size):
a_genotype = evaluator.make_initial_genotype(
img=np.zeros((image_size, image_size, 3), dtype=np.uint8),
sequence_length=sequence_length,
input_spec_size=input_spec_size)
pop.append(a_genotype)
return pop
def evolution_loop(population, worker_pool, evaluator, num_generations,
use_crossover, crossover_prob,
use_projective_transform, projective_transform_coefficient,
plot_every, plot_batch):
"""Create population and run evolution.
Args:
population: Initial population of genotypes
worker_pool: List of workers of parallel evaluations
evaluator: image evaluator to calculate fitnesses
num_generations: number of generations to run
use_crossover: Whether crossover is used for offspring
crossover_prob: Probability that crossover takes place
use_projective_transform: Use projective transforms in evaluation
projective_transform_coefficient: Degree of projective transform
plot_every: number of generations between new plots
plot_batch: whether to show all samples in the batch then plotting
"""
population_size = len(population)
num_workers = len(worker_pool)
print("Population of {} genotypes being evaluated by {} workers".format(
population_size, num_workers))
drawings = {}
fitness_history = []
init_gen = len(fitness_history)
print(f"(Re)starting evolution at generation {init_gen}")
for gen in range(init_gen, num_generations):
# Drawing
t0_loop = time.time()
futures = []
for j in range(0, population_size, num_workers):
for i in range(num_workers):
futures.append(worker_pool[i].compute.remote(
cloudpickle.dumps(population[i+j]), i+j))
data = ray.get(futures)
for i in range(num_workers):
drawings[data[i+j]["id"]] = data[j+i]["drawing"]
batch_drawings = []
for i in range(population_size):
batch_drawings.append(drawings[i])
# Fitness evaluation using CLIP
t1_loop = time.time()
fitnesses = get_fitness(batch_drawings, use_projective_transform,
projective_transform_coefficient)
fitness_history.append(copy.deepcopy(fitnesses))
# Tournament
t2_loop = time.time()
population, best_genotype = truncation_selection(
population, fitnesses, evaluator, use_crossover, crossover_prob)
t3_loop = time.time()
duration_draw = t1_loop - t0_loop
duration_fit = t2_loop - t1_loop
duration_tournament = t3_loop - t2_loop
duration_total = t3_loop - t0_loop
if gen % plot_every == 0:
if VISUALIZE_GENOTYPE:
evaluator.drawing_generator.visualize_genotype(best_genotype)
print("Draw: {:.2f}s fit: {:.2f}s evol: {:.2f}s total: {:.2f}s".format(
duration_draw, duration_fit, duration_tournament, duration_total))
plot_training_res(batch_drawings, fitness_history)
if plot_batch:
num_samples_to_plot = int(math.pow(
math.floor(np.sqrt(population_size)), 2))
plot_samples(batch_drawings, num_samples=num_samples_to_plot)
```
# Configure and Generate
```
#@title Hyperparameters
#@markdown Evolution parameters: population size and number of generations.
POPULATION_SIZE = 10 #@param {type:"slider", min:4, max:100, step:2}
NUM_GENERATIONS = 5000 #@param {type:"integer", min:100}
#@markdown Number of workers working in parallel (should be equal to or smaller than the population size).
NUM_WORKERS = 10 #@param {type:"slider", min:4, max:100, step:2}
#@markdown Crossover in evolution.
USE_CROSSOVER = True #@param {type:"boolean"}
CROSSOVER_PROB = 0.01 #@param {type:"number"}
#@markdown Number of LSTMs, each one encoding a group of strokes.
NUM_LSTMS = 5 #@param {type:"integer", min:1, max:5}
#@markdown Number of inputs for each element in the input sequences.
INPUT_SPEC_SIZE = 10 #@param {type:"integer"}
#@markdown Length of the input sequence fed to the LSTMs (determines number of strokes).
SEQ_LENGTH = 20 #@param {type:"integer", min:20, max:200}
#@markdown Rendering parameter.
ALLOW_STROKES_BEYOND_IMAGE_EDGES = True #@param {type:"boolean"}
#@markdown CLIP evaluation: do we use projective transforms of images?
USE_PROJECTIVE_TRANSFORM = True #@param {type:"boolean"}
PROJECTIVE_TRANSFORM_COEFFICIENT = 0.000001 #@param {type:"number"}
#@markdown These parameters should be edited mostly only for debugging reasons.
NET_LSTM_HIDDENS = 40 #@param {type:"integer"}
NET_MLP_HIDDENS = 20 #@param {type:"integer"}
# Scales the values used in genotype's initialisation.
DNA_SCALE = 1.0 #@param {type:"number"}
IMAGE_SIZE = 224 #@param {type:"integer"}
VERBOSE_CODE = False #@param {type:"boolean"}
VISUALIZE_GENOTYPE = False #@param {type:"boolean"}
VERBOSE_MUTATION = False #@param {type:"boolean"}
#@markdown Number of generations between new plots.
PLOT_EVERY_NUM_GENS = 5 #@param {type:"integer"}
#@markdown Whether to show all samples in the batch when plotting.
PLOT_BATCH = True # @param {type:"boolean"}
assert POPULATION_SIZE % NUM_WORKERS == 0, "POPULATION_SIZE not multiple of NUM_WORKERS"
```
#Running the original evolutionary algorithm
This is the original inefficient version of Arnheim which uses a genetic algorithm to optimize the picture. It takes at least 12 hours to produce an image using 50 workers. In our paper we used 500-1000 GPUs which speeded things up considerably. Refer to Arnheim 2 for a far more efficient way to generate images with a similar architecture.
Try prompts like “A photorealistic chicken”. Feel free to modify this colab to include your own way of generating and evolving images like we did in figure 2 here https://arxiv.org/pdf/2105.00162.pdf.
```
# @title Get text input and run evolution
PROMPT = "an apple" #@param {type:"string"}
# Tokenize prompts and coompute CLIP features.
text_input = clip.tokenize(PROMPT).to(device)
with torch.no_grad():
text_features = model.encode_text(text_input)
ray.shutdown()
ray.init()
drawing_lstm_arch = DrawingLSTMSpec(INPUT_SPEC_SIZE,
NUM_LSTMS,
NET_LSTM_HIDDENS,
NET_MLP_HIDDENS)
workers = create_workers(NUM_WORKERS, IMAGE_SIZE, drawing_lstm_arch,
ALLOW_STROKES_BEYOND_IMAGE_EDGES)
drawing_evaluator = Evaluator(IMAGE_SIZE, drawing_lstm_arch,
ALLOW_STROKES_BEYOND_IMAGE_EDGES)
drawing_population = make_population(POPULATION_SIZE, drawing_evaluator,
IMAGE_SIZE, INPUT_SPEC_SIZE, SEQ_LENGTH)
evolution_loop(drawing_population, workers, drawing_evaluator, NUM_GENERATIONS,
USE_CROSSOVER, CROSSOVER_PROB,
USE_PROJECTIVE_TRANSFORM, PROJECTIVE_TRANSFORM_COEFFICIENT,
PLOT_EVERY_NUM_GENS, PLOT_BATCH)
```
| true |
code
| 0.587292 | null | null | null | null |
|
# CRRT Mortality Prediction
## Model Construction
### Christopher V. Cosgriff, David Sasson, Colby Wilkinson, Kanhua Yin
The purpose of this notebook is to build a deep learning model that predicts ICU mortality in the CRRT population. The data is extracted in the `extract_cohort_and_features` notebook and stored in the `data` folder. This model will be mult-input and use GRUs to model sequence data. See the extraction file for a full description of the data extraction.
## Step 0: Envrionment Setup
```
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from IPython.display import SVG
import os
from keras.optimizers import Adam, SGD, rmsprop
from keras.models import Sequential,Model
from keras.layers import Dense, Activation, Dropout, Input, Dropout, concatenate
from keras.layers.recurrent import GRU
from keras.utils import plot_model
from keras.utils.vis_utils import model_to_dot
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, roc_curve
# for saving images
fig_fp = os.path.join('./', 'figures')
if not os.path.isdir(fig_fp):
os.mkdir(fig_fp)
%matplotlib inline
```
## Step 1: Load and Prepare Data
Here will we load in the data, and create train, validation, and testing splits.
```
# set tensors to float 32 as this is what GPUs expect
features_sequence = np.load('./features_sequence.npy').astype(np.float32)
features_static = np.load('./features_static.npy').astype(np.float32)
labels = np.load('./labels.npy').astype(np.float32)
x_seq_full_train, x_seq_test, x_static_full_train, x_static_test, y_full_train, y_test = train_test_split(
features_sequence, features_static, labels, test_size = 0.20, random_state = 42)
x_seq_train, x_seq_val, x_static_train, x_static_val, y_train, y_val = train_test_split(
x_seq_full_train, x_static_full_train, y_full_train, test_size = 0.10, random_state = 42)
```
Next we need to remove NANs from the data; we'll impute the trianing population mean, the simplest method suggested by David Sontag.
```
def impute_mean(source_data, input_data):
'''
Takes the source data, and uses it to determine means for all
features; it then applies them to the input data.
inputs:
source_data: a tensor to provide means
input_data: the data to fill in NA for
output:
output_data: data with nans imputed for each feature
'''
output_data = input_data.copy()
for feature in range(source_data.shape[1]):
feature_mean = np.nanmean(source_data[:, feature, :][np.where(source_data[:, feature, :] != 0)])
ind_output_data = np.where(np.isnan(output_data[:, feature, :]))
output_data[:, feature, :][ind_output_data] = feature_mean
return output_data
x_seq_train_original = x_seq_train.copy()
x_seq_train = impute_mean(x_seq_train_original, x_seq_train)
x_seq_val = impute_mean(x_seq_train_original, x_seq_val)
x_seq_test = impute_mean(x_seq_train_original, x_seq_test)
```
## Step 2: Build Model
### Model 1
Base model, no regularization.
```
# Define inputs
sequence_input = Input(shape = (x_seq_train.shape[1], x_seq_train.shape[2], ), dtype = 'float32', name = 'sequence_input')
static_input = Input(shape = (x_static_train.shape[1], ), name = 'static_input')
# Network architecture
seq_x = GRU(units = 128)(sequence_input)
# Seperate output for the GRU later
seq_aux_output = Dense(1, activation='sigmoid', name='aux_output')(seq_x)
# Merge dual inputs
x = concatenate([seq_x, static_input])
# We stack a deep fully-connected network on the merged inputs
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
# Sigmoid output layer
main_output = Dense(1, activation='sigmoid', name='main_output')(x)
# optimizer
opt = rmsprop(lr = 0.00001)
# build model
model = Model(inputs = [sequence_input, static_input], outputs = [main_output, seq_aux_output])
model.compile(optimizer = opt, loss = 'binary_crossentropy', metrics = ['accuracy'], loss_weights = [1, 0.1])
# save a plot of the model
plot_model(model, to_file='experiment_GRU-base.svg')
# fit the model
history = model.fit([x_seq_train, x_static_train], [y_train, y_train], epochs = 500, batch_size = 128,\
validation_data=([x_seq_val, x_static_val], [y_val, y_val]),)
# plot the fit
pred_main, pred_aux = model.predict([x_seq_test, x_static_test])
roc = roc_curve(y_test, pred_main)
auc = roc_auc_score(y_test, pred_main)
fig = plt.figure(figsize=(4, 3)) # in inches
plt.plot(roc[0], roc[1], color = 'darkorange', label = 'ROC curve\n(area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color= 'navy', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('%s: ROC' % 'GRU-base')
plt.legend(loc = "lower right")
fig_name = 'gru-base.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
plt.show()
# plot training and validation loss and accuracy
acc = history.history['main_output_acc']
val_acc = history.history['val_main_output_acc']
loss = history.history['main_output_loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
fig_name = 'loss_svg.svg'
fig.savefig('./loss_svg.svg', bbox_inches='tight')
```
### 10% Dropout
```
# Define inputs
sequence_input = Input(shape = (x_seq_train.shape[1], x_seq_train.shape[2], ), dtype = 'float32', name = 'sequence_input')
static_input = Input(shape = (x_static_train.shape[1], ), name = 'static_input')
# Network architecture
seq_x = GRU(units = 128)(sequence_input)
# Seperate output for the GRU later
seq_aux_output = Dense(1, activation='sigmoid', name='aux_output')(seq_x)
# Merge dual inputs
x = concatenate([seq_x, static_input])
# We stack a deep fully-connected network on the merged inputs
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dropout(0.10)(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
# Sigmoid output layer
main_output = Dense(1, activation='sigmoid', name='main_output')(x)
# optimizer
opt = rmsprop(lr = 0.00001)
# build model
model = Model(inputs = [sequence_input, static_input], outputs = [main_output, seq_aux_output])
model.compile(optimizer = opt, loss = 'binary_crossentropy', metrics = ['accuracy'], loss_weights = [1, 0.1])
# save a plot of the model
#plot_model(model, to_file='experiment_GRU-DO.svg')
# fit the model
history = model.fit([x_seq_train, x_static_train], [y_train, y_train], epochs = 500, batch_size = 128,\
validation_data=([x_seq_val, x_static_val], [y_val, y_val]),)
# plot the fit
pred_main, pred_aux = model.predict([x_seq_test, x_static_test])
roc = roc_curve(y_test, pred_main)
auc = roc_auc_score(y_test, pred_main)
fig = plt.figure(figsize=(4, 3)) # in inches
plt.plot(roc[0], roc[1], color = 'darkorange', label = 'ROC curve\n(area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color= 'navy', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('%s: ROC' % 'GRU-base')
plt.legend(loc = "lower right")
fig_name = 'gru-do.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
plt.show()
# plot training and validation loss and accuracy
acc = history.history['main_output_acc']
val_acc = history.history['val_main_output_acc']
loss = history.history['main_output_loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
fig_name = 'do_loss_acc.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
```
| true |
code
| 0.709069 | null | null | null | null |
|
# Emotion recognition using Emo-DB dataset and scikit-learn
### Database: Emo-DB database (free) 7 emotions
The data can be downloaded from http://emodb.bilderbar.info/index-1024.html
Code of emotions
W->Anger->Wut
L->Boredom->Langeweile
E->Disgust->Ekel
A->Anxiety/Fear->Angst
F->Happiness->Freude
T->Sadness->Trauer
N->Neutral

```
import requests
import zipfile
import os
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
import itertools
import sys
sys.path.append("../")
from plots_examples import plot_confusion_matrix, plot_ROC, plot_histogram
# disvoice imports
from phonation.phonation import Phonation
from articulation.articulation import Articulation
from prosody.prosody import Prosody
from phonological.phonological import Phonological
from replearning.replearning import RepLearning
# sklearn methods
from sklearn.model_selection import RandomizedSearchCV, train_test_split
from sklearn import preprocessing
from sklearn import metrics
from sklearn import svm
```
## Download and unzip data
```
def download_url(url, save_path, chunk_size=128):
r = requests.get(url, stream=True)
with open(save_path, 'wb') as fd:
for chunk in r.iter_content(chunk_size=chunk_size):
fd.write(chunk)
PATH_data="http://emodb.bilderbar.info/download/download.zip"
download_url(PATH_data, "./download.zip")
with zipfile.ZipFile("./download.zip", 'r') as zip_ref:
zip_ref.extractall("./emo-db/")
```
## prepare labels from the dataset
we will get labels for two classification problems:
1. high vs. low arousal emotions
2. positive vs. negative emotions
```
PATH_AUDIO=os.path.abspath("./emo-db/wav")+"/"
labelsd='WLEAFTN'
labelshl= [0, 1, 0, 0, 0, 1, 1] # 0 high arousal emotion, 1 low arousal emotions
labelspn= [0, 0, 0, 0, 1, 0, 1] # 0 negative valence emotion, 1 positive valence emotion
hf=os.listdir(PATH_AUDIO)
hf.sort()
yArousal=np.zeros(len(hf))
yValence=np.zeros(len(hf))
for j in range(len(hf)):
name_file=hf[j]
label=hf[j][5]
poslabel=labelsd.find(label)
yArousal[j]=labelshl[poslabel]
yValence[j]=labelspn[poslabel]
```
## compute features using disvoice: phonation, articulation, prosody, phonological
```
phonationf=Phonation()
articulationf=Articulation()
prosodyf=Prosody()
phonologicalf=Phonological()
replearningf=RepLearning('CAE')
```
### phonation features
```
Xphonation=phonationf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xphonation.shape)
```
### articulation features
```
Xarticulation=articulationf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xarticulation.shape)
```
### prosody features
```
Xprosody=prosodyf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xprosody.shape)
```
### phonological features
```
Xphonological=phonologicalf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xphonological.shape)
```
### representation learning features
```
Xrep=replearningf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xrep.shape)
```
### Emotion classification using an SVM classifier
```
def classify(X, y):
# train test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.30, random_state=42)
# z-score standarization
scaler = preprocessing.StandardScaler().fit(Xtrain)
Xtrain=scaler.transform(Xtrain)
Xtest=scaler.transform(Xtest)
Results=[]
# randomized search cross-validation to optimize hyper-parameters of SVM
parameters = {'kernel':['rbf'], 'class_weight': ['balanced'],
'C':st.expon(scale=10),
'gamma':st.expon(scale=0.01)}
svc = svm.SVC()
clf=RandomizedSearchCV(svc, parameters, n_jobs=4, cv=10, verbose=1, n_iter=200, scoring='balanced_accuracy')
clf.fit(Xtrain, ytrain) # train the SVM
accDev= clf.best_score_ # validation accuracy
Copt=clf.best_params_.get('C') # best C
gammaopt=clf.best_params_.get('gamma') # best gamma
# train the SVM with the optimal hyper-parameters
cls=svm.SVC(kernel='rbf', C=Copt, gamma=gammaopt, class_weight='balanced')
cls.fit(Xtrain, ytrain)
ypred=cls.predict(Xtest) # test predictions
# check the results
acc=metrics.accuracy_score(ytest, ypred)
score_test=cls.decision_function(Xtest)
dfclass=metrics.classification_report(ytest, ypred,digits=4)
# display the results
plot_confusion_matrix(ytest, ypred, classes=["class 0", "class 1"], normalize=True)
plot_ROC(ytest, score_test)
plot_histogram(ytest, score_test, name_clases=["class 0", "class 1"])
print("Accuracy: ", acc)
print(dfclass)
```
## classify high vs. low arousal with the different feature sets
```
classify(Xphonation, yArousal)
classify(Xarticulation, yArousal)
classify(Xprosody, yArousal)
classify(Xphonological, yArousal)
classify(Xrep, yArousal)
```
## classify positive vs. negative valence with the different feature sets
```
classify(Xphonation, yValence)
classify(Xarticulation, yValence)
classify(Xprosody, yValence)
classify(Xphonological, yValence)
classify(Xrep, yValence)
```
| true |
code
| 0.459197 | null | null | null | null |
|
# How to make the perfect time-lapse of the Earth
This tutorial shows a detail coverage of making time-lapse animations from satellite imagery like a pro.
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#0.-Prerequisites" data-toc-modified-id="0.-Prerequisites-1">0. Prerequisites</a></span></li><li><span><a href="#1.-Removing-clouds" data-toc-modified-id="1.-Removing-clouds-2">1. Removing clouds</a></span></li><li><span><a href="#2.-Applying-co-registration" data-toc-modified-id="2.-Applying-co-registration-3">2. Applying co-registration</a></span></li><li><span><a href="#3.-Large-Area-Example" data-toc-modified-id="3.-Large-Area-Example-4">3. Large Area Example</a></span></li><li><span><a href="#4.-Split-Image" data-toc-modified-id="4.-Split-Image-5">4. Split Image</a></span></li></ul></div>
Note: This notebook requires an installation of additional packages `ffmpeg-python` and `ipyleaflet`.
```
%load_ext autoreload
%autoreload 2
import datetime as dt
import json
import os
import subprocess
from concurrent.futures import ProcessPoolExecutor
from datetime import date, datetime, time, timedelta
from functools import partial
from glob import glob
import ffmpeg
import geopandas as gpd
import imageio
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shapely
from ipyleaflet import GeoJSON, Map, basemaps
from shapely.geometry import Polygon
from tqdm.auto import tqdm
from eolearn.core import (EOExecutor, EOPatch, EOTask, FeatureType,
LinearWorkflow, LoadTask, OverwritePermission,
SaveTask, ZipFeatureTask)
from eolearn.coregistration import ECCRegistration
from eolearn.features import LinearInterpolation, SimpleFilterTask
from eolearn.io import ExportToTiff, ImportFromTiff, SentinelHubInputTask
from eolearn.mask import CloudMaskTask
from sentinelhub import (CRS, BatchSplitter, BBox, BBoxSplitter,
DataCollection, Geometry, MimeType, SentinelHubBatch,
SentinelHubRequest, SHConfig, bbox_to_dimensions)
```
## 0. Prerequisites
In order to set everything up and make the credentials work, please check [this notebook](https://github.com/sentinel-hub/eo-learn/blob/master/examples/io/SentinelHubIO.ipynb).
```
class AnimateTask(EOTask):
def __init__(self, image_dir, out_dir, out_name, feature=(FeatureType.DATA, 'RGB'), scale_factor=2.5, duration=3, dpi=150, pad_inches=None, shape=None):
self.image_dir = image_dir
self.out_name = out_name
self.out_dir = out_dir
self.feature = feature
self.scale_factor = scale_factor
self.duration = duration
self.dpi = dpi
self.pad_inches = pad_inches
self.shape = shape
def execute(self, eopatch):
images = np.clip(eopatch[self.feature]*self.scale_factor, 0, 1)
fps = len(images)/self.duration
subprocess.run(f'rm -rf {self.image_dir} && mkdir {self.image_dir}', shell=True)
for idx, image in enumerate(images):
if self.shape:
fig = plt.figure(figsize=(self.shape[0], self.shape[1]))
plt.imshow(image)
plt.axis(False)
plt.savefig(f'{self.image_dir}/image_{idx:03d}.png', bbox_inches='tight', dpi=self.dpi, pad_inches = self.pad_inches)
plt.close()
# video related
stream = ffmpeg.input(f'{self.image_dir}/image_*.png', pattern_type='glob', framerate=fps)
stream = stream.filter('pad', w='ceil(iw/2)*2', h='ceil(ih/2)*2', color='white')
split = stream.split()
video = split[0]
# gif related
palette = split[1].filter('palettegen', reserve_transparent=True, stats_mode='diff')
gif = ffmpeg.filter([split[2], palette], 'paletteuse', dither='bayer', bayer_scale=5, diff_mode='rectangle')
# save output
os.makedirs(self.out_dir, exist_ok=True)
video.output(f'{self.out_dir}/{self.out_name}.mp4', crf=15, pix_fmt='yuv420p', vcodec='libx264', an=None).run(overwrite_output=True)
gif.output(f'{self.out_dir}/{self.out_name}.gif').run(overwrite_output=True)
return eopatch
```
## 1. Removing clouds
```
# https://twitter.com/Valtzen/status/1270269337061019648
bbox = BBox(bbox=[-73.558102,45.447728,-73.488750,45.491908], crs=CRS.WGS84)
resolution = 10
time_interval = ('2018-01-01', '2020-01-01')
print(f'Image size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=13
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
mosaicking_order='leastCC',
additional_data=[
(FeatureType.MASK, 'CLM'),
(FeatureType.MASK, 'dataMask')
]
)
def valid_coverage_thresholder_f(valid_mask, more_than=0.95):
coverage = np.count_nonzero(valid_mask)/np.prod(valid_mask.shape)
return coverage > more_than
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
filter_task = SimpleFilterTask((FeatureType.MASK, 'VALID_DATA'), valid_coverage_thresholder_f)
name = 'clm_service'
anim_task = AnimateTask(image_dir = './images', out_dir = './animations', out_name=name, duration=5, dpi=200)
params = {'MaxIters': 500}
coreg_task = ECCRegistration((FeatureType.DATA, 'RGB'), channel=2, params=params)
name = 'clm_service_coreg'
anim_task_after = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
workflow = LinearWorkflow(
download_task,
valid_mask_task,
filter_task,
anim_task,
coreg_task,
anim_task_after
)
result = workflow.execute({
download_task: {'bbox': bbox, 'time_interval': time_interval}
})
```
## 2. Applying co-registration
```
bbox = BBox(bbox=[34.716, 30.950, 34.743, 30.975], crs=CRS.WGS84)
resolution = 10
time_interval = ('2020-01-01', '2021-01-01')
print(f'BBox size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=14
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task_l2a = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l2a')
]
)
download_task_l1c = SentinelHubInputTask(
bands_feature = (FeatureType.DATA, 'BANDS'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L1C,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l1c')
]
)
data_mask_merge = ZipFeatureTask({FeatureType.MASK: ['dataMask_l1c', 'dataMask_l2a']}, (FeatureType.MASK, 'dataMask'),
lambda dm1, dm2: np.all([dm1, dm2], axis=0))
cloud_masking_task = CloudMaskTask(
data_feature=(FeatureType.DATA, 'BANDS'),
is_data_feature='dataMask',
all_bands=True,
processing_resolution=120,
mono_features=None,
mask_feature='CLM',
average_over=16,
dilation_size=12,
mono_threshold=0.2
)
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
filter_task = SimpleFilterTask((FeatureType.MASK, 'VALID_DATA'), valid_coverage_thresholder_f)
name = 'wo_coreg_anim'
anim_task_before = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
params = {'MaxIters': 500}
coreg_task = ECCRegistration((FeatureType.DATA, 'RGB'), channel=2, params=params)
name = 'coreg_anim'
anim_task_after = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
workflow = LinearWorkflow(
download_task_l2a,
download_task_l1c,
data_mask_merge,
cloud_masking_task,
valid_mask_task,
filter_task,
anim_task_before,
coreg_task,
anim_task_after
)
result = workflow.execute({
download_task_l2a: {'bbox': bbox, 'time_interval': time_interval}
})
```
## 3. Large Area Example
```
bbox = BBox(bbox=[21.4,-20.0,23.9,-18.0], crs=CRS.WGS84)
time_interval = ('2017-09-01', '2019-04-01')
# time_interval = ('2017-09-01', '2017-10-01')
resolution = 640
print(f'BBox size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=8
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task_l2a = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l2a')
],
aux_request_args={'dataFilter': {'previewMode': 'PREVIEW'}}
)
download_task_l1c = SentinelHubInputTask(
bands_feature = (FeatureType.DATA, 'BANDS'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L1C,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l1c')
],
aux_request_args={'dataFilter': {'previewMode': 'PREVIEW'}}
)
data_mask_merge = ZipFeatureTask({FeatureType.MASK: ['dataMask_l1c', 'dataMask_l2a']}, (FeatureType.MASK, 'dataMask'),
lambda dm1, dm2: np.all([dm1, dm2], axis=0))
cloud_masking_task = CloudMaskTask(
data_feature='BANDS',
is_data_feature='dataMask',
all_bands=True,
processing_resolution=resolution,
mono_features=('CLP', 'CLM'),
mask_feature=None,
mono_threshold=0.3,
average_over=1,
dilation_size=4
)
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
resampled_range = ('2018-01-01', '2019-01-01', 10)
interp_task = LinearInterpolation(
feature=(FeatureType.DATA, 'RGB'),
mask_feature=(FeatureType.MASK, 'VALID_DATA'),
resample_range=resampled_range,
bounds_error=False
)
name = 'botswana_single_raw'
anim_task_raw = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
name = 'botswana_single'
anim_task = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=3, dpi=200)
workflow = LinearWorkflow(
download_task_l2a,
# anim_task_raw
download_task_l1c,
data_mask_merge,
cloud_masking_task,
valid_mask_task,
interp_task,
anim_task
)
result = workflow.execute({
download_task_l2a:{'bbox': bbox, 'time_interval': time_interval},
})
```
## 4. Split Image
```
bbox = BBox(bbox=[21.3,-20.0,24.0,-18.0], crs=CRS.WGS84)
time_interval = ('2018-09-01', '2020-04-01')
resolution = 120
bbox_splitter = BBoxSplitter([bbox.geometry], bbox.crs, (6,5))
bbox_list = np.array(bbox_splitter.get_bbox_list())
info_list = np.array(bbox_splitter.get_info_list())
print(f'{len(bbox_list)} patches of size: {bbox_to_dimensions(bbox_list[0], resolution)}')
gdf = gpd.GeoDataFrame(None, crs=int(bbox.crs.epsg), geometry=[bbox.geometry for bbox in bbox_list])
geom, crs = gdf.unary_union, CRS.WGS84
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=8
)
for geo in gdf.geometry:
area_geojson = GeoJSON(data=Geometry(geo, crs).geojson)
map1.add_layer(area_geojson)
map1
download_task = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'CLM'),
(FeatureType.DATA, 'CLP'),
(FeatureType.MASK, 'dataMask')
]
)
valid_mask_task = ZipFeatureTask([(FeatureType.MASK, 'dataMask'), (FeatureType.MASK, 'CLM'), (FeatureType.DATA, 'CLP')], (FeatureType.MASK, 'VALID_DATA'),
lambda dm, clm, clp: np.all([dm, clm == 0, clp/255 < 0.3], axis=0))
resampled_range = ('2019-01-01', '2020-01-01', 10)
interp_task = LinearInterpolation(
feature=(FeatureType.DATA, 'RGB'),
mask_feature=(FeatureType.MASK, 'VALID_DATA'),
resample_range=resampled_range,
bounds_error=False
)
export_r = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[0])
export_g = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[1])
export_b = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[2])
convert_to_uint16 = ZipFeatureTask([(FeatureType.DATA, 'RGB')], (FeatureType.DATA, 'RGB'),
lambda x: (x*1e4).astype(np.uint16))
os.system('rm -rf ./tiffs && mkdir ./tiffs')
workflow = LinearWorkflow(
download_task,
valid_mask_task,
interp_task,
convert_to_uint16,
export_r,
export_g,
export_b
)
# Execute the workflow
execution_args = []
for idx, bbox in enumerate(bbox_list):
execution_args.append({
download_task: {'bbox': bbox, 'time_interval': time_interval},
export_r: {'filename': f'r_patch_{idx}.tiff'},
export_g: {'filename': f'g_patch_{idx}.tiff'},
export_b: {'filename': f'b_patch_{idx}.tiff'}
})
executor = EOExecutor(workflow, execution_args, save_logs=True)
executor.run(workers=10, multiprocess=False)
executor.make_report()
# spatial merge
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/r.tiff -co compress=LZW tiffs/r_patch_*.tiff && rm -rf tiffs/r_patch_*.tiff', shell=True);
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/g.tiff -co compress=LZW tiffs/g_patch_*.tiff && rm -rf tiffs/g_patch_*.tiff', shell=True);
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/b.tiff -co compress=LZW tiffs/b_patch_*.tiff && rm -rf tiffs/b_patch_*.tiff', shell=True);
dates = pd.date_range('2019-01-01', '2020-01-01', freq='10D').to_pydatetime()
import_r = ImportFromTiff((FeatureType.DATA, 'R'), f'tiffs/r.tiff', timestamp_size=len(dates))
import_g = ImportFromTiff((FeatureType.DATA, 'G'), f'tiffs/g.tiff', timestamp_size=len(dates))
import_b = ImportFromTiff((FeatureType.DATA, 'B'), f'tiffs/b.tiff', timestamp_size=len(dates))
merge_bands_task = ZipFeatureTask({FeatureType.DATA: ['R', 'G', 'B']}, (FeatureType.DATA, 'RGB'),
lambda r, g, b: np.moveaxis(np.array([r[...,0], g[...,0], b[...,0]]), 0, -1))
def temporal_ma_f(f):
k = np.array([0.05, 0.6, 1, 0.6, 0.05])
k = k/np.sum(k)
w = len(k)//2
return np.array([np.sum([f[(i-w+j)%len(f)]*k[j] for j in range(len(k))], axis=0) for i in range(len(f))])
temporal_smoothing = ZipFeatureTask([(FeatureType.DATA, 'RGB')], (FeatureType.DATA, 'RGB'), temporal_ma_f)
name = 'botswana_multi_ma'
anim_task = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=3,
dpi=400, scale_factor=3.0/1e4)
workflow = LinearWorkflow(
import_r,
import_g,
import_b,
merge_bands_task,
temporal_smoothing,
anim_task
)
result = workflow.execute()
```
## 5. Batch request
Use the evalscript from the [custom scripts repository](https://github.com/sentinel-hub/custom-scripts/tree/master/sentinel-2/interpolated_time_series) and see how to use it in the batch example in our [sentinelhub-py](https://github.com/sentinel-hub/sentinelhub-py/blob/master/examples/batch_processing.ipynb) library.
| true |
code
| 0.571288 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
import linearsolve as ls
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
```
# Class 14: Prescott's Real Business Cycle Model I
In this notebook, we'll consider a centralized version of the model from pages 11-17 in Edward Prescott's article "Theory Ahead of Business Cycle Measurement in the Fall 1986 of the Federal Reserve Bank of Minneapolis' *Quarterly Review* (link to article: https://www.minneapolisfed.org/research/qr/qr1042.pdf). The model is just like the RBC model that we studying in the previous lecture, except that now we include an endogenous labor supply.
## Prescott's RBC Model with Labor
The equilibrium conditions for Prescott's RBC model with labor are:
\begin{align}
\frac{1}{C_t} & = \beta E_t \left[\frac{\alpha A_{t+1}K_{t+1}^{\alpha-1}L_{t+1}^{1-\alpha} +1-\delta }{C_{t+1}}\right]\\
\frac{\varphi}{1-L_t} & = \frac{(1-\alpha)A_tK_t^{\alpha}L_t^{-\alpha}}{C_t} \\
Y_t & = A_t K_t^{\alpha}L_t^{1-\alpha}\\
K_{t+1} & = I_t + (1-\delta) K_t\\
Y_t & = C_t + I_t\\
\log A_{t+1} & = \rho \log A_t + \epsilon_{t+1}
\end{align}
where $\epsilon_{t+1} \sim \mathcal{N}(0,\sigma^2)$.
The objective is use `linearsolve` to simulate impulse responses to a TFP shock using the following parameter values for the simulation:
| $$\rho$$ | $$\sigma$$ | $$\beta$$ | $$\varphi$$ | $$\alpha$$ | $$\delta $$ |
|----------|------------|-------------|-----------|------------|-------------|
| 0.75 | 0.006 | 0.99 | 1.7317 | 0.35 | 0.025 |
The value for $\beta$ implies a steady state (annualized) real interest rate of about 4 percent:
\begin{align}
4 \cdot \left(\beta^{-1} - 1\right) & \approx 0.04040
\end{align}
$\rho = 0.75$ and $\sigma = 0.006$ are consistent with the statistical properties of the cyclical component of TFP in the US. $\alpha$ is set so that, consistent with the long-run average of the US, the labor share of income is about 65 percent of GDP. The deprecation rate of capital is calibrated to be about 10 percent annually. Finally, $\varphi$ was chosen last to ensure that in the steady state households allocate about 33 percent of their available time to labor.
## Model Preparation
Before proceding, let's recast the model in the form required for `linearsolve`. Write the model with all variables moved to the left-hand side of the equations and dropping the expecations operator $E_t$ and the exogenous shock $\epsilon_{t+1}$:
\begin{align}
0 & = \beta\left[\frac{\alpha A_{t+1}K_{t+1}^{\alpha-1}L_{t+1}^{1-\alpha} +1-\delta }{C_{t+1}}\right] - \frac{1}{C_t}\\
0 & = \frac{(1-\alpha)A_tK_t^{\alpha}L_t^{-\alpha}}{C_t} - \frac{\varphi}{1-L_t}\\
0 & = A_t K_t^{\alpha}L_t^{1-\alpha} - Y_t\\
0 & = I_t + (1-\delta) K_t - K_{t+1}\\
0 & = C_t + I_t - Y_t\\
0 & = \rho \log A_t - \log A_{t+1}
\end{align}
Remember, capital and TFP are called *state variables* because they're $t+1$ values are predetermined. Output, consumption, and investment are called a *costate* or *control* variables. Note that the model as 5 equations in 5 endogenous variables.
## Initialization, Approximation, and Solution
The next several cells initialize the model in `linearsolve` and then approximate and solve it.
```
# Create a variable called 'parameters' that stores the model parameter values in a Pandas Series
parameters = pd.Series(dtype=float)
parameters['rho'] = .75
parameters['beta'] = 0.99
parameters['phi'] = 1.7317
parameters['alpha'] = 0.35
parameters['delta'] = 0.025
# Print the model's parameters
print(parameters)
# Create a variable called 'sigma' that stores the value of sigma
sigma = 0.006
# Create variable called 'var_names' that stores the variable names in a list with state variables ordered first
var_names = ['a','k','y','c','i','l']
# Create variable called 'shock_names' that stores an exogenous shock name for each state variable.
shock_names = ['e_a','e_k']
# Define a function that evaluates the equilibrium conditions of the model solved for zero. PROVIDED
def equilibrium_equations(variables_forward,variables_current,parameters):
# Parameters. PROVIDED
p = parameters
# Current variables. PROVIDED
cur = variables_current
# Forward variables. PROVIDED
fwd = variables_forward
# Define variable to store MPK. Will make things easier later.
mpk = p.alpha*fwd.a*fwd.k**(p.alpha-1)*fwd.l**(1-p.alpha)
# Define variable to store MPL. Will make things easier later.
mpl = (1-p.alpha)*fwd.a*fwd.k**p.alpha*fwd.l**-p.alpha
# Euler equation
euler_equation = p.beta*(mpk+1-p.delta)/fwd.c - 1/cur.c
# Labor-labor choice
labor_leisure = mpl/cur.c - p.phi/(1-cur.l)
# Production function
production_function = cur.a*cur.k**p.alpha*cur.l**(1-p.alpha) - cur.y
# Capital evolution. PROVIDED
capital_evolution = cur.i + (1 - p.delta)*cur.k - fwd.k
# Market clearing. PROVIDED
market_clearing = cur.c+cur.i - cur.y
# Exogenous tfp. PROVIDED
tfp_process = p.rho*np.log(cur.a) - np.log(fwd.a)
# Stack equilibrium conditions into a numpy array
return np.array([
euler_equation,
labor_leisure,
production_function,
capital_evolution,
market_clearing,
tfp_process
])
```
Next, initialize the model using `ls.model` which takes the following required arguments:
* `equations`
* `n_states`
* `var_names`
* `shock_names`
* `parameters`
```
# Initialize the model into a variable named 'rbc_model'
rbc_model = ls.model(equations = equilibrium_equations,
n_states=2,
var_names=var_names,
shock_names=shock_names,
parameters=parameters)
# Compute the steady state numerically using .compute_ss() method of rbc_model
guess = [1,4,1,1,1,0.5]
rbc_model.compute_ss(guess)
# Print the computed steady state
print(rbc_model.ss)
# Find the log-linear approximation around the non-stochastic steady state and solve using .approximate_and_solve() method of rbc_model
rbc_model.approximate_and_solve()
```
## Impulse Responses
Compute a 26 period impulse responses of the model's variables to a 0.01 unit shock to TFP in period 5.
```
# Compute impulse responses
rbc_model.impulse(T=26,t0=5,shocks=[0.01,0])
# Print the first 10 rows of the computed impulse responses to the TFP shock
print(rbc_model.irs['e_a'].head(10))
```
Construct a $2\times3$ grid of plots of simulated TFP, output, labor, consumption, investment, and capital. Be sure to multiply simulated values by 100 so that vertical axis units are in "percent deviation from steady state."
```
# Create figure. PROVIDED
fig = plt.figure(figsize=(18,8))
# Create upper-left axis. PROVIDED
ax = fig.add_subplot(2,3,1)
ax.plot(rbc_model.irs['e_a']['a']*100,'b',lw=5,alpha=0.75)
ax.set_title('TFP')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.5,2])
ax.grid()
# Create upper-center axis. PROVIDED
ax = fig.add_subplot(2,3,2)
ax.plot(rbc_model.irs['e_a']['y']*100,'b',lw=5,alpha=0.75)
ax.set_title('Output')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.5,2])
ax.grid()
# Create upper-right axis. PROVIDED
ax = fig.add_subplot(2,3,3)
ax.plot(rbc_model.irs['e_a']['l']*100,'b',lw=5,alpha=0.75)
ax.set_title('Labor')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.5,2])
ax.grid()
# Create lower-left axis. PROVIDED
ax = fig.add_subplot(2,3,4)
ax.plot(rbc_model.irs['e_a']['c']*100,'b',lw=5,alpha=0.75)
ax.set_title('Consumption')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.1,0.4])
ax.grid()
# Create lower-center axis. PROVIDED
ax = fig.add_subplot(2,3,5)
ax.plot(rbc_model.irs['e_a']['i']*100,'b',lw=5,alpha=0.75)
ax.set_title('Investment')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-2,8])
ax.grid()
# Create lower-right axis. PROVIDED
ax = fig.add_subplot(2,3,6)
ax.plot(rbc_model.irs['e_a']['k']*100,'b',lw=5,alpha=0.75)
ax.set_title('Capital')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.2,0.8])
ax.grid()
fig.tight_layout()
```
| true |
code
| 0.639173 | null | null | null | null |
|
# The thermodynamics of ideal solutions
*Authors: Enze Chen (University of California, Berkeley)*
This animation will show how the Gibbs free energy curves correspond to a lens phase diagram.
## Python imports
```
# General libraries
import io
import os
# Scientific computing libraries
import numpy as np
from scipy.misc import derivative
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import matplotlib.animation as animation
from PIL import Image
import cv2
from moviepy.editor import *
```
### Helper functions
```
# analytical function for the solid free energy curve
def curve_s(x, T, beta=0):
"""This function plots the Gibbs free energy curve for the solid solution.
Args:
x (numpy.ndarray): An array of atomic fractions of B.
T (float): The temperature in Kelvin.
beta (float): The interaction parameter in J/mol.
Returns:
G_s (numpy.ndarray): An array of Gibbs free energy values in kJ/mol.
"""
S_mix = -8.314 * (np.multiply(x, np.log(x)) + np.multiply(1 - x, np.log(1 - x)))
H_mix = beta * np.multiply(x, 1 - x)
G_s = -T * S_mix + H_mix
return G_s / 1000
# analytical function for the liquid free energy curve
def curve_l(x, T, beta=0):
"""This function plots the Gibbs free energy curve for the liquid solution.
Args:
x (numpy.ndarray): An array of atomic fractions of B.
T (float): The temperature in Kelvin.
beta (float): The interaction parameter in J/mol.
Returns:
G_l (numpy.ndarray): An array of Gibbs free energy values in kJ/mol.
"""
S_A, S_B = (52.7, 59.9)
T_A, T_B = (1890 + 273, 1205 + 273)
G_A = S_A * (T_A - T)
G_B = S_B * (T_B - T)
S_mix = -8.314 * (np.multiply(x, np.log(x)) + np.multiply(1 - x, np.log(1 - x)))
H_mix = beta * np.multiply(x, 1 - x)
G_l = x * G_B + (1 - x) * G_A - T * S_mix + H_mix
return G_l / 1000
# find the common tangent using intersections and line search
def common_tangent(x, y1, y2, T, beta=0):
"""This function calculates the common tangent of two convex curves.
Args:
x (numpy.ndarray): An array of atomic fractions of B.
y1 (numpy.ndarray): y values for curve 1.
y2 (numpy.ndarray): y values for curve 2.
T (float): The temperature in Kelvin.
beta (float): The interaction parameter for the solid solution.
Returns:
line (numpy.ndarray): y values for the common tangent.
idmin (int): Index of the x-coordinate of the first tangent point.
idmax (int): Index of the x-coordinate of the second tangent point.
"""
# Compute a derivative
dx = 1e-3
dy1 = derivative(func=curve_s, x0=x, dx=dx, args=(T, beta,))
# Make an initial guess at the minimum of curve 1
n = len(x)
idmin, idmax = (0, n)
idx = np.argmin(y1)
yp = y1[idx]
xp = x[idx]
dyp = dy1[idx]
# Construct the tangent line and count intersections with curve 2
line = dyp * x + yp - dyp * xp
diff = np.diff(np.sign(y2 - line))
nnz = np.count_nonzero(diff)
# They're the same curve. Used for finding miscibility gap.
# I'm assuming that the curve is symmetric
if np.linalg.norm(y1 - y2) < 1e-4:
idmin = np.argmin(y1[:int(n/2)])
idmax = np.argmin(y1[int(n/2):]) + int(n/2)
# If the tangent line intersects curve 2, shift tangent point to the left
elif nnz >= 1:
while nnz >= 1:
idx -= 1
# try-except to avoid an out-of-bounds error
try:
yp = y1[idx]
xp = x[idx]
dyp = dy1[idx]
line = dyp * x + yp - dyp * xp
diff = np.diff(np.sign(y2 - line))
nnz = np.count_nonzero(diff)
except:
break
if diff.any():
# Assign left and right indices of the tangent points
# Here we do it each time because once we miss, we can't go back
idmax = np.nonzero(diff)[0][0]
idmin = idx
# If the tangent line misses curve 2, shift tangent point to the right
elif nnz < 1:
while nnz < 1:
idx += 1
# try-except to avoid an out-of-bounds error
try:
yp = y1[idx]
xp = x[idx]
dyp = dy1[idx]
line = dyp * x + yp - dyp * xp
diff = np.diff(np.sign(y2 - line))
nnz = np.count_nonzero(diff)
except:
break
# Assign left and right indices of the tangent points
idmin = idx
idmax = np.nonzero(diff)[0][0]
# Return a tuple
return (line, idmin, idmax)
# plot the Gibbs free energy curves
def plot_Gx(T=1800, beta_s=0, beta_l=0):
"""This function is called by the widget to perform the plotting based on inputs.
Args:
T (float): The temperature in Kelvin.
beta_s (float): The interaction parameter for solids in J/mol.
beta_l (float): The interaction parameter for liquids in J/mol.
Returns:
None, but a pyplot is displayed.
"""
# For the given temperature, calculate the curves and common tangent
n = int(1e4)
xmin, xmax = (0.001, 0.999)
x = np.linspace(xmin, xmax, n)
y_s = curve_s(x, T, beta_s)
y_l = curve_l(x, T, beta_l)
line, idmin, idmax = common_tangent(x, y_s, y_l, T, beta_s)
# Mostly plot settings for visual appeal
plt.rcParams.update({'figure.figsize':(8,6), 'font.size':20, \
'lines.linewidth':4, 'axes.linewidth':2})
fig, ax = plt.subplots()
ymin, ymax = (-39, 19)
ax.plot(x, y_s, c='C0', label='solid')
ax.plot(x, y_l, c='C1', label='liquid')
if abs(idmin) < n and abs(idmax) < n:
ax.plot(x[idmin:idmax], line[idmin:idmax], c='k', lw=5, ls='-.')
ax.vlines(x=[x[idmin], x[idmax]], ymin=ymin, \
ymax=[line[idmin], line[idmax]], linestyles='dotted', linewidth=3)
ax.tick_params(top=True, right=True, direction='in', length=10, width=2)
ax.set_xlim(0, 1)
ax.set_ylim(ymin, ymax)
ax.set_xlabel(r'$x_{B}$')
ax.set_ylabel(r'$\Delta G$ (kJ/mol)')
ax.set_title('Gibbs free energy at T = {} K'.format(T), fontsize=18)
plt.legend()
plt.show()
```
## Animations using `FuncAnimation`
Finally!! VLC/Windows has buggy glitches, but the embedded HTML version looks fine.
Also, **extremely high quality and low memory footprint**!! 🎉
```
# Initialize quantities
n = int(1e4)
xmin, xmax = (0.001, 0.999)
x = np.linspace(xmin, xmax, n)
liquidus = []
solidus = []
Ts = np.arange(1300, 2301, 5)
# Plot settings
plt.rcParams.update({'figure.figsize':(7,9.5), 'font.size':16})
fig, ax = plt.subplots(nrows=2, ncols=1, sharex=True)
# Initialize plot settings
ymin, ymax = -39, 19
ax[0].set_xlim(0, 1)
ax[0].set_ylim(ymin, ymax)
ax[0].set_ylabel(r'$\Delta G$ (kJ/mol)', fontsize=22)
ax[0].set_title('Binary ideal solution\nFree energy vs. composition', fontsize=20)
ax[0].tick_params(axis='both', labelsize=20)
Tmin, Tmax = 1100, 2500
ax[1].set_xlabel(r'$x_{B}$', fontsize=22)
ax[1].set_ylabel(r'$T$ (K)', fontsize=22)
ax[1].set_ylim(Tmin, Tmax)
ax[1].set_title('Phase diagram', fontsize=20)
ax[1].tick_params(axis='both', labelsize=20)
# Initialize the lines
l1, = ax[0].plot([], [], c='C1', label='liquid')
l2, = ax[0].plot([], [], c='C0', label='solid')
l3, = ax[1].plot([], [], c='C1', label='liquidus')
l4, = ax[1].plot([], [], c='C0', label='solidus')
l5, = ax[1].plot([], [], c='gray', ls='dashed', lw=4, alpha=0.5, zorder=-5)
v3, = ax[0].plot([], [], c='k', ls='-.')
v1 = ax[0].vlines(x=[0], ymin=[0], ymax=[0], linestyles='dotted', linewidth=4, color='k')
v2 = ax[1].vlines(x=[0], ymin=[0], ymax=[0], linestyles='dotted', linewidth=4, color='k')
ax[0].legend(loc='upper right')
ax[1].legend(loc='upper right')
plt.tight_layout()
# This is needed to avoid an extra loop
def init():
l1.set_data([], [])
return l1,
# This does the enumeration
def animate(i):
global ymin, ymax, Tmax, liquidus, solidus, x, n, Ts, v1, v2
T = Ts[i]
if T % 100 == 0:
print(T)
y_s = curve_s(x, T)
y_l = curve_l(x, T)
line, idmin, idmax = common_tangent(x, y_s, y_l, T) # compute common tangent
if idmin == 0 or idmin == n-1 or idmax == 0 or idmax == n-1:
liquidus.append(None)
solidus.append(None)
else:
liquidus.append(x[idmax])
solidus.append(x[idmin])
# set the data to be updated each iteration
l1.set_data(x, y_l)
l2.set_data(x, y_s)
l3.set_data(liquidus, Ts[:np.where(Ts==T)[0][0]+1])
l4.set_data(solidus, Ts[:np.where(Ts==T)[0][0]+1])
l5.set_data([0, 1], [T, T])
ax[0].annotate(text=f'$T={T}$ K', xy=(0.70, -33), fontsize=20,
bbox=dict(fc='1.0', boxstyle='round'))
# handle the tangent points
if T == 2170:
v1.remove()
v2.remove()
if abs(idmin) < n and abs(idmax) < n and idmax != 0:
v1.remove()
v2.remove()
v3.set_data(x[idmin:idmax], line[idmin:idmax])
v1 = ax[0].vlines(x=[x[idmin], x[idmax]], ymin=ymin, \
ymax=[line[idmin], line[idmax]], linestyles='dotted', linewidth=4, colors=['C0', 'C1'])
v2 = ax[1].vlines(x=[x[idmin], x[idmax]], ymin=T, ymax=Tmax, linestyles='dotted', linewidth=4, colors=['C0', 'C1'])
# return the artists that get updated (for blitting)
return l1, l2, l3, l4, l5, v3, v2, v1
# Create animation object
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=len(Ts), interval=1000, blit=True, repeat=False)
# Save animation as MP4 (preferred)
# anim.save('C:/Users/Enze/Desktop/test_funcanim.mp4', fps=9, dpi=300, writer='ffmpeg')
# Save animation as GIF (file size MUCH larger!)
# anim.save('C:/Users/Enze/Desktop/test_funcanim.gif', fps=9, dpi=300, writer='pillow')
plt.show()
```
## Other (sub-par) methods that I've tried...
```
# Accumulate images in a list for post-processing
n = int(1e4)
xmin, xmax = (0.001, 0.999)
x = np.linspace(xmin, xmax, n)
liquidus = []
solidus = []
Ts = np.arange(1300, 1450, 10)
plt.rcParams.update({'figure.figsize':(7,9)})
fig, ax = plt.subplots(nrows=2, ncols=1, sharex=True)
fig.tight_layout()
ymin, ymax = -39, 19
ax[0].set_xlim(0, 1)
ax[0].set_ylim(ymin, ymax)
ax[0].set_ylabel(r'$\Delta G$ (kJ/mol)')
Tmin, Tmax = 1100, 2500
ax[1].set_xlabel(r'$x_{B}$')
ax[1].set_ylabel(r'$T$ (K)')
ax[1].set_ylim(Tmin, Tmax)
images = []
for i,T in enumerate(Ts):
if T % 100 == 0:
print(T)
y_s = curve_s(x, T)
y_l = curve_l(x, T)
line, idmin, idmax = common_tangent(x, y_s, y_l, T)
if idmin == 0 or idmin == n-1 or idmax == 0 or idmax == n-1:
liquidus.append(None)
solidus.append(None)
else:
liquidus.append(x[idmax])
solidus.append(x[idmin])
ax[0].plot(x, y_s, c='C0', label='solid')
ax[0].plot(x, y_l, c='C1', label='liquid')
if abs(idmin) < n and abs(idmax) < n and idmax != 0:
ax[0].plot(x[idmin:idmax], line[idmin:idmax], c='k', ls='-.')
v1 = ax[0].vlines(x=[x[idmin], x[idmax]], ymin=ymin, \
ymax=[line[idmin], line[idmax]], linestyles='dotted', linewidth=4, color='k')
v2 = ax[1].vlines(x=[x[idmin], x[idmax]], ymin=T, ymax=Tmax, linestyles='dotted', linewidth=4, color='k')
ax[0].legend(loc='upper right')
ax[1].plot(liquidus, Ts[:i+1], c='C1', label='liquidus')
ax[1].plot(solidus, Ts[:i+1], c='C0', label='solidus')
ax[1].plot([0, 1], [T, T], c='gray', ls='dashed', lw=4, alpha=0.5, zorder=-5)
ax[1].annotate(text=f'$T={T}$ K', xy=(0.7, 2320), fontsize=24,
bbox=dict(fc='1.0', boxstyle='round'))
# fig.savefig(f'C:/Users/Enze/Desktop/plots/fig_{T:4d}')
# Convert to PIL image for GIF
buf = io.BytesIO()
fig.savefig(buf)
buf.seek(0)
images.append(Image.open(buf))
while len(ax[0].lines) > 0:
ax[0].lines.remove(ax[0].lines[0])
while len(ax[1].lines) > 0:
ax[1].lines.remove(ax[1].lines[0])
if abs(idmin) < n and abs(idmax) < n and idmax != 0:
v1.remove()
v2.remove()
# Make a GIF by converting from PIL Image
make_gif = True
if make_gif: # Quality is pretty good!!
images[0].save('C:/Users/Enze/Desktop/test_PIL3.gif', save_all=True, append_images=images[1:], optimize=False, duration=200, loop=0)
print('Finished making GIF')
```
### Convert PIL images to mp4 using [OpenCV](https://docs.opencv.org/master/d6/d00/tutorial_py_root.html)
OK, this works!
Quality could be improved... this is where FuncAnimation native support would probably be better.
```
# This movie is very large in size!!
opencv_images = [cv2.cvtColor(np.array(i), cv2.COLOR_RGB2BGR) for i in images]
height, width, channels = opencv_images[0].shape
fourcc = cv2.VideoWriter_fourcc(*'MP4V') # can also be 'MJPG' or 'MP4V'
video = cv2.VideoWriter(filename='C:/Users/Enze/Desktop/test_opencv.mp4',
fourcc=fourcc, fps=6, frameSize=(width, height))
for i in opencv_images:
video.write(i)
cv2.destroyAllWindows()
video.release()
```
### Convert figure files using [`moviepy`](https://moviepy.readthedocs.io/en/latest/index.html)
Quality seems a little worse than OpenCV.
Also takes a longggg time lol, but the file size is very small!
```
datadir = 'C:/Users/Enze/Desktop/plots/'
clips = [ImageClip(os.path.join(datadir, m)).set_duration(0.2) for m in os.listdir(datadir)]
concat = concatenate_videoclips(clips, method='compose')
concat.write_videofile('C:/Users/Enze/Desktop/test_moviepy.mp4', fps=10)
```
| true |
code
| 0.713482 | null | null | null | null |
|
<center>
<h1>Fetal Health Classification</h1>
<img src="https://blog.pregistry.com/wp-content/uploads/2018/08/AdobeStock_90496738.jpeg">
<small>Source: Google</small>
</center>
<p>
Fetal mortality refers to stillbirths or fetal death. It encompasses any death of a fetus after 20 weeks of gestation.
Cardiotocograms (CTGs) are a simple and cost accessible option to assess fetal health, allowing healthcare professionals to take action in order to prevent child and maternal mortality.
Cardiotocography is a technical means of recording the fetal heartbeat and the uterine contractions during pregnancy. It is most commonly used in the third trimester and its purpose is to monitor fetal well-being and allow early detection of fetal distress. An abnormal CTG may indicate the need for further investigations and potential intervention.
</p>
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('../Datasets/fetal_health.csv')
```
| Variable symbol | Variable description|
| ----------------|---------------------|
|LB | Fetal heart rate baseline (beats per minute)|
|AC | Number of accelerations per second|
|FM | Number of fetal movements per second|
|UC | Number of uterine contractions per second|
|DL | Number of light decelerations per second|
|DS | Number of severe decelerations per second|
|DP | Number of prolonged decelerations per second|
|ASTV | Percentage of time with abnormal short-term variability|
|MSTV | Mean value of short-term variability|
|ALTV | Percentage of time with abnormal long-term variability|
|MLTV | Mean value of long-term variability|
|Width | Width of FHR histogram|
|Min | Minimum of FHR histogram|
|Max | Maximum of FHR histogram|
|Nmax | Number of histogram peaks|
|Nzeros | Number of histogram zeroes|
|Mode | Histogram mode|
|Median | Histogram median|
|Variance | Histogram variance|
|Tendency | Histogram tendency|
|NSP | Fetal state class code (N=Normal, S=Suspected,P=Pathological)|
Reference: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6822315/
```
df.head()
df.info()
df.describe()
df.isna().sum()
```
Thankfully, there are no NaN values in the dataset.
```
sns.countplot(x='fetal_health', data=df)
print(df['fetal_health'].value_counts())
```
We can see that there is the problem of class imbalance in this dataset. This means we cannot use **accuracy** as a metric to evaluate the performance of our model. The most appropiate metric for model evaluation can be:
1. F1 Score
2. Recall
3. Precision
Before diving deep into understanding the data and features, let us first look at what does the three different categories of fetal_health represent. Please refer to the table below for the same.
Reference: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4812878/

```
corr = df.corr()
plt.figure(figsize=(24, 20))
sns.heatmap(corr, annot=True)
plt.title("Correlation Matrix")
plt.show()
```
From the above correlation matrix, we can observe that the following features show some correlation with target variable fetal health:
1. accelerations (negative corr)
2. uterine contractions (negative corr)
3. prolonged_decelerations (positive corr)
4. abnormal short term variability (positive corr)
5. percentage of time with abnormal long term variability (positive corr)
## Model Selection
```
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.svm import LinearSVC
from sklearn.linear_model import SGDClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report, f1_score, recall_score, precision_score
print("There are total "+str(len(df))+" rows in the dataset")
X = df.drop(["fetal_health"],axis=1)
Y = df["fetal_health"]
std_scale = StandardScaler()
X_sc = std_scale.fit_transform(X)
X_train, X_test, y_train,y_test = train_test_split(X_sc, Y, test_size=0.25, random_state=42)
print("There are total "+str(len(X_train))+" rows in training dataset")
print("There are total "+str(len(X_test))+" rows in test dataset")
```
If you remember, in the initial investigation of the data, we found out that we have imbalanced classes.
To handle the problem of imbalanced classes, we can use oversampling techniques. In oversampling, we populate the minority classes with some synthetic data.
Let us try some oversampling techniques and judge their performance on the above dataset.
1. SMOTE Technique
```
from imblearn.over_sampling import SMOTE
smt = SMOTE()
X_train_sm, y_train_sm = smt.fit_resample(X_train, y_train)
```
2. ADASYN
```
from imblearn.over_sampling import ADASYN
ada = ADASYN(random_state=130)
X_train_ada, y_train_ada = ada.fit_resample(X_train, y_train)
```
3. SMOTE + Tomek Links
```
from imblearn.combine import SMOTETomek
smtom = SMOTETomek(random_state=139)
X_train_smtom, y_train_smtom = smtom.fit_resample(X_train, y_train)
```
4. SMOTE + ENN
```
from imblearn.combine import SMOTEENN
smenn = SMOTEENN()
X_train_smenn, y_train_smenn = smenn.fit_resample(X_train, y_train)
def evaluate_model(clf, X_test, y_test, model_name, oversample_type):
print('--------------------------------------------')
print('Model ', model_name)
print('Data Type ', oversample_type)
y_pred = clf.predict(X_test)
f1 = f1_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
precision = precision_score(y_test, y_pred, average='weighted')
print(classification_report(y_test, y_pred))
print("F1 Score ", f1)
print("Recall ", recall)
print("Precision ", precision)
return [model_name, oversample_type, f1, recall, precision]
models = {
'DecisionTrees': DecisionTreeClassifier(random_state=42),
'RandomForest':RandomForestClassifier(random_state=42),
'LinearSVC':LinearSVC(random_state=0),
'AdaBoostClassifier':AdaBoostClassifier(random_state=42),
'SGD':SGDClassifier()
}
oversampled_data = {
'ACTUAL':[X_train, y_train],
'SMOTE':[X_train_sm, y_train_sm],
'ADASYN':[X_train_ada, y_train_ada],
'SMOTE_TOMEK':[X_train_smtom, y_train_smtom],
'SMOTE_ENN':[X_train_smenn, y_train_smenn]
}
final_output = []
for model_k, model_clf in models.items():
for data_type, data in oversampled_data.items():
model_clf.fit(data[0], data[1])
final_output.append(evaluate_model(model_clf, X_test, y_test, model_k, data_type))
final_df = pd.DataFrame(final_output, columns=['Model', 'DataType', 'F1', 'Recall', 'Precision'])
final_df.sort_values(by="F1", ascending=False)
```
### Hyperparameter Tuning
```
param_grid = {
'criterion':['gini', 'entropy'],
'max_depth': [10, 20, 40, 80, 100],
'max_features': ['auto', 'sqrt'],
'n_estimators': [200, 400, 600, 800, 1000, 2000]
}
rfc = RandomForestClassifier(random_state=42)
rfc_cv = GridSearchCV(estimator=rfc, param_grid=param_grid, cv=5, verbose=2)
rfc_cv.fit(X_train_smtom, y_train_smtom)
rfc_cv.best_params_
rf = RandomForestClassifier(n_estimators=2000, criterion='entropy', max_depth=20, max_features='auto')
rf.fit(X_train_smtom, y_train_smtom)
evaluate_model(rf, X_test, y_test, 'RandomForest', 'SMOTE+TOMEK')
import pickle
filename = 'fetal-health-model.pkl'
pickle.dump(rf, open(filename, 'wb'))
```
| true |
code
| 0.46563 | null | null | null | null |
|
# Accessing higher energy states with Qiskit Pulse
In most quantum algorithms/applications, computations are carried out over a 2-dimensional space spanned by $|0\rangle$ and $|1\rangle$. In IBM's hardware, however, there also exist higher energy states which are not typically used. The focus of this section is to explore these states using Qiskit Pulse. In particular, we demonstrate how to excite the $|2\rangle$ state and build a discriminator to classify the $|0\rangle$, $|1\rangle$ and $|2\rangle$ states.
We recommend reviewing the prior [chapter](https://learn.qiskit.org/course/quantum-hardware-pulses/calibrating-qubits-using-qiskit-pulse) before going through this notebook. We also suggest reading the Qiskit Pulse specifications (Ref [1](#refs)).
### Physics Background
We now give some additional background on the physics of transmon qubits, the basis for much of IBM's quantum hardware. These systems contain superconducting circuits composed of a Josephson junction and capacitor. For those unfamiliar with superconducting circuits, see the review [here](https://arxiv.org/pdf/1904.06560.pdf) (Ref. [2](#refs)). The Hamiltonian of this system is given by
$$
H = 4 E_C n^2 - E_J \cos(\phi),
$$
where $E_C, E_J$ denote the capacitor and Josephson energies, $n$ is the reduced charge number operator and $\phi$ is the reduced flux across the junction. We work in units with $\hbar=1$.
Transmon qubits are defined in the regime where $\phi$ is small, so we may expand $E_J \cos(\phi)$ in a Taylor series (ignoring constant terms)
$$
E_J \cos(\phi) \approx \frac{1}{2} E_J \phi^2 - \frac{1}{24} E_J \phi^4 + \mathcal{O}(\phi^6).
$$
The quadratic term $\phi^2$ defines the standard harmonic oscillator. Each additional term contributes an anharmonicity.
Using the relations $n \sim (a-a^\dagger), \phi \sim (a+a^\dagger)$ (for raising, lowering operators $a^\dagger, a$), it can be shown that the system resembles a Duffing oscillator with Hamiltonian
$$
H = \omega a^\dagger a + \frac{\alpha}{2} a^\dagger a^\dagger a a,
$$
where $\omega$ gives the $0\rightarrow1$ excitation frequency ($\omega \equiv \omega^{0\rightarrow1}$) and $\alpha$ is the anharmonicity between the $0\rightarrow1$ and $1\rightarrow2$ frequencies ($\alpha \equiv \omega^{1\rightarrow2} - \omega^{0\rightarrow1}$). Drive terms can be added as needed.
If we choose to specialize to the standard 2-dimensional subspace, we can make $|\alpha|$ sufficiently large or use special control techniques to suppress the higher energy states.
# Contents
[Getting started](#importing)
[Discriminating the 0, 1 and 2 states](#discrim012)
  [Computing the 1->2 Frequency](#freq12)
  [1->2 Rabi Experiment](#rabi12)
  [Build the 0, 1, 2 discriminator](#builddiscrim012)
[References](#refs)
## Getting Started <a id="importing"></a>
We begin by importing dependencies and defining some default variable values. We choose qubit 0 to run our experiments. We perform our experiments on the publicly available single qubit device `ibmq_armonk`.
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from qiskit import pulse # This is where we access all of our Pulse features!
from qiskit.circuit import Parameter # This is Parameter Class for variable parameters.
from qiskit.circuit import QuantumCircuit, Gate
from qiskit import schedule
from qiskit.tools.monitor import job_monitor
from qiskit.tools.jupyter import *
%matplotlib inline
from qiskit import IBMQ
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q', group='open', project='main')
backend = provider.get_backend('ibmq_manila')
backend_defaults = backend.defaults()
backend_properties = backend.properties()
# unit conversion factors -> all backend properties returned in SI (Hz, sec, etc.)
GHz = 1.0e9 # Gigahertz
MHz = 1.0e6 # Megahertz
us = 1.0e-6 # Microseconds
ns = 1.0e-9 # Nanoseconds
qubit = 0 # qubit we will analyze
default_qubit_freq = backend_defaults.qubit_freq_est[qubit] # Default qubit frequency in Hz.
print(f"Qubit {qubit} has an estimated frequency of {default_qubit_freq/ GHz} GHz.")
default_anharmonicity = backend_properties.qubits[qubit][3].value # Default anharmonicity in GHz
print(f"Default anharmonicity is {default_anharmonicity} GHz.")
# scale data (specific to each device)
scale_factor = 1e-7
# number of shots for our experiments
NUM_SHOTS = 1024
```
We define some additional helper functions.
```
def get_job_data(job, average):
"""Retrieve data from a job that has already run.
Args:
job (Job): The job whose data you want.
average (bool): If True, gets the data assuming data is an average.
If False, gets the data assuming it is for single shots.
Return:
list: List containing job result data.
"""
job_results = job.result(timeout = 120) # timeout parameter set to 120 s
result_data = []
for i in range(len(job_results.results)):
if average: # get avg data
result_data.append(np.real(job_results.get_memory(i)[qubit] * scale_factor))
else: # get single data
result_data.append(job_results.get_memory(i)[:, qubit] * scale_factor)
return result_data
def get_closest_multiple_of_16(num):
"""Compute the nearest multiple of 16. Needed because pulse enabled devices require
durations which are multiples of 16 samples.
"""
return int(num + 8 ) - (int(num + 8 ) % 16)
```
Next we include some default parameters for drive pulses.
```
# there are pulse parameters of the single qubit drive in IBM devices
x12_duration = 160
x12_sigma = 40
```
## Discriminating the $|0\rangle$, $|1\rangle$ and $|2\rangle$ states <a id="discrim012"></a>
given we have already calibrated X gate in the qubit subspace, which is available as XGate instruction in the quantum circuit. Here we calibrate transition in the higher energy subspace with pulse gate.
We focus on exciting the $|2\rangle$ state and building a discriminator to classify $|0\rangle$, $|1\rangle$ and $2\rangle$ states from their respective IQ data points. The procedure for even higher states ($|3\rangle$, $|4\rangle$, etc.) should be similar, but we have not tested them explicitly.
The process for building the higher state discriminator is as follows:
1. Compute the $1\rightarrow2$ frequency.
2. Conduct a Rabi experiment to obtain the $\pi$ pulse amplitude for $1\rightarrow2$. To do this, we first apply a $0\rightarrow1$ $\pi$ pulse to get from the $|0\rangle$ to the $|1\rangle$ state. Then, we do a sweep of drive amplitudes at the $1\rightarrow2$ frequency obtained above.
3. Construct 3 schedules:\
a. Zero schedule: just measure the ground state.\
b. One schedule: apply a $0\rightarrow1$ $\pi$ pulse and measure.\
c. Two schedule: apply a $0\rightarrow1$ $\pi$ pulse, then a $1\rightarrow2$ $\pi$ pulse and measure.
4. Separate the data from each schedule into training and testing sets and construct an LDA model for discrimination.
### Computing the 1->2 frequency <a id="freq12"></a>
The first step in our calibration is to compute the frequency needed to go from the $1\rightarrow2$ state. There are two methods to do this:
1. Do a frequency sweep from the ground state and apply very high power. If the applied power is large enough, two peaks should be observed. One at the $0\rightarrow1$ frequency found in section [1](#discrim01) and one at the $0\rightarrow2$ frequency. The $1\rightarrow2$ frequency can be obtained by taking the difference of the two. Unfortunately, for `ibmq_armonk`, the maximum drive power of $1.0$ is not sufficient to see this transition. Instead, we turn to the second method.
2. Excite the $|1\rangle$ state by applying a $0\rightarrow1$ $\pi$ pulse. Then perform the frequency sweep over excitations of the $|1\rangle$ state. A single peak should be observed at a frequency lower than the $0\rightarrow1$ frequency which corresponds to the $1\rightarrow2$ frequency.
We follow the second method described above.
```
# smaller range sweep
num_freqs = 75
drive_power = 0.15
sweep_freqs = default_anharmonicity*GHz + np.linspace(-30*MHz, 30*MHz, num_freqs)
freq = Parameter('freq')
with pulse.build(backend=backend, default_alignment='sequential', name='Frequency sweep') as freq12_sweep_sched:
drive_chan = pulse.drive_channel(qubit)
with pulse.frequency_offset(freq, drive_chan):
pulse.play(pulse.Gaussian(duration=x12_duration,
amp=drive_power,
sigma=x12_sigma,
name='x12_pulse'), drive_chan)
spect_gate = Gate("spect", 1, [freq])
qc_spect = QuantumCircuit(1, 1)
qc_spect.x(0)
qc_spect.append(spect_gate, [0])
qc_spect.measure(0, 0)
qc_spect.add_calibration(spect_gate, (0,), freq12_sweep_sched, [freq])
exp_spect_circs = [qc_spect.assign_parameters({freq: f}) for f in sweep_freqs]
excited_freq_sweep_job = backend.run(exp_spect_circs,
meas_level=1,
meas_return='avg',
shots=NUM_SHOTS)
job_monitor(excited_freq_sweep_job)
# Get the refined data (average)
excited_freq_sweep_data = get_job_data(excited_freq_sweep_job, average=True)
excited_sweep_freqs = default_qubit_freq + default_anharmonicity*GHz + np.linspace(-30*MHz, 30*MHz, num_freqs)
```
Let's plot and fit the refined signal, using the standard Lorentzian curve.
```
def fit_function(x_values, y_values, function, init_params):
"""Fit a function using scipy curve_fit."""
fitparams, conv = curve_fit(function, x_values, y_values, init_params, maxfev = 50000)
y_fit = function(x_values, *fitparams)
return fitparams, y_fit
# do fit in Hz
(excited_sweep_fit_params,
excited_sweep_y_fit) = fit_function(excited_sweep_freqs,
excited_freq_sweep_data,
lambda x, A, q_freq, B, C: (A / np.pi) * (B / ((x - q_freq)**2 + B**2)) + C,
[-20, 4.625*GHz, 0.06*GHz, 3*GHz] # initial parameters for curve_fit
)
# Note: we are only plotting the real part of the signal
plt.scatter(excited_sweep_freqs/GHz, excited_freq_sweep_data, color='black')
plt.plot(excited_sweep_freqs/GHz, excited_sweep_y_fit, color='red')
plt.xlim([min(excited_sweep_freqs/GHz), max(excited_sweep_freqs/GHz)])
plt.xlabel("Frequency [GHz]", fontsize=15)
plt.ylabel("Measured Signal [a.u.]", fontsize=15)
plt.title("1->2 Frequency Sweep (refined pass)", fontsize=15)
plt.show()
_, qubit_12_freq, _, _ = excited_sweep_fit_params
print(f"Our updated estimate for the 1->2 transition frequency is "
f"{round(qubit_12_freq/GHz, 7)} GHz.")
```
### 1->2 Rabi Experiment <a id="rabi12"></a>
Now that we have a good estimate for the $1\rightarrow2$ frequency, we perform a Rabi experiment to obtain the $\pi$ pulse amplitude for the $1\rightarrow2$ transition. To do so, we apply a $0\rightarrow1$ $\pi$ pulse and then sweep over drive amplitudes at the $1\rightarrow2$ frequency.
```
# experimental configuration
num_rabi_points = 75 # number of experiments (ie amplitudes to sweep out)
# Drive amplitude values to iterate over: 75 amplitudes evenly spaced from 0 to 1.0
drive_amp_min = 0
drive_amp_max = 1.0
drive_amps = np.linspace(drive_amp_min, drive_amp_max, num_rabi_points)
amp = Parameter('amp')
with pulse.build(backend=backend, default_alignment='sequential', name='Amp sweep') as rabi_sched:
drive_chan = pulse.drive_channel(qubit)
pulse.set_frequency(qubit_12_freq, drive_chan)
pulse.play(pulse.Gaussian(duration=x12_duration,
amp=amp,
sigma=x12_sigma,
name='x12_pulse'), drive_chan)
rabi_gate = Gate("rabi", 1, [amp])
qc_rabi = QuantumCircuit(1, 1)
qc_rabi.x(0)
qc_rabi.append(rabi_gate, [0])
qc_rabi.measure(0, 0)
qc_rabi.add_calibration(rabi_gate, (0,), rabi_sched, [amp])
exp_rabi_circs = [qc_rabi.assign_parameters({amp: a}) for a in drive_amps]
rabi_12_job = backend.run(exp_rabi_circs,
meas_level=1,
meas_return='avg',
shots=NUM_SHOTS)
job_monitor(rabi_12_job)
# Get the job data (average)
rabi_12_data = get_job_data(rabi_12_job, average=True)
def baseline_remove(values):
"""Center data around 0."""
return np.array(values) - np.mean(values)
# Note: Only real part of data is plotted
rabi_12_data = np.real(baseline_remove(rabi_12_data))
(rabi_12_fit_params,
rabi_12_y_fit) = fit_function(drive_amps,
rabi_12_data,
lambda x, A, B, drive_12_period, phi: (A*np.cos(2*np.pi*x/drive_12_period - phi) + B),
[0.2, 0, 0.3, 0])
plt.scatter(drive_amps, rabi_12_data, color='black')
plt.plot(drive_amps, rabi_12_y_fit, color='red')
drive_12_period = rabi_12_fit_params[2]
pi_amp_12 = drive_12_period/2
plt.axvline(pi_amp_12, color='red', linestyle='--')
plt.axvline(pi_amp_12+drive_12_period/2, color='red', linestyle='--')
plt.annotate("", xy=(pi_amp_12+drive_12_period/2, 0), xytext=(pi_amp_12,0), arrowprops=dict(arrowstyle="<->", color='red'))
plt.annotate("$\pi$", xy=(pi_amp_12-0.03, 0.1), color='red')
plt.xlabel("Drive amp [a.u.]", fontsize=15)
plt.ylabel("Measured signal [a.u.]", fontsize=15)
plt.title('Rabi Experiment (1->2)', fontsize=20)
plt.show()
```
We plot and fit our data as before.
```
print(f"Our updated estimate for the 1->2 transition frequency is "
f"{round(qubit_12_freq/GHz, 7)} GHz.")
print(f"Pi Amplitude (1->2) = {pi_amp_12}")
```
### Build the 0, 1, 2 discriminator <a id="builddiscrim012"></a>
Finally, we build our discriminator for the $|0\rangle$, $|1\rangle$ and $|2\rangle$ states.
As a review, our three circuits are (again, recalling that our system starts in the $|0\rangle$ state):
1. Measure the $|0\rangle$ state directly (obtain $|0\rangle$ centroid).
2. Apply $0\rightarrow1$ $\pi$ pulse and then measure (obtain $|1\rangle$ centroid).
3. Apply $0\rightarrow1$ $\pi$ pulse, then $1\rightarrow2$ $\pi$ pulse, then measure (obtain $|2\rangle$ centroid).
```
with pulse.build(backend=backend, default_alignment='sequential', name='x12 schedule') as x12_sched:
drive_chan = pulse.drive_channel(qubit)
pulse.set_frequency(qubit_12_freq, drive_chan)
pulse.play(pulse.Gaussian(duration=x12_duration,
amp=pi_amp_12,
sigma=x12_sigma,
name='x12_pulse'), drive_chan)
# Create the three circuits
# 0 state
qc_ground = QuantumCircuit(1, 1)
qc_ground.measure(0, 0)
# 1 state
qc_one = QuantumCircuit(1, 1)
qc_one.x(0)
qc_one.measure(0, 0)
# 2 state
x12_gate = Gate("one_two_pulse", 1, [])
qc_x12 = QuantumCircuit(1, 1)
qc_x12.x(0)
qc_x12.append(x12_gate, [0])
qc_x12.measure(0, 0)
qc_x12.add_calibration(x12_gate, (0,), x12_sched, [])
```
We construct the program and plot the centroids in the IQ plane.
```
# Assemble the schedules into a program
IQ_012_job = backend.run([qc_ground, qc_one, qc_x12],
meas_level=1,
meas_return='single',
shots=NUM_SHOTS)
job_monitor(IQ_012_job)
# Get job data (single); split for zero, one and two
IQ_012_data = get_job_data(IQ_012_job, average=False)
zero_data = IQ_012_data[0]
one_data = IQ_012_data[1]
two_data = IQ_012_data[2]
def IQ_012_plot(x_min, x_max, y_min, y_max):
"""Helper function for plotting IQ plane for 0, 1, 2. Limits of plot given
as arguments."""
# zero data plotted in blue
plt.scatter(np.real(zero_data), np.imag(zero_data),
s=5, cmap='viridis', c='blue', alpha=0.5, label=r'$|0\rangle$')
# one data plotted in red
plt.scatter(np.real(one_data), np.imag(one_data),
s=5, cmap='viridis', c='red', alpha=0.5, label=r'$|1\rangle$')
# two data plotted in green
plt.scatter(np.real(two_data), np.imag(two_data),
s=5, cmap='viridis', c='green', alpha=0.5, label=r'$|2\rangle$')
# Plot a large dot for the average result of the 0, 1 and 2 states.
mean_zero = np.mean(zero_data) # takes mean of both real and imaginary parts
mean_one = np.mean(one_data)
mean_two = np.mean(two_data)
plt.scatter(np.real(mean_zero), np.imag(mean_zero),
s=200, cmap='viridis', c='black',alpha=1.0)
plt.scatter(np.real(mean_one), np.imag(mean_one),
s=200, cmap='viridis', c='black',alpha=1.0)
plt.scatter(np.real(mean_two), np.imag(mean_two),
s=200, cmap='viridis', c='black',alpha=1.0)
plt.xlim(x_min, x_max)
plt.ylim(y_min,y_max)
plt.legend()
plt.ylabel('I [a.u.]', fontsize=15)
plt.xlabel('Q [a.u.]', fontsize=15)
plt.title("0-1-2 discrimination", fontsize=15)
x_min = -5
x_max = 5
y_min = -10
y_max = 10
IQ_012_plot(x_min, x_max, y_min, y_max)
```
Now it is time to actually build the discriminator. We will use a machine learning technique called Linear Discriminant Analysis (LDA). LDA classifies an arbitrary data set into a set of categories (here $|0\rangle$, $|1\rangle$ and $|2\rangle$) by maximizing the distance between the means of each category and minimizing the variance within each category. For further detail, see [here](https://scikit-learn.org/stable/modules/lda_qda.html#id4) (Ref. [3](#refs)).
LDA generates a line called a separatrix. Depending on which side of the separatrix a given data point is on, we can determine which category it belongs to.
We use `scikit.learn` for an implementation of LDA; in a future release, this functionality will be added released directly into Qiskit-Ignis (see [here](https://github.com/Qiskit/qiskit-ignis/tree/master/qiskit/ignis/measurement/discriminator)).
We observe a third centroid corresponding to the $|2\rangle$ state. (Note: If the plot looks off, rerun the notebook.)
We begin by reshaping our result data into a format suitable for discrimination.
```
def reshape_complex_vec(vec):
"""Take in complex vector vec and return 2d array w/ real, imag entries. This is needed for the learning.
Args:
vec (list): complex vector of data
Returns:
list: vector w/ entries given by (real(vec], imag(vec))
"""
length = len(vec)
vec_reshaped = np.zeros((length, 2))
for i in range(len(vec)):
vec_reshaped[i]=[np.real(vec[i]), np.imag(vec[i])]
return vec_reshaped
```
We begin by shaping the data for LDA.
```
# Create IQ vector (split real, imag parts)
zero_data_reshaped = reshape_complex_vec(zero_data)
one_data_reshaped = reshape_complex_vec(one_data)
two_data_reshaped = reshape_complex_vec(two_data)
IQ_012_data = np.concatenate((zero_data_reshaped, one_data_reshaped, two_data_reshaped))
print(IQ_012_data.shape) # verify IQ data shape
```
Next, we split our training and testing data. The testing data is a vector containing an array of `0`'s (for the zero schedule, `1`'s (for the one schedule) and `2`'s (for the two schedule).
```
# construct vector w/ 0's, 1's and 2's (for testing)
state_012 = np.zeros(NUM_SHOTS) # shots gives number of experiments
state_012 = np.concatenate((state_012, np.ones(NUM_SHOTS)))
state_012 = np.concatenate((state_012, 2*np.ones(NUM_SHOTS)))
print(len(state_012))
# Shuffle and split data into training and test sets
IQ_012_train, IQ_012_test, state_012_train, state_012_test = train_test_split(IQ_012_data, state_012, test_size=0.5)
```
Finally, we set up our model and train it. The accuracy of our fit is printed.
```
# Set up the LDA
LDA_012 = LinearDiscriminantAnalysis()
LDA_012.fit(IQ_012_train, state_012_train)
# test on some simple data
print(LDA_012.predict([[0, 0], [-10, 0], [-15, -5]]))
# Compute accuracy
score_012 = LDA_012.score(IQ_012_test, state_012_test)
print(score_012)
```
The last step is to plot the separatrix.
```
# Plot separatrix on top of scatter
def separatrixPlot(lda, x_min, x_max, y_min, y_max, shots):
nx, ny = shots, shots
xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),
np.linspace(y_min, y_max, ny))
Z = lda.predict_proba(np.c_[xx.ravel(), yy.ravel()])
Z = Z[:, 1].reshape(xx.shape)
plt.contour(xx, yy, Z, [0.5], linewidths=2., colors='black')
IQ_012_plot(x_min, x_max, y_min, y_max)
separatrixPlot(LDA_012, x_min, x_max, y_min, y_max, NUM_SHOTS)
```
Now that we have 3 centroids, the separatrix is no longer a line, but rather a curve containing a combination of two lines. In order to discriminate between $|0\rangle$, $|1\rangle$ and $|2\rangle$ states, our model checks where the IQ point lies relative to the separatrix and classifies the point accordingly.
## References <a id="refs"></a>
1. D. C. McKay, T. Alexander, L. Bello, M. J. Biercuk, L. Bishop, J. Chen, J. M. Chow, A. D. C ́orcoles, D. Egger, S. Filipp, J. Gomez, M. Hush, A. Javadi-Abhari, D. Moreda, P. Nation, B. Paulovicks, E. Winston, C. J. Wood, J. Wootton, and J. M. Gambetta, “Qiskit backend specifications for OpenQASM and OpenPulse experiments,” 2018, https://arxiv.org/abs/1809.03452.
2. Krantz, P. et al. “A Quantum Engineer’s Guide to Superconducting Qubits.” Applied Physics Reviews 6.2 (2019): 021318, https://arxiv.org/abs/1904.06560.
3. Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011, https://scikit-learn.org/stable/modules/lda_qda.html#id4.
```
import qiskit.tools.jupyter
%qiskit_version_table
```
| true |
code
| 0.697854 | null | null | null | null |
|
# Gaussian feedforward -- analysis
Ro Jefferson<br>
Last updated 2021-05-26
This is the companion notebook to "Gaussian_Feedforward.ipynb", and is designed to read and perform analysis on data generated by that notebook and stored in HDF5 format.
**The user must specify** the `PATH_TO_DATA` (where the HDF5 files to be read are located) and the `PATH_TO_OUTPUT` (where any plots will be written) below.
```
# Numpy, scipy, and plotting:
import numpy as np
from scipy.stats import norm # Gaussian fitting
import scipy.integrate as integrate # integration
import matplotlib.pyplot as plt # plotting
import seaborn as sns; sns.set() # nicer plotting
import pandas as pd # dataframe for use with seaborn
# File i/o:
import pickle # for unpickling MNIST data
import gzip # for opening pickled MNIST data file
import h5py # HDF5
# Miscellaneous:
import math
import random # random number generators
import re # regular expressions
import gc # garbage collection
# symbolic algebra package:
import sympy as sym
from sympy import tanh
```
## Import HDF5 data
Specify the path to the .hdf5 files containing the accuracies and hooks, and define functions to load the data as dictionaries:
```
PATH_TO_DATA = '/full/path/to/HDF5/data/'
PATH_TO_OUTPUT = '/full/path/where/plots/are/to/be/saved/'
# read file of accuracies, return dataset as dictionary:
def read_accuracies(file_name):
with h5py.File(PATH_TO_DATA + file_name, 'r') as file:
# cast elements as np.array, else returns closed file datasets:
acc_dict = {key : np.array(file[key]) for key in file.keys()}
return acc_dict
# read file of inputs/outputs, return dataset as dictionary:
def read_hooks(file_name):
with h5py.File(PATH_TO_DATA + file_name, 'r') as file:
# cast elements as np.array, else returns closed file datasets:
hook_dict = {key : np.array(file[key]) for key in file.keys()}
return hook_dict
# read file of weights, biases; return dataset as dictionary:
def read_parameters(file_name):
with h5py.File(PATH_TO_DATA + file_name, 'r') as file:
# cast elements as np.array, else returns closed file datasets:
for key in file.keys():
para_dict = {key : np.array(file[key]) for key in file.keys()}
return para_dict
# load data, ensuring consistent files:
def load_data(acc_file, hook_file, para_file, verbose=True):
accuracies = read_accuracies(acc_file)
hooks = read_hooks(hook_file)
parameters = read_parameters(para_file)
var_w = accuracies['var_weight'].item()
var_b = accuracies['var_bias'].item()
if var_w != hooks['var_weight'].item() or var_w != parameters['var_weight'].item():
raise Exception('Weight variances do not match!')
elif var_b != hooks['var_bias'].item() or var_b != parameters['var_bias'].item():
raise Exception('Bias variances do not match!')
# extract accuracies corresponding to depth in hook file:
index = np.where(accuracies['depth'] == hooks['depth'])[0] # array of matches
if index.size == 0: # empty array = no match
raise Exception('No matching depth!')
else:
acc = accuracies['accuracies'][index[0]]
print('Successfully loaded network with the following parameters:'
'\nDepth = {}\nvar_w = {}\nvar_b = {}\n'.format(hooks['depth'].item(), var_w, var_b))
# optionally print key lists:
if verbose:
print('Hook keys:\n{}\n'.format(hooks.keys()))
print('Parameter keys:\n{}\n'.format(parameters.keys()))
return acc, hooks, parameters
```
So, for example, we can read in files and extract the hyperparameters as follows:
```
accs, hooks, paras = load_data('acc-150-30.hdf5', 'e14-hooks-150-30.hdf5', 'e14-para-150-30.hdf5')
depth = hooks['depth'].item()
var_w = hooks['var_weight'].item()
var_b = hooks['var_bias'].item()
```
## Analysis functions
Here we'll define some useful functions for analyzing the results. To begin, let's write a simple function that returns the distribution of pre-/post-activations (i.e., inputs/outputs) for each layer, to see whether they remain Gaussian.
```
# return mean and variance for the layer, and optionally plot:
def view_layer(key, plot=False, truncate=1000):
layer = hooks[key][-truncate:] # use last `truncate` samples, else excessive size
sns.distplot(layer, fit=norm)
if not plot: plt.close() # optionally suppress figure
mean, std = norm.fit(layer)
return mean, std**2
# same, but accept layer as array:
def view_array(layer, plot=False):
sns.distplot(layer, fit=norm)
if not plot: plt.close() # optionally suppress figure
mean, std = norm.fit(layer)
return mean, std**2
```
Let's look at a few layers:
```
# current dataset corresponds to `wide` network option, so should remain Gaussian until the last couple layers:
view_layer('in-0', True)
view_layer('in-15', True)
view_layer('in-27', True)
view_layer('in-29', True) # only 10 neurons, don't expect Gaussian
```
Of chief importance is the fixed-point $q^*$. We can find the approximate value with the following process: first, we numerically evaluate the integral expression for $q^{\ell+1}$ as a function of $q^{\ell}$ for a grid of points. We can optionally use this to plot $q^{\ell+1}$ and the unit slope, but all we really need is the nearest datapoint (in the aforementioned grid) to the intersection, which we find by identifying the index at which the difference between these two curves changes sign. Then, we apply linear interpolation to the corresponding line segments to approximate the precise value of the intersection.
Denote the endpoints of the line segment with unit slope $(x_1, y_1=x_1)$ and $(x_2, y_2=x_2)$, and the endpoints of the segment of the $q$-curve $(x_3=x_1, y_3)$ and $(x_4=x_2, y_4)$. Then Cramer's rule reduces to the following expression for the intersection point $x=y$:
\begin{equation}
x=\frac{(x_1y_4-x_2y_3)}{(x_1-x_2)-(y_3-y_4)}
\end{equation}
```
# recursive expression for the variances, eq. (14) in my blog:
def next_q(q, var_w=1, var_b=0):
integral = integrate.quad(lambda z: np.exp(-z**2/2)*np.tanh(np.sqrt(q)*z)**2, -np.inf, np.inf)[0]/np.sqrt(2*np.pi)
return var_w*integral + var_b
# compute q* given variances, and optionally plot q^{l+1} vs. q^l:
def find_qstar(var_weight, var_bias, plot = False, domain = 2): # check between 0 and domain
# grid of points for numerical sampling:
points = np.arange(0,domain,0.05)
qnew = [next_q(q, var_weight, var_bias) for q in points]
# find index (i.e., datapoint) at which difference between curves changes sign:
flip = np.argwhere(np.diff(np.sign(qnew-points)))[0][0]
# extract line segments which contain the intersection:
seg1 = points[flip:flip+2]
seg2 = qnew[flip:flip+2]
# intersection point x=4 via Cramer's rule:
qstar = (seg1[0]*seg2[1] - seg1[1]*seg2[0])/(seg1[0] - seg1[1] - seg2[0] + seg2[1])
if plot:
line_df = pd.DataFrame({'q_l': points, 'q_{l+1}': points})
theory_df = pd.DataFrame({'q_l': points, 'q_{l+1}': qnew})
sns.lineplot('q_l', 'q_{l+1}', data=theory_df, marker='o');
sns.lineplot('q_l', 'q_{l+1}', data=line_df, marker='o');
return qstar
```
For example, for the case above, we have:
```
qstar = find_qstar(var_w, var_b, plot=True)
print(qstar)
```
Similarly, we would like to find the fixed point $\rho^*$, which is found by numerically solving a similar recursion relation, and then applying the flip-interpolation strategy above:
```
# recursive expression for the Pearson correlation coefficient, eq. (23) in my blog:
def next_rho(rho, qstar, var_w=1, var_b=0):
sq = np.sqrt(qstar)
bound = np.inf # integration bound (should be np.inf)
integral = integrate.dblquad(lambda x, y: np.exp(-x**2/2)*np.exp(-y**2/2)*np.tanh(sq*x)*np.tanh(sq*(rho*x+np.sqrt(1-rho**2)*y)),
-bound, bound, lambda x: -bound, lambda x: bound)[0]/(2*np.pi)
return (var_w*integral + var_b)/qstar
# compute rho* given q*, variances; optionally plot rho^{l+1} vs. rho^l:
def find_rhostar(qstar, var_weight, var_bias, plot = False):
# grid of points for numerical sampling:
points = np.arange(0,1.01,0.05)
rhonew = [next_rho(rho, qstar, var_weight, var_bias) for rho in points]
# find index (i.e., datapoint) at which difference between curves changes sign:
where = np.argwhere(np.diff(np.sign(rhonew-points)))
if where.size == 0:
rhostar = 1
else:
flip = np.argwhere(np.diff(np.sign(rhonew-points)))[0][0]
# extract line segments which contain the intersection:
seg1 = points[flip:flip+2]
seg2 = rhonew[flip:flip+2]
# intersection point x=4 via Cramer's rule:
rhostar = (seg1[0]*seg2[1] - seg1[1]*seg2[0])/(seg1[0] - seg1[1] - seg2[0] + seg2[1])
if plot:
line_df = pd.DataFrame({'rho_l': points, 'rho_{l+1}': points})
theory_df = pd.DataFrame({'rho_l': points, 'rho_{l+1}': rhonew})
sns.lineplot('rho_l', 'rho_{l+1}', data=theory_df, marker='o');
sns.lineplot('rho_l', 'rho_{l+1}', data=line_df, marker='o');
return rhostar
```
For example, for the $q^*$ value and associated variances above, we have:
```
rhostar = find_rhostar(qstar, var_w, var_b, True)
print(rhostar)
```
With these values in hand, we can compute the theoretical correlation length, given by eq. (27) in my blog (which is eq. (9) in Schoenholz et al.):
```
# correlation length (for the Pearson correlation coefficient):
def correlation_length(rhostar, qstar, var_w=1):
sq = np.sqrt(qstar)
bound = 100 # integration bound (should be np.inf, but that causes overflow errors)
integral = integrate.dblquad(lambda x, y: np.exp(-x**2/2)*np.exp(-y**2/2)*(1/np.cosh(sq*x))**2*(1/np.cosh(sq*(rhostar*x+np.sqrt(1-rhostar**2)*y))**2),
-bound, bound, lambda x: -bound, lambda x: bound)[0]/(2*np.pi)
return -1/np.log(var_w*integral)
correlation_length(rhostar, qstar, var_w)
```
# Probing fall-off
Theoretically, we should be able to train deeper networks at criticality, and they should all fall-off based on the correlation length. To see how our networks behave, we'll write a function that reads-in a grid-worth of accuracy data (optionally plotting the individual accuracies), and another that uses this function to make the desired scatterplot:
```
# automatically read and plot accuracies from a series of files **with the same variances**:
def read_and_plot_accs(base, start, stop, step, plot=True, write=False):
# file names in format acc-{base}-{dd}.hdf5
filenames = ['acc-{}-{}.hdf5'.format(base, dd) for dd in range(start, stop, step)]
#print('Reading {} files: {}\n'.format(len(filenames), filenames))
# get list of accuracies and corresponding depths:
acc, depth = [], []
for i in range(len(filenames)):
# load data:
acc_dict = read_accuracies(filenames[i])
acc.append(acc_dict['accuracies'])
depth.append(acc_dict['depth'].item())
# get variances from last file:
var_w = acc_dict['var_weight'].item()
var_b = acc_dict['var_bias'].item()
if plot:
#plt.rcParams['figure.figsize'] = [9, 6] # globally (!) adjust figure size
# plot each series, labelled by depth:
list_dict = {'L = {}'.format(dd) : pd.Series(acc[i])
for i,dd in enumerate(depth)}
df = pd.DataFrame(list_dict)
acc_plot = df.plot()
# format legend, title:
acc_legend = acc_plot.legend(loc='upper left', bbox_to_anchor=(1,1))
acc_plot.set_title('var_w = {}'.format(var_w)) # all var_w equal
# optionally save plot as pdf:
if write:
plt.savefig(PATH_TO_OUTPUT+'plot-{}.pdf'.format(base),
bbox_extra_artists=(acc_legend,), bbox_inches='tight')
return acc, depth, var_w, var_b
# read-in accuracies using pre-defined function above, and use this to
# make scatterplot like fig. 5 in Schoenholz et al.:
def probe_falloff(base_list, start, stop, step, plot=True, write=False):
# read accuracies, with plot suppressed:
acc_list, dep_list, w_list, b_list = [], [], [], []
for base in base_list:
acc, dep, w, b = read_and_plot_accs(base, start, stop, step, False, False)
# store final accuracy from run:
acc_list.append([a[-1] for a in acc])
# store list of depths, variances:
dep_list.append(dep)
w_list.append(w)
b_list.append(b)
# var_w gives x-values:
x_vals = []
for i in range(len(w_list)):
# make len(acc_list[i]) copies of w_list[i]:
x_vals.append([w_list[i]]*len(acc_list[i]))
x_vals = np.array(x_vals).flatten()
# depths give y-values:
y_vals = np.array(dep_list).flatten()
# accuracies give z-values (color):
z_vals = np.array(acc_list).flatten()
# optionally make scatterplot:
if plot:
scat_plot = plt.scatter(x_vals, y_vals, c=z_vals, cmap='rainbow', s=50)
plt.colorbar(scat_plot) # add colorbar as legend
# add title, axes labels:
plt.title('var_b = {}'.format(b_list[0])) # all var_b equal
plt.xlabel('var_w')
plt.ylabel('depth')
# optionally save plot as pdf:
if write:
# should all have same bias, so label with that:
plt.savefig(PATH_TO_OUTPUT+'scatterplot-{}.pdf'.format(b_list[0]),)
return x_vals, y_vals, z_vals, b_list
# read and plot:
var_list, dep_list, acc_list, b_list = probe_falloff([x for x in range(100,286,5)], 10, 70, 3, True, False)
```
How does this compare with the theoretical value of the correlation length? We can easily compute this using the $q^*$, $\rho^*$, and `correlation_length` functions above:
```
# same range of var_w values as above, for given var_b:
test_w = np.arange(1.0, 2.86, 0.05)
test_b = 0.05
qstar_test = [find_qstar(ww, test_b, False) for ww in test_w]
#print('q* = ', qstar_test)
rhostar_test = [find_rhostar(qq, ww, test_b, False) for qq, ww in zip(qstar_test, test_w)]
#print('\nrho* = {}\n'.format(rhostar_test))
xi_vals = np.array([correlation_length(rr, qq, ww) for rr,qq,ww in zip(rhostar_test,qstar_test,test_w)])
```
In principle this should never be negative, but the numerics are such that the integral can be greater than 1 near the critical point, which makes $\xi<0$. Since we can't plot infinity, let's just replace this with double the largest positive value for visualization purposes:
```
neg_index = np.where(np.array(xi_vals) < 0)[0].item() # get index of negative value
xis = np.copy(xi_vals)
xis[neg_index] = 2*max(xi_vals)
xi_df = pd.DataFrame({'var_w': test_w, 'xi': xis})
xi_plot = sns.lineplot('var_w', 'xi', data=xi_df, marker='o');
xi_plot.set_ylim(0,100);
```
This is fine, but it would be nice to overlay the theoretical curve on the grid:
```
# re-create and overlay above two plots:
def overlay_falloff(base_list, start, stop, step, write=False):
# ************ load and process data for scatterplot: ************
# read accuracies, with plot suppressed:
acc_list, dep_list, w_list, b_list = [], [], [], []
for base in base_list:
acc, dep, w, b = read_and_plot_accs(base, start, stop, step, False, False)
# store final accuracy from run:
acc_list.append([a[-1] for a in acc])
# store list of depths, variances:
dep_list.append(dep)
w_list.append(w)
b_list.append(b)
# var_w gives x-values:
x_vals = []
for i in range(len(w_list)):
# make len(acc_list[i]) copies of w_list[i]:
x_vals.append([w_list[i]]*len(acc_list[i]))
x_vals = np.array(x_vals).flatten()
# depths give y-values:
y_vals = np.array(dep_list).flatten()
# accuracies give z-values (color):
z_vals = np.array(acc_list).flatten()
# ************ process data for correlation length plot: ************
qstar = [find_qstar(ww, b_list[0], False) for ww in w_list] # all biases equal, so just use first
rhostar = [find_rhostar(qq, ww, b_list[0], False) for qq, ww in zip(qstar, w_list)]
xi_vals = np.array([correlation_length(rr, qq, ww) for rr,qq,ww in zip(rhostar, qstar, w_list)])
# ensure no negative elements (see comment about numerics near critical point above):
artificial_xi = 2*max(xi_vals) # overwrite negative values with this
for i in range(xi_vals.size):
if xi_vals[i] < 0:
xi_vals[i] = artificial_xi
# consider a few different multiples of the correlation length, for comparison with Schoenholz et al.:
three_vals = [np.pi*xx for xx in xi_vals]
six_vals = [2*np.pi*xx for xx in xi_vals]
# ************ overlay correlation length plot on scatterplot: ************
# create combination figure:
fig, ax1 = plt.subplots(figsize=(9,6))
ax2 = ax1.twinx() # share x axis
# make scatterplot:
ax1.set_xlabel(r'$\sigma_w^2$')
ax1.set_ylabel('depth')
scat_plot = ax1.scatter(x=x_vals, y=y_vals, c=z_vals, cmap='rainbow', s=120) # does not return Axes object!
ax1.tick_params(axis='y')
# truncate for cleaner visuals:
ax1.set_ylim(min(y_vals)-1, max(y_vals)+1)
ax1.set_xlim(min(w_list)-0.05, max(w_list)+0.05)
# ax1.set_title('Optional title here')
cbar = plt.colorbar(scat_plot, label='accuracy') # add colorbar as legend
# control labels/ticks position colorbar:
cbar.ax.yaxis.set_ticks_position('right')
cbar.ax.yaxis.set_label_position('left')
# overlay correlation length plot:
xi_df = pd.DataFrame({'var_w': w_list, 'xi': xi_vals})
ax2 = sns.lineplot('var_w', 'xi', data=xi_df, marker=None, color='black')
# n.b., use None instead of False, else pdf still has white horizontal ticks
xi3_df = pd.DataFrame({'var_w': w_list, 'xi': three_vals})
sns.lineplot('var_w', 'xi', data=xi3_df, marker=None, color='grey')
xi6_df = pd.DataFrame({'var_w': w_list, 'xi': six_vals})
sns.lineplot('var_w', 'xi', data=xi6_df, marker=None, color='darkgrey')
# n.b., darkgrey is *lighter* than grey, because what the fuck programmers
# truncate to same range/domain:
ax2.set_ylim(min(y_vals)-1, max(y_vals)+1)
ax2.set_xlim(min(w_list)-0.05, max(w_list)+0.05)
# turn off second labels, ticks, and grid:
ax2.set_ylabel(None)
ax2.grid(False)
ax2.axis('off')
# optionally save plot as pdf:
if write:
# should all have same bias, so label with that:
plt.savefig(PATH_TO_OUTPUT+'scatterplot-{}.pdf'.format(b_list[0]),)
return x_vals, y_vals, z_vals, b_list
overlay_falloff([x for x in range(100,286,5)], 10, 70, 3, xis, False);
```
| true |
code
| 0.626524 | null | null | null | null |
|
# Breast-Cancer Classification
```
#WOHOO already Version 2 I learned How to explore Data
```
# Library
```
# Import Dependencies
%matplotlib inline
# Start Python Imports
import math, time, random, datetime
# Data Manipulation
import numpy as np
import pandas as pd
# Visualization
import matplotlib.pyplot as plt
import missingno
import seaborn as sns
plt.style.use('seaborn-whitegrid')
# Preprocessing
from sklearn.preprocessing import OneHotEncoder, LabelEncoder, label_binarize
# Machine learning
import catboost
from sklearn.model_selection import train_test_split
from sklearn import model_selection, tree, preprocessing, metrics, linear_model
from sklearn.svm import LinearSVC
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LinearRegression, LogisticRegression, SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from catboost import CatBoostClassifier, Pool, cv
# Let's be rebels and ignore warnings for now
import warnings
warnings.filterwarnings('ignore')
```
# Exploring the dataset
```
dataset = pd.read_csv('data.csv')
dataset.drop('Unnamed: 32', inplace=True, axis=1)
dataset.head()
# Plot graphic of missing values
missingno.matrix(dataset, figsize = (30,10))
dataset.columns
print(dataset.shape)
dataset.describe()
dataset.isnull().sum()
X = dataset.iloc[:, 2:].values
y = dataset.iloc[:, 1:2].values
```
# spliting the dataset
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= 0.2)
#categorical values
from sklearn.preprocessing import LabelEncoder
label_y = LabelEncoder()
y_train = label_y.fit_transform(y_train)
y_test = label_y.transform(y_test)
```
# Method 1
## Fitting the model and analysing
```
#fitting
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(n_jobs= -1)
classifier.fit(X_train, y_train)
#predicting
y_pred = classifier.predict(X_test)
#confusion matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred)
# classification analysis
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
# k-fold cross vallidation
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator=classifier, X=X_train, y=y_train,cv= 10, n_jobs=-1)
print(accuracies.mean(), accuracies.std())
```
# Method 2
# Function that runs the requested algorithm and returns the accuracy metrics
```
def fit_ml_algo(algo, X_train, y_train, cv):
# One Pass
model = algo.fit(X_train, y_train)
acc = round(model.score(X_train, y_train) * 100, 2)
# Cross Validation
train_pred = model_selection.cross_val_predict(algo,
X_train,
y_train,
cv=cv,
n_jobs = -1)
# Cross-validation accuracy metric
acc_cv = round(metrics.accuracy_score(y_train, train_pred) * 100, 2)
return train_pred, acc, acc_cv
start_time = time.time()
train_pred_log, acc_log, acc_cv_log = fit_ml_algo(LogisticRegression(),
X_train,
y_train,
10)
log_time = (time.time() - start_time)
print("Accuracy: %s" % acc_log)
print("Accuracy CV 10-Fold: %s" % acc_cv_log)
print("Running Time: %s" % datetime.timedelta(seconds=log_time))
```
| true |
code
| 0.547404 | null | null | null | null |
|
# Exploring Random Forests
```
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.datasets import load_boston, load_iris, load_wine, load_digits, \
load_breast_cancer, load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, precision_score, recall_score
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
from rfpimp import *
from distutils.version import LooseVersion
if LooseVersion(sklearn.__version__) >= LooseVersion("0.24"):
# In sklearn version 0.24, forest module changed to be private.
from sklearn.ensemble._forest import _generate_unsampled_indices
from sklearn.ensemble import _forest as forest
else:
# Before sklearn version 0.24, forest was public, supporting this.
from sklearn.ensemble.forest import _generate_unsampled_indices
from sklearn.ensemble import forest
from sklearn import tree
from dtreeviz.trees import *
def rent(n=None, bootstrap=False):
df_rent = pd.read_csv("data/rent-ideal.csv")
if n is None:
n = len(df_rent)
df_rent = df_rent.sample(n, replace=bootstrap)
X = df_rent[['bedrooms','bathrooms','latitude','longitude']]
y = df_rent['price']
return X, y
def boston():
boston = load_boston()
X = boston.data
y = boston.target
features = boston.feature_names
df = pd.DataFrame(data=X,columns=features)
df['y'] = y
return df
```
## Set up
Get the `rent-ideal.csv` data file from canvas "files area" and store in the data directory underneath your notebook directory.
```
X, y = rent()
X.head(3)
X.shape
```
## Train random forests of different sizes
As we increase the number of trees in the forest, we initially see model bias going down. It will asymptotically approach some minimum error on the testing set.
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
```
Here's how to train a random forest that has a single tree:
```
rf = RandomForestRegressor(n_estimators=1)
rf.fit(X_train, y_train)
```
**Task**: Compute the MAE for the training and the testing set, printing them out.
```
mae_train = mean_absolute_error(...)
mae = mean_absolute_error(...)
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
</pre>
</details>
**Task**: Run the training and testing cycle several times to see the variance: the test scores bounce around a lot.
**Task**: Increase the number of trees (`n_estimators`) to 2, retrain, and print out the results.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=2)
rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
You should notice the both test MAE scores going down and bouncing around less from run to run.
**Q.** Why does the MAE score go down?
<details>
<summary>Solution</summary>
With 2 trees, the chances are that the random forest will have seen (trained on) more of the original training set, despite bootstrapping.
</details>
**Task**: Increase the number of trees (`n_estimators`) to 10, retrain, and print out the results.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=10)
rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
**Q.** What you notice about the MAE scores?
<details>
<summary>Solution</summary>
They are getting smaller.
</details>
**Q.** After running several times, what else do you notice?
<details>
<summary>Solution</summary>
With 10 trees, the prediction from run to run varies a lot less. We have reduced variance, improving generality.
</details>
**Task**: Increase the number of trees (`n_estimators`) to 200, retrain, and print out the results.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=200)
%time rf.fit(X_train, y_train) # how long does this take?
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
**Q.** What you notice about the MAE scores from a single run?
<details>
<summary>Solution</summary>
They are a bit smaller, but not by much.
</details>
**Task**: Notice that it took a long time to train, about 10 seconds. Do the exact same thing again but this time use `n_jobs=-1` as an argument to the `RandomForestRegressor` constructor.
This tells the library to use all processing cores available on the computer processor. As long as the data is not too huge (because it must pass it around), it often goes much faster using this argument. It should take less than two seconds.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=200, n_jobs=-1)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
**Q.** What you notice about the MAE scores from SEVERAL runs?
<details>
<summary>Solution</summary>
The error variance across runs is even lower (tighter).
</details>
## Examining model size and complexity
The structure of a tree is affected by a number of hyper parameters, not just the data. Goal in the section is to see the effect of altering the number of samples per leaf and the maximum number of candidate features per split. Let's start out with a handy function that uses some support code from rfpimp to examine tree size and depth:
```
def showsize(ntrees, max_features=1.0, min_samples_leaf=1):
rf = RandomForestRegressor(n_estimators=ntrees,
max_features=max_features,
min_samples_leaf=min_samples_leaf,
n_jobs=-1)
rf.fit(X_train, y_train)
n = rfnnodes(rf) # from rfpimp
h = np.median(rfmaxdepths(rf)) # rfmaxdepths from rfpimp
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:6.1f}$, test {mae:6.1f}$ using {n:9,d} tree nodes with {h:2.0f} median tree height")
```
### Effect of number of trees
For a single tree, we see about 21,000 nodes and a tree height of around 35:
```
showsize(ntrees=1)
```
**Task**: Look at the metrics for 2 trees and then 100 trees.
<details>
<summary>Solution</summary>
<pre>
showsize(ntrees=2)
showsize(ntrees=100)
</pre>
</details>
**Q.** Why does the median height of a tree stay the same when we increase the number of trees?
<details>
<summary>Solution</summary>
While the number of nodes increases with the number of trees, the height of any individual tree will stay the same because we have not fundamentally changed how it is constructing a single tree.
</details>
### Effect of increasing min samples / leaf
**Task**: Loop around a call to `showsize()` with 10 trees and min_samples_leaf=1..10
```
for i in range(...):
print(f"{i:2d} ",end='')
showsize(...)
```
<details>
<summary>Solution</summary>
<pre>
for i in range(1,10+1):
showsize(ntrees=10, min_samples_leaf=i)
</pre>
</details>
**Q.** Why do the median height of a tree and number of total nodes decrease as we increase the number of samples per leaf?
<details>
<summary>Solution</summary>
Because when the sample size gets down to `min_samples_leaf`, splitting stops, which prevents the tree from getting taller. It also restricts how many nodes total get created for the tree.
</details>
**Q.** Why does the MAE error increase?
<details>
<summary>Solution</summary>
If we include more observations in a single leaf, then the average is taken over more samples. That average is a more general prediction but less accurate.
</details>
It's pretty clear from that print out that `min_samples_leaf=1` is the best choice because it gives the minimum validation error.
### Effect of reducing max_features (rent data)
**Task:** Do another loop from `max_features` = 4 down to 1, with 1 sample per leaf. (There are 4 total features.)
```
p = X_train.shape[1]
for i in range(...):
print(f"{i:2d} ",end='')
showsize(ntrees=10, ...)
```
<details>
<summary>Solution</summary>
<pre>
p = X_train.shape[1]
for i in range(p,0,-1):
print(f"{i:2d} ",end='')
showsize(ntrees=10, max_features=i)
</pre>
</details>
For this data set, changing the available candidate features that each split does not seem to be important as the validation error does not change, nor does the height of the trees.
### Examine effects of hyper parameters on Boston data set
```
df_boston = boston()
df_boston.head(3)
X, y = df_boston.drop('y', axis=1), df_boston['y']
y *= 1000 # y is "Median value of owner-occupied homes in $1000's" so multiply by 1000
# reproducible 20% test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=1)
```
Let's run the metric `showsize()` function to see how many trees we should use:
```
for i in [1,5,30,50,100,150,300]:
print(f"{i:3d} trees: ", end='')
showsize(ntrees=i)
```
Seems like the sweet spot on the validation error is probably 150 trees as it gets a low validation error and has a fairly small set of trees.
Check the effect of increasing the minimum samples per leaf from 1 to 10 as we did before.
```
for i in range(1,10+1):
print(f"{i:2d} ",end='')
showsize(ntrees=150, min_samples_leaf=i)
```
The training error goes up dramatically but the validation error doesn't get too much worse.
**Q.** Which min samples per leaf would you choose?
<details>
<summary>Solution</summary>
After running a few times, it seems that using <tt>min_samples_leaf</tt>=1 or 2 is best for the validation error. But, keep in mind that this data set is pretty small and so our error values will change quite a bit depending on the sample we get for the test set.
</details>
Run a loop from the maximum number of features down to 1 for `max_features` to see the effects.
```
p = X_train.shape[1]
for i in range(p,0,-1):
print(f"{i:2d} ",end='')
showsize(ntrees=150, max_features=i, min_samples_leaf=3)
```
**Q.** Which max features would you choose?
<details>
<summary>Solution</summary>
After running a few times, it seems that using <tt>max_features</tt>=7 or 13 gets best validation error, but again it depends on the randomness of the tree construction and results will vary across runs.
</details>
Here's what the final model would look like:
```
showsize(ntrees=150, max_features=13, min_samples_leaf=1)
```
## RF prediction confidence
A random forest is a collection of decision trees, each of which contributes a prediction. The forest averages those predictions to provide the overall prediction (or takes most common vote for classification). Let's dig inside the random forest to get the individual trees out and ask them what their predictions are.
**Task**: Train a random forest with 10 trees on `X_train`, `y_train`. Use `for t in rf.estimators_` to iterate through the trees making predictions with `t` not `rf`. Print out the usual MAE scores for each tree predictor.
```
rf = RandomForestRegressor(n_estimators=10, n_jobs=-1)
rf.fit(X_train, y_train)
for t in ...:
mae_train = ...
mae = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=10, n_jobs=-1)
rf.fit(X_train, y_train)
for t in rf.estimators_:
mae_train = mean_absolute_error(y_train, t.predict(X_train))
mae = mean_absolute_error(y_test, t.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
Notice that it bounces around quite a bit.
**Task**: Select one of the `X_test` rows and print out the addicted rent price.
```
x = ... # pick single test case
x = x.values.reshape(1,-1) # Needs to be a one-row matrix
print(f"{x} => {rf.predict(x)}$")
```
<details>
<summary>Solution</summary>
<pre>
x = X_test.iloc[3,:] # pick single test case
x = x.values.reshape(1,-1)
print(f"{x} => {rf.predict(x)}$")
</pre>
</details>
**Task**: Now let's see how the forest came to that conclusion. Compute the average of the predictions obtained from every tree.
Compare that to the prediction obtained directly from the random forest (`rf.predict(X_test)`). They should be the same.
```
y_pred = ...
print(f"{x} => {y_pred}$")
```
<details>
<summary>Solution</summary>
<pre>
y_pred = np.mean([t.predict(x) for t in rf.estimators_])
print(f"{x} => {y_pred}$")
</pre>
</details>
**Task**: Compute the standard deviation of the tree estimates and print that out.
<details>
<summary>Solution</summary>
<pre>
np.std([t.predict(x) for t in rf.estimators_])
</pre>
</details>
The lower the standard deviation, the more tightly grouped the predictions were, which means we should have more confidence in our answer.
Different records will often have different standard deviations, which means we could have different levels of confidence in the various answers. This might be helpful to a bank for example that wanted to not only predict whether to give loans, but how confident the model was.
## Altering bootstrap size
**This no longer works with latest versions of scikit-learn... and the feature is not yet implemented by them* See [related github issue](https://github.com/scikit-learn/scikit-learn/issues/11993). Ah [this new features](https://github.com/scikit-learn/scikit-learn/pull/14682) covers it for trees. "Adds a max_samples kwarg to forest ensembles that limits the size of the bootstrap samples used to train each estimator."
```
X, y = rent()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
```
**Task**: There are about 38,000 training records, change that to 19,000 and check the accuracy again.
```
rf = RandomForestRegressor(n_estimators=200) # don't compute in parallel so we can see timing
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
rf = RandomForestRegressor(n_estimators=200, max_samples=1/2)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
It's a bit less accurate, but it's faster.
**Q.** Why is it less accurate?
<details>
<summary>Solution</summary>
Each tree is seeing less of the data set during training.
</details>
**Task**: Turn off bootstrapping by adding `bootstrap=False` to the constructor of the model. This means that it will subsample rather than bootstrap. Remember that bootstrapping gets about two thirds of the data because of replacement.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=200, n_jobs=-1, bootstrap=False)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
That brings the accuracy back up a little bit for the test set but very much so for the training MAE score.
**Task**: Drop that size to one third of the training records then retrain and test.
```
rf = RandomForestRegressor(n_estimators=200, max_samples=1/3, n_jobs=-1)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
Mine is twice as fast as the full bootstrap but continues to have very tight variance because of the number of trees. The accuracy is lower, however, about what we get for the usual random forest with two trees.
| true |
code
| 0.48249 | null | null | null | null |
|
```
from MPyDATA import ScalarField, VectorField, PeriodicBoundaryCondition, Options, Stepper, Solver
import numpy as np
dt, dx, dy = .1, .2, .3
nt, nx, ny = 100, 15, 10
# https://en.wikipedia.org/wiki/Arakawa_grids#Arakawa_C-grid
x, y = np.mgrid[
dx/2 : nx*dx : dx,
dy/2 : ny*dy : dy
]
# vector field (u,v) components
# u - x component of the velocity field
ux, uy = np.mgrid[
0 : (nx+1)*dx : dx,
dy/2 : ny*dy : dy
]
# v - y component of the velocity field
vx, vy = np.mgrid[
dx/2 : nx*dx : dx,
0: (ny+1)*dy : dy
]
from matplotlib import pyplot, rcParams
rcParams['figure.figsize'] = [12, 8]
pyplot.quiver(ux, uy, 1, 0, pivot='mid')
pyplot.quiver(vx, vy, 0, 1, pivot='mid')
pyplot.xticks(ux[:,0])
pyplot.yticks(vy[0,:])
pyplot.scatter(x, y)
pyplot.title('Arakawa-C grid')
pyplot.grid()
pyplot.show()
from MPyDATA import ScalarField, VectorField, PeriodicBoundaryCondition, Options, Stepper, Solver
bc = [PeriodicBoundaryCondition(), PeriodicBoundaryCondition()]
options = Options()
data = np.zeros((nx, ny))
data[1,1] = 10
advectee = ScalarField(data, options.n_halo, boundary_conditions=bc)
# https://en.wikipedia.org/wiki/Stream_function
```
stream function:
$u=-\partial_y \psi$
$v=\partial_x \psi$
example flow field:
$\psi(x,y) = - w_{\text{max}} \frac{X}{\pi}
\sin\left(\pi \frac{y}{Y}\right)
\cos\left(2\pi\frac{x}{X}\right)
$
```
class Psi:
def __init__(self, *, X, Y, w_max):
self.X = X
self.Y = Y
self.w_max = w_max
def __call__(self, x, y):
return - self.w_max * self.X / np.pi * np.sin(np.pi * y/self.Y) * np.cos(2 * np.pi * x/self.X)
psi = Psi(X=nx*dx, Y=ny*dy, w_max=.6)
print(psi(0,0))
print(psi(1,1))
# https://en.wikipedia.org/wiki/Courant%E2%80%93Friedrichs%E2%80%93Lewy_condition
# C_x = u * dt / dx
# C_y = v * dt / dy
u = -(psi(ux, uy+dy/2) - psi(ux, uy-dy/2)) / dy
v = +(psi(vx+dx/2, vy) - psi(vx-dx/2, vy)) / dx
advector = VectorField([u*dt/dx, v*dt/dy], halo=options.n_halo, boundary_conditions=bc)
def plot(advectee, advector):
pyplot.scatter(x, y, s=100, c=advectee.get(), marker='s')
pyplot.quiver(ux, uy, advector.get_component(0), 0, pivot='mid', scale=10)
pyplot.quiver(vx, vy, 0, advector.get_component(1), pivot='mid', scale=10)
pyplot.xticks(ux[:,0])
pyplot.yticks(vy[0,:])
pyplot.colorbar()
pyplot.grid()
pyplot.show()
plot(advectee, advector)
stepper = Stepper(options=options, grid=(nx, ny))
solver = Solver(stepper=stepper, advectee=advectee, advector=advector)
solver.advance(20)
plot(advectee, advector)
# https://en.wikipedia.org/wiki/NetCDF
from scipy.io.netcdf import netcdf_file
with netcdf_file('test.nc', mode='w') as ncdf:
# global attributes (metadata)
ncdf.MPyDATA_options = str(options)
# dimensions
ncdf.createDimension("T", nt)
ncdf.createDimension("X", nx)
ncdf.createDimension("Y", ny)
# variables (defined over defined dimensions)
variables = {}
variables["T"] = ncdf.createVariable("T", "f", ["T"])
variables["T"].units = "seconds"
variables["T"][:] = 0
variables["X"] = ncdf.createVariable("X", "f", ["X"])
variables["X"][:] = x[:, 0]
variables["X"].units = "metres"
variables["Y"] = ncdf.createVariable("Y", "f", ["Y"])
variables["Y"][:] = y[0, :]
variables["Y"].units = "metres"
variables["advectee"] = ncdf.createVariable("advectee", "f", ["T", "X", "Y"])
# attributes (per variable)
# e.g. units above
# note: initial condition not saved
for i in range(nt):
solver.advance(nt=1)
variables["T"][i] = (i+1) * dt
variables["advectee"][i, :, :] = solver.advectee.get()
! ls -lah test.nc
! file test.nc
! ncdump -c test.nc
# https://en.wikipedia.org/wiki/Climate_and_Forecast_Metadata_Conventions
# try opening in Paraview (https://en.wikipedia.org/wiki/ParaView)...
```
| true |
code
| 0.727794 | null | null | null | null |
|
# NLTK
## Sentence and Word Tokenization
```
from nltk.tokenize import sent_tokenize, word_tokenize
EXAMPLE_TEXT = "Hello Mr. Smith, how are you doing today? The weather is great, and Python is awesome. The sky is pinkish-blue. You shouldn't eat cardboard."
# Sentence Tokenization
print(sent_tokenize(EXAMPLE_TEXT))
# Word Tokenization
print(word_tokenize(EXAMPLE_TEXT))
```
## Stopwords
```
from nltk.corpus import stopwords
# Printing all stopwords (english)
set(stopwords.words('english'))
example_sent = "This is a sample sentence, showing off the stop words filtration."
stop_words = set(stopwords.words('english'))
word_tokens = word_tokenize(example_sent)
filtered_sentence = [w for w in word_tokens if not w in stop_words]
print(word_tokens)
print(filtered_sentence)
```
## Stemming words
```
# Porter Stemmer is a stemming algorithm
from nltk.stem import PorterStemmer
from nltk.tokenize import sent_tokenize, word_tokenize
ps = PorterStemmer()
example_words = ["python","pythoner","pythoning","pythoned","pythonly"]
for w in example_words:
print(ps.stem(w))
new_text = "It is important to by very pythonly while you are pythoning with python. All pythoners have pythoned poorly at least once."
words = word_tokenize(new_text)
for w in words:
print(ps.stem(w))
```
## Part of Speech Tagging
# POS tag list:
CC coordinating conjunction
CD cardinal digit
DT determiner
EX existential there (like: "there is" ... think of it like "there exists")
FW foreign word
IN preposition/subordinating conjunction
JJ adjective 'big'
JJR adjective, comparative 'bigger'
JJS adjective, superlative 'biggest'
LS list marker 1)
MD modal could, will
NN noun, singular 'desk'
NNS noun plural 'desks'
NNP proper noun, singular 'Harrison'
NNPS proper noun, plural 'Americans'
PDT predeterminer 'all the kids'
POS possessive ending parent's
PRP personal pronoun I, he, she
PRP\$ possessive pronoun my, his, hers
RB adverb very, silently,
RBR adverb, comparative better
RBS adverb, superlative best
RP particle give up
TO to go 'to' the store.
UH interjection errrrrrrrm
VB verb, base form take
VBD verb, past tense took
VBG verb, gerund/present participle taking
VBN verb, past participle taken
VBP verb, sing. present, non-3d take
VBZ verb, 3rd person sing. present takes
WDT wh-determiner which
WP wh-pronoun who, what
WP$ possessive wh-pronoun whose
WRB wh-abverb where, when
#### PunktSentenceTokenizer
> This tokenizer is capable of unsupervised machine learning, so you can actually train it on any body of text that you use.
```
import nltk
from nltk.corpus import state_union
from nltk.tokenize import PunktSentenceTokenizer
# Create training and testing data
train_text = state_union.raw('2005-GWBush.txt')
sample_text = state_union.raw('2006-GWBush.txt')
# Train Punkt tokenizer
custom_sent_tokenizer = PunktSentenceTokenizer(train_text)
# Actually tokenize
tokenized = custom_sent_tokenizer.tokenize(sample_text)
print(tokenized)
# Create a function that will run through and tag all of the parts of speech per sentence
def process_content():
try:
for i in tokenized[ :5]:
words = nltk.word_tokenize(i)
tagged = nltk.pos_tag(words)
print(tagged)
except Exception as e:
print(str(e))
# Output should be a list of tuples, where the first element in the tuple is the word, and the second is the part of speech tag
process_content()
```
## Lemmatizing
> A very similar operation to stemming is called lemmatizing. The major difference between these is, as you saw earlier, stemming can often create non-existent words, whereas lemmas are actual words.
> So, your root stem, meaning the word you end up with, is not something you can just look up in a dictionary, but you can look up a lemma.
> Some times you will wind up with a very similar word, but sometimes, you will wind up with a completely different word.
```
from nltk.stem import WordNetLemmatizer
lemmatizer = WordNetLemmatizer()
print(lemmatizer.lemmatize("cats"))
print(lemmatizer.lemmatize("cacti"))
print(lemmatizer.lemmatize("geese"))
print(lemmatizer.lemmatize("rocks"))
print(lemmatizer.lemmatize("python"))
print(lemmatizer.lemmatize("better", pos="a"))
print(lemmatizer.lemmatize("best", pos="a"))
print(lemmatizer.lemmatize("run"))
print(lemmatizer.lemmatize("run",'v'))
# Here, we've got a bunch of examples of the lemma for the words that we use.
# The only major thing to note is that lemmatize takes a part of speech parameter, "pos."
# If not supplied, the default is "noun." This means that an attempt will be made to find the closest noun, which can create trouble for you.
# Keep this in mind if you use lemmatizing!
```
## Corpora
> The NLTK corpus is a massive dump of all kinds of natural language data sets
```
# Opening the Gutenberg Bible, and reading the first few lines
from nltk.tokenize import sent_tokenize, PunktSentenceTokenizer
from nltk.corpus import gutenberg
#sample text
sample = gutenberg.raw('bible-kjv.txt')
tok = sent_tokenize(sample)
for x in range(5):
print(tok[x])
```
## Wordnet
> Wordnet is a collection of words, definitions, examples of their use, synonyms, antonyms, and more.
```
# Import wordnet
from nltk.corpus import wordnet
# use the term "program" to find synsets
syns = wordnet.synsets('program')
print(syns)
#Print first synset
print(syns[0].name())
# Print only the word
print(syns[0].lemmas()[0].name())
# Definition for that first synset
print(syns[0].definition())
# Examples of the word in use
print(syns[0].examples())
# Synonyms and Antonyms
# The lemmas will be synonyms,
# and then you can use .antonyms to find the antonyms to the lemmas
synonyms = []
antonyms = []
for syn in wordnet.synsets('good'):
for l in syn.lemmas():
synonyms.append(l.name())
if l.antonyms():
antonyms.append(l.antonyms()[0].name())
print(set(synonyms))
print(set(antonyms))
# compare the similarity of two words and their tenses
w1 = wordnet.synset('ship.n.01')
w2 = wordnet.synset('boat.n.01')
print(w1.wup_similarity(w2))
w1 = wordnet.synset('ship.n.01')
w2 = wordnet.synset('car.n.01')
print(w1.wup_similarity(w2))
w1 = wordnet.synset('ship.n.01')
w2 = wordnet.synset('cat.n.01')
print(w1.wup_similarity(w2))
```
| true |
code
| 0.390621 | null | null | null | null |
|
This notebook presents some code to compute some basic baselines.
In particular, it shows how to:
1. Use the provided validation set
2. Compute the top-30 metric
3. Save the predictions on the test in the right format for submission
```
%pylab inline --no-import-all
import os
from pathlib import Path
import pandas as pd
# Change this path to adapt to where you downloaded the data
DATA_PATH = Path("data")
# Create the path to save submission files
SUBMISSION_PATH = Path("submissions")
os.makedirs(SUBMISSION_PATH, exist_ok=True)
```
We also load the official metric, top-30 error rate, for which we provide efficient implementations:
```
from GLC.metrics import top_30_error_rate
help(top_30_error_rate)
from GLC.metrics import top_k_error_rate_from_sets
help(top_k_error_rate_from_sets)
```
For submissions, we will also need to predict the top-30 sets for which we also provide an efficient implementation:
```
from GLC.metrics import predict_top_30_set
help(predict_top_30_set)
```
We also provide an utility function to generate submission files in the right format:
```
from GLC.submission import generate_submission_file
help(generate_submission_file)
```
# Observation data loading
We first need to load the observation data:
```
df_obs_fr = pd.read_csv(DATA_PATH / "observations" / "observations_fr_train.csv", sep=";", index_col="observation_id")
df_obs_us = pd.read_csv(DATA_PATH / "observations" / "observations_us_train.csv", sep=";", index_col="observation_id")
df_obs = pd.concat((df_obs_fr, df_obs_us))
```
Then, we retrieve the train/val split provided:
```
obs_id_train = df_obs.index[df_obs["subset"] == "train"].values
obs_id_val = df_obs.index[df_obs["subset"] == "val"].values
y_train = df_obs.loc[obs_id_train]["species_id"].values
y_val = df_obs.loc[obs_id_val]["species_id"].values
n_val = len(obs_id_val)
print("Validation set size: {} ({:.1%} of train observations)".format(n_val, n_val / len(df_obs)))
```
We also load the observation data for the test set:
```
df_obs_fr_test = pd.read_csv(DATA_PATH / "observations" / "observations_fr_test.csv", sep=";", index_col="observation_id")
df_obs_us_test = pd.read_csv(DATA_PATH / "observations" / "observations_us_test.csv", sep=";", index_col="observation_id")
df_obs_test = pd.concat((df_obs_fr_test, df_obs_us_test))
obs_id_test = df_obs_test.index.values
print("Number of observations for testing: {}".format(len(df_obs_test)))
df_obs_test.head()
```
# Sample submission file
In this section, we will demonstrate how to generate the sample submission file provided.
To do so, we will use the function `generate_submission_file` from `GLC.submission`.
The sample submission consists in always predicting the first 30 species for all the test observations:
```
first_30_species = np.arange(30)
s_pred = np.tile(first_30_species[None], (len(df_obs_test), 1))
```
We can then generate the associated submission file using:
```
generate_submission_file(SUBMISSION_PATH / "sample_submission.csv", df_obs_test.index, s_pred)
```
# Constant baseline: 30 most observed species
The first baseline consists in predicting the 30 most observed species on the train set which corresponds exactly to the "Top-30 most present species":
```
species_distribution = df_obs.loc[obs_id_train]["species_id"].value_counts(normalize=True)
top_30_most_observed = species_distribution.index.values[:30]
```
As expected, it does not perform very well on the validation set:
```
s_pred = np.tile(top_30_most_observed[None], (n_val, 1))
score = top_k_error_rate_from_sets(y_val, s_pred)
print("Top-30 error rate: {:.1%}".format(score))
```
We will however generate the associated submission file on the test using:
```
# Compute baseline on the test set
n_test = len(df_obs_test)
s_pred = np.tile(top_30_most_observed[None], (n_test, 1))
# Generate the submission file
generate_submission_file(SUBMISSION_PATH / "constant_top_30_most_present_species_baseline.csv", df_obs_test.index, s_pred)
```
# Random forest on environmental vectors
A classical approach in ecology is to train Random Forests on environmental vectors.
We show here how to do so using [scikit-learn](https://scikit-learn.org/).
We start by loading the environmental vectors:
```
df_env = pd.read_csv(DATA_PATH / "pre-extracted" / "environmental_vectors.csv", sep=";", index_col="observation_id")
X_train = df_env.loc[obs_id_train].values
X_val = df_env.loc[obs_id_val].values
X_test = df_env.loc[obs_id_test].values
```
Then, we need to handle properly the missing values.
For instance, using `SimpleImputer`:
```
from sklearn.impute import SimpleImputer
imp = SimpleImputer(
missing_values=np.nan,
strategy="constant",
fill_value=np.finfo(np.float32).min,
)
imp.fit(X_train)
X_train = imp.transform(X_train)
X_val = imp.transform(X_val)
X_test = imp.transform(X_test)
```
We can now start training our Random Forest (as there are a lot of observations, over 1.8M, this can take a while):
```
from sklearn.ensemble import RandomForestClassifier
est = RandomForestClassifier(n_estimators=16, max_depth=10, n_jobs=-1)
est.fit(X_train, y_train)
```
As there are a lot of classes (over 17K), we need to be cautious when predicting the scores of the model.
This can easily take more than 5Go on the validation set.
For this reason, we will be predict the top-30 sets by batches using the following generic function:
```
def batch_predict(predict_func, X, batch_size=1024):
res = predict_func(X[:1])
n_samples, n_outputs, dtype = X.shape[0], res.shape[1], res.dtype
preds = np.empty((n_samples, n_outputs), dtype=dtype)
for i in range(0, len(X), batch_size):
X_batch = X[i:i+batch_size]
preds[i:i+batch_size] = predict_func(X_batch)
return preds
```
We can know compute the top-30 error rate on the validation set:
```
def predict_func(X):
y_score = est.predict_proba(X)
s_pred = predict_top_30_set(y_score)
return s_pred
s_val = batch_predict(predict_func, X_val, batch_size=1024)
score_val = top_k_error_rate_from_sets(y_val, s_val)
print("Top-30 error rate: {:.1%}".format(score_val))
```
We now predict the top-30 sets on the test data and save them in a submission file:
```
# Compute baseline on the test set
s_pred = batch_predict(predict_func, X_test, batch_size=1024)
# Generate the submission file
generate_submission_file(SUBMISSION_PATH / "random_forest_on_environmental_vectors.csv", df_obs_test.index, s_pred)
```
| true |
code
| 0.601652 | null | null | null | null |
|
# Preprocessing for deep learning
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
plt.rcParams['axes.facecolor'] ='w'
plt.rcParams['axes.edgecolor'] = '#D6D6D6'
plt.rcParams['axes.linewidth'] = 2
```
# 1. Background
## A. Variance and covariance
### Example 1.
```
A = np.array([[1, 3, 5], [5, 4, 1], [3, 8, 6]])
print(A)
print(np.cov(A, rowvar=False, bias=True))
```
### Finding the covariance matrix with the dot product
```
def calculateCovariance(X):
meanX = np.mean(X, axis = 0)
lenX = X.shape[0]
X = X - meanX
covariance = X.T.dot(X)/lenX
return covariance
print(calculateCovariance(A))
```
## B. Visualize data and covariance matrices
```
def plotDataAndCov(data):
ACov = np.cov(data, rowvar=False, bias=True)
print('Covariance matrix:\n', ACov)
fig, ax = plt.subplots(nrows=1, ncols=2)
fig.set_size_inches(10, 10)
ax0 = plt.subplot(2, 2, 1)
# Choosing the colors
cmap = sns.color_palette("GnBu", 10)
sns.heatmap(ACov, cmap=cmap, vmin=0)
ax1 = plt.subplot(2, 2, 2)
# data can include the colors
if data.shape[1]==3:
c=data[:,2]
else:
c="#0A98BE"
ax1.scatter(data[:,0], data[:,1], c=c, s=40)
# Remove the top and right axes from the data plot
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
```
## C. Simulating data
### Uncorrelated data
```
np.random.seed(1234)
a1 = np.random.normal(2, 1, 300)
a2 = np.random.normal(1, 1, 300)
A = np.array([a1, a2]).T
A.shape
print(A[:10,:])
sns.distplot(A[:,0], color="#53BB04")
sns.distplot(A[:,1], color="#0A98BE")
plt.show()
plt.close()
plotDataAndCov(A)
plt.show()
plt.close()
```
### Correlated data
```
np.random.seed(1234)
b1 = np.random.normal(3, 1, 300)
b2 = b1 + np.random.normal(7, 1, 300)/2.
B = np.array([b1, b2]).T
plotDataAndCov(B)
plt.show()
plt.close()
```
# 2. Preprocessing
## A. Mean normalization
```
def center(X):
newX = X - np.mean(X, axis = 0)
return newX
BCentered = center(B)
print('Before:\n\n')
plotDataAndCov(B)
plt.show()
plt.close()
print('After:\n\n')
plotDataAndCov(BCentered)
plt.show()
plt.close()
```
## B. Standardization
```
def standardize(X):
newX = center(X)/np.std(X, axis = 0)
return newX
np.random.seed(1234)
c1 = np.random.normal(3, 1, 300)
c2 = c1 + np.random.normal(7, 5, 300)/2.
C = np.array([c1, c2]).T
plotDataAndCov(C)
plt.xlim(0, 15)
plt.ylim(0, 15)
plt.show()
plt.close()
CStandardized = standardize(C)
plotDataAndCov(CStandardized)
plt.show()
plt.close()
```
## C. Whitening
### 1. Zero-centering
```
CCentered = center(C)
plotDataAndCov(CCentered)
plt.show()
plt.close()
```
### 2. Decorrelate
```
def decorrelate(X):
cov = X.T.dot(X)/float(X.shape[0])
# Calculate the eigenvalues and eigenvectors of the covariance matrix
eigVals, eigVecs = np.linalg.eig(cov)
# Apply the eigenvectors to X
decorrelated = X.dot(eigVecs)
return decorrelated
plotDataAndCov(C)
plt.show()
plt.close()
CDecorrelated = decorrelate(CCentered)
plotDataAndCov(CDecorrelated)
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.show()
plt.close()
```
### 3. Rescale the data
```
def whiten(X):
cov = X.T.dot(X)/float(X.shape[0])
# Calculate the eigenvalues and eigenvectors of the covariance matrix
eigVals, eigVecs = np.linalg.eig(cov)
# Apply the eigenvectors to X
decorrelated = X.dot(eigVecs)
# Rescale the decorrelated data
whitened = decorrelated / np.sqrt(eigVals + 1e-5)
return whitened
CWhitened = whiten(CCentered)
plotDataAndCov(CWhitened)
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.show()
plt.close()
```
# 3. Image whitening
```
from keras.datasets import cifar10
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
X_train.shape
X = X_train[:1000]
print(X.shape)
X = X.reshape(X.shape[0], X.shape[1]*X.shape[2]*X.shape[3])
print(X.shape)
def plotImage(X):
plt.rcParams["axes.grid"] = False
plt.figure(figsize=(1.5, 1.5))
plt.imshow(X.reshape(32,32,3))
plt.show()
plt.close()
plotImage(X[12, :])
X_norm = X / 255.
print('X.min()', X_norm.min())
print('X.max()', X_norm.max())
X_norm.mean(axis=0).shape
print(X_norm.mean(axis=0))
X_norm = X_norm - X_norm.mean(axis=0)
print(X_norm.mean(axis=0))
cov = np.cov(X_norm, rowvar=True)
cov.shape
U,S,V = np.linalg.svd(cov)
print(U.shape, S.shape)
print(np.diag(S))
print('\nshape:', np.diag(S).shape)
epsilon = 0.1
X_ZCA = U.dot(np.diag(1.0/np.sqrt(S + epsilon))).dot(U.T).dot(X_norm)
plotImage(X[12, :])
plotImage(X_ZCA[12, :])
X_ZCA_rescaled = (X_ZCA - X_ZCA.min()) / (X_ZCA.max() - X_ZCA.min())
print('min:', X_ZCA_rescaled.min())
print('max:', X_ZCA_rescaled.max())
plotImage(X[12, :])
plotImage(X_ZCA_rescaled[12, :])
```
| true |
code
| 0.634487 | null | null | null | null |
|
# Schooling in Xenopus tadpoles: Power analysis
This is a supplementary notebook that generates some simulated data, and estimates the power analysis for a schooling protocol. The analysis subroutines are the same, or very close to ones from the actual notebook (**schooling_analysis**). The results of power analysis are given, and explained, in the text below, but can also be re-created by the reader, by re-running this notebook.
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.spatial
import scipy.stats as stats
from typing import List,Tuple
```
## 1. Generate simulated data
Data is generated in the following format:
Layout of Tadpole dataframe:
x y tx ty
0 7.391 14.783 -0.159 -0.14
1 8.850 14.623 -0.180 -0.18
2 7.751 12.426 -0.260 -0.24
where each line correponds to a "tadpole"; `x` and `y` columns give the position of the "tadpole's head" (virtual, in this case), and `tx` and `ty` are the positions of the "tail", relative to the "head".
```
def simulate_data(ntads=10, schooling=0.5, alignment=0.6):
"""Simulates tadpole distribution in the dish.
n = how many tadpoles to have
schooling = the probability of being in a school (simplistic, binary approach)
r = aligment radius
alignment = alignment coefficient (1-noise_level)
"""
R_DISH = 7
TAD_LENGTH = 0.4
N_ATTEMPTS = 20 # How many attempts to place each tadpole we would make
JUMP = 1 # Jump, in cm, from one tadpole to another
do_alignment = False # Whether we should align tadpoles to their neighbors. Too fancy?
xy = np.zeros((ntads,2))
tails = np.zeros((ntads,2))
itad = 0
while itad < ntads: # Simplified Bridson’s algorithm for Poisson-disc sampling
if itad==0 or np.random.uniform()>schooling: # First point and non-schooled points placed at random
drop = np.random.uniform(0, 2*R_DISH, 2)
else:
iparent = np.random.randint(itad)
angle = np.random.uniform(0, 2*np.pi)
d = np.random.uniform(JUMP, 2*JUMP)
drop = xy[iparent,:] + np.array([np.cos(angle), np.sin(angle)])*d
if np.sqrt((drop[0]-R_DISH)**2 + (drop[1]-R_DISH)**2) > R_DISH: # Outside of a dish, won't do
continue
good_point = True
for iother in range(itad):
if np.sqrt(np.sum(np.square(drop-xy[iother,:]))) < JUMP: # Too close to another dot; won't do
good_point = False
break
if not good_point:
continue
xy[itad,:] = drop
# Make the tadpole perpendicular to the radius
tails[itad,:] = [xy[itad,1]-R_DISH, -xy[itad,0]+R_DISH]
tails[itad,:] = tails[itad,:]/np.linalg.norm(tails[itad,:])*TAD_LENGTH
if do_alignment: # Fancy mutual alignment; maybe don't use it, as it is too fancy?
if itad>0:
for iother in range(itad):
d = np.linalg.norm(xy[itad,:]-xy[iother,:])
tails[itad,:] += tails[iother,:]/(d**2)
tails[itad,:] = tails[itad,:]/np.linalg.norm(tails[itad,:])*TAD_LENGTH
angle = np.random.uniform(0, 2*np.pi)
randotail = np.array([np.cos(angle), np.sin(angle)])*TAD_LENGTH
tails[itad,:] = tails[itad,:]*alignment + randotail*(1-alignment)
tails[itad,:] = tails[itad,:]/np.linalg.norm(tails[itad,:])*TAD_LENGTH
# This code above with 3 normalizations in a row could have been prettier of course
itad += 1
return pd.DataFrame({'x':xy[:,0] , 'y':xy[:,1] , 'tx':tails[:,0] , 'ty':tails[:,1]})
def arena_plot(t):
for i in range(len(t)):
plt.plot(t.x[i]+np.array([0, t.tx[i]]), t.y[i]+np.array([0, t.ty[i]]), 'r-')
plt.plot(t.x, t.y, '.')
plt.gca().add_artist(plt.Circle((7,7), 6.9, color='blue', fill=False, linestyle='-'))
plt.xlim([0, 14])
plt.ylim([0, 14])
plt.axis('off')
return
schoolings = [1, 0.5, 0]
alignments = [1, 0.5, 0]
names = ['Lawful', 'Neutral', 'Chaotic', 'good', 'neutral', 'evil']
plt.figure(figsize=(9,9))
for i in range(3):
for j in range(3):
t = simulate_data(ntads=20, schooling=schoolings[i], alignment=alignments[j])
plt.subplot(3,3,i*3+j+1)
arena_plot(t)
plt.title(f"Schooling={schoolings[i]}, \n alignment={alignments[j]}")
#plt.title(names[j] + ' ' + names[3+i])
```
## 2. Processing Tools
An exact copy of tools from the "main notebook" (as of 2020.08.01), except that instead of extracing tadpoles from real data, here we simulate this data. (So `exctractTads` function is not actually used).
```
def getNFrames(data):
"""Returns the total number of frames."""
return max(data.Frame)+1
def extractTads(data,frame):
"""Splits the data into XY position of each head, and _relative_ XY position of each tail."""
xy = data.loc[data.Frame==frame,['X','Y']].to_numpy()
heads = xy[0::2,:]
tails = xy[1::2,:]-heads
return pd.DataFrame({'x':heads[:,0] , 'y':heads[:,1] , 'tx':tails[:,0] , 'ty':tails[:,1]})
def findNeighbors(tads): # Returns a new data frame, for edges
"""Triangulates the field, finds "neighbors". No thresholding of distance."""
xy = tads[['x','y']]
tri = scipy.spatial.Delaunay(xy,qhull_options="QJ").simplices # "QJ" is needed to retain
# all tadpoles, including isolated ones
listOfPairs = [] # Array of tuples to describe all pairs of points
flip = lambda x: (x[1],x[0]) # A local function to flip tuples
for i in range(tri.shape[0]): # Go through all edges of Delaunay triangles, include each one only once
triangle = [tuple(tri[i,[0,1]]) , tuple(tri[i,[1,2]]) , tuple(tri[i,[2,0]])]
for p in triangle:
if p not in listOfPairs and flip(p) not in listOfPairs:
listOfPairs += [p]
out = pd.DataFrame({'i':[a for (a,b) in listOfPairs] , 'j':[b for (a,b) in listOfPairs]})
return out
def findDistances(tads,pairs):
"""Calculates distances between pairs of neighboring tadpoles."""
xy = tads[['x','y']].values
dist = [np.linalg.norm(xy[p[0],]-xy[p[1],]) for p in pairs[['i','j']].values.tolist()]
pairs['dist'] = dist
return pairs
# --- Test, for the first frame
tads = simulate_data(ntads=20)
pairs = findNeighbors(tads)
pairs = findDistances(tads,pairs)
print('Layout of Tadpole dataframe:')
print(tads[:3])
print('\nLayout of Pairs dataframe:')
print(pairs[:3])
# Test figure with edge colors proportional to their distance
fig = plt.figure()
ax = fig.add_subplot(111)
xy = tads[['x','y']].values
for i in range(len(pairs)):
p = pairs[['i','j']].values.tolist()[i]
ax.plot([xy[p[0],0] , xy[p[1],0]],[xy[p[0],1] , xy[p[1],1]]) # Point
ax.plot(*([xy[p[i],_] for i in range(2)] for _ in range(2)),
color=np.array([1,0.5,0])*pairs['dist'].iloc[i]/pairs[['dist']].max().values*0.9)
# The awkward construction above draws lines between neighboring tadpoles
ax.set_aspect('equal')
```
## 3. Tools to Process Angles
Exactly same as in the main notebook (as of 2020.08.01)
```
def findAngles(tads,pairs):
'''Angles between pairs of tadpoles'''
tails = tads[['tx','ty']].values # Go from pandas to lists, to utilize list comprehension
norms = [np.linalg.norm(tails[i,]) for i in range(tails.shape[0])]
angle = [np.arccos(np.dot(tails[p[0],],tails[p[1],])/(norms[p[0]]*norms[p[1]]))
for p in pairs[['i','j']].values.tolist()]
pairs['angle'] = np.array(angle)/np.pi*180
return pairs
def niceTadFigure(ax,tads,pairs):
"""Nice picture for troubleshooting."""
xy = tads[['x','y']].values
tails = tads[['tx','ty']].values
ang = pairs[['angle']].values
for i in range(len(pairs)):
p = pairs[['i','j']].values.tolist()[i]
ax.plot(*([xy[p[i],_] for i in range(2)] for _ in range(2)),
color=np.array([0.5,0.8,1])*(1-ang[i]/max(ang))) # Tadpole-tapole Edges
for i in range(xy.shape[0]):
nm = np.linalg.norm(tails[i,])
ax.plot(xy[i,0]+[0,tails[i,0]/nm], xy[i,1]+[0,tails[i,1]/nm] , '-',color='red')
ax.set_aspect('equal')
ax.axis('off')
# --- Test, for the first frame
pairs = findAngles(tads,pairs)
fig = plt.figure()
ax = fig.add_subplot(111)
niceTadFigure(ax,tads,pairs)
#plt.savefig('crystal_pic.svg', format='svg')
```
## 4. Define full processor and dataset visualization
This function is adjusted to look like the procesisng function from the main notebook, but actually we call the simulation several times, to generate the "frames".
```
def processEverything(nsets=12, show_image=False, schooling=0.3, alignment=0.5):
"""Process one full dataset."""
if show_image:
fig = plt.figure(figsize=(10,10));
fullDf = pd.DataFrame()
for iframe in range(nsets):
tads = simulate_data(ntads=20, schooling=schooling, alignment=alignment)
pairs = findNeighbors(tads)
pairs = findDistances(tads,pairs)
angl = findAngles(tads,pairs)
fullDf = fullDf.append(pd.DataFrame({'frame': [iframe]*len(pairs)}).join(pairs))
if show_image:
ax = fig.add_subplot(4,4,iframe+1)
niceTadFigure(ax,tads,pairs)
return fullDf
out = processEverything(show_image=True)
```
## 5. Compare two different simulated datasets
Below, one dataset has high schooling coefficient (0.9), and perfect alignment (1.0), while the other has almost no schooling (0.1), and perfectly random orientation for all tadpoles (alignment=0.0).
```
# Prepare the data
out = processEverything(show_image=False, schooling=0.9, alignment=1.0)
out_treatment = processEverything(show_image=False, schooling=0.1, alignment=0.0)
def two_groups_plot(y1, y2, labels):
"""A basic two-groups plot"""
plt.plot(1+(np.random.uniform(size=y1.shape[0])-0.5)*0.3, y1, '.', alpha=0.2, zorder=-1)
plt.plot(2+(np.random.uniform(size=y2.shape[0])-0.5)*0.3, y2, '.', alpha=0.2, zorder=-1)
# Zorder is set to negative to hack around a bug in matplotlib that places errorbars below plots
plt.errorbar(1, np.mean(y1), np.std(y1), color='k', marker='s', capsize=5)
plt.errorbar(2, np.mean(y2), np.std(y2), color='k', marker='s', capsize=5)
plt.xlim(0,3)
plt.xticks(ticks=[1,2], labels=labels)
def compare_distances(out1,out2,labels):
"""Visualizes distances, reports a stat test"""
N_BINS = 10
d = out1['dist'].values
d2 = out2['dist'].values
plt.figure(figsize=(9,4))
ax = plt.subplot(121)
two_groups_plot(d, d2, labels)
plt.ylabel('Distance, cm')
ax = plt.subplot(122)
#plt.hist(d , bins=30, density=True, alpha=0.5);
#plt.hist(d2, bins=30, density=True, alpha=0.5);
y1,x1 = np.histogram(d, bins=N_BINS, density=True)
y2,x2 = np.histogram(d2, bins=N_BINS, density=True)
centers = lambda x: np.mean(np.vstack((x[:-1],x[1:])), axis=0) # Centers of each bin
plt.plot(centers(x1),y1,'.-')
plt.plot(centers(x2),y2,'.-')
plt.xlabel('Distance, cm')
plt.ylabel('Probability Density')
plt.legend(labels, loc='upper right')
print('Was the average inter-tadpole disctance different between two sets of data?')
print('(were their clumping?)')
test_results = stats.ttest_ind(d,d2)
print('T-test: t = ', test_results.statistic, '; p-value = ',test_results.pvalue)
print('\nWas the distribution shape different between two sets??')
test_results = scipy.stats.ks_2samp(d,d2)
print('Kolmogorov-Smirnov test p-value = ',test_results.pvalue)
compare_distances(out, out_treatment, ['High Schooling','Low schooling'])
#plt.savefig('distances.svg', format='svg')
```
As we can see, non-schooling tadpoles tend to be more uniformly distributed, so we observe more mid-distances and fewer low and high distances. ("More uniformly" doesn't mean that the distribution is actually uniform; it is expected to be closer to $χ^2$). Conversely, schooling tadpoles tend to be closer to each other.
As not all inter-tadpole distances were considered, but rather we rely on the Delaunay triangulation, the shape of the histogram may be rather peculiar, but it is OK. What matters is not the shape itself, but the fact that this shape is sensitive to the configuration of the swarm, as this means that it can be used to statistically compare swarms that were formed differently.
```
def compare_angles(out, out2, labels):
"""Visualizes angles, reports a stat test."""
HIST_BIN = 30 # Histogram step, in degrees
a = out['angle'].values
a2 = out2['angle'].values
#plt.hist(a , bins=np.arange(0,180+10,10), density=True, alpha=0.5);
#plt.hist(a2, bins=np.arange(0,180+10,10), density=True, alpha=0.5);
preset_bins = np.arange(0,180+HIST_BIN, HIST_BIN)
y1,x1 = np.histogram(a, bins=preset_bins, density=True)
y2,x2 = np.histogram(a2, bins=preset_bins, density=True)
centers = lambda x: np.mean(np.vstack((x[:-1],x[1:])), axis=0) # Centers of each bin
plt.plot(centers(x1),y1,'.-')
plt.plot(centers(x2),y2,'.-')
plt.xticks(np.arange(0,180+30,30))
plt.xlabel('Angle, degrees')
plt.ylabel('Probability Density')
plt.legend(labels, loc='upper right')
print('\nWas the distribution of angles different between two sets?')
test_results = scipy.stats.ks_2samp(a,a2)
print('Kolmogorov-Smirnov test p-value = ',test_results.pvalue)
compare_angles(out, out_treatment, ['Alignment','No alignment'])
#plt.savefig('angles.svg', format='svg')
```
As we can see, if tadpoles are oriented at random, the histogram of inter-tadpole angles is flat. If tadpoles school, the distribution of angles drops, as most tadpoles are co-oriented.
## 6. Power analysis
```
ntries = 50
x = np.linspace(0, 1, 21)
y = np.zeros((x.shape[0], 3))
for ival in range(len(x)):
val = x[ival]
print(f'{val:4.1f}', end=' ')
count = np.array([0,0,0])
for iattempt in range(ntries):
print('.', end='')
out1 = processEverything(show_image=False, schooling=0.5, alignment=0.5)
out2 = processEverything(show_image=False, schooling=val, alignment=val)
d = out1['dist'].values
d2 = out2['dist'].values
pttest = stats.ttest_ind(d,d2).pvalue
pks = scipy.stats.ks_2samp(d,d2).pvalue
pangles = scipy.stats.ks_2samp(out['angle'].values, out2['angle'].values).pvalue
count[0] += 1*(pttest<0.05)
count[1] += 1*(pks<0.05)
count[2] += 1*(pangles<0.05)
y[ival,:] = count/ntries
print()
plt.figure(figsize=(8,6));
plt.plot(x,y);
plt.legend(labels=["Distances, t-test","Distances, KS-test","Angles, KS-test"], bbox_to_anchor=(1.3, 1));
plt.xlabel('Coefficients for the 2nd set (1st is fixed at 0.5)');
plt.ylabel('Test power');
```
For every point of the chart above, we compare two simulated datasets. One has the **schooling** coefficient (the probability of joining an existing school) set at 0.5, and the admixture of noise to tadpole orientation (**alignment** coefficient) also set at 0.5. For the other dataset, both parameters assume all values from 0 to 1 with a 0.05 step. The sizes of both datasets are the same as in our real experiments: 20 tadpoles, 12 photos. each simulation is repeated 50 times, to estimate the power 1-β of each of the tests (with α=0.05).
We can see that the angle analysis is much more sensitive, as even a change from 0.50 to 0.55 noise admixture is detected with >95% probability. Yet, the distribution of angles is also arguably more biologically involved, as it can depend on the function of the lateral line, and the distribution of currents in the bowl, while these currents may themselves be affected by the quality of schooling (non-schooling tadpoles won't create a current). To re-iterate, the test for co-alignment is very sensitive mathematically, but may be a bit messy biologically.
The tests of spatial clumping are almost exactly the other way around: they are easy to interpret (if the tadpoles stay together, then phenomenologially the DO schoo, regardless of the mechanism), but they are not that sensitive mathematically. For this sample size, we had to change the probability of "not joining a school" by about 30% to detect a difference with 80% power. We can also see that the t-test is more sensitive to this change than the Kolmogorov-Smirnov test, although this comparison may be sensitive to this particular implementation of a spatial model.
| true |
code
| 0.577674 | null | null | null | null |
|
# OCR (Optical Character Recognition) from Images with Transformers
---
[Github](https://github.com/eugenesiow/practical-ml/) | More Notebooks @ [eugenesiow/practical-ml](https://github.com/eugenesiow/practical-ml)
---
Notebook to recognise text automaticaly from an input image with either handwritten or printed text.
[Optical Character Recognition](https://paperswithcode.com/task/optical-character-recognition) is the task of converting images of typed, handwritten or printed text into machine-encoded text, whether from a scanned document, a photo of a document, a scene-photo (for example the text on signs and billboards in a landscape photo, license plates in cars...) or from subtitle text superimposed on an image (for example: from a television broadcast).
The [transformer models used](https://malaya-speech.readthedocs.io/en/latest/tts-singlish.html) are from Microsoft's TrOCR. The TrOCR models are encoder-decoder models, consisting of an image Transformer as encoder, and a text Transformer as decoder. We utilise the versions hosted on [huggingface.co](https://huggingface.co/models?search=microsoft/trocr) and use the awesome transformers library, for longevity and simplicity.
The notebook is structured as follows:
* Setting up the Environment
* Using the Model (Running Inference)
# Setting up the Environment
#### Dependencies and Runtime
If you're running this notebook in Google Colab, most of the dependencies are already installed and we don't need the GPU for this particular example.
If you decide to run this on many (>thousands) images and want the inference to go faster though, you can select `Runtime` > `Change Runtime Type` from the menubar. Ensure that `GPU` is selected as the `Hardware accelerator`.
We need to install huggingface `transformers` for this example to run, so execute the command below to setup the dependencies. We use the version compiled directly from the latest source (at the time of writing this is the only way to access the transforemrs TrOCR model code).
```
!pip install -q git+https://github.com/huggingface/transformers.git
```
# Using the Model (Running Inference)
Let's define a function for us to get images from the web. We execute this function to download an image with a line of handwritten text and display it.
```
import requests
from IPython.display import display
from PIL import Image
def show_image(url):
img = Image.open(requests.get(url, stream=True).raw).convert("RGB")
display(img)
return img
handwriting1 = show_image('https://fki.tic.heia-fr.ch/static/img/a01-122-02.jpg')
```
Now we want to load the model to recognise handwritten text.
Specifically we are running the following steps:
* Load the processor, `TrOCRProcessor`, which processes our input image and converts it into a sequence of fixed-size patches (resolution 16x16), which are linearly embedded. The processor also adds absolute position embeddings and this sequence is fed to the layers of the Transformer encoder.
* Load the model, `VisionEncoderDecoderModel`, which consists of the image encoder and the text decoder.
* Define `ocr_image` function - We define the function for inferencing which takes our `src_img`, the input image we have downloaded. It will then run both the processor and the model inference and produce the output OCR text that has been recognised from the image.
```
import transformers
from transformers import TrOCRProcessor, VisionEncoderDecoderModel
processor = TrOCRProcessor.from_pretrained('microsoft/trocr-base-handwritten')
model = VisionEncoderDecoderModel.from_pretrained('microsoft/trocr-base-handwritten')
def ocr_image(src_img):
pixel_values = processor(images=src_img, return_tensors="pt").pixel_values
generated_ids = model.generate(pixel_values)
return processor.batch_decode(generated_ids, skip_special_tokens=True)[0]
```
We now run our `ocr_image` function on the line of handwritten text in the image we have downloaded previously (and stored in `handwriting1`).
```
ocr_image(handwriting1)
```
Lets try on another image with handwritten text.
```
ocr_image(show_image('https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcSoolxi9yWGAT5SLZShv8vVd0bz47UWRzQC19fDTeE8GmGv_Rn-PCF1pP1rrUx8kOjA4gg&usqp=CAU'))
import transformers
from transformers import TrOCRProcessor, VisionEncoderDecoderModel
print_processor = TrOCRProcessor.from_pretrained('microsoft/trocr-base-printed')
print_model = VisionEncoderDecoderModel.from_pretrained('microsoft/trocr-base-printed')
def ocr_print_image(src_img):
pixel_values = print_processor(images=src_img, return_tensors="pt").pixel_values
generated_ids = print_model.generate(pixel_values)
return print_processor.batch_decode(generated_ids, skip_special_tokens=True)[0]
```
We download an image with noisy printed text, a scanned receipt.
```
receipt = show_image('https://github.com/zzzDavid/ICDAR-2019-SROIE/raw/master/data/img/000.jpg')
```
As the model processes a line of text, we crop the image to include on of the lines of text in the receipt and send it to our model.
```
receipt_crop = receipt.crop((0, 80, receipt.size[0], 110))
display(receipt_crop)
ocr_print_image(receipt_crop)
```
More Notebooks @ [eugenesiow/practical-ml](https://github.com/eugenesiow/practical-ml) and do star or drop us some feedback on how to improve the notebooks on the [Github repo](https://github.com/eugenesiow/practical-ml/).
| true |
code
| 0.618204 | null | null | null | null |
|
# Implementing an LSTM RNN Model
------------------------
Here we implement an LSTM model on all a data set of Shakespeare works.
We start by loading the necessary libraries and resetting the default computational graph.
```
import os
import re
import string
import requests
import numpy as np
import collections
import random
import pickle
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
```
We start a computational graph session.
```
sess = tf.Session()
```
Next, it is important to set the algorithm and data processing parameters.
---------
Parameter : Descriptions
- min_word_freq: Only attempt to model words that appear at least 5 times.
- rnn_size: size of our RNN (equal to the embedding size)
- epochs: Number of epochs to cycle through the data
- batch_size: How many examples to train on at once
- learning_rate: The learning rate or the convergence paramter
- training_seq_len: The length of the surrounding word group (e.g. 10 = 5 on each side)
- embedding_size: Must be equal to the rnn_size
- save_every: How often to save the model
- eval_every: How often to evaluate the model
- prime_texts: List of test sentences
```
# Set RNN Parameters
min_word_freq = 5 # Trim the less frequent words off
rnn_size = 128 # RNN Model size
embedding_size = 100 # Word embedding size
epochs = 10 # Number of epochs to cycle through data
batch_size = 100 # Train on this many examples at once
learning_rate = 0.001 # Learning rate
training_seq_len = 50 # how long of a word group to consider
embedding_size = rnn_size
save_every = 500 # How often to save model checkpoints
eval_every = 50 # How often to evaluate the test sentences
prime_texts = ['thou art more', 'to be or not to', 'wherefore art thou']
# Download/store Shakespeare data
data_dir = 'temp'
data_file = 'shakespeare.txt'
model_path = 'shakespeare_model'
full_model_dir = os.path.join(data_dir, model_path)
# Declare punctuation to remove, everything except hyphens and apostrophes
punctuation = string.punctuation
punctuation = ''.join([x for x in punctuation if x not in ['-', "'"]])
# Make Model Directory
if not os.path.exists(full_model_dir):
os.makedirs(full_model_dir)
# Make data directory
if not os.path.exists(data_dir):
os.makedirs(data_dir)
```
Download the data if we don't have it saved already. The data comes from the [Gutenberg Project](http://www.gutenberg.org])
```
print('Loading Shakespeare Data')
# Check if file is downloaded.
if not os.path.isfile(os.path.join(data_dir, data_file)):
print('Not found, downloading Shakespeare texts from www.gutenberg.org')
shakespeare_url = 'http://www.gutenberg.org/cache/epub/100/pg100.txt'
# Get Shakespeare text
response = requests.get(shakespeare_url)
shakespeare_file = response.content
# Decode binary into string
s_text = shakespeare_file.decode('utf-8')
# Drop first few descriptive paragraphs.
s_text = s_text[7675:]
# Remove newlines
s_text = s_text.replace('\r\n', '')
s_text = s_text.replace('\n', '')
# Write to file
with open(os.path.join(data_dir, data_file), 'w') as out_conn:
out_conn.write(s_text)
else:
# If file has been saved, load from that file
with open(os.path.join(data_dir, data_file), 'r') as file_conn:
s_text = file_conn.read().replace('\n', '')
# Clean text
print('Cleaning Text')
s_text = re.sub(r'[{}]'.format(punctuation), ' ', s_text)
s_text = re.sub('\s+', ' ', s_text ).strip().lower()
print('Done loading/cleaning.')
```
Define a function to build a word processing dictionary (word -> ix)
```
# Build word vocabulary function
def build_vocab(text, min_word_freq):
word_counts = collections.Counter(text.split(' '))
# limit word counts to those more frequent than cutoff
word_counts = {key:val for key, val in word_counts.items() if val>min_word_freq}
# Create vocab --> index mapping
words = word_counts.keys()
vocab_to_ix_dict = {key:(ix+1) for ix, key in enumerate(words)}
# Add unknown key --> 0 index
vocab_to_ix_dict['unknown']=0
# Create index --> vocab mapping
ix_to_vocab_dict = {val:key for key,val in vocab_to_ix_dict.items()}
return(ix_to_vocab_dict, vocab_to_ix_dict)
```
Now we can build the index-vocabulary from the Shakespeare data.
```
# Build Shakespeare vocabulary
print('Building Shakespeare Vocab')
ix2vocab, vocab2ix = build_vocab(s_text, min_word_freq)
vocab_size = len(ix2vocab) + 1
print('Vocabulary Length = {}'.format(vocab_size))
# Sanity Check
assert(len(ix2vocab) == len(vocab2ix))
# Convert text to word vectors
s_text_words = s_text.split(' ')
s_text_ix = []
for ix, x in enumerate(s_text_words):
try:
s_text_ix.append(vocab2ix[x])
except:
s_text_ix.append(0)
s_text_ix = np.array(s_text_ix)
```
We define the LSTM model. The methods of interest are the `__init__()` method, which defines all the model variables and operations, and the `sample()` method which takes in a sample word and loops through to generate text.
```
# Define LSTM RNN Model
class LSTM_Model():
def __init__(self, embedding_size, rnn_size, batch_size, learning_rate,
training_seq_len, vocab_size, infer_sample=False):
self.embedding_size = embedding_size
self.rnn_size = rnn_size
self.vocab_size = vocab_size
self.infer_sample = infer_sample
self.learning_rate = learning_rate
if infer_sample:
self.batch_size = 1
self.training_seq_len = 1
else:
self.batch_size = batch_size
self.training_seq_len = training_seq_len
self.lstm_cell = tf.contrib.rnn.BasicLSTMCell(self.rnn_size)
self.initial_state = self.lstm_cell.zero_state(self.batch_size, tf.float32)
self.x_data = tf.placeholder(tf.int32, [self.batch_size, self.training_seq_len])
self.y_output = tf.placeholder(tf.int32, [self.batch_size, self.training_seq_len])
with tf.variable_scope('lstm_vars'):
# Softmax Output Weights
W = tf.get_variable('W', [self.rnn_size, self.vocab_size], tf.float32, tf.random_normal_initializer())
b = tf.get_variable('b', [self.vocab_size], tf.float32, tf.constant_initializer(0.0))
# Define Embedding
embedding_mat = tf.get_variable('embedding_mat', [self.vocab_size, self.embedding_size],
tf.float32, tf.random_normal_initializer())
embedding_output = tf.nn.embedding_lookup(embedding_mat, self.x_data)
rnn_inputs = tf.split(axis=1, num_or_size_splits=self.training_seq_len, value=embedding_output)
rnn_inputs_trimmed = [tf.squeeze(x, [1]) for x in rnn_inputs]
# If we are inferring (generating text), we add a 'loop' function
# Define how to get the i+1 th input from the i th output
def inferred_loop(prev, count):
# Apply hidden layer
prev_transformed = tf.matmul(prev, W) + b
# Get the index of the output (also don't run the gradient)
prev_symbol = tf.stop_gradient(tf.argmax(prev_transformed, 1))
# Get embedded vector
output = tf.nn.embedding_lookup(embedding_mat, prev_symbol)
return(output)
decoder = tf.contrib.legacy_seq2seq.rnn_decoder
outputs, last_state = decoder(rnn_inputs_trimmed,
self.initial_state,
self.lstm_cell,
loop_function=inferred_loop if infer_sample else None)
# Non inferred outputs
output = tf.reshape(tf.concat(axis=1, values=outputs), [-1, self.rnn_size])
# Logits and output
self.logit_output = tf.matmul(output, W) + b
self.model_output = tf.nn.softmax(self.logit_output)
loss_fun = tf.contrib.legacy_seq2seq.sequence_loss_by_example
loss = loss_fun([self.logit_output],[tf.reshape(self.y_output, [-1])],
[tf.ones([self.batch_size * self.training_seq_len])],
self.vocab_size)
self.cost = tf.reduce_sum(loss) / (self.batch_size * self.training_seq_len)
self.final_state = last_state
gradients, _ = tf.clip_by_global_norm(tf.gradients(self.cost, tf.trainable_variables()), 4.5)
optimizer = tf.train.AdamOptimizer(self.learning_rate)
self.train_op = optimizer.apply_gradients(zip(gradients, tf.trainable_variables()))
def sample(self, sess, words=ix2vocab, vocab=vocab2ix, num=10, prime_text='thou art'):
state = sess.run(self.lstm_cell.zero_state(1, tf.float32))
word_list = prime_text.split()
for word in word_list[:-1]:
x = np.zeros((1, 1))
x[0, 0] = vocab[word]
feed_dict = {self.x_data: x, self.initial_state:state}
[state] = sess.run([self.final_state], feed_dict=feed_dict)
out_sentence = prime_text
word = word_list[-1]
for n in range(num):
x = np.zeros((1, 1))
x[0, 0] = vocab[word]
feed_dict = {self.x_data: x, self.initial_state:state}
[model_output, state] = sess.run([self.model_output, self.final_state], feed_dict=feed_dict)
sample = np.argmax(model_output[0])
if sample == 0:
break
word = words[sample]
out_sentence = out_sentence + ' ' + word
return(out_sentence)
```
In order to use the same model (with the same trained variables), we need to share the variable scope between the trained model and the test model.
```
# Define LSTM Model
lstm_model = LSTM_Model(embedding_size, rnn_size, batch_size, learning_rate,
training_seq_len, vocab_size)
# Tell TensorFlow we are reusing the scope for the testing
with tf.variable_scope(tf.get_variable_scope(), reuse=True):
test_lstm_model = LSTM_Model(embedding_size, rnn_size, batch_size, learning_rate,
training_seq_len, vocab_size, infer_sample=True)
```
We need to save the model, so we create a model saving operation.
```
# Create model saver
saver = tf.train.Saver(tf.global_variables())
```
Let's calculate how many batches are needed for each epoch and split up the data accordingly.
```
# Create batches for each epoch
num_batches = int(len(s_text_ix)/(batch_size * training_seq_len)) + 1
# Split up text indices into subarrays, of equal size
batches = np.array_split(s_text_ix, num_batches)
# Reshape each split into [batch_size, training_seq_len]
batches = [np.resize(x, [batch_size, training_seq_len]) for x in batches]
```
Initialize all the variables
```
# Initialize all variables
init = tf.global_variables_initializer()
sess.run(init)
```
Training the model!
```
# Train model
train_loss = []
iteration_count = 1
for epoch in range(epochs):
# Shuffle word indices
random.shuffle(batches)
# Create targets from shuffled batches
targets = [np.roll(x, -1, axis=1) for x in batches]
# Run a through one epoch
print('Starting Epoch #{} of {}.'.format(epoch+1, epochs))
# Reset initial LSTM state every epoch
state = sess.run(lstm_model.initial_state)
for ix, batch in enumerate(batches):
training_dict = {lstm_model.x_data: batch, lstm_model.y_output: targets[ix]}
c, h = lstm_model.initial_state
training_dict[c] = state.c
training_dict[h] = state.h
temp_loss, state, _ = sess.run([lstm_model.cost, lstm_model.final_state, lstm_model.train_op],
feed_dict=training_dict)
train_loss.append(temp_loss)
# Print status every 10 gens
if iteration_count % 10 == 0:
summary_nums = (iteration_count, epoch+1, ix+1, num_batches+1, temp_loss)
print('Iteration: {}, Epoch: {}, Batch: {} out of {}, Loss: {:.2f}'.format(*summary_nums))
# Save the model and the vocab
if iteration_count % save_every == 0:
# Save model
model_file_name = os.path.join(full_model_dir, 'model')
saver.save(sess, model_file_name, global_step = iteration_count)
print('Model Saved To: {}'.format(model_file_name))
# Save vocabulary
dictionary_file = os.path.join(full_model_dir, 'vocab.pkl')
with open(dictionary_file, 'wb') as dict_file_conn:
pickle.dump([vocab2ix, ix2vocab], dict_file_conn)
if iteration_count % eval_every == 0:
for sample in prime_texts:
print(test_lstm_model.sample(sess, ix2vocab, vocab2ix, num=10, prime_text=sample))
iteration_count += 1
```
Here is a plot of the training loss across the iterations.
```
# Plot loss over time
plt.plot(train_loss, 'k-')
plt.title('Sequence to Sequence Loss')
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.show()
```
| true |
code
| 0.573738 | null | null | null | null |
|
# Random Forest Classification
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X = df[features]
Y = df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
#### Distribution Of Target Variable
```
plt.figure(figsize = (10,6))
se.countplot(Y)
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 123)#performing datasplitting
```
### Model
A random forest is a meta estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting. The sub-sample size is controlled with the <code>max_samples</code> parameter if <code>bootstrap=True</code> (default), otherwise the whole dataset is used to build each tree.
#### Model Tuning Parameters
1. n_estimators : int, default=100
> The number of trees in the forest.
2. criterion : {“gini”, “entropy”}, default=”gini”
> The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “entropy” for the information gain.
3. max_depth : int, default=None
> The maximum depth of the tree.
4. max_features : {“auto”, “sqrt”, “log2”}, int or float, default=”auto”
> The number of features to consider when looking for the best split:
5. bootstrap : bool, default=True
> Whether bootstrap samples are used when building trees. If False, the whole dataset is used to build each tree.
6. oob_score : bool, default=False
> Whether to use out-of-bag samples to estimate the generalization accuracy.
7. n_jobs : int, default=None
> The number of jobs to run in parallel. fit, predict, decision_path and apply are all parallelized over the trees. <code>None</code> means 1 unless in a joblib.parallel_backend context. <code>-1</code> means using all processors. See Glossary for more details.
8. random_state : int, RandomState instance or None, default=None
> Controls both the randomness of the bootstrapping of the samples used when building trees (if <code>bootstrap=True</code>) and the sampling of the features to consider when looking for the best split at each node (if <code>max_features < n_features</code>).
9. verbose : int, default=0
> Controls the verbosity when fitting and predicting.
```
# Build Model here
model = RandomForestClassifier(n_jobs = -1,random_state = 123)
model.fit(X_train, y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
plot_confusion_matrix(model,X_test,y_test,cmap=plt.cm.Blues)
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* **where**:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(X_test)))
```
#### Feature Importances.
The Feature importance refers to techniques that assign a score to features based on how useful they are for making the prediction.
```
plt.figure(figsize=(8,6))
n_features = len(X.columns)
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), X.columns)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
```
#### Creator: Thilakraj Devadiga , Github: [Profile](https://github.com/Thilakraj1998)
| true |
code
| 0.287718 | null | null | null | null |
|
```
from glob import glob
from os import path
import re
from skbio import DistanceMatrix
import pandas as pd
import numpy as np
from kwipexpt import *
%matplotlib inline
%load_ext rpy2.ipython
%%R
library(tidyr)
library(dplyr, warn.conflicts=F, quietly=T)
library(ggplot2)
```
Calculate performance of kWIP
=============================
The next bit of python code calculates the performance of kWIP against the distance between samples calulcated from the alignments of their genomes.
This code caluclates spearman's $\rho$ between the off-diagonal elements of the triagnular distance matrices.
```
expts = list(map(lambda fp: path.basename(fp.rstrip('/')), glob('data/*/')))
print("Expts:", *expts[:10], "...")
def process_expt(expt):
expt_results = []
def extract_info(filename):
return re.search(r'kwip/(\d\.?\d*)x-(0\.\d+)-(wip|ip).dist', filename).groups()
# dict of scale: distance matrix, populated as we go
truths = {}
for distfile in glob("data/{}/kwip/*.dist".format(expt)):
cov, scale, metric = extract_info(distfile)
if scale not in truths:
genome_dist_path = 'data/{ex}/all_genomes-{sc}.dist'.format(ex=expt, sc=scale)
truths[scale] = load_sample_matrix_to_runs(genome_dist_path)
exptmat = DistanceMatrix.read(distfile)
rho = spearmans_rho_distmats(exptmat, truths[scale])
expt_results.append({
"coverage": cov,
"scale": scale,
"metric": metric,
"rho": rho,
"seed": expt,
})
return expt_results
#process_expt('3662')
results = []
for res in map(process_expt, expts):
results.extend(res)
results = pd.DataFrame(results)
```
Statistical analysis
====================
Is done is R, as that's easier.
Below we see a summary and structure of the data
```
%%R -i results
results$coverage = as.numeric(as.character(results$coverage))
results$scale = as.numeric(as.character(results$scale))
print(summary(results))
str(results)
```
### Experiment design
Below we see the design of the experiment in terms of the two major variables.
We have a series (vertically) that, at 30x coverage, looks at the effect of genetic variation on performance. There is a second series that examines the effect of coverage at an average pairwise genetic distance of 0.001.
There are 100 replicates for each data point, performed as a separate bootstrap across the random creation of the tree and sampling of reads etc.
```
%%R
ggplot(results, aes(x=coverage, y=scale)) +
geom_point() +
scale_x_log10() +
scale_y_log10() +
theme_bw()
```
Effect of Coverage
------------------
Here we show the spread of data across the 100 reps as boxplots per metric and covreage level.
I note that the weighted product seems slightly more variable, particularly at higher coverage. Though the median is nearly always higher
```
%%R
dat = results %>%
filter(scale==0.001, coverage<=30) %>%
select(rho, metric, coverage)
dat$coverage = as.factor(dat$coverage)
ggplot(dat, aes(x=coverage, y=rho, fill=metric)) +
geom_boxplot(aes(fill=metric))
%%R
# AND AGAIN WITHOUT SUBSETTING
dat = results %>%
filter(scale==0.001) %>%
select(rho, metric, coverage)
dat$coverage = as.factor(dat$coverage)
ggplot(dat, aes(x=coverage, y=rho, fill=metric)) +
geom_boxplot(aes(fill=metric))
%%R
dat = subset(results, scale==0.001 & coverage <=15, select=-scale)
ggplot(dat, aes(x=coverage, y=rho, colour=seed, linetype=metric)) +
geom_line()
%%R
summ = results %>%
filter(scale==0.001, coverage <= 50) %>%
select(-scale) %>%
group_by(coverage, metric) %>%
summarise(rho_av=mean(rho), rho_err=sd(rho))
ggplot(summ, aes(x=coverage, y=rho_av, ymin=rho_av-rho_err, ymax=rho_av+rho_err, group=metric)) +
geom_line(aes(linetype=metric)) +
geom_ribbon(aes(fill=metric), alpha=0.2) +
xlab('Genome Coverage') +
ylab(expression(paste("Spearman's ", rho, " +- SD"))) +
scale_x_log10()+
ggtitle("Performance of WIP & IP") +
theme_bw()
%%R
sem <- function(x) sqrt(var(x,na.rm=TRUE)/length(na.omit(x)))
summ = results %>%
filter(scale==0.001) %>%
select(-scale) %>%
group_by(coverage, metric) %>%
summarise(rho_av=mean(rho), rho_err=sem(rho))
ggplot(summ, aes(x=coverage, y=rho_av, ymin=rho_av-rho_err, ymax=rho_av+rho_err, group=metric)) +
geom_line(aes(linetype=metric)) +
geom_ribbon(aes(fill=metric), alpha=0.2) +
xlab('Genome Coverage') +
ylab(expression(paste("Spearman's ", rho))) +
scale_x_log10()+
theme_bw()
%%R
cov_diff = results %>%
filter(scale==0.001) %>%
select(rho, metric, coverage, seed) %>%
spread(metric, rho) %>%
mutate(diff=wip-ip) %>%
select(coverage, seed, diff)
print(summary(cov_diff))
p = ggplot(cov_diff, aes(x=coverage, y=diff, colour=seed)) +
geom_line() +
scale_x_log10() +
ggtitle("Per expt difference in performance (wip - ip)")
print(p)
summ = cov_diff %>%
group_by(coverage) %>%
summarise(diff_av=mean(diff), diff_sd=sd(diff))
ggplot(summ, aes(x=coverage, y=diff_av, ymin=diff_av-diff_sd, ymax=diff_av+diff_sd)) +
geom_line() +
geom_ribbon(alpha=0.2) +
xlab('Genome Coverage') +
ylab(expression(paste("Improvment in Spearman's ", rho, " (wip - IP)"))) +
scale_x_log10() +
theme_bw()
%%R
var = results %>%
filter(coverage == 30) %>%
select(-coverage)
var$scale = as.factor(var$scale)
ggplot(var, aes(x=scale, y=rho, fill=metric)) +
geom_boxplot() +
xlab('Mean pairwise variation') +
ylab(expression(paste("Spearman's ", rho))) +
#scale_x_log10()+
theme_bw()
%%R
summ = results %>%
filter(coverage == 30) %>%
select(-coverage) %>%
group_by(scale, metric) %>%
summarise(rho_av=mean(rho), rho_sd=sd(rho))
ggplot(summ, aes(x=scale, y=rho_av, ymin=rho_av-rho_sd, ymax=rho_av+rho_sd, group=metric)) +
geom_line(aes(linetype=metric)) +
geom_ribbon(aes(fill=metric), alpha=0.2) +
xlab('Mean pairwise variation') +
ylab(expression(paste("Spearman's ", rho))) +
scale_x_log10()+
theme_bw()
```
| true |
code
| 0.349588 | null | null | null | null |
|
# Create redo records
This Jupyter notebook shows how to create a Senzing "redo record".
It assumes a G2 database that is empty.
Essentially the steps are to create very similar records under different data sources,
then delete one of the records. This produces a "redo record".
## G2Engine
### Senzing initialization
Create an instance of G2Engine, G2ConfigMgr, and G2Config.
```
from G2Engine import G2Engine
from G2ConfigMgr import G2ConfigMgr
from G2Config import G2Config
g2_engine = G2Engine()
try:
g2_engine_flags = G2Engine.G2_EXPORT_DEFAULT_FLAGS
g2_engine.initV2(
"pyG2EngineForRedoRecords",
senzing_config_json,
verbose_logging)
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
g2_configuration_manager = G2ConfigMgr()
try:
g2_configuration_manager.initV2(
"pyG2ConfigMgrForRedoRecords",
senzing_config_json,
verbose_logging)
except G2Exception.G2ModuleGenericException as err:
print(g2_configuration_manager.getLastException())
g2_config = G2Config()
try:
g2_config.initV2(
"pyG2ConfigForRedoRecords",
senzing_config_json,
verbose_logging)
config_handle = g2_config.create()
except G2Exception.G2ModuleGenericException as err:
print(g2_config.getLastException())
```
### primeEngine
```
try:
g2_engine.primeEngine()
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Variable initialization
```
load_id = None
```
### Create add data source function
Create a data source with a name having the form `TEST_DATA_SOURCE_nnn`.
```
def add_data_source(datasource_suffix):
datasource_prefix = "TEST_DATA_SOURCE_"
datasource_id = "{0}{1}".format(datasource_prefix, datasource_suffix)
configuration_comment = "Added {}".format(datasource_id)
g2_config.addDataSource(config_handle, datasource_id)
configuration_bytearray = bytearray()
return_code = g2_config.save(config_handle, configuration_bytearray)
configuration_json = configuration_bytearray.decode()
configuration_id_bytearray = bytearray()
g2_configuration_manager.addConfig(configuration_json, configuration_comment, configuration_id_bytearray)
g2_configuration_manager.setDefaultConfigID(configuration_id_bytearray)
g2_engine.reinitV2(configuration_id_bytearray)
```
### Create add record function
Create a record with the id having the form `RECORD_nnn`.
**Note:** this is essentially the same record with only the `DRIVERS_LICENSE_NUMBER` modified slightly.
```
def add_record(record_id_suffix, datasource_suffix):
datasource_prefix = "TEST_DATA_SOURCE_"
record_id_prefix = "RECORD_"
datasource_id = "{0}{1}".format(datasource_prefix, datasource_suffix)
record_id = "{0}{1}".format(record_id_prefix, record_id_suffix)
data = {
"NAMES": [{
"NAME_TYPE": "PRIMARY",
"NAME_LAST": "Smith",
"NAME_FIRST": "John",
"NAME_MIDDLE": "M"
}],
"PASSPORT_NUMBER": "PP11111",
"PASSPORT_COUNTRY": "US",
"DRIVERS_LICENSE_NUMBER": "DL1{:04d}".format(record_id_suffix),
"SSN_NUMBER": "111-11-1111"
}
data_as_json = json.dumps(data)
g2_engine.addRecord(
datasource_id,
record_id,
data_as_json,
load_id)
```
## Redo record
### Print data sources
Print the list of currently defined data sources.
```
try:
datasources_bytearray = bytearray()
g2_config.listDataSources(config_handle, datasources_bytearray)
datasources_dictionary = json.loads(datasources_bytearray.decode())
print(datasources_dictionary)
except G2Exception.G2ModuleGenericException as err:
print(g2_config.getLastException())
```
### Add data sources and records
```
try:
add_data_source(1)
add_record(1,1)
add_record(2,1)
add_data_source(2)
add_record(3,2)
add_record(4,2)
add_data_source(3)
add_record(5,3)
add_record(6,3)
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Delete record
Deleting a record will create a "redo record".
```
try:
g2_engine.deleteRecord("TEST_DATA_SOURCE_3", "RECORD_5", load_id)
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Count redo records
The `count_of_redo_records` will show how many redo records are in Senzing's queue of redo records.
```
try:
count_of_redo_records = g2_engine.countRedoRecords()
print("Number of redo records: {0}".format(count_of_redo_records))
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Print data sources again
Print the list of currently defined data sources.
```
try:
datasources_bytearray = bytearray()
g2_config.listDataSources(config_handle, datasources_bytearray)
datasources_dictionary = json.loads(datasources_bytearray.decode())
print(datasources_dictionary)
except G2Exception.G2ModuleGenericException as err:
print(g2_config.getLastException())
```
| true |
code
| 0.27941 | null | null | null | null |
|
```
%matplotlib inline
```
Neural Transfer Using PyTorch
=============================
**Author**: `Alexis Jacq <https://alexis-jacq.github.io>`_
**Edited by**: `Winston Herring <https://github.com/winston6>`_
**Re-implemented by:** `Shubhajit Das <https://github.com/Shubhajitml>`
Introduction
------------
This tutorial explains how to implement the `Neural-Style algorithm <https://arxiv.org/abs/1508.06576>`__
developed by Leon A. Gatys, Alexander S. Ecker and Matthias Bethge.
Neural-Style, or Neural-Transfer, allows you to take an image and
reproduce it with a new artistic style. The algorithm takes three images,
an input image, a content-image, and a style-image, and changes the input
to resemble the content of the content-image and the artistic style of the style-image.
.. figure:: /_static/img/neural-style/neuralstyle.png
:alt: content1
Underlying Principle
--------------------
The principle is simple: we define two distances, one for the content
($D_C$) and one for the style ($D_S$). $D_C$ measures how different the content
is between two images while $D_S$ measures how different the style is
between two images. Then, we take a third image, the input, and
transform it to minimize both its content-distance with the
content-image and its style-distance with the style-image. Now we can
import the necessary packages and begin the neural transfer.
Importing Packages and Selecting a Device
-----------------------------------------
Below is a list of the packages needed to implement the neural transfer.
- ``torch``, ``torch.nn``, ``numpy`` (indispensables packages for
neural networks with PyTorch)
- ``torch.optim`` (efficient gradient descents)
- ``PIL``, ``PIL.Image``, ``matplotlib.pyplot`` (load and display
images)
- ``torchvision.transforms`` (transform PIL images into tensors)
- ``torchvision.models`` (train or load pre-trained models)
- ``copy`` (to deep copy the models; system package)
```
from google.colab import files
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))
!ls
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from PIL import Image
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
import torchvision.models as models
import copy
```
Next, we need to choose which device to run the network on and import the
content and style images. Running the neural transfer algorithm on large
images takes longer and will go much faster when running on a GPU. We can
use ``torch.cuda.is_available()`` to detect if there is a GPU available.
Next, we set the ``torch.device`` for use throughout the tutorial. Also the ``.to(device)``
method is used to move tensors or modules to a desired device.
```
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
Loading the Images
------------------
Now we will import the style and content images. The original PIL images have values between 0 and 255, but when
transformed into torch tensors, their values are converted to be between
0 and 1. The images also need to be resized to have the same dimensions.
An important detail to note is that neural networks from the
torch library are trained with tensor values ranging from 0 to 1. If you
try to feed the networks with 0 to 255 tensor images, then the activated
feature maps will be unable sense the intended content and style.
However, pre-trained networks from the Caffe library are trained with 0
to 255 tensor images.
.. Note::
Here are links to download the images required to run the tutorial:
`picasso.jpg <https://pytorch.org/tutorials/_static/img/neural-style/picasso.jpg>`__ and
`dancing.jpg <https://pytorch.org/tutorials/_static/img/neural-style/dancing.jpg>`__.
Download these two images and add them to a directory
with name ``images`` in your current working directory.
```
# desired size of the output image
imsize = 512 if torch.cuda.is_available() else 128 # use small size if no gpu
loader = transforms.Compose([
transforms.Resize(imsize), # scale imported image
transforms.ToTensor()]) # transform it into a torch tensor
def image_loader(image_name):
image = Image.open(image_name)
# fake batch dimension required to fit network's input dimensions
image = loader(image).unsqueeze(0)
return image.to(device, torch.float)
style_img = image_loader("colorful.jpg")
content_img = image_loader("shubha.jpg")
assert style_img.size() == content_img.size(), \
"we need to import style and content images of the same size"
```
Now, let's create a function that displays an image by reconverting a
copy of it to PIL format and displaying the copy using
``plt.imshow``. We will try displaying the content and style images
to ensure they were imported correctly.
```
unloader = transforms.ToPILImage() # reconvert into PIL image
plt.ion()
def imshow(tensor, title=None):
image = tensor.cpu().clone() # we clone the tensor to not do changes on it
image = image.squeeze(0) # remove the fake batch dimension
image = unloader(image)
plt.imshow(image)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
plt.figure()
imshow(style_img, title='Style Image')
plt.figure()
imshow(content_img, title='Content Image')
```
Loss Functions
--------------
Content Loss
~~~~~~~~~~~~
The content loss is a function that represents a weighted version of the
content distance for an individual layer. The function takes the feature
maps $F_{XL}$ of a layer $L$ in a network processing input $X$ and returns the
weighted content distance $w_{CL}.D_C^L(X,C)$ between the image $X$ and the
content image $C$. The feature maps of the content image($F_{CL}$) must be
known by the function in order to calculate the content distance. We
implement this function as a torch module with a constructor that takes
$F_{CL}$ as an input. The distance $\|F_{XL} - F_{CL}\|^2$ is the mean square error
between the two sets of feature maps, and can be computed using ``nn.MSELoss``.
We will add this content loss module directly after the convolution
layer(s) that are being used to compute the content distance. This way
each time the network is fed an input image the content losses will be
computed at the desired layers and because of auto grad, all the
gradients will be computed. Now, in order to make the content loss layer
transparent we must define a ``forward`` method that computes the content
loss and then returns the layer’s input. The computed loss is saved as a
parameter of the module.
```
class ContentLoss(nn.Module):
def __init__(self, target,):
super(ContentLoss, self).__init__()
# we 'detach' the target content from the tree used
# to dynamically compute the gradient: this is a stated value,
# not a variable. Otherwise the forward method of the criterion
# will throw an error.
self.target = target.detach()
def forward(self, input):
self.loss = F.mse_loss(input, self.target)
return input
```
.. Note::
**Important detail**: although this module is named ``ContentLoss``, it
is not a true PyTorch Loss function. If you want to define your content
loss as a PyTorch Loss function, you have to create a PyTorch autograd function
to recompute/implement the gradient manually in the ``backward``
method.
Style Loss
~~~~~~~~~~
The style loss module is implemented similarly to the content loss
module. It will act as a transparent layer in a
network that computes the style loss of that layer. In order to
calculate the style loss, we need to compute the gram matrix $G_{XL}$. A gram
matrix is the result of multiplying a given matrix by its transposed
matrix. In this application the given matrix is a reshaped version of
the feature maps $F_{XL}$ of a layer $L$. $F_{XL}$ is reshaped to form $\hat{F}_{XL}$, a $K$\ x\ $N$
matrix, where $K$ is the number of feature maps at layer $L$ and $N$ is the
length of any vectorized feature map $F_{XL}^k$. For example, the first line
of $\hat{F}_{XL}$ corresponds to the first vectorized feature map $F_{XL}^1$.
Finally, the gram matrix must be normalized by dividing each element by
the total number of elements in the matrix. This normalization is to
counteract the fact that $\hat{F}_{XL}$ matrices with a large $N$ dimension yield
larger values in the Gram matrix. These larger values will cause the
first layers (before pooling layers) to have a larger impact during the
gradient descent. Style features tend to be in the deeper layers of the
network so this normalization step is crucial.
```
def gram_matrix(input):
a, b, c, d = input.size() # a=batch size(=1)
# b=number of feature maps
# (c,d)=dimensions of a f. map (N=c*d)
features = input.view(a * b, c * d) # resise F_XL into \hat F_XL
G = torch.mm(features, features.t()) # compute the gram product
# we 'normalize' the values of the gram matrix
# by dividing by the number of element in each feature maps.
return G.div(a * b * c * d)
```
Now the style loss module looks almost exactly like the content loss
module. The style distance is also computed using the mean square
error between $G_{XL}$ and $G_{SL}$.
```
class StyleLoss(nn.Module):
def __init__(self, target_feature):
super(StyleLoss, self).__init__()
self.target = gram_matrix(target_feature).detach()
def forward(self, input):
G = gram_matrix(input)
self.loss = F.mse_loss(G, self.target)
return input
```
Importing the Model
-------------------
Now we need to import a pre-trained neural network. We will use a 19
layer VGG network like the one used in the paper.
PyTorch’s implementation of VGG is a module divided into two child
``Sequential`` modules: ``features`` (containing convolution and pooling layers),
and ``classifier`` (containing fully connected layers). We will use the
``features`` module because we need the output of the individual
convolution layers to measure content and style loss. Some layers have
different behavior during training than evaluation, so we must set the
network to evaluation mode using ``.eval()``.
```
cnn = models.vgg19(pretrained=True).features.to(device).eval()
```
Additionally, VGG networks are trained on images with each channel
normalized by mean=[0.485, 0.456, 0.406] and std=[0.229, 0.224, 0.225].
We will use them to normalize the image before sending it into the network.
```
cnn_normalization_mean = torch.tensor([0.485, 0.456, 0.406]).to(device)
cnn_normalization_std = torch.tensor([0.229, 0.224, 0.225]).to(device)
# create a module to normalize input image so we can easily put it in a
# nn.Sequential
class Normalization(nn.Module):
def __init__(self, mean, std):
super(Normalization, self).__init__()
# .view the mean and std to make them [C x 1 x 1] so that they can
# directly work with image Tensor of shape [B x C x H x W].
# B is batch size. C is number of channels. H is height and W is width.
self.mean = torch.tensor(mean).view(-1, 1, 1)
self.std = torch.tensor(std).view(-1, 1, 1)
def forward(self, img):
# normalize img
return (img - self.mean) / self.std
```
A ``Sequential`` module contains an ordered list of child modules. For
instance, ``vgg19.features`` contains a sequence (Conv2d, ReLU, MaxPool2d,
Conv2d, ReLU…) aligned in the right order of depth. We need to add our
content loss and style loss layers immediately after the convolution
layer they are detecting. To do this we must create a new ``Sequential``
module that has content loss and style loss modules correctly inserted.
```
# desired depth layers to compute style/content losses :
content_layers_default = ['conv_4']
style_layers_default = ['conv_1', 'conv_2', 'conv_3', 'conv_4', 'conv_5']
def get_style_model_and_losses(cnn, normalization_mean, normalization_std,
style_img, content_img,
content_layers=content_layers_default,
style_layers=style_layers_default):
cnn = copy.deepcopy(cnn)
# normalization module
normalization = Normalization(normalization_mean, normalization_std).to(device)
# just in order to have an iterable access to or list of content/syle
# losses
content_losses = []
style_losses = []
# assuming that cnn is a nn.Sequential, so we make a new nn.Sequential
# to put in modules that are supposed to be activated sequentially
model = nn.Sequential(normalization)
i = 0 # increment every time we see a conv
for layer in cnn.children():
if isinstance(layer, nn.Conv2d):
i += 1
name = 'conv_{}'.format(i)
elif isinstance(layer, nn.ReLU):
name = 'relu_{}'.format(i)
# The in-place version doesn't play very nicely with the ContentLoss
# and StyleLoss we insert below. So we replace with out-of-place
# ones here.
layer = nn.ReLU(inplace=False)
elif isinstance(layer, nn.MaxPool2d):
name = 'pool_{}'.format(i)
elif isinstance(layer, nn.BatchNorm2d):
name = 'bn_{}'.format(i)
else:
raise RuntimeError('Unrecognized layer: {}'.format(layer.__class__.__name__))
model.add_module(name, layer)
if name in content_layers:
# add content loss:
target = model(content_img).detach()
content_loss = ContentLoss(target)
model.add_module("content_loss_{}".format(i), content_loss)
content_losses.append(content_loss)
if name in style_layers:
# add style loss:
target_feature = model(style_img).detach()
style_loss = StyleLoss(target_feature)
model.add_module("style_loss_{}".format(i), style_loss)
style_losses.append(style_loss)
# now we trim off the layers after the last content and style losses
for i in range(len(model) - 1, -1, -1):
if isinstance(model[i], ContentLoss) or isinstance(model[i], StyleLoss):
break
model = model[:(i + 1)]
return model, style_losses, content_losses
```
Next, we select the input image. You can use a copy of the content image
or white noise.
```
input_img = content_img.clone()
# if you want to use white noise instead uncomment the below line:
# input_img = torch.randn(content_img.data.size(), device=device)
# add the original input image to the figure:
plt.figure()
imshow(input_img, title='Input Image')
```
Gradient Descent
----------------
As Leon Gatys, the author of the algorithm, suggested `here <https://discuss.pytorch.org/t/pytorch-tutorial-for-neural-transfert-of-artistic-style/336/20?u=alexis-jacq>`__, we will use
L-BFGS algorithm to run our gradient descent. Unlike training a network,
we want to train the input image in order to minimise the content/style
losses. We will create a PyTorch L-BFGS optimizer ``optim.LBFGS`` and pass
our image to it as the tensor to optimize.
```
def get_input_optimizer(input_img):
# this line to show that input is a parameter that requires a gradient
optimizer = optim.LBFGS([input_img.requires_grad_()])
return optimizer
```
Finally, we must define a function that performs the neural transfer. For
each iteration of the networks, it is fed an updated input and computes
new losses. We will run the ``backward`` methods of each loss module to
dynamicaly compute their gradients. The optimizer requires a “closure”
function, which reevaluates the modul and returns the loss.
We still have one final constraint to address. The network may try to
optimize the input with values that exceed the 0 to 1 tensor range for
the image. We can address this by correcting the input values to be
between 0 to 1 each time the network is run.
```
def run_style_transfer(cnn, normalization_mean, normalization_std,
content_img, style_img, input_img, num_steps=500,
style_weight=1000000, content_weight=1):
"""Run the style transfer."""
print('Building the style transfer model..')
model, style_losses, content_losses = get_style_model_and_losses(cnn,
normalization_mean, normalization_std, style_img, content_img)
optimizer = get_input_optimizer(input_img)
print('Optimizing..')
run = [0]
while run[0] <= num_steps:
def closure():
# correct the values of updated input image
input_img.data.clamp_(0, 1)
optimizer.zero_grad()
model(input_img)
style_score = 0
content_score = 0
for sl in style_losses:
style_score += sl.loss
for cl in content_losses:
content_score += cl.loss
style_score *= style_weight
content_score *= content_weight
loss = style_score + content_score
loss.backward()
run[0] += 1
if run[0] % 50 == 0:
print("run {}:".format(run))
print('Style Loss : {:4f} Content Loss: {:4f}'.format(
style_score.item(), content_score.item()))
print()
return style_score + content_score
optimizer.step(closure)
# a last correction...
input_img.data.clamp_(0, 1)
return input_img
```
Finally, we can run the algorithm.
```
output = run_style_transfer(cnn, cnn_normalization_mean, cnn_normalization_std,
content_img, style_img, input_img)
plt.figure()
imshow(output, title='Output Image')
# sphinx_gallery_thumbnail_number = 4
plt.ioff()
plt.show()
```
| true |
code
| 0.757685 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.