code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Copyright 2020 Montvieux Ltd
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#
# +
import requests
from io import BytesIO
import PIL.Image
from IPython.display import display,clear_output,HTML
from IPython.display import Image as DisplayImage
import base64
import json
from io import StringIO
import ipywidgets as widgets
import sys
from plark_game import classes
import time
import imageio
import numpy as np
import matplotlib.pyplot as plt
import io
import os, sys
from stable_baselines.common.env_checker import check_env
from stable_baselines.common.evaluation import evaluate_policy
from gym_plark.envs import plark_env,plark_env_guided_reward,plark_env_top_left
# # %matplotlib inline
# # %load_ext autoreload
# # %autoreload 2
import datetime
basepath = '/data/agents/models'
from stable_baselines import DQN, PPO2, A2C, ACKTR
from stable_baselines.bench import Monitor
from stable_baselines.common.vec_env import DummyVecEnv
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.ERROR)
import helper
display(HTML(data="""
<style>
div#notebook-container { width: 95%; }
div#menubar-container { width: 65%; }
div#maintoolbar-container { width: 99%; }
</style>
"""))
# -
env = plark_env_guided_reward.PlarkEnvGuidedReward()
# +
# It will check your custom environment and output additional warnings if needed
check_env(env)
## Define the player type we are training.
modelplayer = "pelican"
## Define the type of RL algorithm you are using.
modeltype = "dqn"
## Specify the date and time for this training.
basicdate = str(datetime.datetime.now().strftime("%Y%m%d_%H%M%S"))
## Used for generating the json header file which holds details regarding the model.
## This will be used when playing the game from the GUI.
# Instantiate the env
env = plark_env_guided_reward.PlarkEnvGuidedReward()
model = DQN('CnnPolicy', env)
#model = A2C('CnnPolicy', env)
model.learn(500)
retrain_iter = []
retrain_values = []
print("****** STARTING EVALUATION *******")
mean_reward, n_steps = evaluate_policy(model, env, n_eval_episodes=5, deterministic=False, render=False, callback=None, reward_threshold=None, return_episode_rewards=False)
retrain_iter.append(str(0))
retrain_values.append(mean_reward)
def save():
print(str(retrain_iter))
print(str(retrain_values))
plt.figure(figsize=(9, 3))
plt.subplot(131)
plt.bar(retrain_iter, retrain_values)
plt.subplot(132)
plt.scatter(retrain_iter, retrain_values)
plt.subplot(133)
plt.plot(retrain_iter, retrain_values)
plt.suptitle('Retraining Progress')
##plt.show()
model_path,model_dir, modellabel = save_model_with_env_settings(basepath,model,modeltype,env,basicdate)
fig_path = os.path.join(model_dir, 'Training_Progress.png')
plt.savefig(fig_path)
print('Model saved to ', model_path)
def retrain(mean_reward, target_reward, count):
while mean_reward < target_reward:
count = count + 1
retrain_iter.append(str(count))
model.learn(50)
mean_reward, n_steps = evaluate_policy(model, env, n_eval_episodes=1, deterministic=False, render=False, callback=None, reward_threshold=None, return_episode_rewards=False)
retrain_values.append(mean_reward)
if mean_reward > target_reward:
save()
break
if mean_reward < target_reward:
retrain(mean_reward, target_reward, count)
print("Model Training Reached Target Level")
retrain(mean_reward, 10, 1)
# -
| Components/agent-training/agent_training/image-based/benchmark.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# # DENSENET + CTC
# +
#CRNN
#Edit:2017-11-21
#@sima
#%%
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
from keras.layers.convolutional import Conv2D,MaxPooling2D,ZeroPadding2D
from keras.layers.normalization import BatchNormalization
from keras.layers.core import Reshape,Masking,Lambda,Permute
from keras.layers import Input,Dense,Flatten
from keras.preprocessing.sequence import pad_sequences
from keras.layers.recurrent import GRU,LSTM
from keras.layers.wrappers import Bidirectional
from keras.models import Model
from keras import backend as K
from keras.preprocessing import image
from keras.optimizers import Adam,SGD,Adadelta
from keras import losses
from keras.layers.wrappers import TimeDistributed
from keras.callbacks import EarlyStopping,ModelCheckpoint,TensorBoard
from keras.utils import plot_model
from matplotlib import pyplot as plt
import tensorflow as tf
import numpy as np
import os
from PIL import Image
import json
import threading
from imp import reload
import densenet
reload(densenet)
def get_session(gpu_fraction=0.6):
'''''Assume that you have 6GB of GPU memory and want to allocate ~2GB'''
num_threads = os.environ.get('OMP_NUM_THREADS')
gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=gpu_fraction)
if num_threads:
return tf.Session(config=tf.ConfigProto(
gpu_options=gpu_options, intra_op_parallelism_threads=num_threads))
else:
return tf.Session(config=tf.ConfigProto(gpu_options=gpu_options))
K.set_session(get_session())
def ctc_lambda_func(args):
y_pred,labels,input_length,label_length = args
return K.ctc_batch_cost(labels, y_pred, input_length, label_length)
char=''
with open('D:\\char_std_5990.txt',encoding='utf-8') as f:
for ch in f.readlines():
ch = ch.strip('\r\n')
char=char+ch
#caffe_ocr中把0作为blank,但是tf 的CTC the last class is reserved to the blank label.
#https://github.com/tensorflow/tensorflow/blob/master/tensorflow/core/util/ctc/ctc_loss_calculator.h
char =char[1:]+'卍'
print('nclass:',len(char))
id_to_char = {i:j for i,j in enumerate(char)}
print(id_to_char[5988])
maxlabellength = 20
img_h = 32
img_w = 280
nclass = len(char)
rnnunit=256
batch_size =64
class random_uniform_num():
"""
均匀随机,确保每轮每个只出现一次
"""
def __init__(self,total):
self.total = total
self.range = [i for i in range(total)]
np.random.shuffle(self.range)
self.index = 0
def get(self,batchsize):
r_n=[]
if(self.index+batchsize>self.total):
r_n_1 = self.range[self.index:self.total]
np.random.shuffle(self.range)
self.index = (self.index+batchsize)-self.total
r_n_2 = self.range[0:self.index]
r_n.extend(r_n_1)
r_n.extend(r_n_2)
else:
r_n = self.range[self.index:self.index+batchsize]
self.index = self.index+batchsize
return r_n
def readtrainfile(filename):
res=[]
with open(filename,'r') as f:
lines = f.readlines()
for i in lines:
res.append(i.strip('\r\n'))
dic={}
for i in res:
p = i.split(' ')
dic[p[0]] = p[1:]
return dic
def gen3(trainfile,batchsize=64,maxlabellength=10,imagesize=(32,280)):
image_label = readtrainfile(trainfile)
_imagefile = [i for i,j in image_label.items()]
x = np.zeros((batchsize, imagesize[0], imagesize[1], 1), dtype=np.float)
labels = np.ones([batchsize,maxlabellength])*10000
input_length = np.zeros([batchsize,1])
label_length = np.zeros([batchsize,1])
r_n = random_uniform_num(len(_imagefile))
print('图片总量',len(_imagefile))
_imagefile = np.array(_imagefile)
while 1:
shufimagefile = _imagefile[r_n.get(batchsize)]
for i,j in enumerate(shufimagefile):
img1 = Image.open(j).convert('L')
img = np.array(img1,'f')/255.0-0.5
x[i] = np.expand_dims(img,axis=2)
#print('imag:shape',img.shape)
str = image_label[j]
label_length[i] = len(str)
if(len(str)<=0):
print("len<0",j)
input_length[i] = imagesize[1]//8
#caffe_ocr中把0作为blank,但是tf 的CTC the last class is reserved to the blank label.
#https://github.com/tensorflow/tensorflow/blob/master/tensorflow/core/util/ctc/ctc_loss_calculator.h
#
labels[i,:len(str)] =[int(i)-1 for i in str]
inputs = {'the_input': x,
'the_labels': labels,
'input_length': input_length,
'label_length': label_length,
}
outputs = {'ctc': np.zeros([batchsize])}
yield (inputs,outputs)
input = Input(shape=(img_h,None,1),name='the_input')
y_pred= densenet.dense_cnn(input,nclass)
basemodel = Model(inputs=input,outputs=y_pred)
basemodel.summary()
labels = Input(name='the_labels',shape=[maxlabellength],dtype='float32')
input_length = Input(name='input_length', shape=[1], dtype='int64')
label_length = Input(name='label_length', shape=[1], dtype='int64')
loss_out = Lambda(ctc_lambda_func, output_shape=(1,), name='ctc')([y_pred, labels, input_length, label_length])
model = Model(inputs=[input, labels, input_length, label_length], outputs=loss_out)
adam = Adam()
model.compile(loss={'ctc': lambda y_true, y_pred: y_pred}, optimizer=adam,metrics=['accuracy'])
checkpoint = ModelCheckpoint(r'E:\deeplearn\OCR\Sample\model\weights-densent-{epoch:02d}.hdf5',
save_weights_only=True)
earlystop = EarlyStopping(patience=10)
tensorboard = TensorBoard(r'E:\deeplearn\OCR\Sample\model\tflog-densent',write_graph=True)
# +
print('-----------beginfit--')
cc1=gen3(r'D:\train1.txt',batchsize=batch_size,maxlabellength=maxlabellength,imagesize=(img_h,img_w))
cc2=gen3(r'D:\test1.txt',batchsize=batch_size,maxlabellength=maxlabellength,imagesize=(img_h,img_w))
# -
res = model.fit_generator(cc1,
steps_per_epoch =3279601// batch_size,
epochs = 100,
validation_data =cc2 ,
validation_steps = 364400// batch_size,
callbacks =[earlystop,checkpoint,tensorboard],
verbose=1
)
loss = 0.2353 acc = 0.9623
| densent_ocr/densenet-ocr.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Summary
# Try using XGBoost to predict loss. From Kaggle forum [post](https://www.kaggle.com/iglovikov/allstate-claims-severity/xgb-1114).
# +
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cross_validation import train_test_split
from sklearn.metrics import mean_squared_error,mean_absolute_error
from copy import deepcopy
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
# %matplotlib inline
# +
loc = '/Users/elena/Documents/Kaggle/Allstate/data/'
train = pd.read_csv(os.path.join(loc,'train.csv'))
train.drop('id',axis=1,inplace=True)
test = pd.read_csv(os.path.join(loc,'test.csv'))
ids = test['id']
test.drop('id',axis=1,inplace=True)
submission = pd.read_csv(os.path.join(loc,"sample_submission.csv"))
# -
import xgboost as xgb
def convert_strings(pdseries):
# Function inputs a column of a pandas DataFrame,
# determines the number of unique entries, and assigns
# an integer to each entry.
# This is to avoid issues with non-integer data.
array = np.array(pdseries)
vals = np.unique(array)
nums = np.arange(0,len(vals),1)
#new_array = np.zeros(len(array),dtype='int')
new_array = np.zeros(len(array),dtype='float')
#nums = np.linspace(0,1,len(vals))
#new_array = np.zeros(len(array))
for j in range(len(vals)):
ind = np.where(array==vals[j])[0]
new_array[ind]=nums[j]
# Returns a numpy array with an integer for each entry
return new_array
# +
y = np.log1p(train['loss'].values)
full = pd.concat([train,test],ignore_index=True)
full = full.drop('loss',axis=1)
full.head()
to_remove = list(['cont1','cont11','cont6','cat2','cat6','cat8','cat7','cat16'])
for col in full.columns:
if 'cat' in col:
full.loc[:,col]=convert_strings(full.loc[:,col])
somefull = deepcopy(full)
for l in to_remove:
somefull.drop(l,axis=1,inplace=True)
somefull.loc[:,'cont10']=np.log1p(somefull.loc[:,'cont10'])
# +
params = {
'min_child_weight': 1,
'eta': 0.01,
'colsample_bytree': 0.5,
'max_depth': 12,
'subsample': 0.8,
'alpha': 1,
'gamma': 1,
'silent': 1,
'verbose_eval': True,
'seed': 2016
}
X_train, X_test, y_train, y_test = train_test_split(somefull[0:len(train)], y, test_size=.4)
xgtrain = xgb.DMatrix(X_train, label=y_train)
xgtest = xgb.DMatrix(X_test)
model = xgb.train(params, xgtrain, int(2012 / 0.9))
print mean_absolute_error(np.expm1(y_test),np.expm1(model.predict(xgtest)))
sns.set_context('poster')
sns.set_style('white')
sns.distplot(y_train,label='Train')
sns.distplot(model.predict(xgtest),label='Test')
plt.legend(loc='best')
# +
xgtrain = xgb.DMatrix(somefull[0:len(train)], label=y)
xgtest = xgb.DMatrix(somefull[len(train):])
model = xgb.train(params, xgtrain, int(2012 / 0.9))
submission.iloc[:, 1] = np.expm1(model.predict(xgtest))
submission.to_csv(loc+'xgboost1.csv',index=False)
print 'Done'
# -
# Try only using a handful of features:
# +
important = list(["cont10","cat1","cat3","cat4","cat9",
"cat10","cat12","cat27","cat35","cat37",
"cat59","cat66","cat69","cat71","cat79",
"cat80","cat81","cat83"])
keep_df = somefull[important]
X_train, X_test, y_train, y_test = train_test_split(keep_df[0:len(train)], y, test_size=.4)
xgtrain2 = xgb.DMatrix(X_train, label=y_train)
xgtest2 = xgb.DMatrix(X_test)
model2 = xgb.train(params, xgtrain2, int(2012 / 0.9))
sns.set_context('poster')
sns.set_style('white')
sns.distplot(y,label='Train',hist=False)
sns.distplot(model.predict(xgtest),label='Full Dataset',hist=False)
sns.distplot(model2.predict(xgtest2),label='Some Data',hist=False)
plt.legend(loc='best')
# -
| notebooks/20161107_KEW_xgboost.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Implementing a simple standard WebGL scene using feedWebGL2
#
# Display a flat triangle.
#
# Adapted from https://www.tutorialspoint.com/webgl/webgl_sample_application.htm
import feedWebGL2.feedback as fd
from ipywidgets import interact, interactive, fixed, interact_manual
fd.widen_notebook()
# +
vertex_shader = """#version 300 es
uniform float scale;
in vec2 coordinates;
out vec3 output_vertex;
void main() {
vec2 scaled = scale * coordinates;
gl_Position = vec4(scaled, 0.0, 1.0);
output_vertex = gl_Position.xyz;
}
"""
fragment_shader = """#version 300 es
precision highp float;
out vec4 color;
void main() {
color = vec4(1.0, 0.0, 0.0, 1.0);
}
"""
#vertices = [-1, 0, -1, -1, 0, -1];
vectors = [[-1, 0], [-1, -1], [0, -1]]
feedback_program = fd.FeedbackProgram(
context = fd.Context(
buffers = fd.Buffers(
coordinates_buffer = fd.Buffer(
#array=vertices,
vectors=vectors
),
),
width = 600,
show = True,
),
runner = fd.Runner(
vertices_per_instance = 3,
run_type = "TRIANGLES",
uniforms = fd.Uniforms(
scale = fd.Uniform(
default_value = [0.5],
),
),
inputs = fd.Inputs(
coordinates = fd.Input(
num_components = 2,
from_buffer = fd.BufferLocation(
name = "coordinates_buffer",
)
),
),
),
program = fd.Program(
vertex_shader = vertex_shader,
fragment_shader = fragment_shader,
feedbacks = fd.Feedbacks(
output_vertex = fd.Feedback(num_components=3),
),
),
)
# display the widget and debugging information
#feedback_program.debugging_display()
feedback_program.run()
feedback_program
# +
def move_corner(x=-0.5, scale=0.5):
new_vertices = vectors
new_vertices[0][0] = x
feedback_program.change_buffer("coordinates_buffer", new_vertices)
feedback_program.change_uniform_vector("scale", [scale])
feedback_program.run()
interact(move_corner, x=(-1.0, 1.0), scale=(0.0, 1.0))
# -
move_corner(x=-0.1)
feedback_program.get_feedback("output_vertex")
#import time
def ttest():
for i in range(-100, 100):
move_corner(i/100.0)
#time.sleep(0.01)
#print(i)
ttest()
| notebooks/one_triangle.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W2D3_BiologicalNeuronModels/W2D3_Tutorial3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# -
# # Tutorial 3: Synaptic transmission - Models of static and dynamic synapses
# **Week 2, Day 3: Biological Neuron Models**
#
# **By Neuromatch Academy**
#
# __Content creators:__ <NAME>, <NAME>, <NAME>, <NAME>, <NAME>
#
# __Content reviewers:__ <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>
# **Our 2021 Sponsors, including Presenting Sponsor Facebook Reality Labs**
#
# <p align='center'><img src='https://github.com/NeuromatchAcademy/widgets/blob/master/sponsors.png?raw=True'/></p>
# ---
# # Tutorial Objectives
# Synapses connect neurons into neural networks or circuits. Specialized electrical synapses make direct, physical connections between neurons. In this tutorial, however, we will focus on **chemical synapses**, which are more common in the brain. These synapses do not physically join neurons. Instead, a spike in the presynaptic cell causes a chemical, or neurotransmitter, to be released into a small space between the neurons called the synaptic cleft. Once the chemical diffuses across that space, it changes the pearmeability of the postsynaptic membrane, which may result in a positive or negative change in the membrane voltage.
#
# In this tutorial, we will model chemical synaptic transmission and study some interesting effects produced by **static synapses** and **dynamic synapses**.
#
# First, we will start by writing code to simulate static synapses -- whose weight is always fixed.
# Next, we will extend the model and model **dynamic synapses** -- whose synaptic strength is dependent on the recent spike history: synapses can either progressively increase or decrease the size of their effects on the post-synaptic neuron, based on the recent firing rate of its presynaptic partners. This feature of synapses in the brain is called **Short-Term Plasticity** and causes synapses to undergo *Facilitation* or *Depression*.
#
# Our goals for this tutorial are to:
#
# - simulate static synapses and study how excitation and inhibition affect the patterns in the neurons' spiking output
# - define mean- or fluctuation-driven regimes
# - simulate short-term dynamics of synapses (facilitation and depression)
# - study how a change in pre-synaptic firing history affects the synaptic weights (i.e., PSP amplitude)
# + cellView="form"
# @title Video 1: Static and dynamic synapses
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = 'https://player.bilibili.com/player.html?bvid={0}&page={1}'.format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id="", width=854, height=480, fs=1)
print('Video available at https://www.bilibili.com/video/{0}'.format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="Hbz2lj2AO_0", width=854, height=480, fs=1, rel=0)
print('Video available at https://youtube.com/watch?v=' + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
# -
# ---
# # Setup
#
# Import libraries
import matplotlib.pyplot as plt
import numpy as np
# + cellView="form"
# @title Figure Settings
import ipywidgets as widgets # interactive display
# %config InlineBackend.figure_format='retina'
# use NMA plot style
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
my_layout = widgets.Layout()
# + cellView="form"
# @title Helper functions
def my_GWN(pars, mu, sig, myseed=False):
"""
Args:
pars : parameter dictionary
mu : noise baseline (mean)
sig : noise amplitute (standard deviation)
myseed : random seed. int or boolean
the same seed will give the same random number sequence
Returns:
I : Gaussian White Noise (GWN) input
"""
# Retrieve simulation parameters
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
# set random seed
# you can fix the seed of the random number generator so that the results
# are reliable. However, when you want to generate multiple realizations
# make sure that you change the seed for each new realization.
if myseed:
np.random.seed(seed=myseed)
else:
np.random.seed()
# generate GWN
# we divide here by 1000 to convert units to seconds.
I_GWN = mu + sig * np.random.randn(Lt) / np.sqrt(dt / 1000.)
return I_GWN
def Poisson_generator(pars, rate, n, myseed=False):
"""
Generates poisson trains
Args:
pars : parameter dictionary
rate : noise amplitute [Hz]
n : number of Poisson trains
myseed : random seed. int or boolean
Returns:
pre_spike_train : spike train matrix, ith row represents whether
there is a spike in ith spike train over time
(1 if spike, 0 otherwise)
"""
# Retrieve simulation parameters
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
# set random seed
if myseed:
np.random.seed(seed=myseed)
else:
np.random.seed()
# generate uniformly distributed random variables
u_rand = np.random.rand(n, Lt)
# generate Poisson train
poisson_train = 1. * (u_rand < rate * (dt / 1000.))
return poisson_train
def default_pars(**kwargs):
pars = {}
### typical neuron parameters###
pars['V_th'] = -55. # spike threshold [mV]
pars['V_reset'] = -75. # reset potential [mV]
pars['tau_m'] = 10. # membrane time constant [ms]
pars['g_L'] = 10. # leak conductance [nS]
pars['V_init'] = -65. # initial potential [mV]
pars['E_L'] = -75. # leak reversal potential [mV]
pars['tref'] = 2. # refractory time (ms)
### simulation parameters ###
pars['T'] = 400. # Total duration of simulation [ms]
pars['dt'] = .1 # Simulation time step [ms]
### external parameters if any ###
for k in kwargs:
pars[k] = kwargs[k]
pars['range_t'] = np.arange(0, pars['T'], pars['dt']) # Vector of discretized time points [ms]
return pars
def my_illus_LIFSYN(pars, v_fmp, v):
"""
Illustartion of FMP and membrane voltage
Args:
pars : parameters dictionary
v_fmp : free membrane potential, mV
v : membrane voltage, mV
Returns:
plot of membrane voltage and FMP, alongside with the spiking threshold
and the mean FMP (dashed lines)
"""
plt.figure(figsize=(14, 5))
plt.plot(pars['range_t'], v_fmp, 'r', lw=1.,
label='Free mem. pot.', zorder=2)
plt.plot(pars['range_t'], v, 'b', lw=1.,
label='True mem. pot', zorder=1, alpha=0.7)
plt.axhline(-55, 0, 1, color='k', lw=2., ls='--',
label='Spike Threshold', zorder=1)
plt.axhline(np.mean(v_fmp), 0, 1, color='r', lw=2., ls='--',
label='Mean Free Mem. Pot.', zorder=1)
plt.xlabel('Time (ms)')
plt.ylabel('V (mV)')
plt.legend(loc=[1.02, 0.68])
plt.show()
def my_illus_STD(Poi_or_reg=False, rate=20., U0=0.5,
tau_d=100., tau_f=50., plot_out=True):
"""
Only for one presynaptic train
Args:
Poi_or_reg : Poisson or regular input spiking trains
rate : Rate of input spikes, Hz
U0 : synaptic release probability at rest
tau_d : synaptic depression time constant of x [ms]
tau_f : synaptic facilitation time constantr of u [ms]
plot_out : whether ot not to plot, True or False
Returns:
Nothing.
"""
T_simu = 10.0 * 1000 / (1.0 * rate) # 10 spikes in the time window
pars = default_pars(T=T_simu)
dt = pars['dt']
if Poi_or_reg:
# Poisson type spike train
pre_spike_train = Poisson_generator(pars, rate, n=1)
pre_spike_train = pre_spike_train.sum(axis=0)
else:
# Regular firing rate
isi_num = int((1e3/rate)/dt) # number of dt
pre_spike_train = np.zeros(len(pars['range_t']))
pre_spike_train[::isi_num] = 1.
u, R, g = dynamic_syn(g_bar=1.2, tau_syn=5., U0=U0,
tau_d=tau_d, tau_f=tau_f,
pre_spike_train=pre_spike_train,
dt=pars['dt'])
if plot_out:
plt.figure(figsize=(12, 6))
plt.subplot(221)
plt.plot(pars['range_t'], R, 'b', label='R')
plt.plot(pars['range_t'], u, 'r', label='u')
plt.legend(loc='best')
plt.xlim((0, pars['T']))
plt.ylabel(r'$R$ or $u$ (a.u)')
plt.subplot(223)
spT = pre_spike_train > 0
t_sp = pars['range_t'][spT] #spike times
plt.plot(t_sp, 0. * np.ones(len(t_sp)), 'k|', ms=18, markeredgewidth=2)
plt.xlabel('Time (ms)');
plt.xlim((0, pars['T']))
plt.yticks([])
plt.title('Presynaptic spikes')
plt.subplot(122)
plt.plot(pars['range_t'], g, 'r', label='STP synapse')
plt.xlabel('Time (ms)')
plt.ylabel('g (nS)')
plt.xlim((0, pars['T']))
plt.tight_layout()
if not Poi_or_reg:
return g[isi_num], g[9*isi_num]
def plot_volt_trace(pars, v, sp):
"""
Plot trajetory of membrane potential for a single neuron
Args:
pars : parameter dictionary
v : volt trajetory
sp : spike train
Returns:
figure of the membrane potential trajetory for a single neuron
"""
V_th = pars['V_th']
dt = pars['dt']
if sp.size:
sp_num = (sp/dt).astype(int) - 1
v[sp_num] += 10
plt.plot(pars['range_t'], v, 'b')
plt.axhline(V_th, 0, 1, color='k', ls='--', lw=1.)
plt.xlabel('Time (ms)')
plt.ylabel('V (mV)')
# -
# In the `Helper Function`:
#
# - Gaussian white noise generator: `my_GWN(pars, mu, sig, myseed=False)`
# - Poissonian spike train generator: `Poisson_generator(pars, rate, n, myseed=False)`
# - default parameter function (as before) and other plotting utilities
# ---
# # Section 1: Static synapses
# ## Section 1.1: Simulate synaptic conductance dynamics
#
# Synaptic input _in vivo_ consists of a mixture of **excitatory** neurotransmitters, which depolarizes the cell and drives it towards spike threshold, and **inhibitory** neurotransmitters that hyperpolarize it, driving it away from spike threshold. These chemicals cause specific ion channels on the postsynaptic neuron to open, resulting in a change in that neuron's conductance and, therefore, the flow of current in or out of the cell.
#
# This process can be modelled by assuming that the presynaptic neuron's spiking activity produces transient changes in the postsynaptic neuron's conductance ($g_{\rm syn}(t)$). Typically, the conductance transient is modeled as an exponential function.
#
# Such conductance transients can be generated using a simple ordinary differential equation (ODE):
#
# \\
#
# \begin{eqnarray}
# \frac{dg_{\rm syn}(t)}{dt} &=& \bar{g}_{\rm syn} \sum_k \delta(t-t_k) -g_{\rm syn}(t)/\tau_{\rm syn}
# \end{eqnarray}
#
# \\
#
# where $\bar{g}_{\rm syn}$ (often referred to as synaptic weight) is the maximum conductance elicited by each incoming spike, and $\tau_{\rm syn}$ is the synaptic time constant. Note that the summation runs over all spikes received by the neuron at time $t_k$.
#
# Ohm's law allows us to convert conductance changes to the current as:
#
# \\
#
# \begin{align}
# I_{\rm syn}(t) = g_{\rm syn}(t)(V(t)-E_{\rm syn}) \\
# \end{align}
#
# \\
#
# The reversal potential $E_{\rm syn}$ determines the direction of current flow and the excitatory or inhibitory nature of the synapse.
#
# **Thus, incoming spikes are filtered by an exponential-shaped kernel, effectively low-pass filtering the input. In other words, synaptic input is not white noise, but it is, in fact, colored noise, where the color (spectrum) of the noise is determined by the synaptic time constants of both excitatory and inhibitory synapses.**
#
# In a neuronal network, the total synaptic input current $I_{\rm syn}$ is the sum of both excitatory and inhibitory inputs. Assuming the total excitatory and inhibitory conductances received at time $t$ are $g_E(t)$ and $g_I(t)$, and their corresponding reversal potentials are $E_E$ and $E_I$, respectively, then the total synaptic current can be described as:
#
# \\
#
# \begin{align}
# I_{\rm syn}(V(t),t) = -g_E(t) (V-E_E) - g_I(t) (V-E_I)
# \end{align}
#
# \\
#
# Accordingly, the membrane potential dynamics of the LIF neuron under synaptic current drive become:
#
# \\
#
# \begin{eqnarray}
# \tau_m\frac{dV(t)}{dt} = -(V(t)-E_L) - \frac{g_E(t)}{g_L} (V(t)-E_E) - \frac{g_I(t)}{g_L} (V(t)-E_I) + \frac{I_{\rm inj}}{g_L}\quad (2)
# \end{eqnarray}
#
# \\
#
# $I_{\rm inj}$ is an external current injected in the neuron, which is under experimental control; it can be GWN, DC, or anything else.
#
# We will use Eq. (2) to simulate the conductance-based LIF neuron model below.
#
# In the previous tutorials, we saw how the output of a single neuron (spike count/rate and spike time irregularity) changes when we stimulate the neuron with DC and GWN, respectively. Now, we are in a position to study how the neuron behaves when it is bombarded with both excitatory and inhibitory spikes trains -- as happens *in vivo*.
#
# What kind of input is a neuron receiving? When we do not know, we chose the simplest option. The simplest model of input spikes is given when every input spike arrives independently of other spikes, i.e., we assume that the input is Poissonian.
# ## Section 1.2: Simulate LIF neuron with conductance-based synapses
#
# We are now ready to simulate a LIF neuron with conductance-based synaptic inputs! The following code defines the LIF neuron with synaptic input modeled as conductance transients.
# + cellView="form"
# @markdown Execute this cell to get a function for conductance-based LIF neuron (run_LIF_cond)
def run_LIF_cond(pars, I_inj, pre_spike_train_ex, pre_spike_train_in):
"""
Conductance-based LIF dynamics
Args:
pars : parameter dictionary
I_inj : injected current [pA]. The injected current here
can be a value or an array
pre_spike_train_ex : spike train input from presynaptic excitatory neuron
pre_spike_train_in : spike train input from presynaptic inhibitory neuron
Returns:
rec_spikes : spike times
rec_v : mebrane potential
gE : postsynaptic excitatory conductance
gI : postsynaptic inhibitory conductance
"""
# Retrieve parameters
V_th, V_reset = pars['V_th'], pars['V_reset']
tau_m, g_L = pars['tau_m'], pars['g_L']
V_init, E_L = pars['V_init'], pars['E_L']
gE_bar, gI_bar = pars['gE_bar'], pars['gI_bar']
VE, VI = pars['VE'], pars['VI']
tau_syn_E, tau_syn_I = pars['tau_syn_E'], pars['tau_syn_I']
tref = pars['tref']
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
# Initialize
tr = 0.
v = np.zeros(Lt)
v[0] = V_init
gE = np.zeros(Lt)
gI = np.zeros(Lt)
Iinj = I_inj * np.ones(Lt) # ensure Iinj has length Lt
if pre_spike_train_ex.max() == 0:
pre_spike_train_ex_total = np.zeros(Lt)
else:
pre_spike_train_ex_total = pre_spike_train_ex.sum(axis=0) * np.ones(Lt)
if pre_spike_train_in.max() == 0:
pre_spike_train_in_total = np.zeros(Lt)
else:
pre_spike_train_in_total = pre_spike_train_in.sum(axis=0) * np.ones(Lt)
# simulation
rec_spikes = [] # recording spike times
for it in range(Lt - 1):
if tr > 0:
v[it] = V_reset
tr = tr - 1
elif v[it] >= V_th: # reset voltage and record spike event
rec_spikes.append(it)
v[it] = V_reset
tr = tref / dt
# update the synaptic conductance
gE[it + 1] = gE[it] - (dt / tau_syn_E) * gE[it] + gE_bar * pre_spike_train_ex_total[it + 1]
gI[it + 1] = gI[it] - (dt / tau_syn_I) * gI[it] + gI_bar * pre_spike_train_in_total[it + 1]
# calculate the increment of the membrane potential
dv = (dt / tau_m) * (-(v[it] - E_L) \
- (gE[it + 1] / g_L) * (v[it] - VE) \
- (gI[it + 1] / g_L) * (v[it] - VI) + Iinj[it] / g_L)
# update membrane potential
v[it+1] = v[it] + dv
rec_spikes = np.array(rec_spikes) * dt
return v, rec_spikes, gE, gI
print(help(run_LIF_cond))
# -
# ### Exercise 1: Measure the mean free membrane potential
#
# Let's simulate the conductance-based LIF neuron with presynaptic spike trains generated by a `Poisson_generator` with rate 10 Hz for both excitatory and inhibitory inputs. Here, we choose 80 excitatory presynaptic spike trains and 20 inhibitory ones.
#
# Previously, we've already learned that $CV_{\rm ISI}$ can describe the irregularity of the output spike pattern. Now, we will introduce a new descriptor of the neuron membrane, i.e., the **Free Membrane Potential (FMP)** -- the membrane potential of the neuron when its spike threshold is removed.
#
# Although this is completely artificial, calculating this quantity allows us to get an idea of how strong the input is. We are mostly interested in knowing the mean and standard deviation (std.) of the FMP. In the exercise, you can visualize the FMP and membrane voltage with spike threshold.
# +
# To complete the exercise, uncomment the code and fill the missing parts (...)
pars = default_pars(T=1000.)
# Add parameters
pars['gE_bar'] = 2.4 # [nS]
pars['VE'] = 0. # [mV] excitatory reversal potential
pars['tau_syn_E'] = 2. # [ms]
pars['gI_bar'] = 2.4 # [nS]
pars['VI'] = -80. # [mV] inhibitory reversal potential
pars['tau_syn_I'] = 5. # [ms]
# generate presynaptic spike trains
pre_spike_train_ex = Poisson_generator(pars, rate=10, n=80)
pre_spike_train_in = Poisson_generator(pars, rate=10, n=20)
# simulate conductance-based LIF model
v, rec_spikes, gE, gI = run_LIF_cond(pars, 0, pre_spike_train_ex,
pre_spike_train_in)
dt, range_t = pars['dt'], pars['range_t']
if rec_spikes.size:
sp_num = (rec_spikes / dt).astype(int) - 1
v[sp_num] = 10 # draw nicer spikes
####################################################################
## TODO for students: measure the free membrane potential
# In order to measure the free membrane potential, first,
# you should prevent the firing of the LIF neuron
# How to prevent a LIF neuron from firing? Increse the threshold pars['V_th'].
####################################################################
# Change the threshold
# pars['V_th'] = ...
# Calculate FMP
# v_fmp, _, _, _ = run_LIF_cond(pars, ..., ..., ...)
# uncomment when you have filled the exercise
# my_illus_LIFSYN(pars, v_fmp, v)
# +
# to_remove solution
pars = default_pars(T=1000.)
# Add parameters
pars['gE_bar'] = 2.4 # [nS]
pars['VE'] = 0. # [mV] excitatory reversal potential
pars['tau_syn_E'] = 2. # [ms]
pars['gI_bar'] = 2.4 # [nS]
pars['VI'] = -80. # [mV] inhibitory reversal potential
pars['tau_syn_I'] = 5. # [ms]
# generate presynaptic spike trains
pre_spike_train_ex = Poisson_generator(pars, rate=10, n=80)
pre_spike_train_in = Poisson_generator(pars, rate=10, n=20)
# simulate conductance-based LIF model
v, rec_spikes, gE, gI = run_LIF_cond(pars, 0, pre_spike_train_ex,
pre_spike_train_in)
dt, range_t = pars['dt'], pars['range_t']
if rec_spikes.size:
sp_num = (rec_spikes / dt).astype(int) - 1
v[sp_num] = 10 # draw nicer spikes
# Change the threshold
pars['V_th'] = 1e3
# Calculate FMP
v_fmp, _, _, _ = run_LIF_cond(pars, 0, pre_spike_train_ex, pre_spike_train_in)
with plt.xkcd():
my_illus_LIFSYN(pars, v_fmp, v)
# -
# ### Interactive Demo: Conductance-based LIF Explorer with different E/I input
#
# In the following, we can investigate how varying the ratio of excitatory to inhibitory inputs changes the firing rate and the spike time regularity (see the output text).
#
# To change both the excitatory and inhibitory inputs, we will vary their firing rates. *However, if you wish, you can vary the strength and/or the number of these connections as well.*
#
# Pay close attention to the mean free membrane potential (red dotted line) and its location with respect to the spike threshold (black dotted line). Try to develop a heuristic about the mean of the FMP and spike time irregularity ($CV_{\rm ISI}$)
# + cellView="form"
# @title
# @markdown Make sure you execute this cell to enable the widget!
my_layout.width = '450px'
@widgets.interact(
inh_rate=widgets.FloatSlider(20., min=10., max=60., step=5.,
layout=my_layout),
exc_rate=widgets.FloatSlider(10., min=2., max=20., step=2.,
layout=my_layout)
)
def EI_isi_regularity(exc_rate, inh_rate):
pars = default_pars(T=1000.)
# Add parameters
pars['gE_bar'] = 3. # [nS]
pars['VE'] = 0. # [mV] excitatory reversal potential
pars['tau_syn_E'] = 2. # [ms]
pars['gI_bar'] = 3. # [nS]
pars['VI'] = -80. # [mV] inhibitory reversal potential
pars['tau_syn_I'] = 5. # [ms]
pre_spike_train_ex = Poisson_generator(pars, rate=exc_rate, n=80)
pre_spike_train_in = Poisson_generator(pars, rate=inh_rate, n=20) # 4:1
# Lets first simulate a neuron with identical input but with no spike
# threshold by setting the threshold to a very high value
# so that we can look at the free membrane potential
pars['V_th'] = 1e3
v_fmp, rec_spikes, gE, gI = run_LIF_cond(pars, 0, pre_spike_train_ex,
pre_spike_train_in)
# Now simulate a LIP with a regular spike threshold
pars['V_th'] = -55.
v, rec_spikes, gE, gI = run_LIF_cond(pars, 0, pre_spike_train_ex,
pre_spike_train_in)
dt, range_t = pars['dt'], pars['range_t']
if rec_spikes.size:
sp_num = (rec_spikes / dt).astype(int) - 1
v[sp_num] = 10 # draw nicer spikes
spike_rate = 1e3 * len(rec_spikes) / pars['T']
cv_isi = 0.
if len(rec_spikes) > 3:
isi = np.diff(rec_spikes)
cv_isi = np.std(isi) / np.mean(isi)
print('\n')
plt.figure(figsize=(15, 10))
plt.subplot(211)
plt.text(500, -35, f'Spike rate = {spike_rate:.3f} (sp/s), Mean of Free Mem Pot = {np.mean(v_fmp):.3f}',
fontsize=16, fontweight='bold', horizontalalignment='center',
verticalalignment='bottom')
plt.text(500, -38.5, f'CV ISI = {cv_isi:.3f}, STD of Free Mem Pot = {np.std(v_fmp):.3f}',
fontsize=16, fontweight='bold', horizontalalignment='center',
verticalalignment='bottom')
plt.plot(pars['range_t'], v_fmp, 'r', lw=1.,
label='Free mem. pot.', zorder=2)
plt.plot(pars['range_t'], v, 'b', lw=1.,
label='mem. pot with spk thr', zorder=1, alpha=0.7)
plt.axhline(pars['V_th'], 0, 1, color='k', lw=1., ls='--',
label='Spike Threshold', zorder=1)
plt.axhline(np.mean(v_fmp),0, 1, color='r', lw=1., ls='--',
label='Mean Free Mem. Pot.', zorder=1)
plt.ylim(-76, -39)
plt.xlabel('Time (ms)')
plt.ylabel('V (mV)')
plt.legend(loc=[1.02, 0.68])
plt.subplot(223)
plt.plot(pars['range_t'][::3], gE[::3], 'r', lw=1)
plt.xlabel('Time (ms)')
plt.ylabel(r'$g_E$ (nS)')
plt.subplot(224)
plt.plot(pars['range_t'][::3], gI[::3], 'b', lw=1)
plt.xlabel('Time (ms)')
plt.ylabel(r'$g_I$ (nS)')
plt.tight_layout()
# -
# **Mean-driven and Fluctuation-driven regimes**
#
# If we look at the figure above, we note that when the mean FMP is above spike threshold, the fluctuations in the FMP are rather small, and the neuron spikes in a fairly regular fashion. This regime, where the mean FMP is above the spike threshold, is called **mean-driven regime**.
#
#
# When the mean FMP is below the spike threshold, the fluctuations in the FMP are large, and the neuron's spikes are driven by these fluctuations. As a consequence, the neuron spikes in more Poisson-like fashion. This regime, where the mean FMP is below the spike threshold, and spikes are driven by the fluctuations, is called **fluctuation-driven regime**.
# ## Think!
#
# - How much can you increase the spike pattern variability? Under what condition(s) might the neuron respond with Poisson-type spikes? Note that we injected Poisson-type spikes. (Think of the answer in terms of the ratio of the exc. and inh. input spike rates.)
#
# - Link to the balance of excitation and inhibition: one of the definitions of excitation and inhibition balance is that mean free membrane potential remains constant as excitatory and inhibitory input rates are increased. What do you think happens to the neuron firing rate as we change excitatory and inhibitory rates while keeping the neuron in balance? See [Kuhn, Aertsen, and Rotter (2004)](https://www.jneurosci.org/content/jneuro/24/10/2345.full.pdf) for much more on this.
# +
# to_remove explanation
"""
Discussion:
1. We can push the neuron to spike almost like a Poisson neuron. Of course given
that there is a refractoriness it will never spike completely like a Poisson process.
Poisson type spike irregularity will be achieved when mean is small (far from the
spike threshold) and fluctuations are large. This will achieved when excitatory
and inhibitory rates are balanced -- i.e. ratio of exc and inh. spike rate is
constant as you vary the inout rate.
2. Firing rate will increase because fluctuations will increase as we increase
exc. and inh. rates. But if synapses are modelled as conductance as opposed to
currents, fluctuations may start decrease at high input rates because neuron time
constant will drop.
""";
# -
# ---
# # Section 2: Short-term synaptic plasticity
# Above, we modeled synapses with fixed weights. Now we will explore synapses whose weight change in some input conditions.
#
# Short-term plasticity (STP) is a phenomenon in which synaptic efficacy changes over time in a way that reflects the history of presynaptic activity. Two types of STP, with opposite effects on synaptic efficacy, have been experimentally observed. They are known as Short-Term Depression (STD) and Short-Term Facilitation (STF).
#
# The mathematical model (_for more information see [here](http://www.scholarpedia.org/article/Short-term_synaptic_plasticity)_) of STP is based on the concept of a limited pool of synaptic resources available for transmission ($R$), such as, for example, the overall amount of synaptic vesicles at the presynaptic terminals. The amount of presynaptic resource changes in a dynamic fashion depending on the recent history of spikes.
#
# Following a presynaptic spike, (i) the fraction $u$ (release probability) of the available pool to be utilized increases due to spike-induced calcium influx to the presynaptic terminal, after which (ii) $u$ is consumed to increase the post-synaptic conductance. Between spikes, $u$ decays back to zero with time constant $\tau_f$ and $R$ recovers to 1 with time constant $\tau_d$. In summary, the dynamics of excitatory (subscript $E$) STP are given by:
#
# \\
#
# \begin{eqnarray}
# && \frac{du_E}{dt} &=& -\frac{u_E}{\tau_f} + U_0(1-u_E^-)\delta(t-t_{\rm sp}) \\[.5mm]
# && \frac{dR_E}{dt} &=& \frac{1-R_E}{\tau_d} - u_E^+ R_E^- \delta(t-t_{\rm sp}) \qquad (6) \\[.5mm]
# && \frac{dg_E(t)}{dt} &=& -\frac{g_E}{\tau_E} + \bar{g}_E u_E^+ R_E^- \delta(t-t_{\rm sp})
# \end{eqnarray}
#
# \\
#
# where $U_0$ is a constant determining the increment of $u$ produced by a spike. $u_E^-$ and $R_E^-$ denote the corresponding values just before the spike arrives, whereas $u_E^+$ refers to the moment right after the spike. $\bar{g}_E$ denotes the maximum excitatory conductane, and $g_E(t)$ is calculated for all spiketimes $k$, and decays over time with a time constant $\tau_{E}$. Similarly, one can obtain the dynamics of inhibitory STP (i.e., by replacing the subscript $E$ with $I$).
#
#
# The interplay between the dynamics of $u$ and $R$ determines whether the joint effect of $uR$ is dominated by *depression* or *facilitation*. In the parameter regime of $\tau_d \gg \tau_f$ and for large $U_0$, an initial spike incurs a large drop in $R$ that takes a long time to recover; therefore, the synapse is STD-dominated. In the regime of $\tau_d \ll \tau_f$ and for small $U_0$, the synaptic efficacy is increased gradually by spikes, and consequently, the synapse is STF-dominated. This phenomenological model successfully reproduces the kinetic dynamics of depressed and facilitated synapses observed in many cortical areas.
# ## Exercise 2: Compute $du$, $dR$ and $dg$
#
# As we learned in several previous tutorials, the Euler numerical integration method involves the calculation of each derivative at step $n$:
#
# \\
#
# \begin{eqnarray}
# du_E &=& -\frac{u_E[t]}{\tau_f} dt + U_0(1-u_E[t])\cdot \text{sp_or_not[t+dt]} \\
# dR_E &=& \frac{1-R_E[t]}{\tau_d} dt - u_E[t+dt]R_E[t]\cdot \text{sp_or_not[t+dt]} \\
# dg_E &=& -\frac{g_E[t]}{\tau_{E}} dt + \bar{g}_Eu_E[t+dt]R_E[t]\cdot \text{sp_or_not[t+dt]} \\
# \end{eqnarray}
#
# \\
#
# where $\text{sp_or_not}=1$ if there's a spike in the time window $dt$, and $\text{sp_or_not}=0$ otherwise. In addition, note that any spike train generated by our `Poisson_generator` is binary. Then, the values are updated:
#
# \\
#
# \begin{eqnarray}
# u_E[t+dt] &=& u_E[t] + du_E \\
# R_E[t+dt] &=& R_E[t] + dR_E \\
# g_E[t+dt] &=& g_E[t] + dg_E \\
# \end{eqnarray}
#
# \\
#
# Similarly, one can obtain the dynamics of inhibitory conductance.
#
# +
def dynamic_syn(g_bar, tau_syn, U0, tau_d, tau_f, pre_spike_train, dt):
"""
Short-term synaptic plasticity
Args:
g_bar : synaptic conductance strength
tau_syn : synaptic time constant [ms]
U0 : synaptic release probability at rest
tau_d : synaptic depression time constant of x [ms]
tau_f : synaptic facilitation time constantr of u [ms]
pre_spike_train : total spike train (number) input
from presynaptic neuron
dt : time step [ms]
Returns:
u : usage of releasable neurotransmitter
R : fraction of synaptic neurotransmitter resources available
g : postsynaptic conductance
"""
Lt = len(pre_spike_train)
# Initialize
u = np.zeros(Lt)
R = np.zeros(Lt)
R[0] = 1.
g = np.zeros(Lt)
# simulation
for it in range(Lt - 1):
#########################################################################
## TODO for students: compute du, dx and dg, remove NotImplementedError #
# Note pre_spike_train[i] is binary, i.e., sp_or_not in the i-th timebin
# Fill out function and remove
raise NotImplementedError("Student excercise: compute the STP dynamics")
#########################################################################
# Compute du
du = ...
u[it + 1] = u[it] + du
# Compute dR
dR = ...
R[it + 1] = R[it] + dR
# Compute dg
dg = ...
g[it + 1] = g[it] + dg
return u, R, g
# Uncomment this line after completing the dynamic_syn function
# _ = my_illus_STD(Poi_or_reg=False, rate=20., U0=0.5, tau_d=100., tau_f=50.)
# +
# to_remove solution
def dynamic_syn(g_bar, tau_syn, U0, tau_d, tau_f, pre_spike_train, dt):
"""
Short-term synaptic plasticity
Args:
g_bar : synaptic conductance strength
tau_syn : synaptic time constant [ms]
U0 : synaptic release probability at rest
tau_d : synaptic depression time constant of x [ms]
tau_f : synaptic facilitation time constantr of u [ms]
pre_spike_train : total spike train (number) input
from presynaptic neuron
dt : time step [ms]
Returns:
u : usage of releasable neurotransmitter
R : fraction of synaptic neurotransmitter resources available
g : postsynaptic conductance
"""
Lt = len(pre_spike_train)
# Initialize
u = np.zeros(Lt)
R = np.zeros(Lt)
R[0] = 1.
g = np.zeros(Lt)
# simulation
for it in range(Lt - 1):
# Compute du
du = -(dt / tau_f) * u[it] + U0 * (1.0 - u[it]) * pre_spike_train[it + 1]
u[it + 1] = u[it] + du
# Compute dR
dR = (dt / tau_d) * (1.0 - R[it]) - u[it + 1] * R[it] * pre_spike_train[it + 1]
R[it + 1] = R[it] + dR
# Compute dg
dg = -(dt / tau_syn) * g[it] + g_bar * R[it] * u[it + 1] * pre_spike_train[it + 1]
g[it + 1] = g[it] + dg
return u, R, g
with plt.xkcd():
_ = my_illus_STD(Poi_or_reg=False, rate=20., U0=0.5, tau_d=100., tau_f=50.)
# -
# ## Section 2.1: Short-term syaptic depression (STD)
#
# ### Interactive Demo: STD Explorer with input rate
# Below, an interactive demo that shows how Short-term synaptic depression (STD) changes for different firing rates of the presynaptic spike train and how the amplitude synaptic conductance $g$ changes with every incoming spike until it reaches its stationary state.
#
# Does it matter if the neuron fires in a Poisson manner, rather than regularly?
#
# **Note:** `Poi_or_Reg=1`: for *Posisson type* and `Poi_or_Reg=0`: for *regular* presynaptic spikes.
# + cellView="form"
#@title
#@markdown Make sure you execute this cell to enable the widget!
def my_STD_diff_rate(rate, Poi_or_Reg):
_ = my_illus_STD(Poi_or_reg=Poi_or_Reg, rate=rate)
_ = widgets.interact(my_STD_diff_rate, rate=(10., 100.1, 5.),
Poi_or_Reg=(0, 1, 1))
# +
# to_remove explanation
"""
Discussion:
Increasing the input rate, we decrease the synaptic efficacy, i.e., the synaptic
conductance decreases. This is the case for both Poisson or a regular spiking input.
In case of regular spiking, the synaptic conductance reaches a steady state. This
will not happen in the case of Poisson type spikes.
""";
# -
# ### Synaptic depression and presynaptic firing rate
# Once, I asked an experimentalist about the experimental values of the PSP amplitude produced by a connection between two neocortical excitatory neurons. She asked: "At what frequency?" I was confused, but you will understand her question, now that you know that PSP amplitude depends on the spike history, and therefore on the spike rate of the presynaptic neuron.
#
# Here, we will study how the ratio of the synaptic conductance corresponding to the first and 10th spikes change as a function of the presynaptic firing rate (experimentalists often take the ratio of first and second PSPs).
#
# For computational efficiency, we assume that the presynaptic spikes are regular. This assumption means that we do not have to run multiple trials.
# + cellView="form"
# @markdown STD conductance ratio with different input rate
# Regular firing rate
input_rate = np.arange(5., 40.1, 5.)
g_1 = np.zeros(len(input_rate)) # record the the PSP at 1st spike
g_2 = np.zeros(len(input_rate)) # record the the PSP at 10th spike
for ii in range(len(input_rate)):
g_1[ii], g_2[ii] = my_illus_STD(Poi_or_reg=False, rate=input_rate[ii],
plot_out=False, U0=0.5, tau_d=100., tau_f=50)
plt.figure(figsize=(11, 4.5))
plt.subplot(121)
plt.plot(input_rate, g_1, 'm-o', label='1st Spike')
plt.plot(input_rate, g_2, 'c-o', label='10th Spike')
plt.xlabel('Rate [Hz]')
plt.ylabel('Conductance [nS]')
plt.legend()
plt.subplot(122)
plt.plot(input_rate, g_2 / g_1, 'b-o')
plt.xlabel('Rate [Hz]')
plt.ylabel(r'Conductance ratio $g_{10}/g_{1}$')
plt.tight_layout()
# -
# As we increase the input rate the ratio of the first to tenth spike is increased, because the tenth spike conductance becomes smaller. This is a clear evidence of synaptic depression, as using the same amount of current has a smaller effect on the neuron.
# ## Section 2.2: Short-term synaptic facilitation (STF)
# ### Interactive Demo: STF explorer with input rate
# Below, we see an illustration of a short-term facilitation example. Take note of the change in the synaptic variables: `U_0`, `tau_d`, and `tau_f`.
#
# - for STD, `U0=0.5, tau_d=100., tau_f=50.`
#
# - for STP, `U0=0.2, tau_d=100., tau_f=750.`
#
# How does the synaptic conductance change as we change the input rate? What do you observe in the case of a regular input and a Poisson type one?
# + cellView="form"
# @title
# @markdown Make sure you execute this cell to enable the widget!
def my_STD_diff_rate(rate, Poi_or_Reg):
_ = my_illus_STD(Poi_or_reg=Poi_or_Reg, rate=rate, U0=0.2, tau_d=100., tau_f=750.)
_ = widgets.interact(my_STD_diff_rate, rate=(4., 40.1, 2.),
Poi_or_Reg=(0, 1, 1))
# -
# ### Synaptic facilitation and presynaptic firing rate
#
# Here, we will study how the ratio of the synaptic conductance corresponding to the $1^{st}$ and $10^{th}$ spike changes as a function of the presynaptic rate.
# + cellView="form"
# @title STF conductance ratio with different input rates
# Regular firing rate
input_rate = np.arange(2., 40.1, 2.)
g_1 = np.zeros(len(input_rate)) # record the the PSP at 1st spike
g_2 = np.zeros(len(input_rate)) # record the the PSP at 10th spike
for ii in range(len(input_rate)):
g_1[ii], g_2[ii] = my_illus_STD(Poi_or_reg=False, rate=input_rate[ii],
plot_out=False,
U0=0.2, tau_d=100., tau_f=750.)
plt.figure(figsize=(11, 4.5))
plt.subplot(121)
plt.plot(input_rate, g_1, 'm-o', label='1st Spike')
plt.plot(input_rate, g_2, 'c-o', label='10th Spike')
plt.xlabel('Rate [Hz]')
plt.ylabel('Conductance [nS]')
plt.legend()
plt.subplot(122)
plt.plot(input_rate, g_2 / g_1, 'b-o',)
plt.xlabel('Rate [Hz]')
plt.ylabel(r'Conductance ratio $g_{10}/g_{1}$')
plt.tight_layout()
# -
# ## Think!
#
# Why does the ratio of the first and tenth spike conductance changes in a non-monotonic fashion for synapses with STF, even though it decreases monotonically for synapses with STD?
# +
# to_remove explanation
"""
Discussion:
Because we have a facilitatory synapses, as the input rate increases synaptic
resources released per spike also increase. Therefore, we expect that the synaptic
conductance will increase with input rate. However, total synaptic resources are
finite. And they recover in a finite time. Therefore, at high frequency inputs
synaptic resources are rapidly deleted at a higher rate than their recovery, so
after first few spikes, only a small number of synaptic resources are left. This
results in decrease in the steady-state synaptic conductance at high frequency inputs.
""";
# -
# ---
# # Summary
#
# Congratulations! You have just finished the last tutorial of this day. Here, we saw how to model conductance-based synapses and also how to incorporate short-term dynamics in synaptic weights.
#
# We covered the:
#
# - static synapses and how excitation and inhibition affect the neuronal output
# - mean- or fluctuation-driven regimes
# - short-term dynamics of synapses (both facilitation and depression)
#
# Finally, we incorporated all the aforementioned tools to study how a change in presynaptic firing history affects the synaptic weights!
#
# There are many interesting things that you can try on your own to develop a deeper understanding of biological synapses. A couple of those are mentioned below in the optional boxes -- if you have time.
#
# But now it is time to explore another important feature of biological synapses, i.e., spike timing dependent synaptic plasticity (go to the next tutorial).
# ---
# # Bonus 1: Conductance-based LIF with STP
#
# Previously, we looked only at how the presynaptic firing rate affects the presynaptic resource availability and thereby the synaptic conductance. It is straightforward to imagine that, while the synaptic conductances are changing, the output of the postsynaptic neuron will change as well.
#
# So, let's put the STP on synapses impinging on an LIF neuron and see what happens.
# + cellView="form"
# @title Function for conductance-based LIF neuron with STP-synapses
def run_LIF_cond_STP(pars, I_inj, pre_spike_train_ex, pre_spike_train_in):
"""
conductance-based LIF dynamics
Args:
pars : parameter dictionary
I_inj : injected current [pA]
The injected current here can be a value or an array
pre_spike_train_ex : spike train input from presynaptic excitatory neuron (binary)
pre_spike_train_in : spike train input from presynaptic inhibitory neuron (binary)
Returns:
rec_spikes : spike times
rec_v : mebrane potential
gE : postsynaptic excitatory conductance
gI : postsynaptic inhibitory conductance
"""
# Retrieve parameters
V_th, V_reset = pars['V_th'], pars['V_reset']
tau_m, g_L = pars['tau_m'], pars['g_L']
V_init, V_L = pars['V_init'], pars['E_L']
gE_bar, gI_bar = pars['gE_bar'], pars['gI_bar']
U0E, tau_dE, tau_fE = pars['U0_E'], pars['tau_d_E'], pars['tau_f_E']
U0I, tau_dI, tau_fI = pars['U0_I'], pars['tau_d_I'], pars['tau_f_I']
VE, VI = pars['VE'], pars['VI']
tau_syn_E, tau_syn_I = pars['tau_syn_E'], pars['tau_syn_I']
tref = pars['tref']
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
nE = pre_spike_train_ex.shape[0]
nI = pre_spike_train_in.shape[0]
# compute conductance Excitatory synapses
uE = np.zeros((nE, Lt))
RE = np.zeros((nE, Lt))
gE = np.zeros((nE, Lt))
for ie in range(nE):
u, R, g = dynamic_syn(gE_bar, tau_syn_E, U0E, tau_dE, tau_fE,
pre_spike_train_ex[ie, :], dt)
uE[ie, :], RE[ie, :], gE[ie, :] = u, R, g
gE_total = gE.sum(axis=0)
# compute conductance Inhibitory synapses
uI = np.zeros((nI, Lt))
RI = np.zeros((nI, Lt))
gI = np.zeros((nI, Lt))
for ii in range(nI):
u, R, g = dynamic_syn(gI_bar, tau_syn_I, U0I, tau_dI, tau_fI,
pre_spike_train_in[ii, :], dt)
uI[ii, :], RI[ii, :], gI[ii, :] = u, R, g
gI_total = gI.sum(axis=0)
# Initialize
v = np.zeros(Lt)
v[0] = V_init
Iinj = I_inj * np.ones(Lt) # ensure I has length Lt
# simulation
rec_spikes = [] # recording spike times
tr = 0.
for it in range(Lt - 1):
if tr > 0:
v[it] = V_reset
tr = tr - 1
elif v[it] >= V_th: # reset voltage and record spike event
rec_spikes.append(it)
v[it] = V_reset
tr = tref / dt
# calculate the increment of the membrane potential
dv = (dt / tau_m) * (-(v[it] - V_L) \
- (gE_total[it + 1] / g_L) * (v[it] - VE) \
- (gI_total[it + 1] / g_L) * (v[it] - VI) + Iinj[it] / g_L)
# update membrane potential
v[it+1] = v[it] + dv
rec_spikes = np.array(rec_spikes) * dt
return v, rec_spikes, uE, RE, gE, RI, RI, gI
print(help(run_LIF_cond_STP))
# -
# ## Simulation of a postsynaptic neuron with STP synapses driven by Poisson type spike trains
#
# Here we have assumed that both excitatory and inhibitory synapses show short-term depression. Change the nature of synapses and study how spike pattern variability changes.
# In the interactive demo, `tau_d = 500*tau_ratio (ms)` and `tau_f = 300*tau_ratio (ms)`.
#
# You should compare the output of this neuron with what you observed in the previous tutorial when synapses were assumed to be static.
#
# _Note: it will take slightly longer time to run each case_
# ### Interactive Demo: LIF with STP Explorer
# + cellView="form"
# @title
# @markdown Make sure you execute this cell to enable the widget!
def LIF_STP(tau_ratio):
pars = default_pars(T=1000)
pars['gE_bar'] = 1.2 * 4 # [nS]
pars['VE'] = 0. # [mV]
pars['tau_syn_E'] = 5. # [ms]
pars['gI_bar'] = 1.6 * 4 # [nS]
pars['VI'] = -80. # [ms]
pars['tau_syn_I'] = 10. # [ms]
# here we assume that both Exc and Inh synapses have synaptic depression
pars['U0_E'] = 0.45
pars['tau_d_E'] = 500. * tau_ratio # [ms]
pars['tau_f_E'] = 300. * tau_ratio # [ms]
pars['U0_I'] = 0.45
pars['tau_d_I'] = 500. * tau_ratio # [ms]
pars['tau_f_I'] = 300. * tau_ratio # [ms]
pre_spike_train_ex = Poisson_generator(pars, rate=15, n=80)
pre_spike_train_in = Poisson_generator(pars, rate=15, n=20) # 4:1
v, rec_spikes, uE, RE, gE, uI, RI, gI = run_LIF_cond_STP(pars, 0,
pre_spike_train_ex,
pre_spike_train_in)
t_plot_range = pars['range_t'] > 200
plt.figure(figsize=(11, 7))
plt.subplot(211)
plot_volt_trace(pars, v, rec_spikes)
plt.subplot(223)
plt.plot(pars['range_t'][t_plot_range], gE.sum(axis=0)[t_plot_range], 'r')
plt.xlabel('Time (ms)')
plt.ylabel(r'$g_E$ (nS)')
plt.subplot(224)
plt.plot(pars['range_t'][t_plot_range], gI.sum(axis=0)[t_plot_range], 'b')
plt.xlabel('Time (ms)')
plt.ylabel(r'$g_I$ (nS)')
plt.tight_layout()
_ = widgets.interact(LIF_STP, tau_ratio=(0.2, 1.1, 0.2))
# -
# When we vary the tau_ratio we are increasing `tau_f` and `tau_d` i.e. by increasing `tau_ratio` we are increasing the synaptic depression. The effect is same on both Exc and Inh conductances.
# This is visible as a clear decrease in the firing rate of the neuron from 300-400ms onwards.
#
# Not much happens in the beginning because synaptic depression takes some time to become visible.
#
# It is curious that while both excitatory and inhibitory conductances have depressed but output firing rate has still decreased.
#
# There are two explanations of this:
# 1. excitation has depressed more than the inhibition from their starting values.
# 2. because synaptic conductances have depressed, membrane fluctuation size has decreased.
#
# Which is more likely reason? Think.
# ---
# # Bonus 2: STP Synapse Parameter Exploration
#
# Vary the parameters of the above simulation and observe the spiking pattern of the postsynaptic neuron.
# Will the neuron show higher irregularity if the synapses have STP? If yes, what should be the nature of STP on static and dynamic synapses, respectively?
#
# Calculate the $CV_{\rm ISI}$ for different `tau_ratio` after simulating the LIF neuron with STP (Hint:`run_LIF_cond_STP` help you understand the irregularity).
#
# ## Functional implications of short-term dynamics of synapses
# As you have seen above, if the firing rate is stationary, the synaptic conductance quickly reaches a fixed point. On the other hand, if the firing rate transiently changes, synaptic conductance will vary -- even if the change is as short as a single inter-spike-interval. Such small changes can be observed in a single neuron when input spikes are regular and periodic. If the input spikes are Poissonian, then one may have to perform an average over several neurons.
#
# _Come up with other functions that short-term dynamics of synapses can be used to implement and implement them._
| tutorials/W2D3_BiologicalNeuronModels/W2D3_Tutorial3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import seaborn as sns
sns.set()
import pandas as pd
athletes = pd.read_csv('athletes.csv')
athletes = athletes[athletes['sport']
.isin(['wrestling', 'badminton', 'triathlon', 'gymnastics'])]
# # Relational Plots
sns.relplot(data=athletes, x='weight', y='height', col='sport', col_wrap=2, hue='sex',
kind='line')
df = pd.read_csv('weather.csv')
aug = df[df['MONTH'] == 8]
aug.head()
sns.relplot(data=aug, x='TIME', y='TEMP', kind='line')
# # Categorical Plots
sns.catplot(data=athletes, x="sport", y="weight", hue='sex', kind='boxen');
| General/Relational and Categorical Plots.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/bbbb6577/jm/blob/main/Untitled1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="AhDJrBLFYtMK"
import pandas as pd
# + id="EoDiAY1vO0oS" colab={"base_uri": "https://localhost:8080/"} outputId="fd466fcf-453f-4c6e-c010-da41b8bf05bd"
from google.colab import drive
drive.mount('/content/grive')
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="VcmPCYFvYwc-" outputId="9955a77c-a413-4e4a-9029-83fd4e62bdaa"
df= pd.read_csv('/content/auto-mpg.csv')
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="myqHQygjdU59" outputId="b7d842f1-82db-47ab-8aad-b08c21860380"
dataset = df.values
dataset
# + id="7DLLgGAbduwg"
X = dataset[:,0:10]
Y = dataset[:,0:10]
# + id="hw0MXUBmd_g1"
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
X_scale = min_max_scaler.fit_transform(X)
# + colab={"base_uri": "https://localhost:8080/"} id="f-fYGFkleXjj" outputId="629260d9-ce8f-48db-f6c6-7e778fd4eaac"
X_scale
# + colab={"base_uri": "https://localhost:8080/"} id="IXZwyS0VeaBq" outputId="5c3e3dc7-f1f8-4bc8-b9ee-be23c2482b8e"
from sklearn.model_selection import train_test_split
X_train, X_val_and_test, Y_train, Y_val_and_test = train_test_split(X_scale, Y, test_size=0.3)
X_val, X_test, Y_val, Y_test = train_test_split(X_val_and_test, Y_val_and_test, test_size=0.5)
print(X_train.shape, X_val.shape, X_test.shape, Y_train.shape, Y_val.shape, Y_test.shape)
# + id="45M6z-SKeeaz"
from keras.models import Sequential
from keras.layers import Dense
# + id="zHQZnEJRekhj"
model = Sequential([
Dense(32, activation='relu', input_shape=(10,)),
Dense(32, activation='relu'),
Dense(1, activation='sigmoid'),
])
# + id="GKaNDCskeoXy"
model.compile(optimizer='sgd',
loss='binary_crossentropy',
metrics=['accuracy'])
# + colab={"base_uri": "https://localhost:8080/", "height": 595} id="9kXDo1bEewZw" outputId="ceb1cd42-9012-43aa-d950-43c6d94e570b"
hist = model.fit(X_train, Y_train,
batch_size=32, epochs=100,
validation_data=(X_val, Y_val))
# + colab={"base_uri": "https://localhost:8080/", "height": 544} id="UmepZYQCjFkq" outputId="07ce3d91-17f3-4d5f-a39b-2e7633099f5a"
model.evaluate(X_test, Y_test)[1]
| Untitled1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# # Boston Housing Price Prediction with scikit-learn (save model explanations via AML Run History)
# 
# Copyright (c) Microsoft Corporation. All rights reserved.
#
# Licensed under the MIT License.
# Explain a model with the AML explain-model package
#
# 1. Train a GradientBoosting regression model using Scikit-learn
# 2. Run 'explain_model' with AML Run History, which leverages run history service to store and manage the explanation data
# # Save Model Explanation With AML Run History
# +
#Import Iris dataset
from sklearn import datasets
from sklearn.ensemble import GradientBoostingRegressor
import azureml.core
from azureml.core import Workspace, Experiment, Run
from azureml.explain.model.tabular_explainer import TabularExplainer
from azureml.contrib.explain.model.explanation.explanation_client import ExplanationClient
# Check core SDK version number
print("SDK version:", azureml.core.VERSION)
# -
ws = Workspace.from_config()
print('Workspace name: ' + ws.name,
'Azure region: ' + ws.location,
'Subscription id: ' + ws.subscription_id,
'Resource group: ' + ws.resource_group, sep = '\n')
experiment_name = 'explain_model'
experiment = Experiment(ws, experiment_name)
run = experiment.start_logging()
client = ExplanationClient.from_run(run)
# ## Load the Boston house price data
boston_data = datasets.load_boston()
# Split data into train and test
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(boston_data.data, boston_data.target, test_size=0.2, random_state=0)
# ## Train a GradientBoosting Regression model, which you want to explain
clf = GradientBoostingRegressor(n_estimators=100, max_depth=4,
learning_rate=0.1, loss='huber',
random_state=1)
model = clf.fit(x_train, y_train)
# ## Explain predictions on your local machine
tabular_explainer = TabularExplainer(model, x_train, features=boston_data.feature_names)
# ## Explain overall model predictions (global explanation)
# Passing in test dataset for evaluation examples - note it must be a representative sample of the original data
# x_train can be passed as well, but with more examples explanations will take longer although they may be more accurate
global_explanation = tabular_explainer.explain_global(x_test)
# Uploading model explanation data for storage or visualization in webUX
# The explanation can then be downloaded on any compute
client.upload_model_explanation(global_explanation)
# Get model explanation data
explanation = client.download_model_explanation()
local_importance_values = explanation.local_importance_values
expected_values = explanation.expected_values
# Print the values
print('expected values: {}'.format(expected_values))
print('local importance values: {}'.format(local_importance_values))
# Get the top k (e.g., 4) most important features with their importance values
explanation = client.download_model_explanation(top_k=4)
global_importance_values = explanation.get_ranked_global_values()
global_importance_names = explanation.get_ranked_global_names()
print('global importance values: {}'.format(global_importance_values))
print('global importance names: {}'.format(global_importance_names))
# ## Explain individual instance predictions (local explanation) ##### needs to get updated with the new build
local_explanation = tabular_explainer.explain_local(x_test[0,:])
# local feature importance information
local_importance_values = local_explanation.local_importance_values
print('local importance values: {}'.format(local_importance_values))
| how-to-use-azureml/explain-model/explain-tabular-data-run-history/explain-run-history-sklearn-regression.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import glob, os, h5py
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
# PLOTTING OPTIONS
fig_width_pt = 3*246.0 # Get this from LaTeX using \showthe\columnwidth
inches_per_pt = 1.0/72.27 # Convert pt to inch
golden_mean = (np.sqrt(5)-1.0)/2.0 # Aesthetic ratio
fig_width = fig_width_pt*inches_per_pt # width in inches
fig_height = fig_width*golden_mean # height in inches
fig_size = [fig_width,fig_height]
params = { 'axes.labelsize': 24,
'font.family': 'serif',
'font.serif': 'Computer Modern Raman',
'font.size': 24,
'legend.fontsize': 20,
'xtick.labelsize': 24,
'ytick.labelsize': 24,
'axes.grid' : True,
'text.usetex': True,
'savefig.dpi' : 100,
'lines.markersize' : 14,
'figure.figsize': fig_size}
mpl.rcParams.update(params)
# -
# # Reading the file directly from here
fg = pd.read_csv('candidate.csv')
bg = pd.read_csv('background.csv')
# # Making a figure for the paper:
# +
fig = plt.figure()
ax = fig.add_subplot(111)
bgranking = bg['ranking']
fgranking = fg['ranking']
low=-30
bins = np.linspace(low,np.max(bgranking)+1,200)
counts, _ = np.histogram(bgranking,bins=bins)
ax.hist(bins[:-1], bins, weights=counts/100,histtype="step",label='background')
ax.hist(fgranking,bins=bins,alpha=0.7,color='grey',label='candidates')
ax.set_yscale('log')
ax.legend()
ax.set_xlim(-30,35)
ax.set_xlabel('$\lambda_\mathrm{gw+frb}$')
ax.set_ylabel('Number of events / Obs')
#fig.savefig('newstat.png',bbox_inches='tight')
# -
# # FAR
for i in range(3):
print('stat:', fg['ranking'].values[i])
higherbg = bg[bg['ranking']>=fg['ranking'].values[i]]
print( len (higherbg) / 100)
| 2-plot-figure.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import spacy
import pandas as pd
import sklearn
import numpy as np
from scipy.spatial.distance import cosine
import random
import warnings
# from __future__ import unicode_literals
warnings.filterwarnings("ignore", category=DeprecationWarning)
en_nlp = spacy.load('en')
# +
def get_vec(sentence):
vec = np.zeros(96)
for word in sentence:
if word in wordvecs:
vec += wordvecs[word]
return vec
# -
def spacy_get_vec(sentence):
vec = np.zeros(96)
doc = en_nlp((sentence))
for word in doc:
vec += word.vector
return vec
lines = open('./intents.txt').readlines()
vecs = []
intents = []
for line in lines:
tokens = line.split(',')
sentence = tokens[0]
intent = tokens[1]
if intent[-1] == '\n':
intent = intent[:-1]
vecs.append(spacy_get_vec(sentence))
intents.append(intent)
df = pd.DataFrame(vecs, columns=['vec_%d' % i for i in range(96)])
df['intents'] = intents
df.intents = df.intents.astype('category')
X = df.iloc[:, :-1].values
y = df.iloc[:,-1:].values.ravel()
from sklearn.model_selection import train_test_split
X_train,X_val,y_train,y_val = train_test_split(X, y, test_size=0.20)
from sklearn.linear_model import LogisticRegression
logit_model = LogisticRegression(C=1.0)
logit_model.fit(X_train, y_train)
logit_model.score(X_val, y_val)
from sklearn.ensemble import GradientBoostingClassifier
gradboost = GradientBoostingClassifier(n_estimators=500, max_depth=25, max_features='sqrt')
gradboost.fit(X_train, y_train)
gradboost.score(X_val, y_val)
sent = 'hi'
print(gradboost.predict([spacy_get_vec(sent)]))
print(gradboost.predict_proba([spacy_get_vec(sent)]))
sent = 'can you tell the forecast for tomorrow'
print(gradboost.predict([spacy_get_vec(sent)]))
print(gradboost.predict_proba([spacy_get_vec(sent)]))
gradboost.classes_
logit_model.predict_proba(spacy_get_vec('is there a hailstorm outside').reshape(1,-1))
gradboost.fit(X,y)
from sklearn.externals import joblib
joblib.dump(gradboost, 'intent.pkl')
logit_model.predict([spacy_get_vec('Infinity')])
gradboost.predict([spacy_get_vec('Infinity')])
| .ipynb_checkpoints/Intent-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 重置摄像头
# !echo 'jetson' | sudo -S systemctl restart nvargus-daemon && printf '\n'
# ### 初始化
# +
import torch
import torchvision
from torch2trt import torch2trt
from torch2trt import TRTModule
TASK="test"
CATEGORIES = ['apex']
device = torch.device('cuda')
model = torchvision.models.resnet18(pretrained=False)
model.fc = torch.nn.Linear(512, 2 * len(CATEGORIES))
model = model.cuda().eval().half()
model.load_state_dict(torch.load(TASK+'/path/model.pth'))
data = torch.zeros((1, 3, 224, 224)).cuda().half()
model_trt = torch2trt(model, [data], fp16_mode=True)
torch.save(model_trt.state_dict(), TASK+'/road_model_trt.pth')
model_trt = TRTModule()
model_trt.load_state_dict(torch.load(TASK+'/road_model_trt.pth'))
from jetracer.nvidia_racecar import NvidiaRacecar
car = NvidiaRacecar()
# -
# 初始化摄像头
# +
from jetcam.csi_camera import CSICamera
camera = CSICamera(width=224, height=224, capture_fps=65)
# -
# 开始跑
# +
from utils import preprocess
import numpy as np
import threading
import ipywidgets
import time
import cv2
from jetcam.utils import bgr8_to_jpeg
car.steering_gain = -0.55
car.steering_offset = -0.13
car.throttle_gain = 0.5
# car.throttle = 0.25
speed_widget = ipywidgets.IntText(description='速度', value=20)
run_button = ipywidgets.Button(description='启动')
state = 1
prediction_widget = ipywidgets.Image(format='jpeg', width=224, height=224)
def run(car,camera,speed_widget,run_button,prediction_widget):
global state
while True:
image = camera.read()
prediction = image.copy()
image = preprocess(image).half()
output = model_trt(image).detach().cpu().numpy().flatten()
dx = output[0]
dy = output[1]
dx = int(224 * (dx / 2.0 + 0.5))
dy = int(224 * (dy / 2.0 + 0.5))
prediction = cv2.circle(prediction, (dx, dy), 8, (255, 0, 0), 3)
prediction_widget.value = bgr8_to_jpeg(prediction)
if (state == 1):
if car.throttle>0 :
car.throttle = -10
else :
car.throttle = 0
car.steering = 0
time.sleep(0.5)
else:
x = float(output[0])
#car.steering = x * STEERING_GAIN + STEERING_BIAS
car.steering = x
car.throttle = speed_widget.value*0.01
execute_thread = threading.Thread(target=run, args=(car,camera,speed_widget,run_button,prediction_widget))
def runclick(c):
global state
print(run_button.description)
if run_button.description == '启动':
run_button.description = '停止'
state = 0
else:
run_button.description = '启动'
state = 1
run_button.on_click(runclick)
data_collection_widget = ipywidgets.HBox([
run_button,
speed_widget
])
data_display_widget = ipywidgets.VBox([
prediction_widget,
data_collection_widget
])
display(data_display_widget)
execute_thread.start()
# -
| notebooks/record_train/c_racer.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Example Using the Earthquake network
# ================================
# In this example I will try to create the Alarm Bayesian Network using pgmpy and do some simple queries on the network.
# This network is mentioned in Bayesian Artificial Intelligence - Section 2.5.1 (https://bayesian-intelligence.com/publications/bai/book/BAI_Chapter2.pdf)
# Importing Library
from pgmpy.models import BayesianNetwork
from pgmpy.inference import VariableElimination
# +
# Defining network structure
alarm_model = BayesianNetwork(
[
("Burglary", "Alarm"),
("Earthquake", "Alarm"),
("Alarm", "JohnCalls"),
("Alarm", "MaryCalls"),
]
)
# Defining the parameters using CPT
from pgmpy.factors.discrete import TabularCPD
cpd_burglary = TabularCPD(
variable="Burglary", variable_card=2, values=[[0.999], [0.001]]
)
cpd_earthquake = TabularCPD(
variable="Earthquake", variable_card=2, values=[[0.998], [0.002]]
)
cpd_alarm = TabularCPD(
variable="Alarm",
variable_card=2,
values=[[0.999, 0.71, 0.06, 0.05], [0.001, 0.29, 0.94, 0.95]],
evidence=["Burglary", "Earthquake"],
evidence_card=[2, 2],
)
cpd_johncalls = TabularCPD(
variable="JohnCalls",
variable_card=2,
values=[[0.95, 0.1], [0.05, 0.9]],
evidence=["Alarm"],
evidence_card=[2],
)
cpd_marycalls = TabularCPD(
variable="MaryCalls",
variable_card=2,
values=[[0.1, 0.7], [0.9, 0.3]],
evidence=["Alarm"],
evidence_card=[2],
)
# Associating the parameters with the model structure
alarm_model.add_cpds(
cpd_burglary, cpd_earthquake, cpd_alarm, cpd_johncalls, cpd_marycalls
)
# -
# Checking if the cpds are valid for the model
alarm_model.check_model()
# Viewing nodes of the model
alarm_model.nodes()
# Viewing edges of the model
alarm_model.edges()
# Checking independcies of a node
alarm_model.local_independencies("Burglary")
# Listing all Independencies
alarm_model.get_independencies()
| examples/Earthquake.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Autonomous driving - Car detection
#
# Welcome to your week 3 programming assignment. You will learn about object detection using the very powerful YOLO model. Many of the ideas in this notebook are described in the two YOLO papers: Redmon et al., 2016 (https://arxiv.org/abs/1506.02640) and Redmon and Farhadi, 2016 (https://arxiv.org/abs/1612.08242).
#
# **You will learn to**:
# - Use object detection on a car detection dataset
# - Deal with bounding boxes
#
# Run the following cell to load the packages and dependencies that are going to be useful for your journey!
# +
import argparse
import os
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
import scipy.io
import scipy.misc
import numpy as np
import pandas as pd
import PIL
import tensorflow as tf
from keras import backend as K
from keras.layers import Input, Lambda, Conv2D
from keras.models import load_model, Model
from yolo_utils import read_classes, read_anchors, generate_colors, preprocess_image, draw_boxes, scale_boxes
from yad2k.models.keras_yolo import yolo_head, yolo_boxes_to_corners, preprocess_true_boxes, yolo_loss, yolo_body
# %matplotlib inline
# -
# **Important Note**: As you can see, we import Keras's backend as K. This means that to use a Keras function in this notebook, you will need to write: `K.function(...)`.
# ## 1 - Problem Statement
#
# You are working on a self-driving car. As a critical component of this project, you'd like to first build a car detection system. To collect data, you've mounted a camera to the hood (meaning the front) of the car, which takes pictures of the road ahead every few seconds while you drive around.
#
# <center>
# <video width="400" height="200" src="nb_images/road_video_compressed2.mp4" type="video/mp4" controls>
# </video>
# </center>
#
# <caption><center> Pictures taken from a car-mounted camera while driving around Silicon Valley. <br> We would like to especially thank [drive.ai](https://www.drive.ai/) for providing this dataset! Drive.ai is a company building the brains of self-driving vehicles.
# </center></caption>
#
# <img src="nb_images/driveai.png" style="width:100px;height:100;">
#
# You've gathered all these images into a folder and have labelled them by drawing bounding boxes around every car you found. Here's an example of what your bounding boxes look like.
#
# <img src="nb_images/box_label.png" style="width:500px;height:250;">
# <caption><center> <u> **Figure 1** </u>: **Definition of a box**<br> </center></caption>
#
# If you have 80 classes that you want YOLO to recognize, you can represent the class label $c$ either as an integer from 1 to 80, or as an 80-dimensional vector (with 80 numbers) one component of which is 1 and the rest of which are 0. The video lectures had used the latter representation; in this notebook, we will use both representations, depending on which is more convenient for a particular step.
#
# In this exercise, you will learn how YOLO works, then apply it to car detection. Because the YOLO model is very computationally expensive to train, we will load pre-trained weights for you to use.
# ## 2 - YOLO
# YOLO ("you only look once") is a popular algoritm because it achieves high accuracy while also being able to run in real-time. This algorithm "only looks once" at the image in the sense that it requires only one forward propagation pass through the network to make predictions. After non-max suppression, it then outputs recognized objects together with the bounding boxes.
#
# ### 2.1 - Model details
#
# First things to know:
# - The **input** is a batch of images of shape (m, 608, 608, 3)
# - The **output** is a list of bounding boxes along with the recognized classes. Each bounding box is represented by 6 numbers $(p_c, b_x, b_y, b_h, b_w, c)$ as explained above. If you expand $c$ into an 80-dimensional vector, each bounding box is then represented by 85 numbers.
#
# We will use 5 anchor boxes. So you can think of the YOLO architecture as the following: IMAGE (m, 608, 608, 3) -> DEEP CNN -> ENCODING (m, 19, 19, 5, 85).
#
# Lets look in greater detail at what this encoding represents.
#
# <img src="nb_images/architecture.png" style="width:700px;height:400;">
# <caption><center> <u> **Figure 2** </u>: **Encoding architecture for YOLO**<br> </center></caption>
#
# If the center/midpoint of an object falls into a grid cell, that grid cell is responsible for detecting that object.
# Since we are using 5 anchor boxes, each of the 19 x19 cells thus encodes information about 5 boxes. Anchor boxes are defined only by their width and height.
#
# For simplicity, we will flatten the last two last dimensions of the shape (19, 19, 5, 85) encoding. So the output of the Deep CNN is (19, 19, 425).
#
# <img src="nb_images/flatten.png" style="width:700px;height:400;">
# <caption><center> <u> **Figure 3** </u>: **Flattening the last two last dimensions**<br> </center></caption>
# Now, for each box (of each cell) we will compute the following elementwise product and extract a probability that the box contains a certain class.
#
# <img src="nb_images/probability_extraction.png" style="width:700px;height:400;">
# <caption><center> <u> **Figure 4** </u>: **Find the class detected by each box**<br> </center></caption>
#
# Here's one way to visualize what YOLO is predicting on an image:
# - For each of the 19x19 grid cells, find the maximum of the probability scores (taking a max across both the 5 anchor boxes and across different classes).
# - Color that grid cell according to what object that grid cell considers the most likely.
#
# Doing this results in this picture:
#
# <img src="nb_images/proba_map.png" style="width:300px;height:300;">
# <caption><center> <u> **Figure 5** </u>: Each of the 19x19 grid cells colored according to which class has the largest predicted probability in that cell.<br> </center></caption>
#
# Note that this visualization isn't a core part of the YOLO algorithm itself for making predictions; it's just a nice way of visualizing an intermediate result of the algorithm.
#
# Another way to visualize YOLO's output is to plot the bounding boxes that it outputs. Doing that results in a visualization like this:
#
# <img src="nb_images/anchor_map.png" style="width:200px;height:200;">
# <caption><center> <u> **Figure 6** </u>: Each cell gives you 5 boxes. In total, the model predicts: 19x19x5 = 1805 boxes just by looking once at the image (one forward pass through the network)! Different colors denote different classes. <br> </center></caption>
#
# In the figure above, we plotted only boxes that the model had assigned a high probability to, but this is still too many boxes. You'd like to filter the algorithm's output down to a much smaller number of detected objects. To do so, you'll use non-max suppression. Specifically, you'll carry out these steps:
# - Get rid of boxes with a low score (meaning, the box is not very confident about detecting a class)
# - Select only one box when several boxes overlap with each other and detect the same object.
#
#
# ### 2.2 - Filtering with a threshold on class scores
#
# You are going to apply a first filter by thresholding. You would like to get rid of any box for which the class "score" is less than a chosen threshold.
#
# The model gives you a total of 19x19x5x85 numbers, with each box described by 85 numbers. It'll be convenient to rearrange the (19,19,5,85) (or (19,19,425)) dimensional tensor into the following variables:
# - `box_confidence`: tensor of shape $(19 \times 19, 5, 1)$ containing $p_c$ (confidence probability that there's some object) for each of the 5 boxes predicted in each of the 19x19 cells.
# - `boxes`: tensor of shape $(19 \times 19, 5, 4)$ containing $(b_x, b_y, b_h, b_w)$ for each of the 5 boxes per cell.
# - `box_class_probs`: tensor of shape $(19 \times 19, 5, 80)$ containing the detection probabilities $(c_1, c_2, ... c_{80})$ for each of the 80 classes for each of the 5 boxes per cell.
#
# **Exercise**: Implement `yolo_filter_boxes()`.
# 1. Compute box scores by doing the elementwise product as described in Figure 4. The following code may help you choose the right operator:
# ```python
# a = np.random.randn(19*19, 5, 1)
# b = np.random.randn(19*19, 5, 80)
# c = a * b # shape of c will be (19*19, 5, 80)
# ```
# 2. For each box, find:
# - the index of the class with the maximum box score ([Hint](https://keras.io/backend/#argmax)) (Be careful with what axis you choose; consider using axis=-1)
# - the corresponding box score ([Hint](https://keras.io/backend/#max)) (Be careful with what axis you choose; consider using axis=-1)
# 3. Create a mask by using a threshold. As a reminder: `([0.9, 0.3, 0.4, 0.5, 0.1] < 0.4)` returns: `[False, True, False, False, True]`. The mask should be True for the boxes you want to keep.
# 4. Use TensorFlow to apply the mask to box_class_scores, boxes and box_classes to filter out the boxes we don't want. You should be left with just the subset of boxes you want to keep. ([Hint](https://www.tensorflow.org/api_docs/python/tf/boolean_mask))
#
# Reminder: to call a Keras function, you should use `K.function(...)`.
# +
# GRADED FUNCTION: yolo_filter_boxes
def yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = .6):
"""Filters YOLO boxes by thresholding on object and class confidence.
Arguments:
box_confidence -- tensor of shape (19, 19, 5, 1)
boxes -- tensor of shape (19, 19, 5, 4)
box_class_probs -- tensor of shape (19, 19, 5, 80)
threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
Returns:
scores -- tensor of shape (None,), containing the class probability score for selected boxes
boxes -- tensor of shape (None, 4), containing (b_x, b_y, b_h, b_w) coordinates of selected boxes
classes -- tensor of shape (None,), containing the index of the class detected by the selected boxes
Note: "None" is here because you don't know the exact number of selected boxes, as it depends on the threshold.
For example, the actual output size of scores would be (10,) if there are 10 boxes.
"""
# Step 1: Compute box scores
### START CODE HERE ### (≈ 1 line)
box_scores = box_confidence * box_class_probs
### END CODE HERE ###
# Step 2: Find the box_classes thanks to the max box_scores, keep track of the corresponding score
### START CODE HERE ### (≈ 2 lines)
box_classes = K.argmax(box_scores, axis = -1)
box_class_scores = K.max(box_scores, axis = -1)
### END CODE HERE ###
# Step 3: Create a filtering mask based on "box_class_scores" by using "threshold". The mask should have the
# same dimension as box_class_scores, and be True for the boxes you want to keep (with probability >= threshold)
### START CODE HERE ### (≈ 1 line)
filtering_mask = box_class_scores >= threshold
### END CODE HERE ###
# Step 4: Apply the mask to scores, boxes and classes
### START CODE HERE ### (≈ 3 lines)
scores = tf.boolean_mask(box_class_scores, filtering_mask)
boxes = tf.boolean_mask(boxes, filtering_mask)
classes = tf.boolean_mask(box_classes, filtering_mask)
### END CODE HERE ###
return scores, boxes, classes
# -
with tf.Session() as test_a:
box_confidence = tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([19, 19, 5, 4], mean=1, stddev=4, seed = 1)
box_class_probs = tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = 0.5)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.shape))
print("boxes.shape = " + str(boxes.shape))
print("classes.shape = " + str(classes.shape))
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **scores[2]**
# </td>
# <td>
# 10.7506
# </td>
# </tr>
# <tr>
# <td>
# **boxes[2]**
# </td>
# <td>
# [ 8.42653275 3.27136683 -0.5313437 -4.94137383]
# </td>
# </tr>
#
# <tr>
# <td>
# **classes[2]**
# </td>
# <td>
# 7
# </td>
# </tr>
# <tr>
# <td>
# **scores.shape**
# </td>
# <td>
# (?,)
# </td>
# </tr>
# <tr>
# <td>
# **boxes.shape**
# </td>
# <td>
# (?, 4)
# </td>
# </tr>
#
# <tr>
# <td>
# **classes.shape**
# </td>
# <td>
# (?,)
# </td>
# </tr>
#
# </table>
# ### 2.3 - Non-max suppression ###
#
# Even after filtering by thresholding over the classes scores, you still end up a lot of overlapping boxes. A second filter for selecting the right boxes is called non-maximum suppression (NMS).
# <img src="nb_images/non-max-suppression.png" style="width:500px;height:400;">
# <caption><center> <u> **Figure 7** </u>: In this example, the model has predicted 3 cars, but it's actually 3 predictions of the same car. Running non-max suppression (NMS) will select only the most accurate (highest probabiliy) one of the 3 boxes. <br> </center></caption>
#
# Non-max suppression uses the very important function called **"Intersection over Union"**, or IoU.
# <img src="nb_images/iou.png" style="width:500px;height:400;">
# <caption><center> <u> **Figure 8** </u>: Definition of "Intersection over Union". <br> </center></caption>
#
# **Exercise**: Implement iou(). Some hints:
# - In this exercise only, we define a box using its two corners (upper left and lower right): `(x1, y1, x2, y2)` rather than the midpoint and height/width.
# - To calculate the area of a rectangle you need to multiply its height `(y2 - y1)` by its width `(x2 - x1)`.
# - You'll also need to find the coordinates `(xi1, yi1, xi2, yi2)` of the intersection of two boxes. Remember that:
# - xi1 = maximum of the x1 coordinates of the two boxes
# - yi1 = maximum of the y1 coordinates of the two boxes
# - xi2 = minimum of the x2 coordinates of the two boxes
# - yi2 = minimum of the y2 coordinates of the two boxes
# - In order to compute the intersection area, you need to make sure the height and width of the intersection are positive, otherwise the intersection area should be zero. Use `max(height, 0)` and `max(width, 0)`.
#
# In this code, we use the convention that (0,0) is the top-left corner of an image, (1,0) is the upper-right corner, and (1,1) the lower-right corner.
# +
# GRADED FUNCTION: iou
def iou(box1, box2):
"""Implement the intersection over union (IoU) between box1 and box2
Arguments:
box1 -- first box, list object with coordinates (x1, y1, x2, y2)
box2 -- second box, list object with coordinates (x1, y1, x2, y2)
"""
# Calculate the (y1, x1, y2, x2) coordinates of the intersection of box1 and box2. Calculate its Area.
### START CODE HERE ### (≈ 5 lines)
xi1 = max(box1[0], box2[0])
yi1 = max(box1[1], box2[1])
xi2 = min(box1[2], box2[2])
yi2 = min(box1[3], box2[3])
inter_area = max(yi2 - yi1, 0) * max(xi2 - xi1, 0)
### END CODE HERE ###
# Calculate the Union area by using Formula: Union(A,B) = A + B - Inter(A,B)
### START CODE HERE ### (≈ 3 lines)
box1_area = (box1[3] - box1[1]) * (box1[2] - box1[0])
box2_area = (box2[3] - box2[1]) * (box2[2] - box2[0])
union_area = box1_area + box2_area - inter_area
### END CODE HERE ###
# compute the IoU
### START CODE HERE ### (≈ 1 line)
iou = inter_area / union_area
### END CODE HERE ###
return iou
# -
box1 = (2, 1, 4, 3)
box2 = (1, 2, 3, 4)
print("iou = " + str(iou(box1, box2)))
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **iou = **
# </td>
# <td>
# 0.14285714285714285
# </td>
# </tr>
#
# </table>
# You are now ready to implement non-max suppression. The key steps are:
# 1. Select the box that has the highest score.
# 2. Compute its overlap with all other boxes, and remove boxes that overlap it more than `iou_threshold`.
# 3. Go back to step 1 and iterate until there's no more boxes with a lower score than the current selected box.
#
# This will remove all boxes that have a large overlap with the selected boxes. Only the "best" boxes remain.
#
# **Exercise**: Implement yolo_non_max_suppression() using TensorFlow. TensorFlow has two built-in functions that are used to implement non-max suppression (so you don't actually need to use your `iou()` implementation):
# - [tf.image.non_max_suppression()](https://www.tensorflow.org/api_docs/python/tf/image/non_max_suppression)
# - [K.gather()](https://www.tensorflow.org/api_docs/python/tf/gather)
# +
# GRADED FUNCTION: yolo_non_max_suppression
def yolo_non_max_suppression(scores, boxes, classes, max_boxes = 10, iou_threshold = 0.5):
"""
Applies Non-max suppression (NMS) to set of boxes
Arguments:
scores -- tensor of shape (None,), output of yolo_filter_boxes()
boxes -- tensor of shape (None, 4), output of yolo_filter_boxes() that have been scaled to the image size (see later)
classes -- tensor of shape (None,), output of yolo_filter_boxes()
max_boxes -- integer, maximum number of predicted boxes you'd like
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (, None), predicted score for each box
boxes -- tensor of shape (4, None), predicted box coordinates
classes -- tensor of shape (, None), predicted class for each box
Note: The "None" dimension of the output tensors has obviously to be less than max_boxes. Note also that this
function will transpose the shapes of scores, boxes, classes. This is made for convenience.
"""
max_boxes_tensor = K.variable(max_boxes, dtype='int32') # tensor to be used in tf.image.non_max_suppression()
K.get_session().run(tf.variables_initializer([max_boxes_tensor])) # initialize variable max_boxes_tensor
# Use tf.image.non_max_suppression() to get the list of indices corresponding to boxes you keep
### START CODE HERE ### (≈ 1 line)
nms_indices = tf.image.non_max_suppression(boxes, scores, max_boxes, iou_threshold)
### END CODE HERE ###
# Use K.gather() to select only nms_indices from scores, boxes and classes
### START CODE HERE ### (≈ 3 lines)
scores = K.gather(scores, nms_indices)
boxes = K.gather(boxes, nms_indices)
classes = K.gather(classes, nms_indices)
### END CODE HERE ###
return scores, boxes, classes
# -
with tf.Session() as test_b:
scores = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([54, 4], mean=1, stddev=4, seed = 1)
classes = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **scores[2]**
# </td>
# <td>
# 6.9384
# </td>
# </tr>
# <tr>
# <td>
# **boxes[2]**
# </td>
# <td>
# [-5.299932 3.13798141 4.45036697 0.95942086]
# </td>
# </tr>
#
# <tr>
# <td>
# **classes[2]**
# </td>
# <td>
# -2.24527
# </td>
# </tr>
# <tr>
# <td>
# **scores.shape**
# </td>
# <td>
# (10,)
# </td>
# </tr>
# <tr>
# <td>
# **boxes.shape**
# </td>
# <td>
# (10, 4)
# </td>
# </tr>
#
# <tr>
# <td>
# **classes.shape**
# </td>
# <td>
# (10,)
# </td>
# </tr>
#
# </table>
# ### 2.4 Wrapping up the filtering
#
# It's time to implement a function taking the output of the deep CNN (the 19x19x5x85 dimensional encoding) and filtering through all the boxes using the functions you've just implemented.
#
# **Exercise**: Implement `yolo_eval()` which takes the output of the YOLO encoding and filters the boxes using score threshold and NMS. There's just one last implementational detail you have to know. There're a few ways of representing boxes, such as via their corners or via their midpoint and height/width. YOLO converts between a few such formats at different times, using the following functions (which we have provided):
#
# ```python
# boxes = yolo_boxes_to_corners(box_xy, box_wh)
# ```
# which converts the yolo box coordinates (x,y,w,h) to box corners' coordinates (x1, y1, x2, y2) to fit the input of `yolo_filter_boxes`
# ```python
# boxes = scale_boxes(boxes, image_shape)
# ```
# YOLO's network was trained to run on 608x608 images. If you are testing this data on a different size image--for example, the car detection dataset had 720x1280 images--this step rescales the boxes so that they can be plotted on top of the original 720x1280 image.
#
# Don't worry about these two functions; we'll show you where they need to be called.
# +
# GRADED FUNCTION: yolo_eval
def yolo_eval(yolo_outputs, image_shape = (720., 1280.), max_boxes=10, score_threshold=.6, iou_threshold=.5):
"""
Converts the output of YOLO encoding (a lot of boxes) to your predicted boxes along with their scores, box coordinates and classes.
Arguments:
yolo_outputs -- output of the encoding model (for image_shape of (608, 608, 3)), contains 4 tensors:
box_confidence: tensor of shape (None, 19, 19, 5, 1)
box_xy: tensor of shape (None, 19, 19, 5, 2)
box_wh: tensor of shape (None, 19, 19, 5, 2)
box_class_probs: tensor of shape (None, 19, 19, 5, 80)
image_shape -- tensor of shape (2,) containing the input shape, in this notebook we use (608., 608.) (has to be float32 dtype)
max_boxes -- integer, maximum number of predicted boxes you'd like
score_threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (None, ), predicted score for each box
boxes -- tensor of shape (None, 4), predicted box coordinates
classes -- tensor of shape (None,), predicted class for each box
"""
### START CODE HERE ###
# Retrieve outputs of the YOLO model (≈1 line)
box_confidence, box_xy, box_wh, box_class_probs = yolo_outputs
# Convert boxes to be ready for filtering functions
boxes = yolo_boxes_to_corners(box_xy, box_wh)
# Use one of the functions you've implemented to perform Score-filtering with a threshold of score_threshold (≈1 line)
scores, boxes, classes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, score_threshold)
# Scale boxes back to original image shape.
boxes = scale_boxes(boxes, image_shape)
# Use one of the functions you've implemented to perform Non-max suppression with a threshold of iou_threshold (≈1 line)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes, max_boxes, iou_threshold)
### END CODE HERE ###
return scores, boxes, classes
# -
with tf.Session() as test_b:
yolo_outputs = (tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1))
scores, boxes, classes = yolo_eval(yolo_outputs)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **scores[2]**
# </td>
# <td>
# 138.791
# </td>
# </tr>
# <tr>
# <td>
# **boxes[2]**
# </td>
# <td>
# [ 1292.32971191 -278.52166748 3876.98925781 -835.56494141]
# </td>
# </tr>
#
# <tr>
# <td>
# **classes[2]**
# </td>
# <td>
# 54
# </td>
# </tr>
# <tr>
# <td>
# **scores.shape**
# </td>
# <td>
# (10,)
# </td>
# </tr>
# <tr>
# <td>
# **boxes.shape**
# </td>
# <td>
# (10, 4)
# </td>
# </tr>
#
# <tr>
# <td>
# **classes.shape**
# </td>
# <td>
# (10,)
# </td>
# </tr>
#
# </table>
# <font color='blue'>
# **Summary for YOLO**:
# - Input image (608, 608, 3)
# - The input image goes through a CNN, resulting in a (19,19,5,85) dimensional output.
# - After flattening the last two dimensions, the output is a volume of shape (19, 19, 425):
# - Each cell in a 19x19 grid over the input image gives 425 numbers.
# - 425 = 5 x 85 because each cell contains predictions for 5 boxes, corresponding to 5 anchor boxes, as seen in lecture.
# - 85 = 5 + 80 where 5 is because $(p_c, b_x, b_y, b_h, b_w)$ has 5 numbers, and and 80 is the number of classes we'd like to detect
# - You then select only few boxes based on:
# - Score-thresholding: throw away boxes that have detected a class with a score less than the threshold
# - Non-max suppression: Compute the Intersection over Union and avoid selecting overlapping boxes
# - This gives you YOLO's final output.
# ## 3 - Test YOLO pretrained model on images
# In this part, you are going to use a pretrained model and test it on the car detection dataset. As usual, you start by **creating a session to start your graph**. Run the following cell.
sess = K.get_session()
# ### 3.1 - Defining classes, anchors and image shape.
# Recall that we are trying to detect 80 classes, and are using 5 anchor boxes. We have gathered the information about the 80 classes and 5 boxes in two files "coco_classes.txt" and "yolo_anchors.txt". Let's load these quantities into the model by running the next cell.
#
# The car detection dataset has 720x1280 images, which we've pre-processed into 608x608 images.
class_names = read_classes("model_data/coco_classes.txt")
anchors = read_anchors("model_data/yolo_anchors.txt")
image_shape = (720., 1280.)
# ### 3.2 - Loading a pretrained model
#
# Training a YOLO model takes a very long time and requires a fairly large dataset of labelled bounding boxes for a large range of target classes. You are going to load an existing pretrained Keras YOLO model stored in "yolo.h5". (These weights come from the official YOLO website, and were converted using a function written by <NAME>. References are at the end of this notebook. Technically, these are the parameters from the "YOLOv2" model, but we will more simply refer to it as "YOLO" in this notebook.) Run the cell below to load the model from this file.
yolo_model = load_model("model_data/yolo.h5")
# This loads the weights of a trained YOLO model. Here's a summary of the layers your model contains.
yolo_model.summary()
# **Note**: On some computers, you may see a warning message from Keras. Don't worry about it if you do--it is fine.
#
# **Reminder**: this model converts a preprocessed batch of input images (shape: (m, 608, 608, 3)) into a tensor of shape (m, 19, 19, 5, 85) as explained in Figure (2).
# ### 3.3 - Convert output of the model to usable bounding box tensors
#
# The output of `yolo_model` is a (m, 19, 19, 5, 85) tensor that needs to pass through non-trivial processing and conversion. The following cell does that for you.
yolo_outputs = yolo_head(yolo_model.output, anchors, len(class_names))
# You added `yolo_outputs` to your graph. This set of 4 tensors is ready to be used as input by your `yolo_eval` function.
# ### 3.4 - Filtering boxes
#
# `yolo_outputs` gave you all the predicted boxes of `yolo_model` in the correct format. You're now ready to perform filtering and select only the best boxes. Lets now call `yolo_eval`, which you had previously implemented, to do this.
scores, boxes, classes = yolo_eval(yolo_outputs, image_shape)
# ### 3.5 - Run the graph on an image
#
# Let the fun begin. You have created a (`sess`) graph that can be summarized as follows:
#
# 1. <font color='purple'> yolo_model.input </font> is given to `yolo_model`. The model is used to compute the output <font color='purple'> yolo_model.output </font>
# 2. <font color='purple'> yolo_model.output </font> is processed by `yolo_head`. It gives you <font color='purple'> yolo_outputs </font>
# 3. <font color='purple'> yolo_outputs </font> goes through a filtering function, `yolo_eval`. It outputs your predictions: <font color='purple'> scores, boxes, classes </font>
#
# **Exercise**: Implement predict() which runs the graph to test YOLO on an image.
# You will need to run a TensorFlow session, to have it compute `scores, boxes, classes`.
#
# The code below also uses the following function:
# ```python
# image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
# ```
# which outputs:
# - image: a python (PIL) representation of your image used for drawing boxes. You won't need to use it.
# - image_data: a numpy-array representing the image. This will be the input to the CNN.
#
# **Important note**: when a model uses BatchNorm (as is the case in YOLO), you will need to pass an additional placeholder in the feed_dict {K.learning_phase(): 0}.
def predict(sess, image_file):
"""
Runs the graph stored in "sess" to predict boxes for "image_file". Prints and plots the preditions.
Arguments:
sess -- your tensorflow/Keras session containing the YOLO graph
image_file -- name of an image stored in the "images" folder.
Returns:
out_scores -- tensor of shape (None, ), scores of the predicted boxes
out_boxes -- tensor of shape (None, 4), coordinates of the predicted boxes
out_classes -- tensor of shape (None, ), class index of the predicted boxes
Note: "None" actually represents the number of predicted boxes, it varies between 0 and max_boxes.
"""
# Preprocess your image
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
# Run the session with the correct tensors and choose the correct placeholders in the feed_dict.
# You'll need to use feed_dict={yolo_model.input: ... , K.learning_phase(): 0})
### START CODE HERE ### (≈ 1 line)
out_scores, out_boxes, out_classes = sess.run([scores, boxes, classes], feed_dict={yolo_model.input: image_data, K.learning_phase(): 0})
### END CODE HERE ###
# Print predictions info
print('Found {} boxes for {}'.format(len(out_boxes), image_file))
# Generate colors for drawing bounding boxes.
colors = generate_colors(class_names)
# Draw bounding boxes on the image file
draw_boxes(image, out_scores, out_boxes, out_classes, class_names, colors)
# Save the predicted bounding box on the image
image.save(os.path.join("out", image_file), quality=90)
# Display the results in the notebook
output_image = scipy.misc.imread(os.path.join("out", image_file))
imshow(output_image)
return out_scores, out_boxes, out_classes
# Run the following cell on the "test.jpg" image to verify that your function is correct.
out_scores, out_boxes, out_classes = predict(sess, "test.jpg")
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **Found 7 boxes for test.jpg**
# </td>
# </tr>
# <tr>
# <td>
# **car**
# </td>
# <td>
# 0.60 (925, 285) (1045, 374)
# </td>
# </tr>
# <tr>
# <td>
# **car**
# </td>
# <td>
# 0.66 (706, 279) (786, 350)
# </td>
# </tr>
# <tr>
# <td>
# **bus**
# </td>
# <td>
# 0.67 (5, 266) (220, 407)
# </td>
# </tr>
# <tr>
# <td>
# **car**
# </td>
# <td>
# 0.70 (947, 324) (1280, 705)
# </td>
# </tr>
# <tr>
# <td>
# **car**
# </td>
# <td>
# 0.74 (159, 303) (346, 440)
# </td>
# </tr>
# <tr>
# <td>
# **car**
# </td>
# <td>
# 0.80 (761, 282) (942, 412)
# </td>
# </tr>
# <tr>
# <td>
# **car**
# </td>
# <td>
# 0.89 (367, 300) (745, 648)
# </td>
# </tr>
# </table>
# The model you've just run is actually able to detect 80 different classes listed in "coco_classes.txt". To test the model on your own images:
# 1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
# 2. Add your image to this Jupyter Notebook's directory, in the "images" folder
# 3. Write your image's name in the cell above code
# 4. Run the code and see the output of the algorithm!
#
# If you were to run your session in a for loop over all your images. Here's what you would get:
#
# <center>
# <video width="400" height="200" src="nb_images/pred_video_compressed2.mp4" type="video/mp4" controls>
# </video>
# </center>
#
# <caption><center> Predictions of the YOLO model on pictures taken from a camera while driving around the Silicon Valley <br> Thanks [drive.ai](https://www.drive.ai/) for providing this dataset! </center></caption>
# <font color='blue'>
# **What you should remember**:
# - YOLO is a state-of-the-art object detection model that is fast and accurate
# - It runs an input image through a CNN which outputs a 19x19x5x85 dimensional volume.
# - The encoding can be seen as a grid where each of the 19x19 cells contains information about 5 boxes.
# - You filter through all the boxes using non-max suppression. Specifically:
# - Score thresholding on the probability of detecting a class to keep only accurate (high probability) boxes
# - Intersection over Union (IoU) thresholding to eliminate overlapping boxes
# - Because training a YOLO model from randomly initialized weights is non-trivial and requires a large dataset as well as lot of computation, we used previously trained model parameters in this exercise. If you wish, you can also try fine-tuning the YOLO model with your own dataset, though this would be a fairly non-trivial exercise.
# **References**: The ideas presented in this notebook came primarily from the two YOLO papers. The implementation here also took significant inspiration and used many components from Allan Zelener's github repository. The pretrained weights used in this exercise came from the official YOLO website.
# - <NAME>, <NAME>, <NAME>, <NAME> - [You Only Look Once: Unified, Real-Time Object Detection](https://arxiv.org/abs/1506.02640) (2015)
# - <NAME>, <NAME> - [YOLO9000: Better, Faster, Stronger](https://arxiv.org/abs/1612.08242) (2016)
# - <NAME> - [YAD2K: Yet Another Darknet 2 Keras](https://github.com/allanzelener/YAD2K)
# - The official YOLO website (https://pjreddie.com/darknet/yolo/)
# **Car detection dataset**:
# <a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons License" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" property="dct:title">The Drive.ai Sample Dataset</span> (provided by drive.ai) is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>. We are especially grateful to <NAME>, <NAME> and <NAME> for collecting and providing this dataset.
| Convolutional Neural Networks/Week3/Autonomous_driving_application_-_Car_detection_-_v3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: rl_course
# language: python
# name: rl_course
# ---
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:60% !important; }</style>"))
# # Policy Iteration
#
# Here, we implement the grid world example from the RL Lecture 3 by <NAME> for policy iteration [see example](https://youtu.be/Nd1-UUMVfz4?t=1618)
#
# Given an initial policy $\pi$ _Policy iteration_ is done by iteratively evaluating the policy (using policy evaluation) and then improving it by acting greedily w.r.t to $v_\pi$
#
# $$
# \pi' = greedy(v_\pi)
# $$
#
# This algorithm always converges to the optimal policy
import numpy as np
import matplotlib.pyplot as plt
import plotting
plotting.set_layout(drawing_size=15)
# ## Define the Environment
#
# * In every state (except goal state) a moment has a cost of -1
# * In a goal state, thers is no cost for moving
# * If the agent is in a goal state, do not execute any moevement
#
# +
class environment():
""" This class defines all the necessary properties of the environment.
For now, the environment is a nxn rectangular grid"""
def __init__(self,n=5,s_start=(0,0),s_goals=[(4,4)]):
""" n: defines the length and width of the environment
s_start: defines the starting position of the agent (x-,y-position)
"""
# Define the grid
self.n_grid = n
# Agent position
self.x_agent = s_start[0]
self.y_agent = s_start[1]
# Agent actions
self.actions = ['n','e','s','w']
# Define rewards
self.rewards = np.ones((n,n)) * (-1)
# Define goal states
self.s_goals = s_goals
for g_i,g in enumerate(s_goals):
self.rewards[g] = 0
def move(self,a=None,state=None):
""" Moves the agent from its current state to the next state given action a
and returns a reward for that movement (cost of current state or new state ??)
a: is the action
state: is optional and can be the state from which the action is executed
"""
assert(a in self.actions)
# If state is given, use it as an indication that the movement is just simulated.
# Do not update internal states
if state:
x_s = state[0]
y_s = state[1]
else:
x_s = self.x_agent
y_s = self.y_agent
# If agent is in a goal state, do not move anymore
if (x_s, y_s) in self.s_goals:
return x_s,y_s
x = x_s
y = y_s
# execute movement. For now, the environment is deterministic
if a == 'n':
y = y -1
if a == 's':
y = y +1
if a == 'e':
x = x +1
if a == 'w':
x = x -1
# make sure to stay in the environment. if an acion moves the agent outside, just remain in current state
if x < 0 or y < 0 or x >= self.n_grid or y >= self.n_grid:
# do nothing and return rewards of current state
return x_s,y_s
else:
# set new state and return rewards of new state
# update internal variables if its a real movement
if state:
pass
else:
self.x_agent = x
self.y_agent = y
return x,y
def get_reward(self, state):
# Returns the reward for a given state
return self.rewards[state[0],state[1]]
def plot_env(self):
""" Plots the with the agent's position and rewars"""
fig = plt.figure(figsize=(10,5))
axes = fig.subplots(1,2)
# Agent's position
ax = axes[0]
grid = np.zeros((self.n_grid,self.n_grid))
grid[self.y_agent,self.x_agent] = 0.01
ax.matshow(grid, cmap='jet')
ax.set_title('Agent\'s Position')
# Rewards
ax = axes[1]
ax.matshow(self.rewards)
for (i, j), z in np.ndenumerate(self.rewards):
ax.text(j, i, '{:0.1f}'.format(z), ha='center', va='center')
ax.set_title('Rewards')
plt.show()
# -
# ## Define the Agent
#
# Agent stores:
# * The policy
# * value function
# * It has a model of the environment
# +
class agents():
""" This class defines the agent
"""
def __init__(self,n=5, gamma=1, pos_start=(0,0),env=None):
""" n: defines the length and width of the environment
gamma: the discount factor
pos_start: defines the starting position of the agent (x-,y-position)
env: an environment class to use as an internal model
"""
if env:
self.model_env = env
else:
print('No environment given. Cannot simulate movements')
# Store the discount factor
self.gamma = gamma
# Store size of environment
self.n_grid = n
# set the starting position
self.x = pos_start[0]
self.y = pos_start[1]
# Store the value function for each state
# start with zero
self.v = np.zeros((n,n))
# Initialize the policy
# initially the probability to choose an action given a state is 1/4
self.policy = np.ones((self.n_grid,self.n_grid,len(self.model_env.actions))) / 4
# Define transition matrix P^a_ss
self.P = np.zeros((self.n_grid,self.n_grid,len(self.model_env.actions)))
def random_move(self):
# Chooses a random movement (independent of the state)
i = np.random.randint(0,len(self.actions))
return self.actions[i]
def udate_policy(self):
# this function should be called after policy_evaluation
p = np.copy(self.policy)
# For each state check which is the best movement to do. Update the policy accordingly
# walk over all states
for i in range(np.size(self.v,0)):
for ii in range(np.size(self.v,1)):
# walk over all actions calculate the value of the resulting state and store it
l = []
for a_i,a_probability in enumerate(self.policy[i,i]):
# walk over alle possible reachable states given that acion
if a_i == 0:
a = 'n'
if a_i == 1:
a = 'e'
if a_i == 2:
a = 's'
if a_i == 3:
a = 'w'
x,y = self.model_env.move(a,(i,ii))
l.append(self.v[x,y])
# check if all entries are the same
if np.max(l) != np.min(l):
# what about if two entries are similar?
winner = np.argwhere(l == np.amax(l))
p[i,ii] = np.zeros(4)
# update policy
p[i,ii,winner] = 1.0
self.policy = p
def policy_evaluation(self):
# Given the reward update the value function of all states
# self.v[self.y,self.x] = r + self.gamma * np.sum( )
v = np.zeros(self.v.shape)
# walk over all states
for i in range(np.size(self.v,0)):
for ii in range(np.size(self.v,1)):
# walk over all actions accoriding to the policy
for a_i,a_probability in enumerate(self.policy[i,i]):
# walk over alle possible reachable states given that acion
if a_i == 0:
a = 'n'
if a_i == 1:
a = 'e'
if a_i == 2:
a = 's'
if a_i == 3:
a = 'w'
# simulate movement
x,y = self.model_env.move(a,(i,ii))
v[i,ii] += a_probability * ( self.model_env.rewards[i,ii] + self.gamma * self.v[x,y])
self.v = np.copy(v)
# +
# Set up the environmental variables
n = 4
agent_start = (1,1)
goal_states = [(0,0),(3,3)]
gamma = 1
# initialize everything
env = environment(n=n, s_start=agent_start,s_goals=goal_states)
agent = agents(n=n, gamma = gamma, pos_start=agent_start,env=env)
# run the policy iteration
for i in range(100):
agent.policy_evaluation()
agent.udate_policy()
# if i>5:
# agent.udate_policy()
i = i+1
if i==0 or i == 1 or i == 3 or i == 10 or i == 100:
# plot the results
fig =plt.figure(figsize=(7,7))
axes = fig.subplots(1,2)
# if i == 100:
# print(agent.policy)
ax = axes[0]
c = ax.matshow(agent.v)
for (k, j), z in np.ndenumerate(agent.v):
ax.text(j, k, '{:0.1f}'.format(z), ha='center', va='center')
ax.set_ylabel('Run {0:}'.format(i))
ax.set_title('Value Function')
ax = axes[1]
# visualize the policy
p_vis = np.chararray((n,n))
for i in range(np.size(agent.policy,0)):
for ii in range(np.size(agent.policy,1)):
# translate policy into movement characters
if np.all(0.25 == agent.policy[i,ii]):
p_vis[i,ii] = 'R'
else:
# this decoding is upside-down!
a_i = np.argmax(agent.policy[i,ii])
if a_i == 0:
a = 'w'
if a_i == 1:
a = 's'
if a_i == 2:
a = 'e'
if a_i == 3:
a = 'n'
p_vis[i,ii] = a
c = ax.matshow(np.zeros((n,n))* np.nan)
for (k, j), z in np.ndenumerate(p_vis):
ax.text(j, k, z.decode(), ha='center', va='center')
ax.set_title('Policy')
plt.show()
# -
| Lecture 3 Policy Iteration.ipynb |
# <!-- dom:TITLE: PHY321: Classical Mechanics 1 -->
# # PHY321: Classical Mechanics 1
# <!-- dom:AUTHOR: Homework 7, due Monday March 23 -->
# <!-- Author: -->
# **Homework 7, due Monday March 23**
#
# Date: **Mar 23, 2020**
#
# ### Practicalities about homeworks and projects
#
# 1. You can work in groups (optimal groups are often 2-3 people) or by yourself. If you work as a group you can hand in one answer only if you wish. **Remember to write your name(s)**!
#
# 2. Homeworks are available the week before the deadline.
#
# 3. How do I(we) hand in? Due to the corona virus and many of you not being on campus, we recommend that you scan your handwritten notes and upload them to D2L. If you are ok with typing mathematical formulae using say Latex, you can hand in everything as a single jupyter notebook at D2L. The numerical exercise(s) should always be handed in as a jupyter notebook by the deadline at D2L.
#
# ### Introduction to homework 7
#
# This week's sets of classical pen and paper and computational
# exercises are tailored to the topic of two-body problems and central
# forces, following what was discussed during the lectures during week
# 11 (March 9-13) and week 12 (March 16-20). Some of the exercise are
# simple derivations of the equations we discussed during lectures while
# other are applications to specific forces. Plotting the energy-diagram
# is again a very useful exercise. And you will see that many of the
# classical topics like conservation laws, conservative forces, central
# forces, energy, momentum and angular momentum conservation pop up
# again. These are indeed overarching features which allow us to develop
# our intuition about a given physical system.
#
# The relevant reading background is
# 1. Sections 8.1-8.7 of Taylor.
#
# The numerical homework is based on what you did in homework 4 on the Earth-Sun system, but we will add to this the numerical solution of elliptical orbits.
#
#
# ### Exercise 1 (20pt), Center-of-Mass and Relative Coordinates and Reference Frames
#
# We define the two-body center-of-mass coordinate and relative coordinate by expressing the trajectories for
# $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$ into the center-of-mass coordinate
# $\boldsymbol{R}_{\rm cm}$
# $$
# \boldsymbol{R}_{\rm cm}\equiv\frac{m_1\boldsymbol{r}_1+m_2\boldsymbol{r}_2}{m_1+m_2},
# $$
# and the relative coordinate
# $$
# \boldsymbol{r}\equiv\boldsymbol{r}_1-\boldsymbol{r_2}.
# $$
# Here, we assume the two particles interact only with one another, so $\boldsymbol{F}_{12}=-\boldsymbol{F}_{21}$ (where $\boldsymbol{F}_{ij}$ is the force on $i$ due to $j$.
#
# * 1a (5pt) Show that the equations of motion then become $\ddot{\boldsymbol{R}}_{\rm cm}=0$ and $\mu\ddot{\boldsymbol{r}}=\boldsymbol{F}_{12}$, with the reduced mass $\mu=m_1m_2/(m_1+m_2)$.
#
# The first expression simply states that the center of mass coordinate $\boldsymbol{R}_{\rm cm}$ moves at a fixed velocity. The second expression can be rewritten in terms of the reduced mass $\mu$.
#
# * 1b (5pt) Show that the linear momenta for the center-of-mass $\boldsymbol{P}$ motion and the relative motion $\boldsymbol{q}$ are given by $\boldsymbol{P}=M\dot{\boldsymbol{R}}_{\rm cm}$ with $M=m_1+m_2$ and $\boldsymbol{q}=\mu\dot{\boldsymbol{r}}$. The linear momentum of the relative motion is defined $\boldsymbol{q} = (m_2\boldsymbol{p}_1-m_1\boldsymbol{p}_2)/(m_1+m_2)$.
#
# * 1c (5pt) Show then the kinetic energy for two objects can then be written as
# $$
# K=\frac{P^2}{2M}+\frac{q^2}{2\mu}.
# $$
# * 1d (5pt) Show that the total angular momentum for two-particles in the center-of-mass frame $\boldsymbol{R}=0$, is given by
# $$
# \boldsymbol{L}=\boldsymbol{r}\times \mu\dot{\boldsymbol{r}}.
# $$
# ### Exercise 2 (10pt), Conservation of Energy
#
# The equations of motion in the center-of-mass frame in two dimensions with $x=r\cos{(\phi)}$ and $y=r\sin{(\phi)}$ and
# $r\in [0,\infty)$, $\phi\in [0,2\pi]$ and $r=\sqrt{x^2+y^2}$ are given by
# $$
# \mu \ddot{r}=-\frac{dV(r)}{dr}+\mu r\dot{\phi}^2,
# $$
# and
# $$
# \dot{\phi}=\frac{L}{\mu r^2}.
# $$
# Here $V(r)$ is any central force which depends only on the relative coordinate.
# * 2a (5pt) Show that you can rewrite the radial equation in terms of an effective potential $V_{\mathrm{eff}}(r)=V(r)+L^2/(2\mu r^2)$.
#
# * 2b (5pt) Write out the final differential equation for the radial degrees of freedom when we specify that $V(r)=-\alpha/r$. Plot the effective potential. You can choose values for $\alpha$ and $L$ and discuss (see Taylor section 8.4 and example 8.2) the physics of the system for two energies, one larger than zero and one smaller than zero. This is similar to what you did in the first midterm, except that the potential is different.
#
# ### Exercise 3 (40pt), Harmonic oscillator again
#
# See the lecture notes on central forces for a discussion of this problem. It is given as an example in the text.
#
# Consider a particle of mass $m$ in a $2$-dimensional harmonic oscillator with potential
# $$
# V(r)=\frac{1}{2}kr^2=\frac{1}{2}k(x^2+y^2).
# $$
# We assume the orbit has a final non-zero angular momentum $L$. The
# effective potential looks like that of a harmonic oscillator for large
# $r$, but for small $r$, the centrifugal potential repels the particle
# from the origin. The combination of the two potentials has a minimum
# for at some radius $r_{\rm min}$.
#
#
# * 3a (10pt) Set up the effective potential and plot it. Find $r_{\rm min}$ and $\dot{\phi}$. Show that the latter is given by $\dot{\phi}=\sqrt{k/m}$. At $r_{\rm min}$ the particle does not accelerate and $r$ stays constant and the motion is circular. With fixed $k$ and $m$, which parameter can we adjust to change the value of $r$ at $r_{\rm min}$?
#
# * 3b (10pt) Now consider small vibrations about $r_{\rm min}$. The effective spring constant is the curvature of the effective potential. Use the curvature at $r_{\rm min}$ to find the effective spring constant (hint, look at exercise 4 in homework 6) $k_{\mathrm{eff}}$. Show also that $\omega=\sqrt{k_{\mathrm{eff}}/m}=2\dot{\phi}$
#
# * 3c (10pt) The solution to the equations of motion in Cartesian coordinates is simple. The $x$ and $y$ equations of motion separate, and we have $\ddot{x}=-kx/m$ and $\ddot{y}=-ky/m$. The harmonic oscillator is indeed a system where the degrees of freedom separate and we can find analytical solutions. Define a natural frequency $\omega_0=\sqrt{k/m}$ and show that (where $A$, $B$, $C$ and $D$ are arbitrary constants defined by the initial conditions)
# $$
# \begin{eqnarray*}
# x&=&A\cos\omega_0 t+B\sin\omega_0 t,\\
# y&=&C\cos\omega_0 t+D\sin\omega_0 t.
# \end{eqnarray*}
# $$
# * 3d (10pt) With the solutions for $x$ and $y$, and $r^2=x^2+y^2$ and the definitions $\alpha=\frac{A^2+B^2+C^2+D^2}{2}$, $\beta=\frac{A^2-B^2+C^2-D^2}{2}$ and $\gamma=AB+CD$, show that
# $$
# r^2=\alpha+(\beta^2+\gamma^2)^{1/2}\cos(2\omega_0 t-\delta),
# $$
# with
# $$
# \delta=\arctan(\gamma/\beta),
# $$
# ### Exercise 4 (30pt), Numerical Solution of the Harmonic Oscillator
#
# Using the code we developed in homework 4 for the Earth-Sun system, we can solve the above harmonic oscillator problem in two dimensions using our code from this homework. We need however to change the acceleration from the gravitational force to the one given by the harmonic oscillator potential.
#
# The code is given here for the Velocity-Verlet algorithm, with obvious elements to fill in.
# +
# %matplotlib inline
# Common imports
import numpy as np
import pandas as pd
from math import *
import matplotlib.pyplot as plt
import os
# Where to save the figures and data files
PROJECT_ROOT_DIR = "Results"
FIGURE_ID = "Results/FigureFiles"
DATA_ID = "DataFiles/"
if not os.path.exists(PROJECT_ROOT_DIR):
os.mkdir(PROJECT_ROOT_DIR)
if not os.path.exists(FIGURE_ID):
os.makedirs(FIGURE_ID)
if not os.path.exists(DATA_ID):
os.makedirs(DATA_ID)
def image_path(fig_id):
return os.path.join(FIGURE_ID, fig_id)
def data_path(dat_id):
return os.path.join(DATA_ID, dat_id)
def save_fig(fig_id):
plt.savefig(image_path(fig_id) + ".png", format='png')
DeltaT = 0.01
#set up arrays
tfinal = 10.0
n = ceil(tfinal/DeltaT)
# set up arrays for t, a, v, and x
t = np.zeros(n)
v = np.zeros((n,2))
r = np.zeros((n,2))
# Initial conditions as compact 2-dimensional arrays
r0 = np.array([1.0,0.5]) # You need to change these to fit rmin
v0 = np.array([0.0,0.0]) # You need to change these to fit rmin
r[0] = r0
v[0] = v0
k = 0.1 # spring constant
m = 0.1 # mass, you can change these
omega02 = k/m
# Start integrating using the Velocity-Verlet method
for i in range(n-1):
# Set up forces, define acceleration first
a = -r[i]*omega02 # you may need to change this
# update velocity, time and position using the Velocity-Verlet method
r[i+1] = r[i] + DeltaT*v[i]+0.5*(DeltaT**2)*a
# new accelerationfor the Verlet method
anew = -r[i+1]*omega02
v[i+1] = v[i] + 0.5*DeltaT*(a+anew)
t[i+1] = t[i] + DeltaT
# Plot position as function of time
fig, ax = plt.subplots()
ax.set_xlabel('t[s]')
ax.set_ylabel('x[m] and y[m]')
ax.plot(t,r[:,0])
ax.plot(t,r[:,1])
fig.tight_layout()
save_fig("2DimHOVV")
plt.show()
# -
# * 4a (15pt) Use for example the above code to set up the acceleration and use the initial conditions fixed by for example $r_{\rm min}$ from exercise 3. Which value does the initial velocity take if you place yourself at $r_{\rm min}$? Check the solutions as function of different initial conditions (one set suffices) and compare with the analytical solutions for $x$ and $y$. Check also that energy is conserved.
#
# Instead of solving the equations in the cartesian frame we will now rewrite the above code in terms of the radial degrees of freedom only. Our differential equation is now
# $$
# \mu \ddot{r}=-\frac{dV(r)}{dr}+\mu\dot{\phi}^2,
# $$
# and
# $$
# \dot{\phi}=\frac{L}{\mu r^2}.
# $$
# * 4b (15pt) We will use $r_{\rm min}$ to fix a value of $L$, as seen in exercise 3. This fixes also $\dot{\phi}$. Write a code which now implements the radial equation for $r$ using the same $r_{\rm min}$ as you did in 4a. Compare the results with those from 4a with the same initial conditions. Do they agree? Use only one set of initial conditions.
#
# ### Exercise 5, the Bonus Exercise (30pt)
#
# As in previous sets, this exercise is not compulsory but gives you a bonus of 30 points.
# The aim here is to compare the numerical result from 4b with the analytical ones listed in 3d. Do your numerical results agree with the analytical ones? And is energy conserved? For this you need to set up the expression for the energy in terms of the effective potential and the kinetic energy.
| doc/Homeworks/hw7/ipynb/hw7.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
name = input('your name:')
date = float(input('请输入日期格式为1.1:'))
if 4.20<=date<=5.20:
print('',name)
print('是金牛座')
# +
m = int(input('请输入要输入的整数个数,回车结束。'))
max_number = int(input('请输入一个整数,回车结束'))
min_number = max_number
total = 0
i = 1
while i < m:
i += 1
n = int(input('请输入一个整数,回车结束'))
total += n
if n > max_number:
max_number = n
elif n < min_number:
min_number = n
print('最大值是:', max_number)
print('最小值是:', min_number)
print('平均值是:', total/m)
# +
m = int(input('输入第一个数大'))
n= int(input('输入第er个数小'))
print('1求和 2乘积 3求余 4除')
a = int(input('请输入选项'))
product=1
sum=0
if a==1:
while n<=m:
sum+=n
n+=1
print(sum)
elif a==2:
while n<=m:
product *=n
n+=1
print(product)
if a==3:
print(m%n)
elif a==4:
print('m/n')
# -
print('今天的PM2.5指数:')
a = int (input())
if a<=500:
print('空气质量良好')
else :
print('出么你记得戴口罩哈!')
# +
string = input('pls enter a word')
if (string.endswith('s')):
print('right')
else:
print('加s or es')
# -
| chapter1/homework/computer/3-15/201611580924 (2).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.6 64-bit (''sys_tests'': conda)'
# metadata:
# interpreter:
# hash: 75eea971140cd20bf61a98694439aebfe611e1f965354b67c59fd475d54e3010
# name: python3
# ---
# # V0.1.6 - Important notes and examples of how to use Extended Least Squares
#
# Example created by <NAME>
# Here we import the NARMAX model, the metric for model evaluation and the methods to generate sample data for tests. Also, we import pandas for specific usage.
pip install sysidentpy
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sysidentpy.polynomial_basis import PolynomialNarmax
from sysidentpy.metrics import root_relative_squared_error
from sysidentpy.utils.generate_data import get_miso_data, get_siso_data
# ## Generating 1 input 1 output sample data
#
# The data is generated by simulating the following model:
# $y_k = 0.2y_{k-1} + 0.1y_{k-1}x_{k-1} + 0.9x_{k-2} + e_{k}$
#
# If *colored_noise* is set to True:
#
# $e_{k} = 0.8\nu_{k-1} + \nu_{k}$
#
# where $x$ is a uniformly distributed random variable and $\nu$ is a gaussian distributed variable with $\mu=0$ and $\sigma$ is defined by the user.
#
# In the next example we will generate a data with 3000 samples with white noise and selecting 90% of the data to train the model.
x_train, x_valid, y_train, y_valid = get_siso_data(n=1000,
colored_noise=True,
sigma=0.2,
train_percentage=90)
# ## Build the model
#
# First we will train a model without the Extended Least Squares Algorithm for comparison purpose.
model = PolynomialNarmax(non_degree=2,
order_selection=True,
n_info_values=10,
n_terms=3,
extended_least_squares=False,
ylag=2, xlag=2,
info_criteria='aic',
estimator='least_squares',
)
model.fit(x_train, y_train)
yhat = model.predict(x_valid, y_valid)
rrse = root_relative_squared_error(y_valid, yhat)
print(rrse)
# Clearly we have something wrong with the obtained model. See the *basic_steps* notebook to compare the results obtained using the same data but without colored noise. But let take a look in whats is wrong.
# +
results = pd.DataFrame(model.results(err_precision=8,
dtype='dec'),
columns=['Regressors', 'Parameters', 'ERR'])
print(results)
# -
# ## Biased parameter estimation
#
# As we can observe above, the model structure is exact the same the one that generate the data. You can se that the ERR ordered the terms in the correct way. And this is an importante note regarding the Error Reduction Ratio algorithm used here: __it is very robust to colored noise!!__
#
# That is a greate feature! However, although the structure is correct, the model *parameters* are not ok! Here we have a biased estimation! The real parameter for $y_{k-1}$ is $0.2$, not $0.3$.
#
# In this case, we are actually modeling using a NARX model, not a NARMAX. The MA part exists to allow a unbiased estimation of the parameters. To achieve a unbiased estimation of the parameters we have the Extend Least Squares algorithm. Remember, if the data have only white noise, NARX is fine.
#
# Before applying the Extended Least Squares Algorithm we will run several NARX models to check how different the estimated parameters are from the real ones.
# +
import seaborn as sns
import matplotlib.pyplot as plt
parameters = np.zeros([3, 50])
for i in range(50):
x_train, x_valid, y_train, y_valid = get_siso_data(n=3000,
colored_noise=True,
train_percentage=90)
model.fit(x_train, y_train)
parameters[:, i] = list(model.theta)
sns.set()
pal = sns.cubehelix_palette(3, rot=-.5, dark=.3)
ax = sns.kdeplot(parameters.T[:, 0])
ax = sns.kdeplot(parameters.T[:, 1])
ax = sns.kdeplot(parameters.T[:, 2])
# plotting a vertical line where the real values must lie
ax = plt.axvline(x=0.1, c='k')
ax = plt.axvline(x=0.2, c='k')
ax = plt.axvline(x=0.9, c='k')
# -
# ## Using the Extended Least Squares algorithm
#
# As shown in figure above, we have a problem to estimate the parameter for $y_{k-1}$. Now we will use the Extended Least Squares Algorithm.
#
# In SysIdentPy, just set *extended_least_squares* to *True* and the algorithm will be applied.
# +
parameters = np.zeros([3, 50])
for i in range(50):
x_train, x_valid, y_train, y_valid = get_siso_data(n=3000,
colored_noise=True,
train_percentage=90)
model = PolynomialNarmax(non_degree=2,
n_terms=3,
extended_least_squares=True,
ylag=2, xlag=2,
estimator='least_squares',
)
model.fit(x_train, y_train)
parameters[:, i] = list(model.theta)
sns.set()
pal = sns.cubehelix_palette(3, rot=-.5, dark=.3)
ax = sns.kdeplot(parameters.T[:, 0])
ax = sns.kdeplot(parameters.T[:, 1])
ax = sns.kdeplot(parameters.T[:, 2])
# plotting a vertical line where the real values must lie
ax = plt.axvline(x=0.1, c='k')
ax = plt.axvline(x=0.2, c='k')
ax = plt.axvline(x=0.9, c='k')
# -
# Great! Now we have an unbiased estimation of the parameters!
#
# ## Note
#
# Note: The Extended Least Squares is an iterative algorithm. In SysIdentpy we fixed 30 iterations because it is knwon from literature that the algorithm converges quickly (about 10 or 20 iterations). Also, we create a specific set of noise regressors for estimation (order 2 and nonlinearity also equal 2). It is suposed to work in most cases, however we will add the possibility to choose the order and nonlinearity degree for noise regressors in future releases.
| docs/source/examples-v016/extended_least_squares.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Node Colormap
#
#
# Draw a graph with matplotlib, color by degree.
#
# +
import matplotlib.pyplot as plt
import networkx as nx
G = nx.cycle_graph(24)
pos = nx.spring_layout(G, iterations=200)
nx.draw(G, pos, node_color=range(24), node_size=800, cmap=plt.cm.Blues)
plt.show()
| experiments/plot_node_colormap.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # <img style="float: left; padding-right: 10px; width: 45px" src="https://github.com/Harvard-IACS/2018-CS109A/blob/master/content/styles/iacs.png?raw=true"> CS109A Introduction to Data Science
#
#
# ## Lab 3: plotting, K-NN Regression, Simple Linear Regression
#
# **Harvard University**<br>
# **Fall 2019**<br>
# **Instructors:** <NAME>, <NAME>, and <NAME><br>
#
# **Material prepared by**: <NAME>, <NAME>, <NAME>, and <NAME>.
# ## <font color='red'> Extended Edition</font>
#
# Same as the one done in class with the following additions/clarifications:
#
# * I added another example to illustrate the difference between `.iloc` and `.loc` in `pandas` -- > [here](#iloc)
# * I added some notes on why we are adding a constant in our linear regression model --> [here](#constant)
# * How to run the solutions: Uncomment the following line and run the cell:
#
# ```python
# # # %load solutions/knn_regression.py
# ```
# This will bring up the code in the cell but WILL NOT RUN it. You need to run the cell again in order to actually run the code
#
# ---
#RUN THIS CELL
import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/cs109.css").text
HTML(styles)
# ## Learning Goals
#
# By the end of this lab, you should be able to:
# * Review `numpy` including 2-D arrays and understand array reshaping
# * Use `matplotlib` to make plots
# * Feel comfortable with simple linear regression
# * Feel comfortable with $k$ nearest neighbors
#
# **This lab corresponds to lectures 4 and 5 and maps on to homework 2 and beyond.**
# ## Table of Contents
#
# #### <font color='red'> HIGHLIGHTS FROM PRE-LAB </font>
#
# * [1 - Review of numpy](#first-bullet)
# * [2 - Intro to matplotlib plus more ](#second-bullet)
#
# #### <font color='red'> LAB 3 MATERIAL </font>
#
# * [3 - Simple Linear Regression](#third-bullet)
# * [4 - Building a model with `statsmodels` and `sklearn`](#fourth-bullet)
# * [5 - Example: Simple linear regression with automobile data](#fifth-bullet)
# * [6 - $k$Nearest Neighbors](#sixth-bullet)
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import pandas as pd
import time
pd.set_option('display.width', 500)
pd.set_option('display.max_columns', 100)
pd.set_option('display.notebook_repr_html', True)
#import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
# Displays the plots for us.
# %matplotlib inline
# Use this as a variable to load solutions: %load PATHTOSOLUTIONS/exercise1.py. It will be substituted in the code
# so do not worry if it disappears after you run the cell.
PATHTOSOLUTIONS = 'solutions'
# <a class="anchor" id="first-bullet"></a>
# ## 1 - Review of the `numpy` Python library
#
# In lab1 we learned about the `numpy` library [(documentation)](http://www.numpy.org/) and its fast array structure, called the `numpy array`.
# import numpy
import numpy as np
# make an array
my_array = np.array([1,4,9,16])
my_array
print(f'Size of my array: {my_array.size}, or length of my array: {len(my_array)}')
print (f'Shape of my array: {my_array.shape}')
# #### Notice the way the shape appears in numpy arrays
#
# - For a 1D array, .shape returns a tuple with 1 element (n,)
# - For a 2D array, .shape returns a tuple with 2 elements (n,m)
# - For a 3D array, .shape returns a tuple with 3 elements (n,m,p)
# How to reshape a 1D array to a 2D
my_array.reshape(-1,2)
# Numpy arrays support the same operations as lists! Below we slice and iterate.
# +
print("array[2:4]:", my_array[2:4]) # A slice of the array
# Iterate over the array
for ele in my_array:
print("element:", ele)
# -
# Remember `numpy` gains a lot of its efficiency from being **strongly typed** (all elements are of the same type, such as integer or floating point). If the elements of an array are of a different type, `numpy` will force them into the same type (the longest in terms of bytes)
mixed = np.array([1, 2.3, 'eleni', True])
print(type(1), type(2.3), type('eleni'), type(True))
mixed # all elements will become strings
# Next, we push ahead to two-dimensional arrays and begin to dive into some of the deeper aspects of `numpy`.
# +
# create a 2d-array by handing a list of lists
my_array2d = np.array([ [1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
])
my_array2d
# -
# ### Array Slicing (a reminder...)
# Numpy arrays can be sliced, and can be iterated over with loops. Below is a schematic illustrating slicing two-dimensional arrays.
#
# <img src="../images/2dindex_v2.png" alt="Drawing" style="width: 500px;"/>
#
# Notice that the list slicing syntax still works!
# `array[2:,3]` says "in the array, get rows 2 through the end, column 3]"
# `array[3,:]` says "in the array, get row 3, all columns".
# <a class="anchor" id="iloc"></a>
# ### Pandas Slicing (a reminder...)
#
# `.iloc` is by position (position is unique), `.loc` is by label (label is not unique)
# import cast dataframe
cast = pd.read_csv('../data/cast.csv', encoding='utf_8')
cast.head()
# get me rows 10 to 13 (python slicing style : exclusive of end)
cast.iloc[10:13]
# get me columns 0 to 2 but all rows - use head()
cast.iloc[:, 0:2].head()
# get me rows 10 to 13 AND only columns 0 to 2
cast.iloc[10:13, 0:2]
# COMPARE: get me rows 10 to 13 (pandas slicing style : inclusive of end)
cast.loc[10:13]
# give me columns 'year' and 'type' by label but only for rows 5 to 10
cast.loc[5:10,['year','type']]
# #### Another example of positioning with `.iloc` and `loc`
#
# Look at the following data frame. It is a bad example because we have duplicate values for the index but that is legal in pandas. It's just a bad practice and we are doing it to illustrate the difference between positioning with `.iloc` and `loc`. To keep rows unique, though, internally, `pandas` has its own index which in this dataframe runs from `0` to `2`.
index = ['A', 'Z', 'A']
famous = pd.DataFrame({'Elton': ['singer', 'Candle in the wind', 'male'],
'Maraie': ['actress' , 'Do not know', 'female'],
'num': np.random.randn(3)}, index=index)
famous
# accessing elements by label can bring up duplicates!!
famous.loc['A'] # since we want all rows is the same as famous.loc['A',:]
# accessing elements by position is unique - brings up only one row
famous.iloc[1]
# <a class="anchor" id="second-bullet"></a>
# ## 2 - Plotting with matplotlib and beyond
# <br>
# <img style="float: center" src="https://imgs.xkcd.com/comics/convincing.png">
#
# `matplotlib` is a very powerful `python` library for making scientific plots.
#
# We will not focus too much on the internal aspects of `matplotlib` in today's lab. There are many excellent tutorials out there for `matplotlib`. For example,
# * [`matplotlib` homepage](https://matplotlib.org/)
# * [`matplotlib` tutorial](https://github.com/matplotlib/AnatomyOfMatplotlib)
#
# Conveying your findings convincingly is an absolutely crucial part of any analysis. Therefore, you must be able to write well and make compelling visuals. Creating informative visuals is an involved process and we won't cover that in this lab. However, part of creating informative data visualizations means generating *readable* figures. If people can't read your figures or have a difficult time interpreting them, they won't understand the results of your work. Here are some non-negotiable commandments for any plot:
# * Label $x$ and $y$ axes
# * Axes labels should be informative
# * Axes labels should be large enough to read
# * Make tick labels large enough
# * Include a legend if necessary
# * Include a title if necessary
# * Use appropriate line widths
# * Use different line styles for different lines on the plot
# * Use different markers for different lines
#
# There are other important elements, but that list should get you started on your way.
#
# We will work with `matplotlib` and `seaborn` for plotting in this class. `matplotlib` is a very powerful `python` library for making scientific plots. `seaborn` is a little more specialized in that it was developed for statistical data visualization. We will cover some `seaborn` later in class. In the meantime you can look at the [seaborn documentation](https://seaborn.pydata.org)
# First, let's generate some data.
# #### Let's plot some functions
#
# We will use the following three functions to make some plots:
#
# * Logistic function:
# \begin{align*}
# f\left(z\right) = \dfrac{1}{1 + be^{-az}}
# \end{align*}
# where $a$ and $b$ are parameters.
# * Hyperbolic tangent:
# \begin{align*}
# g\left(z\right) = b\tanh\left(az\right) + c
# \end{align*}
# where $a$, $b$, and $c$ are parameters.
# * Rectified Linear Unit:
# \begin{align*}
# h\left(z\right) =
# \left\{
# \begin{array}{lr}
# z, \quad z > 0 \\
# \epsilon z, \quad z\leq 0
# \end{array}
# \right.
# \end{align*}
# where $\epsilon < 0$ is a small, positive parameter.
#
# You are given the code for the first two functions. Notice that $z$ is passed in as a `numpy` array and that the functions are returned as `numpy` arrays. Parameters are passed in as floats.
#
# You should write a function to compute the rectified linear unit. The input should be a `numpy` array for $z$ and a positive float for $\epsilon$.
# +
import numpy as np
def logistic(z: np.ndarray, a: float, b: float) -> np.ndarray:
""" Compute logistic function
Inputs:
a: exponential parameter
b: exponential prefactor
z: numpy array; domain
Outputs:
f: numpy array of floats, logistic function
"""
den = 1.0 + b * np.exp(-a * z)
return 1.0 / den
def stretch_tanh(z: np.ndarray, a: float, b: float, c: float) -> np.ndarray:
""" Compute stretched hyperbolic tangent
Inputs:
a: horizontal stretch parameter (a>1 implies a horizontal squish)
b: vertical stretch parameter
c: vertical shift parameter
z: numpy array; domain
Outputs:
g: numpy array of floats, stretched tanh
"""
return b * np.tanh(a * z) + c
def relu(z: np.ndarray, eps: float = 0.01) -> np.ndarray:
""" Compute rectificed linear unit
Inputs:
eps: small positive parameter
z: numpy array; domain
Outputs:
h: numpy array; relu
"""
return np.fmax(z, eps * z)
# -
# Now let's make some plots. First, let's just warm up and plot the logistic function.
# +
x = np.linspace(-5.0, 5.0, 100) # Equally spaced grid of 100 pts between -5 and 5
f = logistic(x, 1.0, 1.0) # Generate data
# -
plt.plot(x, f)
plt.xlabel('x')
plt.ylabel('f')
plt.title('Logistic Function')
plt.grid(True)
# #### Figures with subplots
#
# Let's start thinking about the plots as objects. We have the `figure` object which is like a matrix of smaller plots named `axes`. You can use array notation when handling it.
# +
fig, ax = plt.subplots(1,1) # Get figure and axes objects
ax.plot(x, f) # Make a plot
# Create some labels
ax.set_xlabel('x')
ax.set_ylabel('f')
ax.set_title('Logistic Function')
# Grid
ax.grid(True)
# -
# Wow, it's *exactly* the same plot! Notice, however, the use of `ax.set_xlabel()` instead of `plt.xlabel()`. The difference is tiny, but you should be aware of it. I will use this plotting syntax from now on.
#
# What else do we need to do to make this figure better? Here are some options:
# * Make labels bigger!
# * Make line fatter
# * Make tick mark labels bigger
# * Make the grid less pronounced
# * Make figure bigger
#
# Let's get to it.
# +
fig, ax = plt.subplots(1,1, figsize=(10,6)) # Make figure bigger
# Make line plot
ax.plot(x, f, lw=4)
# Update ticklabel size
ax.tick_params(labelsize=24)
# Make labels
ax.set_xlabel(r'$x$', fontsize=24) # Use TeX for mathematical rendering
ax.set_ylabel(r'$f(x)$', fontsize=24) # Use TeX for mathematical rendering
ax.set_title('Logistic Function', fontsize=24)
ax.grid(True, lw=1.5, ls='--', alpha=0.75)
# -
# Notice:
# * `lw` stands for `linewidth`. We could also write `ax.plot(x, f, linewidth=4)`
# * `ls` stands for `linestyle`.
# * `alpha` stands for transparency.
# The only thing remaining to do is to change the $x$ limits. Clearly these should go from $-5$ to $5$.
# +
#fig.savefig('logistic.png')
# Put this in a markdown cell and uncomment this to check what you saved.
# 
# -
# #### Resources
# If you want to see all the styles available, please take a look at the documentation.
# * [Line styles](https://matplotlib.org/2.0.1/api/lines_api.html#matplotlib.lines.Line2D.set_linestyle)
# * [Marker styles](https://matplotlib.org/2.0.1/api/markers_api.html#module-matplotlib.markers)
# * [Everything you could ever want](https://matplotlib.org/2.0.1/api/lines_api.html#matplotlib.lines.Line2D.set_marker)
#
# We haven't discussed it yet, but you can also put a legend on a figure. You'll do that in the next exercise. Here are some additional resources:
# * [Legend](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.legend.html)
# * [Grid](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.grid.html)
#
# `ax.legend(loc='best', fontsize=24);`
# <div class="exercise"><b>Exercise</b></div>
#
# Do the following:
# * Make a figure with the logistic function, hyperbolic tangent, and rectified linear unit.
# * Use different line styles for each plot
# * Put a legend on your figure
#
# Here's an example of a figure:
# 
# +
# your code here
# First get the data
f = logistic(x, 2.0, 1.0)
g = stretch_tanh(x, 2.0, 0.5, 0.5)
h = relu(x)
fig, ax = plt.subplots(1,1, figsize=(10,6)) # Create figure object
# Make actual plots
# (Notice the label argument!)
ax.plot(x, f, lw=4, ls='-', label=r'$L(x;1)$')
ax.plot(x, g, lw=4, ls='--', label=r'$\tanh(2x)$')
ax.plot(x, h, lw=4, ls='-.', label=r'$relu(x; 0.01)$')
# Make the tick labels readable
ax.tick_params(labelsize=24)
# Set axes limits to make the scale nice
ax.set_xlim(x.min(), x.max())
ax.set_ylim(h.min(), 1.1)
# Make readable labels
ax.set_xlabel(r'$x$', fontsize=24)
ax.set_ylabel(r'$h(x)$', fontsize=24)
ax.set_title('Activation Functions', fontsize=24)
# Set up grid
ax.grid(True, lw=1.75, ls='--', alpha=0.75)
# Put legend on figure
ax.legend(loc='best', fontsize=24);
fig.savefig('../images/nice_plots.png')
# -
# <div class="exercise"><b>Exercise</b></div>
#
# These figures look nice in the plot and it makes sense for comparison. Now let's put the 3 different figures in separate plots.
#
# * Make a separate plot for each figure and line them up on the same row.
# your code here
# # %load solutions/three_subplots.py
# <div class="exercise"><b>Exercise</b></div>
#
# * Make a grid of 2 x 3 separate plots, 3 will be empty. Just plot the functions and do not worry about cosmetics. We just want you ro see the functionality.
# your code here
# %load solutions/six_subplots.py
# <a class="anchor" id="third-bullet"></a>
# ## 3 - Simple Linear Regression
#
# Linear regression and its many extensions are a workhorse of the statistics and data science community, both in application and as a reference point for other models. Most of the major concepts in machine learning can be and often are discussed in terms of various linear regression models. Thus, this section will introduce you to building and fitting linear regression models and some of the process behind it, so that you can 1) fit models to data you encounter 2) experiment with different kinds of linear regression and observe their effects 3) see some of the technology that makes regression models work.
#
#
# ### Linear regression with a toy dataset
# We first examine a toy problem, focusing our efforts on fitting a linear model to a small dataset with three observations. Each observation consists of one predictor $x_i$ and one response $y_i$ for $i = 1, 2, 3$,
#
# \begin{align*}
# (x , y) = \{(x_1, y_1), (x_2, y_2), (x_3, y_3)\}.
# \end{align*}
#
# To be very concrete, let's set the values of the predictors and responses.
#
# \begin{equation*}
# (x , y) = \{(1, 2), (2, 2), (3, 4)\}
# \end{equation*}
#
# There is no line of the form $\beta_0 + \beta_1 x = y$ that passes through all three observations, since the data are not collinear. Thus our aim is to find the line that best fits these observations in the *least-squares sense*, as discussed in lecture.
# <div class="exercise"><b>Exercise (for home)</b></div>
#
# * Make two numpy arrays out of this data, x_train and y_train
# * Check the dimentions of these arrays
# * Try to reshape them into a different shape
# * Make points into a very simple scatterplot
# * Make a better scatterplot
# +
# your code here
# -
# solution
x_train = np.array([1,2,3])
y_train = np.array([2,3,6])
type(x_train)
x_train.shape
x_train = x_train.reshape(3,1)
x_train.shape
# +
# # %load solutions/simple_scatterplot.py
# Make a simple scatterplot
plt.scatter(x_train,y_train)
# check dimensions
print(x_train.shape,y_train.shape)
# +
# # %load solutions/nice_scatterplot.py
def nice_scatterplot(x, y, title):
# font size
f_size = 18
# make the figure
fig, ax = plt.subplots(1,1, figsize=(8,5)) # Create figure object
# set axes limits to make the scale nice
ax.set_xlim(np.min(x)-1, np.max(x) + 1)
ax.set_ylim(np.min(y)-1, np.max(y) + 1)
# adjust size of tickmarks in axes
ax.tick_params(labelsize = f_size)
# remove tick labels
ax.tick_params(labelbottom=False, bottom=False)
# adjust size of axis label
ax.set_xlabel(r'$x$', fontsize = f_size)
ax.set_ylabel(r'$y$', fontsize = f_size)
# set figure title label
ax.set_title(title, fontsize = f_size)
# you may set up grid with this
ax.grid(True, lw=1.75, ls='--', alpha=0.15)
# make actual plot (Notice the label argument!)
#ax.scatter(x, y, label=r'$my points$')
#ax.scatter(x, y, label='$my points$')
ax.scatter(x, y, label=r'$my\,points$')
ax.legend(loc='best', fontsize = f_size);
return ax
nice_scatterplot(x_train, y_train, 'hello nice plot')
# -
#
# #### Formulae
# Linear regression is special among the models we study because it can be solved explicitly. While most other models (and even some advanced versions of linear regression) must be solved itteratively, linear regression has a formula where you can simply plug in the data.
#
# For the single predictor case it is:
# \begin{align}
# \beta_1 &= \frac{\sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}}{\sum_{i=1}^n{(x_i-\bar{x})^2}}\\
# \beta_0 &= \bar{y} - \beta_1\bar{x}\
# \end{align}
#
# Where $\bar{y}$ and $\bar{x}$ are the mean of the y values and the mean of the x values, respectively.
# ### Building a model from scratch
# In this part, we will solve the equations for simple linear regression and find the best fit solution to our toy problem.
# The snippets of code below implement the linear regression equations on the observed predictors and responses, which we'll call the training data set. Let's walk through the code.
#
# We have to reshape our arrrays to 2D. We will see later why.
# <div class="exercise"><b>Exercise</b></div>
#
# * make an array with shape (2,3)
# * reshape it to a size that you want
# your code here
#solution
xx = np.array([[1,2,3],[4,6,8]])
xxx = xx.reshape(-1,2)
xxx.shape
# +
# Reshape to be a proper 2D array
x_train = x_train.reshape(x_train.shape[0], 1)
y_train = y_train.reshape(y_train.shape[0], 1)
print(x_train.shape)
# +
# first, compute means
y_bar = np.mean(y_train)
x_bar = np.mean(x_train)
# build the two terms
numerator = np.sum( (x_train - x_bar)*(y_train - y_bar) )
denominator = np.sum((x_train - x_bar)**2)
print(numerator.shape, denominator.shape) #check shapes
# -
# * Why the empty brackets? (The numerator and denominator are scalars, as expected.)
# +
#slope beta1
beta_1 = numerator/denominator
#intercept beta0
beta_0 = y_bar - beta_1*x_bar
print("The best-fit line is {0:3.2f} + {1:3.2f} * x".format(beta_0, beta_1))
print(f'The best fit is {beta_0}')
# -
# <div class="exercise"><b>Exercise</b></div>
#
# Turn the code from the above cells into a function called `simple_linear_regression_fit`, that inputs the training data and returns `beta0` and `beta1`.
#
# To do this, copy and paste the code from the above cells below and adjust the code as needed, so that the training data becomes the input and the betas become the output.
#
# ```python
# def simple_linear_regression_fit(x_train: np.ndarray, y_train: np.ndarray) -> np.ndarray:
#
# return
# ```
#
# Check your function by calling it with the training data from above and printing out the beta values.
# +
# Your code here
# -
# # %load solutions/simple_linear_regression_fit.py
def simple_linear_regression_fit(x_train: np.ndarray, y_train: np.ndarray) -> np.ndarray:
"""
Inputs:
x_train: a (num observations by 1) array holding the values of the predictor variable
y_train: a (num observations by 1) array holding the values of the response variable
Returns:
beta_vals: a (num_features by 1) array holding the intercept and slope coeficients
"""
# Check input array sizes
if len(x_train.shape) < 2:
print("Reshaping features array.")
x_train = x_train.reshape(x_train.shape[0], 1)
if len(y_train.shape) < 2:
print("Reshaping observations array.")
y_train = y_train.reshape(y_train.shape[0], 1)
# first, compute means
y_bar = np.mean(y_train)
x_bar = np.mean(x_train)
# build the two terms
numerator = np.sum( (x_train - x_bar)*(y_train - y_bar) )
denominator = np.sum((x_train - x_bar)**2)
#slope beta1
beta_1 = numerator/denominator
#intercept beta0
beta_0 = y_bar - beta_1*x_bar
return np.array([beta_0,beta_1])
# * Let's run this function and see the coefficients
# +
x_train = np.array([1 ,2, 3])
y_train = np.array([2, 2, 4])
betas = simple_linear_regression_fit(x_train, y_train)
beta_0 = betas[0]
beta_1 = betas[1]
print("The best-fit line is {0:8.6f} + {1:8.6f} * x".format(beta_0, beta_1))
# -
# <div class="exercise"><b>Exercise</b></div>
#
# * Do the values of `beta0` and `beta1` seem reasonable?
# * Plot the training data using a scatter plot.
# * Plot the best fit line with `beta0` and `beta1` together with the training data.
# +
# Your code here
# +
# # %load solutions/best_fit_scatterplot.py
fig_scat, ax_scat = plt.subplots(1,1, figsize=(10,6))
# Plot best-fit line
x_train = np.array([[1, 2, 3]]).T
best_fit = beta_0 + beta_1 * x_train
ax_scat.scatter(x_train, y_train, s=300, label='Training Data')
ax_scat.plot(x_train, best_fit, ls='--', label='Best Fit Line')
ax_scat.set_xlabel(r'$x_{train}$')
ax_scat.set_ylabel(r'$y$');
# -
# The values of `beta0` and `beta1` seem roughly reasonable. They capture the positive correlation. The line does appear to be trying to get as close as possible to all the points.
# <a class="anchor" id="fourth-bullet"></a>
# ## 4 - Building a model with `statsmodels` and `sklearn`
#
# Now that we can concretely fit the training data from scratch, let's learn two `python` packages to do it all for us:
# * [statsmodels](http://www.statsmodels.org/stable/regression.html) and
# * [scikit-learn (sklearn)](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html).
#
# Our goal is to show how to implement simple linear regression with these packages. For an important sanity check, we compare the $\beta$ values from `statsmodels` and `sklearn` to the $\beta$ values that we found from above with our own implementation.
#
# For the purposes of this lab, `statsmodels` and `sklearn` do the same thing. More generally though, `statsmodels` tends to be easier for inference \[finding the values of the slope and intercept and dicussing uncertainty in those values\], whereas `sklearn` has machine-learning algorithms and is better for prediction \[guessing y values for a given x value\]. (Note that both packages make the same guesses, it's just a question of which activity they provide more support for.
#
# **Note:** `statsmodels` and `sklearn` are different packages! Unless we specify otherwise, you can use either one.
# <a class="anchor" id="constant"></a>
# ### Why do we need to add a constant in our simple linear regression model?
#
# Let's say we a data set of two obsevations with one predictor and one response variable each. We would then have the following two equations if we run a simple linear regression model. $$y_1=\beta_0 + \beta_1*x_1$$ $$y_2=\beta_0 + \beta_1*x_2$$ <BR> For simplicity and calculation efficiency we want to "absorb" the constant $b_0$ into an array with $b_1$ so we have only multiplication. To do this we introduce the constant ${x}^0=1$<br>$$y_1=\beta_0*{x_1}^0 + \beta_1*x_1$$ $$y_2=\beta_0 * {x_2}^0 + \beta_1*x_2$$ <BR> That becomes:
# $$y_1=\beta_0*1 + \beta_1*x_1$$ $$y_2=\beta_0 * 1 + \beta_1*x_2$$<bR>
#
# In matrix notation:
#
# $$
# \left [
# \begin{array}{c}
# y_1 \\ y_2 \\
# \end{array}
# \right] =
# \left [
# \begin{array}{cc}
# 1& x_1 \\ 1 & x_2 \\
# \end{array}
# \right]
# \cdot
# \left [
# \begin{array}{c}
# \beta_0 \\ \beta_1 \\
# \end{array}
# \right]
# $$
# <BR><BR>
#
# `sklearn` adds the constant for us where in `statsmodels` we need to explicitly add it using `sm.add_constant`
# Below is the code for `statsmodels`. `Statsmodels` does not by default include the column of ones in the $X$ matrix, so we include it manually with `sm.add_constant`.
import statsmodels.api as sm
# +
# create the X matrix by appending a column of ones to x_train
X = sm.add_constant(x_train)
# this is the same matrix as in our scratch problem!
print(X)
# build the OLS model (ordinary least squares) from the training data
toyregr_sm = sm.OLS(y_train, X)
# do the fit and save regression info (parameters, etc) in results_sm
results_sm = toyregr_sm.fit()
# pull the beta parameters out from results_sm
beta0_sm = results_sm.params[0]
beta1_sm = results_sm.params[1]
print(f'The regression coef from statsmodels are: beta_0 = {beta0_sm:8.6f} and beta_1 = {beta1_sm:8.6f}')
# -
# Besides the beta parameters, `results_sm` contains a ton of other potentially useful information.
import warnings
warnings.filterwarnings('ignore')
print(results_sm.summary())
# Now let's turn our attention to the `sklearn` library.
from sklearn import linear_model
# +
# build the least squares model
toyregr = linear_model.LinearRegression()
# save regression info (parameters, etc) in results_skl
results = toyregr.fit(x_train, y_train)
# pull the beta parameters out from results_skl
beta0_skl = toyregr.intercept_
beta1_skl = toyregr.coef_[0]
print("The regression coefficients from the sklearn package are: beta_0 = {0:8.6f} and beta_1 = {1:8.6f}".format(beta0_skl, beta1_skl))
# -
# We should feel pretty good about ourselves now, and we're ready to move on to a real problem!
# ### The `scikit-learn` library and the shape of things
# Before diving into a "real" problem, let's discuss more of the details of `sklearn`.
#
# `Scikit-learn` is the main `Python` machine learning library. It consists of many learners which can learn models from data, as well as a lot of utility functions such as `train_test_split()`.
#
# Use the following to add the library into your code:
#
# ```python
# import sklearn
# ```
#
# In `scikit-learn`, an **estimator** is a Python object that implements the methods `fit(X, y)` and `predict(T)`
#
# Let's see the structure of `scikit-learn` needed to make these fits. `fit()` always takes two arguments:
# ```python
# estimator.fit(Xtrain, ytrain)
# ```
# We will consider two estimators in this lab: `LinearRegression` and `KNeighborsRegressor`.
#
# It is very important to understand that `Xtrain` must be in the form of a **2x2 array** with each row corresponding to one sample, and each column corresponding to the feature values for that sample.
#
# `ytrain` on the other hand is a simple array of responses. These are continuous for regression problems.
# 
#
# <!---->
# ### Practice with `sklearn` and a real dataset
# We begin by loading up the `mtcars` dataset. This data was extracted from the 1974 Motor Trend US magazine, and comprises of fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models). We will load this data to a dataframe with 32 observations on 11 (numeric) variables. Here is an explanation of the features:
#
# - `mpg` is Miles/(US) gallon
# - `cyl` is Number of cylinders,
# - `disp` is Displacement (cu.in.),
# - `hp` is Gross horsepower,
# - `drat` is Rear axle ratio,
# - `wt` is the Weight (1000 lbs),
# - `qsec` is 1/4 mile time,
# - `vs` is Engine (0 = V-shaped, 1 = straight),
# - `am` is Transmission (0 = automatic, 1 = manual),
# - `gear` is the Number of forward gears,
# - `carb` is Number of carburetors.
# +
import pandas as pd
#load mtcars
dfcars = pd.read_csv("../data/mtcars.csv")
dfcars.head()
# -
# Fix the column title
dfcars = dfcars.rename(columns={"Unnamed: 0":"car name"})
dfcars.head()
dfcars.shape
# #### Searching for values: how many cars have 4 gears?
len(dfcars[dfcars.gear == 4].drop_duplicates(subset='car name', keep='first'))
# Next, let's split the dataset into a training set and test set.
# +
# split into training set and testing set
from sklearn.model_selection import train_test_split
#set random_state to get the same split every time
traindf, testdf = train_test_split(dfcars, test_size=0.2, random_state=42)
# -
# testing set is around 20% of the total data; training set is around 80%
print("Shape of full dataset is: {0}".format(dfcars.shape))
print("Shape of training dataset is: {0}".format(traindf.shape))
print("Shape of test dataset is: {0}".format(testdf.shape))
# Now we have training and test data. We still need to select a predictor and a response from this dataset. Keep in mind that we need to choose the predictor and response from both the training and test set. You will do this in the exercises below. However, we provide some starter code for you to get things going.
traindf.head()
# Extract the response variable that we're interested in
y_train = traindf.mpg
y_train
# <div class="exercise"><b>Exercise</b></div>
#
# Use slicing to get the same vector `y_train`
#
# ----
# Now, notice the shape of `y_train`.
y_train.shape, type(y_train)
# ### Array reshape
# This is a 1D array as should be the case with the **Y** array. Remember, `sklearn` requires a 2D array only for the predictor array. You will have to pay close attention to this in the exercises later. `Sklearn` doesn't care too much about the shape of `y_train`.
#
# The whole reason we went through that whole process was to show you how to reshape your data into the correct format.
#
# **IMPORTANT:** Remember that your response variable `ytrain` can be a vector but your predictor variable `xtrain` ***must*** be an array!
# <a class="anchor" id="fifth-bullet"></a>
# ## 5 - Example: Simple linear regression with automobile data
# We will now use `sklearn` to predict automobile mileage per gallon (mpg) and evaluate these predictions. We already loaded the data and split them into a training set and a test set.
# We need to choose the variables that we think will be good predictors for the dependent variable `mpg`.
# <div class="exercise"><b>Exercise in pairs</b></div>
#
# * Pick one variable to use as a predictor for simple linear regression. Discuss your reasons with the person next to you.
# * Justify your choice with some visualizations.
# * Is there a second variable you'd like to use? For example, we're not doing multiple linear regression here, but if we were, is there another variable you'd like to include if we were using two predictors?
x_wt = dfcars.wt
x_wt.shape
# Your code here
# +
# # %load solutions/cars_simple_EDA.py
# -
# <div class="exercise"><b>Exercise</b></div>
#
# * Use `sklearn` to fit the training data using simple linear regression.
# * Use the model to make mpg predictions on the test set.
# * Plot the data and the prediction.
# * Print out the mean squared error for the training set and the test set and compare.
# +
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
dfcars = pd.read_csv("../data/mtcars.csv")
dfcars = dfcars.rename(columns={"Unnamed: 0":"name"})
dfcars.head()
# +
traindf, testdf = train_test_split(dfcars, test_size=0.2, random_state=42)
y_train = np.array(traindf.mpg)
X_train = np.array(traindf.wt)
X_train = X_train.reshape(X_train.shape[0], 1)
# -
y_test = np.array(testdf.mpg)
X_test = np.array(testdf.wt)
X_test = X_test.reshape(X_test.shape[0], 1)
# Let's take another look at our data
dfcars.head()
# And out train and test sets
y_train.shape, X_train.shape
y_test.shape, X_test.shape
# +
#create linear model
regression = LinearRegression()
#fit linear model
regression.fit(X_train, y_train)
predicted_y = regression.predict(X_test)
r2 = regression.score(X_test, y_test)
print(f'R^2 = {r2:.5}')
# +
print(regression.score(X_train, y_train))
print(mean_squared_error(predicted_y, y_test))
print(mean_squared_error(y_train, regression.predict(X_train)))
print('Coefficients: \n', regression.coef_[0], regression.intercept_)
# +
fig, ax = plt.subplots(1,1, figsize=(10,6))
ax.plot(y_test, predicted_y, 'o')
grid = np.linspace(np.min(dfcars.mpg), np.max(dfcars.mpg), 100)
ax.plot(grid, grid, color="black") # 45 degree line
ax.set_xlabel("actual y")
ax.set_ylabel("predicted y")
fig1, ax1 = plt.subplots(1,1, figsize=(10,6))
ax1.plot(dfcars.wt, dfcars.mpg, 'o')
xgrid = np.linspace(np.min(dfcars.wt), np.max(dfcars.wt), 100)
ax1.plot(xgrid, regression.predict(xgrid.reshape(100, 1)))
# -
# <a class="anchor" id="sixth-bullet"></a>
# ## 6 - $k$-nearest neighbors
# Now that you're familiar with `sklearn`, you're ready to do a KNN regression.
#
# Sklearn's regressor is called `sklearn.neighbors.KNeighborsRegressor`. Its main parameter is the `number of nearest neighbors`. There are other parameters such as the distance metric (default for 2 order is the Euclidean distance). For a list of all the parameters see the [Sklearn kNN Regressor Documentation](https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsRegressor.html).
#
# Let's use $5$ nearest neighbors.
# Import the library
from sklearn.neighbors import KNeighborsRegressor
# Set number of neighbors
k = 5
knnreg = KNeighborsRegressor(n_neighbors=k)
# +
# Fit the regressor - make sure your numpy arrays are the right shape
knnreg.fit(X_train, y_train)
# Evaluate the outcome on the train set using R^2
r2_train = knnreg.score(X_train, y_train)
# Print results
print(f'kNN model with {k} neighbors gives R^2 on the train set: {r2_train:.5}')
# -
knnreg.predict(X_test)
# <div class="exercise"><b>Exercise</b></div>
#
# Calculate and print the $R^{2}$ score on the test set
# +
# Your code here
# -
# Not so good? Lets vary the number of neighbors and see what we get.
# +
# Make our lives easy by storing the different regressors in a dictionary
regdict = {}
# Make our lives easier by entering the k values from a list
k_list = [1, 2, 4, 15]
# Do a bunch of KNN regressions
for k in k_list:
knnreg = KNeighborsRegressor(n_neighbors=k)
knnreg.fit(X_train, y_train)
# Store the regressors in a dictionary
regdict[k] = knnreg
# Print the dictionary to see what we have
regdict
# -
# Now let's plot all the k values in same plot.
# +
fig, ax = plt.subplots(1,1, figsize=(10,6))
ax.plot(dfcars.wt, dfcars.mpg, 'o', label="data")
xgrid = np.linspace(np.min(dfcars.wt), np.max(dfcars.wt), 100)
# let's unpack the dictionary to its elements (items) which is the k and Regressor
for k, regressor in regdict.items():
predictions = regressor.predict(xgrid.reshape(-1,1))
ax.plot(xgrid, predictions, label="{}-NN".format(k))
ax.legend();
# -
# <div class="exercise"><b>Exercise</b></div>
#
# Explain what you see in the graph. **Hint** Notice how the $1$-NN goes through every point on the training set but utterly fails elsewhere.
# Lets look at the scores on the training set.
# +
ks = range(1, 15) # Grid of k's
scores_train = [] # R2 scores
for k in ks:
# Create KNN model
knnreg = KNeighborsRegressor(n_neighbors=k)
# Fit the model to training data
knnreg.fit(X_train, y_train)
# Calculate R^2 score
score_train = knnreg.score(X_train, y_train)
scores_train.append(score_train)
# Plot
fig, ax = plt.subplots(1,1, figsize=(12,8))
ax.plot(ks, scores_train,'o-')
ax.set_xlabel(r'$k$')
ax.set_ylabel(r'$R^{2}$')
# -
# <div class="exercise"><b>Exercise</b></div>
#
# * Why do we get a perfect $R^2$ at k=1 for the training set?
# * Make the same plot as above on the *test* set.
# * What is the best $k$?
# Your code here
# +
# # %load solutions/knn_regression.py
# -
# solution to previous exercise
r2_test = knnreg.score(X_test, y_test)
print(f'kNN model with {k} neighbors gives R^2 on the test set: {r2_test:.5}')
| docs/labs/lab03/notebook/cs109a_lab3_extended.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # PCA
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.linear_model import LogisticRegressionCV
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn import metrics
from sklearn.preprocessing import PolynomialFeatures
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import sklearn
print (sklearn.__version__)
def extend(a, b):
return 1.05*a-0.05*b, 1.05*b-0.05*a
# ### 数据说明
#
# | en | zh |
# | :--------: |:-----:|
# |sepal_length|花萼长度|
# |sepal_width |花萼宽度|
# |petal_length|花瓣长度|
# |petal_width |花瓣宽度|
# |class |类别|
iris_data = pd.read_csv('iris.data', header=None)
# print (iris_data)
columns = np.array(['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class'])
iris_data.rename(columns=dict(zip(np.arange(5), columns)), inplace=True)
iris_data['class'] = pd.Categorical(iris_data['class']).codes
print (iris_data[0:5])
# ### load_data
X = iris_data[columns[0:-1]]
y = iris_data[columns[-1]]
#
# ### PCA参数说明:
#
#
# - n_components:
# - 意义:PCA算法中所要保留的主成分个数n,也即保留下来的特征个数n
# - 类型:int 或者 string,缺省时默认为None,所有成分被保留。赋值为int,比如n_components=1,将把原始数据降到一个维度。赋值为string,比如n_components='mle',将自动选取特征个数n,使得满足所要求的方差百分比。
#
#
# - copy:
# - 类型:bool,True或者False,缺省时默认为True。
# - 意义:表示是否在运行算法时,将原始训练数据复制一份。若为True,则运行PCA算法后,原始训练数据的值不会有任何改变,因为是在原始数据的副本上进 行运算;若为False,则运行PCA算法后,原始训练数据的值会改,因为是在原始数据上进行降维计算。
#
#
# - whiten:
# - 类型:bool,缺省时默认为False
# - 意义:白化,使得每个特征具有相同的方差。关于“白化”,
# - 参考:http://deeplearning.stanford.edu/wiki/index.php/%E7%99%BD%E5%8C%96
#
#
# - svd_solver:
# - 即指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。
# - 有4个可以选择的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大,数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD,使用了scipy库对应的实现。arpack和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,而arpack直接使用了scipy库的sparse SVD实现。默认是auto,即PCA类会自己去在前面讲到的三种算法里面去权衡,选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
#
#
# - random_state:
# - 如果是int,random_state是随机数发生器使用的种子; 如果是RandomState实例,random_state是随机数生成器;
#
#
# ### PCA对象的方法:
#
# - fit(X,y=None):
#
# fit()可以说是scikit-learn中通用的方法,每个需要训练的算法都会有fit()方法,它其实就是算法中的“训练”这一步骤。
# 因为PCA是无监督学习算法,此处y自然等于None。fit(X),表示用数据X来训练PCA模型。
# 函数返回值:调用fit方法的对象本身。比如pca.fit(X),表示用X对pca这个对象进行训练。
#
# - fit_transform(X):
#
# 用X来训练PCA模型,同时返回降维后的数据。
# newX=pca.fit_transform(X),newX就是降维后的数据。
#
# - inverse_transform():
#
# 将降维后的数据转换成原始数据,X=pca.inverse_transform(newX)
#
# - transform(X):
#
# 将数据X转换成降维后的数据。当模型训练好后,对于新输入的数据,都可以用transform方法来降维。
#
# - 此外,还有get_covariance()、get_precision()、get_params(deep=True)、score(X, y=None)等方法。
#
# +
method = 'pca'
if method == "pca":
pca = PCA(n_components=2, whiten=True, random_state=0)
x = pca.fit_transform(X)
print ('The composition of the largest variance:', pca.components_)
print ('Variance in all directions:', pca.explained_variance_)
print ('The proportion of variance:', pca.explained_variance_ratio_)
x1_label, x2_label = 'PC1', 'PC2'
title = 'PCA Dimensionality reduction'
else:
fs = SelectKBest(chi2, k=2)
fs.fit(X, y)
idx = fs.get_support(indices=True)
print ('fs.get_support() = ', idx)
x = X[idx]
x = x.values # 为下面使用方便,DataFrame转换成ndarray
x1_label, x2_label = columns[idx]
title = 'Feature selection'
print (x[:5])
# -
# 预测值
cm_light = mpl.colors.ListedColormap(['#FFF68F', '#EEEEE0', '#BCEE68'])
# 实际值
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
# ### 绘制散点图
#
# - `x[:, 0], x[:, 1]`相当于`x,y`坐标
#
# - `c`是色彩或颜色序列
#
# - `True` 显示网格
#
# - `linestyle` 设置线显示的类型(一共四种)
#
# - `color` 设置网格的颜色
#
# - `linewidth` 设置网格的宽度
#
#
# +
plt.figure(facecolor='w')
#plt.scatter(X[u'花萼长度'][:], X[u'花萼宽度'][:], s=30, c=y, marker='o', cmap=cm_dark)
plt.scatter(x[:, 0], x[:, 1], s=30, c=y, marker='o', cmap=cm_dark)
plt.grid(b=True, ls=':')
plt.xlabel(x1_label, fontsize=14)
plt.ylabel(x2_label, fontsize=14)
plt.title(title, fontsize=18)
# plt.savefig('1.png')
plt.show()
# -
# 随机切分训练数据和测试数据
#
# 每次运行的结果会不同
x, x_test, y, y_test = train_test_split(x, y, train_size=0.7,test_size=0.3)
model = Pipeline([
('poly', PolynomialFeatures(degree=4, include_bias=True)),
('lr', LogisticRegressionCV(Cs=np.logspace(-3, 4, 8), cv=5, fit_intercept=False))
])
model.fit(x, y)
# get_params() 取出之前定义的参数
print ('Optimal parameters:', model.get_params('lr')['lr'].C_)
y_hat = model.predict(x)
print ('Training set accuracy:', metrics.accuracy_score(y, y_hat))
y_test_hat = model.predict(x_test)
print ('Test set accuracy:', metrics.accuracy_score(y_test, y_test_hat))
N, M = 500, 500 # 横纵各采样多少个值
x1_min, x1_max = extend(x[:, 0].min(), x[:, 0].max()) # 第0列的范围
x2_min, x2_max = extend(x[:, 1].min(), x[:, 1].max()) # 第1列的范围
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
x_show = np.stack((x1.flat, x2.flat), axis=1) # 测试点
y_hat = model.predict(x_show) # 预测值
y_hat = y_hat.reshape(x1.shape) # 使之与输入的形状相同
plt.figure(facecolor='w')
plt.pcolormesh(x1, x2, y_hat, cmap=cm_light) # 预测值的显示
plt.scatter(x[:, 0], x[:, 1], s=30, c=y, edgecolors='k', cmap=cm_dark) # 样本的显示
plt.xlabel(x1_label, fontsize=14)
plt.ylabel(x2_label, fontsize=14)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid(b=True, ls=':')
# 画各种图
# a = mpl.patches.Wedge(((x1_min+x1_max)/2, (x2_min+x2_max)/2), 1.5, 0, 360, width=0.5, alpha=0.5, color='r')
# plt.gca().add_patch(a)
patchs = [mpatches.Patch(color='#77E0A0', label='Iris-setosa'),
mpatches.Patch(color='#FF8080', label='Iris-versicolor'),
mpatches.Patch(color='#A0A0FF', label='Iris-virginica')]
plt.legend(handles=patchs, fancybox=True, framealpha=0.8, loc='lower right')
plt.title('Logistic Regression result', fontsize=17)
plt.show()
| DSVC-mod/machinelearning/Lesson1/PCA.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.7 64-bit
# language: python
# name: python3
# ---
# # 04_6 OLS Model
#
# Due to NDA agreements no data can be displayed.
# Data Preparation, Data Cleaning, and Preparation for Modelling is the same for all algorithms. To directly go to modelling click [here](#modelling)
# ---
# ## Data preparation
# ### Import libraries and read data
# +
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt
import sys
sys.path.append("..")
import mlflow
from modeling.config import EXPERIMENT_NAME
TRACKING_URI = open("../.mlflow_uri").read().strip()
# -
# read data
df = pd.read_csv('../data/Featureselection03.csv')
df.head()
# ### Create data frame with important features
# So that everyone is on track with the feature selection, we created another csv file to rate the importance and only use important features for training our models and further analysis.
# Only important features are used to train the model. In this case we use 17 features beside the target.
# read list with feature importance
data_log = pd.read_csv('../data/Capstone_features_Features.csv')
data_log.head()
# ### Create data frame with important features
# Only Features with a feature importance smaller than 3 were selected.
# create list of important features (feature importance < 3)
list_imp_feat = list(data_log[data_log['ModelImportance'] < 3]['VarName'])
len(list_imp_feat)
df_model = df[list_imp_feat].copy()
df_model.info()
# ### Fill and drop NaN
# Values for V.SLPOG.act.PRC and ME.SFCI.act.gPkWh contain missing values. The EDA showed that these are mainly caused during harbour times when the main engine was not running. Therefore it makes sense to fill the missing values with 0.
df_model['V.SLPOG.act.PRC'].fillna(0,inplace=True)
df_model['ME.SFCI.act.gPkWh'].fillna(0,inplace=True)
# The remaining rows with missing values are dropped.
df_model.dropna(inplace=True)
df_model.info()
# ### Check correlations
plt.figure(figsize = (30,28))
sns.heatmap(df_model.corr(), annot = True, cmap = 'RdYlGn')
# V.SOG.act.kn is still highly correlated with the target, but this feature is necessary to keep.
# ### Define Target
# For this project the focus is on optimising the fuel consumption. Therefore the supply mass rate is used as target. Target values greater 8 t/h are defined as outlier.
X = df_model.drop(['ME.FMS.act.tPh'], axis = 1)
y = df_model['ME.FMS.act.tPh']
# ### Train Test Split
# Due to the high amount of data, a split into 10% test data and 90% train data is chosen. The random state is set to 42 to have comparable results for diffent models. To account for the imbalance in the distribution of passage types the stratify parameter is used for this feature. This results in approximately the same percentage of the different passage types in each subset.
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify = X['passage_type'], test_size = 0.1, random_state = 42)
# ### Create dummy values for passage type
# Object types need to be transformed to dummy values. For this model this concerns the passage types.
X_train = pd.get_dummies(X_train, drop_first=True)
X_test = pd.get_dummies(X_test, drop_first=True)
# ### Add constant
# For the OLS model an constant for the y axis section needs to be added.
X_train = sm.add_constant(X_train)
X_test = sm.add_constant(X_test)
# ### Set MLFlow connection
# MLFlow is used to track and compare different models and model settings.
# setting the MLFlow connection and experiment
mlflow.set_tracking_uri(TRACKING_URI)
mlflow.set_experiment(EXPERIMENT_NAME)
mlflow.start_run(run_name='OLS_unscaled') # CHANGE!
run = mlflow.active_run()
# ---
# ## Modelling <a id='modelling'></a>
# For all models in this project a MinMaxScaler is applied. For this model a random forrest is used. The hyperparameter are selected based on grid search and offer a reasonable balance between optimal results and overfitting. These settings are used in a pipeline.
X_train.head()
# Linear regression can be done with and without Feature scaling.
# +
#X_train_scaled = scaler.fit_transform(X_train)
#X_test_scaled = scaler.transform(X_test)
# -
# Setting up the OLS model. In the OLS model the formular for a linear regression is being solved. Therefore we can afterwards have a look at the coefficients to understand feature importance.
lin_reg = sm.OLS(y_train, X_train)
# ### Fit and predict
# Training the OLS model.
model = lin_reg.fit()
model.summary()
# Performing model predictions.
y_pred = model.predict(X_test)
y_pred_train = model.predict(X_train)
# ---
# ## Analysis
# ### Errors and residuals
# The root mean squared error (RMSE) is used to evaluate the model.
print('RMSE train: ', mean_squared_error(y_train, y_pred_train, squared= False))
rmse_train = mean_squared_error(y_train, y_pred_train, squared= False)
print('RMSE test: ', mean_squared_error(y_test, y_pred, squared= False))
rmse_test = mean_squared_error(y_test, y_pred, squared= False)
# Plotting actual values against predicted shows that the points are close to the optimal diagonale. However, this plot and the yellowbrick residual plot show some dificulties the model has when predicting low target values.
fig=plt.figure(figsize=(6, 6))
plt.axline([1, 1], [2, 2],color='lightgrey')
plt.scatter(y_train, y_pred_train, color ='#33424F')
plt.scatter(y_test, y_pred, color = '#FF6600')
#plt.xticks(np.arange(0,501,100));
#plt.yticks(np.arange(0,501,100));
plt.xlabel("ME.FMS.act.tPh actual");
plt.ylabel("ME.FMS.act.tPh predicted");
plt.xlim(-2, 8);
plt.ylim(-2, 8);
# Here it can be seen, that especially while trying to predict lower values for the target the model makes some errors in both directions. For higher values the model underpredicts.
# ---
# ### Write to MLFlow
#seting parameters that should be logged on MLFlow
#these parameters were used in feature engineering (inputing missing values)
#or parameters of the model (fit_intercept for Linear Regression model)
params = {
"features drop": 'according to Capstone_features_Features.csv',
"explanation": 'OLS unscaled',
"csv used": 'Featureselection03.csv',
"NaN handling": 'V.SLPOG.act.PRC and ME.SFCI.act.gPkWh filled with 0, rest dropped by row',
'Shape' : df.shape,
'Scaler' : ''
}
#logging params to mlflow
mlflow.log_params(params)
#setting tags
mlflow.set_tag("running_from_jupyter", "True")
#logging metrics
mlflow.log_metric("train-" + "RMSE", rmse_train)
mlflow.log_metric("test-" + "RMSE", rmse_test)
# logging the model to mlflow will not work without a AWS Connection setup.. too complex for now
# but possible if running mlflow locally
# mlflow.log_artifact("../models")
# mlflow.sklearn.log_model(reg, "model")
mlflow.end_run()
# ## Further Analysis
# ### What are the most important features?
model.params
| notebooks/04_6_Model_OLS.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="cpYpeEfnmWKd"
# 
# + [markdown] id="xl3k8bt-mZIc"
# [](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/tutorials/Certification_Trainings/Healthcare/8.Generic_Classifier.ipynb)
# + [markdown] id="xluzxinzKK-L"
# # 8. Generic Classifier
# + id="MdE588BiY3z1"
import json
from google.colab import files
license_keys = files.upload()
with open(list(license_keys.keys())[0]) as f:
license_keys = json.load(f)
# Defining license key-value pairs as local variables
locals().update(license_keys)
# Adding license key-value pairs to environment variables
import os
os.environ.update(license_keys)
# + id="lmHEkaxRYp0g"
# Installing pyspark and spark-nlp
# ! pip install --upgrade -q pyspark==3.1.2 spark-nlp==$PUBLIC_VERSION
# Installing Spark NLP Healthcare
# ! pip install --upgrade -q spark-nlp-jsl==$JSL_VERSION --extra-index-url https://pypi.johnsnowlabs.com/$SECRET
# + id="2vXOoF1LYXLk" colab={"base_uri": "https://localhost:8080/"} outputId="2ea045e8-2c29-4838-9c5f-b90f326ec062"
import json
import os
from pyspark.ml import Pipeline
from pyspark.sql import SparkSession
from sparknlp.annotator import *
from sparknlp_jsl.annotator import *
from sparknlp.base import *
import sparknlp_jsl
import sparknlp
params = {"spark.driver.memory":"16G",
"spark.kryoserializer.buffer.max":"2000M",
"spark.driver.maxResultSize":"2000M"}
spark = sparknlp_jsl.start(license_keys['SECRET'],params=params)
print (sparknlp.version())
print (sparknlp_jsl.version())
# + id="hx2jxxCaVlOV"
# if you want to start the session with custom params as in start function above
def start(secret):
builder = SparkSession.builder \
.appName("Spark NLP Licensed") \
.master("local[*]") \
.config("spark.driver.memory", "16G") \
.config("spark.serializer", "org.apache.spark.serializer.KryoSerializer") \
.config("spark.kryoserializer.buffer.max", "2000M") \
.config("spark.jars.packages", "com.johnsnowlabs.nlp:spark-nlp_2.11:"+version) \
.config("spark.jars", "https://pypi.johnsnowlabs.com/"+secret+"/spark-nlp-jsl-"+jsl_version+".jar")
return builder.getOrCreate()
#spark = start(secret)
# + colab={"base_uri": "https://localhost:8080/", "height": 219} id="7zP-9FcXVzx7" outputId="86734005-fa74-4b3d-cf63-ddfd3ab2aa3a"
spark
# + [markdown] id="kRPlopbi73s0"
# ## load dataset
# + id="x56EZPuwo1dz"
# !wget -q https://raw.githubusercontent.com/JohnSnowLabs/spark-nlp-workshop/master/tutorials/Certification_Trainings/Healthcare/data/petfinder-mini.csv
# + id="BO3kPToCmiEI"
import pandas as pd
dataframe = pd.read_csv('petfinder-mini.csv')
# + id="HAvADhB2pGf2"
# In the original dataset "4" indicates the pet was not adopted.
import numpy as np
dataframe['target'] = np.where(dataframe['AdoptionSpeed']==4, 0, 1)
# + id="-jhLSk4f4vvK"
dataframe = dataframe.drop(['AdoptionSpeed'], axis=1)
# + colab={"base_uri": "https://localhost:8080/", "height": 600} id="WXKq7djqoRYM" outputId="ab05ea81-bdd2-4d60-af7f-a778dbb7dab5"
dataframe.head()
# + colab={"base_uri": "https://localhost:8080/"} id="TU7e3kmfpkuA" outputId="bed06739-5a0a-4ce8-c742-8c61b4014277"
dataframe.columns
# + colab={"base_uri": "https://localhost:8080/"} id="b1-oWmtXqVNR" outputId="94ddabe8-318d-45e4-e568-3158bcaa6d67"
dataframe.info()
# + colab={"base_uri": "https://localhost:8080/"} id="rPkQpA2KpLrM" outputId="5f456cd7-24d8-461d-969b-17fc071a82f0"
dataframe.target.value_counts()
# + id="vl3Ns5KDrZo1"
dataframe.Description = dataframe.Description.fillna('- no description -')
# + [markdown] id="LwPAtkLZ79di"
# ## Featurize with Sklearn Column Transformer
# + id="C3dSJXWJpf-V"
from sklearn.compose import make_column_transformer
from sklearn.compose import ColumnTransformer
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
column_trans = make_column_transformer(
(OneHotEncoder(), ['Type', 'Breed1', 'Gender', 'Color1', 'Color2', 'MaturitySize',
'FurLength', 'Vaccinated', 'Sterilized', 'Health']),
(TfidfVectorizer(max_features=100, norm='l2', ngram_range=(1, 3)), 'Description'),
remainder=StandardScaler())
X = column_trans.fit_transform(dataframe.drop(['target'], axis=1))
y = dataframe.target
# + colab={"base_uri": "https://localhost:8080/"} id="ZOhgYYNy9NKT" outputId="ca21b3c2-4242-4644-cc98-2ae1a2561bf8"
y.nunique()
# + colab={"base_uri": "https://localhost:8080/"} id="IMQQ1CZx9EsF" outputId="73e0a9b1-cacc-46fb-8861-9cf91b7a2009"
X.shape
# + id="QOWmwxtV82rU"
input_dim = X.shape[1]
# + colab={"base_uri": "https://localhost:8080/"} id="2losjq1jsGEO" outputId="883ce831-6f3f-4618-ab6e-ec6c7897bf52"
input_dim
# + colab={"base_uri": "https://localhost:8080/", "height": 299} id="uaCK_qqVrmjg" outputId="bd<PASSWORD>"
df = pd.DataFrame.sparse.from_spmatrix(X)
df.columns = ['col_{}'.format(i) for i in range(input_dim)]
df['target']= y
df.head()
# + [markdown] id="SR_TzUPr8IZW"
# ## Train with Spark NLP Generic Classifier
# + [markdown] id="fSQtVZp0mBik"
# **Building a pipeline**
#
# The FeaturesAssembler is used to collect features from different columns. It can collect features from single value columns (anything which can be cast to a float, if casts fails then the value is set to 0), array columns or SparkNLP annotations (if the annotation is an embedding, it takes the embedding, otherwise tries to cast the 'result' field). The output of the transformer is a FEATURE_VECTOR annotation (the numeric vector is in the 'embeddings' field).
#
# The GenericClassifierApproach takes FEATURE_VECTOR annotations as input, classifies them and outputs CATEGORY annotations. The operation of the classifier is controled by the following methods:
#
# *setEpochsNumber(int)* - Determines how many epochs the model is trained.
#
# *setBatchSize(int)* - Sets the batch size during training.
#
# *setLearningRate(float)* - Sets the learning rate.
#
# *setValidationSplit(float)* - Sets the proportion of examples in the training set used for validation.
#
# *setModelFile(string)* - Loads a model from the specified location and uses it instead of the default model.
#
# *setFixImbalance(boolean)* - If set to true, it tries to balance the training set by weighting the classes according to the inverse of the examples they have.
#
# *setFeatureScaling(string)* - Normalizes the feature factors using the specified method ("zscore", "minmax" or empty for no normalization).
#
# *setOutputLogsPath(string)* - Sets the path to a folder where logs of training progress will be saved. No logs are generated if no path is specified.
# + colab={"base_uri": "https://localhost:8080/"} id="sBY9w03MsSeL" outputId="299bfcbe-4156-40a8-c7b6-afb3bd9d10f1"
spark_df = spark.createDataFrame(df)
spark_df.select(spark_df.columns[-10:]).show(2)
# + colab={"base_uri": "https://localhost:8080/"} id="7K0C1-1ht5ql" outputId="f6efdbcb-da29-45d0-b130-7cb0c9e3f988"
(training_data, test_data) = spark_df.randomSplit([0.8, 0.2], seed = 100)
print("Training Dataset Count: " + str(training_data.count()))
print("Test Dataset Count: " + str(test_data.count()))
# + [markdown] id="tflMPTT5546m"
# ## Create a custom DL architecture with TF
# + colab={"base_uri": "https://localhost:8080/"} id="7O_OSbLZ53g-" outputId="6e6b61ff-48a0-4405-f60c-fd680332d549"
from sparknlp_jsl.training import tf_graph
# !mkdir gc_graph
tf_graph.print_model_params("generic_classifier")
# + colab={"base_uri": "https://localhost:8080/"} id="ACFg2XDVI_oD" outputId="85bdd64e-e7f6-44b3-ceea-f2a7907f3e1f"
# !pip install -q tensorflow_addons
# + colab={"base_uri": "https://localhost:8080/"} id="dP0o09_d6AQ3" outputId="a82632e9-58d6-48b6-9a4d-f4a2bb47a6a0"
DL_params = {"input_dim": input_dim,
"output_dim": y.nunique(),
"hidden_layers": [300, 200, 100],
"hidden_act": "tanh",
'hidden_act_l2':1,
'batch_norm':1}
tf_graph.build("generic_classifier",build_params=DL_params, model_location="/content/gc_graph", model_filename="auto")
# + id="n7C4Hk8z80zH"
#or just use the one we already have in the repo
# !wget -q https://raw.githubusercontent.com/JohnSnowLabs/spark-nlp-workshop/master/tutorials/Certification_Trainings/Healthcare/generic_classifier_graph/pet.in1202D.out2.pb -P /content/gc_graph
# + id="1zgsiTxjaiMd"
from sparknlp_jsl.base import *
# !mkdir logs
features_asm = FeaturesAssembler()\
.setInputCols(['col_{}'.format(i) for i in range(X.shape[1])])\
.setOutputCol("features")
gen_clf = GenericClassifierApproach()\
.setLabelColumn("target")\
.setInputCols(["features"])\
.setOutputCol("prediction")\
.setModelFile('/content/gc_graph/gcl.302.2.pb')\
.setEpochsNumber(50)\
.setBatchSize(100)\
.setFeatureScaling("zscore")\
.setFixImbalance(True)\
.setLearningRate(0.001)\
.setOutputLogsPath("logs")\
.setValidationSplit(0.2) # keep 20% of the data for validation purposes
clf_Pipeline = Pipeline(stages=[
features_asm,
gen_clf])
# + colab={"base_uri": "https://localhost:8080/"} id="7iF7o4pO9gPu" outputId="2253b7da-7e76-4c38-fad5-873e90b0d899"
# %%time
# train 50 epochs (takes around 45 seconds)
clf_model = clf_Pipeline.fit(training_data)
# + colab={"base_uri": "https://localhost:8080/"} id="k5-LqVDxJdan" outputId="8a7283a6-b0e8-4da2-fb60-bac5af8b520c"
log_file_name = os.listdir("logs")[0]
with open("logs/"+log_file_name, "r") as log_file :
print(log_file.read())
# + id="5A4t1Cgoz69r"
pred_df = clf_model.transform(test_data)
# + colab={"base_uri": "https://localhost:8080/"} id="l-XpLuJz0F8B" outputId="7905411f-37bf-4e2a-a40c-0c6b6dc0bfb4"
pred_df.select('target','prediction.result').show()
# + id="fwm80Jp10fKX"
preds_df = pred_df.select('target','prediction.result').toPandas()
# Let's explode the array and get the item(s) inside of result column out
preds_df['result'] = preds_df['result'].apply(lambda x : int(x[0]))
# + colab={"base_uri": "https://localhost:8080/", "height": 423} id="8v65VDgO0q_5" outputId="d65270b7-29fe-4000-bf99-3275808fa191"
preds_df
# + colab={"base_uri": "https://localhost:8080/"} id="yKoNi5-A98ql" outputId="efe1835e-1dd9-46b1-a6ae-a4a35ee3dc8c"
# We are going to use sklearn to evalute the results on test dataset
from sklearn.metrics import classification_report, accuracy_score
print (classification_report(preds_df['result'], preds_df['target'], digits=4))
print (accuracy_score(preds_df['result'], preds_df['target']))
# + [markdown] id="vdGJZ4pM2mJc"
# ## get prediction for random input
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="1wenY10M1f9b" outputId="87e3638f-2b3a-4799-ab53-b243f2a2797f"
pd.DataFrame([dataframe.loc[5191].to_dict()])
# + id="ZBsXH2bA1fKq"
input_X = column_trans.transform(pd.DataFrame([dataframe.loc[0].to_dict()]).drop(['target'], axis=1))
input_y = dataframe.target[0]
# + colab={"base_uri": "https://localhost:8080/", "height": 174} id="4JZXzm0m2KU8" outputId="7f3567bd-3a08-40c4-a0e2-ab17fac9c3cf"
input_df = pd.DataFrame.sparse.from_spmatrix(input_X)
input_df.columns = ['col_{}'.format(i) for i in range(input_X.shape[1])]
input_df['target']= input_y
input_df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="RMViOtUt2Cg1" outputId="12cd9bb2-c347-4f8f-8b6d-0aa309a5d820"
input_spark_df = spark.createDataFrame(input_df)
input_spark_df.show(2)
# + colab={"base_uri": "https://localhost:8080/"} id="lBMTMech2bZI" outputId="1c2e6a91-1f5f-4d47-f6fc-adcaf7fa9d3b"
clf_model.transform(input_spark_df).select('target','prediction.result').show()
# + [markdown] id="09n9FzjNLwmd"
# # Case Study: Alexa Review Classification
# + id="l0zbA3pwLzr_"
# ! wget -q https://raw.githubusercontent.com/JohnSnowLabs/spark-nlp-workshop/master/tutorials/Certification_Trainings/Public/data/amazon_alexa.tsv
# + colab={"base_uri": "https://localhost:8080/", "height": 423} id="-gSO3zKeL8lW" outputId="bc92ac93-b83c-452d-dd6c-2701db00c50d"
import pandas as pd
df = pd.read_csv('amazon_alexa.tsv', sep='\t')
df
# + id="B0IKND1kMhq8"
df.verified_reviews = df.verified_reviews.str.lower()
# + colab={"base_uri": "https://localhost:8080/"} id="570FBEi7Q0gR" outputId="e640ed22-f153-4e0b-c286-04bdb1df5cfa"
df.feedback.value_counts()
# + id="xVzCLRu-MDdg"
from sklearn.compose import make_column_transformer
from sklearn.compose import ColumnTransformer
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
column_trans = make_column_transformer((OneHotEncoder(), ['rating','variation']),
(TfidfVectorizer(max_features=1000, norm='l2', ngram_range=(1, 3)), 'verified_reviews'))
X = column_trans.fit_transform(df.drop(['feedback'], axis=1))
y = df.feedback
# + colab={"base_uri": "https://localhost:8080/", "height": 299} id="sL410lYGMPuO" outputId="870d6f79-0917-444e-b20f-8eb868302f36"
sdf = pd.DataFrame.sparse.from_spmatrix(X)
sdf.columns = ['col_{}'.format(i) for i in range(X.shape[1])]
sdf['feedback']= y
sdf.head()
# + id="MJSlIYryMsKr"
input_spark_df = spark.createDataFrame(sdf)
# + colab={"base_uri": "https://localhost:8080/"} id="SmamGWQHQMNW" outputId="13d25ce7-6959-4a12-8613-972a2c9f3753"
input_spark_df.show(5)
# + colab={"base_uri": "https://localhost:8080/"} id="OgBri1vkNYuv" outputId="8dd5da27-e4b8-4980-edd2-b9a24ce01add"
(training_data, test_data) = input_spark_df.randomSplit([0.8, 0.2], seed = 100)
print("Training Dataset Count: " + str(training_data.count()))
print("Test Dataset Count: " + str(test_data.count()))
# + id="Iyjpg50wM6ZO"
from sparknlp_jsl.base import *
features_asm = FeaturesAssembler()\
.setInputCols(['col_{}'.format(i) for i in range(X.shape[1])])\
.setOutputCol("features")
gen_clf = GenericClassifierApproach()\
.setLabelColumn("feedback")\
.setInputCols(["features"])\
.setOutputCol("prediction")\
.setModelFile('/content/gc_graph/pet.in1202D.out2.pb')\
.setEpochsNumber(50)\
.setBatchSize(100)\
.setFeatureScaling("zscore")\
.setFixImbalance(True)\
.setLearningRate(0.001)\
.setOutputLogsPath("logs")\
clf_Pipeline = Pipeline(stages=[
features_asm,
gen_clf])
clf_model = clf_Pipeline.fit(training_data)
# + colab={"base_uri": "https://localhost:8080/"} id="UrXXGnOoNYY6" outputId="f1c2cfdc-f7fd-4f47-b596-b954db2ca4ae"
pred_df = clf_model.transform(test_data)
preds_df = pred_df.select('feedback','prediction.result').toPandas()
# Let's explode the array and get the item(s) inside of result column out
preds_df['result'] = preds_df['result'].apply(lambda x : int(x[0]))
# We are going to use sklearn to evalute the results on test dataset
from sklearn.metrics import classification_report, accuracy_score
print (classification_report(preds_df['result'], preds_df['feedback'], digits=4))
print (accuracy_score(preds_df['result'], preds_df['feedback']))
| tutorials/Certification_Trainings/Healthcare/8.Generic_Classifier.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Examples for AbslineSystem Class (v1.0)
# +
# imports
import imp
from astropy.coordinates import SkyCoord
from xastropy.igm.abs_sys import ionclms as xionc
from xastropy.igm.abs_sys import abssys_utils as xabsys
from linetools.spectralline import AbsLine
from linetools.lists.linelist import LineList
xa_path = imp.find_module('xastropy')[1]
# -
# ## Simple instantiation
reload(xabsys)
gensys = xabsys.GenericAbsSystem(NHI=16., zabs=1.244)
gensys.coord = SkyCoord(ra=123.1143*u.deg, dec=-12.4321*u.deg)
gensys
# ### Add some absorption lines
ism = LineList('ISM')
few_lines = [1215.6700, 1334.5323, 1808.0129]*u.AA
for ilin in few_lines:
gensys.lines.append(AbsLine(ilin,linelist=ism))
gensys.lines
# ### Grab a lines matching a given transition
Lya = gensys[1215.670*u.AA]
Lya[0]
# ## Fill with IonClms
allfil = xa_path+'/igm/abs_sys/tests/files/UM184.z2929_MAGE.all'
gensys._ionclms = xionc.IonClms(all_file=allfil)
gensys['SiII']
gensys[(14,2)]
| docs/examples/AbslineSystem_examples.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:anaconda3]
# language: python
# name: conda-env-anaconda3-py
# ---
# + [markdown] nbpresent={"id": "ee6dd7e6-42a5-4fb8-8903-20ebd80d131b"}
# Pandas incorporates two additional data structures into Python, namely Pandas Series and Pandas DataFrame.
#
# - How to import Pandas
# - How to create Pandas Series and DataFrames using various methods
# - How to access and change elements in Series and DataFrames
# - How to perform arithmetic operations on Series
# - How to load data into a DataFrame
# - How to deal with Not a Number (NaN) values
#
# [Pandas Documentation](https://pandas.pydata.org/pandas-docs/stable/)
#
# Pandas Series and DataFrames are designed for fast data analysis and manipulation, as well as being flexible and easy to use. Below are just a few features that makes Pandas an excellent package for data analysis:
#
# - Allows the use of labels for rows and columns
# - Can calculate rolling statistics on time series data
# - Easy handling of NaN values
# - Is able to load data of different formats into DataFrames
# - Can join and merge different datasets together
# - It integrates with NumPy and Matplotlib
# + nbpresent={"id": "947107da-668f-4aaf-ae97-719d04d8b157"}
import pandas as pd
groceries = pd.Series(data=[20,6,'Yes','No'], index=['eggs', 'apples', 'milk', 'bread'])
print(groceries)
# + nbpresent={"id": "7f371a18-18a7-412f-9624-de1343677361"}
print("\nShape:", groceries.shape)
print("Number of dimentions:", groceries.ndim)
print("Size:", groceries.size)
# + nbpresent={"id": "258b19f6-25e7-4458-8136-33dd8601de55"}
print(groceries.index)
print(groceries.values)
# + nbpresent={"id": "a3004573-6adf-4798-b494-b39f5c8ca957"}
'banana' in groceries
# + nbpresent={"id": "371dd79a-0c4b-4149-93ee-1bbc9200a949"}
'bread' in groceries
# + [markdown] nbpresent={"id": "ac0cac39-cd00-40be-a900-79a21298de37"}
# # Accessing and Deleting Elements in Pandas Series
# + nbpresent={"id": "d309d8bb-08f4-41aa-b023-e8a67a55afa6"}
groceries['eggs']
# + nbpresent={"id": "5403fc67-8e45-4ce7-bdae-06d7e4c5a5fe"}
groceries[['eggs','milk']]
# + nbpresent={"id": "0a8f3151-3aa7-4bce-bfa4-f462435e6755"}
groceries[0] # first element
# + nbpresent={"id": "a13eb5c7-c2c0-47d2-845d-00273350dd40"}
groceries[-1] # last element
# + nbpresent={"id": "74f493c8-c926-4411-bb9f-53007624a3c1"}
groceries[[0,-1]]
# + nbpresent={"id": "7b6f696d-b715-4d4b-96ba-8e4909a415f7"}
groceries.loc['eggs'] # explicity using a labeled index
# + nbpresent={"id": "de9711dc-30c0-451e-9568-2317cadc1c44"}
groceries.iloc[2] # explicity using a numeric index
# + nbpresent={"id": "c20d3e91-2dd7-44e5-86ed-44187b7fcd9f"}
groceries['eggs'] = 2
groceries
# + nbpresent={"id": "a297aaef-6137-4f7c-ac8c-ae31fc3bd556"}
groceries.drop('apples') # returns groceries without apples
# + nbpresent={"id": "a29a24d3-baea-4c84-9f1c-2a4a89a8a9e2"}
groceries # apples still in groceries
# + nbpresent={"id": "adb2d514-ddbb-4c7d-b71b-d90015efaa30"}
groceries.drop('apples', inplace=True)
groceries
# + nbpresent={"id": "de207e5d-67c8-492e-be5d-ce9502287113"}
fruits = pd.Series([10, 6, 3], ['apples','oranges','bananas'])
fruits
# + nbpresent={"id": "1fc3d8e6-2e12-4735-a144-39ebd72068c8"}
fruits + 2
# + nbpresent={"id": "5d3c6522-c802-4043-8126-9d99110fff28"}
fruits * 2
# + nbpresent={"id": "1be5d51c-3cd9-438e-b4b4-be7d73796b0d"}
import numpy as np
# + nbpresent={"id": "e49cc7f1-96f8-4fbf-814d-e6eafefa4cec"}
np.sqrt(fruits)
# + nbpresent={"id": "9d285cac-5af9-4c98-8444-4b0d954a21b0"}
np.exp(fruits)
# + nbpresent={"id": "bb80ee6b-cec2-4d69-a474-e2c949a4f406"}
np.power(fruits, 2)
# + nbpresent={"id": "94bf8750-e915-4800-86a9-356f7ca732d1"}
fruits
# + nbpresent={"id": "dbd29911-81b9-4e32-92f1-c626e021a2a8"}
fruits['bananas'] + 2
# + nbpresent={"id": "ced4e723-688f-4048-b4b2-c2a2db293f79"}
fruits.iloc[0] + 1
# + nbpresent={"id": "ec701ea3-04f3-4aef-bafb-d53fecbe2286"}
# double apples and oranges
fruits[['apples', 'oranges']] * 2
# + nbpresent={"id": "1133014b-ba0f-4f4f-82bd-ae002b80b8cd"}
import pandas as pd
# Create a Pandas Series that contains the distance of some planets from the Sun.
# Use the name of the planets as the index to your Pandas Series, and the distance
# from the Sun as your data. The distance from the Sun is in units of 10^6 km
distance_from_sun = [149.6, 1433.5, 227.9, 108.2, 778.6]
planets = ['Earth','Saturn', 'Mars','Venus', 'Jupiter']
# Create a Pandas Series using the above data, with the name of the planets as
# the index and the distance from the Sun as your data.
dist_planets = pd.Series(index=planets, data=distance_from_sun)
print(dist_planets)
# + nbpresent={"id": "e977c0de-6047-4169-8639-f75820000fce"}
# Calculate the number of minutes it takes sunlight to reach each planet. You can
# do this by dividing the distance from the Sun for each planet by the speed of light.
# Since in the data above the distance from the Sun is in units of 10^6 km, you can
# use a value for the speed of light of c = 18, since light travels 18 x 10^6 km/minute.
time_light = dist_planets / 18
print(time_light)
# + nbpresent={"id": "582e7806-0a44-4e03-8cad-7041960a2cd0"}
close_planets = time_light[(time_light < 40)]
# + nbpresent={"id": "7dfa9c0e-bb78-4ddc-9146-b22cca52a2c8"}
print(close_planets)
# + [markdown] nbpresent={"id": "38119c3b-5ea6-40d5-9503-9211a7c3d1a4"}
# ## Creating Pandas DataFrames
# + nbpresent={"id": "729310f6-a411-485d-a480-92cc57e1d15e"}
import pandas as pd
# + nbpresent={"id": "6d32d333-ab01-45a0-89a8-3a6913e2d251"}
# dataframe is like a powerfull spreadsheet
items = {'Bob' : pd.Series(data = [245, 25, 55], index = ['bike', 'pants', 'watch']),
'Alice' : pd.Series(data = [40, 110, 500, 45], index = ['book', 'glasses', 'bike', 'pants'])}
# We print the type of items to see that it is a dictionary
print(type(items))
# + nbpresent={"id": "d5d92ead-8d65-4383-9953-266e9376493e"}
shopping_carts = pd.DataFrame(items)
shopping_carts
# + nbpresent={"id": "8f7b16c4-0df9-4275-a4ce-21a447e2ae8f"}
shopping_carts.shape
# + nbpresent={"id": "8901af71-46bb-40e8-84ad-6af2f3f4c3e5"}
shopping_carts.ndim
# + nbpresent={"id": "33679e6a-c155-4c4b-b168-38ed64f7067e"}
shopping_carts.values
# + nbpresent={"id": "088e597c-b38c-4158-8583-fefcea030b04"}
# We create a list of Python dictionaries
items2 = [{'bikes': 20, 'pants': 30, 'watches': 35},
{'watches': 10, 'glasses': 50, 'bikes': 15, 'pants':5}]
# We create a DataFrame
store_items = pd.DataFrame(items2)
# We display the DataFrame
store_items
# + [markdown] nbpresent={"id": "05cd9fd8-48b1-4852-a861-1c50796eea8e"}
# ## Accessing Elements in Pandas DataFrames
# + nbpresent={"id": "62e9bdda-763e-4a71-bf1d-5a64b2e62a7a"}
# We create a list of Python dictionaries
items2 = [{'bikes': 20, 'pants': 30, 'watches': 35},
{'watches': 10, 'glasses': 50, 'bikes': 15, 'pants':5}]
# We create a DataFrame
store_items = pd.DataFrame(items2, index=['store 1', 'store 2'])
# We display the DataFrame
store_items
# -
# access column labels first
store_items['bikes']['store 1']
store_items['shirts'] = [15, 2]
store_items
store_items['suits'] = store_items['shirts'] + store_items['pants']
store_items
new_items = [{'pants': 30}]
new_store = pd.DataFrame(new_items, index=['store 3'])
new_store
store_items = store_items.append(new_store, sort=True)
store_items
# delete a column with pop
store_items.pop('glasses')
store_items
# delete by axis
store_items = store_items.drop(['bikes'], axis=1) # bikes column
store_items
# delete by row label
store_items = store_items.drop(['store 1'], axis=0)
store_items
store_items = store_items.rename(columns={'pants': 'hats'})
store_items
store_items = store_items.rename(index={'store 3': 'fun'})
store_items
# Dealing with NaN
x = store_items.isnull()
print(x)
# numer of NaNs is sum of logical true
x = store_items.isnull().sum()
print(x)
# sum the results
x = store_items.isnull().sum().sum()
print(x)
store_items.count()
# return a frame eliminating rows with NaN values
store_items.dropna(axis=0) # or store_items.dropna(axis=0, inplace=True)
store_items
# return a frame eliminating columns with NaN values
store_items.dropna(axis=1) # or store_items.dropna(axis=1, inplace=True)
# replace NaNs with 0
store_items.fillna(0)
# forward fill
store_items.fillna(method='ffill', axis=0)
store_items
# backward fill
store_items.fillna(method='backfill', axis=0)
store_items.fillna(method='ffill', axis=1)
# +
import pandas as pd
import numpy as np
# Since we will be working with ratings, we will set the precision of our
# dataframes to one decimal place.
pd.set_option('precision', 1)
# Create a Pandas DataFrame that contains the ratings some users have given to a
# series of books. The ratings given are in the range from 1 to 5, with 5 being
# the best score. The names of the books, the authors, and the ratings of each user
# are given below:
books = pd.Series(data = ['Great Expectations', 'Of Mice and Men', 'Romeo and Juliet', 'The Time Machine', 'Alice in Wonderland' ])
authors = pd.Series(data = ['<NAME>', '<NAME>', '<NAME>', ' <NAME>', '<NAME>' ])
user_1 = pd.Series(data = [3.2, np.nan ,2.5])
user_2 = pd.Series(data = [5., 1.3, 4.0, 3.8])
user_3 = pd.Series(data = [2.0, 2.3, np.nan, 4])
user_4 = pd.Series(data = [4, 3.5, 4, 5, 4.2])
# Users that have np.nan values means that the user has not yet rated that book.
# Use the data above to create a Pandas DataFrame that has the following column
# labels: 'Author', 'Book Title', 'User 1', 'User 2', 'User 3', 'User 4'. Let Pandas
# automatically assign numerical row indices to the DataFrame.
# Create a dictionary with the data given above
dat = {
'Author': authors,
'Book Title': books,
'User 1': user_1,
'User 2': user_2,
'User 3': user_3,
'User 4': user_4
}
# Use the dictionary to create a Pandas DataFrame
book_ratings = pd.DataFrame(dat)
# If you created the dictionary correctly you should have a Pandas DataFrame
# that has column labels: 'Author', 'Book Title', 'User 1', 'User 2', 'User 3',
# 'User 4' and row indices 0 through 4.
print(book_ratings)
# Now replace all the NaN values in your DataFrame with the average rating in
# each column. Replace the NaN values in place. HINT: you can use the fillna()
# function with the keyword inplace = True, to do this. Write your code below:
book_ratings['User 1'].fillna(book_ratings['User 1'].mean(), inplace = True)
book_ratings['User 2'].fillna(book_ratings['User 2'].mean(), inplace = True)
book_ratings['User 3'].fillna(book_ratings['User 3'].mean(), inplace = True)
book_ratings
# -
# ## Loading Data into a Pandas DataFrame
# +
# We load Google stock data in a DataFrame
Google_stock = pd.read_csv('~/workspace/udacity-jupyter/GOOG.csv')
# We print some information about Google_stock
print('Google_stock is of type:', type(Google_stock))
print('Google_stock has shape:', Google_stock.shape)
# -
Google_stock.head()
Google_stock.tail()
Google_stock.isnull().any()
Google_stock['Open'].max()
Google_stock['Open'].min()
Google_stock['Open'].mean()
| notebooks/EssentialPandas.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
import matplotlib.pyplot as plt
import csv
# +
x = []
y = []
with open('SongOne_Output_Output_mono.csv','r') as csvfile:
plots = csv.reader(csvfile, delimiter=',')
for row in plots:
x.append(int(row[0]))
y.append(int(row[1])/1000)
plt.plot(x,y, label='Sound level')
plt.xlabel('x')
plt.ylabel('y (x 1000)')
plt.title('Song Plot')
plt.legend()
plt.show()
# -
| csvtograph.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (clean)
# language: python
# name: python3_clean
# ---
# +
import json
import os
import pickle
import yaml
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from src.preprocessing.old_utils import evaluate
from src.preprocessing.preprocessing import get_Xy_from_sheet, spacy_preprocess_texts
# -
clf = pickle.load(open("models/general_decision-tree.pkl", "rb"))
from matplotlib import pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
def plot_dtree(pkl, path, width, height ):
dtree = pickle.load(open(pkl, "rb"))
fig = plt.figure(figsize = (width,height))
_ = tree.plot_tree(clf, filled = True)
fig1= plt.gcf()
fig1.savefig(path+ ".png")
plot_dtree("models/general_decision-tree.pkl", "results/Figures/general_decision_tree_fig", 20, 40)
| Decision Tree Plotting.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # MCMC algorithm - fitting spectral line
#
# +
# Importing Libraries
import numpy as np
import matplotlib.pyplot as plt
import corner
import emcee
import warnings
warnings.filterwarnings('ignore')
# %matplotlib inline
# +
# We create and artificial spectral line
def get_val(x, p):
m, b, sigma, C, lamb_0 = p
return m*x + b - C*np.exp(-(x-lamb_0)**2 / sigma**2)
# Input parameters of the line
m_truth = -0.7
b_truth = 50.5
lamb_0 = 30.
C = 70.
sigma = 6.
truths = m_truth, b_truth, sigma, C, lamb_0
# We will have a wavelength resolution of 1
data = np.zeros((100, 3)) # make an empty matrix with 3 columns and 100 rows
data[:,0] = np.random.uniform(1, 60, size=100)
data[:,2] = np.random.uniform(5, 15, size=100)
data[:,1] = get_val(data[:,0], truths) + np.random.normal(loc=0,scale=data[:,2],size=100)
# Plot data points
plt.errorbar(data[:,0], data[:,1], yerr=data[:,2], label='Observations', fmt='o')
# Plot Input values
x = np.linspace(0,60,200)
y = get_val(x, truths)
plt.plot(x,y, color='r', linewidth=4, label='Input Model')
plt.xlim(0,60)
plt.ylim(-50,90)
plt.xlabel('Wavelength')
plt.ylabel('Amplitude')
plt.legend()
plt.show()
# +
# Now let's define the posterior probability
def ln_prior(p):
m, b, sigma, C, lamb_0 = p
lp = 0.0
return lp
def ln_likelihood(p, data):
x_vals = data[:,0]
y_vals = data[:,1]
y_errs = data[:,2]
y_model = get_val(x_vals, p)
ll = -0.5 * np.sum(((y_vals - get_val(x_vals,p))/y_errs) ** 2)
return ll
def ln_posterior(p,data):
lp = ln_prior(p)
if np.isinf(lp): return -np.inf
ll = ln_likelihood(p, data)
return lp+ll
# +
# Now we are going to use the MCMC
nwalkers = 10
ndim = 50
# The array of initial positions
initial = np.array([0, 10.0, 5.0, 10., 1.0])
ndim = len(initial)
p0 = [np.array(initial) + 1e-8 * np.random.randn(ndim)
for i in xrange(nwalkers)]
# Create sampler object
sampler = emcee.EnsembleSampler(nwalkers=nwalkers, dim=ndim, lnpostfn=ln_posterior, args=(data,))
# Burn-in
pos,prob,state = sampler.run_mcmc(p0, N=1000)
# +
# Plot the trace
fig, ax = plt.subplots(2,1, figsize=(5,8))
# Plot trace
for i in range(2):
for j in range(nwalkers):
ax[i].plot(sampler.chain[j,:,i], alpha=0.1, color='k')
ax[i].axhline(truths[i], color='r')
plt.show()
# +
# Reset the sampler, restart the sampler at this current position, which we saved from before and called "pos"
sampler.reset()
pos,prob,state = sampler.run_mcmc(pos, N=1000)
corner.corner(sampler.flatchain, truths=truths,labels=["m", "b", "$\sigma$", "C","$\lambda_0$"],
quantiles=[0.16, 0.5, 0.84])
plt.show()
# +
# Plot Input values
plt.errorbar(data[:,0], data[:,1], yerr=data[:,2], label='Observations', fmt='o')
x = np.linspace(0,60,200)
y = get_val(x, truths)
# Plot 24 posterior samples.
samples = sampler.flatchain
for s in samples[np.random.randint(len(samples), size=24)]:
plt.plot(x, get_val(x,s), color="#4682b4", alpha=0.3)
plt.xlim(0,60)
plt.ylim(-50,90)
plt.xlabel('Wavelength')
plt.ylabel('Amplitude')
plt.legend()
plt.show()
# -
# A good test of whether or not the sampling went well is to check the mean acceptance fraction of the ensemble
# This number should be between approximately 0.25 and 0.5 if everything went as planned
print("Mean acceptance fraction: {0:.3f}"
.format(np.mean(sampler.acceptance_fraction)))
| fitting_spectral_line_MCMC.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Day 20
#
# https://adventofcode.com/2020/day/20
import collections
import copy
import enum
import itertools
import math
import typing
import aocd
test_data = """
Tile 2311:
..##.#..#.
##..#.....
#...##..#.
####.#...#
##.##.###.
##...#.###
.#.#.#..##
..#....#..
###...#.#.
..###..###
Tile 1951:
#.##...##.
#.####...#
.....#..##
#...######
.##.#....#
.###.#####
###.##.##.
.###....#.
..#.#..#.#
#...##.#..
Tile 1171:
####...##.
#..##.#..#
##.#..#.#.
.###.####.
..###.####
.##....##.
.#...####.
#.##.####.
####..#...
.....##...
Tile 1427:
###.##.#..
.#..#.##..
.#.##.#..#
#.#.#.##.#
....#...##
...##..##.
...#.#####
.#.####.#.
..#..###.#
..##.#..#.
Tile 1489:
##.#.#....
..##...#..
.##..##...
..#...#...
#####...#.
#..#.#.#.#
...#.#.#..
##.#...##.
..##.##.##
###.##.#..
Tile 2473:
#....####.
#..#.##...
#.##..#...
######.#.#
.#...#.#.#
.#########
.###.#..#.
########.#
##...##.#.
..###.#.#.
Tile 2971:
..#.#....#
#...###...
#.#.###...
##.##..#..
.#####..##
.#..####.#
#..#.#..#.
..####.###
..#.#.###.
...#.#.#.#
Tile 2729:
...#.#.#.#
####.#....
..#.#.....
....#..#.#
.##..##.#.
.#.####...
####.#.#..
##.####...
##..#.##..
#.##...##.
Tile 3079:
#.#.#####.
.#..######
..#.......
######....
####.#..#.
.#...#.##.
#.#####.##
..#.###...
..#.......
..#.###...
"""
Lines = typing.List[str]
def parse_tile_items(line: str) -> typing.Tuple[int, Lines]:
first, *rest = line.split('\n')
assert 'Tile ' in first
parts = first.split(' ')
tile_id = int(parts[1][:-1])
assert len(rest) == len(rest[0]) == len(rest[-1]) # square
return tile_id, rest
def parse_data(data: str) -> typing.Dict[int, Lines]:
data = data[1:] if data[0] == '\n' else data
lines = [line.rstrip('\n') for line in data.split('\n\n')]
return dict(parse_tile_items(line) for line in lines)
def pretty_print(lines: Lines) -> None:
print('\n' + '\n'.join(line for line in lines) + '\n')
# tiles = parse_data(test_data)
tiles = parse_data(aocd.get_data(day=20, year=2020))
len(tiles)
def transpose(lines: Lines) -> Lines:
"""Flips across main diagonal."""
return list(''.join(line) for line in zip(*lines))
def test_transpose(tile) -> bool:
return transpose(transpose(tile)) == tile
assert all(test_transpose(tiles[tile]) for tile in tiles)
def flip(lines: Lines) -> Lines:
"""Flips horizontally."""
return [''.join(reversed(line)) for line in lines]
def test_flip(tile) -> bool:
return flip(flip(tile)) == tile
assert all(test_flip(tiles[tile]) for tile in tiles)
def rotate(lines: Lines) -> Lines:
"""Rotates 90 degrees counter-clockwise."""
return transpose(flip(lines))
def test_rotate(tile) -> bool:
return rotate(rotate(rotate(rotate(tile)))) == tile
assert all(test_rotate(tiles[tile]) for tile in tiles)
class Side(enum.Enum):
TOP = 0
RIGHT = 1
BOTTOM = 2
LEFT = 3
def complement(self):
return Side((self.value + 2) % 4)
class Orientation(enum.Enum):
UNCHANGED = 0
ROTATE_90 = 1
ROTATE_180 = 2
ROTATE_270 = 3
FLIP_HORIZONTAL = 4
FLIP_ROTATE_90 = 5
FLIP_ROTATE_180 = 6
FLIP_ROTATE_270 = 7
@property
def flipped(self) -> bool:
return self.value > 3
@property
def rotations(self) -> int:
return self.value % 4
def apply(self, lines: Lines) -> Lines:
lines = copy.deepcopy(lines)
if self.flipped:
lines = flip(lines)
for _ in range(self.rotations):
lines = rotate(lines)
return lines
@staticmethod
def generate_all(lines: Lines) -> typing.List[Lines]:
group = [copy.deepcopy(lines)]
for _ in range(3):
group.append(rotate(group[-1]))
group.append(flip(lines))
for _ in range(3):
group.append(rotate(group[-1]))
return group
class Borders(typing.NamedTuple):
top: str
right: str
bottom: str
left: str
@classmethod
def from_lines(cls, lines: Lines):
top = lines[0]
bottom = lines[-1]
left = ''.join(line[0] for line in lines)
right = ''.join(line[-1] for line in lines)
return cls(top=top, right=right, bottom=bottom, left=left)
def get(self, side: Side) -> str:
return self[side.value]
def pretty_print(self):
n = len(self.top)
lines = [self.top]
for i in range(1, n-1):
lines.append(self.left[i] + ' '*(n-2) + self.right[i])
lines.append(self.bottom)
print('\n'.join(lines))
class BorderGroup:
def __init__(self, group: typing.List[Lines]):
self.borders = {
Orientation(i): Borders.from_lines(lines)
for i, lines in enumerate(group)
}
self.unique_values = set([
border
for value in self.borders.values()
for border in value
])
def __repr__(self):
return repr(self.borders)
def __getitem__(self, orientation: Orientation):
return self.borders[orientation]
def get(self, *, side: Side, orientation: Orientation) -> str:
return self.borders[orientation].get(side)
def overlap(self, other) -> int:
return len(self.unique_values & other.unique_values)
def matches(self, other) -> bool:
for border in self.unique_values:
for other_border in other.unique_values:
if border == other_border:
return True
return False
class Alignment(typing.NamedTuple):
side: Side
orientation: Orientation
neighbor_orientation: Orientation
class Tile(typing.NamedTuple):
raw: Lines
borders: BorderGroup
@classmethod
def from_lines(cls, lines: Lines):
group = Orientation.generate_all(lines)
return cls(raw=lines, borders=BorderGroup(group))
def get_image(self, orientation: Orientation) -> Lines:
image = orientation.apply(self.raw)
return [line[1:-1] for line in image[1:-1]]
def overlap(self, other) -> int:
return self.borders.overlap(other.borders)
def matches(self, other) -> bool:
return self.borders.matches(other.borders)
def find_alignments(
self,
other,
*,
side: Side,
) -> typing.List[Alignment]:
other_side = side.complement()
alignments = []
orientations = itertools.product(Orientation, repeat=2)
for orientation, other_orientation in orientations:
border = self.borders.get(
side=side,
orientation=orientation,
)
other_border = other.borders.get(
side=other_side,
orientation=other_orientation,
)
if border == other_border:
alignments.append(Alignment(
side=side,
orientation=orientation,
neighbor_orientation=other_orientation,
))
return alignments
def preprocess_data(data) -> typing.Dict[int, Tile]:
tiles = parse_data(data)
return {
tile_id: Tile.from_lines(raw)
for tile_id, raw in tiles.items()
}
# tiles = preprocess_data(test_data)
tiles = preprocess_data(aocd.get_data(day=20, year=2020))
len(tiles)
list(tiles.keys())
class CornerType(enum.Enum):
TOP_LEFT = (Side.RIGHT, Side.BOTTOM)
TOP_RIGHT = (Side.LEFT, Side.BOTTOM)
BOTTOM_RIGHT = (Side.LEFT, Side.TOP)
BOTTOM_LEFT = (Side.RIGHT, Side.TOP)
class MatrixTile(typing.NamedTuple):
tile_id: int
orientation: Orientation
image: Lines
class AdjacencyMatrix(collections.abc.Mapping):
def __init__(self, tiles: typing.Dict[int, Tile]):
n = len(tiles)
assert n == math.isqrt(n) ** 2 # grid must be square
self.tiles = dict(tiles)
self._matrix = None
self._image = None
self.adjacency = collections.defaultdict(list)
for i, tile1 in tiles.items():
others = set(tiles.keys())
others.remove(i)
for j in others:
if tile1.matches(tiles[j]):
self.adjacency[i].append(j)
def __repr__(self):
return repr(self._adjacency)
def __getitem__(self, tile_id):
return self.adjacency[tile_id]
def __len__(self):
return len(self.adjacency)
def __iter__(self):
return iter(self.adjacency)
def count_adjacent(self, tile_id: int) -> int:
return len(self[tile_id])
def is_corner(self, tile_id: int) -> bool:
return self.count_adjacent(tile_id) == 2
@property
def overlaps(self) -> typing.DefaultDict:
overlaps = collections.defaultdict(list)
for i in tiles:
for j in tiles:
if j == i:
continue
overlap = self.tiles[i].overlap(tiles[j])
if overlap > 0:
overlaps[i].append((j, overlap))
return overlaps
@property
def corners(self) -> typing.List[int]:
return [tile for tile in self if self.is_corner(tile)]
def _corner_alignment(
self,
*,
corner_number: int,
corner_type: CornerType,
) -> typing.Dict:
corner_id = self.corners[corner_number]
corner_tile = self.tiles[corner_id]
neighbor_ids = self[corner_id]
alignments = [
(n, a)
for n in neighbor_ids
for side in corner_type.value
for a in corner_tile.find_alignments(
self.tiles[n],
side=side,
)
]
candidates = collections.defaultdict(list)
for n, a in alignments:
key = (corner_id, a.orientation)
value = (a.side, (n, a.neighbor_orientation))
candidates[key].append(value)
return {
key: value
for key, value in candidates.items()
if len(value) == 2
}
def adjacent_alignment(
self,
tile: MatrixTile,
*,
side: Side,
exclude_ids: typing.Optional[typing.Set] = None,
) -> MatrixTile:
if exclude_ids is None:
exclude_ids = set()
neighbor_ids = self[tile.tile_id]
alignments = [
(n, a)
for n in neighbor_ids if n not in exclude_ids
for a in self.tiles[tile.tile_id].find_alignments(
self.tiles[n],
side=side,
) if a.orientation == tile.orientation
]
assert len(alignments) == 1
tile = alignments[0]
tile_id = tile[0]
orientation = tile[1].neighbor_orientation
return MatrixTile(
tile_id=tile_id,
orientation=orientation,
image=self.tiles[tile_id].get_image(orientation),
)
def matrix_top_left(self):
n = math.isqrt(len(self.tiles))
matrix = [[None for _ in range(n)] for _ in range(n)]
candidates = self._corner_alignment(
corner_number=0,
corner_type=CornerType.TOP_LEFT,
)
top_left = list(candidates.items())[0]
corner_id, corner_orientation = top_left[0]
neighbors = dict(top_left[1])
right_id, right_orientation = neighbors[Side.RIGHT]
bottom_id, bottom_orientation = neighbors[Side.BOTTOM]
matrix[0][0] = MatrixTile(
tile_id=corner_id,
orientation=corner_orientation,
image=self.tiles[corner_id].get_image(corner_orientation),
)
matrix[0][1] = MatrixTile(
tile_id=right_id,
orientation=right_orientation,
image=self.tiles[right_id].get_image(right_orientation),
)
matrix[1][0] = MatrixTile(
tile_id=bottom_id,
orientation=bottom_orientation,
image=self.tiles[bottom_id].get_image(bottom_orientation),
)
return matrix
@property
def matrix(self) -> typing.List[typing.List[MatrixTile]]:
if self._matrix is not None:
return self._matrix
matrix = self.matrix_top_left()
n = len(matrix)
exclude_ids = set([
tile.tile_id
for row in matrix
for tile in row if tile is not None
])
for j in range(2, n):
matrix[0][j] = self.adjacent_alignment(
matrix[0][j-1],
side=Side.RIGHT,
)
for j in range(1, n):
matrix[1][j] = self.adjacent_alignment(
matrix[1][j-1],
side=Side.RIGHT,
)
for i in range(2, n):
matrix[i][0] = self.adjacent_alignment(
matrix[i-1][0],
side=Side.BOTTOM,
)
for j in range(1, n):
matrix[i][j] = self.adjacent_alignment(
matrix[i][j-1],
side=Side.RIGHT,
)
self._matrix = matrix
return self._matrix
@property
def image(self) -> Lines:
if self._image is not None:
return self._image
image = []
for row in self.matrix:
tiles = iter(row)
tile = next(tiles)
lines = [line for line in tile.image]
for tile in tiles:
for i, line in enumerate(tile.image):
lines[i] = f'{lines[i]}{line}'
image.extend(lines)
self._image = image
return self._image
adj = AdjacencyMatrix(tiles)
len(adj)
# ### Solution to Part 1
math.prod(adj.corners)
# ### Solution to Part 2
pretty_print(adj.image)
SEA_MONSTER = """
#
# ## ## ###
# # # # # #
"""
class SeaMonster:
def __init__(self, pattern: Lines):
self.pattern = pattern
self.rows = len(pattern)
self.cols = len(pattern[0])
assert all(len(row) == self.cols for row in pattern)
self.pounds = ''.join(adj.image).count('#')
@classmethod
def from_text(cls, text: str):
return cls(text.split('\n')[1:-1])
def __repr__(self):
return f'{self.__class__.__name__}({str(self.pattern)})'
def pretty_print(self) -> None:
return pretty_print(self.pattern)
def magnifier(self, image, *, row: int, col: int) -> None:
lines = [
row[col:(col + self.cols + 1)]
for row in image[row:(row + self.rows + 1)]
]
pretty_print(lines)
def mark_pounds(self, *, row: int, col: int) -> typing.Set:
return set(
(row + j, col + i)
for j in range(self.rows)
for i in range(self.cols)
if self.pattern[j][i] == '#'
)
def check_match(self, image: Lines, *, row: int, col: int) -> bool:
return all(
self.pattern[j][i] == ' ' or image[row+j][col+i] == '#'
for j in range(self.rows)
for i in range(self.cols)
)
def count_matches(self, image: Lines) -> int:
sea_monster_pounds = set()
rows = len(image)
cols = len(image[0])
found = 0
for row in range(rows - self.rows + 1):
for col in range(cols - self.cols + 1):
if self.check_match(image, row=row, col=col):
found += 1
sea_monster_pounds |= self.mark_pounds(row=row, col=col)
water_pounds = [
'#' for j in range(rows) for i in range(cols)
if (j, i) not in sea_monster_pounds and image[j][i] == '#'
]
return found, len(water_pounds)
def search_all(self, image: Lines) -> int:
images = {
Orientation(i): transformed
for i, transformed in enumerate(Orientation.generate_all(image))
}
for orientation, transformed in images.items():
found, water_pounds = self.count_matches(transformed)
if found > 0:
return orientation, found, water_pounds
sea_monster = SeaMonster.from_text(SEA_MONSTER)
sea_monster.pretty_print()
sea_monster.search_all(adj.image)
| Day 20.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Unsupervised Methods ##
from __future__ import division
import pandas as pd
import numpy as np
import scipy as sp
import scipy.sparse as ss
import matplotlib.pyplot as plt
import pylab as pl
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.cluster import AgglomerativeClustering #Ward
from sklearn.preprocessing import Binarizer
# %matplotlib inline
# Dataset imported from R using write.csv(USArrests, "/tmp/USArrests.csv", row.names=FALSE)
# Each row in this dataset corresponds to one of the 50 US states.
usa_df = pd.read_csv("../data/USArrests.csv")
usa_df.head()
usa_df.describe()
# ### Principal Components ###
#
# From the output of describe(), Assault has larger variance compared to other features. This would make Assault dominate the Principal component, so we should standardize the variables.
collist = usa_df.columns[1:]
X = usa_df[collist].values
Xdiv = np.linalg.norm(X, ord=2, axis=1)
usa_df[collist] = X / Xdiv[:, None]
usa_df.head()
usa_df.describe()
# The variances are now comparable. Before doing PCA, we compute similarities between the states and represent as a heatmap. Since the matrix is already normalized, cosine similarity can be computed as a product of X and its transpose (the ||x|| and ||y|| are already built in because of the normalization).
X = usa_df[collist].values
cosim = np.matrix(X) * np.matrix(X.T)
cosim
# +
def heatmap(X, labels):
""" Based on this stack overflow discussion """
""" http://stackoverflow.com/questions/14391959/heatmap-in-matplotlib-with-pcolor """
fig, ax = plt.subplots()
heatmap = ax.pcolor(X, cmap=plt.cm.Blues, alpha=0.8)
# Format
fig = plt.gcf()
fig.set_size_inches(8, 11)
# turn off the frame
ax.set_frame_on(False)
# put the major ticks at the middle of each cell
ax.set_yticks(np.arange(X.shape[0]) + 0.5, minor=False)
ax.set_xticks(np.arange(X.shape[1]) + 0.5, minor=False)
# want a more natural, table-like display
ax.invert_yaxis()
ax.xaxis.tick_top()
# Set the labels
ax.set_xticklabels(labels, minor=False)
ax.set_yticklabels(labels, minor=False)
# rotate the xticks
plt.xticks(rotation=90)
ax.grid(False)
# Turn off all the ticks
ax = plt.gca()
for t in ax.xaxis.get_major_ticks():
t.tick1On = False
t.tick2On = False
for t in ax.yaxis.get_major_ticks():
t.tick1On = False
t.tick2On = False
heatmap(np.array(cosim), usa_df["State"].values)
# -
# PCA seems to consider each row as a component. So doing a PCA.fit(X) will decompose
# our 50x4 matrix to 2x4. So we need to fit the transpose of X (4x50) and transpose the
# resulting principal components 2x50.
pca = PCA(n_components=2)
pca.fit(X.T)
print "Explained variance:", pca.explained_variance_ratio_
X_pr = pca.components_.T
X_pr[0:5, :]
# Calculate cosine similarity using X_pr and plot a heat map
X_pdiv = np.linalg.norm(X_pr, ord=2, axis=1)
X_prn = X_pr / X_pdiv[:, None]
cosim_p = np.matrix(X_prn) * np.matrix(X_prn.T)
cosim_p
heatmap(np.array(cosim_p), usa_df["State"].values)
# The resulting heatmap after PCA has more distinct similarities, which is expected, since PCA tends to highlight the differences. The R example shows a biplot. I couldn't find an example of a biplot in Matplotlib, and in any case, I didn't find the biplot to be as compelling a visual as a heatmap, so went for a heatmap instead.
#
# ### K-Means Clustering ###
#
# For illustration and visualization purposes, the example is restricted to 2 dimensions.
# +
X = np.random.rand(100, 2)
X_mean = 8 + (4 * np.random.rand(4, 2)) # N(8,4)
which = np.random.choice(np.array([0,1,2,3]), size=100, replace=True)
for i in range(0, X.shape[0]):
X[i] = X[i] + X_mean[which[i], :]
# Plot the points
fig, ax = plt.subplots()
ax.scatter(X[which == 0][:, 0], X[which == 0][:, 1], c='blue')
ax.scatter(X[which == 1][:, 0], X[which == 1][:, 1], c='green')
ax.scatter(X[which == 2][:, 0], X[which == 2][:, 1], c='red')
ax.scatter(X[which == 3][:, 0], X[which == 3][:, 1], c='cyan')
# -
# We now cluster these points using K-Means (we use the which values to evaluate the performance later).
# +
kmeans = KMeans(n_clusters=4, n_init=15)
kmeans.fit(X)
ypred = kmeans.predict(X)
# Print confusion matrix. Note that the matrix is not aligned because we don't know
# the correspondence between the assigned cluster and the generated cluster, but the
# matrix should show one high value per row and/or column.
confusion_matrix = np.zeros((4, 4))
for i in range(0, which.shape[0]):
actual = which[i]
predicted = ypred[i]
confusion_matrix[actual, predicted] = confusion_matrix[actual, predicted] + 1
print confusion_matrix
# Plot points with cluster centers (marked with +)
fig, ax = plt.subplots()
ax.scatter(X[which == 0][:, 0], X[which == 0][:, 1], c='blue')
ax.scatter(X[which == 1][:, 0], X[which == 1][:, 1], c='green')
ax.scatter(X[which == 2][:, 0], X[which == 2][:, 1], c='red')
ax.scatter(X[which == 3][:, 0], X[which == 3][:, 1], c='cyan')
for cc in kmeans.cluster_centers_:
ax.plot(cc[0], cc[1], marker='+', color='black', markersize=20)
# -
# ### Hierarchical Clustering ###
#
# We reuse the same data to demonstrate Hierarchical Clustering. R has many more options in this area than Scikit-Learn. The only algorithm available is Ward algorithm - one of the 7 methods available in R's hclust() function.
#
# R also has a built-in plot() method which prints out the dendogram for the clustering. It is [possible to draw a dendogram](http://stackoverflow.com/questions/11917779/how-to-plot-and-annotate-hierarchical-clustering-dendrograms-in-scipy-matplotlib) using data returned
# +
# produce a connectivity matrix based on cosine similarity
norms = np.linalg.norm(X, ord=2, axis=1)
X_n = X / norms[:, None]
cosim = np.matrix(X_n) * np.matrix(X_n.T)
binarizer = Binarizer(threshold=0.5).fit_transform(cosim)
cosim_sparse = ss.csr_matrix(cosim)
# run the clustering
ward = AgglomerativeClustering(n_clusters=4, connectivity=cosim_sparse)
ypred = ward.fit_predict(X)
# compute the confusion matrix for hierarchical clustering
confusion_matrix = np.zeros((4, 4))
for i in range(0, which.shape[0]):
actual = which[i]
predicted = ypred[i]
confusion_matrix[actual, predicted] = confusion_matrix[actual, predicted] + 1
confusion_matrix
# -
| src/chapter10.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# https://docs.python.jp/3/library/calendar.html
# -
import calendar
print(calendar.calendar(2017))
print(calendar.month(2100, 1))
l = calendar.monthcalendar(2100, 1)
print(type(l))
print(l)
print(calendar.weekday(2001, 9, 11)) # Monday: 0, Sunday:6
| notebook/calendar_module.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/dvsseed/PyTorch_CNN_MNIST/blob/master/PyTorch_MNIST_v3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="aI-i0nSsEY4m"
# # CNN—PyTorch—MNIST @Date:2020-08-12
# ##### *以下示範碼執行所需時間約160秒(GPU)、535秒(CPU)*
# ---
#
#
# + [markdown] id="pwTLu5bBY_x-" colab_type="text"
# 
# + [markdown] id="UIaEBSbgOk5e" colab_type="text"
# **CNN--PyTorch Coding**
# 1. 匯入套件
# 2. 使用GPU(加速)或CPU
# 3. 圖片轉換(預處理)
# 4. 準備資料集(MNIST):Train(42,000)、Validation(18,000)、Test(10,000)
# 5. 建立CNN模型(3Conv+3FC)
# 6. 設定CNN參數(Epochs, Learning Rate, Loss function, Optimizer)
# 7. 訓練(checkpoint)CNN模型(計算Accuracy, Loss並顯示結果)
# 8. 預測CNN模型(計算Accuracy, Loss並顯示結果)
# 9. 評估CNN模型-驗證指標(Validation index): 混淆矩陣(Confusion Matrix)
# 10. 調參優化
# 11. 儲存(checkpoint)模型相關數據
# 12. 讀取(checkpoint)模型相關數據
# 13. 測試CNN模型(計算Accuracy, Loss並顯示各類別的結果)
#
# ---
#
#
#
# + [markdown] id="wwufO5vTEZnU" colab_type="text"
# 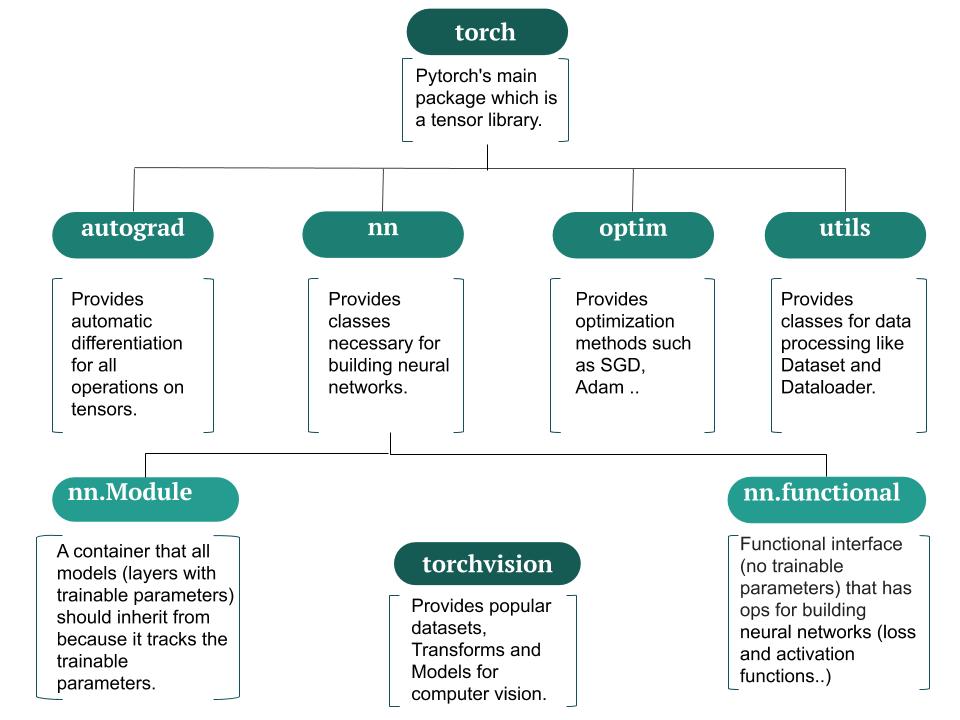
#
# ---
#
#
# + id="IS6ukSuHzHYB" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 101} outputId="99f9be44-6798-4cfc-c5db-8edc9576919d"
# !pip install torch_optimizer # for AdaBound
Checkpoint = 1 # if checkpoint or not
# + [markdown] id="xgC-815gprHN" colab_type="text"
# # **1. 匯入套件**
# + colab_type="code" id="n55IKIvC55w5" colab={}
# Import Libraries
import torch
import torch.nn as nn
# import torch.optim as optim
from torch.optim import lr_scheduler
import torch_optimizer as optim # for AdaBound
import torch.utils.data as dset
import torch.nn.functional as F
from torchvision import datasets, transforms, utils
from torchsummary import summary
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report, confusion_matrix, plot_confusion_matrix
import time
import os
import itertools
from termcolor import colored
# + [markdown] id="cEnbeMu1FSti" colab_type="text"
#
#
# ---
#
#
# 
# + id="tlwz9xQ6SKuB" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 67} outputId="ab46d0a9-6a34-44af-c2e5-5f10519502f9"
model_start = time.time() # start timer
print('PyTorch version:', torch.__version__) # PyTorch version
print('CUDA version:', torch.version.cuda) # Corresponding CUDA version
print('cuDNN version:', torch.backends.cudnn.version()) # Corresponding cuDNN version
# + [markdown] id="Z_JkPhuqFdZ4" colab_type="text"
#
#
# ---
#
#
# 
# + [markdown] id="jfKm0MvNqoAP" colab_type="text"
# # **2. 使用GPU(加速)或CPU**
# + id="484k9_3E8XQn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 84} outputId="816a203e-5b08-4391-8ad7-6c623ddf8be1"
# How many GPUs are there?
if torch.cuda.is_available(): print('GPUs:', torch.cuda.device_count())
# Which GPU Is The Current GPU?
if torch.cuda.is_available(): print('GPU device:', torch.cuda.current_device())
# Get the name of the current GPU
if torch.cuda.is_available(): print('GPU name:', torch.cuda.get_device_name(torch.cuda.current_device()))
# 確認 GPU 是否可用
device = 'cuda:0' if torch.cuda.is_available() else 'cpu'
print('GPU State:', device)
# + [markdown] id="m2jDmBtHFzzO" colab_type="text"
#
#
# ---
#
#
# 
# + [markdown] id="Vf0EKxPkq07T" colab_type="text"
# # **3. 圖片轉換(預處理)**
# + id="Agey2Hm48tY3" colab_type="code" colab={}
# Image Transform
Transform = transforms.Compose(
[
transforms.ToTensor(), # 轉成 Tensor 型態
transforms.Normalize((0.5,), (0.5,)), # 正規化
]
)
# + [markdown] id="UljbzXomGYTq" colab_type="text"
#
#
# ---
#
#
# 
# + [markdown] id="fLbq8-a0q7jc" colab_type="text"
# # **4. 準備資料集(MNIST)**:Train(42,000)、Validation(18,000)、Test(10,000)
# + id="QE5bIq2M9eqd" colab_type="code" colab={}
# Dataset
BatchSize = 16
TrainSet0 = datasets.MNIST(root='MNIST', download=True, train=True, transform=Transform)
TestSet = datasets.MNIST(root='MNIST', download=True, train=False, transform=Transform)
# 切分70%當作訓練集、30%當作驗證集
train_size = int(0.7 * len(TrainSet0))
valid_size = len(TrainSet0) - train_size
TrainSet, ValidSet = torch.utils.data.random_split(TrainSet0, [train_size, valid_size])
TrainLoader = dset.DataLoader(TrainSet, batch_size=BatchSize, shuffle=True) # 打亂數據則將shuffle=True
ValidLoader = dset.DataLoader(ValidSet, batch_size=BatchSize, shuffle=True)
TestLoader = dset.DataLoader(TestSet, batch_size=BatchSize, shuffle=False)
Test10kLoader = dset.DataLoader(TestSet, batch_size=len(TestSet), shuffle=False)
# + [markdown] id="5Ib3L_vNHLEM" colab_type="text"
#
#
# ---
#
#
# 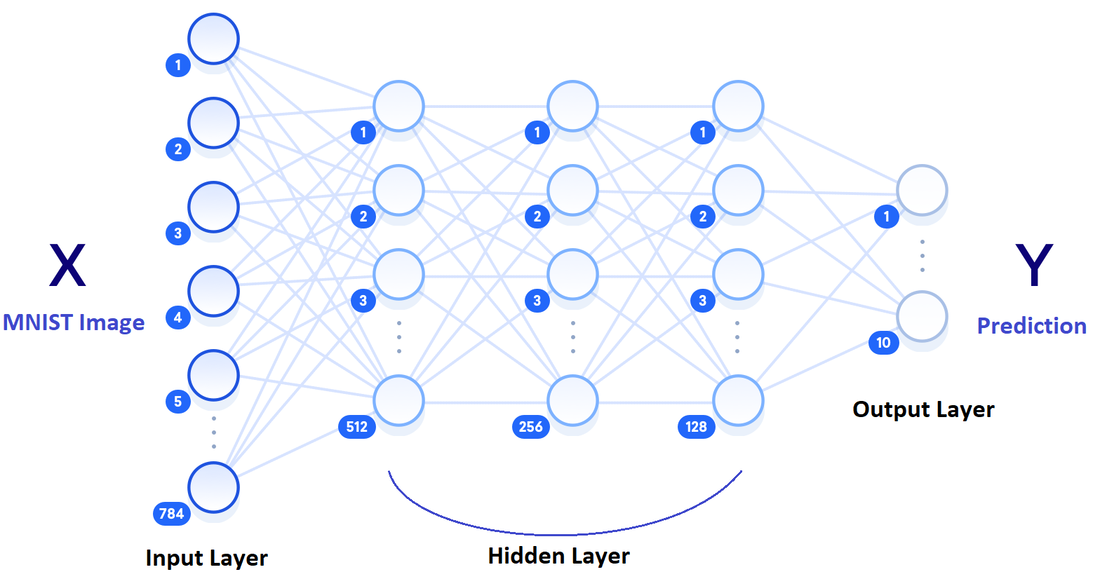
# + [markdown] id="bcnB4oMarLnN" colab_type="text"
# # **5. 建立CNN模型**(3Conv+3FC)
# + colab_type="code" id="A9xVvsbi_OOW" colab={"base_uri": "https://localhost:8080/", "height": 454} outputId="22588da7-c796-4444-d219-36c96a2bda79"
# Define model
class CNNModelClass(nn.Module): # 使用 torch.nn 來建構神經網路
def __init__(self, NumClasses):
super(CNNModelClass, self).__init__()
# # Convolution 1, input_shape=(1,28,28)
self.features = nn.Sequential(
nn.Conv2d(in_channels=1, # input height
out_channels=32, # n_filters
kernel_size=3, # filter size
stride=1, # filter movement/step
padding=1 # if want same width and length of this image after con2d, padding=(kernel_size-1)/2 if stride=1
),
nn.BatchNorm2d(num_features=32),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2, padding=0), # output_shape=(32,14,14)
nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, stride=1, padding=1), # input_shape=(32,14,14)
nn.BatchNorm2d(num_features=64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2, padding=0), # output_shape=(64,7,7)
nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=1, padding=1), # input_shape=(64,7,7)
nn.BatchNorm2d(num_features=128),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2, padding=0) # output_shape=(128,4,4)
)
self.avgpool = nn.AdaptiveAvgPool2d((4, 4))
self.drop_out = nn.Dropout2d(p=0.5)
self.fc_drop = nn.Dropout2d(p=0.5)
self.fc = nn.Sequential(
nn.Linear(in_features=128 * 4 * 4, out_features=512),
nn.ReLU(),
nn.Linear(in_features=512, out_features=512),
nn.ReLU(),
nn.Linear(in_features=512, out_features=NumClasses)
)
def forward(self, x):
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = x.view(-1, 128 * 4 * 4)
# x = self.drop_out(x)
x = self.fc(x)
# x = self.fc_drop(x)
return x
def num_flat_features(self, x):
size = x.size()[1:]
num_features = 1
for s in size:
num_features *= s
return num_features
NumClasses = 10
# Initialize model
model = CNNModelClass(NumClasses).to(device)
print(model) # 列印結構
# + [markdown] id="Fc_0TRv5Knd5" colab_type="text"
#
#
# ---
#
#
# **Dimension Calculations**
#
# * $O=\frac{W−K+2\times P}{S}+1$
# > * O: output height/length
# > * W: input height/length
# > * K: filter size(kernel size)
# > * P: padding, $P=\frac{K−1}{2}$
# > * S: stride
# + [markdown] id="5PqVaSBhI5mn" colab_type="text"
# 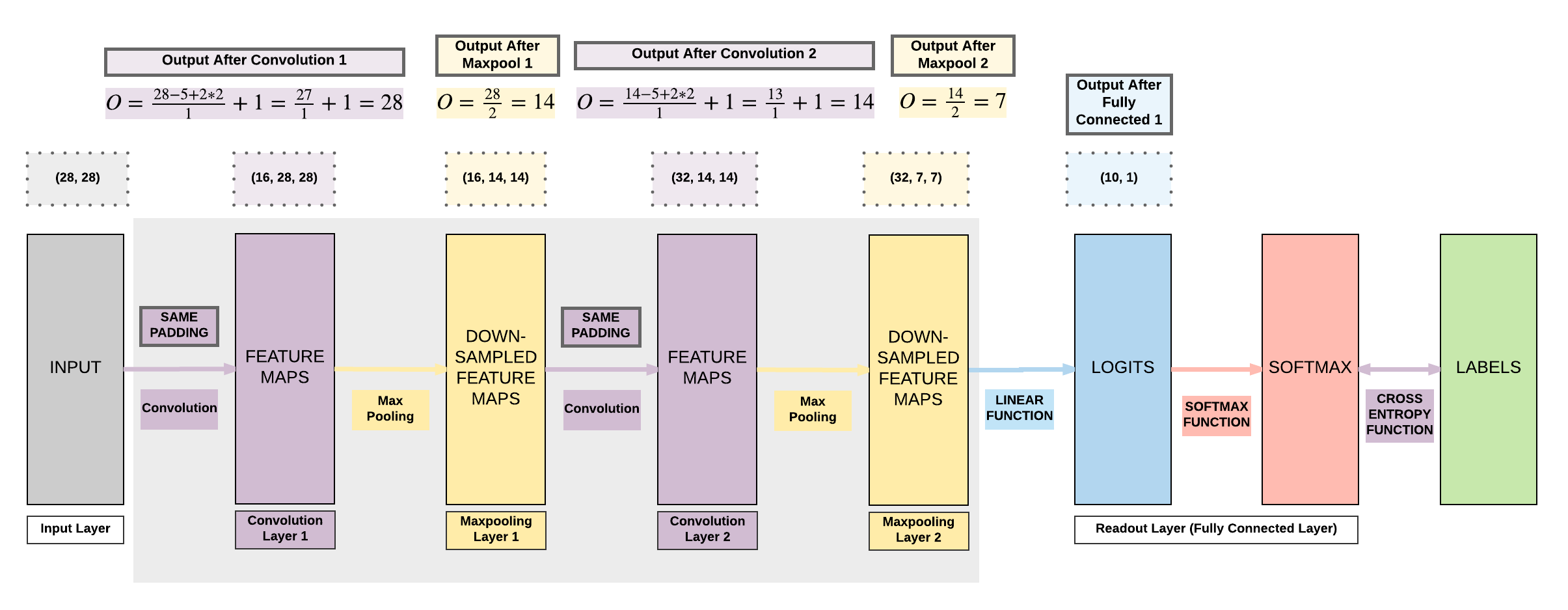
# + id="6y7CxvH9VXuz" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 538} outputId="2df5d18c-6111-42fd-f114-62fd7eef2367"
# 查看模型每層輸出細節, MNIST=(C,H,W)=(1,28,28)
Channels = 1
Height = 28
Width = 28
summary(model, input_size=(Channels, Height, Width), batch_size=BatchSize)
# + id="hYHvZOAlSl8U" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 67} outputId="84647de4-2210-412f-9ffd-1a3f14cf5ec9"
# Counting number parameters in a CNN model
def count_model_layers(model):
conv = 0
fc = 0
for layer in model.modules():
if isinstance(layer, nn.Conv2d):
conv += 1
elif isinstance(layer, nn.Linear):
fc += 1
return conv, fc
num_parameters = sum(torch.numel(parameter) for parameter in model.parameters())
print('Model Params: %.2f M' % (num_parameters / 1e6))
print('Model: Convolutional layer: %s + Fully connected layer: %s' % count_model_layers(model))
params = list(model.parameters())
print(len(params)) # 列印層數
# for name, parameters in model.named_parameters():
# print(name, ':', parameters.size())
# + [markdown] id="qCVL-sDUOTNl" colab_type="text"
#
#
# ---
#
#
# 
# + [markdown] id="YzYeB-9arYi5" colab_type="text"
# # **6. 設定CNN參數**(Epoch, Learning Rate, Loss function, Optimizer)
# + id="lPVuAfm6_4Kd" colab_type="code" colab={}
# Parameters
Epoch = 3 # 訓練的迭代次數
LearningRate = 0.001 # Learning rate,反向傳播的學習率
Criterion = nn.CrossEntropyLoss() # 損失函數(Loss function)
# Initialize optimizer
# Optimizer = optim.Adam(model.parameters(), lr=LearningRate) # 優化器optimize all cnn parameters
Optimizer = optim.AdaBound(model.parameters(), lr=LearningRate, betas=(0.9, 0.999), final_lr=0.1, gamma=1e-3, eps=1e-8, weight_decay=0, amsbound=False)
# change learning rate schedule
Scheduler = lr_scheduler.StepLR(Optimizer, 10, 0.1) # for each 10 epoch, learning rate x 0.1
# + id="M_kmxs_V3qZd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 558} outputId="3549b3cb-93af-47d9-948e-295bcc4e6ca3"
# Print model's state_dict
print('Model\'s state_dict:')
for param_tensor in model.state_dict():
print(param_tensor, '\t', model.state_dict()[param_tensor].size())
# Print optimizer's state_dict
print('Optimizer\'s state_dict:')
for var_name in Optimizer.state_dict():
print(var_name, '\t', Optimizer.state_dict()[var_name])
# + [markdown] id="LKGoFCS1PZkV" colab_type="text"
#
#
# ---
#
#
# 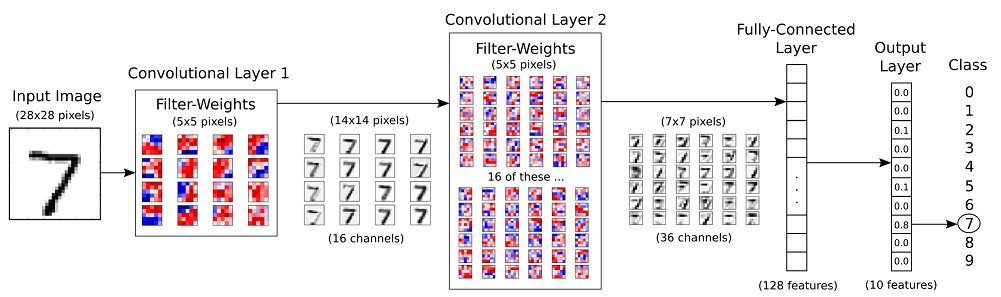
# + [markdown] id="-N4ZKnOTriEz" colab_type="text"
# # **7. 訓練**(checkpoint)**CNN模型**(計算Accuracy, Loss並顯示結果)
# # **8. 預測CNN模型**(計算Accuracy, Loss並顯示結果)
# + colab_type="code" id="5rCbnfZ3VDuN" colab={"base_uri": "https://localhost:8080/", "height": 306} outputId="6088aafe-679c-4270-e95c-b0594aa43240"
# Train、Validation
def training_net(Epoch, trainLoader, Criterion, Optimizer, PATHcp):
if start_epoch == 0:
training_loss = []
validing_loss = []
training_accuracy = []
validing_accuracy = []
else:
checkpoint = torch.load(PATHcp, map_location='cpu')
training_loss = checkpoint['training_loss']
validing_loss = checkpoint['validing_loss']
training_accuracy = checkpoint['training_accuracy']
validing_accuracy = checkpoint['validing_accuracy']
for epoch in range(start_epoch, Epoch):
Scheduler.step()
train_start = time.time()
train_losss = 0.0
t_loss = 0.0
train_correct = 0
train_total = 0
model.train()
for times, tdata in enumerate(TrainLoader):
tinputs, tlabels = tdata[0].to(device), tdata[1].to(device)
# 反向傳播(Backward propagation), 計算loss function更新模型的權重
# Zero the parameter gradients, 將參數、梯度緩衝區歸零
Optimizer.zero_grad()
# Foward + backward + optimize
toutputs = model(tinputs)
_, predicted = torch.max(toutputs.data, 1)
train_total += tlabels.size(0)
train_correct += (predicted == tlabels).sum().item()
train_loss = Criterion(toutputs, tlabels)
train_loss.backward()
train_accuracy = 100 * train_correct / float(train_total)
train_losss += train_loss.item()
t_loss = train_losss / (float(train_total) / BatchSize)
Optimizer.step()
training_accuracy.append(train_accuracy)
training_loss.append(t_loss)
# Print statistics
print('Epoch: [%d/%d, %d/%d] - <Train>, loss: %.6f, accuracy: %.4f %%, duration: %.4f sec' % (
(epoch + 1),
Epoch,
(times + 1),
len(TrainLoader),
t_loss,
train_accuracy,
(time.time() - train_start))
)
valid_start = time.time()
valid_losss = 0.0
v_loss = 0.0
valid_correct = 0
valid_total = 0
model.eval()
for times, vdata in enumerate(ValidLoader):
vinputs, vlabels = vdata[0].to(device), vdata[1].to(device)
voutputs = model(vinputs)
_, predicted = torch.max(voutputs.data, 1)
valid_total += vlabels.size(0)
valid_correct += (predicted == vlabels).sum().item()
valid_loss = Criterion(voutputs, vlabels)
valid_accuracy = 100 * valid_correct / float(valid_total)
valid_losss += valid_loss.item()
v_loss = valid_losss / (float(valid_total) / BatchSize)
validing_accuracy.append(valid_accuracy)
validing_loss.append(v_loss)
# Print statistics
print('Epoch: [%d/%d, %d/%d] - <Validation>, loss: %.6f, accuracy: %.4f %%, duration: %.4f sec' % (
(epoch + 1),
Epoch,
(times + 1),
len(ValidLoader),
v_loss,
valid_accuracy,
(time.time() - valid_start))
)
# Checkpoint
# print('Checkpoint ...')
torch.save({'optimizer_state_dict': Optimizer.state_dict(),
'model_state_dict': model.state_dict(),
'epoch': epoch + 1,
'training_loss': training_loss,
'validing_loss': validing_loss,
'training_accuracy': training_accuracy,
'validing_accuracy': validing_accuracy}, PATHcp)
return training_loss, training_accuracy, validing_loss, validing_accuracy
# Checkpoint
PATHcp = './checkpoint.pth'
if Checkpoint:
if os.path.exists(PATHcp):
os.remove(PATHcp)
if os.path.exists(PATHcp):
print(colored('Restart from checkpoint {}'.format(PATHcp), 'blue'))
checkpoint = torch.load(PATHcp, map_location='cpu')
Optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
model.load_state_dict(checkpoint['model_state_dict'])
if torch.cuda.is_available():
model.cuda()
else:
model = model.cpu()
start_epoch = checkpoint['epoch']
training_loss = checkpoint['training_loss']
validing_loss = checkpoint['validing_loss']
training_accuracy = checkpoint['training_accuracy']
validing_accuracy = checkpoint['validing_accuracy']
else:
print(colored('No checkpoint file at {}'.format(PATHcp), 'blue'))
start_epoch = 0
if torch.cuda.is_available():
model = model.cuda()
else:
model = model.cpu()
print('Started Training.')
training_loss, training_accuracy, validing_loss, validing_accuracy = training_net(Epoch, TrainLoader, Criterion, Optimizer, PATHcp)
print('Finished Training.')
# + colab_type="code" id="TUEEnLZss-GX" colab={"base_uri": "https://localhost:8080/", "height": 573} outputId="9631918e-0c15-45e7-933f-9afc78995470"
# 訓練、預測結果視覺化(visualization)
plt.plot(range(Epoch), training_loss, 'b--', label='Training_loss')
plt.plot(range(Epoch), validing_loss, 'g-', label='Validating_loss')
plt.title('Training & Validating loss')
plt.xlabel('Number of epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.plot(range(Epoch), training_accuracy, 'b--', label='Training_accuracy')
plt.plot(range(Epoch), validing_accuracy, 'g-', label='Validating_accuracy')
plt.title('Training & Validating accuracy')
plt.xlabel('Number of epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
# + [markdown] id="XERAYfg-QuX0" colab_type="text"
#
#
# ---
#
#
# 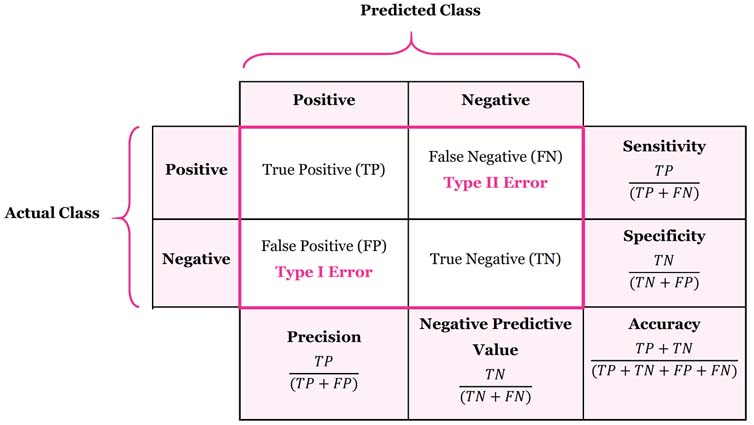
# 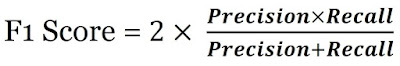
# + [markdown] id="sqb96VB7r9w1" colab_type="text"
# # **9. 評估CNN模型**-驗證指標(Validation index): 混淆矩陣(Confusion Matrix)
# + colab_type="code" id="68bp4VmegUYw" colab={"base_uri": "https://localhost:8080/", "height": 748} outputId="6bdf2b78-6274-4733-8834-25f1023dc9b5"
# 混淆矩陣(Confusion Matrix)
class_names = ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9')
def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion Matrix', cmap=plt.cm.Blues):
if normalize:
cm = cm / cm.sum(axis=1)[:, np.newaxis]
print(title)
# print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.4f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i,
format(cm[i, j], fmt),
horizontalalignment='center',
color='white' if cm[i, j] > thresh else 'black')
def evaluate(ValidLoader):
confusion_matrix = torch.zeros(NumClasses, NumClasses)
with torch.no_grad():
model.eval()
for inputs, labels in ValidLoader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
_, predicted = torch.max(outputs, 1)
for true, pred in zip(labels.view(-1), predicted.view(-1)):
confusion_matrix[true.long(), pred.long()] += 1
# print('Confusion Matrix:\n{}'.format(confusion_matrix.data.numpy()))
precision = confusion_matrix.diag() / confusion_matrix.sum(1)
print('Precision: {}'.format(precision.data.numpy()))
recall = confusion_matrix.diag() / confusion_matrix.sum(0)
print('Recall: {}'.format(recall.data.numpy()))
f1 = 2 * (precision * recall) / (precision + recall)
print('F1 Score: {}'.format(f1.data.numpy()))
mean = f1.mean()
print('Mean: {:.6f}'.format(mean))
# Plot normalized confusion matrix
plt.figure(figsize=(10, 10))
plot_confusion_matrix(confusion_matrix, classes=class_names, normalize=True, title='Normalized Confusion Matrix')
plt.show()
print('Started Evaluating.')
evaluate(ValidLoader)
print('Finished Evaluating.')
# + [markdown] id="C2t8ybjmsEmV" colab_type="text"
# # **11. 儲存**(checkpoint)**模型**相關數據
# + id="P3uzv_9V4ccp" colab_type="code" colab={}
# Saving a General Checkpoint for Inference and/or Resuming Training
# Save final model
PATH = './model.pth'
torch.save({'epoch': Epoch,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': Optimizer.state_dict(),
'loss': Criterion,
'training_loss': training_loss,
'validing_loss': validing_loss,
'training_accuracy': training_accuracy,
'validing_accuracy': validing_accuracy}, PATH)
# + [markdown] id="Q8XdaUgUsPEO" colab_type="text"
# # **12. 讀取**(checkpoint)**模型**相關數據
# + id="o4r2mTFA-VYd" colab_type="code" colab={}
# Loading a General Checkpoint for Inference and/or Resuming Training
model = CNNModelClass(NumClasses).to(device)
# optimizer = TheOptimizerClass(*args, **kwargs)
checkpoint = torch.load(PATH)
model.load_state_dict(checkpoint['model_state_dict'])
Optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
Epoch = checkpoint['epoch']
Criterion = checkpoint['loss']
# + [markdown] id="oH4OJR9WSQ8s" colab_type="text"
#
#
# ---
#
#
# 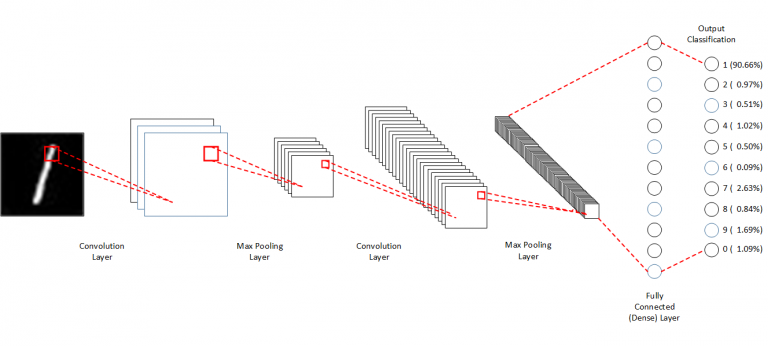
#
# + [markdown] id="K1-HXeL_sY6c" colab_type="text"
# # **13. 測試CNN模型**(計算Accuracy, Loss並顯示各類別的結果)
# + id="R24rvBcNBhPF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 235} outputId="f21049fb-2ba7-4a41-c5cd-0969421c0d50"
# Test
def testing_net(TestLoader):
test_start = time.time()
test_losss = 0.0
t_loss = 0.0
test_correct = 0
test_total = 0
model.eval() # 模型評估模式,沒有要繼續訓練模型、而只拿來應用
with torch.no_grad():
for data in TestLoader:
inputs, labels = data
inputs, labels = inputs.to(device), labels.to(device)
outputs = model(inputs)
_, predicted = torch.max(outputs.data, 1)
test_loss = Criterion(outputs, labels)
test_total += labels.size(0)
test_correct += (predicted == labels).sum().item()
test_accuracy = 100 * test_correct / float(test_total)
test_losss += test_loss.item()
t_loss = test_losss / (float(test_total) / BatchSize)
print('Accuracy of the network on the 10000 test images: %.4f %%, loss: %.4f, duration: %.4f sec' % (
test_accuracy,
t_loss,
(time.time() - test_start)
)
)
print('Started Testing.')
testing_net(TestLoader)
print('Finished Testing.')
class_correct = [0 for i in range(10)]
class_total = [0 for i in range(10)]
with torch.no_grad():
model.eval() # 模型評估模式
for data in TestLoader:
inputs, labels = data[0].to(device), data[1].to(device)
outputs = model(inputs)
_, predicted = torch.max(outputs, 1)
correct = (predicted == labels).squeeze()
for i in range(10):
label = labels[i]
class_correct[label] += correct[i].item()
class_total[label] += 1
# print(class_correct)
# print(class_total)
# 列印10個類別的Accuracy
for i in range(len(class_total)):
print('Accuracy of class[%d]: %3f' % (i, (class_correct[i] / class_total[i])))
# + id="bf08ndI4JH7A" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="b597200c-b1b4-428f-e714-8b2259394e86"
# 只測試一張圖片
correct = 0
total = 0
num = 1000 # 第1000張圖片
model.eval() # 模型評估模式,沒有要繼續訓練模型、而只拿來應用
with torch.no_grad():
for data in Test10kLoader:
inputs, labels = data
inputs, labels = inputs.to(device), labels.to(device)
inputs = inputs[num].view((-1,1,28,28), -1)
outputs = model(inputs)
_, predicted = torch.max(outputs.data, 1)
total += 1
correct += (predicted == labels[num]).sum().item()
break
print('Accuracy of the network on the #%d test image: %f %% -> [predict: %d, label: %d]' % (
num,
(100 * correct / total),
predicted,
labels[num]
)
)
# + id="SoAlPYhWIFLh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 112} outputId="1136018b-7561-49d2-d186-97b0795275d4"
# Test the network on the test data
# functions to show an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
dataiter = iter(TestLoader)
images, labels = dataiter.next()
# print images
imshow(utils.make_grid(images[:8]))
print('GroundTruth:', ''.join('%3s' % class_names[labels[j]] for j in range(8)))
# + id="ZH5la88-AMkC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="521db506-6d36-4a68-fd4b-b6039fe4006a"
# Elapsed time
print('The elapsed time(ET) of this CNN model: [%.4f sec]' % (time.time() - model_start))
| PyTorch_MNIST_v3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
url="https://olympics.com/tokyo-2020/olympic-games/en/results/all-sports/medal-standings.htm"
dfs = pd.read_html(url)
dfs[0].rename(columns={'Unnamed: 2': 'Gold Medal',
'Unnamed: 3': 'Silver Medal',
'Unnamed: 4': 'Bronze Medal',
'RankbyTotal':'Rank by Total'},
inplace=True, errors='raise')
dfs[0]
dfs[0].to_csv('Combined.csv', index = False, header = True)
dfs[1].rename(columns={'Unnamed: 1': 'Gold Medal',
'Unnamed: 2': 'Silver Medal',
'Unnamed: 3': 'Bronze Medal'},
inplace=True, errors='raise')
dfs[1]
dfs[1].to_csv('Men.csv', index = False, header = True)
dfs[2].rename(columns={'Unnamed: 1': 'Gold Medal',
'Unnamed: 2': 'Silver Medal',
'Unnamed: 3': 'Bronze Medal'},
inplace=True, errors='raise')
dfs[2]
dfs[2].to_csv('Women.csv', index = False, header = True)
dfs[3].rename(columns={'Unnamed: 1': 'Gold Medal',
'Unnamed: 2': 'Silver Medal',
'Unnamed: 3': 'Bronze Medal'},
inplace=True, errors='raise')
dfs[3]
dfs[3].to_csv('Mixed.csv', index = False, header = True)
dfs[4].rename(columns={'Unnamed: 1': 'Gold Medal',
'Unnamed: 2': 'Silver Medal',
'Unnamed: 3': 'Bronze Medal'},
inplace=True, errors='raise')
dfs[4]
dfs[4].to_csv('Open.csv', index = False, header = True)
# # by using beautifull soup!!
# +
import requests
from bs4 import BeautifulSoup
page = requests.get(url)
soup = BeautifulSoup(page.text, 'html.parser')
dfs = pd.read_html(page.text)
# -
dfs[0]
| 1-Data-preprocessing-gathering/Untitled2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.5 64-bit
# name: python3
# ---
# # Opals
#
# Explore performance of Opals players using WNBL data
#
# +
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
import wnbl
data_path = "..\\data"
# -
opals_df = wnbl.load_csv(data_path,'opals.csv')
opals_df.head()
# concatenate all teams by season info, drop duplicates to define unique TeamID and name mapping
# select files prefixed with "teams" in "teams" subfolder
teams_df = wnbl.load_csv(os.path.join(data_path,'teams'),'teams')
teams_df = teams_df.drop_duplicates().reset_index()
teams_df.info()
# +
# concatenate all players by season stats
players_df = wnbl.load_csv(os.path.join(data_path,'players'),'players',include_id=True)
# fix html encoded apostrophes iin names
players_df['Player'] = players_df['Player'].str.replace("'","'")
players_df.info()
# +
# load seasons (maps year to competition)
# seasons_df = pd.read_csv(os.path.join(data_path,'seasons.csv'))
seasons_df = wnbl.load_csv(data_path,'seasons.csv')
# identify current seasons
comp_id = seasons_df['CompID'].max()
# -
seasons_df.info()
print(players_df.shape)
print(seasons_df.shape)
print(teams_df.shape)
print(opals_df.shape)
# merge players and seasons so we can plot by date
players_df = players_df.merge(seasons_df,on='CompID',how='left')
players_df = players_df.merge(teams_df,on='TeamID',how='left')
# players_df = players_df.rename(columns={'Team_y':'Team'})
# +
# New features
da = players_df
# efficiency
da['EFF'] = da['PTS'] + da['REB'] + da['AST'] + da['STL'] + da['BLK'] - (da['FGA'] - da['FGM']) - (da['3PA'] - da['3PM']) - (da['FTA'] - da['FTM']) - da['TO']
# efficiency per game
da['EPG'] = da['EFF'] / da['G']
# -
players_df.info()
opals_data_df = pd.merge(da,opals_df,left_on='Player',right_on='Name')
opals_data_df.drop(columns=['Name','Team_y'],inplace=True)
opals_data_df.rename(columns={'Team_x':'Team'},inplace=True)
opals_data_df.info()
# +
# filter by current season to identify current team for each player
tmp = opals_data_df[['Player','Team','CompID']]
tmp = tmp[tmp['CompID']==comp_id]
# identify current team for these top players
current_teams = tmp[['Player','Team']]
# +
tmp = opals_data_df[['Player','Team','CompID']]
a = tmp.groupby(['Player'], sort=False)['CompID'].max()
a
# -
# concatenate current team with player
tmp = opals_data_df[['Player','Team','Year','EPG','Position','Height']]
tmp = tmp.merge(current_teams,on='Player')
tmp['Player-Team'] = tmp['Player'] + ' (' + tmp['Team_y'] + ') ' + '\n Pos: ' + tmp['Position'] + ' '+ ' Height: ' + tmp['Height'].astype('str') + ' '
# order player positions
t = pd.CategoricalDtype(categories=['G', 'F','C'], ordered=True)
tmp['sort']=pd.Series(tmp.Position, dtype=t)
tmp.sort_values(by=['sort','Player','Height'],ascending=[True,True,True],ignore_index=True,inplace=True)
tmp.info()
# +
# facet plot of top player historial EPG
# Create a grid : initialize it
g = sns.FacetGrid(tmp.sort_values(by=['sort','Height','Year']), col='Player-Team', hue='Position', col_wrap=5)
# Add the line over the area with the plot function
g = g.map(plt.plot, 'Year', 'EPG')
# Fill the area with fill_between
g = g.map(plt.fill_between, 'Year', 'EPG', alpha=0.2).set_titles("{col_name} Player-Team")
# Control the title of each facet
g = g.set_titles("{col_name}")
# Add a title for the whole plot
plt.subplots_adjust(top=0.85)
sns.set(rc={'figure.figsize':(12,8)})
g = g.fig.suptitle('Historical Performance of Prospective Opals Players using WNBL Data')
plt.text(2020,-13,"linkedin.com/in/evassiliadis",ha='right',alpha=0.5)
plt.text(2020,-16,"github.com/vass1138/wnbl",ha='right',alpha=0.5)
plt.savefig('wnbl_opals_history.png')
plt.show()
# +
# Repeat for Twitter
# facet plot of top player historial EPG
# Create a grid : initialize it
g = sns.FacetGrid(tmp.sort_values(by=['sort','Height','Year']), col='Player-Team', hue='Position', col_wrap=5)
# Add the line over the area with the plot function
g = g.map(plt.plot, 'Year', 'EPG')
# Fill the area with fill_between
g = g.map(plt.fill_between, 'Year', 'EPG', alpha=0.2).set_titles("{col_name} Player-Team")
# Control the title of each facet
g = g.set_titles("{col_name}")
# Add a title for the whole plot
plt.subplots_adjust(top=0.85)
sns.set(rc={'figure.figsize':(12,6)})
g = g.fig.suptitle('Historical Performance of Prospective Opals Players using WNBL Data')
plt.text(2020,-13,"linkedin.com/in/evassiliadis",ha='right',alpha=0.5)
plt.text(2020,-16,"github.com/vass1138/wnbl",ha='right',alpha=0.5)
plt.savefig('wnbl_opals_history_twitter.png')
| scripts/opals.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Converting Wikipedia Articles for Deletion (*AfD*) dataset into ConvoKit format
# In this notebook we are going to convert Wikipedia Articles for Deletion [dataset](https://github.com/emayfield/AFD_Decision_Corpus) by <NAME> and <NAME> into ConvoKit format.
#
# Here is an example of Wikipedia Article for Deletion page: https://en.wikipedia.org/wiki/Wikipedia:Articles_for_deletion/Andrew_Nellis
import pandas as pd
from convokit import Corpus, Speaker, Utterance
import re
# import glob, os, csv
import json
import numpy as np
from tqdm import tqdm
# ## Load the data
# Instructions on how to download `afd_2019_full_policies.json` as well as `pandas_afd` directory can be found [here](https://github.com/emayfield/AFD_Decision_Corpus).
with open("afd_2019_full_policies.json", 'r') as f:
afd = json.load(f)
afd.keys()
# We are also going to use `users_df.csv` file, as it provides more information on Wikipedia users than `afd_2019_full_policies.json` does.
users_df = pd.read_csv("pandas_afd/users_df.csv")
# ## Create Speaker Objects
users_df = users_df.drop(columns=['Unnamed: 0'])
users_df.head(5)
# Certain users are repeated in the csv file. In cases of duplicates, we will only include the last occurence of the user
pd.concat(g for _, g in users_df.groupby("user_id") if len(g) > 1)
# Modify the dataframe to only contain meta information for speakers and create the speaker objects.
speaker_meta = users_df.replace({np.nan:None}).drop_duplicates(subset=['user_id'], keep='last').set_index('user_id').T.to_dict()
speaker_objects = {}
for s_id in speaker_meta:
speaker_objects[str(s_id)] = Speaker(id=str(s_id), meta=speaker_meta[s_id])
len(speaker_objects)
# Number of speakers in the full dataset is 179859.
#
# Here are examples of speaker objects:
speaker_objects['200000582']
speaker_objects['200000003']
# ## Create Utterance Objects
# Here, we are going to use data from Contributions list of `afd_2019_full_policies.json` dictionary. Mayfield data categorizes contributions into three classes: ***nominations*** for deletion (these tend to happen at the beginning of the disucssion, but not all discussions start with a nomination), ***votes*** by users to delete/keep the article followed by a rationale for the vote, and general ***non-voting comments*** made by users.
#
# Below are examples of a nomination, a vote, and a non-voting comment, in that respective order:
afd['Contributions'][0], afd['Contributions'][1], afd['Contributions'][10]
# **Observe that** `parent` key in each of the contribution dictionaries has a value of `-1`. At this point Mayfield data does not have any information on the conversation structure, from which we can extract reply-to chains. So, to make sure that ConvoKit checks do not throw errors, we are going to introduce the following structure:
# * Every first utterance (nomination, vote, or a non-voting comment) we encounter in the discussion does not have a parent utterance (i.e. reply-to is None)
# * Voting comments and nominations (if they are not already first in the discussion) are replies to the first utterance in the discussion
# * Non-voting comments are replies to either (i) the previous vote or (ii) the first utterance in the discussion if no vote has been cast yet.
# +
utterance_objects = {}
seen_discussions = {}
previous_vote = '', '' #the last voting comments & discussion it occurred in
# We are also going to get citations information for each contributions from Citations list
citations_dct = {str(d['ID']): d['Citations'] for d in afd['Citations']}
for contribution in tqdm(afd['Contributions']):
c_id = str(contribution['ID'])
c_meta = {'citations': citations_dct.get(c_id, [])}
c_speaker = str(contribution['User'])
c_conversation_id = str(contribution['Discussion'])
c_timestamp = contribution['Timestamp']
#keep track of the first contribution in the discussion we encounter
if c_conversation_id not in seen_discussions:
seen_discussions[c_conversation_id] = c_id
#if the contribution is a vote
if c_id[0] == '4':
c_meta.update({'type': 'vote',
'label': contribution['Label'],
'raw_label':contribution['Raw']})
#replace mask the bolded expression with a "VOTE"
c_text = re.sub("\'\'\'[^\']+\'\'\'", "VOTE", contribution['Rationale'])
#votes are replies to the first contribution/utterance in the discussion
c_reply_to = seen_discussions[c_conversation_id]
#keep track of the last voting comments & discussion it occurred in
previous_vote = c_id, c_conversation_id
#if the contribution is a non-voting comment
elif c_id[0] == '5':
c_meta.update({'type':'non-voting comment',
'label': None,
'raw_label': None})
c_text = contribution['Text']
#when a non-voting comment happens before any vote was made, it is a reply to the first contribution in the discussion
if previous_vote[1] != c_conversation_id:
c_reply_to = seen_discussions[c_conversation_id]
#when a comment happens after the vote in the discussion, it is a reply to that vote
else:
c_reply_to = previous_vote[0]
#if contribution is a nomination
elif c_id[0] == '6':
c_meta.update({'type':'nomination',
'label': None,
'raw_label': None})
c_text = contribution['Text']
#c_reply_to = None
#want to make sure that nominations only happen at the very beginning of a discussion
if c_id != seen_discussions[c_conversation_id]:
print("Something wrong")
else:
print(c_id[0])
#The first comment is not a reply to any other contribution
if c_id == seen_discussions[c_conversation_id]:
c_reply_to = None
utterance_objects[c_id] = Utterance(id = c_id,
speaker = speaker_objects[c_speaker],
conversation_id = c_conversation_id,
reply_to = c_reply_to,
timestamp = c_timestamp,
text = c_text,
meta = c_meta
)
# -
# Number of discussions (i.e. ConvoKit conversations) in this data
len(seen_discussions)
# Number of contributions (i.e. ConvoKit utterances) in this data
len(utterance_objects)
# However, note that some of these contributions are empty strings after parsing/cleaning steps completed by authors of the original dataset.
empty_string_contributions = []
for contribution in tqdm(afd['Contributions']):
c_id = str(contribution['ID'])
if (c_id[0] == '4' and len(contribution['Rationale'].split()) != 0) or \
(c_id[0] != '4' and len(contribution['Text'].split()) != 0):
a = 1
else:
empty_string_contributions.append(contribution)
len(empty_string_contributions)
# Here is how examples of a nomination, a vote, and a non-voting comment from above as utterance objects
utterance_objects['600000001']
utterance_objects['400000002']
utterance_objects['500000001']
# ## Create Corpus Object
afd_corpus = Corpus(utterances=list(utterance_objects.values()))
afd_corpus.random_utterance()
# Corpus summary information:
afd_corpus.print_summary_stats()
# Add the dataset name.
afd_corpus.meta['name'] = 'Wikipedia Articles for Deletion Dataset'
# ## Add Metadata for Converastions
# In the metadata field for each conversation we are going to include the title of the Wikipedia page suggested for deletion and information about the outcome of the discussion (as was determined by an admin).
afd['Discussions'][0]
afd['Outcomes'][0]
# +
outcomes_dct = {str(d['Parent']): d for d in afd['Outcomes']}
disc_info_dct = {str(d['ID']): d['Title'] for d in afd['Discussions']}
for conversation in tqdm(afd_corpus.iter_conversations()):
c_id = conversation.get_id()
if c_id not in outcomes_dct:
outcome_id, outcome_label, outcome_label_raw, outcome_user, outcome_timestamp, outcome_rationale = None, None, None, None, None, None
outcome_id = outcomes_dct[c_id]['ID']
outcome_label = outcomes_dct[c_id]['Label']
outcome_label_raw = outcomes_dct[c_id]['Raw']
outcome_user = outcomes_dct[c_id]['User']
outcome_timestamp = outcomes_dct[c_id]['Timestamp']
outcome_rationale = outcomes_dct[c_id]['Rationale']
conversation.meta.update({'article_title': disc_info_dct[c_id],
'outcome_id': str(outcome_id),
'outcome_label': outcome_label,
'outcome_raw_label': outcome_label_raw,
'outcome_decision_maker_id': str(outcome_user),
'outcome_timestamp': outcome_timestamp,
'outcome_rationale': outcome_rationale
})
# -
afd_corpus.get_conversation('100309419').meta
# **Note** that some, but not all, of the outcome decision makers also appear as speakers in this corpus.
#
# User with ID of `'200000595'`, who made the final decision in the example debate above, is also a speaker.
afd_corpus.get_speaker('200000595')
# However, `76` of the outcome decision makers never appeared as contributors/speakers in debates of this corpus.
# +
speaker_ids = []
for speaker in afd_corpus.iter_speakers():
speaker_ids.append(speaker.id)
missing_users = set([])
for conversation in afd_corpus.iter_conversations():
user_id = str(conversation.meta['outcome_decision_maker_id'])
if user_id not in speaker_ids:
missing_users.add(user_id)
len(missing_users)
# -
# ## Verify
afd_corpus.random_utterance()
afd_corpus.random_conversation()
# #### Check reply-to chain integrity
broken = []
for convo in tqdm(afd_corpus.iter_conversations()):
if not convo.check_integrity(verbose=False):
broken.append(convo.id)
print(len(broken))
# So, all conversations were verified to have valid reply-to chains.
# ## Dump the corpus
afd_corpus.dump("wiki-articles-for-deletion-corpus")
| datasets/wiki-articles-for-deletion-corpus/wiki_afd_to_convokit_conversion.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %pylab inline
import pandas as pd
import numpy as np
from scipy.interpolate import RegularGridInterpolator as RS
from interpolation.splines import CubicSpline, LinearSpline
Vgrid = np.load("Vgrid.npy")
cgrid = np.load("cgrid.npy")
bgrid = np.load("bgrid.npy")
kgrid = np.load("kgrid.npy")
hgrid = np.load("hgrid.npy")
ws = np.linspace(0,20000,100)
ns = np.linspace(0,20000,100)
hs = np.linspace(0,20000,100)
a = np.array([0,0,0.0]) # lower boundaries
b = np.array([20000,20000,20000]) # upper boundaries
orders = np.array([100,100,100]) # 50 points along each dimension
values = np.random.random(orders) # values at each node of the grid
S = np.random.random((10**6,3)) # coordinates at which to evaluate the splines
# %timeit spline = LinearSpline(a,b,orders,values)
# %timeit V = spline(S)
# %timeit rs = RS((ws, ns, hs), values,bounds_error=False, fill_value= None)
# %timeit V = rs.ev(S)
# + active=""
#
| 20200612/.ipynb_checkpoints/test-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # **1. meta16S: QIIME2**
#
# Author: <NAME>
# We will work with data from QIIME2's ["Atacama soil microbiome tutorial"](https://docs.qiime2.org/2019.7/tutorials/atacama-soils/). This data is part of [this publication](https://msystems.asm.org/content/2/3/e00195-16).
# **1.0 Working directory**
# If needed update your working directory. This notebook assumes it is located next to the singularity container meta16S.sif.
# cd ../
# **1.1 Get info**
# !singularity exec --app QIIME2 meta16S.sif qiime info
# **1.2 Import data/metadata with QIIME**
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime tools import --help
# -
# What are the available importable types?
# !singularity exec --app QIIME2 meta16S.sif qiime tools import --show-importable-types
# What are the available importable formats?
# !singularity exec --app QIIME2 meta16S.sif qiime tools import --show-importable-formats
# _**Import demultiplexed paired-end data as QIIME2 artifacts**_
# Lets get some example data from QIIME2's tutorial:
# + language="bash"
# mkdir -p data/raw/casava-18-paired-end/fastq
# wget \
# -O 'data/raw/casava-18-paired-end/casava-18-paired-end-demultiplexed.zip' \
# "https://data.qiime2.org/2019.7/tutorials/importing/casava-18-paired-end-demultiplexed.zip"
# unzip -q \
# -d './data/raw/casava-18-paired-end/fastq' \
# 'data/raw/casava-18-paired-end/casava-18-paired-end-demultiplexed.zip'
# rm 'data/raw/casava-18-paired-end/casava-18-paired-end-demultiplexed.zip'
# -
# !ls 'data/raw/casava-18-paired-end/fastq/casava-18-paired-end-demultiplexed/' | head -n5
# The files are named following Casava 1.8 demultiplexed paired-end format. The underscore-separated fields in these file names are:
#
# 1. the sample identifier,
#
# 2. the barcode sequence or a barcode identifier,
#
# 3. the lane number,
#
# 4. the direction of the read (i.e. R1 or R2), and
#
# 5. the set number.
#
# + language="bash"
# # Importing data
# mkdir -p data/interim/qiime/test_dataset
# singularity exec --app QIIME2 meta16S.sif qiime tools import \
# --type 'SampleData[PairedEndSequencesWithQuality]' \
# --input-path ./data/raw/casava-18-paired-end/fastq/casava-18-paired-end-demultiplexed/ \
# --input-format CasavaOneEightSingleLanePerSampleDirFmt \
# --output-path data/interim/qiime/test_dataset/demux-paired-end.qza
# -
# _**Import multiplexed paired-end sequencing data**_
# + language="bash"
# # Lets get some example data
# mkdir -p data/raw/atacama_soil_tutorial/fastq
# # forward reads
# wget \
# -O "./data/raw/atacama_soil_tutorial/fastq/forward.fastq.gz" \
# "https://data.qiime2.org/2019.7/tutorials/atacama-soils/1p/forward.fastq.gz"
# # reverse reads
# wget \
# -O "./data/raw/atacama_soil_tutorial/fastq/reverse.fastq.gz" \
# "https://data.qiime2.org/2019.7/tutorials/atacama-soils/1p/reverse.fastq.gz"
#
# ls data/raw/atacama_soil_tutorial/fastq | head -n 5
# + language="bash"
# # barcodes
# wget \
# -O "./data/raw/atacama_soil_tutorial/fastq/barcodes.fastq.gz" \
# "https://data.qiime2.org/2019.7/tutorials/atacama-soils/1p/barcodes.fastq.gz"
# -
# To analyze these data, we import it as a QIIME artifact:
# + language="bash"
# # Importing data
# mkdir -p data/interim/qiime/atacama_soil_tutorial
# singularity exec --app QIIME2 meta16S.sif qiime tools import \
# --type EMPPairedEndSequences \
# --input-path data/raw/atacama_soil_tutorial/fastq \
# --output-path data/interim/qiime/atacama_soil_tutorial/fastq_pend_seqs.qza
# -
# _**Manifest files**_
# If the fastq files are not named following Casava format, we need to provide a 'manifest file' (a tab-separated text file) that has the following format:
# ```
# sample-id forward-absolute-filepath reverse-absolute-filepath
# sample-1 $PWD/some/filepath/sample0_R1.fastq.gz $PWD/some/filepath/sample1_R2.fastq.gz
# sample-2 $PWD/some/filepath/sample2_R1.fastq.gz $PWD/some/filepath/sample2_R2.fastq.gz
# sample-3 $PWD/some/filepath/sample3_R1.fastq.gz $PWD/some/filepath/sample3_R2.fastq.gz
# sample-4 $PWD/some/filepath/sample4_R1.fastq.gz $PWD/some/filepath/sample4_R2.fastq.gz
# ```
# More details see this [link](https://docs.qiime2.org/2019.7/tutorials/importing/#fastq-manifest-formats)
# _**Import metadata**_
# Lets get some sample metadata file:
# + language="bash"
# wget \
# -O 'data/raw/atacama_soil_tutorial/sample-metadata.tsv' \
# "https://data.qiime2.org/2019.7/tutorials/atacama-soils/sample_metadata.tsv"
# ls data/raw/atacama_soil_tutorial
# -
# !head -n 5 'data/raw/atacama_soil_tutorial/sample-metadata.tsv' | cut -f1-5
# To import this file for visualization with [QIIME2 view](https://view.qiime2.org/), we have to convert it to a qzv file:
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime metadata tabulate \
# --m-input-file ./data/raw/atacama_soil_tutorial/sample-metadata.tsv \
# --o-visualization ./data/interim/qiime/atacama_soil_tutorial/tabulated-sample-metadata.qzv
# -
# In a local machine (a desktop), this file can be visualized with:
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime tools view ./data/interim/qiime/atacama_soil_tutorial/tabulated-sample-metadata.qzv
# -
# WARNING: in a headless server (your HPC university server) or this container, it's not possible to use `qiime tools view`. However this QIIME's visualization output file can be interactively visualized by [**QIIME2 view**](https://view.qiime2.org/), a web application that reads the file and shows it in your browser.
#
# If the visualization file is placed in a file hosting service like dropbox, the link can be provided to **QIIME2 view** wich in turns can generate a perma html link that we can insert in this notebook or share with others:
#
# ```python
# from IPython.display import IFrame
#
# IFrame(src='https://view.qiime2.org/visualization/some_values&type=html', width=700, height=600)
# ```
# **1.3 Demultiplex paired-end reads**
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime demux emp-paired \
# --m-barcodes-file data/raw/atacama_soil_tutorial/sample-metadata.tsv \
# --m-barcodes-column barcode-sequence \
# --p-rev-comp-mapping-barcodes \
# --i-seqs data/interim/qiime/atacama_soil_tutorial/fastq_pend_seqs.qza \
# --o-per-sample-sequences data/interim/qiime/atacama_soil_tutorial/demux.qza \
# --o-error-correction-details data/interim/qiime/atacama_soil_tutorial/demux-details.qza
# -
# **1.4 Quality control**
# + language="bash"
# # Sequence QC inspection
# singularity exec --app QIIME2 meta16S.sif \
# qiime demux summarize \
# --i-data ./data/interim/qiime/atacama_soil_tutorial/demux.qza \
# --o-visualization ./data/interim/qiime/atacama_soil_tutorial/demux.qzv
# -
# With `qiime demux summarize` we obtain a visualization file (demux.qsv). This files provides a quality report and the number of sequences per sample. Visualize it with [**QIIME2 view**](https://view.qiime2.org/).
# **1.5 Obtain feature table by denoising with DADA2 (read-join, denoise, dereplicate, chimera filtering)**
#
# The Feature table in QIIME2 is equivalent to the OTU table (in biom format) generated by QIIME1, see this [link](https://docs.qiime2.org/2019.7/tutorials/pd-mice/#sequence-quality-control-and-feature-table) for further details. The DADA2 method identifies Absolute Sequence Variants (ASVs) instead of Operational Taxonomic Units (OTUs).
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime dada2 denoise-paired --help
# + language="bash"
# singularity exec --app QIIME2 meta16S \
# qiime dada2 denoise-paired \
# --i-demultiplexed-seqs ./data/interim/qiime/atacama_soil_tutorial/demux.qza \
# --p-trim-left-f 13 \
# --p-trim-left-r 13 \
# --p-trunc-len-f 150 \
# --p-trunc-len-r 150 \
# --o-table ./data/interim/qiime/atacama_soil_tutorial/table.qza \
# --o-representative-sequences ./data/interim/qiime/atacama_soil_tutorial/rep-seqs.qza \
# --o-denoising-stats ./data/interim/qiime/atacama_soil_tutorial/denoising-stats.qza
# -
# The output artifacts:
#
# - table.qza : the resulting feature(i.e otu in QIIME1) table is a QIIME2 artifact of type 'FeatureTable[Frequency]'
# - rep-seqs.qza :
# - denoising-stats.qza :
# To generate summaries of the Feature table, corresponding feature sequences and denoising stats:
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime feature-table summarize \
# --i-table ./data/interim/qiime/atacama_soil_tutorial/table.qza \
# --o-visualization ./data/interim/qiime/atacama_soil_tutorial/table.qzv \
# --m-sample-metadata-file ./data/raw/atacama_soil_tutorial/sample-metadata.tsv
#
# singularity exec --app QIIME2 meta16S.sif \
# qiime feature-table tabulate-seqs \
# --i-data ./data/interim/qiime/atacama_soil_tutorial/rep-seqs.qza \
# --o-visualization ./data/interim/qiime/atacama_soil_tutorial/rep-seqs.qzv
#
# singularity exec --app QIIME2 meta16S.sif \
# qiime metadata tabulate \
# --m-input-file ./data/interim/qiime/atacama_soil_tutorial/denoising-stats.qza \
# --o-visualization ./data/interim/qiime/atacama_soil_tutorial/denoising-stats.qzv
# -
# **1.6 Generate phylogenetic tree from Feature sequences**
# This a computationally intensive step.
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime fragment-insertion sepp \
# --i-representative-sequences ./data/interim/qiime/atacama_soil_tutorial/rep-seqs.qza \
# --o-tree ./data/interim/qiime/atacama_soil_tutorial/tree.qza \
# --o-placements ./data/interim/qiime/atacama_soil_tutorial/tree_placements.qza \
# --p-threads 3 # update to a higher number if you can
# -
# **1.7 Taxonomic classification**
# We first download a trained classifier:
# + language="bash"
# wget \
# -O "./data/interim/qiime/gg-13-8-99-515-806-nb-classifier.qza" \
# "https://data.qiime2.org/2019.7/common/gg-13-8-99-515-806-nb-classifier.qza"
# -
# NOTE from QIIME2:
# "Taxonomic classifiers perform best when they are trained based on your specific sample preparation and sequencing parameters, including the primers that were used for amplification and the length of your sequence reads. Therefore in general you should follow the instructions in [Training feature classifiers with q2-feature-classifier](https://docs.qiime2.org/2019.7/tutorials/feature-classifier/) to train your own taxonomic classifiers."
#
# According to [QIIME2's moving pictures tutorial](https://docs.qiime2.org/2019.7/tutorials/moving-pictures/#taxonomic-analysis), the classifier downloaded in this step was trained on the Greengenes 13_8 99% OTUs, where the sequences have been trimmed to only include 250 bases from the region of the 16S that was sequenced in this analysis (the V4 region, bound by the 515F/806R primer pair).
# Now, lets assign taxonomic classifications to our Features (aka OTUs):
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime feature-classifier classify-sklearn \
# --i-classifier ./data/interim/qiime/gg-13-8-99-515-806-nb-classifier.qza \
# --i-reads ./data/interim/qiime/atacama_soil_tutorial/rep-seqs.qza \
# --o-classification ./data/interim/qiime/atacama_soil_tutorial/taxonomy.qza
#
# singularity exec --app QIIME2 meta16S.sif \
# qiime metadata tabulate \
# --m-input-file ./data/interim/qiime/atacama_soil_tutorial/taxonomy.qza \
# --o-visualization ./data/interim/qiime/atacama_soil_tutorial/taxonomy.qzv
# -
# **1.8 Alpha rarefaction**
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime diversity alpha-rarefaction \
# --i-table ./data/interim/qiime/atacama_soil_tutorial/table.qza \
# --i-phylogeny ./data/interim/qiime/atacama_soil_tutorial/tree.qza \
# --p-max-depth 543 \
# --m-metadata-file ./data/raw/atacama_soil_tutorial/sample-metadata.tsv \
# --o-visualization ./data/interim/qiime/atacama_soil_tutorial/alpha-rarefaction.qzv
# -
# **1.9 Export data**
# + language="bash"
# singularity exec --app QIIME2 meta16S.sif \
# qiime tools export \
# --input-path ./data/interim/qiime/atacama_soil_tutorial/table.qza \
# --output-path ./data/interim/qiime/atacama_soil_tutorial/exports/
#
# singularity exec --app QIIME2 meta16S.sif \
# qiime tools export \
# --input-path ./data/interim/qiime/atacama_soil_tutorial/tree.qza \
# --output-path ./data/interim/qiime/atacama_soil_tutorial/exports/
#
# singularity exec --app QIIME2 meta16S.sif \
# qiime tools export \
# --input-path ./data/interim/qiime/atacama_soil_tutorial/taxonomy.qza \
# --output-path ./data/interim/qiime/atacama_soil_tutorial/exports/
#
# singularity exec --app QIIME2 meta16S.sif \
# qiime tools export \
# --input-path ./data/interim/qiime/atacama_soil_tutorial/alpha-rarefaction.qzv \
# --output-path ./data/interim/qiime/atacama_soil_tutorial/exports/alpha-rarefaction/
# -
# !head ./data/interim/qiime/atacama_soil_tutorial/exports/taxonomy.tsv
| meta16S/tutorials/qiime2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
import pandas as pd
# + pycharm={"name": "#%%\n"}
clinical_scores_mrs01_path = '/Users/jk1/OneDrive - unige.ch/stroke_research/scope/output/clinical_scores/mrs01_clinical_scores_results.csv'
clinical_scores_mrs02_path = '/Users/jk1/OneDrive - unige.ch/stroke_research/scope/output/clinical_scores/mrs02_clinical_scores_results.csv'
imaging_results_mrs01_path = '/Users/jk1/temp/keras_scope_server_output/mrs01/cv_20210921-213143/cv_test_results.csv'
imaging_results_mrs02_path = '/Users/jk1/temp/keras_scope_server_output/mrs02/cv_20210909-084904/cv_test_results.csv'
# + pycharm={"name": "#%%\n"}
clinical_scores_mrs01_df = pd.read_csv(clinical_scores_mrs01_path)
clinical_scores_mrs02_df = pd.read_csv(clinical_scores_mrs02_path)
imaging_results_mrs01_df = pd.read_csv(imaging_results_mrs01_path)
imaging_results_mrs02_df = pd.read_csv(imaging_results_mrs02_path)
# + pycharm={"name": "#%%\n"}
overall_results_columns = ['ground truth', 'method', 'auc', 'accuracy', 'f1', 'precision', 'recall']
# + pycharm={"name": "#%%\n"}
overall_results_df = pd.concat([clinical_scores_mrs01_df[overall_results_columns],
clinical_scores_mrs02_df[overall_results_columns]])
overall_results_df = overall_results_df.append(pd.DataFrame([[
'3M mRS 0-1', 'keras_scope 3dcnn',
imaging_results_mrs01_df['auc'].median(),
imaging_results_mrs01_df['acc'].median(),
imaging_results_mrs01_df['f1_m'].median(),
imaging_results_mrs01_df['precision'].median(),
imaging_results_mrs01_df['recall'].median(),
]], columns=overall_results_columns), ignore_index=True)
overall_results_df = overall_results_df.append(pd.DataFrame([[
'3M mRS 0-2', 'keras_scope 3dcnn',
imaging_results_mrs02_df['auc'].median(),
imaging_results_mrs02_df['acc'].median(),
imaging_results_mrs02_df['f1_m'].median(),
imaging_results_mrs02_df['precision'].median(),
imaging_results_mrs02_df['recall'].median(),
]], columns=overall_results_columns), ignore_index=True)
# + pycharm={"name": "#%%\n"}
import seaborn as sns
g = sns.catplot(x="method", y='vals',
hue="method",
col='cols', col_wrap=3,
data=overall_results_df[overall_results_df['ground truth'] == '3M mRS 0-2']\
.melt('method', var_name='cols', value_name='vals')
)
# + pycharm={"name": "#%%\n"}
mrs02_df = overall_results_df[overall_results_df['ground truth'] == '3M mRS 0-2']
# + pycharm={"name": "#%%\n"}
| clinical_scope/result_comparison.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# # Part a
# +
# Loading Dataset
x = []
f = open("data/data/faithful/faithful.txt",'r')
for line in f.readlines():
x.append([float(i) for i in line.strip().split(" ")])
x = np.array(x)
x.shape
# -
#Normalise the data within [-1, 1]
x = (x - np.mean(x, axis=0))*(1/(np.max(x,axis=0) - np.min(x, axis=0)))
plt.scatter(x[:,0], x[:,1])
plt.show()
# +
# Number of clusters
k = 2
# Initialising Cluster parameters
mean = np.array([[-1, 1],[1, -1]])
covariance = np.tile(0.1 * np.eye(2), (k,1,1))
mix = np.ones((k,1))/k
print("Initialisation done. \n mean = \n", mean, "\n covariance = \n", covariance, "\n mixing coefficients = \n", mix)
# +
def e_step(x, k, mean, covariance, mix):
gamma = np.zeros((x.shape[0], k))
for i in range(k):
gamma[:,i] = mix[i]*multivariate_normal.pdf(x=x, mean=mean[i], cov=covariance[i])
temp = np.tile(1/np.sum(gamma, axis=1), (2,1)).transpose()
return(gamma*temp)
def m_step(x, k, gamma):
mix = np.sum(gamma, axis=0)/np.sum(gamma)
mean = np.zeros((k,x.shape[1]))
covariance = np.zeros((k, x.shape[1], x.shape[1]))
for i in range(k):
temp1 = gamma[:,i].reshape(gamma.shape[0],1)
mean[i] = np.sum(x*temp1, axis=0)/np.sum(gamma[:,i])
temp2 = x - mean[i]
temp3 = 0
for j in range(x.shape[0]):
temp3 = temp3+gamma[j,i]*np.matmul(temp2[j].reshape(-1,1), temp2[j].reshape(-1,1).transpose())
covariance[i] = temp3/np.sum(gamma[:,i])
return mean, covariance, mix
# Performing Updates
max_iter = 100
plot_iter = [1,2,5,100]
for i in range(1, max_iter+1):
gamma = e_step(x, k, mean, covariance, mix)
mean, covariance, mix = m_step(x, k, gamma)
# Plotting at desired locations
if(i in plot_iter):
cluster_id = np.argmax(gamma, axis=1)
colours = 'rb'
plt.clf()
for j in range(k):
temp = (cluster_id==j)
plt.scatter(x[temp,0], x[temp,1])
plt.plot(mean[:,0], mean[:,1],'bD')
plt.title("Iteration {}".format(i))
plt.show()
# -
# # Part b
# +
# Loading Dataset
x = []
f = open("data/data/faithful/faithful.txt",'r')
for line in f.readlines():
x.append([float(i) for i in line.strip().split(" ")])
x = np.array(x)
#Normalise the data within [-1, 1]
x = (x - np.mean(x, axis=0))*(1/(np.max(x,axis=0) - np.min(x, axis=0)))
# Number of clusters
k = 2
# Initialising Cluster parameters
mean = np.array([[-1, -1],[1, 1]])
covariance = np.tile(0.5 * np.eye(2), (k,1,1))
mix = np.ones((k,1))/k
print("Initialisation done. \n mean = \n", mean, "\n covariance = \n", covariance, "\n mixing coefficients = \n", mix)
# Performing Updates
max_iter = 100
plot_iter = [1,2,5,100]
for i in range(1, max_iter+1):
gamma = e_step(x, k, mean, covariance, mix)
mean, covariance, mix = m_step(x, k, gamma)
# Plotting at desired locations
if(i in plot_iter):
cluster_id = np.argmax(gamma, axis=1)
colours = 'rb'
plt.clf()
for j in range(k):
temp = (cluster_id==j)
plt.scatter(x[temp,0], x[temp,1])
plt.plot(mean[:,0], mean[:,1],'bD')
plt.title("Iteration {}".format(i))
plt.show()
# -
# # Part c
# +
# Loading Dataset
x = []
f = open("data/data/faithful/faithful.txt",'r')
for line in f.readlines():
x.append([float(i) for i in line.strip().split(" ")])
x = np.array(x)
#Normalise the data within [-1, 1]
x = (x - np.mean(x, axis=0))*(1/(np.max(x,axis=0) - np.min(x, axis=0)))
# Number of clusters
k = 2
# Initialising Cluster parameters
mean = np.array([[0, 0],[0, 0]])
covariance = np.tile(0.5 * np.eye(2), (k,1,1))
mix = np.ones((k,1))/k
print("Initialisation done. \n mean = \n", mean, "\n covariance = \n", covariance, "\n mixing coefficients = \n", mix)
# Performing Updates
max_iter = 100
plot_iter = [1,2,5,100]
for i in range(1, max_iter+1):
gamma = e_step(x, k, mean, covariance, mix)
mean, covariance, mix = m_step(x, k, gamma)
# Plotting at desired locations
if(i in plot_iter):
cluster_id = np.argmax(gamma, axis=1)
colours = 'rb'
plt.clf()
for j in range(k):
temp = (cluster_id==j)
plt.scatter(x[temp,0], x[temp,1])
plt.plot(mean[:,0], mean[:,1],'bD')
plt.title("Iteration {}".format(i))
plt.show()
# -
| assignments/a4/Q3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Vectorization
# +
# load libraries
import numpy as np
a = np.array([1,2,3,4])
print(a)
# +
import time
a = np.random.rand(1000000)
b = np.random.rand(1000000)
t1 = time.time()
c = np.dot(a,b)
t2 = time.time()
print("Vectorized: ", c, str(1000*(t2-t1)) + " ms")
# +
c = 0
t1 = time.time()
for i in range(1000000):
c += a[i]*b[i]
t2 = time.time()
print("Non-Vectorized: ", c, str(1000*(t2-t1)) + " ms")
# -
| deeplearning/basics/vectorization_1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# %pylab inline
# +
from __future__ import print_function, division
from matplotlib import pyplot as plt
import pandas
import src
import gensim
import os
import os.path
import csv
import functools
import itertools
import collections
import scipy
import scipy.stats
from operator import itemgetter
from pprint import pprint
def fake(*args, **kwargs):
print('Fake called with', str(args), str(kwargs))
sys.exit(1)
# fake out the create_model so we don't accidentally attempt to create data
src.common.create_model = fake
# -
print(os.getcwd())
if os.getcwd().endswith('notebooks'):
os.chdir('..')
print(os.getcwd())
def wilcoxon(x, y):
T, p = scipy.stats.wilcoxon(x.dropna(), y.dropna(), correction=True)
nonzeros = sum(1 for a, b in zip(x, y) if (a - b) != 0)
S = sum(range(1, nonzeros + 1))
#assert any([item == 0 for item in x]), "x has 0"
#assert any([item == 0 for item in y]), "y has 0"
assert S >= T, "%f %f" % (S, T)
Td = S - T
rsp1 = Td / S
rsp2 = T / S
r = rsp1 - rsp2
# From this information alone, the remaining rank sum can be computed, because
# it is the total sum S minus T, or in this case 45 - 18 = 27. Next, the two
# rank-sum proportions are 27/45 = 60% and 18/45 = 40%. Finally, the rank
# correlation is the difference between the two proportions (.60 minus .40),
# hence r = .20.
return T, p, r
# +
kwargs = dict(model="lda", level="file", source=["changeset"], force=False, rankpath='', config=dict())
default_model_config, model_config_string = src.main.get_default_model_config(kwargs)
default_changeset_config, changeset_config_string = src.main.get_default_changeset_config()
model_config = dict(default_model_config)
model_config.update({
'alpha_base': 1,
'eta_base': 1,
})
changeset_config = dict(default_changeset_config)
def get_config_string(config):
return '-'.join([unicode(v) for k, v in sorted(config.items()) if not k.endswith("_base")])
def get_config_string2(table):
return "".join(sorted([key.replace('include_', '').upper()[0] for key, value in table.iteritems() if key != "FLT" and key != "DIT" and value]))
alpha_bases = ['auto', 1, 2, 5]
eta_bases = ['auto', 1, 2, 5]
num_topics = [100, 200, 500]
def get_rank_name(kind, experiment, changeset_config, model_config):
"""
kind = [changeset, release, temporal]
experiment = [triage, feature_location]
"""
cs_str = get_config_string(changeset_config)
model_config = dict(model_config)
m_str = get_config_string(model_config)
return '-'.join([kind, experiment, 'lda', cs_str, m_str, 'file', 'ranks']).lower() + '.csv.gz'
model_sweep = list()
for a, e, K in itertools.product(alpha_bases, eta_bases, num_topics):
m = dict(model_config)
m['alpha_base'] = a
m['eta_base'] = e
if a != 'auto':
a /= K
if e != 'auto':
e /= K
m['alpha'] = a
m['eta'] = e
m['num_topics'] = K
model_sweep.append(m)
corpus_sweep = list()
b = [True, False]
for a, c, m, r in itertools.product(b, repeat=4):
conf = dict(changeset_config)
conf['include_additions'] = a
conf['include_context'] = c
conf['include_message'] = m
conf['include_removals'] = r
if any(conf.values()):
corpus_sweep.append(conf)
# -
get_config_string2(corpus_sweep[0])
# +
# All of the sweep files need renaming throughout. The *do* use the seed, it's just not named correctly
model_config_string = model_config_string.replace("seed1-", "")
kwargs.update({'changeset_config': changeset_config,
'changeset_config_string': changeset_config_string})
kwargs.update({'model_config': model_config,
'model_config_string': model_config_string})
# load project info
projects = src.common.load_projects(kwargs)
#projects = src.common.load_projects(dict(model="lda", level="file", rankpath='', config=dict()), "../data")
projects
# +
cs_dit = list()
for project, rankstuff in itertools.product(projects, [
(c, get_rank_name('changeset', 'triage', c, model_config)) for c in corpus_sweep]):
config, rankname = rankstuff
rankpath = os.path.join(project.data_path, project.version, rankname)
if os.path.exists(rankpath):
# cs_dit.append(project._replace(rankpath=rankpath, config=config))
project = project._replace(changeset_config=config, rankpath=rankpath, config=config)
cs_dit.append(
project._replace(
model_config_string=get_config_string(project.model_config),
changeset_config_string=get_config_string(project.changeset_config)
))
else:
print(rankpath)
cs_flt = list()
for project, rankstuff in itertools.product(projects, [
(c, get_rank_name('changeset', 'feature_location', c, model_config)) for c in corpus_sweep]):
config, rankname = rankstuff
rankpath = os.path.join(project.data_path, project.version, rankname)
if os.path.exists(rankpath):
#cs_flt.append(project._replace(rankpath=rankpath, config=config))
project = project._replace(changeset_config=config, rankpath=rankpath, config=config)
cs_flt.append(
project._replace(
model_config_string=get_config_string(project.model_config),
changeset_config_string=get_config_string(project.changeset_config)
))
else:
print(rankpath)
ms_dit = list()
for project, rankstuff in itertools.product(projects, [
(c, get_rank_name('changeset', 'triage', changeset_config, c)) for c in model_sweep]):
config, rankname = rankstuff
rankpath = os.path.join(project.data_path, project.version, rankname)
if os.path.exists(rankpath):
#ms_dit.append(project._replace(rankpath=rankpath, config=config))
project = project._replace(model_config=config, rankpath=rankpath, config=config)
ms_dit.append(
project._replace(
model_config_string=get_config_string(project.model_config),
changeset_config_string=get_config_string(project.changeset_config)
))
else:
print(rankpath)
ms_flt = list()
for project, rankstuff in itertools.product(projects, [
(c, get_rank_name('changeset', 'feature_location', changeset_config, c)) for c in model_sweep]):
config, rankname = rankstuff
rankpath = os.path.join(project.data_path, project.version, rankname)
if os.path.exists(rankpath):
#ms_flt.append(project._replace(rankpath=rankpath, config=config))
project = project._replace(model_config=config, rankpath=rankpath, config=config)
ms_flt.append(
project._replace(
model_config_string=get_config_string(project.model_config),
changeset_config_string=get_config_string(project.changeset_config)
))
else:
print(rankpath)
# -
cs_dit[0]
src.triage.run_experiment(cs_dit[0])
# +
corpus_df = pandas.DataFrame(columns=["Subject", "Task", "Issue", "Rank", "Item", "Additions", "Removals", "Context", "Message"])
for item in cs_dit:
df = pandas.DataFrame(columns=corpus_df.columns)
result = src.triage.run_experiment(item)["changeset"]
df["Rank"] = [x for x, y, z in result]
df["Issue"] = [y for x, y, z in result]
df["Item"] = [z for x, y, z in result]
df["Subject"] = df.Subject.fillna(item.printable_name)
df["Additions"] = df.Additions.fillna(item.config['include_additions'])
df["Removals"] = df.Removals.fillna(item.config['include_removals'])
df["Context"] = df.Context.fillna(item.config['include_context'])
df["Message"] = df.Message.fillna(item.config['include_message'])
df["Task"] = df.Task.fillna("DIT")
corpus_df = corpus_df.append(df, ignore_index=True)
for item in cs_flt:
df = pandas.DataFrame(columns=corpus_df.columns)
result = src.feature_location.run_experiment(item)["changeset"]
df["Rank"] = [x for x, y, z in result]
df["Issue"] = [y for x, y, z in result]
df["Item"] = [z for x, y, z in result]
df["Subject"] = df.Subject.fillna(item.printable_name)
df["Additions"] = df.Additions.fillna(item.config['include_additions'])
df["Removals"] = df.Removals.fillna(item.config['include_removals'])
df["Context"] = df.Context.fillna(item.config['include_context'])
df["Message"] = df.Message.fillna(item.config['include_message'])
df["Task"] = df.Task.fillna("FLT")
corpus_df = corpus_df.append(df, ignore_index=True)
# +
model_df = pandas.DataFrame(columns=["Subject", "Task", "Issue", "Rank", "Item", "alpha", "eta", "K"])
for item in ms_dit:
df = pandas.DataFrame(columns=model_df.columns)
result = src.triage.run_experiment(item)["changeset"]
df["Rank"] = [x for x, y, z in result]
df["Issue"] = [y for x, y, z in result]
df["Item"] = [z for x, y, z in result]
df["Subject"] = df.Subject.fillna(item.printable_name)
df["alpha"] = df.alpha.fillna(item.config['alpha_base'])
df["eta"] = df.eta.fillna(item.config['eta_base'])
df["K"] = df.K.fillna(item.config['num_topics'])
df["Task"] = df.Task.fillna("DIT")
model_df = model_df.append(df, ignore_index=True)
for item in ms_flt:
df = pandas.DataFrame(columns=model_df.columns)
result = src.feature_location.run_experiment(item)["changeset"]
df["Rank"] = [x for x, y, z in result]
df["Issue"] = [y for x, y, z in result]
df["Item"] = [z for x, y, z in result]
df["Subject"] = df.Subject.fillna(item.printable_name)
df["alpha"] = df.alpha.fillna(item.config['alpha_base'])
df["eta"] = df.eta.fillna(item.config['eta_base'])
df["K"] = df.K.fillna(item.config['num_topics'])
df["Task"] = df.Task.fillna("FLT")
model_df = model_df.append(df, ignore_index=True)
# -
# # Corpus analysis
len(corpus_sweep)
# #### These are inequal because of the False, False, False, False configuration being invalid.
corpus_df.groupby(["Subject", "Task", "Additions"]).Issue.apply(len)
(corpus_df.groupby(["Task", "Additions"]).Rank.apply(src.utils.calculate_mrr),
'********************************************',
corpus_df.groupby(["Task", "Removals"]).Rank.apply(src.utils.calculate_mrr),
'********************************************',
corpus_df.groupby(["Task", "Context"]).Rank.apply(src.utils.calculate_mrr),
'********************************************',
corpus_df.groupby(["Task", "Message"]).Rank.apply(src.utils.calculate_mrr),
)
(corpus_df.groupby(["Subject", "Task", "Additions"]).Rank.apply(src.utils.calculate_mrr),
'********************************************',
corpus_df.groupby(["Subject", "Task", "Removals"]).Rank.apply(src.utils.calculate_mrr),
'********************************************',
corpus_df.groupby(["Subject", "Task", "Context"]).Rank.apply(src.utils.calculate_mrr),
'********************************************',
corpus_df.groupby(["Subject", "Task", "Message"]).Rank.apply(src.utils.calculate_mrr),
)
# what the fuck was I doing here?
res = pandas.DataFrame(columns=["Subject", "Task", "Config", "ExcludeMRR", "IncludeMRR", "p"])
for k in ["Additions", "Removals", "Context", "Message"]:
for key, group in corpus_df.groupby(["Subject", "Task"]):
subject, task = key
sub = group.groupby(k).groups
f = corpus_df.ix[sub[False]].Rank
t = corpus_df.ix[sub[True]].Rank
stat, p = scipy.stats.mannwhitneyu(f, t)
# Must use Mann Whitney here instead of Wilcoxon because the FFFF config (all False) creates an offset in the total number of ranks!
res = res.append(
dict(
zip(res.columns,
[subject, task, k, src.utils.calculate_mrr(f), src.utils.calculate_mrr(t), p]))
, ignore_index=True)
sub = corpus_df.groupby(["Task", k]).groups
f = corpus_df.ix[sub[("DIT", False)]].Rank
t = corpus_df.ix[sub[("DIT", True)]].Rank
stat, p = scipy.stats.mannwhitneyu(f, t)
res = res.append(
dict(
zip(res.columns,
["Overall", "DIT", k, src.utils.calculate_mrr(f), src.utils.calculate_mrr(t), p]))
, ignore_index=True)
f = corpus_df.ix[sub[("FLT", False)]].Rank
t = corpus_df.ix[sub[("FLT", True)]].Rank
stat, p = scipy.stats.mannwhitneyu(f, t)
res = res.append(
dict(
zip(res.columns,
["Overall", "FLT", k, src.utils.calculate_mrr(f), src.utils.calculate_mrr(t), p]))
, ignore_index=True)
res[(res.ExcludeMRR > res.IncludeMRR) & (res.p < 0.01)]
res[(res.ExcludeMRR <= res.IncludeMRR) & (res.p < 0.01)]
# +
# for key, group in corpus_df.groupby(["Subject", "Task"]):
# ranks = dict()
# for subkey, subgroup in group.groupby(["Additions", "Removals", "Context", "Message"]):
# ranks[subkey] = subgroup.Rank
# print(key, scipy.stats.friedmanchisquare(*ranks.values()))
# for x, y in itertools.combinations(corpus_df.groupby(["Additions", "Removals", "Context", "Message"]).groups.keys(), r=2):
# stat, p = scipy.stats.wilcoxon(ranks[x], ranks[y])
# if p < 0.01:
# print(x, y, p, "******")
# else:
# print(x, y, p)
# print()
# +
cres = pandas.DataFrame(columns=["Subject", "Task", "Config", "Config2", "MRR", "MRR2", "T", "p", "r"])
for key, group in corpus_df.groupby(["Subject", "Task"]):
for c1, c2 in itertools.combinations(corpus_sweep, r=2):
a = group[
(group.Additions == c1["include_additions"]) &
(group.Removals == c1["include_removals"]) &
(group.Context == c1["include_context"]) &
(group.Message == c1["include_message"])
].Rank
b = group[
(group.Additions == c2["include_additions"]) &
(group.Removals == c2["include_removals"]) &
(group.Context == c2["include_context"]) &
(group.Message == c2["include_message"])
].Rank
stat, p, r = wilcoxon(a,b)
cres = cres.append(
dict(
zip(cres.columns,
[key[0], key[1],
get_config_string2(c1),
get_config_string2(c2),
src.utils.calculate_mrr(a),
src.utils.calculate_mrr(b),
stat, p,r]))
, ignore_index=True)
for key, group in corpus_df.groupby(["Task"]):
for c1, c2 in itertools.combinations(corpus_sweep, r=2):
a = group[
(group.Additions == c1["include_additions"]) &
(group.Removals == c1["include_removals"]) &
(group.Context == c1["include_context"]) &
(group.Message == c1["include_message"])
].Rank
b = group[
(group.Additions == c2["include_additions"]) &
(group.Removals == c2["include_removals"]) &
(group.Context == c2["include_context"]) &
(group.Message == c2["include_message"])
].Rank
stat, p, r = wilcoxon(a,b)
cres = cres.append(
dict(
zip(cres.columns,
["all subject systems", key,
get_config_string2(c1),
get_config_string2(c2),
src.utils.calculate_mrr(a),
src.utils.calculate_mrr(b),
stat, p,r]))
, ignore_index=True)
# -
bon=0.01/len(list(itertools.combinations(range(15),2)))
bon, len(cres[(cres.p < bon)]), len(cres[(cres.p < (0.01))]), len(cres)
bon = 0.01
len(list(itertools.combinations(range(15),2)))
d = cres[(cres.Subject == "all subject systems") &
(cres.Task == "DIT") &
(cres.p < bon)]
len(d), d
f = cres[(cres.Subject == "all subject systems") &
(cres.Task == "FLT") &
(cres.p < bon)]
len(f), f
# +
friedman_df = pandas.DataFrame(columns=["Subject", "Task", "$\chi^2(15)$", "p-value", "Post-hoc Wilcoxon"])
for key, group in corpus_df.groupby(["Task"]):
ranks = dict()
for subkey, subgroup in group.groupby(["Additions", "Removals", "Context", "Message"]):
assert subkey not in ranks
ranks[subkey] = subgroup.Rank
post_hoc = len(cres[(cres.Subject == "all subject systems") &
(cres.Task == key) &
(cres.p < bon)])
stat, p = scipy.stats.friedmanchisquare(*ranks.values())
friedman_df = friedman_df.append(
dict(
zip(friedman_df.columns,
["all subject systems", key, stat, p, post_hoc]))
, ignore_index=True)
for key, group in corpus_df.groupby(["Subject", "Task"]):
ranks = dict()
for subkey, subgroup in group.groupby(["Additions", "Removals", "Context", "Message"]):
assert subkey not in ranks
ranks[subkey] = subgroup.Rank
post_hoc = len(cres[(cres.Subject == key[0]) &
(cres.Task == key[1]) &
(cres.p < bon)])
stat, p = scipy.stats.friedmanchisquare(*ranks.values())
friedman_df = friedman_df.append(
dict(
zip(friedman_df.columns,
[key[0], key[1], stat, p, post_hoc]))
, ignore_index=True)
friedman_df
# +
FIG_TEX = """\\begin{table}
\\begin{spacing}{1.2}
\\centering
\\caption[Friedman test results for %s corpus configuration sweeps (\\ctwo)]{Friedman test results for %s corpus configuration sweeps (\\ctwo). For each system, 105 post-hoc Wilcoxon tests were conducted.}
\\label{table:combo-friedman-%s}
%s
\\end{spacing}
\\end{table}
"""
dit_friedman = friedman_df[friedman_df.Task == "DIT"]
del dit_friedman["Task"]
flt_friedman = friedman_df[friedman_df.Task == "FLT"]
del flt_friedman["Task"]
formatters = {
"p-value": lambda x: ("$p<%f" % bon).rstrip("0") + "$" if x < bon else "$%.4f$" % x ,
"Subject": lambda x: x.replace("all", "\\midrule\nAll") if x.startswith("all") else x,
"$\chi^2(15)$": lambda x: "$%.4f$" % x,
"Optimal MRR": lambda x: "$%.4f$" % x,
"Alternate MRR": lambda x: "$%.4f$" % x,
"Effect size": lambda x: "$%.4f$" % x,
"Post-hoc Wilcoxon": lambda x: "$%d\;(%.1f\\%%)$" % (x, (float(x)/105.0) * 100),
}
flt_tex = flt_friedman.sort("Subject").to_latex(index=False,
escape=False, # needed so it doesn't screw up formatters
formatters=formatters)
dit_tex = dit_friedman.sort("Subject").to_latex(index=False,
escape=False, # needed so it doesn't screw up formatters
formatters=formatters)
print(FIG_TEX % ("FLT", "FLT", "flt", flt_tex))
print(FIG_TEX % ("DIT", "DIT", "dit", dit_tex))
with open(os.path.expanduser("~/git/dissertation/tables/combo_friedman_results.tex"), "wt") as f:
print(FIG_TEX % ("FLT", "FLT", "flt", flt_tex), file=f)
print(FIG_TEX % ("DIT", "DIT", "dit", dit_tex), file=f)
# -
# # Model analysis
model_df[:10]
# +
# for key, group in model_df.groupby(["Subject", "Task"]):
# ranks = dict()
# for subkey, subgroup in group.groupby(["alpha", "eta", "K"]):
# ranks[subkey] = subgroup.Rank
# print(key, scipy.stats.friedmanchisquare(*ranks.values()))
# for x, y in itertools.combinations(model_df.groupby(["alpha", "eta", "K"]).groups.keys(), r=2):
# stat, p = scipy.stats.wilcoxon(ranks[x], ranks[y])
# if p < 0.01:
# print(x, y, p, "******")
# else:
# print(x, y, p)
# print()
# +
for key, group in model_df.groupby(["Task"]):
ranks = dict()
for subkey, subgroup in group.groupby(["alpha", "eta", "K"]):
assert subkey not in ranks
ranks[subkey] = subgroup.Rank
print(key, scipy.stats.friedmanchisquare(*ranks.values()))
print('----')
for key, group in model_df.groupby(["Subject", "Task"]):
ranks = dict()
for subkey, subgroup in group.groupby(["alpha", "eta", "K"]):
assert subkey not in ranks
ranks[subkey] = subgroup.Rank
print(key, scipy.stats.friedmanchisquare(*ranks.values()))
# +
res = pandas.DataFrame(columns=["Subject", "Task", "Config", "Config2", "MRR", "MRR2", "p"])
for k in ["alpha", "eta", "K"]:
for key, group in model_df.groupby(["Subject", "Task"]):
ranks = dict()
for subkey, subgroup in group.groupby(k):
assert subkey not in ranks
ranks[subkey] = subgroup.Rank
for each in itertools.combinations(ranks.keys(), r=2):
f, t = each
stat, p = scipy.stats.wilcoxon(ranks[f], ranks[t], correction=True)
res = res.append(
dict(
zip(res.columns,
[key[0], key[1], k + "=" + str(f), k + "=" + str(t), src.utils.calculate_mrr(ranks[f]), src.utils.calculate_mrr(ranks[t]), p]))
, ignore_index=True)
ores = pandas.DataFrame(columns=["Subject", "Task", "Config", "Config2", "MRR", "MRR2", "p"])
for k in ["alpha", "eta", "K"]:
for key, group in model_df.groupby(["Task"]):
ranks = dict()
for subkey, subgroup in group.groupby(k):
assert subkey not in ranks
ranks[subkey] = subgroup.Rank
for each in itertools.combinations(ranks.keys(), r=2):
f, t = each
stat, p = scipy.stats.wilcoxon(ranks[f], ranks[t], correction=True)
ores = ores.append(
dict(
zip(ores.columns,
["Overall", key, k + "=" + str(f), k + "=" + str(t), src.utils.calculate_mrr(ranks[f]), src.utils.calculate_mrr(ranks[t]), p]))
, ignore_index=True)
# -
len(res[res.p < 0.01]), len(res[res.p >= 0.01])
len(ores[ores.p < 0.01]), len(ores[ores.p >= 0.01])
ores
res[(res.MRR > res.MRR2) & (res.p < 0.01)]
res[(res.MRR < res.MRR2) & (res.p < 0.01)]
t = res[(res.Config == "alpha=1") | (res.Config2 == "alpha=1")]
t
len(t), len(t[t.MRR > t.MRR2]), len(t[t.p < 0.05])
# # table building
model_df[model_df.Rank == 0]
model_all = model_df.groupby(["Task", "alpha", "eta", "K"]).Rank.apply(lambda x: numpy.mean(1/x))
model_all
corpus_all = corpus_df.groupby(["Task", "Additions", "Removals", "Context", "Message"]).Rank.apply(lambda x: numpy.mean(1/x))
corpus_all
# +
names = {'model': {'score': 'score',
'model_base_alpha': 'alpha',
'model_base_eta': 'eta',
'num_topics': 'K'
},
'corpus': {'score': 'score',
'changeset_include_additions': 'Additions',
'changeset_include_context': 'Context',
'changeset_include_message': 'Message',
'changeset_include_removals': 'Removals',
},
}
exps = ['triage', 'feature_location']
table_headers = {
'model':['K', 'alpha', 'eta', 'FLT', 'DIT'], # ['Configuration', 'FLT', 'DIT'],
'corpus': ['Configuration', 'FLT', 'DIT']
}
groups = {
'model': ['K', 'alpha', 'eta'],
'corpus': ['Additions', 'Removals', 'Context', 'Message']
}
full_tex = r"""
\begin{table}
\begin{spacing}{1.2}
\centering
\caption{MRR values of %s %s construction sweep (%s)}
\label{table:%s}
\vspace{0.2em}
%s
\end{spacing}
\end{table}
"""
tex_dir = os.path.expanduser("~/git/dissertation/tables")
def do_great_table(main_df, label_name, rq, caption):
include_fmt = lambda x: "Included" if x else ""
main_df = pandas.DataFrame(main_df)
formatters = {
'FLT': lambda x: r"$\bm{%.4f}$" % x if x == max(main_df["FLT"]) else "$%.4f$" % x,
'alpha': lambda x: "$%s/K$" % x if x != 'auto' else x,
'eta': lambda x: "$%s/K$" % x if x != 'auto' else x,
'K': lambda x: "$%s$" % int(x),
'Additions': include_fmt,
'Removals': include_fmt,
'Context': include_fmt,
'Message': include_fmt,
'DIT': lambda x: r"$\bm{%.4f}$" % x if x == max(main_df["DIT"]) else "$%.4f$" % x,
}
# filter out uninteresting rows, like there was no corpus
main_df = main_df[(main_df["FLT"] != 0) | (main_df["DIT"] != 0)]
if rq == "model":
main_df = main_df.sort(["K", "alpha", "eta"])
"""main_df["Configuration"] = (main_df.K.apply(lambda x: "$(K=%s" % int(x)) +
main_df.alpha.apply(lambda x: r",\alpha=%s/K" % x if x != 'auto' else r',\alpha=auto') +
main_df.eta.apply(lambda x: r",\eta=%s/K)$" % x if x != 'auto' else r',\eta=auto)$'))"""
else:
main_df = main_df.sort(["Additions", "Removals", "Context", "Message"], ascending=False)
main_df["Configuration"] = (main_df.Additions.apply(lambda x: 'A' if x else '') +
main_df.Removals.apply(lambda x: 'R' if x else '') +
main_df.Context.apply(lambda x: 'C' if x else '') +
main_df.Message.apply(lambda x: 'M' if x else ''))
formatters["Configuration"] = lambda x: "$(%s)$" % ','.join(x)
label = "%s_%s_sweep" % (label_name, rq)
op = os.path.join(tex_dir, label + ".tex")
best_flt = main_df[main_df["FLT"] == main_df["FLT"].max()]
best_dit = main_df[main_df["DIT"] == main_df["DIT"].max()]
if len(main_df) > 24:
tex = r"\parbox{.45\linewidth}{\centering %s} \hfill \parbox{.45\linewidth}{\centering %s}"
mid = len(main_df)//2
tex = tex % (main_df[:mid].to_latex(index=False,
escape=False, # needed so it doesn't screw up formatters
formatters=formatters,
columns=table_headers[rq]),
main_df[mid:].to_latex(index=False,
escape=False, # needed so it doesn't screw up formatters
formatters=formatters,
columns=table_headers[rq]))
else:
tex = main_df.to_latex(index=False,
escape=False, # needed so it doesn't screw up formatters
formatters=formatters,
columns=table_headers[rq],)
if (rq == "model"):
blah = "\\cone"
else:
blah = "\\cone and \\ctwo"
# and now the lazy
this_full_tex = full_tex % (caption, rq, blah, label, tex)
this_full_tex = this_full_tex.replace(" alpha ", r" $\alpha$ ")
this_full_tex = this_full_tex.replace(" eta ", r" $\eta$ ")
this_full_tex = this_full_tex.replace(r"\begin{tabular}{rllrr}", r"\begin{tabular}{rll|rr}")
this_full_tex = this_full_tex.replace(r"\begin{tabular}{llllrr}", r"\begin{tabular}{llll|rr}")
this_full_tex = this_full_tex.replace(r"$500$ & $1/K$ & $1/K$ &", r"\myrowcolor $500$ & $1/K$ & $1/K$ &")
this_full_tex = this_full_tex.replace(r"Included & Included & Included & &", r"\myrowcolor Included & Included & Included & &")
#print("Writing to: %s\n%s\n" % (op, this_full_tex))
print("Writing to:", op)
with open(op, 'wt') as f:
f.write(this_full_tex)
return best_dit, best_flt
best_dits = dict({"model": dict(), "corpus": dict()})
best_flts = dict({"model": dict(), "corpus": dict()})
for rq, main_df in [("model", model_all), ("corpus", corpus_all)]:
names[rq]['score'] = 'score'
main_df = main_df.unstack(0).reset_index()
best_dit, best_flt = do_great_table(main_df, "all", rq, "all subject systems")
best_dits[rq]["all subject systems"] = best_dit
best_flts[rq]["all subject systems"] = best_flt
for rq, main_df in [("model", model_df), ("corpus", corpus_df)]:
names[rq]['score'] = 'score'
group = groups[rq]
zz = main_df.groupby(["Subject", "Task"] + group).Rank.apply(lambda x: numpy.mean(1/x))
for each in zz.index.levels[0]:
each_df = zz[each].unstack(0).reset_index()
bad_person = each.split()[0].lower()
best_dit, best_flt = do_great_table(each_df, bad_person, rq, "\\" + bad_person)
best_dits[rq][each] = best_dit
best_flts[rq][each] = best_flt
# -
best_dits['model']['all subject systems'], best_flts['model']['all subject systems']
# +
FIG_TEX="""
%% new fig
\\begin{figure}
\\centering
\\begin{subfigure}{.4\\textwidth}
\\centering
\\includegraphics[height=0.4\\textheight]{%s}
\\caption{Including outliers}\\label{fig:combo:%s_outlier}
\\end{subfigure}%%
\\begin{subfigure}{.4\\textwidth}
\\centering
\\includegraphics[height=0.4\\textheight]{%s_no_outlier}
\\caption{Excluding outliers}\\label{fig:combo:%s_no_outlier}
\\end{subfigure}
\\caption[%s effectiveness measures of optimal and alternate %s configurations for %s]%%
{%s effectiveness measures of optimal ($MRR=%.4f$) and alternate ($MRR=%.4f$) %s configurations for %s}
\\label{fig:combo:%s}
\\end{figure}
"""
def plot_dataframe(df, each, name, kind):
order = ["Optimal", "Alternate"]
kind = kind.lower()
name = name.lower()
size = (len(order)*1.6, 4.5)
limitgrowth = 0.5
fontsize = None
widths = 0.3
lower = 0
kinds = {"flt": "Feature Location", "dit": "Developer Identification"}
rqs = {"flt": {"rq1": "\\cone", "rq2": "\\ctwo", "all": "Overview"},
"dit": {"rq1": "\\cone", "rq2": "\\ctwo", "all": "Overview"}}
config_name = "model" if name == "rq1" else "corpus"
result = df.plot(kind='box',
fontsize=fontsize,
figsize=size,
widths=widths,
y=order)
limit = result.get_ylim()
lower = limit[0] - limitgrowth
if (lower < 0):
lower = 0
result.set_ylim(lower, limit[1] + limitgrowth)
plt.tight_layout()
short_each = each.lower().split(' ')[0]
fig_name = 'figures/combo/%s_%s_%s' % (kind, name, short_each)
path = os.path.expanduser('~/git/dissertation/') + fig_name
plt.savefig(path + ".pdf", dpi=300)
optimal_data = df["Optimal"].dropna()
alternate_data = df["Alternate"].dropna()
optimal_mrr = src.utils.calculate_mrr(optimal_data)
alternative_mrr = src.utils.calculate_mrr(alternate_data)
#T, p, r = wilcoxon(optimal_data, alternate_data)
with open(path + ".tex", "wt") as f:
figlabel = ":".join([x.lower() for x in [kind, name, short_each]])
f.write(FIG_TEX % (fig_name, figlabel,
fig_name, figlabel,
kinds[kind], config_name, each, # toc caption
kinds[kind], # full figure caption
optimal_mrr, alternative_mrr,
config_name, each,
figlabel))
plt.close()
# no outliers
result = df.plot(kind='box',
fontsize=fontsize,
figsize=size,
widths=widths,
y=order,
showfliers=False)
limit = result.get_ylim()
lower = limit[0] - limitgrowth
if (lower < 0):
lower = 0
result.set_ylim(lower, limit[1] + limitgrowth)
plt.tight_layout()
fig_name = 'figures/combo/%s_%s_%s_no_outlier' % (kind, name, short_each)
path = os.path.expanduser('~/git/dissertation/') + fig_name
plt.savefig(path + ".pdf", dpi=300)
plt.close()
# +
corpus_wilcoxon_df = pandas.DataFrame(columns=["Subject", "Task",
"Optimal Configuration", "Alternate Configuration",
"Optimal MRR", "Alternate MRR",
#"T",
"p-value", "Effect size"])
model_wilcoxon_df = pandas.DataFrame(columns=["Subject", "Task",
"Optimal Configuration", "Alternate Configuration",
"Optimal MRR", "Alternate MRR",
#"T",
"p-value", "Effect size"])
for task, best_df, best_alt_df in [("FLT", best_flts, best_dits), ("DIT", best_dits, best_flts)]:
for project, table in best_df['corpus'].items():
alt_table = best_alt_df['corpus'][project]
optimal_config = "$(%s)$" % ", ".join([key[0] for key, value in table.iteritems() if key != "FLT" and key != "DIT" and key != "Configuration" and value.values[0]])
alt_config = "$(%s)$" % ", ".join([key[0] for key, value in alt_table.iteritems() if key != "FLT" and key != "DIT" and key != "Configuration" and value.values[0]])
print(project, task, 'corpus', optimal_config, alt_config)
#print(table.sample(1))
optimal = corpus_df[
(corpus_df.Task == task) &
(corpus_df.Additions == table.Additions.values[0]) &
(corpus_df.Removals == table.Removals.values[0]) &
(corpus_df.Context == table.Context.values[0]) &
(corpus_df.Message == table.Message.values[0])]
#print(alt_table.sample(1))
alternate = corpus_df[
(corpus_df.Task == task) &
(corpus_df.Additions == alt_table.Additions.values[0]) &
(corpus_df.Removals == alt_table.Removals.values[0]) &
(corpus_df.Context == alt_table.Context.values[0]) &
(corpus_df.Message == alt_table.Message.values[0])]
if project != "all subject systems":
optimal = optimal[optimal.Subject == project]
alternate = alternate[alternate.Subject == project]
merge_df = optimal.merge(alternate, on=["Subject", "Task", "Issue"])
optalt_df = pandas.DataFrame()
optalt_df["Optimal"] = merge_df.Rank_x
optalt_df["Alternate"] = merge_df.Rank_y
plot_dataframe(optalt_df, project, "rq2", task)
if((optalt_df.Optimal == optalt_df.Alternate).all()):
corpus_wilcoxon_df = corpus_wilcoxon_df.append({
"Subject": project,
"Task": task,
"Optimal MRR": numpy.mean(1/optalt_df.Optimal),
"Alternate MRR": numpy.mean(1/optalt_df.Alternate),
"Optimal Configuration": optimal_config,
"Alternate Configuration": alt_config,
#"T": numpy.NaN,
"p-value": numpy.NaN,
"Effect size": numpy.NaN
}, ignore_index=True)
else:
T, p, r = wilcoxon(optalt_df.Optimal, optalt_df.Alternate)
corpus_wilcoxon_df = corpus_wilcoxon_df.append({
"Subject": project,
"Task": task,
"Optimal MRR": numpy.mean(1/optalt_df.Optimal),
"Alternate MRR": numpy.mean(1/optalt_df.Alternate),
"Optimal Configuration": optimal_config,
"Alternate Configuration": alt_config,
#"T": T,
"p-value": p,
"Effect size": r
}, ignore_index=True)
for task, best_df, best_alt_df in [("FLT", best_flts, best_dits), ("DIT", best_dits, best_flts)]:
for project, table in best_df['model'].items():
alt_table = best_alt_df['model'][project]
optimal_config = "$(%s)$" % ", ".join(["%s=%s" % (key, int(value.values[0]) if key == "K" else "%s/K" % value.values[0] if value.values[0] != "auto" else value.values[0]) for key, value in sorted(table.iteritems()) if key != "FLT" and key != "DIT" and key != "Configuration"]).replace("alpha", "\\alpha").replace("eta", "\\eta")
alt_config = "$(%s)$" % ", ".join(["%s=%s" % (key, int(value.values[0]) if key == "K" else "%s/K" % value.values[0] if value.values[0] != "auto" else value.values[0]) for key, value in sorted(alt_table.iteritems()) if key != "FLT" and key != "DIT" and key != "Configuration"]).replace("alpha", "\\alpha").replace("eta", "\\eta")
print(project, task, 'model', optimal_config, alt_config)
#print(table.sample(1))
optimal = model_df[
(model_df.Task == task) &
(model_df.alpha == table.alpha.values[0]) &
(model_df.eta == table.eta.values[0]) &
(model_df.K == table.K.values[0])]
#print(alt_table.sample(1))
alternate = model_df[
(model_df.Task == task) &
(model_df.alpha == alt_table.alpha.values[0]) &
(model_df.eta == alt_table.eta.values[0]) &
(model_df.K == alt_table.K.values[0])]
if project != "all subject systems":
optimal = optimal[optimal.Subject == project]
alternate = alternate[alternate.Subject == project]
merge_df = optimal.merge(alternate, on=["Subject", "Task", "Issue"])
optalt_df = pandas.DataFrame()
optalt_df["Optimal"] = merge_df.Rank_x
optalt_df["Alternate"] = merge_df.Rank_y
plot_dataframe(optalt_df, project, "rq1", task)
if((optalt_df.Optimal == optalt_df.Alternate).all()):
model_wilcoxon_df = model_wilcoxon_df.append({
"Subject": project,
"Task": task,
"Optimal MRR": numpy.mean(1/optalt_df.Optimal),
"Alternate MRR": numpy.mean(1/optalt_df.Alternate),
"Optimal Configuration": optimal_config,
"Alternate Configuration": alt_config,
#"T": numpy.NaN,
"p-value": numpy.NaN,
"Effect size": numpy.NaN
}, ignore_index=True)
else:
T, p, r = wilcoxon(optalt_df.Optimal, optalt_df.Alternate)
model_wilcoxon_df = model_wilcoxon_df.append({
"Subject": project,
"Task": task,
"Optimal MRR": numpy.mean(1/optalt_df.Optimal),
"Alternate MRR": numpy.mean(1/optalt_df.Alternate),
"Optimal Configuration": optimal_config,
"Alternate Configuration": alt_config,
#"T": T,
"p-value": p,
"Effect size" : r
}, ignore_index=True)
# -
bon
def print_wilcox(df, task, kind):
WILCOX="""
%% new fig
\\begin{table}
\\begin{spacing}{1.2}
\\centering
\\caption{Wilcoxon test results for %s optimal and alternate %s configurations (%s)}
\\label{table:combo-%s-%s-sweep-wilcox}
%s
\\end{spacing}
\\end{table}
"""
path = os.path.expanduser('~/git/dissertation/tables/')
path += "landscape_%s_sweep_wilcox.tex" % (kind.lower())
with open(path, 'wt') as f:
print("\\begin{landscape}", file=f)
if (kind == "model"):
blah = "\\cone"
else:
blah = "\\cone and \\ctwo"
for task in ["FLT", "DIT"]:
j = df[df.Task == task]
del j["Task"]
j = j.sort(columns=["Subject"])
with open(path, 'at') as f:
print(WILCOX % (task.upper(), kind.lower(), blah, task.lower(), kind.lower(),
j.to_latex(index=False,
escape=False, # needed so it doesn't screw up formatters
formatters=formatters)
.replace('nan', '')
.replace('Optimal MRR & ', '')
.replace('Alternate MRR', '\\multicolumn{2}{c}{MRRs} ')), file=f)
with open(path, 'at') as f:
print("\\end{landscape}", file=f)
print_wilcox(model_wilcoxon_df, "FLT", "model")
print_wilcox(model_wilcoxon_df, "DIT", "model")
print_wilcox(corpus_wilcoxon_df, "FLT", "corpus")
print_wilcox(corpus_wilcoxon_df, "DIT", "corpus")
corpus_wilcoxon_df["Optimal Configuration"].str.contains('A').value_counts()
corpus_wilcoxon_df["Optimal Configuration"].str.contains('C').value_counts()
corpus_wilcoxon_df["Optimal Configuration"].str.contains('M').value_counts()
corpus_wilcoxon_df["Optimal Configuration"].str.contains('R').value_counts()
# +
versus = dict()
for kind in 'ACMR':
versus_r = cres[(cres.Config.str.contains(kind) & ~cres.Config2.str.contains(kind) & (cres.Config.str.replace(kind, '') == cres.Config2))]
# Includes, Excludes
versus[kind] = {'FLT Included': versus_r[(versus_r.MRR > versus_r.MRR2) & (versus_r.Task == "FLT")].Subject.value_counts(),
'FLT Excluded': versus_r[(versus_r.MRR2 > versus_r.MRR) & (versus_r.Task == "FLT")].Subject.value_counts(),
'DIT Included': versus_r[(versus_r.MRR > versus_r.MRR2) & (versus_r.Task == "DIT")].Subject.value_counts(),
'DIT Excluded': versus_r[(versus_r.MRR2 > versus_r.MRR) & (versus_r.Task == "DIT")].Subject.value_counts(),
'Both Included': versus_r[(versus_r.MRR > versus_r.MRR2)].Subject.value_counts(),
'Both Excluded': versus_r[(versus_r.MRR2 > versus_r.MRR)].Subject.value_counts(),
}
versus = pandas.Panel(versus).fillna(0)
# -
versus['A']
versus['C']
versus['M']
versus['R']
# +
versus_wilcox = dict()
for kind in 'ACMR':
versus_r = cres[(cres.Config.str.contains(kind) & ~cres.Config2.str.contains(kind) & (cres.Config.str.replace(kind, '') == cres.Config2))]
del(versus_r["T"])
versus_wilcox[kind] = versus_r
#versus_wilcox["Config"] = versus_wilcox["Config"].apply(lambda x: "$(%s)$" % ", ".join(x))
versus_wilcox = pandas.Panel(versus_wilcox)
versus_wilcox["A"].dropna()
# +
TEX="""
\\begin{table}
\\begin{spacing}{1.2}
\\centering
\\caption{Wilcoxon test results for %s inclusion and exclusion configurations of the %s task for %s (\\ctwo)}
\\label{table:%s}
%s
\\end{spacing}
\\end{table}
"""
kinds = ["additions", "removals", "context", "message"]
def reorg_string(s):
new = ""
s = s.upper()
for each in 'ARCM':
if each in s:
new += each
return new
float_format = lambda x: "$%1.4f$" % x
float_format_bold = lambda x: "$\\bm{%1.4f}$" % x
fasdf = {
"p-value": lambda x: "$p<0.01$" if x < 0.01 else float_format(x) ,
"Effect size": float_format,
"Config": lambda x: "$(%s)$" % ','.join(reorg_string(x)),
"Config2": lambda x: "$(%s)$" % ','.join(reorg_string(x)),
}
for source in ["additions", "removals", "context", "message"]:
df = versus_wilcox[source[0].upper()].dropna()
for key, group in df.groupby(["Subject", "Task"]):
subject, task = key
a = pandas.DataFrame(group) # drops warnings for http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy
a["p-value"] = a["p"].astype(float)
a["Effect size"] = a["r"].astype(float)
a["MRR"] = a["MRR"].astype(float)
a["MRR2"] = a["MRR2"].astype(float)
del[a["p"]]
del[a["r"]]
del[a["Subject"]]
del[a["Task"]]
a = pandas.DataFrame(a)
left = (a.MRR > a.MRR2)
right = (a.MRR <= a.MRR2)
a.MRR.update(a[left].MRR.apply(float_format_bold))
a.MRR.update(a[right].MRR.apply(float_format))
a.MRR2.update(a[left].MRR2.apply(float_format))
a.MRR2.update(a[right].MRR2.apply(float_format_bold))
s = subject.split()[0].lower()
name = "versus-wilcox-%s-%s-%s" % (s, task.lower(), source)
path = os.path.expanduser('~/git/dissertation/tables/')
path += "%s.tex" % (name.lower())
with open(path, 'wt') as f:
print(TEX % (source, task.upper(), subject, name,
a.to_latex(index=False, escape=False, formatters=fasdf)
.replace("Config ", "\\multicolumn{2}{c|}{Configurations} ")
.replace("Config2 &", "")
.replace("MRR ", "\\multicolumn{2}{c|}{MRRs} ")
.replace("MRR2 &", "")
.replace("llllrr", "ll|rr|rr")),
file=f)
# -
| notebooks/sweep analysis.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Machine Learning Engineer Nanodegree
# ## Model Evaluation & Validation
# ## Project 1: Predicting Boston Housing Prices
#
# Welcome to the first project of the Machine Learning Engineer Nanodegree! In this notebook, some template code has already been provided for you, and you will need to implement additional functionality to successfully complete this project. You will not need to modify the included code beyond what is requested. Sections that begin with **'Implementation'** in the header indicate that the following block of code will require additional functionality which you must provide. Instructions will be provided for each section and the specifics of the implementation are marked in the code block with a 'TODO' statement. Please be sure to read the instructions carefully!
#
# In addition to implementing code, there will be questions that you must answer which relate to the project and your implementation. Each section where you will answer a question is preceded by a **'Question X'** header. Carefully read each question and provide thorough answers in the following text boxes that begin with **'Answer:'**. Your project submission will be evaluated based on your answers to each of the questions and the implementation you provide.
#
# >**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. In addition, Markdown cells can be edited by typically double-clicking the cell to enter edit mode.
# ## Getting Started
# In this project, you will evaluate the performance and predictive power of a model that has been trained and tested on data collected from homes in suburbs of Boston, Massachusetts. A model trained on this data that is seen as a *good fit* could then be used to make certain predictions about a home — in particular, its monetary value. This model would prove to be invaluable for someone like a real estate agent who could make use of such information on a daily basis.
#
# The dataset for this project originates from the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Housing). The Boston housing data was collected in 1978 and each of the 506 entries represent aggregated data about 14 features for homes from various suburbs in Boston, Massachusetts. For the purposes of this project, the following preprocessing steps have been made to the dataset:
# - 16 data points have an `'MEDV'` value of 50.0. These data points likely contain **missing or censored values** and have been removed.
# - 1 data point has an `'RM'` value of 8.78. This data point can be considered an **outlier** and has been removed.
# - The features `'RM'`, `'LSTAT'`, `'PTRATIO'`, and `'MEDV'` are essential. The remaining **non-relevant features** have been excluded.
# - The feature `'MEDV'` has been **multiplicatively scaled** to account for 35 years of market inflation.
#
# Run the code cell below to load the Boston housing dataset, along with a few of the necessary Python libraries required for this project. You will know the dataset loaded successfully if the size of the dataset is reported.
# +
# Import libraries necessary for this project
import numpy as np
import pandas as pd
import visuals as vs # Supplementary code
from sklearn.cross_validation import ShuffleSplit
# Pretty display for notebooks
# %matplotlib inline
# Load the Boston housing dataset
data = pd.read_csv('housing.csv')
prices = data['MEDV']
features = data.drop('MEDV', axis = 1)
# Success
print "Boston housing dataset has {} data points with {} variables each.".format(*data.shape)
# -
# ## Data Exploration
# In this first section of this project, you will make a cursory investigation about the Boston housing data and provide your observations. Familiarizing yourself with the data through an explorative process is a fundamental practice to help you better understand and justify your results.
#
# Since the main goal of this project is to construct a working model which has the capability of predicting the value of houses, we will need to separate the dataset into **features** and the **target variable**. The **features**, `'RM'`, `'LSTAT'`, and `'PTRATIO'`, give us quantitative information about each data point. The **target variable**, `'MEDV'`, will be the variable we seek to predict. These are stored in `features` and `prices`, respectively.
# ### Implementation: Calculate Statistics
# For your very first coding implementation, you will calculate descriptive statistics about the Boston housing prices. Since `numpy` has already been imported for you, use this library to perform the necessary calculations. These statistics will be extremely important later on to analyze various prediction results from the constructed model.
#
# In the code cell below, you will need to implement the following:
# - Calculate the minimum, maximum, mean, median, and standard deviation of `'MEDV'`, which is stored in `prices`.
# - Store each calculation in their respective variable.
# +
# TODO: Minimum price of the data
minimum_price = np.amin(prices)
# TODO: Maximum price of the data
maximum_price = np.amax(prices)
# TODO: Mean price of the data
mean_price = np.mean(prices)
# TODO: Median price of the data
median_price = np.median(prices)
# TODO: Standard deviation of prices of the data
std_price = np.std(prices)
# Show the calculated statistics
print "Statistics for Boston housing dataset:\n"
print "Minimum price: ${:,.2f}".format(minimum_price)
print "Maximum price: ${:,.2f}".format(maximum_price)
print "Mean price: ${:,.2f}".format(mean_price)
print "Median price ${:,.2f}".format(median_price)
print "Standard deviation of prices: ${:,.2f}".format(std_price)
# -
# ### Question 1 - Feature Observation
# As a reminder, we are using three features from the Boston housing dataset: `'RM'`, `'LSTAT'`, and `'PTRATIO'`. For each data point (neighborhood):
# - `'RM'` is the average number of rooms among homes in the neighborhood.
# - `'LSTAT'` is the percentage of homeowners in the neighborhood considered "lower class" (working poor).
# - `'PTRATIO'` is the ratio of students to teachers in primary and secondary schools in the neighborhood.
#
# _Using your intuition, for each of the three features above, do you think that an increase in the value of that feature would lead to an **increase** in the value of `'MEDV'` or a **decrease** in the value of `'MEDV'`? Justify your answer for each._
# **Hint:** Would you expect a home that has an `'RM'` value of 6 be worth more or less than a home that has an `'RM'` value of 7?
# **Answer: **
# The use of Data visualization tools (dataset distribution) helped me to understand the relation between the features on our model.
#
# -**RM**: considering we are using the same LSTAT and PTRATIO I could verify that by increasing the RM (number of rooms) it also increased the MEDV (home price).
#
# -**LSTAT**: considering we are using the same RM and PTRATION I could verify that LSTAT have an inverse relation with the MEDV, which means, by increasing the LSTAT (lower class neighborhood) it decreased the MED (home price).
#
# -**PTRATIO**: PTRATIO (students per teacher) behaves almost like the LSTAT (lower class neighborhood), but it is not strong as the LSTAT. I noticed that its distribution was way more spreaded and that sometimes by increasing the PTRATIO it also increased the MEDV. But, the overall tendency showed to be an inverse relation with MEDV, too.
#
# Based on how our features are behaving in our model, I would say that a home with RM 6 will probably worth more than a home with RM 7, when the LSTAT or the PTRATIO of the first home is lower compared with the second home. And also, that a home with RM 6 will probably worth less than a home with RM 7 when both have the same (or close) values for the other features (LSTAT and PTRATION).
#
# ----
#
# ## Developing a Model
# In this second section of the project, you will develop the tools and techniques necessary for a model to make a prediction. Being able to make accurate evaluations of each model's performance through the use of these tools and techniques helps to greatly reinforce the confidence in your predictions.
# ### Implementation: Define a Performance Metric
# It is difficult to measure the quality of a given model without quantifying its performance over training and testing. This is typically done using some type of performance metric, whether it is through calculating some type of error, the goodness of fit, or some other useful measurement. For this project, you will be calculating the [*coefficient of determination*](http://stattrek.com/statistics/dictionary.aspx?definition=coefficient_of_determination), R<sup>2</sup>, to quantify your model's performance. The coefficient of determination for a model is a useful statistic in regression analysis, as it often describes how "good" that model is at making predictions.
#
# The values for R<sup>2</sup> range from 0 to 1, which captures the percentage of squared correlation between the predicted and actual values of the **target variable**. A model with an R<sup>2</sup> of 0 always fails to predict the target variable, whereas a model with an R<sup>2</sup> of 1 perfectly predicts the target variable. Any value between 0 and 1 indicates what percentage of the target variable, using this model, can be explained by the **features**. *A model can be given a negative R<sup>2</sup> as well, which indicates that the model is no better than one that naively predicts the mean of the target variable.*
#
# For the `performance_metric` function in the code cell below, you will need to implement the following:
# - Use `r2_score` from `sklearn.metrics` to perform a performance calculation between `y_true` and `y_predict`.
# - Assign the performance score to the `score` variable.
# +
from sklearn.metrics import r2_score
def performance_metric(y_true, y_predict):
""" Calculates and returns the performance score between
true and predicted values based on the metric chosen. """
# TODO: Calculate the performance score between 'y_true' and 'y_predict'
score = r2_score(y_true, y_predict)
# Return the score
return score
# -
# ### Question 2 - Goodness of Fit
# Assume that a dataset contains five data points and a model made the following predictions for the target variable:
#
# | True Value | Prediction |
# | :-------------: | :--------: |
# | 3.0 | 2.5 |
# | -0.5 | 0.0 |
# | 2.0 | 2.1 |
# | 7.0 | 7.8 |
# | 4.2 | 5.3 |
# *Would you consider this model to have successfully captured the variation of the target variable? Why or why not?*
#
# Run the code cell below to use the `performance_metric` function and calculate this model's coefficient of determination.
# Calculate the performance of this model
score = performance_metric([3, -0.5, 2, 7, 4.2], [2.5, 0.0, 2.1, 7.8, 5.3])
print "Model has a coefficient of determination, R^2, of {:.3f}.".format(score)
# **Answer:** It is visible that the given model is following the target variations. It is not accurate, but it getting close. We can see it represented by the coefficient of determination that is very close to 1, it is in fact 0.92.
# ### Implementation: Shuffle and Split Data
# Your next implementation requires that you take the Boston housing dataset and split the data into training and testing subsets. Typically, the data is also shuffled into a random order when creating the training and testing subsets to remove any bias in the ordering of the dataset.
#
# For the code cell below, you will need to implement the following:
# - Use `train_test_split` from `sklearn.cross_validation` to shuffle and split the `features` and `prices` data into training and testing sets.
# - Split the data into 80% training and 20% testing.
# - Set the `random_state` for `train_test_split` to a value of your choice. This ensures results are consistent.
# - Assign the train and testing splits to `X_train`, `X_test`, `y_train`, and `y_test`.
# +
from sklearn.cross_validation import train_test_split
# TODO: Shuffle and split the data into training and testing subsets
X_train, X_test, y_train, y_test = train_test_split(features, prices, test_size=0.2, random_state=47)
# Success
print "Training and testing split was successful."
# -
# ### Question 3 - Training and Testing
# *What is the benefit to splitting a dataset into some ratio of training and testing subsets for a learning algorithm?*
# **Hint:** What could go wrong with not having a way to test your model?
# **Answer: ** Split the dataset provide us a feedback for comparison. With it we can check if the training data and the testing data are following the same approach on determination and that we are not **overfitting** the model. It works like a double check, in order to make sure that our model was well defined and will be good to provide consistent predictions. By not splitting the dataset there is risk of never validate it with different data, that way becomes hard to guarantee the effectiveness of our model, as we may be assuming data patterns (on our first round of data entry) that are not real patterns for the next set of data that might be applied to our model in the future.
# ----
#
# ## Analyzing Model Performance
# In this third section of the project, you'll take a look at several models' learning and testing performances on various subsets of training data. Additionally, you'll investigate one particular algorithm with an increasing `'max_depth'` parameter on the full training set to observe how model complexity affects performance. Graphing your model's performance based on varying criteria can be beneficial in the analysis process, such as visualizing behavior that may not have been apparent from the results alone.
# ### Learning Curves
# The following code cell produces four graphs for a decision tree model with different maximum depths. Each graph visualizes the learning curves of the model for both training and testing as the size of the training set is increased. Note that the shaded region of a learning curve denotes the uncertainty of that curve (measured as the standard deviation). The model is scored on both the training and testing sets using R<sup>2</sup>, the coefficient of determination.
#
# Run the code cell below and use these graphs to answer the following question.
# Produce learning curves for varying training set sizes and maximum depths
vs.ModelLearning(features, prices)
# ### Question 4 - Learning the Data
# *Choose one of the graphs above and state the maximum depth for the model. What happens to the score of the training curve as more training points are added? What about the testing curve? Would having more training points benefit the model?*
# **Hint:** Are the learning curves converging to particular scores?
# **Answer: ** After analysing the graphs, I decided to use maximum depth equals to 3, for this model, as both curves are converging in to a reasonable score.
#
# Curves analysis when max_depth=3:
# - The training curve starts with score 1 and when we added more training points this curve falls close to 0.9. Furthermore, as more training points are added the curve stabilizes around score 0.8.
# - The testing curve starts with score 0 and then, after the first 50 training points, it raises to score 0.6. As more training points are added the curve stabilizes around score 0.8, as the training curve.
#
# After more than 350 training points both curves seemed to be converging indicating that we found a good generalization model.
#
# I don't think that more training points will benefit this model, considering the graph with depth equals 3, because it is possible to perceive that the testing curve have already stabilized close to the training curve and that both are close to a reasonable score.
# ### Complexity Curves
# The following code cell produces a graph for a decision tree model that has been trained and validated on the training data using different maximum depths. The graph produces two complexity curves — one for training and one for validation. Similar to the **learning curves**, the shaded regions of both the complexity curves denote the uncertainty in those curves, and the model is scored on both the training and validation sets using the `performance_metric` function.
#
# Run the code cell below and use this graph to answer the following two questions.
vs.ModelComplexity(X_train, y_train)
# ### Question 5 - Bias-Variance Tradeoff
# *When the model is trained with a maximum depth of 1, does the model suffer from high bias or from high variance? How about when the model is trained with a maximum depth of 10? What visual cues in the graph justify your conclusions?*
# **Hint:** How do you know when a model is suffering from high bias or high variance?
# **Answer: **
# - With **depth equals 1** we have a scenario of high bias (overfimplified). Both curves are presenting a very poor score, under 0.5. This demonstrate that a model trained like this would have not enought accurancy to predict usefull data.
#
# - With **depth equals 10** we are paying too much attention to the data (overfit) this means we have a high variance what is not good, too, as it will not generalize well. The visual cues of that are that at around depth 4 the curves are behaving in a predictive way and after that, after we increase the depth the curves diverge and we have a much higher error on validation curve than on traninig curve, what is not what we are looking for.
# ### Question 6 - Best-Guess Optimal Model
# *Which maximum depth do you think results in a model that best generalizes to unseen data? What intuition lead you to this answer?*
# **Answer: ** I would say something about 3 or 4 as depth, my intuition leads me to choose 4, as I saw depth 3 decision tree regressor performance scores about 0.8, as the complexity curve remains stable for depth 4, maybe we can achieve scores highers than 0.8 using depth 4.
# -----
#
# ## Evaluating Model Performance
# In this final section of the project, you will construct a model and make a prediction on the client's feature set using an optimized model from `fit_model`.
# ### Question 7 - Grid Search
# *What is the grid search technique and how it can be applied to optimize a learning algorithm?*
# **Answer: **
# Grid Search is a generalization of the traditional search technique that seeks for an optimal hyperparameter that when applied to a given model produces the best predictions (avoiding, as possible, data overfitting).
#
# The big deal about Grid Search is that it can be applied for tuning the models that interact with with more than one hyperparameter, creating complex tuples that when are all combined we give them the name of "grids".
#
# This techinque will loop thru around all set of hyperparameters combinations comparing the effectiveness of the model, by the end it will find the set of parameters that produces the best prediction model (avoiding, as possible, overfitting the data).
# ### Question 8 - Cross-Validation
# *What is the k-fold cross-validation training technique? What benefit does this technique provide for grid search when optimizing a model?*
# **Hint:** Much like the reasoning behind having a testing set, what could go wrong with using grid search without a cross-validated set?
# **Answer: **
# K-fold cross-validation is an evolution of the simple cross-validation that splits data in testing and training datasets. On **K-fold** we divide the dataset into k subsets and we perform cross-validation using k subset as testing and the rest of the k-1 subsets becomes the training data. We then run this **k-times** to calculate the averages. Using k-fold we can use the entire dataset, but it costs more if we take in count the processing time.
#
# The main benefit of K-fold is that its cross-validation method is really good to avoid data overfit, because we can validate the model effectiveness using different subsets of training and testing data **k-times**.
# Adding this technique, that **reduces the overfitting**, as part of the **Grid Search** technique help us to get the best set of hyperparameters that will really generalizes the model, avoiding the model **overtuning** (that is when we the set of parameters we found does not generalize well the entire model, as it was just hooked by the validation set).
# ### Implementation: Fitting a Model
# Your final implementation requires that you bring everything together and train a model using the **decision tree algorithm**. To ensure that you are producing an optimized model, you will train the model using the grid search technique to optimize the `'max_depth'` parameter for the decision tree. The `'max_depth'` parameter can be thought of as how many questions the decision tree algorithm is allowed to ask about the data before making a prediction. Decision trees are part of a class of algorithms called *supervised learning algorithms*.
#
# For the `fit_model` function in the code cell below, you will need to implement the following:
# - Use [`DecisionTreeRegressor`](http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html) from `sklearn.tree` to create a decision tree regressor object.
# - Assign this object to the `'regressor'` variable.
# - Create a dictionary for `'max_depth'` with the values from 1 to 10, and assign this to the `'params'` variable.
# - Use [`make_scorer`](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.make_scorer.html) from `sklearn.metrics` to create a scoring function object.
# - Pass the `performance_metric` function as a parameter to the object.
# - Assign this scoring function to the `'scoring_fnc'` variable.
# - Use [`GridSearchCV`](http://scikit-learn.org/stable/modules/generated/sklearn.grid_search.GridSearchCV.html) from `sklearn.grid_search` to create a grid search object.
# - Pass the variables `'regressor'`, `'params'`, `'scoring_fnc'`, and `'cv_sets'` as parameters to the object.
# - Assign the `GridSearchCV` object to the `'grid'` variable.
# +
# TODO: Import 'make_scorer', 'DecisionTreeRegressor', and 'GridSearchCV'
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import make_scorer
from sklearn.grid_search import GridSearchCV
def fit_model(X, y):
""" Performs grid search over the 'max_depth' parameter for a
decision tree regressor trained on the input data [X, y]. """
# Create cross-validation sets from the training data
cv_sets = ShuffleSplit(X.shape[0], n_iter = 10, test_size = 0.20, random_state = 0)
# TODO: Create a decision tree regressor object
regressor = DecisionTreeRegressor(random_state=0)
# TODO: Create a dictionary for the parameter 'max_depth' with a range from 1 to 10
params = {'max_depth': range(1,11)}
# TODO: Transform 'performance_metric' into a scoring function using 'make_scorer'
scoring_fnc = make_scorer(performance_metric)
# TODO: Create the grid search object
grid = GridSearchCV(regressor, params, scoring = scoring_fnc, cv = cv_sets)
# Fit the grid search object to the data to compute the optimal model
grid = grid.fit(X, y)
# Return the optimal model after fitting the data
return grid.best_estimator_
# -
# ### Making Predictions
# Once a model has been trained on a given set of data, it can now be used to make predictions on new sets of input data. In the case of a *decision tree regressor*, the model has learned *what the best questions to ask about the input data are*, and can respond with a prediction for the **target variable**. You can use these predictions to gain information about data where the value of the target variable is unknown — such as data the model was not trained on.
# ### Question 9 - Optimal Model
# _What maximum depth does the optimal model have? How does this result compare to your guess in **Question 6**?_
#
# Run the code block below to fit the decision tree regressor to the training data and produce an optimal model.
# +
# Fit the training data to the model using grid search
reg = fit_model(X_train, y_train)
# Produce the value for 'max_depth'
print "Parameter 'max_depth' is {} for the optimal model.".format(reg.get_params()['max_depth'])
# -
# **Answer: ** The max_depth is 5, I said on question 6 that my intuition was 4 as it was apparently better than 3 and 6 per our learning curves. But now, using the fit and other techniques it showed to be 5.
# ### Question 10 - Predicting Selling Prices
# Imagine that you were a real estate agent in the Boston area looking to use this model to help price homes owned by your clients that they wish to sell. You have collected the following information from three of your clients:
#
# | Feature | Client 1 | Client 2 | Client 3 |
# | :---: | :---: | :---: | :---: |
# | Total number of rooms in home | 5 rooms | 4 rooms | 8 rooms |
# | Neighborhood poverty level (as %) | 17% | 32% | 3% |
# | Student-teacher ratio of nearby schools | 15-to-1 | 22-to-1 | 12-to-1 |
# *What price would you recommend each client sell his/her home at? Do these prices seem reasonable given the values for the respective features?*
# **Hint:** Use the statistics you calculated in the **Data Exploration** section to help justify your response.
#
# Run the code block below to have your optimized model make predictions for each client's home.
# +
# Produce a matrix for client data
client_data = [[5, 17, 15], # Client 1
[4, 32, 22], # Client 2
[8, 3, 12]] # Client 3
# Show predictions
for i, price in enumerate(reg.predict(client_data)):
print "Predicted selling price for Client {}'s home: ${:,.2f}".format(i+1, price)
# -
# **Answer: ** Considering:<br/>
# **Statistics for Boston housing dataset:**<br/>
# Minimum price: `$`105,000.00 <br/>
# Maximum price: `$`1,024,800.00 <br/>
# Mean price: `$`454,342.94 <br/>
# Median price `$`438,900.00 <br/>
# Standard deviation of prices: `$`165,171.13 <br/>
# ps.:Considering that the Mean and Median are very close, I'm seeing this as an almost normal distribution.
#
# **Home Features**<br/>
# RM (#room): expected to increase the price<br/>
# LSTAT (poverty level): expected to decrease the price<br/>
# PTRATIO (Student-Teacher ratio): expected to decrease the price<br/>
#
# Client 1's home: `$`431,025.00 **(recommended)**
# This home price seems to be very reasonable because there are very good schools. Furthermore the price is compatible with the market and the 5 rooms are fair for this price, not forgetting that the neighborhood is not bad at all.
#
#
# Client 2's home: `$`166,350.00 **(recommended)**
# This home price seems, at first, very low. But it is still far from the Minimum price of our dataset. This price is between the second and the first standard deviation, below the median, what makes this price still acceptable. By checking its features we can see that the level of poverty is high and that Student-teacher ration is also bad.
# Considering this I would, also, trust in the algorithm prediction.
#
# Client 3's home: `$`879,900.00 **(recommended)**
# This home price seems, at first, very high. But when we saw that number of rooms (that is rare these days), this very nice neighborhood and those very selective and good schools, I think the home owner should try to sell it with this price.
#
# :)
#
# ### Sensitivity
# An optimal model is not necessarily a robust model. Sometimes, a model is either too complex or too simple to sufficiently generalize to new data. Sometimes, a model could use a learning algorithm that is not appropriate for the structure of the data given. Other times, the data itself could be too noisy or contain too few samples to allow a model to adequately capture the target variable — i.e., the model is underfitted. Run the code cell below to run the `fit_model` function ten times with different training and testing sets to see how the prediction for a specific client changes with the data it's trained on.
vs.PredictTrials(features, prices, fit_model, client_data)
# ### Question 11 - Applicability
# *In a few sentences, discuss whether the constructed model should or should not be used in a real-world setting.*
# **Hint:** Some questions to answering:
# - *How relevant today is data that was collected from 1978?*
# - *Are the features present in the data sufficient to describe a home?*
# - *Is the model robust enough to make consistent predictions?*
# - *Would data collected in an urban city like Boston be applicable in a rural city?*
# **Answer: **
# I believe that the constructed model is very interesting, but still need to be better validated. We could see that our model is still too sensitive by presenting price variations at a range of $73,357.29 on predictions.<br/>
#
# It is also important to notice that some society values changed since 1978, as the economy, the industry and the immigration, for instance. Just considering the RM, LSTAT and PTRATION as variables to our model definetly is something to revalidate. I'm not saying that we need to add more variables, but that we need to be sure about the ones we are using on our model. I believe that home price predictions should take in count also proximity to business centers/jobs, hospitals and malls, for example.<br/>
#
# Understanding how humans associate a price to an asset, is more complex than just think in superficial items like rooms or poverty. And I also believe that our model, as-is, would not work for rural cities, by the same reason.<br/>
#
# Based on that I think this mode should not be used in a real-world.
#
#
| python/boston_housing/boston_housing.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="nTYnSl6TUMxE" outputId="1f21f89e-f1d0-4cc9-d59c-be0f294cd745"
# gpu_info = !nvidia-smi
gpu_info = '\n'.join(gpu_info)
if gpu_info.find('failed') >= 0:
print('Not connected to a GPU')
else:
print(gpu_info)
# + id="whvcWqRrMTo0"
#Import Stuff here
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import tensorflow.keras as keras
from tensorflow.keras import layers, Model, optimizers
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Conv2D, MaxPooling2D, Flatten, GlobalAveragePooling2D, DepthwiseConv2D, BatchNormalization
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from sklearn.metrics import classification_report, confusion_matrix
import pandas as pd
import numpy as np
import time
from datetime import datetime
from tensorflow.keras.utils import plot_model
from tensorflow.keras.optimizers import RMSprop
# + id="XqHNqmzu9wDE"
from numpy.random import seed
seed(1)
import tensorflow
tensorflow.random.set_seed(2)
# + colab={"base_uri": "https://localhost:8080/"} id="M9l9_5mrcqmV" outputId="71b8b53a-a54e-4254-a895-d7abb50ad889"
from google.colab import drive, files
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="TznxUDLhMTo4" outputId="89216be5-af27-4b0b-cfd2-c70dda705a7b"
def load_data():
datagen = ImageDataGenerator(rescale = 1/255)
train_it = datagen.flow_from_directory ('/content/drive/My Drive/Colab Notebooks/IFFI-dataset-raw/Augmented/', target_size = (256, 256),
class_mode = 'categorical', color_mode="rgb", batch_size=64, seed = 1)
val_it = datagen.flow_from_directory ('/content/drive/My Drive/Colab Notebooks/IFFI-dataset-raw/validation/', target_size = (256, 256),
class_mode = 'categorical', color_mode="rgb", batch_size=64, seed = 1)
test_it = datagen.flow_from_directory ('/content/drive/My Drive/Colab Notebooks/IFFI-dataset-raw/test/', target_size = (256, 256),
class_mode = 'categorical', color_mode="rgb", batch_size=64, seed = 1, shuffle=False)
return train_it, val_it, test_it
train_it, val_it, test_it = load_data()
# + colab={"base_uri": "https://localhost:8080/"} id="AG5LosIcMTo5" outputId="153b3c18-1b54-4ff9-8b0d-2a8c5a43f9cd"
batchX, batchy = train_it.next()
print('Batch shape=%s, min=%.3f, max=%.3f' % (batchX.shape, batchX.min(), batchX.max()))
# + id="xXe51ETCO-h5"
from keras.applications.vgg16 import VGG16
# load model
#model = VGG16()
# summarize the model
#model.summary()
# + id="h8gNLlMKp0ei"
# Fine-tune
# Part 1: Pre train
nclass = len(train_it.class_indices)
# create the base pre-trained model
base_model = VGG16(input_shape = (224, 224, 3), # Shape of our images
include_top = False, # Leave out the last fully connected Layer
weights = 'imagenet',
classes = nclass)
base_model.trainable = False
# add a global spatial average pooling layer
x = base_model.output
x = GlobalAveragePooling2D()(x)
# let's add a fully-connected layer
x = Dense(1024, activation='relu')(x)
predictions = Dense(nclass, activation='softmax')(x)
# this is the model we will train
model = Model(inputs=base_model.input, outputs=predictions)
# first: train only the top layers (which were randomly initialized)
# i.e. freeze all convolutional layers
# for layer in base_model.layers:
# layer.trainable = False
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="H8CA1DRW7uHi" outputId="b80fae5f-a816-4ca1-b2a1-06d8c921ed26"
# model.compile(loss='categorical_crossentropy',
# # optimizer=optimizers.SGD(lr=1e-4, momentum=0.9),
# optimizer = 'Adam',
# metrics=['AUC', 'accuracy'])
model.summary()
plot_model(model, to_file='model.png', show_shapes=True, show_layer_names=True)
# + colab={"base_uri": "https://localhost:8080/"} id="kWrvoj4TflvB" outputId="b10dcf4c-7cd9-47c8-f004-196704fbd39c"
def compile_model(model):
model.compile(optimizer = 'Adam',
loss=keras.losses.CategoricalCrossentropy(),
metrics=['AUC', 'accuracy'])
return model
def train_model(model, train_it, val_it):
callback = keras.callbacks.EarlyStopping(monitor='loss', patience = 5, restore_best_weights = True)
history = model.fit(train_it, epochs = 24, steps_per_epoch = 107, verbose = 2, validation_data= val_it, validation_steps = 27, callbacks=[callback])
return model, history
model = compile_model(model)
model, history = train_model(model, train_it, val_it)
print (model.summary())
# + id="Q9J0I9XRMTo8" colab={"base_uri": "https://localhost:8080/"} outputId="7bc0e638-68cd-4e06-c709-50dd06a0ffe7"
def eval_model(model, test_it):
# TODO: evaluate the model
test_loss, test_auc, test_accuracy = model.evaluate (test_it, steps = 27)
return test_loss, test_auc, test_accuracy
test_loss, test_auc, test_accuracy = eval_model(model, test_it)
# + id="bM7ubAgGMTo9"
test_it.reset()
preds = model.predict(test_it, steps = 27)
# + id="WnjppZFcMTo-"
y_predict = np.argmax(preds,axis=1)
# + id="Jyh9B3eZMTo-" colab={"base_uri": "https://localhost:8080/"} outputId="764404a3-5f74-4d49-c26e-23c469783de2"
print(classification_report(test_it.classes, y_predict, target_names=test_it.class_indices))
# + id="knOvvUM3MTo-" colab={"base_uri": "https://localhost:8080/"} outputId="d88ccd6e-96a4-4a32-cff0-75577664f2e5"
y_predict
# + id="J2JEkSDRMTo_" colab={"base_uri": "https://localhost:8080/"} outputId="1a9aa0d7-813a-474f-8eb4-83692d4f7289"
error_count = 0
for x in range (0,len(y_predict)):
if y_predict[x] != test_it.classes[x]:
error_count += 1
error_count
# + id="MRPmEIKKW_9G"
def plot_result(history):
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend(loc=0)
plt.figure()
plt.show()
# + id="h6yyRIuqMTo_" colab={"base_uri": "https://localhost:8080/", "height": 299} outputId="4391a362-c0b0-4f47-ece9-a87edcf336ee"
plot_result(history)
# + id="smyB6KF_q_7g" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="1dfd1e96-6430-40be-d3aa-376a882610b0"
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="S1e9KZ8JsITW" outputId="283b9774-94a2-4753-9729-2edcf65c3d14"
#Fine-Tune part 2
# Visualize layer names and layer indices to see how many layers need to be freeze
for i, layer in enumerate(base_model.layers):
print(i, layer.name)
# + id="IURanijlzzDm"
# we chose to train the top 2 blocks, try freeze the first 3 layers and unfreeze the rest:
for layer in model.layers[:3]:
layer.trainable = False
for layer in model.layers[3:]:
layer.trainable = True
# + id="7EWoUScrztZn"
# we need to recompile the model for these modifications to take effect
# try a low learning rate
model.compile(optimizer=optimizers.Adam(learning_rate = 0.0001),
loss='categorical_crossentropy',
metrics=['AUC', 'accuracy'])
# + colab={"base_uri": "https://localhost:8080/"} id="E8O587_j0C0L" outputId="feb4478e-e91c-443b-c750-611ef9a41cbc"
# Train our model again (fine-tuning the top 2 blocks alongside the top Dense layers
model, history = train_model(model, train_it, val_it)
print (model.summary())
# + colab={"base_uri": "https://localhost:8080/"} id="2UqBxQGk0L7C" outputId="18a4a9d1-3f8d-4a49-ce47-911359a17da4"
test_loss, test_auc, test_accuracy = eval_model(model, test_it)
# + colab={"base_uri": "https://localhost:8080/"} id="5HU7WtwDE8YW" outputId="5f794a06-7ca6-475d-9106-48d4d483b602"
test_it.reset()
preds = model.predict(test_it, steps = 27)
y_predict = np.argmax(preds,axis=1)
print(classification_report(test_it.classes, y_predict, target_names=test_it.class_indices))
# + colab={"base_uri": "https://localhost:8080/", "height": 299} id="Dn8VDqLLFSRY" outputId="2c18f8bb-ca1c-4dbb-e921-bc014341a576"
plot_result(history)
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="iylie1s5Fb6S" outputId="4cae8601-d5ab-41e5-fffc-faa3a7566ef9"
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# + id="SgrAHy_t-CUv"
model.save('/content/drive/My Drive/Colab Notebooks/VGG16.h5', overwrite = True,
include_optimizer=True)
# + id="KaRv9RK-Flwq"
| Final/TL_Vgg16_augmented 0.90.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="http://landlab.github.io"><img style="float: left" src="../../landlab_header.png"></a>
# # DataRecord Tutorial
# <hr>
# <small>For more Landlab tutorials, click here: <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html</a></small>
# <hr>
#
# This tutorial illustrates how to record variables of a Landlab model using DataRecord.
#
# ## What is DataRecord?
# DataRecord is a data structure that can hold data variables relating to a Landlab model or to items living on the [Landlab grid](../grid_object_demo/grid_object_demo.ipynb).
#
# DataRecord is built on [xarray](http://xarray.pydata.org/en/stable/index.html)'s Dataset structure: a multi-dimensional, in memory, array database. Dataset implements the mapping interface with keys given by variable names and values given by DataArray objects for each variable name. DataRecord inherits all the methods and attributes from xarray.Dataset.
#
# A DataRecord can have one or both (or none) of the following dimensions:
# - `time`: The simulated time in the model.
# - `item_id`: An identifier of a generic item in the model.
#
# Coordinates are one dimensional arrays used for label-based indexing.
#
# The examples below illustrate different use cases for DataRecord.
#
# We start by importing the necessary libraries:
# +
import numpy as np
import xarray as xr
from landlab import RasterModelGrid
from landlab.data_record import DataRecord
from landlab import imshow_grid
import matplotlib.pyplot as plt
from matplotlib.pyplot import plot, subplot, xlabel, ylabel, title, legend, figure
# %matplotlib inline
# -
# ## Case 1. DataRecord with 1 dimension: time
# Let's start with an example where we set DataRecord to have only `time` as a dimension.
# An example variable that varies over time and relates to the Landlab grid could be the mean elevation of the topographic surface. We will store this example variable in DataRecord.
#
# We create a Raster grid, create a field (at nodes) called `topographic__elevation` and populate it with random values.
grid_1 = RasterModelGrid((10, 10), (1., 1.))
z = np.random.rand(100)
_ = grid_1.add_field('topographic__elevation', z, at='node')
# Print the current mean elevation.
current_mean = np.mean(grid_1.at_node['topographic__elevation'])
print(current_mean)
# Now we will create a DataRecord that will hold the data variable `mean_elevation` relating to `grid_1`. The first value, at time=0 is the current mean elevation on the grid.
dr_1 = DataRecord(grid_1,
time=[0.],
items=None,
data_vars={'mean_elevation': (['time'], ([current_mean]))},
attrs={'mean_elevation': 'y'})
# The input arguments passed in this case are: the grid, time (as a 1-element list), a data variable dictionary and an attributes dictionary. Note that `items` is not filled, we will see its use in other cases below.
#
# Note the format of the `data_vars` dictionary:
# ```python
# {'variable_name_1' : (['dimensions'], variable_data_1),
# 'variable_name_2' : (['dimensions'], variable_data_2),
# ...}
# ```
#
# The attributes dictionary `attrs` can be used to store metadata about the variables: in this example, we use it to store the variable units.
#
# So far, our DataRecord `dr_1` holds one variable `mean_elevation` with one record at time=0.
#
dr_1
# We can visualise this data structure as a [pandas dataframe](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html):
dr_1.dataset.to_dataframe()
# Now we will run a simple model where the grid surface is uplifted several times and the mean elevation is recorded at every time step. We use the method `add_record` to put the new value in the DataRecord `dr_1`:
# +
total_time = 100
dt = 20
uplift_rate = 0.01 # m/y
for t in range(20, total_time, dt):
grid_1.at_node['topographic__elevation'] += uplift_rate * dt
dr_1.add_record(time=[t],
new_record={
'mean_elevation':
(['time'],
([np.mean(grid_1.at_node['topographic__elevation'])]))
})
# -
# Let's see what was recorded:
dr_1.dataset['mean_elevation'].values
# The corresponding time coordinates are:
dr_1.dataset.time.values
# Notice the different syntax used here:
# - `time` is a **dimension** and can be called by `dr_1.time` (or `dr_1['time']`)
# - whereas `mean_elevation` is a **variable** and must be called by `dr_1['mean_elevation']`
#
# DataRecord also has the handy property `time_coordinates` that returns these values as a list:
#
#
#
dr_1.time_coordinates
# You can use the methods `get_data` and `set_data` to access and change the data:
dr_1.get_data(time=[20.], data_variable='mean_elevation')
# +
dr_1.set_data(time=[80.], data_variable='mean_elevation', new_value=1.5)
dr_1.dataset['mean_elevation']
# -
# ## Case 2. DataRecord with 1 dimension: item_id
# An important feature of DataRecord is that it allows to create **items** that live on grid elements, and variables describing them. For instance, we can create *boulders* and store information about their *size* and *lithology*.
#
# To create items, we need to instantiate a DataRecord and pass it a dictionary describing where each item lives on the Landlab grid. The format of this dictionary is:
# ```python
# {'grid_element' : [grid_element],
# 'element_id' : [element_id]}
# ```
#
# where:
# - `grid_element` is a str or number-of-items-long array containing strings of the grid element(s) on which the items live (e.g.: node, link). Valid locations depend on the grid type (`my_grid.groups` gives the valid locations for your grid). If `grid_element` is provided as a string, it is assumed that all items live on the same type of grid element.
# - `element_id` is an array of integers identifying the grid element IDs on which each item resides. For each item, `element_id` must be less than the number of this item's `grid_element` that exist on the grid. For example, if the grid has 10 links, no item can live at link 10 or link -3 because only links 0 to 9 exist in this example.
#
# +
grid_2 = RasterModelGrid((5, 5), (2, 2))
boulders = {
'grid_element': 'node',
'element_id': np.array([6, 11, 12, 17, 12])
}
initial_boulder_sizes = np.array([1, 1.5, 3, 1, 2])
boulder_lithologies = np.array(
['sandstone', 'granite', 'sandstone', 'sandstone', 'limestone'])
dr_2 = DataRecord(grid_2,
time=None,
items=boulders,
data_vars={
'boulder_size': (['item_id'], initial_boulder_sizes),
'boulder_litho': (['item_id'], boulder_lithologies)
},
attrs={'boulder_size': 'm'})
dr_2.dataset.to_dataframe()
# -
# Each *item* (in this case, each boulder) is designated by an `item_id`, its position on the grid is described by a `grid_element` and an `element_id`.
#
# We can use the method `add_item` to add new boulders to the record:
# +
dr_2.add_item(
new_item={
'grid_element': np.array(['link', 'node']),
'element_id': np.array([24, 8])
},
new_item_spec={'boulder_size': (['item_id'], np.array([1.2, 2.]))})
dr_2.dataset.to_dataframe()
# -
# Notice that we did not specify the lithologies of the new boulders, their recorded values are thus set as `NaN`. We can use the `set_data` method to report the boulder lithologies:
dr_2.set_data(data_variable='boulder_litho',
item_id=[5, 6],
new_value=['sandstone', 'granite'])
dr_2.dataset.to_dataframe()
# We can use the method `calc_aggregate_value` to apply a function to a variable aggregated at grid elements. For example, we can calculate the mean size of boulders on each node:
mean_size = dr_2.calc_aggregate_value(func=xr.Dataset.mean,
data_variable='boulder_size')
mean_size
# Notice that boulder #5 is on a link so it is not taken into account in this calculation.
# +
# replace nans with 0:
mean_size[np.isnan(mean_size)] = 0
# show unfiltered mean sizes on the grid:
imshow_grid(grid_2, mean_size)
# -
# Before doing this calculation we could filter by lithology and only use the 'sandstone' boulders in the calculation:
# +
# define a filter array:
filter_litho = (dr_2.dataset['boulder_litho'] == 'sandstone')
# aggregate by node and apply function numpy.mean on boulder_size
filtered_mean = dr_2.calc_aggregate_value(func=xr.Dataset.mean,
data_variable='boulder_size',
at='node',
filter_array=filter_litho)
filtered_mean
# -
# ## Case 3. DataRecord with 2 dimensions: item_id and time
#
# We may want to record variables that have both dimensions `time` *and* `item_id`.
#
# In the previous example, some variables that characterize the items (boulders) may not vary with time, such as `boulder_lithology`. Although it can be interesting to keep track of the change in size through time. We will redefine the DataRecord such that the variable `boulder_size` varies among the items/boulders (identified by `item_id`) and through `time`. The variable `boulder_litho` varies only among the items/boulders and this lithogy variable does not vary through time.
# +
grid_3 = RasterModelGrid((5, 5), (2, 2))
initial_boulder_sizes_3 = np.array([[10], [4], [8], [3], [5]])
# boulder_lithologies = np.array(['sandstone', 'granite', 'sandstone', 'sandstone', 'limestone']) #same as above, already run
boulders_3 = {
'grid_element': 'node',
'element_id': np.array([[6], [11], [12], [17], [12]])
}
dr_3 = DataRecord(grid_3,
time=[0.],
items=boulders_3,
data_vars={
'boulder_size': (['item_id',
'time'], initial_boulder_sizes_3),
'boulder_litho': (['item_id'], boulder_lithologies)
},
attrs={'boulder_size': 'm'})
dr_3
# -
# Note that the syntax to define the `initial_boulder_sizes_3` (as well as `element_id`) has changed: they are number-of-items-by-1 arrays because they vary along both `time` and `item_id` (compared to `boulder_lithologies` which is just number-of-items long as it only varies along `item_id`).
boulder_lithologies.shape, initial_boulder_sizes.shape, initial_boulder_sizes_3.shape
# Let's define a very simple erosion law for the boulders:
#
# $$
# \begin{equation}
# \frac{dD}{dt} = -k_{b} . D
# \end{equation}
# $$
#
# where $D$ is the boulder diameter $[L]$ (this value represents the `boulder_size` variable), $t$ is time, and $k_{b}$ is the block erodibility $[L.T^{-1}]$.
#
# We will now model boulder erosion and use DataRecord to store their size through time.
# +
dt = 100
total_time = 100000
time_index = 1
for t in range(dt, total_time, dt):
# create a new time coordinate:
dr_3.add_record(time=np.array([t]))
# this propagates grid_element and element_id values forward in time (instead of the 'nan' default filling):
dr_3.ffill_grid_element_and_id()
for i in range(0, dr_3.number_of_items):
# value of block erodibility:
if dr_3.dataset['boulder_litho'].values[i] == 'limestone':
k_b = 10**-5
elif dr_3.dataset['boulder_litho'].values[i] == 'sandstone':
k_b = 3 * 10**-6
elif dr_3.dataset['boulder_litho'].values[i] == 'granite':
k_b = 3 * 10**-7
else:
print('Unknown boulder lithology')
dr_3.dataset['boulder_size'].values[i, time_index] = dr_3.dataset[
'boulder_size'].values[i, time_index - 1] - k_b * dr_3.dataset[
'boulder_size'].values[i, time_index - 1] * dt
time_index += 1
print('Done')
# +
figure(figsize=(15, 8))
time = range(0, total_time, dt)
boulder_size = dr_3.dataset['boulder_size'].values
subplot(121)
plot(time, boulder_size[1], label='granite')
plot(time, boulder_size[3], label='sandstone')
plot(time, boulder_size[-1], label='limestone')
xlabel('Time (yr)')
ylabel('Boulder size (m)')
legend(loc='lower left')
title('Boulder erosion by lithology')
# normalized plots
subplot(122)
plot(time, boulder_size[1] / boulder_size[1, 0], label='granite')
plot(time, boulder_size[2] / boulder_size[2, 0], label='sandstone')
plot(time, boulder_size[-1] / boulder_size[-1, 0], label='limestone')
xlabel('Time (yr)')
ylabel('Boulder size normalized to size at t=0 (m)')
legend(loc='lower left')
title('Normalized boulder erosion by lithology')
plt.show()
# -
# ## Other properties provided by DataRecord
dr_3.variable_names
dr_3.number_of_items
dr_3.item_coordinates
dr_3.number_of_timesteps
dr_1.time_coordinates
dr_1.earliest_time
dr_1.latest_time
dr_1.prior_time
# # More on DataRecord
#
# DataRecord is the data structure on which the following Landlab components are based:
# - ClastTracker (coming soon)
# - SpeciesEvolver (coming soon)
| notebooks/tutorials/data_record/DataRecord_tutorial.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Overview
#
# This package is a collection of tools to display and analyze 2D and 2D time-lapse microscopy images. In particular it makes it straightforward to create figures containing multi-channel images represented in a *composite* color mode as done in the popular image processing software [Fiji](https://imagej.net/software/fiji/). It also allows to easily complete such figures with standard annotations like **labels** and **scale bars**. In case of time-lapse data, the figures are turned into **animations** which can be interactively browsed from a Jupyter notebook, saved in standard movie formats (mp4, gif etc.) and completed with **time counters**. Finally, figures and animations can easily be combined into larger **panels**. These main functionalities are provided by the ```microfilm.microplot``` and ```microfilm.microanim``` modules.
#
# Following the model of [seaborn](https://seaborn.pydata.org/index.html), ```microfilm``` is entirely based on [Matplotlib](https://matplotlib.org/) and tries to provide good defaults to produce good microcopy figures *out-of-the-box*. It however also offers complete access to the Matplotlib structures like axis and figures underlying the ```microfilm``` objects, allowing thus for the creation of arbitrarily complex plots.
| docs/overview.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #### Install scrapy
# - windows
# - conda install -c conda-forge scrapy
# #### xpath
# - xpath 기본 문법
# - xpath 실습
# - scrapy shell(ipython), jupyter notebook
# - 네이버 키워드 데이터 수집, 다음 키워드 데이터 수집, gmarket 베스트 상품 데이터 수집
# - scrapy project
# - scrapy 파일 디렉토리 구조 및 각 파일에 대한 설명
# - crawler
# - naver 현재 상영 영화 링크
# - 각각의 영화 링크에서 영화 제목, 관객수를 크롤링
# - csv 파일로 저장
# - pipeline을 이용하여 csv 파일로 저장
#
import scrapy
# #### xpath 문법
# - 네이버 영화 제목 xpath - `//*[@id='content']/div[1]/div[2]/div[1]/h3/a[1]`
# - `//`: 가장 상위 엘리먼트
# - `*`: css selector 하위 엘리먼트를 선택할 때 'div a'과 같습니다. 모든 하위 엘리먼트를 검색
# - `[@<key>=<value>]`: @ 속성값 attribute를 의미
# - `[@id='content']` : id가 content인 엘리먼트를 선택
# - `/`: css selector에서 ` > `와 같습니다. 1단계 아래 하위 엘리먼트를 검색
# - div : element 이름
# - `[<number>]`: number 번째의 엘리먼트를 선택 (0부터 시작이 아니라 1부터 시작함)
# - `not`: `not(조건)`, `not(@class='test')` - class test가 아닌 엘리먼트를 선택
# - `.`: 현재 엘리먼트를 의미
# #### Scrapy shell을 이용
# - `$ scrapy shell "<url>"`
# - 네이버 실시간 검색어
# - 다음 실시간 검색어
# - gmarket 베스트 아이템
# #### naver 실시간 검색어
# - `response.xpath('//*[@id="PM_ID_ct"]/div[1]/div[2]/div[2]/div[1]/div/ul/li[1]/a/span[2]')`
# #### Jupyter notebook 사용
# #### naver 실시간 검색어
#
import requests
from scrapy.http import TextResponse
req = requests.get('http://naver.com')
response = TextResponse(req.url, body=req.text, encoding='utf-8')
# 네이버 실시간 검색어 1위 객체 선택
response.xpath('//*[@id="PM_ID_ct"]/div[1]/div[2]/div[2]/div[1]/div/ul/li[1]/a/span[2]')
# 네이버 실시간 검색어 20개 객체 선택
response.xpath('//*[@id="PM_ID_ct"]/div[1]/div[2]/div[2]/div[1]/div/ul/li/a/span[2]')
# 네이버 실시간 검색어 20개 객체에서 문자열 선택
response.xpath('//*[@id="PM_ID_ct"]/div[1]/div[2]/div[2]/div[1]/div/ul/li/a/span[2]/text()').extract()
# 다음에 10개의 문자 키워드 출력
req = requests.get('https://daum.net')
response = TextResponse(req.url, body=req.text, encoding='utf-8')
response.xpath('//*[@id="mArticle"]/div[2]/div[2]/div[3]/div[1]/ol/li/div/div[1]/span[2]/a/text()').extract()
# gmarket 베스트 아이템
req = requests.get('http://corners.gmarket.co.kr/Bestsellers')
response = TextResponse(req.url, body=req.text, encoding='utf-8')
# 베스트 200 아이템의 제목
response.xpath('//*[@id="<PASSWORD>"]/a')
# li 엘리먼트에서 class가 first 인 값만 가져오기
titles = response.xpath('//*[@id="gBestWrap"]/div/div[3]/div[2]/ul/li[@class="first"]/a/text()').extract()
len(titles), titles[:5]
# li 엘리먼트에서 class가 first인 데이터만 빼고 가져오기
titles = response.xpath('//*[@id="gBestWrap"]/div/div[3]/div[2]/ul/li[not(@class="first")]/a/text()').extract()
len(titles), titles[:5]
# #### Scrapy Project
# - 프로젝트 생성
# - `$ scrapy startpoject <프로젝트명>`
# - 프로젝트 파일 설명
# - 네이버 영화에서 현재 상영중인 영화의 제목과 관객수 데이터를 크롤링
# - crawler directory: 프로젝트 디렉토리
# - spiders directory: 크롤링 실행할 클래스와 함수가 모여있는 디렉토리
# - items.py: 크롤링을 할 때 가져오는 데이터를 정의하는 클래스 (MVC - Model)
# - pipeline.py: 여러개의 링크에서 데이터를 가져올 때, 실행하는 함수가 정의 되어 있는 클래스
# - settings.py: scraping을 할 때, 정책과 같은 설정을 할 수 있는 파일 입니다.
# - 예를 들어 robots.txt 정책을 따를 것인지 안 따를 것인지를 결정 할 수 있습니다.
#
# - 네이버 영화에서 현재 상영중인 영화의 제목과 누적 관객수 데이터를 크롤링
req = requests.get('https://movie.naver.com/movie/running/current.nhn')
response = TextResponse(req.url, body=req.text, encoding='utf-8')
links = response.xpath('//*[@id="content"]/div[1]/div[1]/div[3]/ul/li/dl/dt/a/@href').extract()[:10]
for link in links:
link = response.urljoin(link)
print(link)
req = requests.get('https://movie.naver.com/movie/bi/mi/basic.nhn?code=159892')
response = TextResponse(req.url, body=req.text, encoding='utf-8')
response.xpath('//*[@id="content"]/div[1]/div[2]/div[1]/h3/a[1]/text()').extract()[0]
response.xpath('//*[@id="content"]/div[1]/div[2]/div[1]/dl/dd[5]/div/p[2]/text()').extract()[0]
# +
# 프로젝트 디렉토리로 이동
# scrapy crawl NaverMovie
# +
# csv 파일로 저장
# scrapy crawl NaverMovie -o movie.csv
# +
# yield
# Generator
# -
def numbers():
yield 0
yield 1
yield 2
n = numbers()
n
n.__next__()
n.__next__()
n.__next__()
n.__next__()
import csv
csvwrite = csv.writer(open('NaverMovie.csv', 'w'))
csv.close()
| 2018_06_22_scrapy_xpath_practice.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# default_exp trainer.gradtts
# -
# # Trainer
# +
# export
import json
import os
from pathlib import Path
from pprint import pprint
import numpy as np
import torch
from torch.cuda.amp import autocast, GradScaler
import torch.distributed as dist
from torch.nn import functional as F
from torch.nn.parallel import DistributedDataParallel as DDP
from torch.optim.lr_scheduler import ExponentialLR
from torch.utils.data import DataLoader
from tensorboardX import SummaryWriter
import time
from uberduck_ml_dev.models.common import MelSTFT
from uberduck_ml_dev.utils.plot import (
plot_attention,
plot_gate_outputs,
plot_spectrogram,
plot_tensor,
)
from uberduck_ml_dev.text.util import text_to_sequence, random_utterance
from uberduck_ml_dev.text.symbols import symbols_with_ipa
from uberduck_ml_dev.trainer.base import TTSTrainer
from uberduck_ml_dev.data_loader import (
TextAudioSpeakerLoader,
TextMelCollate,
DistributedBucketSampler,
TextMelDataset,
)
from uberduck_ml_dev.vendor.tfcompat.hparam import HParams
from uberduck_ml_dev.utils.plot import save_figure_to_numpy, plot_spectrogram
from uberduck_ml_dev.utils.utils import slice_segments, clip_grad_value_
from uberduck_ml_dev.text.symbols import SYMBOL_SETS
# -
# # Grad TTS Trainer
# +
# export
from tqdm import tqdm
from uberduck_ml_dev.text.util import text_to_sequence, random_utterance
from uberduck_ml_dev.models.gradtts import GradTTS
from uberduck_ml_dev.utils.utils import intersperse
class GradTTSTrainer(TTSTrainer):
REQUIRED_HPARAMS = [
"training_audiopaths_and_text",
"test_audiopaths_and_text",
]
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
for param in self.REQUIRED_HPARAMS:
if not hasattr(self, param):
raise Exception(f"GradTTSTrainer missing a required param: {param}")
self.sampling_rate = self.hparams.sampling_rate
self.checkpoint_path = self.hparams.log_dir
def sample_inference(self, model, timesteps=10, spk=None):
with torch.no_grad():
sequence = text_to_sequence(
random_utterance(),
self.text_cleaners,
1.0,
symbol_set=self.hparams.symbol_set,
)
if self.hparams.intersperse_text:
sequence = intersperse(
sequence, (len(SYMBOL_SETS[self.hparams.symbol_set]))
)
x = torch.LongTensor(sequence).cuda()[None]
x_lengths = torch.LongTensor([x.shape[-1]]).cuda()
y_enc, y_dec, attn = model(
x,
x_lengths,
n_timesteps=50,
temperature=1.5,
stoc=False,
spk=spk,
length_scale=0.91,
)
if self.hparams.vocoder_algorithm == "hifigan":
audio = self.sample(
y_dec,
algorithm=self.hparams.vocoder_algorithm,
hifigan_config=self.hparams.hifigan_config,
hifigan_checkpoint=self.hparams.hifigan_checkpoint,
cudnn_enabled=self.hparams.cudnn_enabled,
)
else:
audio = self.sample(y_dec.cpu()[0])
return audio
def train(self, checkpoint=None):
if self.distributed_run:
self.init_distributed()
train_dataset = TextMelDataset(
self.hparams.training_audiopaths_and_text,
self.hparams.text_cleaners,
1.0,
self.hparams.n_feats,
self.hparams.sampling_rate,
self.hparams.mel_fmin,
self.hparams.mel_fmax,
self.hparams.filter_length,
self.hparams.hop_length,
(self.hparams.filter_length - self.hparams.hop_length) // 2,
self.hparams.win_length,
intersperse_text=self.hparams.intersperse_text,
intersperse_token=(len(SYMBOL_SETS[self.hparams.symbol_set])),
symbol_set=self.hparams.symbol_set,
)
collate_fn = TextMelCollate()
loader = DataLoader(
dataset=train_dataset,
batch_size=self.hparams.batch_size,
collate_fn=collate_fn,
drop_last=True,
num_workers=0,
shuffle=False,
)
test_dataset = TextMelDataset(
self.hparams.test_audiopaths_and_text,
self.hparams.text_cleaners,
1.0,
self.hparams.n_feats,
self.hparams.sampling_rate,
self.hparams.mel_fmin,
self.hparams.mel_fmax,
self.hparams.filter_length,
self.hparams.hop_length,
(self.hparams.filter_length - self.hparams.hop_length) // 2,
self.hparams.win_length,
intersperse_text=self.hparams.intersperse_text,
intersperse_token=(len(SYMBOL_SETS[self.hparams.symbol_set])),
symbol_set=self.hparams.symbol_set,
)
model = GradTTS(self.hparams)
if self.hparams.checkpoint:
model.load_state_dict(torch.load(self.hparams.checkpoint))
model = model.cuda()
print(
"Number of encoder + duration predictor parameters: %.2fm"
% (model.encoder.nparams / 1e6)
)
print("Number of decoder parameters: %.2fm" % (model.decoder.nparams / 1e6))
print("Total parameters: %.2fm" % (model.nparams / 1e6))
print("Initializing optimizer...")
optimizer = torch.optim.Adam(
params=model.parameters(), lr=self.hparams.learning_rate
)
test_batch = test_dataset.sample_test_batch(size=self.hparams.test_size)
for i, item in enumerate(test_batch):
text, mel, spk = item
self.log(
f"image_{i}/ground_truth",
0,
image=plot_tensor(mel.squeeze()),
)
iteration = 0
last_time = time.time()
for epoch in range(0, self.hparams.n_epochs):
model.train()
dur_losses = []
prior_losses = []
diff_losses = []
for batch_idx, batch in enumerate(loader):
model.zero_grad()
x, x_lengths, y, _, y_lengths, speaker_ids = batch
dur_loss, prior_loss, diff_loss = model.compute_loss(
x, x_lengths, y, y_lengths, out_size=self.hparams.out_size
)
loss = sum([dur_loss, prior_loss, diff_loss])
loss.backward()
enc_grad_norm = torch.nn.utils.clip_grad_norm_(
model.encoder.parameters(), max_norm=1
)
dec_grad_norm = torch.nn.utils.clip_grad_norm_(
model.decoder.parameters(), max_norm=1
)
optimizer.step()
self.log("training/duration_loss", iteration, dur_loss.item())
self.log("training/prior_loss", iteration, prior_loss.item())
self.log("training/diffusion_loss", iteration, diff_loss.item())
self.log("training/encoder_grad_norm", iteration, enc_grad_norm)
self.log("training/decoder_grad_norm", iteration, dec_grad_norm)
dur_losses.append(dur_loss.item())
prior_losses.append(prior_loss.item())
diff_losses.append(diff_loss.item())
iteration += 1
log_msg = f"Epoch {epoch}, iter: {iteration}: dur_loss: {np.mean(dur_losses):.4f} | prior_loss: {np.mean(prior_losses):.4f} | diff_loss: {np.mean(diff_losses):.4f} | time: {time.time()-last_time:.2f}s"
last_time = time.time()
with open(f"{self.hparams.log_dir}/train.log", "a") as f:
f.write(log_msg + "\n")
print(log_msg)
if epoch % self.log_interval == 0:
model.eval()
with torch.no_grad():
for i, item in enumerate(test_batch):
x, _y, _speaker_id = item
x = x.to(torch.long).unsqueeze(0)
x_lengths = torch.LongTensor([x.shape[-1]])
y_enc, y_dec, attn = model(x, x_lengths, n_timesteps=50)
self.log(
f"image_{i}/generated_enc",
iteration,
image=plot_tensor(y_enc.squeeze().cpu()),
)
self.log(
f"image_{i}/generated_dec",
iteration,
image=plot_tensor(y_dec.squeeze().cpu()),
)
self.log(
f"image_{i}/alignment",
iteration,
image=plot_tensor(attn.squeeze().cpu()),
)
self.log(
f"audio/inference_{i}",
iteration,
audio=self.sample_inference(model),
)
if epoch % self.save_every == 0:
torch.save(
model.state_dict(),
f=f"{self.hparams.log_dir}/{self.checkpoint_name}_{epoch}.pt",
)
# -
DEFAULTS = HParams(
training_audiopaths_and_text="train.txt",
test_audiopaths_and_text="val.txt",
cudnn_enabled=True,
log_dir="output",
symbol_set="gradtts",
intersperse_text=True,
n_spks=1,
spk_emb_dim=64,
sampling_rate=22050,
hop_length=256,
win_length=1024,
n_enc_channels=192,
filter_channels=768,
filter_channels_dp=256,
n_enc_layers=6,
enc_kernel=3,
enc_dropout=0.1,
n_heads=2,
window_size=4,
dec_dim=64,
beta_min=0.05,
beta_max=20.0,
pe_scale=1000,
test_size=2,
n_epochs=10000,
batch_size=1,
learning_rate=1e-4,
seed=37,
out_size=2 * 22050 // 256,
filter_length=1024,
rank=0,
distributed_run=False,
oversample_weights=None,
text_cleaners=["english_cleaners"],
max_wav_value=32768.0,
n_feats=80,
mel_fmax=8000,
mel_fmin=0.0,
checkpoint=None,
log_interval=100,
save_every=1000,
)
trainer = GradTTSTrainer(DEFAULTS, rank=0)
| nbs/trainer.gradtts.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from pandas import *
import pandas as pd
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
# -
import warnings
warnings.filterwarnings('ignore')
warnings.simplefilter('ignore')
import warnings
warnings.filterwarnings('ignore')
from pycaret.classification import *
exp_clf101 = setup(data = train, target = 'Survived', create_clusters = True , session_id=123)
best_model = compare_models()
models()
top3 = compare_models(n_select = 3)
blender_top3 = blend_models(top3)
gbc1 = create_model('gbc')
r = create_model('ridge')
cat = create_model('catboost')
rf = create_model('rf')
tuned_rf = tune_model(rf)
evaluate_model(blender_2)
titanic2 = predict_model(tuned_cat, data = test)
titanic2.head()
titanic2 = titanic2.drop(['Pclass', 'Name','Sex','Age','SibSp','Parch','Ticket','Fare','Cabin','Embarked','Score'],axis = 1)
titanic2.to_csv('titanic2.csv')
predict_model(cat);
blender = predict_model(blender_top3,data = test)
# +
blender = blender.drop(['Pclass', 'Name','Sex','Age','SibSp','Parch','Ticket','Fare','Cabin','Embarked'],axis = 1)
# -
blender.to_csv('blender.csv')
gbc2 = predict_model(gbc1, data = test);
gbc2.head()
gbc2 = gbc2.drop(['Pclass', 'Name','Sex','Age','SibSp','Parch','Ticket','Fare','Cabin','Embarked','Score'],axis = 1)
predict_model(rf);
rf = predict_model(r, data=test)
predict_model(tuned_rf)
rf.head()
rf = rf = rf.drop(['Pclass', 'Name','Sex','Age','SibSp','Parch','Ticket','Fare','Cabin','Embarked'],axis = 1)
rf.head()
rf.to_csv('rf.csv')
predict_model(r)
ans = predict_model(r, data=test)
ans.head()
ans.to_csv('titanic.csv')
unseen_predictions = predict_model(r, data=train)
unseen_predictions.head()
test.head()
| kaggle-notebooks/titanic.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #### 1. An "ignored" file in git is one that:
# ##### Ans: Is enumerated in a .gitignore file
# #### 2. The command git rm some_file:
# ##### Ans: Removes some_file from the working file tree and the index
# #### 3. The command rm some_file
# ##### Ans: Removes some_file from working file tree, but not from the repository
# #### 4. To list all files in the repository, issue the command:
# ##### Ans: git ls-files
# #### 5. The command git mv some_file new_name_or_location
# ##### Ans: Moves (renames) the file in both the repository and the working tree
| Coursera/Using Git for Distributed Development/Week-2/Quiz/Managing-Files-and-the-Index.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# [View in Colaboratory](https://colab.research.google.com/github/rdenadai/Image-Study-Notebooks/blob/master/notebooks/madelbrot.ipynb)
# + [markdown] id="zg9hPvDmbY_D" colab_type="text"
# ## Mandelbrot
#
# [wiki](https://en.wikipedia.org/wiki/Mandelbrot_set#Computer_drawings)
#
# [Wolfram MathWorld](http://mathworld.wolfram.com/MandelbrotSet.html)
# + [markdown] id="D-285i5qUIY_" colab_type="text"
# ### Numba
#
# Using **numba** one could get even better performance results, without changing much code. It's a excellent libray, with which you will out perform the simplest code.
#
# Check out more about [numba](http://numba.pydata.org/)
# + id="6vrfi0M2QJIO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="93b6c1f9-1790-4a1d-a341-efc139f6e8ef"
# !pip install numba
# + id="RHyVY4OT5Vlh" colab_type="code" colab={}
from functools import lru_cache
from multiprocessing.dummy import Pool as ThreadPool
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from numba import jit
# %matplotlib inline
np.warnings.filterwarnings('ignore')
# + id="EWsuWctNG6fl" colab_type="code" colab={}
@lru_cache(maxsize=10)
def mandelbrot(edges=2, maxiter=100, size=None, dtype='normal', color=True):
N = 2048
if size is None:
x1, x2, y1, y2 = -2, 1, -1.5, 1.5
else:
x1, x2, y1, y2 = size
x, y = np.meshgrid(np.linspace(x1, x2, N), np.linspace(y1, y2, N))
c = x + (1j * y)
@jit(parallel=True, nogil=True)
def normal(z, fractal):
for n in range(maxiter):
z = z**edges + c
if color:
fractal[(np.abs(z) > maxiter)] = n - (np.log(n) / np.log(2)) * .1
return z, fractal
@jit(parallel=True, nogil=True)
def tricorn(z, fractal):
for n in range(maxiter):
z = z.conj()
z = z**edges + c
if color:
fractal[(np.abs(z) > maxiter)] = n - (np.log(n) / np.log(2)) * .1
return z, fractal
@jit(parallel=True, nogil=True)
def mb_sine(z, fractal):
for n in range(maxiter):
z = np.sin(z/c)
if color:
fractal[(np.abs(z) > maxiter)] = n - (np.log(n) / np.log(2)) * .1
return z, fractal
@jit(parallel=True, nogil=True)
def mb_cosine(z, fractal):
for n in range(maxiter):
z = np.cos(z/c)
if color:
fractal[(np.abs(z) > maxiter)] = n - (np.log(n) / np.log(2)) * .1
return z, fractal
z = c.copy()
fractal = np.zeros(z.shape, dtype=np.uint8)
if dtype == 'normal':
z, fractal = normal(z, fractal)
elif dtype == 'tricorn':
z, fractal = tricorn(z, fractal)
elif dtype == 'sine':
z, fractal = mb_sine(z, fractal)
elif dtype == 'cosine':
z, fractal = mb_cosine(z, fractal)
if color:
return (fractal**.3).astype(np.float64)
return np.abs(z)
@lru_cache(maxsize=10)
def mandelbrot_colorless(edges=2, maxiter=100, size=None, dtype='normal', color=True):
N = 2048
if size is None:
x1, x2, y1, y2 = -2, 1, -1.5, 1.5
else:
x1, x2, y1, y2 = size
x, y = np.linspace(x1, x2, N), np.linspace(y1, y2, N)
c = x[:, np.newaxis] + (1j * y[np.newaxis, :])
z = c
if dtype == 'normal':
for _ in range(maxiter):
z = z**edges + c
elif dtype == 'tricorn':
for _ in range(maxiter):
z = z.conj()
z = z**edges + c
elif dtype == 'sine':
for _ in range(maxiter):
z = np.sin(z/c)
elif dtype == 'cosine':
for _ in range(maxiter):
z = np.cos(z/c)
return np.abs(z)
# + [markdown] id="VC2q3FQaOflJ" colab_type="text"
# ### Mandelbrot Set
# + id="MG8gCDQiHaeH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 275} outputId="a5e1ecf0-7399-40dd-aaa4-3f0e980fbef9"
plt.figure(figsize=(15, 15))
for i in [2, 3, 4, 5]:
plt.subplot(1, 4, i-1)
size = (-1.5, 1.5, -1.5, 1.5)
if i == 2:
size = (-2, 1, -1.5, 1.5)
mandel = mandelbrot(edges=i, size=size)
plt.imshow(mandel, extent=size, cmap='jet')
plt.grid(False)
plt.tight_layout()
plt.show()
# + [markdown] id="7-zoIVe-OjUc" colab_type="text"
# ### Tricorn
#
# *"In mathematics, the tricorn, sometimes called the Mandelbar set, is a fractal defined in a similar way to the Mandelbrot set, but using the mapping $z=z^{-2} + c$ instead of $z=z^2 + c$ used for the Mandelbrot set."* [wiki]( https://en.wikipedia.org/wiki/Tricorn_(mathematics) )
# + id="gtxhf3nm6OLU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="80c915da-0b1f-4219-d222-853c5e6e554e"
plt.figure(figsize=(15, 15))
for i in [2, 3, 4, 5]:
plt.subplot(1, 4, i-1)
mandel = mandelbrot(edges=i, size=(-2, 2, -2, 2), dtype='tricorn')
plt.imshow(mandel, extent=[-2, 2, -2, 2], cmap='jet')
plt.grid(False)
plt.tight_layout()
plt.show()
# + [markdown] id="VFJRcuWYOlH_" colab_type="text"
# ### Sine and Cosine
# + id="q5_MzO6wHpbo" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 255} outputId="bb35f223-6bee-492f-c8f3-a3ce5c949b7d"
plt.figure(figsize=(7, 7))
mbscs = mandelbrot(size=(-1, 1, -1, 1), dtype='sine')
mbscc = mandelbrot(size=(-1.5, 1.5, -1.5, 1.5), dtype='cosine')
plt.subplot(1, 2, 1)
plt.imshow(mbscs, extent=[-1, 1, -1, 1], cmap='jet')
plt.grid(False)
plt.subplot(1, 2, 2)
plt.imshow(mbscc, extent=[-1.5, 1.5, -1.5, 1.5], cmap='jet')
plt.grid(False)
plt.tight_layout()
plt.show()
# + id="lDDHj6QRJiXp" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 255} outputId="6ff4d1c0-a0b7-4438-d889-3126969669d2"
plt.figure(figsize=(7, 7))
mbscs = mandelbrot_colorless(size=(-1, 1, -1, 1), dtype='sine')
mbscc = mandelbrot_colorless(size=(-1.5, 1.5, -1.5, 1.5), dtype='cosine')
plt.subplot(1, 2, 1)
plt.imshow(mbscs, extent=[-1, 1, -1, 1], cmap='jet')
plt.grid(False)
plt.subplot(1, 2, 2)
plt.imshow(mbscc.T, extent=[-1.5, 1.5, -1.5, 1.5], cmap='jet')
plt.grid(False)
plt.tight_layout()
plt.show()
# + id="kM2fiTFw_csn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 233} outputId="35c55a96-ee7c-4bc1-ee38-2a2ffabcebfe"
size = (-2, 1, -1.5, 1.5)
print('Mandelbrot with color:')
# %timeit mandelbrot(edges=2, size=size)
print('Mandelbrot without color:')
# %timeit mandelbrot_colorless(edges=2, size=size)
size = (-1, 1, -1, 1)
print('Mandelbrot sine with color:')
# %timeit mandelbrot(edges=2, size=size, dtype='sine')
print('Mandelbrot sine without color:')
# %timeit mandelbrot_colorless(edges=2, size=size, dtype='sine')
# + [markdown] id="GuogId5aMxu-" colab_type="text"
# ## Inefficient way
#
# The bellow examples show mandelbrot calculation (and sine version), but they are very inefficient since we must pass through all positions of the multidimensional image.
#
# But the computation of the colors, allow it to performe more fine grain distinction with a few drawbacks...
# + id="rR2A8R5zsx5l" colab_type="code" colab={}
@lru_cache(maxsize=10)
def mandelbrot(size=2, maxiter=80):
N = 500
x, y = np.linspace(-2, 1, N), np.linspace(-1.25, 1.25, N) * 1j
def mandelbrot_set(c, h, maxiter):
z = c
for n in range(maxiter):
if np.abs(z) > h:
return n - np.log(np.log(z)) / np.log(2)
z = z**size + c
return 0
h = int(np.ceil(maxiter/2))
ms = np.empty([N, N])
for k in range(0, x.size):
for l in range(0, x.size):
ms[k, l] = mandelbrot_set(x[k] + y[l], h, maxiter)
return np.nan_to_num(ms**.3)
@lru_cache(maxsize=10)
def mandelbrot_sine(maxiter=80):
N = 500
x, y = np.linspace(-1, 1, N), np.linspace(-1, 1, N) * 1j
def mandelbrot_set(c, h, maxiter):
z = c
for n in range(maxiter):
if np.abs(z) > h:
return n - np.log(np.log(z)) / np.log(2)
z = np.sin(z/c)
return 0
h = int(np.ceil(maxiter/2))
ms = np.empty([N, N])
for k in range(0, x.size):
for l in range(0, x.size):
ms[k, l] = mandelbrot_set(x[k] + y[l], h, maxiter)
return np.nan_to_num(ms**.3)
# + id="rFimIXfwT-bX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 649} outputId="e12dbc18-3f2d-445f-9cc2-7124196383de"
plt.figure(figsize=(14, 14))
for i, size in enumerate(range(2, 5)):
mandel = mandelbrot(size, 60)
plt.subplot(3, 3, i+1)
plt.imshow(mandel.T, extent=[-2, 1, -1.25, 1.25], cmap='jet')
plt.grid(False)
mbss = mandelbrot_sine(60)
plt.subplot(3, 3, 4)
plt.imshow(mbss.T, extent=[-1, 1, -1, 1], cmap='jet')
plt.grid(False)
plt.tight_layout()
plt.show()
# + id="Vpv9Ln3wE5nr" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 124} outputId="4676c594-167c-421d-c71c-878864bbc8f8"
print('Mandelbrot inefficient with color:')
# %timeit mandelbrot(2, 50)
print('Mandelbrot sine inefficient with color:')
# %timeit mandelbrot_sine(50)
# + id="eIh4du7WQOoh" colab_type="code" colab={}
| notebooks/madelbrot.ipynb |
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .java
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Java
// language: java
// name: java
// ---
// # Contract
//
public enum UnitKind {
MARINE(10), FLAME_THROWER(8)
;
private final int maxPower;
private UnitKind(int maxPower) {
this.maxPower = maxPower;
}
}
public class MilitaryUnit {
private final UnitKind kind;
private final int power;
private IntUnaryOperator bonus;
public MilitaryUnit(UnitKind kind, int power) {
this.kind = Objects.requireNonNull(kind);
if (power < 0 || power >= kind.maxPower) {
throw new IllegalArgumentException("invalid power " + power);
}
this.power = power;
this.bonus = x -> x;
}
public void bonus(IntUnaryOperator bonus) {
this.bonus = Objects.requireNonNull(bonus);
}
public int fightingPower() {
return Math.max(0, Math.min(unit.maxPower, bonus.applyAsInt(power)));
}
}
| jupyter/chapter13-contract.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TestHeader
# <strong>Markdown</strong>
# Write in **md** syntax.
a = 5
# Text ....
#
a = 5 + 6
# **print()** it
print(a)
| CrashCourse/aBasics/00_jupyter.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.3.1
# language: julia
# name: julia-1.3
# ---
# # 5. Mask/Select/Map/Filter/Metaprogramming...
# - Learn how to extract data from the data table with JuliaDB and Mera functions
# - Filter the data table according to one or several conditions
# - Extract data from a filtered data table and use it for further calculations
# - Extend the data table with new columns/variables
# - Mask data with different methods and apply it to some functions
# ## Load The Data
using Mera
info = getinfo(400, "../../testing/simulations/manu_sim_sf_L14");
gas = gethydro(info, lmax=8, smallr=1e-5);
particles = getparticles(info)
clumps = getclumps(info);
# ## Select From Data Table
# ### Select a single column/variable
# ##### By using JuliaDB or Mera functions
using JuliaDB
# The JuliaDB data table is stored in the `data`-field of any `DataSetType`. Extract an existing column (variable):
select(gas.data, :rho) # JuliaDB
# Pass the entire `DataSetType` (here `gas`) to the Mera function `getvar` to extract the selected variable or derived quantity from the data table.
# Call `getvar()` to get a list of the predefined quantities.
getvar(gas, :rho) # MERA
# ### Select several columns
# By selecting several columns a new JuliaDB databse is returned:
select(gas.data, (:rho, :level)) #JuliaDB
# The getvar function returns a dictionary containing the extracted arrays:
getvar(gas, [:rho, :level]) # MERA
# Select one or more columns and get a tuple of vectors:
vtuple = columns(gas.data, (:rho, :level)) # JuliaDB
propertynames(vtuple)
vtuple.rho
# ## Filter by Condition
# ### With JuliaDB (example A)
# Get all the data corresponding to cells/rows with level=6. Here, the variable `p` is used as placeholder for rows. A new JuliaDB data table is returend:
filtered_db = filter(p->p.level==6, gas.data ) # JuliaDB
# see the reduced row number
# ### With Macro Expression (example A)
# (see the documentation at: <https://piever.github.io/JuliaDBMeta.jl/stable/> )
using JuliaDBMeta
filtered_db = @filter gas.data :level==6 # JuliaDBMeta
# ### With JuliaDB (example B)
# Get all cells/rows with densities >= 3 Msol/pc^3. Since the data is given in code units, we need to convert from the given physical units:
density = 3. / gas.scale.Msol_pc3
filtered_db = filter(p->p.rho>= density, gas.data ) # JuliaDB
# ### With Macro Expression (example B)
density = 3. /gas.scale.Msol_pc3
filtered_db = @filter gas.data :rho>= density # JuliaDBMeta
# ### Get a Quantity/Variable from The Filtered Data Table
# Calculate the mass for each cell and the sum:
mass_tot = getvar(gas, :mass, :Msol) # the full data table
sum(mass_tot)
# The same calculation is possible for the filtered data base which has to be passed together with the original object, here: `gas`
mass_filtered_tot = getvar(gas, :mass, :Msol, filtered_db=filtered_db) # the filtered data table
sum(mass_filtered_tot)
# ### Create a New DataSetType from a Filtered Data Table
# A new `DataSetType` can be constructed for the filtered data table that can be passed to the functions.
density = 3. /gas.scale.Msol_pc3
filtered_db = @filter gas.data :rho >= density
gas_new = construct_datatype(filtered_db, gas);
# Both are now of HydroDataType and include the same information about the simulation properties (besides the canged data table)
println( typeof(gas) )
println( typeof(gas_new) )
mass_filtered_tot = getvar(gas_new, :mass, :Msol)
sum(mass_filtered_tot)
# ## Filter by Multiple Conditions
# ### With JuliaDB
# Get the mass of all cells/rows with densities >= 3 Msol/pc^3 that is within the disk radius of 3 kpc and 2 kpc from the plane:
# +
boxlen = info.boxlen
cv = boxlen/2. # box-center
density = 3. /gas.scale.Msol_pc3
radius = 3. /gas.scale.kpc
height = 2. /gas.scale.kpc
# filter cells/rows that contain rho greater equal density
filtered_db = filter(p->p.rho >= density, gas.data )
# filter cells/rows lower equal the defined radius and height
# (convert the cell number to a position according to its cellsize and relative to the box center)
filtered_db = filter(row-> sqrt( (row.cx * boxlen /2^row.level - cv)^2 + (row.cy * boxlen /2^row.level - cv)^2) <= radius &&
abs(row.cz * boxlen /2^row.level - cv) <= height, filtered_db)
var_filtered = getvar(gas, :mass, filtered_db=filtered_db, unit=:Msol)
sum(var_filtered) # [Msol]
# -
# ### Use Pipeline Macros
# +
boxlen = info.boxlen
cv = boxlen/2.
density = 3. /gas.scale.Msol_pc3
radius = 3. /gas.scale.kpc
height = 2. /gas.scale.kpc
filtered_db = @apply gas.data begin
@where :rho >= density
@where sqrt( (:cx * boxlen/2^:level - cv)^2 + (:cy * boxlen/2^:level - cv)^2 ) <= radius
@where abs(:cz * boxlen/2^:level -cv) <= height
end
var_filtered = getvar(gas, :mass, filtered_db=filtered_db, unit=:Msol)
sum(var_filtered) # [Msol]
# -
# ### External Functions With JuliaDB
# +
boxlen = info.boxlen
function r(x,y,level,boxlen)
return sqrt((x * boxlen /2^level - boxlen/2.)^2 + (y * boxlen /2^level - boxlen/2.)^2)
end
function h(z,level,boxlen)
return abs(z * boxlen /2^level - boxlen/2.)
end
density = 3. /gas.scale.Msol_pc3
radius = 3. /gas.scale.kpc
height = 2. /gas.scale.kpc
filtered_db = filter(row-> row.rho >= density &&
r(row.cx,row.cy, row.level, boxlen) <= radius &&
h(row.cz,row.level, boxlen) <= height, gas.data)
var_filtered = getvar(gas, :mass, filtered_db=filtered_db, unit=:Msol)
sum(var_filtered) # [Msol]
# -
# ### External Functions With Macro Expression
# +
boxlen = info.boxlen
cv = boxlen/2.
density = 3. /gas.scale.Msol_pc3
radius = 3. /gas.scale.kpc
height = 2. /gas.scale.kpc
function p(val, level, boxlen)
cv = boxlen/2
return val * boxlen /2^level - cv
end
filtered_db = @apply gas.data begin
@where :rho >= density
@where sqrt( p(:cx, :level, boxlen)^2 + p(:cy, :level, boxlen)^2 ) <= radius
@where abs( p(:cz, :level, boxlen) ) <= height
end
var_filtered = getvar(gas, :mass, filtered_db=filtered_db, unit=:Msol)
sum(var_filtered) # [Msol]
# -
# ### Compare With Predefined Functions
# Compare the previous calculations with the predefined `subregion` function:
# The `subregion` function takes the intersected cells of the range borders into account (default):
# +
density = 3. /gas.scale.Msol_pc3 # in code units
sub_region = subregion(gas, :cylinder, radius=3., height=2., center=[:boxcenter], range_unit=:kpc, verbose=false ) # default: cell=true
filtered_db = @filter sub_region.data :rho >= density
var_filtered = getvar(gas, :mass, :Msol, filtered_db=filtered_db)
sum(var_filtered) # [Msol]
# -
# By setting the keyword `cell=false`, only the cell-centres within the defined region are taken into account (as in the calculations in the previous section).
# +
density = 3. /gas.scale.Msol_pc3 # in code units
sub_region = subregion(gas, :cylinder, radius=3., height=2., center=[:boxcenter], range_unit=:kpc, cell=false, verbose=false )
filtered_db = @filter sub_region.data :rho >= density
var_filtered = getvar(gas, :mass, :Msol, filtered_db=filtered_db)
sum(var_filtered)
# -
# ## Extend the Data Table
# Add costum columns/variables to the data that can be automatically processed in some functions:
# (note: to take advantage of the Mera unit management, store new data in code-units)
# calculate the Mach number in each cell
mach = getvar(gas, :mach);
# add the extracted Mach number (1dim-array) to the data in the object "gas"
# the array has the same length and order (rows/cells) as in the data table
# push a column at the end of the table:
# transform(data-table, key => new-data)
gas.data = transform(gas.data, :mach => mach) # JuliaDB
proj_z = projection(gas, :mach, xrange=[-8.,8.], yrange=[-8.,8.], zrange=[-2.,2.], center=[:boxcenter], range_unit=:kpc);
using PyPlot
imshow( ( permutedims(proj_z.maps[:mach]) ), origin="lower", extent=proj_z.cextent)
colorbar();
# Remove the column :mach from the table:
gas.data = select(gas.data, Not(:mach)) # select all columns, not :mach
# ## Masking
# Many functions in **MERA** provide the opportunity to use a mask on selected data without changing the content in the data table. Here we present several methods to prepare a mask and apply it to some functions. A created mask is an array of type: `MaskType`, which can be Array{Bool,1} or BitArray{1}. A masked cell/row corresponds to a **false**.
# #### Version 1: External Function
# Create an array which represents the cells with the selected condition by true.
# The function checks if the following requirement is true or false for each row/cell in the data table:
# +
function ftest(value)
density = (4. / gas.scale.Msol_pc3)
if value < density
return true
else
return false
end
end
mask_v1 = map(row->ftest(row.rho), gas.data);
println( length(mask_v1) )
println( typeof(mask_v1) )
# -
# #### Version 2: Short Syntax
# ##### Example 1
# +
mask_v2 = map(row->row.rho < 4. / gas.scale.Msol_pc3, gas.data);
println( length(mask_v2) )
println( typeof(mask_v2) )
# -
# ##### Example 2
# +
mask_v2b = getvar(gas, :rho, :Msol_pc3) .> 1. ;
println( length(mask_v2b) )
println( typeof(mask_v2b) )
# -
# #### Version 3: Longer Syntax
# +
rho_array = select(gas.data, :rho);
mask_v3 = rho_array .< 1. / gas.scale.Msol_pc3;
println( length(mask_v3) )
println( typeof(mask_v3) )
# -
# ### Some Functions With Masking Functionality
# The masked rows are not considered in the calculations (mask-element = false ).
# ### Examples
# ### Total Mass
mask = map(row->row.rho < 1. / gas.scale.Msol_pc3, gas.data);
mtot_masked = msum(gas, :Msol, mask=mask)
mtot = msum(gas, :Msol)
println()
println( "Gas Mtot masked: ", mtot_masked , " Msol" )
println( "Gas Mtot: ", mtot , " Msol" )
println()
mask = map(row->row.birth < 100. / particles.scale.Myr, particles.data);
mtot_masked = msum(particles, :Msol, mask=mask)
mtot = msum(particles, :Msol)
println()
println( "Particles Mtot masked: ", mtot_masked , " Msol" )
println( "Particles Mtot: ", mtot , " Msol" )
println()
mask = map(row->row.mass_cl < 1e6 / clumps.scale.Msol, clumps.data);
mtot_masked = msum(clumps, :Msol, mask=mask)
mtot = msum(clumps, :Msol)
println()
println( "Clumps Mtot masked: ", mtot_masked , " Msol" )
println( "Clumps Mtot: ", mtot , " Msol" )
println()
# ### Center-Of-Mass
mask = map(row->row.rho < 100. / gas.scale.nH, gas.data);
com_gas_masked = center_of_mass(gas, :kpc, mask=mask)
com_gas = center_of_mass(gas, :kpc)
println()
println( "Gas COM masked: ", com_gas_masked , " kpc" )
println( "Gas COM: ", com_gas , " kpc" )
println()
mask = map(row->row.birth < 100. / particles.scale.Myr, particles.data);
com_particles_masked = center_of_mass(particles, :kpc, mask=mask)
com_particles = center_of_mass(particles, :kpc)
println()
println( "Particles COM masked: ", com_particles_masked , " kpc" )
println( "Particles COM: ", com_particles , " kpc" )
println()
# +
# calculate joint center-of-mass from gas and particles
mask1 = map(row->row.rho < 100. / gas.scale.nH, gas.data); # mask for the hydro data
mask2 = map(row->row.birth < 100. / particles.scale.Myr, particles.data); # mask for the particle data
println( "Joint COM (Gas + Particles) masked: ", center_of_mass([gas,particles], :kpc, mask=[mask1, mask2]) , " kpc" )
println( "Joint COM (Gas + Particles): ", center_of_mass([gas,particles], :kpc) , " kpc" )
# -
mask = map(row->row.mass_cl < 1e6 / clumps.scale.Msol, clumps.data);
com_clumps_masked = center_of_mass(clumps, mask=mask)
com_clumps = center_of_mass(clumps)
println()
println( "Clumps COM masked:", com_clumps_masked .* clumps.scale.kpc, " kpc" )
println( "Clumps COM: ", com_clumps .* clumps.scale.kpc, " kpc" )
println()
# ### Bulk-Velocity
mask = map(row->row.rho < 100. / gas.scale.nH, gas.data);
bv_gas_masked = bulk_velocity(gas, :km_s, mask=mask)
bv_gas = bulk_velocity(gas, :km_s)
println()
println( "Gas bulk velocity masked: ", bv_gas_masked , " km/s" )
println( "Gas bulk velocity: ", bv_gas , " km/s" )
println()
mask = map(row->row.birth < 100. / particles.scale.Myr, particles.data);
bv_particles_masked = bulk_velocity(particles, :km_s, mask=mask)
bv_particles = bulk_velocity(particles, :km_s)
println()
println( "Particles bulk velocity masked: ", bv_particles_masked , " km/s" )
println( "Particles bulk velocity: ", bv_particles , " km/s" )
println()
# ### Weighted Statistics
# (It is also possible to use the mask within the `getvar` function)
# +
maskgas = map(row->row.rho < 100. / gas.scale.nH, gas.data);
maskpart = map(row->row.birth < 100. / particles.scale.Myr, particles.data);
maskclump = map(row->row.mass_cl < 1e7 / clumps.scale.Msol, clumps.data);
stats_gas_masked = wstat( getvar(gas, :vx, :km_s), weight=getvar(gas, :mass ), mask=maskgas);
stats_particles_masked = wstat( getvar(particles, :vx, :km_s), weight=getvar(particles, :mass ), mask=maskpart);
stats_clumps_masked = wstat( getvar(clumps, :peak_x, :kpc ), weight=getvar(clumps, :mass_cl), mask=maskclump) ;
println( "Gas <vx>_cells masked : ", stats_gas_masked.mean, " km/s (mass weighted)" )
println( "Particles <vx>_particles masked : ", stats_particles_masked.mean, " km/s (mass weighted)" )
println( "Clumps <peak_x>_clumps masked : ", stats_clumps_masked.mean, " kpc (mass weighted)" )
println()
# +
stats_gas = wstat( getvar(gas, :vx, :km_s), weight=getvar(gas, :mass ));
stats_particles = wstat( getvar(particles, :vx, :km_s), weight=getvar(particles, :mass ));
stats_clumps = wstat( getvar(clumps, :peak_x, :kpc ), weight=getvar(clumps, :mass_cl)) ;
println( "Gas <vx>_allcells : ", stats_gas.mean, " km/s (mass weighted)" )
println( "Particles <vx>_allparticles : ", stats_particles.mean, " km/s (mass weighted)" )
println( "Clumps <peak_x>_allclumps : ", stats_clumps.mean, " kpc (mass weighted)" )
println()
# -
| tutorials/version_1/05_multi_Masking_Filtering.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This is an extension to the toy problem listed in Chapter 5 of <NAME>'s Stochastic process book.
# Here we have a `n*n*n` binary matrix, B. At the beginning, 1s and 0s are distributed in a chessboard manner.
# At each Monte Carlo step:
#
# randomly pick a location (i,j) in the matrix
# if B[x][y][z]==0:
# B[x][y][z]=1
# else:
# B[x][y][z]=0
# if 0 is at any of B[x+1][y][z],B[x][y+1][z],B[x][y][z+1],B[x-1][y][z],B[x][y-1][z],B[x][y][z-1]:
# B[x][y][z]=1
#
# The step shown above is then repeated for multiple times till the number of 1s in the matrix hits the target.
#
# Notice: this method can also start from a matrix with only 1s in it.
#
# **Attention: Please cite this paper if you want to use the method described here: Liu, Sizhe, and <NAME>. "Intercalated Cation Disorder in Prussian Blue Analogues: First-Principles and Grand Canonical Analyses." The Journal of Physical Chemistry C 123.16 (2019): 10191-10204.
# +
import numpy as np
n=4
# Prepare starting matrix
B = np.ones((n,n,n), dtype = int)
x = np.zeros((n, n), dtype = int)
x[1::2, ::2] = 1
x[::2, 1::2] = 1
y = np.abs(x-1)
for i in range(n):
if i%2==0:
B[:,:,i]=x
else:
B[:,:,i]=y
# Prepare neighbor array
nbs = np.array([[1,0,0],[0,1,0],[0,0,1],[-1,0,0],[0,-1,0],[0,0,-1]])
# -
def generator(mat, target):
#Target must not be equal to the number of 1s in mat
# maximum value for target is n*n*n
global n, nbs
curr = np.sum(mat)
period = list(range(n))
while curr!=target:
a,b,c = np.random.choice(period, size=3, replace=True)
if mat[a][b][c]==0: # a 0 is picked
mat[a][b][c]=1
curr+=1
else: # a 1 is picked
tempx = a+nbs[:,0]
tempx = [n-1 if x_==-1 else x_ for x_ in tempx]
tempx = [0 if x_==n else x_ for x_ in tempx]
tempy = b+nbs[:,1]
tempy = [n-1 if y_==-1 else y_ for y_ in tempy]
tempy = [0 if y_==n else y_ for y_ in tempy]
tempz = c+nbs[:,2]
tempz = [n-1 if z_==-1 else z_ for z_ in tempz]
tempz = [0 if z_==n else z_ for z_ in tempz]
nn = 0
for t0,t1, t2 in zip(tempx, tempy, tempz):
if mat[t0][t1][t2]==1:
nn+=1
if nn==6: # neighbors' are 1s.
mat[a][b][c]=0
curr-=1
return mat
# +
import time
# %matplotlib inline
import matplotlib.pyplot as plt
tcount = []
for i in range(33, 62):
start = time.time()
generator(B, i)
end = time.time()
tcount.append(end - start)
plt.plot(list(range(33, 62)),tcount,'o-')
plt.xlabel('# of 1s')
plt.ylabel('generating time')
plt.title('generate starting from chessboard pattern')
# -
# **The plot above clearly shows that much more time is needed to generate matrix with nearly all elements are 1s.**
# *Now, let's try to start from matrix with no 0s*
# +
B = np.ones((n,n,n), dtype = int)
tcount = []
for i in range(63, 36,-1):
start = time.time()
generator(B, i)
end = time.time()
tcount.append(end - start)
plt.plot(list(range(63, 36,-1)),tcount,'o-')
plt.xlabel('# of 1s')
plt.ylabel('generating time')
plt.title('generate starting from chessboard pattern')
# -
# **The plot above shows that much more time is needed to generate matrix with nearly half of the elements are 0s.**
| Binary 3D matrix with no adjacent 0s.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### This jupyter notebooks provides the code for classifying signals using the Continuous Wavelet Transform and Convolutional Neural Networks.
# ### To get some more background information, please have a look at the accompanying blog-post:
# ### http://ataspinar.com/2018/12/21/a-guide-for-using-the-wavelet-transform-in-machine-learning/
import pywt
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict, Counter
import keras
from keras.layers import Dense, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.models import Sequential
from keras.callbacks import History
history = History()
# # 1. Loading the UCI HAR dataset into an numpy ndarray
# Download dataset from https://archive.ics.uci.edu/ml/datasets/Human+Activity+Recognition+Using+Smartphones
# +
activities_description = {
1: 'walking',
2: 'walking upstairs',
3: 'walking downstairs',
4: 'sitting',
5: 'standing',
6: 'laying'
}
def read_signals(filename):
with open(filename, 'r') as fp:
data = fp.read().splitlines()
data = map(lambda x: x.strip().split(), data)
data = [list(map(float, line)) for line in data]
return data
def read_labels(filename):
with open(filename, 'r') as fp:
activities = fp.read().splitlines()
activities = list(map(lambda x: int(x)-1, activities))
return activities
def randomize(dataset, labels):
permutation = np.random.permutation(labels.shape[0])
shuffled_dataset = dataset[permutation, :, :]
shuffled_labels = labels[permutation]
return shuffled_dataset, shuffled_labels
DATA_FOLDER = '../datasets/UCI HAR Dataset/'
INPUT_FOLDER_TRAIN = DATA_FOLDER+'train/Inertial Signals/'
INPUT_FOLDER_TEST = DATA_FOLDER+'test/Inertial Signals/'
INPUT_FILES_TRAIN = ['body_acc_x_train.txt', 'body_acc_y_train.txt', 'body_acc_z_train.txt',
'body_gyro_x_train.txt', 'body_gyro_y_train.txt', 'body_gyro_z_train.txt',
'total_acc_x_train.txt', 'total_acc_y_train.txt', 'total_acc_z_train.txt']
INPUT_FILES_TEST = ['body_acc_x_test.txt', 'body_acc_y_test.txt', 'body_acc_z_test.txt',
'body_gyro_x_test.txt', 'body_gyro_y_test.txt', 'body_gyro_z_test.txt',
'total_acc_x_test.txt', 'total_acc_y_test.txt', 'total_acc_z_test.txt']
LABELFILE_TRAIN = DATA_FOLDER+'train/y_train.txt'
LABELFILE_TEST = DATA_FOLDER+'test/y_test.txt'
train_signals, test_signals = [], []
for input_file in INPUT_FILES_TRAIN:
signal = read_signals(INPUT_FOLDER_TRAIN + input_file)
train_signals.append(signal)
train_signals = np.transpose(train_signals, (1, 2, 0))
for input_file in INPUT_FILES_TEST:
signal = read_signals(INPUT_FOLDER_TEST + input_file)
test_signals.append(signal)
test_signals = np.transpose(test_signals, (1, 2, 0))
train_labels = read_labels(LABELFILE_TRAIN)
test_labels = read_labels(LABELFILE_TEST)
[no_signals_train, no_steps_train, no_components_train] = np.shape(train_signals)
[no_signals_test, no_steps_test, no_components_test] = np.shape(test_signals)
no_labels = len(np.unique(train_labels[:]))
print("The train dataset contains {} signals, each one of length {} and {} components ".format(no_signals_train, no_steps_train, no_components_train))
print("The test dataset contains {} signals, each one of length {} and {} components ".format(no_signals_test, no_steps_test, no_components_test))
print("The train dataset contains {} labels, with the following distribution:\n {}".format(np.shape(train_labels)[0], Counter(train_labels[:])))
print("The test dataset contains {} labels, with the following distribution:\n {}".format(np.shape(test_labels)[0], Counter(test_labels[:])))
uci_har_signals_train, uci_har_labels_train = randomize(train_signals, np.array(train_labels))
uci_har_signals_test, uci_har_labels_test = randomize(test_signals, np.array(test_labels))
# -
# # 2. Applying a CWT to UCI HAR signals and saving the resulting scaleogram into an numpy ndarray
# +
scales = range(1,128)
waveletname = 'morl'
train_size = 1000
train_data_cwt = np.ndarray(shape=(train_size, 127, 127, 9))
for ii in range(0,train_size):
if ii % 1000 == 0:
print(ii)
for jj in range(0,9):
signal = uci_har_signals_train[ii, :, jj]
coeff, freq = pywt.cwt(signal, scales, waveletname, 1)
coeff_ = coeff[:,:127]
train_data_cwt[ii, :, :, jj] = coeff_
test_size = 100
test_data_cwt = np.ndarray(shape=(test_size, 127, 127, 9))
for ii in range(0,test_size):
if ii % 100 == 0:
print(ii)
for jj in range(0,9):
signal = uci_har_signals_test[ii, :, jj]
coeff, freq = pywt.cwt(signal, scales, waveletname, 1)
coeff_ = coeff[:,:127]
#coeff_ = coeff
test_data_cwt[ii, :, :, jj] = coeff_
# -
# # 3. Training a Convolutional Neural Network
# +
x_train = train_data_cwt
y_train = list(uci_har_labels_train[:train_size])
x_test = test_data_cwt
y_test = list(uci_har_labels_test[:test_size])
img_x = 127
img_y = 127
img_z = 9
num_classes = 6
batch_size = 16
epochs = 2
# reshape the data into a 4D tensor - (sample_number, x_img_size, y_img_size, num_channels)
# because the MNIST is greyscale, we only have a single channel - RGB colour images would have 3
input_shape = (img_x, img_y, img_z)
# convert the data to the right type
#x_train = x_train.reshape(x_train.shape[0], img_x, img_y, img_z)
#x_test = x_test.reshape(x_test.shape[0], img_x, img_y, img_z)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices - this is for use in the
# categorical_crossentropy loss below
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# +
model = Sequential()
model.add(Conv2D(32, kernel_size=(5, 5), strides=(1, 1), activation='relu', input_shape=input_shape))
model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
model.add(Conv2D(64, (5, 5), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(1000, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adam(),
metrics=['accuracy'])
model.fit(x_train, y_train, batch_size=batch_size,
epochs=epochs, verbose=1,
validation_data=(x_test, y_test),
callbacks=[history])
train_score = model.evaluate(x_train, y_train, verbose=0)
print('Train loss: {}, Train accuracy: {}'.format(train_score[0], train_score[1]))
test_score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss: {}, Test accuracy: {}'.format(test_score[0], test_score[1]))
# -
fig, axarr = plt.subplots(figsize=(12,6), ncols=2)
axarr[0].plot(range(1, epochs+1), history.history['accuracy'], label='train score')
axarr[0].plot(range(1, epochs+1), history.history['val_accuracy'], label='test score')
axarr[0].set_xlabel('Number of Epochs', fontsize=18)
axarr[0].set_ylabel('Accuracy', fontsize=18)
axarr[0].set_ylim([0,1])
axarr[1].plot(range(1, epochs+1), history.history['accuracy'], label='train score')
axarr[1].plot(range(1, epochs+1), history.history['val_accuracy'], label='test score')
axarr[1].set_xlabel('Number of Epochs', fontsize=18)
axarr[1].set_ylabel('Accuracy', fontsize=18)
axarr[1].set_ylim([0.8,1])
plt.legend()
plt.show()
wavlist = pywt.wavelist(kind='continuous')
wavlist
pip list | grep tensorflow
| notebooks/WV3 - Classification of signals using the CWT and CNN.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# This is from a "Getting Started" competition from Kaggle [Titanic competition](https://www.kaggle.com/c/titanic) to showcase how we can use Auto-ML along with datmo and docker, in order to track our work and make machine learning workflow reprocible and usable. Some part of data analysis is inspired from this [kernel](https://www.kaggle.com/sinakhorami/titanic-best-working-classifier)
#
# This approach can be categorized into following methods,
#
# 1. Exploratory Data Analysis (EDA)
# 2. Data Cleaning
# 3. Using Auto-ML to figure out the best algorithm and hyperparameter
#
# During the process of EDA and feature engineering, we would be using datmo to create versions of work by creating snapshot.
# +
# %matplotlib inline
import datmo
import numpy as np
import pandas as pd
import re as re
train = pd.read_csv('./input/train.csv', header = 0, dtype={'Age': np.float64})
test = pd.read_csv('./input/test.csv' , header = 0, dtype={'Age': np.float64})
full_data = [train, test]
print (train.info())
# -
# #### 1. Exploratory Data Analysis
# ###### To understand how each feature has the contribution to Survive
# ###### a. `Sex`
print (train[["Sex", "Survived"]].groupby(['Sex'], as_index=False).mean())
# ###### b. `Pclass`
print (train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean())
# c. `SibSp and Parch`
#
# With the number of siblings/spouse and the number of children/parents we can create new feature called Family Size.
for dataset in full_data:
dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1
print (train[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=False).mean())
# `FamilySize` seems to have a significant effect on our prediction. `Survived` has increased until a `FamilySize` of 4 and has decreased after that. Let's categorize people to check they are alone or not.
for dataset in full_data:
dataset['IsAlone'] = 0
dataset.loc[dataset['FamilySize'] == 1, 'IsAlone'] = 1
print (train[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean())
# d. `Embarked`
#
# we fill the missing values with most occured value `S`
for dataset in full_data:
dataset['Embarked'] = dataset['Embarked'].fillna('S')
print (train[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean())
# e. `Fare`
#
# Fare also has some missing values which will be filled with the median
for dataset in full_data:
dataset['Fare'] = dataset['Fare'].fillna(train['Fare'].median())
train['CategoricalFare'] = pd.qcut(train['Fare'], 4)
print (train[['CategoricalFare', 'Survived']].groupby(['CategoricalFare'], as_index=False).mean())
# It shows the `Fare` has a significant affect on survival, showcasing that people haivng paid higher fares had higher chances of survival
# f. `Age`
#
# There are plenty of missing values in this feature. # generate random numbers between (mean - std) and (mean + std). then we categorize age into 5 range.
# +
for dataset in full_data:
age_avg = dataset['Age'].mean()
age_std = dataset['Age'].std()
age_null_count = dataset['Age'].isnull().sum()
age_null_random_list = np.random.randint(age_avg - age_std, age_avg + age_std, size=age_null_count)
dataset['Age'][np.isnan(dataset['Age'])] = age_null_random_list
dataset['Age'] = dataset['Age'].astype(int)
train['CategoricalAge'] = pd.cut(train['Age'], 5)
print (train[['CategoricalAge', 'Survived']].groupby(['CategoricalAge'], as_index=False).mean())
# -
# g. `Name`
#
# Let's the title of people
# +
def get_title(name):
title_search = re.search(' ([A-Za-z]+)\.', name)
# If the title exists, extract and return it.
if title_search:
return title_search.group(1)
return ""
for dataset in full_data:
dataset['Title'] = dataset['Name'].apply(get_title)
print("=====Title vs Sex=====")
print(pd.crosstab(train['Title'], train['Sex']))
print("")
print("=====Title vs Survived=====")
print (train[['Title', 'Survived']].groupby(['Title'], as_index=False).mean())
# -
# Let's categorize it and check the title impact on survival rate convert the rare titles to `Rare`
# +
for dataset in full_data:
dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
print (train[['Title', 'Survived']].groupby(['Title'], as_index=False).mean())
# -
config = {"features analyzed": ["Sex", "Pclass", "FamilySize", "IsAlone", "Embarked", "Fare", "Age", "Title"]}
# Save the file and run this block
datmo.snapshot.create(message="EDA", config=config)
# #### Creating a datmo snapshot to save my work, this helps me save my current work before proceeding onto data cleaning
# ```bash
# home:~/datmo-tutorials/auto-ml$ datmo snapshot ls
# +---------+-------------+-------------------------------------------+-------+---------+-------+
# | id | created at | config | stats | message | label |
# +---------+-------------+-------------------------------------------+-------+---------+-------+
# | 30803662| 2018-05-15 | {u'features analyzed': [u'Sex', | {} | EDA | None |
# | | 23:15:44 | u'Pclass', u'FamilySize', u'IsAlone', | | | |
# | | | u'Embarked', u'Fare', u'Age', u'Title']} | | | |
# +---------+-------------+-------------------------------------------+-------+---------+-------+
# ```
# #### 2. Data Cleaning
# Now let's clean our data and map our features into numerical values.
# +
train_copy = train.copy()
test_copy = test.copy()
full_data_copy = [train_copy, test_copy]
for dataset in full_data_copy:
# Mapping Sex
dataset['Sex'] = dataset['Sex'].map( {'female': 0, 'male': 1} ).astype(int)
# Mapping titles
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
# Mapping Embarked
dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
# Mapping Fare
dataset.loc[ dataset['Fare'] <= 7.91, 'Fare'] = 0
dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare'] = 2
dataset.loc[ dataset['Fare'] > 31, 'Fare'] = 3
dataset['Fare'] = dataset['Fare'].astype(int)
# Mapping Age
dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
dataset.loc[ dataset['Age'] > 64, 'Age'] = 4
# +
# Feature Selection
drop_elements = ['PassengerId', 'Name', 'Ticket', 'Cabin', 'SibSp',\
'Parch', 'FamilySize']
train_copy = train_copy.drop(drop_elements, axis = 1)
train_copy = train_copy.drop(['CategoricalAge', 'CategoricalFare'], axis = 1)
test_copy = test_copy.drop(drop_elements, axis = 1)
print (train_copy.head(10))
train_copy = train_copy.values
test_copy = test_copy.values
# -
# #### 3. Using Auto-ML to figure out the best algorithm and hyperparameter
# ##### Now we have cleaned our data it's time to use auto-ml in order to get the best algorithm for this data
# 
# +
from tpot import TPOTClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
X = train_copy[0::, 1::]
y = train_copy[0::, 0]
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.75, test_size=0.25)
tpot = TPOTClassifier(generations=5, population_size=50, verbosity=2)
tpot.fit(X_train, y_train)
print(tpot.score(X_test, y_test))
tpot.export('tpot_titanic_pipeline.py')
# +
# Creating a prediction for submission
prediction = tpot.predict(test_copy)
# Creating a submission
submission = pd.DataFrame({
"PassengerId": test["PassengerId"],
"Survived": prediction
})
submission.to_csv('submission.csv', index=False)
submission = pd.read_csv('submission.csv')
submission.head()
# -
config = {"selected features": ["Sex", "Pclass", "Age", "Fare", "Embarked", "Fare", "IsAlone", "Title"]}
stats = {"accuracy": (tpot.score(X_test, y_test))}
datmo.snapshot.create(message="auto-ml-1", config=config, stats=stats)
# ### Let's again create a datmo snapshot to save my work, this helps me save my current work before changing my feature selection
#
# ```bash
# home:~/datmo-tutorials/auto-ml$ datmo snapshot ls
# +---------+-------------+-------------------------------------------+-----------------+---------------+-------+
# | id | created at | config | stats | message | label |
# +---------+-------------+-------------------------------------------+-----------------+---------------+-------+
# | adf76fa7| 2018-05-16 | {u'selected features': [u'Sex', u'Pclass',|{u'accuracy': | auto-ml-1 | None |
# | | 01:24:53 | u'Age', u'Fare', u'Embarked', | 0.7757847} | | |
# | | | u'Fare', u'IsAlone', u'Title']} | | | |
# | 30803662| 2018-05-15 | {u'features analyzed': [u'Sex', | {} | EDA | None |
# | | 23:15:44 | u'Pclass', u'FamilySize', u'IsAlone', | | | |
# | | | u'Embarked', u'Fare', u'Age', u'Title']} | | | |
# +---------+-------------+-------------------------------------------+-----------------+---------------+-------+
# ```
# #### Another feature selection
# 1. Let's leave `FamilySize` rather than just unsing `IsAlone`
# 2. Let's use `Fare_Per_Person` insted of binning `Fare`
# +
train_copy = train.copy()
test_copy = test.copy()
full_data_copy = [train_copy, test_copy]
for dataset in full_data_copy:
# Mapping Sex
dataset['Sex'] = dataset['Sex'].map( {'female': 0, 'male': 1} ).astype(int)
# Mapping titles
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
# Mapping Embarked
dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
# Mapping Fare
dataset['FarePerPerson']=dataset['Fare']/(dataset['FamilySize']+1)
# Mapping Age
dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
dataset.loc[ dataset['Age'] > 64, 'Age'] = 4
# +
# Feature Selection
drop_elements = ['PassengerId', 'Name', 'Ticket', 'Cabin', 'SibSp',\
'Parch', 'IsAlone', 'Fare']
train_copy = train_copy.drop(drop_elements, axis = 1)
train_copy = train_copy.drop(['CategoricalAge', 'CategoricalFare'], axis = 1)
test_copy = test_copy.drop(drop_elements, axis = 1)
print (train_copy.head(10))
train_copy = train_copy.values
test_copy = test_copy.values
# +
from tpot import TPOTClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
X = train_copy[0::, 1::]
y = train_copy[0::, 0]
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.75, test_size=0.25)
tpot = TPOTClassifier(generations=5, population_size=50, verbosity=2)
tpot.fit(X_train, y_train)
print(tpot.score(X_test, y_test))
tpot.export('tpot_titanic_pipeline.py')
# +
# Creating a prediction for submission
prediction = tpot.predict(test_copy)
# Creating a submission
submission = pd.DataFrame({
"PassengerId": test["PassengerId"],
"Survived": prediction
})
submission.to_csv('submission.csv', index=False)
submission = pd.read_csv('submission.csv')
submission.head()
# -
config = {"selected features": ["Sex", "Pclass", "Age", "Fare", "Embarked", "FarePerPerson", "FamilySize", "Title"]}
stats = {"accuracy": (tpot.score(X_test, y_test))}
datmo.snapshot.create(message="auto-ml-2", config=config, stats=stats)
# ### Let's again create a datmo snapshot to save my final work
#
# ```bash
# home:~/datmo-tutorials/auto-ml$ datmo snapshot ls
# +---------+-------------+-------------------------------------------+-----------------+---------------+-------+
# | id | created at | config | stats | message | label |
# +---------+-------------+-------------------------------------------+-----------------+---------------+-------+
# | 30f8366b| 2018-05-16 | {u'selected features': [u'Sex', u'Pclass',|{u'accuracy': | auto-ml-2 | None |
# | | 03:04:06 | u'Age', u'Fare', u'Embarked', u'Title', | 0.8291278} | | |
# | | | u'FarePerPerson', u'FamilySize']} | | | |
# | adf76fa7| 2018-05-16 | {u'selected features': [u'Sex', u'Pclass',|{u'accuracy': | auto-ml-1 | None |
# | | 01:24:53 | u'Age', u'Fare', u'Embarked', | 0.8206278} | | |
# | | | u'Fare', u'IsAlone', u'Title']} | | | |
# | 30803662| 2018-05-15 | {u'features analyzed': [u'Sex', | {} | EDA | None |
# | | 23:15:44 | u'Pclass', u'FamilySize', u'IsAlone', | | | |
# | | | u'Embarked', u'Fare', u'Age', u'Title']} | | | |
# +---------+-------------+-------------------------------------------+-----------------+---------------+-------+
# ```
# #### Let's now move to a different snapshot in order to either get the `experimentation.ipynb`, `submission.csv` or `tpot_titanice_pipeline.py` or any other files in that version
#
# We perform `checkout` command in order to achieve it
#
# ```bash
# home:~/datmo-tutorials/auto-ml$ # Run this command: datmo snapshot checkout --id <snapshot-id>
# home:~/datmo-tutorials/auto-ml$ datmo snapshot checkout --id 30803662
# ```
#
| kaggle-titanic/sdk/experimentation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="dwtgETJhCJSr"
# Задача: напишите исходный код на Python 3 для проверки, является ли введённое число [палиндромом](https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D0%BB%D0%B8%D0%BD%D0%B4%D1%80%D0%BE%D0%BC) (например, 112343211 -- да, 100 -- нет). Программа должна принимать на вход число и печатать на выход ответ "palindrome" или "not palindrome". Решение не должно использовать коллекции, включая строки.
# Предоставьте реализацию в ноутбуке (.ipynb) и обычном файле (.py). Оба файла должны лежать в вашем репозитории на [GitHub](https://github.com). Доступ давать пользователям persdep (Илья) и mr-patty (Олег).
#
| HW1-palindrome.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="hyWXhVMXw82d" outputId="d0c1708e-e2e3-4420-b0bf-3b226af46e22"
import os
from collections import Counter
from itertools import product
from statistics import mean, mode, median
import matplotlib.pyplot as plt
import nltk
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.functional as F
from nltk.tokenize import TweetTokenizer, word_tokenize
from sklearn.metrics import classification_report, f1_score
from sklearn.model_selection import train_test_split
from torch import optim
from tqdm.auto import tqdm
from transformers import AutoModel
from transformers import BertModel, RobertaModel, AlbertModel, BartForSequenceClassification
from transformers import BertTokenizerFast, RobertaTokenizerFast, AlbertTokenizerFast, BartTokenizer
nltk.download('punkt')
# + id="VMnxy56xrHgZ"
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# -
names = ['id', 'json', 'label', 'statement', 'subject', 'speaker', 'job', 'state', 'party', 'credit', 'barely_true',
'false', 'half_true', 'mostly_true', 'pants_on_fire', 'context', 'justification']
df = pd.read_csv('LIAR-PLUS-master/dataset/tsv/train2.tsv', sep='\t', names=names)
df['label'].value_counts()
texts = list(df[df['label'] == 'true']['statement']) + list(df[df['label'] == 'false']['statement'])
labels = list(df[df['label'] == 'true']['label']) + list(df[df['label'] == 'false']['label'])
# +
import random
temp = list(zip(texts, labels))
random.shuffle(temp)
texts, labels = zip(*temp)
# + id="jda1-fKfAnd2"
lengths = [len(text) for text in texts]
# + colab={"base_uri": "https://localhost:8080/"} id="40B7D3MPA5tk" outputId="d52a7076-98e1-4d6c-806a-56aed564c183"
print(sorted(lengths, reverse=True))
# + colab={"base_uri": "https://localhost:8080/"} id="tgfdTOxPAsdN" outputId="f4460656-dfc5-45f3-a8af-249ed36bb139"
print(f"median: {median(lengths)}\nmode: {1}\nmean: {round(mean(lengths))}\nmax: {max(lengths)}\nmin: {min(lengths)}")
# + id="YBR6zktQyDRI"
tokenize = TweetTokenizer()
# -
ready_texts = [tokenize.tokenize(text) for text in texts]
ready_labels = [1 if label == 'true' else 0 for label in labels]
X_train, X_test, y_train, y_test = train_test_split(ready_texts, ready_labels, test_size=0.1)
len(X_train), len(y_train), len(X_test), len(y_test)
X_train, y_train, X_val, y_val = X_train[368:], y_train[368:], X_train[:368], y_train[:368]
# + colab={"base_uri": "https://localhost:8080/"} id="qHTQVgtGAZb4" outputId="60635f11-02ee-4601-b263-69bb4f02683c"
c = Counter(y_train)
print(f"Number of positive examples: {c[0]}\nNumber of negative examples: {c[1]}")
# + colab={"base_uri": "https://localhost:8080/"} id="C5ixUm1kpMrA" outputId="c0415957-9150-4300-c87a-35a7f1bd6b7e"
lengths = [len(x) for x in X_train]
print(
f"median: {median(lengths)}\nmode: {mode(lengths)}\nmean: {round(mean(lengths))}\nmax: {max(lengths)}\nmin: {min(lengths)}")
# -
data = lengths
num_bins = 57
plt.hist(data, num_bins, color='purple', alpha=0.5, rwidth=0.85)
plt.title('Sentence Length Distribution')
plt.xlabel('Sentence Length')
plt.ylabel('Frequency')
plt.show()
# + id="wmr5NPQJxMGw"
word2token = {'PAD': 0, 'UNK': 1}
all_words = set()
for text in X_train:
for word in text:
all_words.add(word)
for word in all_words:
word2token[word] = len(word2token)
# + id="O84HE0_jvVNB"
class RNNclassifier(nn.Module):
def __init__(self, device, emb_size, num_classes=1, dropout=0.4, hidden_size=100):
super(RNNclassifier, self).__init__()
self.device = device
self.hidden_size = hidden_size
self.emb_size = emb_size
self.dropout = nn.Dropout(dropout).to(self.device)
self.num_classes = num_classes
self.embedding = nn.Embedding(self.emb_size, self.hidden_size).to(self.device)
self.rnn = nn.RNN(self.hidden_size, self.hidden_size, batch_first=True).to(self.device)
self.linear = nn.Linear(self.hidden_size, self.num_classes).to(self.device)
def forward(self, tokens, attention_ids, length):
embs = self.embedding(tokens)
rnn_out, hidden = self.rnn(embs)
drop_out = self.dropout(rnn_out)
output_zero_padding = drop_out.permute([2, 0, 1]) * attention_ids
output_zero_padding = output_zero_padding.permute([1, 2, 0])
out = torch.sum(output_zero_padding, 1).T / length
out = out.T
out = self.linear(out)
return out
# + id="1r6tDIh5zwE3"
class Dataset(torch.utils.data.Dataset):
def __init__(self, texts, labels, maxlen, word2token, device):
self.texts = texts
self.labels = labels
self.device = device
self.maxlen = maxlen
self.word2token = word2token
def __getitem__(self, item):
text = self.texts[item]
label = self.labels[item]
transformed_text = [self.word2token.get(word, 1) for word in text][:self.maxlen]
transformed_text = torch.tensor(
transformed_text + [self.word2token['PAD'] for _ in range(self.maxlen - len(transformed_text))],
dtype=torch.long, device=self.device)
attention_ids = torch.tensor(
[1 for _ in range(len(transformed_text))] + [0 for _ in range(self.maxlen - len(transformed_text))],
dtype=torch.long, device=self.device)
return transformed_text, len(transformed_text), attention_ids, label
def __len__(self):
return len(self.texts)
# + id="d0wOLsDTveA8"
def train_model(model, dataloader, dev_dataloader, epoches, optim=optim.RMSprop, lr=0.01):
optimizer = optim(model.parameters(), lr=lr) # Adam, AdamW, Adadelta, Adagrad, SGD, RMSProp
binary = nn.BCEWithLogitsLoss()
best_f = 0
for epoch in range(epoches):
print(epoch + 1, "epoch")
t = tqdm(dataloader)
i = 0
for sentence, length, attention_ids, label in t:
pred = model(sentence, attention_ids, length)
loss = binary(pred.view(-1), label.type(torch.float32))
if i % 10 == 0:
torch.save(model, 'model.pt')
predicted = []
true = []
with torch.no_grad():
for sentence, length, attention_ids, label in dev_dataloader:
pred = model(sentence, attention_ids, length)
idx = (torch.sigmoid(pred) > 0.5).type(torch.int).item()
predicted.append(idx)
true.append(label.item())
f1 = f1_score(true, predicted, average='macro')
if f1 > best_f:
torch.save(model, f"{round(f1, 3)}model.pt")
best_f = f1
print("Saving with score", best_f)
i += 1
t.set_description(f"loss: {round(float(loss), 3)}, f-macro: {round(f1, 3)}")
t.refresh()
loss.backward()
optimizer.step()
model.zero_grad()
return best_f
# + id="QAmT8lhV7JXz"
trainds = Dataset(X_train, y_train, 50, word2token, device)
devds = Dataset(X_val, y_val, 50, word2token, device)
testds = Dataset(X_test, y_test, 50, word2token, device)
# + id="hjbmzhd46hgk"
train_dataloader = torch.utils.data.DataLoader(trainds, batch_size=128)
dev_dataloader = torch.utils.data.DataLoader(devds, batch_size=1)
test_dataloader = torch.utils.data.DataLoader(testds, batch_size=1)
# + id="KyaPQqCGv3LN"
model = RNNclassifier(device, len(word2token), 1, 0.4, 100)
model.train()
train_model(model, train_dataloader, dev_dataloader, epoches=10)
# -
def param_optim(lr_list, optim_list):
best_f = 0
best_params = []
for lr, optim in product(lr_list, optim_list):
model = RNNclassifier(device, len(word2token), 1, 0.4, 100)
model.train()
f1 = train_model(model, train_dataloader, dev_dataloader, epoches=10, optim=optim, lr=lr)
if best_f < f1:
best_f = f1
best_params = [lr, optim]
return best_f, best_params
lr_list = [0.1, 0.01, 0.001, 0.0001]
op_list = [optim.Adam, optim.AdamW, optim.Adadelta, optim.Adagrad, optim.SGD, optim.RMSprop]
best_f, best_params = param_optim(lr_list, op_list)
best_f, best_params
# + id="7tN7Urea7E1M"
model.eval()
# + id="rq0sqVjobliP"
def evaluate(model, test_dataloader):
predicted = []
true = []
with torch.no_grad():
for sentence, length, attention_ids, label in test_dataloader:
pred = model(sentence, attention_ids, length)
idx = (torch.sigmoid(pred) > 0.5).type(torch.int).item()
predicted.append(idx)
true.append(label.item())
print(classification_report(true, predicted))
# + colab={"base_uri": "https://localhost:8080/"} id="uQGaHEiecKEf" outputId="9a7e44ff-b549-42b6-9e2e-f8ae566e0e22"
evaluate(torch.load('0.595model.pt'), test_dataloader)
# + id="t46RtnzEQiH3"
class CNNclassifier(nn.Module):
def __init__(self, device, maxlen, max_pool, emb_size, num_classes=2, hidden_size=100):
super(CNNclassifier, self).__init__()
self.device = device
self.hidden_size = hidden_size
self.maxlen = maxlen
self.max_pool = max_pool
self.emb_size = emb_size
self.embedding = nn.Embedding(self.emb_size, self.hidden_size).to(self.device)
self.cnn = nn.Conv1d(self.hidden_size, int(self.hidden_size / 2), 3)
self.maxpool = nn.MaxPool1d(int(self.maxlen - 2))
self.linear = nn.Linear(int((self.hidden_size / 2)), num_classes).to(self.device)
def forward(self, tokens, attention_ids, length):
embs = self.embedding(tokens)
embs = embs.permute(0, 2, 1)
cnn_out = self.cnn(embs)
max_out = self.maxpool(cnn_out)
max_out = max_out.permute(0, 2, 1)
out = self.linear(max_out)
out = out.squeeze(1)
return out
# + colab={"base_uri": "https://localhost:8080/"} id="uAPtAj8kU7wR" outputId="ae942867-d8f4-442a-d16e-157eb2678cd1"
cn = CNNclassifier(device, 50, 3, len(word2token), 1)
cn.train()
# + colab={"base_uri": "https://localhost:8080/", "height": 356, "referenced_widgets": ["a1b1191ae88447e68a284b65274053e0", "89c9b117c53546ada7dcd78ac234e1d1", "5aeca12e0fce4aeba613b54395a9151f", "<KEY>", "<KEY>", "b1ad670b7c144a6a95e16899da2d92a6", "3bc6ed5865d74c69a37771e673198318", "1086e8ab934746ed91107537ba0997e2", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "922a9cff193f4162a96183d37292b65b", "<KEY>", "71fe7f569da24972859899bff9d1fa17", "55176d9054cc479c86bac3acefe19c55", "b76e687adbfd4159b78e0f991140e048", "380ce323df7649b8b92f9fe189fd5dc0", "<KEY>", "1b78180d6df740b7befc7985706ca895", "<KEY>", "<KEY>", "<KEY>", "e6bd57adfcea40de8a7459e8239d0501"]} id="uO5dgbR4Rww_" outputId="ab5a73e6-7ff8-4ec8-d423-031468732880"
train_model(cn, train_dataloader, dev_dataloader, 10)
# + colab={"base_uri": "https://localhost:8080/"} id="uzytPDoe32Rn" outputId="d783a60d-1ff3-4fa9-9831-95d77a33fd8e"
cn.eval()
# + colab={"base_uri": "https://localhost:8080/"} id="gQ1OYLNk34aw" outputId="19bc1b81-c6a2-4660-ca84-814fc2a3af14"
evaluate(torch.load('0.55model.pt'), test_dataloader)
# + colab={"base_uri": "https://localhost:8080/", "height": 126, "referenced_widgets": ["3f0cc92175b049d5bd419aaae228d1d3", "<KEY>", "6420e6ea360b4326a9a978a235cbea8a", "6d9d5ce6011d44f7929753dffb66260a", "175e50cc03574e01942f693a53185493", "<KEY>", "03cdf7075b9f4b2aba7bbd890d7beabe", "f7eab23f4e53466fa88c33efc542d8cb", "<KEY>", "6b8b4ad714e94445bf5f9efd8f1545c2", "f1f76fc0012c4aefa053739f2efc2f38", "1634ddda44ad40ac8799a2a92b98cc4c", "de03c26b56e44cb7917234e52a3738f1", "526d4a45cd1f4a3d8378d6be178ed6d7", "<KEY>", "c760015b07c04edd9ea2985cd575e564"]} id="7Hm0mNg7mKtI" outputId="91985456-97bf-4a6d-b904-9716365d0439"
model_name = "bert-base-multilingual-cased"
tokenizer = BertTokenizerFast.from_pretrained(model_name)
# + id="2q2SRLYLliMe"
class bertDataset(torch.utils.data.Dataset):
def __init__(self, texts, labels, tokenizer, device):
self.texts = texts
self.labels = labels
self.tokenizer = tokenizer
self.device = device
def __getitem__(self, item):
text = self.texts[item]
label = self.labels[item]
tokens = self.tokenizer(text, padding='max_length', max_length=50, truncation=True, return_tensors='pt',
is_split_into_words=True).to(self.device)
tokens['input_ids'] = torch.squeeze(tokens['input_ids'], 0)[:512]
tokens['attention_mask'] = torch.squeeze(tokens['attention_mask'], 0)[:512]
tokens['token_type_ids'] = torch.squeeze(tokens['token_type_ids'], 0)[:512]
length = sum(tokens['attention_mask']).item()
label = torch.tensor(label, dtype=torch.float32, device=self.device)
return tokens, length, label
def __len__(self):
return len(self.texts)
# + id="abnM4ZN0mP3C"
bert_train = bertDataset(X_train, y_train, tokenizer, device)
bert_dev = bertDataset(X_val, y_val, tokenizer, device)
bert_test = bertDataset(X_test, y_test, tokenizer, device)
bert_tdataloader = torch.utils.data.DataLoader(bert_train, batch_size=64)
bert_ddataloader = torch.utils.data.DataLoader(bert_dev, batch_size=1)
bert_ttdataloader = torch.utils.data.DataLoader(bert_test, batch_size=1)
# + id="Jsgu7fVEvN0e"
class BERT_GRU(nn.Module):
def __init__(self, device, num_classes=1, hidden_size=100, model_name="bert-base-multilingual-cased"):
super(BERT_GRU, self).__init__()
self.device = device
self.bert = BertModel.from_pretrained(model_name).to(self.device)
self.gru = nn.GRU(input_size=768, hidden_size=hidden_size, batch_first=True).to(self.device)
self.dropout = nn.Dropout(0.4).to(self.device)
self.linear = nn.Linear(hidden_size, num_classes).to(self.device)
def forward(self, tokens, length):
with torch.no_grad():
output = self.bert(input_ids=tokens['input_ids'], attention_mask=tokens['attention_mask'],
token_type_ids=tokens['token_type_ids'], return_dict=True)
lstm_out, hidden = self.gru(output[
'last_hidden_state']) #its size is equal to batch_size, sequence_size, embedding_size (in case of this notebook, it's 32, 55, 768)
lstm_out = self.dropout(lstm_out)
output_zero_padding = lstm_out.permute([2, 0, 1]) * tokens['attention_mask']
output_zero_padding = output_zero_padding.permute([1, 2, 0]).to(self.device)
linear = torch.sum(output_zero_padding, 1).to(self.device)
length = length.to(self.device)
linear = linear.T / length
linear = linear.T
out = self.linear(linear)
return out
# + id="rBnjY4YafmVc"
def bert_train_model(model, dataloader, dev_dataloader, epoches):
optimizer = optim.Adam(model.parameters(), lr=1e-5) #lr 1e-5 and adam for roberta and albert
binary = nn.BCEWithLogitsLoss()
best_f = 0
for epoch in range(epoches):
print(epoch + 1, "epoch")
t = tqdm(dataloader)
i = 0
for sentence, length, label in t:
pred = model(sentence, length)
loss = binary(pred.view(-1), label)
if i % 300 == 0:
torch.save(model, 'model.pt')
predicted = []
true = []
with torch.no_grad():
for sentence, length, label in dev_dataloader:
pred = model(sentence, length)
idx = (torch.sigmoid(pred) > 0.5).type(torch.int).item()
predicted.append(idx)
true.append(label.item())
f1 = f1_score(true, predicted, average='macro')
if f1 > best_f:
torch.save(model, f"{round(f1, 3)}model.pt")
best_f = f1
print("Saving with score", best_f)
i += 1
t.set_description(f"loss: {round(float(loss), 3)}, f-macro: {round(f1, 3)}")
t.refresh()
loss.backward()
optimizer.step()
model.zero_grad()
# + id="Qrmw1OuimfUI"
def bert_evaluate(model, test_dataloader):
predicted = []
true = []
with torch.no_grad():
for sentence, length, label in test_dataloader:
pred = model(sentence, length)
idx = (torch.sigmoid(pred) > 0.5).type(torch.int).item()
predicted.append(idx)
true.append(label.item())
print(classification_report(true, predicted))
# + colab={"base_uri": "https://localhost:8080/"} id="Pu4EdIXLe59o" outputId="49eb56c8-9dd7-4d85-9ce6-4b69fb43b8e8"
m = BERT_GRU(device, 1, 100)
m.train()
# + colab={"base_uri": "https://localhost:8080/", "height": 1000, "referenced_widgets": ["f467dd64b3664fde80f1cb23c46c947c", "1f781ab5f43e4dc3999d9ef257b05617", "f4809fa303f945258a9658b83fffc452", "5ec96d7b962c4a5fbbea679810a64661", "4f399134b2d340dc92e246bd49c7e0d6", "<KEY>", "21242fb59d71461abde542917dd4a9a9", "1d535652b3ad47288de9a2bbb45daac4", "667a4c13886444ce8169a313493456fa", "<KEY>", "5b44746ce6184d58b9c42fce4d03d385", "7c6e52cde82641e6b9993b1c57e3ca25", "900888c99f9e4d04a8780324b79ece1f", "dbfc9e4e36c84106ae1834a5a0d203e5", "ef8b68526cb94363bf981920e7002778", "bc3f934926a24a9883478ab38ec87fea", "0f072039f5494c3ca5054ebd3f0ad97d", "1cea2b8619da4f6e9d88702c69aa4040", "<KEY>", "bec93ff8ec20405c9a6b3f8957087d24", "<KEY>", "05d016c40ff648f78c2090a4431dd8fb", "d6befd0a789a47448516bdf4a2d0906f", "<KEY>", "c1efb48bda7d4eb5933efa7a7911761e", "0d58bbbda86449ce8e65ff98a0e24590", "<KEY>", "<KEY>", "1528d8d63673479a903d4cc2ed75ebcc", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "28e445dc54154e4b911a8e33f7dd8076", "<KEY>", "<KEY>", "<KEY>", "578de5aeadf64648b0007b4cbed637e9", "1ef89572fde44de585bfc20506ea3c1e", "<KEY>", "<KEY>", "9c95860749464306ae15e25d99927f4a", "cbeb40676b594a7d8aa2cf6e194da911", "38505cd9d6c24132a1cbac27234e4706", "<KEY>", "<KEY>", "dbe10eca47464683aab646095942a36d", "ea3e069fc0164a5389bf2bb2eee6a28d", "261be75fd1cd40e78d40d9e2c4532f53", "7c227095d4e04d20abcef514421b95d0", "<KEY>", "704f4fbab152421ca11e27dd6f9691f7", "<KEY>", "ef6baf827a7d4b98bf8d6e3ea8dc72ba", "013e4c50866e4799bd5db7bb2a43d221", "0a9f93a1d5fd48a9a72d249160f84a63", "01c8c72beafb4c748e22d3d5c03c29af", "<KEY>", "4021b487d0a04d2e8bcecf3e613a43da", "089a5d45b88d4deb84a3607316384b5c", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "ad352fa05c4e4d91ac25a8799a997422", "2aa01bd7e22f4ad6a12ef1b4d8ceeae6", "4df978b7a8524b488bb0799369a8d665", "ffa78de1cfef4848ad3c12208e6afd7b", "e1fb9236c0e74ee1b3d1acd5133a885b", "81dd96d6b56646a3a8d07ed3540191aa", "<KEY>", "<KEY>", "f4ce18cfd4f047fc9e3acc00952093cd", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "76c0e2ffa729446e98602a741a57229e", "2ba5db7b701b4f2daba2223fecee2d53", "<KEY>"]} id="iVaoY26PfB6N" outputId="aa39c736-b7c3-402b-b034-6851df1bf4b9"
bert_train_model(m, bert_tdataloader, bert_ddataloader, 10)
# + id="cbhBdI6nr9Fe"
class BERTclassifier(nn.Module):
def __init__(self, device, num_classes=1, model_name="bert-base-multilingual-cased"):
super(BERTclassifier, self).__init__()
self.device = device
self.bert = BertModel.from_pretrained(model_name).to(self.device)
self.linear = nn.Linear(768, num_classes).to(self.device)
def forward(self, tokens, length):
output = self.bert(input_ids=tokens['input_ids'], attention_mask=tokens['attention_mask'],
token_type_ids=tokens['token_type_ids'], return_dict=True)
output = output['last_hidden_state'][:,
0] #its size is equal to batch_size, embedding_size (in case of this notebook, it's 32, 768)
out = self.linear(output)
return out
# + colab={"base_uri": "https://localhost:8080/"} id="MAHlUDoWsxC4" outputId="19e2bf74-405a-46b9-c4bf-053b6e04e45b"
b = BERTclassifier(device, 1)
b.train()
# + colab={"base_uri": "https://localhost:8080/", "height": 422, "referenced_widgets": ["cdfd0c3a078e4f76966fefb66aa64e25", "8690bacb590d408e8755d009f3bb9606", "aec2cd1fec7847018fbd7b29b323534b", "cacd84b3cdce4aa199557e47ac7bf1ce", "d9b91ffd223e432f8392a8584d9f079e", "00a10b87d4c74957b045cea4bc2636a9", "05038e69d93944ce9e7c8e1b6350b375", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "715c3066c86d45ec8479070521398933", "f9f69baa441348f88eededafe91b0dd4", "<KEY>", "<KEY>", "3ed67594cda74400ba77e03b1d74be2d", "<KEY>", "<KEY>", "6b97918edf2b456f8e0bc7e3636d5b1c", "779b5c8ad33c4feda8c2f5a3ec22491c", "3e46eb0c49ac4636ad4817259dfa639c", "02992e5315904bd597a54040ca568804", "<KEY>", "8dc31a3a43374b5882b7002fc764890d"]} id="CBh2EmlUs0KA" outputId="1c28d11b-e771-4e1f-a163-daa6450b1e45"
bert_train_model(b, bert_tdataloader, bert_ddataloader, 3)
# + colab={"base_uri": "https://localhost:8080/"} id="46oIu6EC2yoP" outputId="f5b3a9fd-86ee-477b-9a7d-9ad2dfb6041a"
b.eval()
# + colab={"base_uri": "https://localhost:8080/"} id="ex2SJb3smyA-" outputId="cb8ce285-58a8-4d57-93aa-e1b9cdcaca96"
bert_evaluate(b, bert_ttdataloader)
# -
tokenizer = RobertaTokenizerFast.from_pretrained('roberta-base', add_prefix_space=True)
# + id="7sUe6oFLcqxe"
class robertaDataset(torch.utils.data.Dataset):
def __init__(self, texts, labels, tokenizer, device, al=False):
self.texts = texts
self.labels = labels
self.tokenizer = tokenizer
self.device = device
self.al = al
def __getitem__(self, item):
text = self.texts[item]
label = self.labels[item]
tokens = self.tokenizer(text, padding='max_length', max_length=50, truncation=True, return_tensors='pt',
is_split_to_words=True).to(self.device)
tokens['input_ids'] = torch.squeeze(tokens['input_ids'], 0)
tokens['attention_mask'] = torch.squeeze(tokens['attention_mask'], 0)
if self.al:
tokens['token_type_ids'] = torch.squeeze(tokens['token_type_ids'], 0)[:512]
length = sum(tokens['attention_mask']).item()
label = torch.tensor(label, dtype=torch.float32, device=self.device)
return tokens, length, label
def __len__(self):
return len(self.texts)
# + id="PF0aSxowdNX6"
class roBERTaclassifier(nn.Module):
def __init__(self, device, num_classes=1, model_name='roberta-base'):
super(roBERTaclassifier, self).__init__()
self.device = device
self.roberta = RobertaModel.from_pretrained(model_name).to(self.device)
self.linear = nn.Linear(768, num_classes).to(self.device)
def forward(self, tokens, length):
output = self.roberta(**tokens)
output = output.last_hidden_state[:,
0] #its size is equal to batch_size, embedding_size (in case of this notebook, it's 32, 768)
out = self.linear(output)
return out
# + colab={"base_uri": "https://localhost:8080/"} id="kVX61QjodtwD" outputId="5364fa27-6be3-4289-e90c-0069d921e12b"
rob = roBERTaclassifier(device)
rob.train()
# + id="QrgJCzGPeATr"
roberta_train = robertaDataset(X_train, y_train, tokenizer, device)
roberta_dev = robertaDataset(X_val, y_val, tokenizer, device)
roberta_test = robertaDataset(X_test, y_test, tokenizer, device)
roberta_tdataloader = torch.utils.data.DataLoader(roberta_train, batch_size=16)
roberta_ddataloader = torch.utils.data.DataLoader(roberta_dev, batch_size=1)
roberta_ttdataloader = torch.utils.data.DataLoader(roberta_test, batch_size=1)
# + id="RT5uWegceiZW"
bert_train_model(rob, roberta_tdataloader, roberta_ddataloader, 1)
# + colab={"base_uri": "https://localhost:8080/"} id="3z9FLXALmoUB" outputId="3c5ea1e1-f4e4-416b-f053-c1f9e5a5cf09"
rob.eval()
# + colab={"base_uri": "https://localhost:8080/"} id="Z_gX-72Impul" outputId="d8c835eb-e527-4d4a-f2cf-bbb3f113b933"
bert_evaluate(rob, roberta_ttdataloader)
# + id="xASRgBy0o633"
albert_tokenizer = AlbertTokenizerFast.from_pretrained('albert-base-v2')
# + id="OUPcPgf6ohsN"
class ALBERTclassifier(nn.Module):
def __init__(self, device, num_classes=1, model_name='albert-base-v2'):
super(ALBERTclassifier, self).__init__()
self.device = device
self.albert = AlbertModel.from_pretrained(model_name).to(self.device)
self.linear = nn.Linear(768, num_classes).to(self.device)
def forward(self, tokens, length):
output = self.albert(**tokens)
output = output.last_hidden_state[:,
0] #its size is equal to batch_size, embedding_size (in case of this notebook, it's 32, 768)
out = self.linear(output)
return out
# + id="5F2-Gn_WokQC"
albert_train = robertaDataset(X_train, y_train, albert_tokenizer, device, True)
albert_dev = robertaDataset(X_val, y_val, albert_tokenizer, device, True)
albert_test = robertaDataset(X_test, y_test, albert_tokenizer, device, True)
albert_tdataloader = torch.utils.data.DataLoader(albert_train, batch_size=16)
albert_ddataloader = torch.utils.data.DataLoader(albert_dev, batch_size=1)
albert_ttdataloader = torch.utils.data.DataLoader(albert_test, batch_size=1)
# + colab={"base_uri": "https://localhost:8080/"} id="4S0CTFpUpDeg" outputId="b9e1ca0e-0891-468f-ba5c-600435ab35b9"
albert = ALBERTclassifier(device)
albert.train()
# + colab={"base_uri": "https://localhost:8080/", "height": 910, "referenced_widgets": ["895fc3501c7e44cf9a8edd626fa52983", "f867ac8e7abb4829bc6c59d0fda78e28", "dfdb2364841d4e219cf31f487f0ed4ba", "98407a25f7a847378cbf16f82949fcf5", "65ab38dfa30b4d69b0025cf8aec5f4ff", "87ab2409291840198aeb7a547cc3b8ed", "5c4eb744e35a40bcab581cf7826d3e76", "c2d8e57b95094facb6ffb2c390c5fbdb", "20f9d986032442b1885160c41b81a4cf", "2386ebc825334630a67a3863afc531b3", "3578d76f9a2145dcae48faafb5028dec", "<KEY>", "<KEY>", "48f8c9a26ccc4e67a1e2b8d4976f7b28", "<KEY>", "<KEY>", "<KEY>", "4d1decb63d9741ad8df72d8a4d5c1811", "f892f9099cd349acaf8d67511ded0997", "<KEY>", "90d7b42742824b6a80f675dd18e74e4b", "<KEY>", "<KEY>", "d65dfdc57a574cc684a6ba6f3434e306", "<KEY>", "630c6979323e404d856bab781c2181ee", "<KEY>", "8830871b802149a089b494e742e2f359", "<KEY>", "<KEY>", "74b7d007eeb142ef9cb39af26040781f", "<KEY>", "6dc7160de4ad49eda8a2362877849f00", "<KEY>", "0f27fe645e284773a67574c6cff199a6", "8fee41505c414fab92f1efe735034b21", "de417d9d236a40c184abd14e1a2c91d8", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "5891df4585624123b2959e55a3ce6b43", "<KEY>", "5b31901a16d847719eb7fe5ce28757a2", "<KEY>", "<KEY>", "c8ba58d5b17841c28038ea04288da629", "<KEY>", "<KEY>", "<KEY>", "ea203356dda4460ba833b93289878364", "516efd0e7c1949839defee7e373f1e57", "40889519f5fc4e8fb4dc040452fedb33", "<KEY>", "<KEY>", "e3610955286e4f928eb4b1ee125fd044", "fbe52846b8e24a4c9884324ad024363f", "4d22a7e95b7445febb6853ec4de3e8d6", "75c4cff14e9048718f6e1cda713f4ee1", "9f4116917633424f86390a297f7eac05", "<KEY>", "1d3727d3c9654573a06491c64fe2c872", "<KEY>", "<KEY>", "<KEY>", "ac69e4eed8094cd7a7f97334ed93ff7b", "8f9a29d36c344c7b80e6c15d8345d37b", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "81fe6a85241d412fb7e854e61909b925", "ddc23dd99fb241b88a1d4551b0752e50", "<KEY>", "7841f240eb9f4fd2a41afed17644de56", "33d9ce6241f6430787b71a86672f83dd", "bdd029d885f3473ab7030f77494fe53a", "d65bd07160fb4ab59fd07e1aaf8ed8fa", "f38f4a784f1941bea027f1c5f8c8854a"]} id="JMqGMqngpJII" outputId="c6802818-90f3-4aac-cd2d-2ce25775f2fc"
bert_train_model(albert, albert_tdataloader, albert_ddataloader, 1)
# + colab={"base_uri": "https://localhost:8080/"} id="rzaS0kH8xDxm" outputId="b96fbd61-b435-4f9c-e4a3-b880c1779588"
albert.eval()
# + colab={"base_uri": "https://localhost:8080/"} id="szqXNQBhxE_Z" outputId="6b916e73-f6e7-47cc-9331-021c3584652e"
bert_evaluate(albert, albert_ttdataloader)
| app/backend/neural_network_approach/rnn_cnn_bert_roberta_albert.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Importing sibilla
import sibilla
# # Configuring simulation
sibilla_runtime = sibilla.SibillaRuntime()
sibilla_runtime.load_module("population")
sibilla_runtime.load_from_file("split.pm")
sibilla_runtime.set_parameter("scale", 1.0)
sibilla_runtime.set_configuration("stateA")
sibilla_runtime.add_all_measures()
sibilla_runtime.set_deadline(100)
sibilla_runtime.set_dt(1.0)
sibilla_runtime.set_replica(100)
# # Starting simulation
res = sibilla_runtime.simulate("")
# # Saving results
sibilla_runtime.save("results", "split", "__")
| shell/src/dist/scripts/sibilla_docker/workspace/examples/split/.ipynb_checkpoints/split-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Edge Detection - Canny
# ## Import all the necessary libraries
import cv2
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# ## Load and display an image
img = cv2.imread("img/lane_1.jpg") # OpenCV image format is`BGR`.
plt.rcParams['figure.figsize'] = [10, 5]
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
# ## Convert an image into grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
plt.rcParams['figure.figsize'] = [10, 5]
plt.imshow(gray, cmap='gray')
# ## White mask
#
# Sort out the white color out of the image.
# +
# Uncomment or comment and see what happen.
gray_copy = np.copy(gray)
gray_copy[(gray_copy[:,:] < 200)] = 0
plt.rcParams['figure.figsize'] = [20, 10]
plt.subplot(121)
plt.imshow(gray, cmap='gray')
plt.title("Gray Image")
plt.subplot(122)
plt.imshow(gray_copy, cmap='gray')
plt.title("Mask White Image")
# -
# ## Blurring - GaussianBlur
#
# - Smoothing images: reduce noise
#
#blur_gray = cv2.GaussianBlur(gray, (5, 5), 0)
blur_gray = cv2.GaussianBlur(gray_copy, (5, 5), 0)
# ## Canny
# cv2.Canny(src, minVal, maxVal)
edges = cv2.Canny(blur_gray, 50, 150)
#np.set_printoptions(threshold=np.inf)
#print(edges)
# ## Display results
plt.rcParams['figure.figsize'] = [20, 10]
plt.subplot(121)
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.title("Original Image")
plt.subplot(122)
plt.imshow(edges, cmap='gray')
plt.title("Edge Image")
# # Canny Algorithm [Option]
# ## Canny Edge Detector
#
# - [Wiki - Canny edge detector](https://en.wikipedia.org/wiki/Canny_edge_detector)
#
# - [OpenCV - Canny Edge Detection](https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_canny/py_canny.html)
#
# Canny Edge Detection is a popular edge detection algorithm.
# It was developed by <NAME> in 1986. It is a multi-stage algorithm and we will go through each stages.
#
# 1. Noise Reduction:
#
# remove the noise in the image with 5x5 Gaussian filter.
#
#
# 2. Finding Intensity Gradient of the image:
#
# Smoothened image is then filtered with a `Sobel` kernel in both horizontal and vertical direction to get first derivative in horizontal direction (Gx) and vertical direction (Gy).
#
#
# 3. Non-maximum Suppression
#
# 1. Compare the edge strength of the current pixel with the edge strength of the pixel in the positive and negative gradient directions.
# 2. If the edge strength of the current pixel is the largest compared to the other pixels in the mask with the same direction (e.g., a pixel that is pointing in the y-direction will be compared to the pixel above and below it in the vertical axis), the value will be preserved. Otherwise, the value will be suppressed (put to zero).
#
#
# 4. Double Threshold (Hysteresis Thresholding)
#
# `This stage decides which are all edges are really edges and which are not. `
#
# For this, we need two threshold valuse, `high` and `low` (in 2:1 or 3:1):
#
# - If an edge pixel’s gradient value is `higher than the high threshold value`, it is marked as a `strong edge` pixel.
# - If an edge pixel’s gradient value is `smaller than the high threshold value and larger than the low threshold value`, it is marked as a `weak edge` pixel.
# - If an edge pixel's value is `smaller than the low threshold value`, it will be `suppressed`.
| Computer Vision/basics/canny.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="DSPCom-KmApV"
# # Multi-task recommenders
#
# **Learning Objectives**
# 1. Training a model which focuses on ratings.
# 2. Training a model which focuses on retrieval.
# 3. Training a joint model that assigns positive weights to both ratings & retrieval models.
#
# + [markdown] id="Dk8QEc4sIPMi"
# ## Introduction
# In the basic retrieval notebook we built a retrieval system using movie watches as positive interaction signals.
#
# In many applications, however, there are multiple rich sources of feedback to draw upon. For example, an e-commerce site may record user visits to product pages (abundant, but relatively low signal), image clicks, adding to cart, and, finally, purchases. It may even record post-purchase signals such as reviews and returns.
#
# Integrating all these different forms of feedback is critical to building systems that users love to use, and that do not optimize for any one metric at the expense of overall performance.
#
# In addition, building a joint model for multiple tasks may produce better results than building a number of task-specific models. This is especially true where some data is abundant (for example, clicks), and some data is sparse (purchases, returns, manual reviews). In those scenarios, a joint model may be able to use representations learned from the abundant task to improve its predictions on the sparse task via a phenomenon known as [transfer learning](https://en.wikipedia.org/wiki/Transfer_learning). For example, [this paper](https://openreview.net/pdf?id=SJxPVcSonN) shows that a model predicting explicit user ratings from sparse user surveys can be substantially improved by adding an auxiliary task that uses abundant click log data.
#
# In this jupyter notebook, we are going to build a multi-objective recommender for Movielens, using both implicit (movie watches) and explicit signals (ratings).
#
# Each learning objective will correspond to a __#TODO__ in the notebook where you will complete the notebook cell's code before running. Refer to the [solution](https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/deepdive2/recommendation_systems/solutions/multitask.ipynb) for reference.
#
# + [markdown] id="ZwrcZeK7x7xI"
# ## Imports
#
#
# Let's first get our imports out of the way.
#
# + id="izzoRqkGb2Zc"
# Installing the necessary libraries.
# !pip install -q tensorflow-recommenders
# !pip install -q --upgrade tensorflow-datasets
# + [markdown] id="m7KBpffWzlxH"
# **NOTE: Please ignore any incompatibility warnings and errors and re-run the above cell before proceeding.**
#
# + id="SZGYDaF-m5wZ"
# Importing the necessary modules
import os
import pprint
import tempfile
from typing import Dict, Text
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
# + id="BxQ_hy7xPH3N"
import tensorflow_recommenders as tfrs
# + [markdown] id="5PAqjR4a1RR4"
# ## Preparing the dataset
#
# We're going to use the Movielens 100K dataset.
# + id="-ySWtibjm_6a"
ratings = tfds.load('movielens/100k-ratings', split="train")
movies = tfds.load('movielens/100k-movies', split="train")
# Select the basic features.
ratings = ratings.map(lambda x: {
"movie_title": x["movie_title"],
"user_id": x["user_id"],
"user_rating": x["user_rating"],
})
movies = movies.map(lambda x: x["movie_title"])
# + [markdown] id="JRHorm8W1yf3"
# And repeat our preparations for building vocabularies and splitting the data into a train and a test set:
# + id="rS0eDfkjnjJL"
# Randomly shuffle data and split between train and test.
tf.random.set_seed(42)
shuffled = ratings.shuffle(100_000, seed=42, reshuffle_each_iteration=False)
train = shuffled.take(80_000)
test = shuffled.skip(80_000).take(20_000)
movie_titles = movies.batch(1_000)
user_ids = ratings.batch(1_000_000).map(lambda x: x["user_id"])
unique_movie_titles = np.unique(np.concatenate(list(movie_titles)))
unique_user_ids = np.unique(np.concatenate(list(user_ids)))
# + [markdown] id="eCi-seR86qqa"
# ## A multi-task model
#
# There are two critical parts to multi-task recommenders:
#
# 1. They optimize for two or more objectives, and so have two or more losses.
# 2. They share variables between the tasks, allowing for transfer learning.
#
# In this jupyter notebook, we will define our models as before, but instead of having a single task, we will have two tasks: one that predicts ratings, and one that predicts movie watches.
# + [markdown] id="AXHrk_SLzKCM"
# The user and movie models are as before:
#
# ```python
# user_model = tf.keras.Sequential([
# tf.keras.layers.experimental.preprocessing.StringLookup(
# vocabulary=unique_user_ids, mask_token=None),
# # We add 1 to account for the unknown token.
# tf.keras.layers.Embedding(len(unique_user_ids) + 1, embedding_dimension)
# ])
#
# movie_model = tf.keras.Sequential([
# tf.keras.layers.experimental.preprocessing.StringLookup(
# vocabulary=unique_movie_titles, mask_token=None),
# tf.keras.layers.Embedding(len(unique_movie_titles) + 1, embedding_dimension)
# ])
# ```
# + [markdown] id="cWCwkE5z8QBe"
# However, now we will have two tasks. The first is the rating task:
#
# ```python
# tfrs.tasks.Ranking(
# loss=tf.keras.losses.MeanSquaredError(),
# metrics=[tf.keras.metrics.RootMeanSquaredError()],
# )
# ```
# + [markdown] id="xrgQIXEm8UWf"
# Its goal is to predict the ratings as accurately as possible.
#
# The second is the retrieval task:
#
# ```python
# tfrs.tasks.Retrieval(
# metrics=tfrs.metrics.FactorizedTopK(
# candidates=movies.batch(128)
# )
# )
# ```
# + [markdown] id="SCNrv7_gakmF"
# As before, this task's goal is to predict which movies the user will or will not watch.
# + [markdown] id="DSWw3xuq8mGh"
# ### Putting it together
#
# We put it all together in a model class.
#
# The new component here is that - since we have two tasks and two losses - we need to decide on how important each loss is. We can do this by giving each of the losses a weight, and treating these weights as hyperparameters. If we assign a large loss weight to the rating task, our model is going to focus on predicting ratings (but still use some information from the retrieval task); if we assign a large loss weight to the retrieval task, it will focus on retrieval instead.
# + id="YFSkOAMgzU0K"
class MovielensModel(tfrs.models.Model):
def __init__(self, rating_weight: float, retrieval_weight: float) -> None:
# We take the loss weights in the constructor: this allows us to instantiate
# several model objects with different loss weights.
super().__init__()
embedding_dimension = 32
# User and movie models.
self.movie_model: tf.keras.layers.Layer = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_movie_titles, mask_token=None),
tf.keras.layers.Embedding(len(unique_movie_titles) + 1, embedding_dimension)
])
self.user_model: tf.keras.layers.Layer = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_user_ids, mask_token=None),
tf.keras.layers.Embedding(len(unique_user_ids) + 1, embedding_dimension)
])
# A small model to take in user and movie embeddings and predict ratings.
# We can make this as complicated as we want as long as we output a scalar
# as our prediction.
self.rating_model = tf.keras.Sequential([
tf.keras.layers.Dense(256, activation="relu"),
tf.keras.layers.Dense(128, activation="relu"),
tf.keras.layers.Dense(1),
])
# The tasks.
self.rating_task: tf.keras.layers.Layer = tfrs.tasks.Ranking(
loss=tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.RootMeanSquaredError()],
)
self.retrieval_task: tf.keras.layers.Layer = tfrs.tasks.Retrieval(
metrics=tfrs.metrics.FactorizedTopK(
candidates=movies.batch(128).map(self.movie_model)
)
)
# The loss weights.
self.rating_weight = rating_weight
self.retrieval_weight = retrieval_weight
def call(self, features: Dict[Text, tf.Tensor]) -> tf.Tensor:
# We pick out the user features and pass them into the user model.
user_embeddings = self.user_model(features["user_id"])
# And pick out the movie features and pass them into the movie model.
movie_embeddings = self.movie_model(features["movie_title"])
return (
user_embeddings,
movie_embeddings,
# We apply the multi-layered rating model to a concatentation of
# user and movie embeddings.
self.rating_model(
tf.concat([user_embeddings, movie_embeddings], axis=1)
),
)
def compute_loss(self, features: Dict[Text, tf.Tensor], training=False) -> tf.Tensor:
ratings = features.pop("user_rating")
user_embeddings, movie_embeddings, rating_predictions = self(features)
# We compute the loss for each task.
rating_loss = self.rating_task(
labels=ratings,
predictions=rating_predictions,
)
retrieval_loss = self.retrieval_task(user_embeddings, movie_embeddings)
# And combine them using the loss weights.
return (self.rating_weight * rating_loss
+ self.retrieval_weight * retrieval_loss)
# + [markdown] id="ngvn-c0b8lc2"
# ### Rating-specialized model
#
# Depending on the weights we assign, the model will encode a different balance of the tasks. Let's start with a model that only considers ratings.
# + id="NNfB6rYL0VrS"
# Here, configuring the model with losses and metrics.
# TODO 1: Your code goes here.
# + id="I6kjfF1j0iZR"
cached_train = train.shuffle(100_000).batch(8192).cache()
cached_test = test.batch(4096).cache()
# + id="6NWadH1q0c_T"
# Training the ratings model.
model.fit(cached_train, epochs=3)
metrics = model.evaluate(cached_test, return_dict=True)
print(f"Retrieval top-100 accuracy: {metrics['factorized_top_k/top_100_categorical_accuracy']:.3f}.")
print(f"Ranking RMSE: {metrics['root_mean_squared_error']:.3f}.")
# + [markdown] id="lENViv04-i0T"
# The model does OK on predicting ratings (with an RMSE of around 1.11), but performs poorly at predicting which movies will be watched or not: its accuracy at 100 is almost 4 times worse than a model trained solely to predict watches.
# + [markdown] id="yPYd9LtE-4Fm"
# ### Retrieval-specialized model
#
# Let's now try a model that focuses on retrieval only.
# + id="BfnkGd2G--Qt"
# Here, configuring the model with losses and metrics.
# TODO 2: Your code goes here.
# + id="JCCBdM7U_B11"
# Training the retrieval model.
model.fit(cached_train, epochs=3)
metrics = model.evaluate(cached_test, return_dict=True)
print(f"Retrieval top-100 accuracy: {metrics['factorized_top_k/top_100_categorical_accuracy']:.3f}.")
print(f"Ranking RMSE: {metrics['root_mean_squared_error']:.3f}.")
# + [markdown] id="YjM7j7eY_jPh"
# We get the opposite result: a model that does well on retrieval, but poorly on predicting ratings.
# + [markdown] id="hOFwjUus_pLU"
# ### Joint model
#
# Let's now train a model that assigns positive weights to both tasks.
# + id="7xyDbNMf_t8a"
# Here, configuring the model with losses and metrics.
# TODO 3: Your code goes here.
# + id="2pZmM_ub_uEO"
# Training the joint model.
model.fit(cached_train, epochs=3)
metrics = model.evaluate(cached_test, return_dict=True)
print(f"Retrieval top-100 accuracy: {metrics['factorized_top_k/top_100_categorical_accuracy']:.3f}.")
print(f"Ranking RMSE: {metrics['root_mean_squared_error']:.3f}.")
# + [markdown] id="Ni_rkOsaB3f9"
# The result is a model that performs roughly as well on both tasks as each specialized model.
#
# While the results here do not show a clear accuracy benefit from a joint model in this case, multi-task learning is in general an extremely useful tool. We can expect better results when we can transfer knowledge from a data-abundant task (such as clicks) to a closely related data-sparse task (such as purchases).
| courses/machine_learning/deepdive2/recommendation_systems/labs/multitask.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={} colab_type="code" id="uOtwCpbb226Z"
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="o6JF3Q2j28il" outputId="22803595-f674-4bef-faa6-dec298c8f89a"
retail = pd.read_csv('https://raw.githubusercontent.com/Develop-Packt/Exploring-the-Online-Retail-Dataset/master/Datasets/online_retail_II.csv')
retail.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="wd6smOJG3DkT" outputId="9447caca-ea14-454c-bb90-60212f4c66eb"
retail.rename(index = str, columns = {
'Invoice' : 'invoice',
'StockCode' : 'stock_code',
'Quantity' : 'quantity',
'InvoiceDate' : 'date',
'Price' : 'unit_price',
'Country' : 'country',
'Description' : 'desc',
'Customer ID' : 'cust_id'
}, inplace = True)
retail.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 238} colab_type="code" id="4Ty38CBI3Khb" outputId="0cf93b50-706f-4481-e036-52d7657c30bb"
retail.info()
# + colab={"base_uri": "https://localhost:8080/", "height": 170} colab_type="code" id="Ftdl0yR83OAS" outputId="8172560d-7fc2-4874-f890-3081ec4080b3"
retail.isnull().sum().sort_values(ascending = False)
# + colab={"base_uri": "https://localhost:8080/", "height": 297} colab_type="code" id="7mLoj6Kc3Qxc" outputId="9abd4f2f-ef1c-4063-edc2-0450cfe98521"
retail.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 111} colab_type="code" id="_ebHJxaO3WPL" outputId="1361ab4f-6865-4059-f851-43eb414e3f65"
retail.loc[retail['unit_price'] == 25111.090000]
# + colab={"base_uri": "https://localhost:8080/", "height": 80} colab_type="code" id="mSM6ufhJ3YE7" outputId="46a275d7-ed24-4659-8fe2-44019a8484fc"
retail.loc[retail['unit_price'] == -53594.360000]
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="-xsbA5GN3hK4" outputId="0ce2a37b-e18a-4409-98f3-44c9dda9e815"
(retail['unit_price'] <= 0).sum()
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="VCZTw7GA3jEx" outputId="f5d4452e-ccb8-4662-960d-eab41f68ebce"
(retail['quantity'] <= 0).sum()
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="KqpWFgpk3kWA" outputId="585242f4-4407-4d72-8918-8a90365fb73d"
((retail['unit_price'] <= 0) & (retail['quantity'] <= 0) & (retail['cust_id'].isnull())).sum()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="Zcn2wNYo3s-v" outputId="a0ccca99-d769-4211-f5eb-c847373974aa"
null_retail = retail[retail.isnull().any(axis=1)]
null_retail.head()
# + colab={} colab_type="code" id="cpeKtu4W3uUG"
new_retail = retail.dropna()
# + colab={} colab_type="code" id="D-r6Ha4A31lx"
new_retail = new_retail[(new_retail['unit_price'] > 0) & (new_retail['quantity'] > 0)]
# + colab={"base_uri": "https://localhost:8080/", "height": 297} colab_type="code" id="6ZtwuBiE33P-" outputId="44a39bd3-adc2-4886-9b09-6e61c710c35d"
new_retail.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 389} colab_type="code" id="-Dzq-Mbl35e2" outputId="f1a75223-011b-4bf2-98f4-7857a9650893"
plt.subplots(figsize = (12, 6))
up = sns.boxplot(new_retail.unit_price)
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="S0GU-c7S4ANN" outputId="2416fe27-e496-4283-9807-f74c2a54da44"
new_retail = new_retail[new_retail.unit_price < 6000]
# + colab={"base_uri": "https://localhost:8080/", "height": 297} colab_type="code" id="eOyZ38ii4CA2" outputId="f8f4ef7d-f127-4756-d787-3209d352f41b"
new_retail.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 280} colab_type="code" id="lqndq7ep4MlW" outputId="4330ad11-5659-4644-d76a-a3d0238c6b81"
up_new = sns.boxplot(new_retail.unit_price)
# + colab={"base_uri": "https://localhost:8080/", "height": 388} colab_type="code" id="q0EDlr-W4TOF" outputId="8ae3d117-7e17-4593-85e4-0f0c615f4edc"
plt.subplots(figsize = (12, 6))
q = sns.boxplot(new_retail.quantity)
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="gMnvTANe4VdM" outputId="71cba891-9816-4956-d7bc-c9539a464ca3"
new_retail = new_retail[new_retail.quantity < 15000]
# + colab={"base_uri": "https://localhost:8080/", "height": 297} colab_type="code" id="xNsH2Wy94iPm" outputId="5bc4e042-f7c1-411b-93c4-c6a99b579d46"
new_retail.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 279} colab_type="code" id="SS04zP2K4opr" outputId="beee150a-006b-4df7-94f3-75e6327f84f5"
q_new = sns.boxplot(new_retail.quantity)
# + colab={"base_uri": "https://localhost:8080/", "height": 238} colab_type="code" id="-9EuuHow46MR" outputId="8a6d1921-ade7-47e0-f942-7ff28ce81f68"
new_retail[(new_retail.desc.isnull()) & (new_retail.cust_id.isnull())]
new_retail.info()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="WMG5rAHV5AAa" outputId="aff05e4b-dd22-44b8-88e7-627defa42494"
retail = new_retail
retail.head()
# + [markdown] colab_type="text" id="vNZhOcCJzPVm"
# **Exercise 02**
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="GY82ILfK8ndm" outputId="e94246de-2474-4838-9259-b132cdb7fd7d"
retail.desc = retail.desc.str.lower()
retail.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="pULoTQQv8sbx" outputId="bbc8e034-12cd-42c3-c999-72b25826a1c5"
retail['date'] = pd.to_datetime(retail.date, format = '%d/%m/%Y %H:%M')
retail.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="w-aHI__H9Mbh" outputId="db9cc270-f91a-41fd-8d11-4d43f34d5ef7"
retail.insert(loc = 4, column = 'year_month', value = retail.date.map(lambda x: 100 * x.year + x.month))
retail.insert(loc = 5, column = 'year', value = retail.date.dt.year)
retail.insert(loc = 6, column = 'month', value = retail.date.dt.month)
retail.insert(loc = 7, column = 'day', value = retail.date.dt.day)
retail.insert(loc = 8, column ='hour', value = retail.date.dt.hour)
retail.insert(loc = 9, column='day_of_week', value=(retail.date.dt.dayofweek)+1)
retail.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="9A2azKOu9Ryp" outputId="2f403a45-830a-4bf5-c377-1263f09b68a0"
retail.insert(loc = 11, column = 'spent', value = (retail['quantity'] * retail['unit_price']))
retail.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="lVZp548o96jk" outputId="1d4f13eb-6e9c-42ef-a0da-d532a0950944"
retail = retail[['invoice', 'country', 'cust_id', 'stock_code', 'desc','quantity', 'unit_price', 'date', 'spent',
'year_month', 'year', 'month', 'day', 'day_of_week', 'hour']]
retail.head()
# -
| Exercise02/Exercise02.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from collections import deque
d = deque()
print(d)
print(type(d))
d = deque(['m', 'n'])
print(d)
d.append('o')
print(d)
d.appendleft('l')
print(d)
d.extend(['p', 'q'])
print(d)
d.extendleft(['k', 'j'])
print(d)
d.insert(3, 'XXX')
print(d)
d.insert(-1, 'YYY')
print(d)
d.insert(100, 'ZZZ')
print(d)
d.insert(-100, 'XYZ')
print(d)
d = deque(['a', 'b', 'c', 'b', 'd'])
print(d.pop())
print(d)
print(d.popleft())
print(d)
d.remove('b')
print(d)
# +
# d.remove('X')
# ValueError: deque.remove(x): x not in deque
# -
d.clear()
print(d)
# +
# d.pop()
# IndexError: pop from an empty deque
# +
# d.popleft()
# IndexError: pop from an empty deque
# -
d.clear()
print(d)
d = deque(['a', 'b', 'c', 'd', 'e'])
d.rotate()
print(d)
d = deque(['a', 'b', 'c', 'd', 'e'])
d.rotate(2)
print(d)
d = deque(['a', 'b', 'c', 'd', 'e'])
d.rotate(-1)
print(d)
d = deque(['a', 'b', 'c', 'd', 'e'])
d.rotate(6)
print(d)
d = deque(['a', 'b', 'c', 'd', 'e'])
print(d[0])
print(d[-1])
d[2] = 'X'
print(d)
# +
# print(d[2:4])
# TypeError: sequence index must be integer, not 'slice'
# -
import itertools
print(deque(itertools.islice(d, 2, 4)))
d = deque(['a', 'b', 'c', 'c', 'd'])
print(d.index('c'))
# +
# print(d.index('x'))
# ValueError: 'x' is not in deque
# -
d = deque(['a', 'a', 'b', 'c'])
print(len(d))
print(d.count('a'))
print(d.count('x'))
print('b' in d)
print('x' in d)
d = deque(['a', 'b', 'c', 'd', 'e'])
d.reverse()
print(d)
d = deque(['a', 'b', 'c', 'd', 'e'])
print(deque(reversed(d)))
# +
d = deque(['a', 'b', 'c'])
for v in d:
print(v)
# +
d = deque(['a', 'b', 'c'])
l = list(d)
print(l)
# -
print(type(l))
| notebook/collections_deque_basic.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # RGB and CIE
# In this project we'll regularly need to calculate distances between pixels in colour space as a proxy for the visual difference between the colours. The simplest way of doing this is to calculate the Euclidean distance between them (also known as cosine distance or $\ell2$ norm).
# If we have two colours $C_1 = (R_1, G_1, B_1)$ and $C_2 = (R_2, G_2, B_2)$, the Euclidean distance $\Delta C$ is defined as:
#
# ${\displaystyle \Delta C ={\sqrt {(R_{2}-R_{1})^{2}+(G_{2}-G_{1})^{2}+(B_{2}-B_{1})^{2}}}}$
#
# We can implement the function in python as follows
def colour_distance_1(colour_1, colour_2):
return sum([(channel_2 - channel_1) ** 2
for channel_1, channel_2 in
zip(colour_1, colour_2)]) ** 0.5
# The red, green, and blue channels available to us in RGB space are ideally suited for representing colour on pixelated screens. However, our goal is to represent the _ perceptual differences_ between colours, and RGB isn't ideal for this. It's now [pretty well established](https://en.wikipedia.org/wiki/Color_difference) that euclidean distances in RGB space are a bad representation of the distances that our eyes see.
# By stretching the RGB dimensions by different amounts, we can better approximate that difference:
#
# $\displaystyle \Delta C ={ {\sqrt {2\times \Delta R^{2}+4\times \Delta G^{2}+3\times \Delta B^{2}}}}$
#
# Again, here's the python
def colour_distance_2(colour_1, colour_2):
r_1, g_1, b_1 = colour_1
r_2, g_2, b_2 = colour_2
return (2 * (r_1 - r_2) ** 2 +
4 * (g_1 - g_2) ** 2 +
3 * (b_1 - b_2) ** 2) ** 0.5
# We can improve further by adding some extra weirdness to the red and blue channels
#
# ${\displaystyle \Delta C={\sqrt {2\times \Delta R^{2}+4\times \Delta G^{2}+3\times \Delta B^{2}+{{{\bar {r}}\times (\Delta R^{2}-\Delta B^{2})} \over {256}}}}}$
#
# Here it is in python
def colour_distance_3(colour_1, colour_2):
r_1, g_1, b_1 = colour_1
r_2, g_2, b_2 = colour_2
d_r_sq = (r_1 - r_2) ** 2
d_g_sq = (g_1 - g_2) ** 2
d_b_sq = (b_1 - b_2) ** 2
mean_r = (r_1 + r_2) / 2
d_c_sq = (2 * d_r_sq + 4 * d_g_sq + 3 * d_b_sq +
(mean_r * (d_r_sq - d_b_sq) / 256))
return d_c_sq ** 0.5
# The most general and efficient approach (as far as I know) is to transform the image's RGB coordinates into an entirely new space. The _International Commission on Illumination_ (CIE) produced [CIELAB](https://en.wikipedia.org/wiki/CIELAB_color_space#CIELAB) to better approximate human perception of colour distances. The three coordinates of CIELAB represent:
#
# - The lightness of the color. `L` = 0 yields black and `L` = 100 indicates diffuse white.
# - its position between red/magenta and green (`a`, negative values indicate green while positive values indicate magenta)
# - its position between yellow and blue (`b`, negative values indicate blue and positive values indicate yellow).
#
# [CIE76](https://en.wikipedia.org/wiki/Color_difference#CIE76) (ie euclidean distance in LAB space) was the original distance proposed with the space. It's been improved upon since, but the differences are minor and as far as I've seen, are unnecessary complications for such minimal gain.
#
# We can map from RGB to LAB and back again by importing the relevant function from `skimage`
import numpy as np
from skimage.color import rgb2lab, lab2rgb
# In this new space we can use our first, super-simple colour distance function to measure the perceptual difference between colours. Below we're randomly generating two colours, converting them to LAB space and calculating the distance. This distance can be seen as a kind of inverse similarity score (colour pairs with lower distance values are more perceptually similar).
# +
rgb_colour_1 = np.random.randint(0, 255, (1, 1, 3)).astype(np.float64)
rgb_colour_2 = np.random.randint(0, 255, (1, 1, 3)).astype(np.float64)
lab_colour_1 = rgb2lab(rgb_colour_1).squeeze()
lab_colour_2 = rgb2lab(rgb_colour_2).squeeze()
colour_distance_1(lab_colour_1, lab_colour_2)
# -
| data_science/research/palette/notebooks/00 - RGB, LAB, and human colour perception.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Creates copies of data, corrects inhomogeneities and creates a folder for the patient with the CT scan and the ground truth
# +
# #%%writefile preprocess.py
"""
This code was adapted from <NAME>is, available at: https://github.com/ellisdg/3DUnetCNN
Tools for converting, normalizing, and fixing the dataset
"""
import glob
import os
import warnings
import shutil
import SimpleITK as sitk
#from nipype.interfaces.ants import N4BiasFieldCorrection
from train import config
import numpy as np
from preprocess_ipo_utils import read_data, HU_conversion
def append_basename(in_file, append):
dirname, basename = os.path.split(in_file)
base, ext = basename.split(".", 1)
return os.path.join(dirname, base + append + "." + ext)
def get_background_mask(in_folder, out_file, truth_name="GlistrBoost_ManuallyCorrected"):
"""
This function computes a common background mask for all of the data in a subject folder.
:param in_folder: a subject folder from the BRATS dataset.
:param out_file: an image containing a mask that is 1 where the image data for that subject contains the background.
:param truth_name: how the truth file is labeled int he subject folder
:return: the path to the out_file
"""
background_image = None
for name in config["all_modalities"] + [truth_name]:
image = sitk.ReadImage(get_image(in_folder, name))
if background_image:
if name == truth_name and not (image.GetOrigin() == background_image.GetOrigin()):
image.SetOrigin(background_image.GetOrigin())
background_image = sitk.And(image == 0, background_image)
else:
background_image = image == 0
sitk.WriteImage(background_image, out_file)
return os.path.abspath(out_file)
def convert_image_format(in_file, out_file):
sitk.WriteImage(sitk.ReadImage(in_file), out_file)
return out_file
def window_intensities(in_file, out_file, min_percent=1, max_percent=99):
image = sitk.ReadImage(in_file)
image_data = sitk.GetArrayFromImage(image)
out_image = sitk.IntensityWindowing(image, np.percentile(image_data, min_percent), np.percentile(image_data,
max_percent))
sitk.WriteImage(out_image, out_file)
return os.path.abspath(out_file)
def correct_bias(in_file, out_file, image_type=sitk.sitkFloat64):
"""
Corrects the bias using ANTs N4BiasFieldCorrection. If this fails, will then attempt to correct bias using SimpleITK
:param in_file: input file path
:param out_file: output file path
:return: file path to the bias corrected image
"""
correct = N4BiasFieldCorrection()
correct.inputs.input_image = in_file
correct.inputs.output_image = out_file
try:
done = correct.run()
return done.outputs.output_image
except IOError:
warnings.warn(RuntimeWarning("ANTs N4BIasFieldCorrection could not be found."
"Will try using SimpleITK for bias field correction"
" which will take much longer. To fix this problem, add N4BiasFieldCorrection"
" to your PATH system variable. (example: EXPORT PATH=${PATH}:/path/to/ants/bin)"))
input_image = sitk.ReadImage(in_file, image_type)
output_image = sitk.N4BiasFieldCorrection(input_image, input_image > 0)
sitk.WriteImage(output_image, out_file)
return os.path.abspath(out_file)
def rescale(in_file, out_file, minimum=0, maximum=20000):
image = sitk.ReadImage(in_file)
sitk.WriteImage(sitk.RescaleIntensity(image, minimum, maximum), out_file)
return os.path.abspath(out_file)
def background_to_zero(in_file, background_file, out_file):
sitk.WriteImage(sitk.Mask(sitk.ReadImage(in_file), sitk.ReadImage(background_file, sitk.sitkUInt8) == 0),
out_file)
return out_file
def check_origin(in_file, in_file2):
image = sitk.ReadImage(in_file)
image2 = sitk.ReadImage(in_file2)
if not image.GetOrigin() == image2.GetOrigin():
image.SetOrigin(image2.GetOrigin())
sitk.WriteImage(image, in_file)
def normalize_image(in_file, out_file, patient_id,bias_correction=True):
if bias_correction:
correct_bias(in_file, out_file)
print('correcting bias for ', patient_id)
else:
non_corrected=np.copy(in_file)
np.save(out_file+"/"+patient_id+"_ct",non_corrected)
return out_file
def get_truth_image(subject_folder, name):
file_card = os.path.join(subject_folder, name + ".npy")
try:
return glob.glob(file_card)[0]
except IndexError:
raise RuntimeError("Could not find file matching {}".format(file_card))
def convert_brats_folder(patient_id, in_folder, out_folder, mask_folder,truth_name='mask_', no_bias_correction_modalities=None):
slices, affine,first_slice = read_data(in_folder, True)
hu_volume=HU_conversion(slices, first_slice)
hu_array = np.array(hu_volume)
trans = np.flip(hu_array.transpose(2,1,0),2)
data = np.flip(trans,0)
#save data
out_file = os.path.abspath(os.path.join(out_folder))
perform_bias_correction = no_bias_correction_modalities and name not in no_bias_correction_modalities
normalize_image(data, out_file, patient_id,bias_correction=perform_bias_correction) #wether to perform or not correction, if false only copies the image
del out_file, slices, hu_volume, hu_array, trans, data
#save affine matrix
out_file = os.path.abspath(os.path.join(out_folder, patient_id+"_affine.npy"))
np.save(out_file, affine)
del out_file
# copy the truth file
try:
truth_file = get_truth_image(mask_folder, truth_name+patient_id)
except RuntimeError:
truth_file = get_truth_image(mask_folder, truth_name.split("_")[0]+patient_id)
out_file = os.path.abspath(os.path.join(out_folder, patient_id+"_truth.npy"))
truth = np.load(truth_file,mmap_mode='r')
np.save(out_file, truth.copy())
del out_file
del truth_file
del truth
def convert_brats_data(data_folder, out_folder, masks_path,overwrite=False, no_bias_correction_modalities=("flair",)):
"""
Preprocesses the data and writes it to a given output folder. Assumes the original folder structure.
:param brats_folder: folder containing the original brats data
:param out_folder: output folder to which the preprocessed data will be written
:param masks_folder: indices folder containing the masks - needed to only count with the data with ground-truth
:param overwrite: set to True in order to redo all the preprocessing
:param no_bias_correction_modalities: performing bias correction could reduce the signal of certain modalities. If
concerned about a reduction in signal for a specific modality, specify by including the given modality in a list
or tuple.
:return:
"""
masks_folder= os.listdir(masks_path)
for num, subject_folder in enumerate(masks_folder[1:]):
print(subject_folder)
print(num, ' of ', len(masks_folder), ', ', num*100/len(masks_folder),'%')
#subject = os.path.basename(subject_folder)
pre_patient_id = subject_folder.split("_", subject_folder.count(subject_folder))[1]
patient_id = pre_patient_id.split(".")[0]
subject_folder = os.path.basename(patient_id)
original_folder = os.path.join(data_folder, os.path.basename(os.path.dirname(subject_folder)),
patient_id)
preprocessed_folder = os.path.join(out_folder, os.path.basename(os.path.dirname(subject_folder)),
patient_id)
if not os.path.exists(preprocessed_folder) or overwrite:
if not os.path.exists(preprocessed_folder):
os.makedirs(preprocessed_folder)
convert_brats_folder(patient_id,original_folder, preprocessed_folder, masks_path,
no_bias_correction_modalities=None)
def memory_control():
pid = os.getpid()
ps = psutil.Process(pid)
memoryUse = ps.memory_info()
print(memoryUse)
#@profile
def main():
data_folder = "G:/CTimages/original/"
masks_folder ="G:/Masks/testing/"
out_folder = "G:/CTimages/testing/"
convert_brats_data(data_folder, out_folder, masks_folder,overwrite=True,no_bias_correction_modalities=False)
if __name__ == "__main__":
main()
# +
#Code from the Python 3.6 docs:
#https://docs.python.org/3/library/profile.html#profile.Profile
import cProfile, pstats, io
def profile(fnc):
"""A decorator that uses cProfile to profile a function"""
def inner(*args, **kwargs):
pr = cProfile.Profile()
pr.enable()
retval = fnc(*args, **kwargs)
pr.disable()
s = io.StringIO()
sortby = 'cumulative'
ps = pstats.Stats(pr, stream=s).sort_stats(sortby)
ps.print_stats()
print(s.getvalue())
return retval
return inner
# -
| sample/Code/3DUnetCNN-master/brats/Preprocess IPO data.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
'''
This notebook applies several popular regressors of classic machine learning algorithms
to the data set used in network_profile_recommender project
(see https://github.com/fleapapa/network_profile_recommender).
This notebook trains the regressors with 2M data samples of observed network metrics.
Another notebook, https://github.com/fleapapa/network_performance_prediction/blob/master/sklearn/regressors.ipynb,
does similarly, except its training data includes pre-aggregated values of observed metrics.
'''
# %matplotlib inline
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import random
import pandas
import numpy
import tensorflow
import time
from sklearn import metrics
from sklearn import preprocessing
from sklearn import datasets, metrics
from sklearn.cross_validation import train_test_split
# import various kinds of regressors
from sklearn import ensemble
from sklearn import tree
from sklearn import neighbors
from sklearn import linear_model
# +
# %%time
# use the same dataset as used by recommender
df_raw = pandas.read_csv('../data/etl2M.csv',header=None)
df_x = df_raw.ix[:, (1,3,6,9,12,15)] # x = features (observations)
df_y = df_raw.ix[:, 18] # y = labels
x_train, x_test, y_train, y_test = train_test_split(df_x, df_y,
test_size=1000,
random_state=42,
)
# -
algorithms = {
'DecisionTreeRegressor': tree.DecisionTreeRegressor(),
'ExtraTreeRegressor': tree.ExtraTreeRegressor(),
'RandomForestRegressor': ensemble.RandomForestRegressor(n_estimators=40),
'AdaBoostRegressor': ensemble.AdaBoostRegressor(),
'GradientBoostingRegressor': ensemble.GradientBoostingRegressor(),
'KNeighborsRegressor': neighbors.KNeighborsRegressor(5, weights='distance'),
'LinearRegression': linear_model.LinearRegression(),
'LogisticRegression': linear_model.LogisticRegression(),
'BayesianRidge': linear_model.BayesianRidge(),
}
# %%time
for algo_name in algorithms:
tstart = time.time()
algorithm = algorithms[algo_name]
model = algorithm.fit(x_train, y_train)
y_predicted = model.predict(x_test)
tend = time.time()
tsec = tend - tstart
tmin = tsec // 60
tsec = tsec % 60
thrs = tmin // 60
tmin = tmin % 60
tuse = 'time=%02d:%02d:%02d' % (thrs, tmin, tsec)
score = model.score(x_test, y_test)
score = 'score={0:f}'.format(score)
# sort to make plot look not so fuzzy
# intact y_test & y_predicted for next algorithm !!!
p_test, p_predicted = zip(*sorted(zip(y_test, y_predicted)))
fig, ax = plt.subplots()
fig.set_size_inches(16, 8)
plt.scatter(numpy.arange(1, x_test.shape[0]+1, 1), p_test, c='b', label='ground truth')
plt.scatter(numpy.arange(1, x_test.shape[0]+1, 1), p_predicted, c='r', label='prediction')
plt.axis('tight')
plt.legend()
plt.title("%s: %s %s" % (algo_name, tuse, score))
plt.show()
plt.savefig("/data/tmp/%s.png" % algo_name)
| sklearn/regressors-no-avg-delta.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
# -
#export
from exp.nb_08 import *
# ## Image ItemList
# ### Get images
path = datasets.untar_data(datasets.URLs.IMAGENETTE_160)
path
#export
import PIL,os,mimetypes
Path.ls = lambda x: list(x.iterdir())
path.ls()
(path/'val').ls()
path_tench = path/'val'/'n01440764'
img_fn = path_tench.ls()[0]
img_fn
img = PIL.Image.open(img_fn)
img
#export
image_extensions = set(k for k,v in mimetypes.types_map.items() if v.startswith('image/'))
' '.join(image_extensions)
def setify(o): return o if isinstance(o,set) else set(listify(o))
setify('aa'), setify(['aa',1]), setify(None), setify(1), setify({1})
def _get_files(parent, p, fs, extensions=None):
p = Path(p)
extensions = setify(extensions)
low_extensions = [e.lower() for e in extensions]
res = [p/f for f in fs if not f.startswith('.')
and ((not extensions) or f'.{f.split(".")[-1].lower()}' in low_extensions)]
return res
t = [o.name for o in os.scandir(path_tench)]
t = _get_files(path, path, t, extensions=image_extensions)
t[:3]
def get_files(path, extensions=None, recurse=False, include=None):
path = Path(path)
extensions = setify(extensions)
if recurse:
res = []
for p,d,f in os.walk(path): # returns (dirpath, dirnames, filenames)
if include is not None: d[:] = [o for o in d if o in include]
else: d[:] = [o for o in d if not o.startswith('.')]
res += _get_files(path, p, f, extensions)
return res
else:
f = [o.name for o in os.scandir(path) if o.is_file()]
return _get_files(path, path, f, extensions)
get_files(path_tench, image_extensions)[:3]
get_files(path, image_extensions, recurse=True)[:3]
all_fns = get_files(path, image_extensions, recurse=True)
len(all_fns)
# %timeit -n 10 get_files(path, image_extensions, recurse=True)
# ## Prepare for modeling
# What we need to do:
#
# - Get files
# - Split validation set
# - random%, folder name, csv, ...
# - Label:
# - folder name, file name/re, csv, ...
# - Transform per image
# - DataLoader
# - Transform per batch (optional)
# - DataBunch
# - Add test set (optional)
# ### Get files
#export
class IndexedList():
def __init__(self, items): self.items = listify(items)
def __len__(self): return len(self.items)
def __getitem__(self, idx):
if isinstance(idx, (int,slice)): return self.items[idx]
if isinstance(idx[0],bool):
assert len(idx)==len(self) # bool mask
return [o for m,o in zip(idx,self.items) if m]
return [self.items[i] for i in idx]
def __repr__(self):
res = f'{self.__class__.__name__} ({len(self)} items)\n{self.items[:10]}'
if len(self)>10: res += '...'
return res
IndexedList(range(10)), IndexedList(range(100))
t = IndexedList(range(10))
t[[1,2]], t[[False]*8 + [True,False]]
# +
#export
class ItemList(IndexedList):
def __init__(self, items, path='.'):
super().__init__(items)
self.path = Path(path)
def __repr__(self): return f'{super().__repr__()}\nPath: {self.path}'
def get(self, i): return i
def new(self, items): return self.__class__(items, self.path)
def __getitem__(self, idx):
res = super().__getitem__(idx)
if isinstance(res,list): return [self.get(o) for o in res]
return self.get(res)
class ImageItemList(ItemList):
def __init__(self, items, path='.', after_open=None):
super().__init__(items,path)
self.after_open = noop if after_open is None else after_open
@classmethod
def from_files(cls, path, extensions=None, recurse=True, include=None, **kwargs):
if extensions is None: extensions = image_extensions
return cls(get_files(path, extensions, recurse=recurse, include=include), path, **kwargs)
def get(self, fn):
res = PIL.Image.open(fn)
return self.after_open(res)
def new(self, items): return self.__class__(items, self.path, after_open=self.after_open)
# -
make_rgb = lambda o: o.convert('RGB')
il = ImageItemList.from_files(path, after_open=make_rgb)
img = il[0]; img
il[:1]
# ### Split validation set
fn = il.items[0]; fn
fn.parent.parent.name
def grandparent_splitter(fn, valid_name='valid', train_name='train'):
gp = fn.parent.parent.name
return True if gp==valid_name else False if gp==train_name else None
def split_by_func(ds, f):
items = ds.items
mask = [f(o) for o in items]
# `None` values will be filtered out
train = [o for o,m in zip(items,mask) if m==False]
valid = [o for o,m in zip(items,mask) if m==True ]
return train,valid
splitter = partial(grandparent_splitter, valid_name='val')
train,valid = split_by_func(il, splitter)
len(train),len(valid)
class SplitData():
def __init__(self, train, valid): self.train,self.valid = train,valid
@property
def path(self): return self.train.path
@classmethod
def split_by_func(cls, il, f):
lists = map(il.new, split_by_func(il, f))
return cls(*lists)
def __repr__(self): return f'{self.__class__.__name__}\nTrain: {self.train}\nValid: {self.valid}\n'
sd = SplitData.split_by_func(il, splitter); sd
# ### Labeling
def parent_labeler(fn): return fn.parent.name
def _label_by_func(ds, f): return [f(o) for o in ds.items]
class LabeledData():
def __init__(self, x, y): self.x,self.y = x,y
def __repr__(self): return f'{self.__class__.__name__}\nx: {self.x}\ny: {self.y}\n'
def __getitem__(self,idx): return self.x[idx],self.y[idx]
def __len__(self): return len(self.x)
@classmethod
def label_by_func(cls, sd, f): return cls(sd, ItemList(_label_by_func(sd, f), sd.path))
def label_by_func(sd, f):
return SplitData(LabeledData.label_by_func(sd.train, f),
LabeledData.label_by_func(sd.valid, f))
ll = label_by_func(sd, parent_labeler)
ll
# ### Image Transform
def tfm_resize_fixed(im, size):
if isinstance(size,int): size=(size,size)
return im.resize(size, PIL.Image.BILINEAR)
# +
def noop(x, *args, **kwargs): return x
class TransformedImageList():
def __init__(self, il, tfm=None):
if tfm is None: tfm=noop
self.il,self.tfm = il,tfm
def transform(self, img):
res = self.tfm(img)
res = torch.from_numpy(np.array(res, dtype=np.float32))
return res.div_(255.).permute(2,0,1)
def __getitem__(self, idx):
res = self.il[idx]
if isinstance(res,list): return [self.transform(o) for o in res]
return self.transform(res)
def __len__(self): return len(self.il)
def __repr__(self): return f'{self.__class__.__name__}: tfm {self.tfm}\n{self.il}'
# -
tfm = partial(tfm_resize_fixed, size=160)
tl = TransformedImageList(ll.train.x, tfm=tfm)
tl
def show_image(im, figsize=(3,3)):
plt.figure(figsize=figsize)
plt.axis('off')
plt.imshow(im.permute(1,2,0))
show_image(tl[0])
def transform_split_data(sd, tfm):
sd.train.x = TransformedImageList(sd.train.x, tfm=tfm)
sd.valid.x = TransformedImageList(sd.valid.x, tfm=tfm)
transform_split_data(ll, tfm)
show_image(tl[0])
# ### DataBunch
bs=64
train_dl,valid_dl = get_dls(ll.train,ll.valid,bs)
x,y = next(iter(train_dl))
x.shape
def get_cnn_layers(data, nfs, **kwargs):
return [conv2d(nfs[i], nfs[i+1], **kwargs)
for i in range(len(nfs)-1)] + [
nn.AdaptiveAvgPool2d(1), Lambda(flatten), nn.Linear(nfs[-1], data.c)]
class DataBunch():
def __init__(self, train_dl, valid_dl, c):
self.train_dl,self.valid_dl,self.c = train_dl,valid_dl,c
@property
def train_ds(self): return self.train_dl.dataset
@property
def valid_ds(self): return self.valid_dl.dataset
data = DataBunch(train_dl, valid_dl, 10)
nfs = [4,8,16,32,64]
model = nn.Sequential(*get_cnn_layers(data, nfs))
AvgStatsCallback([accuracy])
# +
def init_cnn(m):
for l in m:
if isinstance(l, nn.Sequential): init.kaiming_normal_(l[0].weight, a=0.1)
def get_runner(model, lr=0.6, cbs=None, loss_func = F.cross_entropy):
opt = optim.SGD(model.parameters(), lr=lr)
learn = Learner(model, opt, loss_func, data)
return learn, Runner([AvgStatsCallback([accuracy]), CudaCallback()], listify(cbs))
def get_learn_run(nfs, lr, cbs=None):
model = nn.Sequential(*get_cnn_layers(data, nfs, leak=0.1, sub=0.4, maxv=6.))
init_cnn(model)
return get_runner(model, lr=lr, cbs=cbs)
# -
learn,run = get_learn_run(nfs, 0.1)
| dev_course/dl2/09_images.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Model with Feedback
#
# Example testing a model with both predict and feedback in python. This could be used as a basis for a reinforcement learning model deployment.
#
# # REST
# !s2i build -E environment_rest . seldonio/seldon-core-s2i-python3:0.13 model-with-feedback-rest:0.1
# !docker run --name "model-with-feedback" -d --rm -p 5000:5000 model-with-feedback-rest:0.1
# ## Test predict
# !seldon-core-tester contract.json 0.0.0.0 5000 -p
# ## Test feedback
# !seldon-core-tester contract.json 0.0.0.0 5000 -p --endpoint send-feedback
# !docker rm model-with-feedback --force
# # gRPC
# !s2i build -E environment_grpc . seldonio/seldon-core-s2i-python3:0.13 model-with-feedback-grpc:0.1
# !docker run --name "model-with-feedback" -d --rm -p 5000:5000 model-with-feedback-grpc:0.1
# ## Test predict
# !seldon-core-tester contract.json 0.0.0.0 5000 -p --grpc
# ## Test feedback
# !seldon-core-tester contract.json 0.0.0.0 5000 -p --endpoint send-feedback --grpc
# !docker rm model-with-feedback --force
# # Test using Minikube
#
# **Due to a [minikube/s2i issue](https://github.com/SeldonIO/seldon-core/issues/253) you will need [s2i >= 1.1.13](https://github.com/openshift/source-to-image/releases/tag/v1.1.13)**
# !minikube start --vm-driver kvm2 --memory 4096
# ## Setup Seldon Core
#
# Use the setup notebook to [Setup Cluster](../../seldon_core_setup.ipynb#Setup-Cluster) with [Ambassador Ingress](../../seldon_core_setup.ipynb#Ambassador) and [Install Seldon Core](../../seldon_core_setup.ipynb#Install-Seldon-Core). Instructions [also online](./seldon_core_setup.html).
# # REST
# !eval $(minikube docker-env) && s2i build -E environment_rest . seldonio/seldon-core-s2i-python3:0.13 model-with-feedback-rest:0.1 --loglevel 5
# !kubectl create -f deployment-rest.json
# !kubectl rollout status deploy/mymodel-mymodel-09f8ccd
# ## Test predict
# !seldon-core-api-tester contract.json `minikube ip` `kubectl get svc ambassador -o jsonpath='{.spec.ports[0].nodePort}'` \
# mymodel --namespace default -p
# ## Test feedback
# !seldon-core-api-tester contract.json `minikube ip` `kubectl get svc ambassador -o jsonpath='{.spec.ports[0].nodePort}'` \
# mymodel --namespace default -p --endpoint send-feedback
# !kubectl delete -f deployment-rest.json
# # gRPC
# !eval $(minikube docker-env) && s2i build -E environment_grpc . seldonio/seldon-core-s2i-python3:0.13 model-with-feedback-grpc:0.1
# !kubectl create -f deployment-grpc.json
# !kubectl rollout status deploy/mymodel-mymodel-89dbe9b
# ## Test predict
# !seldon-core-api-tester contract.json `minikube ip` `kubectl get svc ambassador -o jsonpath='{.spec.ports[0].nodePort}'` \
# mymodel --namespace default -p --grpc
# ## Test feedback
# !seldon-core-api-tester contract.json `minikube ip` `kubectl get svc ambassador -o jsonpath='{.spec.ports[0].nodePort}'` \
# mymodel --namespace default -p --endpoint send-feedback --grpc
# !kubectl delete -f deployment-grpc.json
# !minikube delete
| examples/models/template_model_with_feedback/modelWithFeedback.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import argparse
import time
import shutil
import os
os.environ["CUDA_VISIBLE_DEVICES"] = '1'
import os.path as osp
import csv
import numpy as np
np.random.seed(1337)
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim.lr_scheduler import ReduceLROnPlateau, MultiStepLR
from model import SGN
from data import NTUDataLoaders
from data import AverageMeter
import fit
from util import make_dir, get_num_classes
# +
from argparse import ArgumentParser
parser = argparse.ArgumentParser(description='Skeleton-Based Action Recgnition')
fit.add_fit_args(parser)
parser.set_defaults(
network='SGN',
dataset = 'NTU',
case = 0,
batch_size=64,
max_epochs=120,
monitor='val_acc',
lr=0.001,
weight_decay=0.0001,
lr_factor=0.1,
workers=16,
print_freq = 20,
train = 0,
seg = 20,
)
args = parser.parse_args()
def main():
args.num_classes = get_num_classes(args.dataset)
model = SGN(args.num_classes, args.dataset, args.seg, args)
total = get_n_params(model)
print(model)
print('The number of parameters: ', total)
print('The modes is:', args.network)
if torch.cuda.is_available():
print('It is using GPU!')
model = model.cuda()
criterion = LabelSmoothingLoss(args.num_classes, smoothing=0.1).cuda()
optimizer = optim.Adam(model.parameters(), lr=args.lr, weight_decay=args.weight_decay)
if args.monitor == 'val_acc':
mode = 'max'
monitor_op = np.greater
best = -np.Inf
str_op = 'improve'
elif args.monitor == 'val_loss':
mode = 'min'
monitor_op = np.less
best = np.Inf
str_op = 'reduce'
scheduler = MultiStepLR(optimizer, milestones=[60, 90, 110], gamma=0.1)
# Data loading
ntu_loaders = NTUDataLoaders(args.dataset, args.case, seg=args.seg)
train_loader = ntu_loaders.get_train_loader(args.batch_size, args.workers)
val_loader = ntu_loaders.get_val_loader(args.batch_size, args.workers)
train_size = ntu_loaders.get_train_size()
val_size = ntu_loaders.get_val_size()
test_loader = ntu_loaders.get_test_loader(32, args.workers)
print('Train on %d samples, validate on %d samples' % (train_size, val_size))
best_epoch = 0
output_dir = make_dir(args.dataset)
save_path = os.path.join(output_dir, args.network)
if not os.path.exists(save_path):
os.makedirs(save_path)
checkpoint = osp.join(save_path, '%s_best.pth' % args.case)
earlystop_cnt = 0
csv_file = osp.join(save_path, '%s_log.csv' % args.case)
log_res = list()
lable_path = osp.join(save_path, '%s_lable.txt'% args.case)
pred_path = osp.join(save_path, '%s_pred.txt' % args.case)
# Training
if args.train ==1:
for epoch in range(args.start_epoch, args.max_epochs):
print(epoch, optimizer.param_groups[0]['lr'])
t_start = time.time()
train_loss, train_acc = train(train_loader, model, criterion, optimizer, epoch)
val_loss, val_acc = validate(val_loader, model, criterion)
log_res += [[train_loss, train_acc.cpu().numpy(),\
val_loss, val_acc.cpu().numpy()]]
print('Epoch-{:<3d} {:.1f}s\t'
'Train: loss {:.4f}\taccu {:.4f}\tValid: loss {:.4f}\taccu {:.4f}'
.format(epoch + 1, time.time() - t_start, train_loss, train_acc, val_loss, val_acc))
current = val_loss if mode == 'min' else val_acc
####### store tensor in cpu
current = current.cpu()
if monitor_op(current, best):
print('Epoch %d: %s %sd from %.4f to %.4f, '
'saving model to %s'
% (epoch + 1, args.monitor, str_op, best, current, checkpoint))
best = current
best_epoch = epoch + 1
save_checkpoint({
'epoch': epoch + 1,
'state_dict': model.state_dict(),
'best': best,
'monitor': args.monitor,
'optimizer': optimizer.state_dict(),
}, checkpoint)
earlystop_cnt = 0
else:
print('Epoch %d: %s did not %s' % (epoch + 1, args.monitor, str_op))
earlystop_cnt += 1
scheduler.step()
print('Best %s: %.4f from epoch-%d' % (args.monitor, best, best_epoch))
with open(csv_file, 'w') as fw:
cw = csv.writer(fw)
cw.writerow(['loss', 'acc', 'val_loss', 'val_acc'])
cw.writerows(log_res)
print('Save train and validation log into into %s' % csv_file)
### Test
args.train = 0
model = SGN(args.num_classes, args.dataset, args.seg, args)
model = model.cuda()
test(test_loader, model, checkpoint, lable_path, pred_path)
def train(train_loader, model, criterion, optimizer, epoch):
losses = AverageMeter()
acces = AverageMeter()
model.train()
for i, (inputs, target) in enumerate(train_loader):
output = model(inputs.cuda())
target = target.cuda(non_blocking = True)
loss = criterion(output, target)
# measure accuracy and record loss
acc = accuracy(output.data, target)
losses.update(loss.item(), inputs.size(0))
acces.update(acc[0], inputs.size(0))
# backward
optimizer.zero_grad() # clear gradients out before each mini-batch
loss.backward()
optimizer.step()
if (i + 1) % args.print_freq == 0:
print('Epoch-{:<3d} {:3d} batches\t'
'loss {loss.val:.4f} ({loss.avg:.4f})\t'
'accu {acc.val:.3f} ({acc.avg:.3f})'.format(
epoch + 1, i + 1, loss=losses, acc=acces))
return losses.avg, acces.avg
def validate(val_loader, model, criterion):
losses = AverageMeter()
acces = AverageMeter()
model.eval()
for i, (inputs, target) in enumerate(val_loader):
with torch.no_grad():
output = model(inputs.cuda())
target = target.cuda(non_blocking = True)
with torch.no_grad():
loss = criterion(output, target)
# measure accuracy and record loss
acc = accuracy(output.data, target)
losses.update(loss.item(), inputs.size(0))
acces.update(acc[0], inputs.size(0))
return losses.avg, acces.avg
def test(test_loader, model, checkpoint, lable_path, pred_path):
acces = AverageMeter()
# load learnt model that obtained best performance on validation set
model.load_state_dict(torch.load(checkpoint)['state_dict'])
model.eval()
label_output = list()
pred_output = list()
t_start = time.time()
for i, (inputs, target) in enumerate(test_loader):
with torch.no_grad():
output = model(inputs.cuda())
output = output.view((-1, inputs.size(0)//target.size(0), output.size(1)))
output = output.mean(1)
label_output.append(target.cpu().numpy())
pred_output.append(output.cpu().numpy())
acc = accuracy(output.data, target.cuda(non_blocking=True))
acces.update(acc[0], inputs.size(0))
label_output = np.concatenate(label_output, axis=0)
np.savetxt(lable_path, label_output, fmt='%d')
pred_output = np.concatenate(pred_output, axis=0)
np.savetxt(pred_path, pred_output, fmt='%f')
print('Test: accuracy {:.3f}, time: {:.2f}s'
.format(acces.avg, time.time() - t_start))
def accuracy(output, target):
batch_size = target.size(0)
_, pred = output.topk(1, 1, True, True)
pred = pred.t()
correct = pred.eq(target.view(1, -1).expand_as(pred))
correct = correct.view(-1).float().sum(0, keepdim=True)
return correct.mul_(100.0 / batch_size)
def save_checkpoint(state, filename='checkpoint.pth.tar', is_best=False):
torch.save(state, filename)
if is_best:
shutil.copyfile(filename, 'model_best.pth.tar')
def get_n_params(model):
pp=0
for p in list(model.parameters()):
nn=1
for s in list(p.size()):
nn = nn*s
pp += nn
return pp
class LabelSmoothingLoss(nn.Module):
def __init__(self, classes, smoothing=0.0, dim=-1):
super(LabelSmoothingLoss, self).__init__()
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.cls = classes
self.dim = dim
def forward(self, pred, target):
pred = pred.log_softmax(dim=self.dim)
with torch.no_grad():
true_dist = torch.zeros_like(pred)
true_dist.fill_(self.smoothing / (self.cls - 1))
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
return torch.mean(torch.sum(-true_dist * pred, dim=self.dim))
if __name__ == '__main__':
main()
# -
# %tb
| .ipynb_checkpoints/main-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#dibujar en pantalla
# -
import matplotlib.pyplot as plt
import numpy as np
import cv2
imagen = np.zeros((500,500, 3), dtype=np.int16)
imagen.shape
plt.imshow(imagen)
#crear un rectángulo
cv2.rectangle(imagen, pt1=(250, 300), pt2=(320, 400), color=(106,50,255), thickness=10)
cv2.rectangle(imagen, pt1=(150, 150), pt2=(200, 200), color=(116,60,30), thickness=10)
plt.imshow(imagen)
#círculo
cv2.circle(imagen, center=(5, 40), radius=30, color=(220/2, 35*3, 24+5), thickness=5)
cv2.circle(imagen, center=(250, 250), radius=100, color=(220/2, 35*3, 24+5), thickness=5)
plt.imshow(imagen)
#Línea
cv2.line(imagen, pt1=(0,400), pt2=(500,400), color=(225, 50, 75), thickness=10)
cv2.line(imagen, pt1=(25,125), pt2=(25,500), color=(225, 50, 75), thickness=10)
plt.imshow(imagen)
#elipsís
center_coordinates = (120, 100)
axesLength = (100, 50)
startAngle = 0
endAngle = 360
# Blue color in BGR
color = (255, 0, 0)
cv2.ellipse(imagen,center_coordinates,axesLength,45,startAngle,endAngle,color,10)
plt.imshow(imagen)
#polígono
pts = np.array([[100,50],[200,300],[700/2,20],[50,250]], np.int32)
#pts = pts.reshape((-1,1,2))
imagen = cv2.polylines(imagen,[pts],True,(0,255,255), 5)
plt.imshow(imagen)
| ClaseJueves01102020/dibujo.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Using and updating GIS content
#
# The GIS is a warehouse of geographic content and services. Arcgis includes several classes to make use of these content, publish new items and update the them when needed. This sample on updating the content of web maps and web scenes will demonstrate the following
# * **Replace web layers** of a web map. For instance, you can use this to update a web map when the services it points to were deleted. The sample shows how to read a web feature layer as a **FeatureService** object and inspect its properties.
# * **Drive the map widget by code**. In addition to displaying the interactive map widget, you can also set it to load at a particular extent. This is great for presentation purposes. During this process, the sample shows how to create and use a **MapView** object and a **Geocoder** object.
# * Make a **copy of a public web scene** item into your contents and then update it.
# * Edit the list of layers to remove unnecessary ones.
# * **Replace the basemap** of the web scene. In this step the sample shows how to search for **groups** and query the member items.
# * Change visibility of layers.
# +
from arcgis.gis import GIS
from IPython.display import display
gis = GIS("https://python.playground.esri.com/portal", "arcgis_python", "amazing_arcgis_123")
# -
# # Using and updating a web map
# We will search for that web map that has broken layers, render it on the notebook and update it.
search_result = gis.content.search("title:Ebola treatment locations", item_type = "Web Map")
display(search_result)
# Read the web map as a `WebMap` object
# +
wm_item = search_result[1]
from arcgis.mapping import WebMap
web_map_obj = WebMap(wm_item)
# -
# display the web map obj in an interactive widget
web_map_obj
# 
# ## Fix errors in web map
# The widget loads an empty web map with just a basemap. Let us investigate the contents of the web map to determine the issue. You can query the layers in the web map using the `layers` property.
web_map_obj.layers
# The web map has only 1 layer and that points to a feature service named **Ebola_Facilities**. Let us verify if a feature service of that name exists on the server. If not, let us try to find the closest match.
search_result = gis.content.search('title:Ebola_Facilities', item_type = 'Feature Service')
display(search_result)
# Let us change the search query leaving just the word `Ebola` in the title.
search_result = gis.content.search('title:Ebola', item_type='Feature Layer')
search_result[0]
# It is likely the old service was deleted and a new one was with a different name was published. Let us update the web map with the new feature layer
ebola = search_result[0]
ebola.layers
# The new feature service does have a layer with id `1`. Hence we can use the same layer id while switching the url. To remove the old layer, call `remove_layer()` method. Then add the correct `FeatureLayer` object by calling the `add_layer()` method on the `WebMap` object.
# remove the old layer from the web map
web_map_obj.remove_layer(web_map_obj.layers[0])
# add the correct layer. While adding you can customize the title
web_map_obj.add_layer(ebola.layers[1], options={'title':'Ebola_Treatment_Units - Ebola_Treatment_Units_Classed'})
# Check the layers on the web map
for lyr in web_map_obj.layers:
print(lyr.title + " " + lyr.url)
# ## Update the web map
# Now the web map should be fixed as it points to a live service. To update the web map, we call the `update()` method. You have the option to update the thumbnail or any other item properties at this time.
web_map_obj.update(item_properties={'title':'Ebola treatment locations - updated'},
thumbnail = "./data/webmap_thumbnail.png")
# Query the web map object to visualize it in the notebook
web_map_obj
# The web map was sucessfully overwritten with correct operational layers. You can interact with the widget and zoom into the African coast to observe the locations of Ebola treatment centers.
# # Using and updating a web scene
# In the sample above we observed how to update a web map. Updating the web scene is similar, we use the `update()` method. Let us look at the example of a web scene that displays tropical cyclones over the Pacific ocean.
search_result = gis.content.search('title:Western Pacific Typhoons (2005)',
item_type = 'Web Scene', outside_org = True)
search_result[0]
# Lets display the web scene in the notebook.
# +
web_scene_item = search_result[0]
web_scene_obj = arcgis.mapping.WebScene(web_scene_item)
# display web scene in the notebook
web_scene_obj
# -
# 
# This is a great web scene and it displays a lot of hurricane tracks. However, we want to create a new one with only a particular subset of data and customize the basemaps. To modify this web scene, let us first make a copy of it and publish it into your portal.
# ## Make a copy of the public web scene item
# To make a copy, we essentially download the content of the web scene JSON, remove the parts we don't want, add the layers that we want and publish a new item using that information. The publishing steps is similar to what is described earlier in the **data preparation** section and in detail in the sample titled **Publishing web maps and web scenes**.
#
# Let's say, we are only interested in the storms that occur in summer. Summer in tropical Asia is around April-June and that matches with a layer in the existing web scene. Let us query the `operationalLayers` section of the web scene to understand how the layers look like.
#
# ### Update operational layers of new web scene
display(web_scene_obj['operationalLayers'])
# There is a lot of information displayed above. Let us drill into this and display only layer names and their urls. If you notice, some of the layers above are group layers, meaning, they contain sub layers. So let us write a loop like below and print some details.
for layer in web_scene_obj['operationalLayers']:
print(layer['title'] + " :: " + layer['layerType'])
if layer['layerType'] == 'GroupLayer':
for sub_layer in layer['layers']:
print("\t" + sub_layer['title'] + " :: "+ sub_layer['url'])
# We are only interested in the layers that correspond to cyclones in summer. From the above report, we understand that information is in a group layer with two sub layers. Let us extract just that dictionary and compose a new web scene data.
# Let us construct a list comprehension and mine out that group layer.
subset_op_layers = [subset for subset in web_scene_obj['operationalLayers'] if subset['title'] == 'April - June']
display(subset_op_layers)
# Let us apply the changes to a new web scene object.
new_web_scene_obj = web_scene_obj
new_web_scene_obj['operationalLayers'] = subset_op_layers
# ### Update basemap of new web scene
# We now have the necessary `operationalLayers` information. Let us also try to change the basemap to a darker shade. First let us search the basemaps available in the current portal. If no suitable one is found, we can widen the search outside the organization and use a basemap published by Esri.
#
# **Basemaps** are web maps that are stored in a **group** usually called **Basemaps**. Thus to get the list of basemaps available on a portal, we can find the basemaps group and list all web maps that are a part of it.
#
# To get the list of groups on the portal, we use `groups` property of the `GIS` class.
basemap_search = gis.content.search('title:dark',
outside_org=True, item_type='web map')
for item in basemap_search:
display(item)
print(item.tags)
# We have found the basemap of our choice. Let us read it as a **`WebMap`** object and query the `baseMap` dictionary.
dark_basemap_item = basemap_search[1]
dark_basemap_obj = arcgis.mapping.WebMap(dark_basemap_item)
dark_basemap_obj['baseMap']
# Now let us explore how the `baseMap` dictionary of the **web scene** looks like.
new_web_scene_obj['baseMap']
# To get the desired basemap, we need to update the only `url` key-value pair of the web scene's `baseMap` dictionary. Here we will only pick the first layer of the dark basemap web map.
new_web_scene_obj['baseMap']['baseMapLayers'][0]['url'] = \
dark_basemap_obj['baseMap']['baseMapLayers'][0]['url']
# Now that we have performed the necessary updates, we can go ahead and publish this as a new web scene item on our portal.
# +
new_web_scene_properties= {'title':'Toprical Cyclones - Summer',
'type' : 'Web Scene',
'tags' : 'ArcGIS Python API',
'snippet' : str.format('Subset of <a href={2}>{0}</a> published by {1}',
web_scene_item.title, web_scene_item.owner,
"https://www.arcgis.com/home/item.html?id=" + web_scene_item.id),
'text' : json.dumps(new_web_scene_obj)}
new_item = gis.content.add(new_web_scene_properties)
new_item
# -
# We have successfully published the new web scene. Now let us display in an interactive widget and observe if it has the necessary updates.
new_item.share(True)
new_web_scene_obj = arcgis.mapping.WebScene(new_item)
new_web_scene_obj
# 
# Our required updates have been applied to the new web scene. However notice the **April - June** layer is **turned off** by default. Let us fix that and update the web scene.
#
# Let us query the `operationalLayer` dictionary of the new web scene and look for a key called `visibility`.
for layer in new_web_scene_obj['operationalLayers']:
print(layer['visibility'])
# As we know, there is just 1 group layer and it is turned off. Let us change that and update the web scene.
for layer in new_web_scene_obj['operationalLayers']:
layer['visibility'] = True
# To update the web scene call the `update()` method on the web scene object.
new_web_scene_obj.update()
new_web_scene_obj
# 
# # Summary
# In this sample, we observed how to consume web maps, web scenes and how to update them. During this process, the sample showed how to read a web feature layers, how to use geocoding to get co-ordinates of a point of interest, how to modify the map widget using code, how to make copy of an existing item into your account, how to look for basemaps and finally, how to update layer properties within a web scene.
| samples/05_content_publishers/using_and_updating_GIS_content.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import glob
import matplotlib
import math
from matplotlib import colors as mcolors
matplotlib.rcParams['pdf.fonttype'] = 42
matplotlib.rcParams['ps.fonttype'] = 42
# +
# Load the txt-files with with stats from the st-pipeline
path = '../../smomics_data'
filez = ['10015CN108_C1_genes_after_seq_depth_in_spots_under_outside_tissue.txt',
'10015CN108fl_E2_genes_after_seq_depth_in_spots_under_outside_tissue.txt',
'5005CN107_D2_genes_after_seq_depth_in_spots_under_outside_tissue.txt',
'visium_A1_genes_after_seq_depth_in_spots_under_outside_tissue.txt',
'visium_B1_genes_after_seq_depth_in_spots_under_outside_tissue.txt',
'visium_D1_genes_after_seq_depth_in_spots_under_outside_tissue.txt']
sample_type = {'visium_A1':'Visium',
'visium_B1':'Visium',
'visium_D1':'Visium',
'10015CN108_C1': 'sm-omics',
'10015CN108fl_E2': 'sm-omics',
'5005CN107_D2': 'sm-omics'}
stats_list = []
prop_list = [0.001, 0.01, 0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 1]
for file in filez:
filename = os.path.join(path, file)
cond_file = pd.read_csv(filename, sep = '\t')
print(cond_file)
cond_file.sort_values(by='Num reads', inplace=True)
cond_file['Prop_annot_reads'] = prop_list
cond_file['type'] = sample_type[cond_file['Name'][0]]
# normalize uniq counts with # spots under tissue and spot area
cond_file['norm uniq gen inside'] = cond_file['Genes inside']
cond_file['norm uniq gen outside'] = cond_file['Genes outside']
stats_list.append(cond_file)
# Concat all files
cond_merge = pd.concat(stats_list)
print(cond_merge.head())
# Print max value (at Prop_annot_reads == 1)
print(cond_merge[cond_merge['Prop_annot_reads'] == 1])
# +
#Plot
fig = plt.figure(figsize=(20, 10))
x="Prop_annot_reads"
y="norm uniq gen inside"
#y="Genes"
hue='type'
################ LINE PLOT
ax = sns.lineplot(x=x, y=y, data=cond_merge,hue=hue,
palette = ['cadetblue', 'yellowgreen'], hue_order = ['sm-omics', 'Visium'],ci=95)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_color('k')
ax.spines['left'].set_color('k')
# X and y label size
ax.set_xlabel("Proportion annotated reads", fontsize=15)
ax.set_ylabel("Number of unique genes under tissue", fontsize=15)
# Set ticks size
ax.tick_params(axis='y', labelsize=15)
ax.tick_params(axis='x', labelsize=15)
# change background color
back_c = 'white'
ax.set_facecolor(back_c)
ax.grid(False)
# Thousand seprator on y axis
ax.get_yaxis().set_major_formatter(
matplotlib.ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
# LEGEND
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles=handles[0:], labels=['sm-omics', 'Visium'],loc='upper left', ncol=2, fontsize=20)
fig.set_size_inches(20, 10)
# plt.savefig("../../figures/saturation_sm_visium_total_genes_inside.pdf", transparent=True, bbox_inches = 'tight',
# pad_inches = 0, dpi=1200)
plt.show()
# -
cond_merge['Prop_annot_reads'] = 100*cond_merge['Prop_annot_reads']
cond_merge.to_csv('../../smomics_data/sm_visium_unique_genes_under_outside_tissue.csv')
| smomics_performance/Saturation_curve_genes_Visium_vs_SM.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# <h1>Basic test of the wflow BMI interface
# +
import wflow.wflow_bmi as bmi
import logging
reload(bmi)
# %pylab inline
import datetime
from IPython.html.widgets import interact
# -
# Startup two models:
#
# + The wflow_sbm model calculates the runoff from each cell (the LA land-atmosphere model)
# + the wflow_routing model that uses a kinimatic wave for routing the flow (the RT routing model)
# +
# This is the LAnd Atmophere (LA) model
LA_model = bmi.wflowbmi_csdms()
LA_model.initialize('../examples/wflow_rhine_sbm/wflow_sbm_bmi.ini',loglevel=logging.ERROR)
# This is the routing (RT) model
RT_model = bmi.wflowbmi_csdms()
RT_model.initialize('../examples/wflow_rhine_sbm/wflow_routing_bmi.ini',loglevel=logging.ERROR)
# -
# <h3>Now we can investigate some model parameters
print(LA_model.get_value("timestepsecs"))
print LA_model.get_start_time()
aa = LA_model.get_attribute_names()
LA_model.get_attribute_value("run:reinit")
LA_model.set_attribute_value("run:reinit",'1')
LA_model.get_attribute_value("run:reinit")
imshow(LA_model.get_value("Altitude"))
# +
# Save the old dem, chnage the dem in the model and set it back
origdem = LA_model.get_value("Altitude")
newdem = origdem * 1.6
LA_model.set_value('Altitude',newdem)
diff = origdem - LA_model.get_value("Altitude")
imshow(diff)
# -
imshow(LA_model.get_value("FirstZoneDepth"))
imshow(LA_model.get_value("River"))
# <h3>Start and end times
# +
t_end = RT_model.get_end_time()
t_start = RT_model.get_start_time()
t = RT_model.get_current_time()
(t_end - t_start)/(86400)
# -
# <h3>Now start the models
# +
t_end = RT_model.get_end_time()
t = RT_model.get_start_time()
res = []
resq = []
# Loop in time and put output of SBM in seperate routing module - 1way link
while t < t_end:
LA_model.update()
# Now set the output from the LA model (specific Q) as input to the RT model
thevar = LA_model.get_value("InwaterMM")
RT_model.set_value("IW",thevar) # The IW is set in the wflow_routing.ini var as a forcing
RT_model.update()
resq.append(RT_model.get_value("SurfaceRunoff"))
res.append(thevar)
t = RT_model.get_current_time()
print datetime.datetime.fromtimestamp(t)
# -
LA_model.finalize()
RT_model.finalize()
# <h4>Define function to view the results
def browse_res(digits):
n = len(digits)
def view_image(i):
plt.imshow(log(digits[i]+1))
plt.title('Step: %d' % i)
plt.colorbar()
plt.show()
interact(view_image, i=(0,n-1))
# +
browse_res(res)
# -
browse_res(resq)
| wflow/notebooks/BMI-Test.ipynb |
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (Spyder)
# language: python3
# name: python3
# ---
# ## Plot DUACS SSH data for Aviso region
#
# Start by using the subsetted real-time product on the S-MODE server.
# +
import xarray as xr
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import cartopy.crs as ccrs # import projections
import cartopy
import gsw
# import cftime
# +
%matplotlib inline
plt.rcParams['figure.figsize'] = (5,4)
plt.rcParams['figure.dpi'] = 200
plt.rcParams['savefig.dpi'] = 400
plt.close('all')
__figdir__ = '../plots/' + 'SMODE_'
savefig_args = {'bbox_inches':'tight', 'pad_inches':0.2}
plotfiletype='png'
# +
savefig = True
zoom = True
if zoom:
xmin, xmax = (-126,-121)
ymin, ymax = (36.25,38.5)
levels = np.linspace(-.2,.2,41)
else:
xmin, xmax = (-127,-121)
ymin, ymax = (35, 40)
levels = np.linspace(13,18,11)
# -
def plot_ops_area(ax,**kwargs):
""" Add polygon to show S-MODE pilot operations area
Inputs
- matplotlib.pyplot.plot kwargs
return
- exit code (True if OK)
"""
# Add S-MODE pilot operations area
'''
New corners of pentagon:
38° 05.500’ N, 125° 22.067’ W
37° 43.000’ N, 124° 00.067’ W
37° 45.000’ N, 123° 26.000‘ W
36° 58.000’ N, 122° 57.000’ W
36° 20.000’ N, 124° 19.067’ W
'''
coord = [[-(125+22.067/60),38+5.5/60], [-(124+0.067/60),37+43/60], [-(123+26/60),37+45/60], [-(122+57/60),36+58/60], [-(124+19.067/60),36+20/60]]
coord.append(coord[0]) #repeat the first point to create a 'closed loop'
xs, ys = zip(*coord) #create lists of x and y values
if ax is None:
ax = plt.gca()
# ax.plot(xs,ys,transform=ccrs.PlateCarree())
ax.plot(xs,ys,**kwargs)
SF_lon=-(122+25/60)
SF_lat= 37+47/60
# mark a known place to help us geo-locate ourselves
ax.plot(SF_lon, SF_lat, 'o', markersize=3, **kwargs)
ax.text(SF_lon-5/60, SF_lat+5/60, 'San Francisco', fontsize=8, **kwargs)
ax.text(np.mean(xs)-.6, np.mean(ys)-.3, 'S-MODE ops area', fontsize=8, **kwargs)
print(kwargs)
return(xs,ys,ax)
url = 'http://smode.whoi.edu:8080/thredds/dodsC/satellite/AVISO/aviso.nc'
ds = xr.open_dataset(url)
ds
# +
fig = plt.figure()
ax = plt.axes(projection = ccrs.PlateCarree(central_longitude=200)) # Orthographic
extent = [xmin, xmax, ymin, ymax]
tind=-1
day_str = np.datetime_as_string(ds.time[tind], unit='D')
ax.set_extent(extent, crs=ccrs.PlateCarree())
ax.set_title('Sea level anomaly (DUACS), '+ day_str,size = 10.)
#plt.set_cmap(cmap=plt.get_cmap('nipy_spectral'))
plt.set_cmap(cmap=plt.get_cmap('turbo'))
gl = ax.gridlines(draw_labels=True, dms=True, x_inline=False, y_inline=False, alpha=0.5, linestyle='--')
gl.top_labels = False
gl.ylabels_right = False
#gl.xlocator = matplotlib.ticker.MaxNLocator(10)
#gl.xlocator = matplotlib.ticker.AutoLocator
# gl.xlocator = matplotlib.ticker.FixedLocator(np.arange(0, 360 ,30))
cs = ax.contourf(ds.longitude,ds.latitude,np.squeeze(ds.sla.isel(time=tind)), levels, extend='both', transform=ccrs.PlateCarree())
# cs = ax.pcolormesh(ds.longitude,ds.latitude,np.squeeze(ds.sla), vmin=levels[0], vmax=levels[-1], transform=ccrs.PlateCarree())
# cb = plt.colorbar(cs,ax=ax,shrink=.8,pad=.05)
cb = plt.colorbar(cs,fraction = 0.022,extend='both')
cb.set_label('SLA [m]',fontsize = 10)
ax.coastlines()
ax.add_feature(cartopy.feature.LAND, zorder=3, facecolor=[.6,.6,.6], edgecolor='black')
plot_ops_area(ax,transform=ccrs.PlateCarree(),color='w')
# Add a 10 km scale bar
km_per_deg_lat=gsw.geostrophy.distance((125,125), (37,38))/1000
deg_lat_equal_10km=10/km_per_deg_lat
ax.plot(-123.75+np.asarray([0, 0]),36.75+np.asarray([0.,deg_lat_equal_10km]),transform=ccrs.PlateCarree())
if savefig:
plt.savefig(__figdir__+'_SLA'+plotfiletype,**savefig_args)
# -
| notebooks/plot_DUACS.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # autocfg.py
#
# ## This example notebook shows how to use the autocfg.py file in saspy to automatically generate a working saspy config file for connecting to a local SAS install on a Windows system.
# ## autocfg.py can be run as a batch script, or from within python.
#
# ## Even if this works for you, this is no excuse for not reading the install/config doc :)
# ## https://sassoftware.github.io/saspy/install.html
#
# ### There are three optional parameters you can provide.
# * cfgfile - this is the path to the config file that will be created. By default it will be sascfg_personal.py in the saspy install directory
# * SASHome - this is the path to your SASHome directory; the SAS installation directory. It defaults to C:\Program Files\SASHome which is the SAS default install path
# * Java - this is the path to your java.exe on your system. It defaults to java which is usually found in your path when you install java on Windwos
#
# ## These parameters can be specified positionally or by keyword interactivly. For batch, they are positional only, but you can specify None to not specify some. See the examples for that below.
#
#
# ### Here is the signature for the function. The interactive use case follows
# +
#def main(cfgfile: str = None, SASHome: str = None, java: str = None):
# -
# ## You can create a Windows local sascfg_personal.py file using autocfg.py from within Python
# ## Here is the simplest case, for a freshly installed saspy. It will create a config file that works imediatly; assuming I have SAS and Java installed in default locations
from saspy import autocfg
autocfg.main()
import saspy
sas = saspy.SASsession()
sas
fd = open('C:\ProgramData\Anaconda3\lib\site-packages\saspy\sascfg_personal.py')
print(fd.read())
fd.close()
# ## You can create a different sascfg file that you can refer to in SASsession()
# ## Also, lets specify Java ourselves to see that it is used in the config file
from saspy import autocfg
autocfg.main('my_cfg.py', java=r'C:\ProgramData\Oracle\Java\javapath\java.exe')
import saspy
sas = saspy.SASsession(cfgfile='my_cfg.py')
sas
fd = open('my_cfg.py')
print(fd.read())
fd.close()
# ## Now lets see how to run this as a Batch script
#
# ### First, run the default, right after a fresh install of saspy
# ```
# C:\tom1>python \ProgramData\Anaconda3\Lib\site-packages\saspy\autocfg.py
# Generated configurations file: C:\ProgramData\Anaconda3\lib\site-packages\saspy\sascfg_personal.py
#
#
# C:\tom1>type C:\ProgramData\Anaconda3\lib\site-packages\saspy\sascfg_personal.py
# SAS_config_names=["autogen_winlocal"]
#
# SAS_config_options = {
# "lock_down": False,
# "verbose" : True
# }
#
# cpW = "C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\log4j.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.core.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.svc.connection.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.security.sspi.jar"
# cpW += ";C:\\ProgramData\\Anaconda3\\lib\\site-packages\\saspy\\java\\saspyiom.jar"
#
# autogen_winlocal = {
# "java" : "java",
# "encoding" : "windows-1252",
# "classpath" : cpW
# }
#
# import os
# os.environ["PATH"] += ";C:\\Program Files\\SASHome\\SASFoundation\\9.4\\core\\sasext"
#
# C:\tom1>python
# Python 3.6.0 |Anaconda 4.3.0 (64-bit)| (default, Dec 23 2016, 11:57:41) [MSC v.1900 64 bit (AMD64)] on win32
# Type "help", "copyright", "credits" or "license" for more information.
# >>> import saspy
# >>> sas = saspy.SASsession()
# Using SAS Config named: autogen_winlocal
# SAS Connection established. Subprocess id is 27532
#
# >>> sas
# Access Method = IOM
# SAS Config name = autogen_winlocal
# WORK Path = C:\Users\sastpw\AppData\Local\Temp\SAS Temporary Files\_TD27852_d10a626_\Prc2\
# SAS Version = 9.04.01M5P09132017
# SASPy Version = 2.4.0
# Teach me SAS = False
# Batch = False
# Results = Pandas
# SAS Session Encoding = wlatin1
# Python Encoding value = windows-1252
# SAS process Pid value = 27852
#
# >>>
# ```
# ### Now lets create a different sascfg file that you can refer to in SASsession()
# ### And, lets specify Java ourselves to see that it is used in the config file
# * Note that Java is the 3rd positional parm. To skip SASHome, just specify None
# * also, use double quotes to enclose paths, especially when they have spaces in them like "C:\Program Files\SASHome"
# <pre>
# C:\tom1>python \ProgramData\Anaconda3\Lib\site-packages\saspy\autocfg.py batch_cfg.py None "C:\ProgramData\Oracle\Java\javapath\java.exe"
# Generated configurations file: batch_cfg.py
#
#
# C:\tom1>type batch_cfg.py
# SAS_config_names=["autogen_winlocal"]
#
# SAS_config_options = {
# "lock_down": False,
# "verbose" : True
# }
#
# cpW = "C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.core.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.svc.connection.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.security.sspi.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\log4j.jar"
# cpW += ";C:\\ProgramData\\Anaconda3\\lib\\site-packages\\saspy\\java\\saspyiom.jar"
#
# autogen_winlocal = {
# "java" : "C:\\ProgramData\\Oracle\\Java\\javapath\\java.exe",
# "encoding" : "windows-1252",
# "classpath" : cpW
# }
#
# import os
# os.environ["PATH"] += ";C:\\Program Files\\SASHome\\SASFoundation\\9.4\\core\\sasext"
#
# C:\tom1>python
# Python 3.6.0 |Anaconda 4.3.0 (64-bit)| (default, Dec 23 2016, 11:57:41) [MSC v.1900 64 bit (AMD64)] on win32
# Type "help", "copyright", "credits" or "license" for more information.
# >>> import saspy
# >>> sas = saspy.SASsession(cfgfile='batch_cfg.py')
# Using SAS Config named: autogen_winlocal
# SAS Connection established. Subprocess id is 14692
#
# >>> sas
# Access Method = IOM
# SAS Config name = autogen_winlocal
# WORK Path = C:\Users\sastpw\AppData\Local\Temp\SAS Temporary Files\_TD28096_d10a626_\Prc2\
# SAS Version = 9.04.01M5P09132017
# SASPy Version = 2.4.0
# Teach me SAS = False
# Batch = False
# Results = Pandas
# SAS Session Encoding = wlatin1
# Python Encoding value = windows-1252
# SAS process Pid value = 28096
#
# >>>
# </pre>
# ### One last case showing all three parameters.
# <pre>
# C:\tom1>python \ProgramData\Anaconda3\Lib\site-packages\saspy\autocfg.py \ProgramData\Anaconda3\Lib\site-packages\saspy\all_parms.py "C:\Program Files\SASHome" java.exe
# Generated configurations file: \ProgramData\Anaconda3\Lib\site-packages\saspy\all_parms.py
#
#
# C:\tom1>type \ProgramData\Anaconda3\Lib\site-packages\saspy\all_parms.py
# SAS_config_names=["autogen_winlocal"]
#
# SAS_config_options = {
# "lock_down": False,
# "verbose" : True
# }
#
# cpW = "C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\log4j.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.core.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.security.sspi.jar"
# cpW += ";C:\\Program Files\\SASHome\\SASDeploymentManager\\9.4\\products\\deploywiz__94508__prt__xx__sp0__1\\deploywiz\\sas.svc.connection.jar"
# cpW += ";C:\\ProgramData\\Anaconda3\\lib\\site-packages\\saspy\\java\\saspyiom.jar"
#
# autogen_winlocal = {
# "java" : "java.exe",
# "encoding" : "windows-1252",
# "classpath" : cpW
# }
#
# import os
# os.environ["PATH"] += ";C:\\Program Files\\SASHome\\SASFoundation\\9.4\\core\\sasext"
#
# C:\tom1>python
# Python 3.6.0 |Anaconda 4.3.0 (64-bit)| (default, Dec 23 2016, 11:57:41) [MSC v.1900 64 bit (AMD64)] on win32
# Type "help", "copyright", "credits" or "license" for more information.
# >>> import saspy
# >>> sas = saspy.SASsession(cfgfile='c:\\ProgramData\\Anaconda3\\Lib\\site-packages\\saspy\\all_parms.py')
# Using SAS Config named: autogen_winlocal
# SAS Connection established. Subprocess id is 19576
#
# >>> sas
# Access Method = IOM
# SAS Config name = autogen_winlocal
# WORK Path = C:\Users\sastpw\AppData\Local\Temp\SAS Temporary Files\_TD28236_d10a626_\Prc2\
# SAS Version = 9.04.01M5P09132017
# SASPy Version = 2.4.0
# Teach me SAS = False
# Batch = False
# Results = Pandas
# SAS Session Encoding = wlatin1
# Python Encoding value = windows-1252
# SAS process Pid value = 28236
#
# >>>
# </pre>
| SAS_contrib/autocfg.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
from api_keys import g_key
# +
#Import weather data
weather_df = pd.read_csv("..\\WeatherPy\\weather_data.csv")
weather_df.head()
# +
#Store variables to be used in map
locations = weather_df[["Latitude", "Longitude"]].astype(float)
humidity = weather_df["Humidity"].astype(float)
# +
#Create map
gmaps.configure(api_key=g_key)
figure = gmaps.figure()
humidity_heatmap = gmaps.heatmap_layer(locations, weights=humidity,
dissipating=False, max_intensity=100,
point_radius = 2.5)
figure.add_layer(humidity_heatmap)
figure
# -
humidity
# +
#Narrow down dataframe
vacation_df = weather_df.loc[(weather_df["Temperature"] < 85) & (weather_df["Temperature"] > 70) & (weather_df["Wind_Speed"] < 10) & (weather_df["Cloudiness"] < 10)]
vacation_df = vacation_df.dropna()
vacation_df.count()
# +
coords_list = []
for index, row in vacation_df.iterrows():
coords = str(row['Latitude']) + "," + str(row['Longitude'])
coords_list.append(coords)
vacation_df["Locations"] = coords_list
coords_list
# +
#Work with Google APIs to get hotels
hotels_list = []
new_coords = []
for index, row in vacation_df.iterrows():
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
params = {
"location": row["Locations"],
"types": "lodging",
"radius": 5000,
"key": g_key
}
response = requests.get(base_url, params)
full = response.json()
hotels = response.json()["results"]
if hotels:
hotels_list.append(hotels[0]["name"])
new_coords.append(row["Locations"])
hotels
# -
hotel_df = pd.DataFrame({"Hotel Name": hotels_list, "Locations": new_coords})
hotel_df = pd.merge(hotel_df, vacation_df, on='Locations', how='left')
hotel_df
# +
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Latitude", "Longitude"]]
info_layer = gmaps.symbol_layer(
locations, fill_color='rgba(0, 150, 0, 0.4)',
stroke_color='rgba(0, 0, 150, 0.4)', scale=2,
info_box_content=hotel_info
)
figure.add_layer(info_layer)
# -
figure
| VacationPy/VacationPy.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
os.chdir('../src')
# ### load getPretrained module
# %run modules/model/getPretrained.py
ModelFileDict = getModelFileDict()
ModelFileDict
model = modelImageNet('VGG16_includeTop', ModelFileDict['VGG16_includeTop'])
model.summary()
model.layers
conv2D_layer1 = model.layers[1]
conv2D_layer1
block1_conv1_kernel, block1_conv1_bias = conv2D_layer1.variables
conv2D_layer1.variables
conv2D_layer1.weights
conv2D_layer1.kernel, conv2D_layer1.bias
# +
weightsList = model.get_layer ('block1_conv1').get_weights()
for w in weightsList:
print(w.shape)
# -
conv1_kernel, conv1_bias = model.get_layer ('block1_conv1').get_weights()
print(conv1_bias.shape)
print(conv1_bias)
saver = tf.train.Saver(var_list=tf.trainable_variables())
checkPoint = '../notebooks/model_checkpoints/tutorial4/vgg16_model.ckpt'
model.save_weights( checkPoint )
# +
sess = tf.Session()
sess.run( tf.global_variables_initializer() )
saver.restore( sess, checkPoint )
# -
weightsOutput = sess.run( [block1_conv1_kernel, block1_conv1_bias, 'block1_conv1/Relu:0'],
feed_dict={
'input_1:0' : np.random.random(size=(1, 224, 224, 3))
})
conv1_kernel_x = weightsOutput[0]
conv1_bias_x = weightsOutput[1]
conv1_relu_x = weightsOutput[2]
print(conv1_bias_x.shape)
print(conv1_bias_x)
print(np.array_equal(conv1_kernel, conv1_kernel_x))
print(np.array_equal(conv1_bias, conv1_bias_x))
conv2D_layer1.input, conv2D_layer1.output
conv1_output = sess.run( 'block1_conv1/Relu:0',
feed_dict={
'input_1:0' : np.random.random(size=(1, 224, 224, 3))
})
conv1_output.shape
conv1_output
| notebooks/.ipynb_checkpoints/4. extract_from_pretrained_model-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:pytorch]
# language: python
# name: conda-env-pytorch-py
# ---
# +
# # %load_ext autoreload
# %reload_ext autoreload
# %autoreload 2
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
from torchvision import datasets, transforms
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from adamw import AdamW
from nadam import Nadam
from uoptim import UOptimizer
from torch.utils.data import DataLoader
from torch.utils.data.sampler import SubsetRandomSampler
from utils_exp import plot_graphs
import numpy as np
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
import builtins
from IPython.lib import deepreload
builtins.reload = deepreload.reload
stats = (np.array([ 0.4914 , 0.48216, 0.44653]), np.array([ 0.24703, 0.24349, 0.26159]))
# +
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize(stats)])
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
test_loader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=False, num_workers=2)
train_data = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
# train_loader = torch.utils.data.DataLoader(trainset, batch_size=4,
# shuffle=True, num_workers=2)
num_train = len(train_data)
valid = int(0.2*num_train)
indices = list(range(num_train))
split = num_train-valid
np.random.shuffle(indices)
train_idx, valid_idx = indices[:split], indices[split:]
train_sampler = SubsetRandomSampler(train_idx)
valid_sampler = SubsetRandomSampler(valid_idx)
train_loader = DataLoader(train_data, batch_size=32, sampler=train_sampler, num_workers=2)
valid_loader = DataLoader(train_data, batch_size=32, sampler=valid_sampler, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
# +
class BasicBlock(nn.Module):
def __init__(self, in_planes, planes, stride=1):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, planes, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(planes)
)
# SE layers
self.fc1 = nn.Conv2d(planes, planes//16, kernel_size=1) # Use nn.Conv2d instead of nn.Linear
self.fc2 = nn.Conv2d(planes//16, planes, kernel_size=1)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
# Squeeze
w = F.avg_pool2d(out, out.size(2))
w = F.relu(self.fc1(w))
w = F.sigmoid(self.fc2(w))
# Excitation
out = out * w # New broadcasting feature from v0.2!
out += self.shortcut(x)
out = F.relu(out)
return out
class PreActBlock(nn.Module):
def __init__(self, in_planes, planes, stride=1):
super(PreActBlock, self).__init__()
self.bn1 = nn.BatchNorm2d(in_planes)
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
if stride != 1 or in_planes != planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, planes, kernel_size=1, stride=stride, bias=False)
)
# SE layers
self.fc1 = nn.Conv2d(planes, planes//16, kernel_size=1)
self.fc2 = nn.Conv2d(planes//16, planes, kernel_size=1)
def forward(self, x):
out = F.relu(self.bn1(x))
shortcut = self.shortcut(out) if hasattr(self, 'shortcut') else x
out = self.conv1(out)
out = self.conv2(F.relu(self.bn2(out)))
# Squeeze
w = F.avg_pool2d(out, out.size(2))
w = F.relu(self.fc1(w))
w = F.sigmoid(self.fc2(w))
# Excitation
out = out * w
out += shortcut
return out
class SENet(nn.Module):
def __init__(self, block, num_blocks, num_classes=10):
super(SENet, self).__init__()
self.in_planes = 64
self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
self.linear = nn.Linear(512, num_classes)
def _make_layer(self, block, planes, num_blocks, stride):
strides = [stride] + [1]*(num_blocks-1)
layers = []
for stride in strides:
layers.append(block(self.in_planes, planes, stride))
self.in_planes = planes
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = F.avg_pool2d(out, 4)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
def SENet18():
return SENet(PreActBlock, [2,2,2,2])
# -
class Net(nn.Module):
def __init__(self, optim_type='UOptimizer', **optim_params):
super(Net, self).__init__()
self.net = SENet18()
self._loss = None
if optim_type == 'SGD':
self.optim = optim.SGD(self.parameters(), **optim_params)
elif optim_type == 'Adadelta':
self.optim = optim.Adadelta(self.parameters(), **optim_params)
elif optim_type == 'RMSProp':
self.optim = optim.RMSprop(self.parameters(), **optim_params)
elif optim_type == 'Adam':
self.optim = optim.Adam(self.parameters(), **optim_params)
elif optim_type == 'AdamW':
self.optim = AdamW(self.parameters(), **optim_params)
elif optim_type == 'Nadam':
self.optim = Nadam(self.parameters(), **optim_params)
elif optim_type == 'Adamax':
self.optim = optim.Adamax(self.parameters(), **optim_params)
elif optim_type == 'UOptimizer':
self.optim = UOptimizer(params = self.parameters(), **optim_params)
def forward(self, x):
return self.net(x)
def loss(self, output, target, **kwargs):
self._loss = F.cross_entropy(output, target, **kwargs)
self._correct = output.data.max(1, keepdim=True)[1]
self._correct = self._correct.eq(target.data.view_as(self._correct)).to(torch.float).cpu().mean()
return self._loss
models = {'StandardAdam': Net('Adam', lr=3e-3, betas = (0.9, 0.99)).to(device),
'SGD':Net('SGD', lr=0.03, momentum=0.9).to(device),
'Adam_with_adadelta_coeff':Net('UOptimizer',
use_exp_avg_norm = True,
use_exp_avg_sq_norm = True,
use_adadelta_lr = True,
use_bias_correction = True,
lr=1).to(device)
}
train_log = {k: [] for k in models}
test_log = {k: [] for k in models}
def train(epoch, models, log=None):
train_size = len(train_loader.sampler)
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
for model in models.values():
model.optim.zero_grad()
output = model(data)
loss = model.loss(output, target)
loss.backward()
model.optim.step()
if batch_idx % 200 == 0:
line = 'Train Epoch: {} [{}/{} ({:.0f}%)]\tLosses '.format(
epoch, batch_idx * len(data), train_size, 100. * batch_idx / len(train_loader))
losses = ' '.join(['{}: {:.4f}'.format(k, m._loss.item()) for k, m in models.items()])
print(line + losses)
else:
batch_idx += 1
line = 'Train Epoch: {} [{}/{} ({:.0f}%)]\tLosses '.format(
epoch, batch_idx * len(data), train_size, 100. * batch_idx / len(train_loader))
losses = ' '.join(['{}: {:.4f}'.format(k, m._loss.item()) for k, m in models.items()])
if log is not None:
for k in models:
log[k].append((models[k]._loss, models[k]._correct))
print(line + losses)
def test(models, loader, log=None):
test_size = len(loader.sampler)
avg_lambda = lambda l: 'Loss: {:.4f}'.format(l)
acc_lambda = lambda c, p: 'Accuracy: {}/{} ({:.0f}%)'.format(c, test_size, p)
line = lambda i, l, c, p: '{}: '.format(i) + avg_lambda(l) + '\t' + acc_lambda(c, p)
test_loss = {k: 0. for k in models}
correct = {k: 0. for k in models}
with torch.no_grad():
for data, target in loader:
data, target = data.to(device), target.to(device)
output = {k: m(data) for k, m in models.items()}
for k, m in models.items():
test_loss[k] += m.loss(output[k], target, size_average=False).item() # sum up batch loss
pred = output[k].data.max(1, keepdim=True)[1] # get the index of the max log-probability
correct[k] += pred.eq(target.data.view_as(pred)).cpu().sum().item()
for k in models:
test_loss[k] /= test_size
correct_pct = {k: c / test_size for k, c in correct.items()}
lines = '\n'.join([line(k, test_loss[k], correct[k], 100*correct_pct[k]) for k in models]) + '\n'
report = 'Test set:\n' + lines
if log is not None:
for k in models:
log[k].append((test_loss[k], correct_pct[k]))
print(report)
n_epoch = 30
for epoch in range(1, n_epoch+1):
for model in models.values():
model.train()
train(epoch, models, train_log)
for model in models.values():
model.eval()
test(models, valid_loader, test_log)
plot_graphs(test_log, 'loss')
plot_graphs(test_log, 'accuracy')
| testing/experiments_cifar10.ipynb |
# ---
# jupyter:
# jupytext:
# split_at_heading: true
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + hide_input=true
# %matplotlib inline
from fastai.gen_doc.nbdoc import *
from fastai.text import *
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 300
# -
# # Writing the book
# ```python
# def is_cat(x): return x[0].isupper()
# dls = ImageDataLoaders.from_name_func(
# path, get_image_files(path), valid_pct=0.2, seed=42,
# label_func=is_cat, item_tfms=Resize(224))
# ```
#
# The third line tells fastai what kind of dataset we have, and how it is structured. There are various different classes for different kinds of deep learning dataset and problem--here we're using `ImageDataLoaders`. The first part of the class name will generally be the type of data you have, such as image, or text. The second part will generally be the type of problem you are solving, such as classification, or regression.
#
# The other important piece of information that we have to tell fastai is how to get the labels from the dataset. Computer vision datasets are normally structured in such a way that the label for an image is part of the file name, or path, most commonly the parent folder name. Fastai comes with a number of standardized labelling methods, and ways to write your own. Here we define a function `is_cat` which labels cats based on a filename rule provided by the dataset creators.
#
# TK Sylvain. Check conversion here, there is a problem with formatting
#
# Finally, we define the `Transform`s that we need. A `Transform` contains code that is applied automatically during training; fastai includes many pre-defined `Transform`s, and adding new ones is as simple as creating a Python function. There are two kinds: `item_tfms` are applied to each item (in this case, each item is resized to a 224 pixel square); `batch_tfms` are applied to a *batch* of items at a time using the GPU, so they're particularly fast (we'll see many examples of these throughout this book).
#
# Why 224 pixels? This is the standard size for historical reasons (old pretrained models require this size exactly), but you can pass pretty much anything. If you increase the size, you'll often get a model with better results (since it will be able to focus on more details) but at the price of speed and memory consumption; or visa versa if you decrease the size.
#
# ```
# This should be fine
# ```
#
# In this case, there's an extremely convenient mathematical operation that calculates `w*x` for every row of a matrix--it's called *matrix multiplication*. <<matmul>> show what matrix multiplication looks like (diagram from Wikipedia).
# This notebook shows all the special syntax to use to write the book.
for i in range(20):
print('0.9953', end=' ')
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, np.pi*2, 100)
plt.plot(x, np.sin(x));
from fastai.vision.all import *
x = L(tensor(list(range(i, i+6))) for i in range(10))
x
import graphviz
def gv(s): return graphviz.Source('digraph G{ rankdir="LR"' + s + '; }')
gv('''program[shape=box3d width=1 height=0.7]
inputs->program->results''')
# ## Inputs and outputs
# By default inputs and outputs of each code cell are shown (except widgets).
1+1
# You can use the hide input extension to hide an input...
# + hide_input=true
from IPython.display import display,HTML
import pandas as pd
df = pd.DataFrame({'a': ['This', 'an', 'of'], 'b': ['is', 'example', 'table']})
display(HTML(df.to_html(header=False, index=False)))
# -
# Or you can flag it with `#hide_input`
#hide_input
df = pd.DataFrame({'a': ['This', 'an', 'of'], 'b': ['is', 'example', 'table']})
display(HTML(df.to_html(header=False, index=False)))
# You can toggle outputs using `o` in edit mode.
1+1
# Or you can use the `#hide_output` flag (it will be removed from the input).
#hide_output
1+1
# To hide cell entirely, use the flag `#hide`.
#hide
#This cell will be fully removed, input + output
1+1
# ## Formatting
# `backward quotes`, 'single quotes' and "double quotes" are all left as is. Note that in asciidoc, text in single quotes is emphasized.
#
# This is a bullet list. It absolutely needs a new line before beginning.
#
# * one item
# * two items
#
# This is a numbered list. It also needs a new line.
#
# 1. first
# 1. second
#
# This is the syntax for a labeled list (don't forget the new line):
#
# - Term 1:: Definition/description
# - Term 2:: lila
#
# Alternatively, we can write in asciidoc:
# ```asciidoc
# Term 1::
# Definition/description
# Term 2::
# lila
# ```
# Block quotes for special interventions:
#
# > J: Comment from Jeremy
#
# > S: Comment from Sylvain
#
# > A: Comment from Alexis
# Block quotes supported by O'Reilly:
#
# > Warning: This is a warning. Caution gives the same rendering.
#
# > Note: This is a note.
#
# > Tip: This is a tip. Important gives the same rendering.
# For a traditional block quote, you still need to put a colon for correct rendering.
#
# > : The inside of block quotes is not converted so we need to use asciidoc syntax inside.
# You can define a sidebar with title like this:
# #sidebar My intervention
#
# This will be changed to a sidebar when converted in Asciidoc.
#
# It can have several lines, contrary to a block quote.
#
# Here as well you need to use asciidoc syntax.
# Another way to have sidebars is to delimit it between headers cells like this (headers need to be in a cell of their own for this to work).
# ### Sidebar: Another intervention
# All of this will be inside the sidebar. You use normal markdown syntax in this block, and can have code cells or images.
# ### End sidebar
# To write directly in asciidoc, you can use a raw cell or a triple quote enviromnent flagged with `asciidoc`
# + active=""
# This is a raw cell. Things inside are not interpreted.
#
# [[table]]
# .An example of table
# [options="header"]
# |======
# | Myth (don't need) | Truth
# | Lots of math | Just high school math is sufficient
# | Lots of data | We've seen record-breaking results with <50 items of data
# | Lots of expensive computers | You can get what you need for state of the art work for free
# |======
# -
# You can use math as usual in notebooks: $x = \frac{a+b}{2}$
#
# Or
#
# $$x = \frac{a+b}{2}$$
# A footnote[this is a footnote]
# ## Tables and images, caption and references
# To add a caption and a reference to an output table, use `#id` and `#caption` flags
#id fit
#caption A training loop
learn.fit_one_cycle(4)
# For images in markdown, use the HTML syntax. Fields alt, width, caption and id are all interpreted properly.
#
# <img alt="Alternative text" width="700" caption="This is an image" src="puppy.jpg" id="puppy"/>
# Use `<< >>` for references (asciidoc syntax). This is a reference to the puppy in <<puppy>> before.
# To add a label, caption, alternative text or width to an image output, use the following flags
#id puppy1
#alt A cute little doggy
#caption This is an image
#width 200
from fastai.vision.all import *
path = untar_data(URLs.PETS)
fnames = get_image_files(path/'images')
PILImage.create(fnames[0])
# Test an attachment:
# <img src="_test_files/att_00000.png" caption="This is an image" alt="This is an image">
| test/_test.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Extract NECOFS data using NetCDF4-Python and analyze/visualize with Pandas
# Plot forecast water levels from NECOFS model from list of lon,lat locations
# (uses the nearest point, no interpolation)
import netCDF4
import datetime as dt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from StringIO import StringIO
# %matplotlib inline
# +
#model='NECOFS Massbay'
#url='http://www.smast.umassd.edu:8080/thredds/dodsC/FVCOM/NECOFS/Forecasts/NECOFS_FVCOM_OCEAN_MASSBAY_FORECAST.nc'
# GOM3 Grid
#model='NECOFS GOM3'
#url='http://www.smast.umassd.edu:8080/thredds/dodsC/FVCOM/NECOFS/Forecasts/NECOFS_GOM3_FORECAST.nc'
model = 'NECOFS GOM3 Wave'
# forecast
#url = 'http://www.smast.umassd.edu:8080/thredds/dodsC/FVCOM/NECOFS/Forecasts/NECOFS_WAVE_FORECAST.nc'
# archive
url = 'http://www.smast.umassd.edu:8080/thredds/dodsC/fvcom/archives/necofs_gom3_wave'
# +
# Desired time for snapshot
# ....right now (or some number of hours from now) ...
start = dt.datetime.utcnow() + dt.timedelta(hours=-72)
stop = dt.datetime.utcnow() + dt.timedelta(hours=+72)
# ... or specific time (UTC)
start = dt.datetime(1991,1,1,0,0,0) + dt.timedelta(hours=+0)
start = dt.datetime(1992,7,1,0,0,0) + dt.timedelta(hours=+0)
start = dt.datetime(1992,8,1,0,0,0) + dt.timedelta(hours=+0)
start = dt.datetime(2016,1,1,0,0,0) + dt.timedelta(hours=+0)
stop = dt.datetime(2016,6,1,0,0,0) + dt.timedelta(hours=+0)
# -
def dms2dd(d,m,s):
return d+(m+s/60.)/60.
dms2dd(41,33,15.7)
-dms2dd(70,30,20.2)
x = '''
Station, Lat, Lon
Falmouth Harbor, 41.541575, -70.608020
Sage Lot Pond, 41.554361, -70.505611
'''
x = '''
Station, Lat, Lon
Boston, 42.368186, -71.047984
Carolyn Seep Spot, 39.8083, -69.5917
Falmouth Harbor, 41.541575, -70.608020
'''
# Enter desired (Station, Lat, Lon) values here:
x = '''
Station, Lat, Lon
Boston, 42.368186, -71.047984
Scituate Harbor, 42.199447, -70.720090
Scituate Beach, 42.209973, -70.724523
Falmouth Harbor, 41.541575, -70.608020
Marion, 41.689008, -70.746576
Marshfield, 42.108480, -70.648691
Provincetown, 42.042745, -70.171180
Sandwich, 41.767990, -70.466219
Hampton Bay, 42.900103, -70.818510
Gloucester, 42.610253, -70.660570
'''
# Create a Pandas DataFrame
obs=pd.read_csv(StringIO(x.strip()), sep=",\s*",index_col='Station')
obs
# find the indices of the points in (x,y) closest to the points in (xi,yi)
def nearxy(x,y,xi,yi):
ind = np.ones(len(xi),dtype=int)
for i in np.arange(len(xi)):
dist = np.sqrt((x-xi[i])**2+(y-yi[i])**2)
ind[i] = dist.argmin()
return ind
# open NECOFS remote OPeNDAP dataset
nc=netCDF4.Dataset(url).variables
# find closest NECOFS nodes to station locations
obs['0-Based Index'] = nearxy(nc['lon'][:],nc['lat'][:],obs['Lon'],obs['Lat'])
obs
# Get desired time step
time_var = nc['time']
istart = netCDF4.date2index(start,time_var,select='nearest')
istop = netCDF4.date2index(stop,time_var,select='nearest')
# get time values and convert to datetime objects
jd = netCDF4.num2date(time_var[istart:istop],time_var.units)
# get all time steps of water level from each station
nsta = len(obs)
z = np.ones((len(jd),nsta))
for i in range(nsta):
z[:,i] = nc['hs'][istart:istop,obs['0-Based Index'][i]]
# make a DataFrame out of the interpolated time series at each location
zvals=pd.DataFrame(z,index=jd,columns=obs.index)
# list out a few values
zvals.head()
# model blew up producing very high waves on Jan 21, 2016
# eliminate unrealistically high values
mask = zvals>10.
zvals[mask] = np.NaN
# plotting at DataFrame is easy!
ax=zvals.plot(figsize=(16,4),grid=True,title=('Wave Height from %s Forecast' % model),legend=False);
# read units from dataset for ylabel
plt.ylabel(nc['hs'].units)
# plotting the legend outside the axis is a bit tricky
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5));
# what is the maximum over the whole record at a specific location
zvals['Boston'].max()
# make a new DataFrame of maximum water levels at all stations
b=pd.DataFrame(zvals.idxmax(),columns=['time of max value (UTC)'])
# create heading for new column containing max water level
zmax_heading='zmax (%s)' % nc['hs'].units
# Add new column to DataFrame
b[zmax_heading]=zvals.max()
b
| UGRID/NECOFS_wave_levels.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import glob
import pandas as pd
import numpy as np
# import scipy.sparse
from sklearn.preprocessing import normalize
from sklearn.svm import SVC
from sklearn.metrics.pairwise import chi2_kernel
from sklearn.cluster import KMeans
from sklearn.ensemble import AdaBoostClassifier, GradientBoostingClassifier
from sklearn.metrics import average_precision_score
from sklearn.feature_extraction import text
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from xgboost import XGBClassifier
from lightgbm import LGBMClassifier
import re
import time
import os
import warnings
from pandas.core.common import SettingWithCopyWarning
warnings.simplefilter(action="ignore", category=SettingWithCopyWarning)
# -
# ## train_kmeans.py
# +
# python2 scripts/train_kmeans.py select.mfcc.csv $cluster_num kmeans.${cluster_num}.model || exit 1;
# -
sys.argv = ['scripts/train_kmeans.py', 'select.mfcc.csv', '100', 'kmeans.100.model']
# python2 scripts/train_kmeans.py select.mfcc.csv 10 kmeans.10.model || exit 1;
if __name__ == '__main__':
if len(sys.argv) != 4:
print "Usage: {0} mfcc_csv_file cluster_num output_file".format(sys.argv[0])
print "mfcc_csv_file -- path to the mfcc csv file"
print "cluster_num -- number of cluster"
print "output_file -- path to save the k-means model"
exit(1)
mfcc_csv_file = sys.argv[1]; output_file = sys.argv[3]
cluster_num = int(sys.argv[2])
train_sample = pd.read_csv(mfcc_csv_file, header=None, sep=';')
start_time = time.time()
n_clusters = cluster_num
n_init = 5
model = KMeans(n_clusters = n_clusters, random_state = 0, n_init = n_init, n_jobs = -1).fit(train_sample)
filename = output_file+'.sav'
pickle.dump(model, open(filename, 'wb'))
print "===== The time consuming of Kmeans clustering : {} seconds =====".format((time.time() - start_time))
# print mfcc_csv_file
# print output_file
# print cluster_num
print "K-means trained successfully!"
mfcc_csv_file = sys.argv[1]; output_file = sys.argv[3]
cluster_num = int(sys.argv[2])
train_sample = pd.read_csv(mfcc_csv_file, header=None, sep=';')
start_time = time.time()
n_clusters = cluster_num
n_init = 5
output_file = KMeans(n_clusters = n_clusters, random_state = 0, n_init = n_init, n_jobs = -1).fit(train_sample)
print("===== The time consuming of Kmeans clustering : {} seconds =====".format((time.time() - start_time)))
# ## create_kmeans.py
# +
# python2 scripts/create_kmeans.py kmeans.${cluster_num}.model $cluster_num list/all.video || exit 1;
# -
sys.argv = ['scripts/create_kmeans.py', 'kmeans.3.model', '3', 'list/all.video']
# +
# #!/bin/python
import numpy
import os
import cPickle
from sklearn.cluster.k_means_ import KMeans
import sys
# Generate k-means features for videos; each video is represented by a single vector
if __name__ == '__main__':
if len(sys.argv) != 4:
print "Usage: {0} kmeans_model, cluster_num, file_list".format(sys.argv[0])
print "kmeans_model -- path to the kmeans model"
print "cluster_num -- number of cluster"
print "file_list -- the list of videos"
exit(1)
kmeans_model = './'+sys.argv[1]+'.sav'; file_list = sys.argv[3]
cluster_num = int(sys.argv[2])
# load the kmeans model
#kmeans = pickle.load(open(kmeans_model,"rb"))
# model = pickle.load(open(filename, 'rb'))
print kmeans_model
print file_list
print cluster_num
print "K-means features generated successfully!"
# +
if len(sys.argv) != 4:
print "Usage: {0} kmeans_model, cluster_num, file_list".format(sys.argv[0])
print "kmeans_model -- path to the kmeans model"
print "cluster_num -- number of cluster"
print "file_list -- the list of videos"
exit(1)
kmeans_model = './'+sys.argv[1]+'.sav'; file_list = sys.argv[3]
cluster_num = int(sys.argv[2])
# load the kmeans model
kmeans_model = './hw1_git/11775-hws/hw1_code/{}.sav'.format(sys.argv[1])
kmeans = pickle.load(open(kmeans_model,"rb"))
model = kmeans
# +
# path = './hw1_git/11775-hws/videos/*.mp4'
path = './mfcc/*.csv'
filelist = []
for file in glob.glob(path):
filelist.append(file)
# -
filelist
def get_features(k, model, path_list):
loaded_model= model
start_time = time.time()
features_dict = dict()
filelist = path_list
for i in range(len(filelist)):
# for i in range(10):
if i % 1000 == 0:
print('{}th step progressing....'.format(i))
else:
pass
data = pd.read_csv(filelist[i], sep = ';', header = None)
pred_centers = loaded_model.predict(data)
num_clusters = k
bow_preds = np.zeros((1, num_clusters))
for ind in pred_centers:
bow_preds[0, ind] += 1
norm_feat = (1.0 * bow_preds)/np.sum(bow_preds)
features_dict[i] = pd.DataFrame(norm_feat)
features_total = features_dict[0].copy()
for i in range(1, len(features_dict)):
foo = features_dict[i].copy()
features_total = pd.concat([features_total, foo], axis = 0)
features_total = features_total.reset_index().drop('index', axis = 1)
print("===== The time consuming of getting features : {} seconds =====".format((time.time() - start_time)))
return features_total
total_features = get_features(cluster_num, model = model, path_list = filelist)
total_features.to_csv('./hw1_git/11775-hws/hw1_code/total_features_k{}.csv'.format(cluster_num), index=False)
# ## create_asrfeat.py
#python2 scripts/create_asrfeat.py vocab list/all.video || exit 1;
if __name__ == '__main__':
if len(sys.argv) != 3:
print "Usage: {0} vocab_file, file_list".format(sys.argv[0])
print "vocab_file -- path to the vocabulary file"
print "file_list -- the list of videos"
exit(1)
print "ASR features generated successfully!"
# +
# path = './hw1_git/11775-hws/videos/*.mp4'
path = '../asrs/*.txt'
filelist = []
for file in glob.glob(path):
filelist.append(file)
# -
filelist
def concatenate_list_data(list):
result= ''
for element in list:
result += str(element)
return result
text = []
for i in range(len(filelist)):
# for i in range(10):
with open (filelist[i], "r") as myfile:
data=myfile.readlines()
data=concatenate_list_data(data)
text.append(data)
if i % 1000 == 0:
print('{}th txt file reading...'.format(i))
else: pass
vect = CountVectorizer(stop_words="english")
# vect = CountVectorizer()
bow = vect.fit_transform(text).toarray()
norm_bow = normalize(bow, norm = 'l1', axis=1)
norm_data = pd.DataFrame(norm_bow)
norm_data.to_csv('./hw1_git/11775-hws/hw1_code/total_astfeat.csv', index = False)
# ## create_kmeas.py & create_asrfeat.py 이어서
cluster_num = 100
total_features = pd.read_csv('./total_features_k{}.csv'.format(cluster_num))
total_features.head(3)
filelist
i=0
match_front = re.search('mfcc/', filelist[i])
match_end = re.search('.mfcc.csv', filelist[i])
match_front.end()
match_end.start()
filelist[i]
filelist[i][match_front.end()]
# +
# path = './hw1_git/11775-hws/videos/*.mp4'
path = './mfcc/*.csv'
filelist = []
for file in glob.glob(path):
filelist.append(file)
# -
# Making Video name
video_name_ind = []
for i in range(len(filelist)):
import re
match_front = re.search('mfcc/', filelist[i])
match_end = re.search('.mfcc.csv', filelist[i])
video_name_ind.append(filelist[i][match_front.end():match_end.start()])
video_name = pd.DataFrame({'video': video_name_ind})
# +
# Making features columns
k = cluster_num
column_name = ['video']
for i in range(k):
column_name.append('feature_{}'.format(i))
total_data = pd.concat([video_name, total_features], axis = 1)
total_data.columns = column_name
# +
#os.chdir('./hw1_git/11775-hws/hw1_code/')
# +
train_ind = pd.read_csv('./list/train', sep = ' ', header = None)
valid_ind = pd.read_csv('./list/val', sep = ' ', header = None)
test_ind = pd.read_csv('./list/test.video', sep = ' ', header = None)
train_ind['Data'] = 'TRAIN'
valid_ind['Data'] = 'VALID'
test_ind[1] = 'UNK'
test_ind['Data'] = 'TEST'
train_ind.columns = ['video','target','Data']
valid_ind.columns = ['video','target','Data']
test_ind.columns = ['video','target','Data']
# +
data_lable = pd.concat([train_ind, valid_ind, test_ind], axis = 0).reset_index().drop('index', axis = 1)
# data_lable['target_p001'] =
data_lable['target_p001'] = data_lable['target']
data_lable['target_p002'] = data_lable['target']
data_lable['target_p003'] = data_lable['target']
data_lable['target_p001_10'] = 1
data_lable['target_p002_10'] = 1
data_lable['target_p003_10'] = 1
data_lable['target_p001'][data_lable['target'] != 'P001'] = 'Other'
data_lable['target_p002'][data_lable['target'] != 'P002'] = 'Other'
data_lable['target_p003'][data_lable['target'] != 'P003'] = 'Other'
data_lable['target_p001_10'][data_lable['target'] != 'P001'] = 0
data_lable['target_p002_10'][data_lable['target'] != 'P002'] = 0
data_lable['target_p003_10'][data_lable['target'] != 'P003'] = 0
# -
total_mart = total_data.merge(data_lable, how = 'right', on = 'video')
total_mart = total_mart.fillna(0)
train_mart = total_mart[total_mart['Data'] == 'TRAIN']
valid_mart = total_mart[total_mart['Data'] == 'VALID']
test_mart = total_mart[total_mart['Data'] == 'TEST']
# +
# total_mart.to_csv('./datamart_total_k{}.csv'.format(cluster_num), index=False)
# train_mart.to_csv('./datamart_train_k{}.csv'.format(cluster_num), index=False)
# valid_mart.to_csv('./datamart_valid_k{}.csv'.format(cluster_num), index=False)
# test_mart.to_csv('./datamart_test_k{}.csv'.format(cluster_num), index=False)
# -
print(train_mart.shape, valid_mart.shape, test_mart.shape)
# +
def modeling_ap_SVM(k, train_data, valid_data, target = 'target_p001_10'):
start_time = time.time()
k = k
train_mart = train_data
valid_mart = valid_data
target = target
X_train = train_mart.iloc[:,1:k+1]
y_train = train_mart[target]
X_valid = valid_mart.iloc[:,1:k+1]
y_valid = valid_mart[target]
model = SVC(kernel=chi2_kernel, probability=True)
model.fit(X_train, y_train)
y_preds = model.predict(X_valid)
y_probs = model.predict_proba(X_valid)
results = average_precision_score(y_true=y_valid.values, y_score=y_probs[:,1])
print("===== The time consuming of SVM Modeling : {} seconds =====".format((time.time() - start_time)))
print(results)
return results
def modeling_ap_AdaB(k, train_data, valid_data, target = 'target_p001_10'):
start_time = time.time()
k = k
train_mart = train_data
valid_mart = valid_data
target = target
X_train = train_mart.iloc[:,1:k+1]
y_train = train_mart[target]
X_valid = valid_mart.iloc[:,1:k+1]
y_valid = valid_mart[target]
model = AdaBoostClassifier(n_estimators=200, random_state=0)
model.fit(X_train, y_train)
y_preds = model.predict(X_valid)
y_probs = model.predict_proba(X_valid)
results = average_precision_score(y_true=y_valid.values, y_score=y_probs[:,1])
print("===== The time consuming of AdaBoosting Modeling : {} seconds =====".format((time.time() - start_time)))
print(results)
return results
def modeling_ap_Boost(k, train_data, valid_data, target = 'target_p001_10'):
start_time = time.time()
k = k
train_mart = train_data
valid_mart = valid_data
target = target
X_train = train_mart.iloc[:,1:k+1]
y_train = train_mart[target]
X_valid = valid_mart.iloc[:,1:k+1]
y_valid = valid_mart[target]
model = GradientBoostingClassifier(n_estimators=200, random_state=0)
model.fit(X_train, y_train)
y_preds = model.predict(X_valid)
y_probs = model.predict_proba(X_valid)
results = average_precision_score(y_true=y_valid.values, y_score=y_probs[:,1])
print("===== The time consuming of Boosting Modeling : {} seconds =====".format((time.time() - start_time)))
print(results)
return results
def modeling_ap_xgb(k, train_data, valid_data, target = 'target_p001_10'):
start_time = time.time()
k = k
train_mart = train_data
valid_mart = valid_data
target = target
X_train = train_mart.iloc[:,1:k+1]
y_train = train_mart[target]
X_valid = valid_mart.iloc[:,1:k+1]
y_valid = valid_mart[target]
model = XGBClassifier()
model.fit(X_train, y_train)
y_preds = model.predict(X_valid)
y_probs = model.predict_proba(X_valid)
results = average_precision_score(y_true=y_valid.values, y_score=y_probs[:,1])
print("===== The time consuming of XgBoosting Modeling : {} seconds =====".format((time.time() - start_time)))
print(results)
return results
# -
AdaB_results_p001 = modeling_ap_AdaB(k=100, train_data = train_mart, valid_data = valid_mart, target = 'target_p001_10')
Xgb_results_p002 = modeling_ap_xgb(k=100, train_data = train_mart, valid_data = valid_mart, target = 'target_p002_10')
Xgb_results_p003 = modeling_ap_xgb(k=100, train_data = train_mart, valid_data = valid_mart, target = 'target_p003_10')
| hw2_code/99.working_file_ipnb/99.Create_pyfile_km_asrfeat.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten, Dense, Dropout, MaxPooling2D, Conv2D, BatchNormalization
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import cv2
import imutils
import dlib
import os
import matplotlib.pyplot as plt
import numpy as np
# -
# %load_ext autotime
# %matplotlib inline
# +
# loading the model
detector = tf.keras.models.load_model('D:\eye detection\eye_direction.h5')
detector.summary()
# -
face_cascade=cv2.CascadeClassifier(r'D:\eye detection\haarcascade_xml_files\haarcascades\haarcascade_frontalface_default.xml')
right_eye_cascade=cv2.CascadeClassifier(r'D:\eye detection\haarcascade_xml_files\haarcascades\haarcascade_righteye_2splits.xml')
left_eye_cascade=cv2.CascadeClassifier(r'D:\eye detection\haarcascade_xml_files\haarcascades\haarcascade_lefteye_2splits.xml')
# +
eye_img = cv2.imread(r'D:\eye detection\sample_image.jpg')
gray = cv2.cvtColor(eye_img,cv2.COLOR_BGR2GRAY)
gray = cv2.bilateralFilter(gray,9,75,75)
gray = cv2.adaptiveThreshold(gray,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,cv2.THRESH_BINARY,13,3)
plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plt.imshow(eye_img)
plt.subplot(1,2,2)
plt.imshow(gray)
# +
faces = face_cascade.detectMultiScale(gray,1.3,6)
if faces is not None:
for (x,y,w,h) in faces:
roi_gray_face = gray[y:y+h, x:x+w]
roi_color_face = eye_img[y:y+h, x:x+w]
cv2.rectangle(eye_img,(x,y),(x+w,y+h),(0,0,255),1)
cv2.rectangle(gray,(x,y),(x+w,y+h),(0,255,0),1)
left_eye = left_eye_cascade.detectMultiScale(roi_gray_face)
if left_eye is not None:
for (ex,ey,ew,eh) in left_eye:
roi_gray_eye = roi_gray_face[ey:ey+eh, ex:ex+ew]
roi_color_eye = roi_color_face[ey:ey+eh, ex:ex+ew]
cv2.rectangle(roi_gray_face,(ex,ey),(ex+ew,ey+eh),(0,255,0),1)
cv2.rectangle(roi_color_face,(ex,ey),(ex+ew,ey+eh),(0,255,0),1)
right_eye = right_eye_cascade.detectMultiScale(roi_gray_face)
if right_eye is not None:
for (rx,ry,rw,rh) in right_eye:
roi_gray_eye = roi_gray_face[ry:ry+rh, rx:rx+rw]
roi_color_eye = roi_color_face[ry:ry+rh, rx:rx+rw]
cv2.rectangle(roi_gray_face,(rx,ry),(rx+rw,ry+rh),(0,255,0),1)
cv2.rectangle(roi_color_face,(rx,ry),(rx+rw,ry+rh),(255,0,0),1)
plt.figure(figsize=(16,16))
plt.subplot(2,2,1)
plt.imshow(eye_img)
plt.subplot(2,2,2)
plt.imshow(gray)
# -
roi_color_eye.shape
roi_eye = cv2.resize(roi_color_eye,(80,80),interpolation = cv2.INTER_AREA)
roi_eye = np.reshape(roi_color_eye,(1,80,80,3))
pred_cls = detector.predict_classes(roi_color_eye)
# +
cap = cv2.VideoCapture(0)
cv2.namedWindow('PUPIL TRACKER')
while 1:
ret,vid = cap.read()
vid = cv2.flip(vid,1)
gray_vid = cv2.cvtColor(vid,cv2.COLOR_BGR2GRAY)
gray_blur = cv2.bilateralFilter(gray_vid,9,75,75)
gray_blur = cv2.adaptiveThreshold(gray_blur,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,cv2.THRESH_BINARY,13,3)
faces = face_cascade.detectMultiScale(gray_blur,1.2,6)
for (x,y,w,h) in faces:
roi_gray_face = gray_vid[y+20:y+h, x:x+w]
roi_color_face = vid[y+20:y+h, x:x+w]
rcf_zoom = cv2.resize(roi_color_face,(500,500),interpolation = cv2.INTER_AREA)
rgf_zoom = cv2.resize(roi_gray_face,(500,500),interpolation = cv2.INTER_AREA)
left_eye = left_eye_cascade.detectMultiScale(rcf_zoom,1.2,6)
right_eye = right_eye_cascade.detectMultiScale(rcf_zoom,1.2,6)
for (lex,ley,lew,leh) in left_eye:
roi_eye = rcf_zoom[ley:ley+leh,lex:lex+lew]
cv2.rectangle(rcf_zoom,(lex,ley),(lex+lew,ley+leh),(0,255,0),1)
cv2.rectangle(rgf_zoom,(lex,ley),(lex+lew,ley+leh),(0,255,0),1)
eye_pos = cv2.resize(roi_eye,(80,80))
eye_pos = np.array(eye_pos)
eye_pos = eye_pos/255
eye_img = np.reshape(eye_pos,(1,80,80,3))
pred_cls = detector.predict_classes(eye_img)
rgf_zoom = cv2.addWeighted(rgf_zoom,1.7,cv2.blur(rgf_zoom,(5,5),cv2.BORDER_DEFAULT),-1,0)
cv2.imshow('PUPIL TRACKER',rcf_zoom)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cv2.destroyAllWindows()
cap.release()
# -
print(roi_eye.shape)
print(type(roi_eye))
eye_pos = cv2.resize(roi_eye,(80,80))
print(eye_pos.shape)
eye_pos = np.array(eye_pos)
eye_pos = eye_pos/255
eye_img = np.reshape(eye_pos,(1,80,80,3))
print(eye_img.shape)
# +
label_dict = {0:'left',1:'forward',2:'closed',3:'right'}
pred_cls = detector.predict_classes(eye_img)
print(pred_cls)
# -
| model_tester.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Building a model of oxidative ATP synthesis from energetic components
#
# Simulations in the preceding section illustrate how matrix ATP and ADP concentrations are governed by the contributors to the proton motive force. They also show how the matrix ATP/ADP ratio must typically be less than $1$, in contrast to the cytosolic ATP/ADP ratio, which is on the order of $100$. To understand the dependence of ATP synthesis and transport on the proton motive force, the kinetics of the processes that generate it, and the interplay of these processes, we can assemble models of the $\text{F}_0\text{F}_1$ ATP synthase, adenine nucleotide translocase (ANT), mitochondrial phosphate transport, and complexes I, III, and IV of the electron transport chain (ETC) to generate a core model of mitochondrial oxidative ATP synthesis.
# ## Adenine nucleotide translocase
#
# Following synthesis of ATP from ADP and Pi in the matrix, the final step in delivering ATP to the cytosol at physiological free energy levels is the electrically driven exchange of a matrix $\text{ATP}^{4-}$ for a cytosolic $\text{ADP}^{3-}$. This exchange process,
# ```{math}
# (\text{ATP}^{4-})_x + (\text{ADP}^{3-})_c \rightleftharpoons (\text{ATP}^{4-})_c + (\text{ADP}^{3-})_x \, ,
# ```
# is catalyzed by the ANT. Here, we assume rapid transport of species between the cytosol and the IMS, and therefore, equate IMS and cytosol species concentrations.
#
# To simulate the kinetics of this process, we use the Metelkin et al. model {cite}`Metelkin2006`, which accounts for pH and electrochemical dependencies. (Kinetic parameter value estimates for this model were updated by Wu et al. {cite}`Wu2008`.) The steady-state flux of ANT is expressed
# ```{math}
# :label: J_ANT
# J_{\text{ANT}} = E_{\text{ANT}} \dfrac{ \dfrac{ k_2^{\text{ANT}} q }{ K_o^D } [ \text{ATP}^{4-} ]_x [ \text{ADP}^{3-}]_c - \dfrac{ k_3^{\text{ANT}} }{ K_o^T } [ \text{ADP}^{3-} ]_x [ \text{ATP}^{4-} ]_c }{ \left(1 + \dfrac{ [ \text{ATP}^{4-} ]_c }{ K_o^T } + \dfrac{ [ \text{ADP}^{3-} ]_c }{ K_o^D } \right)( [ \text{ADP}^{3-} ]_x + [ \text{ATP}^{4-} ]_x q) },
# ```
# where $E_{\text{ANT}} \ \text{(mol (L mito)}^{-1})$ is the total ANT content of the mitochondria and
# ```{math}
# :label: phi
# k_2^\text{ANT} &=& k_{2,o}^\text{ANT} e^{( -3A - 4B + C) \phi}, \nonumber \\
# k_3^\text{ANT} &=& k_{3,o}^\text{ANT} e^{(-4A - 3B + C) \phi}, \nonumber \\
# K_o^D &=& K_o^{D,0} e^{3 \delta_D \phi}, \nonumber \\
# K_o^T &=& K_o^{T,0} e^{4 \delta_T \phi}, \nonumber \\
# q &=& \dfrac{ k_3^\text{ANT} K_o^D }{ k_2^\text{ANT} K_o^T } e^\phi, \quad \text{and} \nonumber \\
# \phi &=& F \Delta \Psi / R{\rm T}.
# ```
# All parameter values and units can be found in {numref}`table-ANT`, reproduced from {cite}`Bazil2016`.
# ```{list-table} Adenine nucleotide translocase (ANT) parameters.
# :header-rows: 1
# :name: table-ANT
#
# * - Parameter
# - Units
# - Description
# - Value
# * - $E_\text{ANT}$
# - mol (L mito)$^{-1}$
# - ANT activity
# - $0.325$
# * - $\delta_D$
# -
# - ADP displacement binding constant
# - $0.0167 $
# * - $\delta_T$
# -
# - ATP displacement binding constant
# - $0.0699 $
# * - $k_{2,o}^\text{ANT}$
# - s$^{-1}$
# - Forward translocation rate
# - $0.159 $
# * - $k_{3,o}^\text{ANT}$
# - s$^{-1}$
# - Reverse translocation rate
# - $0.501 $
# * - $K_o^{D,0}$
# - $\mu$mol (L cyto water)$^{-1}$
# - ADP binding constant
# - $38.89 $
# * - $K_o^{T,0}$
# - $\mu$mol (L cyto water)$^{-1}$
# - ATP binding constant
# - $56.05$
# * - $A$
# -
# - Translocation displacement constant
# - $0.2829 $
# * - $B$
# -
# - Translocation displacement constant
# - $ -0.2086 $
# * - $C$
# -
# - Translocation displacement constant
# - $0.2372$
# ```
# To simulate ANT and F$_0$F$_1$ ATP synthase activity simultaneously, we extend the system of Equation {eq}`system-ATPase` by adding states for cytosolic species $[\Sigma \text{ATP} ]_c$ and $[\Sigma \text{ADP}]_c$, yielding
# ```{math}
# :label: system-ATP_ANT
# \left\{
# \renewcommand{\arraystretch}{2}
# \begin{array}{rlrl}
# \dfrac{ {\rm d} [\Sigma \text{ATP}]_x }{{\rm d} t} &= (J_\text{F} - J_\text{ANT} ) / W_x, & \dfrac{ {\rm d} [\Sigma \text{ATP}]_c }{{\rm d} t} &= (V_{m2c} J_\text{ANT}) / W_c, \\
# \dfrac{ {\rm d} [\Sigma \text{ADP}]_x }{{\rm d} t} &= (-J_\text{F} + J_\text{ANT}) / W_x, & \dfrac{ {\rm d} [\Sigma \text{ADP}]_c }{{\rm d} t} &= (-V_{m2c} J_\text{ANT}) / W_c, \\
# \dfrac{ {\rm d} [\Sigma \text{Pi}]_x }{{\rm d} t} &= 0 & &\\
# \end{array}
# \renewcommand{\arraystretch}{1}
# \right.
# ```
# where $V_{m2c} \ \text{(L mito) (L cyto)}^{-1}$ is the fraction of the volume of mitochondria per volume cytosol and $W_c \ \text{(L cyto water) (L cyto)}^{-1}$ is the fraction of water volume in the cytoplasm to the total volume of the cytoplasm ({numref}`table-biophysicalconstants`).
# Here, we clamp the matrix phosphate concentration at a constant value since the system of equations in Equation {eq}`system-ATP_ANT` does not account for phosphate transport between the matrix and the cytosol.
# +
import numpy as np
import matplotlib.pyplot as plt
# !pip install scipy
from scipy.integrate import solve_ivp
###### Constants defining metabolite pools ######
# Volume fractions and water space fractions
V_c = 0.6601 # cytosol volume fraction # L cyto (L cell)**(-1)
V_m = 0.2882 # mitochondrial volume fraction # L mito (L cell)**(-1)
V_m2c = V_m / V_c # mito to cyto volume ratio # L mito (L cuvette)**(-1)
W_c = 0.8425 # cytosol water space # L cyto water (L cyto)**(-1)
W_m = 0.7238 # mitochondrial water space # L mito water (L mito)**(-1)
W_x = 0.9*W_m # matrix water space # L matrix water (L mito)**(-1)
# Membrane potential
DPsi = 175/1000
###### Set fixed pH and cation concentrations ######
# pH
pH_x = 7.40
pH_c = 7.20
# K+ concentrations
K_x = 100e-3 # mol (L matrix water)**(-1)
K_c = 140e-3 # mol (L cyto water)**(-1)
# Mg2+ concentrations
Mg_x = 1.0e-3 # mol (L matrix water)**(-1)
Mg_c = 1.0e-3 # mol (L cyto water)**(-1)
###### Parameter vector ######
X_F = 1000 # Synthase activity
E_ANT = 0.325 # Nucleotide transporter activity
activity_array = np.array([X_F, E_ANT]) # Note: This array will be larger in the future parts
###### Initial Conditions ######
# Matrix species
sumATP_x_0 = 0.5e-3 # mol (L matrix water)**(-1)
sumADP_x_0 = 9.5e-3 # mol (L matrix water)**(-1)
sumPi_x_0 = 1e-3 # mol (L matrix water)**(-1)
# Cytoplasmic species
sumATP_c_0 = 0 #9.95e-3 # mol (L cyto water)**(-1)
sumADP_c_0 = 10e-3 #0.05e-3 # mol (L cyto water)**(-1)
X_0 = np.array([sumATP_x_0, sumADP_x_0, sumPi_x_0, sumATP_c_0, sumADP_c_0])
def dXdt(t, X, activity_array):
# Unpack variables
sumATP_x, sumADP_x, sumPi_x, sumATP_c, sumADP_c = X
X_F, E_ANT = activity_array
# Hydrogen ion concentration
H_x = 10**(-pH_x) # mol (L matrix water)**(-1)
H_c = 10**(-pH_c) # mol (L cuvette water)**(-1)
# Thermochemical constants
R = 8.314 # J (mol K)**(-1)
T = 37 + 273.15 # K
F = 96485 # C mol**(-1)
# Proton motive force parameters (dimensionless)
n_F = 8/3
# Dissociation constants
K_MgATP = 10**(-3.88)
K_HATP = 10**(-6.33)
K_KATP = 10**(-1.02)
K_MgADP = 10**(-3.00)
K_HADP = 10**(-6.26)
K_KADP = 10**(-0.89)
K_MgPi = 10**(-1.66)
K_HPi = 10**(-6.62)
K_KPi = 10**(-0.42)
## Binding polynomials
# Matrix species # mol (L mito water)**(-1)
PATP_x = 1 + H_x/K_HATP + Mg_x/K_MgATP + K_x/K_KATP
PADP_x = 1 + H_x/K_HADP + Mg_x/K_MgADP + K_x/K_KADP
PPi_x = 1 + H_x/K_HPi + Mg_x/K_MgPi + K_x/K_KPi
# Cytosol species # mol (L cuvette water)**(-1)
PATP_c = 1 + H_c/K_HATP + Mg_c/K_MgATP + K_c/K_KATP
PADP_c = 1 + H_c/K_HADP + Mg_c/K_MgADP + K_c/K_KADP
## Unbound species
# Matrix species
ATP_x = sumATP_x / PATP_x # [ATP4-]_x
ADP_x = sumADP_x / PADP_x # [ADP3-]_x
# Cytosol species
ATP_c = sumATP_c / PATP_c # [ATP4-]_c
ADP_c = sumADP_c / PADP_c # [ADP3-]_c
###### F0F1-ATPase ######
# ADP3-_x + HPO42-_x + H+_x + n_A*H+_i <-> ATP4- + H2O + n_A*H+_x
# Gibbs energy (J mol**(-1))
DrGo_F = 4990
DrGapp_F = DrGo_F + R * T * np.log( H_x * PATP_x / (PADP_x * PPi_x))
# Apparent equilibrium constant
Kapp_F = np.exp( (DrGapp_F + n_F * F * DPsi ) / (R * T)) * (H_c / H_x)**n_F
# Flux (mol (s * L mito)**(-1))
J_F = X_F * (Kapp_F * sumADP_x * sumPi_x - sumATP_x)
###### ANT ######
# ATP4-_x + ADP3-_i <-> ATP4-_i + ADP3-_x
#Constants
del_D = 0.0167
del_T = 0.0699
k2o_ANT = 9.54/60 # s**(-1)
k3o_ANT = 30.05/60 # s**(-1)
K0o_D = 38.89e-6 # mol (L cuvette water)**(-1)
K0o_T = 56.05e-6 # mol (L cuvette water)**(-1)
A = +0.2829
B = -0.2086
C = +0.2372
phi = F * DPsi / (R * T)
# Reaction rates (s**(-1))
k2_ANT = k2o_ANT * np.exp((A*(-3) + B*(-4) + C)*phi)
k3_ANT = k3o_ANT * np.exp((A*(-4) + B*(-3) + C)*phi)
# Dissociation constants (M)
K0_D = K0o_D * np.exp(3*del_D*phi)
K0_T = K0o_T * np.exp(4*del_T*phi)
q = k3_ANT * K0_D * np.exp(phi) / (k2_ANT * K0_T)
term1 = k2_ANT * ATP_x * ADP_c * q / K0_D
term2 = k3_ANT * ADP_x * ATP_c / K0_T
num = term1 - term2
den = (1 + ATP_c/K0_T + ADP_c/K0_D) * (ADP_x + ATP_x * q)
# Flux (mol (s * L mito)**(-1))
J_ANT = E_ANT * num / den
###### Differential equations (equation 14) ######
# Matrix species
dATP_x = (J_F - J_ANT) / W_x
dADP_x = (-J_F + J_ANT) / W_x
dPi_x = 0
# Cytosol species
dATP_c = ( V_m2c * J_ANT) / W_c
dADP_c = (-V_m2c * J_ANT) / W_c
dX = [dATP_x, dADP_x, dPi_x, dATP_c, dADP_c]
return dX
# Solve ODE
results = solve_ivp(dXdt, [0, 2], X_0, method = 'Radau', args=(activity_array,))
t = results.t
sumATP_x, sumADP_x, sumPi_x, sumATP_c, sumADP_c = results.y
# Plot figures
fig, ax = plt.subplots(1,2, figsize = (10,5))
ax[0].plot(t, sumATP_x*1000, label = '[$\Sigma$ATP]$_x$')
ax[0].plot(t, sumADP_x*1000, label = '[$\Sigma$ADP]$_x$')
ax[0].plot(t, sumPi_x*1000, label = '[$\Sigma$Pi]$_x$')
ax[0].legend(loc="right")
ax[0].set_ylim((-.5,10.5))
ax[0].set_xlabel('Time (s)')
ax[0].set_xticks([0,1,2])
ax[0].set_ylabel('Concentration (mM)')
ax[1].plot(t, sumATP_c*1000, label = '[$\Sigma$ATP]$_c$')
ax[1].plot(t, sumADP_c*1000, label = '[$\Sigma$ADP]$_c$')
ax[1].set_ylim((-0.5,10.5))
ax[1].set_xticks([0,1,2])
ax[1].legend(loc="right")
ax[1].set_xlabel('Time (s)')
plt.show()
# -
# **Figure 4:** Steady state solution from Equation {eq}`system-ATP_ANT` for the (a) matrix and (b) cytosol species with $\Delta \Psi = 175$ mV, $\text{pH}_x = 7.4$, and $\text{pH}_c = 7.2$.
# The above simulations of the system of Equation {eq}`system-ATP_ANT` show how the electrogenic nature of the ANT transport results in the markedly different ATP/ADP ratios in the cytosol compared to the matrix. As we saw in the previous chapter, the ATP hydrolysis potential in the matrix is approximately $\text{-}45 \ \text{kJ mol}^{-1}$. The roughly $100$:$1$ ratio of ATP to ADP in the cytosol is associated with a hydrolysis potential of approximately $\text{-}65 \ \text{kJ mol}^{-1}$. The difference of $20 \ \text{kJ mol}^{-1}$ between the matrix and the cytosolic space is driven primarily by the membrane potential, which is roughly equivalent to $20 \ \text{kJ mol}^{-1}$.
# ## Inorganic phosphate transport
#
# During active ATP synthesis, mitochondrial Pi is replenished via the activity of the phosphate-proton cotransporter (PiC), catalyzing the electroneutral cotransport of protonated inorganic phosphate, $\text{H}_2\text{PO}_4^{-}$, and $\text{H}^{+}$ across the membrane. Again, we assume rapid transport between the cytoplasm and intermembrane space, and hence, we have
# ```{math}
# (\text{H}_2\text{PO}_4^{-})_c + (\text{H}^{+})_c \rightleftharpoons (\text{H}_2\text{PO}_4^{-})_x + (\text{H}^{+})_x.
# ```
# Adopting the flux equation from Bazil et al. {cite}`Bazil2016`, we have
# ```{math}
# :label: J_PiC
# J_\text{PiC} = E_{\text{PiC}} \dfrac{ [\text{H}^{+} ]_{c} [\text{H}_2\text{PO}_4^{-}]_{c} - [\text{H}^{+}]_{x} [\text{H}_2\text{PO}_4^{-}]_{x} }{ [\text{H}_2\text{PO}_4^{-}]_c + k_{\text{PiC}} },
# ```
# where $E_{\text{PiC}} \ \text{(L matrix water) s}^{-1} \text{ (L mito)}^{-1}$ is the PiC activity rate and $k_{\text{PiC}} = 1.61$ mM is an effective Michaelis-Menten constant. The $\text{H}_2\text{PO}_4^{-}$ concentrations in the matrix and cytosol are computed via the relationship
# ```{math}
# [\text{H}_2\text{PO}_4^{-}] = [\Sigma{\rm Pi}] \left( [{\rm H}^+]/K_{\rm HPi} \right) / P_{\rm Pi}
# ```
# from Equation \eqref{sumPi}.
#
#
# To incorporate PiC into Equation {eq}`system-ATP_ANT`, we add a new state $[\Sigma \text{Pi}]_c$ such that at given membrane potential, matrix and cytosolic pH, and cation concentrations, we obtain
# ```{math}
# :label: system-ATP_ANT_PiC
# \left\{
# \renewcommand{\arraystretch}{2}
# \begin{array}{rlrl}
# \dfrac{ {\rm d} [\Sigma \text{ATP}]_x }{{\rm d} t} &= (J_\text{F} - J_\text{ANT} ) / W_x, & \dfrac{ {\rm d} [\Sigma \text{ATP}]_c }{{\rm d} t} &= (V_{m2c} J_\text{ANT}) / W_c \\
# \dfrac{ {\rm d} [\Sigma \text{ADP}]_x }{{\rm d} t} &= (-J_\text{F} + J_\text{ANT}) / W_x, & \dfrac{ {\rm d} [\Sigma \text{ADP}]_c }{{\rm d} t} &= (-V_{m2c} J_\text{ANT}) / W_c, \\
# \dfrac{ {\rm d} [\Sigma \text{Pi}]_x }{{\rm d} t} &= (-J_\text{F} + J_\text{PiC}) / W_x, & \dfrac{ {\rm d} [\Sigma \text{Pi}]_c }{{\rm d} t} &= (- V_{m2c} J_\text{PiC}) / W_c,
# \end{array}
# \renewcommand{\arraystretch}{1}
# \right.
# ```
# The following code simulates the synthesis of ATP from ADP and Pi and their translocation across the IMM under physiological conditions.
# +
import numpy as np
import matplotlib.pyplot as plt
# !pip install scipy
from scipy.integrate import solve_ivp
###### Constants defining metabolite pools ######
# Volume fractions and water space fractions
V_c = 0.6601 # cytosol volume fraction # L cyto (L cell)**(-1)
V_m = 0.2882 # mitochondrial volume fraction # L mito (L cell)**(-1)
V_m2c = V_m / V_c # mito to cyto volume ratio # L mito (L cuvette)**(-1)
W_c = 0.8425 # cytosol water space # L cyto water (L cyto)**(-1)
W_m = 0.7238 # mitochondrial water space # L mito water (L mito)**(-1)
W_x = 0.9*W_m # matrix water space # L matrix water (L mito)**(-1)
# Membrane potential
DPsi = 175/1000
###### Set fixed pH, cation concentrations, and O2 partial pressure ######
# pH
pH_x = 7.40
pH_c = 7.20
# K+ concentrations
K_x = 100e-3 # mol (L matrix water)**(-1)
K_c = 140e-3 # mol (L cyto water)**(-1)
# Mg2+ concentrations
Mg_x = 1.0e-3 # mol (L matrix water)**(-1)
Mg_c = 1.0e-3 # mol (L cyto water)**(-1)
###### Parameter vector ######
X_F = 100 # Synthase activity
E_ANT = 0.325 # Nucleotide transporter activity
E_PiC = 5.0e6 # Phosphate transporter activity
activity_array = np.array([X_F, E_ANT, E_PiC])
###### Initial Conditions ######
# Matrix species
sumATP_x_0 = 0.5e-3 # mol (L matrix water)**(-1)
sumADP_x_0 = 9.5e-3 # mol (L matrix water)**(-1)
sumPi_x_0 = 1e-3 # mol (L matrix water)**(-1)
# Cytosolic species
sumATP_c_0 = 0 # mol (L cyto water)**(-1)
sumADP_c_0 = 10e-3 # mol (L cyto water)**(-1)
sumPi_c_0 = 10e-3 # mol (L cyto water)**(-1)
X_0 = np.array([sumATP_x_0, sumADP_x_0, sumPi_x_0, sumATP_c_0, sumADP_c_0, sumPi_c_0])
def dXdt(t, X, activity_array):
# Unpack variables
sumATP_x, sumADP_x, sumPi_x, sumATP_c, sumADP_c, sumPi_c = X
X_F, E_ANT, E_PiC = activity_array
# Hydrogen ion concentration
H_x = 10**(-pH_x) # mol (L matrix water)**(-1)
H_c = 10**(-pH_c) # mol (L cuvette water)**(-1)
# Thermochemical constants
R = 8.314 # J (mol K)**(-1)
T = 37 + 273.15 # K
F = 96485 # C mol**(-1)
# Proton motive force parameters (dimensionless)
n_F = 8/3
# Dissociation constants
K_MgATP = 10**(-3.88)
K_HATP = 10**(-6.33)
K_KATP = 10**(-1.02)
K_MgADP = 10**(-3.00)
K_HADP = 10**(-6.26)
K_KADP = 10**(-0.89)
K_MgPi = 10**(-1.66)
K_HPi = 10**(-6.62)
K_KPi = 10**(-0.42)
## Binding polynomials
# Matrix species # mol (L mito water)**(-1)
PATP_x = 1 + H_x/K_HATP + Mg_x/K_MgATP + K_x/K_KATP
PADP_x = 1 + H_x/K_HADP + Mg_x/K_MgADP + K_x/K_KADP
PPi_x = 1 + H_x/K_HPi + Mg_x/K_MgPi + K_x/K_KPi
# Cytosol species # mol (L cuvette water)**(-1)
PATP_c = 1 + H_c/K_HATP + Mg_c/K_MgATP + K_c/K_KATP
PADP_c = 1 + H_c/K_HADP + Mg_c/K_MgADP + K_c/K_KADP
PPi_c = 1 + H_c/K_HPi + Mg_c/K_MgPi + K_c/K_KPi
## Unbound species
# Matrix species
ATP_x = sumATP_x / PATP_x # [ATP4-]_x
ADP_x = sumADP_x / PADP_x # [ADP3-]_x
Pi_x = sumPi_x / PPi_x # [HPO42-]_x
# Cytosol species
ATP_c = sumATP_c / PATP_c # [ATP4-]_c
ADP_c = sumADP_c / PADP_c # [ADP3-]_c
Pi_c = sumPi_c / PPi_c # [HPO42-]_c
###### H+-PI2 cotransporter ######
# H2PO42-_x + H+_x = H2PO42-_c + H+_c
# Constant
k_PiC = 1.61e-3 # mol (L cuvette)**(-1)
# H2P04- species
HPi_c = Pi_c * (H_c / K_HPi)
HPi_x = Pi_x * (H_x / K_HPi)
# Flux (mol (s * L mito)**(-1))
J_PiC = E_PiC * (H_c * HPi_c - H_x * HPi_x) / (k_PiC + HPi_c)
###### F0F1-ATPase ######
# ADP3-_x + HPO42-_x + H+_x + n_A*H+_i <-> ATP4- + H2O + n_A*H+_x
# Gibbs energy (J mol**(-1))
DrGo_F = 4990
DrGapp_F = DrGo_F + R * T * np.log( H_x * PATP_x / (PADP_x * PPi_x))
# Apparent equilibrium constant
Kapp_F = np.exp( (DrGapp_F + n_F * F * DPsi ) / (R * T)) * (H_c / H_x)**n_F
# Flux (mol (s * L mito)**(-1))
J_F = X_F * (Kapp_F * sumADP_x * sumPi_x - sumATP_x)
###### ANT ######
# ATP4-_x + ADP3-_i <-> ATP4-_i + ADP3-_x
# Constants
del_D = 0.0167
del_T = 0.0699
k2o_ANT = 9.54/60 # s**(-1)
k3o_ANT = 30.05/60 # s**(-1)
K0o_D = 38.89e-6 # mol (L cuvette water)**(-1)
K0o_T = 56.05e-6 # mol (L cuvette water)**(-1)
A = +0.2829
B = -0.2086
C = +0.2372
phi = F * DPsi / (R * T)
# Reaction rates (s**(-1))
k2_ANT = k2o_ANT * np.exp((A*(-3) + B*(-4) + C)*phi)
k3_ANT = k3o_ANT * np.exp((A*(-4) + B*(-3) + C)*phi)
# Dissociation constants (M)
K0_D = K0o_D * np.exp(3*del_D*phi)
K0_T = K0o_T * np.exp(4*del_T*phi)
q = k3_ANT * K0_D * np.exp(phi) / (k2_ANT * K0_T)
term1 = k2_ANT * ATP_x * ADP_c * q / K0_D
term2 = k3_ANT * ADP_x * ATP_c / K0_T
num = term1 - term2
den = (1 + ATP_c/K0_T + ADP_c/K0_D) * (ADP_x + ATP_x * q)
# Flux (mol (s * L mito)**(-1))
J_ANT = E_ANT * num / den
###### Differential equations (equation 15) ######
# Matrix species
dATP_x = (J_F - J_ANT) / W_x
dADP_x = (-J_F + J_ANT) / W_x
dPi_x = (-J_F + J_PiC) / W_x
# Buffer species
dATP_c = ( V_m2c * J_ANT) / W_c
dADP_c = (-V_m2c * J_ANT) / W_c
dPi_c = (-V_m2c * J_PiC) / W_c
dX = [dATP_x, dADP_x, dPi_x, dATP_c, dADP_c, dPi_c]
return dX
# Solve ODE
t = np.linspace(0,2,100)
results = solve_ivp(dXdt, [0, 2], X_0, method = 'Radau', t_eval = t, args=(activity_array,))
sumATP_x, sumADP_x, sumPi_x, sumATP_c, sumADP_c, sumPi_c = results.y
# Plot figures
fig, ax = plt.subplots(1,2, figsize = (10,5))
ax[0].plot(t, sumATP_x*1000, label = '[$\Sigma$ATP]$_x$')
ax[0].plot(t, sumADP_x*1000, label = '[$\Sigma$ADP]$_x$')
ax[0].plot(t, sumPi_x*1000, label = '[$\Sigma$Pi]$_x$')
ax[0].legend(loc="right")
ax[0].set_ylim((-.5,10.5))
ax[0].set_xlim((0,2))
ax[0].set_xticks([0,1,2])
ax[0].set_xlabel('Time (s)')
ax[0].set_ylabel('Concentration (mM)')
ax[1].plot(t, sumATP_c*1000, label = '[$\Sigma$ATP]$_c$')
ax[1].plot(t, sumADP_c*1000, label = '[$\Sigma$ADP]$_c$')
ax[1].plot(t, sumPi_c*1000, label = '[$\Sigma$Pi]$_c$')
ax[1].set_ylim((-0.5,10.5))
ax[1].set_xlim((0,2))
ax[1].set_xticks([0,1,2])
ax[1].legend(loc="right")
ax[1].set_xlabel('Time (s)')
plt.show()
# -
# **Figure 5:** Steady state solution from Equation {eq}`system-ATP_ANT_PiC` for the (a) matrix and (b) cytosol species with $\Delta \Psi = 175$ mV, $\text{pH}_x = 7.4$, and $\text{pH}_c = 7.2$.
# For the above simulations, cytosolic inorganic phosphate is set to $10 \ \text{mM}$ initially, and all other initial conditions remain unchanged. Driven by $\Delta \text{pH}$, a gradient in phosphate concentration is established, with a steady-state ratio of matrix-to-cytosol concentration of approximately $2.2$. As seen in the previous section, with a constant membrane potential of $175 \ \text{mV}$, the ATP/ADP ratio is maintained at a much higher level in the cytosol than in the matrix.
#
# The final matrix and cytosol ATP and ADP concentrations depend not only on the membrane potential, but also on the total amount of exchangeable phosphate in the system. Here these simulations start with $[\text{Pi}]_c = 10 \ \text{mM}$ and $[\text{Pi}]_x = 1 \ \text{mM}$. The initial $10 \ \text{mM}$ of ADP in the cytosol becomes almost entirely phosphorylated to ATP, leaving $0.32 \ \text{mM}$ of inorganic phosphate in the cytosol in the final steady state. To explore how these steady states depend on $\Delta\Psi$, the following code simulates the steady-state behavior of this system for a range of $\Delta\Psi$ from $100$ to $200 \ \text{mV}$. These simulations, based on a simple, thermodynamically constrained model, show that it is not possible to synthesize ATP at physiological free energy levels for values of $\Delta\Psi$ of lower than approximately $160 \ \text{mV}$.
# +
# !pip install scipy
from scipy.integrate import solve_ivp
### Simulate over a range of Membrane potential from 100 mV to 250 mV ###
# Define array to iterate over
membrane_potential = np.linspace(100,250) # mV
# Define arrays to store steady state results
ATP_x_steady = np.zeros(len(membrane_potential))
ADP_x_steady = np.zeros(len(membrane_potential))
Pi_x_steady = np.zeros(len(membrane_potential))
ATP_c_steady = np.zeros(len(membrane_potential))
ADP_c_steady = np.zeros(len(membrane_potential))
Pi_c_steady = np.zeros(len(membrane_potential))
# Iterate through range of membrane potentials
for i in range(len(membrane_potential)):
DPsi = membrane_potential[i] / 1000 # convert to V
temp_results = solve_ivp(dXdt, [0, 200], X_0, method = 'Radau', args=(activity_array,)).y*1000 # Concentration in mM
ATP_x_steady[i] = temp_results[0,-1]
ADP_x_steady[i] = temp_results[1,-1]
Pi_x_steady[i] = temp_results[2,-1]
ATP_c_steady[i] = temp_results[3,-1]
ADP_c_steady[i] = temp_results[4,-1]
Pi_c_steady[i] = temp_results[5,-1]
# Plot figures
fig, ax = plt.subplots(1,2, figsize = (10,5))
ax[0].plot(membrane_potential, ATP_x_steady, label = '[$\Sigma$ATP]$_x$')
ax[0].plot(membrane_potential, ADP_x_steady, label = '[$\Sigma$ADP]$_x$')
ax[0].plot(membrane_potential, Pi_x_steady, label = '[$\Sigma$Pi]$_x$')
ax[0].legend(loc = "right")
ax[0].set_xlabel('Membrane potential (mV)')
ax[0].set_ylabel('Concentration (mM)')
ax[0].set_xlim([100, 250])
ax[0].set_ylim([-0.5,13])
ax[1].plot(membrane_potential, ATP_c_steady, label = '[$\Sigma$ATP]$_c$')
ax[1].plot(membrane_potential, ADP_c_steady, label = '[$\Sigma$ADP]$_c$')
ax[1].plot(membrane_potential, Pi_c_steady, label = '[$\Sigma$Pi]$_c$')
ax[1].legend(loc = "right")
ax[1].set_xlabel('Membrane potential (mV)')
ax[1].set_ylabel('Concentration (mM)')
ax[1].set_xlim([100, 250])
ax[1].set_ylim([-0.5,13])
plt.show()
# -
# **Figure 6:** Simulation of concentration versus $\Delta \Psi$ for Equation {eq}`system-ATP_ANT_PiC` for the (a) matrix and (b) cytosol species with $\Delta \Psi$ from $100$ to $250$ mV.
# Simulation of this system reinforces the fact that ATP cannot be synthesized at physiological free energy levels for mitochondrial membrane potential of less than approximately $150 \ \text{mV}$.
# ## Respiratory complexes and NADH synthesis
#
# The previous sections have assumed a constant membrane potential. To account for the processes that generate the membrane potential, we model proton pumping associated with the respiratory complexes I, III, and IV of the ETC ({numref}`mitofig`).
# ### ETC complex I
#
# Coupled with the translocation of $n_\text{C1} = 4$ protons across the IMM against the electrochemical gradient, electrons are transferred from NADH to ubiquinone ($Q$) at complex I of the ETC via the reaction
# ```{math}
# :label: reaction_C1
# (\text{NADH}^{2-})_x + (\text{H}^{+})_x + (\text{Q})_x + n_\text{C1} (\text{H}^{+})_x \rightleftharpoons (\text{NAD}^{-})_x + (\text{QH}_2)_x + \text{H}_2\text{O} + n_\text{C1}(\text{H}^+)_c.
# ```
# Since protons move against the gradient when the reaction proceeds in the left-to-right direction, the overall Gibbs energy for the reaction of Equation {eq}`reaction_C1` is
# ```{math}
# \Delta G_\text{C1} &= \Delta_r G_\text{C1} - n_\text{C1} \Delta G_{\rm H} \nonumber \\
# &= \Delta_r G_\text{C1}^\circ + R{\rm T} \ln \left( \dfrac{ [\text{NAD}^{-}]_x [\text{QH}_2]_x }{ [\text{NADH}^{2-}]_x [\text{Q}]_x} \cdot \dfrac{1}{[\text{H}^{+}]_x } \right) + n_\text{C1} F \Delta \Psi - R{\rm T} \ln \left( \dfrac{ [\text{H}^{+}]_x }{ [\text{H}^{+}]_c } \right)^{n_{\text{C1}}} \nonumber \\
# &= \Delta_r G'^{\circ}_\text{C1} + R{\rm T} \ln \left( \dfrac{ [\text{NAD}^{-}]_x [\text{QH}_2]_x }{ [\text{NADH}^{2-}]_x [\text{Q}]_x} \right) + n_\text{C1} F \Delta \Psi - R{\rm T} \ln \left( \dfrac{ [\text{H}^{+}]_x }{ [\text{H}^{+}]_c } \right)^{n_{\text{C1}}},
# ```
# where
# ```{math}
# \Delta_r G'^\circ_\text{C1} = \Delta_r G^\circ_\text{C1} - R \text{T} \ln ( [\text{H}^+]_x )
# ```
# is the apparent Gibbs energy for the reaction in Equation {eq}`reaction_C1`. The apparent equilibrium constant is
# ```{math}
# :label: Kapp_C1
# K'_{eq,\text{C1}} = \left(\dfrac{ [\text{NAD}^{-}]_x [\text{QH}_2]_x }{ [\text{NADH}^{2-}]_x [\text{Q}]_x} \right)_{eq} = \exp \left\{ \dfrac{ - ( \Delta_r G'^\circ_\text{C1} + n_\text{C1} F \Delta \Psi) }{ R \text{T}} \right\} \left( \dfrac{ [\text{H}^{+}]_x }{ [\text{H}^{+}]_c } \right)^{n_\text{C1}}.
# ```
#
# To simulate the flux of complex I, $J_{\text{C1}} \ \text{(mol s}^{-1} \text{ (L mito)}^{-1})$, across the IMM by mass-action kinetics, we have
# ```{math}
# :label: J_C1
# J_{\text{C1}} = X_{\text{C1}} \left( K_{eq,\text{C1}}^\prime [\text{NADH}^{2-}]_x [\text{Q}]_x - [\text{NAD}^{-}]_x [\text{QH}_2]_x \right),
# ```
# for $X_\text{C1} \ \text{(mol s}^{-1} \text{ (L mito)}^{-1})$ the a rate constant. {numref}`table-ETC` lists the constants for complex I.
# ### ETC complex III
#
#
# The reaction catalyzed by complex III reduces two cytochrome c proteins for every $\text{QH}_2$ oxidized
# ```{math}
# :label: reaction_C3
# (\text{QH}_2)_x + 2 \ (\text{c}_{ox}^{3+})_i + n_\text{C3} (\text{H}^+)_x \rightleftharpoons (\text{Q})_x + 2 \ (\text{c}_{red}^{2+})_i + 2 \ (\text{H}^{+})_c + n_\text{C3} (\text{H}^+)_c,
# ```
# where $\text{c}_{ox}^{3+}$ and $\text{c}_{red}^{2+}$ are the oxidized and reduced cytochrome c species and the subscript $i$ indicates that cytochrome c is confined to the IMS. This reaction is coupled with the transport of $n_{\text{C3}} = 2$ protons from the matrix to the cytosol against the electrochemical gradient. Thus, the Gibbs energy for the overall reaction given in Equation {eq}`reaction_C3` is
# ```{math}
# \Delta G_{\text{C3}} &= \Delta_r G_\text{C3} - n_\text{C3} \Delta G_\text{H} \nonumber \\
# &= \Delta_r G_{\text{C3}}^\circ + R{\rm T} \ln \left( \dfrac{ [\text{Q}]_x [\text{c}_{red}^{2+}]_i^2 }{ [\text{QH}_2]_x [\text{c}_{ox}^{3+}]_i^2} \cdot [\text{H}^{+}]_c^2 \right) + n_\text{C3} F \Delta \Psi -
# R{\rm T} \ln \left( \dfrac{ [\text{H}^{+}]_x }{ [\text{H}^{+}]_c} \right)^{n_\text{C3}} \nonumber \\
# &= \Delta_r G'^\circ_\text{C3} + R{\rm T} \ln \left( \dfrac{ [\text{Q}]_x [\text{c}_{red}^{2+}]_i^2 }{ [\text{QH}_2]_x [\text{c}_{ox}^{3+}]_i^2}\right) + n_\text{C3} F \Delta \Psi -
# R{\rm T} \ln \left( \dfrac{ [\text{H}^{+}]_x }{ [\text{H}^{+}]_c} \right)^{n_\text{C3}},
# ```
# where
# ```{math}
# \Delta_r G'^\circ_\text{C3} = \Delta_r G^\circ_\text{C3} + 2 R \text{T} \ln ([\text{H}^+]_c)
# ```
# is the apparent Gibbs energy for complex III. The apparent equilibrium constant is
# ```{math}
# :label: Kapp_C3
# K_{eq,\text{C3}}^\prime = \left( \dfrac{ [\text{Q}]_x [\text{c}_{red}^{2+}]_i^2 }{ [\text{QH}_2]_x [\text{c}_{ox}^{3+}]_i^2 } \right)_{eq} = \exp \left\{ \dfrac{ -(\Delta_r G'^\circ_\text{C3} + n_\text{C3} F
# \Delta \Psi )}{ R \text{T}} \right\} \left( \dfrac{ [\text{H}^{+}]_x}{ [\text{H}^{+}]_c} \right)^{n_\text{C3}}.
# ```
#
# To simulate the flux of complex III, $J_\text{C3} \ \text{(mol s}^{-1} \text{ (L mito)}^{-1})$, by mass-action kinetics, we have
# ```{math}
# :label: J_C3
# J_{\text{C3}} = X_{\text{C3}} \left( K_{eq,\text{C3}}^\prime [\text{QH}_2]_x [\text{c}_{ox}^{3+}]_i^2 - [\text{Q}]_x [\text{c}_{red}^{2+}]_i^2 \right),
# ```
# where $X_{\text{C3}} \ \text{(mol s}^{-1} \text{ (L mito)}^{-1})$ is the rate constant.
# ### ETC complex IV
#
# In the final step of the ETC catalyzed by complex IV, electrons are transferred from cytochrome c to oxygen, forming water
# ```{math}
# :label: reaction_C4
# 2 \ (\text{c}_{red}^{2+})_i + \frac{1}{2} (\text{O}_2)_x + 2 \ (\text{H}^{+})_c + n_\text{C4} ([\text{H}^+])_x \rightleftharpoons 2 \ (\text{c}^{3+}_{ox})_i + \text{H}_2\text{O} + n_\text{C4} ([\text{H}^+])_c,
# ```
# coupled with the translocation of $n_\text{C4} = 4$ protons across the IMM against against the electrochemical gradient. The Gibbs energy of the reaction in Equation {eq}`reaction_C4` is
# ```{math}
# \Delta G_\text{C4} &= \Delta_r G_\text{C4} - n_\text{C4} \Delta G_{\rm H} \nonumber \\
# &= \Delta_r G_{\text{C4}}^o + R{\rm T} \ln \left( \dfrac{ [\text{c}^{3+}_{ox}]^2_i }{ [\text{c}^{2+}_{red}]^2_i [\text{O}_2]^{1/2}_x } \cdot \dfrac{1}{[\text{H}^{+}]^2_c}\right) + n_{\text{C4}} F \Delta \Psi - R{\rm T} \ln \left( \dfrac{ [\text{H}^{+}]_x }{ [\text{H}^{+}]_c} \right)^{n_{\text{C4}}} \nonumber \\
# &= \Delta_r G'^\circ_{\text{C4}} + R{\rm T} \ln \left( \dfrac{ [\text{c}^{3+}_{ox}]^2_i }{ [\text{c}^{2+}_{red}]^2_i [\text{O}_2]^{1/2}_x } \right) + n_{\text{C4}} F \Delta \Psi - R{\rm T} \ln \left( \dfrac{ [\text{H}^{+}]_x }{ [\text{H}^{+}]_c} \right)^{n_{\text{C4}}},
# ```
# where
# ```{math}
# \Delta_r G'^\circ_\text{C4} = \Delta_r G^\circ_\text{C4} - 2 R \text{T} \ln([\text{H}^+]_c)
# ```
# is the apparent Gibbs energy for complex IV. The apparent equilibrium constant is
# ```{math}
# :label: Kapp_C4
# K_{eq,\text{C4}}^\prime = \left( \dfrac{ [\text{c}^{3+}_{ox}]_i^2 }{ [\text{c}^{2+}_{red}]_i^2 [\text{O}_2]_x^{1/2} } \right)_{eq} = \exp \left\{ \dfrac{-(\Delta_r G'^\circ_\text{C4} + n_\text{C4} F \Delta \Psi )}{ R \text{T} } \right\} \left( \dfrac{ [\text{H}^+]_x }{[\text{H}^+]_c} \right)^{n_\text{C4}}.
# ```
#
# To simulate the flux of complex IV, $J_{\text{C4}} \ \text{(mol s}^{-1} \text{ (L mito)}^{-1})$, we use mass-action kinetics and account for binding of oxygen to complex IV as
# ```{math}
# :label: J_C4
# J_{\text{C4}} = X_{\text{C4}} \left( \dfrac{1}{1 + \frac{k_{\text{O}_2}}{[\text{O}_2]
# }} \right) \left( \left(K_{eq,\text{C4}}^\prime\right)^{1/2} [\text{c}_{red}^{2+}]_i [\text{O}_2]_x^{1/4} - [\text{c}_{ox}^{3+}]_i \right),
# ```
# where $X_{\text{C4}} \ \text{(mol s}^{-1} \text{ (L mito)}^{-1})$ is the rate constant and $k_{\text{O}_2}$ is the $\text{O}_2$ binding constant (\ref{table-ETC}). For this study, we assume a partial pressure of $\text{O}_2$ at $25 \ \text{mmHg}$.
# The apparent equilibrium constants for the $\text{F}_0\text{F}_1$ ATPase (Equation {eq}`Kapp_F`), complex I (Equation {eq}`Kapp_C1`), complex III (Equation {eq}`Kapp_C3`), and complex IV (Equation {eq}`Kapp_C4`) depend on $\Delta\Psi$. In the model developed in this section, since $\Delta\Psi$ is a variable, these apparent equilibrium constants are also variables. Thus, the flux expressions in Equations {eq}`J_F`, {eq}`J_C1`, {eq}`J_C3`, and {eq}`J_C4` depend on $\Delta \Psi$. These expressions may be compared to a generalized formulation of rate laws for reversible enzyme-catalyzed reactions {cite}`Noor2013`, where in this case the saturating dependence of flux on substrate concentrations is not accounted for. These expressions may also be compared to the more detailed representations of the underlying catalytic mechanisms used by Bazil et al. {cite}`Bazil2016`. The Bazil et al. model also accounts for side reactions generating reactive oxygen species that are not accounted for here.
# ### Dehydrogenase activity
#
# In this model, we do not explicitly simulate the reactions of the TCA cycle or beta oxidation, but rather the combined action of NADH-producing reactions, that is,
# ```{math}
# (\text{NAD}^{-})_x \rightleftharpoons (\text{NADH}^{2-})_x + (\text{H}^{+})_x
# ```
# From Beard {cite}`Beard2005`, we represent a Pi dependence of NADH production using the following phenomenological expression
# ```{math}
# :label: J_DH
# J_{\text{DH}} = X_{\text{DH}} \left( r [\text{NAD}^-] - [\text{NADH}^{2-}] \right) \left( \dfrac{ 1 + [\Sigma \text{Pi}]_x/k_{\text{Pi},1} }{ 1 + [\Sigma \text{Pi}]_x/k_{\text{Pi},2} } \right),
# ```
# where $X_\text{DH} \text{ (mol s}^{-1} \text{ (L mito)}^{-1})$ is the dehydrogenase activity and $r$ (dimensionless), $k_{\text{Pi},1} \ \text{(mol (L matrix water)}^{-1})$, and $k_{\text{Pi},2} \ \text{(mol (L matrix water)}^{-1})$ are constants. Parameter values are listed in Table {numref}`table-ETC`. The dependence of NADH production on Pi reflects the Pi-dependence of the substrate-level phosphorylation step of the TCA cycle (the succinyl coenzyme-A synthetase reaction) and the fact that Pi drives substrate oxidation via the dicarboxylate carrier.
# ### Proton leak
#
# To simulate proton leak across the IMM, we adopt the Goldman-Hodgkins-Katz formulation from Wu et al. {cite}`Wu2008`,
# ```{math}
# :label: J_H
# J_{\text{H}} = X_\text{H} \left( [\text{H}^{+}]_c \ e^{\phi/2} - [\text{H}^{+}]_x \ e^{-\phi/2} \right)
# ```
# where $X_\text{H} = 1000 \ \text{mol s}^{-1} \text{ (L mito)}^{-1}$ is the proton leak activity and $\phi$ is given in Equation {eq}`phi`. Even though the kinetic constants $X_\text{F}$ and $X_\text{H}$ attain equal values here, under the ATP-producing conditions the proton flux through the $\text{F}_0\text{F}_1$ ATPase ($J_\text{F}$, Equation {eq}`J_F`) is an order of magnitude greater than the proton leak flux ($J_\text{H}$, Equation {eq}`J_H`).
# ```{list-table} Respiratory complex and inorganic phosphate transport parameters
# :header-rows: 1
# :name: table-ETC
#
# * - Parameter
# - Units
# - Description
# - Value
# - Source
# * - $n_{\text{C}1}$
# -
# - Protons translocated by complex I
# - $4 $
# - {cite}`Nicholls2013`
# * - $n_{\text{C}3}$
# -
# - Protons translocated by complex III
# - $2 $
# - {cite}`Nicholls2013`
# * - $n_{\text{C}4}$
# -
# - Protons translocated by complex IV
# - $4 $
# - {cite}`Nicholls2013`
# * - $X_\text{C1}$
# - mol s$^{-1}$ (L mito)$^{-1}$
# - Complex I rate constant
# - $1\text{e}4$
# -
# * - $X_\text{C3}$
# - mol s$^{-1}$ (L mito)$^{-1}$
# - Complex III rate constant
# - $1\text{e}6$
# -
# * - $X_\text{C4}$
# - mol s$^{-1}$ (L mito)$^{-1}$
# - Complex IV rate constant
# - $0.0125$
# -
# * - $X_\text{DH}$
# - mol s$^{-1}$ (L mito)$^{-1}$
# - NADH dehydrogenase rate constant
# - $0.1732$
# -
# * - $X_\text{H}$
# - mol s$^{-1}$ (L mito)$^{-1}$
# - Proton leak activity
# - $1\text{e}3$
# -
# * - $r$
# -
# - Dehydrogenase parameter
# - $6.8385 $
# -
# * - $k_{\text{Pi},1}$
# - mmol (L matrix water)$^{-1}$
# - Dehydrogenase parameter
# - $0.466 $
# -
# * - $k_{\text{Pi},2}$
# - mmol (L matrix water)$^{-1}$
# - Dehydrogenase parameter
# - $0.658 $
# -
# * - $k_{\text{PiC}}$
# - mmol (L cell)$^{-1}$
# - PiC constant
# - $1.61$
# - {cite}`Bazil2016`
# * - $k_{\text{O}_2}$
# - $\mu$mol (L matrix water)$^{-1}$
# - O$_2$ binding constant
# - $120$
# - {cite}`Wu2007`
# * - $\Delta_r G^o_\text{C1}$
# - kJ mol$^{-1}$
# - Gibbs energy of reaction for complex I
# - $ -109.7 $
# - {cite}`Li2011`
# * - $\Delta_r G^o_\text{C3}$
# - kJ mol$^{-1}$
# - Gibbs energy of reaction for complex III
# - $46.7 $
# - {cite}`Li2011`
# * - $\Delta_r G^o_\text{C4}$
# - kJ mol$^{-1}$
# - Gibbs energy of reaction for complex IV
# - $ -202.2 $
# - {cite}`Li2011`
# * - $[\text{NAD}]_{tot}$
# - mmol (L matrix water)$^{-1}$
# - Total NAD pool in the matrix
# - $2.97$
# - {cite}`Wu2007`
# * - $[\text{Q}]_{tot}$
# - mmol (L matrix water)$^{-1}$
# - Total Q pool in the matrix
# - $1.35$
# - {cite}`Wu2007`
# * - $[\text{c}]_{tot}$
# - mmol (L IM water)$^{-1}$
# - Total cytochrome c pool in the IMS
# - $2.70$
# - {cite}`Wu2007`
# ```
# ## Simulating ATP synthesis in vitro
#
# The flux expressions developed above may be used to simulate mitochondrial ATP synthesis in vitro, governed by the system of equations
# ```{math}
# :label: system-singlemito
# \left\{
# \renewcommand{\arraystretch}{2.5}
# \begin{array}{rl}
# \dfrac{ {\rm d} \Delta \Psi }{{\rm d} t} & = ( n_\text{C1} J_\text{C1} + n_\text{C3} J_\text{C3} + n_\text{C4} J_\text{C4} - n_\text{F} J_\text{F} - J_\text{ANT} - J_\text{H}) / C_m \\
# \hline
# \dfrac{ {\rm d} [\Sigma \text{ATP}]_x }{{\rm d} t} &= (J_\text{F} - J_\text{ANT} ) / W_x \\
# \dfrac{ {\rm d} [\Sigma \text{ADP}]_x }{{\rm d} t} &= (-J_\text{F} + J_\text{ANT}) / W_x \\
# \dfrac{ {\rm d} [\Sigma \text{Pi}]_x }{{\rm d} t} &= (-J_\text{F} + J_\text{PiC}) / W_x \quad \text{matrix species}\\
# \dfrac{ {\rm d} [\text{NADH}^{2-}]_x }{{\rm d} t} &= (J_\text{DH} - J_\text{C1}) / W_x \\
# \dfrac{ {\rm d} [\text{QH}_2]_x }{{\rm d} t} &= (J_\text{C1} - J_\text{C3}) / W_x \\
# \hline
# \dfrac{ {\rm d} [\text{c}_{red}^{2+}]_i}{{\rm d} t} &= 2(J_\text{C3} - J_\text{C4}) / W_i \quad \text{intermembrane space species}\\
# \hline
# \dfrac{ {\rm d} [\Sigma \text{ATP}]_c }{{\rm d} t} &= (V_{m2c} J_\text{ANT} - J_\text{AtC} )/ W_c \\
# \dfrac{ {\rm d} [\Sigma \text{ADP}]_c }{{\rm d} t} &= (-V_{m2c} J_\text{ANT} + J_\text{AtC} ) / W_c \quad \text{cytosol species}\\
# \dfrac{ {\rm d} [\Sigma \text{Pi}]_c }{{\rm d} t} &= (- V_{m2c} J_\text{PiC} + J_\text{AtC}) / W_c,
# \end{array}
# \renewcommand{\arraystretch}{1}
# \right.
# ```
# where the fluxes $J_\text{F}$ (Equation {eq}`J_F`), $J_\text{ANT}$ (Equation {eq}`J_ANT`), $J_\text{PiC}$ (Equation {eq}`J_PiC`), $J_\text{C1}$ (Equation {eq}`J_C1`), $J_\text{C3}$ (Equation {eq}`J_C3`), $J_\text{C4}$ (Equation {eq}`J_C4`), $J_\text{DH}$ (Equation {eq}`J_DH`), and $J_\text{H}$ (Equation {eq}`J_H`) are given above and the constants are listed in Tables {numref}`table-biophysicalconstants` and {numref}`table-ETC`. Here, we incorporate a constant ATP consumption flux, $J_\text{AtC} \ \text{(mol s}^{-1} \text{ (L cyto)}^{-1})$, that is
# ```{math}
# J_\text{AtC} = X_\text{AtC}/V_c
# ```
# where $V_c$ is the ratio of the volume of cytosol per L cell. $X_\text{AtC}$ is the ATP consumption rate expressed in units of mmol s$^{-1}$ (L cell)$^{-1}$. Equation {eq}`system-singlemito` does not explicitly treat matrix or external $\text{pH}$, $\text{K}^+$, $\text{Mg}^{2+}$, or $\text{O}_2$ as variables. Reasonable clamped concentrations for these variables are ${\rm pH}_x = 7.4$, ${\rm pH}_c = 7.2$, $[\text{Mg}^{2+}]_x = 1 \ \text{mmol (L matrix water)}^{-1}$, $[\text{Mg}^{2+}]_c = 1 \ \text{mmol (L cyto water)}^{-1}$, $[\text{K}^{+}]_x = 100 \ \text{mmol (L matrix water)}^{-1}$, and $[K^{+}]_c = 140 \ \text{mmol (L cyto water)}^{-1}$, and $\text{O}_2$ partial pressure of $25 \ \text{mmHg}$. Respiratory chain reactants are determined from a total concentration of metabolites within the mitochondrion, that is, the total pools for NAD, cytochrome c, and Q species are
# ```{math}
# [\text{NAD}]_{tot} &= [\text{NAD}^-]_x + [\text{NADH}^{2-}]_x \\
# [\text{c}]_{tot} &= [\text{c}^{2+}_{red}]_i + [\text{c}^{3+}_{ox}]_i, \quad \text{and} \\
# [\text{Q}]_{tot} &= [\text{Q}]_x + [\text{QH}_2]_x.
# ```
# The pools are $[\text{NAD}]_{tot} = 2.97 \ \text{mmol (L matrix water)}^{-1}$, $[\text{c}]_{tot} = 2.7 \ \text{mmol (L IMS water)}^{-1}$, and $[\text{Q}]_{tot} = 1.35$ $\text{mmol}~\text{(L matrix water)}^{-1}$. The finite nature of these metabolite pools constrains the maximal concentrations of substrates available for complexes I, III, and IV. Thus, although the simple mass-action models for these complexes do not account for saturable enzyme kinetics, the fluxes are limited by the availability of substrates. Initial conditions are set under the assumption that the TAN for both the matrix and cytosol is $10 \ \text{mM}$, but the ATP/ADP ratio is $<$$1$ in the matrix and $\sim$$100$ in the cytosol. The following code simulates in vitro mitochondrial function without ATP consumption in the external (cytosolic space).
#
# +
import numpy as np
import matplotlib.pyplot as plt
# !pip install scipy
from scipy.integrate import solve_ivp
###### Constants defining metabolite pools ######
# Volume fractions and water space fractions
V_c = 0.6601 # cytosol volume fraction # L cyto (L cell)**(-1)
V_m = 0.2882 # mitochondrial volume fraction # L mito (L cell)**(-1)
V_m2c = V_m / V_c # mito to cyto volume ratio # L mito (L cuvette)**(-1)
W_c = 0.8425 # cytosol water space # L cyto water (L cyto)**(-1)
W_m = 0.7238 # mitochondrial water space # L mito water (L mito)**(-1)
W_x = 0.9*W_m # matrix water space # L matrix water (L mito)**(-1)
W_i = 0.1*W_m # intermembrane water space # L IM water (L mito)**(-1)
# Total pool concentrations
NAD_tot = 2.97e-3 # NAD+ and NADH conc # mol (L matrix water)**(-1)
Q_tot = 1.35e-3 # Q and QH2 conc # mol (L matrix water)**(-1)
c_tot = 2.7e-3 # cytochrome c ox and red conc # mol (L IM water)**(-1)
# Membrane capacitance ()
Cm = 3.1e-3
###### Set fixed pH, cation concentrations, and O2 partial pressure ######
# pH
pH_x = 7.40
pH_c = 7.20
# K+ concentrations
K_x = 100e-3 # mol (L matrix water)**(-1)
K_c = 140e-3 # mol (L cyto water)**(-1)
# Mg2+ concentrations
Mg_x = 1.0e-3 # mol (L matrix water)**(-1)
Mg_c = 1.0e-3 # mol (L cyto water)**(-1)
# Oxygen partial pressure
PO2 = 25 # mmHg
###### Parameter vector ######
X_DH = 0.1732
X_C1 = 1.0e4
X_C3 = 1.0e6
X_C4 = 0.0125
X_F = 1.0e3
E_ANT = 0.325
E_PiC = 5.0e6
X_H = 1.0e3
X_AtC = 0
activity_array = np.array([X_DH, X_C1, X_C3, X_C4, X_F, E_ANT, E_PiC, X_H, X_AtC])
###### Initial Conditions ######
# Membrane Potential
DPsi_0 = 175/1000 # V
# Matrix species
sumATP_x_0 = 0.5e-3 # mol (L matrix water)**(-1)
sumADP_x_0 = 9.5e-3 # mol (L matrix water)**(-1)
sumPi_x_0 = 1.0e-3 # mol (L matrix water)**(-1)
NADH_x_0 = 2/3 * NAD_tot # mol (L matrix water)**(-1)
QH2_x_0 = 0.1 * Q_tot # mol (L matrix water)**(-1)
# IMS species
cred_i_0 = 0.1 * c_tot # mol (L IMS water)**(-1)
# Cytosolic species
sumATP_c_0 = 0 # mol (L cyto water)**(-1)
sumADP_c_0 = 10e-3 # mol (L cyto water)**(-1)
sumPi_c_0 = 10e-3 # mol (L cyto water)**(-1)
X_0 = np.array([DPsi_0, sumATP_x_0, sumADP_x_0, sumPi_x_0, NADH_x_0, QH2_x_0, cred_i_0, sumATP_c_0, sumADP_c_0, sumPi_c_0])
def dXdt(t, X, activity_array, solve_ode):
# Unpack variables
DPsi, sumATP_x,sumADP_x, sumPi_x, NADH_x, QH2_x, cred_i, sumATP_c, sumADP_c, sumPi_c = X
X_DH, X_C1, X_C3, X_C4, X_F, E_ANT, E_PiC, X_H, X_AtC = activity_array
# Hydrogen ion concentration
H_x = 10**(-pH_x) # mol (L matrix water)**(-1)
H_c = 10**(-pH_c) # mol (L cuvette water)**(-1)
# Oxygen concentration
a_3 = 1.74e-6 # oxygen solubility in cuvette # mol (L matrix water * mmHg)**(-1)
O2_x = a_3*PO2 # mol (L matrix water)**(-1)
# Thermochemical constants
R = 8.314 # J (mol K)**(-1)
T = 37 + 273.15 # K
F = 96485 # C mol**(-1)
# Proton motive force parameters (dimensionless)
n_F = 8/3
n_C1 = 4
n_C3 = 2
n_C4 = 4
# Dissociation constants
K_MgATP = 10**(-3.88)
K_HATP = 10**(-6.33)
K_KATP = 10**(-1.02)
K_MgADP = 10**(-3.00)
K_HADP = 10**(-6.26)
K_KADP = 10**(-0.89)
K_MgPi = 10**(-1.66)
K_HPi = 10**(-6.62)
K_KPi = 10**(-0.42)
# Other concentrations computed from the state variables:
NAD_x = NAD_tot - NADH_x # mol (L matrix water)**(-1)
Q_x = Q_tot - QH2_x # mol (L matrix water)**(-1)
cox_i = c_tot - cred_i # mol (L matrix water)**(-1)
## Binding polynomials
# Matrix species # mol (L mito water)**(-1)
PATP_x = 1 + H_x/K_HATP + Mg_x/K_MgATP + K_x/K_KATP
PADP_x = 1 + H_x/K_HADP + Mg_x/K_MgADP + K_x/K_KADP
PPi_x = 1 + H_x/K_HPi + Mg_x/K_MgPi + K_x/K_KPi
# Cytosol species # mol (L cuvette water)**(-1)
PATP_c = 1 + H_c/K_HATP + Mg_c/K_MgATP + K_c/K_KATP
PADP_c = 1 + H_c/K_HADP + Mg_c/K_MgADP + K_c/K_KADP
PPi_c = 1 + H_c/K_HPi + Mg_c/K_MgPi + K_c/K_KPi
## Unbound species
# Matrix species
ATP_x = sumATP_x / PATP_x # [ATP4-]_x
ADP_x = sumADP_x / PADP_x # [ADP3-]_x
Pi_x = sumPi_x / PPi_x # [HPO42-]_x
# Cytosolic species
ATP_c = sumATP_c / PATP_c # [ATP4-]_c
ADP_c = sumADP_c / PADP_c # [ADP3-]_c
Pi_c = sumPi_c / PPi_c # [HPO42-]_c
###### NADH Dehydrogenase ######
# Constants
r = 6.8385
k_Pi1 = 4.659e-4 # mol (L matrix water)**(-1)
k_Pi2 = 6.578e-4 # mol (L matrix water)**(-1)
# Flux
J_DH = X_DH * (r * NAD_x - NADH_x) * ((1 + sumPi_x / k_Pi1) / (1+sumPi_x / k_Pi2))
###### Complex I ######
# NADH_x + Q_x + 5H+_x <-> NAD+_x + QH2_x + 4H+_i + 4DPsi
# Gibbs energy (J mol**(-1))
DrGo_C1 = -109680
DrGapp_C1 = DrGo_C1 - R * T * np.log(H_x)
# Apparent equilibrium constant
Kapp_C1 = np.exp( -(DrGapp_C1 + n_C1 * F * DPsi) / (R * T)) * ((H_x / H_c)**n_C1)
# Flux (mol (s * L mito)**(-1))
J_C1 = X_C1 * (Kapp_C1 * NADH_x * Q_x - NAD_x * QH2_x)
###### Complex III ######
# QH2_x + 2cuvetteC(ox)3+_i + 2H+_x <-> Q_x + 2cuvetteC(red)2+_i + 4H+_i + 2DPsi
# Gibbs energy (J mol**(-1))
DrGo_C3 = 46690
DrGapp_C3 = DrGo_C3 + 2 * R * T * np.log(H_c)
# Apparent equilibrium constant
Kapp_C3 = np.exp(-(DrGapp_C3 + n_C3 * F * DPsi) / (R * T)) * (H_x / H_c)**n_C3
# Flux (mol (s * L mito)**(-1))
J_C3 = X_C3 * (Kapp_C3 * cox_i**2 * QH2_x - cred_i**2 * Q_x)
###### Complex IV ######
# 2 cytoC(red)2+_i + 0.5O2_x + 4H+_x <-> cytoC(ox)3+_x + H2O_x + 2H+_i +2DPsi
# Constant
k_O2 = 1.2e-4 # mol (L matrix water)**(-1)
# Gibbs energy (J mol**(-1))
DrGo_C4 = -202160 # J mol**(-1)
DrGapp_C4 = DrGo_C4 - 2 * R * T * np.log(H_c)
# Apparent equilibrium constant
Kapp_C4 = np.exp(-(DrGapp_C4 + n_C4 * F * DPsi) / (R * T)) * (H_x / H_c)**n_C4
# Flux (mol (s * L mito)**(-1))
J_C4 = X_C4 *(Kapp_C4**0.5 * cred_i * O2_x**0.25 - cox_i) * (1 / (1 + k_O2 / O2_x))
###### F1F0-ATPase ######
# ADP3-_x + HPO42-_x + H+_x + n_A*H+_i <-> ATP4- + H2O + n_A*H+_x
# Gibbs energy (J mol**(-1))
DrGo_F = 4990
DrGapp_F = DrGo_F + R * T * np.log( H_x * PATP_x / (PADP_x * PPi_x))
# Apparent equilibrium constant
Kapp_F = np.exp( (DrGapp_F + n_F * F * DPsi ) / (R * T)) * (H_c / H_x)**n_F
# Flux (mol (s * L mito)**(-1))
J_F = X_F * (Kapp_F * sumADP_x * sumPi_x - sumATP_x)
###### ANT ######
# ATP4-_x + ADP3-_i <-> ATP4-_i + ADP3-_x
# Constants
del_D = 0.0167
del_T = 0.0699
k2o_ANT = 9.54/60 # s**(-1)
k3o_ANT = 30.05/60 # s**(-1)
K0o_D = 38.89e-6 # mol (L cuvette water)**(-1)
K0o_T = 56.05e-6 # mol (L cuvette water)**(-1)
A = +0.2829
B = -0.2086
C = +0.2372
phi = F * DPsi / (R * T)
# Reaction rates
k2_ANT = k2o_ANT * np.exp((A*(-3) + B*(-4) + C)*phi)
k3_ANT = k3o_ANT * np.exp((A*(-4) + B*(-3) + C)*phi)
# Dissociation constants
K0_D = K0o_D * np.exp(3*del_D*phi)
K0_T = K0o_T * np.exp(4*del_T*phi)
q = k3_ANT * K0_D * np.exp(phi) / (k2_ANT * K0_T)
term1 = k2_ANT * ATP_x * ADP_c * q / K0_D
term2 = k3_ANT * ADP_x * ATP_c / K0_T
num = term1 - term2
den = (1 + ATP_c/K0_T + ADP_c/K0_D) * (ADP_x + ATP_x * q)
# Flux (mol (s * L mito)**(-1))
J_ANT = E_ANT * num / den
###### H+-PI2 cotransporter ######
# H2PO42-_x + H+_x = H2PO42-_c + H+_c
# Constant
k_PiC = 1.61e-3 # mol (L cuvette)**(-1)
# H2P04- species
HPi_c = Pi_c * (H_c / K_HPi)
HPi_x = Pi_x * (H_x / K_HPi)
# Flux (mol (s * L mito)**(-1))
J_PiC = E_PiC * (H_c * HPi_c - H_x * HPi_x) / (k_PiC + HPi_c)
###### H+ leak ######
# Flux (mol (s * L mito)**(-1))
J_H = X_H * (H_c * np.exp(phi/2) - H_x * np.exp(-phi/2))
###### ATPase ######
# ATP4- + H2O = ADP3- + PI2- + H+
#Flux (mol (s * L cyto)**(-1))
J_AtC = X_AtC / V_c
###### Differential equations (equation 23) ######
# Membrane potential
dDPsi = (n_C1 * J_C1 + n_C3 * J_C3 + n_C4 * J_C4 - n_F * J_F - J_ANT - J_H) / Cm
# Matrix species
dATP_x = (J_F - J_ANT) / W_x
dADP_x = (-J_F + J_ANT) / W_x
dPi_x = (-J_F + J_PiC) / W_x
dNADH_x = (J_DH - J_C1) / W_x
dQH2_x = (J_C1 - J_C3) / W_x
# IMS species
dcred_i = 2 * (J_C3 - J_C4) / W_i
# Buffer species
dATP_c = ( V_m2c * J_ANT - J_AtC ) / W_c
dADP_c = (-V_m2c * J_ANT + J_AtC ) / W_c
dPi_c = (-V_m2c * J_PiC + J_AtC) / W_c
dX = [dDPsi, dATP_x, dADP_x, dPi_x, dNADH_x, dQH2_x, dcred_i, dATP_c, dADP_c, dPi_c]
# Calculate state-dependent quantities after model is solved
if solve_ode == 1:
return dX
else:
J = np.array([PATP_x, PADP_x, PPi_x, PATP_c, PADP_c, PPi_c, J_DH, J_C1, J_C3, J_C4, J_F, J_ANT, J_PiC, DrGapp_F])
return dX, J
# Time vector
t = np.linspace(0,5,100)
# Solve ODE
results = solve_ivp(dXdt, [0, 5], X_0, method = 'Radau', t_eval=t, args=(activity_array,1))
DPsi, sumATP_x,sumADP_x, sumPi_x, NADH_x, QH2_x, cred_i, sumATP_c, sumADP_c, sumPi_c = results.y
# Plot figures
fig, ax = plt.subplots(1,2, figsize = (10,5))
ax[0].plot(t, sumATP_x*1000, label = '[$\Sigma$ATP]$_x$')
ax[0].plot(t, sumADP_x*1000, label = '[$\Sigma$ADP]$_x$')
ax[0].plot(t, sumPi_x*1000, label = '[$\Sigma$Pi]$_x$')
ax[0].legend(loc="right")
ax[0].set_xlabel('Time (s)')
ax[0].set_ylabel('Concentration (mM)')
ax[0].set_ylim((-.5,10.5))
ax[1].plot(t, sumATP_c*1000, label = '[$\Sigma$ATP]$_c$')
ax[1].plot(t, sumADP_c*1000, label = '[$\Sigma$ADP]$_c$')
ax[1].plot(t, sumPi_c*1000, label = '[$\Sigma$Pi]$_c$')
ax[1].legend(loc="right")
ax[1].set_xlabel('Time (s)')
ax[1].set_ylabel('Concentration (mM)')
ax[1].set_ylim((-.5,10.5))
plt.show()
# -
# **Figure 7:** Steady state solution from Equation {eq}`system-singlemito` for the (a) matrix and (b) cytosol species with $\text{pH}_x = 7.4$ and $\text{pH}_c = 2$.
# The above simulations reach a final steady state where the phosphate metabolite concentrations are $[\text{ATP}]_x = 0.9 \ \text{mM}$, $[\text{ADP}]_x = 9.1 \ \text{mM} $, $[\text{Pi}]_x = 0.4 \ \text{mM}$, $[\text{ATP}]_c = 9.9 \ \text{mM}$, $[\text{ADP}]_c = 0.1 \ \text{mM}$, $[\text{Pi}]_c = 0.2 \ \text{mM}$, and the membrane potential is $186 \ \text{mV}$. This state represents a *resting* energetic state with no ATP hydrolysis in the cytosol. The Gibbs energy of ATP hydrolysis associated with this predicted state is $\Delta G_{\rm ATP} = \text{-}70 \ \text{kJ mol}^{-1}$, as calculated below.
# +
sumATP_c_ss = sumATP_c[-1]
sumADP_c_ss = sumADP_c[-1]
sumPi_c_ss = sumPi_c[-1]
H_c = 10**(-pH_c) # mol (L cuvette water)**(-1)
# Thermochemical constants
R = 8.314 # J (mol K)**(-1)
T = 37 + 273.15 # K
# Dissociation constants
K_MgATP = 10**(-3.88)
K_HATP = 10**(-6.33)
K_KATP = 10**(-1.02)
K_MgADP = 10**(-3.00)
K_HADP = 10**(-6.26)
K_KADP = 10**(-0.89)
K_MgPi = 10**(-1.66)
K_HPi = 10**(-6.62)
K_KPi = 10**(-0.42)
## Binding polynomials
# Cytosol species # mol (L cuvette water)**(-1)
PATP_c = 1 + H_c/K_HATP + Mg_c/K_MgATP + K_c/K_KATP
PADP_c = 1 + H_c/K_HADP + Mg_c/K_MgADP + K_c/K_KADP
PPi_c = 1 + H_c/K_HPi + Mg_c/K_MgPi + K_c/K_KPi
DrGo_ATP = 4990
# Use equation 9 to calcuate apparent reference cytosolic Gibbs energy
DrGo_ATP_apparent = DrGo_ATP + R * T * np.log(H_c * PATP_c / (PADP_c * PPi_c))
# Use equation 9 to calculate cytosolic Gibbs energy
DrG_ATP = DrGo_ATP_apparent + R * T * np.log((sumADP_c_ss * sumPi_c_ss / sumATP_c_ss))
print('Cytosolic Gibbs energy of ATP hydrolysis (kJ mol^(-1))')
print(DrG_ATP / 1000)
# -
| QAMAS/_build/html/_sources/BuildingModel.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Bibliotecas
# +
# Importar as bibliotecas
# Análise Exploratória de dados
import pandas as pd
import numpy as np
# Visualização
from matplotlib import pyplot as plt
import seaborn as sns
# Pré-processamento e modelos
from sklearn.preprocessing import MinMaxScaler
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import RFE
from sklearn.metrics import classification_report, confusion_matrix, roc_auc_score
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import cross_val_score
from sklearn.metrics import f1_score
from sklearn.feature_selection import SelectKBest, chi2, f_classif
from sklearn import metrics
from sklearn.model_selection import train_test_split, cross_validate, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.naive_bayes import GaussianNB
from lightgbm import LGBMClassifier
import lightgbm as lgbm
pd.set_option("display.max_columns",None) # mostrar todas as colunas
pd.set_option("display.max_rows",None) # mostrar todas as linhas
# -
# 1. Entendimento do negócio
# 1.1. Situação
# - Os clientes são a base de uma instituição financeira. Portanto, é muito importante para uma instituição prever se os seus clientes irão ou não abandonar (churn) o seu serviço. Assim, quanto melhor for a predição, melhor será o direcionamento, por exemplo, em ações financeiras e em ações de marketing para evitar que o cliente abandone a instituição.
# 1.2. Objetivo:
# - Prever o abandono de clientes (churn) de uma instituição financeira
# 1.3. Etapas usadas para solucionar o problema acima:
#
# - Entendimento do negócio (que foi descrito acima);
# - Entendimento dos dados;
# - Preparação dos dados;
# - Modelagem e Avaliação;
# - Previsão.
# 2. Entendimento dos dados (Explorar os conjuntos de dados)
# - 2.1. Importar os conjuntos de dados;
# - 2.2. Informações sobre os conjuntos de dados;
# - 2.3. Estatística das variáveis.
# 2.1. Importar os conjuntos de dados (datasets)
# 2.1.1. Importar o conjunto de dados (dataset) nomeado Abandono_clientes (dados de treino)
df_treino = pd.read_csv("Abandono_clientes.csv", na_values="na")
# 2.1.2. Importar a conjunto de dados (dataset) nomeado Abandono_teste (dados teste). Representam dados que nunca foram vistos
df_teste = pd.read_csv("Abandono_teste.csv",na_values="na")
# 2.2. Informações sobre os conjuntos de dados
# 2.2.1. Dados de treino
df_treino.head() # visualizar as cinco primeiras linhas do conjunto de dados treino
display(df_treino.dtypes) # tipo de cada coluna do conjunto de dados de treino
# 2.2.2 Dados de teste
df_teste.head() # visualizar as cinco primeiras linhas do conjunto de dados
# Conforme mostra acima, todas as informações estão em uma única entrada de coluna. Isso ocorreu porque o read_csv usa um parâmetro sep onde o padrão é ",". Acima as colunas estão separadas por ";", assim, usar sep=";"
df_teste = pd.read_csv("Abandono_teste.csv",sep=';', na_values="na")
df_teste.head()
display(df_teste.dtypes) # tipo de cada coluna do conjunto de dados
# Nos conjuntos de dados acima, cada coluna representa uma informação/variável sobre o cliente.
# Questão 1. O que significa cada variável? Qual é o tipo de cada variável?
#
# a) Variáveis numéricas (int64 ou float64)
# - RowNumber: número de linhas (int64)
# - CustomerId: Id do cliente (int64)
# - CreditScore: score (pontuação) de crédito do cliente (int64)
# - Age: idade do cliente (int64)
# - Tenure: tempo de vínculo do cliente com a instituição financeira (int64). Observação: no conjunto de dados não consta a medida de tempo (são meses ou anos). Vou considerar anos.
# - Balance: montante em dinheiro disponível na conta do cliente (float64). Observação: no conjunto de dados não cosnta a moeda (é dolár, euro, libra, etc). Vou considerar euros, uma vez que os clientes estão localizados em países da Europa.
# - NumbOfProducts: número de produtos da instituição financeira que o cliente possui (int64)
# - HasCrCard: o cliente tem cartão de crédito? 0 = não e 1 = sim (int64)
# - IsActiveMember: o cliente é um membro ativo? 0 = não e 1 = sim (int64)
# - EstimatedSalary: salário estimado do cliente (float64)
# - Exited: o cliente abandonou a instituição financeira? 0 = não e 1 = sim (int64)
#
# b) Variáveis categóricas (object)
# - Surname: sobrenome do cliente
# - Geography: localização do cliente
# - Gender: gênero do cliente (male = masculino e female = feminino)
# Questão 2. Qual a quantidade de variáveis e clientes?
# quantificar as variáveis e clientes do conjunto de dados de treino
print("Número de variáveis:\t {}".format(df_treino.shape[1]))
print("Número de clientes:\t {}".format(df_treino.shape[0]))
# quantificar as variáveis e clientes do conjunto de dados de teste
print("Número de variáveis:\t {}".format(df_teste.shape[1]))
print("Número de clientes:\t {}".format(df_teste.shape[0]))
# Questão 3. Existem valores ausentes nos conjuntos de dados? Qual a quantidade de valores únicos em cada variável?
# criar um dataframe informando a quantidade de valores ausentes e de valores únicos para cada varíavel do conjunto de dados de treino
pd.DataFrame({"Valores Ausentes": df_treino.isna().mean(),
"Valores Únicos": df_treino.nunique()})
# criar um dataframe informando a quantidade de valores ausentes e de valores únicos para cada varíavel do conjunto de dados de teste
pd.DataFrame({"Valores Ausentes": df_teste.isna().mean(),
"Valores Únicos": df_teste.nunique()})
# - Não existem valores ausentes nos conjuntos de dados
# - E quanto aos valores únicos, é sempre bom verificar, especialmente para as variáveis (i) HasCrCard, IsActiveMember e Exited que precisam conter dois tipos de informação (valor): 1 ou 0 e (ii) gender: female ou male. Logo, a quantidade de valores únicos (ou seja, total unitário) precisa ser 2.
# Questão 4. Existem variáveis que não trazem nenhuma informação útil para o objetivo do projeto (prever o churn "abondono de clientes" da instituição financeira)?
# Sim! São as variáveis RowNumber, CustomerId e Surname. Portanto, retirar tais variáveis dos conjuntos de dados. Tais variáveis são apenas para ajudar no gerenciamento do banco de dados da instituição financeira.
print("Número de variáveis:\t {}".format(df_treino.shape[1]))
df_treino= df_treino.drop(columns=["RowNumber","CustomerId","Surname"])
print("Número de variáveis:\t {}".format(df_treino.shape[1])) # verificar se as variáveis foram removidas
df_treino.head() # conjunto de dados de treino sem as variáveis RowNumber, CustomerId e Surname
print("Número de variáveis:\t {}".format(df_teste.shape[1]))
df_teste= df_teste.drop(columns=["RowNumber","CustomerId","Surname"])
print("Número de variáveis:\t {}".format(df_teste.shape[1]))
df_teste.head() # conjunto de dados de teste sem as variáveis RowNumber, CustomerId e Surname
# Questão 5. Existem valores duplicados?
novo_df_treino = df_treino.drop_duplicates() # remover as linhas duplicadas
duplicadas_df_treino = novo_df_treino[novo_df_treino.duplicated()] # calcular o total de linhas duplicadas
print(f"Total de linhas duplicadas: {len(duplicadas_df_treino)}")
novo_df_teste = df_teste.drop_duplicates() # remover as linhas duplicadas
duplicadas_df_teste = novo_df_teste[novo_df_teste.duplicated()] # calcular o total de linhas duplicadas
print(f"Total de linhas duplicadas: {len(duplicadas_df_teste)}")
# Não! Os conjuntos de dados não possuem valores duplicados.
# Questão 6. Existem outliers (valores discrepantes)?
# Variáveis numéricas
sns.boxplot(x="CreditScore",data=df_treino)
# Variáveis numéricas
sns.boxplot(x="Age",data=df_treino)
# Variáveis numéricas
sns.boxplot(x="Tenure",data=df_treino)
# Variáveis numéricas
sns.boxplot(x="Balance",data=df_treino)
# Variáveis numéricas
sns.boxplot(x="NumOfProducts",data=df_treino)
# Variáveis numéricas
sns.boxplot(x="EstimatedSalary",data=df_treino)
# Observação geral sobre a presença de outliers:
# - EstimatedSalary, Balance, Tenure não possuem outliers;
# - NumOfProducts, Age e CreditScore possuem outliers.
#
#
# Outliers podem causar ruídos na análise de dados, ou seja, viesar a(s) análise(s) subsequentes. Então, o que fazer com os outliers?
#
# Listo algumas estratégias:
# - entrar em contato com a equipe responsável pela coleta dos dados para verificar se tais outliers possam ser devido algum erro durante o processo de coleta dos dados. Caso afirmativo, os outliers seriam arrumados;
#
# - remover os outliers. Isso implica perder linha(s) inteira(s) do conjunto de dados. No presente projeto seria perder clientes. Temos uma grande quantidade de observações (n = 10000), porém, a variável alvo (Exited) está desbalanceada (conforme mostrado na etapa posterior), assim, existe o risco de aumentar ainda mais esse desbalanceamento. Portanto, seria preciso avaliar o impacto da remoção dos outliers
#
# - substituir os valores dos outliers por um valor de uma medida de estatística descritiva (por exemplo, média ou moda). Ou também alterar o valor do(s) outlier(s) usando os valores da barra superior e inferior, ou seja, outlier(s) acima da barra superior receberiam o valor da barra superior e outlier(s) abaixo da barra inferior receberiam o valor da barra inferior
#
# - Neste presente projeto, inicialmente, vou continuar com os outliers. Partindo da seguinte premissa: "objetivo é buscar padrões e/ou fazer previsões aos quais não se tem nenhuma informação a priori". Porém, se os modelos apresentarem performances ruins, retorno nesta questão
# 2.3. Estatísticas das variáveis
# 2.3.1. Variável alvo (também conhecida como target, y ou resposta) no conjunto de dados de treino. Exited é a variável alvo e possui dois valores:
# - "1" cliente abandonou a instituição financeira, ou seja, ocorreu churn
# - "0" cliente não abandonou a instituição financeira
# 2.3.1.1. Estatística descritiva da variável alvo
y=df_treino["Exited"]
# Questão 7. Como se comporta a variável alvo?
# Quantidade de clientes que abandonaram a instituição financeira
y_1=sum(y==1)
print("Quantidade de clientes que abandonaram a instituição financeira: {}".format(y_1))
# Quantidade de clientes que não abandonaram a instituição financeira
y_0=sum(y==0)
print("Quantidade de clientes que não abandonaram a instituição financeira: {}".format(y_0))
# +
# Proporção de clientes que abandonaram a instituição financeira
prop_y_1=sum(y==1)*100/y.shape[0]
print("Porcentagem de clientes que abandonaram a instituição financeira: {}".format(prop_y_1))
# Proporção de clientes que não abandonaram a instituição financeira
prop_y_0=sum(y==0)*100/y.shape[0]
print("Porcentagem de clientes que não abandonaram a instituição financeira: {}".format(prop_y_0))
# -
# Criar um dataframe com os dados acima
y_df=pd.DataFrame([["Não",7963,79.63],["Sim",2037,20.37]],index=range(0,2),columns=["Abandono (Churn)","Quantidade de Clientes (N)", "Porcentagem de Clientes (%)"])
display(y_df)
# Mostrar os dados da variável alvo em um gráfico de barras (Quantidade de clientes)
sns.set_color_codes("dark")
g = sns.barplot(x="Quantidade de Clientes (N)", y="Abandono (Churn)",data=y_df, color="green")
g.axes.set_title("Churn", fontsize=16,color="black",alpha=3)
g.set_xlabel("Quantidade de Clientes", size = 14,color="black")
g.set_ylabel("")
sns.despine(left=True, bottom=True)
plt.show()
# Mostrar os dados da variável alvo em um gráfico de barras (Quantidade de clientes)
sns.set_color_codes("dark")
g = sns.barplot(x="Porcentagem de Clientes (%)", y="Abandono (Churn)",data=y_df, color="green")
g.axes.set_title("Churn", fontsize=16,color="black",alpha=3)
g.set_xlabel("Porcentagem de Clientes", size = 14,color="black")
g.set_ylabel("")
plt.text(81,0.1,"79.63%",fontsize=14)
plt.text(21,0.99,"20.37%",fontsize=14)
sns.despine(left=True, bottom=True)
plt.show()
# Através das informações acima podemos verificar que a maioria dos clientes não abandonaram a instituição financeira. Simplesmente, em cada dez clientes, dois abandonaram a instituição financeira. Além disso, está evidente que o conjunto de dados de treino está desbalanceado.
# Consequências de dados desbalanceados na construção de um modelo de aprendizado de máquina (machine learning):
#
# O modelo terá uma tendência a dar muitos "alarmes falsos". Ou seja, na prática o modelo irá responder muito para a classe majoritária (sem abandono = não churn), mas terá um desempenho inferior para a classe minoritária (com abandono = churn). Logo, esse fato merece atenção na hora do pré-processamento dos dados.
# Questão 8. Quem são as outras variáveis?
# São as variáveis explicativas (também conhecidas como preditoras, X ou explanatórias) dos conjuntos de dados. São as variáveis: CredtiScore, Geography, Gender, Age, Tenure, Balance, NumberOfProducts, HasCrCard, IsActiveMember, EstimatedSalary. Total: 10 variáveis
# 2.3.2. Variáveis X
X_treino=df_treino.drop(columns=["Exited"])
X_treino.head()
# Questão 9. Qual o comportamento geral das variáveis X?
# 2.3.2.1. Análise univariada das variáveis X que são numéricas
X_numericas=X_treino.select_dtypes(exclude=["object"])
X_numericas.head()
X_numericas.describe()
# - Acima constam o número de observações (count), média (mean), desvio padrão (std), valor máximo (max) e minimo (min) e os quartis (25%, 50% e 75%) para cada uma das variáveis X numéricas
# - As variáveis possuem escalas de grandezas distintas. Esse fato merece atenção na hora da etapa de pré-processamento
# 2.3.2.2. Análise univariada das variáveis X que são categóricas
X_categoricas=X_treino.select_dtypes(include=["object"])
X_categoricas.head()
X_categoricas.describe(include=object)
fig, ax = plt.subplots(5,2, figsize = (8,10)) # visualizar as variáveis X
sns.countplot(X_numericas["IsActiveMember"], palette = 'Paired', ax = ax[0][0])
sns.countplot(X_numericas["HasCrCard"], palette = 'Paired', ax = ax[0][1])
sns.countplot(X_categoricas["Gender"], palette = "Paired", ax = ax[1][0])
sns.countplot(X_categoricas["Geography"], palette = "Paired", ax = ax[1][1])
sns.boxplot(X_numericas["CreditScore"], palette = 'Paired', ax = ax[2][0])
sns.boxplot(X_numericas["Age"], palette = 'Paired', ax = ax[2][1])
sns.boxplot(X_numericas["Tenure"], palette = "Paired", ax = ax[3][0])
sns.boxplot(X_numericas["Balance"], palette = "Paired", ax = ax[3][1])
sns.countplot(X_numericas["NumOfProducts"], palette = "Paired", ax = ax[4][0])
sns.boxplot(X_numericas["EstimatedSalary"], palette = "Paired", ax = ax[4][1])
plt.tight_layout()
plt.show()
# 2.3.2.3. Análise das variáveis X considerando a variável alvo
fig, ax = plt.subplots(5,2, figsize = (12,10))
sns.histplot(hue= 'Exited', x= 'CreditScore', multiple='stack', data = df_treino, palette = 'Paired', ax = ax[0][0])
sns.histplot(hue= 'Exited', x= 'Age', multiple='stack', data = df_treino, palette = 'Paired', ax = ax[0][1])
sns.histplot(hue= 'Exited', x= 'Tenure', multiple='stack', data = df_treino, palette = 'Paired', ax = ax[1][0])
sns.histplot(hue= 'Exited', x= 'Balance', multiple='stack', data = df_treino, palette = 'Paired', ax = ax[1][1])
sns.histplot(hue= 'Exited', x= 'EstimatedSalary', multiple='stack', data = df_treino, palette = 'Paired', ax = ax[2][0])
sns.countplot(x= 'Gender', hue= 'Exited', data = df_treino, palette = 'Paired', ax = ax[2][1])
sns.countplot(x= 'NumOfProducts', hue= 'Exited', data = df_treino, palette = 'Paired', ax = ax[3][0])
sns.countplot(x= 'HasCrCard', hue= 'Exited', data = df_treino, palette = 'Paired', ax = ax[3][1])
sns.countplot(x= 'IsActiveMember', hue= 'Exited', data = df_treino, palette = 'Paired', ax = ax[4][0])
sns.countplot(x= 'Geography', hue= 'Exited', data = df_treino, palette = 'Paired', ax = ax[4][1])
plt.tight_layout()
plt.show()
# Olhar com mais detalhes determinadas variáveis Xs
df_treino.IsActiveMember.value_counts() # total de clientes em cada categoria de membro ativo
# +
# número de clientes em cada categoria de membro ativo (1 ou 0)
num_yes = len(df_treino[df_treino.IsActiveMember == 1])
num_no = len(df_treino[df_treino.IsActiveMember == 0])
# número de clientes que abandonaram em cada categoria de membro ativo
ex_yes = len(df_treino[(df_treino.IsActiveMember == 1) & (df_treino.Exited == 1)])
ex_no = len(df_treino[(df_treino.IsActiveMember == 0) & (df_treino.Exited == 1)])
yes_ex_rate = ex_yes/num_yes
no_ex_rate = ex_no/num_no
# +
plt.barh(y = ['Yes_Active','No_Active'] , width = [num_yes,num_no], color = 'lightblue')
plt.barh(y = ['Yes_Active','No_Active'] , width = [ex_yes,ex_no] , color = 'darkblue')
plt.xlim(0,5800)
# mostrar a porcentagem de cliente que abandonou em cada categoria de membro ativo
plt.text(5000 , 'No_Active','{:.1f} %'.format(no_ex_rate*100))
plt.text(5200 , 'Yes_Active','{:.1f} %'.format(yes_ex_rate*100))
plt.title('Churn (%) vs Membro Ativo')
plt.xlabel('Número de clientes')
plt.show()
# -
df_treino.HasCrCard.value_counts() # total de clientes que possuem e não possuem cartão de crédito
# +
# número de clientes em cada categoria de membro ativo (1 ou 0)
num_yes = len(df_treino[df_treino.HasCrCard == 1])
num_no = len(df_treino[df_treino.HasCrCard == 0])
# número de clientes que abandonaram em cada categoria de membro ativo
ex_yes = len(df_treino[(df_treino.HasCrCard == 1) & (df_treino.Exited == 1)])
ex_no = len(df_treino[(df_treino.HasCrCard == 0) & (df_treino.Exited == 1)])
yes_ex_rate = ex_yes/num_yes
no_ex_rate = ex_no/num_no
# +
plt.barh(y = ['Yes_CrCard','No_CrCard'] , width = [num_yes,num_no], color = 'lightblue')
plt.barh(y = ['Yes_CrCard','No_CrCard'] , width = [ex_yes,ex_no] , color = 'darkblue')
plt.xlim(0,8000)
# mostrar a porcentagem de cliente que abandonou em cada categoria de membro ativo
plt.text(3000 , 'No_CrCard','{:.1f} %'.format(no_ex_rate*100))
plt.text(7100 , 'Yes_CrCard','{:.1f} %'.format(yes_ex_rate*100))
plt.title('Churn (%) vs Cartão de Crédito')
plt.xlabel('Número de clientes')
plt.show()
# -
df_treino.NumOfProducts.value_counts() # total de clientes em cada categoria de produto
# +
# número de clientes em cada categoria de produto (1, 2, 3 ou 4 produtos)
num_p1 = len(df_treino[df_treino.NumOfProducts == 1])
num_p2 = len(df_treino[df_treino.NumOfProducts == 2])
num_p3 = len(df_treino[df_treino.NumOfProducts == 3])
num_p4 = len(df_treino[df_treino.NumOfProducts == 4])
# número de clientes que abandonaram em cada categoria de produto
ex_p1 = len(df_treino[(df_treino.NumOfProducts == 1) & (df_treino.Exited == 1)])
ex_p2 = len(df_treino[(df_treino.NumOfProducts == 2) & (df_treino.Exited == 1)])
ex_p3 = len(df_treino[(df_treino.NumOfProducts == 3) & (df_treino.Exited == 1)])
ex_p4 = len(df_treino[(df_treino.NumOfProducts == 4) & (df_treino.Exited == 1)])
p1_ex_rate = ex_p1/num_p1
p2_ex_rate = ex_p2/num_p2
p3_ex_rate = ex_p3/num_p3
p4_ex_rate = ex_p4/num_p4
# +
plt.barh(y = ['1_product','2_products','3_products','4_products'] , width = [num_p1,num_p2,num_p3,num_p4], color = 'lightblue')
plt.barh(y = ['1_product','2_products','3_products','4_products'] , width = [ex_p1,ex_p2,ex_p3,ex_p4] , color = 'darkblue')
plt.xlim(0,6000)
# mostrar a porcentagem de cliente que abandonou em cada categoria de produto
plt.text(200 , '4_products','{:.1f} %'.format(p4_ex_rate*100))
plt.text(400 , '3_products','{:.1f} %'.format(p3_ex_rate*100))
plt.text(4700 , '2_products','{:.1f} %'.format(p2_ex_rate*100))
plt.text(5200 , '1_product','{:.1f} %'.format(p1_ex_rate*100))
plt.title('Churn (%) vs Número de produtos')
plt.xlabel('Número de clientes')
plt.show()
# -
# montante médio em dinheiro disponível na conta dos clientes que abandonaram (1) e que não abandonaram a instituição financeira
sns.catplot(data = df_treino , x = 'Exited' , y = 'Balance' , kind = 'bar' , color = 'blue')
plt.plot([0,1.4],[df_treino[df_treino.Exited == 0]['Balance'].mean(),df_treino[df_treino.Exited == 0]['Balance'].mean()],linestyle = '--' , c ='k'
, alpha = 0.8)
plt.show()
# Salário estimado médio dos clientes que abandonaram (1) e que não abandonaram a instituição financeira
sns.catplot(data = df_treino , x = 'Exited' , y = 'EstimatedSalary' , kind = 'bar' , color = 'blue')
plt.plot([0,1.4],[df_treino[df_treino.Exited == 0]['EstimatedSalary'].mean(),df_treino[df_treino.Exited == 0]['EstimatedSalary'].mean()],linestyle = '--' , c ='k'
, alpha = 0.8)
plt.show()
# Salário estimado médio dos clientes que abandonaram (1) e que não abandonaram a instituição financeira
sns.catplot(data = df_treino , x = 'Exited' , y = 'CreditScore' , kind = 'bar' , color = 'blue')
plt.plot([0,1.4],[df_treino[df_treino.Exited == 0]['CreditScore'].mean(),df_treino[df_treino.Exited == 0]['CreditScore'].mean()],linestyle = '--' , c ='k'
, alpha = 0.8)
plt.show()
# - A maioria dos clientes estão localizados na França. Os clientes alemães apresentaram maior número de abandono junto à instituição financeira
# - O maior número de abandono ocorreu entre clientes do sexo feminino
# - Clientes que não são membros ativos abandonaram mais a instituição financeira do que os clientes que são membros ativos
# - Todos os clientes (n = 60) que tinham 4 produtos abandonaram a instituição financeira. Clientes que tinham um (27.7%) e dois (7.6%) produtos abandonaram menos a instituição financeira do que os clientes tinham mais produtos
# - Os clientes que mais abandonaram a instituição financeira foram os que tinham mais dinheiro disponível na conta.
# - Além disso, o salário estimado é praticamente o mesmo entre os clientes que abandonaram e os que permaneceram na instituição financeira. Assim como, a porcentagem de clientes que possui cartão de crédito é a mesma para os clientes que abandonaram e os que não abandonaram
# 3. Preparação dos dados (Pré-processamento)
# 3.1. Tratamento das variáveis categóricas
# Codificando (Encoding) a variável categórica Geography
df_treino = pd.get_dummies(df_treino, columns = ['Geography'])
df_treino.head()
# Codificando (Encoding) a variável categórica "Gender"
df_treino['Gender'] = df_treino['Gender'].map({'Female':0, 'Male':1 })
df_treino.head()
# Encoding a variável categórica
df_teste = pd.get_dummies(df_teste, columns = ['Geography'])
df_teste.head()
# Encoding the categorical data
df_teste['Gender'] = df_teste['Gender'].map({'Female':0, 'Male':1 })
df_teste.head()
# 3.2. Seleção das variáveis X
# Questão 10. Existe correlação entre as variáveis?
plt.figure(figsize=(20,12))
plt.rcParams.update({'font.size': 10})
sns.heatmap(df_treino.corr(), annot=True, cmap='Blues') # criar um heatmap (mapa de calor)
# - não existem variáveis Xs (ou seja, características dos clientes) altamente correlacionadas com a variável alvo (Exited)
# - mas entre todas as variáveis Xs, Age, Geography_Germany, IsActiveMember, Balance e Gender são as que estão mais correlacionadas com a variável alvo
# 3.2.1. Transformação da escala dos dados
df_treino.head()
# As variáveis CreditScore, Balance e EstimatedSalary possuem escalas de grandezas distintas. Portanto, deixar as variáveis numa mesma escala para evitar que análises posteriores fiquem enviesadas para as variáveis de maior grandeza
X_Treino=df_treino.drop(columns=['Exited'])
X_Treino.head()
sc = MinMaxScaler()
X_Treino[['CreditScore','Balance','EstimatedSalary']] = sc.fit_transform(X_Treino[['CreditScore','Balance','EstimatedSalary']])
X_Treino.head()
df_teste[['CreditScore','Balance','EstimatedSalary']] = sc.fit_transform(df_teste[['CreditScore','Balance','EstimatedSalary']])
df_teste.head()
# 3.2.2. Seleção das variáveis X (Redução da dimensionalidade = redução de variáveis)
# Três técnicas usadas: Random Forest, RFE e SelectKBest
# 3.2.2.1. Random Forest (RF)
model = RandomForestClassifier()
model.fit(X_Treino,y)
sns.barplot(y= X_Treino.columns, x = model.feature_importances_)
# 3.2.2.2. Recursive Feature Elimination (RFE) with Random Forest (RF)
selector = RFE(model, n_features_to_select=6)
x_feature_selected = selector.fit_transform(X_Treino, y)
X_Treino.columns[selector.get_support(indices=True)]
# 3.2.2.3. SelectKBest
selector = SelectKBest(f_classif, k=6)
X_Treino_feature_selected = selector.fit_transform(X_Treino, y)
X_Treino.columns[selector.get_support(indices=True)]
sns.barplot(y=X_Treino.columns, x = selector.scores_)
# Geography_Spain e HasCrCard foram as únicas que não apareceram entre as seis variáveis mais importantes nas três abordagens usadas acima. Sendo assim, inicialmente, vou ajustar modelos usando todas as variáveis. Caso não obtenha boa performe dos mesmos, retorno para essa questão, ou seja, , ajustar modelos sem as duas variáveis (Geography_Sapin e HasCrCard)
# 3.2.2. Balanceamento da variável alvo (Exited)
# - Gerar novas observações da classe minoritária usando o algoritmo SMOTE (Synthetic Minority Oversampling Technique). No caso do presente projeto, a classe minoritária é o abandono de clientes (churn) junto à instituição financeira
smote = SMOTE()
X_Treino_balanceado, y_balanceado = smote.fit_resample(X_Treino, y)
y_balanceado = pd.Series(y_balanceado, name=y.name)
y_balanceado.head(1)
# Verificar se gerou novas observações da classe minoritária
ax = sns.countplot(x=y_balanceado)
ax.set_ylabel("Quantidade de clientes")
ax.set_xlabel("Exited");
# 4. Modelagem (Modelo de Classificação, pois a variável alvo (Exited) é binária 0 ou 1)
#
# 4.1. Geração (criação) dos modelos e avaliação dos modelos
# 4.1.1. Primeiro modelo (Regressão Logística)
classifierLR = LogisticRegression(max_iter=500, random_state = 42)
# 4.1.1.1. Dados desbalanceados
# +
# Creating Logistic Regression list of metrics
logistic_regression_sem_balancear = []
# Cross validating the model
cv_result = cross_validate(classifierLR, X_Treino, y, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Logistic Regression list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
logistic_regression_sem_balancear.append(cv_result[i].mean())
# -
# Printing the Logistic Regression metrics
logistic_regression_sem_balancear
# 4.1.1.2. Dados balanceados
# +
# Creating Logistic Regression list of metrics
logistic_regression_balanceado = []
# Cross validating the model
cv_result = cross_validate(classifierLR, X_Treino_balanceado, y_balanceado, cv=10,
# Printing the Logistic Regression metrics
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Logistic Regression list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
logistic_regression_balanceado.append(cv_result[i].mean())
# -
# Printing the Logistic Regression metrics
logistic_regression_balanceado
# 4.1.2. Segundo modelo (Naive Bayes)
classifierNB = GaussianNB()
# 4.1.2.1. Dados desbalanceados
# +
# Creating Gaussian Naive Bayes list of metrics
naive_bayes_sem_balancear = []
# Cross validating the model
cv_result = cross_validate(classifierNB, X_Treino, y, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Gaussian Naive Bayes list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
naive_bayes_sem_balancear.append(cv_result[i].mean())
# -
# Printing the Gaussian Naive Bayes metrics
naive_bayes_sem_balancear
# 4.1.2.2. Dados balanceados
# +
# Creating Gaussian Naive Bayes list of metrics
naive_bayes_balanceado = []
# Cross validating the model
cv_result = cross_validate(classifierNB, X_Treino_balanceado, y_balanceado, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Gaussian Naive Bayes list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
naive_bayes_balanceado.append(cv_result[i].mean())
# -
# Printing the Gaussian Naive Bayes metrics
naive_bayes_balanceado
# 4.1.3. Terceiro modelo (Random Forest - RF)
classifierRF = RandomForestClassifier(random_state = 42)
# 4.1.3.1. Dados desbalanceados
# +
# Creating Random Forest list of metrics
random_forest_sem_balancear = []
# Cross validating the model
cv_result = cross_validate(classifierRF, X_Treino, y, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Random Forest list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
random_forest_sem_balancear.append(cv_result[i].mean())
# -
# Printing the RF metrics
random_forest_sem_balancear
# 4.1.3.2. Dados balanceados
# +
# Creating Random Forest list of metrics
random_forest_balanceado = []
# Cross validating the model
cv_result = cross_validate(classifierRF, X_Treino_balanceado, y_balanceado, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Random Forest list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
random_forest_balanceado.append(cv_result[i].mean())
# -
# Printing the RF metrics
random_forest_balanceado
# 4.1.4. Quarto modelo (Decision Tree)
classifierDT = DecisionTreeClassifier(random_state = 42)
# 4.1.4.1. Dados desbalanceados
# +
# Creating Decision Tree list of metrics
decision_tree_sem_balancear = []
# Cross validating the model
cv_result = cross_validate(classifierDT, X_Treino, y, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Decision Tree list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
decision_tree_sem_balancear.append(cv_result[i].mean())
# -
# Printing the Decision Tree metrics
decision_tree_sem_balancear
# 4.1.4.2. Dados Balanceados
# +
# Creating Decision Tree list of metrics
decision_tree_balanceado = []
# Cross validating the model
cv_result = cross_validate(classifierDT, X_Treino_balanceado, y_balanceado, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to Decision Tree list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
decision_tree_balanceado.append(cv_result[i].mean())
# -
# Printing the Decision Tree metrics
decision_tree_balanceado
# 4.1.5. Quinto modelo (LGBM)
LGBM_model=LGBMClassifier(random_state=42)
# 4.1.5.1. Dados desbalanceados
# +
# Creating LGBM list of metrics
LGBM_model_sem_balancear = []
# Cross validating the model
cv_result = cross_validate(LGBM_model, X_Treino, y, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to LGBM list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
LGBM_model_sem_balancear.append(cv_result[i].mean())
# -
# Printing the LGBM metrics
LGBM_model_sem_balancear
# 4.1.5.2. Dados balanceados
# +
# Creating LGBM list of metrics
LGBM_model_balanceado = []
# Cross validating the model
cv_result = cross_validate(LGBM_model, X_Treino_balanceado, y_balanceado, cv=10,
scoring=['accuracy',
'precision',
'recall',
'f1',
'roc_auc'])
# Appending metrics to LGBM list
for i in ['test_accuracy','test_precision','test_recall','test_f1','test_roc_auc']:
LGBM_model_balanceado.append(cv_result[i].mean())
# -
# Printing the LGBM metrics
LGBM_model_balanceado
# 4.2. Comparar as métricas dos modelos
# +
metricas = (pd.DataFrame([logistic_regression_sem_balancear,logistic_regression_balanceado,naive_bayes_sem_balancear,naive_bayes_balanceado,random_forest_sem_balancear, random_forest_balanceado, decision_tree_sem_balancear,decision_tree_balanceado, LGBM_model_sem_balancear, LGBM_model_balanceado],
index=['Logistic Regression sem balancear','Logistic Regression balanceado','Naive Bayes sem balancear','Naive Bayes balanceado','Random Forest sem balancear', 'Random Forest balanceado','Decision Tree sem balancear','Decision Tree balanceado','LGBM sem balancear','LGBM balanceado'],
columns=['Accuracy','Precision','Recall','F1 Score','AUROC'])*100).round(2)
metricas
# -
# Para o problema de negócio, o mais importante é prever corretamente os clientes que provavelmente abandonarão a instituição financeira (verdadeiros positivos, ou seja, previsão de que ocorre abondono "churn" e, de fato, ocorre) e, também, minimizar o número de clientes erroneamente classificados como sem previsão de abandonar (falsos negativos, ou seja, previsão de que não ocorre abandono "churn", mas ocorre). Portanto, a métrica utilizada será o recall.
metricas['Recall'].sort_values(ascending=False)
# - Melhor modelo: Random Forest balanceado
# - Além disso, o RF balanceado também mostrou maiores performances nas outras métrica
# - Modelos sem balancear: não apresentaram boas performances
# 4.3. Tunagem de hiperparâmetros do Melhor Modelo (RF)
# +
tuned_classifierRF = RandomForestClassifier()
# Parameters to be used
params_RF = {'n_estimators':[100,200],
'min_samples_leaf':[1,2,3],
'max_depth':[None,1,2],
'criterion':['gini','entropy']}
gs_RF = GridSearchCV(estimator=tuned_classifierRF,
param_grid=params_RF,
cv=10,
scoring='recall')
# Fitting the model to the training set
gs_RF.fit(X_Treino_balanceado, y_balanceado)
# Printing the best score adquired from the tunning
best_recall = gs_RF.best_score_
print("Best Recall Score: {:.2f} %".format(best_recall*100))
# Printing the best parameter found
best_parameters = gs_RF.best_params_
print("Best Parameters:", best_parameters)
# +
tuned_classifierRF = RandomForestClassifier()
# Parameters to be used
params_RF = {'n_estimators':[100,200,300],
'min_samples_leaf':[1,2,3],
'max_depth':[None,1,2],
'criterion':['gini','entropy']}
gs_RF = GridSearchCV(estimator=tuned_classifierRF,
param_grid=params_RF,
cv=10,
scoring='recall')
# Fitting the model to the training set
gs_RF.fit(X_Treino_balanceado, y_balanceado)
# Printing the best score adquired from the tunning
best_recall = gs_RF.best_score_
print("Best Recall Score: {:.2f} %".format(best_recall*100))
# Printing the best parameter found
best_parameters = gs_RF.best_params_
print("Best Parameters:", best_parameters)
# -
# 4.4. Treinando com todos os dados de treino
# - Treinar (ajustar) o melhor modelo (RF balanceado) com os melhores hiperparâmetros
# +
RF = RandomForestClassifier(n_estimators=300, max_depth=None,
criterion='gini', random_state=42)
RF.fit(X_Treino_balanceado, y_balanceado)
# -
df_teste.head()
# 5. Previsão usando os dados de teste
pred_RF_test = RF.predict(df_teste)
pred_RF_test
np.savetxt('C:/Users/<NAME>/LightHouse/test1.csv', pred_RF_test, delimiter=',')
| Churn.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="BgeDZxBVawYI" executionInfo={"status": "ok", "timestamp": 1620408372890, "user_tz": -60, "elapsed": 1068, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "15457167959826747159"}} outputId="ac854214-13d0-4316-e6f7-6dfffeb52b7d"
from google.colab import drive
drive.mount("/content/drive")
# + colab={"base_uri": "https://localhost:8080/"} id="lUiiv33-a9-_" executionInfo={"status": "ok", "timestamp": 1620408373486, "user_tz": -60, "elapsed": 1657, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "15457167959826747159"}} outputId="4c9ce6d9-71ef-42bf-9072-42b5be4f665f"
import os
path="/content/drive/MyDrive/UGATIT_without_dg"
os.chdir(path)
os.listdir(path)
# + colab={"base_uri": "https://localhost:8080/"} id="_eU5qzU8bba7" executionInfo={"status": "ok", "timestamp": 1620179703431, "user_tz": -60, "elapsed": 29761133, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "15457167959826747159"}} outputId="a69d84f5-f59e-4ec0-ea74-dcd8e6bce4f6"
# !python main.py --dataset cat2dog --light True --iteration 50000 --save_freq 1000 --print_freq 1000 --resume True
# + colab={"base_uri": "https://localhost:8080/"} id="ITaJoHe3be7n" executionInfo={"status": "ok", "timestamp": 1620408540429, "user_tz": -60, "elapsed": 161114, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "15457167959826747159"}} outputId="b6cfe71b-6398-4ce9-8725-3ad0a5791639"
# !python main.py --dataset cat2dog --phase test --light True
# + colab={"base_uri": "https://localhost:8080/"} id="C1xgWEZd4uTw" executionInfo={"status": "ok", "timestamp": 1620408729579, "user_tz": -60, "elapsed": 5343, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "15457167959826747159"}} outputId="900b0b98-05bb-4f24-8685-24c78ab0b10b"
pip install pytorch-fid
# + id="z_pQqhiG9BWi" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1620408870063, "user_tz": -60, "elapsed": 16077, "user": {"displayName": "GOU PI", "photoUrl": "", "userId": "15457167959826747159"}} outputId="a49dd6b3-8b20-40ac-9493-ce4741d7a913"
# !python -m pytorch_fid "./results/cat2dog/realB" "./results/cat2dog/fakeB"
# + id="9wCtMj0L4sea"
| UGATIT_without_dg/Untitled0.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# %matplotlib inline
import pandas as pd
from keras.preprocessing.sequence import pad_sequences
df = pd.read_excel (r'hindi_modelDataset.xlsx', sheet_name='Sheet1')
df.head(20)
class SentenceGetter(object):
def __init__(self, dataset):
self.n_sent = 1
self.dataset = dataset
self.empty = False
agg_func = lambda s: [(w, t) for w,t in zip(s["word"].values.tolist(),
s["tag"].values.tolist())]
self.grouped = self.dataset.groupby("sent_index").apply(agg_func)
self.sentences = [s for s in self.grouped]
getter = SentenceGetter(df)
sentences = getter.sentences
print(sentences[10])
maxlen = max([len(s) for s in sentences])
print ('Maximum sequence length:', maxlen)
plt.hist([len(s) for s in sentences], bins=50)
plt.show()
words = list(set(df["word"].values))
words.append("end_padding")
n_words = len(words)
n_words
tags = list(set(df["tag"].values))
n_tags = len(tags)
n_tags
# # Feature Generation
word2idx = {w: i for i, w in enumerate(words)}
tag2idx = {t: i for i, t in enumerate(tags)}
print(type(word2idx))
dict_items = word2idx.items()
first_5 = list(dict_items)[:5]
print(first_5)
# +
X = [[word2idx[w[0]] for w in s] for s in sentences]
# -
X = pad_sequences(maxlen=150, sequences=X, padding="post",value=n_words - 1)
y = [[tag2idx[w[1]] for w in s] for s in sentences]
y = pad_sequences(maxlen=150, sequences=y, padding="post", value=tag2idx["O"])
from keras.utils import to_categorical
y = [to_categorical(i, num_classes=n_tags) for i in y]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
from keras.models import Model, Input
from keras.layers import LSTM, Embedding, Dense, TimeDistributed, Dropout, Bidirectional
input = Input(shape=(150,))
model = Embedding(input_dim=n_words, output_dim=150, input_length=150)(input)
model = Dropout(0.1)(model)
model = Bidirectional(LSTM(units=150, return_sequences=True, recurrent_dropout=0.1))(model)
out = TimeDistributed(Dense(n_tags, activation="softmax"))(model)
model = Model(input, out)
model.compile(optimizer="adam", loss="categorical_crossentropy", metrics=["accuracy"])
history = model.fit(X_train, np.array(y_train), batch_size=32, epochs=10, validation_split=0.2, verbose=1)
i = 2
p = model.predict(np.array([X_test[i]]))
p = np.argmax(p, axis=-1)
print("{:14} ({:5}): {}".format("Word", "True", "Pred"))
for w,pred in zip(X_test[i],p[0]):
print("{:15}: {}".format(words[w],tags[pred]))
pred = []
for i in range(len(y_test)):
p = model.predict(np.array([X_test[i]]))
p = np.argmax(p, axis=-1)
pred.append(p)
pred_temp = [x[0] for x in pred]
y_temp = []
for i in range(len(y_test)):
y_temp.append(np.array([np.where(y_test[i][j]==1)[0][0] for j in range(len(y_test[i]))]))
actual = y_temp[0]
for i in range(1, len(y_temp)):
actual = np.concatenate((actual, y_temp[i]), axis=None)
predicted = pred_temp[0]
for i in range(1, len(pred_temp)):
predicted = np.concatenate((predicted, pred_temp[i]), axis=None)
import scikitplot as skplt
from sklearn.metrics import classification_report
skplt.metrics.plot_confusion_matrix(actual, predicted)
print(classification_report(actual, predicted, target_names=tags))
| Base Models/BI-LSTM-Hindi.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Interpolations
# Simulate two macro-spins with anisotropy, where the MEP is given by an asynchronous rotation of the spins
# +
# FIDIMAG:
from fidimag.micro import Sim
from fidimag.common import CuboidMesh
from fidimag.micro import UniformExchange, UniaxialAnisotropy
from fidimag.common.nebm_spherical import NEBM_Spherical
from fidimag.common.nebm_geodesic import NEBM_Geodesic
import fidimag.common.nebm_geodesic
import numpy as np
import matplotlib.pyplot as plt
# +
# Material Parameters
# Parameters
A = 1e-12
Kx = 1e5
# Strong anisotropy
Ms = 3.8e5
"""
We will define two particles using a 4 sites mesh, letting the
sites in the middle as Ms = 0
"""
def two_part(pos):
x = pos[0]
if x > 6 or x < 3:
return Ms
else:
return 0
# Finite differences mesh
mesh = CuboidMesh(nx=3,
ny=1,
nz=1,
dx=3, dy=3, dz=3,
unit_length=1e-9
)
# Prepare simulation
# We define the cylinder with the Magnetisation function
sim = Sim(mesh)
sim.Ms = two_part
# sim.add(UniformExchange(A=A))
# Uniaxial anisotropy along x-axis
sim.add(UniaxialAnisotropy(Kx, axis=(1, 0, 0)))
def mid_m(pos):
if pos[0] > 4:
return (0.5, 0, 0.2)
else:
return (-0.5, 0, 0.2)
init_im = [(-1, 0, 0), mid_m, (1, 0, 0)]
interp = [6, 6]
# Define many initial states close to one extreme. We want to check
# if the images in the last step, are placed mostly in equally positions
init_images = init_im
interpolations = interp
neb = NEBM_Geodesic(sim,
init_images,
interpolations=interpolations,
spring_constant=100,
name='test',
integrator='sundials'
)
neb.relax(max_iterations=2000,
save_vtks_every=1000,
save_npys_every=1000,
stopping_dYdt=1e-4,
dt=1e-6
)
# -
# Get the interpolated data
neb.compute_polynomial_factors()
interp_x, interp_y = neb.compute_polynomial_approximation_energy(200)
plt.plot(interp_x, interp_y)
plt.plot(neb.path_distances, neb.energies, 'o')
# Set the climbing and falling images
neb.climbing_image = [3, 10, -7]
neb.relax(max_iterations=2000,
save_vtks_every=1000,
save_npys_every=1000,
stopping_dYdt=1e-4,
dt=1e-6,
save_initial_state=False
)
# We can see that climbing image and the falling image successfully move to the sadddle point and local minimum
neb.compute_polynomial_factors()
interp_x, interp_y = neb.compute_polynomial_approximation_energy(200)
plt.plot(interp_x, interp_y)
plt.plot(neb.path_distances, neb.energies, 'o')
# We can plot the x component of the spin 0, 1 and 2. Spin 1 has Ms=0 so no component
mx0 = neb.band.reshape(-1, neb.n_dofs_image)[:, 0]
mx1 = neb.band.reshape(-1, neb.n_dofs_image)[:, 3]
mx2 = neb.band.reshape(-1, neb.n_dofs_image)[:, 6]
plt.plot(neb.path_distances, mx0, 'o-')
plt.plot(neb.path_distances, mx1, 'o-')
plt.plot(neb.path_distances, mx2, 'o-')
# # Cubic interpolation
# We can attempt to interpolate every spin component: mx0, mx1, mx2, my0, ... etc. We will start with mx0, which is the 0th component in every band image array
i_factors = [None for i in range(4)]
neb.scale
neb.compute_effective_field_and_energy(neb.band)
# fidimag.common.nebm_geodesic.nebm_clib.project_images(neb.gradientE, neb.band, neb.n_images, neb.n_dofs_image)
# To interpolate the spin component we use: $d m_x / ds = (d m_x^{(0)} / dE) * dE / ds = H_{x(0),\text{eff}}^{-1} (\mathbf{H}_{\text{eff}}\cdot\mathbf{t})$
#
# $dE/ds$ is the energy tangent, which translates into the gradient (wrt to $m$) along the path by the tangents to the curve
#
# Check: https://aip.scitation.org/doi/10.1063/1.1323224
deltas = np.zeros(neb.n_images)
for i in range(neb.n_images):
deltas[i] = np.dot(neb.scale * (neb.gradientE).reshape(neb.n_images, -1)[i],
neb.tangents.reshape(neb.n_images, -1)[i]
)
# Scale by the 0th spin component in the array and
# divide by the x component of the effective field for the 0th spin
den = neb.scale[0] * (neb.gradientE).reshape(neb.n_images, -1)[i][0]
if den != 0:
deltas[i] = deltas[i] / den
else:
print(i, deltas[i])
deltas[i] = 0
i_factors[3] = mx0
i_factors[2] = deltas
i_factors[1] = np.zeros(neb.n_images)
i_factors[0] = np.zeros(neb.n_images)
ds = neb.path_distances
for i in range(neb.n_images - 1):
i_factors[1][i] = -(deltas[i + 1] + 2 * deltas[i]) / (ds[i + 1] - ds[i])
i_factors[1][i] += 3 * (mx0[i + 1] - mx0[i]) / (ds[i + 1] - ds[i]) ** 2.
i_factors[0][i] = (deltas[i + 1] + deltas[i]) / (ds[i + 1] - ds[i]) ** 2.
i_factors[0][i] -= 2 * (mx0[i + 1] - mx0[i]) / (ds[i + 1] - ds[i]) ** 3.
i_factors
# The interpolation:
# +
x = np.linspace(0, neb.path_distances[-1], 200)
y = np.zeros_like(x)
for i, yi in enumerate(y):
# ds = self.path_distances
if x[i] < 0.0 or x[i] > ds[-1]:
raise Exception('x lies outside the valid interpolation range')
# Find index of the ds array for the value that is closest to x
ds_idx = np.abs(x[i] - ds).argmin()
# If x is smaller than the given ds, use the previous ds value so
# that we use ds(i) when x lies in the interval ds(i) < x < ds(i+1)
if x[i] < ds[ds_idx]:
ds_idx -= 1
y[i] = (i_factors[0][ds_idx] * (x[i] - ds[ds_idx]) ** 3 +
i_factors[1][ds_idx] * (x[i] - ds[ds_idx]) ** 2 +
i_factors[2][ds_idx] * (x[i] - ds[ds_idx]) +
i_factors[3][ds_idx]
)
# -
i_factors[3]
# A cubic spline is not the best solution when the curve is linear
plt.figure(figsize=(8, 6))
plt.plot(neb.path_distances, mx0, 'o-')
plt.plot(x, y)
# # Bernstein
import scipy.interpolate as si
# +
derivatives = np.zeros(neb.n_images)
for i in range(neb.n_images):
derivatives[i] = np.dot(
neb.scale * (neb.gradientE).reshape(neb.n_images, -1)[i],
neb.tangents.reshape(neb.n_images, -1)[i])
den = neb.scale[6] * (neb.gradientE).reshape(neb.n_images, -1)[i][6]
if den != 0:
derivatives[i] = derivatives[i] / den
else:
print(i, derivatives[i])
deltas[i] = 0
# = self.energies
# The coefficients for the polynomial approximation
# self.interp_factors[0][:] = E
# self.interp_factors[1][:] = deltas
# Store the polynomial functions
Bernstein_polynomials = []
for i, ds in enumerate(neb.distances):
Bernstein_polynomials.append(
si.BPoly.from_derivatives(
[neb.path_distances[i], neb.path_distances[i + 1]],
[[mx2[i], derivatives[i]],
[mx2[i + 1], derivatives[i + 1]]]
)
)
# -
derivatives
# +
x = np.linspace(0, neb.path_distances[-1], 200)
y = np.zeros_like(x)
for i, yi in enumerate(y):
# ds = self.path_distances
if x[i] < 0.0 or x[i] > neb.path_distances[-1]:
raise Exception('x lies outside the valid interpolation range')
# Find index of the ds array for the value that is closest to x
ds_idx = np.abs(x[i] - ds).argmin()
# If x is smaller than the given ds, use the previous ds value so
# that we use ds(i) when x lies in the interval ds(i) < x < ds(i+1)
if x[i] < neb.path_distances[ds_idx]:
ds_idx -= 1
y[i] = Bernstein_polynomials[ds_idx](x[i])
# +
plt.figure(figsize=(8, 6))
plt.plot(neb.path_distances, mx2, 'o-')
plt.plot(x, y)
plt.ylim([-1.1, 1.1])
# -
# # Hermite polynomial
# As in the Spirit code https://github.com/spirit-code/spirit/
i_factors = [np.zeros(neb.n_images) for i in range(2)]
h00 = lambda x: 2 * x ** 3 - 3 * x ** 2 + 1
h10 = lambda x: -2 * x ** 3 + 3 * x ** 2
h01 = lambda x: x ** 3 - 2 * x ** 2 + x
h11 = lambda x: x ** 3 - x ** 2
i_factors[0][:] = mx0
# +
deltas = np.zeros(neb.n_images)
for i in range(neb.n_images):
i_factors[1][i] = np.dot(neb.scale * (neb.gradientE).reshape(neb.n_images, -1)[i],
neb.tangents.reshape(neb.n_images, -1)[i]
)
den = neb.scale[0] * (neb.gradientE).reshape(neb.n_images, -1)[i][0]
if den != 0:
i_factors[1][i] = i_factors[1][i] / den
else:
print(i, i_factors[1][i])
i_factors[1][i] = 0
i_factors[1][:-1] *= neb.distances
# +
xs = []
ys = []
n_interp = 20
ds = neb.path_distances
for i, xi in enumerate(ds[:-1]):
x0 = ds[i]
x1 = ds[i + 1]
dx = (x1 - x0) / n_interp
for j in range(n_interp):
x = x0 + j * dx
xrel = j / n_interp
# Find index of the ds array for the value that is closest to x
ds_idx = np.abs(x - ds).argmin()
# If x is smaller than the given ds, use the previous ds value so
# that we use ds(i) when x lies in the interval ds(i) < x < ds(i+1)
if x < neb.path_distances[ds_idx]:
ds_idx -= 1
xs.append(x)
y = (h00(xrel) * i_factors[0][ds_idx] +
h10(xrel) * i_factors[0][ds_idx + 1] +
h01(xrel) * i_factors[1][ds_idx] +
h11(xrel) * i_factors[1][ds_idx + 1]
)
ys.append(y)
# +
plt.figure(figsize=(8, 6))
plt.plot(neb.path_distances, mx0, 'o-')
plt.plot(xs, ys)
# -
| sandbox/nebm/energy_and_spin_interpolations.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: openvino_env
# language: python
# name: openvino_env
# ---
# # Super Resolution with PaddleGAN and OpenVINO
#
# This notebook demonstrates converting the RealSR (real-world super-resolution) model from [PaddlePaddle/PaddleGAN](https://github.com/PaddlePaddle/PaddleGAN) to OpenVINO's Intermediate Representation (IR) format, and shows inference results on both the PaddleGAN and IR models.
#
# For more information about the various PaddleGAN superresolution models, see [PaddleGAN's documentation](https://github.com/PaddlePaddle/PaddleGAN/blob/develop/docs/en_US/tutorials/single_image_super_resolution.md). For more information about RealSR, see the [research paper](https://openaccess.thecvf.com/content_CVPRW_2020/papers/w31/Ji_Real-World_Super-Resolution_via_Kernel_Estimation_and_Noise_Injection_CVPRW_2020_paper.pdf) from CVPR 2020.
#
# This notebook works best with small images (up to 800x600).
# ## Preparation
# + tags=[]
import sys
import time
import warnings
from pathlib import Path
import cv2
import matplotlib.pyplot as plt
import numpy as np
import paddle
from IPython.display import HTML, FileLink, ProgressBar, clear_output, display
from IPython.display import Image as DisplayImage
from openvino.inference_engine import IECore
from paddle.static import InputSpec
from PIL import Image
from ppgan.apps import RealSRPredictor
sys.path.append("../utils")
from notebook_utils import NotebookAlert
# -
# ## Settings
# + tags=[]
# The filenames of the downloaded and converted models
MODEL_NAME = "paddlegan_sr"
MODEL_DIR = Path("model")
OUTPUT_DIR = Path("output")
OUTPUT_DIR.mkdir(exist_ok=True)
model_path = MODEL_DIR / MODEL_NAME
ir_path = model_path.with_suffix(".xml")
onnx_path = model_path.with_suffix(".onnx")
# -
# ## Inference on PaddlePaddle model
# ### Investigate PaddleGAN model
#
# The [PaddleGAN documentation](https://github.com/PaddlePaddle/PaddleGAN) explains to run the model with `sr.run()`. Let's see what that function does, and check other relevant functions that are called from that function. Adding `??` to the methods shows the docstring and source code.
# + tags=[]
# Running this cell will download the model weights if they have not been downloaded before
# This may take a while
sr = RealSRPredictor()
# + tags=[]
# sr.run??
# + tags=[]
# sr.run_image??
# + tags=[]
# sr.norm??
# + tags=[]
# sr.denorm??
# -
# The run checks whether the input is an image or a video. For an image, it loads the image as an RGB image, normalizes it, and converts it to a Paddle tensor. It is propagated to the network by calling `self.model()` and then "denormalized". The normalization function simply divides all image values by 255. This converts an image with integer values in the range of 0 to 255 to an image with floating point values in the range of 0 to 1. The denormalization function transforms the output from network shape (C,H,W) to image shape (H,W,C). It then clips the image values between 0 and 255, and converts the image to a standard RGB image with integer values in the range of 0 to 255.
#
# To get more information about the model, we can check what it looks like with `sr.model??`.
# + tags=[]
# # sr.model??
# -
# ### Do Inference
#
# To show inference on the PaddlePaddle model, set PADDLEGAN_INFERENCE to True in the cell below. Performing inference may take some time.
# + tags=[]
# Set PADDLEGAN_INFERENCE to True to show inference on the PaddlePaddle model.
# This may take a long time, especially for larger images.
#
PADDLEGAN_INFERENCE = False
if PADDLEGAN_INFERENCE:
# load the input image and convert to tensor with input shape
IMAGE_PATH = Path("data/coco_tulips.jpg")
image = cv2.cvtColor(cv2.imread(str(IMAGE_PATH)), cv2.COLOR_BGR2RGB)
input_image = image.transpose(2, 0, 1)[None, :, :, :] / 255
input_tensor = paddle.to_tensor(input_image.astype(np.float32))
if max(image.shape) > 400:
NotebookAlert(
f"This image has shape {image.shape}. Doing inference will be slow "
"and the notebook may stop responding. Set PADDLEGAN_INFERENCE to False "
"to skip doing inference on the PaddlePaddle model.",
"warning",
)
# + tags=[]
if PADDLEGAN_INFERENCE:
# Do inference, and measure how long it takes
print(f"Start superresolution inference for {IMAGE_PATH.name} with shape {image.shape}...")
start_time = time.perf_counter()
sr.model.eval()
with paddle.no_grad():
result = sr.model(input_tensor)
end_time = time.perf_counter()
duration = end_time - start_time
result_image = (
(result.numpy().squeeze() * 255).clip(0, 255).astype("uint8").transpose((1, 2, 0))
)
print(f"Superresolution image shape: {result_image.shape}")
print(f"Inference duration: {duration:.2f} seconds")
plt.imshow(result_image);
# -
# ## Convert PaddleGAN Model to ONNX and OpenVINO IR
#
# To convert the PaddlePaddle model to OpenVINO IR, we first convert the model to ONNX, and then convert the ONNX model to the IR format.
#
# ### Convert PaddlePaddle Model to ONNX
# + tags=[]
# Ignore PaddlePaddle warnings:
# The behavior of expression A + B has been unified with elementwise_add(X, Y, axis=-1)
warnings.filterwarnings("ignore")
sr.model.eval()
# ONNX export requires an input shape in this format as parameter
x_spec = InputSpec([None, 3, 299, 299], "float32", "x")
paddle.onnx.export(sr.model, str(model_path), input_spec=[x_spec], opset_version=13)
# -
# ### Convert ONNX Model to OpenVINO IR
# + tags=[]
## Uncomment the command below to show Model Optimizer help, which shows the possible arguments for Model Optimizer
# # ! mo --help
# + tags=[]
if not ir_path.exists():
print("Exporting ONNX model to IR... This may take a few minutes.")
# ! mo --input_model $onnx_path --input_shape "[1,3,299,299]" --model_name $MODEL_NAME --output_dir "$MODEL_DIR" --data_type "FP16" --log_level "CRITICAL"
# -
# ## Do Inference on IR Model
# + tags=[]
# Read network and get input and output names
ie = IECore()
net = ie.read_network(ir_path)
input_layer = next(iter(net.input_info.keys()))
output_layer = next(iter(net.outputs.keys()))
# + tags=[]
# Load and show image
IMAGE_PATH = Path("data/coco_tulips.jpg")
image = cv2.cvtColor(cv2.imread(str(IMAGE_PATH)), cv2.COLOR_BGR2RGB)
if max(image.shape) > 800:
NotebookAlert(
f"This image has shape {image.shape}. The notebook works best with images with "
"a maximum side of 800x600. Larger images may work well, but inference may "
"be slow",
"warning",
)
plt.imshow(image)
# + tags=[]
# Reshape network to image size
net.reshape({input_layer: [1, 3, image.shape[0], image.shape[1]]})
# Load network to the CPU device (this may take a few seconds)
exec_net = ie.load_network(net, "CPU")
# + tags=[]
# Convert image to network input shape and divide pixel values by 255
# See "Investigate PaddleGAN model" section
input_image = image.transpose(2, 0, 1)[None, :, :, :] / 255
start_time = time.perf_counter()
# Do inference
ir_result = exec_net.infer({input_layer: input_image})
end_time = time.perf_counter()
duration = end_time - start_time
print(f"Inference duration: {duration:.2f} seconds")
# + tags=[]
# Get result array in CHW format
result_array = ir_result[output_layer].squeeze()
# Convert array to image with same method as PaddleGAN:
# Multiply by 255, clip values between 0 and 255, convert to HWC INT8 image
# See "Investigate PaddleGAN model" section
image_super = (result_array * 255).clip(0, 255).astype("uint8").transpose((1, 2, 0))
# Resize image with bicubic upsampling for comparison
image_bicubic = cv2.resize(image, tuple(image_super.shape[:2][::-1]), interpolation=cv2.INTER_CUBIC)
# + tags=[]
plt.imshow(image_super)
# -
# ### Show Animated Gif
#
# To visualize the difference between the bicubic image and the superresolution image, we create an imated gif that switches between both versions.
# + tags=[]
result_pil = Image.fromarray(image_super)
bicubic_pil = Image.fromarray(image_bicubic)
gif_image_path = OUTPUT_DIR / Path(IMAGE_PATH.stem + "_comparison.gif")
final_image_path = OUTPUT_DIR / Path(IMAGE_PATH.stem + "_super.png")
result_pil.save(
fp=str(gif_image_path),
format="GIF",
append_images=[bicubic_pil],
save_all=True,
duration=1000,
loop=0,
)
result_pil.save(fp=str(final_image_path), format="png")
DisplayImage(open(gif_image_path, "rb").read(), width=1920 // 2)
# -
# ### Create Comparison Video
#
# Create a video with a "slider", showing the bicubic image to the right and the superresolution image on the left.
#
# For the video, the superresolution and bicubic image are resized by a factor two to improve processing speed. This gives an indication of the superresolution effect. The video is saved as an .avi video. You can click on the link to download the video, or open it directly from the images directory, and play it locally.
# + tags=[]
FOURCC = cv2.VideoWriter_fourcc(*"MJPG")
IMAGE_PATH = Path(IMAGE_PATH)
result_video_path = OUTPUT_DIR / Path(f"{IMAGE_PATH.stem}_comparison_paddlegan.avi")
video_target_height, video_target_width = (
image_super.shape[0] // 2,
image_super.shape[1] // 2,
)
out_video = cv2.VideoWriter(
str(result_video_path),
FOURCC,
90,
(video_target_width, video_target_height),
)
resized_result_image = cv2.resize(image_super, (video_target_width, video_target_height))[
:, :, (2, 1, 0)
]
resized_bicubic_image = cv2.resize(image_bicubic, (video_target_width, video_target_height))[
:, :, (2, 1, 0)
]
progress_bar = ProgressBar(total=video_target_width)
progress_bar.display()
for i in range(2, video_target_width):
# Create a frame where the left part (until i pixels width) contains the
# superresolution image, and the right part (from i pixels width) contains
# the bicubic image
comparison_frame = np.hstack(
(
resized_result_image[:, :i, :],
resized_bicubic_image[:, i:, :],
)
)
# create a small black border line between the superresolution
# and bicubic part of the image
comparison_frame[:, i - 1 : i + 1, :] = 0
out_video.write(comparison_frame)
progress_bar.progress = i
progress_bar.update()
out_video.release()
clear_output()
video_link = FileLink(result_video_path)
video_link.html_link_str = "<a href='%s' download>%s</a>"
display(HTML(f"The video has been saved to {video_link._repr_html_()}"))
# -
| notebooks/207-vision-paddlegan-superresolution/207-vision-paddlegan-superresolution.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # CNTK 206: Part B - Deep Convolutional GAN with MNIST data
#
# **Prerequisites**: We assume that you have successfully downloaded the MNIST data by completing the tutorial titled CNTK_103A_MNIST_DataLoader.ipynb.
#
# ## Introduction
#
# [Generative models](https://en.wikipedia.org/wiki/Generative_model) have gained a [lot of attention](https://openai.com/blog/generative-models/) in deep learning community which has traditionally leveraged [discriminative models](https://en.wikipedia.org/wiki/Discriminative_model) for (semi-supervised) and unsupervised learning.
#
# ## Overview
# In the previous tutorial we introduce the original GAN implementation by [Goodfellow et al](https://arxiv.org/pdf/1406.2661v1.pdf) at NIPS 2014. This pioneering work has since then been extended and many techniques have been published amongst which the Deep Convolutional Generative Adversarial Network a.k.a. DCGAN has become the recommended launch pad in the community.
#
# In this tutorial, we introduce an implementation of the DCGAN with some well tested architectural constraints that improve stability in the GAN training:
#
# - We use [strided convolutions](https://en.wikipedia.org/wiki/Convolutional_neural_network) in the (discriminator) and [fractional-strided convolutions](https://arxiv.org/pdf/1603.07285v1.pdf) in the generator.
# - We have used batch normalization in both the generator and the discriminator
# - We have removed fully connected hidden layers for deeper architectures.
# - We use ReLU activation in generator for all layers except for the output, which uses Tanh.
# - We use LeakyReLU activation in the discriminator for all layers.
#
# +
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os
import cntk as C
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env() # (only needed for our build system)
C.cntk_py.set_fixed_random_seed(1) # fix a random seed for CNTK components
# %matplotlib inline
# -
# There are two run modes:
# - *Fast mode*: `isFast` is set to `True`. This is the default mode for the notebooks, which means we train for fewer iterations or train / test on limited data. This ensures functional correctness of the notebook though the models produced are far from what a completed training would produce.
#
# - *Slow mode*: We recommend the user to set this flag to `False` once the user has gained familiarity with the notebook content and wants to gain insight from running the notebooks for a longer period with different parameters for training.
#
# **Note**
# If the `isFlag` is set to `False` the notebook will take a few hours on a GPU enabled machine. You can try fewer iterations by setting the `num_minibatches` to a smaller number say `20,000` which comes at the expense of quality of the generated images.
isFast = True
# ## Data Reading
# The input to the GAN will be a vector of random numbers. At the end of the traning, the GAN "learns" to generate images of hand written digits drawn from the [MNIST database](https://en.wikipedia.org/wiki/MNIST_database). We will be using the same MNIST data generated in tutorial 103A. A more in-depth discussion of the data format and reading methods can be seen in previous tutorials. For our purposes, just know that the following function returns an object that will be used to generate images from the MNIST dataset. Since we are building an unsupervised model, we only need to read in `features` and ignore the `labels`.
# +
# Ensure the training data is generated and available for this tutorial
# We search in two locations in the toolkit for the cached MNIST data set.
data_found = False
for data_dir in [os.path.join("..", "Examples", "Image", "DataSets", "MNIST"),
os.path.join("data", "MNIST")]:
train_file = os.path.join(data_dir, "Train-28x28_cntk_text.txt")
if os.path.isfile(train_file):
data_found = True
break
if not data_found:
raise ValueError("Please generate the data by completing CNTK 103 Part A")
print("Data directory is {0}".format(data_dir))
# -
def create_reader(path, is_training, input_dim, label_dim):
deserializer = C.io.CTFDeserializer(
filename = path,
streams = C.io.StreamDefs(
labels_unused = C.io.StreamDef(field = 'labels', shape = label_dim, is_sparse = False),
features = C.io.StreamDef(field = 'features', shape = input_dim, is_sparse = False
)
)
)
return C.io.MinibatchSource(
deserializers = deserializer,
randomize = is_training,
max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1
)
# The random noise we will use to train the GAN is provided by the `noise_sample` function to generate random noise samples from a uniform distribution within the interval [-1, 1].
np.random.seed(123)
def noise_sample(num_samples):
return np.random.uniform(
low = -1.0,
high = 1.0,
size = [num_samples, g_input_dim]
).astype(np.float32)
# ## Model Creation
#
# First we provide a brief recap of the basics of GAN. You may skip this block if you are familiar with CNTK 206A.
#
# A GAN network is composed of two sub-networks, one called the Generator ($G$) and the other Discriminator ($D$).
# - The **Generator** takes random noise vector ($z$) as input and strives to output synthetic (fake) image ($x^*$) that is indistinguishable from the real image ($x$) from the MNIST dataset.
# - The **Discriminator** strives to differentiate between the real image ($x$) and the fake ($x^*$) image.
#
# 
#
# In each training iteration, the Generator produces more realistic fake images (in other words *minimizes* the difference between the real and generated counterpart) and the Discriminator *maximizes* the probability of assigning the correct label (real vs. fake) to both real examples (from training set) and the generated fake ones. The two conflicting objectives between the sub-networks ($G$ and $D$) leads to the GAN network (when trained) converge to an equilibrium, where the Generator produces realistic looking fake MNIST images and the Discriminator can at best randomly guess whether images are real or fake. The resulting Generator model once trained produces realistic MNIST image with the input being a random number.
# ### Model config
#
# First, we establish some of the architectural and training hyper-parameters for our model.
#
# - The generator network is fractional strided convolutional network. The input is a 100-dimensional random vector and the output of the generator is a flattened version of a 28 x 28 fake image. The discriminator is strided-convolution network. It takes as input the 784 dimensional output of the generator or a real MNIST image, reshapes into a 28 x 28 image format and outputs a single scalar - the estimated probability that the input image is a real MNIST image.
# ### Model components
# We build a computational graph for our model, one each for the generator and the discriminator. First, we establish some of the architectural parameters of our model.
# +
# architectural parameters
img_h, img_w = 28, 28
kernel_h, kernel_w = 5, 5
stride_h, stride_w = 2, 2
# Input / Output parameter of Generator and Discriminator
g_input_dim = 100
g_output_dim = d_input_dim = img_h * img_w
# We expect the kernel shapes to be square in this tutorial and
# the strides to be of the same length along each data dimension
if kernel_h == kernel_w:
gkernel = dkernel = kernel_h
else:
raise ValueError('This tutorial needs square shaped kernel')
if stride_h == stride_w:
gstride = dstride = stride_h
else:
raise ValueError('This tutorial needs same stride in all dims')
# +
# Helper functions
def bn_with_relu(x, activation=C.relu):
h = C.layers.BatchNormalization(map_rank=1)(x)
return C.relu(h)
# We use param-relu function to use a leak=0.2 since CNTK implementation
# of Leaky ReLU is fixed to 0.01
def bn_with_leaky_relu(x, leak=0.2):
h = C.layers.BatchNormalization(map_rank=1)(x)
r = C.param_relu(C.constant((np.ones(h.shape)*leak).astype(np.float32)), h)
return r
# -
# **Generator**
#
# The generator takes a 100-dimensional random vector (for starters) as input ($z$) and the outputs a 784 dimensional vector, corresponding to a flattened version of a 28 x 28 fake (synthetic) image ($x^*$). In this tutorial, we use fractionally strided convolutions (a.k.a ConvolutionTranspose) with ReLU activations except for the last layer. We use a tanh activation on the last layer to make sure that the output of the generator function is confined to the interval [-1, 1]. The use of ReLU and tanh activation functions are key in addition to using the fractionally strided convolutions.
def convolutional_generator(z):
with C.layers.default_options(init=C.normal(scale=0.02)):
print('Generator input shape: ', z.shape)
s_h2, s_w2 = img_h//2, img_w//2 #Input shape (14,14)
s_h4, s_w4 = img_h//4, img_w//4 # Input shape (7,7)
gfc_dim = 1024
gf_dim = 64
h0 = C.layers.Dense(gfc_dim, activation=None)(z)
h0 = bn_with_relu(h0)
print('h0 shape', h0.shape)
h1 = C.layers.Dense([gf_dim * 2, s_h4, s_w4], activation=None)(h0)
h1 = bn_with_relu(h1)
print('h1 shape', h1.shape)
h2 = C.layers.ConvolutionTranspose2D(gkernel,
num_filters=gf_dim*2,
strides=gstride,
pad=True,
output_shape=(s_h2, s_w2),
activation=None)(h1)
h2 = bn_with_relu(h2)
print('h2 shape', h2.shape)
h3 = C.layers.ConvolutionTranspose2D(gkernel,
num_filters=1,
strides=gstride,
pad=True,
output_shape=(img_h, img_w),
activation=C.sigmoid)(h2)
print('h3 shape :', h3.shape)
return C.reshape(h3, img_h * img_w)
# **Discriminator**
#
# The discriminator takes as input ($x^*$) the 784 dimensional output of the generator or a real MNIST image, re-shapes the input to a 28 x 28 image and outputs the estimated probability that the input image is a real MNIST image. The network is modeled using strided convolution with Leaky ReLU activation except for the last layer. We use a sigmoid activation on the last layer to ensure the discriminator output lies in the inteval of [0,1].
def convolutional_discriminator(x):
with C.layers.default_options(init=C.normal(scale=0.02)):
dfc_dim = 1024
df_dim = 64
print('Discriminator convolution input shape', x.shape)
x = C.reshape(x, (1, img_h, img_w))
h0 = C.layers.Convolution2D(dkernel, 1, strides=dstride)(x)
h0 = bn_with_leaky_relu(h0, leak=0.2)
print('h0 shape :', h0.shape)
h1 = C.layers.Convolution2D(dkernel, df_dim, strides=dstride)(h0)
h1 = bn_with_leaky_relu(h1, leak=0.2)
print('h1 shape :', h1.shape)
h2 = C.layers.Dense(dfc_dim, activation=None)(h1)
h2 = bn_with_leaky_relu(h2, leak=0.2)
print('h2 shape :', h2.shape)
h3 = C.layers.Dense(1, activation=C.sigmoid)(h2)
print('h3 shape :', h3.shape)
return h3
# We use a minibatch size of 128 and a fixed learning rate of 0.0002 for training. In the fast mode (`isFast = True`) we verify only functional correctness with 5000 iterations.
#
# **Note**: In the slow mode, the results look a lot better but it requires in the order of 10 minutes depending on your hardware. In general, the more number of minibatches one trains, the better is the fidelity of the generated images.
# training config
minibatch_size = 128
num_minibatches = 5000 if isFast else 10000
lr = 0.0002
momentum = 0.5 #equivalent to beta1
# ### Build the graph
#
# The rest of the computational graph is mostly responsible for coordinating the training algorithms and parameter updates, which is particularly tricky with GANs for couple reasons. The GANs are sensitive to the choice of learner and the parameters. Many of the parameters chosen here are based on many hard learnt lessons from the community. You may directly go to the code if you have read the basic GAN tutorial.
#
# - First, the discriminator must be used on both the real MNIST images and fake images generated by the generator function. One way to represent this in the computational graph is to create a clone of the output of the discriminator function, but with substituted inputs. Setting `method=share` in the `clone` function ensures that both paths through the discriminator model use the same set of parameters.
#
#
# - Second, we need to update the parameters for the generator and discriminator model separately using the gradients from different loss functions. We can get the parameters for a `Function` in the graph with the `parameters` attribute. However, when updating the model parameters, update only the parameters of the respective models while keeping the other parameters unchanged. In other words, when updating the generator we will update only the parameters of the $G$ function while keeping the parameters of the $D$ function fixed and vice versa.
#
# ### Training the Model
# The code for training the GAN very closely follows the algorithm as presented in the [original NIPS 2014 paper](https://arxiv.org/pdf/1406.2661v1.pdf). In this implementation, we train $D$ to maximize the probability of assigning the correct label (fake vs. real) to both training examples and the samples from $G$. In other words, $D$ and $G$ play the following two-player minimax game with the value function $V(G,D)$:
#
# $$
# \min_G \max_D V(D,G)= \mathbb{E}_{x}[ log D(x) ] + \mathbb{E}_{z}[ log(1 - D(G(z))) ]
# $$
#
# At the optimal point of this game the generator will produce realistic looking data while the discriminator will predict that the generated image is indeed fake with a probability of 0.5. The [algorithm referred below](https://arxiv.org/pdf/1406.2661v1.pdf) is implemented in this tutorial.
#
# 
def build_graph(noise_shape, image_shape, generator, discriminator):
input_dynamic_axes = [C.Axis.default_batch_axis()]
Z = C.input_variable(noise_shape, dynamic_axes=input_dynamic_axes)
X_real = C.input_variable(image_shape, dynamic_axes=input_dynamic_axes)
X_real_scaled = X_real / 255.0
# Create the model function for the generator and discriminator models
X_fake = generator(Z)
D_real = discriminator(X_real_scaled)
D_fake = D_real.clone(
method = 'share',
substitutions = {X_real_scaled.output: X_fake.output}
)
# Create loss functions and configure optimazation algorithms
G_loss = 1.0 - C.log(D_fake)
D_loss = -(C.log(D_real) + C.log(1.0 - D_fake))
G_learner = C.adam(
parameters = X_fake.parameters,
lr = C.learning_parameter_schedule_per_sample(lr),
momentum = C.momentum_schedule(momentum)
)
D_learner = C.adam(
parameters = D_real.parameters,
lr = C.learning_parameter_schedule_per_sample(lr),
momentum = C.momentum_schedule(momentum)
)
# Instantiate the trainers
G_trainer = C.Trainer(X_fake,
(G_loss, None),
G_learner)
D_trainer = C.Trainer(D_real,
(D_loss, None),
D_learner)
return X_real, X_fake, Z, G_trainer, D_trainer
# With the value functions defined we proceed to iteratively train the GAN model. The training of the model can take significantly long depending on the hardware especially if `isFast` flag is turned off.
def train(reader_train, generator, discriminator):
X_real, X_fake, Z, G_trainer, D_trainer = \
build_graph(g_input_dim, d_input_dim, generator, discriminator)
# print out loss for each model for upto 25 times
print_frequency_mbsize = num_minibatches // 25
print("First row is Generator loss, second row is Discriminator loss")
pp_G = C.logging.ProgressPrinter(print_frequency_mbsize)
pp_D = C.logging.ProgressPrinter(print_frequency_mbsize)
k = 2
input_map = {X_real: reader_train.streams.features}
for train_step in range(num_minibatches):
# train the discriminator model for k steps
for gen_train_step in range(k):
Z_data = noise_sample(minibatch_size)
X_data = reader_train.next_minibatch(minibatch_size, input_map)
if X_data[X_real].num_samples == Z_data.shape[0]:
batch_inputs = {X_real: X_data[X_real].data, Z: Z_data}
D_trainer.train_minibatch(batch_inputs)
# train the generator model for a single step
Z_data = noise_sample(minibatch_size)
batch_inputs = {Z: Z_data}
G_trainer.train_minibatch(batch_inputs)
G_trainer.train_minibatch(batch_inputs)
pp_G.update_with_trainer(G_trainer)
pp_D.update_with_trainer(D_trainer)
G_trainer_loss = G_trainer.previous_minibatch_loss_average
return Z, X_fake, G_trainer_loss
# +
reader_train = create_reader(train_file, True, d_input_dim, label_dim=10)
# G_input, G_output, G_trainer_loss = train(reader_train, dense_generator, dense_discriminator)
G_input, G_output, G_trainer_loss = train(reader_train,
convolutional_generator,
convolutional_discriminator)
# -
# Print the generator loss
print("Training loss of the generator is: {0:.2f}".format(G_trainer_loss))
# ## Generating Fake (Synthetic) Images
#
# Now that we have trained the model, we can create fake images simply by feeding random noise into the generator and displaying the outputs. Below are a few images generated from random samples. To get a new set of samples, you can re-run the last cell.
# +
def plot_images(images, subplot_shape):
plt.style.use('ggplot')
fig, axes = plt.subplots(*subplot_shape)
for image, ax in zip(images, axes.flatten()):
ax.imshow(image.reshape(28, 28), vmin=0, vmax=1.0, cmap='gray')
ax.axis('off')
plt.show()
noise = noise_sample(36)
images = G_output.eval({G_input: noise})
plot_images(images, subplot_shape=[6, 6])
# -
# Larger number of iterations should generate more realistic looking MNIST images. A sampling of such generated images are shown below.
#
# 
#
# **Note**: It takes a large number of iterations to capture a representation of the real world signal. Even simple dense networks can be quite effective in modelling data albeit MNIST is a relatively simple dataset as well.
# **Suggested Task**
#
# - Please refer to several hacks presented in this [article](https://github.com/soumith/ganhacks) by <NAME>, Facebook Research. While some of the hacks have been incorporated in this notebook, there are several others I would suggest that you try out.
#
# - Performance is a key aspect to deep neural networks training. Study how the changing the minibatch sizes impact the performance both with regards to quality of the generated images and the time it takes to train a model.
#
# - Try generating fake images using the CIFAR-10 data set as the training data. How does the network above performs? There are other variation in GAN, such as [conditional GAN](https://arxiv.org/pdf/1411.1784.pdf) where the network is additionally conditioned on the input label. Try implementing the labels.
#
| Tutorials/CNTK_206B_DCGAN.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Robot Class
#
# In this project, we'll be localizing a robot in a 2D grid world. The basis for simultaneous localization and mapping (SLAM) is to gather information from a robot's sensors and motions over time, and then use information about measurements and motion to re-construct a map of the world.
#
# ### Uncertainty
#
# As you've learned, robot motion and sensors have some uncertainty associated with them. For example, imagine a car driving up hill and down hill; the speedometer reading will likely overestimate the speed of the car going up hill and underestimate the speed of the car going down hill because it cannot perfectly account for gravity. Similarly, we cannot perfectly predict the *motion* of a robot. A robot is likely to slightly overshoot or undershoot a target location.
#
# In this notebook, we'll look at the `robot` class that is *partially* given to you for the upcoming SLAM notebook. First, we'll create a robot and move it around a 2D grid world. Then, **you'll be tasked with defining a `sense` function for this robot that allows it to sense landmarks in a given world**! It's important that you understand how this robot moves, senses, and how it keeps track of different landmarks that it sees in a 2D grid world, so that you can work with it's movement and sensor data.
#
# ---
#
# Before we start analyzing robot motion, let's load in our resources and define the `robot` class. You can see that this class initializes the robot's position and adds measures of uncertainty for motion. You'll also see a `sense()` function which is not yet implemented, and you will learn more about that later in this notebook.
# import some resources
import numpy as np
import matplotlib.pyplot as plt
import random
# %matplotlib inline
# the robot class
class robot:
# --------
# init:
# creates a robot with the specified parameters and initializes
# the location (self.x, self.y) to the center of the world
#
def __init__(self, world_size = 100.0, measurement_range = 30.0,
motion_noise = 1.0, measurement_noise = 1.0):
self.measurement_noise = 0.0
self.world_size = world_size
self.measurement_range = measurement_range
self.x = world_size / 2.0
self.y = world_size / 2.0
self.motion_noise = motion_noise
self.measurement_noise = measurement_noise
self.landmarks = []
self.num_landmarks = 0
# returns a positive, random float
def rand(self):
return random.random() * 2.0 - 1.0
# --------
# move: attempts to move robot by dx, dy. If outside world
# boundary, then the move does nothing and instead returns failure
#
def move(self, dx, dy):
x = self.x + dx + self.rand() * self.motion_noise
y = self.y + dy + self.rand() * self.motion_noise
if x < 0.0 or x > self.world_size or y < 0.0 or y > self.world_size:
return False
else:
self.x = x
self.y = y
return True
# --------
# sense: returns x- and y- distances to landmarks within visibility range
# because not all landmarks may be in this range, the list of measurements
# is of variable length. Set measurement_range to -1 if you want all
# landmarks to be visible at all times
#
## TODO: complete the sense function
def sense(self):
''' This function does not take in any parameters, instead it references internal variables
(such as self.landamrks) to measure the distance between the robot and any landmarks
that the robot can see (that are within its measurement range).
This function returns a list of landmark indices, and the measured distances (dx, dy)
between the robot's position and said landmarks.
This function should account for measurement_noise and measurement_range.
One item in the returned list should be in the form: [landmark_index, dx, dy].
'''
measurements = []
for ind, landmark in enumerate(self.landmarks):
dx = self.x - landmark[0] + self.rand()*self.measurement_noise
dy = self.y - landmark[1] + self.rand()*self.measurement_noise
if (measurement_range == -1) or ((abs(dx) <= self.measurement_range) and (abs(dy) <= self.measurement_range)):
measurements.append([ind, dx, dy])
## TODO: iterate through all of the landmarks in a world
## TODO: For each landmark
## 1. compute dx and dy, the distances between the robot and the landmark
## 2. account for measurement noise by *adding* a noise component to dx and dy
## - The noise component should be a random value between [-1.0, 1.0)*measurement_noise
## - Feel free to use the function self.rand() to help calculate this noise component
## - It may help to reference the `move` function for noise calculation
## 3. If either of the distances, dx or dy, fall outside of the internal var, measurement_range
## then we cannot record them; if they do fall in the range, then add them to the measurements list
## as list.append([index, dx, dy]), this format is important for data creation done later
## TODO: return the final, complete list of measurements
return measurements
# --------
# make_landmarks:
# make random landmarks located in the world
#
def make_landmarks(self, num_landmarks):
self.landmarks = []
for i in range(num_landmarks):
self.landmarks.append([round(random.random() * self.world_size),
round(random.random() * self.world_size)])
self.num_landmarks = num_landmarks
# called when print(robot) is called; prints the robot's location
def __repr__(self):
return 'Robot: [x=%.5f y=%.5f]' % (self.x, self.y)
# ## Define a world and a robot
#
# Next, let's instantiate a robot object. As you can see in `__init__` above, the robot class takes in a number of parameters including a world size and some values that indicate the sensing and movement capabilities of the robot.
#
# In the next example, we define a small 10x10 square world, a measurement range that is half that of the world and small values for motion and measurement noise. These values will typically be about 10 times larger, but we ust want to demonstrate this behavior on a small scale. You are also free to change these values and note what happens as your robot moves!
# +
world_size = 10.0 # size of world (square)
measurement_range = 5.0 # range at which we can sense landmarks
motion_noise = 0.2 # noise in robot motion
measurement_noise = 0.2 # noise in the measurements
# instantiate a robot, r
r = robot(world_size, measurement_range, motion_noise, measurement_noise)
# print out the location of r
print(r)
# -
# ## Visualizing the World
#
# In the given example, we can see/print out that the robot is in the middle of the 10x10 world at (x, y) = (5.0, 5.0), which is exactly what we expect!
#
# However, it's kind of hard to imagine this robot in the center of a world, without visualizing the grid itself, and so in the next cell we provide a helper visualization function, `display_world`, that will display a grid world in a plot and draw a red `o` at the location of our robot, `r`. The details of how this function wors can be found in the `helpers.py` file in the home directory; you do not have to change anything in this `helpers.py` file.
# +
# import helper function
from helpers import display_world
# define figure size
plt.rcParams["figure.figsize"] = (5,5)
# call display_world and display the robot in it's grid world
print(r)
display_world(int(world_size), [r.x, r.y])
# -
# ## Movement
#
# Now you can really picture where the robot is in the world! Next, let's call the robot's `move` function. We'll ask it to move some distance `(dx, dy)` and we'll see that this motion is not perfect by the placement of our robot `o` and by the printed out position of `r`.
#
# Try changing the values of `dx` and `dy` and/or running this cell multiple times; see how the robot moves and how the uncertainty in robot motion accumulates over multiple movements.
#
# #### For a `dx` = 1, does the robot move *exactly* one spot to the right? What about `dx` = -1? What happens if you try to move the robot past the boundaries of the world?
# +
# choose values of dx and dy (negative works, too)
dx = 1
dy = 2
r.move(dx, dy)
# print out the exact location
print(r)
# display the world after movement, not that this is the same call as before
# the robot tracks its own movement
display_world(int(world_size), [r.x, r.y])
# -
# ## Landmarks
#
# Next, let's create landmarks, which are measurable features in the map. You can think of landmarks as things like notable buildings, or something smaller such as a tree, rock, or other feature.
#
# The robot class has a function `make_landmarks` which randomly generates locations for the number of specified landmarks. Try changing `num_landmarks` or running this cell multiple times to see where these landmarks appear. We have to pass these locations as a third argument to the `display_world` function and the list of landmark locations is accessed similar to how we find the robot position `r.landmarks`.
#
# Each landmark is displayed as a purple `x` in the grid world, and we also print out the exact `[x, y]` locations of these landmarks at the end of this cell.
# +
# create any number of landmarks
num_landmarks = 3
r.make_landmarks(num_landmarks)
# print out our robot's exact location
print(r)
# display the world including these landmarks
display_world(int(world_size), [r.x, r.y], r.landmarks)
# print the locations of the landmarks
print('Landmark locations [x,y]: ', r.landmarks)
# -
# ## Sense
#
# Once we have some landmarks to sense, we need to be able to tell our robot to *try* to sense how far they are away from it. It will be up t you to code the `sense` function in our robot class.
#
# The `sense` function uses only internal class parameters and returns a list of the the measured/sensed x and y distances to the landmarks it senses within the specified `measurement_range`.
#
# ### TODO: Implement the `sense` function
#
# Follow the `##TODO's` in the class code above to complete the `sense` function for the robot class. Once you have tested out your code, please **copy your complete `sense` code to the `robot_class.py` file in the home directory**. By placing this complete code in the `robot_class` Python file, we will be able to refernce this class in a later notebook.
#
# The measurements have the format, `[i, dx, dy]` where `i` is the landmark index (0, 1, 2, ...) and `dx` and `dy` are the measured distance between the robot's location (x, y) and the landmark's location (x, y). This distance will not be perfect since our sense function has some associated `measurement noise`.
#
# ---
#
# In the example in the following cell, we have a given our robot a range of `5.0` so any landmarks that are within that range of our robot's location, should appear in a list of measurements. Not all landmarks are guaranteed to be in our visibility range, so this list will be variable in length.
#
# *Note: the robot's location is often called the **pose** or `[Pxi, Pyi]` and the landmark locations are often written as `[Lxi, Lyi]`. You'll see this notation in the next notebook.*
# +
# try to sense any surrounding landmarks
measurements = r.sense()
# this will print out an empty list if `sense` has not been implemented
print(measurements)
# -
# **Refer back to the grid map above. Do these measurements make sense to you? Are all the landmarks captured in this list (why/why not)?**
# ---
# ## Data
#
# #### Putting it all together
#
# To perform SLAM, we'll collect a series of robot sensor measurements and motions, in that order, over a defined period of time. Then we'll use only this data to re-construct the map of the world with the robot and landmar locations. You can think of SLAM as peforming what we've done in this notebook, only backwards. Instead of defining a world and robot and creating movement and sensor data, it will be up to you to use movement and sensor measurements to reconstruct the world!
#
# In the next notebook, you'll see this list of movements and measurements (which you'll use to re-construct the world) listed in a structure called `data`. This is an array that holds sensor measurements and movements in a specific order, which will be useful to call upon when you have to extract this data and form constraint matrices and vectors.
#
# `data` is constructed over a series of time steps as follows:
# +
data = []
# after a robot first senses, then moves (one time step)
# that data is appended like so:
data.append([measurements, [dx, dy]])
# for our example movement and measurement
print(data)
# +
# in this example, we have only created one time step (0)
time_step = 0
# so you can access robot measurements:
print('Measurements: ', data[time_step][0])
# and its motion for a given time step:
print('Motion: ', data[time_step][1])
# -
# ### Final robot class
#
# Before moving on to the last notebook in this series, please make sure that you have copied your final, completed `sense` function into the `robot_class.py` file in the home directory. We will be using this file in the final implementation of slam!
| 1. Robot Moving and Sensing.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # In-Class Coding Lab: Iterations
#
# The goals of this lab are to help you to understand:
#
# - How loops work.
# - The difference between definite and indefinite loops, and when to use each.
# - How to build an indefinite loop with complex exit conditions.
# - How to create a program from a complex idea.
#
# # Understanding Iterations
#
# Iterations permit us to repeat code until a Boolean expression is `False`. Iterations or **loops** allow us to write succint, compact code. Here's an example, which counts to 3 before [Blitzing the Quarterback in backyard American Football](https://www.quora.com/What-is-the-significance-of-counting-one-Mississippi-two-Mississippi-and-so-on):
i = 1
while i <= 3:
print(i,"Mississippi...")
i=i+1
print("Blitz!")
# ## Breaking it down...
#
# The `while` statement on line 2 starts the loop. The code indented beneath it (lines 3-4) will repeat, in a linear fashion until the Boolean expression on line 2 `i <= 3` is `False`, at which time the program continues with line 5.
#
# ### Some Terminology
#
# We call `i <=3` the loop's **exit condition**. The variable `i` inside the exit condition is the only thing that we can change to make the exit condition `False`, therefore it is the **loop control variable**. On line 4 we change the loop control variable by adding one to it, this is called an **increment**.
#
# Furthermore, we know how many times this loop will execute before it actually runs: 3. Even if we allowed the user to enter a number, and looped that many times, we would still know. We call this a **definite loop**. Whenever we iterate over a fixed number of values, regardless of whether those values are determined at run-time or not, we're using a definite loop.
#
# If the loop control variable never forces the exit condition to be `False`, we have an **infinite loop**. As the name implies, an Infinite loop never ends and typically causes our computer to crash or lock up.
# +
## WARNING!!! INFINITE LOOP AHEAD
## IF YOU RUN THIS CODE YOU WILL NEED TO KILL YOUR BROWSER AND SHUT DOWN JUPYTER NOTEBOOK
i = 1
while i <= 3:
print(i,"Mississippi...")
# i=i+1
print("Blitz!")
# -
# ### For loops
#
# To prevent an infinite loop when the loop is definite, we use the `for` statement. Here's the same program using `for`:
for i in range(1,4):
print(i,"Mississippi...")
print("Blitz!")
# One confusing aspect of this loop is `range(1,4)` why does this loop from 1 to 3? Why not 1 to 4? Well it has to do with the fact that computers start counting at zero. The easier way to understand it is if you subtract the two numbers you get the number of times it will loop. So for example, 4-1 == 3.
#
# ### Now Try It
#
# In the space below, Re-Write the above program to count from 10 to 15. Note: How many times will that loop?
for i in range(1,16):
print(i,"Mississippi...")
print("Blitz!")
# ## Indefinite loops
#
# With **indefinite loops** we do not know how many times the program will execute. This is typically based on user action, and therefore our loop is subject to the whims of whoever interacts with it. Most applications like spreadsheets, photo editors, and games use indefinite loops. They'll run on your computer, seemingly forever, until you choose to quit the application.
#
# The classic indefinite loop pattern involves getting input from the user inside the loop. We then inspect the input and based on that input we might exit the loop. Here's an example:
name = ""
while name != 'mike':
name = input("Say my name! : ")
print("Nope, my name is not %s! " %(name))
# The classic problem with indefinite loops is that its really difficult to get the application's logic to line up with the exit condition. For example we need to set `name = ""` in line 1 so that line 2 start out as `True`. Also we have this wonky logic where when we say `'mike'` it still prints `Nope, my name is not mike!` before exiting.
#
# ### Break statement
#
# The solution to this problem is to use the break statement. **break** tells Python to exit the loop immediately. We then re-structure all of our indefinite loops to look like this:
#
# ```
# while True:
# if exit-condition:
# break
# ```
#
# Here's our program we-written with the break statement. This is the recommended way to write indefinite loops in this course.
while True:
name = input("Say my name!: ")
if name == 'mike':
break
print("Nope, my name is not %s!" %(name))
# ### Multiple exit conditions
#
# This indefinite loop pattern makes it easy to add additional exit conditions. For example, here's the program again, but it now stops when you say my name or type in 3 wrong names. Make sure to run this program a couple of times. First enter mike to exit the program, next enter the wrong name 3 times.
times = 0
while True:
name = input("Say my name!: ")
times = times + 1
if name == 'mike':
print("You got it!")
break
if times == 3:
print("Game over. Too many tries!")
break
print("Nope, my name is not %s!" %(name))
# # Number sums
#
# Let's conclude the lab with you writing your own program which
#
# uses an indefinite loop. We'll provide the to-do list, you write the code. This program should ask for floating point numbers as input and stops looping when **the total of the numbers entered is over 100**, or **more than 5 numbers have been entered**. Those are your two exit conditions. After the loop stops print out the total of the numbers entered and the count of numbers entered.
# +
## TO-DO List
#1 count = 0
#2 total = 0
#3 loop Indefinitely
#4. input a number
#5 increment count
#6 add number to total
#7 if count equals 5 stop looping
#8 if total greater than 100 stop looping
#9 print total and count
# +
# Write Code here:
total = 0
number = 0
count = 0
while number < 100:
number = float(input("Enter a number. "))
total = number + total
print ("Total: " , total)
count = count + 1
if count == 5:
print("Tries exceeded. Exiting.")
break
# -
#
| content/lessons/05/Class-Coding-Lab/CCL-Iterations.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import pandas as pd
from seeq.addons.azureml import backend
from seeq.addons.azureml.utils import AzureMLException
# + pycharm={"name": "#%%\n"}
interactive_index = 0
if spy.jobs._common.running_in_executor():
params = spy.jobs.pull()
else:
params = spy.jobs.pull(interactive_index = interactive_index)
# + pycharm={"name": "#%%\n"}
end = pd.Timestamp.today()
start = end - params.get('Frequency')
# + pycharm={"name": "#%%\n"}
deployment = backend.RunInvestigation(input_signals=params.get('Input Signals'),
result_name=params.get('Result Name'),
az_model_name=params.get('AZ model name'),
az_model_version=params.get('AZ model version'),
start=start,
end=end,
grid=params.get('Grid'),
workbook=params.get('Workbook'),
worksheet=params.get('Worksheet'),
endpoint_uri=params.get('Endpoint'),
aml_primary_key=params.get('aml_primary_key'),
quiet=True)
try:
deployment.run()
deployment.push_to_seeq()
except AzureMLException as e:
raise e
| seeq/addons/azureml/deployment_notebook/azureml_integration_deploy_model.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="xG0TFaIvXy9Z"
# <center>
# <img src="https://gitlab.com/ibm/skills-network/courses/placeholder101/-/raw/master/labs/module%201/images/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
# </center>
#
# + [markdown] id="II_UgQOhXy9l"
# # **Space X Falcon 9 First Stage Landing Prediction**
#
# + [markdown] id="qASGNyPjXy9p"
# ## Assignment: Machine Learning Prediction
#
# + [markdown] id="K7DEP3qcXy9s"
# Estimated time needed: **60** minutes
#
# + [markdown] id="9BJtAFIOXy9s"
# Space X advertises Falcon 9 rocket launches on its website with a cost of 62 million dollars; other providers cost upward of 165 million dollars each, much of the savings is because Space X can reuse the first stage. Therefore if we can determine if the first stage will land, we can determine the cost of a launch. This information can be used if an alternate company wants to bid against space X for a rocket launch. In this lab, you will create a machine learning pipeline to predict if the first stage will land given the data from the preceding labs.
#
# + [markdown] id="c8YYVK0RXy9u"
# 
#
# + [markdown] id="rAowoWRCXy9v"
# Several examples of an unsuccessful landing are shown here:
#
# + [markdown] id="xffB9kjsXy9x"
# 
#
# + [markdown] id="2XRFeBTeXy9y"
# Most unsuccessful landings are planed. Space X; performs a controlled landing in the oceans.
#
# + [markdown] id="qLH5euR4Xy90"
# ## Objectives
#
# + [markdown] id="Dt3NguUkXy91"
# Perform exploratory Data Analysis and determine Training Labels
#
# * create a column for the class
# * Standardize the data
# * Split into training data and test data
#
# \-Find best Hyperparameter for SVM, Classification Trees and Logistic Regression
#
# * Find the method performs best using test data
#
# + [markdown] id="40xsF0geXy93"
#
# + [markdown] id="QkohLV1SXy93"
# ***
#
# + [markdown] id="ngNTQk5rXy94"
# ## Import Libraries and Define Auxiliary Functions
#
# + [markdown] id="Waq1_ue1Xy95"
# We will import the following libraries for the lab
#
# + id="G6fQ5uiPXy95"
# Pandas is a software library written for the Python programming language for data manipulation and analysis.
import pandas as pd
# NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays
import numpy as np
# Matplotlib is a plotting library for python and pyplot gives us a MatLab like plotting framework. We will use this in our plotter function to plot data.
import matplotlib.pyplot as plt
#Seaborn is a Python data visualization library based on matplotlib. It provides a high-level interface for drawing attractive and informative statistical graphics
import seaborn as sns
# Preprocessing allows us to standarsize our data
from sklearn import preprocessing
# Allows us to split our data into training and testing data
from sklearn.model_selection import train_test_split
# Allows us to test parameters of classification algorithms and find the best one
from sklearn.model_selection import GridSearchCV
# Logistic Regression classification algorithm
from sklearn.linear_model import LogisticRegression
# Support Vector Machine classification algorithm
from sklearn.svm import SVC
# Decision Tree classification algorithm
from sklearn.tree import DecisionTreeClassifier
# K Nearest Neighbors classification algorithm
from sklearn.neighbors import KNeighborsClassifier
# + [markdown] id="aqa4luhQXy98"
# This function is to plot the confusion matrix.
#
# + id="3HGIcv5SXy99"
def plot_confusion_matrix(y,y_predict):
"this function plots the confusion matrix"
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y, y_predict)
ax= plt.subplot()
sns.heatmap(cm, annot=True, ax = ax); #annot=True to annotate cells
ax.set_xlabel('Predicted labels')
ax.set_ylabel('True labels')
ax.set_title('Confusion Matrix');
ax.xaxis.set_ticklabels(['did not land', 'land']); ax.yaxis.set_ticklabels(['did not land', 'landed'])
# + [markdown] id="9hM-uE62Xy9-"
# ## Load the dataframe
#
# + [markdown] id="eB5911FNXy9-"
# Load the data
#
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="wzfUM_jxXy9_" outputId="aa82900a-e3a8-4526-bbf2-a0a9ebaeb60f"
data = pd.read_csv("https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/dataset_part_2.csv")
# If you were unable to complete the previous lab correctly you can uncomment and load this csv
# data = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DS0701EN-SkillsNetwork/api/dataset_part_2.csv')
data.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 505} id="9engHLokXy-A" outputId="b096cb5c-248a-4252-a421-f40bd65528b7"
X = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/dataset_part_3.csv')
# If you were unable to complete the previous lab correctly you can uncomment and load this csv
# X = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DS0701EN-SkillsNetwork/api/dataset_part_3.csv')
X.head(100)
# + [markdown] id="ZWKD41sUXy-A"
# ## TASK 1
#
# + [markdown] id="b-2Dgcq7Xy-B"
# Create a NumPy array from the column <code>Class</code> in <code>data</code>, by applying the method <code>to_numpy()</code> then
# assign it to the variable <code>Y</code>,make sure the output is a Pandas series (only one bracket df\['name of column']).
#
# + colab={"base_uri": "https://localhost:8080/"} id="Bbwm4XjFXy-B" outputId="57e25dad-9c66-4e10-dd45-7b19dc53da2e"
Y=data['Class'].to_numpy()
Y
# + [markdown] id="CSgcffRWXy-C"
# ## TASK 2
#
# + [markdown] id="3HLe_LuVXy-C"
# Standardize the data in <code>X</code> then reassign it to the variable <code>X</code> using the transform provided below.
#
# + id="KNc_imsJXy-C"
# students get this
transform = preprocessing.StandardScaler()
# + id="xvhcPWqrXy-D"
X = transform.fit_transform(X)
# + [markdown] id="91zW7mXbXy-D"
# We split the data into training and testing data using the function <code>train_test_split</code>. The training data is divided into validation data, a second set used for training data; then the models are trained and hyperparameters are selected using the function <code>GridSearchCV</code>.
#
# + [markdown] id="ODZvP9jTXy-D"
# ## TASK 3
#
# + [markdown] id="7IkPGlt8Xy-D"
# Use the function train_test_split to split the data X and Y into training and test data. Set the parameter test_size to 0.2 and random_state to 2. The training data and test data should be assigned to the following labels.
#
# + [markdown] id="_5qH-5hEXy-E"
# <code>X_train, X_test, Y_train, Y_test</code>
#
# + colab={"base_uri": "https://localhost:8080/"} id="Zu_f_-JcXy-E" outputId="068ce054-7239-425d-8f02-bc1cbb3ec37a"
X_train, X_test, Y_train, Y_test = train_test_split( X, Y, test_size=0.2, random_state=2)
print ('Train set:', X_train.shape, Y_train.shape)
print ('Test set:', X_test.shape, Y_test.shape)
# + [markdown] id="feTE_QOSXy-E"
# we can see we only have 18 test samples.
#
# + colab={"base_uri": "https://localhost:8080/"} id="Guu9fNvvXy-F" outputId="2e72d860-e217-4a3d-9beb-c7199d820e56"
Y_test.shape
# + [markdown] id="9KgqQYzoXy-F"
# ## TASK 4
#
# + [markdown] id="Pxqy9ki4Xy-G"
# Create a logistic regression object then create a GridSearchCV object <code>logreg_cv</code> with cv = 10. Fit the object to find the best parameters from the dictionary <code>parameters</code>.
#
# + id="2hVyiMDsXy-G"
parameters ={'C':[0.01,0.1,1],
'penalty':['l2'],
'solver':['lbfgs']}
# + colab={"base_uri": "https://localhost:8080/"} id="SlW-fA_SXy-G" outputId="016425ab-9ab1-4c74-96c8-ba45f0f90bed"
parameters ={"C":[0.01,0.1,1],'penalty':['l2'], 'solver':['lbfgs']}# l1 lasso l2 ridge
lr=LogisticRegression()
logreg_cv = GridSearchCV(lr,parameters,cv=10)
logreg_cv.fit(X_train, Y_train)
# + [markdown] id="A2ORCuSqXy-H"
# We output the <code>GridSearchCV</code> object for logistic regression. We display the best parameters using the data attribute <code>best_params\_</code> and the accuracy on the validation data using the data attribute <code>best_score\_</code>.
#
# + colab={"base_uri": "https://localhost:8080/"} id="7YMz8KofXy-H" outputId="4d1f33fc-51d2-46e0-bfa8-5def4e6af93f"
print("tuned hpyerparameters :(best parameters) ",logreg_cv.best_params_)
print("accuracy :",logreg_cv.best_score_)
# + [markdown] id="Sn806tSgXy-H"
# ## TASK 5
#
# + [markdown] id="MAPJ1S_OXy-I"
# Calculate the accuracy on the test data using the method <code>score</code>:
#
# + colab={"base_uri": "https://localhost:8080/"} id="Y_V5l0FFXy-I" outputId="3f32b5c0-d846-40b5-aa99-baee78ac6ece"
print("test set accuracy :",logreg_cv.score(X_test, Y_test))
# + [markdown] id="uaPrBI6ZXy-I"
# Lets look at the confusion matrix:
#
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="V6AEIdVXXy-I" outputId="cee26516-4cf4-4f0c-b4f9-f1c02ee402bf"
yhat=logreg_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
# + [markdown] id="OS_zAFfkXy-J"
# Examining the confusion matrix, we see that logistic regression can distinguish between the different classes. We see that the major problem is false positives.
#
# + [markdown] id="VzIKZOjGXy-J"
# ## TASK 6
#
# + [markdown] id="dDGFaJqTXy-J"
# Create a support vector machine object then create a <code>GridSearchCV</code> object <code>svm_cv</code> with cv - 10. Fit the object to find the best parameters from the dictionary <code>parameters</code>.
#
# + id="WLhTcM3YXy-K"
parameters = {'kernel':('linear', 'rbf','poly','rbf', 'sigmoid'),
'C': np.logspace(-3, 3, 5),
'gamma':np.logspace(-3, 3, 5)}
svm = SVC()
# + colab={"base_uri": "https://localhost:8080/"} id="XT6FKp8gXy-K" outputId="04149654-16ba-45b4-f889-dbbd60898d93"
svm_cv = GridSearchCV(svm,parameters,cv=10)
svm_cv.fit(X_train, Y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="o3jtS4fjXy-L" outputId="1284b20e-ebf2-4af3-d62d-24335a257af6"
print("tuned hpyerparameters :(best parameters) ",svm_cv.best_params_)
print("accuracy :",svm_cv.best_score_)
# + [markdown] id="KmV6sDhUXy-L"
# ## TASK 7
#
# + [markdown] id="zGdgaxCxXy-L"
# Calculate the accuracy on the test data using the method <code>score</code>:
#
# + colab={"base_uri": "https://localhost:8080/"} id="YnhFRZQxXy-M" outputId="98a6c478-92fa-4038-d469-1d81dab18728"
print("test set accuracy :",svm_cv.score(X_test, Y_test))
# + [markdown] id="rRKKIMfCXy-N"
# We can plot the confusion matrix
#
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="OoJOhfCHXy-N" outputId="1d381c24-39c7-4206-c071-a722f76f6412"
yhat=svm_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
# + [markdown] id="B9DehNjUXy-O"
# ## TASK 8
#
# + [markdown] id="1cLSxowrXy-O"
# Create a decision tree classifier object then create a <code>GridSearchCV</code> object <code>tree_cv</code> with cv = 10. Fit the object to find the best parameters from the dictionary <code>parameters</code>.
#
# + id="0TghQgNeXy-P"
parameters = {'criterion': ['gini', 'entropy'],
'splitter': ['best', 'random'],
'max_depth': [2*n for n in range(1,10)],
'max_features': ['auto', 'sqrt'],
'min_samples_leaf': [1, 2, 4],
'min_samples_split': [2, 5, 10]}
tree = DecisionTreeClassifier()
# + colab={"base_uri": "https://localhost:8080/"} id="ldv36C1rXy-P" outputId="4f6d56c3-85d3-456a-ff59-b1e2714f6441"
tree_cv = GridSearchCV(tree,parameters,cv=10)
tree_cv.fit(X_train, Y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="-XgWon8BXy-P" outputId="1157bc41-457b-4c34-8054-76b34f583ffd"
print("tuned hpyerparameters :(best parameters) ",tree_cv.best_params_)
print("accuracy :",tree_cv.best_score_)
# + [markdown] id="IkDfp2FBXy-Q"
# ## TASK 9
#
# + [markdown] id="eSfKiNY7Xy-Q"
# Calculate the accuracy of tree_cv on the test data using the method <code>score</code>:
#
# + colab={"base_uri": "https://localhost:8080/"} id="3XR-haV9Xy-R" outputId="25c3018a-8757-4443-e4e6-018011f67fd6"
print("test set accuracy :",tree_cv.score(X_test, Y_test))
# + [markdown] id="fE6RoVSYXy-R"
# We can plot the confusion matrix
#
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="d9FyyCWjXy-R" outputId="e885c66d-40a9-40a9-a2f3-1aa3b0665f3a"
yhat = svm_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
# + [markdown] id="HGxjTN6-Xy-R"
# ## TASK 10
#
# + [markdown] id="Y25Fclv8Xy-R"
# Create a k nearest neighbors object then create a <code>GridSearchCV</code> object <code>knn_cv</code> with cv = 10. Fit the object to find the best parameters from the dictionary <code>parameters</code>.
#
# + id="DnjTBoEuXy-S"
parameters = {'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
'algorithm': ['auto', 'ball_tree', 'kd_tree', 'brute'],
'p': [1,2]}
KNN = KNeighborsClassifier()
# + colab={"base_uri": "https://localhost:8080/"} id="wPX0BGYbXy-S" outputId="3be277e7-8c3f-474a-8152-ad5d6029e04d"
knn_cv = GridSearchCV(KNN,parameters,cv=10)
knn_cv.fit(X_train, Y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="gkWfJQxpXy-S" outputId="76b0d027-330f-4c29-8a35-c32ea8a0a627"
print("tuned hpyerparameters :(best parameters) ",knn_cv.best_params_)
print("accuracy :",knn_cv.best_score_)
# + [markdown] id="5gEYvxDvXy-S"
# ## TASK 11
#
# + [markdown] id="awVKcRtdXy-S"
# Calculate the accuracy of tree_cv on the test data using the method <code>score</code>:
#
# + colab={"base_uri": "https://localhost:8080/"} id="wI2bBfrWXy-T" outputId="a6388f8e-4111-4c3e-e1db-46906f09ee80"
print("test set accuracy :",knn_cv.score(X_test, Y_test))
# + [markdown] id="MLrgQpxaXy-T"
# We can plot the confusion matrix
#
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="hhm5kyD-Xy-T" outputId="0b017f93-649a-4393-ebc3-9a1c05d31b19"
yhat = knn_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
# + [markdown] id="_VC9KrqUXy-T"
# ## TASK 12
#
# + [markdown] id="xnxDf4BDXy-T"
# Find the method performs best:
#
# + id="zOLQVik8Xy-T"
# After comparing accuracy of above methods, they all preformed practically
# the same, except for tree which fit train data slightly better but test data worse.
# + [markdown] id="7SY4A6NJXy-U"
# ## Authors
#
# + [markdown] id="bk5zXxjcXy-U"
# <a href="https://www.linkedin.com/in/joseph-s-50398b136/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDS0321ENSkillsNetwork26802033-2021-01-01"><NAME></a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
#
# + [markdown] id="6Q_yrWAYXy-U"
# ## Change Log
#
# + [markdown] id="xugIwsfSXy-V"
# | Date (YYYY-MM-DD) | Version | Changed By | Change Description |
# | ----------------- | ------- | ------------- | ----------------------- |
# | 2021-08-31 | 1.1 | <NAME> | Modified markdown |
# | 2020-09-20 | 1.0 | Joseph | Modified Multiple Areas |
#
# + [markdown] id="CNhpnMhBXy-V"
# Copyright © 2020 IBM Corporation. All rights reserved.
#
| Applied Data Science Capstone/4. Predictive Analysis (Classification)/SpaceX_Machine_Learning_Prediction_Part_5.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + papermill={"duration": 0.013212, "end_time": "2021-06-16T07:12:02.365601", "exception": false, "start_time": "2021-06-16T07:12:02.352389", "status": "completed"} tags=[]
import os
# change the value for a different result
num = os.getenv('FACTORIAL_NUMBER', 7)
factorial = 1
# check if the number is negative, positive or zero
if num < 0:
raise RuntimeError('Sorry, factorial does not exist for negative numbers')
elif num == 0:
print('The factorial of 0 is 1')
else:
for i in range(1, num + 1):
factorial = factorial * i
print(f'The factorial of {num} is {factorial}')
# + papermill={"duration": 0.002662, "end_time": "2021-06-16T07:12:02.371176", "exception": false, "start_time": "2021-06-16T07:12:02.368514", "status": "completed"} tags=[]
| scripts/factorial.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import time
import os
import pandas as pd
import numpy as np
import random
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
# %load_ext autoreload
# %autoreload 2
from echoai_pet_measurements.runCFRModel import runCFRModel, Videoconverter
# -
# ### Load list of example videos ###
cfr_data_root = os.path.normpath('/mnt/obi0/andreas/data/cfr')
predict_dir = os.path.join(cfr_data_root, 'predictions_echodata','FirstEchoEvents2repeat')
model = 'cfr_a4c_dgx-1_fc1_global_cfr_calc'
predict_file = os.path.join(predict_dir, 'cfr_models_30fps', model+'.parquet')
predict_df = pd.read_parquet(predict_file)
echo_df = predict_df[predict_df['model_name']==model]
display(echo_df.head(2))
# +
# pick 10 random videos
n_videos=10
np.random.seed(123)
file_list = np.random.choice(echo_df['filename'].unique(), size=n_videos, replace=False)
file_list = [os.path.join(echo_df[echo_df['filename']==file]['dir'].values[0], file) for file in file_list]
def parameter_list(echo_df, file_list, video_attribute):
video_attribute_list = [echo_df[echo_df['filename']==os.path.basename(file)][video_attribute].values[0] \
for file in file_list]
print(f'{len(video_attribute_list)} values for attribute {video_attribute} found.')
return video_attribute_list
deltaX_list = parameter_list(echo_df=echo_df, file_list=file_list, video_attribute='deltaX')
deltaY_list = parameter_list(echo_df=echo_df, file_list=file_list, video_attribute='deltaY')
frame_time_list = parameter_list(echo_df=echo_df, file_list=file_list, video_attribute='frame_time')
VC = Videoconverter(max_frame_time_ms=None, min_frames=None, meta_df=None)
npy_array_list = [VC.load_video(file) for file in file_list]
print(f'{len(npy_array_list)} videos loaded.')
# -
# ### Models and weights ###
checkpoint_dir = os.path.normpath('/mnt/obi0/andreas/data/cfr/checkpoints')
model_output_list = ['global_cfr_calc', 'rest_global_mbf', 'stress_global_mbf']
checkpoint_list = ['global_cfr.h5', 'rest_mbf_ammonia.h5', 'stress_mbf_ammonia.h5']
checkpoint_file_list = [os.path.join(checkpoint_dir, checkpoint_file) for checkpoint_file in checkpoint_list]
checkpoint_dict = dict(zip(model_output_list, checkpoint_file_list))
display(checkpoint_dict)
# ### Predictions from earlier run ####
model_list = ['cfr_a4c_dgx-1_fc1_global_cfr_calc',
'mbf_ammonia_a4c_dgx-1_fc1_rest_global_mbf',
'mbf_ammonia_a4c_dgx-1_fc1_stress_global_mbf']
pred_dict={}
for model in model_list:
predict_file = os.path.join(predict_dir, 'cfr_models_30fps', model+'.parquet')
predict_df = pd.read_parquet(predict_file, columns=['model_name', 'model_output', 'filename', 'predictions'])
predict_df = predict_df[predict_df['model_name']==model]
model_output = predict_df['model_output'].values[0]
model_predictions = [predict_df[predict_df['filename']==os.path.basename(file)]['predictions'].values[0] for file in file_list]
pred_dict_model = {model_output: model_predictions}
pred_dict.update(pred_dict_model)
print(pred_dict.keys())
# ### Predictions from video list and checkpoints ###
qualified_index_list, predictions = runCFRModel(data_array_list=npy_array_list,
frame_time_ms_list=frame_time_list,
deltaX_list=deltaX_list,
deltaY_list=deltaY_list,
checkpoint_dict=checkpoint_dict,
batch_size=1)
# Check the output
for model_output in checkpoint_dict.keys():
df = pd.concat([pd.DataFrame(predictions[model_output]), pd.DataFrame(pred_dict[model_output])], axis=1)
df.columns=['runCFRModel', 'earlier_predictions']
display(df)
| notebooks/testCFRModel.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import numpy as np
def move_is_correct(grid,num):
'''
@param grid: 6x7 grid containing the current game state
@param num: column
returns True if move is allowed on that column
'''
#if 0 is in column
if 0 in grid[:,num]:
#move is allowed
return True
else:
return False
def move_still_possible(S):
'''
@param S: 6x7 grid containing the current game state
returns True if grid contains no 0, therefore no move possible anymore
'''
return not(S[S==0].size == 0)
def move(S,p,col_num):
'''
@param S: 6x7 grid containing the current game state
@param p: current player
@param col_num: column number
sets the player's number on the grid and returns the grid
'''
#sanity check
if 0 in S[:,col_num]:
y = np.where(S[:,col_num]==0)[0][-1]
S[y,col_num] = p
return S , y, col_num
else:
return S, None, None
return
def move_at_random(S):
'''
@param S: 6x7 grid containing the current game state
moves at random
'''
return np.random.randint(0,S.shape[1])
#neat and ugly but the fastest way to search a matrix for a vector is a string find
player1 = '1 1 1 1'
oponent = '2 2 2 2'
def move_was_winning_move(S, p):
'''
@param S: 6x7 grid containing the current game state
@param p: current player
combines all the allowed formations of the grid and string_finds with
the currents player vector. Returns true if match.
'''
if p == 1:
match = player1
else:
match = oponent
l=[]
#for every possible diag
for i in range(-2,4):
l.append(np.diag(S,k = i))
l.append(np.diag(np.fliplr(S),k=i))
#left to right
l.append(S)
#top to bottom
l.append(np.rot90(S))
if ''.join(np.array_str(e) for e in l).find(match) > -1:
return True
return False
# relate numbers (1, -1, 0) to symbols ('x', 'o', ' ')
symbols = {1:'b', 2:'r', 0:' '}
# print game state matrix using symbols
def print_game_state(S):
B = np.copy(S).astype(object)
for n in [1, 2, 0]:
B[B==n] = symbols[n]
print B
if __name__ == '__main__':
# initialize 6x7 connectfour board
gameState = np.zeros((6,7), dtype=int)
# initialize player number, move counter
player = 1
mvcntr = 1
# initialize flag that indicates win
noWinnerYet = True
while move_still_possible(gameState) and noWinnerYet:
while True:
# get player symbol
name = symbols[player]
print '%s moves' % name
# let player move at random
col_num = move_at_random(gameState)
if move_is_correct(gameState, col_num):
gameState, _ , _ = move(gameState,player,col_num)
# print current game state
print_game_state(gameState)
# evaluate game state
if move_was_winning_move(gameState, player):
print 'player %s wins after %d moves' % (name, mvcntr)
noWinnerYet = False
# switch player and increase move counter
if player == 1:
player = 2
elif player == 2:
player = 1
mvcntr += 1
break
if noWinnerYet:
print 'game ended in a draw'
# -
| notebooks/connectfour.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
from IPython.core.display import HTML
with open('../style.css', 'r') as file:
css = file.read()
HTML(css)
# # Die Onkologie-Station
# Auf einer Onkologie-Station liegen fünf Patienten in nebeneinander liegenden Zimmern.
# Bis auf einen der Patienten hat jeder genau eine Zigaretten-Marke geraucht.
# Der Patient, der nicht Zigarette geraucht hat, hat Pfeife geraucht.
# Jeder Patient fährt genau ein Auto und ist
# an genau einer Krebs-Art erkrankt. Zusätzlich haben Sie die folgenden Informationen:
# <ol>
# <li> Im Zimmer neben Michael wird Camel geraucht. </li>
# <li> Der Trabant-Fahrer raucht Ernte 23 und liegt im Zimmer neben dem
# Zungen-Krebs Patienten. </li>
# <li> Rolf liegt im letzten Zimmer und hat Kehlkopf-Krebs. </li>
# <li> Der West-Raucher liegt im ersten Zimmer. </li>
# <li> Der Mazda-Fahrer hat Zungen-Krebs und liegt neben dem Trabant-Fahrer. </li>
# <li> Der Nissan-Fahrer liegt neben dem Zungen-Krebs Patient. </li>
# <li> Rudolf wünscht sich Sterbe-Hilfe und liegt zwischen dem Camel-Raucher und dem Trabant-Fahrer. </li>
# <li> Der Seat Fahrer hat morgen seinen letzten Geburtstag. </li>
# <li> Der Luckies Raucher liegt neben dem Patienten mit Lungen-Krebs. </li>
# <li> Der Camel Raucher liegt neben dem Patienten mit Darm-Krebs. </li>
# <li> Der Nissan Fahrer liegt neben dem Mazda-Fahrer. </li>
# <li> Der Mercedes-Fahrer raucht Pfeife und liegt neben dem Camel Raucher. </li>
# <li> Jens liegt neben dem Luckies Raucher. </li>
# <li> Der Hodenkrebs-Patient hat gestern seine Eier durchs Klo gespült. </li>
# </ol>
# Entwickeln Sie ein <em>Python</em>-Programm, das die folgenden Fragen beantwortet:
# <ol>
# <li> Was raucht der Darmkrebs-Patient? </li>
# <li> Was fährt Kurt für ein Auto? </li>
# </ol>
# ## Importing the Necessary Modules
# Our goal is to solve this puzzle by first coding it as a solvability problem of propositional logic and then to solve the resulting set of clauses using the algorithm of Davis and Putnam.
import davisPutnam as dp
# In order to be able to transform formulas from propositional logic into sets of clauses we import the module <tt>cnf</tt> which implements the function <tt>normalize</tt> that takes a formula and transforms it into a set of clauses.
import cnf
# In order to write formulas conveniently, we use the parser for propositional logic.
import propLogParser as plp
# Using the parser and the module <tt>cnf</tt> we can impement a function $\texttt{parseCNF}(s)$ that takes a string $s$ representing a formula and transforms $s$ into an equivalent set of clauses.
def parseCNF(s):
nestedTuple = plp.LogicParser(s).parse()
Clauses = cnf.normalize(nestedTuple)
return Clauses
# ## Auxiliary Functions
# The function `atMostOne(V)` takes a set of propositional variables `V` as its argument.
# It returns a set of clauses that expresses the fact that at most one of the variables in `V` is true.
def atMostOne(V):
return { frozenset({ ('¬', x), ('¬', y) }) for x in V
for y in V
if x != y
}
atMostOne({'a', 'b', 'c'})
# Given a name $f$ and an index $i \in\{1,2,3,4,5\}$, the function $\texttt{var}(i)$ creates the string
# $f\langle i \rangle$, e.g. the call <tt>var("Japanese", 2)</tt> returns the following string:
#
# <tt>Japanese$\langle$2$\rangle$</tt>.
def var(f, i):
return f + "<" + str(i) + ">"
var("Japanese", 2)
# A call of the form $\texttt{x}$ will return a clause that specifies that the person with property $x$ has to be in one of the rooms from $1$ to $5$.
def somewhere(x):
return frozenset({ var(x, n) for n in range(1, 5+1)})
somewhere("a")
# Given an exclusive set of properties $S$ and a house number $i$, the function $\texttt{atMostOne}(S, i)$ returns a set of clauses that specifies that the person living in house number $i$ has at most one of the properties from the set $S$. For example, if
# $S = \{\texttt{"Japanese"}, \texttt{"Englishman"}, \texttt{"Spaniard"}, \texttt{"Norwegian"}, \texttt{"Ukranian"}\}$,
# then $\texttt{atMostOne}(S, 3)$ specifies that the inhabitant of house number 3 has at most one of the nationalities from the set $S$.
def atMostOneAt(S, i):
return atMostOne({ var(x, i) for x in S })
atMostOneAt({"A", "B", "C"}, 1)
# Implement a function $\texttt{onePerRoom}(S)$ which could be called as follows:
# $$\texttt{onePerRoom}(\{\texttt{"Camel"},
# \texttt{"Ernte"},
# \texttt{"West"},
# \texttt{"Luckies"},
# \texttt{"Pfeife"}\})
# $$
# This function would create a set of clauses that expresses that there has to be a room where the patient smokes Camel, another room where the patient smokes Ernte, a room where the patient smokes West, a room where the patient smokes Luckies lives, and a room where the patient is a pipe smoker.
# Furthermore, the set of clauses would contain clauses that express that these five patient occupy **different** rooms.
def onePerRoom(S):
Clauses = set()
for x in S:
Clauses.add(somewhere(x))
for i in range(1, 5+1):
Clauses |= atMostOneAt(S, i)
return Clauses
onePerRoom({"A", "B", "C", "D", "E"})
# Given to properties $a$ and $b$ the function $\texttt{sameHouse}(a, b)$ computes a set of clauses that specifies that if the inhabitant of house number $i$ has the property $a$, then he also has the property $b$ and vice versa. For example, $\texttt{sameHouse}(\texttt{"Japanese"}, \texttt{"Dog"})$ specifies that the Japanese guy keeps a dog.
def sameRoom(a, b):
Clauses = set()
for i in range(1, 5+1):
Clauses |= parseCNF(f'{var(a, i)} ↔ {var(b, i)}')
return Clauses
sameRoom("Luckies", "Camel")
# Given to properties $a$ and $b$ the function $\texttt{nextTo}(a, b)$ computes a set of clauses that specifies that the inhabitants with properties $a$ and $b$ are direct neighbours. For example, $\texttt{nextTo}(\texttt{'Japanese'}, \texttt{'Dog'})$ specifies that the Japanese guy lives next to the guy who keeps a dog.
def nextTo(a, b):
Clauses = parseCNF(f"{var(a, 1)} → {var(b, 2)}")
for i in range(2, 4+1):
Clauses |= parseCNF(f"{var(a, i)} → {var(b, i-1)} ∨ {var(b, i+1)}")
Clauses |= parseCNF(f"{var(a, 5)} → {var(b, 4)}")
return Clauses
nextTo('A', 'B')
# The function `differentRooms(a, b)` returns a set of clauses expressing the fact that the patients with properties `a` and `b` are in different rooms.
def differentRoom(a, b):
'your code here'
return Clauses
differentRoom('a', 'b')
Brands = { "Camel", "Ernte", "West", "Luckies", "Pfeife" }
Cars = { "Trabant", "Mazda", "Nissan", "Seat", "Mercedes" }
Cancers = { "Zunge", "Kehlkopf", "Lunge", "Darm", "Hoden" }
Names = { "Michael", "Rolf", "Rudolf", "Jens", "Kurt" }
def allClauses():
# In jedem Zimmer wird genau eine Zigaretten-Marke geraucht.
Clauses = 'your code here'
# Jeder Patient hat genau ein Auto.
Clauses |= 'your code here'
# Jeder Patient ist an genau einer Krebsart erkrankt.
Clauses |= 'your code here'
# Jeder Patient hat genau einen Vornamen.
Clauses |= 'your code here'
# Im Zimmer neben Michael wird Camel geraucht.
Clauses |= 'your code here'
# Der Trabant-Fahrer raucht Ernte 23 und liegt im Zimmer neben dem
# Zungen-Krebs Patienten.
Clauses |= 'your code here'
Clauses |= 'your code here'
# Rolf liegt im letzten Zimmer und hat Kehlkopf-Krebs.
Clauses |= 'your code here'
Clauses |= 'your code here'
# Der West-Raucher liegt im ersten Zimmer.
Clauses |= 'your code here'
# Der Mazda-Fahrer hat Zungen-Krebs und liegt neben dem Trabant-Fahrer.
Clauses |= 'your code here'
Clauses |= 'your code here'
# Der Nissan-Fahrer liegt neben dem Zungen-Krebs Patient.
Clauses |= 'your code here'
# Rudolf wünscht sich Sterbe-Hilfe und liegt zwischen dem Camel-Raucher und dem Trabant-Fahrer.
Clauses |= 'your code here'
Clauses |= 'your code here'
Clauses |= 'your code here'
# Der Luckies Raucher liegt neben dem Patienten mit Lungen-Krebs.
Clauses |= 'your code here'
# Der Camel Raucher liegt neben dem Patienten mit Darm-Krebs.
Clauses |= 'your code here'
# Der Nissan Fahrer liegt neben dem Mazda-Fahrer.
Clauses |= 'your code here'
# Der Mercedes-Fahrer raucht Pfeife und liegt neben dem Camel Raucher.
Clauses |= 'your code here'
Clauses |= 'your code here'
# Jens liegt neben dem Luckies Raucher.
Clauses |= 'your code here'
return Clauses
Clauses = allClauses()
Clauses
# There should be 322 different clauses.
len(Clauses)
def solve():
Clauses = allClauses()
return dp.solve(Clauses, set())
# Solving the problem takes about 3 seconds on my computer.
# %%time
Solution = solve()
Solution
# ## Pretty Printing the Solution
from IPython.display import HTML
def arb(S):
for x in S:
return x
def extractAssignment(Solution):
Assignment = {}
for Unit in Solution:
Literal = arb(Unit)
if isinstance(Literal, str):
number = int(Literal[-2])
name = Literal[:-3]
Assignment[name] = number
return Assignment
def showHTML(Solution):
result = '<table style="border:2px solid blue">\n'
result += '<tr>'
for name in ['Room', 'Brands', 'Cars', 'Cancers', 'Names']:
result += '<th style="color:gold; background-color:blue">' + name + '</th>'
result += '</tr>\n'
for chair in range(1, 5+1):
result += '<tr><td style="border:1px solid green">' + str(chair) + '</td>'
for Class in [Brands, Cars, Cancers, Names]:
for x in Class:
if Solution[x] == chair:
result += '<td style="border:1px solid green">' + x + '</td>'
result += '</tr>\n'
result += '</table>'
display(HTML(result))
showHTML(extractAssignment(Solution))
# ## Checking the Uniqueness of the Solution
# Given a set of unit clauses $U$, the function $\texttt{checkUniqueness}(U)$ returns a clause that is the negation of the set $U$.
def negateSolution(UnitClauses):
return { dp.complement(arb(unit)) for unit in UnitClauses }
negateSolution({ frozenset({'a'}), frozenset({('¬', 'b')}) })
# The function $\texttt{checkUniqueness}(\texttt{Solution}, \texttt{Clauses})$ takes a set of $\texttt{Clauses}$ and a $\texttt{Solution}$ for these clauses and checks, whether this is the only solution.
def checkUniqueness(Solution, Clauses):
negation = negateSolution(Solution)
Clauses.add(frozenset(negation))
alternative = dp.solve(Clauses, set())
if alternative == { frozenset() }:
print("Well done: The solution is unique!")
else:
print("ERROR: The solution is not unique!")
checkUniqueness(Solution, Clauses)
| Python/Exercises/Blatt-11-Davis-Putnam.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Knative
#
# Knative (ausgesprochen kay-nay-tiv) erweitert Kubernetes um eine Reihe von Middleware-Komponenten, die für die Erstellung moderner, container-basierter Anwendungen unerlässlich sind.
#
# Knative Komponenten konzentrieren sich auf die Lösung alltäglicher, aber schwieriger Aufgaben wie:
#
# * Bereitstellen eines Containers
# * Routing und Verwaltung des Datenverkehrs mit blue / green Bereitstellung
# * Automatische Skalierung des Workloads
# * Bindung laufender Dienste an mehrere Ökosysteme
# ***
# ## Serving
#
# 
#
# Quelle: knative.dev
# - - -
#
# Knative Serving baut auf Kubernetes und Istio auf, um die Bereitstellung von Anwendungen und Funktionen ohne Server (Serverless, Function as a Service FaaS) zu unterstützen.
#
# Das Knative Serving-Projekt bietet Middleware-Grundelemente, die Folgendes ermöglichen:
#
# * Schnelle Bereitstellung von Services ohne Server
# * Automatische Skalierung auf 0
# * Routing und Netzwerkeinstellungen für Istio-Komponenten
# * Momentaufnahmen von bereitgestelltem Code und bereitgestellten Konfigurationen
#
# ### Installation
# ! kubectl apply --filename https://github.com/knative/serving/releases/download/v0.15.0/serving-crds.yaml
# ! kubectl apply --filename https://github.com/knative/serving/releases/download/v0.15.0/serving-core.yaml
# ! kubectl apply --filename https://github.com/knative/net-istio/releases/download/v0.15.0/release.yaml
# ***
# ### Beispiel Serving - Skalierung auf 0
#
# Nehmen wir an wir haben einen Service welcher nur 1 - 2 im Monat verwendet wird.
#
# Um keine Rechnenleistung zu verschwenden, soll dieser Service nur gestartet werden, wenn er wirklich gebraucht wird.
#
# Deshalb wird der Service "Serverless" implementiert.
# ! kubectl create namespace serving
# + language="bash"
# cat <<%EOF% | kubectl apply -f -
# apiVersion: serving.knative.dev/v1 # Current version of Knative
# kind: Service
# metadata:
# name: helloworld-go # The name of the app
# namespace: serving # The namespace the app will use
# spec:
# template:
# spec:
# containers:
# - image: gcr.io/knative-samples/helloworld-go # The URL to the image of the app
# env:
# - name: TARGET # The environment variable printed out by the sample app
# value: "ich werde nur auf Anforderung gestartet"
# # %EOF%
# -
# Schauen wir uns nun die erstellten Ressourcen an.
#
# Der eigentliche Service (Pods) wird am Anfang gestartet und nach einer bestimmen Leerlaufzeit beendet. Das ReplicaSet setzt die Anzahl Pods auf 0.
# ! kubectl get all --namespace serving
# Der Aufruf des Services erfolgt via Istio. Dabei ist explizit der Hostname (HTTP Header Host:) mit anzugeben.
#
# Das erste Mal dauert der Aufruf relativ lange (Latenzzeit), weil der Pods zuerst gestartet werden muss.
#
# Alternativ könnten wir den Hosteintrag in die `hosts` Datei eintragen oder einen DNS Server verwenden.
#
# **ACHTUNG**: damit es funktioniert müssen oben alle Ressourcen den Status Ready=True haben.
# + language="bash"
# date
# curl -H "Host: helloworld-go.serving.example.com" istio-ingressgateway.istio-system
# date
# # zweiter Start
# curl -H "Host: helloworld-go.serving.example.com" istio-ingressgateway.istio-system
# date
# -
# - - -
# Aufräumen, kann auch Verwendet werden wenn die Ressoucen auf Status Ready=Unknown verbleiben.
# ! kubectl delete namespace serving
| data/jupyter/demo/Serverless-Knative-Serving.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Script To Make Site
#
# This script converts all jupyter notebooks into markdown files, then converts all markdown files (jupyter and note) into a website ready to push to github.
# ## Preliminaries
# +
# Load libraries
import os
import re
import fileinput
import sys
from glob import glob
import shutil
# Create path to content
path = 'content/'
# -
# ## Find All Jupyter Notebooks
# +
# Find all jupyter notebooks in all content folders
all_ipynb_files = [os.path.join(root, name)
for root, dirs, files in os.walk(path)
for name in files
if name.endswith((".ipynb"))]
# Remove all notebooks from checkpoint folders
ipynb_files = [ x for x in all_ipynb_files if ".ipynb_checkpoints" not in x ]
# -
# ## Convert All Jupyter Notebooks To Markdown
# For each file
for file in ipynb_files:
# Convert into markdown
os.system('jupyter nbconvert --to markdown {file}'.format(file=file))
# ## Handle The Folders
#
# This really nasty code finds all the folders generated by the Juypter conversion (they end in `_files`) and then tries to rename them to remove the `_files` part (doing so is required by Hugo so the images can be seen). If an existing folder (without the `_files` part) exists, it moves all the files from the newly generated `_files` into the existing folder (so we retain any manual images like flashcard images in that existing folder) and then deletes the `_files` folder.
# +
# Get all folders in directory
folders = [x[0] for x in os.walk(path)]
# Delete .ipynb checkpoint folders
folders = [ x for x in folders if ".ipynb_checkpoints" not in x ]
# For each folder
for folder_name in folders:
# if _files in folder name
if '_files' in folder_name:
# Create a new folder name
def rchop(thestring, ending):
if thestring.endswith(ending):
return thestring[:-len(ending)]
return thestring
new_folder_name = rchop(folder_name, '_files')
# try to rename original folder
try:
os.rename(folder_name, new_folder_name)
# if error,
except OSError:
existing_base_folder = os.getcwd()+"/"+new_folder_name
justcreated_base_folder = os.getcwd()+"/"+folder_name
# get a list of all files in the folder
generated_files = os.listdir(justcreated_base_folder)
# copy each file to the existing folder
for generated_file in generated_files:
to_copy = justcreated_base_folder+"/"+generated_file
shutil.copy(to_copy, existing_base_folder)
# delete the newly created _files folder
shutil.rmtree(justcreated_base_folder)
# -
# ## Search Through Contents Of All Markdown Files (manually generated and generated by a jupyter notebook) And Fix Links So That They Point To Folders Created Above
# +
def replaceAll(file,searchExp,replaceExp):
for line in fileinput.input(file, inplace=1):
if searchExp in line:
line = line.replace(searchExp,replaceExp)
sys.stdout.write(line)
# Find all markdown files in all content folders
all_md_files = [os.path.join(root, name)
for root, dirs, files in os.walk(path)
for name in files
if name.endswith((".md"))]
for file in all_md_files:
with open(file,'r') as f:
filedata = f.read()
# Find all markdown link syntaxes
md_links = re.findall('!\\[[^\\]]+\\]\\([^)]+\\)', filedata)
# For each markdown link
for link in md_links:
# Replace the full file path
md_image_path = re.search(r'\((.*?)\)', link).group(1)
md_image_filename = os.path.basename(md_image_path)
md_image_title = re.search(r'\[(.*?)\]', link).group(1)
new_link = ""
replaceAll(file, link, new_link)
# -
| make.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
from scipy.stats import norm
from matplotlib import pyplot as plt
# +
N = 100
d = norm(8, 1)
Xᴺ = d.rvs(size=N)
# F̂, Xᴺ は Julia から生成した記号をコピペした.
def F̂(x):
return np.mean(Xᴺ <= x)
F̂=np.vectorize(F̂)
# -
xs = np.linspace(4, 12, 100)
ys = norm.cdf(xs, loc=8, scale=1)
# これブロードキャストさせたいんだけれどん
plt.plot(xs, F̂(xs), label="empirical")
plt.plot(xs, ys, label="true distribution")
plt.legend()
# +
fig,ax=plt.subplots()
xs = np.arange(5, 12, 0.1)
for N in [10, 50, 100, 500, 1000, 10000]:
d = norm(8, 1)
Xᴺ = d.rvs(size=N)
# Remark: F̂=np.vectorize(lambda x:sum(Xᴺ <= x)/N) は非常に遅い
F̂=np.vectorize(lambda x:np.mean(Xᴺ <= x))
ys = F̂(xs)
ax.plot(xs, ys,label=f"N={N}")
ax.plot(xs, norm(8,1).cdf(xs), label="True distribution")
plt.legend()
# -
N = 100000
d = norm(8,1)
Xᴺ = d.rvs(size=N)
def F̂(x):
return np.mean(Xᴺ <= x)
F̂ = np.vectorize(F̂)
domcdf = np.linspace(4,12,num=10000)
imcdf = F̂(domcdf)
# +
xs = []
M = len(domcdf)
for trial in range(100000):
y = np.random.uniform()
idx = np.searchsorted(imcdf, y)
if idx < M:
x = domcdf[idx]
xs.append(x)
plt.xlim([4,12])
plt.hist(xs, density=True,bins=50)
xs = sorted(xs) # d.pdf の描画のために
plt.plot(xs, d.pdf(xs))
| statExer/py_empirical_distribution.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ccClub Class 10: Classifcation with K-Nearest Neighbor
# ---
# **_Author : <NAME>_**
# +
# First thing first. Import packages.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
# -
# # Part 1: Introduction to k-Nearest Neighbor Algorithm
#
# **[From Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)**
#
# In pattern recognition, the k-nearest neighbors algorithm (k-NN) is a non-parametric method used for classification and regression. In both cases, the input consists of the $k$ closest training examples in the feature space. The output depends on whether k-NN is used for classification or regression:
#
# >- In _k-NN classification_, the output is a class membership. An object is classified by a **majority vote** of its neighbors, with the object being assigned to the class most common among its $k$ nearest neighbors ($k$ is a positive integer, typically small). If $k = 1$, then the object is simply assigned to the class of that single nearest neighbor.
#
#
# >- In _k-NN regression_, the output is the property value for the object. This value is the **average of the values** of its $k$ nearest neighbors.
#
# k-NN is a type of instance-based learning, or lazy learning, where the function is only approximated locally and all computation is deferred until classification. The k-NN algorithm is among the simplest of all machine learning algorithms.
# 
#
# [image source](https://upload.wikimedia.org/wikipedia/commons/e/e7/KnnClassification.svg)
# <img src="http://atm.amegroups.com/article/viewFile/10170/html/63653" alt="Drawing" style="width: 500px;"/>
#
# [image source](http://atm.amegroups.com/article/viewFile/10170/html/63653)
# # k-NN classification
#
# ## How to compute majority vote?
#
# To compute the majority vote, we need to come up with a measurement that can tell us how similar two data points are. Therefore, we use **_distance_** between two points to measure their similarity. We can simply use eculidean distance as our measurement.
#
# So for a unseen observation $x'$ (a new data point), we can compute the distance bewteen one training data point $x$ and the unseen data point $x'$ as followed:
#
# $$
# d(x, x') = \sqrt{\sum^n_{i=1} (x_i - x'_i)^2} = \sqrt{(x_1 - x'_1)^2 + (x_2 - x'_2)^2 + ... + (x_n - x'_n)^2}
# $$
#
# Then we compute the distances $d$ for all the training data. Once we have the distance, we choose the top $k$ points that have are closet to our unseen $x'$. Next, we calculate the number of each class and that is the **_votes_** for that class. Finally, we then classify our unseen $x'$ to the class with the highest votes.
# <img src="https://i.pinimg.com/originals/65/36/b9/6536b9a63fc427e0fc3e1a9687b49aff.png" alt="Drawing" style="width: 500px;"/>
#
# [image source](https://i.pinimg.com/originals/65/36/b9/6536b9a63fc427e0fc3e1a9687b49aff.png)
# 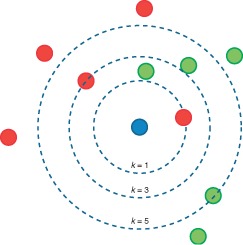
#
# [image source](http://en.proft.me/media/science/r_knn_classify.png)
# # Part 2: Build Your k-NN Model on Iris Data
#
# <img src="https://image.slidesharecdn.com/irisdataanalysiswithr-140801203600-phpapp02/95/iris-data-analysis-example-in-r-3-638.jpg?cb=1406925587" alt="Drawing" style="width: 500px;"/>
#
# [image source](https://image.slidesharecdn.com/irisdataanalysiswithr-140801203600-phpapp02/95/iris-data-analysis-example-in-r-3-638.jpg?cb=1406925587)
#
# We will be using the [Iris Dataset](https://archive.ics.uci.edu/ml/datasets/Iris), which was introduced in 1936 by the famous statistician <NAME>. The data set contains 3 classes of 50 instances each, where each class refers to a type of iris plant (Iris setosa, Iris virginica and Iris versicolor). 4 features were used in this data set and fifth feature is the response (target). Our task is to train a k-NN model to classify the species given their 4 features.
#
# >```text
# 1. sepal length in cm
# 2. sepal width in cm
# 3. petal length in cm
# 4. petal width in cm
# 5. class:
# - Iris Setosa
# - Iris Versicolour
# - Iris Virginica
# ```
# <img src="https://raw.githubusercontent.com/ritchieng/machine-learning-dataschool/master/images/03_iris.png" alt="Drawing" style="width: 200px;"/>
#
# [image source](https://raw.githubusercontent.com/ritchieng/machine-learning-dataschool/master/images/03_iris.png)
# ## 2-1: Read Iris data with Pandas
# +
# define column names
names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class']
# read in data and assign column names
### YOUR CODE HERE ###
data = pd.read_csv('iris.csv', header = None, names=names)
######################
# -
# ## Inspect data
# +
print(data.shape[0], 'rows (instances) X', data.shape[1], 'columns (features)')
display(data.head())
# -
# ## Inspect targets (how many species)
# +
# get unique classes in the dataset
### YOUR CODE HERE ###
classes = data['class'].unique()
######################
print('There are', len(classes), 'classes in the dataset:', ', '.join(list(classes)))
# -
# ## 2-2: Plot the data
# ### `sepal_length` VS `sepal_width`
sns.pairplot(x_vars=["sepal_length"], y_vars=["sepal_width"], data=data, hue="class", size=8)
# ### `petal_length` VS `petal_width`
sns.pairplot(x_vars=["petal_length"], y_vars=["petal_width"], data=data, hue="class", size=8)
# ## 2-3: Split data into training & testing set
#
# - To test the performance of the model, we will need to get testing set.
# - One convention is to split the data into 3 sets: training, development and testing.
# - In this convention, we use development set to test the accuracy of the model.
# - And use real-world data as the testing set to measure the final performance.
# - Another convention is to split the data into 2 sets: training and testing.
# - In this convention, the testing set here is equivalent to the development set.
# ### Here we will use the second convention. To split the data into train and test set, we do the 3 following steps.
#
# - STEP 1: Create a boolean mask to selects our training set.
# - `HINT: use np.random.rand()` to get a probability.
# - This probability is the fraction of data that we want for our training set.
#
#
# - STEP 2: Use the mask as your filter to select your training set.
#
#
# - STEP 3: Last, deselect the indexes to get the testing set.
# - `HINT: use DataFrame[~boolean]`
# +
# to make sure that the random number is always the same (only for checking purpose)
np.random.seed(1)
### YOUR CODE HERE ###
# create a mask to filter training data
mask = np.random.rand(len(data)) < 0.7
# select training data
data_train = data[mask]
# select testing data
data_test = data[~mask]
#######################
print('There are', len(data_train), 'data in your training set.')
print('There are', len(data_test), 'data in your testing set.')
# -
# ## Select Input data and output target
#
# - The input data should be the first 4 columns of the data.
# - The shape of your input data should be `(number of data, 4)`.
#
#
# - The output target should be the last column.
# - Here, we store our output target in a 1D array (ranked 1).
# - The shape of your output target should be `(number of data, )`.
#
#
# - Convert your DataFrame into a numpy array (matrix).
# +
### YOUR CODE HERE ###
X_train = np.array(data_train.iloc[:, :4])
y_train = np.array(data_train.iloc[:, 4])
X_test = np.array(data_test.iloc[:, :4])
y_test = np.array(data_test.iloc[:, 4])
#######################
print('Input data for training:', X_train.shape)
print('Output target for training:', y_train.shape)
print('Input data for testing:', X_test.shape)
print('Output target for testing:', y_test.shape)
# +
# Test cell: to make sure the shape of your data is correct
assert X_train.shape == (len(data_train), 4)
assert y_train.shape == (len(data_train), )
assert X_test.shape == (len(data_test), 4)
assert y_test.shape == (len(data_test), )
# -
# ## 2-4: Build your k-nearest neighbor model from scratch
#
# **_Let the fun part begin!_**
#
# There are 2 main parts for the k nearest neighbor algorithm. The first part is to compute all the distances between the testing data point and the training data points. The second part is to get the prediction based on its $k$ nearest neighbors.
#
# **PART A: COMPUTE DISTANCE**
# - STEP 1: loop over all the points in training data
# - STEP 2: select one data point in the training set, which will be our current `x_train`
# - STEP 3: compute the distance between the testing point `x_test` and `x_train`
# - Hint: use the eculidean distance, see the equation above
# - STEP 4: store the computed distance
#
# **PART B: GET PREDICTION**
# - STEP 1: get the original indexes of the sorted distances.
# - Hint: we use numpy's `argsort` funtion to implement this
# - https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.argsort.html
#
# - STEP 2: get targets based on the sorted distances (increasing order)
# - STEP 3: get top k's targets
# - STEP 4: compute votes for each species and find the majority vote
# - STEP 5: output prediction
# - Hint: we use numpy's `argmax` function to get the index of the maximum vlaue
# - https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.argmax.html
def KNN(X_train, y_train, x_test, k):
# lists to store distance and target
distances = []
# ===== COMPUTE DISTANCE ===== #
### YOUR CODE HERE ###
# STEP 1: loop over all points in training data
for i in range(X_train.shape[0]):
# --- compute distance between testing data 'x_test' and each data point 'x_train' in training data
# STEP 2: select current data point 'x_train'
x_train = X_train[i, :]
# STEP 3: compute euclidean distance (see Hints you are stuck!)
dist = np.sqrt(np.sum((x_test - x_train)**2))
# STEP 4: store distance in the 'distances' list
distances.append(dist)
#######################
# ===== GET PREDICTION ===== #
# STEP 1: get the indexes of the sorted distances (in increasing order)
# convert list to numpy array to use 'argsort' function
indexes = np.array(distances).argsort()
### YOUR CODE HERE ###
# STEP 2: get targets based on sorted distances' indexes
targets = y_train[indexes]
# STEP 3: get the first k's targets (k-neareast neighbor)
k_targets = targets[:k]
# STEP 4: compute votes
# for each species in the classes, compute its votes and store the value in the 'votes' list
classes = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
votes = []
for c in classes:
votes.append(np.sum(k_targets == c))
########################
# STEP 5: get prediction
# get the index of the majority vote, convert list to numpy array to use 'argmax' function
max_index = np.array(votes).argmax()
# get the final prediction that has the most votes
predict = classes[max_index]
return predict
# ## 2-5: Let's test our model
#
# **_Woo-hoo! You've made it. Now let's run your model on the testing data._**
# ### Test on one testing data point
# +
# change the setting to play around with your model
k = 5
x_test = X_test[0,:]
# get prediction using your KNN model
predict = KNN(X_train, y_train, x_test, k)
print('The prediced class for x_test:', predict)
# -
# ### Test on all testing data points
#
# To test on all the testing data, we need to **loop through** all the testing data point and make prediction for each of them.
#
# > Write a function `model` that takes in `X_train`, `y_train`, `X_test`, `y_test` and `k` and calculates the accuracy for the testing data.
#
# >```text
# - STEP 1: loop over all the data points
# - STEP 2: select on testing data point, which will be our current `x_test`
# - STEP 3: get prediction for that data point using your KNN function
# - Hint: see the above code cell if you don't know how to use your function
# - STEP 4: store the prediction
# - STEP 5: compute accuracy
# ```
def model(X_train, y_train, X_test, y_test, k):
# a list to store all the prediction results
predictions = []
### YOUR CODE HERE ###
# STEP 1: loop through all the data point in your testing data 'X_test'
for i in range(X_test.shape[0]):
# STEP 2: get current data point `x_test`
x_test = X_test[i, :]
# STEP 3: make prediction for x_test
predict = KNN(X_train, y_train, x_test, k)
# STEP 4: store the prediction result in the 'predictions' list
predictions.append(predict)
# STEP 5: compute accuracy (number of matches divided by total number of data)
accuracy = np.sum(predictions == y_test) / len(y_test)
#######################
return accuracy
# +
# change the setting to play around with your model
k = 5
# get prediction using your `model` function
accuracy = model(X_train, y_train, X_test, y_test, k)
print('Your KNN model has', str(round(accuracy*100,2)), 'accuracy!')
# -
# ### Test on various value of K
#
# Now that you've built the `KNN` and the `model` function, you can change the value of $k$ to see how different number of $k$ influence the prediction and accuracy. Observe that our model seems to do a pretty good job using only a small number of $k$. As $k$ gets large the accuracy also gets worse.
# +
Ks = [i for i in range(1, 100)] # be careful that k should not exceed the number of training data
test_accuracy = []
for k in Ks:
accuracy = model(X_train, y_train, X_test, y_test, k)
test_accuracy.append(accuracy)
# -
# ### Visualize the results
# +
# plot the testing accuracy with respect to different k
plt.plot(test_accuracy)
plt.title('Accuracy of Various k')
plt.ylabel('Accuracy')
plt.xlabel('Number of neighbors (k)')
| notebooks/KNN_ans.ipynb |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.