code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .scala
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Scala
// language: scala
// name: scala
// ---
// <p style="float: left;"><a href="variances.ipynb" target="_blank">Previous</a></p>
// <p style="float: right;"><a href="lower-type-bounds.ipynb" target="_blank">Next</a></p>
// <p style="text-align:center;">Tour of Scala</p>
// <div style="clear: both;"></div>
//
// # Upper Type Bounds
//
// In Scala, [type parameters](generic-classes.ipynb) and [abstract types](abstract-types.ipynb) may be constrained by a type bound. Such type bounds limit the concrete values of the type variables and possibly reveal more information about the members of such types. An _upper type bound_ `T <: A` declares that type variable `T` refers to a subtype of type `A`.
// Here is an example that demonstrates upper type bound for a type parameter of class `PetContainer`:
// + attributes={"classes": ["tut"], "id": ""}
abstract class Animal {
def name: String
}
abstract class Pet extends Animal {}
class Cat extends Pet {
override def name: String = "Cat"
}
class Dog extends Pet {
override def name: String = "Dog"
}
class Lion extends Animal {
override def name: String = "Lion"
}
class PetContainer[P <: Pet](p: P) {
def pet: P = p
}
val dogContainer = new PetContainer[Dog](new Dog)
val catContainer = new PetContainer[Cat](new Cat)
// + attributes={"classes": ["tut"], "id": ""}
// this would not compile
val lionContainer = new PetContainer[Lion](new Lion)
// -
// The `class PetContainer` take a type parameter `P` which must be a subtype of `Pet`. `Dog` and `Cat` are subtypes of `Pet` so we can create a new `PetContainer[Dog]` and `PetContainer[Cat]`. However, if we tried to create a `PetContainer[Lion]`, we would get the following Error:
//
// `type arguments [Lion] do not conform to class PetContainer's type parameter bounds [P <: Pet]`
//
// This is because `Lion` is not a subtype of `Pet`.
// <p style="float: left;"><a href="variances.ipynb" target="_blank">Previous</a></p>
// <p style="float: right;"><a href="lower-type-bounds.ipynb" target="_blank">Next</a></p>
// <p style="text-align:center;">Tour of Scala</p>
// <div style="clear: both;"></div>
| notebooks/scala-tour/upper-type-bounds.ipynb |
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .scala
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Spark
// language: ''
// name: sparkkernel
// ---
println("Hello World") // make sure we're in a spark kernel
// # Scala for Spark - Assignment
//
// Learning Scala the hard way.
//
// ## Part 1: The Basics
/*
Try the REPL
Scala has a tool called the REPL (Read-Eval-Print Loop) that is analogous to
commandline interpreters in many other languages. You may type any Scala
expression, and the result will be evaluated and printed.
The REPL is a very handy tool to test and verify code. Use it as you read
this tutorial to quickly explore concepts on your own.
*/
// +
// single line comments start with two forward slashes
/*
Multi-line comments look like this
*/
// -
// printing and forcing a new line
println("Hello world")
println(10)
//printing on the same line
print("Hello world")
print(10)
// +
/*
Scala is a statistically typed language, yet note that in the above declarations,
we did not specify a type. THis is due to a language feature called type inference.
In most cases, Scala compiler can guess what type of a variable is, so you don't have to type it every time.
We can explicitly declare the type of a variable like so:
*/
val z: Int = 10
val a: Double = 1.0
// notice automatic convertion from int to double, result is 10.0 not 10
val b: Double = 10
// +
// boolean values
true
false
// boolean operations
!true
!false
true == false
10 > 5
// +
// math operations
1 + 1 // add
2 - 1 // subtract
5 * 3 // multiply
6 / 2 // whole number division
6.0 / 4 // float division
// Evaluating an expression in the REPL gives you the type and value of the result
1 + 7
/* The above line results in:
scala> 1 + 7
res29: Int = 8
This means the result of evaluating 1 + 7 is an object of type Int with a
value of 8
*/
// +
// strings
"Scala strings are surrounded by double quotes"
'a' // a single scala char
// 'Single quote strings don't exist' <- gives an error
// strings have the usual Java methods defined on them
"hello world".length
"hello world".substring(2,6)
"hello world".replace("C", "3")
// they also have extra scala methods
"hello world".take(5)
"hello world".drop(5)
// string interpolation, notice the prefix 's'
val n = 45
s"We have $n apples" // -> we have 45 apples
// expressions inside interpolated strings are also possible
s"Power of 2: ${math.pow(2,2)})"
// some characters need to be "escaped", e.g. a double quote inside a string
"They stood outside the \"Rose and Crown\""
// -
// ## Part 2: Functions
// +
/*
Functions are defined like so:
def functionName(args ...): ReturnType = {body...}
If you come from more traditional programming languages, notice the omission of the
return keyword. In Scala, the last expression in the function block
is the return value
*/
def sumOfSquares(x: Int, y: Int): Int = {
val x2 = x * x
val y2 = y * y
x2 + y2
}
// the { } can be omitted if the function body is a single expression
def sumOfSquaresShort(x: Int, y: Int): Int = x * x + y * y
/// syntax for calling functions is familiar
sumOfSquares(3, 4)
// you can use parameter names to specify them in a different order
def subtract(x: Int, y: Int): Int = x - y
subtract(10, 3)
subtract(y=10, x=3)
/*
In most cases (recursive functions being the most notable exception), function
return type can be omitted. The same type inference we saw with variables will
work with function return values
*/
def sq(x: Int) = x * x
// functions can have default parameters
def addWithDefault(x: Int, y: Int = 5) = x + y
addWithDefault(1, 2)
addWithDefault(1)
// anonymous functions look like this
(x: Int) => x * x
/*
If each argument in an anonymous function is only used once
Scala gives you an even shorter way to define them. These
anonymous functions turn out to be extremely common, as will
be obvious in the data structure section
*/
val addOne: Int => Int = _ + 1
val weirdSum: (Int, Int) => Int= (_ * 2 + _ * 3)
addOne(5)
weirdSum(2, 4)
// -
// ## Part 3: Flow Control
// +
1 to 5
val r = 1 to 5
r.foreach(println)
// NB: Scala is quite lenient when it comes to dots and brckets - study
// the rules separately. This helps write DSLs and APIs that read like English
// Why doesn't println need any parameters here?
// Stay tuned for first-class functions in the Functional programmig section below
(5 to 1 by -1) foreach (println)
// recursion is the idiomatic way of repeating an action in Scala (as in most
// other functiona languages).
// recursive functions need an explicit return type, the compiler can't infer it
// here, it's Unit, which is analagous to a 'void' return type in Java
def showNumbersInRange(a: Int, b: Int): Unit = {
print (a)
if (a < b)
showNumbersInRange(a + 1, b)
}
showNumbersInRange(1, 14)
// conditionals
val x = 10
if (x == 1) println("yeah")
if (x == 10) println("yeah")
if (x == 11) println("yeah")
if (x == 11) println("yeah") else println("nay")
println(if (x == 10) "yeah" else "nope")
val text = if (x == 10) "yeah" else "nope"
// -
// ## Part 4: Data Structures
// +
// arrays
val a = Array(1, 2, 3, 5, 8, 13)
a(0)
a(3)
// a(21) // throws an exception
// sets
val s = Set(1, 3, 7)
s(0) // boolean = false
s(1) // boolean = true
// tuples
(1, 2)
(4, 3, 2)
(1, 2, "three")
(a, 2, "three")
// function to divide integers and store remainder
val divideInts = (x: Int, y: Int) => (x / y, x % y)
// to access the elements of an tuple, use _._n where n is the 1 based
// index of the element
val d = divideInts(10, 3)
d._1
d._2
// alternatively, you can do multiple variable assignment to tuple,
// which is more convenient and readable in many cases
val (div, mod) = divideInts(10, 3)
div
mod
// -
// ## Part 7: Functional Programming
// +
// Scala allows methods and funtions to return, or take as parameters, other
// functions or methods
val add10: Int => Int = _ + 10 // a function taking in an int and returning an int
List(1, 2, 3) map add10 // add ten to each element
// anonymous functions can be used in place of named functions
List(1, 2, 3) map (x => x + 10)
// and the underscore symbol can be used if there is just one argument to the
// anonymous function. It gets bound as the variable
List(1, 2, 3) map (_ + 10)
// if the anonymous block AND the funtion you are applying both take one
// argument, you can even omit the underscore
List("Dom", "Bob", "Natalia") foreach println
// +
// combinators (using s from above)
s.map(sq)
val sSquared = s.map(sq)
sSquared.filter(_ < 10)
sSquared.reduce(_+_)
// the filter function takes a predicate (a function from A -> boolean) and
// selects all elements which satisfy the predicate
List(1, 2, 3) filter (_ > 2)
case class Person(name: String, age: Int)
List(
Person(name = "Dom", age = 23),
Person(name = "Bob", age = 30)
).filter(_.age > 25)
// certain collections (such as List) in Scala have a foreach method,
// which takes as an argument a type returning Unit, that is, a void method
val aListOfNumbers = List(1, 2, 3, 4, 10, 20, 100)
aListOfNumbers foreach (x => println(x))
aListOfNumbers foreach println
// -
// ## Part 9: Misc
// +
// importing things
import scala.collection.immutable.List
// import all sub packages
import scala.collection.immutable._
// import multiple classes in one statement
import scala.collection.immutable.{List, Map}
// rename and import using =>
import scala.collection.immutable.{List => ImmutableList}
// -
| module2-scala-for-spark/scala-practice.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.7 (''venv'': venv)'
# language: python
# name: python3
# ---
# ### Análise de ajustes
# #### Imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from scipy.stats import t
# #### Help functions
# +
def first_analysis_lr(x, y, xlabel, ylabel):
#Cálculos e equação da reta entre duas variáveis aleatórias
df = pd.DataFrame({'x':x, 'y':y})
#x médio:
x_mean = df['x'].mean()
#y médio:
y_mean = df['y'].mean()
#Somatória dos valores de x:
x_sum = df['x'].sum()
#Somatória dos valores de y:
y_sum = df['y'].sum()
#Somatória de x * y:
xy_sum = (df['x'] * df['y']).sum()
#Somatória dos valores de x quadrado:
x2_sum = (df['x']**2).sum()
#Somatória dos valores de y quadrado:
y2_sum = (df['y']**2).sum()
#Número de amostras:
n = df.shape[0]
#Fórnulas complementares para cálculo de b1:
sxy = xy_sum - ((x_sum * y_sum) / n)
sxx = x2_sum - ((x_sum**2) / n)
syy = y2_sum - ( (y_sum**2)/ n)
#Estimativa do coeficiente de inclinação b1(beta 1):
b1 = sxy / sxx
#Estimativa do intercepto b_0(beta 0):
b0 = (y_sum - (b1 * x_sum)) / n
b0 = y_mean - (b1 * x_mean)
#SQE => Soma de Quadrados dos Erros / SQT => Somatória de Quadrados Total / SQR => Soma de quadrados da Regressão:
sqe = y2_sum - (b0 * y_sum) - (b1 * xy_sum)
#alternativa: sqe = syy - (b1 * sxy)
sqt = y2_sum - ( (y_sum**2)/ n)
#alternativa: sqt = syy
sqr = sqt - sqe
#Equação da reta:
print('Equação da reta: y = {} + {}x'.format(b0, b1))
return {xlabel+'_mean':x_mean,
ylabel+'_mean':y_mean,
xlabel+'_sum':x_sum,
ylabel+'_sum':y_sum,
xlabel+'_'+ylabel+'_sum':xy_sum,
xlabel+'2_sum':x2_sum,
ylabel+'2_sum':y2_sum,
'n':n,
'sxy':sxy,
'sxx':sxx,
'syy':syy,
'b1':b1,
'b0':b0,
'sqe':sqe,
'sqt':sqt,
'sqr':sqr}
def var(sqe, n):
#Variância(s2) e Desvio-padrão
s2 = sqe / (n - 2)
return {'variancia':s2}
def std(sqe, n):
s2 = sqe / (n - 2)
s = np.sqrt(s2)
return {'std':s}
def coef_corr(sxy, sxx, syy):
#Cálculo do coeficiente de correlação de Pearson
r = sxy / np.sqrt(sxx*syy)
return {'coef_corr':r}
def coef_det(sqe, sqt):
#Coeficiente de Determinação => Explica se a reta descreve um modelo linear
r2 = 1 - (sqe / sqt)
return {'coef_det':r2}
def confidence_interval(s, sxx, ic, n, b1):
#Intervalo de confiança:
#Obter o erro padrão estimado
sb1_inf = s / np.sqrt(sxx)
print('Erro padrão estimado:', sb1_inf)
#t student => t , alpha/2, n-2 (COnsultar na tabela)
alpha = 1 - (ic / 100)
gl = n - 2
t_student = t.ppf(1 - (alpha / 2), gl)
#b1_inf = b1 +- intervalo
intervalo = t_student * sb1_inf
print('IC de {}% = ({}, {})'.format(ic, b1 - intervalo, b1 + intervalo))
return None
# -
# #### Dataset
df = pd.read_csv('data/carst.csv', delimiter = ',')
df.head()
# #### 1.
# Encontrar os parâmetros e realizar a análise de ajustes de cap_vol (variável preditora) e consumo(variável resposta)
# ##### a.
# Obtenha a reta que descreve a relação entre as variáveis e o interrvalo de confiança para 95%, obtenha o valor esperado de y para x = 3000
# +
x = df['cap_vol']
y = df['consumo']
first_analysis_lr(df['cap_vol'], df['consumo'], 'cap_vol', 'consumo')
x = 3000
b0 = 12.14
b1 = -0.0013
u_y3000 = b0 + (b1 * x)
print('Valor esperado de uy:3000 = {}'.format(u_y3000))
# -
# #### 3.
# Observe a figura que representa um conjunto de dados bivariados, isto é, dados que apresentam informações semelhantes. Os dados, compostos por 20 amostras, estão bem correlacionados porque representam duas metodologias diferentes para obter a concentração de hidrogênio, esperando-se, portanto, que forneçam resultados semelhantes.
# Com esses dados foi realizado o procedimento de regressão obtendo as seguintes informações: reta de regressão Y = -0.9625 + 1.001 x, uma variância estimada de 0,3022 e Sxx = 40925.75.
# Calcule o intervalo de confiança de beta IC a 95%.
# +
y = -0.9625 + (1.001 * x)
s2 = 0.3022
s = pow(s2, 1/2)
sxx = 40925.75
ic = 95
n = 20
b1 = 1.001
b0 = -0.9625
#Intervalo de confiança:
#Obter o erro padrão estimado
sb1_inf = s / pow(sxx, 1/2)
print('Erro padrão estimado:', sb1_inf)
#t student => t , alpha/2, n-2 (COnsultar na tabela)
alpha = 1 - (ic / 100)
gl = n - 2
t_student = t.ppf(1 - (alpha / 2), gl)
#b1_inf = b1 +- intervalo
intervalo = t_student * sb1_inf
print('IC de {}% = ({}, {})'.format(ic, b1 - intervalo, b1 + intervalo))
# -
# #### 4.
# Um conjunto de dados fornece os seguintes valores: Sxx = 1585.2307, Syy = 77.2708, e Sxy = -341.9592, e uma reta de regressão Y = 9.10099 - 0.21572 x. Calcule a soma de quadrados dos erros e o coeficiente de determinação
#
# +
sxx = 1585.2307
syy = 77.2708
sxy = -341.9592
y = 9.10099 - (0.21572 * x)
b1 = -0.21572
b0 = 9.10099
sqe = syy - (b1 * sxy)
print('SQE = {}'.format(sqe))
sqt = syy
coef = coef_det(sqe, sqt)
df['coef_det']
print('Coeficiente de determinação:{}'.format(coef['coef_det']))
# -
# #### 5.
# Considere a seguinte amostra, na qual se apresenta a relação entre a taxa de eficiência de fosfatização de um peça de aço de acordo com a temperatura.
#
# Temp. 76,67 77,78 78,33 78,89 78,89 79,44 80,00 80,56 82,22 82,22 82,22 82,22<br>
# Taxa 0,84 1,31 1,42 1,03 1,07 1,08 1,04 1,80 1,45 1,60 1,61 2,13<br>
# <br>
# Temp. 82,22 82,78 82,78 83,33 83,33 83,33 83,33 84,44 84,44 85,00 85,56 86,67<br>
# Taxa 2,15 0,84 1,43 0,90 1,81 1,94 2,68 1,49 2,52 3,0 1,87 3,08<br>
#
# Aplique o procedimento de regressão linear para obter a reta que descreve esses dados, considere como variável preditora a Temperatura e como variável resposta a Taxa de eficiência, depois calcule os coeficientes de determinação, indique o que ele representa e calcule o valor esperado de Y para x= 80.
# +
#valores
temp = [76.67, 77.78, 78.33, 78.89, 78.89, 79.44, 80.00, 80.56, 82.22, 82.22, 82.22, 82.22, 82.22, 82.78, 82.78, 83.33, 83.33, 83.33, 83.33, 84.44, 84.44, 85.00, 85.56, 86.67]
taxa = [0.84, 1.31, 1.42, 1.03, 1.07, 1.08, 1.04, 1.80, 1.45, 1.60, 1.61, 2.13, 2.15, 0.84, 1.43, 0.90, 1.81, 1.94, 2.68, 1.49, 2.52, 3.0, 1.87, 3.08]
#Análise de regressão linear
df = first_analysis_lr(temp, taxa, 'temp', 'taxa')
#valor esperado
x = 80
u_y80 = -12.232 + (0.17 * x)
print('Valor esperado de y para x = 80: {}'.format(u_y80))
#coeficiente de determinação
coef = coef_det(df['sqe'], df['sqt'])
print('Coeficiente de determinação:{}'.format(coef['coef_det']))
#Baixo coeficiente de determinação, o modelo não exemplifica uma regressão linear simples
| 02_analise_ajustes.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Entrenamiento del Modelo de Asignación Latente de Dirichlet
#
# <img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/4/4d/Wikipedia_15_-_Twitter_wordcloud.png" width="500px" height="300px" />
#
# > Ya que comprendimos el modelo de asignación latente de Dirichlet, veamos como entrenarlo.
#
# > **Objetivos:**
# > - Usar la inferencia variacional para entrenar el modelo de asignación latente de Dirichlet.
# > - Comprender el uso de la asignación latente de Dirichlet mediante un ejemplo.
#
# > **Referencias:**
# > - Bayesian Methods for Machine Learning course, HSE University, Coursera.
# ## 1. Preliminares
#
# Tenemos entonces que la función de verosimilitud conjunta es:
#
# $$
# p(\Theta, Z, X | \Phi) = \prod_{d=1}^{D} p(\theta_d) \prod_{n=1}^{N_d} p(z_{dn} | \theta_d) p(x_{dn} | z_{dn}),
# $$
#
# de donde la log-verosimilitud es:
#
# \begin{align}
# \log p(\Theta, Z, X | \Phi) = \sum_{d=1}^{D} \left[\log p(\theta_d) + \sum_{n=1}^{N_d} \left( \log p(z_{dn} | \theta_d) + \log p(x_{dn} | z_{dn}) \right) \right]
# \end{align}
# Ahora, dado que
#
# - $p(\theta_d) = \text{Dir}(\theta | \alpha)$
# - $p(z_{dn} | \theta_d) = \theta_{d z_{dn}}$
# - $p(x_{dn} | z_{dn}) = \phi_{z_{dn} x_{dn}}$
#
# Es posible notar que:
#
# - $\log p(\theta_d) = \sum_{t=1}^{T} (\alpha_t - 1) \log \theta_{dt} + const.$
# - $\log p(z_{dn} | \theta_d) = \log \theta_{d z_{dn}}$
# - $\log p(x_{dn} | z_{dn}) = \log \phi_{z_{dn} x_{dn}}$
# Con lo cual
#
# \begin{align}
# \log p(\Theta, Z, X | \Phi) = \sum_{d=1}^{D} \left[\sum_{t=1}^T (\alpha_t-1) \log \theta_{dt} + \sum_{n=1}^{N_d} \sum_{t=1}^T \delta(z_{dn} = t) \left( \log \theta_{dt} + \log \phi_{t x_{dn}} \right) \right] + const.
# \end{align}
# Para entrenar los parámetros del modelo $\Phi$, podemos maximizar la verosimilitud marginal:
#
# $$
# \max_{\Phi} p(X | \Phi),
# $$
#
# para lo cual usamos el algoritmo de maximización de la esperanza variancional:
#
# **E-step variacional**
#
# $$
# \min_{q(\Theta), q(Z)}\mathcal{KL}(q(\Theta) q(Z) || p(\Theta, Z | X)).
# $$
#
# **M-Step**
#
# $$
# \max_{\Phi} \mathbb{E}_{q(\Theta)q(Z)}\log p(\Theta, Z, X | \Phi)
# $$
# ## 2. E-step variacional
#
# $$
# \min_{q(\Theta), q(Z)}\mathcal{KL}(q(\Theta) q(Z) || p(\Theta, Z | X)).
# $$
# ### Con respecto a $q(\Theta)$
#
# Usando las ecuaciones de campo media:
#
# $$
# \begin{align}
# \log q(\Theta) & = \mathbb{E}_{q(Z)} \log \underbrace{p(\Theta, Z | X)}_{\frac{p(\Theta, Z, X)}{p(X)}} + const. \\
# & = \mathbb{E}_{q(Z)} \log p(\Theta, Z, X) + const. \\
# & = \mathbb{E}_{q(Z)} \sum_{d=1}^{D} \left[\sum_{t=1}^T (\alpha_t-1) \log \theta_{dt} + \sum_{n=1}^{N_d} \sum_{t=1}^T \delta(z_{dn} = t) \left( \log \theta_{dt} \right) \right] + const. \\
# & = \sum_{d=1}^{D} \left[\sum_{t=1}^T (\alpha_t-1) \log \theta_{dt} + \sum_{n=1}^{N_d} \sum_{t=1}^T \underbrace{\mathbb{E}_{q(Z)}[\delta(z_{dn} = t)]}_{\mathbb{E}_{q(z_{dn})}[\delta(z_{dn} = t)]} \left( \log \theta_{dt} \right) \right] + const. \\
# & = \sum_{d=1}^{D} \left[\sum_{t=1}^T (\alpha_t-1) \log \theta_{dt} + \sum_{n=1}^{N_d} \sum_{t=1}^T q(z_{dn} = t) \left( \log \theta_{dt} \right) \right] + const. \\
# & = \sum_{d=1}^{D} \sum_{t=1}^T \left[ (\alpha_t-1) + \sum_{n=1}^{N_d} q(z_{dn} = t) \right] \log \theta_{dt} + const.
# \end{align}
# $$
# Con lo cual tenemos que:
#
# $$
# \begin{align}
# q(\Theta) & \propto \prod_{d=1}^{D} \prod_{t=1}^T \theta_{dt}^{\sum_{n=1}^{N_d} q(z_{dn} = t) + \alpha_t - 1} + const. \\
# & = \prod_{d=1}^{D} \text{Dir}\left(\theta_d \left\lvert \begin{array}{c} ... \\ \alpha_t + \sum_{n=1}^{N_d} q(z_{dn} = t) \\ ... \end{array}\right. \right)
# \end{align}
# $$
#
# De manera que para encontrar $q(\Theta)$, necesitamos calcular $q(z_{dn} = t)$.
# ### Con respecto a $q(Z)$
#
# Usando las ecuaciones de campo media:
#
# $$
# \begin{align}
# \log q(Z) & = \mathbb{E}_{q(\Theta)} \log p(\Theta, Z, X) + const. \\
# & = \mathbb{E}_{q(\Theta)} \sum_{d=1}^{D} \sum_{n=1}^{N_d} \sum_{t=1}^T \delta(z_{dn} = t) \left( \log \theta_{dt} + \log \phi_{t x_{dn}} \right) + const. \\
# & = \sum_{d=1}^{D} \sum_{n=1}^{N_d} \sum_{t=1}^T \delta(z_{dn} = t) \left(\mathbb{E}_{q(\Theta)} \log \theta_{dt} + \log \phi_{t x_{dn}} \right) + const.
# \end{align}
# $$
# Por tanto:
#
# $$
# \begin{align}
# q(Z) & = \prod_{d=1}^{D} \prod_{n=1}^{N_d} q(z_{dn}),
# \end{align}
# $$
#
# donde
#
# $$
# q(z_{dn} = t) = \frac{\phi_{t x_{dn}} \exp\left(\mathbb{E}_{q(\Theta)} \log \theta_{dt}\right)}{\sum_{t=1}^T \phi_{t x_{dn}} \exp\left(\mathbb{E}_{q(\Theta)} \log \theta_{dt}\right)}.
# $$
# El valor de
#
# $$
# \exp\left(\mathbb{E}_{q(\Theta)} \log \theta_{dt}\right)
# $$
#
# se puede encontrar en:
#
# https://en.wikipedia.org/wiki/Dirichlet_distribution
# **¿Recuerdan el modelo de Iising?**
#
# Debemos iterar para que estas distribuciones converjan.
# ## 3. M-step
# $$
# \max_{\Phi} \mathbb{E}_{q(\Theta)q(Z)}\log p(\Theta, Z, X | \Phi)
# $$
# Conservamos solo los términos que dependen de $\Phi$:
#
# $$
# \begin{align}
# \mathbb{E}_{q(\Theta)q(Z)}\log p(\Theta, Z, X | \Phi) & = \mathbb{E}_{q(\Theta)q(Z)}\sum_{d=1}^{D} \sum_{n=1}^{N_d} \sum_{t=1}^T \delta(z_{dn} = t) \log \phi_{t x_{dn}} + const.
# \end{align}
# $$
#
# Debemos maximizar esta expresión teniendo en cuenta las restricciones:
#
# - $\phi_{tx} \geq 0, \quad \forall t, x$.
# - $\sum_{x} \phi_{tx} = 1, \quad \forall t$
#
# La condición de no negatividad se satisface ya que los términos $\phi$ están dentro del $\log$.
# Definimos el lagrangiano:
#
# $$
# \begin{align}
# L(\Phi, \lambda) & = \mathbb{E}_{q(\Theta)q(Z)}\sum_{d=1}^{D} \sum_{n=1}^{N_d} \sum_{t=1}^T \delta(z_{dn} = t) \log \phi_{t x_{dn}} + \sum_{t=1}^T \lambda_t \left( \sum_{x} \phi_{tx} - 1 \right) \\
# & = \sum_{d=1}^{D} \sum_{n=1}^{N_d} \sum_{t=1}^T q(z_{dn} = t) \log \phi_{t x_{dn}} - \sum_{t=1}^T \lambda_t \left( \sum_{x} \phi_{tx} - 1 \right)
# \end{align}
# $$
# Entonces
#
# $$
# \frac{\partial L(\Phi, \lambda)}{\partial \phi_{tx}} = \sum_{d=1}^{D} \sum_{n=1}^{N_d} q(z_{dn} = t) \frac{1}{\phi_{t x_{dn}}} \delta(x_{dn} = x) - \lambda_t = 0
# $$
#
# si y solo si:
#
# $$
# \phi_{tx} = \frac{\sum_{d=1}^{D} \sum_{n=1}^{N_d} q(z_{dn} = t) \delta(x_{dn} = x)}{\lambda_t}
# $$
# Ahora, imponiendo la restricción $\sum_{x} \phi_{tx} = 1$, nos damos cuenta que:
#
# $$
# \lambda_t = \sum_{x}\sum_{d=1}^{D} \sum_{n=1}^{N_d} q(z_{dn} = t) \delta(x_{dn} = x)
# $$
#
# Con lo cual:
#
# $$
# \phi_{tx} = \frac{\sum_{d=1}^{D} \sum_{n=1}^{N_d} q(z_{dn} = t) \delta(x_{dn} = x)}{\sum_{x}\sum_{d=1}^{D} \sum_{n=1}^{N_d} q(z_{dn} = t) \delta(x_{dn} = x)}.
# $$
# ## 4. Comentarios
#
# Hemos desarrollado las fórmulas para entrenar nuestro modelo. Recordamos que
#
# 1. Hay que iterar varias veces el E-step y el M-step hasta la convergencia de los parámetros en la matriz $\Phi$.
# - La matriz $\Phi$ contiene la distribución tópico-palabras. De acá podemos identificar qué palabras son más importantes para cada tópico y así inferir el tópico.
#
# 2. Dentro del E-step en sí, hay que iterar hasta la convergencia de las distribuciones $q(\Theta), q(Z)$.
#
# 3. Al final, la distribución $q(\Theta)$ modelará las distribuciones de documentos-tópicos. Podremos extraer de los parámetros $\alpha$ la representación de los documentos en los tópicos.
#
# 5. Si quisiéramos predecir para un nuevo documento, podemos reutilizar las ecuaciones del E-step.
# ## 5. Aplicación
#
# Para finalizar todas estas matemáticas, veamos un ejemplo para aterrizar todo lo que hemos visto en este tema.
#
# Para trabajar, utilizaremos [the 20 newsgroups dataset](http://qwone.com/~jason/20Newsgroups/)
# Importamos librerías
# Para obtener los datos
from sklearn.datasets import fetch_20newsgroups
# Para procesar el texto
from sklearn.feature_extraction.text import CountVectorizer
# Latent Dirichlet Allocation
from sklearn.decomposition import LatentDirichletAllocation
# Para graficar
from matplotlib import pyplot as plt
# Obtenemos datos
data, _ = fetch_20newsgroups(shuffle=True, random_state=1,
remove=('headers', 'footers', 'quotes'),
return_X_y=True)
# Visualizamos datos
data[:5]
# ¿Cuántos documentos tenemos?
len(data)
# Definamos algunas cosas
# Número de documentos
n_docs = 3000
# Número de tópicos
n_topics = 10
# Número de palabras en el vocabulario
n_words = 1000
# Vectorizamos el texto por medio de cuentas crudas de palabras
vectorizer = CountVectorizer(max_df=0.95, min_df=2,
max_features=n_words,
stop_words='english')
corpus = vectorizer.fit_transform(data[:n_docs])
# Matriz de documentos vectorizados
corpus
def plot_top_words(model, feature_names, n_top_words, title):
# Malla para graficar 2 filas 5 columnas
fig, axes = plt.subplots(2, 5, figsize=(30, 15), sharex=True)
axes = axes.flatten()
# model.components_ hace referencia a la matriz phi
for topic_idx, topic in enumerate(model.components_):
# La hacemos distribución
topic /= topic.sum()
# Seleccionamos los índices más relevantes del tópico
top_features_ind = topic.argsort()[:-n_top_words - 1:-1]
# Obtenemos las palabras
top_features = [feature_names[i] for i in top_features_ind]
# Obtenemos la ponderación
weights = topic[top_features_ind]
# Graficamos barras horizontales por tópicos con las palabras más relevantes
ax = axes[topic_idx]
ax.barh(top_features, weights, height=0.7)
ax.set_title(f'Topic {topic_idx +1}',
fontdict={'fontsize': 30})
ax.invert_yaxis()
ax.tick_params(axis='both', which='major', labelsize=20)
for i in 'top right left'.split():
ax.spines[i].set_visible(False)
fig.suptitle(title, fontsize=40)
plt.subplots_adjust(top=0.90, bottom=0.05, wspace=0.90, hspace=0.3)
plt.show()
lda = LatentDirichletAllocation(n_components=n_topics)
lda.fit(corpus)
plot_top_words(lda, vectorizer.get_feature_names(), 10, 'Topics in LDA model')
# #### Veamos algunos ejemplos de textos y su categorización en tópicos
print(data[0])
lda.transform(corpus[0])
print(data[101])
lda.transform(corpus[101])
print(data[251])
lda.transform(corpus[251])
# <script>
# $(document).ready(function(){
# $('div.prompt').hide();
# $('div.back-to-top').hide();
# $('nav#menubar').hide();
# $('.breadcrumb').hide();
# $('.hidden-print').hide();
# });
# </script>
#
# <footer id="attribution" style="float:right; color:#808080; background:#fff;">
# Created with Jupyter by <NAME>.
# </footer>
| modulo2/tema4/3_lda_inf_variacional.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sb
# %matplotlib inline
# +
from sklearn.utils.multiclass import unique_labels
from sklearn.metrics import confusion_matrix
def plot_confusion_matrix(y_true, y_pred, classes,
normalize=False,
title=None,
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if not title:
if normalize:
title = 'Normalized confusion matrix'
else:
title = 'Confusion matrix, without normalization'
# Compute confusion matrix
cm = confusion_matrix(y_true, y_pred)
# Only use the labels that appear in the data
classes = classes[unique_labels(y_true, y_pred)]
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
fig, ax = plt.subplots(figsize=(14,7))
im = ax.imshow(cm, interpolation='nearest', cmap=cmap)
ax.grid(False)
ax.figure.colorbar(im, ax=ax)
# We want to show all ticks...
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
# ... and label them with the respective list entries
xticklabels=classes, yticklabels=classes,
title=title,
ylabel='True label',
xlabel='Predicted label')
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
# Loop over data dimensions and create text annotations.
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
fig.tight_layout()
return ax
# -
# # Analysis
# Prepare data
demographic = pd.read_csv('../data/processed/demographic.csv')
severity = pd.read_csv('../data/processed/severity.csv', index_col=0)
features = demographic.columns
X = demographic.astype(np.float64)
y = (severity >= 4).sum(axis=1)
#The definition of the needs were provided by REACH
needs_to_label = {0:'no needs', 1:'low_needs', 2:'moderate needs', 3:'high needs', 4:'very high needs'}
labels = ["no needs", "low needs", "moderate needs", "high needs", "very high needs"]
severity_to_needs = {0:0, 1:1, 2:1, 3:2, 4:2, 5:3, 6:3, 7:4, 8:4}
y = np.array([severity_to_needs[i] for i in y])
# Color vector, for illustration purposes
colors = {0:'b', 1:'r', 2:'g', 3:'c', 4:'y'}
y_c = np.array([colors[i] for i in y])
# ## Understanding the features
from yellowbrick.features import Rank2D
from yellowbrick.features.manifold import Manifold
from yellowbrick.features.pca import PCADecomposition
from yellowbrick.style import set_palette
set_palette('flatui')
# ### Feature covariance plot
visualizer = Rank2D(algorithm='covariance')
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.poof()
# ### Principal Component Projection
visualizer = PCADecomposition(scale=True, color = y_c, proj_dim=3)
visualizer.fit_transform(X, y)
visualizer.poof()
# ### Manifold projections
visualizer = Manifold(manifold='tsne', target='discrete')
visualizer.fit_transform(X, y)
visualizer.poof()
visualizer = Manifold(manifold='modified', target='discrete')
visualizer.fit_transform(X, y)
visualizer.poof()
# No apparent structure from the PCA and Manifold projections.
# ### Class Balance
categories, counts = np.unique(y, return_counts=True)
fig, ax = plt.subplots(figsize=(9, 7))
sb.set(style="whitegrid")
sb.barplot(labels, counts, ax=ax, tick_label=labels)
ax.set(xlabel='Need Categories',
ylabel='Number of HHs');
# Heavy class imbalances. Use appropriate scoring metrics/measures.
# ### Learning and Validation
from sklearn.model_selection import StratifiedKFold
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import RidgeClassifier
from yellowbrick.model_selection import LearningCurve
cv = StratifiedKFold(10)
sizes = np.linspace(0.1, 1., 20)
visualizer = LearningCurve(RidgeClassifier(), cv=cv, train_sizes=sizes,
scoring='balanced_accuracy', n_jobs=-1)
visualizer.fit(X,y)
visualizer.poof()
visualizer = LearningCurve(GaussianNB(), cv=cv, train_sizes=sizes,
scoring='balanced_accuracy', n_jobs=-1)
visualizer.fit(X,y)
visualizer.poof()
# ### Classification
from sklearn.linear_model import RidgeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.utils.class_weight import compute_class_weight
from imblearn.metrics import classification_report_imbalanced
from sklearn.metrics import balanced_accuracy_score
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42, stratify=y)
cv_ = StratifiedKFold(5)
class_weights = compute_class_weight(class_weight='balanced', classes= np.unique(y), y=y)
clf = RidgeClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = KNeighborsClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = GaussianNB()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = ExtraTreesClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = GradientBoostingClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
# ## Voting Classifier
# ### Hard Voting
clf1 = KNeighborsClassifier(weights='distance')
clf2 = GaussianNB()
clf3 = ExtraTreesClassifier(class_weight='balanced_subsample')
clf4 = GradientBoostingClassifier()
vote = VotingClassifier(estimators=[('knn', clf1), ('gnb', clf2), ('ext', clf3), ('gb', clf4)], voting='hard')
params = {'knn__n_neighbors': [2,3,4], 'gb__n_estimators':[50,100,200],
'gb__max_depth':[3,5,7], 'ext__n_estimators': [50,100,200]}
scoring_fns = ['f1_weighted', 'balanced_accuracy']
grid = GridSearchCV(estimator=vote, param_grid=params, cv=cv_,
verbose=2, n_jobs=-1, scoring=scoring_fns, refit='balanced_accuracy')
grid.fit(X_train, y_train)
y_pred = grid.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf1 = KNeighborsClassifier(weights='distance')
clf2 = GaussianNB()
clf3 = ExtraTreesClassifier(class_weight='balanced_subsample')
clf4 = GradientBoostingClassifier()
vote = VotingClassifier(estimators=[('knn', clf1), ('gnb', clf2), ('ext', clf3), ('gb', clf4)], voting='soft')
params = {'knn__n_neighbors': [2,3,4], 'gb__n_estimators':[50,100,200],
'gb__max_depth':[3,5,7], 'ext__n_estimators': [50,100,200]}
scoring_fns = ['f1_weighted', 'balanced_accuracy']
grid_soft = GridSearchCV(estimator=vote, param_grid=params, cv=cv_,
verbose=2, n_jobs=-1, scoring=scoring_fns, refit='balanced_accuracy')
grid_soft.fit(X_train, y_train)
y_pred = grid_soft.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
| notebooks/3) Exploratory Analysis.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Detailed analysis of results.
# This notebook loads the output of the scripts in the directory ``cluster_scripts`` (particularly, the final script, ``run_slurm_pred_error.py``). It produces the Rdata file that is used for the graphs in the paper as well as a number of supplemental analyses.
library(tidyverse)
library(gridExtra)
library(repr) # For setting plot sizes
source("load_python_data_lib.R")
py_main <- InitializePython()
# +
# Choose the initialization method.
init_method <- "kmeans" # This is the choice for the paper.
#init_method <- "warm"
# Choose whether or not to re-run the regressions before calculating test error.
use_rereg <- FALSE # This is the choice for the paper.
#use_rereg <- TRUE
# This is the file that is used in the paper's knitr.
save_dir <- "../../fits"
save_filename <- sprintf("paper_results_init_%s_rereg_%s.Rdata", init_method, use_rereg)
# -
# ### Load the saved data for all dfs and k
#
#
# +
dfs <- list()
metadata_dfs <- list()
for (lo_num_times in 1:3) {
cat("lo_num_times ", lo_num_times)
for (df in 4:8) {
cat(".")
load_res <- LoadPredictionError(df, lo_num_times, init_method)
this_refit_err_df <- load_res$refit_err_df
this_metadata_df <- load_res$metadata_df
this_refit_err_melt <- MeltErrorColumns(this_refit_err_df)
dfs[[length(dfs) + 1]] <- this_refit_err_melt
metadata_dfs[[length(metadata_dfs) + 1]] <- this_metadata_df
}
cat("\n")
}
cat("Done.\n")
refit_err_melt <- do.call(bind_rows, dfs)
metadata_df <- do.call(bind_rows, metadata_dfs)
# -
# ### Metadata (timing, parameter dimensions)
# Make a tidy dataframe with the metadata. The parameter length, Hessian time, and initial optimization time are all reported in the text of the paper. Their values will be derived from this dataframe in knitr.
# +
metadata_df <-
metadata_df %>%
mutate(lr_hess_time=total_lr_time + initial_hess_time,
avg_lr_time=total_lr_time / num_comb,
avg_refit_time=total_refit_time / num_comb,
param_length=gmm_param_length + reg_param_length)
print(names(metadata_df))
select(metadata_df, df, param_length) %>%
group_by(df) %>%
summarize(param_length=unique(param_length))
select(metadata_df, df, initial_hess_time, initial_opt_time) %>%
group_by(df) %>%
summarize(initial_hess_time=median(initial_hess_time),
initial_opt_time=median(initial_opt_time))
round(median(metadata_df$initial_opt_time), digits=-1)
# -
# Make a dataframe for the timing plot from the metadata.
metadata_graph_df <-
metadata_df %>%
select(df, lo_num_times, total_refit_time, lr_hess_time, initial_opt_time) %>%
melt(id.vars=c("lo_num_times", "df"))
head(metadata_graph_df)
ggplot(metadata_graph_df) +
geom_bar(aes(x=lo_num_times, y=value, fill=variable, group=variable),
stat="identity", position=position_dodge()) +
facet_grid( ~ df)
# ### Calculate prediction errors
# Make summaries of prediction error for various methods and datasets.
# +
# In-sample IJ error.
lr_df <-
refit_err_melt %>%
filter(rereg==use_rereg, method=="lin", test==FALSE, measure=="err") %>%
rename(error=value) %>%
mutate(output="lin_in_sample")
# In-sample CV error.
cv_df <-
refit_err_melt %>%
filter(rereg==use_rereg, method=="ref", test==FALSE, measure=="err") %>%
rename(error=value) %>%
mutate(output="cv_in_sample")
# In-sample training error (no points left out).
train_df <-
refit_err_melt %>%
filter(rereg==use_rereg, method=="ref", test==FALSE, measure=="train_err") %>%
rename(error=value) %>%
mutate(output="train_error")
# Out-of-sample test error.
test_df <-
refit_err_melt %>%
filter(rereg==use_rereg, method=="ref", test==TRUE, measure=="train_err") %>%
rename(error=value) %>%
mutate(output="test_error")
refit_for_df_choice <- bind_rows(
lr_df, cv_df, test_df, train_df)
# -
head(refit_for_df_choice)
# Make a tidy dataframe for choosing ``df``. The graph in the paper will be based on this dataframe.
#
# Note that most of the signal for choosing ``df`` is already in the training data error. However, there is an uptick in error in both CV and IJ for ``df=8`` which is not captured by the training data error.
# +
refit_err_summary <-
refit_for_df_choice %>%
group_by(output, df, lo_num_times) %>%
mutate(esize=abs(error)) %>%
summarize(med=median(esize),
mean=mean(esize),
n_obs=n(),
se=sd(esize) / sqrt(n_obs),
qlow=quantile(esize, 0.25),
qhigh=quantile(esize, 0.75))
ggplot(refit_err_summary) +
geom_line(aes(x=df, y=mean, group=output, color=output)) +
geom_errorbar(aes(x=df, ymin=mean - 2 * se, ymax=mean + 2 * se,
group=output, color=output)) +
facet_grid(~ lo_num_times) +
ggtitle(sprintf("%d times left out", lo_num_times))
# -
# ### Gene-by-gene accuracy measures.
refit_err_plot <-
refit_err_melt %>%
filter(rereg==use_rereg) %>%
dcast(df + lo_num_times + test + comb + rereg + gene + time ~ method + measure,
value.var=c("value"))
# We now look at the correlation between the CV and IJ prediction errors across genes. For each ``df`` and ``k``, there are a number of different combinations of left-out points. We report the median, min, and max correlation coefficients across these combinations of left-out points.
# First, we show the correlation between the raw prediction errors. Although the correlation is quite high, this is because the training error at the original optimum is the principle source of variation in the errors across genes, and this quantity is common to both CV and IJ.
# +
err_corr <- refit_err_plot %>%
filter(test==FALSE, rereg==use_rereg) %>%
group_by(df, lo_num_times, comb) %>%
summarize(r=cor(lin_err, ref_err)) %>%
group_by(df, lo_num_times) %>%
summarize(med_r=median(r), min_r=min(r), max_r=max(r))
print("Correlation between error: ")
print(err_corr)
# -
# A more meaningful measure is the correlation in the excess error for IJ and CV over the error at the original fit.
# +
diff_corr <- refit_err_plot %>%
filter(test==FALSE, rereg==use_rereg) %>%
group_by(df, lo_num_times, comb) %>%
summarize(r=cor(lin_e_diff, ref_e_diff)) %>%
group_by(df, lo_num_times) %>%
summarize(med_r=median(r), min_r=min(r), max_r=max(r))
print("Correlation between difference from train error: ")
print(diff_corr)
# -
# For higher degrees of freedom, increasing the number of left-out points seems to decrease the IJ's accuracy, as you might expect.
ggplot(diff_corr) +
geom_bar(aes(x=paste(df, lo_num_times, sep=","),
y=med_r, fill=as.character(df)), stat="identity")
# Plot the densities of the IJ and CV with points to show outliers. This is a graphical version of the results summarized by the correlation tables above.
# +
# There are a few outliers, so limit the extent of the plot so that
# the bulk of the distribution is visible.
qlim <- quantile(refit_err_plot$ref_e_diff, c(0.1, 0.9))
options(repr.plot.width=4, repr.plot.height=20)
# This plot, or ones like it, is probably the best measure of
# the accuracy of the IJ.
ggplot(filter(refit_err_plot, test == FALSE, lo_num_times==1)) +
geom_point(aes(x=ref_e_diff, y=lin_e_diff), alpha=0.01) +
geom_density2d(aes(x=ref_e_diff, y=lin_e_diff)) +
geom_abline(aes(slope=1, intercept=0)) +
facet_grid(df ~ rereg) +
xlim(qlim[1], qlim[2]) + ylim(qlim[1], qlim[2])
# -
# ### Save results for plotting in the paper.
print(sprintf("Saving to %s", file.path(save_dir, save_filename)))
save(refit_err_summary,
metadata_df,
diff_corr,
err_corr,
file=file.path(save_dir, save_filename))
| genomics/jupyter/R/examine_and_save_results.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.optimizers import SGD
import os
import tensorflow as tf
from keras.callbacks import TensorBoard
import time
import matplotlib.pyplot as plt
# %matplotlib inline
# Generate dummy data
import numpy as np
# https://stackoverflow.com/questions/42112260/how-do-i-use-the-tensorboard-callback-of-keras
# tensorboard
# https://www.youtube.com/watch?v=lV09_8432VA
# https://www.youtube.com/watch?v=BqgTU7_cBnk - stydy model
class TrainValTensorBoardF1(TensorBoard):
def __init__(self, log_dir='./logs', name="test", **kwargs):
# Make the original `TensorBoard` log to a subdirectory 'training'
training_log_dir = os.path.join(log_dir, name)
super(TrainValTensorBoardF1, self).__init__(training_log_dir, **kwargs)
self.val_writer = tf.summary.FileWriter(training_log_dir)
self.val_writer1 = tf.summary.FileWriter(training_log_dir)
#self.val_writer_train = tf.summary.FileWriter(training_log_dir)
def dump(self, f1_score_train, f1_score_cv, f1_score_test, x):
# https://github.com/tensorflow/tensorflow/issues/7089
# first
from numpy import random
summary = tf.Summary()
summary_value = summary.value.add()
summary_value.simple_value = f1_score_train
summary_value.tag = "f1_score_train"
self.val_writer.add_summary(summary, x)
# second
if 1:
# summary = tf.Summary()
summary_value = summary.value.add()
summary_value.simple_value = f1_score_cv
summary_value.tag = "f1_score_cv"
# self.val_writer1.add_summary(summary, x)
if 1:
# summary = tf.Summary()
summary_value = summary.value.add()
summary_value.simple_value = f1_score_test
summary_value.tag = "f1_score_test"
self.val_writer.add_summary(summary, x)
# write_op = summary.merge_all()
# log_var = tf.Variable(0.0)
# tf.summary.scalar("loss", log_var)
write_op = tf.summary.merge_all([f1_score_test, f1_score_train])
#session = tf.InteractiveSession()
#session.run(tf.global_variables_initializer())
session = tf.keras.backend.get_session()
# for i in range(100):
# # for writer 1
# summary = session.run(write_op, {log_var: random.rand()})
# self.writer_1.add_summary(summary, i)
# self.writer_1.flush()
# # for writer 2
summary = session.run(write_op, {log_var: random.rand()})
self.val_writer.add_summary(summary, x)
# self.writer_2.flush()
self.val_writer.flush()
# self.val_writer1.flush()
def end_it(self):
self.val_writer.close()
# self.val_writer1.close()
class TrainValTensorBoard(TensorBoard):
def __init__(self, log_dir='./logs', **kwargs):
# Make the original `TensorBoard` log to a subdirectory 'training'
training_log_dir = os.path.join(log_dir, 'training')
super(TrainValTensorBoard, self).__init__(training_log_dir, **kwargs)
# Log the validation metrics to a separate subdirectory
self.val_log_dir = os.path.join(log_dir, 'validation')
def set_model(self, model):
# Setup writer for validation metrics
self.val_writer = tf.summary.FileWriter(self.val_log_dir)
super(TrainValTensorBoard, self).set_model(model)
def on_epoch_end(self, epoch, logs=None):
# Pop the validation logs and handle them separately with
# `self.val_writer`. Also rename the keys so that they can
# be plotted on the same figure with the training metrics
logs = logs or {}
val_logs = {k.replace('val_', ''): v for k, v in logs.items() if k.startswith('val_')}
for name, value in val_logs.items():
summary = tf.Summary()
summary_value = summary.value.add()
summary_value.simple_value = value.item()
summary_value.tag = name
self.val_writer.add_summary(summary, epoch)
self.val_writer.flush()
# Pass the remaining logs to `TensorBoard.on_epoch_end`
logs = {k: v for k, v in logs.items() if not k.startswith('val_')}
super(TrainValTensorBoard, self).on_epoch_end(epoch, logs)
def on_train_end(self, logs=None):
super(TrainValTensorBoard, self).on_train_end(logs)
self.val_writer.close()
# FIXME: load our dataset
# load images
from roadmarks_pipelines import dataset_manager
from roadmarks_pipelines.dataset_manager import to_keras_y
path = '/train_samples/samples_ff128_neg_filtered'
dataset_root = '/mnt/d5/datasets_pa/'
data = dataset_manager.get_all_train_data(path, dataset_root)
#y, X, _ = dataset_manager.unpack_data(data)
# Load and split
size = len(data)
main_ratio = 0.8
print 'main_ratio:', main_ratio
t0 = int(size * main_ratio)
t1 = t0 + int(size * (1 - main_ratio) / 2)
y_train, x_train, fns_train = dataset_manager.unpack_data(data[0:t0])
y_cv, x_cv, fns_cv = dataset_manager.unpack_data(data[t0:t1])
y_test, x_test, _ = dataset_manager.unpack_data(data[t1:])
# conv
y_train = to_keras_y(y_train)
y_cv = to_keras_y(y_cv)
y_test = to_keras_y(y_test)
# FIXME: plain eval
# F1 as metric
# https://stackoverflow.com/questions/43547402/how-to-calculate-f1-macro-in-keras - seems bad idea for opt
input_dim = x_train.shape[1]
print "input_dim:", input_dim
from roadmarks_pipelines.Classifiers import FirstNFeaturesScaler
from roadmarks_pipelines.utils import F1_score_batched
# norm.
featrues_scaler = FirstNFeaturesScaler(input_dim)
featrues_scaler = featrues_scaler.fit(x_train)
# norm immid.
x_cv = featrues_scaler.transform(np.copy(x_cv))
x_test = featrues_scaler.transform(np.copy(x_test))
x_train = featrues_scaler.transform(np.copy(x_train))
# params
decision_thr = 0.5
batch_size = 128
y_train_size = len(y_train)
key = 0
if key == 0:
# Model
tvtb = TrainValTensorBoardF1(name='m'+str(int(time.time())))
for end_ptr in range(batch_size, y_train_size + batch_size * 2, batch_size * 2):
ep = np.clip(end_ptr, 0, y_train_size-1)
y_train_sample = np.copy(y_train[0:ep])
if np.sum(y_train_sample) == 0:
continue
x_train_sample = np.copy(x_train[0:ep])
print 'sz:', len(x_train_sample)
# Build model
model = Sequential()
model.add(Dense(8, input_dim=input_dim, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(16, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
# Fit model
history = model.fit(x_train_sample, y_train_sample,
epochs=2,
batch_size=batch_size, verbose=0)
#, callbacks=[TrainValTensorBoard(write_graph=False)],
# )
# Validation
y_pred_test = np.array(model.predict(x_test) > decision_thr, dtype=np.int)
# predict
y_pred_train = np.array(model.predict(x_train_sample) > decision_thr, dtype=np.int)
y_pred_cv = np.array(model.predict(x_cv) > decision_thr, dtype=np.int)
f1_score_train = F1_score_batched(y_pred_train.ravel(), y_orig=y_train_sample.ravel())
f1_score_cv = F1_score_batched(y_pred_cv.ravel(), y_orig=y_cv.ravel())
f1_score_test = F1_score_batched(y_pred_test.ravel(), y_orig=y_test.ravel())
#f1_scores_train.append(f1_score_train)
#f1_scores_cv.append(f1_score_cv)
#x_axis.append(ep)
tvtb.dump(f1_score_train, f1_score_cv, f1_score_test, ep)
break
tvtb.end_it()
elif key == 2:
# https://www.kaggle.com/eikedehling/keras-nn-scaling-feature-selection-0-548
pass
# -
| keras_theano/test_keras_mlp_graph_join.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SDSS eBOSS Data
# ## Introductory script on reading data, and plotting of the spectrum.
#
# This script explores the data of the spPlate and spZbest fits files.
#
# 1. **Defining the input parameters**
# 2. **Reading the file**
# 3. **Plotting the spectrum**
#
#
# **Data**: 07th Oct, 2019. <br>
# **Author**: <NAME> <br>
# **Script adapted from**: <NAME>, <NAME>
#
# In order to run this script, you would need to download these two files in a folder "**Data**" within your the working directory.
#
# 1. {[Download spPlate file](https://dr14.sdss.org/sas/dr14/eboss/spectro/redux/v5_10_0/9003/spPlate-9003-57488.fits )} General description of file contents can be found [here](https://data.sdss.org/datamodel/files/SPECTRO_REDUX/RUN2D/PLATE4/spPlate.html).
# 2. {[Download spZbest file](https://dr14.sdss.org/sas/dr14/eboss/spectro/redux/v5_10_0/9003/v5_10_0/spZbest-9003-57488.fits)} General description of file contents can be found [here](https://data.sdss.org/datamodel/files/SPECTRO_REDUX/RUN2D/PLATE4/spZbest.html).
# + outputHidden=false inputHidden=false
import astropy.io.fits as fits
import matplotlib.pyplot as plt
import numpy as np
import os
import subprocess
from astropy.convolution import convolve, Box1DKernel
import matplotlib
# %matplotlib inline
font = {'family' : 'arial',
'weight' : 'normal',
'size' : 20}
matplotlib.rc('font', **font)
# -
# ## 1. Defining the input parameters
# + outputHidden=false inputHidden=false
plate = 9003 # 4-digit plate number
mjd = 57488 # 5-digit MJD
fiber = 120 # fibre no. (total 1000)
run2d = "v5_13_0" # version of the pipeline for data-processing
# setting the right path for the directory with the data
current_dir = os.getcwd()
root_dir = os.path.abspath(os.path.join(current_dir, os.pardir))
data_dir = os.path.join(root_dir, "Data")
# -
# ## 2. Reading the file
#
# Functions for reading useful information from the spPlate and spZbest fits files. Refer to links (at the start of the notebook) on general description of the the file contents for further information.
# + outputHidden=false inputHidden=false
def setName(filetype, plate, mjd):
file_name = filetype+'-'+str(plate)+'-'+str(mjd)+'.fits'
data_file = os.path.join(data_dir, file_name)
return data_file
def readSpPlate(plate, mjd):
"""
Function to read the useful headers and data from spPlate fits file
@param place :: 4-digit plate number
@param mjd :: 5-digit MJD
@returns wavelength, bunit, flux, ivar (refer comments for individual meanings)
"""
# opens the file
hdu = fits.open(setName('spPlate', plate, mjd))
c0 = hdu[0].header['coeff0'] # Central wavelength (log10) of first pixel
c1 = hdu[0].header['coeff1'] # Log10 dispersion per pixel
npix = hdu[0].header['naxis1'] # WIDTH (TOTAL!
wavelength = 10.**(c0 + c1 * np.arange(npix))
bunit = hdu[0].header['bunit'] # Units of flux
flux = hdu[0].data # Flux in units of 10^-17^ erg/s/cm^2^/Ang
ivar = hdu[1].data # Inverse variance (1/sigma^2^) for HDU 0
hdu.close()
return wavelength, bunit, flux, ivar
def readspZbest(plate, mjd):
"""
Function to read the useful headers and data from spZbest fits file
@param place :: 4-digit plate number
@param mjd :: 5-digit MJD
@returns wavelength, b
"""
hdu = fits.open(setName('spZbest', plate, mjd))
zspec = hdu[1].data['Z'] # best-fit spectroscopic redshift
zclass = hdu[1].data['CLASS'] # best-fit spectral class
rchi2 = hdu[1].data['RCHI2'] # best-fit reduced chi2
zwarn = hdu[1].data['ZWARNING'] # warning flag
synflux = hdu[2].data # best-fit spectrum
hdu.close()
return zspec, zclass, rchi2, zwarn, synflux
# -
# Calling the functions and reading the data
# + outputHidden=false inputHidden=false
[wave, bunit, flux, ivar] = readSpPlate(plate, mjd)
[zspec, zclass, rchi2, zwarn, synflux] = readspZbest(plate, mjd)
# -
# ## 3. Plotting the spectrum
# + outputHidden=false inputHidden=false
def setLabel(ax, xlabel, ylabel, title, xlim, ylim):
"""
Function defining plot properties
@param ax :: axes to be held
@param xlabel, ylabel :: labels of the x-y axis
@param title :: title of the plot
@param xlim, ylim :: x-y limits for the axis
"""
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
ax.set_xlim(xlim)
ax.set_ylim(ylim)
ax.legend()
ax.grid(True)
ax.set_title(title, fontsize=18)
return
# + outputHidden=false inputHidden=false
fig,ax = plt.subplots(figsize=(8,5))
# we smooth with 50 pixels
tmpflux = convolve(flux[fiber-1,:] * (ivar[fiber-1,:] > 0), Box1DKernel(11))
tmpsynflux = convolve(synflux[fiber-1,:], Box1DKernel(11))
ax.plot(wave, tmpflux, 'k', label='Data')
ax.plot(wave, tmpsynflux, 'r', label='best-fit spectrum')
ax.plot(3727*(1+zspec[fiber-1]+np.zeros(2)),ylim,color='y')
xlabel = r'$\lambda_{obs} (\dot{A})$'
ylabel = r'Flux $\times 10^{-17}$'+'\n'+r'$\rm{(erg\ cm^{-2}\ s^{-1}\ \dot{A}^{-1})}$'
title = r'Z = %.2f, CLASS = %s, ZWARNING = %d, $\chi_{\rm(red)}$ = %.2f'%(zspec[fiber-1], zclass[fiber-1], zwarn[fiber-1], rchi2[fiber-1])
ylim = [-0.05,1.00]
xlim = [4000, 9000]
setLabel(ax, xlabel, ylabel, title, xlim, ylim)
| 01_Intro_to_Reading_Processing_and_Plotting_SDSS_data.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from bs4 import BeautifulSoup
import re
# +
def removeNonAsciiAndNames(s):
bad_chars = [';', ':', '!', '*', '(' , ')', '&']
non_ascii = "".join(i for i in s if ord(i)< 128)
html_decoded_string = BeautifulSoup(non_ascii, "lxml")
string = html_decoded_string.string
non_name = " ".join((filter(lambda x:x[0]!='@', string.split())))
non_badchars = ''.join(filter(lambda i: i not in bad_chars, non_name))
non_links = re.sub(r"http\S+", "", non_badchars)
return non_links
removeNonAsciiAndNames("#NotNotPyramidScheme #MLM's on New Illegal Tender series on Feb. 27 #GigEconomy #SideHustle #BossBabe https://t.co/iml91ExVlB / $HLF $NUS $USNA $MED $TUP #Arbonne #LulaRoe etc. https://t.co/Fj78PqfEJL https://t.co/3unHXPdG3z")
| RemoveNoise.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from keras.models import Sequential
from tensorflow.keras import layers
from keras.layers.core import Flatten, Dense, Dropout
from keras.layers.convolutional import Convolution2D, MaxPooling2D
from keras.models import load_model
import nso_ds_classes.nso_tif_kernel as nso_tif_kernel
import nso_ds_classes.nso_ds_models as nso_ds_models
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder
import tensorflow as tf
onehot_encoder = OneHotEncoder(sparse=False)
label_encoder = LabelEncoder()
# Models.
def VGG_16_inspired_model(size_x_matrix =32 ,size_y_matrix = 32,bands = 4):
model = Sequential()
# model.add(ZeroPadding2D((1,1),input_shape=(31,31, 7)))
model.add(Convolution2D(28, 2, 2, activation='relu',input_shape=((bands, size_x_matrix, size_y_matrix))))
model.add(Convolution2D(56, 2, 2, activation='relu'))
model.add(MaxPooling2D((2,2), strides=(2,2)))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(5, activation='softmax'))
return model
path_to_tif_file = "E:/data/coepelduynen/20210907_112017_SV1-04_SV_RD_11bit_RGBI_50cm_KatwijkAanZee_natura2000_coepelduynen_cropped.tif"
# +
x_kernel_width = 32
y_kernel_height = 32
tif_kernel_generator = nso_tif_kernel.nso_tif_kernel_generator(path_to_tif_file, x_kernel_width , y_kernel_height)
# -
a_generic_model = nso_ds_models.generic_model(tif_kernel_generator)
annotations = a_generic_model.get_annotations(path_to_tif_file.split("/")[-1])
annotations[["label","kernel"]]
model = VGG_16_inspired_model()
model.compile(loss="sparse_categorical_crossentropy",
optimizer= 'rmsprop',
metrics=['accuracy'])
y = label_encoder.fit_transform(annotations['label'].values)
y = y.reshape(len(y), 1)
y = onehot_encoder.fit_transform(y)
print(y)
y = label_encoder.fit_transform(annotations['label'].values)
y.shape
model.fit(tf.cast(np.concatenate(annotations["kernel"]).reshape(5,4,32,32).astype(int), tf.float32),y, epochs=1)
results = model.predict(tf.cast(np.concatenate(annotations["kernel"]).reshape(5,4,32,32).astype(int), tf.float32))
y
results[0]
# +
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D
from tensorflow.keras.losses import sparse_categorical_crossentropy
from tensorflow.keras.optimizers import Adam
# Model configuration
batch_size = 50
img_width, img_height, img_num_channels = 32, 32, 3
loss_function = sparse_categorical_crossentropy
no_classes = 10
no_epochs = 100
optimizer = Adam()
validation_split = 0.2
verbosity = 1
# Load CIFAR-10 data
(input_train, target_train), (input_test, target_test) = cifar10.load_data()
# Determine shape of the data
input_shape = (img_width, img_height, img_num_channels)
# Parse numbers as floats
input_train = input_train.astype('float32')
input_test = input_test.astype('float32')
# Scale data
input_train = input_train / 255
input_test = input_test / 255
# Create the model
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=input_shape))
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dense(no_classes, activation='softmax'))
# Compile the model
model.compile(loss=loss_function,
optimizer=optimizer,
metrics=['accuracy'])
# Fit data to model
history = model.fit(input_train, target_train,
batch_size=batch_size,
epochs=no_epochs,
verbose=verbosity,
validation_split=validation_split)
# Generate generalization metrics
score = model.evaluate(input_test, target_test, verbose=0)
print(f'Test loss: {score[0]} / Test accuracy: {score[1]}')
# -
input_train.shape
target_train.shape
| .ipynb_checkpoints/main_deep_learning-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Lorenz Attractors
#
# The Lorenz attractors are a set of 3 coupled differential equations that, while simple in form, lead to highly nonlinear behavior. These are interesting because, although solutions to these differential equations exhibit divergent behavior and nonlinear effects, they also appear to follow a "global" pattern.
#
# The differential equations are written in terms of three dependent variables ($x$, $y$, $z$) and one independent variable ($t$), as well as three parameters: $\sigma$, $r$, and $b$, with each parameter appearing once in a single differential equation.
#
# $$
# \dfrac{dx}{dt} = \sigma (y-x) \\
# \dfrac{dy}{dt} = rx - y - xz \\
# \dfrac{dz}{dt} = xy - bz
# $$
#
# These equations originally came from numerical experiments run by <NAME>, a meterologist studying the Earth's atmosphere. The equations can be interpreted in that domain as $x$ being the rate of convective overturning, while $y$ and $z$ are the horiziontal and vertical temperature variations in the atmosphere.
#
# Earth's atmosphere is modeled using $\sigma = 10, b = \frac{8}{3}$. The third parameter $r$ controls the nonlinear dynamical behavior.
# +
# #%load_ext base16_mplrc
# #%base16_mplrc dark bespin
# -
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
def lorenz(in_, t, sigma, b, r):
"""Evaluates the RHS of the 3
Lorenz attractor differential equations.
in_ : initial vector of [x_0, y_0, z_0]
t : time vector (not used, but present for odeint() call)
sigma : numerical parameter 1
b : numerical parameter 2
r : numerical parameter 3
"""
x = in_[0]
y = in_[1]
z = in_[2]
return [sigma*(y-x),
r*x - y - x*z,
x*y - b*z]
def get_lorenz_solution(in_0, tmax, nt, args_tuple):
t = np.linspace(0, tmax, nt)
soln = odeint(lorenz, in_0, t, args=args_tuple).T
return t, soln
in_0 = [5.0, 5.0, 5.0]
t_max = 20
t_steps = 20000
t, [solx, soly, solz] = get_lorenz_solution(in_0, t_max, t_steps,
(10.0, 8/3, 28))
fig, ax = plt.subplots(1,1, figsize=(8,8))
ax.plot(t, solx, label='x')
ax.plot(t, soly, label='y')
ax.plot(t, solz, label='z')
ax.legend()
plt.show()
| Lorenz 1 Attractors.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# <div style="height: 79px; margin-right: 110px;"><img src="/static/base/images/TAP-logo.png" align="center" /></div>
#
# ## Welcome
#
# Welcome to the Jupyter Notebooks in TAP.
#
# If you are new to Jupyter we recommend starting with "Help -> User Interface Tour".
#
# Under the [examples](/tree/examples) folder you'll find some example notebooks for working with different libraries:
#
# - [ATK](/tree/examples/atk)
# - [sparktk](/tree/examples/tal/sparktk)
# - [Spark](/tree/examples/spark)
# - [Pandas](/tree/examples/pandas-cookbook)
#
# Visit the [TAP Community](https://community.trustedanalytics.org/) to access forums and get help.
#
#
# ## Help Menus
#
# On the right side of the tool bar you can find the **Help** and **TAP Help** menus. Under the **Help** menu is general documentation for Jupyter, Python, and libraries like pandas. Learn about keyboard shortcuts for Jupyter under "Help -> Keyboard Shortcuts". Under the **TAP Help** menu there is TAP specific help and code snippets for quick and easy reference.
#
# ## Learning Python
#
# If you are new to Python consider starting with the [Hitchhiker's Guide to Python](http://docs.python-guide.org/en/latest/intro/learning/) which lists many resources for learning Python.
#
# ## Installing Python Packages with Conda
#
# Many python packages come pre-installed (pandas, scikit-learn, matplotlib, numpy) but if you need to install additional packages go to the [Jupyter dashboard](/tree) and then choose "New -> Terminal".
#
# Within the Terminal window you can use conda at the command line to install python packages.
#
# ```bash
# # list all packages installed
# conda list
# # search for a package by name
# conda search pandas
# # install a package by name
# conda install pandas
# # get help
# conda --help
# ```
#
# You can also access conda directly in a notebook by prefixing your command with an exclamation point:
# list all packages installed
# !conda list
# See the [Conda Documentation](http://conda.pydata.org/docs/using/index.html) for more information.
#
# [Pip](https://pip.pypa.io/en/stable/) is also available for packages not available via conda.
#
# ## Troubleshooting
#
# If your notebook stops working in an unexpected way try:
# - Restarting the kernel: choose the menu item "Kernel -> Restart".
# - Shutting down your notebook and reopening it: visit the [Jupyter dashboard](/tree), choose "Running" tab, and click the "Shutdown" button.
# - Reaching out for help on the [TAP Community](https://community.trustedanalytics.org/)
#
# ## Links
#
# - [TrustedAnalytics.org](http://trustedanalytics.org/) - the main website for TAP
# - [TAP Community](https://community.trustedanalytics.org/) - forums and community help
# - [TAP Github](https://github.com/trustedanalytics) - source code for TAP
# - [TAP JIRA](https://trustedanalytics.atlassian.net/) - tracking system for bugs and features
# - [ATK](http://trustedanalytics.github.io/atk/) - the TAP Analytics Toolkit documentation
# - [sparktk](http://trustedanalytics.github.io/sparktk) - the Trusted Analytics Libraries, Spark Toolkit documentation
# - [Jupyter](http://jupyter.org/) - project website
# - [Spark](http://spark.apache.org/) - project website
# - [Notebook Viewer](https://nbviewer.jupyter.org/) - a website for sharing Jupyter notebooks, many good examples are available
# ## Using custom DAAL or SparkTK packages
# Both DAAL and SparkTK rely on the following environment variables to be set:
#
# - SPARKTK_HOME
# - DAALTK_HOME
# - LD_LIBRARY_PATH
#
# These variables are listed in the file: "daaltk.sh"
# and they are currently set to the following values:
import os
print os.environ['SPARKTK_HOME']
print os.environ['DAALTK_HOME']
print os.environ['LD_LIBRARY_PATH']
# Once the new packages are uploaded and extracted within Jupyter, above variables need to have new values assigned to them at the begining of the script to overwrite the default values.
| jupyter-default-notebooks/notebooks/README.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from refnx.dataset import Data1D
from refnx.dataset import ReflectDataset
import refnx
import data_in
data = data_in.data_in('d2o/29553_54.dat')
#print(data)
# dataset = data # ...
data = Data1D(data)
#print(data)
from refnx.reflect import SLD, Erf
# simple setup, no tilt, equation or checking
air = SLD(value=0+0j, name='air')
polymer = SLD(4.1,'polymer')
#air-polymer roughness of 17.5, polymer size of 40.5
polymer = polymer(40.5, 17.5)
polymer.thick.setp(vary=True,bounds=(24,55))
#polymer.rough.setp(vary=True,bounds=(11,24))
polymer.sld.real.setp(vary=True,bounds=(1.92,6.21))
polymer.vfsolv.setp(vary=True, bounds=(0,1))
water = SLD(3.5,'water')
water = water(0,13)
water.rough.setp(vary=True, bounds=(0,26))
water.sld.real.setp(vary=True,bounds=(-0.56,6.35))
structure = air | polymer | water
#air-polymer roughness of 4, polymer size of 55
#Erf() <-error function
structure[1].interfaces = Erf() # air-polymer interface
structure[2].interfaces = Erf()
print(structure)
from refnx.reflect import ReflectModel
model = ReflectModel(structure, bkg=0, dq=0)
model.scale.setp(vary=True, bounds=(-1, 1.5))
model.bkg.setp(vary=True,bounds=(-1, 1.5))
#print(model)
from refnx.analysis import CurveFitter, Objective
objective = Objective(model, data)
fitter = CurveFitter(objective)
fitter.fit('differential_evolution')
print(objective,'\n')
#print(fitter)
import matplotlib.pyplot as plt
# %matplotlib notebook
objective.plot()
plt.yscale('log')
plt.xscale('log')
plt.xlabel('Q')
plt.ylabel('Reflectivity')
plt.legend()
print(structure)
| eggs_simple.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Copyright (c) Microsoft Corporation. All rights reserved.
#
# Licensed under the MIT License.
# # Model Development with Custom Weights
# This example shows how to retrain a model with custom weights and fine-tune the model with quantization, then deploy the model running on FPGA. Only Windows is supported. We use TensorFlow and Keras to build our model. We are going to use transfer learning, with ResNet50 as a featurizer. We don't use the last layer of ResNet50 in this case and instead add our own classification layer using Keras.
#
# This Notebook was subsequently edited by <NAME> (<EMAIL>) to accomidate adjustments necessary to apply the methodology for top quark tagging.
#
# The custom wegiths are trained with ImageNet on ResNet50.
#
# Please set up your environment as described in the [quick start](project-brainwave-quickstart.ipynb).
import os
import sys
import tensorflow as tf
import numpy as np
from keras import backend as K
# ## Setup Environment
# After you train your model in float32, you'll write the weights to a place on disk. We also need a location to store the models that get downloaded.
custom_weights_dir = os.path.expanduser("~/custom-weights")
saved_model_dir = os.path.expanduser("~/models")
# ## Prepare Data
# Load the files we are going to use for training and testing. By default this notebook uses only a very small subset of the Cats and Dogs dataset. That makes it run relatively quickly.
# +
import glob
import imghdr
datadir = os.path.expanduser("~/catsanddogs")
cat_files = glob.glob(os.path.join(datadir, 'PetImages', 'Cat', '*.jpg'))
dog_files = glob.glob(os.path.join(datadir, 'PetImages', 'Dog', '*.jpg'))
# Limit the data set to make the notebook execute quickly.
cat_files = cat_files[:64]
dog_files = dog_files[:64]
# The data set has a few images that are not jpeg. Remove them.
cat_files = [f for f in cat_files if imghdr.what(f) == 'jpeg']
dog_files = [f for f in dog_files if imghdr.what(f) == 'jpeg']
if(not len(cat_files) or not len(dog_files)):
print("Please download the Kaggle Cats and Dogs dataset form https://www.microsoft.com/en-us/download/details.aspx?id=54765 and extract the zip to " + datadir)
raise ValueError("Data not found")
else:
print(cat_files[0])
print(dog_files[0])
# -
# Construct a numpy array as labels
image_paths = cat_files + dog_files
total_files = len(cat_files) + len(dog_files)
labels = np.zeros(total_files)
labels[len(cat_files):] = 1
# +
# Split images data as training data and test data
from sklearn.model_selection import train_test_split
onehot_labels = np.array([[0,1] if i else [1,0] for i in labels])
img_train, img_test, label_train, label_test = train_test_split(image_paths, onehot_labels, random_state=42, shuffle=True)
print(len(img_train), len(img_test), label_train.shape, label_test.shape)
# -
# ## Construct Model
# We use ResNet50 for the featuirzer and build our own classifier using Keras layers. We train the featurizer and the classifier as one model. The weights trained on ImageNet are used as the starting point for the retraining of our featurizer. The weights are loaded from tensorflow chkeckpoint files.
# Before passing image dataset to the ResNet50 featurizer, we need to preprocess the input file to get it into the form expected by ResNet50. ResNet50 expects float tensors representing the images in BGR, channel last order. We've provided a default implementation of the preprocessing that you can use.
# +
import azureml.contrib.brainwave.models.utils as utils
def preprocess_images():
# Convert images to 3D tensors [width,height,channel] - channels are in BGR order.
in_images = tf.placeholder(tf.string)
image_tensors = utils.preprocess_array(in_images)
return in_images, image_tensors
# -
# We use Keras layer APIs to construct the classifier. Because we're using the tensorflow backend, we can train this classifier in one session with our Resnet50 model.
def construct_classifier(in_tensor):
from keras.layers import Dropout, Dense, Flatten
K.set_session(tf.get_default_session())
FC_SIZE = 1024
NUM_CLASSES = 2
x = Dropout(0.2, input_shape=(1, 1, 2048,))(in_tensor)
x = Dense(FC_SIZE, activation='relu', input_dim=(1, 1, 2048,))(x)
x = Flatten()(x)
preds = Dense(NUM_CLASSES, activation='softmax', input_dim=FC_SIZE, name='classifier_output')(x)
return preds
# Now every component of the model is defined, we can construct the model. Constructing the model with the project brainwave models is two steps - first we import the graph definition, then we restore the weights of the model into a tensorflow session. Because the quantized graph defintion and the float32 graph defintion share the same node names in the graph definitions, we can initally train the weights in float32, and then reload them with the quantized operations (which take longer) to fine-tune the model.
def construct_model(quantized, starting_weights_directory = None):
from azureml.contrib.brainwave.models import Resnet50, QuantizedResnet50
# Convert images to 3D tensors [width,height,channel]
in_images, image_tensors = preprocess_images()
# Construct featurizer using quantized or unquantized ResNet50 model
if not quantized:
featurizer = Resnet50(saved_model_dir)
else:
featurizer = QuantizedResnet50(saved_model_dir, custom_weights_directory = starting_weights_directory)
features = featurizer.import_graph_def(input_tensor=image_tensors)
# Construct classifier
preds = construct_classifier(features)
# Initialize weights
sess = tf.get_default_session()
tf.global_variables_initializer().run()
featurizer.restore_weights(sess)
return in_images, image_tensors, features, preds, featurizer
# ## Train Model
# First we train the model with custom weights but without quantization. Training is done with native float precision (32-bit floats). We load the traing data set and batch the training with 10 epochs. When the performance reaches desired level or starts decredation, we stop the training iteration and save the weights as tensorflow checkpoint files.
def read_files(files):
""" Read files to array"""
contents = []
for path in files:
with open(path, 'rb') as f:
contents.append(f.read())
return contents
def train_model(preds, in_images, img_train, label_train, is_retrain = False, train_epoch = 10):
""" training model """
from keras.objectives import binary_crossentropy
from tqdm import tqdm
learning_rate = 0.001 if is_retrain else 0.01
# Specify the loss function
in_labels = tf.placeholder(tf.float32, shape=(None, 2))
cross_entropy = tf.reduce_mean(binary_crossentropy(in_labels, preds))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)
def chunks(a, b, n):
"""Yield successive n-sized chunks from a and b."""
if (len(a) != len(b)):
print("a and b are not equal in chunks(a,b,n)")
raise ValueError("Parameter error")
for i in range(0, len(a), n):
yield a[i:i + n], b[i:i + n]
chunk_size = 16
chunk_num = len(label_train) / chunk_size
sess = tf.get_default_session()
for epoch in range(train_epoch):
avg_loss = 0
for img_chunk, label_chunk in tqdm(chunks(img_train, label_train, chunk_size)):
contents = read_files(img_chunk)
_, loss = sess.run([optimizer, cross_entropy],
feed_dict={in_images: contents,
in_labels: label_chunk,
K.learning_phase(): 1})
avg_loss += loss / chunk_num
print("Epoch:", (epoch + 1), "loss = ", "{:.3f}".format(avg_loss))
# Reach desired performance
if (avg_loss < 0.001):
break
def test_model(preds, in_images, img_test, label_test):
"""Test the model"""
from keras.metrics import categorical_accuracy
in_labels = tf.placeholder(tf.float32, shape=(None, 2))
accuracy = tf.reduce_mean(categorical_accuracy(in_labels, preds))
contents = read_files(img_test)
accuracy = accuracy.eval(feed_dict={in_images: contents,
in_labels: label_test,
K.learning_phase(): 0})
return accuracy
# +
# Launch the training
tf.reset_default_graph()
sess = tf.Session(graph=tf.get_default_graph())
with sess.as_default():
in_images, image_tensors, features, preds, featurizer = construct_model(quantized=False)
train_model(preds, in_images, img_train, label_train, is_retrain=False, train_epoch=10)
accuracy = test_model(preds, in_images, img_test, label_test)
print("Accuracy:", accuracy)
featurizer.save_weights(custom_weights_dir + "/rn50", tf.get_default_session())
# -
# ## Test Model
# After training, we evaluate the trained model's accuracy on test dataset with quantization. So that we know the model's performance if it is deployed on the FPGA.
# +
tf.reset_default_graph()
sess = tf.Session(graph=tf.get_default_graph())
with sess.as_default():
print("Testing trained model with quantization")
in_images, image_tensors, features, preds, quantized_featurizer = construct_model(quantized=True, starting_weights_directory=custom_weights_dir)
accuracy = test_model(preds, in_images, img_test, label_test)
print("Accuracy:", accuracy)
# -
# ## Fine-Tune Model
# Sometimes, the model's accuracy can drop significantly after quantization. In those cases, we need to retrain the model enabled with quantization to get better model accuracy.
if (accuracy < 0.93):
with sess.as_default():
print("Fine-tuning model with quantization")
train_model(preds, in_images, img_train, label_train, is_retrain=True, train_epoch=10)
accuracy = test_model(preds, in_images, img_test, label_test)
print("Accuracy:", accuracy)
# ## Service Definition
# Like in the QuickStart notebook our service definition pipeline consists of three stages.
# +
from azureml.contrib.brainwave.pipeline import ModelDefinition, TensorflowStage, BrainWaveStage
model_def_path = os.path.join(saved_model_dir, 'model_def.zip')
model_def = ModelDefinition()
model_def.pipeline.append(TensorflowStage(sess, in_images, image_tensors))
model_def.pipeline.append(BrainWaveStage(sess, quantized_featurizer))
model_def.pipeline.append(TensorflowStage(sess, features, preds))
model_def.save(model_def_path)
print(model_def_path)
# -
# ## Deploy
# Go to our [GitHub repo](https://aka.ms/aml-real-time-ai) "docs" folder to learn how to create a Model Management Account and find the required information below.
# +
from azureml.core import Workspace
ws = Workspace.from_config()
# -
# The first time the code below runs it will create a new service running your model. If you want to change the model you can make changes above in this notebook and save a new service definition. Then this code will update the running service in place to run the new model.
# +
from azureml.core.model import Model
from azureml.core.image import Image
from azureml.core.webservice import Webservice
from azureml.contrib.brainwave import BrainwaveWebservice, BrainwaveImage
from azureml.exceptions import WebserviceException
model_name = "catsanddogs-resnet50-model"
image_name = "catsanddogs-resnet50-image"
service_name = "modelbuild-service"
registered_model = Model.register(ws, model_def_path, model_name)
image_config = BrainwaveImage.image_configuration()
deployment_config = BrainwaveWebservice.deploy_configuration()
try:
service = Webservice(ws, service_name)
service.delete()
service = Webservice.deploy_from_model(ws, service_name, [registered_model], image_config, deployment_config)
service.wait_for_deployment(True)
except WebserviceException:
service = Webservice.deploy_from_model(ws, service_name, [registered_model], image_config, deployment_config)
service.wait_for_deployment(True)
# -
# The service is now running in Azure and ready to serve requests. We can check the address and port.
print(service.ipAddress + ':' + str(service.port))
# ## Client
# There is a simple test client at amlrealtimeai.PredictionClient which can be used for testing. We'll use this client to score an image with our new service.
from azureml.contrib.brainwave.client import PredictionClient
client = PredictionClient(service.ipAddress, service.port)
# You can adapt the client [code](../../pythonlib/amlrealtimeai/client.py) to meet your needs. There is also an example C# [client](../../sample-clients/csharp).
#
# The service provides an API that is compatible with TensorFlow Serving. There are instructions to download a sample client [here](https://www.tensorflow.org/serving/setup).
# ## Request
# Let's see how our service does on a few images. It may get a few wrong.
# Specify an image to classify
print('CATS')
for image_file in cat_files[:8]:
results = client.score_image(image_file)
result = 'CORRECT ' if results[0] > results[1] else 'WRONG '
print(result + str(results))
print('DOGS')
for image_file in dog_files[:8]:
results = client.score_image(image_file)
result = 'CORRECT ' if results[1] > results[0] else 'WRONG '
print(result + str(results))
# ## Cleanup
# Run the cell below to delete your service.
service.delete()
# ## Appendix
# License for plot_confusion_matrix:
#
# New BSD License
#
# Copyright (c) 2007-2018 The scikit-learn developers.
# All rights reserved.
#
#
# Redistribution and use in source and binary forms, with or without
# modification, are permitted provided that the following conditions are met:
#
# a. Redistributions of source code must retain the above copyright notice,
# this list of conditions and the following disclaimer.
# b. Redistributions in binary form must reproduce the above copyright
# notice, this list of conditions and the following disclaimer in the
# documentation and/or other materials provided with the distribution.
# c. Neither the name of the Scikit-learn Developers nor the names of
# its contributors may be used to endorse or promote products
# derived from this software without specific prior written
# permission.
#
#
# THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
# AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
# IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
# ARE DISCLAIMED. IN NO EVENT SHALL THE REGENTS OR CONTRIBUTORS BE LIABLE FOR
# ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL
# DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR
# SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER
# CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT
# LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY
# OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH
# DAMAGE.
#
| project-brainwave/project-brainwave-custom-weights.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Observations and Insights
# The more effective treatments: Capomulin and Ramicane have more data points.
# There's a positive correlation between mouse weight and tumor volume.
# There's a even number of male and female mice in the study.
# The more effective treatments also had smaller variances.
# Ketapril was the worst treatment.
# ## Dependencies
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import scipy.stats as st
import numpy as np
# +
# Study data files
mouse_metadata = "data/Mouse_metadata.csv"
study_results = "data/Study_results.csv"
# Read the mouse data and the study results
mouse_metadata = pd.read_csv(mouse_metadata)
study_results = pd.read_csv(study_results)
# -
# Combine the data into a single dataset
mouse_study_df = pd.merge(mouse_metadata, study_results, on="Mouse ID", how="outer")
mouse_study_df
# ## Summary statistics
# +
# Generate a summary statistics table of mean, median, variance, standard deviation, and SEM of the tumor volume for each regimen
grouped_mouse_study_df = mouse_study_df[["Drug Regimen", "Tumor Volume (mm3)"]].groupby("Drug Regimen")
#Finding mean and median and merging them
mean = grouped_mouse_study_df.mean()
median = grouped_mouse_study_df.median()
Summary_statistics_df = pd.merge(mean, median, on="Drug Regimen", suffixes= [" Mean", " Median"])
# Finding variance and std and merging them
variance = grouped_mouse_study_df.var()
Standard_deviation = grouped_mouse_study_df.std()
var_std_table = pd.merge(variance, Standard_deviation, on="Drug Regimen", suffixes=[" Variance", " Standard Deviation"])
Summary_statistics_df = pd.merge(Summary_statistics_df, var_std_table, on="Drug Regimen")
# Finding SEM and merging it
SEM = grouped_mouse_study_df.sem()
Summary_statistics_df = pd.merge(Summary_statistics_df, SEM, on="Drug Regimen")
Summary_statistics_df.rename(columns={"Tumor Volume (mm3)":"Tumor Volume (mm3) SEM"}, inplace=True)
Summary_statistics_df
# -
# ## Bar plots
# Generate a bar plot showing number of data points for each treatment regimen using pandas
mouse_study_df["Drug Regimen"].value_counts().plot(kind="bar", color = "blue", title="Number of Data Points per Treatment Regimen")
plt.xlabel("Drug Regimen")
plt.ylabel("Number of Data Points")
plt.xlim(-0.75, 9.75)
plt.ylim(0, 260)
plt.tight_layout()
# Generate a bar plot showing number of data points for each treatment regimen using pyplot
plt.bar(mouse_study_df["Drug Regimen"].unique(), mouse_study_df["Drug Regimen"].value_counts(), color ="blue", align="center", width=0.5)
plt.xticks(rotation="vertical")
plt.title("Number of Data Points per Treatment Regimen")
plt.xlabel("Drug Regimen")
plt.ylabel("Number of Data Points")
plt.xlim(-0.75, 9.75)
plt.ylim(0, 260)
plt.tight_layout()
plt.show()
# ## Pie plots
# Generate a pie plot showing the distribution of female versus male mice using pandas
mouse_study_df["Sex"].value_counts().plot(kind="pie", colors=["blue", "red"], shadow=True, autopct="%1.1f%%",
title="Sex Distribution of study")
plt.legend(loc="best")
plt.ylabel("")
plt.axis("equal")
# Generate a pie plot showing the distribution of female versus male mice using pyplot
plt.pie(mouse_study_df["Sex"].value_counts(), labels= mouse_study_df["Sex"].unique(), colors=["blue", "red"], shadow=True,
autopct="%1.1f%%")
plt.title("Sex Distribution of study")
plt.legend(loc="best")
plt.axis("equal")
# ## Quartiles, outliers and boxplots
# +
mouse_ids = mouse_study_df["Mouse ID"].unique()
mouse_ids
last_timepoints = pd.DataFrame({"Mouse ID":[], "Drug Regimen":[], "Sex":[], "Age_months":[], "Weight (g)":[],
"Timepoint":[], "Tumor Volume (mm3)":[], "Metastatic Sites":[]})
for mouse in mouse_ids:
sample_mouse = mouse_study_df.loc[mouse_study_df["Mouse ID"] == mouse,:]
sample_mouse = sample_mouse.sort_values(by="Timepoint", ascending=True)
last_timepoint = sample_mouse.iloc[-1,:]
last_timepoints = last_timepoints.append(last_timepoint, ignore_index=True)
last_timepoints
# +
# Calculate the final tumor volume of each mouse across four of the most promising treatment regimens. Calculate the IQR and quantitatively determine if there are any potential outliers.
last_timepoints_of_top_regimens = last_timepoints.loc[((last_timepoints["Drug Regimen"] == "Capomulin") | \
(last_timepoints["Drug Regimen"] == "Ramicane") | \
(last_timepoints["Drug Regimen"] == "Infubinol") | \
(last_timepoints["Drug Regimen"] == "Ceftamin")),
["Mouse ID", "Drug Regimen", "Tumor Volume (mm3)"]]
last_timepoints_of_top_regimens
# +
quartiles = last_timepoints_of_top_regimens["Tumor Volume (mm3)"].quantile([0.25,0.5,0.75])
lowerq = quartiles[0.25]
upperq = quartiles[0.75]
iqr = upperq - lowerq
lowerbound = lowerq - (1.5*iqr)
upperbound = upperq + (1.5*iqr)
outliers = last_timepoints_of_top_regimens.loc[((last_timepoints_of_top_regimens["Tumor Volume (mm3)"] < lowerbound) | \
(last_timepoints_of_top_regimens["Tumor Volume (mm3)"] > upperbound)),:]
if len(outliers) > 0:
print("There are potential outliers")
else:
print("There are no outliers.")
# +
# Generate a box plot of the final tumor volume of each mouse across four regimens of interest
Capomulin = last_timepoints_of_top_regimens.loc[last_timepoints_of_top_regimens["Drug Regimen"] == "Capomulin",["Tumor Volume (mm3)"]]
Ramicane = last_timepoints_of_top_regimens.loc[last_timepoints_of_top_regimens["Drug Regimen"] == "Ramicane",["Tumor Volume (mm3)"]]
Infubinol = last_timepoints_of_top_regimens.loc[last_timepoints_of_top_regimens["Drug Regimen"] == "Infubinol",["Tumor Volume (mm3)"]]
Ceftamin = last_timepoints_of_top_regimens.loc[last_timepoints_of_top_regimens["Drug Regimen"] == "Ceftamin",["Tumor Volume (mm3)"]]
top_regimens = [Capomulin["Tumor Volume (mm3)"], Ramicane["Tumor Volume (mm3)"], Infubinol["Tumor Volume (mm3)"],
Ceftamin["Tumor Volume (mm3)"]]
# +
red_tri = dict(markerfacecolor="red", markeredgecolor= "red", marker= "1")
fig, ax1 = plt.subplots(sharey=True)
fig.suptitle("Final Tumor Size across top Treatment Regimens")
ax1.boxplot(top_regimens, flierprops=red_tri)
ax1.set_ylabel("Final Tumor Sizes")
ax1.set(xticklabels=["Capomulin", "Ramicane","Infubinol", "Ceftamin"])
ax1.set_ylim(15, 80)
plt.show()
# -
# ## Line and scatter plots
# +
# Generate a line plot of time point versus tumor volume for a mouse treated with Capomulin
mouse = mouse_study_df.loc[mouse_study_df["Drug Regimen"] == "Capomulin",
["Mouse ID", "Timepoint", "Tumor Volume (mm3)"]]
mouse_id = input(f"Which mouse would you like to look for? {mouse['Mouse ID'].unique()} ")
# mouse_id = "s185"
mouse = mouse.loc[mouse["Mouse ID"] == mouse_id, ["Timepoint", "Tumor Volume (mm3)"]]
plt.plot(mouse["Timepoint"], mouse["Tumor Volume (mm3)"], color = "blue", marker="D")
plt.title(f"The tumor size of mouse {mouse_id} over time")
plt.ylabel("Tumor Volume (mm3)")
plt.xlabel("Timepoint")
plt.xlim(-2, 47)
plt.ylim(min(mouse["Tumor Volume (mm3)"])-5, max(mouse["Tumor Volume (mm3)"])+5)
plt.xticks(np.arange(0,50,5))
plt.show()
# -
# Generate a scatter plot of mouse weight versus average tumor volume for the Capomulin regimen
mouse_weight = mouse_study_df.loc[mouse_study_df["Drug Regimen"] == "Capomulin",
["Mouse ID", "Weight (g)", "Tumor Volume (mm3)"]]
mouse_weight = mouse_weight.groupby("Mouse ID").mean()
# +
plt.scatter(mouse_weight["Weight (g)"], mouse_weight["Tumor Volume (mm3)"], marker='o', color='green', label="Tumor Volume by Mouse Weight")
plt.title("Average Tumor Volume vs Mouse Weight")
plt.ylabel("Tumor Volume (mm3)")
plt.xlabel("Mouse Weight (g)")
(slope, intercept, rvalue, pvalue, stderr) = st.linregress(mouse_weight["Weight (g)"], mouse_weight["Tumor Volume (mm3)"])
regress_value = slope * mouse_weight["Weight (g)"] + intercept
plt.plot(mouse_weight["Weight (g)"], regress_value, color="red", label="line of best fit")
plt.legend(loc="best")
plt.show()
# +
# Calculate the correlation coefficient and linear regression model for mouse weight and average tumor volume for the Capomulin regimen
correlation = st.pearsonr(mouse_weight["Weight (g)"], mouse_weight["Tumor Volume (mm3)"])
round(correlation[0],2)
# -
# Pie plot of gender distribution at beginning of trial
gender_survival_at_first = mouse_study_df.loc[(mouse_study_df["Timepoint"] == 0),:]
gender_survival_at_first["Sex"].value_counts().plot(kind="pie", colors=["blue", "red"], shadow=True, autopct="%1.1f%%",
title="Sex Distribution at Beginning of Study")
# Pie plot distribution of survivors' gender at end of trial
gender_survival_at_first = mouse_study_df.loc[(mouse_study_df["Timepoint"] == 45),:]
gender_survival_at_first["Sex"].value_counts().plot(kind="pie", colors=["blue", "red"], shadow=True, autopct="%1.1f%%",
title="Sex Distribution at End of Study")
# Histogram of final timepoints for each mouse
plt.hist(x=last_timepoints["Timepoint"], bins= [0,5,10,15,20,25,30,35,40,45,50])
plt.title("Distribution of Final Timepoints per Mouse")
plt.ylabel("Count of timepoint")
plt.xlabel("Timepoint")
plt.xticks([0,5,10,15,20,25,30,35,40,45])
| Pymaceuticals/.ipynb_checkpoints/pymaceuticals_starter-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# +
def plotCartesian(name, points, file):
fig = plt.figure(figsize=(5,5))
ax1 = fig.add_subplot(111)
ax1.set_title("%s\nCartesian coordinates" % name)
ax1.set_xlabel(r'$x$'); plt.ylabel(r'$y$');
ax1.scatter(points.x, points.y, 2, 'r', 'o')
fig.savefig(file)
plt.show()
def plotPolar(name, points, file):
C = np.cov(points[points.r > 150].theta, points[points.r > 150].r, bias = True)
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(111)
ax1.set_title(name + "\nPolar coordinates, C = %.3f" % C[0,1])
ax1.set_xlabel(r'$\theta$'); plt.ylabel(r'$r$');
ax1.scatter(points.theta, points.r, 2, 'b', 'o')
fig.savefig(file)
plt.show()
# -
circular = pd.read_csv('circular.csv', sep=',')
plotCartesian("Example circular galaxy", circular, 'circular_cartesian.pdf')
plotPolar("Example circular galaxy", circular, 'circular_polar.pdf')
spiral = pd.read_csv('spiral.csv', sep=',')
plotCartesian("Example spiral galaxy", spiral, 'spiral_cartesian.pdf')
plotPolar("Example spiral galaxy", spiral, 'spiral_polar.pdf')
| analysis/spiralAnalysis.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
def loadSimpDat():
simpDat = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return simpDat
simpDat = loadSimpDat()
class treeNode:
def __init__(self, nameValue, numOccur, parentNode):
self.name = nameValue
self.count = numOccur
self.nodeLink = None
self.parent = parentNode #needs to be updated
self.children = {}
#increments the count variable with a given amount
def inc(self, numOccur):
self.count += numOccur
#display tree in text. Useful for debugging
def disp(self, ind=1):
print (' '*ind, self.name, ' ', self.count)
for child in self.children.values():
child.disp(ind+1)
rootNode = treeNode('pyramid',9,None)
rootNode.children['eye'] = treeNode('eye',13,None)
rootNode.children['Axe'] = treeNode('Axe',6,None)
rootNode.disp()
def createTree(dataSet, minSup=1): #create FP-tree from dataset but don't mine
headerTable = {}
#go over dataSet twice
for trans in dataSet:#first pass counts frequency of occurance
#print(trans)
for item in trans:
#print(headerTable)
#print(headerTable.get(item, 0)) #This method return a value for the given key. If key is not available, then returns default value None.
#print(dataSet[trans])
headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
#print('-----------')
#print(headerTable)
#print('-----------')
for k in list(headerTable): #remove items not meeting minSup
if headerTable[k] < minSup:
del(headerTable[k])
freqItemSet = set(headerTable.keys())
#print( 'freqItemSet: ',freqItemSet)
if len(freqItemSet) == 0: return None, None #if no items meet min support -->get out
for k in headerTable:
headerTable[k] = [headerTable[k], None] #reformat headerTable to use Node link
print('headerTable: ',headerTable)
createTree({frozenset({'z'}): 1,
frozenset({'s', 't', 'u', 'v', 'w', 'x', 'y', 'z'}): 1,
frozenset({'e', 'm', 'q', 's', 't', 'x', 'y', 'z'}): 1,
frozenset({'p', 'q', 'r', 't', 'x', 'y', 'z'}): 1,
frozenset({'h', 'j', 'p', 'r', 'z'}): 1,
frozenset({'n', 'o', 'r', 's', 'x'}): 1})
def createTree(dataSet, minSup=1): #create FP-tree from dataset but don't mine
headerTable = {}
#go over dataSet twice
for trans in dataSet:#first pass counts frequency of occurance
for item in trans:
headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
for k in list(headerTable): #remove items not meeting minSup
if headerTable[k] < minSup:
del(headerTable[k])
freqItemSet = set(headerTable.keys())
#print 'freqItemSet: ',freqItemSet
if len(freqItemSet) == 0: return None, None #if no items meet min support -->get out
for k in headerTable:
headerTable[k] = [headerTable[k], None] #reformat headerTable to use Node link
#print 'headerTable: ',headerTable
retTree = treeNode('Null Set', 1, None) #create tree
for tranSet, count in dataSet.items(): #go through dataset 2nd time
localD = {}
for item in tranSet: #put transaction items in order
if item in freqItemSet:
localD[item] = headerTable[item][0]
if len(localD) > 0:
orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)]
updateTree(orderedItems, retTree, headerTable, count)#populate tree with ordered freq itemset
return retTree, headerTable #return tree and header table
| ML/FP-1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import scrapy
import scrapy.crawler as crawler
from multiprocessing import Process, Queue
from twisted.internet import reactor
import logging
# +
import json
class JsonWriterPipeline(object):
def open_spider(self, spider):
self.file = open('quoteresult.jl', 'w')
def close_spider(self, spider):
self.file.close()
def process_item(self, item, spider):
line = json.dumps(dict(item)) + "\n"
self.file.write(line)
return item
# -
# the wrapper to make it run more times
def run_spider(spider):
def f(q):
try:
runner = crawler.CrawlerRunner()
deferred = runner.crawl(spider)
deferred.addBoth(lambda _: reactor.stop())
reactor.run()
q.put(None)
except Exception as e:
q.put(e)
q = Queue()
p = Process(target=f, args=(q,))
p.start()
result = q.get()
p.join()
if result is not None:
raise result
class QuotesSpider(scrapy.Spider):
name = "quotes"
start_urls = [
'http://quotes.toscrape.com/page/1/'
]
custom_settings = {
'LOG_LEVEL': logging.WARNING,
'ITEM_PIPELINES': {'__main__.JsonWriterPipeline': 1}, # Used for pipeline 1
'FEED_FORMAT':'json', # Used for pipeline 2
'FEED_URI': 'quoteresult.json' # Used for pipeline 2
}
def parse(self, response):
for quote in response.css('div.quote'):
yield {
'text': quote.css('span.text::text').get(),
'author': quote.css('small.author::text').get(),
'tags': quote.css('div.tags a.tag::text').getall(),
}
next_page = response.css('li.next a::attr(href)').get()
if next_page is not None:
yield response.follow(next_page, callback=self.parse)
#page = response.url.split("/")[-2]
#filename = 'quotes-%s.html' % page
#with open(filename, 'wb') as f:
# f.write(dic)
# response.follow just returns a Request instance; you still have to yield this Request.
process.crawl(QuotesSpider)
process.start()
# +
print('first run:')
run_spider(QuotesSpider)
#print('\nsecond run:')
#run_spider(QuotesSpider)
# -
# !ls
import pandas as pd
qt = pd.read_json('quoteresult.json')
qt
| crawler/Python-crawler.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Training Batch Reinforcement Learning Policies with Amazon SageMaker RL and Coach library
#
# For many real-world problems, the reinforcement learning (RL) agent needs to learn from historical data that was generated by some deployed policy. For example, we may have historical data of experts playing games, users interacting with a website or sensor data from a control system. This notebook shows an example of how to use batch RL to train a new policy from offline dataset[1]. We use gym `CartPole-v0` as a fake simulated system to generate offline dataset and the RL agents are trained using Amazon SageMaker RL.
#
# We may want to evaluate the policy learned from historical data before deployment. Since simulators may not be available in all use cases, we need to evaluate how good the learned policy by using held out historical data. This is called as off-policy evaluation or counterfactual evaluation. In this notebook, we evaluate the policy during the training using several off-policy evaluation metrics.
#
# We can deploy the policy using SageMaker Hosting endpoint. However, some use cases may not require a persistent serving endpoint with sub-second latency. Here we demonstrate how to deploy the policy with [SageMaker Batch Transform](https://docs.aws.amazon.com/sagemaker/latest/dg/batch-transform.html), where large volumes of input state features can be inferenced with high throughput.
#
# Figure below shows an overview of the entire notebook.
#
# 
# ## Pre-requisites
#
# ### Roles and permissions
#
# To get started, we'll import the Python libraries we need, set up the environment with a few pre-requisites for permissions and configurations.
import sagemaker
import boto3
import sys
import os
import glob
import re
import subprocess
from IPython.display import HTML
import time
from time import gmtime, strftime
sys.path.append("common")
from misc import get_execution_role, wait_for_s3_object
from sagemaker.rl import RLEstimator, RLToolkit, RLFramework
# install gym environments if needed
# !pip install gym
from env_utils import VectoredGymEnvironment
# ### Steup S3 buckets
#
# Setup the linkage and authentication to the S3 bucket that you want to use for checkpoint and the metadata.
# S3 bucket
sage_session = sagemaker.session.Session()
s3_bucket = sage_session.default_bucket()
region_name = sage_session.boto_region_name
s3_output_path = 's3://{}/'.format(s3_bucket) # SDK appends the job name and output folder
print("S3 bucket path: {}".format(s3_output_path))
# ### Define Variables
#
# We define variables such as the job prefix for the training jobs *and the image path for the container (only when this is BYOC).*
# create unique job name
job_name_prefix = 'rl-batch-cartpole'
# ### Configure settings
#
# You can run your RL training jobs on a SageMaker notebook instance or on your own machine. In both of these scenarios, you can run the following in either `local` or `SageMaker` modes. The `local` mode uses the SageMaker Python SDK to run your code in a local container before deploying to SageMaker. This can speed up iterative testing and debugging while using the same familiar Python SDK interface. You just need to set `local_mode = True`.
# +
# %%time
# run in local mode?
local_mode = False
image = '462105765813.dkr.ecr.{}.amazonaws.com/sagemaker-rl-coach-container:coach-1.0.0-tf-cpu-py3'.format(region_name)
print("Use ECR image: {}".format(image))
# -
# ### Create an IAM role
# Either get the execution role when running from a SageMaker notebook `role = sagemaker.get_execution_role()` or, when running from local machine, use utils method `role = get_execution_role()` to create an execution role.
# +
try:
role = sagemaker.get_execution_role()
except:
role = get_execution_role()
print("Using IAM role arn: {}".format(role))
# -
# ### Install docker for `local` mode
#
# In order to work in `local` mode, you need to have docker installed. When running from you local machine, please make sure that you have docker or docker-compose (for local CPU machines) and nvidia-docker (for local GPU machines) installed. Alternatively, when running from a SageMaker notebook instance, you can simply run the following script to install dependenceis.
#
# Note, you can only run a single local notebook at one time.
# only run from SageMaker notebook instance
if local_mode:
# !/bin/bash ./common/setup.sh
# ## Collect offline data
#
# In order to do Batch RL training, we need to first prepare the dataset that is generated by a deployed policy. In real world scenarios, customers can collect these offline data by interacting the live environment using the already deployed agent. In this notebook, we used OpenAI gym `Cartpole-v0` as the environment to mimic a live environment and used a random policy with uniform action distribution to mimic a deployed agent. By interacting with multiple environments simultaneously, we can gather more trajectories from the environments.
#
# Here is a short introduction of the cart-pole balancing problem, where a pole is attached by an un-actuated joint to a cart, moving along a frictionless track.
#
# 1. *Objective*: Prevent the pole from falling over
# 2. *Environment*: The environment used in this example is part of OpenAI Gym, corresponding to the version of the cart-pole problem described by Barto, Sutton, and Anderson [2]
# 3. *State*: Cart position, cart velocity, pole angle, pole velocity at tip
# 4. *Action*: Push cart to the left, push cart to the right
# 5. *Reward*: Reward is 1 for every step taken, including the termination step
# initiate 100 environment to collect rollout data
NUM_ENVS = 100
NUM_EPISODES = 5
vectored_envs = VectoredGymEnvironment('CartPole-v0', NUM_ENVS)
# Now we have 100 environments of `Cartpole-v0` ready. We'll collect 5 episodes from each environment so we’ll have 500 episodes of data for training. We start from a random policy that generates the same uniform action probabilities regardless of the state features.
# initiate a random policy by setting action probabilities as uniform distribution
action_probs = [[1/2, 1/2] for _ in range(NUM_ENVS)]
df = vectored_envs.collect_rollouts_with_given_action_probs(action_probs=action_probs, num_episodes=NUM_EPISODES)
# the rollout dataframes contain attributes: action, action_probs, episode_id, reward, cumulative_rewards, state_features
# only show cumulative rewards at the last step of the episode
df.head()
# We can use the average cumulative reward of the random policy as a baseline for the Batch RL trained policy.
# average cumulative rewards for each episode
avg_rewards = df['cumulative_rewards'].sum() / (NUM_ENVS * NUM_EPISODES)
print("Average cumulative rewards over {} episodes rollouts was {}.".format((NUM_ENVS * NUM_EPISODES), avg_rewards))
# ### Save Dataframe as CSV for Batch RL Training
#
# Coach Batch RL support reading off policy data in CSV format. We will dump our collected rollout data in CSV format.
# dump dataframe as csv file
df.to_csv("src/cartpole_dataset.csv", index=False)
# ## Configure the presets for RL algorithm
#
# The presets that configure the Batch RL training jobs are defined in the `preset-cartpole-ddqnbcq.py` file which is also uploaded on the `/src` directory. Using the preset file, you can define agent parameters to select the specific agent algorithm. You can also set the environment parameters, define the schedule and visualization parameters, and define the graph manager. The schedule presets will define the number of heat up steps, periodic evaluation steps, training steps between evaluations.
#
# These can be overridden at runtime by specifying the `RLCOACH_PRESET` hyperparameter. Additionally, it can be used to define custom hyperparameters.
# !pygmentize src/preset-cartpole-ddqnbcq.py
# In this notebook, we use DDQN[6] to update the policy in an off-policy manner, and combine it with BCQ[5] to address the error induced by inaccurately estimated values for unseen state-action pairs. The training is completely off-line.
# ## Write the Training Code
#
# The training code is written in the file “train-coach.py” which is uploaded in the /src directory.
# First import the environment files and the preset files, and then define the `main()` function.
# !pygmentize src/train-coach.py
# ## Train the RL model using the Python SDK Script mode
#
# If you are using local mode, the training will run on the notebook instance. When using SageMaker for training, you can select a GPU or CPU instance. The RLEstimator is used for training RL jobs.
#
# 1. Specify the source directory where the environment, presets and training code is uploaded.
# 2. Specify the entry point as the training code
# 3. Define the training parameters such as the instance count, job name, S3 path for output and job name.
# 4. Specify the hyperparameters for the RL agent algorithm. The `RLCOACH_PRESET` can be used to specify the RL agent algorithm you want to use.
# +
# %%time
if local_mode:
instance_type = 'local'
else:
instance_type = "ml.m4.xlarge"
estimator = RLEstimator(entry_point="train-coach.py",
source_dir='src',
dependencies=["common/sagemaker_rl"],
image_name=image,
role=role,
train_instance_type=instance_type,
train_instance_count=1,
output_path=s3_output_path,
base_job_name=job_name_prefix,
hyperparameters = {
"RLCOACH_PRESET": "preset-cartpole-ddqnbcq",
"save_model": 1
}
)
estimator.fit()
# -
# ## Store intermediate training output and model checkpoints
#
# The output from the training job above is stored on S3. The intermediate folder contains gifs and metadata of the training. We'll need these metadata for metrics visualization and model evaluations.
# +
job_name=estimator._current_job_name
print("Job name: {}".format(job_name))
s3_url = "s3://{}/{}".format(s3_bucket,job_name)
if local_mode:
output_tar_key = "{}/output.tar.gz".format(job_name)
else:
output_tar_key = "{}/output/output.tar.gz".format(job_name)
intermediate_folder_key = "{}/output/intermediate/".format(job_name)
output_url = "s3://{}/{}".format(s3_bucket, output_tar_key)
intermediate_url = "s3://{}/{}".format(s3_bucket, intermediate_folder_key)
print("S3 job path: {}".format(s3_url))
print("Output.tar.gz location: {}".format(output_url))
print("Intermediate folder path: {}".format(intermediate_url))
tmp_dir = "/tmp/{}".format(job_name)
os.system("mkdir {}".format(tmp_dir))
print("Create local folder {}".format(tmp_dir))
# -
# ## Visualization
# ### Plot metrics for training job
# We can pull the Off Policy Evaluation(OPE) metric of the training and plot it to see the performance of the model over time.
# +
# %matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
csv_file_name = "worker_0.batch_rl_graph.main_level.main_level.agent_0.csv"
key = os.path.join(intermediate_folder_key, csv_file_name)
wait_for_s3_object(s3_bucket, key, tmp_dir, training_job_name=job_name)
csv_file = "{}/{}".format(tmp_dir, csv_file_name)
df = pd.read_csv(csv_file)
df = df.dropna(subset=['Sequential Doubly Robust'])
df.dropna(subset=['Weighted Importance Sampling'])
plt.figure(figsize=(12,5))
plt.xlabel('Number of epochs')
ax1 = df['Weighted Importance Sampling'].plot(color='blue', grid=True, label='WIS')
ax2 = df['Sequential Doubly Robust'].plot(color='red', grid=True, secondary_y=True, label='SDR')
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
plt.legend(h1+h2, l1+l2, loc=1)
plt.show()
# -
# There is a set of methods used to investigate the performance of the current trained policy without interacting with simulator / live environment. They can be used to estimate the goodness of the policy, based on the dataset collected from other policy. Here we showed two of these OPE metrics: WIS (Weighted Importance Sampling) [3] and SDR (Sequential Doubly Robust) [4]. As we can see in the plot, these metrics are improving as the learning agent is iterating over the given dataset.
# ## Evaluation of RL models
#
# To evaluate the model trained with off policy data, we need to see the accumulative rewards of the agent by interacting with the environment. We use the last checkpointed model to run evaluation of the RL Agent. We use a different preset file here `preset-cartpole-ddqnbcq-env.py` to let the RL agent interact with the environment and collect rewards.
#
# ### Load checkpointed model
#
# Checkpoint is passed on for evaluation / inference in the checkpoint channel. In local mode, we can simply use the local directory, whereas in the SageMaker mode, it needs to be moved to S3 first.
# +
wait_for_s3_object(s3_bucket, output_tar_key, tmp_dir, training_job_name=job_name)
if not os.path.isfile("{}/output.tar.gz".format(tmp_dir)):
raise FileNotFoundError("File output.tar.gz not found")
os.system("tar -xvzf {}/output.tar.gz -C {}".format(tmp_dir, tmp_dir))
if local_mode:
checkpoint_dir = "{}/data/checkpoint".format(tmp_dir)
else:
checkpoint_dir = "{}/checkpoint".format(tmp_dir)
print("Checkpoint directory {}".format(checkpoint_dir))
# -
if local_mode:
checkpoint_path = 'file://{}'.format(checkpoint_dir)
print("Local checkpoint file path: {}".format(checkpoint_path))
else:
checkpoint_path = "s3://{}/{}/checkpoint/".format(s3_bucket, job_name)
if not os.listdir(checkpoint_dir):
raise FileNotFoundError("Checkpoint files not found under the path")
os.system("aws s3 cp --recursive {} {}".format(checkpoint_dir, checkpoint_path))
print("S3 checkpoint file path: {}".format(checkpoint_path))
# +
estimator_eval = RLEstimator(entry_point="evaluate-coach.py",
source_dir='src',
dependencies=["common/sagemaker_rl"],
image_name=image,
role=role,
train_instance_type=instance_type,
train_instance_count=1,
output_path=s3_output_path,
base_job_name=job_name_prefix,
hyperparameters = {
"RLCOACH_PRESET": "preset-cartpole-ddqnbcq-env",
"evaluate_steps": 1000
}
)
estimator_eval.fit({'checkpoint': checkpoint_path})
# -
# ### Batch Transform
#
# As we can see from the above evaluation job, the trained agent gets a total reward of around `200` as compared to a total reward around `25` in our offline dataset. Therefore, we can confirm that the agent has learned a better policy from the off-policy data.
#
# After we get the trained model, we can use it to do SageMaker Batch Transform, where customers can provide large volumes of input state features and get predictions with high throughput.
# +
import time
from sagemaker.tensorflow.serving import Model
if local_mode:
sage_session = sagemaker.local.LocalSession()
# Create SageMaker model entity by using model data generated by the estimator
model = Model(model_data=estimator.model_data,
sagemaker_session=sage_session,
role=role)
prefix = "batch_test"
# setup input data prefix and output data prefix for batch transform
batch_input = 's3://{}/{}/{}/input/'.format(s3_bucket, job_name, prefix) # The location of the test dataset
batch_output = 's3://{}/{}/{}/output/'.format(s3_bucket, job_name, prefix) # The location to store the results of the batch transform job
print("Inputpath for batch transform: {}".format(batch_input))
print("Outputpath for batch transform: {}".format(batch_output))
# -
# In this notebook, we use the states of the environments as input for the Batch Transform.
import time
file_name = 'env_states_{}.json'.format(int(time.time()))
# resetting the environments
vectored_envs.reset_all_envs()
# dump environment states into jsonlines file
vectored_envs.dump_environment_states(tmp_dir, file_name)
# In order to use SageMaker Batch Transform, we'll need to first upload the input data from local to S3 bucket
# +
# %%time
from pathlib import Path
local_input_file_path = Path(tmp_dir) / file_name
s3_input_file_path = batch_input + file_name # Path library will remove :// from s3 path
print("Copy file from local path '{}' to s3 path '{}'".format(local_input_file_path, s3_input_file_path))
assert os.system("aws s3 cp {} {}".format(local_input_file_path, s3_input_file_path)) == 0
print("S3 batch input file path: {}".format(s3_input_file_path))
# -
# Similar to how we launch a training job on SageMaker, we can initiate a batch transform job either in `Local` mode or `SageMaker` mode.
# +
if local_mode:
instance_type = 'local'
else:
instance_type = "ml.m4.xlarge"
transformer = model.transformer(instance_count=1, instance_type=instance_type, output_path=batch_output, assemble_with = 'Line', accept = 'application/jsonlines', strategy='SingleRecord')
transformer.transform(data=batch_input, data_type='S3Prefix', content_type='application/jsonlines', split_type='Line', join_source='Input')
transformer.wait()
# -
# After we finished the batch transform job, we can download the prediction output from S3 bucket to local machine.
# +
import subprocess
# get the latest generated output file
cmd = "aws s3 ls {} --recursive | sort | tail -n 1".format(batch_output)
result = subprocess.check_output(cmd, shell=True).decode("utf-8").split(' ')[-1].strip()
local_output_file_path = Path(tmp_dir) / f"{file_name}.out"
s3_output_file_path = 's3://{}/{}'.format(s3_bucket,result)
print("Copy file from s3 path '{}' to local path '{}'".format(s3_output_file_path, local_output_file_path))
os.system("aws s3 cp {} {}".format(s3_output_file_path, local_output_file_path))
print("S3 batch output file local path: {}".format(local_output_file_path))
# +
import subprocess
batcmd="cat {}".format(local_output_file_path)
results = subprocess.check_output(batcmd, shell=True).decode("utf-8").split('\n')
# -
results[:10]
# In this notebook, we use simulated environments to collect rollout data of a random policy. Assuming the updated policy is now deployed, we can use Batch Transform to collect rollout data from this policy.
#
# Here are the steps on how to collect rollout data with Batch Transform:
# 1. Use Batch Transform to get action predictions, provided observation features from the live environment at timestep *t*
# 2. Deployed agent takes suggested actions against the environment (simulator / real) at timestep *t*
# 3. Environment returns new observation features at timestep *t+1*
# 4. Return back to step 1. Use Batch Transform to get action predictions at timestep *t+1*
#
# This iterative procedure enables us to collect a set of data that can cover the whole episode, similar to what we've shown at the beginning of the notebook. Once the data is sufficient, we can use these data to kick off a BatchRL training again.
#
# Batch Transform works well when there are multiple episodes interacting with the environments concurrently. One of the typical use cases is email campaign, where each email user is an independent episode interacting with the deployed policy. Batch Transform can concurrently collect rollout data from millions of user context with efficiency. The collected rollout data can then be supplied to Batch RL Training to train a better policy to serve the email users.
# ### Reference
#
# 1. Batch Reinforcement Learning with Coach: https://github.com/NervanaSystems/coach/blob/master/tutorials/4.%20Batch%20Reinforcement%20Learning.ipynb
# 2. <NAME>, RS Sutton and CW Anderson, "Neuronlike Adaptive Elements That Can Solve Difficult Learning Control Problem", IEEE Transactions on Systems, Man, and Cybernetics, 1983.
# 3. Thomas, Philip, <NAME>, and <NAME>. "High confidence policy improvement." International Conference on Machine Learning. 2015.
# 4. Jiang, Nan, and <NAME>. "Doubly robust off-policy value evaluation for reinforcement learning." arXiv preprint arXiv:1511.03722 (2015).
# 5. Fujimoto, Scott, <NAME>, and <NAME>. "Off-policy deep reinforcement learning without exploration." arXiv preprint arXiv:1812.02900 (2018)
# 6. <NAME>, Hado, <NAME>, and <NAME>. "Deep reinforcement learning with double q-learning." Thirtieth AAAI conference on artificial intelligence. 2016.
| reinforcement_learning/rl_cartpole_batch_coach/rl_cartpole_batch_coach.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="zo3jk2Ckl5bG"
# 範例目標:<br>
# 1. 實做繪製圖表
# 2. 藉由圖表對資料有初步認識,並解釋圖表意義
# + [markdown] id="4DyBUP8RmSmU"
# 範例重點:<br>
# 1. 每一種圖表都有相對應用的情境,分辨情境並繪製對應圖表
# 2. 圖像化展現,方便對於資料有初步的理解
# + id="cu78CXS6mRpg"
import pandas as pd
import numpy as np
# + colab={"base_uri": "https://localhost:8080/", "height": 498} id="qyrd6L2C2Iqw" executionInfo={"status": "ok", "timestamp": 1608446423706, "user_tz": -480, "elapsed": 960, "user": {"displayName": "\u732e\u7ae4\u9ec3", "photoUrl": "", "userId": "07529243043474362942"}} outputId="42f3f150-7ffb-46ae-d587-75dad12414d3"
#單一折線圖
ts = pd.Series(np.random.randn(200), index=pd.date_range('1/1/2020', periods=200))
ts = ts.cumsum()
print(ts)
ts.plot()
# + colab={"base_uri": "https://localhost:8080/", "height": 515} id="EiK8uhbC3TZB" executionInfo={"status": "ok", "timestamp": 1608446709044, "user_tz": -480, "elapsed": 1100, "user": {"displayName": "\u732e\u7ae4\u9ec3", "photoUrl": "", "userId": "07529243043474362942"}} outputId="fb5ccc2e-6110-468d-8569-989aa05bc40b"
#多個折線圖同時畫出
df = pd.DataFrame(np.random.randn(200, 3), index=pd.date_range('1/1/2020', periods=200), columns=["A","B","C"])
df = df.cumsum()
print(df)
df.plot();
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="BuogsoMa5_Q-" executionInfo={"status": "ok", "timestamp": 1608447113712, "user_tz": -480, "elapsed": 999, "user": {"displayName": "\u732e\u7ae4\u9ec3", "photoUrl": "", "userId": "07529243043474362942"}} outputId="eeee4197-f117-46b5-81a1-d95f94cbb350"
#圓餅圖
df = pd.Series(np.random.rand(4), index=["A","B","C","D"],name="title")
print(df)
df.plot.pie()
# + colab={"base_uri": "https://localhost:8080/", "height": 449} id="wd3xpJD731cp" executionInfo={"status": "ok", "timestamp": 1608447501364, "user_tz": -480, "elapsed": 984, "user": {"displayName": "\u732e\u7ae4\u9ec3", "photoUrl": "", "userId": "07529243043474362942"}} outputId="8fc000b9-4ffc-4acf-9abb-3e560ad82757"
#長條圖
df = pd.DataFrame(np.random.rand(10, 2), columns=["A","B"])
print(df)
df.plot.bar();
# + colab={"base_uri": "https://localhost:8080/", "height": 262} id="VaDwfHaD8OqS" executionInfo={"status": "ok", "timestamp": 1608447719250, "user_tz": -480, "elapsed": 1001, "user": {"displayName": "\u732e\u7ae4\u9ec3", "photoUrl": "", "userId": "07529243043474362942"}} outputId="532f7c54-b8eb-4e7e-b907-7233a963dd1e"
df.plot.bar(stacked=True);
# + colab={"base_uri": "https://localhost:8080/", "height": 469} id="2v7kC5CJ9HJm" executionInfo={"status": "ok", "timestamp": 1608448104686, "user_tz": -480, "elapsed": 879, "user": {"displayName": "\u732e\u7ae4\u9ec3", "photoUrl": "", "userId": "07529243043474362942"}} outputId="2005ff3b-65f0-4377-81fd-55539b44c24a"
#箱型圖
df = pd.DataFrame(np.random.rand(10, 2), columns=["A","B"])
print(df)
df.boxplot()
# + colab={"base_uri": "https://localhost:8080/", "height": 485} id="TX9ZBzSl-eyu" executionInfo={"status": "ok", "timestamp": 1608449321661, "user_tz": -480, "elapsed": 905, "user": {"displayName": "\u732e\u7ae4\u9ec3", "photoUrl": "", "userId": "07529243043474362942"}} outputId="2f3385ce-ddeb-4cc1-d654-30e9624bddfc"
#散佈圖
df = pd.DataFrame(np.random.rand(10, 2), columns=["A","B"])
print(df)
df.plot.scatter(x='A', y='B')
| Sample Code/Day_12_SampleCode.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Sentiment Analysis with an RNN
#
# In this notebook, you'll implement a recurrent neural network that performs sentiment analysis.
# >Using an RNN rather than a strictly feedforward network is more accurate since we can include information about the *sequence* of words.
#
# Here we'll use a dataset of movie reviews, accompanied by sentiment labels: positive or negative.
#
# <img src="assets/reviews_ex.png" width=40%>
#
# ### Network Architecture
#
# The architecture for this network is shown below.
#
# <img src="assets/network_diagram.png" width=40%>
#
# >**First, we'll pass in words to an embedding layer.** We need an embedding layer because we have tens of thousands of words, so we'll need a more efficient representation for our input data than one-hot encoded vectors. You should have seen this before from the Word2Vec lesson. You can actually train an embedding with the Skip-gram Word2Vec model and use those embeddings as input, here. However, it's good enough to just have an embedding layer and let the network learn a different embedding table on its own. *In this case, the embedding layer is for dimensionality reduction, rather than for learning semantic representations.*
#
# >**After input words are passed to an embedding layer, the new embeddings will be passed to LSTM cells.** The LSTM cells will add *recurrent* connections to the network and give us the ability to include information about the *sequence* of words in the movie review data.
#
# >**Finally, the LSTM outputs will go to a sigmoid output layer.** We're using a sigmoid function because positive and negative = 1 and 0, respectively, and a sigmoid will output predicted, sentiment values between 0-1.
#
# We don't care about the sigmoid outputs except for the **very last one**; we can ignore the rest. We'll calculate the loss by comparing the output at the last time step and the training label (pos or neg).
# ---
# ### Load in and visualize the data
# +
import numpy as np
# read data from text files
with open('data/reviews.txt', 'r') as f:
reviews = f.read()
with open('data/labels.txt', 'r') as f:
labels = f.read()
# -
print(reviews[:1000])
print()
print(labels[:20])
# ## Data pre-processing
#
# The first step when building a neural network model is getting your data into the proper form to feed into the network. Since we're using embedding layers, we'll need to encode each word with an integer. We'll also want to clean it up a bit.
#
# You can see an example of the reviews data above. Here are the processing steps, we'll want to take:
# >* We'll want to get rid of periods and extraneous punctuation.
# * Also, you might notice that the reviews are delimited with newline characters `\n`. To deal with those, I'm going to split the text into each review using `\n` as the delimiter.
# * Then I can combined all the reviews back together into one big string.
#
# First, let's remove all punctuation. Then get all the text without the newlines and split it into individual words.
# +
from string import punctuation
# get rid of punctuation
reviews = reviews.lower() # lowercase, standardize
all_text = ''.join([c for c in reviews if c not in punctuation])
# split by new lines and spaces
reviews_split = all_text.split('\n')
all_text = ' '.join(reviews_split)
# create a list of words
words = all_text.split()
# -
words[:30]
# ### Encoding the words
#
# The embedding lookup requires that we pass in integers to our network. The easiest way to do this is to create dictionaries that map the words in the vocabulary to integers. Then we can convert each of our reviews into integers so they can be passed into the network.
#
# > **Exercise:** Now you're going to encode the words with integers. Build a dictionary that maps words to integers. Later we're going to pad our input vectors with zeros, so make sure the integers **start at 1, not 0**.
# > Also, convert the reviews to integers and store the reviews in a new list called `reviews_ints`.
# +
# feel free to use this import
from collections import Counter
## Build a dictionary that maps words to integers
counts = Counter(words)
vocab = sorted(counts, key=counts.get, reverse=True)
vocab_to_int = {word: ii for ii, word in enumerate(vocab, 1)}
## use the dict to tokenize each review in reviews_split
## store the tokenized reviews in reviews_ints
reviews_ints = []
for review in reviews_split:
reviews_ints.append([vocab_to_int[word] for word in review.split()])
# -
# **Test your code**
#
# As a text that you've implemented the dictionary correctly, print out the number of unique words in your vocabulary and the contents of the first, tokenized review.
# +
# stats about vocabulary
print('Unique words: ', len((vocab_to_int))) # should ~ 74000+
print()
# print tokens in first review
print('Tokenized review: \n', reviews_ints[:1])
# -
# ### Encoding the labels
#
# Our labels are "positive" or "negative". To use these labels in our network, we need to convert them to 0 and 1.
#
# > **Exercise:** Convert labels from `positive` and `negative` to 1 and 0, respectively, and place those in a new list, `encoded_labels`.
# 1=positive, 0=negative label conversion
labels_split = labels.split('\n')
encoded_labels = np.array([1 if label == 'positive' else 0 for label in labels_split])
# ### Removing Outliers
#
# As an additional pre-processing step, we want to make sure that our reviews are in good shape for standard processing. That is, our network will expect a standard input text size, and so, we'll want to shape our reviews into a specific length. We'll approach this task in two main steps:
#
# 1. Getting rid of extremely long or short reviews; the outliers
# 2. Padding/truncating the remaining data so that we have reviews of the same length.
#
# Before we pad our review text, we should check for reviews of extremely short or long lengths; outliers that may mess with our training.
# outlier review stats
review_lens = Counter([len(x) for x in reviews_ints])
print("Zero-length reviews: {}".format(review_lens[0]))
print("Maximum review length: {}".format(max(review_lens)))
# Okay, a couple issues here. We seem to have one review with zero length. And, the maximum review length is way too many steps for our RNN. We'll have to remove any super short reviews and truncate super long reviews. This removes outliers and should allow our model to train more efficiently.
#
# > **Exercise:** First, remove *any* reviews with zero length from the `reviews_ints` list and their corresponding label in `encoded_labels`.
# +
print('Number of reviews before removing outliers: ', len(reviews_ints))
## remove any reviews/labels with zero length from the reviews_ints list.
# get indices of any reviews with length 0
non_zero_idx = [ii for ii, review in enumerate(reviews_ints) if len(review) != 0]
# remove 0-length reviews and their labels
reviews_ints = [reviews_ints[ii] for ii in non_zero_idx]
encoded_labels = np.array([encoded_labels[ii] for ii in non_zero_idx])
print('Number of reviews after removing outliers: ', len(reviews_ints))
# -
# ---
# ## Padding sequences
#
# To deal with both short and very long reviews, we'll pad or truncate all our reviews to a specific length. For reviews shorter than some `seq_length`, we'll pad with 0s. For reviews longer than `seq_length`, we can truncate them to the first `seq_length` words. A good `seq_length`, in this case, is 200.
#
# > **Exercise:** Define a function that returns an array `features` that contains the padded data, of a standard size, that we'll pass to the network.
# * The data should come from `review_ints`, since we want to feed integers to the network.
# * Each row should be `seq_length` elements long.
# * For reviews shorter than `seq_length` words, **left pad** with 0s. That is, if the review is `['best', 'movie', 'ever']`, `[117, 18, 128]` as integers, the row will look like `[0, 0, 0, ..., 0, 117, 18, 128]`.
# * For reviews longer than `seq_length`, use only the first `seq_length` words as the feature vector.
#
# As a small example, if the `seq_length=10` and an input review is:
# ```
# [117, 18, 128]
# ```
# The resultant, padded sequence should be:
#
# ```
# [0, 0, 0, 0, 0, 0, 0, 117, 18, 128]
# ```
#
# **Your final `features` array should be a 2D array, with as many rows as there are reviews, and as many columns as the specified `seq_length`.**
#
# This isn't trivial and there are a bunch of ways to do this. But, if you're going to be building your own deep learning networks, you're going to have to get used to preparing your data.
def pad_features(reviews_ints, seq_length):
''' Return features of review_ints, where each review is padded with 0's
or truncated to the input seq_length.
'''
# getting the correct rows x cols shape
features = np.zeros((len(reviews_ints), seq_length), dtype=int)
# for each review, I grab that review and
for i, row in enumerate(reviews_ints):
features[i, -len(row):] = np.array(row)[:seq_length]
return features
# +
# Test your implementation!
seq_length = 200
features = pad_features(reviews_ints, seq_length=seq_length)
## test statements - do not change - ##
assert len(features)==len(reviews_ints), "Your features should have as many rows as reviews."
assert len(features[0])==seq_length, "Each feature row should contain seq_length values."
# print first 10 values of the first 30 batches
print(features[:30,:10])
# -
# ## Training, Validation, Test
#
# With our data in nice shape, we'll split it into training, validation, and test sets.
#
# > **Exercise:** Create the training, validation, and test sets.
# * You'll need to create sets for the features and the labels, `train_x` and `train_y`, for example.
# * Define a split fraction, `split_frac` as the fraction of data to **keep** in the training set. Usually this is set to 0.8 or 0.9.
# * Whatever data is left will be split in half to create the validation and *testing* data.
# +
split_frac = 0.8
## split data into training, validation, and test data (features and labels, x and y)
split_idx = int(len(features)*split_frac)
train_x, remaining_x = features[:split_idx], features[split_idx:]
train_y, remaining_y = encoded_labels[:split_idx], encoded_labels[split_idx:]
test_idx = int(len(remaining_x)*0.5)
val_x, test_x = remaining_x[:test_idx], remaining_x[test_idx:]
val_y, test_y = remaining_y[:test_idx], remaining_y[test_idx:]
## print out the shapes of your resultant feature data
print("\t\t\tFeature Shapes:")
print("Train set: \t\t{}".format(train_x.shape),
"\nValidation set: \t{}".format(val_x.shape),
"\nTest set: \t\t{}".format(test_x.shape))
# -
# **Check your work**
#
# With train, validation, and test fractions equal to 0.8, 0.1, 0.1, respectively, the final, feature data shapes should look like:
# ```
# Feature Shapes:
# Train set: (20000, 200)
# Validation set: (2500, 200)
# Test set: (2500, 200)
# ```
# ---
# ## DataLoaders and Batching
#
# After creating training, test, and validation data, we can create DataLoaders for this data by following two steps:
# 1. Create a known format for accessing our data, using [TensorDataset](https://pytorch.org/docs/stable/data.html#) which takes in an input set of data and a target set of data with the same first dimension, and creates a dataset.
# 2. Create DataLoaders and batch our training, validation, and test Tensor datasets.
#
# ```
# train_data = TensorDataset(torch.from_numpy(train_x), torch.from_numpy(train_y))
# train_loader = DataLoader(train_data, batch_size=batch_size)
# ```
#
# This is an alternative to creating a generator function for batching our data into full batches.
# +
import torch
from torch.utils.data import TensorDataset, DataLoader
# create Tensor datasets
train_data = TensorDataset(torch.from_numpy(train_x), torch.from_numpy(train_y))
valid_data = TensorDataset(torch.from_numpy(val_x), torch.from_numpy(val_y))
test_data = TensorDataset(torch.from_numpy(test_x), torch.from_numpy(test_y))
# dataloaders
batch_size = 50
# make sure the SHUFFLE your training data
train_loader = DataLoader(train_data, shuffle=True, batch_size=batch_size)
valid_loader = DataLoader(valid_data, shuffle=True, batch_size=batch_size)
test_loader = DataLoader(test_data, shuffle=True, batch_size=batch_size)
# +
# obtain one batch of training data
dataiter = iter(train_loader)
sample_x, sample_y = dataiter.next()
print('Sample input size: ', sample_x.size()) # batch_size, seq_length
print('Sample input: \n', sample_x)
print()
print('Sample label size: ', sample_y.size()) # batch_size
print('Sample label: \n', sample_y)
# -
# ---
# # Sentiment Network with PyTorch
#
# Below is where you'll define the network.
#
# <img src="assets/network_diagram.png" width=40%>
#
# The layers are as follows:
# 1. An [embedding layer](https://pytorch.org/docs/stable/nn.html#embedding) that converts our word tokens (integers) into embeddings of a specific size.
# 2. An [LSTM layer](https://pytorch.org/docs/stable/nn.html#lstm) defined by a hidden_state size and number of layers
# 3. A fully-connected output layer that maps the LSTM layer outputs to a desired output_size
# 4. A sigmoid activation layer which turns all outputs into a value 0-1; return **only the last sigmoid output** as the output of this network.
#
# ### The Embedding Layer
#
# We need to add an [embedding layer](https://pytorch.org/docs/stable/nn.html#embedding) because there are 74000+ words in our vocabulary. It is massively inefficient to one-hot encode that many classes. So, instead of one-hot encoding, we can have an embedding layer and use that layer as a lookup table. You could train an embedding layer using Word2Vec, then load it here. But, it's fine to just make a new layer, using it for only dimensionality reduction, and let the network learn the weights.
#
#
# ### The LSTM Layer(s)
#
# We'll create an [LSTM](https://pytorch.org/docs/stable/nn.html#lstm) to use in our recurrent network, which takes in an input_size, a hidden_dim, a number of layers, a dropout probability (for dropout between multiple layers), and a batch_first parameter.
#
# Most of the time, you're network will have better performance with more layers; between 2-3. Adding more layers allows the network to learn really complex relationships.
#
# > **Exercise:** Complete the `__init__`, `forward`, and `init_hidden` functions for the SentimentRNN model class.
#
# Note: `init_hidden` should initialize the hidden and cell state of an lstm layer to all zeros, and move those state to GPU, if available.
# +
# First checking if GPU is available
train_on_gpu=torch.cuda.is_available()
if(train_on_gpu):
print('Training on GPU.')
else:
print('No GPU available, training on CPU.')
# +
import torch.nn as nn
class SentimentRNN(nn.Module):
"""
The RNN model that will be used to perform Sentiment analysis.
"""
def __init__(self, vocab_size, output_size, embedding_dim, hidden_dim, n_layers, drop_prob=0.5):
"""
Initialize the model by setting up the layers.
"""
super(SentimentRNN, self).__init__()
self.output_size = output_size
self.n_layers = n_layers
self.hidden_dim = hidden_dim
# embedding and LSTM layers
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim, n_layers,
dropout=drop_prob, batch_first=True)
# dropout layer
self.dropout = nn.Dropout(0.3)
# linear and sigmoid layers
self.fc = nn.Linear(hidden_dim, output_size)
self.sig = nn.Sigmoid()
def forward(self, x, hidden):
"""
Perform a forward pass of our model on some input and hidden state.
"""
batch_size = x.size(0)
# embeddings and lstm_out
x = x.long()
embeds = self.embedding(x)
lstm_out, hidden = self.lstm(embeds, hidden)
# stack up lstm outputs
lstm_out = lstm_out.contiguous().view(-1, self.hidden_dim)
# dropout and fully-connected layer
out = self.dropout(lstm_out)
out = self.fc(out)
# sigmoid function
sig_out = self.sig(out)
# reshape to be batch_size first
sig_out = sig_out.view(batch_size, -1)
sig_out = sig_out[:, -1] # get last batch of labels
# return last sigmoid output and hidden state
return sig_out, hidden
def init_hidden(self, batch_size):
''' Initializes hidden state '''
# Create two new tensors with sizes n_layers x batch_size x hidden_dim,
# initialized to zero, for hidden state and cell state of LSTM
weight = next(self.parameters()).data
if (train_on_gpu):
hidden = (weight.new(self.n_layers, batch_size, self.hidden_dim).zero_().cuda(),
weight.new(self.n_layers, batch_size, self.hidden_dim).zero_().cuda())
else:
hidden = (weight.new(self.n_layers, batch_size, self.hidden_dim).zero_(),
weight.new(self.n_layers, batch_size, self.hidden_dim).zero_())
return hidden
# -
# ## Instantiate the network
#
# Here, we'll instantiate the network. First up, defining the hyperparameters.
#
# * `vocab_size`: Size of our vocabulary or the range of values for our input, word tokens.
# * `output_size`: Size of our desired output; the number of class scores we want to output (pos/neg).
# * `embedding_dim`: Number of columns in the embedding lookup table; size of our embeddings.
# * `hidden_dim`: Number of units in the hidden layers of our LSTM cells. Usually larger is better performance wise. Common values are 128, 256, 512, etc.
# * `n_layers`: Number of LSTM layers in the network. Typically between 1-3
#
# > **Exercise:** Define the model hyperparameters.
#
# +
# Instantiate the model w/ hyperparams
vocab_size = len(vocab_to_int)+1 # +1 for the 0 padding + our word tokens
output_size = 1
embedding_dim = 400
hidden_dim = 256
n_layers = 2
net = SentimentRNN(vocab_size, output_size, embedding_dim, hidden_dim, n_layers)
print(net)
# -
# ---
# ## Training
#
# Below is the typical training code. If you want to do this yourself, feel free to delete all this code and implement it yourself. You can also add code to save a model by name.
#
# >We'll also be using a new kind of cross entropy loss, which is designed to work with a single Sigmoid output. [BCELoss](https://pytorch.org/docs/stable/nn.html#bceloss), or **Binary Cross Entropy Loss**, applies cross entropy loss to a single value between 0 and 1.
#
# We also have some data and training hyparameters:
#
# * `lr`: Learning rate for our optimizer.
# * `epochs`: Number of times to iterate through the training dataset.
# * `clip`: The maximum gradient value to clip at (to prevent exploding gradients).
# +
# loss and optimization functions
lr=0.001
criterion = nn.BCELoss()
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
# +
# training params
epochs = 4 # 3-4 is approx where I noticed the validation loss stop decreasing
counter = 0
print_every = 100
clip=5 # gradient clipping
# move model to GPU, if available
if(train_on_gpu):
net.cuda()
net.train()
# train for some number of epochs
for e in range(epochs):
# initialize hidden state
h = net.init_hidden(batch_size)
# batch loop
for inputs, labels in train_loader:
counter += 1
if(train_on_gpu):
inputs, labels = inputs.cuda(), labels.cuda()
# Creating new variables for the hidden state, otherwise
# we'd backprop through the entire training history
h = tuple([each.data for each in h])
# zero accumulated gradients
net.zero_grad()
# get the output from the model
output, h = net(inputs, h)
# calculate the loss and perform backprop
loss = criterion(output.squeeze(), labels.float())
loss.backward()
# `clip_grad_norm` helps prevent the exploding gradient problem in RNNs / LSTMs.
nn.utils.clip_grad_norm_(net.parameters(), clip)
optimizer.step()
# loss stats
if counter % print_every == 0:
# Get validation loss
val_h = net.init_hidden(batch_size)
val_losses = []
net.eval()
for inputs, labels in valid_loader:
# Creating new variables for the hidden state, otherwise
# we'd backprop through the entire training history
val_h = tuple([each.data for each in val_h])
if(train_on_gpu):
inputs, labels = inputs.cuda(), labels.cuda()
output, val_h = net(inputs, val_h)
val_loss = criterion(output.squeeze(), labels.float())
val_losses.append(val_loss.item())
net.train()
print("Epoch: {}/{}...".format(e+1, epochs),
"Step: {}...".format(counter),
"Loss: {:.6f}...".format(loss.item()),
"Val Loss: {:.6f}".format(np.mean(val_losses)))
# -
# ---
# ## Testing
#
# There are a few ways to test your network.
#
# * **Test data performance:** First, we'll see how our trained model performs on all of our defined test_data, above. We'll calculate the average loss and accuracy over the test data.
#
# * **Inference on user-generated data:** Second, we'll see if we can input just one example review at a time (without a label), and see what the trained model predicts. Looking at new, user input data like this, and predicting an output label, is called **inference**.
# +
# Get test data loss and accuracy
test_losses = [] # track loss
num_correct = 0
# init hidden state
h = net.init_hidden(batch_size)
net.eval()
# iterate over test data
for inputs, labels in test_loader:
# Creating new variables for the hidden state, otherwise
# we'd backprop through the entire training history
h = tuple([each.data for each in h])
if(train_on_gpu):
inputs, labels = inputs.cuda(), labels.cuda()
# get predicted outputs
output, h = net(inputs, h)
# calculate loss
test_loss = criterion(output.squeeze(), labels.float())
test_losses.append(test_loss.item())
# convert output probabilities to predicted class (0 or 1)
pred = torch.round(output.squeeze()) # rounds to the nearest integer
# compare predictions to true label
correct_tensor = pred.eq(labels.float().view_as(pred))
correct = np.squeeze(correct_tensor.numpy()) if not train_on_gpu else np.squeeze(correct_tensor.cpu().numpy())
num_correct += np.sum(correct)
# -- stats! -- ##
# avg test loss
print("Test loss: {:.3f}".format(np.mean(test_losses)))
# accuracy over all test data
test_acc = num_correct/len(test_loader.dataset)
print("Test accuracy: {:.3f}".format(test_acc))
# -
# ### Inference on a test review
#
# You can change this test_review to any text that you want. Read it and think: is it pos or neg? Then see if your model predicts correctly!
#
# > **Exercise:** Write a `predict` function that takes in a trained net, a plain text_review, and a sequence length, and prints out a custom statement for a positive or negative review!
# * You can use any functions that you've already defined or define any helper functions you want to complete `predict`, but it should just take in a trained net, a text review, and a sequence length.
#
# negative test review
test_review_neg = 'The worst movie I have seen; acting was terrible and I want my money back. This movie had bad acting and the dialogue was slow.'
# +
from string import punctuation
def tokenize_review(test_review):
test_review = test_review.lower() # lowercase
# get rid of punctuation
test_text = ''.join([c for c in test_review if c not in punctuation])
# splitting by spaces
test_words = test_text.split()
# tokens
test_ints = []
test_ints.append([vocab_to_int[word] for word in test_words])
return test_ints
# test code and generate tokenized review
test_ints = tokenize_review(test_review_neg)
print(test_ints)
# +
# test sequence padding
seq_length=200
features = pad_features(test_ints, seq_length)
print(features)
# -
# test conversion to tensor and pass into your model
feature_tensor = torch.from_numpy(features)
print(feature_tensor.size())
def predict(net, test_review, sequence_length=200):
net.eval()
# tokenize review
test_ints = tokenize_review(test_review)
# pad tokenized sequence
seq_length=sequence_length
features = pad_features(test_ints, seq_length)
# convert to tensor to pass into your model
feature_tensor = torch.from_numpy(features)
batch_size = feature_tensor.size(0)
# initialize hidden state
h = net.init_hidden(batch_size)
if(train_on_gpu):
feature_tensor = feature_tensor.cuda()
# get the output from the model
output, h = net(feature_tensor, h)
# convert output probabilities to predicted class (0 or 1)
pred = torch.round(output.squeeze())
# printing output value, before rounding
print('Prediction value, pre-rounding: {:.6f}'.format(output.item()))
# print custom response
if(pred.item()==1):
print("Positive review detected!")
else:
print("Negative review detected.")
# positive test review
test_review_pos = 'This movie had the best acting and the dialogue was so good. I loved it.'
# +
# call function
seq_length=200 # good to use the length that was trained on
predict(net, test_review_neg, seq_length)
# -
# ### Try out test_reviews of your own!
#
# Now that you have a trained model and a predict function, you can pass in _any_ kind of text and this model will predict whether the text has a positive or negative sentiment. Push this model to its limits and try to find what words it associates with positive or negative.
#
# Later, you'll learn how to deploy a model like this to a production environment so that it can respond to any kind of user data put into a web app!
| sentiment-rnn/Sentiment_RNN_Solution.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #%%appyter init
from appyter import magic
magic.init(lambda _=globals: _())
# # Enrichr Manhattan Plot Creator
#
# This appyter creates a figure visualizing enrichment analysis results from Enrichr (https://amp.pharm.mssm.edu/Enrichr/) in a manhattan plot.
#
# The resulting figure will contain a manhattan plot of the p-values of all the gene sets in the Enrichr libraries selected.
import pandas as pd
import math
import json
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib.cm as cm
import numpy as np
import requests
import time
import bokeh.io
from operator import itemgetter
from IPython.display import display, FileLink, Markdown, HTML
from bokeh.plotting import ColumnDataSource, figure, output_notebook, show
from bokeh.models import Legend, LegendItem, Span
output_notebook()
# +
# %%appyter hide_code
{% do SectionField(name='section1', title = '1. Submit Your Gene List', subtitle = 'Upload a text file containing your gene list -OR- copy and paste your gene list into the text box below (One gene per row). You can also try the default gene list provided.', img = 'enrichr-icon.png')%}
{% do SectionField(name='section2', title = '2. Choose Enrichr Libraries', subtitle = 'Select the Enrichr libraries you would like in your figure. Choosing somewhere between 1 and 5 libraries is recommended.', img = 'enrichr-icon.png')%}
{% do SectionField(name='section3', title = '3. Other Options', subtitle = 'Choose color scheme of the plot, add a horizontal line to designate a significance level, and choose location of the legend and point labels. NOTE: for the static plot, a legend labeling the libraries will only appear if there is more than one Enrichr library selected.', img = 'enrichr-icon.png')%}
{% do SectionField(name='section4', title = '4. Output Options', subtitle = 'Choose a format and name to save your static figure.', img = 'enrichr-icon.png')%}
# -
# ### Input options
# +
# %%appyter code_eval
gene_list_filename = {{ FileField(name='gene_list_filename', label='Gene List File', default='', description='Upload your gene list as a text file (One gene per row).',section = 'section1') }}
gene_list_input = {{ TextField(name='gene_list_input', label='Gene List', default='NSUN3\<KEY>1\nSFXN5\nZC3H12C\nSLC25A39\nARSG\nDEFB29\nNDUFB6\nZFAND1\nTMEM77\n5730403B10RIK\nRP23-195K8.6\nTLCD1\nPSMC6\nSLC30A6\nLOC100047292\nLRRC40\nORC5L\nMPP7\nUNC119B\nPRKACA\nTCN2\nPSMC3IP\nPCMTD2\nACAA1A\nLRRC1\n2810432D09RIK\nSEPHS2\nSAC3D1\nTMLHE\nLOC623451\nTSR2\nPLEKHA7\nGYS2\nARHGEF12\nHIBCH\nLYRM2\nZBTB44\nENTPD5\nRAB11FIP2\nLIPT1\nINTU\nANXA13\nKLF12\nSAT2\nGAL3ST2\nVAMP8\nFKBPL\nAQP11\nTRAP1\nPMPCB\nTM7SF3\nRBM39\nBRI3\nKDR\nZFP748\nNAP1L1\nDHRS1\nLRRC56\nWDR20A\nSTXBP2\nKLF1\nUFC1\nCCDC16\n9230114K14RIK\nRWDD3\n2610528K11RIK\nACO1\nCABLES1\nLOC100047214\nYARS2\nLYPLA1\nKALRN\nGYK\nZFP787\nZFP655\nRABEPK\nZFP650\n4732466D17RIK\nEXOSC4\nWDR42A\nGPHN\n2610528J11RIK\n1110003E01RIK\nMDH1\n1200014M14RIK\nAW209491\nMUT\n1700123L14RIK\n2610036D13RIK\nCOX15\nTMEM30A\nNSMCE4A\nTM2D2\nRHBDD3\nATXN2\nNFS1\n3110001I20RIK\nBC038156\nLOC100047782\n2410012H22RIK\nRILP\nA230062G08RIK\nPTTG1IP\nRAB1\nAFAP1L1\nLYRM5\n2310026E23RIK\nC330002I19RIK\nZFYVE20\nPOLI\nTOMM70A\nSLC7A6OS\nMAT2B\n4932438A13RIK\nLRRC8A\nSMO\nNUPL2\nTRPC2\nARSK\nD630023B12RIK\nMTFR1\n5730414N17RIK\nSCP2\nZRSR1\nNOL7\nC330018D20RIK\nIFT122\nLOC100046168\nD730039F16RIK\nSCYL1\n1700023B02RIK\n1700034H14RIK\nFBXO8\nPAIP1\nTMEM186\nATPAF1\nLOC100046254\nLOC100047604\nCOQ10A\nFN3K\nSIPA1L1\nSLC25A16\nSLC25A40\nRPS6KA5\nTRIM37\nLRRC61\nABHD3\nGBE1\nPARP16\nHSD3B2\nESM1\nDNAJC18\nDOLPP1\nLASS2\nWDR34\nRFESD\nCACNB4\n2310042D19RIK\nSRR\nBPNT1\n6530415H11RIK\nCLCC1\nTFB1M\n4632404H12RIK\nD4BWG0951E\nMED14\nADHFE1\nTHTPA\nCAT\nELL3\nAKR7A5\nMTMR14\nTIMM44\nSF1\nIPP\nIAH1\nTRIM23\nWDR89\nGSTZ1\nCRADD\n2510006D16RIK\nFBXL6\nLOC100044400\nZFP106\nCD55\n0610013E23RIK\nAFMID\nTMEM86A\nALDH6A1\nDALRD3\nSMYD4\nNME7\nFARS2\nTASP1\nCLDN10\nA930005H10RIK\nSLC9A6\nADK\nRBKS\n2210016F16RIK\nVWCE\n4732435N03RIK\nZFP11\nVLDLR\n9630013D21RIK\n4933407N01RIK\nFAHD1\nMIPOL1\n1810019D21RIK\n1810049H13RIK\nTFAM\nPAICS\n1110032A03RIK\nLOC100044139\nDNAJC19\nBC016495\nA930041I02RIK\nRQCD1\nUSP34\nZCCHC3\nH2AFJ\nPHF7\n4921508D12RIK\nKMO\nPRPF18\nMCAT\nTXNDC4\n4921530L18RIK\nVPS13B\nSCRN3\nTOR1A\nAI316807\nACBD4\nFAH\nAPOOL\nCOL4A4\nLRRC19\nGNMT\nNR3C1\nSIP1\nASCC1\nFECH\nABHD14A\nARHGAP18\n2700046G09RIK\nYME1L1\nGK5\nGLO1\nSBK1\nCISD1\n2210011C24RIK\nNXT2\nNOTUM\nANKRD42\nUBE2E1\nNDUFV1\nSLC33A1\nCEP68\nRPS6KB1\nHYI\nALDH1A3\nMYNN\n3110048L19RIK\nRDH14\nPROZ\nGORASP1\nLOC674449\nZFP775\n5430437P03RIK\nNPY\nADH5\nSYBL1\n4930432O21RIK\nNAT9\nLOC100048387\nMETTL8\nENY2\n2410018G20RIK\nPGM2\nFGFR4\nMOBKL2B\nATAD3A\n4932432K03RIK\nDHTKD1\nUBOX5\nA530050D06RIK\nZDHHC5\nMGAT1\nNUDT6\nTPMT\nWBSCR18\nLOC100041586\nCDK5RAP1\n4833426J09RIK\nMYO6\nCPT1A\nGADD45GIP1\nTMBIM4\n2010309E21RIK\nASB9\n2610019F03RIK\n7530414M10RIK\nATP6V1B2\n2310068J16RIK\nDDT\nKLHDC4\nHPN\nLIFR\nOVOL1\nNUDT12\nCDAN1\nFBXO9\nFBXL3\nHOXA7\nALDH8A1\n3110057O12RIK\nABHD11\nPSMB1\nENSMUSG00000074286\nCHPT1\nOXSM\n2310009A05RIK\n1700001L05RIK\nZFP148\n39509\nMRPL9\nTMEM80\n9030420J04RIK\nNAGLU\nPLSCR2\nAGBL3\nPEX1\nCNO\nNEO1\nASF1A\nTNFSF5IP1\nPKIG\nAI931714\nD130020L05RIK\nCNTD1\nCLEC2H\nZKSCAN1\n1810044D09RIK\nMETTL7A\nSIAE\nFBXO3\nFZD5\nTMEM166\nTMED4\nGPR155\nRNF167\nSPTLC1\nRIOK2\nTGDS\nPMS1\nPITPNC1\nPCSK7\n4933403G14RIK\nEI24\nCREBL2\nTLN1\nMRPL35\n2700038C09RIK\nUBIE\nOSGEPL1\n2410166I05RIK\nWDR24\nAP4S1\nLRRC44\nB3BP\nITFG1\nDMXL1\nC1D\n', description='Paste your gene list (One gene per row).', section = 'section1') }}
transcription_libraries = {{ MultiCheckboxField(name='transcription_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Transcription', default=['ARCHS4_TFs_Coexp', 'ChEA_2016'], section = 'section2',choices=[
'ARCHS4_TFs_Coexp',
'ChEA_2016',
'ENCODE_and_ChEA_Consensus_TFs_from_ChIP-X',
'ENCODE_Histone_Modifications_2015',
'ENCODE_TF_ChIP-seq_2015',
'Epigenomics_Roadmap_HM_ChIP-seq',
'Enrichr_Submissions_TF-Gene_Coocurrence',
'Genome_Browser_PWMs',
'lncHUB_lncRNA_Co-Expression',
'miRTarBase_2017',
'TargetScan_microRNA_2017',
'TF-LOF_Expression_from_GEO',
'TF_Perturbations_Followed_by_Expression',
'Transcription_Factor_PPIs',
'TRANSFAC_and_JASPAR_PWMs',
'TRRUST_Transcription_Factors_2019']) }}
pathways_libraries = {{ MultiCheckboxField(name='pathways_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Pathways', default=[], section = 'section2',choices=[
'ARCHS4_Kinases_Coexp',
'BioCarta_2016',
'BioPlanet_2019',
'BioPlex_2017',
'CORUM',
'Elsevier_Pathway_Collection',
'HMS_LINCS_KinomeScan',
'HumanCyc_2016',
'huMAP',
'KEA_2015',
'KEGG_2019_Human',
'KEGG_2019_Mouse',
'Kinase_Perturbations_from_GEO_down',
'Kinase_Perturbations_from_GEO_up',
'L1000_Kinase_and_GPCR_Perturbations_down',
'L1000_Kinase_and_GPCR_Perturbations_up',
'NCI-Nature_2016',
'NURSA_Human_Endogenous_Complexome',
'Panther_2016',
'Phosphatase_Substrates_from_DEPOD',
'PPI_Hub_Proteins',
'Reactome_2016',
'SILAC_Phosphoproteomics',
'SubCell_BarCode',
'Virus-Host_PPI_P-HIPSTer_2020',
'WikiPathways_2019_Human',
'WikiPathways_2019_Mouse']) }}
ontologies_libraries = {{ MultiCheckboxField(name='ontologies_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Ontologies', default=[], section = 'section2',choices=[
'GO_Biological_Process_2018',
'GO_Cellular_Component_2018',
'GO_Molecular_Function_2018',
'Human_Phenotype_Ontology',
'Jensen_COMPARTMENTS',
'Jensen_DISEASES',
'Jensen_TISSUES',
'MGI_Mammalian_Phenotype_Level_4_2019']) }}
diseases_drugs_libraries = {{ MultiCheckboxField(name='diseases_drugs_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Diseases/Drugs', default=[], section = 'section2',choices=[
'Achilles_fitness_decrease',
'Achilles_fitness_increase',
'ARCHS4_IDG_Coexp',
'ClinVar_2019',
'dbGaP',
'DepMap_WG_CRISPR_Screens_Broad_CellLines_2019',
'DepMap_WG_CRISPR_Screens_Sanger_CellLines_2019',
'DisGeNET',
'DrugMatrix',
'DSigDB',
'GeneSigDB',
'GWAS_Catalog_2019',
'LINCS_L1000_Chem_Pert_down',
'LINCS_L1000_Chem_Pert_up',
'LINCS_L1000_Ligand_Perturbations_down',
'LINCS_L1000_Ligand_Perturbations_up',
'MSigDB_Computational',
'MSigDB_Oncogenic_Signatures',
'Old_CMAP_down',
'Old_CMAP_up',
'OMIM_Disease',
'OMIM_Expanded',
'PheWeb_2019',
'Rare_Diseases_AutoRIF_ARCHS4_Predictions',
'Rare_Diseases_AutoRIF_Gene_Lists',
'Rare_Diseases_GeneRIF_ARCHS4_Predictions',
'Rare_Diseases_GeneRIF_Gene_Lists',
'UK_Biobank_GWAS_v1',
'Virus_Perturbations_from_GEO_down',
'Virus_Perturbations_from_GEO_up',
'VirusMINT']) }}
cell_types_libraries = {{ MultiCheckboxField(name='cell_types_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Cell Types', default=[], section = 'section2',choices=[
'Allen_Brain_Atlas_down',
'Allen_Brain_Atlas_up',
'ARCHS4_Cell-lines',
'ARCHS4_Tissues',
'Cancer_Cell_Line_Encyclopedia',
'CCLE_Proteomics_2020',
'ESCAPE',
'GTEx_Tissue_Sample_Gene_Expression_Profiles_down',
'GTEx_Tissue_Sample_Gene_Expression_Profiles_up',
'Human_Gene_Atlas',
'Mouse_Gene_Atlas',
'NCI-60_Cancer_Cell_Lines',
'ProteomicsDB_2020',
'Tissue_Protein_Expression_from_Human_Proteome_Map']) }}
miscellaneous_libraries = {{ MultiCheckboxField(name='miscellaneous_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Miscellaneous', default=[], section = 'section2',choices=[
'Chromosome_Location_hg19',
'Data_Acquisition_Method_Most_Popular_Genes',
'Enrichr_Libraries_Most_Popular_Genes',
'Genes_Associated_with_NIH_Grants',
'HMDB_Metabolites',
'HomoloGene',
'InterPro_Domains_2019',
'NIH_Funded_PIs_2017_AutoRIF_ARCHS4_Predictions',
'NIH_Funded_PIs_2017_GeneRIF_ARCHS4_Predictions',
'NIH_Funded_PIs_2017_Human_AutoRIF',
'NIH_Funded_PIs_2017_Human_GeneRIF',
'Pfam_Domains_2019',
'Pfam_InterPro_Domains',
'Table_Mining_of_CRISPR_Studies']) }}
legacy_libraries = {{ MultiCheckboxField(name='legacy_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Legacy', default=[], section = 'section2',choices=[
'BioCarta_2013',
'BioCarta_2015',
'ChEA_2013',
'ChEA_2015',
'Chromosome_Location',
'Disease_Signatures_from_GEO_down_2014',
'Disease_Signatures_from_GEO_up_2014',
'Drug_Perturbations_from_GEO_2014',
'ENCODE_Histone_Modifications_2013',
'ENCODE_TF_ChIP-seq_2014',
'GO_Biological_Process_2013',
'GO_Biological_Process_2015',
'GO_Biological_Process_2017',
'GO_Biological_Process_2017b',
'GO_Cellular_Component_2013',
'GO_Cellular_Component_2015',
'GO_Cellular_Component_2017',
'GO_Cellular_Component_2017b',
'GO_Molecular_Function_2013',
'GO_Molecular_Function_2015',
'GO_Molecular_Function_2017',
'GO_Molecular_Function_2017b',
'HumanCyc_2015',
'KEA_2013',
'KEGG_2013',
'KEGG_2015',
'KEGG_2016',
'MGI_Mammalian_Phenotype_2013',
'MGI_Mammalian_Phenotype_2017',
'MGI_Mammalian_Phenotype_Level_3',
'MGI_Mammalian_Phenotype_Level_4',
'NCI-Nature_2015',
'Panther_2015',
'Reactome_2013',
'Reactome_2015',
'TargetScan_microRNA',
'Tissue_Protein_Expression_from_ProteomicsDB',
'WikiPathways_2013',
'WikiPathways_2015',
'WikiPathways_2016']) }}
crowd_libraries = {{ MultiCheckboxField(name='crowd_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Crowd', default=[], section = 'section2',choices=[
'Aging_Perturbations_from_GEO_down',
'Aging_Perturbations_from_GEO_up',
'Disease_Perturbations_from_GEO_down',
'Disease_Perturbations_from_GEO_up',
'Drug_Perturbations_from_GEO_down',
'Drug_Perturbations_from_GEO_up',
'Gene_Perturbations_from_GEO_down',
'Gene_Perturbations_from_GEO_up',
'Ligand_Perturbations_from_GEO_down',
'Ligand_Perturbations_from_GEO_up',
'MCF7_Perturbations_from_GEO_down',
'MCF7_Perturbations_from_GEO_up',
'Microbe_Perturbations_from_GEO_down',
'Microbe_Perturbations_from_GEO_up',
'RNA-Seq_Disease_Gene_and_Drug_Signatures_from_GEO',
'SysMyo_Muscle_Gene_Sets']) }}
color_choice = '{{ ChoiceField(name='color_choice', label='Color Scheme', default='blue/purple/orange', description='Choose the color scheme you want for your plots.', section = 'section3', choices=[
'blue/purple/orange',
'orange',
'red/orange',
'blue/purple',
'purple/pink',
'green',
'rainbow',
'grayscale']) }}'
significance_line = {{ StringField(name='significance_line', label='Significance Line Value', default='', description='Enter a value at which you want a horizontal line to appear (generally used to indicate that values above the line are significant).', section = 'section3') }}
legend_location = '{{ ChoiceField(name='legend_location', label='Legend Location', default='below', description='Choose if you want the plot legend to be to the side or below the figure (static plot).', choices= ['below', 'side'], section = 'section3') }}'
label_location = '{{ ChoiceField(name='label_location', label='Point Label Location', default='right', description='Choose where you want the labels of the significant points to be located (static plot).', choices= ['right', 'above', 'below'], section = 'section3') }}'
figure_file_format = {{ MultiCheckboxField(name='figure_file_format', label='File Format', choices = ['png', 'pdf', 'svg' ], default=['png'], description='Select the format(s) to save your figure (static plot).', section = 'section4') }}
output_file_name = {{ StringField(name='output_file_name', label='File Name', default='Enrichr_results', description='Enter a name/description to save your figure (static plot).', section = 'section4') }}
final_output_file_names = [str(output_file_name+'.'+file_type) for file_type in figure_file_format]
enrichr_libraries = np.sort(transcription_libraries+pathways_libraries+ontologies_libraries+diseases_drugs_libraries+cell_types_libraries+miscellaneous_libraries+legacy_libraries+crowd_libraries)
# -
# ### Import gene list
# Import gene list as file or from text box file
# Will choose file upload over textbox if a file is given
if gene_list_filename != '':
open_gene_list_file = open(gene_list_filename,'r')
lines = open_gene_list_file.readlines()
genes = [x.strip() for x in lines]
open_gene_list_file.close()
else:
genes = gene_list_input.split('\n')
genes = [x.strip() for x in genes]
# ### Get Enrichr Results
#
# Enrichr is an open source web-based application for enrichment analysis and is freely available online at: http://amp.pharm.mssm.edu/Enrichr.
# Function to get Enrichr Results
# Takes a gene list and Enrichr libraries as input
# Returns a dataframe containing gene sets and p-values
def Enrichr_API(enrichr_gene_list, all_libraries):
for library_name in all_libraries :
ENRICHR_URL = 'http://amp.pharm.mssm.edu/Enrichr/addList'
genes_str = '\n'.join(enrichr_gene_list)
description = 'Example gene list'
payload = {
'list': (None, genes_str),
'description': (None, description)
}
response = requests.post(ENRICHR_URL, files=payload)
if not response.ok:
raise Exception('Error analyzing gene list')
data = json.loads(response.text)
time.sleep(0.5)
ENRICHR_URL = 'http://amp.pharm.mssm.edu/Enrichr/enrich'
query_string = '?userListId=%s&backgroundType=%s'
user_list_id = data['userListId']
short_id = data["shortId"]
gene_set_library = library_name
response = requests.get(
ENRICHR_URL + query_string % (user_list_id, gene_set_library)
)
if not response.ok:
raise Exception('Error fetching enrichment results')
data = json.loads(response.text)
#results_df = pd.DataFrame(data[library_name][0:5])
results_df = pd.DataFrame(data[library_name])
# adds library name to the data frame so the libraries can be distinguished
results_df['library'] = library_name.replace('_', '')
return([results_df, str(short_id)])
# ### Assign Color Scheme
# +
colors = []
if color_choice == 'orange':
colors = ['#FF5A00', '#FFA700', '#FF7400', '#FFDB00']
if color_choice == 'red/orange':
colors = ['#FF0000', '#FFCC00', '#FF6600', '#FF9800']
if color_choice == 'blue/purple':
colors = ['#0000FF', '#A3A3FF', '#4949FF', '#7879FF']
if color_choice == 'green':
colors = ['#2eb62c', '#abe098', '#57c84d', '#c5e8b7']
if color_choice == 'rainbow':
colors = ['red', '#fef200', 'green', 'blue', 'purple']
if color_choice == 'blue/purple/orange':
colors = ['#003f5c', '#7a5195', '#ef5675', '#ffa600']
if color_choice == 'purple/pink':
colors = ['#9800b0', '#ef83bd', '#bc37b1', '#d95db5']
if color_choice == 'grayscale':
colors = ['#000000', '#7a7a7a', '#3c3c3c', '#bdbdbd']
# -
# ### Plot Enrichr Results (static)
# Function plots results
def enrichr_figure():
if len(enrichr_libraries) == 1:
results_df = Enrichr_API(genes, enrichr_libraries)[0]
all_terms = []
all_pvalues = []
all_terms.append(list(results_df[1]))
all_pvalues.append(list(results_df[2]))
# make a simple scatterplot
fig, ax = plt.subplots(figsize=(10,4))
# sort the elements alphabetically
x=np.log10(all_pvalues[0])*-1
sorted_terms = list(zip(all_terms[0], x))
sorted_terms = sorted(sorted_terms, key = itemgetter(0))
unzipped_sorted_list = list(zip(*sorted_terms))
data = pd.DataFrame({"Gene Set": unzipped_sorted_list[0], "-log(p value)": unzipped_sorted_list[1]})
# add significance line and label significant points
if significance_line != '':
ax.axes.axhline(y = float(significance_line), color = 'black', lw = 1)
# label points above the significance line
if label_location == 'right':
coords = (6, -3)
elif label_location == 'below':
coords = (-3, -14)
elif label_location == 'above':
coords = (-4, 5)
point_label = 1
sig_point_handles = []
for index, row in data.iterrows():
if row["-log(p value)"] > float(significance_line):
ax.annotate(point_label, xy = (row["Gene Set"], row["-log(p value)"]), xytext = coords, textcoords='offset points')
actual_pvalue = "{:.5e}".format(10**(-1*row["-log(p value)"]))
sig_point_handles += [mpatches.Patch(color = 'white', label = str(point_label) + ": " + row["Gene Set"] + ", " + str(actual_pvalue))]
point_label += 1
# create a legend for the significant points
if point_label != 1:
leg = plt.legend(handles = sig_point_handles, handlelength=0, handletextpad=0, loc='center left', bbox_to_anchor=(1, 0.5), title="Significant Points")
ax.add_artist(leg)
ax.scatter(unzipped_sorted_list[0], unzipped_sorted_list[1], color = colors[0])
ax.axes.get_xaxis().set_ticks([])
plt.ylabel("-log(p value)")
plt.xlabel(enrichr_libraries[0])
elif len(enrichr_libraries) > 1:
# make a manhattan plot
sorted_data = pd.DataFrame({"Gene Set": [], "-log(p value)": [], "Library": []})
fig, ax = plt.subplots(figsize=(10,4))
for i in range(len(enrichr_libraries)):
# get enrichr results from the library selected
results_df = Enrichr_API(genes, [enrichr_libraries[i]])[0]
all_terms = []
all_pvalues = []
library_names = []
all_terms.append(list(results_df[1]))
all_pvalues.append(list(results_df[2]))
library_names.append(list(results_df['library']))
x=np.log10(all_pvalues[0])*-1
sorted_terms = list(zip(all_terms[0], x, library_names[0]))
sorted_terms = sorted(sorted_terms, key = itemgetter(0))
unzipped_sorted_list = list(zip(*sorted_terms))
data = pd.DataFrame({"Gene Set": unzipped_sorted_list[0], "-log(p value)": unzipped_sorted_list[1], "Library": unzipped_sorted_list[2]})
sorted_data = pd.concat([sorted_data, data])
# group data by library
groups = sorted_data.groupby("Library")
# plot points
color_index = 0
for name, group in groups:
if color_index >= len(colors):
color_index = 0
plt.plot(group["Gene Set"], group["-log(p value)"], marker="o", linestyle="", label=name, color = colors[color_index])
color_index += 1
# remove labels and tick marks on the x-axis
ax.axes.get_xaxis().set_ticks([])
# now sort dataframe by p-value so the significant points are labeled in order
sorted_pvalue_data = sorted_data.sort_values(by = ["-log(p value)"], ascending = False)
# add significance line and label significant points
if significance_line != '':
ax.axes.axhline(y = float(significance_line), color = 'black', lw = 1)
# label points above the significance line
if label_location == 'right':
coords = (6, -3)
elif label_location == 'below':
coords = (-3, -14)
elif label_location == 'above':
coords = (-4, 5)
point_label = 1
sig_point_handles = []
for index, row in sorted_pvalue_data.iterrows():
if row["-log(p value)"] > float(significance_line):
ax.annotate(point_label, xy = (row["Gene Set"], row["-log(p value)"]), xytext = coords, textcoords='offset points')
actual_pvalue = "{:.5e}".format(10**(-1*row["-log(p value)"]))
sig_point_handles += [mpatches.Patch(color = 'white', label = str(point_label) + ": " + row["Gene Set"] + ", " + str(actual_pvalue))]
point_label += 1
# create a legend for the significant points
if legend_location == 'side' and point_label != 1:
leg = plt.legend(handles = sig_point_handles, handlelength=0, handletextpad=0, loc='center left', bbox_to_anchor=(1.5, 0.5), title="Significant Points")
ax.add_artist(leg)
elif point_label != 1:
leg = plt.legend(handles = sig_point_handles, handlelength=0, handletextpad=0, loc='center left', bbox_to_anchor=(1, 0.5), title="Significant Points")
ax.add_artist(leg)
# adds a legend for the libraries in the location specified
if legend_location == 'below':
# shrink current axis's height by 10% on the bottom
box = ax.get_position()
ax.set_position([box.x0, box.y0 + box.height * 0.1,
box.width, box.height * 0.9])
# put a legend below current axis
ax.legend(loc='upper center', bbox_to_anchor=(0.5, -0.05),
fancybox=True, shadow=True, ncol=5)
elif legend_location == 'side':
# shrink current axis by 20%
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
# put a legend to the right of the current axis
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.ylabel("-log(p value)")
# save results
for plot_name in final_output_file_names:
plt.savefig(plot_name, bbox_inches = 'tight')
plt.show()
if len(enrichr_libraries) > 1:
return sorted_data, groups
return data
if len(enrichr_libraries) > 1:
sorted_data, groups = enrichr_figure()
else:
data = enrichr_figure()
# download static plots
for i, file in enumerate(final_output_file_names):
display(FileLink(file, result_html_prefix=str('Download ' + figure_file_format[i] + ': ')))
# ### Having trouble with overlapping point labels?
# Try moving the labels to a different location, plotting fewer libraries, or plot only one library at a time.
# ## Interactive plot using Bokeh
# +
if len(enrichr_libraries) > 1:
# split data frame into smaller data frames by library
list_of_df = []
for library_name in enrichr_libraries:
library_name = library_name.replace('_', '')
df_new = sorted_data[sorted_data['Library'] == library_name]
list_of_df += [df_new]
else:
list_of_df = [data]
list_of_xaxis_values = []
for df in list_of_df:
list_of_xaxis_values += df["Gene Set"].values.tolist()
# define the output figure and the features we want
p = figure(x_range = list_of_xaxis_values, plot_height=300, plot_width=1000, tools='pan, box_zoom, hover, reset, save')
# loop over all libraries
r = []
color_index = 0
for df in list_of_df:
if color_index >= len(colors):
color_index = 0
# calculate actual p value from -log(p value)
actual_pvalues = []
for log_value in df["-log(p value)"].values.tolist():
actual_pvalues += ["{:.5e}".format(10**(-1*log_value))]
# define ColumnDataSource with our data for this library
source = ColumnDataSource(data=dict(
x = df["Gene Set"].values.tolist(),
y = df["-log(p value)"].values.tolist(),
pvalue = actual_pvalues,
))
# plot data from this library
r += [p.circle(x = 'x', y = 'y', size=5, fill_color=colors[color_index], line_color= colors[color_index], line_width=1, source = source)]
color_index += 1
if len(enrichr_libraries) > 1:
# create custom legend for the libraries
color_index = 0
renderer_index = 0
legend_items = []
for library_name in enrichr_libraries:
legend_items += [LegendItem(label = library_name, renderers = [r[renderer_index]])]
renderer_index += 1
legend = Legend(items = legend_items, location = (0, 160))
p.add_layout(legend, 'right')
# add significance line
if significance_line != '':
hline = Span(location = float(significance_line), dimension='width', line_color='black', line_width=1)
p.renderers.extend([hline])
p.background_fill_color = 'white'
p.xaxis.major_tick_line_color = None
p.xaxis.major_label_text_font_size = '0pt'
p.y_range.start = 0
p.yaxis.axis_label = '-log(p value)'
p.hover.tooltips = [
("Gene Set", "@x"),
("p value", "@pvalue"),
]
p.output_backend = "svg"
show(p)
# -
# You can hover over the data points in this plot to see their associated gene set and p-value. Also check out the toolbar on the right side of the plot which will allow you to pan, box zoom, reset view, save the plot as an svg, and turn the hover display on/off.
| appyters/Enrichr_Manhattan_Plot/Enrichr_Manhattan_Plot.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''base'': conda)'
# name: python3
# ---
import pandas as pd
import numpy as np
# # 一、导入数据并探索
data = pd.read_excel('初步筛选后数据集.xlsx')
data.info()
data1 = data.copy()
# 重复值
data1.duplicated().sum()
data1.drop_duplicates(inplace=True)
# 有空值的列的空值数量
index = data1.columns[data1.isnull().sum()>0]
data1.isnull().sum()[index]
data1.head(1)
# # 二、交易特征
jiaoyi_features = ['关注人数', '房屋总价', '房屋每平米价', '近七天带看房次数',
'30天带看房次数', '爬取日期', '挂牌时间', '上次交易', '产权所属', '抵押信息',
'房本备件', '小区均价', '小区在售二手房数', '小区在租房数', '小区物业费用', '小区关注人数']+['房屋年限','房屋用途','交易权属']
data_jiaoyi = data1[jiaoyi_features].copy()
# 是原数据的副本,修改data_jiaoyi不会更改data1
# 交易特征中有空值的特征为:
#
# `小区均价、小区在售二手房数、小区在租房数、小区物业费用、小区关注人数`
index = data_jiaoyi.columns[data_jiaoyi.isnull().sum()>0]
data_jiaoyi.isnull().sum()[index]
data_jiaoyi.info()
# ## 2.1 去单位数值化
data_jiaoyi['房屋总价'] = data_jiaoyi['房屋总价'].apply(lambda x:x[:-1]).astype(float)
data_jiaoyi['房屋每平米价'] = data_jiaoyi['房屋每平米价'].apply(lambda x:x[:-4]).astype(float)
data_jiaoyi['小区物业费用'].replace('暂无信息',np.nan,inplace=True)
# np.nan属于float,不能截片,故使用notnull过滤
data_jiaoyi.loc[data_jiaoyi['小区物业费用'].notnull(),'小区物业费用'] = \
data_jiaoyi.loc[data_jiaoyi['小区物业费用'].notnull(),'小区物业费用'].apply(lambda x:x[:-6])
data_jiaoyi.loc[data_jiaoyi['小区物业费用'].notnull(),'小区物业费用'] = \
data_jiaoyi.loc[data_jiaoyi['小区物业费用'].notnull(),'小区物业费用'].apply(lambda x: (np.double(x.split('至')[0])+np.double(x.split('至')[1]))/2 if '至' in x else x)
data_jiaoyi['小区物业费用'] = data_jiaoyi['小区物业费用'].astype('float')
# ## 2.2 时间特征
#
# 感觉爬取日期无意义,删除
data_jiaoyi['上次交易'].replace('暂无数据', np.nan, inplace=True)
data_jiaoyi['上次交易'] = pd.to_datetime(data_jiaoyi['上次交易'],errors = 'coerce')
data_jiaoyi['挂牌时间'] = pd.to_datetime(data_jiaoyi['挂牌时间'],errors = 'coerce')
# 含nan值进行运算得到也是nan
data_jiaoyi['挂牌距上次交易天数'] = (data_jiaoyi['挂牌时间']-data_jiaoyi['上次交易']).apply(lambda x:x.days)
data_jiaoyi[['上次交易','挂牌时间','挂牌距上次交易天数']].head()
data_jiaoyi.drop(['爬取日期','上次交易','挂牌时间'],axis=1,inplace=True)
# ## 2.3 类别特征
data_jiaoyi['房屋年限']
# 房屋年限与税收相关,与房价无关,故删除
data_jiaoyi.drop('房屋年限',axis=1,inplace=True)
# 房屋用途、抵押信息、房本备件、产权所属、交易所属
#
# 属于类别特征,进行标签编码
print(data_jiaoyi['房屋用途'].unique())
print(data_jiaoyi['抵押信息'].unique())
print(data_jiaoyi['房本备件'].unique())
print(data_jiaoyi['产权所属'].unique())
print(data_jiaoyi['交易权属'].unique())
from sklearn.preprocessing import LabelEncoder
# 房屋用途,查资料得到如下等级:别墅>商业>商住两用>普通住宅>平房
# LabelEncoder是从0开始编码
coder = LabelEncoder()
coder.fit(['平房','普通住宅','商住两用','商业','别墅']) # 平房:0,普通住宅:1,。。。
data_jiaoyi['房屋用途'] = coder.transform(data_jiaoyi['房屋用途'])
# coder.inverse_transform(data)可以将编码转为原特征
# 交易权属,暂定使用随机标签编码,等级随机(onehot等编码方式可能会更好)
data_jiaoyi['交易权属'] = coder.fit_transform(data_jiaoyi['交易权属']) # fit_transform = 先fit再transform
# 产权所属、抵押信息、房本备件均0-1编码
# +
# 有空值就不用labelencoder了
data_jiaoyi['是否抵押'] = data_jiaoyi.loc[data_jiaoyi['抵押信息'].notnull(),'抵押信息'].apply(lambda x:x[:3])
data_jiaoyi['是否抵押'] = data_jiaoyi['是否抵押'].replace({'无抵押':0, '有抵押':1, '暂无数':np.nan})
# 后面无空值的特征可用replace也可用coder
data_jiaoyi['是否上传房本照片'] = data_jiaoyi['房本备件'].replace({'未上传房本照片':0,'已上传房本照片':1})
coder.fit(['共有','非共有'])
data_jiaoyi['产权是否共有'] = coder.transform(data_jiaoyi['产权所属'])
# -
(data_jiaoyi.iloc[:,-5:]).head()
data_jiaoyi.drop(['抵押信息','房本备件','产权所属'],axis=1,inplace=True)
data_jiaoyi.info()
# # 三、建筑特征
jianzhu_features = ['建楼时间', '小区建筑年代', 'tag', '户型分间', '小区楼栋数', '房屋图片数量', '建筑面积',
'套内面积', '梯户比例', '房屋户型', '所在楼层', '小区建筑类型', '户型结构', '建筑类型',
'建筑结构', '装修情况', '配备电梯', '房屋朝向']
data_jianzhu = data1[jianzhu_features].copy()
index = data_jianzhu.columns[data_jianzhu.isnull().sum()>0]
data_jianzhu.isnull().sum()[index]
# 建筑特征中含空值的为:
#
# `小区建筑年代、小区楼栋数、房屋图片数量、梯户比例、小区建筑类型、户型结构、建筑类型、配置电梯`
# ## 3.1 时间特征
data_jianzhu['建楼时间'].unique()
# ‘未知年建’
#有nan值和‘未知’
data_jianzhu['小区建筑年代'].unique()
# 提取数字
data_jianzhu['建楼距今年数'] = data_jianzhu['建楼时间'].apply(lambda x:x[:-2])
data_jianzhu.loc[data_jianzhu['小区建筑年代'].notnull(),'小区建成距今年数'] = data_jianzhu.loc[data_jianzhu['小区建筑年代'].notnull(),'小区建筑年代'].apply(lambda x:x[:-1])
# 替换异常值
data_jianzhu['建楼距今年数'].replace('未知',np.nan,inplace=True)
data_jianzhu['小区建成距今年数'].replace('未',np.nan,inplace=True)
this_year = 2021
# 任意数和nan运算结果仍为nan
data_jianzhu['建楼距今年数'] = this_year - data_jianzhu['建楼距今年数'].astype(float)
data_jianzhu['小区建成距今年数'] = this_year - data_jianzhu['小区建成距今年数'].astype(float)
data_jianzhu.iloc[:,-2:].head()
data_jianzhu.drop(['建楼时间','小区建筑年代'],axis=1,inplace=True)
# ## 3.2 房屋标签、小区楼栋数、房屋图片数量、建筑面积、套内面积
#
# 去单位数值化
data_jianzhu[['tag','小区楼栋数','房屋图片数量','建筑面积','套内面积']].head()
# +
index1 = data_jianzhu['小区楼栋数'].notnull() #非空行的索引
data_jianzhu.loc[index1,'小区楼栋数'] = data_jianzhu.loc[index1,'小区楼栋数'].apply(lambda x:x[:-1])
data_jianzhu['小区楼栋数'] = data_jianzhu['小区楼栋数'].astype(float)
data_jianzhu['套内面积'].replace('暂无数据',np.nan,inplace=True)
index2 = data_jianzhu['套内面积'].notnull()
data_jianzhu.loc[index2,'套内面积'] = data_jianzhu.loc[index2,'套内面积'].apply(lambda x:(x.strip())[:-1])
data_jianzhu['套内面积'] = data_jianzhu['套内面积'].astype(float)
data_jianzhu['建筑面积'] = data_jianzhu['建筑面积'].apply(lambda x:x[:-1]).astype(float)
##衍生特征,建筑面积-套内面积=公摊面积
data_jianzhu['公摊面积'] = data_jianzhu['建筑面积']-data_jianzhu['套内面积']
# 计算tag数量
data_jianzhu['房屋标签数量'] = data_jianzhu['tag'].apply(lambda x:len(x.split(',')))
# -
type(data_jianzhu['套内面积'][10])
data_jianzhu[['房屋标签数量','小区楼栋数','房屋图片数量','建筑面积','套内面积','公摊面积']].head()
data_jianzhu.drop('tag',axis=1,inplace=True)
# ## 3.3 户型分间、梯户比例、房屋户型、所在楼层
#
# 较复杂,具体特征具体分析
data_jianzhu[['户型分间','梯户比例','房屋户型','所在楼层']].head()
import cn2an
import re
# +
#梯户比例 将文字转化为比值
data_jianzhu['梯户比例'].fillna('',inplace=True)
re1 = re.compile('(.+)梯(.+)户')
def calculate_ratio(x):
ret = re1.findall(x)
if ret:
ti = cn2an.cn2an(x[0],'smart')
hu = cn2an.cn2an(x[0],'smart') # smart模式下能将‘二’和‘两’都转化为 2
return ti/hu
else:
return np.nan
data_jianzhu['梯户比例'] = data_jianzhu['梯户比例'].apply(calculate_ratio)
# -
#房屋户型 提取房、厅、厨、卫数量
re2 = re.compile('\d+')
temp = data_jianzhu['房屋户型'].apply(re2.findall)
data_jianzhu['卧室数量'] = temp.apply(lambda x:x[0]).astype(float)
data_jianzhu['客厅数量'] = temp.apply(lambda x:x[1]).astype(float)
data_jianzhu['厨房数量'] = temp.apply(lambda x:x[2]).astype(float)
data_jianzhu['卫生间数量'] = temp.apply(lambda x:x[3]).astype(float)
data_jianzhu.drop('房屋户型',axis=1,inplace=True)
# +
#所在楼层 提取总层数和楼层高低程度
re3 = re.compile('.+共(\d+)层.+')
data_jianzhu['总层数'] = data_jianzhu['所在楼层'].apply(lambda x:re3.findall(x)[0]).astype(float)
def rep(x):
pattern = re.compile(r'\s\((.*)\)')
return pattern.sub(r'',x)
data_jianzhu['所在楼层'] = data_jianzhu['所在楼层'].apply(rep)
data_jianzhu['所在楼层'] = data_jianzhu['所在楼层'].replace("nan",np.NAN)
data_jianzhu = pd.concat([data_jianzhu, pd.get_dummies(data_jianzhu[['所在楼层']])], sort=False, axis=1)
data_jianzhu.drop('所在楼层',axis=1,inplace=True)
# -
# 户型分间
print(data_jianzhu['户型分间'][0])
print(data_jianzhu['户型分间'][1])
# ### 户型分间衍生以下特征
# - 1.客厅面积占比
# - 2.卧室面积占比
# - 3.实际使用面积
# - 4.落地窗数量
# - 5.有无储物间
# - 6.有无入室花园
# - 7.窗户数量
# - 8.平均卧室面积
# - 9.客厅、卧室、阳台朝向,采光等级
data_jianzhu['户型分间'].replace('{}',np.nan,inplace=True)
index = data_jianzhu['户型分间'].notnull()
data_jianzhu.loc[index,'是否有储物间'] = data_jianzhu.loc[index,'户型分间'].apply(lambda x:1 if '储物间' in x else 0)
data_jianzhu.loc[index,'是否有入户花园'] = data_jianzhu.loc[index,'户型分间'].apply(lambda x:1 if '入户花园' in x else 0)
data_jianzhu.loc[index,'窗户数量'] = data_jianzhu.loc[index,'户型分间'].apply(lambda x:x.count('窗')-x.count('无窗'))
data_jianzhu.loc[index,'落地窗数量'] = data_jianzhu.loc[index,'户型分间'].apply(lambda x:x.count('落地'))
# +
#朝向以等级分级
#南>东南=西南>东=西>东北=西北>北
rank_direction = {
'南':5,
'东南':4,
'西南':4,
'东':3,
'西':3,
'东北':2,
'西北':2,
'北':1,
'无':np.nan
}
def change_direct(x):
for k,j in rank_direction.items():
if k in x:
return j
# +
act_area = [] # 实际使用面积
livingroom_bili = [] # 客厅面积比例
bedroom_bili = [] # 卧室面积比例
bedroom_avg_area = [] # 卧室平均面积
livingroom_light = [] # 客厅采光等级
bedroom_light = [] # 卧室采光等级
balcony_light = [] # 阳台采光等级
for item in data_jianzhu.loc[index,'户型分间']:
item=eval(item) # 转换为字典
df2=pd.DataFrame(item)
df3=df2.filter(regex='客厅')
df4=df2.filter(regex='卧室')
df5=df2.filter(regex='阳台')
using_area=0
for p in df2.iloc[0]:
p=p.split('平')
p=np.double(p[0])
using_area=using_area+p
act_area.append(using_area)
livingroom_sum=0
for p in df3.iloc[0]:
p=p.split('平')
p=np.double(p[0])
livingroom_sum=livingroom_sum+p
livingroom_bili.append(np.double(livingroom_sum/using_area))
room_sum=0
for p in df4.iloc[0]:
p=p.split('平')
p=np.double(p[0])
room_sum=room_sum+p
bedroom_bili.append(np.double(room_sum/using_area))
m=df4.shape[1]
if m!=0:
room_ave=room_sum/m
else:
room_ave=0
bedroom_avg_area.append(room_ave)
#房屋朝向等级
#客厅
try:
livingroom_light.append(change_direct(df3['客厅'][1]))
except:
livingroom_light.append(np.nan)
#主卧
try:
x1 = df4.iloc[1,np.argmax(df4.loc[0,:].apply(lambda x:x[:-2]).astype(float))]
bedroom_light.append(change_direct(x1))
except:
bedroom_light.append(np.nan)
#主阳台
try:
x1 = df5.iloc[1,np.argmax(df5.loc[0,:].apply(lambda x:x[:-2]).astype(float))]
balcony_light.append(change_direct(x1))
except:
balcony_light.append(np.nan)
# +
data_jianzhu.loc[index,'客厅面积占比'] = livingroom_bili
data_jianzhu.loc[index,'实际使用面积'] = act_area
data_jianzhu.loc[index,'平均卧室面积'] = bedroom_avg_area
data_jianzhu.loc[index,'卧室面积占比'] = bedroom_bili
data_jianzhu.loc[index,'客厅采光程度'] = livingroom_light
data_jianzhu.loc[index,'主卧采光程度'] = bedroom_light
data_jianzhu.loc[index,'阳台采光程度'] = balcony_light
data_jianzhu.drop('户型分间',axis=1,inplace=True)
# -
data_jianzhu.iloc[:,-20:]
# ## 3.4 小区建筑类型、户型结构、房屋建筑类型、建筑结构、装修情况、有无配备电梯、房屋朝向、所在楼层
#
# 小区建筑类型无用删除,房屋朝向与前面特征重复删除,其他特征为类别特征,进行编码
data_jianzhu['小区建筑类型'].unique()
data_jianzhu['房屋朝向'][1000:1005]
data_jianzhu.drop(['小区建筑类型','房屋朝向'],axis=1,inplace=True)
data_jianzhu['户型结构'].unique()
data_jianzhu['建筑类型'].unique()
# +
#户型结构、建筑类型(为无序特征):使用onehot编码
data_jianzhu['户型结构'].replace('暂无数据',np.nan,inplace=True)
data_jianzhu['建筑类型'].replace('暂无数据',np.nan,inplace=True)
data_jianzhu = pd.concat([data_jianzhu,pd.get_dummies(data_jianzhu[['户型结构']])], sort=False, axis=1)
data_jianzhu = pd.concat([data_jianzhu,pd.get_dummies(data_jianzhu[['建筑类型']])], sort=False, axis=1)
data_jianzhu.drop(['户型结构','建筑类型'],axis=1,inplace=True)
# +
#建筑结构、装修情况:定义等级后编码
data_jianzhu['建筑结构'].replace("未知结构",np.NAN,inplace=True)
jiegou_mapping = {
'钢结构': 6,
'钢混结构':5,
'框架结构':4,
'混合结构':3,
'砖混结构':2,
'砖木结构':1}
data_jianzhu['建筑结构'] = data_jianzhu['建筑结构'].map(jiegou_mapping)
data_jianzhu['装修情况'].replace("其他",np.NAN,inplace=True)
zhuangxiu_mapping = {
'精装':3,
'简装':2,
'毛坯':1
}
data_jianzhu['装修情况'] = data_jianzhu['装修情况'].map(zhuangxiu_mapping)
#电梯二值化处理
data_jianzhu['配备电梯'].replace({"暂无数据":np.NAN,'有':1,'无':0},inplace=True)
# -
data_jianzhu[['建筑结构','装修情况','配备电梯']].head()
data_jianzhu.iloc[:,-8:]
data_jianzhu.info()
# # 四、环境特征
# ### 教育设施、交通设施、购物设施、生活设施、娱乐设施、医疗设施
data_huanjing = data1[['幼儿园数','小学数','中学数','大学数','地铁站数','公交站数','商场数','超市数','市场数','银行数',
'ATM数','餐厅数','咖啡馆数','公园数','电影院数','健身房数','体育馆数','医院数','药店数',
'幼儿园平均距离','小学平均距离','中学平均距离','大学平均距离','地铁平均距离','公交平均距离',
'商场平均距离','超市平均距离','市场平均距离','银行平均距离','ATM平均距离','餐厅平均距离',
'咖啡馆平均距离','公园平均距离','电影院平均距离','健身房平均距离','体育馆平均距离','医院平均距离','药店平均距离',
'地铁线数','公交线数','所在广州区域']].copy()
#各设施数量
data_huanjing['教育设施数量'] = data_huanjing['幼儿园数']+data_huanjing['小学数']+data_huanjing['中学数']+data_huanjing['大学数']
data_huanjing['交通设施数量'] = data_huanjing['地铁站数']+data_huanjing['公交站数']
data_huanjing['购物设施数量'] = data_huanjing['商场数']+data_huanjing['超市数']+data_huanjing['市场数']
data_huanjing['生活设施数量'] = data_huanjing['银行数']+data_huanjing['ATM数']+data_huanjing['餐厅数']+data_huanjing['咖啡馆数']
data_huanjing['娱乐设施数量'] = data_huanjing['公园数']+data_huanjing['电影院数']+data_huanjing['健身房数']+data_huanjing['体育馆数']
data_huanjing['医疗设施数量'] = data_huanjing['医院数']+data_huanjing['药店数']
#各设施平均距
data_huanjing['教育设施平均距离'] = (data_huanjing['幼儿园平均距离']+data_huanjing['小学平均距离']+data_huanjing['中学平均距离']+data_huanjing['大学平均距离'])/4
data_huanjing['交通设施平均距离'] = (data_huanjing['地铁平均距离']+data_huanjing['公交平均距离'])/2
data_huanjing['购物设施平均距离'] = (data_huanjing['商场平均距离']+data_huanjing['超市平均距离']+data_huanjing['市场平均距离'])/3
data_huanjing['生活设施平均距离'] = (data_huanjing['银行平均距离']+data_huanjing['ATM平均距离']+data_huanjing['餐厅平均距离']+data_huanjing['咖啡馆平均距离'])/4
data_huanjing['娱乐设施平均距离'] = (data_huanjing['公园平均距离']+data_huanjing['电影院平均距离']+data_huanjing['健身房平均距离']+data_huanjing['体育馆平均距离'])/4
data_huanjing['医疗设施平均距离'] = (data_huanjing['医院平均距离']+data_huanjing['药店平均距离'])/2
data_huanjing.drop(columns = ['地铁站数', '地铁线数','地铁平均距离', '公交站数', '公交线数', '公交平均距离',
'幼儿园数', '幼儿园平均距离', '小学数', '小学平均距离','中学数', '中学平均距离',
'大学数', '大学平均距离', '医院数', '医院平均距离', '药店数', '药店平均距离','商场数',
'商场平均距离', '超市数', '超市平均距离', '市场数', '市场平均距离', '银行数', '银行平均距离',
'ATM数', 'ATM平均距离', '餐厅数', '餐厅平均距离', '咖啡馆数', '咖啡馆平均距离', '公园数', '公园平均距离',
'电影院数', '电影院平均距离', '健身房数', '健身房平均距离', '体育馆数', '体育馆平均距离'],inplace=True)
mapping={'天河':12,'越秀':11,'海珠':10,'荔湾':9,'白云':8,'番禺':7,'黄埔':6,'南沙':5,'顺德':4,'增城':3,'花都':2,'从化':1,'南海':0}
data_huanjing['所在广州区域']=data_huanjing['所在广州区域'].map(mapping)
data_huanjing.info()
# # 五、合并数据
final_data = pd.concat([data1['小区ID'],data_jiaoyi,data_jianzhu,data_huanjing],axis=1)
final_data.info()
# 如上所示,数据全部为数值型
final_data.to_excel('Preprocessed_data.xlsx',index=False)
index = final_data.isnull().sum()>0
final_data.isnull().sum()[index]
# 缺失值处理方法
# - 直接删除
# - 填充(0、最大值、均值、中位数等)
# - 建模预测(knn、Matrix_completion,使用与预测特征较相关的特征建模)
# - 将缺失值作为一个类别进行编码
# - 使用能自动处理缺失值的模型
final_data
data.select_dtypes(exclude='object').columns
data.select_dtypes(include='object').columns
import matplotlib.pyplot as plt
plt.figure(figsize=(20,10))
plt.hist(data['房屋总价'])
plt.show()
| crawler/feature_engineering.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # LiH molecule
#
# ## Origin of this method: Low rank decomposition of the Coulomb operator
# "Low rank representations for quantum simulation of electronic structure"
# <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>-<NAME>
# https://arxiv.org/abs/1808.02625
#
# The code is adapted from OpenFermion-Cirq Tutorial III: Low rank, arbitrary basis molecular simulations https://github.com/quantumlib/OpenFermion-Cirq/blob/master/examples/tutorial_3_arbitrary_basis_trotter.ipynb
#
# In Tutorial III both of those techniques are combined, along with some insights from electronic structure,
# to simulate a Trotter step under the arbitrary basis two-body operator as
# $$
# \prod_{\ell=0}^{L-1} R_\ell \exp\left(-i\sum_{pq} f_{\ell p} f_{\ell q} a^\dagger_p a_p a^\dagger_q a_q\right) R_\ell^\dagger
# $$
# where we note that the operator in the exponential take the form of a diagonal Coulomb operator. Since we can implement the $R_\ell$ circuits in $O(N)$ depth (see Tutorial I) and we can implement Trotter steps under diagonal Coulomb operators in $O(N)$ layers of gates (see Tutorial II) we see that we can implement Trotter steps under arbitrary basis electronic structure Hamiltionians in $O(L N) = O(N^2)$ depth, and all on a linearly connected device.
#
# ## Example implementation: Trotter steps of LiH in molecular orbital basis
#
# We will now use these techniques to implement Trotter steps for an actual molecule. We will focus on LiH at equilibrium geometry, since integrals for that system are provided with every OpenFermion installation. However, by installing [OpenFermion-PySCF](https://github.com/quantumlib/OpenFermion-PySCF) or [OpenFermion-Psi4](https://github.com/quantumlib/OpenFermion-Psi4) one can use these techniques for any molecule at any geometry. We will generate LiH in an active space consisting of 4 qubits. First, we obtain the Hamiltonian as an InteractionOperator.
# +
import openfermion
# Set Hamiltonian parameters for LiH simulation in active space.
diatomic_bond_length = 1.45
geometry = [('Li', (0., 0., 0.)), ('H', (0., 0., diatomic_bond_length))]
basis = 'sto-3g'
multiplicity = 1
active_space_start = 1
active_space_stop = 3
# Generate and populate instance of MolecularData.
molecule = openfermion.MolecularData(geometry, basis, multiplicity, description="1.45")
molecule.load()
# Get the Hamiltonian in an active space.
molecular_hamiltonian = molecule.get_molecular_hamiltonian(
occupied_indices=range(active_space_start),
active_indices=range(active_space_start, active_space_stop))
print("Molecular Hamiltonian with 1 constant and {} 1-body and {} 2-body tensor terms"
.format(molecular_hamiltonian.one_body_tensor.size,
molecular_hamiltonian.two_body_tensor.size))
# obtain the Hamiltonian as matrix
hamiltonian_sparse = openfermion.get_sparse_operator(molecular_hamiltonian)
LiH_matrix = hamiltonian_sparse.todense()
print("Hamiltonian matrix as {} from which {} are not null"
.format( LiH_matrix.shape, hamiltonian_sparse.nnz))
# solve for eigenvalues by matrix algorithms
from scipy.linalg import eigh
eigenvalues , eigenvectors = eigh(LiH_matrix)
print("Eigenvalues (Energies)\n", eigenvalues.round(6))
print("Eigenvectors (Orbitals)\n", eigenvectors.real.round(1))
# -
# We are not yet aiming for chemical accuracy. We could check the Hamiltonian' eigenvalues with experimental data or compare to other computations from https://cccbdb.nist.gov/energy2.asp
# However, in the example the molecule integrals are provided by OpenFermion only for $1,45 \mathring{A}$. If you look up the experimental geometry (correct for the Born-Openheimer approximation), $r_{LiH} = 1.595 \mathring{A}$ for $^7Li$ https://cccbdb.nist.gov/expgeom2.asp.
#
# You can see that the matrix calculation would result in exponential runtimes for larger systems. We convert the Hamiltonian for simulation with a quantum computer into the so-called "second quantized" operator form, as was shown in Tutorial II.
# $$
# H = \sum_{pq} T_{pq} a^\dagger_p a_q + \sum_{pq} V_{pq} a^\dagger_p a_p a^\dagger_q a_q.
# $$
fermion_operator = openfermion.get_fermion_operator(molecular_hamiltonian)
print("Fermionic Hamiltonian with {} terms".format( len(fermion_operator.terms)))
#print(fermion_operator)
# We see from the above output that this is a fairly complex Hamiltonian already. Next we will use the `simulate_trotter` function from Tutorial I, but this time with the built-in `LOW_RANK` Trotter step type, associated with these low rank techniques.
#
# Next we setup the simulation environment with qubits on a line.
# +
import cirq
import openfermioncirq
from openfermioncirq import trotter
# Trotter step parameters.
time = 1.
final_rank = 2
# Initialize circuit qubits in a line.
n_qubits = openfermion.count_qubits(molecular_hamiltonian)
qubits = cirq.LineQubit.range(n_qubits)
# -
# In the cell below, we compile the Trotter step with full rank so $L = N^2$ and depth is actually $O(N^3)$ and repeat the Trotter step multiple times to show that it actually converges to the correct result. Note that the rank of the Coulomb operators is asymptotically $O(N)$ but for very small molecules in small basis sets only a few eigenvalues can be truncated.
# +
# Initialize a random initial state.
import numpy
random_seed = 8317
initial_state = openfermion.haar_random_vector(
2 ** n_qubits, random_seed).astype(numpy.complex64)
# Trotter step paramaters.
n_steps = 3
# Compile the low rank Trotter step using OpenFermion-Cirq.
qubits = cirq.LineQubit.range(n_qubits)
circuit = cirq.Circuit(
trotter.simulate_trotter(
qubits, molecular_hamiltonian,
time=time, n_steps=n_steps,
algorithm=trotter.LOW_RANK),
strategy=cirq.InsertStrategy.EARLIEST)
# Print circuit.
print(f'Before optimization, Circuit has {len(circuit)} moments')
cirq.DropNegligible().optimize_circuit(circuit)
cirq.DropEmptyMoments().optimize_circuit(circuit)
print(f'After optimization, Circuit has {len(circuit)} moments')
#print(circuit.to_text_diagram(transpose=True))
# -
# For comparison we compute the time step with the exact time evolution operator $\psi(t) = e^{ -i H t } \psi(0)$ in matrix form.
#
# We plot the exact values as solid lines and the simulation as dashed lines and include a global phase $e^{i\pi/2}$ for each trotter step.
# Numerically compute the correct circuit output.
import scipy
exact_state = scipy.sparse.linalg.expm_multiply(
-1j * time * hamiltonian_sparse, initial_state)
# %matplotlib
import matplotlib.pyplot as plt
import math, cmath
fig, axs = plt.subplots(2)
axs[1].set_xlabel('basis')
axs[0].set_ylabel('Re(psi)')
axs[1].set_ylabel('Im(psi)')
axs[0].set_title('Simulation')
x = range(exact_state.size)
phase = cmath.exp(1j*math.pi/2)
axs[0].plot(x, (phase*exact_state).real, 'r')
axs[1].plot(x, (phase*exact_state).imag, 'r')
# Compare to complex conjugate state, why?
# And why are Re and Im exchanged between exact and simulated?
# Looks as if a phase factor is there...
# +
# Use Cirq simulator to apply circuit.
simulator = cirq.Simulator()
result = simulator.simulate(circuit, qubit_order=qubits, initial_state=initial_state)
simulated_state = result.final_state
#print( result )
axs[0].plot(x, simulated_state.real, 'r', dashes=[1, 1])
axs[1].plot(x, simulated_state.imag, 'r', dashes=[1, 1])
# Print final fidelity.
fidelity = abs(numpy.dot(simulated_state, numpy.conjugate(exact_state))) ** 2
print('Fidelity with exact result is {}.\n'.format(round(fidelity, 6)))
# -
# Compute next time step
exact_state = scipy.sparse.linalg.expm_multiply(
-1j * time * hamiltonian_sparse, exact_state)
phase *= cmath.exp(1j*math.pi/2)
axs[0].plot(x, (phase*exact_state).real, 'g')
axs[1].plot(x, (phase*exact_state).imag, 'g')
result = simulator.simulate(circuit, qubit_order=qubits, initial_state=simulated_state)
simulated_state = result.final_state
axs[0].plot(x, simulated_state.real, 'g', dashes=[1, 1])
axs[1].plot(x, simulated_state.imag, 'g', dashes=[1, 1])
fidelity = abs(numpy.dot(simulated_state, numpy.conjugate(exact_state))) ** 2
print('Fidelity with exact result is {}.\n'.format(round(fidelity, 6)))
# Compute time step 3
exact_state = scipy.sparse.linalg.expm_multiply(
-1j * time * hamiltonian_sparse, exact_state)
phase *= cmath.exp(1j*math.pi/2)
axs[0].plot(x, (phase*exact_state).real, 'b')
axs[1].plot(x, (phase*exact_state).imag, 'b')
result = simulator.simulate(circuit, qubit_order=qubits, initial_state=simulated_state)
simulated_state = result.final_state
axs[0].plot(x, simulated_state.real, 'b', dashes=[1, 1])
axs[1].plot(x, simulated_state.imag, 'b', dashes=[1, 1])
fidelity = abs(numpy.dot(simulated_state, numpy.conjugate(exact_state))) ** 2
print('Fidelity with exact result is {}.\n'.format(round(fidelity, 6)))
# Compute time step 4
exact_state = scipy.sparse.linalg.expm_multiply(
-1j * time * hamiltonian_sparse, exact_state)
phase *= cmath.exp(1j*math.pi/2)
axs[0].plot(x, (phase*exact_state).real, 'y')
axs[1].plot(x, (phase*exact_state).imag, 'y')
result = simulator.simulate(circuit, qubit_order=qubits, initial_state=simulated_state)
simulated_state = result.final_state
axs[0].plot(x, simulated_state.real, 'y', dashes=[1, 1])
axs[1].plot(x, simulated_state.imag, 'y', dashes=[1, 1])
fidelity = abs(numpy.dot(simulated_state, numpy.conjugate(exact_state))) ** 2
print('Fidelity with exact result is {}.\n'.format(round(fidelity, 6)))
for i, step in enumerate(simulator.simulate_moment_steps(circuit)):
if i == 0:
step.set_state_vector(simulated_state)
else:
color = (float(i/len(circuit)), float(i/len(circuit)), float(i/len(circuit)))
#print('state at step %d: %s' % (i, numpy.around(step.state_vector(), 3)))
#axs[2].plot(x, numpy.real(step.state_vector()), color)
#axs[3].plot(x, numpy.imag(step.state_vector()), color)
plt.show()
| LiH_trotter.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R [conda env:ATACseq_simulation]
# language: R
# name: conda-env-ATACseq_simulation-r
# ---
options(stringsAsFactors=FALSE)
library(data.table)
library(cowplot)
library(Matrix)
library(BuenColors)
# +
metrics_pctcells = read.csv('./peaks_frequency_results/metrics/clustering_scores.csv',
row.names=1)
metrics_pctcells[['cutoff']] = as.numeric(substring(rownames(metrics_pctcells),8))
metrics_nreads = read.csv('./peaks_intensity_results/metrics/clustering_scores.csv',
row.names=1)
metrics_nreads[['cutoff']] = as.numeric(substring(rownames(metrics_pctcells),8))
# -
head(metrics_nreads)
head(metrics_pctcells)
df_merge = rbind(metrics_pctcells,metrics_nreads)
df_merge[['group']] = c(rep('Fequency',dim(metrics_pctcells)[1]),rep('Intensity',dim(metrics_nreads)[1]))
df_merge[['ID']] = rownames(df_merge)
df_merge_new = data.frame(name=character(0),group= character(0), clustering= character(0),
metric = character(0),value = numeric(0),cutoff=numeric(0),stringsAsFactors=FALSE)
for(x in rownames(df_merge)){
for (y in colnames(df_merge)[1:9]){
str_split = strsplit(y,'_')[[1]]
x_metric = str_split[1]
x_clustering = str_split[2]
x_value = df_merge[x,y]
new_row = list(name=x,group=df_merge[x,'group'],clustering=x_clustering,
metric=x_metric,value=x_value,cutoff=df_merge[x,'cutoff'])
df_merge_new = rbind(df_merge_new,new_row)
}
}
df_merge_new[df_merge_new=="louvain"]<-'Louvain'
df_merge_new[df_merge_new=="hc"]<-'HC'
df_merge_new
min(df_merge_new$value)
p <- ggplot(df_merge_new, aes(cutoff, value,color=factor(group))) +
geom_point(size=2,alpha=0.8)+
geom_line(size=1.5,alpha=0.8) +
theme_bw() +
theme(legend.position='top',
text = element_text(colour = "black"),
axis.text.x = element_text(color = "black"),
axis.text.y = element_text(color = "black"),
axis.title.x = element_text(color = 'black'),
axis.title.y = element_text(color = 'black')) +
xlab('Cutoff') + ylab('Score')+
ylim(-0.05, 1)+
labs(color='peak selection')+
scale_x_reverse()
options(repr.plot.width=3*5, repr.plot.height=3*2)
p + facet_grid(vars(clustering), vars(metric))
ggsave(p + facet_grid(vars(clustering), vars(metric)),filename = 'Control_BMp2.pdf',width = 3*5, height = 3*2)
| Extra/BoneMarrow_noisy_p2/test_peaks/Control/make_plots_Control.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Клас контейнер на *Python*
# Створимо базовий клас `String`, який буде зберігатися у класі `Text`
class String:
def __init__(self, value):
self.value = value
def len(self):
return len(self.value)
def all_upper(self):
self.value = self.value.upper()
def compare(self, string):
if string == self.value:
return 1
else:
return 0
def get(self):
return self.value
# Цей клас містить такі методи:
# * `__init__` *конструктор*: передає у клас рядок;
# * `len`: повертає довжину рядка;
# * `all_upper`: переводить рядок у uppercase;
# * `compare`: приймає 1 рядок та порівнює рядок класу з ним. Повертає 1 або 0 якщо вони однакові чи ні відповідно;
# * `get`: повертає значення рядка, що зберігається у класі;
# Створимо клас-контейнер `Text`
class Text:
def __init__(self, string=None):
if string is None:
self.text = []
else:
self.text = [string]
def show(self):
if len(self.text) > 0:
print('\n'.join(list(map(lambda x: x.get(), self.text))))
else:
print("EMPTY!")
def add(self, string: String):
self.text.append(string)
def delete_one(self, index=None):
if index is None:
self.text.pop(-1)
else:
self.text.pop(index)
def delete_all(self):
self.text = []
# That delete_len feels like bad code :|
def delete_len(self, length):
result = []
for i in range(len(self.text)):
if self.text[i].len() == length:
result.append(i)
for i in range(len(result)):
self.text.pop(result[i]-i)
def upper(self):
for string in self.text:
string.all_upper()
def search(self, value):
result = 0
for string in self.text:
result += string.compare(value)
print(f"{result} '{value}' в тексті")
# Цей клас містить наступні методи:
# * `__init__` *конструктор*;
# * `delete_all`: очищує весь клас;
# * `delete_one`: видаляє елемент за індексом чи останній елемент;
# * `delete_len`: видаляє усі елементи заданої довжини;
# * `add`: додає елемент в кінець тексту;
# * `show`: виводить текст у консоль;
# * `upper`: переводить усі елементи у верхній регістр;
# * `search`: приймає рядок, виводить кількість співпадань у тексті;
# Перевіримо роботу классів. Для цього створимо 4 рядка та 4 тексти з них.
# +
s1 = String("Foo Bar")
s2 = String("Spam Eggs")
s3 = String("Pupa Lupa")
s4 = String("C++ is harder")
t1 = Text()
t2 = Text()
t3 = Text()
t4 = Text()
# -
# Циклом додамо до кожного тексту усі рядки
S = [s1, s2, s3, s4]
T = [t1, t2, t3, t4]
for t in T:
for s in S:
t.add(s)
# Повне очищення тексту
t1.delete_all()
t1.show()
# Видалення 1 елементу за індексом та без
t2.delete_one()
t2.delete_one(1)
t2.show()
# Видалення за довжиною
t3.delete_len(9)
t3.show()
# Пошук у тексті, перевод тексту у верхній регістр
t4.add(s3)
t4.search("Spam Eggs")
t4.search("Pupa Lupa")
t4.upper()
t4.show()
| Notebooks/3hird/Python.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import datetime as dt
import matplotlib
import matplotlib.pyplot as plt
import scipy.cluster.hierarchy as shc
from sklearn.cluster import AgglomerativeClustering
import os
import seaborn as sns
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist, pdist
from sklearn.datasets import make_classification
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.cm as cm
from sklearn.mixture import GaussianMixture
from sklearn.cluster import DBSCAN
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
# fileName = 'C:/Users/mcarp/Downloads/usa_00007.csv/usa_00007.csv'
fileName = 'C:/Users/<NAME>/Documents/NYU_CUSP/Capstone/usa_00007.csv'
file = pd.read_csv(fileName)
dfCDI = pd.DataFrame(file)
# fileName2 = 'C:/Users/mcarp/Downloads/county_merged_vals - Sheet1.csv'
fileName2 = 'C:/Users/<NAME>/Documents/NYU_CUSP/Capstone/county_merged_vals - Sheet1.csv'
file2 = pd.read_csv(fileName2)
dfCty = pd.DataFrame(file2)
dfCDI.info()
dfCDI.shape
dfCDI.head()
dfCDI = dfCDI[dfCDI['AGE']>=21]
dfCDI.shape
dfCDI.RENTGRS.value_counts()
dfHomeOwn=dfCDI[dfCDI['OWNERSHP']==1]
dfHomeOwn.RENTGRS.describe()
# This reveals that home owning rows all have 0 values for cost of rent.
dfCDI['OWNERSHP'].value_counts()
dfCDI = dfCDI[dfCDI['OWNERSHP']!=0]
dfCDI.shape
# Removes N/As (~50k rows)
dfCDI['RENTGRS'].value_counts()
dfCDI['affrentdec'] = dfCDI['RENTGRS']*12/dfCDI['HHINCOME']
def housingFunc(own, affrentdec):
if own==1:
housingCat=2
elif own==2 and affrentdec<.3:
housingCat=1
else:
housingCat=0
return housingCat
dfCDI['HousingCat'] = dfCDI.apply(lambda x: housingFunc(x['OWNERSHP'], x['affrentdec']), axis=1)
dfCDI['HousingCat'].value_counts()
# COMBINING aff. rent and home ownership into 1 indicator: 0, 1, 2 scores (0: rent>=30% income, 1: rent<30% income, 2: owner)
dfCDI['EDUCbin'] = [1 if x >=8 else 0 for x in dfCDI['EDUC']]
dfCDI['EDUCbin'].value_counts()
dfCDI['CIHISPEED'].value_counts()
dfCDI = dfCDI[dfCDI['CIHISPEED']!=0]
dfCDI['TRANTIME'].value_counts()
dfCDI.shape
joined2019_2 = dfCDI.merge(dfCty, on='COUNTYFIP')
joined2019_2.shape
print(joined2019_2.columns.get_loc("HousingCat"))
print(joined2019_2.columns.get_loc("EDUCbin"))
print(joined2019_2.columns.get_loc("CIHISPEED"))
print(joined2019_2.columns.get_loc("TRANTIME"))
print(joined2019_2.columns.get_loc("DrinkingWater"))
print(joined2019_2.columns.get_loc("AirQuality"))
print(joined2019_2.columns.get_loc("EarlyEd"))
print(joined2019_2.columns.get_loc("ProspNeigh"))
X = joined2019_2.iloc[:, [41,42,21,39,56,58,57,59,5,19,26,25,28]]
X.head()
scaler=StandardScaler()
scalerNum = scaler.fit(X)
Xstd = scalerNum.transform(X)
Xstd
dfX = pd.DataFrame(Xstd, columns=['HousingCat','EDUCbin','CIHISPEED','TRANTIME','DrinkingWater','AirQuality','EarlyEd','ProspNeigh','HHWT','HHINCOME','RACE','AGE','HISPAN'])
dfX.describe()
dfX.shape
# elbow method:
# +
# wcss = []
# for i in range(1,10):
# kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
# kmeans.fit(dfX)
# wcss.append(kmeans.inertia_)
# +
# plt.figure(figsize=(10,5))
# sns.lineplot(range(1,10), wcss,marker='o',color='red')
# plt.title('The Elbow Method')
# plt.xlabel('Number of clusters')
# plt.ylabel('WCSS')
# plt.show()
# -
# silhouette score:
# +
# for i in range(2,11):
# km = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
# cluster_labels = km.fit_predict(dfX)
# silhouette_avg = silhouette_score(dfX, cluster_labels, metric='euclidean', random_state=None)
# print('For n_clusters = {} the average silhouette_score is: {}'.format(i, silhouette_avg))
# -
kmeans = KMeans(n_clusters = 5, init = 'k-means++', random_state = 42)
kmeans.fit(dfX.iloc[:,0:8])
print(kmeans.labels_)
Xfin = scaler.inverse_transform(dfX)
Xfin
dfXfin = pd.DataFrame(Xfin, columns=['HousingCat','EDUCbin','CIHISPEED','TRANTIME','DrinkingWater','AirQuality','EarlyEd','ProspNeigh','HHWT','HHINCOME','RACE','AGE','HISPAN'])
dfXfin.head()
dfXfin.head()
Xfin
kmeans.labels_
dfXfin
dfXfin['labels'] = kmeans.labels_
cluster_sum = dfXfin.groupby(by = 'labels').mean()
cluster_sum.head()
clust0 = dfXfin[dfXfin['labels']==0]
clust1 = dfXfin[dfXfin['labels']==1]
clust2 = dfXfin[dfXfin['labels']==2]
clust3 = dfXfin[dfXfin['labels']==3]
clust4 = dfXfin[dfXfin['labels']==4]
# clust5 = dfXfin[dfXfin['labels']==5]
# clust6 = dfXfin[dfXfin['labels']==6]
# ## Cluster 0
clust0.describe()
clust0.head()
matplotlib.pyplot.hist(clust0['TRANTIME'])
matplotlib.pyplot.hist(clust0['AirQuality'])
clust0['HousingCat'].value_counts()
# ## Cluster 1
clust1.describe()
matplotlib.pyplot.hist(clust1['TRANTIME'])
matplotlib.pyplot.hist(clust1['AirQuality'])
matplotlib.pyplot.hist(clust1['AGE'])
clust1['HousingCat'].value_counts()
# ## Cluster 2
clust2.describe()
matplotlib.pyplot.hist(clust2['TRANTIME'])
matplotlib.pyplot.hist(clust2['AirQuality'])
matplotlib.pyplot.hist(clust2['AGE'])
clust2['HousingCat'].value_counts()
# ## Cluster 3
clust3.describe()
matplotlib.pyplot.hist(clust3['TRANTIME'])
matplotlib.pyplot.hist(clust3['AirQuality'])
clust3['HousingCat'].value_counts()
# ## Cluster 4
clust4.describe()
matplotlib.pyplot.hist(clust4['TRANTIME'])
matplotlib.pyplot.hist(clust4['AirQuality'])
clust4['HousingCat'].value_counts()
Xcorr=dfXfin.iloc[:, [0,1,2,3,4,5,6,7,8,9,10,11,12]]
Xcorr.head()
# +
#All Clusters Age Demographics chart
# +
fig, axs = plt.subplots(2, 3, sharey=True, figsize=(20,10))
fig.suptitle("AGE")
axs[0, 0].hist(clust0['AGE'])
axs[0, 0].set_title('Cluster 0')
axs[0, 1].hist(clust1['AGE'])
axs[0, 1].set_title('Cluster 1')
axs[0, 2].hist(clust2['AGE'])
axs[0, 2].set_title('Cluster 2')
axs[1, 0].hist(clust3['AGE'])
axs[1, 0].set_title('Cluster 3')
axs[1, 1].hist(clust4['AGE'])
axs[1, 1].set_title('Cluster 4')
for ax in axs.flat[4:]:
ax.set(xlabel='AGE')
# +
fig, axs = plt.subplots(2, 3, sharey=True, figsize=(20,10))
fig.suptitle("RACE")
axs[0, 0].hist(clust0['RACE'])
axs[0, 0].set_title('Cluster 0')
axs[0, 1].hist(clust1['RACE'])
axs[0, 1].set_title('Cluster 1')
axs[0, 2].hist(clust2['RACE'])
axs[0, 2].set_title('Cluster 2')
axs[1, 0].hist(clust3['RACE'])
axs[1, 0].set_title('Cluster 3')
axs[1, 1].hist(clust4['RACE'])
axs[1, 1].set_title('Cluster 4')
for ax in axs.flat[4:]:
ax.set(xlabel='RACE')
# +
fig, axs = plt.subplots(2, 3, sharey=True, figsize=(20,10))
fig.suptitle("HHINCOME")
axs[0, 0].hist(clust0['HHINCOME'])
axs[0, 0].set_title('Cluster 0')
axs[0, 1].hist(clust1['HHINCOME'])
axs[0, 1].set_title('Cluster 1')
axs[0, 2].hist(clust2['HHINCOME'])
axs[0, 2].set_title('Cluster 2')
axs[1, 0].hist(clust3['HHINCOME'])
axs[1, 0].set_title('Cluster 3')
axs[1, 1].hist(clust4['HHINCOME'])
axs[1, 1].set_title('Cluster 4')
for ax in axs.flat[4:]:
ax.set(xlabel='HHINCOME')
# -
plt.subplots(figsize=(12,8))
sns.heatmap(Xcorr.corr(), annot = True)
# ## Cluster Visualizations:
fig, ax = plt.subplots(figsize=(8,8))
scatter = ax.scatter(dfXfin['HousingCat'], dfXfin['EDUCbin'], c=dfXfin['labels'], cmap=plt.cm.cool)
ax.set_xlabel('2 yr college binary')
ax.set_ylabel('% of 3-4 yr olds in preschool')
legend1=ax.legend(*scatter.legend_elements(),loc="lower left", title="Cluster")
plt.gca().add_artist(legend1)
| .ipynb_checkpoints/DescriptiveStatsTest-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.4.5
# language: julia
# name: julia-0.4
# ---
using MultiPolynomials
@variables Rational{BigInt} x y z t
F=[2*x+2*y+2*z+t-1, 2*x*z+z^2+2*y*t-y,
2*x*y+2*y*z+2*z*t-z, 2*x*z+2*y*t+z^2-y,
2*x^2+2*y^2+2*z^2+2*t^2-t]
fgb_qbasis(F, [], [x,y,z,t])
fgb_qbasis(vcat(F,[x+2*y+3*z+4*t-5]), [], [x,y,z,t])
@variables Rational{BigInt} x y z
F=[2*x*z+z^2-4*x*y-4*y^2-4*y*z+y, 2*x*y-2*y*z-4*x*z-4*z^2+z,
2*x*z+z^2-4*x*y-4*y^2-4*y*z+y,
10*x^2+10*y^2+10*z^2+16*x*y+16*x*z-6*x+16*y*z-6*y-6*z+1]
fgb_qbasis(F, [], [x,y,z])
fgb_qbasis_elim(F, [y, z], [x])
| examples/FGb.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pickle
import numpy as np
import pandas as pd
directory = '/mnt/home/jbielecki1/NEMA/'
modelFileName = '10000000/XGB/xgbEstimators1000Depth6'
fileName = 'NEMA_IQ_384str_N0_1000_COINCIDENCES_PREPARED_part'
max_depth = 6
feature_names = ['x1', 'y1', 'z1', 'x2', 'y2', 'z2', 'vol1', 'vol2', 'e1', 'e2', 'dt', 'rX1', 'rY1', 'rZ1', 'volD', 'lorL', 'deg3D', 'deg2D', 'rL', 'eSum']
dataPositiveParts = []
model = pickle.load(open(directory + modelFileName, 'rb'))
def getGOJAFormatPositivePrediction(filePath):
data = pickle.load(open(filePath, 'rb'))
codes = {1:1, 2:0, 3:0, 4:0}
y = data["class"].map(codes)
x = data.drop(["t1", "t2", "sX1", "sY1", "sZ1", "class", "rError"], axis = 1)
x.columns = ["f" + str(x) for x in range(20)]
y_pred_prob = model.predict_proba(x)
y_pred = y_pred_prob > 0.5
pPsPredictedPositive = x[y_pred[:,1]]
dataPositive = data.iloc[list(pPsPredictedPositive.index),:]
return dataPositive.iloc[:,:16]
# +
for i in range(8):
dataPositiveParts.append(getGOJAFormatPositivePrediction(directory + fileName + '0' + str(i+1)))
for i in range(8):
dataPositiveParts.append(getGOJAFormatPositivePrediction(directory + fileName + '1' + str(i)))
dataRec = pd.concat(dataPositiveParts)
# -
len(dataRec)
dataRec.to_csv(directory + 'xgbReconstruction_parts16', sep = "\t", header = False, index = False)
| Notebooks/Reconstrucion/XGBReconstruction.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.8 64-bit (conda)
# name: python3
# ---
# # Introduction to Probability and Statistics
# |
# In this notebook, we will play around with some of the concepts we have previously discussed. Many concepts from probability and statistics are well-represented in major libraries for data processing in Python, such as `numpy` and `pandas`.
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
#
# ## Random Variables and Distributions
#
# Let's start with drawing a sample of 30 variables from a uniform distribution from 0 to 9. We will also compute mean and variance.
sample = [ random.randint(0,10) for _ in range(30) ]
print(f"Sample: {sample}")
print(f"Mean = {np.mean(sample)}")
print(f"Variance = {np.var(sample)}")
# To visually estimate how many different values are there in the sample, we can plot the **histogram**:
plt.hist(sample)
plt.show()
# ## Analyzing Real Data
#
# Mean and variance are very important when analyzing real-world data. Let's load the data about baseball players from [SOCR MLB Height/Weight Data](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights)
df = pd.read_csv("../../data/SOCR_MLB.tsv",sep='\t',header=None,names=['Name','Team','Role','Weight', 'Height', 'Age'])
df
# > We are using a package called **Pandas** here for data analysis. We will talk more about Pandas and working with data in Python later in this course.
#
# Let's compute average values for age, height and weight:
df[['Age','Height','Weight']].mean()
# Now let's focus on height, and compute standard deviation and variance:
print(list(df['Height'][:30]))
mean = df['Height'].mean()
var = df['Height'].var()
std = df['Height'].std()
print(f"Mean = {mean}\nVariance = {var}\nStandard Deviation = {std}")
# In addition to mean, it makes sense to look at median value and quartiles. They can be visualized using **box plot**:
no_nan_height = pd.DataFrame([x for x in df['Height'] if np.isnan(x) == False], columns=['Height'])
plt.figure(figsize=(10,2))
plt.boxplot(no_nan_height,vert=False,showmeans=True)
plt.grid(color='gray',linestyle='dotted')
plt.show()
# We can also make box plots of subsets of our dataset, for example, grouped by player role.
df.boxplot(column='Height',by='Role')
plt.xticks(rotation='vertical')
plt.show()
# > **Note**: This diagram suggests, that on average, height of first basemen is higher that height of second basemen. Later we will learn how we can test this hypothesis more formally, and how to demonstrate that our data is statistically significant to show that.
#
# Age, height and weight are all continuous random variables. What do you think their distribution is? A good way to find out is to plot the histogram of values:
df['Weight'].hist(bins=15)
plt.suptitle('Weight distribution of MLB Players')
plt.xlabel('Weight')
plt.ylabel('Count')
plt.show()
# ## Normal Distribution
#
# Let's create an artificial sample of weights that follows normal distribution with the same mean and variance as real data:
generated = np.random.normal(mean,std,1000)
generated[:20]
plt.hist(generated,bins=15)
plt.show()
plt.hist(np.random.normal(0,1,50000),bins=300)
plt.show()
# Since most values in real life are normally distributed, it means we should not use uniform random number generator to generate sample data. Here is what happens if we try to generate weights with uniform distribution (generated by `np.random.rand`):
wrong_sample = np.random.rand(1000)*2*std+mean-std
plt.hist(wrong_sample)
plt.show()
# ## Confidence Intervals
#
# Let's now calculate confidence intervals for the weights and heights of baseball players. We will use the code [from this stackoverflow discussion](https://stackoverflow.com/questions/15033511/compute-a-confidence-interval-from-sample-data):
# +
import scipy.stats
def mean_confidence_interval(data, confidence=0.95):
a = 1.0 * np.array(data)
n = len(a)
m, se = np.mean(a), scipy.stats.sem(a)
h = se * scipy.stats.t.ppf((1 + confidence) / 2., n-1)
return m, h
for p in [0.85, 0.9, 0.95]:
m, h = mean_confidence_interval(df['Weight'].fillna(method='pad'),p)
print(f"p={p:.2f}, mean = {m:.2f}±{h:.2f}")
# -
# ## Hypothesis Testing
#
# Let's explore different roles in our baseball players dataset:
df.groupby('Role').agg({ 'Height' : 'mean', 'Weight' : 'mean', 'Age' : 'count'}).rename(columns={ 'Age' : 'Count'})
# Let's test the hypothesis that First Basemen are higher then Second Basemen. The simplest way to do it is to test the confidence intervals:
for p in [0.85,0.9,0.95]:
m1, h1 = mean_confidence_interval(df.loc[df['Role']=='First_Baseman',['Height']],p)
m2, h2 = mean_confidence_interval(df.loc[df['Role']=='Second_Baseman',['Height']],p)
print(f'Conf={p:.2f}, 1st basemen height: {m1-h1[0]:.2f}..{m1+h1[0]:.2f}, 2nd basemen height: {m2-h2[0]:.2f}..{m2+h2[0]:.2f}')
# We can see that intervals do not overlap.
#
# More statistically correct way to prove the hypothesis is to use **Student t-test**:
# +
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Second_Baseman',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
# -
# Two values returned by the `ttest_ind` functions are:
# * p-value can be considered as the probability of two distributions having the same mean. In our case, it is very low, meaning that there is strong evidence supporting that first basemen are taller
# * t-value is the intermediate value of normalized mean difference that is used in t-test, and it is compared against threshold value for a given confidence value
# ## Simulating Normal Distribution with Central Limit Theorem
#
# Pseudo-random generator in Python is designed to give us uniform distribution. If we want to create a generator for normal distribution, we can use central limit theorem. To get a normally distributed value we will just compute a mean of a uniform-generated sample.
# +
def normal_random(sample_size=100):
sample = [random.uniform(0,1) for _ in range(sample_size) ]
return sum(sample)/sample_size
sample = [normal_random() for _ in range(100)]
plt.hist(sample)
plt.show()
# -
# ## Correlation and Evil Baseball Corp
#
# Correlation allows us to find inner connection between data sequences. In our toy example, let's pretend there is an evil baseball corporation that pays it's players according to their height - the taller the player is, the more money he/she gets. Suppose there is a base salary of $1000, and an additional bonus from $0 to $100, depending on height. We will take the real players from MLB, and compute their imaginary salaries:
heights = no_nan_height['Height']
salaries = 1000+(heights-heights.min())/(heights.max()-heights.mean())*100
print(list(zip(heights,salaries))[:10])
# Let's now compute covariance and correlation of those sequences. `np.cov` will give us so-called **covariance matrix**, which is an extension of covariance to multiple variables. The element $M_{ij}$ of the covariance matrix $M$ is a correlation between input variables $X_i$ and $X_j$, and diagonal values $M_{ii}$ is the variance of $X_{i}$. Similarly, `np.corrcoef` will give us **correlation matrix**.
print(f"Covariance matrix:\n{np.cov(heights,salaries)}")
print(f"Covariance = {np.cov(heights,salaries)[0,1]}")
print(f"Correlation = {np.corrcoef(heights,salaries)[0,1]}")
# Correlation equal to 1 means that there is a strong **linear relation** between two variables. We can visually see the linear relation by plotting one value against the other:
plt.scatter(heights,salaries)
plt.show()
# Let's see what happens if the relation is not linear. Suppose that our corporation decided to hide the obvious linear dependency between heights and salaries, and introduced some non-linearity into the formula, such as `sin`:
salaries = 1000+np.sin((heights-heights.min())/(heights.max()-heights.mean()))*100
print(f"Correlation = {np.corrcoef(heights,salaries)[0,1]}")
# In this case, the correlation is slightly smaller, but it is still quite high. Now, to make the relation even less obvious, we might want to add some extra randomness by adding some random variable to the salary. Let's see what happens:
salaries = 1000+np.sin((heights-heights.min())/(heights.max()-heights.mean()))*100+np.random.random(size=len(heights))*20-10
print(f"Correlation = {np.corrcoef(heights,salaries)[0,1]}")
plt.scatter(heights, salaries)
plt.show()
# > Can you guess why the dots line up into vertical lines like this?
#
# We have observed the correlation between artificially engineered concept like salary and the observed variable *height*. Let's also see if the two observed variables, such as height and weight, also correlate:
np.corrcoef(df['Height'],df['Weight'])
# Unfortunately, we did not get any results - only some strange `nan` values. This is due to the fact that some of the values in our series are undefined, represented as `nan`, which causes the result of the operation to be undefined as well. By looking at the matrix we can see that `Weight` is problematic column, because self-correlation between `Height` values has been computed.
#
# > This example shows the importance of **data preparation** and **cleaning**. Without proper data we cannot compute anything.
#
# Let's use `fillna` method to fill the missing values, and compute the correlation:
np.corrcoef(df['Height'],df['Weight'].fillna(method='pad'))
# The is indeed a correlation, but not such a strong one as in our artificial example. Indeed, if we look at the scatter plot of one value against the other, the relation would be much less obvious:
plt.scatter(df['Height'],df['Weight'])
plt.xlabel('Height')
plt.ylabel('Weight')
plt.show()
# ## Conclusion
#
# In this notebook, we have learnt how to perform basic operations on data to compute statistical functions. We now know how to use sound apparatus of math and statistics in order to prove some hypotheses, and how to compute confidence intervals for random variable given data sample.
| 1-Introduction/04-stats-and-probability/notebook.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Classification (Bayesian) of the Palmer penguins data
#
# This document is part of the showcase, where I replicate the same brief and simple analyses with different tools.
#
# This particular file focuses on simple (Bayesian multiclass logit) classification of the Palmer penguins data from the tidytuesday project.
#
# The data can be found in https://github.com/rfordatascience/tidytuesday/tree/master/data/2020/2020-07-28. They consist of one documents: penguins.csv contains information and measurements about some penguins.
#
# For the specific analysis I will use Python and pymc3 (plus Jupyter notebook).
#
# We start by loading the packages:
# +
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pymc3 as pm
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
# -
# and the dataset:
penguins = pd.read_csv('https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2020/2020-07-28/penguins.csv')
# We can have a look at the schema of the data:
penguins.info(verbose=True)
# and the summary statistics:
penguins.describe()
# We start by checking for missing values:
penguins.isna().sum()
# We drop all of them:
penguins = penguins.dropna(axis = 0, thresh=4, how = "all")
penguins.isna().sum()
# For this analysis we are going to use only the numeric features, so we drop the categorical:
penguins = penguins.drop(columns=['year','island','sex'])
# We are going to split the data into features and label:
species = penguins.pop('species')
# Now we can split the dataset to training and testing:
X_train, X_test, y_train, y_test = train_test_split(penguins, species, test_size=0.2, random_state=1, stratify=species)
# We extract the classes as a list:
classes = list(y_train.unique())
no_of_classes = len(classes)
no_of_classes
# And we index them (this is useful for the pymc3 model):
y_train = y_train.apply(classes.index)
y_train
# We also need to scale the features (We are going to use a standard Metropolis-Hastings MCMC and scaling would be useful)
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
# We check the training data:
X_train
# Now we can specify and run the multi-logit model in pymc3:
with pm.Model() as model:
# Priors
alpha = pm.Normal('alpha', mu=0, sd=1, shape=no_of_classes)
beta = pm.Normal('beta', mu=0, sd=1, shape=(X_train.shape[1], no_of_classes))
# Likelihood
mu = alpha + pm.math.dot(X_train, beta)
p = pm.math.exp(mu)/pm.math.sum(pm.math.exp(mu), axis=0)
y = pm.Categorical("y", p=p, observed=y_train)
# Sampling
step = pm.Metropolis()
trace = pm.sample(1000, step=step)
# We can plot the traces of the chains to check that they mixed properly:
pm.traceplot(trace)
# That looks decent.
#
# In order to test on the testing data, we need to apply the same data pre-processing (i.e. scaling the features and indexing the label):
X_test = scaler.transform(X_test)
y_test = y_test.apply(classes.index)
y_test
# For the purposes of this showcase project, we are going to use the MAP (maximum a posteriori estimate) for testing, which is effectively the mode of the posterior.
predictions = trace['alpha'].mean(axis=0) + np.dot(X_test, trace['beta'].mean(axis=0))
predicited_classes = np.argmax(np.exp(predictions).T / np.sum(np.exp(predictions), axis=1), axis=0)
# We check the predicted classes:
predicited_classes
# And finally the accuracy:
bayesianTestingAccuracy = accuracy_score(y_test, predicited_classes)
print("Accuracy: " + str(round(bayesianTestingAccuracy,4) * 100) + "%")
| PalmerPenguins_Python_pymc3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Part 1
import pandas as pd
df = pd.read_csv('input.txt', header=None, names=["depth"])
df["dif"] = df.diff()
sum(df.dif>0)
# # Part 2
w3 = df.rolling(window=3).sum()
w3d = w3.diff()
sum(w3d.depth>0)
| 2021/day1/day1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Training Neural Networks
#
# The network we built in the previous part isn't so smart, it doesn't know anything about our handwritten digits. Neural networks with non-linear activations work like universal function approximators. There is some function that maps your input to the output. For example, images of handwritten digits to class probabilities. The power of neural networks is that we can train them to approximate this function, and basically any function given enough data and compute time.
#
# <img src="assets/function_approx.png" width=500px>
#
# At first the network is naive, it doesn't know the function mapping the inputs to the outputs. We train the network by showing it examples of real data, then adjusting the network parameters such that it approximates this function.
#
# To find these parameters, we need to know how poorly the network is predicting the real outputs. For this we calculate a **loss function** (also called the cost), a measure of our prediction error. For example, the mean squared loss is often used in regression and binary classification problems
#
# $$
# \large \ell = \frac{1}{2n}\sum_i^n{\left(y_i - \hat{y}_i\right)^2}
# $$
#
# where $n$ is the number of training examples, $y_i$ are the true labels, and $\hat{y}_i$ are the predicted labels.
#
# By minimizing this loss with respect to the network parameters, we can find configurations where the loss is at a minimum and the network is able to predict the correct labels with high accuracy. We find this minimum using a process called **gradient descent**. The gradient is the slope of the loss function and points in the direction of fastest change. To get to the minimum in the least amount of time, we then want to follow the gradient (downwards). You can think of this like descending a mountain by following the steepest slope to the base.
#
# <img src='assets/gradient_descent.png' width=350px>
# ## Backpropagation
#
# For single layer networks, gradient descent is straightforward to implement. However, it's more complicated for deeper, multilayer neural networks like the one we've built. Complicated enough that it took about 30 years before researchers figured out how to train multilayer networks.
#
# Training multilayer networks is done through **backpropagation** which is really just an application of the chain rule from calculus. It's easiest to understand if we convert a two layer network into a graph representation.
#
# <img src='assets/backprop_diagram.png' width=550px>
#
# In the forward pass through the network, our data and operations go from bottom to top here. We pass the input $x$ through a linear transformation $L_1$ with weights $W_1$ and biases $b_1$. The output then goes through the sigmoid operation $S$ and another linear transformation $L_2$. Finally we calculate the loss $\ell$. We use the loss as a measure of how bad the network's predictions are. The goal then is to adjust the weights and biases to minimize the loss.
#
# To train the weights with gradient descent, we propagate the gradient of the loss backwards through the network. Each operation has some gradient between the inputs and outputs. As we send the gradients backwards, we multiply the incoming gradient with the gradient for the operation. Mathematically, this is really just calculating the gradient of the loss with respect to the weights using the chain rule.
#
# $$
# \large \frac{\partial \ell}{\partial W_1} = \frac{\partial L_1}{\partial W_1} \frac{\partial S}{\partial L_1} \frac{\partial L_2}{\partial S} \frac{\partial \ell}{\partial L_2}
# $$
#
# **Note:** I'm glossing over a few details here that require some knowledge of vector calculus, but they aren't necessary to understand what's going on.
#
# We update our weights using this gradient with some learning rate $\alpha$.
#
# $$
# \large W^\prime_1 = W_1 - \alpha \frac{\partial \ell}{\partial W_1}
# $$
#
# The learning rate $\alpha$ is set such that the weight update steps are small enough that the iterative method settles in a minimum.
# ## Losses in PyTorch
#
# Let's start by seeing how we calculate the loss with PyTorch. Through the `nn` module, PyTorch provides losses such as the cross-entropy loss (`nn.CrossEntropyLoss`). You'll usually see the loss assigned to `criterion`. As noted in the last part, with a classification problem such as MNIST, we're using the softmax function to predict class probabilities. With a softmax output, you want to use cross-entropy as the loss. To actually calculate the loss, you first define the criterion then pass in the output of your network and the correct labels.
#
# Something really important to note here. Looking at [the documentation for `nn.CrossEntropyLoss`](https://pytorch.org/docs/stable/nn.html#torch.nn.CrossEntropyLoss),
#
# > This criterion combines `nn.LogSoftmax()` and `nn.NLLLoss()` in one single class.
# >
# > The input is expected to contain scores for each class.
#
# This means we need to pass in the raw output of our network into the loss, not the output of the softmax function. This raw output is usually called the *logits* or *scores*. We use the logits because softmax gives you probabilities which will often be very close to zero or one but floating-point numbers can't accurately represent values near zero or one ([read more here](https://docs.python.org/3/tutorial/floatingpoint.html)). It's usually best to avoid doing calculations with probabilities, typically we use log-probabilities.
# +
import torch
from torch import nn
import torch.nn.functional as F
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# -
# ### Note
# If you haven't seen `nn.Sequential` yet, please finish the end of the Part 2 notebook.
# +
# Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10))
# Define the loss
criterion = nn.CrossEntropyLoss()
# Get our data
images, labels = next(iter(trainloader))
# Flatten images
images = images.view(images.shape[0], -1)
# Forward pass, get our logits
logits = model(images)
# Calculate the loss with the logits and the labels
loss = criterion(logits, labels)
print(loss)
# -
# In my experience it's more convenient to build the model with a log-softmax output using `nn.LogSoftmax` or `F.log_softmax` ([documentation](https://pytorch.org/docs/stable/nn.html#torch.nn.LogSoftmax)). Then you can get the actual probabilities by taking the exponential `torch.exp(output)`. With a log-softmax output, you want to use the negative log likelihood loss, `nn.NLLLoss` ([documentation](https://pytorch.org/docs/stable/nn.html#torch.nn.NLLLoss)).
#
# >**Exercise:** Build a model that returns the log-softmax as the output and calculate the loss using the negative log likelihood loss. Note that for `nn.LogSoftmax` and `F.log_softmax` you'll need to set the `dim` keyword argument appropriately. `dim=0` calculates softmax across the rows, so each column sums to 1, while `dim=1` calculates across the columns so each row sums to 1. Think about what you want the output to be and choose `dim` appropriately.
# +
# TODO: Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128)
,nn.ReLU()
,nn.Linear(128, 64)
,nn.ReLU()
,nn.Linear(64, 10)
,nn.LogSoftmax(dim=1))
# TODO: Define the loss
criterion = nn.NLLLoss()
### Run this to check your work
# Get our data
images, labels = next(iter(trainloader))
# Flatten images
images = images.view(images.shape[0], -1)
# Forward pass, get our logits
logits = model(images)
# Calculate the loss with the logits and the labels
loss = criterion(logits, labels)
print(loss)
# -
# ## Autograd
#
# Now that we know how to calculate a loss, how do we use it to perform backpropagation? Torch provides a module, `autograd`, for automatically calculating the gradients of tensors. We can use it to calculate the gradients of all our parameters with respect to the loss. Autograd works by keeping track of operations performed on tensors, then going backwards through those operations, calculating gradients along the way. To make sure PyTorch keeps track of operations on a tensor and calculates the gradients, you need to set `requires_grad = True` on a tensor. You can do this at creation with the `requires_grad` keyword, or at any time with `x.requires_grad_(True)`.
#
# You can turn off gradients for a block of code with the `torch.no_grad()` content:
# ```python
# x = torch.zeros(1, requires_grad=True)
# >>> with torch.no_grad():
# ... y = x * 2
# >>> y.requires_grad
# False
# ```
#
# Also, you can turn on or off gradients altogether with `torch.set_grad_enabled(True|False)`.
#
# The gradients are computed with respect to some variable `z` with `z.backward()`. This does a backward pass through the operations that created `z`.
x = torch.randn(2,2, requires_grad=True)
print(x)
y = x**2
print(y)
# Below we can see the operation that created `y`, a power operation `PowBackward0`.
## grad_fn shows the function that generated this variable
print(y.grad_fn)
# The autograd module keeps track of these operations and knows how to calculate the gradient for each one. In this way, it's able to calculate the gradients for a chain of operations, with respect to any one tensor. Let's reduce the tensor `y` to a scalar value, the mean.
z = y.mean()
print(z)
# You can check the gradients for `x` and `y` but they are empty currently.
print(x.grad)
# To calculate the gradients, you need to run the `.backward` method on a Variable, `z` for example. This will calculate the gradient for `z` with respect to `x`
#
# $$
# \frac{\partial z}{\partial x} = \frac{\partial}{\partial x}\left[\frac{1}{n}\sum_i^n x_i^2\right] = \frac{x}{2}
# $$
z.backward()
print(x.grad)
print(x/2)
# These gradients calculations are particularly useful for neural networks. For training we need the gradients of the cost with respect to the weights. With PyTorch, we run data forward through the network to calculate the loss, then, go backwards to calculate the gradients with respect to the loss. Once we have the gradients we can make a gradient descent step.
# ## Loss and Autograd together
#
# When we create a network with PyTorch, all of the parameters are initialized with `requires_grad = True`. This means that when we calculate the loss and call `loss.backward()`, the gradients for the parameters are calculated. These gradients are used to update the weights with gradient descent. Below you can see an example of calculating the gradients using a backwards pass.
# +
# Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
images, labels = next(iter(trainloader))
images = images.view(images.shape[0], -1)
logits = model(images)
loss = criterion(logits, labels)
# +
print('Before backward pass: \n', model[0].weight.grad)
loss.backward()
print('After backward pass: \n', model[0].weight.grad)
# -
# ## Training the network!
#
# There's one last piece we need to start training, an optimizer that we'll use to update the weights with the gradients. We get these from PyTorch's [`optim` package](https://pytorch.org/docs/stable/optim.html). For example we can use stochastic gradient descent with `optim.SGD`. You can see how to define an optimizer below.
# +
from torch import optim
# Optimizers require the parameters to optimize and a learning rate
optimizer = optim.SGD(model.parameters(), lr=0.01)
# -
# Now we know how to use all the individual parts so it's time to see how they work together. Let's consider just one learning step before looping through all the data. The general process with PyTorch:
#
# * Make a forward pass through the network
# * Use the network output to calculate the loss
# * Perform a backward pass through the network with `loss.backward()` to calculate the gradients
# * Take a step with the optimizer to update the weights
#
# Below I'll go through one training step and print out the weights and gradients so you can see how it changes. Note that I have a line of code `optimizer.zero_grad()`. When you do multiple backwards passes with the same parameters, the gradients are accumulated. This means that you need to zero the gradients on each training pass or you'll retain gradients from previous training batches.
# +
print('Initial weights - ', model[0].weight)
images, labels = next(iter(trainloader))
images.resize_(64, 784)
# Clear the gradients, do this because gradients are accumulated
optimizer.zero_grad()
# Forward pass, then backward pass, then update weights
output = model(images)
loss = criterion(output, labels)
loss.backward()
print('Gradient -', model[0].weight.grad)
# -
# Take an update step and few the new weights
optimizer.step()
print('Updated weights - ', model[0].weight)
# ### Training for real
#
# Now we'll put this algorithm into a loop so we can go through all the images. Some nomenclature, one pass through the entire dataset is called an *epoch*. So here we're going to loop through `trainloader` to get our training batches. For each batch, we'll doing a training pass where we calculate the loss, do a backwards pass, and update the weights.
#
# >**Exercise:** Implement the training pass for our network. If you implemented it correctly, you should see the training loss drop with each epoch.
# +
## Your solution here
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003)
epochs = 5
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
# Flatten MNIST images into a 784 long vector
images = images.view(images.shape[0], -1)
# print(output.shape, labels.shape)
# TODO: Training pass
optimizer.zero_grad()
output = model.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
print(f"Training loss: {running_loss/len(trainloader)}")
# -
# With the network trained, we can check out it's predictions.
# +
# %matplotlib inline
import helper
images, labels = next(iter(trainloader))
img = images[0].view(1, 784)
# Turn off gradients to speed up this part
with torch.no_grad():
logps = model(img)
# Output of the network are log-probabilities, need to take exponential for probabilities
ps = torch.exp(logps)
print(img.view(1, 28, 28).shape, ps.shape)
helper.view_classify(img.view(1, 28, 28), ps)
# -
# Now our network is brilliant. It can accurately predict the digits in our images. Next up you'll write the code for training a neural network on a more complex dataset.
| intro-to-pytorch/Part 3 - Training Neural Networks (Exercises).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import matplotlib.pyplot as plt
import os
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.metrics import accuracy_score, mean_squared_error, mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import xgboost as xgb
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
from sklearn.model_selection import StratifiedKFold, KFold
from datetime import datetime
from feature_engineering import compute_ttfl
# -
path_data = os.path.join(os.getcwd(), 'data', 'season_2018_cleaned.csv')
df = pd.read_csv(path_data)
df.head()
df['record'] = df.wins - df.losses
# +
df_opp = df.copy()[['team', 'wins', 'losses', 'opp', 'date']]
df_opp['opp_record'] = df_opp['wins'] - df_opp['losses']
df_opp = df_opp.rename(columns={'team': 'opp', 'opp': 'team'})
df_opp = df_opp.drop_duplicates(subset=['opp', 'team', 'date', 'opp_record'])
df_opp.drop(columns=['wins', 'losses'], inplace=True)
df = df.merge(df_opp)
df = df.fillna(0)
for col in list(df.columns):
col_no_inf = df[df[col] != np.inf][col].max()
df[col] = df[col].replace(np.inf, col_no_inf)
col_no_ninf = df[df[col] != -np.inf][col].min()
df[col] = df[col].replace(-np.inf, col_no_ninf)
# -
int_cols = list(df.dtypes[(df.dtypes == int)].index)
float_cols = list(df.dtypes[(df.dtypes == float)].index)
df[int_cols + float_cols] = df[int_cols + float_cols].round(2)
targets = ['fg', 'fga', 'fg3', 'fg3a', 'ft', 'fta', 'orb', 'drb', 'ast', 'stl', 'blk', 'tov', 'pts', ' trb']
regressions = {'fg': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'orb_lw', 'orb_sn', 'tot_game'],
'fga': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'tot_game'],
'fg3': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'orb_lw', 'orb_sn', 'tot_game'],
'fg3a': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'tot_game'],
'ft': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'orb_lw', 'orb_sn', 'tot_game'],
'fta': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'tot_game'],
'pts': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'orb_lw', 'orb_sn', 'tot_game', 'stl_lw',
'stl_sn'],
'ttfl': ['fg_lw', 'fg_pct_lw', 'fg3_lw', 'fg3_pct_lw', 'fga_lw', 'fg3a_lw', 'ft_lw', 'fta_lw',
'fg_sn', 'fg_pct_sn', 'fg3_sn', 'fg3_pct_sn', 'fga_sn', 'fg3a_sn', 'ft_sn', 'fta_sn',
'last_game', 'mp_lw', 'mp_sn', 'opp_record', 'record', 'plus_minus_lw', 'plus_minus_sn',
'pts_lw', 'pts_sn', 'score_lw', 'score_sn', 'orb_lw', 'orb_sn', 'tot_game', 'stl_lw',
'stl_sn', 'tov_lw', 'tov_sn', 'drb_lw', 'drb_sn', 'blk_lw', 'blk_sn', 'ast_lw', 'ast_sn'],
'tov': ['tov_sn', 'tov_lw', 'opp_record', 'opp_score_lw', 'pls_minus_sn', 'plus_minus_lw']}
not_ttfl_col = not_ttfl_col = list(set(df.columns) - set(targets) - set(['ttfl']))
cols = [col for col in list(not_ttfl_col) if
col.endswith('_sn') or col.endswith('lw')] + ['last_game', 'tot_game' , 'opp_record' , 'record']
def linear_regression(df, target, varbls):
y = df[target]
X = df[varbls]
X = MinMaxScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1337)
model = LinearRegression()
model.fit(X_train, y_train)
#training_score = model.score(X_train, y_train)
#testing_score = model.score(X_test, y_test)
y_pred = model.predict(X_test)
return y_test, y_pred
def linear_regression_ttfl(df, regressions):
reg = {}
for target in targets:
if target != 'ttfl':
reg[target] = linear_regression(df, target, targets)[0]
ttfl_computed = compute_ttfl(reg, missed=False)
return ttfl_computed
def cross_val(df, target, varbls):
y = df[target]
X = df[varbls]
model = LinearRegression()
res = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=5,
verbose=3, n_jobs=3)
print(res)
res = {}
for target, varbls in regressions.items():
reg = linear_regression(df, target, varbls)
reg2 = linear_regression(df, target, cols)
res[target] = np.sqrt(mean_absolute_error(reg[0], reg[1]), mean_absolute_error(reg2[0], reg2[1])
print(target, res[target])
def xgb_cv(df, target, varbls):
y = df[target]
X = df[varbls]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1337)
params = {
'min_child_weight': [1, 3, 5],
'gamma': [0.1, 0.2, 0.3, 0.4, 0.5],
'subsample': [0.5, 0.55, 0.6],
'colsample_bytree': [0.4, 0.5, 0.6],
'max_depth': [3, 4, 5],
'reg_alpha': [0.25, 0.5, 0.75, 1.0, 1.25],
'reg_lambda': [0.8, 0.85, 0.9],
'learning_rate': [0.1, 0.15, 0.2]
}
xgb_reg = xgb.XGBRegressor(objective = 'reg:squarederror',
n_estimators = 200)
folds = 5
param_comb = 10
skf = KFold(n_splits=folds, shuffle = True, random_state = 1001)
random_search = RandomizedSearchCV(xgb_reg, param_distributions=params,
n_iter=param_comb, scoring='neg_median_absolute_error',
n_jobs=4, cv=skf.split(X_train,y_train),
verbose=3, random_state=1001)
# Here we go
# timing starts from this point for "start_time" variable
random_search.fit(X_train, y_train)
# timing ends here for "start_time" variable
preds = random_search.predict(X_test)
mae = (mean_absolute_error(y_test, preds))
bp = random_search.best_params_
return mae, bp
res = xgb_cv(df, 'ttfl', cols)
print(res)
X = df[cols]
y = df['ttfl']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1337)
model_xgb = xgb.XGBRegressor(n_estimators=2200,
random_state =7, nthread = -1, **res[1])
model_xgb.fit(X_train, y_train)
preds = model_xgb.predict(X_test)
np.sqrt(mean_squared_error(y_test, preds))
pd.Series(model_xgb.feature_importances_, index = varbls).sort_values().plot(kind = "barh", figsize=(15,10) ,title='Top Features')
plt.show()
class xgb():
def __init__(self):
self
| src/baseline_regression.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Lateral fill on model grid
#
# This example shows how to apply `pop_tools.lateral_fill` on a model dataset. We use a model grid dataset for illustration purposes.
# +
# %matplotlib inline
import numpy as np
import xarray as xr
import pop_tools
xr.set_options(display_style="html") # fancy HTML repr
# -
ds = pop_tools.get_grid('POP_gx3v7')
ds
# ## Generate a field with some missing values
field = ds.KMT.copy() * 1.0
field = field.where(ds.KMT > 0)
field.values[20:40, :] = np.nan
field.plot()
# ## Fill the missing values
field_filled = pop_tools.lateral_fill(field, isvalid_mask=(ds.KMT > 0))
h = field_filled.plot()
# %load_ext watermark
# %watermark -d -iv -m -g -h
| docs/source/examples/lateral-fill-model-grid.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/statmike/Logistic-Regression/blob/main/02_Feature_Engineering.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="pVDVrSSQ6qlS"
# ## Important Tools for Fitting: Descriptions and Demonstrations
#
# The example above is rather simple: 2 classification levels, single continous factor. No missing data, no rare events, no execess of features, no ability to add more features ....
#
# In real-life we need tools to handle complexity ... messiness
#
# Feature Engineering is all about making the data useful for machine learning!
#
# The following takes common tasks and shows some typical ways of handling them. This is not a detailed or exhaustive list but is a great starting point for understanding.
# + id="eS2-M_2Kxb_d"
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn as sk
from sklearn import linear_model
# + [markdown] id="_ltqR7-N634E"
# ### Categorical Factors - call me a dummy!
#
# One-hot encoding ...
#
# Why one-hot?
#
# + id="fGLl4fns-1vu"
size_format = {0 : 'Small', 1 : 'Medium', 2 : 'Large'}
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="mJrhszEq-B2A" outputId="fb62661a-5e5a-44de-e409-b831035c037d"
np.random.seed(seed=32259)
coffee = pd.DataFrame({'size' : np.random.binomial(1,.5,10)})
coffee['size_code'] = coffee['size'].map(size_format)
coffee
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="FTkL7C1QBuYZ" outputId="2faed755-c885-4dc3-fa11-249e762e4312"
pd.get_dummies(coffee['size_code'])
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="q-_f2tSvAJu9" outputId="b888aa62-ac3d-4f9e-acf5-c6e75acceaec"
np.random.seed(seed=32259)
coffee = pd.DataFrame({'size' : np.random.binomial(2,.5,10)})
coffee['size_code'] = coffee['size'].map(size_format)
coffee
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="b6zQm_LzCM_B" outputId="c0446420-bbca-4327-ecf3-ec9106ad8c14"
pd.get_dummies(coffee['size_code'])
# + [markdown] id="N5RTGspn7yTj"
# ### Continous Factors - stairs can make the hill easier to climb
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="7eZ3vRTXEJaF" outputId="d7f89e86-93b4-4947-c609-56df317f5803"
np.random.seed(seed=32259)
dist = pd.DataFrame(np.random.normal(loc=(10,20), scale=(4,2), size=(1000,2)),columns=['x1','x2'])
dist.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 322} id="_AAf2fg6-dBy" outputId="488a020e-d8c5-4166-fe19-f5c0c189bf6e"
plt.xkcd()
fig, ax = plt.subplots()
dist.plot.kde(ax=ax, legend=True, title='Histogram')
ax.set_ylabel('Probability')
ax.grid(axis='y')
plt.rcdefaults()
# + [markdown] id="7hkxKvl97yGh"
# #### Scale
# + colab={"base_uri": "https://localhost:8080/", "height": 494} id="sBWiEy9w_B_5" outputId="317bdfde-d662-44b3-8693-dc0377403443"
# mean normalization
normalized_dist = (dist-dist.mean())/dist.std()
plt.xkcd()
fig, ax = plt.subplots()
normalized_dist.plot.kde(ax=ax, legend=True, title='Histogram')
ax.set_ylabel('Probability')
ax.grid(axis='y')
plt.rcdefaults()
# + colab={"base_uri": "https://localhost:8080/", "height": 493} id="Sw_EIQZS_n2y" outputId="1032328f-5046-4a1b-8792-55964ec3ae74"
# min/max normalization
normalized_dist = (dist-dist.min())/(dist.max()-dist.min())
plt.xkcd()
fig, ax = plt.subplots()
normalized_dist.plot.kde(ax=ax, legend=True, title='Histogram')
ax.set_ylabel('Probability')
ax.grid(axis='y')
plt.rcdefaults()
# + [markdown] id="62bzI-Zn7xzh"
# #### Divy-Up
# + colab={"base_uri": "https://localhost:8080/", "height": 437} id="6DZbFhv5D2Mr" outputId="2fd04d45-87cc-4182-f321-bc383c18743b"
plt.xkcd()
fig, ax = plt.subplots()
normalized_dist.plot.hist(ax=ax, bins=10, alpha=0.5, legend=True)
plt.rcdefaults()
# + [markdown] id="2v121_kl8z5P"
# ### Missing Points? (must be somewhere in [The Middle](https://youtu.be/M3mJkSqZbX4?t=36))
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="pg8SJFSOFhoD" outputId="72ccefd1-47b3-4926-dd98-abecfd39fffe"
np.random.seed(seed=32259)
coffee['taste'] = pd.DataFrame({'taste' : np.random.normal(10,1,10) * np.random.binomial(1,.8,10)})
coffee.loc[coffee['taste'] == 0, 'taste'] = np.nan
coffee
# + colab={"base_uri": "https://localhost:8080/", "height": 250} id="DcBFsFbIKPqH" outputId="e024016a-b71f-4e6b-f9f2-7543d15915f6"
coffee['taste_mean']= coffee['taste'].fillna(coffee['taste'].mean())
coffee.style.highlight_null(null_color='red')
# + colab={"base_uri": "https://localhost:8080/", "height": 250} id="Zc3fZyGpLMAv" outputId="c23b97cb-36c4-401c-c816-8bbcf15d6c6d"
coffee['taste_med']= coffee['taste'].fillna(coffee['taste'].median())
coffee.style.highlight_null(null_color='red')
# + colab={"base_uri": "https://localhost:8080/", "height": 335} id="eseQXacT6DgL" outputId="404ea0e2-f774-4f70-fe98-4bf303d6ae92"
coffee['size_code2'] = coffee['size_code']
coffee['size_code2'][5] = np.nan
coffee.style.highlight_null(null_color='red')
# + colab={"base_uri": "https://localhost:8080/", "height": 250} id="0r13moBo66bn" outputId="bb8d0324-7a59-4c9b-957a-954b9e9eca36"
coffee['size_code2_mode']= coffee['size_code2'].fillna(coffee['size_code2'].mode()[0])
coffee.style.highlight_null(null_color='red')
# + [markdown] id="WPnXVGg78574"
# ### Get Fit
#
# [](https://www.betterthanpants.com/i-m-into-fitness-fit-ness-taco-in-my-mouth-funny-shirt#)
#
# + [markdown] id="Uud6uCfSTrAV"
# HA! A better example (click it for article):
#
# [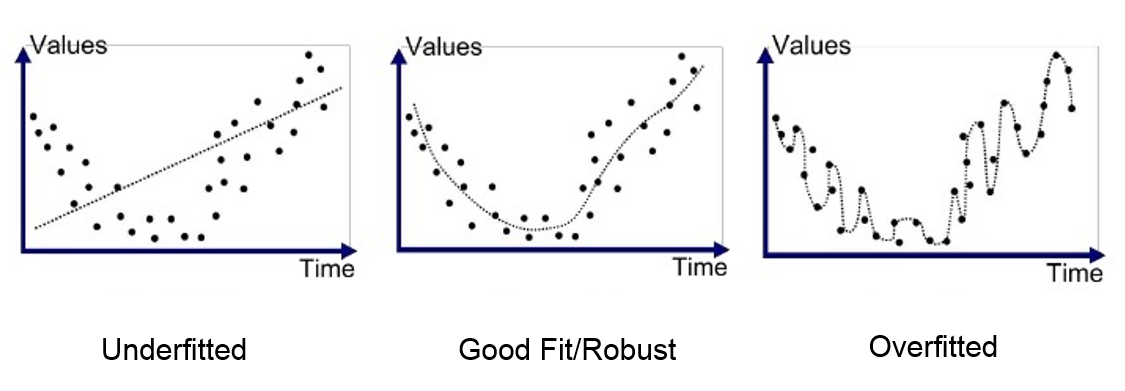](https://medium.com/greyatom/what-is-underfitting-and-overfitting-in-machine-learning-and-how-to-deal-with-it-6803a989c76)
# + [markdown] id="FCuzLoHn9gdG"
# #### Regulate Bad Behavior to get a "Good Fit"
# It's like putting some of your weight in the penalty box:
#
# 
# Photo by <NAME> from Pexels
#
# + [markdown] id="ZqF1mlt8fxzh"
# Types of penalties....
#
# Regulate = build a less complex model
#
# **Common**
#
# Why L1 and L2?
# - names come from [vector norm calculations](https://simple.wikipedia.org/wiki/Norm_(mathematics))
# - both introduce a hyperparameter that is the multiplier of a penalty
# - L1 is Lasso
# - Lasso Regression
# - Lasso = LASSO = Least Aboslute Shrinkage and Selection Operator
# - penalty is on absolute value of magnitude of the coefficient (how far it is from zero)
# - zero is like no regularization
# - large is like over-weighting, ... so underfitting
# - It reins in less important features! Even removes them altogether sometimes.
# - Feature selection!
# - L2 is Ridge
# - Ridge Regression
# - here
# - penalty is on the squared magnitude of the coefficient
# - zero is like no regularization
# - large is like over-weighting, ... so underfitting
# - elastic net?
# - Combination of L1 and L2
# - and it adds another hyperparmeter that adjusts the mixture of L1 and L2
#
#
#
# Is there something else?
# Of Course! It's math so there is always more!
# For instance, Neural networks have
# - L1 and L2!!!
# - and
# - dropout
# - batch-normalization
# - data augmentation
# - early stopping
#
# + colab={"base_uri": "https://localhost:8080/"} id="UsVf1RHd9m35" outputId="b7c46c7b-03c0-4c4d-df8f-28e05ea62313"
from sklearn import datasets
digits = datasets.load_digits()
digits_df = pd.DataFrame(data=digits.data)
digits_df['target'] = digits.target
digits_df['target_OE'] = digits_df['target'].apply(lambda x : 'Odd' if x%2==1 else ('Even' if x%2==0 else ''))
x_train, x_test, y_train, y_test = sk.model_selection.train_test_split(digits_df.iloc[:,:64], digits_df.target_OE, test_size=0.25, random_state=32259)
lr_none = sk.linear_model.LogisticRegression(max_iter=3000, solver='saga', penalty='none') # bump up from default of max_iter=100
lr_none.fit(x_train, y_train)
lr_l1 = sk.linear_model.LogisticRegression(max_iter=3000, solver='saga', penalty='l1') # bump up from default of max_iter=100
lr_l1.fit(x_train, y_train)
lr_l2 = sk.linear_model.LogisticRegression(max_iter=3000, solver='saga', penalty='l2') # bump up from default of max_iter=100
lr_l2.fit(x_train, y_train)
lr_en = sk.linear_model.LogisticRegression(max_iter=3000, solver='saga', penalty='elasticnet', l1_ratio=.5) # bump up from default of max_iter=100
lr_en.fit(x_train, y_train)
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="YNOnex_SYEfh" outputId="19b036f1-2398-40e0-93b3-e38c99365e03"
coef = pd.DataFrame(data=lr_none.coef_.T,columns=['No Regularization'])
coef['L1 Regularization'] = pd.DataFrame(lr_l1.coef_.T)
coef['L2 Regularization'] = pd.DataFrame(lr_l2.coef_.T)
coef['Elastic Net Regularization'] = pd.DataFrame(lr_en.coef_.T)
coef
# + colab={"base_uri": "https://localhost:8080/", "height": 390} id="IE0hd71tewwh" outputId="ea73caed-92e2-4ac0-cc73-c9ccf373b583"
coef[coef['L1 Regularization']==0]
# + colab={"base_uri": "https://localhost:8080/", "height": 492} id="4BKAb8QuaH7n" outputId="357e0348-1b4d-4cae-e115-fc1ce8910126"
plt.xkcd()
plt.axhline(0,color='black')
plt.scatter(coef.index, coef['No Regularization'], alpha=0.5, label='No Regularization')
plt.scatter(coef.index, coef['L1 Regularization'], alpha=0.5, label='L1 Regularization')
plt.scatter(coef.index, coef['L2 Regularization'], alpha=0.5, label='L2 Regularization')
plt.scatter(coef.index, coef['Elastic Net Regularization'], alpha=0.5, label='Elastic Net Regularization')
plt.xlabel("Weight #")
plt.legend()
plt.ylabel("Estimate for Weight")
plt.rcdefaults()
# + colab={"base_uri": "https://localhost:8080/"} id="pTRKvgbRS0ab" outputId="6b0cc341-7d12-4f74-c62b-7db612c8422b"
print("No Regularization: \n",sk.metrics.classification_report(y_test,lr_none.predict(x_test)))
# + colab={"base_uri": "https://localhost:8080/"} id="Li6G-wmQS5D3" outputId="4aa90367-755f-415b-9874-3d5bc1f6e33b"
print("L1 Regularization: \n",sk.metrics.classification_report(y_test,lr_l1.predict(x_test)))
# + colab={"base_uri": "https://localhost:8080/"} id="-_jyVGH0S-_d" outputId="e9962bee-2660-4909-fe95-0b29098af35e"
print("L2 Regularization: \n",sk.metrics.classification_report(y_test,lr_l2.predict(x_test)))
# + colab={"base_uri": "https://localhost:8080/"} id="-OZWmR0nmcav" outputId="373937c1-a6b2-4311-98df-93e5a3b18993"
print("Elastic Net Regularization:",sk.metrics.classification_report(y_test,lr_en.predict(x_test)))
# + [markdown] id="J_L1zREQ01Jv"
# 4 Fits, Three types of regularization, 4 seperate sets of parameter estimates, all have the same accuracy.
| 02_Feature_Engineering.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
self.out = 1/(1+np.exp(-x))
return self.out
def backward(self, dout):
return dout*(1.0-self.out)*self.out
class Affine:
def __init__(self):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dw = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
| DeepLearning/BackPropagation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: ECC
# language: python
# name: ecc
# ---
# +
import numpy as np
import tensorflow as tf
from tensorflow.keras import Model
from tensorflow.keras.layers import Dense, Input, concatenate, BatchNormalization
from tensorflow.keras.losses import MeanSquaredError,MSE
from tensorflow.keras.metrics import MeanAbsoluteError
from tensorflow.keras.optimizers import Adam,RMSprop
from tensorflow.keras.regularizers import l2
from tensorflow.keras.models import load_model
from spektral.data import MixedLoader,Dataset,DisjointLoader,Graph,BatchLoader
from spektral.datasets.mnist import MNIST
from spektral.layers import GCNConv,GlobalSumPool,ECCConv,CrystalConv,GlobalMaxPool
from spektral.layers import GlobalAvgPool,GlobalAttnSumPool,GlobalAttentionPool
from spektral.layers.ops import sp_matrix_to_sp_tensor
from spektral.data import Graph
from spektral.data import Dataset
import rdkit.Chem as Chem
from rdkit.Chem import AllChem
import csv
import warnings
warnings.filterwarnings("ignore")
# +
Index, X_smiles, M_adducts, CCS = [],[],[],[]
f = csv.reader(open('data/Attribute importance data/data.csv','r', encoding='gbk',errors='ignore'))
for i in f:
Index.append(i[0])
X_smiles.append(i[1])
M_adducts.append(i[2])
CCS.append(float(i[3]))
GCN_smiles, GCN_adducts, GCN_Index, GCN_CCS = [],[],[],[]
for i in range(len(X_smiles)):
try:
GCN_smiles.append(X_smiles[i])
GCN_adducts.append(M_adducts[i])
GCN_Index.append(Index[i])
GCN_CCS.append(CCS[i])
except:
;
smiles, ccs, adduct, Coordinate = [], [], [], []
for i in range(len(GCN_Index)):
MOL = Chem.MolFromSmiles(GCN_smiles[i])
atoms = [atom.GetSymbol() for atom in MOL.GetAtoms()]
one_atom = []
f = csv.reader(open('data/Attribute importance data/Coordinate data/'+str(GCN_Index[i])+'.csv','r'))
files = [i for i in f]
for j in range(len(atoms)):
one_atom.append([float(iii) for iii in files[j+1][2:]])
Coordinate.append(one_atom)
smiles.append([GCN_smiles[i]])
ccs.append([GCN_CCS[i]])
adduct.append(GCN_adducts[i])
###########################################################################################
Max_Coor = 15.615155868453662
Min_Coor = -15.475082312818216
for i in range(len(Coordinate)):
Coordinate[i] = (np.array((Coordinate[i])) - Min_Coor) / (Max_Coor - Min_Coor)
Atom_radius = {'N' :71, 'Se':116, 'F':64, 'Co':111, 'O':63,'As':121,
'Br':114,'Cl':99, 'S':103,'C' :75, 'P':111, 'I':133,'H':32}
Atom_radius_list = [Atom_radius[i] for i in Atom_radius]
Max_radius, Min_radius = np.max(Atom_radius_list), np.min(Atom_radius_list)
for i in Atom_radius:
Atom_radius[i] = (Atom_radius[i] - Min_radius) / (Max_radius-Min_radius)
Atom_mass = {'N':14.00674,'Se':78.96,'F':18.9984032,'Co':58.933195,'As':74.92160,
'O':15.9994,'Br':79.904,'Cl':35.453,'S':32.065,'C':12.0107,
'P':30.973762,'I':126.90447,'H':1.00794}
Atom_mass_list = [Atom_mass[i] for i in Atom_mass]
Max_mass, Min_mass = np.max(Atom_mass_list), np.min(Atom_mass_list)
for i in Atom_mass:
Atom_mass[i] = (Atom_mass[i] - Min_mass) / (Max_mass-Min_mass)
All_Atoms = ['As', 'Br', 'C', 'Cl', 'F', 'I', 'N', 'O', 'P', 'S', 'Se']
###########################################################################################
def convertToGraph(smi_lst):
adj,adj_norm, features, edge_features = [], [], [], []
maxNumAtoms = 50
NodeNumFeatures, EdgeNumFeatures, INDEX = 0, 4, -1
for smi in smi_lst:
INDEX += 1
iMol = Chem.MolFromSmiles(smi[0])
maxNumAtoms = iMol.GetNumAtoms()
iAdjTmp = Chem.rdmolops.GetAdjacencyMatrix(iMol)
one_edge_features = edge_feature(iMol)
edge_features.append(one_edge_features)
iFeature = np.zeros((maxNumAtoms, NodeNumFeatures))
iFeatureTmp = []
for atom in iMol.GetAtoms():
iFeatureTmp.append(atom_feature(atom,INDEX))
features.append(np.array(iFeatureTmp))
adj.append(iAdjTmp)
features = np.asarray(features)
edge_features = np.asarray(edge_features)
return adj, features, edge_features
def atom_feature(atom,INDEX):
return np.array(
one_of_k_encoding_unk(atom.GetSymbol() ,All_Atoms) +
one_of_k_encoding_unk(atom.GetDegree(), [0, 1, 2, 3, 4]) +
[Atom_radius[atom.GetSymbol()],Atom_mass[atom.GetSymbol()]] +
one_of_k_encoding_unk(atom.IsInRing(), [0, 1]) +
list(Coordinate[INDEX][atom.GetIdx()])
)
def one_of_k_encoding_unk(x, allowable_set):
if x not in allowable_set:
x = allowable_set[-1]
return list(map(lambda s: x == s, allowable_set))
def edge_feature(iMol):
# 获得分子的邻接矩阵
iAdjTmp = Chem.rdmolops.GetAdjacencyMatrix(iMol)
Edge_feature = []
count = 0
for bond in iMol.GetBonds():
count += 1
bond_feature = np.array(
one_of_k_encoding_unk(bond.GetBondTypeAsDouble(),[1,1.5,2,3])
)
Edge_feature.append(bond_feature)
Edge_feature.append(bond_feature)
Edge_feature = np.array(Edge_feature)
Edge_feature = Edge_feature.astype(np.float)
return Edge_feature
adj, features, edge_features = convertToGraph(smiles)
# +
class MyDataset(Dataset):
def __init__(self, features, adj, edge_features, ccs, **kwargs):
self.features = features
self.adj = adj
self.edge_features = edge_features
self.ccs = ccs
super().__init__(**kwargs)
def read(self):
return [Graph(x = self.features[i],
a = self.adj[i],
e = self.edge_features[i],
y = float(self.ccs[i][0])) for i in range(len(self.adj))]
DataSet = MyDataset(features, adj, edge_features, ccs)
print(DataSet)
adduct_SET = ['[M+H]+', '[M+Na]+', '[M-H]-']
adduct_SET.sort()
print(adduct_SET)
dataset_te = DataSet
adduct_te = adduct
# -
import spektral
import umap
ECC_model = load_model('model/model.h5',
custom_objects = {"ECCConv": spektral.layers.ECCConv,
"GlobalSumPool": spektral.layers.GlobalSumPool})
# +
# 2 : Coordinates
# 3 : Elemental symbols
# 4 : Degree
# 5 : Atomic radius
# 6 : Atomic volume
# 7 : Is on the ring
def convertToGraph_2(smi_lst, SWITCH):
adj,adj_norm, features, edge_features = [], [], [], []
NodeNumFeatures, EdgeNumFeatures, INDEX = 0, 4, -1
for smi in smi_lst:
INDEX += 1
iMol = Chem.MolFromSmiles(smi[0]) # Convert Smiles strings to mol objects
maxNumAtoms = iMol.GetNumAtoms()
iAdjTmp = Chem.rdmolops.GetAdjacencyMatrix(iMol) # Obtain the adjacency matrix of mol
# Characterization of structural chemical bonds
one_edge_features = edge_feature(iMol)
edge_features.append(one_edge_features)
# Constructing node feature data
iFeature = np.zeros((maxNumAtoms, NodeNumFeatures))
iFeatureTmp = []
for atom in iMol.GetAtoms():
if SWITCH == 1:
iFeatureTmp.append(atom_feature_2(atom,INDEX))
elif SWITCH == 2:
iFeatureTmp.append(atom_feature_3(atom,INDEX))
elif SWITCH == 3:
iFeatureTmp.append(atom_feature_4(atom,INDEX))
elif SWITCH == 4:
iFeatureTmp.append(atom_feature_5(atom,INDEX))
elif SWITCH == 5:
iFeatureTmp.append(atom_feature_6(atom,INDEX))
elif SWITCH == 6:
iFeatureTmp.append(atom_feature_7(atom,INDEX))
features.append(np.array(iFeatureTmp))
adj.append(iAdjTmp)
features = np.asarray(features)
edge_features = np.asarray(edge_features)
return adj, features, edge_features
'''Coordinates'''
def atom_feature_2(atom,INDEX):
return np.array(
one_of_k_encoding_unk(atom.GetSymbol() ,All_Atoms) +
one_of_k_encoding_unk(atom.GetDegree(), [0, 1, 2, 3, 4]) +
[Atom_radius[atom.GetSymbol()],Atom_mass[atom.GetSymbol()]] +
one_of_k_encoding_unk(atom.IsInRing(), [0, 1]) +
[0,0,0]
)
'''Elemental symbols'''
def atom_feature_3(atom,INDEX):
return np.array(
[0,0,0,0,0,0,0,0,0,0,0] +
one_of_k_encoding_unk(atom.GetDegree(), [0, 1, 2, 3, 4]) +
[Atom_radius[atom.GetSymbol()],Atom_mass[atom.GetSymbol()]] +
one_of_k_encoding_unk(atom.IsInRing(), [0, 1]) +
list(Coordinate[INDEX][atom.GetIdx()])
)
'''Degree'''
def atom_feature_4(atom,INDEX):
return np.array(
one_of_k_encoding_unk(atom.GetSymbol() ,All_Atoms) +
[0,0,0,0,0] +
[Atom_radius[atom.GetSymbol()],Atom_mass[atom.GetSymbol()]] +
one_of_k_encoding_unk(atom.IsInRing(), [0, 1]) +
list(Coordinate[INDEX][atom.GetIdx()])
)
'''Atomic radius'''
def atom_feature_5(atom,INDEX):
return np.array(
one_of_k_encoding_unk(atom.GetSymbol() ,All_Atoms) +
one_of_k_encoding_unk(atom.GetDegree(), [0, 1, 2, 3, 4]) +
[0,Atom_mass[atom.GetSymbol()]] +
one_of_k_encoding_unk(atom.IsInRing(), [0, 1]) +
list(Coordinate[INDEX][atom.GetIdx()])
)
'''Atomic volume'''
def atom_feature_6(atom,INDEX):
return np.array(
one_of_k_encoding_unk(atom.GetSymbol() ,All_Atoms) +
one_of_k_encoding_unk(atom.GetDegree(), [0, 1, 2, 3, 4]) +
[Atom_radius[atom.GetSymbol()],0] +
one_of_k_encoding_unk(atom.IsInRing(), [0, 1]) +
list(Coordinate[INDEX][atom.GetIdx()])
)
'''Is on the ring'''
def atom_feature_7(atom,INDEX):
return np.array(
one_of_k_encoding_unk(atom.GetSymbol() ,All_Atoms) +
one_of_k_encoding_unk(atom.GetDegree(), [0, 1, 2, 3, 4]) +
[Atom_radius[atom.GetSymbol()],Atom_mass[atom.GetSymbol()]] +
list([0,0]) +
list(Coordinate[INDEX][atom.GetIdx()])
)
# +
adj_2, features_2, edge_features_2 = convertToGraph_2(smiles, 1)
adj_3, features_3, edge_features_3 = convertToGraph_2(smiles, 2)
adj_4, features_4, edge_features_4 = convertToGraph_2(smiles, 3)
adj_5, features_5, edge_features_5 = convertToGraph_2(smiles, 4)
adj_6, features_6, edge_features_6 = convertToGraph_2(smiles, 5)
adj_7, features_7, edge_features_7 = convertToGraph_2(smiles, 6)
DataSet_2 = MyDataset(features_2, adj_2, edge_features_2, ccs)
DataSet_3 = MyDataset(features_3, adj_3, edge_features_3, ccs)
DataSet_4 = MyDataset(features_4, adj_4, edge_features_4, ccs)
DataSet_5 = MyDataset(features_5, adj_5, edge_features_5, ccs)
DataSet_6 = MyDataset(features_6, adj_6, edge_features_6, ccs)
DataSet_7 = MyDataset(features_7, adj_7, edge_features_7, ccs)
dataset_te_2 = DataSet_2
dataset_te_3 = DataSet_3
dataset_te_4 = DataSet_4
dataset_te_5 = DataSet_5
dataset_te_6 = DataSet_6
dataset_te_7 = DataSet_7
# -
def Fun(dataset_te,X):
loader_te = BatchLoader(dataset_te,batch_size=1,epochs=1,shuffle=False); loader_te_data = (); ltd_index = 0;
for i in loader_te.load():
adduct_one_hot = [one_of_k_encoding_unk(adduct_te[ltd_index+ltd_index_i],adduct_SET) for ltd_index_i in range(len(i[1]))]
adduct_one_hot = np.array(adduct_one_hot)
one_sample = ((adduct_one_hot,i[0][0],i[0][1],i[0][2]),i[1])
loader_te_data += (one_sample,)
ltd_index += len(i[1])
loader_te_data = (i for i in loader_te_data)
for batch in loader_te_data:
inputs, target = batch
predictions = ECC_model(inputs, training=False)
predictions = np.array(predictions[0])
X.append(predictions[0])
return np.array(X)
Target = np.array([i[0] for i in ccs])
A = Fun(dataset_te,[])
B = Fun(dataset_te_2,[])
C = Fun(dataset_te_3,[])
D = Fun(dataset_te_4,[])
E = Fun(dataset_te_5,[])
F = Fun(dataset_te_6,[])
G = Fun(dataset_te_7,[])
A2 = abs(Target-A)/Target*100.
B2 = abs(Target-B)/Target*100.
C2 = abs(Target-C)/Target*100.
D2 = abs(Target-D)/Target*100.
E2 = abs(Target-E)/Target*100.
F2 = abs(Target-F)/Target*100.
G2 = abs(Target-G)/Target*100.
# +
from sklearn.metrics import r2_score
R2_Score = r2_score(A,Target)
print(R2_Score,np.median(A2),'\n')
ALL_ARE = [np.mean(B2)-np.mean(A2),
np.mean(C2)-np.mean(A2),
np.mean(D2)-np.mean(A2),
np.mean(E2)-np.mean(A2),
np.mean(F2)-np.mean(A2),
np.mean(G2)-np.mean(A2)]
ALL_ARE_P = [i/np.sum(ALL_ARE) for i in ALL_ARE]
print(ALL_ARE_P)
print(ALL_ARE)
| others/Attribute Analysis.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Annotate Stories against KG
#
# In this notebook, we will annotate 4 random stories scraped manually from [ScienceDaily.com](https://www.sciencedaily.com/) against a company-proprietary Knowledge Graph (KG).
#
# The KG is provided as a TSV file of nodes (concepts) and edges (relationships). We will use the node file to construct a data structure, called an automaton, to support the [Aho-Corasick algorithm](https://en.wikipedia.org/wiki/Aho%E2%80%93Corasick_algorithm). Conceptually, the data structure maps concept names (and synonyms) to the concept ID. As an article text is streamed against it, the algorithm will capture the text spans that match the concept names in the structure.
#
# Output is a single TSV file containing the story ID, the concept ID, and the number of times the concept ID was found in the story.
import ahocorasick
import pandas as pd
import operator
import os
import string
# +
DATA_DIR = "../data"
VERTEX_FILEPATH = os.path.join(DATA_DIR, "emmet-vertices.tsv")
CONCEPTMAP_FILEPATH = os.path.join(DATA_DIR, "story-concepts.tsv")
# -
# ### Build the Aho-Corasick Automaton
#
# We filter out `qualifier` and `event` type concepts since they are somewhat noisy. We also remove acronyms that are 2 characters or less in size. Both are attempts to reduce noisy matches.
# +
def build_annotator(vertices_file):
A = ahocorasick.Automaton()
fvert = open(vertices_file, "r")
for line in fvert:
cols = line.strip().split('\t')
if len(cols) != 5:
continue
if cols[-1] == "qualifier" or cols[-1] == "event":
continue
cid = cols[0]
syns = cols[1]
for syn in syns.split('|'):
if len(syn) < 3:
continue
A.add_word(syn, (cid, syn))
fvert.close()
A.make_automaton()
return A
annotator = build_annotator(VERTEX_FILEPATH)
# -
# ### Read Story, Annotate, Write Concept Frequencies
#
# We loop through each `.story` file, reading the text and doing some cleanup on it.
#
# The `get_story_text` function reads each file, and performs some basic clean-up, mainly removing punctuations from the text. The other thing is to put a leading and trailing space in the text, this is to support the whole word condition in the `annotate_text` function.
# +
def get_story_text(story_file):
text_lines = []
ftext = open(os.path.join(DATA_DIR, story_file))
for line in ftext:
text_lines.append(line.strip())
ftext.close()
text = " ".join(text_lines)
# remove punctuation
translator = str.maketrans('', '', string.punctuation)
text = text.translate(translator)
# add space in front and back (for word check below)
text = " " + text + " "
return text
def annotate_text(annotator, text, debug=False):
matched_concepts = {}
for end_index, (idx, orig_value) in annotator.iter(text):
# make sure word identified is not part of another word
start_index = end_index - len(orig_value) + 1
if text[start_index - 1] != ' ' or text[end_index + 2] != ' ':
continue
if debug:
print(start_index, end_index, idx, orig_value)
if idx in matched_concepts.keys():
matched_concepts[idx] += 1
else:
matched_concepts[idx] = 1
concept_counts = sorted(
[(k, matched_concepts[k]) for k in matched_concepts.keys()],
key=operator.itemgetter(1), reverse=True)
return concept_counts
# +
fconcepts = open(CONCEPTMAP_FILEPATH, "w")
for story_filename in os.listdir(DATA_DIR):
if not story_filename.endswith(".story"):
continue
print("Processing {:s}...".format(story_filename))
story_id = story_filename.split('.')[0]
text = get_story_text(os.path.join(DATA_DIR, story_filename))
concept_map = annotate_text(annotator, text)
for cid, count in concept_map:
fconcepts.write("{:s}\t{:s}\t{:d}\n".format(story_id, cid, count))
fconcepts.close()
# -
# ### Verify Output
story_concepts_df = pd.read_csv(CONCEPTMAP_FILEPATH,
delimiter="\t",
names=["story_id", "concept_id", "concept_count"])
story_concepts_df.head()
| 04-topic-identification/src/01-annotate-stories.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# +
# Data processing libraries
import pandas as pd
import numpy as np
import itertools
# Database libraries
import psycopg2
# Stats libraries
from tableone import TableOne
import statsmodels.api as sm
import statsmodels.formula.api as smf
import scipy.stats
# Image libraries
# https://jakevdp.github.io/pdvega/
# jupyter nbextension enable vega3 --py --sys-prefix
import matplotlib.pyplot as plt
import pdvega
# %matplotlib inline
# -
# Create a database connection
user = 'team_j'
password = '<PASSWORD>'
host = 'hst953.csail.mit.edu'
dbname = 'mimic'
schema = 'mimiciii'
# Connect to the database
con = psycopg2.connect(dbname=dbname, user=user, host=host,
password=password)
cur = con.cursor()
cur.execute('SET search_path to {}'.format(schema))
# +
# Run query and assign the results to a Pandas DataFrame
# Requires the icustay_detail view from:
# https://github.com/MIT-LCP/mimic-code/tree/master/concepts/demographics
# And the OASIS score from:
# https://github.com/MIT-LCP/mimic-code/tree/master/concepts/severityscores
query = \
"""
WITH first_icu AS (
SELECT i.subject_id, i.hadm_id, i.icustay_id, i.gender, i.admittime admittime_hospital,
i.dischtime dischtime_hospital, i.los_hospital, i.age, i.admission_type,
i.hospital_expire_flag, i.intime intime_icu, i.outtime outtime_icu, i.los_icu, i.hospstay_seq, i.icustay_seq,
s.first_careunit,s.last_careunit,s.first_wardid, s.last_wardid
FROM icustay_detail i
LEFT JOIN icustays s
ON i.icustay_id = s.icustay_id
WHERE i.age >= 50 AND i.age <= 60
)
SELECT f.*, o.icustay_expire_flag, o.oasis, o.oasis_prob
FROM first_icu f
LEFT JOIN oasis o
ON f.icustay_id = o.icustay_id;
"""
data = pd.read_sql_query(query,con)
# -
data.columns
data
subj_rows = []
for i,subj_id in enumerate(data['subject_id']):
if subj_id == 13033: # just for a test
subj_rows.append(i)
# +
m_icu_id = (0,0)
for row_i in subj_rows:
d = data['icustay_seq'][row_i]
if d > m_icu_id[1]:
m_icu_id = (row_i,d)
m_icu_id
# -
def create_icu_table():
icu_table = {}
sub_m = {}
for i,subj_id in enumerate(data['subject_id']):
if subj_id not in sub_m:
sub_m[subj_id] = []
sub_m[subj_id].append(i)
for subj,subj_rows in sub_m.items():
for row_i in subj_rows:
d = data['icustay_seq'][row_i]
if d > icu_table.get(subj,(0,0))[1]:
icu_table[subj]=(row_i,d)
return icu_table
it = create_icu_table()
target_rows = []
for row_i, _ in it.values():
target_rows.append(row_i)
data.iloc[target_rows]
len(data['subject_id'].unique())
# +
#writer = pd.ExcelWriter('max_icu_stay.xlsx')
#data.iloc[target_rows].to_excel(writer,'Sheet1')
#writer.save()
# +
item = 228232
query = \
"""
SELECT c.subject_id, c.hadm_id, c.icustay_id, c.charttime,
c.cgid,g.label
FROM chartevents c
LEFT JOIN caregivers g
ON c.cgid = g.cgid
WHERE c.icustay_id = """+str(item)+"""
"""
data_cg = pd.read_sql_query(query,con)
# -
data_cg['cgid'].value_counts()
def get_cgid_label(df, cgid):
return df.loc[df['cgid'] == cgid]['label'].values[0]
get_cgid_label(data_cg,18765)
[get_cgid_label(data_cg,idxx) for idxx in data_cg['cgid'].value_counts().index]
# +
query = \
"""
SELECT g.label
FROM caregivers g
WHERE g.label = 'RN' OR g.label = 'MD' OR g.label = 'Res' OR g.label = 'RO' OR g.label = 'MDs'
"""
data_cglabel = pd.read_sql_query(query,con)
# -
data_cglabel['label'].value_counts()
# +
def get_measure_info(subj_icustay_id):
#Check type for safety
if type(subj_icustay_id)!= int:
raise TypeError
query = \
"""
SELECT c.icustay_id,c.cgid,g.label
FROM chartevents c
LEFT JOIN caregivers g
ON c.cgid = g.cgid
WHERE c.icustay_id = """+str(subj_icustay_id)+"""
"""
data_cg = pd.read_sql_query(query,con)
mea_list = [(get_cgid_label(data_cg,idxx),v) for idxx, v in data_cg['cgid'].value_counts().items()]
#clinic_types = ['RO','MD','Res','RN','MDs']
counts = {"RO":[0,0],"MDs":[0,0],"RN":[0,0],"OTH":[0,0]}
total_meas = 0
for m_inst, m_visit_count in mea_list:
total_meas = total_meas + m_visit_count
if (m_inst == None):
counts["OTH"][0] = counts["OTH"][0] + 1
counts["OTH"][1] = counts["OTH"][1] + m_visit_count
else:
cmp = m_inst.upper()
if (cmp == "RO"):
counts["RO"][0] = counts["RO"][0] + 1
counts["RO"][1] = counts["RO"][1] + m_visit_count
elif (cmp == "MDS"):
counts["MDs"][0] = counts["MDs"][0] + 1
counts["MDs"][1] = counts["MDs"][1] + m_visit_count
elif (cmp == "MD"):
counts["MDs"][0] = counts["MDs"][0] + 1
counts["MDs"][1] = counts["MDs"][1] + m_visit_count
elif (cmp == "RES"):
counts["MDs"][0] = counts["MDs"][0] + 1
counts["MDs"][1] = counts["MDs"][1] + m_visit_count
elif (cmp == "RN"):
counts["RN"][0] = counts["RN"][0] + 1
counts["RN"][1] = counts["RN"][1] + m_visit_count
else:
counts["OTH"][0] = counts["OTH"][0] + 1
counts["OTH"][1] = counts["OTH"][1] + m_visit_count
return (counts,total_meas)
# -
get_measure_info(228232)
data_mro = data.iloc[target_rows]
import datetime
data_slices = []
cur_b = 0
width = 29
while cur_b < len(data_mro):
s = datetime.datetime.now()
d_info = data_mro['icustay_id'][cur_b:cur_b + width].apply(get_measure_info)
data_slices.append(d_info)
e = datetime.datetime.now()
print((e-s).total_seconds(), cur_b)
cur_b = cur_b + width + 1
len(data_mro)
data_slices
plt.hist(data_mro['age'])
import pickle # python serialization
pickle.dump(data_slices,open( "save.p", "wb" ))
| BHI_BSN_test.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Supplementary Practice Problems
#
# These are similar to programming problems you may encounter in the mid-terms. They are not graded but we will review them in lab sessions.
#
# For these questions, you should try to solve the problem manually first (or at least detail out the steps if the algebra is too horrible), then use `scipy.linalg` package routine(s) to solve.
# **1**. Write down the full-matrix, block matrix and outer product forms of the SVD using $\LaTeX$ in a markdown cell.
# **2**. Let
# $$
# u = \begin{bmatrix}
# 1 \\
# 2 \\
# 3
# \end{bmatrix}
# $$
# Find a non-zero vector $v$ that is orthogonal to $u$, and another non-zero vector $w$ that is orthogonal to both $u$ and $v$. Construct an orthogonal matrix $Q$ using the unit versions of $u, v, w$. What is the inverse of $Q$?
# **3**. Find a basis for the 4 fundamental spaces of $A$, where
# $$
# A = \begin{bmatrix}
# 1 & 2 & 3 & 3 \\
# 2 & 0 & 6 & 2 \\
# 3 & 4 & 9 & 7
# \end{bmatrix}
# $$
# State the dimension of each basis, and the dimension of the space of the basis vectors.
# **4**. Find the projection of
# $$
# b = \begin{bmatrix}
# 3 \\
# 2 \\
# 1
# \end{bmatrix}
# $$
# on the column space of $A$ by using the projection matrix, where
# $$
# A = \begin{bmatrix}
# 1 & 2 & 3 & 3 \\
# 2 & 0 & 6 & 2 \\
# 3 & 4 & 9 & 7
# \end{bmatrix}
# $$
# **5**. What is the inverse of
# $$
# A = \begin{bmatrix}
# 0 & 0 & 0 & 1 \\
# 0 & 0 & 1 & 0 \\
# 1 & 0 & 0 & 0 \\
# 0 & 1 & 0 & 0
# \end{bmatrix}
# $$
# **6**. Find the eigenvalues and eigenvectors of $A^TA$, and find an eigendecomposition of $A^TA = V \Lambda V^T$. Finally, construct the SVD of $A$ and use it to generate $A$
# $$
# A = \begin{bmatrix}
# 1 & 2 & 3 & 3 \\
# 2 & 0 & 6 & 11 \\
# 3 & 4 & 9 & 7 \\
# 4 & 4 & 4 & 4
# \end{bmatrix}
# $$
# **7**. Find an orthogonal basis and the QR decomposition for
# $$
# A = \begin{bmatrix}
# 1 & 2 & 0 \\
# 1 & 0 & 2 \\
# 0 & 1 & 2
# \end{bmatrix}
# $$
# **8**. Solve the following problem
# $$
# \begin{bmatrix}
# 1 & 2 & 3 & 3 \\
# 2 & 0 & 6 & 11 \\
# 3 & 4 & 9 & 7 \\
# 4 & 4 & 4 & 4
# \end{bmatrix} \begin{bmatrix}
# x_1 \\
# x_2 \\
# x_3 \\
# x_4
# \end{bmatrix} = \begin{bmatrix}
# 4 \\
# 3 \\
# 2 \\
# 1
# \end{bmatrix}
# $$
# using the following factorizations
# - Gaussian elimination
# - LU
# - LDU
# - QR
# - SVD
# **9**. Let $A$ be the plane spanned by the vectors
#
# $$ v_1
# \begin{bmatrix}
# 1 \\
# 0 \\
# 1 \\
# 0
# \end{bmatrix}, v_2 = \begin{bmatrix}
# 1 \\
# 2 \\
# 3 \\
# 4
# \end{bmatrix}
# $$
# What is the point on the plane nearest to the vectors $b_1$ and $b_2$.
# $$
# b_1 = \begin{bmatrix}
# 3 \\
# 2 \\
# 5 \\
# 4
# \end{bmatrix}, b_2 = \begin{bmatrix}
# 3 \\
# 2 \\
# 0 \\
# 4
# \end{bmatrix}
# $$
# Find the orthogonal distance from $b_1$ and $b_2$ to its nearest point.
# **10**. Let
# $$
# A = \begin{bmatrix}
# 1 & 2 & 3 & 3 \\
# 2 & 0 & 6 & 2 \\
# 3 & 4 & 9 & 7 \\
# 4 & 4 & 4 & 4
# \end{bmatrix}
# $$
# - What is the rank of $A$
# - What is the condition number of $A$?
# - What is the best rank-1 and rank-2 approximation of $A$?
# - What is the distance between $A$ and the best rank-1 and rank-2 approximation of $A$ using the Frobenius norm?
| labs/Lab06S_Notes.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Employing a Multi-target regression (MTR) strategy for predicting horizon-based time series modelling
#
# ### Highlights:
#
# - In this notebook I will present some initial experiments using MTR to model horizon forescating for the S\&P 500 dataset
# - The 3M time series was considered
# - A traditional MTR (Stacked Single-target) method was employed to generate the predictions
# - LASSO, Elastic Net, Support Vector Regression, and Random Forest were employed as regression techniques:
# - Random Forest was selected as the best performer
#
# ### Let's go to the tests:
# #### Firstly, the imports
# Imports
import pandas as pd # Data manipulation
import numpy as np # Algebric operations
import matplotlib.pyplot as plt # Plots
from sklearn.ensemble import RandomForestRegressor # RF regressor
from mtr_time_series import MTRTimeSeries # Golden eggs chicken
import sys
sys.path.append('../')
from utils import hit_count
# #### Data reading
# Read the data
data = pd.read_csv('../../Data/all_stocks_5yr.csv')
data.head(5)
# ### All the actives
# All actives
' '.join(np.unique(data.loc[:, 'Name']).tolist())
# ### Now I'm going to select a single active to apply the MTR strategy (horizon predicting)
# +
select_actv = 'MMM'
s_data = data[data['Name'] == select_actv]
# -
# ### Counting the amount of examples for the active
len(s_data)
# ### Setup time series
#
# #### To this end, only the closing prices were considered
time_serie = s_data['Close'].values.tolist()
time_serie[1:5]
# ### Create and setup MTR evaluator
mtr_ts = MTRTimeSeries(
time_serie=time_serie,
window_size=10,
horizon_size=5,
init_buffer_size=200,
max_buffer_size=300,
sst_method='predictions'
)
# ### Set the regressor for the SST method
mtr_ts.set_regressor(RandomForestRegressor, {'n_estimators': 500, 'n_jobs': 6, 'max_features': 'sqrt'})
# ### Iterate over time serie and get the predictions
predictions = np.array(mtr_ts.iterate_fit_predict())
predictions[1:10]
# ### Do the same thing but applying an exponential smoothing
mtr_ts_decay = MTRTimeSeries(
time_serie=time_serie,
window_size=10,
horizon_size=5,
init_buffer_size=200,
max_buffer_size=300,
use_exp_smoothing=True,
gamma=0.5,
sst_method='predictions'
)
mtr_ts_decay.set_regressor(RandomForestRegressor, {'n_estimators': 500, 'n_jobs': 6, 'max_features': 'sqrt'})
predictions_decay = np.array(mtr_ts_decay.iterate_fit_predict())
# ### Next, I will generate some plots of the predicted values:
pred_start = mtr_ts.init_prediction_index()
observations = np.array(time_serie[pred_start:(pred_start + len(predictions))])
plt.figure(figsize=(10,5))
plt.plot(observations, label='Observed')
plt.plot(predictions, c='r', label='Predicted')
plt.plot(predictions_decay, c='g', label='Exp Smoothing + Prediction')
plt.legend(fontsize=8)
plt.show()
# ### Let's define some error functions
# - MSE
# - RMSE
# - RRMSE
# +
def MSE(obs, pred):
return np.sum((obs - pred) ** 2)/len(obs)
def RMSE(obs, pred):
return np.sqrt(np.sum((obs - pred) ** 2)/len(obs))
def RRMSE(obs, pred):
num = np.sum((obs - pred) ** 2) + 1e-6
den = np.sum((obs - np.mean(obs)) ** 2) + 1e-6
return np.sqrt(num/den)
# -
# ### Observed errors
print('MSE: {}'.format(MSE(observations, predictions)))
print('RMSE: {}'.format(RMSE(observations, predictions)))
print('RRMSE: {}'.format(RRMSE(observations, predictions)))
print()
print('MSE-Decay: {}'.format(MSE(observations, predictions_decay)))
print('RMSE-Decay: {}'.format(RMSE(observations, predictions_decay)))
print('RRMSE-Decay: {}'.format(RRMSE(observations, predictions_decay)))
# ### Length of the observations
len(observations)
# ### Number of hits
print('Hits (without exp smoothing): {}'.format(hit_count(observations, predictions)))
print('Hits (with exp smoothing): {}'.format(hit_count(observations, predictions_decay)))
| src/mtr/mtr_horizon_prediction.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.7 64-bit (''FlyAi_Pytorch1_5Python37'': conda)'
# language: python
# name: python3
# ---
# # 拉普拉斯特征映射(Laplacian Eigenmap, LE)
#
# ## 符号定义
#
# |符号|含义|
# |:-:|:-:|
# |$\pmb{x}$|样本点|
# |$X_i$|样本点$\pmb{x_i}$的k近邻点集合|
# |$N$|总样本数|
# |$N_i$|样本点$\pmb{x_i}$的k近邻点集合的样本总数|
# |$\pmb{X_i^{(j)}}$|样本点$\pmb{x_i}$的k近邻点集合中的第j个样本点|
# |$W$|邻接矩阵|
# |$\pmb{y}$|样本点降维后坐标|
#
# ## 概念
# LE和LLE类似,均是从“局部”的角度来构建数据与数据之间的联系和区别。不同点在于:LLE认为任意一个数据点均可以由其最近邻的k个点线性表示,并且这种线性表示在降维后依然成立;LE认为任意一个数据点和其最近邻的k个点在降维后也应当尽可能相近,即在降维后尽可能保证数据间的结构不发生改变。
#
# 显然,LLE的优化目标和LE的优化目标不同。
#
# 对于LLE来说,降维前后数据点之间的距离变化并不是很重要,只需要降维后依然能够满足降维前的局部线性关系即可。在实际例子中会发现,降维后,某些数据点的k个最近邻点发生了变化(数据之间的结构发生了变化),但是该数据点依然可以由变换前的k个最近邻点的降维结果以相同的权重线性组合得到。
#
# 对于LE来说,降维前后数据点之间的线性关系是否保持并不是很重要,只要降维后相近的数据点依然尽可能相近即可。即降维前后,任意数据点的k个最近邻点不会发生变化。
#
# 上述分析暗示了LE的核心步骤:
#
# 1. 在高维空间中对数据间的结构进行描述
# 2. 在低维空间中寻找满足这一结构的集合
#
# 对于第一步,LE希望关系的描述有如下特点:
# * 数据点A和数据点B关系的描述是唯一的。即无论是从数据点A出发对AB关系进行描述还是从数据点B出发对AB关系进行描述均是相同的(无向图)。
# * 对关系的描述是局部的。即仅描述数据点A与其周围最为接近的数个数据点之间的关系,不会考虑数据点A与所有数据点之间的关系。
#
# 若将关系表示为邻接矩阵,则上述的第一条要求使得邻接矩阵为对称矩阵,上述的第二条要求使得关系矩阵为稀疏矩阵。
#
# 对于第二步,实际上就是解决一个优化问题。其优化目标就是:找到一个集合,使得集合中的元素与高维空间中的数据点一一对应,并且这些元素之间的空间关系与高维空间中数据点之间的关系尽可能相似。
#
# ## 推导
#
# ### 高维空间中的邻接矩阵
#
# k近邻能很方便的找到任意数据点k个最近邻的数据点,这些最近邻的点即为空间中与当前数据点最为接近的数据点的集合。因此用k近邻对定义两个数据点之间是否存在关系是非常合适的。
#
# 但是k近邻存在一个明显的漏洞: **若数据点A是数据点B的最近邻点,那么数据点B不一定是数据点A的最近邻点。** 即两个数据点之间的关系不是相互的。但是根据上一节的分析,对于LE来说,希望关系是相互的。
#
# 这一漏洞有两种处理方法:
#
# 1. 仅考虑互为近邻的关系,即仅认为互为近邻的关系才是有效关系,而其他关系全部置零
# 2. 对于使用矩阵表示的关系,可以简单的使用原关系矩阵和其转置的和的$\frac{1}{2}$来表示
#
# 上述均是在寻找存在“局部”关系的点,对于关系的具体计算也有多种方式
#
# 1. 使用径向基函数(RBF)进行描述。较近的点取值大,较小的点取值较小。例如类似于下式的形式,其中$\gamma>0$为需要给定的参数。
# $$
# \begin{equation}
# \pmb{w_{ij}} = \exp^{-\gamma||\pmb{x_i}-\pmb{x_j}||_2^2}
# \end{equation}
# $$
# 2. 简单使用$\{0, 1\}$描述,对于存在关系取$1$,不存在关系则取$0$
#
# 通过上述两步,即可完成高维空间中局部关系的描述,并得到描述这些关系的邻接矩阵。
#
# ### 低维表示求解
#
# 对于上一步获得的邻接矩阵$W$,希望在降维后依然能够保持,因此可以定义如下的损失函数
#
# $$
# \begin{equation}
# \mathcal{L} = \sum_{ij}||\pmb{y_i}-\pmb{y_j}||_2^2w_{ij}
# \end{equation}
# $$
#
# 上式实际上衡量了在高维空间中存在关系的数据点降维后的距离。当在高维空间中存在关系的两个点尽可能接近时,损失越小。而且不存在关系($w_{ij}=0$)的两个数据点之间的距离并不会影响损失。
#
# 考虑到邻接矩阵为对称矩阵,因此有
#
# $$
# \begin{equation}
# \begin{split}
# \mathcal{L}
# &= \sum_{ij}||\pmb{y_i}-\pmb{y_j}||_2^2w_{ij} \\
# &= \sum_{i=1}^N\sum_{j=1}^N||\pmb{y_i}-\pmb{y_j}||_2^2w_{ij} \\
# &= \sum_{i=1}^N\sum_{j=1}^N(\pmb{y_i}^T\pmb{y_i}-2\pmb{y_i}^T\pmb{y_j}+\pmb{y_j}^T\pmb{y_j})w_{ij} \\
# &= \sum_{i=1}^N(\sum_{j=1}^Nw_{ij})\pmb{y_i}^T\pmb{y_i}+\sum_{j=1}^N(\sum_{i=1}^Nw_{ij})\pmb{y_j}^T\pmb{y_j} - 2\sum_{i=1}^N\sum_{j=1}^N\pmb{y_i}^T\pmb{y_j}w_{ij} \\
# &= 2\sum_{i=1}^N(\sum_{j=1}^Nw_{ij})\pmb{y_i}^T\pmb{y_i} - 2\sum_{i=1}^N\sum_{j=1}^N\pmb{y_i}^T\pmb{y_j}w_{ij} \\
# &= 2\sum_{i=1}^N(\sqrt{\sum_{j=1}^Nw_{ij}}\pmb{y_i})^T(\sqrt{\sum_{j=1}^Nw_{ij}}\pmb{y_i}) - 2\sum_{i=1}^N\pmb{y_i}^T(\sum_{j=1}^N\pmb{y_j}w_{ij}) \\
# &= 2tr(Y^TDY) - 2tr(Y^TWY) \\
# &= 2tr(Y^TLY)
# \end{split}
# \end{equation}
# $$
#
# 其中$L$矩阵即为拉普拉斯矩阵
# $$
# \begin{equation}
# D = diag(\sum_{i=1}^Nw_{i1}, \sum_{i=1}^Nw_{i2}, \cdots, \sum_{i=1}^Nw_{iN})
# \end{equation}
# $$
# $$
# \begin{equation}
# L = D-W
# \end{equation}
# $$
#
# 因此优化目标为
#
# $$
# \begin{equation}
# \begin{split}
# \arg\min\limits_{Y}\mathcal{L}
# &\Rightarrow \arg\min\limits_{Y} tr(Y^TLY)
# \end{split}
# \end{equation}
# $$
#
# 为了消除数据缩放对结果的影响,实际使用时会使用$Y^TDY=\pmb{I}$的限制条件,因此最终的优化目标为
#
# $$
# \begin{equation}
# \arg\min\limits_{Y} tr(Y^TLY), s.t. Y^TDY=\pmb{I}
# \end{equation}
# $$
#
# 考虑使用拉格朗日乘子法对上式进行求解
#
# $$
# \begin{equation}
# \left\{
# \begin{split}
# &\frac{\partial{\mathcal{L}}}{\partial{Y}}-\lambda\frac{\partial{(Y^TDY-\pmb{I})}}{\partial{Y}} = 0 \\
# & Y^TDY-\pmb{I}=0
# \end{split}
# \right.
# \end{equation}
# $$
#
# $$
# \begin{equation}
# \begin{split}
# & LY+L^TY-2\lambda DY=0 \\
# \Rightarrow &LY=\lambda DY
# \end{split}
# \end{equation}
# $$
#
# 上式即为一个广义特征值以及特征向量的求解问题。
#
# 将上式回代到原损失计算式有
# $$
# \begin{equation}
# \begin{split}
# \mathcal{L}
# &= 2tr(Y^TLY) \\
# &= 2tr(\lambda Y^TDY) \\
# &= 2tr(\lambda \pmb{I})
# \end{split}
# \end{equation}
# $$
#
# 考虑到损失应当尽可能小,因此选择前d个最小广义特征值对应的广义特征向量。
#
# 由于矩阵$L$和矩阵$D$均为对称半正定矩阵,因此其特征值必大于等于0
#
# 下面讨论特征值等于0的情况
#
# 若广义特征值等于0,则有
#
# $$
# \begin{equation}
# \begin{split}
# L\pmb{y} &= \pmb{0} \\
# \Rightarrow D\pmb{y} &= W\pmb{y} \\
# \end{split}
# \end{equation}
# $$
#
# 考虑到$D = diag(\sum_{i=1}^Nw_{i1}, \sum_{i=1}^Nw_{i2}, \cdots, \sum_{i=1}^Nw_{iN})$,当$\pmb{y}$为全1矩阵时,上式显然成立。
#
# 若不添加任何限制条件,上述的损失显然存在非常严重的问题: **对没有局部关系的数据点之间的距离没有计算损失。** 这一问题导致若所有的数据点降维后均为同一个点,则$\mathcal{L}=0$,从损失的角度来看有最优解。但是,显然,若任意数据点降维后均为同一个点,这样的降维是没有意义的,此时对应的实际上就是广义特征值为0的情况。
#
# 因此在实际使用时,选择舍弃掉0这个广义特征值对应的广义特征向量,并选用后续的d个广义特征值对应的广义特征向量作为最终的解。
#
# ## 流程
#
# * 定义数据集$X=\{\pmb{x_1}, \pmb{x_2}, \cdots, \pmb{x_N}\}$、邻域大小$k$以及降维后维度$d$
# * 计算邻接矩阵
# * 计算拉普拉斯矩阵和度矩阵
# $$
# \begin{equation}
# L = D-W
# \end{equation}
# $$
# $$
# \begin{equation}
# D = diag(\sum_{i=1}^Nw_{i1}, \sum_{i=1}^Nw_{i2}, \cdots, \sum_{i=1}^Nw_{iN})
# \end{equation}
# $$
# * 计算下式的前d+1个最小广义特征值对应的特征向量,并取$[1, d+1]$个作为最终的解
# $$
# \begin{equation}
# L\pmb{y}=\lambda D\pmb{y}
# \end{equation}
# $$
import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
from sklearn import manifold
from sklearn.neighbors import NearestNeighbors
class MyLE(object):
def __init__(self, input_data, reduction_dims, n_neighbors):
self.input_data = input_data
self.reduction_dims = reduction_dims
self.n_neighbors = n_neighbors
self.samples_num, self.input_dims = self.input_data.shape
# affinity matrix
self.affinity_mat = np.zeros((self.samples_num, self.samples_num))
# reduction result
self.output_mat = np.zeros((self.samples_num, reduction_dims))
def __call__(self):
self.cal_affinity_mat()
self.cal_reduction_result()
return self.output_mat
def cal_affinity_mat(self):
nbrs = NearestNeighbors(n_neighbors=self.n_neighbors).fit(self.input_data)
self.affinity_mat = nbrs.kneighbors_graph(self.input_data).toarray()
self.affinity_mat = 0.5 * (self.affinity_mat + self.affinity_mat.T)
def cal_reduction_result(self):
# cal matrix D
d_mat = np.diag(np.sum(self.affinity_mat, axis=0).reshape(-1))
# cal matrix L
l_mat = d_mat - self.affinity_mat
# cal top k eighvalues and eighvectors
_, topk_e_vecs = self._topk_eigh(l_mat, d_mat, self.reduction_dims)
self.output_mat = np.array(topk_e_vecs)
return self.output_mat
def _topk_eigh(self, mat1, mat2, k, skip_num=1):
e_vals, e_vecs = linalg.eigh(mat1, mat2)
sorted_ind = np.argsort(e_vals)
topk_e_vals = e_vals[sorted_ind[skip_num:k+skip_num]]
topk_e_vecs = e_vecs[:, sorted_ind[skip_num:k+skip_num]]
return topk_e_vals, topk_e_vecs
# +
# ---------------------- create data ----------------------
n_samples = 3000
# Create our sphere.
np.random.seed(1024)
p = np.random.rand(n_samples) * (2 * np.pi - 0.55)
t = np.random.rand(n_samples) * np.pi
# Sever the poles from the sphere.
indices = (t < (np.pi - (np.pi / 8))) & (t > ((np.pi / 8)))
samples_color = p[indices]
x, y, z = (
np.sin(t[indices]) * np.cos(p[indices]),
np.sin(t[indices]) * np.sin(p[indices]),
np.cos(t[indices]),
)
raw_samples = np.array([x, y, z]).T
# ---------------------- sklearn LE ----------------------
sklearn_le = manifold.SpectralEmbedding(n_components=2, n_neighbors=20)
sklearn_le_result = sklearn_le.fit_transform(raw_samples)
# ----------------------- My LE -----------------------
my_le = MyLE(raw_samples, reduction_dims=2, n_neighbors=20)
my_le_result = my_le()
# ----------------------
# draw func
fig = plt.figure(figsize=(20, 20))
ax = fig.add_subplot(221, projection="3d")
ax.set_title("Original data", fontsize=15)
ax.scatter(raw_samples[:, 0], raw_samples[:, 1], raw_samples[:, 2], c=samples_color, cmap=plt.cm.Spectral)
ax = fig.add_subplot(222)
plt.xticks([])
plt.yticks([])
plt.title("Projection of data using Sklearn LE", fontsize=15)
ax.scatter(sklearn_le_result[:, 0], sklearn_le_result[:, 1], c=samples_color, cmap=plt.cm.Spectral)
ax = fig.add_subplot(223, projection="3d")
ax.set_title("Original data", fontsize=15)
ax.scatter(raw_samples[:, 0], raw_samples[:, 1], raw_samples[:, 2], c=samples_color, cmap=plt.cm.Spectral)
ax = fig.add_subplot(224)
plt.xticks([])
plt.yticks([])
plt.title("Projection of data using My LE", fontsize=15)
ax.scatter(my_le_result[:, 0], my_le_result[:, 1], c=samples_color, cmap=plt.cm.Spectral)
plt.show()
| 04_LE/LE.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Housing Case Study
# Problem Statement:
#
# Consider a real estate company that has a dataset containing the prices of properties in the Delhi region. It wishes to use the data to optimise the sale prices of the properties based on important factors such as area, bedrooms, parking, etc.
#
# Essentially, the company wants —
#
#
# - To identify the variables affecting house prices, e.g. area, number of rooms, bathrooms, etc.
#
# - To create a linear model that quantitatively relates house prices with variables such as number of rooms, area, number of bathrooms, etc.
#
# - To know the accuracy of the model, i.e. how well these variables can predict house prices.
# ### Importing and Understanding Data
import pandas as pd
import numpy as np
# Importing Housing.csv
housing = pd.read_csv('Housing.csv')
# Looking at the first five rows
housing.head()
# What type of values are stored in the columns?
housing.info()
# ### Data Preparation
# - You can see that your dataset has many columns with values as 'Yes' or 'No'.
#
# - We need to convert them to 1s and 0s, where 1 is a 'Yes' and 0 is a 'No'.
# Converting Yes to 1 and No to 0
housing['mainroad'] = housing['mainroad'].map({'yes': 1, 'no': 0})
housing['guestroom'] = housing['guestroom'].map({'yes': 1, 'no': 0})
housing['basement'] = housing['basement'].map({'yes': 1, 'no': 0})
housing['hotwaterheating'] = housing['hotwaterheating'].map({'yes': 1, 'no': 0})
housing['airconditioning'] = housing['airconditioning'].map({'yes': 1, 'no': 0})
housing['prefarea'] = housing['prefarea'].map({'yes': 1, 'no': 0})
# Now let's see the head
housing.head()
# The variable 'furnishingstatus' had three levels. We need to convert it to integer.
# Creating a dummy variable for 'furnishingstatus'
status = pd.get_dummies(housing['furnishingstatus'])
# The result has created three variables that are not needed.
status.head()
# we don't need 3 columns.
# we can use drop_first = True to drop the first column from status df.
status = pd.get_dummies(housing['furnishingstatus'],drop_first=True)
#Adding the results to the master dataframe
housing = pd.concat([housing,status],axis=1)
# Now let's see the head of our dataframe.
housing.head()
# Dropping furnishingstatus as we have created the dummies for it
housing.drop(['furnishingstatus'],axis=1,inplace=True)
# Now let's see the head of our dataframe.
housing.head()
# #### Creating a new variable
# Let us create the new metric and assign it to "areaperbedroom"
housing['areaperbedroom'] = housing['area']/housing['bedrooms']
# Metric:bathrooms per bedroom
housing['bbratio'] = housing['bathrooms']/housing['bedrooms']
housing.head()
# ### Rescaling the Features
# It is extremely important to rescale the variables so that they have a comparable scale.
# There are twocoon ways of rescaling
# 1. Normalisation (min-max scaling) and
# 2. standardisation (mean-o, sigma-1)
# Let's try normalisation
# +
#defining a normalisation function
def normalize (x):
return ( (x-np.mean(x))/ (max(x) - min(x)))
# applying normalize ( ) to all columns
housing = housing.apply(normalize)
# -
# ## Splitting Data into Training and Testing Sets
housing.columns
# +
# Putting feature variable to X
X = housing[['area', 'bedrooms', 'bathrooms', 'stories', 'mainroad',
'guestroom', 'basement', 'hotwaterheating', 'airconditioning',
'parking', 'prefarea', 'semi-furnished', 'unfurnished',
'areaperbedroom', 'bbratio']]
# Putting response variable to y
y = housing['price']
# -
#random_state is the seed used by the random number generator, it can be any integer.
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7 ,test_size = 0.3, random_state=100)
# ## Building a linear model
import statsmodels.api as sm # Importing statsmodels
X_train = sm.add_constant(X_train) # Adding a constant column to our dataframe
# create a first fitted model
lm_1 = sm.OLS(y_train,X_train).fit()
#Let's see the summary of our first linear model
print(lm_1.summary())
# ### Checking VIF
# UDF for calculating vif value
def vif_cal(input_data, dependent_col):
vif_df = pd.DataFrame( columns = ['Var', 'Vif'])
x_vars=input_data.drop([dependent_col], axis=1)
xvar_names=x_vars.columns
for i in range(0,xvar_names.shape[0]):
y=x_vars[xvar_names[i]]
x=x_vars[xvar_names.drop(xvar_names[i])]
rsq=sm.OLS(y,x).fit().rsquared
vif=round(1/(1-rsq),2)
vif_df.loc[i] = [xvar_names[i], vif]
return vif_df.sort_values(by = 'Vif', axis=0, ascending=False, inplace=False)
# Calculating Vif value
vif_cal(input_data=housing, dependent_col="price")
# ## Correlation matrix
# Importing matplotlib and seaborn
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# Let's see the correlation matrix
plt.figure(figsize = (16,10)) # Size of the figure
sns.heatmap(housing.corr(),annot = True)
# ### Dropping the Variable and Updating the Model
# Dropping highly correlated variables and insignificant variables
X_train = X_train.drop('bbratio', 1)
# Create a second fitted model
lm_2 = sm.OLS(y_train,X_train).fit()
#Let's see the summary of our second linear model
print(lm_2.summary())
# ### Dropping the Variable and Updating the Model
# Calculating Vif value
vif_cal(input_data=housing.drop(["bbratio"], axis=1), dependent_col="price")
# Dropping highly correlated variables and insignificant variables
X_train = X_train.drop('bedrooms', 1)
# Create a third fitted model
lm_3 = sm.OLS(y_train,X_train).fit()
#Let's see the summary of our third linear model
print(lm_3.summary())
# Calculating Vif value
vif_cal(input_data=housing.drop(["bedrooms","bbratio"], axis=1), dependent_col="price")
# ### Dropping the Variable and Updating the Model
# # Dropping highly correlated variables and insignificant variables
X_train = X_train.drop('areaperbedroom', 1)
# Create a fourth fitted model
lm_4 = sm.OLS(y_train,X_train).fit()
#Let's see the summary of our fourth linear model
print(lm_4.summary())
# Calculating Vif value
vif_cal(input_data=housing.drop(["bedrooms","bbratio","areaperbedroom"], axis=1), dependent_col="price")
# ### Dropping the Variable and Updating the Model
# # Dropping highly correlated variables and insignificant variables
X_train = X_train.drop('semi-furnished', 1)
# Create a fifth fitted model
lm_5 = sm.OLS(y_train,X_train).fit()
#Let's see the summary of our fifth linear model
print(lm_5.summary())
# Calculating Vif value
vif_cal(input_data=housing.drop(["bedrooms","bbratio","areaperbedroom","semi-furnished"], axis=1), dependent_col="price")
# ### Dropping the Variable and Updating the Model
# # Dropping highly correlated variables and insignificant variables
X_train = X_train.drop('basement', 1)
# Create a sixth fitted model
lm_6 = sm.OLS(y_train,X_train).fit()
#Let's see the summary of our sixth linear model
print(lm_6.summary())
# Calculating Vif value
vif_cal(input_data=housing.drop(["bedrooms","bbratio","areaperbedroom","semi-furnished","basement"], axis=1), dependent_col="price")
# #### Assessment question
# #### Design four models by dropping all the variables one by one with high vif (>5). Then, compare the results.
# ## Making Predictions Using the Final Model
# ### Prediction with Model 6
# Adding constant variable to test dataframe
X_test_m6 = sm.add_constant(X_test)
# Creating X_test_m6 dataframe by dropping variables from X_test_m6
X_test_m6 = X_test_m6.drop(["bedrooms","bbratio","areaperbedroom","semi-furnished","basement"], axis=1)
# Making predictions
y_pred_m6 = lm_6.predict(X_test_m6)
# ## Model Evaluation
# Actual vs Predicted
c = [i for i in range(1,165,1)]
fig = plt.figure()
plt.plot(c,y_test, color="blue", linewidth=2.5, linestyle="-") #Plotting Actual
plt.plot(c,y_pred_m6, color="red", linewidth=2.5, linestyle="-") #Plotting predicted
fig.suptitle('Actual and Predicted', fontsize=20) # Plot heading
plt.xlabel('Index', fontsize=18) # X-label
plt.ylabel('Housing Price', fontsize=16) # Y-label
# Plotting y_test and y_pred to understand the spread.
fig = plt.figure()
plt.scatter(y_test,y_pred_m6)
fig.suptitle('y_test vs y_pred', fontsize=20) # Plot heading
plt.xlabel('y_test', fontsize=18) # X-label
plt.ylabel('y_pred', fontsize=16) # Y-label
# Error terms
fig = plt.figure()
c = [i for i in range(1,165,1)]
plt.plot(c,y_test-y_pred_m6, color="blue", linewidth=2.5, linestyle="-")
fig.suptitle('Error Terms', fontsize=20) # Plot heading
plt.xlabel('Index', fontsize=18) # X-label
plt.ylabel('ytest-ypred', fontsize=16) # Y-label
# Plotting the error terms to understand the distribution.
fig = plt.figure()
sns.distplot((y_test-y_pred_m6),bins=50)
fig.suptitle('Error Terms', fontsize=20) # Plot heading
plt.xlabel('y_test-y_pred', fontsize=18) # X-label
plt.ylabel('Index', fontsize=16) # Y-label
import numpy as np
from sklearn import metrics
print('RMSE :', np.sqrt(metrics.mean_squared_error(y_test, y_pred_m6)))
| Linear Regression/Housing Case Study.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # NETCONF/YANG
# This notebook goes through a set of examples with a live platform. The platform should be running IOS-XE 16.3.2. The goal is to show how NETCONF/YANG can be leveraged to perform a range of tasks. We will cover topics like:
# * Basic connectivity
# * Why we really want to use some form of client library
# * Getting started with a Python client like ncclient
# * Capabilities discovery
# * Model discovery
# * Feature discovery
#
# First, let's talk a little about the environment being used here. This is all run inside jupyter notebooks, which some may already be familiar with as iPython notebooks. A jupyter notebook lets us mix text and code and provides a simple way to experiment with Python code.
#
# <span style="color:red">**IMPORTANT for Execution. PLEASE READ**</span>. At its simplest, this is a playbook and execution is top-down. Code cells will look something like "In [#]". That's where you want to single-click. To execute the code, simply hit Shift+Return. The code should execute, and move onto the next cell. It's easy to "execute" an entire notebook, task-by-task, buy continuing to execute Shift+Return. Also, if you ever see "In [*]" in your code cells, it just means things are executing, and you are probably waiting on data to come back. So depending on what you're doing, some patience might be required.
#
# But as well as top-down execution, you can go back to code cells you just executed, tweak the code and run again! This makes it an ideal environment for experimentation and self-education.
#
# ### Connecting to a Device
# First, we need to make sure the device itself has NETCONF/YANG enabled. It's pretty simple:
#
# ``` html
# o22-3850-1#conf t
# Enter configuration commands, one per line. End with CNTL/Z.
# o22-3850-1(config)#netconf-yang
# o22-3850-1(config)#```
#
# Yes, it's that simple! To reference the internal user-guide for pre-requisites though, please see here.
#
# Next, let's define some variables that let us attach to the device. First, let's connect through an SSH tunnel to a device running in the lab. You should replace the variables below with the device of your choice:
#
#
# This is the router you will use for this example notebook, and maybe others.
HOST = '172.26.170.252' (replace with your own IP or your own network device)
PORT = 830
USER = 'admin' (replace with your own user configured on your network device)
PASS = 'password' (replace with .. you get the drift)
# As you can see, NETCONF runs on port 830, via SSH, and needs credentials. Before you ask, these credentials can and should be stored on a AAA server, and not on the router/switch directly. Just depends on how the router is setup in advance. NOTE: In IOS-XE 16.3, keys cannot yet be used.
#
# Now let's establish a NETCONF session to that box using ncclient.
# +
from ncclient import manager
from lxml import etree
def pretty_print(nc_retval):
'''The ncclient library works with XML. It takes XML in and gives XML back.
Yeah, I know it's not JSON, so we need to make it a little easier to read,
so let's define a pretty printer we can use with ncclient responses
'''
print(etree.tostring(etree.fromstring(nc_retval.data_xml), pretty_print=True))
def my_unknown_host_cb(host, fingerprint):
return True
m = manager.connect(host=HOST, port=PORT, username=USER, password=<PASSWORD>,
timeout=600,
allow_agent=False,
look_for_keys=False,
hostkey_verify=False,
unknown_host_cb=my_unknown_host_cb)
# -
# But what is this, and what did it do? It imports the manager class from the ncclient module. It imports whatever functions are in the modules and you can import the namespace into your current namespace (like the notebook here, or in real life, an actual program). Same can be said for the etree library from lxml.
#
# We are also definining a local function called pretty_print (which uses etree functionality) that just makes things easier for you to read!
#
# The execution is in the manager.connect function. It takes in the IP, the PORT, the USER, and the PASS you defined in the preceeding code snippet, and sets up the connetion to the router via NETCONF. As soon as you execute this, you are connected to this router via NETCONF. (congratulations)
#
# ### Capabilities Discovery
#
# Let's look at the capabilities presented by the router you connected to:
for item in iter(m.server_capabilities):
print(item)
# Ok, that is alot of data. What is it anyway?
#
# It is the initial exchange the NETCONF server (aka the router) has with its client (this notebook). Any piece of software (like this notebook, or a controller, etc.) can use this information to understand what the device can do, and possibly more importantly, what it cannot do!
#
# So now, let's tidy up the above and look, initially, at all the base netconf capabilities:
nc_caps = [c for c in m.server_capabilities if c.startswith('urn:ietf:params:netconf')]
for c in nc_caps:
print(c)
# As you might can tell, the code here just filters what was in the preceeding code snippet and makes it look more presentable to you. Either way, this looks better, but what does it mean? Well, if this were a real software program, this piece of software would already now know what the 3850 supports in terms of NETCONF.
#
# For example, the software would know that it supports a writable-running configuration store (via urn:ietf:params:netconf:capability:writable-running:1.0). This is defined by NETCONF, and represents the device's running configuration (you know, what you see when you do 'sho run' on CLI). But since you do NOT see a writable-startup message (which would look like urn:ietf:params:netconf:capability:startup:1.0), this lets you know that your software cannot not save changes to startup config using the standard <copy-config> operation and that you cannot use <edit-config> against the startup config. There are Cisco-specific primitives to work with startup config, but we will save that for later!
#
# Further, since you (or your software) do NOT see a "candiate" capability (which would look like urn:ietf:params:netconf:capability:candidate:1.0), you know that your software cannot stage multiple changes to the configuration (as a separate scratchpad) to be executed later as a single transaction. IOS-XE 16.3 does not yet support this type of capability.
#
# So far, it seems like NETCONF executes configuration just like CLI does (via writable-running) which modifies things directly into the running configuration, but with one **KEY** difference, which is support for the capability urn:ietf:params:netconf:capability:rollback-on-error:1.0. The support for this capability is perhaps one of the most compelling reasons to adopt NETCONF/YANG. This capability tells us that the router guarantees that any one <edit-config> operation will be carried out atomically. IOW, either it **all** happen or **none** of it happens. Just think about that for a moment in the context of how you have to interact with routers and switches over CLI or SNMP!
#
# These are just a few small examples, but also crucial to understand how easily things can now be coded once these initial exchanges take place (and are understood) between client and server (as opposed to the human and the router).
#
# For more details on what these capabilites mean, please reference RFC-6241.
#
# In conclusion, the capabilities exchange here, lets you (or your piece of software) understand **HOW** you can manipulate the router.
# ### Models Discovery
# So now, let's tidy up the above once more, and look at the capabilities that are related to model support:
# +
import re
for c in m.server_capabilities:
model = re.search('module=([^&]*)&', c)
if model is not None:
print("{}".format(model.group(1)))
revision = re.search('revision=([0-9]{4}-[0-9]{2}-[0-9]{2})', c)
if revision is not None:
print(" revision = {}".format(revision.group(1)))
deviations = re.search('deviations=([a-zA-Z0-9_\-,]+)($|&)',c)
if deviations is not None:
print(" deviations = {}".format(deviations.group(1)))
features = re.search('features=([a-zA-Z0-9_\-,]+)($|&)',c)
if features is not None:
print(" features = {}".format(features.group(1)))
# -
# Don't let the code above scare you. We are once more, just using it to make the code snippet from two executions ago (which is the initial capabilities exchange) look more presentable to you. What it techncially does is that it pulls out the model names themselves, the deviations, the versions and the features. Just data parsing here ;-).
#
# Parsing out the models, let's you know what aspects of configuration you have available to work with.
#
# So let's filter it further to explain an example ...
# +
import re
for c in m.server_capabilities:
model = re.search('module=(ietf-interfaces)&', c)
if model is not None:
print("{}".format(model.group(1)))
revision = re.search('revision=([0-9]{4}-[0-9]{2}-[0-9]{2})', c)
if revision is not None:
print(" revision = {}".format(revision.group(1)))
deviations = re.search('deviations=([a-zA-Z0-9_\-,]+)($|&)',c)
if deviations is not None:
print(" deviations = {}".format(deviations.group(1)))
features = re.search('features=([a-zA-Z0-9_\-,]+)($|&)',c)
if features is not None:
print(" features = {}".format(features.group(1)))
break
# -
# Once more, the code above just parses the exchange such that we only see information from one model. In this case, ietf-interfaces. This model has a revision, indicating when it was specified.
#
# Importantly, it also has features and deviations.
#
# **Features** identify which *optional* sections of the YANG model the platform advertising support for ietf-interfaces actually implements.
#
# The presence of **deviations** let us know that Cisco has deviated the model from the standard in some way (as ietf-interfaces (you might guess) is a standard model defined by the IETF). How has Cisco deviated it? We need to go look at the ietf-ip-devs model of course, because YANG provides a standard way to describe these differences!
#
# Ok, so here's some quick code that does that. We could have gone to github, or loaded pyang, but remember, we are connected to our router via NETCONF.
SCHEMA_TO_GET = 'ietf-ip-devs'
c = m.get_schema(SCHEMA_TO_GET)
print c.data
# So we just asked our router for this model directly with the code snippet above. Without going into many details here, the model above tells us how Cisco has deviated form the standard model, and IOS-XE technically does not support a handful of things compared to the standard-model. This is important for software to understand, and NETCONF/YANG supports the standardized exchange of this information.
#
# Further, we are not supporting some of our own augmentations to the ietf-interfaces model. The augmentations of the ietf-interfaces model can be seen by looking at the ietf-ip model (which is shown to be imported by the deviations above). ieft-ip augments ietf-interfaces itself and is defined by RFC-7277
#
# Now, remember this from earlier?
#
# ``` html
# ietf-interfaces
# revision = 2014-05-08
# deviations = ietf-ip-devs
# features = pre-provisioning,if-mib,arbitrary-names```
#
# It told our software the deviations from the standard model, but what about the features?
#
# Pre-provisioning is a feature defined by RFC-7233. This allows software to configure interfaces that might not yet be operable on the system.
#
# IF-MIB is a feature defined by RFC-2863. This allows software to know how the the interface should be managed.
#
# Arbitrary-names is a feature defined by RFC-7233 as well. This allows software to more easily deal with virtual interfaces in addition to interfaces defined by the hardware resident on the platforms. VLANs are a typical example.
#
# The YANG model designers identified these features as optional, and YANG itself provides the mechanism to tell the developer which optional features a platform implements.
# ### Conclusion
# NETCONF presents a number of useful primitives that we looked at, but the two most important are Capabilities Discovery, which tells you HOW you can work with the box, and Model Discovery, which tells you WHAT features the box supports.
#
# With the primitives we ran through, you can do basic model discovery to get the big picture of what you have to work with, understand what optional features are supported, and understand which parts of models are perhaps not supported.
#
# Products such as NSO and open source projects like ODL or the YDK can use these capabilities to work with devices in a much more reliable way. So can the software your customers write.
#
# And remember, we haven't even **DONE** anything yet. Stay tuned for more ...
| netconf/ncc/notebooks/NC-background.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Integrating scATAC-seq data using SCALEX
# The following tutorial demonstrates how to use SCALEX for *integrating* scATAC-seq data.
#
# There are two parts of this tutorial:
#
# * **Seeing the batch effect.** This part will show the batch effects of two adult mouse brain datasets from single nucleus ATAC-seq (snATAC) and droplet-based platform (Mouse Brain 10X) that used in SCALEX manuscript.
# * **Integrating data using SCALEX.** This part will show you how to perform batch correction using [SCALEX](https://scalex.readthedocs.io/en/latest/api/scalex.SCALEX.html#scalex.SCALEX) function in SCALEX.
import scalex
from scalex.function import SCALEX
from scalex.plot import embedding
import scanpy as sc
import pandas as pd
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
import seaborn as sns
import episcanpy as epi
sc.settings.verbosity = 3
sc.settings.set_figure_params(dpi=80, facecolor='white',figsize=(3,3),frameon=True)
sc.logging.print_header()
plt.rcParams['axes.unicode_minus']=False
sns.__version__
scalex.__version__
# ## Seeing the batch effect
# The following data has been used in the [SnapATAC](https://www.nature.com/articles/s41467-021-21583-9) paper, has been used here, and can be downloaded from [here](http://zhanglab.net/scalex-tutorial/mouse_brain_atac.h5ad).
# On a unix system, you can uncomment and run the following to download the count matrix in its anndata format.
# +
# # ! wget http://zhanglab.net/scalex-tutorial/mouse_brain_atac.h5ad
# -
adata_raw=sc.read('mouse_brain_atac.h5ad')
adata_raw
# Inspect the batches contained in the dataset.
adata_raw.obs.batch.value_counts()
# The data processing procedure is according to the epiScanpy tutorial [[Buenrostro_PBMC_data_processing]](https://nbviewer.jupyter.org/github/colomemaria/epiScanpy/blob/master/docs/tutorials/Buenrostro_PBMC_data_processing.html).
epi.pp.filter_cells(adata_raw, min_features=1)
epi.pp.filter_features(adata_raw, min_cells=5)
adata_raw.raw = adata_raw
adata_raw = epi.pp.select_var_feature(adata_raw,
nb_features=30000,
show=False,copy=True)
adata_raw.layers['binary'] = adata_raw.X.copy()
epi.pp.normalize_total(adata_raw)
adata_raw.layers['normalised'] = adata_raw.X.copy()
epi.pp.log1p(adata_raw)
epi.pp.lazy(adata_raw)
epi.tl.leiden(adata_raw)
# We observe a batch effect.
sc.pl.umap(adata_raw,color=['leiden'],legend_fontsize=10)
sc.pl.umap(adata_raw,color=['batch'],legend_fontsize=10)
adata_raw
# ## Integrating data using SCALEX
# The batch effects can be well-resolved using SCALEX.
# <div class="alert alert-info">
#
# **Note**
#
# Here we use GPU to speed up the calculation process, however, you can get the same level of performance only using cpu.
#
# </div>
adata=SCALEX('mouse_brain_atac.h5ad',batch_name='batch',profile='ATAC',
min_features=1, min_cells=5, n_top_features=30000,outdir='ATAC_output/',show=False,gpu=8)
adata
# While there seems to be some strong batch-effect in all cell types, SCALEX can integrate them homogeneously.
sc.settings.set_figure_params(dpi=80, facecolor='white',figsize=(3,3),frameon=True)
sc.pl.umap(adata,color=['leiden'],legend_fontsize=10)
sc.pl.umap(adata,color=['batch'],legend_fontsize=10)
# The integrated data is stored as `adata.h5ad` in the output directory assigned by `outdir` parameter in [SCALE](https://scalex.readthedocs.io/en/latest/api/scalex.SCALEX.html#scalex.SCALEX) function.
| docs/source/tutorial/Integration_scATAC-seq.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Extra New Material BK7
#
# +
# sphinx_gallery_thumbnail_path = '../images/Extra:New-Material-BK7.png'
def run(Plot, Save):
from PyMieSim.Data._Material.utils import LoadOnlineSave
from PyMieSim import Material
LoadOnlineSave(filename='BK7', url='https://refractiveindex.info/data_csv.php?datafile=data/glass/schott/N-BK7.yml')
Mat = Material('BK7')
if Plot:
Mat.Plot()
if Save:
from pathlib import Path
Mat.SaveFig(Path(__file__).stem)
if __name__ == '__main__':
run(Plot=True, Save=False)
| docs/source/auto_examples/Extra/Extra:New-Material-BK7.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # CNN Training
#
# Target of this code is to train a CNN network to classify images of a digital readout to the digits 0 to 9. Additionally a category "NaN" is introduced, to mark images that are not amibiguous.
#
# ### Preparing the training
# * First all libraries are loaded
# * It is assumed, that they are installed during the Python setup
# * matplotlib is set to print the output inline in the jupyter notebook
# +
########### Basic Parameters for Running: ################################
TFliteNamingAndVersion = "dig1320s2" # Used for tflite Filename
Training_Percentage = 0.0 # 0.0 = Use all Images for Training
Epoch_Anz = 500
##########################################################################
import tensorflow as tf
import matplotlib.pyplot as plt
import glob
import os
import numpy as np
from sklearn.utils import shuffle
from tensorflow.python import keras
from tensorflow.python.keras import Sequential
from tensorflow.python.keras.layers import Dense, InputLayer, Conv2D, MaxPool2D, Flatten, BatchNormalization
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from sklearn.model_selection import train_test_split
from tensorflow.keras.callbacks import History
from tensorflow.keras.utils import to_categorical
from PIL import Image
from pathlib import Path
loss_ges = np.array([])
val_loss_ges = np.array([])
# %matplotlib inline
np.set_printoptions(precision=4)
np.set_printoptions(suppress=True)
# -
# ### Load training data
# * The data is expected in the "Input_dir"
# * Inside subdirectories are expected from -1, 0, 1, ... 9 in which the pictures are sorted according to their values (=category)
# * Picture size must be 20x32 with 3 color channels (RGB)
# * The filename can be arbitrary
#
# * The images are stored in the x_data[]
# * The expected category for each image in the corresponding y_data[]
#
# * The last step is a shuffle (from sklearn.utils) and split the data into training and validation data
# +
Input_dir='ziffer_sortiert_resize'
files = glob.glob(Input_dir + '/*.jpg')
x_data = []
y_data = []
for aktfile in files:
base = os.path.basename(aktfile)
target = base[0:1]
if target == "N":
category = 10 # NaN does not work --> convert to 10
else:
category = int(target)
test_image = Image.open(aktfile)
test_image = np.array(test_image, dtype="float32")
x_data.append(test_image)
y_data.append(np.array([category]))
x_data = np.array(x_data)
y_data = np.array(y_data)
y_data = to_categorical(y_data, 11)
print(x_data.shape)
print(y_data.shape)
x_data, y_data = shuffle(x_data, y_data)
if (Training_Percentage > 0):
X_train, X_test, y_train, y_test = train_test_split(x_data, y_data, test_size=Training_Percentage)
else:
X_train = x_data
y_train = y_data
# -
# ### Define the model
#
# The layout of the network ist a typcial CNN network with alternating **Conv2D** and **MaxPool2D** layers. Finished after **flattening** with additional **Dense** layer.
#
# #### Important
# * Shape of the input layer: (32, 20, 3)
# * Number of output layers: 11
# * As loss function "categorical_crossentropy" is choosen, as it is a categories task
# +
model = Sequential()
model.add(BatchNormalization(input_shape=(32,20,3)))
model.add(Conv2D(32, (3, 3), padding='same', activation="relu"))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Conv2D(32, (3, 3), padding='same', activation="relu"))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Conv2D(32, (3, 3), padding='same', activation="relu"))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(256,activation="relu"))
model.add(Dense(11, activation = "softmax"))
model.summary()
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=tf.keras.optimizers.Adadelta(learning_rate=1.0, rho=0.95), metrics = ["accuracy"])
# -
# # Training
# The input pictures are randomly scattered for brightness, pixel shift variations and rotation angle. This is implemented with a ImageDataGenerator.
#
# +
Batch_Size = 4
Shift_Range = 1
Brightness_Range = 0.2
Rotation_Angle = 5
ZoomRange = 0.3
datagen = ImageDataGenerator(width_shift_range=[-Shift_Range,Shift_Range],
height_shift_range=[-Shift_Range,Shift_Range],
brightness_range=[1-Brightness_Range,1+Brightness_Range],
zoom_range=[1-ZoomRange, 1+ZoomRange],
rotation_range=Rotation_Angle)
if (Training_Percentage > 0):
train_iterator = datagen.flow(x_data, y_data, batch_size=Batch_Size)
validation_iterator = datagen.flow(X_test, y_test, batch_size=Batch_Size)
history = model.fit(train_iterator, validation_data = validation_iterator, epochs = Epoch_Anz)
else:
train_iterator = datagen.flow(x_data, y_data, batch_size=Batch_Size)
history = model.fit(train_iterator, epochs = Epoch_Anz)
# -
# ### Learing result
#
# * Visualization of the training and validation results
# +
loss_ges = np.append(loss_ges, history.history['loss'])
plt.semilogy(history.history['loss'])
if (Training_Percentage > 0):
val_loss_ges = np.append(val_loss_ges, history.history['val_loss'])
plt.semilogy(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','eval'], loc='upper left')
plt.show()
# -
# ### Check the model by hand
#
# * The following code uses the trained model to check the deviation for each picture.
# * x-axis walks through each pixel, y-axis shows the result
# ### Check each image for expected and deviation
# * setting the switch "only_deviation = true" will only print the images for which the classification and the CNN-result deviates
#
# The output contains the following information:
#
# | Filename | Expected Category | Predicted Category |
# |------------- |:-----------------------------:|--------------|
# | ziffer_sortiert_resize_NaN/5\Ziffer_4_0034.jpg | 4 | -1 |
#
# +
Input_dir='ziffer_sortiert_resize'
res = []
only_deviation = True
show_wrong_image = True
files = glob.glob(Input_dir + '/*.jpg')
for aktfile in files:
base = os.path.basename(aktfile)
target = base[0:1]
if target == "N":
zw1 = -1
else:
zw1 = int(target)
expected_class = zw1
image_in = Image.open(aktfile)
test_image = np.array(image_in, dtype="float32")
img = np.reshape(test_image,[1,32,20,3])
classes = np.argmax(model.predict(img), axis=-1)
classes = classes[0]
if classes == 10:
classes = -1
zw2 = classes
zw3 = zw2 - zw1
res.append(np.array([zw1, zw2, zw3]))
if only_deviation == True:
if str(classes) != str(expected_class):
print(aktfile + " " + str(expected_class) + " " + str(classes))
if show_wrong_image == True:
display(image_in)
else:
print(aktfile + " " + aktsubdir + " " + str(classes))
res = np.asarray(res)
plt.plot(res[:,0])
plt.plot(res[:,1])
plt.title('Result')
plt.ylabel('Digital Value')
plt.xlabel('#Picture')
plt.legend(['real','model'], loc='upper left')
plt.show()
# -
# ### Save the model
#
# * Save the model to the file with the "h5" file format
# +
FileName = TFliteNamingAndVersion
converter = tf.lite.TFLiteConverter.from_keras_model(model)
tflite_model = converter.convert()
open(FileName + ".tflite", "wb").write(tflite_model)
# +
FileName = TFliteNamingAndVersion + "q.tflite"
import tensorflow as tf
def representative_dataset():
for n in range(x_data[0].size):
data = np.expand_dims(x_data[5], axis=0)
yield [data.astype(np.float32)]
converter2 = tf.lite.TFLiteConverter.from_keras_model(model)
converter2.representative_dataset = representative_dataset
converter2.optimizations = [tf.lite.Optimize.DEFAULT]
converter2.representative_dataset = representative_dataset
tflite_quant_model = converter2.convert()
open(FileName, "wb").write(tflite_quant_model)
print(FileName)
Path(FileName).stat().st_size
# -
# Checking the images shows, that this are border line images, which can be interpreted as a good digit or a faulty one.
| Train_CNN_Digital-Readout-Small-v2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 1. Setup
import sys
sys.path.append('..')
# +
import config
import numpy as np
import warnings
from utils.preprocessing import crop_images_from_dir_and_save_all
# +
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
warnings.filterwarnings('ignore')
# -
DATASET_PATH = f'../datasets/{config.DATASET_NAME}'
# ## 2. Crop images from dir and save all
for split_name in ['train', 'val', 'test']:
for backprop_modifier in ['None', 'deconv', 'guided']:
crop_images_from_dir_and_save_all(images_path=f'{DATASET_PATH}/{split_name}'
f'/{split_name}_{backprop_modifier}'
f'_sal_from_patches',
save_path=f'{DATASET_PATH}/{split_name}'
f'/{split_name}_{backprop_modifier}'
f'_sal_patches',
patch_h=config.INPUT_SHAPE[0],
patch_w=config.INPUT_SHAPE[1],
img_format='png',
append_h_w=False)
| 2018-2019/project/saliency_maps/crop_images_from_dir_and_save_all_for_sal.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ##### Bus
#
# This bus has a passenger entry and exit control system to monitor the number of occupants it carries and thus detect when there is too high a capacity.
#
# At each stop the entry and exit of passengers is represented by a tuple consisting of two integer numbers.
# ```
# bus_stop = (in, out)
# ```
# The succession of stops is represented by a list of these tuples.
# ```
# stops = [(in1, out1), (in2, out2), (in3, out3), (in4, out4)]
# ```
#
# ## Goals:
# * lists, tuples
# * while/for loops
# * minimum, maximum, length
# * average, standard deviation
#
# ## Tasks
# 1. Calculate the number of stops.
# 2. Assign to a variable a list whose elements are the number of passengers at each stop (in-out),
# 3. Find the maximum occupation of the bus.
# 4. Calculate the average occupation. And the standard deviation.
#
# +
# variables
# +
# 1. Calculate the number of stops.
# +
# 2. Assign a variable a list whose elements are the number of passengers in each stop:
# Each item depends on the previous item in the list + in - out.
# +
# 3. Find the maximum occupation of the bus.
# +
# 4. Calculate the average occupation. And the standard deviation.
# -
NOTE FOR THE TEACHERS/COURSE MANAGERS = 0
# I've struggled a lot with this exercise,
# I really do not know how to proceed and resolve it,
# I've made some notes that a guy from the course sent me but
# I would like to have it revised with you. Thank you
# +
number_of_stops = 0
list_of_stops = []
number_of_travels = number_of_stops - 1
number_of_passengers = []
average_of_passenger = 0
SD_passengers = 0
Out = ""
In = ""
print("\n**** I\"m considering that the first stop and the last stop are")
print("the begin and the end of the route respectively. So there are no")
print("passengers exiting the first stop neither entering the last. ****\n")
number_of_stops = 4
is_a_number = 0
while is_a_number == 0:
try:
number_of_stops = 4(number_of_stops)
is_a_number = 1
except:
print("Please enter a number,")
number_of_stops = 4
for i in range(number_of_stops):
if i == 0:
In = 1
is_a_number = 0
while is_a_number == 0:
try:
In = int(In)
is_a_number = 1
except:
print("Please enter a number,")
In = input("How many passengers ENTER the bus at the initial stop? ")
list_of_stops.append((In,0))
elif i < number_of_stops -1:
In = ""
Out = ""
In = input("How many passengers ENTER the bus at the stop number %d ?" % i)
is_a_number = 0
while is_a_number == 0:
try:
In = int(In)
is_a_number = 1
except:
print("Please enter a number,")
In = input("How many passengers ENTER the bus at the stop number %d ?" % i)
Out = input("And how many passengers LEAVE the bus at the stop number %d ?" % i)
is_a_number = 0
while is_a_number == 0:
try:
Out = int(Out)
is_a_number = 1
except:
print("Please enter a number,")
Out = input("How many passengers LEAVE the bus at the stop number %d ?" % i)
list_of_stops.append((In, Out))
else:
a = sum(i[0] for i in list_of_stops)
b = sum(i[1] for i in list_of_stops)
exits_last_stop = a - b
list_of_stops.append((0, exits_last_stop))
list_maximum_occupation = []
for value in range(len(list_of_stops)-1):
a = sum(i[0] for i in list_of_stops[:(value + 1)])
b = sum(i[1] for i in list_of_stops[:(value + 1)])
list_maximum_occupation.append(a-b)
print("\nThe current bus route have %d stops" % number_of_stops)
print("\nThe tuple relative to the bus route is %s" % list_of_stops)
print("\nThe occupation of the bus in-between stops is %s\n" % list_maximum_occupation)
maximum_occupation = max(list_maximum_occupation)
average_ocucupation = sum(list_maximum_occupation) / (len(list_of_stops) - 1)
import math
advance_cm_onexit = []
tin = 0
while tin < len(list_maximum_occupation):
advance_cm_onexit.append(math.pow((list_maximum_occupation[tin] - average_ocucupation), 2))
tin += 1
standard_variation = math.sqrt(sum(advance_cm_onexit)/len(list_maximum_occupation))
print("The maximum occupation is %d" % maximum_occupation)
print("The average occupation is %.2f" % average_ocucupation)
print("The standard variation is %.2f" % standard_variation)
# -
| bus/bus.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# # Copyright 2020 (c) Cognizant Digital Business, Evolutionary AI. All rights reserved. Issued under the Apache 2.0 License.
# -
# # Example Predictor: Linear Rollout Predictor
#
# This example contains basic functionality for training and evaluating a linear predictor that rolls out predictions day-by-day.
#
# First, a training data set is created from historical case and npi data.
#
# Second, a linear model is trained to predict future cases from prior case data along with prior and future npi data.
# The model is an off-the-shelf sklearn Lasso model, that uses a positive weight constraint to enforce the assumption that increased npis has a negative correlation with future cases.
#
# Third, a sample evaluation set is created, and the predictor is applied to this evaluation set to produce prediction results in the correct format.
# ## Training
import pickle
import numpy as np
import pandas as pd
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
# Helpful function to compute mae
def mae(pred, true):
return np.mean(np.abs(pred - true))
# ### Copy the data locally
# Main source for the training data
DATA_URL = 'https://raw.githubusercontent.com/OxCGRT/covid-policy-tracker/master/data/OxCGRT_latest.csv'
# Local file
DATA_FILE = 'data/OxCGRT_latest.csv'
import os
import urllib.request
if not os.path.exists('data'):
os.mkdir('data')
urllib.request.urlretrieve(DATA_URL, DATA_FILE)
# Load historical data from local file
df = pd.read_csv(DATA_FILE,
parse_dates=['Date'],
encoding="ISO-8859-1",
dtype={"RegionName": str,
"RegionCode": str},
error_bad_lines=False)
df.columns
# +
# # For testing, restrict training data to that before a hypothetical predictor submission date
# HYPOTHETICAL_SUBMISSION_DATE = np.datetime64("2020-07-31")
# df = df[df.Date <= HYPOTHETICAL_SUBMISSION_DATE]
# -
# Add RegionID column that combines CountryName and RegionName for easier manipulation of data
df['GeoID'] = df['CountryName'] + '__' + df['RegionName'].astype(str)
# Add new cases column
df['NewCases'] = df.groupby('GeoID').ConfirmedCases.diff().fillna(0)
# Keep only columns of interest
id_cols = ['CountryName',
'RegionName',
'GeoID',
'Date']
cases_col = ['NewCases']
npi_cols = ['C1_School closing',
'C2_Workplace closing',
'C3_Cancel public events',
'C4_Restrictions on gatherings',
'C5_Close public transport',
'C6_Stay at home requirements',
'C7_Restrictions on internal movement',
'C8_International travel controls',
'H1_Public information campaigns',
'H2_Testing policy',
'H3_Contact tracing',
'H6_Facial Coverings']
df = df[id_cols + cases_col + npi_cols]
# Fill any missing case values by interpolation and setting NaNs to 0
df.update(df.groupby('GeoID').NewCases.apply(
lambda group: group.interpolate()).fillna(0))
# Fill any missing NPIs by assuming they are the same as previous day
for npi_col in npi_cols:
df.update(df.groupby('GeoID')[npi_col].ffill().fillna(0))
temp = pd.read_csv('temperature_data.csv')
temp['date_st'] = temp['Date'].apply(lambda e: e[5:])
temp['id'] = temp['GeoID'] + '_' + temp['date_st']
id_temp = dict(zip( temp['id'], temp['temp'] ))
id_holiday = dict(zip( temp['id'], temp['Holiday'] ))
tf = temp[['date_st','temp']]
tf = tf.groupby(['date_st']).mean().reset_index()
date_temp_avg = dict(zip( tf['date_st'], tf['temp'] ))
tf = temp[['date_st','Holiday']]
tf = tf.groupby(['date_st'])['Holiday'].agg(pd.Series.mode).reset_index()
date_holiday_avg = dict(zip( tf['date_st'], tf['Holiday'] ))
id_temp
# +
# Set number of past days to use to make predictions
nb_lookback_days = 30
date_ls = []
geoid_ls = []
country_ls = []
newcase_ls = []
# Create training data across all countries for predicting one day ahead
X_cols = cases_col + npi_cols
y_col = cases_col
X_samples = []
y_samples = []
geo_ids = df.GeoID.unique()
train_geo_ids = [e for e in geo_ids]
geoid_arr = np.zeros(len(train_geo_ids)+1)
for g in geo_ids:
gdf = df[df.GeoID == g]
all_case_data = np.array(gdf[cases_col])
all_npi_data = np.array(gdf[npi_cols])
# Create one sample for each day where we have enough data
# Each sample consists of cases and npis for previous nb_lookback_days
nb_total_days = len(gdf)
for d in range(nb_lookback_days, nb_total_days - 1):
X_cases = all_case_data[d-nb_lookback_days:d]
# Take negative of npis to support positive
# weight constraint in Lasso.
X_npis = -all_npi_data[d - nb_lookback_days:d]
date_ls += [ list(gdf['Date'])[d] ]
geoid_ls += [ list(gdf['GeoID'])[d] ]
country_ls += [ list(gdf['CountryName'])[d] ]
newcase_ls += [ list(gdf['NewCases'])[d] ]
date_st = str(date_ls[-1])[5:10]
id_ = geoid_ls[-1] + '_' + date_st
temperature = date_temp_avg[date_st]
holiday = date_holiday_avg[date_st]
if id_ in id_temp:
temperature = id_temp[id_]
holiday = id_holiday[id_]
# Flatten all input data so it fits Lasso input format.
geoid_arr = np.zeros(len(train_geo_ids)+1)
geoid_arr[ train_geo_ids.index(g) ] = 1
X_sample = np.concatenate([geoid_arr, [temperature,holiday], X_cases.flatten(),
X_npis.flatten()])
y_sample = all_case_data[d]
X_samples.append(X_sample)
y_samples.append(y_sample)
X_samples = np.array(X_samples)
y_samples = np.array(y_samples).flatten()
with open('train_geo_ids.txt', 'w') as f:
f.write('\n'.join(train_geo_ids))
print(X_samples.shape)
# -
X_train, y_train = X_samples,y_samples
print(X_train.shape,y_train.shape)
# +
# import datetime
# train_idx = [i for i in range(len(date_ls)) if date_ls[i] <= datetime.date(2020,7,31) ]
# test_idx = [i for i in range(len(date_ls)) if date_ls[i] >= datetime.date(2020,8,1) ]
# train_idx = np.array(train_idx)
# test_idx = np.array(test_idx)
# +
# # Split data into train and test sets
# X_train, X_test, y_train, y_test = X_samples[train_idx,:], X_samples[test_idx,:],y_samples[train_idx], y_samples[test_idx]
# print(X_train.shape,X_test.shape,y_train.shape,y_test.shape,)
# -
# !pip install lightgbm
import random
def seed_everything(seed=0):
random.seed(seed)
np.random.seed(seed)
seed_everything(42)
# +
# Create and train Lasso model.
# Set positive=True to enforce assumption that cases are positively correlated
# with future cases and npis are negatively correlated.
lasso_model = Lasso(random_state=42)
lasso_model.fit(X_train, y_train)
print('Lasso result:')
# Evaluate model
train_preds = lasso_model.predict(X_train)
train_preds = np.maximum(train_preds, 0) # Don't predict negative cases
print('Train MAE:', mae(train_preds, y_train))
# test_preds = lasso_model.predict(X_test)
# test_preds = np.maximum(test_preds, 0) # Don't predict negative cases
# print('Test MAE:', mae(test_preds, y_test))
with open('models/model_lasso.pkl', 'wb') as model_file:
pickle.dump(lasso_model, model_file)
from lightgbm import LGBMRegressor
lgbm_model = LGBMRegressor(random_state=42)
lgbm_model.fit(X_train, y_train)
# Evaluate model
train_preds = lgbm_model.predict(X_train)
train_preds = np.maximum(train_preds, 0) # Don't predict negative cases
print('lgbm result:')
print('Train MAE:', mae(train_preds, y_train))
# test_preds = lgbm_model.predict(X_test)
# test_preds = np.maximum(test_preds, 0) # Don't predict negative cases
# print('Test MAE:', mae(test_preds, y_test))
with open('models/model_lgbm.pkl', 'wb') as model_file:
pickle.dump(lgbm_model, model_file)
import xgboost as xgb
xgb_model = xgb.XGBRegressor(random_state=42)
xgb_model.fit(X_train, y_train)
# Evaluate model
train_preds = xgb_model.predict(X_train)
train_preds = np.maximum(train_preds, 0) # Don't predict negative cases
print('xgb result:')
print('Train MAE:', mae(train_preds, y_train))
# test_preds = xgb_model.predict(X_test)
# test_preds = np.maximum(test_preds, 0) # Don't predict negative cases
# print('Test MAE:', mae(test_preds, y_test))
with open('models/model_xgb.pkl', 'wb') as model_file:
pickle.dump(xgb_model, model_file)
# +
#with geoid
# Lasso result:
# Train MAE: 118.69420734991954
# Test MAE: 447.06846062728135
# lgbm result:
# Train MAE: 85.51717187475573
# Test MAE: 650.7371662424473
# xgb result:
# Train MAE: 54.2057830354577
# Test MAE: 633.3338386238983
# +
# None geoid result:
# Lasso result:
# Train MAE: 119.2762230373797
# Test MAE: 469.3599710917388
# lgbm result:
# Train MAE: 85.58646245869078
# Test MAE: 665.2549123382636
# xgb result:
# Train MAE: 51.797418546131624
# Test MAE: 650.3725903829637
# -
# Save the best model to file
if not os.path.exists('models'):
os.mkdir('models')
with open('models/model.pkl', 'wb') as model_file:
pickle.dump(lasso_model, model_file)
# ## Evaluation
#
# Now that the predictor has been trained and saved, this section contains the functionality for evaluating it on sample evaluation data.
# Reload the module to get the latest changes
import predict
from importlib import reload
reload(predict)
from predict import predict_df
# %%time
preds_df = predict_df("2020-08-01", "2020-08-31", path_to_ips_file="data/2020-09-30_historical_ip.csv", verbose=True)
# Check the predictions
preds_df.head()
# # Validation
# This is how the predictor is going to be called during the competition.
# !!! PLEASE DO NOT CHANGE THE API !!!
# !python predict.py -s 2020-08-01 -e 2020-08-04 -ip data/2020-09-30_historical_ip.csv -o predictions/2020-08-01_2020-08-04.csv
# !head predictions/2020-08-01_2020-08-04.csv
# # Test cases
# We can generate a prediction file. Let's validate a few cases...
import sys,os,os.path
sys.path.append(os.path.expanduser('/home/thinng/code/2020/covid-xprize/'))
# +
import os
from covid_xprize.validation.predictor_validation import validate_submission
def validate(start_date, end_date, ip_file, output_file):
# First, delete any potential old file
try:
os.remove(output_file)
except OSError:
pass
# Then generate the prediction, calling the official API
# !python predict.py -s {start_date} -e {end_date} -ip {ip_file} -o {output_file}
# And validate it
errors = validate_submission(start_date, end_date, ip_file, output_file)
if errors:
for error in errors:
print(error)
else:
print("All good!")
# -
# ## 4 days, no gap
# - All countries and regions
# - Official number of cases is known up to start_date
# - Intervention Plans are the official ones
validate(start_date="2020-08-01",
end_date="2020-08-04",
ip_file="data/2020-09-30_historical_ip.csv",
output_file="predictions/val_4_days.csv")
# ## 1 month in the future
# - 2 countries only
# - there's a gap between date of last known number of cases and start_date
# - For future dates, Intervention Plans contains scenarios for which predictions are requested to answer the question: what will happen if we apply these plans?
# %%time
validate(start_date="2021-01-01",
end_date="2021-01-31",
ip_file="data/future_ip.csv",
output_file="predictions/val_1_month_future.csv")
# ## 180 days, from a future date, all countries and regions
# - Prediction start date is 1 week from now. (i.e. assuming submission date is 1 week from now)
# - Prediction end date is 6 months after start date.
# - Prediction is requested for all available countries and regions.
# - Intervention plan scenario: freeze last known intervention plans for each country and region.
#
# As the number of cases is not known yet between today and start date, but the model relies on them, the model has to predict them in order to use them.
# This test is the most demanding test. It should take less than 1 hour to generate the prediction file.
# ### Generate the scenario
# +
from datetime import datetime, timedelta
start_date = datetime.now() + timedelta(days=7)
start_date_str = start_date.strftime('%Y-%m-%d')
end_date = start_date + timedelta(days=180)
end_date_str = end_date.strftime('%Y-%m-%d')
print(f"Start date: {start_date_str}")
print(f"End date: {end_date_str}")
# -
from covid_xprize.validation.scenario_generator import get_raw_data, generate_scenario, NPI_COLUMNS
DATA_FILE = 'data/OxCGRT_latest.csv'
latest_df = get_raw_data(DATA_FILE, latest=True)
scenario_df = generate_scenario(start_date_str, end_date_str, latest_df, countries=None, scenario="Freeze")
scenario_file = "predictions/180_days_future_scenario.csv"
scenario_df.to_csv(scenario_file, index=False)
print(f"Saved scenario to {scenario_file}")
# ### Check it
# %%time
validate(start_date=start_date_str,
end_date=end_date_str,
ip_file=scenario_file,
output_file="predictions/val_6_month_future.csv")
# ## predict zero scenario & plot "United States"/"Canada"/"Argentina"
zero_scenario_df = pd.read_csv(scenario_file)
cols = list(zero_scenario_df.columns)[3:]
for col in cols:
zero_scenario_df[col].values[:] = 0
zero_scenario_file = "predictions/180_days_future_scenario_zero.csv"
zero_scenario_df.to_csv(zero_scenario_file, index=False)
print(f"Saved scenario to {zero_scenario_file}")
# %%time
validate(start_date=start_date_str,
end_date=end_date_str,
ip_file=zero_scenario_file,
output_file="predictions/val_6_month_future_zero.csv")
# +
import matplotlib.pyplot as plt
import numpy as np
import datetime
pf = pd.read_csv('predictions/val_6_month_future_zero.csv')
pf = pf[['CountryName','Date','PredictedDailyNewCases']]
pf = pf.groupby(['CountryName','Date']).mean()
pf = pf.reset_index()
tf = pf[pf['CountryName']=='United States']
xdates = list(tf['Date'])
xdates = [datetime.datetime.strptime(date,'%Y-%m-%d') for date in xdates]
usa = list(tf['PredictedDailyNewCases'])
tf = pf[pf['CountryName']=='Canada']
can = list(tf['PredictedDailyNewCases'])
tf = pf[pf['CountryName']=='Argentina']
arg = list(tf['PredictedDailyNewCases'])
fig = plt.figure(figsize=(20,10))
ax = plt.subplot(111)
plt.plot(xdates, usa,label='United States')
plt.plot(xdates, can,label='Canada')
plt.plot(xdates, arg,label='Argentina')
plt.legend(loc=4)
plt.grid()
plt.show()
# -
| thin/work_lgbm_geoid_temp_trainAll/train.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["header"]
# <table width="100%">
# <tr style="border-bottom:solid 2pt #009EE3">
# <td style="text-align:left" width="10%">
# <a href="open_txt.dwipynb" download><img src="../../images/icons/download.png"></a>
# </td>
# <td style="text-align:left" width="10%">
# <a href="https://mybinder.org/v2/gh/biosignalsnotebooks/biosignalsnotebooks/biosignalsnotebooks_binder?filepath=biosignalsnotebooks_environment%2Fcategories%2FLoad%2Fopen_txt.dwipynb" target="_blank"><img src="../../images/icons/program.png" title="Be creative and test your solutions !"></a>
# </td>
# <td></td>
# <td style="text-align:left" width="5%">
# <a href="../MainFiles/biosignalsnotebooks.ipynb"><img src="../../images/icons/home.png"></a>
# </td>
# <td style="text-align:left" width="5%">
# <a href="../MainFiles/contacts.ipynb"><img src="../../images/icons/contacts.png"></a>
# </td>
# <td style="text-align:left" width="5%">
# <a href="https://github.com/biosignalsnotebooks/biosignalsnotebooks" target="_blank"><img src="../../images/icons/github.png"></a>
# </td>
# <td style="border-left:solid 2pt #009EE3" width="15%">
# <img src="../../images/ost_logo.png">
# </td>
# </tr>
# </table>
# + [markdown] tags=["intro_info_title"]
# <link rel="stylesheet" href="../../styles/theme_style.css">
# <!--link rel="stylesheet" href="../../styles/header_style.css"-->
# <link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/font-awesome/4.7.0/css/font-awesome.min.css">
#
# <table width="100%">
# <tr>
# <td id="image_td" width="15%" class="header_image_color_1"><div id="image_img"
# class="header_image_1"></div></td>
# <td class="header_text">Load acquired data from .txt file</td>
# </tr>
# </table>
# + [markdown] tags=["intro_info_tags"]
# <div id="flex-container">
# <div id="diff_level" class="flex-item">
# <strong>Difficulty Level:</strong> <span class="fa fa-star checked"></span>
# <span class="fa fa-star"></span>
# <span class="fa fa-star"></span>
# <span class="fa fa-star"></span>
# <span class="fa fa-star"></span>
# </div>
# <div id="tag" class="flex-item-tag">
# <span id="tag_list">
# <table id="tag_list_table">
# <tr>
# <td class="shield_left">Tags</td>
# <td class="shield_right" id="tags">open☁load☁txt</td>
# </tr>
# </table>
# </span>
# <!-- [OR] Visit https://img.shields.io in order to create a tag badge-->
# </div>
# </div>
# + [markdown] tags=["test"]
#
# A text file is one of the simplest means to store information, being a format outputted by **<span class="color2">OpenSignals</span>**.
#
# In this **<span class="color5">Jupyter Notebook</span>** it will be explained how to load/transpose the data inside .txt file to a **<span class="color1">Python</span>** list, which consists in a step that precedes all processing operations.
#
# -
# <hr>
# + [markdown] tags=[]
# <p class="steps">1 - Importation of the needed packages</p>
# + tags=["hide_out"]
# Package for reading a file when his URL is known
from wget import download
# Package used for loading data from the input text file
from numpy import loadtxt
# biosignalsnotebooks python package
import biosignalsnotebooks as bsnb
# + [markdown] tags=[]
# <p class="steps">2 - Access to electrophysiological signals list</p>
# + [markdown] tags=[]
# <p class="steps">2.1 - Enter <i><span class="color2">biosignalsplux</span></i> url</p>
# + [markdown] tags=[]
# <img src="../../images/open/biosignalsplux_link.png">
# + [markdown] tags=[]
# <p class="steps">2.2 - Navigate through <i><span class="color2">biosignalsplux</span></i> main page menu and enter in "Signal Samples" page</p>
# + [markdown] tags=[]
# <img src="../../images/open/signal_samples_link.png">
# + [markdown] tags=[]
# <p class="steps">2.3 - Interactive buttons for accessing each signal sample file</p>
# + [markdown] tags=[]
# <img src="../../images/open/signal_samples_file_link.png">
# + [markdown] tags=[]
# <p class="steps">2.4 - File url copy (right-click of the mouse in the desired signal file icon)</p>
# + [markdown] tags=[]
# <img src="../../images/open/copy_link.png">
# + tags=[]
copy_link = 'http://biosignalsplux.com/downloads/samples/sensor_samples/biosignalsplux_Blood_Volume_Pulse_(BVP)_Sample.txt'
# + [markdown] tags=[]
# <p class="steps">3 - Get file from URL (<a href="http://biosignalsplux.com/downloads/samples/sensor_samples/biosignalsplux_Blood_Volume_Pulse_(BVP)_Sample.txt">http://biosignalsplux.com/downloads/samples/sensor_samples/biosignalsplux_Blood_Volume_Pulse_(BVP)_Sample.txt</a>)</p>
# + tags=[]
# File download.
txt_file = download(copy_link, out="download_file_name.txt")
# + tags=["hide_in"]
# [Internal code for overwrite file if already exists]
import os
import shutil
if os.path.exists("download_file_name.txt"):
shutil.move(txt_file,"download_file_name.txt")
txt_file = "download_file_name.txt"
# + [markdown] tags=[]
# <p class="steps">4 - Transposition of data to a Python list</p>
# + tags=[]
data = loadtxt(txt_file)
# + [markdown] tags=[]
# <p class="steps">5 - Identification of acquisition sampling rate in the file header ("sampling rate" key)</p>
# + tags=["hide_in"]
# Embedding of .pdf file
from IPython.display import IFrame
IFrame(src="https://biosignalsplux.com/downloads/samples/sensor_samples/biosignalsplux_Blood_Volume_Pulse_(BVP)_Sample.txt", width="100%", height="350")
# + [markdown] tags=[]
# <img src="../../images/open/file_header_sampling_rate.png">
# + tags=[]
sampling_rate = 1000
# + [markdown] tags=[]
# <p class="steps">6 - Generation of time axis for signal plotting</p>
# + tags=[]
time = bsnb.generate_time(data, sampling_rate)
# + [markdown] tags=[]
# <p class="steps">7 - Final Output of the loaded data</p>
# + tags=[]
print (data)
# + [markdown] tags=[]
# Each line of the list defines a sample acquired at a specific time instant and each column can be the sample number (*nSeq* ), digital input (*DI* ) or a sample value (*CH1* ), like described in the file header bellow.
# + tags=["hide_in"]
# Embedding of .pdf file
from IPython.display import IFrame
IFrame(src="https://biosignalsplux.com/downloads/samples/sensor_samples/biosignalsplux_Blood_Volume_Pulse_(BVP)_Sample.txt", width="100%", height="350")
# + [markdown] tags=[]
# <img src="../../images/open/file_header_columns.png">
# + [markdown] tags=[]
# The samples of the signal under analysis are stored at the third entry of each list element (index 2).
# + tags=[]
channel_column = 2
# + [markdown] tags=[]
# <p class="steps">8 - Graphical representation of the signal (raw data)</p>
# -
bsnb.plot(time, data[:, channel_column])
# <i>This procedure can be automatically done by <strong>load</strong> function of <strong><span class="color2">biosignalsnotebooks</span></strong> package</i>
#
# Text files are very popular and, like the name suggests, almost all type of contents can be stored here if they can be translated into a text format.
#
# Numpy <strong>loadtxt</strong> function is very simple and efficient, so, it can be used even for text files not returned by <span class="color2">OpenSignals</span>.
#
# <strong><span class="color7">We hope that you have enjoyed this guide. </span><span class="color2">biosignalsnotebooks</span><span class="color4"> is an environment in continuous expansion, so don't stop your journey and learn more with the remaining <a href="../MainFiles/biosignalsnotebooks.ipynb">Notebooks <img src="../../images/icons/link.png" width="10px" height="10px" style="display:inline"></a></span></strong> !
# + [markdown] tags=["footer"]
# <hr>
# <table width="100%">
# <tr>
# <td style="border-right:solid 3px #009EE3" width="20%">
# <img src="../../images/ost_logo.png">
# </td>
# <td width="40%" style="text-align:left">
# <a href="../MainFiles/aux_files/biosignalsnotebooks_presentation.pdf" target="_blank">☌ Project Presentation</a>
# <br>
# <a href="https://github.com/biosignalsnotebooks/biosignalsnotebooks" target="_blank">☌ GitHub Repository</a>
# <br>
# <a href="https://pypi.org/project/biosignalsnotebooks/" target="_blank">☌ How to install biosignalsnotebooks Python package ?</a>
# <br>
# <a href="../MainFiles/signal_samples.ipynb">☌ Signal Library</a>
# </td>
# <td width="40%" style="text-align:left">
# <a href="../MainFiles/biosignalsnotebooks.ipynb">☌ Notebook Categories</a>
# <br>
# <a href="../MainFiles/by_diff.ipynb">☌ Notebooks by Difficulty</a>
# <br>
# <a href="../MainFiles/by_signal_type.ipynb">☌ Notebooks by Signal Type</a>
# <br>
# <a href="../MainFiles/by_tag.ipynb">☌ Notebooks by Tag</a>
# </td>
# </tr>
# </table>
# + tags=["hide_both"]
from biosignalsnotebooks.__notebook_support__ import css_style_apply
css_style_apply()
# + tags=["hide_both"] language="html"
# <script>
# // AUTORUN ALL CELLS ON NOTEBOOK-LOAD!
# require(
# ['base/js/namespace', 'jquery'],
# function(jupyter, $) {
# $(jupyter.events).on("kernel_ready.Kernel", function () {
# console.log("Auto-running all cells-below...");
# jupyter.actions.call('jupyter-notebook:run-all-cells-below');
# jupyter.actions.call('jupyter-notebook:save-notebook');
# });
# }
# );
# </script>
| notebookToHtml/biosignalsnotebooks_html_publish/Categories/Load/open_txt.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from Vaults_lib import *
import pprint
# +
# Collect TVL and prices of TVL
import csv
n=5 # number of vaults - don't change!!!
with open("vaultstvl5.csv", encoding='utf-8') as r_file:
file_reader = csv.reader(r_file, delimiter = ",")
counter=0
datas=[]
price=[]
tvl=[]
for row in file_reader:
if counter<19:
if counter ==0:
print('Заголовки = ',row)
counter +=1
else:
datas.append(row)
for i in range(0,len(datas)):
price.append([datas[i][0],float(datas[i][4]),float(datas[i][6]),float(datas[i][8]),float(datas[i][10]),float(datas[i][2])])
tvl.append([datas[i][0],int(datas[i][3]), int(datas[i][5]),int(datas[i][7]),int(datas[i][9]),int(datas[i][11])])
#pp.pprint(price)
#pp.pprint(tvl)
print('len(tvl)= ', len(tvl))
print('price(tvl)= ', len(price))
end = len(tvl)
print('tvl[end]= ',tvl[end-1])
for i in range(1,n+1):
print('tvl change ',i,' = ',(tvl[end-1][i]-tvl[0][i])/tvl[0][i]*100/(len(price))*365,' % за год ')
print('Vault 1 = MIM, Vault 2 = FRAX, Vault 3 = USDN, Vault 4= alUSD, Vault 5 = mUSD ' )
for i in range(1,n+1):
print('Profit of Vault ',i,' = ',(price[end-1][i]-price[0][i])/price[0][i]*100/(len(price))*365,' % per year')
print("Указаны проценты в пересчете на 1 год")
# +
# Preparing plot layout - initiate params
total_funds=15000000# Amount of money
delta=1 # Change Parametr Delta This !!!
param1=0
param2=0
param3=0
#-------------------
x=[]#steps
tot_profit1=[]
tot_profit2=[]
tot_profit3=[]
tot_pr1=0
tot_pr2=0
tot_pr3=0
funds11=[]
funds12=[]
funds13=[]
funds14=[]
funds15=[]
funds16=[]
funds21=[]
funds22=[]
funds23=[]
funds24=[]
funds25=[]
funds26=[]
funds31=[]
funds32=[]
funds33=[]
funds34=[]
funds35=[]
funds36=[]
pr_f11=[]
pr_f12=[]
pr_f13=[]
pr_f14=[]
pr_f15=[]
pr_f16=[]
pr_f21=[]
pr_f22=[]
pr_f23=[]
pr_f24=[]
pr_f25=[]
pr_f26=[]
pr_f31=[]
pr_f32=[]
pr_f33=[]
pr_f34=[]
pr_f35=[]
pr_f36=[]
profit_day1=[]
profit_day2=[]
profit_day3=[]
for i in range(0,len(price)-delta, delta):
f1=0
f2=0
f3=0
#print('steps i= ', i)
x.append(i)
funds1 = calc_shares_price_velosity(n, price, i, total_funds, delta, param1) #Strategy 1 - Price Velosity
funds2 = calc_shares_tvl_velosity(n, tvl, i, total_funds, delta, param2)# Strategy 2 - TVL Velosity
funds3= calc_shares_tvl(n, tvl, i, total_funds, delta, param3)# Strategy 3 - TVL
funds11.append(funds1[0])
funds12.append(funds1[1])
funds13.append(funds1[2])
funds14.append(funds1[3])
funds15.append(funds1[4])
#funds16.append(funds1[5])# comment this
tot_f1=0
for k in range(0,n):
tot_f1=tot_f1 + funds1[k]
pr_f11.append(funds1[0]/tot_f1*100)
pr_f12.append(funds1[1]/tot_f1*100)
pr_f13.append(funds1[2]/tot_f1*100)
pr_f14.append(funds1[3]/tot_f1*100)
pr_f15.append(funds1[4]/tot_f1*100)
#pr_f16.append(funds1[5]/tot_f1*100) # comment this
funds21.append(funds2[0])
funds22.append(funds2[1])
funds23.append(funds2[2])
funds24.append(funds2[3])
funds25.append(funds2[4])
#funds26.append(funds2[5])# comment this
tot_f2=0
for k in range(0,n):
tot_f2=tot_f2 + funds2[k]
pr_f21.append(funds2[0]/tot_f2*100)
pr_f22.append(funds2[1]/tot_f2*100)
pr_f23.append(funds2[2]/tot_f2*100)
pr_f24.append(funds2[3]/tot_f2*100)
pr_f25.append(funds2[4]/tot_f2*100)
#pr_f26.append(funds2[5]/tot_f2*100)# comment this
funds31.append(funds3[0])
funds32.append(funds3[1])
funds33.append(funds3[2])
funds34.append(funds3[3])
funds35.append(funds3[4])
#funds36.append(funds3[5])# comment this
tot_f3=0
for k in range(0,n):
tot_f3=tot_f3 + funds3[k]
pr_f31.append(funds3[0]/tot_f3*100)
pr_f32.append(funds3[1]/tot_f3*100)
pr_f33.append(funds3[2]/tot_f3*100)
pr_f34.append(funds3[3]/tot_f3*100)
pr_f35.append(funds3[4]/tot_f3*100)
#pr_f36.append(funds3[5]/tot_f3*100)# comment this
#funds2 = [12540558.371716868, 416968.1746170347, 42473.45366609666, 0.0, 0.0]
#f=calc_profit_step1(n,price, funds2, i, delta)
#print('f= ',f)
profit_day1.append(calc_profit_step(n,price, funds1, i, delta))
profit_day2.append(calc_profit_step(n,price, funds2, i, delta))
profit_day3.append(calc_profit_step(n,price, funds3, i, delta))
tot_pr1=tot_pr1+calc_profit_step(n,price, funds1, i, delta)
tot_pr2=tot_pr2+calc_profit_step(n,price, funds2, i, delta)
#print('f2= ',calc_profit_step(n,price, funds2, i, delta))
tot_pr3=tot_pr3+calc_profit_step(n,price, funds3, i, delta)
#print('f3= ',calc_profit_step(n,price, funds3, i, delta))
tot_profit1.append(tot_pr1)
tot_profit2.append(tot_pr2)
tot_profit3.append(tot_pr3)
#print('funds1 = ', funds1)
print(len(tvl),' days total profit Strategy 1 (Price Velosity) USD', round(tot_pr1) )
print('APR is', round(tot_pr1/len(tvl)*365/total_funds*100, 2),'% per year' )
print(len(tvl),' days total profit Strategy 2 (TVL Velosity) USD', round(tot_pr2) )
print('APR is', round(tot_pr2/len(tvl)*365/total_funds*100, 2),'% per year' )
print(len(tvl),' days total profit Strategy 3 (TVL) USD', round(tot_pr3) )
print('APR is', round(tot_pr3/len(tvl)*365/total_funds*100, 2),'%' )
# +
#проверка
#print(len(price))
print("Контроль изменения цен по валтам")
price1=[[]]
price2=[]
for i in range(0,len(price)-1):
price1.append([])
#print('price[i]=',price[i])
for j in range(1, n+1):
price1[i].append(price[i+1][j]-price[i][j])
print('price1[i], i= ',i, price1[i])
#pp.pprint(price1)
#pp.pprint( price1)
# -
gas_fee = 2000 #2000 USD
pr11=[]
pr22=[]
pr33=[]
pr11_gas=[]
pr22_gas=[]
pr33_gas=[]
z=[]
for delta in range (1,len(tvl)):
pr1=0
pr2=0
pr3=0
z.append(delta)
for i in range(0,len(price)-delta, delta):
funds1 = calc_shares_price_velosity(n, price, i, total_funds, delta, param1) #Strategy 1 - Price Velosity
funds2 = calc_shares_tvl_velosity(n, tvl, i, total_funds, delta, param2)# Strategy 2 - TVL Velosity
funds3 = calc_shares_tvl(n, tvl, i, total_funds, delta, param3)# Strategy 3 - TVL
pr1 = pr1+calc_profit_step(n,price, funds1, i, delta)
pr2 = pr2+calc_profit_step(n,price, funds2, i, delta)
pr3 = pr3+calc_profit_step(n,price, funds3, i, delta)
pr11.append(pr1/total_funds/len(tvl)*365*100)
pr22.append(pr2/total_funds/len(tvl)*365*100)
pr33.append(pr3/total_funds/len(tvl)*365*100)
pr11_gas.append((pr1-gas_fee)/total_funds/len(tvl)*365*100)
pr22_gas.append((pr2-gas_fee)/total_funds/len(tvl)*365*100)
pr33_gas.append((pr3-gas_fee)/total_funds/len(tvl)*365*100)
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=z, y=pr11, line=dict(color='red'), name='Strategy 1 - Price Velosity vs Delta'), secondary_y=False)
fig.add_trace(go.Scatter(x=z, y=pr22, line=dict(color='green'), name='Strategy 2 - TVL Velosity vs Delta'), secondary_y=False)
fig.add_trace(go.Scatter(x=z, y=pr33, line=dict(color='grey'), name='Strategy 3 - TVL vs Delta'), secondary_y=False)
fig.update_layout(title_text='<b>Comparison of Profit of Strategies vs Delta in % APR per year no gas fee </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=z, y=pr33, line=dict(color='red'), name='Strategy 3 - no gas fee'), secondary_y=False)
fig.add_trace(go.Scatter(x=z, y=pr33_gas, line=dict(color='black'), name='Strategy 3 - with gas fee'), secondary_y=False)
#fig.add_trace(go.Scatter(x=z, y=pr22, line=dict(color='green'), name='Strategy 2 - TVL Velosity no gas fee'), secondary_y=True)
#fig.add_trace(go.Scatter(x=z, y=pr22_gas, line=dict(color='green'), name='Strategy 2 - TVL Velosity with gas fee'), secondary_y=True)
#fig.add_trace(go.Scatter(x=z, y=pr33, line=dict(color='grey'), name='Strategy 3 - TVL vs Delta'), secondary_y=False)
fig.update_layout(title_text='<b>Compare of Profit of Strategies vs Delta in % APR per year with gas fee and without gas fee </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# -
#Each Vault as single
def profit_vault_day(price, vault_number, step, total_funds):
return (price[step+1][vault_number]-price[step][vault_number])*total_funds
#---------------
delta = 1
#---------------
profit1=[]
profit2=[]
profit3=[]
profit4=[]
profit5=[]
k=[]
profit_fund1 =[]
profit_fund2 =[]
profit_fund3 =[]
profit_fund4 =[]
profit_fund5 =[]
pf1=1
pf2=1
pf3=1
pf4=1
pf5=1
for step in range(0,len(price)-delta, delta):
k.append(step)
profit1.append(profit_vault_day(price, 1, step, total_funds))
pf1=pf1+profit_vault_day(price, 1, step, total_funds)
profit_fund1.append(pf1)
profit2.append(profit_vault_day(price, 2, step, total_funds))
pf2=pf2+profit_vault_day(price, 2, step, total_funds)
profit_fund2.append(pf2)
profit3.append(profit_vault_day(price, 3, step, total_funds))
pf3=pf3+profit_vault_day(price, 3, step, total_funds)
profit_fund3.append(pf3)
profit4.append(profit_vault_day(price, 4, step, total_funds))
pf4=pf4+profit_vault_day(price, 4, step, total_funds)
profit_fund4.append(pf4)
profit5.append(profit_vault_day(price, 5, step, total_funds))
pf5=pf5+profit_vault_day(price, 5, step, total_funds)
profit_fund5.append(pf5)
#print(profit_fund1)
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=k, y=profit_fund1, line=dict(color='red'), name='MIM Total'), secondary_y=True)
#fig.add_trace(go.Scatter(x=k, y=profit1, line=dict(color='red'), name='USDP'), secondary_y=True)
fig.add_trace(go.Scatter(x=k, y=profit_fund2, line=dict(color='green'), name='FRAX Total'), secondary_y=False)
#fig.add_trace(go.Scatter(x=k, y=profit2, line=dict(color='green'), name='USDN'), secondary_y=True)
fig.add_trace(go.Scatter(x=k, y=profit_fund3, line=dict(color='grey'), name='USDN Total'), secondary_y=False)
#fig.add_trace(go.Scatter(x=k, y=profit3, line=dict(color='grey'), name='IronBank'), secondary_y=True)
fig.add_trace(go.Scatter(x=k, y=profit_fund4, line=dict(color='blue'), name='alUSD Total'), secondary_y=False)
#fig.add_trace(go.Scatter(x=k, y=profit4, line=dict(color='blue'), name='sUSD'), secondary_y=True)
fig.add_trace(go.Scatter(x=k, y=profit_fund5, line=dict(color='brown'), name='mUSD'), secondary_y=False)
fig.update_layout(title_text='<b>Profit of each Vault Total in USD </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
#fig.add_trace(go.Scatter(x=k, y=profit_fund1, line=dict(color='red'), name='USDP Total'), secondary_y=False)
fig.add_trace(go.Scatter(x=k, y=profit1, line=dict(color='red'), name='MIM'), secondary_y=False)
fig.add_trace(go.Scatter(x=k, y=profit2, line=dict(color='green'), name='FRAX'), secondary_y=False)
fig.add_trace(go.Scatter(x=k, y=profit3, line=dict(color='grey'), name='USDN'), secondary_y=False)
#fig.add_trace(go.Scatter(x=k, y=profit_fund4, line=dict(color='blue'), name='sUSD Total'), secondary_y=False)
fig.add_trace(go.Scatter(x=k, y=profit4, line=dict(color='blue'), name='alUSD'), secondary_y=False)
fig.add_trace(go.Scatter(x=k, y=profit5, line=dict(color='brown'), name='mUSD'), secondary_y=False)
fig.update_layout(title_text='<b>Profit of each Vaults per day in USD </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=x, y=tot_profit1, line=dict(color='red'), name='Strategy 1 - Price Velosity'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=tot_profit2, line=dict(color='green'), name='Strategy 2 - TVL Velosity'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=tot_profit3, line=dict(color='grey'), name='Strategy 3 - TVL'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=profit_fund1, line=dict(color='black'), name='MIM Total'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=profit_fund3, line=dict(color='blue'), name='USDN Total'), secondary_y=False)
fig.add_trace(go.Scatter(x=k, y=profit_fund5, line=dict(color='brown'), name='mUSD'), secondary_y=False)
fig.update_layout(title_text='<b>Comparison total income of Strategies and The Best Vault USDN </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=x, y=profit1, line=dict(color='green'), name='MIM'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=profit2, line=dict(color='grey'), name='FRAX'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=profit3, line=dict(color='blue'), name='USDN'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=profit4, line=dict(color='coral'), name='alUSD'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=profit5, line=dict(color='brown'), name='mUSD'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=profit_day1, line=dict(color='red'), name='Strategy 1- Price Velosity'), secondary_y=False)
#fig.add_trace(go.Scatter(x=k, y=profit1, line=dict(color='red'), name='MIM'), secondary_y=False)
fig.update_layout(title_text='<b>Comparison of every day Profit of USDN Vault and Best Strategy in USD </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# -
# На рисунке выше видно, как стратегия поймала два скачка в разных Vaults - не знаю, осуществимо ли это на практике, но на картинке красиво !
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=x, y=pr_f11, line=dict(color='red'), name='MIM'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f12, line=dict(color='green'), name='FRAX'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f13, line=dict(color='grey'), name='USDN'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f14, line=dict(color='blue'), name='alUSD'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f15, line=dict(color='brown'), name='mUSD'), secondary_y=False)
#fig.add_trace(go.Scatter(x=x, y=pr_f16, line=dict(color='light green'), name='BUSD'), secondary_y=False)
fig.update_layout(yaxis_range=[-5,110])
fig.update_layout(xaxis_range=[-3,len(tvl)+1])
fig.update_layout(title_text='<b>Strategies 1 - Vaults Price Velosity - Percentage of Shares </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=x, y=pr_f21, line=dict(color='red'), name='MIM'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f22, line=dict(color='green'), name='FRAX'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f23, line=dict(color='grey'), name='USDN'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f24, line=dict(color='blue'), name='alUSD'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f25, line=dict(color='brown'), name='mUSD'), secondary_y=False)
#fig.add_trace(go.Scatter(x=x, y=pr_f26, line=dict(color='light green'), name='BUSD'), secondary_y=False)
fig.update_layout(yaxis_range=[-2,105])
fig.update_layout(xaxis_range=[-3,len(tvl)+1])
fig.update_layout(title_text='<b>Strategies 2 - TVL Velosity - Percentage of Shares </b>')
fig.update_xaxes(title_text='Step')
fig.show()
# +
fig = make_subplots(subplot_titles=('' ), specs=[[{"secondary_y": True}]])
fig.add_trace(go.Scatter(x=x, y=pr_f31, line=dict(color='red'), name='MIM'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f32, line=dict(color='green'), name='FRAX'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f33, line=dict(color='grey'), name='USDN'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f34, line=dict(color='blue'), name='alUSD'), secondary_y=False)
fig.add_trace(go.Scatter(x=x, y=pr_f35, line=dict(color='brown'), name='mUSD'), secondary_y=False)
#fig.add_trace(go.Scatter(x=x, y=pr_f36, line=dict(color='light green'), name='BUSD'), secondary_y=False)
fig.update_layout(yaxis_range=[-3,105])
fig.update_layout(xaxis_range=[-3,len(tvl)+1])
fig.update_layout(title_text='<b>Strategies 3 - TVL - Percentage of Shares</b>')
fig.update_xaxes(title_text='Step')
fig.show()
# -
| YearnVaultsSimulation/old/v4/v4gasfee/funds5_1-with gas fee-211021.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jainnipun/MachineLearning/blob/master/TextAnalytics/NLP_Text_classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="VVv4MAOTpyBJ" colab_type="text"
# #Natural Language Processing (NLP)
# + [markdown] id="j_-ZFWO1-AyZ" colab_type="text"
# ## Text Classification
# + [markdown] id="puMtCKWdvHvj" colab_type="text"
# **Identifying wether a name is of a Male or Female **
# + [markdown] id="CzrO3jlhpu5q" colab_type="text"
# I am using the NLTK’s names corpus as the labeled training data. The names corpus contains a total of around 8K male and female names.
# It’s compiled by <NAME>.
#
# So, we have two categories for classification. They are male and female. Our training data (the “names” corpus) has names that are already labeled as male and names that are already labeled as female.
# + id="txKKVW2ZnnVB" colab_type="code" outputId="67586113-91df-4264-bae5-83809ae0461d" colab={"base_uri": "https://localhost:8080/", "height": 68}
import nltk
nltk.download('names')
# + id="sWFqMakWnbWZ" colab_type="code" outputId="298fb9ce-8105-4e69-8338-cff7bbf1262d" colab={"base_uri": "https://localhost:8080/", "height": 34}
from nltk.corpus import names
#Viewing fields present in names
print (names.fileids()) # Output: ['female.txt', 'male.txt']
# + id="UqACRh4X9k1W" colab_type="code" outputId="a7f0e5ae-d231-44bf-f00b-7adaefac9d67" colab={"base_uri": "https://localhost:8080/", "height": 85}
male_names = names.words('male.txt')
female_names = names.words('female.txt')
print (len(male_names)) # Output: 2943
print (len(female_names)) # Output: 5001
# print 15 female names
print (female_names[1200:1215])
# print 15 male names
print (male_names[1200:1215])
# + [markdown] id="ia6PexHxqRAf" colab_type="text"
# **Feature Extraction**
#
# To classify the text into any category, we need to define some criteria. On the basis of those criteria, our classifier will learn that a particular kind of text falls in a particular category. This kind of criteria is known as feature. We can define one or more feature to train our classifier.
#
# In this example, we will use the last letter of the names as the feature.
#
# We will define a function that extracts the last letter of any provided word. The function will return a dictionary containing the last letter information of the given word.
# + id="T5GSU4FTnxRr" colab_type="code" outputId="8bdd22d0-f65b-43a0-eb9c-5ccaa5424a40" colab={"base_uri": "https://localhost:8080/", "height": 34}
def gender_features(word):
return {'last_letter' : word[-1:]}
print (gender_features('Nipun')) # Output: {'last_letter': 'n'}
# + [markdown] id="zU2dq4eLrvev" colab_type="text"
# The dictionary returned by the above function is called a feature set. This feature set is used to train the classifier.
#
# We will now create a feature set using all the male and female names.
#
# For this, we first combine the male and female names and shuffle the combined array.
# + id="4wJ8qKPNnxXn" colab_type="code" outputId="3cc79c20-8ee7-4063-cf6c-fa46fc1bb639" colab={"base_uri": "https://localhost:8080/", "height": 71}
from nltk.corpus import names
import random
names_masculine = names.words('male.txt')
names_feminine = names.words('female.txt')
labeled_names_feminine = [(str(name), 'female') for name in names_feminine]
# printing 15 labeled female names
print (labeled_names_feminine[1200:1215])
print('No of Female names :',len(labeled_names_feminine))
# + id="Xx_BHaUjDeWU" colab_type="code" outputId="8b5cd3f8-78f8-4912-c29a-142d2bc2fa37" colab={"base_uri": "https://localhost:8080/", "height": 71}
labeled_names_masculine = [(str(name), 'male') for name in names_masculine]
# printing 15 labeled male names
print (labeled_names_masculine[1200:1215])
print('No of Male names :',len(labeled_names_masculine))
# + id="1kw17hBUDfv9" colab_type="code" outputId="1f6a186d-ac4c-44c5-e85c-2774f0551fce" colab={"base_uri": "https://localhost:8080/", "height": 34}
# combine labeled male and labeled female names
labeled_all_names = labeled_names_masculine + labeled_names_feminine
print('Total Names : ',len(labeled_all_names))
# + id="Z9nyOProDiIa" colab_type="code" outputId="f180dbe6-603f-48e8-8234-ae0e84f15f32" colab={"base_uri": "https://localhost:8080/", "height": 54}
# shuffle the labeled names array
random.shuffle(labeled_all_names)
# printing 10 labeled all/combined names
print (labeled_all_names[1200:1215])
# + [markdown] id="0IIN5ja3sjf5" colab_type="text"
# **Extracting Feature & Creating Feature Set**
#
# We use the gender_features function that we defined above to extract the feature from the labeled names data. As mentioned above, the feature for this example will be the last letter of the names. So, we extract the last letter of all the labeled names and create a new array with the last letter of each name and the associated label for that particular name. This new array is called the feature set.
# + id="ZRvchnM3nxaw" colab_type="code" outputId="d9ca2137-6821-42aa-b207-8e63178848c5" colab={"base_uri": "https://localhost:8080/", "height": 71}
feature_set = [(gender_features(name), gender) for (name, gender) in labeled_all_names]
print (labeled_all_names[:15])
print (feature_set[:15])
# + [markdown] id="J24K6WR0tr6u" colab_type="text"
# **Training Classifier**
#
# From the feature set we created above, we now create a separate training set and a separate testing/validation set. The train set is used to train the classifier and the test set is used to test the classifier to check how accurately it classifies the given text.
#
# **Creating Train and Test Dataset**
#
# Now we will be splitting the dataset using scikit learn test-train split.
# We split data in 80/20 percentage split between training and testing set, i.e. 80 percent training set and 20 percent testing set.
#
# test_size : = 0.25 represents the percent of test samples, rest is training set
#
# random_state : 73 The seed used by the random number generator
# + id="gjQ2S_conxeI" colab_type="code" outputId="3a5f0da3-db6f-4a51-cf76-23b7201fcf91" colab={"base_uri": "https://localhost:8080/", "height": 51}
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(feature_set, test_size=0.20, random_state=73)
print ('Train set Length',len(train_set)) # Output: 6355
print ('Test set Length',len(test_set)) # Output: 1589
# + [markdown] id="L7kjM0RvuKZT" colab_type="text"
# **Training a Classifier**
#
# Now, we train a classifier using the training dataset. There are different kind of classifiers namely Naive Bayes Classifier, Maximum Entropy Classifier, Decision Tree Classifier, Support Vector Machine Classifier, etc.
#
# In this example, we use the Naive Bayes Classifier. It’s a simple, fast, and easy classifier which performs well for small datasets. It’s a simple probabilistic classifier based on applying Bayes’ theorem. Bayes’ theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event.
# + id="SixfPVihn6WJ" colab_type="code" colab={}
from nltk import NaiveBayesClassifier
classifier = NaiveBayesClassifier.train(train_set)
# + [markdown] id="GlRJZmA3uQPs" colab_type="text"
# **Testing the trained Classifier**
#
# Let’s see the output of the classifier by providing some names to it.
# + id="K2QW6tUyn6ZH" colab_type="code" outputId="fe35e4f7-73b1-45aa-cde2-482c486e59d2" colab={"base_uri": "https://localhost:8080/", "height": 51}
print (classifier.classify(gender_features('Nipun'))) # Output: male
print (classifier.classify(gender_features('Roxie'))) # Output: female
# + [markdown] id="KmDZevPIuVyu" colab_type="text"
# Let’s see the accuracy percentage of the trained classifier. The accuracy value changes each time you run the program because of the names array being shuffled above.
#
#
# + id="AnR-pHvln6b_" colab_type="code" outputId="7e45fda0-419d-4358-8db4-adc420dbf12a" colab={"base_uri": "https://localhost:8080/", "height": 34}
from nltk import classify
accuracy = classify.accuracy(classifier, test_set)
print (accuracy)
# + [markdown] id="cNjXkMI9ugSy" colab_type="text"
# Let’s see the most informative features among the entire features in the feature set.
#
# The result shows that the names ending with letter “a” are females 40.3 times more often than they are female but the names ending with the letter “k” are males 39.0 times more often than they are male. Similarly, for other letters. These ratios are also called likelihood ratios.
#
# Therefore, if you provide a name ending with letter “k” to the above trained classifier then it will predict it as “male” and if you provide a name ending with the letter “a” to the classifier then it will predict it as “female”.
#
# + id="afZZWG10n6e5" colab_type="code" outputId="e7a593bf-7d91-4a5a-b4fc-03017b4289fc" colab={"base_uri": "https://localhost:8080/", "height": 187}
# show 5 most informative features
print (classifier.show_most_informative_features(5))
print ('Rock : ',classifier.classify(gender_features('Rock'))) # Output: male
print ('Sara : ',classifier.classify(gender_features('Sara'))) # Output: female
print ('Nipun : ',classifier.classify(gender_features('Nipun'))) # Output: male
# + [markdown] id="7LGidBDquo4a" colab_type="text"
# **Note**:
# We can modify the *gender_features* function to generate the feature set which can improve the accuracy of the trained classifier.
# For example,
# we can use last two letters instead of 1
# or we can use both first and last letter of the names as the feature.
# Feature extractors are built through a process of trial-and-error & guided by intuitions.
| TextAnalytics/NLP_Text_classification.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Project 8: Backtesting
#
# In this project, you will build a fairly realistic backtester that uses the Barra data. The backtester will perform portfolio optimization that includes transaction costs, and you'll implement it with computational efficiency in mind, to allow for a reasonably fast backtest. You'll also use performance attribution to identify the major drivers of your portfolio's profit-and-loss (PnL). You will have the option to modify and customize the backtest as well.
#
#
# ## Instructions
#
# Each problem consists of a function to implement and instructions on how to implement the function. The parts of the function that need to be implemented are marked with a `# TODO` comment. Your code will be checked for the correct solution when you submit it to Udacity.
#
#
# ## Packages
#
# When you implement the functions, you'll only need to you use the packages you've used in the classroom, like [Pandas](https://pandas.pydata.org/) and [Numpy](http://www.numpy.org/). These packages will be imported for you. We recommend you don't add any import statements, otherwise the grader might not be able to run your code.
#
# ### Install Packages
import sys
# !{sys.executable} -m pip install -r requirements.txt
# ### Load Packages
# +
import scipy
import patsy
import pickle
import numpy as np
import pandas as pd
import scipy.sparse
import matplotlib.pyplot as plt
from statistics import median
from scipy.stats import gaussian_kde
from statsmodels.formula.api import ols
from tqdm import tqdm
# -
# ## Load Data
#
# We’ll be using the Barra dataset to get factors that can be used to predict risk. Loading and parsing the raw Barra data can be a very slow process that can significantly slow down your backtesting. For this reason, it's important to pre-process the data beforehand. For your convenience, the Barra data has already been pre-processed for you and saved into pickle files. You will load the Barra data from these pickle files.
#
# In the code below, we start by loading `2004` factor data from the `pandas-frames.2004.pickle` file. We also load the `2003` and `2004` covariance data from the `covaraince.2003.pickle` and `covaraince.2004.pickle` files. You are encouraged to customize the data range for your backtest. For example, we recommend starting with two or three years of factor data. Remember that the covariance data should include all the years that you choose for the factor data, and also one year earlier. For example, in the code below we are using `2004` factor data, therefore, we must include `2004` in our covariance data, but also the previous year, `2003`. If you don't remember why must include this previous year, feel free to review the lessons.
# +
barra_dir = '../../data/project_8_barra/'
data = {}
for year in [2004]:
fil = barra_dir + "pandas-frames." + str(year) + ".pickle"
data.update(pickle.load( open( fil, "rb" ) ))
covariance = {}
for year in [2004]:
fil = barra_dir + "covariance." + str(year) + ".pickle"
covariance.update(pickle.load( open(fil, "rb" ) ))
daily_return = {}
for year in [2004, 2005]:
fil = barra_dir + "price." + str(year) + ".pickle"
daily_return.update(pickle.load( open(fil, "rb" ) ))
# -
# ## Shift Daily Returns Data (TODO)
#
# In the cell below, we want to incorporate a realistic time delay that exists in live trading, we’ll use a two day delay for the `daily_return` data. That means the `daily_return` should be two days after the data in `data` and `cov_data`. Combine `daily_return` and `data` together in a dict called `frames`.
#
# Since reporting of PnL is usually for the date of the returns, make sure to use the two day delay dates (dates that match the `daily_return`) when building `frames`. This means calling `frames['20040108']` will get you the prices from "20040108" and the data from `data` at "20040106".
#
# Note: We're not shifting `covariance`, since we'll use the "DataDate" field in `frames` to lookup the covariance data. The "DataDate" field contains the date when the `data` in `frames` was recorded. For example, `frames['20040108']` will give you a value of "20040106" for the field "DataDate".
# +
frames ={}
dlyreturn_n_days_delay = 2
# TODO: Implement
d_shifts = zip(
sorted(data.keys()),
sorted(daily_return.keys())[dlyreturn_n_days_delay:len(data) + dlyreturn_n_days_delay])
for data_date, price_date in d_shifts:
frames[price_date] = data[data_date].merge(daily_return[price_date], on='Barrid')
# -
# ## Add Daily Returns date column (Optional)
# Name the column `DlyReturnDate`.
# **Hint**: create a list containing copies of the date, then create a pandas series.
# Optional
for DlyReturnDate, df in daily_return.items():
n_rows = df.shape[0]
df['DlyReturnDate'] = pd.Series([DlyReturnDate]*n_rows)
# ## Winsorize
#
# As we have done in other projects, we'll want to avoid extremely positive or negative values in our data. Will therefore create a function, `wins`, that will clip our values to a minimum and maximum range. This process is called **Winsorizing**. Remember that this helps us handle noise, which may otherwise cause unusually large positions.
def wins(x,a,b):
return np.where(x <= a,a, np.where(x >= b, b, x))
# ## Density Plot
#
# Let's check our `wins` function by taking a look at the distribution of returns for a single day `20040102`. We will clip our data from `-0.1` to `0.1` and plot it using our `density_plot` function.
# +
def density_plot(data):
density = gaussian_kde(data)
xs = np.linspace(np.min(data),np.max(data),200)
density.covariance_factor = lambda : .25
density._compute_covariance()
plt.plot(xs,density(xs))
plt.xlabel('Daily Returns')
plt.ylabel('Density')
plt.show()
test = frames['20040108']
test['DlyReturn'] = wins(test['DlyReturn'],-0.1,0.1)
density_plot(test['DlyReturn'])
# -
# ## Factor Exposures and Factor Returns
#
# Recall that:
#
# $r_{i,t} = \sum_{j=1}^{k} (\beta_{i,j,t-2} \times f_{j,t})$
# where $i=1...N$ (N assets),
# and $j=1...k$ (k factors).
#
# where $r_{i,t}$ is the return, $\beta_{i,j,t-2}$ is the factor exposure, and $f_{j,t}$ is the factor return. Since we get the factor exposures from the Barra data, and we know the returns, it is possible to estimate the factor returns. In this notebook, we will use the Ordinary Least Squares (OLS) method to estimate the factor exposures, $f_{j,t}$, by using $\beta_{i,j,t-2}$ as the independent variable, and $r_{i,t}$ as the dependent variable.
# +
def get_formula(factors, Y):
L = ["0"]
L.extend(factors)
return Y + " ~ " + " + ".join(L)
def factors_from_names(n):
return list(filter(lambda x: "USFASTD_" in x, n))
def estimate_factor_returns(df):
## build universe based on filters
estu = df.loc[df.IssuerMarketCap > 1e9].copy(deep=True)
## winsorize returns for fitting
estu['DlyReturn'] = wins(estu['DlyReturn'], -0.25, 0.25)
all_factors = factors_from_names(list(df))
form = get_formula(all_factors, "DlyReturn")
model = ols(form, data=estu)
results = model.fit()
return results
# +
facret = {}
for date in frames:
facret[date] = estimate_factor_returns(frames[date]).params
# -
my_dates = sorted(list(map(lambda date: pd.to_datetime(date, format='%Y%m%d'), frames.keys())))
# ## Choose Alpha Factors
#
# We will now choose our alpha factors. Barra's factors include some alpha factors that we have seen before, such as:
#
# * **USFASTD_1DREVRSL** : Reversal
#
# * **USFASTD_EARNYILD** : Earnings Yield
#
# * **USFASTD_VALUE** : Value
#
# * **USFASTD_SENTMT** : Sentiment
#
# We will choose these alpha factors for now, but you are encouraged to come back to this later and try other factors as well.
# +
alpha_factors = ["USFASTD_1DREVRSL", "USFASTD_EARNYILD", "USFASTD_VALUE", "USFASTD_SENTMT"]
facret_df = pd.DataFrame(index = my_dates)
for dt in my_dates:
for alp in alpha_factors:
facret_df.at[dt, alp] = facret[dt.strftime('%Y%m%d')][alp]
for column in facret_df.columns:
plt.plot(facret_df[column].cumsum(), label=column)
plt.legend(loc='upper left')
plt.xlabel('Date')
plt.ylabel('Cumulative Factor Returns')
plt.show()
# -
# ## Merge Previous Portfolio Holdings
#
# In order to optimize our portfolio we will use the previous day's holdings to estimate the trade size and transaction costs. In order to keep track of the holdings from the previous day we will include a column to hold the portfolio holdings of the previous day. These holdings of all our assets will be initialized to zero when the backtest first starts.
def clean_nas(df):
numeric_columns = df.select_dtypes(include=[np.number]).columns.tolist()
for numeric_column in numeric_columns:
df[numeric_column] = np.nan_to_num(df[numeric_column])
return df
# +
previous_holdings = pd.DataFrame(data = {"Barrid" : ["USA02P1"], "h.opt.previous" : np.array(0)})
df = frames[my_dates[0].strftime('%Y%m%d')]
df = df.merge(previous_holdings, how = 'left', on = 'Barrid')
df = clean_nas(df)
df.loc[df['SpecRisk'] == 0]['SpecRisk'] = median(df['SpecRisk'])
# -
# ## Build Universe Based on Filters (TODO)
#
# In the cell below, implement the function `get_universe` that creates a stock universe by selecting only those companies that have a market capitalization of at least 1 billion dollars **OR** that are in the previous day's holdings, even if on the current day, the company no longer meets the 1 billion dollar criteria.
#
# When creating the universe, make sure you use the `.copy()` attribute to create a copy of the data. Also, it is very important to make sure that we are not looking at returns when forming the portfolio! to make this impossible, make sure to drop the column containing the daily return.
# +
def get_universe(df):
"""
Create a stock universe based on filters
Parameters
----------
df : DataFrame
All stocks
Returns
-------
universe : DataFrame
Selected stocks based on filters
"""
# TODO: Implement
#making copy of data
data_copy = df.copy()
universe = data_copy.loc[(data_copy['IssuerMarketCap']>=1e9)]
return universe.drop(columns='DlyReturn')
universe = get_universe(df)
# -
date = str(int(universe['DataDate'][1]))
# ## Factors
#
# We will now extract both the risk factors and alpha factors. We begin by first getting all the factors using the `factors_from_names` function defined previously.
all_factors = factors_from_names(list(universe))
# We will now create the function `setdiff` to just select the factors that we have not defined as alpha factors
def setdiff(temp1, temp2):
s = set(temp2)
temp3 = [x for x in temp1 if x not in s]
return temp3
risk_factors = setdiff(all_factors, alpha_factors)
# We will also save the column that contains the previous holdings in a separate variable because we are going to use it later when we perform our portfolio optimization.
h0 = universe['h.opt.previous']
# ## Matrix of Risk Factor Exposures
#
# Our dataframe contains several columns that we'll use as risk factors exposures. Extract these and put them into a matrix.
#
# The data, such as industry category, are already one-hot encoded, but if this were not the case, then using `patsy.dmatrices` would help, as this function extracts categories and performs the one-hot encoding. We'll practice using this package, as you may find it useful with future data sets. You could also store the factors in a dataframe if you prefer.
#
# #### How to use patsy.dmatrices
#
# `patsy.dmatrices` takes in a formula and the dataframe. The formula tells the function which columns to take. The formula will look something like this:
# `SpecRisk ~ 0 + USFASTD_AERODEF + USFASTD_AIRLINES + ...`
# where the variable to the left of the ~ is the "dependent variable" and the others to the right are the independent variables (as if we were preparing data to be fit to a model).
#
# This just means that the `pasty.dmatrices` function will return two matrix variables, one that contains the single column for the dependent variable `outcome`, and the independent variable columns are stored in a matrix `predictors`.
#
# The `predictors` matrix will contain the matrix of risk factors, which is what we want. We don't actually need the `outcome` matrix; it's just created because that's the way patsy.dmatrices works.
formula = get_formula(risk_factors, "SpecRisk")
def model_matrix(formula, data):
outcome, predictors = patsy.dmatrices(formula, data)
return predictors
B = model_matrix(formula, universe)
BT = B.transpose()
# ## Calculate Specific Variance
#
# Notice that the specific risk data is in percent:
universe['SpecRisk'][0:2]
# Therefore, in order to get the specific variance for each stock in the universe we first need to multiply these values by `0.01` and then square them:
specVar = (0.01 * universe['SpecRisk']) ** 2
# ## Factor covariance matrix (TODO)
#
# Note that we already have factor covariances from Barra data, which is stored in the variable `covariance`. `covariance` is a dictionary, where the key is each day's date, and the value is a dataframe containing the factor covariances.
covariance['20040102'].head()
# In the code below, implement the function `diagonal_factor_cov` to create the factor covariance matrix. Note that the covariances are given in percentage units squared. Therefore you must re-scale them appropriately so that they're in decimals squared. Use the given `colnames` function to get the column names from `B`.
#
# When creating factor covariance matrix, you can store the factor variances and covariances, or just store the factor variances. Try both, and see if you notice any differences.
def colnames(B):
if type(B) == patsy.design_info.DesignMatrix:
return B.design_info.column_names
if type(B) == pandas.core.frame.DataFrame:
return B.columns.tolist()
return None
# +
def diagonal_factor_cov(date, B):
"""
Create the factor covariance matrix
Parameters
----------
date : string
date. For example 20040102
B : patsy.design_info.DesignMatrix OR pandas.core.frame.DataFrame
Matrix of Risk Factors
Returns
-------
Fm : Numpy ndarray
factor covariance matrix
"""
# TODO: Implement
factor_cov_matrix = np.zeros([B.shape[1],B.shape[1]])
for i in range(0,B.shape[1]):
factor = colnames(B)[i]
factor_cov_matrix[i,i] = (0.01**2) * covariance[date].loc[(covariance[date].Factor1==factor) & (covariance[date].Factor2==factor),"VarCovar"].iloc[0]
return factor_cov_matrix
Fvar = diagonal_factor_cov(date, B)
# -
# ## Transaction Costs
#
# To get the transaction cost, or slippage, we have to multiply the price change due to market impact by the amount of dollars traded:
#
# $$
# \mbox{tcost_{i,t}} = \% \Delta \mbox{price}_{i,t} \times \mbox{trade}_{i,t}
# $$
#
# In summation notation it looks like this:
# $$
# \mbox{tcost}_{i,t} = \sum_i^{N} \lambda_{i,t} (h_{i,t} - h_{i,t-1})^2
# $$
# where
# $$
# \lambda_{i,t} = \frac{1}{10\times \mbox{ADV}_{i,t}}
# $$
#
# Note that since we're dividing by ADV, we'll want to handle cases when ADV is missing or zero. In those instances, we can set ADV to a small positive number, such as 10,000, which, in practice assumes that the stock is illiquid. In the code below if there is no volume information we assume the asset is illiquid.
# +
def get_lambda(universe, composite_volume_column = 'ADTCA_30'):
universe.loc[np.isnan(universe[composite_volume_column]), composite_volume_column] = 1.0e4
universe.loc[universe[composite_volume_column] == 0, composite_volume_column] = 1.0e4
adv = universe[composite_volume_column]
return 0.1 / adv
Lambda = get_lambda(universe)
# -
# ## Alpha Combination (TODO)
#
# In the code below create a matrix of alpha factors and return it from the function `get_B_alpha`. Create this matrix in the same way you created the matrix of risk factors, i.e. using the `get_formula` and `model_matrix` functions we have defined above. Feel free to go back and look at the previous code.
# +
def get_B_alpha(alpha_factors, universe):
# TODO: Implement
return model_matrix(get_formula(alpha_factors, "SpecRisk"), data = universe)
B_alpha = get_B_alpha(alpha_factors, universe)
# -
# Now that you have the matrix containing the alpha factors we will combine them by adding its rows. By doing this we will collapse the `B_alpha` matrix into a single alpha vector. We'll multiply by `1e-4` so that the expression of expected portfolio return, $\alpha^T \mathbf{h}$, is in dollar units.
# +
def get_alpha_vec(B_alpha):
"""
Create an alpha vecrtor
Parameters
----------
B_alpha : patsy.design_info.DesignMatrix
Matrix of Alpha Factors
Returns
-------
alpha_vec : patsy.design_info.DesignMatrix
alpha vecrtor
"""
# TODO: Implement
return 1e-4* B_alpha.sum(axis=1)
alpha_vec = get_alpha_vec(B_alpha)
# -
# #### Optional Challenge
#
# You can also try to a more sophisticated method of alpha combination, by choosing the holding for each alpha based on the same metric of its performance, such as the factor returns, or sharpe ratio. To make this more realistic, you can calculate a rolling average of the sharpe ratio, which is updated for each day. Remember to only use data that occurs prior to the date of each optimization, and not data that occurs in the future. Also, since factor returns and sharpe ratios may be negative, consider using a `max` function to give the holdings a lower bound of zero.
# ## Objective function (TODO)
#
# The objective function is given by:
#
# $$
# f(\mathbf{h}) = \frac{1}{2}\kappa \mathbf{h}_t^T\mathbf{Q}^T\mathbf{Q}\mathbf{h}_t + \frac{1}{2} \kappa \mathbf{h}_t^T \mathbf{S} \mathbf{h}_t - \mathbf{\alpha}^T \mathbf{h}_t + (\mathbf{h}_{t} - \mathbf{h}_{t-1})^T \mathbf{\Lambda} (\mathbf{h}_{t} - \mathbf{h}_{t-1})
# $$
#
# Where the terms correspond to: factor risk + idiosyncratic risk - expected portfolio return + transaction costs, respectively. We should also note that $\textbf{Q}^T\textbf{Q}$ is defined to be the same as $\textbf{BFB}^T$. Review the lessons if you need a refresher of how we get $\textbf{Q}$.
#
# Our objective is to minimize this objective function. To do this, we will use Scipy's optimization function:
#
# `scipy.optimize.fmin_l_bfgs_b(func, initial_guess, func_gradient)`
#
# where:
#
# * **func** : is the function we want to minimize
#
# * **initial_guess** : is out initial guess
#
# * **func_gradient** : is the gradient of the function we want to minimize
#
# So, in order to use the `scipy.optimize.fmin_l_bfgs_b` function we first need to define its parameters.
#
# In the code below implement the function `obj_func(h)` that corresponds to the objective function above that we want to minimize. We will set the risk aversion to be `1.0e-6`.
# +
risk_aversion = 1.0e-6
def get_obj_func(h0, risk_aversion, Q, specVar, alpha_vec, Lambda):
def obj_func(h):
# TODO: Implement
f = 0.5 * risk_aversion * np.sum( np.matmul(Q, h) ** 2 ) \
+ 0.5 * risk_aversion * np.dot(h ** 2, specVar) \
- np.dot(h, alpha_vec) \
+ np.dot( (h - h0) ** 2, Lambda)
return f
return obj_func
# -
# ## Gradient (TODO)
#
# Now that we can generate the objective function using `get_obj_func`, we can now create a similar function with its gradient. The reason we're interested in calculating the gradient is so that we can tell the optimizer in which direction, and how much, it should shift the portfolio holdings in order to improve the objective function (minimize variance, minimize transaction cost, and maximize expected portfolio return).
#
# Before we implement the function we first need to know what the gradient looks like. The gradient, or derivative of the objective function, with respect to the portfolio holdings h, is given by:
#
# $$
# f'(\mathbf{h}) = \frac{1}{2}\kappa (2\mathbf{Q}^T\mathbf{Qh}) + \frac{1}{2}\kappa (2\mathbf{Sh}) - \mathbf{\alpha} + 2(\mathbf{h}_{t} - \mathbf{h}_{t-1}) \mathbf{\Lambda}
# $$
#
# In the code below, implement the function `grad(h)` that corresponds to the function of the gradient given above.
def get_grad_func(h0, risk_aversion, Q, QT, specVar, alpha_vec, Lambda):
def grad_func(h):
# TODO: Implement
g = risk_aversion * (np.matmul(QT, np.matmul(Q,h)) + (specVar * h) ) \
- alpha_vec \
+ 2 * (h-h0) * Lambda
return np.asarray(g)
return grad_func
# ## Optimize (TODO)
#
# Now that we can generate the objective function using `get_obj_func`, and its corresponding gradient using `get_grad_func` we are ready to minimize the objective function using Scipy's optimization function. For this, we will use out initial holdings as our `initial_guess` parameter.
#
# In the cell below, implement the function `get_h_star` that optimizes the objective function. Use the objective function (`obj_func`) and gradient function (`grad_func`) provided within `get_h_star` to optimize the objective function using the `scipy.optimize.fmin_l_bfgs_b` function.
# +
risk_aversion = 1.0e-6
Q = np.matmul(scipy.linalg.sqrtm(Fvar), BT)
QT = Q.transpose()
def get_h_star(risk_aversion, Q, QT, specVar, alpha_vec, h0, Lambda):
"""
Optimize the objective function
Parameters
----------
risk_aversion : int or float
Trader's risk aversion
Q : patsy.design_info.DesignMatrix
Q Matrix
QT : patsy.design_info.DesignMatrix
Transpose of the Q Matrix
specVar: Pandas Series
Specific Variance
alpha_vec: patsy.design_info.DesignMatrix
alpha vector
h0 : Pandas Series
initial holdings
Lambda : Pandas Series
Lambda
Returns
-------
optimizer_result[0]: Numpy ndarray
optimized holdings
"""
obj_func = get_obj_func(h0, risk_aversion, Q, specVar, alpha_vec, Lambda)
grad_func = get_grad_func(h0, risk_aversion, Q, QT, specVar, alpha_vec, Lambda)
# TODO: Implement
return scipy.optimize.fmin_l_bfgs_b(obj_func, h0, fprime=grad_func) [0]
h_star = get_h_star(risk_aversion, Q, QT, specVar, alpha_vec, h0, Lambda)
# -
# After we have optimized our objective function we can now use, `h_star` to create our optimal portfolio:
opt_portfolio = pd.DataFrame(data = {"Barrid" : universe['Barrid'], "h.opt" : h_star})
# ## Risk Exposures (TODO)
#
# We can also use `h_star` to calculate our portfolio's risk and alpha exposures.
#
# In the cells below implement the functions `get_risk_exposures` and `get_portfolio_alpha_exposure` that calculate the portfolio's risk and alpha exposures, respectively.
# +
def get_risk_exposures(B, BT, h_star):
"""
Calculate portfolio's Risk Exposure
Parameters
----------
B : patsy.design_info.DesignMatrix
Matrix of Risk Factors
BT : patsy.design_info.DesignMatrix
Transpose of Matrix of Risk Factors
h_star: Numpy ndarray
optimized holdings
Returns
-------
risk_exposures : Pandas Series
Risk Exposures
"""
# TODO: Implement
return pd.Series(np.matmul(B.T, h_star), index = colnames(B))
risk_exposures = get_risk_exposures(B, BT, h_star)
# +
def get_portfolio_alpha_exposure(B_alpha, h_star):
"""
Calculate portfolio's Alpha Exposure
Parameters
----------
B_alpha : patsy.design_info.DesignMatrix
Matrix of Alpha Factors
h_star: Numpy ndarray
optimized holdings
Returns
-------
alpha_exposures : Pandas Series
Alpha Exposures
"""
# TODO: Implement
return pd.Series(np.matmul(B_alpha.transpose(), h_star), index = colnames(B_alpha))
portfolio_alpha_exposure = get_portfolio_alpha_exposure(B_alpha, h_star)
# -
# ## Transaction Costs (TODO)
#
# We can also use `h_star` to calculate our total transaction costs:
# $$
# \mbox{tcost} = \sum_i^{N} \lambda_{i} (h_{i,t} - h_{i,t-1})^2
# $$
#
# In the cell below, implement the function `get_total_transaction_costs` that calculates the total transaction costs according to the equation above:
# +
def get_total_transaction_costs(h0, h_star, Lambda):
"""
Calculate Total Transaction Costs
Parameters
----------
h0 : Pandas Series
initial holdings (before optimization)
h_star: Numpy ndarray
optimized holdings
Lambda : Pandas Series
Lambda
Returns
-------
total_transaction_costs : float
Total Transaction Costs
"""
# TODO: Implement
return np.dot(Lambda, (h_star-h0)**2)
total_transaction_costs = get_total_transaction_costs(h0, h_star, Lambda)
# -
# ## Putting It All Together
#
# We can now take all the above functions we created above and use them to create a single function, `form_optimal_portfolio` that returns the optimal portfolio, the risk and alpha exposures, and the total transactions costs.
def form_optimal_portfolio(df, previous, risk_aversion):
df = df.merge(previous, how = 'left', on = 'Barrid')
df = clean_nas(df)
df.loc[df['SpecRisk'] == 0]['SpecRisk'] = median(df['SpecRisk'])
universe = get_universe(df)
date = str(int(universe['DataDate'][1]))
all_factors = factors_from_names(list(universe))
risk_factors = setdiff(all_factors, alpha_factors)
h0 = universe['h.opt.previous']
B = model_matrix(get_formula(risk_factors, "SpecRisk"), universe)
BT = B.transpose()
specVar = (0.01 * universe['SpecRisk']) ** 2
Fvar = diagonal_factor_cov(date, B)
Lambda = get_lambda(universe)
B_alpha = get_B_alpha(alpha_factors, universe)
alpha_vec = get_alpha_vec(B_alpha)
Q = np.matmul(scipy.linalg.sqrtm(Fvar), BT)
QT = Q.transpose()
h_star = get_h_star(risk_aversion, Q, QT, specVar, alpha_vec, h0, Lambda)
opt_portfolio = pd.DataFrame(data = {"Barrid" : universe['Barrid'], "h.opt" : h_star})
risk_exposures = get_risk_exposures(B, BT, h_star)
portfolio_alpha_exposure = get_portfolio_alpha_exposure(B_alpha, h_star)
total_transaction_costs = get_total_transaction_costs(h0, h_star, Lambda)
return {
"opt.portfolio" : opt_portfolio,
"risk.exposures" : risk_exposures,
"alpha.exposures" : portfolio_alpha_exposure,
"total.cost" : total_transaction_costs}
# ## Build tradelist
#
# The trade list is the most recent optimal asset holdings minus the previous day's optimal holdings.
def build_tradelist(prev_holdings, opt_result):
tmp = prev_holdings.merge(opt_result['opt.portfolio'], how='outer', on = 'Barrid')
tmp['h.opt.previous'] = np.nan_to_num(tmp['h.opt.previous'])
tmp['h.opt'] = np.nan_to_num(tmp['h.opt'])
return tmp
# ## Save optimal holdings as previous optimal holdings.
#
# As we walk through each day, we'll re-use the column for previous holdings by storing the "current" optimal holdings as the "previous" optimal holdings.
def convert_to_previous(result):
prev = result['opt.portfolio']
prev = prev.rename(index=str, columns={"h.opt": "h.opt.previous"}, copy=True, inplace=False)
return prev
# ## Run the backtest
#
# Walk through each day, calculating the optimal portfolio holdings and trade list. This may take some time, but should finish sooner if you've chosen all the optimizations you learned in the lessons.
# +
trades = {}
port = {}
for dt in tqdm(my_dates, desc='Optimizing Portfolio', unit='day'):
date = dt.strftime('%Y%m%d')
result = form_optimal_portfolio(frames[date], previous_holdings, risk_aversion)
trades[date] = build_tradelist(previous_holdings, result)
port[date] = result
previous_holdings = convert_to_previous(result)
# -
# ## Profit-and-Loss (PnL) attribution (TODO)
#
# Profit and Loss is the aggregate realized daily returns of the assets, weighted by the optimal portfolio holdings chosen, and summed up to get the portfolio's profit and loss.
#
# The PnL attributed to the alpha factors equals the factor returns times factor exposures for the alpha factors.
#
# $$
# \mbox{PnL}_{alpha}= f \times b_{alpha}
# $$
#
# Similarly, the PnL attributed to the risk factors equals the factor returns times factor exposures of the risk factors.
#
# $$
# \mbox{PnL}_{risk} = f \times b_{risk}
# $$
#
# In the code below, in the function `build_pnl_attribution` calculate the PnL attributed to the alpha factors, the PnL attributed to the risk factors, and attribution to cost.
# +
## assumes v, w are pandas Series
def partial_dot_product(v, w):
common = v.index.intersection(w.index)
return np.sum(v[common] * w[common])
def build_pnl_attribution():
df = pd.DataFrame(index = my_dates)
for dt in my_dates:
date = dt.strftime('%Y%m%d')
p = port[date]
fr = facret[date]
mf = p['opt.portfolio'].merge(frames[date], how = 'left', on = "Barrid")
mf['DlyReturn'] = wins(mf['DlyReturn'], -0.5, 0.5)
df.at[dt,"daily.pnl"] = np.sum(mf['h.opt'] * mf['DlyReturn'])
# TODO: Implement
df.at[dt,"attribution.alpha.pnl"] = partial_dot_product(p['alpha.exposures'], fr)
df.at[dt,"attribution.risk.pnl"] = partial_dot_product(p['risk.exposures'], fr)
df.at[dt,"attribution.cost"] = p['total.cost']
return df
# +
attr = build_pnl_attribution()
for column in attr.columns:
plt.plot(attr[column].cumsum(), label=column)
plt.legend(loc='upper left')
plt.xlabel('Date')
plt.ylabel('PnL Attribution')
plt.show()
# -
# ## Build portfolio characteristics (TODO)
# Calculate the sum of long positions, short positions, net positions, gross market value, and amount of dollars traded.
#
# In the code below, in the function `build_portfolio_characteristics` calculate the sum of long positions, short positions, net positions, gross market value, and amount of dollars traded.
def build_portfolio_characteristics():
df = pd.DataFrame(index = my_dates)
for dt in my_dates:
date = dt.strftime('%Y%m%d')
p = port[date]
tradelist = trades[date]
h = p['opt.portfolio']['h.opt']
# TODO: Implement
df.at[dt,"long"] = np.sum(h[h > 0])
df.at[dt,"short"] = np.sum(h[h < 0])
df.at[dt,"net"] = np.sum(h)
df.at[dt,"gmv"] = np.sum(abs(h))
df.at[dt,"traded"] = np.sum(np.abs(tradelist['h.opt'] - tradelist['h.opt.previous']))
return df
# +
pchar = build_portfolio_characteristics()
for column in pchar.columns:
plt.plot(pchar[column], label=column)
plt.legend(loc='upper left')
plt.xlabel('Date')
plt.ylabel('Portfolio')
plt.show()
# -
# #### Optional
# Choose additional metrics to evaluate your portfolio.
# Optional
# ## Submission
# Now that you're done with the project, it's time to submit it. Click the submit button in the bottom right. One of our reviewers will give you feedback on your project with a pass or not passed grade.
| Building a Bactester/home/project_8_starter.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Importing and prepping data
import pandas as pd
import numpy as np
import diff_classifier.aws as aws
import diff_classifier.pca as pca
# +
features = []
featofvar = 'Type and Serum'
remote_folder = '10_04_18_COOH_PEG_serum' #Folder in AWS S3 containing files to be analyzed
bucket = 'rhodese.data'
vids = 10
types = ['COOH', 'COOH_serum', 'PEG', 'PEG_serum']
counter2 = 0
counter = 0
for typ in types:
for num in range(1, vids+1):
try:
filename = 'features_{}_XY{}.csv'.format(typ, '%02d' % num)
print(filename)
aws.download_s3('{}/{}'.format(remote_folder, filename), filename, bucket_name=bucket)
fstats = pd.read_csv(filename, encoding = "ISO-8859-1", index_col='Unnamed: 0')
print('{} size: {}'.format(filename, fstats.shape))
fstats['Type and Serum'] = pd.Series(fstats.shape[0]*[typ], index=fstats.index)
if 'serum' in typ:
fstats['Serum'] = pd.Series(fstats.shape[0]*['serum'], index=fstats.index)
else:
fstats['Serum'] = pd.Series(fstats.shape[0]*['no serum'], index=fstats.index)
if 'COOH' in typ:
fstats['Type'] = pd.Series(fstats.shape[0]*['COOH'], index=fstats.index)
else:
fstats['Type'] = pd.Series(fstats.shape[0]*['PEG'], index=fstats.index)
fstats['Video Number'] = pd.Series(fstats.shape[0]*[num], index=fstats.index)
counter = counter + 1
if counter == 1:
fstats_tot = fstats
else:
fstats_tot = fstats_tot.append(fstats, ignore_index=True)
except:
print('Skipped!: {}'.format(filename))
counter2 = counter2 + 1
# +
#PCA analyses with too many datapoints fail. You get rows with lots of NAs. I'm going to try making a subset of the data first
#and then do a PCA analysis on that.
#include all in analysis
import random
subset = np.sort(np.array(random.sample(range(fstats_tot.shape[0]), 500000)))
fstats_sub = fstats_tot.loc[subset, :].reset_index(drop=True)
# -
fstats_tot['Type and Serum'].unique()
for typ in fstats_tot['Type and Serum'].unique():
fstats_type = fstats_tot[fstats_tot['Type and Serum']==typ].reset_index(drop=True)
print(fstats_type.shape)
#with equal sample sizes for each particle type
import random
counter = 0
for typ in fstats_tot['Type and Serum'].unique():
fstats_type = fstats_tot[fstats_tot['Type and Serum']==typ].reset_index(drop=True)
print(fstats_type.shape)
subset = np.sort(np.array(random.sample(range(fstats_type.shape[0]), 50000)))
if counter == 0:
fstats_sub = fstats_type.loc[subset, :].reset_index(drop=True)
else:
fstats_sub = fstats_sub.append(fstats_type.loc[subset, :].reset_index(drop=True), ignore_index=True)
counter = counter + 1
#fstats = pd.read_csv(filename, encoding = "ISO-8859-1", index_col='Unnamed: 0')
nonnum = ['Type and Serum', 'Type', 'Serum', 'Video Number', 'Track_ID', 'Mean Mean_Intensity', 'Std Mean_Intensity', 'X', 'Y',
'Mean X', 'Mean Y', 'Std X', 'Std Y']
fstats_num = fstats_sub.drop(nonnum, axis=1)
fstats_raw = fstats_num.as_matrix()
#fstats
# ## PCA analysis
# The pca.pca_analysis function provides a completely contained PCA analysis of the input trajectory features dataset. It includes options to impute NaN values (fill in with average values or drop them), and to scale features. Read the docstring for more information.
ncomp = 14
pcadataset = pca.pca_analysis(fstats_tot, dropcols=nonnum, n_components=ncomp)
pcadataset.components.to_csv('components.csv')
aws.upload_s3('components.csv', '{}/components.csv'.format(remote_folder, filename), bucket_name=bucket)
fstats_num.columns
pcadataset.prcomps
# The pca.kmo function calculates the Kaiser-Meyer-Olkin statistic, a measure of sampling adequacy. Check the docstring for more information.
kmostat = pca.kmo(pcadataset.scaled)
# ## Visualization
# Users can then compare average principle component values between subgroups of the data. In this case, all particles were taken from the same sample, so there are no experimental subgroups. I chose to compare short trajectories to long trajectories, as I would expect differences between the two groups.
import numpy as np
featofvar = 'Type and Serum'
#ncomp = 14
dicti = {}
#test = np.exp(np.nanmean(np.log(pcadataset.final[pcadataset.final['Particle Size']==200].as_matrix()), axis=0))[-6:]
#test1 = np.exp(np.nanmean(np.log(pcadataset.final[pcadataset.final['Particle Size']==500].as_matrix()), axis=0))[-6:]
dicti[0] = np.nanmean(pcadataset.final[pcadataset.final[featofvar]=='COOH'].values[:, -ncomp:], axis=0)
dicti[1] = np.nanmean(pcadataset.final[pcadataset.final[featofvar]=='COOH_serum'].values[:, -ncomp:], axis=0)
dicti[2] = np.nanmean(pcadataset.final[pcadataset.final[featofvar]=='PEG'].values[:, -ncomp:], axis=0)
dicti[3] = np.nanmean(pcadataset.final[pcadataset.final[featofvar]=='PEG_serum'].values[:, -ncomp:], axis=0)
labels = ['COOH', 'COOH_serum', 'PEG', 'PEG_serum']
pca.plot_pca(dicti, savefig=True, labels=labels, rticks=np.linspace(-4, 4, 9))
# The variable pcadataset.prcomps shows the user the major contributions to each of the new principle components. When observing the graph above, users can see that there are some differences between short trajectories and long trajectories in component 0 (asymmetry1 being the major contributor) and component 1 (elongation being the major contributor).
#labels=['10K', '5K', '1K', 'COOH']
feats = pca.feature_violin(pcadataset.final, label=featofvar, lvals=labels, fsubset=ncomp, yrange=[-12, 12])
fstats1 = pca.feature_plot_3D(pcadataset.final, label=featofvar, lvals=labels, randcount=400, ylim=[-12, 12],
xlim=[-12, 12], zlim=[-12, 12], features=[0, 2, 3])
fstats1 = pca.feature_plot_3D(pcadataset.final, label='Serum', lvals=['serum', 'no serum'], randcount=800, ylim=[-12, 12],
xlim=[-12, 12], zlim=[-12, 12], features=[0, 2, 3])
fstats1 = pca.feature_plot_3D(pcadataset.final, label='Type', lvals=['COOH', 'PEG'], randcount=800, ylim=[-12, 12],
xlim=[-12, 12], zlim=[-12, 12], features=[0, 2, 3])
# +
#ncomp = 14
trainp = np.array([])
testp = np.array([])
labels3 = ['COOH', 'PEG']
labels = ['COOH', 'COOH_serum', 'PEG', 'PEG_serum']
for i in range(0, 3):
KNNmod, X, y = pca.build_model(pcadataset.final, featofvar, labels, equal_sampling=True,
tsize=2000, input_cols=ncomp, model='MLP', NNhidden_layer=(6, 5, 3))
trainp = np.append(trainp, pca.predict_model(KNNmod, X, y))
X2 = pcadataset.final.values[:, -ncomp:]
y2 = pcadataset.final[featofvar].values
testp = np.append(testp, pca.predict_model(KNNmod, X2, y2))
print('Run {}: {}'.format(i, testp[i]))
# -
# +
#ncomp = 14
trainp = np.array([])
testp = np.array([])
labels3 = ['COOH', 'PEG']
labels = ['COOH', 'COOH_serum', 'PEG', 'PEG_serum']
for i in range(0, 5):
KNNmod, X, y = pca.build_model(pcadataset.final, featofvar, labels, equal_sampling=True,
tsize=2000, input_cols=ncomp, model='MLP', NNhidden_layer=(6, 5, 3))
trainp = np.append(trainp, pca.predict_model(KNNmod, X, y))
X2 = pcadataset.final.values[:, -ncomp:]
y2 = pcadataset.final[featofvar].values
testp = np.append(testp, pca.predict_model(KNNmod, X2, y2))
print('Run {}: {}'.format(i, testp[i]))
# -
print('{} +/ {}'.format(np.mean(trainp), np.std(trainp)))
print('{} +/ {}'.format(np.mean(testp), np.std(testp)))
ypred = pd.Series(KNNmod.predict(X2)).str.split('_', expand=True)
# +
ya = np.copy(yact[0].values)
ya[ya == 'COOH'] = 1
ya[ya != 1] = 0
yp = np.copy(ypred[0].values)
yp[yp == 'COOH'] = 1
yp[yp != 1] = 0
# +
from sklearn import metrics
def mod_roc_curve(y_true, y_score, pos_label):
ya = np.copy(y_true)
ya[ya == pos_label] = 1
ya[ya != 1] = 0
yp = np.copy(y_score)
yp[yp == pos_label] = 1
yp[yp != 1] = 0
fpr, tpr, thresholds = metrics.roc_curve(ya, yp, drop_intermediate=False)
return fpr, tpr, thresholds
# -
fpr, tpr, thresholds = mod_roc_curve(yact[1].values, ypred[1].values, pos_label=None)
import matplotlib.pyplot as plt
plt.plot(fpr, tpr)
plt.plot(fpr, tpr)
plt.plot(fpr, tpr)
plt.plot(fpr, tpr)
yr1 = np.random.randint(0, 2, size=400)
yr2 = np.random.rand(400)
fpr, tpr, thresholds = metrics.roc_curve(yr1, yr2)
plt.plot(fpr, tpr)
noise = 10
size = 400
yr1 = np.random.randint(0, 2, size=size)
yr2 = yr1 + noise*np.random.rand(size) - 0.5*noise
fpr, tpr, thresholds = metrics.roc_curve(yr1, yr2)
plt.plot(fpr, tpr)
noise = 5
size = 400
yr1 = np.random.randint(0, 2, size=size)
yr2 = yr1 + noise*np.random.rand(size) - 0.5*noise
fpr, tpr, thresholds = metrics.roc_curve(yr1, yr2)
plt.plot(fpr, tpr)
noise = 2.5
size = 400
yr1 = np.random.randint(0, 2, size=size)
yr2 = yr1 + noise*np.random.rand(size) - 0.5*noise
fpr, tpr, thresholds = metrics.roc_curve(yr1, yr2)
plt.plot(fpr, tpr)
noise = 1.5
size = 400
yr1 = np.random.randint(0, 2, size=size)
yr2 = yr1 + noise*np.random.rand(size) - 0.5*noise
fpr, tpr, thresholds = metrics.roc_curve(yr1, yr2)
plt.plot(fpr, tpr)
KNNmod.score(X2, y2)
from sklearn.neural_network import MLPClassifier
from sklearn.multiclass import OneVsRestClassifier
from sklearn import svm
from sklearn import metrics
ynew = label_binarize(y, classes=labels)
y2new = label_binarize(y2, classes=labels)
n_classes = ynew.shape[1]
ynew
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True))
y_score = classifier.fit(X, ynew).decision_function(X2)
y_scorep = pd.DataFrame(data=y_score.transpose()).idxmax()
y2newp = pd.DataFrame(data=y2new.transpose()).idxmax()
ycorrect = y_scorep == y2newp
ycorrect.mean()
# +
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = metrics.roc_curve(y2new[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = metrics.roc_curve(y2new.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# -
tclass = 0
plt.figure()
lw = 4
plt.plot(fpr[tclass], tpr[tclass], color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[tclass])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
classifier.score(X2, y2new)
roc_auc[0]*roc_auc[1]*roc_auc[2]*roc_auc[3]
# +
# Compute macro-average ROC curve and ROC area
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# Plot all ROC curves
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue', 'slategray'])
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0, 0.4])
plt.ylim([0.5, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
# -
# I found a standard way of implementing ROC curves with non-binary data called the one versus all method. It essentially breaks a n-class system into n-1 binary systems, and you make an n-1 roc curves for each case. I can't use MLP methods this way, but it looks like I can get high predictive power as-is? Kind of? I can get
fpr, tpr, _ = metrics.roc_curve(y, y_score)
# +
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from scipy import interp
# -
# Import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]
y
# +
# Add noisy features to make the problem harder
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
# shuffle and split training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5,
random_state=0)
# -
# Learn to predict each class against the other
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True,
random_state=random_state))
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# +
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
| notebooks/development/10_11_18_pca_Emily_corona_roc_curve.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import cv2
import numpy as np
import matplotlib.pylab as plt
def region_of_interest(img, vertices):
mask = np.zeros_like(img)
channel_count = img.shape[2]
match_mask_color = (255,) * channel_count
cv2.fillPoly(mask, vertices, match_mask_color)
masked_img = cv2.bitwise_and(img, mask)
return masked_img
img = cv2.imread('road.jpg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
print(img.shape)
height = img.shape[0]
width = img.shape[1]
region_of_interest_vertices = [
(0, height),
(width/2, height/2),
(width, height)
]
cropped_img = region_of_interest(img, np.array([region_of_interest_vertices], np.int32))
img_gray = cv2.cvtColor(cropped_img, cv2.COLOR_RGB2GRAY)
canny_image = cv2.Canny(img_gray, 100, 200)
plt.imshow(canny_image)
plt.imshow(cropped_img)
plt.imshow(img)
plt.show()
# -
| opencv/Road line detection.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# Importing libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Read data
df = pd.read_csv("../Data.csv")
df
# +
# dependent variable, y = Purchased
# independent variables, X = Country, age, salary
# -
X = df.iloc[:,:-1].values
X
y = df.iloc[:,3:].values
y
# +
# As you can see there are missing values in independent variables
# as they are continous valued we can imput them
# -
from sklearn.preprocessing import Imputer
imputer = Imputer(missing_values='NaN', strategy='mean')
imputer = imputer.fit(X[:,1:3])
X[:,1:3] = imputer.transform(X[:,1:3])
X
# +
# or directly use fit_transform
# -
X[:,1:3] = imputer.fit_transform(X[:,1:3])
X
# +
# Categorical Data
# the country and Purchased are categorical that needs to be changed to numerical
# -
from sklearn.preprocessing import LabelEncoder
labelencoder_country = LabelEncoder()
X[:,0] = labelencoder_country.fit_transform(X[:,0])
X[:,0]
labelencoder_purchased = LabelEncoder()
y[:,0] = labelencoder_country.fit_transform(y[:,0])
y
# +
# encoding the categorical data
# -
from sklearn.preprocessing import OneHotEncoder
onehotencoder = OneHotEncoder(categorical_features=[0])
X = onehotencoder.fit_transform(X).toarray()
X
# +
# get dummies in pandas can also be used for OHE
# pandas get_dummies can work with string
# -
pd.get_dummies(df)
df.columns
# +
#splitting train test
# -
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=0 )
X_train, X_test
# +
# Scaling
# -
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
X_train
| Part 1 - Data Preprocessing/Section 2 - Part 1 - Data Preprocessing/mine/Data Preprocessing.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# 
# The normal distribution is commonly associated with the normal distribution with the 68-95-99.7 rule which you can see in the image above. 68% of the data is within 1 standard deviation (σ) of the mean (μ), 95% of the data is within 2 standard deviations (σ) of the mean (μ), and 99.7% of the data is within 3 standard deviations (σ) of the mean (μ).
# This notebook explains how those numbers were derived in the hope that they can be more interpretable for your future endeavors.
# ## Probability Density Function
# To be able to understand where the percentages come from in the 68-95-99.7 rule, it is important to know about the probability density function (PDF). A PDF is used to specify the probability of the random variable falling within a particular range of values, as opposed to taking on any one value. This probability is given by the integral of this variable’s PDF over that range — that is, it is given by the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. This definition might not make much sense so let’s clear it up by graphing the probability density function for a normal distribution. The equation below is the probability density function for a normal distribution
# 
# Let’s simplify it by assuming we have a mean (μ) of 0 and a standard deviation (σ) of 1.
# 
# Now that the function is simpler, let’s graph this function with a range from -3 to 3.
# +
# Import all libraries for the rest of the blog post
from scipy.integrate import quad
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
# %matplotlib inline
x = np.linspace(-3, 3, num = 100)
constant = 1.0 / np.sqrt(2*np.pi)
pdf_normal_distribution = constant * np.exp((-x**2) / 2.0)
fig, ax = plt.subplots(figsize=(10, 5));
ax.plot(x, pdf_normal_distribution);
ax.set_ylim(0);
ax.set_title('Normal Distribution', size = 20);
ax.set_ylabel('Probability Density', size = 20);
# -
# The graph above does not show you the probability of events but their probability density. To get the probability of an event within a given range we will need to integrate. Suppose we are interested in finding the probability of a random data point landing within 1 standard deviation of the mean, we need to integrate from -1 to 1. This can be done with SciPy.
# ## Within 1 Standard Deviation
# <b>Math Expression</b> $$\int_{-1}^{1}\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2}\mathrm{d}x$$
# +
# Make a PDF for the normal distribution a function
def normalProbabilityDensity(x):
constant = 1.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) )
# Integrate PDF from -1 to 1
result_n1_1, _ = quad(normalProbabilityDensity, -1, 1, limit = 1000)
print(result_n1_1)
# +
a, b = -1, 1 # integral limits
x = np.linspace(-3, 3)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(a, b)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0, .08, r"$\int_{-1}^{1} f(x)\mathrm{d}x = $" + "{0:.1f}%".format(result_n1_1*100),
horizontalalignment='center', fontsize=18);
ax.set_title(r'68% of Values are within 1 STD', fontsize = 24);
ax.set_ylabel(r'Probability Density', fontsize = 18);
fig.savefig('images/68_1_std.png', dpi = 1200)
# -
# 68% of the data is within 1 standard deviation (σ) of the mean (μ).
# ## Within 2 Standard Deviations
# <b>Math Expression</b> $$\int_{-2}^{2}\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2}\mathrm{d}x$$
# +
# Make the PDF for the normal distribution a function
def normalProbabilityDensity(x):
constant = 1.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) )
# Integrate PDF from -2 to 2
result_n2_2, _ = quad(normalProbabilityDensity, -2, 2, limit = 1000)
print(result_n2_2)
# +
a, b = -2, 2 # integral limits
x = np.linspace(-3, 3)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(a, b)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0, .08, r"$\int_{-2}^{2} f(x)\mathrm{d}x = $" + "{0:.1f}%".format(result_n2_2*100),
horizontalalignment='center', fontsize=18);
ax.set_title(r'95% of Values are within 2 STD', fontsize = 24);
ax.set_ylabel(r'Probability Density', fontsize = 18);
fig.savefig('images/95_2_std.png', dpi = 1200)
# -
# 95% of the data is within 2 standard deviations (σ) of the mean (μ).
# ## Within 3 Standard Deviations
# <b>Math Expression</b> $$\int_{-3}^{3}\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2}\mathrm{d}x$$
# +
# Make the PDF for the normal distribution a function
def normalProbabilityDensity(x):
constant = 1.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) )
# Integrate PDF from -3 to 3
result_n3_3, _ = quad(normalProbabilityDensity, -3, 3, limit = 1000)
print(result_n3_3)
# +
a, b = -3, 3 # integral limits
x = np.linspace(-3, 3)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(a, b)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0, .08, r"$\int_{-3}^{3} f(x)\mathrm{d}x = $" + "{0:.1f}%".format(result_n3_3*100),
horizontalalignment='center', fontsize=18);
ax.set_title(r'99.7% of Values are within 3 STD', fontsize = 24);
ax.set_ylabel(r'Probability Density', fontsize = 18);
fig.savefig('images/99_3_std.png', dpi = 1200)
# -
# 99.7% of the data is within 3 standard deviations (σ) of the mean (μ).
# ## Negative Infinity to Positive Infinity
# For any PDF, the area under the curve must be 1 (the probability of drawing any number from the function's range is always 1).
# +
def normalProbabilityDensity(x):
constant = 1.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) )
result_all, _ = quad(normalProbabilityDensity, np.NINF, np.inf)
print(result_all)
# +
# This should really be -inf to positive inf, but graph can only be so big.
# Currently it is plus or minus 4 std deviations
a, b = -4, 4 # integral limits
x = np.linspace(a, b)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(a, b)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0, .08, r"$\int_{-\infty}^{\infty} f(x)\mathrm{d}x = 1$",
horizontalalignment='center', fontsize=20);
ax.set_title(r'99.7% of Values are within 3 STD', fontsize = 24);
ax.set_ylabel(r'Probability Density', fontsize = 18);
# -
# <b>You will also find that it is also possible for observations to fall 4, 5 or even more standard deviations from the mean, but this is very rare if you have a normal or nearly normal distribution.</b>
# ## 68-95-99.7 Rule
# Most of the code below is just matplotlib. It is a bit difficult to understand, but I figured somebody would appreciate the code for their endeavors.
# +
x = np.linspace(-3, 3)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
#############################
a, b = -1, 1 # integral limits
# Make the shaded region
ix = np.linspace(-1, 1)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0.0, .28, r'{0:.2f}%'.format((result_n1_1)*100),
horizontalalignment='center', fontsize=18);
##############################
# Bounding the make arrow
ax.annotate(r'',
xy=(-1, .27), xycoords='data',
xytext=(1, .27), textcoords='data',
arrowprops=dict(arrowstyle="|-|",
connectionstyle="arc3")
);
##############################
a, b = 1, 2 # integral limits
# Make the shaded region
ix = np.linspace(1, 2)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='blue', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
##############################
a, b = -2, -1 # integral limits
# Make the shaded region
ix = np.linspace(-2, -1)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='blue', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
#ax.text(-1.5, .04, r'{0:.2f}%'.format(result_n2_n1*100),
# horizontalalignment='center', fontsize=14);
ax.text(0.0, .18, r'{0:.2f}%'.format((result_n2_2)*100),
horizontalalignment='center', fontsize=18);
##############################
# Bounding the make arrow
ax.annotate(r'',
xy=(-2, .17), xycoords='data',
xytext=(2, .17), textcoords='data',
arrowprops=dict(arrowstyle="|-|",
connectionstyle="arc3")
);
##############################
a, b = 2, 3 # integral limits
# Make the shaded region
ix = np.linspace(2, 3)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='green', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
##############################
a, b = -3, -2 # integral limits
# Make the shaded region
ix = np.linspace(-3, -2)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='green', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
### This is the middle part
ax.text(0.0, .08, r'{0:.2f}%'.format((result_n3_3)*100),
horizontalalignment='center', fontsize=18);
# Bounding the make arrow
ax.annotate(r'',
xy=(-3, .07), xycoords='data',
xytext=(3, .07), textcoords='data',
arrowprops=dict(arrowstyle="|-|",
connectionstyle="arc3")
);
ax.set_title(r'68-95-99.7 Rule', fontsize = 24)
ax.set_ylabel(r'Probability Density', fontsize = 18)
xTickLabels = ['',
r'$\mu - 3\sigma$',
r'$\mu - 2\sigma$',
r'$\mu - \sigma$',
r'$\mu$',
r'$\mu + \sigma$',
r'$\mu + 2\sigma$',
r'$\mu + 3\sigma$']
yTickLabels = ['0.00',
'0.05',
'0.10',
'0.15',
'0.20',
'0.25',
'0.30',
'0.35',
'0.40']
ax.set_xticklabels(xTickLabels, fontsize = 16)
ax.set_yticklabels(yTickLabels, fontsize = 16)
fig.savefig('images/68_95_99_rule.png', dpi = 1200)
# -
# # Code to look at Different Regions
# ## Mean (0) to Mean + STD (1)
# Integrate normal distribution from 0 to 1
result, error = quad(normalProbabilityDensity, 0, 1, limit = 1000)
result
# +
# This should really be -inf to positive inf, but graph can only be so big.
# Currently it is plus or minus 5 std deviations
a, b = 0, 1 # integral limits
x = np.linspace(-4, 4)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(0, 1)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0.5, .05, r'{0:.2f}%'.format(result*100),
horizontalalignment='center', fontsize=15);
# -
# ## Looking at Between 1 STD
result, _ = quad(normalProbabilityDensity, -1, 1)
result
# +
# This should really be -inf to positive inf, but graph can only be so big.
# Currently it is plus or minus 5 std deviations
a, b = -1, 1 # integral limits
x = np.linspace(-4, 4)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(-1, 1)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0.0, .05, r'{0:.1f}%'.format(result*100),
horizontalalignment='center', fontsize=15);
# -
# ## (Mean + STD) to Mean + (2STD)
result, error = quad(normalProbabilityDensity, 1, 2, limit = 1000)
result
# +
# This should really be -inf to positive inf, but graph can only be so big.
# Currently it is plus or minus 5 std deviations
a, b = 1, 2 # integral limits
x = np.linspace(-4, 4)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(a, b)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(1.5, .02, r'{0:.2f}%'.format(result*100),
horizontalalignment='center', fontsize=15);
# -
# ## (Mean + 2STD) to (Mean + 3STD)
result, error = quad(normalProbabilityDensity, 2, 3, limit = 1000)
result
# +
# This should really be -inf to positive inf, but graph can only be so big.
# Currently it is plus or minus 5 std deviations
a, b = 2, 3 # integral limits
x = np.linspace(-4, 4)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(a, b)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
#ax.text(1.5, .02, r'{0:.1f}%'.format(result*100),
# horizontalalignment='center', fontsize=15);
ax.annotate(r'{0:.2f}%'.format(result*100),
xy=(2.5, 0.001), xycoords='data',
xytext=(2.5, 0.05), textcoords='data',
arrowprops=dict(arrowstyle="-",
connectionstyle="arc3"),
);
# -
# ## (Mean + 3STD) to (Mean + 4STD)
result, error = quad(normalProbabilityDensity, 3, 4, limit = 1000)
result
# +
# This should really be -inf to positive inf, but graph can only be so big.
# Currently it is plus or minus 5 std deviations
a, b = 3, 4 # integral limits
x = np.linspace(-4, 4)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
# Make the shaded region
ix = np.linspace(a, b)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.annotate(r'{0:.2f}%'.format(result*100),
xy=(3.3, 0.001), xycoords='data',
xytext=(3.2, 0.05), textcoords='data',
arrowprops=dict(arrowstyle="-",
connectionstyle="arc3"),
);
# -
# ## Mean + 4STD (4) to Infinity
# This is the area under the curve that wont fit in my picture. Notice the probability is so small
result, error = quad(normalProbabilityDensity, 4, np.inf, limit = 1000)
result
# ## Lets put together the Entire Graph
# If you think this is too much code, next section will make this better.
def normalProbabilityDensity(x):
constant = 1.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) )
# +
# Area under curve for entire Graph
result, _ = quad(normalProbabilityDensity, np.NINF, np.inf)
# Integrate normal distribution from 0 to 1
result_0_1, _ = quad(normalProbabilityDensity, 0, 1, limit = 1000)
# Integrate normal distribution from -1 to 0
result_n1_0, _ = quad(normalProbabilityDensity, -1, 0, limit = 1000)
# Integrate normal distribution from 1 to 2
result_1_2, _ = quad(normalProbabilityDensity, 1, 2, limit = 1000)
# Integrate normal distribution from -2 to -1
result_n2_n1, _ = quad(normalProbabilityDensity, -2, -1, limit = 1000)
# Integrate normal distribution from 2 to 3
result_2_3, _ = quad(normalProbabilityDensity, 2, 3, limit = 1000)
# Integrate normal distribution from -3 to -2
result_n3_n2, _ = quad(normalProbabilityDensity, -3, -2, limit = 1000)
# Integrate normal distribution from 3 to 4
result_3_4, _ = quad(normalProbabilityDensity, 3, 4, limit = 1000)
# Integrate normal distribution from -4 to -3
result_n4_n3, _ = quad(normalProbabilityDensity, -4, -3, limit = 1000)
# Integrate normal distribution from 4 to inf
result_4_inf, error = quad(normalProbabilityDensity, 4, np.inf, limit = 1000)
# +
# This should really be -inf to positive inf, but graph can only be so big.
# Currently it is plus or minus 5 std deviations
x = np.linspace(-4, 4)
y = normalProbabilityDensity(x)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y, 'k', linewidth=.5)
ax.set_ylim(ymin=0)
#############################
a, b = 0, 1 # integral limits
# Make the shaded region
ix = np.linspace(0, 1)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(0.5, .04, r'{0:.2f}%'.format(result_0_1*100),
horizontalalignment='center', fontsize=14);
##############################
a, b = -1, 0 # integral limits
# Make the shaded region
ix = np.linspace(-1, 0)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='red', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(-0.5, .04, r'{0:.2f}%'.format(result_n1_0*100),
horizontalalignment='center', fontsize=14);
##############################
a, b = 1, 2 # integral limits
# Make the shaded region
ix = np.linspace(1, 2)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='blue', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(1.5, .04, r'{0:.2f}%'.format(result_1_2*100),
horizontalalignment='center', fontsize=14);
##############################
a, b = -2, -1 # integral limits
# Make the shaded region
ix = np.linspace(-2, -1)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='blue', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(-1.5, .04, r'{0:.2f}%'.format(result_n2_n1*100),
horizontalalignment='center', fontsize=14);
##############################
a, b = 2, 3 # integral limits
# Make the shaded region
ix = np.linspace(2, 3)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='green', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(2.6, .04, r'{0:.2f}%'.format(result_2_3*100),
horizontalalignment='center', fontsize=14);
##############################
a, b = -3, -2 # integral limits
# Make the shaded region
ix = np.linspace(-3, -2)
iy = normalProbabilityDensity(ix)
verts = [(a, 0)] + list(zip(ix, iy)) + [(b, 0)]
poly = Polygon(verts, facecolor='green', edgecolor='0.2', alpha = .4)
ax.add_patch(poly);
ax.text(-2.6, .04, r'{0:.2f}%'.format(result_2_3*100),
horizontalalignment='center', fontsize=14);
##############################
a, b = 3, 4 # integral limits
# Region from 3 to 4
ix = np.linspace(3, 4)
iy = normalProbabilityDensity(ix)
verts = [(3, 0)] + list(zip(ix, iy)) + [(4, 0)]
poly = Polygon(verts, facecolor='orange', edgecolor='.2', alpha = 1)
ax.add_patch(poly);
ax.text(3.6, .04, r'{0:.2f}%'.format(result_3_4*100),
horizontalalignment='center', fontsize=14);
# Region from -4 to -3
ix = np.linspace(-4, -3)
iy = normalProbabilityDensity(ix)
verts = [(-4, 0)] + list(zip(ix, iy)) + [(-3, 0)]
poly = Polygon(verts, facecolor='orange', edgecolor='.2', alpha = 1)
ax.add_patch(poly);
ax.text(-3.6, .040, r'{0:.2f}%'.format(result_n4_n3*100),
horizontalalignment='center', fontsize=14);
ax.set_title(r'Normal Distribution', fontsize = 24)
ax.set_ylabel(r'Probability Density', fontsize = 18)
xTickLabels = ['',
r'$\mu - 4\sigma$',
r'$\mu - 3\sigma$',
r'$\mu - 2\sigma$',
r'$\mu - \sigma$',
r'$\mu$',
r'$\mu + \sigma$',
r'$\mu + 2\sigma$',
r'$\mu + 3\sigma$',
r'$\mu + 4\sigma$']
yTickLabels = ['0.00',
'0.05',
'0.10',
'0.15',
'0.20',
'0.25',
'0.30',
'0.35',
'0.40']
ax.set_xticklabels(xTickLabels, fontsize = 16)
ax.set_yticklabels(yTickLabels, fontsize = 16)
fig.savefig('images/NormalDistribution.png', dpi = 1200)
| Statistics/normal_Distribution_Area_Under_Curve.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
from timeit import default_timer as timer
from datetime import timedelta
import os
import sys
import pickle
from timeit import default_timer as timer
from datetime import timedelta
from IPython.display import clear_output
import gym
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, Sequential, optimizers
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# tf.config.list_physical_devices(device_type='GPU')
# +
seed = 1
random.seed(seed)
np.random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed) # 为了禁止hash随机化,使得实验可复现。
tf.random.set_seed(seed)
# tensorflow 如何设置在GPU上能够复现结果还不太清楚怎么弄
# -
path = os.path.abspath('..')
if path not in sys.path:
sys.path.append(path)
from configs import Config
from replay_memories import PrioritizedReplayMemory
from networks_tensorflow import MLP_tensorflow
from agents_tensorflow import DQNAgentTensorflow
# # Training Loop
#
# - replay_memories里导入的replaybuffer不一样了
# - DQNAgent里的`prioritized`参数要修改一下
#
# 结果很不错,我愿称之为最强trick
# +
name = 'CartPole-v0'
env_eval = gym.make(name)
env_eval.seed(seed)
config = Config()
start = timer()
dqn_agent = DQNAgentTensorflow(env_name=name, network=MLP_tensorflow, prioritized=True, config=config)
obs = dqn_agent.env.reset()
for step in range(1, config.max_steps+1):
epsilon = config.epsilon_by_step(step)
action = dqn_agent.get_action(obs, epsilon)
pre_obs = obs
obs, reward, done, _ = dqn_agent.env.step(action)
dqn_agent.memory.add((pre_obs, action, reward, obs, done))
dqn_agent.train(step)
if done:
obs = dqn_agent.env.reset()
if step % 1000 == 0:
mean_returns, max_returns, mean_lengths, max_lengths = dqn_agent.eval_(env_eval, 5)
print('step: {}, epsilon: {}, lr: {}, time: {}'.format(step, epsilon, dqn_agent.optimizer.lr(step).numpy(), timedelta(seconds=int(timer()-start))))
print('episode reward mean: {}, epsisode reward max: {}, episode length mean: {}, episode length max: {}, loss: {}'.format(
mean_returns,
max_returns,
mean_lengths,
max_lengths,
np.array(dqn_agent.losses[-10:]).mean()))
# print('==========================================')
# print([(tf.reduce_max(param).numpy(), tf.reduce_min(param).numpy(), tf.reduce_max(grad).numpy(), tf.reduce_min(grad).numpy()) for (grad, param) in zip(dqn_agent.grads, dqn_agent.model.trainable_variables)])
# print('==========================================')
if step % 10000 == 0:
clear_output(True)
clear_output(True)
plt.figure(figsize=(20, 5))
plt.subplot(121)
plt.title('step: {}, epsilon: {}, time: {}, episode reward mean'.format(step, epsilon, timedelta(seconds=int(timer()-start))))
plt.plot(pd.Series(dqn_agent.rewards).rolling(10, 2).mean())
plt.subplot(122)
plt.title('loss')
plt.plot(pd.Series(dqn_agent.losses).rolling(100, 20).mean())
plt.show()
if np.array(dqn_agent.rewards[-20:]).mean() > 195: # 一开始会报一个warning: RuntimeWarning: Mean of empty slice, 可以忽略
print('a new render begins')
mean_returns, max_returns, mean_lengths, max_lengths = dqn_agent.eval_(env_eval, 100)
print('step: {}, epsilon: {}, time: {}'.format(step, epsilon, timedelta(seconds=int(timer()-start))))
print('episode reward mean: {}, epsisode reward max: {}, episode length mean: {}, episode length max: {}'.format(
mean_returns,
max_returns,
mean_lengths,
max_lengths))
if mean_returns > 195:
print('Solved!')
break
# dqn_agent.render(env_eval)
# -
plt.figure(figsize=(20, 5))
plt.subplot(121)
plt.title('step: {}, epsilon: {}, time: {}, episode reward mean'.format(step, epsilon, timedelta(seconds=int(timer()-start))))
plt.plot(pd.Series(dqn_agent.rewards).rolling(10, 2).mean())
plt.subplot(122)
plt.title('loss')
plt.plot(pd.Series(dqn_agent.losses).rolling(100, 20).mean())
plt.show()
dqn_agent.model.save_weights('./dqn_prioritized_cartpole.ckpt')
dqn_agent.render(env_eval)
# ## LunarLander-v2
# +
name = 'LunarLander-v2'
env_eval = gym.make(name)
env_eval.seed(seed)
config = Config()
start = timer()
dqn_agent = DQNAgentTensorflow(env_name=name, network=MLP_tensorflow, prioritized=True, config=config)
obs = dqn_agent.env.reset()
for step in range(1, config.max_steps+1):
epsilon = config.epsilon_by_step(step)
action = dqn_agent.get_action(obs, epsilon)
pre_obs = obs
obs, reward, done, _ = dqn_agent.env.step(action)
dqn_agent.memory.add((pre_obs, action, reward, obs, done))
dqn_agent.train(step)
if done:
obs = dqn_agent.env.reset()
if step % 1000 == 0:
mean_returns, max_returns, mean_lengths, max_lengths = dqn_agent.eval_(env_eval, 5)
print('step: {}, epsilon: {}, lr: {}, time: {}'.format(step, epsilon, dqn_agent.optimizer.lr(step).numpy(), timedelta(seconds=int(timer()-start))))
print('episode reward mean: {}, epsisode reward max: {}, episode length mean: {}, episode length max: {}, loss: {}'.format(
mean_returns,
max_returns,
mean_lengths,
max_lengths,
np.array(dqn_agent.losses[-10:]).mean()))
# print('==========================================')
# print([(tf.reduce_max(param).numpy(), tf.reduce_min(param).numpy(), tf.reduce_max(grad).numpy(), tf.reduce_min(grad).numpy()) for (grad, param) in zip(dqn_agent.grads, dqn_agent.model.trainable_variables)])
# print('==========================================')
if step % 10000 == 0:
clear_output(True)
clear_output(True)
plt.figure(figsize=(20, 5))
plt.subplot(121)
plt.title('step: {}, epsilon: {}, time: {}, episode reward mean'.format(step, epsilon, timedelta(seconds=int(timer()-start))))
plt.plot(pd.Series(dqn_agent.rewards).rolling(10, 2).mean())
plt.subplot(122)
plt.title('loss')
plt.plot(pd.Series(dqn_agent.losses).rolling(100, 20).mean())
plt.show()
if np.array(dqn_agent.rewards[-20:]).mean() > 195: # 一开始会报一个warning: RuntimeWarning: Mean of empty slice, 可以忽略
print('a new render begins')
mean_returns, max_returns, mean_lengths, max_lengths = dqn_agent.eval_(env_eval, 100)
print('step: {}, epsilon: {}, time: {}'.format(step, epsilon, timedelta(seconds=int(timer()-start))))
print('episode reward mean: {}, epsisode reward max: {}, episode length mean: {}, episode length max: {}'.format(
mean_returns,
max_returns,
mean_lengths,
max_lengths))
if mean_returns > 195:
print('Solved!')
break
# dqn_agent.render(env_eval)
# -
plt.figure(figsize=(20, 5))
plt.subplot(121)
plt.title('step: {}, epsilon: {}, time: {}, episode reward mean'.format(step, epsilon, timedelta(seconds=int(timer()-start))))
plt.plot(pd.Series(dqn_agent.rewards).rolling(10, 2).mean())
plt.subplot(122)
plt.title('loss')
plt.plot(pd.Series(dqn_agent.losses).rolling(100, 20).mean())
plt.show()
dqn_agent.model.save_weights('./dqn_prioritized_lunarlander.ckpt')
dqn_agent.render(env_eval)
| tensorflow2.0/Prioritized-ReplayBuffer/Prioritized ReplayBuffer.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''data-science-playground'': conda)'
# language: python
# name: python3
# ---
# ### Strength of ice cream
# - Easy installation ```pip install ice cream```
# - Easy to inspect order of program ```from icecream import ic;ic()```
# - Retrieve input and output in logging
# - Easy to log with filename, line number, and parent function ```ic.configureOutput(includeContext=True)```
# - Installin one file and run in all without calling it.
#
# ### To use icecream or builtinlogging
# - Light debugging use ic
# - Package building use builtinlogging
# ### ic helps to identify the order of program
# - Without arguments, ic() inspects itself and prints the calling filename, line number, and parent function.
# - Check [this](programorder.py) out
# ### includeContext, if provided and True, adds the ic() call's filename, line number, and parent function to ic()'s output.
#
# - check [this](logwithcontext.py) out
# ### To make ic() available in every file without needing to be imported in every file, you can install() it.
# - For example, in a root A.py:
# ```
# # #!/usr/bin/env python3
# # -*- coding: utf-8 -*-
#
# from icecream import install
# install()
#
# from B import foo
# foo()
# ```
#
# - and then in B.py, which is imported by A.py, just call ic():
#
# ```
# # -*- coding: utf-8 -*-
#
# def foo():
# x = 3
# ic(x)
# ```
# +
from icecream import ic
def foo(i):
return i + 333
ic(foo(123))
# -
# ### ic prints the function and the output
# +
d = {'key': {1: 'one'}}
ic(d['key'][1])
class klass():
attr = 'yep'
ic(klass.attr)
# -
# ### ic() returns its argument(s), so ic() can easily be inserted into pre-existing code.
# +
a = 6
def half(i):
return i / 2
b = half(ic(a))
ic(b)
# -
#
#
| notebooks/logging/icecream/summary.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Requires ImageMagick
# To add text, you must install ImageMagic.
#
# ##### macOS:
#
# Use [homebrew](http://brew.sh)
#
# ```
# brew update && brew install imagemagick
# ```
# #### Linux:
# Download [here](https://imagemagick.org/script/download.php)
#
# #### Windows:
# Use the [binary or exe](https://imagemagick.org/script/download.php#windows)
# +
import shutil
from conf import (SAMPLE_INPUTS, SAMPLE_OUTPUTS)
from moviepy.editor import *
from PIL import Image # pipenv install pillow
video_path = os.path.join(SAMPLE_INPUTS, 'sample.mp4')
output_video = os.path.join(SAMPLE_OUTPUTS, "with-text.mp4")
video_audio = os.path.join(SAMPLE_OUTPUTS, "og-audio.mp3")
audio_path = os.path.join(SAMPLE_INPUTS, 'audio.mp3')
temp_dir = os.path.join(SAMPLE_OUTPUTS,'temp')
os.makedirs(temp_dir, exist_ok=True)
temp_audio = os.path.join(temp_dir, 'temp-audio.m4a')
# -
clip = VideoFileClip(video_path)
og_audio = clip.audio
og_audio = og_audio.set_duration(clip.duration)
og_audio.write_audiofile(video_audio)
intro_duration = 5 # seconds
intro_text = TextClip("Hello world!", fontsize=70,color='white', size=clip.size)
intro_text = intro_text.set_duration(intro_duration)
intro_text = intro_text.set_fps(clip.fps)
intro_text = intro_text.set_pos("center")
intro_audio = AudioFileClip(audio_path)
intro_audio = intro_audio.set_duration(intro_duration)
intro_text = intro_text.set_audio(intro_audio)
# +
w, h = clip.size
text = TextClip("CFE", fontsize=70,color='white', align='East', size=(w, 70))
text = text.set_fps(clip.fps)
text = text.set_duration(clip.duration)
text = text.margin(right=2, bottom=2, opacity=0)
text = text.set_position(("bottom"))
cvc = CompositeVideoClip( [text],
size=clip.size)
cvc = cvc.set_duration(clip.duration)
cvc = cvc.set_fps(clip.fps)
# +
overlay_clip = CompositeVideoClip([clip, cvc], size=clip.size)
overlay_clip = overlay_clip.set_audio(None)
overlay_clip = overlay_clip.set_duration(clip.duration)
overlay_clip = overlay_clip.set_fps(clip.fps)
overlay_clip = overlay_clip.set_audio(AudioFileClip(video_audio))
# -
final_clip = concatenate_videoclips([intro_text, overlay_clip])
final_clip.write_videofile(output_video, temp_audiofile=temp_audio, remove_temp=True, codec="libx264", audio_codec="aac")
| tutorial-reference/Day 15/notebooks/5 - Overlay Text, Image or Video.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:prova]
# language: python
# name: conda-env-prova-py
# ---
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from lightgbm import LGBMClassifier
from shaphypetune import BoostSearch, BoostBoruta, BoostRFE
import warnings
warnings.simplefilter('ignore')
# -
def binary_performances(y_true, y_prob, thresh=0.5, labels=['Positives','Negatives']):
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix, auc, roc_curve
shape = y_prob.shape
if len(shape) > 1:
if shape[1] > 2:
raise ValueError('A binary class problem is required')
else:
y_prob = y_prob[:,1]
plt.figure(figsize=[15,4])
#1 -- Confusion matrix
cm = confusion_matrix(y_true, (y_prob>thresh).astype(int))
plt.subplot(131)
ax = sns.heatmap(cm, annot=True, cmap='Blues', cbar=False,
annot_kws={"size": 14}, fmt='g')
cmlabels = ['True Negatives', 'False Positives',
'False Negatives', 'True Positives']
for i,t in enumerate(ax.texts):
t.set_text(t.get_text() + "\n" + cmlabels[i])
plt.title('Confusion Matrix', size=15)
plt.xlabel('Predicted Values', size=13)
plt.ylabel('True Values', size=13)
#2 -- Distributions of Predicted Probabilities of both classes
plt.subplot(132)
plt.hist(y_prob[y_true==1], density=True, bins=25,
alpha=.5, color='green', label=labels[0])
plt.hist(y_prob[y_true==0], density=True, bins=25,
alpha=.5, color='red', label=labels[1])
plt.axvline(thresh, color='blue', linestyle='--', label='Boundary')
plt.xlim([0,1])
plt.title('Distributions of Predictions', size=15)
plt.xlabel('Positive Probability (predicted)', size=13)
plt.ylabel('Samples (normalized scale)', size=13)
plt.legend(loc="upper right")
#3 -- ROC curve with annotated decision point
fp_rates, tp_rates, _ = roc_curve(y_true, y_prob)
roc_auc = auc(fp_rates, tp_rates)
plt.subplot(133)
plt.plot(fp_rates, tp_rates, color='orange',
lw=1, label='ROC curve (area = %0.3f)' % roc_auc)
plt.plot([0, 1], [0, 1], lw=1, linestyle='--', color='grey')
tn, fp, fn, tp = [i for i in cm.ravel()]
plt.plot(fp/(fp+tn), tp/(tp+fn), 'bo', markersize=8, label='Decision Point')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate', size=13)
plt.ylabel('True Positive Rate', size=13)
plt.title('ROC Curve', size=15)
plt.legend(loc="lower right")
plt.subplots_adjust(wspace=.3)
plt.show()
tn, fp, fn, tp = [i for i in cm.ravel()]
precision = tp / (tp + fp)
recall = tp / (tp + fn)
F1 = 2*(precision * recall) / (precision + recall)
results = {
"Precision": precision, "Recall": recall,
"F1 Score": F1, "AUC": roc_auc
}
prints = [f"{kpi}: {round(score, 3)}" for kpi,score in results.items()]
prints = ' | '.join(prints)
print(prints)
return results
# +
### CREATE SYNTHETIC DATA ###
X, y = make_classification(n_samples=150_000,
n_features=50, n_informative=11, n_redundant=10,
n_classes=2, weights=[0.9, 0.1], class_sep=0.5,
random_state=33, shuffle=True)
X = pd.DataFrame(X, columns=[f"feat_{c}" for c in range(X.shape[1])])
X.shape, y.shape
# +
### CREATE CATEGORICAL COLUMNS ###
cat_col = [f"feat_{c}" for c in range(10)]
X[cat_col] = X[cat_col].round(2).astype("category")
# +
### TRAIN TEST SPLIT ###
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, shuffle=True, random_state=33)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train, y_train, test_size=0.2, shuffle=True, random_state=33)
# +
### DEFINE TUNING VARIABLES ###
param_grid = {
'n_estimators': 200,
'learning_rate': [0.3, 0.2, 0.1],
'num_leaves': [20, 25, 30, 35]
}
def AUC(y_true, y_hat):
return 'auc', roc_auc_score(y_true, y_hat), True
results = {}
lgbm = LGBMClassifier(random_state=0, n_jobs=-1)
# +
### HYPERPARAM TUNING WITH GRID-SEARCH ###
model = BoostSearch(lgbm, param_grid=param_grid, greater_is_better=True)
model.fit(X_train, y_train, eval_set=[(X_valid, y_valid)], eval_metric=AUC, early_stopping_rounds=3, verbose=0)
# +
### PLOT AND STORE RESULTS ###
results['Param Tuning'] = binary_performances(y_test, model.predict_proba(X_test))
# +
### HYPERPARAM TUNING WITH GRID-SEARCH + RECURSIVE FEATURE ELIMINATION (RFE) ###
model = BoostRFE(lgbm, param_grid=param_grid, min_features_to_select=10, step=3, greater_is_better=True)
model.fit(X_train, y_train, eval_set=[(X_valid, y_valid)], eval_metric=AUC, early_stopping_rounds=3, verbose=0)
# +
### PLOT AND STORE RESULTS ###
results['Param Tuning + RFE'] = binary_performances(y_test, model.predict_proba(X_test))
# +
### HYPERPARAM TUNING WITH GRID-SEARCH + RECURSIVE FEATURE ELIMINATION (RFE) WITH SHAP ###
model = BoostRFE(lgbm, param_grid=param_grid, min_features_to_select=10, step=3, greater_is_better=True,
importance_type='shap_importances', train_importance=False)
model.fit(X_train, y_train, eval_set=[(X_valid, y_valid)], eval_metric=AUC, early_stopping_rounds=3, verbose=0)
# +
### PLOT AND STORE RESULTS ###
results['Param Tuning + RFE w/ SHAP'] = binary_performances(y_test, model.predict_proba(X_test))
# +
### PLOT AND COMPARE RESULTS ###
plt.figure(figsize=(12,5))
plt.bar(np.arange(4)-0.05, results['Param Tuning'].values(),
alpha=0.5, width=0.1, label='Param Tuning')
plt.bar(np.arange(4)+0.05, results['Param Tuning + RFE'].values(),
alpha=0.5, width=0.1, label='Param Tuning + RFE')
plt.bar(np.arange(4)+0.15, results['Param Tuning + RFE w/ SHAP'].values(),
alpha=0.5, width=0.1, label='Param Tuning + RFE w/ SHAP')
plt.xticks(range(4), results['Param Tuning'].keys())
plt.ylabel('scores'); plt.legend()
plt.show()
| Shap_FeatureSelection/Shap_FeatureSelection.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] editable=true
# # Part I. ETL Pipeline for Pre-Processing the Files
# + [markdown] editable=true
# ## PLEASE RUN THE FOLLOWING CODE FOR PRE-PROCESSING THE FILES
# + [markdown] editable=true
# #### Import Python packages
# + editable=true
# Import Python packages
import pandas as pd
import cassandra
import re
import os
import glob
import numpy as np
import json
import csv
# + [markdown] editable=true
# #### Creating list of filepaths to process original event csv data files
# + editable=true
# checking your current working directory
print(os.getcwd())
# Get your current folder and subfolder event data
filepath = os.getcwd() + '/event_data'
# Create a for loop to create a list of files and collect each filepath
for root, dirs, files in os.walk(filepath):
# join the file path and roots with the subdirectories using glob
file_path_list = glob.glob(os.path.join(root,'*'))
#print(file_path_list)
# + [markdown] editable=true
# #### Processing the files to create the data file csv that will be used for Apache Casssandra tables
# + editable=true
# initiating an empty list of rows that will be generated from each file
full_data_rows_list = []
# for every filepath in the file path list
for f in file_path_list:
# reading csv file
with open(f, 'r', encoding = 'utf8', newline='') as csvfile:
# creating a csv reader object
csvreader = csv.reader(csvfile)
next(csvreader)
# extracting each data row one by one and append it
for line in csvreader:
#print(line)
full_data_rows_list.append(line)
# uncomment the code below if you would like to get total number of rows
#print(len(full_data_rows_list))
# uncomment the code below if you would like to check to see what the list of event data rows will look like
#print(full_data_rows_list)
# creating a smaller event data csv file called event_datafile_full csv that will be used to insert data into the \
# Apache Cassandra tables
csv.register_dialect('myDialect', quoting=csv.QUOTE_ALL, skipinitialspace=True)
with open('event_datafile_new.csv', 'w', encoding = 'utf8', newline='') as f:
writer = csv.writer(f, dialect='myDialect')
writer.writerow(['artist','firstName','gender','itemInSession','lastName','length',\
'level','location','sessionId','song','userId'])
for row in full_data_rows_list:
if (row[0] == ''):
continue
writer.writerow((row[0], row[2], row[3], row[4], row[5], row[6], row[7], row[8], row[12], row[13], row[16]))
# + editable=true
# check the number of rows in your csv file
with open('event_datafile_new.csv', 'r', encoding = 'utf8') as f:
print(sum(1 for line in f))
# + [markdown] editable=true
# # Part II. Complete the Apache Cassandra coding portion of your project.
#
# ## Now you are ready to work with the CSV file titled <font color=red>event_datafile_new.csv</font>, located within the Workspace directory. The event_datafile_new.csv contains the following columns:
# - artist
# - firstName of user
# - gender of user
# - item number in session
# - last name of user
# - length of the song
# - level (paid or free song)
# - location of the user
# - sessionId
# - song title
# - userId
#
# The image below is a screenshot of what the denormalized data should appear like in the <font color=red>**event_datafile_new.csv**</font> after the code above is run:<br>
#
# <img src="images/image_event_datafile_new.jpg">
# + [markdown] editable=true
# ## Begin writing your Apache Cassandra code in the cells below
# + [markdown] editable=true
# #### Creating a Cluster
# + editable=true
# This should make a connection to a Cassandra instance your local machine
# (127.0.0.1)
from cassandra.cluster import Cluster
cluster = Cluster()
# To establish connection and begin executing queries, need a session
session = cluster.connect()
# + [markdown] editable=true
# #### Create Keyspace
# + editable=true
# TO-DO: Create a Keyspace
# + [markdown] editable=true
# #### Set Keyspace
# + editable=true
# TO-DO: Set KEYSPACE to the keyspace specified above
# + [markdown] editable=true
# ### Now we need to create tables to run the following queries. Remember, with Apache Cassandra you model the database tables on the queries you want to run.
# + [markdown] editable=true
# ## Create queries to ask the following three questions of the data
#
# ### 1. Give me the artist, song title and song's length in the music app history that was heard during sessionId = 338, and itemInSession = 4
#
#
# ### 2. Give me only the following: name of artist, song (sorted by itemInSession) and user (first and last name) for userid = 10, sessionid = 182
#
#
# ### 3. Give me every user name (first and last) in my music app history who listened to the song 'All Hands Against His Own'
#
#
#
# + editable=true
## TO-DO: Query 1: Give me the artist, song title and song's length in the music app history that was heard during \
## sessionId = 338, and itemInSession = 4
# + editable=true
# We have provided part of the code to set up the CSV file. Please complete the Apache Cassandra code below#
file = 'event_datafile_new.csv'
with open(file, encoding = 'utf8') as f:
csvreader = csv.reader(f)
next(csvreader) # skip header
for line in csvreader:
## TO-DO: Assign the INSERT statements into the `query` variable
query = "<ENTER INSERT STATEMENT HERE>"
query = query + "<ASSIGN VALUES HERE>"
## TO-DO: Assign which column element should be assigned for each column in the INSERT statement.
## For e.g., to INSERT artist_name and user first_name, you would change the code below to `line[0], line[1]`
session.execute(query, (line[#], line[#]))
# + [markdown] editable=true
# #### Do a SELECT to verify that the data have been inserted into each table
# + editable=true
## TO-DO: Add in the SELECT statement to verify the data was entered into the table
# + [markdown] editable=true
# ### COPY AND REPEAT THE ABOVE THREE CELLS FOR EACH OF THE THREE QUESTIONS
# + editable=true
## TO-DO: Query 2: Give me only the following: name of artist, song (sorted by itemInSession) and user (first and last name)\
## for userid = 10, sessionid = 182
# + editable=true
## TO-DO: Query 3: Give me every user name (first and last) in my music app history who listened to the song 'All Hands Against His Own'
# + editable=true
# + editable=true
# + [markdown] editable=true
# ### Drop the tables before closing out the sessions
# + editable=true
## TO-DO: Drop the table before closing out the sessions
# + editable=true
# + [markdown] editable=true
# ### Close the session and cluster connection¶
# + editable=true
session.shutdown()
cluster.shutdown()
# + editable=true
# + editable=true
| Project_1B_ Project_Template.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/VaibhavDS19/ML-DSC/blob/master/DataStufW/Pandas_assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="ndCuPhfASjT4"
# # Pandas assignment
# - Different tasks will be detailed by comments or text.
# - It should be noted there may be more than one different way to answer a question or complete an exercise.
# - For further reference and resources, it's advised to check out the pandas documnetation.
# + id="KycwQxf8SjT6"
# Import pandas
import pandas as pd
# + id="MtiusXejPt31" outputId="c78c6486-db51-4e14-fcb5-7dd901f0bbe3" colab={"base_uri": "https://localhost:8080/", "height": 54}
from google.colab import drive
drive.mount('/content/drive')
# + id="O5DHslCDSjUB" outputId="feee85d5-f1ef-41ba-b9af-231e81462d52" colab={"base_uri": "https://localhost:8080/", "height": 221}
# Create a series of fruits(string) of length 5 and view it
# Create a series of prices(int) of length 5 and view it
fruits = pd.Series(['Apple', 'Banana','Mango','Orange','Strawberry'])
prices = pd.Series([100,50,200,300,400])
print(fruits)
print(prices)
# + id="UsKBgGGfSjUI" outputId="a34db395-d43b-4762-b859-c5af0b1294e7" colab={"base_uri": "https://localhost:8080/", "height": 204}
# Create a fruit_prices dataframe out of the 2 series you just made and view it
fruit_prices = pd.DataFrame({"fruits":fruits,"prices":prices})
fruit_prices
# + id="kVaxqXd1SjUR" outputId="28a0a88c-926b-4460-e4ea-c7f14fa69c4f" colab={"base_uri": "https://localhost:8080/", "height": 85}
# Find the mean, sum, standard deviation, variance of the prices
print("mean: ", fruit_prices['prices'].mean())
print("sum: ", fruit_prices['prices'].sum())
print("std: ", fruit_prices['prices'].std())
print("var: ", fruit_prices['prices'].var())
# + [markdown] id="a2KsYtSRSjUX"
# ### CSV - Cereal data
# - Download the csv file given to you and place it in the same directory as your notebook if you are using Jupyter notebooks.
# - If you are using Google colab mount the google drive to your colab notebook. Upload your csv file into any folder in your drive. Then do a right click on csv file and copy the file path and paste this path while importing this csv with Pandas
# + id="KuBuK03BSjUZ"
# import the csv file given to you and turn it into a DataFrame
data = pd.read_csv('/content/drive/My Drive/cereal.csv')
# + id="MvH7G7_-SjUg" outputId="cc47f721-680c-4dcc-8068-4a84e439d7b9" colab={"base_uri": "https://localhost:8080/", "height": 306}
# Find the different datatypes of the DataFrame
data.dtypes
# + id="y1_E_cpRSjUl" outputId="ac0f8798-6cf5-4486-d5e2-892176e0b4c7" colab={"base_uri": "https://localhost:8080/", "height": 317}
# Describe your current DataFrame using describe()
data.describe()
# + id="lvpcJK9OSjUw" outputId="5cd967c4-ebfe-4c93-ee85-3f172c7d365d" colab={"base_uri": "https://localhost:8080/", "height": 408}
# Get information about your DataFrame using info()
data.info()
# + id="dREw7PZ-SjU3" outputId="872e6976-cd2a-46b1-83f9-732768fe3784" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Find the length of the DataFrame
len(data)
# + id="bL3ydLwuSjU9" outputId="b224bf50-b0d6-4786-fbf0-69f8b39c4f8d" colab={"base_uri": "https://localhost:8080/", "height": 221}
# Find the unique values in shelf column
data['shelf'].unique
# + id="uG_CKZcpSjVC" outputId="23a4ea9e-b753-46bf-da6d-9a35bd24bc43" colab={"base_uri": "https://localhost:8080/", "height": 439}
# Show the first 7 rows of the DataFrame
data.head(7)
# + id="pi-oqk9RSjVH" outputId="dd12be7c-659f-4971-c43d-f425332fa426" colab={"base_uri": "https://localhost:8080/", "height": 405}
# Show the last 7 rows of the DataFrame
data.tail(7)
# + id="jLj_RCkESjVM" outputId="fd8308a3-e91a-49df-d1d6-e8fb870405d0" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Use .loc to find the sodium value of the 4th item
data['sodium'].loc[3]
# + id="BJ9rj9F3SjVR" outputId="cdeb888e-52f7-4675-986f-5eff8132f946" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Use .iloc to find the value of the 7th row and 7th column
data.iloc[6][6]
# + id="CUxL39xTSjVW" outputId="f34c9bf5-3dc6-4dfd-e65f-c17d9fa316b7" colab={"base_uri": "https://localhost:8080/", "height": 221}
# Select the "name" column from the DataFrame
data.loc[:,'name']
# + id="yaDI0CoLSjVc" outputId="f882e19f-9225-4360-9bac-d54e48d4ac38" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Select the rows which have more than 100 calories
data[data['calories']>100]
# + id="sDR-opdVSjVh" outputId="3e4ac9df-6785-40ad-aea7-bb387686af0b" colab={"base_uri": "https://localhost:8080/", "height": 450}
# Create a crosstab of the name and vitamins columns
ct = pd.crosstab(data['name'], data['vitamins'])
ct
# + id="z-457M_ISjVm" outputId="72c00898-0844-4755-c417-ba7f4f1bb95a" colab={"base_uri": "https://localhost:8080/", "height": 317}
# Group columns of the DataFrame by the manufacturer(mfr column) and find the average
data.groupby('mfr').mean()
# + id="FQILQhCvSjVt" outputId="f0f24fdd-d757-42a8-bb18-d8cc6ef9f1b3" colab={"base_uri": "https://localhost:8080/", "height": 221}
# Get rid of the decimal digits in ratings. #For example: 68.402973 -> 68
data['rating'] = data['rating'].astype(int)
data['rating']
# + id="H0CiyhaeSjV0" outputId="60dae93a-0048-40d2-9711-b0da45ec0191" colab={"base_uri": "https://localhost:8080/", "height": 306}
# Check for missing values in the dataframe
data.isnull().sum()
# + id="qDCJZhPfSjV5" outputId="21b1c0fd-a26b-4b42-e0b5-df3562ad6c09" colab={"base_uri": "https://localhost:8080/", "height": 626}
# Create a "Safe for consumption" column with boolean value True
data['safe for consumption'] = True
data
# + id="ihqJz8n0SjV_" outputId="e7824f4b-3200-4286-ba6f-9cc068429e5c" colab={"base_uri": "https://localhost:8080/", "height": 626}
# Remove the sugars column
data.drop('sugars', axis=1)
# + id="BcOdm4QbSjWE" outputId="5211e48e-0042-4824-b415-3291232f17af" colab={"base_uri": "https://localhost:8080/", "height": 660}
# Shuffle the DataFrame using sample() with the frac parameter set to 1
data = data.sample(frac=1)
data
# + id="TnBtri48SjWI" outputId="2dc3af91-99f2-49e5-b814-ba28fbeb0a01" colab={"base_uri": "https://localhost:8080/", "height": 660}
# Save the the shuffled DataFrame to a new variable
sdata = data
sdata
| DataHandling/Assignment4.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !pip install mitdeeplearning
# +
# Import Tensorflow 2.0
import tensorflow as tf
# Download and import the MIT 6.S191 package
import mitdeeplearning as mdl
# Import all remaining packages
import numpy as np
import re
import os
import time
import functools
from IPython import display as ipythondisplay
from tqdm import tqdm
# #!apt-get install abcmidi timidity > /dev/null 2>&1
# Check that we are using a GPU, if not switch runtimes
# using Runtime > Change Runtime Type > GPU
assert len(tf.config.list_physical_devices('GPU')) > 0
# +
# Download the dataset
songs = mdl.lab1.load_training_data()
# Print one of the songs to inspect it in greater detail!
example_song = songs[0]
print("\nExample song: ")
print(example_song)
# -
# Convert the ABC notation to audio file and listen to it
mdl.lab1.play_song(example_song)
# +
# Join our list of song strings into a single string containing all songs
songs_joined = "\n\n".join(songs)
# Find all unique characters in the joined string
vocab = sorted(set(songs_joined))
print("There are", len(vocab), "unique characters in the dataset")
print(songs_joined)
# +
### Define numerical representation of text ###
# Create a mapping from character to unique index.
# For example, to get the index of the character "d",
# we can evaluate `char2idx["d"]`.
char2idx = {u:i for i, u in enumerate(vocab)}
# Create a mapping from indices to characters. This is
# the inverse of char2idx and allows us to convert back
# from unique index to the character in our vocabulary.
idx2char = np.array(vocab)
print(idx2char)
# +
### Vectorize the songs string ###
def vectorize_string(songs):
numeric_rep = list()
for char in songs:
numeric_rep.append(char2idx[char])
vectorized_songs = np.array(numeric_rep)
return vectorized_songs
vectorized_songs = vectorize_string(songs_joined)
# +
print ('{} ---- characters mapped to int ----> {}'.format(repr(songs_joined[:10]), vectorized_songs[:10]))
# check that vectorized_songs is a numpy array
assert isinstance(vectorized_songs, np.ndarray), "returned result should be a numpy array"
# +
### Batch definition to create training examples ###
def get_batch(vectorized_songs, seq_length, batch_size):
input_batch = list()
output_batch = list()
# the length of the vectorized songs string
n = vectorized_songs.shape[0] - 1
# randomly choose the starting indices for the examples in the training batch
idx = np.random.choice(n-seq_length, batch_size)
print(idx)
# Construct a list of input sequences for the training batch
for index in idx:
for id in range(seq_length):
input_batch.append(vectorized_songs[id+index])
# Construct a list of output sequences for the training batch
for index in idx:
for id in range(seq_length):
output_batch.append(vectorized_songs[id+index+1])
# x_batch, y_batch provide the true inputs and targets for network training
x_batch = np.reshape(input_batch, [batch_size, seq_length])
y_batch = np.reshape(output_batch, [batch_size, seq_length])
return x_batch, y_batch
# Perform some simple tests to make sure your batch function is working properly!
test_args = (vectorized_songs, 10, 2)
if not mdl.lab1.test_batch_func_types(get_batch, test_args) or \
not mdl.lab1.test_batch_func_shapes(get_batch, test_args) or \
not mdl.lab1.test_batch_func_next_step(get_batch, test_args):
print("======\n[FAIL] could not pass tests")
else:
print("======\n[PASS] passed all tests!")
# +
x_batch, y_batch = get_batch(vectorized_songs, seq_length=5, batch_size=1)
for i, (input_idx, target_idx) in enumerate(zip(np.squeeze(x_batch), np.squeeze(y_batch))):
print("Step {:3d}".format(i))
print(" input: {} ({:s})".format(input_idx, repr(idx2char[input_idx])))
print(" expected output: {} ({:s})".format(target_idx, repr(idx2char[target_idx])))
# -
def LSTM(rnn_units):
return tf.keras.layers.LSTM(
rnn_units,
return_sequences=True,
recurrent_initializer='glorot_uniform',
recurrent_activation='sigmoid',
stateful=True,
)
# +
### Defining the RNN Model ###
dropout_rate = 0.2;
def build_model(vocab_size, embedding_dim, rnn_units, batch_size):
model = tf.keras.Sequential([
# Layer 1: Embedding layer to transform indices into dense vectors
# of a fixed embedding size
tf.keras.layers.Embedding(vocab_size, embedding_dim, batch_input_shape=[batch_size, None]),
# Layer 2: LSTM with `rnn_units` number of units.
LSTM(rnn_units),
tf.keras.layers.Dropout(dropout_rate),
LSTM(rnn_units),
tf.keras.layers.Dropout(dropout_rate),
# Layer 3: Dense (fully-connected) layer that transforms the LSTM output
# into the vocabulary size.
tf.keras.layers.Dense(vocab_size)
])
return model
# Build a simple model with default hyperparameters. You will get the
# chance to change these later.
model = build_model(len(vocab), embedding_dim=256, rnn_units=1024, batch_size=32)
# -
model.summary()
# +
x, y = get_batch(vectorized_songs, seq_length=100, batch_size=32)
pred = model(x)
print("Input shape: ", x.shape, " # (batch_size, sequence_length)")
print("Prediction shape: ", pred.shape, "# (batch_size, sequence_length, vocab_size)")
# -
sampled_indices = tf.random.categorical(pred[0], num_samples=1)
sampled_indices = tf.squeeze(sampled_indices,axis=-1).numpy()
sampled_indices
print("Input: \n", repr("".join(idx2char[x[0]])))
print()
print("Next Char Predictions: \n", repr("".join(idx2char[sampled_indices])))
# +
### Defining the loss function ###
def compute_loss(labels, logits):
loss = tf.keras.losses.sparse_categorical_crossentropy(labels, logits, from_logits=True)
return loss
example_batch_loss = compute_loss(y, pred)
print("Prediction shape: ", pred.shape, " # (batch_size, sequence_length, vocab_size)")
print("scalar_loss: ", example_batch_loss.numpy().mean())
# +
### Hyperparameter setting and optimization ###
# Optimization parameters:
num_training_iterations = 2000 # Increase this to train longer
batch_size = 4 # Experiment between 1 and 64
seq_length = 200 # Experiment between 50 and 500
learning_rate = 1e-3 # Experiment between 1e-5 and 1e-1
# Model parameters:
vocab_size = len(vocab)
embedding_dim = 256
rnn_units = 200 # Experiment between 1 and 2048
# Checkpoint location:
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "my_ckpt")
# +
### Define optimizer and training operation ###
model = build_model(vocab_size, embedding_dim, rnn_units, batch_size)
#optimizer = tf.keras.optimizers.Adam(learning_rate)
optimizer = tf.keras.optimizers.RMSprop(learning_rate)
@tf.function
def train_step(x, y):
with tf.GradientTape() as tape:
# Feed the current input into the model and generate predictions'''
y_hat = model(x)
# Compute the loss!
loss = compute_loss(y, y_hat)
# Now, compute the gradients
grads = tape.gradient(loss, model.trainable_variables)
# Apply the gradients to the optimizer so it can update the model accordingly
optimizer.apply_gradients(zip(grads, model.trainable_variables))
return loss
##################
# Begin training!#
##################
history = []
plotter = mdl.util.PeriodicPlotter(sec=2, xlabel='Iterations', ylabel='Loss')
if hasattr(tqdm, '_instances'): tqdm._instances.clear() # clear if it exists
for iter in tqdm(range(num_training_iterations)):
# Grab a batch and propagate it through the network
x_batch, y_batch = get_batch(vectorized_songs, seq_length, batch_size)
loss = train_step(x_batch, y_batch)
# Update the progress bar
history.append(loss.numpy().mean())
plotter.plot(history)
# Update the model with the changed weights!
if iter % 100 == 0:
model.save_weights(checkpoint_prefix)
# Save the trained model and the weights
model.save_weights(checkpoint_prefix)
# +
# Rebuild the model using a batch_size=1
model = build_model(vocab_size, embedding_dim, rnn_units, batch_size=1)
# Restore the model weights for the last checkpoint after training
model.load_weights(tf.train.latest_checkpoint(checkpoint_dir))
model.build(tf.TensorShape([1, None]))
model.summary()
# +
### Prediction of a generated song ###
def generate_text(model, start_string, generation_length=1000):
# Evaluation step (generating ABC text using the learned RNN model)
# Convert the start string to numbers (vectorize)
input_eval = [char2idx[s] for s in start_string]
input_eval = tf.expand_dims(input_eval, 0)
# Empty string to store our results
text_generated = []
# Here batch size == 1
model.reset_states()
tqdm._instances.clear()
for i in tqdm(range(generation_length)):
# Evaluate the inputs and generate the next character predictions
predictions = model(input_eval)
# Remove the batch dimension
predictions = tf.squeeze(predictions, 0)
# Use a multinomial distribution to sample
predicted_id = tf.random.categorical(predictions, num_samples=1)[-1,0].numpy()
# Pass the prediction along with the previous hidden state
# as the next inputs to the model
input_eval = tf.expand_dims([predicted_id], 0)
# Add the predicted character to the generated text!
text_generated.append(idx2char[predicted_id])
print(start_string + ''.join(text_generated))
return (start_string + ''.join(text_generated))
# -
start_string="X:1\nT:"
generated_text = generate_text(model, start_string, generation_length=500)
# +
generated_songs = mdl.lab1.extract_song_snippet('\n\n'+example_song+'\n\n')
for i, song in enumerate(generated_songs):
# Synthesize the waveform from a song
waveform = mdl.lab1.play_song(song)
# If its a valid song (correct syntax), lets play it!
if waveform:
print("Generated song", i)
ipythondisplay.display(waveform)
# -
# © <NAME> and <NAME>
# MIT 6.S191: Introduction to Deep Learning
# IntroToDeepLearning.com
#
# Instructions for lab obtained from:
# https://github.com/aamini/introtodeeplearning/
| code/RNN Practice (MIT 6.S191).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
def maxProfit(prices):
if prices == [] or len(prices) == 1:
return 0
max_prof = 0
val1 = prices[0]
for index, val in enumerate(prices[1:], 1):
val2 = prices[index]
max_prof = val2 - val1 if max_prof < val2 - val1 else max_prof
val1 = min(val1, val2)
return max_prof
maxProfit([1, 2, 4])
| 121_Best_Time_to_Buy_and_Sell_Stock.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Bayesian Convolutional Neural Network
#
# > In this post, we will create a Bayesian convolutional neural network to classify the famous MNIST handwritten digits. This will be a probabilistic model, designed to capture both aleatoric and epistemic uncertainty. You will test the uncertainty quantifications against a corrupted version of the dataset. This is the assignment of lecture "Probabilistic Deep Learning with Tensorflow 2" from Imperial College London.
#
# - toc: true
# - badges: true
# - comments: true
# - author: <NAME>
# - categories: [Python, Coursera, Tensorflow_probability, ICL]
# - image: images/mnist_corrupted.png
# ## Packages
# +
import tensorflow as tf
import tensorflow_probability as tfp
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D, MaxPooling2D
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.optimizers import RMSprop
import numpy as np
import os
import matplotlib.pyplot as plt
tfd = tfp.distributions
tfpl = tfp.layers
plt.rcParams['figure.figsize'] = (10, 6)
# -
print("Tensorflow Version: ", tf.__version__)
print("Tensorflow Probability Version: ", tfp.__version__)
# 
#
# ## The MNIST and MNIST-C datasets
#
# In this notebook, you will use the [MNIST](http://yann.lecun.com/exdb/mnist/) and [MNIST-C](https://github.com/google-research/mnist-c) datasets, which both consist of a training set of 60,000 handwritten digits with corresponding labels, and a test set of 10,000 images. The images have been normalised and centred. The MNIST-C dataset is a corrupted version of the MNIST dataset, to test out-of-distribution robustness of computer vision models.
#
# - <NAME>, <NAME>, <NAME>, and <NAME>. "Gradient-based learning applied to document recognition." Proceedings of the IEEE, 86(11):2278-2324, November 1998.
# - <NAME> and <NAME>. "MNIST-C: A Robustness Benchmark for Computer Vision" https://arxiv.org/abs/1906.02337
#
# Our goal is to construct a neural network that classifies images of handwritten digits into one of 10 classes.
# ### Load the datasets
#
# We'll start by importing two datasets. The first is the MNIST dataset of handwritten digits, and the second is the MNIST-C dataset, which is a corrupted version of the MNIST dataset. This dataset is available on [TensorFlow datasets](https://www.tensorflow.org/datasets/catalog/mnist_corrupted). We'll be using the dataset with "spatters". We will load and inspect the datasets below. We'll use the notation `_c` to denote `corrupted`. The images are the same as in the original MNIST, but are "corrupted" by some grey spatters.
# +
# Function to load training and testing data, with labels in integer and one-hot form
def load_data(name):
data_dir = os.path.join('dataset', name)
x_train = 1 - np.load(os.path.join(data_dir, 'x_train.npy')) / 255.
x_train = x_train.astype(np.float32)
y_train = np.load(os.path.join(data_dir, 'y_train.npy'))
y_train_oh = tf.keras.utils.to_categorical(y_train)
x_test = 1 - np.load(os.path.join(data_dir, 'x_test.npy')) / 255.
x_test = x_test.astype(np.float32)
y_test = np.load(os.path.join(data_dir, 'y_test.npy'))
y_test_oh = tf.keras.utils.to_categorical(y_test)
return (x_train, y_train, y_train_oh), (x_test, y_test, y_test_oh)
# +
# Function to inspect dataset digits
def inspect_images(data, num_images):
fig, ax = plt.subplots(nrows=1, ncols=num_images, figsize=(2*num_images, 2))
for i in range(num_images):
ax[i].imshow(data[i, ..., 0], cmap='gray')
ax[i].axis('off')
plt.show()
# +
# Load and inspect the MNIST dataset
(x_train, y_train, y_train_oh), (x_test, y_test, y_test_oh) = load_data('MNIST')
inspect_images(data=x_train, num_images=8)
# +
# Load and inspect the MNIST-C dataset
(x_c_train, y_c_train, y_c_train_oh), (x_c_test, y_c_test, y_c_test_oh) = load_data('MNIST_corrupted')
inspect_images(data=x_c_train, num_images=8)
# -
# ### Create the deterministic model
#
# We will first train a standard deterministic CNN classifier model as a base model before implementing the probabilistic and Bayesian neural networks.
def get_deterministic_model(input_shape, loss, optimizer, metrics):
"""
This function should build and compile a CNN model according to the above specification.
The function takes input_shape, loss, optimizer and metrics as arguments, which should be
used to define and compile the model.
Your function should return the compiled model.
"""
model = Sequential([
Conv2D(kernel_size=(5, 5), filters=8, activation='relu', padding='VALID', input_shape=input_shape),
MaxPooling2D(pool_size=(6, 6)),
Flatten(),
Dense(units=10, activation='softmax')
])
model.compile(loss=loss, optimizer=optimizer, metrics=metrics)
return model
# +
# Run your function to get the benchmark model
tf.random.set_seed(0)
deterministic_model = get_deterministic_model(
input_shape=(28, 28, 1),
loss=SparseCategoricalCrossentropy(),
optimizer=RMSprop(),
metrics=['accuracy']
)
# +
# Print the model summary
deterministic_model.summary()
# +
# Train the model
deterministic_model.fit(x_train, y_train, epochs=5)
# +
# Evaluate the model
print('Accuracy on MNIST test set: ',
str(deterministic_model.evaluate(x_test, y_test, verbose=False)[1]))
print('Accuracy on corrupted MNIST test set: ',
str(deterministic_model.evaluate(x_c_test, y_c_test, verbose=False)[1]))
# -
# As you might expect, the pointwise performance on the corrupted MNIST set is worse. This makes sense, since this dataset is slightly different, and noisier, than the uncorrupted version. Furthermore, the model was trained on the uncorrupted MNIST data, so has no experience with the spatters.
# ### Probabilistic CNN model
#
# You'll start by turning this deterministic network into a probabilistic one, by letting the model output a distribution instead of a deterministic tensor. This model will capture the aleatoric uncertainty on the image labels. You will do this by adding a probabilistic layer to the end of the model and training using the negative loglikelihood.
#
# Note that, our NLL loss function has arguments `y_true` for the correct label (as a one-hot vector), and `y_pred` as the model prediction (a `OneHotCategorical` distribution). It should return the negative log-likelihood of each sample in `y_true` given the predicted distribution `y_pred`. If `y_true` is of shape `[B, E]` and `y_pred` has batch shape `[B]` and event shape `[E]`, the output should be a Tensor of shape `[B]`.
def nll(y_true, y_pred):
"""
This function should return the negative log-likelihood of each sample
in y_true given the predicted distribution y_pred. If y_true is of shape
[B, E] and y_pred has batch shape [B] and event_shape [E], the output
should be a Tensor of shape [B].
"""
return -y_pred.log_prob(y_true)
# Now we need to build probabilistic model.
def get_probabilistic_model(input_shape, loss, optimizer, metrics):
"""
This function should return the probabilistic model according to the
above specification.
The function takes input_shape, loss, optimizer and metrics as arguments, which should be
used to define and compile the model.
Your function should return the compiled model.
"""
model = Sequential([
Conv2D(kernel_size=(5, 5), filters=8, activation='relu', padding='VALID', input_shape=input_shape),
MaxPooling2D(pool_size=(6, 6)),
Flatten(),
Dense(tfpl.OneHotCategorical.params_size(10)),
tfpl.OneHotCategorical(10, convert_to_tensor_fn=tfd.Distribution.mode)
])
model.compile(loss=loss, optimizer=optimizer, metrics=metrics)
return model
# +
# Run your function to get the probabilistic model
tf.random.set_seed(0)
probabilistic_model = get_probabilistic_model(
input_shape=(28, 28, 1),
loss=nll,
optimizer=RMSprop(),
metrics=['accuracy']
)
# +
# Print the model summary
probabilistic_model.summary()
# -
# Now, you can train the probabilistic model on the MNIST data using the code below.
#
# Note that the target data now uses the one-hot version of the labels, instead of the sparse version. This is to match the categorical distribution you added at the end.
# +
# Train the model
probabilistic_model.fit(x_train, y_train_oh, epochs=5)
# +
# Evaluate the model
print('Accuracy on MNIST test set: ',
str(probabilistic_model.evaluate(x_test, y_test_oh, verbose=False)[1]))
print('Accuracy on corrupted MNIST test set: ',
str(probabilistic_model.evaluate(x_c_test, y_c_test_oh, verbose=False)[1]))
# -
# #### Analyse the model predictions
#
# We will now do some deeper analysis by looking at the probabilities the model assigns to each class instead of its single prediction.
#
# The function below will be useful to help us analyse the probabilistic model predictions.
# +
# Function to make plots of the probabilities that the model estimates for an image
def analyse_model_prediction(data, true_labels, model, image_num, run_ensemble=False):
if run_ensemble:
ensemble_size = 200
else:
ensemble_size = 1
image = data[image_num]
true_label = true_labels[image_num, 0]
predicted_probabilities = np.empty(shape=(ensemble_size, 10))
for i in range(ensemble_size):
predicted_probabilities[i] = model(image[np.newaxis, :]).mean().numpy()[0]
model_prediction = model(image[np.newaxis, :])
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(10, 2),
gridspec_kw={'width_ratios': [2, 4]})
# Show the image and the true label
ax1.imshow(image[..., 0], cmap='gray')
ax1.axis('off')
ax1.set_title('True label: {}'.format(str(true_label)))
# Show a 95% prediction interval of model predicted probabilities
pct_2p5 = np.array([np.percentile(predicted_probabilities[:, i], 2.5) for i in range(10)])
pct_97p5 = np.array([np.percentile(predicted_probabilities[:, i], 97.5) for i in range(10)])
bar = ax2.bar(np.arange(10), pct_97p5, color='red')
bar[int(true_label)].set_color('green')
ax2.bar(np.arange(10), pct_2p5-0.02, color='white', linewidth=1, edgecolor='white')
ax2.set_xticks(np.arange(10))
ax2.set_ylim([0, 1])
ax2.set_ylabel('Probability')
ax2.set_title('Model estimated probabilities')
plt.show()
# +
# Prediction examples on MNIST
for i in [0, 1577]:
analyse_model_prediction(x_test, y_test, probabilistic_model, i)
# -
# The model is very confident that the first image is a 6, which is correct. For the second image, the model struggles, assigning nonzero probabilities to many different classes.
#
# Run the code below to do the same for 2 images from the corrupted MNIST test set.
# +
# Prediction examples on MNIST-C
for i in [0, 3710]:
analyse_model_prediction(x_c_test, y_c_test, probabilistic_model, i)
# -
# The first is the same 6 as you saw above, but the second image is different. Notice how the model can still say with high certainty that the first image is a 6, but struggles for the second, assigning an almost uniform distribution to all possible labels.
#
# Finally, have a look at an image for which the model is very sure on MNIST data but very unsure on corrupted MNIST data:
# +
# Prediction examples from both datasets
for i in [9241]:
analyse_model_prediction(x_test, y_test, probabilistic_model, i)
analyse_model_prediction(x_c_test, y_c_test, probabilistic_model, i)
# -
# It's not surprising what's happening here: the spatters cover up most of the number. You would hope a model indicates that it's unsure here, since there's very little information to go by. This is exactly what's happened.
# ### Uncertainty quantification using entropy
#
# We can also make some analysis of the model's uncertainty across the full test set, instead of for individual values. One way to do this is to calculate the [entropy](https://en.wikipedia.org/wiki/Entropy_%28information_theory%29) of the distribution. The entropy is the expected information (or informally, the expected 'surprise') of a random variable, and is a measure of the uncertainty of the random variable. The entropy of the estimated probabilities for sample $i$ is defined as
#
# $$
# H_i = -\sum_{j=1}^{10} p_{ij} \text{log}_{2}(p_{ij})
# $$
#
# where $p_{ij}$ is the probability that the model assigns to sample $i$ corresponding to label $j$. The entropy as above is measured in _bits_. If the natural logarithm is used instead, the entropy is measured in _nats_.
#
# The key point is that the higher the value, the more unsure the model is. Let's see the distribution of the entropy of the model's predictions across the MNIST and corrupted MNIST test sets. The plots will be split between predictions the model gets correct and incorrect.
# +
# Functions to plot the distribution of the information entropy across samples,
# split into whether the model prediction is correct or incorrect
def get_correct_indices(model, x, labels):
y_model = model(x)
correct = np.argmax(y_model.mean(), axis=1) == np.squeeze(labels)
correct_indices = [i for i in range(x.shape[0]) if correct[i]]
incorrect_indices = [i for i in range(x.shape[0]) if not correct[i]]
return correct_indices, incorrect_indices
def plot_entropy_distribution(model, x, labels):
probs = model(x).mean().numpy()
entropy = -np.sum(probs * np.log2(probs), axis=1)
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
for i, category in zip(range(2), ['Correct', 'Incorrect']):
entropy_category = entropy[get_correct_indices(model, x, labels)[i]]
mean_entropy = np.mean(entropy_category)
num_samples = entropy_category.shape[0]
title = category + 'ly labelled ({:.1f}% of total)'.format(num_samples / x.shape[0] * 100)
axes[i].hist(entropy_category, weights=(1/num_samples)*np.ones(num_samples))
axes[i].annotate('Mean: {:.3f} bits'.format(mean_entropy), (0.4, 0.9), ha='center')
axes[i].set_xlabel('Entropy (bits)')
axes[i].set_ylim([0, 1])
axes[i].set_ylabel('Probability')
axes[i].set_title(title)
plt.show()
# +
# Entropy plots for the MNIST dataset
print('MNIST test set:')
plot_entropy_distribution(probabilistic_model, x_test, y_test)
# +
# Entropy plots for the MNIST-C dataset
print('Corrupted MNIST test set:')
plot_entropy_distribution(probabilistic_model, x_c_test, y_c_test)
# -
# There are two main conclusions:
# - The model is more unsure on the predictions it got wrong: this means it "knows" when the prediction may be wrong.
# - The model is more unsure for the corrupted MNIST test than for the uncorrupted version. Futhermore, this is more pronounced for correct predictions than for those it labels incorrectly.
#
# In this way, the model seems to "know" when it is unsure. This is a great property to have in a machine learning model, and is one of the advantages of probabilistic modelling.
# ### Bayesian CNN model
#
# The probabilistic model you just created considered only aleatoric uncertainty, assigning probabilities to each image instead of deterministic labels. The model still had deterministic weights. However, as you've seen, there is also 'epistemic' uncertainty over the weights, due to uncertainty about the parameters that explain the training data.
def get_convolutional_reparameterization_layer(input_shape, divergence_fn):
"""
This function should create an instance of a Convolution2DReparameterization
layer according to the above specification.
The function takes the input_shape and divergence_fn as arguments, which should
be used to define the layer.
Your function should then return the layer instance.
"""
layer = tfpl.Convolution2DReparameterization(
input_shape=input_shape, filters=8, kernel_size=(5, 5),
activation='relu', padding='VALID',
kernel_prior_fn=tfpl.default_multivariate_normal_fn,
kernel_posterior_fn=tfpl.default_mean_field_normal_fn(is_singular=False),
kernel_divergence_fn=divergence_fn,
bias_prior_fn=tfpl.default_multivariate_normal_fn,
bias_posterior_fn=tfpl.default_mean_field_normal_fn(is_singular=False),
bias_divergence_fn=divergence_fn
)
return layer
# ### Custom prior
#
# For the parameters of the `DenseVariational` layer, we will use a custom prior: the "spike and slab" (also called a *scale mixture prior*) distribution. This distribution has a density that is the weighted sum of two normally distributed ones: one with a standard deviation of 1 and one with a standard deviation of 10. In this way, it has a sharp spike around 0 (from the normal distribution with standard deviation 1), but is also more spread out towards far away values (from the contribution from the normal distribution with standard deviation 10). The reason for using such a prior is that it is like a standard unit normal, but makes values far away from 0 more likely, allowing the model to explore a larger weight space. Run the code below to create a "spike and slab" distribution and plot its probability density function, compared with a standard unit normal.
# +
# Function to define the spike and slab distribution
def spike_and_slab(event_shape, dtype):
distribution = tfd.Mixture(
cat=tfd.Categorical(probs=[0.5, 0.5]),
components=[
tfd.Independent(tfd.Normal(
loc=tf.zeros(event_shape, dtype=dtype),
scale=1.0*tf.ones(event_shape, dtype=dtype)),
reinterpreted_batch_ndims=1),
tfd.Independent(tfd.Normal(
loc=tf.zeros(event_shape, dtype=dtype),
scale=10.0*tf.ones(event_shape, dtype=dtype)),
reinterpreted_batch_ndims=1)],
name='spike_and_slab')
return distribution
# +
# Plot the spike and slab distribution pdf
x_plot = np.linspace(-5, 5, 1000)[:, np.newaxis]
plt.plot(x_plot, tfd.Normal(loc=0, scale=1).prob(x_plot).numpy(), label='unit normal', linestyle='--')
plt.plot(x_plot, spike_and_slab(1, dtype=tf.float32).prob(x_plot).numpy(), label='spike and slab')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.show()
# -
def get_prior(kernel_size, bias_size, dtype=None):
"""
This function should create the prior distribution, consisting of the
"spike and slab" distribution that is described above.
The distribution should be created using the kernel_size, bias_size and dtype
function arguments above.
The function should then return a callable, that returns the prior distribution.
"""
n = kernel_size+bias_size
prior_model = Sequential([tfpl.DistributionLambda(lambda t : spike_and_slab(n, dtype))])
return prior_model
def get_posterior(kernel_size, bias_size, dtype=None):
"""
This function should create the posterior distribution as specified above.
The distribution should be created using the kernel_size, bias_size and dtype
function arguments above.
The function should then return a callable, that returns the posterior distribution.
"""
n = kernel_size + bias_size
return Sequential([
tfpl.VariableLayer(tfpl.IndependentNormal.params_size(n), dtype=dtype),
tfpl.IndependentNormal(n)
])
def get_dense_variational_layer(prior_fn, posterior_fn, kl_weight):
"""
This function should create an instance of a DenseVariational layer according
to the above specification.
The function takes the prior_fn, posterior_fn and kl_weight as arguments, which should
be used to define the layer.
Your function should then return the layer instance.
"""
return tfpl.DenseVariational(
units=10, make_posterior_fn=posterior_fn, make_prior_fn=prior_fn, kl_weight=kl_weight
)
# Now, you're ready to use the functions you defined to create the convolutional reparameterization and dense variational layers, and use them in your Bayesian convolutional neural network model.
tf.random.set_seed(0)
divergence_fn = lambda q, p, _ : tfd.kl_divergence(q, p) / x_train.shape[0]
convolutional_reparameterization_layer = get_convolutional_reparameterization_layer(
input_shape=(28, 28, 1), divergence_fn=divergence_fn
)
dense_variational_layer = get_dense_variational_layer(
get_prior, get_posterior, kl_weight=1/x_train.shape[0]
)
# +
# Build and compile the Bayesian CNN model
bayesian_model = Sequential([
convolutional_reparameterization_layer,
MaxPooling2D(pool_size=(6, 6)),
Flatten(),
dense_variational_layer,
tfpl.OneHotCategorical(10, convert_to_tensor_fn=tfd.Distribution.mode)
])
bayesian_model.compile(loss=nll,
optimizer=RMSprop(),
metrics=['accuracy'],
experimental_run_tf_function=False)
# +
# Print the model summary
bayesian_model.summary()
# +
# Train the model
bayesian_model.fit(x=x_train, y=y_train_oh, epochs=10, verbose=True)
# +
# Evaluate the model
print('Accuracy on MNIST test set: ',
str(bayesian_model.evaluate(x_test, y_test_oh, verbose=False)[1]))
print('Accuracy on corrupted MNIST test set: ',
str(bayesian_model.evaluate(x_c_test, y_c_test_oh, verbose=False)[1]))
# -
# ### Analyse the model predictions
#
# Now that the model has trained, run the code below to create the same plots as before, starting with an analysis of the predicted probabilities for the same images.
#
# This model now has weight uncertainty, so running the forward pass multiple times will not generate the same estimated probabilities. For this reason, the estimated probabilities do not have single values. The plots are adjusted to show a 95% prediction interval for the model's estimated probabilities.
# +
# Prediction examples on MNIST
for i in [0, 1577]:
analyse_model_prediction(x_test, y_test, bayesian_model, i, run_ensemble=True)
# -
# For the first image, the model assigns a probability of almost one for the 6 label. Furthermore, it is confident in this probability: this probability remains close to one for every sample from the posterior weight distribution (as seen by the horizontal green line having very small height, indicating a narrow prediction interval). This means that the epistemic uncertainty on this probability is very low.
#
# For the second image, the epistemic uncertainty on the probabilities is much larger, which indicates that the estimated probabilities may be unreliable. In this way, the model indicates whether estimates may be inaccurate.
# +
# Prediction examples on MNIST-C
for i in [0, 3710]:
analyse_model_prediction(x_c_test, y_c_test, bayesian_model, i, run_ensemble=True)
# -
# Even with the spatters, the Bayesian model is confident in predicting the correct label for the first image above. The model struggles with the second image, which is reflected in the range of probabilities output by the network.
# +
# Prediction examples from both datasets
for i in [9241]:
analyse_model_prediction(x_test, y_test, bayesian_model, i, run_ensemble=True)
analyse_model_prediction(x_c_test, y_c_test, bayesian_model, i, run_ensemble=True)
# -
# Similar to before, the model struggles with the second number, as it is mostly covered up by the spatters. However, this time is clear to see the epistemic uncertainty in the model.
# ### Uncertainty quantification using entropy
#
# We also again plot the distribution of distribution entropy across the different test sets below. In these plots, no consideration has been made for the epistemic uncertainty, and the conclusions are broadly similar to those for the previous model.
# +
# Entropy plots for the MNIST dataset
print('MNIST test set:')
plot_entropy_distribution(bayesian_model, x_test, y_test)
# +
# Entropy plots for the MNIST-C dataset
print('Corrupted MNIST test set:')
plot_entropy_distribution(bayesian_model, x_c_test, y_c_test)
| _notebooks/2021-08-26-01-Bayesian-Convolutional-Neural-Network.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction to Deep Learning with PyTorch
#
# In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
#
#
# ## Neural Networks
#
# Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
#
# <img src="assets/simple_neuron.png" width=400px>
#
# Mathematically this looks like:
#
# $$
# \begin{align}
# y &= f(w_1 x_1 + w_2 x_2 + b) \\
# y &= f\left(\sum_i w_i x_i +b \right)
# \end{align}
# $$
#
# With vectors this is the dot/inner product of two vectors:
#
# $$
# h = \begin{bmatrix}
# x_1 \, x_2 \cdots x_n
# \end{bmatrix}
# \cdot
# \begin{bmatrix}
# w_1 \\
# w_2 \\
# \vdots \\
# w_n
# \end{bmatrix}
# $$
# ## Tensors
#
# It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
#
# <img src="assets/tensor_examples.svg" width=600px>
#
# With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
# +
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
# -
# Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
#
# `features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
#
# `weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
#
# Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
#
# PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
# > **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
# +
### Solution
# Now, make our labels from our data and true weights
y = activation(torch.sum(features * weights) + bias)
y = activation((features * weights).sum() + bias)
# -
# You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
#
# Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
#
# ```python
# >> torch.mm(features, weights)
#
# ---------------------------------------------------------------------------
# RuntimeError Traceback (most recent call last)
# <ipython-input-13-15d592eb5279> in <module>()
# ----> 1 torch.mm(features, weights)
#
# RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
# ```
#
# As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
#
# **Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
#
# There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
#
# * `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
# * `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
# * `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
#
# I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
#
# > **Exercise**: Calculate the output of our little network using matrix multiplication.
# +
## Solution
y = activation(torch.mm(features, weights.view(5,1)) + bias)
# -
# ### Stack them up!
#
# That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
#
# <img src='assets/multilayer_diagram_weights.png' width=450px>
#
# The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
#
# $$
# \vec{h} = [h_1 \, h_2] =
# \begin{bmatrix}
# x_1 \, x_2 \cdots \, x_n
# \end{bmatrix}
# \cdot
# \begin{bmatrix}
# w_{11} & w_{12} \\
# w_{21} &w_{22} \\
# \vdots &\vdots \\
# w_{n1} &w_{n2}
# \end{bmatrix}
# $$
#
# The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
#
# $$
# y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
# $$
# +
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
# -
# > **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
# +
### Solution
h = activation(torch.mm(features, W1) + B1)
output = activation(torch.mm(h, W2) + B2)
print(output)
# -
# If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
#
# The number of hidden units a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
# ## Numpy to Torch and back
#
# Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
# The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
| intro-to-pytorch/Part 1 - Tensors in PyTorch (Solution).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from matplotlib import pyplot as plt
track = pd.read_csv(r'C:\Users\User\Downloads\20181120_track_features\track_features\tf_000000000001.csv')
session = pd.read_csv(r'E:\logdata\test_set\log_prehistory_20180715_000000000000.csv')
session.rename(columns = {'track_id_clean':'track_id'}, inplace = True)
track.head()
session.head()
track = track.drop_duplicates(keep='first')
session = session.drop_duplicates(keep='first')
track.describe
session.describe
track.columns
session.columns
session = session.dropna()
track = track.dropna()
track.shape
session.shape
track.info()
session.info()
most_heard_tracks = track.sort_values(by ='us_popularity_estimate', ascending=False)
most_heard_tracks['track_id']
tracks_per_session = session.groupby('session_id')['track_id'].count().reset_index(name="count")
tracks_per_session
tracks_per_session['count'].unique()
plt.hist(tracks_per_session['count'], bins = 10, facecolor='blue', alpha=0.5)
plt.xlabel("Count of tracks per session")
plt.ylabel("Number of sessions")
plt.title("Tracks vs Sessions")
plt.show()
plt.figure(figsize = (15, 7))
track.boxplot(column = ['acousticness', 'beat_strength', 'bounciness', 'danceability',
'energy', 'liveness', 'organism', 'speechiness'])
plt.show()
temp = session.drop_duplicates(subset = 'session_id', keep='first')
temp
track.corr()
session.corr()
df = track[['acousticness', 'beat_strength', 'bounciness', 'danceability',
'energy', 'liveness', 'organism', 'speechiness']]
sns.heatmap(df)
df = track[['beat_strength', 'bounciness', 'danceability',
'energy', 'organism']]
sns.heatmap(df)
df = track[['acoustic_vector_0','acoustic_vector_1','acoustic_vector_2','acoustic_vector_3',
'acoustic_vector_4','acoustic_vector_5','acoustic_vector_6', 'acoustic_vector_7']]
sns.heatmap(df)
df = track[['acoustic_vector_1','acoustic_vector_2','acoustic_vector_5', 'acoustic_vector_7']]
sns.heatmap(df)
sns.distplot(track['us_popularity_estimate'])
sns.distplot(track['acousticness'])
sns.distplot(track['beat_strength'])
sns.distplot(track['bounciness'])
sns.distplot(track['danceability'])
sns.distplot(track['energy'])
sns.distplot(track['organism'])
sns.distplot(track['speechiness'])
sns.distplot(track['liveness'])
df = np.where((session['not_skipped'] == 'False'),0,1)
sns.distplot(df)
| EDA_old_dataset.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={} tags=[]
# <img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# + [markdown] colab_type="text" id="NFm_zRA1PE2e" papermill={} tags=[]
# # WorldBank - GDP per country and evolution
# <a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/WorldBank/WorldBank_GDP_per_country_and_evolution.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
# + [markdown] papermill={} tags=[]
# **Tags:** #worldbank #opendata #snippet #plotly
# + [markdown] papermill={} tags=["naas"]
# **Author:** [<NAME>](https://www.linkedin.com/in/ACoAAAJHE7sB5OxuKHuzguZ9L6lfDHqw--cdnJg/)
# + [markdown] colab_type="text" id="eHA8sVa24OON" papermill={} tags=[]
# Objective : allows to visualize the distribution of GDP per capita and the GDP growth in the world. Click on the country on the map or select it to see the details info
#
# Data :
# GDP PER CAPITA (CURRENT US$)
# GDP GROWTH (ANNUAL %)
#
# by countries, agregated by region
#
# Sources:
#
# World Bank national accounts data,
# OECD National Accounts data files.
#
#
# Production : Team Denver 2020/04/20 (MyDigitalSchool)
# + [markdown] colab_type="text" id="7DurCJtH4YWL" papermill={} tags=[]
# **source des données:** data.worldbank.org
#
#
#
# + [markdown] colab_type="text" id="UDK3v1kJe3Ku" papermill={} tags=[]
# **Introduction**: https://drive.google.com/file/d/1kM7_P18bwEPrsZSk8YsvOdiuJyLN1_3H/view?usp=sharing
# + [markdown] papermill={} tags=[]
# ## Input
# + [markdown] colab_type="text" id="JDQhKKXgQ3z7" papermill={} tags=[]
# ### Get the data
#
# *Récupération des données sur le PIB par pays:*
# https://data.worldbank.org/indicator/NY.GDP.PCAP.CD
#
# *Récupération des données sur l'évolution du PIB par an par pays:*
# https://data.worldbank.org/indicator/NY.GDP.PCAP.KD.ZG
# + [markdown] colab_type="text" id="kISsuJL15JqX" papermill={} tags=[]
# ### Import libraries
# + colab={} colab_type="code" id="PxNbb9bE5Py_" papermill={} tags=[]
import pandas as pd
import numpy as np
import plotly.graph_objects as go
# + [markdown] papermill={} tags=[]
# ## Model
# + [markdown] colab_type="text" id="w4BwPJoDErL1" papermill={} tags=[]
# ### Data formatting
# + colab={"base_uri": "https://localhost:8080/", "height": 419} colab_type="code" id="0ksZHPdp6JgN" outputId="152bded3-95ee-4729-9c77-0fedbcc2a41a" papermill={} tags=[]
from pandas_datareader import wb
indicators = wb.download(indicator=['NY.GDP.PCAP.CD', 'NY.GDP.PCAP.KD.ZG'], country='all', start=2013, end=2018)
indicators = indicators.reset_index()
indicators = indicators[['country', 'year', 'NY.GDP.PCAP.CD', 'NY.GDP.PCAP.KD.ZG']]
indicators.columns = ['country', 'year', 'GDP_PER_CAPITAL', 'GDP_GROWTH_PER_CAPITAL']
indicators = indicators.fillna(0)
countries = wb.get_countries()
countries = countries[['name', 'region', 'iso3c']]
master_table = pd.merge(indicators, countries, left_on='country', right_on='name')
master_table = master_table[master_table['region'] != 'Aggregates']
master_table = master_table.drop(columns=['name'])
master_table = master_table.dropna()
# Création de l'ensemble final
xls_formatted = pd.DataFrame(columns=['COUNTRY', 'YEAR', 'GDP_PER_CAPITAL', 'GDP_GROWTH_PER_CAPITAL', 'REGION', 'ISO3C'])
for index, line in master_table.iterrows():
xls_formatted = xls_formatted.append(
{
'COUNTRY': line['country'],
'YEAR': line['year'],
'GDP_PER_CAPITAL': line['GDP_PER_CAPITAL'],
'GDP_GROWTH_PER_CAPITAL': line['GDP_GROWTH_PER_CAPITAL'],
'REGION': line['region'],
'ISO3C': line['iso3c'],
}, ignore_index=True
)
master_table = xls_formatted
master_table
# + [markdown] papermill={} tags=[]
# ## Output
# + [markdown] colab_type="text" id="YFRXBt3QRGyV" papermill={} tags=[]
# ### Display the plot with plotly
# + colab={"base_uri": "https://localhost:8080/", "height": 917} colab_type="code" id="iq6gJ2MwedAL" outputId="7633a002-78cf-465d-a859-617c4b1e5bf8" papermill={} tags=[]
# Variable à changer pour avoir les autres années
year = "2018"
master_year_table = master_table[master_table['YEAR'] == year]
GDP_GROWTH_PER_CAPITAL = "GDP GROWTH PER CAPITAL"
GDP_PER_CAPITAL = "GDP PER CAPITAL"
fig = go.Figure()
fig.add_trace(go.Choropleth(
locations=master_year_table['ISO3C'],
z = master_year_table['GDP_PER_CAPITAL'],
colorscale = [(0,"black"), (0.01,"red"),(0.1,"yellow"),(0.3,"green"),(1,"green")],
colorbar_title = "GDP PER CAPITAL",
customdata = master_year_table['COUNTRY'],
hovertemplate = '<b>%{customdata}: %{z:,.0f}</b><extra></extra>'
))
fig.add_trace(go.Choropleth(
locations=master_year_table['ISO3C'],
visible= False,
z = master_year_table['GDP_GROWTH_PER_CAPITAL'],
colorscale = [(0,"red"),(0.5,"red"),(0.75,"rgb(240,230,140)"), (1,"green")],
colorbar_title = "GDP GROWTH PER CAPITAL",
customdata = master_year_table['COUNTRY'],
hovertemplate = '<b>%{customdata}: %{z:0.2f}%</b><extra></extra>'
))
fig.update_layout(
autosize=False,
width= 1600,
height= 900,
title=f"GDP per capital in {year}",
title_x=0.5,
updatemenus=[
dict(
type = "buttons",
active=0,
buttons=list([
dict(
args=[{"visible": [True, False]}, {"title": f"{GDP_PER_CAPITAL} in {year}"}],
label=GDP_PER_CAPITAL,
method="update"
),
dict(
args=[{"visible": [False, True]}, {"title": f"{GDP_GROWTH_PER_CAPITAL} in {year}"}],
label=GDP_GROWTH_PER_CAPITAL,
method="update"
)
]),
showactive=True,
x=1,
xanchor="right",
y=1.1,
yanchor="top"
),
]
)
fig.show()
| WorldBank/WorldBank_GDP_per_country_and_evolution.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="jagco6YcuMT4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 462} outputId="e7d260cf-0325-4471-ac91-6121496bf5c7" executionInfo={"status": "ok", "timestamp": 1583361880310, "user_tz": -60, "elapsed": 9568, "user": {"displayName": "kom<NAME>", "photoUrl": "", "userId": "02416341188871661815"}}
# !pip install --upgrade tables
# !pip install eli5
# + id="OIQ8vfbYrXzc" colab_type="code" colab={}
import pandas as pd
import numpy as np
from sklearn.dummy import DummyRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error as mae
from sklearn.model_selection import cross_val_score
import eli5
from eli5.sklearn import PermutationImportance
# + id="e0PWJYY0ujSD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="9cb3071b-c0ef-4c91-8b76-40aaef9e5995" executionInfo={"status": "ok", "timestamp": 1583361982983, "user_tz": -60, "elapsed": 420, "user": {"displayName": "kom<NAME>", "photoUrl": "", "userId": "02416341188871661815"}}
# cd "/content/drive/My Drive/Colab Notebooks/dw_matrix/matrix_two"
# + [markdown] id="XeDCZDNLuePI" colab_type="text"
# #Wczytywanie danych
# + id="I5sSbUJztvrs" colab_type="code" colab={}
df = pd.read_hdf('data/car.h5')
# + id="wcPXRenMutUY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 187} outputId="d6e6d326-4c2d-48ed-9ae2-cf9a8da850c3" executionInfo={"status": "ok", "timestamp": 1583362033248, "user_tz": -60, "elapsed": 485, "user": {"displayName": "kombinator kombinator", "photoUrl": "", "userId": "02416341188871661815"}}
df.columns
# + id="C3SjUdAxu0QX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="a34dd9cf-eaaa-48f5-9b01-bb629db5dd59" executionInfo={"status": "ok", "timestamp": 1583362244618, "user_tz": -60, "elapsed": 508, "user": {"displayName": "kombinator kombinator", "photoUrl": "", "userId": "02416341188871661815"}}
df.select_dtypes(np.number).columns
# + id="eJjhMB-yvn2f" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="0f6a4015-82eb-40c1-8f9a-bc1716e8f98e" executionInfo={"status": "ok", "timestamp": 1583362360333, "user_tz": -60, "elapsed": 497, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "02416341188871661815"}}
feats = ['car_id']
X = df[feats].values
y = df['price_value'].values
model = DummyRegressor()
model.fit(X,y)
y_pred = model.predict(X)
mae(y,y_pred)
# + id="JURcaGlAwEGO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="3cf24a09-a1fb-4e20-d7a7-8f7ba94bfe7f" executionInfo={"status": "ok", "timestamp": 1583362432753, "user_tz": -60, "elapsed": 459, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "02416341188871661815"}}
[x for x in df.columns if 'price' in x]
# + id="gskpqBjDwVyw" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="3e147961-0328-495f-81c7-168d8868fe12" executionInfo={"status": "ok", "timestamp": 1583362570117, "user_tz": -60, "elapsed": 607, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "02416341188871661815"}}
df['price_currency'].value_counts(normalize=True)
# + id="64JVbkRFwbgI" colab_type="code" colab={}
df = df[df ['price_currency'] != 'EUR']
# + [markdown] id="3D-6gitD6TWo" colab_type="text"
# # Features
# + id="7SEbk5z4w2qe" colab_type="code" colab={}
SUFFIX_CAT = '__cat'
for feat in df.columns:
if isinstance(df[feat][0],list): continue
factorized_values = df[feat].factorize()[0]
if SUFFIX_CAT is feat :
df[feat] = factorized_values
else:
df[feat + SUFFIX_CAT] = factorized_values
# + id="n9kyOHLH7yj2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="88882caf-812b-47d0-ac42-5f330b6231c7" executionInfo={"status": "ok", "timestamp": 1583365539408, "user_tz": -60, "elapsed": 431, "user": {"displayName": "kombinator kombinator", "photoUrl": "", "userId": "02416341188871661815"}}
cat_feats = [x for x in df.columns if SUFFIX_CAT in x]
cat_feats = [x for x in cat_feats if 'price' not in x]
len(cat_feats)
# + id="QsfOWB1T8MQ5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="05c6f168-17e6-486b-f08c-608349f7a605" executionInfo={"status": "ok", "timestamp": 1583365657908, "user_tz": -60, "elapsed": 4248, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "02416341188871661815"}}
X = df[cat_feats].values
y = df['price_value'].values
model = DecisionTreeRegressor(max_depth=5)
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
np.mean(scores)
# + id="sNEh8y5x8oQH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 391} outputId="148e5472-84ff-444b-eba9-4780599e9626" executionInfo={"status": "ok", "timestamp": 1583365898221, "user_tz": -60, "elapsed": 43538, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "02416341188871661815"}}
m = DecisionTreeRegressor(max_depth=5)
m.fit(X,y)
imp = PermutationImportance(m).fit(X,y)
eli5.show_weights(imp,feature_names=cat_feats)
# + id="NK43pw2E9GQa" colab_type="code" colab={}
# + id="mfDRDAJm-7j5" colab_type="code" colab={}
| matrix_two/day3_feature_engenering.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import glob
import os
import keras
#save the models to model_folder
model_folder=''
#output folder of trajactory got from the simulation
output_folder='
#create energy_folder to save the prediction results
energy_folder=''
# # Select scenario for weather condition
#weather option: rainy, sunny, windy, and snowy
weather = 'sunny'
# # Load microscopic energy eatimation model for different vehicle classes
#
model_diesel = keras.models.load_model(f'{model_folder}/diesel.model')
model_hybrid = keras.models.load_model(f'{model_folder}/hybrid.model')
model_electric = keras.models.load_model(f'{model_folder}/electric.model')
# # Predict energy consumption of each trip
# +
path = f'{output_folder}'
all_files = glob.glob(os.path.join(path, "Trajectory*.csv"))
colnames=['time_ms','speed','acceleration','vehicle_ref','actorConfig_id','actorConfig_emissionClass','actorConfig_fuel','actorConfig_ref','actorConfig_vehicleClass']
for f in all_files:
trip=pd.read_csv(f,names=colnames, header=None)
#trip=pd.read_csv(f)
trip = trip[trip.speed != 'speed']
trip = trip[trip.acceleration != 'acceleration']
trip['speed']=trip['speed'].astype(float)*0.036 #km/h
#find the vehicle class of this trip based on the column "actorConfig_ref"
vtype = ['Gillig_LF_2014','Gillig_HF_2006','Gillig_HF_2002','Gillig_HF_1998','Gillig_Hybrids_2014',
'Gillig_Hybrids_2009','Gillig_LF_2009','BYD_BEV']
diesel = ['Gillig_LF_2014','Gillig_HF_2006','Gillig_HF_2002','Gillig_HF_1998','Gillig_LF_2009']
hybrid = ['Gillig_Hybrids_2014', 'Gillig_Hybrids_2009']
electric = ['BYD_BEV']
if trip['actorConfig_fuel'].iloc[2] in diesel:
Vclass = 'diesel'
elif trip['actorConfig_fuel'].iloc[2] in hybrid:
Vclass = 'hybrid'
elif trip['actorConfig_fuel'].iloc[2] in electric:
Vclass = 'electric'
if Vclass == 'electric':
trip['acceleration']=trip['acceleration'].astype(float)*0.001*3.28084
#ft/s2
else:
trip['acceleration']=trip['acceleration'].astype(float)*0.001
#m/s2
if weather == 'rainy':
trip['temperature']= 60
trip['humidity']= 0.9 #range[0,1]
if weather == 'sunny':
trip['temperature']= 70
trip['humidity']= 0.5
if weather == 'windy':
trip['temperature']= 60
trip['humidity']= 0.6
if weather == 'snowy':
trip['temperature']= 30
trip['humidity']= 0.4
trip['roadGrade']= 0
input2esti=trip[['speed','acceleration','temperature','humidity','roadGrade']]
#prdiction
if Vclass == 'electric':
pre = model_electric.predict(input2esti)
tripf=pd.concat([trip,pd.DataFrame(pre,columns=['energyrate_'+Vclass])], axis=1)
tripf['energy_gal'] = tripf['energyrate_'+Vclass]/33.7 #gal
path_new = os.path.join(energy_folder, Vclass)
try:
os.mkdir(path_new)
except:
pass
with open(f'{path_new}'+ f[len(output_folder):] + '.csv', 'w', newline='') as oFile:
tripf.to_csv(oFile, index = False)
elif Vclass == 'hybrid':
pre = model_hybrid.predict(input2esti)
pre[pre<0]=0
tripf=pd.concat([trip,pd.DataFrame(pre,columns=['energyrate_'+Vclass])], axis=1)
tripf['energy_gal'] = tripf['energyrate_'+Vclass]/3600 #gal
path_new = os.path.join(energy_folder, Vclass)
try:
os.mkdir(path_new)
except:
pass
with open(f'{path_new}' + f[len(output_folder):] + '.csv', 'w', newline='') as oFile:
tripf.to_csv(oFile, index = False)
elif Vclass == 'diesel':
pre = model_diesel.predict(input2esti)
pre[pre<0]=0
tripf=pd.concat([trip,pd.DataFrame(pre,columns=['energyrate_'+Vclass])], axis=1)
tripf['energy_gal'] = tripf['energyrate_'+Vclass]/3600 #gal
path_new = os.path.join(energy_folder, Vclass)
try:
os.mkdir(path_new)
except:
pass
#write the predicted results
with open(f'{path_new}' + f[len(output_folder):] + '.csv', 'w', newline='') as oFile:
tripf.to_csv(oFile, index = False)
# -
# # Estimate energy consumption of each route
Route = ['Route1','Route2A','Route3','Route4','Route7','Route8','Route9','Route10C','Route10A','Route10G','Route16','Route21','Route33','Route34','Route13','Route15_A','Route21_A','Route28','RouteDTS']
path = f'{energy_folder}'
route_summary = pd.DataFrame()
b=0
for r in Route:
allfiles = glob.glob(os.path.join(path, "*"+r+"*.csv"))
if len(allfiles) > 0:
colnames=['time_ms','speed','acceleration','vehicle_ref','actorConfig_id','actorConfig_emissionClass','actorConfig_fuel','actorConfig_ref','actorConfig_vehicleClass','temperature','humidity','roadGrade','energyrate','energy_gal']
route_energy = pd.DataFrame()
c=0
for f in allfiles:
df=pd.read_csv(f,names=colnames, header=None)
df['speed']=pd.to_numeric(df['speed'],errors='coerce')
df['energy_gal']=pd.to_numeric(df['energy_gal'],errors='coerce')
df['speed_mile_s']=df['speed']*0.000172603 #mile/s
energy=df['speed_mile_s'].sum()/df['energy_gal'].sum() #mi/gal
sum_gal = df['energy_gal'].sum()
route_energy.loc[c,'energy_mpg']=energy
route_energy.loc[c,'sum_energy_gal']=sum_gal
with open(f'{energy_folder}'+'_'+ r + 'energy.csv', 'w', newline='') as wFile:
route_energy.to_csv(wFile, index = False)
c+=1
route_energy['trip_id']=[f[-21:-8] for f in allfiles]
route_summary.loc[b,'sum_energy_gal']=route_energy['sum_energy_gal'].sum()
route_summary.loc[b,'route']=r
b+=1
print(route_summary)
| energy_estimation/Energy_estimation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## [教學重點]
# 學習使用 sklearn 中的 linear regression 模型,並理解各項參數的意義
# ## [範例重點]
# 觀察丟進模型訓練的資料格式,輸入 linear regression 與 Logistic regression 的資料有甚麼不同?
# ## import 需要的套件
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, linear_model
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score, accuracy_score
# ### Linear regssion
# +
# 讀取糖尿病資料集
diabetes = datasets.load_diabetes()
# 為方便視覺化,我們只使用資料集中的 1 個 feature (column)
X = diabetes.data[:, np.newaxis, 2]
print("Data shape: ", X.shape) # 可以看見有 442 筆資料與我們取出的其中一個 feature
# 切分訓練集/測試集
x_train, x_test, y_train, y_test = train_test_split(X, diabetes.target, test_size=0.1, random_state=4)
# 建立一個線性回歸模型
regr = linear_model.LinearRegression()
# 將訓練資料丟進去模型訓練
regr.fit(x_train, y_train)
# 將測試資料丟進模型得到預測結果
y_pred = regr.predict(x_test)
# +
# 可以看回歸模型的參數值
print('Coefficients: ', regr.coef_)
# 預測值與實際值的差距,使用 MSE
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
# -
# 畫出回歸模型與實際資料的分佈
plt.scatter(x_test, y_test, color='black')
plt.plot(x_test, y_pred, color='blue', linewidth=3)
plt.show()
# ### Logistics regression
# +
# 讀取鳶尾花資料集
iris = datasets.load_iris()
# 切分訓練集/測試集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.1, random_state=4)
# 建立模型
logreg = linear_model.LogisticRegression()
# 訓練模型
logreg.fit(x_train, y_train)
# 預測測試集
y_pred = logreg.predict(x_test)
# -
acc = accuracy_score(y_test, y_pred)
print("Accuracy: ", acc)
# ## [作業重點]
# 了解其他資料集的使用方法,如何將資料正確地送進模型訓練
# ## 練習時間
# 試著使用 sklearn datasets 的其他資料集 (wine, boston, ...),來訓練自己的線性迴歸模型。
wine = datasets.load_wine()
boston = datasets.load_boston()
breast_cancer = datasets.load_breast_cancer()
# ### HINT: 注意 label 的型態,確定資料集的目標是分類還是回歸,在使用正確的模型訓練!
| homeworks/D038/Day_038_regression_model.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# 10727109 林亞岑
fileTitleNum = ""
# +
class SchoolType():
def __init__(self):
self.record = "" # 一整行資料
self.name = "" # 學校名稱
self.numOfGra = 0 # 畢業人數
class BinaryTree():
def __init__(self):
self.school = SchoolType()
self.right = None # 較大(含)
self.left = None # 較小
# +
class SchoolList() :
# constructor
def __init__( self ):
self.sList = []
self.fileID = ""
self.rootGra = None # 根(頭) 數字排序的
self.rootName = None # 根(頭) 名稱排序的
# 計算樹高
def __Heights( self , root ):
if ( root == None ):
return 0
else :
left = self.__Heights( root.left )
right = self.__Heights( root.right )
if ( right >= left ):
return right + 1
else :
return left + 1
# 放置一個物件至以畢業人數為基準的二元樹
def PutByGra( self, root, aSchool ):
# 沒東西 就新增一個
if ( root == None ):
root = BinaryTree()
root.school = aSchool
root.right = None
root.left = None
# 要放進來的 大於或等於 樹的頭-> 放右邊
elif ( aSchool.numOfGra >= root.school.numOfGra ):
root.right = self.PutByGra( root.right, aSchool )
# 要放進來的 小於 樹的頭- -> 放左邊
else :
root.left = self.PutByGra( root.left, aSchool )
return root
# 放置一個物件至以畢業人數為基準的二元樹
def PutByName( self, root, aSchool ):
# 沒東西 就新增一個
if ( root == None ):
root = BinaryTree()
root.school = aSchool
root.right = None
root.left = None
# 要放進來的 大於或等於 樹的頭-> 放右邊
elif ( aSchool.name >= root.school.name ):
root.right = self.PutByName( root.right, aSchool )
# 要放進來的 小於 樹的頭- -> 放左邊
else :
root.left = self.PutByName( root.left, aSchool )
return root
# 依畢業人數做基準的二元樹
def BuildByGra( self ):
# 先設定好root
self.rootGra = None
# 把每個school放進樹裡
for i in range( 0, len(self.sList) ):
self.rootGra = self.PutByGra( self.rootGra, self.sList[i] )
print( "{Number of graduates} = ", self.__Heights( self.rootGra ) )
# 依學校名稱做基準的二元樹
def BuildByName( self ):
# 先設定好root
self.rootName = None
# 把每個school放進樹裡
for i in range( 0, len(self.sList) ):
self.rootName = self.PutByName( self.rootName, self.sList[i] )
print( "{School name} = ", self.__Heights( self.rootName ) )
# 印出所有學校資訊(7項而已)
def Show( self ):
print( "\t學校名稱\t科系名稱\t日間/進修別\t等級別\t學生數\t教師數\t上學年度畢業生數" )
for i in range ( 0, len( self.sList ) ):
print( "[", i+1, "]\t" + self.sList[i].record )
# 讀取檔案資料
def ReadFile( self, fileName ):
self.sList.clear()
try: # { try
file = open( fileName, 'r' )
# 先把前三行讀掉
for i in range (0, 3) :
aLine = file.readline()
for aLine in file : # { 如果檔案還沒讀完 讀一行(含換行)
aSchool = SchoolType()
numOfTab = 0
# 此句從頭到尾檢查
for i in range( 0, len(aLine) ): # {
# 讀record 只需讀 2 4 5 6 7 8 9 項
if ( numOfTab >= 1 and numOfTab <= 8 and numOfTab != 2 and aLine[i] != '\n' ):
aSchool.record = aSchool.record + aLine[i]
if ( aLine[i] == '\t' ): # 計算Tab數量
numOfTab = numOfTab + 1
elif ( numOfTab == 1 ): # 把第2項(學校名稱)存下來
aSchool.name = aSchool.name + aLine[i]
elif ( numOfTab == 8 ): # 把第9項(畢業人數)存下來
aSchool.numOfGra = aSchool.numOfGra * 10 + ( int(aLine[i]) - int('0') )
# } for 此句從頭到尾檢查
if ( aSchool.record != "" ): # 有資料
self.sList.append( aSchool ) # 將此筆資料存進sList
# } 讀檔案
file.close()
return True
# } try
except:
return False
# -
# 指令說明文字
def Tip():
print("\n*** University Graduate Information System ***")
print("* 0. Quit *")
print("* 1. Create Two Binary Search Trees *")
print("**********************************************")
# Main
Tip()
command = str( input("Input a command(0, 1):") )
while command != "0" :
if command == "1" :
fileName = ""
fileTitleNum = str( input( "\n輸入檔案名稱:\n601, 602,.....\n>" ) )
fileName = "input" + fileTitleNum + ".txt"
sList = SchoolList()
readSuccess = sList.ReadFile( fileName ) # 取得檔案資訊
if readSuccess == False :
print( "### " + fileName + " does not exist! ###" )
else:
sList.Show() # 列出所有檔案內容到螢幕
print( "\nTree heights:\n" )
sList.BuildByGra()
sList.BuildByName()
else :
print( "Command does not exist!" ) # 非正常指令
Tip()
command = str( input("Input a command(0, 1):") )
| ex06/10727109/DS1ex#6_10727109.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Learning Objectives
#
# 1. Plotting a dataframe
# 2. Kind of plot
# 3. Default is line plot
# 4. Plotting random data from a dataframe
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
plt.rcParams["figure.figsize"] = (12,8)
# -
# ## Plotting random data from a dataframe
# +
df = pd.DataFrame(np.random.randn(100,3).cumsum(axis=0),
columns=["X1", "X2", "X3"],
index = np.arange(100))
df
# -
df.plot(use_index=False)
# ## Kind of plots
series = pd.Series(np.random.randn(100).cumsum())
series
series.plot(kind='hist')
series.plot.line()
| module_5_visualization/line_plots.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !pip install tensorflow
# !pip install tensorflow-hub
# !pip install tensorflow-text
# !pip install youtube-dl
# !pip install datetime
# +
import tensorflow as tf
import tensorflow_hub as hub
import tensorflow_text as text
import os
from datetime import timedelta, datetime, date, time
import youtube_dl
import requests
import re
import uuid
from youtube_transcript_api import YouTubeTranscriptApi
import json
# -
model_path = r''+os.getcwd()+'\\jerma_model\\'
model = tf.keras.models.load_model(model_path)
# Testing
model.summary()
cand = {"[Laughter]":"","[Music]":"","[Applause]":""}
mid_bit = "="
drift = 0.0
def createTimestampFile(youtubeID):
global mid_bit
name = "timestamp" + mid_bit
index = 1
url = "https://www.youtube.com/watch?v={}".format(youtubeID)
change = mid_bit+ str(uuid.uuid4().hex)
ydl = youtube_dl.YoutubeDL({'writesubtitles': True, 'allsubtitles': True, 'writeautomaticsub': True})
res = ydl.extract_info(url, download=False)
if not os.path.exists(os.getcwd() + "\\temp\\" + name + res.get("id", None) + ".txt"):
change = ""
if res['requested_subtitles'] and res['requested_subtitles']['en']:
print('Grabbing vtt file from ' + res['requested_subtitles']['en']['url'])
response = requests.get(res['requested_subtitles']['en']['url'], stream=True)
'''
Regex:
\d = digit
{} = {# of digits}
\W = any word character
\s = white spaces
'''
timeStampRegex = re.compile(r'\d{2}\W\d{2}\W\d{2}\W\d{3}\s\W{3}\s\d{2}\W\d{2}\W\d{2}\W\d{3}')
print(response.text)
new = timeStampRegex.findall(response.text)
# f1 = open(name + res.get("id", None) + change + ".txt", "a+")
# f1.write("{")
# f1.close()
if new is None:
print("Found instance of none")
else:
for i in new:
i = re.sub(" --> ","\",\"end\":\"",i)
# line = '\"'+str(index)+"\":"+"{\"start\":" + str(i)+"},\n"
line = "{\"start\":\"" + str(i)+"\"}\n"
# print(line)
f1 = open(os.getcwd() + "\\temp\\" + name + res.get("id", None) + change + ".txt", "a+")
f1.write(line)
f1.close()
index += 1
# f1 = open(name + res.get("id", None) + change + ".txt", "a+")
# f1.write("}")
# f1.close()
if len(res['subtitles']) > 0:
print('manual captions')
else:
print('automatic_captions')
return name + res.get("id", None) + change + ".txt"
else:
print('Youtube Video does not have any english captions')
return None
def createTranscriptFile(video_id):
global mid_bit
global cand
name = "trans" + mid_bit
change = mid_bit+ str(uuid.uuid4().hex)
if not os.path.exists(os.getcwd() + "\\temp\\" + name + video_id + ".txt"):
change = ""
file_name = name + video_id + change
transcript_list = YouTubeTranscriptApi.list_transcripts(video_id)
try:
transcript = transcript_list.find_manually_created_transcript(['en'])
except Exception:
transcript = transcript_list.find_generated_transcript(['en'])
tran = transcript.fetch()
with open(os.getcwd() + "\\temp\\" +'{}.txt'.format(file_name),'w+') as file:
for line in tran:
newLine = line.get("text")
i = "" if not [k for k,v in cand.items() if line.get("text") == k] else [k for k,v in cand.items() if line.get("text") == k][0]
newLine = line.get("text").replace(i,"")
newLine = newLine.replace("\n","")
print(newLine)
if newLine.strip():
file.write(newLine+"\n")
return file_name + ".txt"
def createCommandFile(timestamp_file_name,trans_file_name):
global mid_bit
global drift
video_id = timestamp_file_name.split(mid_bit)[1]
name = "command"+ mid_bit
change = mid_bit+ str(uuid.uuid4().hex)
if not os.path.exists(os.getcwd() + "\\temp\\" + name + video_id + ".txt"):
change = ""
file_name = name + video_id + change
with open(os.getcwd() + "\\temp\\" +timestamp_file_name,"r") as timestamp_file:
timestamp_allLines = timestamp_file.readlines()
with open(os.getcwd() + "\\temp\\" +trans_file_name,"r") as trans_file:
trans_allLines = trans_file.readlines()
timestamp_max_line = len(timestamp_allLines)
trans_max_line = len(trans_allLines)
print(timestamp_max_line)
print(trans_max_line )
for line in range(trans_max_line):
print(timestamp_allLines[line])
time_dic = json.loads(timestamp_allLines[line])
if(not trans_allLines[line].strip()):
continue
text = trans_allLines[line]
predict = model.predict([text])
print(predict)
if predict > 0.2 + drift:
with open(os.getcwd() + "\\temp\\" +'{}.txt'.format(file_name),'a+') as command_file:
command_file.write(get_command(youtubeID,time_dic["start"],time_dic["end"],str(line)+ ".mp4"))
return file_name + ".txt"
def get_command(url,start,end,output_dir):
# format of start and end
## e.g
# format needed
## 00:13:00.00
# format style: url duration start
duration = datetime.combine(date.min, time.fromisoformat(end)) - datetime.combine(date.min, time.fromisoformat(start))
return "ffmpeg $(youtube-dl -g '{}' | sed 's/^/-ss {} -i /') -t {} -c copy {}\n".format(
url,duration,start,output_dir
)
if __name__ == '__main__':
youtubeID = "DDg9TGHoPUU"
timestamp_file_name = createTimestampFile(youtubeID)
trans_file_name = createTranscriptFile(youtubeID)
command_file_name = createCommandFile(timestamp_file_name,trans_file_name)
| .ipynb_checkpoints/JermaHighlightVideoMaker-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 加载预训练的 Inception V3 模型
from keras.applications import inception_v3
from keras import backend as K
K.set_learning_phase(0)
model = inception_v3.InceptionV3(weights='imagenet',
include_top=False)
# 设置 DeepDream 配置
layer_contributions = {
'mixed2': 0.2,
'mixed3': 3.,
'mixed4': 2.,
'mixed5': 1.5,
}
# 定义需要最大化的损失
layer_dict = dict([(layer.name, layer) for layer in model.layers])
loss = K.variable(0.)
for layer_name in layer_contributions:
coeff = layer_contributions[layer_name]
activation = layer_dict[layer_name].output
scaling = K.prod(K.cast(K.shape(activation), 'float32'))
loss += coeff * K.sum(K.square(activation[:, 2: -2, 2: -2, :])) / scaling
# +
# 梯度上升过程
dream = model.input
grads = K.gradients(loss, dream)[0]
grads /= K.maximum(K.mean(K.abs(grads)), 1e-7)
outputs = [loss, grads]
fetch_loss_and_grads = K.function([dream], outputs)
def eval_loss_and_grads(x):
outs = fetch_loss_and_grads([x])
loss_value = outs[0]
grad_values = outs[1]
return loss_value, grad_values
def gradient_ascent(x, iterations, step, max_loss=None):
for i in range(iterations):
loss_value, grad_values = eval_loss_and_grads(x)
if max_loss is not None and loss_value > max_loss:
break
print('...Loss value at', i, ':', loss_value)
x += step * grad_values
return x
# +
# 辅助函数
import scipy
from keras.preprocessing import image
def resize_img(img, size):
img = np.copy(img)
factors = (1,
float(size[0]) / img.shape[1],
float(size[1]) / img.shape[2],
1)
return scipy.ndimage.zoom(img, factors, order=1)
def save_img(img, fname):
pil_img = deprocess_image(np.copy(img))
scipy.misc.imsave(fname, pil_img)
def preprocess_image(image_path):
img = image.load_img(image_path)
img = image.img_to_array(img)
img = np.expand_dims(img, axis=0)
img = inception_v3.preprocess_input(img)
return img
def deprocess_image(x):
if K.image_data_format() == 'channels_first':
x = x.reshape((3, x.shape[2], x.shape[3]))
x = x.transpose((1, 2, 0))
else:
x = x.reshape((x.shape[1], x.shape[2], 3))
x /= 2.
x += 0.5
x *= 255.
x = np.clip(x, 0, 255).astype('uint8')
return x
# +
# 在多个连续尺度上运行梯度上升
import numpy as np
step = 0.01
num_octave = 3
octave_scale = 1.4
iterations = 20
max_loss = 10.
base_image_path = '/home/fc/Downloads/fengjing.jpg'
img = preprocess_image(base_image_path)
original_shape = img.shape[1:3]
successive_shapes = [original_shape]
for i in range(1, num_octave):
shape = tuple([int(dim / (octave_scale ** i))
for dim in original_shape])
successive_shapes.append(shape)
successive_shapes = successive_shapes[::-1]
original_img = np.copy(img)
shrunk_original_img = resize_img(img, successive_shapes[0])
for shape in successive_shapes:
print('Processing image shape', shape)
img = resize_img(img, shape)
img = gradient_ascent(img,
iterations=iterations,
step=step,
max_loss=max_loss)
upscaled_shrunk_original_img = resize_img(shrunk_original_img, shape)
same_size_original = resize_img(original_img, shape)
lost_detail = same_size_original - upscaled_shrunk_original_img
img += lost_detail
shrunk_original_img = resize_img(original_img, shape)
save_img(img, fname='dream_at_scale_' + str(shape) + '.png')
save_img(img, fname='final_dream.png')
# -
| 8.2 使用keras实现DeepDream.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
# %run analysis.py
RESULTS_PATH = '../ops/results'
SERVERS = ['node%d' % i for i in range(90, 93)]
CLIENTS = ['node%d' % i for i in range(41, 45) if i != 43]
single_experiment_overview(RESULTS_PATH, SERVERS, CLIENTS)
# -
| analysis/Experiment Analysis.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Welter issue #1
# ## Telluric Absorption Lines and Spectral Shape
# ### Part 1- Spectral response functions overview
#
# <NAME>
# Thursday, November 26, 2015
#
#
# In the [previous notebook](welter_issue002-Spot_Check_the_Pipeline_Spectra_01.ipynb), we spot-checked the $H-$band data. It looked OK, so we can proceed with our analysis of the telluric absorption lines.
#
# In this notebook, we will characterize the spectral response.
import warnings
warnings.filterwarnings("ignore")
import numpy as np
from astropy.io import fits
import matplotlib.pyplot as plt
% matplotlib inline
% config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set_context('notebook')
# ## Read in all the data.
# No spot-checking necessary, since we already did that in the previous notebook.
hdu_raw = fits.open('../data/raw/LkCa4_gully/outdata/20151117/SDCH_20151117_0199.spec.fits')
hdu_f = fits.open('../data/raw/LkCa4_gully/outdata/20151117/SDCH_20151117_0199.spec_flattened.fits')
hdu_var = fits.open('../data/raw/LkCa4_gully/outdata/20151117/SDCH_20151117_0199.variance.fits')
hdu_tar = fits.open('../data/raw/LkCa4_gully/outdata/20151117/SDCH_20151117_0205.spec.fits')
hdr = hdu_tar[0].header
# ## The problem: What is the "spectral response function"?
#
# What we *want* is the **stellar spectrum**: $f_{\star}$.
# What we *get* is the **raw observed spectrum**: $f_{raw}$.
#
# We have to convert between $f_{raw}$ and $f_{\star}$.
#
o=10
plt.plot(hdu_tar[1].data[o, :], hdu_tar[0].data[o, :], label='LkCa4')
plt.plot(hdu_raw[1].data[o, :], hdu_raw[0].data[o, :]/2.0+5000.0, label='A0V + const.')
plt.legend(loc='best')
plt.ylim(ymin=0)
plt.xlabel("$\lambda$ ($\mu$m)")
plt.ylabel("Raw signal (ADU)");
plt.title('{OBJECT} raw spectrum'.format(OBJECT=hdr['OBJECT']));
# **Figure 1**: The spectral response of IGRINS includes both instrumental and telluric effects.
# ## Estimating the spectral response
# The net spectral response is composed of many terms. The main features can be broken up into the immersion grating blaze function, $t_{IG}$, which depends on wavelength and spectral order $m$. The telluric transmission, $t_{\oplus}$, is mostly in fine-grained lines.
#
# $$f_{raw} = f_{\star} \cdot t_{net} \\
# t_{net} = t_{inst} \cdot t_{\oplus} \\
# t_{inst} = t_{IG}(m) \cdot t_{VPH} \cdot t_{dichroic} \cdot t_{HJST} \cdot t_{optics} $$
#
# Where:
# $t_{net}$ is the **net spectral response** including all known calibration effects.
# $t_{inst}$ is the component of the spectral response attributable to the **instrument and telescope**.
# $t_{\oplus}$ is the component of the spectral response attributable to **Earth's atmospheric absorption** (i.e. *telluric* absorption).
# $t_{IG}$ is the component of the spectral response attributable to the **silicon immersion grating**.
# $t_{VPH}$ is the component of the spectral response attributable to the **volume phase holographic grating**.
# $t_{dichroic}$ is the component of the spectral response attributable to the **dichroic**.
# $t_{HJST}$ is the component of the spectral response attributable to the **<NAME>. Smith Telescope**.
# $t_{optics}$ is a catch-all for everything else in IGRINS, including camera, mirrors, detector, etc.
# and
# $f_{raw}$ is the **observed raw flux**, measured in analog-to-digital units (ADUs).
# $f_{\star}$ is the **absolute stellar flux** above the Earth's atmosphere.
# ### Ideal scenario, or *The Right Thing to Do ™*
#
# #### 1. Determine the instrumental response and chatacterize how it varies in time.
# We would use high precision lab data of each component to estimate each component's contribution, and multiply them together to get a lab-based predicted $\hat t_{inst, lab}$. We would then compare $\hat t_{net, lab}$ to on-sky measurements $\hat t_{inst, sky}$, and then refine and adopt a fixed $\hat t_{inst}$. Lastly, we would monitor whether $\hat t_{inst}$ changes based on temperature, time, observing run, etc., and then refine our model for $\hat t_{inst}(t)$.
#
# #### 2. Determine the telluric response and characterize how it varies with atmospheric properties.
# We would make many observations of the sky in different atmospheric conditions and airmasses. We would fit atmospheric models to these spectra to see how well the models perform. We could build semi-empirical models, and use near-contemporaneous observations of relatively-featureless A0V spectra to determine a $\hat t_{\oplus}$ for the moment of the target star observations.
# ### Pragmatic scenario, or *What We Actually Do ™*
# We estimate a spectral shape from a single, near-contemporaneous, A0V star spectrum and apply it to the target star spectrum. The noise $\epsilon$ from the standard star observation is included in the estimated response function.
#
# $$\hat t_{inst} = \mathcal{F}_{LPF} \left[ \frac{f_{std, raw}+ \epsilon}{f_{std \star}} \right]$$
#
# $$\hat t_{\oplus} = \frac{f_{std, raw}+ \epsilon}{\hat t_{inst}}$$
#
# Where:
# $f_{std, raw}$ is the observed A0V star spectrum.
# $f_{std \star}$ is a nearly-perfect **model of the standard star** (*e.g* Vega).
# $\mathcal{F}_{LPF}$ is a **low-pass-filter** algorithm, that pools information from specral flat fields.
# and
# $\hat t_{inst}$ is the estimator for the instrumental response function.
# $\hat t_{\oplus}$ is the estimator for the telluric response function.
#
# The IGRINS pipeline package provides $\hat t_{net}$ broken into a low-pass and high-pass components to approximate $\hat t_{inst}$ and $\hat t_{\oplus}$, respectively.
# ### Let's look at the two components:
# +
fig = plt.figure(figsize=(10, 5))
#Plot 1: $t_{inst}$
ax = fig.add_subplot(121)
t_inst = hdu_raw[0].data[o, :] / hdu_f[0].data[o, :]
ax.plot(hdu_raw[1].data[o, :], t_inst)
ax.set_xlabel('$\lambda$ ($\mu$m)'); ax.set_ylabel('$t$'); ax.set_title('$\hat t_{inst}$')
#Plot 2: $t_{\oplus}$
ax = fig.add_subplot(122)
t_oplus = hdu_f[0].data[o, :]
ax.plot(hdu_raw[1].data[o, :], t_oplus)
ax.set_xlabel('$\lambda$ ($\mu$m)'); ax.set_ylabel('$t$'); ax.set_title('$\hat t_{\oplus}$');
# -
# **Figure 2:** *Left-* $\hat t_{inst}$ is probably a **biased** estimator, as <NAME> described at the IGRINS workshop.
# *Right-* It is clear that $\hat t_{\oplus}$ is a *noisy* estimator, i.e. it has high **variance**.
# ## Can we include the variance data to reduce the noise at the edges of orders?
# +
fig = plt.figure(figsize=(10, 5))
#Plot 1: $t_{inst}$
ax = fig.add_subplot(121)
t_oplus = hdu_f[0].data[o, :]
ax.plot(hdu_raw[1].data[o, :], t_oplus)
ax.set_xlabel('$\lambda$ ($\mu$m)'); ax.set_ylabel('$t$'); ax.set_title('$\hat t_{\oplus}$');
#Plot 2: $t_{\oplus}$
ax = fig.add_subplot(122)
t_oplus = hdu_f[0].data[o, :]
sig = np.sqrt(hdu_var[0].data[o, :]) / t_inst
#ax.plot(hdu_raw[1].data[o, :], t_oplus)
ax.fill_between(hdu_raw[1].data[o, :], t_oplus - 1.96 * sig, t_oplus + 1.96 * sig,
alpha=0.2, color='r', label='95% confidence interval')
ax.set_ylim(0.6, 1.3)
ax.set_xlabel('$\lambda$ ($\mu$m)'); ax.set_ylabel('$t$'); ax.set_title('$\hat t_{\oplus}$ 95% CI');
# -
# ## Let's clean the data.
# Plot the flattened target spectrum:
# ### $\frac{f_{raw}}{\hat t_{inst}}$
dx0, dx1 = 1500, 1900 #Pick the middle 1000 pixels
sub_sample_y = hdu_f[0].data[o, dx0:dx1]
sub_sample_x = hdu_raw[1].data[o, dx0:dx1]
# +
o=10
plt.figure(figsize=(15, 5))
plt.subplot(131)
tar_f = hdu_tar[0].data[o, :] / t_inst
plt.plot(hdu_tar[1].data[o, :], tar_f, label='LkCa4 flattened')
plt.plot(hdu_raw[1].data[o, :], hdu_f[0].data[o, :], label='A0V flattened')
plt.plot(sub_sample_x, sub_sample_y, label='sub sample')
plt.legend(loc='best')
plt.ylim(ymin=0)
plt.xlabel("$\lambda$ ($\mu$m)")
plt.ylabel("Normalized signal");
plt.title('{OBJECT} raw spectrum'.format(OBJECT=hdr['OBJECT']));
plt.subplot(132)
tar_f = hdu_tar[0].data[o, :] / t_inst
plt.plot(hdu_tar[1].data[o, :], tar_f/0.5+0.2, label='LkCa4 flattened')
plt.plot(hdu_raw[1].data[o, :], hdu_f[0].data[o, :], label='A0V flattened')
plt.legend(loc='best')
plt.xlim(1.650, 1.655)
plt.xlabel("$\lambda$ ($\mu$m)")
plt.ylabel("Normalized signal");
plt.title('detail');
plt.subplot(133)
tar_f = hdu_tar[0].data[o, :] / t_inst
plt.step(hdu_tar[1].data[o, :], tar_f/0.5, label='LkCa4 flattened')
plt.step(hdu_raw[1].data[o, :], hdu_f[0].data[o, :], label='A0V flattened')
plt.legend(loc='best')
plt.xlim(1.6507, 1.6512)
plt.ylim(0.6, 1.1)
plt.xlabel("$\lambda$ ($\mu$m)")
plt.ylabel("Normalized signal");
plt.title('high detail');
# -
from scipy import signal
# +
#dx0, dx1 = 500, 1500 #Pick the middle 1000 pixels
cor1 = signal.correlate(tar_f/0.5, hdu_f[0].data[o, dx0:dx1], mode='same')
cor2 = signal.correlate(tar_f/0.5, tar_f[dx0:dx1]/0.5, mode='same')
x = np.arange(2048)
plt.step(x, cor1/np.nanmax(cor1), label='self')
plt.step(x, cor2/np.nanmax(cor2), label='target')
plt.ylim(0.9999, 1.00005)
#plt.xlim(1160, 1180)
plt.xlim(1060, 1075)
plt.legend(loc='best')
# -
# ### The end for now.
| notebooks/welter_issue001-01_Spectral_Response_Functions.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sys
sys.path.append("../")
# +
from pathlib import Path
from functools import partial
import joblib
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from fastai.core import T
from fastai.rnn_reg import EmbeddingDropout
from torch.optim import Adam
import torch.nn as nn
import torch
import torch.nn.functional as F
import sentencepiece as spm
from cnlp.fastai_extended import LanguageModelLoader, LanguageModelData, ShuffledLanguageModelLoader
# -
tokens = joblib.load("../data/tokens_unigram.pkl")
# Filter out empty texts
tokens = [x for x in tokens if x.shape[0] > 0]
# Set shuffle = False to keep sentences from the same paragraph together
trn_tokens, val_tokens = train_test_split(tokens, test_size=0.2, shuffle=False)
val_tokens, tst_tokens = train_test_split(val_tokens, test_size=0.5, shuffle=False)
def get_voc_stats(tokens):
total_tokens = np.sum([x.shape[0] for x in tokens])
unks = np.sum([np.sum(x == 0) for x in tokens])
print("Total tokens: %d\nUnknown Percentage: %.2f %%" % (total_tokens, unks * 100 / total_tokens))
get_voc_stats(tokens)
bptt = 100
batch_size = 64
n_tok = int(np.max([np.max(x) for x in tokens]) + 1)
trn_loader = ShuffledLanguageModelLoader(
np.concatenate(trn_tokens), batch_size, bptt, target_length=90, batch_first=True)
val_loader = ShuffledLanguageModelLoader(
np.concatenate(val_tokens), batch_size, bptt, target_length=90, batch_first=True)
tst_loader = ShuffledLanguageModelLoader(
np.concatenate(tst_tokens), batch_size, bptt, target_length=90, batch_first=True)
sp = spm.SentencePieceProcessor()
sp.Load("../data/unigram_model.model")
np.sum([np.sum(x == 2) for x in tokens]) # </s>
sp.DecodeIds(trn_tokens[0].tolist())
path = Path("../data/cache/lm_unigram_transformer/")
path.mkdir(parents=True, exist_ok=True)
model_data = LanguageModelData(
path, pad_idx=2, n_tok=n_tok, trn_dl=trn_loader, val_dl=val_loader, test_dl=tst_loader
)
n_tok
# ### Transformer Model
drops = np.array([0.1, 0.1, 0.05, 0, 0.1])
learner = model_data.get_model(
partial(Adam, betas=(0.8, 0.999)),
emb_sz=300, n_hid=500, n_layers=3,
dropouti=drops[0], dropout=drops[1], wdrop=drops[2],
dropoute=drops[3], dropouth=drops[4], qrnn=False
)
# Courtesy of https://stackoverflow.com/questions/49201236/check-the-total-number-of-parameters-in-a-pytorch-model
pytorch_total_params = sum(p.numel() for p in learner.model.parameters())
pytorch_trainable_params = sum(p.numel() for p in learner.model.parameters() if p.requires_grad)
pytorch_total_params, pytorch_trainable_params
learner = model_data.get_transformer_model(
partial(Adam, betas=(0.8, 0.99)),
max_seq_len=trn_loader.max_possible_seq_len,
emb_sz=480,
n_head=12,
n_layer=6,
embd_pdrop=0.1,
attn_pdrop=0.1,
resid_pdrop=0.1
)
pytorch_total_params = sum(p.numel() for p in learner.model.parameters())
pytorch_trainable_params = sum(p.numel() for p in learner.model.parameters() if p.requires_grad)
pytorch_total_params, pytorch_trainable_params
learner.clip = 10.
learner.lr_find(start_lr=1e-4, end_lr=1e-2, linear=False)
# %time learner.sched.plot()
lrs = 1e-3
learner.clip = 20.
# %time learner.fit(lrs, 1, wds=0, use_clr=(50, 4), cycle_len=5, use_wd_sched=False)
learner.sched.plot_lr()
learner.save("lm_transformer")
learner.save_encoder("lm_transformer_enc")
tmp_iter = iter(trn_loader)
next(tmp_iter)[0].shape
learner.load("lm_transformer")
# ## Test the model
learner.model.eval()
# ### Next Character Inference
tokens = sp.EncodeAsIds("德国 是 世界 大国 之 一 , 其 国内 生产 总 值 以 国际 汇率 计")
tokens
iterator = iter(tst_loader)
x, y = next(iterator)
x.shape, y.shape
logits = learner.model(x.to("cuda"))
logits.shape
def eval_tensors(x, y):
logits = learner.model(x.to("cuda"))
sorted_idx = np.argsort(logits.data.cpu().numpy(), 1)
preds = []
for i in range(1, 4):
preds.append([sp.IdToPiece(x) for x in sorted_idx[:, -i].tolist()])
print(x.shape, len(preds[0]))
return pd.DataFrame({
"orig": [sp.IdToPiece(int(i)) for i in x[0, 10:].numpy()] + [""],
"pred_1": [""] + preds[0], "pred_2": [""] + preds[1], "pred_3": [""] + preds[2],
"actual": [""] + [sp.IdToPiece(int(i)) for i in y.numpy()]
})
tmp = eval_tensors(x[:1, :], y[:90])
tmp[:20]
tmp.iloc[-20:]
tmp = eval_tensors(x[1:2, :], y[90:180])
tmp[-20:]
def eval_text(texts):
tokens = sp.EncodeAsIds(texts)[:100]
logits = learner.model(T(tokens).unsqueeze(0))
sorted_idx = np.argsort(logits.data.cpu().numpy(), 1)
preds = []
for i in range(1, 4):
preds.append([sp.IdToPiece(x) for x in sorted_idx[:, -i].tolist()])
# preds = list(map(lambda x: itos[x], np.argmax(logits.data.cpu().numpy(), 1)))
print(len(preds[0]))
return pd.DataFrame({"orig": sp.EncodeAsPieces(texts)[-90:] + [""],
"pred_1": [""] + preds[0][-90:], "pred_2": [""] + preds[1][-90:], "pred_3": [""] + preds[2][-90:]})
sp.DecodeIds(x[0, :].numpy().tolist())
tmp = eval_text(sp.DecodeIds(x[6, :].numpy().tolist()))
tmp
eval_text("特朗普 政府 以为 加征 关税 会 令 中国 屈服 , 这种 策略 肯定 会 适得其反 , 如果 就业 和 财富")
eval_text("对 中国 与 南洋 发动 全面 的 战争 。 1990 年代 , 中")
| legacy/notebooks/Language Model - Unigram - Transformer.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### CIR model for interest rates and liability hedging
# - Cox Ingersoll Ross model is used to model dynamics of interest rates
# - It is an extension of basic Vasicek Model to prevent negative interest rates
# +
import ipywidgets as widgets
from IPython.display import display
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
import risk_kit as rk
import pandas as pd
import numpy as np
import matplotlib as plt
# +
def inst_to_ann(r):
"""
Converts short rate to an annualized rate
"""
return np.expm1(r)
def ann_to_inst(r):
"""
Converts annualized to a short rate
"""
return np.log1p(r)
# -
def cir(n_years=10, n_scenarios=1, a=0.05, b=0.03, sigma=0.05,
steps_per_year=12, r_0=None):
"""Implements the CIR model"""
if r_0 is None: r_0 = b
r_0 = ann_to_inst(r_0)
dt = 1 / steps_per_year
num_steps = int(n_years * steps_per_year) + 1
shock = np.random.normal(0, scale=np.sqrt(dt), size=(num_steps, n_scenarios))
rates = np.empty_like(shock)
rates[0] = r_0
for step in range(1, num_steps):
r_t = rates[step - 1]
d_r_t = a*(b - r_t)*dt + sigma*np.sqrt(r_t)*shock[step]
rates[step] = abs(r_t + d_r_t)
return pd.DataFrame(data=inst_to_ann(rates), index=range(num_steps))
cir(n_scenarios=100, sigma=0.1).plot(figsize=(8,5), legend=False)
# +
def show_cir_prices(r_0=0.03, a=0.05, b=0.03, sigma=0.05, n_scenarios=5):
rk.cir(r_0=r_0, a=a, b=b, sigma=sigma,
n_scenarios=n_scenarios)[1].plot(legend=False, figsize=(8,5))
controls = widgets.interactive(show_cir_prices,
r_0=(0, 0.15, 0.01),
a=(0, 1, 0.1),
b=(0, 0.15, 0.01),
sigma=(0, 0.1, 0.01),
n_scenarios=(0, 100))
display(controls)
# -
a_0 = 750000 # asset
rates, bond_prices = rk.cir(n_years=10, r_0=0.03, b=0.03, n_scenarios=10)
liabilities = bond_prices
zcbond_10 = pd.Series(data=[1], index=[10])
zc_0 = rk.pv(zcbond_10, r=0.03)
n_bonds = a_0 / zc_0
av_zc_bonds = n_bonds * bond_prices
av_cash = a_0 * (rates/12 + 1).cumprod()
av_zc_bonds.head()
av_cash.plot(legend=False, figsize=(8, 5))
av_zc_bonds.plot(legend=False, figsize=(8, 5))
#rk.discount(30, 0.01)
50* 1.03**(-20)
(411681 / 7257519) #* 1700000
2000000 * 0.05
110000 / 1750123
# ### Monte Carlo Sims of Bond Prices with Cox-Ingersoll-Ross
rk.bond_price(5, 100, 0.05, 12, 0.03)
rates, zc_prices = rk.cir(10, 500, b=0.03, r_0=0.03)
rk.bond_price(5, 100, 0.05, 12, rates.iloc[1][[1,2,3]])
rates[[1,2,3]].head()
# ### Homework #4
# B1 is a 15 Year Bond with a Face Value of $1000 that pays
# a 5% coupon semi-annually (2 times a year)
#
# B2 is a 5 Year Bond with a Face value of $1000 that pays a 6% coupon quarterly (4 times a year)
#
# B3 is a 10 Year Zero-Coupon Bond with a Face Value of $1000
#
#
# (Hint: you can still use the erk.bond_cash_flows() and erk.bond_price() by setting the coupon amount to 0% and coupons_per_year to 1) Assume the yield curve is flat at 5%.
rk.bond_price(15, 1000, 0.05, 2, 0.05)
rk.bond_price(5, 1000, 0.06, 4, 0.05)
rk.bond_price(10, 1000, 0, 1, 0.05)
# What is the price of the 10 Year Zero Coupon Bond B3?
# Duration refers to Macaulay Duration
# Hint: the macaulay_duration function gives as output the duration expressed in periods and not in years. If you want to get the yearly duration you need to divide the duration for coupons_per_year; e.g.: duarion_B2 = erk.macaulay_duration(flows_B2, 0.05/4)/4
b1_flows = rk.bond_cash_flows(15, 1000, 0.05, 2)
rk.macaulay_duration(b1_flows, 0.05/2)/2
b2_flows = rk.bond_cash_flows(5, 1000, 0.06, 4)
rk.macaulay_duration(b2_flows, 0.05/4)/4
b3_flows = rk.bond_cash_flows(10, 1000, 0, 1)
rk.macaulay_duration(b3_flows, 0.05)/1
# Assume a sequence of 3 liabilities of $100,000, $200,000 and $300,000 that are 3, 5 and 10 years away, respectively. What is the Duration of the liabilities?
#
# (Reminder: Assume the yield curve is flat at 5%. Duration refers to Macaulay Duration)
liabilities = pd.DataFrame(data=[100000, 200000, 300000], index=[3, 5, 10])
rk.macaulay_duration(liabilities, 0.05)
# Assuming the same liabilities as the previous questions (i.e. a sequence of 3 liabilities of
# $100,000, $200,000 and $300,000 that are 3, 5 and 10 years away, respectively), build a Duration Matched Portfolio of B2 and B3 to match the liabilities.
#
# What is the weight of B2 in this portfolio?
# +
liabs = pd.Series(data=[100000, 200000, 300000], index=[3, 5, 10])
b1 = rk.bond_cash_flows(15, 1000, coupon_rate=0.05, coupons_per_year=1)
b2 = rk.bond_cash_flows(5, 1000, coupon_rate=0.06, coupons_per_year=1)
ws = rk.match_durations(liabs, b1, b2, 0.05)
# -
ws.all()
b3 = rk.bond_cash_flows(10, 1000, 0, 1)
b3
| cir.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# LSTM for international airline passengers problem with window regression framing
import numpy
import numpy as np
import keras
import matplotlib.pyplot as plt
from pandas import read_csv
import math
from keras.models import Sequential
from keras.layers import Dense,Dropout
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import OneHotEncoder
from sklearn.cross_validation import train_test_split
from keras.utils.vis_utils import plot_model
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return numpy.array(dataX), numpy.array(dataY)
def create_dataset2(dataset, look_back=1):
dataX, dataY = [], []
dataZ=[]
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 1]
dataX.append(a)
b = dataset[i + look_back, 0]
dataZ.append(b)
dataY.append(dataset[i + look_back, 1])
return numpy.array(dataX), numpy.array(dataY),numpy.array(dataZ)
# +
# fix random seed for reproducibility
numpy.random.seed(7)
# load the dataset
# dataframe = read_csv('w_d_v.csv', usecols=[7], engine='python', skipfooter=3)
dataframe = read_csv('t6192.csv', usecols=[8,0], engine='python',dtype=np.int32,skiprows=1,header=None,skipfooter=3)
pattern = read_csv('t6192.csv', usecols=[7], engine='python',dtype=np.int32,skiprows=1,header=None,skipfooter=3)
Matrix = read_csv('matrix621.csv', usecols=[2,3,4,5,6,7,8,9,10,11,12,13], engine='python',header=None)
all_data = read_csv('all_data.csv', usecols=[7], engine='python', skipfooter=3)
dataset = dataframe.values
Matrix = Matrix.values
pattern=pattern.values
allData=all_data.values
Matrix=np.append([[-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1]],Matrix,axis=0)
week_info = read_csv('t6192.csv', usecols=[11], engine='python',dtype=np.int32,skiprows=1,header=None,skipfooter=3)
Start_info = read_csv('t6192.csv', usecols=[12], engine='python',dtype=np.int32,skiprows=1,header=None,skipfooter=3)
End_info = read_csv('t6192.csv', usecols=[13], engine='python',dtype=np.int32,skiprows=1,header=None,skipfooter=3)
Stay_info = read_csv('t6192.csv', usecols=[14], engine='python',dtype=np.int32,skiprows=1,header=None,skipfooter=3)
week_info = week_info.values
Start_info = Start_info.values
End_info=End_info.values
Stay_info=Stay_info.values
week_info=week_info[:-4]
Start_info=Start_info[:-4]
End_info=End_info[:-4]
Stay_info=Stay_info[:-4]
# +
look_back = 3
trainX, trainY, trainZ = create_dataset2(dataset, look_back)
AllX, AllY = create_dataset(allData, look_back)
patternX, patternY = create_dataset(pattern, look_back)
trainY=numpy.reshape(trainY,(trainY.shape[0],-1))
AllY=numpy.reshape(AllY,(AllY.shape[0],-1))
# -
Location_info=trainY
encX = OneHotEncoder()
encX.fit(trainX)
encY = OneHotEncoder()
encY.fit(trainY)
trainX_one=encX.transform(trainX).toarray()
train_X=numpy.reshape(trainX_one,(trainX_one.shape[0],look_back,-1))
train_Y=encY.transform(trainY).toarray()
# #还没能直接拆分,其他维度没有做对应
# a_train, a_test, b_train, b_test = train_test_split(train_X, train_Y, test_size=0.1, random_state=42)
emdedding_size=Matrix.shape[1] #
vo_len=look_back #
vocab_size=Matrix.shape[0] #
a_train=trainX.reshape(-1,3,1)
a_train=a_train.reshape(-1,3)
b_train=train_Y
k=trainZ
pretrained_weights=Matrix
LSTM_size=32
pretrained_weights.shape
print("------------------------")
print("in size:")
print(a_train.shape)
print("------------------------")
print("out size:")
print(b_train.shape)
print("------------------------")
print("user size:")
print(k.shape)
print("------------------------")
# +
print("------------------------")
print("input encode example1:")
print(train_X[0])
print("------------------------")
print("input encode example2:")
for x in a_train[0]:
print(pretrained_weights[x])
print("------------------------")
print("input decode example:")
print(a_train[0])
print("------------------------")
print("output encode example:")
print(b_train[0])
print("------------------------")
print("output decode example:")
print(trainY[0])
print("------------------------")
print("user_id example:")
print(k[0])
print("------------------------")
# +
print("------------------------")
print("emdedding_size:")
print(emdedding_size)
print("------------------------")
print("vocab_length:")
print(vo_len)
print("------------------------")
print("vocab_size:")
print(vocab_size)
print("------------------------")
# +
print("使用 T+S")
from keras.layers import Input, Embedding, LSTM, Dense,Merge,Flatten
from keras.models import Model
# a_train=a_train.reshape(-1,3)
emdedding_size=100
Location_size=201
User_size=183
LSTM_size=200
Time_size=5
Week_size=8
Stay_size=1440
pretrained_weights_size=12
# Move_Pattern Sequences
input_pattern = Input(shape=(3, ),name="Move_Pattern_Input")
# User-Id
User_id = Input(shape=(1,),name="User_id_Input")
# Temporary
Start_Time = Input(shape=(1,),name="Start_Time_Input")
End_Time = Input(shape=(1,),name="End_Time_Input")
Stay_Time = Input(shape=(1,),name="Stay_Time_Input")
Date_Info = Input(shape=(1,),name="Date_Info_Input")#1-7 Monday to Sunday
# Spatial
Location_Info = Input(shape=(3,),name="Semantic_Location_Info_Input")#12 categories Interest_point
# Weather
Weather_Info = Input(shape=(1,),name="Weather_Info_Input")#1-7 Weather Type
#Spatial
em = Embedding(input_dim=Location_size, output_dim=emdedding_size,input_length=vo_len,name="Spatial_Pattern")(input_pattern)
lstm_out = LSTM(LSTM_size,name="Spatial_Feature")(em)
lstm_out = Dropout(0.2)(lstm_out)
#User_id
em2 = Embedding(input_dim=User_size, output_dim=emdedding_size,input_length=1,name="User_id")(User_id)
em2=Flatten(name="User_Feature")(em2)
#Temporary
emStart_Time = Embedding(input_dim=Time_size, output_dim=emdedding_size,input_length=1,name="Start_Time")(Start_Time)
emEnd_Time = Embedding(input_dim=Time_size, output_dim=emdedding_size,input_length=1,name="End_Time")(End_Time)
emStay_Time = Embedding(input_dim=Stay_size, output_dim=emdedding_size,input_length=1,name="Stay_Time")(Stay_Time)
emDate_Info = Embedding(input_dim=Week_size, output_dim=emdedding_size,input_length=1,name="Date_Info")(Date_Info)
Temporary = keras.layers.concatenate([emStart_Time, emEnd_Time,emStay_Time,emDate_Info],name="Temporary_Feature_Model")
Temporary = Flatten(name="Temporary_Feature")(Temporary)
#Semantic
Location_Semantic=Embedding(input_dim=Location_size, output_dim=pretrained_weights_size,input_length=vo_len,weights=[pretrained_weights],name="Semantic_Location_Info")(Location_Info)
Semantic_lstm = LSTM(36,return_sequences=True,name="Semantic_Model")(Location_Semantic)
Location_Semantic=Flatten(name="Semantic_Feature")(Semantic_lstm)
#Weather
x = keras.layers.concatenate([lstm_out, em2, Temporary,Location_Semantic])
x=Dense(808,activation='relu',name="C")(x)
x=Dense(404,activation='relu',name="C2")(x)
x=Dense(202,activation='relu',name="C3")(x)
x=Dropout(0.2)(x)
x=Dense(b_train.shape[1],activation='softmax',name='x')(x)
model = Model(inputs=[input_pattern,User_id,Start_Time,End_Time,Stay_Time,Date_Info,Location_Info], outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
# print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm_T+S.png',show_shapes=True)
# -
# print(a_train.shape)
# print(Location_info.shape)
# print(week_info.shape)
# Location_info[0:10]
history_T_S = model.fit([a_train,k,Start_info,End_info,Stay_info,week_info,a_train], b_train, epochs=100, batch_size=512, verbose=2)
# +
print("使用 encode2 (语义权重 pretrained_weights)方法")
from keras.layers import Input, Embedding, LSTM, Dense,Merge,Flatten
from keras.models import Model
# a_train=a_train.reshape(-1,3)
emdedding_size=100
Location_size=201
User_size=183
LSTM_size=200
Time_size=5
Week_size=8
Stay_size=1440
# Move_Pattern Sequences
input_pattern = Input(shape=(3, ),name="Move_Pattern")
# User-Id
User_id = Input(shape=(1,),name="User_id")
# Temporary
Start_Time = Input(shape=(1,),name="Start_Time")
End_Time = Input(shape=(1,),name="End_Time")
Stay_Time = Input(shape=(1,),name="Stay_Time")
Date_Info = Input(shape=(1,),name="Date_Info")#1-7 Monday to Sunday
# Spatial
Location_Info = Input(shape=(12,),name="Location_Info")#12 categories Interest_point
# Weather
Weather_Info = Input(shape=(1,),name="Weather_Info")#1-7 Weather Type
em = Embedding(input_dim=Location_size, output_dim=emdedding_size,input_length=vo_len)(input_pattern)
lstm_out = LSTM(LSTM_size)(em)
lstm_out = Dropout(0.2)(lstm_out)
em2 = Embedding(input_dim=User_size, output_dim=emdedding_size,input_length=1)(User_id)
emStart_Time = Embedding(input_dim=Time_size, output_dim=emdedding_size,input_length=1)(Start_Time)
emEnd_Time = Embedding(input_dim=Time_size, output_dim=emdedding_size,input_length=1)(End_Time)
emStay_Time = Embedding(input_dim=Stay_size, output_dim=emdedding_size,input_length=1)(Stay_Time)
emDate_Info = Embedding(input_dim=Week_size, output_dim=emdedding_size,input_length=1)(Date_Info)
Temporary = keras.layers.concatenate([emStart_Time, emEnd_Time,emStay_Time,emDate_Info])
Temporary = Flatten()(Temporary)
em2=Flatten()(em2)
x = keras.layers.concatenate([lstm_out, em2, Temporary])
x=Dense(700,activation='relu',name="C")(x)
x=Dense(400,activation='relu',name="C2")(x)
x=Dense(250,activation='relu',name="C3")(x)
x=Dropout(0.2)(x)
x=Dense(b_train.shape[1],activation='softmax',name='x')(x)
model = Model(inputs=[input_pattern,User_id,Start_Time,End_Time,Stay_Time,Date_Info], outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
# print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm624.png',show_shapes=True)
# -
history_nopre = model.fit([a_train,k,Start_info,End_info,Stay_info,week_info], b_train, epochs=100, batch_size=512, verbose=2)
# +
print("使用 encode2 (语义权重 pretrained_weights)方法")
from keras.layers import Input, Embedding, LSTM, Dense,Merge,Flatten
from keras.models import Model
# a_train=a_train.reshape(-1,3)
emdedding_size=100
Location_size=201
User_size=183
LSTM_size=200
Time_size=5
Week_size=8
Stay_size=1440
# Move_Pattern Sequences
input_pattern = Input(shape=(3, ),name="Move_Pattern")
# User-Id
User_id = Input(shape=(1,),name="User_id")
# Temporary
Start_Time = Input(shape=(1,),name="Start_Time")
End_Time = Input(shape=(1,),name="End_Time")
Stay_Time = Input(shape=(1,),name="Stay_Time")
Date_Info = Input(shape=(1,),name="Date_Info")#1-7 Monday to Sunday
# Spatial
Location_Info = Input(shape=(12,),name="Location_Info")#12 categories Interest_point
# Weather
Weather_Info = Input(shape=(1,),name="Weather_Info")#1-7 Weather Type
em = Embedding(input_dim=Location_size, output_dim=emdedding_size,input_length=vo_len)(input_pattern)
lstm_out = LSTM(LSTM_size)(em)
lstm_out = Dropout(0.2)(lstm_out)
em2 = Embedding(input_dim=User_size, output_dim=emdedding_size,input_length=1)(User_id)
emStart_Time = Embedding(input_dim=Time_size, output_dim=emdedding_size,input_length=1)(Start_Time)
emEnd_Time = Embedding(input_dim=Time_size, output_dim=emdedding_size,input_length=1)(End_Time)
emStay_Time = Embedding(input_dim=Stay_size, output_dim=emdedding_size,input_length=1)(Stay_Time)
emDate_Info = Embedding(input_dim=Week_size, output_dim=emdedding_size,input_length=1)(Date_Info)
# Temporary = keras.layers.concatenate([emStart_Time, emEnd_Time,emStay_Time,emDate_Info])
# Temporary = Flatten()(Temporary)
em2=Flatten()(em2)
x = keras.layers.concatenate([lstm_out, em2])
x=Dense(700,activation='relu',name="C")(x)
x=Dense(400,activation='relu',name="C2")(x)
x=Dense(250,activation='relu',name="C3")(x)
x=Dropout(0.2)(x)
x=Dense(b_train.shape[1],activation='softmax',name='x')(x)
model = Model(inputs=[input_pattern,User_id,Start_Time,End_Time,Stay_Time,Date_Info], outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
# print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm624_notem.png',show_shapes=True)
history_notem = model.fit([a_train,k,Start_info,End_info,Stay_info,week_info], b_train, epochs=100, batch_size=512, verbose=2)
# +
fig = plt.figure()
plt.plot(history_nopre.history['acc'])
plt.plot(history_notem.history['acc'])
plt.plot(history_T_S.history['acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['None', 'T','T+S'], loc='upper left')
# +
print("使用 encode1 方法")
aa_train=train_X
from keras.layers import Input, Embedding, LSTM, Dense,Merge
from keras.models import Model
input_pattern = Input(shape=(3, aa_train.shape[2]),name="Move_Pattern")
input_id = Input(shape=(1,),name="User_id")
lstm_out = LSTM(units=200,return_sequences=False)(input_pattern)
lstm_out = Dropout(0.2)(lstm_out)
em2 = Embedding(input_dim=User_size, output_dim=emdedding_size,input_length=1)(input_id)
em2=Flatten()(em2)
x = keras.layers.concatenate([lstm_out, em2])
x=Dense(400,activation='relu',name="C")(x)
x=Dense(300,activation='relu',name="C2")(x)
x=Dense(250,activation='relu',name="C3")(x)
x=Dropout(0.2)(x)
x=Dense(b_train.shape[1],activation='softmax')(x)
model = Model(inputs=[input_pattern,input_id], outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
# print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm_encode1.png',show_shapes=True)
# -
history_encode1 = model.fit([aa_train,k], b_train, epochs=100, batch_size=512, verbose=2)
# +
aa_train=train_X
from keras.layers import Input, Embedding, LSTM, Dense,Merge
from keras.models import Model
input_pattern = Input(shape=(3, aa_train.shape[2]),name="Move_Pattern")
input_id = Input(shape=(1,),name="User_id")
lstm_out = LSTM(units=300,return_sequences=False)(input_pattern)
lstm_out = Dropout(0.2)(lstm_out)
# em2 = Embedding(input_dim=User_size, output_dim=emdedding_size,input_length=1)(input_id)
# em2=Flatten()(em2)
# x = keras.layers.concatenate([lstm_out, em2])
x=Dense(400,activation='relu',name="C1")(lstm_out)
x=Dense(300,activation='relu',name="C2")(x)
x=Dense(250,activation='relu',name="C3")(x)
x=Dropout(0.2)(x)
x=Dense(b_train.shape[1],activation='softmax')(x)
model = Model(inputs=[input_pattern,input_id], outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
# print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm_encode1.png',show_shapes=True)
# -
history_encode1 = model.fit([aa_train,k], b_train, epochs=100, batch_size=512, verbose=2)
# +
from keras.layers import Input, Embedding, LSTM, Dense,Merge
from keras.models import Model
emdedding_size=12 #
vo_len=3 #
vocab_size=11000 #
a_train=patternX
b_train=train_Y
k=trainZ
pretrained_weights=Matrix
input_pattern = Input(shape=(3, ),name="input_pattern")
em = Embedding(input_dim=vocab_size, output_dim=emdedding_size,input_length=vo_len, weights=[pretrained_weights])(input_pattern)
lstm_out = LSTM(units=emdedding_size)(em)
lstm_out = Dropout(0.2)(lstm_out)
x=Dense(250,activation='relu',name="C")(lstm_out)
x=Dropout(0.2)(x)
x=Dense(180,activation='softmax')(x)
model = Model(inputs=input_pattern, outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm_test.png',show_shapes=True)
history_withpre2 = model.fit(a_train, b_train, epochs=100, batch_size=16, verbose=2)
# -
# plot_model(model, to_file='t_lstm_test.png',show_shapes=True)
# history_nopre = model.fit(a_train, b_train, epochs=100, batch_size=16, verbose=2)
# +
from keras.layers import Input, Embedding, LSTM, Dense,Merge
from keras.models import Model
emdedding_size=12 #
vo_len=3 #
vocab_size=11000 #
a_train=trainX.reshape(-1,3)
b_train=train_Y
k=trainZ
pretrained_weights=Matrix
input_pattern = Input(shape=(3, ),name="input_pattern")
em = Embedding(input_dim=vocab_size, output_dim=emdedding_size,input_length=vo_len, weights=[pretrained_weights])(input_pattern)
lstm_out = LSTM(units=emdedding_size)(em)
lstm_out = Dropout(0.2)(lstm_out)
x=Dense(250,activation='relu',name="C")(lstm_out)
x=Dropout(0.2)(x)
x=Dense(180,activation='softmax')(x)
model = Model(inputs=input_pattern, outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm_test.png',show_shapes=True)
history_withpre2 = model.fit(a_train, b_train, epochs=100, batch_size=16, verbose=2)
# +
from keras.layers import Input, Embedding, LSTM, Dense,Merge
from keras.models import Model
emdedding_size=12 #
vo_len=3 #
vocab_size=11000 #
a_train=patternX.reshape(-1,3,1)
b_train=train_Y
k=trainZ
pretrained_weights=Matrix
input_pattern = Input(shape=(3, 1),name="input_pattern")
lstm_out = LSTM(units=64)(input_pattern)
lstm_out = Dropout(0.2)(lstm_out)
x=Dense(250,activation='relu',name="C")(lstm_out)
x=Dropout(0.2)(x)
x=Dense(180,activation='softmax')(x)
model = Model(inputs=input_pattern, outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm_test.png',show_shapes=True)
history_withpre2 = model.fit(a_train, b_train, epochs=100, batch_size=16, verbose=2)
# -
# plot_model(model, to_file='t_lstm_test.png',show_shapes=True)
# history1 = model.fit(a_train, b_train, epochs=100, batch_size=16, verbose=2)
# +
from keras.layers import Input, Embedding, LSTM, Dense,Merge
from keras.models import Model
input_pattern = Input(shape=(3, a_train.shape[2]),name="input_pattern")
lstm_out = LSTM(512,input_shape=(3, a_train.shape[2]))(input_pattern)
# lstm_out = LSTM(512,return_sequences=True,input_shape=(3, a_train.shape[2]))(input_pattern)
# lstm_out = LSTM(300)(lstm_out)
lstm_out = Dropout(0.2)(lstm_out)
x=Dense(250,activation='relu',name="C")(lstm_out)
x=Dropout(0.2)(x)
x=Dense(a_train.shape[2],activation='softmax')(x)
model = Model(inputs=input_pattern, outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm_test.png',show_shapes=True)
# -
history = model.fit(a_train, b_train, epochs=100, batch_size=16, verbose=2, validation_data=(a_test, b_test))
print(history.history.keys())
fig = plt.figure()
plt.plot(history.history['acc'])
plt.plot(history1.history['acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['1-lstm', '2-lstm'], loc='upper left')
fig = plt.figure()
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='lower left')
train_X=train_X.reshape(-1,200)
train_Y.reshape(-1,200)
train_X.shape
train_Y.shape
# +
from keras.layers import Input, Embedding, LSTM, Dense,Merge
from keras.models import Model
a_train=train_X
b_train=train_Y
k=trainZ
input_pattern = Input(shape=(3, a_train.shape[2]),name="input_pattern")
input_id = Input(shape=(1,),name="input_id")
lstm_out = LSTM(250,input_shape=(3, a_train.shape[2]))(input_pattern)
lstm_out = Dropout(0.2)(lstm_out)
x = keras.layers.concatenate([lstm_out, input_id])
x=Dense(250,activation='relu',name="C")(x)
x=Dropout(0.2)(x)
x=Dense(a_train.shape[2],activation='softmax',name='x')(x)
model = Model(inputs=[input_pattern,input_id], outputs=x)
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
print(model.summary()) # Summarize Model
plot_model(model, to_file='t_lstm.png',show_shapes=True)
# +
k=np.zeros(a_train.shape[0],dtype=np.int16)
k=k.reshape(-1,1)
k1=np.zeros(train_X.shape[0],dtype=np.int16)
k1=k1.reshape(-1,1)
# -
history = model.fit({'input_pattern': a_train, 'input_id' : k}, {'x': b_train}, epochs=100, batch_size=64, verbose=2)
# +
fig = plt.figure()
Accuracy=[42.00,47.15 ,48.36, 49.35,47.42, 50.82, 52.31,56.93 ,57.15 ]
x2=(20,30,40,50,60,70,80,90,100)
plt.plot(x2,Accuracy)
x1=range(0,100)
plt.plot(x1,history.history['acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['100% total_data Yu','100% total_data Mine'], loc='upper left')
# -
fig = plt.figure()
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['90% train_data', '100% total_data'], loc='upper left')
# model.fit(a_train, b_train, epochs=100, batch_size=16, verbose=2, validation_data=(a_test, b_test))
model.evaluate(train_X, train_Y, batch_size=64, verbose=2, sample_weight=None)
trainPredict = model.predict(train_X)
D=np.argmax(train_Y,axis = 1)
E=np.argmax(trainPredict,axis = 1)
print(D)
print(E)
A=0 #total number of right
for i,t in enumerate(E):
if D[i]==t :
A=A+1
print(A/D.shape[0])
| 2018-06-27.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="ELNDFgkVdPcr"
# # Artificial Neural Networks
#
# It consists of a supervised learning algorithm, that consists of the reception of input and computation of a function with weights (in layers).
#
# It can sort of mimmic a natural brain neural net, because of its structure with neurons and connections between them.
#
# ## Why use them?
#
# In traditional Machine Learning, to compute predictions, one must feed input; perform feature engineering; feed features; perform the model; output, whereas in AI (Neural Nets), one must only feed input to the net to receive output.
#
# Neural Nets with multiple layers can in each node or in each layer detect different aspects of the input (specific patterns), for example if you feed dog images, a region of the net can form patterns for the eyes, another for the nose, et cetera. So basically the only requirement for learning is sufficient quantity of data.
#
#
# ## Perceptron
#
# The Perceptron is the simplest ANN, since it only has one neuron and one output value. We will use it to start .
#
#
# So, given the input matrix $X$, and weights $\mathbf{W} = \{w_j\}_{j=1}^N$ and bias $w_0$ we have the **activation function** $g: \mathbb{R}^{N+1} \rightarrow \mathbb{R}^M$:
#
# \begin{equation}
# \hat{y} = g( w_0 + \mathbf{X}^T \mathbf{W} )
# \end{equation}
#
# One of the most simple and popular activation functions is the sigmoid function:
# \begin{equation}
# \sigma(x) = \frac{1}{1 + e^{-x}}
# \end{equation}
#
# Is is useful because it receibes a certain value $x$ and maps its value into the interval $[0,1]$, therefore possibily computing a probability measure.
# Also, multiple activation functions can be used in different layers, to induce complexity to the model.
#
# 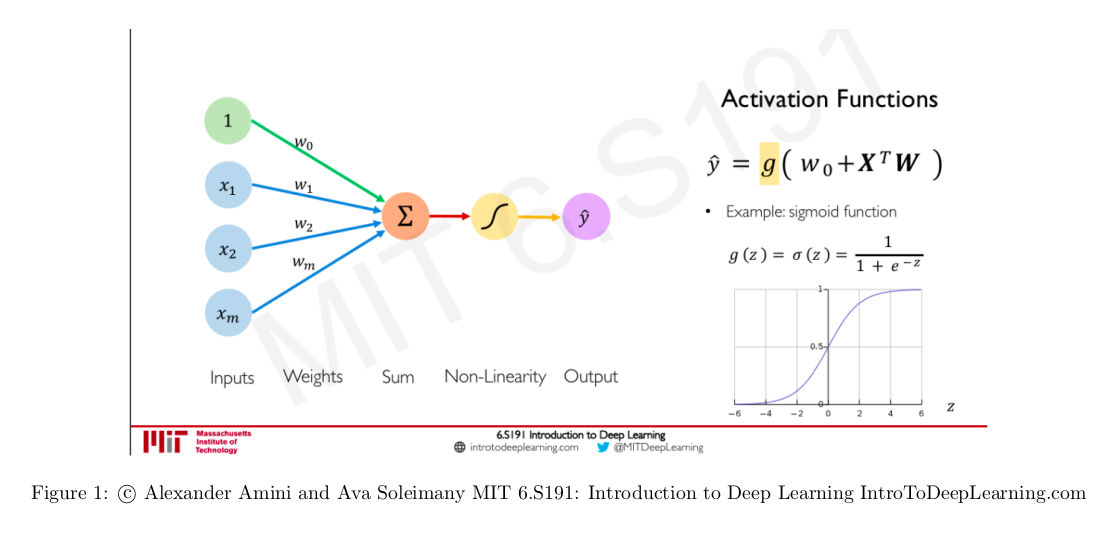
#
# - The activation function can help us to introduce "non-linearity" into the model, which is important when dealing with real data, that is not usually linear.
#
# - The weigths can be adjusted (and must be!), and this process is the training process: by adjusting our weights, model performance can improve ("and learn").
#
# - $w_0$ is our bias. It can alter our activation function argument independantly from the input $\mathbf{X}$.
#
# + colab={"base_uri": "https://localhost:8080/", "height": 625} id="dVSieJoudLGf" outputId="a88ecee7-e772-4bfd-ab5b-d7f724c2e3ca"
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def hyperbolic_tanget(x):
return (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))
def relu(x):
return max(0, x)
def plot_af():
activation_functions = {
'sigmoid': sigmoid, 'hyperbolic tangent': hyperbolic_tanget, 'relu': relu
}
plt.figure(figsize=(12,8))
plt.suptitle('Some common activation functions', fontsize=25, y=1.05)
c=0
for f in list(activation_functions.keys()):
c+=1
plt.subplot(3,1,c)
x = np.linspace(-10, 10, 200)
y = list(map(activation_functions[f], x))
plt.title(f, fontsize=18)
plt.plot(x, y)
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.tight_layout()
plt.show()
plot_af()
# + [markdown] id="4JSDGBsOgfO7"
#
#
# <br>
#
#
# + [markdown] id="LCKTays4iPIS"
#
# ## Multioutput Neural Net
#
# Generalizing our Neural Net, let us say we have $N$ input values, $K$ layers
# and $J$ output classes (taking it is a classification problem), our output expression would be:
#
# \begin{equation}
# \hat{y}_j = g(w_{0, j}^{(k)} + \sum_{i=1}^N x_i w_{i, j}^{(k)}) \quad \begin{cases}
# \text{layers} & k=1, ..., K \\
# \text{outputs} & j = 1, 2, ..., J
# \end{cases}
# \end{equation}
#
#
# In the cases that we have an intermediate layer (neither input nor output), it can be called a "hidden layer".
#
#
# + [markdown] id="ieirsEr8bTjx"
#
# ## Deep Neural Nets
#
# They are ANNs with a large quantity of hidden layers.
#
#
# + [markdown] id="hYzE2cYJbYIx"
#
#
# ## Loss
#
# To quantify the error and accuracy of a prediction (output of the net) $\hat{y}_j$, comparing to the real value $y_j$, we must define a Cost function
#
# \begin{equation}
# \mathcal{L} (\hat{y}_j, y_j): \mathbb{R}^n \rightarrow \mathbb{R}
# \end{equation}
#
# ### Empirical Loss
#
# Also called Objective Function, Cost Function, Empirical Risk.
# Taking $f$ as the function of the ANN.
#
# \begin{equation}
# J(\mathbf{W}) = \frac{1}{N} \sum_{i=1}^N \mathcal{L} \left( f(x^{(i)}; \mathbf{W}), y^{(i)} \right)
# \end{equation}
#
# ### Binary Cross Entropy Loss
#
# \begin{equation}
# J(\mathbf{W}) = \frac{1}{N} \sum_{i=1}^N y^{(i)} log \left(f(x^{(i)}; \mathbf{W}) \right) + (1 - y^{(i)}) log \left( 1 - f(x^{(i)}; \mathbf{W}) \right)
# \end{equation}
#
# - can be used for binary classification problems, since it computes a probability value.
#
# ### MSE
#
# The Mean Squared Error (MSE) is computed by
#
# \begin{equation}
# J(\mathbf{W}) = \frac{1}{N} \sum_{i=1}^N \left( f(x^{(i)}; \mathbf{W})- y^{(i)} \right)^2
# \end{equation}
#
# - This can be used for regression problems, to compute a Loss value in the continuous real line.
#
#
# + [markdown] id="-Mf8WLoUbZ6T"
#
# ## Example
#
# Let us see a simple example with 2 input nodes, 1 hidden layer and 1 output node
# + colab={"base_uri": "https://localhost:8080/"} id="wtUc_a0Npq1v" outputId="16157856-9d35-49ef-c143-553de0ca48ec"
# given the input data X
X = [
[0.7, 0.4],
[0.2, 0.8],
[0.3, 0.9],
[0.01, 0.01]
]
# weigths
W = [[1, 1],
[1, 1],
[1, 1],
[1, 1]]
def simple_net(X, W, w0, hidden_layers=1):
""" Simple Net with sigmoid activation function """
y = []
for j in range(len(X)): # for each sequence of inputs {x_j}_{j=1}^I, with I input nodes
s=0
for k in range(np.array(W).shape[1]): # for each hidden layer
s += W[j][k] * X[j][k]
print("j={}, k= {}, W[j][k]={}, X[j][k]={}, W[j][k] * X[j][k]={}".format(j, k, W[j][k], X[j][k], s))
y.append(sigmoid(s + w0))
print("Final Layer values: ", y)
print('Output: ', sum(y))
simple_net(X, W, w0=0)
# + [markdown] id="ZTdYjOWdxyHY"
# This simple example shows us that if we don't use a activation function, we simply compute a linear relationship to our data, and that our weights must be adjusted for us to leave random computations and achieve pattern recognition.
# + [markdown] id="yo65gATdwe2L"
# ## Training - Loss Optimization
#
# The training process consists of a optimization process, since, given our weigths, we have want to minimize a given cost function , to improve accuracy, by adjusting our weights.
#
# \begin{equation}
# \mathbf{W}^* = \underset{W}{argmin} \frac{1}{N} \sum_{i=1}^N \mathcal{L} \left( f(x^{(i)}; \mathbf{W}), y^{(i)} \right) = \underset{W}{argmin} J(\mathbf{W})
# \end{equation}
#
# 
#
# + [markdown] id="tYw0vS5Hbuwr"
#
# ## Gradient Descent
#
# A simple algorithm for optimizing our Loss function through gradient computation, given a learning rate $\eta$:
#
# - 1) Initialize pseudo-random weights $\mathbf{W} \sim \mathcal{N}(0, \sigma^2)$
# - 2) while $\nabla J(\mathbf{W}) \neq 0 $ (loop until convergence)
# - 2.1) Compute $\nabla J(\mathbf{W})$
# - 2.2) Update weights $\mathbf{W} \leftarrow \mathbf{W} - \eta \nabla J(\mathbf{W})$
# - 3) return optimized weigths $\mathbf{W}^*$
#
# <br>
#
#
# #### Notes:
#
# - Note that in our algorithm steps, with
# \begin{equation}
# x^{k+1} = x^k + t_k d^k
# \end{equation}
# we are taking a step $t_k$ (relative to the learning rate), in the direction $d^k$. In gradient descent, the direction is $d^k = - \nabla J(\mathbf{W})$, because the gradient points to the maximum, so we take orthogonal steps, searching for a minimum.
#
# - The Loss Surfice (as in the figure above with $J(w_0, w_1)$ x $w_0$ x $w_1$ can have multiple local minimals, and we want the global minimal. So one must be careful to decide the learning rate $\eta$, for not to take too little steps (increasing computational time), nor too large steps (and skipping the minimal region).
#
# - In gradient descent backpropagation, basically we update each weight by a small amount, considering a learning rate.
#
# <br>
#
# + [markdown] id="N9yFTKZVbxFd"
#
# ### Stochastic Gradient Descent
#
# In this method, random samples are selected to compute the gradient.
# Algorithm:
#
# - 1) Initialize weights $\mathbf{W} \sim \mathcal{N}(0,\sigma^2)$
# - 2) while $\nabla J(\mathbf{W}) \neq 0$ (loop until co
# nvergence)
# - 2.1) sample a batch of $B$ data points
# - 2.2) Compute the gradient at the selected batch $\frac{\partial J(\mathbf{W})}{\partial \mathbf{W}} = \frac{1}{B} \sum_{k=1}^B \frac{\partial J_k(\mathbf{W})}{\partial \mathbf{W}}$
# - 2.3) update weights $\mathbf{W} \leftarrow \mathbf{W} - \eta \nabla J(\mathbf{W})$
# - 3) return weights $\mathbf{W}^*$
#
#
# <br>
#
#
# + [markdown] id="8g_U9pA8byLY"
# ## Backpropagation
#
# It is the process of computing the gradients and training feedforward neural networks
# + colab={"base_uri": "https://localhost:8080/"} id="jn8j-BTLSb4D" outputId="fee79c0f-8722-477a-ad32-304c82481e86"
import random
def create_random_weights(rowdim=4, coldim=2):
""" Given the dimensions of rows and columns, create a matrix with values:
u_1 (-1)^(u_2), u_1, u_2 \sim U[0,1]
i.e. a uniform number that might have a minus sign
"""
W = []
for r in range(rowdim):
W.append([])
for c in range(coldim):
W[r].append(np.random.uniform()*((-1)**round(np.random.uniform())))
return W
create_random_weights()
# + id="T544KOkFEGjJ"
#implementing Gradient Descent and backpropagation
import numpy as np
from copy import deepcopy
# activation function
def sigmoid(x):
return 1/(1+np.exp(-x))
# loss function
def mse(y, y_pred):
return np.mean(np.square(np.array(y) - np.array(y_pred)))
def simple_net(X, y, W, w0, hidden_layers=1, y_true=0, verbose=False):
""" Simple Net with sigmoid activation function """
y_pred = []
for j in range(len(X)): # for each sequence of inputs {x_j}_{j=1}^I, with I input nodes
s=0
for k in range(np.array(W).shape[1]): # for each hidden layer
s += W[j][k] * X[j][k]
if verbose:
print("j={}, k= {}, W[j][k]={}, X[j][k]={}, W[j][k] * X[j][k]={}".format(j, k, W[j][k], X[j][k], s))
y_pred.append(sigmoid(s + w0))
if verbose:
print("Final Layer values: ", y)
print('Output: ', sum(y))
return mse(y=y, y_pred=y_pred)
def backprop(X, y, W,
dif=0.0001,
eta=0.01,
w0 = -0.5516,
verbose=False
):
loss_0 = simple_net(X, y, W, w0, verbose=verbose)
w_update = deepcopy(W)
adj_w = deepcopy(W)
for i, layer in enumerate(W):
for j, w_j in np.ndenumerate(layer):
if verbose:
print('i: {}, j: {}, w_j: {}'.format(i, j, w_j))
j=j[0]
# small difference in weights
adj_w[i][j] += dif
aditional_loss = simple_net(X, y, adj_w, w0, verbose=verbose)
# \nabla J(W) = \frac{\partial J(\mathbf{W})}{\partial \mathbf{W}}
grad = (aditional_loss - loss_0) / dif
# W <- W - \eta * \nabla J(W)
w_update[i][j] -= eta * grad
return w_update, loss_0
# + colab={"base_uri": "https://localhost:8080/", "height": 52} id="NQxgpWxgGBc7" outputId="c8b9aa87-a695-46ee-cdb5-9e1cda4cf9e8"
def test_loss(X, y, W, w0, epochs=100):
loss=[]
for epoch in range(epochs):
W, l = backprop(X, y, W, w0)
loss.append(l)
plt.figure(figsize=(15,4))
plt.title('Loss function x epochs')
plt.plot(loss)
plt.show()
'''
W = np.array([[-0.0053, 0.3793],
[-0.5820, -0.5204],
[-0.2723, 0.1896]])
w0 = -0.5516
X = [[1, 1]]
y = np.array([[0]])
test_loss(X, y, W, w0, epochs=3000)
'''
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="n68SipKAWSM3" outputId="442fc919-948d-422f-d8eb-29520d45049b"
# generating random weights and bias
W = create_random_weights(3, 2)
w0 = create_random_weights(1,1)[0][0]
# given the input
X = [[1, 1]]
# and the actual value
y = np.array([[0]])
# adjust weight through gradient descent backpropagation to minimize loss
test_loss(X, y, W, w0, epochs=3000)
# + colab={"base_uri": "https://localhost:8080/"} id="XKBXAF-9XPcP" outputId="7f0076ef-dfa1-4b50-8c9b-d5fbdd4e9c4a"
# given the input data X
X = [
[0.7, 0.4],
[0.2, 0.8],
[0.3, 0.9],
[0.01, 0.01]
]
y = np.array([[0]])
# weigths
W = create_random_weights(4, 2)
w0 = -0.5516
backprop(X, y, W, w0, verbose=True)
# + [markdown] id="8-GU6p9J0e24"
# Another way of looking at the gradient descent computing is trought the chain rule, in which
#
# \begin{equation}
# \frac{ \partial J(\mathbf{W})}{\partial w_j} = \frac{ \partial J(\mathbf{W})}{\partial \hat{y_j}} \frac{\partial \hat{y}}{\partial w_j} = \frac{ \partial J(\mathbf{W})}{\partial \hat{y_j}} \frac{\partial \hat{y}}{\partial z_j} \frac{\partial z_j}{\partial w_j}
# \end{equation}
#
# In a chain operation
# \begin{equation}
# (x) \overset{w_1}{\rightarrow} (z_1) \overset{w_2}{\rightarrow} (\hat{y}) \rightarrow J(\mathbf{W})
# \end{equation}
# + [markdown] id="8qSZdZm2cSPN"
# ## Authors:
# - <NAME>
#
# ## Repository:
# https://github.com/pedroblossbraga/NeuralNets
#
# ## LICENSE:
# - MIT
| 1_Artificial_Neural_Nets.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + slideshow={"slide_type": "skip"}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
#output_notebook()
resultados = list()
ejecuciones = list()
for i in range(30):
resultados.append(pd.read_csv('./Ejecuciones/' + str(i + 1) + 'output.csv'))
resultados[i]['ejecucion'] = (i + 1)
ejecuciones.append(resultados[i].tail(200)[['ejecucion', 'aptitud']])
# + [markdown] slideshow={"slide_type": "slide"}
# # Evaluación Algoritmo Genético G9
#
# **Minimizar:**
# $$f(\vec{x})=(x_{1} − 10)^2 + 5(x_{2} − 12)^{2} + x_{3}^{4} + 3(x_{4} − 11)^2 +
# 10x_{5}^{6} + 7x_{6}^2 + x_{7}^{4} − 4x_{6}x_{7} − 10x_{6} − 8x_{7}$$
#
# Sujeta a:
#
# - $g1(\vec{x}) : −127 + 2x_{1}^{2} + 3x_{2}^{4} + x_{3} + 4x_{4}^{2} + 5x_{5} ≤ 0$
#
# - $g2(\vec{x}) : −282 + 7x_{1} + 3x_{2} + 10x_{3}^{2} + x_{4} − x_{5} ≤ 0$
#
# - $g3(\vec{x}) : −196 + 23x_{1} + x_{2}^{2} + 6x_{6}^{2} − 8x_{7} ≤ 0$
#
# - $g4(\vec{x}) : 4x_{1}^{2} + x_{2}^{2} − 3x_{1}x_{2} + 2x_{3}^2 + 5x_{6} − 11x_{7} ≤ 0$
#
# Donde $−10 ≤ x_{i} ≤ 10(i = 1, ..., 7)$.
#
# ## Características del Algoritmo
#
# - 30 ejecuciones independientes.
# - Tamaño de población = 200.
# - Número de evaluaciones máximas: 220,000.
# - **Reportar:** Mejor, mediana, peor, desviación estándar, de los mejores y gráfica de convergencia del mejor, peor y mediana.
#
# ### Ejecución
#
# ```python
# import os
# for i in range(30):
# os.system("python algoritmo_g9.py " + str((i + 1)))
#
# for i in range(30):
# os.system("mv " + str((i + 1)) + "output.csv ./Ejecuciones")
#
# ```
# + [markdown] slideshow={"slide_type": "slide"}
# ## Tabla Descriptiva de la Solución
#
# | Atributo | Solución |
# | - | - |
# | Representación | Lista de números reales |
# | Recombinación | Primeros 4 del padre o madre. Siguientes 4 mitad padre y mitad madre |
# | Probabilidad de recombinación | 1 |
# | Mutación | Generación aleatoria de número |
# | Probabilidad de mutación | 1 |
# | Selección de padres | Mejores 20 por Torneo |
# | Reemplazo | Eliminar peores 20 |
# | Tamaño de población | 200 |
# | Número de descendientes | 20 |
# | Inicialización | Aleatoria |
# | Condición de paro | Solución o 220,000 evaluaciones |
# + slideshow={"slide_type": "skip"}
df = pd.DataFrame
df = pd.concat(ejecuciones, ignore_index=True)
pd.options.display.float_format = "{:.2f}".format
TOOLTIPS = [
("Generación", "$index"),
("Aptitud del Mejor", "($y)"),
]
# + [markdown] slideshow={"slide_type": "slide"}
# ## Tabla Comparativa de las 30 Ejecuciones
# + slideshow={"slide_type": "slide"}
promedio = []
mejor = []
peor = []
desviacion = []
mediana = []
for i in range(30):
mejor.append(df.loc[df['ejecucion'] == i + 1].min().values[1])
promedio.append(df.loc[df['ejecucion'] == i + 1].mean().values[1])
desviacion.append(df.loc[df['ejecucion'] == i + 1].std().values[1])
mediana.append(df.loc[df['ejecucion'] == i + 1].median().values[1])
peor.append(df.loc[df['ejecucion'] == i + 1].max().values[1])
data = {'Número de Ejecución': list(range(1, 31)),\
'Mejor':mejor, \
'Promedio':promedio, \
'Mediana':mediana, \
'Desviación Estándar':desviacion, \
'Peor':peor}
df = pd.DataFrame(data)
df.set_index(['Número de Ejecución'], inplace=True)
df
# + [markdown] slideshow={"slide_type": "slide"}
# ## Descripción General de las Ejecuciones
# + slideshow={"slide_type": "slide"}
df.describe()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Mejor Ejecución
# + slideshow={"slide_type": "subslide"}
df_mejor = df.loc[df["Mejor"] == df["Mejor"].min()].head(1)
df_mejor
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Ejecución 26
# + slideshow={"slide_type": "subslide"}
mejor_ejecucion = df_mejor.index.values[0]
df2 = pd.read_csv('Ejecuciones/' + str(mejor_ejecucion) + 'output.csv')
promedio = []
mejor = []
peor = []
desviacion = []
mediana = []
gen = []
for i in range(len(df2['generacion'].unique().tolist())):
mejor.append(df2.loc[df2['generacion'] == i + 1].min().values[1])
promedio.append(df2.loc[df2['generacion'] == i + 1].mean().values[1])
desviacion.append(df2.loc[df2['generacion'] == i + 1].std().values[1])
mediana.append(df2.loc[df2['generacion'] == i + 1].median().values[1])
peor.append(df2.loc[df2['generacion'] == i + 1].max().values[1])
gen.append(i+1)
data = {'Generación': gen,\
'Mejor':mejor, \
'Promedio':promedio, \
'Mediana':mediana, \
'Desviación Estándar':desviacion, \
'Peor':peor}
df2 = pd.DataFrame(data)
df2.head()
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Gráfica de Convergencia
# + slideshow={"slide_type": "subslide"}
df2.plot(x='Generación', y=['Mejor'], figsize=(10,5), grid=True)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Peor Ejecución
# + slideshow={"slide_type": "subslide"}
df_peor = df.loc[df["Mejor"] == df["Peor"].max()].head(1)
df_peor
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Ejecución 22
# + slideshow={"slide_type": "subslide"}
peor_ejecucion = df_peor.index.values[0]
df3 = pd.read_csv('Ejecuciones/' + str(peor_ejecucion) + 'output.csv')
promedio = []
mejor = []
peor = []
desviacion = []
mediana = []
gen = []
for i in range(len(df3['generacion'].unique().tolist())):
mejor.append(df3.loc[df3['generacion'] == i].min().values[1])
promedio.append(df3.loc[df3['generacion'] == i].mean().values[1])
desviacion.append(df3.loc[df3['generacion'] == i].std().values[1])
mediana.append(df3.loc[df3['generacion'] == i].median().values[1])
peor.append(df3.loc[df3['generacion'] == i].max().values[1])
gen.append(i+1)
data = {'Generación': gen,\
'Mejor':mejor, \
'Promedio':promedio, \
'Mediana':mediana, \
'Desviación Estándar':desviacion, \
'Peor':peor}
df3 = pd.DataFrame(data)
df3.head()
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Gráfica de Convergencia
# + slideshow={"slide_type": "subslide"}
df3.plot(x='Generación', y=['Mejor'], figsize=(10,5), grid=True)
# -
# ## Mediana Ejecución
df_mediana = df.loc[df["Mediana"] == df["Mediana"].median()].head(1)
df_mediana
# ### Ejecución 1
# + slideshow={"slide_type": "subslide"}
mediana_ejecucion = df_mediana.index.values[0]
df4 = pd.read_csv('Ejecuciones/' + str(mediana_ejecucion) + 'output.csv')
promedio = []
mejor = []
peor = []
desviacion = []
mediana = []
gen = []
for i in range(len(df4['generacion'].unique().tolist())):
mejor.append(df4.loc[df4['generacion'] == i].min().values[1])
promedio.append(df4.loc[df4['generacion'] == i].mean().values[1])
desviacion.append(df4.loc[df4['generacion'] == i].std().values[1])
mediana.append(df4.loc[df4['generacion'] == i].median().values[1])
peor.append(df4.loc[df4['generacion'] == i].max().values[1])
gen.append(i + 1)
data = {'Generación': gen,\
'Mejor':mejor, \
'Promedio':promedio, \
'Mediana':mediana, \
'Desviación Estándar':desviacion, \
'Peor':peor}
df4 = pd.DataFrame(data)
df4.head()
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Gráfica de Convergencia
# + slideshow={"slide_type": "subslide"}
df4.plot(x='Generación', y=['Mejor'], figsize=(10,5), grid=True)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Comparación Gráficas de Convergencia
# + slideshow={"slide_type": "slide"}
fig, ax = plt.subplots(1, figsize=(10, 5))
fig.suptitle('Comparación de las Tres Ejecuciones')
ax.plot(df2['Generación'], df2['Mejor'], label="Mejor Aptitud")
ax.plot(df4['Generación'], df4['Mejor'], label="Mediana Aptitud")
plt.grid(b=True, which='major', color='#666666', linestyle='-')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.show()
# -
| Resultados-G9.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/mrdbourke/tensorflow-deep-learning/blob/main/01_neural_network_regression_in_tensorflow.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="UPgo18-N1gSi"
# # 01. Neural Network Regression with TensorFlow
#
# There are many definitions for a [regression problem](https://en.wikipedia.org/wiki/Regression_analysis) but in our case, we're going to simplify it to be: predicting a number.
#
# For example, you might want to:
# - Predict the selling price of houses given information about them (such as number of rooms, size, number of bathrooms).
# - Predict the coordinates of a bounding box of an item in an image.
# - Predict the cost of medical insurance for an individual given their demographics (age, sex, gender, race).
#
# In this notebook, we're going to set the foundations for how you can take a sample of inputs (this is your data), build a neural network to discover patterns in those inputs and then make a prediction (in the form of a number) based on those inputs.
#
# ## What we're going to cover
#
# Specifically, we're going to go through doing the following with TensorFlow:
# - Architecture of a regression model
# - Input shapes and output shapes
# - `X`: features/data (inputs)
# - `y`: labels (outputs)
# - Creating custom data to view and fit
# - Steps in modelling
# - Creating a model
# - Compiling a model
# - Defining a loss function
# - Setting up an optimizer
# - Creating evaluation metrics
# - Fitting a model (getting it to find patterns in our data)
# - Evaluating a model
# - Visualizng the model ("visualize, visualize, visualize")
# - Looking at training curves
# - Compare predictions to ground truth (using our evaluation metrics)
# - Saving a model (so we can use it later)
# - Loading a model
#
# Don't worry if none of these make sense now, we're going to go through each.
#
# ## How you can use this notebook
#
# You can read through the descriptions and the code (it should all run), but there's a better option.
#
# Write all of the code yourself.
#
# Yes. I'm serious. Create a new notebook, and rewrite each line by yourself. Investigate it, see if you can break it, why does it break?
#
# You don't have to write the text descriptions but writing the code yourself is a great way to get hands-on experience.
#
# Don't worry if you make mistakes, we all do. The way to get better and make less mistakes is to **write more code**.
# + [markdown] id="etAu7oCZ8r_G"
# ## Typical architecture of a regresison neural network
#
# The word *typical* is on purpose.
#
# # Why?
#
# Because there are many different ways (actually, there's almost an infinite number of ways) to write neural networks.
#
# But the following is a generic setup for ingesting a collection of numbers, finding patterns in them and then outputing some kind of target number.
#
# Yes, the previous sentence is vague but we'll see this in action shortly.
#
# | **Hyperparameter** | **Typical value** |
# | --- | --- |
# | Input layer shape | Same shape as number of features (e.g. 3 for # bedrooms, # bathrooms, # car spaces in housing price prediction) |
# | Hidden layer(s) | Problem specific, minimum = 1, maximum = unlimited |
# | Neurons per hidden layer | Problem specific, generally 10 to 100 |
# | Output layer shape | Same shape as desired prediction shape (e.g. 1 for house price) |
# | Hidden activation | Usually [ReLU](https://www.kaggle.com/dansbecker/rectified-linear-units-relu-in-deep-learning) (rectified linear unit) |
# | Output activation | None, ReLU, logistic/tanh |
# | Loss function | [MSE](https://en.wikipedia.org/wiki/Mean_squared_error) (mean square error) or [MAE](https://en.wikipedia.org/wiki/Mean_absolute_error) (mean absolute error)/Huber (combination of MAE/MSE) if outliers |
# | Optimizer | [SGD](https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/SGD) (stochastic gradient descent), [Adam](https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/Adam) |
#
# ***Table 1:*** *Typical architecture of a regression network.* ***Source:*** *Adapted from page 293 of [Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow Book by <NAME>](https://www.oreilly.com/library/view/hands-on-machine-learning/9781492032632/)*
#
# Again, if you're new to neural networks and deep learning in general, much of the above table won't make sense. But don't worry, we'll be getting hands-on with all of it soon.
#
# > 🔑 **Note:** A **hyperparameter** in machine learning is something a data analyst or developer can set themselves, where as a **parameter** usually describes something a model learns on its own (a value not explicitly set by an analyst).
#
# Okay, enough talk, let's get started writing code.
#
# To use TensorFlow, we'll import it as the common alias `tf` (short for TensorFlow).
# + colab={"base_uri": "https://localhost:8080/"} id="FMqsqKpk7TrH" outputId="319b5f13-6fff-47a3-fd8b-f7e85e7a67d0"
import tensorflow as tf
print(tf.__version__) # check the version (should be 2.x+)
# + [markdown] id="8clMYxrF6Mzv"
# ## Creating data to view and fit
#
# Since we're working on a **regression problem** (predicting a number) let's create some linear data (a straight line) to model.
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="G43tWFof6i7T" outputId="04bc42be-84b7-43e6-f10e-41e0a06ca1b0"
import numpy as np
import matplotlib.pyplot as plt
# Create features
X = np.array([-7.0, -4.0, -1.0, 2.0, 5.0, 8.0, 11.0, 14.0])
# Create labels
y = np.array([3.0, 6.0, 9.0, 12.0, 15.0, 18.0, 21.0, 24.0])
# Visualize it
plt.scatter(X, y);
# + [markdown] id="9ONZF8un7_xy"
# Before we do any modelling, can you calculate the pattern between `X` and `y`?
#
# For example, say I asked you, based on this data what the `y` value would be if `X` was 17.0?
#
# Or how about if `X` was -10.0?
#
# This kind of pattern discover is the essence of what we'll be building neural networks to do for us.
# + [markdown] id="zNCXxHnF6jjZ"
# ## Regression input shapes and output shapes
#
# One of the most important concepts when working with neural networks are the input and output shapes.
#
# The **input shape** is the shape of your data that goes into the model.
#
# The **output shape** is the shape of your data you want to come out of your model.
#
# These will differ depending on the problem you're working on.
#
# Neural networks accept numbers and output numbers. These numbers are typically represented as tensors (or arrays).
#
# Before, we created data using NumPy arrays, but we could do the same with tensors.
# + colab={"base_uri": "https://localhost:8080/"} id="XrXQ3m0prWXa" outputId="c8fd3447-9379-44cf-b671-ee1c0f82813f"
# Example input and output shapes of a regresson model
house_info = tf.constant(["bedroom", "bathroom", "garage"])
house_price = tf.constant([939700])
house_info, house_price
# + colab={"base_uri": "https://localhost:8080/"} id="Yi3VWKH6sRrZ" outputId="4d32f5e9-7f93-46e9-a1c1-8106d21cca39"
house_info.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="kOxyr9sR6m9X" outputId="02b5e416-6b5b-4429-b73b-0ca19f5c34e7"
import numpy as np
import matplotlib.pyplot as plt
# Create features (using tensors)
X = tf.constant([-7.0, -4.0, -1.0, 2.0, 5.0, 8.0, 11.0, 14.0])
# Create labels (using tensors)
y = tf.constant([3.0, 6.0, 9.0, 12.0, 15.0, 18.0, 21.0, 24.0])
# Visualize it
plt.scatter(X, y);
# + [markdown] id="zaPxco6E9i1_"
# Our goal here will be to use `X` to predict `y`.
#
# So our **input** will be `X` and our **output** will be `y`.
#
# Knowing this, what do you think our input and output shapes will be?
#
# Let's take a look.
# + colab={"base_uri": "https://localhost:8080/"} id="j1oT1gmB9iX-" outputId="c4aa34e4-c04c-4032-d55b-91676f199387"
# Take a single example of X
input_shape = X[0].shape
# Take a single example of y
output_shape = y[0].shape
input_shape, output_shape # these are both scalars (no shape)
# + [markdown] id="m4txxFTL_EEX"
# # Huh?
#
# From this it seems our inputs and outputs have no shape?
#
# How could that be?
#
# It's because no matter what kind of data we pass to our model, it's always going to take as input and return as ouput some kind of tensor.
#
# But in our case because of our dataset (only 2 small lists of numbers), we're looking at a special kind of tensor, more specificially a rank 0 tensor or a scalar.
# + colab={"base_uri": "https://localhost:8080/"} id="Dag5y4MPaTmc" outputId="4e041946-1095-479a-8db1-b19a390cab3f"
# Let's take a look at the single examples invidually
X[0], y[0]
# + [markdown] id="fKtihU57_cOY"
# In our case, we're trying to build a model to predict the pattern between `X[0]` equalling `-7.0` and `y[0]` equalling `3.0`.
#
# So now we get our answer, we're trying to use 1 `X` value to predict 1 `y` value.
#
# You might be thinking, "this seems pretty complicated for just predicting a straight line...".
#
# And you'd be right.
#
# But the concepts we're covering here, the concepts of input and output shapes to a model are fundamental.
#
# In fact, they're probably two of the things you'll spend the most time on when you work with neural networks: **making sure your input and outputs are in the correct shape**.
#
# If it doesn't make sense now, we'll see plenty more examples later on (soon you'll notice the input and output shapes can be almost anything you can imagine).
#
# 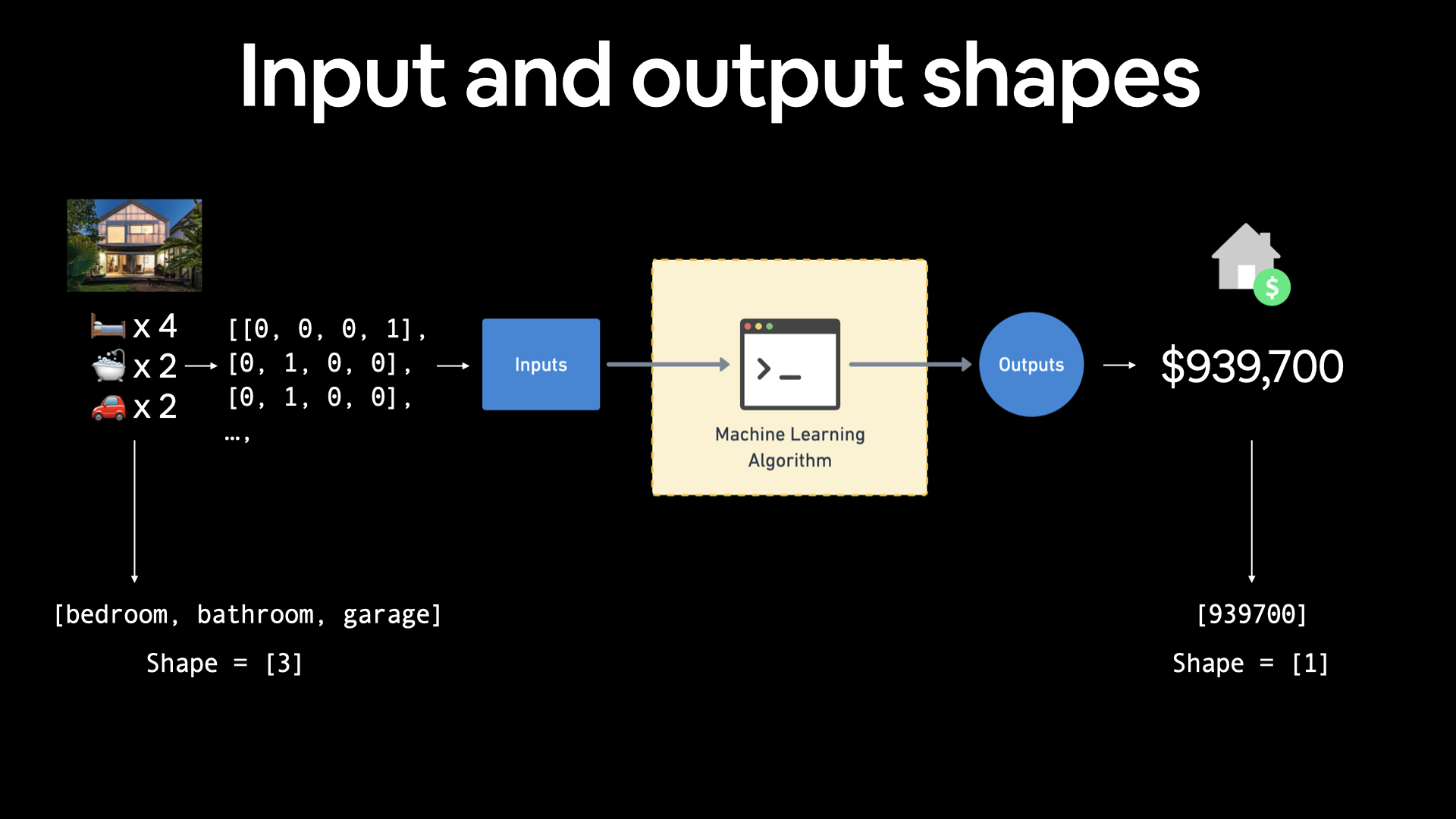
# *If you were working on building a machine learning algorithm for predicting housing prices, your inputs may be number of bedrooms, number of bathrooms and number of garages, giving you an input shape of 3 (3 different features). And since you're trying to predict the price of the house, your output shape would be 1.*
# + [markdown] id="PhAIqjrn6olF"
# ## Steps in modelling with TensorFlow
#
# Now we know what data we have as well as the input and output shapes, let's see how we'd build a neural network to model it.
#
# In TensorFlow, there are typically 3 fundamental steps to creating and training a model.
#
# 1. **Creating a model** - piece together the layers of a neural network yourself (using the [Functional](https://www.tensorflow.org/guide/keras/functional) or [Sequential API](https://www.tensorflow.org/api_docs/python/tf/keras/Sequential)) or import a previously built model (known as transfer learning).
# 2. **Compiling a model** - defining how a models performance should be measured (loss/metrics) as well as defining how it should improve (optimizer).
# 3. **Fitting a model** - letting the model try to find patterns in the data (how does `X` get to `y`).
#
# Let's see these in action using the [Keras Sequential API](https://www.tensorflow.org/api_docs/python/tf/keras/Sequential) to build a model for our regression data. And then we'll step through each.
#
# > **Note:** If you're using [TensorFlow 2.7.0](https://github.com/tensorflow/tensorflow/releases/tag/v2.7.0)+, the `fit()` function no longer upscales input data to go from `(batch_size, )` to `(batch_size, 1)`. To fix this, you'll need to expand the dimension of input data using `tf.expand_dims(input_data, axis=-1)`.
# >
# > In our case, this means instead of using `model.fit(X, y, epochs=5)`, use `model.fit(tf.expand_dims(X, axis=-1), y, epochs=5)`.
# + colab={"base_uri": "https://localhost:8080/"} id="P9jj-OE16yCn" outputId="63cf816f-16af-4867-f71a-242682033473"
# Set random seed
tf.random.set_seed(42)
# Create a model using the Sequential API
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])
# Compile the model
model.compile(loss=tf.keras.losses.mae, # mae is short for mean absolute error
optimizer=tf.keras.optimizers.SGD(), # SGD is short for stochastic gradient descent
metrics=["mae"])
# Fit the model
# model.fit(X, y, epochs=5) # this will break with TensorFlow 2.7.0+
model.fit(tf.expand_dims(X, axis=-1), y, epochs=5)
# + [markdown] id="bbjCwkEtetB9"
# Boom!
#
# We've just trained a model to figure out the patterns between `X` and `y`.
#
# How do you think it went?
# + colab={"base_uri": "https://localhost:8080/"} id="VWLpG2U3erWo" outputId="16076fb8-e754-4edb-b18b-3e5c30d6e2be"
# Check out X and y
X, y
# + [markdown] id="0ZpkaI_Oe6no"
# What do you think the outcome should be if we passed our model an `X` value of 17.0?
# + colab={"base_uri": "https://localhost:8080/"} id="X86cD66Qeo-8" outputId="29b569e6-90ce-46c7-8842-4ca69c5144a3"
# Make a prediction with the model
model.predict([17.0])
# + [markdown] id="2YoKIqhffq33"
# It doesn't go very well... it should've output something close to 27.0.
#
# > 🤔 **Question:** What's Keras? I thought we were working with TensorFlow but every time we write TensorFlow code, `keras` comes after `tf` (e.g. `tf.keras.layers.Dense()`)?
#
# Before TensorFlow 2.0+, [Keras](https://keras.io/) was an API designed to be able to build deep learning models with ease. Since TensorFlow 2.0+, its functionality has been tightly integrated within the TensorFlow library.
# + [markdown] id="qAPk1T3xgOm4"
# ## Improving a model
#
# How do you think you'd improve upon our current model?
#
# If you guessed by tweaking some of the things we did above, you'd be correct.
#
# To improve our model, we alter almost every part of the 3 steps we went through before.
#
# 1. **Creating a model** - here you might want to add more layers, increase the number of hidden units (also called neurons) within each layer, change the activation functions of each layer.
# 2. **Compiling a model** - you might want to choose optimization function or perhaps change the **learning rate** of the optimization function.
# 3. **Fitting a model** - perhaps you could fit a model for more **epochs** (leave it training for longer) or on more data (give the model more examples to learn from).
#
# 
# *There are many different ways to potentially improve a neural network. Some of the most common include: increasing the number of layers (making the network deeper), increasing the number of hidden units (making the network wider) and changing the learning rate. Because these values are all human-changeable, they're referred to as [hyperparameters](https://en.wikipedia.org/wiki/Hyperparameter_(machine_learning)) and the practice of trying to find the best hyperparameters is referred to as [hyperparameter tuning](https://en.wikipedia.org/wiki/Hyperparameter_optimization).*
#
# Woah. We just introduced a bunch of possible steps. The important thing to remember is how you alter each of these will depend on the problem you're working on.
#
# And the good thing is, over the next few problems, we'll get hands-on with all of them.
#
# For now, let's keep it simple, all we'll do is train our model for longer (everything else will stay the same).
# + colab={"base_uri": "https://localhost:8080/"} id="MI0LammMgWcN" outputId="0c01661d-6495-476a-b71e-bc63aa7e9ffe"
# Set random seed
tf.random.set_seed(42)
# Create a model (same as above)
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])
# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=["mae"])
# Fit model (this time we'll train for longer)
model.fit(tf.expand_dims(X, axis=-1), y, epochs=100) # train for 100 epochs not 10
# + [markdown] id="1CIKSm7filgj"
# You might've noticed the loss value decrease from before (and keep decreasing as the number of epochs gets higher).
#
# What do you think this means for when we make a prediction with our model?
#
# How about we try predict on 17.0 again?
# + colab={"base_uri": "https://localhost:8080/"} id="_YcacZsfi4zZ" outputId="011ee264-7e6e-47f6-cd8e-26627befb2b5"
# Remind ourselves of what X and y are
X, y
# + colab={"base_uri": "https://localhost:8080/"} id="e6k5V08ZivNO" outputId="9f703f97-1b6d-41af-b408-18a99aa6c8dc"
# Try and predict what y would be if X was 17.0
model.predict([17.0]) # the right answer is 27.0 (y = X + 10)
# + [markdown] id="sYi5V8ZYi_dy"
# Much better!
#
# We got closer this time. But we could still be better.
#
# Now we've trained a model, how could we evaluate it?
# + [markdown] id="HvC98q_h6zvG"
# ## Evaluating a model
#
# A typical workflow you'll go through when building neural networks is:
#
# ```
# Build a model -> evaluate it -> build (tweak) a model -> evaulate it -> build (tweak) a model -> evaluate it...
# ```
#
# The tweaking comes from maybe not building a model from scratch but adjusting an existing one.
#
# ### Visualize, visualize, visualize
#
# When it comes to evaluation, you'll want to remember the words: "visualize, visualize, visualize."
#
# This is because you're probably better looking at something (doing) than you are thinking about something.
#
# It's a good idea to visualize:
# * **The data** - what data are you working with? What does it look like?
# * **The model itself** - what does the architecture look like? What are the different shapes?
# * **The training of a model** - how does a model perform while it learns?
# * **The predictions of a model** - how do the predictions of a model line up against the ground truth (the original labels)?
#
# Let's start by visualizing the model.
#
# But first, we'll create a little bit of a bigger dataset and a new model we can use (it'll be the same as before, but the more practice the better).
#
# + colab={"base_uri": "https://localhost:8080/"} id="srxuqbeYopns" outputId="85d3bffc-9c4c-40e7-8223-25ff0209e395"
# Make a bigger dataset
X = np.arange(-100, 100, 4)
X
# + colab={"base_uri": "https://localhost:8080/"} id="pQcC0nSko3kJ" outputId="4fc242dc-0da9-499f-8f42-de2a0c837202"
# Make labels for the dataset (adhering to the same pattern as before)
y = np.arange(-90, 110, 4)
y
# + [markdown] id="KNIw5tgGpKjb"
# Since $y=X+10$, we could make the labels like so:
# + colab={"base_uri": "https://localhost:8080/"} id="ACgbmrAOpJwW" outputId="de9805da-e70b-4dba-ace3-b18ea0e277db"
# Same result as above
y = X + 10
y
# + [markdown] id="ax3MnQDupeBp"
# ## Split data into training/test set
#
# One of the other most common and important steps in a machine learning project is creating a training and test set (and when required, a validation set).
#
# Each set serves a specific purpose:
# * **Training set** - the model learns from this data, which is typically 70-80% of the total data available (like the course materials you study during the semester).
# * **Validation set** - the model gets tuned on this data, which is typically 10-15% of the total data available (like the practice exam you take before the final exam).
# * **Test set** - the model gets evaluated on this data to test what it has learned, it's typically 10-15% of the total data available (like the final exam you take at the end of the semester).
#
# For now, we'll just use a training and test set, this means we'll have a dataset for our model to learn on as well as be evaluated on.
#
# We can create them by splitting our `X` and `y` arrays.
#
# > 🔑 **Note:** When dealing with real-world data, this step is typically done right at the start of a project (the test set should always be kept separate from all other data). We want our model to learn on training data and then evaluate it on test data to get an indication of how well it **generalizes** to unseen examples.
# + colab={"base_uri": "https://localhost:8080/"} id="5G0RDMnZrgvK" outputId="d7bffb88-c10b-47fd-cd68-b1d678f8647f"
# Check how many samples we have
len(X)
# + colab={"base_uri": "https://localhost:8080/"} id="4Q9ptcQkrGfO" outputId="402152b7-1abe-4eae-fc85-b7aa5224e966"
# Split data into train and test sets
X_train = X[:40] # first 40 examples (80% of data)
y_train = y[:40]
X_test = X[40:] # last 10 examples (20% of data)
y_test = y[40:]
len(X_train), len(X_test)
# + [markdown] id="Rz2cIdECsLH5"
# ## Visualizing the data
#
# Now we've got our training and test data, it's a good idea to visualize it.
#
# Let's plot it with some nice colours to differentiate what's what.
# + colab={"base_uri": "https://localhost:8080/", "height": 428} id="os30CXBHsOAH" outputId="44a785b8-7535-4d44-8075-2e507e26e11a"
plt.figure(figsize=(10, 7))
# Plot training data in blue
plt.scatter(X_train, y_train, c='b', label='Training data')
# Plot test data in green
plt.scatter(X_test, y_test, c='g', label='Testing data')
# Show the legend
plt.legend();
# + [markdown] id="cxRcHZFgtS_B"
# Beautiful! Any time you can visualize your data, your model, your anything, it's a good idea.
#
# With this graph in mind, what we'll be trying to do is build a model which learns the pattern in the blue dots (`X_train`) to draw the green dots (`X_test`).
#
# Time to build a model. We'll make the exact same one from before (the one we trained for longer).
# + id="4qpe0eSStSm-"
# Set random seed
tf.random.set_seed(42)
# Create a model (same as above)
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])
# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=["mae"])
# Fit model (same as above)
#model.fit(X_train, y_train, epochs=100) # commented out on purpose (not fitting it just yet)
# + [markdown] id="hc2RHCCfqlAc"
# ## Visualizing the model
#
# After you've built a model, you might want to take a look at it (especially if you haven't built many before).
#
# You can take a look at the layers and shapes of your model by calling [`summary()`](https://www.tensorflow.org/api_docs/python/tf/keras/Model#summary) on it.
#
# > 🔑 **Note:** Visualizing a model is particularly helpful when you run into input and output shape mismatches.
# + colab={"base_uri": "https://localhost:8080/", "height": 334} id="OlgJj0cFwChH" outputId="44547880-60d0-4070-8a8e-af3ebbbcff74"
# Doesn't work (model not fit/built)
model.summary()
# + [markdown] id="SJj6KLe8xsyF"
# Ahh, the cell above errors because we haven't fit our built our model.
#
# We also haven't told it what input shape it should be expecting.
#
# Remember above, how we discussed the input shape was just one number?
#
# We can let our model know the input shape of our data using the `input_shape` parameter to the first layer (usually if `input_shape` isn't defined, Keras tries to figure it out automatically).
# + id="zMXKFtFBuWgJ"
# Set random seed
tf.random.set_seed(42)
# Create a model (same as above)
model = tf.keras.Sequential([
tf.keras.layers.Dense(1, input_shape=[1]) # define the input_shape to our model
])
# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=["mae"])
# + colab={"base_uri": "https://localhost:8080/"} id="24Q325x2yCoi" outputId="316b4790-abb8-4d16-c2a8-11087e8ca8ca"
# This will work after specifying the input shape
model.summary()
# + [markdown] id="jdurWKlryl6b"
# Calling `summary()` on our model shows us the layers it contains, the output shape and the number of parameters.
# * **Total params** - total number of parameters in the model.
# * **Trainable parameters** - these are the parameters (patterns) the model can update as it trains.
# * **Non-trainable parameters** - these parameters aren't updated during training (this is typical when you bring in the already learned patterns from other models during transfer learning).
#
# > 📖 **Resource:** For a more in-depth overview of the trainable parameters within a layer, check out [MIT's introduction to deep learning video](https://youtu.be/njKP3FqW3Sk).
#
# > 🛠 **Exercise:** Try playing around with the number of hidden units in the `Dense` layer (e.g. `Dense(2)`, `Dense(3)`). How does this change the Total/Trainable params? Investigate what's causing the change.
#
# For now, all you need to think about these parameters is that their learnable patterns in the data.
#
# Let's fit our model to the training data.
# + colab={"base_uri": "https://localhost:8080/"} id="-Kywg4q9u051" outputId="32d2564b-0383-4688-ab1c-0711573b4e2a"
# Fit the model to the training data
model.fit(X_train, y_train, epochs=100, verbose=0) # verbose controls how much gets output
# + colab={"base_uri": "https://localhost:8080/"} id="-jWuOwj961ri" outputId="5f1717a8-c183-492d-e8ef-45ad5368f9de"
# Check the model summary
model.summary()
# + [markdown] id="RrrkHEkMYh5A"
# Alongside summary, you can also view a 2D plot of the model using [`plot_model()`](https://www.tensorflow.org/api_docs/python/tf/keras/utils/plot_model).
# + colab={"base_uri": "https://localhost:8080/", "height": 201} id="liIg5WqDfdK4" outputId="05654e49-d1cc-4c5c-c80a-f9b27b552f8b"
from tensorflow.keras.utils import plot_model
plot_model(model, show_shapes=True)
# + [markdown] id="ygw7V8OVYxQS"
# In our case, the model we used only has an input and an output but visualizing more complicated models can be very helpful for debugging.
# + [markdown] id="gebj2eptqwg8"
# ## Visualizing the predictions
#
# Now we've got a trained model, let's visualize some predictions.
#
# To visualize predictions, it's always a good idea to plot them against the ground truth labels.
#
# Often you'll see this in the form of `y_test` vs. `y_pred` (ground truth vs. predictions).
#
# First, we'll make some predictions on the test data (`X_test`), remember the model has never seen the test data.
# + colab={"base_uri": "https://localhost:8080/"} id="RRzj7LJMYftb" outputId="ba064840-2194-4147-e5cd-998aa4c73933"
# Make predictions
y_preds = model.predict(X_test)
# + colab={"base_uri": "https://localhost:8080/"} id="_hKpW-KOZiAW" outputId="f31dea6e-0f76-4662-bcba-7cc64ccd8932"
# View the predictions
y_preds
# + [markdown] id="aPRaFncaZnT-"
# Okay, we get a list of numbers but how do these compare to the ground truth labels?
#
# Let's build a plotting function to find out.
#
# > 🔑 **Note:** If you think you're going to be visualizing something a lot, it's a good idea to functionize it so you can use it later.
# + id="56euC69rZvNJ"
def plot_predictions(train_data=X_train,
train_labels=y_train,
test_data=X_test,
test_labels=y_test,
predictions=y_preds):
"""
Plots training data, test data and compares predictions.
"""
plt.figure(figsize=(10, 7))
# Plot training data in blue
plt.scatter(train_data, train_labels, c="b", label="Training data")
# Plot test data in green
plt.scatter(test_data, test_labels, c="g", label="Testing data")
# Plot the predictions in red (predictions were made on the test data)
plt.scatter(test_data, predictions, c="r", label="Predictions")
# Show the legend
plt.legend();
# + colab={"base_uri": "https://localhost:8080/", "height": 428} id="Fug5_B6Ab7Ah" outputId="8ab057a0-528a-43ad-cdee-078608c58da4"
plot_predictions(train_data=X_train,
train_labels=y_train,
test_data=X_test,
test_labels=y_test,
predictions=y_preds)
# + [markdown] id="H63NPcgPcwZV"
# From the plot we can see our predictions aren't totally outlandish but they definitely aren't anything special either.
# + [markdown] id="orAfIWOrgRDA"
# ## Evaluating predictions
#
# Alongisde visualizations, evaulation metrics are your alternative best option for evaluating your model.
#
# Depending on the problem you're working on, different models have different evaluation metrics.
#
# Two of the main metrics used for regression problems are:
# * **Mean absolute error (MAE)** - the mean difference between each of the predictions.
# * **Mean squared error (MSE)** - the squared mean difference between of the predictions (use if larger errors are more detrimental than smaller errors).
#
# The lower each of these values, the better.
#
# You can also use [`model.evaluate()`](https://www.tensorflow.org/api_docs/python/tf/keras/Model#evaluate) which will return the loss of the model as well as any metrics setup during the compile step.
# + colab={"base_uri": "https://localhost:8080/"} id="DPgTdF3ddxiY" outputId="635fd3f4-00bf-4412-e959-917c831ae5bf"
# Evaluate the model on the test set
model.evaluate(X_test, y_test)
# + [markdown] id="DAXIRyVzegFd"
# In our case, since we used MAE for the loss function as well as MAE for the metrics, `model.evaulate()` returns them both.
#
# TensorFlow also has built in functions for MSE and MAE.
#
# For many evaluation functions, the premise is the same: compare predictions to the ground truth labels.
# + colab={"base_uri": "https://localhost:8080/"} id="gqoMQ0dJeD2S" outputId="f8938dff-e7d9-4a64-f99f-c62c65413f18"
# Calculate the mean absolute error
mae = tf.metrics.mean_absolute_error(y_true=y_test,
y_pred=y_preds)
mae
# + [markdown] id="7pYp3XNYfkyC"
# Huh? That's strange, MAE should be a single output.
#
# Instead, we get 10 values.
#
# This is because our `y_test` and `y_preds` tensors are different shapes.
# + colab={"base_uri": "https://localhost:8080/"} id="zeUHwOc2gIV4" outputId="b5f2e2c8-8bf9-469c-aff2-fbbca656fe54"
# Check the test label tensor values
y_test
# + colab={"base_uri": "https://localhost:8080/"} id="3aJwlTxugPyc" outputId="cfa714b2-f083-4d35-c8c0-6dc31b4a9f03"
# Check the predictions tensor values (notice the extra square brackets)
y_preds
# + colab={"base_uri": "https://localhost:8080/"} id="xolZ-lmge_ES" outputId="0ae30863-314f-4699-9ad8-951df7f4d55d"
# Check the tensor shapes
y_test.shape, y_preds.shape
# + [markdown] id="eW1qleu5gHyZ"
# Remember how we discussed dealing with different input and output shapes is one the most common issues you'll come across, this is one of those times.
#
# But not to worry.
#
# We can fix it using [`squeeze()`](https://www.tensorflow.org/api_docs/python/tf/squeeze), it'll remove the the `1` dimension from our `y_preds` tensor, making it the same shape as `y_test`.
#
# > 🔑 **Note:** If you're comparing two tensors, it's important to make sure they're the right shape(s) (you won't always have to manipulate the shapes, but always be on the look out, *many* errors are the result of mismatched tensors, especially mismatched input and output shapes).
# + colab={"base_uri": "https://localhost:8080/"} id="tVtMyw70g4aF" outputId="1345aaa4-c6da-468f-91a2-4f9151ab2a46"
# Shape before squeeze()
y_preds.shape
# + colab={"base_uri": "https://localhost:8080/"} id="qnYaBnCng-Nq" outputId="5d5a33d4-1fae-4a40-ba2f-06b93d9e208c"
# Shape after squeeze()
y_preds.squeeze().shape
# + colab={"base_uri": "https://localhost:8080/"} id="HxvVeD64hEX8" outputId="21c20781-b6cf-4d35-c6a7-c32882a9baf0"
# What do they look like?
y_test, y_preds.squeeze()
# + [markdown] id="mfUCIeHyhLk7"
# Okay, now we know how to make our `y_test` and `y_preds` tenors the same shape, let's use our evaluation metrics.
# + colab={"base_uri": "https://localhost:8080/"} id="TvjY6GIJvXBO" outputId="e5617649-57f9-4304-9b66-1f77edf74695"
# Calcuate the MAE
mae = tf.metrics.mean_absolute_error(y_true=y_test,
y_pred=y_preds.squeeze()) # use squeeze() to make same shape
mae
# + colab={"base_uri": "https://localhost:8080/"} id="EwA9nGJzvbMT" outputId="9a1c0403-36b3-4a89-f0bc-9d36a83dd8fc"
# Calculate the MSE
mse = tf.metrics.mean_squared_error(y_true=y_test,
y_pred=y_preds.squeeze())
mse
# + [markdown] id="X06oo_CIjPbL"
# We can also calculate the MAE using pure TensorFlow functions.
# + colab={"base_uri": "https://localhost:8080/"} id="YxiD6-QBYSzd" outputId="459b3159-56b8-4067-e548-dd4a2677cc9d"
# Returns the same as tf.metrics.mean_absolute_error()
tf.reduce_mean(tf.abs(y_test-y_preds.squeeze()))
# + [markdown] id="rmEho4lYofOa"
# Again, it's a good idea to functionize anything you think you might use over again (or find yourself using over and over again).
#
# Let's make functions for our evaluation metrics.
# + id="bs1Z2jgNol5f"
def mae(y_test, y_pred):
"""
Calculuates mean absolute error between y_test and y_preds.
"""
return tf.metrics.mean_absolute_error(y_test,
y_pred)
def mse(y_test, y_pred):
"""
Calculates mean squared error between y_test and y_preds.
"""
return tf.metrics.mean_squared_error(y_test,
y_pred)
# + [markdown] id="zub5zK7bcl40"
# ## Running experiments to improve a model
#
# After seeing the evaluation metrics and the predictions your model makes, it's likely you'll want to improve it.
#
# Again, there are many different ways you can do this, but 3 of the main ones are:
# 1. **Get more data** - get more examples for your model to train on (more opportunities to learn patterns).
# 2. **Make your model larger (use a more complex model)** - this might come in the form of more layers or more hidden units in each layer.
# 3. **Train for longer** - give your model more of a chance to find the patterns in the data.
#
# Since we created our dataset, we could easily make more data but this isn't always the case when you're working with real-world datasets.
#
# So let's take a look at how we can improve our model using 2 and 3.
#
# To do so, we'll build 3 models and compare their results:
# 1. `model_1` - same as original model, 1 layer, trained for 100 epochs.
# 2. `model_2` - 2 layers, trained for 100 epochs.
# 3. `model_3` - 2 layers, trained for 500 epochs.
#
# **Build `model_1`**
# + colab={"base_uri": "https://localhost:8080/"} id="StVHIIM9csyS" outputId="b9c87603-1d3f-4d74-b246-bb9f567d8fa3"
# Set random seed
tf.random.set_seed(42)
# Replicate original model
model_1 = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])
# Compile the model
model_1.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
# Fit the model
model_1.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=100)
# + colab={"base_uri": "https://localhost:8080/", "height": 465} id="A-Da56xspOrY" outputId="97967485-83f2-4463-b2e1-acfac187ac3e"
# Make and plot predictions for model_1
y_preds_1 = model_1.predict(X_test)
plot_predictions(predictions=y_preds_1)
# + colab={"base_uri": "https://localhost:8080/"} id="EXxHBAtHoSh2" outputId="7dee67ef-1c5c-4011-e332-656dece0a41b"
# Calculate model_1 metrics
mae_1 = mae(y_test, y_preds_1.squeeze()).numpy()
mse_1 = mse(y_test, y_preds_1.squeeze()).numpy()
mae_1, mse_1
# + [markdown] id="XXELOpdBrE9_"
# **Build `model_2`**
#
# This time we'll add an extra dense layer (so now our model will have 2 layers) whilst keeping everything else the same.
# + colab={"base_uri": "https://localhost:8080/"} id="05vcgEP3rEFi" outputId="36aea698-e728-4ce4-a41f-9ed0d9f7368f"
# Set random seed
tf.random.set_seed(42)
# Replicate model_1 and add an extra layer
model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tf.keras.layers.Dense(1) # add a second layer
])
# Compile the model
model_2.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
# Fit the model
model_2.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=100, verbose=0) # set verbose to 0 for less output
# + colab={"base_uri": "https://localhost:8080/", "height": 428} id="9xCbDcoDraux" outputId="5c0391b8-2bbe-4d4f-c1ea-090ee6d93ff5"
# Make and plot predictions for model_2
y_preds_2 = model_2.predict(X_test)
plot_predictions(predictions=y_preds_2)
# + [markdown] id="GxMYu5Frri6o"
# Woah, that's looking better already! And all it took was an extra layer.
# + colab={"base_uri": "https://localhost:8080/"} id="9LnPuGaBrcrP" outputId="76d99ae4-14e6-4547-86b6-3847d64af935"
# Calculate model_2 metrics
mae_2 = mae(y_test, y_preds_2.squeeze()).numpy()
mse_2 = mse(y_test, y_preds_2.squeeze()).numpy()
mae_2, mse_2
# + [markdown] id="R8i9yfQGrwHx"
# **Build `model_3`**
#
# For our 3rd model, we'll keep everything the same as `model_2` except this time we'll train for longer (500 epochs instead of 100).
#
# This will give our model more of a chance to learn the patterns in the data.
# + colab={"base_uri": "https://localhost:8080/"} id="ABGwQFsbrvUS" outputId="94ff92ba-7f6b-4ec3-db2c-c0864285205f"
# Set random seed
tf.random.set_seed(42)
# Replicate model_2
model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tf.keras.layers.Dense(1)
])
# Compile the model
model_3.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
# Fit the model (this time for 500 epochs, not 100)
model_3.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=500, verbose=0) # set verbose to 0 for less output
# + colab={"base_uri": "https://localhost:8080/", "height": 428} id="jEz4bVmasbFk" outputId="45f04bb9-3057-4f1c-c9a6-a6a038ed5701"
# Make and plot predictions for model_3
y_preds_3 = model_3.predict(X_test)
plot_predictions(predictions=y_preds_3)
# + [markdown] id="38Ki8ZHcsztG"
# Strange, we trained for longer but our model performed worse?
#
# As it turns out, our model might've trained too long and has thus resulted in worse results (we'll see ways to prevent training for too long later on).
# + colab={"base_uri": "https://localhost:8080/"} id="BPTUcFe4sbfk" outputId="4cba4687-3bf7-479d-f901-3c4d5cef0dfc"
# Calculate model_3 metrics
mae_3 = mae(y_test, y_preds_3.squeeze()).numpy()
mse_3 = mse(y_test, y_preds_3.squeeze()).numpy()
mae_3, mse_3
# + [markdown] id="UPEeM3UsrxGB"
# ## Comparing results
#
# Now we've got results for 3 similar but slightly different results, let's compare them.
# + id="mw5RZk-BqLZd"
model_results = [["model_1", mae_1, mse_1],
["model_2", mae_2, mse_2],
["model_3", mae_3, mae_3]]
# + colab={"base_uri": "https://localhost:8080/", "height": 142} id="Ip7bKH83p5X0" outputId="200a4d09-1220-4d14-8327-e3d22f768814"
import pandas as pd
all_results = pd.DataFrame(model_results, columns=["model", "mae", "mse"])
all_results
# + [markdown] id="o_AtUiwuuLGo"
# From our experiments, it looks like `model_2` performed the best.
#
# And now, you might be thinking, "wow, comparing models is tedious..." and it definitely can be, we've only compared 3 models here.
#
# But this is part of what machine learning modelling is about, trying many different combinations of models and seeing which performs best.
#
# Each model you build is a small experiment.
#
# > 🔑 **Note:** One of your main goals should be to minimize the time between your experiments. The more experiments you do, the more things you'll figure out which don't work and in turn, get closer to figuring out what does work. Remember the machine learning practitioner's motto: "experiment, experiment, experiment".
#
# Another thing you'll also find is what you thought may work (such as training a model for longer) may not always work and the exact opposite is also often the case.
#
# ## Tracking your experiments
#
# One really good habit to get into is tracking your modelling experiments to see which perform better than others.
#
# We've done a simple version of this above (keeping the results in different variables).
#
# > 📖 **Resource:** But as you build more models, you'll want to look into using tools such as:
# * [**TensorBoard**](https://tensorboard.dev/) - a component of the TensorFlow library to help track modelling experiments (we'll see this later).
# * [**Weights & Biases**](https://www.wandb.com/) - a tool for tracking all kinds of machine learning experiments (the good news for Weights & Biases is it plugs into TensorBoard).
# + [markdown] id="Fe5DgNbX6192"
# ## Saving a model
#
# Once you've trained a model and found one which performs to your liking, you'll probably want to save it for use elsewhere (like a web application or mobile device).
#
# You can save a TensorFlow/Keras model using [`model.save()`](https://www.tensorflow.org/tutorials/keras/save_and_load#save_the_entire_model).
#
# There are two ways to save a model in TensorFlow:
# 1. The [SavedModel format](https://www.tensorflow.org/tutorials/keras/save_and_load#savedmodel_format) (default).
# 2. The [HDF5 format](https://www.tensorflow.org/tutorials/keras/save_and_load#hdf5_format).
#
# The main difference between the two is the SavedModel is automatically able to save custom objects (such as special layers) without additional modifications when loading the model back in.
#
# Which one should you use?
#
# It depends on your situation but the SavedModel format will suffice most of the time.
#
# Both methods use the same method call.
# + colab={"base_uri": "https://localhost:8080/"} id="gg0jD2cUoPsg" outputId="bde421a5-d4b1-4d8e-9212-c7824f14dcc7"
# Save a model using the SavedModel format
model_2.save('best_model_SavedModel_format')
# + colab={"base_uri": "https://localhost:8080/"} id="dsCpDYrU7D1j" outputId="7f1b842b-cebb-46a7-ff9c-f6017fabf8eb"
# Check it out - outputs a protobuf binary file (.pb) as well as other files
# !ls best_model_SavedModel_format
# + [markdown] id="NGKmWco_SOEU"
# Now let's save the model in the HDF5 format, we'll use the same method but with a different filename.
# + id="97J6GJMBSM2j"
# Save a model using the HDF5 format
model_2.save("best_model_HDF5_format.h5") # note the addition of '.h5' on the end
# + colab={"base_uri": "https://localhost:8080/"} id="vB7TmsSGSjdv" outputId="a82e9aa8-2391-461c-d3d5-cf31c9d7eaed"
# Check it out
# !ls best_model_HDF5_format.h5
# + [markdown] id="OGA02tY97EUI"
# ## Loading a model
#
# We can load a saved model using the [`load_model()`](https://www.tensorflow.org/api_docs/python/tf/keras/models/load_model) method.
#
# Loading a model for the different formats (SavedModel and HDF5) is the same (as long as the pathnames to the particuluar formats are correct).
# + colab={"base_uri": "https://localhost:8080/"} id="FzyLIWfs7Fvh" outputId="9dbc900f-bc63-436b-ba1a-60cf7ed7d793"
# Load a model from the SavedModel format
loaded_saved_model = tf.keras.models.load_model("best_model_SavedModel_format")
loaded_saved_model.summary()
# + [markdown] id="MfGO0dCQTeQh"
# Now let's test it out.
# + colab={"base_uri": "https://localhost:8080/"} id="7rehN8ZxTy43" outputId="6696ffb8-7470-41aa-a83e-778c41241dfa"
# Compare model_2 with the SavedModel version (should return True)
model_2_preds = model_2.predict(X_test)
saved_model_preds = loaded_saved_model.predict(X_test)
mae(y_test, saved_model_preds.squeeze()).numpy() == mae(y_test, model_2_preds.squeeze()).numpy()
# + [markdown] id="prjkfX6rUZ6a"
# Loading in from the HDF5 is much the same.
# + colab={"base_uri": "https://localhost:8080/"} id="dQfx-bWKUfRQ" outputId="7983df59-27f5-4715-d3a4-6da88b055ebe"
# Load a model from the HDF5 format
loaded_h5_model = tf.keras.models.load_model("best_model_HDF5_format.h5")
loaded_h5_model.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="L0kT91h-Uru-" outputId="44af4a8c-7aab-468a-f6e3-e94f447610f8"
# Compare model_2 with the loaded HDF5 version (should return True)
h5_model_preds = loaded_h5_model.predict(X_test)
mae(y_test, h5_model_preds.squeeze()).numpy() == mae(y_test, model_2_preds.squeeze()).numpy()
# + [markdown] id="ABtsYBDtr5Zz"
# ## Downloading a model (from Google Colab)
#
# Say you wanted to get your model from Google Colab to your local machine, you can do one of the following things:
# * Right click on the file in the files pane and click 'download'.
# * Use the code below.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} id="JV0onjIIr9XC" outputId="328e1446-c184-40cc-d1bf-bb931b0c5cc6"
# Download the model (or any file) from Google Colab
from google.colab import files
files.download("best_model_HDF5_format.h5")
# + [markdown] id="7xpVdMtKw6X4"
# ## A larger example
#
# Alright, we've seen the fundamentals of building neural network regression models in TensorFlow.
#
# Let's step it up a notch and build a model for a more feature rich datase.
#
# More specifically we're going to try predict the cost of medical insurance for individuals based on a number of different parameters such as, `age`, `sex`, `bmi`, `children`, `smoking_status` and `residential_region`.
#
# To do, we'll leverage the pubically available [Medical Cost dataset](https://www.kaggle.com/mirichoi0218/insurance) available from Kaggle and [hosted on GitHub](https://github.com/stedy/Machine-Learning-with-R-datasets/blob/master/insurance.csv).
#
# > 🔑 **Note:** When learning machine learning paradigms, you'll often go through a series of foundational techniques and then practice them by working with open-source datasets and examples. Just as we're doing now, learn foundations, put them to work with different problems. Every time you work on something new, it's a good idea to search for something like "problem X example with Python/TensorFlow" where you substitute X for your problem.
# + id="WWK1LBxapgc2"
# Import required libraries
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt
# + id="JrnTr5N9blFo"
# Read in the insurance dataset
insurance = pd.read_csv("https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="QtXPN7cfb4Nm" outputId="d859454e-45c9-4e6a-e919-65edf4cd139b"
# Check out the insurance dataset
insurance.head()
# + [markdown] id="s55oIsYv0KkZ"
# We're going to have to turn the non-numerical columns into numbers (because a neural network can't handle non-numerical inputs).
#
# To do so, we'll use the [`get_dummies()`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.get_dummies.html) method in pandas.
#
# It converts categorical variables (like the `sex`, `smoker` and `region` columns) into numerical variables using one-hot encoding.
# + colab={"base_uri": "https://localhost:8080/", "height": 224} id="MqM_BmPkdon8" outputId="c6a4b1bf-3042-4702-bf7f-bce155e64310"
# Turn all categories into numbers
insurance_one_hot = pd.get_dummies(insurance)
insurance_one_hot.head() # view the converted columns
# + [markdown] id="zOHoPzgqgZPq"
# Now we'll split data into features (`X`) and labels (`y`).
# + id="W_EGj3FxhkAb"
# Create X & y values
X = insurance_one_hot.drop("charges", axis=1)
y = insurance_one_hot["charges"]
# + colab={"base_uri": "https://localhost:8080/", "height": 224} id="-QQFJmDn5ATV" outputId="eb53df6b-4461-4251-f1c7-47cf81c99da7"
# View features
X.head()
# + [markdown] id="kudhkM-0giS1"
# And create training and test sets. We could do this manually, but to make it easier, we'll leverage the already available [`train_test_split`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html) function available from Scikit-Learn.
# + id="WPGZGk0jhxCZ"
# Create training and test sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=0.2,
random_state=42) # set random state for reproducible splits
# + [markdown] id="W8wEC0FPglnN"
# Now we can build and fit a model (we'll make it the same as `model_2`).
# + colab={"base_uri": "https://localhost:8080/"} id="OCXTmz6oh_T6" outputId="da476651-b453-4465-d8ee-9c16961b8ce1"
# Set random seed
tf.random.set_seed(42)
# Create a new model (same as model_2)
insurance_model = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tf.keras.layers.Dense(1)
])
# Compile the model
insurance_model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
# Fit the model
insurance_model.fit(X_train, y_train, epochs=100)
# + colab={"base_uri": "https://localhost:8080/"} id="B1U7LqpKid0r" outputId="0e322c1b-6c8a-49cd-f724-67afc65bba7f"
# Check the results of the insurance model
insurance_model.evaluate(X_test, y_test)
# + [markdown] id="H9doNDToqDru"
# Our model didn't perform very well, let's try a bigger model.
#
# We'll try 3 things:
# - Increasing the number of layers (2 -> 3).
# - Increasing the number of units in each layer (except for the output layer).
# - Changing the optimizer (from SGD to Adam).
#
# Everything else will stay the same.
# + id="W59EqfqYimnR"
# Set random seed
tf.random.set_seed(42)
# Add an extra layer and increase number of units
insurance_model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(100), # 100 units
tf.keras.layers.Dense(10), # 10 units
tf.keras.layers.Dense(1) # 1 unit (important for output layer)
])
# Compile the model
insurance_model_2.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(), # Adam works but SGD doesn't
metrics=['mae'])
# Fit the model and save the history (we can plot this)
history = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)
# + colab={"base_uri": "https://localhost:8080/"} id="k9IbYWnOqmoT" outputId="eab558fc-8905-42fe-89b4-eb6576eae14c"
# Evaluate our larger model
insurance_model_2.evaluate(X_test, y_test)
# + [markdown] id="o9Rf3NosqriS"
# Much better! Using a larger model and the Adam optimizer results in almost half the error as the previous model.
#
# > 🔑 **Note:** For many problems, the [Adam optimizer](https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/Adam) is a great starting choice. See <NAME>'s "Adam is safe" point from [*A Recipe for Training Neural Networks*](http://karpathy.github.io/2019/04/25/recipe/) for more.
#
# Let's check out the loss curves of our model, we should see a downward trend.
# + colab={"base_uri": "https://localhost:8080/", "height": 279} id="9SE55ANojcF_" outputId="1c145cb3-71ef-4f0f-bf8e-26e95f3398f0"
# Plot history (also known as a loss curve)
pd.DataFrame(history.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs");
# + [markdown] id="ckHqtn0srQ5q"
# From this, it looks like our model's loss (and MAE) were both still decreasing (in our case, MAE and loss are the same, hence the lines in the plot overlap eachother).
#
# What this tells us is the loss might go down if we try training it for longer.
#
# > 🤔 **Question:** How long should you train for?
#
# > It depends on what problem you're working on. Sometimes training won't take very long, other times it'll take longer than you expect. A common method is to set your model training for a very long time (e.g. 1000's of epochs) but set it up with an [EarlyStopping callback](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/EarlyStopping) so it stops automatically when it stops improving. We'll see this in another module.
#
# Let's train the same model as above for a little longer. We can do this but calling fit on it again.
# + id="Ucs62jV8jl6N"
# Try training for a little longer (100 more epochs)
history_2 = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)
# + [markdown] id="L2FZA1z1sxxs"
# How did the extra training go?
# + colab={"base_uri": "https://localhost:8080/"} id="cxtiYB3qs0PZ" outputId="9d479dec-66d0-4e02-9b2f-316910fa7b95"
# Evaluate the model trained for 200 total epochs
insurance_model_2_loss, insurance_model_2_mae = insurance_model_2.evaluate(X_test, y_test)
insurance_model_2_loss, insurance_model_2_mae
# + [markdown] id="MzUySYEOs-O_"
# Boom! Training for an extra 100 epochs we see about a 10% decrease in error.
#
# How does the visual look?
# + colab={"base_uri": "https://localhost:8080/", "height": 279} id="BtYKSLeQjuzL" outputId="49c03b0b-a5ce-49ac-b7e8-4f9e69ea17b9"
# Plot the model trained for 200 total epochs loss curves
pd.DataFrame(history_2.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs"); # note: epochs will only show 100 since we overrid the history variable
# + [markdown] id="HS8xYkvIuVZZ"
# ## Preprocessing data (normalization and standardization)
#
# A common practice when working with neural networks is to make sure all of the data you pass to them is in the range 0 to 1.
#
# This practice is called **normalization** (scaling all values from their original range to, e.g. between 0 and 100,000 to be between 0 and 1).
#
# There is another process call **standardization** which converts all of your data to unit variance and 0 mean.
#
# These two practices are often part of a preprocessing pipeline (a series of functions to prepare your data for use with neural networks).
#
# Knowing this, some of the major steps you'll take to preprocess your data for a neural network include:
# * Turning all of your data to numbers (a neural network can't handle strings).
# * Making sure your data is in the right shape (verifying input and output shapes).
# * [**Feature scaling**](https://scikit-learn.org/stable/modules/preprocessing.html#preprocessing-scaler):
# * Normalizing data (making sure all values are between 0 and 1). This is done by subtracting the minimum value then dividing by the maximum value minus the minmum. This is also referred to as min-max scaling.
# * Standardization (making sure all values have a mean of 0 and a variance of 1). This is done by substracting the mean value from the target feature and then dividing it by the standard deviation.
# * Which one should you use?
# * **With neural networks you'll tend to favour normalization** as they tend to prefer values between 0 and 1 (you'll see this espcially with image processing), however, you'll often find a neural network can perform pretty well with minimal feature scaling.
#
# > 📖 **Resource:** For more on preprocessing data, I'd recommend reading the following resources:
# * [Scikit-Learn's documentation on preprocessing data](https://scikit-learn.org/stable/modules/preprocessing.html#preprocessing-data).
# * [Scale, Standardize or Normalize with Scikit-Learn by <NAME>](https://towardsdatascience.com/scale-standardize-or-normalize-with-scikit-learn-6ccc7d176a02).
#
# We've already turned our data into numbers using `get_dummies()`, let's see how we'd normalize it as well.
# + id="9v7P20A2d7H6"
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
# Read in the insurance dataset
insurance = pd.read_csv("https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="vir8UAIwlUOo" outputId="306bc0ed-8038-4822-b69e-c0181f5c8f88"
# Check out the data
insurance.head()
# + [markdown] id="SHMQiNosg3J3"
# Now, just as before, we need to transform the non-numerical columns into numbers and this time we'll also be normalizing the numerical columns with different ranges (to make sure they're all between 0 and 1).
#
# To do this, we're going to use a few classes from Scikit-Learn:
# * [`make_column_transformer`](https://scikit-learn.org/stable/modules/generated/sklearn.compose.make_column_transformer.html) - build a multi-step data preprocessing function for the folllowing trnasformations:
# * [`MinMaxScaler`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html) - make sure all numerical columns are normalized (between 0 and 1).
# * [`OneHotEncoder`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html) - one hot encode the non-numerical columns.
#
# Let's see them in action.
# + id="-x9JwbV0hqWh"
from sklearn.compose import make_column_transformer
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder
# Create column transformer (this will help us normalize/preprocess our data)
ct = make_column_transformer(
(MinMaxScaler(), ["age", "bmi", "children"]), # get all values between 0 and 1
(OneHotEncoder(handle_unknown="ignore"), ["sex", "smoker", "region"])
)
# Create X & y
X = insurance.drop("charges", axis=1)
y = insurance["charges"]
# Build our train and test sets (use random state to ensure same split as before)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Fit column transformer on the training data only (doing so on test data would result in data leakage)
ct.fit(X_train)
# Transform training and test data with normalization (MinMaxScalar) and one hot encoding (OneHotEncoder)
X_train_normal = ct.transform(X_train)
X_test_normal = ct.transform(X_test)
# + [markdown] id="Tz58y3nPiBJ-"
# Now we've normalized it and one-hot encoding it, what does our data look like now?
# + colab={"base_uri": "https://localhost:8080/"} id="VODt2YiziK45" outputId="0aacd372-5097-40d5-d27c-daf5cc32255a"
# Non-normalized and non-one-hot encoded data example
X_train.loc[0]
# + colab={"base_uri": "https://localhost:8080/"} id="mMYDXdwUnNVt" outputId="793a3869-9588-4861-8923-ae8adbb530fc"
# Normalized and one-hot encoded example
X_train_normal[0]
# + [markdown] id="9iI4KtfWib44"
# How about the shapes?
# + colab={"base_uri": "https://localhost:8080/"} id="SFmxzqrWntj7" outputId="e13b80e2-e9c6-443b-8178-520113ced7b9"
# Notice the normalized/one-hot encoded shape is larger because of the extra columns
X_train_normal.shape, X_train.shape
# + [markdown] id="MST951aYijTS"
# Our data is normalized and numerical, let's model it.
#
# We'll use the same model as `insurance_model_2`.
# + colab={"base_uri": "https://localhost:8080/"} id="TdHnIQqll83Y" outputId="2efbfe2f-b476-4f39-a35d-3a3f3c7fa81b"
# Set random seed
tf.random.set_seed(42)
# Build the model (3 layers, 100, 10, 1 units)
insurance_model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(100),
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
# Compile the model
insurance_model_3.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(),
metrics=['mae'])
# Fit the model for 200 epochs (same as insurance_model_2)
insurance_model_3.fit(X_train_normal, y_train, epochs=200, verbose=0)
# + [markdown] id="-DjwktO6jW41"
# Let's evaluate the model on normalized test set.
# + colab={"base_uri": "https://localhost:8080/"} id="sBcXZu9AnZfP" outputId="d42dbf4e-807b-4de2-c38c-b3cf2dbb5e70"
# Evaulate 3rd model
insurance_model_3_loss, insurance_model_3_mae = insurance_model_3.evaluate(X_test_normal, y_test)
# + [markdown] id="ZlHro290jhtX"
# And finally, let's compare the results from `insurance_model_2` (trained on non-normalized data) and `insurance_model_3` (trained on normalized data).
# + colab={"base_uri": "https://localhost:8080/"} id="ybZtnVlNjCJO" outputId="ef1d85b1-f6e5-4d54-9e9a-509040916288"
# Compare modelling results from non-normalized data and normalized data
insurance_model_2_mae, insurance_model_3_mae
# + [markdown] id="gUttViY4jzi8"
# From this we can see normalizing the data results in 10% less error using the same model than not normalizing the data.
#
# This is **one of the main benefits of normalization: faster convergence time** (a fancy way of saying, your model gets to better results faster).
#
# `insurance_model_2` may have eventually achieved the same results as `insurance_model_3` if we left it training for longer.
#
# Also, the results may change if we were to alter the architectures of the models, e.g. more hidden units per layer or more layers.
#
# But since our main goal as neural network practioners is to decrease the time between experiments, anything that helps us get better results sooner is a plus.
# + [markdown] id="NhIPO_KqocHP"
# ## 🛠 Exercises
#
# We've a covered a whole lot pretty quickly.
#
# So now it's time to have a **play around** with a few things and start to build up your initution.
#
# I emphasise the words play around because that's very important. Try a few things out, run the code and see what happens.
#
# 1. Create your own regression dataset (or make the one we created in "Create data to view and fit" bigger) and build fit a model to it.
# 2. Try building a neural network with 4 Dense layers and fitting it to your own regression dataset, how does it perform?
# 3. Try and improve the results we got on the insurance dataset, some things you might want to try include:
# * Building a larger model (how does one with 4 dense layers go?).
# * Increasing the number of units in each layer.
# * Lookup the documentation of [Adam](https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/Adam) and find out what the first parameter is, what happens if you increase it by 10x?
# * What happens if you train for longer (say 300 epochs instead of 200)?
# 4. Import the [Boston pricing dataset](https://www.tensorflow.org/api_docs/python/tf/keras/datasets/boston_housing/load_data) from TensorFlow [`tf.keras.datasets`](https://www.tensorflow.org/api_docs/python/tf/keras/datasets) and model it.
#
# + [markdown] id="AyiHG2nubmu7"
# ## 📖 Extra curriculum
#
# If you're looking for extra materials relating to this notebook, I'd check out the following:
#
# * [MIT introduction deep learning lecture 1](https://youtu.be/njKP3FqW3Sk) - gives a great overview of what's happening behind all of the code we're running.
# * Reading: 1-hour of [Chapter 1 of Neural Networks and Deep Learning](http://neuralnetworksanddeeplearning.com/chap1.html) by <NAME> - a great in-depth and hands-on example of the intuition behind neural networks.
#
# To practice your regression modelling with TensorFlow, I'd also encourage you to look through [Lion Bridge's collection of datasets](https://lionbridge.ai/datasets/) or [Kaggle's datasets](https://www.kaggle.com/data), find a regression dataset which sparks your interest and try to model.
| 2_neural_network_regression_in_tensorflow.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Conventions
#
# Here, we will outline some of the conventions used by prysm. These will be useful to understand if extending the library, or performing custom analysis.
#
# prysm uses a large number of classes which carry data and metadata about the signals with their namesakes. They can be divided loosely into two caregories,
#
# * phases
# * images
#
# Both have common properties of `x` and `y`, which are one dimensional arrays giving the gridded coordinates in x and y.
# +
# an example of a phase-type object and an image-type object
from prysm import Pupil, Slit
pu = Pupil()
sl = Slit(1, sample_spacing=0.075, samples=64)
pu.x[:3], sl.y[:3] # only first three elements for brevity
# -
# Each has an array that holds the numerical representation of the signal itself, for phaes-type objects this is `phase` and for image-type objects this is `data`. The convention is `y,x` indices, consistent with numpy. This is the opposite convention used by matlab.
pu.phase[:3,:3], sl.data[:3,:3]
# both inherit from BasicData (in fact, just about every class in prysm does) which imbues them with a brevy of properties:
from prysm._basicdata import BasicData
help(BasicData)
# prysm is a metadata-heavy library, with many functions and procedures taking a several arguments, most of which populated with sane default values. A number of these defaults can be controlled through prysm's config object,
from prysm import config
controlled_properties = [i for i in dir(config) if not i.startswith('_') and not i == 'initialized']
print(controlled_properties)
# To change the value used by prysm, simply assign to the property,
# use 32-bit floats instead of 64-bit, ~50% speedup to all operations in exchange for accuracy
config.precision = 32
#
| docs/source/user_guide/Conventions.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # How Python Manages Memory #
#
# Python is a *dynamic* language. Not only do you not need to declare the types of variables, function results/arguments and so on, but for the most part you don’t even need to worry about allocating and freeing memory for objects—Python manages that automatically.
#
# Allocating memory is easy, but when do you free up the memory? How does Python know when you have finished with an object, so the storage for it can be reclaimed?
#
# There are two common techniques for keeping track of memory allocations:
# * *Reference counting*, where the number of variables or other objects that refer to this one is stored in a field in the object. This is incremented every time a new reference to this object is stored somewhere, and decremented every time such a reference is removed (whether because it has been replaced with a reference to something else, or the containing object has been reclaimed). When this goes to zero, the object can be deleted and its storage reused.
# * *Garbage collection*, which scans through all the variables in your program, looking for what objects they hold references to, and what other objects those in turn hold references to, and so on. Any objects for which storage is allocated, but which are not encountered in such a scan, can be deallocated.
#
# CPython (which is the Python implementation in most common use, the one maintained by the Python Software Foundation and available from `python.org`, and is the one you’re using now in this notebook) uses both techniques.
# The following demonstrates how each object has a reference count attached, which can be accessed with the `sys.getrefcount()` function:
# +
import sys
class MyObj :
def __init__(self, name) :
self.name = name
#end __init__
def __repr__(self) :
return "%s(%s)" % (type(self).__name__, repr(self.name))
#end __repr__
#end MyObj
a = MyObj("a")
print("initial refcount:", sys.getrefcount(a))
b = a
print("after assigning to b:", sys.getrefcount(a))
b = None
print("after deassigning from b:", sys.getrefcount(a))
# -
# Why is the initial refcount 2 and not 1? Probably because `sys.getrefcount()`, like any normal function, needs to have another reference to the object in its function argument. Here is what the reference count looks like for an object which is created only to be passed to `sys.getrefcount()`, and then discarded:
print("refcount for throwaway object:", sys.getrefcount(MyObj("throwaway")))
# Besides the normal kind of object reference you get when you assign an object to a variable as above, there is another kind of object reference, called a *weak* reference. These are basically saying “I only want to keep this reference as long as the object actually exists, but I don’t want my reference to count towards the reasons for not deleting it”. As soon as the object disappears (because all the regular kind of references have disappeared), then any weak references to that object will also automatically disappear.
#
# Weak references have many uses, one of which is as a diagnostic tool. Here we obtain a weak reference to the object above, and as soon as the last reference to this object is overwritten, the object disappears. This uses the `weakref.ref()` function, which creates a callable that will return a strong reference to the object as long as it exists, otherwise it returns (a strong reference to) `None`:
#
# +
import weakref
c = weakref.ref(a)
print("before nulling a:", c())
a = None
print("after nulling a:", c())
# -
# Why does CPython use both memory-management techniques? The reason for this is that the two techniques have pros and cons.
#
# As you can see above, reference counting usually frees up storage quickly. If an object is only assigned to one variable, its reference count will be 1. As soon as the variable is assigned something else (or goes out of scope), the object reference count goes to 0 and the object can be freed.
#
# However, it is possible to have *reference cycles*, where object A contains a reference to object B, while object B in turn contains a reference to object A (longer chains with more than two such links are also possible); in this case, even when nothing else holds any references to either object, they each still have a reference count of 1, and so reference counting alone will not determine that they can both be freed.
#
# The following example uses a `WeakSet`, which every time it is examined will be seen to contain (strong) references to members which still exist. As those members disappear, they will also disappear from the set the next time it is examined.
a = MyObj("a")
b = MyObj("b")
c = MyObj("c")
a.link = b
b.link = a
x = weakref.WeakSet((a, b, c))
print("before losing strong refs:", list(x))
a = b = c = None
print("after losing strong refs:", list(x))
# As you can see, while the object in `c` has disappeared, even after variables `a` and `b` have lost their references to the other two interlinked objects, they haven’t gone away.
#
# The only way to get rid of such “orphaned” objects is via garbage collection. This will often happen automatically during the run of a Python program, but it is possible to force it to run:
# +
import gc
gc.collect()
print("after gc:", list(x))
# -
# A further disadvantage of reference-counting is the infamous *Global Interpreter Lock* (“GIL”) in the CPython implementation. What this means is that the CPython interpreter cannot multithread references to objects. In order to ensure that the reference counts are correctly updated, other threads have to be locked out of the interpreter, to prevent them from accessing any Python objects at the same time. So pure-Python code cannot make use of modern multi-CPU hardware, at least when running under CPython, since only one thread will be able to run at any one time!
#
# Garbage collection deals correctly with reference cycles, and it has no problem with multithreaded interpreters. So why not use it all the time, and dispense with reference-counting? The big problem is deciding when to run it. Running it frequently adds to CPU overhead. But then, running it infrequently means the program’s memory usage might grow; even though it does not need a lot of memory for live objects at any particular time, it might be allocating new objects (and forgetting old ones) at a high rate, so these will be hanging around, consuming excess memory, in-between garbage-collection runs.
#
# Some languages that rely purely on garbage collection for memory management, like Java, have to impose a limit on maximum process memory size, in order to keep the program from gobbling up all available system memory. Then this becomes another configuration chore: how big do you make the memory size? You have to decide how much is needed for “real” memory usage by objects with significant lifetimes, instead of letting the program automatically ask the system for how much it needs.
#
# CPython gives you the choice. You can rely on garbage collection if you want. Or, if you write your code carefully enough, you can exploit its use of reference-counting to keep your program’s memory usage down.
# ## Suddenly Cycles I ##
#
# Reference cycles can often be introduced in subtle ways. Consider the following very simple class, which allows the caller to attach callbacks which are invoked in response to a particular method call:
# +
class MessageHandler :
def __init__(self) :
self.handlers = []
#end __init__
def send(self, val) :
for h in self.handlers :
h[0](h[1], val)
#end for
#end send
#end MessageHandler
# -
# Looks pretty straightforward so far? Here is an example use of this class:
# +
def my_handle1(obj, val) :
print("%s got val = %s" % (repr(obj), repr(val)))
#end my_handle1
mh = MessageHandler()
mh.handlers.append((my_handle1, "some val"))
mh.send("hello 1")
# -
# Now, let’s check that discarding the only known reference to our `MessageHandler` object causes it to disappear:
w_mh = weakref.ref(mh)
print("before nulling:", w_mh())
mh = None
print("after nulling:", w_mh())
# Yup, looks good. Let’s try another use of the same class, this time passing a reference to the object itself to the callback as the first argument:
mh = MessageHandler()
mh.handlers.append((my_handle1, mh))
mh.send("hello 2")
# But watch what happens when I try to make the `MessageHandler` object go away:
w_mh = weakref.ref(mh)
print("before nulling:", w_mh())
mh = None
print("after nulling:", w_mh())
# It doesn’t go away! Why not? Can you see the reference cycle?
#
# mh → mh.handlers → [my_handle1, mh]
#
# How do we fix this? We need to break the reference cycle. How? By finding another use for weak refs, substituting one of them in place of one of the strong refs in the above chain.
# The obvious place is the parent object in the callback entry:
# +
def my_handle2(w_obj, val) :
obj = w_obj()
assert obj != None
print("%s got val = %s" % (repr(obj), repr(val)))
#end my_handle2
mh = MessageHandler()
mh.handlers.append((my_handle2, weakref.ref(mh)))
mh.send("hello 2")
# -
# As you can see, the output looks exactly the same as before.
#
# Does the `MessageHandler` now correctly go away?
w_mh = weakref.ref(mh)
print("before nulling:", w_mh())
mh = None
print("after nulling:", w_mh())
# Yes, it does!
# ## Suddenly Cycles II ##
#
# Here is another, possibly even more subtle situation I recently encountered, where a reference cycle is introduced during execution of an object’s `__del__()` method, which has the effect of bringing the object back to life.
# +
class ZombieObj :
def __init__(self, key) :
self.key = key
#end __init__
def __del__(self) :
def subdel(level) :
# doesn’t do anything useful, except demonstrate the problem
if level > 0 :
subdel(level - 1)
#end if
something = self.key
#end subdel
#begin __del__
subdel(1)
#end __del__
#end ZombieObj
obj = ZombieObj(99)
w_obj = weakref.ref(obj)
print("before nulling: %s" % repr(w_obj()))
obj = None
print("after nulling: %s" % repr(w_obj()))
# -
# You should see that the `ZombieObj` instance still remains after `obj` is set to `None`.
#
# What is happening here? It seems that the reference to the nonlocal `self` variable within the nested `subdel` function is creating references to the `ZombieObj` object that do not immediately disappear when the `__del__()` method finishes execution. Hence the object is not deleted.
#
# Try playing with the above example a bit before proceeding: does the zombie effect remain if the recursive call to `subdel` is removed? If the call is left in, but the outer call gives a `level` of 0, so the inner call never gets executed? (The answers are no and yes.)
#
# Here is a fixed version: the fix consists in explicitly passing `self` as an argument to the nested function. Does this make sense to you? All I can say is, it works ...
# +
class NonZombieObj :
def __init__(self, key) :
self.key = key
#end __init__
def __del__(self) :
def subdel(self, level) :
# doesn’t do anything useful, except demonstrate the problem
if level > 0 :
subdel(self, level - 1)
#end if
something = self.key
#end subdel
#begin __del__
subdel(self, 1)
#end __del__
#end NonZombieObj
obj = NonZombieObj(99)
w_obj = weakref.ref(obj)
print("before nulling: %s" % repr(w_obj()))
obj = None
print("after nulling: %s" % repr(w_obj()))
# -
# Now the `NonZombieObj` instance goes away when you expect it to.
# ## To Garbage Collect, Or Not To Garbage Collect? ##
#
# Given some of the intricacies in avoiding cycles with reference counting, it seems tempting to give up and simply fall back on garbage collection all the time. As mentioned, some languages (and some alternative Python implementations) already take this approach. But that doesn’t get you completely out of the woods: besides the performance and resource-usage issues already discussed, it is still possible to get memory leaks, even in a purely garbage-collected language. And they can be just as tricky to track down.
#
# But that discussion is for another day.
| How Python Manages Memory.ipynb |
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
library(ggfortify) # autoplot
library(dplyr) # select
library(ggplot2) # ggplot
library(gridExtra) # grid
library(olsrr) # hadi
# Data Load
setwd('D:/Working/03.Korea/회귀분석/Final-Report/google-play-store-apps')
gplay_data <- read.csv(file="googleplaystore.csv", header=TRUE, sep=",")
gplay_data <- subset(gplay_data, Category == "GAME") # Category 항목을 GAME 데이터만 사용
gplay_data <- subset(gplay_data, Type == "Paid") # Type 항목을 Paid 데이터만 사용
gplay_data <- subset(gplay_data, Last_Updated == "2017") # 업데이트 2017 년도의 데이터만 사용
rownames(gplay_data) <- 1:nrow(gplay_data) # index 초기화.
gplay_data <- gplay_data %>% dplyr::select(-Category, -Type, -Last_Updated) # 결정 된 항목의 열을 삭제
# 전체 적합
gplay_reg = lm(Rating ~ ., gplay_data)
summary(gplay_reg)
# +
p1 <- ols_plot_resid_stand(gplay_reg)$plot # Standardized Residuals Chart
p2 <- ols_plot_cooksd_chart(gplay_reg)$plot # Cook's D Chart
p3 <- ols_plot_dffits(gplay_reg)$plot # DFFITS
p4 <- ols_plot_hadi(gplay_reg) # H
grid.arrange(p1, p2, p3, p4, ncol=2, nrow=2)
# -
par(mfrow=c(2,2))
plot(gplay_reg)
gplay_data <- gplay_data[c(-13,-14,-19),] # 13, 14, 19 데이터 제거
gplay_reg = lm(Rating ~ ., gplay_data)
summary(gplay_reg)
par(mfrow=c(2,2))
plot(gplay_reg)
panel.cor <- function(x,y,digits=2, prefix="", cex.cor,...)
{
usr <- par("usr"); on.exit(par(usr))
par(usr=c(0,1,0,1))
r <- abs(cor(x,y))
txt <- format(c(r,0.123456789),digits=digits)[1]
txt <- paste0(prefix,txt)
if(missing(cex.cor))
cex.cor <- 1.5/strwidth(txt)
text(0.5,0.5,txt, cex=cex.cor*r)
}
# panel.cor 함수는 pairs 함수 사용할때 상관계수 크기에 따라 텍스트크기가 변하도록 해주는 사용자 정의 함수
pairs(gplay_data ,
lower.panel=function(x,y){
points(x,y);
abline(lm(y ~ x), col='red')
},
upper.panel = panel.cor
)
library(usdm)
vif(gplay_data)
gplay_paid_cor <- cor(gplay_data)
gplay_eigen <- eigen(gplay_paid_cor)$val
c_index_gplay <- sqrt(gplay_eigen[1]/gplay_eigen)
c_index_gplay
step(gplay_reg, direction="both")
gplay_data <- gplay_data %>% dplyr::select(-Installs)
vif(gplay_data)
gplay_paid_cor <- cor(gplay_data)
gplay_eigen <- eigen(gplay_paid_cor)$val
c_index_gplay <- sqrt(gplay_eigen[1]/gplay_eigen)
c_index_gplay
gplay_reg = lm(Rating ~ ., gplay_data)
summary(gplay_reg)
par(mfrow=c(2,2))
plot(gplay_reg)
autoplot(gplay_reg
, colour = "black"
, label.colour ="red"
, smooth.colour = "blue"
, ad.colour = "red")
| 1st semester/01.LinearRegression/Final-Test/Final-GooglePlay-Game.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Data exploration, feature engineering и prediction с линейна регресия.
# ### Разгледан [dataset](https://www.kaggle.com/thec03u5/fifa-18-demo-player-dataset/data) от Kaggle съдържа информация за атрибутите на над 17 хиляди футболисти в играта Fifa 18.
# Нека първо добавим нужните библиотеки и други неща.
# +
import sys
import sklearn
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import warnings
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.linear_model import (LinearRegression, Ridge, Lasso)
from sklearn.ensemble import RandomForestRegressor
# %matplotlib inline
warnings.filterwarnings('ignore')
pd.options.display.max_rows = 20
# -
# Целият dataset съдържа 4 файла. Ние ще използваме *CompleteDataset.csv*
#
# Нека да заредим и видим данните.
data = pd.read_csv('../data/fifa/CompleteDataset.csv', index_col=0, low_memory=False)
data
# Нека видим какви колони имаме и какви са техните стойности.
data.info()
# Нека проверим за NaN/Null стойности.
data.isnull().sum().sort_values()
# Доста постоянно число на липсващи данни.
2029 / data.shape[0]
# Около 11%. От първото принтиране на данните забелязваме, че записите на индекси 4 и 6 съдържат NaN. Това са [<NAME>](https://en.wikipedia.org/wiki/Manuel_Neuer) и [de Gea](https://en.wikipedia.org/wiki/David_de_Gea), които са вратари. Дали това не важи за всички вратари?
data.loc[data['Preferred Positions'] == 'GK ']
# Точно 2029. Явно всички вратари нямат рейтинг за различните позиции. Доста трудно бихме попълнили тези колони. Нека се ограничим до използването на качесвените характеривики за всеки футболист.
#
# Това са следните колони от Acceleration до Volleys.
#
# Нека си ги запишем в някаква променлива.
data.columns
attributes = ['Acceleration', 'Aggression', 'Agility', 'Balance', 'Ball control', 'Composure',
'Crossing', 'Curve', 'Dribbling', 'Finishing', 'Free kick accuracy', 'GK diving',
'GK handling', 'GK kicking', 'GK positioning', 'GK reflexes', 'Heading accuracy',
'Interceptions', 'Jumping', 'Long passing', 'Long shots', 'Marking', 'Penalties',
'Positioning', 'Reactions', 'Short passing', 'Shot power', 'Sliding tackle',
'Sprint speed', 'Stamina', 'Standing tackle', 'Strength', 'Vision', 'Volleys']
# Целта ни е на база на тези качества за всеки футболист да предвидим неговия рейтинг (Overall). Нека видим разпределението на Overall.
sns.distplot(data['Overall'])
# Изглежда доста равномерно разпределено. Да видим атрибутите.
data[attributes].info()
# Очаквахме числови стойности, а колоните са от тип object.
# Нека видим какви стойности се съдържат в произволна колона.
data['Jumping'].unique()
# Явно някой не си е сметнал стойностите.
# Нека преобразуваме колоните до числов тип. Но преди това проверка за NaN/Null.
# +
player_attributes_df = data[attributes]
player_attributes_df.isnull().sum().sort_values()
# -
for attribute in player_attributes_df.columns:
player_attributes_df[attribute] = player_attributes_df[attribute].apply(lambda x: eval(str(x)))
# Нека проверим дали колоните вече съдържат числови стойности.
player_attributes_df.info()
# Изглежда наред. Да проверим за NaN/Null стойности.
player_attributes_df.isnull().sum().sort_values()
# Да добавим колона за рейтинг и да пробваме линейна регресия.
player_attributes_df['Overall'] = data.Overall
def data_and_target(df):
X = df
X = X.drop('Overall',1)
y = df['Overall']
print('X shape: {}, y shape {}'.format(X.shape, y.shape))
return (X, y)
(X, y) = data_and_target(player_attributes_df)
# +
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=12345)
y_train.mean(), y_test.mean()
# -
model = LinearRegression().fit(X_train, y_train)
print("train score:", model.score(X_train, y_train))
print("test score: ", model.score(X_test, y_test))
# Доста добре. Всеки футболист обаче играе на определена позиция. Нека разгледаме колоната preferred position.
data['Preferred Positions'].unique()
data['Preferred Positions']
# Забелязваме, че някой футболисти имат по повече от една предпочитана позиция.
# Нека вземем всички уникални позиции.
positions = set(''.join(data['Preferred Positions'].unique()).split())
positions
# Нека добавим колоната за предпочината позиция като преобразуваме string до списък с предпочитани позиции.
player_attributes_df['Preferred Positions'] = data['Preferred Positions'].str[0:-1].str.split(' ').astype('object')
player_attributes_df['Preferred Positions']
# Това изглежда добре. Нека да one-hot-нем предпочината позиция.
#
# Първо ще създадем колоните за всяка позиция и ще ги попълним с 0.
#
# След това ще сложим 1 само на позициите, на които футболистът предпочита да играе.
# +
player_attributes_df_enc = player_attributes_df
positions = list(positions)
positions.sort()
for position in positions:
player_attributes_df_enc[position] = 0.0
for index, row in player_attributes_df_enc.iterrows():
for position in row['Preferred Positions']:
player_attributes_df_enc.set_value(index, position, 1.0)
player_attributes_df_enc = player_attributes_df_enc.drop('Preferred Positions', 1)
# -
# На ред 17972 - футболистът имаше следните предпочитани позиции \[CB, LW, LWB, LB\]. Нека видим дали нашия one-hot e сработил.
player_attributes_df_enc[player_attributes_df_enc.index == 17972][positions]
# Да тренираме отново.
(X, y) = data_and_target(player_attributes_df_enc)
# +
(X_train, X_test, y_train, y_test) = train_test_split(X, y, random_state=12345)
y_train.mean(), y_test.mean()
# -
model = LinearRegression().fit(X_train, y_train)
print("train score:", model.score(X_train, y_train))
print("test score: ", model.score(X_test, y_test))
# Подобрихме с около 3%
#
# Нека видим, кои колони не сме използвали.
set(data.columns) - (set(player_attributes_df_enc.columns) | set('Preferred Positions'))
# Възрастта, стойността и заплатата на футболиста изглеждат интересни колони.
#
# Нека пробваме.
player_attributes_df_enc['Age'] = data['Age']
player_attributes_df_enc['Value'] = data['Value']
player_attributes_df_enc['Wage'] = data['Wage']
# Нека видим какво се съдържа в тях.
player_attributes_df_enc['Age'].unique()
sns.factorplot('Age', 'Overall', data=player_attributes_df_enc, size=10);
# Забелязваме някаква аномалия около 44 години. Нека видим какви са тези футболисти.
player_attributes_df_enc[player_attributes_df_enc['Age'] == 44][positions]
# Явно са вратари. Понякога вратарите играят на добро ниво и в напреднала футболна възраст. Приемаме го за нормално.
player_attributes_df_enc['Value'].unique()
# Очевидно имаме някой футболисти, които струват милиони, някой хиляди а някой са доста евтини.
# Нека превърнем тези стойности до числови.
player_attributes_df_enc['Value'] = data['Value'].apply(lambda x: float(x[1:-1]) * 10**6 if x[-1] == 'M'
else float(x[1:-1]) * 10**3 if x[-1] == 'K'
else float(x[1:]))
sns.factorplot('Value', 'Overall', data=player_attributes_df_enc, size=8);
# Футболистите с висок рейтинг са скъпи. Закономерно. Но има футболисти с висок рейтинг и ниска цена. Нека видим дали има такив с цена €0.
player_attributes_df_enc[player_attributes_df_enc['Value'] == 0]['Overall'].mean()
# Ред е на заплатите.
player_attributes_df_enc['Wage'].unique()
player_attributes_df_enc['Wage'] = data['Wage'].apply(lambda x: float(x[1:-1]) * 10**3
if x[-1] == 'K'
else float(x[1:]))
sns.factorplot('Wage', 'Overall', data=player_attributes_df_enc, size=8);
# При заплатите положението изглежда същото. Нека видим колко получават заплата €0.
len(player_attributes_df_enc[player_attributes_df_enc['Wage'] == 0])
# Нека тренираме отново.
(X, y) = data_and_target(player_attributes_df_enc)
# +
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=12345)
y_train.mean(), y_test.mean()
# -
model = LinearRegression().fit(X_train, y_train)
print("train score:", model.score(X_train, y_train))
print("test score: ", model.score(X_test, y_test))
# Подобрихме с 1.5%.
# Нека разгледаме колоната Special. Създава усещатането, че е просто сумата на всички атрибути. Нека проверим.
player_attributes_df_enc[attributes].sum(axis=1) - data['Special']
# Нека приложим разликата на тези като наша колона за Special
player_attributes_df_enc['Special'] = player_attributes_df_enc[attributes].sum(axis=1) - data['Special']
# Да тренираме.
(X, y) = data_and_target(player_attributes_df_enc)
# +
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=12345)
y_train.mean(), y_test.mean()
# -
model = LinearRegression().fit(X_train, y_train)
print("train score:", model.score(X_train, y_train))
print("test score: ", model.score(X_test, y_test))
# Почти без промяна. Нека пробваме без футболистите оценени на €0 и със заплата €0.
player_attributes_df_enc = player_attributes_df_enc.drop(player_attributes_df_enc[player_attributes_df_enc['Value'] == 0].index)
player_attributes_df_enc = player_attributes_df_enc.drop(player_attributes_df_enc[player_attributes_df_enc['Wage'] == 0].index)
(X, y) = data_and_target(player_attributes_df_enc)
# +
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=12345)
y_train.mean(), y_test.mean()
# -
model = LinearRegression().fit(X_train, y_train)
print("train score:", model.score(X_train, y_train))
print("test score: ", model.score(X_test, y_test))
# Почти без промяна. Нека пробваме някаква регуляризация.
# +
alphas = [0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
for alpha in alphas:
model = Ridge(alpha = alpha).fit(X_train, y_train)
print('alpha = ', alpha)
print("train score:", model.score(X_train, y_train))
print("test score: ", model.score(X_test, y_test))
# -
# Без промяна. Lasso?
# +
alphas = [0.0001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
for alpha in alphas:
lasso = Lasso(alpha = alpha, max_iter=100000).fit(X_train, y_train)
print('alpha = ', alpha)
print("Features used: {}/{}".format(np.sum(lasso.coef_ != 0), np.shape(X_train)[1]))
print("train score:", lasso.score(X_train, y_train))
print("test score: ", lasso.score(X_test, y_test))
# -
# Регуляризацията не помогна. Нека пробваме с гора.
# +
forest = RandomForestRegressor(criterion='mse',
min_samples_leaf=3,
min_samples_split=3,
max_depth=50,
n_estimators=20)
forest.fit(X_train, y_train)
print('train score: {}'.format(forest.score(X_train, y_train)))
print('test score: {}'.format(forest.score(X_test, y_test)))
# -
# Явно нашата гора разгада тайната формула на [EA sports](https://en.wikipedia.org/wiki/EA_Sports) за изчисляване на рейтинга на футболистите в играта.
# Нека видим теглата на feature-ите.
def linear_regression_features(X, model):
plt.figure(figsize=(12,8))
barplot = sns.barplot(x=X.columns, y=model.coef_, orient='vertical')
plt.setp(barplot.get_xticklabels(), rotation=90)
plt.grid(True)
# Преди това да нормализираме всички feature-и, за да видидим равнопоставени тегла.
# +
player_attributes_df_norm = (player_attributes_df_enc - player_attributes_df_enc.mean()) / (player_attributes_df_enc.max() - player_attributes_df_enc.min())
(X, y) = data_and_target(player_attributes_df_norm)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=12345)
model = LinearRegression().fit(X_train, y_train)
print("train score:", model.score(X_train, y_train))
print("test score: ", model.score(X_test, y_test))
# -
linear_regression_features(X, model);
| notebooks/Fifa18-explore.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Agenda:
#
# - What is micropython
#
# ### Using MicroPython
#
# #### micropython-lib
# ### Getting started
#
# - ampy
# - webrepl
# - upip
#
# #### compiling:
# - modules/: pre-compiled and frozen into the runtime
# - scripts/: source frozen into the runtime
#
#
# ### Demo
#
# - boot.py, main.py
# - WLAN
# - HTTP server (done)
# - MQTT (done)
# - deep sleep?
# - External interrupts
# - Beeper (irq)
# - 8x8 matrix display (SPI)
# - microSD
# - Music (PWM)
# - Tank (ADC)
# - Asyncio
# - src/NDC demo/tank_async.py
# ### Network (WLAN)
#
# http://claytondarwin.com/projects/ESP32/MicroPython/#C4toc
| OVERVIEW.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + pycharm={"is_executing": false}
import pandas as pd
import numpy as np
import csv
import string
import nltk
import re
import time
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
import os
import matplotlib.pyplot as plt
import seaborn as sns
from nltk.corpus import stopwords
from nltk.stem.snowball import SnowballStemmer
from sklearn.feature_extraction.text import CountVectorizer
import sys
import warnings
from os import path
import ast
from PIL import Image
from wordcloud import WordCloud, STOPWORDS, ImageColorGenerator
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from skmultilearn.problem_transform import BinaryRelevance
from skmultilearn.problem_transform import LabelPowerset
from skmultilearn.problem_transform import ClassifierChain
from sklearn.preprocessing import MultiLabelBinarizer
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import f1_score, average_precision_score, precision_recall_fscore_support
from sklearn.metrics import accuracy_score
from sklearn.metrics import multilabel_confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import zero_one_loss
from sklearn.metrics import jaccard_score
import sklearn.metrics as skm
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy as np
from sklearn.multiclass import OneVsRestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
import time
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import StratifiedKFold
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
from skmultilearn.adapt import MLkNN
from sklearn.model_selection import GridSearchCV
from sklearn.svm import LinearSVC
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from skmultilearn.adapt import BRkNNaClassifier
from sklearn.linear_model import RidgeClassifierCV
pd.options.display.max_seq_items = 2000
pd.options.display.max_colwidth = 90
pd.options.display.max_rows = 999
loggingFile = './experiment//TitleBody3GramTFIDF.txt'
binaryBodyTitle = './experiment/binaryBodyTitle.csv'
template = './experiment/dfTeste.csv'
# -
#organizing data_frame to issue order
def organize():
data_classes = pd.read_csv(binaryBodyTitle, header = 0, sep=";")
data_classes
del data_classes['prIssue']
del data_classes['issueTitle']
del data_classes['issueBody']
data_classes.rename(columns={'issueComments': 'prComments','Comments': 'prCodeReviewComments','issueTitleLink': 'issueTitle','issueBodyLink': 'issueBody','issueCommentsLink': 'issue_Comments','pr': 'prNumber','issue': 'issueNumber', 'Title': 'prTitle','Body': 'prBody'}, inplace=True)
categories = data_classes.columns.values.tolist()
data_classes = data_classes[['issueNumber', 'prNumber', 'issueTitle', 'issueBody', 'issue_Comments',
'prTitle','prBody','prComments','prCodeReviewComments','commitMessage','isPR','isTrain',
'Google Common','Test','SO','IO','UI','Network','Security',
'OpenOffice Documents','Database','Utils','PDF','Logging','Latex']]
data_classes['issueNumber'] = data_classes['issueNumber'].astype('Int64')
return data_classes
# +
#data_classes = organize()
# -
#Filtering issues with PRs
def filtering(data_classes):
IssuePRDataset = data_classes[data_classes["isTrain"] == 0]
#invalid number of issue = NaN
IssuePRDataset = IssuePRDataset.drop([1805])
categories = IssuePRDataset.columns.values.tolist()
return categories, IssuePRDataset
# +
#categories, IssuePRDataset = filtering(data_classes)
# -
# RQ1.a - o quão sensível o resultado é em relação ao algoritmo?
#vários algoritmos - BinaryRelevance
#todas as palavras, bootstrap, unigram
#somente o título
def dataset_config(IssuePRDataset):
data_test1 = IssuePRDataset[['issueNumber','prNumber','issueTitle','Google Common', 'Test', 'SO', 'IO', 'UI', 'Network', 'Security',
'OpenOffice Documents', 'Database', 'Utils', 'PDF', 'Logging', 'Latex']].copy()
data_test1["corpus"] = data_test1["issueTitle"].map(str)
del data_test1["issueTitle"]
#removing utils because we won't to predict a so simple API that is basically used in all PRs
del data_test1["Utils"]
data_test1 = data_test1.reset_index(drop=True)
return data_test1
# +
#data_test1 = dataset_config(IssuePRDataset)
# +
#preprocessing text
#We first convert the comments to lower-case
#then use custom made functions to remove html-tags, punctuation and non-alphabetic characters from the TitleBody.
def clean_data(data_test1):
if not sys.warnoptions:
warnings.simplefilter("ignore")
def cleanHtml(sentence):
cleanr = re.compile('<.*?>')
cleantext = re.sub(cleanr, ' ', str(sentence))
return cleantext
def cleanPunc(sentence): #function to clean the word of any punctuation or special characters
cleaned = re.sub(r'[?|!|\'|"|#]',r'',sentence)
cleaned = re.sub(r'[.|,|)|(|\|/]',r' ',cleaned)
cleaned = cleaned.strip()
cleaned = cleaned.replace("\n"," ")
return cleaned
def keepAlpha(sentence):
alpha_sent = ""
for word in sentence.split():
alpha_word = re.sub('[^a-z A-Z]+', ' ', word)
alpha_sent += alpha_word
alpha_sent += " "
alpha_sent = alpha_sent.strip()
return alpha_sent
#function pra remover palavras com menos de 3 tokens
data_test1['corpus'] = data_test1['corpus'].str.lower()
data_test1['corpus'] = data_test1['corpus'].apply(cleanHtml)
data_test1['corpus'] = data_test1['corpus'].apply(cleanPunc)
data_test1['corpus'] = data_test1['corpus'].apply(keepAlpha)
return data_test1
# +
#data_test1 = clean_data(data_test1)
# +
#### removing stopwords
def remove_stop_words():
stop_words = set(stopwords.words('english'))
stop_words.update(['pr','zero','one','two','three','four','five','six','seven','eight','nine','ten','may','also','across','among','beside','however','yet','within','jabref','org','github','com','md','https','ad','changelog','','joelparkerhenderson','localizationupd',' localizationupd','localizationupd ','i', 'me', 'my', 'myself', 'we', 'our', 'ours', 'ourselves', 'you', 'your', 'yours', 'yourself', 'yourselves', 'he', 'him', 'his', 'himself', 'she', 'her', 'hers', 'herself', 'it', 'its', 'itself', 'they', 'them', 'their', 'theirs', 'themselves', 'what', 'which', 'who', 'whom', 'this', 'that', 'these', 'those', 'am', 'is', 'are', 'was', 'were', 'be', 'been', 'being', 'have', 'has', 'had', 'having', 'do', 'does', 'did', 'doing', 'a', 'an', 'the','Mr', 'and', 'but', 'if', 'or', 'because', 'as', 'until', 'while', 'of', 'at', 'by', 'for', 'with', 'about', 'against', 'between', 'into', 'through', 'during', 'before', 'after', 'above', 'below', 'to', 'from', 'up', 'down', 'in', 'out', 'on', 'off', 'over', 'under', 'again', 'further', 'then', 'once', 'here', 'there', 'when', 'where', 'why', 'how', 'all', 'any', 'both', 'each', 'few', 'more', 'most', 'other', 'some', 'such', 'no', 'nor', 'not', 'only', 'own', 'same', 'so', 'than', 'too', 'very', 's', 't', 'can', 'will', 'just', 'don', 'should', 'now'])
#stop_words.update(['i', 'me", "my", "myself", "we", "our", "ours", "ourselves", "you", "your", "yours", "yourself", "yourselves", "he", "him", "his", "himself", "she", "her", "hers", "herself", "it", "its", "itself", "they", "them", "their", "theirs", "themselves", "what", "which", "who", "whom", "this", "that", "these", "those", "am", "is", "are", "was", "were", "be", "been", "being", "have", "has", "had", "having", "do", "does", "did", "doing", "a", "an", "the","Mr", "and", "but", "if", "or", "because", "as", "until", "while", "of", "at", "by", "for", "with", "about", "against", "between", "into", "through", "during", "before", "after", "above", "below", "to", "from", "up", "down", "in", "out", "on", "off", "over", "under", "again", "further", "then", "once", "here", "there", "when", "where", "why", "how", "all", "any", "both", "each", "few", "more", "most", "other", "some", "such", "no", "nor", "not", "only", "own", "same", "so", "than", "too", "very", "s", "t", "can", "will", "just", "don", "should", "now"])
re_stop_words = re.compile(r"\b(" + "|".join(stop_words) + ")\\W", re.I)
return re_stop_words
# +
#re_stop_words = remove_stop_words()
# +
def removeStopWords(sentence, re_stop_words):
#global re_stop_words
#print(sentence)
return re_stop_words.sub(" ", sentence)
#removing words with less than 3 characters
#data_classes['titleBody'] = data_classes['titleBody'].str.findall('\w{3,}').str.join(' ')
# -
#data_test1['corpus'] = data_test1['corpus'].apply(removeStopWords, re_stop_words=re_stop_words)
def apply_stem(data_test1):
stemmer = SnowballStemmer("english")
def stemming(sentence):
stemSentence = ""
for word in sentence.split():
stem = stemmer.stem(word)
stemSentence += stem
stemSentence += " "
stemSentence = stemSentence.strip()
return stemSentence
data_test1['corpus'] = data_test1['corpus'].apply(stemming)
print(data_test1['corpus'])
return data_test1
# +
#data_test1 = apply_stem(data_test1)
# -
#TF-ID
def run_tf_idf(data, configurationTFIDF, num_feature, tfIDFoutputFile):
#we need to text max_feature with 10, 20, 25, 50
#, max_features=num_feature
vectorizer = TfidfVectorizer(strip_accents='unicode', analyzer='word', ngram_range = configurationTFIDF, max_features=num_feature)
tf_idf_results = vectorizer.fit_transform(data['corpus'])
features = vectorizer.get_feature_names()
print(features)
scores = (tf_idf_results.toarray())
output_tf_idf = pd.DataFrame(scores)
output_tf_idf = pd.concat([data['issueNumber'], output_tf_idf], axis=1)
output_tf_idf.to_csv(tfIDFoutputFile, encoding='utf-8', header=False, index=False, sep=',')
# remove words occuring less than 5 times
#tfidf = TfidfVectorizer(min_df=5)
#you can also remove common words:
# remove words occuring in more than half the documents
#tfidf = TfidfVectorizer(max_df=0.5)
#you can also remove stopwords like this:
# +
#use one of the data_test's (1 to 11) e.g data_test5
#run_tf_idf(data_test1, configurationTFIDF, num_feature, tfIDFoutputFile)
# +
#analyzing frequency of TOP 50 terms
def analyze_top(data, termFrequencyTop50):
docs = data['corpus'].tolist()
cv = CountVectorizer()
cv_fit=cv.fit_transform(docs)
#print(cv.get_feature_names())
#print(cv_fit.toarray())
word_list = cv.get_feature_names()
count_list = cv_fit.toarray().sum(axis=0)
term_frequency = dict(zip(word_list,count_list))
a = sorted(term_frequency.items(), key=lambda x: x[1], reverse=True)
top50 = a[:100]
df_frequency = pd.DataFrame(top50, columns =['term', 'frequency'])
print(df_frequency)
df_frequency.to_csv(termFrequencyTop50, encoding='utf-8', header=False, index=False, sep=',')
sns.set(font_scale = 2)
plt.figure(figsize=(18,17))
plt.xticks(rotation=90)
plt.title("Frequency of terms ")
plt.ylabel('term', fontsize=20)
plt.xlabel('frequency', fontsize=20)
ax = sns.barplot(x="frequency", y="term", data=df_frequency)
return docs
# +
#docs = analyze_top(data_test1, termFrequencyTop50)
# -
#merging features TF-IDF with data_frame
def merging(data_test1, tfIDFoutputFile):
feature = pd.read_csv(tfIDFoutputFile, header=None, sep=",")
feature.rename(columns={0: 'issueNumber'}, inplace=True)
data_classifier = data_test1.join(feature, lsuffix='issueNumber', rsuffix='issueNumber')
categories = data_classifier.columns.values.tolist()
return data_classifier, categories
# +
#data_classifier, categories = merging(data_test1)
# -
def eval_metrics(predictions, probabilities, y_test):
y_pred = predictions.values
y_proba = probabilities.values
#receiving the y_test true value from each pull request
y_true = y_test.to_numpy()
print("Accuracy Score")
acc_ml = accuracy_score(y_true, y_pred)
print(acc_ml)
print("---------")
print("")
print("Accuracy Score not normalized")
acc_score = accuracy_score(y_true, y_pred, normalize=False)
print(acc_score)
print("---------")
print("")
print("zero_one_loss")
zeroOne = zero_one_loss(y_true, y_pred)
print(zeroOne)
print("---------")
print("")
print("Fmeasure Score")
fmeasure_score = f1_score(y_true,y_pred, average='micro')
#fmeasure_score = f1_score(y_true,y_pred, average='macro')
print(fmeasure_score)
print("---------")
print("")
#AUC-PR
print("AUC-PR")
pr_score = average_precision_score(y_true,y_proba,average='micro')
print(pr_score)
#pr_score = average_precision_score(y_true,y_proba,average='macro')
print("---------")
print("")
print("hamming loss average")
hamming_loss = skm.hamming_loss(y_true, y_pred)
print(hamming_loss)
print("---------")
print("")
print("Jaccard samples")
jaccard_score_samples = jaccard_score(y_true, y_pred, average='samples')
print(jaccard_score_samples)
print("---------")
print("")
print("Jaccard macro")
jaccard_macro = jaccard_score(y_true, y_pred, average='micro')
print(jaccard_macro)
#jaccard_score(y_true, y_pred, average=None)
print("---------")
print("")
return y_true, y_proba, y_pred, acc_ml, acc_score, zeroOne, fmeasure_score, pr_score, hamming_loss, jaccard_score_samples, jaccard_macro
def plot_classes(probability, y_true, y_test):
precision = dict()
recall = dict()
average_precision = dict()
n_classes = y_test.shape[1]
for i in range(n_classes):
precision[i], recall[i], _ = precision_recall_curve(y_true[:, i], probability[:, i])
average_precision[i] = average_precision_score(y_true[:, i], probability[:, i])
precision["micro"], recall["micro"], _ = precision_recall_curve(y_true.ravel(),probability.ravel())
average_precision["micro"] = average_precision_score(y_true, probability, average="micro")
print('Average precision score, micro-averaged over all classes: {0:0.2f}'
.format(average_precision["micro"]))
plt.figure()
plt.step(recall['micro'], precision['micro'], where='post')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title(
'Average precision score, micro-averaged over all classes: AP={0:0.2f}'
.format(average_precision["micro"]))
import io
def confusion_matrix(y_true, y_pred, confusionMatrix, i):
data = multilabel_confusion_matrix(y_true, y_pred)
labels = ['Google Common', 'Test', 'SO', 'IO', 'UI', 'Network',
'Security', 'OpenOffice Documents', 'Database','PDF',
'Logging','Latex']
metrics = pd.DataFrame()
line = []
dataLine = ""
dataLine = "Label, TN, FP, FN, TP"
line.append((dataLine))
for j in range (0,12):
print(j)
row = data[j]
dataLine=""
dataLine = labels[j]
print(dataLine)
for x in np.nditer(row):
dataLine = dataLine + "," + str(x)
print(dataLine)
line.append((dataLine))
print(line)
metrics = pd.DataFrame(line)
metrics.to_csv(confusionMatrix + str(i) +'.csv' , encoding='utf-8', header=True, index=False , sep=',')
# +
#build the model
def build_model(test_type):
if test_type == "DecisionTree":
clf = BinaryRelevance(classifier=DecisionTreeClassifier(), require_dense = [False, True])
#clf = ClassifierChain(classifier=DecisionTreeClassifier(), require_dense = [False, True])
if test_type == "LogisticRegression":
clf = BinaryRelevance(classifier=LogisticRegression(random_state=0), require_dense = [False, True])
#clf = ClassifierChain(classifier=LogisticRegression(random_state=0), require_dense = [False, True])
if test_type == "RandomForest":
clf = BinaryRelevance(classifier=RandomForestClassifier(criterion='entropy',max_depth= 50, min_samples_leaf= 1, min_samples_split= 3, n_estimators= 50), require_dense = [False, True])
#clf = ClassifierChain(classifier=RandomForestClassifier(criterion='entropy',max_depth= 50, min_samples_leaf= 1, min_samples_split= 3, n_estimators= 50), require_dense = [False, True])
if test_type == "MLPClassifier":
clf = BinaryRelevance(classifier=MLPClassifier(hidden_layer_sizes=(150,100,50), max_iter=300,activation = 'relu',solver='adam',random_state=1), require_dense = [False, True])
#clf = ClassifierChain(classifier=MLPClassifier(hidden_layer_sizes=(150,100,50), max_iter=300,activation = 'relu',solver='adam',random_state=1), require_dense = [False, True])
if test_type == "MLkNN":
clf = BinaryRelevance(MLkNN(k=3))
#clf = ClassifierChain(classifier=MLkNN(k=3))
#This three works without probability
if test_type == "LinearSVC":
clf = BinaryRelevance(classifier=LinearSVC(), require_dense = [False, True])
if test_type == "GaussianNB":
clf = BinaryRelevance(classifier=GaussianNB(), require_dense = [False, True])
if test_type == "RidgeClassifierCV":
clf = BinaryRelevance(classifier=RidgeClassifierCV(alphas=[1e-3, 1e-2, 1e-1, 1]), require_dense = [False, True])
if test_type == "BRkNNaClassifier":
clf = BinaryRelevance(BRkNNaClassifier(k=3))
return clf
# -
def save_metrics(y_true, y_pred, acc_ml,acc_score,zeroOne,pr_score,hamming_loss,jaccard_score_samples,jaccard_macro, modelMatrix, metrics_by_class, i, configurationTFIDF ,num_feature ,stop_word ,size_test,test_type):
line=[]
# line to csv report file
names = ['Google Common',
'Test',
'SO',
'IO',
'UI',
'Network',
'Security',
'OpenOffice Documents',
'Database',
'PDF',
'Logging',
'Latex']
prec, rec, fscore, sup = precision_recall_fscore_support(y_true,y_pred, average='micro')
arr = [acc_ml,acc_score,zeroOne,pr_score,hamming_loss,jaccard_score_samples,jaccard_macro,prec,rec, fscore]
columns = ['Accuracy','Acc-Score','zero_one_loss','AUC-PR','hamming loss average','Jaccard samples','Jaccard macro','Precision','Recall','Fmeasure']
df_metrics2 = pd.DataFrame([arr],columns=columns)
print(df_metrics2)
print("---------")
print("")
x = precision_recall_fscore_support(y_true,y_pred, average=None)
print("")
print("")
df_metrics_by_class = pd.DataFrame.from_records(x, columns=names, index=['precision','recall','f-measure','samples_tested'])
print(df_metrics_by_class)
print("---------")
print("")
df_metrics2.to_csv(modelMatrix, encoding='utf-8', header=True, index=False, sep=',')
df_metrics_by_class.to_csv(metrics_by_class, encoding='utf-8', header=True, index=False, sep=',')
dataLine = ""
dataLine = "tf-IDFMin, tf-IDFMax, #_TopTerms,Stop_Word,Train/Test_Size,Algorithm,Accuracy_Score,Accuracy_Score_not_normalized,zero_one_loss, AUC-PR,hamming_loss_avg,Jaccard_samples,Jaccard_macro,Precision,Recall,Fmeasure_Score, i"
line.append((dataLine))
dataLine = str(configurationTFIDF) + "," + str(num_feature) + "," + stop_word + "," + str(size_test) + "," + str(test_type) + "," + str(acc_ml) + ","+ str(acc_score) + ","+ str(zeroOne) + "," + str(pr_score) + ","+ str(hamming_loss) + ","+ str(jaccard_score_samples) + ","+ str(jaccard_macro)+"," + str(prec)+","+str(rec)+","+str(fscore)+","+str(i)
line.append((dataLine))
print(line)
metrics = pd.DataFrame(line)
metrics.to_csv('./experiment/report'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+str(i)+'.csv', encoding='utf-8', header=False, index=False, sep=',')
np.savetxt(r'./experiment/report'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+str(i)+'.txt', metrics.values, fmt='%s', delimiter=',')
return prec, rec, fscore, sup
# +
import datetime
def persist_data(configurationTFIDF ,num_feature , stop_word , size_test , test_type , acc_ml ,
acc_score , zeroOne , pr_score, hamming_loss, jaccard_score_samples,
jaccard_macro , prec , rec, fscore, i):
now = datetime.datetime.now()
templateData = pd.read_csv(template, sep=',')
print ("Current date and time : ")
print (now.strftime("%Y-%m-%d %H:%M:%S"))
headerdf = ['date_time','tf-IDF', '#_TopTerms','Stop_Word','Train/Test_Size','Algorithm','Accuracy_Score',
'Accuracy_Score_not_normalized','zero_one_loss', 'AUC-PR','hamming_loss_avg','Jaccard_samples',
'Jaccard_macro','Precision','Recall','Fmeasure_Score','i']
tup = ( now,str(configurationTFIDF) ,str(num_feature) , stop_word , str(size_test) , str(test_type) , str(acc_ml) ,
str(acc_score) , str(zeroOne) , str(pr_score) , str(hamming_loss) , str(jaccard_score_samples) ,
str(jaccard_macro) , str(prec) , str(rec) , str(fscore) ,str(i))
print("tupla:", tup)
print(len(tup))
list_tup = [ now,str(configurationTFIDF) ,str(num_feature) , stop_word , str(size_test) , str(test_type) , str(acc_ml) ,
str(acc_score) , str(zeroOne) , str(pr_score) , str(hamming_loss) , str(jaccard_score_samples) ,
str(jaccard_macro) , str(prec) , str(rec) , str(fscore) ,str(i)]
dfTeste = pd.DataFrame.from_records(data=[tup], columns=[headerdf])
data_list = templateData.values.tolist()
data_list.append(list_tup)
new_data = pd.DataFrame(data_list)
for row in templateData.itertuples():
print(row)
new_data.to_csv('./experiment/dfTeste.csv', encoding='utf-8', index=False, sep=',', header=headerdf)
# -
def run_split(data_classifier, test_type, confusionMatrix, modelMatrix, metrics_by_class, configurationTFIDF ,num_feature ,stop_word ,size_test):
train = []
test = []
X = data_classifier
rs = ShuffleSplit(n_splits=splits, test_size= size_test, random_state=52)
rs.get_n_splits(X)
for train_index, test_index in rs.split(X):
#print("%s %s" % (train_index, test_index))
train.append(train_index)
test.append(test_index)
for i in range(0, len(train)):
size_features = len(X.columns)
data = data_classifier.ix[train[i]]
X_train = data.iloc[:,15:size_features]
#del X_train['issueNumberissueNumber']
y_train = data.loc[:,'Google Common':'Latex']
data = data_classifier.ix[test[i]]
X_test = data.iloc[:,15:size_features]
y_test = data.loc[:,'Google Common':'Latex']
categories = y_test.columns.values.tolist()
ids = y_test.index
classifier_setup = build_model(test_type)
clf = classifier_setup
clf.fit(X_train,y_train)
predict = clf.predict(X_test).toarray()
probability = clf.predict_proba(X_test).toarray()
predictions = pd.DataFrame(predict, index=ids, columns=categories) # with header
probabilities = pd.DataFrame(probability, index=ids, columns=categories) # with header
y_pred = predictions.values
y_proba = probabilities.values
y_true = y_test.to_numpy()
y_true, y_proba, y_pred, acc_ml, acc_score, zeroOne, fmeasure_score, pr_score, hamming_loss, jaccard_score_samples, jaccard_macro = eval_metrics(predictions, probabilities, y_test)
plot_classes(probability, y_true, y_test)
confusion_matrix(y_true, y_pred, confusionMatrix, i)
prec, rec, fscore, sup = save_metrics(y_true, y_pred, acc_ml,acc_score,zeroOne,pr_score,hamming_loss,jaccard_score_samples,jaccard_macro, modelMatrix, metrics_by_class, i, configurationTFIDF ,num_feature ,stop_word ,size_test,test_type)
persist_data(configurationTFIDF ,num_feature , stop_word , size_test , test_type , acc_ml ,
acc_score , zeroOne , pr_score, hamming_loss, jaccard_score_samples,
jaccard_macro , prec , rec, fscore, i)
# + pycharm={"is_executing": false}
# +
#number of shuffles (folds)
splits=10
#defining paths
loggingFile = './experiment//TitleBody3GramTFIDF.txt'
binaryBodyTitle = './experiment/binaryBodyTitle.csv'
template = './experiment/dfTeste.csv'
configurationTFIDFList = [(1,1)]
#configurationTFIDFList = [(1,1),(2,2),(3,3),(4,4)]
#num_featureList = [25,50,100,500,1000,2500,5000]
num_featureList = [900]
size_testList = [0.2]
#size_testList = [0.2,0.3,0.4]
stop_wordList = ["Yes"]
#test_typeList = ["RandomForest","DecisionTree","LogisticRegression","MLPClassifier","MLkNN"]
test_typeList = ["RandomForest"]
#examples
#configurationTFIDFList = [(1,1),(2,2)]
#num_featureList = [25,50]
#size_testList = [0.2,0.3]
#stop_wordList = ["Yes","No"]
#test_typeList = ["RandomForest","DecisionTree"]
configurationTFIDF=(1,1)
num_feature=25
size_test=0.2
#stop_word = stop_wordList[i]
stop_word = "Yes"
test_type = "RandomForest"
# dont forget to have the file dfTeste.csv ready in the files folder only with the header!
def __main__():
# getting length of list
lengthT = len(configurationTFIDFList)
lengthF = len(num_featureList)
lengthS = len(size_testList)
lengthY = len(test_typeList)
# Iterating the index
# same as 'for i in range(len(list))'
for t in range(lengthT):
for f in range(lengthF):
for s in range(lengthS):
for y in range(lengthY):
print("----------------")
print(configurationTFIDFList[t])
print(num_featureList[f])
print(size_testList[s])
print(test_typeList[y])
print("----------------")
configurationTFIDF=configurationTFIDFList[t]
num_feature=num_featureList[f]
size_test=size_testList[s]
#stop_word = stop_wordList[i]
stop_word = "Yes"
test_type = test_typeList[y]
tfIDFoutputFile = './experiment/tfIDFoutputFile'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+'.csv'
classifierFeatureInput='./experiment/train_file_test'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+'.csv'
termFrequencyTop50 = './experiment/termFrequencyTop50'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+'.csv'
predictions_result = './experiment/predict_file_'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+'.csv'
probabilities_result = './experiment/probability_file_'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+'.csv'
modelMatrix = './experiment/modelMatrix'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+'.csv'
metrics_by_class = './experiment/metrics_By_Class'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)+'.csv'
confusionMatrix = './experiment/CM'+ str(configurationTFIDF) + str(num_feature) + stop_word + str(size_test)+ str(test_type)
data_classes = organize()
categories, IssuePRDataset = filtering(data_classes)
data_test1 = dataset_config(IssuePRDataset)
data_test1 = clean_data(data_test1)
re_stop_words = remove_stop_words()
data_test1['corpus'] = data_test1['corpus'].apply(removeStopWords, re_stop_words=re_stop_words)
data = data_test1
data_test1 = apply_stem(data)
run_tf_idf(data_test1, configurationTFIDF, num_feature, tfIDFoutputFile)
docs = analyze_top(data_test1, termFrequencyTop50)
data_classifier, categories = merging(data_test1, tfIDFoutputFile)
run_split(data_classifier, test_type, confusionMatrix, modelMatrix, metrics_by_class, configurationTFIDF ,num_feature ,stop_word ,size_test)
# -
__main__()
| experiment/Baseline/ClassifierV5-scenarioBaseline.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import os
traindf= pd.read_csv("train.csv")
testdf= pd.read_csv("test.csv")
traindf.var()
for k in traindf.keys():
print('{0}: {1}'.format(k, len(traindf[k].unique())))
for k in traindf.keys():
if len(traindf[k].unique())<=10:
print(k)
import math
def forAge(row):
if row['Age'] < 10:
return '<10'
elif math.isnan(row['Age']):
return "nan"
else:
dec = str(int(row['Age']/10))
return "{0}0's".format(dec)
decade=traindf.apply(forAge, axis=1)
print("Decade: {1}".format(k, len(decade.unique())))
import numpy as np
def pretreat(df):
# create a df with discrete variables (len<10)
filt=[k for k in df.keys() if len(df[k].unique())<=10]
filtr2=df[filt].copy()
forAge = lambda row: int(row['Age']/10) if not math.isnan(row['Age']) else np.nan
filtr2['Decade']=df.apply(forAge, axis=1)
filtr2=filtr2.dropna()
filtr2['Decade']=filtr2['Decade'].astype('int32')
return filtr2
ptraindf= pretreat(traindf)
ptestdf=pretreat(testdf)
ptraindf.to_csv('post_train.csv', index=False)
ptestdf.to_csv( 'post_test.csv', index=False)
import pyAgrum as gum
import matplotlib.pyplot as plt
import pyAgrum.lib.notebook as gnb
df=pd.read_csv('post_train.csv')
for k in df.keys():
print("{} : {}".format(k, df[k].unique()))
template=gum.BayesNet()
template.add(gum.RangeVariable("Survived", "Survived",0,1))
template.add(gum.RangeVariable("Pclass", "Pclass",1,3))
template.add(gum.LabelizedVariable("Gender", "Gender",0).addLabel("female").addLabel("male"))
template.add(gum.RangeVariable("SibSp", "SibSp",0,8))
template.add(gum.RangeVariable("Parch", "Parch",0,9))
template.add(gum.LabelizedVariable("Embarked", "Embarked",0).addLabel('').addLabel('C').addLabel('Q').addLabel('S'))
template.add(gum.RangeVariable("Decade", "Calculated decade", 0,9))
gnb.showBN(template)
learner = gum.BNLearner('post_train.csv', template)
bn = learner.learnBN()
bn
gnb.showInformation(bn,{},size="20")
gnb.showInference(bn)
gnb.showPosterior(bn,evs={},target='Survived')
gnb.showPosterior(bn,evs={"Sex": "male", "Decade": 3},target='Survived')
gnb.showPosterior(bn,evs={"Sex": "female", "Decade": 8},target='Survived')
gnb.sideBySide(bn, gum.MarkovBlanket(bn, 'Survived'), captions=["Learned Bayesian Network", "Markov blanket of 'Survived'"])
from pyAgrum.lib.bn2roc import showROC
showROC(bn, 'post_train.csv','Survived',"1",True,True)
# +
vars=[var for var in ptestdf.keys() if var != "Survived" ]
ie=gum.LazyPropagation(bn)
testdf=pd.read_csv('post_test.csv')
def init_belief():
# Initialize evidence
for var in vars:
ie.addEvidence(var, 0)
def update_beliefs(row):
# Update beliefs from a given row less the Survived variable
for var in vars:
label = str(row.to_dict()[var])
idx = bn.variable(var).index(str(row.to_dict()[var]))
ie.chgEvidence(var, idx)
ie.makeInference()
def is_well_predicted(row):
update_beliefs(row)
marginal = ie.posterior('Survived')
outcome = row.to_dict()['Survived']
if outcome == 0: # Did not survived
if marginal.toarray()[1] < 0.46576681:
return "True Positive"
else:
return "False Negative"
else: # Survived
if marginal.toarray()[1] >= 0.46576681:
return "True Negative"
else:
return "False Positive"
init_belief()
ie.addTarget('Survived')
result = testdf.apply(is_well_predicted, axis=1)
result.value_counts(True)
# -
| Chapter08/BN.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Descarga de datos del fichero de Indicadores de Seguimiento publicado por Ministerio de Sanidad
# ## Objetivo
# Vamos a hacer una lectura de los datos publicados en el informe https://t.co/KOFUAhUynL?amp=1 publicado por Sanidad el 30 Noviembre:
#
# <NAME>
# [@walyt](https://twitter.com/walyt)
#
# [#escovid19data](https://github.com/montera34/escovid19data)
#
#
# ## Código
# Como siempre importamos las librerías con las que vamos a trabajar:
# +
import os.path as pth
import datetime as dt
import time
from glob import glob
import re
import pandas as pd
import numpy as np
import requests
from shutil import copyfile
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
from matplotlib import cm
import matplotlib.dates as mdates
import matplotlib.ticker as ticker
from matplotlib.dates import (YEARLY, MONTHLY, DateFormatter, WeekdayLocator, MonthLocator,DayLocator,
rrulewrapper, RRuleLocator, drange)
import seaborn as sns
import matplotlib.colors as colors
from pdfminer.pdfinterp import PDFResourceManager, PDFPageInterpreter
from pdfminer.pdfpage import PDFPage
from pdfminer.converter import TextConverter
from pdfminer.layout import LAParams
from io import StringIO
import numpy as np
from datetime import datetime,timedelta
import seaborn as sns
# %matplotlib inline
# -
# Definimos variables que nos ayuden en la gestión de los nombres de los ficheros, nombres de columnas e indices.
datadir='pdf_ext/'
URL_reg='https://saludextremadura.ses.es/filescms/web/uploaded_files/CasosPositivos/Datos%20Covid-19.pdf'
conversion_mes={'ENERO':1,'FEBRERO':2,'MARZO':3,
'ABRIL':4,'MAYO':5,'JUNIO':6,
'JULIO':7,'AGOSTO':8,'SEPTIEMBRE':9,
'OCTUBRE':10,'NOVIEMBRE':11,'DICIEMBRE':12}
#generamos un pandas vacío con esas columnas e indice tal que las zonas
datos_pos.shape
pueblos=['BADAJOZ',
'<NAME>',
'MONTIJO',
'ZAHINOS',
'OLIVENZA',
'<NAME>',
'PUE<NAME>',
'PARRA (LA)',
'ALBUERA (LA)',
'TALAVERA LA REAL',
'<NAME>',
'<NAME>',
'ALCUESCAR',
'CACERES',
'TORREORGAZ',
'<NAME>',
'<NAME>',
'LOGROSAN',
'MIAJADAS',
'VILLAMESIAS',
'CUMBRE (LA)',
'TRUJILLO',
'JOLA',
'CORIA',
'CASTUERA',
'MONTERRUBIO DE LA SERENA',
'<NAME>' ,
'<NAME>JA',
'<NAME>' ,
'VILLANUEVA DE LA SERENA' ,
'PUEBLA DEL MAESTRE' ,
'ALCONERA',
'VALENCIA DEL, VENTOSO',
'ZAFRA' ,
'ACEUCHAL',
'ALMENDRALEJO',
'<NAME>' ,
'ESPARRAGALEJO' ,
'MERIDA',
'<NAME>',
'MIRANDILLA',
'<NAME>' ,
'<NAME>',
'<NAME>',
'<NAME>',
'<NAME>',
'<NAME>',
'<NAME>',
'<NAME>',
'TALAYUELA',
'<NAME>',
'PINOFRANQUEADO',
'PLASENCIA',
'<NAME>']
datos_pos=pd.DataFrame()
datos_pos.loc[:,'pueblo']=pueblos
historico=pd.read_csv(datadir+'positivos.csv',index_col=0)
historico.head(5)
# ### Función para descargar un fichero pdf
# Definimos a continuación una función para descargar el fichero pdf de web
def descarga(url,guardarlo_como):
'''
Devuelve True si éxito descargando el pdf del link url, grabándolo como guardarlo_como
Parametros:
url: url del fichero a descargar
guardarlo_como : nombre del fichero a grabar, sin extensión.
'''
print('Descargando:', url)
nombre_a_guardar=datadir+guardarlo_como+'.pdf'
headers = {'User-Agent': 'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_10_1) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/39.0.2171.95 Safari/537.36'}
with requests.Session() as s:
r = s.get(url, headers=headers)
if r.status_code == requests.codes.ok:
with open(nombre_a_guardar, 'wb') as fp:
fp.write(r.content)
print('Guardándolo como:', nombre_a_guardar)
return True
else:
print ('Error con el ',nombre_a_guardar)
return False
# Vamos a llamar a los ficheros tal que su día de publicación en formato `%Y-%m-%d`, "2020-12-05" por ejemplo...
un_dia=timedelta(days=1)
hoy=datetime.today().strftime('%d-%m-%Y')
#descargamos el del 30-11
fecha_str='2020-11-30'
descarga(URL_reg,hoy)
# ### Extraemos el texto de la pagina concreta del pdf
# Extract PDF text using PDFMiner. Adapted from
# http://stackoverflow.com/questions/5725278/python-help-using-pdfminer-as-a-library
# codigo copiado del script de @alfonsotwr
# desde
def pdf_to_text(pdfname, pagenum=None):
'''
Devuelve el texto de la página pagenum extraído del pdf de path=pdfname
Parametros:
pdfname:pdf del fichero pdf
pagenum : página del fichero
'''
# PDFMiner boilerplate
rsrcmgr = PDFResourceManager()
sio = StringIO()
laparams = LAParams()
device = None
try:
device = TextConverter(rsrcmgr, sio, laparams=laparams)
interpreter = PDFPageInterpreter(rsrcmgr, device)
# Extract text
with open(pdfname, 'rb') as fp:
for i, page in enumerate(PDFPage.get_pages(fp)):
if pagenum is None or pagenum == i:
interpreter.process_page(page)
# Get text from StringIO
text = sio.getvalue()
finally:
# Cleanup
sio.close()
if device is not None:
device.close()
return text
# Tras estudiar el formato de `text` hemos generado unas RegEx para leer las series de números: basicamente se compone de una cabezera (IA x 100.000....) seguida de una lista de 30 números ó `NA`..
loc_pdf=datadir+hoy+'.pdf'
#sacamos la tabla de la página 3, aprox la mitad de las zonas
primera_pagina = pdf_to_text(loc_pdf, pagenum=0) #con que pagina queremos trabajar?
segunda_pagina = pdf_to_text(loc_pdf, pagenum=1)
# extraemos la fecha del documento
# +
#regex_fecha_publicacion='(CASOS POSITIVOS Y BROTES – )(\d{1,2} DE (\w)* DE \d{4} )'
regex_fecha_publicacion='(CASOS POSITIVOS Y BROTES – )((\d{1,2}) DE (\w*) DE (\d{4}))'
regex_fecha_casos='del día (\d{2}) de (\w*)'
match_fecha_casos=re.search(re.compile(r'{}'.format(regex_fecha_casos)),primera_pagina)
match_fecha_publicacion=re.search(re.compile(r'{}'.format(regex_fecha_publicacion)),primera_pagina)
#datos=list(match.group(2).rstrip().lstrip().replace('\n','').split(' '))
#eliminamos el primer elemento
#indicadores.loc[zonas[0]:zonas[len(datos)-1],columnas[i]]=datos
print (0,'-->',match_fecha_casos.group(2))
print (0,'-->',match_fecha_casos.groups())
print (0,'-->',match_fecha_publicacion.group(2))
print (0,'-->',match_fecha_publicacion.groups())
fecha_casos=datetime(year=2020,
month=conversion_mes[match_fecha_casos.groups()[1].upper()],
day=int(match_fecha_casos.groups()[0]))
fecha_publicacion=datetime(year=int(match_fecha_publicacion.groups()[4]),
month=conversion_mes[match_fecha_publicacion.groups()[3]],
day=int(match_fecha_publicacion.groups()[2]))
nombre_columna=datetime.strftime(fecha_casos,'%d-%m-%Y')
# -
# extraemos la primera lista de casos positivos, página nº 1
# +
regex_casos=['(CASOS \+ )((\n\d* ){45})','(CASOS \+ )((\n\d* ){9})']
match=re.search(re.compile(r'{}'.format(regex_casos[0])),primera_pagina)
datos1=list(match.group(2).rstrip().lstrip().replace('\n','').split(' '))
print ('-->',datos1)
# -
# extraemos la segunda lista de casos positivos, página nº 2
match=re.search(re.compile(r'{}'.format(regex_casos[1])),segunda_pagina)
datos2=list(match.group(2).rstrip().lstrip().replace('\n','').split(' '))
#indicadores.loc[zonas[0]:zonas[len(datos)-1],columnas[i]]=datos
print ('-->',datos2)
datos_pos.loc[:,nombre_columna]=datos1+datos2
datos_pos.head(5)
datos_tabla=datos_pos.set_index('pueblo').unstack().reset_index()
datos_tabla.columns=['Fecha','pueblo','positivos']
datos_tabla.head(20)
datos_tabla.to_csv(datadir+'positivos.csv')
| .ipynb_checkpoints/scrap_pdf_extremadura-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import requests
import json
import time
import math
import re
import calendar
import dateutil.parser as parser
from dateutil.relativedelta import relativedelta
from datetime import datetime, timezone
import yaml
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
import plotly.graph_objects as go
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
from sklearn.neighbors import NearestNeighbors
from yellowbrick.cluster import KElbowVisualizer, SilhouetteVisualizer
import os, sys, glob
import kaleido
from PIL import Image
from fpdf import FPDF
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
from scipy.signal import argrelextrema
now = datetime.now()
def convert_date(utc_time):
parsed_date = parser.parse(utc_time)
var_date=parsed_date.date()
var_time=parsed_date.time()
var_f_time=var_time.hour
var_julian_date=parsed_date.timetuple().tm_yday
var_weekday=parsed_date.weekday()
var_weekday_name=calendar.day_name[parsed_date.weekday()]
return var_date, var_time, var_f_time, var_julian_date, var_weekday, var_weekday_name
def eda(data):
output=[]
for col in data.columns:
duplicatedvalue = data[col].duplicated().sum()
duplicatedrows = data.duplicated().sum()
missingvalue = np.sum(pd.isna(data[col]))
uniquevalue = data[col].nunique()
datatype = str(data[col].dtype)
output.append([col, duplicatedvalue, duplicatedrows, missingvalue, uniquevalue, datatype])
output = pd.DataFrame(output)
output.columns = ['Features', 'Duplicated Values', 'Duplicated Rows', 'Missing Values', 'Unique Values', 'Data Type']
display(output)
def perc_on_bar(plot, feature):
total = len(feature)
for p in ax.patches:
percentage = "{:.1f}%".format(100 * p.get_height() / total)
x = p.get_x() + p.get_width() / 2 - 0.05
y = p.get_y() + p.get_height()
ax.annotate(percentage, (x, y), size=12)
plt.show()
def viz(data, indice):
fig = go.Figure(data=[go.Candlestick(x=data['UTC_Time'],
open=data['Open'],
high=data['High'],
low=data['Low'],
close=data['Close'])])
fig.update_layout(xaxis_rangeslider_visible=False,
title="Neighbor: " + indice + " " + pair + " " + timeframe + " " + now.strftime("%Y-%m-%d %H:%M:%S"),
title_font_color="blue",
title_font_size = 20)
fig.update_xaxes(rangebreaks=[dict(bounds=["sat", "mon"])])
fig.write_image(path + "/" + indice + "_chart.png")
fig.show()
def market_order(instrument, units, take_profit, stop_loss):
login_request_body = {
"order": {
"type": "MARKET",
"instrument": instrument,
"units": units,
"timeInForce": "IOC",
"positionFill": "DEFAULT",
"takeProfitOnFill": {
"price": take_profit
},
"stopLossOnFill": {
"price": stop_loss
}
}
}
response = requests.post(provider_api_url, data=json.dumps(login_request_body),
headers=request_headers,
verify=False)
response
response.status_code
def find_candle_trend (candle_no):
if candle_no < 10:
return 0
data = pd.read_csv(filename)
data = data.iloc[candle_no-5:candle_no+1]
# display (data[['Open','Close','Low','High']])
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['Close'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
Current_Market_Fit = int(r2_score(Y, y_pred)*100)
# print(Current_Market_Fit)
coeficient = (linear_regressor.coef_)
if coeficient > 0:
Current_Market = 1 * Current_Market_Fit## Bullish / Buy ##
else:
Current_Market = -1 * Current_Market_Fit ## Bearish / Sell ##
return Current_Market
# ### The Configs for Run:
with open ('config.yml') as ymlfile:
cfg = yaml.safe_load(ymlfile)
oanda_api_key = cfg['creds']['oanda_api']
account_number = cfg['creds']['account_number_1']
# # <font color='red'>Currency Pair</font>
# +
Load_10K_Records=True
currency_pairs = ['EUR_USD','EUR_GBP','EUR_NZD','EUR_AUD','EUR_CHF','EUR_CAD',
'GBP_USD','GBP_CHF','GBP_NZD','GBP_AUD','GBP_CAD','AUD_USD',
'AUD_CAD','AUD_CHF','AUD_NZD','NZD_USD','NZD_CHF','NZD_CAD',
'USD_CAD','USD_CHF','CAD_CHF']
currency_pairs = ["USD_CHF"]
timeframe = "H4"
#D #H1 #H4 M30
# https://developer.oanda.com/rest-live-v20/instrument-df/#CandlestickGranularity
price_char = "M"
#M(midpoint candles) #B(bid candles) #A(ask candles) #BA
price_com = "mid"
#mid #bid #ask
# def of OANDA request variable
provider_api_url = 'https://api-fxpractice.oanda.com/v3/accounts/{}/orders'.format(account_number)
request_headers = {
"Authorization": oanda_api_key,
"Accept-Datetime-Format": "RFC3339",
"Connection": "Keep-Alive",
"Content-Type": "application/json;charset=UTF-8"
}
# +
provider_authorization = 'Bearer {0}'.format(oanda_api_key)
headers = {
'Content-Type': 'application/json',
'Authorization': provider_authorization,
}
# -
# ### Logging
now = datetime.now()
for pair in currency_pairs:
Log_Folder = now.strftime("%d-%m-%Y_%I-%M_%p")
path = os.path.join(Log_Folder+"_"+pair)
os.mkdir(path)
# # Get Candlesticks Data
# ### Pricing & Spread Cost
for pair in currency_pairs:
pricing_params = (
('instruments', pair),
)
response = requests.get('https://api-fxpractice.oanda.com/v3/accounts/{}/pricing'.format(account_number),
headers=headers,
params=pricing_params).json()
time = response['time']
ask = response['prices'][0]['closeoutAsk']
bid = response['prices'][0]['closeoutBid']
print ('Date:', time, 'Ask:', ask, 'Bid:', bid)
# ### Open Positions
# + active=""
# response = requests.get('https://api-fxpractice.oanda.com/v3/accounts/{}/openPositions'.format(account_number),
# headers=headers,
# params=pricing_params).json()
# response['positions']
# -
# ### Candlestick Data
params_count = (
('price', price_char),
('count', '5000'),
('granularity', timeframe),
)
for pair in currency_pairs:
first_response = requests.get('https://api-fxpractice.oanda.com/v3/instruments/{}/candles'.format(pair),
headers=headers,
params=params_count).json()
if Load_10K_Records:
datetime_object = parser.parse(first_response['candles'][0]['time'])
date= datetime_object - relativedelta(years=3)
from_date = date.replace(tzinfo=timezone.utc).timestamp()
params_date = (
('count', '5000'),
('price', price_char),
('from', from_date),
('granularity', timeframe),)
second_response = requests.get('https://api-fxpractice.oanda.com/v3/instruments/{}/candles'.format(pair),
headers=headers,
params=params_date).json()
first_response= first_response['candles']
second_response= second_response['candles']
second_response.extend(first_response)
response=second_response
else:
response=first_response['candles']
# +
filename = "{}_{}.csv".format(pair, timeframe)
output = []
all_candlesticks = response
for i in range (len(all_candlesticks)):
result= (convert_date(response[i]['time']))
output.append([(result[0]),(result[1]),(result[2]),(result[3]),(result[4]),(result[5]),
response[i]['time'],
response[i]['volume'],
response[i][price_com]['o'],
response[i][price_com]['h'],
response[i][price_com]['l'],
response[i][price_com]['c']])
output = pd.DataFrame(output)
output.columns = ['Date','Time','f_time','julian_date','Weekday','Weekday_Name','UTC_Time', 'Volume', 'Open', 'High', 'Low', 'Close']
data = output.to_csv(filename, header = True, index = False)
data = pd.read_csv(filename)
# -
data = data.drop_duplicates()
data = data.to_csv(filename, header = True, index = False)
data = pd.read_csv(filename)
data.shape
data.describe()
data.head(5)
data.tail(5)
# ## Simple Moving Average (SMA)
data['SMA_5'] = data['Close'].rolling(window=5).mean().round(4)
data['SMA_10'] = data['Close'].rolling(window=10).mean().round(4)
data['SMA_20'] = data['Close'].rolling(window=20).mean().round(4)
# ## Simple Moving Average Range
data['F_SMA_5'] = data['Close'] - data['SMA_5']
data['F_SMA_10'] = data['Close'] - data['SMA_10']
data['F_SMA_20'] = data['Close'] - data['SMA_20']
data = data.drop_duplicates()
data = data.to_csv(filename, header = True, index = False)
data = pd.read_csv(filename)
data.tail()
# ## Price Range
# +
data['O-H'] = data['Open'] - data['High']
data['O-L'] = data['Open'] - data['Low']
data['O-C'] = data['Open'] - data['Close']
data['H-L'] = data['High'] - data['Low']
data['H-C'] = data['High'] - data['Close']
data['L-C'] = data['Low'] - data['Close']
data['Direction'] = data['O-C'].apply(lambda x: 1 if x<0 else 0)
data['col_1'] = data['Open'] - data['Close']
for value in data['col_1']:
if value > 0:
data['col_2'] = data['High'] - data['Open']
data['col_3'] = data['Close'] - data['Low']
else:
data['col_2'] = data['High'] - data['Close']
data['col_3'] = data['Open'] - data['Low']
#Two Previous Candlesticks
data['col_4'] = data['col_1'].shift(1)
data['col_5'] = data['col_1'].shift(2)
# + active=""
# %%time
# for candle_no in data.index.tolist():
# # print (candle_no)
# data.at[candle_no, "Trend"] = find_candle_trend(candle_no)
# -
data = data.dropna()
data = data.to_csv(filename, header = True, index = False)
data = pd.read_csv(filename)
data['Volume'].median()
data.shape
# ## Relative Strength Index (RSI)
delta = data['Close'].diff()
up = delta.clip(lower=0)
down = -1*delta.clip(upper=0)
ema_up = up.ewm(com=13, adjust=False).mean()
ema_down = down.ewm(com=13, adjust=False).mean()
rs = ema_up/ema_down
data['RSI'] = 100 - (100/(1 + rs))
# ## Calculate Average True Range (ATR)
high_low = data['High'] - data['Low']
high_cp = np.abs(data['High'] - data['Close'].shift())
low_cp = np.abs(data['Low'] - data['Close'].shift())
df = pd.concat([high_low, high_cp, low_cp], axis=1)
true_range = np.max(df, axis=1)
data['ATR_14'] = true_range.rolling(14).mean()
# # <font color='red'>CANDLE INDEX NUMBER</font>
candle_no = len(data) - 2
candle_no
# # Stop Loss & TakeProfit
ATR = data.iloc[candle_no]['ATR_14']
CLOSED_PRICE = data.iloc[candle_no]['Close']
BUY_SL = (CLOSED_PRICE - ATR).round(5)
SELL_SL = (CLOSED_PRICE + ATR).round(5)
BUY_TP = (CLOSED_PRICE + ATR).round(5)
SELL_TP = (CLOSED_PRICE - ATR).round(5)
print('StopLoss for Sell:', SELL_SL)
print('StopLoss for Buy:', BUY_SL)
print('TakeProfit for Sell:', SELL_TP)
print('TakeProfit for Sell:', BUY_TP)
# # Modeling
data = pd.read_csv(filename)
# ### Feature Selection and Reduction
data.columns
data = data[[
# 'col_1', 'col_2', 'col_3',
'O-H', 'O-L', 'O-C', 'H-L','H-C', 'L-C',
# 'col_4', 'col_5',
'F_SMA_10', 'F_SMA_20',
# 'Trend',
]]
# ### Feature Being Fit to the Model
data.head()
# ### Scaling using Standard Scaler
# + active=""
# all_col = data.iloc[:,0:].columns.tolist()
# scaler=StandardScaler()
# subset=data[all_col].copy()
# subset_scaled=scaler.fit_transform(subset)
# subset_scaled_df=pd.DataFrame(subset_scaled,columns=subset.columns)
# subset_scaled_df
# + active=""
# clusters=range(1,10)
# meanDistortions=[]
#
# for k in clusters:
# model=KMeans(n_clusters=k)
# model.fit(subset_scaled_df)
# prediction=model.predict(subset_scaled_df)
# distortion=sum(np.min(cdist(subset_scaled_df, model.cluster_centers_, 'euclidean'), axis=1)) / subset_scaled_df.shape[0]
#
# meanDistortions.append(distortion)
#
# print('Number of Clusters:', k, '\tAverage Distortion:', distortion)
#
# plt.plot(clusters, meanDistortions, 'bx-')
# plt.xlabel('k')
# plt.ylabel('Average Distortion')
# plt.title('Selecting k with the Elbow Method', fontsize=20)
# + active=""
# visualizer = KElbowVisualizer(KMeans(random_state = 1))
# visualizer.fit(subset_scaled_df)
# visualizer.show()
# -
def find_k_similar_candles(candle_id, dataset, k=5):
indices=[]
distances = []
output = []
model_knn = NearestNeighbors(metric = 'euclidean', algorithm = 'auto')
model_knn.fit(dataset)
#metric = 'euclidean' or 'cosine' or 'manhattan' or 'mahalanobis'
distances, indices = model_knn.kneighbors(dataset.iloc[candle_id,:].values.reshape(1,-1),
n_neighbors = k)
for i in range(0,len(distances.flatten())):
if i==0:
display (pd.DataFrame(data.iloc[candle_id]).transpose())
#print("Recommendation for {0}:\n".format(eurusd_data.index[candle_id]))
else:
#print("{0}: {1}, with distance of {2}".format(i,
# dataset.index[indices.flatten()[i]],
# distances.flatten()[i]))
output.append ([dataset.index[indices.flatten()[i]],
distances.flatten()[i],
dataset.iloc[indices.flatten()[i]]['O-H'],dataset.iloc[indices.flatten()[i]]['O-L'],dataset.iloc[indices.flatten()[i]]['O-C'],dataset.iloc[indices.flatten()[i]]['H-L'],dataset.iloc[indices.flatten()[i]]['H-C'],dataset.iloc[indices.flatten()[i]]['L-C'],
# dataset.iloc[indices.flatten()[i]]['col_1'],dataset.iloc[indices.flatten()[i]]['col_2'],dataset.iloc[indices.flatten()[i]]['col_3'],
# dataset.iloc[indices.flatten()[i]]['col_4'],dataset.iloc[indices.flatten()[i]]['col_5'],
dataset.iloc[indices.flatten()[i]]['F_SMA_10'],
dataset.iloc[indices.flatten()[i]]['F_SMA_20'],
# dataset.iloc[indices.flatten()[i]]['F_SMA_20'],
# dataset.iloc[indices.flatten()[i]]['Trend'],
# dataset.iloc[indices.flatten()[i]]['RSI'],
])
output = pd.DataFrame(output)
output.columns = ['Indice','Distance',
'O-H','O-L','O-C','H-L','H-C','L-C',
# 'col_1','col_2','col_3',
# 'col_4','col_5',
'F_SMA_10',
'F_SMA_20',
# 'F_SMA_20',
# 'Trend',
# 'RSI',
]
display (output)
return indices, distances
# ### Top 5 Similar Candlesticks
indices, distances = find_k_similar_candles (candle_no,data)
indices = indices[0:1][0]
indices
# ### Currnet Market/Candlestick (Last Candlestick)
# +
closed_candle = "currnet_market_data.csv"
data = pd.read_csv(filename)
data = data.iloc[candle_no-6:candle_no+1]
#data.to_csv(path + "/" + closed_candle, header = True, index = False)
viz(data, "current_market")
print("BEFORE: ", "Close:", data.iloc[0]['Close'] , "High: ", data['High'].max(), 'Low: ', data['Low'].min())
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['Close'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print("Trend:", r2_score(Y, y_pred).round(2)*100*1)
else:
print("Trend:",r2_score(Y, y_pred).round(2)*100*-1)
# -
# ### Recommendations
print(datetime.now())
for indice in indices[1:5]:
data = pd.read_csv(filename)
print ("")
print ('------------------- Neighbor:', indice, '-------------------')
print ("")
data = data.iloc[indice:indice+9]
print("BEFORE: ", "Close:", data.iloc[0]['Close'] , "High: ", data['High'].max(), 'Low: ', data['Low'].min())
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['Close'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print(r2_score(Y, y_pred).round(2)*100*1)
else:
print(r2_score(Y, y_pred).round(2)*100*-1)
data = pd.read_csv(filename)
data = data.iloc[indice:indice+7]
print("")
print("AFTER: ", "Close:", data.iloc[0]['Close'] , "High: ", data['High'].max(), 'Low: ', data['Low'].min())
print("")
print("Date:", data.iloc[0]['Date'])
print("")
print("C - H:", (data.iloc[0]['Close'] - data['High'].min()).round(4) )
print("C - L:", (data.iloc[0]['Close'] - data['Low'].min()).round(4) )
print("")
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['Close'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print('Trend - Close:', r2_score(Y, y_pred).round(2)*100*1)
else:
print('Trend - Close:', r2_score(Y, y_pred).round(2)*100*-1)
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['High'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print('Trend - Low:', r2_score(Y, y_pred).round(2)*100*1)
else:
print('Trend - Low:', r2_score(Y, y_pred).round(2)*100*-1)
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['Low'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print('Trend - High:', r2_score(Y, y_pred).round(2)*100*1)
else:
print('Trend - High:', r2_score(Y, y_pred).round(2)*100*-1)
# +
for indice in indices[1:5]:
recommendation_log = "{}_data.csv".format(indice)
data = pd.read_csv(filename)
data = data.iloc[indice:indice+7]
# data.to_csv(path + "/" + recommendation_log, header = True, index = False)
display(data[['Open','High','Low','Close']])
print ('Neighbor:', indice, '|', '10K Records:', Load_10K_Records)
viz(data, indice.astype(str))
# data['local_max'] = data['Close'][
# (data['Close'].shift(1) < data['Close']) &
# (data['Close'].shift(-1) < data['Close'])]
# data['local_min'] = data['Close'][
# (data['Close'].shift(1) > data['Close']) &
# (data['Close'].shift(-1) > data['Close'])]
# max_idx = argrelextrema(data['Close'].values, np.greater, order=5)[0]
# min_idx = argrelextrema(data['Close'].values, np.less, order=5)[0]
# plt.figure(figsize=(15, 6))
# plt.plot(data['Close'], zorder=0)
# plt.scatter(data.iloc[max_idx].index, data.iloc[max_idx]['Close'], label='Maxima', s=100, color="green", marker='^')
# plt.scatter(data.iloc[min_idx].index, data.iloc[min_idx]['Close'], label='Minima', s=100, color="red", marker='v')
# plt.legend()
# plt.show()
print ("")
print ("---------- Linear Regression based on Close ----------")
print ("")
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['Close'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
plt.figure(figsize=(15, 6))
plt.scatter(X, Y)
plt.plot(X, y_pred, color='red')
plt.show()
print(r2_score(Y, y_pred).round(2)*100, '% Fit')
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print('Action: BUY')
print('STOP LOSS:', BUY_SL, 'TAKE PROFIT:', BUY_TP)
else:
print('Action: SELL')
print('STOP LOSS:', SELL_SL, 'TAKE PROFIT:', SELL_TP)
print ("")
print ("---------- Linear Regression based on High ----------")
print ("")
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['High'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
plt.figure(figsize=(15, 6))
plt.scatter(X, Y)
plt.plot(X, y_pred, color='red')
plt.show()
print(r2_score(Y, y_pred).round(2)*100, '% Fit')
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print('Action: BUY')
print('STOP LOSS:', BUY_SL, 'TAKE PROFIT:', BUY_TP)
else:
print('Action: SELL')
print('STOP LOSS:', SELL_SL, 'TAKE PROFIT:', SELL_TP)
print ("")
print ("---------- Linear Regression based on Low ----------")
print ("")
data['candleno'] = range (1, len(data) + 1)
X = data['candleno'].values.reshape(-1, 1)
Y = data['Low'].values.reshape(-1, 1)
linear_regressor = LinearRegression()
linear_regressor.fit(X, Y)
y_pred = linear_regressor.predict(X)
plt.figure(figsize=(15, 6))
plt.scatter(X, Y)
plt.plot(X, y_pred, color='red')
plt.show()
print(r2_score(Y, y_pred).round(2)*100, '% Fit')
coeficient = (linear_regressor.coef_)
if coeficient > 0:
print('Action: BUY')
print('STOP LOSS:', BUY_SL, 'TAKE PROFIT:', BUY_TP)
else:
print('Action: SELL')
print('STOP LOSS:', SELL_SL, 'TAKE PROFIT:', SELL_TP)
# -
# ### Save the Recommendations
# + active=""
# currentpath = os.path.join(sys.path[0])
# pngfiles = []
# pngfiles = glob.glob(currentpath+"/"+path+"/*.png")
# pdf = FPDF()
#
# for pngfile in pngfiles:
# pdf.add_page()
# pdf.image(pngfile, w=200, h=130)
#
# pdf.output(path+"/recommendations.pdf", "F")
| Master_Pipeline/Forexience_Main.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.12 (''.venv'': pipenv)'
# language: python
# name: python3
# ---
# # pip install matplotlib ipympl
# # Test for issue 9418
import numpy as np
from matplotlib import pyplot as plt
# %matplotlib widget
x = np.linspace(start=0, stop=2*np.pi, num=5000)
sine = np.sin(x)
plt.figure(figsize=(1,1))
plt.plot(sine)
plt.show()
x = np.linspace(start=10, stop=5*np.pi, num=500)
sine = np.sin(x)
plt.figure()
plt.plot(sine)
plt.show()
| src/test/datascience/widgets/notebooks/matplotlib_multiple_cells_widgets.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
"""Tutorial: Introduction to the Spin-Orbital Formulation of Post-HF Methods"""
__author__ = "<NAME>"
__credit__ = ["<NAME>", "<NAME>"]
__copyright__ = "(c) 2014-2018, The Psi4NumPy Developers"
__license__ = "BSD-3-Clause"
__date__ = "2017-05-23"
# -
# # Introduction to the Spin Orbital Formulation of Post-HF Methods
# ## Notation
#
# Post-HF methods such as MPn, coupled cluster theory, and configuration interaction improve the accuracy of our Hartree-Fock wavefunction by including terms corresponding to excitations of electrons from occupied (i, j, k..) to virtual (a, b, c...) orbitals. This recovers some of the dynamic electron correlation previously neglected by Hartree-Fock.
#
# It is convenient to introduce new notation to succinctly express the complex mathematical expressions encountered in these methods. This tutorial will cover this notation and apply it to a spin orbital formulation of conventional MP2. This code will also serve as a starting template for other tutorials which use a spin-orbital formulation, such as CEPA0, CCD, CIS, and OMP2.
#
#
#
# ### I. Physicist's Notation for Two-Electron Integrals
# Recall from previous tutorials the form for the two-electron integrals over spin orbitals ($\chi$) and spatial orbitals ($\phi$):
# \begin{equation}
# [pq|rs] = [\chi_p\chi_q|\chi_r\chi_s] = \int dx_{1}dx_2 \space \chi^*_p(x_1)\chi_q(x_1)\frac{1}{r_{12}}\chi^*_r(x_2)\chi_s(x_2) \\
# (pq|rs) = (\phi_p\phi_q|\phi_r\phi_s) = \int dx_{1}dx_2 \space \phi^*_p(x_1)\phi_q(x_1)\frac{1}{r_{12}}\phi^*_r(x_2)\phi_s(x_2)
# \end{equation}
#
# Another form of the spin orbital two electron integrals is known as physicist's notation. By grouping the complex conjugates on the left side, we may express them in Dirac ("bra-ket") notation:
# \begin{equation}
# \langle pq \mid rs \rangle = \langle \chi_p \chi_q \mid \chi_r \chi_s \rangle = \int dx_{1}dx_2 \space \chi^*_p(x_1)\chi^*_q(x_2)\frac{1} {r_{12}}\chi_r(x_1)\chi_s(x_2)
# \end{equation}
#
# The antisymmetric form of the two-electron integrals in physcist's notation is given by
#
# \begin{equation}
# \langle pq \mid\mid rs \rangle = \langle pq \mid rs \rangle - \langle pq \mid sr \rangle
# \end{equation}
#
#
# ### II. Kutzelnigg-Mukherjee Tensor Notation and the Einstein Summation Convention
#
# Kutzelnigg-Mukherjee (KM) notation provides an easy way to express and manipulate the tensors (two-electron integrals, $t$-amplitudes, CI coefficients, etc.) encountered in post-HF methods. Indices which appear in the bra are expressed as subscripts, and indices which appear in the ket are expressed as superscripts:
# \begin{equation}
# g_{pq}^{rs} = \langle pq \mid rs \rangle \quad \quad \quad \overline{g}_{pq}^{rs} = \langle pq \mid\mid rs \rangle
# \end{equation}
#
# The upper and lower indices allow the use of the Einstein Summation convention. Under this convention, whenever an indice appears in both the upper and lower position in a product, that indice is implicitly summed over. As an example, consider the MP2 energy expression:
#
# \begin{equation}
# E_{MP2} = \frac{1}{4} \sum_{i a j b} \frac{ [ia \mid\mid jb] [ia \mid\mid jb]} {\epsilon_i - \epsilon_a + \epsilon_j - \epsilon_b}
# \end{equation}
# Converting to physicist's notation:
#
# \begin{equation}
# E_{MP2} = \frac{1}{4} \sum_{i j a b} \frac{ \langle ij \mid\mid ab \rangle \langle ij \mid \mid ab \rangle} {\epsilon_i - \epsilon_a + \epsilon_j - \epsilon_b}
# \end{equation}
# KM Notation, taking advantage of the permutational symmetry of $g$:
# \begin{equation}
# E_{MP2} = \frac{1}{4} \overline{g}_{ab}^{ij} \overline{g}_{ij}^{ab} (\mathcal{E}_{ab}^{ij})^{-1}
# \end{equation}
#
# where $\mathcal{E}_{ab}^{ij}$ is the sum of orbital energies $\epsilon_i - \epsilon_a + \epsilon_j - \epsilon_b$. Upon collecting every possible orbital energy sum into a 4-dimensional tensor, this equation can be solved with a simple tensor-contraction, as done in our MP2 tutorial.
#
# The notation simplication here is minor, but the value of this notation becomes obvious with more complicated expressions encountered in later tutorials such as CCD. It is also worth noting that KM notation is deeply intertwined with the second quantization and diagrammatic expressions of methods in advanced electronic structure theory. For our purposes, we will shy away from the details and simply use the notation to write out readily-programmable expressions.
#
#
# ### III. Coding Spin Orbital Methods Example: MP2
#
# In the MP2 tutorial, we used spatial orbitals in our two-electron integral tensor, and this appreciably decreased the computational cost. However, this code will only work when using an RHF reference wavefunction. We may generalize our MP2 code (and other post-HF methods) to work with any reference by expressing our integrals, MO coefficients, and orbital energies obtained from Hartree-Fock in a spin orbital formulation. As an example, we will code spin orbital MP2, and this will serve as a foundation for later tutorials.
#
#
# ### Implementation of Spin Orbital MP2
# As usual, we import Psi4 and NumPy, and set the appropriate options. However, in this code, we will be free to choose open-shell molecules which require UHF or ROHF references. We will stick to RHF and water for now.
# +
# ==> Import statements & Global Options <==
import psi4
import numpy as np
psi4.set_memory(int(2e9))
numpy_memory = 2
psi4.core.set_output_file('output.dat', False)
# +
# ==> Molecule & Psi4 Options Definitions <==
mol = psi4.geometry("""
0 1
O
H 1 1.1
H 1 1.1 2 104
symmetry c1
""")
psi4.set_options({'basis': '6-31g',
'scf_type': 'pk',
'reference': 'rhf',
'mp2_type': 'conv',
'e_convergence': 1e-8,
'd_convergence': 1e-8})
# -
# For convenience, we let Psi4 take care of the Hartree-Fock procedure, and return the wavefunction object.
# Get the SCF wavefunction & energies
scf_e, scf_wfn = psi4.energy('scf', return_wfn=True)
# We also need information about the basis set and orbitals, such as the number of basis functions, number of spin orbitals, number of alpha and beta electrons, the number of occupied spin orbitals, and the number of virtual spin orbitals. These can be obtained with MintsHelper and from the wavefunction.
mints = psi4.core.MintsHelper(scf_wfn.basisset())
nbf = mints.nbf()
nso = 2 * nbf
nalpha = scf_wfn.nalpha()
nbeta = scf_wfn.nbeta()
nocc = nalpha + nbeta
nvirt = 2 * nbf - nocc
# For MP2, we need the MO coefficients, the two-electron integral tensor, and the orbital energies. But, since we are using spin orbitals, we have to manipulate this data accordingly. Let's get our MO coefficients in the proper form first. Recall in restricted Hartree-Fock, we obtain one MO coefficient matrix **C**, whose columns are the molecular orbital coefficients, and each row corresponds to a different atomic orbital basis function. But, in unrestricted Hartree-Fock, we obtain separate matrices for the alpha and beta spins, **Ca** and **Cb**. We need a general way to build one **C** matrix regardless of our Hartree-Fock reference. The solution is to put alpha and beta MO coefficients into a block diagonal form:
# +
Ca = np.asarray(scf_wfn.Ca())
Cb = np.asarray(scf_wfn.Cb())
C = np.block([
[ Ca , np.zeros_like(Cb) ],
[np.zeros_like(Ca) , Cb ]
])
# Result: | Ca 0 |
# | 0 Cb|
# -
# It's worth noting that for RHF and ROHF, the Ca and Cb given by Psi4 are the same.
#
# Now, for this version of MP2, we also need the MO-transformed two-electron integral tensor in physicist's notation. However, Psi4's default two-electron integral tensor is in the AO-basis, is not "spin-blocked" (like **C**, above!), and is in chemist's notation, so we have a bit of work to do.
#
# First, we will spin-block the two electron integral tensor in the same way that we spin-blocked our MO coefficients above. Unfortunately, this transformation is impossible to visualize for a 4-dimensional array.
#
# Nevertheless, the math generalizes and can easily be achieved with NumPy's kronecker product function `np.kron`. Here, we take the 2x2 identity, and place the two electron integral array into the space of the 1's along the diagonal. Then, we transpose the result and do the same. The result doubles the size of each dimension, and we obtain a "spin-blocked" two electron integral array.
# +
# Get the two electron integrals using MintsHelper
I = np.asarray(mints.ao_eri())
def spin_block_tei(I):
"""
Function that spin blocks two-electron integrals
Using np.kron, we project I into the space of the 2x2 identity, tranpose the result
and project into the space of the 2x2 identity again. This doubles the size of each axis.
The result is our two electron integral tensor in the spin orbital form.
"""
identity = np.eye(2)
I = np.kron(identity, I)
return np.kron(identity, I.T)
# Spin-block the two electron integral array
I_spinblock = spin_block_tei(I)
# -
# From here, converting to antisymmetrized physicists notation is simply:
# Converts chemist's notation to physicist's notation, and antisymmetrize
# (pq | rs) ---> <pr | qs>
# Physicist's notation
tmp = I_spinblock.transpose(0, 2, 1, 3)
# Antisymmetrize:
# <pr||qs> = <pr | qs> - <pr | sq>
gao = tmp - tmp.transpose(0, 1, 3, 2)
# We also need the orbital energies, and just as with the MO coefficients, we combine alpha and beta together. We also want to ensure that the columns of **C** are sorted in the same order as the corresponding orbital energies.
# +
# Get orbital energies
eps_a = np.asarray(scf_wfn.epsilon_a())
eps_b = np.asarray(scf_wfn.epsilon_b())
eps = np.append(eps_a, eps_b)
# Before sorting the orbital energies, we can use their current arrangement to sort the columns
# of C. Currently, each element i of eps corresponds to the column i of C, but we want both
# eps and columns of C to be in increasing order of orbital energies
# Sort the columns of C according to the order of increasing orbital energies
C = C[:, eps.argsort()]
# Sort orbital energies in increasing order
eps = np.sort(eps)
# -
# Finally, we transform our two-electron integrals to the MO basis. For the sake of generalizing for other methods, instead of just transforming the MP2 relevant subsection as before:
# ~~~python
# tmp = np.einsum('pi,pqrs->iqrs', Cocc, I, optimize=True)
# tmp = np.einsum('qa,iqrs->iars', Cvirt, tmp, optimize=True)
# tmp = np.einsum('iars,rj->iajs', tmp, Cocc, optimize=True)
# I_mo = np.einsum('iajs,sb->iajb', tmp, Cvirt, optimize=True)
# ~~~
#
# we instead transform the full array so it can be used for terms from methods other than MP2. The nested `einsum`'s work the same way as the method above. Here, we denote the integrals as `gmo` to differentiate from the chemist's notation integrals `I_mo`.
# Transform gao, which is the spin-blocked 4d array of physicist's notation,
# antisymmetric two-electron integrals, into the MO basis using MO coefficients
gmo = np.einsum('pQRS, pP -> PQRS',
np.einsum('pqRS, qQ -> pQRS',
np.einsum('pqrS, rR -> pqRS',
np.einsum('pqrs, sS -> pqrS', gao, C, optimize=True), C, optimize=True), C, optimize=True), C, optimize=True)
# And just as before, construct the 4-dimensional array of orbital energy denominators. An alternative to the old method:
# ~~~python
# e_ij = eps[:nocc]
# e_ab = eps[nocc:]
# e_denom = 1 / (e_ij.reshape(-1, 1, 1, 1) - e_ab.reshape(-1, 1, 1) + e_ij.reshape(-1, 1) - e_ab)
# ~~~
# is the following:
# Define slices, create 4 dimensional orbital energy denominator tensor
n = np.newaxis
o = slice(None, nocc)
v = slice(nocc, None)
e_abij = 1 / (-eps[v, n, n, n] - eps[n, v, n, n] + eps[n, n, o, n] + eps[n, n, n, o])
# These slices will also be used to define the occupied and virtual space of our two electron integrals.
#
# For example, $\bar{g}_{ab}^{ij}$ can be accessed with `gmo[v, v, o, o]`
# We now have all the pieces we need to compute the MP2 correlation energy. Our energy expression in KM notation is
#
# \begin{equation}
# E_{MP2} = \frac{1}{4} \bar{g}_{ab}^{ij} \bar{g}_{ij}^{ab} (\mathcal{E}_{ab}^{ij})^{-1}
# \end{equation}
#
# which may be easily read-off as an einsum in NumPy. Here, for clarity, we choose to read the tensors from left to right (bra to ket). We also are sure to take the appropriate slice of the two-electron integral array:
# +
# Compute MP2 Correlation Energy
E_MP2_corr = (1 / 4) * np.einsum('abij, ijab, abij ->', gmo[v, v, o, o], gmo[o, o, v, v], e_abij, optimize=True)
E_MP2 = E_MP2_corr + scf_e
print('MP2 correlation energy: ', E_MP2_corr)
print('MP2 total energy: ', E_MP2)
# -
# Finally, compare our answer with Psi4:
# ==> Compare to Psi4 <==
psi4.compare_values(psi4.energy('mp2'), E_MP2, 6, 'MP2 Energy')
# ## References
#
# 1. Notation and Symmetry of Integrals:
# > <NAME>, "Permutational Symmetries of One- and Two-Electron Integrals" Accessed with http://vergil.chemistry.gatech.edu/notes/permsymm/permsymm.pdf
# 2. Useful Notes on Kutzelnigg-Mukherjee Notation:
# > <NAME>, "Kutzelnigg-Mukherjee Tensor Notation" Accessed with https://github.com/CCQC/chem-8950/tree/master/2017
#
# 3. Original paper on MP2: "Note on an Approximation Treatment for Many-Electron Systems"
# > [[Moller:1934:618](https://journals.aps.org/pr/abstract/10.1103/PhysRev.46.618)] <NAME> and <NAME>, *Phys. Rev.* **46**, 618 (1934)
#
#
| Example/Psi4Numpy/08-CEPA0andCCD/8a_Intro_to_spin_orbital_postHF.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Lab 5: Simulations
#
# Welcome to lab 5! This week, we will go over iteration and simulations, and introduce the concept of randomness. All of this material is covered in [Chapter 9](https://www.inferentialthinking.com/chapters/09/randomness.html) and [Chapter 10](https://www.inferentialthinking.com/chapters/10/sampling-and-empirical-distributions.html) of the textbook.
#
# The data used in this lab will contain salary data and statistics for basketball players from the 2018-2019 NBA season. This data was collected from sports analytic sites [basketball-reference](http://www.basketball-reference.com) and [spotrac](http://www.spotrac.com). Since the salary data and statistics come from two separate websites, we cross-compared using the players' names and only kept the intersection of them.
#
# In this lab you will be using
# * Boolean operators
# * `if` / `else` / `elif` conditional statements
# * `np.random.choice(array_name)`
# * functions that you defined yourself
# * `apply` method for tables
# * iterating over arrays using `for` loops
# * simulation steps to compute different statistics
# * `in` and `not in` operators to check for presence of values
# * `np.append` method to add values to an array
#
# First, set up the tests and imports by running the cell below.
# +
# Run this cell, but please don't change it.
# These lines import the Numpy and Datascience modules.
import numpy as np
from datascience import *
# These lines do some fancy plotting magic
import matplotlib
# %matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
# Don't change this cell; just run it.
from client.api.notebook import Notebook
ok = Notebook('lab05.ok')
_ = ok.auth(inline=True)
# -
# ## Booleans and Conditionals
#
# **Reminder**: whenever you are writing your code, pay attention to the requested **type of input and the type of output**. Make sure that you are **reading the instructions _carefully_**.
# In Python, Boolean values can either be `True` or `False`. We get Boolean values when using comparison operators, among which are `<` (less than), `>` (greater than), and `==` (equal to). For a complete list, refer to [Booleans and Comparison](https://www.inferentialthinking.com/chapters/09/randomness.html#Booleans-and-Comparison) at the start of Chapter 9.
#
# Run the cell below to see an example of a comparison operator in action.
3 > 1 + 1
# We can even assign the result of a comparison operation to a variable.
#
# _Note that due to the operator precedence, Python will first evaluate the division `10 / 2`, then compare the result to 5, and finally assign the Boolean result of the comparison to the variable `result`._
result = 10 / 2 == 5
result
# Arrays are compatible with comparison operators. The output is an array of boolean values.
make_array(1, 5, 7, 8, 3, -1) > 3
# What does the code in the previous cell do? Well, the comparison operator `>` looks at each element of the array, compare the element with 3, and returns a new array with each element corresponding to the result of the comparison. To be specific, the comparison operator `>` firstly takes 1, the first element in the array and compares 1 with 3. 1 is not greater than 3, so in the resulting array, the first element is `False`. And then `>` takes the second element 5 and does the same thing. This time 5 is greater than 3, so in the resulting array, the second element is `True`. This process goes on until it reaches the last element. That is how we get an array of boolean values.
# ## 1. Nachos and Conditionals
#
# Waiting on the dining table just for you is a hot bowl of nachos! Let's say that whenever you take a nacho, it will have cheese, salsa, both, or neither (just a plain tortilla chip).
#
# Using the function call `np.random.choice(array_name)`, let's simulate taking nachos from the bowl at random. Start by running the cell below several times, and observe how the results change.
nachos = make_array('cheese', 'salsa', 'both', 'neither')
np.random.choice(nachos)
# Here we introduce `np.count_nonzero(array_name)` which will be used in **Quesiton 1**. This function counts the nonzero values in an array with numerical values or counts the number of `True` values in an array with Boolean values.
np.count_nonzero(make_array(1, 0, 7, 0, 2, 0, -10))
np.count_nonzero(make_array(True, False, False, False, True))
np.count_nonzero(make_array(1, 5, 7, 8, 3, -1) > 3)
# +
some_nachos = make_array('cheese', 'salsa', 'salsa')
print(np.count_nonzero(some_nachos == 'salsa'))
# Now complete the code below to count the number of nachos with cheese.
print(np.count_nonzero(some_nachos == ...))
# -
# Make sure you understand what is going on in the previous cells before proceeding to **Question 1**!
# **Question 1.** Assume we took ten nachos at random, and stored the results in an array called `ten_nachos` as done below. Write a Python expression to count the number of nachos with only cheese (do not hardcode a number).
#
# *Hint:* Our solution involves a comparison operator and the `np.count_nonzero` method.
ten_nachos = make_array('neither', 'cheese', 'both', 'both', 'cheese', 'salsa', 'both', 'neither', 'cheese', 'both')
number_cheese = ...
number_cheese
_ = ok.grade('q1_1')
# ### Conditional Statements
#
# A conditional statement is made up of many lines that allow Python to choose from different alternatives based on whether some condition is true.
#
# Here is a basic example.
#
# ```
# def sign(x):
# if x > 0:
# return 'Positive'
# ```
#
# The way the function works is this: if the input `x` is greater than `0`, we get the string `'Positive'` back.
#
# If we want to test multiple conditions at once, we use the following general format.
#
# ```
# if <if expression>:
# <if body>
# elif <elif expression 0>:
# <elif body 0>
# elif <elif expression 1>:
# <elif body 1>
# ...
# else:
# <else body>
# ```
#
# **Only one** of the `<elif body>` statements will ever be executed. Each `if` and `elif` expression is evaluated and considered in order, starting at the top. As soon as a true value is found, the corresponding body is executed, and **the rest of the expression is skipped**. If none of the `if` or `elif` expressions are true, then the `else body` is executed. For more examples and explanation, refer to [Section 9.1](https://www.inferentialthinking.com/chapters/09/1/conditional-statements.html).
# **Question 2.** Complete the following conditional statement so that the string `'More please'` is assigned to `say_please` if the number of nachos with cheese in `ten_nachos` is less than `5`.
#
# *Hint*: You should not have to directly reference the variable `ten_nachos`. Why? Remember that you already counted how many nachos with cheese you have in the previous question, so you should use the same variable here.
# + for_assignment_type="student"
say_please = '?'
if ...:
say_please = 'More please'
say_please
# -
_ = ok.grade('q1_2')
# **Question 3.** Write a function called `nacho_reaction` that returns a string based on the type of nacho passed in as an argument. From top to bottom, the conditions should correspond to: `'cheese'`, `'salsa'`, `'both'`, `'neither'`.
# + for_assignment_type="student"
def nacho_reaction(nacho):
if ...:
return 'Cheesy'
# next condition should return 'Spicy'
...
# next condition should return 'Wow'
...
# next condition should return 'Meh'
...
spicy_nacho = nacho_reaction('salsa')
spicy_nacho
# -
_ = ok.grade('q1_3')
# ### Using the `apply` method
#
# Let's review how to use `apply` method since **Question 4** needs it. Suppose we have a table with humidity (the concentration of water vapor in the air) with values between 0 and 1. We would like to add another column to the table with those values (which are proportions) converted to percentage string. First, we define the following function `to_percentage_string` whose input is a float and output is a percentage string.
def to_percentage_string(proportion):
percentage = proportion * 100
# You don't have to understand what is happening in the next line of code.
# This is the syntax for formatting a string so that the float is displayed
# up to two decimal places followed by a percentage sign.
percentage_string = "{0:.2f}%".format(percentage)
return percentage_string
# Try running this function with a sample input
to_percentage_string(0.4)
# Let's create a table with the sample humidity values.
humidity_table = Table().with_column('proportion', make_array(0.2, 0.354, 0.1239, 0.56))
humidity_table
# Next, we use the `apply` method below to get an array where each element is the result of applying the function `to_percentage_string` to each element in the column "proportion".
humidity_in_percentage_string = humidity_table.apply(to_percentage_string, 'proportion')
humidity_in_percentage_string
# Lastly, we create a new table `humidity_table_with_percentage` by adding a new column called "percentage" to `humidity_table`.
humidity_table_with_percentage = humidity_table.with_column('percentage', humidity_in_percentage_string)
humidity_table_with_percentage
# **Question 4.** Add a column `'Reactions'` to the table `ten_nachos_reactions` that consists of reactions for each of the nachos in `ten_nachos`.
#
# *Hint:* Use the `apply` method.
#
# *Hint 1:* Remember, you already wrote a function that generates the reactions.
# + for_assignment_type="student"
ten_nachos_reactions = Table().with_column('Nachos', ten_nachos)
...
ten_nachos_reactions
# -
_ = ok.grade('q1_4')
# **Question 5.** Use Python functions to find the number of `'Wow'` reactions for the nachos in `ten_nachos_reactions`.
number_wow_reactions = ...
number_wow_reactions
_ = ok.grade('q1_5')
# **Question 6.** Complete the function `both_or_neither`, which takes in a table of nachos with reactions (just like the one from Question 4) and returns `'Wow'` if there are more nachos with both cheese and salsa, or `'Meh'` if there are more nachos with neither. If there are an equal number of each, return `'Okay'`.
# + for_assignment_type="student"
def both_or_neither(nacho_table):
reactions = ...
number_wow_reactions = ...
number_meh_reactions = ...
if ...:
return 'Wow'
# next condition should return 'Meh'
...
# next condition should return 'Okay'
...
many_nachos = Table().with_column('Nachos', np.random.choice(nachos, 250))
many_nachos = many_nachos.with_column('Reactions', many_nachos.apply(nacho_reaction, 'Nachos'))
result = both_or_neither(many_nachos)
result
# -
_ = ok.grade('q1_6')
# ## 2. Simulations
# Using a `for` statement, we can perform a task multiple times. This is known as **iteration**. Here, we'll simulate drawing different suits from a deck of cards. Drawing different suits from a deck of cards means picking a card of a specific shape (suit) from the stack (deck) of cards. For example, if we draw a ♤3, we say we have picked a suit ♤.
# +
suits = make_array("♤", "♡", "♢", "♧")
draws = make_array()
repetitions = 6
for i in np.arange(repetitions):
draws = np.append(draws, np.random.choice(suits))
draws
# -
# In the example above, the `for` loop appends a random draw to the `draws` array for every number in `np.arange(repetitions)`.
#
# **Make sure that you understand what is happening with this example**, since it will be the basis for the solutions in the questions below.
#
# > Here's a nice way to think of what we did above. We had a deck of 4 cards of different suits, we randomly drew one card, saw the suit, kept track of it in `draws` array, and put the card back into the deck. We repeated this for a total of 6 times without having to manually repeat code, thanks to the `for` loop. We simulated this experiment using a `for` loop.
#
# Another use of iteration is to loop through a set of values. For instance, we can print out all of the colors of the rainbow (and capitalize each word while we are at it!).
#
# +
rainbow = make_array("red", "orange", "yellow", "green", "blue", "indigo", "violet")
for color in rainbow:
print(color.title())
# -
# We can see that the indented part of the `for` loop, known as the **body**, is executed **once for each item** in `rainbow`. Notice that each time through the loop, `color` takes on (i.e., stores) the next value stored in the array `rainbow` that it is looping through.
#
# Note that the name `color` is arbitrary; we could easily have named it something else. The important thing is that inside the body of the `for` loop, we always use the same variable name to access the elements that the loop is iterating through. In the cell above, we should always use the same variable name `color` in the body of the `for` loop. In the cell below, we should always use the same variable name `another_name` in the body of the `for` loop.
for another_name in rainbow:
print(another_name)
# In general, however, we would like the variable name to be somewhat informative.
# Let's do an example of summing all the elements in an array. Replace the ellipsis with the code according to the instructions in the cell below. **Make sure you understand this example before moving on to Question 1!**
# +
# Create an array such that it contains 0, 1, 2, ..., 9
my_array = ...
# my_sum is initialized to 0. It will be incremented/increased inside the for loop.
my_sum = 0
for i in np.arange(len(my_array)):
my_sum = my_sum + ... # Get the i-th element in the array here
my_sum
# -
# **Question 1.** Clay is playing darts. His dartboard contains ten equal-sized zones with point values from 1 to 10. Write code that simulates his total score after 1000 dart tosses. Make sure to use a `for` loop.
#
# *Hint:* There are a few steps to this problem (and most simulations):
# 1. Figuring out **the big picture** of what we want to simulate (the total score after 1000 dart tosses)
# 2. Deciding the possible values you can take in the experiment (point values in this case) and **simulating one example** (throwing one dart)
# 3 Deciding **how many times to run through the experiment** (1000 tosses in our case) and **keeping track** of the total information of **each time you ran through the experiment** (the total score in this case)
# 4. Coding up the whole simulation!
#
# Take a look at the [Chapter 9.3](https://www.inferentialthinking.com/chapters/09/3/Simulation.html) to read more about Simulations.
# + for_assignment_type="student"
possible_point_values = ...
tosses = 1000
total_score = ...
# a for loop would be useful here
total_score
# -
_ = ok.grade('q2_1')
# **Question 2.** In the following cell, we've loaded the text of _Pride and Prejudice_ by <NAME>, split it into individual words, and stored these words in an array (that we called `p_and_p_words`). Using a `for` loop, assign `longer_than_five` to the number of words in the novel that are more than 5 letters long.
#
# *Hint*: You can find the number of letters in a word with the `len` function.
# + for_assignment_type="student"
austen_string = open('Austen_PrideAndPrejudice.txt', encoding='utf-8').read()
p_and_p_words = np.array(austen_string.split())
longer_than_five = ...
# a for loop would be useful here
longer_than_five
# -
_ = ok.grade('q2_2')
# **Question 3.** Using simulation with 10,000 trials, assign `chance_of_all_different` to an estimate of the chance that if you pick three words from _Pride and Prejudice_ uniformly at random (with replacement), they all have different lengths.
#
# *Hint 1:* How do we compute chance? The chance of something happening is the number of instances where it happens divided by the number of total instances.
#
# *Hint 2*: Remember that `!=` only checks for non-equality between two items, not three. However, you can use `!=` more than once in the same line. For example, `2 != 3 != 4` first checks for non-equality between `2` and `3`, then `3` and `4`, but NOT `2` and `4`.
# +
trials = 10000
different = ...
for ... in ...:
...
chance_of_all_different = ...
chance_of_all_different
# -
_ = ok.grade('q2_3')
# **Question 4.** In this question, we ask you to count the number of unique words in *Pride and Prejudice*.
#
# To do this, first of all, you need to maintain an array of unique words you have already seen, which we will call `seen_words`. Initially this array is empty, because you have not seen anything yet. As you loop through every word in the array `p_and_p_word`, if the word has never appeared before (which means you cannot find it `seen_words`), you add it into `seen_words`.
#
# To determine whether an item is in an array, we use the `in` operator. Below are different ways that you can structure your code. Play around with the values to make sure you understand how the code works.
# +
fruits = make_array('orange', 'banana', 'watermelon')
if 'apple' in fruits:
print('apple is in the array')
else:
print('apple is not in the array')
if 'kiwi' not in fruits:
print('banana is not in the array')
# -
# To add an item into an array, we use the method `np.append`.
old_array = make_array('orange', 'banana', 'watermelon')
new_array = np.append(old_array, 'apple')
new_array
# Now try to count the number of unique words in *Pride and Prejudice*! Note that it will take a while for the code to run completely. Wait at least a minute for the code to run!
# + for_assignment_type="student"
num_unique_words = ...
seen_words = ...
for ... in ...:
if ... not in ...:
...
num_unique_words
# -
_ = ok.grade('q2_4')
# **Question 5.** Have you ever wondered how many times letter 'q' has occured in *Pride and Prejudice*? Well, wonder no more! Count the number of times the letter 'q' appears in *Pride and Prejudice*.
#
# *Hint:* Firstly, you need to know how to count the letter 'q' in an arbitrary string. (The next cell tells you how it can be done.) Then, you will need to do this for every word in `p_and_p_words`.
# +
# In this cell, we count the number of times the letter 'p' appears in the word "appropriate".
my_word = "appropriate" # a sample word
num_p_in_my_word = 0 # a counter that keeps a running sum
for letter in my_word: #for each letter in the given word
if letter == 'p':
num_p_in_my_word = num_p_in_my_word + 1 # update the counter/sum
num_p_in_my_word
# -
# Now, try to count the number of times the letter 'q' appears in *Pride and Prejudice*!
# + for_assignment_type="student"
num_q = ...
for ... in ...:
for ... in ...:
...
num_q
# -
_ = ok.grade('q2_5')
# Now suppose we want to count the number of times any arbitrary letter in the alphabet appears in *Pride and Prejudice*. Can we write a function that counts the number of occurrences of a given letter in *Pride and Prejudice*?
#
# *Hint:* Test your function by seeing if you get the same result when you count the number of 'q's.
# +
def find_num_letter(letter):
num_letter = ...
for ... in ...:
for ... in ...:
...
return ...
find_num_letter(...)
# -
# We can test and play with our function `find_num_letter` some more below using the interactive widget.
# +
from ipywidgets import widgets, interact
_ = interact(find_num_letter, letter=widgets.Text())
# -
# Which letter is the most common? Which letter is the least common? Type your answer in the cell below.
# *Write your answer here, replacing this text.*
# **Question 6.** In preparation for the next question, let's see if we can run another simulation.
#
# <NAME> is drafting Basketball Players for his NBA Fantasy League. He chooses 10 times randomly from a list of players, and drafts the players from this list regardless of whether the player has been chosen before (You could have ten Kevin Durants on a team!). Count how many times <NAME> is chosen in a version of LeBron's draft.
# + for_assignment_type="student"
players = ["<NAME>", "<NAME>", "<NAME>", "<NAME>", "<NAME>"]
draft_picks = ...
num_wall = ...
for ... in ...:
...
num_wall
# -
_ = ok.grade('q2_6')
# ## 3. Sampling Basketball Data
#
#
# Run the cell below to load the player and salary data.
player_data = Table().read_table("player_data_2018_2019.csv")
salary_data = Table().read_table("salary_data_2018_2019.csv")
# Both tables share a column containing the names of the players, so we can create a new table that contains the data from both, `player_data` and `salary_data`. We'll call the new, combined table `full_data`.
full_data = salary_data.join("PlayerName", player_data, "Name")
# The show method immediately displays the contents of a table.
# This way, we can display the top of two tables using a single cell.
player_data.show(3)
salary_data.show(3)
full_data.show(3)
# Let's look at the distribution of the player ages stored in the `player_data` table by drawing a histogram.
player_data.hist("Age")
# What's the age of the youngest player? What's the age of the oldest player? What functions can you use to extract this information?
youngest_age = ...
oldest_age = ...
# Does the histogram above capture the age of the oldest person? How do you know? How can you use the `.bin()` method to verify that the histogram contains the oldest player's age? See [Chapter 7.2](https://www.inferentialthinking.com/chapters/07/2/Visualizing_Numerical_Distributions.html) if you need to look up how to use the method and what parameters it takes.
player_data.bin(...)
# Let's visualize the same information for salaries. Draw the histogram of the salaries and find out the smallest and largest salary a player earns.
full_data.hist("Salary")
smallest_salary = ...
top_salary = ...
_ = ok.grade('q3_0') # Just a sanity check
# Rather than getting data on every player, imagine that we had gotten data on only a smaller subset of the players. For 398 players, it's not so unreasonable to expect to see all the data, but usually we aren't so lucky. Instead, we often make *statistical inferences* about a large underlying population using a smaller sample.
#
# A **statistical inference** is a statement about some statistic of the underlying population, such as "the average salary of NBA players from the 2018-2019 season was $3". You may have heard the word "inference" used in other contexts. It's important to keep in mind that statistical inferences, unlike, say, logical inferences, can be wrong.
#
# A general strategy for inference using samples is to _estimate statistics of **the population**_ by computing _the **same** statistics on **a sample**_. This strategy sometimes works well and sometimes doesn't. The degree to which it gives us useful answers depends on several factors, and we'll touch lightly on a few of those today.
#
# One very important factor in the utility of samples is **how** they were gathered. We have prepared some example datasets to simulate inference from different kinds of samples for the NBA player dataset. Later we'll ask you to create your own samples to see how they behave.
# To save typing and increase the clarity of your code, we will package the loading and analysis code into two functions. This will be useful in the rest of the lab as we will repeatedly need to create histograms and collect summary statistics from that data.
#
# **Remember: Histograms are inclusive on the left hand side of the interval, but not the right.** More information about histograms are in [Chapter 7.2](https://www.inferentialthinking.com/chapters/07/2/Visualizing_Numerical_Distributions.html).
# **Question 3.1**. Complete the `histograms` function, which takes **a table** with columns `Age` and `Salary` and draws a histogram for each one. Use the `min` and `max` functions to pick the bin boundaries so that **all data** appears on the histogram for any table passed to your function. For bin width, use 1 year for `Age` and $1,000,000 for `Salary`.
#
# *Hint*: When creating the bins for the the histograms, think critically about what the stop argument should be for `np.arange`. **Histograms are inclusive on the left hand side of the interval, but not the right.** So, if we have a maximum age of 80, we need a 80-81 bin in order to capture this in the histogram.
# +
def histograms(t):
ages = t.column('Age')
salaries = t.column('Salary')
age_bins = ...
salary_bins = ...
t.hist('Age', bins=age_bins, unit='year')
t.hist('Salary', bins=salary_bins, unit='$')
return age_bins # Keep this statement so that your work can be checked
histograms(full_data)
print('Two histograms should be displayed below')
# -
_ = ok.grade('q3_1') # Warning: Charts will be displayed while running this test
# **Question 3.2**. Create a function called `compute_statistics` that takes a Table containing ages and salaries and:
# - Draws a histogram of ages
# - Draws a histogram of salaries
# - Returns a two-element array containing the average age and average salary
#
# You can call your `histograms` function to draw the histograms!
# +
def compute_statistics(age_and_salary_data):
...
age = ...
salary = ...
...
full_stats = compute_statistics(full_data)
# -
_ = ok.grade('q3_2') # Warning: Charts will be displayed while running this test
# ### Convenience sampling
# One sampling methodology, which is **generally a bad idea**, is to choose players who are somehow convenient to sample. For example, you might choose players from one team that's near your house, since it's easier to survey them. This is called, somewhat pejoratively, *convenience sampling*.
#
# Suppose you survey only *relatively new* players with ages less than 22. (The more experienced players didn't bother to answer your surveys about their salaries.)
#
# **Question 3.3** Assign `convenience_sample_data` to a subset of `full_data` that contains only the rows for players under the age of 22.
convenience_sample = ...
convenience_sample
_ = ok.grade('q3_3')
# **Question 3.4** Assign `convenience_stats` to a list of the average age and average salary of your convenience sample, using the `compute_statistics` function. Since they're computed on a sample, these are called *sample averages*.
convenience_stats = ...
convenience_stats
_ = ok.grade('q3_4')
# Next, we'll compare the convenience sample salaries with the full data salaries in a single histogram. To do that, we'll need to use the `bin_column` option of the `hist` method, which indicates that all columns are counts of the bins in a particular column. The following cell should not require any changes; just run it.
# +
def compare_salaries(first, second, first_title, second_title):
"""Compare the salaries in two tables."""
max_salary = max(np.append(first.column('Salary'), second.column('Salary')))
bins = np.arange(0, max_salary+1e6+1, 1e6)
first_binned = first.bin('Salary', bins=bins).relabeled(1, first_title)
second_binned = second.bin('Salary', bins=bins).relabeled(1, second_title)
first_binned.join('bin', second_binned).hist(bin_column='bin')
compare_salaries(full_data, convenience_sample, 'All Players', 'Convenience Sample')
# -
# **Question 3.5** Does the convenience sample give us an accurate picture of the age and salary of the full population of NBA players in 2018-2019? Would you expect it to, in general? Before you move on, write a short answer in English below. You can refer to the statistics calculated above or perform your own analysis.
# *Write your answer here, replacing this text.*
# Congratulations, you're done with Lab 5! Be sure to
# - **run all the tests** (the next cell has a shortcut for that),
# - **Save and Checkpoint** from the `File` menu,
# - **run the cell below to submit your work**,
# - and ask one of the staff members to check you off.
# For your convenience, you can run this cell to run all the tests at once!
import os
_ = [ok.grade(q[:-3]) for q in os.listdir("tests") if q.startswith('q')]
_ = ok.submit()
| lab05/lab05.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/amilkh/cs230-fer/blob/master/datasets/affectnet_to_png.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="PWC1w1-0xJlE" colab_type="code" outputId="bc030a88-0696-4088-b847-2cf038382011" colab={"base_uri": "https://localhost:8080/", "height": 128}
from google.colab import drive
drive.mount('/content/drive')
# + id="J76fXHTw-FCU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 72} outputId="5d3c3b27-4581-4b4c-d8ea-d3d42a7e5f1e"
# ! rm -rf /content/affectnet && mkdir /content/affectnet
# ! unrar e -idq '/content/drive/My Drive/cs230 project/dataset/affectnet/Manually_Annotated.part01.rar' /content/affectnet
# + id="a3gZOJmkEpcX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="3c4eb36e-e54b-4e75-902c-7f6a636b2492"
# ! ls -1 /content/affectnet | wc -l
# + id="cJgl4RTOzaSu" colab_type="code" colab={}
import pandas as pd
train_csv = pd.read_csv('/content/drive/My Drive/cs230 project/dataset/affectnet/training.csv')
# FER2013 = {0:'angry', 1:'disgust', 2:'fear', 3:'happy', 4:'sad', 5:'surprise', 6:'neutral'}
# AffectNet = 0: Neutral, 1: Happiness, 2: Sadness, 3: Surprise, 4: Fear, 5: Disgust, 6: Anger, 7: Contempt, 8: None, 9: Uncertain, 10: No-Face
def reindex_labels(y):
label_mapping = {0:6,1:3,2:4,3:5,4:2,5:1,6:0,7:7,8:8,9:9,10:10}
for label in label_mapping.keys():
y[y == label] = label_mapping[label]
return y
# + id="bqSj7t1MFde5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 98} outputId="2a700724-edd9-44be-d24d-450a196443f2"
train_csv[train_csv['subDirectory_filePath']=='163/7b5d3644888582a32c7896e7f58f400f179f1fd8c48feb286e2cd8d4.jpg']
# + id="zd3pBrfRWLCs" colab_type="code" colab={}
train_csv['subDirectory_filePath'] = train_csv['subDirectory_filePath'].apply(lambda fp: [fp.split('/')[1]])
# + id="Uu4HDJJtFukB" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="f7c53ecb-f659-4952-abd3-383456296355"
train_csv(0)
# + id="3pk_IV0LaqPn" colab_type="code" colab={}
from PIL import Image
for i, row in train_csv.iterrows():
try:
fn=row['subDirectory_filePath'].split('/')[1][0]
img=Image.open('/content/affectnet/'+fn)
except IOError as e:
pass
else:
img.show()
break
# + id="REQj2eX6Y7ZJ" colab_type="code" outputId="d550066b-8d9d-459d-f007-b576f586e81e" colab={"base_uri": "https://localhost:8080/", "height": 35}
train_csv[train_csv['subDirectory_filePath'] == train_csv.iloc[0]['subDirectory_filePath'][0]]['subDirectory_filePath']
# + id="BVwlKRu-9qSN" colab_type="code" colab={}
from os import listdir
for fn in listdir('/content/affectnet'):
if fn.endswith(".jpg"):
print(train_csv['subDirectory_filePath'==fn])
break
else:
continue
# + id="bezzV2CF8c6o" colab_type="code" outputId="46ac3c6a-b68f-4b93-e4d3-b42dfb57a173" colab={"base_uri": "https://localhost:8080/", "height": 35}
#e = 0
#train_csv_e=train_csv[train_csv['expression']==e]
# + id="7thKHuzr4enP" colab_type="code" colab={}
import numpy as np
X = np.load('/content/ck-output/npy_files/X.npy')
y8 = np.load('/content/ck-output/npy_files/y.npy')
y = reindex_labels(y8)
# + id="GSH3CX8IE5yj" colab_type="code" colab={}
import matplotlib.pyplot as plt
emotions = {0:'angry', 1:'disgust', 2:'fear', 3:'happy', 4:'sad', 5:'surprise', 6:'neutral'}
for i in range(0,10):
plt.xlabel(emotions[y[i]])
plt.imshow(X[i].reshape(96,96),cmap='gray')
plt.figure()
# + id="Rd-enGupIs_1" colab_type="code" outputId="362718e2-8d0d-423c-9595-8b3963f600d3" colab={"base_uri": "https://localhost:8080/", "height": 35}
X.shape
# + id="ZvgocTG4KF1v" colab_type="code" colab={}
from os import mkdir
mkdir('/content/ck-images/')
for emotion in emotions:
mkdir(f'/content/ck-images/' + f'{emotion} ' + f'{emotions[emotion]}')
# + id="ojFKvNRXFA5G" colab_type="code" colab={}
from PIL import Image
count = 0
for i in range(0,X.shape[0]):
count_string = str(count).zfill(7)
fname = '/content/ck-images/' + f'{y[i]} ' + f'{emotions[y[i]]}/' + f'{emotions[y[i]]}-{count_string}.png'
img = Image.fromarray(X[i].reshape(96,96))
img=img.resize((48,48))
img.save(fname)
count += 1
# + id="b-lZOMv4JCPC" colab_type="code" colab={}
# ! cd ck-images && zip -r ck-plus.zip *
# + id="pCsREeBHK2N7" colab_type="code" colab={}
# ! mv ck-images/ck-plus.zip '/content/drive/My Drive/cs230 project/dataset/'
# + id="lZlxu8ciL0Y4" colab_type="code" outputId="d39db1b8-ab03-4606-c47b-377b7882939f" colab={"base_uri": "https://localhost:8080/", "height": 326}
# ! ls -lh '/content/drive/My Drive/cs230 project/dataset/'
# + id="uAA7hlqTL-el" colab_type="code" colab={}
| datasets/affectnet_to_png.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/StarAtNyte1/ml-basics/blob/main/random_forest_regression.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="LeamvpPVXuS_"
# # Random Forest Regression
# + [markdown] id="O2wvZ7SKXzVC"
# ## Importing the libraries
# + id="PVmESEFZX4Ig"
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# + [markdown] id="zgbK_F8-X7em"
# ## Importing the dataset
# + id="adBE4tjQX_Bh"
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:-1].values
y = dataset.iloc[:, -1].values
# + [markdown] id="v4S2fyIBYDcu"
# ## Training the Random Forest Regression model on the whole dataset
# + id="o8dOCoJ1YKMc" colab={"base_uri": "https://localhost:8080/"} outputId="c41dd0e8-8d4e-403c-e567-adc24cbddea9"
from sklearn.ensemble import RandomForestRegressor
regressor = RandomForestRegressor(n_estimators = 10, random_state = 0)
regressor.fit(X, y)
# + [markdown] id="8IbsXbK3YM4M"
# ## Predicting a new result
# + id="pTXrS8FEYQlJ" colab={"base_uri": "https://localhost:8080/"} outputId="123aa7eb-52f7-4ed4-b285-1a576de205dc"
regressor.predict([[6.5]])
# + [markdown] id="kLqF9yMbYTon"
# ## Visualising the Random Forest Regression results (higher resolution)
# + id="BMlTBifVYWNr" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="11bd09f5-37da-4b96-ee9d-7e3f7e55afd3"
X_grid = np.arange(min(X), max(X), 0.01)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, regressor.predict(X_grid), color = 'blue')
plt.title('Truth or Bluff (Random Forest Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()
| random_forest_regression.ipynb |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.