title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python Solution O(n^2) Solution Beats 94% | construct-quad-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThink of how you would do divide and conquer on an array if we had to divide the array in half everytime we do a recursion.\n\nWe will typically have a start index and number of elements from the start. \nFor example if our array is like this - \n\n[0,1,2,3,4,5,6,7]\n\nIn our first stack our recursive calls will look like -\nstart = 0, num_items = 4 # [0,1,2,3]\nstart = 4, num_items = 4 # [4,5,6,7]\n\nOur next recursive call for [4,5,6,7] will look like -\nstart = 4, num_items = 2 # [4,5]\nstart = 6, num_items = 2 # [6,7]\n\nOur base case will be when num_items == 1.\n\nUsing this understanding above, how can we equally divide a 2D array.\nFrom the above example we see that we need a `start` point and `num_items` to describe a 1D array.\n\nTherefore to describe a 2D array we will need a start point in the form of a tuple `(start_row, start_col)` and `size` of our grid, since we will always have `nxn` grid.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInorder to keep track of the grid that we are evalulating we will keep 4 variables - \n`pos` - This will be our starting point (described above). For simplicity we will unpack our tuple `r, c = pos` and use `r` as our starting row and `c` as starting column.\n`grid` - This is our original grid\n`size` - number of rows and columns we want to evaluate (described above)\n\nLet\'s understand our base cases here -\n- We will stop recursing if the grid size that we are evaluating is 1x1. Since each grid that we divide has equal number of rows and columns, we will use `abs(c-num_cols) == 1`\n - Create a node and return it `return Node(grid[r][c], True, None, None, None, None)`. Our leaf is set to `True` and we use the first element of the grid as the marker.\n- The second scenario is when all nodes in our current grid is same.\n - We start from `r` (our starting row) and loop until `r+size`\n - For the column we start from `c` and loop until `c+size`\n - If at any point our current element doesn\'t match with the first element of our current grid `grid[row][col] != grid[r][c]:` We break out of the loop and recurse further (See below)\n - Otherwise return same as above `return Node(grid[r][c], True, None, None, None, None)`\n```\nif abs(c-size) == 1:\n return Node(grid[r][c], True, None, None, None, None)\nfor row in range(r, r+size):\n is_break = False\n for col in range(c, c+size):\n if grid[row][col] != grid[r][c]:\n is_break = True\n break\n if is_break:\n break\nelse:\n return Node(grid[r][c], True, None, None, None, None)\n```\nAlternatively you can merge these 2 cases, but I left it there for understanding sake.\n\nLet\'s go over how we are going to recursive if the elements of our current grid are not the same.\n\nWe have 4 cases for recursion\n- Top left `top_left = helper((r,c), grid, size//2)`\n\n ```\n [x o - -]\n [o o - -]\n [- - - -]\n [- - - -]\n ``` \n - Here our `x` represets our starting point, and squares marked with `o` represet our grid that we wil evaluate in next recursion which is of size `n // 2`\n - In our next recursive stack our `(r,c)` is (0,0) our `size` drops from 4 - > 2\n\n\n- Top right `top_right = helper((r,c+size//2), grid, size//2)`\n ```\n [- - x o]\n [- - o o]\n [- - - -]\n [- - - -]\n ``` \n - Here `x` x starts from our original column `c` + half the size of the grid `size//2` our `size` stays the same as before\n - In our next recursive stack our `(r,c)` is (0,2) our `size` drops from 4 - > 2\n\n\n- Bottom Left `bottom_left = helper((r+size//2,c), grid, size//2)`\n ```\n [- - - -]\n [- - - -]\n [x o - -]\n [o o - -]\n ``` \n - Here `x` x starts from our original row `r` + half the size of the grid `size//2` our `size` stays the same as before.\n - In our next recursive stack our `(r,c)` is (2,0) our `size` drops from 4 - > 2\n\n\n- Bottom Right `bottom_right = helper((r+size//2,c+size//2), grid, size//2)`\n ```\n [- - - -]\n [- - - -]\n [- - x o]\n [- - o o]\n ``` \n - Here `x` x starts from our original row `r` and original column `c` + half the size of the grid `size//2` our `size` stays the same as before.\n - In our next recursive stack our `(r,c)` is (2,2) our `size` drops from 4 - > 2\n\nFinally we create a `Node` and populate it with the variables `above`. Our leaf will be set to `False` and since we are allowed to pick any value for `val` we will pick our current grid\'s starting cell value - `grid[r][c]`.\n```\n top_left = helper((r,c), grid, size//2)\n top_right = helper((r,c+size//2), grid, size//2)\n bottom_left = helper((r+size//2,c), grid, size//2)\n bottom_right = helper((r+size//2,c+size//2), grid, size//2)\n return Node(grid[r][c], False, top_left, top_right, bottom_left, bottom_right)\n```\n\nNote: Our first call will have a starting point `(0,0)` and `size` will be `len(grid)`\n```\n return helper((0,0), grid, len(grid))\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2) \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) \n\n# Code\n```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n\n def helper(pos, grid, size):\n r, c = pos\n if abs(c-size) == 1:\n return Node(grid[r][c], True, None, None, None, None)\n for row in range(r, r+size):\n is_break = False\n for col in range(c, c+size):\n if grid[row][col] != grid[r][c]:\n is_break = True\n break\n if is_break:\n break\n else:\n return Node(grid[r][c], True, None, None, None, None)\n top_left = helper((r,c), grid, size//2)\n top_right = helper((r,c+size//2), grid, size//2)\n bottom_left = helper((r+size//2,c), grid, size//2)\n bottom_right = helper((r+size//2,c+size//2), grid, size//2)\n return Node(grid[r][c], False, top_left, top_right, bottom_left, bottom_right)\n return helper((0,0), grid, len(grid))\n``` | 1 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Простое решение на Петухоне | construct-quad-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\ndef is_leaf(grid: List[List[int]]) -> bool:\n N = len(grid)\n k = grid[0][0]\n for i in range(N):\n for j in range(N):\n if grid[i][j] == k:\n continue\n return False\n return True\n\n\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n N = len(grid)\n if is_leaf(grid):\n return Node(\n val=bool(grid[0][0]),\n isLeaf=True,\n topLeft=None,\n topRight=None,\n bottomLeft=None,\n bottomRight=None,\n )\n else:\n return Node(\n val=False,\n isLeaf=False,\n topLeft=self.construct([i[:N//2] for i in grid[:N//2]]),\n topRight=self.construct([i[N//2:] for i in grid[:N//2]]),\n bottomLeft=self.construct([i[:N//2] for i in grid[N//2:]]),\n bottomRight=self.construct([i[N//2:] for i in grid[N//2:]]),\n )\n``` | 1 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Простое решение на Петухоне | construct-quad-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\ndef is_leaf(grid: List[List[int]]) -> bool:\n N = len(grid)\n k = grid[0][0]\n for i in range(N):\n for j in range(N):\n if grid[i][j] == k:\n continue\n return False\n return True\n\n\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n N = len(grid)\n if is_leaf(grid):\n return Node(\n val=bool(grid[0][0]),\n isLeaf=True,\n topLeft=None,\n topRight=None,\n bottomLeft=None,\n bottomRight=None,\n )\n else:\n return Node(\n val=False,\n isLeaf=False,\n topLeft=self.construct([i[:N//2] for i in grid[:N//2]]),\n topRight=self.construct([i[N//2:] for i in grid[:N//2]]),\n bottomLeft=self.construct([i[:N//2] for i in grid[N//2:]]),\n bottomRight=self.construct([i[N//2:] for i in grid[N//2:]]),\n )\n``` | 1 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Python || Dividing matrix recursively | construct-quad-tree | 0 | 1 | # Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n\n def makeTree(self,mat):\n s = sum([sum(x) for x in mat])\n n = len(mat)\n if s==0 or s==n*n:\n return Node(s//(n*n),1,None,None,None,None)\n \n topm = mat[:n//2]\n botm = mat[n//2:]\n\n topml = list(map(lambda x:x[:n//2],topm))\n topmr = list(map(lambda x:x[n//2:],topm))\n botml = list(map(lambda x:x[:n//2],botm))\n botmr = list(map(lambda x:x[n//2:],botm))\n\n tl = self.makeTree(topml)\n tr = self.makeTree(topmr)\n bl = self.makeTree(botml)\n br = self.makeTree(botmr)\n\n return Node(1,0,tl,tr,bl,br)\n\n def construct(self, grid: List[List[int]]) -> \'Node\':\n\n return self.makeTree(grid)\n``` | 1 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Python || Dividing matrix recursively | construct-quad-tree | 0 | 1 | # Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n\n def makeTree(self,mat):\n s = sum([sum(x) for x in mat])\n n = len(mat)\n if s==0 or s==n*n:\n return Node(s//(n*n),1,None,None,None,None)\n \n topm = mat[:n//2]\n botm = mat[n//2:]\n\n topml = list(map(lambda x:x[:n//2],topm))\n topmr = list(map(lambda x:x[n//2:],topm))\n botml = list(map(lambda x:x[:n//2],botm))\n botmr = list(map(lambda x:x[n//2:],botm))\n\n tl = self.makeTree(topml)\n tr = self.makeTree(topmr)\n bl = self.makeTree(botml)\n br = self.makeTree(botmr)\n\n return Node(1,0,tl,tr,bl,br)\n\n def construct(self, grid: List[List[int]]) -> \'Node\':\n\n return self.makeTree(grid)\n``` | 1 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Python one liner | construct-quad-tree | 0 | 1 | # Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n return Node(val=1 if sum([sum(row) for row in grid]) else 0, isLeaf=1, topLeft=None, topRight=None, bottomLeft=None, bottomRight=None) if sum([sum(row) for row in grid]) == 0 or sum([sum(row) for row in grid]) == len(grid)*len(grid) else Node(val=1 if sum([sum(row) for row in grid]) else 0, isLeaf=0, topLeft=self.construct([row[:len(grid)//2] for row in grid[:len(grid)//2]]), topRight=self.construct([row[len(grid)//2:] for row in grid[:len(grid)//2]]), bottomLeft=self.construct([row[:len(grid)//2] for row in grid[len(grid)//2:]]), bottomRight=self.construct([row[len(grid)//2:] for row in grid[len(grid)//2:]]))\n\n``` | 0 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Python one liner | construct-quad-tree | 0 | 1 | # Code\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n return Node(val=1 if sum([sum(row) for row in grid]) else 0, isLeaf=1, topLeft=None, topRight=None, bottomLeft=None, bottomRight=None) if sum([sum(row) for row in grid]) == 0 or sum([sum(row) for row in grid]) == len(grid)*len(grid) else Node(val=1 if sum([sum(row) for row in grid]) else 0, isLeaf=0, topLeft=self.construct([row[:len(grid)//2] for row in grid[:len(grid)//2]]), topRight=self.construct([row[len(grid)//2:] for row in grid[:len(grid)//2]]), bottomLeft=self.construct([row[:len(grid)//2] for row in grid[len(grid)//2:]]), bottomRight=self.construct([row[len(grid)//2:] for row in grid[len(grid)//2:]]))\n\n``` | 0 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Python | Beats 100% | Simple and Efficient Solution | DFS | construct-quad-tree | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n def dfs(n, r, c):\n allSame = True\n for i in range(n):\n for j in range(n):\n if grid[r][c] != grid[r+i][c+j]:\n allSame = False\n break\n if allSame:\n return Node(grid[r][c], True)\n n = n // 2\n topleft = dfs(n, r, c)\n topright = dfs(n, r, c+n)\n bottomleft = dfs(n, r+n, c)\n bottomright = dfs(n, r+n, c+n)\n return Node(0, False, topleft, topright, bottomleft, bottomright)\n return dfs(len(grid), 0, 0) \n``` | 1 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Python | Beats 100% | Simple and Efficient Solution | DFS | construct-quad-tree | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n def dfs(n, r, c):\n allSame = True\n for i in range(n):\n for j in range(n):\n if grid[r][c] != grid[r+i][c+j]:\n allSame = False\n break\n if allSame:\n return Node(grid[r][c], True)\n n = n // 2\n topleft = dfs(n, r, c)\n topright = dfs(n, r, c+n)\n bottomleft = dfs(n, r+n, c)\n bottomright = dfs(n, r+n, c+n)\n return Node(0, False, topleft, topright, bottomleft, bottomright)\n return dfs(len(grid), 0, 0) \n``` | 1 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Clean Codes🔥🔥|| Full Explanation✅|| Helper Method✅|| C++|| Java|| Python3 | construct-quad-tree | 1 | 1 | # Intuition :\n- Here we have to construct a Quadtree from a 2D binary grid, where each node of the Quadtree represents a square of the grid. \n\n# What is Quad Tree ?\n- A Quadtree is represented by a tree of Node objects, where each Node has four children (topLeft, topRight, bottomLeft, and bottomRight) that represent the four quadrants of its square.\n- A Quadtree is a way of dividing the picture into smaller and smaller sections, with each node in the tree representing a section of the picture. The tree is built recursively, which means it keeps calling itself until it reaches the smallest possible section.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Detail Explanation to Approach :\n**Class Solution :**\n- Here we have to create a tree-like structure called a Quadtree from a picture that is made up of only black and white squares. \n```\nclass Solution {\n public Node construct(int[][] grid) {\n return helper(grid, 0, 0, grid.length);\n }\n\n```\n- This is the class definition for the solution, which contains one public method called construct. \n- This method takes a 2D integer array called grid as input, and it returns a Node object that represents the root of the Quadtree for that grid. \n- The helper method (defined later) is used to construct the Quadtree recursively, starting from the entire grid.\n\n**Helper Function :**\n- See , first start with the entire picture and check if all the squares in that section are the same color. \n- If they are, create a single node in the Quadtree to represent that section of the picture. \n- If they aren\'t, split that section into four smaller squares and repeats the process for each one. \n- Keep doing this until you reach a point where all the squares in a section are the same color, and create a node to represent that section.\n```\n private Node helper(int[][] grid, int i, int j, int w) {\n if (allSame(grid, i, j, w))\n return new Node(grid[i][j] == 1 ? true : false, true);\n\n Node node = new Node(true, false);\n node.topLeft = helper(grid, i, j, w / 2);\n node.topRight = helper(grid, i, j + w / 2, w / 2);\n node.bottomLeft = helper(grid, i + w / 2, j, w / 2);\n node.bottomRight = helper(grid, i + w / 2, j + w / 2, w / 2);\n return node;\n }\n\n```\n- This is the helper method, which is a private recursive function used to construct the Quadtree. It takes four parameters:\n\n1. grid: the 2D integer array representing the current sub-grid.\n2. i: the row index of the top-left corner of the current sub-grid.\n3. j: the column index of the top-left corner of the current sub-grid.\n4. w: the width of the current sub-grid.\n\n**allSame Method :**\n- The `allSame` method is a way of checking if all the squares in a section of the picture are the same color. \n- It checks each square in the section and compares it to the top-left square to see if they are the same color. \n- If any square is a different color, it returns false, which means that the section is not all the same color. \n- If it gets to the end of the loop and all squares are the same color, it returns true, which means that the section is all the same color.\n```\n private boolean allSame(int[][] grid, int i, int j, int w) {\n for (int x = i; x < i + w; ++x)\n for (int y = j; y < j + w; ++y)\n if (grid[x][y] != grid[i][j])\n return false;\n return true;\n }\n\n```\n- This is the allSame helper method, which checks if all the squares in a given sub-grid are the same color. It takes four parameters:\n\n1. grid: the 2D integer array representing the full grid.\n2. i: the row index of the top-left corner of the sub-grid.\n3. j: the column index of the top-left corner of the sub-grid.\n4. w: the width of the sub-grid.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : O(n^2 * log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n*Let\'s Code it Up .\nThere may be minor syntax difference in C++ and Python*\n# Codes [C++ |Java |Python3] : \n```C++ []\nclass Solution {\n public:\n Node* construct(vector<vector<int>>& grid) {\n return helper(grid, 0, 0, grid.size());\n }\n\n private:\n Node* helper(const vector<vector<int>>& grid, int i, int j, int w) {\n if (allSame(grid, i, j, w))\n return new Node(grid[i][j], true);\n\n Node* node = new Node(true, false);\n node->topLeft = helper(grid, i, j, w / 2);\n node->topRight = helper(grid, i, j + w / 2, w / 2);\n node->bottomLeft = helper(grid, i + w / 2, j, w / 2);\n node->bottomRight = helper(grid, i + w / 2, j + w / 2, w / 2);\n return node;\n }\n\n bool allSame(const vector<vector<int>>& grid, int i, int j, int w) {\n return all_of(begin(grid) + i, begin(grid) + i + w,\n [&](const vector<int>& row) {\n return all_of(begin(row) + j, begin(row) + j + w,\n [&](int num) { return num == grid[i][j]; });\n });\n }\n};\n```\n```Java []\nclass Solution {\n public Node construct(int[][] grid) {\n return helper(grid, 0, 0, grid.length);\n }\n\n private Node helper(int[][] grid, int i, int j, int w) {\n if (allSame(grid, i, j, w))\n return new Node(grid[i][j] == 1 ? true : false, true);\n\n Node node = new Node(true, false);\n node.topLeft = helper(grid, i, j, w / 2);\n node.topRight = helper(grid, i, j + w / 2, w / 2);\n node.bottomLeft = helper(grid, i + w / 2, j, w / 2);\n node.bottomRight = helper(grid, i + w / 2, j + w / 2, w / 2);\n return node;\n }\n\n private boolean allSame(int[][] grid, int i, int j, int w) {\n for (int x = i; x < i + w; ++x)\n for (int y = j; y < j + w; ++y)\n if (grid[x][y] != grid[i][j])\n return false;\n return true;\n }\n}\n```\n```Python []\nclass Node:\n def __init__(self, val, isLeaf, topLeft=None, topRight=None, bottomLeft=None, bottomRight=None):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> Node:\n return self.helper(grid, 0, 0, len(grid))\n\n def helper(self, grid, i, j, w):\n if self.allSame(grid, i, j, w):\n return Node(grid[i][j] == 1, True)\n\n node = Node(True, False)\n node.topLeft = self.helper(grid, i, j, w // 2)\n node.topRight = self.helper(grid, i, j + w // 2, w // 2)\n node.bottomLeft = self.helper(grid, i + w // 2, j, w // 2)\n node.bottomRight = self.helper(grid, i + w // 2, j + w // 2, w // 2)\n return node\n\n def allSame(self, grid, i, j, w):\n for x in range(i, i + w):\n for y in range(j, j + w):\n if grid[x][y] != grid[i][j]:\n return False\n return True\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n | 71 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Clean Codes🔥🔥|| Full Explanation✅|| Helper Method✅|| C++|| Java|| Python3 | construct-quad-tree | 1 | 1 | # Intuition :\n- Here we have to construct a Quadtree from a 2D binary grid, where each node of the Quadtree represents a square of the grid. \n\n# What is Quad Tree ?\n- A Quadtree is represented by a tree of Node objects, where each Node has four children (topLeft, topRight, bottomLeft, and bottomRight) that represent the four quadrants of its square.\n- A Quadtree is a way of dividing the picture into smaller and smaller sections, with each node in the tree representing a section of the picture. The tree is built recursively, which means it keeps calling itself until it reaches the smallest possible section.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Detail Explanation to Approach :\n**Class Solution :**\n- Here we have to create a tree-like structure called a Quadtree from a picture that is made up of only black and white squares. \n```\nclass Solution {\n public Node construct(int[][] grid) {\n return helper(grid, 0, 0, grid.length);\n }\n\n```\n- This is the class definition for the solution, which contains one public method called construct. \n- This method takes a 2D integer array called grid as input, and it returns a Node object that represents the root of the Quadtree for that grid. \n- The helper method (defined later) is used to construct the Quadtree recursively, starting from the entire grid.\n\n**Helper Function :**\n- See , first start with the entire picture and check if all the squares in that section are the same color. \n- If they are, create a single node in the Quadtree to represent that section of the picture. \n- If they aren\'t, split that section into four smaller squares and repeats the process for each one. \n- Keep doing this until you reach a point where all the squares in a section are the same color, and create a node to represent that section.\n```\n private Node helper(int[][] grid, int i, int j, int w) {\n if (allSame(grid, i, j, w))\n return new Node(grid[i][j] == 1 ? true : false, true);\n\n Node node = new Node(true, false);\n node.topLeft = helper(grid, i, j, w / 2);\n node.topRight = helper(grid, i, j + w / 2, w / 2);\n node.bottomLeft = helper(grid, i + w / 2, j, w / 2);\n node.bottomRight = helper(grid, i + w / 2, j + w / 2, w / 2);\n return node;\n }\n\n```\n- This is the helper method, which is a private recursive function used to construct the Quadtree. It takes four parameters:\n\n1. grid: the 2D integer array representing the current sub-grid.\n2. i: the row index of the top-left corner of the current sub-grid.\n3. j: the column index of the top-left corner of the current sub-grid.\n4. w: the width of the current sub-grid.\n\n**allSame Method :**\n- The `allSame` method is a way of checking if all the squares in a section of the picture are the same color. \n- It checks each square in the section and compares it to the top-left square to see if they are the same color. \n- If any square is a different color, it returns false, which means that the section is not all the same color. \n- If it gets to the end of the loop and all squares are the same color, it returns true, which means that the section is all the same color.\n```\n private boolean allSame(int[][] grid, int i, int j, int w) {\n for (int x = i; x < i + w; ++x)\n for (int y = j; y < j + w; ++y)\n if (grid[x][y] != grid[i][j])\n return false;\n return true;\n }\n\n```\n- This is the allSame helper method, which checks if all the squares in a given sub-grid are the same color. It takes four parameters:\n\n1. grid: the 2D integer array representing the full grid.\n2. i: the row index of the top-left corner of the sub-grid.\n3. j: the column index of the top-left corner of the sub-grid.\n4. w: the width of the sub-grid.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : O(n^2 * log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n*Let\'s Code it Up .\nThere may be minor syntax difference in C++ and Python*\n# Codes [C++ |Java |Python3] : \n```C++ []\nclass Solution {\n public:\n Node* construct(vector<vector<int>>& grid) {\n return helper(grid, 0, 0, grid.size());\n }\n\n private:\n Node* helper(const vector<vector<int>>& grid, int i, int j, int w) {\n if (allSame(grid, i, j, w))\n return new Node(grid[i][j], true);\n\n Node* node = new Node(true, false);\n node->topLeft = helper(grid, i, j, w / 2);\n node->topRight = helper(grid, i, j + w / 2, w / 2);\n node->bottomLeft = helper(grid, i + w / 2, j, w / 2);\n node->bottomRight = helper(grid, i + w / 2, j + w / 2, w / 2);\n return node;\n }\n\n bool allSame(const vector<vector<int>>& grid, int i, int j, int w) {\n return all_of(begin(grid) + i, begin(grid) + i + w,\n [&](const vector<int>& row) {\n return all_of(begin(row) + j, begin(row) + j + w,\n [&](int num) { return num == grid[i][j]; });\n });\n }\n};\n```\n```Java []\nclass Solution {\n public Node construct(int[][] grid) {\n return helper(grid, 0, 0, grid.length);\n }\n\n private Node helper(int[][] grid, int i, int j, int w) {\n if (allSame(grid, i, j, w))\n return new Node(grid[i][j] == 1 ? true : false, true);\n\n Node node = new Node(true, false);\n node.topLeft = helper(grid, i, j, w / 2);\n node.topRight = helper(grid, i, j + w / 2, w / 2);\n node.bottomLeft = helper(grid, i + w / 2, j, w / 2);\n node.bottomRight = helper(grid, i + w / 2, j + w / 2, w / 2);\n return node;\n }\n\n private boolean allSame(int[][] grid, int i, int j, int w) {\n for (int x = i; x < i + w; ++x)\n for (int y = j; y < j + w; ++y)\n if (grid[x][y] != grid[i][j])\n return false;\n return true;\n }\n}\n```\n```Python []\nclass Node:\n def __init__(self, val, isLeaf, topLeft=None, topRight=None, bottomLeft=None, bottomRight=None):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> Node:\n return self.helper(grid, 0, 0, len(grid))\n\n def helper(self, grid, i, j, w):\n if self.allSame(grid, i, j, w):\n return Node(grid[i][j] == 1, True)\n\n node = Node(True, False)\n node.topLeft = self.helper(grid, i, j, w // 2)\n node.topRight = self.helper(grid, i, j + w // 2, w // 2)\n node.bottomLeft = self.helper(grid, i + w // 2, j, w // 2)\n node.bottomRight = self.helper(grid, i + w // 2, j + w // 2, w // 2)\n return node\n\n def allSame(self, grid, i, j, w):\n for x in range(i, i + w):\n for y in range(j, j + w):\n if grid[x][y] != grid[i][j]:\n return False\n return True\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n | 71 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Python Fully Optimized Recursion || O(n^2) | construct-quad-tree | 0 | 1 | # Intuition\nWe will recursively construct the quadtree. Given some grid, we divide it into 4 subgrids, construct the nodes for those subgrids, then combine those children nodes into a tree. These base case is when we reach a grid of size 1, we know this must be a leaf node.\n\n\n# Approach\n### Case 1: Grid contains single value\nHow do we combine the children into a tree? If all children are leaves and they all have the same `val`, then the current grid contains all the same values! We can just represent this grid as a single leaf node.\nExample:\n```\nGrid:\n1 | 1\n--+---\n1 | 1\ntopLeft returns Node(val=1, isLeaf=True)\ntopRight returns Node(val=1, isLeaf=True)\nbotLeft returns Node(val=1, isLeaf=True)\nbotRight returns Node(val=1, isLeaf=True)\n\nThe entire grid is all the same value, and can be represented by a single node.\nReturn Node(val=1, isLeaf=True)\n```\n\n### Case 2: Grid contains multiple values\nIf one of the children is not a leaf, then that subgrid contains multiple values. If all children are leaves but their values differ, then the grid contains different values. In these cases, we create a parent node and connect them to each child.\nExample:\n```\nGrid:\n0 | 1\n--+---\n1 | 1\ntopLeft returns Node(val=0, isLeaf=True)\ntopRight returns Node(val=1, isLeaf=True)\nbotLeft returns Node(val=1, isLeaf=True)\nbotRight returns Node(val=1, isLeaf=True)\n\nThe grid contains multiple values. The current node needs children nodes.\nReturn Node(0, True, topLeft, topRight, botLeft, botRight)\n```\n\n\n# Complexity\n- Time complexity: `O(n^2)`. The reason this approach is optimized is because we don\'t check to see if the grid contains all the same values at each recursive call. We check a grid only in the base case, and we do this for each cell. Since there are `n^2` cells in total, the time complexity is `O(n^2)`.\n\n- Space complexity: `O(logn)`. The space to store the output is usually not considered. The space taken by the recursive call stack is the number of times we can divide the grid, which is at most `O(logn)` times.\n\n# Code\n```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n def construct_range(top, left, l):\n """\n Construct a node representing the subgrid with\n top left corner at (top, left) and side length l\n """\n if l == 1:\n return Node(grid[top][left], True)\n topLeft = construct_range(top, left, l // 2)\n topRight = construct_range(top, left + l // 2, l // 2)\n botLeft = construct_range(top + l // 2, left, l // 2)\n botRight = construct_range(top + l // 2, left + l // 2, l // 2)\n\n children = [topLeft, topRight, botLeft, botRight]\n # Check if all subgrids have the same value\n if all(child.isLeaf and child.val == topLeft.val for child in children):\n return Node(topLeft.val, True)\n \n return Node(0, False, topLeft, topRight, botLeft, botRight)\n \n return construct_range(0, 0, len(grid))\n``` | 24 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Python Fully Optimized Recursion || O(n^2) | construct-quad-tree | 0 | 1 | # Intuition\nWe will recursively construct the quadtree. Given some grid, we divide it into 4 subgrids, construct the nodes for those subgrids, then combine those children nodes into a tree. These base case is when we reach a grid of size 1, we know this must be a leaf node.\n\n\n# Approach\n### Case 1: Grid contains single value\nHow do we combine the children into a tree? If all children are leaves and they all have the same `val`, then the current grid contains all the same values! We can just represent this grid as a single leaf node.\nExample:\n```\nGrid:\n1 | 1\n--+---\n1 | 1\ntopLeft returns Node(val=1, isLeaf=True)\ntopRight returns Node(val=1, isLeaf=True)\nbotLeft returns Node(val=1, isLeaf=True)\nbotRight returns Node(val=1, isLeaf=True)\n\nThe entire grid is all the same value, and can be represented by a single node.\nReturn Node(val=1, isLeaf=True)\n```\n\n### Case 2: Grid contains multiple values\nIf one of the children is not a leaf, then that subgrid contains multiple values. If all children are leaves but their values differ, then the grid contains different values. In these cases, we create a parent node and connect them to each child.\nExample:\n```\nGrid:\n0 | 1\n--+---\n1 | 1\ntopLeft returns Node(val=0, isLeaf=True)\ntopRight returns Node(val=1, isLeaf=True)\nbotLeft returns Node(val=1, isLeaf=True)\nbotRight returns Node(val=1, isLeaf=True)\n\nThe grid contains multiple values. The current node needs children nodes.\nReturn Node(0, True, topLeft, topRight, botLeft, botRight)\n```\n\n\n# Complexity\n- Time complexity: `O(n^2)`. The reason this approach is optimized is because we don\'t check to see if the grid contains all the same values at each recursive call. We check a grid only in the base case, and we do this for each cell. Since there are `n^2` cells in total, the time complexity is `O(n^2)`.\n\n- Space complexity: `O(logn)`. The space to store the output is usually not considered. The space taken by the recursive call stack is the number of times we can divide the grid, which is at most `O(logn)` times.\n\n# Code\n```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n def construct_range(top, left, l):\n """\n Construct a node representing the subgrid with\n top left corner at (top, left) and side length l\n """\n if l == 1:\n return Node(grid[top][left], True)\n topLeft = construct_range(top, left, l // 2)\n topRight = construct_range(top, left + l // 2, l // 2)\n botLeft = construct_range(top + l // 2, left, l // 2)\n botRight = construct_range(top + l // 2, left + l // 2, l // 2)\n\n children = [topLeft, topRight, botLeft, botRight]\n # Check if all subgrids have the same value\n if all(child.isLeaf and child.val == topLeft.val for child in children):\n return Node(topLeft.val, True)\n \n return Node(0, False, topLeft, topRight, botLeft, botRight)\n \n return construct_range(0, 0, len(grid))\n``` | 24 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Python short and clean. Divide and Conquer. Optimized DFS. | construct-quad-tree | 0 | 1 | # Approach\nSimilar to the [Official solution](https://leetcode.com/problems/construct-quad-tree/editorial/).\n\n# Complexity\n- Time complexity: $$O(m * n)$$\n\n- Space complexity: $$O(log\u2084(m * n))$$\n\nwhere, `m x n is the size of the grid`.\n\n# Code\n```python\nclass Solution:\n def construct(self, grid: list[list[int]]) -> \'Node\':\n def build_quad(i1: int, j1: int, i2: int, j2: int) -> \'Node\':\n if (i1, j1) == (i2, j2): return Node(grid[i1][j1], True)\n\n im, jm = i1 + (i2 - i1) // 2, j1 + (j2 - j1) // 2\n tl = build_quad(i1, j1, im, jm)\n tr = build_quad(i1, jm + 1, im, j2)\n bl = build_quad(im + 1, j1, i2, jm)\n br = build_quad(im + 1, jm + 1, i2, j2)\n\n sub_trees = (tl, tr, bl, br)\n val_ = tl.val\n are_leaves = all(node.isLeaf == True for node in sub_trees)\n are_same_val = all(node.val == val_ for node in sub_trees)\n\n return Node(val_, True) if are_leaves and are_same_val else Node(val_, False, tl, tr, bl, br)\n\n m, n = len(grid), len(grid[0])\n return build_quad(0, 0, m - 1, n - 1)\n\n\n``` | 3 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Python short and clean. Divide and Conquer. Optimized DFS. | construct-quad-tree | 0 | 1 | # Approach\nSimilar to the [Official solution](https://leetcode.com/problems/construct-quad-tree/editorial/).\n\n# Complexity\n- Time complexity: $$O(m * n)$$\n\n- Space complexity: $$O(log\u2084(m * n))$$\n\nwhere, `m x n is the size of the grid`.\n\n# Code\n```python\nclass Solution:\n def construct(self, grid: list[list[int]]) -> \'Node\':\n def build_quad(i1: int, j1: int, i2: int, j2: int) -> \'Node\':\n if (i1, j1) == (i2, j2): return Node(grid[i1][j1], True)\n\n im, jm = i1 + (i2 - i1) // 2, j1 + (j2 - j1) // 2\n tl = build_quad(i1, j1, im, jm)\n tr = build_quad(i1, jm + 1, im, j2)\n bl = build_quad(im + 1, j1, i2, jm)\n br = build_quad(im + 1, jm + 1, i2, j2)\n\n sub_trees = (tl, tr, bl, br)\n val_ = tl.val\n are_leaves = all(node.isLeaf == True for node in sub_trees)\n are_same_val = all(node.val == val_ for node in sub_trees)\n\n return Node(val_, True) if are_leaves and are_same_val else Node(val_, False, tl, tr, bl, br)\n\n m, n = len(grid), len(grid[0])\n return build_quad(0, 0, m - 1, n - 1)\n\n\n``` | 3 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
📌📌Python3 || ⚡103 ms, faster than 96.69% of Python3 | construct-quad-tree | 0 | 1 | \n\n```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n def is_same(grid, x, y, length):\n val = grid[x][y]\n for i in range(x, x+length):\n for j in range(y, y+length):\n if val != grid[i][j]:\n return False\n return True\n\n def solve(grid, x, y, length):\n if is_same(grid, x,y, length):\n return Node(grid[x][y], True)\n else:\n root = Node(None, False)\n root.topLeft = solve(grid, x, y, length//2)\n root.topRight = solve(grid, x, y+length//2, length//2)\n root.bottomLeft = solve(grid, x+length//2, y, length//2)\n root.bottomRight = solve(grid, x+length//2, y+length//2, length//2)\n return root\n return solve(grid, 0, 0, len(grid))\n```\nThis code constructs a Quad-Tree from a matrix of 0\'s and 1\'s.\nA Quad-Tree is a tree data structure where each internal node has exactly four children. The Quad-Tree is used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. In this case, the matrix is recursively subdivided into four quadrants until each quadrant contains only 0\'s or 1\'s. Then, each quadrant is represented by a node in the Quad-Tree.\n\nHere\'s how the code works step by step:\n1. Define a helper function is_same(grid, x, y, length) that checks if a square in the matrix is all 0\'s or all 1\'s.\n1. Define a recursive function solve(grid, x, y, length) that takes in a matrix, a starting row index x, a starting column index y, and the length of the square. The function checks if the current square is all 0\'s or all 1\'s. If it is, then it returns a leaf node with the value of the square. Otherwise, it creates an internal node with a value of None and recursively calls itself on each of the four quadrants. The result of each call is assigned to one of the four children of the current node.\n1. Call solve(grid, 0, 0, len(grid)) to construct the Quad-Tree. This starts the recursive calls on the entire matrix.\n1. Return the root of the Quad-Tree that was constructed.\n\nThe time complexity of this code is O(n^2 log n), where n is the size of the matrix, because the code performs log n recursive calls and checks n^2 elements in the matrix. | 5 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
📌📌Python3 || ⚡103 ms, faster than 96.69% of Python3 | construct-quad-tree | 0 | 1 | \n\n```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n def is_same(grid, x, y, length):\n val = grid[x][y]\n for i in range(x, x+length):\n for j in range(y, y+length):\n if val != grid[i][j]:\n return False\n return True\n\n def solve(grid, x, y, length):\n if is_same(grid, x,y, length):\n return Node(grid[x][y], True)\n else:\n root = Node(None, False)\n root.topLeft = solve(grid, x, y, length//2)\n root.topRight = solve(grid, x, y+length//2, length//2)\n root.bottomLeft = solve(grid, x+length//2, y, length//2)\n root.bottomRight = solve(grid, x+length//2, y+length//2, length//2)\n return root\n return solve(grid, 0, 0, len(grid))\n```\nThis code constructs a Quad-Tree from a matrix of 0\'s and 1\'s.\nA Quad-Tree is a tree data structure where each internal node has exactly four children. The Quad-Tree is used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. In this case, the matrix is recursively subdivided into four quadrants until each quadrant contains only 0\'s or 1\'s. Then, each quadrant is represented by a node in the Quad-Tree.\n\nHere\'s how the code works step by step:\n1. Define a helper function is_same(grid, x, y, length) that checks if a square in the matrix is all 0\'s or all 1\'s.\n1. Define a recursive function solve(grid, x, y, length) that takes in a matrix, a starting row index x, a starting column index y, and the length of the square. The function checks if the current square is all 0\'s or all 1\'s. If it is, then it returns a leaf node with the value of the square. Otherwise, it creates an internal node with a value of None and recursively calls itself on each of the four quadrants. The result of each call is assigned to one of the four children of the current node.\n1. Call solve(grid, 0, 0, len(grid)) to construct the Quad-Tree. This starts the recursive calls on the entire matrix.\n1. Return the root of the Quad-Tree that was constructed.\n\nThe time complexity of this code is O(n^2 log n), where n is the size of the matrix, because the code performs log n recursive calls and checks n^2 elements in the matrix. | 5 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
Python 3 || 6 lines, recursion, w/ explanation || T/M: 99.8% / 30% | construct-quad-tree | 0 | 1 | ```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> Node:\n\n def dfs(x = 0, y = 0, n = len(grid)): # <- (x,y) is the upper-left corner of the quad\n # and n is the length of the side of the quad\n\n if all (grid[i+x][j+y] == grid[x][y] # <- check whether all elements in the quad are the \n for i in range(n) for j in range(n)): # same, thenthe same. If so, then the quad is a leaf ... \n \n return Node(grid[x][y] == 1, True)\n\n n//= 2 \n \n return Node(False, False, # <- ... if not, then divide the quad in four and recuse.\n dfs(x,y,n), dfs(x,y+n,n), \n dfs(x+n,y,n), dfs(x+n,y+n,n))\n\n return dfs() # <- initial case is the entire grid\n\n```\n[https://leetcode.com/problems/construct-quad-tree/submissions/856266978/](http://)\n\nPython 3 || 6 lines, recursion, w/ explanation || T/M: 99.8% / 30%\n\nI could be wrong, but I think that time is, worst case, *O*(*N*^2). Because there\'s no slices, I thnk space is *O*(1). (But recusion baffles me.) | 10 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
Python 3 || 6 lines, recursion, w/ explanation || T/M: 99.8% / 30% | construct-quad-tree | 0 | 1 | ```\nclass Solution:\n def construct(self, grid: List[List[int]]) -> Node:\n\n def dfs(x = 0, y = 0, n = len(grid)): # <- (x,y) is the upper-left corner of the quad\n # and n is the length of the side of the quad\n\n if all (grid[i+x][j+y] == grid[x][y] # <- check whether all elements in the quad are the \n for i in range(n) for j in range(n)): # same, thenthe same. If so, then the quad is a leaf ... \n \n return Node(grid[x][y] == 1, True)\n\n n//= 2 \n \n return Node(False, False, # <- ... if not, then divide the quad in four and recuse.\n dfs(x,y,n), dfs(x,y+n,n), \n dfs(x+n,y,n), dfs(x+n,y+n,n))\n\n return dfs() # <- initial case is the entire grid\n\n```\n[https://leetcode.com/problems/construct-quad-tree/submissions/856266978/](http://)\n\nPython 3 || 6 lines, recursion, w/ explanation || T/M: 99.8% / 30%\n\nI could be wrong, but I think that time is, worst case, *O*(*N*^2). Because there\'s no slices, I thnk space is *O*(1). (But recusion baffles me.) | 10 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
427: Solution with step by step explanation | construct-quad-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the Node class with val, isLeaf, topLeft, topRight, bottomLeft, and bottomRight attributes.\n\n2. Define the Solution class with the construct method that takes in a 2D list of 0\'s and 1\'s as input.\n\n3. Within the construct method, define a recursive function construct_helper that takes in a 2D list of 0\'s and 1\'s as input.\n\n4. Check if the length of the input grid is 1. If so, create a leaf node with isLeaf set to True and val set to the value of the only element in the grid. Return this node.\n\n5. Check if all elements in the input grid are the same. If so, create a leaf node with isLeaf set to True and val set to the value of the first element in the grid. Return this node.\n\n6. If the input grid is not a leaf node and does not contain all the same elements, create a new node with isLeaf set to False.\n\n7. Calculate the mid-point of the grid.\n\n8. Divide the input grid into four sub-grids using the mid-point calculated in step 7. These sub-grids are the top left, top right, bottom left, and bottom right sub-grids.\n\n9. Recurse on each sub-grid by calling the construct_helper function with the appropriate sub-grid as input.\n\n10. Assign the resulting nodes to the appropriate child of the newly created node in step 6 (i.e. node.topLeft = construct_helper(top_left), node.topRight = construct_helper(top_right), etc.).\n\n11. Return the newly created node.\n\n12. Call the construct_helper function with the input grid as argument within the construct method of the Solution class.\n\n13. Return the root node of the constructed Quad-Tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Node:\n def __init__(self, val=False, isLeaf=False, topLeft=None, topRight=None, bottomLeft=None, bottomRight=None):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> Node:\n \n # Define a recursive function to construct the Quad-Tree\n def construct_helper(grid):\n # Check if the grid has length 1\n if len(grid) == 1:\n return Node(val=bool(grid[0][0]), isLeaf=True)\n \n # Check if all elements in the grid are the same\n all_same = all(all(val == grid[0][0] for val in row) for row in grid)\n if all_same:\n return Node(val=bool(grid[0][0]), isLeaf=True)\n \n # Otherwise, create a new node with isLeaf=False\n node = Node(isLeaf=False)\n \n # Divide the grid into four sub-grids\n n = len(grid)\n mid = n // 2\n top_left = [row[:mid] for row in grid[:mid]]\n top_right = [row[mid:] for row in grid[:mid]]\n bottom_left = [row[:mid] for row in grid[mid:]]\n bottom_right = [row[mid:] for row in grid[mid:]]\n \n # Recurse on each sub-grid and assign the resulting node to the appropriate child\n node.topLeft = construct_helper(top_left)\n node.topRight = construct_helper(top_right)\n node.bottomLeft = construct_helper(bottom_left)\n node.bottomRight = construct_helper(bottom_right)\n \n return node\n \n # Call the recursive function and return the root node\n return construct_helper(grid)\n\n``` | 4 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
427: Solution with step by step explanation | construct-quad-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the Node class with val, isLeaf, topLeft, topRight, bottomLeft, and bottomRight attributes.\n\n2. Define the Solution class with the construct method that takes in a 2D list of 0\'s and 1\'s as input.\n\n3. Within the construct method, define a recursive function construct_helper that takes in a 2D list of 0\'s and 1\'s as input.\n\n4. Check if the length of the input grid is 1. If so, create a leaf node with isLeaf set to True and val set to the value of the only element in the grid. Return this node.\n\n5. Check if all elements in the input grid are the same. If so, create a leaf node with isLeaf set to True and val set to the value of the first element in the grid. Return this node.\n\n6. If the input grid is not a leaf node and does not contain all the same elements, create a new node with isLeaf set to False.\n\n7. Calculate the mid-point of the grid.\n\n8. Divide the input grid into four sub-grids using the mid-point calculated in step 7. These sub-grids are the top left, top right, bottom left, and bottom right sub-grids.\n\n9. Recurse on each sub-grid by calling the construct_helper function with the appropriate sub-grid as input.\n\n10. Assign the resulting nodes to the appropriate child of the newly created node in step 6 (i.e. node.topLeft = construct_helper(top_left), node.topRight = construct_helper(top_right), etc.).\n\n11. Return the newly created node.\n\n12. Call the construct_helper function with the input grid as argument within the construct method of the Solution class.\n\n13. Return the root node of the constructed Quad-Tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Node:\n def __init__(self, val=False, isLeaf=False, topLeft=None, topRight=None, bottomLeft=None, bottomRight=None):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> Node:\n \n # Define a recursive function to construct the Quad-Tree\n def construct_helper(grid):\n # Check if the grid has length 1\n if len(grid) == 1:\n return Node(val=bool(grid[0][0]), isLeaf=True)\n \n # Check if all elements in the grid are the same\n all_same = all(all(val == grid[0][0] for val in row) for row in grid)\n if all_same:\n return Node(val=bool(grid[0][0]), isLeaf=True)\n \n # Otherwise, create a new node with isLeaf=False\n node = Node(isLeaf=False)\n \n # Divide the grid into four sub-grids\n n = len(grid)\n mid = n // 2\n top_left = [row[:mid] for row in grid[:mid]]\n top_right = [row[mid:] for row in grid[:mid]]\n bottom_left = [row[:mid] for row in grid[mid:]]\n bottom_right = [row[mid:] for row in grid[mid:]]\n \n # Recurse on each sub-grid and assign the resulting node to the appropriate child\n node.topLeft = construct_helper(top_left)\n node.topRight = construct_helper(top_right)\n node.bottomLeft = construct_helper(bottom_left)\n node.bottomRight = construct_helper(bottom_right)\n \n return node\n \n # Call the recursive function and return the root node\n return construct_helper(grid)\n\n``` | 4 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
[Java/C++/Python/JavaScript/Swift]O(n)time/BEATS 99.97% MEMORY/SPEED 0ms APRIL 2022 | construct-quad-tree | 1 | 1 | ```\n```\n\n(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, ***please upvote*** this post.)\n***Take care brother, peace, love!***\n\n```\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 38.2MB*** (beats 92.04% / 24.00%).\n* ***Java***\n```\n public Node construct(int[][] grid) {\n return make(grid, 0, 0, grid.length);\n }\n private Node make(int grid[][], int r, int c, int length) {\n if(length == 1)\n return new Node(grid[r][c] == 1? true : false, true);\n Node topLeft = make(grid, r, c, length/2);\n Node topRight = make(grid, r, c + length/2, length/2);\n Node bottomLeft = make(grid, r + length/2, c, length/2);\n Node bottomRight = make(grid, r + length/2, c + length/2, length/2);\n if(topLeft.val == topRight.val && bottomLeft.val == bottomRight.val && topLeft.val == bottomLeft.val && topLeft.isLeaf && topRight.isLeaf && bottomLeft.isLeaf && bottomRight.isLeaf)\n return new Node(topLeft.val, true);\n else\n return new Node(true, false, topLeft, topRight, bottomLeft, bottomRight);\n }\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 7.0MB*** (beats 100.00% / 100.00%).\n* ***C++***\n```\nclass Solution {\npublic:\n Node* construct(vector<vector<int>>& grid) {\n grid_ = move(grid);\n leafNodes_[0] = new Node(false, true, nullptr, nullptr, nullptr, nullptr);\n leafNodes_[1] = new Node(true, true, nullptr, nullptr, nullptr, nullptr);\n return construct(0, 0, grid_.size());\n }\n \n Node* construct(int r, int c, int s) {\n if (s == 1)\n return leafNodes_[grid_[r][c]];\n s /= 2;\n Node* tl = construct(r, c, s);\n Node* tr = construct(r, c+s, s);\n Node* bl = construct(r+s, c, s);\n Node* br = construct(r+s, c+s, s);\n if (tl == tr && tl == bl && tl == br)\n return tl;\n return new Node(false, false, tl, tr, bl, br);\n }\n \nprivate:\n vector<vector<int>> grid_;\n array<Node*, 2> leafNodes_;\n};\n```\n\n```\n```\n\n```\n```\n\n\nThe best result for the code below is ***26ms / 12.2MB*** (beats 95.42% / 82.32%).\n* ***Python***\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n \n \'\'\'\n Make a helper function helper(x, y, size) where x,y is coord of top left. \n \n If size is 1, set val to grid[x][y], isLeaf true, and children to None.\n \n Create node for all children.\n \n If all children are leaves with same value, set same value, set isLeaf to True and children to None. \n Otherwise value can be whatever, set isLeaf false.\n \n topleft : helper(x, y, size // 2)\n topright : helper(x, y + size // 2, size // 2)\n bottomleft: helper(x + size // 2, y, size // 2)\n bottomright: helper(x + size // 2, y + size // 2, size // 2)\n \n \'\'\'\n \n def helper(x, y, size):\n if size == 1:\n return Node(grid[x][y], True, None, None, None, None)\n \n half = size // 2\n topLeft = helper(x, y, half)\n topRight = helper(x, y + half, half)\n bottomLeft = helper(x + half, y, half)\n bottomRight = helper(x + half, y + half, half)\n \n children = [topLeft, topRight, bottomLeft, bottomRight]\n \n allLeaves = all(c.isLeaf for c in children)\n allMatch = all(c.val == topLeft.val for c in children)\n \n isLeaf = allLeaves and allMatch\n \n if isLeaf:\n return Node(topLeft.val, True, None, None, None, None)\n else:\n return Node(1, False, topLeft, topRight, bottomLeft, bottomRight)\n \n return helper(0, 0, len(grid))\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***51ms / 34.2MB*** (beats 100.00% / 84.12%).\n* ***JavaScript***\n```\nvar construct = function(grid) {\n const len = grid.length;\n \n function split(matrix) {\n const [[rowStart, colStart], [rowEnd, colEnd]] = matrix;\n const halfWidth = (rowEnd - rowStart) / 2 \n const midRow = rowStart + halfWidth;\n const midCol = colStart + halfWidth;\n \n const topLeft = [[rowStart, colStart], [midRow, midCol]];\n const topRight = [[rowStart, midCol], [midRow, colEnd]];\n const bottomLeft = [[midRow, colStart], [rowEnd, midCol]];\n const bottomRight = [[midRow, midCol], [rowEnd, colEnd]]\n \n return {topLeft, topRight, bottomLeft, bottomRight}\n }\n \n function recurse(matrix) {\n const [[rowStart, colStart], [rowEnd, colEnd]] = matrix;\n \n if(rowEnd - rowStart === 1) return new Node(grid[rowStart][colStart], true)\n \n const {topLeft, topRight, bottomLeft, bottomRight} = split(matrix);\n \n const nodeTL = recurse(topLeft);\n const nodeTR = recurse(topRight);\n const nodeBL = recurse(bottomLeft);\n const nodeBR = recurse(bottomRight);\n \n // if all 4 quadrants are leaf nodes and have the same value \n // they can be merge into one quadrant\n if(nodeTL.isLeaf && nodeTR.isLeaf && nodeBL.isLeaf && nodeBR.isLeaf && \n (nodeTL.val === nodeTR.val && nodeTR.val === nodeBL.val && nodeBL.val === nodeBR.val)) {\n return new Node(nodeTL.val, true);\n }\n return new Node(false, false, nodeTL, nodeTR, nodeBL, nodeBR);\n }\n return recurse([[0, 0], [len, len]])\n};\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***12ms / 32.2MB*** (beats 95% / 84%).\n* ***Swift***\n```\nfinal class Solution {\n func construct(_ grid: [[Int]]) -> Node? {\n return helper(grid, 0,0, grid.count)\n }\n \n func helper(_ grid: [[Int]], _ x: Int, _ y: Int, _ len: Int) -> Node {\n if len == 1 {\n return Node(grid[x][y] != 0, true)\n }\n let result = Node(true, false)\n let topLeft = helper(grid, x, y, len/2)\n let topRight = helper(grid, x, y + len/2, len/2)\n let bottomLeft = helper(grid, x + len/2, y, len/2)\n let bottomRight = helper(grid, x + len/2, y + len/2, len/2)\n \n if (topLeft.isLeaf && topRight.isLeaf && bottomLeft.isLeaf && bottomRight.isLeaf && topLeft.val == topRight.val && topRight.val == bottomLeft.val && bottomLeft.val == bottomRight.val) {\n result.isLeaf = true\n result.val = topLeft.val\n } else {\n result.topLeft = topLeft\n result.topRight = topRight\n result.bottomLeft = bottomLeft\n result.bottomRight = bottomRight\n }\n return result\n }\n }\n```\n\n```\n```\n\n```\n```\n\n***"Open your eyes. Expect us." - \uD835\uDCD0\uD835\uDCF7\uD835\uDCF8\uD835\uDCF7\uD835\uDD02\uD835\uDCF6\uD835\uDCF8\uD835\uDCFE\uD835\uDCFC*** | 4 | Given a `n * n` matrix `grid` of `0's` and `1's` only. We want to represent `grid` with a Quad-Tree.
Return _the root of the Quad-Tree representing_ `grid`.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
* `val`: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the `val` to True or False when `isLeaf` is False, and both are accepted in the answer.
* `isLeaf`: True if the node is a leaf node on the tree or False if the node has four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
1. If the current grid has the same value (i.e all `1's` or all `0's`) set `isLeaf` True and set `val` to the value of the grid and set the four children to Null and stop.
2. If the current grid has different values, set `isLeaf` to False and set `val` to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.
If you want to know more about the Quad-Tree, you can refer to the [wiki](https://en.wikipedia.org/wiki/Quadtree).
**Quad-Tree format:**
You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where `null` signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list `[isLeaf, val]`.
If the value of `isLeaf` or `val` is True we represent it as **1** in the list `[isLeaf, val]` and if the value of `isLeaf` or `val` is False we represent it as **0**.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** \[\[0,1\],\[1,0\],\[1,1\],\[1,1\],\[1,0\]\]
**Explanation:** The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,1,1,1,1\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\],\[1,1,1,1,0,0,0,0\]\]
**Output:** \[\[0,1\],\[1,1\],\[0,1\],\[1,1\],\[1,0\],null,null,null,null,\[1,0\],\[1,0\],\[1,1\],\[1,1\]\]
**Explanation:** All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:
**Constraints:**
* `n == grid.length == grid[i].length`
* `n == 2x` where `0 <= x <= 6` | null |
[Java/C++/Python/JavaScript/Swift]O(n)time/BEATS 99.97% MEMORY/SPEED 0ms APRIL 2022 | construct-quad-tree | 1 | 1 | ```\n```\n\n(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, ***please upvote*** this post.)\n***Take care brother, peace, love!***\n\n```\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 38.2MB*** (beats 92.04% / 24.00%).\n* ***Java***\n```\n public Node construct(int[][] grid) {\n return make(grid, 0, 0, grid.length);\n }\n private Node make(int grid[][], int r, int c, int length) {\n if(length == 1)\n return new Node(grid[r][c] == 1? true : false, true);\n Node topLeft = make(grid, r, c, length/2);\n Node topRight = make(grid, r, c + length/2, length/2);\n Node bottomLeft = make(grid, r + length/2, c, length/2);\n Node bottomRight = make(grid, r + length/2, c + length/2, length/2);\n if(topLeft.val == topRight.val && bottomLeft.val == bottomRight.val && topLeft.val == bottomLeft.val && topLeft.isLeaf && topRight.isLeaf && bottomLeft.isLeaf && bottomRight.isLeaf)\n return new Node(topLeft.val, true);\n else\n return new Node(true, false, topLeft, topRight, bottomLeft, bottomRight);\n }\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 7.0MB*** (beats 100.00% / 100.00%).\n* ***C++***\n```\nclass Solution {\npublic:\n Node* construct(vector<vector<int>>& grid) {\n grid_ = move(grid);\n leafNodes_[0] = new Node(false, true, nullptr, nullptr, nullptr, nullptr);\n leafNodes_[1] = new Node(true, true, nullptr, nullptr, nullptr, nullptr);\n return construct(0, 0, grid_.size());\n }\n \n Node* construct(int r, int c, int s) {\n if (s == 1)\n return leafNodes_[grid_[r][c]];\n s /= 2;\n Node* tl = construct(r, c, s);\n Node* tr = construct(r, c+s, s);\n Node* bl = construct(r+s, c, s);\n Node* br = construct(r+s, c+s, s);\n if (tl == tr && tl == bl && tl == br)\n return tl;\n return new Node(false, false, tl, tr, bl, br);\n }\n \nprivate:\n vector<vector<int>> grid_;\n array<Node*, 2> leafNodes_;\n};\n```\n\n```\n```\n\n```\n```\n\n\nThe best result for the code below is ***26ms / 12.2MB*** (beats 95.42% / 82.32%).\n* ***Python***\n```\n"""\n# Definition for a QuadTree node.\nclass Node:\n def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):\n self.val = val\n self.isLeaf = isLeaf\n self.topLeft = topLeft\n self.topRight = topRight\n self.bottomLeft = bottomLeft\n self.bottomRight = bottomRight\n"""\n\nclass Solution:\n def construct(self, grid: List[List[int]]) -> \'Node\':\n \n \'\'\'\n Make a helper function helper(x, y, size) where x,y is coord of top left. \n \n If size is 1, set val to grid[x][y], isLeaf true, and children to None.\n \n Create node for all children.\n \n If all children are leaves with same value, set same value, set isLeaf to True and children to None. \n Otherwise value can be whatever, set isLeaf false.\n \n topleft : helper(x, y, size // 2)\n topright : helper(x, y + size // 2, size // 2)\n bottomleft: helper(x + size // 2, y, size // 2)\n bottomright: helper(x + size // 2, y + size // 2, size // 2)\n \n \'\'\'\n \n def helper(x, y, size):\n if size == 1:\n return Node(grid[x][y], True, None, None, None, None)\n \n half = size // 2\n topLeft = helper(x, y, half)\n topRight = helper(x, y + half, half)\n bottomLeft = helper(x + half, y, half)\n bottomRight = helper(x + half, y + half, half)\n \n children = [topLeft, topRight, bottomLeft, bottomRight]\n \n allLeaves = all(c.isLeaf for c in children)\n allMatch = all(c.val == topLeft.val for c in children)\n \n isLeaf = allLeaves and allMatch\n \n if isLeaf:\n return Node(topLeft.val, True, None, None, None, None)\n else:\n return Node(1, False, topLeft, topRight, bottomLeft, bottomRight)\n \n return helper(0, 0, len(grid))\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***51ms / 34.2MB*** (beats 100.00% / 84.12%).\n* ***JavaScript***\n```\nvar construct = function(grid) {\n const len = grid.length;\n \n function split(matrix) {\n const [[rowStart, colStart], [rowEnd, colEnd]] = matrix;\n const halfWidth = (rowEnd - rowStart) / 2 \n const midRow = rowStart + halfWidth;\n const midCol = colStart + halfWidth;\n \n const topLeft = [[rowStart, colStart], [midRow, midCol]];\n const topRight = [[rowStart, midCol], [midRow, colEnd]];\n const bottomLeft = [[midRow, colStart], [rowEnd, midCol]];\n const bottomRight = [[midRow, midCol], [rowEnd, colEnd]]\n \n return {topLeft, topRight, bottomLeft, bottomRight}\n }\n \n function recurse(matrix) {\n const [[rowStart, colStart], [rowEnd, colEnd]] = matrix;\n \n if(rowEnd - rowStart === 1) return new Node(grid[rowStart][colStart], true)\n \n const {topLeft, topRight, bottomLeft, bottomRight} = split(matrix);\n \n const nodeTL = recurse(topLeft);\n const nodeTR = recurse(topRight);\n const nodeBL = recurse(bottomLeft);\n const nodeBR = recurse(bottomRight);\n \n // if all 4 quadrants are leaf nodes and have the same value \n // they can be merge into one quadrant\n if(nodeTL.isLeaf && nodeTR.isLeaf && nodeBL.isLeaf && nodeBR.isLeaf && \n (nodeTL.val === nodeTR.val && nodeTR.val === nodeBL.val && nodeBL.val === nodeBR.val)) {\n return new Node(nodeTL.val, true);\n }\n return new Node(false, false, nodeTL, nodeTR, nodeBL, nodeBR);\n }\n return recurse([[0, 0], [len, len]])\n};\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***12ms / 32.2MB*** (beats 95% / 84%).\n* ***Swift***\n```\nfinal class Solution {\n func construct(_ grid: [[Int]]) -> Node? {\n return helper(grid, 0,0, grid.count)\n }\n \n func helper(_ grid: [[Int]], _ x: Int, _ y: Int, _ len: Int) -> Node {\n if len == 1 {\n return Node(grid[x][y] != 0, true)\n }\n let result = Node(true, false)\n let topLeft = helper(grid, x, y, len/2)\n let topRight = helper(grid, x, y + len/2, len/2)\n let bottomLeft = helper(grid, x + len/2, y, len/2)\n let bottomRight = helper(grid, x + len/2, y + len/2, len/2)\n \n if (topLeft.isLeaf && topRight.isLeaf && bottomLeft.isLeaf && bottomRight.isLeaf && topLeft.val == topRight.val && topRight.val == bottomLeft.val && bottomLeft.val == bottomRight.val) {\n result.isLeaf = true\n result.val = topLeft.val\n } else {\n result.topLeft = topLeft\n result.topRight = topRight\n result.bottomLeft = bottomLeft\n result.bottomRight = bottomRight\n }\n return result\n }\n }\n```\n\n```\n```\n\n```\n```\n\n***"Open your eyes. Expect us." - \uD835\uDCD0\uD835\uDCF7\uD835\uDCF8\uD835\uDCF7\uD835\uDD02\uD835\uDCF6\uD835\uDCF8\uD835\uDCFE\uD835\uDCFC*** | 4 | Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, `'+'`, `'-'`, `'*'`, `'/'` operators, and open `'('` and closing parentheses `')'`. The integer division should **truncate toward zero**.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1+1 "
**Output:** 2
**Example 2:**
**Input:** s = "6-4/2 "
**Output:** 4
**Example 3:**
**Input:** s = "2\*(5+5\*2)/3+(6/2+8) "
**Output:** 21
**Constraints:**
* `1 <= s <= 104`
* `s` consists of digits, `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* `s` is a **valid** expression. | null |
429: Space 92.13%, Solution with step by step explanation | n-ary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We start by checking if the input root is empty. If it is, we return an empty list.\n```\n if not root:\n return []\n```\n2. We initialize two lists, result and level. result will store the final level order traversal of the nodes\' values, and level will store the current level of nodes we are traversing.\n```\n result = []\n level = [root]\n```\n3. We enter a loop that will continue as long as there are nodes in level. At each iteration, we will add the values of the nodes in the current level to result, and add their children to next_level for the next iteration.\n```\n while level:\n current_level = []\n next_level = []\n \n for node in level:\n current_level.append(node.val)\n next_level += node.children\n \n result.append(current_level)\n level = next_level\n``` \n4. Inside the loop, we initialize an empty list current_level to store the values of the nodes in the current level, and another empty list next_level to store the children of the nodes in the current level for the next iteration.\n\n5. We iterate over each node in level, append its value to current_level, and add its children to next_level.\n\n6. After iterating over all nodes in level, we append current_level to result.\n\n7. Finally, we update level to be next_level, which will contain all the children of the nodes in the current level for the next iteration.\n\n8. Once the loop has completed, we have successfully traversed all levels of the tree and stored the values of the nodes in result. We simply return result as the final output.\n```\n return result\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root:\n return []\n \n result = []\n level = [root]\n \n while level:\n current_level = []\n next_level = []\n \n for node in level:\n current_level.append(node.val)\n next_level += node.children\n \n result.append(current_level)\n level = next_level\n \n return result\n\n``` | 2 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
429: Space 92.13%, Solution with step by step explanation | n-ary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We start by checking if the input root is empty. If it is, we return an empty list.\n```\n if not root:\n return []\n```\n2. We initialize two lists, result and level. result will store the final level order traversal of the nodes\' values, and level will store the current level of nodes we are traversing.\n```\n result = []\n level = [root]\n```\n3. We enter a loop that will continue as long as there are nodes in level. At each iteration, we will add the values of the nodes in the current level to result, and add their children to next_level for the next iteration.\n```\n while level:\n current_level = []\n next_level = []\n \n for node in level:\n current_level.append(node.val)\n next_level += node.children\n \n result.append(current_level)\n level = next_level\n``` \n4. Inside the loop, we initialize an empty list current_level to store the values of the nodes in the current level, and another empty list next_level to store the children of the nodes in the current level for the next iteration.\n\n5. We iterate over each node in level, append its value to current_level, and add its children to next_level.\n\n6. After iterating over all nodes in level, we append current_level to result.\n\n7. Finally, we update level to be next_level, which will contain all the children of the nodes in the current level for the next iteration.\n\n8. Once the loop has completed, we have successfully traversed all levels of the tree and stored the values of the nodes in result. We simply return result as the final output.\n```\n return result\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root:\n return []\n \n result = []\n level = [root]\n \n while level:\n current_level = []\n next_level = []\n \n for node in level:\n current_level.append(node.val)\n next_level += node.children\n \n result.append(current_level)\n level = next_level\n \n return result\n\n``` | 2 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
N-ary Tree Level Order Traversal | n-ary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n l=defaultdict(list)\n def level(temp ,h):\n if temp is None:\n return\n l[h].append(temp.val)\n for i in temp.children:\n level(i,h+1)\n level(root,0)\n return l.values()\n``` | 1 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
N-ary Tree Level Order Traversal | n-ary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n l=defaultdict(list)\n def level(temp ,h):\n if temp is None:\n return\n l[h].append(temp.val)\n for i in temp.children:\n level(i,h+1)\n level(root,0)\n return l.values()\n``` | 1 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
Solution | n-ary-tree-level-order-traversal | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root) {\n queue<Node*>q;\n vector<vector<int>> ans;\n if(!root) return ans;\n q.push(root);\n while(!q.empty()){\n int size=q.size();\n vector<int>temp;\n while(size--){\n Node *curr=q.front();\n temp.push_back(curr->val);\n q.pop();\n for(int i=0;i<curr->children.size();i++){\n q.push(curr->children[i]);\n }\n }\n ans.push_back(temp);\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root:\n return []\n result = collections.defaultdict(list)\n def helper(node, level):\n if not node:\n return\n result[level].append(node.val)\n for child in node.children:\n helper(child, level+1)\n helper(root, 0)\n return result.values()\n```\n\n```Java []\nclass Solution {\n List<List<Integer>> res;\n void solve(Node cur, int level){\n if(cur == null)\n return ;\n if(level >= res.size()){\n res.add(new ArrayList<Integer>());\n }\n res.get(level).add(cur.val);\n for(int i=0;i<cur.children.size();i++){\n solve(cur.children.get(i), level+1);\n }\n }\n public List<List<Integer>> levelOrder(Node root) {\n res = new ArrayList<>();\n solve(root, 0);\n return res;\n }\n}\n```\n | 1 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
Solution | n-ary-tree-level-order-traversal | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root) {\n queue<Node*>q;\n vector<vector<int>> ans;\n if(!root) return ans;\n q.push(root);\n while(!q.empty()){\n int size=q.size();\n vector<int>temp;\n while(size--){\n Node *curr=q.front();\n temp.push_back(curr->val);\n q.pop();\n for(int i=0;i<curr->children.size();i++){\n q.push(curr->children[i]);\n }\n }\n ans.push_back(temp);\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root:\n return []\n result = collections.defaultdict(list)\n def helper(node, level):\n if not node:\n return\n result[level].append(node.val)\n for child in node.children:\n helper(child, level+1)\n helper(root, 0)\n return result.values()\n```\n\n```Java []\nclass Solution {\n List<List<Integer>> res;\n void solve(Node cur, int level){\n if(cur == null)\n return ;\n if(level >= res.size()){\n res.add(new ArrayList<Integer>());\n }\n res.get(level).add(cur.val);\n for(int i=0;i<cur.children.size();i++){\n solve(cur.children.get(i), level+1);\n }\n }\n public List<List<Integer>> levelOrder(Node root) {\n res = new ArrayList<>();\n solve(root, 0);\n return res;\n }\n}\n```\n | 1 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
PYTHON3 beats 95% using queue and None method space and time O(N) | n-ary-tree-level-order-traversal | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe can have a queue which holds the root node and then a None node,this None node being the point where a level ends\nfrom here we attach the values of node to an array b \n for the children each child is similarly appended to the queue and it repeats till a None is found\n when this None is found,we can attach the b array to answer \nthe loop ends when all elements are exhausted and only None is left in the q ,after popping q will be empty and we can return\n#pop(0) acts similar to popleft() in deque\nwe can use deque() can perform the same\n\n\n\n# Complexity\nN being number of elements\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n______**O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n______**O(N)**\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root:return \n q=[root,None]\n ans=[]\n b=[]\n while q:\n node=q.pop(0)\n if not node:\n ans.append(b)\n b=[]\n if not q:\n return ans\n q.append(None)\n else:\n b.append(node.val)\n for i in node.children:\n q.append(i)\n``` | 1 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
PYTHON3 beats 95% using queue and None method space and time O(N) | n-ary-tree-level-order-traversal | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe can have a queue which holds the root node and then a None node,this None node being the point where a level ends\nfrom here we attach the values of node to an array b \n for the children each child is similarly appended to the queue and it repeats till a None is found\n when this None is found,we can attach the b array to answer \nthe loop ends when all elements are exhausted and only None is left in the q ,after popping q will be empty and we can return\n#pop(0) acts similar to popleft() in deque\nwe can use deque() can perform the same\n\n\n\n# Complexity\nN being number of elements\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n______**O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n______**O(N)**\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val=None, children=None):\n self.val = val\n self.children = children\n"""\n\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root:return \n q=[root,None]\n ans=[]\n b=[]\n while q:\n node=q.pop(0)\n if not node:\n ans.append(b)\n b=[]\n if not q:\n return ans\n q.append(None)\n else:\n b.append(node.val)\n for i in node.children:\n q.append(i)\n``` | 1 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
✅Python3 57ms 🔥🔥🔥 easy detailed explanation. | n-ary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimple BFS can solve this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- store nodes by level.\n- traverse all children.\n- if current node is None return.\n- return answer\n\n# Approach for array\n- here using array instade of dictionary is helpful.\n- because if we use dictionary then insertion is easy but getting values at last is O(N).\n- so we to save this time we can use something of this type.\n\n# Complexity\n- Time complexity: O(H)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n ans = []\n def helper(curr = root, level = 0):\n nonlocal ans\n if curr:\n if len(ans) > level:\n ans[level].append(curr.val)\n else:\n ans.append([curr.val])\n for i in curr.children:\n helper(i, level + 1)\n return\n helper()\n return ans\n```\n# Please like and comment below.\n# (\u3063\uFF3E\u25BF\uFF3E)\u06F6\uD83C\uDF78\uD83C\uDF1F\uD83C\uDF7A\u0669(\u02D8\u25E1\u02D8 ) | 5 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
✅Python3 57ms 🔥🔥🔥 easy detailed explanation. | n-ary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimple BFS can solve this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- store nodes by level.\n- traverse all children.\n- if current node is None return.\n- return answer\n\n# Approach for array\n- here using array instade of dictionary is helpful.\n- because if we use dictionary then insertion is easy but getting values at last is O(N).\n- so we to save this time we can use something of this type.\n\n# Complexity\n- Time complexity: O(H)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n ans = []\n def helper(curr = root, level = 0):\n nonlocal ans\n if curr:\n if len(ans) > level:\n ans[level].append(curr.val)\n else:\n ans.append([curr.val])\n for i in curr.children:\n helper(i, level + 1)\n return\n helper()\n return ans\n```\n# Please like and comment below.\n# (\u3063\uFF3E\u25BF\uFF3E)\u06F6\uD83C\uDF78\uD83C\uDF1F\uD83C\uDF7A\u0669(\u02D8\u25E1\u02D8 ) | 5 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
🍀Java 🔥 | | Python 🔥| | C++ 🔥| | Easy 🔥🍀 | n-ary-tree-level-order-traversal | 1 | 1 | # N-ary Tree level Order Traversal \n> ### *Try to understand the code line by line. Easy BFS solution.* \n```java []\nclass Solution {\n public List<List<Integer>> levelOrder(Node root) {\n Queue<Node> queue = new LinkedList<>();\n List<List<Integer>> result = new ArrayList<>();\n if(root == null)\n return result;\n queue.offer(root);\n while(queue.size() > 0)\n {\n List<Integer> arr = new ArrayList<>();\n int length = queue.size();\n for(int i = 0;i<length;i++)\n {\n Node curr = queue.poll();\n arr.add(curr.val);\n for(Node child : curr.children)\n {\n queue.offer(child);\n }\n }\n result.add(arr);\n }\n return result;\n }\n}\n```\n```python []\nfrom collections import deque\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n queue = deque()\n result = []\n if not root:\n return result\n queue.append(root)\n while queue:\n arr = []\n length = len(queue)\n for i in range(length):\n curr = queue.popleft()\n arr.append(curr.val)\n for child in curr.children:\n queue.append(child)\n result.append(arr)\n return result\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root) {\n queue<Node*> q;\n vector<vector<int>> res;\n if(root == NULL)\n return res;\n q.push(root);\n while(!q.empty())\n {\n vector<int> arr;\n int length = q.size();\n for(int i = 0;i<length;i++)\n {\n Node* curr = q.front();\n q.pop();\n arr.push_back(curr->val);\n for(Node* child : curr->children)\n {\n q.push(child);\n }\n }\n res.push_back(arr);\n }\n return res;\n }\n};\n```\n---\n#### *Please don\'t forget to upvote if you\'ve liked my solution.* \u2B06\uFE0F\n--- | 5 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
🍀Java 🔥 | | Python 🔥| | C++ 🔥| | Easy 🔥🍀 | n-ary-tree-level-order-traversal | 1 | 1 | # N-ary Tree level Order Traversal \n> ### *Try to understand the code line by line. Easy BFS solution.* \n```java []\nclass Solution {\n public List<List<Integer>> levelOrder(Node root) {\n Queue<Node> queue = new LinkedList<>();\n List<List<Integer>> result = new ArrayList<>();\n if(root == null)\n return result;\n queue.offer(root);\n while(queue.size() > 0)\n {\n List<Integer> arr = new ArrayList<>();\n int length = queue.size();\n for(int i = 0;i<length;i++)\n {\n Node curr = queue.poll();\n arr.add(curr.val);\n for(Node child : curr.children)\n {\n queue.offer(child);\n }\n }\n result.add(arr);\n }\n return result;\n }\n}\n```\n```python []\nfrom collections import deque\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n queue = deque()\n result = []\n if not root:\n return result\n queue.append(root)\n while queue:\n arr = []\n length = len(queue)\n for i in range(length):\n curr = queue.popleft()\n arr.append(curr.val)\n for child in curr.children:\n queue.append(child)\n result.append(arr)\n return result\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root) {\n queue<Node*> q;\n vector<vector<int>> res;\n if(root == NULL)\n return res;\n q.push(root);\n while(!q.empty())\n {\n vector<int> arr;\n int length = q.size();\n for(int i = 0;i<length;i++)\n {\n Node* curr = q.front();\n q.pop();\n arr.push_back(curr->val);\n for(Node* child : curr->children)\n {\n q.push(child);\n }\n }\n res.push_back(arr);\n }\n return res;\n }\n};\n```\n---\n#### *Please don\'t forget to upvote if you\'ve liked my solution.* \u2B06\uFE0F\n--- | 5 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
🔥 [LeetCode The Hard Way]🔥 Easy BFS Explained Line By Line | n-ary-tree-level-order-traversal | 0 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. I\'ll explain my solution line by line daily. \nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\nYou may check out my recent BFS solutions on other problems.\n\nhttps://leetcode.com/problems/average-of-levels-in-binary-tree/discuss/2516577/leetcode-the-hard-way-bfs-explained-line-by-line\nhttps://leetcode.com/problems/numbers-with-same-consecutive-differences/discuss/2521519/leetcode-the-hard-way-easy-bfs-100-explained-line-by-line\n\n**Someone keeps downvoting my posts recently for no reason. Instead of just downvoting, please leave a useful comment to let me know what I could make better. Thanks.**\n\n**C++**\n\n```cpp\n// Time Complexity: O(N) where N is the number of nodes in the tree\n// Space Complexity: O(M): where M is the maximum number in the tree at any level\nclass Solution {\npublic:\n // The idea is to use BFS, which is a common way to traverse the tree level by level\n // For a standard BFS, we can use queue to push the first root node into a queue\n // Then remove the front of the queue, add its children to back of the queue\n // Do the above steps until the queue is empty\n // In this question, we need to extra thing which is to push the each value of the nodes level by level\n // We can simply use `level` to store the values of the nodes at current level, \n // and add it back to `ans` once we\'ve processed all nodes at that level\n vector<vector<int>> levelOrder(Node* root) {\n // the total number of nodes is between [0, 10 ^ 4]\n // check if root is nullptr to cover 0 node case\n if(!root) return {};\n // init ans\n vector<vector<int>> ans;\n // standard bfs approach\n queue<Node*> q;\n // start with the root node\n q.push(root); \n // do the following logic when the queue is not empty\n while(!q.empty()) {\n // get the queue size\n int n = q.size(); \n // level is used to store all the node values at the current level\n vector<int> level;\n // for each element in the current queue\n for(int i = 0; i < n; i++){\n //get the first node from the queue\n Node* node = q.front();\n // pop it\n q.pop();\n // add it to level\n level.push_back(node->val);\n // this node may include other nodes, we add them all to the queue\n for(auto n : node->children) q.push(n); \n }\n // we\'ve processed this level, add it to ans\n ans.push_back(level);\n }\n // return final ans\n return ans;\n }\n};\n```\n\n**Python**\n\n```py\n# Time Complexity: O(N) where N is the number of nodes in the tree\n# Space Complexity: O(M): where M is the maximum number in the tree at any level\nclass Solution:\n # The idea is to use BFS, which is a common way to traverse the tree level by level\n # For a standard BFS, we can use queue to push the first root node into a queue\n # Then remove the front of the queue, add its children to back of the queue\n # Do the above steps until the queue is empty\n # In this question, we need to extra thing which is to push the each value of the nodes level by level\n # We can simply use `level` to store the values of the nodes at current level, \n # and add it back to `ans` once we\'ve processed all nodes at that level\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n # the total number of nodes is between [0, 10 ^ 4]\n # check if root is None to cover 0 node case\n if not root: return []\n # init ans\n ans = []\n # standard bfs approach\n # start with the root node\n q = deque([root])\n # do the following logic when the queue is not empty\n while q:\n # level is used to store all the node values at the current level\n level = []\n # for each element in the current queue\n for _ in range(len(q)):\n # get the first node from the queue and pop it\n node = q.popleft()\n # add it to level\n level += [node.val]\n # this node may include other nodes, we add them all to the queue\n for n in node.children: q.append(n)\n # we\'ve processed this level, add it to ans\n ans += [level]\n # return final ans\n return ans\n``` | 48 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
🔥 [LeetCode The Hard Way]🔥 Easy BFS Explained Line By Line | n-ary-tree-level-order-traversal | 0 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. I\'ll explain my solution line by line daily. \nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\nYou may check out my recent BFS solutions on other problems.\n\nhttps://leetcode.com/problems/average-of-levels-in-binary-tree/discuss/2516577/leetcode-the-hard-way-bfs-explained-line-by-line\nhttps://leetcode.com/problems/numbers-with-same-consecutive-differences/discuss/2521519/leetcode-the-hard-way-easy-bfs-100-explained-line-by-line\n\n**Someone keeps downvoting my posts recently for no reason. Instead of just downvoting, please leave a useful comment to let me know what I could make better. Thanks.**\n\n**C++**\n\n```cpp\n// Time Complexity: O(N) where N is the number of nodes in the tree\n// Space Complexity: O(M): where M is the maximum number in the tree at any level\nclass Solution {\npublic:\n // The idea is to use BFS, which is a common way to traverse the tree level by level\n // For a standard BFS, we can use queue to push the first root node into a queue\n // Then remove the front of the queue, add its children to back of the queue\n // Do the above steps until the queue is empty\n // In this question, we need to extra thing which is to push the each value of the nodes level by level\n // We can simply use `level` to store the values of the nodes at current level, \n // and add it back to `ans` once we\'ve processed all nodes at that level\n vector<vector<int>> levelOrder(Node* root) {\n // the total number of nodes is between [0, 10 ^ 4]\n // check if root is nullptr to cover 0 node case\n if(!root) return {};\n // init ans\n vector<vector<int>> ans;\n // standard bfs approach\n queue<Node*> q;\n // start with the root node\n q.push(root); \n // do the following logic when the queue is not empty\n while(!q.empty()) {\n // get the queue size\n int n = q.size(); \n // level is used to store all the node values at the current level\n vector<int> level;\n // for each element in the current queue\n for(int i = 0; i < n; i++){\n //get the first node from the queue\n Node* node = q.front();\n // pop it\n q.pop();\n // add it to level\n level.push_back(node->val);\n // this node may include other nodes, we add them all to the queue\n for(auto n : node->children) q.push(n); \n }\n // we\'ve processed this level, add it to ans\n ans.push_back(level);\n }\n // return final ans\n return ans;\n }\n};\n```\n\n**Python**\n\n```py\n# Time Complexity: O(N) where N is the number of nodes in the tree\n# Space Complexity: O(M): where M is the maximum number in the tree at any level\nclass Solution:\n # The idea is to use BFS, which is a common way to traverse the tree level by level\n # For a standard BFS, we can use queue to push the first root node into a queue\n # Then remove the front of the queue, add its children to back of the queue\n # Do the above steps until the queue is empty\n # In this question, we need to extra thing which is to push the each value of the nodes level by level\n # We can simply use `level` to store the values of the nodes at current level, \n # and add it back to `ans` once we\'ve processed all nodes at that level\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n # the total number of nodes is between [0, 10 ^ 4]\n # check if root is None to cover 0 node case\n if not root: return []\n # init ans\n ans = []\n # standard bfs approach\n # start with the root node\n q = deque([root])\n # do the following logic when the queue is not empty\n while q:\n # level is used to store all the node values at the current level\n level = []\n # for each element in the current queue\n for _ in range(len(q)):\n # get the first node from the queue and pop it\n node = q.popleft()\n # add it to level\n level += [node.val]\n # this node may include other nodes, we add them all to the queue\n for n in node.children: q.append(n)\n # we\'ve processed this level, add it to ans\n ans += [level]\n # return final ans\n return ans\n``` | 48 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
Python, BFS | n-ary-tree-level-order-traversal | 0 | 1 | ```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n result = [] \n q = deque([root] if root else [])\n while q:\n result.append([])\n for _ in range(len(q)):\n node = q.popleft()\n result[-1].append(node.val)\n q.extend(node.children)\n \n return result\n``` | 15 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
Python, BFS | n-ary-tree-level-order-traversal | 0 | 1 | ```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n result = [] \n q = deque([root] if root else [])\n while q:\n result.append([])\n for _ in range(len(q)):\n node = q.popleft()\n result[-1].append(node.val)\n q.extend(node.children)\n \n return result\n``` | 15 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
Python Elegant & Short | BFS + DFS | Generators | n-ary-tree-level-order-traversal | 0 | 1 | # BFS solution\n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tdef levelOrder(self, root: Optional[\'Node\']) -> List[List[int]]:\n\t\t\tif root is None:\n\t\t\t\treturn []\n\n\t\t\tqueue = deque([root])\n\t\t\tlevels = []\n\n\t\t\twhile queue:\n\t\t\t\tlevels.append([])\n\t\t\t\tfor _ in range(len(queue)):\n\t\t\t\t\tnode = queue.popleft()\n\t\t\t\t\tlevels[-1].append(node.val)\n\t\t\t\t\tqueue.extend(node.children)\n\n\t\t\treturn levels\n# DFS solution\n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tdef levelOrder(self, root: Optional[\'Node\']) -> List[List[int]]:\n\t\t\tlevels = defaultdict(list)\n\n\t\t\tfor node, depth in self._walk(root):\n\t\t\t\tlevels[depth].append(node.val)\n\n\t\t\treturn [levels[d] for d in sorted(levels)]\n\n\t\t@classmethod\n\t\tdef _walk(cls, root: Optional[\'Node\'], depth: int = 0) -> Generator:\n\t\t\tif root is None:\n\t\t\t\treturn\n\n\t\t\tyield root, depth\n\t\t\tfor child in root.children:\n\t\t\t\tyield from cls._walk(child, depth + 1)\n | 2 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
Python Elegant & Short | BFS + DFS | Generators | n-ary-tree-level-order-traversal | 0 | 1 | # BFS solution\n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tdef levelOrder(self, root: Optional[\'Node\']) -> List[List[int]]:\n\t\t\tif root is None:\n\t\t\t\treturn []\n\n\t\t\tqueue = deque([root])\n\t\t\tlevels = []\n\n\t\t\twhile queue:\n\t\t\t\tlevels.append([])\n\t\t\t\tfor _ in range(len(queue)):\n\t\t\t\t\tnode = queue.popleft()\n\t\t\t\t\tlevels[-1].append(node.val)\n\t\t\t\t\tqueue.extend(node.children)\n\n\t\t\treturn levels\n# DFS solution\n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tdef levelOrder(self, root: Optional[\'Node\']) -> List[List[int]]:\n\t\t\tlevels = defaultdict(list)\n\n\t\t\tfor node, depth in self._walk(root):\n\t\t\t\tlevels[depth].append(node.val)\n\n\t\t\treturn [levels[d] for d in sorted(levels)]\n\n\t\t@classmethod\n\t\tdef _walk(cls, root: Optional[\'Node\'], depth: int = 0) -> Generator:\n\t\t\tif root is None:\n\t\t\t\treturn\n\n\t\t\tyield root, depth\n\t\t\tfor child in root.children:\n\t\t\t\tyield from cls._walk(child, depth + 1)\n | 2 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
Simplest Python code [Just do level-order] | n-ary-tree-level-order-traversal | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n a = []\n\n def dfs(node, h):\n if not node: return\n if len(a) == h: a.append([])\n\n a[h].append(node.val)\n\n for child in node.children:\n dfs(child, h+1)\n\n dfs(root, 0)\n\n return a\n``` | 2 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
Simplest Python code [Just do level-order] | n-ary-tree-level-order-traversal | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n a = []\n\n def dfs(node, h):\n if not node: return\n if len(a) == h: a.append([])\n\n a[h].append(node.val)\n\n for child in node.children:\n dfs(child, h+1)\n\n dfs(root, 0)\n\n return a\n``` | 2 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
[Python] Recursive DFS Solution | n-ary-tree-level-order-traversal | 0 | 1 | ```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root: return []\n res = []\n levels = set()\n def dfs(node, level):\n if level not in levels:\n levels.add(level)\n res.append([])\n res[level].append(node.val)\n for child in node.children:\n dfs(child, level + 1)\n \n dfs(root, 0)\n return res\n``` | 1 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
[Python] Recursive DFS Solution | n-ary-tree-level-order-traversal | 0 | 1 | ```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if not root: return []\n res = []\n levels = set()\n def dfs(node, level):\n if level not in levels:\n levels.add(level)\n res.append([])\n res[level].append(node.val)\n for child in node.children:\n dfs(child, level + 1)\n \n dfs(root, 0)\n return res\n``` | 1 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
🌻 100% | Classic BFS . 2 ways in each language (C++, Go, Python, Ts/Js, Java) | n-ary-tree-level-order-traversal | 0 | 1 | There are two ways to add values of each level to the `result` array \n1. add one at a time, when we have finished iterating through the children of a particular node to the `deque`, like this:\n```\nfor (Node *n: node->children)\n{\n\tdq.push_back(n);\n}\ntemp.push_back(node->val);\n```\n2. or, we can add them as we iterate through children, \n```\nfor (Node *n: node->children)\n{\n\tdq.push_back(n);\n\ttemp.push_back(n->val); // added\n}\n```\nNote: in the 2nd way, result should be initiated with the `root.val` inside.\n```\nvector<vector<int>> r;\n\nr.push_back({root->val}); /* Here */\n```\nAlso on each level traversal, before we add `temp` to the `result` array, we have to make sure that `temp` is not empty. \n\n-----\n# C++ . 1\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root)\n {\n vector<vector<int>> r;\n deque<Node*> dq;\n\n if (!root)\n return r;\n dq.push_back(root);\n while (!dq.empty())\n {\n vector<int>\ttemp;\n int\t\tlen;\n\n\t len = dq.size();\n while (len--)\n {\n Node *node = dq.front();\n\n dq.pop_front();\n for (Node *n: node->children)\n {\n dq.push_back(n);\n }\n temp.push_back(node->val);\n }\n r.push_back(temp);\n }\n return r;\n }\n};\n```\nC++ . 2\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root)\n {\n vector<vector<int>> r;\n deque<Node*> dq;\n\n if (!root)\n return r;\n dq.push_back(root);\n r.push_back({root->val}); // added\n while (!dq.empty())\n {\n int len = dq.size();\n vector<int> temp;\n\n while (len--)\n {\n Node *node = dq.front();\n\n dq.pop_front();\n for (Node *n: node->children)\n {\n dq.push_back(n);\n temp.push_back(n->val); // added\n }\n }\n if (!temp.empty())\n r.push_back(temp);\n }\n return r;\n }\n};\n```\nPython . 1\n```py\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n r = []\n if not root:\n return r\n dq = deque()\n dq.append(root)\n while dq:\n temp = []\n size = len(dq)\n for _ in range(size):\n node = dq.popleft()\n for n in node.children:\n dq.append(n)\n temp.append(node.val)\n r.append(temp)\n return r\n```py\n# Python . 2\n```py\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n r = []\n if not root:\n return r\n r.append([root.val])\n dq = deque()\n dq.append(root)\n while dq:\n temp = []\n size = len(dq)\n for _ in range(size):\n node = dq.popleft()\n for n in node.children:\n dq.append(n)\n temp.append(n.val)\n if temp:\n r.append(temp)\n return r\n```\n# Go . 1\n```go\nfunc levelOrder(root *Node) [][]int {\n r := [][] int {}\n dq := [] *Node {}\n if root == nil {\n return r\n }\n dq = append(dq, root)\n for len(dq) > 0 {\n temp := [] int {}\n size := len(dq)\n for i := 0; i < size; i++ {\n node := dq[0]\n dq = dq[1:]\n temp = append(temp, node.Val)\n for _, child := range node.Children {\n dq = append(dq, child)\n }\n }\n r = append(r, temp)\n }\n return r\n}\n```\n# Go . 2\n```go\n\nfunc levelOrder(root *Node) [][]int {\n r := [][] int {}\n dq := [] *Node {}\n if root == nil {\n return r\n }\n r = append(r, [] int { root.Val })\n dq = append(dq, root)\n for len(dq) > 0 {\n temp := [] int {}\n size := len(dq)\n for i := 0; i < size; i++ {\n node := dq[0]\n dq = dq[1:]\n for _, child := range node.Children {\n dq = append(dq, child)\n temp = append(temp, child.Val)\n }\n }\n if len(temp) != 0 {\n r = append(r, temp)\n }\n }\n return r\n}\n```\n# TS / Js . 1\n```js\n/**\n * // Definition for a Node.\n * function Node(val,children) {\n * this.val = val;\n * this.children = children;\n * };\n */\n\n/**\n * @param {Node|null} root\n * @return {number[][]}\n */\n\nvar levelOrder = function(root) {\n let r = []\n if (!root) {\n return r\n }\n let dq = [root]\n while (dq.length > 0) {\n let temp = []\n let len = dq.length\n while (len-- > 0) {\n let node = dq.shift()\n for (let n of node.children) {\n dq.push(n)\n }\n temp.push(node.val)\n }\n r.push(temp)\n }\n return r\n};\n```\n# TS/Js . 2\n```ts\nvar levelOrder = function(root) {\n let r = []\n if (!root) {\n return r\n }\n r.push([root.val])\n let dq = [root]\n while (dq.length > 0) {\n let temp = []\n let len = dq.length\n while (len-- > 0) {\n let node = dq.shift()\n for (let n of node.children) {\n dq.push(n)\n temp.push(n.val)\n }\n }\n if (temp.length > 0) {\n r.push(temp)\n }\n }\n return r\n};\n```\nJava\n```java\nclass Solution {\n public List<List<Integer>> levelOrder(Node root) {\n List<List<Integer>> r = new LinkedList<>();\n LinkedList<Node> dq = new LinkedList<>();\n\n if (root == null)\n return r;\n dq.add(root);\n while (! dq.isEmpty())\n {\n LinkedList<Integer> temp = new LinkedList<>();\n int len = dq.size();\n\n while (len-- > 0)\n {\n System.out.println(len);\n Node node = dq.pollFirst();\n\n for (Node n: node.children)\n dq.addLast(n);\n temp.add(node.val);\n }\n r.add(temp);\n }\n return r;\n }\n}\n``` | 1 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
🌻 100% | Classic BFS . 2 ways in each language (C++, Go, Python, Ts/Js, Java) | n-ary-tree-level-order-traversal | 0 | 1 | There are two ways to add values of each level to the `result` array \n1. add one at a time, when we have finished iterating through the children of a particular node to the `deque`, like this:\n```\nfor (Node *n: node->children)\n{\n\tdq.push_back(n);\n}\ntemp.push_back(node->val);\n```\n2. or, we can add them as we iterate through children, \n```\nfor (Node *n: node->children)\n{\n\tdq.push_back(n);\n\ttemp.push_back(n->val); // added\n}\n```\nNote: in the 2nd way, result should be initiated with the `root.val` inside.\n```\nvector<vector<int>> r;\n\nr.push_back({root->val}); /* Here */\n```\nAlso on each level traversal, before we add `temp` to the `result` array, we have to make sure that `temp` is not empty. \n\n-----\n# C++ . 1\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root)\n {\n vector<vector<int>> r;\n deque<Node*> dq;\n\n if (!root)\n return r;\n dq.push_back(root);\n while (!dq.empty())\n {\n vector<int>\ttemp;\n int\t\tlen;\n\n\t len = dq.size();\n while (len--)\n {\n Node *node = dq.front();\n\n dq.pop_front();\n for (Node *n: node->children)\n {\n dq.push_back(n);\n }\n temp.push_back(node->val);\n }\n r.push_back(temp);\n }\n return r;\n }\n};\n```\nC++ . 2\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(Node* root)\n {\n vector<vector<int>> r;\n deque<Node*> dq;\n\n if (!root)\n return r;\n dq.push_back(root);\n r.push_back({root->val}); // added\n while (!dq.empty())\n {\n int len = dq.size();\n vector<int> temp;\n\n while (len--)\n {\n Node *node = dq.front();\n\n dq.pop_front();\n for (Node *n: node->children)\n {\n dq.push_back(n);\n temp.push_back(n->val); // added\n }\n }\n if (!temp.empty())\n r.push_back(temp);\n }\n return r;\n }\n};\n```\nPython . 1\n```py\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n r = []\n if not root:\n return r\n dq = deque()\n dq.append(root)\n while dq:\n temp = []\n size = len(dq)\n for _ in range(size):\n node = dq.popleft()\n for n in node.children:\n dq.append(n)\n temp.append(node.val)\n r.append(temp)\n return r\n```py\n# Python . 2\n```py\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n r = []\n if not root:\n return r\n r.append([root.val])\n dq = deque()\n dq.append(root)\n while dq:\n temp = []\n size = len(dq)\n for _ in range(size):\n node = dq.popleft()\n for n in node.children:\n dq.append(n)\n temp.append(n.val)\n if temp:\n r.append(temp)\n return r\n```\n# Go . 1\n```go\nfunc levelOrder(root *Node) [][]int {\n r := [][] int {}\n dq := [] *Node {}\n if root == nil {\n return r\n }\n dq = append(dq, root)\n for len(dq) > 0 {\n temp := [] int {}\n size := len(dq)\n for i := 0; i < size; i++ {\n node := dq[0]\n dq = dq[1:]\n temp = append(temp, node.Val)\n for _, child := range node.Children {\n dq = append(dq, child)\n }\n }\n r = append(r, temp)\n }\n return r\n}\n```\n# Go . 2\n```go\n\nfunc levelOrder(root *Node) [][]int {\n r := [][] int {}\n dq := [] *Node {}\n if root == nil {\n return r\n }\n r = append(r, [] int { root.Val })\n dq = append(dq, root)\n for len(dq) > 0 {\n temp := [] int {}\n size := len(dq)\n for i := 0; i < size; i++ {\n node := dq[0]\n dq = dq[1:]\n for _, child := range node.Children {\n dq = append(dq, child)\n temp = append(temp, child.Val)\n }\n }\n if len(temp) != 0 {\n r = append(r, temp)\n }\n }\n return r\n}\n```\n# TS / Js . 1\n```js\n/**\n * // Definition for a Node.\n * function Node(val,children) {\n * this.val = val;\n * this.children = children;\n * };\n */\n\n/**\n * @param {Node|null} root\n * @return {number[][]}\n */\n\nvar levelOrder = function(root) {\n let r = []\n if (!root) {\n return r\n }\n let dq = [root]\n while (dq.length > 0) {\n let temp = []\n let len = dq.length\n while (len-- > 0) {\n let node = dq.shift()\n for (let n of node.children) {\n dq.push(n)\n }\n temp.push(node.val)\n }\n r.push(temp)\n }\n return r\n};\n```\n# TS/Js . 2\n```ts\nvar levelOrder = function(root) {\n let r = []\n if (!root) {\n return r\n }\n r.push([root.val])\n let dq = [root]\n while (dq.length > 0) {\n let temp = []\n let len = dq.length\n while (len-- > 0) {\n let node = dq.shift()\n for (let n of node.children) {\n dq.push(n)\n temp.push(n.val)\n }\n }\n if (temp.length > 0) {\n r.push(temp)\n }\n }\n return r\n};\n```\nJava\n```java\nclass Solution {\n public List<List<Integer>> levelOrder(Node root) {\n List<List<Integer>> r = new LinkedList<>();\n LinkedList<Node> dq = new LinkedList<>();\n\n if (root == null)\n return r;\n dq.add(root);\n while (! dq.isEmpty())\n {\n LinkedList<Integer> temp = new LinkedList<>();\n int len = dq.size();\n\n while (len-- > 0)\n {\n System.out.println(len);\n Node node = dq.pollFirst();\n\n for (Node n: node.children)\n dq.addLast(n);\n temp.add(node.val);\n }\n r.add(temp);\n }\n return r;\n }\n}\n``` | 1 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
Easy python solution 18 lines only | n-ary-tree-level-order-traversal | 0 | 1 | ```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if root is None:\n return []\n #print(root.children)\n valList=[[root.val]]\n flst=[]\n xlst=[]\n lst=[root]\n while lst:\n x=lst.pop(0)\n if x.children:\n for i in x.children:\n flst.append(i)\n xlst.append(i.val)\n if len(lst)==0:\n lst=flst[:]\n flst=[]\n if xlst:\n valList.append(xlst)\n xlst=[]\n return valList\n``` | 1 | Given an n-ary tree, return the _level order_ traversal of its nodes' values.
_Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)._
**Example 1:**
**Input:** root = \[1,null,3,2,4,null,5,6\]
**Output:** \[\[1\],\[3,2,4\],\[5,6\]\]
**Example 2:**
**Input:** root = \[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14\]
**Output:** \[\[1\],\[2,3,4,5\],\[6,7,8,9,10\],\[11,12,13\],\[14\]\]
**Constraints:**
* The height of the n-ary tree is less than or equal to `1000`
* The total number of nodes is between `[0, 104]` | null |
Easy python solution 18 lines only | n-ary-tree-level-order-traversal | 0 | 1 | ```\nclass Solution:\n def levelOrder(self, root: \'Node\') -> List[List[int]]:\n if root is None:\n return []\n #print(root.children)\n valList=[[root.val]]\n flst=[]\n xlst=[]\n lst=[root]\n while lst:\n x=lst.pop(0)\n if x.children:\n for i in x.children:\n flst.append(i)\n xlst.append(i.val)\n if len(lst)==0:\n lst=flst[:]\n flst=[]\n if xlst:\n valList.append(xlst)\n xlst=[]\n return valList\n``` | 1 | You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The `ith` element of the array `mines` is defined as `mines[i] = [xi, yi]` where `grid[xi][yi] == 0`.
Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
**Example 1:**
**Input:** n = 5, mines = \[\[4,2\]\]
**Output:** 2
**Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
**Example 2:**
**Input:** n = 1, mines = \[\[0,0\]\]
**Output:** 0
**Explanation:** There is no plus sign, so return 0.
**Constraints:**
* `1 <= n <= 500`
* `1 <= mines.length <= 5000`
* `0 <= xi, yi < n`
* All the pairs `(xi, yi)` are **unique**. | null |
Unlocking the Mysteries of the Squiggly List: A Tale of Flattening Multilevel Doubly Linked Lists | flatten-a-multilevel-doubly-linked-list | 0 | 1 | # Intuition\nWhen reading the question to flatten a multilevel doubly linked list, a first intuition would be to use recursion or iteration to traverse the list and handle the child nodes.\n\n# Approach\nThe approach used in this code is a recursive traversal of the multilevel doubly linked list to flatten it.\nThe flatten function takes the head of the multilevel doubly linked list as input and returns the flattened version of the list.\n\n- Check if the head is None. If it is, return None.\n- Initialize an empty list T to store the values of the nodes in the desired order.\n- Invoke the traverse function with the head node and the T list as arguments.\n- The traverse function recursively traverses the multilevel doubly linked list and appends the values of the nodes to the result list.\n-- If the current node is None, return.\n-- Append the value of the current node to the result list.\n-- Recursively traverse the child node by calling the traverse function with the child node and result.\n-- Recursively traverse the next node by calling the traverse function with the next node and result.\n- After the traverse function completes, the T list contains the values of the nodes in the desired order.\n- Create a new node ret_head using the first value from the T list.\n- Initialize curr as the ret_head node.\n- Set the child pointer of ret_head to None.\n- Iterate over the remaining values in the T list from index 1.\n -- Create a new node new_node with the current value.\n -- Set the prev pointer of new_node to curr.\n -- Set the child pointer of new_node to None.\n -- Set the next pointer of curr to new_node.\n -- Update curr to the newly created new_node.\n- Return ret_head, which is the head of the flattened linked list.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if head is None:\n return \n T = self.traverse(head,[])\n ret_head = Node(T[0])\n curr = ret_head\n ret_head.child = None\n for i in range(1,len(T)):\n new_node = Node(T[i])\n new_node.prev = curr\n new_node.child = None\n curr.next = new_node\n curr = curr.next\n return ret_head\n def traverse(self,head,result):\n if head is None:\n return\n result.append(head.val)\n self.traverse(head.child,result)\n self.traverse(head.next,result)\n return result\n``` | 2 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
Unlocking the Mysteries of the Squiggly List: A Tale of Flattening Multilevel Doubly Linked Lists | flatten-a-multilevel-doubly-linked-list | 0 | 1 | # Intuition\nWhen reading the question to flatten a multilevel doubly linked list, a first intuition would be to use recursion or iteration to traverse the list and handle the child nodes.\n\n# Approach\nThe approach used in this code is a recursive traversal of the multilevel doubly linked list to flatten it.\nThe flatten function takes the head of the multilevel doubly linked list as input and returns the flattened version of the list.\n\n- Check if the head is None. If it is, return None.\n- Initialize an empty list T to store the values of the nodes in the desired order.\n- Invoke the traverse function with the head node and the T list as arguments.\n- The traverse function recursively traverses the multilevel doubly linked list and appends the values of the nodes to the result list.\n-- If the current node is None, return.\n-- Append the value of the current node to the result list.\n-- Recursively traverse the child node by calling the traverse function with the child node and result.\n-- Recursively traverse the next node by calling the traverse function with the next node and result.\n- After the traverse function completes, the T list contains the values of the nodes in the desired order.\n- Create a new node ret_head using the first value from the T list.\n- Initialize curr as the ret_head node.\n- Set the child pointer of ret_head to None.\n- Iterate over the remaining values in the T list from index 1.\n -- Create a new node new_node with the current value.\n -- Set the prev pointer of new_node to curr.\n -- Set the child pointer of new_node to None.\n -- Set the next pointer of curr to new_node.\n -- Update curr to the newly created new_node.\n- Return ret_head, which is the head of the flattened linked list.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if head is None:\n return \n T = self.traverse(head,[])\n ret_head = Node(T[0])\n curr = ret_head\n ret_head.child = None\n for i in range(1,len(T)):\n new_node = Node(T[i])\n new_node.prev = curr\n new_node.child = None\n curr.next = new_node\n curr = curr.next\n return ret_head\n def traverse(self,head,result):\n if head is None:\n return\n result.append(head.val)\n self.traverse(head.child,result)\n self.traverse(head.next,result)\n return result\n``` | 2 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
[Python 3] Using recursion || beats 98% || 36ms 🥷🏼 | flatten-a-multilevel-doubly-linked-list | 0 | 1 | \n```python3 []\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n def unpack(head):\n cur = tail = head\n while cur:\n if cur.child:\n start, end = unpack(cur.child)\n if cur.next: cur.next.prev = end\n cur.next, start.prev, end.next, cur.child = start, cur, cur.next, None\n cur = end\n tail = cur\n cur = cur.next\n return (head, tail)\n\n return unpack(head)[0]\n```\n\n | 3 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
[Python 3] Using recursion || beats 98% || 36ms 🥷🏼 | flatten-a-multilevel-doubly-linked-list | 0 | 1 | \n```python3 []\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n def unpack(head):\n cur = tail = head\n while cur:\n if cur.child:\n start, end = unpack(cur.child)\n if cur.next: cur.next.prev = end\n cur.next, start.prev, end.next, cur.child = start, cur, cur.next, None\n cur = end\n tail = cur\n cur = cur.next\n return (head, tail)\n\n return unpack(head)[0]\n```\n\n | 3 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
Python || 99.36% Faster || Recursive Solution | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\nclass Solution:\n def child(self,node,bottom,nexx):\n curr=bottom\n while curr.next:\n if curr.child:\n self.child(curr,curr.child,curr.next)\n curr=curr.next\n node.next=bottom\n bottom.prev=node\n node.child=None\n curr.next=nexx\n if nexx:\n nexx.prev=curr\n \n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\': \n temp=head\n while temp:\n if temp.child:\n nexx=temp.next\n self.child(temp,temp.child,nexx)\n temp=temp.next\n return head\n```\n**An upvote will be encouraging** | 1 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
Python || 99.36% Faster || Recursive Solution | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\nclass Solution:\n def child(self,node,bottom,nexx):\n curr=bottom\n while curr.next:\n if curr.child:\n self.child(curr,curr.child,curr.next)\n curr=curr.next\n node.next=bottom\n bottom.prev=node\n node.child=None\n curr.next=nexx\n if nexx:\n nexx.prev=curr\n \n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\': \n temp=head\n while temp:\n if temp.child:\n nexx=temp.next\n self.child(temp,temp.child,nexx)\n temp=temp.next\n return head\n```\n**An upvote will be encouraging** | 1 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
430: Solution with step by step explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the function flattenDFS which takes a Node object as input and returns a Node object.\n2. Check if the node object is None. If it is, return None.\n3. Check if node object has no child and no next pointers. If it does not, return the node object.\n4. Check if the node object has no child pointer. If it does not, call flattenDFS with the next node and return its result.\n5. Call flattenDFS with the child node and store its result in childTail.\n6. Get the next node of node and store it in nextNode.\n7. If nextNode is not None, set childTail.next to nextNode and set nextNode.prev to childTail.\n8. Set node.next to node.child and set node.child.prev to node.\n9. Set node.child to None.\n10. Call flattenDFS with nextNode if it is not None, otherwise call it with childTail. Store the result in a variable.\n11. Return the head of the flattened linked list after calling flattenDFS with the input head and completing the process.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n def flattenDFS(node):\n if not node:\n return None\n if not node.child and not node.next:\n return node\n if not node.child:\n return flattenDFS(node.next)\n childTail = flattenDFS(node.child)\n nextNode = node.next\n if nextNode:\n childTail.next = nextNode\n nextNode.prev = childTail\n node.next = node.child\n node.child.prev = node\n node.child = None\n return flattenDFS(nextNode) if nextNode else childTail\n flattenDFS(head)\n return head\n\n``` | 6 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
430: Solution with step by step explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the function flattenDFS which takes a Node object as input and returns a Node object.\n2. Check if the node object is None. If it is, return None.\n3. Check if node object has no child and no next pointers. If it does not, return the node object.\n4. Check if the node object has no child pointer. If it does not, call flattenDFS with the next node and return its result.\n5. Call flattenDFS with the child node and store its result in childTail.\n6. Get the next node of node and store it in nextNode.\n7. If nextNode is not None, set childTail.next to nextNode and set nextNode.prev to childTail.\n8. Set node.next to node.child and set node.child.prev to node.\n9. Set node.child to None.\n10. Call flattenDFS with nextNode if it is not None, otherwise call it with childTail. Store the result in a variable.\n11. Return the head of the flattened linked list after calling flattenDFS with the input head and completing the process.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n def flattenDFS(node):\n if not node:\n return None\n if not node.child and not node.next:\n return node\n if not node.child:\n return flattenDFS(node.next)\n childTail = flattenDFS(node.child)\n nextNode = node.next\n if nextNode:\n childTail.next = nextNode\n nextNode.prev = childTail\n node.next = node.child\n node.child.prev = node\n node.child = None\n return flattenDFS(nextNode) if nextNode else childTail\n flattenDFS(head)\n return head\n\n``` | 6 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
Implementation using stack and dummy pointer [99% Space Complexity] | flatten-a-multilevel-doubly-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy First thoughts upon viewing the questions is to some how save the `head.next` nodes when encountering the nodes with the `head.child` nodes. As saving the `head.next` once we continue moving forward in the child node and reach the end I can pop the stack, make curent node.next to the pop and pop.prev to current and can finish the problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. The `end` list is used to keep track of nodes next to the nodes with children that need to be reconnected after flattening. `res` is used to store the original head of the linked list, and it will be returned as the result.\n\n2. The solution enters a while loop that iterates through the linked list, starting with the `head`.\n\n3. Inside the loop, it checks if the current node has a child (the `child` attribute is not None). If it does have a child, it performs the following steps:\n - If the current node also has a next node (`head.next` is not None), it pushes the next node onto the `end` stack for later reconnection.\n - It updates the `head.next` to point to the child node and sets the child node\'s `prev` pointer to the current `head`.\n - Finally, it sets the current node\'s `child` attribute to None, effectively detaching the child.\n\n4. The solution then checks if the current node has reached the end of the list (`head.next` is None) and if there are nodes in the `end` stack waiting to be reconnected. If both conditions are met, it pops a node (`no`) from the `end` stack, and if `no` is not None, it reconnects it to the current node as the next node, and updates the `prev` pointer accordingly.\n\n5. The `head` pointer is then moved to the next node in the original list, and the loop continues until it reaches the end of the list.\n\n6. Finally, the `res` (original head) is returned as the flattened doubly linked list.\n\nThis approach effectively flattens a multilevel doubly linked list while maintaining the original order of nodes. It uses a stack (`end`) to keep track of nodes next to the nodes with children, and it modifies the pointers accordingly to achieve the desired result.\n\n\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<small>In only the wort case scenario it will be $$O(n)$$, which is the case where every node has a child. Excluding that every other case will have much better time complexity.</small>\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n\n end = []\n res = head\n while head:\n if head.child:\n if head.next:\n end.append(head.next)\n head.next = head.child\n head.next.prev = head\n head.child=None\n if not head.next and end:\n no = end.pop() if end else None\n if no :\n head.next = no\n no.prev = head\n head = head.next\n\n return res\n``` | 1 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
Implementation using stack and dummy pointer [99% Space Complexity] | flatten-a-multilevel-doubly-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy First thoughts upon viewing the questions is to some how save the `head.next` nodes when encountering the nodes with the `head.child` nodes. As saving the `head.next` once we continue moving forward in the child node and reach the end I can pop the stack, make curent node.next to the pop and pop.prev to current and can finish the problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. The `end` list is used to keep track of nodes next to the nodes with children that need to be reconnected after flattening. `res` is used to store the original head of the linked list, and it will be returned as the result.\n\n2. The solution enters a while loop that iterates through the linked list, starting with the `head`.\n\n3. Inside the loop, it checks if the current node has a child (the `child` attribute is not None). If it does have a child, it performs the following steps:\n - If the current node also has a next node (`head.next` is not None), it pushes the next node onto the `end` stack for later reconnection.\n - It updates the `head.next` to point to the child node and sets the child node\'s `prev` pointer to the current `head`.\n - Finally, it sets the current node\'s `child` attribute to None, effectively detaching the child.\n\n4. The solution then checks if the current node has reached the end of the list (`head.next` is None) and if there are nodes in the `end` stack waiting to be reconnected. If both conditions are met, it pops a node (`no`) from the `end` stack, and if `no` is not None, it reconnects it to the current node as the next node, and updates the `prev` pointer accordingly.\n\n5. The `head` pointer is then moved to the next node in the original list, and the loop continues until it reaches the end of the list.\n\n6. Finally, the `res` (original head) is returned as the flattened doubly linked list.\n\nThis approach effectively flattens a multilevel doubly linked list while maintaining the original order of nodes. It uses a stack (`end`) to keep track of nodes next to the nodes with children, and it modifies the pointers accordingly to achieve the desired result.\n\n\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<small>In only the wort case scenario it will be $$O(n)$$, which is the case where every node has a child. Excluding that every other case will have much better time complexity.</small>\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n\n end = []\n res = head\n while head:\n if head.child:\n if head.next:\n end.append(head.next)\n head.next = head.child\n head.next.prev = head\n head.child=None\n if not head.next and end:\n no = end.pop() if end else None\n if no :\n head.next = no\n no.prev = head\n head = head.next\n\n return res\n``` | 1 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
Python O(n), O(1) easy solution with explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | Easy iterative approach without using extra memory.\nO(n) time complexity\nO(1) space complexity\n\n```\n"""\n# Definition for a Node.\nclass Node(object):\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution(object):\n def flatten(self, head):\n """\n :type head: Node\n :rtype: Node\n """\n # traverse the list and look for nodes, where self.child is not None\n # keep the pointer to the previous node and to the original next node\n # merge a child list to the parent list - connect prev and next pointers\n # continue traversing until encountering another node where self.child is not None, \n # or reaching the end of the main list\n \n current = head\n \n while current is not None:\n # check for child node\n if current.child is not None:\n # merge child list into the parent list\n self.merge(current)\n \n # move to the next node\n current = current.next\n \n return head\n \n \n def merge(self, current):\n child = current.child\n \n # traverse child list until we get the last node\n while child.next is not None:\n child = child.next\n \n # child is now pointing at the last node of the child list\n # we need to connect child.next to current.next, if there is any\n if current.next is not None:\n child.next = current.next\n current.next.prev = child\n \n # now, we have to connect current to the child list\n # child is currently pointing at the last node of the child list, \n # so we need to use pointer (current.child) to get to the first node of the child list\n current.next = current.child\n current.child.prev = current\n \n # at the end remove self.child pointer\n current.child = None\n \n``` | 21 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
Python O(n), O(1) easy solution with explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | Easy iterative approach without using extra memory.\nO(n) time complexity\nO(1) space complexity\n\n```\n"""\n# Definition for a Node.\nclass Node(object):\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution(object):\n def flatten(self, head):\n """\n :type head: Node\n :rtype: Node\n """\n # traverse the list and look for nodes, where self.child is not None\n # keep the pointer to the previous node and to the original next node\n # merge a child list to the parent list - connect prev and next pointers\n # continue traversing until encountering another node where self.child is not None, \n # or reaching the end of the main list\n \n current = head\n \n while current is not None:\n # check for child node\n if current.child is not None:\n # merge child list into the parent list\n self.merge(current)\n \n # move to the next node\n current = current.next\n \n return head\n \n \n def merge(self, current):\n child = current.child\n \n # traverse child list until we get the last node\n while child.next is not None:\n child = child.next\n \n # child is now pointing at the last node of the child list\n # we need to connect child.next to current.next, if there is any\n if current.next is not None:\n child.next = current.next\n current.next.prev = child\n \n # now, we have to connect current to the child list\n # child is currently pointing at the last node of the child list, \n # so we need to use pointer (current.child) to get to the first node of the child list\n current.next = current.child\n current.child.prev = current\n \n # at the end remove self.child pointer\n current.child = None\n \n``` | 21 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
Solution | flatten-a-multilevel-doubly-linked-list | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n Node* flat(Node* head) {\n if (!head)\n return NULL;\n Node* temp1=NULL;\n while(head) {\n if (head->child) {\n Node* tail = flat(head->child);\n Node* temp = head->next;\n head->next = head->child;\n head->child->prev = head;\n head->child = NULL;\n if (tail) {\n tail->next = temp;\n if (temp)\n temp->prev = tail;\n }\n temp1=tail;\n head = temp;\n } else {\n temp1=head;\n head = head->next;\n }\n }\n return temp1;\n }\n Node* flatten(Node* head) {\n flat(head);\n return head;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n def recurse(node: \'Optional[Node]\') -> \'Optional[Node]\' :\n while node:\n nxt = node.next\n \n if not node.child and not node.next:\n return node\n elif node.child:\n node.next = node.child\n node.child.prev = node\n \n child_tail = recurse(node.child)\n node.child = None\n \n if nxt:\n child_tail.next = nxt\n nxt.prev = child_tail\n else:\n return child_tail\n\n node = nxt\n \n recurse(head)\n return head\n```\n\n```Java []\nclass Solution {\n public Node flatten(Node head) {\n Stack<Node> stk = new Stack<>();\n Node curr = head;\n if(curr==null)\n return null;\n while(curr.next !=null || curr.child!=null)\n {\n while(curr.child==null)\n {\n if(curr.next ==null)\n break;\n curr= curr.next; \n }\n if(curr.next!=null)\n {\n curr.next.prev = null;\n stk.add(curr.next);\n curr.next = null;\n }\n if(curr.child!=null)\n {\n Node temp = curr.child;\n temp.prev = curr;\n curr.child = null;\n curr.next = temp;\n curr = temp;\n }\n }\n while(!stk.isEmpty()) \n {\n Node rem = stk.pop();\n rem.prev = curr;\n curr.next = rem;\n while(curr.next!=null)\n {\n curr = curr.next;\n }\n }\n return head; \n }\n}\n```\n | 2 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
Solution | flatten-a-multilevel-doubly-linked-list | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n Node* flat(Node* head) {\n if (!head)\n return NULL;\n Node* temp1=NULL;\n while(head) {\n if (head->child) {\n Node* tail = flat(head->child);\n Node* temp = head->next;\n head->next = head->child;\n head->child->prev = head;\n head->child = NULL;\n if (tail) {\n tail->next = temp;\n if (temp)\n temp->prev = tail;\n }\n temp1=tail;\n head = temp;\n } else {\n temp1=head;\n head = head->next;\n }\n }\n return temp1;\n }\n Node* flatten(Node* head) {\n flat(head);\n return head;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n def recurse(node: \'Optional[Node]\') -> \'Optional[Node]\' :\n while node:\n nxt = node.next\n \n if not node.child and not node.next:\n return node\n elif node.child:\n node.next = node.child\n node.child.prev = node\n \n child_tail = recurse(node.child)\n node.child = None\n \n if nxt:\n child_tail.next = nxt\n nxt.prev = child_tail\n else:\n return child_tail\n\n node = nxt\n \n recurse(head)\n return head\n```\n\n```Java []\nclass Solution {\n public Node flatten(Node head) {\n Stack<Node> stk = new Stack<>();\n Node curr = head;\n if(curr==null)\n return null;\n while(curr.next !=null || curr.child!=null)\n {\n while(curr.child==null)\n {\n if(curr.next ==null)\n break;\n curr= curr.next; \n }\n if(curr.next!=null)\n {\n curr.next.prev = null;\n stk.add(curr.next);\n curr.next = null;\n }\n if(curr.child!=null)\n {\n Node temp = curr.child;\n temp.prev = curr;\n curr.child = null;\n curr.next = temp;\n curr = temp;\n }\n }\n while(!stk.isEmpty()) \n {\n Node rem = stk.pop();\n rem.prev = curr;\n curr.next = rem;\n while(curr.next!=null)\n {\n curr = curr.next;\n }\n }\n return head; \n }\n}\n```\n | 2 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
[Python3] Recursion | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n res = head\n \n def flatLayer(node):\n pre = node\n while node:\n if node.child is not None:\n end = flatLayer(node.child)\n end.next = node.next\n if node.next:\n node.next.prev = end\n node.next = node.child\n node.child.prev = node\n pre = end\n node.child = None\n node = end.next\n else:\n pre = node\n node = node.next\n return pre\n \n flatLayer(head)\n return res\n``` | 1 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
[Python3] Recursion | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n res = head\n \n def flatLayer(node):\n pre = node\n while node:\n if node.child is not None:\n end = flatLayer(node.child)\n end.next = node.next\n if node.next:\n node.next.prev = end\n node.next = node.child\n node.child.prev = node\n pre = end\n node.child = None\n node = end.next\n else:\n pre = node\n node = node.next\n return pre\n \n flatLayer(head)\n return res\n``` | 1 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
TC: O(n), SC: O(1) No stack, No recursion Simple One Pass Python Solution | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\ndef flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head: return\n curr = head\n while curr:\n if curr.child:\n childNode = curr.child\n childNode.prev = curr #setting previous pointer\n \n while childNode.next:\n childNode = childNode.next\n \n childNode.next = curr.next\n \n if childNode.next: childNode.next.prev = childNode\n \n curr.next = curr.child\n curr.child = None\n \n curr = curr.next\n \n return head\n```\nThe traversal technique used here is known as Morris Traversal.\nMorris traversal is generally used to traverse binary trees, but if you give it some thought, the doubly linked list given in this problem is just like a Binary Tree with previous pointers.\nChild pointer and next pointer can be thought of as left pointer and right pointer of a tree respectively.\nOnce we look at the problem like this it becomes similar to flattening a binary tree to a linked list, just with two extra steps to set the previous pointers.\n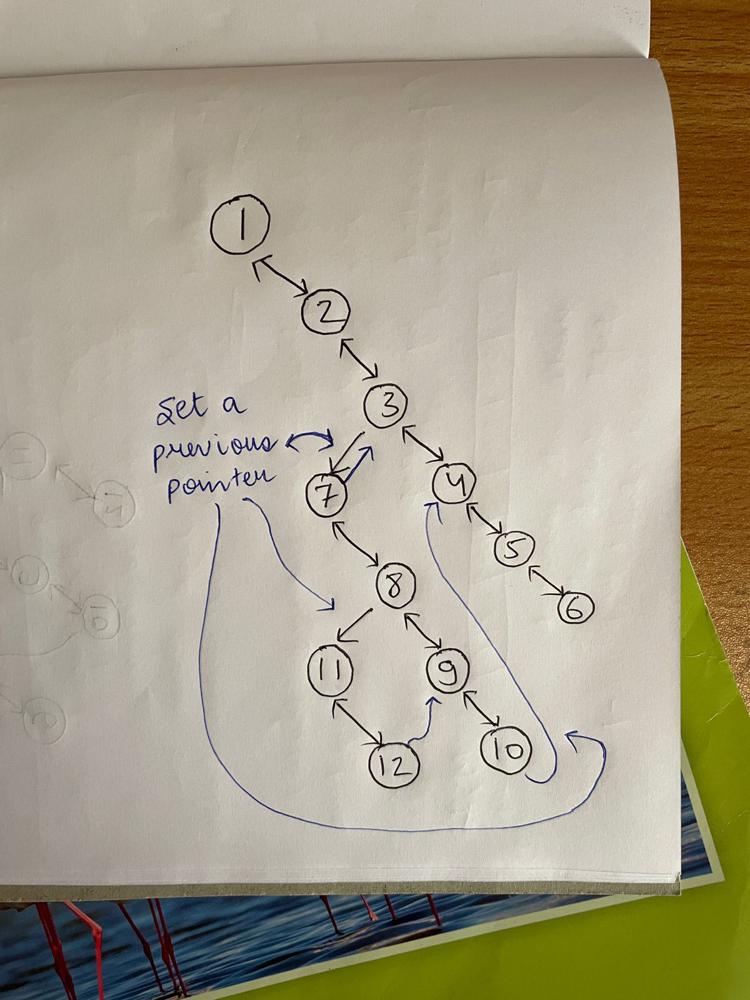\n\nIf you remove the two extra steps where you set the previous pointers, you get a solution to this problem: https://leetcode.com/problems/flatten-binary-tree-to-linked-list/\n```\ndef flatten(self, root: Optional[TreeNode]) -> None:\n if root == None: return\n curr = root\n while curr:\n if curr.left:\n childNode = curr.left\n while childNode.right:\n childNode = childNode.right\n childNode.right = curr.right\n curr.right = curr.left\n curr.left = None\n curr = curr.right\n```\n\n | 9 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
TC: O(n), SC: O(1) No stack, No recursion Simple One Pass Python Solution | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\ndef flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head: return\n curr = head\n while curr:\n if curr.child:\n childNode = curr.child\n childNode.prev = curr #setting previous pointer\n \n while childNode.next:\n childNode = childNode.next\n \n childNode.next = curr.next\n \n if childNode.next: childNode.next.prev = childNode\n \n curr.next = curr.child\n curr.child = None\n \n curr = curr.next\n \n return head\n```\nThe traversal technique used here is known as Morris Traversal.\nMorris traversal is generally used to traverse binary trees, but if you give it some thought, the doubly linked list given in this problem is just like a Binary Tree with previous pointers.\nChild pointer and next pointer can be thought of as left pointer and right pointer of a tree respectively.\nOnce we look at the problem like this it becomes similar to flattening a binary tree to a linked list, just with two extra steps to set the previous pointers.\n\n\nIf you remove the two extra steps where you set the previous pointers, you get a solution to this problem: https://leetcode.com/problems/flatten-binary-tree-to-linked-list/\n```\ndef flatten(self, root: Optional[TreeNode]) -> None:\n if root == None: return\n curr = root\n while curr:\n if curr.left:\n childNode = curr.left\n while childNode.right:\n childNode = childNode.right\n childNode.right = curr.right\n curr.right = curr.left\n curr.left = None\n curr = curr.right\n```\n\n | 9 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
Python Intuitive Recursive Approach with Detailed Explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return\n \n def dfs(node):\n if node.child: #if node has a child, we go down\n temp = node.next # store the next node to temp \n node.next = node.child # current node\'s next points to its child \n node.child.prev = node # current node\'s child\'s prev points to current node\n last = dfs(node.child) # dfs the list that starts with current node\'s child (i.e., list with one level down), this will return the end node of the list one level below\n node.child = None # assign null to child\n if temp and last: # if the original next node is not null and the last node of the list one level below are both not null, we should connect them\n last.next = temp\n temp.prev = last\n return dfs(temp) # after connection, we should keep searching down the list on the current level\n else: # if the original next node is Null, we can\'t append it to our current list. As a result, we can simply return the last node from below so we can connect it with the list one level above. \n return last \n \n elif node.next: # if there is a next element, go right\n return dfs(node.next)\n else: # we\'ve hit the end of the current list, return the last node\n return node\n \n dfs(head)\n \n return(head)\n ``\n``` | 2 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
Python Intuitive Recursive Approach with Detailed Explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ```\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return\n \n def dfs(node):\n if node.child: #if node has a child, we go down\n temp = node.next # store the next node to temp \n node.next = node.child # current node\'s next points to its child \n node.child.prev = node # current node\'s child\'s prev points to current node\n last = dfs(node.child) # dfs the list that starts with current node\'s child (i.e., list with one level down), this will return the end node of the list one level below\n node.child = None # assign null to child\n if temp and last: # if the original next node is not null and the last node of the list one level below are both not null, we should connect them\n last.next = temp\n temp.prev = last\n return dfs(temp) # after connection, we should keep searching down the list on the current level\n else: # if the original next node is Null, we can\'t append it to our current list. As a result, we can simply return the last node from below so we can connect it with the list one level above. \n return last \n \n elif node.next: # if there is a next element, go right\n return dfs(node.next)\n else: # we\'ve hit the end of the current list, return the last node\n return node\n \n dfs(head)\n \n return(head)\n ``\n``` | 2 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
Python Recursion: Easy-to-understand with Explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ### Intuition\n\nSince we are working with a doubly-linked list, for every `node.child` that we handle, we need to obtain the end `node` of the list at that particular level, so that we can assign its `node.next` appropriately. We can thus write a recursive function that does the following:\n\n- Loop through each `node` in the list (at that particular level).\n- Upon encountering a `node` with a `child`, call the function again starting with `node.child`.\n- Once we reach the end of the list (at that particular level), return the end `node` so we can handle it accordingly on the previous level.\n\n---\n\n### Code\n\n```python\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n def getTail(node):\n prev = None\n while node:\n _next = node.next\n if node.child:\n\t\t\t\t\t# ... <-> node <-> node.child <-> ...\n node.next = node.child\n node.child = None\n node.next.prev = node\n\t\t\t\t\t# get the end node of the node.child list\n prev = getTail(node.next)\n if _next:\n\t\t\t\t\t\t# ... <-> prev (end node) <-> _next (originally node.next) <-> ...\n _next.prev = prev\n prev.next = _next\n else:\n prev = node\n node = _next # loop through the list of nodes\n return prev # return end node\n \n getTail(head)\n return head\n```\n\n---\n\n### Final Result\n\n\n\nPlease upvote if this has helped you! Appreciate any comments as well ;) | 8 | You are given a doubly linked list, which contains nodes that have a next pointer, a previous pointer, and an additional **child pointer**. This child pointer may or may not point to a separate doubly linked list, also containing these special nodes. These child lists may have one or more children of their own, and so on, to produce a **multilevel data structure** as shown in the example below.
Given the `head` of the first level of the list, **flatten** the list so that all the nodes appear in a single-level, doubly linked list. Let `curr` be a node with a child list. The nodes in the child list should appear **after** `curr` and **before** `curr.next` in the flattened list.
Return _the_ `head` _of the flattened list. The nodes in the list must have **all** of their child pointers set to_ `null`.
**Example 1:**
**Input:** head = \[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\]
**Output:** \[1,2,3,7,8,11,12,9,10,4,5,6\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 2:**
**Input:** head = \[1,2,null,3\]
**Output:** \[1,3,2\]
**Explanation:** The multilevel linked list in the input is shown.
After flattening the multilevel linked list it becomes:
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Explanation:** There could be empty list in the input.
**Constraints:**
* The number of Nodes will not exceed `1000`.
* `1 <= Node.val <= 105`
**How the multilevel linked list is represented in test cases:**
We use the multilevel linked list from **Example 1** above:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
The serialization of each level is as follows:
\[1,2,3,4,5,6,null\]
\[7,8,9,10,null\]
\[11,12,null\]
To serialize all levels together, we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
\[1, 2, 3, 4, 5, 6, null\]
|
\[null, null, 7, 8, 9, 10, null\]
|
\[ null, 11, 12, null\]
Merging the serialization of each level and removing trailing nulls we obtain:
\[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12\] | null |
Python Recursion: Easy-to-understand with Explanation | flatten-a-multilevel-doubly-linked-list | 0 | 1 | ### Intuition\n\nSince we are working with a doubly-linked list, for every `node.child` that we handle, we need to obtain the end `node` of the list at that particular level, so that we can assign its `node.next` appropriately. We can thus write a recursive function that does the following:\n\n- Loop through each `node` in the list (at that particular level).\n- Upon encountering a `node` with a `child`, call the function again starting with `node.child`.\n- Once we reach the end of the list (at that particular level), return the end `node` so we can handle it accordingly on the previous level.\n\n---\n\n### Code\n\n```python\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n def getTail(node):\n prev = None\n while node:\n _next = node.next\n if node.child:\n\t\t\t\t\t# ... <-> node <-> node.child <-> ...\n node.next = node.child\n node.child = None\n node.next.prev = node\n\t\t\t\t\t# get the end node of the node.child list\n prev = getTail(node.next)\n if _next:\n\t\t\t\t\t\t# ... <-> prev (end node) <-> _next (originally node.next) <-> ...\n _next.prev = prev\n prev.next = _next\n else:\n prev = node\n node = _next # loop through the list of nodes\n return prev # return end node\n \n getTail(head)\n return head\n```\n\n---\n\n### Final Result\n\n\n\nPlease upvote if this has helped you! Appreciate any comments as well ;) | 8 | Given an `m x n` `matrix`, return _`true` if the matrix is Toeplitz. Otherwise, return `false`._
A matrix is **Toeplitz** if every diagonal from top-left to bottom-right has the same elements.
**Example 1:**
**Input:** matrix = \[\[1,2,3,4\],\[5,1,2,3\],\[9,5,1,2\]\]
**Output:** true
**Explanation:**
In the above grid, the diagonals are:
"\[9\] ", "\[5, 5\] ", "\[1, 1, 1\] ", "\[2, 2, 2\] ", "\[3, 3\] ", "\[4\] ".
In each diagonal all elements are the same, so the answer is True.
**Example 2:**
**Input:** matrix = \[\[1,2\],\[2,2\]\]
**Output:** false
**Explanation:**
The diagonal "\[1, 2\] " has different elements.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 20`
* `0 <= matrix[i][j] <= 99`
**Follow up:**
* What if the `matrix` is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
* What if the `matrix` is so large that you can only load up a partial row into the memory at once? | null |
Solution O(1). Runtime > 99% | all-oone-data-structure | 0 | 1 | \n\n```\nclass ListCount:\n def __init__(self, set_string, count, prev= None, next= None):\n self.set_string = set_string\n self.count = count\n self.next = next\n self.prev = prev\n\nclass AllOne:\n def __init__(self):\n self.head = ListCount({""}, count= 0)\n self.tail = ListCount({""}, count= inf, prev= self.head)\n self.head.next = self.tail\n self.dic_string = {}\n\n def inc(self, key: str) -> None:\n if key in self.dic_string:\n node = self.dic_string[key]\n inc_cnt = node.count+1 \n if len(node.set_string) == 1:\n if inc_cnt == node.next.count:\n node.next.set_string.add(key)\n self.dic_string[key] = node.next\n node.next.prev, node.prev.next = node.prev, node.next \n else:\n node.count = inc_cnt \n else:\n node.set_string.remove(key)\n if inc_cnt == node.next.count:\n node.next.set_string.add(key)\n self.dic_string[key] = node.next\n else:\n new_node = ListCount(set_string= {key}, count= inc_cnt, prev= node, next= node.next)\n node.next.prev = new_node\n node.next = new_node\n self.dic_string[key] = new_node\n else:\n if self.head.next.count == 1:\n self.head.next.set_string.add(key)\n self.dic_string[key] = self.head.next\n else: \n node = ListCount(set_string= {key}, count= 1, prev= self.head, next= self.head.next)\n self.head.next.prev = node\n self.head.next = node\n self.dic_string[key] = node\n\n def dec(self, key: str) -> None:\n node = self.dic_string[key]\n if node.count == 1: \n if len(node.set_string) == 1: \n node.next.prev, node.prev.next = node.prev, node.next \n else:\n node.set_string.remove(key)\n del self.dic_string[key] \n else:\n dec_cnt = node.count-1\n if len(node.set_string) == 1:\n if dec_cnt == node.prev.count:\n node.prev.set_string.add(key)\n self.dic_string[key] = node.prev\n node.next.prev, node.prev.next = node.prev, node.next \n else:\n node.count = dec_cnt \n else:\n node.set_string.remove(key)\n if dec_cnt == node.prev.count:\n node.prev.set_string.add(key)\n self.dic_string[key] = node.prev\n else:\n new_node = ListCount(set_string= {key}, count= dec_cnt, prev= node.prev, next= node)\n node.prev.next = new_node\n node.prev = new_node\n self.dic_string[key] = new_node\n\n def getMaxKey(self) -> str:\n return next(iter(self.tail.prev.set_string))\n \n def getMinKey(self) -> str:\n return next(iter(self.head.next.set_string))\n```\n###### Another quick solution (runtime > 96%). But contains one small loop in def getMinKey\n```\nclass AllOne:\n def __init__(self):\n self.dic_counter = {}\n self.dic_string = defaultdict(set)\n self.max_cnt = 1\n\n def inc(self, key: str) -> None: \n if key in self.dic_counter:\n cnt = self.dic_counter[key]\n self.dic_counter[key] = cnt+1 \n self.dic_string[cnt].remove(key)\n self.dic_string[cnt+1].add(key)\n self.max_cnt = max(cnt+1, self.max_cnt)\n else:\n self.dic_counter[key] = 1\n self.dic_string[1].add(key)\n\n def dec(self, key: str) -> None:\n cnt = self.dic_counter[key]\n if cnt == 1:\n del self.dic_counter[key]\n self.dic_string[cnt].remove(key)\n else:\n self.dic_counter[key] = cnt-1 \n self.dic_string[cnt-1].add(key)\n if self.max_cnt == cnt and len(self.dic_string[cnt]) == 1:\n self.max_cnt -= 1\n del self.dic_string[cnt]\n else:\n self.dic_string[cnt].remove(key)\n\n def getMaxKey(self) -> str:\n return next(iter(self.dic_string[self.max_cnt])) if self.dic_counter else ""\n \n def getMinKey(self) -> str:\n if not self.dic_counter:\n return ""\n for min_cnt in iter(self.dic_string):\n if self.dic_string[min_cnt]:\n return next(iter(self.dic_string[min_cnt]))\n```\n\n | 4 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Solution | all-oone-data-structure | 1 | 1 | ```C++ []\nclass AllOne {\npublic:\nunordered_map<string, int> m;\n AllOne() {\n ios_base::sync_with_stdio(0);\n cin.tie(0); cout.tie(0);\n }\n void updateMin() { \n _min.second = INT_MAX;\n for(auto & nd : m) {\n if(_min.second > nd.second) {\n _min.second = nd.second;\n _min.first = nd.first;\n }\n }\n }\n void updateMax() { \n _max.second = INT_MIN;\n for(auto & nd : m) {\n if(_max.second < nd.second) {\n _max.second = nd.second;\n _max.first = nd.first;\n }\n }\n }\n void inc(string key) {\n auto & v = m[key];\n ++v;\n if(v > _max.second) {\n _max.second = v;\n _max.first = key;\n }\n if(key == _min.first) {\n updateMin();\n }\n if(_min.second > v || _min.first.empty()) {\n _min.first = key;\n _min.second = v;\n }\n }\n void dec(string key) {\n m[key]--;\n if(m[key] ==0)\n m.erase(key);\n _min.first = _max.first = "";\n }\n string getMaxKey() {\n if(!_max.first.empty())\n return _max.first;\n updateMax();\n return _max.first;\n }\n string getMinKey() {\n if(!_min.first.empty())\n return _min.first;\n\n updateMin();\n return _min.first;\n }\n pair<string, int> _min{{}, 0};\n pair<string, int> _max{{}, 0};\n};\n```\n\n```Python3 []\nclass AllOne:\n\n def __init__(self):\n self.mem = dict()\n self.prev_max = None\n self.prev_min = None\n \n def inc(self, key: str) -> None:\n self.prev_max, self.prev_min = None, None\n\n if key not in self.mem:\n self.mem[key] = 1\n else:\n self.mem[key] += 1\n\n def dec(self, key: str) -> None:\n self.prev_max, self.prev_min = None, None\n\n if self.mem[key] == 1:\n self.mem.pop(key)\n else:\n self.mem[key] -= 1\n \n def getMaxKey(self) -> str:\n if len(self.mem) == 0:\n return ""\n else:\n if self.prev_max != None:\n return self.prev_max\n \n output = sorted(self.mem.items(), key=lambda x:x[1])[-1][0]\n self.prev_max = output\n\n return output\n \n def getMinKey(self) -> str:\n if len(self.mem) == 0:\n return ""\n else:\n if self.prev_min != None:\n return self.prev_min\n output = sorted(self.mem.items(), key=lambda x:x[1])[0][0]\n self.prev_min = output\n return output\n```\n\n```Java []\nimport java.util.HashMap;\nimport java.util.Map;\n\nclass AllOne {\n static class Node {\n String string;\n int count;\n Node prev;\n Node next;\n\n Node() {\n this.string = "";\n }\n Node(String string, int count) {\n this.string = string;\n this.count = count;\n }\n }\n Map<String, Node> stringNodeMap;\n Node head;\n Node tail;\n\n public AllOne() {\n this.stringNodeMap = new HashMap<>();\n this.head = new Node();\n this.tail = new Node();\n\n this.head.next = this.tail;\n this.tail.prev = this.head;\n }\n private Node insertKeyAtBeginning(String key) {\n Node node = new Node(key, 1);\n\n this.head.next.prev = node;\n node.next = this.head.next;\n this.head.next = node;\n node.prev = this.head;\n\n return node;\n }\n public void inc(String key) {\n if (stringNodeMap.containsKey(key)) {\n \n Node node = stringNodeMap.get(key);\n node.count++;\n\n while (node.next != this.tail && node.count > node.next.count) {\n Node prev = node.prev;\n Node next = node.next;\n\n prev.next = next;\n next.prev = prev;\n\n node.next = next.next;\n next.next.prev = node;\n\n next.next = node;\n node.prev = next;\n }\n } else {\n Node node = insertKeyAtBeginning(key);\n this.stringNodeMap.put(key, node);\n }\n }\n private void removeNode(Node node) {\n Node prev = node.prev;\n Node next = node.next;\n\n prev.next = next;\n next.prev = prev;\n\n node.next = null;\n node.prev = null;\n }\n public void dec(String key) {\n Node node = stringNodeMap.get(key);\n if (node.count == 1) {\n \n removeNode(node);\n this.stringNodeMap.remove(key);\n } else {\n \n node.count--;\n\n while (node.prev != this.head && node.count < node.prev.count) {\n Node prev = node.prev;\n Node next = node.next;\n\n prev.next = next;\n next.prev = prev;\n\n node.prev = prev.prev;\n prev.prev.next = node;\n\n prev.prev = node;\n node.next = prev;\n }\n }\n }\n public String getMaxKey() {\n return this.tail.prev.string;\n }\n public String getMinKey() {\n return this.head.next.string;\n }\n}\n```\n | 2 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Python3 Solution Using Counter and Cache (Runtime Beating 98%, Memory Beating 100%) | all-oone-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe prompt told us that "each function must run in O(1) average time complexity", which suggests that we must be using a hashmap to achieve this. What is tricky though, is that ordinary dictionaries are not really suited for the getMaxKey/getMinKey methods, forcing us to a) Save up a sorted frequency list of all the strings, or b) Finding a data structure that\'s suited for the task (that is, returning the most and least frequent key).\n\nThis alone, however, will not be enough to handle the demanding testcases towards the end. Even with the appropriate data structure, checking the min/maxkey is still a costly operation. However, we know that the result of such queries won\'t change as long as there\'s no change to the data between two queries. This allows us to implement a simple cache that will save us from a lot of unnecessary calculations.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nhttps://docs.python.org/3/library/collections.html#collections.Counter\n\n*Counter* is a container datatype in Python\'s standard library that\'s well suited for the task. Normally, it is used to track the frequency of elements in a list or a string. However, we can easily use it as our frequency dictionary. This provides us with two benefits:\n\n1. "Counter objects have a dictionary interface except that they return a zero count for missing items instead of raising a KeyError". This means that we don\'t need to worry about the existence or not of a key when checking any key. If a key doesn\'t exist, it will just return 0.\n\n(Nevertheless, I still recommend deleting keys when their counter drops to 0, since it could mess up with getMinKey)\n\n2. Counter provides the most_common([n]) which is well suited for finding the most and least frequent keys. When most_common() is called without an argument, it will return a sorted(descending) list of tuples in the form of (key, occurences). Example:\n```\nCounter(\'abracadabra\').most_common(3)\n[(\'a\', 5), (\'b\', 2), (\'r\', 2)]\n```\nThis makes it very easy to implement the getMinKey/getMaxKey method by returning most_common()[-1]/most_common()[0]\n\n\nThe most important optimization to pass the testcases is to implement a simple cache for the min and max keys. We will clear the cache when any change is done to the data (inc() and dec()). However, if there has not been any change, our queries will just return the cached value.\n\n# Complexity\n- Time complexity: $$O(1)$$ for inc and dec. $$O(k log k)$$ (k being the unique number of keys) for getMaxKey and getMinKey when the results are not cached, but $$O(1)$$ when the results are.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$ (k being the unique number of keys), since all instances of a unique key would only be stored in one tuple in our counter.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nclass AllOne:\n c = None\n max_cache = None\n min_cache = None\n def __init__(self):\n self.c = Counter()\n\n def inc(self, key: str) -> None:\n self.c[key]+=1\n self.max_cache = None\n self.min_cache = None \n\n def dec(self, key: str) -> None:\n if self.c[key] == 1:\n del self.c[key]\n else:\n self.c[key]-=1\n self.max_cache = None\n self.min_cache = None \n\n def getMaxKey(self) -> str:\n if self.max_cache is not None:\n return self.max_cache\n res = self.c.most_common()\n if len(res) == 0:\n return ""\n self.max_cache = res[0][0]\n return self.max_cache\n\n def getMinKey(self) -> str:\n if self.min_cache is not None:\n return self.min_cache\n res = self.c.most_common()\n if len(res) == 0:\n return ""\n self.min_cache = res[-1][0]\n return self.min_cache\n\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n``` | 1 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
DoubleLinkedList | all-oone-data-structure | 0 | 1 | # Intuition\nUsing Doublelinklist to achieve O(1) retrieval. Using hashmap to help with O(1) add or remove list nodes.\n\n# Approach\ncreate dummy head and tail for better implementation of the double linkedlist. (avoid edge cases when adding or removing nodes). Head is the smallest and tail is the largest, hence using head.next to find the min and tail.prev to get the max.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Node:\n def __init__(self, key=None, freq=0):\n self.freq = freq\n self.prev = None\n self.next = None\n self.keys = set()\n if key:\n self.keys.add(key)\n\n\nclass AllOne:\n\n def __init__(self):\n\n self.head = Node(None, 0)\n self.tail = Node(None, inf)\n self.head.next = self.tail\n self.tail.prev = self.head\n self.map = {} #key:node\n self.map[0] = self.head\n self.map[inf] = self.tail\n\n def removeNode(self, node):\n\n # node = self.map[key]\n node.prev.next = node.next\n node.next.prev = node.prev\n # del self.map[key]\n return\n \n def addNode(self, prevNode, newNode):\n\n nxtNode = prevNode.next\n prevNode.next = newNode\n newNode.prev = prevNode\n\n newNode.next = nxtNode\n nxtNode.prev = newNode\n return \n\n \n def inc(self, key: str) -> None:\n\n if key in self.map:\n # print(key)\n node = self.map[key]\n prevNode = node\n f = node.freq\n newF = f+1\n node.keys.remove(key)\n del self.map[key]\n\n if not node.keys:\n prevNode = node.prev\n self.removeNode(node)\n\n nxt = node.next\n if nxt.freq != newF:\n newNode = Node(key, newF)\n self.addNode(prevNode, newNode)\n self.map[key] = newNode\n else:\n self.map[key] = nxt\n nxt.keys.add(key)\n else:\n node = self.head.next\n if node.freq == 1:\n node.keys.add(key)\n self.map[key] = node\n else:\n newNode = Node(key, 1)\n self.addNode(self.head, newNode)\n self.map[key] = newNode\n\n return \n \n def dec(self, key: str) -> None:\n\n node = self.map[key]\n f = node.freq\n newF = f-1\n prevNode = node.prev\n node.keys.remove(key)\n del self.map[key]\n\n if not node.keys:\n self.removeNode(node)\n \n if newF >= 1:\n if prevNode.freq == newF:\n prevNode.keys.add(key)\n self.map[key] = prevNode\n else:\n newNode = Node(key, newF)\n self.addNode(prevNode, newNode)\n self.map[key] = newNode\n # print(self.map)\n return \n \n\n def getMaxKey(self) -> str:\n\n return list(self.tail.prev.keys)[0] if len(self.tail.prev.keys) >= 1 else ""\n \n\n def getMinKey(self) -> str:\n return list(self.head.next.keys)[0] if len(self.head.next.keys) >= 1 else ""\n \n\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
LeetCodeLegends | all-oone-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need constant time search so a hash table must be involved.\nWe need constant time access to a min and a max key. Heap maybe?\nWe need be able to move elements to max/min locatoin in constant time when they are incremented/decremented and become maximal/minimal.\nLinkList is probably the way to go.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n<iframe width="560" height="315" src="https://www.youtube.com/embed/GTDQgL2VQns?si=tzDRyWHuTvZwWpkD" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe>\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass AllOne:\n \n # DoublyLinkedList Node\n # Encapsulates a set of all keys with the same count\n class AllOneNode:\n def __init__(self):\n self.prev = None\n self.next = None\n self.count = -1\n self.keys = set()\n\n # Initialize DoublyLinkedList Head/Tail and our HashMaps\n def __init__(self):\n self.head_ = self.AllOneNode()\n self.tail_ = self.AllOneNode()\n self.head_.next = self.tail_\n self.tail_.prev = self.head_\n self.count2Node_ = {}\n self.key2Count_ = {}\n\n # Utility function for inserting a new node inbetween predecessor and successor\n def insertNodeBetween(self, predecessor, successor, node):\n predecessor.next = node\n node.prev = predecessor\n successor.prev = node\n node.next = successor\n\n # Utility function for deleting a node when it has no more keys\n def removeNode(self, node):\n node.prev.next = node.next\n node.next.prev = node.prev\n del self.count2Node_[node.count]\n del node\n\n def inc(self, key: str) -> None:\n # - Key doesn\'t exist\n if key not in self.key2Count_:\n count = 1\n if count not in self.count2Node_:\n node = self.AllOneNode()\n node.count = 1\n self.insertNodeBetween(self.tail_.prev, self.tail_, node)\n self.count2Node_[count] = node\n self.key2Count_[key] = count\n self.count2Node_[count].keys.add(key)\n # - Key exists\n else:\n currentCount = self.key2Count_[key]\n updatedCount = currentCount+1\n\n self.key2Count_[key] = updatedCount\n\n # Get handle to currentCountNode\n currentCountNode = self.count2Node_[currentCount]\n\n # Insert key at updatedCountNode\n if updatedCount not in self.count2Node_:\n node = self.AllOneNode()\n node.count = updatedCount\n self.insertNodeBetween(currentCountNode.prev, currentCountNode, node)\n self.count2Node_[updatedCount] = node\n updatedCountNode = self.count2Node_[updatedCount]\n updatedCountNode.keys.add(key)\n\n # Remove key from currentCount\n currentCountNode = self.count2Node_[currentCount]\n currentCountNode.keys.remove(key)\n # Check if removal left the node empty\n if len(currentCountNode.keys) == 0:\n self.removeNode(currentCountNode)\n\n def dec(self, key: str) -> None:\n # - Key doesn\'t exist\n if key not in self.key2Count_:\n pass\n # - Key exists\n else:\n currentCount = self.key2Count_[key]\n updatedCount = currentCount-1\n\n # Get handle to currentCountNode\n currentCountNode = self.count2Node_[currentCount]\n\n if updatedCount != 0:\n self.key2Count_[key] = updatedCount\n # Insert key at updatedCountNode\n if updatedCount not in self.count2Node_:\n node = self.AllOneNode()\n node.count = updatedCount\n self.insertNodeBetween(currentCountNode, currentCountNode.next, node)\n self.count2Node_[updatedCount] = node\n updatedCountNode = self.count2Node_[updatedCount]\n updatedCountNode.keys.add(key)\n else:\n del self.key2Count_[key]\n\n # Remove key from currentCount\n currentCountNode = self.count2Node_[currentCount]\n currentCountNode.keys.remove(key)\n # Check if removal left the node empty\n if len(currentCountNode.keys) == 0:\n self.removeNode(currentCountNode)\n \n\n def getMaxKey(self) -> str:\n maxNode = self.getMaxNode()\n if maxNode is self.tail_:\n return ""\n for key in maxNode.keys:\n return key\n \n def getMinKey(self) -> str:\n minNode = self.getMinNode()\n if minNode is self.head_:\n return ""\n for key in minNode.keys:\n return key\n\n def getMaxNode(self):\n return self.head_.next\n\n def getMinNode(self):\n return self.tail_.prev\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Hack It Up | all-oone-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass AllOneNode:\n def __init__(self):\n self.prev = None\n self.next = None\n self.count = -1\n self.keys = set()\n\nclass AllOne:\n def __init__(self):\n self.head_ = AllOneNode()\n self.tail_ = AllOneNode()\n self.head_.next = self.tail_\n self.tail_.prev = self.head_\n self.count2Node_ = {}\n self.key2Count_ = {}\n\n def insertNodeBetween(self, predecessor, successor, node):\n predecessor.next = node\n node.prev = predecessor\n successor.prev = node\n node.next = successor\n\n def removeNode(self, node):\n node.prev.next = node.next\n node.next.prev = node.prev\n del self.count2Node_[node.count]\n del node\n\n def inc(self, key: str) -> None:\n # - Key doesn\'t exist\n if key not in self.key2Count_:\n count = 1\n if count not in self.count2Node_:\n node = AllOneNode()\n node.count = 1\n self.insertNodeBetween(self.tail_.prev, self.tail_, node)\n self.count2Node_[count] = node\n self.key2Count_[key] = count\n self.count2Node_[count].keys.add(key)\n # - Key exists\n else:\n currentCount = self.key2Count_[key]\n updatedCount = currentCount+1\n\n self.key2Count_[key] = updatedCount\n\n # Get handle to currentCountNode\n currentCountNode = self.count2Node_[currentCount]\n\n # Insert key at updatedCountNode\n if updatedCount not in self.count2Node_:\n node = AllOneNode()\n node.count = updatedCount\n self.insertNodeBetween(currentCountNode.prev, currentCountNode, node)\n self.count2Node_[updatedCount] = node\n updatedCountNode = self.count2Node_[updatedCount]\n updatedCountNode.keys.add(key)\n\n # Remove key from currentCount\n currentCountNode = self.count2Node_[currentCount]\n currentCountNode.keys.remove(key)\n # Check if removal left the node empty\n if len(currentCountNode.keys) == 0:\n self.removeNode(currentCountNode)\n\n def dec(self, key: str) -> None:\n # - Key doesn\'t exist\n if key not in self.key2Count_:\n pass\n # - Key exists\n else:\n currentCount = self.key2Count_[key]\n updatedCount = currentCount-1\n\n # Get handle to currentCountNode\n currentCountNode = self.count2Node_[currentCount]\n\n if updatedCount != 0:\n self.key2Count_[key] = updatedCount\n # Insert key at updatedCountNode\n if updatedCount not in self.count2Node_:\n node = AllOneNode()\n node.count = updatedCount\n self.insertNodeBetween(currentCountNode, currentCountNode.next, node)\n self.count2Node_[updatedCount] = node\n updatedCountNode = self.count2Node_[updatedCount]\n updatedCountNode.keys.add(key)\n else:\n del self.key2Count_[key]\n\n # Remove key from currentCount\n currentCountNode = self.count2Node_[currentCount]\n currentCountNode.keys.remove(key)\n # Check if removal left the node empty\n if len(currentCountNode.keys) == 0:\n self.removeNode(currentCountNode)\n \n\n def getMaxKey(self) -> str:\n maxNode = self.getMaxNode()\n if maxNode is self.tail_:\n return ""\n for key in maxNode.keys:\n return key\n \n def getMinKey(self) -> str:\n minNode = self.getMinNode()\n if minNode is self.head_:\n return ""\n for key in minNode.keys:\n return key\n\n def getMaxNode(self):\n return self.head_.next\n\n def getMinNode(self):\n return self.tail_.prev\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Very easy and simple using Hashing Technique + beat 97% both in Time and Space | all-oone-data-structure | 0 | 1 | # Intuition\nThis code implements an "All O(1) Data Structure" using two dictionaries, self.keys and self.count, to manage keys and their counts efficiently. The keys dictionary is organized by counts, and the count dictionary tracks the count of each key. The inc and dec methods adjust counts and update dictionaries, while getMaxKey and getMinKey retrieve keys based on counts.\n\n# Approach\n_init_: Create two dictionaries. self.keys will store keys grouped by their counts, and self.count will store the count of each key.\n\n*inc()*: Increase the count of a given key in self.count. Update self.keys by removing the key from its previous count group and adding it to the new count group.\n\n_dec()_: Decrease the count of a given key in self.count. Update self.keys similarly to the increment method.\n\n_getMaxKey() and getMinKey()_: Retrieve the keys with maximum and minimum counts by accessing the corresponding entries in self.keys\n\n# Complexity\n- Time complexity:\ninc and dec methods have a time complexity of O(1)\ngetMaxKey and getMinKey have a time complexity of O(1)\n\nso All have O(1) Time Complexity\n\n- Space complexity:\nThe space complexity is O(N), where N is the number of unique keys\n\n# Code\n```\nclass AllOne:\n\n def __init__(self):\n self.keys = {}\n self.count = {}\n\n def inc(self, key: str) -> None:\n if key in self.count:\n self.count[key] = self.count[key] + 1\n else:\n self.count[key] = 1\n\n c = self.count[key]\n\n if c - 1 in self.keys:\n self.keys[c - 1].remove(key)\n if not self.keys[c - 1]:\n del self.keys[c - 1]\n\n if c in self.keys:\n self.keys[c].append(key)\n else:\n self.keys[c] = [key]\n\n def dec(self, key: str) -> None:\n if key in self.count:\n self.count[key] = self.count[key] - 1\n\n c = self.count[key]\n if c + 1 in self.keys:\n self.keys[c + 1].remove(key)\n if not self.keys[c + 1]:\n del self.keys[c + 1]\n\n if c == 0:\n del self.count[key]\n else:\n if c in self.keys:\n self.keys[c].append(key)\n else:\n self.keys[c] = [key]\n\n def getMaxKey(self) -> str:\n if self.keys:\n lst = max(self.keys.keys())\n return self.keys[lst][0]\n else:\n return ""\n\n def getMinKey(self) -> str:\n if self.keys:\n lst = min(self.keys.keys())\n return self.keys[lst][0]\n else:\n return ""\n\n\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Python3 O(1) amortized | dictionary + arraylist only - no linked list or deque | 64 ms (beats 93%) | all-oone-data-structure | 1 | 1 | \n\n# Code\n```\nclass AllOne:\n\n def __init__(self):\n self.key_count = {}\n self.count_key = {}\n\n def inc(self, key: str) -> None:\n count = self.key_count.get(key, 0)\n new_count = count + 1\n\n # Update key_count dictionary\n self.key_count[key] = new_count\n\n # Update count_key dictionary\n if new_count not in self.count_key:\n self.count_key[new_count] = [key]\n else:\n self.count_key[new_count].append(key)\n\n # Remove key from its previous count in count_key\n if count > 0:\n self.count_key[count].remove(key)\n if not self.count_key[count]:\n del self.count_key[count]\n\n def dec(self, key: str) -> None:\n count = self.key_count.get(key, 0)\n\n if count == 0:\n return\n\n # Update key_count dictionary\n new_count = count - 1\n if new_count > 0:\n self.key_count[key] = new_count\n else:\n del self.key_count[key]\n\n # Update count_key dictionary\n self.count_key[count].remove(key)\n if not self.count_key[count]:\n del self.count_key[count]\n\n if new_count > 0:\n if new_count not in self.count_key:\n self.count_key[new_count] = [key]\n else:\n self.count_key[new_count].append(key)\n\n def getMaxKey(self) -> str:\n if not self.count_key:\n return ""\n max_count = max(self.count_key.keys())\n return self.count_key[max_count][0]\n\n def getMinKey(self) -> str:\n if not self.count_key:\n return ""\n min_count = min(self.count_key.keys())\n return self.count_key[min_count][0]\n\n\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
python code with comments | all-oone-data-structure | 0 | 1 | \n\n# Code\n```\nfrom sortedcontainers import SortedDict\nfrom collections import defaultdict\n\nclass AllOne:\n def __init__(self):\n # Dictionary to store the frequency of each word\n self.word_to_count = {}\n # Sorted dictionary to map a count to a set of words with that count\n self.count_to_words = SortedDict()\n print(self.word_to_count)\n\n def inc(self, key: str):\n """Increment the count of the given key."""\n if key not in self.word_to_count:\n self.word_to_count[key] = 1\n if 1 in self.count_to_words:\n self.count_to_words[1].add(key)\n else:\n self.count_to_words[1] = set()\n self.count_to_words[1].add(key)\n else:\n self.adjust_count(key, True)\n\n def dec(self, key: str):\n """Decrement the count of the given key."""\n if key in self.word_to_count:\n self.adjust_count(key, False)\n\n def getMinKey(self) -> str:\n """Return the key with the minimum count."""\n if self.count_to_words:\n data = self.count_to_words.peekitem(index=0)[1]\n return next(iter(data))\n return ""\n\n def getMaxKey(self) -> str:\n """Return the key with the maximum count."""\n if self.count_to_words:\n data = self.count_to_words.peekitem()[1]\n return next(iter(data))\n return ""\n\n def adjust_count(self, key: str, isInc: bool):\n """Adjust the count for the given key."""\n prev_count = self.word_to_count[key]\n new_count = prev_count + 1 if isInc else prev_count - 1\n\n # Remove the old count and possibly delete the empty set\n self.count_to_words[prev_count].remove(key)\n if not self.count_to_words[prev_count]:\n del self.count_to_words[prev_count]\n \n # Update the new count\n if new_count == 0:\n del self.word_to_count[key]\n else:\n if new_count in self.count_to_words:\n self.count_to_words[new_count].add(key)\n else:\n self.count_to_words[new_count] = set()\n self.count_to_words[new_count].add(key)\n self.word_to_count[key] = new_count\n\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Using two dictionaries - O(1) average | all-oone-data-structure | 0 | 1 | # Intuition\nThe idea is to keep track of the minimum occurrence number of greater than 1. This keeps the retrievals O(1)-average.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsed two dictionaries: d_count[i]: retains the set of words with i occurrence\n d_word[key]: retains the number of occurrence of word key\n# Complexity\n- Time complexity: O(1)-average\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Code\n```\nfrom collections import defaultdict\nclass AllOne:\n def __init__(self):\n self.Max = 10**4 * 5 + 2\n ##self.count = [0] * self.Max\n self.d_word = defaultdict(int)\n self.d_count = defaultdict(set)\n self.tot_count = 0\n self.max_index = 0\n self.min_index = self.Max\n def inc(self, key: str) -> None:\n self.tot_count +=1\n\n self.d_word[key]+=1\n if self.d_word[key]!=1:\n self.min_index = min(self.min_index,self.d_word[key])\n self.max_index = max(self.max_index, self.d_word[key])\n \n if self.d_word[key]!=1:\n self.d_count[self.d_word[key]-1].remove(key)\n if len(self.d_count[self.d_word[key]-1])==0:\n self.d_count.pop(self.d_word[key]-1)\n self.d_count[self.d_word[key]].add(key)\n\n if self.min_index!=self.Max:\n if len(self.d_count[self.min_index])==0:\n self.min_index+=1\n\n def dec(self, key: str) -> None:\n self.tot_count -=1\n \n self.d_word[key]-=1\n self.d_count[self.d_word[key]+1].remove(key)\n if self.d_word[key]!=0:\n self.d_count[self.d_word[key]].add(key)\n if len(self.d_count[self.max_index])==0:\n self.max_index-=1\n if len(self.d_count[self.min_index])==0:\n if self.tot_count == len(self.d_count[1]):\n self.min_index = self.Max \n else:\n self.min_index = 2\n while(len(self.d_count[self.min_index])==0):\n self.min_index+=1\n def getMaxKey(self) -> str:\n if self.tot_count == 0:\n return ""\n x = self.d_count[self.max_index].pop()\n self.d_count[self.max_index].add(x)\n return x\n def getMinKey(self) -> str:\n if self.tot_count == 0:\n return ""\n index = self.min_index\n if len(self.d_count[1])!=0:\n index = 1\n \n x = self.d_count[index].pop()\n self.d_count[index].add(x)\n return x\n\n# Your AllOne object will be instantiated and called as such:\n# obj = AllOne()\n# obj.inc(key)\n# obj.dec(key)\n# param_3 = obj.getMaxKey()\n# param_4 = obj.getMinKey()\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Functions to add/delete in linkedlist to keep things simple | all-oone-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCreating quick handy functions for addition and deletion of a node from the frequency doubly linked list makes the solution very handy\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(n) (for storing all the keys)\n\n# Code\n```\nclass LinkedListNode:\n def __init__(self, freq=0, prev = None, next = None):\n self.freq = freq\n self.keys = set()\n self.next = next\n self.prev = prev\n\n\nclass AllOne:\n\n def __init__(self):\n self.string_to_freq = {}\n self.freq_list_head = None\n self.freq_list_tail = None\n\n def add_freq_node(self, new_node, prev_node=None, next_node=None):\n new_node.prev = prev_node\n new_node.next = next_node\n if prev_node:\n prev_node.next = new_node\n else:\n self.freq_list_head = new_node\n\n if next_node:\n next_node.prev = new_node\n else:\n self.freq_list_tail = new_node\n\n def del_freq_node(self, node_to_del):\n prev_node = node_to_del.prev\n next_node = node_to_del.next\n\n if prev_node:\n prev_node.next = next_node\n else:\n self.freq_list_head = next_node\n\n if next_node:\n next_node.prev = prev_node\n else:\n self.freq_list_tail = prev_node\n\n\n\n def inc(self, key: str) -> None:\n\n freq_node = self.string_to_freq.get(key, None)\n if freq_node is None:\n # Either head has freq of 1 or we add a new head\n if self.freq_list_head and self.freq_list_head.freq == 1:\n self.freq_list_head.keys.add(key)\n self.string_to_freq[key] = self.freq_list_head\n return\n else:\n new_freq_node = LinkedListNode(1)\n new_freq_node.keys.add(key)\n self.string_to_freq[key] = new_freq_node\n self.add_freq_node(new_freq_node, None, self.freq_list_head)\n return\n\n new_freq = freq_node.freq + 1\n next_node = freq_node.next\n\n # Check next node exists and has freq = new_freq\n if next_node and next_node.freq == new_freq:\n next_node.keys.add(key)\n self.string_to_freq[key] = next_node\n freq_node.keys.remove(key)\n if len(freq_node.keys) == 0:\n self.del_freq_node(freq_node)\n return\n\n # New node has to be added after current freq node\n new_freq_node = LinkedListNode(new_freq)\n new_freq_node.keys.add(key)\n self.string_to_freq[key] = new_freq_node\n self.add_freq_node(new_freq_node, freq_node, next_node)\n freq_node.keys.remove(key)\n if len(freq_node.keys) == 0:\n self.del_freq_node(freq_node)\n\n\n def dec(self, key: str) -> None:\n\n freq_node = self.string_to_freq.get(key, None)\n # Key does not exsit\n if freq_node is None:\n return\n\n # Key exists\n new_freq = freq_node.freq - 1\n prev_node = freq_node.prev\n\n if new_freq == 0:\n del self.string_to_freq[key]\n freq_node.keys.remove(key)\n if len(freq_node.keys) == 0:\n self.del_freq_node(freq_node)\n return\n\n if prev_node and prev_node.freq == new_freq:\n prev_node.keys.add(key)\n self.string_to_freq[key] = prev_node\n freq_node.keys.remove(key)\n if len(freq_node.keys) == 0:\n # Delete this node\n self.del_freq_node(freq_node)\n return\n\n # New freq node has to be added before current\n new_freq_node = LinkedListNode(new_freq)\n new_freq_node.keys.add(key)\n self.string_to_freq[key] = new_freq_node\n self.add_freq_node(new_freq_node, prev_node, freq_node)\n freq_node.keys.remove(key)\n # Del current node as it is empty\n if len(freq_node.keys) == 0:\n self.del_freq_node(freq_node)\n\n\n def getMaxKey(self) -> str:\n return list(self.freq_list_tail.keys)[0] if self.freq_list_tail else ""\n \n\n def getMinKey(self) -> str:\n return list(self.freq_list_head.keys)[0] if self.freq_list_head else ""\n \n\n``` | 0 | Design a data structure to store the strings' count with the ability to return the strings with minimum and maximum counts.
Implement the `AllOne` class:
* `AllOne()` Initializes the object of the data structure.
* `inc(String key)` Increments the count of the string `key` by `1`. If `key` does not exist in the data structure, insert it with count `1`.
* `dec(String key)` Decrements the count of the string `key` by `1`. If the count of `key` is `0` after the decrement, remove it from the data structure. It is guaranteed that `key` exists in the data structure before the decrement.
* `getMaxKey()` Returns one of the keys with the maximal count. If no element exists, return an empty string `" "`.
* `getMinKey()` Returns one of the keys with the minimum count. If no element exists, return an empty string `" "`.
**Note** that each function must run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "AllOne ", "inc ", "inc ", "getMaxKey ", "getMinKey ", "inc ", "getMaxKey ", "getMinKey "\]
\[\[\], \[ "hello "\], \[ "hello "\], \[\], \[\], \[ "leet "\], \[\], \[\]\]
**Output**
\[null, null, null, "hello ", "hello ", null, "hello ", "leet "\]
**Explanation**
AllOne allOne = new AllOne();
allOne.inc( "hello ");
allOne.inc( "hello ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "hello "
allOne.inc( "leet ");
allOne.getMaxKey(); // return "hello "
allOne.getMinKey(); // return "leet "
**Constraints:**
* `1 <= key.length <= 10`
* `key` consists of lowercase English letters.
* It is guaranteed that for each call to `dec`, `key` is existing in the data structure.
* At most `5 * 104` calls will be made to `inc`, `dec`, `getMaxKey`, and `getMinKey`. | null |
Python DFS, easy understanding | minimum-genetic-mutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTreat the problem as a graph traversal problem, such that you have to traverse from start to end with the help of bank.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCollect all edges b/n 2 bank strings having one mutation and also with start(0) and end(n+1).\n\n\n# Code\n```\nclass Solution:\n def minMutation(self, start: str, end: str, bank: List[str]) -> int:\n n=len(bank)\n graph=[[] for _ in range(n+1)]\n # 0-> start , 1->bank[0] ,2->bank[1],....,n+1->end\n def check(s1,s2):\n c=0\n for i,j in zip(s1,s2):\n if i!=j:\n c+=1\n if c==2:\n return False\n return True\n if end in bank:\n if check(start,end):\n # n+1->end\n graph[0].append(n+1)\n # graph[n+1].append(0)\n for i in range(n):\n if check(start,bank[i]):\n graph[0].append(i+1)\n graph[i+1].append(0)\n if (end in bank) and check(end,bank[i]):\n # graph[n+1].append(i+1)\n # n+1->end\n graph[i+1].append(n+1)\n for j in range(i+1,n):\n if check(bank[i],bank[j]):\n graph[i+1].append(j+1)\n graph[j+1].append(i+1)\n # print(graph)\n visited=set()\n def helper(ind):\n # n+1->end\n if ind==(n+1):\n return 0\n count=float("inf")\n visited.add(ind)\n for i in graph[ind]:\n if i not in visited:\n count=min(count,1+helper(i))\n visited.remove(ind)\n return count\n x=helper(0)\n if x==float("inf"):\n return -1\n return x\n \n\n``` | 1 | A gene string can be represented by an 8-character long string, with choices from `'A'`, `'C'`, `'G'`, and `'T'`.
Suppose we need to investigate a mutation from a gene string `startGene` to a gene string `endGene` where one mutation is defined as one single character changed in the gene string.
* For example, `"AACCGGTT " --> "AACCGGTA "` is one mutation.
There is also a gene bank `bank` that records all the valid gene mutations. A gene must be in `bank` to make it a valid gene string.
Given the two gene strings `startGene` and `endGene` and the gene bank `bank`, return _the minimum number of mutations needed to mutate from_ `startGene` _to_ `endGene`. If there is no such a mutation, return `-1`.
Note that the starting point is assumed to be valid, so it might not be included in the bank.
**Example 1:**
**Input:** startGene = "AACCGGTT ", endGene = "AACCGGTA ", bank = \[ "AACCGGTA "\]
**Output:** 1
**Example 2:**
**Input:** startGene = "AACCGGTT ", endGene = "AAACGGTA ", bank = \[ "AACCGGTA ", "AACCGCTA ", "AAACGGTA "\]
**Output:** 2
**Constraints:**
* `0 <= bank.length <= 10`
* `startGene.length == endGene.length == bank[i].length == 8`
* `startGene`, `endGene`, and `bank[i]` consist of only the characters `['A', 'C', 'G', 'T']`. | null |
433: Solution with step by step explanation | minimum-genetic-mutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. The first line of the method converts the list of strings bank into a set for faster lookup.\n\n2. The second line checks if the end string is not present in the bank set. If it\'s not present, then there\'s no way to reach the end gene through valid mutations, so the method returns -1.\n\n3. The third line defines a dictionary called mutations that maps each character in a gene to the set of possible mutations that can be made to that character. For example, if the character is \'A\', then it can be mutated to either \'C\', \'G\', or \'T\'.\n\n4. The fourth line checks if the first character of the start gene is a valid character according to the mutations dictionary. If it\'s not valid, then there\'s no way to reach any valid mutation path from the start gene, so the method returns -1.\n\n5. The fifth line initializes a queue called queue with the start gene and a mutations count of 0.\n\n6. The sixth line initializes a set called visited with the start gene, since we have already visited the start gene.\n\n7. The next few lines perform a breadth-first search (BFS) to find the minimum number of mutations required to reach the end gene from the start gene.\n\n8. Inside the while loop, we pop the gene and the mutations count from the left end of the queue.\n\n9. We then iterate over all the characters in the gene and all the possible mutations that can be made to that character.\n\n10. For each mutation, we create a new gene by replacing the character at the current index with the mutated character.\n\n11. We then check if the new gene is in the bank set and if it has not been visited before.\n\n12. If the new gene is in the bank set and has not been visited before, we add it to the visited set, add it to the queue with a mutations count of 1 more than the previous gene, and check if it\'s the end gene. If it\'s the end gene, we return the mutations count plus 1, since we need to include the mutation that was just made.\n\n13. If we reach the end of the while loop without finding the end gene, then there is no valid mutation path from start to end, so the method returns -1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def minMutation(self, startGene: str, endGene: str, bank: List[str]) -> int:\n \n # Create a set of all valid genes in the bank for faster access\n bankSet = set(bank)\n \n # Define the possible mutations for each character\n options = [\'A\', \'C\', \'G\', \'T\']\n \n # Create a queue to store the genes to be checked\n queue = deque()\n queue.append(startGene)\n \n # Create a set to mark visited genes\n visited = set()\n visited.add(startGene)\n \n # Counter to keep track of the minimum mutations required to reach end gene\n count = 0\n \n # Perform BFS\n while queue:\n size = len(queue)\n for i in range(size):\n gene = queue.popleft()\n if gene == endGene:\n return count\n for j in range(8):\n for option in options:\n newGene = gene[:j] + option + gene[j+1:]\n if newGene in bankSet and newGene not in visited:\n visited.add(newGene)\n queue.append(newGene)\n count += 1\n \n # If end gene not found\n return -1\n\n``` | 8 | A gene string can be represented by an 8-character long string, with choices from `'A'`, `'C'`, `'G'`, and `'T'`.
Suppose we need to investigate a mutation from a gene string `startGene` to a gene string `endGene` where one mutation is defined as one single character changed in the gene string.
* For example, `"AACCGGTT " --> "AACCGGTA "` is one mutation.
There is also a gene bank `bank` that records all the valid gene mutations. A gene must be in `bank` to make it a valid gene string.
Given the two gene strings `startGene` and `endGene` and the gene bank `bank`, return _the minimum number of mutations needed to mutate from_ `startGene` _to_ `endGene`. If there is no such a mutation, return `-1`.
Note that the starting point is assumed to be valid, so it might not be included in the bank.
**Example 1:**
**Input:** startGene = "AACCGGTT ", endGene = "AACCGGTA ", bank = \[ "AACCGGTA "\]
**Output:** 1
**Example 2:**
**Input:** startGene = "AACCGGTT ", endGene = "AAACGGTA ", bank = \[ "AACCGGTA ", "AACCGCTA ", "AAACGGTA "\]
**Output:** 2
**Constraints:**
* `0 <= bank.length <= 10`
* `startGene.length == endGene.length == bank[i].length == 8`
* `startGene`, `endGene`, and `bank[i]` consist of only the characters `['A', 'C', 'G', 'T']`. | null |
Faster Than 90% Python Sol | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n n=len(s)\n c=0\n i=0\n while(i<n):\n while(i<n and s[i]==\' \'):i+=1\n count=False\n while(i<n and s[i]!=\' \'):\n i+=1\n count=True\n if(count):c+=1 \n i+=1 \n return c\n \n``` | 1 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
😎Brute Force to Efficient Method 100% beat🤩 | Java | C++ | Python | JavaScript | number-of-segments-in-a-string | 1 | 1 | 1. Java\n2. C++\n3. Python\n4. JavaScript\n\n\n# Java\n## Java 1st Method :- Brute force\n\n1. We split the input string s into an array of words using the split method with a space as the delimiter. This will give us an array of substrings separated by spaces.\n2. We initialize a variable count to keep track of the number of segments.\n3. We iterate through each word in the words array.\n4. For each word, we check if it\'s not empty (i.e., it contains at least one non-space character). If it\'s not empty, we increment the count variable.\n5. Finally, we return the count as the number of segments in the string.\n\n>While this brute force approach works, it\'s not the most efficient way to solve this problem. We can optimize it by avoiding the split operation and iterating through the characters of the string, counting segments as we go.\n\n\n## Code\n``` Java []\nclass Solution {\n public int countSegments(String s) {\n // Split the string into words using spaces as separators\n String[] words = s.split(" ");\n int count = 0;\n\n // Count non-empty words\n for (String word : words) {\n if (!word.isEmpty()) {\n count++;\n }\n }\n\n return count;\n }\n}\n```\n\n## Complexity\n#### Time complexity: O(n + k);\n- The `split` method is used to `split` the string into words using spaces as separators. The `split` method generally has a time complexity of O(n), where n is the length of the input string `s`.\n- The subsequent loop iterates over the array of words, which has a length equal to the number of segments in the string. In the worst case, if there are k segments, this loop has a time complexity of O(k), as it iterates through each word.\n\nSo, the overall time complexity of this solution is O(n + k), where n is the length of the input string `s`, and k is the number of segments in the string.\n#### Space complexity: O(k);\n- The `split` method creates an array of strings to store the words. The space required for this array is proportional to the number of words in the string, which is equal to the number of segments. So, the space complexity for the `words` array is O(k).\n- The integer variable `count` and the `word` variable used in the loop have constant space requirements and do not depend on the input size.\n\nTherefore, the overall space complexity of this solution is O(k), where k is the number of segments in the string.\n\n## Java 2nd Method :- Efficient Method\n1. We initialize the `count` variable to keep track of the number of segments and a boolean `inSegment` to track whether we are currently inside a segment.\n2. We iterate through each character in the input string `s` using a for-each loop.\n3. For each character, we check if it\'s not a space (`\' \'`). If it\'s not a space and we were not previously in a segment, we set `inSegment` to `true` and increment the `count`. This accounts for the start of a new segment.\n4. If the character is a space, we set `inSegment` to `false`. This indicates that we are not inside a segment.\n5. Finally, we return the `count` as the number of segments in the string.\n\n>This more efficient approach does not require splitting the string into an array, making it faster and using less memory.\n\n\n\n## Code\n``` Java []\nclass Solution {\n public int countSegments(String s) {\n int count = 0;\n boolean inSegment = false;\n\n // Iterate through the characters in the string\n for (char c : s.toCharArray()) {\n if (c != \' \') {\n // If the character is not a space, we are in a segment\n if (!inSegment) {\n inSegment = true;\n count++;\n }\n } else {\n // If the character is a space, we are not in a segment\n inSegment = false;\n }\n }\n return count;\n }\n}\n```\n## Complexity\n#### Time complexity: O(n);\n- The code iterates through each character in the input string, where "n" is the length of the string.\n- For each character, it performs constant-time operations to check whether the character is a space and to update the count and inSegment variables.\n\nTherefore, the time complexity of this solution is O(n), where "n" is the length of the input string.\n#### Space complexity: O(1);\n- The code uses a constant amount of extra space for the integer variable count and the boolean variable inSegment. These variables do not depend on the size of the input string.\n- It also uses the enhanced for loop, which does not create any additional data structures or arrays. The s.toCharArray() operation is done in place and does not allocate extra memory.\n\nAs a result, the space complexity of this solution is O(1), indicating that the space used is constant and does not depend on the input size.\n\n# C++\n## C++ 1st Method :- Brute force\n\n1. We include the necessary header files for `std::istringstream` and `std::string`.\n2. In the `countSegments` function, we create an `istringstream` object `iss` and initialize it with the input string `s`. This allows us to treat the input string as a stream of words.\n3. We declare a `string` variable `word` to hold each word as we extract them from the stream.\n4. We initialize a variable `count` to keep track of the number of segments.\n5. Using a `while` loop, we extract words from the `istringstream` object `iss` one by one using the `>>` operator. The loop continues until there are no more words to extract.\n6. For each word extracted, we increment the `count` variable.\n7. Finally, we return the `count` as the number of segments in the string.\n\n## Code\n``` C++ []\nclass Solution {\npublic:\n int countSegments(string s) {\n istringstream iss(s);\n string word;\n int count = 0;\n\n while (iss >> word) {\n count++;\n }\n\n return count;\n }\n};\n```\n\n## Complexity\n#### Time complexity: O(n + k);\n- Creating the `istringstream` object takes O(n) time, where n is the length of the input string `s`.\n- The while loop iterates over the words in the string. In the worst case, if there are `k` words in the string, it will run `k` times.\n\nTherefore, the overall time complexity of this solution is O(n + k), where n is the length of the input string, and k is the number of segments (words) in the string.\n#### Space complexity: O(n);\n- The `istringstream` object stores a copy of the input string, which contributes to additional space usage. The space required for `istringstream` is O(n), where n is the length of the input string.\n- The space required for the `word` variable is constant and doesn\'t depend on the input size.\n\nTherefore, the overall space complexity of this solution is O(n) because of the `istringstream` object.\n\n## C++ 2nd Method :- Efficient Method\n1. In the efficient approach, we include the necessary header file for `std::string`.\n2. We declare the `countSegments` function, which takes a string `s` as input.\n3. We initialize the `count` variable to keep track of the number of segments and a boolean `inSegment` to track whether we are currently inside a segment.\n4. Using a `for` loop to iterate through each character in the input string `s`.\n5. For each character, we check if it\'s not a space (`\' \'`). If it\'s not a space and we were not previously in a segment, we set `inSegment` to `true` and increment the `count`, which accounts for the start of a new segment.\n6. If the character is a space, we set `inSegment` to `false`, indicating that we are not inside a segment.\n7. Finally, we return the `count` as the number of segments in the string.\n\n## Code\n``` C++ []\nclass Solution {\npublic:\n int countSegments(string s) {\n int count = 0;\n bool inSegment = false;\n\n for (char c : s) {\n if (c != \' \') {\n // If the character is not a space, we are in a segment\n if (!inSegment) {\n inSegment = true;\n count++;\n }\n } else {\n // If the character is a space, we are not in a segment\n inSegment = false;\n }\n }\n\n return count;\n }\n};\n```\n## Complexity\n#### Time complexity: O(n);\n- The code iterates through each character in the input string s exactly once. During each iteration, it performs a constant amount of work, which includes checking whether the character is a space and updating the count and inSegment variables accordingly. Therefore, the time complexity is O(n), where n is the length of the input string s.\n#### Space complexity: O(1);\n- The code uses a constant amount of extra space to store the count and inSegment variables, regardless of the size of the input string s. It doesn\'t use any additional data structures or memory allocation that depends on the input size. Therefore, the space complexity is O(1), which means it has constant space complexity.\n\n# Python\n## Py 1st Method :- Brute force\nThe brute force approach is simple. We can iterate through each character in the string and count the segments based on the following conditions:\n\n1. Start counting when we encounter a non-space character after a space.\n2. Keep counting until we encounter a space character.\n## Code\n``` Python []\nclass Solution:\n def countSegments(self, s: str) -> int:\n # Initialize a variable to keep track of the count of segments.\n count = 0\n # Initialize a flag to check if we are inside a segment.\n inside_segment = False\n \n # Iterate through each character in the string.\n for char in s:\n # If the current character is not a space and we are not inside a segment, start a new segment.\n if char != \' \' and not inside_segment:\n count += 1\n inside_segment = True\n # If the current character is a space and we are inside a segment, mark the end of the segment.\n elif char == \' \' and inside_segment:\n inside_segment = False\n \n return count\n\n```\n## Complexity\n#### Time complexity: O(n);\n- The algorithm iterates through each character in the input string exactly once.\n- In each iteration, it performs some constant-time operations such as comparisons and updates.\n- Therefore, the time complexity of this solution is O(n), where n is the length of the input string `s`.\n#### Space complexity: O(1);\n- The algorithm uses a constant amount of extra space to store the `count` and `inside_segment` variables, regardless of the input size.\n- Therefore, the space complexity of this solution is O(1), indicating that it uses constant space.\n\n## Py 2nd Method :- Efficient Method\n>We can optimize the solution by splitting the string using the built-in split() method in Python and counting the non-empty segments. This method is more concise and efficient.\n\n\n## Code\n``` Python []\nclass Solution:\n def countSegments(self, s: str) -> int:\n # Use the split() method to split the string into segments based on spaces.\n segments = s.split()\n # Return the count of non-empty segments.\n return len(segments)\n\n```\nThe `split()` method splits the string into a list of segments based on spaces. We then count the non-empty segments using `len()`. This approach has a time complexity of O(n) due to the `split()` operation but is generally faster and more concise than the brute force approach.\n## Complexity\n#### Time complexity: O(n);\n- The split() method takes O(n) time, where n is the length of the input string s. It needs to iterate through the string to identify and split segments.\n- The len() function takes O(1) time because it simply returns the length of the segments list, which has already been created.\n\nOverall, the time complexity of the countSegments function is O(n) due to the split() operation.\n#### Space complexity: O(n);\n- The `segments` list is created, which stores the `segments` produced by splitting the input string. In the worst case, if there are no spaces in the input string, the `segments` list would contain a single element with the entire input string. \nTherefore, the space complexity for the `segments` list is O(n), where n is the length of the input string.\n- The `len()` function and other variables used have constant space requirements.\n\nOverall, the space complexity of the `countSegments` function is O(n) due to the `segments` list.\n\n# JavaScript\n## Js 1st Method :- Brute force\n>We can split the input string by spaces, and then count the number of non-empty segments. \n\n>In this approach, we split the string by spaces, and then iterate through the resulting array to count non-empty segments. This approach works but may not be the most efficient, especially for large input strings.\n## Code\n``` JavaScript []\nvar countSegments = function(s) {\n // Split the input string by spaces\n const segments = s.split(\' \');\n \n let count = 0;\n // Iterate through the segments and count non-empty ones\n for (const segment of segments) {\n if (segment !== \'\') {\n count++;\n }\n }\n \n return count;\n};\n``` \n## Complexity\n#### Time complexity: O(n + m);\n- Splitting the string using `s.split(\' \')` takes O(n) time, where \'n\' is the length of the input string \'s\'. This is because we need to go through the entire string to identify spaces and split it accordingly.\n- Iterating through the segments using a `for...of` loop takes O(m) time, where \'m\' is the number of segments.\n- Inside the loop, the check `if (segment !== \'\')` is a constant-time operation.\n\nCombining these steps, the overall time complexity of the function is O(n + m), where \'n\' is the length of the input string, and \'m\' is the number of segments.\n\n#### Space complexity: O(n);\n- The `segments` array stores the segments of the input string, so its space complexity is O(m), where \'m\' is the number of segments.\n- In the worst case, if the input string has no spaces, the number of segments \'m\' will be equal to the length of the input string \'n\'. Therefore, the space complexity is O(n).\n \n## Js 2nd Method :- Efficient Method\n>To optimize the solution, we can count the segments without explicitly splitting the string. We can iterate through the characters of the string and check for transitions from space to non-space characters. Here\'s the code for the more efficient approach:\n## Code\n``` JavaScript []\nvar countSegments = function(s) {\n let count = 0;\n \n for (let i = 0; i < s.length; i++) {\n // Check if the current character is a non-space character and the previous character is a space or the start of the string\n if (s[i] !== \' \' && (i === 0 || s[i - 1] === \' \')) {\n count++;\n }\n }\n \n return count;\n}\n```\n>In this efficient approach, we iterate through the characters of the string, and whenever we encounter a non-space character that is preceded by a space or is at the beginning of the string, we increment the count. This avoids splitting the string and is more efficient for large input strings with many spaces.java\n# Complexity\n#### Time complexity: O(n);\n- where n is the length of the input string s. This is because the function iterates through each character in the string once.\n#### Space complexity: O(1);\n- it uses a constant amount of extra space regardless of the size of the input string. The function only uses a few variables (e.g., count, i), and the space required for these variables does not depend on the size of the input string. Therefore, the space complexity is constant.\n | 12 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
EASY TO UNDERSTAND NOOB CODE | number-of-segments-in-a-string | 0 | 1 | # Intuition\n- Using split() function store the strings into a list \n# Approach\n- Splits the input string into segments, filters out the empty segments, and returns the count of non-empty segments. \n- This approach ensures that multiple consecutive spaces are treated as a single delimiter, and empty segments (resulting from consecutive spaces or leading/trailing spaces) are not counted.\n\n# Complexity\n- Time complexity: **o(n)**\n\n- Space complexity: **o(n)**\n\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n c=[]\n if(len(s)==0):\n return(0)\n else:\n k=s.split(" ")\n for j in k:\n if len(j)!=0:\n c.append(j)\n return(len(c))\n\n``` | 2 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Python 91% Faster - Simple Solution | number-of-segments-in-a-string | 0 | 1 | An easy to follow solution\n\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n \n #create a list based on a space split\n slist = list(s.split(" "))\n \n #return the len of list minus empty item\n return(len(slist)-slist.count(""))\n``` | 1 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
434: Space 90.14%, Solution with step by step explanation | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the count variable to 0. This variable will keep track of the number of segments in the input string.\n```\ncount = 0\n```\n2. Iterate over each character in the input string using a for loop and the range function. The for loop will loop through the string character by character.\n```\nfor i in range(len(s)):\n```\n3. Inside the for loop, check if the current character is not a space and if the previous character is a space or if the current character is the first character in the string. If this condition is true, it means that a new segment has started, so we increment the count variable.\n```\nif s[i] != \' \' and (i == 0 or s[i-1] == \' \'):\n count += 1\n```\n4. Once the for loop has completed, we have counted all the segments in the input string, so we return the count variable.\n```\nreturn count\n```\nThe logic of the code is counting the number of segments in the input string, which is defined as a sequence of non-space characters that are separated by spaces. The code is iterating through each character in the string and checking if it\'s the start of a new segment. If it is, it increments the count variable. Finally, it returns the count variable which represents the number of segments in the input string.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n # Initialize the segment count to 0\n count = 0\n \n # Iterate over each character in the string\n for i in range(len(s)):\n # If the current character is not a space and the previous character is a space or it\'s the first character, increment the count\n if s[i] != \' \' and (i == 0 or s[i-1] == \' \'):\n count += 1\n \n # Return the segment count\n return count\n\n``` | 7 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Python || easy to understand | number-of-segments-in-a-string | 0 | 1 | easy simple solution\n\n\tcount = 0\n for i in (s.strip(\' \').split(\' \')):\n if i != \'\':\n count += 1\n \n return count | 5 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
✅ One Line Solution || Easy to Understand || RegExp || Javascript || Python3 || Go | number-of-segments-in-a-string | 0 | 1 | # Intuition\nUse RegExp to find all matched string and return the length of result.\n\n# Approach\nUse ([^\\s]+) for matching strings that not contain spaces.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Javascript\n```javascript\n/**\n * @param {string} s\n * @return {number}\n */\nvar countSegments = function(s) {\n return s.match(/([^\\s]+)/g)?.length ?? 0;\n};\n\n```\n\n# Python3\n```python\nclass Solution:\n def countSegments(self, s: str) -> int:\n return len(re.findall(\'([^\\s]+)\', s))\n```\n\n# Golang\n```golang\nimport (\n "regexp"\n)\n\nfunc countSegments(s string) int {\n return len(regexp.MustCompile(`([^\\s]+)`).FindAll([]byte(s), -1))\n}\n```\n | 1 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Different one-liners in Python | number-of-segments-in-a-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n return len(s.split())\n```\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n return len([word for word in s.split() if word])\n```\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n return len(re.findall(r\'\\S+\', s))\n``` | 2 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Number of segments in a string | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n return len(s.split())\n``` | 4 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Number of Segments in a String | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n l = len(s) # \u5C06\u5B57\u7B26\u4E32 s \u7684\u957F\u5EA6\u8D4B\u503C\u7ED9\u53D8\u91CF l \n # j = not s.isspace() # \u67E5\u770B\u5B57\u7B26\u4E32 s \u662F\u5426\u53EA\u542B\u6709\u7A7A\u884C\uFF0C\u662F\u7684\u8BDD\u8FD4\u56DE False \u7528\u4E8E if \u5224\u65AD\u4E0D\u6267\u884C\uFF1B\u4E0D\u53EA\u542B\u7A7A\u884C\u8FD4\u56DE True \u6267\u884C if \u8BED\u53E5\u3002\u5C06\u5E03\u5C14\u503C\u8D4B\u7ED9\u53D8\u91CF j\n if l != 0: # \u5982\u679C\u4E0D\u53EA\u6709\u7A7A\u884C\n n = len(s.split())\n else:\n n = 0\n return n\n \n``` | 0 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Simple python answer | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n elecount = 0\n x = s.split(" ")\n \n for i in x:\n if i != "":\n elecount += 1\n return elecount\n \n \n \n``` | 0 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
A python3 solution | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n count=0\n ju=True\n # \u904D\u5386\u5168\u90E8s\u4E2D\u5168\u90E8\u5B57\u7B26\n for i in s:\n # \u5224\u65ADi\u662F\u5426\u975E" "\n if i!=" ":\n # \u5224\u65AD\u524D\u4E00\u6B21\u8FED\u4EE3\u662F\u5426\u4E3A" ", \u662F\u5219\u8BA1\u6570\u52A01\n if ju:\n count+=1\n ju=False\n continue\n # i\u4E3A" "\u5219\u8BB0\u5F55\u672C\u6B21\u8FED\u4EE3\u4E3A" "\n else:\n ju=True\n # \u8FD4\u56DE\u5355\u8BCD\u6570\n return count\n``` | 0 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
One-liner | 4 ms | Beats 98.29% of users with Python | number-of-segments-in-a-string | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a list from the string using split function (delimiter space). And return the length.\n\n# Complexity\n- Time complexity: *O(n), where n is the length of the string*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: *O(w), where w is the number of words in the input string*\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def countSegments(self, s):\n """\n :type s: str\n :rtype: int\n """\n return len(s.split())\n \n``` | 0 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Single Line Code Faster than 93% of Solutions | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSplit the given string with respect to " " and return the count of non empty strings.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n-> Split the string with respect to " " and convert it into list.\n-> This list may contain empty string because of the spaces more than one present consecutively in the original string like " ".\n-> Return the Lenght of list and subtract the empty strings.\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n return (len(list(s.split(" ")))-list(s.split(" ")).count(""))\n``` | 0 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
One Line Solution | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n return len(s.split())\n``` | 0 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Simple intuition | number-of-segments-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf you pad the string with a space in the beginning, then each segment starts after a space\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse a helper variable called `prev_char`. Initialize it to `\' \'`. Then iterate over the characters in the string, if you run into the case that prev_char is `\' \'` but curr_char is not `\' \' `, then you have hit a new segment. Otherwise you are either in a whitespace or just continuing a segment you already counted. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def countSegments(self, s: str) -> int:\n count = 0\n prev_char = \' \'\n for c in s:\n if prev_char == \' \' and c != \' \':\n count += 1\n\n prev_char = c\n\n return count\n\n \n``` | 0 | Given a string `s`, return _the number of segments in the string_.
A **segment** is defined to be a contiguous sequence of **non-space characters**.
**Example 1:**
**Input:** s = "Hello, my name is John "
**Output:** 5
**Explanation:** The five segments are \[ "Hello, ", "my ", "name ", "is ", "John "\]
**Example 2:**
**Input:** s = "Hello "
**Output:** 1
**Constraints:**
* `0 <= s.length <= 300`
* `s` consists of lowercase and uppercase English letters, digits, or one of the following characters `"!@#$%^&*()_+-=',.: "`.
* The only space character in `s` is `' '`. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.