title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution | arithmetic-slices-ii-subsequence | 1 | 1 | ```C++ []\nusing ll = long;\nconst uint max_n = 1000;\nuint dp[max_n][max_n];\n\nclass Solution {\npublic:\n int numberOfArithmeticSlices(vector<int>& a) {\n uint n = a.size();\n uint res = 0;\n unordered_map<int, vector<uint>> ai = {};\n for (uint i = 0; i < n; i++) ai[a[i]].push_back(i);\n for (uint i = 1; i < n; i++) {\n for (uint j = 0; j < i; j++) {\n dp[i][j] = 0;\n auto p = 2l * a[j] - a[i];\n if (p < INT_MIN || p > INT_MAX)\n continue;\n auto ii = ai.find(p);\n if (ii != ai.end()) {\n for (auto k : ai[p]) {\n if (k >= j)\n break;\n dp[i][j] += dp[j][k] + 1;\n }\n }\n res += dp[i][j];\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nimport bisect\n\nclass Solution:\n def helper(self, v, d, stt):\n key = v, d, stt\n if key in self.mem:\n return self.mem[key]\n \n ps = self.v_to_ps[v]\n loc = bisect.bisect_left(ps, stt)\n if loc >= len(ps):\n self.mem[key] = 0\n return self.mem[key]\n idx = ps[loc]\n r = 1 + self.helper(v, d, idx+1)\n if v+d in self.v_to_ps:\n r += self.helper(v+d, d, idx+1)\n self.mem[key] = r\n return self.mem[key]\n \n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n self.v_to_ps = {}\n for i, v in enumerate(nums):\n self.v_to_ps.setdefault(v, [])\n self.v_to_ps[v].append(i)\n \n self.mem = {}\n rst = 0\n n = len(nums)\n for i in range(n-1):\n for j in range(i+1, n):\n d = nums[j]-nums[i]\n v = nums[j]+d\n if v in self.v_to_ps:\n rst += self.helper(v, d, j+1)\n \n return rst\n```\n\n```Java []\nclass Solution {\n public int numberOfArithmeticSlices(int[] nums) {\n int n = nums.length;\n int[][] dp = new int[n][n];\n Map<Long, List<Integer>> map = new HashMap<>();\n for(int i = 0; i < n; i++) {\n map.putIfAbsent((long) nums[i], new ArrayList<>());\n map.get((long) nums[i]).add(i);\n }\n int result = 0;\n for(int i = 0; i < n; i++) {\n for(int j = 0; j < i; j++) {\n long target = 2 * (long) nums[j] - nums[i];\n if(map.containsKey(target)) {\n for(int k : map.get(target)) {\n if(k < j) {\n dp[i][j] += (dp[j][k] + 1);\n }\n }\n }\n result += dp[i][j];\n }\n }\n return result;\n }\n}\n```\n | 1 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
8 lines solution in Python | arithmetic-slices-ii-subsequence | 0 | 1 | \n\n# Complexity\n- Time complexity: $$O(n**2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n**2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n n = len(nums);ans = 0\n dp = defaultdict(Counter)\n for i in range(1,n):\n for j in range(i):\n d = nums[i] - nums[j]\n dp[i][d] += dp[j][d] + 1\n ans += sum(dp[i].values()) - i\n return ans\n``` | 1 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
Arithmetic Slices II - Subsequence - Python Simple Solution | arithmetic-slices-ii-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* Think about dp solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* Storing all subsequence ending at i\'th index with all possible arithimetic difference at nums[i]\n\n# Complexity\n- Time complexity: O(n*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n n = len(nums)\n dp = [defaultdict(int) for i in range(n)]\n for i in range(1, n):\n for j in range(i-1, -1, -1):\n d = nums[i] - nums[j]\n dp[i][d] = dp[i].get(d, 0) + dp[j].get(d, 0) + 1\n ans = 0\n for d in dp:\n ans += sum(d.values())\n return ans - (n*(n-1))//2\n\n``` | 1 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
Python3 solution | arithmetic-slices-ii-subsequence | 0 | 1 | \n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, A):\n total, n = 0, len(A)\n dp = [Counter() for item in A]\n for i in range(n):\n for j in range(i):\n dp[i][A[i] - A[j]] += (dp[j][A[i] - A[j]] + 1) \n total += sum(dp[i].values())\n \n return total - (n-1)*n//2 \n``` | 1 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
Python3 - Recursion + Memoization | arithmetic-slices-ii-subsequence | 0 | 1 | # Intuition\nForce the first and second item of the subsequence. This will force a delta. Then you can recurse looking for expected values moving right. At each point you can continue or stop, so keep adding one.\n\n\n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n cnt = 0\n c = Counter(nums)\n m = {n:[] for n in c}\n for i, n in enumerate(nums):\n m[n].append(i)\n\n @lru_cache(None)\n def r(i, n, delta):\n if i >= len(nums) or n not in c:\n return 0\n arr = m[n]\n tot = 0\n for j in range(bisect_left(arr, i), len(arr)):\n tot += 1\n tot += r(arr[j] + 1, n + delta, delta)\n return tot\n\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n d = nums[j] - nums[i]\n cnt += r(j+1, nums[j] + d, d)\n return cnt\n\n``` | 1 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
Python3 | Freq Tables | arithmetic-slices-ii-subsequence | 0 | 1 | \n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n if len(nums) <= 2:\n return 0\n\n rst = 0\n freq = [defaultdict(int) for _ in range(len(nums))] # arithmetic sub-seqs\n for i, x in enumerate(nums):\n for j in range(i):\n diff = x - nums[j]\n rst += freq[j].get(diff, 0)\n freq[i][diff] += (1 + freq[j][diff])\n\n return rst\n\n\n``` | 1 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
FASTEST || BEATS 96% SUBMISSIONS || EASIEST || DP | arithmetic-slices-ii-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDYNAMIC PROGRAMMING\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCREATE A HASHMAP OF THE DIFFERENCE AND COUNT OF SUBSEQUENCE AND STORE THEM IN DP ARRAY.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N*2)\n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n n=len(nums)\n dp=[defaultdict(int)for _ in range(n)]\n output=0\n for i in range(n):\n for j in range(i):\n d=nums[i]-nums[j]\n dp[i][d] +=(1+dp[j][d])\n output +=dp[j][d]\n return output\n\n``` | 1 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
Python3 Solution with freq table | arithmetic-slices-ii-subsequence | 0 | 1 | \nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n \n n=len(nums)\n dp=[defaultdict(int) for _ in range(n)]\n res=0\n for i in range(n):\n for j in range(i):\n diff=nums[i]-nums[j]\n dp[i][diff]+=(1+dp[j][diff])\n res+=dp[j][diff]\n \n return res \n``` | 3 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
[Python] Recursion with Memoization | arithmetic-slices-ii-subsequence | 0 | 1 | # Intuition\nRecursion with Memoization\n\n# Approach\nConsider an element to be part of an Arithmetic Progression with\ndiffence d. See if the next term(s) exists in the array, get their\nindexes and recursively call for them increasing the count by 1.\nRecursive function will have 3 parameters- index,difference and count.\nIgnore the dp memoization and understand the recursion for better intuition. \n\n# Complexity\n- Time complexity:\n- O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n import numpy as np \n #storing the indexes of the elements in dictionary a with values as a key\n counter={}\n for i in range(len(nums)):\n if nums[i] not in counter:\n counter[nums[i]]=[i]\n else:\n counter[nums[i]].append(i)\n dp={}\n def rec(i,d,c):\n if (i,d,c) in dp:\n return dp[(i,d,c)]\n \n total=0\n if c>=3:\n total+=1\n if nums[i]+d in counter:\n for j in counter[nums[i]+d]:\n if j>i:\n total+=rec(j,d,c+1)\n dp[(i,d,c)]=total\n return total\n ans=0\n for i in range(len(nums)):\n for j in range(i+1,len(nums)): \n ans+=rec(j,nums[j]-nums[i],2)\n return ans\n \n\n \n``` | 4 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
10 line short Python Solution - 98% Faster | arithmetic-slices-ii-subsequence | 1 | 1 | \tclass Solution:\n\t\tdef numberOfArithmeticSlices(self, nums: List[int]) -> int:\n\t\t\td = [defaultdict(int) for _ in range(len(nums))]\n\t\t\tans=0\n\t\t\tfor i in range(1,len(nums)):\n\t\t\t\tfor j in range(i):\n\t\t\t\t\tcd = nums[i]-nums[j]\n\t\t\t\t\tjj = d[j][cd]\n\t\t\t\t\tii = d[i][cd]\n\t\t\t\t\tans+=jj\n\t\t\t\t\td[i][cd]=jj+ii+1\n\t\t\treturn ans | 3 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
Intuitive DP || Python | arithmetic-slices-ii-subsequence | 0 | 1 | \n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n \n \n dp = [defaultdict(int) for _ in range(len(nums))]\n count = 0\n \n for ind, num in enumerate(nums):\n for sec_ind in range(ind):\n dif = num - nums[sec_ind]\n dp[ind][dif] += dp[sec_ind][dif] + 1\n count += dp[sec_ind][dif]\n \n return count\n \n``` | 0 | Given an integer array `nums`, return _the number of all the **arithmetic subsequences** of_ `nums`.
A sequence of numbers is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1, 3, 5, 7, 9]`, `[7, 7, 7, 7]`, and `[3, -1, -5, -9]` are arithmetic sequences.
* For example, `[1, 1, 2, 5, 7]` is not an arithmetic sequence.
A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
* For example, `[2,5,10]` is a subsequence of `[1,2,1,**2**,4,1,**5**,**10**]`.
The test cases are generated so that the answer fits in **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,4,6,8,10\]
**Output:** 7
**Explanation:** All arithmetic subsequence slices are:
\[2,4,6\]
\[4,6,8\]
\[6,8,10\]
\[2,4,6,8\]
\[4,6,8,10\]
\[2,4,6,8,10\]
\[2,6,10\]
**Example 2:**
**Input:** nums = \[7,7,7,7,7\]
**Output:** 16
**Explanation:** Any subsequence of this array is arithmetic.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1` | null |
Solution | number-of-boomerangs | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numberOfBoomerangs(vector<vector<int>>& points) {\n int n = points.size ();\n \n vector <vector <int>> dis (n, vector <int> (n, 0));\n for (int i = 1; i < n; i++)\n for (int j = 0; j < i; j++)\n {\n int dist = distinct (points, i, j);\n dis [i][j] = dist;\n dis [j][i] = dist;\n }\n int res = 0;\n for (int i = 0; i < n; i++)\n {\n vector <int>& len = dis[i];\n sort (len.begin (), len.end ());\n int last = len [0], count = 1;\n for (int j = 1; j < len.size (); j++)\n {\n if (len [j] == last)\n count++;\n else\n {\n res += count * (count - 1);\n count = 1;\n last = len [j];\n }\n }\n res += count * (count - 1);\n }\n return res;\n }\n int distinct (vector<vector<int>>& points, int i, int j)\n {\n vector<int>& a = points[i];\n vector<int>& b = points[j];\n return (a[0]-b[0])*(a[0]-b[0]) + (a[1]-b[1])*(a[1]-b[1]);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n ans=0\n for x1, y1 in points:\n dist=[(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2) for x2, y2 in points ]\n count=collections.Counter(dist)\n for c in count.values():\n ans+=c*(c-1)\n return ans\n```\n\n```Java []\nclass Solution {\n public int numberOfBoomerangs(int[][] points) {\n HashMap<Integer, Integer> map = new HashMap();\n int boomerangs = 0;\n for (int[] p1 : points) {\n for (int[] p2 : points)\n boomerangs += map.merge((p1[0] - p2[0]) * (p1[0] - p2[0]) + (p1[1] - p2[1]) * (p1[1] - p2[1]), 1, Integer::sum) - 1;\n map.clear();\n }\n return boomerangs * 2;\n }\n}\n```\n | 1 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Fast Python Solution | number-of-boomerangs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to find the number of boomerangs in a given set of points. A boomerang is a set of three points such that the middle point is equidistant from the other two points.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach that is taken in this problem is to iterate over each point in the given set of points, and for each point, calculate the distance between that point and every other point in the set. The distances are stored in a dictionary, where the key is the distance and the value is the number of points that have that distance from the current point. The number of boomerangs that can be formed with the current point as the middle point is then calculated by taking the number of points at each distance and multiplying it by (number of points at that distance - 1). This calculation is done for each point, and the final count of boomerangs is returned.\n\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n count = 0\n for p in points:\n d = {}\n for q in points:\n dist = (p[0] - q[0]) ** 2 + (p[1] - q[1]) ** 2\n d[dist] = d.get(dist, 0) + 1\n for k in d:\n count += d[k] * (d[k] - 1)\n return count\n\n``` | 2 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
447: Solution with step by step explanation | number-of-boomerangs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function named numberOfBoomerangs that takes in a list of lists called points and returns an integer.\n2. Initialize a variable called boomerangs to 0 to keep track of the number of boomerangs.\n3. Iterate through each point, p1, in the points list.\n4. Create a defaultdict called distances to keep track of the number of points that are a certain distance away from p1.\n5. Iterate through each point, p2, in the points list.\n6. If p1 is the same as p2, continue to the next iteration of the loop.\n7. Calculate the squared distance between p1 and p2.\n8. Increment the value in distances corresponding to the squared distance by 1.\n9. Iterate through each value in distances.\n10. For each value dist in distances, calculate the number of boomerangs that can be formed with p1 as the center point and dist as the distance.\n11. Add the number of boomerangs calculated in step 10 to boomerangs.\n12. Return the final value of boomerangs.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n boomerangs = 0\n for p1 in points:\n distances = defaultdict(int)\n for p2 in points:\n if p1 == p2:\n continue\n dist = (p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2\n distances[dist] += 1\n for dist in distances.values():\n boomerangs += dist * (dist - 1)\n return boomerangs\n\n``` | 5 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python | High Speed | Fast O(n^2) | number-of-boomerangs | 0 | 1 | **Python | High Speed | Fast O(n^2)**\n\n```\nclass Solution:\n def numberOfBoomerangs(self, points):\n n = 0\n for a,b in points:\n counter = {}\n for x,y in points:\n # NOTE: x,y == a,b can only be registered once, so...\n\t\t\t\t# radius=0 never has enough points to make a false triplet\n key = (x-a)**2 + (y-b)**2\n if key in counter:\n n += 2*counter[key]\n counter[key] += 1\n else:\n counter[key] = 1\n return n\n``` | 12 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Easy, with Process, explanation | number-of-boomerangs | 0 | 1 | 1. You just need the distance, not that very point.\n2. Store the distance in a way, you can have the ans.\n3. If m points are located a x distance from a point, you can choose 2 of them in m*(m-1) ways.(m c 2)\n4. All done, ya very simple.\n```\nn = len(points)\nt = [defaultdict(int) for _ in range(n)]\nfor i in range(n):\n\tx1, y1 = points[i]\n\tfor j in range(n):\n\t\tif(i != j):\n\t\t\tx2, y2 = points[j]\n\t\t\td = ((x2-x1)**2 + (y2-y1)**2)**0.5\n\t\t\tt[i][d] += 1\nans = 0\nfor i in range(n):\n\tfor j in t[i]:\n\t\tans += t[i][j] * (t[i][j] - 1)\nreturn ans\n``` | 1 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python3 oneliner | number-of-boomerangs | 0 | 1 | # Intuition\nFor each potential point i, we can calculate the frequencies of distances to i and then use formula for the partial sum. \n\n# Approach\nAfter solving it iterativley I tought I could make it a oneliner using generators.\n\n# Complexity\n- Time complexity: O(n^2)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n return sum(freq * (freq - 1) for x1, y1 in points for freq in Counter((x1 - x2)**2 + (y1 - y2)**2 for x2, y2 in points).values())\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python Counter and permutations solution | number-of-boomerangs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nfrom itertools import permutations\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n def cal_distance(p1, p2):\n x_diff = p2[0]-p1[0]\n y_diff = p2[1]-p1[1]\n return x_diff * x_diff + y_diff * y_diff\n\n ans = 0\n size = len(points)\n for i in range(size):\n dist_list = []\n for j in range(size):\n if i == j:\n continue\n dist_list.append(cal_distance(points[i], points[j]))\n count_dist = Counter(dist_list)\n # print(count_dist)\n for val in count_dist.values():\n if val > 1:\n ans += len(list(permutations(list(range(val)), 2))) \n return ans\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Math Equation, O(n^2) | number-of-boomerangs | 0 | 1 | # Intuition\nEach points $$p_i$$ has distinct boomerangs $$(p_i, p_j,p_q)$$, i.e. different points cannot have the same boomerangs $$(p_i, p_j,p_q)$$ since the order is matter and it\'s defined by the distance from $$p_i$$.\nTherefore, the total number of boomerangs is the sum of each point total boomerang $$Result=\\sum_{i=1}^{n}Boomerangs(p_i)$$.\nFor some point $p_i$, if it has 2 other points with same distance to $p_i$ then it adds up 2 boomerang, if it has 3 other points with same distance to $p_i$ then it adds up 6 boomerang (Select 2 items from a group of 3 where the order is matter).\nGeneral speaking, if point $p_i$ has $x$ items with the same distance to $p_i$, then they add up $x\\cdot (x-1)$ boomerangs.\n\n# Complexity\n- Time complexity: $O(n^2)$ - Finding total boomerang per point is $O(n)$ and we apply it on $n$ points.\n\n- Space complexity: $O(n)$ - We store how many items have distance $x$ from point $p_i$, you can have maximum $n$ distinct distances.\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n if len(points) < 3:\n return 0\n import math\n\n def distance(p1, p2):\n x1, y1 = p1\n x2, y2 = p2\n return math.sqrt((x1 - x2)**2 + (y1 - y2) ** 2)\n \n def getBoomerangs(p1_idx):\n p1 = points[p1_idx]\n \n distances = defaultdict(lambda: 0)\n for p2_idx, p2 in enumerate(points):\n if p2_idx == p1_idx:\n continue\n \n dist = distance(p1, p2)\n distances[dist] += 1\n \n return sum(\n val * (val-1)\n for val in distances.values()\n if val >= 2\n )\n \n result = sum(\n getBoomerangs(idx)\n for idx in range(len(points))\n )\n return result\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python3 - 598ms, O(n^2) | number-of-boomerangs | 0 | 1 | ```\ndef numberOfBoomerangs(self, points: List[List[int]]) -> int:\n res = 0\n for p1 in points:\n d = {}\n for p2 in points:\n distance = math.dist(p1, p2)\n if distance not in d: d[distance] = 1\n else: d[distance] += 1\n for val in d.values():\n if val > 1: res += math.comb(val, 2) * 2\n return res\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python Easy Solution | number-of-boomerangs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n ans = 0\n for p in points:\n \n cmap = {}\n for q in points:\n \n f = p[0] - q[0]\n s = p[1] - q[1]\n cmap[f*f + s*s] = 1 + cmap.get(f*f + s*s , 0 )\n \n for k in cmap:\n ans += cmap[k] * (cmap[k]-1)\n \n return ans\n \n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
hash map + distance as key | number-of-boomerangs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthe idea is to keep a distance as key, check how many points in the same key\n# Approach\n<!-- Describe your approach to solving the problem. -->\nres += 2 * counter[key] if to check a new points with the same key, if add 1 point, we need to res + counter[key]\n\ne.g.: 3 points: a, x, b, the distance of a and x is the same as x, b\nthen we add another d points, we need to add (a, d), (d, a), (b, d), (d, b) with x, 2 * 2 = 4, we need to add 4\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n res = 0\n for x1, y1 in points:\n counter = {}\n for x2, y2 in points:\n key = (x1-x2) ** 2 + (y1-y2) ** 2\n if key in counter:\n res += 2 * counter[key]\n counter[key] += 1\n else:\n counter[key] = 1\n return res\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python in 5 lines | number-of-boomerangs | 0 | 1 | ```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n ans = 0\n for p in points:\n cnt = collections.Counter([(p[0] - q[0]) ** 2 + (p[1] - q[1]) ** 2 for q in points])\n ans += sum([n*(n-1) for n in cnt.values()])\n return ans\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Easy and Simple Approach in Python | number-of-boomerangs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHHashmap and iteration\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nfrom math import*\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n c=0\n for i in range(len(points)):\n di={}\n for j in range(len(points)):\n if points[i]!=points[j]:\n d=sqrt((points[i][0]-points[j][0])**2+(points[i][1]-points[j][1])**2)\n if d not in di:\n di[d]=1\n else:\n di[d]+=1\n for x,y in di.items():\n if y>=2:\n c+=(y*(y-1))\n return c\n \n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python Solution | number-of-boomerangs | 0 | 1 | \n\n\n# Approach\nThe solution calculates the number of boomerangs in a given set of points in the plane. A boomerang is a tuple of three points (i, j, k) such that the distance between i and j is equal to the distance between i and k.\n\nThe solution uses a default dictionary to store the distances between each point i and every other point j. For each point i, it calculates the distances between it and every other point j, and stores it in the default dictionary. The key of the dictionary is the distance and the value is the number of points that have that distance from point i.\n\nAfter counting the distances, the solution iterates over the values of the dictionary and calculates the number of boomerangs for each distance. The number of boomerangs for each distance d is calculated as k * (k - 1), where k is the number of points with the distance d from point i. Finally, the result is accumulated and returned as the output.\n\n# Complexity\n- Time complexity:\nThe time complexity of the solution is O(n^2), where n is the number of points. This is because for each point i, the solution calculates the distance between it and every other point j, which takes O(n) time, and this operation is repeated n times, giving a total time complexity of O(n^2). \n\n- Space complexity:\nThe space complexity of the solution is O(n), as it uses a default dictionary with at most n keys to store the distances.\n\n# More\nMore LeetCode problems of mine at https://github.com/aurimas13/Solutions-To-Problems\n\n# Code\n```\nfrom collections import defaultdict\nfrom typing import List\n\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n res = 0\n for i in range(len(points)):\n d = defaultdict(int)\n for j in range(len(points)):\n if i == j:\n continue\n dist = (points[i][0] - points[j][0]) ** 2 + (points[i][1] - points[j][1]) ** 2\n d[dist] += 1\n for k in d.values():\n res += k * (k - 1)\n return res\n\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Number of Boomerangs | number-of-boomerangs | 0 | 1 | # Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n def distance(p1, p2):\n x1, y1 = p1\n x2, y2 = p2\n return sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)\n\n\n if len(points) <= 2:\n return 0\n\n ans = 0\n\n hashtable = {}\n for i in range(len(points)):\n for j in range(len(points)):\n if i != j:\n dis = distance(points[i], points[j])\n if dis in hashtable:\n hashtable[dis] += 1\n else:\n hashtable[dis] = 1\n\n # print(hashtable)\n \n for d in hashtable:\n if hashtable[d] > 1:\n ans += hashtable[d] * (hashtable[d] - 1)\n \n hashtable = {}\n\n\n\n return ans\n\n \n \n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
<easy solution using hash table and math> | number-of-boomerangs | 0 | 1 | \n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n def distance(p1, p2):\n x1, y1 = p1\n x2, y2 = p2\n return sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)\n\n\n if len(points) <= 2:\n return 0\n\n ans = 0\n\n hashtable = {}\n for i in range(len(points)):\n for j in range(len(points)):\n if i != j:\n dis = distance(points[i], points[j])\n if dis in hashtable:\n hashtable[dis] += 1\n else:\n hashtable[dis] = 1\n\n # print(hashtable)\n \n for d in hashtable:\n if hashtable[d] > 1:\n ans += hashtable[d] * (hashtable[d] - 1)\n \n hashtable = {}\n\n\n\n return ans\n\n \n \n\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Easy Python Solution | number-of-boomerangs | 0 | 1 | # Intuition\nUsed dictionary to store the mapping between the distances\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nCalculate all possible combination which can be formed if new equal distance is found\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dis(self,a,b):\n return (a[0]-b[0])**2+(a[1]-b[1])**2\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n count=0\n if len(points)<3:\n return 0\n for i in points:\n d={}\n for j in points:\n if i==j:\n continue\n bis=self.dis(i,j)\n if d.get(bis) is None:\n d[bis]=1\n else:\n d[bis]+=1\n count+=d[bis]*2-2\n return count\n \n \n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Python | number-of-boomerangs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfBoomerangs(self, points: List[List[int]]) -> int:\n\n def dist(a,b):\n return math.sqrt( (a[0]-b[0])**2 + (a[1]-b[1])**2 )\n\n def sum_func(n):\n if n == 1:\n return 1\n return n + sum_func(n-1)\n \n n = len(points)\n c = 0\n temp3 = []\n if n < 3:\n return 0\n d = {}\n for i in points:\n temp = i\n for j in points:\n if i!=j:\n if dist(i,j) in d:\n d[dist(i,j)] += 1\n else:\n d[dist(i,j)] = 1\n temp3.append(list(d.values()))\n d = {}\n for i in temp3:\n for j in i:\n if j>=0:\n c+=(sum_func(j)-j)\n print(temp3)\n return c*2\n``` | 0 | You are given `n` `points` in the plane that are all **distinct**, where `points[i] = [xi, yi]`. A **boomerang** is a tuple of points `(i, j, k)` such that the distance between `i` and `j` equals the distance between `i` and `k` **(the order of the tuple matters)**.
Return _the number of boomerangs_.
**Example 1:**
**Input:** points = \[\[0,0\],\[1,0\],\[2,0\]\]
**Output:** 2
**Explanation:** The two boomerangs are \[\[1,0\],\[0,0\],\[2,0\]\] and \[\[1,0\],\[2,0\],\[0,0\]\].
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 2
**Example 3:**
**Input:** points = \[\[1,1\]\]
**Output:** 0
**Constraints:**
* `n == points.length`
* `1 <= n <= 500`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the points are **unique**. | null |
Easy-to-understand approach using hashtable. | find-all-numbers-disappeared-in-an-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n \n d = {}\n for i in range(1, len(nums)+1): \n d[i] = 0\n for i in nums:\n d[i] += 1\n result = []\n for key, val in d.items():\n if val == 0:\n result.append(key)\n return result\n \n``` | 0 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
✔Beats 99.45% TC || Python Solution | find-all-numbers-disappeared-in-an-array | 0 | 1 | \n\n# Complexity\n- Time complexity:\nBeats 99.45%\n\n# Do Upvote if you like it :)\n\n# Code\n```\n\nclass Solution:\n def findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n set_nums = set(nums)\n missing = []\n\n for i in range(1,len(nums)+1):\n if i not in set_nums:\n missing.append(i)\n\n return missing\n# Do upvote if you like it\n``` | 17 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
🐍 python solution; O(N) with no extra space | find-all-numbers-disappeared-in-an-array | 0 | 1 | # Approach\nwe use cycle sort. Each number after cycle sort should be at its relevant index (which here is value-1). If that is not the case, then that index+1 is missing. \n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n\n for i in range(len(nums)):\n while nums[i]!=i+1:\n next_index = nums[i]-1\n if nums[next_index]==nums[i]: # we put this since we do not want to get stuck in a cycle. \n break\n nums[i], nums[next_index] = nums[next_index], nums[i]\n\n ans = []\n for i in range(len(nums)):\n if nums[i]!=i+1:\n ans.append(i+1)\n return ans\n\n \n``` | 1 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
Python3 0(n) optimal Solution Negative marking | find-all-numbers-disappeared-in-an-array | 0 | 1 | ```\nclass Solution(object):\n def findDisappearedNumbers(self, nums):\n """\n :type nums: List[int]\n :rtype: List[int]\n """\n \n for i in range(len(nums)):\n \n x = abs(nums[i])\n \n if x-1 < len(nums) and nums[x-1] > 0:\n \n # x-1 <len(nums) to avoid out of index \n \n # nums[x-1] > 0 to check whether it is already negative(marked)\n \n nums[x-1] = -nums[x-1]\n \n # Mark element as negative\n \n return [i+1 for i in range(len(nums)) if nums[i]>0]\n | 1 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
448: Solution with step by step explanation | find-all-numbers-disappeared-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Iterate through the input list nums, and for each element nums[i]:\na. Calculate the index of nums[i] in the list by taking the absolute value of nums[i] and subtracting 1. This is because the input list contains integers in the range [1, n].\nb. Update the value at the calculated index to its negative absolute value using nums[index] = -abs(nums[index]). This is because the input list can contain duplicates, so we need to mark the value as visited using its absolute value.\n3. Iterate through the updated list nums, and for each element nums[i]:\na. If the value at index i is positive, it means that the number i+1 did not appear in the input list. Append i+1 to the list of missing numbers.\n3. Return the list of missing numbers.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n \n # iterate through the input list and mark the values as visited\n for i in range(len(nums)):\n index = abs(nums[i]) - 1\n nums[index] = -abs(nums[index])\n \n # collect the missing values which are still positive\n missing = []\n for i in range(len(nums)):\n if nums[i] > 0:\n missing.append(i+1)\n \n return missing\n\n``` | 9 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
Python 3 solutions || O(1) SC || One Line Solution | find-all-numbers-disappeared-in-an-array | 0 | 1 | **Python :**\n\n\nTime complexity : *O(n)*\nSpace complexity : *O(n)*\n```\ndef findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n\tallNums = [0] * len(nums)\n\tfor i in nums:\n\t\tallNums[i - 1] = i\n\n\treturn [i + 1 for i in range(len(allNums)) if allNums[i] == 0]\n```\n\nTime complexity : *O(n)*\nSpace complexity : *O(1)*\n```\ndef findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n for i in nums:\n nums[abs(i) - 1] = -abs(nums[abs(i) - 1])\n \n return [i + 1 for i in range(len(nums)) if nums[i] > 0]\n```\n\nTricky one line solution :\n\n```\ndef findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n\treturn set(range(1, len(nums) + 1)) - set(nums)\n```\n\n**Like it ? please upvote !** | 28 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
Python | Easy Solution✅ | find-all-numbers-disappeared-in-an-array | 0 | 1 | ```\ndef findDisappearedNumbers(self, nums: List[int]) -> List[int]: # nums = [4,3,2,7,8,2,3,1]\n full_list = [i for i in range(1,len(nums)+1)] # [1, 2, 3, 4, 5, 6, 7, 8]\n return list(set(full_list) - set(nums)) # {1, 2, 3, 4, 5, 6, 7, 8} - {1, 2, 3, 4, 7, 8} = [5,6]\n``` | 16 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
Python 3 | find-all-numbers-disappeared-in-an-array | 0 | 1 | ```\nclass Solution:\n def findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n for n in nums:\n a = abs(n) - 1\n if nums[a] > 0: nums[a] *= -1\n return [i+1 for i in range(len(nums)) if nums[i] > 0]\n```\n\nPlease let me know if any improvements can be made.\n\nThank you! | 58 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
Python3|| Beats 98.89%|| Simple solution | find-all-numbers-disappeared-in-an-array | 0 | 1 | # Please upvote\n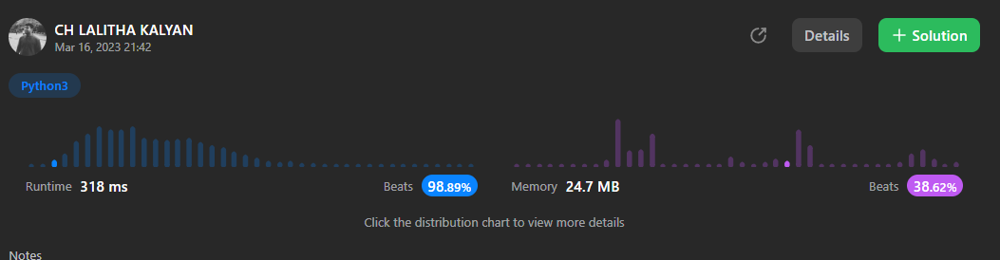\n\n\n# Code\n```\nclass Solution:\n def findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n nums1 = set(nums)\n lst=[]\n for i in range(1,len(nums)+1):\n if i in nums1:\n continue\n lst.append(i)\n return lst\n``` | 2 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
1 liner no brainer - fast than 95% | find-all-numbers-disappeared-in-an-array | 0 | 1 | ```\nclass Solution:\n def findDisappearedNumbers(self, nums: List[int]) -> List[int]:\n return set(nums) ^ set(range(1,len(nums)+1))\n``` | 2 | Given an array `nums` of `n` integers where `nums[i]` is in the range `[1, n]`, return _an array of all the integers in the range_ `[1, n]` _that do not appear in_ `nums`.
**Example 1:**
**Input:** nums = \[4,3,2,7,8,2,3,1\]
**Output:** \[5,6\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= n`
**Follow up:** Could you do it without extra space and in `O(n)` runtime? You may assume the returned list does not count as extra space. | This is a really easy problem if you decide to use additional memory. For those trying to write an initial solution using additional memory, think counters! However, the trick really is to not use any additional space than what is already available to use. Sometimes, multiple passes over the input array help find the solution. However, there's an interesting piece of information in this problem that makes it easy to re-use the input array itself for the solution. The problem specifies that the numbers in the array will be in the range [1, n] where n is the number of elements in the array. Can we use this information and modify the array in-place somehow to find what we need? |
449: Time 91.2%, Solution with step by step explanation | serialize-and-deserialize-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFor the serialize function:\n\n1. If the given root is None, return an empty string.\n2. Create an empty stack and push the root node to it.\n3. Create an empty string called serialized.\n4. While the stack is not empty, pop a node from the stack.\n5. If the node is None, append "$," to the serialized string.\n6. Otherwise, append the node\'s value followed by "," to the serialized string.\n7. Push the node\'s right child to the stack (if it exists).\n8. Push the node\'s left child to the stack (if it exists).\n9. Return the serialized string without the last comma.\n\nFor the deserialize function:\n\n1. If the given data string is empty, return None.\n2. Split the data string by comma and create a deque called queue from the resulting list.\n3. Call the _deserialize function with queue as the argument and return its result.\n\nFor the _deserialize function:\n\n1. Pop the leftmost value from the queue and store it in a variable called value.\n2. If value is "$", return None.\n3. Create a new TreeNode with the integer value of value.\n4. Set the node\'s left child to the result of calling _deserialize recursively with queue.\n5. Set the node\'s right child to the result of calling _deserialize recursively with queue.\n6. Return the node.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Codec:\n def serialize(self, root: Optional[TreeNode]) -> str:\n """Encodes a tree to a single string."""\n if not root:\n return ""\n stack = [root]\n serialized = ""\n while stack:\n node = stack.pop()\n if not node:\n serialized += "$,"\n else:\n serialized += str(node.val) + ","\n stack.append(node.right)\n stack.append(node.left)\n return serialized[:-1]\n\n def deserialize(self, data: str) -> Optional[TreeNode]:\n """Decodes your encoded data to tree."""\n if not data:\n return None\n values = data.split(",")\n queue = deque(values)\n return self._deserialize(queue)\n\n def _deserialize(self, queue: Deque[str]) -> Optional[TreeNode]:\n value = queue.popleft()\n if value == "$":\n return None\n node = TreeNode(int(value))\n node.left = self._deserialize(queue)\n node.right = self._deserialize(queue)\n return node\n``` | 2 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
mY BfS | serialize-and-deserialize-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> bfs with \'N\'\n\n# Approach\n<!-- Describe your approach to solving the problem. --> bfs\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n # \u043F\u0440\u0435\u0432\u0440\u0430\u0442\u0438\u0442\u044C \u0434\u0435\u0440\u0435\u0432\u0443 \u0432 \u0441\u0442\u0440\u043E\u043A\u0443\n def serialize(self, root: Optional[TreeNode]) -> str:\n mas = []\n stack = [root]\n while stack:\n temp = stack.pop()\n if temp:\n left = temp.left \n right = temp.right\n left_val = \'N\' if left is None else left.val\n right_val = \'N\' if right is None else right.val\n line = f"{temp.val} {left_val} {right_val}"\n mas.append(line)\n stack.append(right)\n stack.append(left)\n return "\\n".join(mas)\n\n # \u043F\u043E\u043B\u0443\u0447\u0438\u0442\u044C \u0438\u0437 \u0441\u0442\u0440\u043E\u043A\u0438 \u043E\u0431\u0440\u0430\u0442\u043D\u043E \u0434\u0435\u0440\u0435\u0432\u043E\n def deserialize(self, data: str) -> Optional[TreeNode]:\n dct = {}\n first = None\n for elem in data.split(\'\\n\'):\n # \u043F\u043E\u0442\u043E\u0442\u043C \u043D\u0430\u0448\u0435\u043B \u0431\u0430\u0433\u0443, \u0447\u0442\u043E \u043F\u0430\u0434\u0430\u0435\u0442 \u0434\u043B\u044F \u043F\u0443\u0441\u0442\u043E\u0433\u043E \u043C\u0430\u0441\u0441\u0438\u0432\u0430\n if not elem:\n continue\n a, b, c = elem.split()\n if first is None:\n first = int(a)\n dct[int(a)] = [int(b) if b != \'N\' else None, int(c) if c != \'N\' else None]\n \n if first is None:\n return []\n head = root = TreeNode(first)\n stack = [root]\n while stack:\n temp = stack.pop()\n \n if dct[temp.val][1] is not None:\n temp.right = TreeNode(dct[temp.val][1])\n stack.append(temp.right)\n\n if dct[temp.val][0] is not None:\n temp.left = TreeNode(dct[temp.val][0])\n stack.append(temp.left)\n \n return head\n``` | 1 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Python solution | serialize-and-deserialize-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking to implement a serialization and deserialization method for a binary tree. The serialization method should take a binary tree and convert it into a string format, while the deserialization method should take the string format and convert it back into a binary tree.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe serialization method can be done by doing a breadth-first traversal of the tree and appending the values of the nodes to a list. If a node is None, append "null" to the list. After the traversal, join the list into a string using "," as the delimiter.\n\nThe deserialization method can be done by splitting the string into a list using "," as the delimiter. Create the root node using the first element in the list and append it to a queue. Then, for each element in the list, starting from the second element, check if the element is "null" or not. If it is not "null", create a new node with that value and append it to the left or right of the current node in the queue, depending on whether it is the left or right child. Append the new node to the queue as well. Repeat this process until all elements in the list have been processed.\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root: Optional[TreeNode]) -> str:\n """Encodes a tree to a single string.\n """\n if not root:\n return ""\n queue = [root]\n output = []\n while queue:\n current = queue.pop(0)\n if current:\n output.append(str(current.val))\n queue.append(current.left)\n queue.append(current.right)\n else:\n output.append("null")\n return ",".join(output)\n \n\n def deserialize(self, data: str) -> Optional[TreeNode]:\n """Decodes your encoded data to tree.\n """\n if not data:\n return None\n data = data.split(",")\n root = TreeNode(int(data[0]))\n queue = [root]\n i = 1\n while queue:\n current = queue.pop(0)\n if data[i] != "null":\n current.left = TreeNode(int(data[i]))\n queue.append(current.left)\n i += 1\n if data[i] != "null":\n current.right = TreeNode(int(data[i]))\n queue.append(current.right)\n i += 1\n return root\n\n# Your Codec object will be instantiated and called as such:\n# Your Codec object will be instantiated and called as such:\n# ser = Codec()\n# deser = Codec()\n# tree = ser.serialize(root)\n# ans = deser.deserialize(tree)\n# return ans\n``` | 2 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Python, BFS > 90% | serialize-and-deserialize-bst | 0 | 1 | ```\nclass Codec:\n\n def serialize(self, root: TreeNode) -> str:\n """Encodes a tree to a single string.\n """\n if not root: return \'\'\n tree = []\n queue = deque([root])\n while queue:\n node = queue.popleft()\n if node:\n tree.append(str(node.val))\n queue.extend([node.left, node.right])\n else:\n tree.append(\'*\')\n return \',\'.join(tree)\n \n\n def deserialize(self, data: str) -> TreeNode:\n """Decodes your encoded data to tree.\n """\n if not data: return None\n tree = deque(data.split(\',\'))\n root = TreeNode(int(tree.popleft()))\n queue = deque([root])\n while queue:\n node = queue.popleft()\n \n if (left := tree.popleft()) != \'*\':\n node.left = TreeNode(int(left))\n queue.append(node.left)\n \n if (right := tree.popleft()) != \'*\':\n node.right = TreeNode(int(right))\n queue.append(node.right)\n \n return root\n``` | 18 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Simple solution, beats 65%, 59% | serialize-and-deserialize-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root: Optional[TreeNode]) -> str:\n """Encodes a tree to a single string.\n """\n def get_nodes(node):\n if not node:\n return ["N"]\n\n left = get_nodes(node.left)\n right = get_nodes(node.right)\n return [str(node.val)] + left + right\n\n return ",".join(get_nodes(root))\n\n def deserialize(self, data: str) -> Optional[TreeNode]:\n """Decodes your encoded data to tree.\n """\n data = data.split(\',\')\n if len(data) == 1:\n return None\n\n idx = 0\n def build():\n nonlocal idx\n if data[idx] == \'N\':\n idx += 1\n return None\n new_node = TreeNode(data[idx])\n idx += 1\n new_node.left = build()\n new_node.right = build()\n return new_node\n\n return build()\n\n# Your Codec object will be instantiated and called as such:\n# Your Codec object will be instantiated and called as such:\n# ser = Codec()\n# deser = Codec()\n# tree = ser.serialize(root)\n# ans = deser.deserialize(tree)\n# return ans\n``` | 0 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Simple DFS solution | serialize-and-deserialize-bst | 0 | 1 | ```\nclass Codec:\n def serialize(self, root: Optional[TreeNode]) -> str:\n """Encodes a tree to a single string.\n """\n \n def dfs(root):\n return [] if not root else [str(root.val)] + dfs(root.left) + dfs(root.right)\n \n return \' \'.join(reversed(dfs(root)))\n \n\n def deserialize(self, data: str) -> Optional[TreeNode]:\n """Decodes your encoded data to tree.\n """\n \n def dfs(preorder, bound):\n if not preorder or int(preorder[-1]) > bound:\n return None\n node = TreeNode(int(preorder.pop()))\n node.left = dfs(preorder, node.val)\n node.right = dfs(preorder, bound)\n return node\n\n return dfs(data.split(), inf)\n \n\n\n\n# Your Codec object will be instantiated and called as such:\n# Your Codec object will be instantiated and called as such:\n# ser = Codec()\n# deser = Codec()\n# tree = ser.serialize(root)\n# ans = deser.deserialize(tree)\n# return ans\n``` | 0 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Python3 - preorder + stack | serialize-and-deserialize-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n- Space complexity: O(N)\n\n# Code\n```\nclass Codec:\n def serialize(self, root) -> str:\n preorder = []\n def preorderTraversal(root, preorder):\n if not root:\n return\n preorder.append(str(root.val))\n preorderTraversal(root.left, preorder)\n preorderTraversal(root.right, preorder)\n preorderTraversal(root, preorder)\n return \',\'.join(preorder)\n\n\n def deserialize(self, data: str):\n if data == \'\':\n return None\n nodeValues = list(map(int, data.split(\',\')))\n stack = []\n root = None\n for value in nodeValues:\n node = TreeNode(value)\n lastPop = None\n while len(stack) and stack[-1].val <= value:\n lastPop = stack.pop()\n if lastPop:\n lastPop.right = node\n elif len(stack) == 0:\n root = node\n else:\n stack[-1].left = node\n stack.append(node)\n return root\n\n``` | 0 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Python O(N): deserialize from pre order using Stack | serialize-and-deserialize-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- To serialize: pre order traversal\n- To deserialize: If next value is less than current node value, we create new node to the left of current node and move down. Else if next value is greater than current node value, we move up to find the approciate node using a stack.\n\n# Complexity\n- Time complexity: O(N) for both serialization and deserialization\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Codec:\n def serialize(self, root: Optional[TreeNode]) -> str:\n """Encodes a tree to a single string.\n """\n if not root:\n return \'\'\n\n st, ans = [root], \'\'\n while st:\n node: TreeNode = st.pop()\n ans += str(node.val) + \',\'\n if node.right:\n st.append(node.right)\n if node.left:\n st.append(node.left)\n \n return ans[:-1]\n\n def deserialize(self, data: str) -> Optional[TreeNode]:\n """Decodes your encoded data to tree.\n """\n if not data:\n return None\n \n vals = [int(v) for v in data.split(\',\')]\n root = TreeNode(vals[0])\n\n st = [root]\n for v in vals[1:]:\n if v <= st[-1].val:\n node = TreeNode(v)\n st[-1].left = node\n st.append(node)\n else:\n while st and st[-1].val < v:\n node = st.pop() \n\n new_node = TreeNode(v)\n node.right = new_node\n st.append(new_node)\n\n return root\n``` | 0 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Begineer friendly Python3 solution using BFS | serialize-and-deserialize-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root: Optional[TreeNode]) -> str:\n """Encodes a tree to a single string.\n """\n dummy = root \n ans = ""\n\n queue = deque()\n queue.append([root])\n while queue:\n pop = queue.popleft()\n row = [] \n queueRow = []\n ansLen = len(ans)\n for node in pop:\n if node != None:\n ans += str(node.val) + "-"\n if node.left:\n queueRow.append(node.left) \n else:\n queueRow.append(None) \n if node.right:\n queueRow.append(node.right)\n else:\n queueRow.append(None) \n else:\n ans += str(\'N\') + "-"\n if ansLen != len(ans):\n ans += ","\n queue.append(queueRow)\n return(ans)\n \n # def serializeInOrder(self, root, ans):\n # if not root:\n # return \n # self.serializeInOrder(root.left, ans)\n # ans[0] += str(root.val)+ ","\n # self.serializeInOrder(root.right, ans)\n\n \n\n def deserialize(self, data: str) -> Optional[TreeNode]:\n """Decodes your encoded data to tree.\n """\n temp = data.split(\',\')[:-1]\n # print(temp) \n if temp[0].split(\'-\')[0] != \'N\':\n dummy = TreeNode(int(temp.pop(0).split(\'-\')[0]))\n else:\n return []\n\n # print(dummy)\n queue = deque()\n queue.append([dummy])\n while temp:\n upperRow = queue.popleft()\n lowerRow = temp.pop(0).split(\'-\')[:-1]\n print(lowerRow)\n newRow = []\n for upperNode in upperRow:\n if lowerRow[0] != \'N\':\n upperNode.left = TreeNode(int(lowerRow.pop(0)))\n newRow.append(upperNode.left)\n else:\n # print("pop: ", lowerRow.pop(0))\n lowerRow.pop(0)\n if lowerRow[0] != \'N\':\n upperNode.right = TreeNode(int(lowerRow.pop(0)))\n newRow.append(upperNode.right)\n else:\n # print("pop: ", lowerRow.pop(0)) \n lowerRow.pop(0)\n queue.append(newRow)\n return(dummy)\n\n\n\n\n\n \n \n\n \n\n# Your Codec object will be instantiated and called as such:\n# Your Codec object will be instantiated and called as such:\n# ser = Codec()\n# deser = Codec()\n# tree = ser.serialize(root)\n# ans = deser.deserialize(tree)\n# return ans\n``` | 0 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
🐍 python, O(N) | serialize-and-deserialize-bst | 0 | 1 | # Approach\nThe serialization is very similar to inorder traversal DFS. \nAnd for deserialize we can take a very similar apporach to [1008. Construct Binary Search Tree from Preorder Traversal\n](https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/)\n\nKeep in mind the fact that we know it is a BST made this solution possible. \n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root: Optional[TreeNode]) -> str:\n self.ans = []\n def dfs(node):\n if node:\n self.ans.append(node.val)\n dfs(node.left)\n dfs(node.right)\n if not root:\n return \'[]\'\n dfs(root)\n return \'{}\'.format(self.ans)\n \n \n\n def deserialize(self, preorder: str) -> Optional[TreeNode]:\n def helper(pp_min, pp_max):\n nonlocal i\n node = TreeNode(preorder[i])\n i+=1\n if i<len(preorder) and pp_min<preorder[i]<node.val:\n node.left=helper(pp_min, node.val)\n if i<len(preorder) and node.val<preorder[i]<pp_max: \n node.right=helper(node.val, pp_max)\n return node\n i = 0\n if preorder==\'[]\':\n return None\n preorder = preorder[1:-1].split(\',\')\n preorder = [int(j) for j in preorder]\n return helper(-float(\'inf\'), float(\'inf\')) \n \n\n# Your Codec object will be instantiated and called as such:\n# Your Codec object will be instantiated and called as such:\n# ser = Codec()\n# deser = Codec()\n# tree = ser.serialize(root)\n# ans = deser.deserialize(tree)\n# return ans\n``` | 0 | Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a **binary search tree**. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
**The encoded string should be as compact as possible.**
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `0 <= Node.val <= 104`
* The input tree is **guaranteed** to be a binary search tree. | null |
Recursive solution with o(found node) space complexity and o(n) time complexity | delete-node-in-a-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthis is based on two problems. first one is to find the node that is required and second one is to remove it \n\nto remove it we can observe three scenerios:\n1) it will have no children\n2) it has 2 childrens\n3) it has both childrens\n\nwe only need to address last scenerio as it is demanding us to shift the left children in the right tree\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nstep 1 -> initialize a var to keep the found node \nstep 2 -> search the node and if found then send its right children if its present or else send left children\nstep 3 -> we will only initialize the var with found node if its both children are present\nstep 4 -> if it doesn\'t have both childrens return asit is because we have successfully deleted the node\n\nstep 5 -> take out leftfound and rightfound children out of the found node \nstep 6 -> by using bst logic if left children is less than current right node then it will go to left of the rightfound children \nstep 7 -> we will repeat the process until we find a null place to keep this left node according to bst rules (left is small and right is big than root)\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n \n- Space complexity: O(f) where f is the found node (not considering the stack space for recursive function)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:\n self.actual_node_found = None\n def find_val(node, key):\n if node == None:\n return node\n\n if node.val == key:\n if node.right and node.left:\n self.actual_node_found = node\n if node.right:\n return node.right\n else:\n return node.left\n return None\n \n node.left = find_val(node.left, key)\n node.right = find_val(node.right, key)\n\n return node\n\n root = find_val(root, key)\n \n if self.actual_node_found is None or \\\n self.actual_node_found.left is None:\n return root\n\n #now the problem becomes of attaching left subtree of found val to this right child of the found val\n\n #how to do this \n\n right = self.actual_node_found.right\n left = self.actual_node_found.left\n prev_node = right\n while True:\n prev = right\n if right.val > left.val:\n right = right.left\n else:\n right = right.right\n\n if right == None:\n break\n \n if prev.val > left.val:\n prev.left = left\n else:\n prev.right = left\n\n return root\n\n\n\n\n\n \n\n \n\n \n\n\n \n \n\n\n\n \n \n``` | 2 | Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return _the **root node reference** (possibly updated) of the BST_.
Basically, the deletion can be divided into two stages:
1. Search for a node to remove.
2. If the node is found, delete the node.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 3
**Output:** \[5,4,6,2,null,null,7\]
**Explanation:** Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is \[5,4,6,2,null,null,7\], shown in the above BST.
Please notice that another valid answer is \[5,2,6,null,4,null,7\] and it's also accepted.
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 0
**Output:** \[5,3,6,2,4,null,7\]
**Explanation:** The tree does not contain a node with value = 0.
**Example 3:**
**Input:** root = \[\], key = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* Each node has a **unique** value.
* `root` is a valid binary search tree.
* `-105 <= key <= 105`
**Follow up:** Could you solve it with time complexity `O(height of tree)`? | null |
[ Python ] | Simple & Clean Solution | delete-node-in-a-bst | 0 | 1 | \n# Code\n```\nclass Solution:\n def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:\n if not root: return root\n\n if root.val > key:\n root.left = self.deleteNode(root.left, key)\n elif root.val < key:\n root.right = self.deleteNode(root.right, key)\n else:\n if not root.left: return root.right\n if not root.right: return root.left\n\n if root.left and root.right:\n temp = root.right\n while temp.left: temp = temp.left\n root.val = temp.val\n root.right = self.deleteNode(root.right, root.val)\n \n return root \n\n``` | 14 | Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return _the **root node reference** (possibly updated) of the BST_.
Basically, the deletion can be divided into two stages:
1. Search for a node to remove.
2. If the node is found, delete the node.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 3
**Output:** \[5,4,6,2,null,null,7\]
**Explanation:** Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is \[5,4,6,2,null,null,7\], shown in the above BST.
Please notice that another valid answer is \[5,2,6,null,4,null,7\] and it's also accepted.
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 0
**Output:** \[5,3,6,2,4,null,7\]
**Explanation:** The tree does not contain a node with value = 0.
**Example 3:**
**Input:** root = \[\], key = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* Each node has a **unique** value.
* `root` is a valid binary search tree.
* `-105 <= key <= 105`
**Follow up:** Could you solve it with time complexity `O(height of tree)`? | null |
450: Solution with step by step explanation | delete-node-in-a-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. If the root is None, return None.\n2. If the key to be deleted is less than the root\'s key, then recursively call the function with the left subtree as the new root.\n3. If the key to be deleted is greater than the root\'s key, then recursively call the function with the right subtree as the new root.\n4. If the key to be deleted is equal to the root\'s key:\n 1. If the root has no child or only one child, replace the root with its child (if any).\n 2. If the root has two children, find the inorder successor of the root (i.e., the smallest value in the right subtree). Set the value of the root to be the value of the inorder successor. Recursively call the function to delete the inorder successor from the right subtree.\n5. Return the modified root.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def deleteNode(self, root: TreeNode, key: int) -> TreeNode:\n \n # If the root is None, return None\n if not root:\n return None\n \n # If the key to be deleted is less than the root\'s key,\n # then the function is recursively called with the left subtree\n if key < root.val:\n root.left = self.deleteNode(root.left, key)\n # If the key to be deleted is greater than the root\'s key,\n # then the function is recursively called with the right subtree\n elif key > root.val:\n root.right = self.deleteNode(root.right, key)\n else:\n # If the root has no child or only one child, then the root is replaced with its child\n if not root.left:\n return root.right\n elif not root.right:\n return root.left\n # If the root has two children, then the inorder successor of the root is found\n else:\n node = root.right\n while node.left:\n node = node.left\n # The value of the inorder successor is copied to the root\n root.val = node.val\n # The inorder successor is then deleted from the right subtree of the root\n root.right = self.deleteNode(root.right, node.val)\n \n return root\n\n``` | 11 | Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return _the **root node reference** (possibly updated) of the BST_.
Basically, the deletion can be divided into two stages:
1. Search for a node to remove.
2. If the node is found, delete the node.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 3
**Output:** \[5,4,6,2,null,null,7\]
**Explanation:** Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is \[5,4,6,2,null,null,7\], shown in the above BST.
Please notice that another valid answer is \[5,2,6,null,4,null,7\] and it's also accepted.
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 0
**Output:** \[5,3,6,2,4,null,7\]
**Explanation:** The tree does not contain a node with value = 0.
**Example 3:**
**Input:** root = \[\], key = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* Each node has a **unique** value.
* `root` is a valid binary search tree.
* `-105 <= key <= 105`
**Follow up:** Could you solve it with time complexity `O(height of tree)`? | null |
Python 3 -> 97.55% faster. Explanation added | delete-node-in-a-bst | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\nKey Learnings for me:\n1. First find the node that we need to delete.\n2. After it\'s found, think about ways to keep the tree BST after deleting the node. \n\t1. If there\'s no left or right subtree, we found the leaf. Delete this node without any further traversing.\n\t2. If it\'s not a leaf node, what node we can use from the subtree that can replace the delete node and still maintain the BST property? We can either replace the delete node with the minimum from the right subtree (if right exists) or we can replace the delete node with the maximum from the left subtree (if left exists).\n\n```\ndef deleteNode(self, root: TreeNode, key: int) -> TreeNode:\n\tif not root:\n\t\treturn None\n\n\tif key > root.val:\n\t\troot.right = self.deleteNode(root.right, key)\n\telif key < root.val:\n\t\troot.left = self.deleteNode(root.left, key)\n\telse:\n\t\tif not root.left and not root.right:\n\t\t\troot = None\n\t\telif root.right:\n\t\t\troot.val = self.successor(root)\n\t\t\troot.right = self.deleteNode(root.right, root.val)\n\t\telse:\n\t\t\troot.val = self.predecessor(root)\n\t\t\troot.left = self.deleteNode(root.left, root.val)\n\treturn root\n\ndef successor(self, root: TreeNode) -> TreeNode:\n\troot = root.right\n\twhile root.left:\n\t\troot = root.left\n\treturn root.val\n\ndef predecessor(self, root: TreeNode) -> TreeNode:\n\troot = root.left\n\twhile root.right:\n\t\troot = root.right\n\treturn root.val\n```\n\n**I hope that you\'ve found this useful.\nIn that case, please upvote. It only motivates me to write more such posts\uD83D\uDE03** | 42 | Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return _the **root node reference** (possibly updated) of the BST_.
Basically, the deletion can be divided into two stages:
1. Search for a node to remove.
2. If the node is found, delete the node.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 3
**Output:** \[5,4,6,2,null,null,7\]
**Explanation:** Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is \[5,4,6,2,null,null,7\], shown in the above BST.
Please notice that another valid answer is \[5,2,6,null,4,null,7\] and it's also accepted.
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 0
**Output:** \[5,3,6,2,4,null,7\]
**Explanation:** The tree does not contain a node with value = 0.
**Example 3:**
**Input:** root = \[\], key = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* Each node has a **unique** value.
* `root` is a valid binary search tree.
* `-105 <= key <= 105`
**Follow up:** Could you solve it with time complexity `O(height of tree)`? | null |
Solution | delete-node-in-a-bst | 1 | 1 | ```C++ []\nclass Solution {\npublic:\nTreeNode* helper(TreeNode* root){\n if(root->left==NULL){\n return root->right;\n }\n else if(root->right==NULL){\n return root->left;\n }\n else{\n TreeNode* rightchild = root->right;\n TreeNode* lastright = find(root->left);\n lastright->right = rightchild;\n return root->left;\n } \n}\nTreeNode* find(TreeNode* root){\n if(root->right==NULL){\n return root;\n }\n return find(root->right);\n}\n TreeNode* deleteNode(TreeNode* root, int key) {\n if(root==NULL){\n return root;\n }\n if(root->val==key){\n return helper(root);\n }\n TreeNode* cur = root;\n while(root!=NULL){\n if(root->val > key){\n if(root->left!=NULL && root->left->val==key){\n root->left = helper(root->left);\n break;\n }\n else{\n root= root->left;\n }\n }\n else{\n if(root->right!=NULL && root->right->val==key){\n root->right = helper(root->right);\n break;\n }\n else{\n root= root->right;\n }\n }\n }\n return cur;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:\n if root == None:\n return root\n \n if key < root.val:\n root.left = self.deleteNode(root.left,key)\n \n elif key > root.val:\n root.right = self.deleteNode(root.right,key)\n \n else:\n if root.left == None and root.right == None:\n return None\n \n if root.left == None:\n temp = root.right\n root = None\n return temp\n\n if root.right == None:\n temp = root.left\n root = None\n return temp\n \n temp = self.minNode(root.right)\n root.val = temp.val\n root.right = self.deleteNode(root.right,temp.val)\n\n return root\n \n def minNode(self,node):\n curr = node\n\n while curr.left != None:\n curr = curr.left\n\n return curr\n```\n\n```Java []\nclass Solution {\n public TreeNode deleteNode(TreeNode root, int key) {\n if(root==null) return root;\n if(key<root.val){\n root.left=deleteNode(root.left,key);\n }\n else if(key>root.val){\n root.right=deleteNode(root.right,key);\n }\n else{\n if(root.left==null) return root.right;\n if(root.right==null) return root.left;\n\n root.val=minvalue(root.right);//to find inorder succesor\n\n root.right=deleteNode(root.right,root.val);\n }\n return root;\n }\n public int minvalue(TreeNode root){\n int min=root.val;\n while(root.left!=null){\n min=root.left.val;\n root=root.left;\n }\n return min;\n }\n}\n```\n | 5 | Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return _the **root node reference** (possibly updated) of the BST_.
Basically, the deletion can be divided into two stages:
1. Search for a node to remove.
2. If the node is found, delete the node.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 3
**Output:** \[5,4,6,2,null,null,7\]
**Explanation:** Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is \[5,4,6,2,null,null,7\], shown in the above BST.
Please notice that another valid answer is \[5,2,6,null,4,null,7\] and it's also accepted.
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,7\], key = 0
**Output:** \[5,3,6,2,4,null,7\]
**Explanation:** The tree does not contain a node with value = 0.
**Example 3:**
**Input:** root = \[\], key = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* Each node has a **unique** value.
* `root` is a valid binary search tree.
* `-105 <= key <= 105`
**Follow up:** Could you solve it with time complexity `O(height of tree)`? | null |
Easy Dictionary approach | Python 3 | Beats 84.6% ( time ) | sort-characters-by-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nusing dictionary to find all the frequencies of alphabets\nO(n)\nfor loop in sorted dictionary (sort by values)\nO(n*log(n))\nFinally we return the string in reverse order as it is sorted in ascending order\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBeats 84.6%\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nBeats 40.63%\n\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n #first we create a dictionary and find all the frequencies\n dic = {}\n for i in s:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n st = ""\n #we iterate through the dictionary items where it is sorted by value \n #sorting is done in ascending order\n for i in sorted(dic.items(), key=lambda x:x[1]):\n # print(i)\n #then we add the character by multiplying item*frequency\n st += i[0] * i[1]\n # print(st)\n #as the sorting is done in ascending order we reverse the string for output\n return st[::-1]\n \n``` | 1 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Python3|| O(N) | sort-characters-by-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n d = {}\n for char in s:\n d[char] = d.get(char,0) + 1\n \n sortedList = sorted(d.items(), key = lambda x:x[1])[::-1]\n res = \'\'\n \n for tupleEle in sortedList:\n res = res+tupleEle[0]*tupleEle[1]\n return res\n``` | 1 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
🐍 Python | Easy Explantation | 3 line | sort-characters-by-frequency | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- Count frequency of each character in input string.\n- Sort dictionary was get in descending \n- Loop dictionary and append that in result\n# Complexity\n\n\n\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n dct = {i : s.count(i) for i in set(s)}\n dct = sorted(dct.items(),key=lambda x:x[1], reverse=True)\n return \'\'.join([k*v for k,v in dct])\n``` | 1 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Easy Approach , For beginners 🔥🔥, Medium Question made Easy for all Python beginners | sort-characters-by-frequency | 0 | 1 | # Intuition\nCounter function , gives the key value pair where the values are the frequencies in which the key occured.\n\n# Approach\nFirst we are converting the key value pairs into list of key value pairs and then trying to sort it in a descending order and then changing it back into dictionary using "dict" consturctor. After returning the dict into a descending order we took a variable "newstr" and started appending the characters according to their frequencies.**This approach is easy to understand and also fits the beginner coders.**\n\n# Complexity\n- Time complexity:\nTime complexity is **O(n * log(n))** in the worst case\n\n- Space complexity:\n**O(n)**\n\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n dict1 = Counter(s)\n dict1 = dict(sorted(dict1.items(), key=lambda item: item[1], reverse=True))\n newstr = ""\n for i in dict1.keys():\n newstr = newstr + i*dict1[i]\n return newstr\n \n``` | 2 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Python Easy Solution || Sorting || Hashmap | sort-characters-by-frequency | 0 | 1 | # Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def sort(self,nums: list)-> list:\n i=0\n while(i<len(nums)):\n swapped=0\n j=0\n while(j<len(nums)-i-1):\n if nums[j]>nums[j+1]:\n \n nums[j+1],nums[j]=nums[j],nums[j+1]\n swapped=1\n j+=1\n if swapped==0:\n break\n i+=1\n return(nums)\n\n def frequencySort(self, s: str) -> str:\n dic=dict()\n res=[]\n new=""\n for i in s:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n for i in dic:\n res.append(dic[i])\n res=Solution.sort(self,res)\n for i in res:\n for j in dic:\n if dic[j]==i:\n if j not in new:\n new+=j*i \n return new[::-1]\n\n\n``` | 1 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Simple Python solution using Hashmaps | sort-characters-by-frequency | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n d = {}\n for i in s:\n if i in d:\n d[i] += 1\n else:\n d[i] = 1\n \n c = [[i, d[i]] for i in d ]\n c.sort(key = lambda x: x[1], reverse = True)\n\n res = \'\'\n for i in c:\n res += i[0]*i[1]\n return res\n``` | 1 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Python Easy Solution with simple explaination | sort-characters-by-frequency | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n<b>step 1 :</b> Create a dictionary to store the frequency of elements\n<b>step 2 :</b> Define a helper method inside. which returns the key associated with the frequency\n<b>step 3 :</b> create an empty string, the fetch the dictionary values in decreased order.\n<b>step 4 :</b> get the corresponding key using `get_key()` method attach the key (character) to empty string.\n\n\n\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n # frequency count\n count = {}\n for i in s:\n if i not in count:\n count[i] = 1\n else:\n count[i] += 1\n \n # (helper method) to get the key of corresponding value\n def get_key(val, dic):\n for i in dic:\n if dic[i] == val:\n dic.pop(i)\n return i, val\n\n out = \'\'\n # taking the keys in reverse order of frequency\n for i in reversed(sorted(count.values())):\n key, value = get_key(i, count)\n # appending (frequecy * key) to the string\n out += key * value\n return out\n``` | 3 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Simple solution using dictionary/hashmap in O(n). Beginners Friendly approach!! 🔥🔥 | sort-characters-by-frequency | 1 | 1 | \n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n count_dict={}\n for i in s:\n count_dict[i]=count_dict.get(i,0)+1\n sorted_dict=dict(sorted(count_dict.items(),key = lambda item : item[1], reverse=True))\n ans=\'\'\n print(sorted_dict)\n for i,j in sorted_dict.items():\n ans+=i*j\n return ans\n``` | 2 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Python Easy Solution ^_____^ | sort-characters-by-frequency | 0 | 1 | # **PLEASE UPVOTE ^_^ \u2764**\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n l={}\n for i in s:\n l[i]=l.get(i,0)+1\n l=[[k,v] for k,v in (sorted(l.items(),key=lambda a: a[1],reverse=True))]\n ans=""\n for i,j in l:\n ans+=i*j\n return ans\n``` | 1 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Grasping LOGICAL Solution | sort-characters-by-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:99%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:75%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n m=Counter(s)\n s1=dict(sorted(m.items(),key=lambda x:x[1],reverse=True))\n string=""\n for i,j in s1.items():\n string+=i*j\n return string\n#please upvote,it would encourage me to solve in further problem\n\n\n\n``` | 3 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Python || Hash Table || 96% | sort-characters-by-frequency | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n\n# Code\n> # Use lambda function to sort Dict in Descending Order by Value\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n d = {}\n for char in s:\n d[char] = d.get(char,0) + 1\n\n sorted_d = sorted(d.items(), key=lambda x: x[1], reverse=True)\n\n ans = \'\'\n for pair in sorted_d:\n # key = pair[0]\n # value = pair[1]\n ans += (pair[0] * pair[1])\n\n return ans\n\n#\n```\n\n> # Use Simple way to sort Dict in Descending Order by Value\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n d = {}\n for char in s:\n d[char] = d.get(char,0) + 1\n \n value_key = ((value, key) for (key,value) in d.items())\n value_key = sorted(value_key, reverse= True)\n\n key_value = {key:value for (value, key) in value_key }\n\n ans = \'\'\n for key, value in key_value.items():\n ans += (key*value)\n\n return ans\n\n#\n``` | 2 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
[Python/Java] HashTable + Heap/Sort, Easy to understand and Detailed Explanation | sort-characters-by-frequency | 1 | 1 | I understand there are a tons of solution like mine, but here I offered a clean and detailed explanation on this kind of problem.\n\nFirst, the idea of solution as follows.\n1. HashTable + Sort: We use HashTable to count the occurence and sort the entries based on the occurence, then build the string.\n2. HashTable + Heap(Maxheap): We use HashTable to count the occurence and build the heap based on the occurence, then build the string.\n\n\n**Java**\n\n1. HashTable + Sort:\n```java\npublic String frequencySort(String s) {\n\t// Count the occurence on each character\n\tHashMap<Character, Integer> cnt = new HashMap<>();\n\tfor (char c : s.toCharArray()) {\n\t\tcnt.put(c, cnt.getOrDefault(c, 0) + 1);\n\t}\n\t\n\t// Sorting\n\tList<Character> chars = new ArrayList(cnt.keySet());\n\tCollections.sort(chars, (a, b) -> (cnt.get(b) - cnt.get(a)));\n\n\t// Build string\n\tStringBuilder sb = new StringBuilder();\n\tfor (Object c : chars) {\n\t\tfor (int i = 0; i < cnt.get(c); i++) {\n\t\t\tsb.append(c);\n\t\t}\n\t}\n\treturn sb.toString();\n}\n```\n\nTime Complexity: O(nlogn), since we sort the characters\nSpace Complexity: O(n)\n\n2. HashTable + Heap:\n```java\npublic String frequencySort(String s) {\n\t// Count the occurence on each character\n\tHashMap<Character, Integer> cnt = new HashMap<>();\n\tfor (char c: s.toCharArray()) {\n\t\tcnt.put(c, cnt.getOrDefault(c, 0) + 1);\n\t}\n\n\t// Build heap\n\tPriorityQueue<Character> heap = new PriorityQueue<>((a, b) -> (cnt.get(b) - cnt.get(a)));\n\theap.addAll(cnt.keySet());\n\n\t// Build string\n\tStringBuilder sb = new StringBuilder();\n\twhile (!heap.isEmpty()) {\n\t\tchar c = heap.poll();\n\t\tfor (int i = 0; i < cnt.get(c); i++) {\n\t\t\tsb.append(c);\n\t\t}\n\t}\n\treturn sb.toString();\n}\n```\nTime Complexity: O(nlogk), where k is the number of distinct character.\nSpace Complexity: O(n)\n\n**Python**\n1. HashTable + Sort:\n```python\ndef frequencySort(self, s: str) -> str:\n\t# Count the occurence on each character\n\tcnt = collections.defaultdict(int)\n\tfor c in s:\n\t\tcnt[c] += 1\n\t\n\t# Sort and Build string\n\tres = []\n\tfor k, v in sorted(cnt.items(), key = lambda x: -x[1]):\n\t\tres += [k] * v\n\treturn "".join(res)\n```\nTime Complexity: O(nlogn)\nSpace Complexity: O(n)\n\nNote that we can optimize the first solution to O(n) by using `Counter()` in Python\n```python\ndef frequencySort(self, s: str) -> str:\n\t# Count the occurence on each character\n\tcnt = collections.Counter(s)\n\t\n\t# Build string\n\tres = []\n\tfor k, v in cnt.most_common():\n\t\tres += [k] * v\n\treturn "".join(res)\n```\nTime Complexity: O(nlogk), we don\'t need to sort here, the `most_common()` cost O(nlogk) based on source code. In fact, the `most_common` used `heapq` on th implementation. Thus, we can consider this solution is the same as solution 2.\nSpace Complexity: O(n)\n\n2. HashTable + Heap:\n```python\ndef frequencySort(self, s: str) -> str:\n\t# Count the occurence on each character\n\tcnt = collections.Counter(s)\n\t\n\t# Build heap\n\theap = [(-v, k) for k, v in cnt.items()]\n\theapq.heapify(heap)\n\t\n\t# Build string\n\tres = []\n\twhile heap:\n\t\tv, k = heapq.heappop(heap)\n\t\tres += [k] * -v\n\treturn \'\'.join(res)\n```\nTime Complexity: O(nlogk), where k is the number of distinct character.\nSpace Complexity: O(n)\n\nRemember that if you want to achieve `Heap` structure in **Python**, you can use `heapq` and `PriorityQueue` in **Java**\n | 74 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Python Bucket Sort - Video Solution | sort-characters-by-frequency | 0 | 1 | I have tried to explain the intution behind Bucket Sort and other similar solutions in this [video](https://youtu.be/ofCIa35IIEI).\n\n```\nclass Solution:\n def frequencySort(self, s: str) -> str:\n n = len(s)\n \n c = Counter(s)\n \n bucket = [[] for _ in range(n+1)]\n \n for ch, freq in c.items():\n bucket[freq].append(ch)\n \n res = \'\'\n for freq in reversed(range(n+1)):\n for ch in bucket[freq]:\n res += (freq * ch)\n \n return res | 3 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Two approaches 94% faster one using dictionary and counter . Another one using map and then sorting | sort-characters-by-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nin first one i optimised the second code using counter from collections. WHta it does is counts the occurence a particular string and stores it in a dictionary. then i did the basic steps for sorting the dictionary using lambda and array extension for returning the output.\nFIrst code is much faster than the 2nd code as it saves so many for loops just for doing a simple sort.\nHope you like it \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(n)\n\n# Code\n```\n\nclass Solution:\n def frequencySort(self, s: str) -> str:\n \n d= Counter(s)\n sorted_dict = sorted(d.keys() , key = lambda k:(-d[k], k))\n jod = [k*d[k] for k in sorted_dict]\n jod2 = "".join(jod)\n return jod2\n """\n d = {}\n for i in s:\n if i in d:\n d[i] += 1\n else:\n d[i] = 1\n\n sorted_keys = sorted(d.keys(), key=lambda k: (-d[k], k))\n sorted_dict = {k: d[k] for k in sorted_keys}\n jod = []\n for k, v in sorted_dict.items():\n jod.extend([k] * v)\n jod2 = "".join(jod)\n return(jod2)\n \n """\n \n \n \n``` | 2 | Given a string `s`, sort it in **decreasing order** based on the **frequency** of the characters. The **frequency** of a character is the number of times it appears in the string.
Return _the sorted string_. If there are multiple answers, return _any of them_.
**Example 1:**
**Input:** s = "tree "
**Output:** "eert "
**Explanation:** 'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr " is also a valid answer.
**Example 2:**
**Input:** s = "cccaaa "
**Output:** "aaaccc "
**Explanation:** Both 'c' and 'a' appear three times, so both "cccaaa " and "aaaccc " are valid answers.
Note that "cacaca " is incorrect, as the same characters must be together.
**Example 3:**
**Input:** s = "Aabb "
**Output:** "bbAa "
**Explanation:** "bbaA " is also a valid answer, but "Aabb " is incorrect.
Note that 'A' and 'a' are treated as two different characters.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s` consists of uppercase and lowercase English letters and digits. | null |
Python3: Counter Intersections | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Intuition\nthe number of arrows == the number of intersections among all ranges\n\n# Approach\n1. Sort (as you need)\n2. Kinda the same approach for finding the unions: use heapq to track the rightmost intersection (since the heapq implementation in Python library is minheap, I took the negative to make sure the rightmost intersection is always on the top of the heap)\n\n# Complexity\n- Time complexity:\nO(n * nlog(n))\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x: (x[0], x[1]))\n intervals = []\n for point in points:\n if (len(intervals) == 0):\n heapq.heappush(intervals, [-point[1], -point[0]])\n else:\n leftmost = intervals[0]\n start = -leftmost[1]\n end = -leftmost[0]\n if (point[0] <= start and point[1] >= start):\n new_interval = [-min(point[1], end), -max(point[0], start)]\n heapq.heappushpop(intervals, new_interval)\n elif (point[0] >= start and point[1] <= end):\n new_interval = [-min(point[1], end), -max(point[0], start)]\n heapq.heappushpop(intervals, new_interval)\n elif (point[0] <= end and point[1] >= end):\n new_interval = [-min(point[1], end), -max(point[0], start)]\n heapq.heappushpop(intervals, new_interval)\n else:\n heapq.heappush(intervals, [-point[1], -point[0]])\n return len(intervals)\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
easy python solution | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n points.sort()\n c=1\n m=points[0]\n for i in range(1,len(points)):\n if(m[1]>=points[i][0]):\n m=[max(m[0],points[i][0]),min(m[1],points[i][1])]\n else:\n m=points[i]\n c=c+1\n return c\n \n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Python3 Solution | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Intuition\nWe can sort our points array, loop through our sorted values and find overlap by keeping track of lower and upper bounds.\n\n# Approach\nFirst sort the array, initialize variables lower and upper, loop through values and update lower and upper bounds as we go. If we find overlap, update our lower and upper bounds, if no overlap we shoot another arrow and set our lower and upper bounds to the current point values.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n points.sort()\n\n arrows = 0\n lower, upper = float(\'inf\'), float(\'-inf\')\n\n for xstart, xend in points:\n if xstart >= lower and xstart <= upper: #we can pop\n lower, upper = max(xstart, lower), min(xend, upper)\n else:\n lower, upper = xstart, xend\n arrows += 1\n return arrows\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Using Disjoint Set Union (DSU), Python3 | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDisjoint Set Union\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing Disjoint Set Union approach for maintaining tree that serves intersections.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n*log(n)) complexity\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) linear complexity\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n points = sorted(points, key=lambda x: x[0])\n\n class DSU:\n def __init__(self, points):\n self.points = points\n self.n = len(points)\n\n # representative\n self.repr = dict()\n # size\n self.size = dict()\n # intersection\n self.intr = dict()\n\n # filling default values\n for i in range(self.n):\n self.repr[i] = i\n self.size[i] = 1\n self.intr[i] = self.points[i]\n\n def find(self, u):\n if u == self.repr[u]:\n return u\n self.repr[u] = self.find(self.repr[u])\n return self.repr[u]\n\n def combine(self, u, v):\n u = self.find(u) \n v = self.find(v)\n if self.size[u] > self.size[v]:\n u, v = v, u\n\n self.repr[u] = v\n self.size[v] += self.size[u]\n\n # changing intersection of new representative\n self.intr[v] = [max(self.intr[u][0], self.intr[v][0]), \\\n min(self.intr[u][1], self.intr[v][1])]\n \n def answer(self):\n s = set()\n for i in range(self.n):\n # referring to intersection of representative\'s tree\n val = self.intr[self.find(i)]\n s.add(tuple(val))\n return len(s)\n\n\n dsu = DSU(points=points)\n for i in range(len(points)-1):\n # only representatives contain real\n # intersection value for all childs in DSU tree\n left = dsu.intr[dsu.find(i)]\n right = dsu.intr[dsu.find(i+1)]\n if left[1] >= right[0]:\n # we only combine representatives\n dsu.combine(dsu.find(i), dsu.find(i+1))\n\n # getting answer\n return dsu.answer()\n\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Python Lambda Sorting Maths Solution | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n n=len(points)\n points = sorted(points, key = lambda x: x[1])\n maxa=-float(\'inf\')\n \n ans=0\n\n for i in range(0,n):\n if maxa<points[i][0]:\n ans+=1\n maxa=points[i][1]\n\n return ans\n\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Python3 Simple Solution Using Sort and Greedy | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBy looking at the question and points input we figure its a range type question in which we have to find common intervals\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn any range or interval type related problem the first thing we do is sort our input array In Python we can use arr.sort() method which uses tim sort,\n\nThen we choose points[0] xend as our limit i.e when we encounter some other point whose xstart is greater than limit we update our limit and we increase the count of arrows by 1. \n\nConsider example : [[3,9],[7,12],[3,8],[6,8],[9,10],[2,9],[0,9],[3,9],[0,6],[2,8]]\n\nStep 1: First we sort our array\n[[0, 6], [0, 9], [2, 8], [2, 9], [3, 8], [3, 9], [3, 9], [6, 8], [7, 12], [9, 10]]\n\nStep 2: Initialize limit to our first xend in this case limit = 6\n\nThere can be following cases:\n1. If our xstart is greater than limit: update limit and increment arrows count by 1 \n2. If our limit is in between current xstart and xend do nothing\n3. If our limit is greater than xstart and xend do nothing (because we sorted the array as per 0th Index). \n\nIn above example, at point = [9,10] our limit would 12 because we updated limit at previous point ([7,12]). Even though our limit doesnt fall in between xstart and xend. We would not be updating the arrows count since we can just shoot at x = 9 or some other value which is still smaller than our limit and we will update limit to 10 since if for some future point if xstart is greater than 10 we would be requiring another arrow. \n\n\n\n# Complexity\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nSorting Space Complexity for Python (Tim Sort) : $$O(N)$$\nSorting Time Complexity : $$O(N Log N) $$\n\nIterating an for loop for each point : $$O(N)$$\n\nSo Overall Time Complexity is $$O(N)$$ \n\nSpace complexity:$$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n points.sort()\n arrows = 1\n limit = points[0][1]\n \n for point in points:\n if (limit >= point[0] and limit <= point[1]) or (limit >= point[0]):\n limit = min(limit,point[1])\n else:\n arrows += 1\n limit = point[1]\n \n return arrows\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Greedy 🔥Approach Python | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | \n# Approach\nGreedy Appoach\n\n# Complexity\n- Time complexity:\nO(N logN)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, p: List[List[int]]) -> int:\n lp=(p[0][1])\n cnt=0\n for i in sorted(p):\n if i[0]>lp:\n cnt+=1\n lp=i[1]\n lp=min(i[1],lp)\n return cnt+1\n\n\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
SIMPLE PYTHON GREEDY SOLUTION | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSort the point according to their ending point.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x:(x[1],x[0]))\n n=len(points)\n st=points[0][0]\n end=points[0][1]\n ct=1\n for i in range(1,n):\n if points[i][0]<=end:\n st=max(st,points[i][0])\n end=min(end,points[i][1])\n else:\n st=points[i][0]\n end=points[i][1]\n ct+=1\n return ct\n\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Easy to understand Python3 solution with Commentsssss!!😸 | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n # Sort the list of points by their starting positions.\n points = sorted(points)\n # Initialize the answer counter to 1 since we\'ll always need at least one arrow.\n ans = 1\n # Create a stack to keep track of overlapping intervals.\n stack = []\n # Add the first point to the stack.\n stack.append(points[0])\n for i in range(1, len(points)):\n # If the current point overlaps with the interval at the top of the stack:\n if stack[-1][0] <= points[i][0] <= stack[-1][1]:\n # Update the end of the interval to the minimum of the two intervals.\n stack[-1][1] = min(points[i][1], stack[-1][1])\n else:\n # If the current point doesn\'t overlap, pop the top interval from the stack,\n # increment the answer counter, and add the current point to the stack.\n stack.pop()\n ans += 1\n stack.append(points[i])\n # Return the total number of arrows needed to burst all balloons.\n return ans\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Python | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | ```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x: x[0])\n xstart = points[0][0]\n xend = points[0][1]\n arrow = 1\n for i in range(1,len(points)):\n if points[i][0] <= xend:\n xstart = max(xstart, points[i][0])\n xend = min(xend, points[i][1])\n else:\n arrow+=1\n xstart = points[i][0]\n xend = points[i][1]\n return arrow\n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Python Elegant & Short | Greedy | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | ```\ndef findMinArrowShots(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x: x[1])\n\n arrows = 0\n end = -maxsize\n\n for s, e in points:\n if s > end:\n arrows += 1\n end = e\n\n return arrows\n\n``` | 3 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
🎀✨ Easy Code with Kawaii Illustration | 10 lines only | Python | O(n) Complexity ✨🎀 | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Visualization\n\n\nConsider the first example: \nInput: points = [[10,16],[2,8],[1,6],[7,12]]\nOutput: 2\nExplanation: The balloons can be burst by 2 arrows:\n- Shoot an arrow at x = 6, bursting the balloons [2,8] and [1,6].\n- Shoot an arrow at x = 11, bursting the balloons [10,16] and [7,12].\nCode help from kiut frenn - @Aratrik_\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinArrowShots(self, intv: List[List[int]]) -> int:\n intv.sort(key=lambda x:(x[1],x[0]))\n pl=intv[0][1]\n i=ans=1\n for cf, cl in intv[1:]:\n if not (pl >= cf and pl <= cl):\n ans += 1\n pl = cl \n return ans\n \n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Easy Python Code in O(NlogN) Time Complexity | minimum-number-of-arrows-to-burst-balloons | 0 | 1 | # Code\n```\nclass Solution:\n def findMinArrowShots(self, points: List[List[int]]) -> int:\n\n points = sorted(points, key = lambda x:x[1])\n cnt = len(points)\n\n #x = points[0][0]\n #Just imagine of maintaining a range like merge intervals\n y = points[0][1]\n\n for i in range(1,len(points)):\n if points[i][0]<=y:\n #x = max(x,points[i][0])\n y = min(y,points[i][1])\n cnt-=1\n else:\n #x = points[i][0]\n y = points[i][1]\n return cnt\n\n\n \n \n``` | 1 | There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array `points` where `points[i] = [xstart, xend]` denotes a balloon whose **horizontal diameter** stretches between `xstart` and `xend`. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up **directly vertically** (in the positive y-direction) from different points along the x-axis. A balloon with `xstart` and `xend` is **burst** by an arrow shot at `x` if `xstart <= x <= xend`. There is **no limit** to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array `points`, return _the **minimum** number of arrows that must be shot to burst all balloons_.
**Example 1:**
**Input:** points = \[\[10,16\],\[2,8\],\[1,6\],\[7,12\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons \[2,8\] and \[1,6\].
- Shoot an arrow at x = 11, bursting the balloons \[10,16\] and \[7,12\].
**Example 2:**
**Input:** points = \[\[1,2\],\[3,4\],\[5,6\],\[7,8\]\]
**Output:** 4
**Explanation:** One arrow needs to be shot for each balloon for a total of 4 arrows.
**Example 3:**
**Input:** points = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\]\]
**Output:** 2
**Explanation:** The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons \[1,2\] and \[2,3\].
- Shoot an arrow at x = 4, bursting the balloons \[3,4\] and \[4,5\].
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `-231 <= xstart < xend <= 231 - 1` | null |
Simplest Approach✔ || Easy and Understandable (Java / Python) Code | minimum-moves-to-equal-array-elements | 1 | 1 | # Approach\nA simple approach could be to find out the minimum element of the array in the first traversal and then in the next traversal find the difference between each element of the array with the minimum one and sum them up.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n# Code\n\n```java []\nclass Solution {\n public int minMoves(int[] nums) {\n int sum = 0;\n Arrays.sort(nums);\n\n for(int i = nums.length;i >= 0;i--){\n int diff = nums[i] - nums[0];\n sum += diff;\n }\n return sum;\n }\n}\n```\n```python []\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n sum = 0\n nums.sort()\n for i in range(len(nums)-1,0,-1):\n diff = nums[i] - nums[0]\n sum = sum + diff\n return sum\n```\n | 4 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
[Python] 2 Short and Simple Approaches with Explanation | minimum-moves-to-equal-array-elements | 0 | 1 | ### Introduction\n\nWe want to find the minimum number of moves needed to make the elements of `nums` equal. A move is defined by incrementing any `n - 1` elements in `nums` by 1, where `n` is the number of elements in `nums`. This can be re-written to incrementing **all elements but one** in `nums` by 1.\n\n---\n\n### Approach 1: Determine the Method\n\nWe want to ask: Just how exactly are we going to achieve our goal by incrementing `n - 1` elements? One way of doing it is by **making elements equal one-by-one**. This is best described by an illustration:\n\nConsider the array `[0, 1, 2, 3]`. Let\'s first try to **make the second-largest element equal to the largest element**; i.e., we want to make `nums[2] = nums[3]`. This can be done simply by incrementing all elements except the largest element until the second-largest element is equal.\n\n```text\nMove:\n 0 [ 0, 1, 2, 3 ]\n v v v\n 1 [ 1, 2, 3, 3 ]\n```\n\nOnce that\'s done, we want to **make the third-largest element (which has now become the second-largest) equal to the largest elements**. However, we can\'t simply employ the strategy we just used, since we would need to select one of the two largest elements to increment along with the other elements. We cannot select one of the largest elements randomly to increment, since that would revert the previous steps of making the two largest elements equal.\n\nTo fix this problem, we can **alternate between the largest elements when performing the increments**. This ensures a balanced increment of the elements such that, when all is complete, the largest elements remain equal while the next-largest element becomes equal.\n\n```text\nMove:\n 1 [ 1, 2, 3, 3 ]\n v v v\n 2 [ 2, 3, 4, 3 ]\n v v v\n 3 [ 3, 4, 4, 4 ]\n```\n\nThis strategy can then be repeated for the remaining elements until all elements are equal. Note that for any given \'cycle\' of increments with `n` largest elements, each of the largest elements will increment by `n - 1` while the target next-largest element will increment by `n`. Thus, after every \'cycle\', **the next-largest element will be 1 closer to the largest elements**.\n\n```text\nMove: <------ n elements ------>\n m [ 0 , 1 , 1 , 1 , ..., 1 , 1 ]\n v v v v v v\n m+1 [ 1 , 2 , 2 , 2 , ..., 2 , 1 ]\n v v v v v v\n m+2 [ 2 , 3 , 3 , 3 , ..., 2 , 2 ]\n v v v v v v\n ...\n v v v v v v\nm+n-2 [ n-2, n-1, n-1, n-2, ..., n-2, n-2 ]\n v v v v v v\nm+n-1 [ n-1, n , n-1, n-1, ..., n-1, n-1 ]\n v v v v v v\n m+n [ n , n , n , n , ..., n , n ]\n```\n\nAs such, it is important to know the number of such \'cycles\' each element requires. This, multiplied by the number of largest elements, will give the total number of moves required for the next-largest element to be made equal with the largest elements. In a sorted array, this will look something like:\n\n```text\nMove: Required:\n 0 [ 6, 3, 1, 0 ] For 3->6, given 1 6: 6-3=3 moves\n ^\n\n 3 [ 6, 6, 4, 3 ] For 4->6, given 2 6s: (6-4)*2=4 moves\n ^\n\n 7 [ 8, 8, 8, 7 ] For 7->8, given 3 8s: (8-7)*3=3 moves\n ^\n\n 10 [ 10, 10, 10, 10 ]\n```\n\nThe last step in all of this is that we **require `nums` to be sorted**. Once done, we can perform the calculations without actually having to modify the elements, since the relative difference between two consecutive elements will not change during the increment process.\n\n```python\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n return sum((nums[i-1]-nums[i])*i for i in range(1, len(nums)))\n```\n\n**TC: <img src="https://latex.codecogs.com/png.image?\\dpi{110}&space;O(nlog(n))" title="O(nlog(n))" />**, since we need to sort `nums`.\n**SC: <img src="https://latex.codecogs.com/png.image?\\dpi{110}&space;O(1)" title="O(1)" />**, no additional data structures used.\n\n---\n\n### Approach 2: Mathematical Equivalence\n\nEarlier, we approached the definition of each move as incrementing all elements but one by one. The mathematical equivalent of this definition is to **decrement one element by one**, since the relative difference between the elements is the same for both definitions. Since we are not interested in the final number, this definition is useful for calculating the number of moves as it makes the calculation much more intuitive.\n\nIn Approach 1, we used the largest element as a reference point and made all other elements equal to it. Here, we can similarly **use the smallest element as a reference point and decrement all other elements** until all elements are equal to the smallest element.\n\n```python\nclass Solution:\n\tdef minMoves(self, nums: List[int]) -> int:\n\t\t_min, _sum = min(nums), 0\n\t\tfor num in nums:\n\t\t\t_sum += num-_min # for num->_min, -1 per move takes (num-_min) moves\n\t\treturn _sum\n```\n\nThis can be simplified to the following one-liner (which is cleaner also):\n\n```python\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n return sum(nums)-min(nums)*len(nums)\n```\n\nOf course, you can remove the need to loop through `nums` twice to further optimise the solution:\n\n```python\nclass Solution:\n\tdef minMoves(self, nums: List[int]) -> int:\n\t\t_sum, _min = 0, float(\'inf\')\n\t\tfor num in nums:\n\t\t\t_sum += num\n\t\t\t_min = _min if _min < num else num\n\t\treturn _sum-_min*len(nums)\n```\n\n**TC: <img src="https://latex.codecogs.com/png.image?\\dpi{110}&space;O(n)" title="O(n)" />**, simple loop through `nums`.\n**SC: <img src="https://latex.codecogs.com/png.image?\\dpi{110}&space;O(1)" title="O(1)" />**, as previously discussed.\n\n---\n\n### Conclusion\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 10 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
1 line solution; beats 98% O(N) time and 96% O(1) space; easy to understand | minimum-moves-to-equal-array-elements | 0 | 1 | Let,\n\t`k` = number of elements in `nums`\n\t`s` = sum of elements in `nums` \n\t`m` = minumum number of moves \n\t`e` = element at all indices in final array (Eg., [a, b, d, a, c] will turn to [e, e, e, e, e])\n\n\nSum of all elements in the final array is going to be `k * e`.\n\nOn each move, the sum of the original array is going to increase by `k - 1`. So after `m` moves, the sum will increase by `m(k - 1)`. \n\nHence, we have,\n`s + m(k - 1) = k * e` ---- equation (i)\n\nIn this equation, `e` is the only unknown other than `m`. How can we find `e`? Whatever the smallest integer is in `nums`, plus the number of moves `m`, will be equal to `e`. This is because with each `m`, we only increment the value by 1. So, \n\n`min + m = e` ---- equation (ii)\n\nCombining (i) and (ii), \n\n`s + m(k - 1) = k(min + m)`\n\nSimplify for m, \n\n`m = s - (k * min)`\n\nHence, we return the `sum(nums)`, minus the product of the number of elements in nums and the smallest element in `nums`.\n```\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n return sum(nums) - (len(nums) * min(nums))\n``` | 16 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
453: Solution with step by step explanation | minimum-moves-to-equal-array-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a class named Solution.\n2. Define a method named minMoves that takes an input array nums of integers and returns an integer.\n3. Find the minimum element in the input array nums using the min() function and store it in a variable named min_element.\n4. Calculate the sum of the differences between each element and the minimum element using the sum() function and subtracting the product of the length of the input array nums and the minimum element.\n5. Return the sum of the differences as the minimum number of moves required to make all array elements equal.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n # Find the minimum element in the input array\n min_element = min(nums)\n \n # Calculate the sum of the differences between each element and the minimum element\n sum_diff = sum(nums) - len(nums) * min_element\n \n # Return the sum of the differences as the minimum number of moves required to make all array elements equal\n return sum_diff\n\n``` | 5 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
Simple solution with description of the intuitive approach | minimum-moves-to-equal-array-elements | 0 | 1 | ```\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n\t\t# If we observe some sample arrays we will see that the minimum number has to equal the maximum number so that they are equal\n\t\t# However during this time (n - 2) elements will also increase by 1 for each step where n is the length of the array.\n\t\t# Example 1 :- [1, 2, 3]\n\t\t# For 1 to increase to 3 it will take exactly 2 steps but during these 2 steps 2 will also increase by 2 taking it to 4. Thus we would have to again take the two resulting 3s and make them into 4s in the next step.\n\t\t# Example 2:- [2, 2, 4]\n\t\t# 1st iteration : [3, 3, 4]\n\t\t# 2nd iteration : [4, 4, 4]\n\t\t# Let us now see the pattern. If we do abs(4 - 2 ) + abs (2 - 2) + abs (2 - 2) we get 2.\n\t\t# For [1, 2, 3] its abs(1 - 1) + abs(1 - 2) + abs(1 - 3) = 3\n\t\t# After the pattern is decoded, the implementation becomes simple.\n\t\tsteps = 0\n min_num = min(nums)\n for num in nums:\n steps += abs(min_num - num)\n return steps\n```\n\n | 6 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
Python3 Detailed Explanation in comments O(N), O(1) | minimum-moves-to-equal-array-elements | 0 | 1 | ***Please upvote if this helps!***\n```\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n\t\n # Approach:\n # we want to make all the elements equal ; question does not \n # say "to which element" they should be made equal so that means\n # we can "choose" to what element they all should finally reach\n \n # Choose the minimum element of the array as a starting point\n # because the statement says - \n # we can increment all elements except one element \n # which can be interpreted as "decreasing that one element" in each\n # move to make all the elements equal\n \n # for eg: \n # [1,2,3] -> [1,1,3] -> [1,1,2] -> [1,1,1]\n # at each step, we decrement one element towards the smallest\n _min = min(nums)\n ans = 0\n \n # if all elements are already equal; ans = 0\n if all(ele == nums[0] for ele in nums):\n return 0\n else:\n for ele in nums:\n ans = ans + (ele - _min)\n # ele - _min because it takes ele - _min steps to make ele \n # equal to the minimum element\n return ans\n```\nTC = O(N); because we iterate through the array once\nSC = O(1); we are not using any extra space\n | 2 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
Intuitive approach with Python example | minimum-moves-to-equal-array-elements | 0 | 1 | We are only trying to match all the numbers in an array, so operations should be viewed by how they effect elements relative to the rest. Subtracting 1 to a single element is relatively equivalent to adding 1 to all the others. So the question is equivalent to asking "How many time must we subtract 1 to any element to make all elements equal." \n\nLet us never decrease the minimum value in the array, and decrement all other elements to match that minimum value. The amount that we decrease each element is equal to x - min_e where x is the current element and min_e is the value of the minimum element. We then sum the total amount of decreases.\n\nNotice: Since we must calculate this value once per element in the array, we are subtracting min_e once per the size of the array. This means we are subtracting a total value of min_e * len(array), and adding the total value of the array. If we arrange this so that the subtracting of min_e * n is outside of our for loop, we can avoid having to loop twice through the array: once to find the minimum value and once to find the number of times we must decrement each value to reach the minimum.\n\nThis leads to the following:\n```\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n total = 0\n min_num = None\n for x in nums:\n if min_num == None or x < min_num:\n min_num = x\n total += x\n return total - min_num * len(nums)\n```\nO(n) time complexity for the single loop through, and O(1) space complexity for storing the sum and minimum element. | 3 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
One line Python solution with clear explanation | minimum-moves-to-equal-array-elements | 0 | 1 | Here is the simple idea.\nEach time we increase n-1 elements by 1, which equals to decrease the one which is not increased by 1, then the idea is clear.\n```\nclass Solution:\n def minMoves(self, nums: List[int]) -> int:\n return sum(nums) - min(nums)*len(nums)\n``` | 9 | Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment `n - 1` elements of the array by `1`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Explanation:** Only three moves are needed (remember each move increments two elements):
\[1,2,3\] => \[2,3,3\] => \[3,4,3\] => \[4,4,4\]
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* The answer is guaranteed to fit in a **32-bit** integer. | null |
✔️ [Python3] O(n^2) ¯\_( ͡👁️ ͜ʖ ͡👁️)_/¯, Explained | 4sum-ii | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe simple bruteforce solution would take `n^4` time complexity here. We can do better by dividing given lists into two groups and precalculating all possible sums for the first group. Results go to a hashmap where keys are sums and values are frequencies. It will take `n^2` time and space. After that, we iterate over elements of the second group, and for every pair check whether their sum can add up to zero with a sum from the first group using a hashmap.\n\nTime: **O(n^2)** - double n^2 scan\nSpace: **O(n^2)** - for hashmap\n\nRuntime: 716 ms, faster than **85.08%** of Python3 online submissions for 4Sum II.\nMemory Usage: 14.1 MB, less than **98.30%** of Python3 online submissions for 4Sum II.\n\n```\ndef fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n\tn, hm, res = len(nums1), defaultdict(int), 0\n\n\tfor i in range(n):\n\t\tfor j in range(n):\n\t\t\thm[nums1[i] + nums2[j]] += 1 \n\n\tfor k in range(n):\n\t\tfor l in range(n):\n\t\t\tres += hm[0 - (nums3[k] + nums4[l])]\n\n\treturn res\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 107 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
Solution | 4sum-ii | 1 | 1 | ```C++ []\nint smallest(vector<int> const &v)\n{\n return *min_element(begin(v), end(v));\n}\nint greatest(vector<int> const &v)\n{\n return *max_element(begin(v), end(v));\n}\nclass Solution\n{\npublic:\n int fourSumCount(vector<int> &nums1, vector<int> &nums2, vector<int> &nums3, vector<int> &nums4)\n {\n const int left = min(smallest(nums1) + smallest(nums2), -greatest(nums3) - greatest(nums4));\n const int right = max(greatest(nums1) + greatest(nums2), -smallest(nums3) - smallest(nums4));\n static vector<uint16_t> counts;\n counts.resize(0);\n counts.resize(right - left + 1, 0);\n\n for(auto i : nums1) \n {\n for(auto j : nums2)\n {\n ++counts[i + j - left];\n }\n }\n int ans = 0;\n auto end = counts.end();\n\n for(auto i : nums3) \n {\n for(auto j : nums4)\n {\n ans += counts[-(i + j) - left];\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n n1 = Counter(nums1)\n n2 = Counter(nums2)\n n3 = Counter(nums3)\n n4 = Counter(nums4)\n a, b = defaultdict(int), defaultdict(int)\n for k1, v1 in n1.items():\n for k2, v2 in n2.items():\n a[k1+k2] += v1 * v2\n for k1, v1 in n3.items():\n for k2, v2 in n4.items():\n b[k1+k2] += v1 * v2\n result = 0\n for k, v in a.items():\n result += b.get(-k, 0) * v\n return result\n```\n\n```Java []\nclass Solution {\n public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {\n int[] m1 = getMaxMin(nums1);\n int[] m2 = getMaxMin(nums2);\n int[] m3 = getMaxMin(nums3);\n int[] m4 = getMaxMin(nums4);\n\n int max = Math.max((m1[0]+m2[0]), -(m3[1]+m4[1]));\n int min = Math.min((m1[1]+m2[1]), -(m3[0]+m4[0]));\n\n int[] dp = new int[max-min+1];\n for(int i: nums1){\n for(int j: nums2){\n dp[i+j-min]++;\n }\n }\n int res = 0;\n for(int x: nums3){\n for(int y: nums4){\n res += dp[-(x+y)-min];\n }\n }\n return res;\n }\n private int[] getMaxMin(int[] nums){\n int[] res = new int[2];\n res[0] = Integer.MIN_VALUE;\n res[1] = Integer.MAX_VALUE;\n for(int n: nums){\n res[0] = Math.max(res[0], n);\n res[1] = Math.min(res[1], n);\n }\n return res;\n }\n}\n```\n | 1 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
[Python] Clean and concise | Detail explanation | One linear | 4sum-ii | 0 | 1 | The first things to note is unlike the prevoius variation of this problem (3 Sum, 2 Sum) where they asked us to return the indexes of the array, here we are supposed to return only the no of ways in which we can achieve it. \n\nSo, first lets loop through any of the two array and store all possible combination of sum which can be achived by those two arrays. So lets take an example below,\n```\nnums1 = [1,2] \nnums2 = [-1,-2]\nnums3 = [-1,2]\nnums4 = [0,2]\n```\nIn this case lets choose nums1 and nums2, so our hasmap after we store all possible combination of sum will be \n\n`Map<sum, count> = {-1: 1, 0: 2, 1: 1}`\n\nNow that we have these values and also we know the final sum to be zero, we can do the similar iteration with other two arrays to get all possible combination sums of those, now if we encounter negation of the same value in our Map (-x +x = 0), that will indeed result to a pair of values resulting in total sum 0, so we can increase our result by 1. \n\n**Talking is cheap,**\n```\nclass Solution:\n def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n \n # hashmap and final result count\n nums12, res = defaultdict(int), 0\n \n # storing all possible combinations of sum\n for i in nums1:\n for j in nums2:\n nums12[i+j] += 1\n \n # iterating the left out two array to find negation of same value\n for k in nums3:\n for l in nums4:\n res += nums12[-(k+l)]\n \n return res\n```\n\nWe can also convert it more pythonic using a one linear, here you go\n```\nclass Solution:\n def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n return sum(counts[-(c + d)] for counts in [Counter(a + b for a in nums1 for b in nums2)] for c in nums3 for d in nums4)\n```\n\n*Time complexity*: **O(n^2)**\n*Space complexity*: **O(n^2)**\n\n***Upvote if this helped!***\n | 22 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
Python3 two-liner | 4sum-ii | 0 | 1 | Instead of using a usual dictionary to store 2-sums and their counts we can use standard Counter class that does that automatically and write solution in the most pythonic way possible:\n\n```\nclass Solution:\n def fourSumCount(self, A: List[int], B: List[int], C: List[int], D: List[int]) -> int:\n sums = collections.Counter(c+d for c in C for d in D)\n return sum(sums.get(-(a+b), 0) for a in A for b in B)\n``` | 33 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
Python || 96.13% Faster || O(n) || Counter | 4sum-ii | 0 | 1 | ```\nclass Solution:\n def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n AB = Counter(a + b for a in nums1 for b in nums2)\n CD = Counter(c + d for c in nums3 for d in nums4)\n count = 0\n for key in AB:\n count += AB[key] * CD[-key] #[(a+b)-(c+d)=0]\n return count \n```\n**An upvote will be encouraging** | 1 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
Python 3 (500ms) | N^2 Approach | Easy to Understand | 4sum-ii | 0 | 1 | ```\nclass Solution:\n def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n ht = defaultdict(int)\n for n1 in nums1:\n for n2 in nums2:\n ht[n1 + n2] += 1\n ans = 0\n c=0\n for n3 in nums3:\n for n4 in nums4:\n c=ht[-n3 - n4]\n ans +=c\n return ans\n``` | 3 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
454: Solution with step by step explanation | 4sum-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create a defaultdict(int) called sums12 to store the counts of all possible sums of elements in nums1 and nums2.\n\n2. For each pair of elements num1 and num2 in nums1 and nums2, calculate their sum num1 + num2 and increment the corresponding count in sums12.\n\n3. Set a variable count to 0.\n\n4. For each pair of elements num3 and num4 in nums3 and nums4, calculate their complement -num3 - num4.\n\n5. Check if the complement exists in sums12. If it does, increment count by the corresponding count in sums12.\n\n6. Return count.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n \n # Use a defaultdict to store the counts of all possible sums of elements in nums1 and nums2\n sums12 = defaultdict(int)\n for num1 in nums1:\n for num2 in nums2:\n sums12[num1 + num2] += 1\n \n count = 0\n \n # For each pair of elements in nums3 and nums4, check if their complement exists in sums12\n for num3 in nums3:\n for num4 in nums4:\n complement = -num3 - num4\n count += sums12.get(complement, 0)\n \n return count\n\n``` | 2 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
4 Sum II | Python | Easy to understand | 4sum-ii | 0 | 1 | ```\ndef fourSumCount(self, A: List[int], B: List[int], C: List[int], D: List[int]) -> int:\n \n h = dict()\n \n for a in A:\n for b in B:\n p = -(a+b)\n if p in h:\n h[p]+=1\n else:\n h[p]=1\n count=0\n \n for c in C:\n for d in D:\n p = c+d\n if p in h:\n count+=h[p]\n \n return count\n``` | 10 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
Python3 Solution || Beats 92.70% || Dictionary Approach | 4sum-ii | 0 | 1 | ```\nclass Solution:\n def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:\n dictionary = defaultdict(int)\n for n1 in nums1:\n for n2 in nums2:\n numberNeeded = -(n1 + n2)\n dictionary[numberNeeded] += 1\n \n numberOfTuples = 0\n for n3 in nums3:\n for n4 in nums4:\n numberOfTuples += dictionary[n3 + n4]\n \n return numberOfTuples\n``` | 2 | Given four integer arrays `nums1`, `nums2`, `nums3`, and `nums4` all of length `n`, return the number of tuples `(i, j, k, l)` such that:
* `0 <= i, j, k, l < n`
* `nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0`
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[-2,-1\], nums3 = \[-1,2\], nums4 = \[0,2\]
**Output:** 2
**Explanation:**
The two tuples are:
1. (0, 0, 0, 1) -> nums1\[0\] + nums2\[0\] + nums3\[0\] + nums4\[1\] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1\[1\] + nums2\[1\] + nums3\[0\] + nums4\[0\] = 2 + (-1) + (-1) + 0 = 0
**Example 2:**
**Input:** nums1 = \[0\], nums2 = \[0\], nums3 = \[0\], nums4 = \[0\]
**Output:** 1
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `n == nums3.length`
* `n == nums4.length`
* `1 <= n <= 200`
* `-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228` | null |
455: Solution with step by step explanation | assign-cookies | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the findContentChildren function that takes in two lists of integers, g and s, and returns an integer representing the number of content children.\n2. Sort the lists g and s in non-decreasing order using the sort() method.\n3. Initialize two indices i and j to 0.\n4. While i is less than the length of g and j is less than the length of s, do the following:\na. Check if the current cookie s[j] is large enough to satisfy the current child\'s greed g[i].\nb. If the current cookie is large enough, increment i to indicate that the current child has been assigned a cookie.\nc. Regardless of whether a cookie was assigned or not, increment j to move to the next cookie.\n5. Return the value of i as the number of content children.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int:\n g.sort()\n s.sort()\n i, j = 0, 0\n while i < len(g) and j < len(s):\n if s[j] >= g[i]:\n i += 1\n j += 1\n return i\n\n``` | 19 | Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1` | null |
Simple Explanation 😎 | assign-cookies | 0 | 1 | # Intuition\nThink like dad\uD83D\uDC68\u200D\uD83D\uDC66\u200D\uD83D\uDC66!\n- You have a cookies & you first think how to give cookies to childrens :\n- case1 : Random order\n- case2 : Give minimum size cookie which child have minimum greed & then jump into another child (when first child satisfy).\n- At the end you have maximum child feed.\n# Approach\n### case2\n- Sort both g & s.\n- Loop over cookie(s) & check it is satisy greed of child then increment child.\n- return child.\n\n# Complexity\n- Time complexity:\nO(Nlog(N)) (sorting)\n- Space complexity:\nO(N) (sorting)\n\n# Code\n```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int:\n\n # Sort g & s\n g.sort()\n s.sort()\n \n # Set child to zero\n child = 0\n \n # Loop over s(cookies)\n for cookie in s:\n \n # If child greed satisfy\n if cookie >= g[child]:\n \n # Then increment child\n child += 1\n \n # If no child left\n if child == len(g):\n \n # Then return child\n return child\n \n # Return child\n return child\n``` | 5 | Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.