title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
1-Line Python Solution || 96% Faster (68ms) || Memory less than 90% | range-addition-ii | 0 | 1 | ```\nclass Solution:\n def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:\n return min([x for x,y in ops])*min([y for x,y in ops]) if ops else m*n\n```\n-------------------\n***----- Taha Choura -----***\n*[email protected]* | 4 | You are given an `m x n` matrix `M` initialized with all `0`'s and an array of operations `ops`, where `ops[i] = [ai, bi]` means `M[x][y]` should be incremented by one for all `0 <= x < ai` and `0 <= y < bi`.
Count and return _the number of maximum integers in the matrix after performing all the operations_.
**Example 1:**
**Input:** m = 3, n = 3, ops = \[\[2,2\],\[3,3\]\]
**Output:** 4
**Explanation:** The maximum integer in M is 2, and there are four of it in M. So return 4.
**Example 2:**
**Input:** m = 3, n = 3, ops = \[\[2,2\],\[3,3\],\[3,3\],\[3,3\],\[2,2\],\[3,3\],\[3,3\],\[3,3\],\[2,2\],\[3,3\],\[3,3\],\[3,3\]\]
**Output:** 4
**Example 3:**
**Input:** m = 3, n = 3, ops = \[\]
**Output:** 9
**Constraints:**
* `1 <= m, n <= 4 * 104`
* `0 <= ops.length <= 104`
* `ops[i].length == 2`
* `1 <= ai <= m`
* `1 <= bi <= n` | null |
Python Brute Force Solution | minimum-index-sum-of-two-lists | 0 | 1 | # Intuition\nbeats 99.9%\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nBrute force\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n n(log n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n d2={}\n l=[]\n for i in range(len(list2)):\n d2[list2[i]]=i\n for i in range(len(list1)):\n if list1[i] in d2:\n l.append([i+d2[list1[i]],list1[i]])\n l1=[]\n l.sort()\n l1.append(l[0][1])\n for i in range(1,len(l)):\n if l[i][0]==l[i-1][0]:\n l1.append(l[i][1])\n else:\n break\n return l1\n \n``` | 1 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
Easily Understandable Python Code || Brute Force Approach | minimum-index-sum-of-two-lists | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n m = len(list1) + len(list2)\n list3 = []\n \n for i in range(len(list1)):\n for j in range(len(list2)):\n if list1[i] == list2[j]:\n if (i+j)<=m:\n if list3 == None:\n list3.append(list2[j])\n \n elif m == i+j:\n list3.append(list2[j])\n \n else:\n list3=[]\n list3.append(list2[j])\n \n m = i + j\n return list3\n``` | 2 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
Solution | minimum-index-sum-of-two-lists | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<string> findRestaurant(vector<string>& list1, vector<string>& list2) {\n unordered_map<string,int> mp,m;\n vector<string> v;\n int mini =INT_MAX;\n int mi;\n int sum;\n for(int i=0;i<list1.size();i++)\n m[list1[i]] = i;\n for(int j=0;j<list2.size();j++)\n {\n if(m.find(list2[j]) != m.end())\n {\n sum = j + m[list2[j]];\n if(sum<mini)\n {\n v.clear();\n mini = sum;\n v.push_back(list2[j]);\n }\n else if( sum == mini)\n v.push_back(list2[j]);\n }\n }\n return v;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n\n def result(l1, l2) -> List[str]:\n hashmap, res, minInd = {}, [], len(list1) + len(list2) - 2\n\n for ind, val in enumerate(l1):\n hashmap[val] = ind\n\n for ind, val in enumerate(l2):\n if val in hashmap and hashmap[val] + ind <= minInd:\n if hashmap[val] + ind < minInd:\n res.clear()\n minInd = hashmap[val] + ind\n res.append(val)\n\n return res\n\n return result(list1, list2) if len(list1) < len(list2) else result(list2, list1)\n```\n\n```Java []\nclass Solution {\n public String[] findRestaurant(String[] list1, String[] list2) {\n if (list1.length > list2.length) {\n return findRestaurant(list2, list1);\n }\n HashMap <String, Integer> hm = new HashMap<>();\n for(int i=0;i< list1.length;i++) {\n hm.put(list1[i], i);\n }\n int count=0;\n int minval = Integer.MAX_VALUE;\n List<String> op = new ArrayList<>();\n for(int i=0;i< list2.length&& i <= minval;i++) {\n Integer x = hm.get(list2[i]);\n if(x!=null) {\n if(minval> x+i){\n op.add(0,list2[i]);\n minval=x+i;\n count=1;\n } else if(minval == x+i) {\n op.add(count++, list2[i]);\n }\n }\n }\n return op.subList(0, count).toArray(new String[0]);\n }\n}\n```\n | 2 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
Python3 easy-peasy solution | minimum-index-sum-of-two-lists | 0 | 1 | # Intuition\nThe time complexity of both solutions is O(m * n), where m and n are the lengths of the two input lists. In the worst case, we have to compare every element of list1 to every element of list2 to find the common strings, which requires m * n comparisons. However, both solutions use a dictionary to keep track of the index sum for each common string, which allows them to identify the minimum index sum in O(m * n) time. Therefore, the overall time complexity is O(m * n).\n\nThe space complexity of both solutions is also O(m * n), because in the worst case, every element of list1 is a common string with every element of list2, and we need to store the index sum for each pair of common strings in the dictionary. However, in practice, the space complexity is likely to be much lower, because we will usually have only a small number of common strings.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\n0(1)\n\n# Code\n```\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n \'\'\'\n # Solution 1: Brute force\n min_val = -1\n res = {}\n tmp = []\n for i, l1 in enumerate(list1):\n for j, l2 in enumerate(list2):\n if l1 == l2:\n res[l1] = i+j\n if min_val == -1:\n min_val = i+j \n else:\n min_val = min(min_val, i+j)\n \n \n for k, v in res.items():\n if v == min_val:\n tmp.append(k) \n return tmp\'\'\'\n\n # Solution 2: Optimised\n\n l1 = {list1[i]: i for i in range(len(list1))}\n l2 = {list2[i]: i for i in range(len(list2))}\n min_val = float(\'inf\')\n res = []\n for k, v in l1.items():\n if k in l2:\n if (l1[k] + l2[k]) < min_val:\n res = [k]\n min_val = l1[k] + l2[k]\n elif (l1[k] + l2[k]) == min_val:\n res.append(k)\n\n return res\n\n``` | 1 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
Python3|| Beats 99.13% || Using Dictionary(simple solution). | minimum-index-sum-of-two-lists | 0 | 1 | # Please do upvote if you find the solution helpful.\n\n\n\n# Code\n```\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n d={}\n for i in range(len(list1)):\n for j in range(len(list2)):\n if list1[i] == list2[j]:\n d[list1[i]] = i+j\n lst=[]\n for i,j in d.items():\n if j == min(d.values()):\n lst.append(i)\n return lst\n``` | 4 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
599: Solution with step by step explanation | minimum-index-sum-of-two-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFind the common elements between both lists using the set intersection operator & and store the result in a variable called common.\n\nInitialize a dictionary called index_sum to store the index sum of common elements in list1.\n\nIterate through each element r in list1 and for each element:\n\nIf r is in common, store the index sum of r in index_sum.\nIterate through each element r in list2 and for each element:\n\nIf r is in common, add the index sum of r to its corresponding value in index_sum.\nFind the minimum value in index_sum and store it in a variable called min_sum.\n\nReturn a list of elements in index_sum whose value is equal to min_sum.\n\nEnd of the algorithm.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n common = set(list1) & set(list2) # Find common elements between both lists\n index_sum = {}\n for i, r in enumerate(list1):\n if r in common:\n index_sum[r] = i # Store index sum of common elements in list1\n for i, r in enumerate(list2):\n if r in common:\n index_sum[r] += i # Add index sum of common elements in list2\n min_sum = min(index_sum.values()) # Find minimum index sum\n return [r for r, s in index_sum.items() if s == min_sum] # Return elements with minimum index sum\n\n``` | 8 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
easy solution | minimum-index-sum-of-two-lists | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public String[] findRestaurant(String[] list1, String[] list2) {\n Map<String,Integer> map=new HashMap<>();\n List<String> list=new ArrayList<>();\n int sum=Integer.MAX_VALUE;\n for(int i=0;i<list1.length;i++) map.put(list1[i],i);\n for(int i=0;i<list2.length;i++){\n Integer k=map.get(list2[i]);\n if(k!=null && k+i<sum ){\n list.clear();\n sum=k+i;\n list.add(list2[i]);\n }\n else if(k!=null && k+i<=sum){\n list.add(list2[i]);\n }\n }\n return list.toArray(new String[list.size()]);\n }\n}\n```\n```c++ []\n vector<string> findRestaurant(vector<string>& list1, vector<string>& list2) {\n vector<string>res;\n unordered_map<string,int>m;\n int min = INT_MAX;\n for(int i = 0; i < list1.size(); i++) m[list1[i]] = i;\n for(int i = 0; i < list2.size(); i++)\n if(m.count(list2[i]) != 0)\n if(m[list2[i]] + i < min) min = m[list2[i]] + i, res.clear(), res.push_back(list2[i]);\n else if(m[list2[i]] + i == min) res.push_back(list2[i]);\n return res;\n }\n```\n```python3 []\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n m = len(list1) + len(list2)\n list3 = []\n \n for i in range(len(list1)):\n for j in range(len(list2)):\n if list1[i] == list2[j]:\n if (i+j)<=m:\n if list3 == None:\n list3.append(list2[j])\n \n elif m == i+j:\n list3.append(list2[j])\n \n else:\n list3=[]\n list3.append(list2[j])\n \n m = i + j\n return list3\n```\n\n | 2 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
Python3 || Dictionary || single loop || Easy solution | minimum-index-sum-of-two-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\nUse dict .\n\n1.In for loop iterarte either list1 or list2 by using enumerate().\n\n2.Ckeck if word exists in second list, if so assign word as dict`s key and sum of word`s index and index given by index() as dict`s value.\n\n3.Sort dict by lambda in sorted() according to dict`s value.Obtain minimum value from sorted dic. Finally, load word with minimum value in list comprehension.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRestaurant(self, list1: list[str], list2: list[str]) -> list[str]:\n dic = {}\n\n for x, val in enumerate(list1):\n if val in list2:\n dic[val] = x + list2.index(val)\n\n dic = sorted(dic.items(), key=lambda x: x[1])\n minimum = dic[0][1]\n return [x[0] for x in dic if x[1]==minimum]\n\n\n\n``` | 1 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
Python easy solution for beginners using lists only | minimum-index-sum-of-two-lists | 0 | 1 | ```\nclass Solution:\n def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:\n res = []\n min_ind_sum = -1\n if len(list1) < len(list2):\n for i in range(len(list1)):\n if list1[i] in list2:\n ind_sum = i + list2.index(list1[i])\n if min_ind_sum == -1 or ind_sum < min_ind_sum:\n res.clear()\n res.append(list1[i])\n min_ind_sum = ind_sum\n elif ind_sum == min_ind_sum:\n res.append(list1[i])\n else:\n for i in range(len(list2)):\n if list2[i] in list1:\n ind_sum = i + list1.index(list2[i])\n if min_ind_sum == -1 or ind_sum < min_ind_sum:\n res.clear()\n res.append(list2[i])\n min_ind_sum = ind_sum\n elif ind_sum == min_ind_sum:\n res.append(list2[i])\n return res | 1 | Given two arrays of strings `list1` and `list2`, find the **common strings with the least index sum**.
A **common string** is a string that appeared in both `list1` and `list2`.
A **common string with the least index sum** is a common string such that if it appeared at `list1[i]` and `list2[j]` then `i + j` should be the minimum value among all the other **common strings**.
Return _all the **common strings with the least index sum**_. Return the answer in **any order**.
**Example 1:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "Piatti ", "The Grill at Torrey Pines ", "Hungry Hunter Steakhouse ", "Shogun "\]
**Output:** \[ "Shogun "\]
**Explanation:** The only common string is "Shogun ".
**Example 2:**
**Input:** list1 = \[ "Shogun ", "Tapioca Express ", "Burger King ", "KFC "\], list2 = \[ "KFC ", "Shogun ", "Burger King "\]
**Output:** \[ "Shogun "\]
**Explanation:** The common string with the least index sum is "Shogun " with index sum = (0 + 1) = 1.
**Example 3:**
**Input:** list1 = \[ "happy ", "sad ", "good "\], list2 = \[ "sad ", "happy ", "good "\]
**Output:** \[ "sad ", "happy "\]
**Explanation:** There are three common strings:
"happy " with index sum = (0 + 1) = 1.
"sad " with index sum = (1 + 0) = 1.
"good " with index sum = (2 + 2) = 4.
The strings with the least index sum are "sad " and "happy ".
**Constraints:**
* `1 <= list1.length, list2.length <= 1000`
* `1 <= list1[i].length, list2[i].length <= 30`
* `list1[i]` and `list2[i]` consist of spaces `' '` and English letters.
* All the strings of `list1` are **unique**.
* All the strings of `list2` are **unique**.
* There is at least a common string between `list1` and `list2`. | null |
600: Solution with step by step explanation | non-negative-integers-without-consecutive-ones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nInitialize a list f to store the fibonacci numbers 1 and 2.\n\nUse a loop to append the next 29 fibonacci numbers to f.\n\nInitialize two variables ans and last_seen to 0.\n\nUse a loop to iterate through all 31 bits of n, starting with the most significant bit.\n\nIf the current bit is set to 1:\n\nAdd the corresponding fibonacci number to ans.\nIf last_seen is also 1, subtract 1 from ans, set last_seen to 0, and break out of the loop.\nOtherwise, set last_seen to 1.\nIf the current bit is set to 0:\n\nSet last_seen to 0.\nReturn ans + 1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findIntegers(self, n: int) -> int:\n # f stores the fibonacci numbers\n f = [1, 2]\n for i in range(2, 31):\n f.append(f[-1] + f[-2])\n # last_seen tells us if there was a one right before. \n # If that is the case, we are done then and there!\n # ans is the answer\n ans, last_seen = 0, 0\n for i in reversed(range(31)):\n if (1 << i) & n: # is the ith bit set?\n ans += f[i]\n if last_seen: \n ans -= 1\n break\n last_seen = 1\n else:\n last_seen = 0\n return ans + 1\n\n\n``` | 2 | Given a positive integer `n`, return the number of the integers in the range `[0, n]` whose binary representations **do not** contain consecutive ones.
**Example 1:**
**Input:** n = 5
**Output:** 5
**Explanation:**
Here are the non-negative integers <= 5 with their corresponding binary representations:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
Among them, only integer 3 disobeys the rule (two consecutive ones) and the other 5 satisfy the rule.
**Example 2:**
**Input:** n = 1
**Output:** 2
**Example 3:**
**Input:** n = 2
**Output:** 3
**Constraints:**
* `1 <= n <= 109` | null |
Solution | non-negative-integers-without-consecutive-ones | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findIntegers(int n) {\n int fib[31];\n fib[0] = 1;\n fib[1] = 2;\n\n for(int i=2; i<30; i++){\n fib[i] = fib[i-1]+fib[i-2];\n }\n int count = 30, ans = 0, prevOne = 0;\n while(count >= 0){\n if(n&(1<<count)){\n ans += fib[count];\n if(prevOne) return ans;\n prevOne = 1;\n }\n else{\n prevOne = 0;\n }\n count--;\n }\n return ans+1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findIntegers(self, n: int) -> int:\n binary = []\n while n:\n binary.append(n % 2)\n n = n // 2\n k = len(binary)\n\n count = [0] * (k + 1)\n count[0], count[1] = 1, 2\n for i in range(2, k + 1):\n count[i] = count[i - 1] + count[i - 2]\n \n binary.reverse()\n print(binary)\n ans = 0\n for i, c in enumerate(binary):\n if c == 1:\n ans += count[k - i - 1]\n if i > 0 and binary[i - 1] == 1:\n return ans\n \n return ans + 1\n```\n\n```Java []\nclass Solution {\n public int findIntegers(int num) {\n StringBuilder bits = new StringBuilder();\n for (; num > 0; num >>= 1)\n bits.append(num & 1);\n\n final int n = bits.length();\n int[] zero = new int[n];\n int[] one = new int[n];\n\n zero[0] = 1;\n one[0] = 1;\n\n for (int i = 1; i < n; ++i) {\n zero[i] = zero[i - 1] + one[i - 1];\n one[i] = zero[i - 1];\n }\n int ans = zero[n - 1] + one[n - 1];\n\n for (int i = n - 2; i >= 0; --i) {\n if (bits.charAt(i) == \'1\' && bits.charAt(i + 1) == \'1\')\n break;\n if (bits.charAt(i) == \'0\' && bits.charAt(i + 1) == \'0\')\n ans -= one[i];\n }\n return ans;\n }\n}\n```\n | 1 | Given a positive integer `n`, return the number of the integers in the range `[0, n]` whose binary representations **do not** contain consecutive ones.
**Example 1:**
**Input:** n = 5
**Output:** 5
**Explanation:**
Here are the non-negative integers <= 5 with their corresponding binary representations:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
Among them, only integer 3 disobeys the rule (two consecutive ones) and the other 5 satisfy the rule.
**Example 2:**
**Input:** n = 1
**Output:** 2
**Example 3:**
**Input:** n = 2
**Output:** 3
**Constraints:**
* `1 <= n <= 109` | null |
python clean & simple solution ✅ | | fibonacci approach 39ms 🔥🔥🔥 | non-negative-integers-without-consecutive-ones | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findIntegers(self, n: int) -> int:\n f = [1,2]\n for i in range(2,30):\n f.append(f[-1] + f[-2])\n \n ans = last_seen = 0\n\n for i in range(29,-1,-1):\n if (1 << i) & n:\n ans += f[i]\n if last_seen :\n return ans\n last_seen = 1\n else:\n last_seen = 0\n return ans + 1\n``` | 3 | Given a positive integer `n`, return the number of the integers in the range `[0, n]` whose binary representations **do not** contain consecutive ones.
**Example 1:**
**Input:** n = 5
**Output:** 5
**Explanation:**
Here are the non-negative integers <= 5 with their corresponding binary representations:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
Among them, only integer 3 disobeys the rule (two consecutive ones) and the other 5 satisfy the rule.
**Example 2:**
**Input:** n = 1
**Output:** 2
**Example 3:**
**Input:** n = 2
**Output:** 3
**Constraints:**
* `1 <= n <= 109` | null |
[Python3] Official Solution Explained Simply with Diagrams | non-negative-integers-without-consecutive-ones | 0 | 1 | ## 0. Introduction\nThe problem is hard, but looks deceptively easy. The solution is easy, but hard to understand. I\'ll attempt to explain the [official solution](https://leetcode.com/problems/non-negative-integers-without-consecutive-ones/solution/) with diagrams.\n\n## 1. The World of Bits\nThe single constraint given to us is of **no consecutive set bits**. Set bits meaning bits with value of 1. Since the question is in terms of bits, let\'s think in terms of bits.\n\nSay we have two bits worth of space, `xx`. What all are the valid combinations? `00, 01, 10`. \n\n\n\nSimilarly, for 3 bits as `xxx`:\n\n\n\nThe paths reaching till the end with green are counted as valid.\n\n## 2. Observations\n- One thing is glaringly obvious: Only a sequence of `0` and `10` is able to produce both `0, 1` as the output, giving us full freedom over what to pick next. This is marked as yellow.\n- Note how the trees are similar. Take the case of 4 bits as: `xxxx`.\n\n\nThat\'s right, its a fibonacci sequence! This is the core of the solution.\n\n## 3. Examples\nNow we know that its a world of bits with `0` and `10` as the minimum viable sequences giving us fibonacci numbers as the answer. \n\nSince all the numbers can be formed using 1s and 0s, let\'s take a look at some of the samples.\n\ninput: n = "1010"\noutput: In this case we can think of "1010" as "1000+10". We add the answers of "1000" and "10", which can be given by `f[3]+f[1]+1`. We add the additional 1 because "1010" itself is a valid number!\n\ninput: n = "1110"\noutput: Something intersting happends here. Consider "1110 = 1000+110". Answer for "1000" is `f[3]`.\nWhat about "110"? Can we break it down as "110 = 100+10"? Not so fast! \nThe issue is, "110" has a hidden 1 behind it. Meaning, we can consider numbers **upto** "100", sure (*not* inlcuding "100"), but any number beyond that is simply invalid by the condition. So, we only consider "1110 as 1000+100". The answer is thus `f[3]+f[2]`. Note how we didn\'t do `+1` because "1100" is an invalid number.\n\ninput: n = "101 1010"\noutput: "101 1010 = 100 0000 + 1 0000 + 1000" => `f[6]+f[4]+f[3]`. The rest would become invalid. If you are confued, reread! This combines elements of both of the above.\n\n## 4. Code\nThis code is a direct translation of the official solution, but this time, it should make sense!\n\n```\nclass Solution:\n def findIntegers(self, n: int) -> int:\n # f stores the fibonacci numbers\n f = [1, 2]\n for i in range(2, 30):\n f.append(f[-1]+f[-2])\n \n # last_seen tells us if there was a one right before. \n # If that is the case, we are done then and there!\n # ans is the answer\n ans, last_seen = 0, 0\n for i in reversed(range(30)):\n if (1 << i) & n: # is the ith bit set?\n ans += f[i]\n if last_seen: \n ans -= 1\n break\n last_seen = 1\n else:\n last_seen = 0\n return ans+1\n```\n\nAny questions? Ask! Any comments/criticisms? I\'m happy to hear! An upvote let\'s me know it was helpful for you :D\n | 109 | Given a positive integer `n`, return the number of the integers in the range `[0, n]` whose binary representations **do not** contain consecutive ones.
**Example 1:**
**Input:** n = 5
**Output:** 5
**Explanation:**
Here are the non-negative integers <= 5 with their corresponding binary representations:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
Among them, only integer 3 disobeys the rule (two consecutive ones) and the other 5 satisfy the rule.
**Example 2:**
**Input:** n = 1
**Output:** 2
**Example 3:**
**Input:** n = 2
**Output:** 3
**Constraints:**
* `1 <= n <= 109` | null |
Solution to 600. Non-negative Integers without Consecutive Ones | non-negative-integers-without-consecutive-ones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the count of non-negative integers in the range [0, n] whose binary representations do not contain consecutive ones. To achieve this, we need a strategy to count the valid binary representations efficiently.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use dynamic programming to build an array `dp`, where `dp[i]` represents the count of valid binary representations of length `i`. We initialize base cases for empty string and single-digit strings. Then, we iteratively build the array based on the recurrence relation: `dp[i] = dp[i-1] + dp[i-2]`.\n\nNext, we convert the given integer `n` to its binary representation and traverse its bits. While traversing, we accumulate the count of valid representations based on the dynamic programming array. If two consecutive 1s are encountered, we adjust the count accordingly.\n\nFinally, we return the count, considering the binary representation of `n` itself.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is $$O(log(n))$$ for converting the integer to binary and $$O(log(n))$$ for traversing its bits. The dynamic programming array is built in $$O(log(n))$$ time. Therefore, the overall time complexity is $$O(log(n))$$.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is $$O(log(n))$$ as it is dominated by the dynamic programming array used to store the counts of valid binary representations of different lengths.\n# Code\n```\nclass Solution:\n def findIntegers(self, n: int) -> int:\n # Convert n to binary\n binary_n = bin(n)[2:]\n \n # Initialize dp array to store the count of valid binary representations of length i\n dp = [0] * (len(binary_n) + 1)\n \n # Initialize base cases\n dp[0] = 1 # Empty string is a valid binary representation\n dp[1] = 2 # "0" and "1" are valid\n \n # Build the dp array\n for i in range(2, len(dp)):\n dp[i] = dp[i - 1] + dp[i - 2]\n \n # Count the valid representations for n\n count = 0\n prev_bit = 0\n \n for i in range(len(binary_n)):\n if binary_n[i] == \'1\':\n count += dp[len(binary_n) - i - 1]\n if prev_bit == 1:\n count -= 1 # Subtract 1 for the case where two consecutive 1s are encountered\n break\n prev_bit = 1\n else:\n prev_bit = 0\n \n return count + 1 # Add 1 for the binary representation of n itself\n``` | 0 | Given a positive integer `n`, return the number of the integers in the range `[0, n]` whose binary representations **do not** contain consecutive ones.
**Example 1:**
**Input:** n = 5
**Output:** 5
**Explanation:**
Here are the non-negative integers <= 5 with their corresponding binary representations:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
Among them, only integer 3 disobeys the rule (two consecutive ones) and the other 5 satisfy the rule.
**Example 2:**
**Input:** n = 1
**Output:** 2
**Example 3:**
**Input:** n = 2
**Output:** 3
**Constraints:**
* `1 <= n <= 109` | null |
Time and space complexity very cool | can-place-flowers | 0 | 1 | if you want to help, you can subscribe to my twitch: www.twitch.tv/edexade\n\n# Code\n```\nclass Solution:\n def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:\n if n == 0:\n return True\n flowerbed.append(0)\n k = 0\n i = 0\n while i < len(flowerbed)-1:\n if flowerbed[i+1] == 0:\n if flowerbed[i] == 0:\n k += 1\n if k == n:\n return True\n\n i += 2\n else:\n i += 3\n \n return False\n\'\'\'\n if flowerbed[i] == 0:\n if flowerbed[i+1] == 0:\n k += 1\n i += 2\n if k == n:\n return True\n else:\n \n i += 3\n else:\n if flowerbed[i+1] == 0:\n i += 2\n else:\n i += 3\n\'\'\'\n \n``` | 1 | You have a long flowerbed in which some of the plots are planted, and some are not. However, flowers cannot be planted in **adjacent** plots.
Given an integer array `flowerbed` containing `0`'s and `1`'s, where `0` means empty and `1` means not empty, and an integer `n`, return `true` _if_ `n` _new flowers can be planted in the_ `flowerbed` _without violating the no-adjacent-flowers rule and_ `false` _otherwise_.
**Example 1:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 1
**Output:** true
**Example 2:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 2
**Output:** false
**Constraints:**
* `1 <= flowerbed.length <= 2 * 104`
* `flowerbed[i]` is `0` or `1`.
* There are no two adjacent flowers in `flowerbed`.
* `0 <= n <= flowerbed.length` | null |
Simple Python3 Solution || Brute Force || O(n) || Upto 50% Faster | can-place-flowers | 0 | 1 | # Intuition\nOne possible solution to the problem is to iterate over the elements of the flowerbed array and check if the current plot and its adjacent plots are empty. If they are, plant a flower and increase the value of valid_slots. \nAt the end, return True if n is less than or equal to valid_slots, otherwise return False.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:\n valid_slots = -1\n i = 0\n while i < len(flowerbed):\n #print(flowerbed[i])\n # Checking if any empty plots are beside any planted plots\n # if not we increase valid_slots by 1\n if flowerbed[i] == 0:\n #We check if the left slot is empty\n left = 0\n if i-1 >= 0:\n if flowerbed[i-1] == 0:\n left = 1\n else:\n left = 1\n\n #We check if the right slot is empty\n right = 0\n if i+1 < len(flowerbed):\n if flowerbed[i+1] == 0:\n right = 1\n else:\n right = 1\n\n\n # If both the slots are empty we increase valid_slots\n if right and left:\n if valid_slots == -1:\n valid_slots = 0\n valid_slots += 1\n # We next check next.next slot instead of next slot \n # so Increase i +1\n i += 1\n \n i += 1\n \n # If no new plantations return True\n if n == 0:\n return True\n\n if valid_slots == -1:\n return False\n\n #if Valid slots are equal to n return True\n return valid_slots >= n\n \n``` | 1 | You have a long flowerbed in which some of the plots are planted, and some are not. However, flowers cannot be planted in **adjacent** plots.
Given an integer array `flowerbed` containing `0`'s and `1`'s, where `0` means empty and `1` means not empty, and an integer `n`, return `true` _if_ `n` _new flowers can be planted in the_ `flowerbed` _without violating the no-adjacent-flowers rule and_ `false` _otherwise_.
**Example 1:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 1
**Output:** true
**Example 2:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 2
**Output:** false
**Constraints:**
* `1 <= flowerbed.length <= 2 * 104`
* `flowerbed[i]` is `0` or `1`.
* There are no two adjacent flowers in `flowerbed`.
* `0 <= n <= flowerbed.length` | null |
✅✅Python Simple Solution 🔥🔥 Easy to Understand🔥🔥 | can-place-flowers | 0 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am Giving away my premium content videos related to computer science and data science and also will be sharing well-structured assignments and study materials to clear interviews at top companies to my first 1000 Subscribers. So, **DON\'T FORGET** to Subscribe\n\nhttps://www.youtube.com/@techwired8/?sub_confirmation=1\n\n**Solution Video Search \uD83D\uDC49 "Can Place Flowers by Tech Wired leetcode" on YouTube**\n\n\n\n```\nclass Solution:\n def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:\n if n == 0:\n return True\n for i in range(len(flowerbed)):\n if flowerbed[i] == 0 and (i == 0 or flowerbed[i-1] == 0) and (i == len(flowerbed)-1 or flowerbed[i+1] == 0):\n flowerbed[i] = 1\n n -= 1\n if n == 0:\n return True\n return False\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D | 256 | You have a long flowerbed in which some of the plots are planted, and some are not. However, flowers cannot be planted in **adjacent** plots.
Given an integer array `flowerbed` containing `0`'s and `1`'s, where `0` means empty and `1` means not empty, and an integer `n`, return `true` _if_ `n` _new flowers can be planted in the_ `flowerbed` _without violating the no-adjacent-flowers rule and_ `false` _otherwise_.
**Example 1:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 1
**Output:** true
**Example 2:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 2
**Output:** false
**Constraints:**
* `1 <= flowerbed.length <= 2 * 104`
* `flowerbed[i]` is `0` or `1`.
* There are no two adjacent flowers in `flowerbed`.
* `0 <= n <= flowerbed.length` | null |
Not a optimized solution | can-place-flowers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:\n if n==0:\n return True\n for i in range(len(flowerbed)):\n if flowerbed[i]==0 and (i==0 or flowerbed[i-1]==0)and (i==len(flowerbed)-1 or flowerbed[i+1]==0):\n flowerbed[i]=1\n n-=1\n if n==0:\n return True\n return False\n``` | 1 | You have a long flowerbed in which some of the plots are planted, and some are not. However, flowers cannot be planted in **adjacent** plots.
Given an integer array `flowerbed` containing `0`'s and `1`'s, where `0` means empty and `1` means not empty, and an integer `n`, return `true` _if_ `n` _new flowers can be planted in the_ `flowerbed` _without violating the no-adjacent-flowers rule and_ `false` _otherwise_.
**Example 1:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 1
**Output:** true
**Example 2:**
**Input:** flowerbed = \[1,0,0,0,1\], n = 2
**Output:** false
**Constraints:**
* `1 <= flowerbed.length <= 2 * 104`
* `flowerbed[i]` is `0` or `1`.
* There are no two adjacent flowers in `flowerbed`.
* `0 <= n <= flowerbed.length` | null |
🔥More Than One Method🔥| Java | C++ | Python | JavaScript | | construct-string-from-binary-tree | 1 | 1 | # 1st Method :- DFS\uD83D\uDD25\n\n## \u2712\uFE0FCode\n``` Java []\nclass Solution {\n public String tree2str(TreeNode root) {\n if (root == null) {\n return "";\n }\n \n // Step 1: Start with an empty result string\n StringBuilder result = new StringBuilder();\n \n // Step 2: Perform preorder traversal\n preorderTraversal(root, result);\n \n // Step 3: Return the final result string\n return result.toString();\n }\n\n private void preorderTraversal(TreeNode node, StringBuilder result) {\n if (node == null) {\n return;\n }\n \n // Step 4: Append the current node\'s value to the result\n result.append(node.val);\n \n // Step 5: Check if the current node has a left child or a right child\n if (node.left != null || node.right != null) {\n \n // Step 6: If there is a left child, add empty parentheses for it\n result.append("(");\n preorderTraversal(node.left, result);\n result.append(")");\n }\n \n // Step 7: If there is a right child, process it similarly\n if (node.right != null) {\n result.append("(");\n preorderTraversal(node.right, result);\n result.append(")");\n }\n \n // Step 8: The recursion will handle all the child nodes\n }\n}\n\n```\n``` C++ []\n\nclass Solution {\npublic:\n string tree2str(TreeNode* root) {\n if (root == nullptr) {\n return "";\n }\n\n // Step 1: Start with an empty result string\n stringstream result;\n\n // Step 2: Perform preorder traversal\n preorderTraversal(root, result);\n\n // Step 3: Return the final result string\n return result.str();\n }\n\nprivate:\n void preorderTraversal(TreeNode* node, stringstream& result) {\n if (node == nullptr) {\n return;\n }\n\n // Step 4: Append the current node\'s value to the result\n result << node->val;\n\n // Step 5: Check if the current node has a left child or a right child\n if (node->left != nullptr || node->right != nullptr) {\n\n // Step 6: If there is a left child, add empty parentheses for it\n result << "(";\n preorderTraversal(node->left, result);\n result << ")";\n }\n\n // Step 7: If there is a right child, process it similarly\n if (node->right != nullptr) {\n result << "(";\n preorderTraversal(node->right, result);\n result << ")";\n }\n\n // Step 8: The recursion will handle all the child nodes\n }\n};\n\n```\n``` Python []\nclass Solution:\n def tree2str(self, root):\n if root is None:\n return ""\n\n # Step 1: Start with an empty result string\n result = []\n\n # Step 2: Perform preorder traversal\n self.preorderTraversal(root, result)\n\n # Step 3: Return the final result string\n return \'\'.join(result)\n\n def preorderTraversal(self, node, result):\n if node is None:\n return\n\n # Step 4: Append the current node\'s value to the result\n result.append(str(node.val))\n\n # Step 5: Check if the current node has a left child or a right child\n if node.left is not None or node.right is not None:\n\n # Step 6: If there is a left child, add empty parentheses for it\n result.append("(")\n self.preorderTraversal(node.left, result)\n result.append(")")\n\n # Step 7: If there is a right child, process it similarly\n if node.right is not None:\n result.append("(")\n self.preorderTraversal(node.right, result)\n result.append(")")\n\n # Step 8: The recursion will handle all the child nodes\n\n```\n``` JavaScript []\nvar tree2str = function(root) {\n // Step 1: Start with an empty result array\n let result = [];\n\n // Step 2: Perform preorder traversal\n preorderTraversal(root, result);\n\n // Step 3: Return the final result string\n return result.join(\'\');\n\n // Step 4: Define the preorderTraversal function\n function preorderTraversal(node, result) {\n // Step 5: Check if the current node is null\n if (node === null) {\n return;\n }\n\n // Step 6: Append the current node\'s value to the result\n result.push(node.val);\n\n // Step 7: Check if the current node has a left child or a right child\n if (node.left !== null || node.right !== null) {\n\n // Step 8: If there is a left child, add empty parentheses for it\n result.push("(");\n preorderTraversal(node.left, result);\n result.push(")");\n }\n\n // Step 9: If there is a right child, process it similarly\n if (node.right !== null) {\n result.push("(");\n preorderTraversal(node.right, result);\n result.push(")");\n }\n\n // Step 10: The recursion will handle all the child nodes\n }\n};\n\n```\n``` C# []\npublic class Solution {\n public string Tree2str(TreeNode root) {\n if (root == null) {\n return "";\n }\n \n // Step 1: Start with an empty result string\n StringBuilder result = new StringBuilder();\n \n // Step 2: Perform preorder traversal\n PreorderTraversal(root, result);\n \n // Step 3: Return the final result string\n return result.ToString();\n }\n\n private void PreorderTraversal(TreeNode node, StringBuilder result) {\n if (node == null) {\n return;\n }\n \n // Step 4: Append the current node\'s value to the result\n result.Append(node.val);\n \n // Step 5: Check if the current node has a left child or a right child\n if (node.left != null || node.right != null) {\n \n // Step 6: If there is a left child, add empty parentheses for it\n result.Append("(");\n PreorderTraversal(node.left, result);\n result.Append(")");\n }\n \n // Step 7: If there is a right child, process it similarly\n if (node.right != null) {\n result.Append("(");\n PreorderTraversal(node.right, result);\n result.Append(")");\n }\n \n // Step 8: The recursion will handle all the child nodes\n }\n}\n```\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9Time complexity: O(n)\n- The time complexity is determined by the number of nodes in the binary tree.\n- In the worst case, the algorithm visits each node once during the preorder traversal.\n- Therefore, the time complexity is O(n), where n is the number of nodes in the binary tree.\n\n### \uD83C\uDFF9Space complexity: O(n)\n- The space complexity is determined by the maximum depth of the recursion stack.\n- In the worst case, when the binary tree is skewed (essentially a linked list), the maximum depth of the recursion stack is equal to the number of nodes.\n- Therefore, the space complexity is O(n) in the worst case.\n\n\n\n---\n# 2nd Method :- DFS\uD83D\uDD25\n\n## \u2712\uFE0FCode\n``` Java []\npublic class Solution {\n public String tree2str(TreeNode root) {\n // Step 1: Base case - if the root is null, return an empty string\n if (root == null) return "";\n \n // Step 2: Start with the value of the current node as the result string\n String result = root.val + "";\n \n // Step 3: Recursively process the left and right subtrees\n String leftSubtree = tree2str(root.left);\n String rightSubtree = tree2str(root.right);\n \n // Step 4: Check conditions to determine the final result\n if (leftSubtree.equals("") && rightSubtree.equals("")) {\n // Both left and right subtrees are empty, return the current result\n return result;\n }\n if (leftSubtree.equals("")) {\n // Left subtree is empty, include empty parentheses for it\n return result + "()" + "(" + rightSubtree + ")";\n }\n if (rightSubtree.equals("")) {\n // Right subtree is empty, include the left subtree\n return result + "(" + leftSubtree + ")";\n }\n \n // Both left and right subtrees are non-empty, include both in the result\n return result + "(" + leftSubtree + ")" + "(" + rightSubtree + ")";\n }\n}\n\n```\n``` C++ []\n\nclass Solution {\npublic:\n std::string tree2str(TreeNode* root) {\n // Step 1: Base case - if the root is null, return an empty string\n if (root == nullptr) {\n return "";\n }\n\n // Step 2: Start with the value of the current node as the result string\n std::string result = std::to_string(root->val);\n\n // Step 3: Recursively process the left and right subtrees\n std::string leftSubtree = tree2str(root->left);\n std::string rightSubtree = tree2str(root->right);\n\n // Step 4: Check conditions to determine the final result\n if (leftSubtree.empty() && rightSubtree.empty()) {\n // Both left and right subtrees are empty, return the current result\n return result;\n }\n if (leftSubtree.empty()) {\n // Left subtree is empty, include empty parentheses for it and the right subtree\n return result + "()" + "(" + rightSubtree + ")";\n }\n if (rightSubtree.empty()) {\n // Right subtree is empty, include the left subtree\n return result + "(" + leftSubtree + ")";\n }\n\n // Both left and right subtrees are non-empty, include both in the result\n return result + "(" + leftSubtree + ")" + "(" + rightSubtree + ")";\n }\n};\n```\n``` Python []\nclass Solution:\n def tree2str(self, root):\n # Step 1: Base case - if the root is None, return an empty string\n if root is None:\n return ""\n\n # Step 2: Start with the value of the current node as the result string\n result = str(root.val)\n\n # Step 3: Recursively process the left and right subtrees\n left_subtree = self.tree2str(root.left)\n right_subtree = self.tree2str(root.right)\n\n # Step 4: Check conditions to determine the final result\n if not left_subtree and not right_subtree:\n # Both left and right subtrees are empty, return the current result\n return result\n if not left_subtree:\n # Left subtree is empty, include empty parentheses for it and the right subtree\n return result + "()" + "(" + right_subtree + ")"\n if not right_subtree:\n # Right subtree is empty, include the left subtree\n return result + "(" + left_subtree + ")"\n\n # Both left and right subtrees are non-empty, include both in the result\n return result + "(" + left_subtree + ")" + "(" + right_subtree + ")"\n```\n``` JavaScript []\nvar tree2str = function(root) {\n // Step 1: Base case - if the root is null, return an empty string\n if (root === null) return "";\n\n // Step 2: Start with the value of the current node as the result string\n let result = root.val.toString();\n\n // Step 3: Recursively process the left and right subtrees\n let leftSubtree = tree2str(root.left);\n let rightSubtree = tree2str(root.right);\n\n // Step 4: Check conditions to determine the final result\n if (leftSubtree === "" && rightSubtree === "") {\n // Both left and right subtrees are empty, return the current result\n return result;\n }\n if (leftSubtree === "") {\n // Left subtree is empty, include empty parentheses for it and the right subtree\n return result + "()" + "(" + rightSubtree + ")";\n }\n if (rightSubtree === "") {\n // Right subtree is empty, include the left subtree\n return result + "(" + leftSubtree + ")";\n }\n\n // Both left and right subtrees are non-empty, include both in the result\n return result + "(" + leftSubtree + ")" + "(" + rightSubtree + ")";\n};\n\n```\n``` C# []\npublic class Solution {\n public string Tree2str(TreeNode root) {\n // Step 1: Base case - if the root is null, return an empty string\n if (root == null) return "";\n\n // Step 2: Start with the value of the current node as the result string\n string result = root.val.ToString();\n\n // Step 3: Recursively process the left and right subtrees\n string leftSubtree = Tree2str(root.left);\n string rightSubtree = Tree2str(root.right);\n\n // Step 4: Check conditions to determine the final result\n if (leftSubtree == "" && rightSubtree == "") {\n // Both left and right subtrees are empty, return the current result\n return result;\n }\n if (leftSubtree == "") {\n // Left subtree is empty, include empty parentheses for it and the right subtree\n return result + "()" + "(" + rightSubtree + ")";\n }\n if (rightSubtree == "") {\n // Right subtree is empty, include the left subtree\n return result + "(" + leftSubtree + ")";\n }\n\n // Both left and right subtrees are non-empty, include both in the result\n return result + "(" + leftSubtree + ")" + "(" + rightSubtree + ")";\n }\n}\n```\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9Time complexity: O(n)\nThe time complexity is primarily determined by the recursive function `tree2str`. In each recursive call, the code performs constant-time operations, and the recursion is called once for each node in the binary tree. Therefore, the time complexity is O(n), where n is the number of nodes in the binary tree.\n\n### \uD83C\uDFF9Space complexity: O(n)\n\nThe space complexity is influenced by the recursive calls and the depth of the recursion stack. In each recursive call, a constant amount of space is used for the local variables (result, leftSubtree, rightSubtree). The maximum depth of the recursion stack is equal to the height of the binary tree.\n\nIn the worst case, for a skewed binary tree (essentially a linked list), the height is n (number of nodes), leading to a space complexity of O(n). In the average case for a balanced binary tree, the height is log(n), resulting in a space complexity of O(log n).\n | 39 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
✅☑[C++/Java/Python/JavaScript] || Easy Approach || EXPLAINED🔥 | construct-string-from-binary-tree | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n\n\n1. **Preorder Traversal (pre Function):**\n\n - The `pre` function performs a preorder traversal of the binary tree.\n - At each node, it appends the node\'s value to the `ans` string.\n - If the node has either a left child or a right child (or both), it includes parentheses around the subtree represented by that child.\n - It recursively calls itself for the left and right subtrees.\n1. **String Representation:**\n\n - The `tree2str` function initiates the preorder traversal (`pre` function) and constructs the string representation of the binary tree.\n - After traversing and forming the string, it returns the final constructed string.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n string ans = ""; // Variable to store the final string representation of the tree\n\n // Helper function to perform preorder traversal of the tree and construct the string\n void pre(TreeNode* root) {\n if (root == nullptr) {\n return; // Base case: If the node is null, return\n }\n\n // Append the current node\'s value to the string\n ans += to_string(root->val);\n\n // If the current node has a left child or a right child, include parentheses\n if (root->left != nullptr || root->right != nullptr) {\n ans += "(";\n pre(root->left); // Recursive call to process the left subtree\n ans += ")";\n }\n\n // If the current node has a right child, include parentheses\n if (root->right != nullptr) {\n ans += "(";\n pre(root->right); // Recursive call to process the right subtree\n ans += ")";\n }\n }\n\n // Main function to convert the binary tree to the required string format\n string tree2str(TreeNode* root) {\n pre(root); // Call the helper function to construct the string\n return ans; // Return the final string representation of the tree\n }\n};\n\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\nstruct TreeNode {\n int val;\n struct TreeNode *left;\n struct TreeNode *right;\n};\n\nchar ans[1000]; // Variable to store the final string representation of the tree\n\n// Helper function to perform preorder traversal of the tree and construct the string\nvoid pre(struct TreeNode* root) {\n if (root == NULL) {\n return; // Base case: If the node is null, return\n }\n\n // Append the current node\'s value to the string\n sprintf(ans + strlen(ans), "%d", root->val);\n\n // If the current node has a left child or a right child, include parentheses\n if (root->left != NULL || root->right != NULL) {\n sprintf(ans + strlen(ans), "(");\n pre(root->left); // Recursive call to process the left subtree\n sprintf(ans + strlen(ans), ")");\n }\n\n // If the current node has a right child, include parentheses\n if (root->right != NULL) {\n sprintf(ans + strlen(ans), "(");\n pre(root->right); // Recursive call to process the right subtree\n sprintf(ans + strlen(ans), ")");\n }\n}\n\n// Main function to convert the binary tree to the required string format\nchar* tree2str(struct TreeNode* root) {\n ans[0] = \'\\0\'; // Initialize the string\n pre(root); // Call the helper function to construct the string\n return ans; // Return the final string representation of the tree\n}\n\n\n\n```\n```Java []\nclass Solution {\n StringBuilder ans = new StringBuilder(); // StringBuilder to store the final string representation\n\n // Helper function to perform preorder traversal of the tree and construct the string\n public void pre(TreeNode root) {\n if (root == null) {\n return; // Base case: If the node is null, return\n }\n\n // Append the current node\'s value to the StringBuilder\n ans.append(root.val);\n\n // If the current node has a left child or a right child, include parentheses\n if (root.left != null || root.right != null) {\n ans.append("(");\n pre(root.left); // Recursive call to process the left subtree\n ans.append(")");\n }\n\n // If the current node has a right child, include parentheses\n if (root.right != null) {\n ans.append("(");\n pre(root.right); // Recursive call to process the right subtree\n ans.append(")");\n }\n }\n\n // Main function to convert the binary tree to the required string format\n public String tree2str(TreeNode root) {\n pre(root); // Call the helper function to construct the string\n return ans.toString(); // Return the final string representation of the tree\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def tree2str(self, root):\n def pre(node):\n if not node:\n return\n\n # Append the current node\'s value to the string\n self.ans += str(node.val)\n\n # If the current node has a left child or a right child, include parentheses\n if node.left or node.right:\n self.ans += "("\n pre(node.left) # Recursive call to process the left subtree\n self.ans += ")"\n\n # If the current node has a right child, include parentheses\n if node.right:\n self.ans += "("\n pre(node.right) # Recursive call to process the right subtree\n self.ans += ")"\n\n self.ans = "" # String to store the final string representation\n pre(root) # Call the helper function to construct the string\n return self.ans # Return the final string representation of the tree\n\n\n\n```\n```javascript []\nlet ans = \'\'; // Variable to store the final string representation of the tree\n\n// Helper function to perform preorder traversal of the tree and construct the string\nfunction pre(root) {\n if (root === null) {\n return; // Base case: If the node is null, return\n }\n\n // Append the current node\'s value to the string\n ans += root.val.toString();\n\n // If the current node has a left child or a right child, include parentheses\n if (root.left !== null || root.right !== null) {\n ans += \'(\';\n pre(root.left); // Recursive call to process the left subtree\n ans += \')\';\n }\n\n // If the current node has a right child, include parentheses\n if (root.right !== null) {\n ans += \'(\';\n pre(root.right); // Recursive call to process the right subtree\n ans += \')\';\n }\n}\n\n// Main function to convert the binary tree to the required string format\nfunction tree2str(root) {\n ans = \'\'; // Initialize the string\n pre(root); // Call the helper function to construct the string\n return ans; // Return the final string representation of the tree\n}\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 11 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
😎 𝖇𝖊𝖆𝖙𝖘 100% | 𝕾𝖎𝖒𝖕𝖑𝖊 𝕻𝖗𝖊𝖔𝖗𝖉𝖊𝖗 𝕿𝖗𝖆𝖛𝖊𝖗𝖘𝖆𝖑 🚀💖 | construct-string-from-binary-tree | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires constructing a string representation of a binary tree using the preorder traversal approach. The challenge is to omit unnecessary empty parenthesis pairs without affecting the one-to-one mapping relationship between the string and the original binary tree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Base Case Check:**\n - If the current node is null (`root == nullptr`), return from the `preorder` function as there\'s nothing to process.\n\n2. **Process Current Node:**\n - Append the value of the current node to the result string (`ans`).\n\n3. **Handle Left Subtree:**\n - If there is a left child (`root->left`), add an opening parenthesis `"("` to the result string.\n - Recursively call `preorder` on the left child.\n - Add a closing parenthesis `")"` to the result string.\n\n4. **Handle Right Subtree:**\n - If there is a right child (`root->right`), add an opening parenthesis `"("` to the result string.\n - Recursively call `preorder` on the right child.\n - Add a closing parenthesis `")"` to the result string.\n\n**Visualization: \uD83C\uDF32**\n\nConsider the example: Input: `[1, 2, 3, null, 4]`\n\n```\n 1\n / \\\n 2 3\n /\n 4\n```\n\n**Preorder Traversal:**\n- Start at the root (1), then go left (2), then go right (3).\n- For each node, append its value and handle its left and right subtrees.\n\n**Construction Steps:**\n- 1 (append 1)\n- 1 (append "(" for left subtree) 2 (append ")" for left subtree)\n- 1 (append "(" for right subtree) 3 (append "(" for left subtree) 4 (append ")" for left subtree) (append ")" for right subtree)\n\n**Resulting String:**\n"1(2()(4))(3)"\n\n**Note:**\n- Empty parenthesis pairs are omitted where there are no child nodes.\n- The first pair cannot be omitted to maintain the one-to-one mapping relationship.\n\n**Code Explanation: \uD83E\uDDD1\u200D\uD83D\uDCBB**\n\n- The `tree2str` function initializes an empty string (`ans`) and calls `preorder` to construct the result.\n- The `preorder` function processes each node as described above, updating the result string accordingly.\n\nThis approach ensures that unnecessary empty parenthesis pairs are omitted while maintaining the correct one-to-one mapping relationship between the string and the original binary tree.\n\n# Complexity\n- Time complexity: O(N), where N is the number of nodes in the binary tree.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(H), where H is the height of the binary tree.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n void preorder(TreeNode* root,string& ans)\n {\n if(root == 0) return;\n\n ans += to_string(root->val);\n if(root->left or root->right)\n {\n ans += "(";\n preorder(root->left,ans);\n ans += ")";\n }\n if(root->right)\n {\n ans += "(";\n preorder(root->right,ans);\n ans += ")";\n }\n }\n string tree2str(TreeNode* root) {\n string ans;\n preorder(root,ans);\n return ans;\n }\n};\n```\n\n | 4 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
【Video】Give me 7 minutes - Recursion and Stack solution(Bonus) - How we think about a solution | construct-string-from-binary-tree | 1 | 1 | # Intuition\nCheck right child first.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/gV7MkiwMDS8\n\n\u25A0 Timeline of the video\n\n`0:05` How we create an output string\n`2:07` Coding\n`4:30` Time Complexity and Space Complexity\n`4:49` Step by step of recursion process\n`7:27` Step by step algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,377\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nThe description says "preorder traversal way", so we should traverse the tree in preorder way.\n\n```\nInput: root = [1,2,3,4]\nOutput: "1(2(4))(3)"\n```\nWe need to create output string with node value and parenthesis.\n\n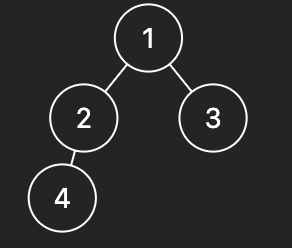\n\nBased on example 1 in the description, output string should be\n```\n"1(2(4))(3)"\nroot(= 1)(left(= 2)(left(= 4)))(right(= 3))\n```\nSo, when we have right child, we should create output string like this.\n\n```\nroot(left)(right)\n1(2)(3)\n```\nIf we don\'t have right child, we should create output string like this\n```\nroot(left)\n2(4)\n```\nWe will repeat those process.\n\nAnd when we create output string, we will check right child first. Why? Look at my solution code.\n```\nif root.right:\n return str(root.val) + \'(\' + dfs(root.left) + \')(\' + dfs(root.right) + \')\'\nif root.left:\n return str(root.val) + \'(\' + dfs(root.left) + \')\'\n\n```\nLet\'s change order of `root.left` and `root.right`.\n```\nif root.left:\n return str(root.val) + \'(\' + dfs(root.left) + \')\'\nif root.right:\n return str(root.val) + \'(\' + dfs(root.left) + \')(\' + dfs(root.right) + \')\'\n```\n\nWhat if we have both children and we check left child first, in that case, we cannot create right child because this program is executed.\n\n```\nreturn str(root.val) + \'(\' + dfs(root.left) + \')\'\n```\nNo right child in the string.\n\nLet\'s see dfs function one by one.\n\n\n\n```\nInput: root = [1,2,3,4]\n```\n\n```\nroot = 1\nWe have right child(= 3) \n\nroot(left)(right)\n1(left)(right)\n\n "1" Execute \u2193\nreturn str(root.val) + \'(\' + dfs(root.left) + \')(\' + dfs(root.right) + \')\'\n```\nGo to left\n```\nroot = 2\nWe don\'t have right child\n\nroot(left)\n2(left)\n "2" Execute \u2193\nreturn str(root.val) + \'(\' + dfs(root.left) + \')\'\n```\nGo to left.\n```\nroot = 4\nWe don\'t have both children, so return "4"\n\n "4"\nExecute return str(root.val)\n```\nGo back to root = 2\n```\nroot = 2\n\nroot(left)\nreturn 2(4)\n "2" "4" \nExecute return str(root.val) + \'(\' + dfs(root.left) + \')\'\n```\nGo back to root = 1\n```\nroot = 1\n\nroot(left)(right)\n1(2(4))(right)\n "1" Done\u2193 "2(4)" Execute \u2193\nreturn str(root.val) + \'(\' + dfs(root.left) + \')(\' + dfs(root.right) + \')\'\n```\nGo to right (= 3). No children. Just return "3"\n```\nroot = 3\nreturn "3"\n "3"\nExecute return str(root.val)\n```\nGo back to root = 1\n```\nroot = 1\n\nroot(left)(right)\n1(2(4))(3)\n "1" Done\u2193 "(2(4))" Done \u2193 "(3)"\nExecute return str(root.val) + \'(\' + dfs(root.left) + \')(\' + dfs(root.right) + \')\'\n\n```\n```\nOutput: 1(2(4))(3)\n```\n\nEasy!\uD83D\uDE04\nLet\'s see real algorithm!\n\n\n---\n\n1. **Base Case Check:**\n - The DFS function checks if the current node (`root`) is `None` (i.e., if it doesn\'t exist). If so, it returns an empty string.\n\n2. **String Construction:**\n - If the current node has a right child (`root.right` exists), the function constructs a string by combining the value of the current node (`str(root.val)`) with its left subtree (`dfs(root.left)`) and right subtree (`dfs(root.right)`). The substrings are enclosed in parentheses.\n\n ```python\n if root.right:\n return str(root.val) + \'(\' + dfs(root.left) + \')(\' + dfs(root.right) + \')\'\n ```\n\n3. **Alternative String Construction:**\n - If the current node doesn\'t have a right child but has a left child, the function constructs a string by combining the value of the current node (`str(root.val)`) with its left subtree (`dfs(root.left)`). The substrings are enclosed in parentheses.\n\n ```python\n if root.left:\n return str(root.val) + \'(\' + dfs(root.left) + \')\'\n ```\n\n4. **Leaf Node Case:**\n - If the current node is a leaf node (i.e., it has neither left nor right child), the function returns a string containing only the value of the leaf node.\n\n ```python\n return str(root.val)\n ```\n\n5. **Return Result:**\n - The `tree2str` method returns the result of the DFS function applied to the root of the binary tree.\n\n ```python\n return dfs(root)\n ```\n\n### Summary:\n\n- The algorithm uses DFS to traverse the binary tree and construct a string representation based on the specified rules.\n- The conditions in the DFS function are designed to skip unnecessary parentheses pairs and create a compact, one-to-one mapping relationship between the string and the original binary tree.\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\nEach node is visited exactly once, so the time complexity is $$O(n)$$, where n is the number of nodes in the tree.\n\n- Space complexity: $$O(n)$$\n\nIn the worst case, we have a skewed tree.\n\n```python []\nclass Solution:\n def tree2str(self, root: Optional[TreeNode]) -> str:\n\n def dfs(root):\n if not root:\n return \'\'\n if root.right:\n return str(root.val) + \'(\' + dfs(root.left) + \')(\' + dfs(root.right) + \')\'\n if root.left:\n return str(root.val) + \'(\' + dfs(root.left) + \')\'\n \n return str(root.val)\n \n return dfs(root) \n```\n```javascript []\nvar tree2str = function(root) {\n function dfs(node) {\n if (!node) {\n return \'\';\n }\n if (node.right) {\n return `${node.val}(${dfs(node.left)})(${dfs(node.right)})`;\n }\n if (node.left) {\n return `${node.val}(${dfs(node.left)})`;\n }\n return `${node.val}`;\n }\n\n return dfs(root); \n};\n```\n```java []\nclass Solution {\n public String tree2str(TreeNode root) {\n if (root == null) {\n return "";\n }\n\n StringBuilder result = new StringBuilder();\n\n dfs(root, result);\n\n return result.toString(); \n }\n\n private void dfs(TreeNode node, StringBuilder result) {\n if (node == null) {\n return;\n }\n\n result.append(node.val);\n\n if (node.left != null || node.right != null) {\n result.append("(");\n dfs(node.left, result);\n result.append(")");\n\n if (node.right != null) {\n result.append("(");\n dfs(node.right, result);\n result.append(")");\n }\n }\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n string tree2str(TreeNode* root) {\n if (!root) {\n return "";\n }\n\n string result;\n dfs(root, result);\n\n return result; \n }\n\nprivate:\n void dfs(TreeNode* node, string& result) {\n if (!node) {\n return;\n }\n\n result += to_string(node->val);\n\n if (node->left || node->right) {\n result += "(";\n dfs(node->left, result);\n result += ")";\n\n if (node->right) {\n result += "(";\n dfs(node->right, result);\n result += ")";\n }\n }\n }\n};\n```\n\n---\n\n\n# Bonus - Stack solution\n\nIn most posts, the problems were solved using recursion, so I tried solving it using a stack.\n\nIf possible, please let me know about any optimizations or improvements, since I didn\'t have time to think too much. lol\n\n```python []\nclass Solution:\n def tree2str(self, root: Optional[TreeNode]) -> str:\n # Check if the tree is empty\n if not root:\n return ""\n \n # Initialize an empty result string\n res = ""\n # Initialize a stack for iterative traversal\n stack = [root]\n # Use a set to track visited nodes\n visited = set()\n \n # Iterate through the tree using a stack\n while stack:\n # Get the current node from the top of the stack\n cur = stack[-1]\n \n # If the current node is already visited, pop it from the stack and close the parenthesis\n if cur in visited:\n stack.pop()\n res += ")"\n else:\n # If the current node is not visited, mark it as visited and add its value to the result\n visited.add(cur)\n res += f"({cur.val}"\n \n # If the current node has no left child and a right child, add an empty pair of parentheses\n if not cur.left and cur.right:\n res += "()"\n \n # Add the right child to the stack if it exists\n if cur.right:\n stack.append(cur.right)\n # Add the left child to the stack if it exists\n if cur.left:\n stack.append(cur.left)\n \n # Return the result string with leading \'(\' and trailing \')\' removed\n return res[1:-1]\n\n```\n```javascript []\nvar tree2str = function(root) {\n // Check if the tree is empty\n if (!root) {\n return "";\n }\n \n // Initialize an empty result string\n let res = "";\n // Initialize a stack for iterative traversal\n const stack = [root];\n // Use a set to track visited nodes\n const visited = new Set();\n \n // Iterate through the tree using a stack\n while (stack.length > 0) {\n // Get the current node from the top of the stack\n const cur = stack[stack.length - 1];\n \n // If the current node is already visited, pop it from the stack and close the parenthesis\n if (visited.has(cur)) {\n stack.pop();\n res += ")";\n } else {\n // If the current node is not visited, mark it as visited and add its value to the result\n visited.add(cur);\n res += `(${cur.val}`;\n \n // If the current node has no left child and a right child, add an empty pair of parentheses\n if (!cur.left && cur.right) {\n res += "()";\n }\n \n // Add the right child to the stack if it exists\n if (cur.right) {\n stack.push(cur.right);\n }\n \n // Add the left child to the stack if it exists\n if (cur.left) {\n stack.push(cur.left);\n }\n }\n }\n \n // Return the result string with leading \'(\' and trailing \')\' removed\n return res.substring(1, res.length - 1); \n};\n\n```\n```java []\nclass Solution {\n public String tree2str(TreeNode root) {\n // Check if the tree is empty\n if (root == null) {\n return "";\n }\n\n // Initialize a StringBuilder to efficiently build the result string\n StringBuilder res = new StringBuilder();\n // Initialize a stack for iterative traversal\n Stack<TreeNode> stack = new Stack<>();\n // Use a set to track visited nodes\n Set<TreeNode> visited = new HashSet<>();\n stack.push(root);\n\n // Iterate through the tree using a stack\n while (!stack.isEmpty()) {\n // Get the current node from the top of the stack\n TreeNode cur = stack.peek();\n\n // If the current node is already visited, pop it from the stack and close the parenthesis\n if (visited.contains(cur)) {\n stack.pop();\n res.append(")");\n } else {\n // If the current node is not visited, mark it as visited and add its value to the result\n visited.add(cur);\n res.append("(").append(cur.val);\n\n // If the current node has no left child and a right child, add an empty pair of parentheses\n if (cur.left == null && cur.right != null) {\n res.append("()");\n }\n\n // Add the right child to the stack if it exists\n if (cur.right != null) {\n stack.push(cur.right);\n }\n\n // Add the left child to the stack if it exists\n if (cur.left != null) {\n stack.push(cur.left);\n }\n }\n }\n\n // Return the result string with leading \'(\' and trailing \')\' removed\n return res.substring(1, res.length() - 1);\n } \n}\n\n```\n```C++ []\nclass Solution {\npublic:\n string tree2str(TreeNode* root) { // Time: O(n), Space: O(n)\n // Check if the tree is empty\n if (!root) return "";\n \n // Initialize an empty result string\n string res;\n // Initialize a stack for iterative traversal\n stack<TreeNode*> st;\n // Use a set to track visited nodes\n unordered_set<TreeNode*> visited;\n // Push the root onto the stack\n st.push(root);\n \n // Iterate through the tree using a stack\n while (!st.empty()) {\n // Get the current node from the top of the stack\n TreeNode* cur = st.top();\n \n // If the current node is already visited, pop it from the stack and close the parenthesis\n if (visited.count(cur)) {\n st.pop();\n res += ")";\n } else {\n // If the current node is not visited, mark it as visited and add its value to the result\n visited.insert(cur);\n res += "(" + to_string(cur->val);\n \n // If the current node has no left child and a right child, add an empty pair of parentheses\n if (!cur->left && cur->right) {\n res += "()";\n }\n \n // Add the right child to the stack if it exists\n if (cur->right) st.push(cur->right);\n \n // Add the left child to the stack if it exists\n if (cur->left) st.push(cur->left);\n }\n }\n \n // Return the result string with leading \'(\' and trailing \')\' removed\n return res.substr(1, res.length() - 2);\n }\n};\n\n```\n\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/binary-tree-inorder-traversal/solutions/4380244/video-give-me-5-minutes-recursive-and-stack-solutionbonus-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/TKMxiXRzDZ0\n\n\u25A0 Timeline of the video\n`0:04` How to implement inorder, preorder and postorder\n`1:16` Coding (Recursive)\n`2:14` Time Complexity and Space Complexity\n`2:37` Explain Stack solution\n`7:22` Coding (Stack)\n`8:45` Time Complexity and Space Complexity\n`8:59` Step by step algorithm with my stack solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/largest-odd-number-in-string/solutions/4372831/video-give-me-1-minute-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/f-hyawcTl8U\n\n\u25A0 Timeline of the video\n\n`0:04` Coding\n`1:18` Time Complexity and Space Complexity\n`1:31` Step by step algorithm with my solution code\n\n | 56 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Python DFS recursion return f string directly | construct-string-from-binary-tree | 0 | 1 | # Intuition\nUse recursion. Instead of building the string by appending a list or using +=, we return the string directly in our recursive call using f strings.\n\n# Approach\nAt each recursive call, we assume that the next call "just works" and returns the correct answer. So when we are in the dfs call, we need to ask what are the cases.\n\nBase case: \nnode is None, so return ""\n\nCase 1: Right child exists.\nMeans there will be own val(left stuff)(right stuff)\n\nCase 2: if not case 1, check if left child exists. Means we do not need the brackets for the right child. So the form will be own val(left stuff)\n\nCase 3: means no child. Just return the value itself\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def tree2str(self, root: Optional[TreeNode]) -> str:\n\n def dfs(node):\n if not node:\n return ""\n if node.right:\n return f"{node.val}({dfs(node.left)})({dfs(node.right)})"\n elif node.left:\n return f"{node.val}({dfs(node.left)})"\n else:\n return f"{node.val}"\n return dfs(root)\n\n \n \n``` | 4 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Simple DFS code | construct-string-from-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def tree2str(self, root: Optional[TreeNode]) -> str:\n res = []\n def preorder(root):\n if not root:\n return \n res.append(\'(\')\n res.append(str(root.val))\n if not root.left and root.right: #only condition when we are not going to eliminate empty parentheses \n res.append("()") \n preorder(root.left)\n preorder(root.right)\n res.append(")")\n preorder(root)\n return "".join(res[1:-1])\n``` | 2 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Python3 Solution | construct-string-from-binary-tree | 0 | 1 | \n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def tree2str(self, root: Optional[TreeNode]) -> str:\n ans=[]\n def preorder(root):\n if not root:\n return\n ans.append("(")\n ans.append(str(root.val))\n if not root.left and root.right:\n ans.append("()")\n preorder(root.left)\n preorder(root.right)\n ans.append(")")\n preorder(root) \n return "".join(ans)[1:-1]\n``` | 2 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
✅ One Line Solution | construct-string-from-binary-tree | 0 | 1 | # Code #1.1 - Oneliner\nTime complexity: $$O(n^2)$$. Space complexity: $$O(n)$$.\nDisclaimer: this code is not a good example to use in a real project, it is written for fun mostly.\n```\nclass Solution:\n def tree2str(self, r: Optional[TreeNode]) -> str:\n return f\'{r.val}\' + (f\'({self.tree2str(r.left)})\' if r.left or r.right else \'\') + (f\'({self.tree2str(r.right)})\' if r.right else \'\') if r else \'\'\n```\n\n# Code #1.2 - Unwrapped\n\n```\nclass Solution:\n def tree2str(self, r: Optional[TreeNode]) -> str:\n if not r:\n return \'\'\n\n s = f\'{r.val}\'\n if r.left or r.right:\n s += f\'({self.tree2str(r.left)})\'\n if r.right:\n s += f\'({self.tree2str(r.right)})\'\n \n return s\n```\n\n# Code #2 - Using One List To Build A Result\nTime complexity: $$O(n)$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def tree2str(self, r: Optional[TreeNode]) -> str:\n def dfs(r, result):\n if not r:\n return\n\n result.append(f\'{r.val}\')\n if r.left or r.right:\n result.append(\'(\')\n dfs(r.left, result)\n result.append(\')\')\n if r.right:\n result.append(\'(\')\n dfs(r.right, result)\n result.append(\')\')\n\n return result\n \n return \'\'.join(dfs(r, []))\n```\n\n# Code #3 - Using Generator\nTime complexity: $$O(n)$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def tree2str(self, r: Optional[TreeNode]) -> str:\n def dfs(r):\n if not r:\n return\n\n yield f\'{r.val}\'\n if r.left or r.right:\n yield \'(\'\n yield from dfs(r.left)\n yield \')\'\n if r.right:\n yield \'(\'\n yield from dfs(r.right)\n yield \')\'\n \n return \'\'.join(dfs(r))\n``` | 1 | Given the `root` of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.
Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
**Example 1:**
**Input:** root = \[1,2,3,4\]
**Output:** "1(2(4))(3) "
**Explanation:** Originally, it needs to be "1(2(4)())(3()()) ", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3) "
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:** "1(2()(4))(3) "
**Explanation:** Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Solution | find-duplicate-file-in-system | 1 | 1 | ```C++ []\nstruct trie {\n trie* content[75] {};\n vector<string> files;\n};\nclass Solution {\n trie root;\n void dfs(vector<vector<string>>& res, trie* node) {\n if(node->files.size() >= 2) {\n res.push_back(node->files);\n }\n for(int i = 0; i < 75; ++i) {\n if(node->content[i] != nullptr) dfs(res, node->content[i]);\n }\n }\npublic:\n vector<vector<string>> findDuplicate(vector<string>& paths) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n\n for(auto& files : paths) {\n int i = 0, n = files.length();\n while(files[i] != \' \') ++i;\n string dir(files.substr(0, i++));\n\n while(i < n) {\n int j = i;\n while(files[i] != \'(\') ++i;\n string filename(files.substr(j, i++ - j));\n \n trie* node = &root;\n while(files[i] != \')\') {\n char c = files[i++] - \'0\';\n if(node->content[c] == nullptr) {\n node->content[c] = new trie;\n }\n node = node->content[c];\n }\n node->files.push_back(dir + \'/\' + filename);\n i += 2;\n } \n }\n vector<vector<string>> res;\n dfs(res, &root); //Collect the duplicates using dfs\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n D = defaultdict(list)\n for path in paths:\n directory, *files = path.split()\n for file in files:\n filename, content = file.split(\'(\')\n D[content].append(directory + \'/\' + filename)\n return [paths for paths in D.values() if len(paths) > 1]\n```\n\n```Java []\nclass Solution {\n public List<List<String>> findDuplicate(String[] paths) {\n \tList<List<String>> res = new ArrayList<>();\n \tMap<String, List<String>> map = new HashMap<>();\n \tfor (String path : paths) {\n \t\tString[] files = path.split(" ");\n String filePath = files[0] + "/";\n \t\tfor (int i = 1; i < files.length; i++) {\n \t\t\tint start = files[i].indexOf(\'(\'), end = files[i].length() - 1;\n \t\t\tif (start < 0 || files[i].charAt(end) != \')\')\n \t\t\t\tcontinue;\n \t\t\tString fileContent = files[i].substring(start + 1, end);\n \t\t\tmap.computeIfAbsent(fileContent, x -> new ArrayList<String>()).add(filePath + files[i].substring(0, start));\n \t\t}\n \t}\n \tfor (List<String> list : map.values())\n \t\tif (list.size() > 1)\n \t\t\tres.add(list);\n \treturn res;\n }\n}\n```\n | 1 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
609: Time 95.76%, Solution with step by step explanation | find-duplicate-file-in-system | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create a defaultdict object named "content_dict" that will store the file contents as keys and the file paths as values.\n2. Iterate over each path in the "paths" list.\n3. Split the path string into separate parts based on spaces, so that the first part is the directory and the remaining parts are individual files.\n4. For each file in the path, split the file string into separate parts based on the opening parenthesis. The first part is the file name, and the second part (without the closing parenthesis) is the file content.\n5. Append the directory path and file name together as a string, and add it to the list of file paths stored under the corresponding file content key in the "content_dict" dictionary.\n6. After iterating over all paths, create a new list of lists by iterating over each unique file content key in the "content_dict" dictionary.\n7. If the list of file paths stored under the current file content key has a length greater than 1 (meaning there are at least two files with the same content), add it to the new list of lists.\n8. Return the new list of lists of file paths.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n content_dict = defaultdict(list)\n \n for path in paths:\n files = path.split(\' \')\n directory = files[0]\n \n for file in files[1:]:\n name, content = file.split(\'(\')\n content_dict[content[:-1]].append(directory + \'/\' + name)\n \n return [content_dict[content] for content in content_dict if len(content_dict[content]) > 1]\n\n``` | 1 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | find-duplicate-file-in-system | 0 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n**C++**\n\n```cpp\nclass Solution {\npublic:\n // custom split template\n vector<string> split(string str, char delim) {\n string line;\n vector<string> res;\n stringstream ss(str);\n while (getline(ss, line, delim)) res.push_back(line);\n return res;\n }\n \n // steps\n // 1. for each path, split by the \' \', then get the directory path, file name and file content\n // 2. combine the directory path and file name\n // 3. group directoryPath/fileName by file content using hash map\n // 4. build the final ans \n vector<vector<string>> findDuplicate(vector<string>& paths) {\n vector<vector<string>> ans;\n unordered_map<string, vector<string>> m;\n for (auto p : paths) {\n vector<string> path = split(p, \' \');\n string directoryPath;\n for (int i = 0; i < path.size(); i++) {\n if (i == 0) {\n directoryPath = path[i];\n } else {\n // e.g. 1.txt\n string fileName = path[i].substr(0, path[i].find(\'(\'));\n // e.g. abcd\n string fileContent = path[i].substr(path[i].find(\'(\') + 1, path[i].find(\')\') - path[i].find(\'(\') - 1);\n // e.g. efgh: ["root/a/2.txt","root/c/d/4.txt","root/4.txt"]\n m[fileContent].push_back(directoryPath + "/" + fileName);\n }\n }\n }\n // build the final answer\n for (auto x : m) {\n // check if there is duplicate\n // e.g. ["root/a 1.txt(abcd) 2.txt(efsfgh)","root/c 3.txt(abdfcd)","root/c/d 4.txt(efggdfh)"]\n if (x.second.size() > 1) {\n // x.second is already the full list of paths\n ans.push_back(x.second); \n }\n }\n return ans;\n }\n};\n```\n\n**Python**\n\n```py\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n m = defaultdict(list)\n for p in paths:\n # 1. split the string by \' \'\n path = p.split()\n # the first string is the directory path\n # the rest of them are just file names with content\n directoryPath, rest = path[0], path[1:]\n # for each file names with content\n for f in rest:\n # we retrieve the file name and the file content\n fileName, fileContent = f.split(\'(\')[0], f.split(\'(\')[1][:-1]\n # then group {directoryPath}/{fileName} by file content\n m[fileContent].append("{}/{}".format(directoryPath, fileName))\n # return the file list only when the size is greater than 1, meaning they are duplicate files\n return [m[k] for k in m.keys() if len(m[k]) > 1]\n``` | 28 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
Easy python 10 lines solution using hashmap | find-duplicate-file-in-system | 0 | 1 | ```\nfrom collections import defaultdict\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n dic=defaultdict(lambda :[])\n for i in range(len(paths)):\n st=paths[i]\n lst=st.split(" ")\n for j in range(1,len(lst)):\n sp=lst[j].index("(")\n dic[lst[j][sp:]].append(lst[0]+"/"+lst[j][:sp])\n return [dic[i] for i in dic if len(dic[i])>1]\n``` | 12 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
Regex Solution Python [Easy] | find-duplicate-file-in-system | 0 | 1 | ```\nimport re\n\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n \n\t\t# this regex has two group: \n\t\t# 1. a file name group \n\t\t# 2. a content group\n\t\t#\n\t\t# Ex: "root/a 1.txt(abcd) 2.txt(efgh)"\n\t\t# \n\t\t# Output: [(\'1.txt\', \'abcd\'), (\'2.txt\', \'efgh\')]\n #\n\t\tcontent_regex = re.compile("(\\w+.txt)\\((.*?)\\)", re.IGNORECASE)\n\t\t\n\t\t# hashmap to keep everything\n\t\t#\n d = defaultdict(list)\n\t\t\n\t\t# go through each path\n\t\t# \n for path in paths:\n\t\t\t\n\t\t\t# a regex expression is not needed as the dir path\n\t\t\t# is always the first item and is seperated by a space\n\t\t\t#\n root = path.split(" ")[0]\n file = re.findall(content_regex, path)\n \n for file_name, content in file:\n \n\t\t\t\t# store a list of file plus its directory under the content of each file\n\t\t\t\t#\n d[content].append(root + "/" + file_name) \n \n\t\t# filtering out anything that has a length that is smaller than 1\n\t\t# since it wouldn\'t be a group\n\t\t#\n return list(filter(lambda x: len(x) > 1, d.values())) \n``` | 2 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
[ Python ] ✅✅ Simple Python Solution Using Dictionary | HashMap🥳✌👍 | find-duplicate-file-in-system | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 175 ms, faster than 35.76% of Python3 online submissions for Find Duplicate File in System.\n# Memory Usage: 23.6 MB, less than 76.61% of Python3 online submissions for Find Duplicate File in System.\n\n\tclass Solution:\n\t\tdef findDuplicate(self, paths: List[str]) -> List[List[str]]:\n\n\t\t\tresult = []\n\n\t\t\tdirectory = {}\n\n\t\t\tfor path in paths:\n\n\t\t\t\tpath = path.split()\n\n\t\t\t\tdir_name = path[0]\n\n\t\t\t\tfor file in path[1:]:\n\n\t\t\t\t\tstart_index = file.index(\'(\')\n\t\t\t\t\tend_index = file.index(\')\')\n\n\t\t\t\t\tcontent = file[start_index + 1 : end_index ]\n\n\t\t\t\t\tif content not in directory:\n\n\t\t\t\t\t\tdirectory[content] = [dir_name + \'/\' + file[ : start_index]]\n\t\t\t\t\telse:\n\t\t\t\t\t\tdirectory[content].append(dir_name + \'/\' + file[ : start_index])\n\n\n\t\t\tfor key in directory:\n\n\t\t\t\tif len(directory[key]) > 1:\n\t\t\t\t\tresult.append(directory[key])\n\n\t\t\treturn result\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D | 2 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
Python || Dictionary || Easy Approach | find-duplicate-file-in-system | 0 | 1 | ```\n\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n contents = defaultdict(list)\n res = list()\n for direc in paths:\n d = direc.split()\n for i in range(1, len(d)):\n x = d[i].split("(")\n cont = x[1][:-1]\n file_name = d[0] + "/" + x[0]\n contents[cont].append(file_name)\n \n for file in contents:\n if len(contents[file]) > 1:\n res.append(contents[file])\n \n return res\n \n \n | 1 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
pythonic | find-duplicate-file-in-system | 0 | 1 | ```\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n data = defaultdict(list)\n for path in paths:\n directory, files = path.split(" ", 1)\n for file in files.split():\n file_content = file[file.index("("):-1]\n data[file_content].append(directory+"/"+file[0:file.index("(")])\n \n return [v for k, v in data.items() if len(v) >= 2]\n``` | 1 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
pretty short python solution using hashmap | find-duplicate-file-in-system | 0 | 1 | ```\nclass Solution:\n def findDuplicate(self, paths: List[str]) -> List[List[str]]:\n d=defaultdict(list)\n for i in paths:\n dirs=i.split()\n files=[dirs[k] for k in range(1,len(dirs))]\n for j in range(len(files)):\n val=files[j].split(\'(\')\n d[val[-1]].append("".join([dirs[0],\'/\',val[0]]))\n res=[d[i] for i in d if len(d[i])>1]\n return res | 1 | Given a list `paths` of directory info, including the directory path, and all the files with contents in this directory, return _all the duplicate files in the file system in terms of their paths_. You may return the answer in **any order**.
A group of duplicate files consists of at least two files that have the same content.
A single directory info string in the input list has the following format:
* `"root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content) "`
It means there are `n` files `(f1.txt, f2.txt ... fn.txt)` with content `(f1_content, f2_content ... fn_content)` respectively in the directory "`root/d1/d2/.../dm "`. Note that `n >= 1` and `m >= 0`. If `m = 0`, it means the directory is just the root directory.
The output is a list of groups of duplicate file paths. For each group, it contains all the file paths of the files that have the same content. A file path is a string that has the following format:
* `"directory_path/file_name.txt "`
**Example 1:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)","root 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt","root/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Example 2:**
**Input:** paths = \["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"\]
**Output:** \[\["root/a/2.txt","root/c/d/4.txt"\],\["root/a/1.txt","root/c/3.txt"\]\]
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 3000`
* `1 <= sum(paths[i].length) <= 5 * 105`
* `paths[i]` consist of English letters, digits, `'/'`, `'.'`, `'('`, `')'`, and `' '`.
* You may assume no files or directories share the same name in the same directory.
* You may assume each given directory info represents a unique directory. A single blank space separates the directory path and file info.
**Follow up:**
* Imagine you are given a real file system, how will you search files? DFS or BFS?
* If the file content is very large (GB level), how will you modify your solution?
* If you can only read the file by 1kb each time, how will you modify your solution?
* What is the time complexity of your modified solution? What is the most time-consuming part and memory-consuming part of it? How to optimize?
* How to make sure the duplicated files you find are not false positive? | null |
Solution | valid-triangle-number | 1 | 1 | ```C++ []\ntypedef vector<int>::iterator vit;\nclass Solution {\npublic:\n int triangleNumber(vector<int>& nums) {\n if ( nums.size() < 3 ) return 0;\n vit b = nums.begin(), e = nums.end();\n sort(b, e);\n int res = 0;\n for ( vit k = b+2; k != e; ++k ){\n vit i = b, j = k-1;\n while ( i < j ){\n if ( *i + *j > *k ){\n res += j - i;\n --j;\n }\n else{\n ++i;\n }\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def triangleNumber(self, nums: List[int]) -> int:\n nums.sort()\n \n fgtoe = [-1] * (2000+1)\n j = 0\n for i in range(len(fgtoe)):\n while j < len(nums) and nums[j] < i:\n j += 1\n fgtoe[i] = j\n \n ctr = 0\n rs = len(nums) * (len(nums) - 1) // 2 - 1\n rss = 0\n for ai in range(0, len(nums)-2):\n nai = nums[ai]\n if nai != 0:\n ctr += sum(fgtoe[nai + nums[bi]] for bi in range(ai+1, len(nums)-1))\n rss += rs\n rs -= ai+2\n return ctr - rss\n```\n\n```Java []\nclass Solution {\n public int triangleNumber(int[] nums) {\n if (nums == null || nums.length <= 2) {\n return 0;\n }\n Arrays.sort(nums);\n\n int[] indexMap = new int[2001];\n for (int i = 0; i < indexMap.length; ++i) {\n indexMap[i] = -1;\n }\n for (int i = 0; i < nums.length; ++i) {\n indexMap[nums[i]] = i;\n }\n for (int i = 1; i < indexMap.length; ++i) {\n if (indexMap[i] == -1) {\n indexMap[i] = indexMap[i - 1];\n }\n }\n int res = 0;\n for (int i = 0; i < nums.length; ++i) {\n for (int j = i + 1; j < nums.length; ++j) {\n if (nums[i] + nums[j] - 1 >= 0 && nums[i] + nums[j] - 1 <= 2000) {\n res += Math.max(0, indexMap[nums[i] + nums[j] - 1] - j);\n }\n }\n }\n return res;\n }\n}\n```\n | 1 | Given an integer array `nums`, return _the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle_.
**Example 1:**
**Input:** nums = \[2,2,3,4\]
**Output:** 3
**Explanation:** Valid combinations are:
2,3,4 (using the first 2)
2,3,4 (using the second 2)
2,2,3
**Example 2:**
**Input:** nums = \[4,2,3,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000` | null |
Full Explanation + Python 2 line | valid-triangle-number | 0 | 1 | ## Solution 1 :\n## What Q asked to do :\n```\nnums = [0,0,10,15,17,19,20,22,25,26,30,31,37] (sorted version)\n\nIf nums[i] is not 0 as with 0 length a triangle is not possible :\n_________________________________________________________________\n\nfor a triangle we need 3 length and if a+b>c and a+c>b and b+c>a BUT since we are \'sorting\'\nwe need to check only one condition, "a+b>c"\n\n nums[2] + nums[3] = 10 + 15 = 25. \n Now with this summation of these TWO FIXED VALUE we will compare it with other values :\n \nnums = [0,0, 10,15, 17,19,20,22, 25,26,30,31,37] (sorted version)\n |___| |__________| |\n | | |_____ We stop here as it defies the rule "a+b>c"\nFixed Value ---| These 4 values (25>25 -- False)\nSummation = 25 are less than 25\n and satisfy the \n rule a+b>c\n\nSince the list is sorted, we can find the FIRST VALUE WHICH IS EQUAL OR GREATER THAN THE \nSUMMATION with lower_bound IN CPP and bisect_left in Python.\n\nWe checked for 10,15,17 10,15,19 10,15,20 ...... what about for 10,17,19 10,17,20?\n\nI believe you got the idea now.\n```\n```CPP []\nclass Solution \n{\npublic:\n int triangleNumber(vector<int>& nums) \n {\n sort(begin(nums), end(nums));\n int lb, count = 0, ni = nums.size()-2, nj = nums.size()-1;\n for(int i=0; i<ni; i++)\n {\n for(int j=i+1; j<nj ;j++)\n {\n lb = lower_bound(nums.begin()+j+1, nums.end(), nums[i]+nums[j]) - nums.begin();\n count += lb - j -1;\n }\n }\n return count;\n }\n};\n```\n```Python []\nclass Solution:\n def triangleNumber(self, nums: List[int]) -> int:\n nums.sort()\n return sum( bisect_left(nums, nums[i]+nums[j]) - j-1 for i in range(len(nums)-2) if nums[i]!=0 for j in range(i+1, len(nums)-1) )\n```\n```\nTime complexity : O(n^2 logn) as for every O(n^2) we did logn operation\nSpace complexity : O(1)\n```\n\n## Modification in solution 1\n```\nnums = [0,0, 10,15, 17,19,20,22, 25,26,30,31,37] (sorted version)\n |___| |__________| |\n | |_____ We stop here.\n 25 \n\nnums = [0,0, 10,15,17,19,20,22, 25,26,30,31,37] (sorted version)\n |_____| |\n | |_____ For 27 start from here.\n 27\n\nIf for the summation of 25, 17,19,20,22 are true, then for 27 19,20,22 already true as 27>25\n |_________|\nso start from previous inside the loop of \'j\'. for every \'i\', lb = i+2.\nNow the lower_bound won\'t even run O(n) inside the nested loop till j stops, so TC is O(n^2) \n\nfor testcases : nums = [1,2,3,4,5]\nfor i = 0, j = 1 : bisect_left/lower_bound will return 1 for searching 1+2 = 3\nsince the index of 3 is 2, then j will be 2 also, but we don\'t want to start our\nlower_bound/bisect_left at the same index of j, so I added (lb == j) which will handle this. \n``` \n```CPP []\nclass Solution \n{\npublic:\n int triangleNumber(vector<int>& nums) \n {\n sort(begin(nums), end(nums));\n int lb = 0, count = 0, ni = nums.size()-2, nj = nums.size()-1;\n for(int i=0; i<ni; i++)\n {\n if(nums[i] == 0) continue;\n lb = i+2;\n for(int j=i+1; j<nj; j++)\n {\n lb = lower_bound(begin(nums)+lb+(lb==j), end(nums), nums[i]+nums[j]) - begin(nums);\n count += lb - j-1;\n }\n }\n return count;\n }\n};\n```\n```CPP []\nclass Solution \n{\npublic:\n int triangleNumber(vector<int>& nums) \n {\n sort(begin(nums), end(nums));\n int lb = 0, count = 0, ni = nums.size()-2, nj = nums.size()-1;\n for(int i=0; i<ni; i++)\n {\n if(nums[i] == 0) continue;\n lb = i+2;\n for(int j=i+1; j<nj; j++)\n {\n // without lower bound\n while(lb<nums.size() && nums[i]+nums[j]>nums[lb])\n lb++;\n count += lb - j-1;\n }\n }\n return count;\n }\n};\n```\n```Python []\nclass Solution:\n def triangleNumber(self, nums: List[int]) -> int:\n nums.sort()\n count = lb = 0\n for i in range(len(nums)-2):\n if nums[i] == 0: continue\n lb = i + 2\n for j in range(i+1, len(nums)-1):\n lb = bisect_left(nums, nums[i]+nums[j], lb+(lb==j))\n count += lb - j - 1\n \n return count\n```\n```\nTime Complexity : O(n^2) which i explained why.\nSpace Complexity : O(1)\n```\n## If the post was helpful to you, an upvote will really make me happy:) | 2 | Given an integer array `nums`, return _the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle_.
**Example 1:**
**Input:** nums = \[2,2,3,4\]
**Output:** 3
**Explanation:** Valid combinations are:
2,3,4 (using the first 2)
2,3,4 (using the second 2)
2,2,3
**Example 2:**
**Input:** nums = \[4,2,3,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000` | null |
[Python3] | binary-search | valid-triangle-number | 0 | 1 | ```\nclass Solution:\n def triangleNumber(self, nums: List[int]) -> int:\n n=len(nums)\n ans=0\n nums.sort()\n for i in range(n):\n for j in range(i+1,n):\n s2s=nums[i]+nums[j]\n ind=bisect.bisect_left(nums,s2s)\n ans+=max(0,ind-j-1)\n return ans\n``` | 3 | Given an integer array `nums`, return _the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle_.
**Example 1:**
**Input:** nums = \[2,2,3,4\]
**Output:** 3
**Explanation:** Valid combinations are:
2,3,4 (using the first 2)
2,3,4 (using the second 2)
2,2,3
**Example 2:**
**Input:** nums = \[4,2,3,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000` | null |
611: Solution with step by step explanation | valid-triangle-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Sort the input array "nums" in ascending order.\n2. Initialize a variable "count" to 0, which will keep track of the number of valid triangles.\n3. Loop through all possible triplets in the array, using two pointers "i" and "j".\n4. For each triplet, initialize a third pointer "k" to "i + 2".\n5. If the first element of the triplet is 0, skip to the next element by using the "continue" statement.\n6. If all remaining elements in the array are zero, break out of the loop by using the "break" statement.\n7. Loop through all possible second elements of the triplet, starting at "j = i + 1" and ending at "len(nums) - 1".\n8. Move the third pointer "k" to the first element that is greater than or equal to the sum of the first two elements.\n9. Calculate the number of valid triangles that can be formed with the current pair of first two elements as "k - j - 1", and add it to the "count" variable.\n10. Return the final value of "count", which represents the total number of valid triangles that can be formed from the input array.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def triangleNumber(self, nums: List[int]) -> int:\n nums.sort() # Sort the input array\n count = 0 # Initialize count of valid triangles\n \n # Loop through all possible triplets using two pointers\n for i in range(len(nums) - 2):\n k = i + 2 # Initialize third pointer to i + 2\n \n # If the first element of the triplet is 0, move to the next element\n if nums[i] == 0:\n continue\n \n # If all remaining elements in the array are zero, break out of the loop\n if nums[i+1] == 0 and nums[-1] == 0:\n break\n \n # Loop through all possible second elements of the triplet\n for j in range(i + 1, len(nums) - 1):\n \n # Move the third pointer to the first element that is greater than or equal to the sum of the first two elements\n while k < len(nums) and nums[i] + nums[j] > nums[k]:\n k += 1\n \n # The number of valid triangles that can be formed with the current pair of first two elements is the difference between the third pointer and the second pointer minus 1\n count += k - j - 1\n \n return count\n\n``` | 4 | Given an integer array `nums`, return _the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle_.
**Example 1:**
**Input:** nums = \[2,2,3,4\]
**Output:** 3
**Explanation:** Valid combinations are:
2,3,4 (using the first 2)
2,3,4 (using the second 2)
2,2,3
**Example 2:**
**Input:** nums = \[4,2,3,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000` | null |
Python Iterative solution | merge-two-binary-trees | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:\n\n stack1 = [root1]\n stack2 = [root2]\n if not root1:\n return root2\n\n while stack1:\n n1 = stack1.pop()\n n2 = stack2.pop()\n\n if n1 and n2:\n n1.val += n2.val\n\n if n2.left and not n1.left:\n n1.left = TreeNode()\n if n2.right and not n1.right:\n n1.right = TreeNode()\n\n stack1.append(n1.left)\n stack1.append(n1.right)\n stack2.append(n2.left)\n stack2.append(n2.right)\n\n return root1\n\n\n \n``` | 2 | You are given two binary trees `root1` and `root2`.
Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.
Return _the merged tree_.
**Note:** The merging process must start from the root nodes of both trees.
**Example 1:**
**Input:** root1 = \[1,3,2,5\], root2 = \[2,1,3,null,4,null,7\]
**Output:** \[3,4,5,5,4,null,7\]
**Example 2:**
**Input:** root1 = \[1\], root2 = \[1,2\]
**Output:** \[2,2\]
**Constraints:**
* The number of nodes in both trees is in the range `[0, 2000]`.
* `-104 <= Node.val <= 104` | null |
[Python] Simple Create New Tree By Joining Two Input Trees | merge-two-binary-trees | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:\n\n def dfs(node1, node2):\n if node1 and node2:\n # If both node exists, combine their values to form a new super node\n root = TreeNode(node1.val + node2.val)\n # And add its children by joining the children from both nodes\n root.left = dfs(node1.left, node2.left)\n root.right = dfs(node1.right, node2.right)\n # Finally return this super node\n return root\n else:\n # Otherwise return either that exists or None if neither exists\n return node1 or node2\n \n # Start the search in the head or roots of both trees\n return dfs(root1, root2)\n``` | 20 | You are given two binary trees `root1` and `root2`.
Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.
Return _the merged tree_.
**Note:** The merging process must start from the root nodes of both trees.
**Example 1:**
**Input:** root1 = \[1,3,2,5\], root2 = \[2,1,3,null,4,null,7\]
**Output:** \[3,4,5,5,4,null,7\]
**Example 2:**
**Input:** root1 = \[1\], root2 = \[1,2\]
**Output:** \[2,2\]
**Constraints:**
* The number of nodes in both trees is in the range `[0, 2000]`.
* `-104 <= Node.val <= 104` | null |
Python,Recursive Solution Beats 100% | merge-two-binary-trees | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:\n if not t1:\n return t2\n elif not t2:\n return t1\n else:\n res = TreeNode(t1.val + t2.val)\n res.left = self.mergeTrees(t1.left, t2.left)\n res.right = self.mergeTrees(t1.right, t2.right)\n return res\n``` | 54 | You are given two binary trees `root1` and `root2`.
Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.
Return _the merged tree_.
**Note:** The merging process must start from the root nodes of both trees.
**Example 1:**
**Input:** root1 = \[1,3,2,5\], root2 = \[2,1,3,null,4,null,7\]
**Output:** \[3,4,5,5,4,null,7\]
**Example 2:**
**Input:** root1 = \[1\], root2 = \[1,2\]
**Output:** \[2,2\]
**Constraints:**
* The number of nodes in both trees is in the range `[0, 2000]`.
* `-104 <= Node.val <= 104` | null |
very easy solution 🔥🔥 || Python uwu | merge-two-binary-trees | 0 | 1 | \n```\nclass Solution:\n def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:\n if not root1:\n return root2\n if not root2:\n return root1\n\n root1.val += root2.val\n root1.left = self.mergeTrees(root1.left, root2.left)\n root1.right = self.mergeTrees(root1.right, root2.right)\n\n return root1\n``` | 3 | You are given two binary trees `root1` and `root2`.
Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.
Return _the merged tree_.
**Note:** The merging process must start from the root nodes of both trees.
**Example 1:**
**Input:** root1 = \[1,3,2,5\], root2 = \[2,1,3,null,4,null,7\]
**Output:** \[3,4,5,5,4,null,7\]
**Example 2:**
**Input:** root1 = \[1\], root2 = \[1,2\]
**Output:** \[2,2\]
**Constraints:**
* The number of nodes in both trees is in the range `[0, 2000]`.
* `-104 <= Node.val <= 104` | null |
Python O(n) time, count it directly | task-scheduler | 0 | 1 | \n# Code\n```\nclass Solution:\n def leastInterval(self, tasks: List[str], n: int) -> int:\n cnt = [0] * 26\n for i in tasks: cnt[ord(i) - ord(\'A\')] += 1\n mx, mxcnt = max(cnt), 0\n for i in cnt: \n if i == mx: mxcnt += 1\n return max((mx - 1) * (n + 1) + mxcnt, len(tasks))\n``` | 12 | Given a characters array `tasks`, representing the tasks a CPU needs to do, where each letter represents a different task. Tasks could be done in any order. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer `n` that represents the cooldown period between two **same tasks** (the same letter in the array), that is that there must be at least `n` units of time between any two same tasks.
Return _the least number of units of times that the CPU will take to finish all the given tasks_.
**Example 1:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 2
**Output:** 8
**Explanation:**
A -> B -> idle -> A -> B -> idle -> A -> B
There is at least 2 units of time between any two same tasks.
**Example 2:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 0
**Output:** 6
**Explanation:** On this case any permutation of size 6 would work since n = 0.
\[ "A ", "A ", "A ", "B ", "B ", "B "\]
\[ "A ", "B ", "A ", "B ", "A ", "B "\]
\[ "B ", "B ", "B ", "A ", "A ", "A "\]
...
And so on.
**Example 3:**
**Input:** tasks = \[ "A ", "A ", "A ", "A ", "A ", "A ", "B ", "C ", "D ", "E ", "F ", "G "\], n = 2
**Output:** 16
**Explanation:**
One possible solution is
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> idle -> idle -> A -> idle -> idle -> A
**Constraints:**
* `1 <= task.length <= 104`
* `tasks[i]` is upper-case English letter.
* The integer `n` is in the range `[0, 100]`. | null |
[Python] Very detailed explanation with examples | task-scheduler | 0 | 1 | ```\nclass Solution:\n def leastInterval(self, tasks: List[str], n: int) -> int:\n ## RC ##\n ## APPROACH : HASHMAP ##\n ## LOGIC : TAKE THE MAXIMUM FREQUENCY ELEMENT AND MAKE THOSE MANY NUMBER OF SLOTS ##\n ## Slot size = (n+1) if n= 2 => slotsize = 3 Example: {A:5, B:1} => ABxAxxAxxAxxAxx => indices of A = 0,2 and middle there should be n elements, so slot size should be n+1\n \n ## Ex: {A:6,B:4,C:2} n = 2\n ## final o/p will be\n ## slot size / cycle size = 3\n ## Number of rows = number of A\'s (most freq element)\n # [\n # [A, B, C],\n # [A, B, C],\n # [A, B, idle],\n # [A, B, idle],\n # [A, idle, idle],\n # [A - - ],\n # ]\n #\n # so from above total time intervals = (max_freq_element - 1) * (n + 1) + (all elements with max freq)\n # ans = rows_except_last * columns + last_row\n \n \n ## but consider {A:5, B:1, C:1, D:1, E:1, F:1, G:1, H:1, I:1, J:1, K:1, L:1} n = 1\n ## total time intervals by above formula will be 4 * 2 + 1 = 9, which is less than number of elements, which is not possible. so we have to return max(ans, number of tasks)\n \n \n\t\t## TIME COMPLEXITY : O(N) ##\n\t\t## SPACE COMPLEXITY : O(1) ##\n\n freq = collections.Counter(tasks)\n max_freq = max(freq.values())\n freq = list(freq.values())\n max_freq_ele_count = 0 # total_elements_with_max_freq, last row elements\n i = 0\n while( i < len(freq)):\n if freq[i] == max_freq:\n max_freq_ele_count += 1\n i += 1\n \n ans = (max_freq - 1) * (n+1) + max_freq_ele_count\n \n return max(ans, len(tasks))\n```\nPLEASE UPVOTE IF YOU LIKE MY SOLUTION | 81 | Given a characters array `tasks`, representing the tasks a CPU needs to do, where each letter represents a different task. Tasks could be done in any order. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer `n` that represents the cooldown period between two **same tasks** (the same letter in the array), that is that there must be at least `n` units of time between any two same tasks.
Return _the least number of units of times that the CPU will take to finish all the given tasks_.
**Example 1:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 2
**Output:** 8
**Explanation:**
A -> B -> idle -> A -> B -> idle -> A -> B
There is at least 2 units of time between any two same tasks.
**Example 2:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 0
**Output:** 6
**Explanation:** On this case any permutation of size 6 would work since n = 0.
\[ "A ", "A ", "A ", "B ", "B ", "B "\]
\[ "A ", "B ", "A ", "B ", "A ", "B "\]
\[ "B ", "B ", "B ", "A ", "A ", "A "\]
...
And so on.
**Example 3:**
**Input:** tasks = \[ "A ", "A ", "A ", "A ", "A ", "A ", "B ", "C ", "D ", "E ", "F ", "G "\], n = 2
**Output:** 16
**Explanation:**
One possible solution is
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> idle -> idle -> A -> idle -> idle -> A
**Constraints:**
* `1 <= task.length <= 104`
* `tasks[i]` is upper-case English letter.
* The integer `n` is in the range `[0, 100]`. | null |
Explanation of the Greedy Solution | task-scheduler | 0 | 1 | This is my explanation of the [Official Greedy Solution](https://leetcode.com/problems/task-scheduler/editorial/) \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe arrange the task with the maximium occurence with a cooldown period of n. Then we insert the remaining tasks into the idle time slots.\n\n# Approach \n<!-- Describe your approach to solving the problem. -->\nFor example, \n> input: [\'A\', \'A\', \'A\', \'B\', \'B\', \'B\', \'C\', \'C\', \'D\', \'D\'], n=2\n\n1. We first pick tasks marked with \'A\' and arrange them like the description in the last section, which results:\n\n| A | | | A | | | A |\n|---|---|---|---|---|---|---|\n\nFor convienice, we call the area between the first and the last \'A\' as the `scope`.\n\n2. Then we can pick the task type with maximium occurence and insert tasks and let them take up as many idle time as possible.\n\n| A | B | | A | B | | A | B |\n|---|---|---|---|---|---|---|---|\n\nNotice that there is one task B outside the original scope, we will look back at this case later.\n\n3. Repeat step 2, suppose we pick task type C. \n\n| A | B | C | A | B | C | A | B |\n|---|---|---|---|---|---|---|---|\n\n4. Finally we pick task type D, this is most tricky part. Do we need to put them at the tail, which results more idle slots? No! We can put them just right to each of the \'A\'s:\n\n| A | D | B | C | A | D | B | C | A | B |\n|---|---|---|---|---|---|---|---|---|---|\n\nWe can always do like this to avoid extra idle time slots even if there are remaining \'E\'s, \'F\'s... \n\nNow let\'s calculate the total length. Intuitively, \n- if the idle time slots can all be filled with tasks and there are `X` extra tasks, we need a new scope with a length of `original scope length`+`X` slots in tatal. \n- if the idle time slots can not be filled, since no tasks is out of the original scope, we need `original scope length`\n\nBut remember in step 2, we have a task \'B\' out of scope. \'A\' is one of the task type with the maximium occurence, so we can conclude that\n- if there are extra task types share the maximium occurence, for each type, we need to add 1 to the tatal length.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def leastInterval(self, tasks: List[str], n: int) -> int:\n occurences = [0] * 26\n for t in tasks:\n occurences[ord(t)-ord(\'A\')] += 1\n max_occurence = max(occurences)\n\n # arrange task with max occurence evenly with a distance of n\n idle_time = (max_occurence-1) * n\n occurences.remove(max_occurence) # remove one max_occurence which is picked to arrange evenly\n remain_task_time_in_scope = 0\n remain_task_time_out_scope = 0\n for task in occurences:\n if task == max_occurence:\n remain_task_time_in_scope += task-1\n remain_task_time_out_scope += 1\n else:\n remain_task_time_in_scope += task\n\n extra_time = max(0, remain_task_time_in_scope - idle_time) + remain_task_time_out_scope\n return (max_occurence-1)*(n+1)+1 + extra_time\n\n```\n\n# Improvement - The Math Approach\n\nHowever, we do not really need to \'simulate\' the fill progress. When using the greedy thinking like decribed above, results can be divided into 2 situations:\n\n1. The `scope` is filled and there is no idle time slot.\n2. The `scope` is not filled and there exists idle time slots.\n\nIn situation 1, since there is no idle slot, the total length equal to the lengh of `tasks`, which is the input list.\n\nIn situation 2, because the original `scope` is not filled, which means the `scope` is not extended, we can calculate the total length with `original scope length` and `num of maximiun-occurence task type`\n\n```python\nclass Solution:\n def leastInterval(self, tasks: List[str], n: int) -> int:\n cnts = [0] * 26\n for t in tasks:\n cnts[ord(t)-ord(\'A\')] += 1\n max_occurence = max(cnts)\n max_occurence_cnt = cnts.count(max_occurence)\n len_full_fill = len(tasks)\n len_part_fill = (max_occurence-1)*(n+1)+max_occurence_cnt\n return max(len_full_fill, len_part_fill)\n``` | 6 | Given a characters array `tasks`, representing the tasks a CPU needs to do, where each letter represents a different task. Tasks could be done in any order. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer `n` that represents the cooldown period between two **same tasks** (the same letter in the array), that is that there must be at least `n` units of time between any two same tasks.
Return _the least number of units of times that the CPU will take to finish all the given tasks_.
**Example 1:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 2
**Output:** 8
**Explanation:**
A -> B -> idle -> A -> B -> idle -> A -> B
There is at least 2 units of time between any two same tasks.
**Example 2:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 0
**Output:** 6
**Explanation:** On this case any permutation of size 6 would work since n = 0.
\[ "A ", "A ", "A ", "B ", "B ", "B "\]
\[ "A ", "B ", "A ", "B ", "A ", "B "\]
\[ "B ", "B ", "B ", "A ", "A ", "A "\]
...
And so on.
**Example 3:**
**Input:** tasks = \[ "A ", "A ", "A ", "A ", "A ", "A ", "B ", "C ", "D ", "E ", "F ", "G "\], n = 2
**Output:** 16
**Explanation:**
One possible solution is
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> idle -> idle -> A -> idle -> idle -> A
**Constraints:**
* `1 <= task.length <= 104`
* `tasks[i]` is upper-case English letter.
* The integer `n` is in the range `[0, 100]`. | null |
Python | Heavily visualized + Detailed explanation | task-scheduler | 0 | 1 | I took some time to understand the logic behind it so I\'m sharing my understanding here with some graphs. Hopefully it would help you if are still confused.\n\nPlease upvote if you like.\n\nTaking ```tasks=[A,A,A,B,B,B,C,C,D,D],n=3``` as an example, we have a variable ```mx```: the maximum frequency of tasks. In this case, ```mx=3``` (3 A and 3 B). Besides, there are totally ```x``` tasks appear ```mx```. We can divide the arrangement into two parts: the first one consist of ```mx-1``` chunks with the length equals to ```n+1```; the second part consist of ```x``` tasks.\n\n\n\nThen we use greedy when filling in the idle times. We put the remaining tasks sequentially to the chunks and evenly filled in idle times.\n\n\n\nIn this case, it\u2019s easy to find out that the total time is ```(mx-1)*(n+1)+x```. This is actually the lower bound to process these tasks: when ```n``` gets really large, we have to hold this much time to satisfy that there are ```n``` timeslots between two same tasks.\n\n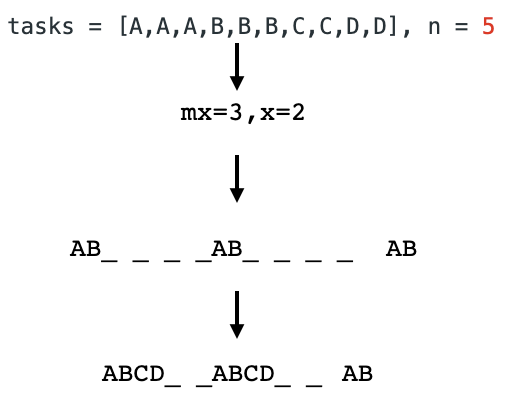\n\n\nWhen ```n``` is small and after taking all idle times, however, we can safely place remaining tasks into the chunks, and the chunk size expands. In this case, there\u2019s no idle time and the answer is simply the number of tasks.\n\n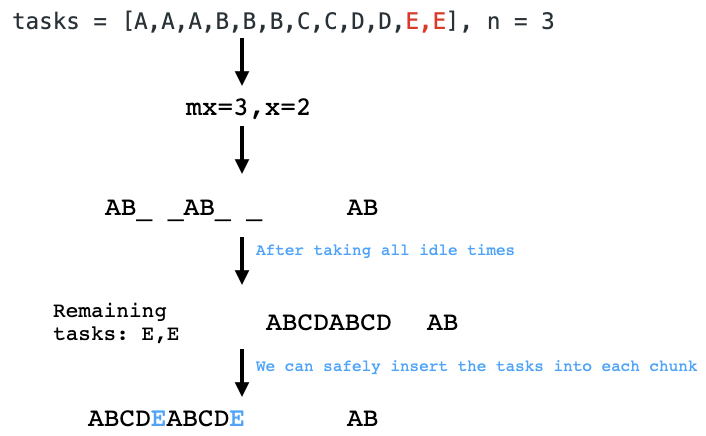\n\n | 52 | Given a characters array `tasks`, representing the tasks a CPU needs to do, where each letter represents a different task. Tasks could be done in any order. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer `n` that represents the cooldown period between two **same tasks** (the same letter in the array), that is that there must be at least `n` units of time between any two same tasks.
Return _the least number of units of times that the CPU will take to finish all the given tasks_.
**Example 1:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 2
**Output:** 8
**Explanation:**
A -> B -> idle -> A -> B -> idle -> A -> B
There is at least 2 units of time between any two same tasks.
**Example 2:**
**Input:** tasks = \[ "A ", "A ", "A ", "B ", "B ", "B "\], n = 0
**Output:** 6
**Explanation:** On this case any permutation of size 6 would work since n = 0.
\[ "A ", "A ", "A ", "B ", "B ", "B "\]
\[ "A ", "B ", "A ", "B ", "A ", "B "\]
\[ "B ", "B ", "B ", "A ", "A ", "A "\]
...
And so on.
**Example 3:**
**Input:** tasks = \[ "A ", "A ", "A ", "A ", "A ", "A ", "B ", "C ", "D ", "E ", "F ", "G "\], n = 2
**Output:** 16
**Explanation:**
One possible solution is
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> idle -> idle -> A -> idle -> idle -> A
**Constraints:**
* `1 <= task.length <= 104`
* `tasks[i]` is upper-case English letter.
* The integer `n` is in the range `[0, 100]`. | null |
✔Beats 94.89% TC || Python Solution | design-circular-queue | 0 | 1 | # Code\n```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.queue = []\n self.k = k\n\n def enQueue(self, value: int) -> bool:\n if self.isFull():\n return False \n if len(self.queue) < self.k:\n self.queue.append(value)\n return True\n\n def deQueue(self) -> bool:\n if self.isEmpty():\n return False\n if len(self.queue) > 0:\n self.queue.pop(0)\n return True\n\n def Front(self) -> int:\n if len(self.queue) > 0:\n return self.queue[0]\n return -1\n\n def Rear(self) -> int:\n if len(self.queue) > 0:\n return self.queue[-1]\n return -1\n\n def isEmpty(self) -> bool:\n if len(self.queue) == 0:\n return True\n\n def isFull(self) -> bool:\n if len(self.queue) == self.k:\n return True\n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 1 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
✔Beats 94.89% TC || Python Solution | design-circular-queue | 0 | 1 | # Code\n```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.queue = []\n self.k = k\n\n def enQueue(self, value: int) -> bool:\n if self.isFull():\n return False \n if len(self.queue) < self.k:\n self.queue.append(value)\n return True\n\n def deQueue(self) -> bool:\n if self.isEmpty():\n return False\n if len(self.queue) > 0:\n self.queue.pop(0)\n return True\n\n def Front(self) -> int:\n if len(self.queue) > 0:\n return self.queue[0]\n return -1\n\n def Rear(self) -> int:\n if len(self.queue) > 0:\n return self.queue[-1]\n return -1\n\n def isEmpty(self) -> bool:\n if len(self.queue) == 0:\n return True\n\n def isFull(self) -> bool:\n if len(self.queue) == self.k:\n return True\n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 1 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python || 99.49% Faster || Explained with comments | design-circular-queue | 0 | 1 | ```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.size=k\n self.q=[0]*k\n self.front=-1\n self.rear=-1\n\n def enQueue(self, value: int) -> bool:\n if self.isFull():\n return False\n if self.isEmpty():\n self.front=self.rear=0\n else:\n self.rear=(self.rear+1)%self.size #To maintain the cyclic nature of the queue\n self.q[self.rear]=value\n return True\n\n def deQueue(self) -> bool:\n if self.isEmpty():\n return False\n item=self.q[self.front]\n if self.front==self.rear: #if there is only one element in the queue\n self.front=self.rear=-1\n else:\n self.front=(self.front+1)%self.size #To maintain the cyclic nature of the queue\n return True\n\n def Front(self) -> int:\n if self.front==-1:\n return -1\n return self.q[self.front]\n\n def Rear(self) -> int:\n if self.rear==-1:\n return -1\n return self.q[self.rear]\n\n def isEmpty(self) -> bool:\n return self.front==-1\n\n def isFull(self) -> bool:\n if self.front==0 and self.rear==self.size-1: #if we don\'t write this condition then also second condition will manage everything\n return True\n if self.rear==(self.front-1)%(self.size):\n return True\n return False\n```\n**An upvote will be encouraging** | 2 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
Python || 99.49% Faster || Explained with comments | design-circular-queue | 0 | 1 | ```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.size=k\n self.q=[0]*k\n self.front=-1\n self.rear=-1\n\n def enQueue(self, value: int) -> bool:\n if self.isFull():\n return False\n if self.isEmpty():\n self.front=self.rear=0\n else:\n self.rear=(self.rear+1)%self.size #To maintain the cyclic nature of the queue\n self.q[self.rear]=value\n return True\n\n def deQueue(self) -> bool:\n if self.isEmpty():\n return False\n item=self.q[self.front]\n if self.front==self.rear: #if there is only one element in the queue\n self.front=self.rear=-1\n else:\n self.front=(self.front+1)%self.size #To maintain the cyclic nature of the queue\n return True\n\n def Front(self) -> int:\n if self.front==-1:\n return -1\n return self.q[self.front]\n\n def Rear(self) -> int:\n if self.rear==-1:\n return -1\n return self.q[self.rear]\n\n def isEmpty(self) -> bool:\n return self.front==-1\n\n def isFull(self) -> bool:\n if self.front==0 and self.rear==self.size-1: #if we don\'t write this condition then also second condition will manage everything\n return True\n if self.rear==(self.front-1)%(self.size):\n return True\n return False\n```\n**An upvote will be encouraging** | 2 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | design-circular-queue | 1 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n\n<iframe src="https://leetcode.com/playground/7pfwXKft/shared" frameBorder="0" width="100%" height="500"></iframe>\n | 90 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | design-circular-queue | 1 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n\n<iframe src="https://leetcode.com/playground/7pfwXKft/shared" frameBorder="0" width="100%" height="500"></iframe>\n | 90 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
✔️✔️✔️EASY Solution || Python | design-circular-queue | 0 | 1 | ```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.q = []\n self.k = k\n def enQueue(self, value: int) -> bool:\n if not self.isFull():\n self.q.append(value)\n return True\n \n \n def deQueue(self) -> bool:\n if not self.isEmpty():\n self.q.pop(0)\n return True\n \n \n def Front(self) -> int:\n if self.isEmpty(): return -1\n return self.q[0]\n \n\n def Rear(self) -> int:\n if self.isEmpty(): return -1\n \n return self.q[-1]\n\n def isEmpty(self) -> bool:\n return len(self.q) == 0\n \n\n def isFull(self) -> bool:\n return len(self.q) == self.k\n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 5 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
✔️✔️✔️EASY Solution || Python | design-circular-queue | 0 | 1 | ```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.q = []\n self.k = k\n def enQueue(self, value: int) -> bool:\n if not self.isFull():\n self.q.append(value)\n return True\n \n \n def deQueue(self) -> bool:\n if not self.isEmpty():\n self.q.pop(0)\n return True\n \n \n def Front(self) -> int:\n if self.isEmpty(): return -1\n return self.q[0]\n \n\n def Rear(self) -> int:\n if self.isEmpty(): return -1\n \n return self.q[-1]\n\n def isEmpty(self) -> bool:\n return len(self.q) == 0\n \n\n def isFull(self) -> bool:\n return len(self.q) == self.k\n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 5 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python3 - Concise Readable Solution. | design-circular-queue | 0 | 1 | ```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.queue = [-1] * k\n self.front = self.rear = -1\n self.size = 0 #current size of the queue\n self.maxsize = k #max size of the queue\n\n def enQueue(self, value: int) -> bool:\n if self.front == -1:\n self.front = 0\n if self.size < self.maxsize:\n self.rear = (self.rear + 1) % self.maxsize # for making it circular\n self.queue[self.rear] = value\n self.size += 1\n return True\n else:\n return False\n\n def deQueue(self) -> bool:\n if self.size > 0:\n self.front = (self.front + 1) % self.maxsize # for making it circular\n self.size -= 1\n return True\n else:\n return False\n\n def Front(self) -> int:\n return self.queue[self.front] if self.size > 0 else -1\n\n def Rear(self) -> int:\n return self.queue[self.rear] if self.size > 0 else -1\n\n def isEmpty(self) -> bool:\n return True if self.size == 0 else False\n\n def isFull(self) -> bool:\n return True if self.size == self.maxsize else False\n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 5 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
Python3 - Concise Readable Solution. | design-circular-queue | 0 | 1 | ```\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.queue = [-1] * k\n self.front = self.rear = -1\n self.size = 0 #current size of the queue\n self.maxsize = k #max size of the queue\n\n def enQueue(self, value: int) -> bool:\n if self.front == -1:\n self.front = 0\n if self.size < self.maxsize:\n self.rear = (self.rear + 1) % self.maxsize # for making it circular\n self.queue[self.rear] = value\n self.size += 1\n return True\n else:\n return False\n\n def deQueue(self) -> bool:\n if self.size > 0:\n self.front = (self.front + 1) % self.maxsize # for making it circular\n self.size -= 1\n return True\n else:\n return False\n\n def Front(self) -> int:\n return self.queue[self.front] if self.size > 0 else -1\n\n def Rear(self) -> int:\n return self.queue[self.rear] if self.size > 0 else -1\n\n def isEmpty(self) -> bool:\n return True if self.size == 0 else False\n\n def isFull(self) -> bool:\n return True if self.size == self.maxsize else False\n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 5 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Beats 99.98%|C++ Python | design-circular-queue | 0 | 1 | # Code C++\n```\nstruct Node {\n int val;\n Node* next;\n};\n\nclass MyCircularQueue {\nprivate:\n Node* last = nullptr;\n int maxSize = 0;\n int curSize = 0;\n\npublic:\n MyCircularQueue(int k) {\n maxSize = k;\n }\n\n bool enQueue(int value) {\n if (curSize == maxSize) {\n return false; // Queue is full, cannot enqueue\n }\n\n Node* newNode = new Node;\n newNode->val = value;\n newNode->next = nullptr;\n\n if (last == nullptr) {\n last = newNode;\n last->next = last; // Circular linkage for the first element\n } else {\n newNode->next = last->next;\n last->next = newNode;\n last = newNode;\n }\n\n curSize++;\n return true;\n }\n\n bool deQueue() {\n if (curSize == 0) {\n return false; // Queue is empty, cannot dequeue\n }\n\n Node* front = last->next;\n if (curSize == 1) {\n last = nullptr;\n } else {\n last->next = front->next;\n }\n\n delete front;\n curSize--;\n return true;\n }\n\n int Front() {\n if (curSize == 0) {\n return -1; // Queue is empty\n }\n return last->next->val;\n }\n\n int Rear() {\n if (curSize == 0) {\n return -1; // Queue is empty\n }\n return last->val;\n }\n\n bool isEmpty() {\n return curSize == 0;\n }\n\n bool isFull() {\n return curSize == maxSize;\n }\n};\n\n/**\n * Your MyCircularQueue object will be instantiated and called as such:\n * MyCircularQueue* obj = new MyCircularQueue(k);\n * bool param_1 = obj->enQueue(value);\n * bool param_2 = obj->deQueue();\n * int param_3 = obj->Front();\n * int param_4 = obj->Rear();\n * bool param_5 = obj->isEmpty();\n * bool param_6 = obj->isFull();\n */\n```\n\n# Code Python\n```\nclass MyCircularQueue:\n \n def __init__(self, k: int):\n self.maxSize = k\n self.queue = []\n\n def enQueue(self, value: int) -> bool:\n if len(self.queue) == self.maxSize:\n return False\n self.queue.append(value)\n return True\n \n def deQueue(self) -> bool:\n if len(self.queue) == 0:\n return False\n self.queue.pop(0)\n return True\n \n\n def Front(self) -> int:\n return -1 if len(self.queue)==0 else self.queue[0]\n\n def Rear(self) -> int:\n if len(self.queue)==0:\n return -1 \n return self.queue[len(self.queue)-1]\n\n def isEmpty(self) -> bool:\n return 1 if len(self.queue)==0 else 0\n\n def isFull(self) -> bool:\n return 1 if len(self.queue)==self.maxSize else 0\n \n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 1 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
Beats 99.98%|C++ Python | design-circular-queue | 0 | 1 | # Code C++\n```\nstruct Node {\n int val;\n Node* next;\n};\n\nclass MyCircularQueue {\nprivate:\n Node* last = nullptr;\n int maxSize = 0;\n int curSize = 0;\n\npublic:\n MyCircularQueue(int k) {\n maxSize = k;\n }\n\n bool enQueue(int value) {\n if (curSize == maxSize) {\n return false; // Queue is full, cannot enqueue\n }\n\n Node* newNode = new Node;\n newNode->val = value;\n newNode->next = nullptr;\n\n if (last == nullptr) {\n last = newNode;\n last->next = last; // Circular linkage for the first element\n } else {\n newNode->next = last->next;\n last->next = newNode;\n last = newNode;\n }\n\n curSize++;\n return true;\n }\n\n bool deQueue() {\n if (curSize == 0) {\n return false; // Queue is empty, cannot dequeue\n }\n\n Node* front = last->next;\n if (curSize == 1) {\n last = nullptr;\n } else {\n last->next = front->next;\n }\n\n delete front;\n curSize--;\n return true;\n }\n\n int Front() {\n if (curSize == 0) {\n return -1; // Queue is empty\n }\n return last->next->val;\n }\n\n int Rear() {\n if (curSize == 0) {\n return -1; // Queue is empty\n }\n return last->val;\n }\n\n bool isEmpty() {\n return curSize == 0;\n }\n\n bool isFull() {\n return curSize == maxSize;\n }\n};\n\n/**\n * Your MyCircularQueue object will be instantiated and called as such:\n * MyCircularQueue* obj = new MyCircularQueue(k);\n * bool param_1 = obj->enQueue(value);\n * bool param_2 = obj->deQueue();\n * int param_3 = obj->Front();\n * int param_4 = obj->Rear();\n * bool param_5 = obj->isEmpty();\n * bool param_6 = obj->isFull();\n */\n```\n\n# Code Python\n```\nclass MyCircularQueue:\n \n def __init__(self, k: int):\n self.maxSize = k\n self.queue = []\n\n def enQueue(self, value: int) -> bool:\n if len(self.queue) == self.maxSize:\n return False\n self.queue.append(value)\n return True\n \n def deQueue(self) -> bool:\n if len(self.queue) == 0:\n return False\n self.queue.pop(0)\n return True\n \n\n def Front(self) -> int:\n return -1 if len(self.queue)==0 else self.queue[0]\n\n def Rear(self) -> int:\n if len(self.queue)==0:\n return -1 \n return self.queue[len(self.queue)-1]\n\n def isEmpty(self) -> bool:\n return 1 if len(self.queue)==0 else 0\n\n def isFull(self) -> bool:\n return 1 if len(self.queue)==self.maxSize else 0\n \n\n\n# Your MyCircularQueue object will be instantiated and called as such:\n# obj = MyCircularQueue(k)\n# param_1 = obj.enQueue(value)\n# param_2 = obj.deQueue()\n# param_3 = obj.Front()\n# param_4 = obj.Rear()\n# param_5 = obj.isEmpty()\n# param_6 = obj.isFull()\n``` | 1 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python3 - AddOne method | design-circular-queue | 0 | 1 | \'\'\'\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.data = [None] * (k + 1) # only k seats can be taken\n self.head = 1\n self.tail = 0\n self.MAX_SIZE = k + 1\n\n def enQueue(self, value: int) -> bool:\n if self.isFull(): return False\n self.tail = self.addOne(self.tail)\n self.data[self.tail] = value\n \n return True\n\n def deQueue(self) -> bool:\n if self.isEmpty(): return False\n value = self.data[self.head]\n self.head = self.addOne(self.head)\n \n return True\n\n def Front(self) -> int:\n if self.isEmpty(): return -1\n return self.data[self.head]\n\n def Rear(self) -> int:\n if self.isEmpty(): return -1\n return self.data[self.tail]\n\n def isEmpty(self) -> bool:\n return self.addOne(self.tail) == self.head\n\n def isFull(self) -> bool:\n return self.addOne(self.addOne(self.tail)) == self.head\n \n def addOne(self, x: int) -> int:\n return (1 + x) % self.MAX_SIZE\n\'\'\' | 1 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
Python3 - AddOne method | design-circular-queue | 0 | 1 | \'\'\'\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.data = [None] * (k + 1) # only k seats can be taken\n self.head = 1\n self.tail = 0\n self.MAX_SIZE = k + 1\n\n def enQueue(self, value: int) -> bool:\n if self.isFull(): return False\n self.tail = self.addOne(self.tail)\n self.data[self.tail] = value\n \n return True\n\n def deQueue(self) -> bool:\n if self.isEmpty(): return False\n value = self.data[self.head]\n self.head = self.addOne(self.head)\n \n return True\n\n def Front(self) -> int:\n if self.isEmpty(): return -1\n return self.data[self.head]\n\n def Rear(self) -> int:\n if self.isEmpty(): return -1\n return self.data[self.tail]\n\n def isEmpty(self) -> bool:\n return self.addOne(self.tail) == self.head\n\n def isFull(self) -> bool:\n return self.addOne(self.addOne(self.tail)) == self.head\n \n def addOne(self, x: int) -> int:\n return (1 + x) % self.MAX_SIZE\n\'\'\' | 1 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
✅ [Python] Simple, Clean 2 approach LinkedList & Array | design-circular-queue | 0 | 1 | ### \u2714\uFE0F1. Using Linked-List\n\n```\n\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\n \n\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.k = k\n self.head = None\n self.counter = 0\n self.pointer = None\n\n def append(self, val):\n if self.head is None:\n self.head = ListNode(val)\n self.head.next = self.head\n self.pointer = self.head\n else:\n self.pointer.next = ListNode(val, self.head)\n self.pointer = self.pointer.next\n self.counter+=1\n return True\n \n def remove(self):\n if self.head is None:\n return False\n if self.counter == 1:\n self.head = None\n self.pointer = None\n self.counter-=1\n return True\n self.head = self.head.next\n self.pointer.next = self.head\n self.counter-=1\n return True\n \n def enQueue(self, value: int) -> bool:\n return self.append(value) if self.counter < self.k else False\n\n def deQueue(self) -> bool:\n return self.remove() if self.counter > 0 else False\n \n def Front(self) -> int:\n if self.head is None:\n return -1\n return self.head.val\n\n def Rear(self) -> int:\n if self.head is None:\n return -1\n return self.pointer.val\n\n def isEmpty(self) -> bool:\n return self.counter==0\n\n def isFull(self) -> bool:\n return self.counter==self.k\n\n\n```\n.\n### \u2714\uFE0F2. Using Array\n.\n\n```\n\n\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.queue=[]\n self.size=k\n\n def enQueue(self, value: int) -> bool:\n if self.isFull(): return False\n self.queue.append(value)\n return True \n\n def deQueue(self) -> bool:\n if self.isEmpty(): return False\n self.queue.pop(0)\n return True\n\n def Front(self) -> int:\n return -1 if len(self.queue)==0 else self.queue[0]\n\n def Rear(self) -> int:\n return -1 if len(self.queue)==0 else self.queue[-1] \n\n def isEmpty(self) -> bool:\n return True if len(self.queue)==0 else False \n\n def isFull(self) -> bool:\n return True if len(self.queue)==self.size else False\n```\n\nIf you think this post is **helpful** for you, hit a **thums up.** Any questions or discussions are welcome!\n\nThank a lot. | 1 | Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer ".
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Implement the `MyCircularQueue` class:
* `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
* `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
* `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
* `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
* `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
* `boolean isEmpty()` Checks whether the circular queue is empty or not.
* `boolean isFull()` Checks whether the circular queue is full or not.
You must solve the problem without using the built-in queue data structure in your programming language.
**Example 1:**
**Input**
\[ "MyCircularQueue ", "enQueue ", "enQueue ", "enQueue ", "enQueue ", "Rear ", "isFull ", "deQueue ", "enQueue ", "Rear "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 3, true, true, true, 4\]
**Explanation**
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear(); // return 3
myCircularQueue.isFull(); // return True
myCircularQueue.deQueue(); // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`. | null |
✅ [Python] Simple, Clean 2 approach LinkedList & Array | design-circular-queue | 0 | 1 | ### \u2714\uFE0F1. Using Linked-List\n\n```\n\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\n \n\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.k = k\n self.head = None\n self.counter = 0\n self.pointer = None\n\n def append(self, val):\n if self.head is None:\n self.head = ListNode(val)\n self.head.next = self.head\n self.pointer = self.head\n else:\n self.pointer.next = ListNode(val, self.head)\n self.pointer = self.pointer.next\n self.counter+=1\n return True\n \n def remove(self):\n if self.head is None:\n return False\n if self.counter == 1:\n self.head = None\n self.pointer = None\n self.counter-=1\n return True\n self.head = self.head.next\n self.pointer.next = self.head\n self.counter-=1\n return True\n \n def enQueue(self, value: int) -> bool:\n return self.append(value) if self.counter < self.k else False\n\n def deQueue(self) -> bool:\n return self.remove() if self.counter > 0 else False\n \n def Front(self) -> int:\n if self.head is None:\n return -1\n return self.head.val\n\n def Rear(self) -> int:\n if self.head is None:\n return -1\n return self.pointer.val\n\n def isEmpty(self) -> bool:\n return self.counter==0\n\n def isFull(self) -> bool:\n return self.counter==self.k\n\n\n```\n.\n### \u2714\uFE0F2. Using Array\n.\n\n```\n\n\nclass MyCircularQueue:\n\n def __init__(self, k: int):\n self.queue=[]\n self.size=k\n\n def enQueue(self, value: int) -> bool:\n if self.isFull(): return False\n self.queue.append(value)\n return True \n\n def deQueue(self) -> bool:\n if self.isEmpty(): return False\n self.queue.pop(0)\n return True\n\n def Front(self) -> int:\n return -1 if len(self.queue)==0 else self.queue[0]\n\n def Rear(self) -> int:\n return -1 if len(self.queue)==0 else self.queue[-1] \n\n def isEmpty(self) -> bool:\n return True if len(self.queue)==0 else False \n\n def isFull(self) -> bool:\n return True if len(self.queue)==self.size else False\n```\n\nIf you think this post is **helpful** for you, hit a **thums up.** Any questions or discussions are welcome!\n\nThank a lot. | 1 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Solution | add-one-row-to-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* addOneRow(TreeNode* root, int val, int depth) {\n if (depth == 1)\n return new TreeNode(val, root, NULL);\n if (!root) \n return NULL;\n\n root -> left = addOneRow(root -> left, val, depth - 1, true);\n root -> right = addOneRow(root -> right, val, depth - 1, false);\n \n return root;\n }\n TreeNode *addOneRow(TreeNode *root, int val, int depth, bool isLeft)\n {\n if (!root && depth > 1)\n return root;\n\n if (depth > 1)\n {\n root -> left = addOneRow(root -> left, val, depth - 1, true);\n root -> right = addOneRow(root -> right, val, depth - 1, false);\n return root;\n } \n return new TreeNode(val, isLeft ? root : NULL, isLeft ? NULL : root); \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:\n if depth == 1:\n newRoot = TreeNode(val, root, None)\n return newRoot\n self.DFS(root, val, 1, depth)\n return root\n \n def DFS(self, node, val, currDepth, targetDepth):\n if node != None:\n if currDepth == targetDepth-1:\n newNodeLeft = TreeNode(val, node.left, None)\n newNodeRight = TreeNode(val, None, node.right)\n node.left = newNodeLeft\n node.right = newNodeRight\n else:\n self.DFS(node.left, val, currDepth+1, targetDepth)\n self.DFS(node.right, val, currDepth+1, targetDepth)\n```\n\n```Java []\nclass Solution {\n public TreeNode addOneRow(TreeNode root, int val, int depth) {\n if(depth == 1){\n TreeNode ans = new TreeNode(val);\n ans.left= root;\n return ans;\n }\n process(root, val, 1, depth);\n return root;\n }\n public void process(TreeNode root, int val, int curDepth, int targetDepth){\n if(curDepth == (targetDepth-1)){\n TreeNode curLeft = new TreeNode();\n TreeNode curRight = new TreeNode();\n curLeft.left = root.left;\n curRight.right = root.right;\n curLeft.val = val;\n curRight.val = val;\n root.left=curLeft;\n root.right=curRight;\n return;\n }\n curDepth++;\n if(root.left != null){\n process(root.left, val, curDepth, targetDepth);\n }\n if(root.right != null){\n process(root.right, val, curDepth, targetDepth);\n }\n }\n}\n```\n | 1 | Given the `root` of a binary tree and two integers `val` and `depth`, add a row of nodes with value `val` at the given depth `depth`.
Note that the `root` node is at depth `1`.
The adding rule is:
* Given the integer `depth`, for each not null tree node `cur` at the depth `depth - 1`, create two tree nodes with value `val` as `cur`'s left subtree root and right subtree root.
* `cur`'s original left subtree should be the left subtree of the new left subtree root.
* `cur`'s original right subtree should be the right subtree of the new right subtree root.
* If `depth == 1` that means there is no depth `depth - 1` at all, then create a tree node with value `val` as the new root of the whole original tree, and the original tree is the new root's left subtree.
**Example 1:**
**Input:** root = \[4,2,6,3,1,5\], val = 1, depth = 2
**Output:** \[4,1,1,2,null,null,6,3,1,5\]
**Example 2:**
**Input:** root = \[4,2,null,3,1\], val = 1, depth = 3
**Output:** \[4,2,null,1,1,3,null,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* The depth of the tree is in the range `[1, 104]`.
* `-100 <= Node.val <= 100`
* `-105 <= val <= 105`
* `1 <= depth <= the depth of tree + 1` | null |
623: Solution with step by step explanation | add-one-row-to-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the depth is 1. If it is, create a new root node with value val, make its left subtree the original tree, and return the new root.\n2. Create a queue q and add a tuple containing the root node and its level (which is 1) to it.\n3. While q is not empty:\na. Dequeue a node and its level from q.\nb. If the level is equal to depth - 1, then we have reached the level above where we want to add a new row. Save the current left and right subtrees of this node.\nc. Create two new nodes with value val.\nd. Link the new left node to the saved left subtree and the new right node to the saved right subtree.\ne. Update the left and right subtrees of the current node to be the new left and right nodes.\nf. If we haven\'t reached the target depth yet, add the children of the current node to the queue with their level incremented by 1.\n4. Return the modified tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOneRow(self, root: TreeNode, val: int, depth: int) -> TreeNode:\n # If depth is 1, create a new root node with left subtree as original tree\n if depth == 1:\n new_root = TreeNode(val)\n new_root.left = root\n return new_root\n \n # Create a queue to perform BFS\n q = collections.deque([(root, 1)])\n \n # Traverse the tree level by level until we reach depth-1\n while q:\n node, level = q.popleft()\n if level == depth - 1:\n # Save the current left and right subtrees\n left, right = node.left, node.right\n # Create new nodes with value val\n new_left, new_right = TreeNode(val), TreeNode(val)\n # Link the new nodes to the saved subtrees\n new_left.left, new_right.right = left, right\n # Update the node\'s left and right subtrees\n node.left, node.right = new_left, new_right\n else:\n # If we haven\'t reached the target depth yet, add the children of the current node to the queue\n if node.left:\n q.append((node.left, level + 1))\n if node.right:\n q.append((node.right, level + 1))\n \n # Return the modified tree\n return root\n\n``` | 1 | Given the `root` of a binary tree and two integers `val` and `depth`, add a row of nodes with value `val` at the given depth `depth`.
Note that the `root` node is at depth `1`.
The adding rule is:
* Given the integer `depth`, for each not null tree node `cur` at the depth `depth - 1`, create two tree nodes with value `val` as `cur`'s left subtree root and right subtree root.
* `cur`'s original left subtree should be the left subtree of the new left subtree root.
* `cur`'s original right subtree should be the right subtree of the new right subtree root.
* If `depth == 1` that means there is no depth `depth - 1` at all, then create a tree node with value `val` as the new root of the whole original tree, and the original tree is the new root's left subtree.
**Example 1:**
**Input:** root = \[4,2,6,3,1,5\], val = 1, depth = 2
**Output:** \[4,1,1,2,null,null,6,3,1,5\]
**Example 2:**
**Input:** root = \[4,2,null,3,1\], val = 1, depth = 3
**Output:** \[4,2,null,1,1,3,null,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* The depth of the tree is in the range `[1, 104]`.
* `-100 <= Node.val <= 100`
* `-105 <= val <= 105`
* `1 <= depth <= the depth of tree + 1` | null |
✅ [Python] Simple Solutions Bfs [ 98%] | add-one-row-to-tree | 0 | 1 | Main idea:\n\nif at depth-1, we\'ll need children nodes of value val.\nIf the current node has a child, the child must be removed and made a child of the new node.\nIf the current node does not have a child, we can simply add the new node as a new node.\nif not at depth-1, go to the children and check if they are at depth-1.\n```\nclass Solution:\n def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:\n if depth == 1:\n return TreeNode(val=val, left=root) \n \n def dfs(node, level):\n if level == depth - 1: \n node.left = TreeNode(val, left=node.left) if node.left else TreeNode(val)\n node.right = TreeNode(val, right=node.right) if node.right else TreeNode(val)\n return node\n else: \n if node.left: node.left = dfs(node.left, level+1)\n if node.right: node.right = dfs(node.right, level+1)\n return node\n \n root = dfs(root, 1) \n return root\n```\n\n\n\n**UP VOTE IF HELPFUL** | 1 | Given the `root` of a binary tree and two integers `val` and `depth`, add a row of nodes with value `val` at the given depth `depth`.
Note that the `root` node is at depth `1`.
The adding rule is:
* Given the integer `depth`, for each not null tree node `cur` at the depth `depth - 1`, create two tree nodes with value `val` as `cur`'s left subtree root and right subtree root.
* `cur`'s original left subtree should be the left subtree of the new left subtree root.
* `cur`'s original right subtree should be the right subtree of the new right subtree root.
* If `depth == 1` that means there is no depth `depth - 1` at all, then create a tree node with value `val` as the new root of the whole original tree, and the original tree is the new root's left subtree.
**Example 1:**
**Input:** root = \[4,2,6,3,1,5\], val = 1, depth = 2
**Output:** \[4,1,1,2,null,null,6,3,1,5\]
**Example 2:**
**Input:** root = \[4,2,null,3,1\], val = 1, depth = 3
**Output:** \[4,2,null,1,1,3,null,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* The depth of the tree is in the range `[1, 104]`.
* `-100 <= Node.val <= 100`
* `-105 <= val <= 105`
* `1 <= depth <= the depth of tree + 1` | null |
Easy To Understand | 3 Lines 🚀🚀 | maximum-product-of-three-numbers | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n Use this test case for better understanding --> [-100,-98,-1,2,3,4]\n\n# Complexity\n- Time complexity: O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumProduct(vector<int>& nums) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n sort(nums.begin(),nums.end());\n int n = nums.size();\n\n return max(nums[n-1] * nums[n-2] * nums[n-3], nums[0] * nums[1] * nums[n-1]);\n }\n};\n``` | 2 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
PYTHON SIMPLE | maximum-product-of-three-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort(reverse = True)\n return max(nums[0] * nums[1] * nums[2], nums[0] * nums[-1] * nums[-2])\n \n``` | 1 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
easiest two lines of code#python3 | maximum-product-of-three-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort()\n return max(nums[-1]*nums[-2]*nums[-3],nums[0]*nums[1]*nums[-1])\n #please do upvote as it makes me to code more.\n```\n# consider upvoting\n\n | 17 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
[Python] O(N) | maximum-product-of-three-numbers | 0 | 1 | Time Complexcity O(N)\nSpace Complexcity O(1)\n```\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort()\n h3=nums[-1]*nums[-2]*nums[-3]\n l3=nums[0]*nums[1]*nums[-1]\n return max(h3,l3)\n \n``` | 1 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
Simple solution in python using sort | maximum-product-of-three-numbers | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maximumProduct(self, A: List[int]) -> int:\n A.sort()\n return max(A[0]*A[1]*A[-1], A[-1]*A[-2]*A[-3])\n``` | 3 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
2 Lines of Code-->Powerful Heap Concept | maximum-product-of-three-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n #Math Approach\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort()\n return max(nums[0]*nums[1]*nums[-1],nums[-1]*nums[-2]*nums[-3])\n\n #please upvote me it would encourage me alot\n\n```\n\n```\n #Heap Approach\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n pos=heapq.nlargest(3,nums)\n neg=heapq.nsmallest(2,nums)\n return max(neg[0]*neg[1]*pos[0],pos[0]*pos[1]*pos[2])\n #please upvote me it would encourage me alot\n\n\n | 9 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
Python Easy Solution || Sorting | maximum-product-of-three-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort()\n n=len(nums)\n return max(nums[n-1]*nums[n-2]*nums[n-3],nums[0]*nums[1]*nums[n-1])\n \n``` | 2 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
4 Lines of Python code | maximum-product-of-three-numbers | 0 | 1 | ```\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort()\n l1 = nums[-1]*nums[-2]*nums[-3]\n l2 = nums[0]*nums[1]*nums[-1]\n return max(l1,l2) | 4 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
Solution | maximum-product-of-three-numbers | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maximumProduct(vector<int>& nums) {\n int max1 = INT32_MIN, max2 = INT32_MIN, max3 = INT32_MIN;\n int min1 = INT32_MAX, min2 = INT32_MAX;\n for(int& num : nums) {\n if(num > max1) {\n max3 = max2, max2 = max1, max1 = num;\n }\n else if(num > max2) {\n max3 = max2, max2 = num;\n }\n else if(num > max3) {\n max3 = num;\n }\n if(num < min1) {\n min2 = min1, min1 = num;\n }\n else if(num < min2) {\n min2 = num;\n }\n }\n return std::max(max1*max2*max3, max1*min1*min2);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maximumProduct(self, nums):\n a, b = heapq.nlargest(3, nums), heapq.nsmallest(2, nums)\n return max(a[0] * a[1] * a[2], b[0] * b[1] * a[0])\n```\n\n```Java []\nclass Solution {\n int maxi(int[] a,int n)\n {\n int max=(int)-9999999;\n int f=-1;\n for(int i=0;i<n;i++)\n {\n if(max<=a[i])\n {\n max=a[i];\n f=i;\n }\n }\n a[f]=(int)-9999999;\n return max;\n }\n int min(int[] a,int n)\n {\n int max=(int)999999;\n int f=-1;\n for(int i=0;i<n;i++)\n {\n if(a[i]!=-9999999)\n {\n if(max>=a[i])\n {\n max=a[i];\n f=i;\n }\n }\n }\n a[f]=(int)999999;\n return max;\n }\n public int maximumProduct(int[] a) {\n int n=a.length;\n int aa=maxi(a,n);\n int b=maxi(a,n);\n int c=maxi(a,n);\n if(n==3)\n {\n return aa*b*c;\n }\n int x=min(a,n);\n int y=min(a,n);\n if(n==4)\n {\n y=c;\n }\n return Math.max(aa*b*c,aa*x*y);\n }\n}\n```\n | 3 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
Superb Logic in java and Python(Heap concept) | maximum-product-of-three-numbers | 1 | 1 | \n\n# Superb Solution in JAVA\n```\nclass Solution {\n public int maximumProduct(int[] nums) {\n Arrays.sort(nums);\n int n=nums.length;\n return Math.max(nums[0]*nums[1]*nums[n-1],nums[n-1]*nums[n-2]*nums[n-3]); \n }\n}\n```\n# Excellent Solution in Python Using Heap Concept\n```\nclass Solution:\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort()\n pos=heapq.nlargest(3,nums)\n neg=heapq.nsmallest(2,nums)\n return max(neg[0]*neg[1]*pos[0],pos[-1]*pos[-2]*pos[-3])\n``` | 4 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
python 2 liner code faster | maximum-product-of-three-numbers | 0 | 1 | ```\n def maximumProduct(self, nums: List[int]) -> int:\n nums.sort()\n return max((nums[-1]*nums[-2]*nums[-3]),(nums[0]*nums[1]*nums[-1]))\n``` | 3 | Given an integer array `nums`, _find three numbers whose product is maximum and return the maximum product_.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 6
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 24
**Example 3:**
**Input:** nums = \[-1,-2,-3\]
**Output:** -6
**Constraints:**
* `3 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000` | null |
Solution | k-inverse-pairs-array | 1 | 1 | ```C++ []\nconstexpr long MODULUS = 1\'000\'000\'007;\n\nstatic int ANSWERS[1001][1001] = {};\nstatic bool CALCULATED = false;\n\nclass Solution {\npublic:\n int kInversePairs(int in_n, int in_k) {\n if (CALCULATED) {\n return ANSWERS[in_n][in_k];\n }\n for (int n = 1; n <= 1000; n++) {\n const int* prev_row = ANSWERS[n - 1];\n int* out = ANSWERS[n];\n int* it = out;\n int* end = out + 1001;\n *it = 1;\n ++it;\n *it = n - 1;\n int prev = *it;\n ++it;\n int limit = min(1000, n * (n - 1) / 2);\n for (int k = 2; k <= limit; k++, ++it) {\n prev = *it = (prev + prev_row[k] - (k >= n ? prev_row[k - n] : 0) + MODULUS) % MODULUS;\n }\n }\n CALCULATED = true;\n return ANSWERS[in_n][in_k];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def kInversePairs(self, n: int, k: int) -> int:\n M = 1000_000_007\n if k == 0:\n return 1\n if n == 1:\n return 1 if k == 0 else 0\n\n dpp = [0] * (k+1)\n dpp[0] = 1\n dpc = [0] * (k+1)\n for i in range(n-2, -1, -1):\n v = 0\n t = n - i\n for j in range(0, k+1):\n v += dpp[j]\n if j >= t:\n v -= dpp[j - t]\n v %= M\n dpc[j] = v\n dpc, dpp = dpp, dpc\n return dpp[k]\n```\n\n```Java []\nclass Solution {\n public int kInversePairs(int n, int k) {\n int[][] dp = new int[n + 1][k + 1];\n dp[0][0] = 1;\n int mod = 1000000007;\n\n for(int i = 1; i <= n; i++) {\n int val = 0;\n for(int j = 0; j <= k; j++) {\n val += dp[i - 1][j];\n if(j >= i) val -= dp[i - 1][j - i];\n if(val < 0) val += mod;\n val = (val % mod);\n dp[i][j] = val;\n }\n }\n return (int)(dp[n][k]);\n }\n}\n```\n | 1 | For an integer array `nums`, an **inverse pair** is a pair of integers `[i, j]` where `0 <= i < j < nums.length` and `nums[i] > nums[j]`.
Given two integers n and k, return the number of different arrays consist of numbers from `1` to `n` such that there are exactly `k` **inverse pairs**. Since the answer can be huge, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 0
**Output:** 1
**Explanation:** Only the array \[1,2,3\] which consists of numbers from 1 to 3 has exactly 0 inverse pairs.
**Example 2:**
**Input:** n = 3, k = 1
**Output:** 2
**Explanation:** The array \[1,3,2\] and \[2,1,3\] have exactly 1 inverse pair.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= k <= 1000` | null |
Easy Solution || Beats 99% || Python | k-inverse-pairs-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kInversePairs(self, n: int, k: int) -> int:\n M = 1000000007\n if k == 0:\n return 1\n if n == 1:\n return 1 if k == 0 else 0\n\n current_count = [0] * (k + 1)\n current_count[0] = 1\n previous_count = [0] * (k + 1)\n\n for i in range(n - 2, -1, -1):\n total_count = 0\n threshold = n - i\n\n for j in range(0, k + 1):\n total_count += current_count[j]\n\n if j >= threshold:\n total_count -= current_count[j - threshold]\n\n total_count %= M\n previous_count[j] = total_count\n\n current_count, previous_count = previous_count, current_count\n\n return current_count[k]\n #Upvote me if it helps\n\n``` | 1 | For an integer array `nums`, an **inverse pair** is a pair of integers `[i, j]` where `0 <= i < j < nums.length` and `nums[i] > nums[j]`.
Given two integers n and k, return the number of different arrays consist of numbers from `1` to `n` such that there are exactly `k` **inverse pairs**. Since the answer can be huge, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 0
**Output:** 1
**Explanation:** Only the array \[1,2,3\] which consists of numbers from 1 to 3 has exactly 0 inverse pairs.
**Example 2:**
**Input:** n = 3, k = 1
**Output:** 2
**Explanation:** The array \[1,3,2\] and \[2,1,3\] have exactly 1 inverse pair.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= k <= 1000` | null |
Python3 || dp,1D array, 10 lines, w/ explanation || T/M: 95%/86% | k-inverse-pairs-array | 0 | 1 | ```\nclass Solution:\n # A very good description of the dp solution is at\n # https://leetcode.com/problems/k-inverse-pairs-array/solution/ \n # The code below uses two 1D arrays--dp and tmp--instead if a \n # 2D array. tmp replaces dp after each i-iteration.\n def kInversePairs(self, n: int, k: int) -> int:\n dp, mod = [1]+[0] * k, 1000000007\n \n for i in range(n):\n tmp, sm = [], 0\n for j in range(k + 1):\n sm+= dp[j]\n if j-i >= 1: sm-= dp[j-i-1]\n sm%= mod\n tmp.append(sm)\n dp = tmp\n #print(dp) # <-- uncomment this line to get a sense of dp from the print output\n\t\t\t # try n = 6, k = 4; your answer should be 49.\n return dp[k] | 8 | For an integer array `nums`, an **inverse pair** is a pair of integers `[i, j]` where `0 <= i < j < nums.length` and `nums[i] > nums[j]`.
Given two integers n and k, return the number of different arrays consist of numbers from `1` to `n` such that there are exactly `k` **inverse pairs**. Since the answer can be huge, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 0
**Output:** 1
**Explanation:** Only the array \[1,2,3\] which consists of numbers from 1 to 3 has exactly 0 inverse pairs.
**Example 2:**
**Input:** n = 3, k = 1
**Output:** 2
**Explanation:** The array \[1,3,2\] and \[2,1,3\] have exactly 1 inverse pair.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= k <= 1000` | null |
PYTHON 95% FASTER EASY BEGINER FRIENDLY Multiple Solutions | k-inverse-pairs-array | 0 | 1 | # DON\'T FORGET TO UPVOTE.\n\n# 1. 95% Faster solution:\n\n\n\t\tclass Solution:\n\t\t\tdef kInversePairs(self, n: int, k: int) -> int:\n\t\t\t\tm = 10 ** 9 + 7\n\n\t\t\t\tdp0 = [0] * (k + 1)\n\t\t\t\tdp0[0] = 1\n\n\t\t\t\tfor i in range(n):\n\t\t\t\t\tdp1 = []\n\t\t\t\t\ts = 0\n\t\t\t\t\tfor j in range(k + 1):\n\t\t\t\t\t\ts += dp0[j]\n\t\t\t\t\t\tif j >= i + 1:\n\t\t\t\t\t\t\ts -= dp0[j - i - 1]\n\t\t\t\t\t\ts %= m\n\t\t\t\t\t\tdp1.append(s)\n\t\t\t\t\tdp0 = dp1\n\n\t\t\t\treturn dp0[-1]\n\t\t\n\t\t\n# 2 An Average Time Solution:\n\n\t\tfrom functools import cache\n\n\t\tMOD = 10**9 + 7\n\n\t\tdef generateDP(n, k):\n\t\t\tdp = [[0 for _ in range(k + 1)] for _ in range(n + 1)]\n\t\t\tdp[0][0] = 1\n\t\t\tdpSums = [1] * (k + 2)\n\t\t\tdpSums[0] = 0\n\t\t\tfor emptySpaces in range(1, n + 1):\n\t\t\t\tdpPrevSums = dpSums\n\t\t\t\tdpSums = [0] * (k + 2)\n\t\t\t\tfor remainingInversePairs in range(emptySpaces):\n\t\t\t\t\tresult = dpPrevSums[remainingInversePairs+1]\n\t\t\t\t\tdp[emptySpaces][remainingInversePairs] = result\n\t\t\t\t\tdpSums[remainingInversePairs+1] = (dpSums[remainingInversePairs] + result) % MOD\n\t\t\t\tfor remainingInversePairs in range(emptySpaces, k + 1):\n\t\t\t\t\tresult = (dpPrevSums[remainingInversePairs+1] - dpPrevSums[remainingInversePairs-emptySpaces+1]) % MOD\n\t\t\t\t\tdp[emptySpaces][remainingInversePairs] = result\n\t\t\t\t\tdpSums[remainingInversePairs+1] = (dpSums[remainingInversePairs] + result) % MOD\n\t\t\treturn dp\n\n\t\tDP = generateDP(1000, 1000)\n\n\t\tclass Solution:\n\t\t\tdef kInversePairs(self, n: int, k: int) -> int:\n\t\t\t\treturn DP[n][k] | 5 | For an integer array `nums`, an **inverse pair** is a pair of integers `[i, j]` where `0 <= i < j < nums.length` and `nums[i] > nums[j]`.
Given two integers n and k, return the number of different arrays consist of numbers from `1` to `n` such that there are exactly `k` **inverse pairs**. Since the answer can be huge, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 0
**Output:** 1
**Explanation:** Only the array \[1,2,3\] which consists of numbers from 1 to 3 has exactly 0 inverse pairs.
**Example 2:**
**Input:** n = 3, k = 1
**Output:** 2
**Explanation:** The array \[1,3,2\] and \[2,1,3\] have exactly 1 inverse pair.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= k <= 1000` | null |
Python3 || Heapq || Faster Solution with explanation | course-schedule-iii | 0 | 1 | We start learning courses with earliest closing date first. If we find a course that can\'t fit into its close date, we can un-learn one of the previous course in order to fit it in. We can safely un-learn a previous course because it closes earlier and there is no way for it to be picked up again later. We pick up the one with longest learning time to un-learn, if the longest learning time happend to be the newly added course, then it is equivalent to not learning the newly added course.\n\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n courses.sort(key=lambda c: c[1])\n A, curr = [], 0\n for dur, ld in courses:\n heapq.heappush(A,-dur)\n curr += dur\n if curr > ld: curr += heapq.heappop(A)\n return len(A)\n``` | 33 | There are `n` different online courses numbered from `1` to `n`. You are given an array `courses` where `courses[i] = [durationi, lastDayi]` indicate that the `ith` course should be taken **continuously** for `durationi` days and must be finished before or on `lastDayi`.
You will start on the `1st` day and you cannot take two or more courses simultaneously.
Return _the maximum number of courses that you can take_.
**Example 1:**
**Input:** courses = \[\[100,200\],\[200,1300\],\[1000,1250\],\[2000,3200\]\]
**Output:** 3
Explanation:
There are totally 4 courses, but you can take 3 courses at most:
First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
**Example 2:**
**Input:** courses = \[\[1,2\]\]
**Output:** 1
**Example 3:**
**Input:** courses = \[\[3,2\],\[4,3\]\]
**Output:** 0
**Constraints:**
* `1 <= courses.length <= 104`
* `1 <= durationi, lastDayi <= 104` | During iteration, say I want to add the current course, currentTotalTime being total time of all courses taken till now, but adding the current course might exceed my deadline or it doesn’t.
1. If it doesn’t, then I have added one new course. Increment the currentTotalTime with duration of current course. 2. If it exceeds deadline, I can swap current course with current courses that has biggest duration.
* No harm done and I might have just reduced the currentTotalTime, right?
* What preprocessing do I need to do on my course processing order so that this swap is always legal? |
Python3 || Heapq || Faster Solution with explanation | course-schedule-iii | 0 | 1 | We start learning courses with earliest closing date first. If we find a course that can\'t fit into its close date, we can un-learn one of the previous course in order to fit it in. We can safely un-learn a previous course because it closes earlier and there is no way for it to be picked up again later. We pick up the one with longest learning time to un-learn, if the longest learning time happend to be the newly added course, then it is equivalent to not learning the newly added course.\n\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n courses.sort(key=lambda c: c[1])\n A, curr = [], 0\n for dur, ld in courses:\n heapq.heappush(A,-dur)\n curr += dur\n if curr > ld: curr += heapq.heappop(A)\n return len(A)\n``` | 33 | There are `n` different online courses numbered from `1` to `n`. You are given an array `courses` where `courses[i] = [durationi, lastDayi]` indicate that the `ith` course should be taken **continuously** for `durationi` days and must be finished before or on `lastDayi`.
You will start on the `1st` day and you cannot take two or more courses simultaneously.
Return _the maximum number of courses that you can take_.
**Example 1:**
**Input:** courses = \[\[100,200\],\[200,1300\],\[1000,1250\],\[2000,3200\]\]
**Output:** 3
Explanation:
There are totally 4 courses, but you can take 3 courses at most:
First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
**Example 2:**
**Input:** courses = \[\[1,2\]\]
**Output:** 1
**Example 3:**
**Input:** courses = \[\[3,2\],\[4,3\]\]
**Output:** 0
**Constraints:**
* `1 <= courses.length <= 104`
* `1 <= durationi, lastDayi <= 104` | During iteration, say I want to add the current course, currentTotalTime being total time of all courses taken till now, but adding the current course might exceed my deadline or it doesn’t.
1. If it doesn’t, then I have added one new course. Increment the currentTotalTime with duration of current course. 2. If it exceeds deadline, I can swap current course with current courses that has biggest duration.
* No harm done and I might have just reduced the currentTotalTime, right?
* What preprocessing do I need to do on my course processing order so that this swap is always legal? |
Python Max Heap O(NlogN) very straighforward and explained well | course-schedule-iii | 0 | 1 | Solution Explanation: \n Intuition: Move forward till you can and when you can\'t move leave out something from behind that will optimize the current state. Dropping a longer duration course that we took before and taking in a shorter duration will optimize our current state. Reason is because it will leave more room for future courses.\n1. \tKeep track of current time with \'time\' variable\n2. Sort courses by their last day.\n3. Take the current course like this:\n heapq.heappush(maxHeap, -duration)\n time += duration\n4. If we can\'t take the current course, it is a shame, we can\'t fit all courses before this last day. We can just move on, but wouldn\'t it make sense to drop a longer duration course we took before and instead taking in the current course that is shorter (especially if we know that that this current course will fit after dropping that longer duration course). So, we better get rid of that heavy course that we took before in favor of this shorter duration. Hopefully, this will leave more room for future courses. We can check if dropping the largest duration course that we took before will whether fit this current course that is shorter like this:\n```py\nelif max_heap and -max_heap[0] > duration and time + duration - (-max_heap[0]) < last_day:\n\ttime += duration - (-heapq.heappop(max_heap))\n heapq.heappush(max_heap, -duration)\n```\nPython only supports min heap. So negate the value when popped/pushed to treat min heap as max heap.\n5. max_heap trackes the number of courses we took. So, return len(max_heap) \n \nTC: O(NlogN)\nSC: O(N)\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n time, max_heap = 0, []\n for duration, last_day in sorted(courses, key=lambda c:c[1]):\n # we can take the course\n if time + duration <= last_day:\n time += duration\n heapq.heappush(max_heap, -duration)\n\t\t\t# we can\'t take the course. Drop the largest duration course we took before and add \n # this current shorter course which will fit now due to dropping the other largest one\n elif max_heap and -max_heap[0] > duration and time + duration - (-max_heap[0]) < last_day:\n time += duration - (-heapq.heappop(max_heap))\n heapq.heappush(max_heap, -duration)\n return len(max_heap)\n``` | 4 | There are `n` different online courses numbered from `1` to `n`. You are given an array `courses` where `courses[i] = [durationi, lastDayi]` indicate that the `ith` course should be taken **continuously** for `durationi` days and must be finished before or on `lastDayi`.
You will start on the `1st` day and you cannot take two or more courses simultaneously.
Return _the maximum number of courses that you can take_.
**Example 1:**
**Input:** courses = \[\[100,200\],\[200,1300\],\[1000,1250\],\[2000,3200\]\]
**Output:** 3
Explanation:
There are totally 4 courses, but you can take 3 courses at most:
First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
**Example 2:**
**Input:** courses = \[\[1,2\]\]
**Output:** 1
**Example 3:**
**Input:** courses = \[\[3,2\],\[4,3\]\]
**Output:** 0
**Constraints:**
* `1 <= courses.length <= 104`
* `1 <= durationi, lastDayi <= 104` | During iteration, say I want to add the current course, currentTotalTime being total time of all courses taken till now, but adding the current course might exceed my deadline or it doesn’t.
1. If it doesn’t, then I have added one new course. Increment the currentTotalTime with duration of current course. 2. If it exceeds deadline, I can swap current course with current courses that has biggest duration.
* No harm done and I might have just reduced the currentTotalTime, right?
* What preprocessing do I need to do on my course processing order so that this swap is always legal? |
Python Max Heap O(NlogN) very straighforward and explained well | course-schedule-iii | 0 | 1 | Solution Explanation: \n Intuition: Move forward till you can and when you can\'t move leave out something from behind that will optimize the current state. Dropping a longer duration course that we took before and taking in a shorter duration will optimize our current state. Reason is because it will leave more room for future courses.\n1. \tKeep track of current time with \'time\' variable\n2. Sort courses by their last day.\n3. Take the current course like this:\n heapq.heappush(maxHeap, -duration)\n time += duration\n4. If we can\'t take the current course, it is a shame, we can\'t fit all courses before this last day. We can just move on, but wouldn\'t it make sense to drop a longer duration course we took before and instead taking in the current course that is shorter (especially if we know that that this current course will fit after dropping that longer duration course). So, we better get rid of that heavy course that we took before in favor of this shorter duration. Hopefully, this will leave more room for future courses. We can check if dropping the largest duration course that we took before will whether fit this current course that is shorter like this:\n```py\nelif max_heap and -max_heap[0] > duration and time + duration - (-max_heap[0]) < last_day:\n\ttime += duration - (-heapq.heappop(max_heap))\n heapq.heappush(max_heap, -duration)\n```\nPython only supports min heap. So negate the value when popped/pushed to treat min heap as max heap.\n5. max_heap trackes the number of courses we took. So, return len(max_heap) \n \nTC: O(NlogN)\nSC: O(N)\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n time, max_heap = 0, []\n for duration, last_day in sorted(courses, key=lambda c:c[1]):\n # we can take the course\n if time + duration <= last_day:\n time += duration\n heapq.heappush(max_heap, -duration)\n\t\t\t# we can\'t take the course. Drop the largest duration course we took before and add \n # this current shorter course which will fit now due to dropping the other largest one\n elif max_heap and -max_heap[0] > duration and time + duration - (-max_heap[0]) < last_day:\n time += duration - (-heapq.heappop(max_heap))\n heapq.heappush(max_heap, -duration)\n return len(max_heap)\n``` | 4 | There are `n` different online courses numbered from `1` to `n`. You are given an array `courses` where `courses[i] = [durationi, lastDayi]` indicate that the `ith` course should be taken **continuously** for `durationi` days and must be finished before or on `lastDayi`.
You will start on the `1st` day and you cannot take two or more courses simultaneously.
Return _the maximum number of courses that you can take_.
**Example 1:**
**Input:** courses = \[\[100,200\],\[200,1300\],\[1000,1250\],\[2000,3200\]\]
**Output:** 3
Explanation:
There are totally 4 courses, but you can take 3 courses at most:
First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
**Example 2:**
**Input:** courses = \[\[1,2\]\]
**Output:** 1
**Example 3:**
**Input:** courses = \[\[3,2\],\[4,3\]\]
**Output:** 0
**Constraints:**
* `1 <= courses.length <= 104`
* `1 <= durationi, lastDayi <= 104` | During iteration, say I want to add the current course, currentTotalTime being total time of all courses taken till now, but adding the current course might exceed my deadline or it doesn’t.
1. If it doesn’t, then I have added one new course. Increment the currentTotalTime with duration of current course. 2. If it exceeds deadline, I can swap current course with current courses that has biggest duration.
* No harm done and I might have just reduced the currentTotalTime, right?
* What preprocessing do I need to do on my course processing order so that this swap is always legal? |
Python Recursive + Memoization + Bottom-UP - Greedy + Heap | course-schedule-iii | 0 | 1 | Typical Knapsack Problem, either take the course or not, calculate total number of days by taking course and choose the maximum number of courses taken at that point of time.\n***Recursion: Time Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n return self.scheduleCourseHelper(courses, 0, 0)\n # Hypothesis, will return maximum number of courses taken\n def scheduleCourseHelper(self, courses, totalDays, index) -> int:\n # Returning 0, if no courses to take\n if index >= len(courses):\n return 0\n # Curr Course\n currCourse = courses[index]\n # We will have two choices now, after sorting, Either take the current course or not\n courseTaken = 0\n courseNotTaken = 0\n # If we take the course, we will increase the count by 1\n if totalDays + currCourse[0] <= currCourse[1]:\n courseTaken = 1 + self.scheduleCourseHelper(courses, totalDays + currCourse[0], index + 1)\n # If not taking course, go to next course, and dont increase the count\n courseNotTaken = self.scheduleCourseHelper(courses, totalDays, index + 1)\n # return maximum of course Taken and not taken\n return max(courseTaken, courseNotTaken)\n \n```\n\n***Memoization: Memory Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n memo = [[-1 for _ in range(courses[-1][1] + 1)] for _ in range(len(courses) + 1)]\n return self.scheduleCourseHelper(courses, 0, 0, memo)\n # Hypothesis, will return maximum number of courses taken\n def scheduleCourseHelper(self, courses, totalDays, index, memo) -> int:\n # Returning 0, if no courses to take\n if index >= len(courses):\n return 0\n if memo[index][totalDays] != -1:\n return memo[index][totalDays]\n # Curr Course\n currCourse = courses[index]\n # We will have two choices now, after sorting, Either take the current course or not\n courseTaken = 0\n courseNotTaken = 0\n # If we take the course, we will increase the count by 1\n if totalDays + currCourse[0] <= currCourse[1]:\n courseTaken = 1 + self.scheduleCourseHelper(courses, totalDays + currCourse[0], index + 1, memo)\n # If not taking course, go to next course, and dont increase the count\n courseNotTaken = self.scheduleCourseHelper(courses, totalDays, index + 1, memo)\n # return maximum of course Taken and not taken\n memo[index][totalDays] = max(courseTaken, courseNotTaken)\n return memo[index][totalDays] \n```\n\n***Bottom Up DP: Time Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n dp = [[0 for _ in range(courses[-1][1] + 1)] for _ in range(len(courses) + 1)]\n for i in range(1, len(courses) + 1):\n for j in range(1, courses[-1][1] + 1):\n courseIndex = i - 1\n duration = courses[courseIndex][0]\n lastDay = courses[courseIndex][1]\n # Take the course\n # only if current day is less than lastDay and duration is less than equal to time\n if j <= lastDay and j >= duration:\n # Now, refer the calculation for remaining day\n dp[i][j] = 1 + dp[i - 1][j - duration]\n # Now, take the maximum if course taken or not taken\n dp[i][j] = max(dp[i][j], max(dp[i][j - 1], dp[i - 1][j]))\n # Dont take the course\n else:\n dp[i][j] = max(dp[i][j], max(dp[i][j - 1], dp[i - 1][j]))\n return dp[len(courses)][courses[-1][1]]\n```\n***Greedy: Time Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n totalDays = 0\n count = 0\n for i in range(len(courses)):\n # If course can be taken, keep adding course\n if totalDays + courses[i][0] <= courses[i][1]:\n totalDays += courses[i][0]\n count += 1\n # if we cant take course, we will try to fit this course, by replacing it with the course\n # which we have already taken but have higher duration\n else:\n currCourseIndexWhichCantFit = i\n for j in range(i):\n # Find the course which is already present and have duration higher than\n # currCourseIndexWhichCantFit and have max last day\n if courses[j][0] > courses[currCourseIndexWhichCantFit][0]:\n currCourseIndexWhichCantFit = j\n # Now take the currCourseIndexWhichCantFit course and replace it with the max Duration course found\n if courses[currCourseIndexWhichCantFit][0] > courses[i][0]:\n totalDays += courses[i][0] - courses[currCourseIndexWhichCantFit][0]\n # ALready, considered this, so wont take in future\n # assign, any non positive value\n courses[currCourseIndexWhichCantFit][0] = float("-inf")\n return count\n```\n\n***Heap: Accepted***\n```\nimport heapq\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n totalDays = 0\n maxHeap = []\n for i in range(len(courses)):\n # If course can be taken, keep adding course\n totalDays += courses[i][0]\n # Python default is minHEap, so adding -ve of that value\n heapq.heappush(maxHeap, -courses[i][0])\n # Now, if totalDays exceeds the last day after taking that course,\n # remove the course with maximum duration\n if courses[i][1] < totalDays:\n courseWithMaxDuration = heapq.heappop(maxHeap)\n # Since, we added the negative values because of maxHeap in Python\n totalDays += courseWithMaxDuration\n # Length of heap will determine number of courses taken,\n # as it will only contain courses taken\n return len(maxHeap)\n``` | 3 | There are `n` different online courses numbered from `1` to `n`. You are given an array `courses` where `courses[i] = [durationi, lastDayi]` indicate that the `ith` course should be taken **continuously** for `durationi` days and must be finished before or on `lastDayi`.
You will start on the `1st` day and you cannot take two or more courses simultaneously.
Return _the maximum number of courses that you can take_.
**Example 1:**
**Input:** courses = \[\[100,200\],\[200,1300\],\[1000,1250\],\[2000,3200\]\]
**Output:** 3
Explanation:
There are totally 4 courses, but you can take 3 courses at most:
First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
**Example 2:**
**Input:** courses = \[\[1,2\]\]
**Output:** 1
**Example 3:**
**Input:** courses = \[\[3,2\],\[4,3\]\]
**Output:** 0
**Constraints:**
* `1 <= courses.length <= 104`
* `1 <= durationi, lastDayi <= 104` | During iteration, say I want to add the current course, currentTotalTime being total time of all courses taken till now, but adding the current course might exceed my deadline or it doesn’t.
1. If it doesn’t, then I have added one new course. Increment the currentTotalTime with duration of current course. 2. If it exceeds deadline, I can swap current course with current courses that has biggest duration.
* No harm done and I might have just reduced the currentTotalTime, right?
* What preprocessing do I need to do on my course processing order so that this swap is always legal? |
Python Recursive + Memoization + Bottom-UP - Greedy + Heap | course-schedule-iii | 0 | 1 | Typical Knapsack Problem, either take the course or not, calculate total number of days by taking course and choose the maximum number of courses taken at that point of time.\n***Recursion: Time Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n return self.scheduleCourseHelper(courses, 0, 0)\n # Hypothesis, will return maximum number of courses taken\n def scheduleCourseHelper(self, courses, totalDays, index) -> int:\n # Returning 0, if no courses to take\n if index >= len(courses):\n return 0\n # Curr Course\n currCourse = courses[index]\n # We will have two choices now, after sorting, Either take the current course or not\n courseTaken = 0\n courseNotTaken = 0\n # If we take the course, we will increase the count by 1\n if totalDays + currCourse[0] <= currCourse[1]:\n courseTaken = 1 + self.scheduleCourseHelper(courses, totalDays + currCourse[0], index + 1)\n # If not taking course, go to next course, and dont increase the count\n courseNotTaken = self.scheduleCourseHelper(courses, totalDays, index + 1)\n # return maximum of course Taken and not taken\n return max(courseTaken, courseNotTaken)\n \n```\n\n***Memoization: Memory Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n memo = [[-1 for _ in range(courses[-1][1] + 1)] for _ in range(len(courses) + 1)]\n return self.scheduleCourseHelper(courses, 0, 0, memo)\n # Hypothesis, will return maximum number of courses taken\n def scheduleCourseHelper(self, courses, totalDays, index, memo) -> int:\n # Returning 0, if no courses to take\n if index >= len(courses):\n return 0\n if memo[index][totalDays] != -1:\n return memo[index][totalDays]\n # Curr Course\n currCourse = courses[index]\n # We will have two choices now, after sorting, Either take the current course or not\n courseTaken = 0\n courseNotTaken = 0\n # If we take the course, we will increase the count by 1\n if totalDays + currCourse[0] <= currCourse[1]:\n courseTaken = 1 + self.scheduleCourseHelper(courses, totalDays + currCourse[0], index + 1, memo)\n # If not taking course, go to next course, and dont increase the count\n courseNotTaken = self.scheduleCourseHelper(courses, totalDays, index + 1, memo)\n # return maximum of course Taken and not taken\n memo[index][totalDays] = max(courseTaken, courseNotTaken)\n return memo[index][totalDays] \n```\n\n***Bottom Up DP: Time Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n dp = [[0 for _ in range(courses[-1][1] + 1)] for _ in range(len(courses) + 1)]\n for i in range(1, len(courses) + 1):\n for j in range(1, courses[-1][1] + 1):\n courseIndex = i - 1\n duration = courses[courseIndex][0]\n lastDay = courses[courseIndex][1]\n # Take the course\n # only if current day is less than lastDay and duration is less than equal to time\n if j <= lastDay and j >= duration:\n # Now, refer the calculation for remaining day\n dp[i][j] = 1 + dp[i - 1][j - duration]\n # Now, take the maximum if course taken or not taken\n dp[i][j] = max(dp[i][j], max(dp[i][j - 1], dp[i - 1][j]))\n # Dont take the course\n else:\n dp[i][j] = max(dp[i][j], max(dp[i][j - 1], dp[i - 1][j]))\n return dp[len(courses)][courses[-1][1]]\n```\n***Greedy: Time Limit Exceeded***\n```\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n totalDays = 0\n count = 0\n for i in range(len(courses)):\n # If course can be taken, keep adding course\n if totalDays + courses[i][0] <= courses[i][1]:\n totalDays += courses[i][0]\n count += 1\n # if we cant take course, we will try to fit this course, by replacing it with the course\n # which we have already taken but have higher duration\n else:\n currCourseIndexWhichCantFit = i\n for j in range(i):\n # Find the course which is already present and have duration higher than\n # currCourseIndexWhichCantFit and have max last day\n if courses[j][0] > courses[currCourseIndexWhichCantFit][0]:\n currCourseIndexWhichCantFit = j\n # Now take the currCourseIndexWhichCantFit course and replace it with the max Duration course found\n if courses[currCourseIndexWhichCantFit][0] > courses[i][0]:\n totalDays += courses[i][0] - courses[currCourseIndexWhichCantFit][0]\n # ALready, considered this, so wont take in future\n # assign, any non positive value\n courses[currCourseIndexWhichCantFit][0] = float("-inf")\n return count\n```\n\n***Heap: Accepted***\n```\nimport heapq\nclass Solution:\n def scheduleCourse(self, courses: List[List[int]]) -> int:\n # First, sorting according to the lastday.\n courses.sort(key=lambda x: x[1])\n totalDays = 0\n maxHeap = []\n for i in range(len(courses)):\n # If course can be taken, keep adding course\n totalDays += courses[i][0]\n # Python default is minHEap, so adding -ve of that value\n heapq.heappush(maxHeap, -courses[i][0])\n # Now, if totalDays exceeds the last day after taking that course,\n # remove the course with maximum duration\n if courses[i][1] < totalDays:\n courseWithMaxDuration = heapq.heappop(maxHeap)\n # Since, we added the negative values because of maxHeap in Python\n totalDays += courseWithMaxDuration\n # Length of heap will determine number of courses taken,\n # as it will only contain courses taken\n return len(maxHeap)\n``` | 3 | There are `n` different online courses numbered from `1` to `n`. You are given an array `courses` where `courses[i] = [durationi, lastDayi]` indicate that the `ith` course should be taken **continuously** for `durationi` days and must be finished before or on `lastDayi`.
You will start on the `1st` day and you cannot take two or more courses simultaneously.
Return _the maximum number of courses that you can take_.
**Example 1:**
**Input:** courses = \[\[100,200\],\[200,1300\],\[1000,1250\],\[2000,3200\]\]
**Output:** 3
Explanation:
There are totally 4 courses, but you can take 3 courses at most:
First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
**Example 2:**
**Input:** courses = \[\[1,2\]\]
**Output:** 1
**Example 3:**
**Input:** courses = \[\[3,2\],\[4,3\]\]
**Output:** 0
**Constraints:**
* `1 <= courses.length <= 104`
* `1 <= durationi, lastDayi <= 104` | During iteration, say I want to add the current course, currentTotalTime being total time of all courses taken till now, but adding the current course might exceed my deadline or it doesn’t.
1. If it doesn’t, then I have added one new course. Increment the currentTotalTime with duration of current course. 2. If it exceeds deadline, I can swap current course with current courses that has biggest duration.
* No harm done and I might have just reduced the currentTotalTime, right?
* What preprocessing do I need to do on my course processing order so that this swap is always legal? |
Solution | smallest-range-covering-elements-from-k-lists | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n std::vector<int> smallestRange(std::vector<std::vector<int>> const &nums)\n {\n auto S = nums.size();\n std::vector<std::pair<std::vector<int>::const_iterator,\n std::vector<int>::const_iterator>>\n ps(S);\n std::transform(nums.begin(),\n nums.end(),\n ps.begin(),\n [](auto const &num)\n {\n return std::make_pair(std::begin(num), std::end(num));\n });\n auto less_val = [](auto i, auto j)\n {\n return *(i.first) < *(j.first);\n };\n auto max_i = std::max_element(ps.begin(), ps.end(), less_val);\n auto best_max = max_i->first;\n auto best_min = std::min_element(ps.begin(), ps.end(), less_val)->first;\n while (max_i->first != max_i->second)\n {\n for (auto &[begin, end] : ps)\n {\n begin = std::upper_bound(begin, end, *(max_i->first)) - 1;\n }\n auto min_i = std::min_element(ps.begin(), ps.end(), less_val);\n if (*max_i->first - *min_i->first < *best_max - *best_min)\n {\n best_max = max_i->first;\n best_min = min_i->first;\n }\n min_i->first++;\n max_i = min_i;\n }\n return std::vector<int>({ *best_min, *best_max });\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def smallestRange(self, nums: List[List[int]]) -> List[int]:\n d = defaultdict(list)\n for i, evs in enumerate(nums):\n for v in evs:\n d[v].append(i)\n keys = sorted(d.keys())\n lo = 0\n n = len(nums)\n dd = defaultdict(int)\n le, ri = -1, float(\'Inf\')\n have = 0\n for hi in range(len(keys)):\n for x in d[keys[hi]]:\n dd[x] += 1\n if dd[x] == 1:\n have += 1\n while have == n:\n curr = keys[hi] - keys[lo]\n if ri - le > curr:\n ri = keys[hi]\n le = keys[lo]\n for x in d[keys[lo]]:\n dd[x] -= 1\n if dd[x] == 0:\n have -= 1\n lo += 1\n return [le, ri]\n```\n\n```Java []\nclass Solution {\n private int[] bestRange;\n public int[] smallestRange(List<List<Integer>> nums) {\n List<Integer> firstList = nums.get(0);\n for (int elem : firstList) {\n int[] range = new int[2];\n range[0] = elem;\n range[1] = elem;\n expandRange(nums, 1, range);\n }\n return bestRange; \n }\n private void expandRange(List<List<Integer>> nums, int listIndex, int[] currentRange) {\n if (listIndex >= nums.size()) {\n checkBest(currentRange);\n return;\n }\n if (shouldPrune(currentRange)) {\n return;\n }\n List<Integer> newList = nums.get(listIndex);\n\n int leftIndex = findIndex(newList, currentRange[0], 0, newList.size() - 1);\n int rightIndex = findIndex(newList, currentRange[1], 0, newList.size() - 1);\n\n boolean needsExpanding = leftIndex == rightIndex && \n (leftIndex == newList.size() || \n (newList.get(leftIndex) != currentRange[0] && newList.get(rightIndex) != currentRange[1]));\n\n if (needsExpanding) {\n int originalLeft = currentRange[0];\n int originalRight = currentRange[1];\n \n if (rightIndex < newList.size()) {\n currentRange[1] = newList.get(rightIndex);\n expandRange(nums, listIndex + 1, currentRange);\n currentRange[0] = originalLeft;\n currentRange[1] = originalRight;\n }\n if (leftIndex > 0) {\n currentRange[0] = newList.get(leftIndex - 1);\n expandRange(nums, listIndex + 1, currentRange);\n }\n } else {\n expandRange(nums, listIndex + 1, currentRange);\n }\n }\n private static int findIndex(List<Integer> list, int value, int left, int right) {\n if (left > right) {\n return left;\n }\n int mid = right - (right - left) / 2;\n int candidate = list.get(mid);\n\n if (candidate >= value) {\n if (mid == 0 || list.get(mid - 1) < value) {\n return mid;\n }\n return findIndex(list, value, left, mid - 1);\n } else {\n return findIndex(list, value, mid + 1, right);\n }\n }\n private void checkBest(int[] currentRange) {\n if (isBest(currentRange)) {\n if (bestRange == null) {\n bestRange = new int[2];\n }\n bestRange[0] = currentRange[0];\n bestRange[1] = currentRange[1];\n }\n }\n private boolean isBest(int[] currentRange) {\n if (bestRange == null) {\n return true;\n }\n int currentRangeSize = currentRange[1] - currentRange[0];\n int bestRangeSize = bestRange[1] - bestRange[0];\n return currentRangeSize < bestRangeSize || (currentRangeSize == bestRangeSize && currentRange[0] < bestRange[0]);\n }\n private boolean shouldPrune(int[] currentRange) {\n return !isBest(currentRange);\n }\n}\n```\n | 1 | You have `k` lists of sorted integers in **non-decreasing order**. Find the **smallest** range that includes at least one number from each of the `k` lists.
We define the range `[a, b]` is smaller than range `[c, d]` if `b - a < d - c` **or** `a < c` if `b - a == d - c`.
**Example 1:**
**Input:** nums = \[\[4,10,15,24,26\],\[0,9,12,20\],\[5,18,22,30\]\]
**Output:** \[20,24\]
**Explanation:**
List 1: \[4, 10, 15, 24,26\], 24 is in range \[20,24\].
List 2: \[0, 9, 12, 20\], 20 is in range \[20,24\].
List 3: \[5, 18, 22, 30\], 22 is in range \[20,24\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[1,2,3\],\[1,2,3\]\]
**Output:** \[1,1\]
**Constraints:**
* `nums.length == k`
* `1 <= k <= 3500`
* `1 <= nums[i].length <= 50`
* `-105 <= nums[i][j] <= 105`
* `nums[i]` is sorted in **non-decreasing** order. | null |
Very inituive solution with sorting. | smallest-range-covering-elements-from-k-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe leverage the requirement that range has to include at least one number. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIf we get a sorted list that contains every numbers from each k list, we only need to keep the range to cover those numbers just coming from each k. This converts to the min window to include k unique numbers. \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlog(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def smallestRange(self, nums: List[List[int]]) -> List[int]:\n temp = []\n for i, arr in enumerate(nums):\n for n in arr:\n temp.append((n, i))\n\n temp.sort()\n\n k = len(nums)\n ans = (temp[0][0], temp[-1][0])\n best = temp[-1][0] - temp[0][0]\n\n seen = defaultdict(int)\n start = 0\n for i, (x, idx) in enumerate(temp):\n seen[idx] += 1\n if i == 0:\n continue\n\n if len(seen) < k:\n continue\n else:\n while len(seen) == k:\n if x - temp[start][0] < best:\n best = x - temp[start][0]\n ans = (temp[start][0], x)\n \n y = temp[start][1]\n seen[y] -= 1\n if seen[y] == 0:\n del seen[y]\n start += 1\n\n return ans\n``` | 0 | You have `k` lists of sorted integers in **non-decreasing order**. Find the **smallest** range that includes at least one number from each of the `k` lists.
We define the range `[a, b]` is smaller than range `[c, d]` if `b - a < d - c` **or** `a < c` if `b - a == d - c`.
**Example 1:**
**Input:** nums = \[\[4,10,15,24,26\],\[0,9,12,20\],\[5,18,22,30\]\]
**Output:** \[20,24\]
**Explanation:**
List 1: \[4, 10, 15, 24,26\], 24 is in range \[20,24\].
List 2: \[0, 9, 12, 20\], 20 is in range \[20,24\].
List 3: \[5, 18, 22, 30\], 22 is in range \[20,24\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[1,2,3\],\[1,2,3\]\]
**Output:** \[1,1\]
**Constraints:**
* `nums.length == k`
* `1 <= k <= 3500`
* `1 <= nums[i].length <= 50`
* `-105 <= nums[i][j] <= 105`
* `nums[i]` is sorted in **non-decreasing** order. | null |
Using min heap to get min of current nums and tracking a max val to enumerate valid ranges | smallest-range-covering-elements-from-k-lists | 0 | 1 | # Code\n```\nclass Solution:\n # T = O(Nlog(K)) for the heap popping happening n times \n # S = O(K) for the heap\n def smallestRange(self, nums: List[List[int]]) -> List[int]:\n ans = -math.inf, math.inf # max range to start with\n\n heap = []\n \n high = -math.inf\n # track max out of first starting list of numbers \n # and also add them to min heap\n for i in range(len(nums)):\n heapq.heappush(heap, (nums[i][0], i, 0))\n high = max(high, nums[i][0])\n\n # Logic: At each iteration we have max element in list\n # and heap pop gives us min element in list and we go left to \n # right.\n # Between these min and max we will cover at least one element in the array as we \n # got the min and max out of taking one element from each array \n # Now to reduce this window \n # 1. we can reduce max -> but this will lead to an array from which this max \n # came getting skipped \n # 2. so we can only try to increase min as this can give us new window to consider\n # So we use min heap to get min out of current window and replace it with \n # next element in the array that gave min\n # This will give use a new set of values to consider \n # We will also track if this next element is greater than current max and update max\n # This way at each level we have \n # 1. 1 element from each array \n # 2. min from them and max from them \n # and as we go from left to right we consider ranges with smaller start first \n # as this is what we want (eg: 11 over 33) in [[1,2,3], [1,2,3], [1,2,3]]\n # This also is complete as we are not missing any range. Each time we only increment \n # the smalest of all the numbers. Which means we are consiering the widest possible \n # allowed range that has an element from each array and trying to reducing it.\n while True:\n low, id, ind = heapq.heappop(heap)\n\n # if new range is smaller then update ans\n if high - low < ans[1] - ans[0]:\n ans = (low, high)\n\n # if we reached the end of an array then we need to stop\n # as going further we will miss elements from this array\n if ind + 1 == len(nums[id]):\n return ans\n\n next = nums[id][ind+1]\n\n # find new max\n high = max(high, next)\n\n heapq.heappush(heap, (next, id, ind+1))\n``` | 1 | You have `k` lists of sorted integers in **non-decreasing order**. Find the **smallest** range that includes at least one number from each of the `k` lists.
We define the range `[a, b]` is smaller than range `[c, d]` if `b - a < d - c` **or** `a < c` if `b - a == d - c`.
**Example 1:**
**Input:** nums = \[\[4,10,15,24,26\],\[0,9,12,20\],\[5,18,22,30\]\]
**Output:** \[20,24\]
**Explanation:**
List 1: \[4, 10, 15, 24,26\], 24 is in range \[20,24\].
List 2: \[0, 9, 12, 20\], 20 is in range \[20,24\].
List 3: \[5, 18, 22, 30\], 22 is in range \[20,24\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[1,2,3\],\[1,2,3\]\]
**Output:** \[1,1\]
**Constraints:**
* `nums.length == k`
* `1 <= k <= 3500`
* `1 <= nums[i].length <= 50`
* `-105 <= nums[i][j] <= 105`
* `nums[i]` is sorted in **non-decreasing** order. | null |
Awesome Logic With Heap Concept | smallest-range-covering-elements-from-k-lists | 0 | 1 | # Using Heap Concept:\n```\nclass Solution:\n def smallestRange(self, nums: List[List[int]]) -> List[int]:\n heap=[]\n maxvalue=0\n for i in range(len(nums)):\n heapq.heappush(heap,[nums[i][0],i,0])\n maxvalue=max(maxvalue,nums[i][0])\n answer=[heap[0][0],maxvalue]\n while True:\n _,row,col=heapq.heappop(heap)\n if col==len(nums[row])-1:\n break\n next_num=nums[row][col+1]\n heapq.heappush(heap,[next_num,row,col+1])\n maxvalue=max(maxvalue,next_num)\n if maxvalue-heap[0][0]<answer[1]-answer[0]:\n answer=[heap[0][0],maxvalue]\n return answer\n```\n# please upvote me it would encourage me alot\n | 9 | You have `k` lists of sorted integers in **non-decreasing order**. Find the **smallest** range that includes at least one number from each of the `k` lists.
We define the range `[a, b]` is smaller than range `[c, d]` if `b - a < d - c` **or** `a < c` if `b - a == d - c`.
**Example 1:**
**Input:** nums = \[\[4,10,15,24,26\],\[0,9,12,20\],\[5,18,22,30\]\]
**Output:** \[20,24\]
**Explanation:**
List 1: \[4, 10, 15, 24,26\], 24 is in range \[20,24\].
List 2: \[0, 9, 12, 20\], 20 is in range \[20,24\].
List 3: \[5, 18, 22, 30\], 22 is in range \[20,24\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[1,2,3\],\[1,2,3\]\]
**Output:** \[1,1\]
**Constraints:**
* `nums.length == k`
* `1 <= k <= 3500`
* `1 <= nums[i].length <= 50`
* `-105 <= nums[i][j] <= 105`
* `nums[i]` is sorted in **non-decreasing** order. | null |
python using heap | | smallest-range-covering-elements-from-k-lists | 0 | 1 | ```\nclass Solution:\n def smallestRange(self, nums: List[List[int]]) -> List[int]:\n \n n = len(nums)\n \n pq = []\n ma = 0\n \n for i in range(n):\n \n heappush(pq, (nums[i][0] , i, 0))\n ma = max(ma , nums[i][0])\n \n ans = [pq[0][0] , ma]\n while True:\n \n _,i,j = heappop(pq)\n \n \n if j == len(nums[i])-1:\n break\n \n next_num = nums[i][j+1]\n \n ma = max( ma , next_num)\n \n heappush(pq,(next_num, i , j+1))\n \n if ma-pq[0][0] < ans[1] - ans[0]:\n ans= [pq[0][0], ma]\n return ans\n``` | 18 | You have `k` lists of sorted integers in **non-decreasing order**. Find the **smallest** range that includes at least one number from each of the `k` lists.
We define the range `[a, b]` is smaller than range `[c, d]` if `b - a < d - c` **or** `a < c` if `b - a == d - c`.
**Example 1:**
**Input:** nums = \[\[4,10,15,24,26\],\[0,9,12,20\],\[5,18,22,30\]\]
**Output:** \[20,24\]
**Explanation:**
List 1: \[4, 10, 15, 24,26\], 24 is in range \[20,24\].
List 2: \[0, 9, 12, 20\], 20 is in range \[20,24\].
List 3: \[5, 18, 22, 30\], 22 is in range \[20,24\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[1,2,3\],\[1,2,3\]\]
**Output:** \[1,1\]
**Constraints:**
* `nums.length == k`
* `1 <= k <= 3500`
* `1 <= nums[i].length <= 50`
* `-105 <= nums[i][j] <= 105`
* `nums[i]` is sorted in **non-decreasing** order. | null |
Solution | sum-of-square-numbers | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool judgeSquareSum(int c) {\n if(c==1)\n return true;\n long long int left=0, right = sqrt(c);\n while(left<=right){\n long long int sum = (left*left) + (right*right);\n if(sum==c)\n return true;\n else if(sum<c)\n left++;\n else\n right--;\n }\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def judgeSquareSum(self, c: int) -> bool:\n i = 2\n while i * i <= c:\n count = 0\n if c % i == 0:\n while c % i == 0:\n count += 1\n c //= i\n if count % 2 and i % 4 == 3:\n return False\n i += 1\n return c % 4 != 3\n```\n\n```Java []\nclass Solution {\n public boolean judgeSquareSum(int c) {\n for (int i = 2; i * i <= c; i++) {\n int count = 0;\n if (c % i == 0) {\n while (c % i == 0) {\n count++;\n c /= i;\n }\n if (i % 4 == 3 && count % 2 != 0)\n return false;\n }\n }\n return c % 4 != 3;\n }\n}\n```\n | 3 | Given a non-negative integer `c`, decide whether there're two integers `a` and `b` such that `a2 + b2 = c`.
**Example 1:**
**Input:** c = 5
**Output:** true
**Explanation:** 1 \* 1 + 2 \* 2 = 5
**Example 2:**
**Input:** c = 3
**Output:** false
**Constraints:**
* `0 <= c <= 231 - 1` | null |
Easy python solution using binary Search || 2 different Solution using BS | sum-of-square-numbers | 0 | 1 | # #Solution 1\n\n\n# Code\n```\nclass Solution:\n def judgeSquareSum(self, c: int) -> bool:\n i=0\n j=int(c**(1/2))\n while i<=j:\n m=i*i+j*j\n if m==c:\n return True\n elif m>c:\n j-=1\n else:i+=1\n return False\n```\n## #Solution 2\n\n\n```\nclass Solution(object):\n def judgeSquareSum(self, c):\n """\n :type c: int\n :rtype: bool\n """\n val=c\n if c>2000:val=sqrt(c)\n lst=[i*i for i in range(int(val)+1)]\n def bs(val,lst):\n i=0\n j=len(lst)-1\n while i<=j:\n m=(i+j)//2\n if lst[m]==val:\n return 1\n elif lst[m]>val:\n j=m-1\n else:i=m+1\n return 0\n for i in lst:\n val=c-i\n if val<0:break\n ans=bs(val,lst)\n if val==0 or ans==True:\n return True\n return False\n``` | 3 | Given a non-negative integer `c`, decide whether there're two integers `a` and `b` such that `a2 + b2 = c`.
**Example 1:**
**Input:** c = 5
**Output:** true
**Explanation:** 1 \* 1 + 2 \* 2 = 5
**Example 2:**
**Input:** c = 3
**Output:** false
**Constraints:**
* `0 <= c <= 231 - 1` | null |
Python3 Easy Solution |One Pointer | faster thar 91% | sum-of-square-numbers | 0 | 1 | \n\n\n```\n for a in range(int(sqrt(c))+1):\n b=sqrt(c-a*a)\n if b==int(b): return True\n```\n | 4 | Given a non-negative integer `c`, decide whether there're two integers `a` and `b` such that `a2 + b2 = c`.
**Example 1:**
**Input:** c = 5
**Output:** true
**Explanation:** 1 \* 1 + 2 \* 2 = 5
**Example 2:**
**Input:** c = 3
**Output:** false
**Constraints:**
* `0 <= c <= 231 - 1` | null |
Binary Search and Two Pointers Approach----->Python3 | sum-of-square-numbers | 0 | 1 | # 1. Two Pointers Approach\n``` \nclass Solution:\n def judgeSquareSum(self, c: int) -> bool:\n i,j=0,int(sqrt(c))\n while i<=j:\n if i*i+j*j==c:\n return True\n if i*i+j*j>c:\n j-=1\n else:\n i+=1\n return False\n```\n\n# 2. Binary search Approach----->O(NLogN)\n```\nclass Solution:\n def judgeSquareSum(self, c: int) -> bool:\n for i in range(int(sqrt(c))+1):\n left,right=0,c\n while left<=right:\n mid=(left+right)//2\n if i*i+mid*mid==c:\n return True\n if i*i + mid*mid > c:\n right=mid-1\n else:\n left=mid+1\n return False\n```\n# please upvote me it would encourage me alot\n | 5 | Given a non-negative integer `c`, decide whether there're two integers `a` and `b` such that `a2 + b2 = c`.
**Example 1:**
**Input:** c = 5
**Output:** true
**Explanation:** 1 \* 1 + 2 \* 2 = 5
**Example 2:**
**Input:** c = 3
**Output:** false
**Constraints:**
* `0 <= c <= 231 - 1` | null |
633: Solution with step by step explanation | sum-of-square-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize left and right pointers to 0 and the integer square root of c respectively.\n2. While the left pointer is less than or equal to the right pointer, compute the current sum of squares.\n3. If the current sum is equal to c, return True.\n4. If the current sum is less than c, increment the left pointer by 1.\n5. If the current sum is greater than c, decrement the right pointer by 1.\n6. If the loop completes without finding a valid pair of integers, return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def judgeSquareSum(self, c: int) -> bool:\n left, right = 0, int(c**0.5) # initialize left and right pointers\n while left <= right:\n curr_sum = left**2 + right**2\n if curr_sum == c:\n return True\n elif curr_sum < c:\n left += 1\n else:\n right -= 1\n return False\n\n``` | 1 | Given a non-negative integer `c`, decide whether there're two integers `a` and `b` such that `a2 + b2 = c`.
**Example 1:**
**Input:** c = 5
**Output:** true
**Explanation:** 1 \* 1 + 2 \* 2 = 5
**Example 2:**
**Input:** c = 3
**Output:** false
**Constraints:**
* `0 <= c <= 231 - 1` | null |
[Python][Stack]Easy to Understand] | exclusive-time-of-functions | 0 | 1 | In this solution, we calculate the time in place rather than waiting for the **endtime** of the process. \n\nWe always keep track of current time **currt**\n\n\nWhenever a new process is started, we calculate the time taken by the previus process till now ( **timestamp -currt**) and and add that to the stack along with its **fid**. \n\nWhenever a process ends, we pop the the previous element from the stack(which is its starttime log) and update the **res[fid]** with **time -currt + 1**\n\n\n\n\n\n\n\n\n\n\n```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n\t # Store total time of fid\n res = [0 for _ in range(n)]\n\t\t# stack\n s = []\n\t\t# store the current time\n currt = 0\n\t\t\n\t\t# iterate through the logs\n for log in logs: \n \n\t\t\t# Get thefid , state and timestamp from the log\t\n fid, state, timestamp = log.split(":")\n \n fid = int(fid)\n timestamp = int(timestamp)\n \n if state == "end":\n\t\t\t\t# since the process is ended, we pop out its start log\n s.pop()\n\t\t\t\t# Update the time of the log. We add **+1** as the process gets over at the end of timestamp. \n\t\t\t\t# So adding that **1**\n res[fid] += timestamp - currt+1\n\t\t\t\t# updating the current time\n currt = timestamp + 1\n else:\n if (s):\n\t\t\t\t # if another process is strating before the previious process has been ended, \n\t\t\t\t\t # we get the fid anf time of previouse proces\n fidprev,time = s[-1]\n\t\t\t\t\t# add the time taken by previouse process till now before a new process is spawned\n res[fidprev] += timestamp - currt\n\t\t\t\t# add the start log to the stack \n s.append((fid,timestamp))\n\t\t\t\t# update the current time\n currt = timestamp\n \n return res\n```\n\nTC: O(N)\nSC: O(N)\n\n | 3 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
Python 3 || 12 lines, stack, w/example || T/M: 95% / 94% | exclusive-time-of-functions | 0 | 1 | ```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n\n stack, ans = deque(), [0]*n # Example: ["0:start:0", "0:start:2", "0:end:5",\n # "1:start:6", "1:end :6", "0:end:7"]\n \n for log in logs: # time-\n id, action, timestamp = log.split(":") # id action stamp ans stack\n id, timestamp = int(id), int(timestamp) # \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\n # 0 start 0 [0,0] [(0,0)]\n if action == "start": # 0 start 2 [0,0] [(0,0),(0,2)]\n stack.append((id, timestamp)) # 0 end 5 [0,0] [(0,0)]\n # 1 start 6 [0,0] [(0,0),(1,6)]\n else: # 1 end 6 [0,1] [(0,0)]\n id, initTime = stack.pop() # 0 end 7 [7,1] []\n elapsedTime = timestamp + 1 - initTime\n ans[id]+= elapsedTime\n\n if stack: ans[stack[-1][0]]-= elapsedTime\n \n return ans\n\n```\n[https://leetcode.com/problems/exclusive-time-of-functions/submissions/894946824/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 6 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.