title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 3 | Clean, Simple Stack | Explanation | exclusive-time-of-functions | 0 | 1 | ### Explanation\n- Split a function call to 2 different type of states\n\t- Before nested call was made\n\t- After nested call was made\n- Record time spent on these 2 types of states\n- e.g. for `n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]`\n\t- Initially stack is empty, then it will record `[[0, 0]]` meaning function `0` start at timestamp `0`\n\t- Then nested call happens, we record time spent on function `0` in `ans`, then append to stack\n\t\t- record time spent before nested call `ans[s[-1][0]] += timestamp - s[-1][1]`\n\t- now stack has `[[0, 0], [1, 2]]`\n\t- when a `end` is met, pop top of stack and record time as `timestamp - s.pop()[1] + 1`\n\t- now stack is back to `[[0, 0]]`, but before we end this iteration, we need to update the start time of this record\n\t\t- because time spent on it before nested call is recorded, so now it\'s like a new start\n\t\t- update start time: `s[-1][1] = timestamp+1`\n### Implementation\n```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n helper = lambda log: (int(log[0]), log[1], int(log[2])) # to covert id and time to integer\n logs = [helper(log.split(\':\')) for log in logs] # convert [string] to [(,,)]\n ans, s = [0] * n, [] # initialize answer and stack\n for (i, status, timestamp) in logs: # for each record\n if status == \'start\': # if it\'s start\n if s: ans[s[-1][0]] += timestamp - s[-1][1] # if s is not empty, update time spent on previous id (s[-1][0])\n s.append([i, timestamp]) # then add to top of stack\n else: # if it\'s end\n ans[i] += timestamp - s.pop()[1] + 1 # update time spend on `i`\n if s: s[-1][1] = timestamp+1 # if s is not empty, udpate start time of previous id; \n return ans\n``` | 18 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
very very simple solution | stacks | exclusive-time-of-functions | 0 | 1 | ```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n\n result = [0]*n\n stack = []\n \n for i, log in enumerate(logs):\n curr_fid, curr_event, curr_time = log.split(":")\n if curr_event == "start":\n stack.append(log)\n elif curr_event == "end":\n prev_fid, prev_event, prev_time = stack.pop().split(":")\n result[int(curr_fid)] += int(curr_time)-int(prev_time)+1\n if stack:\n prev_fid1, prev_event1, prev_time1 = stack[-1].split(":")\n result[int(prev_fid1)] -= (int(curr_time)-int(prev_time))+1\n \n return result\n``` | 4 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
Python, simple solution with stack using defaultdict | exclusive-time-of-functions | 0 | 1 | Please upvote!!!\n\nTime: O(n), since you need to travel the entire list of logs\nSpace: O(n/2) so O(n), if you have n/2 start processes, then you would have n/2 end processes too. So at most you have n/2 processes in stack. \n\n```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n output = [0] * n\n \n # initialize stack for each function_id\n record = collections.defaultdict(list)\n \n for log in logs:\n f_id, f_type, ts = log.split(\':\')\n \n #convert ts into integer for array indexing\n cur_ts = int(ts)\n \n # start is straightforward, just push it to stack\n if f_type == \'start\':\n record[f_id].append(cur_ts)\n \n # end needs to adjust any start ts if records are present\n elif f_type == \'end\':\n prev_ts = record[f_id].pop()\n diff = cur_ts - prev_ts + 1\n output[int(f_id)] += diff\n \n # adjust time elapsed for each pending process in stack\n for key in record:\n record[key] = [item + diff for item in record[key]]\n\n return output\n``` | 2 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
Python stack easy to understand | exclusive-time-of-functions | 0 | 1 | \n```\ndef exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n \n stack = []\n prev_time = 0\n ans = [0 for i in range(n)]\n \n for i in range(0,len(logs)):\n fid, state, time = logs[i].split(\':\')\n fid, time = int(fid), int(time)\n \n if state == "start":\n if stack:\n ans[stack[-1]] += time - prev_time\n \n stack.append(fid)\n prev_time = time\n \n else:\n ans[stack.pop()] += time - prev_time + 1\n prev_time = time + 1\n \n return ans\n``` | 8 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
Solution | exclusive-time-of-functions | 1 | 1 | ```C++ []\nclass Solution {\n enum Event {kStart, kEnd};\n vector<int> ans;\n tuple<int, enum Event, int> parseLog(const string &log)\n {\n tuple<int, enum Event, int> ret;\n int pos = log.find(\':\');\n get<0>(ret) = stoi(log.substr(0, pos));\n int prev = pos; pos = log.find(\':\', prev+1);\n\n get<1>(ret) = (log.substr(prev+1, pos-prev-1) == "start") ? kStart : kEnd;\n get<2>(ret) = stoi(log.substr(pos+1));\n return ret;\n }\npublic:\n vector<int> exclusiveTime(int n, vector<string>& logs) {\n ans = vector<int>(n, 0);\n stack<pair<int, int> > s;\n stack<pair<int, int> > res;\n int level = 0;\n\n for (int i = 0; i < logs.size(); i++)\n {\n auto[fid, event, timestamp] = parseLog(logs[i]);\n if (event == kStart)\n {\n level++;\n s.push({fid, timestamp});\n }\n else \n {\n level--;\n pair<int, int> top = s.top();\n ans[top.first] += timestamp-top.second+1;\n int temp = timestamp-top.second+1;\n s.pop();\n while (!res.empty() && res.top().second > level)\n {\n ans[top.first] -= res.top().first;\n res.pop();\n }\n res.push({temp, level});\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n res = [0 for _ in range(n)]\n s = []\n currt = 0\n\t\t\n for log in logs: \n \n fid, state, timestamp = log.split(":")\n \n fid = int(fid)\n timestamp = int(timestamp)\n \n if state == "end":\n s.pop()\n res[fid] += timestamp - currt+1\n currt = timestamp + 1\n else:\n if (s):\n fidprev,time = s[-1]\n res[fidprev] += timestamp - currt\n s.append((fid,timestamp))\n currt = timestamp\n \n return res\n```\n\n```Java []\nclass Solution {\n public int[] exclusiveTime(int n, List<String> logs) {\n int[] result = new int[n];\n if (n == 0 || logs == null || logs.size() == 0) {\n return result;\n }\n Deque<Integer> stack = new ArrayDeque<>();\n int prevTime = 0;\n\n for (String log : logs) {\n String[] logParts = log.split(":");\n int curTime = Integer.parseInt(logParts[2]);\n\n if ("start".equals(logParts[1])) {\n if (!stack.isEmpty()) {\n result[stack.peek()] += curTime - prevTime;\n }\n stack.push(Integer.parseInt(logParts[0]));\n prevTime = curTime;\n } else {\n result[stack.pop()] += curTime - prevTime + 1;\n prevTime = curTime + 1;\n }\n }\n return result;\n }\n}\n```\n | 1 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
python | stack | easy | O(n) | exclusive-time-of-functions | 0 | 1 | ```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n \n \n f = [0]*(n)\n \n \n stack=[]\n \n \n for i in logs:\n \n ID,pos,time = i.split(\':\')\n \n ID= int(ID)\n time= int(time)\n if pos == \'start\':\n \n stack.append([ID,time])\n else:\n \n prID, prtime = stack.pop()\n \n timespent = time-prtime+1\n f[ID]+= timespent\n \n #remove the overlapping time \n \n if stack:\n f[stack[-1][0]]-= timespent\n \n return f\n \n \n \n \n \n``` | 5 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
O(n) Python, Faster than 99.39%, easy to understand | exclusive-time-of-functions | 0 | 1 | The easy is easy to build if we understand the boundry conditions. \n1. The function that starts or ends claims the time stamp\n2. if a new method is starting we claim the duration of previous method as it has run till that time\n\nwe can build a simple timeline as \n0,0,1,1,1,...\nwhere 0, 1 represent the function id however it is not necessary to build this if we directly keep the count in the result array\n\n```\nclass Solution: \n \n\tdef exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n # memory efficient implementation\n # We basically mark the array at that time stamp as the one starting or ending \n stk = []\n current = -1\n res_count = [0 for _ in range(n)]\n for i in range(len(logs)):\n curr = logs[i]\n fid_str, op, time = curr.split(":")\n t_int = int(time)\n fid = int(fid_str)\n if op == "start":\n if not stk:\n res_count[fid] += t_int - current # base case, start a new function\n else:\n res_count[stk[-1]] += (t_int - current - 1) # increment the runtime for last function till the t-1\n res_count[fid] += 1 # claim the runtime of 1 for new function started \n stk.append(fid)\n elif op == "end":\n fid_old = stk.pop() # pop the last function as it is the one ended\n res_count[fid_old] += (t_int - current - 1) # increment the runtime for last function till the t-1\n res_count[fid] += 1 # claim the runtime of 1 for the function ended\n current = t_int\n return res_count\n``` | 2 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
[Python] Simple solution with comments | exclusive-time-of-functions | 0 | 1 | ```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n ## RC ##\n\t\t## APPROACH : STACK ##\n stack, res = [], [0] * n\n for log in logs:\n id, func, curr_time = log.split(":")\n id, curr_time = int(id), int(curr_time)\n if func == "start":\n stack.append((id, curr_time))\n elif func == "end" and id == stack[-1][0]:\n pop_id, insert_time = stack.pop()\n time_taken = curr_time - insert_time + 1\n res[pop_id] += time_taken\n \n # gist, we have remove overlap time, if a process is in the stack indicates there is overlap with the last process\n if stack:\n res[stack[-1][0]] -= time_taken # time taken by this process is the overlap time for prev process in stack\n return res\n \n``` | 11 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
Python intuitive approach with comments | exclusive-time-of-functions | 0 | 1 | ```\nclass Solution:\n def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:\n \n result = [0] * n\n p_num, _, p_timestamp = logs[0].split(\':\')\n stack = [[int(p_num), int(p_timestamp)]]\n \n i = 1\n while i < len(logs):\n # c_ variables are current index\'s log entry\n c_num, c_status, c_timestamp = logs[i].split(\':\')\n c_num = int(c_num)\n c_timestamp = int(c_timestamp)\n \n if c_status == \'start\':\n # append to stack if start\n stack.append([c_num, c_timestamp])\n else:\n # p_ variables are from top of the stack\n p_num, p_timestamp = stack.pop()\n curr_time = c_timestamp - p_timestamp + 1\n result[p_num] += curr_time\n \n # Since we need exclusive time, subract curr function\'s time \n # from prev function that is paused\n if stack:\n pp_num, pp_timestamp = stack[-1]\n result[pp_num] -= curr_time\n prev_end = p_timestamp\n i += 1\n \n return result\n``` | 2 | On a **single-threaded** CPU, we execute a program containing `n` functions. Each function has a unique ID between `0` and `n-1`.
Function calls are **stored in a [call stack](https://en.wikipedia.org/wiki/Call_stack)**: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is **the current function being executed**. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list `logs`, where `logs[i]` represents the `ith` log message formatted as a string `"{function_id}:{ "start " | "end "}:{timestamp} "`. For example, `"0:start:3 "` means a function call with function ID `0` **started at the beginning** of timestamp `3`, and `"1:end:2 "` means a function call with function ID `1` **ended at the end** of timestamp `2`. Note that a function can be called **multiple times, possibly recursively**.
A function's **exclusive time** is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for `2` time units and another call executing for `1` time unit, the **exclusive time** is `2 + 1 = 3`.
Return _the **exclusive time** of each function in an array, where the value at the_ `ith` _index represents the exclusive time for the function with ID_ `i`.
**Example 1:**
**Input:** n = 2, logs = \[ "0:start:0 ", "1:start:2 ", "1:end:5 ", "0:end:6 "\]
**Output:** \[3,4\]
**Explanation:**
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
**Example 2:**
**Input:** n = 1, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "0:start:6 ", "0:end:6 ", "0:end:7 "\]
**Output:** \[8\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
**Example 3:**
**Input:** n = 2, logs = \[ "0:start:0 ", "0:start:2 ", "0:end:5 ", "1:start:6 ", "1:end:6 ", "0:end:7 "\]
**Output:** \[7,1\]
**Explanation:**
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
**Constraints:**
* `1 <= n <= 100`
* `1 <= logs.length <= 500`
* `0 <= function_id < n`
* `0 <= timestamp <= 109`
* No two start events will happen at the same timestamp.
* No two end events will happen at the same timestamp.
* Each function has an `"end "` log for each `"start "` log. | null |
Store node's level, bfs through and track sums | average-of-levels-in-binary-tree | 0 | 1 | \nIf you know what a BFS is, and that a queue stores a tree\'s nodes level by level, the only thing to think about in this problem is the edge cases and making sure we\'re updating our array in the right places.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nimport collections\nclass Solution:\n def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:\n\n\n res = []\n if root: res = [root.val] \n else: return res\n queue = collections.deque()\n if root.right:\n queue.append((root.right, 1))\n if root.left:\n queue.append((root.left, 1))\n if len(queue) == 0: return res\n prevLevel = 1\n currSum = 0\n currCount = 0\n while queue:\n\n node = queue.popleft()\n val, level = node[0].val, node[1]\n if level != prevLevel:\n res.append(currSum / currCount)\n currSum = val\n currCount = 1\n prevLevel = level\n\n else:\n currSum += val\n currCount += 1\n\n if node[0].left:\n queue.append((node[0].left, level + 1))\n if node[0].right:\n queue.append((node[0].right, level + 1))\n\n res.append(currSum / currCount)\n return res\n\n# keep track of levels for each node\n# 3 -> 0\n# 9 20 -> 1\n\n# when we reach a new level, divide the count by sum for the previous level and store in an array\n\n# when adding children to queue, add 1 to the current level for new children\n\n \n``` | 0 | Given the `root` of a binary tree, return _the average value of the nodes on each level in the form of an array_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[3.00000,14.50000,11.00000\]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return \[3, 14.5, 11\].
**Example 2:**
**Input:** root = \[3,9,20,15,7\]
**Output:** \[3.00000,14.50000,11.00000\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
15 lines of code very easy approach | average-of-levels-in-binary-tree | 0 | 1 | # Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:\n if not root: return []\n s=defaultdict(int)\n n=defaultdict(int)\n def dfs(root,depth):\n s[depth]+=root.val\n n[depth]+=1\n if root.left: dfs(root.left,depth+1)\n if root.right: dfs(root.right,depth+1)\n dfs(root,0)\n ar=[]\n for i in s.keys():\n ar.append(s[i]/n[i])\n return ar\n``` | 1 | Given the `root` of a binary tree, return _the average value of the nodes on each level in the form of an array_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[3.00000,14.50000,11.00000\]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return \[3, 14.5, 11\].
**Example 2:**
**Input:** root = \[3,9,20,15,7\]
**Output:** \[3.00000,14.50000,11.00000\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Solution | shopping-offers | 1 | 1 | ```C++ []\nbool operator >= (const vector<int>& a, const vector<int>& b)\n{\n for (int i = 0; i < a.size(); ++i)\n {\n if (a[i] < b[i]) return false;\n }\n return true;\n}\nint operator* (const vector<int>& a, const vector<int>& b)\n{\n int res = 0;\n for (int i = 0; i < a.size(); ++i)\n {\n res += a[i] * b[i];\n }\n return res;\n}\nvoid operator-= (vector<int>& a, vector<int>& b)\n{\n for (int i = 0; i < a.size(); ++i)\n {\n a[i] -= b[i];\n }\n}\nvoid operator += (vector<int>& a, vector<int>& b)\n{\n for (int i = 0; i < a.size(); ++i)\n {\n a[i] += b[i];\n }\n}\nclass Solution123 {\npublic:\n int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {\n int cost = needs * price;\n for (auto s : special)\n {\n if (cost < s.back()) continue;\n if (needs > s)\n {\n needs -= s;\n cost = min(cost, s.back() + shoppingOffers(price, special, needs));\n needs += s;\n }\n }\n return cost;\n }\n};\nclass Solution {\npublic:\n unordered_map<string, int> m;\n int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {\n string s;\n for (int i : needs)\n {\n s.append(1, i);\n }\n if (m.count(s)) \n return m[s];\n\n int cost = needs * price;\n\n for (auto& spe : special) {\n if (spe.back() > cost) continue;\n if (needs >= spe) {\n needs -= spe;\n cost = min(cost, spe.back() + shoppingOffers(price, special, needs));\n needs += spe;\n }\n }\n m[s] = cost;\n return cost;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def shoppingOffers(\n self, price: List[int], special: List[List[int]], needs: List[int]\n ) -> int:\n def _impl(current_needs, dp_table):\n if current_needs in dp_table:\n return dp_table[current_needs]\n length = len(price)\n min_price = float("inf")\n for spec in special:\n can_use = True\n for i in range(length):\n if spec[i] > current_needs[i]:\n can_use = False\n break\n if can_use:\n current_price = spec[-1] + _impl(\n tuple([need - consume for consume, need in zip(spec, current_needs)]),\n dp_table\n )\n if current_price < min_price:\n min_price = current_price\n if not math.isinf(min_price):\n dp_table[current_needs] = min_price\n return min_price\n current_price = 0\n for i, n in enumerate(current_needs):\n current_price += n * price[i]\n dp_table[current_needs] = current_price\n return current_price\n length = len(price)\n useful_special = []\n for spec in special:\n current = 0\n for i in range(length):\n current += price[i] * spec[i]\n if current > spec[-1]:\n useful_special.append(spec)\n special = useful_special\n return _impl(tuple(needs), {})\n```\n\n```Java []\nclass Solution {\n int minPrice;\n public int shoppingOffers(List<Integer> price, List<List<Integer>> special, List<Integer> needs) {\n minPrice=directlyBuy(price,needs);\n help(price,special,needs,0,0);\n return minPrice;\n }\n private int directlyBuy(List<Integer> price,List<Integer> needs){\n int total=0;\n int n=needs.size();\n for(int i=0;i<n;i++){\n total+=price.get(i)*needs.get(i);\n }\n return total;\n }\n private boolean canUse(List<Integer> offer,List<Integer> needs){\n int n=needs.size();\n for(int i=0;i<n;i++){\n if(offer.get(i)>needs.get(i))return false;\n }\n return true;\n }\n private void help(List<Integer> price,List<List<Integer>> special,List<Integer> needs,int used,int index){\n if(used>=minPrice)return;\n if(index==special.size()){\n used+=directlyBuy(price,needs);\n if(used<minPrice){\n minPrice=used;\n }\n return;\n }\n List<Integer> offer=special.get(index);\n if(canUse(offer,needs)){\n int n=needs.size();\n List<Integer> updatedNeeds=new ArrayList<>();\n for(int i=0;i<n;i++){\n updatedNeeds.add(needs.get(i)-offer.get(i));\n }\n help(price,special,updatedNeeds,used+offer.get(n),index);\n }\n help(price,special,needs,used,index+1);\n }\n}\n```\n | 1 | In LeetCode Store, there are `n` items to sell. Each item has a price. However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given an integer array `price` where `price[i]` is the price of the `ith` item, and an integer array `needs` where `needs[i]` is the number of pieces of the `ith` item you want to buy.
You are also given an array `special` where `special[i]` is of size `n + 1` where `special[i][j]` is the number of pieces of the `jth` item in the `ith` offer and `special[i][n]` (i.e., the last integer in the array) is the price of the `ith` offer.
Return _the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers_. You are not allowed to buy more items than you want, even if that would lower the overall price. You could use any of the special offers as many times as you want.
**Example 1:**
**Input:** price = \[2,5\], special = \[\[3,0,5\],\[1,2,10\]\], needs = \[3,2\]
**Output:** 14
**Explanation:** There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
**Example 2:**
**Input:** price = \[2,3,4\], special = \[\[1,1,0,4\],\[2,2,1,9\]\], needs = \[1,2,1\]
**Output:** 11
**Explanation:** The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
**Constraints:**
* `n == price.length == needs.length`
* `1 <= n <= 6`
* `0 <= price[i], needs[i] <= 10`
* `1 <= special.length <= 100`
* `special[i].length == n + 1`
* `0 <= special[i][j] <= 50` | null |
Easy Solution|| Beats 98%|| Easy to Understand💯🔥 | shopping-offers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shoppingOffers(self, price: List[int], special: List[List[int]], needs: List[int]) -> int:\n def _impl(current_needs, dp_table):\n if current_needs in dp_table:\n return dp_table[current_needs]\n length = len(price)\n min_price = float("inf")\n\n for spec in special:\n can_use = True\n for i in range(length):\n if spec[i] > current_needs[i]:\n can_use = False\n break\n if can_use:\n current_price = spec[-1] + _impl(\n tuple([need - consume for consume, need in zip(spec, current_needs)]),\n dp_table\n )\n if current_price < min_price:\n min_price = current_price\n\n if not math.isinf(min_price):\n dp_table[current_needs] = min_price\n return min_price\n\n current_price = 0\n for i, n in enumerate(current_needs):\n current_price += n * price[i]\n\n dp_table[current_needs] = current_price\n return current_price\n\n length = len(price)\n useful_special = []\n for spec in special:\n current = 0\n for i in range(length):\n current += price[i] * spec[i]\n if current > spec[-1]:\n useful_special.append(spec)\n special = useful_special\n return _impl(tuple(needs), {})\n\n``` | 1 | In LeetCode Store, there are `n` items to sell. Each item has a price. However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given an integer array `price` where `price[i]` is the price of the `ith` item, and an integer array `needs` where `needs[i]` is the number of pieces of the `ith` item you want to buy.
You are also given an array `special` where `special[i]` is of size `n + 1` where `special[i][j]` is the number of pieces of the `jth` item in the `ith` offer and `special[i][n]` (i.e., the last integer in the array) is the price of the `ith` offer.
Return _the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers_. You are not allowed to buy more items than you want, even if that would lower the overall price. You could use any of the special offers as many times as you want.
**Example 1:**
**Input:** price = \[2,5\], special = \[\[3,0,5\],\[1,2,10\]\], needs = \[3,2\]
**Output:** 14
**Explanation:** There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
**Example 2:**
**Input:** price = \[2,3,4\], special = \[\[1,1,0,4\],\[2,2,1,9\]\], needs = \[1,2,1\]
**Output:** 11
**Explanation:** The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
**Constraints:**
* `n == price.length == needs.length`
* `1 <= n <= 6`
* `0 <= price[i], needs[i] <= 10`
* `1 <= special.length <= 100`
* `special[i].length == n + 1`
* `0 <= special[i][j] <= 50` | null |
Cleanest, easiest, fastest [Memoization] | shopping-offers | 0 | 1 | # Intuition\nTry all ways.\n\n# Approach\n1. There are 2 ways of purchasing.\n - special offers: we need to check if we can purchase an offer by checking do we need the number of items the offer is offering.\n - just buy at direct price\n2. **(Base case)** Once the needs becomes 0, we stop.\n3. We also memoize the needs to handle the overlapping subproblems.\n\n# Complexity\nPlease comment down below if anyone can figure out the time complexity for this algorithm. \n- Time complexity:\n**TBD**\n\n- Space complexity:\n**TBD**\n\n# Code\n```\nclass Solution:\n def shoppingOffers(self, price: List[int], special: List[List[int]], needs: List[int]) -> int:\n dp = {}\n def dfs(needs):\n if sum(needs)==0: return 0\n key = tuple(needs)\n if key in dp: return dp[key]\n\n best = self.buyOut(needs,price)\n for offer in special:\n new_needs = self.canTake(offer,needs[:])\n \n if new_needs: best = min(best,offer[-1] + dfs(new_needs))\n \n dp[key] = best\n return best\n\n return dfs(needs)\n\n def buyOut(self,needs,prices):\n return sum([n*p for n,p in zip(needs,prices)])\n\n def canTake(self,offer,needs):\n for i in range(len(needs)):\n needs[i] -= offer[i]\n if needs[i] < 0: return []\n return needs\n \n``` | 1 | In LeetCode Store, there are `n` items to sell. Each item has a price. However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given an integer array `price` where `price[i]` is the price of the `ith` item, and an integer array `needs` where `needs[i]` is the number of pieces of the `ith` item you want to buy.
You are also given an array `special` where `special[i]` is of size `n + 1` where `special[i][j]` is the number of pieces of the `jth` item in the `ith` offer and `special[i][n]` (i.e., the last integer in the array) is the price of the `ith` offer.
Return _the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers_. You are not allowed to buy more items than you want, even if that would lower the overall price. You could use any of the special offers as many times as you want.
**Example 1:**
**Input:** price = \[2,5\], special = \[\[3,0,5\],\[1,2,10\]\], needs = \[3,2\]
**Output:** 14
**Explanation:** There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
**Example 2:**
**Input:** price = \[2,3,4\], special = \[\[1,1,0,4\],\[2,2,1,9\]\], needs = \[1,2,1\]
**Output:** 11
**Explanation:** The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
**Constraints:**
* `n == price.length == needs.length`
* `1 <= n <= 6`
* `0 <= price[i], needs[i] <= 10`
* `1 <= special.length <= 100`
* `special[i].length == n + 1`
* `0 <= special[i][j] <= 50` | null |
✅✔️Easy implementation using dfs with memorziable dictionary || Python Fast Solution✈️✈️✈️✈️✈️ | shopping-offers | 0 | 1 | ## 638. Shopping Offers\n\nIn LeetCode Store, there are n items to sell. Each item has a price. However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.\n\nYou are given an integer array price where price[i] is the price of the ith item, and an integer array needs where needs[i] is the number of pieces of the ith item you want to buy.\n\nYou are also given an array special where special[i] is of size n + 1 where special[i][j] is the number of pieces of the jth item in the ith offer and special[i][n] (i.e., the last integer in the array) is the price of the ith offer.\n\nReturn the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers. You are not allowed to buy more items than you want, even if that would lower the overall price. You could use any of the special offers as many times as you want.\n\nConstraints:\n\n* n == price.length == needs.length\n* 1 <= n <= 6\n* 0 <= price[i], needs[i] <= 10\n* 1 <= special.length <= 100\n* special[i].length == n + 1\n* 0 <= special[i][j] <= 50\n\n### Intuition\nWhen seeing the function array which represent the price and nums. It definitely will be a dynamic programming problem, because we can it has a iteration property. Easyly to see. A knapsack problem. \n* First, we have special offer - quantity1,q2,q3.. and the total price for this offer, price for each item and needed.\n* You are not allowed to buy more items than you want, even if that would lower the overall price. But I don\'t know how to build dp equation. Let me see the std solution.\n* Because it\'s a DP problem, we definitely can write a iteration solution, but it\'s a little bit complex. So we can use recursion with memorizable variable to solve it.\n\n### Approach\n* step 1:each time first we calculate if we all use the original without special offer, what\'s the price.\n* step 2: then we try to use each special offer, if we can use it, we will use it, and then we will dfs to next level with the new needs which the items we purchased has been deducted.\n* step 3: we will compare the price we get from step 1 and step 2, and return the min one.\n\n\n### Complexity\n- Time complexity:\nBecause we need to iterate all possible combination of special offer, so the time complexity is $$O(2^n)$$\n\n- Space complexity:\nfor the recursion, we need to store the needs, so the space complexity is $$O(n^n)$$ because each elements in dict is a list with n elements, it has 0 - n possibilities, therefore in total we may have $$n^n$$ possibilities.\n\n### Code\n```python\nclass Solution:\n def shoppingOffers(self, price: List[int], special: List[List[int]], needs: List[int]) -> int:\n d = {}\n def dfs(price, special, needs):\n if not needs:\n return 0\n # calculate the price without special offer\n res = sum([price[i] * needs[i] for i in range(len(needs))])\n # try to use each special offer\n for offer in special:\n # check if we can use this offer\n for i in range(len(needs)):\n if needs[i] < offer[i]:\n break\n else:\n # use this offer\n tmp = [needs[j] - offer[j] for j in range(len(needs))]\n if tuple(tmp) not in d:\n d[tuple(tmp)] = dfs(price, special, tmp)\n res = min(res, offer[-1] + d[tuple(tmp)])\n return res\n return dfs(price, special, needs)\n```\n | 1 | In LeetCode Store, there are `n` items to sell. Each item has a price. However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given an integer array `price` where `price[i]` is the price of the `ith` item, and an integer array `needs` where `needs[i]` is the number of pieces of the `ith` item you want to buy.
You are also given an array `special` where `special[i]` is of size `n + 1` where `special[i][j]` is the number of pieces of the `jth` item in the `ith` offer and `special[i][n]` (i.e., the last integer in the array) is the price of the `ith` offer.
Return _the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers_. You are not allowed to buy more items than you want, even if that would lower the overall price. You could use any of the special offers as many times as you want.
**Example 1:**
**Input:** price = \[2,5\], special = \[\[3,0,5\],\[1,2,10\]\], needs = \[3,2\]
**Output:** 14
**Explanation:** There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
**Example 2:**
**Input:** price = \[2,3,4\], special = \[\[1,1,0,4\],\[2,2,1,9\]\], needs = \[1,2,1\]
**Output:** 11
**Explanation:** The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
**Constraints:**
* `n == price.length == needs.length`
* `1 <= n <= 6`
* `0 <= price[i], needs[i] <= 10`
* `1 <= special.length <= 100`
* `special[i].length == n + 1`
* `0 <= special[i][j] <= 50` | null |
Python 3 || 10 lines, dfs, w/ comments || T/M: 75% / 34% | shopping-offers | 0 | 1 | ```\nclass Solution:\n def shoppingOffers(self, price: List[int], specials: List[List[int]], needs: List[int]) -> int:\n\n @lru_cache(None)\n def dfs(needs):\n\n cost = sum(map(mul, needs, price)) # cost with no specials applied\n\n for special in specials:\n specPrice = special.pop()\n tmp = tuple(map(sub, needs, special)) # reset need if special applied\n\n if min(tmp) < 0: continue # special cannot be applied\n\n cost = min(cost, dfs(tmp)) + specPrice # id special best buy?\n\n return cost # return best cost for needs\n\n return dfs(tuple(needs))\n```\n[https://leetcode.com/problems/shopping-offers/submissions/894987964/](http://) | 3 | In LeetCode Store, there are `n` items to sell. Each item has a price. However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given an integer array `price` where `price[i]` is the price of the `ith` item, and an integer array `needs` where `needs[i]` is the number of pieces of the `ith` item you want to buy.
You are also given an array `special` where `special[i]` is of size `n + 1` where `special[i][j]` is the number of pieces of the `jth` item in the `ith` offer and `special[i][n]` (i.e., the last integer in the array) is the price of the `ith` offer.
Return _the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers_. You are not allowed to buy more items than you want, even if that would lower the overall price. You could use any of the special offers as many times as you want.
**Example 1:**
**Input:** price = \[2,5\], special = \[\[3,0,5\],\[1,2,10\]\], needs = \[3,2\]
**Output:** 14
**Explanation:** There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
**Example 2:**
**Input:** price = \[2,3,4\], special = \[\[1,1,0,4\],\[2,2,1,9\]\], needs = \[1,2,1\]
**Output:** 11
**Explanation:** The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
**Constraints:**
* `n == price.length == needs.length`
* `1 <= n <= 6`
* `0 <= price[i], needs[i] <= 10`
* `1 <= special.length <= 100`
* `special[i].length == n + 1`
* `0 <= special[i][j] <= 50` | null |
python3 dfs | shopping-offers | 0 | 1 | \n# Code\n```\nclass Solution:\n def shoppingOffers(self, price: List[int], special: List[List[int]], needs: List[int]) -> int:\n freq = {}\n for offer in special:\n a = tuple(offer[:-1])\n if a not in freq:\n freq[a] = float(\'inf\')\n freq[a] = min(freq[a],offer[-1])\n special = [list(a)+[freq[a]] for a in freq] # select out the best offers.Crucial in that you have to shorten the offer list to avoid TLE\n self.needs = needs\n n = len(needs)\n def dfs():\n res = sum([a*b for a,b in zip(price,self.needs)])\n for offer in special:\n if all(a<=b for a,b in zip(offer[:-1],self.needs)):\n for i in range(n):\n self.needs[i] -= offer[i]\n res = min(offer[-1] + dfs(), res)\n for i in range(n):\n self.needs[i] += offer[i]\n #print(self.needs,res)\n return res\n return dfs()\n``` | 0 | In LeetCode Store, there are `n` items to sell. Each item has a price. However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given an integer array `price` where `price[i]` is the price of the `ith` item, and an integer array `needs` where `needs[i]` is the number of pieces of the `ith` item you want to buy.
You are also given an array `special` where `special[i]` is of size `n + 1` where `special[i][j]` is the number of pieces of the `jth` item in the `ith` offer and `special[i][n]` (i.e., the last integer in the array) is the price of the `ith` offer.
Return _the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers_. You are not allowed to buy more items than you want, even if that would lower the overall price. You could use any of the special offers as many times as you want.
**Example 1:**
**Input:** price = \[2,5\], special = \[\[3,0,5\],\[1,2,10\]\], needs = \[3,2\]
**Output:** 14
**Explanation:** There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
**Example 2:**
**Input:** price = \[2,3,4\], special = \[\[1,1,0,4\],\[2,2,1,9\]\], needs = \[1,2,1\]
**Output:** 11
**Explanation:** The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
**Constraints:**
* `n == price.length == needs.length`
* `1 <= n <= 6`
* `0 <= price[i], needs[i] <= 10`
* `1 <= special.length <= 100`
* `special[i].length == n + 1`
* `0 <= special[i][j] <= 50` | null |
Simple and precise Top-down DP approach (Memoization) | decode-ways-ii | 0 | 1 | # Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def numDecodings(self, s: str) -> int:\n M = 10**9 + 7\n \n def dp(s, i, memo):\n if i == len(s):\n return 1\n\n if memo[i] is not None:\n return memo[i]\n\n if s[i] == "0":\n memo[i] = 0\n return memo[i]\n\n result = 0\n\n if s[i] == "*":\n if i + 1 < len(s) and s[i + 1] != "*":\n if s[i + 1] > "6":\n result = (9 * dp(s, i + 1, memo) + dp(s, i + 2, memo)) % M\n else:\n result = (9 * dp(s, i + 1, memo) + 2 * dp(s, i + 2, memo)) % M\n\n elif i + 1 < len(s) and s[i + 1] == "*":\n result = (9 * dp(s, i + 1, memo) + 15 * dp(s, i + 2, memo)) % M\n\n else:\n result = 9 * dp(s, i + 1, memo)\n\n elif s[i] != "*":\n result = dp(s, i + 1, memo)\n\n if i + 1 < len(s) and s[i + 1] == "*":\n if s[i] == "1":\n result = (result + 9 * dp(s, i + 2, memo)) % M\n elif s[i] == "2":\n result = (result + 6 * dp(s, i + 2, memo)) % M\n\n elif i + 1 < len(s):\n two_digits = int(s[i:i + 2])\n if 10 <= two_digits <= 26:\n result = (result + dp(s, i + 2, memo)) % M\n\n memo[i] = result\n return memo[i]\n\n\n return dp(s, 0, [None] * (len(s) + 1))\n\n\n \n``` | 2 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
**In addition** to the mapping above, an encoded message may contain the `'*'` character, which can represent any digit from `'1'` to `'9'` (`'0'` is excluded). For example, the encoded message `"1* "` may represent any of the encoded messages `"11 "`, `"12 "`, `"13 "`, `"14 "`, `"15 "`, `"16 "`, `"17 "`, `"18 "`, or `"19 "`. Decoding `"1* "` is equivalent to decoding **any** of the encoded messages it can represent.
Given a string `s` consisting of digits and `'*'` characters, return _the **number** of ways to **decode** it_.
Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "\* "
**Output:** 9
**Explanation:** The encoded message can represent any of the encoded messages "1 ", "2 ", "3 ", "4 ", "5 ", "6 ", "7 ", "8 ", or "9 ".
Each of these can be decoded to the strings "A ", "B ", "C ", "D ", "E ", "F ", "G ", "H ", and "I " respectively.
Hence, there are a total of 9 ways to decode "\* ".
**Example 2:**
**Input:** s = "1\* "
**Output:** 18
**Explanation:** The encoded message can represent any of the encoded messages "11 ", "12 ", "13 ", "14 ", "15 ", "16 ", "17 ", "18 ", or "19 ".
Each of these encoded messages have 2 ways to be decoded (e.g. "11 " can be decoded to "AA " or "K ").
Hence, there are a total of 9 \* 2 = 18 ways to decode "1\* ".
**Example 3:**
**Input:** s = "2\* "
**Output:** 15
**Explanation:** The encoded message can represent any of the encoded messages "21 ", "22 ", "23 ", "24 ", "25 ", "26 ", "27 ", "28 ", or "29 ".
"21 ", "22 ", "23 ", "24 ", "25 ", and "26 " have 2 ways of being decoded, but "27 ", "28 ", and "29 " only have 1 way.
Hence, there are a total of (6 \* 2) + (3 \* 1) = 12 + 3 = 15 ways to decode "2\* ".
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a digit or `'*'`. | null |
Solution | decode-ways-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numDecodings(string s) {\n long long MOD = 1e9+7;\n int n=s.length();\n long long dp[n+1];\n if(s[0]==\'0\')\n return 0;\n dp[0]=1;\n dp[1]=s[0]==\'*\'?9:1;\n for(int i=2;i<=n;i++){\n dp[i]=0;\n if(s[i-1]==\'*\'){\n dp[i]=(9ll*dp[i-1])%MOD;\n \n if(s[i-2]==\'1\'){\n dp[i] = (dp[i] + (9ll*dp[i-2])%MOD)%MOD;\n }\n if(s[i-2]==\'2\'){\n dp[i] = (dp[i] + (6ll*dp[i-2])%MOD)%MOD;\n }\n if(s[i-2]==\'*\'){\n dp[i] = (dp[i] + (15ll*dp[i-2])%MOD)%MOD;\n }\n }\n else if(s[i-1]==\'0\'){\n if(s[i-2]==\'1\'||s[i-2]==\'2\')\n dp[i] = dp[i-2];\n else if(s[i-2]==\'*\')\n dp[i]=(2ll*dp[i-2])%MOD;\n } else {\n dp[i] = dp[i-1];\n if(s[i-2]==\'*\'){\n if(s[i-1]<=\'6\'){\n dp[i] = (dp[i]+ (2ll*dp[i-2])%MOD)%MOD;\n }\n else{\n dp[i] = (dp[i] + (1ll*dp[i-2])%MOD)%MOD;\n }\n } else {\n int num = (s[i-2]-\'0\')*10 +(s[i-1]-\'0\');\n if(num<=26&&num>=10)\n dp[i] = (dp[i]+ dp[i-2])%MOD;\n }\n }\n }\n return dp[n];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numDecodings(self, s: str) -> int:\n mod = 10 ** 9 + 7\n o0 = ord(\'0\')\n prev = None\n count = 1\n prev_count = 0\n for c in s:\n o = ord(c) - o0\n\n cur = count if o else 0\n if c == \'*\':\n cur *= 9\n if prev == \'*\':\n cur += prev_count * 15\n elif prev == \'1\':\n cur += prev_count * 9\n elif prev == \'2\':\n cur += prev_count * 6\n else:\n if prev == \'*\':\n if o < 7:\n cur += 2 * prev_count\n else:\n cur += prev_count\n else:\n if o < 7 and prev == \'2\':\n cur += prev_count\n elif prev == \'1\':\n cur += prev_count\n prev_count, count = count, cur % mod\n prev = c\n if not count:\n return 0\n return count\n```\n\n```Java []\nclass Solution {\n private static final int MOD = 1000000007;\n public int numDecodings(String s) {\n if (s == null) {\n throw new IllegalArgumentException("Input string is null");\n }\n int len = s.length();\n if (len == 0 || s.charAt(0) == \'0\') {\n return 0;\n }\n char preChar = s.charAt(0);\n long pre = 1;\n long cur = preChar == \'*\' ? 9 : 1;\n \n for (int i = 1; i < len; i++) {\n char curChar = s.charAt(i);\n if (preChar == \'0\' && curChar == \'0\') {\n return 0;\n }\n long ways = 0;\n if (curChar != \'0\') {\n ways += cur * (curChar == \'*\' ? 9 : 1);\n }\n if (preChar == \'*\') {\n if (curChar == \'*\') {\n ways += 15 * pre;\n } else if (curChar <= \'6\') {\n ways += 2 * pre;\n } else {\n ways += pre;\n }\n } else if (preChar == \'2\') {\n if (curChar == \'*\') {\n ways += 6 * pre;\n } else if (curChar <= \'6\') {\n ways += pre;\n }\n } else if (preChar == \'1\') {\n ways += pre * (curChar == \'*\' ? 9 : 1);\n }\n pre = cur;\n cur = ways % MOD;\n preChar = curChar;\n }\n return (int) cur;\n }\n}\n```\n | 1 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
**In addition** to the mapping above, an encoded message may contain the `'*'` character, which can represent any digit from `'1'` to `'9'` (`'0'` is excluded). For example, the encoded message `"1* "` may represent any of the encoded messages `"11 "`, `"12 "`, `"13 "`, `"14 "`, `"15 "`, `"16 "`, `"17 "`, `"18 "`, or `"19 "`. Decoding `"1* "` is equivalent to decoding **any** of the encoded messages it can represent.
Given a string `s` consisting of digits and `'*'` characters, return _the **number** of ways to **decode** it_.
Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "\* "
**Output:** 9
**Explanation:** The encoded message can represent any of the encoded messages "1 ", "2 ", "3 ", "4 ", "5 ", "6 ", "7 ", "8 ", or "9 ".
Each of these can be decoded to the strings "A ", "B ", "C ", "D ", "E ", "F ", "G ", "H ", and "I " respectively.
Hence, there are a total of 9 ways to decode "\* ".
**Example 2:**
**Input:** s = "1\* "
**Output:** 18
**Explanation:** The encoded message can represent any of the encoded messages "11 ", "12 ", "13 ", "14 ", "15 ", "16 ", "17 ", "18 ", or "19 ".
Each of these encoded messages have 2 ways to be decoded (e.g. "11 " can be decoded to "AA " or "K ").
Hence, there are a total of 9 \* 2 = 18 ways to decode "1\* ".
**Example 3:**
**Input:** s = "2\* "
**Output:** 15
**Explanation:** The encoded message can represent any of the encoded messages "21 ", "22 ", "23 ", "24 ", "25 ", "26 ", "27 ", "28 ", or "29 ".
"21 ", "22 ", "23 ", "24 ", "25 ", and "26 " have 2 ways of being decoded, but "27 ", "28 ", and "29 " only have 1 way.
Hence, there are a total of (6 \* 2) + (3 \* 1) = 12 + 3 = 15 ways to decode "2\* ".
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a digit or `'*'`. | null |
Python 3 || 11 lines, dp, defaultdict || T/M: 97% / 31% | decode-ways-ii | 0 | 1 | ```\nclass Solution:\n def numDecodings(self, s: str) -> int:\n \n d = defaultdict(int)\n for i in range(1,27): d[str(i)] = 1\n for i in range(10): d["*"+str(i)] = 1 + (i< 7)\n d[\'*\'], d[\'**\'], d[\'1*\'], d[\'2*\'] = 9,15,9,6\n\n n, M = len(s)-1, 10**9+7\n dp = [d[s[0]]] + [0]*n + [1]\n\n for i in range(n):\n one, two = s[i+1], s[i]+s[i+1]\n\n dp[i+1] = (d[one] * dp[i ] + \n d[two] * dp[i-1])%M\n if not dp[i+1]: return 0\n \n return dp[-2]\n```\n[https://leetcode.com/problems/decode-ways-ii/submissions/1000396570/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `len(s)`. | 3 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
**In addition** to the mapping above, an encoded message may contain the `'*'` character, which can represent any digit from `'1'` to `'9'` (`'0'` is excluded). For example, the encoded message `"1* "` may represent any of the encoded messages `"11 "`, `"12 "`, `"13 "`, `"14 "`, `"15 "`, `"16 "`, `"17 "`, `"18 "`, or `"19 "`. Decoding `"1* "` is equivalent to decoding **any** of the encoded messages it can represent.
Given a string `s` consisting of digits and `'*'` characters, return _the **number** of ways to **decode** it_.
Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "\* "
**Output:** 9
**Explanation:** The encoded message can represent any of the encoded messages "1 ", "2 ", "3 ", "4 ", "5 ", "6 ", "7 ", "8 ", or "9 ".
Each of these can be decoded to the strings "A ", "B ", "C ", "D ", "E ", "F ", "G ", "H ", and "I " respectively.
Hence, there are a total of 9 ways to decode "\* ".
**Example 2:**
**Input:** s = "1\* "
**Output:** 18
**Explanation:** The encoded message can represent any of the encoded messages "11 ", "12 ", "13 ", "14 ", "15 ", "16 ", "17 ", "18 ", or "19 ".
Each of these encoded messages have 2 ways to be decoded (e.g. "11 " can be decoded to "AA " or "K ").
Hence, there are a total of 9 \* 2 = 18 ways to decode "1\* ".
**Example 3:**
**Input:** s = "2\* "
**Output:** 15
**Explanation:** The encoded message can represent any of the encoded messages "21 ", "22 ", "23 ", "24 ", "25 ", "26 ", "27 ", "28 ", or "29 ".
"21 ", "22 ", "23 ", "24 ", "25 ", and "26 " have 2 ways of being decoded, but "27 ", "28 ", and "29 " only have 1 way.
Hence, there are a total of (6 \* 2) + (3 \* 1) = 12 + 3 = 15 ways to decode "2\* ".
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a digit or `'*'`. | null |
Solution to 639. Decode Ways II | decode-ways-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves decoding a string that contains digits and `*` characters. We aim to count the possible ways to interpret the string. `*` can represent any digit from `1` to `9`, and the task is to determine the total number of valid interpretations. This requires considering different groupings of digits and `*` to calculate the final count. The dynamic programming approach will help keep track of counts at each step, leading to the desired result.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize two variables, `prev` and `curr`, to keep track of the counts.\n2. Iterate through the string, and for each character:\n2.2. If it\'s `*`, update `curr` based on the possibilities.\n2.3. If it\'s a digit, update `curr` based on the digit and the previous character.\n3. Return the final count `curr`.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numDecodings(self, s: str) -> int:\n mod = 10**9 + 7\n prev, curr = 1, 1\n\n for i in range(1, len(s) + 1):\n temp = curr\n if s[i-1] == \'*\':\n curr = 9 * curr % mod\n if i > 1:\n if s[i-2] == \'1\':\n curr = (curr + 9 * prev) % mod\n elif s[i-2] == \'2\':\n curr = (curr + 6 * prev) % mod\n elif s[i-2] == \'*\':\n curr = (curr + 15 * prev) % mod\n else:\n curr = (curr if s[i-1] != \'0\' else 0)\n if i > 1:\n if s[i-2] == \'1\':\n curr = (curr + prev) % mod\n elif s[i-2] == \'2\' and s[i-1] <= \'6\':\n curr = (curr + prev) % mod\n elif s[i-2] == \'*\':\n curr = (curr + (2 if s[i-1] <= \'6\' else 1) * prev) % mod\n\n prev = temp\n\n return curr\n\n``` | 0 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
**In addition** to the mapping above, an encoded message may contain the `'*'` character, which can represent any digit from `'1'` to `'9'` (`'0'` is excluded). For example, the encoded message `"1* "` may represent any of the encoded messages `"11 "`, `"12 "`, `"13 "`, `"14 "`, `"15 "`, `"16 "`, `"17 "`, `"18 "`, or `"19 "`. Decoding `"1* "` is equivalent to decoding **any** of the encoded messages it can represent.
Given a string `s` consisting of digits and `'*'` characters, return _the **number** of ways to **decode** it_.
Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "\* "
**Output:** 9
**Explanation:** The encoded message can represent any of the encoded messages "1 ", "2 ", "3 ", "4 ", "5 ", "6 ", "7 ", "8 ", or "9 ".
Each of these can be decoded to the strings "A ", "B ", "C ", "D ", "E ", "F ", "G ", "H ", and "I " respectively.
Hence, there are a total of 9 ways to decode "\* ".
**Example 2:**
**Input:** s = "1\* "
**Output:** 18
**Explanation:** The encoded message can represent any of the encoded messages "11 ", "12 ", "13 ", "14 ", "15 ", "16 ", "17 ", "18 ", or "19 ".
Each of these encoded messages have 2 ways to be decoded (e.g. "11 " can be decoded to "AA " or "K ").
Hence, there are a total of 9 \* 2 = 18 ways to decode "1\* ".
**Example 3:**
**Input:** s = "2\* "
**Output:** 15
**Explanation:** The encoded message can represent any of the encoded messages "21 ", "22 ", "23 ", "24 ", "25 ", "26 ", "27 ", "28 ", or "29 ".
"21 ", "22 ", "23 ", "24 ", "25 ", and "26 " have 2 ways of being decoded, but "27 ", "28 ", and "29 " only have 1 way.
Hence, there are a total of (6 \* 2) + (3 \* 1) = 12 + 3 = 15 ways to decode "2\* ".
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a digit or `'*'`. | null |
Solution to 639. Decode Ways II | decode-ways-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves counting the number of ways to decode a given string. We need to handle the presence of `*` as a wildcard character, which can represent any digit from `1` to `9`. The goal is to return the count of possible decodings.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a dynamic programming array dp of length n+1, where n is the length of the input string s. `dp[i]` will represent the number of ways to decode the substring `s[:i]`.\n2. Set `dp[0] = 1` since an empty string has one decoding (empty string).\n3. Iterate from index 1 to n:\n3.1. If the current character `s[i-1]` is `*`, calculate the possibilities for a single character and two adjacent characters, and update `dp[i]` accordingly.\n3.2. If the current character `s[i-1]` is `0`, check if the previous character `s[i-2]` is `1` or `2`. If true, update `dp[i]` using the possibilities for two adjacent characters; otherwise, set `dp[i]` to `0`.\n3.3 If the current character s[i-1] is a digit from \'1\' to \'9\', update dp[i] using the possibilities for a single character and two adjacent characters.\n4. Return the value of `dp[n]`, which represents the number of ways to decode the entire string s.\n# Complexity\n- Time complexity: $$O(n)$$, where n is the length of the input string.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$, for the dynamic programming array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numDecodings(self, s: str) -> int:\n MOD = 10**9 + 7\n \n def ways(char: str) -> int:\n if char == \'0\':\n return 0\n if char == \'*\':\n return 9\n return 1\n \n def ways_two_chars(first: str, second: str) -> int:\n if first == \'1\':\n if second == \'*\':\n return 9\n return 1\n elif first == \'2\':\n if second == \'*\':\n return 6\n elif \'0\' <= second <= \'6\':\n return 1\n elif first == \'*\':\n if second == \'*\':\n return 15\n elif \'0\' <= second <= \'6\':\n return 2\n return 1\n return 0\n \n length = len(s)\n dp = [0] * (length + 1)\n dp[0] = 1\n \n for i in range(1, length + 1):\n dp[i] = (dp[i] + dp[i - 1] * ways(s[i - 1])) % MOD\n if i > 1:\n dp[i] = (dp[i] + dp[i - 2] * ways_two_chars(s[i - 2], s[i - 1])) % MOD\n \n return dp[length]\n\n``` | 0 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
**In addition** to the mapping above, an encoded message may contain the `'*'` character, which can represent any digit from `'1'` to `'9'` (`'0'` is excluded). For example, the encoded message `"1* "` may represent any of the encoded messages `"11 "`, `"12 "`, `"13 "`, `"14 "`, `"15 "`, `"16 "`, `"17 "`, `"18 "`, or `"19 "`. Decoding `"1* "` is equivalent to decoding **any** of the encoded messages it can represent.
Given a string `s` consisting of digits and `'*'` characters, return _the **number** of ways to **decode** it_.
Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "\* "
**Output:** 9
**Explanation:** The encoded message can represent any of the encoded messages "1 ", "2 ", "3 ", "4 ", "5 ", "6 ", "7 ", "8 ", or "9 ".
Each of these can be decoded to the strings "A ", "B ", "C ", "D ", "E ", "F ", "G ", "H ", and "I " respectively.
Hence, there are a total of 9 ways to decode "\* ".
**Example 2:**
**Input:** s = "1\* "
**Output:** 18
**Explanation:** The encoded message can represent any of the encoded messages "11 ", "12 ", "13 ", "14 ", "15 ", "16 ", "17 ", "18 ", or "19 ".
Each of these encoded messages have 2 ways to be decoded (e.g. "11 " can be decoded to "AA " or "K ").
Hence, there are a total of 9 \* 2 = 18 ways to decode "1\* ".
**Example 3:**
**Input:** s = "2\* "
**Output:** 15
**Explanation:** The encoded message can represent any of the encoded messages "21 ", "22 ", "23 ", "24 ", "25 ", "26 ", "27 ", "28 ", or "29 ".
"21 ", "22 ", "23 ", "24 ", "25 ", and "26 " have 2 ways of being decoded, but "27 ", "28 ", and "29 " only have 1 way.
Hence, there are a total of (6 \* 2) + (3 \* 1) = 12 + 3 = 15 ways to decode "2\* ".
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a digit or `'*'`. | null |
Soln | decode-ways-ii | 0 | 1 | # Intuition/Approach\n<!-- Describe your approach to solving the problem. -->\n$ Let ,\n\\newline\\quad \n\\left. \n \\begin{matrix*}[l]\n ways(pattern) & {\n size( \n \\underbrace{n}_{\n\n \\left\\{\n \\begin{matrix*}[l]\n\n {n \\in\\{1...26\\}}) \\\\\n n \\text{ mathes } pattern\n \\end{matrix*}\n \\right.\n }\n )\n } \\\\\ndp[i] & {\\text{\\# ways upto }i^{th} \\text{ index}}\n \\end{matrix*}\n\\right.\n$\n\n---\n$Recurrence \\space relations:\n\\\\dp[i] += dp[i-1] * ways(s[i])\n\\\\dp[i+1] += dp[i-1] * ways(s[i:i+2])\n$\n\n# Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict as dd\nfrom functools import cache\nimport re\nclass Solution:\n def numDecodings(self, s: str) -> int:\n MOD = int(1e9 + 7)\n STAR="*"\n N= len(s)\n @cache\n def ways(s):\n if(s=="0"):\n """\n As per PS , A - 1 , B -1 ... z -26 \n so single digit number zero doesnt represent anything \n but double digit number can have a zero (eg. "10" , "20")\n """\n return 0\n s = "^"+s+"$"\n STAR_REPLACE = "[1-9]"\n regex_pattern= re.compile(s.replace(STAR, STAR_REPLACE))\n matches = [ \n (str(i), regex_pattern.match(str(i))) \n for i in range(27) \n if(regex_pattern.match(str(i)) is not None)\n ]\n # print(s,regex_pattern,len(matches))\n return len(matches)\n\n dp = dd(lambda : 0)\n p_ix = None\n dp[p_ix] = 1 \n for i in range(N):\n """\n ways[current_index+1] += ways[previous_index] * calc_ways(to add 1 digit number as per pattern in s[current_index] )\n """\n if(i < N):\n c1 = ways(s[i])\n dp[i] += dp[p_ix] * c1\n dp[i] %=MOD\n """\n ways[current_index+2] += ways[previous_index] * calc_ways(to add 2 digit number as per pattern in s[current_index: currentindex +2] )\n """\n if(i+1 < N):\n c2 = ways(s[i] + s[i+1])\n dp[i+1] += dp[p_ix] * c2\n dp[i] %=MOD\n del dp[p_ix]\n p_ix = i\n return dp[N-1]\n``` | 0 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
**In addition** to the mapping above, an encoded message may contain the `'*'` character, which can represent any digit from `'1'` to `'9'` (`'0'` is excluded). For example, the encoded message `"1* "` may represent any of the encoded messages `"11 "`, `"12 "`, `"13 "`, `"14 "`, `"15 "`, `"16 "`, `"17 "`, `"18 "`, or `"19 "`. Decoding `"1* "` is equivalent to decoding **any** of the encoded messages it can represent.
Given a string `s` consisting of digits and `'*'` characters, return _the **number** of ways to **decode** it_.
Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "\* "
**Output:** 9
**Explanation:** The encoded message can represent any of the encoded messages "1 ", "2 ", "3 ", "4 ", "5 ", "6 ", "7 ", "8 ", or "9 ".
Each of these can be decoded to the strings "A ", "B ", "C ", "D ", "E ", "F ", "G ", "H ", and "I " respectively.
Hence, there are a total of 9 ways to decode "\* ".
**Example 2:**
**Input:** s = "1\* "
**Output:** 18
**Explanation:** The encoded message can represent any of the encoded messages "11 ", "12 ", "13 ", "14 ", "15 ", "16 ", "17 ", "18 ", or "19 ".
Each of these encoded messages have 2 ways to be decoded (e.g. "11 " can be decoded to "AA " or "K ").
Hence, there are a total of 9 \* 2 = 18 ways to decode "1\* ".
**Example 3:**
**Input:** s = "2\* "
**Output:** 15
**Explanation:** The encoded message can represent any of the encoded messages "21 ", "22 ", "23 ", "24 ", "25 ", "26 ", "27 ", "28 ", or "29 ".
"21 ", "22 ", "23 ", "24 ", "25 ", and "26 " have 2 ways of being decoded, but "27 ", "28 ", and "29 " only have 1 way.
Hence, there are a total of (6 \* 2) + (3 \* 1) = 12 + 3 = 15 ways to decode "2\* ".
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a digit or `'*'`. | null |
Solution | solve-the-equation | 1 | 1 | ```C++ []\nclass Solution {\n public:\n string solveEquation(string equation) {\n const string lhsEquation = equation.substr(0, equation.find(\'=\'));\n const string rhsEquation = equation.substr(equation.find(\'=\') + 1);\n const auto& [lhsCoefficient, lhsConstant] = calculate(lhsEquation);\n const auto& [rhsCoefficient, rhsConstant] = calculate(rhsEquation);\n const int coefficient = lhsCoefficient - rhsCoefficient;\n const int constant = rhsConstant - lhsConstant;\n\n if (coefficient == 0 && constant == 0)\n return "Infinite solutions";\n if (coefficient == 0 && constant != 0)\n return "No solution";\n return "x=" + to_string(constant / coefficient);\n }\n private:\n pair<int, int> calculate(const string& s) {\n int coefficient = 0;\n int constant = 0;\n int num = 0;\n int sign = 1;\n\n for (int i = 0; i < s.length(); ++i) {\n const char c = s[i];\n if (isdigit(c))\n num = num * 10 + (c - \'0\');\n else if (c == \'+\' || c == \'-\') {\n constant += sign * num;\n sign = c == \'+\' ? 1 : -1;\n num = 0;\n } else {\n if (i > 0 && num == 0 && s[i - 1] == \'0\')\n continue;\n coefficient += num == 0 ? sign : sign * num;\n num = 0;\n }\n }\n return {coefficient, constant + sign * num};\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def solveEquation(self, equation):\n x = a = 0\n side = 1\n for eq, sign, num, isx in re.findall(\'(=)|([-+]?)(\\d*)(x?)\', equation):\n if eq:\n side = -1\n elif isx:\n x += side * int(sign + \'1\') * int(num or 1)\n elif num:\n a -= side * int(sign + num)\n return \'x=%d\' % (a / x) if x else \'No solution\' if a else \'Infinite solutions\'\n```\n\n```Java []\nclass Solution {\n public String solveEquation(String equation) {\n int x1 = 0,x2 = 0;\n int sum1=0,sum2=0;\n int sign = 1;\n int i=0;\n boolean flag = true;\n for(i=0;i<equation.length();i++){\n char ch = equation.charAt(i);\n if(ch == \'=\') flag = false;\n else if(ch == \'x\'){\n if(flag) x1 += sign;\n else x2 += sign;\n sign = 1;\n }\n else if(Character.isDigit(ch)){\n int val =0;\n while(i<equation.length() && Character.isDigit(equation.charAt(i))){\n val = val*10 + Character.getNumericValue(equation.charAt(i)); \n i++;\n }\n i--;\n if(i<equation.length()-1 && equation.charAt(i+1) == \'x\'){\n i++;\n if(flag) x1+=sign * val;\n else x2 += sign * val;\n }\n else{\n if(flag)sum1 += sign * val;\n else sum2 += sign * val;\n }\n sign = 1;\n }else if(ch == \'-\') sign = -1;\n }\n StringBuilder sb = new StringBuilder();\n if(x1==x2 && sum1 == sum2) return "Infinite solutions";\n else if(sum1 == 0 && sum2 == 0) return "x=0";\n else if(x1 == x2 && ((sum1!=0)||(sum2!=0))) return "No solution";\n int sum=0;\n int x=0;\n if(x1>x2){\n x = x1 - x2;\n sum = sum2-sum1;\n sum = sum/x;\n }\n else if(x2>x1){\n x = x2 - x1;\n sum = sum1-sum2;\n sum = sum/x;\n }\n sb.append("x=");\n sb.append(sum);\n return sb.toString();\n }\n}\n```\n | 2 | Solve a given equation and return the value of `'x'` in the form of a string `"x=#value "`. The equation contains only `'+'`, `'-'` operation, the variable `'x'` and its coefficient. You should return `"No solution "` if there is no solution for the equation, or `"Infinite solutions "` if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of `'x'` is an integer.
**Example 1:**
**Input:** equation = "x+5-3+x=6+x-2 "
**Output:** "x=2 "
**Example 2:**
**Input:** equation = "x=x "
**Output:** "Infinite solutions "
**Example 3:**
**Input:** equation = "2x=x "
**Output:** "x=0 "
**Constraints:**
* `3 <= equation.length <= 1000`
* `equation` has exactly one `'='`.
* `equation` consists of integers with an absolute value in the range `[0, 100]` without any leading zeros, and the variable `'x'`. | null |
Basic simulation (R-95%+, M-70%+) | solve-the-equation | 0 | 1 | # Complexity\n- Time complexity: **O(n)**\nn - length of input string `equation`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def solveEquation(self, equation: str) -> str:\n left: str\n right: str\n # All \'x\' goes to left, all \'vals\' goes to right.\n # Because we only have \'-\', \'+\' operations.\n left, right = equation.split(\'=\')\n\n def rebuild_part(part: str) -> str:\n """\n Rebuild one part of the equation into: +-val*x+-vals\n :param part: part of the equation to change\n :return: rebuild version of the given part\n """\n part_x: int = 0\n part_else: int = 0\n cur_val: str = \'\'\n part += \'+\' # we\'re always ignoring last value we built, so it\'s faster to add extra trigger.\n for x in range(len(part)):\n # Resets for new value.\n if part[x] == \'-\':\n if cur_val:\n part_else += int(cur_val)\n cur_val = \'\'\n cur_val += \'-\'\n elif part[x] == \'+\':\n if cur_val:\n part_else += int(cur_val)\n cur_val = \'\'\n # \'x\' on current part.\n elif part[x] == \'x\':\n if cur_val:\n if cur_val == \'-\':\n part_x += -1\n else:\n part_x += int(cur_val)\n else:\n part_x += 1\n cur_val = \'\'\n # Everything else on this part.\n else:\n cur_val += part[x]\n return f\'{part_x}x+{part_else}\' if part_else >= 0 else f\'{part_x}x{part_else}\'\n\n new_left: str = rebuild_part(left)\n new_right: str = rebuild_part(right)\n # Both sides will lead to 0=0.\n if new_left == new_right:\n return \'Infinite solutions\'\n # New parts are always in style: +-val*x+-vals\n # So, we care about value before \'x\' and after.\n left_x_ind: int = new_left.index(\'x\')\n right_x_ind: int = new_right.index(\'x\')\n x_side: int = int(new_left[:left_x_ind]) - int(new_right[:right_x_ind])\n # Both sides will lead to 0*x=w.e.\n if x_side == 0:\n return \'No solution\'\n # Transfer left_part -> right_part => (left_part values * -1).\n else_side: int = int(new_right[right_x_ind + 1:]) - int(new_left[left_x_ind + 1:])\n if x_side == 1:\n return f\'x={else_side}\'\n # ! If there is exactly one solution for the equation,\n # we ensure that the value of \'x\' is an integer. !\n # So, it\'s always floor, and ALL test cases bugs out if one of them results in => x=float.\n return f\'x={else_side // x_side}\'\n``` | 0 | Solve a given equation and return the value of `'x'` in the form of a string `"x=#value "`. The equation contains only `'+'`, `'-'` operation, the variable `'x'` and its coefficient. You should return `"No solution "` if there is no solution for the equation, or `"Infinite solutions "` if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of `'x'` is an integer.
**Example 1:**
**Input:** equation = "x+5-3+x=6+x-2 "
**Output:** "x=2 "
**Example 2:**
**Input:** equation = "x=x "
**Output:** "Infinite solutions "
**Example 3:**
**Input:** equation = "2x=x "
**Output:** "x=0 "
**Constraints:**
* `3 <= equation.length <= 1000`
* `equation` has exactly one `'='`.
* `equation` consists of integers with an absolute value in the range `[0, 100]` without any leading zeros, and the variable `'x'`. | null |
python3 , tokenize expression and pass over tokens. | solve-the-equation | 0 | 1 | # Intuition\nparse input into tokens, and one pass over tokens. Gather the sum of the factors of X and the sum of the constants, solve it.\n\n\n# Complexity\n- Time complexity:\nO(n) - pass once over the input to parse the tokens, second pass over the tokens (number of tokens is usually smaller than n, but close to n)\n\n- Space complexity:\nconstant \n\n# Code\n```\nimport re\n\nclass Solution:\n def solveEquation(self, equation: str) -> str:\n tokens = re.findall(r\'x|\\+|\\-|=|\\d+\', equation)\n\n sign = 1\n factor = 1\n\n x_count = 0 \n const_count = 0 \n\n idx = 0\n while idx < len(tokens):\n if tokens[idx] == \'+\':\n sign = 1\n elif tokens[idx] == \'-\':\n sign = -1\n elif tokens[idx] == \'=\':\n factor = -1\n sign = 1\n elif tokens[idx] == \'x\':\n x_count += factor * sign\n else:\n # number\n if idx + 1 < len(tokens) and tokens[idx+1] == \'x\':\n x_count += int(tokens[idx]) * factor * sign\n idx += 1\n else:\n const_count += int(tokens[idx]) * -factor * sign\n\n idx += 1\n\n\n if x_count == 0:\n if const_count == 0:\n return "Infinite solutions"\n return "No solution" \n \n return f"x={int(const_count / x_count)}"\n``` | 0 | Solve a given equation and return the value of `'x'` in the form of a string `"x=#value "`. The equation contains only `'+'`, `'-'` operation, the variable `'x'` and its coefficient. You should return `"No solution "` if there is no solution for the equation, or `"Infinite solutions "` if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of `'x'` is an integer.
**Example 1:**
**Input:** equation = "x+5-3+x=6+x-2 "
**Output:** "x=2 "
**Example 2:**
**Input:** equation = "x=x "
**Output:** "Infinite solutions "
**Example 3:**
**Input:** equation = "2x=x "
**Output:** "x=0 "
**Constraints:**
* `3 <= equation.length <= 1000`
* `equation` has exactly one `'='`.
* `equation` consists of integers with an absolute value in the range `[0, 100]` without any leading zeros, and the variable `'x'`. | null |
Python Solution || Easy to Understand | solve-the-equation | 0 | 1 | * **Time Complexity: *O(n)***\n# Methodology:\nI have framed different equations for x-coefficients and constants on both sides\nSay equation: *3x-2-2x=5x+3*,\nthen x1 = 3-2 (**3x**-2 **-2x**)\n\t\tx2 = 5 ( **5x**+3x)\n\t\tn1 = -2 ( 3x **-2**-2x)\n\t\tn2 = 3 (5x **+3x**)\n\ttotal (x) = (3-2)-(5) => -4 (coefficient of final x)\n\ttotal (n) = (-2) + (3) => 1\nnow I these and solved it.\n\t\t\n\n```python\nclass Solution:\n def solveEquation(self, eqn: str) -> str:\n if eqn == "x=x": return "Infinite solutions"\n\n x1 = ""; x2 = ""\n n1 = ""; n2 = ""\n flg = ""\n e = 0; coeff = "";\n n = len(eqn); i = 0;\n while i < n:\n if e: # after "="\n \n if eqn[i] == "x":\n if coeff:\n x2 = x2 + flg + coeff; coeff = ""\n else:\n x2 = x2 + flg + "1";\n elif 48 <= ord(eqn[i]) <= 57:\n if i < n-1:\n temp = ""; xfound = 0\n while i < n and eqn[i] not in [\'+\',\'-\']:\n if eqn[i] == \'x\':\n xfound = 1;\n coeff = temp; temp = ""; break;\n temp += eqn[i]; i += 1;\n if not xfound: \n n2 = n2 + flg + temp;\n i -= 1;\n else: n2 = n2 + flg + eqn[i]; \n else:\n flg = eqn[i]; \n else: \n if eqn[i] == "=": \n e = 1; flg = ""\n \n elif eqn[i] == "x":\n if coeff:\n x1 = x1 + flg + coeff; coeff = ""\n else: x1 = x1 + flg + "1";\n\n elif 48 <= ord(eqn[i]) <= 57:\n if i < n-1:\n temp = ""; xfound = 0\n while i < n and eqn[i] not in [\'+\',\'-\', "="]:\n if eqn[i] == \'x\':\n xfound = 1;\n coeff = temp; temp = ""; break;\n temp += eqn[i]; i += 1;\n if not xfound:\n n1 = n1 + flg + temp;\n i -= 1;\n else: n1 = n1 + flg + eqn[i];\n else:\n flg = eqn[i];\n i += 1;\n \n # now evaluate thus formed eqn\'s::\n if not x1: x1 = "0"\n if not x2: x2 = "0"\n if not n1: n1 = "0"\n if not n2: n2 = "0"\n \n x = eval(x1) - eval(x2)\n num = eval(n2) - eval(n1)\n \n print(x1, x2, n1, n2, x,num)\n if not x and not num: return "Infinite solutions"\n if not x: return "No solution"\n \n return "x="+ str(num//x)\n \n``` | 0 | Solve a given equation and return the value of `'x'` in the form of a string `"x=#value "`. The equation contains only `'+'`, `'-'` operation, the variable `'x'` and its coefficient. You should return `"No solution "` if there is no solution for the equation, or `"Infinite solutions "` if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of `'x'` is an integer.
**Example 1:**
**Input:** equation = "x+5-3+x=6+x-2 "
**Output:** "x=2 "
**Example 2:**
**Input:** equation = "x=x "
**Output:** "Infinite solutions "
**Example 3:**
**Input:** equation = "2x=x "
**Output:** "x=0 "
**Constraints:**
* `3 <= equation.length <= 1000`
* `equation` has exactly one `'='`.
* `equation` consists of integers with an absolute value in the range `[0, 100]` without any leading zeros, and the variable `'x'`. | null |
Simple python3 solution | solve-the-equation | 0 | 1 | ```\nclass Solution:\n def solveEquation(self, equation: str) -> str:\n def parse(expr):\n zero = False\n sign, curr = 1, 0\n coeff, val = 0, 0\n \n for i in range(len(expr)):\n if expr[i] == \'+\' or expr[i] == \'-\':\n val += sign * curr\n curr = 0\n sign = 1 if expr[i] == \'+\' else -1\n\n elif expr[i].isdigit():\n curr = curr*10 + ord(expr[i]) - 48\n if curr == 0: zero = True\n\n else:\n if not zero:\n coeff += sign * (curr if curr != 0 else 1)\n curr = 0\n zero = False\n\n if expr[-1] != \'x\': \n val += sign * curr\n\n return coeff, val\n\n\n left_part, right_part = equation.split(\'=\')\n\n a, c = parse(left_part)\n b, d = parse(right_part)\n\n if a == b:\n return \'No solution\' if c != d else \'Infinite solutions\'\n \n return f\'x={(d - c) // (a - b)}\'\n\n``` | 0 | Solve a given equation and return the value of `'x'` in the form of a string `"x=#value "`. The equation contains only `'+'`, `'-'` operation, the variable `'x'` and its coefficient. You should return `"No solution "` if there is no solution for the equation, or `"Infinite solutions "` if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of `'x'` is an integer.
**Example 1:**
**Input:** equation = "x+5-3+x=6+x-2 "
**Output:** "x=2 "
**Example 2:**
**Input:** equation = "x=x "
**Output:** "Infinite solutions "
**Example 3:**
**Input:** equation = "2x=x "
**Output:** "x=0 "
**Constraints:**
* `3 <= equation.length <= 1000`
* `equation` has exactly one `'='`.
* `equation` consists of integers with an absolute value in the range `[0, 100]` without any leading zeros, and the variable `'x'`. | null |
Python Solution Using RE | solve-the-equation | 0 | 1 | \n# Code\n```\nclass Solution:\n def solveEquation(self, equation: str) -> str:\n coef = [0, 0] # coefficient of x and constant\n left = 1\n for item in re.findall("=|[\\+-]?[0-9x]+", equation):\n if item == "=":\n left = -1\n elif "x" in item:\n item = item.replace("x", "")\n coef[0] += left * int(item + "1") if item in ["", "+", "-"] else left * int(item)\n else:\n coef[1] += left * int(item)\n if coef[0] == 0:\n return "Infinite solutions" if coef[1] == 0 else "No solution"\n else:\n return "x={0}".format(-coef[1]//coef[0])\n``` | 0 | Solve a given equation and return the value of `'x'` in the form of a string `"x=#value "`. The equation contains only `'+'`, `'-'` operation, the variable `'x'` and its coefficient. You should return `"No solution "` if there is no solution for the equation, or `"Infinite solutions "` if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of `'x'` is an integer.
**Example 1:**
**Input:** equation = "x+5-3+x=6+x-2 "
**Output:** "x=2 "
**Example 2:**
**Input:** equation = "x=x "
**Output:** "Infinite solutions "
**Example 3:**
**Input:** equation = "2x=x "
**Output:** "x=0 "
**Constraints:**
* `3 <= equation.length <= 1000`
* `equation` has exactly one `'='`.
* `equation` consists of integers with an absolute value in the range `[0, 100]` without any leading zeros, and the variable `'x'`. | null |
Simple regexp solution | solve-the-equation | 0 | 1 | # Intuition\n\nUsing the regexp `(^|[+-=])([0-9]*)(x|)` one can split the string into token triples. Each consists of an `op` a coefficient and optionally `x`. Then we can compute the total constant on both side and the coefficient of `x`. \n \n\n# Code\n```\nimport re\nclass Solution:\n def solveEquation(self, equation: str) -> str:\n pat = "(^|[+-=])([0-9]*)(x|)"\n coeff = [0, 0]\n sign = 1\n for op, a, x in re.findall(pat, equation):\n default = 1 if x==\'x\' else 0\n a = int(a) if a != \'\' else default\n if op == \'=\':\n sign = -1\n elif op == \'-\':\n a = -a\n a = sign*a\n if x == \'x\':\n coeff[1] += a\n else:\n coeff[0] += a\n if coeff[1]==0:\n return "Infinite solutions" if coeff[0]==0 else "No solution"\n return f"x={-coeff[0]//coeff[1]}"\n\n\n\n \n``` | 0 | Solve a given equation and return the value of `'x'` in the form of a string `"x=#value "`. The equation contains only `'+'`, `'-'` operation, the variable `'x'` and its coefficient. You should return `"No solution "` if there is no solution for the equation, or `"Infinite solutions "` if there are infinite solutions for the equation.
If there is exactly one solution for the equation, we ensure that the value of `'x'` is an integer.
**Example 1:**
**Input:** equation = "x+5-3+x=6+x-2 "
**Output:** "x=2 "
**Example 2:**
**Input:** equation = "x=x "
**Output:** "Infinite solutions "
**Example 3:**
**Input:** equation = "2x=x "
**Output:** "x=0 "
**Constraints:**
* `3 <= equation.length <= 1000`
* `equation` has exactly one `'='`.
* `equation` consists of integers with an absolute value in the range `[0, 100]` without any leading zeros, and the variable `'x'`. | null |
✔Beats 97.6% TC || Python Solution | design-circular-deque | 0 | 1 | # Complexity\n- Time complexity:\n97.6%\n- Space complexity:\n88.24%\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.deque = []\n self.k = k\n\n def insertFront(self, value: int) -> bool:\n if len(self.deque) < self.k:\n self.deque = [value] + self.deque\n return True\n return False \n\n def insertLast(self, value: int) -> bool:\n if len(self.deque) < self.k:\n self.deque.append(value)\n return True\n return False\n\n def deleteFront(self) -> bool:\n if len(self.deque) > 0:\n self.deque.pop(0)\n return True\n return False\n\n def deleteLast(self) -> bool:\n if len(self.deque) > 0:\n self.deque.pop()\n return True\n return False\n\n def getFront(self) -> int:\n if len(self.deque) > 0:\n front = self.deque[0]\n return front\n return -1\n\n def getRear(self) -> int:\n if len(self.deque) > 0:\n rear = self.deque[-1]\n return rear\n return -1\n\n def isEmpty(self) -> bool:\n if len(self.deque) == 0:\n return True\n\n def isFull(self) -> bool:\n if len(self.deque) == self.k:\n return True\n\n\n# Your MyCircularDeque object will be instantiated and called as such:\n# obj = MyCircularDeque(k)\n# param_1 = obj.insertFront(value)\n# param_2 = obj.insertLast(value)\n# param_3 = obj.deleteFront()\n# param_4 = obj.deleteLast()\n# param_5 = obj.getFront()\n# param_6 = obj.getRear()\n# param_7 = obj.isEmpty()\n# param_8 = obj.isFull()\n``` | 1 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
✔Beats 97.6% TC || Python Solution | design-circular-deque | 0 | 1 | # Complexity\n- Time complexity:\n97.6%\n- Space complexity:\n88.24%\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.deque = []\n self.k = k\n\n def insertFront(self, value: int) -> bool:\n if len(self.deque) < self.k:\n self.deque = [value] + self.deque\n return True\n return False \n\n def insertLast(self, value: int) -> bool:\n if len(self.deque) < self.k:\n self.deque.append(value)\n return True\n return False\n\n def deleteFront(self) -> bool:\n if len(self.deque) > 0:\n self.deque.pop(0)\n return True\n return False\n\n def deleteLast(self) -> bool:\n if len(self.deque) > 0:\n self.deque.pop()\n return True\n return False\n\n def getFront(self) -> int:\n if len(self.deque) > 0:\n front = self.deque[0]\n return front\n return -1\n\n def getRear(self) -> int:\n if len(self.deque) > 0:\n rear = self.deque[-1]\n return rear\n return -1\n\n def isEmpty(self) -> bool:\n if len(self.deque) == 0:\n return True\n\n def isFull(self) -> bool:\n if len(self.deque) == self.k:\n return True\n\n\n# Your MyCircularDeque object will be instantiated and called as such:\n# obj = MyCircularDeque(k)\n# param_1 = obj.insertFront(value)\n# param_2 = obj.insertLast(value)\n# param_3 = obj.deleteFront()\n# param_4 = obj.deleteLast()\n# param_5 = obj.getFront()\n# param_6 = obj.getRear()\n# param_7 = obj.isEmpty()\n# param_8 = obj.isFull()\n``` | 1 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
Python || 92.92% Faster || Explained with comments | design-circular-deque | 0 | 1 | ```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.size=k\n self.q=[0]*self.size\n self.front=-1\n self.rear=-1\n\n def insertFront(self, value: int) -> bool:\n if self.isFull():\n return False\n if self.isEmpty():\n self.front=self.rear=0\n else:\n self.front=(self.front-1)%self.size #To maintain the cyclic nature of the queue\n self.q[self.front]=value\n return True\n\n def insertLast(self, value: int) -> bool:\n if self.isFull():\n return False\n if self.isEmpty():\n self.front=self.rear=0\n else:\n self.rear=(self.rear+1)%self.size #To maintain the cyclic nature of the queue\n self.q[self.rear]=value\n return True\n\n def deleteFront(self) -> bool:\n if self.isEmpty():\n return False\n item=self.q[self.front]\n if self.front==self.rear: #if there is only one element in the queue\n self.front=self.rear=-1\n else:\n self.front=(self.front+1)%self.size #To maintain the cyclic nature of the queue\n return True\n\n def deleteLast(self) -> bool:\n if self.isEmpty():\n return False\n item=self.q[self.rear]\n if self.front==self.rear: #if there is only one element in the queue\n self.front=self.rear=-1\n else:\n self.rear=(self.rear-1)%self.size #To maintain the cyclic nature of the queue\n return True\n\n def getFront(self) -> int:\n if self.front==-1:\n return -1\n return self.q[self.front]\n\n def getRear(self) -> int:\n if self.rear==-1:\n return -1\n return self.q[self.rear]\n\n def isEmpty(self) -> bool:\n return self.front==self.rear==-1\n\n def isFull(self) -> bool:\n if (self.rear + 1) % self.size == self.front:\n return True\n return False\n```\n**An upvote will be encouraging** | 1 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
Python || 92.92% Faster || Explained with comments | design-circular-deque | 0 | 1 | ```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.size=k\n self.q=[0]*self.size\n self.front=-1\n self.rear=-1\n\n def insertFront(self, value: int) -> bool:\n if self.isFull():\n return False\n if self.isEmpty():\n self.front=self.rear=0\n else:\n self.front=(self.front-1)%self.size #To maintain the cyclic nature of the queue\n self.q[self.front]=value\n return True\n\n def insertLast(self, value: int) -> bool:\n if self.isFull():\n return False\n if self.isEmpty():\n self.front=self.rear=0\n else:\n self.rear=(self.rear+1)%self.size #To maintain the cyclic nature of the queue\n self.q[self.rear]=value\n return True\n\n def deleteFront(self) -> bool:\n if self.isEmpty():\n return False\n item=self.q[self.front]\n if self.front==self.rear: #if there is only one element in the queue\n self.front=self.rear=-1\n else:\n self.front=(self.front+1)%self.size #To maintain the cyclic nature of the queue\n return True\n\n def deleteLast(self) -> bool:\n if self.isEmpty():\n return False\n item=self.q[self.rear]\n if self.front==self.rear: #if there is only one element in the queue\n self.front=self.rear=-1\n else:\n self.rear=(self.rear-1)%self.size #To maintain the cyclic nature of the queue\n return True\n\n def getFront(self) -> int:\n if self.front==-1:\n return -1\n return self.q[self.front]\n\n def getRear(self) -> int:\n if self.rear==-1:\n return -1\n return self.q[self.rear]\n\n def isEmpty(self) -> bool:\n return self.front==self.rear==-1\n\n def isFull(self) -> bool:\n if (self.rear + 1) % self.size == self.front:\n return True\n return False\n```\n**An upvote will be encouraging** | 1 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
Using List Simple || Python3 | design-circular-deque | 0 | 1 | # Intuition\nYou can perform all operations as same as using a normal deque just for pushing an element from front\ndeque uses -> appendleft\nfor list -> [value] + arr\n\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.q = []\n self.k = k\n \n def insertFront(self, value: int) -> bool:\n if len(self.q) < self.k:\n self.q = [value] + self.q\n # self.q.appendleft(value) #push in front if using deque\n return True\n return False\n\n def insertLast(self, value: int) -> bool:\n if len(self.q) < self.k:\n self.q.append(value) #push in last\n return True\n return False\n \n def deleteFront(self) -> bool:\n if len(self.q) > 0:\n self.q.pop(0)\n return True\n return False\n\n def deleteLast(self) -> bool:\n if len(self.q) > 0:\n self.q.pop()\n return True\n return False\n\n def getFront(self) -> int:\n if len(self.q) > 0:\n front = self.q[0]\n return front\n return -1\n\n def getRear(self) -> int:\n if len(self.q) > 0:\n last = self.q[-1]\n return last\n return -1\n \n def isEmpty(self) -> bool:\n if len(self.q) == 0:\n return True\n return False\n \n def isFull(self) -> bool:\n if len(self.q) == self.k:\n return True\n return False\n \n\n\n# Your MyCircularDeque object will be instantiated and called as such:\n# obj = MyCircularDeque(k)\n# param_1 = obj.insertFront(value)\n# param_2 = obj.insertLast(value)\n# param_3 = obj.deleteFront()\n# param_4 = obj.deleteLast()\n# param_5 = obj.getFront()\n# param_6 = obj.getRear()\n# param_7 = obj.isEmpty()\n# param_8 = obj.isFull()\n``` | 1 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
Using List Simple || Python3 | design-circular-deque | 0 | 1 | # Intuition\nYou can perform all operations as same as using a normal deque just for pushing an element from front\ndeque uses -> appendleft\nfor list -> [value] + arr\n\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.q = []\n self.k = k\n \n def insertFront(self, value: int) -> bool:\n if len(self.q) < self.k:\n self.q = [value] + self.q\n # self.q.appendleft(value) #push in front if using deque\n return True\n return False\n\n def insertLast(self, value: int) -> bool:\n if len(self.q) < self.k:\n self.q.append(value) #push in last\n return True\n return False\n \n def deleteFront(self) -> bool:\n if len(self.q) > 0:\n self.q.pop(0)\n return True\n return False\n\n def deleteLast(self) -> bool:\n if len(self.q) > 0:\n self.q.pop()\n return True\n return False\n\n def getFront(self) -> int:\n if len(self.q) > 0:\n front = self.q[0]\n return front\n return -1\n\n def getRear(self) -> int:\n if len(self.q) > 0:\n last = self.q[-1]\n return last\n return -1\n \n def isEmpty(self) -> bool:\n if len(self.q) == 0:\n return True\n return False\n \n def isFull(self) -> bool:\n if len(self.q) == self.k:\n return True\n return False\n \n\n\n# Your MyCircularDeque object will be instantiated and called as such:\n# obj = MyCircularDeque(k)\n# param_1 = obj.insertFront(value)\n# param_2 = obj.insertLast(value)\n# param_3 = obj.deleteFront()\n# param_4 = obj.deleteLast()\n# param_5 = obj.getFront()\n# param_6 = obj.getRear()\n# param_7 = obj.isEmpty()\n# param_8 = obj.isFull()\n``` | 1 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
python3-solution using list | design-circular-deque | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.deque=[]\n self.len=k\n\n def insertFront(self, value: int) -> bool:\n if len(self.deque)<self.len:\n self.deque.insert(0,value) \n return True\n else:\n return False\n\n def insertLast(self, value: int) -> bool:\n if len(self.deque)<self.len:\n self.deque.append(value) \n return True\n else:\n return False\n\n def deleteFront(self) -> bool:\n if self.deque:\n self.deque=self.deque[1:]\n return True\n\n def deleteLast(self) -> bool:\n if self.deque:\n self.deque=self.deque[:-1]\n return True\n\n def getFront(self) -> int:\n if self.deque:\n return self.deque[0]\n else:return -1\n\n\n def getRear(self) -> int:\n if self.deque:\n return self.deque[-1]\n else:return -1\n\n def isEmpty(self) -> bool:\n if self.deque:\n return False\n return True\n\n def isFull(self) -> bool:\n if self.len==len(self.deque):return True\n\n\n# Your MyCircularDeque object will be instantiated and called as such:\n# obj = MyCircularDeque(k)\n# param_1 = obj.insertFront(value)\n# param_2 = obj.insertLast(value)\n# param_3 = obj.deleteFront()\n# param_4 = obj.deleteLast()\n# param_5 = obj.getFront()\n# param_6 = obj.getRear()\n# param_7 = obj.isEmpty()\n# param_8 = obj.isFull()\n``` | 2 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
python3-solution using list | design-circular-deque | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.deque=[]\n self.len=k\n\n def insertFront(self, value: int) -> bool:\n if len(self.deque)<self.len:\n self.deque.insert(0,value) \n return True\n else:\n return False\n\n def insertLast(self, value: int) -> bool:\n if len(self.deque)<self.len:\n self.deque.append(value) \n return True\n else:\n return False\n\n def deleteFront(self) -> bool:\n if self.deque:\n self.deque=self.deque[1:]\n return True\n\n def deleteLast(self) -> bool:\n if self.deque:\n self.deque=self.deque[:-1]\n return True\n\n def getFront(self) -> int:\n if self.deque:\n return self.deque[0]\n else:return -1\n\n\n def getRear(self) -> int:\n if self.deque:\n return self.deque[-1]\n else:return -1\n\n def isEmpty(self) -> bool:\n if self.deque:\n return False\n return True\n\n def isFull(self) -> bool:\n if self.len==len(self.deque):return True\n\n\n# Your MyCircularDeque object will be instantiated and called as such:\n# obj = MyCircularDeque(k)\n# param_1 = obj.insertFront(value)\n# param_2 = obj.insertLast(value)\n# param_3 = obj.deleteFront()\n# param_4 = obj.deleteLast()\n# param_5 = obj.getFront()\n# param_6 = obj.getRear()\n# param_7 = obj.isEmpty()\n# param_8 = obj.isFull()\n``` | 2 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
Solution | design-circular-deque | 1 | 1 | ```C++ []\nclass MyCircularDeque {\n public:\n MyCircularDeque(int k) : k(k), q(k), rear(k - 1) {}\n bool insertFront(int value) {\n if (isFull())\n return false;\n\n front = (--front + k) % k;\n q[front] = value;\n ++size;\n return true;\n }\n bool insertLast(int value) {\n if (isFull())\n return false;\n\n rear = ++rear % k;\n q[rear] = value;\n ++size;\n return true;\n }\n bool deleteFront() {\n if (isEmpty())\n return false;\n\n front = ++front % k;\n --size;\n return true;\n }\n bool deleteLast() {\n if (isEmpty())\n return false;\n\n rear = (--rear + k) % k;\n --size;\n return true;\n }\n int getFront() {\n return isEmpty() ? -1 : q[front];\n }\n int getRear() {\n return isEmpty() ? -1 : q[rear];\n }\n bool isEmpty() {\n return size == 0;\n }\n bool isFull() {\n return size == k;\n }\n private:\n const int k;\n vector<int> q;\n int size = 0;\n int front = 0;\n int rear;\n};\n```\n\n```Python3 []\nclass Node:\n def __init__(self, val, p=None, n=None):\n self.val = val\n self.prev = p\n self.next = n\nclass MyCircularDeque:\n def __init__(self, k: int):\n self.k = k\n self.l = 0\n self.head = self.tail = None\n\n def insertFront(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.head.prev, curr.next = curr, self.head\n self.head = curr\n self.l += 1\n return 1\n \n\n def insertLast(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.tail.next, curr.prev = curr, self.tail\n self.tail = curr\n self.l += 1\n return 1\n\n def deleteFront(self) -> bool:\n if(self.l == 0):\n return 0\n self.head = self.head.next\n self.l -= 1\n return 1\n\n def deleteLast(self) -> bool:\n if(self.l == 0):\n return 0\n self.tail = self.tail.prev\n self.l -= 1\n return 1\n\n def getFront(self) -> int:\n if(self.l == 0):\n return -1\n return self.head.val\n\n def getRear(self) -> int:\n if(self.l == 0):\n return -1\n return self.tail.val\n\n def isEmpty(self) -> bool:\n return self.l == 0\n\n def isFull(self) -> bool:\n return self.l == self.k\n```\n\n```Java []\nclass MyCircularDeque {\n int[] a;\n int head;\n int size;\n int cap;\n public MyCircularDeque(int k) {\n a = new int[k];\n head = 0;\n size = 0;\n cap = k;\n }\n public boolean insertFront(int value) {\n if(size == cap) return false;\n if(head == 0)\n {\n a[cap-1] = value;\n head = cap -1;\n }\n else\n {\n a[--head] = value;\n }\n ++size;\n return true;\n }\n public boolean insertLast(int value) {\n if(size == cap) return false;\n a[(head + (size++)) % cap] = value;\n return true;\n }\n public boolean deleteFront() {\n if(size == 0) return false;\n\n head = ++head % cap;\n --size;\n return true;\n }\n public boolean deleteLast() {\n if(size == 0) return false;\n --size;\n return true;\n }\n public int getFront() {\n if(size == 0) return -1;\n return a[head];\n }\n public int getRear() {\n if(size == 0) return -1;\n\n return a[(head + size - 1) % cap];\n }\n public boolean isEmpty() {\n return size == 0;\n }\n public boolean isFull() {\n return size == cap;\n }\n}\n```\n | 2 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
Solution | design-circular-deque | 1 | 1 | ```C++ []\nclass MyCircularDeque {\n public:\n MyCircularDeque(int k) : k(k), q(k), rear(k - 1) {}\n bool insertFront(int value) {\n if (isFull())\n return false;\n\n front = (--front + k) % k;\n q[front] = value;\n ++size;\n return true;\n }\n bool insertLast(int value) {\n if (isFull())\n return false;\n\n rear = ++rear % k;\n q[rear] = value;\n ++size;\n return true;\n }\n bool deleteFront() {\n if (isEmpty())\n return false;\n\n front = ++front % k;\n --size;\n return true;\n }\n bool deleteLast() {\n if (isEmpty())\n return false;\n\n rear = (--rear + k) % k;\n --size;\n return true;\n }\n int getFront() {\n return isEmpty() ? -1 : q[front];\n }\n int getRear() {\n return isEmpty() ? -1 : q[rear];\n }\n bool isEmpty() {\n return size == 0;\n }\n bool isFull() {\n return size == k;\n }\n private:\n const int k;\n vector<int> q;\n int size = 0;\n int front = 0;\n int rear;\n};\n```\n\n```Python3 []\nclass Node:\n def __init__(self, val, p=None, n=None):\n self.val = val\n self.prev = p\n self.next = n\nclass MyCircularDeque:\n def __init__(self, k: int):\n self.k = k\n self.l = 0\n self.head = self.tail = None\n\n def insertFront(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.head.prev, curr.next = curr, self.head\n self.head = curr\n self.l += 1\n return 1\n \n\n def insertLast(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.tail.next, curr.prev = curr, self.tail\n self.tail = curr\n self.l += 1\n return 1\n\n def deleteFront(self) -> bool:\n if(self.l == 0):\n return 0\n self.head = self.head.next\n self.l -= 1\n return 1\n\n def deleteLast(self) -> bool:\n if(self.l == 0):\n return 0\n self.tail = self.tail.prev\n self.l -= 1\n return 1\n\n def getFront(self) -> int:\n if(self.l == 0):\n return -1\n return self.head.val\n\n def getRear(self) -> int:\n if(self.l == 0):\n return -1\n return self.tail.val\n\n def isEmpty(self) -> bool:\n return self.l == 0\n\n def isFull(self) -> bool:\n return self.l == self.k\n```\n\n```Java []\nclass MyCircularDeque {\n int[] a;\n int head;\n int size;\n int cap;\n public MyCircularDeque(int k) {\n a = new int[k];\n head = 0;\n size = 0;\n cap = k;\n }\n public boolean insertFront(int value) {\n if(size == cap) return false;\n if(head == 0)\n {\n a[cap-1] = value;\n head = cap -1;\n }\n else\n {\n a[--head] = value;\n }\n ++size;\n return true;\n }\n public boolean insertLast(int value) {\n if(size == cap) return false;\n a[(head + (size++)) % cap] = value;\n return true;\n }\n public boolean deleteFront() {\n if(size == 0) return false;\n\n head = ++head % cap;\n --size;\n return true;\n }\n public boolean deleteLast() {\n if(size == 0) return false;\n --size;\n return true;\n }\n public int getFront() {\n if(size == 0) return -1;\n return a[head];\n }\n public int getRear() {\n if(size == 0) return -1;\n\n return a[(head + size - 1) % cap];\n }\n public boolean isEmpty() {\n return size == 0;\n }\n public boolean isFull() {\n return size == cap;\n }\n}\n```\n | 2 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
641: Solution with step by step explanation | design-circular-deque | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize an array with size k, set the head and tail pointers to 0, and set the size to 0.\n2. Implement insertFront by checking if the deque is full, if not, decrement the head pointer (using modular arithmetic to wrap around the array), insert the value at the head, and increment the size.\n3. Implement insertLast by checking if the deque is full, if not, insert the value at the tail pointer (using modular arithmetic to wrap around the array), increment the tail pointer, and increment the size.\n4. Implement deleteFront by checking if the deque is empty, if not, increment the head pointer (using modular arithmetic to wrap around the array), and decrement the size.\n5. Implement deleteLast by checking if the deque is empty, if not, decrement the tail pointer (using modular arithmetic to wrap around the array), and decrement the size.\n6. Implement getFront by checking if the deque is empty, if not, return the value at the head pointer.\n7. Implement getRear by checking if the deque is empty, if not, return the value at the tail pointer minus 1 (using modular arithmetic to wrap around the array).\n8. Implement isEmpty by checking if the size is equal to 0.\n9. Implement isFull by checking if the size is equal to k.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MyCircularDeque:\n def __init__(self, k: int):\n self.queue = [None] * k\n self.max_size = k\n self.head = 0\n self.tail = 0\n self.size = 0\n\n def insertFront(self, value: int) -> bool:\n if self.isFull():\n return False\n self.head = (self.head - 1) % self.max_size\n self.queue[self.head] = value\n self.size += 1\n return True\n\n def insertLast(self, value: int) -> bool:\n if self.isFull():\n return False\n self.queue[self.tail] = value\n self.tail = (self.tail + 1) % self.max_size\n self.size += 1\n return True\n\n def deleteFront(self) -> bool:\n if self.isEmpty():\n return False\n self.head = (self.head + 1) % self.max_size\n self.size -= 1\n return True\n\n def deleteLast(self) -> bool:\n if self.isEmpty():\n return False\n self.tail = (self.tail - 1) % self.max_size\n self.size -= 1\n return True\n\n def getFront(self) -> int:\n if self.isEmpty():\n return -1\n return self.queue[self.head]\n\n def getRear(self) -> int:\n if self.isEmpty():\n return -1\n return self.queue[(self.tail - 1) % self.max_size]\n\n def isEmpty(self) -> bool:\n return self.size == 0\n\n def isFull(self) -> bool:\n return self.size == self.max_size\n\n``` | 4 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
641: Solution with step by step explanation | design-circular-deque | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize an array with size k, set the head and tail pointers to 0, and set the size to 0.\n2. Implement insertFront by checking if the deque is full, if not, decrement the head pointer (using modular arithmetic to wrap around the array), insert the value at the head, and increment the size.\n3. Implement insertLast by checking if the deque is full, if not, insert the value at the tail pointer (using modular arithmetic to wrap around the array), increment the tail pointer, and increment the size.\n4. Implement deleteFront by checking if the deque is empty, if not, increment the head pointer (using modular arithmetic to wrap around the array), and decrement the size.\n5. Implement deleteLast by checking if the deque is empty, if not, decrement the tail pointer (using modular arithmetic to wrap around the array), and decrement the size.\n6. Implement getFront by checking if the deque is empty, if not, return the value at the head pointer.\n7. Implement getRear by checking if the deque is empty, if not, return the value at the tail pointer minus 1 (using modular arithmetic to wrap around the array).\n8. Implement isEmpty by checking if the size is equal to 0.\n9. Implement isFull by checking if the size is equal to k.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MyCircularDeque:\n def __init__(self, k: int):\n self.queue = [None] * k\n self.max_size = k\n self.head = 0\n self.tail = 0\n self.size = 0\n\n def insertFront(self, value: int) -> bool:\n if self.isFull():\n return False\n self.head = (self.head - 1) % self.max_size\n self.queue[self.head] = value\n self.size += 1\n return True\n\n def insertLast(self, value: int) -> bool:\n if self.isFull():\n return False\n self.queue[self.tail] = value\n self.tail = (self.tail + 1) % self.max_size\n self.size += 1\n return True\n\n def deleteFront(self) -> bool:\n if self.isEmpty():\n return False\n self.head = (self.head + 1) % self.max_size\n self.size -= 1\n return True\n\n def deleteLast(self) -> bool:\n if self.isEmpty():\n return False\n self.tail = (self.tail - 1) % self.max_size\n self.size -= 1\n return True\n\n def getFront(self) -> int:\n if self.isEmpty():\n return -1\n return self.queue[self.head]\n\n def getRear(self) -> int:\n if self.isEmpty():\n return -1\n return self.queue[(self.tail - 1) % self.max_size]\n\n def isEmpty(self) -> bool:\n return self.size == 0\n\n def isFull(self) -> bool:\n return self.size == self.max_size\n\n``` | 4 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
89% TC easy python solution | design-circular-deque | 0 | 1 | ```\nclass Node:\n def __init__(self, val, p=None, n=None):\n self.val = val\n self.prev = p\n self.next = n\nclass MyCircularDeque:\n def __init__(self, k: int):\n self.k = k\n self.l = 0\n self.head = self.tail = None\n\n def insertFront(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.head.prev, curr.next = curr, self.head\n self.head = curr\n self.l += 1\n return 1\n \n\n def insertLast(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.tail.next, curr.prev = curr, self.tail\n self.tail = curr\n self.l += 1\n return 1\n\n def deleteFront(self) -> bool:\n if(self.l == 0):\n return 0\n self.head = self.head.next\n self.l -= 1\n return 1\n\n def deleteLast(self) -> bool:\n if(self.l == 0):\n return 0\n self.tail = self.tail.prev\n self.l -= 1\n return 1\n\n def getFront(self) -> int:\n if(self.l == 0):\n return -1\n return self.head.val\n\n def getRear(self) -> int:\n if(self.l == 0):\n return -1\n return self.tail.val\n\n def isEmpty(self) -> bool:\n return self.l == 0\n\n def isFull(self) -> bool:\n return self.l == self.k\n``` | 3 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
89% TC easy python solution | design-circular-deque | 0 | 1 | ```\nclass Node:\n def __init__(self, val, p=None, n=None):\n self.val = val\n self.prev = p\n self.next = n\nclass MyCircularDeque:\n def __init__(self, k: int):\n self.k = k\n self.l = 0\n self.head = self.tail = None\n\n def insertFront(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.head.prev, curr.next = curr, self.head\n self.head = curr\n self.l += 1\n return 1\n \n\n def insertLast(self, value: int) -> bool:\n if(self.l == self.k):\n return 0\n if(self.l == 0):\n self.head = self.tail = Node(value)\n else:\n curr = Node(value)\n self.tail.next, curr.prev = curr, self.tail\n self.tail = curr\n self.l += 1\n return 1\n\n def deleteFront(self) -> bool:\n if(self.l == 0):\n return 0\n self.head = self.head.next\n self.l -= 1\n return 1\n\n def deleteLast(self) -> bool:\n if(self.l == 0):\n return 0\n self.tail = self.tail.prev\n self.l -= 1\n return 1\n\n def getFront(self) -> int:\n if(self.l == 0):\n return -1\n return self.head.val\n\n def getRear(self) -> int:\n if(self.l == 0):\n return -1\n return self.tail.val\n\n def isEmpty(self) -> bool:\n return self.l == 0\n\n def isFull(self) -> bool:\n return self.l == self.k\n``` | 3 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
Ring Buffer - ArrayLen + 1 - O(1) | design-circular-deque | 0 | 1 | ## Approach\n```haskell\n f\nempty: [#,#,#,#,#], when f == b\n b\n```\n```haskell\n f\nfull: [#,#,#,#,#], when f == b + 1\n b\n```\n\n## Complexity\n```haskell\nTime complexity (all ops): O(1)\nSpace complexity: O(n)\n```\n\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.q = [0 for _ in range(k + 1)]\n self.f = 0\n self.b = 0\n self.len = k + 1\n\n def insertFront(self, value: int) -> bool:\n if (self.b + 1) % self.len == (self.f) % self.len: return False\n self.f = (self.f - 1) % self.len\n self.q[self.f] = value\n return True\n\n def insertLast(self, value: int) -> bool:\n if (self.b + 1) % self.len == (self.f) % self.len: return False\n self.q[self.b] = value\n self.b = (self.b + 1) % self.len\n return True\n\n\n def deleteFront(self) -> bool:\n if self.b == self.f: return False\n self.f = (self.f + 1) % self.len\n return True\n \n\n def deleteLast(self) -> bool:\n if self.b == self.f: return False\n self.b = (self.b - 1) % self.len\n return True\n \n\n def getFront(self) -> int:\n if self.b == self.f: return -1\n return self.q[self.f]\n\n def getRear(self) -> int:\n if self.b == self.f: return -1\n return self.q[(self.b - 1) % self.len]\n \n\n def isEmpty(self) -> bool:\n return self.b == self.f\n \n\n def isFull(self) -> bool:\n return (self.b + 1) % self.len == self.f\n``` | 0 | Design your implementation of the circular double-ended queue (deque).
Implement the `MyCircularDeque` class:
* `MyCircularDeque(int k)` Initializes the deque with a maximum size of `k`.
* `boolean insertFront()` Adds an item at the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean insertLast()` Adds an item at the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteFront()` Deletes an item from the front of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `boolean deleteLast()` Deletes an item from the rear of Deque. Returns `true` if the operation is successful, or `false` otherwise.
* `int getFront()` Returns the front item from the Deque. Returns `-1` if the deque is empty.
* `int getRear()` Returns the last item from Deque. Returns `-1` if the deque is empty.
* `boolean isEmpty()` Returns `true` if the deque is empty, or `false` otherwise.
* `boolean isFull()` Returns `true` if the deque is full, or `false` otherwise.
**Example 1:**
**Input**
\[ "MyCircularDeque ", "insertLast ", "insertLast ", "insertFront ", "insertFront ", "getRear ", "isFull ", "deleteLast ", "insertFront ", "getFront "\]
\[\[3\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[4\], \[\]\]
**Output**
\[null, true, true, true, false, 2, true, true, true, 4\]
**Explanation**
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1); // return True
myCircularDeque.insertLast(2); // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear(); // return 2
myCircularDeque.isFull(); // return True
myCircularDeque.deleteLast(); // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront(); // return 4
**Constraints:**
* `1 <= k <= 1000`
* `0 <= value <= 1000`
* At most `2000` calls will be made to `insertFront`, `insertLast`, `deleteFront`, `deleteLast`, `getFront`, `getRear`, `isEmpty`, `isFull`. | null |
Ring Buffer - ArrayLen + 1 - O(1) | design-circular-deque | 0 | 1 | ## Approach\n```haskell\n f\nempty: [#,#,#,#,#], when f == b\n b\n```\n```haskell\n f\nfull: [#,#,#,#,#], when f == b + 1\n b\n```\n\n## Complexity\n```haskell\nTime complexity (all ops): O(1)\nSpace complexity: O(n)\n```\n\n# Code\n```\nclass MyCircularDeque:\n\n def __init__(self, k: int):\n self.q = [0 for _ in range(k + 1)]\n self.f = 0\n self.b = 0\n self.len = k + 1\n\n def insertFront(self, value: int) -> bool:\n if (self.b + 1) % self.len == (self.f) % self.len: return False\n self.f = (self.f - 1) % self.len\n self.q[self.f] = value\n return True\n\n def insertLast(self, value: int) -> bool:\n if (self.b + 1) % self.len == (self.f) % self.len: return False\n self.q[self.b] = value\n self.b = (self.b + 1) % self.len\n return True\n\n\n def deleteFront(self) -> bool:\n if self.b == self.f: return False\n self.f = (self.f + 1) % self.len\n return True\n \n\n def deleteLast(self) -> bool:\n if self.b == self.f: return False\n self.b = (self.b - 1) % self.len\n return True\n \n\n def getFront(self) -> int:\n if self.b == self.f: return -1\n return self.q[self.f]\n\n def getRear(self) -> int:\n if self.b == self.f: return -1\n return self.q[(self.b - 1) % self.len]\n \n\n def isEmpty(self) -> bool:\n return self.b == self.f\n \n\n def isFull(self) -> bool:\n return (self.b + 1) % self.len == self.f\n``` | 0 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
Py3 | Beginner friendly with details and explanation | maximum-average-subarray-i | 0 | 1 | # Approach\n\nThis problem uses sliding window concept.\nYou can solve this problem using two loops in $O(n^2)$ time complexity. However, with sliding window approach, you can easily resolve this in O(n) time.\n\n\nFollow the images below to look at how this works:\n1. Our given input\n\n2. Initialization\n\n\n3. Operations\n\n\n3. Final operation\n\n4. We now return the `maxSum / k` to return the max average.\n\n# Complexity\n Time: O(n)\nSpace: O(1)\n\n# Code\n``` Python []\nclass Solution:\n def findMaxAverage(self, nums: List[int], k: int) -> float:\n \n # Initialize currSum and maxSum to the sum of the initial k elements\n currSum = maxSum = sum(nums[:k])\n\n # Start the loop from the kth element \n # Iterate until you reach the end\n for i in range(k, len(nums)):\n\n # Subtract the left element of the window\n # Add the right element of the window\n currSum += nums[i] - nums[i - k]\n \n # Update the max\n maxSum = max(maxSum, currSum)\n\n # Since the problem requires average, we return the average\n return maxSum / k\n\n```\n``` C++ []\nclass Solution {\npublic:\n double findMaxAverage(vector<int>& nums, int k) {\n double currSum = 0, maxSum = 0;\n \n // Initialize currSum and maxSum to the sum of the initial k elements\n for (int i = 0; i < k; i++)\n currSum += nums[i];\n maxSum = currSum;\n \n // Start the loop from the kth element \n // Iterate until you reach the end\n for (int i = k; i < nums.size(); i++) {\n // Subtract the left element of the window\n // Add the right element of the window\n currSum += nums[i] - nums[i - k];\n \n // Update the max\n maxSum = max(maxSum, currSum);\n }\n \n // Since the problem requires average, we return the average\n return maxSum / k;\n }\n};\n\n``` | 55 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
The solution is easy to understand complexity O(n) | maximum-average-subarray-i | 0 | 1 | # Approach\nThe simplest idea is to slightly optimize the most obvious approach with iterating under an array and just move forward element by element. \n\n# Complexity\n- Time complexity:\nComplexity of the algorithm O(n)\n\n\n# Code\n```\nclass Solution:\n def findMaxAverage(self, nums: List[int], k: int) -> float:\n i = 0\n n = len(nums)\n max_avg = float("-inf")\n cur_avg = sum(nums[:k])\n max_avg = cur_avg / k\n \n\n while i + k + 1 <= n:\n cur_avg -= nums[i]\n cur_avg += nums[i+k]\n\n if max_avg < cur_avg / k:\n max_avg = cur_avg / k\n\n i += 1\n return max_avg\n``` | 4 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
Python|| Easiest Solution || Leetcode 75 | maximum-average-subarray-i | 0 | 1 | \n# Approach\nWe calculate the sum of first k elements and for with k+1 th element we keep on adding elements and subtracting i-kth elements ( basically keeping the window between i+1 to k+1)\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findMaxAverage(self, nums: List[int], k: int) -> float:\n sum=0\n \n for i in range(k):\n sum+=nums[i]\n max_sum=sum\n for i in range(k,len(nums)):\n sum+=nums[i] - nums[i-k]\n max_sum=max(max_sum,sum)\n return max_sum/k\n\n```\n# **PLEASE DO UPVOTE!!!** | 2 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
✅Python | Sliding Window : Explained | Easy & Fast 🔥🔥 | maximum-average-subarray-i | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs we are given we need to find k elements average which is contigious i thought we make a window and move it till end.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- first we find sum of first k elements and make it Sum and MaxSum.\n- now define two pointers i and j which are end and start of window where i = k and j = 0\n- now for each iteration add nums[i] and remove nums[j] from Sum and save max of Sum and maxSum. \n- increment i and j for each iteration because window is of size k.\n- as we know which is simple Math if sum is maximum we will get maximum average.\n- so return maxSum/k gives max average.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaxAverage(self, nums: List[int], k: int) -> float:\n Sum = 0\n for i in range(k):\n Sum += nums[i]\n\n maxSum = Sum\n i = k\n j = 0\n while i < len(nums):\n Sum -= nums[j]\n Sum += nums[i]\n maxSum = max(maxSum, Sum)\n i += 1\n j += 1\n return maxSum/k\n\n```\n# Please UPVOTE \uD83D\uDC4D if you find it helpful.\n | 15 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
Python O(n) solution | beats 99% | maximum-average-subarray-i | 0 | 1 | # Approach\nSliding sum of k elements.\n\n# Code\n```\nclass Solution:\n def findMaxAverage(self, nums: List[int], k: int) -> float:\n n = len(nums)\n s = sum(nums[:k])\n answer = s\n for i in range(k, n):\n s += nums[i]\n s -= nums[i-k]\n answer = max(answer, s)\n return answer/k\n\n``` | 7 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
Sliding Window | maximum-average-subarray-i | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n \n def findMaxAverage(self, nums: List[int], k: int) -> float:\n\n s = sum(nums[0 : k])\n mx = s\n\n # [1,12,-5,-6,50,3], k = 4\n\n \n\n for i in range(0, len(nums) - k):\n s = s + nums[i + k] - nums[i]\n mx = max(mx, s)\n\n return mx / k\n\n # 1,12,-5,-6,50,3\n # [1 ,13, 8, 2, 52, 55]\n\n\n``` | 3 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
Both Brute force and Sliding Window Approaches | maximum-average-subarray-i | 0 | 1 | # Approach\n###### Sliding Window Approach\n\n# Complexity\n\n##### Brute force Approach\n\n- Time complexity: O((n-k+1) * k)\n\n- Space complexity: O(1)\n\n\n##### Sliding Window Approach\n\n- Time complexity: O(n-k+1)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def findMaxAverage(self, nums: List[int], k: int) -> float:\n\n curr_arr = nums[:k]\n curr_avg = sum(nums[:k])/k\n res = [curr_avg]\n j = 1\n\n for i in range(1,len(nums)-k+1):\n curr_avg -= nums[i-1]/k\n curr_arr = nums[i:k+j]\n j += 1\n curr_avg += curr_arr[-1]/k\n # curr_avg /= k\n res.append(curr_avg)\n\n return max(res)\n```\n\n\n# Brute force Approach\n\nWe can just iterate along all the numbers in the array and in each iteration we can just grab k elements from the current number\n\n\nLet us take an example,\n\nnums = [1,2,3,4,5,6] and k = 3\n\nIn each iteration,\n\n1st iteration ==> 1,2,3\n1st iteration ==> 2,3,4\n1st iteration ==> 3,4,5\n1st iteration ==> 4,5,6\n\n\nThe time complexity of the **brute force approach** described above is **O((n-k+1) * k)**, where n is the length of the input array nums.\n\nIn the worst case, when k is close to n, the time complexity can be approximated to O(n^2). This is because, for each starting index of the subarray (n-k+1 possible starting indices), we need to iterate over k elements to calculate the sum. Therefore, the total number of iterations is (n-k+1) * k.\n\nHowever, note that this brute force approach is not the most efficient solution for this problem. There is an optimized approach that can solve this problem with a time complexity of O(n) using a sliding window technique.\n\n\n# Sliding Window Approach\n\n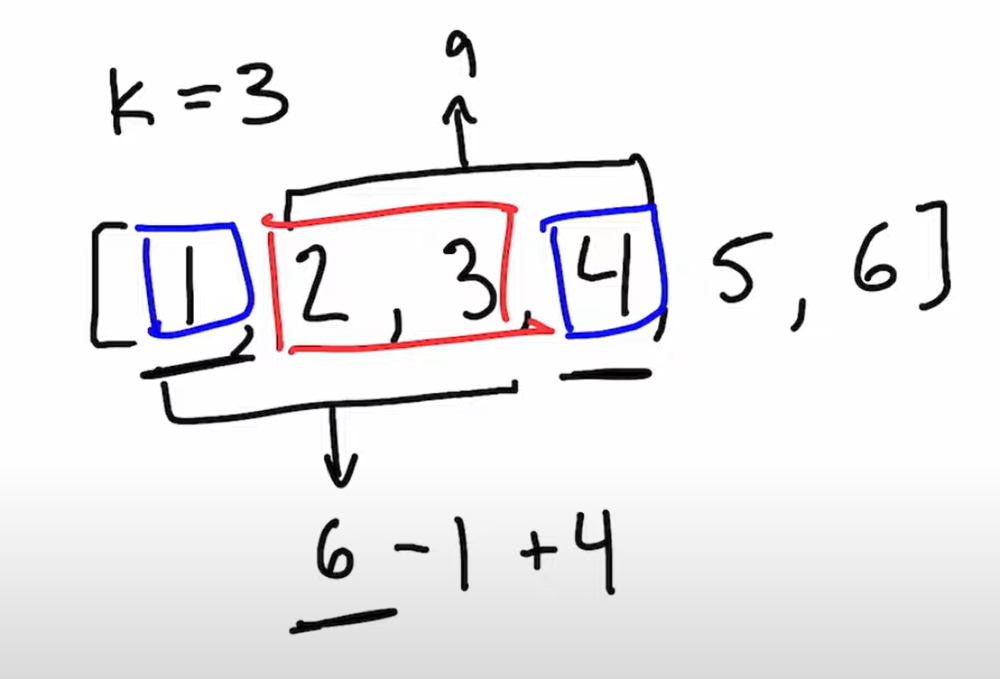\n\n\nHere in this example,\n\nFor 1st sub-array 1,2,3 and for the 2nd sub-array 2,3,4 we are calculating the sum (average in our case) of 2 and 3 twice (once in the sub-array 1,2,3 and once in the sub-array 2,3,4) \n\nInstead,\n\n###### After getting the first-subarray sum i.e, 1+2+3 = 6 we can just subract 1 and add 4 to get the 2nd sub-array sum i.e, 6-1+4 = 9 (also 2nd sub-array sum i.e, 2+3+4 = 9).\n\n##### So, as a result it will only take n-k+1 iterations \n\ni.e,\n\nAt 1,\n1,2,3 ==> Sum = 6\n\nAt 2,\n2,3,4 ==> Sum = 6-1+4 = 9\n\nAt 3,\n3,4,5 ==> Sum = 9-2+5 = 12\n\nAt 4,\n4,5,6 ==> Sum = 12-3+6 = 15\n\nn-k+1 iterations i.e, 6-3+1 = 4 iterations.\n\n##### Note:\n##### I have explained the Sliding Window technique by the sum, where as in our case it\'s average. But, the technique remains the same.\n\n\n# Explanation of the Code\n\n1) Assign current array to the first k elemenets ans store the average of it and push it to a list\n\n2) Now,\n Iterate along the array n-k+1 times\n\n3) Each time, \n (i) Subract the before number/k from the current avg \n (ii) Add the next number/k after updating the current array\n (iii) Append current average to the list\n\n4) Return maximum of the list\n\n\n\n##### If you find my solution helpful and worthy, please consider upvoting my solution. Upvotes play a crucial role in ensuring that this valuable content reaches others and helps them as well.\n\n##### Only your support motivates me to continue contributing more solutions and assisting the community further.\n\n##### Thank You for spending your valuable time.\n | 2 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
Simple Sliding Window Approach, O(n) | maximum-average-subarray-i | 0 | 1 | # Approach\nHere\'s a breakdown of how the function works:\n\n1. Calculate the sum of the first `k` elements in the `nums` list and assign it to the variable `windowSum`. This represents the sum of the elements in the initial window of size `k`.\n\n2. Calculate the initial maximum average by dividing `windowSum` by `k` and assign it to the variable `maxAverage`.\n\n3. Iterate over the range from `0 to len(nums) - k` (inclusive) using the index `i`. This loop represents sliding the window over the `nums` list.\n\n4. In each iteration, update the `windowSum` by subtracting the element at index `i` and adding the element at index `i + k`. This effectively moves the window one step to the right.\n\n5. Update the `maxAverage` by comparing the current `maxAverage` with the average of the current window (i.e., `windowSum / k`), and taking the maximum of the two.\n\n6. After the loop, return the `maxAverage`, which represents the maximum average of any contiguous subarray of length `k`.\n\nOverall, this code efficiently finds the maximum average subarray of length `k` by using a sliding window approach. \n\n# Complexity\n- Time complexity: $O(n)$\nThe time complexity of this function is $O(n)$, where `n` is the length of the input list `nums`, since it iterates through the list once.\n\n- Space complexity: $O(1)$\nThe space complexity is $O(1)$, as the code uses a constant amount of additional space regardless of the input size.\n\n# Code\n```\nclass Solution:\n def findMaxAverage(self, nums: List[int], k: int) -> float:\n windowSum = sum(nums[:k])\n maxAverage = windowSum/k\n for i in range(len(nums)-k):\n windowSum = windowSum-nums[i]+nums[i+k]\n maxAverage = max(maxAverage, windowSum/k)\n return maxAverage\n``` | 4 | You are given an integer array `nums` consisting of `n` elements, and an integer `k`.
Find a contiguous subarray whose **length is equal to** `k` that has the maximum average value and return _this value_. Any answer with a calculation error less than `10-5` will be accepted.
**Example 1:**
**Input:** nums = \[1,12,-5,-6,50,3\], k = 4
**Output:** 12.75000
**Explanation:** Maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
**Example 2:**
**Input:** nums = \[5\], k = 1
**Output:** 5.00000
**Constraints:**
* `n == nums.length`
* `1 <= k <= n <= 105`
* `-104 <= nums[i] <= 104` | null |
Easy Python Solution | set-mismatch | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nDeclare a Counter before the for loop, so that you don\'t need to use the count() function inside of the for loop, that would have the raised the complexity of the function form $$O(n)$$ to $$O(n^2)$$. Now initilaize an array with [0,0] so that you can reuse the index to store the values, 0th index for the dual number, 1st position for the non-existing number in nums. Inside of the for loop, now check if the number exists twice or once, using the counter that we declared before and then intialize the values accordingly.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findErrorNums(self, nums: List[int]) -> List[int]:\n c=Counter(nums)\n l=[0,0]\n for i in range(1,len(nums)+1):\n if c[i]==2:\n l[0]=i\n if c[i]==0:\n l[1]=i\n return l\n``` | 20 | You have a set of integers `s`, which originally contains all the numbers from `1` to `n`. Unfortunately, due to some error, one of the numbers in `s` got duplicated to another number in the set, which results in **repetition of one** number and **loss of another** number.
You are given an integer array `nums` representing the data status of this set after the error.
Find the number that occurs twice and the number that is missing and return _them in the form of an array_.
**Example 1:**
**Input:** nums = \[1,2,2,4\]
**Output:** \[2,3\]
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[1,2\]
**Constraints:**
* `2 <= nums.length <= 104`
* `1 <= nums[i] <= 104` | null |
Python 3 || 7 lines, w/ explanation || T/M: 100% / 90% | maximum-length-of-pair-chain | 0 | 1 | Here\'s the plan:\n\n- We initialize two variables: `ans` to store the length of the longest chain; and `chainEnd` to keep track of the ending value of the current chain.\n\n- We sort `pairs` based on the second element of each pair and then iterate through the sorted pairs using a loop.\n\n- If `l` is greater than `chainEnd`, then a new chain is formed, starting from the current pair. `ans` is incremented, and the \'chainEnd\' is updated to `r`. If not, then the current pair can be added to the current chain.\n\n- We return `ans`.\n```\nclass Solution:\n def findLongestChain(self, pairs: list[list[int]]) -> int:\n\n ans, chainEnd = 0, -inf\n pairs.sort(key = lambda x: x[1])\n\n for l, r in pairs:\n if l > chainEnd:\n ans+= 1\n chainEnd = r\n\n return ans\n```\n[https://leetcode.com/problems/maximum-length-of-pair-chain/submissions/1031847359/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*log*N*) and space complexity is *O*(1), in which *N* ~ `len(nums)`. | 5 | You are given an array of `n` pairs `pairs` where `pairs[i] = [lefti, righti]` and `lefti < righti`.
A pair `p2 = [c, d]` **follows** a pair `p1 = [a, b]` if `b < c`. A **chain** of pairs can be formed in this fashion.
Return _the length longest chain which can be formed_.
You do not need to use up all the given intervals. You can select pairs in any order.
**Example 1:**
**Input:** pairs = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The longest chain is \[1,2\] -> \[3,4\].
**Example 2:**
**Input:** pairs = \[\[1,2\],\[7,8\],\[4,5\]\]
**Output:** 3
**Explanation:** The longest chain is \[1,2\] -> \[4,5\] -> \[7,8\].
**Constraints:**
* `n == pairs.length`
* `1 <= n <= 1000`
* `-1000 <= lefti < righti <= 1000` | null |
Python || Greedy || Easy || key || 99% | maximum-length-of-pair-chain | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key observation here is that for a chain of pairs to be formed, the second element of each pair should be strictly smaller than the first element of the next pair. This way, you can keep selecting pairs in such a way that they form a valid chain.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Sorting by Second Element:** The first step is to sort the given pairs based on their second element. This sorting ensures that pairs with smaller second elements come first in the sorted list. This is crucial for building a valid chain.\n\n2. **Greedy Chain Formation:** Now that the pairs are sorted by the second element, you can start forming a chain greedily. You begin with the first pair (smallest second element) and then keep looking for pairs that have a first element greater than or equal to the second element of the current pair. This guarantees that you\'re forming a chain where each subsequent pair is compatible with the previous one.\n\n3. **Updating Chain and Count:** For each compatible pair you find, you update the c variable to be the second element of the current pair. This keeps track of the upper bound of the chain formed so far. Additionally, you increment the a variable, which counts the number of pairs in the longest chain.\n\n4. **Return the Count:** After iterating through all pairs, the value of a will represent the length of the longest chain of pairs that can be formed while following the given conditions.\n\n# Overall Intuition:\nBy sorting the pairs and then iteratively forming a chain by selecting the compatible pairs, you ensure that you\'re building the longest possible chain. The greedy approach of always picking the next compatible pair with the smallest second element leads to an optimal solution for this problem.\n\nThe solution leverages the properties of the input pairs and the requirement that chains are formed by selecting pairs with specific relationships between their first and second elements. This allows the algorithm to efficiently find the longest chain possible.\n\n\n\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n log n)\n\n1. pairs.sort(key=lambda x: x[1]): Sorting the pairs based on the second element of each pair (in increasing order of the second element) takes O(n log n) time complexity, where \'n\' is the number of pairs.\n\n2. The loop that follows iterates through the sorted pairs exactly once, performing constant-time operations in each iteration. Therefore, it takes O(n) time complexity.\n\nThe dominant factor here is the sorting operation, so the overall time complexity of the findLongestChain method is O(n log n), where \'n\' is the number of pairs.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n1. The space required for the input pairs list is not considered in the complexity analysis since it\'s part of the input.\n\n2. The additional space used for variables like c and a is constant and doesn\'t depend on the input size.\n\nTherefore, the space complexity of the findLongestChain method is O(1), which means it uses a constant amount of extra space regardless of the input size.\n\n# PLEASE UPVOTE ME!!!\n\n# Code\n```\nclass Solution:\n def findLongestChain(self, pairs: List[List[int]]) -> int:\n pairs.sort(key= lambda x: x[1])\n c=pairs[0][1]\n a=1\n for i in pairs:\n if c<i[0]:\n c=i[1]\n a+=1\n return a\n``` | 2 | You are given an array of `n` pairs `pairs` where `pairs[i] = [lefti, righti]` and `lefti < righti`.
A pair `p2 = [c, d]` **follows** a pair `p1 = [a, b]` if `b < c`. A **chain** of pairs can be formed in this fashion.
Return _the length longest chain which can be formed_.
You do not need to use up all the given intervals. You can select pairs in any order.
**Example 1:**
**Input:** pairs = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The longest chain is \[1,2\] -> \[3,4\].
**Example 2:**
**Input:** pairs = \[\[1,2\],\[7,8\],\[4,5\]\]
**Output:** 3
**Explanation:** The longest chain is \[1,2\] -> \[4,5\] -> \[7,8\].
**Constraints:**
* `n == pairs.length`
* `1 <= n <= 1000`
* `-1000 <= lefti < righti <= 1000` | null |
SELF SOLVED 95%🤩. Therefore The simplest explanation with THOUGHT PROCESS . | maximum-length-of-pair-chain | 0 | 1 | # Intuition\nI swear\uD83E\uDD1E I didnt look the solution.The only intution that came to my mind was I might have to sort the elements . So I sorted them by their x values . Each pair is represented by (x,y) or (X,Y)\n\n\nAnd I started dry running them on the first testcase,\nand then some more and then some more . This went on for the first 15 minutes.\n\nI kept on thinking\uD83E\uDD14\uD83E\uDD14 If I have sorted by x . Can I rely on my\nmy sorted list\'s first element as being the first element of my chain. But each time the answer was NOOOOOO \uD83D\uDE35\u200D\uD83D\uDCAB\uD83D\uDE35\u200D\uD83D\uDCAB. \n\n\nThink about it\uD83E\uDD14\uD83E\uDD14 ....... If the y value corresponding to the first element is really large it might end up being the worst chain of length 1. For eg:\n\n```\npairs=[[2,3],[4,5],[6,7],[1,1000]]:\nSort By X:\npairs=[[1,1000],[2,3],[4,5],[6,7]].\n```\n\nCan I take my sorted array\'s first element No right? It will lead to a chain of length 1 (i.e. [[1,1000]]), But the actual ans is length 3(i.e. [[2,3],[4,5],[6,7]] )..\n\n\n*That\'s when I got the idea that no matter what the first element of my chain will be the one with smallest Y not smallest X.(X,Y) being the pair.\uD83D\uDCA5\uD83D\uDCA5 BOOOMMM \uD83D\uDCA5\uD83D\uDCA5*\n\nI was reallly really happy I though this might be the revolutionary idea to solve the question. I got all the world\'s happiness in that one minute \uD83D\uDE00\uD83D\uDE00.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThere after it was all easy. Sort by y values to keep linking the chain to max length:\nI got my first solution:\n```\nclass Solution:\n def findLongestChain(self, pairs: List[List[int]]) -> int:\n # First elem in the chain will always be the lowest y\n pairs=sorted(pairs, key=lambda x: x[1]) #O(nlogn) time\n ans=[] #O(nlogn) space max\n ans.append(pairs[0])\n i=1\n while i <len(pairs):\n elem=pairs[i]\n top=ans[-1]\n # append\n if elem[0]>top[1]:\n ans.append(elem)\n i+=1\n return len(ans)\n```\nIt was obvious the space complexity was O(n) due to maintaining ans array\nBut do I really need an ans array? All I need to track is the last element. SO this is my final solution:\n\n# Complexity\n- Time complexity:\nThe major time taking is Sorting and while loop wich takes O(NLogN) and O(N) . So time complexity is O(NlogN)\n\n- Space complexity:\nO(1) easy I am sure u can figure that out even if u are a noob like me.\n\n# Code\n```\nclass Solution:\n def findLongestChain(self, pairs: List[List[int]]) -> int:\n pairs = sorted(pairs, key=lambda x: x[1])\n count = 1 # Minimum length is at least 1\n prev_elem = pairs[0]\n \n for i in range(1, len(pairs)):\n if pairs[i][0] > prev_elem[1]:\n count += 1\n prev_elem = pairs[i]\n \n return count\n\n```\n\n# Show Off\n\n\nAll suggestions are welcome.\nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97 it. Thank you:-)\nHappy Learning, Cheers Guys \uD83D\uDE0A\nKeep Grinding \uD83D\uDE00\uD83D\uDE00\n\n | 2 | You are given an array of `n` pairs `pairs` where `pairs[i] = [lefti, righti]` and `lefti < righti`.
A pair `p2 = [c, d]` **follows** a pair `p1 = [a, b]` if `b < c`. A **chain** of pairs can be formed in this fashion.
Return _the length longest chain which can be formed_.
You do not need to use up all the given intervals. You can select pairs in any order.
**Example 1:**
**Input:** pairs = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The longest chain is \[1,2\] -> \[3,4\].
**Example 2:**
**Input:** pairs = \[\[1,2\],\[7,8\],\[4,5\]\]
**Output:** 3
**Explanation:** The longest chain is \[1,2\] -> \[4,5\] -> \[7,8\].
**Constraints:**
* `n == pairs.length`
* `1 <= n <= 1000`
* `-1000 <= lefti < righti <= 1000` | null |
🌟 Python Simple Solution | Greedy Approach ⚡ | maximum-length-of-pair-chain | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n```\nclass Solution:\n def findLongestChain(self, pairs: List[List[int]]) -> int:\n pairs.sort(key = lambda x: x[1])\n res = 1\n end = pairs[0][1]\n \n for i in range(1, len(pairs)):\n \n if end < pairs[i][0]:\n res+=1\n end = pairs[i][1]\n \n return res\n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 2 | You are given an array of `n` pairs `pairs` where `pairs[i] = [lefti, righti]` and `lefti < righti`.
A pair `p2 = [c, d]` **follows** a pair `p1 = [a, b]` if `b < c`. A **chain** of pairs can be formed in this fashion.
Return _the length longest chain which can be formed_.
You do not need to use up all the given intervals. You can select pairs in any order.
**Example 1:**
**Input:** pairs = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The longest chain is \[1,2\] -> \[3,4\].
**Example 2:**
**Input:** pairs = \[\[1,2\],\[7,8\],\[4,5\]\]
**Output:** 3
**Explanation:** The longest chain is \[1,2\] -> \[4,5\] -> \[7,8\].
**Constraints:**
* `n == pairs.length`
* `1 <= n <= 1000`
* `-1000 <= lefti < righti <= 1000` | null |
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | maximum-length-of-pair-chain | 1 | 1 | # Intuition\nSorting pairs with the seocond element.\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 248 videos as of August 26th.\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/agYDE4CcKNc\n\n## In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. **Sort the Pairs List Based on the Second Element:**\n - Main Point: The pairs list is sorted in ascending order based on the second element of each sub-list.\n - Explanation: Sorting the pairs based on the second element ensures that we process pairs in ascending order of their ending values, which is essential for finding the longest chain.\n\n2. **Initialize Variables:**\n - Main Point: Initialize the variables `prev` and `res`.\n - Explanation: `prev` stores the current pair under consideration, and `res` counts the length of the longest chain.\n\n3. **Iterate Through Sorted Pairs:**\n - Main Point: Iterate through the sorted pairs starting from the second pair.\n - Explanation: Starting from the second pair (index 1), compare each current pair (`cur`) with the previous pair (`prev`) to check if the current pair\'s starting value is greater than the previous pair\'s ending value.\n\n4. **Check if Current Pair Extends the Chain:**\n - Main Point: Check if the starting value of the current pair is greater than the ending value of the previous pair.\n - Explanation: If the current pair\'s starting value is greater than the previous pair\'s ending value, it indicates that the current pair can be added to the chain without overlap. Therefore, increment the `res` counter and update `prev` to the current pair.\n\n5. **Return the Result:**\n - Main Point: Return the value of the `res` variable.\n - Explanation: After iterating through all the pairs, the value of `res` will represent the length of the longest chain of non-overlapping pairs.\n\nIn summary, this algorithm sorts the pairs based on their second element, then iterates through the sorted pairs, adding each eligible pair to the chain, and finally returns the length of the longest chain. This approach guarantees the optimal solution by always selecting the non-overlapping pairs with the smallest ending values.\n\n# Complexity\n- Time complexity: O(n log n)\nWe use sorting.\n\n- Space complexity: O(1) or could be O(n)\nDepends on language you use\n\n```python []\nclass Solution:\n def findLongestChain(self, pairs: List[List[int]]) -> int:\n pairs.sort(key=lambda x: x[1])\n\n prev = pairs[0]\n res = 1\n\n for cur in pairs[1:]:\n if cur[0] > prev[1]:\n res += 1\n prev = cur\n\n return res\n```\n```javascript []\n/**\n * @param {number[][]} pairs\n * @return {number}\n */\nvar findLongestChain = function(pairs) {\n pairs.sort((a, b) => a[1] - b[1]);\n\n let prev = pairs[0];\n let res = 1;\n\n for (let i = 1; i < pairs.length; i++) {\n const cur = pairs[i];\n if (cur[0] > prev[1]) {\n res++;\n prev = cur;\n }\n }\n\n return res; \n};\n```\n```Java []\nclass Solution {\n public int findLongestChain(int[][] pairs) {\n Arrays.sort(pairs, Comparator.comparingInt(a -> a[1]));\n\n int[] prev = pairs[0];\n int res = 1;\n\n for (int i = 1; i < pairs.length; i++) {\n int[] cur = pairs[i];\n if (cur[0] > prev[1]) {\n res++;\n prev = cur;\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findLongestChain(vector<vector<int>>& pairs) {\n std::sort(pairs.begin(), pairs.end(), [](const std::vector<int>& a, const std::vector<int>& b) {\n return a[1] < b[1];\n });\n\n std::vector<int> prev = pairs[0];\n int res = 1;\n\n for (int i = 1; i < pairs.size(); i++) {\n const std::vector<int>& cur = pairs[i];\n if (cur[0] > prev[1]) {\n res++;\n prev = cur;\n }\n }\n\n return res; \n }\n};\n```\n | 20 | You are given an array of `n` pairs `pairs` where `pairs[i] = [lefti, righti]` and `lefti < righti`.
A pair `p2 = [c, d]` **follows** a pair `p1 = [a, b]` if `b < c`. A **chain** of pairs can be formed in this fashion.
Return _the length longest chain which can be formed_.
You do not need to use up all the given intervals. You can select pairs in any order.
**Example 1:**
**Input:** pairs = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The longest chain is \[1,2\] -> \[3,4\].
**Example 2:**
**Input:** pairs = \[\[1,2\],\[7,8\],\[4,5\]\]
**Output:** 3
**Explanation:** The longest chain is \[1,2\] -> \[4,5\] -> \[7,8\].
**Constraints:**
* `n == pairs.length`
* `1 <= n <= 1000`
* `-1000 <= lefti < righti <= 1000` | null |
Greedy approach using "championship interval" | maximum-length-of-pair-chain | 0 | 1 | # Intuition\nThe first thought: can we find a start interval in advance to be sure **THIS can be the first in the chain?**\nThe second thought is: we\'ve found a start interval, assume that we can choose **any interval NEXT** to the starting **if it MEET the conditions**:\n```\nfor [A,B] and [C, D] \n=> B must be less then C \n=> let\'s consider an example\n\na = [1, 2]\nb = [2, 3]\nc = [3, 4]\n\nThe resulting chain will be [a, c], because\na and c interval NON-OVERLAP each other, and the next interval\ncan be any of them, if it meet the conditions, respectively.\n```\nThis tell us we need to look up for next interval as **GREEDY** as we can.\n\n---\n\nIf you\'ve never heard about **championship interval**, it\'s time to break down into details.\n\n# Approach\n**The championship interval** is **that**, whose ending point will be **THE FIRST ENDING** point in chain.\n1. be sure to sort intervals by **LAST point**\n2. create variables, that store last and count of excluded intervals\n3. any time the last interval is **FIT** the condition, we **SET** the current index to **last** and move forward, otherwise **EXCLUDE** the **current** interval\n4. the final answer is to **extract** count of **excluded** intervals\n\n# Complexity\n- Time complexity: O(n(log n)), since we need to sort the intervals by last point\n- Space complexity: O(1), because we don\'t use any additional extra space.\n\n# Code\n```\nclass Solution:\n def findLongestChain(self, intervals: List[List[int]]) -> int:\n intervals.sort(key=lambda x: x[1])\n last = 0\n excluded = 0\n\n for i in range(1, len(intervals)):\n if intervals[last][1] >= intervals[i][0]:\n excluded += 1\n else:\n last = i\n\n return len(intervals) - excluded\n``` | 1 | You are given an array of `n` pairs `pairs` where `pairs[i] = [lefti, righti]` and `lefti < righti`.
A pair `p2 = [c, d]` **follows** a pair `p1 = [a, b]` if `b < c`. A **chain** of pairs can be formed in this fashion.
Return _the length longest chain which can be formed_.
You do not need to use up all the given intervals. You can select pairs in any order.
**Example 1:**
**Input:** pairs = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The longest chain is \[1,2\] -> \[3,4\].
**Example 2:**
**Input:** pairs = \[\[1,2\],\[7,8\],\[4,5\]\]
**Output:** 3
**Explanation:** The longest chain is \[1,2\] -> \[4,5\] -> \[7,8\].
**Constraints:**
* `n == pairs.length`
* `1 <= n <= 1000`
* `-1000 <= lefti < righti <= 1000` | null |
Simplest easy to understand Python solution O(n^2) time. | palindromic-substrings | 0 | 1 | # Approach\nFirst time I made a solution that was way better than the other answers. I can\'t believe all of the other complicated ones are getting so many views/upvotes. Time complexity is O(n^2) which if I am not mistaken is the best you can do in a timely manner.\n\nTrust me, no explanation for the code needed. The code speaks for itself.\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n count = 0\n for i in range(len(s)):\n for l, r in [(i, i), (i, i + 1)]:\n while l >= 0 and r < len(s) and s[l] == s[r]:\n count += 1\n l -= 1\n r += 1\n return count\n``` | 0 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Simplest easy to understand Python solution O(n^2) time. | palindromic-substrings | 0 | 1 | # Approach\nFirst time I made a solution that was way better than the other answers. I can\'t believe all of the other complicated ones are getting so many views/upvotes. Time complexity is O(n^2) which if I am not mistaken is the best you can do in a timely manner.\n\nTrust me, no explanation for the code needed. The code speaks for itself.\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n count = 0\n for i in range(len(s)):\n for l, r in [(i, i), (i, i + 1)]:\n while l >= 0 and r < len(s) and s[l] == s[r]:\n count += 1\n l -= 1\n r += 1\n return count\n``` | 0 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Easy Python solution | palindromic-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n sub = []\n for indi, i in enumerate(s):\n for indj, j in enumerate(s[indi:], start=indi):\n if i == j and s[indi:indj+1] == s[indi:indj+1][::-1]:\n sub.append(s[indi:indj+1])\n return len(sub)\n``` | 1 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Easy Python solution | palindromic-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n sub = []\n for indi, i in enumerate(s):\n for indj, j in enumerate(s[indi:], start=indi):\n if i == j and s[indi:indj+1] == s[indi:indj+1][::-1]:\n sub.append(s[indi:indj+1])\n return len(sub)\n``` | 1 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Python Easy approach Beats ~97% | palindromic-substrings | 0 | 1 | #### Expand around Center\n\nThe main idea is **to pick a center and then extend towards the bounds** of the input string. With this approach, we count all valid pallindrome substrings which are based on the specified center. \n\nThere are **two valid cases of centers** for finding pallindrome substrings:\n1. If it\'s an odd-lengthed pallindrome string, then our centers will expand from same center and will match the criteria `i=j`. eg: for string `"aba"`, center is `i=j=1`.\n2. If it\'s an even-lengthed pallindrome string, then our centers will not expand from same center and will match the criteria `i+1=j` eg: for string `"abba"`,` i=1, j=2`.\n\nBelow is the code, with documentation:\n```\nclass Solution: \n def expandAndCountPallindromes(self, i, j, s):\n \'\'\'Counts the number of pallindrome substrings from a given center i,j \n 1. when i=j, it\'s an odd-lengthed pallindrome string. \n eg: for string "aba", i=j=1.\n 2. when i+1=j, it\'s an even-lengthed pallindrome string. \n eg: for string "abba", i=1, j=2.\n \n Parameters:\n i,j - centers from which the code will expand to find number of pallindrome substrings.\n s - the string in which the code needs to find the pallindrome substrings. \n \n Returns:\n cnt - The number of pallindrome substrings from the given center i,j \n \'\'\'\n \n length=len(s)\n cnt=0\n \n while 0<=i and j<length and s[i]==s[j]:\n i-=1\n j+=1\n cnt+=1\n \n return cnt\n \n def countSubstrings(self, s: str) -> int:\n \n return sum(self.expandAndCountPallindromes(i,i,s) + self.expandAndCountPallindromes(i,i+1,s) for i in range(len(s)))\n \n```\n\n**Time - O(len(s)^2) \nSpace - O(1)\n**\n\n---\n\n***Please upvote if you find it useful*** | 39 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Python Easy approach Beats ~97% | palindromic-substrings | 0 | 1 | #### Expand around Center\n\nThe main idea is **to pick a center and then extend towards the bounds** of the input string. With this approach, we count all valid pallindrome substrings which are based on the specified center. \n\nThere are **two valid cases of centers** for finding pallindrome substrings:\n1. If it\'s an odd-lengthed pallindrome string, then our centers will expand from same center and will match the criteria `i=j`. eg: for string `"aba"`, center is `i=j=1`.\n2. If it\'s an even-lengthed pallindrome string, then our centers will not expand from same center and will match the criteria `i+1=j` eg: for string `"abba"`,` i=1, j=2`.\n\nBelow is the code, with documentation:\n```\nclass Solution: \n def expandAndCountPallindromes(self, i, j, s):\n \'\'\'Counts the number of pallindrome substrings from a given center i,j \n 1. when i=j, it\'s an odd-lengthed pallindrome string. \n eg: for string "aba", i=j=1.\n 2. when i+1=j, it\'s an even-lengthed pallindrome string. \n eg: for string "abba", i=1, j=2.\n \n Parameters:\n i,j - centers from which the code will expand to find number of pallindrome substrings.\n s - the string in which the code needs to find the pallindrome substrings. \n \n Returns:\n cnt - The number of pallindrome substrings from the given center i,j \n \'\'\'\n \n length=len(s)\n cnt=0\n \n while 0<=i and j<length and s[i]==s[j]:\n i-=1\n j+=1\n cnt+=1\n \n return cnt\n \n def countSubstrings(self, s: str) -> int:\n \n return sum(self.expandAndCountPallindromes(i,i,s) + self.expandAndCountPallindromes(i,i+1,s) for i in range(len(s)))\n \n```\n\n**Time - O(len(s)^2) \nSpace - O(1)\n**\n\n---\n\n***Please upvote if you find it useful*** | 39 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
python simple solution with explanation, 95% fast | palindromic-substrings | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n #helper fxn to expand from centre and count palindromic substring\n def expander(l,r):\n res = 0\n #condition for valid palindromic substring, if yes then increase the counter of res\n while (l>=0 and r<len(s) and s[l] == s[r]):\n res += 1\n l-=1\n r+=1\n return res\n \n res=0\n for i in range(len(s)):\n #for odd len strings, call by taking each iteration as center\n res+= expander(i,i)\n #for even len strings, call by taking each iteration as center\n res+= expander(i,i+1)\n return res\n``` | 1 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
python simple solution with explanation, 95% fast | palindromic-substrings | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n #helper fxn to expand from centre and count palindromic substring\n def expander(l,r):\n res = 0\n #condition for valid palindromic substring, if yes then increase the counter of res\n while (l>=0 and r<len(s) and s[l] == s[r]):\n res += 1\n l-=1\n r+=1\n return res\n \n res=0\n for i in range(len(s)):\n #for odd len strings, call by taking each iteration as center\n res+= expander(i,i)\n #for even len strings, call by taking each iteration as center\n res+= expander(i,i+1)\n return res\n``` | 1 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Solution in Python 3 (beats ~94%) (six lines) (With Detaiiled Explanation) | palindromic-substrings | 0 | 1 | _Explanation:_\n\nThis method uses an expand around center approach. The program iterates through each central point of a potential palindrome. moving left to right in the original input string. It then expands outward (left and right) from the center point and checks if the two characters match. This is done by moving _a_ to the left by one and moving _b_ to the right by one. It keeps doing this until they don\'t match (i.e. ```s[a] == s[b]``` fails to be true) or either end of the input string is reached. This expansion of the palindrome from its center outward occurs inside of the while loop. Once the while loop exits, we have expanded as far as we could and the length of the palindrome is equal to (b - a - 1). It is useful at this point to find the pattern between the length of a palindrome and the number of palindromes it contains (_with the same center_). Notice the following pattern:\n\n- Palindromes of length 1 and 2 contain 1 palindrome:\na and aa each contain one palindrome with the same center: a contains itself and aa contains itself\n- Palindromes of length 3 and 4 contain 2 palindromes:\naba and abba each contain two palindromes with the same center: aba contains b and itself and abba contains bb and itself\n- Palindromes of length 5 and 6 contain 3 palindromes:\nabcba and abccba each contain three palindromes with the same center: abcba contains c, bcb, and itself and abccba contains cc, bccb, and itself\netc. ...\n\nThe reason we are only counting palindromes with the same center and not other palindromes it may contain is because we will have already counted them earlier in the for loop or will encounter them later in the for loop. It is important that we do not double count. Reflecting at the pattern above we can easily see that a palindrome of length L will contain (L+1)//2 palindromes within it that have the same center. Since the length of our palindrome is (b - a - 1), it follows that the number of palindromes withint it will be (b - a)//2. Thus at the end of the while loop, we add (b-a)//2 to r which is counting the total number of palindromes found thus far.\n\nPerhaps the most important (and most challenging) part of the program occurs in the structure of the inner for loop: ```for a,b in [(i,i),(i,i+1)]``` This part may take a little explanation to fully understand. A palindrome can be centered in one of two places. The palindrome _dad_ is centered on one of its letters, specifcally the letter _a_. If you had to pick two indices to describe where the palindrome _dad_ is centered you would say that it was centered at the indices 1 and 1, since 1 is the index of _a_. In general such palindromes (palindromes with an odd number of elements) are centered at (_i_,_i_) for some index _i_. The other type of palindrome, _abba_ is centered in between two identical letters, specifcally it is centered between the letters _b_ and _b_. If you had to pick two indices to describe where the palindrome _abba_ is centered you would say that it was centered at the indices 1 and 2, since 1 and 2 are the indices of the central two _b_\'s. In general such palindromes (palindromes with an even number of elements) are centered at (_i_,_i+1_) for some index _i_. To correctly look at all the palindrome substrings, for each index _i_ in the for loop we have to consider both centeral pivoting points. This is why the inner for loop iterates through both (_i_,_i_) and (_i_,_i+1_).\n\nThe program ends by returning r, the final total count of palindromes found within the original string s.\n\n_Glossary of Variables:_\nL = length of original input string\nr = total current count of palindromic substrings\na = number of units left of center of palindrome\nb = number of units right of center of palindrome\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n\t L, r = len(s), 0\n\t for i in range(L):\n\t \tfor a,b in [(i,i),(i,i+1)]:\n\t \t\twhile a >= 0 and b < L and s[a] == s[b]: a -= 1; b += 1\n\t \t\tr += (b-a)//2\n\t return r\n\t\t\n\t\t\n- Junaid Mansuri\n(LeetCode ID)@hotmail.com | 76 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Solution in Python 3 (beats ~94%) (six lines) (With Detaiiled Explanation) | palindromic-substrings | 0 | 1 | _Explanation:_\n\nThis method uses an expand around center approach. The program iterates through each central point of a potential palindrome. moving left to right in the original input string. It then expands outward (left and right) from the center point and checks if the two characters match. This is done by moving _a_ to the left by one and moving _b_ to the right by one. It keeps doing this until they don\'t match (i.e. ```s[a] == s[b]``` fails to be true) or either end of the input string is reached. This expansion of the palindrome from its center outward occurs inside of the while loop. Once the while loop exits, we have expanded as far as we could and the length of the palindrome is equal to (b - a - 1). It is useful at this point to find the pattern between the length of a palindrome and the number of palindromes it contains (_with the same center_). Notice the following pattern:\n\n- Palindromes of length 1 and 2 contain 1 palindrome:\na and aa each contain one palindrome with the same center: a contains itself and aa contains itself\n- Palindromes of length 3 and 4 contain 2 palindromes:\naba and abba each contain two palindromes with the same center: aba contains b and itself and abba contains bb and itself\n- Palindromes of length 5 and 6 contain 3 palindromes:\nabcba and abccba each contain three palindromes with the same center: abcba contains c, bcb, and itself and abccba contains cc, bccb, and itself\netc. ...\n\nThe reason we are only counting palindromes with the same center and not other palindromes it may contain is because we will have already counted them earlier in the for loop or will encounter them later in the for loop. It is important that we do not double count. Reflecting at the pattern above we can easily see that a palindrome of length L will contain (L+1)//2 palindromes within it that have the same center. Since the length of our palindrome is (b - a - 1), it follows that the number of palindromes withint it will be (b - a)//2. Thus at the end of the while loop, we add (b-a)//2 to r which is counting the total number of palindromes found thus far.\n\nPerhaps the most important (and most challenging) part of the program occurs in the structure of the inner for loop: ```for a,b in [(i,i),(i,i+1)]``` This part may take a little explanation to fully understand. A palindrome can be centered in one of two places. The palindrome _dad_ is centered on one of its letters, specifcally the letter _a_. If you had to pick two indices to describe where the palindrome _dad_ is centered you would say that it was centered at the indices 1 and 1, since 1 is the index of _a_. In general such palindromes (palindromes with an odd number of elements) are centered at (_i_,_i_) for some index _i_. The other type of palindrome, _abba_ is centered in between two identical letters, specifcally it is centered between the letters _b_ and _b_. If you had to pick two indices to describe where the palindrome _abba_ is centered you would say that it was centered at the indices 1 and 2, since 1 and 2 are the indices of the central two _b_\'s. In general such palindromes (palindromes with an even number of elements) are centered at (_i_,_i+1_) for some index _i_. To correctly look at all the palindrome substrings, for each index _i_ in the for loop we have to consider both centeral pivoting points. This is why the inner for loop iterates through both (_i_,_i_) and (_i_,_i+1_).\n\nThe program ends by returning r, the final total count of palindromes found within the original string s.\n\n_Glossary of Variables:_\nL = length of original input string\nr = total current count of palindromic substrings\na = number of units left of center of palindrome\nb = number of units right of center of palindrome\n```\nclass Solution:\n def countSubstrings(self, s: str) -> int:\n\t L, r = len(s), 0\n\t for i in range(L):\n\t \tfor a,b in [(i,i),(i,i+1)]:\n\t \t\twhile a >= 0 and b < L and s[a] == s[b]: a -= 1; b += 1\n\t \t\tr += (b-a)//2\n\t return r\n\t\t\n\t\t\n- Junaid Mansuri\n(LeetCode ID)@hotmail.com | 76 | Given a string `s`, return _the number of **palindromic substrings** in it_.
A string is a **palindrome** when it reads the same backward as forward.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** s = "abc "
**Output:** 3
**Explanation:** Three palindromic strings: "a ", "b ", "c ".
**Example 2:**
**Input:** s = "aaa "
**Output:** 6
**Explanation:** Six palindromic strings: "a ", "a ", "a ", "aa ", "aa ", "aaa ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation? |
Python3 brute force solution | replace-words | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def replaceWords(self, dictionary: List[str], sentence: str) -> str:\n \n \n words = sentence.split()\n dic_set = set(dictionary)\n ans=[]\n \n for word in words:\n flag=False\n for i in range(len(word)):\n sub=word[:i+1]\n if sub in dic_set:\n ans.append(sub)\n flag=True\n break\n \n if flag==False:\n ans.append(word)\n\n return " ".join(ans)\n``` | 1 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
Easy and Simple Python Solution using Trie | replace-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TireNode:\n def __init__(self) -> None:\n self.children = {}\n self.endOfWord = False\nclass Tire:\n def __init__(self): \n self.root = TireNode()\n\n def insert(self, word):\n cur = self.root\n for char in word:\n if char not in cur.children:\n cur.children[char] = TireNode()\n cur = cur.children[char]\n cur.endOfWord = True\n\nclass Solution:\n def replaceWords(self, dictionary: List[str], sentence: str) -> str:\n tire = Tire()\n for root in dictionary:\n tire.insert(root)\n \n words = sentence.split(\' \')\n res = []\n for word in words:\n cur = tire.root \n temp = \'\'\n prefix_exist_in_d = False \n for char in word:\n # Case1: found root of the word in the tire, break out early\n if cur.endOfWord: \n prefix_exist_in_d = True\n break\n if char in cur.children:\n temp += char\n cur = cur.children[char]\n # Case 2: if the char is not in the tire, directly break out\n else: \n break\n \n # Case3: the word exactly exist in the tire\n if cur.endOfWord:\n prefix_exist_in_d = True\n \n # Depend on above 3 cases, decide on what to add in the list\n if not temp or not prefix_exist_in_d: \n res.append(word)\n elif temp and prefix_exist_in_d: \n res.append(temp)\n\n return \' \'.join(res)\n\n``` | 4 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
Python, easy solution with explanation | replace-words | 0 | 1 | \n\n```\n# The TNode class represents node for our Trie \n# We will store all the children for each node and a state\n# All the \'is_complete\' state does is marks it to show where the inserted \'root\' finished\n# E.g if we insert ABC as root we will end up with 3 nodes: \n# A -> B -> C\n# Where B is a child of A and C is a child of B and in our program we will set is_complete in node B to True \n# so that we know it represents a complete word ( This will allow us to stop traversing and get the shortest root )\nclass TNode:\n def __init__(self):\n self.children = {}\n self.is_complete = False\n \nclass Solution:\n def replaceWords(self, dictionary: List[str], sentence: str) -> str:\n # Store all roots in a tire \n tire_root = self.dict_to_trie(dictionary)\n\t\t# Split the sentence into individual words \n words = sentence.split(\' \')\n results = []\n \n\t\t# Replace each word in a sentence with either the root of itself when no prefix matches\n for word in words:\n results.append(self.get_replacement(tire_root, word))\n \n # return result as a string\n return \' \'.join(results)\n \n # Store roots in a trie\n def dict_to_trie(self, dictionary: List[str]) -> TNode:\n root = TNode()\n \n\t\t# We have to go through each character in each word \n for word in dictionary:\n node = root\n for char in word:\n\t\t\t\t# Add a new node if doesn\'t exist\n if char not in node.children:\n node.children[char] = TNode()\n\t\t\t\t# move to next node \n node = node.children[char]\n\t\t\t# finally, set the last inserted node as complete\n node.is_complete = True \n \n return root\n \n # Get replacement for each word, this will either return \n # the root or the successor if no matching prefix is found\n def get_replacement(self, root: TNode, word: str) -> str:\n replacement = \'\'\n node = root\n \n for char in word:\n if char not in node.children or node.is_complete:\n break\n \n replacement += char\n node = node.children[char]\n \n return replacement if node.is_complete == True else word\n \n \n \n \n``` | 1 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
[Python] - Trie Implementation | replace-words | 0 | 1 | ```\nclass TrieNode:\n def __init__(self):\n self.children = collections.defaultdict(TrieNode)\n self.isWord = False\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, word):\n node = self.root\n for w in word:\n node = node.children[w]\n node.isWord = True\n \n def search(self, word):\n node = self.root\n osf = \'\'\n for c in word:\n if c not in node.children: break\n node = node.children[c]\n osf += c\n if node.isWord: return osf\n return word\n\nclass Solution:\n def replaceWords(self, dict: List[str], sentence: str) -> str:\n trie = Trie()\n for words in dict:\n trie.insert(words)\n res = \'\'\n for sent in sentence.split():\n if res:\n res += \' \'\n res += trie.search(sent)\n return res\n``` | 11 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
Fast solution beats 97% submissions | replace-words | 0 | 1 | ```\nclass Solution:\n def replaceWords(self, dictionary: List[str], sentence: str) -> str:\n d = {w:len(w) for w in dictionary}\n mini, maxi = min(d.values()), max(d.values())\n wd = sentence.split()\n rt = []\n for s in wd:\n c = s \n for k in range(mini,min(maxi,len(s))+1):\n ss = s[:k]\n if ss in d:\n c = ss \n break \n rt.append(c)\n return " ".join(rt)\n```\nPlease upvote :) | 4 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
Python 3 | Trie Variation | Explanation | replace-words | 0 | 1 | ### Explanation\n- Replace `word` with the shortest `root` of it in `dictionary`\n- Add every `root` from `dictionary` to a `trie`\n- Search prefix for each `word` in `sentence` \n\t- If a `root` is found, return `root` (this guarantees the shortest)\n\t- Else, return `word` itself\n### Implementation\n```\nclass TrieNode:\n def __init__(self):\n self.children = dict()\n self.is_word = False\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, word): \n node = self.root\n for c in word:\n if c not in node.children:\n node.children[c] = TrieNode()\n node = node.children[c] \n node.is_word = True \n \n def root_of(self, word): \n node, prefix = self.root, \'\'\n for c in word:\n if c not in node.children:\n return word\n prefix += c \n node = node.children[c] \n if node.is_word:\n return prefix\n return word \n \nclass Solution:\n def replaceWords(self, dictionary: List[str], sentence: str) -> str:\n trie = Trie()\n for root in dictionary:\n trie.insert(root)\n \n return \' \'.join([trie.root_of(word) for word in sentence.split(\' \')])\n``` | 4 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
97% speed, Trie Python3 | replace-words | 0 | 1 | ```\nclass Trie:\n def __init__(self):\n self.root = {}\n \n def insert(self, word):\n p = self.root\n for char in word:\n if char not in p:\n p[char] = {}\n p = p[char]\n p[\'#\'] = True\n \n def search(self, word):\n p = self.root\n res = \'\'\n for char in word:\n if char in p:\n res += char\n p = p[char]\n if \'#\' in p:\n break\n else:\n break\n return res if \'#\' in p else word\n \nclass Solution:\n def replaceWords(self, roots: List[str], sentence: str) -> str:\n t = Trie()\n for root in roots:\n t.insert(root)\n return \' \'.join(map(t.search, sentence.split()))\n``` | 8 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
Remember its a sentence not an array. Trie solution with python | replace-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TrieNode:\n def __init__(self):\n self.children={}\n self.root=False\n self.value=""\n \n\n \nclass Solution:\n def __init__(self):\n self.root=TrieNode()\n def insert(self,val):\n cur=self.root\n for v in val:\n if v not in cur.children:\n cur.children[v]=TrieNode()\n cur=cur.children[v]\n cur.root=True\n cur.value=val\n \n def checkRoot(self,val):\n cur=self.root\n \n for v in val:\n \n if cur.root==True:\n \n return cur.value\n if v not in cur.children:\n \n return val\n cur=cur.children[v]\n \n return val\n \n \n def replaceWords(self, dictionary: List[str], sentence: str) -> str:\n for items in dictionary:\n self.insert(items)\n arr=[]\n \n s=sentence.split(" ")\n \n for items in s:\n \n arr.append(self.checkRoot(items))\n return " ".join(arr)\n \n \n \n``` | 0 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
Python easy solution, clean code | replace-words | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def replaceWords(self, dictionary: List[str], sentence: str) -> str:\n dictionary = sorted(dictionary,key = lambda x : len(x))\n words = sentence.split(" ")\n stack = []\n for word in words:\n stack.append(word)\n for keyword in dictionary :\n if word.startswith(keyword) : \n stack.pop()\n stack.append(keyword)\n break\n return " ".join(stack)\n\n \n``` | 0 | In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an "` is followed by the **successor** word `"other "`, we can form a new word `"another "`.
Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
Return _the `sentence`_ after the replacement.
**Example 1:**
**Input:** dictionary = \[ "cat ", "bat ", "rat "\], sentence = "the cattle was rattled by the battery "
**Output:** "the cat was rat by the bat "
**Example 2:**
**Input:** dictionary = \[ "a ", "b ", "c "\], sentence = "aadsfasf absbs bbab cadsfafs "
**Output:** "a a b c "
**Constraints:**
* `1 <= dictionary.length <= 1000`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case letters.
* `1 <= sentence.length <= 106`
* `sentence` consists of only lower-case letters and spaces.
* The number of words in `sentence` is in the range `[1, 1000]`
* The length of each word in `sentence` is in the range `[1, 1000]`
* Every two consecutive words in `sentence` will be separated by exactly one space.
* `sentence` does not have leading or trailing spaces. | null |
Simple Diagram Explanation | dota2-senate | 1 | 1 | # Idea\n- **We will use a two queue approach.**\n- Recall, each senator has a position to exercise their right. \n- The ones to the left have an earlier turn than the ones to the right. \n- `rad` is queue that holds all positions of **active** senators in "Radiant"\n- `dir` is queue that holds all positions of **active** senators in "Dire".\n- **Active** being that they still have the right to vote. \n- Our queue will be ordered so that the senators with earlier voting power come first (to the left of the queue). \n- To goal is to have the earliest senator of each queue *fight* each other to see who gets to eliminate the other depending on their position. \n- Obviously, the one with the earlier position will win. \n- The loser is removed from the queue since they are no longer **active.**\n- The winner will go to the end of the queue for the next round. \n- We keep doing this until one queue is empty which means there are no more senators on the team. \n\n# Everything is easier with an example: \n- `senate = "RDDDRDRRDR"`\n\n\n\n\n\n\n\n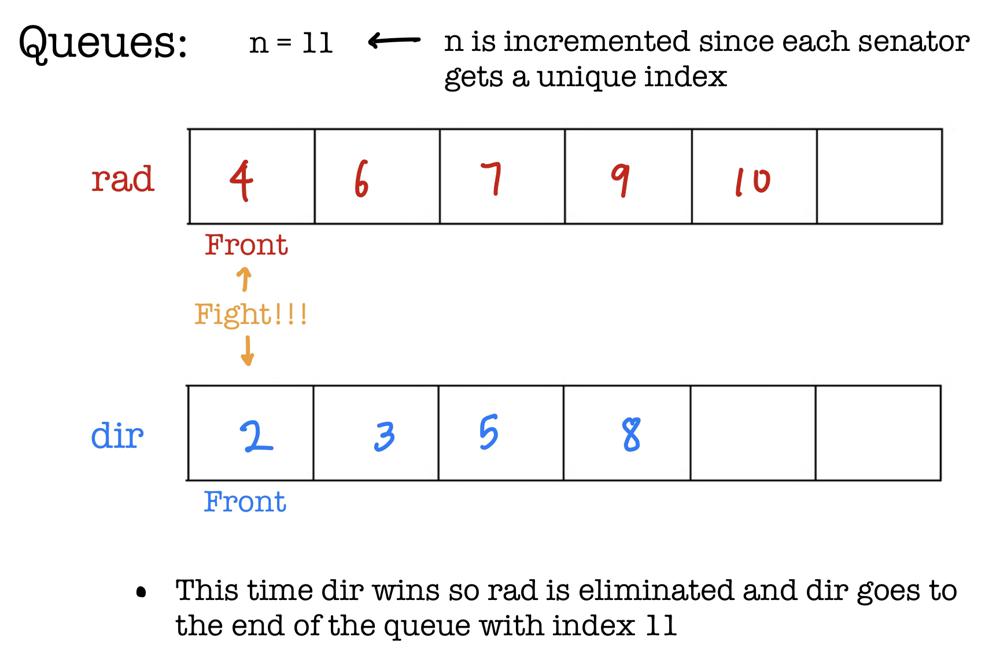\n\n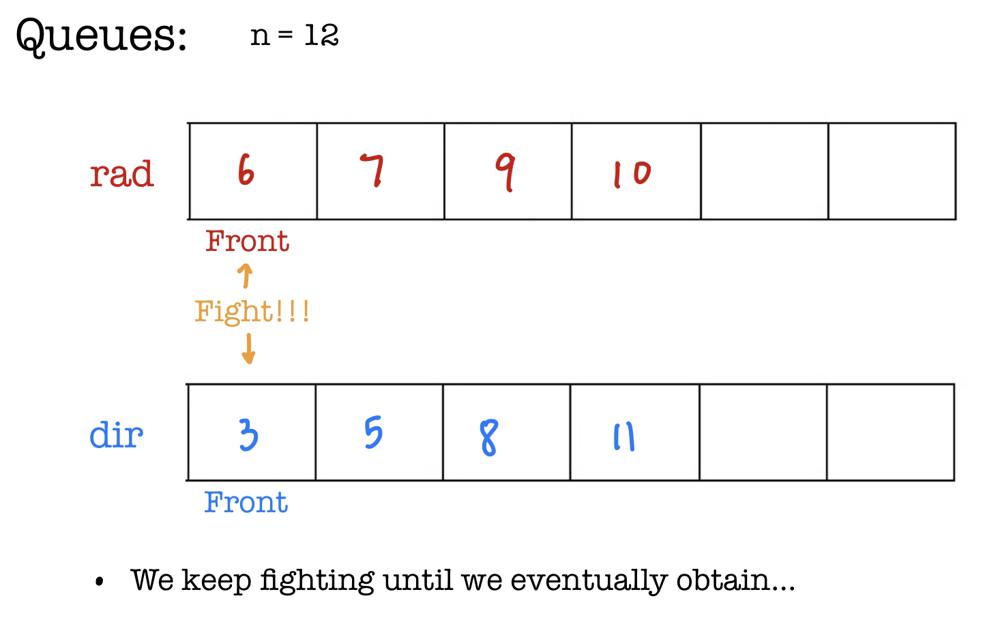\n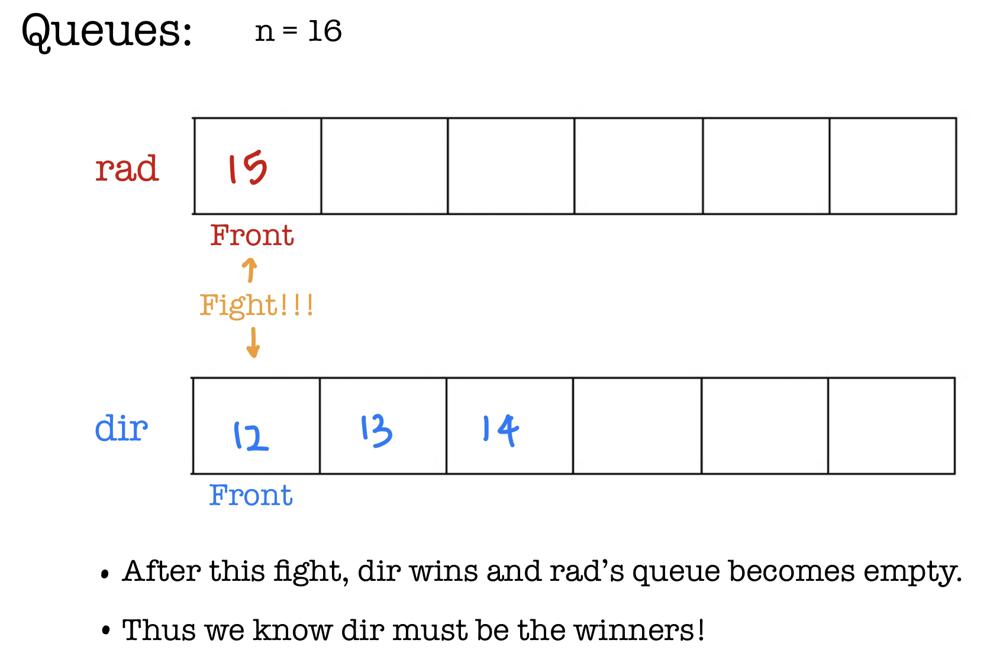\n\n# Code\n```\nclass Solution {\npublic:\n string predictPartyVictory(string senate) {\n queue<int> rad, dir;\n int n = senate.length();\n // Add all senators to respect queue with index\n for (int i = 0; i < n; i++){\n if (senate[i] == \'R\'){\n rad.push(i);\n }\n else {\n dir.push(i);\n }\n }\n // Use increasing n to keep track of position\n while (!rad.empty() && !dir.empty()){\n // Only "winner" stays in their queue\n if (rad.front() < dir.front()){\n rad.push(n++);\n }\n else {\n dir.push(n++);\n }\n rad.pop(), dir.pop();\n }\n return (rad.empty()) ? ("Dire") : ("Radiant");\n }\n};\n```\n### Why does the winner go to the end of the queue?\n- Since the voting is done such that both sides perform the most optimal strategy, the senators who have already voted will not be a problem to the other team for that round. \n- So, instead of eliminating a senator who has already moved, the best move for each team is to eliminate the next senator who has the power to vote. \n- This works perfectly with the queue approach since we can just place the senators who have voted at the end. \n## If this helped, please leave an upvote! Much appreciated!\n##### edit: Thanks all for the kind comments; it definitely motivates me to make more of these diagram solutions! | 450 | In the world of Dota2, there are two parties: the Radiant and the Dire.
The Dota2 senate consists of senators coming from two parties. Now the Senate wants to decide on a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise **one** of the two rights:
* **Ban one senator's right:** A senator can make another senator lose all his rights in this and all the following rounds.
* **Announce the victory:** If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and decide on the change in the game.
Given a string `senate` representing each senator's party belonging. The character `'R'` and `'D'` represent the Radiant party and the Dire party. Then if there are `n` senators, the size of the given string will be `n`.
The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party. Predict which party will finally announce the victory and change the Dota2 game. The output should be `"Radiant "` or `"Dire "`.
**Example 1:**
**Input:** senate = "RD "
**Output:** "Radiant "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And in round 2, the first senator can just announce the victory since he is the only guy in the senate who can vote.
**Example 2:**
**Input:** senate = "RDD "
**Output:** "Dire "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And the third senator comes from Dire and he can ban the first senator's right in round 1.
And in round 2, the third senator can just announce the victory since he is the only guy in the senate who can vote.
**Constraints:**
* `n == senate.length`
* `1 <= n <= 104`
* `senate[i]` is either `'R'` or `'D'`. | null |
Python 3 solution with approach and time complexity analysis | dota2-senate | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirstly noticeable thing is that there are only two types of parties in here Radiant and Dire. We can make use of this property and we just need to keep count of who is coming early and who is banned already. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**step 1:** first of all we need some variables to store certain parameters like count_R, count_D (total members), banned_R, banned_D (banned members count), total_banned_D, total_banned_R (this is for maintaining the total count so that we can check if any one has won)\n\n**step 2:** Now we\'ll create a queue as we need to simulate the rounds so we need to push back the members that still have right to vote\n\n**step 3:** Now loop over queue take the first member and check if its right has been banned , if not than increase the banned count of opposite party.\n\n**step 4:** Lastly just check if any of the parties total banned count is equal to their all members count. If yes, we got a winner.\n\n\n# Complexity\n- Time complexity: O(n) since all members will be once in the queue\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) again cause of the queue\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def predictPartyVictory(self, senate: str) -> str:\n banned_R = 0\n banned_D = 0\n total_banned_D = 0\n total_banned_R = 0\n count_R = 0\n count_D = 0\n for sen in senate:\n if sen == "R": \n count_R += 1\n else:\n count_D += 1\n\n queue = deque(senate)\n\n while queue:\n sen = queue.popleft()\n if sen == "R":\n if banned_R > 0:\n banned_R -= 1\n else:\n total_banned_D += 1\n banned_D += 1\n queue.append(sen)\n else: \n if banned_D > 0:\n banned_D -= 1\n else:\n total_banned_R += 1\n banned_R += 1\n queue.append(sen)\n\n if total_banned_D >= count_D:\n return "Radiant"\n elif total_banned_R >= count_R:\n return "Dire"\n return -1\n``` | 2 | In the world of Dota2, there are two parties: the Radiant and the Dire.
The Dota2 senate consists of senators coming from two parties. Now the Senate wants to decide on a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise **one** of the two rights:
* **Ban one senator's right:** A senator can make another senator lose all his rights in this and all the following rounds.
* **Announce the victory:** If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and decide on the change in the game.
Given a string `senate` representing each senator's party belonging. The character `'R'` and `'D'` represent the Radiant party and the Dire party. Then if there are `n` senators, the size of the given string will be `n`.
The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party. Predict which party will finally announce the victory and change the Dota2 game. The output should be `"Radiant "` or `"Dire "`.
**Example 1:**
**Input:** senate = "RD "
**Output:** "Radiant "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And in round 2, the first senator can just announce the victory since he is the only guy in the senate who can vote.
**Example 2:**
**Input:** senate = "RDD "
**Output:** "Dire "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And the third senator comes from Dire and he can ban the first senator's right in round 1.
And in round 2, the third senator can just announce the victory since he is the only guy in the senate who can vote.
**Constraints:**
* `n == senate.length`
* `1 <= n <= 104`
* `senate[i]` is either `'R'` or `'D'`. | null |
Python Without Queues | dota2-senate | 0 | 1 | \n```\nclass Solution:\n def predictPartyVictory(self, senate: str) -> str:\n\n # The main observation is that we have to remove the\n # senators of the remaning bans from the begining\n # of the remaning list and so we can also use queue\'s here\n\n n = len(senate)\n bans,arr = [0,0],[]\n for i in range(len(senate)):\n arr.append( 0 if senate[i]==\'R\' else 1 )\n while( len(set(arr)) > 1 ):\n temp = []\n for c in arr:\n if bans[c] >0:bans[c]-=1\n else:\n temp.append(c)\n bans[~c]+=1 \n arr = []\n # The remaning bans.. remove from the front \n for c in temp:\n if bans[c] >0:bans[c]-=1\n else:arr.append(c)\n \n return \'Radiant\' if arr[0] == 0 else \'Dire\'\n \n\n``` | 2 | In the world of Dota2, there are two parties: the Radiant and the Dire.
The Dota2 senate consists of senators coming from two parties. Now the Senate wants to decide on a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise **one** of the two rights:
* **Ban one senator's right:** A senator can make another senator lose all his rights in this and all the following rounds.
* **Announce the victory:** If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and decide on the change in the game.
Given a string `senate` representing each senator's party belonging. The character `'R'` and `'D'` represent the Radiant party and the Dire party. Then if there are `n` senators, the size of the given string will be `n`.
The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party. Predict which party will finally announce the victory and change the Dota2 game. The output should be `"Radiant "` or `"Dire "`.
**Example 1:**
**Input:** senate = "RD "
**Output:** "Radiant "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And in round 2, the first senator can just announce the victory since he is the only guy in the senate who can vote.
**Example 2:**
**Input:** senate = "RDD "
**Output:** "Dire "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And the third senator comes from Dire and he can ban the first senator's right in round 1.
And in round 2, the third senator can just announce the victory since he is the only guy in the senate who can vote.
**Constraints:**
* `n == senate.length`
* `1 <= n <= 104`
* `senate[i]` is either `'R'` or `'D'`. | null |
Easy to understand, Simulation with nicely written comments. Step by step method. | dota2-senate | 0 | 1 | # Intuition\n- Initially we count the number of Ds and number of Rs\n- Then we loop until we see that all of Ds or all of Rs are banned.\n- If we encounter a D, and we see that there are bans on D, then we enforce that. Similarly with R.\n- Finally, whichever team got banned, we return the other.\n\n# Code\n```\nclass Solution:\n def predictPartyVictory(self, senate: str) -> str:\n num_r = 0\n num_d = 0\n\n # Count the number of D and Rs\n for mem in senate:\n if mem == "R":\n num_r += 1\n else:\n num_d += 1\n ban_r = 0\n ban_d = 0\n senate = list(senate)\n floating_d_bans = 0\n floating_r_bans = 0\n # Loop until all D\'s are banned or all Rs are banned\n while ban_d!=num_d and ban_r!=num_r:\n for i,mem in enumerate(senate):\n\n # Member is R\n if mem == \'R\':\n # There is a ban on R that isn\'t enforced yet\n if floating_r_bans > 0:\n floating_r_bans -= 1\n senate[i] = \'X\'\n ban_r += 1\n else:\n floating_d_bans += 1\n if mem == \'D\':\n if floating_d_bans > 0:\n floating_d_bans -= 1\n senate[i] = \'X\'\n ban_d += 1\n else:\n floating_r_bans += 1\n if ban_r == num_r:\n return "Dire"\n return "Radiant"\n``` | 1 | In the world of Dota2, there are two parties: the Radiant and the Dire.
The Dota2 senate consists of senators coming from two parties. Now the Senate wants to decide on a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise **one** of the two rights:
* **Ban one senator's right:** A senator can make another senator lose all his rights in this and all the following rounds.
* **Announce the victory:** If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and decide on the change in the game.
Given a string `senate` representing each senator's party belonging. The character `'R'` and `'D'` represent the Radiant party and the Dire party. Then if there are `n` senators, the size of the given string will be `n`.
The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party. Predict which party will finally announce the victory and change the Dota2 game. The output should be `"Radiant "` or `"Dire "`.
**Example 1:**
**Input:** senate = "RD "
**Output:** "Radiant "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And in round 2, the first senator can just announce the victory since he is the only guy in the senate who can vote.
**Example 2:**
**Input:** senate = "RDD "
**Output:** "Dire "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And the third senator comes from Dire and he can ban the first senator's right in round 1.
And in round 2, the third senator can just announce the victory since he is the only guy in the senate who can vote.
**Constraints:**
* `n == senate.length`
* `1 <= n <= 104`
* `senate[i]` is either `'R'` or `'D'`. | null |
Solutions in C++, Python, and Java | dota2-senate | 1 | 1 | # Code\n<iframe src="https://leetcode.com/playground/7gyLhdmK/shared" frameBorder="0" width="700" height="400"></iframe>\n | 52 | In the world of Dota2, there are two parties: the Radiant and the Dire.
The Dota2 senate consists of senators coming from two parties. Now the Senate wants to decide on a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise **one** of the two rights:
* **Ban one senator's right:** A senator can make another senator lose all his rights in this and all the following rounds.
* **Announce the victory:** If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and decide on the change in the game.
Given a string `senate` representing each senator's party belonging. The character `'R'` and `'D'` represent the Radiant party and the Dire party. Then if there are `n` senators, the size of the given string will be `n`.
The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party. Predict which party will finally announce the victory and change the Dota2 game. The output should be `"Radiant "` or `"Dire "`.
**Example 1:**
**Input:** senate = "RD "
**Output:** "Radiant "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And in round 2, the first senator can just announce the victory since he is the only guy in the senate who can vote.
**Example 2:**
**Input:** senate = "RDD "
**Output:** "Dire "
**Explanation:**
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And the third senator comes from Dire and he can ban the first senator's right in round 1.
And in round 2, the third senator can just announce the victory since he is the only guy in the senate who can vote.
**Constraints:**
* `n == senate.length`
* `1 <= n <= 104`
* `senate[i]` is either `'R'` or `'D'`. | null |
Top-down Memoization [Python3] | 2-keys-keyboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI think top down is more intuitive, and easier to understand.\nFor every operation, we either copy all or paste the current result.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHowever, we cannot let the user to keep copying/pasting nothing forever. We need a stopping condition to check if the user is doing either that:\n\n`if curr == saved` checks if the user has already copied.\n`if saved == 0` checks if the user pasting empty string.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(2^n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(2^n)$$\n\n\n# Code\n```\nclass Solution:\n def minSteps(self, n: int) -> int:\n @lru_cache(None)\n def dp(ops, curr, saved):\n if curr == n: return ops\n if curr > n: return inf\n if curr == saved: return dp(ops + 1, curr + saved, saved)\n if saved == 0: return dp(ops + 1, curr, curr)\n return min(dp(ops + 1, curr + saved, saved), dp(ops + 1, curr, curr))\n return dp(0, 1, 0) \n \n``` | 1 | There is only one character `'A'` on the screen of a notepad. You can perform one of two operations on this notepad for each step:
* Copy All: You can copy all the characters present on the screen (a partial copy is not allowed).
* Paste: You can paste the characters which are copied last time.
Given an integer `n`, return _the minimum number of operations to get the character_ `'A'` _exactly_ `n` _times on the screen_.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** Initially, we have one character 'A'.
In step 1, we use Copy All operation.
In step 2, we use Paste operation to get 'AA'.
In step 3, we use Paste operation to get 'AAA'.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `1 <= n <= 1000` | How many characters may be there in the clipboard at the last step if n = 3? n = 7? n = 10? n = 24? |
[Python] Simple Recursion + Memoization Solution with Explanation | 2-keys-keyboard | 0 | 1 | * We start with 1 A on screen and with an empty clipboard, \n* In every iteration we have two options either we paste previously copied data or copy the current data and then paste it\n* Now, keep in mind that we can only paste if we have something in clipboard, if clipboard is empty we cannot paste\n* For base case, since out target is to get n A\'s on screen, we return 0 when screen == n and if A\'s on screen becomes greater than n then we need to discard this so we return Infinty, since we take min this will be discarded\n```\nclass Solution:\n def minSteps(self, n: int) -> int:\n cache = {}\n def helper(screen, clipboard):\n if (screen, clipboard) in cache: return cache[(screen, clipboard)]\n if screen == n: return 0\n if screen > n: return float("Inf")\n \n copy_paste = helper(screen+screen, screen) + 2\n paste = float("Inf")\n if clipboard:\n paste = helper(screen + clipboard, clipboard) + 1\n\n cache[(screen, clipboard)] = min(copy_paste, paste) \n return cache[(screen, clipboard)]\n \n return helper(1, 0)\n``` | 20 | There is only one character `'A'` on the screen of a notepad. You can perform one of two operations on this notepad for each step:
* Copy All: You can copy all the characters present on the screen (a partial copy is not allowed).
* Paste: You can paste the characters which are copied last time.
Given an integer `n`, return _the minimum number of operations to get the character_ `'A'` _exactly_ `n` _times on the screen_.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** Initially, we have one character 'A'.
In step 1, we use Copy All operation.
In step 2, we use Paste operation to get 'AA'.
In step 3, we use Paste operation to get 'AAA'.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `1 <= n <= 1000` | How many characters may be there in the clipboard at the last step if n = 3? n = 7? n = 10? n = 24? |
📌📌Python3 || ⚡42 ms, faster than 97.10% of Python3 | find-duplicate-subtrees | 0 | 1 | \n```\nclass Solution:\n def findDuplicateSubtrees(self, root: Optional[TreeNode]) -> List[Optional[TreeNode]]:\n map = {}\n res = set()\n def check(node):\n if not node:\n return \'#\'\n s = \'\'\n if not node.left and not node.right:\n s += str(node.val)\n map[s] = map.get(s,0)+1\n if map[s]==2:\n res.add(node)\n return s\n s = s + str(node.val)\n s = s + "," + check(node.left)\n s = s+ "," + check(node.right)\n map[s] = map.get(s,0)+1\n if map[s]==2:\n res.add(node)\n return s\n \n check(root)\n return res\n```\nThe given code finds all the duplicate subtrees in a given binary tree. Here\'s a step-by-step explanation of the code:\n1. Define a class named Solution.\n1. Define a function findDuplicateSubtrees that takes the root of the binary tree as input and returns a list of nodes that are duplicate.\n1. Create a dictionary named \'map\' that will store the subtree string and its frequency.\n1. Create a set named \'res\' that will store the duplicate subtrees.\n1. Define a nested function named \'check\' that takes a node as input and returns a string.\n1. If the node is None, return a string \'#\'. This represents a null node in the subtree string.\n1. Create an empty string \'s\'.\n1. If the node has no children (i.e., it is a leaf node), append its value to \'s\' as a string.\n1. Add the subtree string \'s\' to the dictionary \'map\' with its frequency increased by 1.\n1. If the frequency of the subtree \'s\' in the dictionary is 2, add the current node to the set \'res\'.\n1. Return the subtree string \'s\'.\n1. If the node has children, append the value of the node to \'s\' as a string.\n1. Recursively call the \'check\' function on the left and right subtrees of the node.\n1. Append the result of calling the \'check\' function on the left and right subtrees to \'s\' with \',\' as a separator.\n1. Add the subtree string \'s\' to the dictionary \'map\' with its frequency increased by 1.\n1. If the frequency of the subtree \'s\' in the dictionary is 2, add the current node to the set \'res\'.\n1. Return the subtree string \'s\'.\n1. Call the \'check\' function with the root of the binary tree as input.\n1. Return the set \'res\' containing the duplicate subtrees. | 3 | Given the `root` of a binary tree, return all **duplicate subtrees**.
For each kind of duplicate subtrees, you only need to return the root node of any **one** of them.
Two trees are **duplicate** if they have the **same structure** with the **same node values**.
**Example 1:**
**Input:** root = \[1,2,3,4,null,2,4,null,null,4\]
**Output:** \[\[2,4\],\[4\]\]
**Example 2:**
**Input:** root = \[2,1,1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[2,2,2,3,null,3,null\]
**Output:** \[\[2,3\],\[3\]\]
**Constraints:**
* The number of the nodes in the tree will be in the range `[1, 5000]`
* `-200 <= Node.val <= 200` | null |
Solution | find-duplicate-subtrees | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n unordered_map<string,int> m;\n string generate(TreeNode *root,vector<TreeNode*> &res){\n if(!root) return "#";\n string s=generate(root->left,res) +\',\'+generate(root->right,res)+\',\'+to_string(root->val);\n m[s]++;\n if(m[s]==2) res.push_back(root);\n return s;\n }\n vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {\n vector<TreeNode*> ans;\n generate(root,ans);\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findDuplicateSubtrees(self, root: Optional[TreeNode]) -> List[Optional[TreeNode]]:\n def traverse(node):\n if not node:\n return 0\n triplet = (traverse(node.left), node.val, traverse(node.right))\n if triplet not in triplet_to_id:\n triplet_to_id[triplet] = len(triplet_to_id) + 1\n tid = triplet_to_id[triplet]\n cnt[tid] += 1\n if cnt[tid] == 2:\n res.append(node)\n return tid\n triplet_to_id = dict()\n cnt = defaultdict(int)\n res = []\n traverse(root)\n return res\n```\n\n```Java []\nimport java.util.AbstractList;\n\nclass Solution {\n List<TreeNode> _duplicatedTrees = null;\n public List<TreeNode> findDuplicateSubtrees(TreeNode root) {\n return new AbstractList<TreeNode>() {\n public TreeNode get(int index) {\n init(); return _duplicatedTrees.get(index);\n }\n public int size() {\n init(); return _duplicatedTrees.size();\n }\n private void init() {\n if (_duplicatedTrees != null)\n return;\n \n final HashMap<String,Integer> treeMap = new HashMap<String,Integer>();\n _duplicatedTrees = new ArrayList<TreeNode>();\n stringRepresentationOfTree(root, treeMap, _duplicatedTrees);\n }\n };\n }\n private final StringBuilder stringRepresentationOfTree(final TreeNode root, final HashMap<String,Integer> treeRepMap, final List<TreeNode> duplciatedTrees) {\n if (root == null) \n return new StringBuilder("#");\n StringBuilder rep1 = stringRepresentationOfTree(root.left, treeRepMap, duplciatedTrees);\n StringBuilder rep2 = stringRepresentationOfTree(root.right, treeRepMap, duplciatedTrees);\n final StringBuilder treeRep = rep1.append(",").append(rep2).append(",").append(root.val);\n\n treeRepMap.put(treeRep.toString(), treeRepMap.getOrDefault(treeRep.toString(), 0) + 1);\n \n if (treeRepMap.get(treeRep.toString()) >= 2) {\n duplciatedTrees.add(root); treeRepMap.put(treeRep.toString(), Integer.MIN_VALUE);\n } \n return treeRep;\n }\n}\n```\n | 1 | Given the `root` of a binary tree, return all **duplicate subtrees**.
For each kind of duplicate subtrees, you only need to return the root node of any **one** of them.
Two trees are **duplicate** if they have the **same structure** with the **same node values**.
**Example 1:**
**Input:** root = \[1,2,3,4,null,2,4,null,null,4\]
**Output:** \[\[2,4\],\[4\]\]
**Example 2:**
**Input:** root = \[2,1,1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[2,2,2,3,null,3,null\]
**Output:** \[\[2,3\],\[3\]\]
**Constraints:**
* The number of the nodes in the tree will be in the range `[1, 5000]`
* `-200 <= Node.val <= 200` | null |
Python || Easy Solution | find-duplicate-subtrees | 0 | 1 | \n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def __init__(self):\n self.hash = defaultdict(bool)\n self.ans = []\n \n def get_ans(self, root, s):\n if root:\n lst = self.get_ans(root.left, -1) + [root.val] + self.get_ans(root.right, 1)\n tpl = tuple(lst)\n if tpl in self.hash:\n if self.hash[tpl] == True:\n self.ans.append(root)\n self.hash[tpl] = False\n else:\n self.hash[tpl] = True\n return lst\n return [s]\n \n \n\n def findDuplicateSubtrees(self, root: Optional[TreeNode]) -> List[Optional[TreeNode]]:\n self.get_ans(root, 0)\n return self.ans\n\n``` | 1 | Given the `root` of a binary tree, return all **duplicate subtrees**.
For each kind of duplicate subtrees, you only need to return the root node of any **one** of them.
Two trees are **duplicate** if they have the **same structure** with the **same node values**.
**Example 1:**
**Input:** root = \[1,2,3,4,null,2,4,null,null,4\]
**Output:** \[\[2,4\],\[4\]\]
**Example 2:**
**Input:** root = \[2,1,1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[2,2,2,3,null,3,null\]
**Output:** \[\[2,3\],\[3\]\]
**Constraints:**
* The number of the nodes in the tree will be in the range `[1, 5000]`
* `-200 <= Node.val <= 200` | null |
[Python] Hash map with serialization; Explained | find-duplicate-subtrees | 0 | 1 | We can recursively traverse the tree. However, in order to find duplicated subtrees, we need to maintain a hash map which can easily help us to compare two subtrees with only 1 traverse.\n\nThe key of the hashmap is the serialization of the visited subtree. Whenever we have a new serialization string, we just add it into the hashmap, and increase the count of it. If the count a serialization string is larger than 2, we found a duplicated subtree.\n\nSee the code for details:\n\n```\nclass Solution:\n def findDuplicateSubtrees(self, root: Optional[TreeNode]) -> List[Optional[TreeNode]]:\n # in order traverse and keep tracking of subtrees visited\n self.subtree_set = collections.defaultdict(int)\n self.ans = []\n if root:\n self.dfs(root)\n return self.ans\n \n \n def dfs(self, root):\n if root.left is None and root.right is None:\n # this is a leaf node\n tree_str = "(#)" + str(root.val) + "(#)"\n self.subtree_set[tree_str] += 1\n if self.subtree_set[tree_str] == 2:\n # only returns one of the duplicated subtrees\n self.ans.append(root)\n return tree_str\n \n left_ts = "#"\n if root.left:\n left_ts = self.dfs(root.left)\n \n left_ts = "(" + left_ts + ")" + str(root.val)\n right_ts = "#"\n if root.right:\n right_ts = self.dfs(root.right)\n \n tree_str = left_ts + "(" + right_ts + ")"\n self.subtree_set[tree_str] += 1\n if self.subtree_set[tree_str] == 2:\n self.ans.append(root)\n return tree_str\n``` | 1 | Given the `root` of a binary tree, return all **duplicate subtrees**.
For each kind of duplicate subtrees, you only need to return the root node of any **one** of them.
Two trees are **duplicate** if they have the **same structure** with the **same node values**.
**Example 1:**
**Input:** root = \[1,2,3,4,null,2,4,null,null,4\]
**Output:** \[\[2,4\],\[4\]\]
**Example 2:**
**Input:** root = \[2,1,1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[2,2,2,3,null,3,null\]
**Output:** \[\[2,3\],\[3\]\]
**Constraints:**
* The number of the nodes in the tree will be in the range `[1, 5000]`
* `-200 <= Node.val <= 200` | null |
Clean Codes🔥🔥|| Full Explanation✅|| Depth First Search✅|| C++|| Java|| Python3 | find-duplicate-subtrees | 1 | 1 | # Intuition :\n- Here we have to find all the subtrees in a binary tree that occur more than once and return their roots.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Detail Explanation to Approach :\n- Here we are using a `depth-first search` approach to traverse the tree and encode each subtree into a string using a preorder traversal.\n- The encoding includes the value of the current node and the encoding of its left and right subtrees, separated by a special character ("#").\n- **For example,** the subtree consisting of just the root node with value `1` would be encoded as `"1##"` (with two "#" characters to indicate that there are no left or right subtrees).\n```\nfinal String encoded = root.val + "#" + encode(root.left, count,ans)\n + "#" + encode(root.right, count, ans);\n```\n**OR YOU CAN WRITE IT AS**\n```\nString left = encode(root.left, count, ans);\nString right = encode(root.right, count, ans);\nfinal String encoded = root.val + "#" + left + "#" + right;\n```\n- The encoding is then added to a HashMap that counts the number of occurrences of each subtree.\n- If the encoding already exists in the map, its count is incremented by 1 using the `Integer::sum` function. \n- If it doesn\'t exist, a new entry is added with a count of 1. This ensures that each subtree encoding is counted exactly once in the map.\n```\ncount.merge(encoded, 1, Integer::sum);\n```\n- If a subtree\'s encoding appears more than once (i.e., its count in the HashMap is 2), its root is added to a result list. \n```\nif (count.get(encoded) == 2)//duplicate subtree\n ans.add(root);//add the roots\n```\n- Finally, return the list of duplicate subtrees.\n```\nreturn ans;\n```\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity :\n- Time complexity : O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n\n```\n*Let\'s Code it Up .\nThere may be minor syntax difference in C++ and Python*\n# Codes [C++ |Java |Python3] : With Comments\n\n```C++ []\nclass Solution {\n public:\n vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {\n vector<TreeNode*> ans;\n unordered_map<string, int> count;\n encode(root, count, ans);\n return ans;\n }\n\n private:\n string encode(TreeNode* root, unordered_map<string, int>& count,\n vector<TreeNode*>& ans) {\n if (root == nullptr)\n return "";\n\n const string encoded = to_string(root->val) + "#" +\n encode(root->left, count, ans) + "#" +\n encode(root->right, count, ans);\n //# for encoding null left and right childs\n if (++count[encoded] == 2)//duplicate subtree\n ans.push_back(root);//add the roots\n return encoded;\n }\n};\n```\n```Java []\nclass Solution \n{\n public List<TreeNode> findDuplicateSubtrees(TreeNode root) \n {\n List<TreeNode> ans = new ArrayList<>();\n Map<String, Integer> count = new HashMap<>();\n\n encode(root, count, ans);\n return ans;\n }\n private String encode(TreeNode root, Map<String, Integer> count, List<TreeNode> ans)\n {\n if (root == null)\n return "";\n \n final String encoded = root.val + "#" + encode(root.left, count, ans) + "#" + encode(root.right, count, ans);//# for encoding null left and right childs\n count.merge(encoded, 1, Integer::sum);\n //used to add the encoding to the count map. If the encoding already exists in the map, its count is incremented by 1 using the Integer::sum function. If it doesn\'t exist, a new entry is added with a count of 1. This ensures that each subtree encoding is counted exactly once in the map.\n if (count.get(encoded) == 2)//duplicate subtree\n ans.add(root);//add the roots\n return encoded;\n }\n}\n```\n```Python []\nclass Solution:\n def findDuplicateSubtrees(self, root: Optional[TreeNode]) -> List[Optional[TreeNode]]:\n ans = []\n count = collections.Counter()\n\n def encode(root: Optional[TreeNode]) -> str:\n if not root:\n return \'\'\n\n encoded = str(root.val) + \'#\' + \\\n encode(root.left) + \'#\' + \\\n encode(root.right)\n count[encoded] += 1\n if count[encoded] == 2:\n ans.append(root)\n return encoded\n\n encode(root)\n return ans\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 52 | Given the `root` of a binary tree, return all **duplicate subtrees**.
For each kind of duplicate subtrees, you only need to return the root node of any **one** of them.
Two trees are **duplicate** if they have the **same structure** with the **same node values**.
**Example 1:**
**Input:** root = \[1,2,3,4,null,2,4,null,null,4\]
**Output:** \[\[2,4\],\[4\]\]
**Example 2:**
**Input:** root = \[2,1,1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[2,2,2,3,null,3,null\]
**Output:** \[\[2,3\],\[3\]\]
**Constraints:**
* The number of the nodes in the tree will be in the range `[1, 5000]`
* `-200 <= Node.val <= 200` | null |
Beginner-friendly || Construct a Tree with Divide-and-conquer algorithm in Python3 | maximum-binary-tree | 0 | 1 | # Intuition\nThe problem description is the following:\n- given the integer list of `nums`, that represents **node values** of a tree\n- our goal is to **construct a Binary Tree** using this `nums` list\n\nLet\'s have a look a little closer:\n```\n# Example\nnums = [3,2,1,6,0,5]\n\n# The algorithm to build a tree is:\n# 1. find a maximum value of a list and store it\'s index\n# 2. divide a collection of list into left and right\n# 3. continue to eval the algorithm until the nums count == 0\n\n# Iterations\n# 1. \nmax = 6, left = [3, 2, 1], right = [0, 5]\n\n# 2. \nmax = 3, left = [], right = [2, 1]\n\n# etc\n```\n\n---\n\nIf you haven\'t already familiar with [divide-and-conquer algorithm\n](https://en.wikipedia.org/wiki/Divide-and-conquer_algorithm), follow the link.\n\n\n# Approach\n1. the base case for recursion is to check how many `nums` do we have, otherwise return `None`\n2. initialize `index` and `curMax` to **store** index and max value from `nums`\n3. iterate over all `nums` to find a maximum value\n4. divide a list into `left` and `right` slices\n5. construct a current `TreeNode` with `left` and `right` nodes \n\n# Complexity\n- Time complexity: **O(n^2)** in worst case scenario, because of n-iterations * n-elements in `nums`\n\n- Space complexity: **O(n)**, because `constructMaximumBinaryTree` requires at least `n` recursive calls inside of a stack \n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:\n if not nums:\n return None\n\n index = 0\n curMax = -float(\'inf\')\n \n for i in range(len(nums)):\n if nums[i] > curMax:\n curMax = nums[i]\n index = i\n \n left = self.constructMaximumBinaryTree(nums[:index])\n right = self.constructMaximumBinaryTree(nums[index + 1:])\n \n return TreeNode(curMax, left, right) \n``` | 2 | You are given an integer array `nums` with no duplicates. A **maximum binary tree** can be built recursively from `nums` using the following algorithm:
1. Create a root node whose value is the maximum value in `nums`.
2. Recursively build the left subtree on the **subarray prefix** to the **left** of the maximum value.
3. Recursively build the right subtree on the **subarray suffix** to the **right** of the maximum value.
Return _the **maximum binary tree** built from_ `nums`.
**Example 1:**
**Input:** nums = \[3,2,1,6,0,5\]
**Output:** \[6,3,5,null,2,0,null,null,1\]
**Explanation:** The recursive calls are as follow:
- The largest value in \[3,2,1,6,0,5\] is 6. Left prefix is \[3,2,1\] and right suffix is \[0,5\].
- The largest value in \[3,2,1\] is 3. Left prefix is \[\] and right suffix is \[2,1\].
- Empty array, so no child.
- The largest value in \[2,1\] is 2. Left prefix is \[\] and right suffix is \[1\].
- Empty array, so no child.
- Only one element, so child is a node with value 1.
- The largest value in \[0,5\] is 5. Left prefix is \[0\] and right suffix is \[\].
- Only one element, so child is a node with value 0.
- Empty array, so no child.
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[3,null,2,null,1\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
* All integers in `nums` are **unique**. | null |
654: Solution with step by step explanation | maximum-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a stack to store nodes.\n2. Loop through each number in the input array.\n3. Create a new node with the current number as its value.\n4. While the stack is not empty and the current number is greater than the value of the top node on the stack, pop the top node from the stack and set it as the left child of the current node.\n5. If the stack is not empty, set the current node as the right child of the top node on the stack.\n6. Push the current node onto the stack.\n7. Once the loop is finished, the last remaining node on the stack is the root node of the maximum binary tree.\n8. Return the root node.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:\n # We will use a stack to keep track of the nodes we have created so far\n stack = []\n for num in nums:\n node = TreeNode(num) \n # If the stack is not empty and the current number is greater than the top of the stack,\n # we need to pop the stack until we find a node with a value greater than the current number.\n # The last popped node will be the parent of the current node.\n while stack and num > stack[-1].val:\n node.left = stack.pop()\n \n # If the stack is not empty, the top node is the parent of the current node.\n # We set the right child of the parent to be the current node.\n if stack:\n stack[-1].right = node\n \n # We push the current node onto the stack.\n stack.append(node)\n \n # The last node on the stack is the root of the tree.\n return stack[0]\n\n``` | 10 | You are given an integer array `nums` with no duplicates. A **maximum binary tree** can be built recursively from `nums` using the following algorithm:
1. Create a root node whose value is the maximum value in `nums`.
2. Recursively build the left subtree on the **subarray prefix** to the **left** of the maximum value.
3. Recursively build the right subtree on the **subarray suffix** to the **right** of the maximum value.
Return _the **maximum binary tree** built from_ `nums`.
**Example 1:**
**Input:** nums = \[3,2,1,6,0,5\]
**Output:** \[6,3,5,null,2,0,null,null,1\]
**Explanation:** The recursive calls are as follow:
- The largest value in \[3,2,1,6,0,5\] is 6. Left prefix is \[3,2,1\] and right suffix is \[0,5\].
- The largest value in \[3,2,1\] is 3. Left prefix is \[\] and right suffix is \[2,1\].
- Empty array, so no child.
- The largest value in \[2,1\] is 2. Left prefix is \[\] and right suffix is \[1\].
- Empty array, so no child.
- Only one element, so child is a node with value 1.
- The largest value in \[0,5\] is 5. Left prefix is \[0\] and right suffix is \[\].
- Only one element, so child is a node with value 0.
- Empty array, so no child.
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[3,null,2,null,1\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
* All integers in `nums` are **unique**. | null |
Use Stack (Python, O(n) time/space) | maximum-binary-tree | 0 | 1 | Hi everyone. I liked this problem so much that I decided to write this article about my approach to solving this problem. So let us dive into it.\n\nMy first thoughts about a recursive solution were exactly the same as in the official guide:\n1. Find the maximum `max` and make it the `root` of the tree\n1. Divide the array into two parts. Generate left child from left subarray, and right child from right subarray.\n1. Return the `root`\n\nBut it turns out that time complexity in the worst case was `O(n ** 2)`. That is definitely not good... The problem is that despite the fact that you will traverse the array just once to create all the nodes, you will have to traverse it several times to find the maximum element in each recursive call. Then I came up with idea that I do not have to know the maximum of the range of values in the array. I just have to know that at the left side of the current node there are just nodes with bigger values, and at the right side with smaller values.\n\n**The algorithm:**\n```\nclass Solution:\n def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:\n nodes = []\n for num in nums:\n node = TreeNode(num)\n while nodes and nodes[-1].val < num:\n node.left = nodes.pop()\n\n if nodes:\n nodes[-1].right = node\n\n nodes.append(node)\n\n return nodes[0]\n```\n\n**Complexity:**\nTime: in the worst case, you will access the initial array or stack elements `O(2n)` times, or just `O(n)`.\nSpace: it is obvious that the result will take space proportional to the length of the initial array, hence space complexity is `O(n)`.\n\n\uD83D\uDCE2 *If you think that that solution is good enough to be recommended to other LeetCoders then upvote.* | 42 | You are given an integer array `nums` with no duplicates. A **maximum binary tree** can be built recursively from `nums` using the following algorithm:
1. Create a root node whose value is the maximum value in `nums`.
2. Recursively build the left subtree on the **subarray prefix** to the **left** of the maximum value.
3. Recursively build the right subtree on the **subarray suffix** to the **right** of the maximum value.
Return _the **maximum binary tree** built from_ `nums`.
**Example 1:**
**Input:** nums = \[3,2,1,6,0,5\]
**Output:** \[6,3,5,null,2,0,null,null,1\]
**Explanation:** The recursive calls are as follow:
- The largest value in \[3,2,1,6,0,5\] is 6. Left prefix is \[3,2,1\] and right suffix is \[0,5\].
- The largest value in \[3,2,1\] is 3. Left prefix is \[\] and right suffix is \[2,1\].
- Empty array, so no child.
- The largest value in \[2,1\] is 2. Left prefix is \[\] and right suffix is \[1\].
- Empty array, so no child.
- Only one element, so child is a node with value 1.
- The largest value in \[0,5\] is 5. Left prefix is \[0\] and right suffix is \[\].
- Only one element, so child is a node with value 0.
- Empty array, so no child.
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[3,null,2,null,1\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
* All integers in `nums` are **unique**. | null |
Marvellous Code Technique Python3 | maximum-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:\n def BFS(nums):\n if not nums: return None\n maxvalue,index=float(\'-inf\'),-1\n for i in range(len(nums)):\n if nums[i]>maxvalue:\n maxvalue=nums[i]\n index=i\n root=TreeNode(maxvalue)\n root.left,root.right=BFS(nums[0:index]),BFS(nums[index+1:]\n return root\n return BFS(nums)\n #please upvote me it would encourage me alot\n\n\n``` | 6 | You are given an integer array `nums` with no duplicates. A **maximum binary tree** can be built recursively from `nums` using the following algorithm:
1. Create a root node whose value is the maximum value in `nums`.
2. Recursively build the left subtree on the **subarray prefix** to the **left** of the maximum value.
3. Recursively build the right subtree on the **subarray suffix** to the **right** of the maximum value.
Return _the **maximum binary tree** built from_ `nums`.
**Example 1:**
**Input:** nums = \[3,2,1,6,0,5\]
**Output:** \[6,3,5,null,2,0,null,null,1\]
**Explanation:** The recursive calls are as follow:
- The largest value in \[3,2,1,6,0,5\] is 6. Left prefix is \[3,2,1\] and right suffix is \[0,5\].
- The largest value in \[3,2,1\] is 3. Left prefix is \[\] and right suffix is \[2,1\].
- Empty array, so no child.
- The largest value in \[2,1\] is 2. Left prefix is \[\] and right suffix is \[1\].
- Empty array, so no child.
- Only one element, so child is a node with value 1.
- The largest value in \[0,5\] is 5. Left prefix is \[0\] and right suffix is \[\].
- Only one element, so child is a node with value 0.
- Empty array, so no child.
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[3,null,2,null,1\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
* All integers in `nums` are **unique**. | null |
Solution | print-binary-tree | 1 | 1 | ```C++ []\nclass Solution {\n public:\n vector<vector<string>> printTree(TreeNode* root) {\n const int m = maxHeight(root);\n const int n = pow(2, m) - 1;\n vector<vector<string>> ans(m, vector<string>(n));\n dfs(root, 0, 0, ans[0].size() - 1, ans);\n return ans;\n }\n private:\n int maxHeight(TreeNode* root) {\n if (root == nullptr)\n return 0;\n return 1 + max(maxHeight(root->left), maxHeight(root->right));\n }\n void dfs(TreeNode* root, int row, int left, int right,\n vector<vector<string>>& ans) {\n if (root == nullptr)\n return;\n\n const int mid = (left + right) / 2;\n ans[row][mid] = to_string(root->val);\n dfs(root->left, row + 1, left, mid - 1, ans);\n dfs(root->right, row + 1, mid + 1, right, ans);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def getTreeHeight(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n return max(self.getTreeHeight(root.left), self.getTreeHeight(root.right)) + 1\n\n def place(self, root: Optional[TreeNode],row: int, col: int,\n height:int, mat:List[List[str]]) -> None:\n if not root:\n return\n mat[row][col] = str(root.val)\n self.place(root.left, row+1, int(col-2**(height-row-1)), height, mat)\n self.place(root.right, row+1, int(col+2**(height-row-1)), height, mat)\n\n def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:\n height = int(self.getTreeHeight(root) - 1)\n mrows = height + 1\n mcols = 2**(height+1) - 1\n mat = [["" for _ in range(mcols)] for _ in range(mrows)]\n if not root:\n return mat\n self.place(root, 0,int((mcols-1)/2), height, mat)\n return mat\n```\n\n```Java []\nclass Solution {\n public List<List<String>> printTree(TreeNode root) {\n int height = getHeight(root);\n int width = (int)Math.pow(2,height)-1;\n String[][] matrix = new String[height][width];\n for(String[] r : matrix){\n Arrays.fill(r,"");\n }\n List<List<String>> list = new ArrayList<>();\n getBinary(matrix, root, 0, 0, width-1);\n for(String[] r : matrix){\n list.add(Arrays.asList(r));\n }\n return list;\n }\n public void getBinary(String[][] matrix, TreeNode root, int row, int left, int right){\n if(root == null) return;\n int mid = left + (right - left)/2;\n matrix[row][mid] = String.valueOf(root.val);\n getBinary(matrix, root.left, row+1, left, mid-1);\n getBinary(matrix, root.right, row+1, mid+1, right);\n }\n public int getHeight(TreeNode root){\n if(root == null) return 0;\n return 1 + Math.max(getHeight(root.left), getHeight(root.right));\n }\n}\n```\n | 1 | Given the `root` of a binary tree, construct a **0-indexed** `m x n` string matrix `res` that represents a **formatted layout** of the tree. The formatted layout matrix should be constructed using the following rules:
* The **height** of the tree is `height` and the number of rows `m` should be equal to `height + 1`.
* The number of columns `n` should be equal to `2height+1 - 1`.
* Place the **root node** in the **middle** of the **top row** (more formally, at location `res[0][(n-1)/2]`).
* For each node that has been placed in the matrix at position `res[r][c]`, place its **left child** at `res[r+1][c-2height-r-1]` and its **right child** at `res[r+1][c+2height-r-1]`.
* Continue this process until all the nodes in the tree have been placed.
* Any empty cells should contain the empty string `" "`.
Return _the constructed matrix_ `res`.
**Example 1:**
**Input:** root = \[1,2\]
**Output:**
\[\[ " ", "1 ", " "\],
\[ "2 ", " ", " "\]\]
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:**
\[\[ " ", " ", " ", "1 ", " ", " ", " "\],
\[ " ", "2 ", " ", " ", " ", "3 ", " "\],
\[ " ", " ", "4 ", " ", " ", " ", " "\]\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 210]`.
* `-99 <= Node.val <= 99`
* The depth of the tree will be in the range `[1, 10]`. | null |
655: Time 94.44%, Solution with step by step explanation | print-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Calculate the height of the given binary tree using the get_height function, which takes a node as input and returns the height of the tree. Here, the height is defined as the length of the longest path from the root to a leaf node.\n\n2. Calculate the width of the matrix using the formula (1 << height) - 1, where height is the height of the tree. Here, << is the bitwise left shift operator, which shifts the bits of the number to the left by the specified number of bits.\n\n3. Create a 2D list res of size height x width filled with empty strings.\n\n4. Define a recursive function fill that takes a node, a level, a left index, and a right index as input. This function fills the matrix with the values of the binary tree nodes according to the given rules.\n\n5. If the given node is None, return from the function.\n\n6. Calculate the middle index of the current row using the formula (left + right) >> 1, where >> is the bitwise right shift operator, which shifts the bits of the number to the right by the specified number of bits.\n\n7. Set the value of res[level][mid] to the string representation of the value of the node.\n\n8. Recursively call the fill function for the left child of the current node with level + 1, left, and mid - 1 as the input parameters.\n\n9. Recursively call the fill function for the right child of the current node with level + 1, mid + 1, and right as the input parameters.\n\n10. Call the fill function with the root node, level = 0, left = 0, and right = width - 1.\n\n11. Return the matrix res.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def printTree(self, root: TreeNode) -> List[List[str]]:\n height = self.get_height(root)\n width = (1 << height) - 1\n res = [[\'\'] * width for _ in range(height)]\n \n def fill(node, level, left, right):\n if not node:\n return\n mid = (left + right) >> 1\n res[level][mid] = str(node.val)\n fill(node.left, level + 1, left, mid - 1)\n fill(node.right, level + 1, mid + 1, right)\n \n fill(root, 0, 0, width - 1)\n return res\n \n def get_height(self, node):\n return 0 if not node else 1 + max(self.get_height(node.left), self.get_height(node.right))\n\n``` | 3 | Given the `root` of a binary tree, construct a **0-indexed** `m x n` string matrix `res` that represents a **formatted layout** of the tree. The formatted layout matrix should be constructed using the following rules:
* The **height** of the tree is `height` and the number of rows `m` should be equal to `height + 1`.
* The number of columns `n` should be equal to `2height+1 - 1`.
* Place the **root node** in the **middle** of the **top row** (more formally, at location `res[0][(n-1)/2]`).
* For each node that has been placed in the matrix at position `res[r][c]`, place its **left child** at `res[r+1][c-2height-r-1]` and its **right child** at `res[r+1][c+2height-r-1]`.
* Continue this process until all the nodes in the tree have been placed.
* Any empty cells should contain the empty string `" "`.
Return _the constructed matrix_ `res`.
**Example 1:**
**Input:** root = \[1,2\]
**Output:**
\[\[ " ", "1 ", " "\],
\[ "2 ", " ", " "\]\]
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:**
\[\[ " ", " ", " ", "1 ", " ", " ", " "\],
\[ " ", "2 ", " ", " ", " ", "3 ", " "\],
\[ " ", " ", "4 ", " ", " ", " ", " "\]\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 210]`.
* `-99 <= Node.val <= 99`
* The depth of the tree will be in the range `[1, 10]`. | null |
Python BFS simple | print-binary-tree | 0 | 1 | ```python\ndef printTree(self, root: TreeNode) -> List[List[str]]:\n \n def getHeight(node=root):\n return 1+max(getHeight(node.left), getHeight(node.right)) if node else 0\n \n height = getHeight()-1\n columns = 2**(height+1)-1\n res = [[""]*columns for _ in range(height+1)]\n \n queue = deque([(root, (columns-1)//2)])\n r = 0\n \n while queue:\n for _ in range(len(queue)):\n node, c = queue.popleft()\n res[r][c] = str(node.val)\n if node.left:\n queue.append((node.left, c-2**(height-r-1)))\n if node.right:\n queue.append((node.right, c+2**(height-r-1)))\n r += 1\n \n return res\n``` | 6 | Given the `root` of a binary tree, construct a **0-indexed** `m x n` string matrix `res` that represents a **formatted layout** of the tree. The formatted layout matrix should be constructed using the following rules:
* The **height** of the tree is `height` and the number of rows `m` should be equal to `height + 1`.
* The number of columns `n` should be equal to `2height+1 - 1`.
* Place the **root node** in the **middle** of the **top row** (more formally, at location `res[0][(n-1)/2]`).
* For each node that has been placed in the matrix at position `res[r][c]`, place its **left child** at `res[r+1][c-2height-r-1]` and its **right child** at `res[r+1][c+2height-r-1]`.
* Continue this process until all the nodes in the tree have been placed.
* Any empty cells should contain the empty string `" "`.
Return _the constructed matrix_ `res`.
**Example 1:**
**Input:** root = \[1,2\]
**Output:**
\[\[ " ", "1 ", " "\],
\[ "2 ", " ", " "\]\]
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:**
\[\[ " ", " ", " ", "1 ", " ", " ", " "\],
\[ " ", "2 ", " ", " ", " ", "3 ", " "\],
\[ " ", " ", "4 ", " ", " ", " ", " "\]\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 210]`.
* `-99 <= Node.val <= 99`
* The depth of the tree will be in the range `[1, 10]`. | null |
Easy O(n) approach for beginner, 73% | print-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nGet height of tree in first traverse.\nCreate matrix.\nAssign value to matrix in second traver.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:\n def traverse(n:TreeNode) -> int:\n if not n:\n return 0\n return max(traverse(n.left), traverse(n.right))+1\n\n def assign(n:TreeNode, matrix:List[List[str]], r:int, c:int):\n if not n:\n return\n matrix[r][c] = str(n.val)\n assign(n.left, matrix, r+1, c-2**(self.height-r-1))\n assign(n.right, matrix, r+1, c+2**(self.height-r-1))\n \n row = traverse(root)\n col = 2**row - 1\n self.height = row - 1\n ans = [[""]*col for _ in range(row)]\n\n assign(root, ans, 0, col//2)\n return ans\n``` | 0 | Given the `root` of a binary tree, construct a **0-indexed** `m x n` string matrix `res` that represents a **formatted layout** of the tree. The formatted layout matrix should be constructed using the following rules:
* The **height** of the tree is `height` and the number of rows `m` should be equal to `height + 1`.
* The number of columns `n` should be equal to `2height+1 - 1`.
* Place the **root node** in the **middle** of the **top row** (more formally, at location `res[0][(n-1)/2]`).
* For each node that has been placed in the matrix at position `res[r][c]`, place its **left child** at `res[r+1][c-2height-r-1]` and its **right child** at `res[r+1][c+2height-r-1]`.
* Continue this process until all the nodes in the tree have been placed.
* Any empty cells should contain the empty string `" "`.
Return _the constructed matrix_ `res`.
**Example 1:**
**Input:** root = \[1,2\]
**Output:**
\[\[ " ", "1 ", " "\],
\[ "2 ", " ", " "\]\]
**Example 2:**
**Input:** root = \[1,2,3,null,4\]
**Output:**
\[\[ " ", " ", " ", "1 ", " ", " ", " "\],
\[ " ", "2 ", " ", " ", " ", "3 ", " "\],
\[ " ", " ", "4 ", " ", " ", " ", " "\]\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 210]`.
* `-99 <= Node.val <= 99`
* The depth of the tree will be in the range `[1, 10]`. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.