title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Simple simulation in Python3 | robot-return-to-origin | 0 | 1 | # Intuition\nHere we have:\n- `moves` string and a robot\n- our goal is to move a robot from **origin**, which is `[0, 0]` by `moves` and check, if after all of the moves robot **returned** to a basic origin\n\nAn algorithm is quite simple: **simulate the process**, via mapping directions with integers (`U` and `L` as `-1`, and `R` and `D` as 1 respectively). \n\n# Approach\n1. define `steps` HashMap to store moves\n2. define `origin`\n3. traverse over `moves` and move a robot, according to a particular direction\n4. return `true`, if a robot **returned to the origin** and `false` otherwise\n\n# Complexity\n- Time complexity: **O(N)** to traverse over `moves`\n\n- Space complexity: **O(1)**, since we store only `steps` as in count of `4`, that leads to **constant**\n\n# Code\n```\nclass Solution:\n def judgeCircle(self, moves: str) -> bool:\n steps = {\n \'U\': [0, -1],\n \'D\': [0, 1],\n \'L\': [1, -1],\n \'R\': [1, 1]\n }\n origin = [0, 0]\n\n for move in moves:\n dir, diff = steps[move]\n origin[dir]+= diff\n\n return origin[0] == origin[1] == 0\n``` | 1 | There is a robot starting at the position `(0, 0)`, the origin, on a 2D plane. Given a sequence of its moves, judge if this robot **ends up at** `(0, 0)` after it completes its moves.
You are given a string `moves` that represents the move sequence of the robot where `moves[i]` represents its `ith` move. Valid moves are `'R'` (right), `'L'` (left), `'U'` (up), and `'D'` (down).
Return `true` _if the robot returns to the origin after it finishes all of its moves, or_ `false` _otherwise_.
**Note**: The way that the robot is "facing " is irrelevant. `'R'` will always make the robot move to the right once, `'L'` will always make it move left, etc. Also, assume that the magnitude of the robot's movement is the same for each move.
**Example 1:**
**Input:** moves = "UD "
**Output:** true
**Explanation**: The robot moves up once, and then down once. All moves have the same magnitude, so it ended up at the origin where it started. Therefore, we return true.
**Example 2:**
**Input:** moves = "LL "
**Output:** false
**Explanation**: The robot moves left twice. It ends up two "moves " to the left of the origin. We return false because it is not at the origin at the end of its moves.
**Constraints:**
* `1 <= moves.length <= 2 * 104`
* `moves` only contains the characters `'U'`, `'D'`, `'L'` and `'R'`. | null |
Easy to understand Simple | robot-return-to-origin | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def judgeCircle(self, moves: str) -> bool:\n def move(a,i,j):\n if(a==\'L\'):\n j-=1\n elif(a==\'R\'):\n j+=1\n elif(a==\'U\'):\n i-=1\n else:\n i+=1\n return i,j\n i=j=0\n for a in moves:\n i,j=move(a,i,j)\n return i==0 and j==0\n\n \n``` | 2 | There is a robot starting at the position `(0, 0)`, the origin, on a 2D plane. Given a sequence of its moves, judge if this robot **ends up at** `(0, 0)` after it completes its moves.
You are given a string `moves` that represents the move sequence of the robot where `moves[i]` represents its `ith` move. Valid moves are `'R'` (right), `'L'` (left), `'U'` (up), and `'D'` (down).
Return `true` _if the robot returns to the origin after it finishes all of its moves, or_ `false` _otherwise_.
**Note**: The way that the robot is "facing " is irrelevant. `'R'` will always make the robot move to the right once, `'L'` will always make it move left, etc. Also, assume that the magnitude of the robot's movement is the same for each move.
**Example 1:**
**Input:** moves = "UD "
**Output:** true
**Explanation**: The robot moves up once, and then down once. All moves have the same magnitude, so it ended up at the origin where it started. Therefore, we return true.
**Example 2:**
**Input:** moves = "LL "
**Output:** false
**Explanation**: The robot moves left twice. It ends up two "moves " to the left of the origin. We return false because it is not at the origin at the end of its moves.
**Constraints:**
* `1 <= moves.length <= 2 * 104`
* `moves` only contains the characters `'U'`, `'D'`, `'L'` and `'R'`. | null |
Easy to understand Simple | robot-return-to-origin | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def judgeCircle(self, moves: str) -> bool:\n def move(a,i,j):\n if(a==\'L\'):\n j-=1\n elif(a==\'R\'):\n j+=1\n elif(a==\'U\'):\n i-=1\n else:\n i+=1\n return i,j\n i=j=0\n for a in moves:\n i,j=move(a,i,j)\n return i==0 and j==0\n\n \n``` | 1 | There is a robot starting at the position `(0, 0)`, the origin, on a 2D plane. Given a sequence of its moves, judge if this robot **ends up at** `(0, 0)` after it completes its moves.
You are given a string `moves` that represents the move sequence of the robot where `moves[i]` represents its `ith` move. Valid moves are `'R'` (right), `'L'` (left), `'U'` (up), and `'D'` (down).
Return `true` _if the robot returns to the origin after it finishes all of its moves, or_ `false` _otherwise_.
**Note**: The way that the robot is "facing " is irrelevant. `'R'` will always make the robot move to the right once, `'L'` will always make it move left, etc. Also, assume that the magnitude of the robot's movement is the same for each move.
**Example 1:**
**Input:** moves = "UD "
**Output:** true
**Explanation**: The robot moves up once, and then down once. All moves have the same magnitude, so it ended up at the origin where it started. Therefore, we return true.
**Example 2:**
**Input:** moves = "LL "
**Output:** false
**Explanation**: The robot moves left twice. It ends up two "moves " to the left of the origin. We return false because it is not at the origin at the end of its moves.
**Constraints:**
* `1 <= moves.length <= 2 * 104`
* `moves` only contains the characters `'U'`, `'D'`, `'L'` and `'R'`. | null |
Simplest Approach || Easily Understandable || Python and Java Solution | robot-return-to-origin | 1 | 1 | # Code\n```python []\nclass Solution:\n def judgeCircle(self, moves: str) -> bool:\n lr , ud = 0 , 0\n\n for move in moves:\n if move == \'U\':\n ud += 1\n elif move == \'D\':\n ud -= 1\n elif move == \'L\':\n lr += 1\n elif move == \'R\':\n lr -= 1\n\n if lr == 0 and ud == 0:\n return True\n```\n```Java []\nclass Solution {\n public boolean judgeCircle(String moves) {\n int x = 0, y = 0;\n for (int i = 0; i < moves.length(); i++) {\n char move = moves.charAt(i);\n if (move == \'U\') y--;\n else if (move == \'D\') y++;\n else if (move == \'L\') x--;\n else if (move == \'R\') x++;\n }\n return x == 0 && y == 0;\n }\n}\n``` | 8 | There is a robot starting at the position `(0, 0)`, the origin, on a 2D plane. Given a sequence of its moves, judge if this robot **ends up at** `(0, 0)` after it completes its moves.
You are given a string `moves` that represents the move sequence of the robot where `moves[i]` represents its `ith` move. Valid moves are `'R'` (right), `'L'` (left), `'U'` (up), and `'D'` (down).
Return `true` _if the robot returns to the origin after it finishes all of its moves, or_ `false` _otherwise_.
**Note**: The way that the robot is "facing " is irrelevant. `'R'` will always make the robot move to the right once, `'L'` will always make it move left, etc. Also, assume that the magnitude of the robot's movement is the same for each move.
**Example 1:**
**Input:** moves = "UD "
**Output:** true
**Explanation**: The robot moves up once, and then down once. All moves have the same magnitude, so it ended up at the origin where it started. Therefore, we return true.
**Example 2:**
**Input:** moves = "LL "
**Output:** false
**Explanation**: The robot moves left twice. It ends up two "moves " to the left of the origin. We return false because it is not at the origin at the end of its moves.
**Constraints:**
* `1 <= moves.length <= 2 * 104`
* `moves` only contains the characters `'U'`, `'D'`, `'L'` and `'R'`. | null |
Python 3, Very Easy | robot-return-to-origin | 0 | 1 | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def judgeCircle(self, moves: str) -> bool:\n x: int = 0\n y: int = 0\n for move in moves:\n if move == \'U\':\n x += 1\n elif move == \'D\':\n x -= 1\n elif move == \'L\':\n y += 1\n elif move == \'R\':\n y -= 1\n return x == 0 and y == 0\n\n``` | 2 | There is a robot starting at the position `(0, 0)`, the origin, on a 2D plane. Given a sequence of its moves, judge if this robot **ends up at** `(0, 0)` after it completes its moves.
You are given a string `moves` that represents the move sequence of the robot where `moves[i]` represents its `ith` move. Valid moves are `'R'` (right), `'L'` (left), `'U'` (up), and `'D'` (down).
Return `true` _if the robot returns to the origin after it finishes all of its moves, or_ `false` _otherwise_.
**Note**: The way that the robot is "facing " is irrelevant. `'R'` will always make the robot move to the right once, `'L'` will always make it move left, etc. Also, assume that the magnitude of the robot's movement is the same for each move.
**Example 1:**
**Input:** moves = "UD "
**Output:** true
**Explanation**: The robot moves up once, and then down once. All moves have the same magnitude, so it ended up at the origin where it started. Therefore, we return true.
**Example 2:**
**Input:** moves = "LL "
**Output:** false
**Explanation**: The robot moves left twice. It ends up two "moves " to the left of the origin. We return false because it is not at the origin at the end of its moves.
**Constraints:**
* `1 <= moves.length <= 2 * 104`
* `moves` only contains the characters `'U'`, `'D'`, `'L'` and `'R'`. | null |
Python3 my first explained solution ✅✅✅ || Faster than 74.98% ⏩ || Memory beats 62.34(need help) 🧠 | robot-return-to-origin | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI thought tracking the robot\'s coordinate would help me find it\'s current place, so I did track it\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can track every move the robot does. Since tuples are **immutable**, we have to use an array.\n1. If the robot moves up, the y coordinate should **add one**.\n2. Down, y coordinate should **go down by one**.\n3. Left, x coordinate **goes down by one**.\n4. Right, x coordinate **adds one**.\n# Complexity\n- Time complexity: O(n) time bro\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: need expert. maybe O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n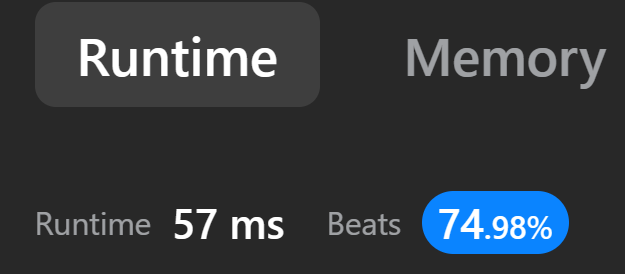\n\n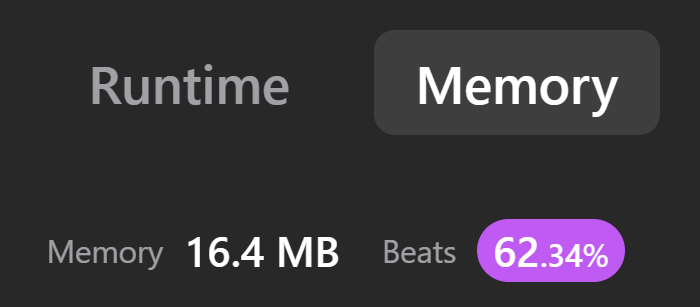\n\n\n# Code\n```\nclass Solution:\n def judgeCircle(self, moves: str) -> bool:\n original = [0, 0]\n robot = [0, 0]\n for m in moves:\n if m == "U":\n robot[1] += 1\n elif m == "D":\n robot[1] -= 1\n elif m == "L":\n robot[0] -= 1\n else:\n robot[0] += 1\n return original == robot\n``` | 2 | There is a robot starting at the position `(0, 0)`, the origin, on a 2D plane. Given a sequence of its moves, judge if this robot **ends up at** `(0, 0)` after it completes its moves.
You are given a string `moves` that represents the move sequence of the robot where `moves[i]` represents its `ith` move. Valid moves are `'R'` (right), `'L'` (left), `'U'` (up), and `'D'` (down).
Return `true` _if the robot returns to the origin after it finishes all of its moves, or_ `false` _otherwise_.
**Note**: The way that the robot is "facing " is irrelevant. `'R'` will always make the robot move to the right once, `'L'` will always make it move left, etc. Also, assume that the magnitude of the robot's movement is the same for each move.
**Example 1:**
**Input:** moves = "UD "
**Output:** true
**Explanation**: The robot moves up once, and then down once. All moves have the same magnitude, so it ended up at the origin where it started. Therefore, we return true.
**Example 2:**
**Input:** moves = "LL "
**Output:** false
**Explanation**: The robot moves left twice. It ends up two "moves " to the left of the origin. We return false because it is not at the origin at the end of its moves.
**Constraints:**
* `1 <= moves.length <= 2 * 104`
* `moves` only contains the characters `'U'`, `'D'`, `'L'` and `'R'`. | null |
(Java/Python3/JavaScript) three solutions | find-k-closest-elements | 1 | 1 | ```\n# python3\nclass Solution:\n def findClosestElements(self, arr: List[int], k: int, x: int) -> List[int]:\n\t\t# It\'s easy to write, but we need to sort it twice, so it\'s not the best way\n return sorted(sorted(arr, key = lambda v: abs(v-x))[:k])\n```\n```\n# python3\nclass Solution:\n def findClosestElements(self, arr: List[int], k: int, x: int) -> List[int]:\n\t\t# Here is the better way, we only need to search once, and then enlarge the border pointers to find what we want\n\t\tright = bisect_left(arr,x)\n left = right-1\n for _ in range(k):\n if left < 0: right += 1\n elif right >= len(arr): left -= 1\n else:\n if x-arr[left] <= arr[right]-x: left -= 1\n else: right += 1\n return arr[left+1:right]\n```\n```\n// java\nclass Solution {\n public List<Integer> findClosestElements(int[] arr, int k, int x) {\n PriorityQueue<Integer> queue = new PriorityQueue<>((a,b)->{\n int a1 = Math.abs(a-x), b1 = Math.abs(b-x);\n return a1 == b1 ? a-b : a1-b1;\n });\n for (int a : arr) queue.offer(a);\n List<Integer> ans = new ArrayList<>();\n for (int i=0; i<k; i++) {\n ans.add(queue.poll());\n }\n Collections.sort(ans);\n return ans;\n }\n}\n```\n```\n// javaScript\nvar findClosestElements = function(arr, k, x) {\n arr.sort((a,b)=>{\n const a1 = Math.abs(a-x), b1 = Math.abs(b-x);\n return a1 == b1 ? a-b : a1-b1;\n });\n const ans = arr.slice(0,k);\n ans.sort((a,b)=>a-b);\n return ans;\n};\n``` | 3 | Given a **sorted** integer array `arr`, two integers `k` and `x`, return the `k` closest integers to `x` in the array. The result should also be sorted in ascending order.
An integer `a` is closer to `x` than an integer `b` if:
* `|a - x| < |b - x|`, or
* `|a - x| == |b - x|` and `a < b`
**Example 1:**
**Input:** arr = \[1,2,3,4,5\], k = 4, x = 3
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** arr = \[1,2,3,4,5\], k = 4, x = -1
**Output:** \[1,2,3,4\]
**Constraints:**
* `1 <= k <= arr.length`
* `1 <= arr.length <= 104`
* `arr` is sorted in **ascending** order.
* `-104 <= arr[i], x <= 104` | null |
Python || 2 Approaches || Min and Max Heap | find-k-closest-elements | 0 | 1 | ```\n#Using Max Heap\nclass Solution:\n def findClosestElements(self, arr: List[int], k: int, x: int) -> List[int]:\n pq=[]\n for i in range(len(arr)):\n d = -abs(x-arr[i]) \n if len(pq) < k: \n heapq.heappush(pq,(d,arr[i]))\n else:\n if -d < -pq[0][0]:\n heapq.heappop(pq)\n heapq.heappush(pq,(d,arr[i]))\n result=[]\n for i in range(k):\n result.append(pq[i][1])\n print(result)\n return sorted(result)\n \n#Using Min Heap\nclass Solution:\n def findClosestElements(self, arr: List[int], k: int, x: int) -> List[int]:\n pq = []\n for num in arr:\n heapq.heappush(pq, (abs(num-x), num))\n ans = []\n while k:\n tup = heapq.heappop(pq)\n ans.append(tup[1])\n k-=1\n ans.sort()\n return ans\n```\n**An upvote will be encouraging** | 1 | Given a **sorted** integer array `arr`, two integers `k` and `x`, return the `k` closest integers to `x` in the array. The result should also be sorted in ascending order.
An integer `a` is closer to `x` than an integer `b` if:
* `|a - x| < |b - x|`, or
* `|a - x| == |b - x|` and `a < b`
**Example 1:**
**Input:** arr = \[1,2,3,4,5\], k = 4, x = 3
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** arr = \[1,2,3,4,5\], k = 4, x = -1
**Output:** \[1,2,3,4\]
**Constraints:**
* `1 <= k <= arr.length`
* `1 <= arr.length <= 104`
* `arr` is sorted in **ascending** order.
* `-104 <= arr[i], x <= 104` | null |
Solution | split-array-into-consecutive-subsequences | 1 | 1 | ```C++ []\nclass Solution {\n bool isSegmentPossible(vector<int>& nums, int startIdx, int endIdx)\n {\n vector<int> freq(nums[endIdx] - nums[startIdx] + 1);\n for (int i = startIdx; i <= endIdx; ++i)\n ++freq[nums[i]-nums[startIdx]];\n int lengthOneSubsequence = 0, lengthTwoSubsequence = 0, totalFreq = 0;\n for (int i = 0; i <= nums[endIdx] - nums[startIdx]; ++i)\n {\n if (freq[i] < lengthOneSubsequence + lengthTwoSubsequence)\n {\n return false;\n }\n lengthTwoSubsequence = lengthOneSubsequence;\n lengthOneSubsequence = max(0, freq[i] - totalFreq);\n totalFreq = freq[i];\n }\n return lengthOneSubsequence == 0 and lengthTwoSubsequence == 0;\n }\npublic:\n bool isPossible(vector<int>& nums) {\n int start = 0;\n for (int i = 1; i < nums.size(); ++i)\n {\n if (nums[i] - nums[i - 1] > 1)\n {\n if (!isSegmentPossible(nums, start, i - 1))\n return false;\n start = i;\n }\n }\n return isSegmentPossible(nums, start, nums.size() - 1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isPossible(self, nums: List[int]) -> bool:\n pre, k1, k2, k3 = float(\'-inf\'), 0, 0, 0\n i = 0; n = len(nums)\n\n while i < n:\n cur = nums[i]\n tmp = i\n while i < n and nums[i] == cur:\n i += 1\n cnt = i - tmp\n\n if cur > (pre + 1):\n if k1 or k2:\n return False\n k1, k2, k3 = cnt, 0, 0\n\n else:\n if cnt < (k1 + k2):\n return False\n # k1, k2, k3 = max(0, cnt - (k1 + k2 + k3)), k1, min(cnt - k1, k2 + k3)\n elif cnt <= (total := (k1 + k2 + k3)):\n k1, k2, k3 = 0, k1, cnt - k1\n else:\n k1, k2, k3 = cnt - total, k1, k2 + k3\n\n pre = cur\n\n return (k1 == 0 and k2 == 0)\n\n end = defaultdict(lambda: [0, 0, 0])\n for num in nums:\n flag = True\n if (num - 1) in end:\n for l in range(3):\n if end[num - 1][l] != 0:\n end[num - 1][l] -= 1\n end[num][min(l + 1, 2)] += 1\n flag = False\n break\n if flag:\n end[num][0] += 1\n\n for pre in end:\n if pre < (num - 1):\n if end[pre][0] or end[pre][1]:\n return False\n\n return all(end[num][0] == 0 and end[num][1] == 0 for num in end)\n\n end = defaultdict(lambda: [0, 0, 0])\n for num in nums:\n flag = True\n if (num - 1) in end:\n for l in range(3):\n if end[num - 1][l] != 0:\n end[num - 1][l] -= 1\n end[num][min(l + 1, 2)] += 1\n flag = False\n break\n if flag:\n end[num][0] += 1\n if end[num - 2][0] or end[num - 2][1]:\n return False\n del end[num - 2]\n return all(end[num][0] == 0 and end[num][1] == 0 for num in end)\n\n rem, end = Counter(nums), Counter()\n for num in nums:\n if not rem[num]:\n continue\n if end[num - 1]:\n end[num - 1] -= 1\n end[num] += 1\n elif rem[num + 1] and rem[num + 2]:\n rem[num + 1] -= 1\n rem[num + 2] -= 1\n end[num + 2] += 1\n else:\n return False\n rem[num] -= 1\n return True\n\n end = defaultdict(list)\n for num in nums:\n if end[num - 1]:\n heappush(end[num], heappop(end[num - 1]) + 1)\n else:\n heappush(end[num], 1)\n return all(end[num][0] > 2 for num in end if end[num])\n```\n\n```Java []\nclass Solution {\n public boolean isPossible(int[] nums) {\n int pre = Integer.MIN_VALUE;\n\tint p1 = 0;\n\tint p2 = 0;\n\tint p3 = 0;\n\t\n int cur = 0;\n\tint cnt = 0;\n\tint c1 = 0;\n\tint c2 = 0;\n\tint c3 = 0;\n \n for (int i = 0; i < nums.length; pre = cur, p1 = c1, p2 = c2, p3 = c3) {\n for (cur = nums[i], cnt = 0; i < nums.length && cur == nums[i]; i++) {\n\t\t\tcnt++;\n\t\t}\n if (cur != pre + 1) {\n if (p1 != 0 || p2 != 0) {\n\t\t\t\treturn false;\n\t\t\t}\n c1 = cnt;\n\t\t\tc2 = 0;\n\t\t\tc3 = 0;\n } else {\n if (cnt < p1 + p2) {\n\t\t\t\treturn false;\n\t\t\t}\n c2 = p1;\n c3 = p2;\n if (cnt - (p1 + p2) > 0) {\n c3 += Math.min(p3, cnt - (p1 + p2));\n }\n c1 = Math.max(0, cnt - (p1 + p2 + p3));\n }\n }\n return (p1 == 0 && p2 == 0); \n }\n}\n```\n | 1 | You are given an integer array `nums` that is **sorted in non-decreasing order**.
Determine if it is possible to split `nums` into **one or more subsequences** such that **both** of the following conditions are true:
* Each subsequence is a **consecutive increasing sequence** (i.e. each integer is **exactly one** more than the previous integer).
* All subsequences have a length of `3` **or more**.
Return `true` _if you can split_ `nums` _according to the above conditions, or_ `false` _otherwise_.
A **subsequence** of an array is a new array that is formed from the original array by deleting some (can be none) of the elements without disturbing the relative positions of the remaining elements. (i.e., `[1,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,3,2]` is not).
**Example 1:**
**Input:** nums = \[1,2,3,3,4,5\]
**Output:** true
**Explanation:** nums can be split into the following subsequences:
\[**1**,**2**,**3**,3,4,5\] --> 1, 2, 3
\[1,2,3,**3**,**4**,**5**\] --> 3, 4, 5
**Example 2:**
**Input:** nums = \[1,2,3,3,4,4,5,5\]
**Output:** true
**Explanation:** nums can be split into the following subsequences:
\[**1**,**2**,**3**,3,**4**,4,**5**,5\] --> 1, 2, 3, 4, 5
\[1,2,3,**3**,4,**4**,5,**5**\] --> 3, 4, 5
**Example 3:**
**Input:** nums = \[1,2,3,4,4,5\]
**Output:** false
**Explanation:** It is impossible to split nums into consecutive increasing subsequences of length 3 or more.
**Constraints:**
* `1 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000`
* `nums` is sorted in **non-decreasing** order. | null |
Python 524ms 98.3% Faster Multiple solutions 94% memory efficient | split-array-into-consecutive-subsequences | 0 | 1 | # DON\'T FORGET TO UPVOTE!!!\n# 1. 98% faster 524 ms solution:\n\n\t\tclass Solution:\n\t\t\tdef isPossible(self, nums: List[int]) -> bool:\n\t\t\t\tlen1 = len2 = absorber = 0\n\t\t\t\tprev_num = nums[0] - 1\n\t\t\t\tfor streak_len, streak_num in Solution.get_streaks(nums):\n\t\t\t\t\tif streak_num == prev_num + 1:\n\t\t\t\t\t\tspillage = streak_len - len1 - len2\n\t\t\t\t\t\tif spillage < 0:\n\t\t\t\t\t\t\treturn False\n\t\t\t\t\t\tabsorber = min(absorber, spillage)\n\t\t\t\t\t\tlen1, len2, absorber = spillage - absorber, len1, absorber + len2\n\t\t\t\t\telse:\n\t\t\t\t\t\tif len1 or len2:\n\t\t\t\t\t\t\treturn False\n\t\t\t\t\t\tabsorber = 0\n\t\t\t\t\tprev_num = streak_num\n\t\t\t\treturn len1 == len2 == 0\n\n\t\t\t@staticmethod\n\t\t\tdef get_streaks(nums: List[int]):\n\t\t\t\tstreak_num = nums[0]\n\t\t\t\tstreak_len = 0\n\t\t\t\tfor num in nums:\n\t\t\t\t\tif num == streak_num:\n\t\t\t\t\t\tstreak_len += 1\n\t\t\t\t\telse:\n\t\t\t\t\t\tyield streak_len, streak_num\n\t\t\t\t\t\tstreak_num = num\n\t\t\t\t\t\tstreak_len = 1\n\t\t\t\tyield streak_len, streak_num\n\t\t\t\t\n\t\t\t\t\n# 2. Memory Efficient solution:\n\n\t\t\tclass Solution:\n\t\t\t\tdef isPossible(self, nums: List[int]) -> bool:\n\t\t\t\t\tcounter = collections.Counter(nums)\n\t\t\t\t\tfor i in sorted(counter.keys()):\n\t\t\t\t\t\twhile counter[i] > 0:\n\t\t\t\t\t\t\tlast = 0\n\t\t\t\t\t\t\tj = i\n\t\t\t\t\t\t\tk = 0\n\t\t\t\t\t\t\twhile counter[j] >= last:\n\t\t\t\t\t\t\t\tlast = counter[j]\n\t\t\t\t\t\t\t\tcounter[j] -= 1\n\t\t\t\t\t\t\t\tj += 1\n\t\t\t\t\t\t\t\tk += 1\n\t\t\t\t\t\t\tif k < 3:\n\t\t\t\t\t\t\t\treturn False\n\t\t\t\t\treturn True\n\t\t\t\t\t\n# 3 Easy explained approach:\n\n\tclass Solution:\n\t\tdef isPossible(self, nums: List[int]) -> bool:\n\n\t\t\tif len(nums) < 3: return False\n\n\t\t\tfrequency = collections.Counter(nums)\n\t\t\tsubsequence = collections.defaultdict(int)\n\n\t\t\tfor i in nums:\n\n\t\t\t\tif frequency[i] == 0:\n\t\t\t\t\tcontinue\n\n\t\t\t\tfrequency[i] -= 1\n\n\t\t\t\t# option 1 - add to an existing subsequence\n\t\t\t\tif subsequence[i-1] > 0:\n\t\t\t\t\tsubsequence[i-1] -= 1\n\t\t\t\t\tsubsequence[i] += 1\n\n\t\t\t\t# option 2 - create a new subsequence \n\t\t\t\telif frequency[i+1] and frequency[i+2]:\n\t\t\t\t\tfrequency[i+1] -= 1\n\t\t\t\t\tfrequency[i+2] -= 1\n\t\t\t\t\tsubsequence[i+2] += 1\n\n\t\t\t\telse:\n\t\t\t\t\treturn False\n\n\t\t\treturn True\n\n\t\t# TC: O(n), SC: O(n) | 45 | You are given an integer array `nums` that is **sorted in non-decreasing order**.
Determine if it is possible to split `nums` into **one or more subsequences** such that **both** of the following conditions are true:
* Each subsequence is a **consecutive increasing sequence** (i.e. each integer is **exactly one** more than the previous integer).
* All subsequences have a length of `3` **or more**.
Return `true` _if you can split_ `nums` _according to the above conditions, or_ `false` _otherwise_.
A **subsequence** of an array is a new array that is formed from the original array by deleting some (can be none) of the elements without disturbing the relative positions of the remaining elements. (i.e., `[1,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,3,2]` is not).
**Example 1:**
**Input:** nums = \[1,2,3,3,4,5\]
**Output:** true
**Explanation:** nums can be split into the following subsequences:
\[**1**,**2**,**3**,3,4,5\] --> 1, 2, 3
\[1,2,3,**3**,**4**,**5**\] --> 3, 4, 5
**Example 2:**
**Input:** nums = \[1,2,3,3,4,4,5,5\]
**Output:** true
**Explanation:** nums can be split into the following subsequences:
\[**1**,**2**,**3**,3,**4**,4,**5**,5\] --> 1, 2, 3, 4, 5
\[1,2,3,**3**,4,**4**,5,**5**\] --> 3, 4, 5
**Example 3:**
**Input:** nums = \[1,2,3,4,4,5\]
**Output:** false
**Explanation:** It is impossible to split nums into consecutive increasing subsequences of length 3 or more.
**Constraints:**
* `1 <= nums.length <= 104`
* `-1000 <= nums[i] <= 1000`
* `nums` is sorted in **non-decreasing** order. | null |
Solution | image-smoother | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n\tvector<vector<int>> imageSmoother(vector<vector<int>>& img) {\n\t\tint m=img.size();\n\t\tint n=img[0].size();\n\t\tvector<vector<int>>mat=img;\n\t\tfor(int i=0;i<m;i++){\n\t\t\tfor(int j=0;j<n;j++){\n\t\t\t\tint sum=img[i][j];\n\t\t\t\tint count=1;\n\t\t\t\tif(i-1>=0){\n\t\t\t\t\tsum+=img[i-1][j];\n\t\t\t\t\tcount++;\n\t\t\t\t\tif(j+1<n){\n\t\t\t\t\t\tsum+=img[i-1][j+1];\n\t\t\t\t\t\tcount++;\n\t\t\t\t\t}\n\t\t\t\t\tif(j-1>=0){\n\t\t\t\t\t\tsum+=img[i-1][j-1];\n\t\t\t\t\t\tcount++;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tif(i+1<m){\n\t\t\t\t\tsum+=img[i+1][j];\n\t\t\t\t\tcount++;\n\t\t\t\t\tif(j-1>=0){\n\t\t\t\t\t\tsum+=img[i+1][j-1];\n\t\t\t\t\t\tcount++;\n\t\t\t\t\t}\n\t\t\t\t\tif(j+1<n){\n\t\t\t\t\t\tsum+=img[i+1][j+1];\n\t\t\t\t\t\tcount++;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tif(j-1>=0){\n\t\t\t\t\tsum+=img[i][j-1];\n\t\t\t\t\tcount++;\n\t\t\t\t}\n\t\t\t\tif(j+1<n){\n\t\t\t\t\tsum+=img[i][j+1];\n\t\t\t\t\tcount++;\n\t\t\t\t}\n\t\t\t\tmat[i][j]=(int)(sum/count);\n\t\t\t}\n\t\t}\n\t\treturn mat;\n\t}\n};\n```\n\n```Python3 []\nfrom itertools import product\nimport numpy as np \n\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n m, n = len(img), len(img[0])\n img_np = np.zeros((m+2, n+2), dtype=np.int32)\n img_np[1:-1, 1:-1] = img\n cnt_np = np.zeros((m+2, n+2), dtype=np.int32)\n cnt_np[1:-1, 1:-1] = 1\n\n reduce_img = lambda x: sum([x[o1:m+o1, o2:n+o2] for o1, o2 in product(range(3), range(3))])\n\n\n ans = reduce_img(img_np) // reduce_img(cnt_np)\n return ans.tolist()\n```\n\n```Java []\nclass Solution {\n public int[][] imageSmoother(int[][] img) {\n int rowLast = img.length - 1;\n int colLast = img[0].length - 1;\n if (rowLast == 0) { \n if (colLast != 0) singleRow(img[0], colLast);\n }\n else if (colLast == 0) { \n singleCol(img, rowLast);\n }\n else { \n for (int row = 0; row <= rowLast; row++) \n sumRow(img[row], colLast);\n sumCol(img, 0, 4, 6, rowLast); \n sumCol(img, colLast, 4, 6, rowLast); \n for (int col = 1; col < colLast; col++) \n sumCol(img, col, 6, 9, rowLast);\n }\n return img;\n }\n private void singleRow(int[] MR, int colLast) {\n int prev = 0;\n int curr = MR[0];\n int next = MR[1];\n MR[0] = (curr + next) / 2;\n for (int col = 1; col < colLast; col++) {\n prev = curr;\n curr = next;\n next = MR[col+1];\n MR[col] = (prev + curr + next) / 3;\n }\n MR[colLast] = (next + curr) / 2;\n }\n private void singleCol(int[][] M, int rowLast) {\n int prev = 0;\n int curr = M[0][0];\n int next = M[1][0];\n M[0][0] = (curr + next) / 2;\n for (int row = 1; row < rowLast; row++) {\n prev = curr;\n curr = next;\n next = M[row+1][0];\n M[row][0] = (prev + curr + next) / 3;\n }\n M[rowLast][0] = (next + curr) / 2;\n }\n private void sumRow(int[] MR, int colLast) {\n int prev = 0;\n int curr = 0;\n int next = MR[0];\n for (int col = 0; col < colLast; col++) {\n prev = curr;\n curr = next;\n next = MR[col+1];\n MR[col] = prev + curr + next;\n }\n MR[colLast] = next + curr;\n }\n private void sumCol(int[][] M, int col, int endDiv, int midDiv, int rowLast) {\n int prev = 0;\n int curr = M[0][col];\n int next = M[1][col];\n M[0][col] = (curr + next) / endDiv;\n for (int row = 1; row < rowLast; row++) {\n prev = curr;\n curr = next;\n next = M[row+1][col];\n M[row][col] = (prev + curr + next) / midDiv;\n }\n M[rowLast][col] = (next + curr) / endDiv;\n}\n}\n```\n | 1 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
661: Solution with step by step explanation | image-smoother | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function called imageSmoother that takes in a 2D list of integers called img and returns a 2D list of integers.\n2. Get the dimensions of the original image by getting the length of img (number of rows) and the length of the first row in img (number of columns).\n3. Initialize the output matrix called res with zeros. The size of res is the same as img.\n4. Iterate through each cell in the image using two nested for loops that go from 0 to m-1 and from 0 to n-1, respectively.\n5. For each cell, calculate the sum of the cells in the 3x3 neighborhood by creating two nested for loops that go from i-1 to i+1 and from j-1 to j+1, respectively.\n6. Check if the current cell is inside the image by using an if statement. If the cell is inside the image, add its value to the total variable and increment the count variable by 1.\n7. Calculate the smoothed value for the cell by dividing the total by the count and rounding down to the nearest integer using the // operator.\n8. Return the output matrix res.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n # dimensions of original image\n m, n = len(img), len(img[0])\n # initialize output matrix with zeros\n res = [[0] * n for _ in range(m)]\n # iterate through each cell in the image\n for i in range(m):\n for j in range(n):\n # calculate the sum of the cells in the 3x3 neighborhood\n total = 0\n count = 0\n for x in range(i-1, i+2):\n for y in range(j-1, j+2):\n # check if the cell is inside the image\n if 0 <= x < m and 0 <= y < n:\n total += img[x][y]\n count += 1\n # calculate the smoothed value for the cell\n res[i][j] = total // count\n return res\n\n``` | 5 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
Python solution beats 90% | image-smoother | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this problem is to smooth an image by averaging the value of each pixel with its surrounding pixels. One way to achieve this is to iterate through each pixel in the image and average the values of the 8 neighboring pixels.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used in the provided code is to iterate through each pixel in the image, and for each pixel, iterate through its 8 neighboring pixels. If the neighboring pixel is within the bounds of the image, its value is added to a running total for the current pixel, and a count is incremented to keep track of how many neighboring pixels were used in the average. Once all neighboring pixels have been considered, the running total is divided by the count to find the average value, which is then assigned as the new value for the current pixel.\n# Complexity\n- Time complexity: $$O(m*n) $$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nwhere m is the number of rows in the image and n is the number of columns in the image. This is because the algorithm iterates through each pixel in the image once, and for each pixel, it iterates through its 8 neighboring pixels.\n- Space complexity: $$O(m*n) $$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere m is the number of rows in the image and n is the number of columns in the image. This is because the algorithm creates a new 2D list of the same size as the input image to store the smoothed image.\n# Code\n```\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n m, n = len(img), len(img[0])\n res = [[0] * n for _ in range(m)]\n for i in range(m):\n for j in range(n):\n count = 0\n for x in range(i-1, i+2):\n for y in range(j-1, j+2):\n if 0 <= x < m and 0 <= y < n:\n res[i][j] += img[x][y]\n count += 1\n res[i][j] //= count\n return res\n``` | 3 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
python 3 || clean and efficient solution | image-smoother | 0 | 1 | ```\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n m, n = len(img), len(img[0])\n \n def avg(i, j):\n s = squares = 0\n top, bottom = max(0, i - 1), min(m, i + 2)\n left, right = max(0, j - 1), min(n, j + 2)\n\n for x in range(top, bottom):\n for y in range(left, right):\n s += img[x][y]\n squares += 1\n \n return s // squares\n \n return [[avg(i, j) for j in range(n)] for i in range(m)] | 9 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
Python3 simple solution | image-smoother | 0 | 1 | ```\nclass Solution:\n def imageSmoother(self, M: List[List[int]]) -> List[List[int]]:\n row, col = len(M), len(M[0])\n res = [[0]*col for i in range(row)]\n dirs = [[0,0],[0,1],[0,-1],[1,0],[-1,0],[1,1],[-1,-1],[-1,1],[1,-1]]\n for i in range(row):\n for j in range(col):\n temp = [M[i+m][j+n] for m,n in dirs if 0<=i+m<row and 0<=j+n<col]\n res[i][j] = sum(temp)//len(temp)\n return res\n``` | 16 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
Simple intuitive method | image-smoother | 0 | 1 | # Intuition\nRead the code.\nIf you cant understand it, get off of leetcode and go back to doing scratch; This is literally the most simple solution you will find.\n\n\n# Approach\nInitialise a zero matrix with the same dimensions as img, go through the matrix and take the average of all available surround points, set the value in that zero matrix to the floor of the average, return the filled out zero matrix.\n# Complexity\n- Time complexity:\n$$O(n^2)$$ its not efficient but it gets the job done and its intuive.\n\n\n# Code\n```\nimport numpy\n\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n m = len(img)\n n = len(img[0])\n\n ans = [[0]*n for _ in range(m)]\n\n for i in range(m):\n for j in range(n):\n total = 0\n count = 0\n for x in range(i-1, i+2):\n for y in range(j-1, j+2):\n if 0 <= x < m and 0 <= y < n:\n total += img[x][y]\n count += 1\n ans[i][j] = total//count\n return ans\n \n \n\n```\n\nUpvote or else Stackoverflow will break for you.\nDon\'t act like you\'ve never used it. I know you have. | 0 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
Intuitive approach - Python! | image-smoother | 0 | 1 | # Code\n```\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n m, n, c = len(img), len(img[0]), 0\n ans = [[0 for _ in range(n)] for _ in range(m)]\n \n for i in range(m):\n rowStart, rowEnd = max(0, i - 1), min(m, i + 2)\n for j in range(n):\n colStart, colEnd = max(0, j - 1), min(n, j + 2)\n for l in range(rowStart, rowEnd):\n c += len(img[l][colStart:colEnd])\n ans[i][j] += sum(img[l][colStart:colEnd])\n ans[i][j] //= c\n c = 0\n \n return ans\n```\n\n | 0 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
Dead Easy Python Solution...!!!!! | image-smoother | 0 | 1 | # Dead Easy Python Solution\n\n# Code\n```\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n n = len(img)\n m = len(img[0])\n ans = [[0]*m for i in range(n)]\n for row in range(n):\n for col in range(m):\n s = 0\n c = 0\n for i in range(-1,2):\n for j in range(-1,2):\n nrow = row + i\n ncol = col + j\n if 0<=nrow<n and 0<=ncol<m:\n s += img[nrow][ncol]\n c += 1\n ans[row][col] = s//c\n return ans\n\n```\n\n# Upvote if it helped you.....! | 0 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
EASY PEASY PYTHON SOLUTION | image-smoother | 0 | 1 | # Code\n```\nclass Solution:\n def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:\n m = len(img)\n n = len(img[0])\n def apply(img,start,end,m,n):\n i,j = start\n s,c = 0,0\n if i<0: i=0\n if i>m: i=m\n if j<0: j=0\n if j>n: j=n\n for row in range(i,end[0]+1):\n if row>=m:continue\n for col in range(j,end[1]+1):\n if col>=n:continue\n s += img[row][col]\n c += 1\n return s//c\n ans = []\n for row in range(m):\n temp = []\n for col in range(n):\n temp.append(apply(img,(row-1,col-1),(row+1,col+1),m,n))\n ans.append(temp)\n return ans\n \n\n\n``` | 0 | An **image smoother** is a filter of the size `3 x 3` that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).
Given an `m x n` integer matrix `img` representing the grayscale of an image, return _the image after applying the smoother on each cell of it_.
**Example 1:**
**Input:** img = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
**Example 2:**
**Input:** img = \[\[100,200,100\],\[200,50,200\],\[100,200,100\]\]
**Output:** \[\[137,141,137\],\[141,138,141\],\[137,141,137\]\]
**Explanation:**
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138
**Constraints:**
* `m == img.length`
* `n == img[i].length`
* `1 <= m, n <= 200`
* `0 <= img[i][j] <= 255` | null |
Simple solution with Python (BFS) | maximum-width-of-binary-tree | 0 | 1 | \n# Complexity\n- Time complexity: O(N+K) -> O(N), where N is count of root nodes and K is root depth\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(K) -> O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n lvls = []\n\n def helper(node, lvl, num):\n if not node:\n return\n\n if len(lvls) == lvl:\n lvls.append([float(\'+inf\'), 0])\n\n lvls[lvl][0] = min(lvls[lvl][0], num)\n lvls[lvl][1] = max(lvls[lvl][1], num)\n\n helper(node.left, lvl + 1, num * 2)\n helper(node.right, lvl + 1, num * 2 + 1)\n\n helper(root, 0, 0)\n\n return max(lvl[1] - lvl[0] + 1 for lvl in lvls)\n``` | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python solution with node numbering | maximum-width-of-binary-tree | 0 | 1 | ```\nJust number the nodes, like what we do to keep a tree in an array. \n\n root:x \nleft:2*x+1 right:2*x+2\n\nNow, this can get above the integer limit, but since our \nanswer is always withing the integer range, we can use mod \nhere. the difference of the rightmost and leftmost number is within in. \n\n*Also the numbering of nodes in a particual level are in a sequence from left to right \neg \n1\n2 3 \n4 5 6 7 \n... so on \n\n```\n# Code\n```\n\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n level = defaultdict(lambda : [pow(2,32),0])\n def rec(node,h,num):\n if(node == None): return ""\n else:\n if(level[h][0] > num%pow(2,31) ): level[h][0] = num%pow(2,31)\n if(level[h][1] < num%pow(2,31) ): level[h][1] = num%pow(2,31)\n rec(node.left,h+1,num*2+1)\n rec(node.right,h+1,num*2+2)\n rec(root,0,0)\n res = 0\n \n for key in level.keys():\n res = max( res , level[key][1]-level[key][0])\n print(level[key]) \n return res +1\n``` | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python3 👍||⚡89/95 faster beats 🔥|| clean solution || simple explain || | maximum-width-of-binary-tree | 0 | 1 | \n\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n queue = deque([([root],[1])])\n ans = 1\n while queue:\n q,i = [],[]\n cur_lv = queue.popleft()\n for cur,index in zip(cur_lv[0],cur_lv[1]):\n if cur.left:\n q.append(cur.left)\n i.append(2*index)\n if cur.right:\n q.append(cur.right)\n i.append(2*index+1)\n if q:\n ans = max(ans,i[-1]-i[0]+1)\n queue = deque([(q,i)])\n continue\n queue.clear()\n return ans\n``` | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
BFS || Binary Tree || Day 11 || PLEASE UPVOTE | maximum-width-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n res = 0\n q = deque([[root,1,0]])\n prevLevel, prevNum = 0, 1\n\n while q:\n node, num, level = q.popleft()\n if level > prevLevel:\n prevLevel = level\n prevNum = num\n res = max(res, num-prevNum+1)\n\n if node.left:\n q.append([node.left, 2* num, level + 1])\n if node.right:\n q.append([node.right, 2*num + 1, level+1])\n return res\n```\n**CORRECT IF ANYTHING WRONG**\n**PLEASE UPVOTE** | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
✅✅Python🔥Java 🔥C++🔥Simple Solution🔥Easy to Understand🔥 | maximum-width-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach to solve this problem is to perform a level-order traversal of the binary tree using a queue. For each node, we calculate its corresponding index value based on the level order traversal. We keep track of the start index of each level to calculate the width of the level. Finally, we return the maximum width of all levels.\n\nWe can see that the width of each level can be calculated using the index values of the nodes in the level-order traversal. For example, the first level contains only one node with index 0, so its width is 1. The second level contains nodes with indices 1 and 2, so its width is 2-1+1=2. The third level contains nodes with indices 3, 4, and 5, so its width is 5-2+1=4. Therefore, the maximum width of this binary tree is 4.\n\nWe can use a queue to perform a level-order traversal of the binary tree. For each node, we calculate its corresponding index value based on its level order traversal. We keep track of the start index of each level to calculate the width of the level. Finally, we return the maximum width of all levels.\n\nThe intuition behind this approach is that the level-order traversal of the binary tree allows us to calculate the index values of the nodes in a left-to-right order. We can use these index values to calculate the width of each level and find the maximum width of all levels.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n if not root: \n return 0\n res = 0\n q = collections.deque() \n q.append((0, root))\n while q:\n res = max(res, q[-1][0] - q[0][0] + 1)\n for i in range(len(q)):\n index, current_node = q.popleft()\n if current_node.left: \n q.append(( 2 * index, current_node.left))\n if current_node.right: \n q.append((2 * index + 1, current_node.right)) \n return res\n\n\n\n\n```\n\n\n\n\n\n | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python3 Solution | maximum-width-of-binary-tree | 0 | 1 | \n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n if root is None:\n return 0\n\n q=[(root,0)]\n width=1\n while len(q)!=0:\n if len(q)>1:\n width=max(width,q[-1][1]-q[0][1]+1)\n\n temp_q=[]\n while len(q)!=0:\n node,position=q.pop(0)\n\n if node.left!=None:\n temp_q.append((node.left,position*2))\n\n if node.right!=None:\n temp_q.append((node.right,position*2+1))\n\n q=temp_q \n \n return width\n``` | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python BFS | maximum-width-of-binary-tree | 0 | 1 | # Approach\nBFS traversal while keeping track of each nodes index. The trick is that the index of the left child of a node x is 2 * index_of_x, and the index of the right child of a node x is (2 * index_of_x) + 1.\n\nThen, since we\'re doing BFS, we can just check the first (left) and last (right) node of each level. This is O(1) time complexity in Python because a deque is a double ended linked list, meaning that operations at the front and back are O(1).\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N), where N = number of nodes.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N) because last level may contain N/2 nodes.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n\n queue = deque([(root, 1)])\n ans = 0\n while queue:\n\n left_index = queue[0][1]\n right_index = queue[-1][1]\n ans = max(ans, right_index - left_index + 1)\n\n for _ in range(len(queue)):\n node, index = queue.popleft()\n if node.left:\n queue.append((node.left, index * 2))\n if node.right:\n queue.append((node.right, index * 2 + 1))\n \n return ans\n``` | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Solution | maximum-width-of-binary-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int widthOfBinaryTree(TreeNode* root) {\n long long int ans=0;\n if(root==NULL)return 0;\n \n queue<pair<TreeNode*,long long>> q;\n q.push({root,0});\n\n while(!q.empty()){\n int sz = q.size();\n long long int mini = q.front().second;\n long long int first,last;\n for(int i =0;i<sz;i++){\n long long cur_idx = q.front().second-mini;\n TreeNode * cur = q.front().first;\n q.pop();\n if(i==0)first = cur_idx;\n if(i==sz-1)last = cur_idx;\n\n if(cur->left){\n q.push({cur->left,2*cur_idx+1});\n }\n if(cur->right){\n q.push({cur->right,2*cur_idx+2});\n }\n } \n ans = max(ans,last-first+1); \n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n res = []\n queue= collections.deque()\n queue.append((root,0))\n maxw = 0\n while queue:\n qlen = len(queue)\n nl,base = queue[0]\n for i in range(qlen):\n node,indx = queue.popleft()\n if node.left:\n queue.append((node.left,2*indx))\n if node.right:\n queue.append((node.right,(2*indx)+1))\n maxw = max(maxw,indx-base+1)\n return maxw\n```\n\n```Java []\nclass Pair{\n TreeNode node;\n int pos;\n Pair(TreeNode node,int pos){\n this.node=node;\n this.pos=pos;\n }\n}\nclass Solution {\n public int widthOfBinaryTree(TreeNode root) {\n Queue<Pair> q=new LinkedList<>();\n int max=0;\n q.add(new Pair(root,0));\n while(!q.isEmpty()){\n int size=q.size();\n int min=q.peek().pos;\n int first=0; int last=0;\n for(int i=0;i<size;i++){\n int curr=q.peek().pos-min;\n TreeNode node=q.poll().node;\n if(i==0) first=curr;\n if(i==size-1) last=curr;\n if(node.left!=null) q.add(new Pair(node.left,(2*curr)+1));\n if(node.right!=null) q.add(new Pair(node.right,(2*curr)+2));\n }\n max=Math.max(max,last-first+1);\n }\n return max;\n }\n}\n```\n | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python Solution With Diagrams and Explanation | maximum-width-of-binary-tree | 0 | 1 | # Intuition\nInstead of keeping track of distance between each node.\nKeep track of "what could be the possible index"\n\nFor example \nIf we look at the example tree\n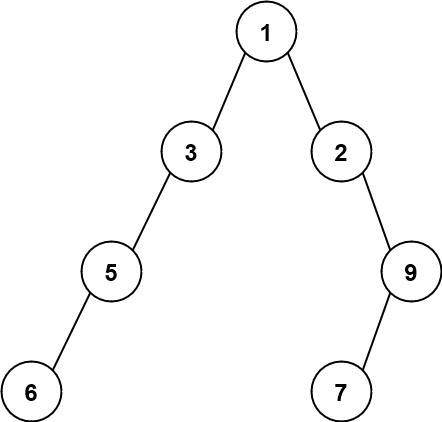\n\nWe could fill out our indexes as such \n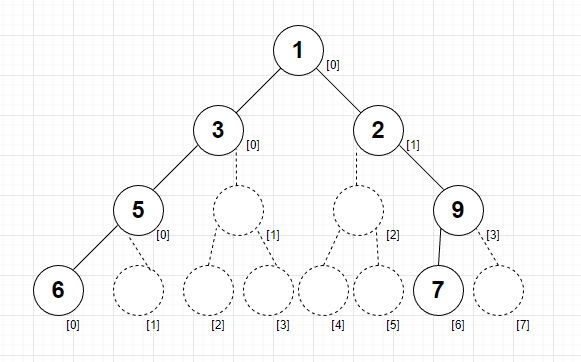\n\nNotice how relation between a node\'s index and it\'s left child index is (2 node\'s index) and it\'s right child is (2 X node+1).\nFor example at `node=9` which is at `index=3`. So it\'s left child is at `index=3*2` for `node=7` and its possible right child would be at `index=(3*2)+1`\nLet\'s see how we can use this to our advantage.\n\n# Approach\nStore the left and right index in a dictionary of 2 elements `dic` and a `self.max_diff` to keep track of maximum diff in a level.\n\nAt every level we update the level\'s maximum and minimum index and set our `self.max_diff` accordingly\n```\ndic.setdefault(level, [index, index])\ndic[level][0] = min(dic[level][0], index)\ndic[level][1] = max(dic[level][1], index)\nself.max_diff = max(self.max_diff, dic[level][1] - dic[level][0])\n```\nWe are using index at `0` to keep our minimum index and `1` to keep our maximum index.\n\nEverytime we traverse left we take our node\'s current index, and multiply it by 2.\n```\ntraversal(root.left, 2*index, level+1, dic)\n```\nEverytime we traverse right we take the node\'s current index, multiply it by 2 and add 1 (Check initution section)\n```\ntraversal(root.right, 2*index+1, level+1, dic)\n```\n\nSimply start the call by passing the original root, index as `0` and level as `0`.\n```\ntraversal(root, 0, 0, dic)\n```\n\nIn the end return \n```\nreturn self.max_diff+1\n```\nWhy the +1? Since we need to also include the node in our distance calculation.\n\n\n# Complexity\n- Time complexity:\nO(n) Since we need to take into account every node.\nNote: It might be intuitive to think that just traversing the left and right boundary is enough. However that doesn\'t seem to be the case, as a larger subtree can be found from one of the middle nodes of the tree.\n\n- Space complexity:\nO(log n) Since our dictionary size is same as level size.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n dic = {}\n self.max_diff = 0\n def traversal(root, index, level, dic):\n if root is None:\n return \n dic.setdefault(level, [index, index])\n dic[level][0] = min(dic[level][0], index)\n dic[level][1] = max(dic[level][1], index)\n self.max_diff = max(self.max_diff, dic[level][1] - dic[level][0])\n\n traversal(root.left, 2*index, level+1, dic)\n traversal(root.right, 2*index+1, level+1, dic)\n traversal(root, 0, 0, dic)\n return self.max_diff+1\n``` | 8 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python BFS | maximum-width-of-binary-tree | 0 | 1 | ```\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n q, width = deque([(root, 0)]), 0\n while q:\n width = max(width, q[-1][1] - q[0][1])\n for _ in range(len(q)):\n node, k = q.popleft()\n if node.left:\n q.append((node.left, k * 2 - 1))\n if node.right:\n q.append((node.right, k * 2))\n return width + 1\n\n``` | 12 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Image Explanation🏆- [Why long to int ??] - C++/Java/Python | maximum-width-of-binary-tree | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Maximum Width of Binary Tree` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n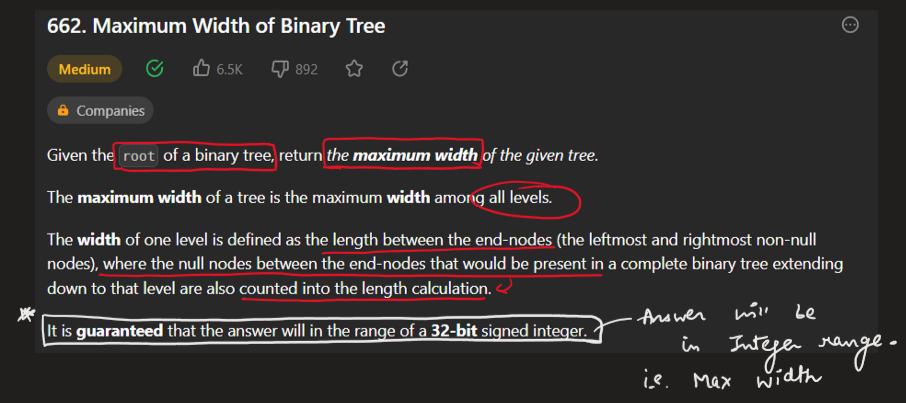\n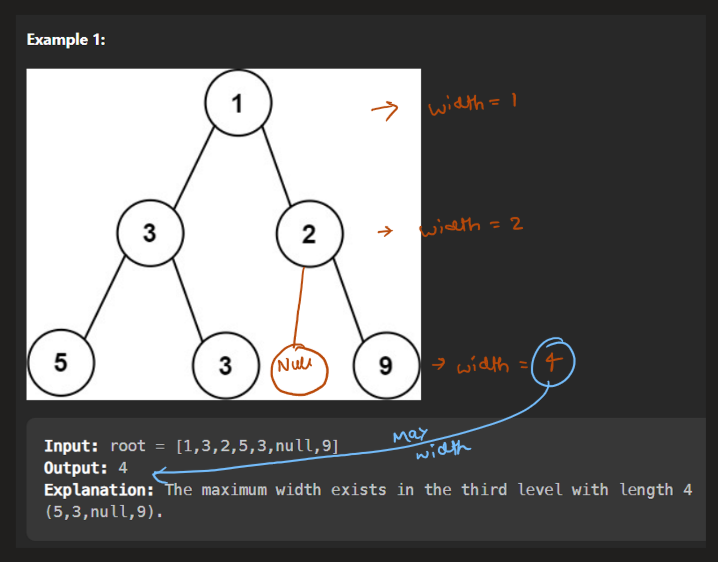\n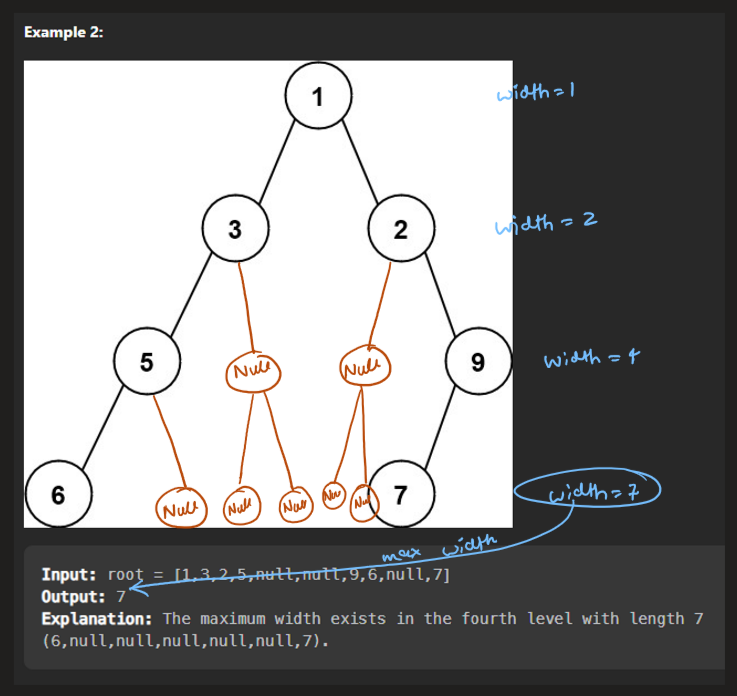\n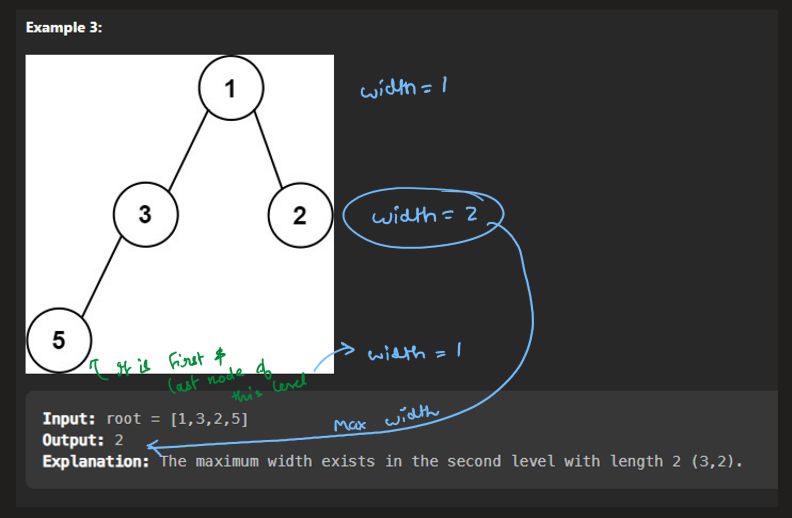\n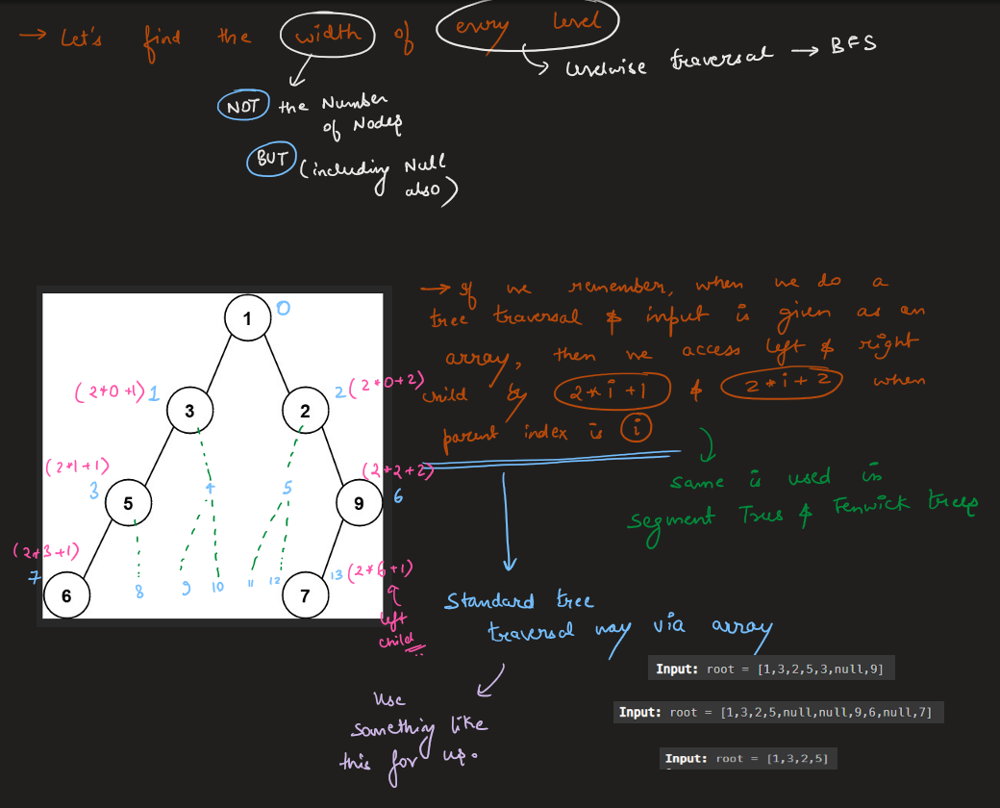\n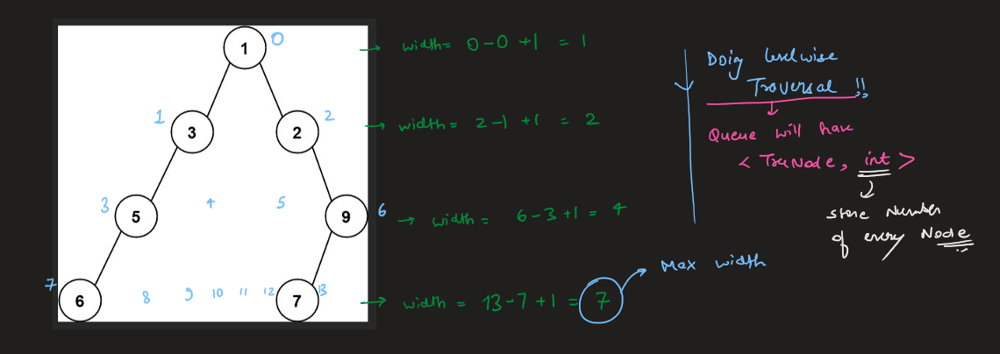\n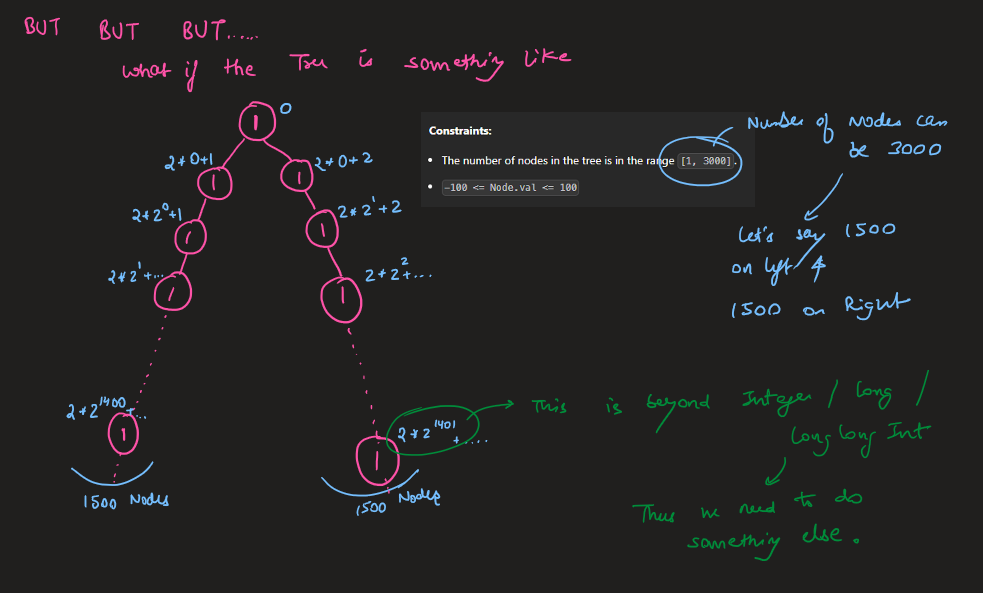\n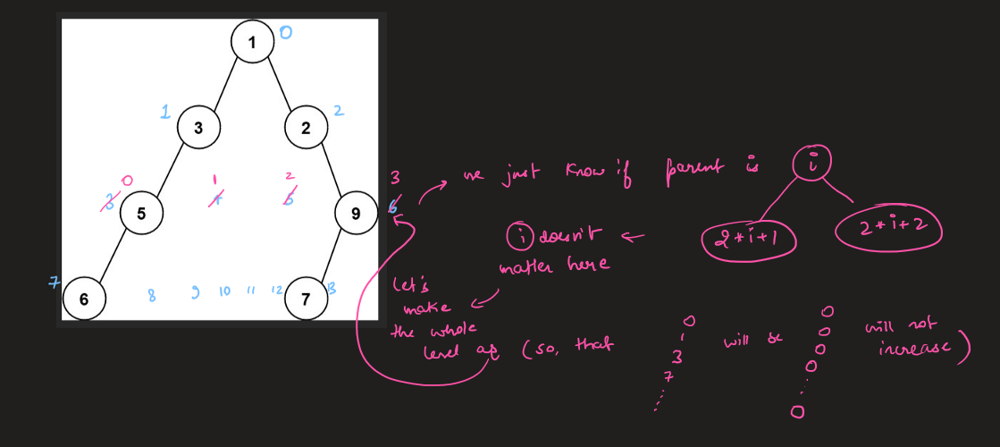\n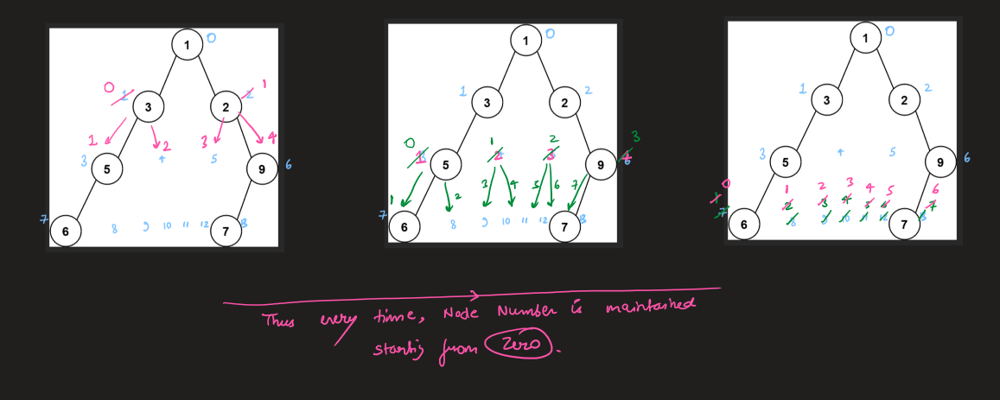\n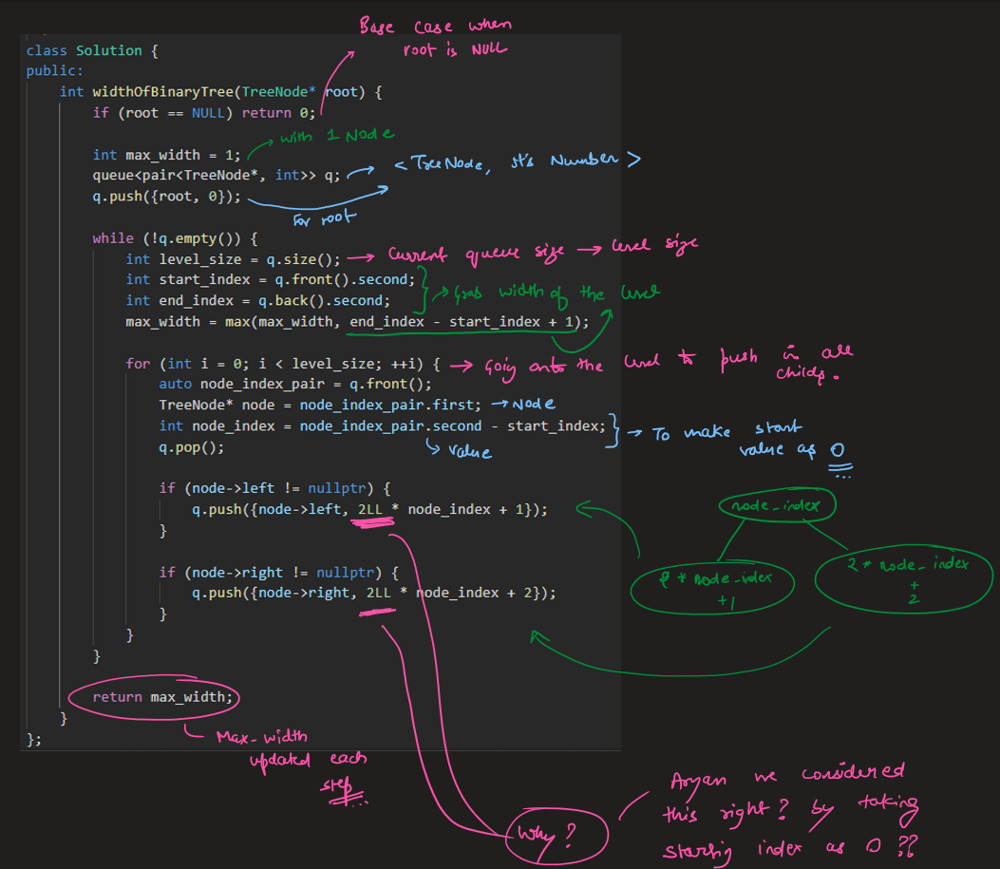\n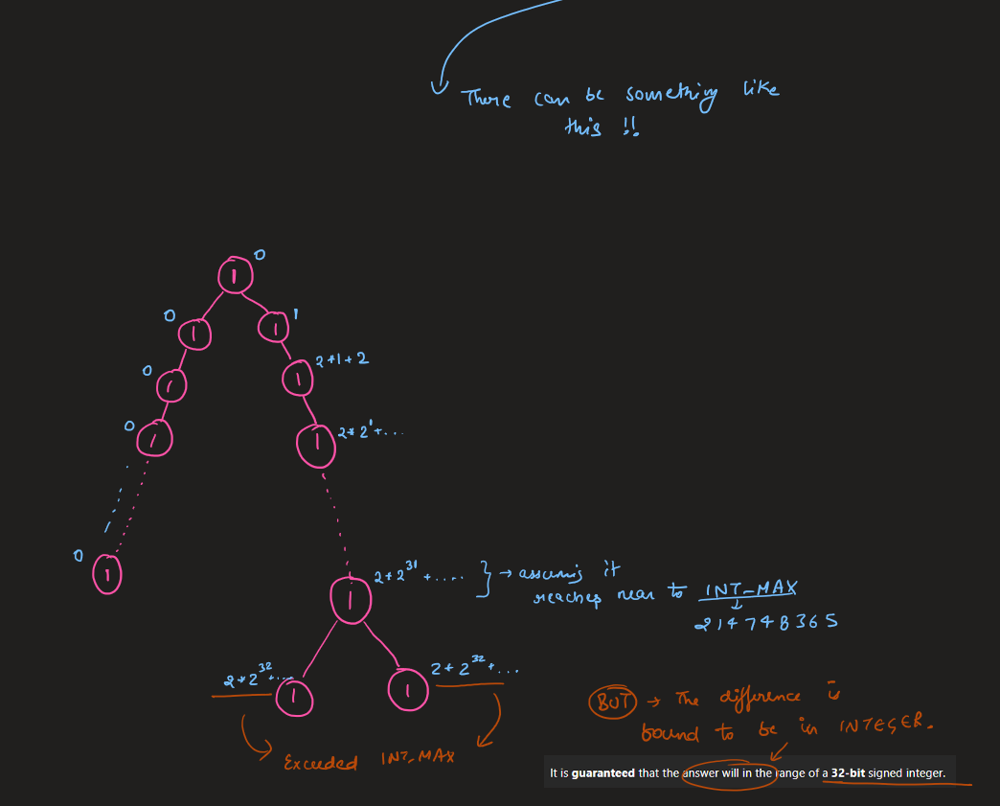\n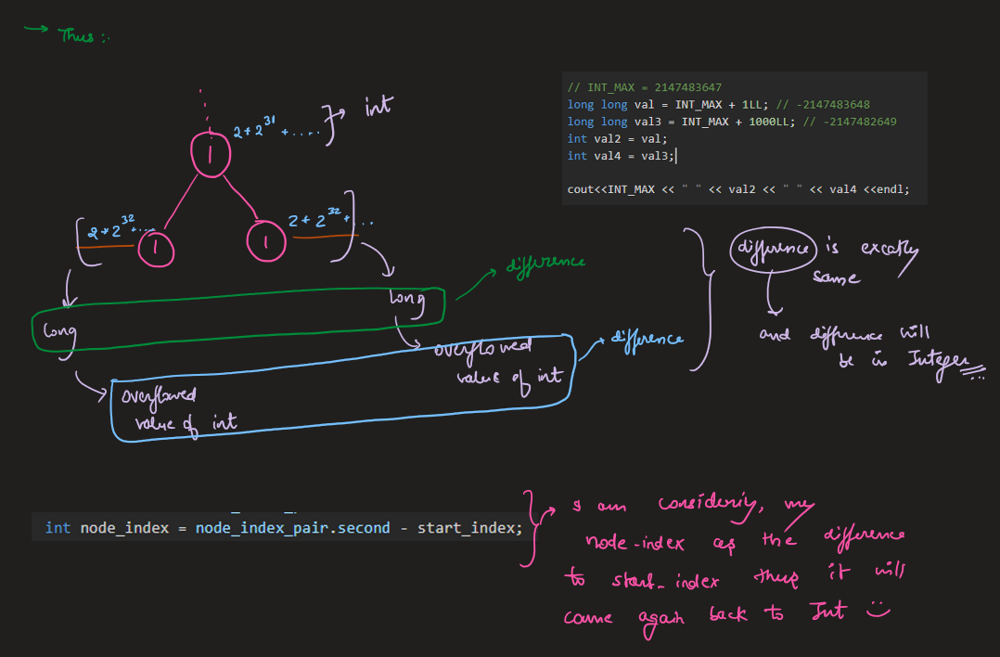\n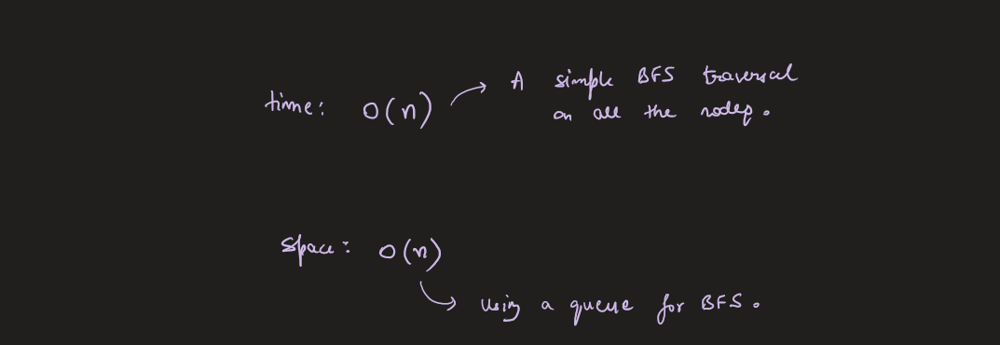\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int widthOfBinaryTree(TreeNode* root) {\n if (root == NULL) return 0;\n \n int max_width = 1;\n queue<pair<TreeNode*, int>> q;\n q.push({root, 0});\n\n while (!q.empty()) {\n int level_size = q.size();\n int start_index = q.front().second;\n int end_index = q.back().second;\n max_width = max(max_width, end_index - start_index + 1);\n \n for (int i = 0; i < level_size; ++i) {\n auto node_index_pair = q.front();\n TreeNode* node = node_index_pair.first;\n int node_index = node_index_pair.second - start_index;\n q.pop();\n \n if (node->left != nullptr) {\n q.push({node->left, 2LL * node_index + 1});\n }\n \n if (node->right != nullptr) {\n q.push({node->right, 2LL * node_index + 2});\n }\n }\n }\n \n return max_width;\n }\n};\n```\n```Java []\nclass Solution {\n public int widthOfBinaryTree(TreeNode root) {\n if (root == null) return 0;\n \n Queue<Pair<TreeNode, Integer>> queue = new LinkedList<>();\n queue.add(new Pair<>(root, 0));\n int maxWidth = 0;\n \n while (!queue.isEmpty()) {\n int levelLength = queue.size();\n int levelStart = queue.peek().getValue();\n int index = 0;\n \n for (int i = 0; i < levelLength; i++) {\n Pair<TreeNode, Integer> pair = queue.poll();\n TreeNode node = pair.getKey();\n index = pair.getValue();\n \n if (node.left != null) {\n queue.add(new Pair<>(node.left, 2*index));\n }\n \n if (node.right != null) {\n queue.add(new Pair<>(node.right, 2*index+1));\n }\n }\n \n maxWidth = Math.max(maxWidth, index - levelStart + 1);\n }\n \n return maxWidth;\n }\n}\n```\n```Python []\nclass Solution:\n def widthOfBinaryTree(self, root: TreeNode) -> int:\n if not root:\n return 0\n \n queue = deque([(root, 0)])\n max_width = 0\n \n while queue:\n level_length = len(queue)\n _, level_start = queue[0]\n \n for i in range(level_length):\n node, index = queue.popleft()\n \n if node.left:\n queue.append((node.left, 2*index))\n \n if node.right:\n queue.append((node.right, 2*index+1))\n \n max_width = max(max_width, index - level_start + 1)\n \n return max_width\n```\n | 139 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python || Easy || BFS || O(n) Solution | maximum-width-of-binary-tree | 0 | 1 | ```\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n q=deque([[root,0]])\n ans=0\n while q:\n n=len(q)\n m=q[0][1]\n for i in range(n):\n node,index=q.popleft()\n index-=m\n if i==0:\n first=index\n if i==n-1:\n last=index\n if node.left:\n q.append([node.left,2*index+1])\n if node.right:\n q.append([node.right,2*index+2])\n ans=max(ans,last-first+1)\n return ans\n```\n**An upvote will be encouraging** | 1 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Most efficient solution using bfs | maximum-width-of-binary-tree | 1 | 1 | \n\n# Approach\n- BFS Traversal with Position Tracking: Use BFS traversal to visit nodes in the binary tree. For each node, track its position in the current level. Nodes in the left subtree have positions 2 * curr - 1, and nodes in the right subtree have positions 2 * curr.\n\n- Position Calculation: When traversing the nodes, calculate their positions based on the parent\'s position. This ensures that nodes in the left and right subtrees have consecutive positions.\n\n- Width Calculation: For each level, calculate the width as the difference between the first and last node positions, plus one. Update the maximum width seen so far (ans) during the traversal.\n\n- Return Maximum Width: Return the maximum width (ans) after traversing the entire tree.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n int widthOfBinaryTree(TreeNode* root) {\n if (!root) return 0;\n int ans = 0;\n queue<pair<TreeNode*, long long>> q;\n q.push({root, 0});\n while (!q.empty()) {\n int size = q.size();\n long long mini = q.front().second;\n long long first, last;\n for (int i = 0; i < size; i++) {\n long long curr = q.front().second - mini;\n TreeNode* node = q.front().first;\n q.pop();\n if (i == 0) first = curr;\n if (i == size - 1) last = curr;\n if (node->left) q.push({node->left, curr * 2 + 1});\n if (node->right) q.push({node->right, curr * 2 + 2});\n }\n ans = max(ans, static_cast<int>(last - first + 1));\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n \n ans = 0\n queue = SimpleQueue()\n queue.put((root, 0))\n \n while not queue.empty():\n size = queue.qsize()\n mini = queue.queue[0][1]\n first, last = 0, 0\n \n for _ in range(size):\n node, curr = queue.get()\n if not first:\n first = curr\n last = curr\n \n if node.left:\n queue.put((node.left, curr * 2 + 1))\n if node.right:\n queue.put((node.right, curr * 2 + 2))\n \n ans = max(ans, last - first + 1)\n \n return ans\n```\n```Java []\npublic class Solution {\n public int widthOfBinaryTree(TreeNode root) {\n if (root == null) return 0;\n int ans = 0;\n Queue<Pair<TreeNode, Long>> q = new LinkedList<>();\n q.offer(new Pair<>(root, 0L));\n while (!q.isEmpty()) {\n int size = q.size();\n long mini = q.peek().getValue();\n long first, last;\n for (int i = 0; i < size; i++) {\n long curr = q.poll().getValue() - mini;\n TreeNode node = q.peek().getKey();\n if (i == 0) first = curr;\n if (i == size - 1) last = curr;\n if (node.left != null) q.offer(new Pair<>(node.left, curr * 2 + 1));\n if (node.right != null) q.offer(new Pair<>(node.right, curr * 2 + 2));\n }\n ans = Math.max(ans, (int)(last - first + 1));\n }\n return ans;\n }\n}\n```\n | 2 | Given the `root` of a binary tree, return _the **maximum width** of the given tree_.
The **maximum width** of a tree is the maximum **width** among all levels.
The **width** of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is **guaranteed** that the answer will in the range of a **32-bit** signed integer.
**Example 1:**
**Input:** root = \[1,3,2,5,3,null,9\]
**Output:** 4
**Explanation:** The maximum width exists in the third level with length 4 (5,3,null,9).
**Example 2:**
**Input:** root = \[1,3,2,5,null,null,9,6,null,7\]
**Output:** 7
**Explanation:** The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
**Example 3:**
**Input:** root = \[1,3,2,5\]
**Output:** 2
**Explanation:** The maximum width exists in the second level with length 2 (3,2).
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `-100 <= Node.val <= 100` | null |
Python3 Solution | strange-printer | 0 | 1 | \n```\nclass Solution:\n def strangePrinter(self, s: str) -> int:\n n=len(s)\n if not s:\n return 0\n\n dp=[[sys.maxsize]*n for _ in range(n)]\n\n for i in range(n):\n dp[i][i]=1\n\n for l in range(2,n+1):\n for i in range(n-l+1):\n j=i+l-1\n dp[i][j]=dp[i+1][j]+1\n\n for k in range(i+1,j+1):\n if s[i]==s[k]:\n dp[i][j]=min(dp[i][j],dp[i][k-1]+(dp[k+1][j] if j>k else 0))\n\n return dp[0][n-1] \n``` | 3 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
[C++/Python/Rust] Divide and Conquer DP Solution | strange-printer | 0 | 1 | # Complexity\n- Time complexity: $$O(n ^ 3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n ^ 2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nconst int INF = 1e9;\n\nclass Solution {\npublic:\n int strangePrinter(string s) {\n int n = s.length();\n vector<vector<int>> dp(n, vector<int>(n, 0));\n\n for (int d = 0; d < n; ++d) {\n for (int idx = 0; idx < n; ++idx) {\n int l = idx, r = idx + d;\n if (r >= n) {\n break;\n }\n dp[l][r] = INF;\n if (l == r) {\n dp[l][r] = 0;\n } else if (s[l] != s[l + 1]) {\n dp[l][r] = min(dp[l][r], dp[l + 1][r] + 1);\n for (int i = l + 1; i <= r; ++i) {\n if (s[l] == s[i]) {\n dp[l][r] = min(dp[l][r], dp[l][i - 1] + dp[i][r]);\n }\n }\n } else {\n dp[l][r] = dp[l + 1][r];\n }\n }\n }\n\n return dp[0][n - 1] + 1;\n }\n};\n```\n```python3 []\nINF = 1_000_000_000\n\nclass Solution:\n def strangePrinter(self, s: str) -> int:\n n = len(s)\n dp = [[0] * n for _ in range(n)]\n\n for d in range(n):\n for idx in range(n):\n l, r = idx, idx + d\n if r >= n:\n break\n dp[l][r] = INF\n if l == r:\n dp[l][r] = 0\n elif s[l] != s[l + 1]:\n dp[l][r] = min(dp[l][r], dp[l + 1][r] + 1)\n for i in range(l + 1, r + 1):\n if s[l] == s[i]:\n dp[l][r] = min(dp[l][r], dp[l][i - 1] + dp[i][r])\n else:\n dp[l][r] = dp[l + 1][r]\n\n return dp[0][n - 1] + 1\n```\n```rust []\nuse std::cmp;\n\nconst INF: i32 = 1_000_000_000;\n\nimpl Solution {\n pub fn strange_printer(s: String) -> i32 {\n let s = s.as_bytes();\n let n = s.len();\n let mut dp = vec![vec![0 as i32; n]; n];\n for d in 0..n {\n for idx in 0..n {\n let (l, r) = (idx, idx + d);\n if r >= n {\n break;\n } \n dp[l][r] = INF;\n if l == r {\n dp[l][r] = 0;\n } else if s[l] != s[l + 1] {\n dp[l][r] = cmp::min(dp[l][r], dp[l + 1][r] + 1);\n for i in (l + 1)..=r {\n if s[l] == s[i] {\n dp[l][r] = cmp::min(dp[l][r], dp[l][i - 1] + dp[i][r]);\n }\n }\n } else {\n dp[l][r] = dp[l + 1][r];\n }\n } \n }\n return dp[0][n - 1] + 1; \n }\n}\n``` | 1 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
Python easy solutions || time & memory efficient | strange-printer | 0 | 1 | # Intuition\nThe problem seems to involve finding the minimum number of turns required to print a given string using a "strange printer." The printer can print a character on any substring of the given string and it can overlap with the existing characters. The objective is to minimize the number of turns to print the entire string.\n\n# Approach\nTo solve this problem, we use dynamic programming. It initializes a 2D DP array, where dp[i][j] represents the minimum number of turns required to print the substring from index i to index j of the original string s.\n\nThe base case is when i == j, which means there is only one character in the substring, and in this case, dp[i][i] is set to 1 as it takes 1 turn to print a single character.\n\nFor substrings with more than one character, the solution iterates from the end of the string (n-1) to the start (0). For each i and j, it checks if the characters at these positions in the string are the same. If they are, then the minimum turns required to print the substring from i to j is the same as the minimum turns required to print the substring from i to j-1.\n\nIf the characters at i and j are different, it means a new turn is required to print the character at position j. In this case, the solution tries different partition points k between i and j and calculates the minimum turns required to print the substring from i to j. It takes the minimum of all such values as the final minimum turns required for dp[i][j].\n\nIn the end, dp[0][n-1] represents the minimum turns required to print the entire original string.\n\n# Code\n```\nclass Solution:\n def strangePrinter(self, s: str) -> int:\n n = len(s)\n dp = [[0] * n for _ in range(n)]\n\n for i in range(n - 1, -1, -1):\n dp[i][i] = 1 # Base case: single character needs 1 turn\n for j in range(i + 1, n):\n if s[i] == s[j]:\n dp[i][j] = dp[i][j - 1] # If s[i] and s[j] are the same, no extra turn needed\n else:\n dp[i][j] = dp[i][j - 1] + 1 # Initialize to maximum turns\n for k in range(i, j):\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j])\n\n return dp[0][n - 1]\n``` | 1 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
Solution | strange-printer | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int dp[101][101];\n int helper(int l, int r, string &s){\n if(l>r) return 0;\n if(dp[l][r] != -1) return dp[l][r];\n int ans = INT_MAX;\n ans = min(ans, 1+helper(l+1, r, s));\n for(int i=l+1; i<=r; i++){\n if(s[i]==s[l]){\n ans = min(ans, helper(i, r, s)+helper(l+1, i-1, s));\n }\n }\n return dp[l][r] = ans;\n }\n int strangePrinter(string s) {\n memset(dp, -1, sizeof(dp));\n string str;\n for(int i=0; i<s.size();){\n char ch = s[i];\n while(i<s.size() and ch==s[i]) i++;\n str.push_back(ch);\n } \n return helper(0, str.size()-1, str);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n\tdef strangePrinter(self, s: str) -> int:\n\t\t\n\t\ts = \'\'.join([c for i, c in enumerate(s)\n\t\t\t\t\t if i == 0 or c != s[i - 1]])\n\n\t\tnext_occ_search = {}\n\t\tnext_occurrence_of_letter = list(range(len(s)))\n\t\tfor i, c in enumerate(s):\n\t\t\tif c in next_occ_search:\n\t\t\t\tnext_occurrence_of_letter[next_occ_search[c]] = i\n\t\t\tnext_occ_search[c] = i\n\n\t\tfor v in next_occ_search.values():\n\t\t\tnext_occurrence_of_letter[v] = 10**10\n\n\t\[email protected]_cache(None)\n\t\tdef dp(left_ind: int, right_ind: int) -> int:\n\n\t\t\tif left_ind >= right_ind:\n\t\t\t\treturn 0\n\n\t\t\tif s[right_ind] == s[left_ind]:\n\t\t\t\treturn dp(left_ind + 1, right_ind)\n\n\t\t\tans = 1 + dp(left_ind + 1, right_ind)\n\n\t\t\tpivot_index = next_occurrence_of_letter[left_ind]\n\t\t\twhile pivot_index <= right_ind:\n\t\t\t\tans = min(ans, 1 + dp(left_ind + 1, pivot_index)\n\t\t\t\t\t\t + dp(pivot_index + 1, right_ind))\n\t\t\t\tpivot_index = next_occurrence_of_letter[pivot_index]\n\n\t\t\treturn ans\n\n\t\ts += \'#\'\n\t\treturn dp(0, len(s) - 1)\n```\n\n```Java []\nclass Solution {\n private int[][] memo;\n private char[] array;\n public int strangePrinter(String s) {\n if (s.isEmpty()) {\n return 0;\n }\n array = squash(s);\n int N = array.length;\n memo = new int[N][];\n\n for (int i = 0; i < N; i++) {\n memo[i] = new int[N];\n memo[i][i] = 1;\n if (i != N - 1) {\n int next = i + 1;\n memo[i][next] = array[i] == array[next] ? 1 : 2;\n }\n }\n return strangePrinter(0, array.length - 1);\n }\n public int strangePrinter(int i, int j) {\n if (i > j) {\n return 0;\n }\n if (memo[i][j] == 0) {\n\n int nextIdx = i + 1;\n int letter = array[i];\n\n int answer = 1 + strangePrinter(nextIdx, j);\n\n for (int k = nextIdx; k <= j; k++) {\n if (array[k] == letter) {\n\n int betterAnswer = strangePrinter(i, k - 1) + strangePrinter(k + 1, j);\n answer = Math.min(answer, betterAnswer);\n }\n }\n memo[i][j] = answer;\n }\n return memo[i][j];\n }\n char[] squash(String s) {\n char[] chars = s.toCharArray();\n int last = 0;\n int fullLength = chars.length;\n for (int i = 1; i < fullLength; i++) {\n if (chars[i] != chars[last]) {\n chars[++last] = chars[i];\n }\n }\n return Arrays.copyOf(chars, last + 1);\n }\n}\n```\n | 1 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
🖨️ 100% Printer [VIDEO] 🔀 Peculiar : Minimizing Prints with Dynamic Programming 🔄📜 | strange-printer | 1 | 1 | ## Intuition\nWhen first encountering this problem, it seems to be a task of finding an optimal strategy for a sequence of actions. This is often a cue for a dynamic programming approach. In particular, the "strange" behavior of the printer (being able to print on top of existing characters and only printing the same character at a time) suggests that we can benefit from considering smaller subproblems (i.e., substrings of the input) in order to construct the solution for the whole string.\n\nhttps://youtu.be/f4diE_0zYs4\n\n## Approach\n\nThe solution to this problem involves setting up a dynamic programming (DP) table, where each cell \\( dp[i][j] \\) represents the minimum number of turns the printer needs to print the substring from \\( i \\) to \\( j \\). \n\n1. **Initialization**: We start by initializing the diagonal of the DP table with 1, as the printer only needs one turn to print a single character. So, if we have the string "abc", the printer can print "a", "b", or "c" each in one turn. As such, the diagonal of our DP table (which represents substrings of length 1) is filled with 1s.\n\n2. **Filling the DP Table**: We adopt a bottom-up approach to fill in the DP table. For every \\( i \\) (from \\( n-1 \\) to 0) and \\( j \\) (from \\( i+1 \\) to \\( n \\)), we initially set \\( dp[i][j] \\) to \\( dp[i][j-1] + 1 \\). This equates to printing the substring from \\( i \\) to \\( j-1 \\) first, followed by printing the character at \\( j \\) separately. For example, if we have the string "abc", the printer can print "ab" in two turns and then print "c" in an additional turn, making a total of 3 turns.\n\n3. **Considering Overlapping Characters**: If there are overlapping characters, we may be able to print the substring from \\( i \\) to \\( j \\) in fewer turns. This is where \\( k \\) comes into play. We introduce \\( k \\) to divide the substring from \\( i \\) to \\( j \\) into two parts at \\( k \\), namely the left part from \\( i \\) to \\( k \\) and the right part from \\( k+1 \\) to \\( j \\). For each \\( k \\) from \\( i \\) to \\( j \\), if \\( s[k] \\) is the same as \\( s[j] \\), we can first print the substring from \\( i \\) to \\( k \\), and then print the character at \\( j \\), which will also cover \\( s[k] \\). For instance, if we have the string "aba", the printer can print "aa" in one turn and then print "b" in another turn, making a total of 2 turns. In this case, we update \\( dp[i][j] \\) to be the minimum of its current value and \\( dp[i][k] + dp[k+1][j-1] \\) (or just \\( dp[i][k] \\) if \\( k+1 > j-1 \\)).\n\n4. **Final Output**: After filling the DP table, we can find the minimum number of turns needed to print the entire string at \\( dp[0][n-1] \\). This cell represents the minimum number of turns to print the entire string since it covers the substring from the first character (0) to the last character (\\( n-1 \\)) of the string.\n\n## Complexity\n\n- Time complexity: \\(O(n^3)\\). The algorithm needs to fill a \\(n \\times n\\) DP table. For each cell in the DP table, it goes through a loop of size \\(n\\) to consider all possible values of \\(k\\).\n\n- Space complexity: \\(O(n^2)\\). The space complexity is determined by the size of the DP table, which is \\(n \\times n\\).\n\n## Code\n```Python []\nclass Solution:\n def strangePrinter(self, s: str) -> int:\n n = len(s)\n dp = [[0]*n for _ in range(n)]\n \n for i in range(n-1, -1, -1):\n dp[i][i] = 1\n for j in range(i+1, n):\n dp[i][j] = dp[i][j-1] + 1\n for k in range(i, j):\n if s[k] == s[j]:\n dp[i][j] = min(dp[i][j], dp[i][k] + (dp[k+1][j-1] if k+1<=j-1 else 0))\n\n return dp[0][n-1]\n```\n``` C++ []\nclass Solution {\npublic:\n int strangePrinter(string s) {\n int n = s.size();\n vector<vector<int>> dp(n, vector<int>(n, 0));\n \n for (int i = n-1; i >= 0; --i) {\n dp[i][i] = 1;\n for (int j = i+1; j < n; ++j) {\n dp[i][j] = dp[i][j-1] + 1;\n for (int k = i; k < j; ++k) {\n if (s[k] == s[j]) {\n dp[i][j] = min(dp[i][j], dp[i][k] + (k+1<=j-1 ? dp[k+1][j-1] : 0));\n }\n }\n }\n }\n return dp[0][n-1];\n }\n};\n```\n``` Java []\nclass Solution {\n public int strangePrinter(String s) {\n int n = s.length();\n int[][] dp = new int[n][n];\n \n for (int i = n-1; i >= 0; --i) {\n dp[i][i] = 1;\n for (int j = i+1; j < n; ++j) {\n dp[i][j] = dp[i][j-1] + 1;\n for (int k = i; k < j; ++k) {\n if (s.charAt(k) == s.charAt(j)) {\n dp[i][j] = Math.min(dp[i][j], dp[i][k] + (k+1<=j-1 ? dp[k+1][j-1] : 0));\n }\n }\n }\n }\n return dp[0][n-1];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar strangePrinter = function(s) {\n let n = s.length;\n let dp = Array.from(Array(n), () => new Array(n).fill(0));\n \n for (let i = n-1; i >= 0; --i) {\n dp[i][i] = 1;\n for (let j = i+1; j < n; ++j) {\n dp[i][j] = dp[i][j-1] + 1;\n for (let k = i; k < j; ++k) {\n if (s[k] == s[j]) {\n dp[i][j] = Math.min(dp[i][j], dp[i][k] + (k+1<=j-1 ? dp[k+1][j-1] : 0));\n }\n }\n }\n }\n return dp[0][n-1];\n};\n```\n``` C# []\npublic class Solution {\n public int StrangePrinter(string s) {\n int n = s.Length;\n int[,] dp = new int[n,n];\n \n for (int i = n-1; i >= 0; --i) {\n dp[i,i] = 1;\n for (int j = i+1; j < n; ++j) {\n dp[i,j] = dp[i,j-1] + 1;\n for (int k = i; k < j; ++k) {\n if (s[k] == s[j]) {\n dp[i,j] = Math.Min(dp[i,j], dp[i,k] + (k+1<=j-1 ? dp[k+1,j-1] : 0));\n }\n }\n }\n }\n return dp[0,n-1];\n }\n}\n```\n## Video for JavaScript & C++\nhttps://youtu.be/bazV0MMaFQI\nhttps://youtu.be/dBtekOl0ofE\n | 48 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | strange-printer | 1 | 1 | # Intuition\nUsing dynamic programming to keep how many times the strange printer should print characters in current range between start and end.\n\n\n---\n\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/bAS9rmAxBnI\n\n# Subscribe to my channel from here. I have 235 videos as of July 31th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python solution. Other might be different a bit.\n\n1. Initialize an empty dictionary `memo` to store the results of subproblems for memoization.\n\n2. Define a recursive function `min_turns_to_print(start, end)` that calculates the minimum number of turns needed to print the substring `s[start:end+1]`.\n\n3. In the `min_turns_to_print` function:\n a. Base case: If `start` is greater than `end`, there are no characters to print, so return 0 turns.\n b. Check if the result for the current subproblem `(start, end)` is already memoized in `memo`. If yes, return the memoized result to avoid redundant computations.\n c. Initialize the minimum number of turns `res` for the current subproblem by assuming that the last character `s[end]` is printed separately. Therefore, `res = min_turns_to_print(start, end - 1) + 1`.\n\n4. Try to improve the minimum turns `res` by considering all possible break points (middle) between `start` and `end - 1`. For each `middle`:\n a. If the character at `s[middle]` is the same as the character at `s[end]`, it means that we can potentially print the substring `s[start:end+1]` in a single operation. In this case, try to combine the turns needed to print `s[start:middle]` and `s[middle+1:end]` separately. Calculate `min_turns_to_print(start, middle) + min_turns_to_print(middle + 1, end - 1)`.\n b. Update `res` to be the minimum of the current `res` and the value calculated in the previous step, i.e., `res = min(res, min_turns_to_print(start, middle) + min_turns_to_print(middle + 1, end - 1))`.\n\n5. Memoize the result `res` for the current subproblem `(start, end)` in the `memo` dictionary, so that we can use it for future computations.\n\n6. Return the minimum number of turns needed to print the entire string `s`, which is the result of calling `min_turns_to_print(0, len(s) - 1)`.\n\nThe main idea of this algorithm is to recursively divide the string into smaller subproblems and use memoization to avoid redundant calculations. By considering all possible break points, we can find the optimal way to print the string with the minimum number of turns.\n\n# Complexity\nThis is based on Python solution. Other might be different a bit.\n\n- Time complexity: O(n^3)\n\nn is the length of the input string s. The reason for this time complexity is due to the recursive nature of the min_turns_to_print function and the memoization technique used.\n\nIn the min_turns_to_print function, we are considering all possible subproblems by iterating through all possible start and end positions of substrings of s. For each substring, we also consider all possible break points (middle) to find the optimal way to print it. This leads to three nested loops, resulting in a cubic time complexity.\n\n- Space complexity: O(n^2)\n\nn is the length of the input string s. The main reason for this space complexity is the memoization dictionary memo. Since we are memoizing the results of all possible subproblems (start and end positions of substrings), the space required for the memo dictionary grows quadratically with the length of the input string. Additionally, the recursion stack also contributes to the space complexity, but it is limited to O(n) in this case.\n\n```python []\nclass Solution:\n def strangePrinter(self, s: str) -> int:\n memo = {}\n\n def min_turns_to_print(start, end):\n if start > end:\n return 0\n \n if (start, end) in memo:\n return memo[(start, end)]\n \n res = min_turns_to_print(start, end - 1) + 1\n\n for middle in range(start, end):\n if s[middle] == s[end]:\n res = min(res, min_turns_to_print(start, middle) + min_turns_to_print(middle + 1, end - 1))\n \n memo[(start, end)] = res\n return res\n\n return min_turns_to_print(0, len(s) - 1) \n```\n```javascript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar strangePrinter = function(s) {\n const memo = {};\n\n function min_turns_to_print(start, end) {\n if (start > end) {\n return 0;\n }\n \n if (memo.hasOwnProperty(`${start}-${end}`)) {\n return memo[`${start}-${end}`];\n }\n \n let res = min_turns_to_print(start, end - 1) + 1;\n\n for (let middle = start; middle < end; middle++) {\n if (s[middle] === s[end]) {\n res = Math.min(res, min_turns_to_print(start, middle) + min_turns_to_print(middle + 1, end - 1));\n }\n }\n \n memo[`${start}-${end}`] = res;\n return res;\n }\n\n return min_turns_to_print(0, s.length - 1); \n};\n```\n```java []\nclass Solution {\n public int strangePrinter(String s) {\n Map<String, Integer> memo = new HashMap<>();\n\n return min_turns_to_print(0, s.length() - 1, s, memo); \n }\n\n private int min_turns_to_print(int start, int end, String s, Map<String, Integer> memo) {\n if (start > end) {\n return 0;\n }\n \n String key = start + "-" + end;\n if (memo.containsKey(key)) {\n return memo.get(key);\n }\n \n int res = min_turns_to_print(start, end - 1, s, memo) + 1;\n\n for (int middle = start; middle < end; middle++) {\n if (s.charAt(middle) == s.charAt(end)) {\n res = Math.min(res, min_turns_to_print(start, middle, s, memo) + min_turns_to_print(middle + 1, end - 1, s, memo));\n }\n }\n \n memo.put(key, res);\n return res;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int strangePrinter(string s) {\n std::unordered_map<std::string, int> memo;\n return min_turns_to_print(0, s.length() - 1, s, memo); \n }\n\nprivate:\n int min_turns_to_print(int start, int end, const std::string& s, std::unordered_map<std::string, int>& memo) {\n if (start > end) {\n return 0;\n }\n \n std::string key = std::to_string(start) + "-" + std::to_string(end);\n if (memo.count(key)) {\n return memo[key];\n }\n \n int res = min_turns_to_print(start, end - 1, s, memo) + 1;\n\n for (int middle = start; middle < end; middle++) {\n if (s[middle] == s[end]) {\n res = std::min(res, min_turns_to_print(start, middle, s, memo) + min_turns_to_print(middle + 1, end - 1, s, memo));\n }\n }\n \n memo[key] = res;\n return res;\n } \n};\n```\n | 16 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
Python | Easy to Understand | Hard Problem | 664. Strange Printer | strange-printer | 0 | 1 | # Python | Easy to Understand | Hard Problem | 664. Strange Printer\n```\nclass Solution:\n def strangePrinter(self, s: str) -> int:\n N = len(s)\n @cache\n def calc(left, right): \n if left >= right: \n return 0\n best = calc(left + 1, right) + 1\n for index in range(left + 1, right + 1): \n if s[left] == s[index]: \n best = min(best, calc(left, index - 1) + calc(index, right))\n return best\n return calc(0, N - 1) + 1\n``` | 24 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
664: Space 93.43%, Solution with step by step explanation | strange-printer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Get the length of the input string and store it in variable n.\n2. Create a n x n matrix called dp to store the minimum number of turns needed to print s[i:j+1].\n3. Loop backwards over the matrix to fill in the upper diagonal (i.e., the values above the diagonal).\n4. For each index i on the diagonal, set dp[i][i] to 1, since it takes one turn to print a single character.\n5. Loop forwards over the matrix to fill in the lower diagonal (i.e., the values below the diagonal).\n6. For each pair of indices (i,j) in the lower diagonal, check if s[i] and s[j] are the same character. If so, we can print them together in one turn and set dp[i][j] to dp[i][j-1], which represents the minimum number of turns needed to print s[i:j] plus the additional character s[j].\n7. If s[i] and s[j] are different characters, we need to try all possible k values between i and j, and find the minimum number of turns needed to print s[i:j+1] by combining s[i:k+1] and s[k+1:j+1]. To do this, set dp[i][j] to infinity and loop over all k values between i and j. For each k value, update dp[i][j] to the minimum of its current value and dp[i][k] + dp[k+1][j], which represents the minimum number of turns needed to print s[i:k+1] plus the minimum number of turns needed to print s[k+1:j+1].\n8. Once all values in the matrix have been computed, the minimum number of turns needed to print the entire string s is stored in dp[0][n-1]. Return this value.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def strangePrinter(self, s: str) -> int:\n # Get the length of the input string\n n = len(s)\n \n # Create a n x n matrix to store the minimum number of turns needed to print s[i:j+1]\n dp = [[0] * n for _ in range(n)]\n \n # Loop backwards over the matrix to fill in the upper diagonal\n for i in range(n-1, -1, -1):\n # Initialize the diagonal values to 1, since it takes one turn to print a single character\n dp[i][i] = 1\n \n # Loop forwards over the matrix to fill in the lower diagonal\n for j in range(i+1, n):\n # If s[i] and s[j] are the same character, we can print them together in one turn\n if s[i] == s[j]:\n dp[i][j] = dp[i][j-1]\n else:\n # If s[i] and s[j] are different characters, we try to use the previously computed dp values\n # and update the current dp value by taking the minimum value of the two possible options\n dp[i][j] = float(\'inf\')\n for k in range(i, j):\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j])\n \n # The minimum number of turns needed to print the entire string s is stored in dp[0][n-1]\n return dp[0][n-1]\n``` | 7 | There is a strange printer with the following two special properties:
* The printer can only print a sequence of **the same character** each time.
* At each turn, the printer can print new characters starting from and ending at any place and will cover the original existing characters.
Given a string `s`, return _the minimum number of turns the printer needed to print it_.
**Example 1:**
**Input:** s = "aaabbb "
**Output:** 2
**Explanation:** Print "aaa " first and then print "bbb ".
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation:** Print "aaa " first and then print "b " from the second place of the string, which will cover the existing character 'a'.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | null |
Python Easy Greedy w/ explanation - O(1) space | non-decreasing-array | 0 | 1 | The approach that we will be taking is **greedy**. From the problem statement, it\'s clear that we have to count the number of violations i.e. **nums[i-1]>nums[i]**.\n\n> Input Array - **[1, 2, 4, 3]**\n> \nIn above case, we find one violation at index `3`. So this is a valid case, as we can make it non-decreasing by just modifying the violation which is \n> After fixing the violation - **[1, 2, 3, 3]**\n> \n\nAs you can see, I just did **nums[i-1]=nums[i]** to fix the violation. After fixing the violation, the array is non-decreasing.\n\nNow let\'s pick an invalid case.\n> Input Array - **[3, 4, 2, 3]**\n> \nHere if you see, there is only one violation at index `2`. \n> Fixed violation at index `2` - **[3, 2, 2, 3]**\n> \nBut after fixing the violation, the array is still not in non-decreasing order. Hence, it\'s an invalid case. So from this example we can observe that we need to take into account **nums[i-2]** as well.\n\nNow let\'s take another example.\n> Input array - **[3, 4, 2]**\n> \nWe find one violation at index `2`. Here instead of doing **nums[i-1]=nums[i]**, we do **nums[i]=nums[i-1]**.\n> resultant array - **[3, 4, 4]**\n> \n\nFrom the above details, we can observe the following:\n1. We **need** the **count of violations** in the input array. If at any point **count > 1**, we return **False**\n2. For any violation, we have to make an **additional check for nums[i-2]**. If **nums[i-2]>nums[i]**, we perform **nums[i]=nums[i-1]** to fix the violation.\n\nTaking above things into consideration, below is my implemenation using greeedy.\n\n\n```\nclass Solution:\n def checkPossibility(self, nums: List[int]) -> bool:\n cnt_violations=0 \n for i in range(1, len(nums)): \n if nums[i]<nums[i-1]:\n if cnt_violations==1:\n return False\n cnt_violations+=1\n if i>=2 and nums[i-2]>nums[i]:\n nums[i]=nums[i-1] \n return True\n```\n\n**Time - O(n)**\n**Space - O(1)**\n\n\n___\n\n\n***Please upvote if you find it useful*** | 64 | Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
**Example 1:**
**Input:** nums = \[4,2,3\]
**Output:** true
**Explanation:** You could modify the first 4 to 1 to get a non-decreasing array.
**Example 2:**
**Input:** nums = \[4,2,1\]
**Output:** false
**Explanation:** You cannot get a non-decreasing array by modifying at most one element.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `-105 <= nums[i] <= 105` | null |
Just Change the element | non-decreasing-array | 0 | 1 | ```\nclass Solution:\n def checkPossibility(self, nums: List[int]) -> bool:\n count=0\n n=len(nums)\n for i in range(1,n):\n if nums[i]<nums[i-1]:\n count+=1\n if count>1:\n return False\n if i>=2 and nums[i-2]>nums[i]:\n nums[i]=nums[i-1]\n return True\n ```\n # please upvote me it would encourage me alot\n | 3 | Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
**Example 1:**
**Input:** nums = \[4,2,3\]
**Output:** true
**Explanation:** You could modify the first 4 to 1 to get a non-decreasing array.
**Example 2:**
**Input:** nums = \[4,2,1\]
**Output:** false
**Explanation:** You cannot get a non-decreasing array by modifying at most one element.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `-105 <= nums[i] <= 105` | null |
THE BEST SOLUTION ON THE PLANET | non-decreasing-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkPossibility(self, nums: List[int]) -> bool:\n if nums==sorted(nums):return True\n count=0\n for i in range(len(nums)-1):\n if nums[i+1]<nums[i]:\n lol=nums[i]\n nums[i]=nums[i+1]\n if not nums==sorted(nums):\n nums[i]=lol\n nums[i+1]=lol\n count+=1\n if count==1:break\n return nums==sorted(nums)\n\n \n``` | 0 | Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
**Example 1:**
**Input:** nums = \[4,2,3\]
**Output:** true
**Explanation:** You could modify the first 4 to 1 to get a non-decreasing array.
**Example 2:**
**Input:** nums = \[4,2,1\]
**Output:** false
**Explanation:** You cannot get a non-decreasing array by modifying at most one element.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `-105 <= nums[i] <= 105` | null |
665: Time 96.74%, Solution with step by step explanation | non-decreasing-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We start by initializing a count variable to keep track of the number of modifications we make.\n2. We then iterate through the array starting from the second element.\n3. For each element, we check if it is less than the previous element. If it is, we increment the count.\n4. If the count is greater than 1, we know that we have made more than one modification, so we can return False.\n5. If the current element is less than or equal to the element before the previous element, we modify the current element to be equal to the previous element. This ensures that the array is non-decreasing, as the previous element is guaranteed to be less than or equal to the next element.\n6. If the current element is greater than the element before the previous element, we modify the previous element to be equal to the current element. This ensures that the array is still non-decreasing, as the current element is guaranteed to be greater than or equal to the next element.\n7. At the end of the loop, if we have not returned False, we know that we have made at most one modification, so we can return True.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkPossibility(self, nums: List[int]) -> bool:\n # variable to keep track of the number of modifications\n count = 0\n # iterate through the array starting from the second element\n for i in range(1, len(nums)):\n # check if the current element is less than the previous element\n if nums[i] < nums[i-1]:\n # if it is, increment the count\n count += 1\n # if we have already made a modification, return False\n if count > 1:\n return False\n # if the current element is less than or equal to the element before the previous element\n # we modify the current element to be equal to the previous element\n if i < 2 or nums[i] >= nums[i-2]:\n nums[i-1] = nums[i]\n # otherwise, we modify the previous element to be equal to the current element\n else:\n nums[i] = nums[i-1]\n # if we reach the end of the loop without returning False, return True\n return True\n\n``` | 3 | Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
**Example 1:**
**Input:** nums = \[4,2,3\]
**Output:** true
**Explanation:** You could modify the first 4 to 1 to get a non-decreasing array.
**Example 2:**
**Input:** nums = \[4,2,1\]
**Output:** false
**Explanation:** You cannot get a non-decreasing array by modifying at most one element.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `-105 <= nums[i] <= 105` | null |
Python3 | Explained | Easy to Understand | Non-decreasing Array | non-decreasing-array | 0 | 1 | ```\nclass Solution:\n def checkPossibility(self, nums: List[int]) -> bool:\n is_modified = False # to check for multiple occurances of False condition(non increasing)\n index = -1 # to get the index of false condition\n n = len(nums)\n if n==1:return True\n for i in range(1, n):\n if nums[i] < nums[i-1] and not is_modified: # check if nums[i-1] is greater than nums[i]\n index = i # stores the index\n is_modified = True # mark the change which is to be modified\n elif nums[i] < nums[i-1] and is_modified: # if another false occurs return false (atmost 1 false cond.)\n return False\n if index != -1:\n v = nums[index-1]\n nums[index-1] = nums[index] # modifying index value and check for sort\n idx = index-1\n if idx-1>=0 and idx<n and nums[idx-1]<=nums[idx]<=nums[idx+1]: # check if modified array is sorted or not\n return True\n elif idx==0 and idx+1<n and nums[idx]<=nums[idx+1]: # check if modified array is sorted or not\n return True\n nums[index-1]=v\n nums[index] = nums[index-1]+1\n if index-1>=0 and index+1<n and nums[index-1]<=nums[index]<=nums[index+1]: # check if modified array is sorted or not\n return True\n elif index==n-1 and nums[index-1]<=nums[index]:\n return True\n if index==-1: # if array is already sorted\n return True\n return False\n \n``` | 3 | Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
**Example 1:**
**Input:** nums = \[4,2,3\]
**Output:** true
**Explanation:** You could modify the first 4 to 1 to get a non-decreasing array.
**Example 2:**
**Input:** nums = \[4,2,1\]
**Output:** false
**Explanation:** You cannot get a non-decreasing array by modifying at most one element.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `-105 <= nums[i] <= 105` | null |
✔ Short & Easy Python3 Solution | non-decreasing-array | 0 | 1 | > Python3 Solution\n\n# Approach\n> Greedy\n\n\n# Code\n```\nclass Solution:\n def checkPossibility(self, nums: List[int]) -> bool:\n dummy=nums.copy()\n for i in range(1,len(nums)):\n if nums[i-1]>nums[i]:\n nums[i]=nums[i-1]\n dummy[i-1]=dummy[i]\n break\n\n return nums==sorted(nums) or dummy==sorted(dummy)\n``` | 1 | Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
**Example 1:**
**Input:** nums = \[4,2,3\]
**Output:** true
**Explanation:** You could modify the first 4 to 1 to get a non-decreasing array.
**Example 2:**
**Input:** nums = \[4,2,1\]
**Output:** false
**Explanation:** You cannot get a non-decreasing array by modifying at most one element.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `-105 <= nums[i] <= 105` | null |
Python 3, after 7 "Wrong Answer" attempts, explained with diagrams, O(n) | non-decreasing-array | 0 | 1 | After 7 failed attempts, here is the solution.\nBelow table shows a cople of simple examples with 1 and two elements in the array\n\n\nBelow table shows a couple of examples with 3 elements.\n\n\nLast but not least, the most complicated scenario which is the array length larger than 3 and also the decrease is just once. You will see how the solution takes the advantage of the array diff. Here are a couple of examples with result false.\n\n\nHere are a couple of examples with result true.\n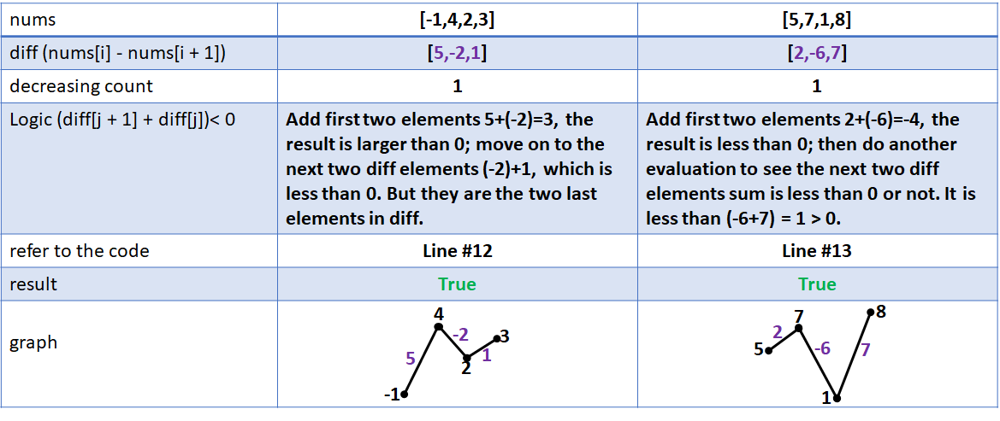\n\nFeel free to comment on.\n\n~~~\n1 class Solution:\n2 def checkPossibility(self, nums: List[int]) -> bool:\n3 if len(nums) == 1 or len(nums) == 2: return True\n4 count, diff = 0, []\n5 for i in range(len(nums)-1):\n6 diff.append(nums[i+1] - nums[i])\n7 if nums[i] > nums[i + 1]:\n8 count += 1\n9 if count > 1: return False\n10 if len(diff) > 2:\n11 for j in range(len(diff)-1):\n12 if ((diff[j+1] + diff[j]) < 0) and (j < len(diff)-2):\n13 if (diff[j+2] + diff[j+1]) < 0: return False\n14 return True\n~~~\n\n#Runtime: 176 ms, faster than 81.80% of Python3 online submissions for Non-decreasing Array.\n#Memory Usage: 15.3 MB, less than 26.80% of Python3 online submissions for Non-decreasing Array.\n | 18 | Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
**Example 1:**
**Input:** nums = \[4,2,3\]
**Output:** true
**Explanation:** You could modify the first 4 to 1 to get a non-decreasing array.
**Example 2:**
**Input:** nums = \[4,2,1\]
**Output:** false
**Explanation:** You cannot get a non-decreasing array by modifying at most one element.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `-105 <= nums[i] <= 105` | null |
Solution | beautiful-arrangement-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> constructArray(int n, int k) {\n vector<int> ans;\n int i;\n for(i = 1; i <= n - k; i++)\n {\n ans.push_back(i);\n }\n int count = 0;\n for(int j = 0; j < k; j++)\n {\n if(j%2==0)\n ans.push_back(n-count), count++;\n else ans.push_back(i), i++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def constructArray(self, n: int, k: int) -> List[int]:\n\n ans = list(range(1, n - k)) \n for i in range(k+1):\n if i % 2 == 0:\n ans.append(n-k + i//2)\n else:\n ans.append(n - i//2)\n\n return ans\n```\n\n```Java []\nclass Solution {\n public int[] constructArray(int n, int k) {\n int ans[]=new int[n];\n int low=1,high=n,index=0;\n boolean isHigh=false;\n ans[index++]=low++;\n while(k>1){\n ans[index++]=high--;\n k--;\n isHigh=true;\n if(k>1){\n ans[index++]=low++;\n k--;\n isHigh=false;\n }\n }\n while(index<n){\n if(isHigh) ans[index++]=high--;\n else ans[index++]=low++;\n }\n return ans;\n }\n}\n```\n | 1 | Given two integers `n` and `k`, construct a list `answer` that contains `n` different positive integers ranging from `1` to `n` and obeys the following requirement:
* Suppose this list is `answer = [a1, a2, a3, ... , an]`, then the list `[|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|]` has exactly `k` distinct integers.
Return _the list_ `answer`. If there multiple valid answers, return **any of them**.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** \[1,2,3\]
Explanation: The \[1,2,3\] has three different positive integers ranging from 1 to 3, and the \[1,1\] has exactly 1 distinct integer: 1
**Example 2:**
**Input:** n = 3, k = 2
**Output:** \[1,3,2\]
Explanation: The \[1,3,2\] has three different positive integers ranging from 1 to 3, and the \[2,1\] has exactly 2 distinct integers: 1 and 2.
**Constraints:**
* `1 <= k < n <= 104` | null |
667: Solution with step by step explanation | beautiful-arrangement-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create an empty list called "ans".\n\n2. Add integers 1 through (n-k) to the "ans" list using the range() function.\n\n3. For each value of i in the range of 0 to k-1:\na. Calculate the difference between i and the nearest even number using the floor division operator "//". This value represents the distance of the current element from the previous element in the result array.\nb. If i is even, append the value n minus the calculated difference plus 1 to the "ans" list. This will ensure that the difference between this value and the previous value is equal to the difference calculated in step 3a.\nc. If i is odd, append the value n-k plus the calculated difference to the "ans" list. This will ensure that the difference between this value and the previous value is equal to the difference calculated in step 3a.\n\n4. Return the "ans" list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def constructArray(self, n: int, k: int) -> List[int]:\n ans = list(range(1, n - k + 1))\n for i in range(k):\n diff = i // 2 + 1\n if i % 2 == 0:\n ans.append(n - diff + 1)\n else:\n ans.append(n - k + diff)\n\n return ans\n\n``` | 2 | Given two integers `n` and `k`, construct a list `answer` that contains `n` different positive integers ranging from `1` to `n` and obeys the following requirement:
* Suppose this list is `answer = [a1, a2, a3, ... , an]`, then the list `[|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|]` has exactly `k` distinct integers.
Return _the list_ `answer`. If there multiple valid answers, return **any of them**.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** \[1,2,3\]
Explanation: The \[1,2,3\] has three different positive integers ranging from 1 to 3, and the \[1,1\] has exactly 1 distinct integer: 1
**Example 2:**
**Input:** n = 3, k = 2
**Output:** \[1,3,2\]
Explanation: The \[1,3,2\] has three different positive integers ranging from 1 to 3, and the \[2,1\] has exactly 2 distinct integers: 1 and 2.
**Constraints:**
* `1 <= k < n <= 104` | null |
Python solution | beautiful-arrangement-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def constructArray(self, n: int, k: int) -> List[int]:\n\n ans = list(range(1, n - k)) \n for i in range(k+1):\n if i % 2 == 0:\n ans.append(n-k + i//2)\n else:\n ans.append(n - i//2)\n\n return ans\n``` | 0 | Given two integers `n` and `k`, construct a list `answer` that contains `n` different positive integers ranging from `1` to `n` and obeys the following requirement:
* Suppose this list is `answer = [a1, a2, a3, ... , an]`, then the list `[|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|]` has exactly `k` distinct integers.
Return _the list_ `answer`. If there multiple valid answers, return **any of them**.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** \[1,2,3\]
Explanation: The \[1,2,3\] has three different positive integers ranging from 1 to 3, and the \[1,1\] has exactly 1 distinct integer: 1
**Example 2:**
**Input:** n = 3, k = 2
**Output:** \[1,3,2\]
Explanation: The \[1,3,2\] has three different positive integers ranging from 1 to 3, and the \[2,1\] has exactly 2 distinct integers: 1 and 2.
**Constraints:**
* `1 <= k < n <= 104` | null |
Not fast, but more explainable than original question! | Commented and Explained | beautiful-arrangement-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOur goal is to get all numbers in range 1 to n+1 \nWe need them in a \'beautiful\' order \nTo start, we know we can get the beginning of an answer by going from 1 to n-k values \nSo, we start our answer there \nThen, we know that we want distint values in that range, and so we want to have the values marked when we have used them \nTo accomplish this, we can mark their availability \nWe build this by first marking all of our start answer components as False\nThen, we loop from where we stopped/1 to n+1 that those values are available. \n\nTo find our final answer we now do two steps \nFirst, we get our current value to consider as the last value of answer + 1 or just 1 if we have no answer built due to range considerations \nWe mark that as unavailable, and then add it to the answer \n\nWe can then loop over k from current to 0 and determine next updates as detailed in approach, before finally adding any missed values still available and then returning. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe get our original problem space with a list from 1 to n-k \nWe then set up values available and mark the original problem space considerations as unavailable \nWe then set up from our stopping point in original problem space to n+1 as available in our mapping \n\nWe select the current value based on either final of original problem space solution + 1 or 1 if no problem space set up yet \nMark it as unavailable and then add it to the answer \n\nNow while we have k > 1 \n- We could find an update at current value - k -> points to left end of range \n- Or we could find an update current value + k -> points to right end of range \n- If we have a value on left that is gt 0 and is available, we\'ll use that, otherwise we\'ll use the addition valuation \n- Once we know our next value, mark it\'s available status as false, set current value to it and update our answer \n- decrement k when done \n\nAt the end of the while loop, update answer with every value in value available we have not yet considered \n\nreturn when completed \n\nThis works by first eliminating the base case considered \nThen, does so by marking and udpates within range with consideration for which end of the \'total\' list we\'d be pulling from at any point \nThen finalizes with a final update for all unused values \n\n# Complexity\n- Time complexity : O(N + K) \n - O(N) to build answer at start \n - O(N) to build up value available \n - O(N) to finalize value available \n - O(K) to conduct while loop \n - O(N) to finalize answer \n\n- Space complexity : O(N) \n - O(N) values stored \n\n# Code\n```\nclass Solution :\n def constructArray(self, n: int, k: int) -> List[int] :\n # build array \n answer = list(range(1, n-k))\n # by first mapping if values are used or not \n value_available = dict() \n # mark initial considerations \n for value in answer : \n value_available[value] = False\n\n # loop over values we may use \n for value in range(min(1, n-k), n+1) : \n # and since we have not used them, mark as True \n value_available[value] = True\n \n # use either last value + 1 to start or 1 if no answer built yet \n current_value = answer[-1]+1 if answer else 1 \n value_available[current_value] = False\n answer.append(current_value)\n\n # loop while you have k to consider \n while k > 1 : \n # get subtraction by k and addition by k update \n subtraction = current_value - k\n addition = current_value + k \n # go with subtraction if subtraction is positive and we haven\'t used that value, otherwise addition \n next_value = subtraction if (subtraction > 0 and value_available[subtraction]) else addition\n # whatever it was, it\'s now not available \n value_available[next_value] = False\n # update current, add to answer and decrement k \n current_value = next_value \n answer.append(current_value)\n k -= 1 \n\n # add to answer all values still True for values in range we need and have not yet done\n answer += [value for value in value_available.keys() if value_available[value] == True]\n # return completed answer \n return answer \n\n \n``` | 0 | Given two integers `n` and `k`, construct a list `answer` that contains `n` different positive integers ranging from `1` to `n` and obeys the following requirement:
* Suppose this list is `answer = [a1, a2, a3, ... , an]`, then the list `[|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|]` has exactly `k` distinct integers.
Return _the list_ `answer`. If there multiple valid answers, return **any of them**.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** \[1,2,3\]
Explanation: The \[1,2,3\] has three different positive integers ranging from 1 to 3, and the \[1,1\] has exactly 1 distinct integer: 1
**Example 2:**
**Input:** n = 3, k = 2
**Output:** \[1,3,2\]
Explanation: The \[1,3,2\] has three different positive integers ranging from 1 to 3, and the \[2,1\] has exactly 2 distinct integers: 1 and 2.
**Constraints:**
* `1 <= k < n <= 104` | null |
Solution | kth-smallest-number-in-multiplication-table | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findKthNumber(int m, int n, int k) {\n int l=1, L=m*n;\n while (L) {\n int d=L>>1;\n int x=l+d;\n int y=0;\n for (int a=n, b=0; a>0; --a) {\n while (b<=m and a*b<=x) ++b;\n y+=b-1;\n }\n if (y<k) {\n l=x+1;\n L-=d+1;\n } else\n L=d;\n }\n return l;\n }\n};\n```\n\n```Python3 []\nclass Solution(object):\n def findKthNumber(self, m, n, k):\n if m==1 or n==1:\n return k\n l,r = 1,m*n\n if m>n:\n m,n = n,m\n def check(v):\n res = v//n*n\n if res>=k:\n return True\n for i in range(v//n+1,min(v,m)+1):\n res += v//i\n if res>=k:\n return True\n return res>=k\n while l<r:\n mid = (l+r)>>1\n if check(mid):\n r = mid\n else:\n l = mid+1\n return l\n```\n\n```Java []\nclass Solution {\n public int countlessthanmid(int n ,int m, int mid){\n int count=0;\n int i=1;\n int j =m;\n while(i<=n && j>=1){\n if(i*j<=mid){\n count+=j;\n i++;\n }else{\n j--;\n }\n }\n return count;\n }\n public int findKthNumber(int m, int n, int k) {\n int l = 1;\n int h = m*n;\n int mid =0;\n int res = 0;\n while(l<=h){\n mid = l+(h-l)/2;\n int count = countlessthanmid(m, n, mid);\n if(count<k){\n l = mid+1;\n }else{\n res = mid;\n h = mid-1;\n }\n }\n return res;\n }\n}\n```\n | 1 | Nearly everyone has used the [Multiplication Table](https://en.wikipedia.org/wiki/Multiplication_table). The multiplication table of size `m x n` is an integer matrix `mat` where `mat[i][j] == i * j` (**1-indexed**).
Given three integers `m`, `n`, and `k`, return _the_ `kth` _smallest element in the_ `m x n` _multiplication table_.
**Example 1:**
**Input:** m = 3, n = 3, k = 5
**Output:** 3
**Explanation:** The 5th smallest number is 3.
**Example 2:**
**Input:** m = 2, n = 3, k = 6
**Output:** 6
**Explanation:** The 6th smallest number is 6.
**Constraints:**
* `1 <= m, n <= 3 * 104`
* `1 <= k <= m * n` | null |
668: Time 96.19%, Solution with step by step explanation | kth-smallest-number-in-multiplication-table | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Inside the binary_search function, use a while loop to iterate until left is no longer less than right.\n\n2. Calculate the middle index mid using the formula (left + right) // 2.\n\n3. Initialize a variable count to 0 and another variable j to n.\n\n4. Use a for loop to iterate through the range 1 to m+1.\n\n5. Inside the for loop, use a while loop to iterate until j is greater than or equal to 1 and i*j is greater than mid.\n\n6. Decrement j by 1 inside the while loop.\n\n7. Add the value of j to count.\n\n8. After the for loop, check if count is less than k.\n\n9. If count is less than k, update left to mid + 1.\n\n10. If count is greater than or equal to k, update right to mid.\n\n11. Return left outside the while loop.\n\n12. Finally, call the binary_search function with the initial values of left as 1 and right as m*n, and return the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findKthNumber(self, m: int, n: int, k: int) -> int:\n \n # Define binary search function to find the kth smallest element\n def binary_search(left, right):\n while left < right:\n mid = (left + right) // 2\n count = 0\n j = n\n for i in range(1, m+1):\n while j >= 1 and i*j > mid:\n j -= 1\n count += j\n if count < k:\n left = mid + 1\n else:\n right = mid\n return left\n \n # Call binary search function with appropriate left and right bounds\n return binary_search(1, m*n)\n\n``` | 2 | Nearly everyone has used the [Multiplication Table](https://en.wikipedia.org/wiki/Multiplication_table). The multiplication table of size `m x n` is an integer matrix `mat` where `mat[i][j] == i * j` (**1-indexed**).
Given three integers `m`, `n`, and `k`, return _the_ `kth` _smallest element in the_ `m x n` _multiplication table_.
**Example 1:**
**Input:** m = 3, n = 3, k = 5
**Output:** 3
**Explanation:** The 5th smallest number is 3.
**Example 2:**
**Input:** m = 2, n = 3, k = 6
**Output:** 6
**Explanation:** The 6th smallest number is 6.
**Constraints:**
* `1 <= m, n <= 3 * 104`
* `1 <= k <= m * n` | null |
[ Python ] Clean & Most Efficient Binary Solution Beats 87.25% in runtime | kth-smallest-number-in-multiplication-table | 0 | 1 | \n# Code\n```\nclass Solution:\n def findKthNumber(self, m: int, n: int, k: int) -> int:\n def count(x):\n return sum(min(x//i, n) for i in range(1, m+1))\n\n l, r, mid, ans = 0, m*n, 0, 0\n while l <= r:\n mid = (l + r) >> 1\n if count(mid) < k:\n l = mid + 1\n else:\n r, ans = mid - 1, mid\n return ans\n``` | 2 | Nearly everyone has used the [Multiplication Table](https://en.wikipedia.org/wiki/Multiplication_table). The multiplication table of size `m x n` is an integer matrix `mat` where `mat[i][j] == i * j` (**1-indexed**).
Given three integers `m`, `n`, and `k`, return _the_ `kth` _smallest element in the_ `m x n` _multiplication table_.
**Example 1:**
**Input:** m = 3, n = 3, k = 5
**Output:** 3
**Explanation:** The 5th smallest number is 3.
**Example 2:**
**Input:** m = 2, n = 3, k = 6
**Output:** 6
**Explanation:** The 6th smallest number is 6.
**Constraints:**
* `1 <= m, n <= 3 * 104`
* `1 <= k <= m * n` | null |
[C++/Java/Python] Short Binary Search Solution with Explanation | kth-smallest-number-in-multiplication-table | 1 | 1 | ### Introduction\n\nGiven a `m x n` multiplication table, we need to find the <code>k<sup>th</sup></code> smallest number in that table, where `1 <= k <= m*n`. But first, let\'s consider a different point-of-view: **if we are given a number `num` where `1 <= num <= m*n`, how do we find the number of numbers in the table smaller than `num`?** As an example, consider the following table:\n\n```text\nm=5, n=4: 5 x 4 multiplication table\n\n 1 2 3 4 5\n1 1 2 3 4 5\n2 2 4 6 8 10 [ 1, 2, 2, 3, 3, 4, 4, 4, 5, 6, 6, 8, 8, 9, 10, 12, 12, 15, 16, 20 ]\n3 3 6 9 12 15\n4 4 8 12 16 20\n```\n\nSay we want to find how many numbers are smaller than `12` in the table. We can break up the problem further and check the columns (or rows): how many numbers in each column is smaller than `12`? The more intuitive way is to **count the number of numbers that are strictly smaller than `12`.** For example:\n\n```text\nm=5, n=4: 5 x 4 multiplication table\n\n 1 2 3 4 5\n1 1 2 3 4 5\n2 2 4 6 8 10 [ 1, 2, 2, 3, 3, 4, 4, 4, 5, 6, 6, 8, 8, 9, 10, 12, 12, 15, 16, 20 ]\n3 3 6 9 12 15 ^\n4 4 8 12 16 20 |\n v v v v v |\n 4 4 3 2 2 --> 15 -------------------------------------------\n```\n\nNotice that, since we excluded `12` itself from the count, the final number that the total count points to will be the number just before `12`. I.e., since we obtain `15` from the total count of numbers less than `12`, we can assert that `12` is the <code>16<sup>th</sup></code> smallest number.\n\n```text\nPseudocode:\ncounter = 0\nfor each column number i (there are m columns)\n for each row number j (there are n columns)\n\t check if i*j < num (12 in our example)\n\t\t counter = counter + 1 if so\nnum is the (counter+1)-th smallest number\n```\n\nThis will work, but it is quite slow (rough time complexity is O(mn) here). We can do better by **obtaining the expected number of numbers smaller than `12` in each column** (i.e. determine what `j` should be) by rounding down `12 / i`. Then, since there is only a maximum of `n` rows, we need to account for this upper limit.\n\n```text\nPseudocode:\ncounter = 0\nfor each column number i (there are m columns)\n determine expected value of j: num / i, rounded down\n\tcounter = counter + (j, but n if j > n)\n\tcheck if i*j is num\n\t\tcount = counter - 1 if so\nnum is the (counter+1)-th smallest number\n```\n\nThe new time complexity is O(m), which will run much faster. One final optimisation is to do away with the strict checking and allow `12` itself to be included in the count:\n\n```text\nPseudocode:\ncounter = 0\nfor each column number i (there are m columns)\n determine expected value of j: num / i, rounded down\n\tcounter = counter + (j, but n if j > n)\nnum is the (counter)-th smallest number\n```\n\n```text\nm=5, n=4: 5 x 4 multiplication table\n\n 1 2 3 4 5\n1 1 2 3 4 5\n2 2 4 6 8 10 [ 1, 2, 2, 3, 3, 4, 4, 4, 5, 6, 6, 8, 8, 9, 10, 12, 12, 15, 16, 20 ]\n3 3 6 9 12 15 ^\n4 4 8 12 16 20 |\n v v v v v |\n 4 4 4 3 2 --> 17 ---------------------------------------------------\n```\n\nThis excludes all numbers that are strictly greater than `12`. Notice that `16 =/= 17`; we obtained two different indexes since there are duplicate `12`s. If `k = 16`, however, we would still need to return `12`. This suggests that we need to accomodate for duplicate numbers by allowing `counter >= k`, provided that the number we obtain in the <code>counter<sup>th</sup></code> index is equal to our target `num`.\n\n---\n\n### Binary Search\n\nHow does binary search fit into all of this? Continuing from the POV we are using (determining how many numbers are smaller than a given `num`), we now want to know: how we can obtain this `num`? For that, we can use binary search to give us numbers to check through. How does this work?\n\n- **`num` must be bounded; `1 <= num <= m*n`**. This is not to say that `num` must be in the table, rather, we can safely assume that the <code>k<sup>th</sup></code> smallest number must fall in `[1, m*n]` since `1 <= k <= m*n`.\n- **We are able to derive exactly 2 cases:** either `counter >= k` is satisfied and `num` could be the correct number that we\'re looking for, or `counter >= k` is not satisfied and `num` is smaller than the target number. This dichotomous nature of the conditional checking of `num` forms the basis of binary search, as we can discard/disregard one half of the search space based on this condition.\n\nBut wait, if `num` doesn\'t need to be in the table, how can we be sure that the resultant `num` obtained is in the table? We could perform a check after the binary search, but thanks to the way that we computed `counter`, we don\'t have to. Consider the following example:\n\n```text\nm=3, n=3, k=7\n 1 2 3\n1 1 2 3\n2 2 4 6 -> [ 1, 2, 2, 3, 3, 4, 6, 6, 9 ]\n3 3 6 9 ^\n\ncounter\n ^\n | 9\n | 8 _____________\n | __________________| | |\n | 6 | | | | | |\n | 5 ____________| | | | | |\n | ______| | | | | | | |\n | 3 | | | | | | | | |\n | ______| | | | | | | | |\n | 1 | | | | | | | | | |\n |_____| | | | | | | | | |\n | | | | | | | | | | |\n -------------------------------------------------------------> num\n 1 2 3 4 5 6 7 8 9 10\n```\n\nLet\'s start by defining some variables. First, denote the <code>k<sup>th</sup></code> smallest element in the table as `target`. We know from definition that `1 <= target <= m*n`. Next, denote the previous adjacent element in the table as `prev`, where `1 <= prev < target <= m*n`, and let\'s assume that it exists; i.e., `k > 1` (we can assert that `k = 1` is trivial, since `k = 1` always returns `1`). Finally, define `btwn` as all numbers such that `prev < btwn < target`, and note that `btwn` does not exist in the table.\n\nWe can therefore note 3 key observations:\n\n1. The number of elements in the table that are smaller than `target` is given by <code>counter<sub>target</sub> >= k</code>. Note then that **<code>counter<sub>target</sub></code> is the closest we have that fulfils the criteria of `counter >= k`**, i.e. any smaller valid counter will result in <code>counter < k <= counter<sub>target</sub></code>.\n2. **For each `btwn`, <code>counter<sub>btwn</sub> = counter<sub>prev</sub></code>**. This is because `btwn` is not found in the table, and <code>counter<sub>prev</sub></code> includes `prev` in the count.\n3. Since `prev < target`, <code>counter<sub>prev</sub> < counter<sub>target</sub></code>. **Therefore, from observations 1 and 2, <code>counter<sub>prev</sub> = counter<sub>btwn</sub> < k <= counter<sub>target</sub></code>**.\n\nFrom observation 3, it is clear that any number below `target` can be eliminated successfully by binary search since `counter < k`. From observation 1, we therefore conclude that `target` is the minimum possible number that satisfies `counter >= k`, and can therefore eliminate the upper search space if we obtain a number that is greater than `target`. **Both of these work together so that, in the end, the binary search limits the search space down to the final `target`**. Hence, this is why binary search is able to obtain a number from the table despite not having explicit checks for that condition.\n\nSo, now that we\'ve established that binary search works, our implementation can be as follows:\n\n- Obtain a number from the middle of the search space `[1, m*n]`.\n- Check if this number fulfils `counter >= k`.\n - If so, our targer number must lie in the lower half of the search space.\n - Otherwise, our target number must lie in the upper half of the search space.\n- Shrink the search space accordingly, and iterate until our search space reduces to a single number.\n\n---\n\n### Code\n\n<iframe src="https://leetcode.com/playground/m8DfwKhi/shared" frameBorder="0" width="900" height="400"></iframe>\n\n**TC: O(<img src="http://latex.codecogs.com/svg.image?mlog(mn)" title="mlog(mn)" />)**. The binary search is O(<img src="http://latex.codecogs.com/svg.image?log(mn)" title="log(mn)" />), and the nested counter computations runs in O(m) time.\n**SC: O(1)**, since no additional data structures are used.\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 110 | Nearly everyone has used the [Multiplication Table](https://en.wikipedia.org/wiki/Multiplication_table). The multiplication table of size `m x n` is an integer matrix `mat` where `mat[i][j] == i * j` (**1-indexed**).
Given three integers `m`, `n`, and `k`, return _the_ `kth` _smallest element in the_ `m x n` _multiplication table_.
**Example 1:**
**Input:** m = 3, n = 3, k = 5
**Output:** 3
**Explanation:** The 5th smallest number is 3.
**Example 2:**
**Input:** m = 2, n = 3, k = 6
**Output:** 6
**Explanation:** The 6th smallest number is 6.
**Constraints:**
* `1 <= m, n <= 3 * 104`
* `1 <= k <= m * n` | null |
python3 solution | kth-smallest-number-in-multiplication-table | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findKthNumber(self, m: int, n: int, k: int) -> int:\n\n def feasible(mid):\n count = 0\n for v in range(1,m+1):\n add = min(mid//v , n)\n if add == 0:\n break\n count+=add\n return count >= k\n\n l = 1\n r = m*n\n while l < r:\n mid = (l+r) // 2\n if feasible(mid):\n r = mid\n else:\n l = mid + 1\n return l \n``` | 0 | Nearly everyone has used the [Multiplication Table](https://en.wikipedia.org/wiki/Multiplication_table). The multiplication table of size `m x n` is an integer matrix `mat` where `mat[i][j] == i * j` (**1-indexed**).
Given three integers `m`, `n`, and `k`, return _the_ `kth` _smallest element in the_ `m x n` _multiplication table_.
**Example 1:**
**Input:** m = 3, n = 3, k = 5
**Output:** 3
**Explanation:** The 5th smallest number is 3.
**Example 2:**
**Input:** m = 2, n = 3, k = 6
**Output:** 6
**Explanation:** The 6th smallest number is 6.
**Constraints:**
* `1 <= m, n <= 3 * 104`
* `1 <= k <= m * n` | null |
Solution | trim-a-binary-search-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* trimBST(TreeNode* root, int low, int high) {\n if(root==NULL) return NULL;\n if(root->val>=low&&root->val<=high){\n root->left=trimBST(root->left,low,high);\n root->right=trimBST(root->right,low,high);\n return root;\n }\n else if(root->val<low){\n return trimBST(root->right,low,high);\n }\n else return trimBST(root->left,low,high);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:\n \n def trim(node):\n if not node:\n return\n \n if node.val < low:\n return trim(node.right)\n elif high < node.val:\n return trim(node.left)\n \n node.left = trim(node.left)\n node.right = trim(node.right)\n return node\n \n return trim(root)\n```\n\n```Java []\nclass Solution {\n public TreeNode trimBST(TreeNode root, int low, int high) {\n if(root == null){\n return null;\n }\n if(root.val < low){\n return trimBST(root.right, low, high);\n }\n if(root.val > high){\n return trimBST(root.left, low, high);\n }\n root.left = trimBST(root.left, low, high);\n root.right = trimBST(root.right, low, high);\n return root;\n }\n}\n```\n | 2 | Given the `root` of a binary search tree and the lowest and highest boundaries as `low` and `high`, trim the tree so that all its elements lies in `[low, high]`. Trimming the tree should **not** change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a **unique answer**.
Return _the root of the trimmed binary search tree_. Note that the root may change depending on the given bounds.
**Example 1:**
**Input:** root = \[1,0,2\], low = 1, high = 2
**Output:** \[1,null,2\]
**Example 2:**
**Input:** root = \[3,0,4,null,2,null,null,1\], low = 1, high = 3
**Output:** \[3,2,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104`
* The value of each node in the tree is **unique**.
* `root` is guaranteed to be a valid binary search tree.
* `0 <= low <= high <= 104` | null |
Recurssive solution using post order traversal | trim-a-binary-search-tree | 0 | 1 | # Approach\nKeep doing `post order traversal` and check for below conditions:\n`root.val < low`\nThis means current root and all the left node should be trimmed\n`root.val > high`\nThis means current root and all the right nodes should be trimmed\n`low <= root.val <= high`\nIn this case curretn root should be returned\n\n\n# Complexity\n- Time complexity: `O(n)`\n- Space complexity: `O(n)` in worst case if the tree is skewed\n\n# Code\n```\nclass Solution:\n def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:\n if root is None:\n return None\n \n root.left = self.trimBST(root.left, low, high)\n root.right = self.trimBST(root.right, low, high)\n\n if root.val < low:\n return root.right\n elif root.val > high:\n return root.left\n return root\n``` | 1 | Given the `root` of a binary search tree and the lowest and highest boundaries as `low` and `high`, trim the tree so that all its elements lies in `[low, high]`. Trimming the tree should **not** change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a **unique answer**.
Return _the root of the trimmed binary search tree_. Note that the root may change depending on the given bounds.
**Example 1:**
**Input:** root = \[1,0,2\], low = 1, high = 2
**Output:** \[1,null,2\]
**Example 2:**
**Input:** root = \[3,0,4,null,2,null,null,1\], low = 1, high = 3
**Output:** \[3,2,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104`
* The value of each node in the tree is **unique**.
* `root` is guaranteed to be a valid binary search tree.
* `0 <= low <= high <= 104` | null |
Python. faster than 98.05%. recursive. 6 lines. DFS. | trim-a-binary-search-tree | 0 | 1 | \tclass Solution:\n\t\tdef trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:\n\t\t\tif not root: return root\n\t\t\tif root.val < low: return self.trimBST(root.right, low, high)\n\t\t\tif root.val > high: return self.trimBST(root.left, low, high)\n\t\t\troot.left = self.trimBST(root.left, low, high)\n\t\t\troot.right = self.trimBST(root.right, low, high)\n\t\t\treturn root | 30 | Given the `root` of a binary search tree and the lowest and highest boundaries as `low` and `high`, trim the tree so that all its elements lies in `[low, high]`. Trimming the tree should **not** change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a **unique answer**.
Return _the root of the trimmed binary search tree_. Note that the root may change depending on the given bounds.
**Example 1:**
**Input:** root = \[1,0,2\], low = 1, high = 2
**Output:** \[1,null,2\]
**Example 2:**
**Input:** root = \[3,0,4,null,2,null,null,1\], low = 1, high = 3
**Output:** \[3,2,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104`
* The value of each node in the tree is **unique**.
* `root` is guaranteed to be a valid binary search tree.
* `0 <= low <= high <= 104` | null |
669: Solution with step by step explanation | trim-a-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a while loop to find the new root of the trimmed tree. Iterate through the tree until we find a node that is within the boundaries of low and high.\n\n2. Check if the root is None. If it is, return None.\n\n3. Set a variable node to root.\n\n4. Initialize a nested while loop to trim the left subtree of the new root. While node is not None, check if its left child is not None and its value is less than low. If it is, set the left child of node to its right child. Continue to traverse the left subtree by setting node to its left child.\n\n5. Reset node to root.\n\n6. Initialize another nested while loop to trim the right subtree of the new root. While node is not None, check if its right child is not None and its value is greater than high. If it is, set the right child of node to its left child. Continue to traverse the right subtree by setting node to its right child.\n\n7. Return the new root of the trimmed tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:\n while root and (root.val < low or root.val > high):\n if root.val < low:\n root = root.right\n else:\n root = root.left\n \n if not root:\n return None\n \n node = root\n while node:\n while node.left and node.left.val < low:\n node.left = node.left.right\n \n node = node.left\n \n node = root\n while node:\n while node.right and node.right.val > high:\n node.right = node.right.left\n \n node = node.right\n \n return root\n\n``` | 3 | Given the `root` of a binary search tree and the lowest and highest boundaries as `low` and `high`, trim the tree so that all its elements lies in `[low, high]`. Trimming the tree should **not** change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a **unique answer**.
Return _the root of the trimmed binary search tree_. Note that the root may change depending on the given bounds.
**Example 1:**
**Input:** root = \[1,0,2\], low = 1, high = 2
**Output:** \[1,null,2\]
**Example 2:**
**Input:** root = \[3,0,4,null,2,null,null,1\], low = 1, high = 3
**Output:** \[3,2,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104`
* The value of each node in the tree is **unique**.
* `root` is guaranteed to be a valid binary search tree.
* `0 <= low <= high <= 104` | null |
✅ Python || Easy Solution || 5 lines use recursive! || 100% | trim-a-binary-search-tree | 0 | 1 | * class Solution:\n\t\t\tdef trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:\n\t\t\t\tif(root == None) : \n\t\t\t\t\treturn None; \n\t\t\t\troot.left = self.trimBST(root.left,low,high);\n\t\t\t\troot.right = self.trimBST(root.right,low,high); \n\t\t\t\tif( low <= root.val and root.val <= high ) :\n\t\t\t\t\treturn root;\n\t\t\t\tif root.left != None :\n\t\t\t\t\treturn root.left;\n\t\t\t\telse:\n\t\t\t\t\treturn root.right; | 7 | Given the `root` of a binary search tree and the lowest and highest boundaries as `low` and `high`, trim the tree so that all its elements lies in `[low, high]`. Trimming the tree should **not** change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a **unique answer**.
Return _the root of the trimmed binary search tree_. Note that the root may change depending on the given bounds.
**Example 1:**
**Input:** root = \[1,0,2\], low = 1, high = 2
**Output:** \[1,null,2\]
**Example 2:**
**Input:** root = \[3,0,4,null,2,null,null,1\], low = 1, high = 3
**Output:** \[3,2,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104`
* The value of each node in the tree is **unique**.
* `root` is guaranteed to be a valid binary search tree.
* `0 <= low <= high <= 104` | null |
Easy to understand Python3 code with full explanation - O(n) time & O(n) space | maximum-swap | 0 | 1 | # Intuition\nBy eye-balling the question, we immediately have the intuition to swap the smallest left-most digit with the largest right-most digit in order to maximize the number . But how can we translate this into code?\n\nIf we iterate from left to right, we have to keep track of the left-most smallest digit and we also have to keep track of the right-most largest digit. This requires look back & look forward logic which can be expensive.\n\nIs there a simpler approach? What if we iterate from right to left? In that scenario, we have to keep track of the largest digit encountered so far and then swap it with right-most digit which is smaller than it. \n\nWhy does this work? Because we are guaranteed to find the left-most largest digit and replace it with the right-most smallest digit. Since this is a greedy approach, we don\'t need any look backs and only need to iterate through all the digits just once.\n\n\n# Code\n```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n num_list = list(str(num))\n\n # initialize tuple which stores value of maximum digit and its index and set this to rightmost digit\n max_digit = (int(num_list[len(num_list) - 1]), len(num_list) - 1)\n\n # initialize tuple which stores indices of digits to be swapped\n swap_indices = (0, 0)\n\n # iterate through the number list from right to left\n for idx in range(len(num_list) - 2, -1, -1):\n digit = int(num_list[idx])\n\n # if current digit is smaller than max digit, register current index to be swapped with index of max digit encounted so far\n if digit < max_digit[0]:\n swap_indices = (max_digit[1], idx)\n\n # if current digit is greater than max digit, register new max_digit\n elif digit > max_digit[0]:\n max_digit = (digit, idx)\n\n # if the current digit is equal to max digit, then don\'t make any changes because we always want to swap rightmost largest digit\n\n # swap digits\n num_list[swap_indices[0]], num_list[swap_indices[1]] = num_list[swap_indices[1]], num_list[swap_indices[0]]\n return(int(\'\'.join(num_list)))\n\n# Unit tests\nfrom unittest import TestCase\nclass TestSolution(TestCase):\n def test_solution(self):\n input_output = [\n [2736, 7236],\n [9973, 9973],\n [98368, 98863]\n ]\n input = [Solution().maximumSwap(ip_op[0]) for ip_op in input_output]\n output = [ip_op[1] for ip_op in input_output]\n self.assertEqual(input, output)\n\n```\n\n# Complexity:\n Consider an int with N digits\n Time: O(N) - we iterate through all the digits exactly once\n Space: O(N) - we split the int into string of digits which takes O(N) space | 0 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
String manipulation | Python3 | O(n) | maximum-swap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nConvert the number to a string: The first step is to convert the given integer num into a string. This allows us to work with individual digits easily, making it convenient to iterate through the number digit by digit.\n\nFind the rightmost smaller digit: To maximize the number, we want to swap a digit with a larger digit to its right (higher index) while maintaining the order of the other digits. To do this, we iterate through the digits from left to right. We need to find the rightmost digit that is smaller than its right neighbor because swapping any other digit would not lead to a larger number.\n\nLocate the maximum digit to the right: Once we find the rightmost smaller digit, we want to find the largest digit to its right that is smaller than the identified digit. This is because swapping with this larger digit will result in the maximum value.\n\nSwap and return the result: Once we find the two digits to swap, we create a new list containing the digits and perform the swap. After the swap, we convert the list back to an integer and return the maximum value.\n\nNo swap needed: If no suitable digits are found to swap (i.e., the number is already in its maximum value form), we can simply return the original number.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nConvert the given integer to a string to work with individual digits.\nIterate through the digits and find the rightmost digit (higher index) that is smaller than its right neighbor.\nIf such a digit is found, we search for the maximum digit to its right (higher index) that is smaller than itself. This is done to find the digit with which we can swap to get the maximum value.\nSwap the two identified digits.\nConvert the modified string back to an integer and return the result.\n# Complexity\nThis code has a time complexity of O(n) where n is the number of digits in the input number. It efficiently finds the digits to swap and constructs the maximum value accordingly.\n\n# Code\n```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n num_str = str(num)\n n = len(num_str)\n last_occurrence = [-1] * 10\n\n # Store the last occurrence of each digit in the number\n for i in range(n):\n last_occurrence[int(num_str[i])] = i\n\n # Iterate through the digits and find the rightmost smaller digit\n for i in range(n):\n digit = int(num_str[i])\n # Check if there\'s any larger digit to the right\n for j in range(9, digit, -1):\n if last_occurrence[j] > i:\n # Swap the digits and return the result\n num_list = list(num_str)\n num_list[i], num_list[last_occurrence[j]] = num_list[last_occurrence[j]], num_list[i]\n return int(\'\'.join(num_list))\n\n # If no swap is possible, the number itself is the maximum\n return num\n``` | 1 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
Python 3 | Greedy, Math | Explanations | maximum-swap | 0 | 1 | ### Explanation\n- Basic idea:\n\t- Find a index `i`, where there is a increasing order \n\t- On the right side of `i`, find the max value (`max_val`) and its index (`max_idx`)\n\t- On the left side of `i`, find the most left value and its index (`left_idx`), which is less than `max_val`\n\t- Swap above `left_idx` and `max_idx` if necessary\n- Please check the comments for more detail\n### Implementation\n```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n s = list(str(num))\n n = len(s)\n for i in range(n-1): # find index where s[i] < s[i+1], meaning a chance to flip\n if s[i] < s[i+1]: break\n else: return num # if nothing find, return num\n max_idx, max_val = i+1, s[i+1] # keep going right, find the maximum value index\n for j in range(i+1, n):\n if max_val <= s[j]: max_idx, max_val = j, s[j]\n left_idx = i # going right from i, find most left value that is less than max_val\n for j in range(i, -1, -1): \n if s[j] < max_val: left_idx = j\n s[max_idx], s[left_idx] = s[left_idx], s[max_idx] # swap maximum after i and most left less than max\n return int(\'\'.join(s)) # re-create the integer\n``` | 62 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
670: Solution with step by step explanation | maximum-swap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Convert the input integer num to a list of digits by using list(str(num)). This allows us to access each digit individually.\n\n2. Create a dictionary called last_seen that keeps track of the last index of each digit in the number. To do this, we iterate over the digits and add each digit as a key in the dictionary with its index as the value. For example, if digits is [2, 7, 3, 6], last_seen will be {2: 0, 7: 1, 3: 2, 6: 3}.\n\n3. Iterate over each digit in the number using enumerate(digits). We will use the index i and the digit digit in our algorithm.\n\n4. For each digit, check if there is a larger digit after it by using a for loop that counts down from 9 to digit (exclusive). If the larger digit exists in last_seen and its last occurrence is after the current index i, we can swap the digits to get a larger number.\n\n5. If we swap the digits, we return the maximum valued number by converting the list of digits back to an integer with int(\'\'.join(digits)).\n\n6. If we don\'t make any swaps, we return the original number num.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n # Convert the integer to a list of digits\n digits = list(str(num))\n \n # Keep track of the last index of each digit in the number\n last_seen = {int(digit): i for i, digit in enumerate(digits)}\n \n # Iterate over each digit in the number\n for i, digit in enumerate(digits):\n # Check if there is a larger digit after the current digit\n for j in range(9, int(digit), -1):\n if j in last_seen and last_seen[j] > i:\n # Swap the digits and return the result\n digits[i], digits[last_seen[j]] = digits[last_seen[j]], digits[i]\n return int(\'\'.join(digits))\n \n # If no swap was made, return the original number\n return num\n\n``` | 4 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
Solution | maximum-swap | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maximumSwap(int num) {\n string digits = to_string(num);\n int left = 0, right = 0;\n int max_idx = digits.length() - 1;\n for (int i = digits.length() - 1; i >= 0; --i) {\n if (digits[i] > digits[max_idx]) {\n max_idx = i;\n } else if (digits[max_idx] > digits[i]) {\n left = i;\n right = max_idx;\n }\n }\n swap(digits[left], digits[right]);\n return stoi(digits);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maximumSwap(self, num):\n num = list(str(num))\n max_idx = len(num) - 1\n small = large = 0\n \n for i in range(len(num) - 1, -1, -1): \n if num[i] > num[max_idx]:\n max_idx = i # this is the right side max number index\n elif num[i] < num[max_idx]:\n small = i\n large = max_idx\n \n num[small], num[large] = num[large], num[small]\n return int(\'\'.join(num)) # join a list of string/charaters\n```\n\n```Java []\nclass Solution {\n public int maximumSwap(int num) {\n if(num < 10) return num;\n char[] arr = String.valueOf(num).toCharArray();\n int[] rightIndex = new int[10]; \n for(int i=0; i<arr.length; i++){\n rightIndex[arr[i] - \'0\'] = i;\n }\n for(int i=0; i<arr.length; i++){\n for(int j=9; j>arr[i] - \'0\'; j--){\n if(rightIndex[j] > i){\n char temp = arr[i];\n arr[i] = arr[rightIndex[j]];\n arr[rightIndex[j]] = temp;\n return Integer.valueOf(new String(arr));\n }\n }\n }\n return num;\n }\n}\n```\n | 4 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
Intuitive | recursive | python 3 | maximum-swap | 0 | 1 | Approach: \n1. Find the max of given array of digits.\n2. If max matches with the first digit (index 0) then there is no benefit of swapping, so recursively solve for remaining array i.e. index 1 onwards\n3. Else if - digit at index 0 is not equal to max of that array then swap it with the last occurance of max in the given array.\n\n```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n \n num = [int(digit) for digit in str(num)]\n \n \n def solve(num):\n if not num:\n return num\n max_num = max(num)\n if max_num == num[0]:\n return [num[0]] + solve(num[1:])\n else:\n # get the last occurance index of max element - use index() on reversed list\n index = num[::-1].index(max_num) \n\t\t\t\t\n\t\t\t\t# add 1 to the index so that we can use the index for negetive indexing on non reversed list while swapping\n index = index+1\n\t\t\t\t\n num[0], num[-index] = num[-index], num[0]\n return num\n\t\t\t\t\n return int(\'\'.join(str(digit) for digit in solve(num)))\n``` | 3 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
Python 3 O(n) time, O(1) space, without using strings, with comments | maximum-swap | 0 | 1 | ```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n # larger digit to swap, digit position of this digit\n high_digit = high_pos = 0\n \n # smaller digit to swap, digit position of this digit\n low_digit = low_pos = 0\n \n # greatest digit seen so far, digit postion of this digit\n cur_high_digit, cur_high_pos = -1, 0\n \n # current digit position\n pos = 1\n \n res = num\n while num: # iterate through digits from right to left\n digit = num % 10\n \n # if digit is greatest digit yet\n if digit > cur_high_digit:\n cur_high_digit, cur_high_pos = digit, pos\n \n # if digit is less than greatest digit yet\n elif digit < cur_high_digit:\n # set the digits to swap as the greatest digit yet, and this digit\n high_digit, high_pos = cur_high_digit, cur_high_pos\n low_digit, low_pos = digit, pos\n \n pos *= 10\n num //= 10\n \n # swap the digits\n res += high_digit*(low_pos - high_pos) + low_digit*(high_pos - low_pos)\n return res | 10 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
Two Pointers || Explanation || Python | maximum-swap | 0 | 1 | # Intuition\nFirstly, I was thinking to appproach this problem as next greater but it will give wrong ans. Why? Suppose u found a bigger number later in string which can be interchanged with first one then that ans will give u correct ans.\neg => 782349\nnext greater swap will give == 872349\nans == 982347 \nhence u have to maintain two pointers to find the biggest number from the remaining list from the curr pointer\n\n# Approach\nMaintain a left pointer as your curr Pointer and assume the it as the minimum by default and run a right pointer till left + 1 index and find the max in it.\nNow check if the found max is actually greater than our assumed minimum if not, u already have the current left index num at correct pos and doesnt need to be swapped so increment ur left pointer.\nonce u find a larger element swap them and break from the loop(as u can only swap exactly once)\nthe resultant is ur final ans.\n\n# Code\n```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n #convert into list\n nums = []\n for n in str(num):\n nums.append(int(n))\n left = 0\n\n while left < len(nums):\n #assume curr left as min\n mini = nums[left]\n maxi = 0\n #check for max\n for right in range(len(nums) -1, left, -1):\n if nums[right] > maxi:\n maxIndex = right\n maxi = nums[right]\n #if the max found is greater than assumed min => swap\n if maxi > mini: \n nums[maxIndex], nums[left] = nums[left], nums[maxIndex]\n break\n #no need to swap with curr left\n left += 1\n # print(nums)\n ans = ""\n for n in nums:\n ans += str(n)\n return int(ans)\n\n``` | 3 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
python3 simple logic (with explanation) | maximum-swap | 0 | 1 | The greedy solution is to swap the leftmost digit with a larger digit to the right of it. For example, in 2237, 2 is swapped with 7, the largest digit to its right. \n\nHowever, what if there are multiple larger digits that are the same to the right? You should always swap with the rightmost one. For example, 89999 should become 99998, not 98999. Thus, we find the rightmost max.\n```\nclass Solution:\n def maximumSwap(self, num: int) -> int:\n num = [int(i) for i in str(num)]\n for i in range(len(num)-1):\n m = max(num[i+1:])\n if num[i] < m:\n for j in range(len(num)-1, i, -1):\n if num[j] == m:\n break\n num[i], num[j] = num[j], num[i]\n break\n return int("".join([str(i) for i in num]))\n``` | 16 | You are given an integer `num`. You can swap two digits at most once to get the maximum valued number.
Return _the maximum valued number you can get_.
**Example 1:**
**Input:** num = 2736
**Output:** 7236
**Explanation:** Swap the number 2 and the number 7.
**Example 2:**
**Input:** num = 9973
**Output:** 9973
**Explanation:** No swap.
**Constraints:**
* `0 <= num <= 108` | null |
671: Space 95.86%, Solution with step by step explanation | second-minimum-node-in-a-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the minimum value and second minimum value to be the root value.\n\n2. Define a recursive helper function to explore the tree, taking a node as input.\n\n3. Within the helper function, use the nonlocal keyword to access the minimum and second minimum values from the outer function scope.\n\n4. Check if the node value is less than the current minimum value. If it is, update the second minimum value to be the previous minimum value, and update the minimum value to be the node value.\n\n5. If the node value is not less than the current minimum value but is less than the current second minimum value, update the second minimum value to be the node value.\n\n6. Recursively call the helper function on the left and right subtrees of the current node if they exist.\n\n7. Call the helper function on the root node to start exploring the tree.\n\n8. Check if the second minimum value was updated during the exploration. If it was, return the second minimum value. Otherwise, return -1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSecondMinimumValue(self, root: TreeNode) -> int:\n # initialize minimum and second minimum values to be the root value\n min_val = root.val\n second_min_val = float(\'inf\')\n \n # recursive helper function to explore the tree\n def dfs(node: TreeNode) -> None:\n nonlocal min_val, second_min_val\n \n # check if node value is less than current minimum value\n if node.val < min_val:\n second_min_val = min_val\n min_val = node.val\n # check if node value is not less than minimum value but less than second minimum value\n elif node.val != min_val and node.val < second_min_val:\n second_min_val = node.val\n \n # explore left and right subtrees if they exist\n if node.left:\n dfs(node.left)\n if node.right:\n dfs(node.right)\n \n # explore the tree starting from the root\n dfs(root)\n \n # check if second minimum value was updated and return it, otherwise return -1\n return second_min_val if second_min_val != float(\'inf\') else -1\n\n``` | 2 | Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly `two` or `zero` sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property `root.val = min(root.left.val, root.right.val)` always holds.
Given such a binary tree, you need to output the **second minimum** value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
**Example 1:**
**Input:** root = \[2,2,5,null,null,5,7\]
**Output:** 5
**Explanation:** The smallest value is 2, the second smallest value is 5.
**Example 2:**
**Input:** root = \[2,2,2\]
**Output:** -1
**Explanation:** The smallest value is 2, but there isn't any second smallest value.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 25]`.
* `1 <= Node.val <= 231 - 1`
* `root.val == min(root.left.val, root.right.val)` for each internal node of the tree. | null |
Simple Python Solution | second-minimum-node-in-a-binary-tree | 0 | 1 | # Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findSecondMinimumValue(self, root: Optional[TreeNode]) -> int:\n def inorderTraversal(node):\n if not node:\n return\n inorderTraversal(node.left)\n unique_values.add(node.val)\n inorderTraversal(node.right)\n unique_values = set()\n inorderTraversal(root)\n sorted_values = sorted(unique_values)\n if len(sorted_values) < 2:\n return -1\n return sorted_values[1] \n``` | 2 | Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly `two` or `zero` sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property `root.val = min(root.left.val, root.right.val)` always holds.
Given such a binary tree, you need to output the **second minimum** value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
**Example 1:**
**Input:** root = \[2,2,5,null,null,5,7\]
**Output:** 5
**Explanation:** The smallest value is 2, the second smallest value is 5.
**Example 2:**
**Input:** root = \[2,2,2\]
**Output:** -1
**Explanation:** The smallest value is 2, but there isn't any second smallest value.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 25]`.
* `1 <= Node.val <= 231 - 1`
* `root.val == min(root.left.val, root.right.val)` for each internal node of the tree. | null |
Python3 (DFS/DFS Recursive/ BFS) | second-minimum-node-in-a-binary-tree | 0 | 1 | \n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findSecondMinimumValue(self, root: Optional[TreeNode]) -> int:\n #DFS\n a = []\n if not root: return -1\n stack = [(root, root.val)]\n while stack:\n node, val = stack.pop()\n if node.val not in a:\n a.append(node.val)\n if node.left: stack.append((node.left, node.left.val))\n if node.right: stack.append((node.right, node.right.val))\n a.sort()\n return a[1] if len(a) >= 2 else -1\n\n self.ans = float(\'inf\')\n min1 = root.val\n #Recursive DFS\n def dfs(node):\n if node:\n if min1 < node.val < self.ans:\n self.ans = node.val\n elif node.val == min1:\n dfs(node.left)\n dfs(node.right)\n\n dfs(root)\n return self.ans if self.ans < float(\'inf\') else -1\n #BFS\n a = []\n if not root: return -1\n dq = collections.deque([(root, root.val)])\n while dq:\n node, val = dq.popleft()\n if node.val not in a:\n a.append(node.val)\n if node.left: dq.append((node.left, node.left.val))\n if node.right: dq.append((node.right, node.right.val))\n a.sort()\n return a[1] if len(a) >= 2 else -1\n``` | 2 | Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly `two` or `zero` sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property `root.val = min(root.left.val, root.right.val)` always holds.
Given such a binary tree, you need to output the **second minimum** value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
**Example 1:**
**Input:** root = \[2,2,5,null,null,5,7\]
**Output:** 5
**Explanation:** The smallest value is 2, the second smallest value is 5.
**Example 2:**
**Input:** root = \[2,2,2\]
**Output:** -1
**Explanation:** The smallest value is 2, but there isn't any second smallest value.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 25]`.
* `1 <= Node.val <= 231 - 1`
* `root.val == min(root.left.val, root.right.val)` for each internal node of the tree. | null |
11 lines of code very easy approach | second-minimum-node-in-a-binary-tree | 0 | 1 | # Code\n```\nclass Solution:\n def findSecondMinimumValue(self, root: Optional[TreeNode]) -> int:\n if not root: return -1\n ar=set()\n def dfs(root):\n ar.add(root.val)\n if root.left: dfs(root.left)\n if root.right: dfs(root.right)\n dfs(root)\n ar.remove(min(ar))\n return min(ar) if ar else -1\n``` | 1 | Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly `two` or `zero` sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property `root.val = min(root.left.val, root.right.val)` always holds.
Given such a binary tree, you need to output the **second minimum** value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
**Example 1:**
**Input:** root = \[2,2,5,null,null,5,7\]
**Output:** 5
**Explanation:** The smallest value is 2, the second smallest value is 5.
**Example 2:**
**Input:** root = \[2,2,2\]
**Output:** -1
**Explanation:** The smallest value is 2, but there isn't any second smallest value.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 25]`.
* `1 <= Node.val <= 231 - 1`
* `root.val == min(root.left.val, root.right.val)` for each internal node of the tree. | null |
Simplest Python solution | second-minimum-node-in-a-binary-tree | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findSecondMinimumValue(self, root: Optional[TreeNode]) -> int:\n a = []\n\n def dfs(root):\n if not root:\n return\n dfs(root.left)\n a.append(root.val)\n dfs(root.right)\n\n dfs(root)\n\n return (sorted(set(a)))[1] if len(set(a)) >= 2 else -1\n``` | 4 | Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly `two` or `zero` sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property `root.val = min(root.left.val, root.right.val)` always holds.
Given such a binary tree, you need to output the **second minimum** value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
**Example 1:**
**Input:** root = \[2,2,5,null,null,5,7\]
**Output:** 5
**Explanation:** The smallest value is 2, the second smallest value is 5.
**Example 2:**
**Input:** root = \[2,2,2\]
**Output:** -1
**Explanation:** The smallest value is 2, but there isn't any second smallest value.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 25]`.
* `1 <= Node.val <= 231 - 1`
* `root.val == min(root.left.val, root.right.val)` for each internal node of the tree. | null |
74% TC and 65% SC easy python solution | second-minimum-node-in-a-binary-tree | 0 | 1 | ```\ndef findSecondMinimumValue(self, root: Optional[TreeNode]) -> int:\n\tleaf = set()\n\tdef dfs(node):\n\t\tif not(node.left):\n\t\t\tleaf.add(node.val)\n\t\t\treturn\n\t\tdfs(node.left)\n\t\tdfs(node.right)\n\tdfs(root)\n\treturn -1 if(len(leaf) < 2) else sorted(list(leaf))[1]\n``` | 2 | Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly `two` or `zero` sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property `root.val = min(root.left.val, root.right.val)` always holds.
Given such a binary tree, you need to output the **second minimum** value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
**Example 1:**
**Input:** root = \[2,2,5,null,null,5,7\]
**Output:** 5
**Explanation:** The smallest value is 2, the second smallest value is 5.
**Example 2:**
**Input:** root = \[2,2,2\]
**Output:** -1
**Explanation:** The smallest value is 2, but there isn't any second smallest value.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 25]`.
* `1 <= Node.val <= 231 - 1`
* `root.val == min(root.left.val, root.right.val)` for each internal node of the tree. | null |
SIMPLE PYTHON SOLUTION || UPTO 98 % FASTER | second-minimum-node-in-a-binary-tree | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findSecondMinimumValue(self, root: Optional[TreeNode]) -> int:\n def trav(root, final):\n if not root:\n return None\n if root.val not in final:\n final.append(root.val)\n\n if root.left:\n trav(root.left,final)\n \n if root.right:\n trav(root.right,final)\n \n return final\n\n final = trav(root,[])\n final = sorted(final)\n #print(final)\n if len(final)>=2:\n return final[1]\n else:\n return -1\n\n \n\n\n\n``` | 1 | Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly `two` or `zero` sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property `root.val = min(root.left.val, root.right.val)` always holds.
Given such a binary tree, you need to output the **second minimum** value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
**Example 1:**
**Input:** root = \[2,2,5,null,null,5,7\]
**Output:** 5
**Explanation:** The smallest value is 2, the second smallest value is 5.
**Example 2:**
**Input:** root = \[2,2,2\]
**Output:** -1
**Explanation:** The smallest value is 2, but there isn't any second smallest value.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 25]`.
* `1 <= Node.val <= 231 - 1`
* `root.val == min(root.left.val, root.right.val)` for each internal node of the tree. | null |
672: Time 96.77%, Solution with step by step explanation | bulb-switcher-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Reduce n to at most 3, since any action performed more than 3 times will result in a pattern that has already been counted.\n2. If m is 0, return 1 as there is only one possible outcome (all lights off).\n3. If m is 1, return the number of possible outcomes for the given value of n and m.\n4. If m is 2, return the number of possible outcomes for the given value of n and m.\n5. If m is greater than or equal to 3, return the number of possible outcomes for the given value of n and m.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipLights(self, n: int, m: int) -> int:\n # Reduce n to at most 3, since any action performed more than 3 times\n # will result in a pattern that has already been counted\n n = min(n, 3)\n if m == 0:\n return 1\n elif m == 1:\n # For m=1, there are only 2 outcomes for n=1, 3 outcomes for n=2, and 4 outcomes for n=3\n return [2, 3, 4][n - 1]\n elif m == 2:\n # For m=2, there are only 2 outcomes for n=1, 4 outcomes for n=2, and 7 outcomes for n=3\n return [2, 4, 7][n - 1]\n else:\n # For m>=3, there are only 2 outcomes for n=1, 4 outcomes for n=2, and 8 outcomes for n=3\n return [2, 4, 8][n - 1]\n\n``` | 3 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Python, BFS | bulb-switcher-ii | 0 | 1 | # Intuition\nWe need to traverse the states graph for exactly ``presses`` levels and get the total number of states discovered on the last level.\n\n# Approach\nWe can do either BFS or DFS. We also need an efficient way to represent a state and to calculate next states. \nWe can represent states as binary numbers where ith bit is set to ``1`` if the ith bulb is switched on and ``0`` otherwise. \nThen, for the state transitions, we have: \n1. Toggle all bulbs - perform an bitwise XOR on the state with all bits set to 1\n2. Toggle even bulbs - perform an bitwise XOR on the state with all even bits set to 1 \n3. Toggle odd bulbs - perform an bitwise XOR on the state with all odd bits set to 1 \n4. Toggle ``3*k+1`` bulbs - perform an bitwise XOR on the state with all ith bits set to 1, where ``i % 3 == 1``\n\nSince ``n <= 1000`` we would need big numbers to represent those states. Luckily Python has an out of the box support for big numbers.\n\n\n# Complexity\n- Time complexity: $$O(presses)$$\nWe need to perform ``presses`` steps traversing the states graph, each step has $$O(1)$$ operations.\n\n- Space complexity:\nSpace complexity is trickier here. On each step we discover 4 states from each state, however there are a lot of duplicated states. It can be proven that because of the operations that we have we wouldn\'t get more than ``8`` different states on each level. \n\nIntuition:\nWe can divide the whole state in groups of 3 digits and only have following operations:\n1. Switch all 3 bits\n2. Switch odd bits\n3. Switch even bits\n4. Switch only last bit\n\nRest bits will be changed in the same way. The only problem is that we would change odd and even groups of 3 differently for odd and even bits toggles.\n\nI don\'t have a better explanation yet, but my guess is that only ``8`` different states are possible at most.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipLights(self, n: int, presses: int) -> int:\n\n all_ones, evens, odds, three = 0, 0, 0, 0\n for i in range(n):\n all_ones = (all_ones << 1) + 1\n evens = (evens << 1) + (1 if (i+1) % 2 == 0 else 0)\n odds = (odds << 1) + (1 if (i+1) % 2 == 1 else 0)\n three = (three << 1) + (1 if (i+1) % 3 == 1 else 0)\n\n state = all_ones\n\n level = {state}\n for i in range(presses):\n next_level = set()\n for state in level:\n states = [state ^ all_ones,\n state ^ evens,\n state ^ odds,\n state ^ three]\n for next_state in states:\n next_level.add(next_state)\n level = next_level\n\n return len(level)\n``` | 2 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
O(1) with python. Pointless Question | bulb-switcher-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMost stupid question I have ever done. First I thought it was recursion, then I thought it was a counting problem. Finally just found out it is just listing out all the cases. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipLights(self, n: int, presses: int) -> int:\n # n > 2 means all presses are unique\n if presses == 0:\n return 1\n if n == 1:\n return 2\n if n == 2:\n if presses > 1:\n return 4\n else:\n return 3\n if n > 2:\n if presses == 1:\n return 4\n if presses == 2:\n return 7\n else:\n return 8\n``` | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Consider all cases, O(1) | bulb-switcher-ii | 0 | 1 | Straightforward to know that what matters is only n % 6.\nSuppose we have a,b,c,d operations of 1,2,3,4.\nBulb1 = (a+b+d) % 2\nBulb2 = (a+c) % 2\nBulb3 = (a+b) % 2\nand bulb 4 same as 1, 5 same as 3, 6 same as 2\n\nTherefore, what really matters is only the first three bulbs. \n\nIf we have only 1 bulb, in on step we have the two states 0 and 1 reachable. And so on, we just return 2.\n\nIn the case where we have 2 bulbs, step 1 would lead us to states 11,10,01 but not 00. After step 2 we can get 00 again, and so on we can reach whaterver we want.\n\n3 bulb, draw on your paper and easily we see in one step we got 4 states, and 2 steps we have all 8 states but 100, which can be reached after the 3 step. \n\nTherefore, just a few ifelses, O(1).\n\n# Code\n```\nclass Solution:\n def flipLights(self, n: int, presses: int) -> int:\n n = min(3,n)\n state = 0\n if presses == 0:\n return 1\n if n == 1:\n return 2\n if n == 2:\n return 4 if presses > 1 else 3\n if n == 3:\n if presses > 2:return 8\n elif presses == 2: return 7\n else: return 4\n\n\n\n\n\n \n``` | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Easiest Solution | bulb-switcher-ii | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n\n public int flipLights(int n, int p) {\n n = Math.min(n, 4); \n p = Math.min(p, 4);\n int thre = (1<<n)-1;\n\n int[] flips = new int[] {\n Integer.parseInt("1111", 2)&thre,\n Integer.parseInt("0101", 2)&thre,\n Integer.parseInt("1010", 2)&thre,\n Integer.parseInt("1001", 2)&thre\n };\n\n if(p==0) return 1;\n\n int ans = 0;\n boolean[] used = new boolean[(1<<10)+1];\n\n Queue<int[]> q = new LinkedList();\n q.add(new int[] {0, 0});\n\n while(!q.isEmpty()){\n int[] val = q.remove();\n int cur = val[0];\n int presses = val[1];\n\n if(presses==p) {\n if(!used[cur]) ans++;\n used[cur] = true;\n continue;\n }\n\n for(int flip : flips){\n q.add(new int[] {flip ^ cur, presses + 1});\n } \n }\n\n return ans;\n }\n}\n```\n\n```python3 []\nuse std::collections::{HashSet, VecDeque};\n\nimpl Solution {\n fn flip_bit(number: i32, position: u32) -> i32 {\n let mask = 1 << position;\n let flipped_number = number ^ mask;\n flipped_number\n }\n \n fn y_function(x: i32) -> i32 {\n 3 * x + 1\n }\n \n fn get_neighbors(state: i32, n: i32) -> Vec<i32> {\n let mut nbrs: Vec<i32> = vec![];\n \n let mut curr_num = state;\n for i in 1..n {\n curr_num = Solution::flip_bit(curr_num, i as u32);\n }\n nbrs.push(curr_num);\n \n curr_num = state;\n for i in (1..n).step_by(2) {\n curr_num = Solution::flip_bit(curr_num, i as u32);\n }\n nbrs.push(curr_num);\n \n curr_num = state;\n for i in (0..n).step_by(2) {\n curr_num = Solution::flip_bit(curr_num, i as u32);\n }\n nbrs.push(curr_num);\n \n let mut i = 0;\n while Solution::y_function(i) < n {\n curr_num = Solution::flip_bit(curr_num, Solution::y_function(i) as u32);\n i += 1;\n }\n nbrs.push(curr_num);\n \n nbrs\n }\n \n // O(n*press) time,\n // O(n*space) space,\n // Approach: bfs, bit manipulation\n fn flip_lights(n: i32, presses: i32) -> i32 {\n let mut answer: HashSet<i32> = HashSet::new();\n let mut queue: VecDeque<i32> = VecDeque::new();\n queue.push_back((2_i32.pow(n as u32) - 1));\n answer.insert(queue[0]);\n \n let mut presses = presses;\n \n while presses > 0 && !queue.is_empty() {\n presses -= 1;\n let queue_len = queue.len();\n answer = HashSet::new();\n for _ in 0..queue_len {\n let state = queue.pop_front().unwrap();\n let nbrs = Solution::get_neighbors(state, n);\n for nbr in nbrs {\n if answer.contains(&nbr) {\n continue;\n }\n answer.insert(nbr);\n queue.push_back(nbr);\n }\n }\n }\n\n answer.len() as i32\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n int flipLights(int n, int presses) {\n vector<bitset<1000>> m(4);\n\n for (int i=1;i<n;i+=2) {\n m[1].flip(i);\n m[2].flip(i-1);\n }\n if (n%2==1) m[2].flip(n-1);\n m[0]=m[1];\n m[0]|=m[2];\n\n \n for (int i=0;i<n;i+=3) m[3].flip(i);\n\n //for(auto& a:m) cout << a << endl;\n\n unordered_set<bitset<1000>> q;\n q.insert(m[0]);\n\n for (int i=0;i<presses;i++){\n unordered_set<bitset<1000>> temp;\n for (auto& item:q){\n for (int j=0;j<4;j++){\n auto t = bitset<1000>{item};\n t ^= m[j];\n temp.insert(t);\n }\n }\n q = temp;\n }\n return q.size();\n\n }\n};\n```\n | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Bit manipulation solution | bulb-switcher-ii | 0 | 1 | # Complexity\n- Time complexity:\n$$O(1)$$\n\n- Space complexity:\n$$O(m)$$. m is number of different states.\n\n# Code\n```\nclass Solution:\n def flipLights(self, n: int, presses: int) -> int:\n if presses == 0:\n return 1\n length = min(10, n)\n state = (1 << length) - 1\n buttons = [(1 << length) - 1, 0, 0, 0]\n for i in range(length):\n if i % 2 != 0:\n buttons[1] |= 1 << i\n if i % 2 == 0:\n buttons[2] |= 1 << i\n if 3 * i + 1 < length:\n buttons[3] |= 1 << (3 * i)\n states = set()\n visited = set()\n q = deque()\n q.append([state, presses])\n while q:\n for _ in range(len(q)):\n currentState, currentPresses = q.popleft()\n for button in buttons:\n newState = currentState ^ button\n if newState not in states and (newState, currentPresses - 1) not in visited:\n if currentPresses - 1 > 0:\n q.append([newState, currentPresses - 1])\n visited.add((newState, currentPresses - 1))\n else:\n states.add(newState)\n return len(states)\n\n\n``` | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Bit manipulation + BFS Rust and Python3 Solution | bulb-switcher-ii | 0 | 1 | ### Rust Solution (passes)\n\n```\nuse std::collections::{HashSet, VecDeque};\n\nimpl Solution {\n fn flip_bit(number: i32, position: u32) -> i32 {\n let mask = 1 << position;\n let flipped_number = number ^ mask;\n flipped_number\n }\n \n fn y_function(x: i32) -> i32 {\n 3 * x + 1\n }\n \n fn get_neighbors(state: i32, n: i32) -> Vec<i32> {\n let mut nbrs: Vec<i32> = vec![];\n \n let mut curr_num = state;\n for i in 1..n {\n curr_num = Solution::flip_bit(curr_num, i as u32);\n }\n nbrs.push(curr_num);\n \n curr_num = state;\n for i in (1..n).step_by(2) {\n curr_num = Solution::flip_bit(curr_num, i as u32);\n }\n nbrs.push(curr_num);\n \n curr_num = state;\n for i in (0..n).step_by(2) {\n curr_num = Solution::flip_bit(curr_num, i as u32);\n }\n nbrs.push(curr_num);\n \n let mut i = 0;\n while Solution::y_function(i) < n {\n curr_num = Solution::flip_bit(curr_num, Solution::y_function(i) as u32);\n i += 1;\n }\n nbrs.push(curr_num);\n \n nbrs\n }\n \n // O(n*press) time,\n // O(n*space) space,\n // Approach: bfs, bit manipulation\n fn flip_lights(n: i32, presses: i32) -> i32 {\n let mut answer: HashSet<i32> = HashSet::new();\n let mut queue: VecDeque<i32> = VecDeque::new();\n queue.push_back((2_i32.pow(n as u32) - 1));\n answer.insert(queue[0]);\n \n let mut presses = presses;\n \n while presses > 0 && !queue.is_empty() {\n presses -= 1;\n let queue_len = queue.len();\n answer = HashSet::new();\n for _ in 0..queue_len {\n let state = queue.pop_front().unwrap();\n let nbrs = Solution::get_neighbors(state, n);\n for nbr in nbrs {\n if answer.contains(&nbr) {\n continue;\n }\n answer.insert(nbr);\n queue.push_back(nbr);\n }\n }\n }\n\n answer.len() as i32\n }\n}\n```\n\n### Python3 Solution (TLE)\n```\nclass Solution:\n \n def flipBit(self, number, position):\n mask = 1 << position\n flipped_number = number ^ mask\n return flipped_number\n \n def yFunction(self, x: int) -> int:\n return 3*x + 1\n \n def getNeighbors(self, state: int, n: int,) -> List[int]:\n nbrs = []\n \n curr_num = state\n for i in range(1, n):\n curr_num = self.flipBit(curr_num, i)\n nbrs.append(curr_num)\n \n curr_num = state\n for i in range(1, n, 2):\n curr_num = self.flipBit(curr_num, i)\n nbrs.append(curr_num)\n \n curr_num = state\n for i in range(0, n, 2):\n curr_num = self.flipBit(curr_num, i)\n nbrs.append(curr_num)\n \n i = 0\n while self.yFunction(i) < n:\n curr_num = self.flipBit(curr_num, self.yFunction(i))\n i += 1\n nbrs.append(curr_num) \n \n return nbrs\n \n \n # O(n*press) time,\n # O(n*space) space,\n # Approach: bfs, bit manipulation, \n def flipLights(self, n: int, presses: int) -> int:\n answer = set()\n queue = deque()\n queue.append(2**n - 1)\n answer.add(queue[0])\n \n while presses and queue:\n presses -= 1\n queue_len = len(queue)\n answer = set()\n for _ in range(queue_len):\n state = queue.popleft()\n nbrs = self.getNeighbors(state, n)\n for nbr in nbrs:\n if nbr in answer:\n continue\n answer.add(nbr)\n queue.append(nbr)\n\n return len(answer)\n``` | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Python3 Interview Feasible Solution | bulb-switcher-ii | 0 | 1 | ## Inspired by [awice\'s post](https://leetcode.com/problems/bulb-switcher-ii/solutions/107267/Python-Straightforward-with-Explanation/)\n\n### 1. Observations:\n1. pressing a button twice -> nothing happen\n2. buttons order doesn\'t matter -> `Button1 + Button2` = `Button2 + Button1` \n\n### 2. Thought Processes:\nFor each of the 4 buttons, it will either be pressed or not pressed at the end (pressing twice equal to nothing happen). \n\nHence, we can construct a list of combinations of whether each button is pressed or not, and then validate if we can get that `combination`, like `(1, 0, 0, 1)` meaning `Button1` and `Button4` are pressed. We only have 16 such combinations (2 ** 4)\n\nAnd how are we gonna validate the combination? \n1. `sum(combination) % 2` == `presses % 2` \n\n\tsum of all presses in the combination should be the same as `presses`, ignoring the case pressing the same button even times.\n\t\n\tLet say testcase `presses=6` and we are validating `combination=(2, 1, 3, 0)`. We can reduce the combination to `(0, 1, 1, 0)` (`Observation 1`). In this case `sum(combination) % 2` = `presses % 2` = `0`, hence, this should be a potential valid combination.\n\t\n2. `sum(combination`) <= `presses` \n\tif `presses` <= 4, we should not expect more than `presses` buttons being pressed in the combination.\n\n\n\n#### 3. Code\n```python\nclass Solution:\n def flipLights(self, n: int, presses: int) -> int:\n """\n https://leetcode.com/problems/bulb-switcher-ii/discuss/107267\n """\n result = set()\n\n # we can find out that the pattern is repeated each 6 bulbs (least common multiple of 2 and 3)\n # 1 is light on, and 0 is off for each bulb\n # each of the following represents the operation of the 4 buttons\n switches = [\n int(\'111111\'[-n:], 2),\n int(\'101010\'[-n:], 2),\n int(\'010101\'[-n:], 2),\n int(\'001001\'[-n:], 2),\n ]\n\n for combination in itertools.product((0, 1), repeat=4):\n # validate operation\n if sum(combination) % 2 == presses % 2 and sum(combination) <= presses:\n # all lights on initially\n bulbs = int(\'111111\', 2)\n for i, op in enumerate(combination):\n if op == 1:\n bulbs ^= switches[i]\n\n result.add(bulbs)\n \n return len(result)\n``` | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Python | one-line O(1) | bulb-switcher-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust try small cases and find a pattern. \n\n# Complexity\n- Time complexity: ```O(1)```\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ```O(1)```\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipLights(self,n,p):\n return [[1,1,1],[2,3,4],[2,4,7],[2,4,8]][min(p,3)][min(n-1,2)]\n``` | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Identify the states of bulb for n=1,2,3 | O(1) | bulb-switcher-ii | 0 | 1 | ```\nclass Solution:\n def flipLights(self, n: int, presses: int) -> int:\n """\n the trick to problem is that only 3 bulbs are indicative of all the n bulbs\n this is because, sequence repeats every 3 bulbs\n\n if n>3, then we can consider sequence of 3 bubls since that will reprsent the \n entire sequence\n\n (1, 1, 1) -> (0, 0, 0), (0, 1, 0), (1, 0, 1), (0, 1, 1) [for n>=3, k=1, ans=4]\n\n (0, 0, 0) -> (1, 1, 1), (1, 0, 1), (0, 1, 0), (1, 0, 0)\n (0, 1, 0) -> (1, 0, 1), (1, 1, 1), (0, 0, 0), (1, 1, 0)\n (1, 0, 1) -> (0, 1, 0), (0, 0, 0), (1, 1, 1), (0, 0, 1)\n (0, 1, 1) -> (1, 0, 0), (1, 1, 0), (0, 0, 1), (1, 1, 1) [for n>=3, k=2, ans=7]\n\n for n>=3, k>=3, there will be one more state added i.e. (0, 1, 1)\n along with the other 7 states, so ans=8\n\n when n = 1, k>=1\n (1) -> (0), (1), (0), (0) [for n=1, for every k, ans=2]\n\n when n=2, k=1\n (1,1) -> (0, 0), (1, 0), (0, 1), (0, 1) [for n=2, k=1, ans=3]\n\n (0, 0) -> (1, 1), (1, 0), (0, 1), (0, 0)\n (1, 0) -> (0, 1), (1, 1), (0, 0), (0, 0)\n (0, 1) -> (1, 0), (1, 1), (0, 0), (1, 1) [for n=2, k>=2, ans=4]\n """\n if presses == 0:\n return 1\n if n == 1:\n return 2\n if n == 2:\n if presses==1:\n return 3\n else:\n return 4\n if n >= 3:\n if presses == 1:\n return 4\n elif presses == 2:\n return 7\n else:\n return 8\n``` | 0 | There is a room with `n` bulbs labeled from `1` to `n` that all are turned on initially, and **four buttons** on the wall. Each of the four buttons has a different functionality where:
* **Button 1:** Flips the status of all the bulbs.
* **Button 2:** Flips the status of all the bulbs with even labels (i.e., `2, 4, ...`).
* **Button 3:** Flips the status of all the bulbs with odd labels (i.e., `1, 3, ...`).
* **Button 4:** Flips the status of all the bulbs with a label `j = 3k + 1` where `k = 0, 1, 2, ...` (i.e., `1, 4, 7, 10, ...`).
You must make **exactly** `presses` button presses in total. For each press, you may pick **any** of the four buttons to press.
Given the two integers `n` and `presses`, return _the number of **different possible statuses** after performing all_ `presses` _button presses_.
**Example 1:**
**Input:** n = 1, presses = 1
**Output:** 2
**Explanation:** Status can be:
- \[off\] by pressing button 1
- \[on\] by pressing button 2
**Example 2:**
**Input:** n = 2, presses = 1
**Output:** 3
**Explanation:** Status can be:
- \[off, off\] by pressing button 1
- \[on, off\] by pressing button 2
- \[off, on\] by pressing button 3
**Example 3:**
**Input:** n = 3, presses = 1
**Output:** 4
**Explanation:** Status can be:
- \[off, off, off\] by pressing button 1
- \[off, on, off\] by pressing button 2
- \[on, off, on\] by pressing button 3
- \[off, on, on\] by pressing button 4
**Constraints:**
* `1 <= n <= 1000`
* `0 <= presses <= 1000` | null |
Python3 Solution | number-of-longest-increasing-subsequence | 0 | 1 | \n```\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n n=len(nums)\n dp=[1]*n\n count=[1]*n\n for i in range(1,n):\n for j in range(i):\n if nums[i]>nums[j]:\n if 1+dp[j]>dp[i]:\n dp[i]=dp[j]+1\n\n count[i]=count[j]\n\n elif dp[j]+1==dp[i]:\n count[i]+=count[j]\n longest_len=max(dp)\n return sum([count[i] for i in range(n) if dp[i]==longest_len]) \n``` | 4 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
BEST PYTHON SOLUTION FULL EXPLANATION 100% | number-of-longest-increasing-subsequence | 0 | 1 | # Intuition\n\nTo solve this problem, we can use dynamic programming to find the number of longest increasing subsequences (LIS) in the input list nums. We can maintain two arrays, dp1 and dp2, where dp1[i] represents the length of the LIS ending at index i, and dp2[i] represents the count of such LIS. We initialize both arrays with all 1\'s, as the minimum length of an LIS is 1, and each element can form an LIS of length 1.\n\n# Approach\n\nInitialize two arrays, dp1 and dp2, with all 1\'s to store the length and count of LIS respectively.\nInitialize count and maxval variables to track the maximum length and count of LIS found so far.\nLoop through the elements of the nums list starting from the second element.\nCompare the current element with all the previous elements (from 0 to i-1).\nIf the current element is greater than a previous element, it can be part of an increasing subsequence. Update the dp1 and dp2 arrays accordingly to keep track of the length and count of LIS ending at each index.\nTrack the maximum length of LIS (maxval) and the count of LIS of that length (count) found so far.\nIf we encounter an LIS of greater length, update maxval and reset the count to the count of LIS for the current element. If we encounter an LIS of the same length, add the count of LIS for the current element to the existing count.\nFinally, return the final count of longest increasing subsequences, which is stored in the count variable.\nComplexity\n\n# Time complexity: The time complexity of this approach is O(n^2), where n is the length of the input list nums. This is because we have nested loops to compare each element with all previous elements.\nSpace complexity: The space complexity is O(n) since we use two arrays, dp1 and dp2, to store the length and count of LIS, each of size n.\n\n# Code\n```\nclass Solution(object):\n def findNumberOfLIS(self, nums):\n # Check if the input list \'nums\' is empty\n if not nums:\n return 0\n \n # Initialize two arrays, dp1 and dp2, with all 1\'s to store the length and count of LIS respectively\n dp1, dp2 = [1] * len(nums), [1] * len(nums)\n \n # Initialize \'count\' and \'maxval\' variables to track the maximum length and count of LIS found so far\n count, maxval = 1, 1\n \n # Loop through the \'nums\' list starting from the second element\n for i in range(1, len(nums)):\n # Compare the current element with all the previous elements (from 0 to i-1)\n for j in range(i):\n # If the current element is greater than the previous element, it can be part of the LIS\n if nums[i] > nums[j]:\n # If the LIS ending at the current element (i) is longer than the LIS ending at the previous element (j),\n # update the length and count of LIS for the current element (i)\n if dp1[j] + 1 > dp1[i]:\n dp1[i], dp2[i] = dp1[j] + 1, dp2[j]\n # If the LIS ending at the current element (i) has the same length as the LIS ending at the previous element (j),\n # add the count of LIS ending at the previous element (j) to the count of LIS for the current element (i)\n elif dp1[j] + 1 == dp1[i]:\n dp2[i] += dp2[j]\n\n # Update \'maxval\' and \'count\' if the length of LIS for the current element (i) is greater than or equal to \'maxval\'\n if dp1[i] > maxval:\n maxval, count = dp1[i], dp2[i]\n elif dp1[i] == maxval:\n count += dp2[i]\n\n # Return the final count of longest increasing subsequences\n return count\n\n``` | 2 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Python short and clean. 3 solutions. O(n . log(n)). Functional programming. | number-of-longest-increasing-subsequence | 0 | 1 | # Approach 1: Recursive DP\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def findNumberOfLIS(self, nums: list[int]) -> int:\n n = len(nums)\n get = lambda xs, i: xs[i] if i < n else inf # To avoid using nums.append(inf)\n\n @cache\n def lis_len_count(i: int) -> tuple[int, int]: # Index -> (LIS length, LIS count) ending at Index\n len_counts = [lis_len_count(j) for j in range(min(i, n)) if get(nums, j) < get(nums, i)]\n m_len = max(len_counts, default=(0, 0))[0]\n return m_len + 1, max(sum(c for l, c in len_counts if l == m_len), 1)\n \n return lis_len_count(n)[1]\n\n\n```\n\n---\n\n# Approach 2: Iterative DP\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\n n = len(nums)\n get = lambda xs, i: xs[i] if i < n else inf # To avoid using nums.append(inf)\n\n lis_len_count = [(0, 0)] * (n + 1) # Index -> (LIS length, LIS count) ending at Index\n lis_len_count[0] = (1, 1)\n\n for i in range(n + 1):\n len_counts = [lis_len_count[j] for j in range(min(i, n)) if get(nums, j) < get(nums, i)]\n m_len = max(len_counts, default=(0, 0))[0]\n lis_len_count[i] = (m_len + 1, max(sum(c for l, c in len_counts if l == m_len), 1))\n \n return lis_len_count[-1][1]\n\n\n```\n\n---\n\n# Approach 3: Segment tree\n\n# Complexity\n- Time complexity: $$O(n \\cdot log(n))$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n\n```python\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n default_value = (0, 1) # (lts_length, lts_count)\n \n def merge(x, y):\n return (x[0], x[1] + y[1]) if x[0] == y[0] and x[0] != 0 else max(x, y)\n \n if not nums: return 0\n \n start, end = min(nums), max(nums)\n st = SegmentTree(start, end, default_value, merge)\n for num in nums:\n res = st.query(start, num - 1)\n st.insert(num, (res[0] + 1, res[1]))\n return st.root.value[1]\n \n\nfrom typing import Callable, TypeVar\n\nT = TypeVar("T")\n\n\nclass SegmentTree:\n class Node:\n def __init__(self, value: T, start: int, end: int, left=None, right=None):\n self.value = value\n self.start = start\n self.end = end\n self.left = left\n self.right = right\n\n @property\n def mid(self):\n return (self.start + self.end) // 2\n\n def __init__(\n self, start: int, end: int, default_value: T, func: Callable[[T, T], T]\n ):\n self.func = func\n self.default_value = default_value\n self.root = SegmentTree.Node(default_value, start, end)\n\n def safe_left(self, node: Node):\n node.left = (\n node.left\n if node.left\n else SegmentTree.Node(self.default_value, node.start, node.mid)\n )\n return node.left\n\n def safe_right(self, node: Node):\n node.right = (\n node.right\n if node.right\n else SegmentTree.Node(self.default_value, node.mid + 1, node.end)\n )\n return node.right\n\n def insert(self, key: int, value: T) -> None:\n def insert_segment(node: SegmentTree.Node):\n if node.start == node.end:\n node.value = self.func(value, node.value)\n return\n\n if key <= node.mid:\n insert_segment(self.safe_left(node))\n elif key > node.mid:\n insert_segment(self.safe_right(node))\n\n node.value = self.func(\n self.safe_left(node).value, self.safe_right(node).value\n )\n\n insert_segment(self.root)\n\n def update(self, key: int, value: T) -> None:\n self.insert(key, value)\n\n def query(self, start: int, end: int) -> int:\n def query_segment(node: SegmentTree.Node):\n if start <= node.start <= node.end <= end:\n return node.value\n\n if end < start or end < node.start or node.end < start:\n return self.default_value\n\n left_value = query_segment(self.safe_left(node))\n right_value = query_segment(self.safe_right(node))\n\n return self.func(left_value, right_value)\n\n return query_segment(self.root)\n\n\n``` | 1 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Python3 👍||⚡92% faster beats (984ms) 🔥|| different from other popular answers || | number-of-longest-increasing-subsequence | 0 | 1 | \n\n\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n ct = defaultdict(list)\n ct[0] = [1,1]\n length,longest,ans = len(nums),1,1\n\n for right in range(1,length):\n map,cur_longest = defaultdict(lambda:1),1\n for left in range(right-1,-1,-1):\n if nums[right] > nums[left] and ct[left][0]+1>=cur_longest:\n temp_long,temp_ct = ct[left]\n cur_longest = temp_long+1\n map[cur_longest] += temp_ct\n if map:\n map[cur_longest]-=1\n ct[right] = [cur_longest,map[cur_longest]]\n else:\n ct[right] = ct[0]\n if cur_longest > longest:\n longest,ans = cur_longest,map[cur_longest]\n elif cur_longest == longest:\n ans += map[cur_longest]\n return ans\n``` | 1 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Python | Easy to Understand | number-of-longest-increasing-subsequence | 0 | 1 | # Intuition\nWe will use a dynamic programming approach to track the lengths and counts of increasing subsequences ending at each position in the array. The final answer will be the sum of the counts of subsequences with the maximum length.\n\n# Approach\n\n\n1. We initialize two lists `lengths` and `counts`, each with a length equal to the number of elements in the input array `nums`.\n2. We iterate through the array with two nested loops. For each element at index `i`, we compare it with all previous elements at indices `j < i`.\n3. If `nums[i] > nums[j]`, it means we can extend the increasing subsequence ending at index `j` by adding element `i`. We then check if this extension results in a longer subsequence (`lengths[j] + 1 > lengths[i]`), and update the `lengths` and `counts` lists accordingly.\n4. After the iteration, we have the length of the longest increasing subsequence in the variable `max_length`. We then calculate the total count of subsequences with that length and return it.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n n=len(nums)\n if n == 0:\n return 0\n \n lengths = [1] * n\n counts = [1] * n\n for i in range(1,n):\n for j in range(i):\n if nums[i] > nums[j]:\n if lengths[j] + 1 > lengths[i]:\n lengths[i] = lengths[j] + 1\n counts[i] = counts[j]\n elif lengths[j] + 1 == lengths[i]:\n counts[i] += counts[j]\n\n \n max_length= max(lengths)\n total_count= sum(count for length , count in zip(lengths,counts) if length == max_length)\n\n return total_count\n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Python | Easy to Understand | Medium Problem | 673. Number of Longest Increasing Subsequence | number-of-longest-increasing-subsequence | 0 | 1 | # Python | Easy to Understand | Medium Problem | 673. Number of Longest Increasing Subsequence\n```\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n if not nums: return 0\n n = len(nums)\n m, dp, cnt = 0, [1] * n, [1] * n\n for i in range(n):\n for j in range(i):\n if nums[j] < nums[i]:\n if dp[i] < dp[j]+1: dp[i], cnt[i] = dp[j]+1, cnt[j]\n elif dp[i] == dp[j]+1: cnt[i] += cnt[j]\n m = max(m, dp[i]) \n return sum(c for l, c in zip(dp, cnt) if l == m)\n``` | 1 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
🚀Beats 99.4% [VIDEO] | Cracking the Code DP - Longest Increasing Subsequences🔥 | number-of-longest-increasing-subsequence | 0 | 1 | # Intuition\nUpon seeing this problem, I realized that it was a classic dynamic programming problem. It\'s about finding the number of longest strictly increasing subsequences in an array. A sequence is increasing if every number is larger than the one before. The intuition here was to keep track of two lists: one for the length of the longest increasing subsequence ending at each index, and another for the count of such subsequences.\n\nhttps://youtu.be/yqAwQtoT9jk\n\n# Approach\nMy approach involves initializing two lists: `dp` and `count`, both filled initially with ones, representing the length and count of the longest subsequence ending at each index. \n\nThen, using a nested loop, every pair of indices are compared. If a number larger than the current one is found, it means we can extend the subsequence. In this case, `dp` and `count` lists are updated accordingly. \n\nFinally, the maximum length of the subsequences is found using the `max` function on the `dp` list. Then the counts of subsequences that have this maximum length are summed up, which yields our final answer.\n\n# Complexity\n- Time complexity: \nThe time complexity for this approach is O(n^2), where n is the size of the input list. This is due to the nested loop comparing each pair of indices.\n\n- Space complexity: \nThe space complexity is O(n), which is used to store the `dp` and `count` lists.\n\n# Code\n``` Python []\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n dp = [1] * len(nums) \n count = [1] * len(nums) \n for i in range(len(nums)): \n for j in range(i): \n if nums[i] > nums[j]: \n if dp[j] >= dp[i]: \n dp[i] = dp[j] + 1 \n count[i] = count[j] \n elif dp[j] + 1 == dp[i]: \n count[i] += count[j] \n max_length = max(dp) \n return sum(c for d, c in zip(dp, count) if d == max_length)\n```\n``` JavaScript []\nvar findNumberOfLIS = function(nums) {\n let n = nums.length, res = 0, max_len = 0; \n let len = new Array(n).fill(0), cnt = new Array(n).fill(0); \n for(let i = 0; i < n; i++){ \n len[i] = cnt[i] = 1; \n for(let j = 0; j < i; j++){ \n if(nums[i] > nums[j]){ \n if(len[i] == len[j] + 1) \n cnt[i] += cnt[j]; \n if(len[i] < len[j] + 1){ \n len[i] = len[j] + 1; \n cnt[i] = cnt[j]; \n } \n } \n } \n if(max_len == len[i]) \n res += cnt[i]; \n if(max_len < len[i]){ \n max_len = len[i]; \n res = cnt[i]; \n } \n } \n return res; \n};\n```\n``` C++ []\nclass Solution {\npublic:\n int findNumberOfLIS(vector<int>& nums) {\n\n int n = nums.size(), res = 0, max_len = 0; \n vector<int> len(n, 0), cnt(n, 0); \n for(int i=0; i<n; i++){ \n len[i] = cnt[i] = 1; \n for(int j=0; j <i; j++){ \n if(nums[i] > nums[j]){ \n if(len[i] == len[j] + 1) \n cnt[i] += cnt[j]; \n if(len[i] < len[j] + 1){ \n len[i] = len[j] + 1; \n cnt[i] = cnt[j]; \n } \n } \n } \n if(max_len == len[i]) \n res += cnt[i]; \n if(max_len < len[i]){ \n max_len = len[i]; \n res = cnt[i]; \n } \n } \n return res; \n \n }\n};\n```\nI hope this approach provides a clear solution to the problem. Please comment below if you have any questions! | 2 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
🌿Efficient DP Solution | LIS | Beats 98.4% | number-of-longest-increasing-subsequence | 1 | 1 | # Intuition\nThe given problem can be efficiently solved using a dynamic programming approach. We maintain two arrays, dp and count, to keep track of the length of the longest increasing subsequence and the count of such subsequences, respectively. The idea is to iterate through the input array, updating these arrays as we go along.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize the dp and count arrays with all elements set to 1, as each element is a valid subsequence of length 1.\n2. For each element at index i in the input array, iterate through all elements before it (index j from 0 to i-1).\n3. Compare the values of nums[i] and nums[j]:\n - If nums[i] is greater than nums[j], we have a potential increasing subsequence.\n - Check if dp[j] + 1 (the length of the LIS ending at index j plus the current element) is greater than dp[i] (the current length of the LIS ending at index i). If so, update dp[i] to dp[j] + 1, and set count[i] to count[j] since we have found a new longer subsequence ending at i.\n - If dp[j] + 1 is equal to dp[i], it means we have found another subsequence with the same length as the one ending at i. In this case, we add count[j] to the existing count[i], as we have multiple ways to form subsequences with the same length.\n4. Keep track of the maxLength of the LIS encountered during the process.\n5. Finally, iterate through the dp array again, and for each index i, if dp[i] equals maxLength, add the corresponding count[i] to the result.\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n public int findNumberOfLIS(int[] nums) {\n int n = nums.length;\n if (n == 0) return 0;\n\n int[] dp = new int[n]; \n int[] count = new int[n];\n Arrays.fill(dp, 1);\n Arrays.fill(count, 1);\n\n int maxLength = 1; \n\n for (int i = 1; i < n; i++) {\n for (int j = 0; j < i; j++) {\n if (nums[i] > nums[j]) {\n if (dp[j] + 1 > dp[i]) {\n dp[i] = dp[j] + 1;\n count[i] = count[j];\n } else if (dp[j] + 1 == dp[i]) {\n count[i] += count[j];\n }\n }\n }\n maxLength = Math.max(maxLength, dp[i]);\n }\n\n int result = 0;\n for (int i = 0; i < n; i++) {\n if (dp[i] == maxLength) {\n result += count[i];\n }\n }\n\n return result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int findNumberOfLIS(vector<int>& nums) {\n int n = nums.size();\n if (n == 0) return 0;\n\n vector<int> lengths(n, 1); \n vector<int> counts(n, 1); \n vector<int> bit(n + 1, 0); \n\n int max_length = 1; \n\n for (int i = 0; i < n; ++i) {\n for (int j = 0; j < i; ++j) {\n if (nums[i] > nums[j]) {\n if (lengths[j] + 1 > lengths[i]) {\n lengths[i] = lengths[j] + 1;\n counts[i] = counts[j];\n } else if (lengths[j] + 1 == lengths[i]) {\n counts[i] += counts[j];\n }\n }\n }\n max_length = max(max_length, lengths[i]);\n }\n\n int result = 0;\n for (int i = 0; i < n; ++i) {\n if (lengths[i] == max_length) {\n result += counts[i];\n }\n }\n\n return result;\n }\n};\n\n```\n```Python3 []\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n n = len(nums)\n if n <= 1:\n return n\n\n lengths = [1] * n\n counts = [1] * n\n\n for i in range(1, n):\n for j in range(i):\n if nums[i] > nums[j]:\n if lengths[j] + 1 > lengths[i]:\n lengths[i] = lengths[j] + 1\n counts[i] = counts[j]\n elif lengths[j] + 1 == lengths[i]:\n counts[i] += counts[j]\n\n max_length = max(lengths)\n return sum(count for length, count in zip(lengths, counts) if length == max_length)\n\n```\n```C []\nint findNumberOfLIS(int* nums, int numsSize) {\n if (numsSize == 0) return 0;\n\n int dp[numsSize];\n for (int i = 0; i < numsSize; i++) {\n dp[i] = 1;\n }\n\n int maxLength = 1;\n int result = 0;\n\n for (int i = 1; i < numsSize; i++) {\n for (int j = 0; j < i; j++) {\n if (nums[i] > nums[j]) {\n if (dp[j] + 1 > dp[i]) {\n dp[i] = dp[j] + 1;\n }\n }\n }\n if (dp[i] > maxLength) {\n maxLength = dp[i];\n }\n }\n\n for (int i = 0; i < numsSize; i++) {\n if (dp[i] == maxLength) {\n result++;\n }\n }\n\n return result;\n}\n```\n\n> If you find my solution helpful, I would greatly appreciate your one upvote. | 66 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Solution | number-of-longest-increasing-subsequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findNumberOfLIS(vector<int>& nums) {\n if (nums.empty()) {\n return 0;\n }\n vector<vector<pair<int, int>>> dyn(nums.size() + 1);\n int max_so_far = 0;\n for (int i = 0; i < nums.size(); ++i) {\n int l = 0, r = max_so_far;\n while (l < r) {\n int mid = l + (r - l) / 2;\n if (dyn[mid].back().first < nums[i]) {\n l = mid + 1;\n } else {\n r = mid;\n }\n }\n int options = 1;\n int row = l - 1;\n if (row >= 0) {\n int l1 = 0, r1 = dyn[row].size();\n while (l1 < r1) {\n int mid = l1 + (r1 - l1) / 2;\n if (dyn[row][mid].first < nums[i]) {\n r1 = mid;\n } else {\n l1 = mid + 1;\n }\n }\n options = dyn[row].back().second; \n options -= (l1 == 0) ? 0 : dyn[row][l1 - 1].second;\n }\n dyn[l].push_back({nums[i], (dyn[l].empty() ? options : dyn[l].back().second + options)});\n if (l == max_so_far) {\n max_so_far++;\n }\n }\n return dyn[max_so_far-1].back().second;\n }\n};\n```\n\n```Python3 []\nfrom typing import List\nimport bisect\n\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n if not nums: return 0\n \n decks, ends_decks, paths = [], [], []\n for num in nums:\n deck_idx = bisect.bisect_left(ends_decks, num)\n n_paths = 1\n if deck_idx > 0:\n l = bisect.bisect(decks[deck_idx-1], -num)\n n_paths = paths[deck_idx-1][-1] - paths[deck_idx-1][l]\n \n if deck_idx == len(decks):\n decks.append([-num])\n ends_decks.append(num)\n paths.append([0,n_paths])\n else:\n decks[deck_idx].append(-num)\n ends_decks[deck_idx] = num\n paths[deck_idx].append(n_paths + paths[deck_idx][-1])\n \n return paths[-1][-1]\n```\n\n```Java []\nclass Solution {\n public int findNumberOfLIS(int[] nums) {\n int num = nums.length;\n List<int[]>[] len = new ArrayList[num];\n for(int i = 0; i< num ; i++){\n len[i] = new ArrayList<>();\n }\n int size = 0;\n for(int n : nums){\n int index = bSearchLength(len,size,n);\n int count = 1;\n\n if(index > 0){\n List<int[]> t = len[index-1];\n int p = bSearchIndex(t,n);\n count = t.get(t.size()-1)[1] - (p == 0 ? 0 : t.get(p-1)[1]);\n }\n if(len[index].size()==0){\n len[index].add(new int[]{n,count});\n size++;\n } else {\n List<int[]> t = len[index];\n int[] last = t.get(t.size()-1);\n int ch = last[1]+count;\n if(last[0] == n){\n last[1]+=count;\n } else {\n t.add(new int[]{n,last[1]+count});\n }\n }\n }\n return len[size-1].get(len[size-1].size()-1)[1];\n }\n public int bSearchLength(List<int[]>[] len,int right,int n){\n int left = 0;\n while(left<right){\n int mid = (left+right)/2;\n if(n > len[mid].get(len[mid].size()-1)[0])\n left = mid + 1;\n else\n right = mid;\n }\n return left;\n }\n public int bSearchIndex(List<int[]> t,int num){\n int left = 0 , right = t.size()-1;\n while(left<right){\n int mid = left + (right-left)/2;\n if(num <= t.get(mid)[0])\n left = mid + 1;\n else\n right = mid;\n }\n return left;\n }\n}\n```\n | 2 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Python 3 | DP | Explanation | number-of-longest-increasing-subsequence | 0 | 1 | ### Intuition\n- To find the frequency of the longest increasing sequence, we need \n\t- First, know how long is the longest increasing sequence\n\t- Second, count the frequency\n- Thus, we create 2 lists with length `n`\n\t- `dp[i]`: meaning length of longest increasing sequence\n\t- `cnt[i]`: meaning frequency of longest increasing sequence\n- If `dp[i] < dp[j] + 1` meaning we found a longer sequence and `dp[i]` need to be updated, then `cnt[i]` need to be updated to `cnt[j]`\n- If `dp[i] == dp[j] + 1` meaning `dp[j] + 1` is one way to reach longest increasing sequence to `i`, so simple increment by `cnt[j]` like this `cnt[i] = cnt[i] + cnt[j]`\n- Finally, sum up `cnt` of all longest increase sequence will be the solution\n- This is a pretty standard DP question. Just like most sequence type of DP question, we need to loop over each element and check all previous stored information to update current. \n- Time complexity is `O(n*n)`\n### Implementation\n```\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n if not nums: return 0\n n = len(nums)\n m, dp, cnt = 0, [1] * n, [1] * n\n for i in range(n):\n for j in range(i):\n if nums[j] < nums[i]:\n if dp[i] < dp[j]+1: dp[i], cnt[i] = dp[j]+1, cnt[j]\n elif dp[i] == dp[j]+1: cnt[i] += cnt[j]\n m = max(m, dp[i]) \n return sum(c for l, c in zip(dp, cnt) if l == m)\n``` | 106 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | number-of-longest-increasing-subsequence | 1 | 1 | # Intuition\nUsing Dynamic Programming to keep longest subsequences every iteration.\nThis solution beats 97%. \n\n\n\n---\n\n# Solution Video\n*** Please upvote for this article. *** \n\nhttps://youtu.be/EP4CeEoxkwY\n\n# Subscribe to my channel from here. I have 226 videos as of July 22th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python code. Other languages might be different.\n\n1. Initialize the `dp` dictionary with a `defaultdict` of `Counter`. This dictionary will store the number of increasing subsequences (LIS) of different lengths, and each LIS length will be associated with a Counter object that counts the occurrences of different ending numbers for that LIS length.\n\n2. Initialize `dp[-1][-float("inf")] = 1`. This is a special entry in the `dp` dictionary to handle the case when the LIS length is 0. Here, `-float("inf")` is used as a unique key to represent LIS length 0, and the count is set to 1, as there is only one empty LIS.\n\n3. Initialize an empty list `sorted_nums`. This list will be used to keep track of the elements of the input `nums` list in sorted order, to find the correct insertion position for each number.\n\n4. Loop through each number `num` in the `nums` list:\n a. Find the index `insert_index` using `bisect.bisect_left(sorted_nums, num)` where `sorted_nums` is treated as a sorted list. This index represents the correct position to insert the current number `num` to maintain the sorted order.\n b. If `insert_index` is equal to the length of `sorted_nums`, it means the current number is greater than all elements in `sorted_nums`, so we append it to the end of `sorted_nums`.\n c. Otherwise, if `insert_index` is within the range of `sorted_nums`, it means the current number needs to be inserted at a specific position in `sorted_nums`, so we update the element at `insert_index` with the current number.\n d. Initialize `total` to 0, which will be used to store the count of all possible LIS of length `insert_index` ending with the current number `num`.\n e. Loop through each previous number `prev_num` in the LIS of length `insert_index - 1`:\n - If `prev_num` is less than the current number `num`, then it can be a valid ending number for the LIS of length `insert_index`.\n - We add the count of LIS of length `insert_index - 1` ending with `prev_num` to the `total`.\n f. Update the `dp[insert_index][num]` entry by adding the `total` to it. This represents the count of LIS of length `insert_index` ending with the current number `num`.\n\n5. Finally, return the sum of all values in the `dp` dictionary for the last length `len(sorted_nums) - 1`, which represents the total count of all possible LIS of the longest length.\n\nIn summary, the algorithm dynamically computes the number of increasing subsequences of different lengths using a combination of `sorted_nums` to find the correct position for each number and the `dp` dictionary to store the counts. The approach efficiently calculates the number of LIS by considering the increasing property and reusing the counts of shorter subsequences to determine the counts of longer subsequences.\n\n# Complexity\nThis is based on Python code. Other languages might be different.\n\n- Time complexity: O(n log n) or O(n^2)\nTheoretically, O(n^2) but in reality O(n log n). I didn\'t come up with O(n^2) case. Let me know if you find the case.\n\n- Space complexity: O(n)\nThere is possiblity that I put data into dp and sorted_nums at most n.\n\n```python []\nclass Solution:\n def findNumberOfLIS(self, nums: List[int]) -> int:\n dp = defaultdict(Counter)\n dp[-1][-float("inf")] = 1\n sorted_nums = []\n\n for num in nums:\n insert_index = bisect.bisect_left(sorted_nums, num)\n if insert_index == len(sorted_nums):\n sorted_nums.append(num)\n else:\n sorted_nums[insert_index] = num\n\n total = 0\n for prev_num in dp[insert_index - 1]:\n if prev_num < num:\n total += dp[insert_index - 1][prev_num]\n \n dp[insert_index][num] += total\n \n return sum(dp[len(sorted_nums) - 1].values())\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findNumberOfLIS = function(nums) {\n var dp = new Map();\n dp.set(-1, new Map());\n dp.get(-1).set(-Infinity, 1);\n var sortedNums = [];\n\n for (var num of nums) {\n var insertIndex = bisectLeft(sortedNums, num);\n if (insertIndex === sortedNums.length) {\n sortedNums.push(num);\n } else {\n sortedNums[insertIndex] = num;\n }\n\n var total = 0;\n for (var [prevNum, count] of dp.get(insertIndex - 1).entries()) {\n if (prevNum < num) {\n total += count;\n }\n }\n dp.set(insertIndex, dp.get(insertIndex) || new Map());\n dp.get(insertIndex).set(num, (dp.get(insertIndex).get(num) || 0) + total);\n }\n\n var result = 0;\n for (var count of dp.get(sortedNums.length - 1).values()) {\n result += count;\n }\n return result; \n};\n\nvar bisectLeft = function(arr, target) {\n var left = 0;\n var right = arr.length;\n\n while (left < right) {\n var mid = Math.floor((left + right) / 2);\n if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return left;\n};\n```\n```java []\nclass Solution {\n public int findNumberOfLIS(int[] nums) {\n Map<Integer, Map<Integer, Integer>> dp = new HashMap<>();\n dp.put(-1, new HashMap<>());\n dp.get(-1).put(Integer.MIN_VALUE, 1);\n List<Integer> sortedNums = new ArrayList<>();\n\n for (int num : nums) {\n int insertIndex = bisectLeft(sortedNums, num);\n if (insertIndex == sortedNums.size()) {\n sortedNums.add(num);\n } else {\n sortedNums.set(insertIndex, num);\n }\n\n int total = 0;\n for (Map.Entry<Integer, Integer> entry : dp.getOrDefault(insertIndex - 1, new HashMap<>()).entrySet()) {\n int prevNum = entry.getKey();\n int count = entry.getValue();\n if (prevNum < num) {\n total += count;\n }\n }\n dp.putIfAbsent(insertIndex, new HashMap<>());\n dp.get(insertIndex).put(num, dp.getOrDefault(insertIndex, new HashMap<>()).getOrDefault(num, 0) + total);\n }\n\n int result = 0;\n for (int count : dp.getOrDefault(sortedNums.size() - 1, new HashMap<>()).values()) {\n result += count;\n }\n return result; \n }\n\n private int bisectLeft(List<Integer> arr, int target) {\n int left = 0;\n int right = arr.size();\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr.get(mid) < target) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return left;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int findNumberOfLIS(vector<int>& nums) {\n std::unordered_map<int, std::map<int, int>> dp;\n dp[-1][-INT_MAX] = 1;\n std::vector<int> sortedNums;\n\n for (int num : nums) {\n int insertIndex = bisectLeft(sortedNums, num);\n if (insertIndex == sortedNums.size()) {\n sortedNums.push_back(num);\n } else {\n sortedNums[insertIndex] = num;\n }\n\n int total = 0;\n for (const auto& entry : dp[insertIndex - 1]) {\n int prevNum = entry.first;\n int count = entry.second;\n if (prevNum < num) {\n total += count;\n }\n }\n dp[insertIndex][num] += total;\n }\n\n int result = 0;\n for (const auto& entry : dp[sortedNums.size() - 1]) {\n result += entry.second;\n }\n return result; \n }\n\nprivate:\n int bisectLeft(const std::vector<int>& arr, int target) {\n int left = 0;\n int right = arr.size();\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return left;\n } \n};\n```\n | 7 | Given an integer array `nums`, return _the number of longest increasing subsequences._
**Notice** that the sequence has to be **strictly** increasing.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 2
**Explanation:** The two longest increasing subsequences are \[1, 3, 4, 7\] and \[1, 3, 5, 7\].
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 5
**Explanation:** The length of the longest increasing subsequence is 1, and there are 5 increasing subsequences of length 1, so output 5.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-106 <= nums[i] <= 106` | null |
Python short 1-liner. Functional programming. | longest-continuous-increasing-subsequence | 0 | 1 | # Approach\n1. For each adjacent `pairwise` numbers in `nums` check if $$nums_i < nums_{i + 1}$$ to form a boolean array. (Useful to see bools as 1 and 0).\n`lt_bools = starmap(lt, pairwise(nums))`\n\n2. Calculate `running_sums` on the array of bools and reset every time a `0` is found.\n`run_sums = accumulate(lt_bools, lambda a, x: a * x + 1, initial=1)`\n\n3. Return the `max(run_sums) + 1`\n\nExample:\n```python\nnums = [1, 3, 5, 4, 7, 2, 4, 5, 7, 9]\nlt_bools = [1, 1, 0, 1, 0, 1, 1, 1, 1]\nrun_sums = [1, 2, 3, 1, 2, 1, 2, 3, 4, 5] # Extra 1 added at the beginning\nlcis_len = 5\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is length of nums`.\n\n# Code\n```python\nclass Solution:\n def findLengthOfLCIS(self, nums: list[int]) -> int:\n return max(accumulate(starmap(lt, pairwise(nums)), lambda a, x: a * x + 1, initial=1))\n\n\n``` | 1 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
Beginners Python Code | longest-continuous-increasing-subsequence | 0 | 1 | # Code\n```\nclass Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n n = len(nums)\n ans = 1\n curr_len = 1\n for i in range(1,n):\n if nums[i] > nums[i-1]:\n curr_len = curr_len + 1\n ans = max(ans,curr_len)\n else:\n curr_len = 1\n return ans\n \n``` | 2 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.