title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Two python solutions using dp and a straightforward soln | longest-continuous-increasing-subsequence | 0 | 1 | 1. DP solution.\n```class Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n dp=[1]*len(nums)\n for i in range(1,len(nums)):\n if nums[i]>nums[i-1]:\n dp[i]+=dp[i-1]\n return max(dp)\n ```\n2\n```\nclass Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n counter=1\n temp=1\n for i in range(0,len(nums)-1):\n if nums[i]<nums[i+1]:\n temp+=1\n if temp>counter:\n counter=temp\n else:\n temp=1\n return counter | 6 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
Python O(n) Solution - O(1) Space Complexity | longest-continuous-increasing-subsequence | 0 | 1 | ```\nclass Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n if not nums:\n return 0\n \n cur_len = 1\n max_len = 1\n \n for i in range(1,len(nums)):\n if nums[i] > nums[i-1]:\n cur_len += 1\n else:\n max_len = max(max_len,cur_len)\n cur_len = 1\n \n return max(max_len,cur_len)\n``` | 19 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
674: Solution with step by step explanation | longest-continuous-increasing-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We handle the base cases where the input list is empty or has only one element. In both cases, the length of the longest continuous in1.creasing subsequence is the length of the input list itself, so we simply return that length.\n\n2. We initialize two variables cur_len and max_len to keep track of the length of the current increasing subsequence and the maximum length seen so far, respectively. We set both variables to 1 because the first element of the input list is always part of a subsequence of length 1.\n\n3. We iterate through the input list starting from the second element. For each element, we check if it is greater than the previous element. If it is, then it is part of the current increasing subsequence, so we increase the length of the subsequence by 1 (cur_len += 1). We also update the maximum length seen so far (max_len = max(max_len, cur_len)) if necessary. If the current element is not greater than the previous element, then it is the start of a new increasing subsequence, so we reset the length of the subsequence to 1 (cur_len = 1).\n\n4. After iterating through the entire input list, we return the maximum length of any increasing subsequence seen (return max_len).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n # Base case: empty list or single element list\n if len(nums) == 0 or len(nums) == 1:\n return len(nums)\n \n # Initialize variables to keep track of current length and max length\n cur_len = 1 # current length of increasing subsequence\n max_len = 1 # maximum length of increasing subsequence\n \n # Iterate through the list starting from the second element\n for i in range(1, len(nums)):\n # If the current element is greater than the previous element, it is part of the increasing subsequence\n if nums[i] > nums[i-1]:\n cur_len += 1 # increase the length of the subsequence\n max_len = max(max_len, cur_len) # update the maximum length if necessary\n else:\n cur_len = 1 # reset the length of the subsequence if the current element is not greater than the previous element\n \n return max_len\n\n``` | 4 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
O(N) solution | longest-continuous-increasing-subsequence | 0 | 1 | ```\nclass Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n maxLen = count = 1\n for i in range(len(nums) - 1):\n if nums[i] < nums[i + 1]:\n count += 1\n else:\n count = 1\n \n maxLen = max(count, maxLen)\n \n return maxLen\n``` | 2 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
Solution | longest-continuous-increasing-subsequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findLengthOfLCIS(vector<int>& nums) {\n int maxlength = 1;\n int length = 1;\n int n = nums.size();\n for(int i= 1; i<n;i++){\n if (nums[i-1]<nums[i]){\n length++;\n }\n else{\n if(maxlength<length){\n maxlength = length;\n }\n length = 1;\n }\n }\n return max(length, maxlength);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n l, r, curMax = 0, 1, 1\n while r < len(nums):\n if nums[r] > nums[r-1]:\n curMax = max(curMax, r-l+1)\n else:\n l = r\n r += 1\n return curMax\n```\n\n```Java []\nclass Solution {\n public int findLengthOfLCIS(int[] nums) \n {\n int maxCount = 1;\n int currentCount = 1;\n int i = 0 ;\n int j = 1;\n while(j<nums.length)\n {\n if(nums[j]>nums[i])\n {\n currentCount++;\n i++;\n j++;\n }\n else\n {\n i = j;\n j++;\n currentCount = 1;\n }\n if(maxCount<currentCount)\n {\n maxCount = currentCount;\n }\n } \n return maxCount; \n }\n}\n```\n | 2 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
python3 || easy | longest-continuous-increasing-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->easy \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findLengthOfLCIS(self, nums: List[int]) -> int:\n k=1\n ans=0\n for i in range(1,len(nums)):\n if nums[i]>nums[i-1]:\n k+=1\n else:\n ans=max(k,ans)\n k=1\n ans=max(k,ans)\n return ans\n \n``` | 0 | Given an unsorted array of integers `nums`, return _the length of the longest **continuous increasing subsequence** (i.e. subarray)_. The subsequence must be **strictly** increasing.
A **continuous increasing subsequence** is defined by two indices `l` and `r` (`l < r`) such that it is `[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]` and for each `l <= i < r`, `nums[i] < nums[i + 1]`.
**Example 1:**
**Input:** nums = \[1,3,5,4,7\]
**Output:** 3
**Explanation:** The longest continuous increasing subsequence is \[1,3,5\] with length 3.
Even though \[1,3,5,7\] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\]
**Output:** 1
**Explanation:** The longest continuous increasing subsequence is \[2\] with length 1. Note that it must be strictly
increasing.
**Constraints:**
* `1 <= nums.length <= 104`
* `-109 <= nums[i] <= 109` | null |
Python 3 || 19 lines bfs || T/M: 91% / 21% | cut-off-trees-for-golf-event | 0 | 1 | This code is similar to those in other posts, with one exception. We use `unseen` to prune out the zero cells initially, and then keep track of the cells *not* visited.\n```\nclass Solution:\n\n def cutOffTree(self, forest: List[List[int]]) -> int:\n\n def bfs(beg, end):\n queue, uns = deque([(beg,0)]), unseen.copy()\n uns.discard(beg)\n\n while queue:\n (r,c), steps = queue.popleft()\n\n if (r,c) == end: return steps\n\n for R,C in ((r-1,c), (r,c-1), (r+1,c), (r,c+1)):\n\n if (R,C) not in uns: continue\n\n queue.append(((R,C),steps+1))\n uns.discard((R,C))\n\n return -1\n \n m, n, ans = len(forest), len(forest[0]), 0\n start, trees = (0,0), []\n\n grid = tuple(product(range(m), range(n)))\n unseen = set(filter(lambda x: forest[x[0]][x[1]] != 0, grid))\n\n for r,c in grid:\n if forest[r][c] > 1: heappush(trees,(forest[r][c], (r,c)))\n\n while trees:\n if (res:= bfs(start,(pos:= heappop(trees)[1]))) < 0: return -1\n\n ans += res\n start = pos\n\n return ans\n```\n[https://leetcode.com/problems/cut-off-trees-for-golf-event/submissions/1025189951/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*log*N*), in which *N* ~ number of cells in the 2D array`forest` (which is `len(forest)*len(forest[0])`). | 4 | You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an `m x n` matrix. In this matrix:
* `0` means the cell cannot be walked through.
* `1` represents an empty cell that can be walked through.
* A number greater than `1` represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes `1` (an empty cell).
Starting from the point `(0, 0)`, return _the minimum steps you need to walk to cut off all the trees_. If you cannot cut off all the trees, return `-1`.
**Note:** The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
**Example 1:**
**Input:** forest = \[\[1,2,3\],\[0,0,4\],\[7,6,5\]\]
**Output:** 6
**Explanation:** Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
**Example 2:**
**Input:** forest = \[\[1,2,3\],\[0,0,0\],\[7,6,5\]\]
**Output:** -1
**Explanation:** The trees in the bottom row cannot be accessed as the middle row is blocked.
**Example 3:**
**Input:** forest = \[\[2,3,4\],\[0,0,5\],\[8,7,6\]\]
**Output:** 6
**Explanation:** You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
**Constraints:**
* `m == forest.length`
* `n == forest[i].length`
* `1 <= m, n <= 50`
* `0 <= forest[i][j] <= 109`
* Heights of all trees are **distinct**. | null |
Solution | cut-off-trees-for-golf-event | 1 | 1 | ```C++ []\nclass Solution {\n static constexpr int DIR[4][2] = {{-1,0},{1,0},{0,-1},{0,1}};\n struct Cell {\n short r : 8;\n short c : 8;\n };\n int doit(const vector<vector<int>>& forest, Cell start, vector<int> &curr, vector<int> &prev, vector<Cell> &bfs) {\n const int M = forest.size(), N = forest[0].size();\n int steps = 0;\n swap(curr, prev);\n fill(begin(curr), end(curr), -1);\n curr[start.r * N + start.c] = steps;\n if (prev[start.r * N + start.c] != -1) {\n return prev[start.r * N + start.c];\n }\n bfs.clear();\n bfs.push_back(start);\n while (!bfs.empty()) {\n int size = bfs.size();\n steps++;\n while (size--) {\n auto [r0, c0] = bfs[size];\n swap(bfs[size], bfs.back());\n bfs.pop_back();\n for (auto [dr, dc] : DIR) {\n short r1 = r0 + dr, c1 = c0 + dc;\n int pos = r1 * N + c1;\n if (r1 >= 0 && r1 < M && c1 >= 0 && c1 < N && forest[r1][c1] > 0 && curr[pos] == -1) {\n if (prev[pos] != -1) {\n return steps + prev[pos];\n }\n curr[pos] = steps;\n bfs.push_back({r1, c1});\n }\n }\n }\n }\n return -1;\n }\n int manhattan_distance(vector<Cell> &cells) {\n int result = 0;\n Cell prev{0, 0};\n for (auto &cell : cells) {\n result += abs(prev.r - cell.r) + abs(prev.c - cell.c);\n prev = cell;\n }\n return result;\n }\npublic:\n int cutOffTree(vector<vector<int>>& forest) {\n const int M = forest.size(), N = forest[0].size();\n if (forest[0][0] == 0) {\n return -1;\n }\n int obstacles = 0;\n vector<Cell> cells;\n cells.reserve(8);\n\n for (short r = 0; r < M; r++) {\n for (short c = 0; c < N; c++) {\n if (forest[r][c] > 1) {\n cells.push_back({r, c});\n } else if (forest[r][c] == 0) {\n obstacles++;\n }\n }\n }\n sort(begin(cells), end(cells), [&forest](const Cell &a, const Cell &b){\n return forest[a.r][a.c] < forest[b.r][b.c];\n });\n if (obstacles == 0) {\n return manhattan_distance(cells);\n }\n vector<int> curr(M * N, -1), prev = curr;\n curr[0] = 0;\n\n vector<Cell> bfs;\n bfs.reserve(8);\n\n int steps = 0;\n\n for (auto &cell : cells) {\n int result = doit(forest, cell, curr, prev, bfs);\n\n if (result != -1) {\n steps += result;\n } else {\n return -1;\n }\n }\n return steps;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def cutOffTree(self, forest: List[List[int]]) -> int:\n if forest[0][0] == 0 :\n return -1\n m = len(forest)\n n = len(forest[0])\n def distance(node1, node2):\n now = [node1]\n soon = []\n expanded = set()\n manhattan = abs(node1[0] - node2[0]) + abs(node1[1] - node2[1])\n detours = 0\n while True:\n if len(now) == 0:\n now = soon\n soon = []\n detours += 1\n node = now.pop()\n if node == node2:\n return manhattan + 2 * detours\n if node not in expanded:\n expanded.add(node)\n x, y = node\n if x - 1 >= 0 and forest[x - 1][y] >= 1:\n if x > node2[0]:\n now.append((x - 1, y))\n else:\n soon.append((x - 1, y))\n if y + 1 < n and forest[x][y + 1] >= 1:\n if y < node2[1]:\n now.append((x, y + 1))\n else:\n soon.append((x, y + 1))\n if x + 1 < m and forest[x + 1][y] >= 1:\n if x < node2[0]:\n now.append((x + 1, y))\n else:\n soon.append((x + 1, y))\n if y - 1 >= 0 and forest[x][y - 1] >= 1:\n if y > node2[1]:\n now.append((x, y - 1))\n else:\n soon.append((x, y - 1))\n trees = []\n for i in range(m):\n for j in range(n):\n if forest[i][j] > 1:\n trees.append(((i, j), forest[i][j]))\n trees.sort(key=lambda x: x[1])\n can_reach = {(0, 0)}\n stack = [(0, 0)]\n while len(stack) > 0:\n x, y = stack.pop()\n if x - 1 >= 0 and forest[x - 1][y] >= 1 and (x - 1, y) not in can_reach:\n can_reach.add((x - 1, y))\n stack.append((x - 1, y))\n if y + 1 < n and forest[x][y + 1] >= 1 and (x, y + 1) not in can_reach:\n can_reach.add((x, y + 1))\n stack.append((x, y + 1))\n if x + 1 < m and forest[x + 1][y] >= 1 and (x + 1, y) not in can_reach:\n can_reach.add((x + 1, y))\n stack.append((x + 1, y))\n if y - 1 >= 0 and forest[x][y - 1] >= 1 and (x, y - 1) not in can_reach:\n can_reach.add((x, y - 1))\n stack.append((x, y - 1))\n for t in trees:\n if t[0] not in can_reach:\n return -1\n start = (0, 0)\n num_step = 0\n for t in trees: \n num_step += distance(start, t[0])\n forest[t[0][0]][t[0][1]] = 1\n start = t[0]\n return num_step\n```\n\n```Java []\nclass Solution {\n public int cutOffTree(List<List<Integer>> forest) {\n PriorityQueue<int[]> pq=new PriorityQueue<>((a,b)->(forest.get(a[0]).get(a[1])-forest.get(b[0]).get(b[1])));\n for(int i=0;i<forest.size();i++){\n for(int j=0;j<forest.get(0).size();j++){\n if(forest.get(i).get(j)>1)\n pq.add(new int[]{i,j});\n }\n }\n int ans=0;\n int curr[]={0,0};\n while(pq.size()>0){\n int[] temp=pq.poll();\n int dis=calcDis(forest,curr,temp);\n if(dis==-1)\n return -1;\n ans+=dis;\n curr=temp;\n }\n return ans;\n }\n int calcDis(List<List<Integer>> forest,int start[],int end[]){\n int n=forest.size(),m=forest.get(0).size();\n boolean vis[][]=new boolean[n][m];\n Queue<int[]> queue=new LinkedList<>();\n queue.add(start);\n vis[start[0]][start[1]]=true;\n int dis=0;\n while(queue.size()>0){\n int len =queue.size();\n while(len-->0){\n int temp[]=queue.remove();\n int r=temp[0],c=temp[1];\n if(r==end[0] && c==end[1])\n return dis;\n if(r+1<n && !vis[r+1][c] && forest.get(r+1).get(c)!=0){\n queue.add(new int[]{r+1,c});\n vis[r+1][c]=true;\n }if(r-1>=0 && !vis[r-1][c] && forest.get(r-1).get(c)!=0){\n queue.add(new int[]{r-1,c});\n vis[r-1][c]=true;\n }if(c-1>=0 && !vis[r][c-1] && forest.get(r).get(c-1)!=0){\n queue.add(new int[]{r,c-1});\n vis[r][c-1]=true;\n }if(c+1<m && !vis[r][c+1] && forest.get(r).get(c+1)!=0){\n queue.add(new int[]{r,c+1});\n vis[r][c+1]=true;\n }\n }\n dis++;\n }\n return -1;\n }\n}\n```\n | 2 | You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an `m x n` matrix. In this matrix:
* `0` means the cell cannot be walked through.
* `1` represents an empty cell that can be walked through.
* A number greater than `1` represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes `1` (an empty cell).
Starting from the point `(0, 0)`, return _the minimum steps you need to walk to cut off all the trees_. If you cannot cut off all the trees, return `-1`.
**Note:** The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
**Example 1:**
**Input:** forest = \[\[1,2,3\],\[0,0,4\],\[7,6,5\]\]
**Output:** 6
**Explanation:** Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
**Example 2:**
**Input:** forest = \[\[1,2,3\],\[0,0,0\],\[7,6,5\]\]
**Output:** -1
**Explanation:** The trees in the bottom row cannot be accessed as the middle row is blocked.
**Example 3:**
**Input:** forest = \[\[2,3,4\],\[0,0,5\],\[8,7,6\]\]
**Output:** 6
**Explanation:** You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
**Constraints:**
* `m == forest.length`
* `n == forest[i].length`
* `1 <= m, n <= 50`
* `0 <= forest[i][j] <= 109`
* Heights of all trees are **distinct**. | null |
675: Solution with step by step explanation | cut-off-trees-for-golf-event | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We first initialize the size of the forest m and n. We also create an empty list called trees which will contain tuples of (height, x, y) where x and y are the coordinates of the tree in the forest.\n\n2. We iterate through every cell in the forest and if the value is greater than 1, we append a tuple of (height, x, y) to the trees list. We sort the list by the height of the trees in ascending order.\n\n3. We define a bfs function which takes in the starting coordinates sx and sy, and the target coordinates tx and ty. We use a heap to implement Dijkstra\'s algorithm for finding the shortest path. We keep track of the minimum distance d, current coordinates x and y, and push the tuple (d, x, y) into the heap.\n\n4. We create a visited set to keep track of cells that have been visited. We add the starting coordinates to the set.\n\n5. While the heap is not empty, we pop the cell with the minimum distance d from the heap. If the current coordinates are the target coordinates, we return the minimum distance d.\n\n6. Otherwise, we iterate through all possible directions (north, east, south, west) and check if the next cell is within the boundaries of the forest, not in the visited set, and not blocked by a tree. If the conditions are met, we add the next cell to the visited set and push the tuple (d+1, nx, ny) into the heap.\n\n7. If the target coordinates cannot be reached, we return -1.\n\n8. We initialize ans to 0, and the starting coordinates sx and sy to (0, 0).\n\n9. We iterate through every tree in the trees list in ascending order of height. For each tree,\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def cutOffTree(self, forest: List[List[int]]) -> int:\n m, n = len(forest), len(forest[0])\n trees = []\n for i in range(m):\n for j in range(n):\n if forest[i][j] > 1:\n trees.append((forest[i][j], i, j))\n trees.sort()\n\n def bfs(sx, sy, tx, ty):\n queue = [(0, sx, sy)]\n visited = set()\n visited.add((sx, sy))\n while queue:\n d, x, y = heapq.heappop(queue)\n if x == tx and y == ty:\n return d\n for dx, dy in [(0, 1), (1, 0), (0, -1), (-1, 0)]:\n nx, ny = x + dx, y + dy\n if 0 <= nx < m and 0 <= ny < n and (nx, ny) not in visited and forest[nx][ny]:\n visited.add((nx, ny))\n heapq.heappush(queue, (d+1, nx, ny))\n return -1\n\n ans = 0\n sx, sy = 0, 0\n for _, tx, ty in trees:\n d = bfs(sx, sy, tx, ty)\n if d == -1:\n return -1\n ans += d\n sx, sy = tx, ty\n return ans\n\n``` | 2 | You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an `m x n` matrix. In this matrix:
* `0` means the cell cannot be walked through.
* `1` represents an empty cell that can be walked through.
* A number greater than `1` represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes `1` (an empty cell).
Starting from the point `(0, 0)`, return _the minimum steps you need to walk to cut off all the trees_. If you cannot cut off all the trees, return `-1`.
**Note:** The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
**Example 1:**
**Input:** forest = \[\[1,2,3\],\[0,0,4\],\[7,6,5\]\]
**Output:** 6
**Explanation:** Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
**Example 2:**
**Input:** forest = \[\[1,2,3\],\[0,0,0\],\[7,6,5\]\]
**Output:** -1
**Explanation:** The trees in the bottom row cannot be accessed as the middle row is blocked.
**Example 3:**
**Input:** forest = \[\[2,3,4\],\[0,0,5\],\[8,7,6\]\]
**Output:** 6
**Explanation:** You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
**Constraints:**
* `m == forest.length`
* `n == forest[i].length`
* `1 <= m, n <= 50`
* `0 <= forest[i][j] <= 109`
* Heights of all trees are **distinct**. | null |
[Python] BFS & PriorityQueue - w/ comments and prints for visualization | cut-off-trees-for-golf-event | 0 | 1 | Approach: \nHave priority queue that stores (height,x,y) for each tree in order of min to max.\nUse BFS to find the next available smallest height in priority queue.\n\nComplexity:\nLet m=len(forest), n=len(forest[0])\nO(mnlog(mn) + 3^(m+n)) runtime - 692ms (45.50%)\nO(mn) space - 14.9MB (56.88%)\n\n```Python\nfrom typing import List \nimport heapq\nimport collections\nimport numpy as np #for printing\nclass Solution:\n def cutOffTree(self, forest: List[List[int]]) -> int:\n #print("forest at start: \\n{}".format(np.array(forest)))\n m = len(forest)\n n = len(forest[0])\n \n #store all trees in priority queue in (height,x,y) format\n pq = []\n for x in range(m):\n for y in range(n):\n height = forest[x][y]\n if height > 1:\n heapq.heappush(pq,(height,x,y))\n #print("heap: {}".format(pq))\n \n #takes in starting position and next tree position, returns min steps to get to that next tree position\n def bfs(x,y,nextX,nextY) -> int:\n queue = collections.deque([(x,y,0)])\n seen = {(x,y)}\n #print("starting at: ({},{})".format(x,y))\n #keep BFS searching until we find target tree or tried all paths\n while queue:\n x,y,steps = queue.popleft()\n\n if x == nextX and y == nextY:\n #found the next tree, chop it down and return depth\n forest[x][y] = 1\n #print("ending at: ({},{}) after {} steps".format(x,y,steps))\n return steps\n\n #append adjacent nodes (if they are a valid position i.e. height >= 1, within bounds of forest, and not already used)\n for dx,dy in [(-1,0),(0,1),(0,-1),(1,0)]:\n adjX,adjY = x+dx, y+dy\n if (0 <= adjX < m and 0 <= adjY < n) and (forest[adjX][adjY] >= 1) and ((adjX,adjY) not in seen):\n # if (nextX,nextY) == (0,0):\n # #print("seen for reaching {},{}: {}".format(nextX,nextY,seen))\n # print("queue: {}".format(queue))\n queue.append((adjX,adjY,steps+1))\n seen.add((adjX,adjY))\n #print("seen: {}".format(seen))\n\n #no such path exists\n return -1\n \n #start from 0,0 and have next be the first smallest tree, and use BFS for the others\n x,y = 0,0\n steps = 0\n #while there are still trees to cut\n while pq:\n _,nextX,nextY = heapq.heappop(pq)\n \n #find the shortest path to the next tree\n shortestPath = bfs(x,y,nextX,nextY)\n if shortestPath == -1:\n #print("forest: \\n{}".format(np.array(forest)))\n return -1\n steps += shortestPath\n #print("total steps taken: {}".format(steps))\n x,y = nextX,nextY\n\n #print("forest at end: \\n{}".format(np.array(forest)))\n return steps\n``` | 8 | You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an `m x n` matrix. In this matrix:
* `0` means the cell cannot be walked through.
* `1` represents an empty cell that can be walked through.
* A number greater than `1` represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes `1` (an empty cell).
Starting from the point `(0, 0)`, return _the minimum steps you need to walk to cut off all the trees_. If you cannot cut off all the trees, return `-1`.
**Note:** The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
**Example 1:**
**Input:** forest = \[\[1,2,3\],\[0,0,4\],\[7,6,5\]\]
**Output:** 6
**Explanation:** Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
**Example 2:**
**Input:** forest = \[\[1,2,3\],\[0,0,0\],\[7,6,5\]\]
**Output:** -1
**Explanation:** The trees in the bottom row cannot be accessed as the middle row is blocked.
**Example 3:**
**Input:** forest = \[\[2,3,4\],\[0,0,5\],\[8,7,6\]\]
**Output:** 6
**Explanation:** You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
**Constraints:**
* `m == forest.length`
* `n == forest[i].length`
* `1 <= m, n <= 50`
* `0 <= forest[i][j] <= 109`
* Heights of all trees are **distinct**. | null |
Python, normal and priority BFS, faster than 99% and faster than 77% | cut-off-trees-for-golf-event | 0 | 1 | ## normal bfs\n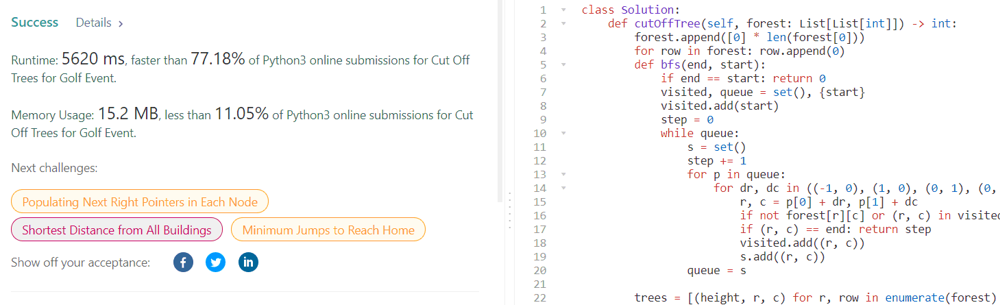\n\n```\nclass Solution:\n def cutOffTree(self, forest: List[List[int]]) -> int:\n forest.append([0] * len(forest[0]))\n for row in forest: row.append(0)\n def bfs(end, start):\n if end == start: return 0\n visited, queue = set(), {start}\n visited.add(start)\n step = 0\n while queue:\n s = set()\n step += 1\n for p in queue: \n for dr, dc in ((-1, 0), (1, 0), (0, 1), (0, -1)):\n r, c = p[0] + dr, p[1] + dc\n if not forest[r][c] or (r, c) in visited: continue\n if (r, c) == end: return step\n visited.add((r, c))\n s.add((r, c))\n queue = s\n\n trees = [(height, r, c) for r, row in enumerate(forest) for c, height in enumerate(row) if forest[r][c] > 1]\n # check\n queue = [(0, 0)]\n reached = set()\n reached.add((0, 0))\n while queue:\n r, c = queue.pop()\n for dr, dc in ((-1, 0), (1, 0), (0, -1), (0, 1)):\n row, col = r + dr, c + dc\n if forest[row][col] and (row, col) not in reached:\n queue.append((row, col))\n reached.add((row,col))\n if not all([(i, j) in reached for (height, i, j) in trees]): return -1\n trees.sort()\n return sum([bfs((I,J),(i,j)) for (_, i, j), (_, I, J) in zip([(0, 0, 0)] + trees, trees)])\n```\n## priority bfs\n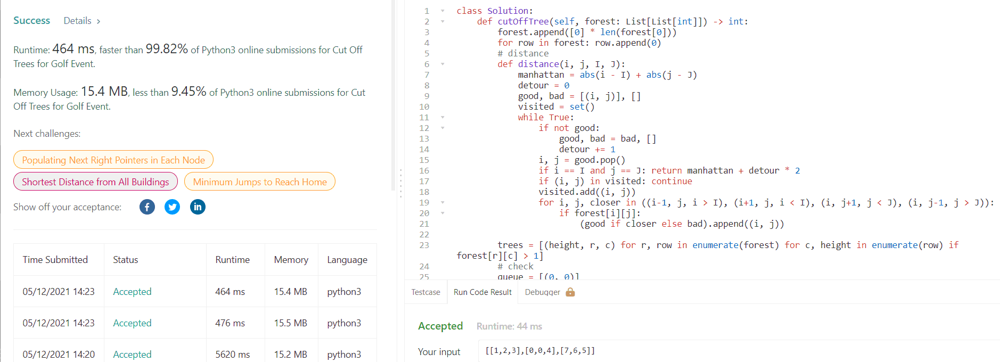\n\n```\nclass Solution:\n def cutOffTree(self, forest: List[List[int]]) -> int:\n forest.append([0] * len(forest[0]))\n for row in forest: row.append(0)\n # distance\n def distance(i, j, I, J):\n manhattan = abs(i - I) + abs(j - J)\n detour = 0\n good, bad = [(i, j)], []\n visited = set()\n while True:\n if not good:\n good, bad = bad, []\n detour += 1\n i, j = good.pop()\n if i == I and j == J: return manhattan + detour * 2\n if (i, j) in visited: continue\n visited.add((i, j))\n for i, j, closer in ((i-1, j, i > I), (i+1, j, i < I), (i, j+1, j < J), (i, j-1, j > J)):\n if forest[i][j]:\n (good if closer else bad).append((i, j))\n \n trees = [(height, r, c) for r, row in enumerate(forest) for c, height in enumerate(row) if forest[r][c] > 1]\n # check\n queue = [(0, 0)]\n reached = set()\n reached.add((0, 0))\n while queue:\n r, c = queue.pop()\n for dr, dc in ((-1, 0), (1, 0), (0, -1), (0, 1)):\n row, col = r + dr, c + dc\n if forest[row][col] and (row, col) not in reached:\n queue.append((row, col))\n reached.add((row,col))\n if not all([(i, j) in reached for (height, i, j) in trees]): return -1\n trees.sort()\n return sum([distance(i, j, I, J) for (_, i, j), (_, I, J) in zip([(0, 0, 0)] + trees, trees)])\n``` | 4 | You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an `m x n` matrix. In this matrix:
* `0` means the cell cannot be walked through.
* `1` represents an empty cell that can be walked through.
* A number greater than `1` represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes `1` (an empty cell).
Starting from the point `(0, 0)`, return _the minimum steps you need to walk to cut off all the trees_. If you cannot cut off all the trees, return `-1`.
**Note:** The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
**Example 1:**
**Input:** forest = \[\[1,2,3\],\[0,0,4\],\[7,6,5\]\]
**Output:** 6
**Explanation:** Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
**Example 2:**
**Input:** forest = \[\[1,2,3\],\[0,0,0\],\[7,6,5\]\]
**Output:** -1
**Explanation:** The trees in the bottom row cannot be accessed as the middle row is blocked.
**Example 3:**
**Input:** forest = \[\[2,3,4\],\[0,0,5\],\[8,7,6\]\]
**Output:** 6
**Explanation:** You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
**Constraints:**
* `m == forest.length`
* `n == forest[i].length`
* `1 <= m, n <= 50`
* `0 <= forest[i][j] <= 109`
* Heights of all trees are **distinct**. | null |
Average solution | cut-off-trees-for-golf-event | 0 | 1 | # Intuition\n1. Sort order of trees\n2. Call bfs to reach next tree from current pos\n - Increment total steps whilst doing so\n \n# Code\n```\nclass Solution:\n def cutOffTree(self, forest: List[List[int]]) -> int:\n order = []\n m = len(forest)\n n = len(forest[0])\n directions = [(1,0),(-1,0),(0,1),(0,-1)]\n\n for i in range(m):\n for j in range(n):\n if forest[i][j] > 1:\n order.append(forest[i][j])\n order.sort()\n res = 0\n\n def bfs(start, target):\n if forest[start[0]][start[1]] == target: return start\n nonlocal res\n q = deque([start])\n v = set([start])\n while q:\n res += 1\n for _ in range(len(q)):\n r, c = q.popleft()\n for dr, dc in directions:\n nr = dr + r\n nc = dc + c\n if 0 <= nr < m and 0 <= nc < n and (nr,nc) not in v and forest[nr][nc] != 0:\n q.append((nr,nc))\n v.add((nr,nc))\n if forest[nr][nc] == target:\n forest[nr][nc] = 1\n return (nr, nc)\n return -1\n \n curPos = (0,0)\n for i in range(len(order)):\n curPos = bfs(curPos,order[i])\n if curPos == -1: return -1\n return res\n``` | 0 | You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an `m x n` matrix. In this matrix:
* `0` means the cell cannot be walked through.
* `1` represents an empty cell that can be walked through.
* A number greater than `1` represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes `1` (an empty cell).
Starting from the point `(0, 0)`, return _the minimum steps you need to walk to cut off all the trees_. If you cannot cut off all the trees, return `-1`.
**Note:** The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
**Example 1:**
**Input:** forest = \[\[1,2,3\],\[0,0,4\],\[7,6,5\]\]
**Output:** 6
**Explanation:** Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
**Example 2:**
**Input:** forest = \[\[1,2,3\],\[0,0,0\],\[7,6,5\]\]
**Output:** -1
**Explanation:** The trees in the bottom row cannot be accessed as the middle row is blocked.
**Example 3:**
**Input:** forest = \[\[2,3,4\],\[0,0,5\],\[8,7,6\]\]
**Output:** 6
**Explanation:** You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
**Constraints:**
* `m == forest.length`
* `n == forest[i].length`
* `1 <= m, n <= 50`
* `0 <= forest[i][j] <= 109`
* Heights of all trees are **distinct**. | null |
Python BFS Solution using `deque` | cut-off-trees-for-golf-event | 0 | 1 | # Intuition\n<!-- -->\nConduct BFS repeatedly to find each point in ascending order, next time starting from the point you found in previous execution of BFS.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort all tree position in ascending order\n2. Set initial node = `(0, 0)`\n3. Run BFS to find path to first tree with shortest height (first item in list)\n4. With each new level from current node, keep track of steps, neighbour of current node will be at position `step + 1` (if it took `step` steps to get to current node)\n5. When you find destination node, add total steps to global `total_steps` variable. Repeat steps 3-5 now with initial node as the current node you are on (the position of the tree you arrived at which you were initially after) and destination as the next heighest tree in the sorted list\n6. Once all trees have been found return `total_steps`. If all trees are not found or anywhere in between a tree is not found / not reachable return `-1`.\n# Complexity\n##### Time complexity:\n<!-- \n -->\nO(V+E) * O(K) = O(K*(V + E))\n\nExplanatation of terms\n- where K = number of trees in grid, \n- V = number of vertices which is n*m for a n x m grid,\n- E = number of edges between nodes, where only adjacent nodes can have an edge between them (nodes which have a side in common) which is 2 * n * m - (n + m)\n\n##### Time complexity:\n- O(n * m): For storing the visited 2D grid.\n<!-- O(n * m) -->\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def __init__(self):\n self.queue = deque()\n self.width = 0\n self.height = 0\n self.visited = [ [False]*self.width for i in range(self.height) ]\n # self.queue.pop\n \n def cutTrees(self, forest: List[List[int]], locs: List[List[int]]):\n reachable = True\n initial_loc = (0, 0)\n tot_steps = 0\n for i in range(len(locs)):\n self.queue.clear()\n steps = self.bfs(initial_loc, (locs[i][0], locs[i][1],), forest)\n if steps == -1:\n return -1\n tot_steps += steps\n initial_loc = (locs[i][0], locs[i][1],)\n return tot_steps\n\n def bfs(self, curr, destination, forest):\n count = 0\n self.visited = [ [False]*self.width for i in range(self.height) ]\n self.queue.append(curr + (count,))\n curr_min = float(\'inf\')\n found = False\n while len(self.queue) != 0:\n curr_loc = self.queue.popleft()\n if self.visited[curr_loc[0]][curr_loc[1]]:\n continue\n self.visited[curr_loc[0]][curr_loc[1]] = True\n neighbours = self.get_valid_neighbours(curr_loc[0], curr_loc[1], forest, self.visited)\n if (curr_loc[0], curr_loc[1],) == destination:\n forest[curr_loc[0]][curr_loc[1]] = 1\n found = True\n return curr_loc[2]\n for neighbour in neighbours:\n self.queue.append(neighbour + (curr_loc[2]+1,))\n if not found:\n return -1\n return curr_min\n \n def get_valid_neighbours(self, x, y, forest, visited):\n neighbours = []\n top = (x-1, y) if x >= 1 and forest[x-1][y] >= 1 and not visited[x-1][y] else None\n bottom = (x+1, y) if x < self.height-1 and forest[x+1][y] >= 1 and not visited[x+1][y] else None\n left = (x, y-1) if y >= 1 and forest[x][y-1] >= 1 and not visited[x][y-1] else None\n right = (x, y+1) if y < self.width-1 and forest[x][y+1] >= 1 and not visited[x][y+1] else None\n neighbours.append(top) if top is not None else None\n neighbours.append(bottom) if bottom is not None else None\n neighbours.append(left) if left is not None else None\n neighbours.append(right) if right is not None else None\n return neighbours\n \n \n def cutOffTree(self, forest: List[List[int]]) -> int:\n all_tree_locations_with_heights = []\n self.height = len(forest)\n self.width = len(forest[0])\n for i in range(len(forest)):\n for j in range(len(forest[i])):\n if forest[i][j] > 1:\n loc = (i, j, forest[i][j])\n all_tree_locations_with_heights.append(loc)\n all_tree_locations_with_heights = sorted(all_tree_locations_with_heights, key=lambda x: x[2])\n self.queue.append([0, 0])\n return self.cutTrees(forest, all_tree_locations_with_heights)\n \n \n \n``` | 0 | You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an `m x n` matrix. In this matrix:
* `0` means the cell cannot be walked through.
* `1` represents an empty cell that can be walked through.
* A number greater than `1` represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes `1` (an empty cell).
Starting from the point `(0, 0)`, return _the minimum steps you need to walk to cut off all the trees_. If you cannot cut off all the trees, return `-1`.
**Note:** The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
**Example 1:**
**Input:** forest = \[\[1,2,3\],\[0,0,4\],\[7,6,5\]\]
**Output:** 6
**Explanation:** Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
**Example 2:**
**Input:** forest = \[\[1,2,3\],\[0,0,0\],\[7,6,5\]\]
**Output:** -1
**Explanation:** The trees in the bottom row cannot be accessed as the middle row is blocked.
**Example 3:**
**Input:** forest = \[\[2,3,4\],\[0,0,5\],\[8,7,6\]\]
**Output:** 6
**Explanation:** You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.
**Constraints:**
* `m == forest.length`
* `n == forest[i].length`
* `1 <= m, n <= 50`
* `0 <= forest[i][j] <= 109`
* Heights of all trees are **distinct**. | null |
Solution | implement-magic-dictionary | 1 | 1 | ```C++ []\nclass MagicDictionary {\n public:\n void buildDict(vector<string> dictionary) {\n for (const string& word : dictionary)\n for (int i = 0; i < word.length(); ++i) {\n const string replaced = getReplaced(word, i);\n dict[replaced] = dict.count(replaced) ? \'*\' : word[i];\n }\n }\n bool search(string searchWord) {\n for (int i = 0; i < searchWord.length(); ++i) {\n const string replaced = getReplaced(searchWord, i);\n if (dict.count(replaced) && dict[replaced] != searchWord[i])\n return true;\n }\n return false;\n }\n private:\n unordered_map<string, char> dict;\n\n string getReplaced(const string& s, int i) {\n return s.substr(0, i) + \'*\' + s.substr(i + 1);\n }\n};\n```\n\n```Python3 []\nclass MagicDictionary:\n\n def __init__(self):\n self.countDict = {}\n\n def buildDict(self, dictionary: List[str]) -> None:\n for word in dictionary:\n if len(word) not in self.countDict: self.countDict[len(word)] = []\n self.countDict[len(word)].append(word)\n\n def isOneOff(self, word, searchWord) -> bool:\n numDiffs = 0\n for i in range(len(word)):\n if word[i] != searchWord[i]: numDiffs += 1\n if numDiffs > 1: return False\n return numDiffs == 1\n\n def search(self, searchWord: str) -> bool:\n if len(searchWord) not in self.countDict: return False\n candidates = self.countDict[len(searchWord)]\n for c in candidates:\n if self.isOneOff(c, searchWord): return True\n return False\n```\n\n```Java []\nclass MagicDictionary {\n private HashMap<Integer, ArrayList<String>> lenMap;\n public MagicDictionary() {\n lenMap = new HashMap<>();\n }\n public void buildDict(String[] dictionary) {\n lenMap.clear();\n for(String word: dictionary){\n if(!lenMap.containsKey(word.length())){\n lenMap.put(word.length(), new ArrayList<>());\n }\n lenMap.get(word.length()).add(word);\n }\n }\n public boolean search(String searchWord) {\n if(!lenMap.containsKey(searchWord.length())){\n return false;\n }\n ArrayList<String> arr = lenMap.get(searchWord.length());\n for(String word: arr){\n if(checkAlmostSame(searchWord, word)){\n return true;\n }\n }\n return false;\n }\n private boolean checkAlmostSame(String searchWord, String word){\n boolean foundDiff = false;\n for(int i = 0; i < word.length(); i++){\n if(word.charAt(i) != searchWord.charAt(i)){\n if(foundDiff == true){\n return false;\n } else {\n foundDiff = true;\n }\n }\n }\n return foundDiff;\n }\n}\n```\n | 1 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
[Python 3] - Trie - Simple Solution | implement-magic-dictionary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N*K)$$ with N is the number of word and K is length of each word\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N*K)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TrieNode:\n\n def __init__(self):\n self.children = collections.defaultdict(TrieNode)\n self.is_end = False\n\n\nclass MagicDictionary:\n\n def __init__(self):\n self.trie = TrieNode()\n self.s = set()\n \n\n def buildDict(self, dictionary: List[str]) -> None:\n for word in dictionary:\n self.s.add(word)\n cur = self.trie\n for ch in word:\n cur = cur.children[ch]\n cur.is_end = True\n \n\n def search(self, searchWord: str) -> bool:\n n = len(searchWord)\n def dfs(root: TrieNode, cnt: int, i: int) -> bool:\n if cnt > 1 or i == n: return cnt == 1 and root.is_end\n return any([dfs(root.children[c], cnt + int(c != searchWord[i]), i + 1) for c in root.children])\n \n return dfs(self.trie, 0, 0)\n\n# Your MagicDictionary object will be instantiated and called as such:\n# obj = MagicDictionary()\n# obj.buildDict(dictionary)\n# param_2 = obj.search(searchWord)\n``` | 3 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
676: Solution with step by step explanation | implement-magic-dictionary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. __init__ method\n 1. Create an empty dictionary to hold the words and their replacements.\n 2. Store the dictionary in the class attribute self.dict.\n2. buildDict method\n 1. For each word in the dictionary argument:\n - For each index i in the range 0 to len(word):\n - Replace the character at index i with *.\n - Store the new string in a variable named replaced.\n - If replaced is already a key in the dictionary:\n - Append the original word to the list of words associated with the replaced key.\n - Otherwise, create a new key-value pair in the dictionary where the key is replaced and the value is a list containing word.\n 2. Store the updated dictionary in the class attribute self.dict.\n3. search method\n1. For each index i in the range 0 to len(searchWord):\n 1. Replace the character at index i with *.\n 2. Store the new string in a variable named replaced.\n 3. If replaced is a key in the dictionary:\n - Get the list of words associated with the replaced key.\n - For each word in the list:\n - If the word is not equal to searchWord and has the same length as searchWord:\n - Initialize a variable match to True.\n - For each index j in the range 0 to len(searchWord):\n - If the characters at index j in searchWord and word are not equal and the character at index j in replaced is not *, set match to False and break out of the loop.\n - If match is still True after the loop, return True.\n2. Return False if no matches were found.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MagicDictionary:\n def __init__(self):\n self.dict = {}\n\n def buildDict(self, dictionary: List[str]) -> None:\n for word in dictionary:\n for i in range(len(word)):\n replaced = word[:i] + \'*\' + word[i+1:]\n if replaced in self.dict:\n self.dict[replaced].append(word)\n else:\n self.dict[replaced] = [word]\n\n def search(self, searchWord: str) -> bool:\n for i in range(len(searchWord)):\n replaced = searchWord[:i] + \'*\' + searchWord[i+1:]\n if replaced in self.dict:\n words = self.dict[replaced]\n for word in words:\n if word != searchWord and len(word) == len(searchWord):\n match = True\n for j in range(len(searchWord)):\n if searchWord[j] != word[j] and replaced[j] != \'*\':\n match = False\n break\n if match:\n return True\n return False\n\n``` | 3 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
2 Solution Beginner Friendly Set and simple array using Zip (Python3) | implement-magic-dictionary | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- 1. Array and Zip \n- 2. Set method\n\n# Complexity\n\n- Array and Zip\n - Time complexity: O(n * m)\n\n - Space complexity: O(n + m)\n- Set \n - Time complexity: O(26M) \n\n - Space complexity: O(n * m)\n\n# 1. Simple Array and zip method\n```\nclass MagicDictionary:\n\n def __init__(self):\n self.dict = []\n\n def buildDict(self, dictionary: List[str]) -> None:\n for ch in dictionary:\n self.dict.append((ch))\n \n\n def search(self, searchWord: str) -> bool:\n for word in self.dict:\n if len(word) == len(searchWord) and sum(c1 != c2 for c1, c2 in zip(word, searchWord)) == 1: return True\n return False\n```\n- explaination of if statement in Search()\n```\nfor word in self.dict:\n count = 0\n for c1, c2 in zip(word, searchWord): #if word is \'hello\' and searchWord is \'hhllo\', zip(word, searchWord) would produce ->\n if c1 != c2: #(\'h\', \'h\'), (\'e\', \'h\'), (\'l\', \'l\'), (\'l\', \'l\'), (\'o\', \'o\')\n count += 1\n\n if count == 1: return True\n else: return False\n\n\n```\n\n# 2 . Set method\n```\nclass MagicDictionary:\n\n def __init__(self):\n self.words = set()\n\n def buildDict(self, dictionary: List[str]) -> None:\n self.words = set(dictionary)\n\n def search(self, searchWord: str) -> bool:\n for i in range(len(searchWord)):\n for char in \'abcdefghijklmnopqrstuvwxyz\':\n if char == searchWord[i]:\n continue\n replaced_word = searchWord[:i] + char + searchWord[i + 1:]\n if replaced_word in self.words:\n return True\n return False\n```\n | 3 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
Python 97.27% speed | Hashmap only | Simple code | implement-magic-dictionary | 0 | 1 | For each word, length is the key. For each searchWord, only need to check the words with same length\n\n```\nclass MagicDictionary:\n\n def __init__(self):\n self.myDict = defaultdict(set)\n\n def buildDict(self, dictionary: List[str]) -> None:\n for word in dictionary:\n n = len(word)\n self.myDict[n].add(word)\n\n def search(self, searchWord: str) -> bool:\n n = len(searchWord)\n if n not in self.myDict: return False\n \n def diff(word1, word2):\n count = 0\n for i in range(len(word1)):\n if word1[i] != word2[i]:\n count += 1 \n if count > 1:\n return count\n return count\n \n \n for word in self.myDict[n]:\n if diff(word, searchWord) == 1:\n return True\n return False\n``` | 5 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
My fast Python solution | implement-magic-dictionary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thoughts on how to solve this problem is to create a data structure that stores all the words in the dictionary. Then, when searching for a word, I will iterate through each word in the data structure and compare it to the search word. If the two words have a difference of only one character, I will return true.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach I will take is to first create a data structure to store the dictionary words, in this case a set. Then, I will implement the search function which will iterate through each word in the data structure and compare it to the search word. If the two words have a difference of only one character, the function will return true, otherwise it will return false.\n\n\n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MagicDictionary:\n\n def __init__(self):\n """\n Initialize your data structure here.\n """\n self.dic = set()\n\n def buildDict(self, dictionary: List[str]) -> None:\n self.dic = set(dictionary)\n\n def search(self, searchWord: str) -> bool:\n for word in self.dic:\n if len(word) == len(searchWord):\n diff = 0\n for i in range(len(word)):\n if word[i] != searchWord[i]:\n diff += 1\n if diff == 1:\n return True\n return False\n# Your MagicDictionary object will be instantiated and called as such:\n# obj = MagicDictionary()\n# obj.buildDict(dictionary)\n# param_2 = obj.search(searchWord)\n``` | 2 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
Easy to read solution using a dictionary of set of candidate words with a length as key | implement-magic-dictionary | 0 | 1 | \n# Code\n```\nclass MagicDictionary:\n\n def __init__(self):\n self.dct = collections.defaultdict(set) # key:value = length:set of words with length\n \n\n def buildDict(self, dictionary: List[str]) -> None:\n for word in dictionary:\n n = len(word)\n self.dct[n].add(word)\n \n\n def findWord(self, query: str, candidate: str) -> bool:\n n = len(query)\n seen_diff = False\n for i in range(len(query)):\n if query[i] != candidate[i]:\n if seen_diff:\n return False\n seen_diff = True\n return seen_diff\n \n\n def search(self, searchWord: str) -> bool:\n n = len(searchWord)\n for item in self.dct[n]:\n if self.findWord(searchWord, item):\n return True\n return False\n \n \n\n\n# Your MagicDictionary object will be instantiated and called as such:\n# obj = MagicDictionary()\n# obj.buildDict(dictionary)\n# param_2 = obj.search(searchWord)\n``` | 0 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
Python | Trie | implement-magic-dictionary | 0 | 1 | # Code\n```\nclass MagicDictionary:\n\n def __init__(self):\n self.trie = {}\n\n def buildDict(self, dictionary: List[str]) -> None:\n for word in dictionary:\n node = self.trie\n for ch in word:\n if ch not in node:\n node[ch] = {}\n node = node[ch]\n # mark as word end\n node[\'#\'] = {}\n\n def search(self, searchWord: str) -> bool:\n\n def check(k, node, diff):\n for i in range(k, len(searchWord)):\n ch = searchWord[i]\n for avail in node:\n if diff == 0 and avail != ch and check(i + 1, node[avail], diff + 1):\n return True\n if ch not in node:\n return False\n node = node[ch]\n return \'#\' in node and diff == 1\n\n return check(0, self.trie, 0)\n\n# Your MagicDictionary object will be instantiated and called as such:\n# obj = MagicDictionary()\n# obj.buildDict(dictionary)\n# param_2 = obj.search(searchWord)\n``` | 0 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
use hashmap and hamming distance | implement-magic-dictionary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. we first build a hashmap using string length as key and a list of strings in the dictionary of that length as the value\n2. we then build a mini function to calculate hamming distance of two strings with equal length\n3. given a new search word, if the length is not found in our hashmap we would know it\'s impossible to change one character to achieve a match. so we return False immediately\n4. if the length of the search word is found from the hashmap, it means we have at least one word in the dictionary which would have the same length. Thus this pair of strings are eligible for hamming distance calculation.\n5. since there could be multiple strings in hashmap which have identical length, we would tally up the total # of cases where the hamming distance of the pair is exactly 1 (i.e. modifying one character of search word would make it identical to the given string from the dictionary)\n6. if the total number of disctionary words with 1 hamming distance from the search word is 1 or more, we know the operation could be carried out successfully. Thus we return True. It\'d be False, otherwise\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MagicDictionary:\n\n def __init__(self):\n self.hashmap={}\n\n def buildDict(self, dictionary: List[str]) -> None:\n for e in dictionary:\n if len(e) not in self.hashmap:\n self.hashmap[len(e)] = [e]\n else:\n self.hashmap[len(e)].append(e)\n\n def hamming(self,s1,s2):\n result=0\n for x,(i,j) in enumerate(zip(s1,s2)):\n if i!=j:\n result+=1\n return result\n\n def search(self, searchWord: str) -> bool:\n res = 0\n if len(searchWord) not in self.hashmap:\n return False\n for e in self.hashmap[len(searchWord)]:\n if self.hamming(e, searchWord) == 1:\n res += 1\n if res > 0:\n return True\n else:\n return False\n\n\n# Your MagicDictionary object will be instantiated and called as such:\n# obj = MagicDictionary()\n# obj.buildDict(dictionary)\n# param_2 = obj.search(searchWord)\n``` | 0 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
easy and fast python solution. | implement-magic-dictionary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nworst case `O(N*k)` where N is num of words in dictionary, k is the length of the search word. Worst case == we must search all dict ionary words. \n- Space complexity:\n`O(N*k)` chars, where k is the average word length.\n\n# Code\n```\nfrom collections import Counter, defaultdict\nclass MagicDictionary:\n\n def __init__(self):\n # len -> words \n self.d = defaultdict(list)\n\n\n def buildDict(self, dictionary: List[str]) -> None:\n # populate len -> words dictionary \n for word in dictionary: \n self.d[len(word)].append(word)\n\n def search(self, sw: str) -> bool:\n # find words with equal length\n candidates = self.d.get(len(sw), None)\n if not candidates: \n return False \n\n for cand in candidates: \n # try each candidate\n if one_char_diff(cand, sw): \n return True \n return False \n \ndef one_char_diff(c1, c2) : \n count = 0\n for a,b in zip(c1, c2): \n if a != b: \n count += 1 \n if count > 1: \n # more than 2 chars diff, return False \n return False \n # return exactly one char diff. \n return count == 1 \n\n``` | 0 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
Python Trie BFS Solution 🎄 | implement-magic-dictionary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MagicDictionary:\n\n def __init__(self):\n self.magic = {}\n\n def buildDict(self, dictionary: List[str]) -> None:\n for word in dictionary:\n temp = self.magic\n for char in word:\n if char in temp:\n temp = temp[char]\n else:\n temp[char] = {}\n temp = temp[char]\n \n temp[\':)\'] = \':)\' #signifies end of word\n\n def search(self, searchWord: str) -> bool:\n queue = [(0,0,self.magic)]\n while queue:\n index, numWrong, dictionary = queue.pop(0)\n \n if index == len(searchWord) and \':)\' in dictionary and type(dictionary) != str and numWrong == 1:\n print(index, dictionary)\n return True\n \n if index < len(searchWord):\n if searchWord[index] in dictionary:\n queue.append((index+1, numWrong, dictionary[searchWord[index]]))\n\n if numWrong == 0:\n for character in dictionary:\n if character != searchWord[index]:\n queue.append((index+1, 1, dictionary[character]))\n\n return False\n \n\n \n\n\n# Your MagicDictionary object will be instantiated and called as such:\n# obj = MagicDictionary()\n# obj.buildDict(dictionary)\n# param_2 = obj.search(searchWord)\n``` | 0 | Design a data structure that is initialized with a list of **different** words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.
Implement the `MagicDictionary` class:
* `MagicDictionary()` Initializes the object.
* `void buildDict(String[] dictionary)` Sets the data structure with an array of distinct strings `dictionary`.
* `bool search(String searchWord)` Returns `true` if you can change **exactly one character** in `searchWord` to match any string in the data structure, otherwise returns `false`.
**Example 1:**
**Input**
\[ "MagicDictionary ", "buildDict ", "search ", "search ", "search ", "search "\]
\[\[\], \[\[ "hello ", "leetcode "\]\], \[ "hello "\], \[ "hhllo "\], \[ "hell "\], \[ "leetcoded "\]\]
**Output**
\[null, null, false, true, false, false\]
**Explanation**
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(\[ "hello ", "leetcode "\]);
magicDictionary.search( "hello "); // return False
magicDictionary.search( "hhllo "); // We can change the second 'h' to 'e' to match "hello " so we return True
magicDictionary.search( "hell "); // return False
magicDictionary.search( "leetcoded "); // return False
**Constraints:**
* `1 <= dictionary.length <= 100`
* `1 <= dictionary[i].length <= 100`
* `dictionary[i]` consists of only lower-case English letters.
* All the strings in `dictionary` are **distinct**.
* `1 <= searchWord.length <= 100`
* `searchWord` consists of only lower-case English letters.
* `buildDict` will be called only once before `search`.
* At most `100` calls will be made to `search`. | null |
677: Solution with step by step explanation | map-sum-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nDefine a TrieNode class with two attributes: children (a dictionary mapping characters to child nodes) and value (an integer representing the sum of values stored at or below this node in the Trie).\n\nDefine a MapSum class with two attributes: root (a TrieNode representing the root of the Trie) and map (a dictionary mapping keys to values).\n\nDefine an insert method that takes a key (a string) and a value (an integer) as input. Calculate the difference between the new value and the old value for the given key (if it exists), and store the new value in the map dictionary.\n\nTraverse the Trie from the root to the node that represents the prefix of the key, and update the node value with the new value. Start by initializing a variable node to the root node and adding the difference to node.value. Then, iterate through each character in the key string. If the character is not in node.children, create a new TrieNode and add it to node.children. Update node to be the child node corresponding to the current character, and add the difference to node.value.\n\nDefine a sum method that takes a prefix (a string) as input and returns the sum of values stored in the Trie at or below the node that represents the prefix. Start by initializing a variable node to the root node. Then, iterate through each character in the prefix string. If the character is not in node.children, return 0 (indicating that no keys with this prefix exist in the Trie). Otherwise, update node to be the child node corresponding to the current character. Once the loop is finished, return node.value (the sum of values stored at or below the node representing the prefix).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.value = 0\n\nclass MapSum:\n def __init__(self):\n self.root = TrieNode()\n self.map = {}\n\n def insert(self, key: str, val: int) -> None:\n # Calculate the difference between the new value and the old value\n # for the given key, if it exists.\n diff = val - self.map.get(key, 0)\n self.map[key] = val\n \n # Traverse the Trie from the root to the node that represents\n # the prefix of the key, and update the node value with the new value.\n node = self.root\n node.value += diff\n for char in key:\n if char not in node.children:\n node.children[char] = TrieNode()\n node = node.children[char]\n node.value += diff\n\n def sum(self, prefix: str) -> int:\n # Traverse the Trie from the root to the node that represents\n # the prefix, and return the value of that node.\n node = self.root\n for char in prefix:\n if char not in node.children:\n return 0\n node = node.children[char]\n return node.value\n\n``` | 2 | Design a map that allows you to do the following:
* Maps a string key to a given value.
* Returns the sum of the values that have a key with a prefix equal to a given string.
Implement the `MapSum` class:
* `MapSum()` Initializes the `MapSum` object.
* `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
* `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
**Example 1:**
**Input**
\[ "MapSum ", "insert ", "sum ", "insert ", "sum "\]
\[\[\], \[ "apple ", 3\], \[ "ap "\], \[ "app ", 2\], \[ "ap "\]\]
**Output**
\[null, null, 3, null, 5\]
**Explanation**
MapSum mapSum = new MapSum();
mapSum.insert( "apple ", 3);
mapSum.sum( "ap "); // return 3 (apple = 3)
mapSum.insert( "app ", 2);
mapSum.sum( "ap "); // return 5 (apple + app = 3 + 2 = 5)
**Constraints:**
* `1 <= key.length, prefix.length <= 50`
* `key` and `prefix` consist of only lowercase English letters.
* `1 <= val <= 1000`
* At most `50` calls will be made to `insert` and `sum`. | null |
Solution | map-sum-pairs | 1 | 1 | ```C++ []\nstruct TrieNode {\n vector<shared_ptr<TrieNode>> children;\n int sum = 0;\n TrieNode() : children(26) {}\n};\nclass MapSum {\n public:\n void insert(string key, int val) {\n const int diff = val - keyToVal[key];\n shared_ptr<TrieNode> node = root;\n for (const char c : key) {\n const int i = c - \'a\';\n if (node->children[i] == nullptr)\n node->children[i] = make_shared<TrieNode>();\n node = node->children[i];\n node->sum += diff;\n }\n keyToVal[key] = val;\n }\n int sum(string prefix) {\n shared_ptr<TrieNode> node = root;\n for (const char c : prefix) {\n const int i = c - \'a\';\n if (node->children[i] == nullptr)\n return 0;\n node = node->children[i];\n }\n return node->sum;\n }\n private:\n shared_ptr<TrieNode> root = make_shared<TrieNode>();\n unordered_map<string, int> keyToVal;\n};\n```\n\n```Python3 []\nclass MapSum:\n\n def __init__(self):\n self.trie = {}\n\n def insert(self, key: str, val: int) -> None:\n node = self.trie\n for ch in key:\n node = node.setdefault(ch, {})\n node[\'val\'] = val\n return\n\n def sum(self, prefix: str) -> int:\n def traverse(node):\n nonlocal res\n if not node:\n return\n if \'val\' in node:\n res += node[\'val\']\n for child in node:\n if child == \'val\': continue\n traverse(node[child])\n return\n \n node = self.trie\n for ch in prefix:\n node = node.get(ch, {})\n if not node:\n return 0\n res = 0\n traverse(node)\n return res\n```\n\n```Java []\nclass MapSum {\n class TrieNode {\n TrieNode next[] = new TrieNode[26];\n int val = 0;\n int sum = 0;\n }\n TrieNode head;\n public MapSum() {\n head = new TrieNode();\n }\n public void insert(String key, int val) {\n int n = key.length();\n TrieNode tmp = head;\n for (int i = 0; i < n; i++) {\n int now = key.charAt(i) - \'a\';\n if (tmp.next[now] == null) tmp.next[now] = new TrieNode();\n tmp = tmp.next[now];\n }\n int diff = val - tmp.val;\n tmp.val = val;\n tmp = head;\n\n for (int i = 0; i < n && diff != 0; i++) {\n int now = key.charAt(i) - \'a\';\n tmp.sum += diff;\n tmp = tmp.next[now];\n }\n tmp.sum += diff;\n }\n public int sum(String key) {\n int n = key.length();\n TrieNode tmp = head;\n for (int i = 0; i < n; i++) {\n int now = key.charAt(i) - \'a\';\n if (tmp.next[now] == null) return 0;\n tmp = tmp.next[now];\n }\n return tmp.sum;\n }\n}\n```\n | 2 | Design a map that allows you to do the following:
* Maps a string key to a given value.
* Returns the sum of the values that have a key with a prefix equal to a given string.
Implement the `MapSum` class:
* `MapSum()` Initializes the `MapSum` object.
* `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
* `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
**Example 1:**
**Input**
\[ "MapSum ", "insert ", "sum ", "insert ", "sum "\]
\[\[\], \[ "apple ", 3\], \[ "ap "\], \[ "app ", 2\], \[ "ap "\]\]
**Output**
\[null, null, 3, null, 5\]
**Explanation**
MapSum mapSum = new MapSum();
mapSum.insert( "apple ", 3);
mapSum.sum( "ap "); // return 3 (apple = 3)
mapSum.insert( "app ", 2);
mapSum.sum( "ap "); // return 5 (apple + app = 3 + 2 = 5)
**Constraints:**
* `1 <= key.length, prefix.length <= 50`
* `key` and `prefix` consist of only lowercase English letters.
* `1 <= val <= 1000`
* At most `50` calls will be made to `insert` and `sum`. | null |
[Python] TRIE Solution easy to understand | map-sum-pairs | 0 | 1 | ```\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.prefixCount = 0\n \n \nclass MapSum: \n\n def __init__(self):\n self.root = TrieNode()\n self.dic = {}\n\n def insert(self, key: str, val: int) -> None: \n delta = val\n if key in self.dic: # key already existed, the original key-value pair will be overridden to the new one. And val - self.dic[key] does this thing\n delta = val - self.dic[key]\n self.dic[key] = val\n cur = self.root\n for c in key:\n if c not in cur.children:\n cur.children[c] = TrieNode()\n cur = cur.children[c]\n cur.prefixCount += delta\n\n def sum(self, prefix: str) -> int:\n cur = self.root\n for c in prefix:\n if c not in cur.children:\n cur.children[c] = TrieNode()\n cur = cur.children[c]\n return cur.prefixCount\n\n\'\'\'\nTime complexity: O(m) to insert key of length m as well it is O(m) to evaluate sum for prefix of length m. \nSpace complexity: O(T) where T it total length of all words.\n\'\'\'\n``` | 6 | Design a map that allows you to do the following:
* Maps a string key to a given value.
* Returns the sum of the values that have a key with a prefix equal to a given string.
Implement the `MapSum` class:
* `MapSum()` Initializes the `MapSum` object.
* `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
* `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
**Example 1:**
**Input**
\[ "MapSum ", "insert ", "sum ", "insert ", "sum "\]
\[\[\], \[ "apple ", 3\], \[ "ap "\], \[ "app ", 2\], \[ "ap "\]\]
**Output**
\[null, null, 3, null, 5\]
**Explanation**
MapSum mapSum = new MapSum();
mapSum.insert( "apple ", 3);
mapSum.sum( "ap "); // return 3 (apple = 3)
mapSum.insert( "app ", 2);
mapSum.sum( "ap "); // return 5 (apple + app = 3 + 2 = 5)
**Constraints:**
* `1 <= key.length, prefix.length <= 50`
* `key` and `prefix` consist of only lowercase English letters.
* `1 <= val <= 1000`
* At most `50` calls will be made to `insert` and `sum`. | null |
88% TC and 92% SC easy python solution using map | map-sum-pairs | 0 | 1 | ```\nclass MapSum:\n def __init__(self):\n self.d = defaultdict(int)\n self.s = dict()\n\n def insert(self, key: str, val: int) -> None:\n if(key in self.s):\n val, self.s[key] = val - self.s[key], val\n else:\n self.s[key] = val\n for i in range(1, len(key)+1):\n self.d[key[:i]] += val\n \n def sum(self, prefix: str) -> int:\n return self.d[prefix]\n``` | 1 | Design a map that allows you to do the following:
* Maps a string key to a given value.
* Returns the sum of the values that have a key with a prefix equal to a given string.
Implement the `MapSum` class:
* `MapSum()` Initializes the `MapSum` object.
* `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
* `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
**Example 1:**
**Input**
\[ "MapSum ", "insert ", "sum ", "insert ", "sum "\]
\[\[\], \[ "apple ", 3\], \[ "ap "\], \[ "app ", 2\], \[ "ap "\]\]
**Output**
\[null, null, 3, null, 5\]
**Explanation**
MapSum mapSum = new MapSum();
mapSum.insert( "apple ", 3);
mapSum.sum( "ap "); // return 3 (apple = 3)
mapSum.insert( "app ", 2);
mapSum.sum( "ap "); // return 5 (apple + app = 3 + 2 = 5)
**Constraints:**
* `1 <= key.length, prefix.length <= 50`
* `key` and `prefix` consist of only lowercase English letters.
* `1 <= val <= 1000`
* At most `50` calls will be made to `insert` and `sum`. | null |
Python - Modifying the standard Trie concept | map-sum-pairs | 0 | 1 | ```\nclass TrieNode:\n def __init__(self):\n self.children = collections.defaultdict(TrieNode)\n self.value = 0\n \nclass MapSum:\n def __init__(self):\n self.t = TrieNode()\n self.m = {}\n\n def insert(self, key: str, val: int) -> None:\n delta = val - self.m.get(key,0)\n self.m[key] = val\n node = self.t\n for char in key:\n node = node.children[char]\n node.value += delta\n \n def sum(self, prefix: str) -> int:\n node = self.t\n for char in prefix:\n node = node.children.get(char)\n if not node:\n return 0\n return node.value\n \n``` | 6 | Design a map that allows you to do the following:
* Maps a string key to a given value.
* Returns the sum of the values that have a key with a prefix equal to a given string.
Implement the `MapSum` class:
* `MapSum()` Initializes the `MapSum` object.
* `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
* `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
**Example 1:**
**Input**
\[ "MapSum ", "insert ", "sum ", "insert ", "sum "\]
\[\[\], \[ "apple ", 3\], \[ "ap "\], \[ "app ", 2\], \[ "ap "\]\]
**Output**
\[null, null, 3, null, 5\]
**Explanation**
MapSum mapSum = new MapSum();
mapSum.insert( "apple ", 3);
mapSum.sum( "ap "); // return 3 (apple = 3)
mapSum.insert( "app ", 2);
mapSum.sum( "ap "); // return 5 (apple + app = 3 + 2 = 5)
**Constraints:**
* `1 <= key.length, prefix.length <= 50`
* `key` and `prefix` consist of only lowercase English letters.
* `1 <= val <= 1000`
* At most `50` calls will be made to `insert` and `sum`. | null |
✅ Easy Python 3 O(k) Beats 90% Trie + Dictionary ✅ | map-sum-pairs | 0 | 1 | # Intuition\nWe use a trie to store all the keys. The trie nodes are associated with their corresponding character but also holds a value field. This value feild tracks the sum of all keys who uses this particular node in the trie.\n\n# Approach\nWrite a separate TrieNode class: the children field is implemented with a dictionary which maps characters to other TrieNodes. In the insert method, update down the trie character chain. Since insertions of the same key should override the previous value, we also keep a dictionary to store keys that are currently present in the trie. For the sum method, traverse down to the desired TrieNode and retrieve the sum.\n\n# Complexity\n- Time complexity:\nO(k) where k is the length of the key to be inserted or prefix to be checked\n\n# Code\n```\nclass TrieNode:\n def __init__(self, val):\n self.value = val\n self.children = {}\n\nclass MapSum:\n\n def __init__(self):\n self.root = TrieNode(0)\n self.words = {}\n \n\n def insert(self, key: str, val: int) -> None:\n toAdd = val\n if key in self.words:\n toAdd -= self.words[key]\n self.words[key] = val\n curr = self.root\n for c in key:\n if c in curr.children:\n curr = curr.children[c]\n curr.value += toAdd\n else:\n curr.children[c] = TrieNode(val)\n curr = curr.children[c]\n\n def sum(self, prefix: str) -> int:\n curr = self.root\n for c in prefix:\n if c in curr.children:\n curr = curr.children[c]\n else:\n return 0\n return curr.value\n\n\n# Your MapSum object will be instantiated and called as such:\n# obj = MapSum()\n# obj.insert(key,val)\n# param_2 = obj.sum(prefix)\n``` | 0 | Design a map that allows you to do the following:
* Maps a string key to a given value.
* Returns the sum of the values that have a key with a prefix equal to a given string.
Implement the `MapSum` class:
* `MapSum()` Initializes the `MapSum` object.
* `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
* `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
**Example 1:**
**Input**
\[ "MapSum ", "insert ", "sum ", "insert ", "sum "\]
\[\[\], \[ "apple ", 3\], \[ "ap "\], \[ "app ", 2\], \[ "ap "\]\]
**Output**
\[null, null, 3, null, 5\]
**Explanation**
MapSum mapSum = new MapSum();
mapSum.insert( "apple ", 3);
mapSum.sum( "ap "); // return 3 (apple = 3)
mapSum.insert( "app ", 2);
mapSum.sum( "ap "); // return 5 (apple + app = 3 + 2 = 5)
**Constraints:**
* `1 <= key.length, prefix.length <= 50`
* `key` and `prefix` consist of only lowercase English letters.
* `1 <= val <= 1000`
* At most `50` calls will be made to `insert` and `sum`. | null |
Python Trie | map-sum-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TrieNode:\n def __init__(self):\n self.count=0\n self.children={}\n \n\nclass MapSum:\n\n def __init__(self):\n self.root=TrieNode()\n self.hashmap={}\n \n \n\n def insert(self, key: str, val: int) -> None:\n cur=self.root\n minus=0\n if key in self.hashmap:\n minus=self.hashmap[key]\n \n for k in key:\n if k not in cur.children:\n cur.children[k]=TrieNode()\n cur=cur.children[k]\n cur.count+=val-minus\n self.hashmap[key]=val\n\n \n\n def sum(self, prefix: str) -> int:\n cur=self.root\n for i in prefix:\n if i not in cur.children:\n return 0 \n cur=cur.children[i]\n return cur.count\n \n\n\n# Your MapSum object will be instantiated and called as such:\n# obj = MapSum()\n# obj.insert(key,val)\n# param_2 = obj.sum(prefix)\n``` | 0 | Design a map that allows you to do the following:
* Maps a string key to a given value.
* Returns the sum of the values that have a key with a prefix equal to a given string.
Implement the `MapSum` class:
* `MapSum()` Initializes the `MapSum` object.
* `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
* `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
**Example 1:**
**Input**
\[ "MapSum ", "insert ", "sum ", "insert ", "sum "\]
\[\[\], \[ "apple ", 3\], \[ "ap "\], \[ "app ", 2\], \[ "ap "\]\]
**Output**
\[null, null, 3, null, 5\]
**Explanation**
MapSum mapSum = new MapSum();
mapSum.insert( "apple ", 3);
mapSum.sum( "ap "); // return 3 (apple = 3)
mapSum.insert( "app ", 2);
mapSum.sum( "ap "); // return 5 (apple + app = 3 + 2 = 5)
**Constraints:**
* `1 <= key.length, prefix.length <= 50`
* `key` and `prefix` consist of only lowercase English letters.
* `1 <= val <= 1000`
* At most `50` calls will be made to `insert` and `sum`. | null |
Python 3, Brute Force Recursive + memo | valid-parenthesis-string | 0 | 1 | # Intuition\nrecursive + memo\n\n\n# Complexity\n- Time complexity: O(n^3)\n- Space complexity: O(n^3)\n\n# Code\n```\nclass Solution:\n def checkValidString(self, s: str) -> bool:\n n: int = len(s)\n\n memo = {}\n def f(i: int, left: int):\n\n if (i, left) in memo:\n return memo[(i, left)]\n\n if i == n:\n if left == 0:\n return True\n else:\n return False\n\n if left < 0:\n memo[(i, left)] = False\n elif s[i] == "(":\n memo[(i, left)] = f(i + 1, left + 1)\n elif s[i] == ")":\n memo[(i, left)] = f(i + 1, left - 1)\n else:\n memo[(i, left)] = f(i + 1, left - 1) | f(i + 1, left + 1) | f(i + 1, left)\n\n return memo[(i, left)]\n\n return f(0, 0)\n\n\n``` | 1 | Given a string `s` containing only three types of characters: `'('`, `')'` and `'*'`, return `true` _if_ `s` _is **valid**_.
The following rules define a **valid** string:
* Any left parenthesis `'('` must have a corresponding right parenthesis `')'`.
* Any right parenthesis `')'` must have a corresponding left parenthesis `'('`.
* Left parenthesis `'('` must go before the corresponding right parenthesis `')'`.
* `'*'` could be treated as a single right parenthesis `')'` or a single left parenthesis `'('` or an empty string `" "`.
**Example 1:**
**Input:** s = "()"
**Output:** true
**Example 2:**
**Input:** s = "(\*)"
**Output:** true
**Example 3:**
**Input:** s = "(\*))"
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is `'('`, `')'` or `'*'`. | null |
Python O(n) by stack. 85%+ [w/ Comment] | valid-parenthesis-string | 0 | 1 | [\u4E2D\u6587\u8A73\u89E3 \u89E3\u984C\u6587\u7AE0](https://vocus.cc/article/6541ed1afd89780001044ee2)\n\nPython O(n) by stack. \n\n---\n\n```\nclass Solution:\n def checkValidString(self, s: str) -> bool:\n \n # store the indices of \'(\'\n stk = []\n \n # store the indices of \'*\'\n star = []\n \n \n for idx, char in enumerate(s):\n \n if char == \'(\':\n stk.append( idx )\n \n elif char == \')\':\n \n if stk:\n stk.pop()\n elif star:\n star.pop()\n else:\n return False\n \n else:\n star.append( idx )\n \n \n # cancel ( and * with valid positions, i.e., \'(\' must be on the left hand side of \'*\'\n while stk and star:\n if stk[-1] > star[-1]:\n return False\n \n stk.pop()\n star.pop()\n \n \n # Accept when stack is empty, which means all braces are paired\n # Reject, otherwise.\n return len(stk) == 0\n \n```\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #20 Valid Parentheses](https://leetcode.com/problems/valid-parentheses/) | 48 | Given a string `s` containing only three types of characters: `'('`, `')'` and `'*'`, return `true` _if_ `s` _is **valid**_.
The following rules define a **valid** string:
* Any left parenthesis `'('` must have a corresponding right parenthesis `')'`.
* Any right parenthesis `')'` must have a corresponding left parenthesis `'('`.
* Left parenthesis `'('` must go before the corresponding right parenthesis `')'`.
* `'*'` could be treated as a single right parenthesis `')'` or a single left parenthesis `'('` or an empty string `" "`.
**Example 1:**
**Input:** s = "()"
**Output:** true
**Example 2:**
**Input:** s = "(\*)"
**Output:** true
**Example 3:**
**Input:** s = "(\*))"
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is `'('`, `')'` or `'*'`. | null |
678: Solution with step by step explanation | valid-parenthesis-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nInitialize two empty stacks, left_paren_stack and asterisk_stack, to keep track of indices of left parentheses and asterisks, respectively.\n\nIterate through each character s[i] in the string:\n\nIf s[i] is \'(\', append the index i to the left_paren_stack.\nIf s[i] is \'*\', append the index i to the asterisk_stack.\nIf s[i] is \')\', check if there is a left parenthesis in the left_paren_stack. If there is, pop it. Otherwise, check if there is an asterisk in the asterisk_stack. If there is, pop it. If there is neither a left parenthesis nor an asterisk to match the right parenthesis, return False.\nIterate through the remaining elements in the left_paren_stack and asterisk_stack:\n\nIf the index of the left parenthesis is greater than the index of the asterisk, return False.\nPop the top elements from both stacks.\nIf there are no more left parentheses to match the asterisks, return True. Otherwise, return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkValidString(self, s: str) -> bool:\n # Initialize two stacks to keep track of indices of left parentheses and asterisks\n left_paren_stack, asterisk_stack = [], []\n \n # Iterate through each character in the string\n for i in range(len(s)):\n if s[i] == \'(\':\n # Add the index of the left parenthesis to the left_paren_stack\n left_paren_stack.append(i)\n elif s[i] == \'*\':\n # Add the index of the asterisk to the asterisk_stack\n asterisk_stack.append(i)\n else: # s[i] == \')\'\n # If there is a left parenthesis in the left_paren_stack, pop it\n if left_paren_stack:\n left_paren_stack.pop()\n # Otherwise, if there is an asterisk in the asterisk_stack, pop it\n elif asterisk_stack:\n asterisk_stack.pop()\n # If there is neither a left parenthesis nor an asterisk to match the right parenthesis, the string is invalid\n else:\n return False\n \n # Iterate through the remaining elements in the left_paren_stack and asterisk_stack\n while left_paren_stack and asterisk_stack:\n # If the index of the left parenthesis is greater than the index of the asterisk, the string is invalid\n if left_paren_stack[-1] > asterisk_stack[-1]:\n return False\n left_paren_stack.pop()\n asterisk_stack.pop()\n \n # If there are no more left parentheses to match the asterisks, the string is valid\n return not left_paren_stack\n\n``` | 9 | Given a string `s` containing only three types of characters: `'('`, `')'` and `'*'`, return `true` _if_ `s` _is **valid**_.
The following rules define a **valid** string:
* Any left parenthesis `'('` must have a corresponding right parenthesis `')'`.
* Any right parenthesis `')'` must have a corresponding left parenthesis `'('`.
* Left parenthesis `'('` must go before the corresponding right parenthesis `')'`.
* `'*'` could be treated as a single right parenthesis `')'` or a single left parenthesis `'('` or an empty string `" "`.
**Example 1:**
**Input:** s = "()"
**Output:** true
**Example 2:**
**Input:** s = "(\*)"
**Output:** true
**Example 3:**
**Input:** s = "(\*))"
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is `'('`, `')'` or `'*'`. | null |
Python Time O(n) Space O(1) Greedy Solution with Detailed Explanation and some proof | valid-parenthesis-string | 0 | 1 | \nFirst, if we do not have asterisk\uFF0Cin order to be vaild\n* obs1: "(" should be more or equal to ")" when we check the string from left to right\n* obs2: At the end, there is no open "(" ( i.e. equal number of "(" and ")")\n\nFor example,\n* "(()))("-> False, index = 4, two "(" and three ")" then ")" at index 4 will never be canceled out\n* "(((())"-> False, at the end two unclosed "("\n\nThus, to solve the problem, we can just count the open "(" by \n* openleft = 0\n* meet "(", openleft += 1\n* meet ")", openleft -= 1 once openleft < 0 -> "(" is less than ")" return False\n* At the end, if openleft = 0 -> no open "(" and return True\n\nNow, let\'s consider the asterisk. It can be "(", ")" or "". Thus, there are more possibilities. The openleft can have different numbers by tunning the asterisk. Let the openleft be within [leftmin, leftmax] if go through the string left to right (now we do not consider the valid just count openleft range for each index)\n* if "(", leftmin, leftmax += 1\n* if ")", leftmin, leftmax -=1\n* if "asterisk", leftmin -=1 , leftmax += 1\n\n* obs3: Openleft can take any value within [leftmin, leftmax]. leftmin can make all "asterisk" to ")", leftmax can make all "asterisk" to "(", other numbers can just tune the "asterisk"\n\n\nHowever there some additional constrains to let the string to be vaild\n* obs4: According to obs1, openleft shold be greater or equal to 0 at each index. If leftmax < 0, there is no possible openleft. If leftmax >= 0, the range becomes [max(leftmin,0), leftmax]. Since openleft can not take any negative value at each index, we need to truncate the range to above 0\n* obs5: According to obs 2, at the end openleft should be 0, then the range should contain 0. Under obs4 constraint, here it is just leftmin =0\n\nHere is the code. We only use two constant space leftmin and leftmax, thus space O(1). We need to go through one loop of the string thus time 0(n).\n```\nclass Solution:\n def checkValidString(self, s: str) -> bool:\n leftmin = leftmax = 0\n for c in s:\n if c == "(":\n leftmax += 1\n leftmin += 1\n if c == ")":\n leftmax -= 1\n leftmin = max(0, leftmin-1)\n if c == "*":\n leftmax +=1\n leftmin = max(0, leftmin-1)\n if leftmax < 0:\n return False\n if leftmin == 0:\n return True\n``` | 19 | Given a string `s` containing only three types of characters: `'('`, `')'` and `'*'`, return `true` _if_ `s` _is **valid**_.
The following rules define a **valid** string:
* Any left parenthesis `'('` must have a corresponding right parenthesis `')'`.
* Any right parenthesis `')'` must have a corresponding left parenthesis `'('`.
* Left parenthesis `'('` must go before the corresponding right parenthesis `')'`.
* `'*'` could be treated as a single right parenthesis `')'` or a single left parenthesis `'('` or an empty string `" "`.
**Example 1:**
**Input:** s = "()"
**Output:** true
**Example 2:**
**Input:** s = "(\*)"
**Output:** true
**Example 3:**
**Input:** s = "(\*))"
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is `'('`, `')'` or `'*'`. | null |
Python 3 || 9 lines, dfs || T/M: 37% / 99% | 24-game | 0 | 1 | ```\ndiv = lambda x,y: reduce(truediv,(x,y)) if y else inf\nops = (add, sub, mul, div)\n\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n\n def dfs(c: list) -> bool:\n\n if len(c) <2 : return isclose(c[0], 24)\n \n for p in set(permutations(c)):\n for num in {reduce(op,p[:2]) for op in ops}:\n if dfs([num] + list(p[2:])): return True\n\n return False \n \n return dfs(cards)\n```\n[https://leetcode.com/problems/24-game/submissions/992130414/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(1) and space complexity is *O*(1). (The time and space will improve with fewer distinct digits in cards.) | 3 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
Python || Solver can optionally print *all* solutions | 24-game | 0 | 1 | # Intuition\nPick any two numbers apply any operation, and replace the two numbers with their result. We now have a smaller problem.\n\n# Code\n```\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n def compute(a,b,op):\n if op==0:\n return a+b\n if op==1:\n return a-b\n if op==2:\n return a*b\n return a/b\n\n def solve(nums: List[int]):\n nonlocal solCount\n n = len(nums)\n if n==1:\n if goal-e < nums[0] < goal+e:\n # print(sol)\n solCount += 1\n return\n # stop at one solution\n if solCount>0:\n return\n for i in range(n):\n for j in range(n):\n if i==j: continue\n for op in range(3 + (nums[j]!=0)):\n if i>j and op%2==0: continue\n x = compute(nums[i], nums[j], op)\n nums2 = [x]\n for k in range(n):\n if k!=i and k!=j:\n nums2.append(nums[k])\n # sol.append("%s = %s%s%s"%(x,nums[i],operator[op],nums[j]))\n solve(nums2)\n # sol.pop()\n\n e = 10**-5\n goal = 24\n operator = "+-*/"\n sol = []\n solCount = 0\n solve(cards)\n # print(solCount)\n return solCount>0\n\n``` | 1 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
Python - 80ms | 24-game | 0 | 1 | ```\nimport itertools as it\n\nclass Solution:\n def judgePoint24(self, nums: List[int]) -> bool:\n if len(nums) == 1:\n return round(nums[0], 4) == 24\n else:\n for (i, m), (j, n) in it.combinations(enumerate(nums), 2):\n new_nums = [x for t, x in enumerate(nums) if i != t != j]\n inter = {m+n, abs(m-n), n*m}\n if n != 0: inter.add(m/n)\n if m != 0: inter.add(n/m)\n \n if any(self.judgePoint24(new_nums + [x]) for x in inter):\n return True\n \n return False\n``` | 20 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
679: Solution with step by step explanation | 24-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a helper function called "generate" that takes in two float values "a" and "b" and returns a list of float values that represent all possible arithmetic combinations of "a" and "b".\n2. Define another helper function called "dfs" that takes in a list of float values "nums" and returns a boolean value.\n3. In the "dfs" function, check if the length of the input list is equal to 1. If it is, return True if the absolute difference between the first element in the list and 24.0 is less than 0.001, else return False.\n4. Iterate through all possible pairs of indices in the input list using two nested loops.\n5. For each pair of indices, call the "generate" function to get a list of all possible arithmetic combinations of the values at the two indices.\n6. For each value in the list generated in step 6, create a new list called "nextRound" that contains the value from step 6 and all the other values in the input list except the ones at the indices used in step 5.\n7. Recursively call the "dfs" function with the "nextRound" list as the input.\n8. If the recursive call in step 8 returns True, return True in the current call, else continue with the loop in step 5.\n9. If none of the recursive calls in step 8 returned True, return False after the loops in step 5 have completed.\n10. In the "judgePoint24" function, call the "dfs" function with the input list "nums" and return the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def judgePoint24(self, nums: List[int]) -> bool:\n def generate(a: float, b: float) -> List[float]:\n return [a * b,\n math.inf if b == 0 else a / b,\n math.inf if a == 0 else b / a,\n a + b, a - b, b - a]\n\n def dfs(nums: List[float]) -> bool:\n if len(nums) == 1:\n return abs(nums[0] - 24.0) < 0.001\n\n for i in range(len(nums)):\n for j in range(i + 1, len(nums)):\n for num in generate(nums[i], nums[j]):\n nextRound = [num]\n for k in range(len(nums)):\n if k == i or k == j:\n continue\n nextRound.append(nums[k])\n if dfs(nextRound):\n return True\n\n return False\n\n return dfs(nums)\n``` | 4 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
Python: DFS (Very fast) | 24-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom functools import lru_cache\nfrom itertools import permutations, product\nfrom math import isclose, inf\n\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n binary_ops = [\n lambda a, b: a + b,\n lambda a, b: a * b,\n lambda a, b: a - b,\n lambda a, b: a / b if b else inf\n ]\n\n @lru_cache(None)\n def dfs(c: Tuple[int]) -> List[float]:\n if len(c) == 1:\n return [c[0]]\n elif len(c) == 2:\n return [op(*c) for op in binary_ops]\n else:\n ret = []\n for i in range(1, len(c)):\n for a, b in product(dfs(c[:i]), dfs(c[i:])):\n ret.extend(dfs((a, b)))\n return ret\n\n for perm in set(permutations(cards)):\n if any([isclose(24, num) for num in dfs(perm)]):\n return True\n return False\n\n``` | 0 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
[Python3] 9 lines, DFS | runtime 94 ms; beats 46.15% | 24-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndiv = lambda x,y: reduce(truediv,(x,y)) if y else inf\nops = (add, sub, mul, div)\n\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n def dfs(c: list) -> bool:\n if len(c) <2 : return isclose(c[0], 24)\n \n for p in set(permutations(c)):\n for num in {reduce(op,p[:2]) for op in ops}:\n if dfs([num] + list(p[2:])): return True\n\n return False \n \n return dfs(cards)\n``` | 0 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
python solution | 24-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI don\'t know whether i over complicated the problem....\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef gcd(a, b):\n if a < b:\n a, b = b, a\n while b != 0:\n a, b = b, a % b\n return a \n\ndef lcm(a, b):\n return a * b // gcd(a, b)\n\nclass Num:\n def __init__(self, n, d):\n self.n = n\n self.d = d\n\n def __repr__(self):\n return f\'{self.n}/{self.d}\'\n\n def __add__(self, other):\n if isinstance(other, (int, float)):\n other = Num(other, 1)\n common_d = lcm(self.d, other.d)\n common_n = (common_d // self.d * self.n) + (common_d // other.d * other.n)\n common_gcd = gcd(common_d, common_n)\n return Num(common_n // common_gcd, common_d // common_gcd)\n\n def __radd__(self, other):\n return self + other\n\n def __sub__(self, other):\n if isinstance(other, (int, float)):\n other = Num(other, 1)\n common_d = lcm(self.d, other.d)\n common_n = (common_d // self.d * self.n) - (common_d // other.d * other.n)\n common_gcd = gcd(common_d, common_n)\n return Num(common_n // common_gcd, common_d // common_gcd)\n\n def __rsub__(self, other):\n return -(self - other)\n\n def __mul__(self, other):\n if isinstance(other, (int, float)):\n return Num(self.n * other, self.d)\n\n common_d = self.d * other.d\n common_n = self.n * other.n\n common_gcd = gcd(common_d, common_n)\n return Num(common_n // common_gcd, common_d // common_gcd)\n\n def __rmul__(self, other):\n return self * other \n\n\n def __truediv__(self, other):\n if isinstance(other, (int, float)):\n return Num(self.n / other, self.d)\n\n common_d = self.d * other.n\n common_n = self.n * other.d\n common_gcd = gcd(common_d, common_n)\n return Num(common_n // common_gcd, common_d // common_gcd)\n\n def __rtruediv__(self, other):\n a = self/other\n if a.n == 0:\n raise ZeroDivisionError("Divide by Zero")\n return Num(a.d, a.n)\n\n def __neg__(self):\n return Num(-self.n, self.d)\n\n def __eq__(self, other):\n if isinstance(other, int) or isinstance(other, float):\n return other == (self.n/self.d)\n if isinstance(other, Num):\n return (other.d * self.n) == (self.d * other.n)\n\n\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n ret = [False]\n def test_cards(cards, tmp):\n cards.append(tmp)\n dfs(cards)\n cards.pop()\n def dfs(cards):\n if len(cards) == 1:\n if cards[0] == 24:\n ret[0] = True\n return\n for idx in range(len(cards)):\n for idx2 in range(idx+1, len(cards)):\n new_cards = [cards[i] for i in range(len(cards)) if i not in (idx2, idx)]\n test_cards(new_cards, cards[idx]+cards[idx2])\n test_cards(new_cards, cards[idx]*cards[idx2])\n test_cards(new_cards, cards[idx]-cards[idx2])\n test_cards(new_cards, cards[idx2]-cards[idx])\n if cards[idx2] != 0:\n if isinstance(cards[idx], (int, float)):\n cards[idx] = Num(cards[idx], 1)\n test_cards(new_cards, cards[idx]/cards[idx2])\n if cards[idx] != 0:\n if isinstance(cards[idx2], (int, float)):\n cards[idx2] = Num(cards[idx2], 1)\n test_cards(new_cards, cards[idx2]/cards[idx])\n dfs(cards)\n return ret[0]\n\n\n \n``` | 0 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
Python 3 || Two Pointer Approach || Self-Understandable | valid-palindrome-ii | 0 | 1 | ```\nclass Solution:\n def validPalindrome(self, s: str) -> bool:\n p1=0\n p2=len(s)-1\n while p1<=p2:\n if s[p1]!=s[p2]:\n string1=s[:p1]+s[p1+1:]\n string2=s[:p2]+s[p2+1:]\n return string1==string1[::-1] or string2==string2[::-1]\n p1+=1\n p2-=1\n return True\n```\n\n***Do Upvote If you found my solution helpful :)*** | 115 | Given a string `s`, return `true` _if the_ `s` _can be palindrome after deleting **at most one** character from it_.
**Example 1:**
**Input:** s = "aba "
**Output:** true
**Example 2:**
**Input:** s = "abca "
**Output:** true
**Explanation:** You could delete the character 'c'.
**Example 3:**
**Input:** s = "abc "
**Output:** false
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Simple python Two-Pointer approach | valid-palindrome-ii | 0 | 1 | # Approach\nApply two pointer and increment the left pointer whenever the left value != right value\nRepeat the same by decrementing the right value.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validPalindrome(self, s: str) -> bool:\n c = 0\n p1 = 0\n n = len(s)\n p2 = n - 1\n while p1 < p2 and c <= 1:\n if s[p1] != s[p2]:\n c += 1\n else:\n p2 -= 1\n p1 += 1\n if c <= 1:\n return 1\n c = 0\n p1 = 0\n p2 = n - 1\n while p1 < p2 and c <= 1:\n if s[p1] != s[p2]:\n c += 1\n else:\n p1 += 1\n p2 -= 1\n return c <= 1\n\n``` | 2 | Given a string `s`, return `true` _if the_ `s` _can be palindrome after deleting **at most one** character from it_.
**Example 1:**
**Input:** s = "aba "
**Output:** true
**Example 2:**
**Input:** s = "abca "
**Output:** true
**Explanation:** You could delete the character 'c'.
**Example 3:**
**Input:** s = "abc "
**Output:** false
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Python Readable and Intuitive Solution (Generalizable to n deletes) | valid-palindrome-ii | 0 | 1 | Simply checking if character at left matches corresponding right until it doesn\'t. At that point we have a choice of either deleting the left or right character. If either returns Palindrome, we return true. To generalize this to more than one deletes, we can simply replace the flag "deleted" to be a counter initialized to how many characters we are allowed to delete and stop allowing for recursive calls when it reaches 0.\n\n```\ndef validPalindrome(self, s: str) -> bool:\n def verify(s, left, right, deleted):\n while left < right:\n if s[left] != s[right]:\n if deleted:\n return False\n else:\n return verify(s, left+1, right, True) or verify(s, left, right-1, True)\n else:\n left += 1\n right -= 1\n return True\n return verify(s, 0, len(s)-1, False)\n``` | 130 | Given a string `s`, return `true` _if the_ `s` _can be palindrome after deleting **at most one** character from it_.
**Example 1:**
**Input:** s = "aba "
**Output:** true
**Example 2:**
**Input:** s = "abca "
**Output:** true
**Explanation:** You could delete the character 'c'.
**Example 3:**
**Input:** s = "abc "
**Output:** false
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Easy python recursive solution, easy to understand | valid-palindrome-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n\n def ispalindrome(self,s,i,j,skip1):\n while(i<j):\n if s[i]==s[j]:\n i+=1\n j-=1\n elif s[i]!=s[j] and not skip1:\n return self.ispalindrome(s,i+1,j,skip1=True) or self.ispalindrome(s,i,j-1,skip1=True)\n else:\n return False\n return True\n\n def validPalindrome(self, s: str) -> bool:\n i=0\n j=len(s)-1\n skip1=False\n\n return self.ispalindrome(s,i,j,skip1)\n\n \n``` | 1 | Given a string `s`, return `true` _if the_ `s` _can be palindrome after deleting **at most one** character from it_.
**Example 1:**
**Input:** s = "aba "
**Output:** true
**Example 2:**
**Input:** s = "abca "
**Output:** true
**Explanation:** You could delete the character 'c'.
**Example 3:**
**Input:** s = "abc "
**Output:** false
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
PythonnohtyP Palindrome Solution | valid-palindrome-ii | 0 | 1 | ```\nclass Solution:\n # Classic 2 pointer solution\n # Start travelling from start and ends\n # The first mismatch gives us 2 options\n # We can either remove the first or the end character and the remaining string must be a plindrome\n # Else return False\n def validPalindrome(self, s: str) -> bool:\n l, r = 0, len(s) - 1\n while l < r:\n if s[l] == s[r]:\n l, r = l + 1, r - 1\n else:\n p1 = s[l + 1: r + 1]\n p2 = s[l: r]\n if p1 == p1[:: -1] or p2 == p2[:: -1]: return True\n else: return False\n return True\n``` | 1 | Given a string `s`, return `true` _if the_ `s` _can be palindrome after deleting **at most one** character from it_.
**Example 1:**
**Input:** s = "aba "
**Output:** true
**Example 2:**
**Input:** s = "abca "
**Output:** true
**Explanation:** You could delete the character 'c'.
**Example 3:**
**Input:** s = "abc "
**Output:** false
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Python 94.65% faster ||Simplest solution with explanation|| Beg to Adv|| Two Pointer | valid-palindrome-ii | 0 | 1 | ```python\nclass Solution:\n def validPalindrome(self, s: str) -> bool:\n left = 0 # pointer one\n right = len(s) - 1 # pointer two\n \n while left < right: # index should be less then right one, not even equal, as we dont need to compare same index\n if s[left] == s[right]: # if both the ends value are equal.\n left += 1 # if yes increase them both\n right -= 1\n else: # if not, we will check if it is after removing either right of left value\n return s[left:right] == s[left:right][::-1] or s[left+1:right+1] == s[left+1:right+1][::-1] # return true if either situation is True.\n \n return True # True as both ends values are same.\n```\n\nLemme explain this line too, to make it easy for you:-\n```\nreturn s[left:right] == s[left:right][::-1] or s[left+1:right+1] == s[left+1:right+1][::-1]\n```\nThe first part is \n> s[left:right] == s[left:right][::-1]\n> In this we are taking whole list, starting from start to the end. Though list slicing doesn`t consider last element, so automatically right value will be removed, then we`ll compare it with reverse of it.\n\nThe second part is \n>s[left+1:right+1] == s[left+1:right+1][::-1]\n>In this we are removing left most element.\n\n\nFound helpful, Do upvote !! | 31 | Given a string `s`, return `true` _if the_ `s` _can be palindrome after deleting **at most one** character from it_.
**Example 1:**
**Input:** s = "aba "
**Output:** true
**Example 2:**
**Input:** s = "abca "
**Output:** true
**Explanation:** You could delete the character 'c'.
**Example 3:**
**Input:** s = "abc "
**Output:** false
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
using stack | baseball-game | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n stack=[]\n for i in operations:\n if i ==\'D\':\n stack.append(2*stack[-1])\n elif i==\'C\':\n stack.pop()\n elif i==\'+\':\n stack.append(stack[-1]+stack[-2])\n else:\n stack.append(int(i))\n return sum(stack)\n``` | 1 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Easy python solution using stack | baseball-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n lst=[]\n for i in operations:\n if i=="C":\n lst.pop()\n elif i=="D":\n lst.append(lst[-1]*2)\n elif i=="+":\n sm=lst[-2]+lst[-1]\n lst.append(sm)\n else:\n lst.append(int(i))\n print(lst)\n return sum(lst)\n``` | 3 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
baseball-game | baseball-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def calPoints(self, o: List[str]) -> int:\n i = 0\n l = []\n p = []\n while i<len(o):\n if o[i]!= "C" and o[i]!= "D" and o[i]!= "+":\n l.append(int(o[i]))\n # print(l)\n elif o[i]=="C":\n l.remove(l[-1])\n # print(l)\n elif o[i] == "D":\n l.append(l[-1]*2)\n # print(l)\n elif o[i] == "+":\n l.append(l[-1] + l[-2])\n # print(l)\n i+=1\n return (sum(l))\n``` | 1 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Python Easy Solution | baseball-game | 0 | 1 | # Code\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n res=[]\n for i in operations:\n if i=="C":\n res.pop()\n elif i=="D":\n res.append(2*(res[len(res)-1]))\n elif i=="+":\n res.append(res[len(res)-1]+res[len(res)-2])\n else:\n res.append(int(i))\n return sum(res)\n``` | 1 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Easy python solution got 98%run time|| Using Stacks | baseball-game | 0 | 1 | # Code\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n lst=[]\n for i in operations:\n if i=="C":\n lst.pop()\n elif i=="D":\n lst.append(lst[-1]*2)\n elif i=="+":\n sm=lst[-2]+lst[-1]\n lst.append(sm)\n else:\n lst.append(int(i))\n print(lst)\n return sum(lst)\n``` | 4 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Stack Solution beats 98% | baseball-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n stack = []\n for operation in operations:\n if operation == \'+\':\n stack.append(stack[-1] + stack[-2])\n elif operation == \'D\':\n stack.append(stack[-1]*2)\n elif operation == \'C\':\n stack.pop(-1)\n else:\n stack.append(int(operation))\n return sum(stack)\n\n``` | 1 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Easy Python🐍 code!! | baseball-game | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n stack = []\n for i in range(len(operations)):\n if operations[i]=="D":\n stack.append(stack[-1]*2)\n elif operations[i]=="C":\n stack.pop(-1)\n elif operations[i]=="+":\n stack.append(stack[-1]+stack[-2])\n else:\n stack.append(int(operations[i]))\n print(stack)\n return sum(stack)\n\n\n\n``` | 1 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Solution | baseball-game | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int calPoints(vector<string>&o)\n {\n stack<int>s;\n for(int i=0;i<o.size();i++)\n {\n if(o[i]=="C")\n s.pop();\n else if(o[i]=="D")\n s.push(s.top()*2);\n else if(o[i]=="+")\n {\n int e1=s.top();\n s.pop();\n int e2=s.top();\n s.push(e1);\n s.push(e1+e2);\n }\n else\n s.push(stoi(o[i]));\n }\n int sum=0;\n while(!s.empty())\n {\n sum+=s.top();\n s.pop();\n }\n return sum;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n stack = []\n\n for c in operations:\n if c == "C":\n stack.pop()\n elif c == "D":\n stack.append(stack[-1] * 2)\n elif c == "+":\n stack.append(stack[-1] + stack[-2])\n else:\n stack.append(int(c))\n return sum(stack)\n```\n\n```Java []\nclass Solution {\n public int calPoints(String[] operations) {\n int sum=0;\n int[] arr = new int[operations.length];\n int count=0;\n\n for(int i=0;i<operations.length;i++){\n if(operations[i].equals("C")){\n arr[--count]=0;\n }\n else if(operations[i].equals("D")){\n arr[count] = 2 * arr[count-1];\n count++;\n }\n else if(operations[i].equals("+")){\n arr[count]= arr[count-1] + arr[count-2];\n count++;\n } else {\n arr[count] = Integer.parseInt(operations[i]);\n count++;\n } \n }\n for(int j=0;j<arr.length;j++){\n sum += arr[j];\n }\n return sum;\n }\n}\n```\n | 3 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Very Simple Python Solution | baseball-game | 0 | 1 | Time and Space Complexcity O(n)\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n ans=[]\n a=0\n for i in operations:\n if i=="C":\n a=ans.pop()\n elif i=="D":\n ans.append(2*ans[-1])\n elif i=="+":\n ans.append(ans[-1]+ans[-2])\n else:\n ans.append(int(i))\n return sum(ans)\n \n``` | 2 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Baseball Game | baseball-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def calPoints(self, operations: List[str]) -> int:\n res=[]\n for i in operations:\n if i==\'C\':\n res.pop()\n elif i==\'D\':\n res.append(int(res[-1])*2)\n elif i==\'+\':\n res.append(int(res[-1])+int(res[-2]))\n else:\n res.append(i)\n ans=0\n for i in res:\n ans+=int(i)\n return ans\n``` | 2 | You are keeping the scores for a baseball game with strange rules. At the beginning of the game, you start with an empty record.
You are given a list of strings `operations`, where `operations[i]` is the `ith` operation you must apply to the record and is one of the following:
* An integer `x`.
* Record a new score of `x`.
* `'+'`.
* Record a new score that is the sum of the previous two scores.
* `'D'`.
* Record a new score that is the double of the previous score.
* `'C'`.
* Invalidate the previous score, removing it from the record.
Return _the sum of all the scores on the record after applying all the operations_.
The test cases are generated such that the answer and all intermediate calculations fit in a **32-bit** integer and that all operations are valid.
**Example 1:**
**Input:** ops = \[ "5 ", "2 ", "C ", "D ", "+ "\]
**Output:** 30
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"2 " - Add 2 to the record, record is now \[5, 2\].
"C " - Invalidate and remove the previous score, record is now \[5\].
"D " - Add 2 \* 5 = 10 to the record, record is now \[5, 10\].
"+ " - Add 5 + 10 = 15 to the record, record is now \[5, 10, 15\].
The total sum is 5 + 10 + 15 = 30.
**Example 2:**
**Input:** ops = \[ "5 ", "-2 ", "4 ", "C ", "D ", "9 ", "+ ", "+ "\]
**Output:** 27
**Explanation:**
"5 " - Add 5 to the record, record is now \[5\].
"-2 " - Add -2 to the record, record is now \[5, -2\].
"4 " - Add 4 to the record, record is now \[5, -2, 4\].
"C " - Invalidate and remove the previous score, record is now \[5, -2\].
"D " - Add 2 \* -2 = -4 to the record, record is now \[5, -2, -4\].
"9 " - Add 9 to the record, record is now \[5, -2, -4, 9\].
"+ " - Add -4 + 9 = 5 to the record, record is now \[5, -2, -4, 9, 5\].
"+ " - Add 9 + 5 = 14 to the record, record is now \[5, -2, -4, 9, 5, 14\].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
**Example 3:**
**Input:** ops = \[ "1 ", "C "\]
**Output:** 0
**Explanation:**
"1 " - Add 1 to the record, record is now \[1\].
"C " - Invalidate and remove the previous score, record is now \[\].
Since the record is empty, the total sum is 0.
**Constraints:**
* `1 <= operations.length <= 1000`
* `operations[i]` is `"C "`, `"D "`, `"+ "`, or a string representing an integer in the range `[-3 * 104, 3 * 104]`.
* For operation `"+ "`, there will always be at least two previous scores on the record.
* For operations `"C "` and `"D "`, there will always be at least one previous score on the record. | null |
Simple intuition explained. | redundant-connection | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWith `n` edges and `n` vertices we are guaranteed to have a cycle. To find the redundant edge we can apply the "union-find" data structure. union-find is the most optimal data structure for combining disjoint graphs. We can keep unioning each edge till an edge\'s two vertices are in the same graph\u2014a redundant edge.\n\nFor each vertex, it has a parent and a rank. Rank measure its size, so it starts at 1. Parent is itself at the start. When we union two vertices due to an edge btwn them, we perform a find and a union:\n1. Find: we find their parents. If we apply path compression, this becomes O(1) time since we can just access their parent via an array.\n2. Union: we set the parent with a lower rank (if equal rank, order doesn\'t matter) to now point to the higher rank parent as its new parent. We also update rank with sum since the new parent just parented some new vertices.\n\nWhen we union an edge and detect that both vertices\' parents are equal, then that edge is a redundant edge. And, for some reason, this also happens to be the "last redundant edge" in the `n` edges we get as input (if you know why, please add in comments).\n\n# Complexity\n- Time complexity:`O(n)` union has O(1) time complexity and find has O(1) as well, due to path compression and storing rank, and we call union n times in worst case.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:`O(n)` we store parent and rank arrays, each n long\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n parent = [i for i in range(len(edges) + 1)]\n rank = [1] * (len(edges) + 1) # rank measure size of graph\n\n def find(v): # finds the parent of v\n p = parent[v]\n while p != parent[p]:\n parent[p] = parent[parent[p]] # path compression\n p = parent[p]\n return p\n\n def union(v1, v2):\n p1, p2 = find(v1), find(v2)\n\n if p1 == p2: return False\n \n # p1 should be the larger disjoint graph (e.g. tree)\n if rank[p1] < rank[p2]: p1, p2 = p2, p1\n\n rank[p1] += rank[p2]\n parent[p2] = p1\n\n return True\n \n # since we don\'t create the full graph, but rather union iteratively\n # the redundant connection will be the first and last in edges\n for a, b in edges:\n if not union(a, b):\n return (a, b)\n\n\n``` | 1 | In this problem, a tree is an **undirected graph** that is connected and has no cycles.
You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the graph.
Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[1,4\],\[1,5\]\]
**Output:** \[1,4\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ai < bi <= edges.length`
* `ai != bi`
* There are no repeated edges.
* The given graph is connected. | null |
SIMPLE PYTHON SOLUTION | redundant-connection | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n$$ Disjoint Set $$\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Disjoint:\n def __init__(self,n):\n self.rank=[0]*(n+1)\n self.parent=[i for i in range(n+1)]\n \n def findUpar(self,node):\n if node==self.parent[node]:\n return node\n self.parent[node]=self.findUpar(self.parent[node])\n return self.parent[node]\n\n def byRank(self,u,v):\n ulp_u=self.findUpar(u)\n ulp_v=self.findUpar(v)\n if ulp_u==ulp_v:\n return False\n if self.rank[ulp_u]>self.rank[ulp_v]:\n self.parent[ulp_v]=ulp_u\n elif self.rank[ulp_v]<self.rank[ulp_u]:\n self.parent[ulp_u]=ulp_v\n else:\n self.parent[ulp_v]=ulp_u\n self.rank[ulp_u]+=1\n return True\n\n\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n n=len(edges)\n disjoint=Disjoint(n)\n for x,y in edges:\n if disjoint.byRank(x,y)==False:\n lst=[x,y]\n return lst\n``` | 1 | In this problem, a tree is an **undirected graph** that is connected and has no cycles.
You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the graph.
Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[1,4\],\[1,5\]\]
**Output:** \[1,4\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ai < bi <= edges.length`
* `ai != bi`
* There are no repeated edges.
* The given graph is connected. | null |
Easy union-find solution in python🐍 | redundant-connection | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n parent = [i for i in range(len(edges)+1)]\n rank = [1]* (len(edges)+1)\n\n def find(n):\n temp = parent[n]\n while temp!=parent[temp]:\n temp=parent[temp]\n return temp\n \n def union(n1,n2):\n p1 , p2 = find(n1),find(n2)\n\n if p1 == p2:\n return False\n \n if rank[p1] > rank[p2]:\n parent[p2] = p1\n rank[p1]+=rank[p2]\n else: \n parent[p1] = p2\n rank[p2] += rank[p1]\n return True\n \n for i,j in edges:\n if not union(i,j):\n return [i,j]\n\n\n\n \n``` | 1 | In this problem, a tree is an **undirected graph** that is connected and has no cycles.
You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the graph.
Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[1,4\],\[1,5\]\]
**Output:** \[1,4\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ai < bi <= edges.length`
* `ai != bi`
* There are no repeated edges.
* The given graph is connected. | null |
Python short and clean solution. DSU (Disjoint-Set-Union | Union-Find) | redundant-connection | 0 | 1 | # Approach\n1. Initialize a Disjoint-Set-Union (`DSU`) data structure.\n2. Iterate through the `edges` in the graph.\n3. Check if the edge makes a cycle by checking if the two vertices of the edge are already `connected`. If they are connected then return that edge as it is the edge that causes a cycle in the tree.\n4. If they are not connected, use the `DSU.union` to connect the two vertices of the edge.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n = number of edges`\n\n# Code\n```Python\nclass Solution:\n def findRedundantConnection(self, edges: list[list[int]]) -> list[int]:\n dsu = DSU()\n for u, v in edges:\n if dsu.is_connected(u, v): return [u, v]\n dsu.union(u, v)\n \nclass DSU:\n T = Hashable\n\n def __init__(self, xs: Iterable[T] = tuple()) -> None:\n self.parents = {x: x for x in xs}\n self.sizes = {x: 1 for x in xs}\n \n def add(self, x: T) -> None:\n if x in self.parents: return\n self.parents[x] = x\n self.sizes[x] = 1\n \n def make_safe(func: Callable) -> Callable:\n """Decorator used to ensure input values are added to parents using in func"""\n def wrapper(self, *xs):\n for x in xs: self.add(x)\n return func(self, *xs)\n return wrapper\n \n @make_safe\n def union(self, u: T, v: T) -> None:\n ur, vr = self.find(u), self.find(v)\n short_t, long_t = (ur, vr) if self.sizes[ur] < self.sizes[vr] else (vr, ur)\n\n self.parents[short_t] = long_t\n self.sizes[long_t] += self.sizes[short_t]\n \n @make_safe\n def find(self, x: T) -> T:\n self.parents[x] = self.find(self.parents[x]) if self.parents[x] != x else x\n return self.parents[x]\n \n @make_safe\n def is_connected(self, u: T, v: T) -> bool:\n return self.find(u) == self.find(v)\n \n``` | 1 | In this problem, a tree is an **undirected graph** that is connected and has no cycles.
You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the graph.
Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[1,4\],\[1,5\]\]
**Output:** \[1,4\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ai < bi <= edges.length`
* `ai != bi`
* There are no repeated edges.
* The given graph is connected. | null |
Python3 | DFS | with clear explanation | redundant-connection | 0 | 1 | # Intuition\nRedundant edge will always be the one which is responsible for forming a cycle within graph. And we can be ensured that a cycle will be formed because number of edges >= number of nodes. \n\n\nLet\'s consider the input -\n[[1,2],[1,3],[2,3]]\n\nLet\'s form the graph - \n\n\n# Pseudo Code\n1. keep track of graph constructed so far\n2. for each pair of nodes (u,v) provided in input\n - check if path exists between u and v using dfs\n - if it exists it means that adding the current edge will create a cycle hence return (u,v) as answer\n - else add that to graph\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ because for each pair of nodes we run dfs.\n=> $$O(n)$$ during **for loop** and $$O(n)$$ during **dfs** \n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\ndef findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n # variable to keep track of graph constructed so far\n graph_so_far = collections.defaultdict(lambda: [])\n \n # dfs function to check if path exists between nodes u and v\n def path_exists(u, v):\n # we reached to v from u\n if u == v:\n return True\n\n # mark u as visited\n visited.add(u)\n\n # iterate through all the neighbors of u and if they are not visited call dfs on them\n for neighbor in graph_so_far[u]:\n if neighbor not in visited:\n if path_exists(neighbor, v):\n return True\n \n return False\n\n # iterate through all the pairs of edges\n for u, v in edges:\n # we make a fresh visited because we call dfs for every pair of edges\n visited = set()\n # if path exists between u and v return that\'s the answer\n if path_exists(u,v):\n return [u,v]\n else:\n # if path does not exist we add edges to graph\n graph_so_far[u].append(v)\n graph_so_far[v].append(u)\n\n return None\n``` | 10 | In this problem, a tree is an **undirected graph** that is connected and has no cycles.
You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the graph.
Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[1,4\],\[1,5\]\]
**Output:** \[1,4\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ai < bi <= edges.length`
* `ai != bi`
* There are no repeated edges.
* The given graph is connected. | null |
✅[Python] Simple and Clean, beats 88%✅ | redundant-connection | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n*This is an NFT*\n# Intuition\nThe problem asks us to find an edge in a graph that can be removed to make it a tree. A tree is an undirected graph that is connected and has no cycles. So, we need to find an edge that creates a cycle in the graph. One way to detect cycles in an undirected graph is to use the `Union-Find algorithm.`\n\n# Approach\n1. Initialize the `parent` array with each node being its own parent and the `rank` array with all elements set to 1.\n2. Define the `find` function that takes a node as input and returns its root parent using path compression.\n3. Define the `union` function that takes two nodes as input and merges their sets if they are not already in the same set. The function returns `False` if the two nodes are already in the same set (i.e., there is a cycle), otherwise it returns `True`.\n4. Iterate over each edge in the `edges` array and call the `union` function with the two nodes of the edge as input.\n5. If the `union` function returns `False`, return the current edge as it creates a cycle in the graph.\n\n# Complexity\n- Time complexity: $$O(n \\alpha(n))$$ where $$n$$ is the number of nodes in the graph and $$\\alpha(n)$$ is the inverse Ackermann function which grows very slowly and can be considered a constant for all practical purposes.\n- Space complexity: $$O(n)$$ where $$n$$ is the number of nodes in the graph.\n\n# Code\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n # Initialize the parent array with each node being its own parent\n # and the rank array with all elements set to 1\n parent = [i for i in range(len(edges)+1)]\n rank = [1]*(len(edges)+1)\n \n # Define the find function that takes a node as input\n # and returns its root parent using path compression\n def find(n):\n p = parent[n]\n while p != parent[p]:\n parent[p] = parent[parent[p]]\n p = parent[p]\n return p\n \n # Define the union function that takes two nodes as input\n # and merges their sets if they are not already in the same set\n # The function returns False if the two nodes are already in the same set (i.e., there is a cycle)\n # otherwise it returns True\n def union(n1,n2):\n p1,p2 = find(n1),find(n2)\n if p1==p2:\n return False\n if rank[p1]>rank[p2]:\n parent[p2]=p1\n rank[p1]+=rank[p2]\n else:\n parent[p1]=p2\n rank[p2]+=rank[p1]\n return True\n \n # Iterate over each edge in the edges array and call the union function with the two nodes of the edge as input\n for n1,n2 in edges:\n if not union(n1,n2):\n # If the union function returns False, return the current edge as it creates a cycle in the graph\n return [n1,n2]\n``` | 3 | In this problem, a tree is an **undirected graph** that is connected and has no cycles.
You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the graph.
Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[1,4\],\[1,5\]\]
**Output:** \[1,4\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ai < bi <= edges.length`
* `ai != bi`
* There are no repeated edges.
* The given graph is connected. | null |
Python - Union Find - Easy | redundant-connection | 0 | 1 | ```\nclass Solution(object):\n def findRedundantConnection(self, edges):\n self.parent = dict()\n \n for e in edges:\n \n f0 = self.find(e[0])\n f1 = self.find(e[1])\n if f0 == f1:\n return e\n \n self.parent[f0] = f1\n \n def find(self, x):\n if x not in self.parent:\n return x\n \n return self.find(self.parent[x])\n``` | 1 | In this problem, a tree is an **undirected graph** that is connected and has no cycles.
You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the graph.
Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[1,4\],\[1,5\]\]
**Output:** \[1,4\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ai < bi <= edges.length`
* `ai != bi`
* There are no repeated edges.
* The given graph is connected. | null |
Solution | redundant-connection-ii | 1 | 1 | ```C++ []\nclass DSU{\n private:\n vector<int>parent,size;\n public:\n DSU(int n){\n parent.resize(n + 1);\n size.resize(n + 1, 1);\n for(int i = 0; i <= n; i++)\n parent[i] = i;\n }\n int findPar(int a){\n if(a == parent[a])\n return a;\n return parent[a] = findPar(parent[a]);\n }\n bool join(int a, int b){\n int par_a = findPar(a);\n int par_b = findPar(b);\n if(par_a == par_b)\n return false;\n parent[par_a] = par_b;\n size[par_b] += size[par_a];\n return true;\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n DSU dsu(n);\n vector<int>ans;\n\n int ans1 = -1 , ans2 = -1;\n vector<int>indegree(n+ 1, -1);\n for(int i = 0; i < n; i++){\n if(indegree[edges[i][1]] != -1){\n ans1 = i;\n ans2 = indegree[edges[i][1]];\n }\n indegree[edges[i][1]] = i; \n }\n for(int i =0; i < n; i++){\n if(i != ans1 && !dsu.join(edges[i][0], edges[i][1])){\n if(ans2 != -1)\n return edges[ans2];\n return edges[i];\n }\n }\n return ans = edges[ans1];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:\n l = [*range(len(edges)+1)]\n def find(x):\n if l[x]!=x:\n l[x] = find(l[x])\n return l[x]\n def union(x1,x2):\n r1 = find(x1)\n r2 = find(x2)\n if r1!=r2:\n l[r2] = r1\n return False\n return True\n last = []\n p = {}\n can = []\n for u,v in edges:\n if v in p:\n can.append([p[v],v])\n can.append([u,v])\n else:\n p[v] = u\n if union(u,v): # hasSameRoot?\n last = [u,v]\n if not can:\n return last\n return can[0] if last else can[1]\n```\n\n```Java []\nclass Solution {\n public int[] findRedundantDirectedConnection(int[][] edges) {\n int n = edges.length;\n\n int[] parent = new int[n+1], ds = new int[n+1];\n Arrays.fill(parent ,-1);\n int first = -1, second = -1, last = -1;\n for(int i = 0; i < n; i++){\n int p = edges[i][0], c = edges[i][1];\n if(parent[c] != -1){\n first = parent[c];\n second = i;\n continue;\n }\n parent[c] = i;\n int p2 = find(ds, p);\n if(p2 == c)\n last = i;\n else ds[c] = p2;\n }\n if(last == -1) return edges[second];\n if(second == -1)return edges[last];\n return edges[first];\n }\n private int find(int[] ds, int p){\n return ds[p] == 0?p:(ds[p] = find(ds,ds[p]));\n }\n}\n```\n | 2 | In this problem, a rooted tree is a **directed** graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents.
The given input is a directed graph that started as a rooted tree with `n` nodes (with distinct values from `1` to `n`), with one additional directed edge added. The added edge has two different vertices chosen from `1` to `n`, and was not an edge that already existed.
The resulting graph is given as a 2D-array of `edges`. Each element of `edges` is a pair `[ui, vi]` that represents a **directed** edge connecting nodes `ui` and `vi`, where `ui` is a parent of child `vi`.
Return _an edge that can be removed so that the resulting graph is a rooted tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the given 2D-array.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[4,1\],\[1,5\]\]
**Output:** \[4,1\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* `ui != vi` | null |
685: Solution with step by step explanation | redundant-connection-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nCreate a UnionFind object with a size equal to the number of edges in the input graph plus one.\n\nCreate a parent list of size n+1, initialized to all zeros.\n\nInitialize two variables candidate1 and candidate2 to None.\n\nLoop through the edges in the input list, and for each edge (u, v), if the parent[v] is not zero, then we have found a node with two parents. In this case, set candidate1 to the first parent of v (i.e. parent[v]) and candidate2 to the current edge (i.e. [u, v]). Break out of the loop.\n\nLoop through the edges in the input list again, and for each edge (u, v), if it is equal to candidate2, skip to the next iteration. Otherwise, call the union() method of the UnionFind object with u and v as arguments. If the union() method returns False, then we have found a cycle in the graph, and we can return candidate1 if it is not None, otherwise we return the current edge (i.e. [u, v]).\n\nIf we have not found a cycle by the end of the loop, then the graph must be a tree with a node with two parents. In this case, we can return candidate2.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n))\n self.rank = [0] * n\n\n def find(self, u: int) -> int:\n if self.parent[u] != u:\n self.parent[u] = self.find(self.parent[u])\n return self.parent[u]\n\n def union(self, u: int, v: int) -> bool:\n pu, pv = self.find(u), self.find(v)\n if pu == pv:\n return False\n if self.rank[pu] < self.rank[pv]:\n self.parent[pu] = pv\n elif self.rank[pv] < self.rank[pu]:\n self.parent[pv] = pu\n else:\n self.parent[pu] = pv\n self.rank[pv] += 1\n return True\n\n\nclass Solution:\n def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:\n uf = UnionFind(len(edges) + 1)\n parent = [0] * (len(edges) + 1)\n candidate1 = candidate2 = None\n \n for u, v in edges:\n if parent[v]:\n candidate1 = [parent[v], v]\n candidate2 = [u, v]\n break\n parent[v] = u\n\n for u, v in edges:\n if [u, v] == candidate2:\n continue\n if not uf.union(u, v):\n return candidate1 if candidate1 else [u, v]\n\n return candidate2\n\n``` | 4 | In this problem, a rooted tree is a **directed** graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents.
The given input is a directed graph that started as a rooted tree with `n` nodes (with distinct values from `1` to `n`), with one additional directed edge added. The added edge has two different vertices chosen from `1` to `n`, and was not an edge that already existed.
The resulting graph is given as a 2D-array of `edges`. Each element of `edges` is a pair `[ui, vi]` that represents a **directed** edge connecting nodes `ui` and `vi`, where `ui` is a parent of child `vi`.
Return _an edge that can be removed so that the resulting graph is a rooted tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the given 2D-array.
**Example 1:**
**Input:** edges = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** \[2,3\]
**Example 2:**
**Input:** edges = \[\[1,2\],\[2,3\],\[3,4\],\[4,1\],\[1,5\]\]
**Output:** \[4,1\]
**Constraints:**
* `n == edges.length`
* `3 <= n <= 1000`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* `ui != vi` | null |
Solution | repeated-string-match | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void filllps(vector<int> &lps,string B){\n lps[0] = 0;\n int len = 0;\n\n for(int i=1; i<B.size();){\n if(B[i]==B[len]) {\n len++;\n lps[i++] = len; \n }\n else {\n if(len == 0) lps[i++] = len;\n else len = lps[len-1];\n }\n }\n }\n int repeatedStringMatch(string A, string B) {\n int a = A.size(), b = B.size();\n vector<int>lps(b,0);\n filllps(lps,B);\n\n for(int i=0,j=0;i<a;){\n if(B[j]==A[(i+j) % a]) j++;\n if(j==b){\n if((i+j) % a) return (i+j) / a+1;\n else return (i+j) / a;\n }\n else if(i<a && B[j]!=A[(i+j) % a]) {\n if(j!=0){\n i += (j-lps[j-1]);\n j = lps[j-1];\n }\n else i++;\n }\n }\n return -1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def repeatedStringMatch(self, a: str, b: str) -> int:\n for i in range(len(b)//len(a), len(b)//len(a)+3):\n if b in a*(i):\n return i\n return -1\n```\n\n```Java []\nclass Solution {\n public int repeatedStringMatch(String a, String b) {\n boolean[] bucket = new boolean[26];\n for (char c : a.toCharArray()) bucket[c - \'a\'] = true;\n for (char c : b.toCharArray()) \n if (!bucket[c - \'a\']) return -1;\n \n int cnt = b.length() / a.length();\n\n StringBuilder sb = new StringBuilder(a.repeat(cnt));\n\n for (int i = 0;i < 3;i++) {\n if (sb.indexOf(b) >= 0) return cnt + i;\n sb.append(a);\n }\n return -1;\n }\n}\n```\n | 2 | Given two strings `a` and `b`, return _the minimum number of times you should repeat string_ `a` _so that string_ `b` _is a substring of it_. If it is impossible for `b` to be a substring of `a` after repeating it, return `-1`.
**Notice:** string `"abc "` repeated 0 times is `" "`, repeated 1 time is `"abc "` and repeated 2 times is `"abcabc "`.
**Example 1:**
**Input:** a = "abcd ", b = "cdabcdab "
**Output:** 3
**Explanation:** We return 3 because by repeating a three times "ab**cdabcdab**cd ", b is a substring of it.
**Example 2:**
**Input:** a = "a ", b = "aa "
**Output:** 2
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist of lowercase English letters. | null |
686: Solution with step by step explanation | repeated-string-match | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nCompute the number of times a needs to be repeated to have a string with length at least as long as b.\nCheck if b is a substring of the repeated a string of length n. If yes, return n.\nIf b is not a substring of a repeated n times, check if it is a substring of a repeated n+1 times. If yes, return n+1.\nIf b is not a substring of either a repeated n times or a repeated n+1 times, return -1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def repeatedStringMatch(self, a: str, b: str) -> int:\n n, m = divmod(len(b), len(a))\n if m:\n n += 1\n if b in a * n:\n return n\n elif b in a * (n+1):\n return n+1\n else:\n return -1\n\n``` | 4 | Given two strings `a` and `b`, return _the minimum number of times you should repeat string_ `a` _so that string_ `b` _is a substring of it_. If it is impossible for `b` to be a substring of `a` after repeating it, return `-1`.
**Notice:** string `"abc "` repeated 0 times is `" "`, repeated 1 time is `"abc "` and repeated 2 times is `"abcabc "`.
**Example 1:**
**Input:** a = "abcd ", b = "cdabcdab "
**Output:** 3
**Explanation:** We return 3 because by repeating a three times "ab**cdabcdab**cd ", b is a substring of it.
**Example 2:**
**Input:** a = "a ", b = "aa "
**Output:** 2
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist of lowercase English letters. | null |
Python || Easy || 96.76% Faster || O(n) Solution | repeated-string-match | 0 | 1 | ```\nclass Solution:\n def repeatedStringMatch(self, a: str, b: str) -> int:\n if b in a:\n return 1\n c,n=1,len(b)\n t=a\n while b!=t and len(t)<=n:\n c+=1\n t=a*c\n if b in t:\n return c\n if b in a*(c+1):\n return c+1\n return -1\n```\n\n**Upvote if you like the solution or ask if there is any query** | 2 | Given two strings `a` and `b`, return _the minimum number of times you should repeat string_ `a` _so that string_ `b` _is a substring of it_. If it is impossible for `b` to be a substring of `a` after repeating it, return `-1`.
**Notice:** string `"abc "` repeated 0 times is `" "`, repeated 1 time is `"abc "` and repeated 2 times is `"abcabc "`.
**Example 1:**
**Input:** a = "abcd ", b = "cdabcdab "
**Output:** 3
**Explanation:** We return 3 because by repeating a three times "ab**cdabcdab**cd ", b is a substring of it.
**Example 2:**
**Input:** a = "a ", b = "aa "
**Output:** 2
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist of lowercase English letters. | null |
[Python3] Knuth Morris Pratt Algorithm - O(|a| + |b|) time, O(|b|) space | repeated-string-match | 0 | 1 | View the \'a\' string as a circular object. In the normal KMP algorithm, the string \'a\' will have an end. But in this case \'a\' is circular, how do you know when to stop searching for a match? Well, you know if there exists a match, b[0] must match with one of the characters in the first copy of \'a\' (otherwise you have a useless copy of \'a\' at the beginning for no reason). The maximum number of times you must repeat \'a\' is in the case where b[0] matches with the last character of \'a\'. So you can stop searching when you\'ve hopped around |a| + |b| times.\n```\nclass Solution:\n def repeatedStringMatch(self, a: str, b: str) -> int:\n \n def kmp_failure(pattern):\n # kmp failure function\n m = len(pattern)\n f = [0] * m\n i = 1\n j = 0\n while i < m:\n if pattern[j] == pattern[i]:\n f[i] = j+1\n i += 1\n j += 1\n elif j > 0:\n j = f[j-1]\n else:\n f[i] = 0\n i += 1\n return f\n \n f = kmp_failure(b)\n n = len(a)\n m = len(b)\n i = 0\n j = 0\n while i < n + m: # worst case, start of b begins at end of a\n if b[j] == a[i%n]:\n if j == m-1:\n return math.ceil((i+1) / n)\n i += 1\n j += 1\n elif j > 0:\n j = f[j-1]\n else:\n i += 1\n return -1\n``` | 2 | Given two strings `a` and `b`, return _the minimum number of times you should repeat string_ `a` _so that string_ `b` _is a substring of it_. If it is impossible for `b` to be a substring of `a` after repeating it, return `-1`.
**Notice:** string `"abc "` repeated 0 times is `" "`, repeated 1 time is `"abc "` and repeated 2 times is `"abcabc "`.
**Example 1:**
**Input:** a = "abcd ", b = "cdabcdab "
**Output:** 3
**Explanation:** We return 3 because by repeating a three times "ab**cdabcdab**cd ", b is a substring of it.
**Example 2:**
**Input:** a = "a ", b = "aa "
**Output:** 2
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist of lowercase English letters. | null |
Simple C++ & Python solution with explanation | longest-univalue-path | 0 | 1 | This question is definitely not `easy` question. Its `medium` at best.\nWe will do post-order traversal to compute paths so that at each parent node there will be information about the paths from left and right child.\nWe will maintain following variables:\nglobal: `max_val` which will always have the max value.\nlocal: `cur_val` which will compute the value at the node.\nlocal: `ret_val` which will compute the value to be returned to parent.\n\nTo compute the solution of this question we have to consider 4 possible conditions at each level.\n1. if left_child.val == right_child.val == root.val\n```\n 4\n / \\\n4 4\n\t\t\\\n\t\t 4\n```\nIn this case, \n`cur_val = lval + rval + 2` (+ 2 because two paths are now added from right and left)\n`ret_val = max(lval, rval) + 1` (because we can only send one path to the parent. To get the longest path we will have to send the max(lval, rval)\n2. if only left_child.val == root.val\n```\n 4\n / \\\n4 5\n```\n`cur_val = ret_val = lval + 1`\n3. If only right_child.val == root.val\n```\n 5\n / \\\n4 5\n```\n`cur_val = ret_val = rval + 1`\n4. If both right_child and left_child don\'t match with root.val\n```\n 3\n / \\\n4 5\n```\n`cur_val = ret_val = 0` Since there no path between the child and parent node.\n\n\nC++\n```\nclass Solution {\npublic:\n int max_val {0};\n int longestUnivaluePath(TreeNode* root);\n int helper(TreeNode* root);\n \n};\n\nint Solution::longestUnivaluePath(TreeNode* root) {\n int cur_val {helper(root)};\n return this->max_val;\n}\n\nint Solution::helper(TreeNode* root){\n if (!root) return 0;\n \n int lval = helper(root->left);\n int rval = helper(root->right);\n int cur_val {0};\n int ret_val {0};\n if (root->left != NULL && root->right != NULL && \n (root->left->val == root->val) &&\n (root->right->val == root->val)){\n cur_val = lval + rval + 2;\n ret_val = std::max(lval, rval) + 1;\n }\n else if (root->left && (root->left->val == root->val)){\n cur_val = lval + 1;\n ret_val = cur_val;\n }\n else if (root->right && (root->right->val == root->val)){\n cur_val = rval + 1;\n ret_val = cur_val;\n }\n else{\n cur_val = 0;\n ret_val = cur_val;\n \n }\n \n this->max_val = std::max(this->max_val, cur_val);\n return ret_val;\n \n}\n```\n\nPython3:\n```\nclass Solution:\n def longestUnivaluePath(self, root: TreeNode) -> int:\n if not root: return 0\n self.res = 0\n self.postOrder(root)\n return self.res\n \n def postOrder(self, node):\n if not node: return 0\n l_val = r_val = b_val = 0\n l_val = self.postOrder(node.left)\n r_val = self.postOrder(node.right)\n \n if node.left and node.right and (node.val == node.left.val == node.right.val):\n self.res = max(self.res, l_val + r_val + 2)\n return (max(l_val, r_val) + 1)\n \n elif node.left and (node.val == node.left.val):\n l_val += 1\n self.res = max(self.res, l_val)\n return l_val\n elif node.right and (node.val == node.right.val):\n r_val += 1\n self.res = max(self.res, r_val)\n return r_val\n else:\n return 0\n | 30 | Given the `root` of a binary tree, return _the length of the longest path, where each node in the path has the same value_. This path may or may not pass through the root.
**The length of the path** between two nodes is represented by the number of edges between them.
**Example 1:**
**Input:** root = \[5,4,5,1,1,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 5).
**Example 2:**
**Input:** root = \[1,4,5,4,4,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 4).
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000`
* The depth of the tree will not exceed `1000`. | null |
Solution | longest-univalue-path | 1 | 1 | ```C++ []\nclass Solution {\n int maxi;\npublic:\n int longestUnivaluePath(TreeNode* root) {\n if(!root)\n return maxi;\n DFS(root, root->val);\n return maxi-1;\n }\nprivate:\n int DFS(TreeNode* root, int prev){\n if(!root)\n return 0;\n int l = DFS(root->left, root->val);\n int r = DFS(root->right, root->val);\n int tmp = max(l, r) + 1;\n maxi = max(maxi, l + r + 1);\n return (root->val == prev ? tmp : 0);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:\n A=[1]\n def b(n):\n if n.left is None and n.right is None: return 1\n crosslen = 1\n singret = 1\n if n.left is not None :\n leftres = b(n.left)\n if n.left.val==n.val:\n singret+=leftres\n crosslen += leftres\n if n.right is not None:\n rres = b(n.right)\n if n.right.val==n.val:\n singret=max(singret,rres+1)\n crosslen += rres\n if crosslen>A[0]:A[0]=crosslen\n return singret\n if root is None:return 0\n b(root)\n return A[0]-1\n```\n\n```Java []\nclass Solution {\n int len = 0;\n public int longestUnivaluePath(TreeNode root) {\n len = 0;\n helper(root,-1);\n \n if(len > 0){\n len = len - 1;\n }\n return len;\n }\n public int helper(TreeNode node,int val){\n if(node == null){\n return 0;\n }\n int left = helper(node.left,node.val);\n int right = helper(node.right,node.val);\n \n if(left + right + 1 > len){\n len = left+right+1;\n } \n if(val == node.val){\n return Math.max(left,right) + 1;\n }else{\n return 0;\n }\n } \n}\n```\n | 2 | Given the `root` of a binary tree, return _the length of the longest path, where each node in the path has the same value_. This path may or may not pass through the root.
**The length of the path** between two nodes is represented by the number of edges between them.
**Example 1:**
**Input:** root = \[5,4,5,1,1,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 5).
**Example 2:**
**Input:** root = \[1,4,5,4,4,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 4).
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000`
* The depth of the tree will not exceed `1000`. | null |
Recursion || Python3 | longest-univalue-path | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:\n max_len = 0 \n def recursive(prev, root):\n nonlocal max_len\n if not root:\n return 0\n left = recursive(root, root.left)\n right = recursive(root, root.right)\n max_len = max(max_len, right + left)\n if prev and root.val == prev.val:\n return 1 + max(left, right)\n return 0\n recursive(None, root)\n return max_len\n \n``` | 1 | Given the `root` of a binary tree, return _the length of the longest path, where each node in the path has the same value_. This path may or may not pass through the root.
**The length of the path** between two nodes is represented by the number of edges between them.
**Example 1:**
**Input:** root = \[5,4,5,1,1,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 5).
**Example 2:**
**Input:** root = \[1,4,5,4,4,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 4).
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000`
* The depth of the tree will not exceed `1000`. | null |
687: Solution with step by step explanation | longest-univalue-path | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nInside the function, define a variable max_len and initialize it to 0.\nDefine a nested function helper that takes node and parent_val as parameters.\nIf the node is None, return 0.\nRecursively call the helper function on the left and right child nodes, passing the current node\'s value as the parent_val.\nDefine left_len and right_len as the return values of the recursive calls.\nIf the node\'s value equals the value of its left child node, increment left_len by 1, else set left_len to 0.\nIf the node\'s value equals the value of its right child node, increment right_len by 1, else set right_len to 0.\nSet max_len to the maximum value between max_len and left_len + right_len.\nReturn 1 + the maximum value between left_len and right_len if the node\'s value equals the parent_val, else return 0.\nCall the helper function on the root node with parent_val set to None.\nReturn max_len.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestUnivaluePath(self, root: TreeNode) -> int:\n self.max_len = 0\n def helper(node: TreeNode, parent_val: int) -> int:\n if not node:\n return 0\n \n left_len = helper(node.left, node.val)\n right_len = helper(node.right, node.val)\n \n self.max_len = max(self.max_len, left_len + right_len)\n \n return 1 + max(left_len, right_len) if node.val == parent_val else 0\n \n helper(root, None)\n return self.max_len\n\n``` | 3 | Given the `root` of a binary tree, return _the length of the longest path, where each node in the path has the same value_. This path may or may not pass through the root.
**The length of the path** between two nodes is represented by the number of edges between them.
**Example 1:**
**Input:** root = \[5,4,5,1,1,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 5).
**Example 2:**
**Input:** root = \[1,4,5,4,4,null,5\]
**Output:** 2
**Explanation:** The shown image shows that the longest path of the same value (i.e. 4).
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000`
* The depth of the tree will not exceed `1000`. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript and Java | knight-probability-in-chessboard | 1 | 1 | # Intuition\nCreating two boards and keep current and next probability.\nThis Python solution beats 92%.\n\n\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/e3oSatmeAPo\n\n# Subscribe to my channel from here. I have 227 videos as of July 22th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other language might be different a bit.\n\n1. Define a list `moves` that contains all possible directions a knight can move to. Each element in `moves` is a tuple representing the relative coordinates for each direction.\n\n2. Create two 2D lists `cur_board` and `next_board`, both of size `n x n`, and initialize all elements to 0.0.\n\n3. Set the starting position `next_board[row][column]` to 1.0, as the knight is initially at this cell.\n\n4. Iterate `k` times, where `k` represents the number of moves the knight can take.\n\n5. For each iteration, update `cur_board` with the values from `next_board`, and reset `next_board` to a new 2D list of size `n x n` filled with zeros.\n\n6. For each cell `(r, c)` in the `cur_board` (representing the current state of the knight at each position), calculate the probability of reaching the neighboring cells by taking all possible moves (as specified in `moves`).\n\n7. If the current cell is not reachable (`cur_board[r][c] == 0.0`), continue to the next cell.\n\n8. If the neighboring cell `(next_row, next_col)` is within the chessboard (0 <= next_row < n and 0 <= next_col < n), update the probability of reaching that cell in `next_board` by adding the probability from the current cell divided by 8.0. This is because there are 8 possible moves the knight can take from the current cell.\n\n9. Repeat steps 6-8 for all cells in the `cur_board`, updating the `next_board` with the new probabilities.\n\n10. After `k` iterations, the `next_board` will contain the probabilities of the knight being at each cell on the chessboard after `k` moves.\n\n11. Calculate the total probability of the knight being on the chessboard by summing up all the probabilities in `next_board`.\n\n12. Return the total probability as the final result.\n\nThe code uses dynamic programming to calculate the probabilities efficiently and stores the intermediate results in `cur_board` and `next_board` for each iteration to avoid redundant calculations.\n\n# Complexity\nThis is based on Python. Other language might be different a bit.\n\n- Time complexity: O(k * n^2)\nThe outer loop runs k times, and the two nested loops run n^2 times each\n\n- Space complexity: O(n^2)\nTwo 2D arrays, cur_board and next_board, are created with dimensions n x n, each occupying n^2 space.\n\nk represents the number of moves the knight can take, and n is the size of the chessboard. \n\n```python []\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n moves = [(-2, -1), (-2, 1), (-1, -2), (-1, 2), (1, -2), (1, 2), (2, -1), (2, 1)]\n\n cur_board = [[0.0] * n for _ in range(n)]\n next_board = [[0.0] * n for _ in range(n)]\n next_board[row][column] = 1.0\n\n for _ in range(k):\n cur_board, next_board = next_board, [[0.0] * n for _ in range(n)]\n\n for r in range(n):\n for c in range(n):\n if cur_board[r][c] == 0.0:\n continue\n \n for dr, dc in moves:\n next_row, next_col = r + dr, c + dc\n\n if 0 <= next_row < n and 0 <= next_col < n:\n next_board[next_row][next_col] += cur_board[r][c] / 8.0\n \n total = 0.0\n for r in range(n):\n for c in range(n):\n total += next_board[r][c]\n \n return total\n```\n``` javascript []\n/**\n * @param {number} n\n * @param {number} k\n * @param {number} row\n * @param {number} column\n * @return {number}\n */\nvar knightProbability = function(n, k, row, column) {\n const moves = [[-2, -1], [-2, 1], [-1, -2], [-1, 2], [1, -2], [1, 2], [2, -1], [2, 1]];\n\n let curBoard = Array.from({ length: n }, () => Array(n).fill(0.0));\n let nextBoard = Array.from({ length: n }, () => Array(n).fill(0.0));\n nextBoard[row][column] = 1.0;\n\n for (let i = 0; i < k; i++) {\n [curBoard, nextBoard] = [nextBoard, Array.from({ length: n }, () => Array(n).fill(0.0))];\n\n for (let r = 0; r < n; r++) {\n for (let c = 0; c < n; c++) {\n if (curBoard[r][c] === 0.0) {\n continue;\n }\n\n for (const [dr, dc] of moves) {\n const nextRow = r + dr;\n const nextCol = c + dc;\n\n if (nextRow >= 0 && nextRow < n && nextCol >= 0 && nextCol < n) {\n nextBoard[nextRow][nextCol] += curBoard[r][c] / 8.0;\n }\n }\n }\n }\n }\n\n let total = 0.0;\n for (let r = 0; r < n; r++) {\n for (let c = 0; c < n; c++) {\n total += nextBoard[r][c];\n }\n }\n\n return total; \n};\n```\n```java []\nclass Solution {\n\n public double knightProbability(int n, int k, int row, int column) {\n int[][] moves = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};\n\n double [][] curBoard;\n double [][] nextBoard = new double[n][n];\n nextBoard[row][column] = 1.0;\n \n for (int i = 0; i < k; i++) {\n curBoard = nextBoard;\n nextBoard = new double[n][n];\n \n for (int r = 0; r < n; r++) {\n for (int c = 0; c < n; c++) {\n if (curBoard[r][c] == 0.0)\n continue;\n \n for (int [] dir : moves) {\n int nextRow = r + dir[0];\n int nextCol = c + dir[1];\n \n if (nextRow >= 0 && nextRow < n && nextCol >= 0 && nextCol < n) {\n nextBoard[nextRow][nextCol] += curBoard[r][c] / 8.0;\n }\n }\n }\n }\n }\n \n double total = 0.0;\n for (int r = 0; r < n; r++)\n for (int c = 0; c < n; c++)\n total += nextBoard[r][c];\n \n return total;\n }\n}\n```\n | 8 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
EASY PYTHON SOLUTION USING DFS | knight-probability-in-chessboard | 0 | 1 | # Code\n```\nclass Solution:\n def dp(self,x,y,n,visited,k):\n if k<0:\n return 1\n if (x<0 or x>=n) or (y<0 or y>=n):\n return 0\n if (x,y,k) in visited:\n return visited[(x,y,k)]\n a=self.dp(x+2,y+1,n,visited,k-1)*1/8\n b=self.dp(x+2,y-1,n,visited,k-1)*1/8\n c=self.dp(x-2,y+1,n,visited,k-1)*1/8\n d=self.dp(x-2,y-1,n,visited,k-1)*1/8\n e=self.dp(x+1,y+2,n,visited,k-1)*1/8\n f=self.dp(x+1,y-2,n,visited,k-1)*1/8\n g=self.dp(x-1,y+2,n,visited,k-1)*1/8\n h=self.dp(x-1,y-2,n,visited,k-1)*1/8\n visited[(x,y,k)]=a+b+c+d+e+f+g+h\n return a+b+c+d+e+f+g+h\n \n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n return self.dp(row,column,n,{},k)\n\n``` | 4 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
🔥 [VIDEO] Conquer The Chess Knight Challenge with Python and Dynamic Programming! | knight-probability-in-chessboard | 1 | 1 | # Intuition\nWhen first approaching this problem, I thought of the knight\'s eight possible moves on a chessboard and how some of these moves can cause it to fall off the board. I recognized the probability aspect of the problem and the fact that each move the knight makes is independent of the others. This made me think about using dynamic programming to solve this problem as it involves computing the probabilities of independent events and has overlapping sub-problems, which are characteristics that dynamic programming excels at.\n\nhttps://youtu.be/tp5UqIarBGQ\n\n# Approach\nI used a dynamic programming approach to solve this problem. The idea is to use a 3D array to keep track of the probability of the knight being on each cell after a certain number of moves. The dp[i][j][k] cell in this array represents the probability of the knight being in cell (j, k) after i moves. For each cell, I calculate its probability by averaging the probabilities of the knight reaching that cell from each of its possible previous positions. The base case is that the knight is on the board (with a probability of 1) if it starts on the board. Finally, I sum up the probabilities in all cells after k moves to get the total probability of the knight remaining on the board.\n\n# Complexity\n- Time complexity: The time complexity of this solution is $$O(n^2 * k)$$ where n is the size of the board and k is the number of moves. This is because for each move, I iterate over all cells in the n by n board, and for each cell, I calculate its probability based on the probabilities of its previous positions.\n \n- Space complexity: The space complexity of this solution is $$O(n^2 * k)$$ due to the 3D dp array used to store the probabilities of the knight being on each cell after a certain number of moves.\n\n# Code\n``` Python []\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n moves = [(1, 2), (2, 1), (-1, 2), (2, -1), (-1, -2), (-2, -1), (1, -2), (-2, 1)] \n dp = [[0 for _ in range(n)] for _ in range(n)]\n dp_prev = [[0 for _ in range(n)] for _ in range(n)]\n dp_prev[row][column] = 1\n\n for step in range(k):\n for r in range(n):\n for c in range(n):\n dp[r][c] = 0\n for dr, dc in moves:\n prev_r, prev_c = r - dr, c - dc\n if 0 <= prev_r < n and 0 <= prev_c < n:\n dp[r][c] += dp_prev[prev_r][prev_c] / 8.0\n dp, dp_prev = dp_prev, dp \n\n total_probability = sum(sum(dp_prev[r][c] for c in range(n)) for r in range(n))\n return total_probability\n```\n``` JavaScript []\nvar knightProbability = function(n, k, r, c) {\n const moves = [[1,2], [2,1], [-1,2], [2,-1], [-1,-2], [-2,-1], [1,-2], [-2,1]];\n let dp = Array.from({length: n}, () => new Array(n).fill(0));\n let dpPrev = Array.from({length: n}, () => new Array(n).fill(0));\n dpPrev[r][c] = 1;\n\n for(let step = 0; step < k; step++) {\n for(let i = 0; i < n; i++) {\n for(let j = 0; j < n; j++) {\n dp[i][j] = 0;\n for(let [dr, dc] of moves) {\n let prevR = i - dr;\n let prevC = j - dc;\n if(prevR >= 0 && prevR < n && prevC >= 0 && prevC < n) {\n dp[i][j] += dpPrev[prevR][prevC] / 8.0;\n }\n }\n }\n }\n [dp, dpPrev] = [dpPrev, dp];\n }\n\n let totalProbability = 0;\n for(let i = 0; i < n; i++) {\n for(let j = 0; j < n; j++) {\n totalProbability += dpPrev[i][j];\n }\n }\n\n return totalProbability;\n};\n```\n``` C++ []\nclass Solution {\npublic:\n double knightProbability(int n, int k, int row, int column) {\n vector<vector<int>> moves = {{1, 2}, {2, 1}, {-1, 2}, {2, -1}, {-1, -2}, {-2, -1}, {1, -2}, {-2, 1}};\n vector<vector<double>> dp(n, vector<double>(n, 0));\n vector<vector<double>> dpPrev(n, vector<double>(n, 0));\n dpPrev[row][column] = 1;\n \n for (int step = 0; step < k; step++) {\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n dp[i][j] = 0;\n for (auto& move : moves) {\n int prevR = i - move[0];\n int prevC = j - move[1];\n if (prevR >= 0 && prevR < n && prevC >= 0 && prevC < n) {\n dp[i][j] += dpPrev[prevR][prevC] / 8.0;\n }\n }\n }\n }\n swap(dp, dpPrev);\n }\n \n double totalProbability = 0;\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n totalProbability += dpPrev[i][j];\n }\n }\n \n return totalProbability;\n }\n};\n```\n``` Java []\nclass Solution {\n public double knightProbability(int n, int k, int r, int c) {\n int[][] moves = {{1, 2}, {2, 1}, {-1, 2}, {2, -1}, {-1, -2}, {-2, -1}, {1, -2}, {-2, 1}};\n double[][] dp = new double[n][n];\n double[][] dpPrev = new double[n][n];\n dpPrev[r][c] = 1;\n \n for (int step = 0; step < k; step++) {\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n dp[i][j] = 0;\n for (int[] move : moves) {\n int prevR = i - move[0];\n int prevC = j - move[1];\n if (prevR >= 0 && prevR < n && prevC >= 0 && prevC < n) {\n dp[i][j] += dpPrev[prevR][prevC] / 8.0;\n }\n }\n }\n }\n double[][] temp = dp;\n dp = dpPrev;\n dpPrev = temp;\n }\n \n double totalProbability = 0;\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n totalProbability += dpPrev[i][j];\n }\n }\n \n return totalProbability;\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn knight_probability(n: i32, k: i32, r: i32, c: i32) -> f64 {\n let moves = [(1, 2), (2, 1), (-1, 2), (2, -1), (-1, -2), (-2, -1), (1, -2), (-2, 1)];\n let mut dp = vec![vec![0.0; n as usize]; n as usize];\n let mut dp_prev = vec![vec![0.0; n as usize]; n as usize];\n dp_prev[r as usize][c as usize] = 1.0;\n\n for _step in 0..k {\n for i in 0..n {\n for j in 0..n {\n dp[i as usize][j as usize] = 0.0;\n for &(dr, dc) in &moves {\n let prev_r = i - dr;\n let prev_c = j - dc;\n if prev_r >= 0 && prev_r < n && prev_c >= 0 && prev_c < n {\n dp[i as usize][j as usize] += dp_prev[prev_r as usize][prev_c as usize] / 8.0;\n }\n }\n }\n }\n std::mem::swap(&mut dp, &mut dp_prev);\n }\n\n let mut total_probability = 0.0;\n for i in 0..n {\n for j in 0..n {\n total_probability += dp_prev[i as usize][j as usize];\n }\n }\n total_probability\n }\n}\n``` | 2 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
Python3 Solution | knight-probability-in-chessboard | 0 | 1 | \n```\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n @lru_cache(None)\n def dp(cur_r,cur_c,k):\n if k==0:\n return 1\n\n else:\n ans=0\n for r,c in moves:\n now_r=cur_r+r\n now_c=cur_c+c\n if 0<=now_r<=n-1 and 0<=now_c<=n-1:\n ans+=dp(now_r,now_c,k-1)\n\n return ans\n\n if k==0:\n return 1\n\n moves=[[1,2],[2,1],[1,-2],[2,-1],[-1,2],[-2,1],[-1,-2],[-2,-1]]\n return dp(row,column,k)/8**k \n\n``` | 5 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
Python short and clean. Multiple solutions. Functional programming. | knight-probability-in-chessboard | 0 | 1 | # Approach 1:\n###### Top-Down, Recursive, Functional DP\nGiven a board `n * n`. Let `on_board_prob` be a function which returns the probability of knight to stay on the board after `k` steps, starting from row `i` and column `j`. (Exactly what the problem asks)\n\nIf `k > 0`, i.e some moves are left: Try out the `8` equivi-probable `moves` from `i, j` that are `on_board` and add `1/8 th` of the probabilities from each of them.\n\nIf `k == 0`, return `prob = 1 if (i, j) is on_board else 0`\n\nMake sure to memoize `on_board_prob` to exploit overlapping subproblems and optimal substructure of the problem.\n\nNote: The first 3 lines defining `on_board`, `moves`, `next_positions` are copy pasted in all solutions.\n\n# Complexity\n- Time complexity: $$O(k \\cdot n^2)$$\n\n- Space complexity: $$O(k \\cdot n^2)$$\n\n# Code\n```python\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n on_board = lambda i, j: 0 <= i < n and 0 <= j < n\n moves = ((1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1), (-2, 1), (-1, 2))\n next_positions = lambda i, j: ((i + di, j + dj) for di, dj in moves)\n\n @cache\n def on_board_prob(k: int, i: int, j: int) -> float:\n return sum(on_board_prob(k - 1, ni, nj) for ni, nj in next_positions(i, j) if on_board(ni, nj)) / 8 if k else on_board(i, j)\n \n return on_board_prob(k, row, column)\n\n\n```\n\n---\n\n# Approach 2:\n###### Bottom-Up, Imperative DP\nUse explicit `probs` 3-dimensional `k * n * n` DP array to replace `on_board_prob(k, i, j)` function above.\n\n# Complexity\n- Time complexity: $$O(k \\cdot n^2)$$\n\n- Space complexity: $$O(k \\cdot n^2)$$\n\n# Code\n```python\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n on_board = lambda i, j: 0 <= i < n and 0 <= j < n\n moves = ((1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1), (-2, 1), (-1, 2))\n next_positions = lambda i, j: ((i + di, j + dj) for di, dj in moves)\n\n probs = [[[1] * n for _ in range(n)] for _ in range(k + 1)]\n for k, i, j in product(range(1, k + 1), range(n), range(n)):\n probs[k][i][j] = sum(probs[k - 1][ni][nj] for ni, nj in next_positions(i, j) if on_board(ni, nj)) / 8\n \n return probs[k][row][column]\n\n\n```\n\n---\n\n# Approach 3:\n###### Bottom-Up, Imperative, Space optimized DP\nNotice, we only ever use `probs[k - 1][..][..]` to calculate `probs[k][..][..]`.\nReduce `probs` to 2-dimensional `n * n` DP array by keeping only the previous values of first dimension.\n\n# Complexity\n- Time complexity: $$O(k \\cdot n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\n# Code\n```python\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n on_board = lambda i, j: 0 <= i < n and 0 <= j < n\n moves = ((1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1), (-2, 1), (-1, 2))\n next_positions = lambda i, j: ((i + di, j + dj) for di, dj in moves)\n\n probs = [[1] * n for _ in range(n)]\n for k in range(1, k + 1):\n probs = [[sum(probs[ni][nj] for ni, nj in next_positions(i, j) if on_board(ni, nj)) / 8 for j in range(n)] for i in range(n)]\n \n return probs[row][column]\n\n\n```\n\n---\n\n# Approach 4:\n###### Bottom-Up, Declarative, Functional, Space optimized DP\nUse `functools.reduce` to eliminate imperative coding in the above solution.\n\nNote: At this point, the code is purely functional and can technically also be written as a 1-liner, albeit a very long one!\n\n# Complexity\n- Time complexity: $$O(k \\cdot n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\n# Code\n```python\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n on_board = lambda i, j: 0 <= i < n and 0 <= j < n\n moves = ((1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1), (-2, 1), (-1, 2))\n next_positions = lambda i, j: ((i + di, j + dj) for di, dj in moves)\n\n next_probs = lambda prob, k: [[sum(prob[ni][nj] for ni, nj in next_positions(i, j) if on_board(ni, nj)) / 8 for j in range(n)] for i in range(n)]\n probs = reduce(next_probs, range(1, k + 1), [[1] * n for _ in range(n)])\n return probs[row][column]\n\n\n``` | 1 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
10 lines Python3 | knight-probability-in-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse DFS and sum the probabilities of in each step.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse DFS and cache to accelerate.\n\n# Complexity\n- Time complexity: $$O(n^2k)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```=python3\nfrom functools import cache\n\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n moves = ((1, 2), (1, -2), (-1, 2), (-1, -2), (2, 1), (2, -1), (-2, 1), (-2, -1))\n\n @cache\n def helper(k, i, j):\n if i < 0 or i >= n or j < 0 or j >= n:\n return 0.0\n if k == 0:\n return 1.0\n return sum(helper(k - 1, i + _i, j + _j) for _i, _j in moves) / 8\n \n return helper(k, row, column)\n``` | 1 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
Python 3 || BFS in a linearised grid | Very efficient | knight-probability-in-chessboard | 0 | 1 | \n\n## Intuition\nWe use a linearised grid for fast access and low memory use.\nValue in the graph is probability to attend the case.\nWhen a knight move from a white case, it attends a black case. One only grid can be used. It\'s not possible to overwrite a probability in an inappropriate case.\n\n## Complexity\n- Time complexity:\n$O(k\u22C5n\xB2)$\n\n- Space complexity:\n$O(n\xB2)$\n\n## Code\n```\nclass Solution:\n\n def knightProbability(self, n, k, row, column):\n # We make a linearised grid\n lin_grid = []\n BOUNDARY = -1\n for i in range(n):\n lin_grid.extend([0] * n + [BOUNDARY] * 2)\n n += 2\n lin_grid.extend([BOUNDARY] * 2 * n)\n START = row * n + column\n lin_grid[START] = 1\n \n # Moves in this grid\n moves = (-n - 2, -n + 2, -2 * n - 1, -2 * n + 1, n - 2, n + 2, 2 * n - 1, 2 * n + 1)\n \n # BFS\n to_process = deque([START])\n for _ in range(k):\n for __ in range(len(to_process)):\n i = to_process.popleft()\n p = lin_grid[i] / 8\n lin_grid[i] = 0\n for m in moves:\n ni = i + m\n if lin_grid[ni] != BOUNDARY:\n # Add ni only once in the queue\n if lin_grid[ni] == 0:\n to_process.append(ni)\n lin_grid[ni] += p\n return sum(p for p in lin_grid if p > 0)\n\n\n``` | 1 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
Python | DFS | Easy to Understand | Optimal Solution | 688. Knight Probability in Chessboard | knight-probability-in-chessboard | 0 | 1 | # Python | DFS | Easy to Understand | Optimal Solution | Medium Problem | 688. Knight Probability in Chessboard\n```\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n if k == 0:\n return 1\n\n @cache\n def dfs(r: int, c: int, cur_moves: int) -> int:\n if r < 0 or r >= n or c < 0 or c >= n:\n return 0\n if cur_moves == k:\n return 1\n on_board = 0\n for rd, cd in [(-2, -1), (-2, 1), (-1, -2), (-1, 2), (2, -1), (2, 1), (1, -2), (1, 2)]:\n on_board += dfs(r + rd, c + cd, cur_moves + 1)\n return on_board\n \n on_board = dfs(row, column, 0)\n return on_board / pow(8, k)\n``` | 1 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
✅DP + Memoization || JAVA/C++/Python Beginner Friendly🔥🔥🔥 | knight-probability-in-chessboard | 1 | 1 | # Approach\nThe `knightProbability` function initializes a memoization array `memo`, and then calls the recursive function `dp`. The dp function calculates the probability of the knight remaining on the board after k moves from a given position. It considers all eight possible moves and recursively calls itself for each move with reduced k and updated position. The probabilities are stored in the memo array to avoid redundant computations. Finally, the function returns the probability of the knight remaining on the board after k moves, starting from the given position. The time complexity is O(k * n^2), and the space complexity is O(k * n^2) due to the memoization array.\nWhen we **return** the original code should be return `(possibleCellCounts/8)*(sum/possibleCellCounts)` then we simplify it to `sum/8`.\n\nExaample: `n = 3, k = 2, row = 0, column = 0`\n- for the first move the probability for the knight that remains on the board is `2/8`\n- for the second move we need to consider for those two cells([1,2], [2,1]) and for both of the cells th probability is `2/8`. So, (2/8 + 2/8)/8 => 1/16 = 0.06250\n```java []\npublic class Solution {\n private double[][][] memo;\n\n public double knightProbability(int n, int k, int row, int column) {\n this.memo = new double[k + 1][n][n];\n return dp(n, k, row, column);\n }\n\n private double dp(int n, int k, int row, int column) {\n if (k == 0) return 1.0;\n if (memo[k][row][column] != 0) return memo[k][row][column];\n\n double sum = 0;\n int[][] moves = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};\n for (int[] move : moves) {\n int r = row + move[0];\n int c = column + move[1];\n if (r >= 0 && r < n && c >= 0 && c < n) {\n sum += dp(n, k - 1, r, c);\n }\n }\n\n memo[k][row][column] = sum / 8;\n return sum / 8;\n }\n}\n\n```\n```python []\ndef knightProbability(n, k, row, column):\n memo = [[[0 for _ in range(n)] for _ in range(n)] for _ in range(k + 1)]\n return dp(n, k, row, column, memo)\n\ndef dp(n, k, row, column, memo):\n if k == 0:\n return 1.0\n if memo[k][row][column] != 0:\n return memo[k][row][column]\n \n sum_prob = 0\n moves = [(-2, -1), (-2, 1), (-1, -2), (-1, 2), (1, -2), (1, 2), (2, -1), (2, 1)]\n for dr, dc in moves:\n nr, nc = row + dr, column + dc\n if 0 <= nr < n and 0 <= nc < n:\n sum_prob += dp(n, k - 1, nr, nc, memo)\n\n memo[k][row][column] = sum_prob / 8\n return sum_prob / 8\n\n```\n```C++ []\nclass Solution {\npublic:\n double knightProbability(int n, int k, int row, int column) {\n vector<vector<vector<double>>> memo(k + 1, vector<vector<double>>(n, vector<double>(n, 0)));\n return dp(n, k, row, column, memo);\n }\n \n double dp(int n, int k, int row, int column, vector<vector<vector<double>>>& memo) {\n if (k == 0) {\n return 1.0;\n }\n if (memo[k][row][column] != 0) {\n return memo[k][row][column];\n }\n \n double sum_prob = 0;\n vector<pair<int, int>> moves = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};\n for (auto move : moves) {\n int nr = row + move.first;\n int nc = column + move.second;\n if (nr >= 0 && nr < n && nc >= 0 && nc < n) {\n sum_prob += dp(n, k - 1, nr, nc, memo);\n }\n }\n \n memo[k][row][column] = sum_prob / 8;\n return sum_prob / 8;\n }\n};\n\n```\n\n\n# Complexity\n- Time/Space complexity:\nO(k * n^2)\n\n# *Upvote would be appreciated!*\n\n\n``` | 1 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
[Python3] Two Different Techniques. Double The Fun. | knight-probability-in-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOne can solve this problem with either of these techniques.\n1. Dynamic Programming - DP[i][j] means the probability for a knight to stay on board with index (i, j). \n2. Graph with DFS - Construct an adjacency list of all indexes that a knight can move, and perform DFS to calculate the number of cells, finally divided such number by `8^k`. The reason is a knight have 8 paths to choose from, and we need to choose `k` times.\n\nBoth tenhniques require\nTC - $$O(n * n * k)$$\nSC - $$O(n * n)$$\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor DP Solution- \n1. For DP solution, we set a 2D array `dp` first with values `0`.\n2. `dp[row][column]` is the starting point, so the probability is `1`.\n3. Keep in mind that probability is `cumulative`, that is, the probability of a cell can be expressed as `probability of a cell = sum of probability of previous cells`.\n4. To do so, we need to initialize a new 2D array to keep track of currently calculated probability for this iteration.\n\nFor Graph Solution -\n1. Consider all cells connected to index `(row, column)` a graph, we can create an adjacency list.\n2. Perform DFS for all cells and calculate the number of reachable cells, the depth of the recursion call is `k`\n3. Divide that number by `8^k` since a knight have 8 paths to choose from, and we need to choose `k` times.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n * n * k)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n * n)$$\n\n# Code\n```\n# This is DP\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n directions = [\n (2, 1),\n (2, -1),\n (-2, 1),\n (-2, -1),\n (1, 2),\n (1, -2),\n (-1, 2),\n (-1, -2)\n ]\n\n # Dynamic Programming\n dp = [[0 for _ in range(n)] for _ in range(n)]\n dp[row][column] = 1\n\n for dk in range(k):\n # For each iteration, we need curr_dp_prob to keep track of currently calcuated probability\n curr_dp_prob = [[0 for j in range(n)] for i in range(n)]\n for i in range(n):\n for j in range(n):\n if dp[i][j] == 0:\n continue\n for x, y in directions:\n delta_x, delta_y = i + x, j + y\n if 0 <= delta_x < n and 0 <= delta_y < n:\n curr_dp_prob[delta_x][delta_y] += dp[i][j] / 8\n # After calculating current iteration, we update original dp table\n dp = curr_dp_prob\n return sum([sum(l) for l in dp])\n```\n\n# Code\n```\n# This is DFS\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n adj_list = defaultdict(list)\n directions = [\n (2, 1),\n (2, -1),\n (-2, 1),\n (-2, -1),\n (1, 2),\n (1, -2),\n (-1, 2),\n (-1, -2)\n ]\n # Create an adjaency list for reachable cells from each indexes\n for i in range(n):\n for j in range(n):\n for x, y in directions:\n delta_x, delta_y = i + x, j + y\n if 0 <= delta_x < n and 0 <= delta_y < n:\n adj_list[(i, j)].append((delta_x, delta_y))\n @cache\n def dfs(x, y, depth):\n nonlocal adj_list, k\n if depth == k:\n return 1\n res = 0\n for next_x, next_y in adj_list[(x, y)]:\n res += dfs(next_x, next_y, depth + 1)\n return res\n\n # Calculate all reachable cells from (row, column)\n total_num_of_reachable_cells = dfs(row, column, 0)\n return total_num_of_reachable_cells / 8 ** k\n```\n\n\n\n\n | 1 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
Very Simple DP Soultion | knight-probability-in-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe just needs to count the number times the knight will end up in board after all the moves and divide it by total possible moves.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe base condition would be we have to return 0 if it lands on the borad and we have to return 1 if the knight is in board after all moves.\n\ntotal moves = 8^k\n# Code\n```\nclass Solution:\n def knightProbability(self, n: int, k: int, row: int, column: int) -> float:\n\n all_dir = [(-2, 1), (-1, 2), (1,2), (2,1) , (2,-1), (1,-2), (-1, -2), (-2,-1)]\n\n cache = {}\n \n def dp(x, y, remain):\n\n if (x, y, remain) in cache:\n return cache[(x, y, remain)]\n\n if not (0 <= x < n and 0 <= y < n):\n return 0\n\n \n if remain == 0:\n return 1\n \n wins = 0\n\n for dx, dy in all_dir:\n nx , ny = x + dx, y + dy\n wins += dp(nx, ny , remain-1)\n \n \n cache[(x, y, remain)] = wins\n return cache[(x, y, remain)]\n \n tot_wins = dp(row, column, k)\n\n return tot_wins / (8**k)\n\n``` | 1 | On an `n x n` chessboard, a knight starts at the cell `(row, column)` and attempts to make exactly `k` moves. The rows and columns are **0-indexed**, so the top-left cell is `(0, 0)`, and the bottom-right cell is `(n - 1, n - 1)`.
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly `k` moves or has moved off the chessboard.
Return _the probability that the knight remains on the board after it has stopped moving_.
**Example 1:**
**Input:** n = 3, k = 2, row = 0, column = 0
**Output:** 0.06250
**Explanation:** There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.
**Example 2:**
**Input:** n = 1, k = 0, row = 0, column = 0
**Output:** 1.00000
**Constraints:**
* `1 <= n <= 25`
* `0 <= k <= 100`
* `0 <= row, column <= n - 1` | null |
689: Solution with step by step explanation | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Get the length of the input list nums.\n2. Create an array sums to store the sums of all possible subarrays of length k in nums. The array will have length n - k + 1.\n3. Loop through the indices i of sums, where i ranges from 0 to n - k. For each index i, calculate the sum of the subarray of length k starting at index i in nums, and store it in sums[i].\n4. Create two arrays left and right to store the starting index of the maximum sum subarray of length k to the left and right of each index i in nums. Both arrays will have length n - k + 1.\n5. Loop through the indices i of left and right, where i ranges from 0 to n - k. For each index i, if the sum of the subarray of length k starting at index i in nums is greater than the maximum sum subarray to its left (i.e., at index i-1), set left[i] to i. Otherwise, set left[i] to left[i-1]. Similarly, if the sum of the subarray of length k starting at index n - k - i in nums is greater than the maximum sum subarray to its right (i.e., at index n - k - i + 1), set right[n - k - i] to n - k - i. Otherwise, set right[n - k - i] to right[n - k - i + 1].\n6. Initialize max_sum to negative infinity and res to [0, k, 2*k], which are the starting indices of the three subarrays with maximum sum if no other subarrays are found.\n7. Loop through the indices i of sums, where i ranges from k to n - 2*k. For each index i, calculate the sum of the subarrays starting at left[i-k], i, and right[i+k], and store it in total_sum.\n8. If total_sum is greater than max_sum, update max_sum to total_sum and update res to [left[i-k], i, right[i+k]].\n9. Return res.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n n = len(nums)\n \n # Create an array to store the sums of all possible subarrays of length k in nums.\n sums = [sum(nums[i:i+k]) for i in range(n-k+1)]\n \n # Create two arrays to store the starting index of the maximum sum subarray of length k to the left and to the right of each index in nums.\n left = [0] * (n-k+1)\n right = [n-k] * (n-k+1)\n for i in range(1, n-k+1):\n if sums[i] > sums[left[i-1]]:\n left[i] = i\n else:\n left[i] = left[i-1]\n if sums[n-k-i] >= sums[right[n-k-i+1]]:\n right[n-k-i] = n-k-i\n else:\n right[n-k-i] = right[n-k-i+1]\n \n # Initialize the maximum sum and the starting indices of the three subarrays.\n max_sum = float(\'-inf\')\n res = [0, k, 2*k]\n \n # Iterate through the sums array from index k to n-2k and calculate the sum of three subarrays starting at i-k, i and i+k using the sums array and the left and right arrays.\n for i in range(k, n-2*k+1):\n left_sum = sums[left[i-k]]\n right_sum = sums[right[i+k]]\n mid_sum = sums[i]\n total_sum = left_sum + mid_sum + right_sum\n \n # If the sum of three subarrays is greater than the current maximum sum, update the maximum sum and the starting indices of the three subarrays.\n if total_sum > max_sum:\n max_sum = total_sum\n res = [left[i-k], i, right[i+k]]\n \n return res\n\n``` | 1 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
Standard Python Knapsack DP -- generalized max_sum_of_d_subarrays | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | key idea:\n- calculate all subarray sums efficiently, select d (or 3 in this case) with the largest sum such that they don\'t overlap\n- "calculate all subarray sums efficiently" should imply prefix sums\n- "select d elements such that X" should imply knapsack\n\n```python\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n\n p = [0] + list(accumulate(nums))\n a = [(u, u + k - 1, (p[u + k] - p[u])) for u in range(0, len(nums) - k + 1)]\n\n n, d = len(a), 3\n\n dp = [[-inf for _ in range(d + 1)] for _ in range(n + 1)]\n for i in range(n + 1): dp[i][0] = 0\n\n h = defaultdict(list)\n for i in range(1, n + 1):\n for dd in range(1, d + 1):\n dp[i][dd] = max(dp[i][dd], dp[i - 1][dd])\n pv = (dp[i - k][dd - 1] if i - k >= 0 else 0)\n if dp[i][dd] < a[i - 1][2] + pv:\n dp[i][dd] = a[i - 1][2] + pv\n h[dp[i][dd]] = h[dp[i - k][dd - 1]] + [a[i - 1][0]]\n\n return h[dp[n][dd]]\n```\n\n`d` is the number of subarrays to partition into\n`p` is a prefix sum array for constant time range sums\n`a` is a list of all possible subarrays with their sums (`O(n)`)\n\nThe DP component is standard for knapsack problems\n\nWe maintain a separate dictionary `h` to store the indices associated with solutions to subproblems | 2 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
Python 3 || 10 lines, prefix sum, zip || T/S: 100% / 98% | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | Here\'s the plan:\n\n- We use `acc`, a prefix-sum array, in lieu of a sliding window.\n\n- We iterate though an enumerated zip to determine the sums of three contiguous subarrays starting at index `i`. The three subarrays are demarcated by `a0, a1, a2, a3`.\n\n- We initialize and update `sm1`, `sm2`, `sm3` to keep track of the currently optimum subarrays as we iterate through `acc`.\n\n- We use`idx1, idx2, idx3`to store the indices of the current optimum triple of subarrays. We return idx3 after the loop completes.\n\n```\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums, k):\n \n sm1 = sm2 = sm3 = 0\n \n acc = list(accumulate(nums, initial = 0))\n\n for i, (a0,a1,a2,a3) in enumerate(zip(acc ,\n acc[k:] , \n acc[2*k:], \n acc[3*k:])):\n if a1 - a0 > sm1:\n sm1, idx1 = a1 - a0, i\n\n if a2 - a1 > sm2 - sm1:\n sm2, idx2 = sm1 + a2 - a1, (idx1, i+k)\n\n if a3 - a2 > sm3 - sm2:\n sm3, idx3 = sm2 + a3 - a2, (*idx2, i+2*k)\n\n return idx3\n```\n[https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/submissions/1048581491/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `len(nums)`. | 4 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
Python top down DP in various forms | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | If you\'re like me, you probably didn\'t easily understand the problem, or understand the greedy window solutions. A more intuitive approach is outlined below. Maybe this is one you might actually be able to remember in an interview.\n\n**Brute force**\nThis will TLE but it helps to see the brute force and how it might play out.\n\nOne thing you\'ll notice, if you do the brute force, is how many overlapping sub problems there are. This is a good place to start, because it can lead into the intuition for how DP might work. You try every index, and every non overlapping kth window offset from that window, and then every kth window offset from the offset window. You literally try every solution.\n\nTime complexity: n ^ 3\nspace: O(1) (we store almost nothing)\n\n```python\n maxS = float(\'-inf\')\n res = []\n\n\t\t# e1, e2, e3 are ending indices of first, second and third intervals.\n for e1 in range(k-1, N - 2*k):\n s1 = e1 - k + 1\n for e2 in range(e1+k, N - k):\n s2 = e2 - k + 1\n for e3 in range(e2+k, N):\n s3 = e3 - k + 1\n tsum = dp[e1] + dp[e2] + dp[e3] \n if tsum > maxS:\n maxS = tsum\n res = [s1, s2, s3]\n return res\n```\n\n**Top Down Without Memo**\n\nThe idea here is similar, but implemented in a recursive top down approach. Note that this will also TLE, but gives use a better understanding of how caching might be implemented to save overlapping sub problems.\n\nTime complexity: 2 ^ n\nSpace: O(n)\n\n```python\n def maxSumOfThreeSubarraysCustom(self, nums: List[int], k: int) -> List[int]:\n res = self.window_sum(nums, k, 0, 0)\n return res[1]\n\n def window_sum(self, nums, k, idx, used):\n # we can only have 3 windows at a time\n if used == 3:\n return 0, []\n\n # are we going to overflow over our nums array?\n if idx - (used * k) > (len(nums)):\n return 0, []\n\n take_curr_sum, take_curr_indices = self.window_sum(nums, k, idx + k, used + 1)\n take_curr_sum += sum(nums[idx:idx + k])\n\n skip_curr_sum, skip_curr_indices = self.window_sum(nums, k, idx + 1, used)\n\n if take_curr_sum >= skip_curr_sum:\n return take_curr_sum, ([idx] + take_curr_indices)\n else:\n return skip_curr_sum, skip_curr_indices\n```\n\n\n**Top down with Memo**\n\nIt\'s very slow, but with the memo solution this is close to a true O(n) sol. Note that this can be sped up using a prefix sum array, which will allow us to look up the sums of any interval between indices.\n\nTime: O(n ^ 2) due to the `sum(nums[idx:idx + k])` could be O(n) using prefix sum.\nSpace: O(n)\n\n```python\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n memo = {}\n res = self.window_sum(nums, k, 0, 0, memo)\n return res[1]\n\n def window_sum(self, nums, k, idx, used, memo):\n # we can only have 3 windows at a time\n if used == 3:\n return 0, []\n\n # are we going to overflow over our nums array?\n if idx - (used * k) > (len(nums)):\n return 0, []\n\n if (idx, used) in memo:\n return memo[(idx, used)]\n\n take_curr_sum, take_curr_indices = self.window_sum(nums, k, idx + k, used + 1, memo)\n take_curr_sum += sum(nums[idx:idx + k])\n\n skip_curr_sum, skip_curr_indices = self.window_sum(nums, k, idx + 1, used, memo)\n\n if take_curr_sum >= skip_curr_sum:\n memo[(idx, used)] = (take_curr_sum, ([idx] + take_curr_indices))\n return memo[(idx, used)]\n else:\n memo[(idx, used)] = (skip_curr_sum, skip_curr_indices)\n return memo[(idx, used)]\n```\n | 16 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
Solution | maximum-sum-of-3-non-overlapping-subarrays | 1 | 1 | ```C++ []\n#include<iostream>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {\n int n = nums.size()-k+1;\n int subArraySum[n];\n subArraySum[0] = 0;\n for (int i = 0; i < k; i++)\n subArraySum[0] += nums[i];\n \n for (int i = 1; i < n; i++)\n subArraySum[i] = subArraySum[i-1]-nums[i-1]+nums[i+k-1];\n\n int leftBest[n];\n int best = 0;\n for (int i = 0; i < n; i++){\n if(subArraySum[i] > subArraySum[best])\n best = i;\n leftBest[i] = best;\n }\n int rightBest[n];\n best = n-1;\n for (int i = n-1; i >= 0; i--){\n if(subArraySum[i] >= subArraySum[best])\n best = i;\n rightBest[i] = best;\n }\n vector<int> res = {0,k,2*k};\n best = subArraySum[0] + subArraySum[k] + subArraySum[k*2];\n\n for(int i = k; i <= (nums.size()-(2*k)); i++){\n int actual = subArraySum[leftBest[i-k]] + subArraySum[i] + subArraySum[rightBest[i+k]]; \n if (actual > best){\n best = actual;\n res[0] = leftBest[i-k];\n res[1] = i;\n res[2] = rightBest[i+k];\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n w1, w2, w3 = sum(nums[0:k]), sum(nums[k:2*k]), sum(nums[2*k:3*k])\n maxw1, maxw2, maxw3 = w1, w1 + w2, w1 + w2 + w3\n\n maxw1index, maxw2index, maxw3index = [0], [0, k], [0, k, 2*k]\n\n for i in range(1, len(nums) - 3*k + 1):\n w1 += nums[i+k-1] - nums[i-1]\n w2 += nums[i+2*k-1] - nums[i+k-1]\n w3 += nums[i+3*k-1] - nums[i+2*k-1]\n\n if w1 > maxw1:\n maxw1, maxw1index = w1, [i]\n\n if maxw1 + w2 > maxw2:\n maxw2, maxw2index = maxw1 + w2, maxw1index + [i+k]\n\n if maxw2 + w3 > maxw3:\n maxw3, maxw3index = maxw2 + w3, maxw2index + [i+2*k]\n\n return maxw3index\n```\n\n```Java []\nclass Solution {\n public int[] maxSumOfThreeSubarrays(int[] nums, int k) {\n \n int n = nums.length;\n int[] sum = new int[n + 1];\n for (int i = 0; i < n; ++i) sum[i + 1] = sum[i] + nums[i];\n int[] left = new int[n];\n int[] right = new int[n];\n int[] ans = new int[3];\n for (int i = k, tot = sum[k] - sum[0]; i < n; ++i) {\n if (sum[i + 1] - sum[i + 1 - k] > tot) {\n left[i] = i + 1 - k;\n tot = sum[i + 1] - sum[i + 1 - k];\n } else {\n left[i] = left[i - 1];\n }\n }\n right[n - k] = n - k;\n for (int i = n - k - 1, tot = sum[n] - sum[n - k]; i >= 0; --i) {\n if (sum[i + k] - sum[i] >= tot) {\n right[i] = i;\n tot = sum[i + k] - sum[i];\n } else {\n right[i] = right[i + 1];\n }\n }\n int best = 0;\n for (int i = k; i <= n - 2 * k; ++i) {\n int l = left[i - 1], r = right[i + k];\n int tot = (sum[i + k] - sum[i]) + (sum[l + k] - sum[l]) + (sum[r + k] - sum[r]);\n if (tot > best) {\n ans[0] = l; ans[1] = i; ans[2] = r;\n best = tot;\n }\n }\n return ans;\n }\n}\n```\n | 3 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
Generalized DP Solution - Maximum of N Non Overlapping Subarrays with length K | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(m*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nO(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n m,n = len(nums), 3\n dp = [[[0,0] for i in range(m)] for j in range(n+1)]\n\n prefix_sum = [0]*m\n curr_sum = 0\n\n for index,num in enumerate(nums):\n curr_sum += num\n prefix_sum[index] = curr_sum\n\n for i in range(1,n+1):\n for j in range(k-1,m):\n total = prefix_sum[j] - prefix_sum[j-k] + dp[i-1][j-k][0] if j - k >= 0 else prefix_sum[j]\n if total > dp[i][j-1][0]:\n dp[i][j] = [total, j-k+1]\n else:\n dp[i][j] = [dp[i][j-1][0], dp[i][j-1][1]]\n \n u,v,result = n,m,[]\n while u > 0:\n index = dp[u][v-1][1]\n result.append(index)\n u -= 1\n v = index\n\n return result[::-1]\n``` | 0 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
General DP Solution | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(n*k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(n*K)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n m, n = len(nums), 3\n dp = [[[0, -1] for _ in range(m)] for _ in range(n + 1)]\n prefix_sum = [0] * m\n curr_sum = 0\n\n for index, num in enumerate(nums):\n curr_sum += num\n prefix_sum[index] = curr_sum\n\n for i in range(1, n + 1):\n for j in range(k - 1, m):\n ai = prefix_sum[j] - prefix_sum[j - k] + dp[i - 1][j - k][0] if j - k >= 0 else prefix_sum[j]\n if ai > dp[i][j - 1][0]:\n dp[i][j] = [ai, j - k + 1]\n else:\n dp[i][j] = [dp[i][j-1][0], dp[i][j - 1][1]]\n\n third = dp[n][m-1][1]\n second = dp[n-1][third-1][1]\n first = dp[n-2][second-1][1]\n return [first, second, third]\n``` | 0 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
DP, O(n) here but generalizes to any k | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | # Intuition\nThis is a typical dynamic programming question: at every index `i`, we can either use the last k-sized array ending at `i` or skip it. Some additional tricks are that: \n- We store the locations of the 3 arrays in the dp table itself. \n- We use cumulative sums to precompute the sums of the subarrays.\n\n# Approach\nWe try to maximize the sum obtained up to index i (`dp[i]`) for up to 3 arrays of length k (i.e. `dp[i][1], dp[i][2], dp[i][3]`). \n\n# Complexity\n- Time complexity: $O(n)$ where $n$ is the length of the array\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$ for the additional cumulative sums table as well as the main dp table.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n s,cumsum=0,[0]\n for n in nums:\n s+=n\n cumsum.append(s)\n dp=[[(0,[]) for _ in range(4)] for _ in range(len(nums)+1)]\n for i in range(k,len(nums)+1):\n for arrs in range(1,4):\n skip = dp[i-1][arrs][0]\n use = dp[i-k][arrs-1][0]+cumsum[i]-cumsum[i-k] if i>=k else 0\n if skip>=use:\n dp[i][arrs]=(skip, dp[i-1][arrs][1])\n else:\n incl_i=dp[i-k][arrs-1][1].copy()\n incl_i.append(i-k)\n dp[i][arrs]=(use, incl_i)\n return dp[len(nums)][3][1]\n``` | 0 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
Time: O(n)O(n) Space: O(n)O(n) | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n ans = [-1] * 3\n subarrayCount = len(nums) - k + 1\n dp = [0] * subarrayCount\n summ = 0\n\n for i, num in enumerate(nums):\n summ += num\n if i >= k:\n summ -= nums[i - k]\n if i >= k - 1:\n dp[i - k + 1] = summ\n\n left = [0] * subarrayCount\n maxIndex = 0\n\n for i in range(subarrayCount):\n if dp[i] > dp[maxIndex]:\n maxIndex = i\n left[i] = maxIndex\n\n right = [0] * subarrayCount\n maxIndex = subarrayCount - 1\n\n for i in reversed(range(subarrayCount)):\n if dp[i] >= dp[maxIndex]:\n maxIndex = i\n right[i] = maxIndex\n\n for i in range(k, subarrayCount - k):\n if ans[0] == -1 or dp[left[i - k]] + dp[i] + dp[right[i + k]] > dp[ans[0]] + dp[ans[1]] + dp[ans[2]]:\n ans = [left[i - k], i, right[i + k]]\n\n return ans\n\n``` | 0 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
Sliding Windows and Lexicographic Indexing | Commented and Explained | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to keep track of all of the sliding window subarrays of size k in our array. So, we want to set up a list of windows in order index wise. We then want to track arrays going from left to right by sum and find the strictly best first instance when doing so, and record that index up to each index in a left hand array of subarray indices. We then do the same from right to left, this time tracking as good or better. The reason for this difference is to preserve the lexicographic ordering and allow for a definite gap between left and right to be formed. \n\nOnce we have done this, we can go over our windows, and get the index from left prior to here and index on right after here. This gives us left hand side indice, current indice and right hand side indice. The first time this occurs, we will record these in indices, which is our return value. After the first time, we will set a current indices array of these three indices at current, then compare the sum of the window sums at these indices with those we have stored prior in indices. If we have a strictly better winner, we should update. Otherwise, we should not as we want the first lexicographically better instance, as preserved by our comparison methodology described above. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nk is not very clear aobut what it represents, which is the max size of the given windows of subarrays in the array. Set a local variable max size to value of k, then init a list of window sums and a current sum as an empty list and 0 respectively. \n\nAfter that, enumerate nums and as you go \n- increment current sum by value here \n- if your index is now greater than max size, decrement current sum by the item at index - max size that has just dropped out of the sum \n- if your index is at least the size of the array needed (max size - 1) \n - append the current sum to your list of window sums \n\nSet W as the size of the list of your window sums \nleft_windows are window indices of windows from left to right of our list of window sums. They start as an array of 0s of size W. Similar is for right windows but from right to left and with same start of 0s of size W. \n\nGoing from left to right by index \n- if the window sum at current index is strictly greater than window sum at best left index so far, swap best left index so far with current index \n- set left windows at window index to best window index \n\nSimilar process on the right, but with greater than or equal to for comparison and going from right to left of window sums \n\nSet indices as None \n\nOur window indices range is going to be of at least max size and go to W - max size. This allows us to access windows that do not overlap. \nFor window index in range max_size to W - max_size \n- index_1 is left windows at window index - max size \n- index_3 is right windows at window index + max size \n- window index is index_2 \n- if indices is None, set indices to index_1, window_index, index_3 \n- otherwise \n - current indices is [index_1, window_index, index_3]\n - get sum of list of window sums for index in indices \n - get sum of list of window sums for index in current indices \n - if current sum is strictly greater than prior sum, set indices to current indices \n\nAt end return indices \n\n# Complexity\n- Time complexity: O(N + W)\n - O(N) going over list and building windows \n - O(W) going over windows from left to right and right to left \n - O(W) doing final evaluation \n - Total is O(N + W)\n\n- Space complexity: O(W) \n - O(W) windows in list of window sums, left window and right window \n\n\n# Code\n```\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n # get max window size \n max_size = k \n # get list of window sums set up \n list_of_window_sums = []\n # current sum is 0 \n current_sum = 0\n # enumerate nums and slide window of max size over it \n for index, value in enumerate(nums) : \n current_sum += value \n # once you\'re past the maximal size, update \n if index >= max_size : \n current_sum -= nums[index - max_size]\n if index >= max_size - 1 : \n # once you\'re at the right size, start appending \n list_of_window_sums.append(current_sum)\n \n # get the length of the windows for easier addressing \n W = len(list_of_window_sums)\n\n left_windows = [0] * W\n best_window_index = 0\n # left windows go left to right, and in here the first occurrence of the largest value of window sums \n # will take place at the best index, which is why we default to 0 \n # on the left we care about strictly greater than, as we want the greatest unique such value \n # the an equal value later in the list may be subsumed by index on the right \n # due to this, we do not wish to block that from occurring \n for window_index in range(W) : \n if list_of_window_sums[window_index] > list_of_window_sums[best_window_index] : \n best_window_index = window_index \n left_windows[window_index] = best_window_index\n \n # right windows will then track from right to left \n # though it would hurt readability you could push these two into the same loop if you felt like it \n right_windows = [0] * W \n best_window_index = W - 1 \n # here we want to snag the last such that it is greater or equal then, as we will be moving backwards\n # when we consider occurrences on the right. This means we use greater than or equal to in this case \n for window_index in range(W-1, -1, -1) : \n if list_of_window_sums[window_index] >= list_of_window_sums[best_window_index] : \n best_window_index = window_index \n right_windows[window_index] = best_window_index\n \n # set up your indices \n indices = None \n\n # window index is from max size to W minus max size so we consider all valid window ranges \n for window_index in range(max_size, W-max_size) : \n # index 1 and index 3 are the current index then shifted by max size \n in_1, in_3 = left_windows[window_index - max_size], right_windows[window_index + max_size]\n # if indices is None, set these ones in to start, then go on from there \n if indices is None : \n indices = in_1, window_index, in_3\n else : \n # otherwise, get your current indices in a nice lists form \n current_indices = [in_1, window_index, in_3]\n # sum current and priors using list notation \n current_sum = 0 \n for index in current_indices : \n current_sum += list_of_window_sums[index]\n prior_sum = 0\n for index in indices : \n prior_sum += list_of_window_sums[index]\n # if current sum is better, set indices to current indices \n # But only if strictly better. \n # If not strictly better, the earlier the indices are lexicographically the better off we are \n if current_sum > prior_sum : \n indices = current_indices\n # at end, return indices \n return indices \n``` | 0 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
[Python] Generic K Non overlapping Subarrays DP | Clean | maximum-sum-of-3-non-overlapping-subarrays | 0 | 1 | \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n\n# Code\n```\nclass Solution:\n def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:\n K,n = 3,len(nums) # K subarrays \n dp = [[0]*(n+1) for i in range(K+1)] # dp[i][j] - max sum of i non overapping subarrays till jth index\n dec = [[0]*(n+1) for i in range(K+1)] # dec[i][j] whose last index caused dp[i][j]\n pref = [0]*(n+1) # prefix sum for convience\n for i in range(1,n+1): pref[i] = pref[i-1]+nums[i-1] # we can use sliding window to calculate k sum but this is more clean imo\n for i in range(1,K+1):\n for j in range(k,n+1):\n dp[i][j] = max(dp[i][j-1],pref[j]-pref[j-k]+dp[i-1][j-k]) # generic dp either continue with previous max or choose this sum with prev max\n if(dp[i][j]>dp[i][j-1]): dec[i][j] = j # to build ans we need to track decision made during dp\n else: dec[i][j] = dec[i][j-1]\n res = []\n cur,m = n,K # backtrack dp to get ans\n while(m>0 and cur>0):\n cur = dec[m][cur]-k\n res.append(cur)\n m -=1\n return reversed(res) \n``` | 0 | Given an integer array `nums` and an integer `k`, find three non-overlapping subarrays of length `k` with maximum sum and return them.
Return the result as a list of indices representing the starting position of each interval (**0-indexed**). If there are multiple answers, return the lexicographically smallest one.
**Example 1:**
**Input:** nums = \[1,2,1,2,6,7,5,1\], k = 2
**Output:** \[0,3,5\]
**Explanation:** Subarrays \[1, 2\], \[2, 6\], \[7, 5\] correspond to the starting indices \[0, 3, 5\].
We could have also taken \[2, 1\], but an answer of \[1, 3, 5\] would be lexicographically larger.
**Example 2:**
**Input:** nums = \[1,2,1,2,1,2,1,2,1\], k = 2
**Output:** \[0,2,4\]
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] < 216`
* `1 <= k <= floor(nums.length / 3)` | null |
97% Readable Python DFS | employee-importance | 0 | 1 | # Intuition\nThis is a graph problem, where there is a directed edge between an employee and their subordinate; specifically, this is a tree. We can solve this with DFS and just keep a running sum of the importance values.\n\n# Approach\nThe non-trivial part is defining the graph. I assumed earlier that the index positions of the employee matched their ID, but this was not the case. Instead, I create an employee directory that is a dictionary with the employee id as keys and the employee object as the value.\n\nThe neighbors of the employee node can be left in the subordinates attribute of the employee.\n\nI decided to use an iterative DFS approach; it doesn\'t matter if we do DFS or BFS.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$ to hold the employee directory.\n\n# Code\n```\n"""\n# Definition for Employee.\nclass Employee:\n def __init__(self, id: int, importance: int, subordinates: List[int]):\n self.id = id\n self.importance = importance\n self.subordinates = subordinates\n"""\n\nclass Solution:\n def getImportance(self, employees: List[\'Employee\'], id: int) -> int:\n # do a DFS and and just add the importance as you see them\n \n queue = [id]\n directory = {}\n for e in employees:\n directory[e.id] = e\n\n total = 0\n \n while queue:\n emp_id = queue.pop()\n emp = directory[emp_id]\n total += emp.importance\n\n for sub in emp.subordinates:\n queue.append(sub)\n\n return total\n```\n\n# Footnote\nYes, I know the times are volatile, and you can have 97% one time and get 60% the next run with the same go!\n | 0 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
690: Time 98.69% and Space 100%, Solution with step by step explanation | employee-importance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a class called Employee with attributes: id, importance, and subordinates.\n2. Define a class called Solution.\n3. In the Solution class, define a method called getImportance that takes two arguments: employees (a list of Employee objects) and id (an integer representing the ID of an employee).\n4. Create a dictionary called employee_dict to map each employee ID to its corresponding Employee object.\n5. Define a recursive DFS function called dfs that takes an employee ID and returns the total importance value of that employee and all their subordinates.\n6. In the dfs function, retrieve the corresponding Employee object using the employee_dict dictionary.\n7. Initialize a variable called total_importance to the importance value of the employee.\n8. Iterate through the list of subordinates of the employee and add the result of calling the dfs function recursively on each subordinate to the total_importance variable.\n9. Return the total_importance variable.\n10. Call the dfs function on the given employee ID and return the result.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Employee:\n def __init__(self, id: int, importance: int, subordinates: List[int]):\n self.id = id\n self.importance = importance\n self.subordinates = subordinates\n\nclass Solution:\n def getImportance(self, employees: List[Employee], id: int) -> int:\n # Build a dictionary to map each employee ID to their corresponding Employee object.\n employee_dict = {employee.id: employee for employee in employees}\n \n # Define a recursive DFS function to get the total importance value of an employee and all their subordinates.\n def dfs(employee_id):\n employee = employee_dict[employee_id]\n total_importance = employee.importance\n for subordinate_id in employee.subordinates:\n total_importance += dfs(subordinate_id)\n return total_importance\n \n # Call the DFS function on the given employee ID.\n return dfs(id)\n\n``` | 2 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
Python, a short and easy DFS solution. | employee-importance | 0 | 1 | ```\nclass Solution:\n def getImportance(self, employees: List[\'Employee\'], id: int) -> int:\n def dfs(emp):\n imp = emps[emp].importance \n for s in emps[emp].subordinates:\n imp += dfs(s)\n return imp\n \n emps= {emp.id: emp for emp in employees}\n \n return dfs(id)\n``` | 17 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.