markdown
stringlengths 0
1.02M
| code
stringlengths 0
832k
| output
stringlengths 0
1.02M
| license
stringlengths 3
36
| path
stringlengths 6
265
| repo_name
stringlengths 6
127
|
|---|---|---|---|---|---|
Shapiro-Wilk Test | # define Shapiro Wilk Test function
def shapiro_test(data):
'''calculate K-S Test for and out results in table'''
data = data._get_numeric_data()
data_shapiro_test = pd.DataFrame()
# Iterate over columns, calculate test statistic & create table
for column in data:
column_shapiro_test = shapiro(data[column])
shapiro_pvalue_column = column_shapiro_test.pvalue
if column_shapiro_test.pvalue < .05:
shapiro_pvalue_column = '{:.6f}'.format(shapiro_pvalue_column) + '*'
column_distr = 'non-normal'
else:
column_distr = 'normal'
new_row = {'variable': column,
'Shapiro Wilk p-value': shapiro_pvalue_column,
'Shapiro Wilk statistic': column_shapiro_test.statistic,
'distribution': column_distr
}
data_shapiro_test = data_shapiro_test.append(new_row, ignore_index=True)
data_shapiro_test = data_shapiro_test[['variable', 'Shapiro Wilk statistic', 'Shapiro Wilk p-value', 'distribution']]
return data_shapiro_test
shapiro_test(df.dropna()) | _____no_output_____ | MIT | 210601 gca data analyses.ipynb | rbnjd/gca_data_analyses |
Histograms **Histograms: Likert-scale variables** | for column in df._get_numeric_data().drop(columns=['assessed PEB','age']):
sns.set(rc={'figure.figsize':(5,5)})
data = df[column]
sns.histplot(data, bins=np.arange(1,9)-.5)
plt.xlabel(column)
plt.show() | _____no_output_____ | MIT | 210601 gca data analyses.ipynb | rbnjd/gca_data_analyses |
**Histogramm: age** | sns.histplot(df['age'], bins=10) | _____no_output_____ | MIT | 210601 gca data analyses.ipynb | rbnjd/gca_data_analyses |
**Histogramm: assessed PEB** | sns.histplot(df['assessed PEB'], bins=np.arange(0,8)-.5) | _____no_output_____ | MIT | 210601 gca data analyses.ipynb | rbnjd/gca_data_analyses |
Kendall's Tau correlation | # create df with correlation coefficient and p-value indication
def kendall_pval(x,y):
return kendalltau(x,y)[1]
# calculate kendall's tau correlation with p values ( < .01 = ***, < .05 = **, < .1 = *)
tau = df.corr(method = 'kendall').round(decimals=2)
pval = df.corr(method=kendall_pval) - np.eye(*tau.shape)
p = pval.applymap(lambda x: ''.join(['*' for t in [0.1,0.05] if x<=t]))
tau_corr_with_p_values = tau.round(4).astype(str) + p
# set colored highlights for correlation matri
def color_sig_blue(val):
"""
color all significant values in blue
"""
color = 'blue' if val.endswith('*') else 'black'
return 'color: %s' % color
tau_corr_with_p_values.style.applymap(color_sig_blue) | _____no_output_____ | MIT | 210601 gca data analyses.ipynb | rbnjd/gca_data_analyses |
Correlation Heatmap All not significant correlations (p < .05) are not shown. | # calculate correlation coefficient
corr = df.corr(method='kendall')
# calculate column correlations and make a seaborn heatmap
sns.set(rc={'figure.figsize':(12,12)})
ax = sns.heatmap(
corr,
vmin=-1, vmax=1, center=0,
cmap=sns.diverging_palette(20, 220, n=200),
square=True
)
ax.set_xticklabels(
ax.get_xticklabels(),
rotation=45,
horizontalalignment='right'
);
heatmap = ax.get_figure()
# calculate correlation coefficient and p-values
corr_p_values = df.corr(method = kendall_pval)
corr = df.corr(method='kendall')
# calculate column correlations and make a seaborn heatmap
sns.set(rc={'figure.figsize':(12,12)})
#set mask for only significant values (p <= .05)
mask = np.invert(np.tril(corr_p_values<.05))
ax = sns.heatmap(
corr,
vmin=-1, vmax=1, center=0,
cmap=sns.diverging_palette(20, 220, n=200),
square=True,
annot=True,
mask=mask
)
ax.set_xticklabels(
ax.get_xticklabels(),
rotation=45,
horizontalalignment='right'
);
heatmap = ax.get_figure() | _____no_output_____ | MIT | 210601 gca data analyses.ipynb | rbnjd/gca_data_analyses |
Cherry Blossoms!If we travel back in time a few months, [cherry blossoms](https://en.wikipedia.org/wiki/Cherry_blossom) were in full bloom! We don't live in Japan or DC, but we do have our fair share of the trees - buuut you sadly missed [Brooklyn Botanic Garden's annual festival](https://www.bbg.org/visit/event/sakura_matsuri_2019).We'll have to make up for it with data-driven cherry blossoms instead. Once upon a time [Data is Plural](https://tinyletter.com/data-is-plural) linked to [a dataset](http://atmenv.envi.osakafu-u.ac.jp/aono/kyophenotemp4/) about when the cherry trees blossom each year. It's a little out of date, but it's quirky in a real nice way so we're sticking with it. 0. Do all of your importing/setup stuff | import pandas as pd
import numpy as np
%matplotlib inline | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
1. Read in the file using pandas, and look at the first five rows | df = pd.read_excel("KyotoFullFlower7.xls")
df.head(5) | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
2. Read in the file using pandas CORRECTLY, and look at the first five rowsHrm, how do your column names look? Read the file in again but this time add a parameter to make sure your columns look right.**TIP: The first year should be 801 AD, and it should not have any dates or anything.** | df=df[25:]
df
df.dtypes
df.head(5)
| _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
3. Look at the final five rows of the data | df.tail(5) | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
4. Add some more NaN values It looks like you should probably have some NaN/missing values earlier on in the dataset under "Reference name." Read in the file *one more time*, this time making sure all of those missing reference names actually show up as `NaN` instead of `-`. | df.replace("-", np.nan, inplace=True)
df
df.rename(columns={'Full-flowering dates of Japanese cherry (Prunus jamasakura) at Kyoto, Japan. (Latest version, Jun. 12, 2012)': 'AD', 'Unnamed:_1': 'Full-flowering date'}, inplace=True)
df.rename(columns={'Unnamed: 1': 'DOY', 'Unnamed: 2': 'Full_flowering_date', 'Unnamed: 3': 'Source_code'}, inplace=True)
df.rename(columns={'Unnamed: 4': 'Data_type_code', 'Unnamed: 5': 'Reference_Name'}, inplace=True)
df | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
5. What source is the most common as a reference? | df.dtypes
df.Source_code.value_counts() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
6. Filter the list to only include columns where the `Full-flowering date (DOY)` is not missingIf you'd like to do it in two steps (which might be easier to think through), first figure out how to test whether a column is empty/missing/null/NaN, get the list of `True`/`False` values, and then later feed it to your `df`. | df.DOY.value_counts(dropna=False) | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
7. Make a histogram of the full-flowering dateIs it not showing up? Remember the "magic" command that makes graphs show up in matplotlib notebooks! | df.DOY.value_counts().hist() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
8. Make another histogram of the full-flowering date, but with 39 bins instead of 10 | df.DOY.value_counts().hist(bins=39) | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
9. What's the average number of days it takes for the flowers to blossom? And how many records do we have?Answer these both with one line of code. | df.DOY.describe() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
10. What's the average days into the year cherry flowers normally blossomed before 1900? | (df.AD>=1900).mean() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
11. How about after 1900? | (df.AD<=1900).mean() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
12. How many times was our data from a title in Japanese poetry?You'll need to read the documentation inside of the Excel file. | #Data_type_code
#4=poetry
df.Data_type_code.value_counts() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
13. Show only the years where our data was from a title in Japanese poetry | df[df.Data_type_code == 4]
| _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
14. Graph the full-flowering date (DOY) over time | df.DOY.plot(x="DOY", y="AD", figsize=(10,7)) | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
15. Smooth out the graphIt's so jagged! You can use `df.rolling` to calculate a rolling average.The following code calculates a **10-year mean**, using the `AD` column as the anchor. If there aren't 20 samples to work with in a row, it'll accept down to 5. Neat, right?(We're only looking at the final 5) | df.rolling(10, on='AD', min_periods=5)['DOY'].mean().tail()
df.rolling(10, on='AD', min_periods=5)['DOY'].mean().tail().plot(ylim=(80, 120)) | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
Use the code above to create a new column called `rolling_date` in our dataset. It should be the 20-year rolling average of the flowering date. Then plot it, with the year on the x axis and the day of the year on the y axis.Try adding `ylim=(80, 120)` to your `.plot` command to make things look a little less dire. 16. Add a month columnRight now the "Full-flowering date" column is pretty rough. It uses numbers like '402' to mean "April 2nd" and "416" to mean "April 16th." Let's make a column to explain what month it happened in.* Every row that happened in April should have 'April' in the `month` column.* Every row that happened in March should have 'March' as the `month` column.* Every row that happened in May should have 'May' as the `month` column.**I've given you March as an example**, you just need to add in two more lines to do April and May. | df.loc[df['Full_flowering_date'] < 400, 'month'] = 'March'
df.loc[df['Full_flowering_date'] < 500, 'month'] = 'April'
df.loc[df['Full_flowering_date'] < 600, 'month'] = 'May' | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
17. Using your new column, how many blossomings happened in each month? | df.month.value_counts() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
18. Graph how many blossomings happened in each month. | df.month.value_counts().hist() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
19. Adding a day-of-month columnNow we're going to add a new column called "day of month." It's actually a little tougher than it should be since the `Full-flowering date` column is a *float* instead of an integer. | df.Full_flowering_date.astype(int) | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
And if you try to convert it to an int, **pandas yells at you!** That's because, as you can read, you can't have an `NaN` be an integer. But, for some reason, it *can* be a float. Ugh! So what we'll do is **drop all of the na values, then convert them to integers to get rid of the decimals.**I'll show you the first 5 here. | df['Full_flowering_date'].dropna().astype(int).head() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
On the next line, I take the first character of the row and add a bunch of exclamation points on it. I want you to edit this code to **return the last TWO digits of the number**. This only shows you the first 5, by the way.You might want to look up 'list slicing.' | df['Full_flowering_date'].dropna().astype(int).astype(str).apply(lambda value: value[0] + "!!!").head() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
Now that you've successfully extracted the last two letters, save them into a new column called `'day-of-month'` | df['day-of-month'] = df['Full_flowering_date'].dropna().astype(int).astype(str).apply(lambda value: value[0] + "!!!")
df.head() | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
20. Adding a date columnNow take the `'month'` and `'day-of-month'` columns and combine them in order to create a new column called `'date'` | df["date"] = df["month"] + df["day-of-month"]
df | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
YOU ARE DONE.And **incredible.** | !!!!!!!!!!! | _____no_output_____ | MIT | 07-homework/cherry-blossoms/Cherry Blossoms.ipynb | giovanafleck/foundations_homework |
Tarea N°02 Instrucciones1.- Completa tus datos personales (nombre y rol USM) en siguiente celda.**Nombre**: Fabián Rubilar Álvarez **Rol**: 201510509-K2.- Debes pushear este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.3.- Se evaluará:- Soluciones- Código- Que Binder esté bien configurado.- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error. I.- Clasificación de dígitosEn este laboratorio realizaremos el trabajo de reconocer un dígito a partir de una imagen. 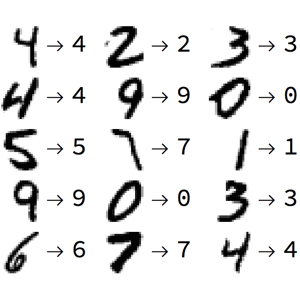 El objetivo es a partir de los datos, hacer la mejor predicción de cada imagen. Para ellos es necesario realizar los pasos clásicos de un proyecto de _Machine Learning_, como estadística descriptiva, visualización y preprocesamiento. * Se solicita ajustar al menos tres modelos de clasificación: * Regresión logística * K-Nearest Neighbours * Uno o más algoritmos a su elección [link](https://scikit-learn.org/stable/supervised_learning.htmlsupervised-learning) (es obligación escoger un _estimator_ que tenga por lo menos un hiperparámetro). * En los modelos que posean hiperparámetros es mandatorio buscar el/los mejores con alguna técnica disponible en `scikit-learn` ([ver más](https://scikit-learn.org/stable/modules/grid_search.htmltuning-the-hyper-parameters-of-an-estimator)).* Para cada modelo, se debe realizar _Cross Validation_ con 10 _folds_ utilizando los datos de entrenamiento con tal de determinar un intervalo de confianza para el _score_ del modelo.* Realizar una predicción con cada uno de los tres modelos con los datos _test_ y obtener el _score_. * Analizar sus métricas de error (**accuracy**, **precision**, **recall**, **f-score**) Exploración de los datosA continuación se carga el conjunto de datos a utilizar, a través del sub-módulo `datasets` de `sklearn`. | import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
%matplotlib inline
digits_dict = datasets.load_digits()
print(digits_dict["DESCR"])
digits_dict.keys()
digits_dict["target"] | _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
A continuación se crea dataframe declarado como `digits` con los datos de `digits_dict` tal que tenga 65 columnas, las 6 primeras a la representación de la imagen en escala de grises (0-blanco, 255-negro) y la última correspondiente al dígito (`target`) con el nombre _target_. | digits = (
pd.DataFrame(
digits_dict["data"],
)
.rename(columns=lambda x: f"c{x:02d}")
.assign(target=digits_dict["target"])
.astype(int)
)
digits.head() | _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Ejercicio 1**Análisis exploratorio:** Realiza tu análisis exploratorio, no debes olvidar nada! Recuerda, cada análisis debe responder una pregunta.Algunas sugerencias:* ¿Cómo se distribuyen los datos?* ¿Cuánta memoria estoy utilizando?* ¿Qué tipo de datos son?* ¿Cuántos registros por clase hay?* ¿Hay registros que no se correspondan con tu conocimiento previo de los datos? | #Primero veamos los tipos de datos del DF y cierta información que puede ser de utilidad
digits.info()
#Veamos si hay valores nulos en las columnas
if True not in digits.isnull().any().values:
print('No existen valores nulos')
#Veamos que elementos únicos tenemos en la columna target del DF
digits.target.unique()
#Veamos cuantos registros por clase existen luego de saber que hay 10 tipos de clase en la columna target
(u,v) = np.unique(digits['target'] , return_counts = True)
for i in range(0,10):
print ('Tenemos', v[i], 'registros para', u[i])
#Como tenemos 10 tipos de elementos en target, veamos las caracteristicas que poseen los datos
caract_datos = [len(digits[digits['target'] ==i ].target) for i in range(0,10)]
print ('El total de los datos es:', sum(caract_datos))
print ('El máximo de los datos es:', max(caract_datos))
print ('El mínimo de los datos es:', min(caract_datos))
print ('El promedio de los datos es:', 0.1*sum(caract_datos)) | El total de los datos es: 1797
El máximo de los datos es: 183
El mínimo de los datos es: 174
El promedio de los datos es: 179.70000000000002
| MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Por lo tanto, tenemos un promedio de 180 (aproximando por arriba) donde el menor valor es de 174 y el mayor valor es de 183. | #Para mejorar la visualización, construyamos un histograma
digits.target.plot.hist(bins=12, alpha=0.5) | _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Sabemos que cada dato corresponde a una matriz cuadrada de dimensión 8 con entradas de 0 a 16. Cada dato proviene de otra matriz cuadrada de dimensión 32, el cual ha sido procesado por un método de reducción de dimensiones. Además, cada dato es una imagen de un número entre 0 a 9, por lo tanto se utilizan 8$\times$8 = 64 bits, sumado al bit para guardar información. Así, como tenemos 1797 datos, calculamos 1797$\times$65 = 116805 bits en total. Ahora, si no se aplica la reducción de dimensiones, tendriamos 32$\times$32$\times$1797 = 1840128 bits, que es aproximadamente 15,7 veces mayor. Ejercicio 2**Visualización:** Para visualizar los datos utilizaremos el método `imshow` de `matplotlib`. Resulta necesario convertir el arreglo desde las dimensiones (1,64) a (8,8) para que la imagen sea cuadrada y pueda distinguirse el dígito. Superpondremos además el label correspondiente al dígito, mediante el método `text`. Esto nos permitirá comparar la imagen generada con la etiqueta asociada a los valores. Realizaremos lo anterior para los primeros 25 datos del archivo. | digits_dict["images"][0] | _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Visualiza imágenes de los dígitos utilizando la llave `images` de `digits_dict`. Sugerencia: Utiliza `plt.subplots` y el método `imshow`. Puedes hacer una grilla de varias imágenes al mismo tiempo! | nx, ny = 5, 5
fig, axs = plt.subplots(nx, ny, figsize=(12, 12))
for x in range(0,5):
for y in range(0,5):
axs[x,y].imshow(digits_dict['images'][5*x+y], cmap = 'plasma')
axs[x,y].text(3,4,s = digits['target'][5*x+y], fontsize = 30) | _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Ejercicio 3**Machine Learning**: En esta parte usted debe entrenar los distintos modelos escogidos desde la librería de `skelearn`. Para cada modelo, debe realizar los siguientes pasos:* **train-test** * Crear conjunto de entrenamiento y testeo (usted determine las proporciones adecuadas). * Imprimir por pantalla el largo del conjunto de entrenamiento y de testeo. * **modelo**: * Instanciar el modelo objetivo desde la librería sklearn. * *Hiper-parámetros*: Utiliza `sklearn.model_selection.GridSearchCV` para obtener la mejor estimación de los parámetros del modelo objetivo.* **Métricas**: * Graficar matriz de confusión. * Analizar métricas de error.__Preguntas a responder:__* ¿Cuál modelo es mejor basado en sus métricas?* ¿Cuál modelo demora menos tiempo en ajustarse?* ¿Qué modelo escoges? | X = digits.drop(columns="target").values
y = digits["target"].values
from sklearn import datasets
from sklearn.model_selection import train_test_split
#Ahora vemos los conjuntos de testeo y entrenamiento
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
print('El conjunto de testeo tiene la siguiente cantidad de datos:', len(y_test))
print('El conjunto de entrenamiento tiene la siguiente cantidad de datos:', len(y_train))
#REGRESIÓN LOGÍSTICA
from sklearn.linear_model import LogisticRegression
from metrics_classification import *
from sklearn.metrics import r2_score
from sklearn.metrics import confusion_matrix
#Creando el modelo
rlog = LogisticRegression()
rlog.fit(X_train, y_train) #Ajustando el modelo
#Matriz de confusión
y_true = list(y_test)
y_pred = list(rlog.predict(X_test))
print('\nMatriz de confusion:\n ')
print(confusion_matrix(y_true,y_pred))
#Métricas
df_temp = pd.DataFrame(
{
'y':y_true,
'yhat':y_pred
}
)
df_metrics = summary_metrics(df_temp)
print("\nMetricas para los regresores")
print("")
print(df_metrics)
#K-NEAREST NEIGHBORS
from sklearn.neighbors import KNeighborsClassifier
from sklearn import neighbors
from sklearn import preprocessing
#Creando el modelo
knn = neighbors.KNeighborsClassifier()
knn.fit(X_train,y_train) #Ajustando el modelo
#Matriz de confusión
y_true = list(y_test)
y_pred = list(knn.predict(X_test))
print('\nMatriz de confusion:\n ')
print(confusion_matrix(y_true,y_pred))
#Métricas
df_temp = pd.DataFrame(
{
'y':y_true,
'yhat':y_pred
}
)
df_metrics = summary_metrics(df_temp)
print("\nMetricas para los regresores")
print("")
print(df_metrics)
#ÁRBOL DE DECISIÓN
from sklearn.tree import DecisionTreeClassifier
#Creando el modelo
add = DecisionTreeClassifier(max_depth=10)
add = add.fit(X_train, y_train) #Ajustando el modelo
#Matriz de confusión
y_true = list(y_test)
y_pred = list(add.predict(X_test))
print('\nMatriz de confusion:\n ')
print(confusion_matrix(y_true,y_pred))
#Métricas
df_temp = pd.DataFrame(
{
'y':y_true,
'yhat':y_pred
}
)
df_metrics = summary_metrics(df_temp)
print("\nMetricas para los regresores")
print("")
print(df_metrics)
#GRIDSEARCH
from sklearn.model_selection import GridSearchCV
model = DecisionTreeClassifier()
# rango de parametros
rango_criterion = ['gini','entropy']
rango_max_depth = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 20, 30, 40, 50, 70, 90, 120, 150])
param_grid = dict(criterion = rango_criterion, max_depth = rango_max_depth)
print(param_grid)
print('\n')
gs = GridSearchCV(estimator=model,
param_grid=param_grid,
scoring='accuracy',
cv=10,
n_jobs=-1)
gs = gs.fit(X_train, y_train)
print(gs.best_score_)
print('\n')
print(gs.best_params_)
| {'criterion': ['gini', 'entropy'], 'max_depth': array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15,
20, 30, 40, 50, 70, 90, 120, 150])}
0.8761308281141267
{'criterion': 'entropy', 'max_depth': 11}
| MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Ejercicio 4__Comprensión del modelo:__ Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, debe comprender e interpretar minuciosamente los resultados y gráficos asocados al modelo en estudio, para ello debe resolver los siguientes puntos: * **Cross validation**: usando **cv** (con n_fold = 10), sacar una especie de "intervalo de confianza" sobre alguna de las métricas estudiadas en clases: * $\mu \pm \sigma$ = promedio $\pm$ desviación estandar * **Curva de Validación**: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.htmlsphx-glr-auto-examples-model-selection-plot-validation-curve-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. * **Curva AUC–ROC**: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.htmlsphx-glr-auto-examples-model-selection-plot-roc-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. | #Cross Validation
from sklearn.model_selection import cross_val_score
model = KNeighborsClassifier()
precision = cross_val_score(estimator = model, X = X_train, y = y_train, cv = 10)
med = precision.mean()#Media
desv = precision.std()#Desviación estandar
a = med - desv
b = med + desv
print('(',a,',', b,')')
#Curva de Validación
from sklearn.model_selection import validation_curve
knn.get_params()
parameters = np.arange(1,10)
train_scores, test_scores = validation_curve(model,
X_train,
y_train,
param_name = 'n_neighbors',
param_range = parameters,
scoring = 'accuracy',
n_jobs = -1)
train_scores_mean = np.mean(train_scores, axis = 1)
train_scores_std = np.std(train_scores, axis = 1)
test_scores_mean = np.mean(test_scores, axis = 1)
test_scores_std = np.std(test_scores, axis = 1)
plt.figure(figsize=(12,8))
plt.title('Validation Curve (KNeighbors)')
plt.xlabel('n_neighbors')
plt.ylabel('scores')
#Train
plt.semilogx(parameters,
train_scores_mean,
label = 'Training Score',
color = 'red',
lw =2)
plt.fill_between(parameters,
train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std,
alpha = 0.2,
color = 'red',
lw = 2)
#Test
plt.semilogx(parameters,
test_scores_mean,
label = 'Cross Validation Score',
color = 'navy',
lw =2)
plt.fill_between(parameters,
test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std,
alpha = 0.2,
color = 'navy',
lw = 2)
plt.legend(loc = 'Best')
plt.show()
#Curva AUC–ROC
| _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Ejercicio 5__Reducción de la dimensión:__ Tomando en cuenta el mejor modelo encontrado en el `Ejercicio 3`, debe realizar una reducción de dimensionalidad del conjunto de datos. Para ello debe abordar el problema ocupando los dos criterios visto en clases: * **Selección de atributos*** **Extracción de atributos**__Preguntas a responder:__Una vez realizado la reducción de dimensionalidad, debe sacar algunas estadísticas y gráficas comparativas entre el conjunto de datos original y el nuevo conjunto de datos (tamaño del dataset, tiempo de ejecución del modelo, etc.) | #Selección de atributos
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
df = pd.DataFrame(X)
df.columns = [f'P{k}' for k in range(1,X.shape[1]+1)]
df['y']=y
print('Vemos que el df respectivo es de la forma:')
print('\n')
print(df.head())
# Separamos las columnas objetivo
x_training = df.drop(['y',], axis=1)
y_training = df['y']
# Aplicando el algoritmo univariante de prueba F.
k = 40 # número de atributos a seleccionar
columnas = list(x_training.columns.values)
seleccionadas = SelectKBest(f_classif, k=k).fit(x_training, y_training)
catrib = seleccionadas.get_support()
atributos = [columnas[i] for i in list(catrib.nonzero()[0])]
print('\n')
print('Los atributos quedan como:')
print('\n')
print(atributos)
#Veamos que pasa si entrenamos un nuevo modelo K-NEAREST NEIGHBORS con los atributos seleccionados anteriormente
x=df[atributos]
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=42)
#Creando el modelo
knn = neighbors.KNeighborsClassifier()
knn.fit(x_train,y_train) #Ajustando el modelo
#Matriz de confusión
y_true = list(y_test)
y_pred = list(knn.predict(x_test))
print('\nMatriz de confusion:\n ')
print(confusion_matrix(y_true,y_pred))
#Métricas
df_temp = pd.DataFrame(
{
'y':y_true,
'yhat':y_pred
}
)
df_metrics = summary_metrics(df_temp)
print("\nMetricas para los regresores ")
print("")
print(df_metrics)
#Extracción de atributos
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
x = StandardScaler().fit_transform(X)
n_components = 50
pca = PCA(n_components)
principalComponents = pca.fit_transform(x)
# Graficar varianza por componente
percent_variance = np.round(pca.explained_variance_ratio_* 100, decimals =2)
columns = [ 'P'+str(i) for i in range(n_components)]
plt.figure(figsize=(20,4))
plt.bar(x= range(0,n_components), height=percent_variance, tick_label=columns)
plt.ylabel('Percentate of Variance Explained')
plt.xlabel('Principal Component')
plt.title('PCA Scree Plot')
plt.show()
# graficar varianza por la suma acumulada de los componente
percent_variance_cum = np.cumsum(percent_variance)
columns = [ 'P' + str(0) + '+...+P' + str(i) for i in range(n_components) ]
plt.figure(figsize=(20,4))
plt.bar(x= range(0,n_components), height=percent_variance_cum, tick_label=columns)
plt.xticks(range(len(columns)), columns, rotation=90)
plt.xlabel('Principal Component Cumsum')
plt.title('PCA Scree Plot')
plt.show()
| _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Ejercicio 6__Visualizando Resultados:__ A continuación se provee código para comparar las etiquetas predichas vs las etiquetas reales del conjunto de _test_. | def mostar_resultados(digits,model,nx=5, ny=5,label = "correctos"):
"""
Muestra los resultados de las prediciones de un modelo
de clasificacion en particular. Se toman aleatoriamente los valores
de los resultados.
- label == 'correcto': retorna los valores en que el modelo acierta.
- label == 'incorrecto': retorna los valores en que el modelo no acierta.
Observacion: El modelo que recibe como argumento debe NO encontrarse
'entrenado'.
:param digits: dataset 'digits'
:param model: modelo de sklearn
:param nx: numero de filas (subplots)
:param ny: numero de columnas (subplots)
:param label: datos correctos o incorrectos
:return: graficos matplotlib
"""
X = digits.drop(columns = "target").values
y = digits["target"].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
model.fit(X_train, y_train) # ajustando el modelo
y_pred = model.predict(X_test)
# Mostrar los datos correctos
if label == "correctos":
mask = (y_pred == y_test)
color = "green"
# Mostrar los datos correctos
elif label == "incorrectos":
mask = (y_pred != y_test)
color = "red"
else:
raise ValueError("Valor incorrecto")
X_aux = X_test[mask]
y_aux_true = y_test[mask]
y_aux_pred = y_pred[mask]
# We'll plot the first 100 examples, randomly choosen
fig, ax = plt.subplots(nx, ny, figsize=(12,12))
for i in range(nx):
for j in range(ny):
index = j + ny * i
data = X_aux[index, :].reshape(8,8)
label_pred = str(int(y_aux_pred[index]))
label_true = str(int(y_aux_true[index]))
ax[i][j].imshow(data, interpolation = 'nearest', cmap = 'gray_r')
ax[i][j].text(0, 0, label_pred, horizontalalignment = 'center', verticalalignment = 'center', fontsize = 10, color = color)
ax[i][j].text(7, 0, label_true, horizontalalignment = 'center', verticalalignment = 'center', fontsize = 10, color = 'blue')
ax[i][j].get_xaxis().set_visible(False)
ax[i][j].get_yaxis().set_visible(False)
plt.show()
| _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
**Pregunta*** Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, grafique los resultados cuando: * el valor predicho y original son iguales * el valor predicho y original son distintos * Cuando el valor predicho y original son distintos , ¿Por qué ocurren estas fallas? | mostar_resultados(digits, KNeighborsClassifier(), nx=5, ny=5,label = "correctos")
mostar_resultados(digits, neighbors.KNeighborsClassifier(), nx=5, ny=5,label = "incorrectos")
| _____no_output_____ | MIT | homeworks/tarea_02/tarea_02.ipynb | FabianSaulRubilarAlvarez/mat281_portfolio_template |
Ocean heat transport in CMIP5 models Read data | import matplotlib.pyplot as plt
import iris
import iris.plot as iplt
import iris.coord_categorisation
import cf_units
import numpy
%matplotlib inline
infile = '/g/data/ua6/DRSv2/CMIP5/NorESM1-M/rcp85/mon/ocean/r1i1p1/hfbasin/latest/hfbasin_Omon_NorESM1-M_rcp85_r1i1p1_200601-210012.nc'
cube = iris.load_cube(infile)
print(cube)
dim_coord_names = [coord.name() for coord in cube.dim_coords]
print(dim_coord_names)
cube.coord('latitude').points
aux_coord_names = [coord.name() for coord in cube.aux_coords]
print(aux_coord_names)
cube.coord('region')
global_cube = cube.extract(iris.Constraint(region='global_ocean'))
def convert_to_annual(cube):
"""Convert data to annual timescale.
Args:
cube (iris.cube.Cube)
full_months(bool): only include years with data for all 12 months
"""
iris.coord_categorisation.add_year(cube, 'time')
iris.coord_categorisation.add_month(cube, 'time')
cube = cube.aggregated_by(['year'], iris.analysis.MEAN)
cube.remove_coord('year')
cube.remove_coord('month')
return cube
global_cube_annual = convert_to_annual(global_cube)
print(global_cube_annual)
iplt.plot(global_cube_annual[5, ::])
iplt.plot(global_cube_annual[20, ::])
plt.show() | _____no_output_____ | MIT | development/hfbasin.ipynb | DamienIrving/ocean-analysis |
So for any given year, the annual mean shows ocean heat transport away from the tropics. Trends | def convert_to_seconds(time_axis):
"""Convert time axis units to seconds.
Args:
time_axis(iris.DimCoord)
"""
old_units = str(time_axis.units)
old_timestep = old_units.split(' ')[0]
new_units = old_units.replace(old_timestep, 'seconds')
new_unit = cf_units.Unit(new_units, calendar=time_axis.units.calendar)
time_axis.convert_units(new_unit)
return time_axis
def linear_trend(data, time_axis):
"""Calculate the linear trend.
polyfit returns [a, b] corresponding to y = a + bx
"""
masked_flag = False
if type(data) == numpy.ma.core.MaskedArray:
if type(data.mask) == numpy.bool_:
if data.mask:
masked_flag = True
elif data.mask[0]:
masked_flag = True
if masked_flag:
return data.fill_value
else:
return numpy.polynomial.polynomial.polyfit(time_axis, data, 1)[-1]
def calc_trend(cube):
"""Calculate linear trend.
Args:
cube (iris.cube.Cube)
running_mean(bool, optional):
A 12-month running mean can first be applied to the data
yr (bool, optional):
Change units from per second to per year
"""
time_axis = cube.coord('time')
time_axis = convert_to_seconds(time_axis)
trend = numpy.ma.apply_along_axis(linear_trend, 0, cube.data, time_axis.points)
trend = numpy.ma.masked_values(trend, cube.data.fill_value)
return trend
trend_data = calc_trend(global_cube_annual)
trend_cube = global_cube_annual[0, ::].copy()
trend_cube.data = trend_data
trend_cube.remove_coord('time')
#trend_unit = ' yr-1'
#trend_cube.units = str(global_cube_annual.units) + trend_unit
iplt.plot(trend_cube)
plt.show() | _____no_output_____ | MIT | development/hfbasin.ipynb | DamienIrving/ocean-analysis |
So the trends in ocean heat transport suggest reduced transport in the RCP 8.5 simulation (i.e. the trend plot is almost the inverse of the climatology plot). Convergence | print(global_cube_annual)
diffs_data = numpy.diff(global_cube_annual.data, axis=1)
lats = global_cube_annual.coord('latitude').points
diffs_lats = (lats[1:] + lats[:-1]) / 2.
print(diffs_data.shape)
print(len(diffs_lats))
plt.plot(diffs_lats, diffs_data[0, :])
plt.plot(lats, global_cube_annual[0, ::].data / 10.0)
plt.show() | _____no_output_____ | MIT | development/hfbasin.ipynb | DamienIrving/ocean-analysis |
Convergence trend | time_axis = global_cube_annual.coord('time')
time_axis = convert_to_seconds(time_axis)
diffs_trend = numpy.ma.apply_along_axis(linear_trend, 0, diffs_data, time_axis.points)
diffs_trend = numpy.ma.masked_values(diffs_trend, global_cube_annual.data.fill_value)
print(diffs_trend.shape)
plt.plot(diffs_lats, diffs_trend * -1)
plt.axhline(y=0)
plt.show()
plt.plot(diffs_lats, diffs_trend * -1, color='black')
plt.axhline(y=0)
plt.axvline(x=30)
plt.axvline(x=50)
plt.axvline(x=77)
plt.xlim(20, 90)
plt.show() | _____no_output_____ | MIT | development/hfbasin.ipynb | DamienIrving/ocean-analysis |
Baseline | def customVectorizer(df, toRemove):
# leEmbarked.fit(df_raw['Embarked'])
leSex = preprocessing.LabelEncoder()
leEmbarked = preprocessing.LabelEncoder()
df.fillna(inplace=True, value=0)
leSex.fit(df['Sex'])
# leEmbarked.fit(df['Embarked'])
# df['Embarked'] = leEmbarked.transform(df['Embarked'])
df['Sex'] = leSex.transform(df['Sex'])
return df.drop(labels=toRemove, axis=1)
X = customVectorizer(X, ['Embarked', 'PassengerId', 'Name', 'Age', 'Ticket', 'Cabin'])
print(X.shape)
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(random_state=42)
from sklearn.model_selection import cross_val_score
lr_model = LogisticRegression()
cv_scores = cross_val_score(lr_model, X=X, y=y, cv=5, n_jobs=4)
print(cv_scores)
model.fit(X,y)
df_raw_test = pd.read_csv('test.csv')
df_test = baselineVectorizer(df_raw_test)
y_test_predicted = model.predict(df_test)
print('\n'.join(["{},{}".format(892 + i, y_test_predicted[i]) for i in range(len(y_test_predicted))]) , file=open('test_pred.csv', 'w'))
import matplotlib.pyplot as plt
plt.hist(X['Age'], bins=30) | _____no_output_____ | MIT | titanic/Titanic Clean.ipynb | bhi5hmaraj/Applied-ML |
Train a classifer for Age and use it to fill gapsSo first we split the train.csv into 2 parts (one with non null age and the other with null) . We train a regressor on the non null data points to predict age and use this trained regressor to fill the missing ages. Now we combine the 2 split data sets into a single dataset and train a logistic regression classifier. | X = pd.read_csv('train.csv')
age_present = X['Age'] > 0
age_present.describe()
False in age_present
X_age_p = X[age_present]
X_age_p.shape
age = X_age_p['Age']
# X_age_p
X_age_p = customVectorizer(X_age_p, ['Embarked', 'Age', 'PassengerId', 'Name', 'Ticket', 'Cabin'])
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X_age_p, age)
X_null_age = X[X['Age'].isnull()]
pred_age = reg.predict(customVectorizer(X_null_age, ['Embarked', 'Age', 'PassengerId', 'Name', 'Ticket', 'Cabin']))
age.mean()
pred_age = list(map(lambda x : max(0, x), pred_age))
X_null_age['Age'] = pred_age
y = X['Survived']
# from sklearn.model_selection import cross_val_score
# lr_model = LogisticRegression()
X_age_p['Age'] = age
X_age_p.shape
X = pd.concat([X_age_p, customVectorizer(X_null_age, ['Embarked', 'PassengerId', 'Name', 'Ticket', 'Cabin'])])
y = X['Survived']
X = X.drop(labels=['Survived'], axis=1)
lr_model = LogisticRegression()
cv_scores = cross_val_score(lr_model, X=X, y=y, cv=10, n_jobs=4)
print(cv_scores) | [0.76666667 0.76666667 0.85393258 0.7752809 0.80898876 0.78651685
0.79775281 0.80898876 0.86516854 0.79545455]
| MIT | titanic/Titanic Clean.ipynb | bhi5hmaraj/Applied-ML |
Try ensemble with LR, SVC, RF | # taken from https://machinelearningmastery.com/ensemble-machine-learning-algorithms-python-scikit-learn/
from sklearn import model_selection
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
kfold = model_selection.KFold(n_splits=10, random_state=42)
# create the sub models
estimators = []
model1 = LogisticRegression()
estimators.append(('logistic', model1))
model2 = DecisionTreeClassifier()
estimators.append(('cart', model2))
model3 = SVC()
estimators.append(('svm', model3))
# create the ensemble model
ensemble = VotingClassifier(estimators)
results = model_selection.cross_val_score(ensemble, X, y, cv=kfold)
print(results.mean())
print(results)
| /home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
FutureWarning)
/home/bhishma/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
| MIT | titanic/Titanic Clean.ipynb | bhi5hmaraj/Applied-ML |
Notebook BasicsIn this lesson we'll learn how to work with **notebooks**. Notebooks allow us to do interactive and visual computing which makes it a great learning tool. We'll use notebooks to code in Python and learn the basics of machine learning. View on practicalAI Run in Google Colab View code on GitHub Set Up 1. Sign into your [Google](https://accounts.google.com/signin) account to start using the notebook. If you don't want to save your work, you can skip the steps below.2. If you do want to save your work, click the **COPY TO DRIVE** button on the toolbar. This will open a new notebook in a new tab.  3. Rename this new notebook by removing the words `Copy of` from the title (change "`Copy of 00_Notebooks`" to "`00_Notebooks`").  4. Now you can run the code, make changes and it's all saved to your personal Google Drive. Types of cells Notebooks are made up of cells. Each cell can either be a **code cell** or a **text cell**. * **code cell**: used for writing and executing code.* **text cell**: used for writing text, HTML, Markdown, etc. Creating cells First, let's create a text cell. Click on a desired location in the notebook and create the cell by clicking on the **➕TEXT** (located in the top left corner). Once you create the cell, click on it and type the following inside it:``` This is a headerHello world!``` This is a headerHello world! Running cells Once you type inside the cell, press the **SHIFT** and **RETURN** (enter key) together to run the cell. Editing cells To edit a cell, double click on it and you can edit it. Moving cells Once you create the cell, you can move it up and down by clicking on the cell and then pressing the ⬆️ and ⬇️ button on the top right of the cell. Deleting cells You can delete the cell by clicking on it and pressing the trash can button 🗑️ on the top right corner of the cell. Alternatively, you can also press ⌘/Ctrl + M + D. Creating a code cell You can repeat the steps above to create and edit a *code* cell. You can create a code cell by clicking on the ➕CODE (located in the top left corner).Once you've created the code cell, double click on it, type the following inside it and then press `Shift + Enter` to execute the code.```print ("Hello world!")``` | print ("Hello world!") | Hello world!
| MIT | notebooks/00_Notebooks.ipynb | raidery/practicalAI |
Tutorial 2: Learning Hyperparameters**Week 1, Day 2: Linear Deep Learning****By Neuromatch Academy**__Content creators:__ Saeed Salehi, Andrew Saxe__Content reviewers:__ Polina Turishcheva, Antoine De Comite, Kelson Shilling-Scrivo__Content editors:__ Anoop Kulkarni__Production editors:__ Khalid Almubarak, Spiros Chavlis **Our 2021 Sponsors, including Presenting Sponsor Facebook Reality Labs** --- Tutorial Objectives* Training landscape* The effect of depth* Choosing a learning rate* Initialization matters | # @title Tutorial slides
# @markdown These are the slides for the videos in the tutorial
# @markdown If you want to locally dowload the slides, click [here](https://osf.io/sne2m/download)
from IPython.display import IFrame
IFrame(src=f"https://mfr.ca-1.osf.io/render?url=https://osf.io/sne2m/?direct%26mode=render%26action=download%26mode=render", width=854, height=480) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
--- SetupThis a GPU-Free tutorial! | # @title Install dependencies
!pip install git+https://github.com/NeuromatchAcademy/evaltools --quiet
from evaltools.airtable import AirtableForm
# Imports
import time
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# @title Figure settings
from ipywidgets import interact, IntSlider, FloatSlider, fixed
from ipywidgets import HBox, interactive_output, ToggleButton, Layout
from mpl_toolkits.axes_grid1 import make_axes_locatable
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/content-creation/main/nma.mplstyle")
# @title Plotting functions
def plot_x_y_(x_t_, y_t_, x_ev_, y_ev_, loss_log_, weight_log_):
"""
"""
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.scatter(x_t_, y_t_, c='r', label='training data')
plt.plot(x_ev_, y_ev_, c='b', label='test results', linewidth=2)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.subplot(1, 3, 2)
plt.plot(loss_log_, c='r')
plt.xlabel('epochs')
plt.ylabel('mean squared error')
plt.subplot(1, 3, 3)
plt.plot(weight_log_)
plt.xlabel('epochs')
plt.ylabel('weights')
plt.show()
def plot_vector_field(what, init_weights=None):
"""
"""
n_epochs=40
lr=0.15
x_pos = np.linspace(2.0, 0.5, 100, endpoint=True)
y_pos = 1. / x_pos
xx, yy = np.mgrid[-1.9:2.0:0.2, -1.9:2.0:0.2]
zz = np.empty_like(xx)
x, y = xx[:, 0], yy[0]
x_temp, y_temp = gen_samples(10, 1.0, 0.0)
cmap = matplotlib.cm.plasma
plt.figure(figsize=(8, 7))
ax = plt.gca()
if what == 'all' or what == 'vectors':
for i, a in enumerate(x):
for j, b in enumerate(y):
temp_model = ShallowNarrowLNN([a, b])
da, db = temp_model.dloss_dw(x_temp, y_temp)
zz[i, j] = temp_model.loss(temp_model.forward(x_temp), y_temp)
scale = min(40 * np.sqrt(da**2 + db**2), 50)
ax.quiver(a, b, - da, - db, scale=scale, color=cmap(np.sqrt(da**2 + db**2)))
if what == 'all' or what == 'trajectory':
if init_weights is None:
for init_weights in [[0.5, -0.5], [0.55, -0.45], [-1.8, 1.7]]:
temp_model = ShallowNarrowLNN(init_weights)
_, temp_records = temp_model.train(x_temp, y_temp, lr, n_epochs)
ax.scatter(temp_records[:, 0], temp_records[:, 1],
c=np.arange(len(temp_records)), cmap='Greys')
ax.scatter(temp_records[0, 0], temp_records[0, 1], c='blue', zorder=9)
ax.scatter(temp_records[-1, 0], temp_records[-1, 1], c='red', marker='X', s=100, zorder=9)
else:
temp_model = ShallowNarrowLNN(init_weights)
_, temp_records = temp_model.train(x_temp, y_temp, lr, n_epochs)
ax.scatter(temp_records[:, 0], temp_records[:, 1],
c=np.arange(len(temp_records)), cmap='Greys')
ax.scatter(temp_records[0, 0], temp_records[0, 1], c='blue', zorder=9)
ax.scatter(temp_records[-1, 0], temp_records[-1, 1], c='red', marker='X', s=100, zorder=9)
if what == 'all' or what == 'loss':
contplt = ax.contourf(x, y, np.log(zz+0.001), zorder=-1, cmap='coolwarm', levels=100)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)
cbar = plt.colorbar(contplt, cax=cax)
cbar.set_label('log (Loss)')
ax.set_xlabel("$w_1$")
ax.set_ylabel("$w_2$")
ax.set_xlim(-1.9, 1.9)
ax.set_ylim(-1.9, 1.9)
plt.show()
def plot_loss_landscape():
"""
"""
x_temp, y_temp = gen_samples(10, 1.0, 0.0)
xx, yy = np.mgrid[-1.9:2.0:0.2, -1.9:2.0:0.2]
zz = np.empty_like(xx)
x, y = xx[:, 0], yy[0]
for i, a in enumerate(x):
for j, b in enumerate(y):
temp_model = ShallowNarrowLNN([a, b])
zz[i, j] = temp_model.loss(temp_model.forward(x_temp), y_temp)
temp_model = ShallowNarrowLNN([-1.8, 1.7])
loss_rec_1, w_rec_1 = temp_model.train(x_temp, y_temp, 0.02, 240)
temp_model = ShallowNarrowLNN([1.5, -1.5])
loss_rec_2, w_rec_2 = temp_model.train(x_temp, y_temp, 0.02, 240)
plt.figure(figsize=(12, 8))
ax = plt.subplot(1, 1, 1, projection='3d')
ax.plot_surface(xx, yy, np.log(zz+0.5), cmap='coolwarm', alpha=0.5)
ax.scatter3D(w_rec_1[:, 0], w_rec_1[:, 1], np.log(loss_rec_1+0.5),
c='k', s=50, zorder=9)
ax.scatter3D(w_rec_2[:, 0], w_rec_2[:, 1], np.log(loss_rec_2+0.5),
c='k', s=50, zorder=9)
plt.axis("off")
ax.view_init(45, 260)
plt.show()
def depth_widget(depth):
if depth == 0:
depth_lr_init_interplay(depth, 0.02, 0.9)
else:
depth_lr_init_interplay(depth, 0.01, 0.9)
def lr_widget(lr):
depth_lr_init_interplay(50, lr, 0.9)
def depth_lr_interplay(depth, lr):
depth_lr_init_interplay(depth, lr, 0.9)
def depth_lr_init_interplay(depth, lr, init_weights):
n_epochs = 600
x_train, y_train = gen_samples(100, 2.0, 0.1)
model = DeepNarrowLNN(np.full((1, depth+1), init_weights))
plt.figure(figsize=(10, 5))
plt.plot(model.train(x_train, y_train, lr, n_epochs),
linewidth=3.0, c='m')
plt.title("Training a {}-layer LNN with"
" $\eta=${} initialized with $w_i=${}".format(depth, lr, init_weights), pad=15)
plt.yscale('log')
plt.xlabel('epochs')
plt.ylabel('Log mean squared error')
plt.ylim(0.001, 1.0)
plt.show()
def plot_init_effect():
depth = 15
n_epochs = 250
lr = 0.02
x_train, y_train = gen_samples(100, 2.0, 0.1)
plt.figure(figsize=(12, 6))
for init_w in np.arange(0.7, 1.09, 0.05):
model = DeepNarrowLNN(np.full((1, depth), init_w))
plt.plot(model.train(x_train, y_train, lr, n_epochs),
linewidth=3.0, label="initial weights {:.2f}".format(init_w))
plt.title("Training a {}-layer narrow LNN with $\eta=${}".format(depth, lr), pad=15)
plt.yscale('log')
plt.xlabel('epochs')
plt.ylabel('Log mean squared error')
plt.legend(loc='lower left', ncol=4)
plt.ylim(0.001, 1.0)
plt.show()
class InterPlay:
def __init__(self):
self.lr = [None]
self.depth = [None]
self.success = [None]
self.min_depth, self.max_depth = 5, 65
self.depth_list = np.arange(10, 61, 10)
self.i_depth = 0
self.min_lr, self.max_lr = 0.001, 0.105
self.n_epochs = 600
self.x_train, self.y_train = gen_samples(100, 2.0, 0.1)
self.converged = False
self.button = None
self.slider = None
def train(self, lr, update=False, init_weights=0.9):
if update and self.converged and self.i_depth < len(self.depth_list):
depth = self.depth_list[self.i_depth]
self.plot(depth, lr)
self.i_depth += 1
self.lr.append(None)
self.depth.append(None)
self.success.append(None)
self.converged = False
self.slider.value = 0.005
if self.i_depth < len(self.depth_list):
self.button.value = False
self.button.description = 'Explore!'
self.button.disabled = True
self.button.button_style = 'danger'
else:
self.button.value = False
self.button.button_style = ''
self.button.disabled = True
self.button.description = 'Done!'
time.sleep(1.0)
elif self.i_depth < len(self.depth_list):
depth = self.depth_list[self.i_depth]
# assert self.min_depth <= depth <= self.max_depth
assert self.min_lr <= lr <= self.max_lr
self.converged = False
model = DeepNarrowLNN(np.full((1, depth), init_weights))
self.losses = np.array(model.train(self.x_train, self.y_train, lr, self.n_epochs))
if np.any(self.losses < 1e-2):
success = np.argwhere(self.losses < 1e-2)[0][0]
if np.all((self.losses[success:] < 1e-2)):
self.converged = True
self.success[-1] = success
self.lr[-1] = lr
self.depth[-1] = depth
self.button.disabled = False
self.button.button_style = 'success'
self.button.description = 'Register!'
else:
self.button.disabled = True
self.button.button_style = 'danger'
self.button.description = 'Explore!'
else:
self.button.disabled = True
self.button.button_style = 'danger'
self.button.description = 'Explore!'
self.plot(depth, lr)
def plot(self, depth, lr):
fig = plt.figure(constrained_layout=False, figsize=(10, 8))
gs = fig.add_gridspec(2, 2)
ax1 = fig.add_subplot(gs[0, :])
ax2 = fig.add_subplot(gs[1, 0])
ax3 = fig.add_subplot(gs[1, 1])
ax1.plot(self.losses, linewidth=3.0, c='m')
ax1.set_title("Training a {}-layer LNN with"
" $\eta=${}".format(depth, lr), pad=15, fontsize=16)
ax1.set_yscale('log')
ax1.set_xlabel('epochs')
ax1.set_ylabel('Log mean squared error')
ax1.set_ylim(0.001, 1.0)
ax2.set_xlim(self.min_depth, self.max_depth)
ax2.set_ylim(-10, self.n_epochs)
ax2.set_xlabel('Depth')
ax2.set_ylabel('Learning time (Epochs)')
ax2.set_title("Learning time vs depth", fontsize=14)
ax2.scatter(np.array(self.depth), np.array(self.success), c='r')
# ax3.set_yscale('log')
ax3.set_xlim(self.min_depth, self.max_depth)
ax3.set_ylim(self.min_lr, self.max_lr)
ax3.set_xlabel('Depth')
ax3.set_ylabel('Optimial learning rate')
ax3.set_title("Empirically optimal $\eta$ vs depth", fontsize=14)
ax3.scatter(np.array(self.depth), np.array(self.lr), c='r')
plt.show()
# @title Helper functions
atform = AirtableForm('appn7VdPRseSoMXEG','W1D2_T2','https://portal.neuromatchacademy.org/api/redirect/to/9c55f6cb-cdf9-4429-ac1c-ec44fe64c303')
def gen_samples(n, a, sigma):
"""
Generates `n` samples with `y = z * x + noise(sgma)` linear relation.
Args:
n : int
a : float
sigma : float
Retutns:
x : np.array
y : np.array
"""
assert n > 0
assert sigma >= 0
if sigma > 0:
x = np.random.rand(n)
noise = np.random.normal(scale=sigma, size=(n))
y = a * x + noise
else:
x = np.linspace(0.0, 1.0, n, endpoint=True)
y = a * x
return x, y
class ShallowNarrowLNN:
"""
Shallow and narrow (one neuron per layer) linear neural network
"""
def __init__(self, init_ws):
"""
init_ws: initial weights as a list
"""
assert isinstance(init_ws, list)
assert len(init_ws) == 2
self.w1 = init_ws[0]
self.w2 = init_ws[1]
def forward(self, x):
"""
The forward pass through netwrok y = x * w1 * w2
"""
y = x * self.w1 * self.w2
return y
def loss(self, y_p, y_t):
"""
Mean squared error (L2) with 1/2 for convenience
"""
assert y_p.shape == y_t.shape
mse = ((y_t - y_p)**2).mean()
return mse
def dloss_dw(self, x, y_t):
"""
partial derivative of loss with respect to weights
Args:
x : np.array
y_t : np.array
"""
assert x.shape == y_t.shape
Error = y_t - self.w1 * self.w2 * x
dloss_dw1 = - (2 * self.w2 * x * Error).mean()
dloss_dw2 = - (2 * self.w1 * x * Error).mean()
return dloss_dw1, dloss_dw2
def train(self, x, y_t, eta, n_ep):
"""
Gradient descent algorithm
Args:
x : np.array
y_t : np.array
eta: float
n_ep : int
"""
assert x.shape == y_t.shape
loss_records = np.empty(n_ep) # pre allocation of loss records
weight_records = np.empty((n_ep, 2)) # pre allocation of weight records
for i in range(n_ep):
y_p = self.forward(x)
loss_records[i] = self.loss(y_p, y_t)
dloss_dw1, dloss_dw2 = self.dloss_dw(x, y_t)
self.w1 -= eta * dloss_dw1
self.w2 -= eta * dloss_dw2
weight_records[i] = [self.w1, self.w2]
return loss_records, weight_records
class DeepNarrowLNN:
"""
Deep but thin (one neuron per layer) linear neural network
"""
def __init__(self, init_ws):
"""
init_ws: initial weights as a numpy array
"""
self.n = init_ws.size
self.W = init_ws.reshape(1, -1)
def forward(self, x):
"""
x : np.array
input features
"""
y = np.prod(self.W) * x
return y
def loss(self, y_t, y_p):
"""
mean squared error (L2 loss)
Args:
y_t : np.array
y_p : np.array
"""
assert y_p.shape == y_t.shape
mse = ((y_t - y_p)**2 / 2).mean()
return mse
def dloss_dw(self, x, y_t, y_p):
"""
analytical gradient of weights
Args:
x : np.array
y_t : np.array
y_p : np.array
"""
E = y_t - y_p # = y_t - x * np.prod(self.W)
Ex = np.multiply(x, E).mean()
Wp = np.prod(self.W) / (self.W + 1e-9)
dW = - Ex * Wp
return dW
def train(self, x, y_t, eta, n_epochs):
"""
training using gradient descent
Args:
x : np.array
y_t : np.array
eta: float
n_epochs : int
"""
loss_records = np.empty(n_epochs)
loss_records[:] = np.nan
for i in range(n_epochs):
y_p = self.forward(x)
loss_records[i] = self.loss(y_t, y_p).mean()
dloss_dw = self.dloss_dw(x, y_t, y_p)
if np.isnan(dloss_dw).any() or np.isinf(dloss_dw).any():
return loss_records
self.W -= eta * dloss_dw
return loss_records
#@title Set random seed
#@markdown Executing `set_seed(seed=seed)` you are setting the seed
# for DL its critical to set the random seed so that students can have a
# baseline to compare their results to expected results.
# Read more here: https://pytorch.org/docs/stable/notes/randomness.html
# Call `set_seed` function in the exercises to ensure reproducibility.
import random
import torch
def set_seed(seed=None, seed_torch=True):
if seed is None:
seed = np.random.choice(2 ** 32)
random.seed(seed)
np.random.seed(seed)
if seed_torch:
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
print(f'Random seed {seed} has been set.')
# In case that `DataLoader` is used
def seed_worker(worker_id):
worker_seed = torch.initial_seed() % 2**32
np.random.seed(worker_seed)
random.seed(worker_seed)
#@title Set device (GPU or CPU). Execute `set_device()`
# especially if torch modules used.
# inform the user if the notebook uses GPU or CPU.
def set_device():
device = "cuda" if torch.cuda.is_available() else "cpu"
if device != "cuda":
print("GPU is not enabled in this notebook. \n"
"If you want to enable it, in the menu under `Runtime` -> \n"
"`Hardware accelerator.` and select `GPU` from the dropdown menu")
else:
print("GPU is enabled in this notebook. \n"
"If you want to disable it, in the menu under `Runtime` -> \n"
"`Hardware accelerator.` and select `None` from the dropdown menu")
return device
SEED = 2021
set_seed(seed=SEED)
DEVICE = set_device() | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
--- Section 1: A Shallow Narrow Linear Neural Network*Time estimate: ~30 mins* | # @title Video 1: Shallow Narrow Linear Net
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1F44y117ot", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"6e5JIYsqVvU", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('video 1: Shallow Narrow Linear Net')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Section 1.1: A Shallow Narrow Linear Net To better understand the behavior of neural network training with gradient descent, we start with the incredibly simple case of a shallow narrow linear neural net, since state-of-the-art models are impossible to dissect and comprehend with our current mathematical tools.The model we use has one hidden layer, with only one neuron, and two weights. We consider the squared error (or L2 loss) as the cost function. As you may have already guessed, we can visualize the model as a neural network:or by its computation graph:or on a rare occasion, even as a reasonably compact mapping:$$ loss = (y - w_1 \cdot w_2 \cdot x)^2 $$Implementing a neural network from scratch without using any Automatic Differentiation tool is rarely necessary. The following two exercises are therefore **Bonus** (optional) exercises. Please ignore them if you have any time-limits or pressure and continue to Section 1.2. Analytical Exercise 1.1: Loss Gradients (Optional)Once again, we ask you to calculate the network gradients analytically, since you will need them for the next exercise. We understand how annoying this is.$\dfrac{\partial{loss}}{\partial{w_1}} = ?$$\dfrac{\partial{loss}}{\partial{w_2}} = ?$--- Solution$\dfrac{\partial{loss}}{\partial{w_1}} = -2 \cdot w_2 \cdot x \cdot (y - w_1 \cdot w_2 \cdot x)$$\dfrac{\partial{loss}}{\partial{w_2}} = -2 \cdot w_1 \cdot x \cdot (y - w_1 \cdot w_2 \cdot x)$--- Coding Exercise 1.1: Implement simple narrow LNN (Optional)Next, we ask you to implement the `forward` pass for our model from scratch without using PyTorch.Also, although our model gets a single input feature and outputs a single prediction, we could calculate the loss and perform training for multiple samples at once. This is the common practice for neural networks, since computers are incredibly fast doing matrix (or tensor) operations on batches of data, rather than processing samples one at a time through `for` loops. Therefore, for the `loss` function, please implement the **mean** squared error (MSE), and adjust your analytical gradients accordingly when implementing the `dloss_dw` function.Finally, complete the `train` function for the gradient descent algorithm:\begin{equation}\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \eta \nabla loss (\mathbf{w}^{(t)})\end{equation} | class ShallowNarrowExercise:
"""Shallow and narrow (one neuron per layer) linear neural network
"""
def __init__(self, init_weights):
"""
Args:
init_weights (list): initial weights
"""
assert isinstance(init_weights, (list, np.ndarray, tuple))
assert len(init_weights) == 2
self.w1 = init_weights[0]
self.w2 = init_weights[1]
def forward(self, x):
"""The forward pass through netwrok y = x * w1 * w2
Args:
x (np.ndarray): features (inputs) to neural net
returns:
(np.ndarray): neural network output (prediction)
"""
#################################################
## Implement the forward pass to calculate prediction
## Note that prediction is not the loss
# Complete the function and remove or comment the line below
raise NotImplementedError("Forward Pass `forward`")
#################################################
y = ...
return y
def dloss_dw(self, x, y_true):
"""Gradient of loss with respect to weights
Args:
x (np.ndarray): features (inputs) to neural net
y_true (np.ndarray): true labels
returns:
(float): mean gradient of loss with respect to w1
(float): mean gradient of loss with respect to w2
"""
assert x.shape == y_true.shape
#################################################
## Implement the gradient computation function
# Complete the function and remove or comment the line below
raise NotImplementedError("Gradient of Loss `dloss_dw`")
#################################################
dloss_dw1 = ...
dloss_dw2 = ...
return dloss_dw1, dloss_dw2
def train(self, x, y_true, lr, n_ep):
"""Training with Gradient descent algorithm
Args:
x (np.ndarray): features (inputs) to neural net
y_true (np.ndarray): true labels
lr (float): learning rate
n_ep (int): number of epochs (training iterations)
returns:
(list): training loss records
(list): training weight records (evolution of weights)
"""
assert x.shape == y_true.shape
loss_records = np.empty(n_ep) # pre allocation of loss records
weight_records = np.empty((n_ep, 2)) # pre allocation of weight records
for i in range(n_ep):
y_prediction = self.forward(x)
loss_records[i] = loss(y_prediction, y_true)
dloss_dw1, dloss_dw2 = self.dloss_dw(x, y_true)
#################################################
## Implement the gradient descent step
# Complete the function and remove or comment the line below
raise NotImplementedError("Training loop `train`")
#################################################
self.w1 -= ...
self.w2 -= ...
weight_records[i] = [self.w1, self.w2]
return loss_records, weight_records
def loss(y_prediction, y_true):
"""Mean squared error
Args:
y_prediction (np.ndarray): model output (prediction)
y_true (np.ndarray): true label
returns:
(np.ndarray): mean squared error loss
"""
assert y_prediction.shape == y_true.shape
#################################################
## Implement the MEAN squared error
# Complete the function and remove or comment the line below
raise NotImplementedError("Loss function `loss`")
#################################################
mse = ...
return mse
#add event to airtable
atform.add_event('Coding Exercise 1.1: Implement simple narrow LNN')
set_seed(seed=SEED)
n_epochs = 211
learning_rate = 0.02
initial_weights = [1.4, -1.6]
x_train, y_train = gen_samples(n=73, a=2.0, sigma=0.2)
x_eval = np.linspace(0.0, 1.0, 37, endpoint=True)
## Uncomment to run
# sn_model = ShallowNarrowExercise(initial_weights)
# loss_log, weight_log = sn_model.train(x_train, y_train, learning_rate, n_epochs)
# y_eval = sn_model.forward(x_eval)
# plot_x_y_(x_train, y_train, x_eval, y_eval, loss_log, weight_log) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D2_LinearDeepLearning/solutions/W1D2_Tutorial2_Solution_46492cd6.py)*Example output:* Section 1.2: Learning landscapes | # @title Video 2: Training Landscape
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Nv411J71X", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"k28bnNAcOEg", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 2: Training Landscape')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
As you may have already asked yourself, we can analytically find $w_1$ and $w_2$ without using gradient descent:\begin{equation}w_1 \cdot w_2 = \dfrac{y}{x}\end{equation}In fact, we can plot the gradients, the loss function and all the possible solutions in one figure. In this example, we use the $y = 1x$ mapping:**Blue ribbon**: shows all possible solutions: $~ w_1 w_2 = \dfrac{y}{x} = \dfrac{x}{x} = 1 \Rightarrow w_1 = \dfrac{1}{w_2}$**Contour background**: Shows the loss values, red being higher loss**Vector field (arrows)**: shows the gradient vector field. The larger yellow arrows show larger gradients, which correspond to bigger steps by gradient descent.**Scatter circles**: the trajectory (evolution) of weights during training for three different initializations, with blue dots marking the start of training and red crosses ( **x** ) marking the end of training. You can also try your own initializations (keep the initial values between `-2.0` and `2.0`) as shown here:```pythonplot_vector_field('all', [1.0, -1.0])```Finally, if the plot is too crowded, feel free to pass one of the following strings as argument:```pythonplot_vector_field('vectors') for vector fieldplot_vector_field('trajectory') for training trajectoryplot_vector_field('loss') for loss contour```**Think!**Explore the next two plots. Try different initial values. Can you find the saddle point? Why does training slow down near the minima? | plot_vector_field('all') | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Here, we also visualize the loss landscape in a 3-D plot, with two training trajectories for different initial conditions.Note: the trajectories from the 3D plot and the previous plot are independent and different. | plot_loss_landscape()
# @title Student Response
from ipywidgets import widgets
text=widgets.Textarea(
value='Type your answer here and click on `Submit!`',
placeholder='Type something',
description='',
disabled=False
)
button = widgets.Button(description="Submit!")
display(text,button)
def on_button_clicked(b):
atform.add_answer('q1', text.value)
print("Submission successful!")
button.on_click(on_button_clicked)
# @title Video 3: Training Landscape - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1py4y1j7cv", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"0EcUGgxOdkI", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 3: Training Landscape - Discussiond')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
--- Section 2: Depth, Learning rate, and initialization*Time estimate: ~45 mins* Successful deep learning models are often developed by a team of very clever people, spending many many hours "tuning" learning hyperparameters, and finding effective initializations. In this section, we look at three basic (but often not simple) hyperparameters: depth, learning rate, and initialization. Section 2.1: The effect of depth | # @title Video 4: Effect of Depth
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1z341167di", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"Ii_As9cRR5Q", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 4: Effect of Depth')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Why might depth be useful? What makes a network or learning system "deep"? The reality is that shallow neural nets are often incapable of learning complex functions due to data limitations. On the other hand, depth seems like magic. Depth can change the functions a network can represent, the way a network learns, and how a network generalizes to unseen data. So let's look at the challenges that depth poses in training a neural network. Imagine a single input, single output linear network with 50 hidden layers and only one neuron per layer (i.e. a narrow deep neural network). The output of the network is easy to calculate:$$ prediction = x \cdot w_1 \cdot w_2 \cdot \cdot \cdot w_{50} $$If the initial value for all the weights is $w_i = 2$, the prediction for $x=1$ would be **exploding**: $y_p = 2^{50} \approx 1.1256 \times 10^{15}$. On the other hand, for weights initialized to $w_i = 0.5$, the output is **vanishing**: $y_p = 0.5^{50} \approx 8.88 \times 10^{-16}$. Similarly, if we recall the chain rule, as the graph gets deeper, the number of elements in the chain multiplication increases, which could lead to exploding or vanishing gradients. To avoid such numerical vulnerablities that could impair our training algorithm, we need to understand the effect of depth. Interactive Demo 2.1: Depth widgetUse the widget to explore the impact of depth on the training curve (loss evolution) of a deep but narrow neural network.**Think!**Which networks trained the fastest? Did all networks eventually "work" (converge)? What is the shape of their learning trajectory? | # @markdown Make sure you execute this cell to enable the widget!
_ = interact(depth_widget,
depth = IntSlider(min=0, max=51,
step=5, value=0,
continuous_update=False))
# @title Video 5: Effect of Depth - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Qq4y1H7uk", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"EqSDkwmSruk", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 5: Effect of Depth - Discussion')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Section 2.2: Choosing a learning rate The learning rate is a common hyperparameter for most optimization algorithms. How should we set it? Sometimes the only option is to try all the possibilities, but sometimes knowing some key trade-offs will help guide our search for good hyperparameters. | # @title Video 6: Learning Rate
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV11f4y157MT", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"w_GrCVM-_Qo", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 6: Learning Rate')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Interactive Demo 2.2: Learning rate widgetHere, we fix the network depth to 50 layers. Use the widget to explore the impact of learning rate $\eta$ on the training curve (loss evolution) of a deep but narrow neural network.**Think!**Can we say that larger learning rates always lead to faster learning? Why not? | # @markdown Make sure you execute this cell to enable the widget!
_ = interact(lr_widget,
lr = FloatSlider(min=0.005, max=0.045, step=0.005, value=0.005,
continuous_update=False, readout_format='.3f',
description='eta'))
# @title Video 7: Learning Rate - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Aq4y1p7bh", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"cmS0yqImz2E", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 7: Learning Rate - Discussion')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Section 2.3: Depth vs Learning Rate | # @title Video 8: Depth and Learning Rate
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1V44y1177e", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"J30phrux_3k", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 8: Depth and Learning Rate')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Interactive Demo 2.3: Depth and Learning-Rate **Important instruction**The exercise starts with 10 hidden layers. Your task is to find the learning rate that delivers fast but robust convergence (learning). When you are confident about the learning rate, you can **Register** the optimal learning rate for the given depth. Once you press register, a deeper model is instantiated, so you can find the next optimal learning rate. The Register button turns green only when the training converges, but does not imply the fastest convergence. Finally, be patient :) the widgets are slow.**Think!**Can you explain the relationship between the depth and optimal learning rate? | # @markdown Make sure you execute this cell to enable the widget!
intpl_obj = InterPlay()
intpl_obj.slider = FloatSlider(min=0.005, max=0.105, step=0.005, value=0.005,
layout=Layout(width='500px'),
continuous_update=False,
readout_format='.3f',
description='eta')
intpl_obj.button = ToggleButton(value=intpl_obj.converged, description='Register')
widgets_ui = HBox([intpl_obj.slider, intpl_obj.button])
widgets_out = interactive_output(intpl_obj.train,
{'lr': intpl_obj.slider,
'update': intpl_obj.button,
'init_weights': fixed(0.9)})
display(widgets_ui, widgets_out)
# @title Video 9: Depth and Learning Rate - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV15q4y1p7Uq", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"7Fl8vH7cgco", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 9: Depth and Learning Rate - Discussion')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Section 2.4: Why initialization is important | # @title Video 10: Initialization Matters
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1UL411J7vu", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"KmqCz95AMzY", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 10: Initialization Matters')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
We’ve seen, even in the simplest of cases, that depth can slow learning. Why? From the chain rule, gradients are multiplied by the current weight at each layer, so the product can vanish or explode. Therefore, weight initialization is a fundamentally important hyperparameter.Although in practice initial values for learnable parameters are often sampled from different $\mathcal{Uniform}$ or $\mathcal{Normal}$ probability distribution, here we use a single value for all the parameters.The figure below shows the effect of initialization on the speed of learning for the deep but narrow LNN. We have excluded initializations that lead to numerical errors such as `nan` or `inf`, which are the consequence of smaller or larger initializations. | # @markdown Make sure you execute this cell to see the figure!
plot_init_effect()
# @title Video 11: Initialization Matters Explained
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1hM4y1T7gJ", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"vKktGdiQDsE", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 11: Initialization Matters Explained')
display(out) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
--- SummaryIn the second tutorial, we have learned what is the training landscape, and also we have see in depth the effect of the depth of the network and the learning rate, and their interplay. Finally, we have seen that initialization matters and why we need smart ways of initialization. | # @title Video 12: Tutorial 2 Wrap-up
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1P44y117Pd", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"r3K8gtak3wA", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 12: Tutorial 2 Wrap-up')
display(out)
# @title Airtable Submission Link
from IPython import display as IPydisplay
IPydisplay.HTML(
f"""
<div>
<a href= "{atform.url()}" target="_blank">
<img src="https://github.com/NeuromatchAcademy/course-content-dl/blob/main/tutorials/static/AirtableSubmissionButton.png?raw=1"
alt="button link to Airtable" style="width:410px"></a>
</div>""" ) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
--- Bonus Hyperparameter interactionFinally, let's put everything we learned together and find best initial weights and learning rate for a given depth. By now you should have learned the interactions and know how to find the optimal values quickly. If you get `numerical overflow` warnings, don't be discouraged! They are often caused by "exploding" or "vanishing" gradients.**Think!**Did you experience any surprising behaviour or difficulty finding the optimal parameters? | # @markdown Make sure you execute this cell to enable the widget!
_ = interact(depth_lr_init_interplay,
depth = IntSlider(min=10, max=51, step=5, value=25,
continuous_update=False),
lr = FloatSlider(min=0.001, max=0.1,
step=0.005, value=0.005,
continuous_update=False,
readout_format='.3f',
description='eta'),
init_weights = FloatSlider(min=0.1, max=3.0,
step=0.1, value=0.9,
continuous_update=False,
readout_format='.3f',
description='initial weights')) | _____no_output_____ | CC-BY-4.0 | tutorials/W1D2_LinearDeepLearning/student/W1D2_Tutorial2.ipynb | eduardojdiniz/course-content-dl |
Web scraping with PythonThis notebook demonstrates how you can use the Python programming language to scrape information from a web page. The goal today: Scrape the main table on [the first page of Maryland's list of WARN letters](https://www.dllr.state.md.us/employment/warn.shtml) and, if time, write the data to a CSV.If you're relatively new to Python, it might be helpful to have [this Python syntax cheat sheet](Python%20syntax%20cheat%20sheet.ipynb) open in another tab as you work through this notebook. Table of contents- [Using Jupyter notebooks](Using-Jupyter-notebooks)- [What _is_ a web page, anyway?](What-is-a-web-page,-anyway?)- [Inspect the source](Inspect-the-source)- [Import libraries](Import-libraries)- [Request the page](Request-the-page)- [Turn your HTML into soup](Turn-your-HTML-into-soup)- [Targeting and extracting data](Targeting-and-extracting-data)- [Write the results to file](Write-the-results-to-file) Using Jupyter notebooksThere are several ways to write and run Python code on your computer. One way -- the method we're using today -- is to use [Jupyter notebooks](https://jupyter.org/), which run in your browser and allow you to intersperse documentation with your code. They're handy for bundling your code with a human-readable explanation of what's happening at each step. Check out some examples from the [L.A. Times](https://github.com/datadesk/notebooks) and [BuzzFeed News](https://github.com/BuzzFeedNews/everythingdata-and-analyses).**To add a new cell to your notebook**: Click the + button in the menu or press the `b` button on your keyboard.**To run a cell of code**: Select the cell and click the "Run" button in the menu, or you can press Shift+Enter.**One common gotcha**: The notebook doesn't "know" about code you've written until you've _run_ the cell containing it. For example, if you define a variable called `my_name` in one cell, and later, when you try to access that variable in another cell but get an error that says `NameError: name 'my_name' is not defined`, the most likely solution is to run (or re-run) the cell in which you defined `my_name`. What _is_ a web page, anyway?Generally, a web page consists of a bunch of specifically formatted text files stored on a computer (a _server_) that's probably sitting on a rack in a giant data center somewhere.Mostly you'll be dealing with `.html` (HyperText Markup Language) files that might include references to `.css` (Cascading Style Sheet) files, which determine how the page looks, and/or `.js` (JavaScript) files, which add interactivity, and other specially formatted text files.Today, we'll focus on the HTML, which gives structure to the page.Most HTML elements are represented by a pair of tags -- an opening tag and a closing tag.A table, for example, starts with `` and ends with ``. The first tag tells the browser: "Hey! I got a table here! Render it as a table." The closing tag (note the forward slash!) tells the browser: "Hey! I'm all done with that table, thanks." Inside the table are nested more HTML tags representing rows (``) and cells (``).HTML elements can have any number of attributes, such as classes --``-- styles --``-- hyperlinks to other pages --`Click here to visit IRE's website`-- and IDs --``-- that will be useful to know about when we're scraping. Inspect the sourceYou can look at the HTML that makes up a web page by _inspecting the source_ in a web browser. We like Chrome and Firefox for this; today, we'll use Chrome.You can inspect specific elements on the page by right-clicking on the page and selecting "Inspect" or "Inspect Element" from the context menu that pops up. Hover over elements in the "Elements" tab to highlight them on the page.To examine all of the source code that makes up a page, you can "view source." In Chrome, hit `Ctrl+U` on a PC or `⌘+Opt+U` on a Mac. (It's also in the menu bar: View > Developer > View Page Source.)You'll get a page showing you all of the HTML code that makes up that page. Ignore 99% of it and try to locate the element(s) that you want to target (use `Ctrl+F` on a PC and `⌘+F` to find).Open up a Chrome browser and inspect the table on the [the first page of Maryland's list of WARN letters](https://www.dllr.state.md.us/employment/warn.shtml). Find the table we want to scrape.Is it the only table on the page? If not, does it have any attributes that would allow you to target it? Import librariesStep one is to _import_ two third-party Python libraries that will help us scrape this page:- `requests` is the de facto standard for making HTTP requests, similar to what happens when you type a URL into a browser window and hit enter.- `bs4`, or BeautifulSoup, is a popular library for parsing HTML into a data structure that Python can work with.These libraries are installed separately from Python on a per-project basis ([read more about our recommendations for setting up Python projects here](https://docs.google.com/document/d/1cYmpfZEZ8r-09Q6Go917cKVcQk_d0P61gm0q8DAdIdg/editheading=h.od2v1nkge5t1)).Run this cell (you'll only have to do this once): | import requests
import bs4 | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Request the pageNext, we'll use the `get()` method of the `requests` library (which we just imported) to grab the web page.While we're at it, we'll _assign_ all the stuff that comes back to a new variable using `=`.The variable name is arbitrary, but it's usually good to pick something that describes the value it's pointing to.Notice that the URL we're grabbing is wrapped in quotes, making it a _string_ that Python will interepret as text (as opposed to numbers, booleans, etc.). You can read up more on Python data types and variable assignment [here](Python%20syntax%20cheat%20sheet.ipynb).Run these two cells: | URL = 'http://www.dllr.state.md.us/employment/warn.shtml'
warn_page = requests.get(URL) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Nothing appears to have happened, which is (usually) a good sign.If you want to make sure that your request was successful, you can check the `status_code` attribute of the Python object that was returned: | warn_page.status_code | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
A `200` code means all is well. `404` means the page wasn't found, etc. ([Here's one of our favorite lists of HTTP status codes](https://http.cat/) ([or here, if you prefer dogs](https://httpstatusdogs.com/)).)The object being stored as the `warn_page` variable came back with a lot of potentially useful information we could access. Today, we're mostly interested in the `.text` attribute -- the HTML that makes up the web page, same as if we'd viewed the page source. Let's take a look: | warn_page.text | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
✍️ Try it yourselfUse the code blocks below to experiment with requesting web pages and checking out the HTML that gets returned.Some ideas to get you started:- `'http://ire.org'`- `'https://web.archive.org/web/20031202214318/http://www.tdcj.state.tx.us:80/stat/finalmeals.htm'`- `'https://www.nrc.gov/reactors/operating/list-power-reactor-units.html'` Turn your HTML into soupThe HTML in the `.text` attribute of the request object is just a string -- a big ol' chunk of text.Before we start targeting and extracting pieces of data in the HTML, we need to turn that chunk of text into a data structure that Python can work with. That's where the [BeautifulSoup](https://www.crummy.com/software/BeautifulSoup/bs4/doc/) (`bs4`) library comes in.We'll create a new instance of a `BeautifulSoup` object, which lives under the top-level `bs4` library that we imported earlier. We need to give it two things:- The HTML we'd like to parse -- `warn_page.text`- A string with the name of the type of parser to use -- `html.parser` is the default and usually fine, but [there are other options](https://www.crummy.com/software/BeautifulSoup/bs4/doc/installing-a-parser)We'll save the parsed HTML as a new variable, `soup`. | soup = bs4.BeautifulSoup(warn_page.text, 'html.parser') | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Nothing happened, which is good! You can take a look at what `soup` is, but it looks pretty much like `warn_page.text`: | soup | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
If you want to be sure, you can use the Python function `type()` to check what sort of object you're dealing with: | # the `str` type means a string, or text
type(warn_page.text)
# the `bs4.BeautifulSoup` type means we successfully created the object
type(soup) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
✍️ Try it yourselfUse the code blocks below to experiment fetching HTML and turning it into soup (if you fetched some pages earlier and saved them as variables, that'd be a good start). Targeting and extracting dataNow that we have BeautifulSoup object loaded up, we can go hunting for the specific HTML elements that contain the data we need. Our general strategy:1. Find the main table with the data we want to grab2. Get a list of rows (the `tr` element, which stands for "table row") in that table3. Use a Python `for loop` to go through each table row and find the data inside it (`td`, or "table data")To accomplish this, we'll use two `bs4` methods:- [`find()`](https://www.crummy.com/software/BeautifulSoup/bs4/doc/find), which returns the first element that matches whatever criteria you hand it- [`find_all()`](https://www.crummy.com/software/BeautifulSoup/bs4/doc/find-all), which returns a _list_ of elements that match the criteria. ([Here's how Python lists work](Python%20syntax%20cheat%20sheet.ipynbLists).) Find the tableTo start with, we need to find the table. There are several ways to accomplish this, but because this is the only table on the page (view source and `Ctrl+F` to search for `<table` to confirm), we can simply say, "Look through the `soup` object and find the table tag."Translated, the code is: `soup.find('table')`. While we're at it, save the results of that search to a new variable, `table`.Run these cells: | table = soup.find('table')
table | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Find the rows in the tableNext, use the `find_all()` method to drill down and get a list of rows in the table: | rows = table.find_all('tr')
rows | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
To see how many items are in this list -- in other words, how many rows are in the table -- you can use the `len()` function: | len(rows) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Loop through the rows and extract the dataNext, we can use a [`for` loop](Python%20syntax%20cheat%20sheet.ipynbfor-loops) to go through the list of rows and start grabbing data from each one.Quick refresher on _for loop_ syntax: Start with the word `for` (lowercase), then a variable name to stand in for each item in the list that you're looping over, then the word `in` (lowercase), then the name of the list holding the items (`rows`, in our case), then a colon, then an indented block of code describing what we're doing to each item in the list.Each piece of data in the row will be stored in a `td` tag, which stands for "table data." So inside the loop -- in the indented block -- we'll use the `find_all()` method to get a list of every `td` tag inside the row. And from there, we can access the content inside each tag.Our goal is to end up with a _list_ of data for each row that we will eventually write out to a file. Typically you'd probably do the work of looping and inspecting the results, step by step, in one code cell. But to show the thinking of how you might approach this (and to practice the syntax), we'll start by just printing out each row and then build from there. (`print('='*80)` will print a line of 80 equals signs -- a way to help us see exactly what we're working with in each row.) | for row in rows:
print(row)
print('='*80) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Notice that the first item that prints is the header row with the column labels. You are free to keep these headers if you want, but I typically skip that row and define my own list of column names.(Another thing to consider: On better-constructed web pages, the cells in the header row will be represented by `th` ("table header") tags, not `td` ("table data") tags. The next step in our `for` loop is, "Find all of the `td` tags in this row," so that would be something you would need to deal with.)We can skip the first row by using _list slicing_: adding square brackets after the name of the list with some instructions about which items in the list we want to select.Here, the syntax would be: `rows[1:]`, which means, take everything in the `rows` list starting with the item in position 1 (the second item) to the end of the list. Like many programming languages, Python starts counting at 0, so the result will leave off the first item in the list -- i.e. the item in position 0, i.e. the headers. | for row in rows[1:]:
print(row)
print('='*80) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Now we're cooking with gas. Let's start pulling out the data in each row. Start by using `find_all()` to grab a list of `td` tags: | for row in rows[1:]:
cells = row.find_all('td')
print(cells)
print('='*80) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Now we have, for each row, a _list_ of `td` tags. Next step is to look at the table and start grabbing specific values based on their position in the list and assigning them to human-readable variable names.Quick refresher on list syntax: To access a specific item in a list, use square brackets `[]` and the index number of the item you'd like to access. For instance, to get the first cell in the row -- the date that each WARN report was issued -- use `[0]`. | for row in rows[1:]:
cells = row.find_all('td')
warn_date = cells[0]
print(warn_date)
print('='*80) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
This is returning the entire `Tag` object -- we just want the contents inside it. You can access the `.text` attribute of the tag to get the text inside: | for row in rows[1:]:
cells = row.find_all('td')
warn_date = cells[0].text
print(warn_date) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
In the next cell (`[1]`), the `.text` attribute will give you the NAICS code. In the third cell (`[2]`) you'll get the name of the business. Etc.It's also generally good practice to trim off external whitespace for each value, and you can use the Python built-in string method `strip()` to accomplish this as you march across the row.Which gets us this far: | for row in rows[1:]:
cells = row.find_all('td')
warn_date = cells[0].text.strip()
naics_code = cells[1].text.strip()
biz = cells[2].text.strip()
print(warn_date, naics_code, biz) | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
✍️ Try it yourselfNow that you've gotten this far, see if you can isolate the other pieces of data in each row. | for row in rows[1:]:
cells = row.find_all('td')
warn_date = cells[0].text.strip()
naics_code = cells[1].text.strip()
biz = cells[2].text.strip()
# address
# wia_code
# total_employees
# effective_date
# type_code
# print() | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Write the results to fileNow that we've targeted our lists of data for each row, we can use Python's built-in [`csv`](https://docs.python.org/3/library/csv.html) module to write each list to a CSV file.First, import the csv module. | import csv | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Now define a list of headers to match the data (each column header will be a string) -- run this cell: | HEADERS = [
'warn_date',
'naics_code',
'biz',
'address',
'wia_code',
'total_employees',
'effective_date',
'type_code'
] | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Now, using something called a `with` block, open a new CSV file to write to and write some code to do the following things:- Create a `csv.writer` object- Write out the list of headers using the `writerow()` method of the `csv.writer` object- Drop in the `for` loop you just wrote and, instead of just printing the contents of each cell, create a list of items and use the `writerow()` method of the `csv.writer` object to write your list of data to file | # create a file called 'warn-data.csv' in write ('w') mode
# specify that newlines are terminated by an empty string (this deals with a PC-specific problem)
# and use the `as` keyword to name the open file handler (the variable name `outfile` is arbitrary)
with open('warn-data.csv', 'w', newline='') as outfile:
# go to the csv module we imported and make a new .writer object attached to the open file
# and save it to a variable
writer = csv.writer(outfile)
# write out the list of headers
writer.writerow(HEADERS)
# paste in the for loop you wrote earlier here -- watch the indentation!
# it should be at this indentation level =>
# for row in rows[1:]:
# cells = row.find_all('td')
# etc. ...
# but at the end, instead of `print(warn_date, naics_code, ...etc.)`
# make it something like
# data_out = [warn_date, naics_code, ...etc.]
# `writer.writerow(data_out)` | _____no_output_____ | MIT | Web scraping with Python.ipynb | allanjamesvestal/teaching-guide-python-scraping |
Lambda School Data Science, Unit 2: Predictive Modeling Kaggle Challenge, Module 3 Assignment- [ ] [Review requirements for your portfolio project](https://lambdaschool.github.io/ds/unit2/portfolio-project/ds6), then choose your dataset, and [submit this form](https://forms.gle/nyWURUg65x1UTRNV9), due today at 4pm Pacific.- [ ] Continue to participate in our Kaggle challenge.- [ ] Try xgboost.- [ ] Get your model's permutation importances.- [ ] Try feature selection with permutation importances.- [ ] Submit your predictions to our Kaggle competition. (Go to our Kaggle InClass competition webpage. Use the blue **Submit Predictions** button to upload your CSV file. Or you can use the Kaggle API to submit your predictions.)- [ ] Commit your notebook to your fork of the GitHub repo. Stretch Goals Doing- [ ] Add your own stretch goal(s) !- [ ] Do more exploratory data analysis, data cleaning, feature engineering, and feature selection.- [ ] Try other categorical encodings.- [ ] Try other Python libraries for gradient boosting.- [ ] Look at the bonus notebook in the repo, about monotonic constraints with gradient boosting.- [ ] Make visualizations and share on Slack. ReadingTop recommendations in _**bold italic:**_ Permutation Importances- _**[Kaggle / Dan Becker: Machine Learning Explainability](https://www.kaggle.com/dansbecker/permutation-importance)**_- [Christoph Molnar: Interpretable Machine Learning](https://christophm.github.io/interpretable-ml-book/feature-importance.html) (Default) Feature Importances - [Ando Saabas: Selecting good features, Part 3, Random Forests](https://blog.datadive.net/selecting-good-features-part-iii-random-forests/) - [Terence Parr, et al: Beware Default Random Forest Importances](https://explained.ai/rf-importance/index.html) Gradient Boosting - [A Gentle Introduction to the Gradient Boosting Algorithm for Machine Learning](https://machinelearningmastery.com/gentle-introduction-gradient-boosting-algorithm-machine-learning/) - _**[A Kaggle Master Explains Gradient Boosting](http://blog.kaggle.com/2017/01/23/a-kaggle-master-explains-gradient-boosting/)**_ - [_An Introduction to Statistical Learning_](http://www-bcf.usc.edu/~gareth/ISL/ISLR%20Seventh%20Printing.pdf) Chapter 8 - [Gradient Boosting Explained](http://arogozhnikov.github.io/2016/06/24/gradient_boosting_explained.html) - _**[Boosting](https://www.youtube.com/watch?v=GM3CDQfQ4sw) (2.5 minute video)**_ Categorical encoding for trees- [Are categorical variables getting lost in your random forests?](https://roamanalytics.com/2016/10/28/are-categorical-variables-getting-lost-in-your-random-forests/)- [Beyond One-Hot: An Exploration of Categorical Variables](http://www.willmcginnis.com/2015/11/29/beyond-one-hot-an-exploration-of-categorical-variables/)- _**[Categorical Features and Encoding in Decision Trees](https://medium.com/data-design/visiting-categorical-features-and-encoding-in-decision-trees-53400fa65931)**_- _**[Coursera — How to Win a Data Science Competition: Learn from Top Kagglers — Concept of mean encoding](https://www.coursera.org/lecture/competitive-data-science/concept-of-mean-encoding-b5Gxv)**_- [Mean (likelihood) encodings: a comprehensive study](https://www.kaggle.com/vprokopev/mean-likelihood-encodings-a-comprehensive-study)- [The Mechanics of Machine Learning, Chapter 6: Categorically Speaking](https://mlbook.explained.ai/catvars.html) Imposter Syndrome- [Effort Shock and Reward Shock (How The Karate Kid Ruined The Modern World)](http://www.tempobook.com/2014/07/09/effort-shock-and-reward-shock/)- [How to manage impostor syndrome in data science](https://towardsdatascience.com/how-to-manage-impostor-syndrome-in-data-science-ad814809f068)- ["I am not a real data scientist"](https://brohrer.github.io/imposter_syndrome.html)- _**[Imposter Syndrome in Data Science](https://caitlinhudon.com/2018/01/19/imposter-syndrome-in-data-science/)**_ Python libraries for Gradient Boosting- [scikit-learn Gradient Tree Boosting](https://scikit-learn.org/stable/modules/ensemble.htmlgradient-boosting) — slower than other libraries, but [the new version may be better](https://twitter.com/amuellerml/status/1129443826945396737) - Anaconda: already installed - Google Colab: already installed- [xgboost](https://xgboost.readthedocs.io/en/latest/) — can accept missing values and enforce [monotonic constraints](https://xiaoxiaowang87.github.io/monotonicity_constraint/) - Anaconda, Mac/Linux: `conda install -c conda-forge xgboost` - Windows: `conda install -c anaconda py-xgboost` - Google Colab: already installed- [LightGBM](https://lightgbm.readthedocs.io/en/latest/) — can accept missing values and enforce [monotonic constraints](https://blog.datadive.net/monotonicity-constraints-in-machine-learning/) - Anaconda: `conda install -c conda-forge lightgbm` - Google Colab: already installed- [CatBoost](https://catboost.ai/) — can accept missing values and use [categorical features](https://catboost.ai/docs/concepts/algorithm-main-stages_cat-to-numberic.html) without preprocessing - Anaconda: `conda install -c conda-forge catboost` - Google Colab: `pip install catboost` Categorical Encodings**1.** The article **[Categorical Features and Encoding in Decision Trees](https://medium.com/data-design/visiting-categorical-features-and-encoding-in-decision-trees-53400fa65931)** mentions 4 encodings:- **"Categorical Encoding":** This means using the raw categorical values as-is, not encoded. Scikit-learn doesn't support this, but some tree algorithm implementations do. For example, [Catboost](https://catboost.ai/), or R's [rpart](https://cran.r-project.org/web/packages/rpart/index.html) package.- **Numeric Encoding:** Synonymous with Label Encoding, or "Ordinal" Encoding with random order. We can use [category_encoders.OrdinalEncoder](https://contrib.scikit-learn.org/categorical-encoding/ordinal.html).- **One-Hot Encoding:** We can use [category_encoders.OneHotEncoder](http://contrib.scikit-learn.org/categorical-encoding/onehot.html).- **Binary Encoding:** We can use [category_encoders.BinaryEncoder](http://contrib.scikit-learn.org/categorical-encoding/binary.html).**2.** The short video **[Coursera — How to Win a Data Science Competition: Learn from Top Kagglers — Concept of mean encoding](https://www.coursera.org/lecture/competitive-data-science/concept-of-mean-encoding-b5Gxv)** introduces an interesting idea: use both X _and_ y to encode categoricals.Category Encoders has multiple implementations of this general concept:- [CatBoost Encoder](http://contrib.scikit-learn.org/categorical-encoding/catboost.html)- [James-Stein Encoder](http://contrib.scikit-learn.org/categorical-encoding/jamesstein.html)- [Leave One Out](http://contrib.scikit-learn.org/categorical-encoding/leaveoneout.html)- [M-estimate](http://contrib.scikit-learn.org/categorical-encoding/mestimate.html)- [Target Encoder](http://contrib.scikit-learn.org/categorical-encoding/targetencoder.html)- [Weight of Evidence](http://contrib.scikit-learn.org/categorical-encoding/woe.html)Category Encoder's mean encoding implementations work for regression problems or binary classification problems. For multi-class classification problems, you will need to temporarily reformulate it as binary classification. For example:```pythonencoder = ce.TargetEncoder(min_samples_leaf=..., smoothing=...) Both parameters > 1 to avoid overfittingX_train_encoded = encoder.fit_transform(X_train, y_train=='functional')X_val_encoded = encoder.transform(X_train, y_val=='functional')```**3.** The **[dirty_cat](https://dirty-cat.github.io/stable/)** library has a Target Encoder implementation that works with multi-class classification.```python dirty_cat.TargetEncoder(clf_type='multiclass-clf')```It also implements an interesting idea called ["Similarity Encoder" for dirty categories](https://www.slideshare.net/GaelVaroquaux/machine-learning-on-non-curated-data-154905090).However, it seems like dirty_cat doesn't handle missing values or unknown categories as well as category_encoders does. And you may need to use it with one column at a time, instead of with your whole dataframe.**4. [Embeddings](https://www.kaggle.com/learn/embeddings)** can work well with sparse / high cardinality categoricals._**I hope it’s not too frustrating or confusing that there’s not one “canonical” way to encode categorcals. It’s an active area of research and experimentation! Maybe you can make your own contributions!**_ | # If you're in Colab...
import os, sys
in_colab = 'google.colab' in sys.modules
if in_colab:
# Install required python packages:
# category_encoders, version >= 2.0
# eli5, version >= 0.9
# pandas-profiling, version >= 2.0
# plotly, version >= 4.0
!pip install --upgrade category_encoders eli5 pandas-profiling plotly
# Pull files from Github repo
os.chdir('/content')
!git init .
!git remote add origin https://github.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge.git
!git pull origin master
# Change into directory for module
os.chdir('module3')
import pandas as pd
from sklearn.model_selection import train_test_split
# Merge train_features.csv & train_labels.csv
train = pd.merge(pd.read_csv('../data/tanzania/train_features.csv'),
pd.read_csv('../data/tanzania/train_labels.csv'))
# Read test_features.csv & sample_submission.csv
test = pd.read_csv('../data/tanzania/test_features.csv')
sample_submission = pd.read_csv('../data/tanzania/sample_submission.csv') | _____no_output_____ | MIT | module3/assignment_kaggle_challenge_3.ipynb | mikedcurry/DS-Unit-2-Kaggle-Challenge |
Dealing with Outliers Sometimes outliers can mess up an analysis; you usually don't want a handful of data points to skew the overall results. Let's revisit our example of income data, with some random billionaire thrown in: | %matplotlib inline
import numpy as np
incomes = np.random.normal(27000, 15000, 10000)
incomes = np.append(incomes, [1000000000])
import matplotlib.pyplot as plt
plt.hist(incomes, 50)
plt.show() | _____no_output_____ | MIT | Outliers.ipynb | wf539/MLDataSciDeepLearningPython |
That's not very helpful to look at. One billionaire ended up squeezing everybody else into a single line in my histogram. Plus it skewed my mean income significantly: | incomes.mean() | _____no_output_____ | MIT | Outliers.ipynb | wf539/MLDataSciDeepLearningPython |
It's important to dig into what is causing your outliers, and understand where they are coming from. You also need to think about whether removing them is a valid thing to do, given the spirit of what it is you're trying to analyze. If I know I want to understand more about the incomes of "typical Americans", filtering out billionaires seems like a legitimate thing to do.Here's something a little more robust than filtering out billionaires - it filters out anything beyond two standard deviations of the median value in the data set: | def reject_outliers(data):
u = np.median(data)
s = np.std(data)
filtered = [e for e in data if (u - 2 * s < e < u + 2 * s)]
return filtered
filtered = reject_outliers(incomes)
plt.hist(filtered, 50)
plt.show() | _____no_output_____ | MIT | Outliers.ipynb | wf539/MLDataSciDeepLearningPython |
That looks better. And, our mean is more, well, meangingful now as well: | np.mean(filtered) | _____no_output_____ | MIT | Outliers.ipynb | wf539/MLDataSciDeepLearningPython |
Building your Recurrent Neural Network - Step by StepWelcome to Course 5's first assignment! In this assignment, you will implement your first Recurrent Neural Network in numpy.Recurrent Neural Networks (RNN) are very effective for Natural Language Processing and other sequence tasks because they have "memory". They can read inputs $x^{\langle t \rangle}$ (such as words) one at a time, and remember some information/context through the hidden layer activations that get passed from one time-step to the next. This allows a uni-directional RNN to take information from the past to process later inputs. A bidirection RNN can take context from both the past and the future. **Notation**:- Superscript $[l]$ denotes an object associated with the $l^{th}$ layer. - Example: $a^{[4]}$ is the $4^{th}$ layer activation. $W^{[5]}$ and $b^{[5]}$ are the $5^{th}$ layer parameters.- Superscript $(i)$ denotes an object associated with the $i^{th}$ example. - Example: $x^{(i)}$ is the $i^{th}$ training example input.- Superscript $\langle t \rangle$ denotes an object at the $t^{th}$ time-step. - Example: $x^{\langle t \rangle}$ is the input x at the $t^{th}$ time-step. $x^{(i)\langle t \rangle}$ is the input at the $t^{th}$ timestep of example $i$. - Lowerscript $i$ denotes the $i^{th}$ entry of a vector. - Example: $a^{[l]}_i$ denotes the $i^{th}$ entry of the activations in layer $l$.We assume that you are already familiar with `numpy` and/or have completed the previous courses of the specialization. Let's get started! Let's first import all the packages that you will need during this assignment. | import numpy as np
from rnn_utils import * | _____no_output_____ | MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
1 - Forward propagation for the basic Recurrent Neural NetworkLater this week, you will generate music using an RNN. The basic RNN that you will implement has the structure below. In this example, $T_x = T_y$. **Figure 1**: Basic RNN model Here's how you can implement an RNN: **Steps**:1. Implement the calculations needed for one time-step of the RNN.2. Implement a loop over $T_x$ time-steps in order to process all the inputs, one at a time. Let's go! 1.1 - RNN cellA Recurrent neural network can be seen as the repetition of a single cell. You are first going to implement the computations for a single time-step. The following figure describes the operations for a single time-step of an RNN cell. **Figure 2**: Basic RNN cell. Takes as input $x^{\langle t \rangle}$ (current input) and $a^{\langle t - 1\rangle}$ (previous hidden state containing information from the past), and outputs $a^{\langle t \rangle}$ which is given to the next RNN cell and also used to predict $y^{\langle t \rangle}$ **Exercise**: Implement the RNN-cell described in Figure (2).**Instructions**:1. Compute the hidden state with tanh activation: $a^{\langle t \rangle} = \tanh(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a)$.2. Using your new hidden state $a^{\langle t \rangle}$, compute the prediction $\hat{y}^{\langle t \rangle} = softmax(W_{ya} a^{\langle t \rangle} + b_y)$. We provided you a function: `softmax`.3. Store $(a^{\langle t \rangle}, a^{\langle t-1 \rangle}, x^{\langle t \rangle}, parameters)$ in cache4. Return $a^{\langle t \rangle}$ , $y^{\langle t \rangle}$ and cacheWe will vectorize over $m$ examples. Thus, $x^{\langle t \rangle}$ will have dimension $(n_x,m)$, and $a^{\langle t \rangle}$ will have dimension $(n_a,m)$. | # GRADED FUNCTION: rnn_cell_forward
def rnn_cell_forward(xt, a_prev, parameters):
"""
Implements a single forward step of the RNN-cell as described in Figure (2)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
"""
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ### (≈2 lines)
# compute next activation state using the formula given above
a_next = np.tanh(np.matmul(Waa, a_prev) + np.matmul(Wax, xt) + ba)
# compute output of the current cell using the formula given above
yt_pred = softmax(np.matmul(Wya, a_next) + by)
### END CODE HERE ###
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape) | a_next[4] = [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978
-0.18887155 0.99815551 0.6531151 0.82872037]
a_next.shape = (5, 10)
yt_pred[1] = [ 0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
0.36920224 0.9966312 0.9982559 0.17746526]
yt_pred.shape = (2, 10)
| MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
**Expected Output**: **a_next[4]**: [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978 -0.18887155 0.99815551 0.6531151 0.82872037] **a_next.shape**: (5, 10) **yt[1]**: [ 0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212 0.36920224 0.9966312 0.9982559 0.17746526] **yt.shape**: (2, 10) 1.2 - RNN forward pass You can see an RNN as the repetition of the cell you've just built. If your input sequence of data is carried over 10 time steps, then you will copy the RNN cell 10 times. Each cell takes as input the hidden state from the previous cell ($a^{\langle t-1 \rangle}$) and the current time-step's input data ($x^{\langle t \rangle}$). It outputs a hidden state ($a^{\langle t \rangle}$) and a prediction ($y^{\langle t \rangle}$) for this time-step. **Figure 3**: Basic RNN. The input sequence $x = (x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, ..., x^{\langle T_x \rangle})$ is carried over $T_x$ time steps. The network outputs $y = (y^{\langle 1 \rangle}, y^{\langle 2 \rangle}, ..., y^{\langle T_x \rangle})$. **Exercise**: Code the forward propagation of the RNN described in Figure (3).**Instructions**:1. Create a vector of zeros ($a$) that will store all the hidden states computed by the RNN.2. Initialize the "next" hidden state as $a_0$ (initial hidden state).3. Start looping over each time step, your incremental index is $t$ : - Update the "next" hidden state and the cache by running `rnn_cell_forward` - Store the "next" hidden state in $a$ ($t^{th}$ position) - Store the prediction in y - Add the cache to the list of caches4. Return $a$, $y$ and caches | # GRADED FUNCTION: rnn_forward
def rnn_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network described in Figure (3).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of caches, x)
"""
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and parameters["Wya"]
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
### START CODE HERE ###
# initialize "a" and "y" with zeros (≈2 lines)
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# Initialize a_next (≈1 line)
a_next = a0
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈1 line)
a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y_pred[:,:,t] = yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])
print("len(caches) = ", len(caches)) | a[4][1] = [-0.99999375 0.77911235 -0.99861469 -0.99833267]
a.shape = (5, 10, 4)
y_pred[1][3] = [ 0.79560373 0.86224861 0.11118257 0.81515947]
y_pred.shape = (2, 10, 4)
caches[1][1][3] = [-1.1425182 -0.34934272 -0.20889423 0.58662319]
len(caches) = 2
| MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
**Expected Output**: **a[4][1]**: [-0.99999375 0.77911235 -0.99861469 -0.99833267] **a.shape**: (5, 10, 4) **y[1][3]**: [ 0.79560373 0.86224861 0.11118257 0.81515947] **y.shape**: (2, 10, 4) **cache[1][1][3]**: [-1.1425182 -0.34934272 -0.20889423 0.58662319] **len(cache)**: 2 Congratulations! You've successfully built the forward propagation of a recurrent neural network from scratch. This will work well enough for some applications, but it suffers from vanishing gradient problems. So it works best when each output $y^{\langle t \rangle}$ can be estimated using mainly "local" context (meaning information from inputs $x^{\langle t' \rangle}$ where $t'$ is not too far from $t$). In the next part, you will build a more complex LSTM model, which is better at addressing vanishing gradients. The LSTM will be better able to remember a piece of information and keep it saved for many timesteps. 2 - Long Short-Term Memory (LSTM) networkThis following figure shows the operations of an LSTM-cell. **Figure 4**: LSTM-cell. This tracks and updates a "cell state" or memory variable $c^{\langle t \rangle}$ at every time-step, which can be different from $a^{\langle t \rangle}$. Similar to the RNN example above, you will start by implementing the LSTM cell for a single time-step. Then you can iteratively call it from inside a for-loop to have it process an input with $T_x$ time-steps. About the gates - Forget gateFor the sake of this illustration, lets assume we are reading words in a piece of text, and want use an LSTM to keep track of grammatical structures, such as whether the subject is singular or plural. If the subject changes from a singular word to a plural word, we need to find a way to get rid of our previously stored memory value of the singular/plural state. In an LSTM, the forget gate lets us do this: $$\Gamma_f^{\langle t \rangle} = \sigma(W_f[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_f)\tag{1} $$Here, $W_f$ are weights that govern the forget gate's behavior. We concatenate $[a^{\langle t-1 \rangle}, x^{\langle t \rangle}]$ and multiply by $W_f$. The equation above results in a vector $\Gamma_f^{\langle t \rangle}$ with values between 0 and 1. This forget gate vector will be multiplied element-wise by the previous cell state $c^{\langle t-1 \rangle}$. So if one of the values of $\Gamma_f^{\langle t \rangle}$ is 0 (or close to 0) then it means that the LSTM should remove that piece of information (e.g. the singular subject) in the corresponding component of $c^{\langle t-1 \rangle}$. If one of the values is 1, then it will keep the information. - Update gateOnce we forget that the subject being discussed is singular, we need to find a way to update it to reflect that the new subject is now plural. Here is the formulat for the update gate: $$\Gamma_u^{\langle t \rangle} = \sigma(W_u[a^{\langle t-1 \rangle}, x^{\{t\}}] + b_u)\tag{2} $$ Similar to the forget gate, here $\Gamma_u^{\langle t \rangle}$ is again a vector of values between 0 and 1. This will be multiplied element-wise with $\tilde{c}^{\langle t \rangle}$, in order to compute $c^{\langle t \rangle}$. - Updating the cell To update the new subject we need to create a new vector of numbers that we can add to our previous cell state. The equation we use is: $$ \tilde{c}^{\langle t \rangle} = \tanh(W_c[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_c)\tag{3} $$Finally, the new cell state is: $$ c^{\langle t \rangle} = \Gamma_f^{\langle t \rangle}* c^{\langle t-1 \rangle} + \Gamma_u^{\langle t \rangle} *\tilde{c}^{\langle t \rangle} \tag{4} $$ - Output gateTo decide which outputs we will use, we will use the following two formulas: $$ \Gamma_o^{\langle t \rangle}= \sigma(W_o[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_o)\tag{5}$$ $$ a^{\langle t \rangle} = \Gamma_o^{\langle t \rangle}* \tanh(c^{\langle t \rangle})\tag{6} $$Where in equation 5 you decide what to output using a sigmoid function and in equation 6 you multiply that by the $\tanh$ of the previous state. 2.1 - LSTM cell**Exercise**: Implement the LSTM cell described in the Figure (3).**Instructions**:1. Concatenate $a^{\langle t-1 \rangle}$ and $x^{\langle t \rangle}$ in a single matrix: $concat = \begin{bmatrix} a^{\langle t-1 \rangle} \\ x^{\langle t \rangle} \end{bmatrix}$2. Compute all the formulas 1-6. You can use `sigmoid()` (provided) and `np.tanh()`.3. Compute the prediction $y^{\langle t \rangle}$. You can use `softmax()` (provided). | # GRADED FUNCTION: lstm_cell_forward
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
"""
Implement a single forward step of the LSTM-cell as described in Figure (4)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
c_next -- next memory state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)
Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),
c stands for the memory value
"""
# Retrieve parameters from "parameters"
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
### START CODE HERE ###
# Concatenate a_prev and xt (≈3 lines)
concat = np.zeros((n_x + n_a, m))
concat[: n_a, :] = a_prev
concat[n_a :, :] = xt
# Compute values for ft, it, cct, c_next, ot, a_next using the formulas given figure (4) (≈6 lines)
ft = sigmoid(np.matmul(Wf, concat) + bf)
it = sigmoid(np.matmul(Wi, concat) + bi)
cct = np.tanh(np.matmul(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
ot = sigmoid(np.matmul(Wo, concat) + bo)
a_next = ot * np.tanh(c_next)
# Compute prediction of the LSTM cell (≈1 line)
yt_pred = softmax(np.matmul(Wy, a_next) + by)
### END CODE HERE ###
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
print("cache[1][3] =", cache[1][3])
print("len(cache) = ", len(cache)) | a_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape = (5, 10)
c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape = (5, 10)
yt[1] = [ 0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape = (2, 10)
cache[1][3] = [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874
0.07651101 -1.03752894 1.41219977 -0.37647422]
len(cache) = 10
| MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
**Expected Output**: **a_next[4]**: [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482 0.76566531 0.34631421 -0.00215674 0.43827275] **a_next.shape**: (5, 10) **c_next[2]**: [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942 0.76449811 -0.0981561 -0.74348425 -0.26810932] **c_next.shape**: (5, 10) **yt[1]**: [ 0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381 0.00943007 0.12666353 0.39380172 0.07828381] **yt.shape**: (2, 10) **cache[1][3]**: [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874 0.07651101 -1.03752894 1.41219977 -0.37647422] **len(cache)**: 10 2.2 - Forward pass for LSTMNow that you have implemented one step of an LSTM, you can now iterate this over this using a for-loop to process a sequence of $T_x$ inputs. **Figure 4**: LSTM over multiple time-steps. **Exercise:** Implement `lstm_forward()` to run an LSTM over $T_x$ time-steps. **Note**: $c^{\langle 0 \rangle}$ is initialized with zeros. | # GRADED FUNCTION: lstm_forward
def lstm_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (3).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)
"""
# Initialize "caches", which will track the list of all the caches
caches = []
### START CODE HERE ###
# Retrieve dimensions from shapes of x and parameters['Wy'] (≈2 lines)
n_x, m, T_x = x.shape
n_y, n_a = parameters['Wy'].shape
# initialize "a", "c" and "y" with zeros (≈3 lines)
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
# Initialize a_next and c_next (≈2 lines)
a_next = a0
c_next = np.zeros((n_a, m))
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
a_next, c_next, yt, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t] = yt
# Save the value of the next cell state (≈1 line)
c[:,:,t] = c_next
# Append the cache into caches (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, caches
np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a, y, c, caches = lstm_forward(x, a0, parameters)
print("a[4][3][6] = ", a[4][3][6])
print("a.shape = ", a.shape)
print("y[1][4][3] =", y[1][4][3])
print("y.shape = ", y.shape)
print("caches[1][1[1]] =", caches[1][1][1])
print("c[1][2][1]", c[1][2][1])
print("len(caches) = ", len(caches)) | a[4][3][6] = 0.172117767533
a.shape = (5, 10, 7)
y[1][4][3] = 0.95087346185
y.shape = (2, 10, 7)
caches[1][1[1]] = [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.855544916718
len(caches) = 2
| MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
**Expected Output**: **a[4][3][6]** = 0.172117767533 **a.shape** = (5, 10, 7) **y[1][4][3]** = 0.95087346185 **y.shape** = (2, 10, 7) **caches[1][1][1]** = [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139 0.41005165] **c[1][2][1]** = -0.855544916718 **len(caches)** = 2 Congratulations! You have now implemented the forward passes for the basic RNN and the LSTM. When using a deep learning framework, implementing the forward pass is sufficient to build systems that achieve great performance. The rest of this notebook is optional, and will not be graded. 3 - Backpropagation in recurrent neural networks (OPTIONAL / UNGRADED)In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers do not need to bother with the details of the backward pass. If however you are an expert in calculus and want to see the details of backprop in RNNs, you can work through this optional portion of the notebook. When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in recurrent neural networks you can to calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are quite complicated and we did not derive them in lecture. However, we will briefly present them below. 3.1 - Basic RNN backward passWe will start by computing the backward pass for the basic RNN-cell. **Figure 5**: RNN-cell's backward pass. Just like in a fully-connected neural network, the derivative of the cost function $J$ backpropagates through the RNN by following the chain-rule from calculas. The chain-rule is also used to calculate $(\frac{\partial J}{\partial W_{ax}},\frac{\partial J}{\partial W_{aa}},\frac{\partial J}{\partial b})$ to update the parameters $(W_{ax}, W_{aa}, b_a)$. Deriving the one step backward functions: To compute the `rnn_cell_backward` you need to compute the following equations. It is a good exercise to derive them by hand. The derivative of $\tanh$ is $1-\tanh(x)^2$. You can find the complete proof [here](https://www.wyzant.com/resources/lessons/math/calculus/derivative_proofs/tanx). Note that: $ \text{sech}(x)^2 = 1 - \tanh(x)^2$Similarly for $\frac{ \partial a^{\langle t \rangle} } {\partial W_{ax}}, \frac{ \partial a^{\langle t \rangle} } {\partial W_{aa}}, \frac{ \partial a^{\langle t \rangle} } {\partial b}$, the derivative of $\tanh(u)$ is $(1-\tanh(u)^2)du$. The final two equations also follow same rule and are derived using the $\tanh$ derivative. Note that the arrangement is done in a way to get the same dimensions to match. | def rnn_cell_backward(da_next, cache):
"""
Implements the backward pass for the RNN-cell (single time-step).
Arguments:
da_next -- Gradient of loss with respect to next hidden state
cache -- python dictionary containing useful values (output of rnn_cell_forward())
Returns:
gradients -- python dictionary containing:
dx -- Gradients of input data, of shape (n_x, m)
da_prev -- Gradients of previous hidden state, of shape (n_a, m)
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dba -- Gradients of bias vector, of shape (n_a, 1)
"""
# Retrieve values from cache
(a_next, a_prev, xt, parameters) = cache
# Retrieve values from parameters
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ###
# compute the gradient of tanh with respect to a_next (≈1 line)
dtanh = (1 - a_next ** 2) * da_next
# compute the gradient of the loss with respect to Wax (≈2 lines)
dxt = np.matmul(Wax.T, dtanh)
dWax = np.matmul(dtanh, xt.T)
# compute the gradient with respect to Waa (≈2 lines)
da_prev = np.matmul(Waa.T, dtanh)
dWaa = np.matmul(dtanh, a_prev.T)
# compute the gradient with respect to b (≈1 line)
dba = np.sum(dtanh, keepdims=True, axis=1)
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
b = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)
da_next = np.random.randn(5,10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape) | gradients["dxt"][1][2] = -0.460564103059
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = 0.0842968653807
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.393081873922
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = -0.28483955787
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [ 0.80517166]
gradients["dba"].shape = (5, 1)
| MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
**Expected Output**: **gradients["dxt"][1][2]** = -0.460564103059 **gradients["dxt"].shape** = (3, 10) **gradients["da_prev"][2][3]** = 0.0842968653807 **gradients["da_prev"].shape** = (5, 10) **gradients["dWax"][3][1]** = 0.393081873922 **gradients["dWax"].shape** = (5, 3) **gradients["dWaa"][1][2]** = -0.28483955787 **gradients["dWaa"].shape** = (5, 5) **gradients["dba"][4]** = [ 0.80517166] **gradients["dba"].shape** = (5, 1) Backward pass through the RNNComputing the gradients of the cost with respect to $a^{\langle t \rangle}$ at every time-step $t$ is useful because it is what helps the gradient backpropagate to the previous RNN-cell. To do so, you need to iterate through all the time steps starting at the end, and at each step, you increment the overall $db_a$, $dW_{aa}$, $dW_{ax}$ and you store $dx$.**Instructions**:Implement the `rnn_backward` function. Initialize the return variables with zeros first and then loop through all the time steps while calling the `rnn_cell_backward` at each time timestep, update the other variables accordingly. | def rnn_backward(da, caches):
"""
Implement the backward pass for a RNN over an entire sequence of input data.
Arguments:
da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x)
caches -- tuple containing information from the forward pass (rnn_forward)
Returns:
gradients -- python dictionary containing:
dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x)
da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m)
dWax -- Gradient w.r.t the input's weight matrix, numpy-array of shape (n_a, n_x)
dWaa -- Gradient w.r.t the hidden state's weight matrix, numpy-arrayof shape (n_a, n_a)
dba -- Gradient w.r.t the bias, of shape (n_a, 1)
"""
### START CODE HERE ###
# Retrieve values from the first cache (t=1) of caches (≈2 lines)
(caches, x) = caches
(a1, a0, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈6 lines)
dx = np.zeros((n_x, m, T_x))
dWax = np.zeros((n_a, n_x))
dWaa = np.zeros((n_a, n_a))
dba = np.zeros((n_a, 1))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
# Loop through all the time steps
for t in reversed(range(T_x)):
# Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t])
# Retrieve derivatives from gradients (≈ 1 line)
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
# Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line)
da0 = da_prevt
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape) | gradients["dx"][1][2] = [-2.07101689 -0.59255627 0.02466855 0.01483317]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.314942375127
gradients["da0"].shape = (5, 10)
gradients["dWax"][3][1] = 11.2641044965
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 2.30333312658
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [-0.74747722]
gradients["dba"].shape = (5, 1)
| MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
**Expected Output**: **gradients["dx"][1][2]** = [-2.07101689 -0.59255627 0.02466855 0.01483317] **gradients["dx"].shape** = (3, 10, 4) **gradients["da0"][2][3]** = -0.314942375127 **gradients["da0"].shape** = (5, 10) **gradients["dWax"][3][1]** = 11.2641044965 **gradients["dWax"].shape** = (5, 3) **gradients["dWaa"][1][2]** = 2.30333312658 **gradients["dWaa"].shape** = (5, 5) **gradients["dba"][4]** = [-0.74747722] **gradients["dba"].shape** = (5, 1) 3.2 - LSTM backward pass 3.2.1 One Step backwardThe LSTM backward pass is slighltly more complicated than the forward one. We have provided you with all the equations for the LSTM backward pass below. (If you enjoy calculus exercises feel free to try deriving these from scratch yourself.) 3.2.2 gate derivatives$$d \Gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*(1-\Gamma_o^{\langle t \rangle})\tag{7}$$$$d\tilde c^{\langle t \rangle} = dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * i_t * da_{next} * \tilde c^{\langle t \rangle} * (1-\tanh(\tilde c)^2) \tag{8}$$$$d\Gamma_u^{\langle t \rangle} = dc_{next}*\tilde c^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * \tilde c^{\langle t \rangle} * da_{next}*\Gamma_u^{\langle t \rangle}*(1-\Gamma_u^{\langle t \rangle})\tag{9}$$$$d\Gamma_f^{\langle t \rangle} = dc_{next}*\tilde c_{prev} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * c_{prev} * da_{next}*\Gamma_f^{\langle t \rangle}*(1-\Gamma_f^{\langle t \rangle})\tag{10}$$ 3.2.3 parameter derivatives $$ dW_f = d\Gamma_f^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{11} $$$$ dW_u = d\Gamma_u^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{12} $$$$ dW_c = d\tilde c^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{13} $$$$ dW_o = d\Gamma_o^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{14}$$To calculate $db_f, db_u, db_c, db_o$ you just need to sum across the horizontal (axis= 1) axis on $d\Gamma_f^{\langle t \rangle}, d\Gamma_u^{\langle t \rangle}, d\tilde c^{\langle t \rangle}, d\Gamma_o^{\langle t \rangle}$ respectively. Note that you should have the `keep_dims = True` option.Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.$$ da_{prev} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c^{\langle t \rangle} + W_o^T * d\Gamma_o^{\langle t \rangle} \tag{15}$$Here, the weights for equations 13 are the first n_a, (i.e. $W_f = W_f[:n_a,:]$ etc...)$$ dc_{prev} = dc_{next}\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh(c_{next})^2)*\Gamma_f^{\langle t \rangle}*da_{next} \tag{16}$$$$ dx^{\langle t \rangle} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c_t + W_o^T * d\Gamma_o^{\langle t \rangle}\tag{17} $$where the weights for equation 15 are from n_a to the end, (i.e. $W_f = W_f[n_a:,:]$ etc...)**Exercise:** Implement `lstm_cell_backward` by implementing equations $7-17$ below. Good luck! :) | def lstm_cell_backward(da_next, dc_next, cache):
"""
Implement the backward pass for the LSTM-cell (single time-step).
Arguments:
da_next -- Gradients of next hidden state, of shape (n_a, m)
dc_next -- Gradients of next cell state, of shape (n_a, m)
cache -- cache storing information from the forward pass
Returns:
gradients -- python dictionary containing:
dxt -- Gradient of input data at time-step t, of shape (n_x, m)
da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x)
dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
dWo -- Gradient w.r.t. the weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
dbo -- Gradient w.r.t. biases of the output gate, of shape (n_a, 1)
"""
# Retrieve information from "cache"
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
### START CODE HERE ###
# Retrieve dimensions from xt's and a_next's shape (≈2 lines)
n_x, m = xt.shape
n_a, m = a_next.shape
# Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
dot = da_next * np.tanh(c_next) * ot * (1 - ot)
dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
dft = (dc_next * c_prev + ot * (1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)
# Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
temp = np.concatenate((a_prev, xt), axis=0).T
dWf = np.dot(dft, temp)
dWi = np.dot(dit, temp)
dWc = np.dot(dcct, temp)
dWo = np.dot(dot, temp)
dbf = np.sum(dft, axis=1, keepdims=True)
dbi = np.sum(dit, axis=1, keepdims=True)
dbc = np.sum(dcct, axis=1, keepdims=True)
dbo = np.sum(dot, axis=1, keepdims=True)
# Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
da_prev = np.dot(parameters['Wf'][:,:n_a].T, dft) + np.dot(parameters['Wi'][:,:n_a].T, dit) + np.dot(parameters['Wc'][:,:n_a].T, dcct) + np.dot(parameters['Wo'][:,:n_a].T, dot)
dc_prev = dc_next * ft + ot * (1 - np.square(np.tanh(c_next))) * ft * da_next
dxt = np.dot(parameters['Wf'][:,n_a:].T, dft) + np.dot(parameters['Wi'][:,n_a:].T, dit) + np.dot(parameters['Wc'][:,n_a:].T, dcct) + np.dot(parameters['Wo'][:,n_a:].T, dot)
### END CODE HERE ###
# Save gradients in dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
da_next = np.random.randn(5,10)
dc_next = np.random.randn(5,10)
gradients = lstm_cell_backward(da_next, dc_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape) | gradients["dxt"][1][2] = 3.23055911511
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.0639621419711
gradients["da_prev"].shape = (5, 10)
gradients["dc_prev"][2][3] = 0.797522038797
gradients["dc_prev"].shape = (5, 10)
gradients["dWf"][3][1] = -0.147954838164
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 1.05749805523
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 2.30456216369
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.331311595289
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [ 0.18864637]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.40142491]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [ 0.25587763]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [ 0.13893342]
gradients["dbo"].shape = (5, 1)
| MIT | Course-5-Sequence-Models/week1/Building+a+Recurrent+Neural+Network+-+Step+by+Step+-+v3.ipynb | xnone/coursera-deep-learning |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.