question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
stone-game-iv | Simple DP solution(O(n*sqrt(n))) with explaination (Java) | simple-dp-solutiononsqrtn-with-explainat-oej6 | This quesion is actually about the best strategy. \nFirstly, let us write down the first couple of cases:\n\n|Stone | Alice can win by some strategy| Explain|\n | troydad | NORMAL | 2020-07-12T01:56:53.236601+00:00 | 2020-07-13T17:41:10.133648+00:00 | 99 | false | This quesion is actually about the best strategy. \nFirstly, let us write down the first couple of cases:\n\n|Stone | Alice can win by some strategy| Explain|\n|---|---|---|\n|1|true|Trivial|\n|2|false|Alice can only take 1 and bob win|\n|3|true|Alice 1, bob 1, alice win|\n|4|true|Alice 4|\n|5|false|Alice take 1 or 4, Bob take 4 or 1, ie (1,4) or (4,1)|\n|6|true|(4,1,1) or (1,4,1)|\n|7|false|As (4,1,1,1) or (1,4,1,1)|\n|8|true|Alice cannot take 4 because it will be (4,4) and bob will win. So it must start from 1, as (1,4,1,1,1) or (1,1,1,1,4)|\n\nWait a sec here. Easily to notice, every "false" there is a "true" after it. Why is it? Look at the solution of `8`, `6`. the solution for `8`, (1,4,1,1,1) can be understood as:\n(1), (4,1,1,1)\n```\nAlice: Let me take only 1, and leave a 7 to bob. I\'ve know that 7 is a bad situation for first drawer.\nBob: hmmm 7 is impossible to win.\n```\nOk from here, let us conclude:\n- For every must-lose situation `n`, every number `n + i * i` will be a must-win situation.\n- f(1) = true, f(2) = false\n\nNow the solution will be trivial:\n```java\npublic boolean winnerSquareGame(int n) {\n if (n == 1) return true;\n if (n == 2) return false;\n int m = (int) Math.sqrt(n);\n Set<Integer> sqs = new HashSet<>();\n boolean[] res = new boolean[n+1];\n for (int i = 1; i <= m; i++) {\n sqs.add(i*i);\n res[i*i] = true;\n }\n res[1] = true;\n res[2] = false;\n for (int i = 1; i <= n ; i++) {\n if (!res[i]) {\n for (Integer sq: sqs) {\n if (i+sq <=n) res[i+sq] = true;\n }\n }\n }\n return res[n];\n}\n```\n\nForgive my ugly edge case handling, and please commend if you have suggestion.\n\n\n\n | 2 | 1 | ['Dynamic Programming'] | 1 |
stone-game-iv | DP solution in Python | dp-solution-in-python-by-k0ush1k-alrl | \nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [0 for i in range(n+1)]\n dp[0] = 0\n dp[1] = 1\n for i in | k0ush1k | NORMAL | 2020-07-11T17:06:42.851752+00:00 | 2020-07-11T17:06:42.851797+00:00 | 49 | false | ```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [0 for i in range(n+1)]\n dp[0] = 0\n dp[1] = 1\n for i in range(2,n+1):\n x = int(math.sqrt(i))\n for j in range(1,x+1):\n if dp[i-j*j] == 0:\n dp[i] = 1\n \n \n if dp[n] == 1:\n return True\n return False\n \n\t\t``` | 2 | 0 | [] | 0 |
stone-game-iv | [Python] O(n*sqrt*(n)) time O(n) space - DP solution | python-onsqrtn-time-on-space-dp-solution-ie90 | Explanation: First, we compute all square numbers, so we know which numbers are square numbers.\n Then we have the DP table (denoted as C):\n | theleetman | NORMAL | 2020-07-11T16:07:13.401595+00:00 | 2020-07-11T16:07:13.401648+00:00 | 198 | false | Explanation: First, we compute all square numbers, so we know which numbers are square numbers.\n Then we have the DP table (denoted as C):\n C[i][b] - i is current number of stones in the pile\n b is 0 or 1 (player 0 or player 1, defined as ALICE or BOB)\n\n the meaning of C[i][b] is - does player b win when it\'s his turn and there are i stones in the pile. (Boolean)\n So C[0][b] = False (0 piles = lose)\n Then just calculate bottom up using all possible moves\n\n Each subproblem computation time: at most O(sqrt(n))\n number of subproblems: O(n)\n\n Time complexity: O(n * sqrt(n))\n Space complexity: O(n) (the table)\n Note: size of the pre-computed sqrs is floor(sqrt(10**5)) which is 316\n\n Note: could simply compute the table until 10**5 in the precomputation stage and then just return the relevant table location when queried.\n\nCode:\n```\nfrom math import sqrt, floor\n\nALICE = 0\nBOB = 1\n\nsqrs = []\nfor i in range(1, floor(sqrt(10 ** 5)) + 1):\n sqrs.append(i ** 2)\n\n\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n C = [[False for _ in range(2)] for _ in range(n + 1)]\n\n C[0][ALICE] = False # Alise loses\n C[0][BOB] = False # Bob loses\n\n for i in range(1, n + 1):\n for b in range(2):\n j = 0\n while sqrs[j] <= i:\n if not C[i - sqrs[j]][1 - b]:\n C[i][b] = True\n break\n j += 1\n\n return C[n][ALICE]\n``` | 2 | 0 | [] | 0 |
stone-game-iv | [C++] DP Solution (5 Lines Clean Code) | c-dp-solution-5-lines-clean-code-by-appl-14za | \n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false); \n for(int i = 1; i <= n; i++)\n for(int j = 1; j * j <= i; j++){ | applefanboi | NORMAL | 2020-07-11T16:05:04.855051+00:00 | 2020-07-11T16:20:11.572024+00:00 | 208 | false | ```\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false); \n for(int i = 1; i <= n; i++)\n for(int j = 1; j * j <= i; j++){\n dp[i] = !dp[i - (j * j)];\n if(dp[i]) break;\n }\n return dp[n];\n }\n\n``` | 2 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
stone-game-iv | easy dp c++ | easy-dp-c-by-diveyk-7dj5 | \nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<int> dp(n+1);\n for(int i=1; i<=n; ++i) {\n for(int j=1; j*j<= | diveyk | NORMAL | 2020-07-11T16:02:25.207323+00:00 | 2020-07-11T16:02:25.207354+00:00 | 175 | false | ```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<int> dp(n+1);\n for(int i=1; i<=n; ++i) {\n for(int j=1; j*j<=i; ++j)\n dp[i]|=!dp[i-j*j];\n }\n return dp[n];\n }\n};\n``` | 2 | 1 | [] | 1 |
stone-game-iv | Game theory + DP, Simple solution | Recursive | My screen recording | game-theory-dp-simple-solution-recursive-yuwa | \nclass Solution {\npublic:\n \n int dp[100009];\n \n // check if a number if a square or not\n bool isSq(int x) {\n int y = sqrt(x);\n | rachilies | NORMAL | 2020-07-11T16:01:38.315770+00:00 | 2020-07-11T23:00:31.140163+00:00 | 346 | false | ```\nclass Solution {\npublic:\n \n int dp[100009];\n \n // check if a number if a square or not\n bool isSq(int x) {\n int y = sqrt(x);\n return (y * y == x);\n }\n \n bool flag = false;\n \n bool winnerSquareGame(int n) {\n // this step is run only once to initialize my dp array with -1;\n if(!flag) {\n memset(dp, -1, sizeof(dp));\n flag = true;\n }\n \n // if the number is a square then person who\'s turn it is will be the winner\n if(isSq(n)) \n return true; \n \n // return memoized answer if pre calculated\n if(dp[n] != -1)\n return dp[n];\n \n bool ans = false;\n \n // otherwise try to subtract each possible square (x) in range [1, n] from n and recursively check the answer for n - x;\n \n for(int i = 1; i*i <= n; i++) {\n // and now as we will be asking the game result for next player with value (n - i*i), the result will be reverse for this player. hence ans |= !(winner..(n - (i * i)));\n ans |= !(winnerSquareGame(n - (i*i)));\n // if any of the x gives me false for the next player, meaning current player can subtract this x and the remaining value n - x will force the next player to loose the game.\n }\n \n // store the result in dp array for future reference;\n dp[n] = ans ? 1: 0; \n \n return ans;\n }\n};\n```\n\nIn case if you\'re interested in a boaring recording https://youtu.be/8TgT77Ijei8\n\n | 2 | 0 | [] | 0 |
stone-game-iv | Java 5 lines | java-5-lines-by-mayank12559-di9d | \npublic boolean winnerSquareGame(int n) {\n boolean []dp = new boolean[n+1];\n for(int i=1; i<=n; i++)\n for(int j = (int)Math.sqrt(i) | mayank12559 | NORMAL | 2020-07-11T16:00:53.552469+00:00 | 2020-07-11T16:00:53.552544+00:00 | 298 | false | ```\npublic boolean winnerSquareGame(int n) {\n boolean []dp = new boolean[n+1];\n for(int i=1; i<=n; i++)\n for(int j = (int)Math.sqrt(i); !dp[i] && j >= 1; j--)\n dp[i] = !dp[i -j*j];\n return dp[n];\n }\n``` | 2 | 0 | [] | 1 |
stone-game-iv | DP and Math, with explanation! O(N *square_root(N)) / O(N) | dp-and-math-with-explanation-on-square_r-08tr | Intuition\n Describe your first thoughts on how to solve this problem. \nBuilding the solution from the start 0 to end N. Alice tries her best to make Bob lose | Kai_XD | NORMAL | 2024-08-08T03:43:37.414441+00:00 | 2024-08-08T03:43:37.414467+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBuilding the solution from the start 0 to end N. Alice tries her best to make Bob lose by picking some square number of stone which makes Bob in a losing state.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse DP to realize the above idea!\n\n# Complexity\n- Time complexity:O(N*square_root(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n \n dp = [0,1] + [0] * (n-1)\n squares = [1]\n for i in range(2, n+1):\n new_square = squares[-1] + 1\n if (new_square) ** 2 <= i:\n squares.append(new_square)\n\n for square in squares:\n if dp[i-square ** 2] == 0:\n dp[i] = 1\n break\n\n return dp[-1]\n``` | 1 | 0 | ['Python3'] | 0 |
stone-game-iv | C++ Code | c-code-by-lucifer_2214-5c6k | class Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector dp(n + 1, false);\n for (int i = 1; i <= n; ++i) {\n for (int k | lucifer_2214 | NORMAL | 2024-07-03T04:21:30.317189+00:00 | 2024-07-03T04:21:30.317227+00:00 | 28 | false | class Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false);\n for (int i = 1; i <= n; ++i) {\n for (int k = 1; k * k <= i; ++k) {\n if (!dp[i - k * k]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n}; | 1 | 0 | ['C++'] | 0 |
stone-game-iv | Beats 100%🔥|| DP🔥|| Memoization🔥|| easy ✅ | beats-100-dp-memoization-easy-by-priyans-kdau | Simple if current index is false than every perfect square+current index will be true because Alice will put bob on a losing position.\n# 1st Method\n\nclass So | priyanshu1078 | NORMAL | 2024-01-11T17:22:51.774935+00:00 | 2024-01-11T17:22:51.774969+00:00 | 450 | false | Simple if current index is **false** than every perfect square+current index will be **true** because Alice will put bob on a losing position.\n# 1st Method\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean dp[]=new boolean[n+1];\n for(int i=0;i<=n;i++){\n if(dp[i]) continue;\n for(int j=1;i+j*j<=n;j++){\n dp[i+j*j]=true;\n }\n }\n return dp[n];\n }\n}\n```\nIn this method we are check if there is any losing position before current index. If there is any losing position than Alice can win. \n# 2nd Method\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean dp[]=new boolean[n+1];\n for(int i=1;i<=n;i++){\n for(int j=1;j*j<=i;j++){\n if(!dp[i-(j*j)]){\n dp[i]=true;\n break;\n }\n }\n }\n return dp[n];\n }\n}\n```\n# 3rd Method(Memoization)\n```\nclass Solution {\n Boolean[] memo;\n public boolean winnerSquareGame(int n) {\n memo=new Boolean[n+1];\n return sol(n);\n }\n public boolean sol(int n){\n if(n<=0) return false;\n if(memo[n]!=null) return memo[n];\n for(int i=1;i*i<=n;i++){\n if(!sol(n-i*i)) return memo[n]=true;\n }\n return memo[n]=false;\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 0 |
stone-game-iv | C++ | c-by-ankita2905-ra6f | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ankita2905 | NORMAL | 2023-10-03T13:07:59.097657+00:00 | 2023-10-03T13:07:59.097677+00:00 | 161 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false);\n for (int i = 1; i <= n; ++i) {\n for (int k = 1; k * k <= i; ++k) {\n if (!dp[i - k * k]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
stone-game-iv | C++ | c-by-ankita2905-rwi1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ankita2905 | NORMAL | 2023-10-03T13:07:56.945432+00:00 | 2023-10-03T13:07:56.945457+00:00 | 44 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false);\n for (int i = 1; i <= n; ++i) {\n for (int k = 1; k * k <= i; ++k) {\n if (!dp[i - k * k]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
stone-game-iv | A simple solution for C | a-simple-solution-for-c-by-zsbxp-gp8s | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | zsbxp | NORMAL | 2023-06-14T16:00:23.205700+00:00 | 2023-06-14T16:00:23.205718+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nbool winnerSquareGame(int n){\n bool flag[n+2];\n memset(flag, false, n+2);\n for(int i=0; i<=n+1; i++){\n if(!flag[i]){\n for(int j = 1; j*j+i<=n;j++){\n flag[i+j*j] = true;\n }\n }\n }\n return flag[n];\n}\n``` | 1 | 0 | ['C'] | 1 |
stone-game-iv | ✅✅ C++ || JAVA || GO || easy & simple | c-java-go-easy-simple-by-tamim447-yd31 | C++ Solution:\n\n\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool>dp(n+1, 0);\n for(int i=1; i<=n; i++) {\n | tamim447 | NORMAL | 2022-09-22T19:54:05.315329+00:00 | 2022-11-01T16:36:54.792084+00:00 | 321 | false | **C++ Solution:**\n\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool>dp(n+1, 0);\n for(int i=1; i<=n; i++) {\n for(int j=1; j*j<=i; j++) {\n if(!dp[i-j*j]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n```\n\n**Java Solution:**\n\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean[] dp = new boolean[n+1];\n for(int i = 1; i <= n; i++) {\n for(int j = 1; j*j <= i; j++) {\n if(!dp[i-j*j]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n}\n```\n\n**Go Solution:**\n\n```\nfunc winnerSquareGame(n int) bool {\n dp:= make([]bool, n+1);\n \n for i:= 1; i<=n; i++ {\n for j:= 1; j*j<=i; j++ {\n if !dp[i-j*j] {\n dp[i] = true;\n }\n }\n }\n return dp[n];\n}\n``` | 1 | 0 | ['C', 'Java', 'Go'] | 1 |
stone-game-iv | Beats 100% Memory and 91% Speed | Python | DP | beats-100-memory-and-91-speed-python-dp-yf9qr | \n\n\n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp=[False](n+1)\n w=[]\n for i in range(1,int((n).5)+1):\n | abhishekm-001 | NORMAL | 2022-08-23T09:22:17.077158+00:00 | 2022-08-23T09:35:15.632920+00:00 | 111 | false | \n\n\n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp=[False]*(n+1)\n w=[]\n for i in range(1,int((n)**.5)+1):\n w+=[i*i]\n for i in range(n):\n if dp[i]==False:\n for j in w:\n if i+j<n+1:\n dp[i+j]=True\n return dp[-1]\n | 1 | 0 | ['Dynamic Programming', 'Python'] | 0 |
stone-game-iv | C++ Tabulation + Memoization | c-tabulation-memoization-by-omhardaha1-2fl8 | Tabulation \n\nbool winnerSquareGame(int n)\n{\n vector<int> dp(n + 1, -1);\n dp[0] = false;\n for (int k = 1; k <= n; k++)\n {\n bool f = 0; | omhardaha1 | NORMAL | 2022-06-24T19:34:58.189392+00:00 | 2022-06-24T19:34:58.189438+00:00 | 156 | false | # Tabulation \n```\nbool winnerSquareGame(int n)\n{\n vector<int> dp(n + 1, -1);\n dp[0] = false;\n for (int k = 1; k <= n; k++)\n {\n bool f = 0;\n for (int i = sqrt(n); i >= 1; i--)\n {\n if (i * i <= k)\n {\n if (!dp[k - i * i])\n {\n f = 1;\n break;\n }\n }\n }\n dp[k] = f;\n }\n return dp[n];\n};\n```\n\n# Memoization\n\n```\nclass Solution\n{\npublic:\n vector<int> dp;\n bool win(int n)\n {\n if (n == 0)\n {\n return false;\n }\n if (dp[n] == false)\n {\n return false;\n }\n for (int i = sqrt(n); i >= 1; i--)\n {\n if (i * i <= n)\n {\n if (!win(n - (i * i)))\n {\n return true;\n }\n }\n }\n return dp[n] = false;\n }\n bool winnerSquareGame(int n)\n {\n dp = vector<int>(n + 1, -1);\n return win(n);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C'] | 1 |
stone-game-iv | C++|| EASY TO UNDERSTAND || 3 Approaches || Memoization+Tabulaton | c-easy-to-understand-3-approaches-memoiz-rhgq | Memoization\n\nclass Solution {\npublic:\n bool fun(int n,vector<int> &memo)\n {\n bool res=false;\n if(memo[n]!=-1)\n return mem | aarindey | NORMAL | 2022-04-12T17:44:07.161665+00:00 | 2022-04-12T17:52:51.631486+00:00 | 75 | false | **Memoization**\n```\nclass Solution {\npublic:\n bool fun(int n,vector<int> &memo)\n {\n bool res=false;\n if(memo[n]!=-1)\n return memo[n];\n for(int i=1;i*i<=n;i++)\n {\n res=res|(!fun(n-i*i,memo));\n }\n return memo[n]=res;\n }\n bool winnerSquareGame(int n) {\n vector<int> memo(n+1,-1);\n return fun(n,memo);\n \n }\n};\n```\n**Tabulation**\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1,false);\n for(int i=1;i<=n;i++)\n {\n bool res=false;\n for(int j=1;j*j<=i;j++)\n {\n res|=!(dp[i-j*j]);\n }\n dp[i]=res;\n }\n return dp[n];\n }\n};\n```\n**Tabultaion 2(with &)**\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1,false);\n for(int i=1;i<=n;i++)\n {\n bool res=true;\n for(int j=1;j*j<=i;j++)\n {\n res&=(dp[i-j*j]);\n }\n dp[i]=!res;\n }\n return dp[n];\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome** | 1 | 0 | [] | 0 |
stone-game-iv | Dynamic Programming | TC: O(n * sqrt(n)) SC: O(n) | dynamic-programming-tc-on-sqrtn-sc-on-by-emd1 | Intution is to find a state where the other player can lose. If such a state exists, the current player can win the game (both players play optimally). We know | sks_15 | NORMAL | 2022-01-23T12:28:04.803399+00:00 | 2022-01-23T12:28:04.803433+00:00 | 50 | false | Intution is to find a state where the other player can lose. If such a state exists, the current player can win the game (both players play optimally). We know that in order to maintain these states, we need to do this problem dynamically. \n\nIf we have a state from all the `k` where k ranges from [1, sqrt(i)]. This is because we are only allowed to remove a perfect square number of stones at a given state. So we simply check all the states which are perfect squares less than the current number of stones. \n\nThe above works simply because if both players play optimally and there can be a state where the other player can lose even playing optimally, then surely the current player wins in the current state.\n```\nbool winnerSquareGame(int n) {\n\tvector<bool> dp(n+1);\n\n\tfor(int i = 1; i <= n; i++) {\n\t\tfor(int k = 1; k*k <= i; k++) {\n\t\t\tif(dp[i - k*k] == false) {\n\t\t\t\tdp[i] = true;\n\t\t\t\tbreak;\n\t\t\t}\n\t\t}\n\t}\n\n\treturn dp[n];\n}\n``` | 1 | 0 | ['Dynamic Programming', 'C', 'Game Theory'] | 0 |
stone-game-iv | very easy solution c++ will understand | very-easy-solution-c-will-understand-by-d2kg0 | \nclass Solution {\npublic:\n \n bool stonegame(int n,vector<int> &vec)\n{\n if(n==0)\n return false;\n if(vec[n]!=-1)\n return vec[n];\n \ | AdityaAlugani_ | NORMAL | 2022-01-22T17:57:40.190904+00:00 | 2022-01-22T17:57:40.190952+00:00 | 40 | false | ```\nclass Solution {\npublic:\n \n bool stonegame(int n,vector<int> &vec)\n{\n if(n==0)\n return false;\n if(vec[n]!=-1)\n return vec[n];\n \n for(int i=1;i*i<=n;i++)\n {\n if(!stonegame(n-i*i,vec))\n return vec[n]=true;\n }\n return vec[n]=false;\n}\n bool winnerSquareGame(int n) {\n \n vector<int> vec(n+1,-1);\n return stonegame(n,vec);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming'] | 0 |
stone-game-iv | Detailed explanation with examples using pen and paper || DP | detailed-explanation-with-examples-using-n4yn | Explanation\n\n\n\n\n\nJAVA CODE\n\n\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean dp[] = new boolean[n + 1];\n //No s | rachana_raut | NORMAL | 2022-01-22T17:02:36.476341+00:00 | 2022-01-22T17:02:36.476382+00:00 | 88 | false | **Explanation**\n\n\n\n\n\n**JAVA CODE**\n\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean dp[] = new boolean[n + 1];\n //No stones, Then since is first to make the move, she loses\n dp[0] = false;\n for(int i = 1; i <= n; i++){\n for(int sqrtNum = 1; sqrtNum * sqrtNum <= i; sqrtNum++){\n\t\t\t//check prev case if Bob had lost through dp[i - sqrtNum * sqrtNum] = false\n if(!dp[i - sqrtNum * sqrtNum]){\n //find atleast 1 case where Alice can win\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n]; \n }\n}\n```\n\n<br>\n<br>\n\nString yourReaction;\nif("understood".equals(yourReaction) || "liked it".equals(yourReaction))\nSystem.out.println(**"Please upvote!"**) | 1 | 0 | ['Dynamic Programming', 'Java'] | 1 |
stone-game-iv | [C++] Intuitive Solution | DP | Tabulation | Memorization | c-intuitive-solution-dp-tabulation-memor-gw5w | APPROACH : DP Tabulation\n\n Alice wins if he can make Bob lose the game.\n\nAlice plays first :\n\nFor example :\n\nn = 1 ---> Alice picks 1 stone & wins the g | Mythri_Kaulwar | NORMAL | 2022-01-22T16:25:34.951361+00:00 | 2022-01-22T16:25:34.951389+00:00 | 189 | false | **APPROACH : DP Tabulation**\n\n* Alice wins if he can make Bob lose the game.\n\nAlice plays first :\n\n*For example :*\n```\nn = 1 ---> Alice picks 1 stone & wins the game\nn = 2 ---> Alice picks 1 stone, Bob picks one stone, Alice is left with nothing so he loses.\nn = 3 ---> Alice picks 1 stone, Bob picks 1 stone, Alice picks 1 stone again --> He made Bob lose the game - so he wins.\nn = 4 ---> Alice picks up 4 stones directly. Bob is left with nothing, so he wins.\nn = 5 ---> Alice picks 4 stones, Bob picks 1, So Alex loses.\nn = 4 ----> Alice picks 4 stones, Bob picks 1 stone, Alex picks 1 stone again --> He makes Bob lose, so he wins\n``` \nSo we understand that Alice can win if Bob is left with no choice.\n\nSo, we\'ll create a 1D array ```dp``` where we\'ll store the winning chances of Alice starting from1 stone. If dp[n] = true, we\'ll return true.\n\n**Time Complexity :** O(n^1.5) -> O(n*x*n^0.5) - Because there are ```floor(sqrt(n))``` perfect squares less than or equal to n.\n\n**Space Complexity :** O(n) - For the dp array.\n\n**Code :**\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1);\n \n for(int i=1; i <= n; i++){\n for(int j=1; j*j <=i; j++){\n if(!dp[i-j*j]){ \n dp[i]=true; \n break;\n }\n }\n }\n return dp[n];\n }\n};\n```\n\n**APPROACH : DP Memorization**\n\n* The same can be done using memorization also.\n* The approach is pretty similar.\n\n**Time Complexity :** O(n^1.5)\n\n**Space Complexity :** O(n)\n\n**Code :**\n```\nclass Solution {\n bool dp[100001] = {false};\npublic:\n bool winnerSquareGame(int n){\n if(n==0) return false;\n \n if(dp[n]) return dp[n];\n \n bool winner = false;\n for(int i=1; i*i <= n; i++){\n if(!winnerSquareGame(n - i*i)){\n winner = true;\n break;\n } \n }\n return dp[n] = winner;\n }\n};\n```\n\n**Do upvote if you like :)** | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 0 |
stone-game-iv | Easy C++ solution | easy-c-solution-by-kunal_sihare-w9hv | \n bool winnerSquareGame(int n) {\n vector<bool>dp(n+1,false);\n if(n==1)\n return true;\n if(n==2)\n return false;\n | Kunal_Sihare | NORMAL | 2022-01-22T15:26:08.468127+00:00 | 2022-01-22T15:26:08.468168+00:00 | 46 | false | ```\n bool winnerSquareGame(int n) {\n vector<bool>dp(n+1,false);\n if(n==1)\n return true;\n if(n==2)\n return false;\n dp[0]=false;\n dp[1]=true;\n dp[2]=false;\n for(int i=3;i<=n;i++)\n {\n for(int k=1;k*k<=i;k++)\n {\n dp[i]=dp[i]||!dp[i-k*k];\n if(dp[i])\n break;\n }\n }\n return dp[n];\n }\n``` | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
stone-game-iv | C++ : 3 Accepted Solutions with clear explanation | c-3-accepted-solutions-with-clear-explan-3e4d | Points to consider:\n\nA. Zero is a losing position.\nB. A state is a WinningState if at least one of the positions that can be obtained from this position by a | MayankAtLeetcode | NORMAL | 2022-01-22T15:02:28.008668+00:00 | 2022-01-22T15:03:06.102746+00:00 | 42 | false | Points to consider:\n\nA. Zero is a losing position.\nB. A state is a WinningState if at least one of the positions that can be obtained from this position by a single move is a LosingSate.\nC. A state is a LosingState if every position that can be obtained from this position by a single move is a WinningState.\n\n**1st Solution:**\nIdea: Keep 2 sets one which keeps the winning state and one which keeps the losing state.\nBase case would be 0 is a losing state.\nIf we can reach in one move to a losing state means this is a winningState.\nAfter considering all if we don\'t have it in a WinningState then add it to losingState.\nAt the end check if n is in winning or losing state.\n```\n bool winnerSquareGame(int n) {\n set<int> winningState, losingState;\n losingState.insert(0); // Base case\n \n for (int i=1; i<=n ; i++) {\n for (int j=1; j*j<=i; j++) {\n if (losingState.find(i-j*j) != losingState.end()) {\n winningState.insert(i);\n break;\n }\n }\n if (winningState.find(i) == winningState.end())\n losingState.insert(i);\n }\n if (winningState.find(n) != winningState.end()) return true;\n return false;\n \n }\n```\n\n**2nd Solution:**\nCheck if we can reach to some losing condition from current position then this becomes a winning point. Return dp[n] which would tell if it is winning or losing state.\n```\n bool winnerSquareGame(int n) {\n vector<bool>dp(n+1, false);\n if (n <= 0) return false;\n \n for (int i=1; i<n+1; i++) {\n for (int j=1; j*j < i+1; j++) {\n if (!dp[i-j*j]) {\n dp[i] = true; \n }}}\n return dp[n];\n }\n```\n\n**3rd Solution:**\n**This one is the Fastest of the all 3 solutions**\nIdea: Base case dp[1] is true and dp[0] is false.\nTry to reach to a position whcih is winning position from positions which are marked as losing positions. As per our initial points:\nA state is a WinningState if at least one of the positions that can be obtained from this position by a single move is a LosingSate.\nReturn state of n.\n\n```\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1,false);\n dp[1]=true;\n int i,j;\n for(i=0;i<=n;i++)\n {\n if(dp[i])\n continue;\n for(j=1;i+j*j<=n;j++)\n {\n dp[i+j*j]=true;\n }\n }\n return dp[n];\n }\n```\n\n// Please upvote if it helped. :-) | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
stone-game-iv | C++ solution with inline comments | c-solution-with-inline-comments-by-rix23-ke3o | The idea is to keep track of the game states. A state is a winner state if we can reach a looser state.\nTime complexity: O(n^1.5)\nSpace complexity: O(n)\n\n`` | Rix2323 | NORMAL | 2022-01-22T14:50:02.492948+00:00 | 2022-01-22T15:00:51.535938+00:00 | 26 | false | The idea is to keep track of the game states. A state is a winner state if we can reach a looser state.\nTime complexity: O(n^1.5)\nSpace complexity: O(n)\n\n````\nclass Solution { \npublic: \n bool winnerSquareGame(int n) {\n vector<int> square;\n for(int i=1;i<=sqrt(n);i++) square.push_back(i*i); // vector of squares less or equal than n\n \n vector<bool> v(n+1,false); // we set each state as looser\n v[1]=true;\n for(int i=2;i<=n;i++){\n int j = 0;\n while(j<square.size() && i>=square[j]){ // we try all possible moves (removing each square less or equal than i)\n if(!v[i-square[j]]){ // if we can reach a looser state, then Bob will lose and so \'i\' is a winner state\n v[i]=true; \n break; // we can go to the next element\n } \n j++;\n } \n }\n return v[n];\n }\n}; | 1 | 0 | [] | 0 |
stone-game-iv | Memoization | Python| Readable | Detailed Comments and naming | No crazy tricks | memoization-python-readable-detailed-com-wqst | Search all possible moves but memoization saves the day,\nDynamic programming solution also possible, give it a try.\n\nclass Solution(object):\n def winnerS | delcin | NORMAL | 2022-01-22T14:19:34.958823+00:00 | 2022-01-22T14:19:34.958853+00:00 | 102 | false | Search all possible moves but memoization saves the day,\nDynamic programming solution also possible, give it a try.\n```\nclass Solution(object):\n def winnerSquareGame(self, n):\n """\n :type n: int\n :rtype: bool\n """\n starterWins = dict()\n # This dictionary stores the result of whether a player can win starting from n stones\n starterWins[1] = True # Alice wins when she moves with 1 stones left\n starterWins[0] = False # Alice loses if it\'s her turn to play and no stones are left\n \n def canWin(x):\n # This function searches for all possible ways that a player can win given\n # ... x stones\n if x in starterWins:\n return starterWins[x]\n \n one = 1\n square = 1\n while square <= x:\n res = not canWin(x-square)\n # square is a valid move as it is less than x\n # After this move if the next player canWin then it means the current\n # player cannot win. But if the next player can\'t win then the current player\n # definitely wins.\n if res:\n starterWins[x] = True\n return True\n one += 1\n square = one*one\n # We have tried all possible squares and could not win\n starterWins[x] = False\n return False\n \n return canWin(n)\n``` | 1 | 0 | ['Recursion', 'Memoization', 'Python'] | 1 |
stone-game-iv | C++ | Dp | Fast and easy | c-dp-fast-and-easy-by-dr_strange_10-wcoy | \nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n int dp[n+1];\n dp[0] = false;\n for(int i = 1;i<=n;i++)\n {\n | Dr_Strange_10 | NORMAL | 2022-01-22T08:21:45.590446+00:00 | 2022-01-22T08:21:45.590477+00:00 | 31 | false | ```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n int dp[n+1];\n dp[0] = false;\n for(int i = 1;i<=n;i++)\n {\n dp[i] = false;\n for(int j = 1; j*j<=i;j++)\n {\n if(dp[i - j*j] == false)\n {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n``` | 1 | 0 | ['Dynamic Programming'] | 0 |
stone-game-iv | C++||1-D DP Solution Commented || Based on few test cases || | c1-d-dp-solution-commented-based-on-few-m6kxj | ```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n \n // Few test cases to build intuition\n // 1 2 3 4 5 6 7 8 9 10 11 1 | Kishan_Srivastava | NORMAL | 2022-01-22T08:17:15.906240+00:00 | 2022-01-22T08:17:15.906266+00:00 | 32 | false | ```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n \n // Few test cases to build intuition\n // 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20\n // T F T T F T F T T F T F T T F T F T T F\n \n // dp[i] simply means if no. of stones are i\n // then player with turn can win or not\n vector<bool> dp(n+1,false);\n dp[0]=false;\n dp[1]=true;\n dp[2]=false;\n \n for(int i=3;i<=n;i+=1)\n {\n int root= sqrt(i);\n // if i is perfect square then Alice wins\n if((root*root)==i)\n dp[i]=true;\n \n // if for (i-1) no. of stones alice cannot win\n // then it is for sure that for i no. of stones\n // Alice will win, as firstly Alice will pick 1 stone\n // and because next turn will be of Bob and for (i-1)\n // stones player cannot win so Bob loses hence Alice wins\n else if(dp[i-1]==false)\n dp[i]=true;\n \n // Else we loop to check if there for i no. of stones \n // Alice can win or not\n else\n {\n for(int j=1;j<=root;j+=1)\n { \n // dp[i-j*j] is for Bob\'s turn\n dp[i]= dp[i]|(!dp[i-j*j]);\n }\n \n }\n \n }\n \n return dp[n];\n \n }\n};\n\n | 1 | 0 | ['Dynamic Programming'] | 0 |
stone-game-iv | C++ | DP | c-dp-by-chikzz-m5av | PLEASE UPVOTE IF U LIKE MY SOLUTION\n\n\nclass Solution {\n bool dp[100001];\npublic:\n bool winnerSquareGame(int n) {\n \n if(n==0)return 0 | chikzz | NORMAL | 2022-01-22T07:52:46.732159+00:00 | 2022-01-22T07:52:46.732204+00:00 | 72 | false | **PLEASE UPVOTE IF U LIKE MY SOLUTION**\n\n```\nclass Solution {\n bool dp[100001];\npublic:\n bool winnerSquareGame(int n) {\n \n if(n==0)return 0;\n \n if(dp[n])return 1;\n \n bool f=0;\n for(int i=1;i*i<=n;i++)\n {\n f|=(!winnerSquareGame(n-i*i)); \n }\n return dp[n]=f; \n }\n};\n``` | 1 | 0 | ['Dynamic Programming'] | 0 |
stone-game-iv | Easy solution || Dynamic Programming || Comments | easy-solution-dynamic-programming-commen-zz96 | \nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n // accumulate all perfect squares less than n\n vector<int> squares;\n fo | utsavslife | NORMAL | 2022-01-22T07:50:09.347843+00:00 | 2022-01-22T07:50:09.347872+00:00 | 42 | false | ```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n // accumulate all perfect squares less than n\n vector<int> squares;\n for(int i=1; i*i<=n; i++){\n squares.push_back(i*i);\n }\n \n // create a dp in which ith position\n // stores the posblilitiy of game win\n // if a person starts with i stones in that chance\n vector<bool> dp(n+1, false);\n // player will always win if only 1 stone is \n // present initially\n dp[1]=true;\n for(int i=2; i<=n; i++){\n // to check ith position is winning or not\n // dependes upon wether your opponent \n // wins or not after you remove squares[j] stones\n // squares[j]<=i\n for(int j=0; j<squares.size() && squares[j]<=i; j++){\n dp[i]=dp[i] || !(dp[i-squares[j]]);\n }\n }\n return dp[n];\n }\n};\n``` | 1 | 0 | [] | 0 |
stone-game-iv | Simple DP with explanation | simple-dp-with-explanation-by-as468579-be8p | \n\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool>dp (n+1, true);\n\t\t// Stores the encountered perfect square numbers\n | as468579 | NORMAL | 2022-01-22T07:37:19.276853+00:00 | 2022-01-22T07:38:18.842419+00:00 | 51 | false | ```\n\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool>dp (n+1, true);\n\t\t// Stores the encountered perfect square numbers\n vector<int> squares;\n squares.push_back(1);\n \n\t\t// Since Alice and Bob are symmetric, they have the same strategy\n\t\t// That is checking any possible next steps \n\t\t// i.e. (dp[i - num], for all num in squares)\n\t\t\n\t\t// Furthermore, since Alice and Bob have optimal strategies, \n\t\t// he/she will win the game if any next step is false (i.e. another player losses the game)\n\t\t\n\t\t// Pseudo code\n\t\t// if all dp[i - squared_num] are true, dp[i] = false, \n\t\t// else dp[i] = true\n for(int i=2; i<=n; ++i){\n double square_root = sqrt(i);\n if(int(square_root) == square_root) { \n dp[i] = true;\n squares.push_back(i);\n continue;\n }\n \n bool res = true;\n for(vector<int>::iterator it=squares.begin(); it!=squares.end(); it++){\n res = (res && dp[i - (*it)]);\n if(!res){ \n dp[i] = true;\n break;\n }\n }\n if(res){\n dp[i] = false;\n }\n }\n return dp[n];\n }\n};\n\n``` | 1 | 0 | ['Dynamic Programming', 'C++'] | 0 |
stone-game-iv | Easy Explanation C++ solution | easy-explanation-c-solution-by-mikki123-opg0 | We are checking if in our first move we can remove a square from number such that the resultant number obtained is always losing irrespective of the number remo | mikki123 | NORMAL | 2022-01-22T06:40:36.748731+00:00 | 2022-01-22T06:45:37.452196+00:00 | 35 | false | We are checking if in our first move we can remove a square from number such that the resultant number obtained is always losing irrespective of the number removed, so we created a boolean array to get outcome for different numbers. \nTC= O(N^1.5)\nSC=O(N)\n\n```\n bool winnerSquareGame(int n) {\n vector<bool>mid(n+1,0);\n for(int i=1;i<=n;i++) \n {\n for(int j=1;j*j<=i;j++)\n {\n if(mid[i-(j*j)]==0)\n {\n mid[i]=1;\n break;\n }\n }\n }\n return mid[n];\n }\n``` | 1 | 0 | [] | 1 |
shortest-impossible-sequence-of-rolls | [Java/C++/Python] One Pass, O(K) Space | javacpython-one-pass-ok-space-by-lee215-qw7w | Intuition\nFor the first number, it could be any number from 1 to k.\nSo my intuition is to check the first occurrence of all number from 1 to k.\n\n\n# Explana | lee215 | NORMAL | 2022-07-23T16:00:50.948543+00:00 | 2022-07-23T16:00:50.948598+00:00 | 8,204 | false | # **Intuition**\nFor the first number, it could be any number from 1 to k.\nSo my intuition is to check the first occurrence of all number from 1 to k.\n<br>\n\n# **Explanation**\nWe check the first occurrences of all number from `A[0]`.\nAssume `A[i]` is the rightmost one among them,\nwhich is the first occurrence of a number in `[1,k]`.\n\nThat means from `A[0]` to `A[i]`,\nwe have seen all numbers at least once.\nIn other words, `A[0]` to `A[i]` forms our first **complete set** including all numbers.\n\nThis complete set can satisfy any number from 1 to `k`,\nas the first number in the sequence.\n\nThen we continue this process, to find out the next complete set.\nWe continue doing this, and assume we can find `x` complete sets in total.\nThere may ramian some elements, but the rest can not form one more set of all numebr.\n\nThen we can take any sequence of length `x`,\n`x + 1` is the length of the shortest sequence of rolls,\nthat cannot be taken from rolls.\n\nWe simply returns `x + 1`.\n\n\n# **Prove**\nAssume there are `x` complete sets in the rolls.\n\n1) We can take any sequence of length `x`\nwe can take any number from a complete set\n\n2) We can\'t take all sequence of length `x + 1`\nWe can contruct one sequence `S` that we can\'t take.\n\n`S[0]` is the last element in the first complet set\n`S[1]` is the last element in the second complet set\n...\n\n`S[x]` is one element which is not in the incomplete set after `x` complete set\n\nWith 1) and 2),\nwe prove that `x + 1` is the length of the shortest sequence of rolls\nthat cannot be taken from rolls.\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(k)`\n<br>\n\n**Java**\n```java\n public int shortestSequence(int[] A, int k) {\n int res = 1;\n Set<Integer> s = new HashSet<>();\n for (int a : A) {\n s.add(a);\n if (s.size() == k) {\n res++;\n s.clear();\n }\n }\n return res;\n }\n```\n\n**C++**\n```cpp\n int shortestSequence(vector<int>& A, int k) {\n int res = 1;\n unordered_set<int> s;\n for (int& a : A) {\n s.insert(a);\n if (s.size() == k) {\n res++;\n s.clear();\n }\n }\n return res;\n }\n```\n\n**Python**\n```py\n def shortestSequence(self, rolls, k):\n res = 1\n s = set()\n for a in rolls:\n s.add(a)\n if len(s) == k:\n res += 1\n s.clear()\n return res\n```\n | 283 | 2 | ['C', 'Python', 'Java'] | 37 |
shortest-impossible-sequence-of-rolls | C++ | O(N) | SIMPLE TO UNDERSTAND | c-on-simple-to-understand-by-iamcoderrr-zchl | \n It looks like a very heavy Question but believes me It is Not,\n It may be difficult for you to understand why it is Working but, DRY RUN for 1-2 times and | IAmCoderrr | NORMAL | 2022-07-23T16:01:30.827872+00:00 | 2022-07-23T17:46:23.716915+00:00 | 3,819 | false | \n It looks like a very heavy Question but believes me It is Not,\n It may be difficult for you to understand why it is Working but, DRY RUN for 1-2 times and you will understand,\n \n LOGIC:\n First, I found the number which had the last occurrence in rolls means the first point where all the elements are visited for once,\n so by this, I conclude, that the sequence of length 1 is always possible,\n Then I continue doing this and continue to increase my and, as I found the all number from 1 - K\n AT last, I return The ANS,\n\t\nSummary :\nTo make all combinations of length len of k numbers we need to have numbers 1-k atleast appearing len times in the array :\nExample : for k = 3 len = 2\nAll possible sequences :\n=> 1 1, 1 2, 1 3, 2 1, 2 2, 2 3, 3 1, 3 2, 3 3\nto create all those possibilities of arrangements we need to have 1,2,3,1,2,3 in the array as a subsequence (single 1-k group of numbers can be in any order i.e, we\ncan also have 3,2,1,3,2,1 or 2,3,1,1,3,2 etc.)\nwhich is numbers from 1-k must be appearing len times in the array as a subsequence.\n\nHAPPY CODING :)\n***IF YOU LEARN SOMETHING FROM THIS POST, PLEASE UPVOTE IT***\n\n\t```\n int shortestSequence(vector<int>& rolls, int k) {\n map<int,int> m;\n int c=0,ans=0;\n for(auto a:rolls){\n m[a]++;\n if(m[a]==1) c++;\n if(c==k){\n c=0;\n m.clear();\n ans++;\n }\n }\n return ans+1;\n }\n\t``` | 123 | 3 | [] | 19 |
shortest-impossible-sequence-of-rolls | Count Subarrays with All Dice | count-subarrays-with-all-dice-by-votruba-scer | \nFor a sequence of size 1, all k dice must appear in rolls.\nFor a sequence of size 2, all k dice must appear after all k dice appear in rolls.\n... and so on. | votrubac | NORMAL | 2022-07-23T16:01:26.981486+00:00 | 2022-07-23T16:17:44.912050+00:00 | 3,101 | false | \nFor a sequence of size 1, all `k` dice must appear in `rolls`.\nFor a sequence of size 2, all `k` dice must appear after all `k` dice appear in `rolls`.\n... and so on.\n \nSo, we go through `rolls` and count unique dice.\n \nWhen we have all `k` dice, we increase the number of sequences `seq` and reset the counter.\n\n> Implementation note: instead of resetting the counter, we use the sequence number to check if a dice has appeared for the current sequence.\n> When we have all dice, we increase `seq`, so all dice must appear again.\n\n **Java**\n ```java\n public int shortestSequence(int[] rolls, int k) {\n int seq = 0, cnt = 0, dice[] = new int[k + 1];\n for (var r : rolls)\n if (dice[r] == seq) {\n dice[r] = seq + 1;\n if (++cnt % k == 0)\n ++seq;\n }\n return seq + 1;\n}\n ```\n**C++**\n```cpp\nint shortestSequence(vector<int>& rolls, int k) {\n int seq = 0, cnt = 0, dice[100001] = {};\n for (auto r : rolls)\n if (dice[r] == seq) {\n dice[r] = seq + 1;\n if (++cnt % k == 0)\n ++seq;\n }\n return seq + 1;\n}\n``` | 81 | 0 | ['C', 'Java'] | 10 |
shortest-impossible-sequence-of-rolls | Easy To Understand || Java Solution || O(n) || With Explanation || With Question Explain | easy-to-understand-java-solution-on-with-80l5 | Since i found it difficult to understand the question in the first go, so we will begin from understanding the question.\n\n#### Understanding the question:\n\n | Utkarsh_09 | NORMAL | 2022-07-23T18:05:20.077794+00:00 | 2022-07-23T18:06:09.508991+00:00 | 1,035 | false | Since i found it difficult to understand the question in the first go, so we will begin from understanding the question.\n\n#### Understanding the question:\n\nIn our question we are given an **integer array rolls** where **rolls[i] is the result of i\'th roll**. **We have a dice which has k sides number from 1 to k(inclusive)**.\n\nBasically we need to **find the length of shortest sequence that cannot be created using our rolls array**.\nEg: \n```\nInput: rolls = [4,2,1,2,3,3,2,4,1], k = 4\nOutput: 3\n```\nAll sequence of length 1 : [1], [2] , [3] , [4] can be formed since all these are present in our rolls array\nAll sequence of length 2 : \n\t[1,1] : (Pos 3, Pos 9)\n\t[1,2] : (Pos 3, Pos 7)\n\t[1,3] : (Pos 3, Pos 6)\n\t[1,4] : (Pos 3, Pos 8)\n\t[2,1] : (Pos 2, Pos 9)\n\t[2,2] : (Pos 2, Pos 7)\n\t[2,3] : (Pos 2, Pos 6)\n\t[2,4] : (Pos 2, Pos 8)\n\t.\n\t.\n\t.\nAll sequence of length 3:\n\t[1,1,1] : (Pos 3, Pos 9, Not Found ) : **This results in an impossible sequence** .\n\t[2,2,2] : (Pos 2, Pos 7, **Not Found** ) : **This results in an impossible sequence**.\n\t[1,4,2] : (Pos 3, Pos 8, **Not found**) : **This results in an impossible sequence**.\n\t\nTherefore the **shortest length of imossible sequence is 3**.\n\n\n#### Deriving intution for the solution :\n\n**If any of the element in the range [1,k] is not present in our rolls array then the length of shortest impossible sequence will be 1**.\n\nEg:\n```\nInput: rolls = [1,1,3,2,2,2,3,3], k = 4\nOutput: 1\n```\n\nSince for this it would be **impossible to find a sequence [4] therefore the answer is 1** .\n\n***Thus we can say that if suppose we get an index i upto which we have find all our elements from [1,k] i.e (rolls[0]....rolls[i] contains all the elements from [1,k]) then we can ensure that all the sequences of length 1 are possible, lets mark this index as idx1.***\n\n***Now let us suppose we get an index i (i>idx1) upto which we have find all our elemnts from [1,k] i.e (rolls[idx1+1]..........rolls[i] contains all the elements from [1,k]) then we can ensure that all the sequences of length 2 are possible.***\n\nHere ***we can surely say that all our sequence of length 2 will be possible because we can surely say that all the integers in the range[0,idx1] contains all our integers from range[1,k] (This subarray will contribute for the first element of our sequence) and all the integers in the range[idx1+1,idx2] again contains all the integers (This subarray will contribute for the second element of our sequence).***\n\nLet us consider an example : \n\n```\nInput: rolls = [4,2,1,2,3,3,2,4,1], k = 4\nOutput: 3\n\n```\n\n (Digit 1) (Digit 2)\n|--------| |------|\n4 2 1 2 3 3 2 4 1\n\nHere our subarray **(Digit1) can make all the sequences of length 1**.\n\nIf we consider taking **first digit from digit1 and second digit from digit2 then all the combinations of length 2 can be created**. Thus all the sequences of **length 2 are also be created and thus possible**.\n\nSince we are **unable to find third such subarray which contains all the elements**. Therefore it would be **impossible to create all the sequences of length 3**.\n\nThus our ***answer is 3***.\n\n### Final Solution\n\nBy doing this we can calculate the maximum length upto which all our sequences will be valid and thus our answer will be maximum sequence length + 1;\n\n```\nclass Solution {\n public int shortestSequence(int[] rolls, int k) {\n int len = 0;\n Set<Integer> set = new HashSet<>();\n for(int i:rolls)\n {\n set.add(i);\n if(set.size()==k)\n {\n set = new HashSet<>();\n len++;\n }\n }\n return len+1;\n }\n}\n```\n\nTime Complexity : O(n) \n\nSpace Complexity : O(k) \n\nFeel free to ask any doubts in the comment section.\n\n***Hope this helps :)*** | 49 | 0 | ['Java'] | 12 |
shortest-impossible-sequence-of-rolls | Greedy | Easy To Understand | With Approach | greedy-easy-to-understand-with-approach-u2uwr | Approach\n\nThe idea is if you\'re given that you can create a L length array of all permutation of k numbers, with atleast M length of given array used from th | codeanzh | NORMAL | 2022-07-23T16:02:26.550907+00:00 | 2022-07-23T18:52:12.102453+00:00 | 1,397 | false | **Approach**\n\nThe idea is if you\'re given that you can create a L length array of all permutation of k numbers, with atleast M length of given array used from the begining, then if you do not find all the k numbers after this m length then L + 1 length can not be created.\n\n**Let me elaborate**\nThink of it a bit recurcively, In a Dynamic Programing manner but not exactly DP, rather greedily.\n\nYou\'ve the array rolls, and a number k, which is the number of dice outcome that each roll can consist of, Now if you want to check if you can create all permutation of L length of K numbers, this is, you can create every possible permutation of k numbers with length L for that consider if you know that you can create L - 1 length of permutation with at least m length of the given array that is, it requires at least m length of the given array to create all permutaion of L - 1 length, then to check if you can create a L length array or not is by checking if you can get all the k numbers after m index, in the array so that you can put every number in the L - 1 length permutation to make a L length permutation with every posibility.\n\n**Example**\n\nrolls = [4,2,1,2,3,3,2,4,1], k = 4\n\nNow if I tell you that you can create 1 length permutaion by at least using 5 length of given array, then to check if we can create a 2 length array or not, we have to check if there exist all the 4 numbers in the array or not after 5 length, and in our case there exist all the 4 numbers after 5 ;ength this is in between 6 to 9 length, therefore we can create all the 2 length array, but as it requires atleast 9 length of our given array to make 2 length permutaion, you can not create all the 3 length permutaion as there are not all the numbers to insert after every 2 length permutaion.\n\n**Implementation**\n\n* Initially consider you can make (len = 1) length permutation subsequence array with starting of the given array.\n* To hold the above statement true there should be all k numbers to the right.\n* Make an empty set (data) of numbers.\n* Iterate untill you make the size of the set equals k this is, you find all the k numbers.\n* There can be two case\n1. * If you don\'t find all the k numbers after iterating all the numbers this means this length permutation can not be created, therefore this is the answer else.\n2. * If you find all the k numbers before completing the whole iteration, then the current length permutation is fixed that you can create all the permutation of given length, therefore you should make your set empty and increment length by one (len = len + 1) and continue iterating the array with above conditions for incremented length.\n\n**Time Complexity**\n* If you use C++ set then you\'ll get a time complexity of O(nlogk)\n\n**Space Compexity**\n* O(k) for the set of size k.\n\n**C++**\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int len = 1;\n set<int> data ;\n \n for (int i = 0; i < rolls.size(); i++) {\n data.insert(rolls[i]);\n \n if (data.size() == k) {\n len++;\n data = set<int>();\n }\n }\n \n return len;\n }\n};\n```\n\n**Python**\n```\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n ans = 1\n data = set()\n \n for roll in rolls:\n data.add(roll)\n \n if len(data) == k:\n ans += 1\n data.clear()\n \n return ans\n``` | 27 | 2 | ['Greedy', 'C', 'Python'] | 6 |
shortest-impossible-sequence-of-rolls | logic and catch behind that five line code | logic-and-catch-behind-that-five-line-co-6c18 | so basically we have to make sure that of size 1,2,3,4...k and numbers from[1,2,3,4,.....k] we have every possible permutation.so how will we solve that,\nlet s | karna001 | NORMAL | 2022-07-23T19:01:54.848059+00:00 | 2022-07-24T07:03:27.115785+00:00 | 633 | false | so basically we have to make sure that of size 1,2,3,4...k and numbers from[1,2,3,4,.....k] we have every possible permutation.so how will we solve that,\nlet say for size 2 we have to find out for k =3, so what are all the combinations, [1,1],[1,2] ,[1,3],[2,1],[2,2],[2,3],[3,1],[3,2],[3,3]....since there are 9 cases only here we can check for all but what if k is large like 7 or 8 ,how will we make sure that till what size we are getting every possible combination,so the catch is separate it into sets of size k , let say about out first test case[4,2,1,2,3,3,2,4,1]\nwe will iterate till our set size is 4 so we will go like\n4 - set size 1\n4,2 - set size 2\n4,2,1 - set size 3\n4,2,1,2 - set size 3 (set only contains unique elements)\n4,2,1,2,3 - set size 4 \nso now we have one pack of set of size 4 \nso if someone say bro can u make any combination of size 1 - i\'ll say yes!! i can make because i have all values present from 1 to k in my first pack\nnow let\'s start making other pack so,\n3 - set size 1\n3,2 - set size 2\n3,2,4 - set size 3\n3,2,4,1 - set size 4\nso now i have two packs of set each of size k\nso if you will ask for any combination of size two i can make ................why?? \nbecause i have all elements present in both my pack\nif you will say make 2 3\nill take 2 from first and 3 from second pack similarly i can make all. therefore the answer is the number of packs we can make +1\nsince we can\'t 3 packs there always will be one combination of 3 which we can\'t make, and here goes the code!!!!\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& A, int k) {\n \n int res = 1;\n unordered_set<int> s;\n for (int& a : A) {\n s.insert(a);\n if (s.size() == k) {\n res++;\n s.clear();\n }\n }\n return res;\n \n }\n};\n```\ni hope you get the whole picture around this short code, if you also think that it\'s too tricky to strike in our mind in live contest , kindly upvote :3 | 26 | 0 | ['C', 'Ordered Set'] | 9 |
shortest-impossible-sequence-of-rolls | C++ | Easy to understand | CPP code | c-easy-to-understand-cpp-code-by-sach400-a7o9 | \n \n int shortestSequence(vector & rolls, int k) {\n int n=rolls.size();\n set st;\n int ans=1;\n \n for(int i=0;i<n;i++) | sach4008 | NORMAL | 2022-07-23T16:33:20.099244+00:00 | 2022-07-23T16:33:37.619020+00:00 | 861 | false | \n \n int shortestSequence(vector<int> & rolls, int k) {\n int n=rolls.size();\n set<int> st;\n int ans=1;\n \n for(int i=0;i<n;i++){\n st.insert(rolls[i]);\n \n if(st.size()==k){\n\t\t\t\t// we are updating our ans as we our forming all sub-sequence of size ans\n ans++;\n st.clear();\n }\n }\n return ans;\n }\n | 12 | 1 | ['Greedy', 'C', 'Ordered Set', 'C++'] | 7 |
shortest-impossible-sequence-of-rolls | C++ || 100% faster || 100% less memory || Full Explanation with Intuition. | c-100-faster-100-less-memory-full-explan-dcjh | \n\n\nLet\'s start by building the intuition around the problem,\n\nObservation:\nSo, if we want to build a sequence of size 1. Then all the possible ways are { | AniTheSin | NORMAL | 2022-07-24T09:28:41.066802+00:00 | 2022-07-24T10:35:33.926025+00:00 | 373 | false | \n\n\nLet\'s start by building the intuition around the problem,\n\n**Observation:**\nSo, if we want to build a sequence of size 1. Then all the possible ways are **{1}, {2}, {3}, {4}**.\nSimilarly, if we want to check for size 2, Then for each of the 1st possible ways i.e({1}, {2}, {3}, {4} )we will have to append all four numbers at the end. i.e\nFor {1}\n{1,1} appends 1,\n{1,2} appends 2,\n{1,3} appends 3,\n{1,4} appends 4. \n\nSimilarly, for 2 3 4 you can do it yourself.\n\nSo we can observe that for making a sequence of size one we needed 1,2,3,4 to occur then we again need 1,2,3,4 for the sequence of size two. \n\nFor ex: **3 2 1 4 1 2 3 4** this is the given array then, we can say the first 1,2,3,4 will help us make the sequence of size one and the next 1,2,3,4 will help us make a sequence of size two & so on.\n\n**Code Explanation**\n\n**Step 1:** Make an unordered set that will help us track the occurrence of distinct numbers.\n**Step 2:** Loop through the array and insert each element in the set(i.e. unordered_set ).\n**Step 3:** Count each time the size of the set is == k, and clear the set.\n**Step 4:** No of counts + 1 is your desired answer.\n\n**Practice**\n* Go and run the test cases on the copy to get the gist of it. \n* Try now to find examples and make your own, so better understand the logic.\n\n**Solution**\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n \n unordered_set<int> s;\n int cnt_size = 0;\n \n for(int i=0 ; i<rolls.size() ; i++){\n s.insert(rolls[i]);\n if(s.size() == k){\n cnt_size++;\n s.clear();\n } \n }\n \n return ++cnt_size;\n }\n};\n```\n\n**Happy Leetcoding, please upvote if it helps you.** | 11 | 0 | ['Ordered Set'] | 1 |
shortest-impossible-sequence-of-rolls | [Python O(n) 1 pass] Explanation | Intuition | Code | python-on-1-pass-explanation-intuition-c-9di0 | Question\nWe have to find the smallest length such that there exists at least one subsequence of that length which can not be formed by the given array.\n\nIntu | surajajaydwivedi | NORMAL | 2022-07-23T16:02:28.878783+00:00 | 2022-07-23T16:45:56.702241+00:00 | 548 | false | **Question**\nWe have to find the smallest length such that there exists at least one subsequence of that length which can not be formed by the given array.\n\n**Intuition**\nLets say **magically** we know that all the subsequence of length x-1 can be formed between index *i->len(rolls)-1* (both inclusive).\nWe need to check if all elements **exists** between 0->i-1 (both inclusive), \nto know that we can form all subsequences of length x.\n\nThis is true as \n- We can pick a element from between 0->i-1 \n- Add it to a subsequence of length x-1, \n*that we magically know exists between index i->len(rolls)-1 (both inclusive).*\n\n**If all elements exists between index j->i-1 (both inclusive),**\n - **We now are at same subproblem as above** \n - **We know that all the subsequence of length x can be formed between index *j->len(rolls)-1* (both inclusive).** \n - **So we just repeat for length x+1 and so on**\n\n*We can start by assuming the length x=1 then subsequently increasing it. (As subsequence of length 0 can always be formed, i.e. [])*\n\n**For Example**\n**for array = [4,2,1,2,3,3,2,4,1], k=4**\n\n*subsequence length =1,*\n- at index =5, arr[index]=3. |*Righmost index*\n- We can form all possible subsequences of length 1 between 5->8(both inclusive), i.e. [1],[2],[3],[4]\n\n*subsequence length =2,*\nAt index=4, arr[index] =3\n- We already know that all of the subsequences of length = 1 can be formed from index 5.\n- We can now deduce that all of subsequences of length = 2, starting with *3* can be formed from index 4 onwards.\ni.e. [3,1],[3,2],[3,3],[3,4]\n\nSo Similarly, \n*subsequence length = 2*\n- at index = 2, arr[index]=1.\n- We can form all possible subsequences of length 2, i.e. [1,1],[1,2],[1,3],[1,4]....[4,3],[4,4]. \n\n*subsequence length = 3* \n- Can not be validated at even index = 0, as we still can not form all possible subsequences starting with 1,3.\n\n**Explanation**\n\nStarting from level = 1 (Assuming all subsequences of level 0 can be formed as [])\nWe just need to find the rightmost indexes for each level, where we have found all the elements upto k atleast 1 time excluding the previous level.\n\nThis works because as soon as we find the rightmost index where all elements have been found at least once for this level, we know we can start from all the elements in this level, without using any of the previous levels. Also we know we can form all the subsequences of level-1 afterwards as we have already formed them in the previous level.\n\n**Note : - Same algorithm can be adjusted to work with leftmost indexes.**\n\n**Complexity**\nTime O(n)\nSpace O(k)\n\n**Code**\n\n```\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n \n i=len(rolls)-1\n visit=set()\n c=1\n while i>=0:\n visit.add(rolls[i])\n if len(visit)==k:\n c+=1\n visit=set()\n i-=1\n return c\n \n``` | 10 | 1 | ['Python'] | 0 |
shortest-impossible-sequence-of-rolls | Greedy solution [EXPLAINED] | greedy-solution-explained-by-r9n-ku0p | IntuitionFind the shortest sequence that cannot be formed, we observe that once all dice values (1 to k) are used in a subsequence, it is impossible to extend b | r9n | NORMAL | 2024-12-19T02:52:26.629923+00:00 | 2024-12-19T02:52:26.629923+00:00 | 36 | false | # Intuition\nFind the shortest sequence that cannot be formed, we observe that once all dice values (1 to k) are used in a subsequence, it is impossible to extend beyond sequences of that length using the current rolls.\n\n# Approach\nKeep adding dice rolls to a set until it contains all numbers from 1 to k, increment the count when it does, and reset the set to start a new subsequence until the rolls are exhausted.\n\n# Complexity\n- Time complexity:\nO(n) because we iterate through the rolls once.\n\n- Space complexity:\nO(k) for the set to store up to k dice values.\n\n# Code\n```csharp []\nclass Solution {\n public int ShortestSequence(int[] rolls, int k) {\n // Use a HashSet to track unique dice values in the current subsequence\n var currentSet = new System.Collections.Generic.HashSet<int>();\n int result = 0;\n\n // Iterate through the rolls array\n foreach (var roll in rolls) {\n // Add the current roll to the set\n currentSet.Add(roll);\n\n // If the set contains all dice values (1 to k), increment the result\n if (currentSet.Count == k) {\n result++;\n currentSet.Clear(); // Reset the set for the next subsequence\n }\n }\n\n // The result represents the shortest impossible sequence length\n return result + 1;\n }\n}\n\n``` | 8 | 0 | ['Array', 'Hash Table', 'Greedy', 'C#'] | 0 |
shortest-impossible-sequence-of-rolls | C++ | Detailed and easy to understand with diagram | c-detailed-and-easy-to-understand-with-d-o3io | 1. Whats being asked?\nIn simple words the question is asking for what minimum length L, a sequence of possible dice moves of length L is not possible. This als | WTEF_adititiwari02 | NORMAL | 2022-07-25T17:25:46.394092+00:00 | 2022-07-26T17:21:59.128368+00:00 | 533 | false | #### 1. Whats being asked?\nIn simple words the question is asking for what minimum length L, a sequence of possible dice moves of length L is not possible. This also mean that for length < L, all possible dice moves of that length are allowed.\n\n#### 2. Brute force approach\nAfter being clear about what is being asked one can think of the brute force way of doing this.\nFor each length lets generate all possible dice moves.\nFor eg: Let rolls = [1, 2, 2, 3, 1] and for L = 2, and k = 3 we generate [1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3, 1], [3, 2], [3, 3]\nWe can then check if each of the generated possible dice moved of length L can be found as a [subsequence](https://en.wikipedia.org/wiki/Subsequence) within the rolls array.\n\nNow lets think what will be the time complexity for doing this check for a length L, k sided dice and rolls array of length n.\n\nFor generating the possible dice moves of length L we have [(k possibility), (k possibility) ... (k possibility)], i.e L^k possible dice moves.\nFor checking if it occurs as a subsequence, N comparisions at max with the rolls array.\nThus overall it takes for a checking a particular length L is, O(n * L^k) \n\nWe can do better than this.\n\n#### 3. Some observations\nFor rolls = [1, 2, 2, 3, 1, 3, 2, 2,1, 1], k = 3\n\n\n\n\n#### 4. Solution\nIf we carefully oberserve all ways for generating the possible dice moves in the brute force and the observations we can see that essentially for being able to generate all possible moves of length L we need to find L non overlapping subarrays such that it they each contains all elements from 1 to k.\n\n#### 5. Implementation details\n1. Keep a variable maxPossibleLength to keep track of number of subarrays found. Initialized to zero.\n2. Interate over the rolls array and keep a set to track the elements visited.\n3. Keep on inserting the elements of rolls in the set.\n4. Once the size of set is equal to k, increment maxPossibleLength and clear the set.\n5. After finishing the iteration, return maxPossibleLength + 1. We add 1 as all dice moves of this length is not possible.\n\n#### 6. Code\n```\nclass Solution {\npublic:\n\tint shortestSequence(vector<int>& rolls, int k) {\n\t\tint maxPossibleLength = 0;\n\t\tset<int> st;\n\t\tfor (int& r : rolls) {\n\t\t\tst.insert(r);\n\t\t\tif ((int)st.size() == k) {\n\t\t\t\tmaxPossibleLength++;\n\t\t\t\tst.clear();\n\t\t\t}\n\t\t}\n\t\treturn maxPossibleLength + 1;\n\t}\n};\n```\n\n#### 7. Time and space complexity analysis\n##### Space Complexity:\nO(k) (As at max k elements are stored in the set at a point of time)\n##### Time Complexity:\n1. When using ordered set: O(nlogk)\n2. When using unordered set: O(n) | 8 | 0 | ['C'] | 1 |
shortest-impossible-sequence-of-rolls | C++ | Easy | Full Explains | c-easy-full-explains-by-nitin23rathod-dlbq | We can look at the examples and find out the algorithm:\n\nInput: rolls = [4,2,1,2,3,3,2,4,1], k = 4:\n\n\n\nOutput: 2 , because only 1 level is fully filled\n\ | nitin23rathod | NORMAL | 2022-07-23T16:00:35.027869+00:00 | 2022-07-23T16:25:37.072223+00:00 | 573 | false | We can look at the examples and find out the algorithm:\n\nInput: rolls = [4,2,1,2,3,3,2,4,1], k = 4:\n\n\n\n**Output: 2 , because only 1 level is fully filled**\n\n**Algorithm:**\n* iterate through rolls\n* every new roll value possibly "extends" the set of values of current level\n* if current level contains all possible roll values {1, ..., k} - current level is fully filled, we can start a new level\n* the shortest sequence which cannot be taken from rolls is longer by 1 than our count of fully filled levels\n\n* **Time complexity** : `O(N)` - linear in rolls size\n* **Space complexity** : `O(K)` - the curLevelNumbers set can contain up to K numbers.\n\n```\nint shortestSequence(vector<int>& rolls, int k) {\n unordered_set<int> curLevelNumbers; // roll values of current level\n int fullLevelsCount = 0;\n for (int roll : rolls) {\n curLevelNumbers.insert(roll);\n if (curLevelNumbers.size() == k) {\n // If current level is fully filled with `k` numbers {1, ..., k} - start a new level, increment the `fullLevelsCount`:\n ++fullLevelsCount;\n curLevelNumbers.clear();\n }\n }\n return fullLevelsCount + 1; // the shortest sequence is longer by `1` than the `full levels count`.\n}\n```\n**If you like please upvote ** | 8 | 1 | ['C'] | 1 |
shortest-impossible-sequence-of-rolls | (My thought process during contest Explained) and clean cpp code using map. | my-thought-process-during-contest-explai-qn2a | My intution for this solution was that we will be able to compute permutaion of any particular size when we will have that much basket of number from 1 to k in | Srivaliii | NORMAL | 2022-07-23T18:11:22.771646+00:00 | 2022-07-24T09:36:03.840234+00:00 | 308 | false | My intution for this solution was that we will be able to compute permutaion of any particular size when we will have that much basket of number from 1 to k in continous order.\nex: [1, 2, 3, 4, 1, 2, 3, 4] \nhere we can generate all permuation of two size because we can pick one element from first basket (index 0 to 3) and another from 2nd basket (index 4 to 7).\nEx: [1, 2], [4, 4], [3, 2], [2, 3],....\nNote: in the above example array could be [2, 3, 4, 1, 1, 2, 3, 4] .\n```\nint shortestSequence(vector<int>& rolls, int k) {\n int n = rolls.size();\n int cnt = 0;\n map<int, int>mp;\n for(auto i: rolls){\n mp[i]++;\n\t\t\t//my basket is having numbers from 1 to k\n if(mp.size() == k){\n mp.clear();\n cnt++;\n }\n }\n return cnt+1;\n }\n\t```\n\tUpvote if u like this :)\n\tComment if any doubt. | 6 | 0 | ['C++'] | 2 |
shortest-impossible-sequence-of-rolls | c++ easy short and concise | c-easy-short-and-concise-by-abhay1707-1w09 | ``` \nint shortestSequence(vector& rolls, int k) {\n int ans=0,i;\n int n=size(rolls);\n unordered_mapm;\n for(i=n-1; i>=0; i--){ | abhay1707 | NORMAL | 2022-07-23T16:08:11.096720+00:00 | 2022-07-23T16:08:11.096757+00:00 | 206 | false | ``` \nint shortestSequence(vector<int>& rolls, int k) {\n int ans=0,i;\n int n=size(rolls);\n unordered_map<int,int>m;\n for(i=n-1; i>=0; i--){\n m[rolls[i]]++;\n if(m.size()==k){\n ans++;\n m.clear();\n }\n }\n return ans+1;\n }\n | 6 | 1 | [] | 1 |
shortest-impossible-sequence-of-rolls | CPP | Easy | cpp-easy-by-amirkpatna-f61t | \nclass Solution {\npublic:\n \n int shortestSequence(vector<int>& rolls, int k) {\n set<int> st;\n int ans=1;\n for(int x:rolls){\n | amirkpatna | NORMAL | 2022-07-23T16:02:39.788070+00:00 | 2022-07-23T16:02:39.788110+00:00 | 215 | false | ```\nclass Solution {\npublic:\n \n int shortestSequence(vector<int>& rolls, int k) {\n set<int> st;\n int ans=1;\n for(int x:rolls){\n if(!st.count(x))st.insert(x);\n if(st.size()==k){\n st.clear();\n ans++;\n }\n }\n return ans;\n }\n};\n``` | 6 | 1 | ['C++'] | 0 |
shortest-impossible-sequence-of-rolls | C++ || SET | c-set-by-ganeshkumawat8740-sjgn | get no of segment which has all [1..k] element\'s of array.\n# Code\n\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n | ganeshkumawat8740 | NORMAL | 2023-05-24T11:54:45.591370+00:00 | 2023-05-24T11:54:45.591410+00:00 | 201 | false | get no of segment which has all [1..k] element\'s of array.\n# Code\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n unordered_set<int> s;\n int a = 1;\n for(auto &i: rolls){\n s.insert(i);\n if(s.size()==k){\n a++;\n s.clear();\n }\n }\n return a;\n }\n};\n``` | 4 | 0 | ['Array', 'Hash Table', 'Greedy', 'Ordered Set', 'C++'] | 1 |
shortest-impossible-sequence-of-rolls | ✅ [C++] O(N) Intuitive approach w/sets | c-on-intuitive-approach-wsets-by-bit_leg-fy1e | This is agruably one of the Easiest-Hard problem. \nWe are asked to find the shortest subsequence which can not be formed from the given array, given that the a | biT_Legion | NORMAL | 2022-07-25T04:01:47.925063+00:00 | 2022-07-25T04:01:47.925108+00:00 | 116 | false | This is agruably one of the Easiest-Hard problem. \nWe are asked to find the shortest subsequence which can not be formed from the given array, given that the array only contains elements from 1 to k. From this, we can think of the fact that if we have exactly one occurance of each element from 1 to k, then it is possible to form evey possible subsequence of size 1 from the array. Similiarly, if we are asked to form a subsequence of size 2, then we will check if we have atleast two occurences of each element from 1 to k. If we do have alteast 2 occurences, we can form every possible subsequence of size 2, else we willl have atleast one subsequence of size 2 which will not be possible. \n____________________________________________________________________________________________________________________\nFor ex.\n```\nk = 6\nnums = [5, 6, 6, 2, 3, 6, 4, 6, 1, 5, 4, 5, 3, 3, 5, 4, 3, 1, 3, 5, 4, 2]\n\n "[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21]"\n\nAnswer will be 2 because [1,6] is not possible.\n```\nNow, we can see that the last occurance of 6 is at index 7 and the first occurance of 1 is at index 8. So, subsequence [1,6] is simply not possible. To achieve our goal, i used set, where i keep pushing elements inside set and once i have all the k elements in it, I increase our answer length by 1 because we have atleast one occurance of each element, thus a subsequence of 1 length is unavoidable. In above example, we will see that, at index 8, we will have atleast one occurance of each element, therefore our ans will be incremented by 1 here, but after this index, we will never have all the elements in our set, and therefore, our final answer will be 2.\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set <int> s;\n int count = 0;\n for(int i = 0; i<rolls.size(); i++){\n s.insert(rolls[i]);\n if(s.size()==k){\n count++;\n s.clear();\n }\n }\n return count+1;\n }\n};\n``` | 4 | 0 | ['Greedy', 'C', 'Ordered Set'] | 0 |
shortest-impossible-sequence-of-rolls | JAVA using set | java-using-set-by-aditya_jain_2584550188-rpbo | \nclass Solution {\n\tpublic int shortestSequence(int[] arr, int k) {\n\t\tint res = 1;\n\t\tint index = 0;\n\t\twhile (true) {\n\t\t\tint count = 0;\n\t\t\tint | Aditya_jain_2584550188 | NORMAL | 2022-07-23T17:54:59.012731+00:00 | 2022-07-23T17:54:59.012774+00:00 | 96 | false | ```\nclass Solution {\n\tpublic int shortestSequence(int[] arr, int k) {\n\t\tint res = 1;\n\t\tint index = 0;\n\t\twhile (true) {\n\t\t\tint count = 0;\n\t\t\tint max = 0;\n\t\t\tHashSet<Integer> set = new HashSet<>();\n\t\t\tfor (int i = index; i < arr.length; i++) {\n\t\t\t\tif (set.contains(arr[i]))\n\t\t\t\t\tcontinue;\n\t\t\t\telse {\n\t\t\t\t\tset.add(arr[i]);\n\t\t\t\t\tcount++;\n\t\t\t\t\tmax = Math.max(max, i);\n\t\t\t\t\tif (set.size() == k) {\n\t\t\t\t\t\tbreak;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\tif (count < k) {\n\t\t\t\treturn res;\n\t\t\t}\n\t\t\tindex = max + 1;\n\t\t\tres++;\n\t\t}\n\t}\n}\n``` | 3 | 0 | ['Java'] | 0 |
shortest-impossible-sequence-of-rolls | [c++ / javascript] solution | c-javascript-solution-by-dilipsuthar60-1k2g | \nclass Solution {\npublic:\n int shortestSequence(vector<int>& nums, int k) {\n unordered_set<int>s;\n int n=nums.size();\n int ans=0;\ | dilipsuthar17 | NORMAL | 2022-07-23T17:31:12.159695+00:00 | 2022-07-23T17:32:13.457529+00:00 | 121 | false | ```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& nums, int k) {\n unordered_set<int>s;\n int n=nums.size();\n int ans=0;\n for(int i=0;i<n;i++)\n {\n s.insert(nums[i]);\n if(s.size()==k)\n {\n ans++;\n s.clear();\n }\n }\n return ans+1;\n }\n};\n```\n\n```\nvar shortestSequence = function(nums, k) {\n let ans=0;\n let st=new Set();\n for(let it of nums){\n st.add(it);\n if(st.size===k){\n ans++;\n st=new Set();\n }\n }\n return ans+1;\n};\n``` | 3 | 0 | ['C', 'C++', 'JavaScript'] | 0 |
shortest-impossible-sequence-of-rolls | C++ O(n) iterative solution using set | c-on-iterative-solution-using-set-by-ary-wll6 | Algorithm -\n\nThe basic idea behind this algorithim is that every sequence of (x) rolls can be obtained be appending every number from 1 to k to all sequences | AryanMalpani | NORMAL | 2022-07-23T16:20:02.694331+00:00 | 2022-07-26T14:48:14.716034+00:00 | 43 | false | # Algorithm -\n\nThe basic idea behind this algorithim is that every sequence of (x) rolls can be obtained be appending every number from 1 to `k` to all sequences of (x-1) rolls \n\neg - Let k be 4. Now the possible sequences for two rolls are as follows. If taken a closer look each column is a number from 1 to k added to the possible sequences for 1 roll.\n<img src="https://assets.leetcode.com/users/images/4927b255-9061-4b00-a71b-56b2c77c37f0_1658735150.5346284.png" alt="closed_paren" title="Closed Parenthesis" width="425" height="350"/><img src="https://assets.leetcode.com/users/images/dd758175-5d56-425c-ad44-7436db91b051_1658735284.9261305.png" alt="closed_paren" title="Closed Parenthesis" width="425" height="340"/>\n\n\n\n\n\n\n\n\n\n\n\nSo a solution can be formed as follows -\nWe traverse the vector `rolls` from left to right and keep a count on the numbers found.\n1. If all numbers from 1 to `k` are not present in `rolls` atleast once, then the answer is 1.\n2. As soon as all numbers from 1 to `k` have occured atleast once, we can say that answer is = 1 + shortestSequence(of the remaning vector).\n(this is done because once we find that all k numbers have occured atleast once, then we can append each one to the sequences formed by the numbers ahead)\n\nThis gives us a recursive solution.\n\nAn iterative approach can also be made as follows -\n\n\n\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int ret=1;\n unordered_set<int> s;\n for(int i=0;i<rolls.size();i++)\n {\n s.insert(rolls[i]);\n if(s.size()==k)\n {\n s.clear();\n ret++;\n }\n \xA0 \xA0 \xA0 \xA0} \n\t\treturn ret;\n }\n};\n```\n\n# Complexity Analysis -\n\nRuntime Complexity - O(n)\n(Since the vector `rolls` is only traversed once and all set operations inside the loop have an average of O(1) complexity, the overall complexity of the algorithm is O(n), where n is the size of the vector `rolls`)\n\nSpace Complexity - O(k)\n(Since the set is the only componenet occupying space and as it can fill up to a maximum of k elements only, the overall space complexity is O(k), where `k` is the given integer) | 3 | 0 | [] | 1 |
shortest-impossible-sequence-of-rolls | Easy C++ one pass Solution With Explaination and Approach | easy-c-one-pass-solution-with-explainati-rsal | Intuition and Approach: Suppose if we can make sequences of length 2 till some index \nFor eg, if we can make all sequences of length 2({1,1}{1,2}{1,3}{1,4}{2,1 | karan252 | NORMAL | 2022-07-23T16:03:19.750671+00:00 | 2022-07-23T16:09:38.169031+00:00 | 154 | false | **Intuition and Approach:** Suppose if we can make sequences of length 2 till some index \nFor eg, if we can make all sequences of length 2({1,1}{1,2}{1,3}{1,4}{2,1}{2,2}{2,3}{2,4}{3,1}{3,2}{3,3}{3,4}{4,1}{4,2}{4,3}{4,4}) till some index m, then to make sequence of length 3 we will need all the numbers to be present after index m\nFor this purpose, we initialise a set and remove the number whenever we see it in a set and when set becomes empty we increment the ans, in order to avoid initialising the set again we choose other set to copy the values.\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n \n int n=rolls.size();\n int ans=1;\n set<int> s1,s2;\n for(int i=1;i<=k;i++)\n s1.insert(i);\n for(int i=0;i<n;i++)\n {\n if(s1.find(rolls[i])!=s1.end())\n {\n s1.erase(rolls[i]); //remove from set s1 and insert in s2\n s2.insert(rolls[i]); \n }\n if(s1.empty())\n {\n ans++; // when s1 is empty increment the ans and initialise it with s2;\n s1=s2;\n }\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 1 |
shortest-impossible-sequence-of-rolls | [Easy C++] Thinking process | easy-c-thinking-process-by-coding_mess-8ixa | Longest increase sub-sequence should start with some number b/w 1 and k\n2. If there are 2 number and i and j (i < j), if sub-sequence of len x is possible star | coding_mess | NORMAL | 2022-07-23T16:02:18.665631+00:00 | 2022-07-23T16:03:31.064860+00:00 | 166 | false | 1. Longest increase sub-sequence should start with some number b/w 1 and k\n2. If there are 2 number and i and j (i < j), if sub-sequence of len x is possible starting with jth element, then it is definitely possible starting with ith but not vice-versa.\n\nExample [1,1,4,3,4,2,1,2,3, 4] k = 4\nLets take i = 4, j = 5\nWe see sub-sequence of len(2) are possible starting with jth element [2, 1], [2,2]...\nThis confirms that sub-sequence of len(2) are possible starting with ith element because with can take take ith element and all len(1) sub-sequences from previous sub-sequences.\n\n3. So, for all the possible starting number, if we take the last occurring starting number, it has most chances of having first impossible sub-sequence. \n\nExample \n[1,1,4,3,4,2,1,2,3, 4]\n\nWe take first starting index j = 5. \nNow we have to keep doing same for the remaining array starting from (j+1)\n```\n\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int n = rolls.size();\n set<int> myset;\n int ans = 0;\n for(int i=0;i<n;i++){\n myset.insert(rolls[i]);\n if(myset.size() == k){\n ans++;\n myset.clear();\n }\n }\n return (ans+1);\n }\n};\n\n```\n | 3 | 0 | ['Ordered Set'] | 0 |
shortest-impossible-sequence-of-rolls | Counting groups. | counting-groups-by-akshay_gupta_7-6b6g | Intuition\nPehle 12 ando ko acche se fete. Phir omlate ki jageh tehelka omlate banaayee.\n\n# Approach\nFind first group which have all eleemnts atleast ones. a | akshay_gupta_7 | NORMAL | 2024-07-09T19:26:50.229110+00:00 | 2024-07-10T04:17:21.697318+00:00 | 64 | false | # Intuition\nPehle 12 ando ko acche se fete. Phir omlate ki jageh tehelka omlate banaayee.\n\n# Approach\nFind first group which have all eleemnts atleast ones. any extra element in this group won\'t make an extra length group because last element in this group is unique and to make an new subsequence it needs all elements after it. So jsut find groups with all elements in it which are sequential.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n public int shortestSequence(int[] omlate, int bklYeeLee) {\n Set<Integer> tehelkaOmlate=new HashSet<>();\n int yeeLee=0;\n for(int i=0;i<omlate.length;i++){\n tehelkaOmlate.add(omlate[i]);\n if(tehelkaOmlate.size()==bklYeeLee){\n tehelkaOmlate.clear();\n yeeLee++;\n }\n }\n return yeeLee+1;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
shortest-impossible-sequence-of-rolls | Easiest approach using map | easiest-approach-using-map-by-aayu_t-454s | Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n | aayu_t | NORMAL | 2024-05-28T20:21:59.362160+00:00 | 2024-05-28T20:21:59.362177+00:00 | 20 | false | # Complexity\n- Time complexity: **O(n)**\n\n- Space complexity: **O(n)**\n\n# Code\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int n = rolls.size();\n int cnt = 0;\n unordered_map<int, int>mp;\n for(auto i: rolls){\n mp[i]++;\n if(mp.size() == k){\n mp.clear();\n cnt++;\n }\n }\n return cnt+1;\n }\n};\n``` | 2 | 0 | ['Ordered Map', 'C++'] | 0 |
shortest-impossible-sequence-of-rolls | C based implementation | c-based-implementation-by-prabhatravi-fcqw | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks to find the length of the shortest sequence of rolls that cannot be ta | prabhatravi | NORMAL | 2024-04-28T14:58:30.352868+00:00 | 2024-04-28T14:58:30.352904+00:00 | 38 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks to find the length of the shortest sequence of rolls that cannot be taken from the given rolls array. To solve this problem efficiently, we need to track the frequency of each roll and count how many different rolls have been encountered in each sequence.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We initialize an array m of size k + 1 to track the frequency of each roll. We also initialize variables c to count the distinct rolls encountered and ans to store the answer.\n2. We iterate through the rolls array:\n- For each roll, we increment its frequency in the m array.\n- If the frequency of a roll becomes 1, we increment c.\n- If c becomes equal to k, it means we have encountered all possible rolls in the current sequence. We increment ans and reset the frequency array m to zeros.\n3. After processing all rolls, the answer is ans + 1 because the last sequence may not reach k distinct rolls.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the program is $$O(k)$$, where k is the maximum possible value of a roll.\n\n# Code\n```\nint shortestSequence(int* rolls, int rollsSize, int k) {\n int m[k + 1];\n int c = 0, ans = 0;\n for (int i = 0; i <= k; ++i) m[i] = 0;\n for (int i = 0; i < rollsSize; ++i) {\n int a = rolls[i];\n if (m[a] == 0) c++;\n m[a]++;\n if (c == k) {\n c = 0;\n for (int j = 0; j <= k; ++j) m[j] = 0;\n ans++;\n }\n }\n return ans + 1;\n}\n``` | 2 | 0 | ['C'] | 1 |
shortest-impossible-sequence-of-rolls | hint is the best to look for easiest solution | hint-is-the-best-to-look-for-easiest-sol-doxv | Intuition\n Describe your first thoughts on how to solve this problem. \nif i am not getting that any number that many time that i am looking for\n\n# Approach\ | Amanr_nitw | NORMAL | 2024-03-20T17:44:46.902847+00:00 | 2024-03-20T17:44:46.902868+00:00 | 37 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nif i am not getting that any number that many time that i am looking for\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nsimply traverse through rolls array and check the size of map if it is equal to k and increase the count if you got it and at last simply return the count;\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n unordered_map<int,int> mp;\n int c=1;\n for(auto it:rolls)\n {\n mp[it]++;\n if(mp.size()==k)\n {\n mp.clear();\n c++;\n }\n \n }\n return c;\n }\n};\n``` | 2 | 0 | ['Hash Table', 'C++'] | 0 |
shortest-impossible-sequence-of-rolls | c++ | easy | short | c-easy-short-by-venomhighs7-r0qi | \n\n# Code\n\nclass Solution {\npublic:\n int shortestSequence(vector<int>& A, int k) {\n int res = 1;\n unordered_set<int> s;\n for (in | venomhighs7 | NORMAL | 2022-10-25T05:53:35.379216+00:00 | 2022-10-25T05:53:35.379253+00:00 | 717 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& A, int k) {\n int res = 1;\n unordered_set<int> s;\n for (int& a : A) {\n s.insert(a);\n if (s.size() == k) {\n res++;\n s.clear();\n }\n }\n return res;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
shortest-impossible-sequence-of-rolls | simple logic, greedy+hashing | simple-logic-greedyhashing-by-ritzverma0-a9v5 | ->if we can make a subarray of length X with all k elements till index ix ,than the answer will be (X+1) if we can\'t find at least one of the array element af | ritzverma08 | NORMAL | 2022-09-18T14:59:45.779882+00:00 | 2022-09-18T14:59:45.779937+00:00 | 109 | false | ->if we can make a subarray of length X with all k elements till index ix ,than the answer will be (X+1) if we can\'t find at least one of the array element after the index ix\n->this can be done using set \n\n```\n int n = rolls.size();\n int cur= 1 ; \n set<int>st;\n for(int i = 0;i<n;i++){\n st.insert(rolls[i]);\n if(st.size()==k){\n st.clear();//we were able to make all the subarray of size cur so answer will be atleast cur+1\n cur++;\n }\n \n }\n return cur;\n \n```\nexample :\n 1 2 1 1 2 1 1 1 1 1 1 k=2\n the extra ones don\'t matter here cause 2 is the bottle neck \n set(1 2) set.clear -> set(1 2) set.clear -> set(1) ->2 is missing \n1 2 1 1 2 1 1 1 1 1 1 k=3\n 3 is missing so answer =3 | 2 | 0 | ['Greedy'] | 0 |
shortest-impossible-sequence-of-rolls | Easy Solution in CPP | easy-solution-in-cpp-by-sanket_jadhav-1fqv | ```\nclass Solution {\npublic:\n int shortestSequence(vector& rolls, int k) {\n unordered_sets;\n \n int ans=0;\n for(auto ele:ro | Sanket_Jadhav | NORMAL | 2022-08-09T17:06:40.713592+00:00 | 2022-08-09T17:06:40.713634+00:00 | 61 | false | ```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n unordered_set<int>s;\n \n int ans=0;\n for(auto ele:rolls){\n s.insert(ele);\n if(s.size()==k){\n ans++;\n s.clear();\n }\n }\n \n return ans+1;\n }\n}; | 2 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | just medium question !!!! just analyze for atleast 10 test cases | just-medium-question-just-analyze-for-at-r23h | ```\ndef shortestSequence(self, rolls: List[int], k: int) -> int:\n #what are thoughts coming in mind?\n #lets check for k=5 what are minimum poss | yaswanthkosuru | NORMAL | 2022-08-03T09:49:41.727042+00:00 | 2022-08-08T10:39:36.258930+00:00 | 100 | false | ```\ndef shortestSequence(self, rolls: List[int], k: int) -> int:\n #what are thoughts coming in mind?\n #lets check for k=5 what are minimum possible values requrie {1,2,3,4,5} for 1st combination\n #lets check for k=5 what are minimum possible values require {1,2,3,4,5,1,2,3,4,5} is it make sense \n #similarly k=3 we want{1,2,3,4,5,1,2,3,4,5,1,2,3,4,5}\n #we get a solution thats fine (count the number of [1:k] values present in rolls in a sequential manner(one after another as i said above))\n res=1\n s=set()\n for i in rolls:\n s.add(i)\n if len(s)==k:\n res+=1\n s.clear()\n return res | 2 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | [C++] Masterpiece Solution || O(N) time | c-masterpiece-solution-on-time-by-prosen-lssq | If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nWe are trying to break the | _pros_ | NORMAL | 2022-08-02T09:04:13.047304+00:00 | 2022-08-02T09:05:35.354648+00:00 | 154 | false | # **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nWe are trying to break the list into max number of groups that consist of [1, k] elements. \nThe length of the group+1 is the combination that is not possible\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int n = rolls.size(), ans = 1;\n unordered_map<int, int> um;\n for(int i = 0; i < n; i++)\n {\n um[rolls[i]]++;\n if(um.size() == k)\n {\n ans++;\n um.clear();\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Greedy', 'C', 'C++'] | 0 |
shortest-impossible-sequence-of-rolls | CPP | JAVA Solutions | O(N) | Using bitset | cpp-java-solutions-on-using-bitset-by-ia-qak1 | CPP Solution\n\nTime Complexity : O(N)\nSpace Complexity : O(N)\n\n\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n b | iambharatks | NORMAL | 2022-07-26T04:09:28.643115+00:00 | 2022-07-26T04:09:28.643151+00:00 | 31 | false | **CPP Solution**\n\nTime Complexity : O(N)\nSpace Complexity : O(N)\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n bitset<100005> b;\n int res = 0,cnt = 0;\n for(int &i: rolls){\n if(b[i] == 0){\n b[i] = 1;\n cnt++;\n }\n if(cnt== k){\n b.reset();\n res++;\n cnt = 0;\n }\n }\n return res+1;\n }\n};\n```\n\n**Java Solution**\n\nTime Complexity : O(N)\nSpace Complexity : O(k)\n\n```\nclass Solution {\n public int shortestSequence(int[] rolls, int k) {\n BitSet b = new BitSet(k+1);\n int cnt = 0,res = 1;\n for(int i = 0 ; i < rolls.length ;i++){\n if(b.get(rolls[i]) == false){\n b.set(rolls[i]);\n cnt++;\n }\n if(cnt == k){\n res++;\n cnt = 0;\n b.clear();\n }\n }\n return res;\n }\n}\n``` | 2 | 0 | ['Bit Manipulation'] | 0 |
shortest-impossible-sequence-of-rolls | C++ unordered_set | c-unordered_set-by-omhardaha1-x3cx | - if we have all k element together we can make sub seq of size 1.\n# - so count no. of time all k elements are together.\n\nclass Solution {\npublic:\n int | omhardaha1 | NORMAL | 2022-07-23T19:41:44.763277+00:00 | 2022-07-23T19:41:44.763317+00:00 | 47 | false | # - if we have all k element together we can make sub seq of size 1.\n# - so count no. of time all k elements are together.\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int> & rolls, int k) {\n \n unordered_set<int> st;\n int ans=1;\n\n for(int i=0;i<rolls.size();i++){\n st.insert(rolls[i]);\n if(st.size()==k){\n ans++;\n st.clear();\n }\n }\n\n return ans;\n }\n};\n``` | 2 | 0 | ['C', 'Ordered Set'] | 0 |
shortest-impossible-sequence-of-rolls | 10lines C++ code | Concise | Simple | Greedy | 10lines-c-code-concise-simple-greedy-by-fm4r2 | \n int shortestSequence(vector<int>& rolls, int k) {\n set<int> s;\n int co=0;\n for(auto it:rolls)\n {\n if(s.find(it)= | nm1605 | NORMAL | 2022-07-23T16:11:59.021184+00:00 | 2022-07-23T16:15:56.060734+00:00 | 81 | false | ```\n int shortestSequence(vector<int>& rolls, int k) {\n set<int> s;\n int co=0;\n for(auto it:rolls)\n {\n if(s.find(it)==s.end()) s.insert(it);\n if(s.size()==k)\n {\n s.clear();\n co++;\n }\n }\n return co+1;\n }\n\t``` | 2 | 0 | ['Greedy', 'C++'] | 1 |
shortest-impossible-sequence-of-rolls | Very Simple and Easy to Understand C++ Solution - O(n) time complexity | very-simple-and-easy-to-understand-c-sol-dqff | Up Vote if you like the solution\n\nclass Solution {\npublic:\n //ans is 1 + no. of times 1 to k appers in any sequence\n int shortestSequence(vector<int | kreakEmp | NORMAL | 2022-07-23T16:02:56.186980+00:00 | 2022-07-23T16:16:39.817244+00:00 | 68 | false | <b> Up Vote if you like the solution\n```\nclass Solution {\npublic:\n //ans is 1 + no. of times 1 to k appers in any sequence\n int shortestSequence(vector<int>& rolls, int k) {\n int m = 1, n = k, ans = 0;\n unordered_set<int> st;\n for(auto r: rolls){\n tst.insert(r);\n if(tst.size() == k){\n ans++;\n st.clear();\n }\n }\n return ans + 1;\n }\n};\n``` | 2 | 0 | ['C', 'Ordered Set'] | 0 |
shortest-impossible-sequence-of-rolls | Python easy understanding solution | python-easy-understanding-solution-by-by-yro6 | For example, k = 3, rolls = [1, 1, 2, 2, 3, 1]\nUse a set to record if all possible numbers has appeared at least once.\nIn this case, when iterate to 3 in [1 | byroncharly3 | NORMAL | 2022-07-23T16:02:29.487867+00:00 | 2022-07-24T03:39:32.920509+00:00 | 158 | false | For example, k = 3, rolls = [1, 1, 2, 2, 3, 1]\nUse a set to record if all possible numbers has appeared at least once.\nIn this case, when iterate to 3 in [1, 1, 2, 2, **3**, 1], all possible numbers (1-3) has appeared at least once,\nso you must at least take 1 number from interval [1, 1, 2, 2, 3], in practice, take 3.\n\nIn the remain array [1], it cannot fill the set again. It means there exists a number you can take to make the sequence impossible, in this case, take either 2 or 3. So both [3, 2] and [3, 3] are impossible array.\n\n```\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n s = set()\n res = 0\n \n for r in rolls:\n s.add(r)\n if len(s) == k: # All possible number has appeared once.\n res += 1 # So you must "at least" use one more place to store it.\n s.clear() # Clear the set.\n \n \n return res + 1 | 2 | 0 | ['Ordered Set', 'Python', 'Python3'] | 0 |
shortest-impossible-sequence-of-rolls | C++ || Set || Greedy | c-set-greedy-by-akash92-ytjk | Intuition\n Describe your first thoughts on how to solve this problem. \nIf all k numbers exist then we can form all subsequences of length 1.\nAfter this if ag | akash92 | NORMAL | 2024-07-22T13:36:44.258336+00:00 | 2024-07-22T13:36:44.258370+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf all k numbers exist then we can form all subsequences of length 1.\nAfter this if again all k numbers exist, then we can form all subseq of length 2.\nAfter this if again all k numbers exist, then we can form all subseq of length 3.\nAnd so on...\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStart with minLen = 1\nStore every number in a set, untill the size if the set becomes equal to k, ie, all k numbers are found.\nIncrease minLen and clear the set.\nAgain repeat the same process from the next index.\nUse unordered_set for insertion in $$O(1)$$ time.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int minLen = 1;\n unordered_set<int> st;\n for(auto it: rolls){\n st.insert(it);\n\n if(st.size()==k){ // if we are able to find all k numbers, then that minLen is possible\n // so increase minLen by 1 and again search if all k numbers exist after that\n // repeat this process till the end of the array\n minLen+=1;\n st.clear();\n }\n }\n\n return minLen;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
shortest-impossible-sequence-of-rolls | [JavaScript] 2350. Shortest Impossible Sequence of Rolls | javascript-2350-shortest-impossible-sequ-9ibg | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n\nFrom Question\n "sequence taken does not have to be consecutive as l | pgmreddy | NORMAL | 2023-07-22T13:11:29.649802+00:00 | 2023-07-22T13:15:35.247136+00:00 | 45 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n```\nFrom Question\n "sequence taken does not have to be consecutive as long as it is in order."\n so order of elements is important\n\nExample 1\n when 1,2,3,4 1,2,3,4 occur in sequence\n then [1,2,3,4] [1,2,3,4] groups that has (all 4 elements), are formed\n then all possible 2 element sequences are possible\n 1,1 1,2 1,3 1,4\n 2,1 2,2 2,3 2,4\n 3,1 3,2 3,3 3,4\n 4,1 4,2 4,3 4,4\n then some 3 element is not possible like 1,1,1\n\nExample 2\n when 1,1, 2,2 3,3, 4,4 occur in sequence\n then [1,1, 2,2 3,3, 4] [4] groups that has (all 4, or, rest of elments) are formed\n then some 2 element is not possible like 2,1\n\nConclusion\n so number of (all element) groups are important\n +1 is answer ( that is shortest seq not possible - 1,1,1 & 2,1 above)\n```\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\nSee above, for explanation\n\n```\nvar shortestSequence = function (a, k) {\n let allElementGroups = 0;\n let set = new Set()\n\n for (let e of a) {\n set.add(e);\n if (set.size === k) {\n allElementGroups += 1; // all possible distinct elements (1 to k) occured, another group formed, in order\n set = new Set(); // now, reset the set, with no elements to see if another group forms, in order\n }\n }\n return allElementGroups + 1;\n};\n```\n\nSome tests:\n```\n[1,1,2,2,3,3,4,4]\n4\n[1,2,3,4,1,2,3,4]\n4\n[4,3,2,1,4,3,2,1]\n4\n\n[ 1,2,1,2]\n2\n[ 1,1,1,2,2,2,3,3,3,4,4 ]\n4\n[ 1,2,3,4 ]\n4\n[ 1,2,3,4, 1,2,3,4 ]\n4\n[ 1,1,2,2,3,3,4,4 ]\n4\n[ 1,1,2,2,3,3,4,4, 1,2,3 ]\n4\n[ 1,1,2,2,3,3,4,4, 3,2,1 ]\n4\n\n[1]\n1\n[1,1]\n1\n[1,1,1]\n1\n[1,1]\n2\n[2,2]\n2\n[1,2]\n2\n[2,1]\n2\n[1,1,1]\n3\n\n[1,2,3,4]\n4\n[4,3,2,1]\n4\n\n[1]\n1\n[1,1]\n1\n[1,1,1]\n1\n[1,2]\n2\n[1,1,2,2]\n2\n[1,2,1,2]\n2\n[1,2,2,1]\n2\n[2,1,1,1]\n2\n[2,1,1,1]\n2\n```\n | 1 | 0 | ['JavaScript'] | 1 |
shortest-impossible-sequence-of-rolls | Java O(N) tricky Solution | java-on-tricky-solution-by-adarsh2dubey-4u5w | \n\n\n\n\n# To make all combinations of length len of k numbers we need to have numbers 1-k atleast appearing len times in the array :\nExample:\nfor k = 3 len | adarsh2dubey | NORMAL | 2022-07-30T11:26:59.870484+00:00 | 2022-07-30T11:33:03.842485+00:00 | 99 | false | \n\n\n\n\n# To make all combinations of length len of k numbers we need to have numbers 1-k atleast appearing len times in the array :\n**Example**:\nfor k = 3 len = 2\nAll possible sequences :\n=> 1 1, 1 2, 1 3, 2 1, 2 2, 2 3, 3 1, 3 2, 3 3\n to create all those possibilities of arrangements we need to have 1,2,3,1,2,3 in the array as a subsequence (single 1-k group of numbers can be in any order i.e, we can also have 3,2,1,3,2,1 or 2,3,1,1,3,2 etc.) which is numbers from 1-k must be appearing len times in the array as a subsequence.\n\n```\nclass Solution {\n public int shortestSequence(int[] A, int k) {\n int res = 1;\n Set<Integer> s = new HashSet<>();\n for (int a : A) {\n s.add(a);\n if (s.size() == k) {\n res++;\n s.clear();\n }\n }\n return res;\n }\n}\n```\n*P.S. : I couldn\'t solve this in first attempt then I saw discuss and after reading some solutions and comment I became able to solve this*\n**Credit to : @lee215 *and* @x21svge**\n | 1 | 1 | ['Java'] | 0 |
shortest-impossible-sequence-of-rolls | Simplest Detailed Explanation-Simple Logic | simplest-detailed-explanation-simple-log-eu9r | This problem is actually straightforward.\nAll we need is a little insight into how we form the sequences\n\nSuppose k=3\nLet\'s search for all 1 length sequenc | Kogarashi | NORMAL | 2022-07-26T18:12:50.368566+00:00 | 2022-07-26T18:12:50.368619+00:00 | 50 | false | This problem is actually straightforward.\nAll we need is a little insight into how we form the sequences\n\n**Suppose k=3**\nLet\'s search for all **1 length** sequences\nWe will have the following possible sequences->{1}, {2}, {3}.\nNow suppose in the rolls array we found these sequences , which means we can\'t have our answer as 1 because we are able to form all possible sequences for k=3.\n\n**Now let\'s look at all 2 length possible sequences**\n\nSuppose we iterated further on the rolls array and we again found the sequences **{1}, {2}, {3}**.\nWe have already found the the same sequences already then this means:\nfor {1,2,3}->**found before** and {1,2,3} **found in this iteration,** we can make the following combinations of 2 length sequences->**{1,1},{1,2},{1,3},{2,1},{2,2},{2,3},{3,1},{3,2},{3,3}**\n\nTherfore we just realized that we can form all possible sequences of length 2 until now. So our answer cannot be of length 2. Our answer might be of length 3 though.\n\nSo we further check if we again find these k number which are {1,2,3} further in the rolls array.\n\nIf we find these k numbers again then we can make all possible 3 length sequences therefore our answer can\'t be 3. But if we did not found these k number until the end for the 3rd time now therefore there must be some 3 length sequence which is not present in the rolls array.\n\nSo we return our answer as 3\n\nI used a simple hashset to check whether I am able to find the k numbers uptil now.\nAs soon as I find the k numbers I increment my possible answer and clear the set.\n\n```\nclass Solution {\n public int shortestSequence(int[] rolls, int k) {\n \n int n=rolls.length;\n int res=0;\n HashSet<Integer> set=new HashSet<>();\n \n for(int i=0;i<n;i++){\n set.add(rolls[i]);\n if(set.size()==k){\n res++;\n set.clear();\n }\n }\n \n return res+1;\n }\n}\n``` | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | One Pass solution | one-pass-solution-by-itsyaswanth-rtb2 | \nTime : O(nlogn)\nSpace :O(n)\n\n#define ll long long \nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int>s;\n | itsyaswanth | NORMAL | 2022-07-26T17:21:58.644087+00:00 | 2022-07-26T17:21:58.644191+00:00 | 37 | false | \nTime : `O(nlogn)`\nSpace :` O(n)`\n```\n#define ll long long \nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int>s;\n ll ans = 0;\n for(ll i=0;i<rolls.size();i++){\n s.insert(rolls[i]);\n if(s.size()==k){\n ans++;\n s.clear();\n }\n }\n return ans+1;\n }\n};\n``` | 1 | 0 | ['Ordered Set'] | 1 |
shortest-impossible-sequence-of-rolls | C++/JavaScript || TC:O(N) | cjavascript-tcon-by-pradeeptosarkar-dieu | This problem can be easily solved using a clever use of Set data structure and thinking greedily. Other approaches like DP might not yield the desired results a | pradeeptosarkar | NORMAL | 2022-07-25T09:37:41.773103+00:00 | 2022-07-25T09:37:41.773149+00:00 | 64 | false | This problem can be easily solved using a clever use of Set data structure and thinking greedily. Other approaches like DP might not yield the desired results and will be slower.\n\nThe intution is we need to create sets of complete elements such that all the numbers from 1 to K appear atleast once in such a complete set. The number of complete and sequential sets we are able to form, will give us the length of the largest possible sequence we can make. For eg, in a given case the number of complete sets are 3 that means we can derive any sequence of 3 digits from our array. The answer in that case will be 4 because there exists atleast one sequence of length 4 that cannot be derived from the given array. \n\nTo create complete sets we can use the Set available in C++ STL as well as JavaScript. The unique quality of a set is it always contains unique elements. For eg: if an element \'3\' is pushed 4 times into a set, it will appear only once in the set and therefore will only occupy one unit of space and any subsequent pushes of the same element doesn\'t increase the size of our set. Hence sets are useful to keep count of unique elements especially when we know our elements always belong to a particular range.\n\nWe start iterating from the first element in our rolls array with an empty set and keep pushing each element into the set. The moment our set reaches a size of k, we increment our answer variable and a complete set is said to have been formed in the process. Then we can clear the set to look for a new complete set. Also since our array consists of numbers in the range 1 to k, we can be sure that a complete set consists of all natural numbers upto k where each element exists atleast once.\n\n**C++ Code:**\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) \n {\n int ans=1;\n set<int> s;\n \n for(auto i:rolls)\n {\n s.insert(i);\n if(s.size()==k)\n {\n ans++;\n s.clear();\n }\n }\n return ans;\n }\n};\n\n```\n\n**JavaScript Code:**\n\n```\nvar shortestSequence = function(rolls, k) \n{\n let ans=1;\n let sett=new Set();\n \n for(let i of rolls)\n {\n sett.add(i);\n if(sett.size===k)\n {\n ans++;\n sett=new Set();\n }\n }\n return ans;\n};\n```\n | 1 | 0 | ['Greedy', 'C', 'Ordered Set', 'JavaScript'] | 0 |
shortest-impossible-sequence-of-rolls | java - easy & small (sliding window) | java-easy-small-sliding-window-by-zx007j-vcgi | Runtime: 6 ms, faster than 100.00% of Java online submissions for Shortest Impossible Sequence of Rolls.\nMemory Usage: 74.8 MB, less than 80.00% of Java online | ZX007java | NORMAL | 2022-07-25T07:02:51.738228+00:00 | 2022-07-25T07:02:51.738276+00:00 | 79 | false | Runtime: 6 ms, faster than 100.00% of Java online submissions for Shortest Impossible Sequence of Rolls.\nMemory Usage: 74.8 MB, less than 80.00% of Java online submissions for Shortest Impossible Sequence of Rolls.\n```\nclass Solution {\n public int shortestSequence(int[] rolls, int k) {\n int table[] = new int[k+1], tot = 0, level = 1;\n \n for(int j = 0; j != rolls.length; j++){\n if(table[rolls[j]]++ == 0) tot++;\n if(tot == k){\n level++;\n tot = 0;\n Arrays.fill(table, 0);\n }\n }\n \n return level;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
shortest-impossible-sequence-of-rolls | 😎Very interesting problem with easy and logical solution// CPP | very-interesting-problem-with-easy-and-l-hztw | \n\n/// EX: rolls= [1,2,3,4, 3,2,4,1, 1,1,2,2,4,3, 2,1]\n// _______ _______ ___________ ___\n// | | | rishi800900 | NORMAL | 2022-07-24T13:25:59.858684+00:00 | 2022-07-24T13:55:13.087357+00:00 | 25 | false | 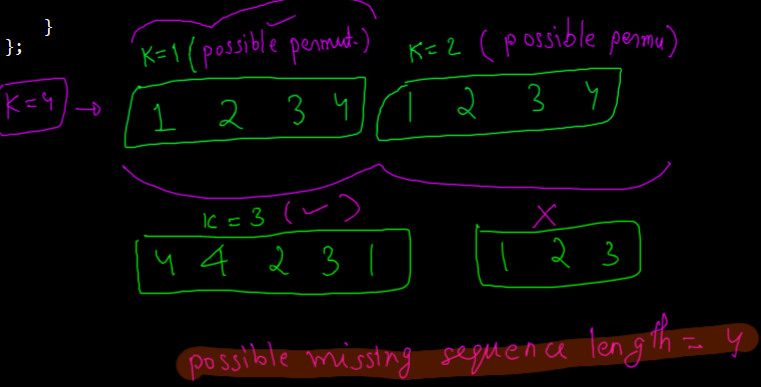\n```\n/// EX: rolls= [1,2,3,4, 3,2,4,1, 1,1,2,2,4,3, 2,1]\n// _______ _______ ___________ ___\n// | | | |\n// set = 1,2,3,4 1,2,3,4 1,2,3,4 1,2\n// ________ _______ ________ ____\n// k=1 \u2705 k=2\u2705 k=3\u2705 k=4\u274C // shortest sequence of rolls that cannot be taken from rolls=4\n\n\n/// EX: rolls= [1,2,3,4, 3,2,4,1, 2,1,1,1,2,2,4,3] // shortest sequence of rolls that cannot be taken from rolls=4\n// _______ _______ _______________ \n// | | |\n// set = 1,2,3,4 1,2,3,4 1,2,3,4\n// ________ _______ __________\n// k=1 \u2705 k=2\u2705 k=3\u2705 \n\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int>data;\n int sz_ans=1;\n for(int i=0;i<rolls.size();i++){\n data.insert(rolls[i]); // you need 1,2,3,4 for every k\n // for k=2 means need [1][2][1,2][2,1]\n if(data.size()==k){ // we should have rolls array like in set we get k times [1,2][1,2] in any order\n sz_ans++;\n data.clear();\n }\n }\n return sz_ans;\n \n }\n};\n``` | 1 | 0 | ['Greedy', 'C'] | 0 |
shortest-impossible-sequence-of-rolls | [Java/Python/Golang] One pass | javapythongolang-one-pass-by-sahil_77-u37o | Python\n\nclass Solution:\n def shortestSequence(self, rolls, k):\n """\n [4,2,1,2,3,3,2,4,1]\n \n we first find the index of a | sahil_77 | NORMAL | 2022-07-24T08:22:23.806884+00:00 | 2022-07-24T08:22:23.806922+00:00 | 103 | false | Python\n```\nclass Solution:\n def shortestSequence(self, rolls, k):\n """\n [4,2,1,2,3,3,2,4,1]\n \n we first find the index of a complete set\n \n i= 4 (first occurence of three) \n \n next we iterate through the i-->len(nums)\n finding the next index of complete set that ensures that elemts is resetn atleast two times\n \n i=8\n \n Now since we have reached to end we return how completeset was found +1\n """\n res = 1\n s = set()\n for a in rolls:\n s.add(a)\n if len(s) == k:\n res += 1\n s.clear()\n return res\n```\n\nJava\n```\nclass Solution {\n public int shortestSequence(int[] A, int k) {\n int res = 1;\n Set<Integer> s = new HashSet<>();\n for (int a : A) {\n s.add(a);\n if (s.size() == k) {\n res++;\n s.clear();\n }\n }\n return res;\n }\n}\n```\n\nGolang\n```\nfunc shortestSequence(rolls []int, k int) int {\n var s = map[int]bool{}\n var curr, res int = 0, 1\n for _, a := range rolls {\n if !s[a] {\n curr ++\n s[a] = true\n }\n // when we\'ve collected all k nums, ++\n if curr == k {\n res ++\n curr = 0\n s = map[int]bool{}\n }\n }\n return res\n}\n``` | 1 | 0 | ['Ordered Set', 'Python', 'Java', 'Go'] | 1 |
shortest-impossible-sequence-of-rolls | A simple interview style explanation | a-simple-interview-style-explanation-by-jyasu | \n\n\n\n\n\n\n\nI post solutions like this on LinkedIn, you can follow me there - https://www.linkedin.com/posts/mayank-singh-1004981a4_shortest-impossible-sequ | mayank17081998 | NORMAL | 2022-07-24T07:01:04.070261+00:00 | 2022-07-24T07:01:04.070328+00:00 | 26 | false | \n\n\n\n\n\n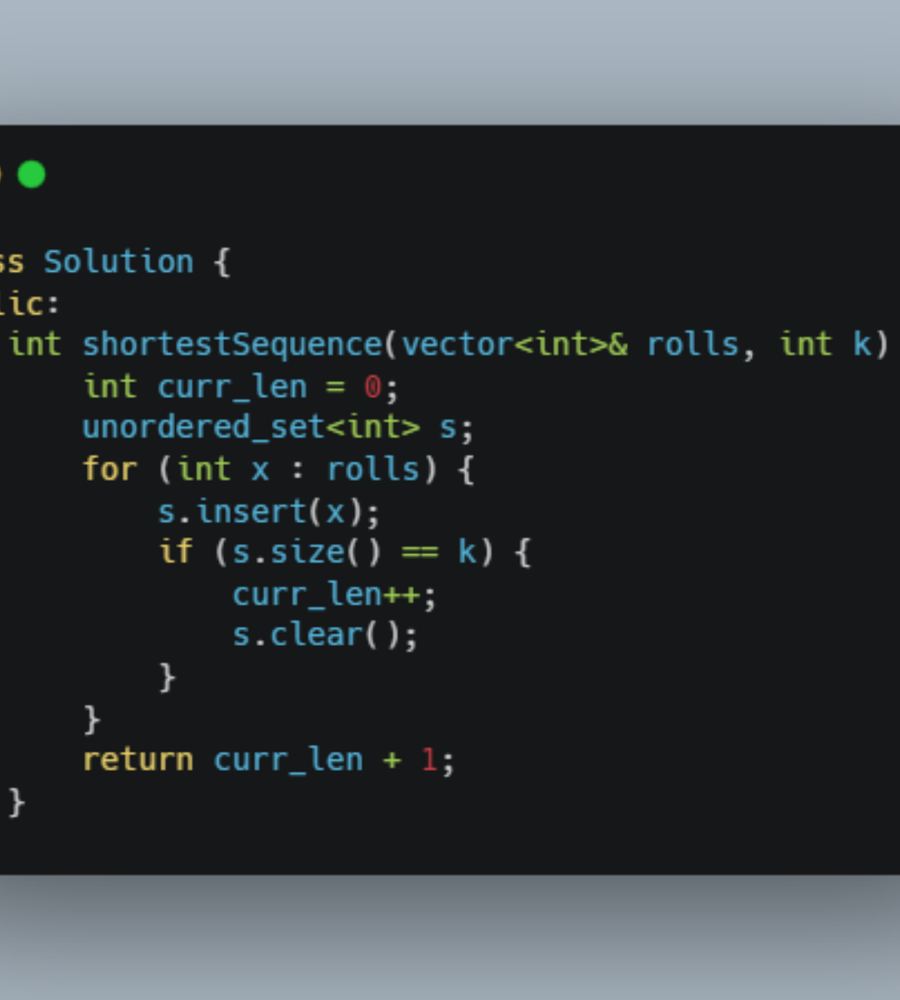\n\nI post solutions like this on LinkedIn, you can follow me there - https://www.linkedin.com/posts/mayank-singh-1004981a4_shortest-impossible-sequence-of-rolls-activity-6956860374616846336-XfzI?utm_source=linkedin_share&utm_medium=member_desktop_web | 1 | 0 | ['C', 'Ordered Set'] | 0 |
shortest-impossible-sequence-of-rolls | Java, O(n)|O(k), 3ms | java-onok-3ms-by-vkochengin-2xqe | \npublic int shortestSequence(int[] rolls, int k) {\n\tboolean[] s = new boolean[k+1];\n\tint count = k;\n\tboolean v = true;\n\tint result = 1;\n\tfor(int i:ro | vkochengin | NORMAL | 2022-07-24T06:24:14.881073+00:00 | 2022-07-24T06:24:14.881336+00:00 | 15 | false | ```\npublic int shortestSequence(int[] rolls, int k) {\n\tboolean[] s = new boolean[k+1];\n\tint count = k;\n\tboolean v = true;\n\tint result = 1;\n\tfor(int i:rolls){\n\t\tif(s[i]!=v){\n\t\t\ts[i]=v;\n\t\t\tcount--;\n\t\t\tif(count == 0){\n\t\t\t\tresult++;\n\t\t\t\tcount = k;\n\t\t\t\tv=!v;\n\t\t\t}\n\t\t}\n\t}\n\treturn result;\n}\n``` | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | Greedy Solution using SET | greedy-solution-using-set-by-_v3n0m-2l5u | Iterate untill you make the size of the set equals k this is, you find all the k numbers.\nThere can be two case :\n->If you don\'t find all the k numbers after | _V3N0M | NORMAL | 2022-07-24T04:18:00.835594+00:00 | 2022-10-21T15:05:14.209175+00:00 | 34 | false | Iterate untill you make the size of the set equals k this is, you find all the k numbers.\n*There can be two case :*\n->If you don\'t find all the k numbers after iterating all the numbers \n->If you find all the k numbers before completing the whole iteration, then the current length permutation is fixed that you can create all the permutation of given length, therefore you should make your set empty and increment length by one (count = count + 1) and continue iterating the array.\n\n**CODE:**\n``` \nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int> mp;\n int cnt=0;\n for(auto it: rolls){\n mp.insert(it);\n if(mp.size()==k){\n cnt++;\n mp.clear();\n }\n }\n return cnt+1;\n }\n}; | 1 | 0 | ['Greedy', 'C', 'Ordered Set', 'C++'] | 0 |
shortest-impossible-sequence-of-rolls | [Python3] hash set | python3-hash-set-by-ye15-6hjs | \n\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n ans = 1\n seen = set()\n for x in rolls: \n | ye15 | NORMAL | 2022-07-24T01:34:38.089234+00:00 | 2022-07-24T01:34:38.089265+00:00 | 42 | false | \n```\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n ans = 1\n seen = set()\n for x in rolls: \n seen.add(x)\n if len(seen) == k: \n ans += 1\n seen.clear()\n return ans\n``` | 1 | 1 | ['Python3'] | 0 |
shortest-impossible-sequence-of-rolls | C++ O(n) solution || easy to understand | c-on-solution-easy-to-understand-by-adit-hvq5 | Approach : we have to find the shortest impossible sequence that is if dice has all numbers occuring once then the impossible length will be two.\nif all number | aditya0203 | NORMAL | 2022-07-23T18:06:36.865028+00:00 | 2022-07-23T18:06:36.865059+00:00 | 26 | false | Approach : we have to find the shortest impossible sequence that is if dice has all numbers occuring once then the impossible length will be two.\nif all numbers are occuring twice when we divide the array then the impossible length will be 3.. and so on. \n\nwith the code itself you will understand the intution.\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int>st;\n int ans = 1;\n int n = rolls.size();\n \n for(int i=0;i<n;i++){\n if(st.find(rolls[i]) == st.end()){\n st.insert(rolls[i]);\n \n if(st.size() == k){\n ans++;\n st.clear();\n }\n }\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C', 'Ordered Set'] | 1 |
shortest-impossible-sequence-of-rolls | Python Solution linear time and space | python-solution-linear-time-and-space-by-vtxh | \nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n s = set()\n ans = 1\n for r in rolls:\n s. | user6397p | NORMAL | 2022-07-23T17:45:49.445043+00:00 | 2022-07-23T17:46:08.425971+00:00 | 15 | false | ```\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n s = set()\n ans = 1\n for r in rolls:\n s.add(r)\n if len(s) == k:\n ans += 1\n s = set()\n \n return ans\n``` | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | C++ || Set || Explained With Example || I will not say , it was easy || Thinking Based Q. | c-set-explained-with-example-i-will-not-ruev6 | \n // Intuition \n \n // check for this one -> [4,2,1,2,3,3,2,4,1], k = 4\n \n // Take the element till it has at least one occurences of distinc | KR_SK_01_In | NORMAL | 2022-07-23T17:45:47.785853+00:00 | 2022-07-23T17:48:04.709039+00:00 | 27 | false | ```\n // Intuition \n \n // check for this one -> [4,2,1,2,3,3,2,4,1], k = 4\n \n // Take the element till it has at least one occurences of distinct k values\n \n // Take a set , we will start inserting the value in the set which have values [ 4 , 2 , 1 , 2 , 3] upto \n // index 4 , \n \n // next elements from index = 5 to n-1 , [ 3 , 2 , 4 , 1] has at least one \n // occurences of distinct k values \n \n //set1 - [ 4 , 2 , 1 , 2 , 3] , set2- [ 3 , 2 , 4 , 1] -> there will exist a sequence \n //such that \n // u take element e1 from set1 , e2 from set , but there is no set3 \n // so a sequence of length 3 will not possible in that case \n \n // Remember we are not claiming that any sequence of length 3 will not exist .\n // There can exist but , there will atleast one sequence of length 3 \n // which cannot be formed as no of distinct set is only 2.\n int shortestSequence(vector<int>& nums, int k) {\n \n int n=nums.size();\n \n set<int> st;\n \n int ans=0;\n \n for(int i=0;i<n;i++)\n {\n if(st.find(nums[i])==st.end())\n {\n st.insert(nums[i]);\n \n if(st.size()==k)\n {\n st.clear();\n ans++;\n }\n }\n }\n \n return ans+1;;\n }\n``` | 1 | 0 | ['C', 'Ordered Set', 'C++'] | 0 |
shortest-impossible-sequence-of-rolls | Short & Concise | C++ | short-concise-c-by-tusharbhart-va0g | \nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n unordered_set<int> s;\n int ans = 1;\n \n for(i | TusharBhart | NORMAL | 2022-07-23T16:57:22.376125+00:00 | 2022-07-23T16:57:22.376151+00:00 | 24 | false | ```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n unordered_set<int> s;\n int ans = 1;\n \n for(int i : rolls) {\n s.insert(i);\n if(s.size() == k) s.clear(), ans++;\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Greedy', 'C', 'Ordered Set'] | 0 |
shortest-impossible-sequence-of-rolls | C++ Greedy | c-greedy-by-harem_jutsu-8rmz | We Can Notice That for all sequence of length 1 we need all k numbers once,\nSimilarly for all length 2 sequence we need all k numbers again after we have found | harem_jutsu | NORMAL | 2022-07-23T16:50:54.542261+00:00 | 2022-07-23T16:50:54.542285+00:00 | 36 | false | We Can Notice That for all sequence of length 1 we need all k numbers once,\nSimilarly for all length 2 sequence we need all k numbers again after we have found them already once because\nas we have found out all k elements once again, we can pair them up such that they form every length 2 sequence.\n```\nSay k=4\nnums=[1,2,3,4,1,2,3,4]\nwe find 1,2,3,4 once. Now after that we again find them all.\nin the first occurence of k elements 4 is at last position let its index be 3. Now after that we again find all k elements so element at index 3(=4) can pair with all the newly found k elements to form sequence of length 2. Can i Say if i can pair index 3, i can pair all index before it? Answer is Obviously Yes.\n```\nSimilarly we need all k numbers again for all length 3 sequence after we are done with length 2 sequence.\n\nThis can be easily done using set. first we fill set until we encounter all k numbers, after that once size reaches k we clear set and track for next length sequence of k element. this can be done using multiset also by keeping only one occurence of each element until size is k and then repeating the same process till we reach the end and final answer wold be size/4 ceil value. In our case of set answer would be number of times we hit k size in set+1. Obviously set implementation would be more easier so i did it that way.\nStill if it is not clear then look at example below\nExample:\n```\nnums=[1,2,3,4,4,3,2,1,1,2] \nk=4\nwe first keep a var result=1 supposing we cannot form 1 length sequence.\nfirst we insert 1,2,3,4, in set and size is now k so we conclude that we can make all 1 length sequence and so we increase result supposing that we cannot form length 2 sequence and clear set. Now again we insert 4,3,2,1 in set now again size is 4 so we again conclude that we can form length 2 sequence and now we again increment result supposing that we can not form 3 length sequence and our elements end up as we insert 1,2 in set and we reach end of array.So, we conclude that we cannot make sequence of length 3, hence our Answer is 3.\n```\nCode:\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int>st;\n int ans=1,q=0;\n for(int i=0;i<rolls.size();i++){\n if(st.find(rolls[i])==st.end())\n {\n st.insert(rolls[i]);\n if(st.size()==k)\n {\n ans++;\n st.clear();\n }\n }\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Greedy', 'C'] | 1 |
shortest-impossible-sequence-of-rolls | Short and Simple Solution | short-and-simple-solution-by-chaturvedip-yxm5 | \nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int res=1;\n unordered_set<int> s;\n for(int &i:rolls) | ChaturvediParth | NORMAL | 2022-07-23T16:47:44.655008+00:00 | 2022-07-23T16:47:44.655045+00:00 | 15 | false | ```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int res=1;\n unordered_set<int> s;\n for(int &i:rolls) {\n s.insert(i);\n if(s.size()==k) {\n res++;\n s.clear();\n }\n }\n return res;\n }\n};\n```\n\n# Please upvote if you liked the solution\n\n# \uD83D\uDCBB\uD83D\uDC31\u200D\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, please do comment below \uD83D\uDC47 | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | C++ One Pass | c-one-pass-by-mandelakalam12364-7r0m | This solution has been taken from @penguinhacker\nWorld class solution\nJust do the dry run and you will understand the logic\nIf you have any confusion, please | mandelakalam12364 | NORMAL | 2022-07-23T16:20:37.448352+00:00 | 2022-07-23T16:22:05.875529+00:00 | 20 | false | This solution has been taken from @penguinhacker\nWorld class solution\nJust do the dry run and you will understand the logic\nIf you have any confusion, please comment below\n\nTime Complexity :O(n)\nSpace Complexity : O(k)\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n vector<bool> vis(k+1);\n int cnt=0;\n int ans=1;\n for (int i : rolls) {\n if (!vis[i]) {\n vis[i]=1;\n ++cnt;\n if (cnt==k) {\n vis=vector<bool>(k+1);\n ++ans;\n cnt=0;\n }\n }\n }\n return ans;\n }\n}; | 1 | 0 | ['C'] | 0 |
shortest-impossible-sequence-of-rolls | C++ Easy Intutive , Contest solution | c-easy-intutive-contest-solution-by-thea-s52l | \n First we store all indices corresponding with the number\n Now for len=1 , get minimum indices from (1 to k)\n now for len=2 , (1 to k ) should exist before | TheAkkirana | NORMAL | 2022-07-23T16:11:53.999821+00:00 | 2022-07-23T16:11:53.999848+00:00 | 29 | false | \n* First we store all indices corresponding with the number\n* Now for len=1 , get minimum indices from (1 to k)\n* now for len=2 , (1 to k ) should exist before the last length index \n* now for len=3 , get minimum index from len=2 , and check whether (1 to k ) exist before last index\n* BUT WHY THIS ??\n* len =1 {1,2,3,4}\n* len=2 { _ _ _ _ 1 , 2 , 3 , 4} empty spaces should contain (1,2,3,4) to achieve (1,1) (1,2)(1,3)(1,4) | (2,1) (2,2)(2,3)(2,4) | (3,1) (3,2) (3,3) (3,4) | (4,1) (4,2)(4,3)(4,4) \n```\nvector<vector<int>>v(k+1);\n for(int i=0;i<rolls.size();i++){\n v[rolls[i]].push_back(i);\n }\n \n int last=INT_MAX;\n for(int len=1;len<=rolls.size();len++){\n int curr=INT_MAX;\n for(int i=1;i<=k;i++){\n while(v[i].size()>0 and v[i].back()>last) v[i].pop_back(); // get index which exist before last\n if(v[i].size()==0) return len;\n curr=min(curr,v[i].back());\n v[i].pop_back();\n }\n last=curr;\n }\n return rolls.size()+1;\n``` | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | Python - Just count complete sets of numbers 1 to k | python-just-count-complete-sets-of-numbe-xky7 | What a wonderful problem! You need to recognize that for each \u201Cposition\u201D in a sequence of x rolls to be produced, you are going to need to have found | jamzz8 | NORMAL | 2022-07-23T16:05:46.848817+00:00 | 2022-07-23T16:05:46.848845+00:00 | 36 | false | What a wonderful problem! You need to recognize that for each \u201Cposition\u201D in a sequence of x rolls to be produced, you are going to need to have found at least one each of the numbers from 1 to k (in any order). So, basically, all you have to do is create a set s, and iterate through the items in rolls, keeping a count of the number of times the length of the set becomes equal to k, and at that point begin again with an empty set. The answer is just one more than that count.\n\nHere is my code: \n```\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n count = 0\n i = 0\n found = set()\n while i < len(rolls):\n found.add(rolls[i])\n if len(found) == k:\n count += 1\n i += 1\n found = set()\n continue\n i += 1\n return count +1\n```\n | 1 | 0 | [] | 1 |
shortest-impossible-sequence-of-rolls | Easiest Solution Possible + Explanation | easiest-solution-possible-explanation-by-jr8s | Explantion:\n\nJust go and insert all unique elements in unordered set (Bcoz order is not matter here), After that when set size == k means we can create for on | amanchowdhury046 | NORMAL | 2022-07-23T16:04:09.195050+00:00 | 2022-07-23T16:04:09.195095+00:00 | 48 | false | Explantion:\n\nJust go and insert all unique elements in unordered set (Bcoz order is not matter here), After that when set size == k means we can create for one more len i.e., len + 1.\n \nEg:\n [4,2,1,2,3,3,2,4,1]\n i=0, set{4};\ni=1, set{4,2};\ni=2, set{4,2,1};\ni=3, set{4,2,1};\ni=5, set{4,2,1,3}; That\'s mean we can create one size rolls, increment count by 1 and clear the set.\ni=6, set{3};\ni=7, set{3,2};\ni=8, set{3,2,4};\ni=9, set{3,2,4,1}; That\'s mean we again able to form every number in this therefore, we will able to create any rolls with length 2.\n \nEnd of array. That\'s mean we will not able to form roll of size 3 (atleast one roll).\n \n \n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n int n=rolls.size();\n int cnt=0;\n unordered_set<int>s;\n for(int i=0;i<n;i++){\n s.insert(rolls[i]);\n if(s.size()==k){\n cnt++;\n s.clear();\n }\n }\n return cnt+1;\n }\n};\n``` | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | With explanation | C++ | Easy to understand | | with-explanation-c-easy-to-understand-by-il13 | Explanation:-\n1. You have to calculate number of subarrays that contains all numbers from 1 to k. \n2. Eg;- Let k=5; then for len=1 you need all number from 1 | aman282571 | NORMAL | 2022-07-23T16:02:02.346308+00:00 | 2022-07-23T16:02:02.346339+00:00 | 33 | false | **Explanation:-**\n1. You have to calculate number of subarrays that contains all numbers from 1 to k. \n2. Eg;- Let k=5; then for len=1 you need all number from 1 to 5. Now for len=2:- 1...5 numbers need 1...5 numbers again to form all the possible 2 length sequences.\n3. You can think that first subarray 1...5 can also contain some 2 len sequences. That is also correct but think of 5 from len 1 .It needs all 1...5 numbers again to form length 2 possible sequences. . If len=3 we need 1...5 1...5 1...5 ... so on for other lengths\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& nums, int k) {\n int sz=nums.size(),ans=1;\n unordered_set<int>st;\n for(int i=0;i<sz;i++){\n st.insert(nums[i]);\n if(st.size()==k){\n st.clear();\n ans++;\n }\n }\n return ans;\n \n }\n};\n```\n\nDo **UPVOTE** if it helps :) | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | O(N) simple C++ approach, observation based | on-simple-c-approach-observation-based-b-mgdp | \nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int>s;\n int n = rolls.size(), ans = 1;\n for(int | aryan1995 | NORMAL | 2022-07-23T16:02:00.147952+00:00 | 2022-07-23T16:02:16.480137+00:00 | 38 | false | ```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& rolls, int k) {\n set<int>s;\n int n = rolls.size(), ans = 1;\n for(int i = n-1; i>=0; i--){\n s.insert(rolls[i]);\n if(s.size() == k){\n //sequence of length ans is possible(as we have got all the k numbers), now check for the next length\n ans++;\n set<int>temp;\n swap(s, temp);\n }\n }\n return ans;\n }\n};\n```\n\n\n | 1 | 0 | ['C', 'Ordered Set'] | 0 |
shortest-impossible-sequence-of-rolls | Python | Greedy | Set | O(n) | python-greedy-set-on-by-aryonbe-dpcr | My code is originated from the following idea.\nMain Idea: to make all the sequences of rolls of length q, the given array rolls should be split into q segments | aryonbe | NORMAL | 2022-07-23T16:01:04.934413+00:00 | 2022-07-23T16:26:04.395942+00:00 | 122 | false | My code is originated from the following idea.\nMain Idea: to make all the sequences of rolls of length q, the given array rolls should be split into q segments where each segment contains all the numbers from 1 to k.\n```\nclass Solution:\n def shortestSequence(self, rolls: List[int], k: int) -> int:\n V = set()\n res = 1\n for roll in rolls:\n V.add(roll)\n if len(V) == k:\n res += 1\n V = set()\n return res | 1 | 0 | ['Greedy', 'Python'] | 0 |
shortest-impossible-sequence-of-rolls | [C++] unordered_set, one pass, O(n) | c-unordered_set-one-pass-on-by-kevin1010-67tu | Explanation\nIf every sequence of rolls of length len can be taken from rolls, then the rolls can be divided to len group and every groups must contains every n | kevin1010607 | NORMAL | 2022-07-23T16:00:36.767779+00:00 | 2022-07-23T16:00:36.767815+00:00 | 147 | false | **Explanation**\nIf every sequence of rolls of length `len` can be taken from rolls, then the rolls can be divided to `len` group and every groups must contains every number from `1` to `k`.\nSo we just traverse the rolls and use a set to store number, when meet every number from `1` to `k`, clear the set and `res++`.\nThe answer is `res` after traversal.\n\n**Example**\nrolls = [4,2,1,2,3,3,2,4,1], k = 4\n--> <u>4</u>,<u>2</u>,<u>1</u>,2,<u>3</u> | <u>3</u>,<u>2</u>,<u>4</u>,<u>1</u>\n--> The answer is 3\n\n```\nclass Solution {\npublic:\n int shortestSequence(vector<int>& A, int k) {\n int res = 1;\n unordered_set<int> s;\n for(auto i : A){\n s.insert(i);\n if(s.size() == k){\n s.clear();\n res++;\n }\n } \n return res;\n }\n};\n``` | 1 | 0 | [] | 0 |
shortest-impossible-sequence-of-rolls | Simple Greedy Solution C++ ✅✅ | simple-greedy-solution-c-by-jayesh_06-1zsx | Code | Jayesh_06 | NORMAL | 2025-03-27T11:43:18.001151+00:00 | 2025-03-27T11:43:18.001151+00:00 | 2 | false |
# Code
```cpp []
class Solution {
public:
int shortestSequence(vector<int>& rolls, int k) {
int n=rolls.size(),curr_k=1,c=0;
vector<int> v(k+1);
for(int i=0;i<n;i++){
if(v[rolls[i]]!=curr_k){
v[rolls[i]]=curr_k;
c++;
}
if(c==k){
c=0;
curr_k++;
}
//cout<<i<<" "<<c<<" "<<curr_k<<endl;
}
return curr_k;
}
};
``` | 0 | 0 | ['Array', 'Hash Table', 'Greedy', 'C++'] | 0 |
shortest-impossible-sequence-of-rolls | JAVA easy | java-easy-by-navalbihani15-8e1d | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | navalbihani15 | NORMAL | 2025-03-27T10:23:57.607170+00:00 | 2025-03-27T10:23:57.607170+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int shortestSequence(int[] rolls, int k) {
Set<Integer> s = new HashSet<>();
int c = 0 ;
for(int i = 0 ;i<rolls.length;i++){
s.add(rolls[i]);
if(s.size()==k){
c++;
s.clear();
}
}
return c+1;
}
}
``` | 0 | 0 | ['Java'] | 0 |
shortest-impossible-sequence-of-rolls | 2350. Shortest Impossible Sequence of Rolls | 2350-shortest-impossible-sequence-of-rol-u7di | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-18T10:37:28.319678+00:00 | 2025-01-18T10:37:28.319678+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int shortestSequence(vector<int>& rolls, int k) {
unordered_set<int> unique_rolls;
int result = 0;
for (int roll : rolls) {
unique_rolls.insert(roll);
if (unique_rolls.size() == k) {
result++;
unique_rolls.clear();
}
}
return result + 1;
}
};
``` | 0 | 0 | ['C++'] | 0 |
shortest-impossible-sequence-of-rolls | Easy simple solution | c++ | small code | easy-simple-solution-c-small-code-by-vin-rz1g | IntuitionThe problem requires finding the shortest impossible sequence length that can be formed using the rolls. The key observation is that a sequence of leng | vinayjaiswal9919 | NORMAL | 2025-01-04T14:50:07.103886+00:00 | 2025-01-04T14:50:07.103886+00:00 | 10 | false | # Intuition
The problem requires finding the shortest impossible sequence length that can be formed using the rolls. The key observation is that a sequence of length n requires at least k^n unique combinations of rolls. By tracking how many unique numbers from 1 to k have been seen, we can determine when it is no longer possible to form a sequence of the current length
# Approach
1. Use a hash set (seen) to track the unique numbers encountered in the current iteration.
2. Iterate through the rolls array:
- Add each number to the set.
- When the size of the set equals 𝑘 (i.e., all numbers from 1 to k have been seen), increment the result and clear the set.
3. The result represents the shortest sequence length that cannot be formed.
# Complexity
- Time complexity:
O(n), where 𝑛 is the length of the rolls array. Each element is processed once, and operations on the set are O(1) on average.
- Space complexity:
O(1)w,here k is the size of the set. The set stores at most k unique elements.
# Code
```cpp []
class Solution {
public:
int shortestSequence(vector<int>& rolls, int k) {
unordered_set<int> seen;
int result = 1;
for (int roll : rolls) {
seen.insert(roll);
if (seen.size() == k) {
result++;
seen.clear();
}
}
return result;
}
};
``` | 0 | 0 | ['C++'] | 1 |
shortest-impossible-sequence-of-rolls | Easy simple solution | c++ | small code | easy-simple-solution-c-small-code-by-vin-llyy | IntuitionThe problem requires finding the shortest impossible sequence length that can be formed using the rolls. The key observation is that a sequence of leng | vinayjaiswal9919 | NORMAL | 2025-01-04T14:50:04.649396+00:00 | 2025-01-04T14:50:04.649396+00:00 | 2 | false | # Intuition
The problem requires finding the shortest impossible sequence length that can be formed using the rolls. The key observation is that a sequence of length n requires at least k^n unique combinations of rolls. By tracking how many unique numbers from 1 to k have been seen, we can determine when it is no longer possible to form a sequence of the current length
# Approach
1. Use a hash set (seen) to track the unique numbers encountered in the current iteration.
2. Iterate through the rolls array:
- Add each number to the set.
- When the size of the set equals 𝑘 (i.e., all numbers from 1 to k have been seen), increment the result and clear the set.
3. The result represents the shortest sequence length that cannot be formed.
# Complexity
- Time complexity:
O(n), where 𝑛 is the length of the rolls array. Each element is processed once, and operations on the set are O(1) on average.
- Space complexity:
O(1)w,here k is the size of the set. The set stores at most k unique elements.
# Code
```cpp []
class Solution {
public:
int shortestSequence(vector<int>& rolls, int k) {
unordered_set<int> seen;
int result = 1;
for (int roll : rolls) {
seen.insert(roll);
if (seen.size() == k) {
result++;
seen.clear();
}
}
return result;
}
};
``` | 0 | 0 | ['C++'] | 1 |
shortest-impossible-sequence-of-rolls | Java Python3 C++ || 2ms 11ms 0ms || Bitmask or array to find 1..k groups | java-python3-c-2ms-11ms-0ms-bitmask-or-a-1ddd | Note: The leetcode problem description did not give its definition of a "subsequence". For this problem, a "subsequence" is defined as deleting any number of | dudeandcat | NORMAL | 2024-12-21T06:56:50.997246+00:00 | 2024-12-21T07:45:58.017319+00:00 | 6 | false | *Note: The leetcode problem description did not give its definition of a "subsequence". For this problem, a "subsequence" is defined as deleting any number of values from any indexes in `rolls[]`, but the remaining `rolls[]` values must keep the same relative order.*\n\nThe code below is available in both Java and Python3, both in clean (uncommented) code, and highly commented code.\n\n**Basic Concept:**\n\nThe basic concept is to scan through the values in `rolls[]`, until found all values from 1 to k. If all values 1..k were found, then the answer sequence length must be greater than 1, since the value in any length 1 sequence would be in the 1..k values that were found in `rolls[]`. Continue scanning `rolls[]` to find a second group of all 1..k values. If the second group of all 1..k values were found, then the answer sequence length must be greater than 2, since two separate 1..k groups were found, and any length 2 sequence could be formed from a value from the first 1..k group, followed by a value from the second 1..k group. This can be continued, finding as many separate 1..k groups as possible from `rolls[]`.\n\n**Algorithm:**\n\n1. If k==1, then return `rolls.length+1`.\n2. Initialize shortest sequence length to 1\n3. Scan through `rolls[]` one element at a time, trying to find groups of all values 1..k.\n\t3a. Mark current roll value as used.\n\t3b. If used all values 1..k, then increment shortest sequence\'s length, and reset used status for finding next group of all the 1..k values.\n4. Return calculated shortest sequence length.\n\n**Optimization: k==1**\n\nIf k==1, then using a 1-sided dice that can only roll the value "1". Therefore, `roll[]` can only contain the value 1. The shortest sequence of values 1..k that is *not* a subsequence of `rolls[]`, can only contain the value 1,\n\n**Optimization: Detecting used values 1..k**\n\nThe algorithm requires keeping information about which values 1..k have been "used", because when all values 1..k have been "used", then the answer sequence length must be incremented. Different data structures can be used to detect when all 1..k valued have been used, some of which are listed in order from fastest to slowest:\n\n- **Bitmask** -- Use a bitmask of k bits, with each bit indicating when the corresponding 1..k value is used. Keep a variable with all bits 1..k set to compare to the bitmask to determine when done finding all 1..k values. In the bitmask, bit-0 will always be zero because the dice can never roll a zero.\n. \nUsed in the code below to gain execution speed, but only when k<=62, because values of 62 bits can be handled by single CPU instructions. In Java, this would be a `long` value. In C++, it would be a `long long` value. In Python the bitmask is simply a numeric value, and Python bitmasks can contain the max k==100_000 bits, but bitmasks this large are slower than the other following data structures.\n\n- **Integer array** -- Use an array of k integers, indexed by a roll value, to indicate when that 1..k roll value is "used". Also keep a separate variable as a down-counter of how many of the 1..k values are remaining to be found. Used in the code below when k>62, when the bitmask data structures are not efficient. The C++ code will occasionally have a runtime of 0ms using only the integer array, *without* using the faster bitmask section of the code.\n\n- **Boolean array** -- Use an array of boolean values, similar to the integer array above, and also including a separate down-counter to indicate when all 1..k values are found. Not used in the code below.\n\n- **HashSet** -- Use a HashSet (`set()` in Python) that contains the 1..k values already "used". When the HashSet size equals k, then all 1..k values have been used. Clear the HashSet to start looking for the next 1..k group. Not used in the code below.\n\n**Runtimes**\nC++: 0ms to 8ms, December 2024\nJava: 2ms to 3ms, December 2024:\nPython3: 11ms to 27ms, December 2024:\n\n**--- Clean code ---**\n<iframe src="https://leetcode.com/playground/GF2FGbiC/shared" frameBorder="0" width="600" height="450"></iframe>\n\n**--- Commented code ---**\n<iframe src="https://leetcode.com/playground/kYug76jh/shared" frameBorder="0" width="600" height="450"></iframe> | 0 | 0 | ['C', 'Java', 'Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.