question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
smallest-index-with-equal-value | Java Solution faster than 94% | java-solution-faster-than-94-by-vishwaje-dko2 | \nclass Solution {\n public int smallestEqual(int[] nums) {\n for(int i = 0;i<nums.length;i++)\n if(i%10==nums[i])\n return | vishwajeet_rauniyar | NORMAL | 2022-05-27T13:31:37.584636+00:00 | 2022-05-27T13:31:37.584668+00:00 | 37 | false | ```\nclass Solution {\n public int smallestEqual(int[] nums) {\n for(int i = 0;i<nums.length;i++)\n if(i%10==nums[i])\n return i;\n return -1;\n }\n}\n``` | 1 | 0 | [] | 0 |
smallest-index-with-equal-value | Easy python solution | easy-python-solution-by-rupeshmohanty-e54w | \nclass Solution:\n def smallestEqual(self, nums: List[int]) -> int:\n res = []\n \n for i in range(len(nums)):\n if i % 10 = | rupeshmohanty | NORMAL | 2022-05-10T15:09:04.434948+00:00 | 2022-05-10T15:09:04.434977+00:00 | 108 | false | ```\nclass Solution:\n def smallestEqual(self, nums: List[int]) -> int:\n res = []\n \n for i in range(len(nums)):\n if i % 10 == nums[i]:\n res.append(i)\n \n if len(res) > 0:\n return min(res)\n else:\n return -1\n``` | 1 | 0 | ['Python'] | 0 |
smallest-index-with-equal-value | C++ beginner friendly solution | c-beginner-friendly-solution-by-pratium-072t | \nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n int n=nums.size();\n for(int i=0;i<n;i++){\n if(i%10==nums[i] | pratium | NORMAL | 2022-05-02T09:21:32.889686+00:00 | 2022-05-02T09:21:32.889737+00:00 | 28 | false | ```\nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n int n=nums.size();\n for(int i=0;i<n;i++){\n if(i%10==nums[i]){\n return i;\n break;}\n }\n return -1;\n }\n};\n``` | 1 | 0 | [] | 0 |
smallest-index-with-equal-value | Java Solution - O(N) | java-solution-on-by-solved-fxbj | \nclass Solution {\n public int smallestEqual(int[] nums) {\n for (int i = 0; i < nums.length; i++) {\n if (i % 10 == nums[i]) {\n | solved | NORMAL | 2022-03-21T16:41:03.903853+00:00 | 2022-03-21T16:41:03.903899+00:00 | 28 | false | ```\nclass Solution {\n public int smallestEqual(int[] nums) {\n for (int i = 0; i < nums.length; i++) {\n if (i % 10 == nums[i]) {\n return i;\n }\n }\n return -1;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
smallest-index-with-equal-value | Without Modular operator | follow-up question | without-modular-operator-follow-up-quest-hm74 | With modulus it\'s easy, here is without modulus\n\nclass Solution {\n public int smallestEqual(int[] nums) {\n int index = 0;\n for (int i = 0 | nishantk3101 | NORMAL | 2022-03-12T22:13:56.080135+00:00 | 2022-03-12T22:13:56.080163+00:00 | 56 | false | **With modulus it\'s easy, here is without modulus**\n```\nclass Solution {\n public int smallestEqual(int[] nums) {\n int index = 0;\n for (int i = 0 ; i < nums.length; i++) {\n if (index == nums[i]) {\n return i;\n }\n if (++index== 10) {\n index = 0;\n }\n }\n return -1;\n }\n}\n```\n | 1 | 0 | ['Java'] | 0 |
smallest-index-with-equal-value | C++ | Easy Solution | O(n) time complexity | Clean Code | c-easy-solution-on-time-complexity-clean-foa7 | Please Upvote if you found this useful.\n\n\nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) \n {\n for(int i=0; i<nums.size(); i+ | saketgautam | NORMAL | 2022-02-19T22:57:38.746586+00:00 | 2022-02-19T22:57:38.746613+00:00 | 61 | false | **Please Upvote if you found this useful.**\n\n```\nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) \n {\n for(int i=0; i<nums.size(); i++)\n {\n if(i % 10== nums[i])\n {\n return i;\n }\n }\n return -1;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 0 |
smallest-index-with-equal-value | Java Solution | Memory Usage is less than 73.35% of online submissions | | java-solution-memory-usage-is-less-than-d7gq2 | class Solution {\n public int smallestEqual(int[] nums) {\n int smallIndex = -1;\n for (int i=nums.length-1; i>=0; i--){\n int help | m1502 | NORMAL | 2022-01-14T12:23:29.171413+00:00 | 2022-01-14T12:23:29.171454+00:00 | 78 | false | class Solution {\n public int smallestEqual(int[] nums) {\n int smallIndex = -1;\n for (int i=nums.length-1; i>=0; i--){\n int help = i % 10;\n if (help == nums[i]){\n smallIndex = i;\n }\n }\n return smallIndex;\n }\n} | 1 | 1 | ['Array', 'Java'] | 0 |
smallest-index-with-equal-value | c++ one loop | c-one-loop-by-amarp-92od | \nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n for (int i = 0; i < nums.size(); i++) {\n if ( (i % 10) == nums[i]) | amarp | NORMAL | 2021-12-31T07:20:36.235498+00:00 | 2021-12-31T07:20:36.235537+00:00 | 43 | false | ```\nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n for (int i = 0; i < nums.size(); i++) {\n if ( (i % 10) == nums[i]) return i; \n } \n return -1; \n }\n};\n``` | 1 | 0 | [] | 0 |
smallest-index-with-equal-value | C++ / NO MOD NO MULTI , ONLY ADD / simple solution | c-no-mod-no-multi-only-add-simple-soluti-wxwt | \nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n int idx = 0;\n for (int i = 0 ; i < nums.size(); ++i) {\n if | pat333333 | NORMAL | 2021-12-11T07:08:36.104419+00:00 | 2021-12-11T07:09:23.772255+00:00 | 39 | false | ```\nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n int idx = 0;\n for (int i = 0 ; i < nums.size(); ++i) {\n if (idx == nums[i]) {\n return i;\n }\n if (++idx == 10) {\n idx = 0;\n }\n }\n return -1;\n }\n};\n``` | 1 | 0 | [] | 0 |
smallest-index-with-equal-value | [JAVA] Runtime 100% && Simple 3-Line Solution | java-runtime-100-simple-3-line-solution-3wrb8 | if you find it useful, please upvote it)\n\n public int smallestEqual(int[] nums) {\n for(int i=0; i<nums.length; i++)\n if((i-nums[i])%10= | 7akhongir | NORMAL | 2021-11-26T21:07:24.752163+00:00 | 2021-11-26T21:07:49.149782+00:00 | 213 | false | if you find it useful, please upvote it)\n```\n public int smallestEqual(int[] nums) {\n for(int i=0; i<nums.length; i++)\n if((i-nums[i])%10==0) return i;\n return -1;\n }\n``` | 1 | 0 | ['Java'] | 1 |
smallest-index-with-equal-value | [Python3] 1 line | python3-1-line-by-nuno-dev1-9lig | \nclass Solution:\n def smallestEqual(self, nums: List[int]) -> int:\n return min([i for i,el in enumerate(nums) if i%10==el],default=-1)\n | nuno-dev1 | NORMAL | 2021-11-22T12:09:20.584291+00:00 | 2021-11-22T12:09:20.584355+00:00 | 60 | false | ```\nclass Solution:\n def smallestEqual(self, nums: List[int]) -> int:\n return min([i for i,el in enumerate(nums) if i%10==el],default=-1)\n``` | 1 | 0 | [] | 0 |
smallest-index-with-equal-value | C++ || easy solution with 1 for loop + explanation | c-easy-solution-with-1-for-loop-explanat-uqvn | class Solution {\npublic:\n int smallestEqual(vector& nums) \n {\n* int ans=INT_MAX;\n for(int i=0;i<nums.size();i++)\n {\n | mayanksamadhiya12345 | NORMAL | 2021-11-11T17:08:39.636709+00:00 | 2021-11-11T17:09:05.513003+00:00 | 61 | false | class Solution {\npublic:\n int smallestEqual(vector<int>& nums) \n {\n* int ans=INT_MAX;\n for(int i=0;i<nums.size();i++)\n {\n if(i%10==nums[i])\n {\n ans = min(ans,i);\n }\n }\n if(ans==INT_MAX)\n {\n return -1;\n }\n return ans;\n }\n} | 1 | 0 | [] | 0 |
smallest-index-with-equal-value | Python easy code, beats 100% | python-easy-code-beats-100-by-vistrit-ahuc | \ndef smallestEqual(self, nums: List[int]) -> int:\n for i in range(len(nums)):\n if i%10==nums[i]: return i\n return -1\n | vistrit | NORMAL | 2021-11-09T04:24:08.707997+00:00 | 2021-11-09T04:24:08.708049+00:00 | 169 | false | ```\ndef smallestEqual(self, nums: List[int]) -> int:\n for i in range(len(nums)):\n if i%10==nums[i]: return i\n return -1\n``` | 1 | 0 | ['Python'] | 0 |
smallest-index-with-equal-value | Surprise from leetcode | surprise-from-leetcode-by-avinash1320-slh1 | \nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n int i=0, ans=-1;\n for(i=0;i<nums.size();i++){\n if(i%10==num | avinash1320 | NORMAL | 2021-11-05T06:26:40.948718+00:00 | 2021-11-05T06:26:40.948776+00:00 | 48 | false | ```\nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n int i=0, ans=-1;\n for(i=0;i<nums.size();i++){\n if(i%10==nums[i]){\n ans=i;\n break;}\n }\n return ans;\n }\n};\n```\n\n##### I know it is a easy question but there is some thing we can explore more like\n##### Since modullo operator is a very heavy operator , so instead of doing modullo every time ,\n##### We can just skip the elements who are greater than 9 and the code\'s execution time comes down\n##### from 16ms to 8ms . \n\n\t for(int i=0 ; i< nums.size() ; i++)\n\t {\n\t\t if(nums[i] >= 10 ) continue;\n\t\t if(nums[i] == i%10)\n\t\t\t return i ;\n\t }\n\t return -1 ;\n\t \n Please **Upvote** | 1 | 1 | ['C', 'C++'] | 1 |
smallest-index-with-equal-value | EZ Python Code For Beginners O(N) | ez-python-code-for-beginners-on-by-saumy-7hf6 | \nclass Solution:\n def smallestEqual(self, nums: List[int]) -> int:\n val=-1\n for i in range(len(nums)):\n if i%10==nums[i]:\n | SaumyaRai29 | NORMAL | 2021-11-05T06:18:42.141640+00:00 | 2021-11-05T06:18:42.141679+00:00 | 31 | false | ```\nclass Solution:\n def smallestEqual(self, nums: List[int]) -> int:\n val=-1\n for i in range(len(nums)):\n if i%10==nums[i]:\n val=i\n return val\n return val\n``` | 1 | 1 | ['Python'] | 0 |
smallest-index-with-equal-value | Kotlin | kotlin-by-armat-qpip | \nclass Solution {\n fun smallestEqual(nums: IntArray): Int =\n nums.withIndex()\n .find { (index, num) -> index % 10 == num }\n | armat | NORMAL | 2021-11-04T14:31:08.203316+00:00 | 2021-11-04T14:31:08.203348+00:00 | 27 | false | ```\nclass Solution {\n fun smallestEqual(nums: IntArray): Int =\n nums.withIndex()\n .find { (index, num) -> index % 10 == num }\n ?.index ?: -1\n}\n``` | 1 | 0 | [] | 0 |
smallest-index-with-equal-value | Easy Java Solution | easy-java-solution-by-debankakhan-17ej | \nclass Solution {\n public int smallestEqual(int[] nums) {\n int k=0;\n int flag=0;\n int arr[]= new int[nums.length];\n for(int | DebankaKhan | NORMAL | 2021-11-04T04:50:05.894831+00:00 | 2021-11-04T04:50:05.894881+00:00 | 65 | false | ```\nclass Solution {\n public int smallestEqual(int[] nums) {\n int k=0;\n int flag=0;\n int arr[]= new int[nums.length];\n for(int i=0;i<nums.length;i++){\n arr[k]= i%10;\n k++;\n }\n for(int i=0;i<nums.length;i++){\n if(nums[i]==arr[i]){\n flag=1;\n return i;\n }\n }\n return -1;\n }\n}\n\n``` | 1 | 0 | [] | 1 |
smallest-index-with-equal-value | C++ | c-by-ujjwal2001kant-fnum | ```\nclass Solution {\npublic:\n int smallestEqual(vector& nums) {\n for(int i=0; i<nums.size(); i++)\n {\n if(i%10==nums[i])\n | ujjwal2001kant | NORMAL | 2021-11-02T20:05:40.305344+00:00 | 2021-11-02T20:05:40.305400+00:00 | 54 | false | ```\nclass Solution {\npublic:\n int smallestEqual(vector<int>& nums) {\n for(int i=0; i<nums.size(); i++)\n {\n if(i%10==nums[i])\n return i;\n }\n return -1;\n }\n}; | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | who dont understand code | who-dont-understand-code-by-yaswanthkosu-yrcc | why these type of problems in contest \ni dont even understand problem | yaswanthkosuru | NORMAL | 2022-09-03T16:11:46.217406+00:00 | 2022-09-03T16:11:46.217446+00:00 | 4,613 | false | why these type of problems in contest \ni dont even understand problem | 125 | 10 | [] | 16 |
maximum-rows-covered-by-columns | Brute-Force + Bit Magic | brute-force-bit-magic-by-votrubac-f5b2 | \nLow constraints give away a brute-force solution.\n \nWe try all combinations of columns (using a bit mask), where the number of columns does not exceed co | votrubac | NORMAL | 2022-09-03T16:00:17.929657+00:00 | 2022-09-03T16:00:17.929688+00:00 | 5,633 | false | \nLow constraints give away a brute-force solution.\n \nWe try all combinations of columns (using a bit mask), where the number of columns does not exceed `cols`.\n \nFor each combination, we count covered rows, and return the maximum.\n \nAs an optimization, we can only consider bit masks with `cols` bits. We start from `(1 << cols) - 1`.\n\nThen, we use `next_popcount` to get the next mask with the same number of bits.\n \n**C++**\n```cpp\nint next_popcount(int n) {\n int c = (n & -n), r = n + c;\n return (((r ^ n) >> 2) / c) | r;\n}\nint maximumRows(vector<vector<int>>& mat, int cols) {\n int m = mat.size(), n = mat[0].size(), res = 0;\n for (int mask = (1 << cols) - 1; mask < (1 << n); mask = next_popcount(mask)) {\n int rows = 0;\n for (int i = 0, j = 0; i < m; ++i) {\n for (j = 0; j < n; ++j)\n if (mat[i][j] && (mask & (1 << j)) == 0)\n break;\n rows += j == n;\n }\n res = max(res, rows);\n }\n return res;\n} | 62 | 1 | [] | 15 |
maximum-rows-covered-by-columns | Bit Masking | bit-masking-by-surajthapliyal-o7dt | Idea : Generate all possible combinations to select columns, then check what asked.\ni\'th bit in mask is set if we are considering taking that column, otherwis | surajthapliyal | NORMAL | 2022-09-03T16:02:44.193744+00:00 | 2022-09-03T16:25:01.185064+00:00 | 1,893 | false | **Idea** : Generate all possible combinations to select columns, then check what asked.\n*i\'th* bit in mask is set if we are considering taking that column, otherwise it will be zero.\n-Total of \'2 power columns\' `(1<<total_columns)` combinations are possible.\n\n```\nclass Solution {\n\n public int maximumRows(int[][] mat, int cols) {\n int max = 0;\n for (int mask = 0; mask < (1 << mat[0].length); mask++) {\n if (Integer.bitCount(mask) != cols) continue; // restricted to select ony cols columns\n int c = 0;\n for (int i = 0; i < mat.length; i++) {\n boolean take = true;\n for (int j = 0; j < mat[0].length; j++) {\n if ((mask >> j & 1) == 0 && mat[i][j] == 1) {\n take = false;\n break;\n }\n }\n if (take) c++;\n }\n max = Math.max(max, c);\n }\n return max;\n }\n}\n```\n | 31 | 0 | [] | 6 |
maximum-rows-covered-by-columns | [C++] || Backtracking | c-backtracking-by-4byx-fnje | What is Asked ?\n We have to find the maximum rows in which all cells having 1 should be covered by column we picking\n\nHow to Do ?\n\n1. We make a recursive f | 4byx | NORMAL | 2022-09-03T16:23:29.741654+00:00 | 2022-09-03T16:43:58.189673+00:00 | 3,040 | false | **What is Asked ?**\n `We have to find the maximum rows in which all cells having 1 should be covered by column we picking`\n\n**How to Do ?**\n```\n1. We make a recursive function in which we will pick column and not pick it\n2. picking a column means we marked it as visited\n3. When we reached base case we will traverse whole matrix which tells us that\nwhether we can pick a row or not , we can pick a row only when \'1\' s in it are visited which \nwe can verify by visited arrray\n```\n\n**Code**\n```\nclass Solution {\npublic:\n int maxi = INT_MIN;\n void helper(vector<vector<int>> &mat , int m , int n , int cols , int idx , vector<int> &vis){\n if(cols == 0 or idx==n){\n int cnt = 0;\n for(int p = 0 ; p < m ; p++){\n bool check = true;\n for(int q = 0 ; q < n; q++){\n // if cell is 1 and not visited then we cannot take this row\n if(mat[p][q] == 1 and vis[q] == 0){\n check = false;\n break;\n }\n }\n if(check) cnt++;\n }\n maxi = max(maxi,cnt);\n return;\n }\n \n // picking idx th column and marking column as visited\n vis[idx]=1;\n helper(mat,m,n,cols-1,idx+1,vis);\n vis[idx]=0;\n \n // not picking\n helper(mat,m,n,cols,idx+1,vis);\n return;\n \n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int m = mat.size();\n int n = mat[0].size();\n \n vector<int> vis(n);\n \n helper(mat,m,n,cols,0,vis);\n return maxi;\n }\n};\n``` | 24 | 1 | ['C'] | 7 |
maximum-rows-covered-by-columns | Python 3 || 5 lines, combinations || T/S: 99% / 92% | python-3-5-lines-combinations-ts-99-92-b-a05n | \nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n\t\n m, n, ans = len(mat), len(mat[0]), -inf\n \n fo | Spaulding_ | NORMAL | 2022-10-06T19:42:01.410134+00:00 | 2024-06-14T16:13:52.281465+00:00 | 480 | false | ```\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n\t\n m, n, ans = len(mat), len(mat[0]), -inf\n \n for comb in combinations(range(n),n-cols):\n \n ct = len(set(r for r in range(m) for c in comb if mat[r][c] == 1))\n\n ans = max(ans,m-ct)\n\n return ans\n```\n[https://leetcode.com/problems/maximum-rows-covered-by-columns/submissions/1287518760/](https://leetcode.com/problems/maximum-rows-covered-by-columns/submissions/1287518760/)\n\nI could be wrong, but I think that time complexity is *O*(*M* * *N*^2) and space complexity is *O*(1), in which *N* ~ `m` and *N* ~ `n`.\n\n | 16 | 0 | ['Python'] | 0 |
maximum-rows-covered-by-columns | C++ Easy to Understand BackTracking Solution | c-easy-to-understand-backtracking-soluti-tvlu | Intuition: We will consider all possible combinations of choosing the "cols" amount of columns. For each such combination, we will find the number of covered r | n0IQ | NORMAL | 2022-09-03T17:33:01.777008+00:00 | 2024-10-09T18:48:01.173999+00:00 | 972 | false | Intuition: We will consider all possible combinations of choosing the "cols" amount of columns. For each such combination, we will find the number of covered rows and choose the combination that gives the maximum number of covered rows.\n\nApproach: For considering all possible combinations of choosing columns, let\'s use recursion + backtracking. On each call, we will have two options: \n1. Not to Choose this Column - make a call on the next column.\n2. Choose this Column - mark this column as selected and call on the next column.\n\nBase Cases:\n1. We have selected all required columns.\n2. Columns size is exhausted and we haven\'t chosen the required amount of columns.\n\nRemember that we **must** choose "cols" number of columns.\n\n**C++**\n```\nclass Solution {\nprivate:\n int ans;\n \n void helper(vector<vector<int>>& mat, vector<int> &chose, int c, int n, int m, int cols) {\n if(cols == 0) { // We choose all required columns\n int cntRows = calcRow(mat, chose, n, m);\n ans = max(ans, cntRows);\n return;\n }\n \n if(c >= m) { // if column size is exhausted and we haven\'t chosen the required amount of columns\n return;\n }\n \n helper(mat, chose, c + 1, n, m, cols); // not choosing this column\n \n\t\t// choose this column\n chose[c] = 1; // mark this column\n helper(mat, chose, c + 1, n, m, cols - 1);\n chose[c] = 0; // unmark this column\n }\n \n int calcRow(vector<vector<int>>& mat, vector<int> &chose, int n, int m) {\n int cnt = 0;\n \n for(int i = 0; i < n; i++) {\n bool ok = 1;\n for(int j = 0; j < m; j++) {\n\t\t\t\t// If this cell in the ith row contains \'1\' but we haven\'t chosen this column, thus we cannot consider this row as covered\n if(mat[i][j] == 1 && chose[j] == 0) {\n\t\t\t\t\tok = 0;\n\t\t\t\t\tbreak;\n\t\t\t\t}\n }\n if(ok) cnt++;\n }\n \n return cnt;\n }\n \npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n ans = 0;\n int n = mat.size(), m = mat[0].size();\n vector<int> chose(m, 0); // to track the chosen columns \n helper(mat, chose, 0, n, m, cols);\n return ans;\n }\n};\n```\n\nN = rows, M = columns\n\nTC: O(N * M * 2^M)\nSC: O(M * 2 ^ M) | 16 | 1 | ['Backtracking', 'Recursion', 'C'] | 4 |
maximum-rows-covered-by-columns | Brute Force || Java | brute-force-java-by-abdulazizms-6s4k | \n static int maximumRows(int[][] mat, int cols) {\n return getResult(mat, cols, new HashSet<Integer>(),0) ;\n }\n static int getResult(int [][] | abdulazizms | NORMAL | 2022-09-03T16:02:01.758973+00:00 | 2022-09-03T19:01:05.164300+00:00 | 1,058 | false | ```\n static int maximumRows(int[][] mat, int cols) {\n return getResult(mat, cols, new HashSet<Integer>(),0) ;\n }\n static int getResult(int [][] mat, int cols, Set<Integer> set, int x){\n int maxResult = 0;\n if(cols == 0){\n int count = 0;\n for(int i = 0; i < mat.length; i++) {\n int [] row = mat[i];\n boolean flag = true;\n for(int col = 0; col < row.length; col++){\n if(row[col] == 1 && !set.contains(col)){\n flag = false; break;\n }\n }\n if(flag) count++;\n\n }\n return count;\n }\n\n for(int i = x; i < mat[0].length; i++) {\n set.add(i);\n maxResult = Math.max(maxResult, getResult(mat, cols - 1, set, i+1));\n set.remove(i);\n }\n return maxResult;\n }\n``` | 9 | 2 | [] | 2 |
maximum-rows-covered-by-columns | C++ solution using backtracking DFS | c-solution-using-backtracking-dfs-by-dha-hs6y | We can use DFS with backtracking to fetch all the valid combinations for this problem that would be C(m, cols) = m! / ((m - cols)! * cols!) here C denotes Combi | dhavalkumar | NORMAL | 2022-09-03T22:12:21.774161+00:00 | 2022-09-03T22:12:21.774201+00:00 | 351 | false | We can use **DFS** with **backtracking** to fetch all the **valid combinations** for this problem that would be C(m, cols) = m! / ((m - cols)! * cols!) here C denotes Combination or Binomial Coefficient and m denotes number of columns. Then we calculate the answer for each valid combination and return the maximum of all the valid answers. \n\nThis DFS trick can also be used to find all the premutations too. I saw this trick first used in an atcoder contest by tourist. I have mentioned that problem below this along with tourist\'s solution and editorial.\n\n**Similar Problem**\nProblem Link: https://atcoder.jp/contests/abc236/tasks/abc236_d\nTourist\'s Solution: https://atcoder.jp/contests/abc236/submissions/28725135\nEditorial: https://atcoder.jp/contests/abc236/editorial/3304\n\n**Note:** Learn to use lambda funtions if you code in C++ it makes your code many time easier to type then passing all the values by referance. References: https://usaco.guide/general/lambda-funcs?lang=cpp https://codeforces.com/blog/entry/89790.\n\n**Solution:**\n```Cpp\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n const int n = (int)mat.size(), m = (int)mat[0].size();\n int ans = 0;\n vector<bool> vis(m, false);\n function<void(int, int)> dfs = [&](int u, int cnt) -> void {\n if(cnt == cols) {\n int cur = 0;\n for(int i = 0; i < n; i++) {\n bool flag = true;\n for(int j = 0; j < m; j++) {\n if(!vis[j] and mat[i][j]) flag = false;\n if(!flag) break;\n }\n cur += flag;\n }\n ans = max(ans, cur);\n } else {\n for(int i = u + 1; i < m; i++) {\n vis[i] = true;\n dfs(i, cnt + 1);\n vis[i] = false;\n }\n }\n };\n dfs(-1, 0);\n return ans;\n }\n}; | 8 | 1 | ['Backtracking', 'Depth-First Search', 'C'] | 0 |
maximum-rows-covered-by-columns | C++ | Bit Masking | Faster than 100% | O(2^n * n) | c-bit-masking-faster-than-100-o2n-n-by-a-kd5j | Approach\n1. Convert each row into a decimal number and store in a vector.\n2. Then traverse over range 1 << size of column, to go through all permutations havi | ama29n | NORMAL | 2022-09-03T16:10:16.133917+00:00 | 2022-09-03T17:35:01.073071+00:00 | 901 | false | **Approach**\n1. Convert each row into a decimal number and store in a vector.\n2. Then traverse over range 1 << size of column, to go through all permutations having set_bits = cols. \n3. For each such permutation count number of elements in above generated vector which have set bits at same position.\n4. Store the maximum answer.\n```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int m = mat.size(), n = mat[0].size();\n vector<int> nums;\n for(int i = 0; i < m; i++) {\n string str;\n for(int j = 0; j < n; j++) {\n str += (mat[i][j] + \'0\');\n }\n int number = stoi(str, nullptr, 2);\n nums.push_back(number);\n }\n int range = 1 << n;\n int ans = 0;\n for(int i = 0; i < range; i++) {\n int count = 0;\n if(__builtin_popcount(i) == cols) {\n for(auto it : nums) {\n if((it | i) == i)\n count++;\n }\n }\n ans = max(ans, count);\n }\n return ans;\n }\n};\n``` | 8 | 2 | ['C', 'Bitmask'] | 2 |
maximum-rows-covered-by-columns | C++ || Backtracking | c-backtracking-by-kbp12-cr8n | \nclass Solution {\npublic:\n int n,m,ans = 0;\n void recur(vector<vector<int>>& mat, vector<int>& col_arr, int idx, int remaining_cols){\n //if we | kbp12 | NORMAL | 2022-09-03T16:01:20.469517+00:00 | 2022-09-03T16:01:20.469566+00:00 | 948 | false | ```\nclass Solution {\npublic:\n int n,m,ans = 0;\n void recur(vector<vector<int>>& mat, vector<int>& col_arr, int idx, int remaining_cols){\n //if we have not selected cols columns then remaining_cols will be non zero and no updatation in ans;\n if(idx==m and remaining_cols!=0) return;\n //if we have selected cols columns then we check how many rows satisfies the given condions and update ans\n if(idx==m and remaining_cols==0){\n int res = 0;\n for(int j=0;j<n;j++){\n bool yes = true;\n for(int k=0;k<m;k++){\n if(mat[j][k] and col_arr[k]==0){\n yes = false;\n break;\n }\n }\n if(yes) res++;\n }\n ans = max(ans,res);\n return;\n }\n //lets skip this column and recur next\n recur(mat,col_arr,idx+1,remaining_cols);\n //or select this column and recur next\n col_arr[idx] = 1;\n recur(mat,col_arr,idx+1,remaining_cols-1);\n col_arr[idx] = 0;\n return;\n }\n \n int maximumRows(vector<vector<int>>& mat, int cols) {\n n = mat.size();\n m = mat[0].size();\n vector<int>col_arr(m,0);\n recur(mat,col_arr,0,cols);\n return ans;\n }\n};\n``` | 8 | 0 | ['Backtracking', 'C'] | 1 |
maximum-rows-covered-by-columns | Anyone has difficulty in understanding ? | anyone-has-difficulty-in-understanding-b-13an | A lot of time is wasted for the problem understanding! | vincent_great | NORMAL | 2022-09-03T16:29:48.883549+00:00 | 2022-09-03T16:31:17.589971+00:00 | 296 | false | A lot of time is wasted for the problem understanding! | 6 | 0 | [] | 1 |
maximum-rows-covered-by-columns | ✅C++ || EXPLAINED && CLEAN CODE || Pick-NotPick | c-explained-clean-code-pick-notpick-by-a-9hq0 | \n\nwe have to apple pick-notpick on the columns of the matrix and we have to select \'cols\' number of subsequence lets say you selected 0th and 2nd col in the | abhinav_0107 | NORMAL | 2022-09-03T16:02:58.608540+00:00 | 2022-09-03T16:29:15.136085+00:00 | 994 | false | 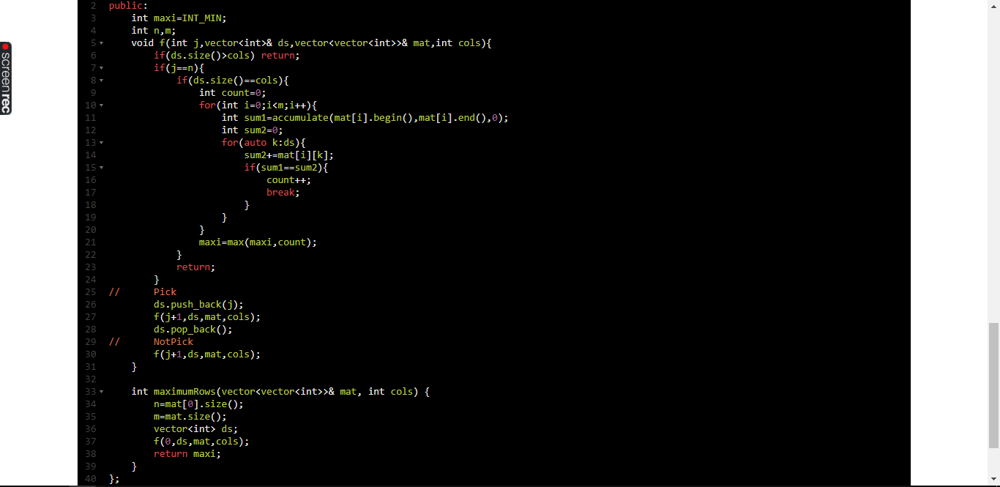\n\n***we have to apple pick-notpick on the columns of the matrix and we have to select \'cols\' number of subsequence lets say you selected 0th and 2nd col in the Example -1. Then we have to iterate over rows of the selected columns and have to check weather in a particular row the number of 1\'s is equal to the number of selected columns (in other words whether all the 1\'s of a particular is covered or not) if all the 1\'s are covered then that row will be counted. and at last we have to take the max count out of it!***\n\n\tclass Solution {\n\tpublic:\n\t\tint maxi=INT_MIN;\n\t\tint n,m;\n\t\tvoid f(int j,vector<int>& ds,vector<vector<int>>& mat,int cols){\n\t\t\tif(ds.size()>cols) return;\n\t\t\tif(j==n){\n\t\t\t\tif(ds.size()==cols){\n\t\t\t\t\tint count=0;\n\t\t\t\t\tfor(int i=0;i<m;i++){\n\t\t\t\t\t\tint sum1=accumulate(mat[i].begin(),mat[i].end(),0);\n\t\t\t\t\t\tint sum2=0;\n\t\t\t\t\t\tfor(auto k:ds){\n\t\t\t\t\t\t\tsum2+=mat[i][k];\n\t\t\t\t\t\t\tif(sum1==sum2){\n\t\t\t\t\t\t\t\tcount++;\n\t\t\t\t\t\t\t\tbreak; \n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t\tmaxi=max(maxi,count);\n\t\t\t\t}\n\t\t\t\treturn;\n\t\t\t}\n\t// Pick\n\t\t\tds.push_back(j);\n\t\t\tf(j+1,ds,mat,cols);\n\t\t\tds.pop_back();\n\t// NotPick\n\t\t\tf(j+1,ds,mat,cols);\n\t\t}\n\n\t\tint maximumRows(vector<vector<int>>& mat, int cols) {\n\t\t\tn=mat[0].size();\n\t\t\tm=mat.size();\n\t\t\tvector<int> ds;\n\t\t\tf(0,ds,mat,cols);\n\t\t\treturn maxi;\n\t\t}\n\t}; | 6 | 3 | ['Backtracking', 'Recursion', 'C', 'C++'] | 1 |
maximum-rows-covered-by-columns | Python Simple Solution | python-simple-solution-by-redheadphone-aa9i | \nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n n,m = len(mat),len(mat[0])\n ans = 0\n\n def check( | redheadphone | NORMAL | 2022-09-03T16:01:48.946715+00:00 | 2022-09-03T16:01:48.946761+00:00 | 900 | false | ```\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n n,m = len(mat),len(mat[0])\n ans = 0\n\n def check(state,row,rowIncludedCount):\n nonlocal ans\n if row==n:\n if sum(state)<=cols:\n ans = max(ans,rowIncludedCount)\n return\n \n check(state[::],row+1,rowIncludedCount)\n for j in range(m):\n if mat[row][j]==1:\n state[j] = 1\n check(state,row+1,rowIncludedCount+1)\n \n check([0]*m,0,0)\n return ans\n``` | 6 | 1 | ['Python', 'Python3'] | 0 |
maximum-rows-covered-by-columns | Recursion Solution , Pick and NotPick Accepted | recursion-solution-pick-and-notpick-acce-h0kv | \n public int maximumRows(int[][] mat, int cols) {\n\n return helper(0, cols, mat);\n }\n\n Set<Integer> set = new HashSet<>();\n\n int helper | mufassir | NORMAL | 2022-09-03T16:09:41.326680+00:00 | 2022-09-03T16:09:41.326713+00:00 | 481 | false | ```\n public int maximumRows(int[][] mat, int cols) {\n\n return helper(0, cols, mat);\n }\n\n Set<Integer> set = new HashSet<>();\n\n int helper(int col, int cols, int[][] mat) {\n if (cols == 0 || col == mat[0].length) {\n int res = count(mat);\n return res;\n }\n set.add(col);\n int pick = helper(col + 1, cols-1, mat);\n set.remove(col);\n int notPick = helper(col + 1, cols, mat);\n return Math.max(pick, notPick);\n }\n\n int count(int[][] mat) {\n int m = mat.length;\n int n = mat[0].length;\n int res = 0;\n for (int i = 0; i < m; i++) {\n int ones = 0;\n for (int j = 0; j < n; j++) {\n if (mat[i][j] == 1 && !set.contains(j))\n ones++;\n }\n if (ones == 0)\n res++;\n }\n return res;\n }\n\t``` | 5 | 0 | ['Recursion', 'Java'] | 1 |
maximum-rows-covered-by-columns | Simple solution | easy to understand | Combinations | simple-solution-easy-to-understand-combi-6qn3 | Just check all the combinations of column\n\n\n\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n m, n = len(mat), l | thoufic | NORMAL | 2022-09-03T16:04:27.879395+00:00 | 2022-09-03T16:57:48.810085+00:00 | 812 | false | Just check all the combinations of column\n\n```\n\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n m, n = len(mat), len(mat[0])\n maxRows = 0\n \n colToChoose = list(combinations(list(range(n)), cols))\n \n for col in colToChoose:\n col = set(col)\n rowHidden = 0\n for row in mat:\n canHide = True\n for i in range(n):\n if(row[i] and i not in col):\n canHide = False\n break\n if(canHide):\n rowHidden += 1\n maxRows = max(maxRows, rowHidden)\n return maxRows\n \n \n``` | 5 | 1 | ['Python'] | 2 |
maximum-rows-covered-by-columns | generate every possible subset and check | generate-every-possible-subset-and-check-59p2 | \nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int m=mat.size(),n=mat[0].size(),ans=0;\n int mask=((1<<n | aman282571 | NORMAL | 2022-09-03T16:01:04.196884+00:00 | 2022-09-03T16:03:05.122011+00:00 | 840 | false | ```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int m=mat.size(),n=mat[0].size(),ans=0;\n int mask=((1<<n)-1);\n // use mask to generate every possible columns combination\n while(mask){\n unordered_set<int>select;\n for(int i=0;i<n;i++){\n if(((mask>>i)&1)==1)\n select.insert(i);\n }\n // if subset contains exaclty "cols" columns then we can use this subset\n if(select.size()==cols){\n int cnt=0;\n for(int j=0;j<m;j++){\n bool flag=true;\n for(int k=0;k<n;k++){\n // if any row contains 1 in column other than columns which we have in "select" then this row is not valid row for our answer\n if(mat[j][k]==1 && select.count(k)==0){\n flag=false;\n break;\n }\n }\n if(flag)\n cnt++;\n }\n ans=max(ans,cnt);\n }\n mask--;\n }\n return ans;\n }\n};\n```\nDo **UPVOTE** is it helps :) | 5 | 0 | [] | 2 |
maximum-rows-covered-by-columns | Simple C++ solution | simple-c-solution-by-tars2412-ehpb | simple backtracking problem!!!\n\n1. mark the current column\'s 1\'s and reduce the number of cols you have and move onwards to other columns\n2. unmark the cur | tars2412 | NORMAL | 2022-09-03T16:00:46.781495+00:00 | 2022-09-03T16:04:10.247980+00:00 | 597 | false | simple backtracking problem!!!\n\n1. mark the current column\'s 1\'s and reduce the number of cols you have and move onwards to other columns\n2. unmark the current column\'s 1\'s and move onwards to other columns.\n3. base case is when you reach the end column or you don\'t have cols left to mark 1\'s.\n4. I later realised that you can flip steps 1 and 2 to make implementation easier but I am presenting the contest solution to you.\n```\nclass Solution {\npublic:\n void backtrack(vector<vector<int>>& mat,int colno,int m,int n,int rem,int &res){\n if(rem==0||colno==n){\n int count = 0;\n for(int i=0;i<m;i++){\n bool flag = false;\n for(int j=0;j<n;j++){\n if(mat[i][j]){\n flag = true;\n break;\n }\n }\n if(!flag)\n count++;\n }\n res = max(count,res);\n return;\n }\n vector<bool> markedpos(m,false);\n //choose this column and proceed\n for(int i=0;i<m;i++){\n if(mat[i][colno]==1){\n mat[i][colno] = 0;\n markedpos[i] = true;\n }\n }\n backtrack(mat,colno+1,m,n,rem-1,res);\n //undo \n for(int i=0;i<m;i++){\n if(markedpos[i]){\n mat[i][colno] = 1;\n }\n }\n backtrack(mat,colno+1,m,n,rem,res);\n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int res = 0;\n int m = mat.size(),n = mat[0].size();\n backtrack(mat,0,m,n,cols,res);\n return res;\n }\n};\n```\n\nPlease upvote if you found this helpful! | 5 | 0 | ['Backtracking'] | 0 |
maximum-rows-covered-by-columns | Brute-Force + Backtracking | brute-force-backtracking-by-pk_87-kgt4 | \nclass Solution {\nprivate:\n int n,m;\n unordered_map<int,vector<int>> col;\n int maxRow=0;\n \n void selectCol(int currCol,vector<int> selecte | pawan_mehta | NORMAL | 2022-11-15T07:58:39.660321+00:00 | 2022-11-15T07:58:39.660352+00:00 | 770 | false | ```\nclass Solution {\nprivate:\n int n,m;\n unordered_map<int,vector<int>> col;\n int maxRow=0;\n \n void selectCol(int currCol,vector<int> selectedCol,int numSelect,int colSize)\n {\n if(selectedCol.size() == numSelect)\n {\n unordered_set<int> selectedColSet;\n for(int col : selectedCol) selectedColSet.insert(col);\n \n int count=0;\n \n for(int i=0; i<n; i++)\n {\n if(col[i].size() == 0)\n count++;\n else\n {\n bool flag=true;\n \n for(auto& tempCol : col[i])\n {\n if(selectedColSet.find(tempCol) == selectedColSet.end())\n {\n flag=false;\n break;\n }\n }\n \n if(flag)\n count++;\n }\n }\n \n maxRow=max(maxRow,count);\n }\n else\n {\n for(int i=currCol; i<colSize; i++)\n {\n selectedCol.push_back(i);\n selectCol(i+1,selectedCol,numSelect,colSize);\n selectedCol.pop_back();\n selectCol(i+1,selectedCol,numSelect,colSize);\n }\n }\n }\n \npublic:\n int maximumRows(vector<vector<int>>& matrix, int numSelect) {\n n=matrix.size();\n m=matrix[0].size(); \n \n for(int i=0; i<n; i++)\n {\n for(int j=0; j<m; j++)\n {\n if(matrix[i][j] == 1)\n col[i].push_back(j);\n }\n }\n \n selectCol(0,{},numSelect,m);\n \n return maxRow;\n }\n};\n``` | 4 | 0 | ['C'] | 0 |
maximum-rows-covered-by-columns | 100% faster ,Brute force C++,Easy to Understand | 100-faster-brute-force-ceasy-to-understa-nuwq | Simply check for all the combinations of columns i.e, check for a set of coulms taken that how many rows are covered tht can be furthur checked by checking all | Xahoor72 | NORMAL | 2022-09-04T06:49:50.932373+00:00 | 2022-09-04T06:52:55.002275+00:00 | 81 | false | **Simply check for all the combinations of columns i.e, check for a set of coulms taken that how many rows are covered tht can be furthur checked by checking all the ones in a row are present in the selected columns or not if yes count++ and at last take the maximum of this count for all the combinations of coulmns generated.**\n*Just use a function to generate all the combinations of columns and then check the ones in a row for all these combinations generated .\nlook the code for more understanding*\n* And one thing also since the contraints are not big so we will not get tle for using brute force.\n```\n void solve(vector<vector<int>>&mat,vector<int>temp,int i,int j,int cols){\n if(i==j){\n if(temp.size()==cols)mat.push_back(temp);return;\n }\n solve(mat,temp,i+1,j,cols);\n temp.push_back(i);\n solve(mat,temp,i+1,j,cols);\n temp.pop_back();\n }\n \n int maximumRows(vector<vector<int>>& mat, int cols) {\n int r=mat.size(),c=mat[0].size();\n if(cols>=c){\n return r;\n }\n vector<vector<int>>tot;\n vector<int>temp;\n solve(tot,temp,0,c,cols);\n \n\n int ans=0;\n \n \n for(auto x: tot){\n map<int,int>mp;\n for(auto it:x)mp[it]++;\n int res=0;\n for(int i=0;i<r;i++){\n \n bool ok=true;\n for(int j=0;j<c;j++){\n \n if(mat[i][j]==1 and mp.find(j)==mp.end())ok=false;\n }\n \n if(ok)res++;\n \n }\n ans=max(res,ans);\n }\n \n \n\n \n return ans;\n }\n``` | 4 | 0 | ['Backtracking', 'C'] | 0 |
maximum-rows-covered-by-columns | C++ Bitmask O(n*2^n) 7ms | c-bitmask-on2n-7ms-by-pisces311-loq1 | Whenever you see n <= 12, start typing for (int mask = 0; mask < (1 << n); mask++).\nc++\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& ma | Pisces311 | NORMAL | 2022-09-03T16:02:48.747227+00:00 | 2022-09-03T19:27:48.406029+00:00 | 340 | false | Whenever you see `n <= 12`, start typing `for (int mask = 0; mask < (1 << n); mask++)`.\n``` c++\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int n = mat.size(), m = mat[0].size();\n vector<int> rows(n);\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (mat[i][j] == 1) {\n rows[i] |= (1 << j);\n }\n }\n }\n int ans = 0;\n for (int mask = 0; mask < (1 << m); mask++) {\n if (__builtin_popcount(mask) != cols) continue;\n int cur = 0;\n for (int i = 0; i < n; i++) {\n if ((mask | rows[i]) == mask) cur++;\n }\n ans = max(ans, cur);\n }\n return ans;\n }\n};\n``` | 4 | 1 | ['C', 'Bitmask'] | 2 |
maximum-rows-covered-by-columns | Backtracking | Simple | C++ | backtracking-simple-c-by-adi193-bdio | \nclass Solution {\npublic:\n void func(vector<vector<int>>& mat, int cols,vector <int> v,int idx,int &ans){\n if(cols==0){\n int cnt=0;\n | adi193 | NORMAL | 2022-09-03T16:01:25.590935+00:00 | 2022-09-03T16:01:25.590968+00:00 | 358 | false | ```\nclass Solution {\npublic:\n void func(vector<vector<int>>& mat, int cols,vector <int> v,int idx,int &ans){\n if(cols==0){\n int cnt=0;\n for(int i=0;i<mat.size();i++){\n int f=1;\n for(int j=0;j<mat[i].size();j++){\n if(mat[i][j]==1 && v[j]==0){\n f=0;\n break;\n }\n }\n if(f==1){\n cnt++;\n }\n }\n ans=max(cnt,ans);\n return;\n }\n \n for(int i=idx;i<mat[0].size();i++){\n v[i]=1;\n func(mat,cols-1,v,i+1,ans);\n v[i]=0;\n }\n }\n \n int maximumRows(vector<vector<int>>& mat, int cols) {\n int ans=0;\n int n=mat[0].size();\n vector <int> v(n,0);\n func(mat,cols,v,0,ans);\n return ans;\n }\n};\n``` | 4 | 1 | ['Backtracking', 'C++'] | 0 |
maximum-rows-covered-by-columns | ✅ One Line Solution | one-line-solution-by-mikposp-onfv | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1.1 - One LineTime complexity: O(comb∗m∗n). Sp | MikPosp | NORMAL | 2024-02-24T14:20:10.849061+00:00 | 2025-03-16T11:16:06.811973+00:00 | 48 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1.1 - One Line
Time complexity: $$O(comb*m*n)$$. Space complexity: $$O(n)$$
```
class Solution:
def maximumRows(self, g: List[List[int]], k: int) -> int:
return max(sum(all(r[c]==0 for c in q) for r in g) for q in combinations(range(len(g[0])),len(g[0])-k))
```
# Code #1.2 - Unwrapped
```
class Solution:
def maximumRows(self, g: List[List[int]], k: int) -> int:
n = len(g[0])
result = 0
for q in combinations(range(n), n-k):
res = 0
for r in g:
res += all(r[c] == 0 for c in q)
result = max(result, res)
return result
```
(Disclaimer 2: all code above is just a product of fantasy put into one line, it is not considered as 'true' oneliners - please, remind about drawbacks only if you know how to make it better) | 3 | 0 | ['Array', 'Matrix', 'Combinatorics', 'Python', 'Python3'] | 0 |
maximum-rows-covered-by-columns | Check all subsets using Bit Masking | check-all-subsets-using-bit-masking-by-h-4cwl | According to the problem if we select a set of columns then \n\nFor ith row(matrix[i]) to be valid:\n\n1. If the jth col is selected: \n we don\'t care if th | Harshyd26 | NORMAL | 2024-01-27T09:46:59.909793+00:00 | 2024-01-27T10:00:48.197128+00:00 | 116 | false | According to the problem if we select a set of columns then \n\n**For ith row(matrix[i]) to be valid:**\n\n**1. If the jth col is selected:** \n we don\'t care if there are `0` or `1` in matrix[i][j].\n**2. If the jth column is not selected**\n`if(matrix[i][j]==1)` then that row will be invalid for those set of selected columns\n\n**# Conclusion:**\nFind no. of valid rows i.e `mat[i][j] = 0 for all unselected coloumns` for all possible combinations of columns and take the maximum of all combinations.\n\nI commented the code so that it become easy for you to understand, a basic understanding of bit operations is required.\n\n# Code\n```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& matrix, int k) {\n \n int m = matrix.size();\n int n = matrix[0].size();\n\t\tint subset_ct = (1<<n); //Total subset (2^n)\n\n int ans = 0;\n\t\tfor(int mask = 1; mask < subset_ct; mask++){ //Iterate for each subset possible\n\t\t\tif(__builtin_popcount(mask)==k){ //If exact k col are selected\n int temp = m; //Initially mark all the row valid\n for(int i=0;i<m;i++){ //For a possible combination of col check the no. of valid rows\n for(int j=0;j<n;j++){\n if(!(mask&(1<<j)) && matrix[i][n-j-1]==1) {temp--; break;}\n }\n }\n ans = max(ans,temp);\n }\n\t\t}\n\n return ans;\n }\n};\n``` | 3 | 0 | ['Bit Manipulation', 'C++'] | 0 |
maximum-rows-covered-by-columns | [java] ✔one the easiest solution with Explanation [Pick || notPick] Approach. | java-one-the-easiest-solution-with-expla-5uez | Approach - if you look at problem in little deep , you can directly see that for each column we have two option\n1. pick that column (if picked then, go to next | atul-chaudhary | NORMAL | 2022-09-05T16:17:04.638298+00:00 | 2022-09-05T16:17:04.638340+00:00 | 150 | false | Approach - if you look at problem in little deep , you can directly see that for each column we have two option\n1. pick that column (if picked then, go to next index and increased the count of total picked column)\n2. Not pick that column (if not picked, got to next step in this case since we have not picked it total count is not going to increase).\n\n**Base Condition Explanation**\nThink logically when we are going to hit base i,e {index == matrix[0].length} simple.\nand if base condition is met that we need to do, we need to calculate total of rows covered with currently selected column.\n\n```\npublic int maximumRows(int[][] mat, int cols) {\n boolean[] visited = new boolean[mat[0].length];\n return solve(mat, cols, 0, 0, visited);\n }\n private static int solve(int[][] arr, int cols, int index, int curTotalPicked, boolean[] visited) {\n if (index == arr[0].length) {\n int count = 0;\n for (int i = 0; i < arr.length; i++) {\n boolean flag = true;\n for (int j = 0; j < arr[0].length; j++) {\n if (arr[i][j] == 1) {\n if (!visited[j]) {\n flag = false;\n }\n }\n }\n\n if (flag) {\n count++;\n }\n }\n return count;\n }\n\n int pick = 0;\n if (curTotalPicked < cols) {\n visited[index] = true;\n pick = solve(arr, cols, index + 1, curTotalPicked + 1, visited);\n visited[index] = false;\n }\n int notPick = solve(arr, cols, index +1, curTotalPicked, visited);\n return Math.max(pick, notPick);\n }\n``` | 3 | 0 | ['Java'] | 0 |
maximum-rows-covered-by-columns | C++ Solution | Easy to Understand | Using Backtracking | c-solution-easy-to-understand-using-back-lzur | In this problem we apply concept of recursion of take and non take because of small constraint.\nSteps\n1. first we make a recursive function \'fun\' in which w | devil_pratihar | NORMAL | 2022-09-04T06:27:22.162850+00:00 | 2022-09-04T06:28:42.816094+00:00 | 25 | false | In this problem we apply concept of recursion of take and non take because of small constraint.\n**Steps**\n**1.** first we make a recursive function \'fun\' in which we pass current index, given matrix, given cols and visited array.\n**2.** So visited array take care of column of matrix that which column is selected or which is not.\n**3.** So mainly in recursive function, we try out all possible column which are possible for given cols value. we will do this with the help of take and non take method. and we update our visited array for that column which is taken.\n**4.** For Base case, if our cols value become 0 or if we cover all column means now we check for covered row.\n**5.** So Now we traverse our matrix and check if that column is unvisited and value of that mat[row][col]==1 means that row is not a covered row so we come out of loop of column.\n**6.** otherwise we update the value of covered row by 1 (count++).\n**7.** At last we take maximum of count and ans. because we have to calculate maximum row covered.\n\n**Code**\n\t\t\n\t\tclass Solution {\n\t\t\tpublic:\n\t\t\t\tint m,n;\n\t\t\t\tint ans=INT_MIN;\n\t\t\t\tvoid fun(int i,vector<vector<int>> &mat,int col,vector<int> vis){\n\t\t\t\t\tint count=0;\n\t\t\t\t\tif(col==0 || i==n){\n\n\t\t\t\t\t\tfor(int p=0;p<m;p++){\n\t\t\t\t\t\t\tint f=0;\n\t\t\t\t\t\t\tfor(int q=0;q<n;q++){\n\t\t\t\t\t\t\t\tif(mat[p][q]==1 && vis[q]==0){\n\t\t\t\t\t\t\t\t\tf=1;\n\t\t\t\t\t\t\t\t\tbreak;\n\t\t\t\t\t\t\t\t}\n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t\tif(f==0) count++;\n\t\t\t\t\t\t}\n\t\t\t\t\t\tans=max(ans,count);\n\t\t\t\t\t\treturn;\n\t\t\t\t\t}\n\n\t\t\t\t\tfun(i+1,mat,col,vis);\n\t\t\t\t\tvis[i]=1;\n\t\t\t\t\tcol--;\n\t\t\t\t\tfun(i+1,mat,col,vis);\n\t\t\t\t\treturn;\n\t\t\t\t}\n\n\t\t\t\tint maximumRows(vector<vector<int>>& mat, int cols) {\n\t\t\t\t\tm=mat.size();\n\t\t\t\t\tn=mat[0].size();\n\t\t\t\t\tvector<int> vis(n,0);\n\t\t\t\t\tfun(0,mat,cols,vis);\n\t\t\t\t\treturn ans;\n\t\t\t\t}\n\t\t\t};\n\t\t\t\n**Please upvote if you like the explanation ** | 3 | 0 | ['Backtracking', 'Recursion', 'C'] | 0 |
maximum-rows-covered-by-columns | Python || recursion || backtracking | python-recursion-backtracking-by-1md3nd-lj9a | Backtracking + recursion\n## Time -> O(2^N) {N is length of columns}\n## Space -> O(cols)\n\n\nclass Solution:\n def maximumRows(self, mat: List[List[int]], | 1md3nd | NORMAL | 2022-09-03T20:52:07.091533+00:00 | 2022-09-03T20:52:07.091566+00:00 | 516 | false | # Backtracking + recursion\n## Time -> O(2^N) {N is length of columns}\n## Space -> O(cols)\n\n```\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n res = []\n M = len(mat)\n N = len(mat[0])\n def check(seen):\n count = 0\n for row in mat:\n flag = True\n for c in range(N): \n if row[c] == 1:\n if c in seen:\n continue\n else:\n flag = False\n break\n if flag: \n count +=1 \n res.append(count)\n \n def solve(c,seen,cols):\n if cols == 0:\n check(seen)\n return\n if c == N:\n return\n else:\n seen.add(c)\n solve(c+1,seen,cols-1)\n seen.remove(c)\n solve(c+1,seen,cols)\n seen = set()\n solve(0,seen,cols)\n return max(res)\n``` | 3 | 0 | ['Backtracking', 'Recursion', 'Python', 'Python3'] | 0 |
maximum-rows-covered-by-columns | Easy C++ Explanation with comment | easy-c-explanation-with-comment-by-imdhr-4jpn | \n\nclass Solution {\n \n int f(vector<vector<int>>& mat, vector<int> &v, int r){\n \n int ans = 0;\n bool flag = true;\n \n | ImDhruba | NORMAL | 2022-09-03T18:01:09.243655+00:00 | 2022-09-03T18:06:55.296377+00:00 | 28 | false | ```\n\nclass Solution {\n \n int f(vector<vector<int>>& mat, vector<int> &v, int r){\n \n int ans = 0;\n bool flag = true;\n \n for(int i = 0; i < r; i++){\n \n\t\t\t/*\n\t\t\twe are taking each row at one time and iterating through it\t\t\t\n\t\t\t*/\n vector<int> row = mat[i];\n \n for(int j = 0; j < row.size(); j++){\n \n\t\t\t\t/*\n\t\t\t\tif all the element in that particular row are 0, then flag will remain true and ans will get increased.\n\t\t\t\tif any element is 1 in that particular row then we will check if that 1 is covered by coloumn or not\n\t\t\t\tif yes flag will remain true\n\t\t\t\tif no flag will be false\n\t\t\t\t*/\n if(row[j] == 1){\n if(!count(v.begin(), v.end(), j)){\n flag = false;\n }\n }\n }\n\t\t\t/*\n\t\t\tit remains true , it means all 1 are covered by coloums\n\t\t\tor there are no 1 ie all are Zero\n\t\t\tSo, we will increased our ans, since one more row is covered .\n\t\t\t*/\n if(flag) ans++;\n\t\t\t/*\n\t\t\tnow we have to check the next row , so we are again making it true\n\t\t\t*/\n flag = true;\n }\n \n \n return ans;\n \n }\n \n /*\n https://stackoverflow.com/questions/12991758/creating-all-possible-k-combinations-of-n-items-in-c\n Refer this to understand comb function.\n */\nvoid comb(int N, int K, vector<vector<int>> &combi)\n{\n string bitmask(K, 1); // K leading 1\'s\n \n bitmask.resize(N, 0); // N-K trailing 0\'s\n \n vector<int> ans;\n // print integers and permute bitmask\n do {\n for (int i = 0; i < N; ++i) // [0..N-1] integers\n {\n if (bitmask[i]) {\n ans.push_back(i);\n }\n }\n // cout << std::endl;\n combi.push_back(ans);\n ans.clear();\n \n } while (prev_permutation(bitmask.begin(), bitmask.end()));\n}\n \npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n int r = mat.size();\n \n int maxi = 0;\n \n vector<vector<int>> combi;\n \n\t\t/*comb function will generates all possible column combination \n\t\teg if cols = 2, mat[0].size() = 3 (if the matrix has 3 columns)\n\t\tit means we have to select any 2 columns out of 3 columns(0,1,2)\t\t\n\t\t*/\n comb(mat[0].size(), cols, combi);\n \n \n\t\t/*\n\t\tcombi will have:\n\t\t\t0, 1\n\t\t\t0, 2\n\t\t\t1, 2\t\t\n\t\t*/\n \n for(int i = 0; i < combi.size(); i++){\n \t\t\t\n /*\n\t\t\tNow we are passing each combination of column to the f function\n\t\t\twhen i = 0 : 0, 1\n\t\t\t\t i = 1 : 0, 2\n\t\t\t\t i = 2 : 1, 2\n\t\t\t*/\n maxi = max(f(mat,combi[i],r),maxi);\n }\n \n \n return maxi;\n }\n};\n```\nIf anything is not understandable, comment it . I will try to explain.\nPlease, upvote it if it helps you :) | 3 | 0 | ['C++'] | 1 |
maximum-rows-covered-by-columns | C++ || 100% Fast || Easy To Understand | c-100-fast-easy-to-understand-by-geeksme-l3l9 | \nclass Solution {\npublic:\n // Global Vector to all possible column combinations\n vector<vector<int>>comb;\n\t\n // Function to find the number of r | geeksme123 | NORMAL | 2022-09-03T17:58:02.889857+00:00 | 2022-09-03T17:58:02.889922+00:00 | 352 | false | ```\nclass Solution {\npublic:\n // Global Vector to all possible column combinations\n vector<vector<int>>comb;\n\t\n // Function to find the number of rows a particular column combination can capture\n int find(vector<vector<int>>& mat1)\n {\n int c = 0;\n for(int i = 0; i < mat1.size(); i++)\n {\n int flg = 0;\n for(int j = 0; j < mat1[0].size(); j++)\n if(mat1[i][j] == 1)\n flg = 1;\n if(flg == 0)\n c++;\n }\n return c;\n }\n \n\t// Function to Traverse for each Column Combination Present\n int find_ans(vector<vector<int>>& mat)\n {\n int ans = 0;\n for(int i = 0; i < comb.size(); i++)\n {\n vector<int>temp = comb[i];\n vector<vector<int>> mat1 = mat;\n for(int j = 0; j < temp.size(); j++)\n {\n int col_val = temp[j];\n for(int k = 0; k < mat1.size(); k++)\n mat1[k][col_val] = 0;\n }\n ans = max(ans, find(mat1));\n }\n return ans;\n }\n // Function to Find all possible column combinations\n void helper(vector<vector<int>>& mat, int cols, int count, int idx, vector<int>tans)\n {\n int col = mat[0].size();\n if(count == cols)\n {\n comb.push_back(tans);\n return;\n }\n if(idx >= col)\n return;\n \n helper(mat, cols, count, idx+1, tans);\n tans.push_back(idx);\n helper(mat, cols, count+1, idx+1, tans);\n }\n \n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n vector<int>tans;\n helper(mat, cols, 0, 0, tans);\n return find_ans(mat);\n }\n};\n``` | 3 | 0 | ['Backtracking', 'C', 'C++'] | 0 |
maximum-rows-covered-by-columns | 🤯 Simplest Python Solution | Brute Force | Combinations | simplest-python-solution-brute-force-com-qj20 | Upvote if you like\n\n\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n columns = [i for i in range(len(mat[0]))]\n | ramsudharsan | NORMAL | 2022-09-03T16:34:56.622828+00:00 | 2022-09-17T21:25:49.623071+00:00 | 201 | false | Upvote if you like\n\n```\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n columns = [i for i in range(len(mat[0]))]\n\t\t# All combinations of columns to select\n combos = combinations(columns, cols)\n ans = 0\n \n\t\t# For every combo try to count number of valid rows\n for combo in combos:\n combo = set(combo)\n selectedRows = 0\n \n for r in range(len(mat)):\n for c in range(len(mat[0])):\n if mat[r][c] == 1 and c not in combo:\n break\n else:\n\t\t\t\t# select a row only if it has 1s in the selected columns(combo) i.e. if loop never breaks\n selectedRows += 1\n \n ans = max(ans, selectedRows)\n \n return ans\n``` | 3 | 0 | ['Python'] | 1 |
maximum-rows-covered-by-columns | Backtracking | Java Solution | Code with comments | backtracking-java-solution-code-with-com-vwso | Idea is to use backtraking. But before trying that we should know how to calculate which all rows are not covered by choosen columns. For that we can store this | anuj0503 | NORMAL | 2022-09-03T16:00:52.564621+00:00 | 2022-09-03T16:01:11.836938+00:00 | 401 | false | Idea is to use backtraking. But before trying that we should know how to calculate which all rows are not covered by choosen columns. For that we can store this info in a map (column index to set of row indices haiving one). For each possible combination in backtraking we calculate which all rows were missed and substract if from total number of rows.\n\n\n```\nclass Solution {\n int result;\n public int maximumRows(int[][] mat, int cols) {\n int m = mat.length; // number of rows\n int n = mat[0].length; // number of columns\n result = -1;\n\n // if cols is equal to number of columns andswer will be number of rows.\n if(cols == n) return m;\n\n // Map to store which column index covers which all rows having value 1.\n Map<Integer, Set<Integer>> columnIndexToRowHavingOnes = new HashMap<>();\n\n for(int i = 0; i < n; i++) columnIndexToRowHavingOnes.put(i, new HashSet<>());\n for(int i = 0; i < m; i++){\n for(int j = 0; j < n; j++){\n if(mat[i][j] == 1) {\n Set<Integer> set = columnIndexToRowHavingOnes.get(j);\n set.add(i);\n columnIndexToRowHavingOnes.put(j, set);\n }\n }\n }\n\n getAnswer(0, new ArrayList<Integer>(), cols, columnIndexToRowHavingOnes, m, n);\n\n return result;\n }\n\n // Backtracking function\n private void getAnswer(int index, ArrayList<Integer> colChoosen, int cols, Map<Integer, Set<Integer>> columnIndexToRowHavingOnes, int m, int n){\n\n // If we have chossed cols number of columns\n if(colChoosen.size() == cols){\n Set<Integer> rowNotCoveredByChoosenColumns = new HashSet<>();\n // For each column\n for(int i = 0; i < n; i++){\n // find which all rows were missed which have value 1\n if(!colChoosen.contains(i)){\n rowNotCoveredByChoosenColumns.addAll(columnIndexToRowHavingOnes.get(i));\n }\n }\n\n result = Math.max(result, m - rowNotCoveredByChoosenColumns.size());\n return;\n }\n\n if(index == n) return;\n\n // pick the column\n colChoosen.add(index);\n getAnswer(index + 1, colChoosen, cols, columnIndexToRowHavingOnes, m, n);\n\n // unpick the column\n colChoosen.remove(colChoosen.size() - 1);\n getAnswer(index + 1, colChoosen, cols, columnIndexToRowHavingOnes, m, n);\n\n }\n}\n``` | 3 | 0 | ['Backtracking', 'Java'] | 0 |
maximum-rows-covered-by-columns | Permutations v/s Subsets | permutations-vs-subsets-by-jay_1410-8f0a | 1. Using Subsets - \n- We can just simply Check all subsets which have K setbits (i.e K columns selected)\n- Time Complexity : O(2^(Columns) * Rows * Columns)\n | Jay_1410 | NORMAL | 2024-06-09T13:19:45.434426+00:00 | 2024-06-09T13:22:54.031545+00:00 | 249 | false | # 1. Using Subsets - \n- We can just simply Check all subsets which have K setbits (i.e K columns selected)\n- **Time Complexity :** O(2^(Columns) * Rows * Columns)\n- **Space Complexity :** O(1)\n```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>> &A , int K){\n int Rows = A.size() , Cols = A[0].size();\n int maxRowsCovered = 0;\n for(int mask = (1 << K) - 1 ; mask < (1 << Cols) ; mask++){\n if(__builtin_popcount(mask) == K){\n int currRowsCovered = 0;\n for(int Row = 0 ; Row < Rows ; Row++){\n int isRowCovered = 1;\n for(int Col = 0 ; Col < Cols ; Col++){\n if(A[Row][Col] && (mask >> Col & 1 ^ 1)){\n isRowCovered = 0;\n break;\n }\n }\n if(isRowCovered) currRowsCovered += 1;\n }\n maxRowsCovered = max(maxRowsCovered , currRowsCovered);\n }\n }\n return maxRowsCovered;\n }\n};\n```\n\n# 2. Using Permutations - \n- `Idea :` Subsets with K-SetBits = PermuationsOf(`000111....(K-times)`)\n- Instead of going through all subsets and considering Subsets with K-SetBits , we can `skip Non-K-SetBits Subsets Using Permutations `\n- In subsets approach our first mask with K-SetBits is `000111....(K-times)`\nAnd it will be same in permutations approach as well ,\nbecause `000111....(K-times)` is the lexicographically smallest valid permutation and from this permutation we can get all Subets with K-SetBits using Next Permutation.\n- **Time Complexity :** O(NCR(Columns , K) * Rows * Columns)\n- **Space Complexity :** O(1)\n- `NOTE : NCR(Columns , K) will be atmask 924 which is NCR(12 , 6)`\n```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>> &A , int K){\n int Rows = A.size() , Cols = A[0].size();\n int maxRowsCovered = 0;\n string P = string(Cols - K , \'0\') + string(K , \'1\');\n do{\n int currRowsCovered = 0;\n for(int Row = 0 ; Row < Rows ; Row++){\n int isRowCovered = 1;\n for(int Col = 0 ; Col < Cols ; Col++){\n if(A[Row][Col] && P[Col] == \'0\'){\n isRowCovered = 0;\n break;\n }\n }\n if(isRowCovered) currRowsCovered += 1;\n }\n maxRowsCovered = max(maxRowsCovered , currRowsCovered);\n }while(next_permutation(P.begin() , P.end()));\n return maxRowsCovered;\n }\n};\n``` | 2 | 0 | ['Bit Manipulation', 'Combinatorics', 'Bitmask', 'C++', 'Java', 'Python3'] | 0 |
maximum-rows-covered-by-columns | C++ | Easy-Understanding Backtracking Solution | c-easy-understanding-backtracking-soluti-pt5x | \t#define ll int\n\tclass Solution {\n\tpublic:\n ll maxi =0;\n ll n,m;\n void f (ll col,ll curcol, vector> &mat, vector> &dummy){ \n if( | Kaustubh01 | NORMAL | 2022-09-07T16:44:14.762146+00:00 | 2022-09-07T16:44:14.762187+00:00 | 95 | false | \t#define ll int\n\tclass Solution {\n\tpublic:\n ll maxi =0;\n ll n,m;\n void f (ll col,ll curcol, vector<vector<int>> &mat, vector<vector<int>> &dummy){ \n if(col==0){\n ll rows =0; \n // count how many rows are filled with 0 values\n for(int i=0;i<n;i++){\n bool ok = true;\n for(ll j=0;j<m;j++){ \n if(dummy[i][j]==1) {\n ok=false; \n break;\n }\n } \n if(ok) rows++;\n }\n maxi=max(maxi,rows);\n return;\n }\n if(curcol==m) return;\n for(int i=0;i<n;i++){\n dummy[i][curcol]=0;\n // if we are taking the current col fill that col with 0 \n }\n // take the current col \n f(col-1,curcol+1,mat,dummy);\n \n for(int i=0;i<n;i++){\n dummy[i][curcol]= mat[i][curcol]; \n // backtrack the original values \n }\n // ignore the current col\n f(col,curcol+1,mat,dummy);\n\n }\n int maximumRows(vector<vector<int>>& matrix, int numSelect) {\n n = matrix.size(), m = matrix[0].size();\n vector<vector<ll>> dummy;\n dummy = matrix;\n f(numSelect,0,matrix,dummy);\n return maxi;\n }\n}; | 2 | 0 | ['Backtracking', 'Recursion', 'C'] | 0 |
maximum-rows-covered-by-columns | JAVA | BACKTRACK | RECURSION | Runtime 1ms | 100% faster | java-backtrack-recursion-runtime-1ms-100-s7gz | This question is similar to 698. Partition to K Equal Sum Subsets.\nWe try all possible combinations of columns, once we select the given number of columns, we | raghavtilak | NORMAL | 2022-09-06T07:52:35.860829+00:00 | 2022-09-06T11:59:35.566174+00:00 | 200 | false | This question is similar to [698. Partition to K Equal Sum Subsets](https://leetcode.com/problems/partition-to-k-equal-sum-subsets/).\nWe try all possible combinations of columns, once we select the given number of columns, we check that for how many rows in the matrix, the below condition is true:-\n1. Each cell of the row is \'0\', or\n2. If the cell of the row is \'1\', then the cell\'s column value(say, \'j\') should be \'1\'(i.e. this column is selected by us) in the \'s\' array. (s[j]==1).\n\nWe return the count of the rows.\nIn order to get our answer we maintain the maximum value(max number of rows that could be selected) in \'ans\'.\n```\nclass Solution {\n public int maximumRows(int[][] mat, int cols) {\n \n int m=mat.length;\n int n=mat[0].length;\n \n int[] s=new int[n];\n \n return f(0,m,n,cols,mat,s);\n }\n \n public int f(int ind,int m,int n,int cols,int[][] mat,int[] s){\n \n if(cols==0){\n int count=0;\n for(int i=0; i<m; i++){\n\t\t\t//supposing that this row is valid\n boolean selected=true;\n for(int j=0; j<n; j++){\n\t\t\t\t//if any cell of this row violates the given two conditions, then the row is discarded\n if(mat[i][j]==1 && s[j]!=1)\n selected=false;\n }\n if(selected)\n count+=1;\n }\n \n return count;\n }\n \n int ans=-1;\n for(int i=ind; i<n; i++){\n \n s[i]=1; //do\n ans=Math.max(ans,f(i+1,m,n,cols-1,mat,s));\n s[i]=0; //undo / backtrack\n }\n \n return ans;\n }\n}\n``` | 2 | 0 | ['Backtracking', 'Recursion', 'Java'] | 0 |
maximum-rows-covered-by-columns | Simple backtracking java solution | simple-backtracking-java-solution-by-uts-zjsv | \nclass Solution { \n public int calculateNumberOfRows(int [][]mat,Set<Integer> cols){\n int n=mat.length,m=mat[0].length;\n int cnt=0;\n | utsavvjain | NORMAL | 2022-09-05T18:56:07.881895+00:00 | 2022-09-05T18:56:07.881932+00:00 | 139 | false | ```\nclass Solution { \n public int calculateNumberOfRows(int [][]mat,Set<Integer> cols){\n int n=mat.length,m=mat[0].length;\n int cnt=0;\n int i,j;\n for(i=0;i<n;i++){\n for(j=0;j<m;j++) {\n if(mat[i][j]==1 && !cols.contains(j)) break;\n }\n if(j==m) cnt+=1;\n }\n return cnt;\n }\n public int maximumRows(int[][] mat, int cols,Set<Integer> col,int colNum,int n) {\n if(cols==0 ){\n return calculateNumberOfRows(mat,col); \n }\n if(colNum>=n) return Integer.MIN_VALUE;\n \n //pick\n col.add(colNum);\n int pick=maximumRows(mat,cols-1,col,colNum+1,n); \n col.remove(colNum);\n \n //not pick\n int notPick=maximumRows(mat,cols,col,colNum+1,n); \n return Math.max(pick,notPick);\n }\n public int maximumRows(int[][] mat, int cols) {\n Set<Integer> col=new HashSet<>();\n return maximumRows(mat,cols,col,0,mat[0].length);\n }\n}\n``` | 2 | 0 | ['Backtracking', 'Java'] | 0 |
maximum-rows-covered-by-columns | C++ Easy Solution | c-easy-solution-by-mdaparnay23-j46n | \nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& v, int k) {\n int n=v.size(),m=v[0].size();\n int ans=0;\n for(int i= | mdaparnay23 | NORMAL | 2022-09-04T05:30:11.398814+00:00 | 2022-09-04T05:30:11.398858+00:00 | 90 | false | ```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& v, int k) {\n int n=v.size(),m=v[0].size();\n int ans=0;\n for(int i=0;i<(1<<12);i++){\n string s="";\n int c=0;\n for(int j=0;j<12;j++){\n if(i&(1<<j)) s+=\'1\';\n else s+=\'0\';\n if(s[j]==\'1\') c++;\n }\n if(c!=k) continue;\n int cnt=0;\n for(int x=0;x<n;x++){\n bool ok=true;\n for(int y=0;y<m;y++){\n if(v[x][y]==1 and s[y]!=\'1\') {ok=false;break;}\n }if(ok) cnt++;\n }ans=max(ans,cnt);\n }return ans;\n }\n};\n``` | 2 | 0 | [] | 0 |
maximum-rows-covered-by-columns | C++ | Simple Next Permutation | No Bit Masking or Back Tracking | c-simple-next-permutation-no-bit-masking-iocm | The idea is to just try all the combinations of the columns(with maximum cols columns selected) and see how many rows are being covered.\n\nWe can generate all | nisaanthdunnu | NORMAL | 2022-09-03T23:43:39.315862+00:00 | 2022-09-03T23:43:39.315897+00:00 | 52 | false | The idea is to just try all the combinations of the columns(with maximum ***cols*** columns selected) and see how many rows are being covered.\n\nWe can generate all the permutations using C++ next_permutation() algorithm starting from the first permutation when lexicographically sorted.\n\n\n```\nint maximumRows(vector<vector<int>>& mat, int cols) {\n int n = mat.size(), m = mat[0].size(), ans=0;\n vector<int> perm(m,0);\n // Our initial arrangement should be the first arrangement in the lexicographically sorted permutations.\n // This helps us to loop over the next_permutations until all the permutations are covered .\n for(int i=0;i<cols;i++) perm[m-i-1]=1;\n do {\n int rows = 0, good;\n for(int i=0;i<n;i++) {\n good = 1;\n for(int j=0;j<m;j++) {\n if(mat[i][j]==1 && perm[j]!=1) { \n good=0; break; \n }\n }\n if(good==1) rows++;\n }\n ans = max(ans, rows);\n } while(next_permutation(perm.begin(),perm.end()));\n \n return ans;\n }\n``` | 2 | 0 | ['C'] | 0 |
maximum-rows-covered-by-columns | python brute force | python-brute-force-by-akaghosting-9tg5 | \tclass Solution:\n\t\tdef maximumRows(self, mat: List[List[int]], cols: int) -> int:\n\t\t\tm = len(mat)\n\t\t\tn = len(mat[0])\n\t\t\tres = 0\n\t\t\tfor combi | akaghosting | NORMAL | 2022-09-03T19:47:13.551883+00:00 | 2022-09-03T20:38:28.406153+00:00 | 68 | false | \tclass Solution:\n\t\tdef maximumRows(self, mat: List[List[int]], cols: int) -> int:\n\t\t\tm = len(mat)\n\t\t\tn = len(mat[0])\n\t\t\tres = 0\n\t\t\tfor combination in combinations(range(n), cols):\n\t\t\t\tcnt = 0\n\t\t\t\tfor i in range(m):\n\t\t\t\t\tcheck = True\n\t\t\t\t\tfor j in range(n):\n\t\t\t\t\t\tif mat[i][j] == 1 and j not in combination:\n\t\t\t\t\t\t\tcheck = False\n\t\t\t\t\t\t\tbreak\n\t\t\t\t\tif check:\n\t\t\t\t\t\tcnt += 1\n\t\t\t\tres = max(res, cnt)\n\t\t\treturn res | 2 | 0 | [] | 1 |
maximum-rows-covered-by-columns | C++ Solution | c-solution-by-travanj05-h3zo | cpp\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>> &mat, int cols) {\n int m = mat.size(), n = mat[0].size();\n int perm = po | travanj05 | NORMAL | 2022-09-03T18:25:36.034676+00:00 | 2022-09-03T18:25:36.034721+00:00 | 34 | false | ```cpp\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>> &mat, int cols) {\n int m = mat.size(), n = mat[0].size();\n int perm = pow(2, n) - 1;\n vector<vector<int>> grid(perm + 1, vector<int>(n, 0));\n for (int i = 0; i <= perm; i++) {\n for (int j = 0; j < n; j++) {\n if ((i & (1 << j)) >= 1) {\n grid[i][j] = 1;\n }\n }\n }\n int mx = 0;\n for (int i = 0; i <= perm; i++) {\n int cnt = 0, temp = 0;\n unordered_set<int> st;\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == 1) {\n st.insert(j);\n cnt++;\n }\n }\n if (cnt == cols) {\n for (int i = 0; i < m; i++) {\n bool flag = false;\n for (int j = 0; j < n; j++) {\n if (st.count(j) == 0) {\n if (mat[i][j] == 1) {\n flag = true;\n }\n }\n }\n if (!flag) temp++;\n }\n }\n mx = max(mx, temp);\n }\n return mx;\n }\n};\n``` | 2 | 0 | ['C', 'C++'] | 0 |
maximum-rows-covered-by-columns | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-keah | Backtracking\n\n Time Complexity :- O(N * M * 2 ^ M)\n\n Space Complexity :- O(N * M * 2 ^ M)\n\n\nclass Solution {\npublic:\n \n // res will store all th | __KR_SHANU_IITG | NORMAL | 2022-09-03T17:32:16.885316+00:00 | 2022-09-03T17:32:16.885364+00:00 | 142 | false | * ***Backtracking***\n\n* ***Time Complexity :- O(N * M * 2 ^ M)***\n\n* ***Space Complexity :- O(N * M * 2 ^ M)***\n\n```\nclass Solution {\npublic:\n \n // res will store all the subsequence of size k\n \n vector<vector<int>> res;\n \n vector<int> curr;\n \n // function for finding subsequence of an array\n \n void dfs(vector<int>& arr, int i, int n, int k)\n {\n // base case\n \n if(i == n)\n {\n if(curr.size() == k)\n {\n res.push_back(curr);\n }\n \n return;\n }\n \n // for every no. we have two options either we can include or exclude\n \n // inclusion part\n \n curr.push_back(arr[i]);\n \n dfs(arr, i + 1, n, k);\n \n curr.pop_back();\n \n // exclusion part\n \n dfs(arr, i + 1, n, k);\n }\n \n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n int n = mat.size();\n \n int m = mat[0].size();\n \n // declare and initialize a col_arr\n \n vector<int> col_arr(m, 0);\n \n for(int i = 0; i < m; i++)\n {\n col_arr[i] = i;\n }\n \n // find all the subsequece of columns of size cols\n \n dfs(col_arr, 0, m, cols);\n \n // now for every column combination find the maximum row we can covered\n \n int maxi = INT_MIN;\n \n for(int k = 0; k < res.size(); k++)\n {\n vector<int> temp = res[k];\n \n unordered_set<int> s(temp.begin(), temp.end());\n \n int count = 0;\n \n // check every row can we covered or not\n \n for(int i = 0; i < n; i++)\n {\n bool flag = true;\n \n for(int j = 0; j < m; j++)\n {\n if(mat[i][j])\n {\n if(s.count(j) == 0)\n {\n flag = false;\n \n break;\n }\n }\n }\n \n if(flag)\n {\n count++;\n }\n }\n \n // update maxi\n \n maxi = max(maxi, count);\n }\n \n return maxi;\n }\n};\n``` | 2 | 0 | ['Backtracking', 'Recursion', 'C', 'C++'] | 0 |
maximum-rows-covered-by-columns | Backtracking C++ | backtracking-c-by-07ritvik-x1m2 | Logic :\n1. We have to take cols no. of columns so we have choice whether to take a particular column or not.\n2. If we chose a particular column ind then we ma | 07ritvik | NORMAL | 2022-09-03T16:45:36.685332+00:00 | 2022-09-03T16:46:23.259752+00:00 | 73 | false | Logic :\n1. We have to take **cols** no. of columns so we have choice whether to take a particular column or not.\n2. If we chose a particular column **ind** then we make all the elements of the rows in which column value is **ind**.\n3. If we do not chose this column then we will backtrack and unvisit the elements which we visited.\n\n```\nclass Solution {\npublic:\n \n void solve(int ind,int cnt,vector<vector<int>>& mat,int cols,int &ans,vector<vector<bool>>& vis){\n if(ind>mat[0].size()) return;\n\t\t\n\t\t// calculating the rows which are not covered by the chosen columns and substracting from the total rows ,\n\t\t//then we will get the no. of rows covered by the selected columns and then checking for the max value of ans;\n\t\t\n if(cnt==cols && ind==mat[0].size()){\n int t=0;\n for(int i=0;i<mat.size();i++){\n \n for(int j=0;j<mat[0].size();j++){\n if(vis[i][j]==0&&mat[i][j]==1){\n t++;\n break;\n }\n }\n }\n if(ans<mat.size()-t) ans=mat.size()-t;\n return;\n }\n //taken the current column\n for(int i=0;i<mat.size();i++){\n vis[i][ind]=1;\n }\n solve(ind+1,cnt+1,mat,cols,ans,vis);\n //not taken the current column \n for(int i=0;i<mat.size();i++){\n vis[i][ind]=0;\n }\n solve(ind+1,cnt,mat,cols,ans,vis);\n \n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int n=mat.size();\n int m=mat[0].size();\n vector<vector<bool>> vis(n,vector<bool>(m,false));\n int ans=0;\n solve(0,0,mat,cols,ans,vis);\n return ans;\n }\n};\n``` | 2 | 0 | ['C'] | 1 |
maximum-rows-covered-by-columns | Python | Simple and straightforward | Combinations | Explained | python-simple-and-straightforward-combin-zjks | \nfrom itertools import combinations\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n rows = 0\n \n # | kajabraz | NORMAL | 2022-09-03T16:33:28.649526+00:00 | 2023-08-30T00:19:51.363709+00:00 | 227 | false | ```\nfrom itertools import combinations\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n rows = 0\n \n # iterate over each combintion of the given numer of columns\n # the first argument passed to combinations is the list of columns\' indices\n # the second argumnet is the number of columns we need to consider\n # e.g., if mat consists of 3 columns, we\'ll iterate over the following list [(0,1), (0,2), (1,2)]\n for c in combinations(range(len(mat[0])), cols):\n \n # initialise temp which is the number of valid rows for the current iteration\n temp = 0\n \n # iterate over each row in mat\n for r in mat:\n valid = True\n \n # iterate over each number in the row (we use enumerate; the index of the number is the column\'s index)\n # check if each number 1 present in the row is also present among columns we consider in the current most outer iteration (c)\n # if that\'s not the case, the row is not valid\n for col, n in enumerate(r):\n if valid and n == 1 and col not in c:\n valid = False\n if valid:\n temp += 1\n \n # at the end of the current most outer iteration (c), check if the current number of valid rows (temp) is bigger then the previous one\n rows = max(rows, temp)\n return rows\n```\n | 2 | 0 | ['Python', 'Python3'] | 1 |
maximum-rows-covered-by-columns | Cpp solution | cpp-solution-by-user2349xl-lt20 | \nclass Solution {\npublic:\n \n typedef long long ll;\n vector<int> v;\n int dp[13][4097][13];\n int m, n;\n\t\n int maximumRows(vector<vecto | ninaiway | NORMAL | 2022-09-03T16:22:40.567613+00:00 | 2022-09-03T16:36:16.103617+00:00 | 117 | false | ```\nclass Solution {\npublic:\n \n typedef long long ll;\n vector<int> v;\n int dp[13][4097][13];\n int m, n;\n\t\n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n m = mat.size();\n n = mat[0].size();\n \n for (int i =0; i < m; i++) {\n \n int a = 0;\n for (int j = 0; j < n; j++) {\n a *= 2;\n a += mat[i][j];\n }\n v.push_back(a);\n }\n \n memset(dp, -1, sizeof(dp));\n return dfs(0, 0, cols);\n }\n \n int dfs(int i, int j, int cols) {\n \n if (dp[i][j][cols] != -1) return dp[i][j][cols];\n \n if (cols == 0 | i == n) {\n int ans = 0;\n for (auto& num : v) {\n if ((~j) & num) continue;\n ans += 1;\n }\n \n return dp[i][j][cols] = ans;\n }\n \n int case1 = dfs(i+1, j | (1 << i), cols - 1);\n int case2 = dfs(i+1, j, cols);\n \n return dp[i][j][cols] = max(case1, case2);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'Depth-First Search', 'C++'] | 0 |
maximum-rows-covered-by-columns | Whoever understand this is a god ✅ JavaScript | Combinations | whoever-understand-this-is-a-god-javascr-xoph | FYI, I wrote this solutions and got accepted (just 4 sec before end time) in biweekly contest 86. I understand the code is very brute force. Anyway I\'m trying | thakurballary | NORMAL | 2022-09-03T16:13:08.566598+00:00 | 2022-09-03T17:43:28.206191+00:00 | 338 | false | FYI, I wrote this solutions and got accepted (just 4 sec before end time) in biweekly contest 86. I understand the code is very brute force. Anyway I\'m trying to improve my skills. So, ya enjoy reading my solution and if you understand it, now only god, you and I know it :)\n```\n/**\n * @param {number[][]} mat\n * @param {number} cols\n * @return {number}\n */\nfunction getCombinations(n, k) {\n const ans = [];\n const arr = [];\n \n function dfs(i) {\n arr.push(i);\n \n if (arr.length === k) {\n ans.push(Array.from(arr));\n arr.pop();\n return;\n }\n \n for (let j = i + 1; j < n; j++) {\n dfs(j);\n }\n \n arr.pop();\n }\n \n for (let i = 0; i < n; i++) {\n dfs(i);\n }\n \n return ans;\n}\n\nvar maximumRows = function(mat, cols) {\n const m = mat.length;\n const n = mat[0].length;\n \n let min = 0; // to store no. of rows with all 0\'s\n let ans = 0;\n \n const map = {}; // to store rows with column numbers having 1\'s. From ex 1 :- {1: [0, 2], 2: [1, 2]}\n \n for (let i = 0; i < m; i++) {\n for (let j = 0; j < n; j++) {\n if (mat[i][j]) {\n if (map[i]) {\n map[i].push(j); // at row i, jth column is having 1\n } else {\n map[i] = [j];\n }\n }\n }\n if (!map[i]) { // if all values in row i are 0\'s\n min++;\n }\n }\n\t\n\t// I need more practice on bit masking so I choose backtracking way to get combinations \n // https://leetcode.com/problems/combinations/discuss/2523710/JavaScript-or-TC-O(n!)-or-SC-O(n)\n const combinations = getCombinations(n, cols); \n const rows = Object.values(map);\n \n\t// loop through each combination and see if rows having cell value 1 is chosen or not\n for (const comb of combinations) {\n // assigned min because min contains the count of rows with all 0\'s (which indicates covered)\n\t\tlet combAns = min;\n for (const row of rows) {\n // count to check if we reached end of row (all 1\'s cell of this row are in chosen column combination\n\t\t\tlet count = 0; \n for (let i = 0; i < row.length; i++) {\n\t\t\t// row[i] holds the cell with value 1, and if that doesn\'t include in the chosen combination, we break the loop. So, this row is not covered.\n if (!comb.includes(row[i])) { \n break;\n } else {\n count++;\n }\n }\n if (count === row.length) {\n combAns++;\n }\n }\n\t\t// once we have rows count (combAns) covered by this combination (comb), we take max \n ans = Math.max(ans, combAns);\n }\n \n return ans;\n};\n``` | 2 | 0 | ['JavaScript'] | 5 |
maximum-rows-covered-by-columns | easy short clean code | easy-short-clean-code-by-maverick09-yvst | \nclass Solution {\npublic:\n int m, n, res;\n long long func(const vector<vector<int>>& v, int c, const int&x, int bm) {\n if (__builtin_popcount( | maverick09 | NORMAL | 2022-09-03T16:02:52.346877+00:00 | 2022-09-03T16:02:52.346965+00:00 | 235 | false | ```\nclass Solution {\npublic:\n int m, n, res;\n long long func(const vector<vector<int>>& v, int c, const int&x, int bm) {\n if (__builtin_popcount(bm) == x) {\n int ans = m;\n for (int i = 0;i < m;++i) {\n for (int j = 0;j < n;++j) {\n if (v[i][j] == 1 && !(bm & (1 << j))) {\n --ans;\n break;\n }\n }\n }\n return ans;\n }\n if (c == n) {\n return LLONG_MIN;\n }\n return max(func(v, c + 1, x, bm), func(v, c + 1, x, bm | (1 << c)));\n }\n int maximumRows(vector<vector<int>>& v, int x) {\n m = v.size(), n = v[0].size();\n return func(v, 0, x, 0);\n }\n};\n``` | 2 | 0 | ['Backtracking', 'C'] | 0 |
maximum-rows-covered-by-columns | Basic C++ Backtracking & Recursive Approach. | basic-c-backtracking-recursive-approach-njr04 | Intuition
Given a binary matrix (matrix) and a number numSelect, we need to select numSelect columns such that the maximum number of fully covered rows is achi | Sujal049 | NORMAL | 2025-04-03T18:17:49.984327+00:00 | 2025-04-03T18:17:49.984327+00:00 | 11 | false | # Intuition
- Given a binary matrix (matrix) and a number numSelect, we need to select numSelect columns such that the maximum number of fully covered rows is achieved.
- A row is covered if all 1s in that row exist in at least one of the selected columns.
- The goal is to maximize the number of fully covered rows.
# Approach
- The algorithm tries all possible ways to select numSelect columns and finds the best selection.
- 1️⃣ Recursively Try Selecting Columns
mxrows(idx, matrix, num, cnt, selected) is the main recursive function.
- We either pick the current column or skip it.
- Base conditions:
If we selected numSelect columns → count covered rows.
If we ran out of columns → return 0.
- 2️⃣ Counting Fully Covered Rows
Function cntrows(selected, matrix) counts how many rows are fully covered by selected columns.
For each row, check if all 1s in that row are covered by some selected column.
- 3️⃣ Take the Maximum
Try both picking and not picking the current column.
Return max(pick, notpick) to ensure we get the best result.
# Complexity
- Time complexity:
$$O(2^n)$$ n=number of columns
- Space complexity:
$$O(n)$$ stack space
# Code
```cpp []
class Solution {
public:
int cntrows(set<int>& selected, vector<vector<int>>& matrix)
{
int coveredRows = 0;
for (int i = 0; i < matrix.size(); i++)
{
bool covered = true;
for (int j = 0; j < matrix[0].size(); j++)
{
if (matrix[i][j] == 1 && selected.find(j) == selected.end())
{
covered = false;
break;
}
}
if (covered) coveredRows++;
}
return coveredRows;
}
int mxrows(int idx, vector<vector<int>>& matrix, int num, int cnt, set<int>& selected)
{
if (cnt == num)
{
return cntrows(selected, matrix);
}
if (idx >= matrix[0].size())
{
return 0;
}
selected.insert(idx);
int pick = mxrows(idx + 1, matrix, num, cnt + 1, selected);
selected.erase(idx);
int notpick = mxrows(idx + 1, matrix, num, cnt, selected);
return max(pick, notpick);
}
int maximumRows(vector<vector<int>>& matrix, int numSelect) {
set<int> selected;
return mxrows(0, matrix, numSelect, 0, selected);
}
};
``` | 1 | 0 | ['Backtracking', 'Recursion', 'Matrix', 'C++'] | 0 |
maximum-rows-covered-by-columns | Easy C++ Solution using Bitmask and Backtracking | easy-c-solution-using-bitmask-and-backtr-wysp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ronit_0109 | NORMAL | 2024-06-13T19:47:54.791604+00:00 | 2024-06-13T19:47:54.791635+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint ans=0;\nvoid helper(vector<vector<int>> &matrix,int k,int selectedcol,int index){\n if(index>=matrix[0].size()){\n if(k==0){\n int t=0;\n for(int i=0;i<matrix.size();i++){\n bool cantake=true;\n for(int j=0;j<matrix[0].size();j++){\n if(matrix[i][j]==1 and ((selectedcol>>j)&1)==0){\n cantake=false;\n break;\n }\n }\n if(cantake)t++;\n }\n ans=max(ans,t);\n }\n return;\n }\n helper(matrix,k,selectedcol,index+1);\n selectedcol=(selectedcol | (1<<index));\n helper(matrix,k-1,selectedcol,index+1);\n selectedcol=(selectedcol & (~(1<<index)));\n}\n int maximumRows(vector<vector<int>>& matrix, int numSelect) {\n // vector<bool> selectedcol(matrix[0].size(),false); \n int selectedcol=0;\n helper(matrix,numSelect,selectedcol,0);\n return ans;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Bit Manipulation', 'Bitmask', 'C++'] | 0 |
maximum-rows-covered-by-columns | Brute force using Backtracking | C++ | brute-force-using-backtracking-c-by-whoa-9qfr | I tried generating all possible combination of numSelect columns using the f( ) function using backtracking. Then just iteraterd over the matrix for each combin | whoami950 | NORMAL | 2023-06-01T18:15:14.713242+00:00 | 2023-06-01T18:15:14.713279+00:00 | 16 | false | I tried generating all possible combination of **numSelect** columns using the `f( )` function using backtracking. Then just iteraterd over the matrix for each combination of columns, checked the given condition which just says that if the cell is equal to 1 then it has to be a part of the column selected by current combination of columns.\n\n```\nclass Solution\n{\n int rows, cols;\n\n void f(int idx, int numSelect, vector<vector<int>> &combs, vector<int> cur)\n {\n if (numSelect <= 0 or idx>=cols)\n {\n if(numSelect<=0)\n combs.push_back(cur);\n return;\n }\n for (int i = idx; i < cols; i++)\n {\n cur.push_back(i);\n f(i+1, numSelect - 1, combs, cur);\n cur.pop_back();\n f(i+1, numSelect, combs, cur);\n }\n }\n\n int help(vector<vector<int>> &matrix, int numSelect)\n {\n vector<vector<int>> combs;\n vector<int> cur;\n f(0, numSelect, combs, cur);\n int maxi= 0;\n for (auto &v : combs)\n {\n int cnt = 0;\n for (int j = 0; j < rows; j++)\n {\n bool is=true;\n for (int k = 0; k < cols; k++)\n {\n if(find(v.begin(), v.end(), k) == v.end() and matrix[j][k]==1){\n is =false;\n break;\n }\n }\n if(is)\n {\n cnt++;\n }\n }\n maxi=max(maxi,cnt);\n }\n return maxi;\n }\n\npublic:\n int maximumRows(vector<vector<int>> &matrix, int numSelect)\n {\n rows = matrix.size(), cols = matrix[0].size();\n return help(matrix, numSelect);\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
maximum-rows-covered-by-columns | c++ | easy to undersatand | step by step | c-easy-to-undersatand-step-by-step-by-ve-jc95 | ```\nclass Solution {\npublic:\n int n, ans=0;\n vector row_sums;\n \n int sumOfRow(vector &vec){\n int res=0;\n for(auto a:vec) res+= | venomhighs7 | NORMAL | 2022-09-27T12:15:45.377501+00:00 | 2022-09-27T12:15:45.377536+00:00 | 47 | false | ```\nclass Solution {\npublic:\n int n, ans=0;\n vector<int> row_sums;\n \n int sumOfRow(vector<int> &vec){\n int res=0;\n for(auto a:vec) res+=a;\n return res;\n }\n \n int isPossible(vector<int> &a, vector<int> &b){\n int res=0;\n for(int i=0; i<a.size(); i++){\n if(a[i]==b[i]) res++;\n else continue;\n }\n return res;\n }\n \n void helper(vector<vector<int>>& matrix, int c, int count, vector<int> c_sums){\n if(c==matrix[0].size()){\n if(count==n){\n int temp=isPossible(c_sums, row_sums);\n if(temp)\n ans=max(ans, temp);\n }\n return;\n }\n \n helper(matrix, c+1, count, c_sums);\n \n for(int i=0; i<matrix.size(); i++){\n c_sums[i]+=matrix[i][c];\n }\n helper(matrix, c+1, count+1, c_sums);\n }\n \n int maximumRows(vector<vector<int>>& matrix, int numSelect) {\n n=numSelect;\n for(auto a:matrix){\n row_sums.push_back(sumOfRow(a));\n }\n \n vector<int> c_sums(matrix.size(), 0);\n helper(matrix, 0, 0, c_sums);\n return ans;\n }\n}; | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | Maximum Rows Covered by Columns Solution Java | maximum-rows-covered-by-columns-solution-3v2a | class Solution {\n public int maximumRows(int[][] matrix, int numSelect) {\n dfs(matrix, /colIndex=/0, numSelect, /mask=/0);\n return ans;\n }\n\n priv | bhupendra786 | NORMAL | 2022-09-18T12:07:30.631514+00:00 | 2022-09-18T12:07:30.631559+00:00 | 47 | false | class Solution {\n public int maximumRows(int[][] matrix, int numSelect) {\n dfs(matrix, /*colIndex=*/0, numSelect, /*mask=*/0);\n return ans;\n }\n\n private int ans = 0;\n\n private void dfs(int[][] matrix, int colIndex, int leftColsCount, int mask) {\n if (leftColsCount == 0) {\n ans = Math.max(ans, getAllZerosRowCount(matrix, mask));\n return;\n }\n if (colIndex == matrix[0].length)\n return;\n\n // choose this column\n dfs(matrix, colIndex + 1, leftColsCount - 1, mask | 1 << colIndex);\n // not choose this column\n dfs(matrix, colIndex + 1, leftColsCount, mask);\n }\n\n int getAllZerosRowCount(int[][] matrix, int mask) {\n int count = 0;\n for (int[] row : matrix) {\n boolean isAllZeros = true;\n for (int i = 0; i < row.length; ++i) {\n if (row[i] == 1 && (mask >> i & 1) == 0) {\n isAllZeros = false;\n break;\n }\n }\n if (isAllZeros)\n ++count;\n }\n return count;\n }\n}\n | 1 | 0 | ['Array', 'Backtracking', 'Bit Manipulation', 'Matrix', 'Enumeration'] | 0 |
maximum-rows-covered-by-columns | No backtracking ❌ | Do bit manipulation✅ | no-backtracking-do-bit-manipulation-by-n-0sr1 | \n\t\tclass Solution:\n\t\t\tdef maximumRows(self, matrix: List[List[int]], numSelect: int) -> int:\n\t\t\t\tn = len(matrix)\n\t\t\t\ta = [int(\'\'.join([str(j) | NaveenprasanthSA | NORMAL | 2022-09-16T11:54:32.802077+00:00 | 2022-09-16T11:54:32.802119+00:00 | 72 | false | \n\t\tclass Solution:\n\t\t\tdef maximumRows(self, matrix: List[List[int]], numSelect: int) -> int:\n\t\t\t\tn = len(matrix)\n\t\t\t\ta = [int(\'\'.join([str(j) for j in matrix[i]]),2) for i in range(n)]\n\t\t\t\tres = 0\n\t\t\t\tfor i in range(n):\n\t\t\t\t\tans = a[i] \n\t\t\t\t\tcur = 0\n\t\t\t\t\tfor j in range(n):\n\t\t\t\t\t\tif bin(ans|a[j]).count(\'1\') <= numSelect:\n\t\t\t\t\t\t\tans|=a[j]\n\t\t\t\t\t\t\tcur+=1 \n\t\t\t\t\tres = max(cur,res)\n\t\t\t\treturn res | 1 | 0 | ['Python'] | 0 |
maximum-rows-covered-by-columns | Combinations and issubset(), 77% speed | combinations-and-issubset-77-speed-by-ev-e6nv | \n\nclass Solution:\n def maximumRows(self, matrix: List[List[int]], numSelect: int) -> int:\n ans = 0\n m_ones = [{i for i, v in enumerate(row | evgenysh | NORMAL | 2022-09-12T10:49:21.250389+00:00 | 2022-09-12T10:52:17.712809+00:00 | 65 | false | \n```\nclass Solution:\n def maximumRows(self, matrix: List[List[int]], numSelect: int) -> int:\n ans = 0\n m_ones = [{i for i, v in enumerate(row) if v} for row in matrix]\n for comb in combinations(range(len(matrix[0])), numSelect):\n set_comb = set(comb)\n ans = max(ans, sum(s.issubset(set_comb) for s in m_ones))\n return ans\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
maximum-rows-covered-by-columns | How is it in the medium category | how-is-it-in-the-medium-category-by-hash-shod | Like seiously, after wasting a day and a half pondering upon a consize and effective approach, this problem turns out to be a basic bruteforce backtracking prob | Hash_coder27 | NORMAL | 2022-09-11T19:31:52.769392+00:00 | 2022-09-11T19:32:33.598720+00:00 | 73 | false | Like seiously, after wasting a day and a half pondering upon a consize and effective approach, this problem turns out to be a basic bruteforce backtracking problem!!!\nTotally annoying | 1 | 1 | [] | 1 |
maximum-rows-covered-by-columns | Python Brute Force | python-brute-force-by-maelseifi-3w21 | ```\nm = len(matrix)\n n = len(matrix[0])\n colcombs = list(itertools.combinations(list(range(n)), numSelect))\n \n maxcovered = 0\n | maelseifi | NORMAL | 2022-09-09T18:43:30.869550+00:00 | 2022-09-09T18:43:30.869599+00:00 | 76 | false | ```\nm = len(matrix)\n n = len(matrix[0])\n colcombs = list(itertools.combinations(list(range(n)), numSelect))\n \n maxcovered = 0\n for i in range(len(colcombs)):\n covered = 0\n for j in range(m):\n flag = 0\n if all(x == 0 for x in matrix[j]):\n flag = 1\n \n if all (k in colcombs[i] for k in range(n) if matrix[j][k] == 1):\n flag = 1\n \n if flag == 1:\n covered+=1\n maxcovered = max(covered, maxcovered)\n \n return(maxcovered)\n | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | C++| Brute-Force | c-brute-force-by-kumarabhi98-i8jr | \nclass Solution {\npublic:\n int no(int n){\n int re = 0;\n while(n){ n = n&(n-1); re++;} return re;\n }\n \n int find(vector<vector | kumarabhi98 | NORMAL | 2022-09-06T13:39:32.085297+00:00 | 2022-09-06T13:39:32.085322+00:00 | 56 | false | ```\nclass Solution {\npublic:\n int no(int n){\n int re = 0;\n while(n){ n = n&(n-1); re++;} return re;\n }\n \n int find(vector<vector<int>>& nums,int bit){\n unordered_set<int> st;\n for(int i = 0; i<nums.size();++i){\n for(int j = 0; j<nums[0].size();++j){\n if(nums[i][j] && !bool(bit&(1<<j))) st.insert(i);\n }\n }\n return nums.size()-st.size();\n }\n \n int maximumRows(vector<vector<int>>& nums, int numSelect) {\n int n = nums.size(), m = nums[0].size();\n int bit = (1<<m)-1, re = 0;\n for(int i = bit; i>0; i = bit&(i-1)){\n if(no(i)==numSelect){\n re = max(find(nums,i),re);\n }\n }\n return re;\n }\n};\n``` | 1 | 0 | ['C', 'Bitmask'] | 0 |
maximum-rows-covered-by-columns | My Java Solution | my-java-solution-by-akash_nad-2i2q | Time Complexity is probably Exponential but I can\'t say the exact figure.\nSpace Complexity: O(N - cols)\n\nclass Solution {\n int M, N;\n public int max | Akash_Nad | NORMAL | 2022-09-06T09:44:42.188605+00:00 | 2022-09-06T09:44:42.188648+00:00 | 64 | false | ***Time Complexity is probably Exponential but I can\'t say the exact figure.***\n***Space Complexity: O(N - cols)***\n```\nclass Solution {\n int M, N;\n public int maximumRows(int[][] mat, int cols) {\n M = mat.length;\n N = mat[0].length;\n if(cols == N) return M;\n return findMaxRow(N - cols, mat, new ArrayList<>());\n }\n private int findMaxRow(int cols, int[][] mat, List<Integer> list) {\n if(cols == 0) {\n int rows = 0;\n for(int i=0 ;i<M ;i++) {\n boolean isAdded = true;\n for(int j : list) {\n if(mat[i][j] == 1) {\n isAdded = false;\n break;\n }\n }\n if(isAdded) rows++;\n }\n return rows;\n }\n \n int last = list.size() != 0 ? list.get(list.size() - 1) : -1;\n int maxRow = -1;\n \n for(int i=last + 1 ;i<N ;i++) {\n list.add(i);\n maxRow = Math.max(maxRow, findMaxRow(cols - 1, mat, list));\n list.remove(list.size() - 1);\n }\n return maxRow;\n }\n}\n``` | 1 | 0 | ['Backtracking', 'Java'] | 0 |
maximum-rows-covered-by-columns | Python3 Solution | Very Easy Approach | python3-solution-very-easy-approach-by-t-wx91 | The solution is very simple:\nFirst we will find all the combinations, and then we will iterate over all the combinations of the array. At each iteration, check | triposat | NORMAL | 2022-09-05T10:08:15.189845+00:00 | 2022-09-05T10:09:28.730566+00:00 | 75 | false | *The solution is very simple:*\n**First we will find all the combinations, and then we will iterate over all the combinations of the array. At each iteration, check every row and cols.**\n\n\tclass Solution:\n\t\tdef maximumRows(self, mat: List[List[int]], cols: int) -> int:\n\t\t\tallCombinations = []\n\n\t\t\tdef combina(nums, k, path):\n\t\t\t\tif len(path) == k:\n\t\t\t\t\tallCombinations.append((path))\n\t\t\t\t\treturn\n\t\t\t\tfor i in range(len(nums)):\n\t\t\t\t\tcombina(nums[i+1:], k, path+[nums[i]])\n\n\t\t\tcol = len(mat[0])\n\t\t\tans = 0\n\t\t\tcombina(list(range(0, col)), cols, [])\n\t\t\tfor comb in allCombinations:\n\t\t\t\ttot = 0\n\t\t\t\tcomb = set(comb)\n\t\t\t\tfor row in mat:\n\t\t\t\t\tflag = True\n\t\t\t\t\tfor i in range(col):\n\t\t\t\t\t\tif row[i] and i not in comb:\n\t\t\t\t\t\t\tflag = False\n\t\t\t\t\t\t\tbreak\n\t\t\t\t\tif flag:\n\t\t\t\t\t\ttot += 1\n\t\t\t\tans = max(ans, tot)\n\t\t\treturn ans | 1 | 0 | ['Python', 'Python3'] | 0 |
maximum-rows-covered-by-columns | Accepted Solution | Using Recursion | C++ | accepted-solution-using-recursion-c-by-p-olvz | \nclass Solution {\nprivate:\n int maxi = INT_MIN;\n int checkMax(int& m, int& n, vector<vector<int>>& mat, vector<bool>& visCols){\n int count=0;\ | parasgaur24 | NORMAL | 2022-09-05T08:00:29.071064+00:00 | 2022-09-05T08:01:39.592549+00:00 | 14 | false | ```\nclass Solution {\nprivate:\n int maxi = INT_MIN;\n int checkMax(int& m, int& n, vector<vector<int>>& mat, vector<bool>& visCols){\n int count=0;\n \n for(int i=0;i<m;i++){\n bool flag=true;\n for(int j=0;j<n;j++){\n if(mat[i][j]==1 && visCols[j]==false){\n flag=false;\n break;\n }\n }\n if(flag==true)\n count++;\n }\n return count;\n }\n \n void solve(int& m, int& n, vector<vector<int>>& mat, int col, vector<bool>& visCols, int cols){\n //base case\n if(cols==0){\n maxi = max(maxi,checkMax(m,n,mat,visCols));\n return;\n }\n \n for(int j=col;j<n;j++){\n \n //choose this col\n visCols[j]=true;\n solve(m,n,mat,j+1,visCols,cols-1);\n visCols[j]=false;\n \n //skip this col\n solve(m,n,mat,j+1,visCols,cols);\n }\n }\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int m = mat.size();\n int n = mat[0].size();\n \n maxi = INT_MIN;\n vector<bool> visCols(n,false);\n solve(m,n,mat,0,visCols,cols);\n return maxi;\n }\n};\n``` | 1 | 0 | ['Recursion', 'C'] | 0 |
maximum-rows-covered-by-columns | C++ | Bitmask | c-bitmask-by-rachit759-7de8 | \nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int m(size(mat)), n(size(mat[0]));\n int ans = 0, rows;\n | rachit759 | NORMAL | 2022-09-05T00:27:14.913618+00:00 | 2022-09-05T01:00:03.750933+00:00 | 44 | false | ```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int m(size(mat)), n(size(mat[0]));\n int ans = 0, rows;\n bool flag;\n for(int mask = 1; mask <= (1<<n); mask++) {\n if(__builtin_popcount(mask) != cols) continue; \n vector<int> col_set(n,0);\n rows = 0;\n for(int i = 0; i < n; i++) {\n if(mask & (1<<i)) {\n col_set[i] = 1;\n }\n }\n for(int i = 0; i < m; i++) {\n flag = true;\n for(int j = 0; j < n; j++) {\n\t if(!col_set[j] and mat[i][j]) {\n flag = false;\n break;\n }\n }\n if(flag) rows += 1;\n }\n ans = max(ans,rows);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C', 'Bitmask'] | 0 |
maximum-rows-covered-by-columns | Simple Backtracking c++ | simple-backtracking-c-by-aditya_h-r34s | ```\nclass Solution {\npublic:\n void pickcolumn(int i,vector>& mat, int cols,int currcols, vector&visited, int &ans){\n if(i==mat[0].size()){\n | Aditya_H | NORMAL | 2022-09-04T16:14:41.266163+00:00 | 2022-09-04T16:14:41.266202+00:00 | 32 | false | ```\nclass Solution {\npublic:\n void pickcolumn(int i,vector<vector<int>>& mat, int cols,int currcols, vector<bool>&visited, int &ans){\n if(i==mat[0].size()){\n int count=0;\n for(int i=0;i<mat.size();i++){\n bool flag=true;\n for(int j=0;j<mat[0].size();j++){\n if(mat[i][j]==1){\n if(!visited[j]){\n flag=false;\n break;\n }\n }\n }\n if(flag){\n count++;\n }\n }\n ans=max(ans,count);\n return;\n }\n \n if(currcols<cols){\n visited[i]=true; \n pickcolumn(i+1,mat,cols,currcols+1,visited,ans); \n visited[i]=false;\n }\n pickcolumn(i+1,mat,cols,currcols,visited,ans);\n \n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n int currcols=0;\n int ans=0;\n vector<bool>visited(mat[0].size(),0);\n pickcolumn(0,mat, cols,currcols,visited,ans);\n \n return ans;\n \n }\n}; | 1 | 0 | ['Backtracking', 'Recursion'] | 0 |
maximum-rows-covered-by-columns | C++ || backtracking || intuitive approach || 4 ms | c-backtracking-intuitive-approach-4-ms-b-z9ea | Try all possible combination of columns \n* Check against each combination of columns for the maximum covered rows\n\n\nclass Solution {\npublic:\n int solve | gourav0sharma1 | NORMAL | 2022-09-04T07:10:28.228518+00:00 | 2022-09-04T07:10:28.228570+00:00 | 23 | false | * Try all possible combination of columns \n* Check against each combination of columns for the maximum covered rows\n\n```\nclass Solution {\npublic:\n int solve(vector<vector<int>> &mat, int curCol , int column, vector<int> &selectedColumn){\n \n if(column == 0){\n int count = 0;\n int selectedRows = mat.size();\n for(int i =0; i< mat.size(); i++){\n for(int j = 0; j < mat[0].size();j++){\n if(selectedColumn[j]) continue;\n if(mat[i][j] == 1){\n selectedRows--;\n break; \n }\n \n }\n }\n return selectedRows;\n }\n if(curCol >= mat[0].size()) return 0;\n selectedColumn[curCol] =1;\n int pick = solve(mat, curCol+1, column-1, selectedColumn);\n \n selectedColumn[curCol] =0;\n int notPick = solve(mat, curCol+1, column, selectedColumn);\n return max(pick, notPick);\n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n vector<int> selectedColumn(mat[0].size());\n return solve(mat, 0, cols, selectedColumn);\n }\n};\n``` | 1 | 0 | ['Backtracking', 'C'] | 0 |
maximum-rows-covered-by-columns | Super Easy Recursive Code || Java | super-easy-recursive-code-java-by-lil_to-aeau | \nclass Solution {\n int m,n,res = 0, arr[], cols,mat[][];\n public int maximumRows(int[][] mat, int cols) {\n m = mat.length;\n n = mat[0]. | Lil_ToeTurtle | NORMAL | 2022-09-04T06:30:08.460959+00:00 | 2022-09-04T06:30:08.461000+00:00 | 241 | false | ```\nclass Solution {\n int m,n,res = 0, arr[], cols,mat[][];\n public int maximumRows(int[][] mat, int cols) {\n m = mat.length;\n n = mat[0].length;\n this.cols = cols;\n arr = new int[cols];\n this.mat = mat;\n recurse(-1,-1);\n return res;\n }\n \n void recurse(int i, int donetill){\n i++; donetill++;\n if(i == cols) check();\n else{\n for(int j = donetill;j<n;j++){\n arr[i] = j;\n recurse(i,j);\n }\n }\n }\n \n void check(){\n int count = 0,i,j;\n boolean flag;\n HashSet<Integer> colsSelected = new HashSet<Integer>();\n for(int col : arr) colsSelected.add(col);\n for(i=0;i<m;i++){\n flag = true;\n for(j=0;j<n;j++){\n if(mat[i][j]==1 && !colsSelected.contains(j)){\n flag = false;\n break;\n }\n }\n if(flag) count++;\n }\n res = Math.max(res, count);\n }\n}\n\n``` | 1 | 0 | ['Recursion', 'Java'] | 1 |
maximum-rows-covered-by-columns | brute force recursive solution || 100%fast | brute-force-recursive-solution-100fast-b-0ved | \n | Am_Shubh_07_06 | NORMAL | 2022-09-03T20:33:00.974000+00:00 | 2022-09-03T20:33:00.974036+00:00 | 13 | false | \n | 1 | 0 | ['Backtracking', 'Recursion'] | 1 |
maximum-rows-covered-by-columns | Backtracking || Trying all combinations of cols | backtracking-trying-all-combinations-of-29l9u | \nclass Solution {\npublic:\n void solve(vector<vector<int>>&nums, vector<int> temp, int i, int cols, int m){\n \n if(i==m){\n if(te | bhomik23 | NORMAL | 2022-09-03T20:26:57.461152+00:00 | 2022-09-03T20:26:57.461182+00:00 | 62 | false | ```\nclass Solution {\npublic:\n void solve(vector<vector<int>>&nums, vector<int> temp, int i, int cols, int m){\n \n if(i==m){\n if(temp.size() == cols)\n nums.push_back(temp);\n \n return ;\n }\n \n // dont take this column\n solve(nums, temp, i+1, cols, m);\n \n // take this column\n temp.push_back(i);\n solve(nums, temp, i+1, cols, m);\n \n temp.pop_back();\n \n }\n \n int check(vector<vector<int>>& mat, unordered_set<int> &st, int n, int m){\n int count = 0;\n for(int i = 0; i<n; i++){\n bool notValidRow = false;\n \n for(int j = 0; j<m; j++){\n \n if(mat[i][j]==1 && st.find(j)==st.end()){\n \n notValidRow = true;\n break;\n \n }\n }\n \n if(!notValidRow)\n count++;\n }\n \n return count;\n \n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int n = mat.size();\n int m = mat[0].size();\n vector<vector<int>> nums;\n vector<int> temp;\n solve( nums, temp, 0, cols, m);\n int res = 0;\n \n for(auto it: nums){\n \n unordered_set<int> st;\n \n for(auto i: it)\n st.insert(i);\n \n res = max(res,check(mat, st, n, m));\n \n }\n \n return res;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Recursion', 'C', 'C++'] | 0 |
maximum-rows-covered-by-columns | JAVA EASY SOLUTION | java-easy-solution-by-abhizz-tha2 | \nclass Solution {\n public int maximumRows(int[][] mat, int cols) {\n int rows = mat.length;\n int col = mat[0].length;\n int res = 0;\ | abhizz | NORMAL | 2022-09-03T18:40:11.884790+00:00 | 2022-09-03T18:40:11.884837+00:00 | 115 | false | ```\nclass Solution {\n public int maximumRows(int[][] mat, int cols) {\n int rows = mat.length;\n int col = mat[0].length;\n int res = 0;\n for(int i = 0; i < (1<<col); i++) {\n if(getCount(i) == cols) {\n int cnt = 0;\n for(int r = 0; r < rows; r++) {\n int flag = 0;\n for(int c = 0; c < col; c++) {\n if(mat[r][c] == 1 && !isPresent(i,c)){\n flag = 1;\n break;\n }\n }\n if(flag == 0) {\n cnt++; \n }\n }\n res = Math.max(res,cnt);\n }\n }\n return res; \n }\n public static int getCount(int i) {\n int cnt = 0;\n while(i>0) {\n cnt += (i&1);\n i = i>>1;\n }\n return cnt;\n }\n public static boolean isPresent(int mask, int i) {\n return ((mask>>i)&1) == 1;\n }\n \n}\n\n``` | 1 | 0 | ['Bitmask', 'Java'] | 0 |
maximum-rows-covered-by-columns | Bit Masking+ Implementation (Easy understanding) | C++ | bit-masking-implementation-easy-understa-t2zm | I have used concept of bitmasking:\n1. Convert each row into a number(convert binary to decimal)\n2. Then we select column by using set bits of 1 to 2^(number o | automata_1 | NORMAL | 2022-09-03T18:09:44.058686+00:00 | 2022-09-03T18:09:44.058733+00:00 | 49 | false | I have used concept of bitmasking:\n1. Convert each row into a number(convert binary to decimal)\n2. Then we select column by using set bits of 1 to 2^(number of columns)[concept of subset generation]\n3. Then take ```AND``` and then see if the count of bits is same or not. \n\nEx: \n0 0 0 -> 0\n1 0 1 -> 5\n0 1 1 -> 3\n0 0 1 -> 1\n\n\n```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n int n=mat.size();\n int m=mat[0].size();\n \n vector<int> bit; // to store number formed from each row\n \n for(int i=0;i<n;i++){\n \n int num=0;\n int b=0;\n for(int j=m-1;j>=0;j--){\n \n \n int pow=(1<<b);\n \n num=num+(mat[i][j]*pow);// converting binary to decimal\n b++;\n \n }\n bit.push_back(num);//storing formed number in bit array\n }\n \n int loop=(1<<m);\n \n int mx=INT_MIN;\n for(int i=1;i<loop;i++){// loop to generate all subsets\n int bit_count=__builtin_popcount(i);\n \n \n int cnt=0;\n if(bit_count==cols){\n \n for(int j=0;j<bit.size();j++){\n \n int check=bit[j]&i;\n int bit1=__builtin_popcount(bit[j]);\n int bit2=__builtin_popcount(check);\n \n \n if(bit1==bit2 || bit[j]==0){\n cnt++;\n }\n }\n \n }\n mx=max(cnt,mx);\n }\n \n return mx;\n }\n};\n``` | 1 | 0 | ['C', 'Bitmask'] | 0 |
maximum-rows-covered-by-columns | Simple Intuition NO BITS - Backtracking | simple-intuition-no-bits-backtracking-by-vfxd | \nclass Solution {\n public int maximumRows(int[][] mat, int cols) {\n int m = mat.length;\n int n = mat[0].length;\n \n int ones | vedwaj | NORMAL | 2022-09-03T18:04:36.865386+00:00 | 2022-09-03T18:04:36.865432+00:00 | 322 | false | ```\nclass Solution {\n public int maximumRows(int[][] mat, int cols) {\n int m = mat.length;\n int n = mat[0].length;\n \n int onesInRow[] = new int[m];\n //counting number of ones in each row \n List<List<Integer>> onesInCol = new ArrayList<>();\n \n for(int i=1; i<=n; i++)\n onesInCol.add(new ArrayList<Integer>());\n \n for(int i=0; i<m; i++){\n for(int j=0; j<n; j++){\n if(mat[i][j] == 1){\n onesInRow[i]++;\n onesInCol.get(j).add(i);\n }\n }\n }\n \n if(cols >= n) return m;\n int ans=0;\n for(int i:onesInRow)\n ans+= i==0 ? 1 : 0;\n return ans+removeCols(0, m, n, cols, onesInRow, onesInCol, mat);\n }\n \n private int removeCols(int curr, int m, int n, int cols, int []onesInRow, List<List<Integer>> onesInCol, int[][] mat){\n if(cols == 0 || curr==n) return 0;\n \n \n //hataaya\n int ans=0;\n for(Integer i : onesInCol.get(curr)){ \n if(--onesInRow[i] == 0) ans++;\n }\n int h = ans + removeCols(curr+1, m, n, cols-1, onesInRow, onesInCol, mat);\n for(Integer i : onesInCol.get(curr)){ \n ++onesInRow[i];\n }\n //nahi hataaya\n int nh = removeCols(curr+1, m, n, cols, onesInRow, onesInCol, mat);\n\t\t\n return Math.max(h, nh);\n }\n}\n``` | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | Plz Anyone explain me the question first! | plz-anyone-explain-me-the-question-first-yjpy | Please anyone explain me the question. Thanks in advance! | cube_red | NORMAL | 2022-09-03T17:38:30.731606+00:00 | 2022-09-03T17:38:30.731644+00:00 | 23 | false | Please anyone explain me the question. Thanks in advance! | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | [JAVA] Beats 100%, BitMask + Backtraking, O(N!/(N-C)!) | java-beats-100-bitmask-backtraking-onn-c-lf4i | \nclass Solution {\n \n private int ans;\n \n public int maximumRows(int[][] mat, int cols) {\n var masks = new int[mat.length];\n // | yurokusa | NORMAL | 2022-09-03T17:24:23.915471+00:00 | 2022-09-03T17:45:01.276209+00:00 | 31 | false | ```\nclass Solution {\n \n private int ans;\n \n public int maximumRows(int[][] mat, int cols) {\n var masks = new int[mat.length];\n // convert every row to bitmask\n for (int r = 0; r < mat.length; r++) {\n var mask = 0;\n for (int c = 0; c < mat[r].length; c++)\n if (mat[r][c] == 1)\n mask |= 1 << (mat[r].length - c - 1);\n masks[r] = mask;\n } \n // brute force all combination of columns\n backtrack(0, 0, cols, mat[0].length, masks);\n return ans;\n }\n \n private void backtrack(int idx, int mask, int c, int limit, int[] masks) {\n if (c == 0) {\n // calculate ans\n var count = 0;\n for (int m : masks)\n if ((mask | m) == mask)\n count++;\n ans = Math.max(ans, count);\n return;\n }\n\n if (idx == limit)\n return; // nothing to do\n\n // include current element\n backtrack(idx + 1, mask | (1 << (limit - idx - 1)), c - 1, limit, masks);\n \n // exclude current element\n backtrack(idx + 1, mask, c, limit, masks);\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
maximum-rows-covered-by-columns | I did not understand the question.....please help | i-did-not-understand-the-questionplease-0q2b7 | Did anyone understand the problem????? | pratosh | NORMAL | 2022-09-03T17:19:26.944589+00:00 | 2022-09-03T17:19:26.944629+00:00 | 13 | false | Did anyone understand the problem????? | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | Bit Manipulation + Brute Force | bit-manipulation-brute-force-by-draxkira-8n77 | \nclass Solution {\npublic:\n \n int nost(int &n){\n int a=0;\n for(int i = 0 ; i<32; i++){\n if(n&(1<<i))a++;\n \n | draxkira | NORMAL | 2022-09-03T17:11:46.978534+00:00 | 2022-09-03T17:11:46.978573+00:00 | 28 | false | ```\nclass Solution {\npublic:\n \n int nost(int &n){\n int a=0;\n for(int i = 0 ; i<32; i++){\n if(n&(1<<i))a++;\n \n }\n return a;\n }\n \n int maximumRows(vector<vector<int>>& mat, int cols) {\n int n = mat[0].size();\n int m = mat.size();\n int ans =0;\n for(int i =0 ; i< (1<<n); i++){\n if(nost(i)==cols){\n int temp =m;\n for(int j =0 ; j< m ;j++){\n for(int k=0 ; k<n; k++){\n if(mat[j][k]){\n if(!(i&(1<<(n-k-1)))){\n temp--;\n break; \n }\n }\n }\n }\n ans= max(ans,temp);\n }\n }\n return ans;\n \n \n }\n};\n``` | 1 | 0 | ['Bit Manipulation'] | 0 |
maximum-rows-covered-by-columns | For those who are finding it difficult to understand the problem statement! | for-those-who-are-finding-it-difficult-t-61ny | To simplify this question \nGiven a matrix of n rows and m columns, and provided input coll(which is the number of columns you have to pick) , you can choose a | ninja_01 | NORMAL | 2022-09-03T17:05:48.793831+00:00 | 2022-09-03T17:11:07.989562+00:00 | 27 | false | ## To simplify this question \nGiven a matrix of **n** rows and **m** columns, and provided input **col**l(*which is the number of columns you have to pick*) , you can choose any combination of colums (example say you have a matrix of columns 3) and given col input is 2 you can either choose **(12 , 13 , 23)** ie **3C2** for these elements in the set you have find max rows covered \n**Definition of Row covered:** For a given row for every cell which contains 1 it has to belong to one of the columns in the chosen combination of colums in the set ,if 0 is present you can neglect those cells.\nFor the maximum Row covered you have to iterate through all the combination of the column set possible **[12 , 13 , 23]** in this case and check the rows covered in these sets and return the maximum of them\n\nExample test case\n<img width="200" src = "https://assets.leetcode.com/uploads/2022/07/14/rowscovered.png">\n\nHere choosing **(1,3)** out of **(12,13,23)** will yield you max rows covered \n\nLets take **(13)**\n**First row** : [0 , 0 , 0 ] all zeroes no need to check already covered - **1** row covered\n**Second row** : [1 , 0 , 1] : both 1\'s are at column 1 and column 3 which are in your column combination **(13)** - **2** rows covered\n**Third row** : [0 , 1 , 1] : first 1 is at 2nd column which is not in our column combination **(13)** so not covered ,no need to check for other cells\n**Fourth row** [0 , 0 , 1] first 1 at **3** which is in our column combination **(13)** so covered\n\nThe maximum rows covered is **3**, you can try for other column combinations **12** and **23** and the result will be less than or equal to 3 so return **3** as the answer. | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | forcest brute of all brute forces | forcest-brute-of-all-brute-forces-by-abh-8ohf | \nclass Solution {\npublic:\n int ans = -1;\n int res(int i,vector<int> v,vector<vector<int>>& mat,int cols)\n {\n if(i==mat[0].size())\n | abhinavsingh15682 | NORMAL | 2022-09-03T16:53:01.282860+00:00 | 2022-09-03T16:53:01.282894+00:00 | 19 | false | ```\nclass Solution {\npublic:\n int ans = -1;\n int res(int i,vector<int> v,vector<vector<int>>& mat,int cols)\n {\n if(i==mat[0].size())\n {\n int ch=0;\n for(int i=0;i<v.size();i++)\n if(v[i]==1)\n ch++;\n if(ch==cols)\n {\n int val = 0;\n for(int i=0;i<mat.size();i++){int c=0;\n for(int j=0;j<mat[0].size();j++){\n if(mat[i][j]==1&&v[j]!=1)\n c=-1;}\n if(c==0)\n val++;\n }\n ans = max(val,ans);\n return -1;\n }\n else\n return -1;\n }\n else\n {\n v[i]=0;\n res(i+1,v,mat,cols);\n v[i]=1;\n res(i+1,v,mat,cols);\n return -1;\n }\n return -1;\n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n vector<int> v;\n for(int i=0;i<mat[0].size();i++)\n v.push_back(-1);\n res(0,v,mat,cols);\n return ans;\n }\n \n};\n``` | 1 | 0 | [] | 1 |
maximum-rows-covered-by-columns | Bitmasking | C++ | bitmasking-c-by-mostafa_abdullah-di8w | \nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int n = mat.size(), m = mat[0].size();\n int len = (1 << | mostafa_abdullah | NORMAL | 2022-09-03T16:37:55.302856+00:00 | 2022-09-03T16:40:27.238183+00:00 | 17 | false | ```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n int n = mat.size(), m = mat[0].size();\n int len = (1 << m), ans = 0;\n for (int x = 1; x < len; x++)\n {\n // if the number of chosen columns does not equal cols skip it\n if (__builtin_popcount(x) != cols)\n continue;\n set<int> invalid;\n for (int i = 0; i < n; i++)\n for (int j = 0; j < m; j++)\n if (mat[i][j] == 1 && !((x >> j) & 1))\n invalid.emplace(i);\n ans = max(ans, n - (int)invalid.size());\n }\n return ans;\n }\n};\n``` | 1 | 0 | [] | 0 |
maximum-rows-covered-by-columns | C++| Backtracking | Very Easy Code | c-backtracking-very-easy-code-by-ankit46-cm99 | Please Upvote :)\n\n\nclass Solution {\npublic:\n int res=0;\n int maximumRows(vector<vector<int>>& mat, int cols) {\n unordered_map<int,int> m;\n | ankit4601 | NORMAL | 2022-09-03T16:30:38.521984+00:00 | 2022-09-03T16:30:38.522014+00:00 | 84 | false | Please Upvote :)\n\n```\nclass Solution {\npublic:\n int res=0;\n int maximumRows(vector<vector<int>>& mat, int cols) {\n unordered_map<int,int> m;\n fun(mat,m,cols,0);\n return res;\n }\n void fun(vector<vector<int>>& mat,unordered_map<int,int>& m,int cols,int i)\n {\n if(cols==0)\n {\n int c=0;\n for(int p=0;p<mat.size();p++)\n {\n int f=1;\n for(int q=0;q<mat[p].size();q++)\n {\n // if for a row the element at col i is 1 and this column was not choosen then break\n if(mat[p][q] && !m[q])\n {\n f=0;\n break;\n }\n }\n c+=f;\n }\n res=max(res,c);\n return;\n }\n if(i>=mat[0].size())\n return;\n \n // choose the column i or don\'t choose the column i\n fun(mat,m,cols,i+1);\n m[i]=1;\n fun(mat,m,cols-1,i+1);\n m[i]=0;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Recursion', 'C', 'C++'] | 0 |
maximum-rows-covered-by-columns | Backtracking+ set | backtracking-set-by-comder_00-52fh | Okay so, I will tell you my simple approach for this question.\nI came up with this approach after I saw theconstraints at the contest.\nBasically the solution | comder_00 | NORMAL | 2022-09-03T16:27:44.333870+00:00 | 2022-09-03T16:27:44.333902+00:00 | 10 | false | Okay so, I will tell you my simple approach for this question.\nI came up with this approach after I saw theconstraints at the contest.\nBasically the solution is:-\n1. select all the sets of columns of size cols.\n2. For each set count the number of covered rows \n3. keep a counter to count the maximum.\n```\nclass Solution {\npublic:\n int res=0;\n int find_rows(vector<vector<int>>& mat,unordered_set<int> &col_set)\n {\n int ans=0;\n int m=mat.size();\n int n=mat[0].size();\n for(int i=0;i<m;i++)\n {\n bool val=true;\n for(int j=0;j<n;j++)\n {\n if(mat[i][j]==1 and col_set.find(j)==col_set.end())\n val=false;\n }\n if(val)\n ans++;\n }\n return ans;\n }\n void add_col(unordered_set<int> &col_set,int n,int cols,int idx,vector<vector<int>> &mat)\n {\n if(col_set.size()==cols)\n {\n res=max(find_rows(mat,col_set),res);\n return;\n }\n for(int j=idx;j<n;j++)\n {\n col_set.insert(j);\n add_col(col_set,n,cols,j+1,mat);\n col_set.erase(j);\n }\n }\n int maximumRows(vector<vector<int>>& mat, int cols) \n {\n int m=mat.size();\n int n=mat[0].size();\n unordered_set<int> col_set;\n for(int j=0;j<=n-cols;j++)\n {\n col_set.insert(j);\n add_col(col_set,n,cols,j+1,mat);\n col_set.erase(j);\n }\n return res;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Ordered Set'] | 0 |
maximum-rows-covered-by-columns | Ruby | 100% | Bit mask | ruby-100-bit-mask-by-agentivan-lyao | Runtime: 192 ms, faster than 100.00% of Ruby online submissions\n#### Memory Usage: 211.1 MB, less than 100.00% of Ruby online submissions\nruby\ndef maximum_ro | AgentIvan | NORMAL | 2022-09-03T16:23:29.859604+00:00 | 2022-09-03T17:44:40.726137+00:00 | 16 | false | #### Runtime: 192 ms, faster than 100.00% of Ruby online submissions\n#### Memory Usage: 211.1 MB, less than 100.00% of Ruby online submissions\n```ruby\ndef maximum_rows(mat, cols)\n m, n, max = mat.length, mat[0].length, 0\n ints = mat.map{ _1.reduce(0) { |s, n| s * 2 + n }} # int form line of bits\n [*0...n].combination(cols).map { |comb| # comibations of columns of `cols` length \n mask = comb.reduce(0) { |sum, n| sum + (1 << n) } # convert to bit mask (reversed order of bits doesn\'t metter)\n ints.count { |i| mask & i == i } # count of mask covers i\n }.max # return max\nend\n``` | 1 | 0 | ['Bitmask', 'Ruby'] | 2 |
maximum-rows-covered-by-columns | C# Solution .✅❇️ | c-solution-by-arafatsabbir-4b23 | \npublic int MaximumRows(int[][] mat, int cols) {\n var m = mat.Length;\n var n = mat[0].Length;\n var max = 0;\n for (var i = 0; i | arafatsabbir | NORMAL | 2022-09-03T16:13:33.222196+00:00 | 2022-09-04T15:49:40.170082+00:00 | 72 | false | ```\npublic int MaximumRows(int[][] mat, int cols) {\n var m = mat.Length;\n var n = mat[0].Length;\n var max = 0;\n for (var i = 0; i < 1 << n; i++)\n {\n var count = 0;\n var set = new HashSet<int>();\n for (var j = 0; j < n; j++)\n {\n if ((i & (1 << j)) != 0)\n {\n set.Add(j);\n }\n }\n if (set.Count != cols) continue;\n for (var j = 0; j < m; j++)\n {\n var flag = true;\n for (var k = 0; k < n; k++)\n {\n if (mat[j][k] == 1 && !set.Contains(k))\n {\n flag = false;\n break;\n }\n }\n if (flag) count++;\n }\n max = Math.Max(max, count);\n }\n return max;\n }\n``` | 1 | 0 | ['Bit Manipulation'] | 0 |
maximum-rows-covered-by-columns | c++ solution using bitmasking | c-solution-using-bitmasking-by-dilipsuth-vh0t | \nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) \n {\n int n=mat.size();\n int m=mat[0].size();\n i | dilipsuthar17 | NORMAL | 2022-09-03T16:12:35.365473+00:00 | 2022-09-03T16:12:35.365518+00:00 | 45 | false | ```\nclass Solution {\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) \n {\n int n=mat.size();\n int m=mat[0].size();\n int val=0;\n for(int i=0;i<(1<<m);i++)\n {\n if(__builtin_popcount(i)==cols)\n {\n int cov=0;\n for(int x=0;x<n;x++)\n {\n int ans=true;\n int zero=0;\n int count=0;\n for(int y=0;y<m;y++)\n {\n if(mat[x][y]==0)\n {\n zero++;\n }\n else\n {\n if(i&(1<<y))\n {\n if(mat[x][y]==1)\n {\n count++;\n }\n }\n else\n {\n ans=false;\n }\n }\n }\n if(zero==m)\n {\n cov++;\n }\n else\n {\n if(ans&&count)\n {\n cov++;\n }\n }\n }\n val=max(val,cov);\n }\n }\n return val;\n }\n};\n``` | 1 | 0 | ['Bitmask', 'C++'] | 0 |
maximum-rows-covered-by-columns | Brute Force + Bitmasking | brute-force-bitmasking-by-placementtohmi-gcsx | \nclass Solution {\n\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n int mx = 0;\n \n for(int mask=0,cur = 0; | placementTohMilneSeRaha | NORMAL | 2022-09-03T16:06:50.473817+00:00 | 2022-09-03T16:10:56.350596+00:00 | 63 | false | ```\nclass Solution {\n\npublic:\n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n int mx = 0;\n \n for(int mask=0,cur = 0;mask<(1ll<<(mat[0].size()+1));mask++)\n {\n\t\t\t\tif(__builtin_popcount(mask) > cols) // basically checking if no of chosen \n\t\t\t\t\tcontinue; //columns is exceeding the value of cols\n \n cur = 0;\n \n for(int i=0;i<mat.size();i++)\n {\n \n int cnt = 0;\n bool flag = 1;\n \n for(int j=0;j<mat[0].size();j++)\n {\n\t\t\t\t\tif(((mask&(1<<j))==0) and mat[i][j]==1) // this is cutting the loop off, \n\t\t\t\t\t\t\t\t\t\t\t//because the current bit is not set but the current column is set\n {\n flag = 0;\n break;\n }\n }\n \n if(flag)\n cur++; // if the current row gets checked by the condition then increment cur\n }\n \n mx = max(mx,cur);\n }\n \n return mx;\n }\n};\n``` | 1 | 0 | ['C', 'Bitmask'] | 0 |
maximum-rows-covered-by-columns | Brute - Backtracking [C++] | brute-backtracking-c-by-hehehiiiiuuhuu-0sbe | \nclass Solution {\npublic:\n int ans = 0;\n \n int countRow(vector<int>&temp,vector<vector<int>>&mat)\n {\n int cnt = 0;\n unordered_ | hehehiiiiuuhuu | NORMAL | 2022-09-03T16:04:44.564837+00:00 | 2022-09-03T16:04:44.564889+00:00 | 59 | false | ```\nclass Solution {\npublic:\n int ans = 0;\n \n int countRow(vector<int>&temp,vector<vector<int>>&mat)\n {\n int cnt = 0;\n unordered_map<int,int>mpp;\n for(auto x:temp)mpp[x]++;\n \n for(auto row : mat)\n {\n bool flag = true;\n for(int i=0 ; i<row.size() ; i++)\n {\n if(row[i]==1)\n {\n if(mpp.find(i)==mpp.end())\n {\n flag = false;\n break;\n }\n }\n }\n if(flag == true)\n {\n cnt++;\n }\n }\n return cnt;\n }\n \n void solve(int col , vector<int>&temp ,int cols , vector<vector<int>>&mat )\n {\n if(col>=mat[0].size())\n {\n if(cols==0)\n {\n ans = max(ans , countRow(temp,mat));\n }\n return ;\n }\n \n // take that column \n temp.push_back(col);\n solve(col+1,temp,cols-1,mat);\n temp.pop_back();\n \n // don\'t take\n solve(col+1,temp,cols,mat);\n \n \n }\n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n vector<int>temp;\n solve(0,temp,cols,mat);\n return ans;\n \n }\n};\n``` | 1 | 0 | ['Backtracking', 'C'] | 1 |
maximum-rows-covered-by-columns | [Python3] enumeration | python3-enumeration-by-ye15-ba2g | Please pull this commit for solutions of biweekly 86. \n\n\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n m, n = | ye15 | NORMAL | 2022-09-03T16:03:09.186205+00:00 | 2022-09-03T18:11:15.709226+00:00 | 129 | false | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/35b262c16bc702edbad6adc895bc8321a037ebaa) for solutions of biweekly 86. \n\n```\nclass Solution:\n def maximumRows(self, mat: List[List[int]], cols: int) -> int:\n m, n = len(mat), len(mat[0])\n masks = []\n for i in range(m): \n mask = reduce(xor, (1<<j for j in range(n) if mat[i][j]), 0)\n masks.append(mask)\n ans = 0 \n for x in range(1<<n): \n if x.bit_count() <= cols: \n ans = max(ans, sum(mask & x == mask for mask in masks))\n return ans \n``` | 1 | 0 | ['Python3'] | 1 |
maximum-rows-covered-by-columns | C++ Brute force using recursion backtracking | c-brute-force-using-recursion-backtracki-vfzl | \nclass Solution {\npublic:\n int maxi = 0;\n vector<int>v;\n \n void count(vector<vector<int>>&mat){\n int c = 0;\n for(int i = 0;i<m | mohitdbst | NORMAL | 2022-09-03T16:03:06.779073+00:00 | 2022-09-03T16:03:06.779121+00:00 | 154 | false | ```\nclass Solution {\npublic:\n int maxi = 0;\n vector<int>v;\n \n void count(vector<vector<int>>&mat){\n int c = 0;\n for(int i = 0;i<mat.size();i++){\n int t = 0;\n int co= 0 ;\n for(int j = 0;j<mat[i].size();j++){\n if(mat[i][j] == 1)t++;\n if(mat[i][j]==1 && v[j] == 1)co++;\n }\n if(t == co)c++;\n }\n \n maxi = max(maxi,c);\n return;\n }\n \n void dfs(vector<vector<int>>&mat,int c,int cols){\n if(cols == 0){\n count(mat);\n return;\n }\n if(c >= mat[0].size())return ;\n \n v[c] = 1;\n \n dfs(mat,c+1,cols-1);\n v[c]=0;\n dfs(mat,c+1,cols);\n return;\n }\n \n int maximumRows(vector<vector<int>>& mat, int cols) {\n \n if(cols == mat[0].size())return mat.size();\n v = vector<int>(mat[0].size(),0);\n dfs(mat,0,cols);\n \n return maxi;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Recursion', 'C'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.