question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-containers-on-a-ship | Easiest solution | easiest-solution-by-prajapatiabhishek150-59lb | Complexity
Time complexity:
Code | PrajapatiAbhishek1504 | NORMAL | 2025-03-28T20:56:16.086303+00:00 | 2025-03-28T20:56:16.086303+00:00 | 2 | false |
# Complexity
- Time complexity:
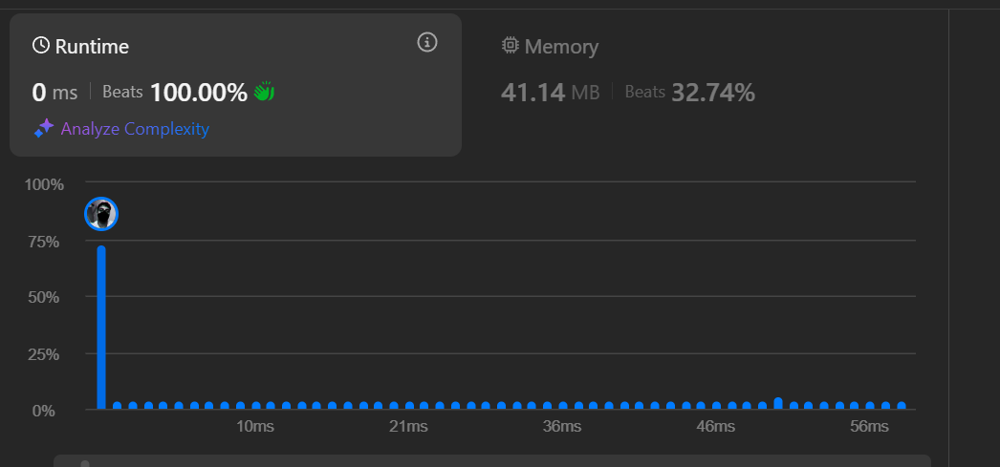
# Code
```java []
class Solution {
public int maxContainers(int n, int w, int maxWeight) {
return Math.min(n*n,maxWeight/w);
}
}
``` | 0 | 0 | ['Math', 'C++', 'Java', 'Python3'] | 0 |
maximum-containers-on-a-ship | Easiest Solution using Math | easiest-solution-using-math-by-prajapati-wgtg | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | PrajapatiAbhishek1504 | NORMAL | 2025-03-28T20:54:03.570635+00:00 | 2025-03-28T20:54:03.570635+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
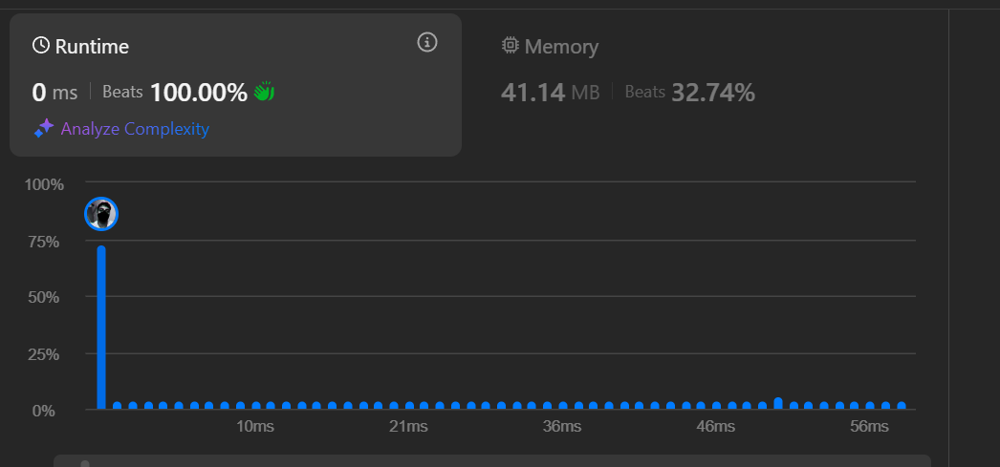
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maxContainers(int n, int w, int maxWeight) {
return Math.min(n*n,maxWeight/w);
}
}
``` | 0 | 0 | ['Math', 'Java'] | 0 |
maximum-containers-on-a-ship | Very Easy Understandable Solution || JAVA | very-easy-understandable-solution-java-b-btp2 | Code | sumo25 | NORMAL | 2025-03-28T17:37:13.929025+00:00 | 2025-03-28T17:37:13.929025+00:00 | 2 | false |
# Code
```java []
class Solution {
public int maxContainers(int n, int w, int maxWeight) {
int cell=n*n;
int count=0;
while(count+1<=cell && maxWeight-w>=0){
count++;
maxWeight-=w;
}
return count;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-containers-on-a-ship | Simple solution -> Beats 100.00% | simple-solution-beats-10000-by-developer-yx7m | IntuitionApproachComplexity
Time complexity:
O(1)
Space complexity:
O(1)
Code | DevelopersUsername | NORMAL | 2025-03-28T17:08:22.013212+00:00 | 2025-03-28T17:08:22.013212+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public int maxContainers(int n, int w, int maxWeight) {
return Math.min((int) Math.pow(n, 2), maxWeight / w);
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-containers-on-a-ship | C | c-by-n97rvh-z9fw | Code | N97RVH | NORMAL | 2025-03-28T16:13:48.762212+00:00 | 2025-03-28T16:13:48.762212+00:00 | 5 | false | # Code
```c []
int maxContainers(int n, int w, int maxWeight) {
int ans = maxWeight / w;
return (ans > (n * n) ? n * n: ans);
}
``` | 0 | 0 | ['C'] | 0 |
maximum-containers-on-a-ship | [Python] min(maxWeight // w, n*n) | python-minmaxweight-w-nn-by-pbelskiy-5d7b | null | pbelskiy | NORMAL | 2025-03-28T14:16:05.536732+00:00 | 2025-03-28T14:16:05.536732+00:00 | 1 | false | ```python3 []
class Solution:
def maxContainers(self, n: int, w: int, maxWeight: int) -> int:
return min(maxWeight // w, n*n)
``` | 0 | 0 | ['Python3'] | 0 |
maximum-containers-on-a-ship | single line output | single-line-output-by-vijayakumar-1728-c33n | Code | vijayakumar-1728 | NORMAL | 2025-03-28T04:53:08.481172+00:00 | 2025-03-28T04:53:08.481172+00:00 | 1 | false |
# Code
```java []
class Solution {
public int maxContainers(int n, int w, int maxWeight) {
return Math.min(n*n,maxWeight/w);
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-containers-on-a-ship | Python3 O(1) Approach | kotlin-o1-approach-by-curenosm-b7mz | Code | curenosm | NORMAL | 2025-03-28T00:25:02.862420+00:00 | 2025-03-28T00:25:14.026429+00:00 | 3 | false | # Code
```python3 []
class Solution:
def maxContainers(self, n: int, w: int, maxWeight: int) -> int:
return min(n * n, maxWeight // w)
``` | 0 | 0 | ['Python3'] | 0 |
maximum-containers-on-a-ship | One Line Solution | one-line-solution-by-s_piyushhh-b19h | Complexity
Time complexity: O[1]
Space complexity: O[1]
Code | s_piyushhh | NORMAL | 2025-03-27T18:55:14.287536+00:00 | 2025-03-27T18:55:14.287536+00:00 | 1 | false | # Complexity
- Time complexity: O[1]
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O[1]
# Code
```cpp []
class Solution {
public:
int maxContainers(int n, int w, int maxWeight) {
return min(n*n, maxWeight/w);
}
};
```
```python []
class Solution(object):
def maxContainers(self, n, w, maxWeight):
return min(n*n, maxWeight/w)
``` | 0 | 0 | ['C++'] | 0 |
maximum-containers-on-a-ship | beginner level easy c solution 0 ms 100% beats | beginner-level-easy-c-solution-0-ms-100-bbaw0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kunsh2301 | NORMAL | 2025-03-27T18:03:43.684598+00:00 | 2025-03-27T18:03:43.684598+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
int maxContainers(int n, int w, int maxWeight) {
n*=n;
if(n*w<=maxWeight) return n;
return (int)maxWeight/w;
}
``` | 0 | 0 | ['C'] | 0 |
maximum-containers-on-a-ship | C++ one-liner, beats 100% | c-one-liner-beats-100-by-akshar-jhxu | Code | akshar_ | NORMAL | 2025-03-27T16:32:27.179404+00:00 | 2025-03-27T16:32:27.179404+00:00 | 1 | false | # Code
```cpp []
class Solution {
public:
int maxContainers(int n, int w, int maxWeight) {
return min(n * n, maxWeight / w);
}
};
``` | 0 | 0 | ['Math', 'C++'] | 0 |
maximum-containers-on-a-ship | Most easiest question ever solved. Best for beginners | most-easiest-question-ever-solved-best-f-8cp7 | IntuitionIt is quite difficult but after clearly understanding the question.it just few seconds to solve this oneApproachMathematical ApproachComplexity
Time co | PradeepSS25 | NORMAL | 2025-03-27T15:21:16.313629+00:00 | 2025-03-27T15:21:16.313629+00:00 | 1 | false | # Intuition
It is quite difficult but after clearly understanding the question.it just few seconds to solve this one
# Approach
Mathematical Approach
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```python []
class Solution(object):
def maxContainers(self, n, w, maxWeight):
return min(n*n,maxWeight/w)
``` | 0 | 0 | ['Python'] | 0 |
maximum-containers-on-a-ship | Go | go-by-marcdidom-rkj0 | Code | marcdidom | NORMAL | 2025-03-27T14:43:47.307996+00:00 | 2025-03-27T14:43:47.307996+00:00 | 3 | false |
# Code
```golang []
func maxContainers(n, w, maxWeight int) int {
totalCells := n * n
possibleByWeight := maxWeight / w
if totalCells < possibleByWeight {
return totalCells
}
return possibleByWeight
}
``` | 0 | 0 | ['Go'] | 0 |
maximum-containers-on-a-ship | Beats 100%, 1 LOC | beats-100-1-loc-by-nisargshahh-kvl2 | Code | nisargshahh | NORMAL | 2025-03-27T13:12:31.044149+00:00 | 2025-03-27T13:12:31.044149+00:00 | 1 | false | # Code
```cpp []
class Solution {
public:
int maxContainers(int n, int w, int maxWeight) {
return min(n*n, maxWeight / w);
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-containers-on-a-ship | [C++] Simple Check | c-simple-check-by-lokeshpaidi-c3mq | Intuition / Approach
Simple Check
Complexity
Time complexity: O(1)
Space complexity: O(1)
Code | LokeshPaidi | NORMAL | 2025-03-27T07:03:46.983521+00:00 | 2025-03-27T07:03:46.983521+00:00 | 1 | false | # Intuition / Approach
- Simple Check
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maxContainers(int n, int w, int maxWeight) {
if(n*n*w<=maxWeight)
return n*n;
return maxWeight/w;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-containers-on-a-ship | python | python-by-alex72112-cx3o | Code | alex72112 | NORMAL | 2025-03-27T05:42:15.714952+00:00 | 2025-03-27T05:42:15.714952+00:00 | 3 | false |
# Code
```python3 []
class Solution:
def maxContainers(self, n: int, w: int, maxWeight: int) -> int:
return int(min(n * n, maxWeight / w))
``` | 0 | 0 | ['Python3'] | 0 |
maximum-containers-on-a-ship | 1 liner | Beats 100% | | 1-liner-beats-100-by-shoryasethia-j2b9 | Approach(n*n*w<=maxWeight) is true then n*n else maxWeight/w.Complexity
Time complexity:
O(1)
Space complexity:
None
Code | shoryasethia | NORMAL | 2025-03-26T22:02:35.943295+00:00 | 2025-03-26T22:02:35.943295+00:00 | 2 | false | # Approach
`(n*n*w<=maxWeight)` is true then `n*n` else `maxWeight/w`.
# Complexity
- Time complexity:
O(1)
- Space complexity:
None
# Code
```cpp []
class Solution {
public:
int maxContainers(int n, int w, int maxWeight) {
return (n*n*w<=maxWeight) ? n*n:maxWeight/w;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-containers-on-a-ship | one liner super easy | one-liner-super-easy-by-antarab-gfw1 | Intuitionmax of contanier present and container that can holdApproachn*n = max container presentComplexity
Time complexity: | antarab | NORMAL | 2025-03-26T20:31:04.672910+00:00 | 2025-03-26T20:31:04.672910+00:00 | 2 | false | # Intuition
max of contanier present and container that can hold
# Approach
n*n = max container present
# Complexity
- Time complexity:
$$O(1)
- Space complexity:
O(1)
# Code
```python3 []
class Solution:
def maxContainers(self, n: int, w: int, maxWeight: int) -> int:
ans1= maxWeight //w
return min(n*n, int(ans1))
``` | 0 | 0 | ['Python3'] | 0 |
stone-game-vii | C++/Python O(n * n) | cpython-on-n-by-votrubac-0l5y | Sounds like a search problem. Try a stone from each side, and recursively calculate the difference. Maximize the difference among two choices to play optimally. | votrubac | NORMAL | 2020-12-13T04:01:20.830837+00:00 | 2020-12-14T01:10:44.901437+00:00 | 12,431 | false | Sounds like a search problem. Try a stone from each side, and recursively calculate the difference. Maximize the difference among two choices to play optimally. \n\nWe can memoise the results for the start (`i`) and end(`j`) of the remaining stones.\n\n**C++**\n```cpp\nint dp[1001][1001] = {};\nint dfs(vector<int>& s, int i, int j, int sum) {\n if (i == j)\n return 0;\n return dp[i][j] ? dp[i][j] : dp[i][j] = max(sum - s[i] - dfs(s, i + 1, j, sum - s[i]),\n sum - s[j] - dfs(s, i, j - 1, sum - s[j]));\n}\nint stoneGameVII(vector<int>& s) {\n return dfs(s, 0, s.size() - 1, accumulate(begin(s), end(s), 0));\n}\n```\n**Python, Recursion**\nIt looks like something going on with Python on LeetCode, folks need to do manual memo to get it accepted.\n\n> I added the tabulation solution below, its runtime is twice as fast as of the recursive solution.\n\nHere, we are using the prefix sum array to get the subarray sum in O(1). We are not passing the remaining sum as a parameters (like in C++ code above), so it\'s easier to replace manual memo with` @lru_cache(None)`.\n\n```python\nclass Solution:\n def stoneGameVII(self, s: List[int]) -> int:\n dp = [[0] * len(s) for _ in range(len(s))]\n p_sum = [0] + list(accumulate(s))\n def dfs(i: int, j: int) -> int:\n if i == j:\n return 0\n if dp[i][j] == 0:\n sum = p_sum[j + 1] - p_sum[i]\n dp[i][j] = max(sum - s[i] - dfs(i + 1, j), sum - s[j] - dfs(i, j - 1))\n return dp[i][j]\n res = dfs(0, len(s) - 1)\n return res\n\n```\n\n**Python, Tabulation**\n```python\nclass Solution:\n def stoneGameVII(self, s: List[int]) -> int:\n dp = [[0] * len(s) for _ in range(len(s))]\n p_sum = [0] + list(accumulate(s))\n for i in range(len(s) - 2, -1, -1):\n for j in range(i + 1, len(s)):\n dp[i][j] = max(p_sum[j + 1] - p_sum[i + 1] - dp[i + 1][j], \n p_sum[j] - p_sum[i] - dp[i][j - 1]);\n return dp[0][len(s) - 1]\n``` | 136 | 6 | [] | 18 |
stone-game-vii | [C++/Java/Python] Minimax, Top down, Bottom up DP - Clean & Concise | cjavapython-minimax-top-down-bottom-up-d-pqb3 | Approach 1: Minimax Algorithm\nIdea\n- Let\'s Alice be a maxPlayer and Bob be a minPlayer. On each turn, we need to maximize score of the maxPlayer and minimize | hiepit | NORMAL | 2020-12-13T04:02:03.390492+00:00 | 2021-06-11T18:46:41.821075+00:00 | 9,082 | false | **Approach 1: Minimax Algorithm**\n**Idea**\n- Let\'s `Alice` be a `maxPlayer` and `Bob` be a `minPlayer`. On each turn, we need to maximize score of the `maxPlayer` and minimize score of the `minPlayer`. After all, the final score is the difference in Alice and Bob\'s score if they both play optimally.\n- More about detail Minimax: https://en.wikipedia.org/wiki/Minimax\n\n**Simillar problem**\n- [1406. Stone Game III](https://leetcode.com/problems/stone-game-iii/discuss/564896)\n\n<iframe src="https://leetcode.com/playground/XXxTroDy/shared" frameBorder="0" width="100%" height="550"></iframe>\n\n**Complexity**\n- Time: `O(4*n^2)` ~ `O(n^2)`\n- Space: `O(2 * n^2)` ~ `O(n^2)`\n\n\n**Approach 2: Optimized Top down DP**\n**Idea**\n- There is another way of thinking about this problem.\n- Since both Alice and Bob play optimally, they are trying to maximize their score.\n\t- Alice is trying to maximize her score so that she has a maximum difference from Bob\'s score. \n\t- Bob is also trying to maximize his score so that he is as close to Alice as possible.\n- Our goal is to return the maximum difference in score between Alice and Bob where Alice go first.\n- The difference in score between Alice and Bob can be given by:\n\t- If the current player is Alice: `Difference = Current Score - Difference returned by Bob`\n\t- If the current player is Bob: `Difference = Current Score - Difference returned by Alice`\n- Now, both players have a common goal, that is, to return maximum difference in score to the opponent. We don\'t care who is the current player.\n- Let `dp(left, right)` is the maximum different between the current player and their opponent.\n- We have:\n\t```\n\tdp(left, right) = max(\n\t\tscoreRemoveLeftMost - dp(left+1, right), // case remove left most stone\n\t\tscoreRemoveRightMost - dp(left, right-1) // case remove right most stone\n\t)\n\t```\n- Finally, `dp(0, n-1)` is the maximum difference in score of the whole stones between Alice and Bob, where Alice go first.\n\n<iframe src="https://leetcode.com/playground/WmgNfsoh/shared" frameBorder="0" width="100%" height="500"></iframe>\n\n**Complexity**\n- Time: `O(2*n^2)` ~ `O(n^2)`\n- Space: `O(n^2)`\n\n\n**Appoach 3: Bottom up DP**\n- Exactly same idea with approach 2, just convert Top-down DP into Bottom-up DP.\n<iframe src="https://leetcode.com/playground/CJfwSFVv/shared" frameBorder="0" width="100%" height="480"></iframe>\n\n**Complexity**\n- Time: `O(n^2)`\n- Space: `O(n^2)` | 115 | 5 | [] | 19 |
stone-game-vii | JS, Python, Java, C++ | Easy DP Solution w/ Explanation | js-python-java-c-easy-dp-solution-w-expl-oimp | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-06-11T08:05:03.344628+00:00 | 2021-06-14T19:21:58.123150+00:00 | 5,074 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nLike most of the Stone Game problems, this one boils down to a system of ever-repeating subproblems, as the there are many different ways to get to the same board condition as we move towards the end of the game. This naturally points to a **dynamic programming** (**DP**) solution.\n\nIn order to represent the different board positions, we\'d normally build an **N * N** DP matrix where **N** is the length of the stones array (**S**). In this DP array, **dp[i][j]** would represent the best score difference with **i** representing the leftmost remaining stone\'s index and **j** representing the rightmost remaining stone\'s index.\n\nWe\'ll start at **i = N - 2** and iterate backwards and start each nested **for** loop at **j = i + 1**. This ensures that we\'re building the pyramid of DP results downward, always starting each row with **i** and **j** next to each other.\n\nFor each row, we\'ll keep track of the sum **total** of the stones in the range **[i,j]** by adding **S[j]** at each iteration of **j**. Then, we can represent the current player\'s ideal play by choosing the best value between picking the stone at **i** (**total - S[i]**) and picking the stone at **j** (**total - S[j]**). For each option, we have to also subtract the best value that the other player will get from the resulting board position (**dp[i+1][j]** or **dp[i][j-1]**).\n\nSince we will only be building off the cells to the left and above the current cell, however, we can actually eliminate the DP matrix and instead just one array representing the current row, reusing it each time. This will drop the **space complexity** from **O(N^2)** to **O(N)**.\n\nThis approach works because, when evaluating a new cell, the cell to the left will already have been overwritten and will accurately represent the previous cell on the same row. The not-yet-overwritten current cell value still represents the cell that would have been in the row above in a full DP matrix.\n\nAt the end, the solution will be the value stored in the DP array representing the board position with all stones present. We should therefore **return dp[N-1]**.\n\n - _**Time Complexity: O(N^2)** where **N** is the length of **S**_\n - _**Space Complexity: O(N)** for **dp**_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **108ms / 37.9MB** (beats 100% / 100%).\n```javascript\nvar stoneGameVII = function(S) {\n let N = S.length, dp = new Uint32Array(N)\n for (let i = N - 2; ~i; i--) {\n let total = S[i]\n for (let j = i + 1; j < N; j++) {\n total += S[j]\n dp[j] = Math.max(total - S[i] - dp[j], total - S[j] - dp[j-1])\n }\n }\n return dp[N-1]\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **2668ms / 14.3MB** (beats 97% / 99%).\n```python\nclass Solution:\n def stoneGameVII(self, S: List[int]) -> int:\n N, dp = len(S), [0] * len(S)\n for i in range(N - 2, -1, -1):\n total = S[i]\n for j in range(i + 1, N):\n total += S[j]\n dp[j] = max(total - S[i] - dp[j], total - S[j] - dp[j-1])\n return dp[-1]\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **16ms / 38.2MB** (beats 100% / 99%).\n```java\nclass Solution {\n public int stoneGameVII(int[] S) {\n int N = S.length;\n int[] dp = new int[N];\n for (int i = N - 2; i >= 0; i--) {\n int total = S[i];\n for (int j = i + 1; j < N; j++) {\n total += S[j];\n dp[j] = Math.max(total - S[i] - dp[j], total - S[j] - dp[j-1]);\n }\n }\n return dp[N-1];\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **124ms / 9.9MB** (beats 96% / 100%).\n```c++\nclass Solution {\npublic:\n int stoneGameVII(vector<int>& S) {\n int N = S.size();\n vector<int> dp(N);\n for (int i = N - 2; ~i; i--) {\n int total = S[i];\n for (int j = i + 1; j < N; j++) {\n total += S[j];\n dp[j] = max(total - S[i] - dp[j], total - S[j] - dp[j-1]);\n }\n }\n return dp[N-1];\n }\n};\n``` | 83 | 6 | ['C', 'Python', 'Java', 'JavaScript'] | 0 |
stone-game-vii | C++ Bottom-up DP O(N^2) time | c-bottom-up-dp-on2-time-by-lzl124631x-jsyw | \nSee my latest update in repo LeetCode\n\n## Solution 1. Bottom-up DP\n\nLet dp[i][j] be the maximum difference the first player can get if the players play on | lzl124631x | NORMAL | 2020-12-13T04:01:06.312247+00:00 | 2021-01-19T05:56:18.248276+00:00 | 5,484 | false | \nSee my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Bottom-up DP\n\nLet `dp[i][j]` be the maximum difference the first player can get if the players play on `A[i..j]`.\n\n```\ndp[i][j] = max(\n sum(i + 1, j) - dp[i + 1][j], // if the first player choose `A[i]`\n sum(i, j - 1) - dp[i][j - 1] // if the first player choose `A[j]`\n )\n```\nwhere `sum(i, j)` is `A[i] + ... + A[j]`. We can get `sum(i, j)` using prefix sum array.\n\n```cpp\n// OJ: https://leetcode.com/contest/weekly-contest-219/problems/stone-game-vii/\n// Author: github.com/lzl124631x\n// Time: O(N^2)\n// Space: O(N^2)\nclass Solution {\npublic:\n int stoneGameVII(vector<int>& A) {\n int N = A.size();\n vector<int> sum(N + 1);\n for (int i = 0; i < N; ++i) sum[i + 1] = sum[i] + A[i];\n vector<vector<int>> dp(N, vector<int>(N));\n for (int len = 2; len <= N; ++len) {\n for (int i = 0; i <= N - len; ++i) {\n int j = i + len - 1;\n dp[i][j] = max(sum[j + 1] - sum[i + 1] - dp[i + 1][j], sum[j] - sum[i] - dp[i][j - 1]);\n }\n }\n return dp[0][N - 1];\n }\n};\n```\n\n---\n\nUpdate 1/18/2021:\n\nAdding some explanation.\n\nEach player needs to play optimally to get as many points as possible and make the other player get as less as possible. So the game is actually the same for both of them.\n\nAfter Alice finshes the her first round, ignoring the points Alice made there, the game to Bob is exactly the same as if he is the first player.\n\nSo each round on `A[i..j]`, no matter who plays first, the first player always has two options:\n1. pick `A[i]`, the first player get `sum(i + 1, j)` points, and we need to deduct the maximum point difference the next player can get in the remaining game, i.e. `dp[i + 1][j]`\n2. pick `A[j]`, the first player get `sum(i, j - 1)` points, and we need to deduct the maximum point difference the next player can get in the remaining game, i.e. `dp[i][j - 1]`\n\nAnd the first player simply pick the option more advantageous to him/her. | 72 | 3 | [] | 14 |
stone-game-vii | C++ memoization code with proper explanation | c-memoization-code-with-proper-explanati-m24q | \n\nclass Solution {\npublic:\n int dp[1001][1001];\n int solve(vector<int>& stones, int i, int j, int sum){\n if(i>=j){\n return 0;\n | roger2001 | NORMAL | 2021-06-03T10:01:00.578298+00:00 | 2021-08-16T08:21:22.263856+00:00 | 3,512 | false | \n```\nclass Solution {\npublic:\n int dp[1001][1001];\n int solve(vector<int>& stones, int i, int j, int sum){\n if(i>=j){\n return 0;\n }\n if(sum<=0){\n return 0;\n }\n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n \n // both the player have two options either they can choose the first element\n // or they can choose the last element\n // they will choose that particular element which will give them the maximum profit\n // as player A wants to maximize its profit\n // and player B wants to minimize the difference between them\n // hence both will choose the maximum value only\n int choose_front = sum-stones[i]-solve(stones,i+1,j,sum-stones[i]);\n int choose_back = sum-stones[j]-solve(stones,i,j-1,sum-stones[j]);\n \n int profit = max(choose_front,choose_back);\n return dp[i][j] = profit;\n }\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n int sum = 0;\n for(int i=0;i<n;i++){\n sum+=stones[i];\n }\n memset(dp,-1,sizeof(dp));\n // same as stone game-II, III \n // here value is the difference between profit of A and profit of B\n int value = solve(stones,0,n-1,sum);\n return value;\n }\n};\n```\n\n---------------------------------------------------------------------------------------------------------------\nfor any state[i,j] ,\nthere are two things either i can choose front element or back element.\n\nlet us take example for front -> int choose_front = sum-stones[i]-solve(stones,i+1,j,sum-stones[i]); \n1. sum-stones[i] => this is the profit that current player make if he choose the front element\n2. solve(stones,i+1,j,sum-stones[i]) => the value of this function represent the optimal profit that the opponent can make\nhence equation [ int choose_front = sum-stones[i]-solve(stones,i+1,j,sum-stones[i]) ] represents the difference between current player\'s profit and opponent\'s profit.\n* same for choose_back case.\n\nAs question required, difference in Alice and Bob\'s score if they both play optimally. So by maximum profit for current state[i,j] we mean, the maximum difference between current player\'s profit and opponent\'s profit (that can come from either choosing back_element or the front_element).\n**Time complexity -> O(n*n)**\n\n---------------------------------------------------------------------------------------------------------------\n\n**Try these questions also**\n*logic is 80% same*\n[1140. Stone Game II](https://leetcode.com/problems/stone-game-ii/discuss/1247693/C%2B%2B-memoization-with-proper-explanation)\n[1406. Stone Game III](https://leetcode.com/problems/stone-game-iii/)\n\n**Please upvote 0\'_\'0** | 51 | 1 | ['Memoization', 'C', 'C++'] | 3 |
stone-game-vii | [Python] O(n*n) dp solution, how to avoid TLE, explained | python-onn-dp-solution-how-to-avoid-tle-d2lz9 | We can see dynamic programming structure in this problem: each time we take some stones from the left or from the left side, what is rest is always contigious a | dbabichev | NORMAL | 2021-06-11T08:24:48.686919+00:00 | 2021-06-11T08:24:48.686968+00:00 | 2,135 | false | We can see dynamic programming structure in this problem: each time we take some stones from the left or from the left side, what is rest is always contigious array. So, let us denote by `dp(i, j)` the biggest difference in scores for the person who start with this position.\n\n1. If `i > j`, then we have empty array and result is zero.\n2. In the opposite case, we have two options: we can take either leftmost stone or rightmost stone. We also precomputed `CSum`: cumulative sums to evaluate sums in ranges in `O(1)` time. We can either can gain sum from `[i+1, j]` and subtract `dp(i+1, j)` or we can gain sum from `[i, j-1]` and subtract `dp(i, j-1)`. Why we need to subtract here? Because `dp(i+1, j)` and `dp(i, j-1)` is maximum difference of scores **another** player can gain, so for current player we need to take negative value.\n\n#### Complexity\nWe have `O(n^2)` states with `2` transactions from every state, so total time and space is `O(n^2)`.\n\n#### Code\n```python\nclass Solution:\n def stoneGameVII(self, A):\n CSum = [0] + list(accumulate(A))\n @lru_cache(2000)\n def dp(i, j):\n if i > j: return 0\n sm = CSum[j + 1] - CSum[i]\n return sm - min(A[i] + dp(i+1, j), A[j] + dp(i, j-1))\n \n return dp(0, len(A) - 1)\n```\n\n#### Important remark\nSometimes when we use `lru_cache`, it works slower than memoisation by hands, and in this problem you will get TLE if you use usual `@lru_cache(None)`, because restrictions in this problem are quite tight on python. So, what you can do during contest to avoid this?\n1. Do memorisation by hands: it is the quickest and working way to do it: instead of `lru_cache`, use say dictionary `d` and each time in the beginning check if we have element in `d` or not.\n2. Change `None` in `lru_cache` to some magical constant, here `1000` to `10000` will work fine, but I do not have explanation why. And on the contest you can not be lucky to get it or you get it and then it will be rejudged and you will get TLE or MLE. So, it is not safe in my opinion.\n3. Use classical table dp, where you have here `2d` list of lists and then fill it with usual ways. It is also safe way, but I am so used to `lru_cache`, so for this one I would have spend more time on contest, but if method `1` is not working, you should definitely go to this one.\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 44 | 1 | ['Dynamic Programming'] | 3 |
stone-game-vii | Stone Game VII | JS, Python, Java, C++ | Easy DP Solution w/ Explanation | stone-game-vii-js-python-java-c-easy-dp-zcq1w | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-06-11T08:05:36.898260+00:00 | 2021-06-14T19:22:26.858569+00:00 | 1,923 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nLike most of the Stone Game problems, this one boils down to a system of ever-repeating subproblems, as the there are many different ways to get to the same board condition as we move towards the end of the game. This naturally points to a **dynamic programming** (**DP**) solution.\n\nIn order to represent the different board positions, we\'d normally build an **N * N** DP matrix where **N** is the length of the stones array (**S**). In this DP array, **dp[i][j]** would represent the best score difference with **i** representing the leftmost remaining stone\'s index and **j** representing the rightmost remaining stone\'s index.\n\nWe\'ll start at **i = N - 2** and iterate backwards and start each nested **for** loop at **j = i + 1**. This ensures that we\'re building the pyramid of DP results downward, always starting each row with **i** and **j** next to each other.\n\nFor each row, we\'ll keep track of the sum **total** of the stones in the range **[i,j]** by adding **S[j]** at each iteration of **j**. Then, we can represent the current player\'s ideal play by choosing the best value between picking the stone at **i** (**total - S[i]**) and picking the stone at **j** (**total - S[j]**). For each option, we have to also subtract the best value that the other player will get from the resulting board position (**dp[i+1][j]** or **dp[i][j-1]**).\n\nSince we will only be building off the cells to the left and above the current cell, however, we can actually eliminate the DP matrix and instead just one array representing the current row, reusing it each time. This will drop the **space complexity** from **O(N^2)** to **O(N)**.\n\nThis approach works because, when evaluating a new cell, the cell to the left will already have been overwritten and will accurately represent the previous cell on the same row. The not-yet-overwritten current cell value still represents the cell that would have been in the row above in a full DP matrix.\n\nAt the end, the solution will be the value stored in the DP array representing the board position with all stones present. We should therefore **return dp[N-1]**.\n\n - _**Time Complexity: O(N^2)** where **N** is the length of **S**_\n - _**Space Complexity: O(N)** for **dp**_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **108ms / 37.9MB** (beats 100% / 100%).\n```javascript\nvar stoneGameVII = function(S) {\n let N = S.length, dp = new Uint32Array(N)\n for (let i = N - 2; ~i; i--) {\n let total = S[i]\n for (let j = i + 1; j < N; j++) {\n total += S[j]\n dp[j] = Math.max(total - S[i] - dp[j], total - S[j] - dp[j-1])\n }\n }\n return dp[N-1]\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **2668ms / 14.3MB** (beats 97% / 99%).\n```python\nclass Solution:\n def stoneGameVII(self, S: List[int]) -> int:\n N, dp = len(S), [0] * len(S)\n for i in range(N - 2, -1, -1):\n total = S[i]\n for j in range(i + 1, N):\n total += S[j]\n dp[j] = max(total - S[i] - dp[j], total - S[j] - dp[j-1])\n return dp[-1]\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **16ms / 38.2MB** (beats 100% / 99%).\n```java\nclass Solution {\n public int stoneGameVII(int[] S) {\n int N = S.length;\n int[] dp = new int[N];\n for (int i = N - 2; i >= 0; i--) {\n int total = S[i];\n for (int j = i + 1; j < N; j++) {\n total += S[j];\n dp[j] = Math.max(total - S[i] - dp[j], total - S[j] - dp[j-1]);\n }\n }\n return dp[N-1];\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **124ms / 9.9MB** (beats 96% / 100%).\n```c++\nclass Solution {\npublic:\n int stoneGameVII(vector<int>& S) {\n int N = S.size();\n vector<int> dp(N);\n for (int i = N - 2; ~i; i--) {\n int total = S[i];\n for (int j = i + 1; j < N; j++) {\n total += S[j];\n dp[j] = max(total - S[i] - dp[j], total - S[j] - dp[j-1]);\n }\n }\n return dp[N-1];\n }\n};\n``` | 44 | 1 | [] | 4 |
stone-game-vii | [Python] Top Down and Bottom Up DP - explained | python-top-down-and-bottom-up-dp-explain-71z4 | Approach:\n\nEach player is trying to maximize their score so\nwhen Alice picks up a stone[i] she gains the \nremaining points in the array knowing that Bob\nwi | rowe1227 | NORMAL | 2020-12-13T04:12:50.360777+00:00 | 2020-12-13T18:17:12.252597+00:00 | 2,607 | false | **Approach:**\n\nEach player is trying to maximize their score so\nwhen Alice picks up a stone[i] she gains the \nremaining points in the array knowing that Bob\nwill pick the optimal stone next round.\n\nRather than giving Bob the points, we subtract\nBob\'s points from Alice\'s points.\n\n***think of it like Bob gets negative points and Alice gets\npositive points and the sum of Bob\'s and Alice\'s points\nequals the amount of points Alice will win by***\n\n**Implementation:**\n\nUse two pointers i and j to mark the start and end\nof the remaining stones. \n\nIf the left stone is picked, increment i by 1 and \nif the right stone is picked increment j by -1.\n\nWhen i == j then there is only one stone to pick from.\nAnd if i > j return 0 because there are no more stones.\n\n\n**Optimizations:**\n\nUse a presum array to calculate the sum of the stones\nremaining in O(1) time. \n\nThis can be done because ```presum[i]``` tells us\nthe sum of all the stones to the left of i (inclusive).\n\nAnd ```presum[j]``` tells us the sum of all the stones to\nthe left of j (inclusive).\n\nSo ```presum[j] - presum[i-1]``` equals sum(stones[i:j+1]) which is\nthe amount of points from the remaining stoens in the range [i,j].\n\n**Recursive Visualization:**\n\nSay A<sub>N</sub> and B<sub>N</sub> is Alice and Bob\'s score for picking up the N<sup>th</sup> stone.\nThe recursive function will look like this:\n\n```html5\nA<sub>1</sub> - (B<sub>2</sub> - (A<sub>3</sub> - (B<sub>4</sub> - (A<sub>5</sub> - (B<sub>6</sub> - ...)))))\n```\n\nWhich simplifies to:\n\n```html5\nA<sub>1</sub> + A<sub>3</sub> + A<sub>5</sub> + ... - (B<sub>2</sub> + B<sub>4</sub> + B<sub>6</sub> + ...)\n```\n\n<br>\n\n```python\ndef stoneGameVII(self, stones: List[int]) -> int:\n\t\n\tpresum = [0] + stones[:]\n\tfor i in range(1, len(presum)):\n\t\tpresum[i] += presum[i-1]\n\t\t\n\tdef score(i, j):\n\t\tj += 1\n\t\treturn presum[j] - presum[i]\n\t\n\tn = len(stones)\n\tdp = [[0 for _ in range(n)] for _ in range(n)]\n\tfor i in range(n-1, -1, -1):\n\t\tfor j in range(i+1, n):\n\t\t\tdp[i][j] = max(score(i+1, j) - dp[i+1][j], score(i, j-1) - dp[i][j-1])\n\t\n\treturn dp[0][n-1]\n```\n\n<br>\n\n<details>\n\n<summary>Top Down DP: <b>remember to clear the cache</b> (click to show)</summary>\n\n```python\ndef stoneGameVII(self, stones: List[int]) -> int:\n\t\n\tpresum = [0] + stones[:]\n\tfor i in range(1, len(presum)):\n\t\tpresum[i] += presum[i-1]\n\t\t\n\tdef score(i, j):\n\t\tj += 1\n\t\treturn presum[j] - presum[i]\n\t\t\n\[email protected]_cache(None)\n\tdef helper(i, j):\n\t\tif i >= j:\n\t\t\treturn 0\n\t\treturn max(score(i+1, j) - helper(i+1, j), score(i, j-1) - helper(i, j-1))\n\n\tres = helper(0, len(stones) - 1)\n\thelper.cache_clear()\n\treturn res\n```\n\n</details> | 34 | 2 | [] | 9 |
stone-game-vii | Unfriendly to python, why my python O(n^2) topdown dp got MLE; | unfriendly-to-python-why-my-python-on2-t-rxr6 | conclusion\n\ndiff\nclass Solution:\n def stoneGameVII(self,A) -> int:\n n = len(A)\n @lru_cache(None)\n def dp(i,j):\n if j- | migeater | NORMAL | 2020-12-13T04:04:04.439028+00:00 | 2022-02-14T08:35:30.433159+00:00 | 1,692 | false | ## conclusion\n\n```diff\nclass Solution:\n def stoneGameVII(self,A) -> int:\n n = len(A)\n @lru_cache(None)\n def dp(i,j):\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2: return max(dp(i+1,j),dp(i,j-1))\n return min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n- return dp(0,n-1)\n+ ret = dp(0,n-1)\n+ del dp # or `dp.cache_clear()`\n+ return ret\n```\n\n## main part\n-----\n\nWhy my python O(n^2) topdown dp got MLE(**(2020, 12, 17)currently it\'s TLE**) if I use a `2d dict` or use `@lru_cache(None)`?\n\n```\nclass Solution:\n def stoneGameVII(self,A) -> int:\n n = len(A)\n cac = {}\n def dp(i,j):\n """\n if (j-i+1) %2 == n%2, Alice choose first; \n\t\t\totherwise Bob choose first.\n return the maximum difference of Alice score - Bob score, choosing from A[i:j+1], by playing stoneGameVII\n\t\t\tI don\'t want to explain why this algorithm is correct, this is what I submit on the contest. \n\t\t\tThe main point is why MLE/TLE.\n\t\t\tCompare to dp using prefix sum, this algorithm is obscure and not recommend\n """\n if (i,j) not in cac:\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2:\n # Alice choose, but what she choose don\'t credit to return value\n r = max(dp(i+1,j),dp(i,j-1))\n else:\n # Bob choose\n r = min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n cac[i,j]=r\n return r\n else:\n return cac[i,j]\n return dp(0,n-1)\n```\n\t\n~~I know I can change that to 1d dp, but this is really the first time I need to use dp space compression in a contest.~~\n\n-----\nLeetcodeOJ create a `Solution` object for every testcases, in order to solve this problem, there are serveral ways:\n+ <b> combine `@lru_cache(None)` with `.cache_clear()` or `del` topdown function </b>\n+ `import gc; gc.collect()`\n+ `del` the data structure at the end of a method or call the `.clear()` method of the memorization hashdict\n+ change to a space 1d topdown dp if possible(`@lru_cache(n)` check example code below)\n+ use another dp status calculation order\n + bottom-up dp\n\t+ bfs order, store status layer by layer(if possible, such as #1770)\n+ ~~change to c++ or java~~\n\nBelow is a table record my experiment results based on python3. This experiment result happens in a specific time point, the results are expected to has the same runtime and memory as if the same code was submitted on weekly contest 219, currently maybe the OJ have added more testcases so the experiment results can\'t repeated.\nYou can find some code at the bottom of this post.\nI don\'t know why `dict` maybe TLE when declared as a global variable.\n\n|runtime(s)/memory(MB) |(no action)|`del` operator or<sup>[1][f1]</sup> <br>`clear()` method<sup>[2][f2]</sup> or `cache_clear()` method<sup>[3][f3]</sup>|global|`__init__`<sup>[4][f4]</sup>|\n|---|---|---|---|---|---|\ntopdown `lru_cache(None)`|MLE|5.8/111|~~--------------~~|~~--------------~~\ntopdown 2d list|5.9/89|6/32|6.4/32|9.1/94\ntopdown 2d dict|MLE|7.3/111|TLE or 7.3/111|TLE or 7.2/111\nbottomup 2d list|3.9/30|3.9/30|5/30|4.7/30\n\nFor those code cost memory <20 MB above methods are not meaningful.\n\n[f1]: # (only slightly difference)\n[f2]: # (combined with dict or list)\n[f3]: # (combined with lru_cache)\n[f4]: # (declare in `Solution.__init__` function )\n\n<details><summary>A space 1d dp code:(14.5 MB)</summary>\n<p>\n\n```\nclass Solution:\n def stoneGameVII(self,A) -> int:\n n = len(A)\n dp=[0]*(n+1)\n for j in range(n):\n for ri in range(n-j,n+1):\n i=n-ri\n assert 0<=i<=j\n if (j-i+1)%2==n%2:\n dp[ri]=max(dp[ri-1] if ri>=1 else 0,dp[ri])\n else:\n dp[ri]=min(A[i]+(dp[ri-1] if ri>=1 else 0) ,A[j]+dp[ri])\n return dp[n]\n```\n\n</p>\n</details>\n\n<details>\n\n<summary>Use lru_cache(n+10) code (17 MB)</summary>\n Since this can be reduced to a space 1d dp you can use `lru_cache(maxsize=n+10)` by a proper function calling sequence.\n Ensure(at least in my code) calling `dp(i+1,j)` before calling `dp(i,j-1)`, otherwise you will got a TLE. \n<p>\n\n```\ndef stoneGameVII(self,A) -> int:\n n = len(A)\n @lru_cache(maxsize=n+10)\n def dp(i,j):\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2:\n return max(dp(i+1,j),dp(i,j-1))\n else:\n return min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n\n return dp(0,n-1)\n```\n<blockquote>\n<details><summary>A TLE test code mentioned above</summary>\n<p>\n\n```\nclass Solution:\n def stoneGameVII(self,A) -> int:\n n = len(A)\n @lru_cache(maxsize=3000)\n def dp(i,j):\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2:\n return max(dp(i,j-1),dp(i+1,j))\n else:\n return min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n\n return dp(0,n-1)\n```\n</p>\n</details>\n</blockquote>\n\n</p></details>\n\n<details><summary>A global 2d dict TLE code</summary><p>\n\n```\ncac = {}\nclass Solution:\n def stoneGameVII(self,A) -> int:\n n = len(A)\n def dp(i,j):\n if (i,j) not in cac:\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2:\n r = max(dp(i+1,j),dp(i,j-1))\n else:\n r = min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n cac[i,j]=r\n return r\n else:\n return cac[i,j]\n r = dp(0,n-1)\n cac.clear()\n return r\n```\n</p>\n</details>\n\n<details><summary>A global 2d dict AC code</summary><p>\n\n```\ncac = {}\nclass Solution:\n def stoneGameVII(self,A) -> int:\n cac.clear()\n n = len(A)\n def dp(i,j):\n if (i,j) not in cac:\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2:\n r = max(dp(i+1,j),dp(i,j-1))\n else:\n r = min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n cac[i,j]=r\n return r\n else:\n return cac[i,j]\n return dp(0,n-1)\n```\n</p>\n</details>\n\n<details><summary>`__init__` 2d dict AC</summary><p>\n\n```\nclass Solution:\n def __init__(self):\n self.cac = {}\n def stoneGameVII(self,A) -> int:\n cac = self.cac\n n = len(A)\n def dp(i,j):\n if (i,j) not in cac:\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2:\n r = max(dp(i+1,j),dp(i,j-1))\n else:\n r = min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n cac[i,j]=r\n return r\n else:\n return cac[i,j]\n r = dp(0,n-1)\n cac.clear()\n return r\n```\n</p></details>\n\n<details><summary>`__init__` 2d dict TLE</summary><p>\n\n```\nclass Solution:\n def __init__(self):\n self.cac = {}\n def stoneGameVII(self,A) -> int:\n cac = self.cac\n cac.clear()\n n = len(A)\n def dp(i,j):\n if (i,j) not in cac:\n if j-i+1<=0: return 0\n if (j-i+1) %2 == n%2:\n r = max(dp(i+1,j),dp(i,j-1))\n else:\n r = min(A[i]+dp(i+1,j),A[j]+dp(i,j-1))\n cac[i,j]=r\n return r\n else:\n return cac[i,j]\n r = dp(0,n-1)\n \n return r\n```\n</p></details>\n\n## similar python topdown TLE problem\n#516. Longest Palindromic Subsequence\n#1770. Maximum Score from Performing Multiplication Operations\n\n----\nThanks to @rowe1227 @infmount . | 29 | 3 | [] | 8 |
stone-game-vii | [Java] DP with a bit of explanation, O(n^2) time, O(n) space | java-dp-with-a-bit-of-explanation-on2-ti-10sa | First a bit of analysis:\n\n\n\n\n\nFrom the table we can find the state transfer function:\n\nresult(stones[0 .. n]) = max(\n\tsum(stones[1 .. n]) - result(sto | joor | NORMAL | 2020-12-13T04:06:55.045829+00:00 | 2020-12-13T10:55:52.963418+00:00 | 1,595 | false | First a bit of analysis:\n\n\n\n\n\nFrom the table we can find the state transfer function:\n```\nresult(stones[0 .. n]) = max(\n\tsum(stones[1 .. n]) - result(stones[1 .. n]),\n\tsum(stones[0 .. n - 1]) - result(stones[0 .. n - 1])\n)\n```\n\nNotice this function holds for `n >= 3`, so we need special consideration for the case where `n == 2`, where the result calculation is reduced to max(A, B).\n\nOptimisation 1: since the results of stones of length `l` is only related to that with length `l - 1`, we only need to maintain a 1-D array.\n\nOptimisation 2: a quick way to calculate `sum(stones[i .. j])` is to first calculate the prefix sum of stones, such that `prefix[i] = sum(stones[0 .. i])`, then we can easily find `sum(stones[i .. j]) == prefix[j] - prefix[i - 1]`\n\nThus the full solution:\n\n```\nclass Solution {\n public int stoneGameVII(int[] stones) {\n int n = stones.length, prefix[] = new int[n], dp[] = new int[n];\n\n for (var i = 0; i < n; i ++) {\n prefix[i] = stones[i] + (i > 0 ? prefix[i - 1] : 0);\n }\n\n for (var i = 0; i < n - 1; i ++) {\n dp[i]= Math.max(stones[i], stones[i + 1]);\n }\n \n for (var l = 2; l < n; l ++) {\n // length of current stone array = l + 1\n for (var i = 0; i < n - l; i ++) {\n dp[i] = Math.max(\n prefix[i + l - 1] - (i > 0 ? prefix[i - 1] : 0) - dp[i], // sum(i, i + l - 1)\n prefix[i + l] - prefix[i] - dp[i + 1]\n );\n }\n }\n \n return dp[0];\n }\n}\n``` | 28 | 0 | [] | 5 |
stone-game-vii | JAVA - Journey from Brute Force to Most Optimized DP (✅) | java-journey-from-brute-force-to-most-op-wbi6 | Let\'s try to understand the problem first. \nI think that one statement of Bob always losing and trying to get minimum score difference might lead to confusion | techtutelage | NORMAL | 2021-06-11T18:10:36.142743+00:00 | 2021-06-11T18:12:41.585474+00:00 | 1,197 | false | Let\'s try to understand the problem first. \nI think that one statement of Bob always losing and trying to get minimum score difference might lead to confusion. But it is simple what it meant is that Bob wants to mininum his loss score i.e. `minimize(Alice\'s Winnings - Bob\'s Winnings)` while Alice wants this to maximize `maximize(Alice\'s Winnings - Bob\'s Winnings)`. After defining these 2 statements it is implicit that the way both play is same i.e. if Bob tries to score more he would be able to minimize the score difference. Similarly, if Alice tries score more he would be able to lead and increase the gap between his and Bob\'s winnings.\n\nLet\'s start our discussion from the most obvious thought looking at this problem. We need to try out all possible combinations and at each step we want to take out that element out of leftmost and righmost elements that would lead to maximum score for him in future after the game is over. Let\'s start from the initial thought and on the way pick up all the optimizations as we can and reach the final accepted solution. \u2705\n\nBefore starting Iet\'s recall what the score at a given turn is. It is defined as the (`sum of all remaining elements in the array - score obtained by the opponent`).\n# **BruteForce (Time Limited Exceed)**\nIn this approach we try out the above thought and try to process both `leftmost` and `rightmost` node at each turn of the game.\n\n```\npublic int stoneGameVII(int[] stones) {\n return playTurn(stones, 0, stones.length - 1);\n }\n \n\t/**\n\t\tThis method gives the sum of elements from the range [left, right] inclusive. \n\t*/\n private int getScore(int[] stones, int left, int right) {\n int sum = 0;\n for(int i = left; i <= right; i++)\n sum += stones[i];\n \n return sum;\n }\n \n private int playTurn(int[] stones, int left, int right) {\n if (left > right) return 0;\n \n int lScore = getScore(stones, left + 1, right) - playTurn(stones, left + 1, right); // if leftmost element is picked\n int rScore = getScore(stones, left, right - 1) - playTurn(stones, left, right - 1); // if rightmost element is picked\n \n return Math.max(lScore, rScore);\n }\n```\n\n*Time Complexity* - `O(2^n)` - As at each node we are making 2 recursive calls. We also have complexity of calculating the score within a window.\n\n# **Recursive + Memoization -- Top-Down DP (Accepted) 130ms \u2705**\n\nAs it might be evident that we are performing many computations again and again while their solution would remain the same. So, this calls for introducing a memory to store the already processed nodes and just provide a lookup of `O(1)`.\n\nAlso, their is an interesting take from the above solution. If we somehow reduce the amortized cost of finding the score that would be helpful as well as it would prevent so many repetitive additions. For this we have prefix sum as the rescue. At each node we would store the sum of elements starting from index 0 to the current element(both inclusive). So, to calculate a sum of a window we subtract cummulative sum(CS) of lower index bound from the CS of upper index bound.\n\n```\nprivate int[] preSum;\n private Integer[][] mem;\n \n public int stoneGameVII(int[] stones) {\n int size = stones.length;\n preSum = new int[size + 1];\n mem = new Integer[size][size];\n \n for(int i = 0; i < size; i++) // Calculating prefix sum\n preSum[i + 1] = preSum[i] + stones[i];\n \n return playTurn(stones, 0, size - 1);\n }\n \n private int getScore(int left, int right) {\n return preSum[right + 1] - preSum[left];\n }\n \n private int playTurn(int[] stones, int left, int right) {\n if (left > right) return 0;\n \n if(mem[left][right] != null) return mem[left][right];\n \n int lScore = getScore(left + 1, right) - playTurn(stones, left + 1, right);\n int rScore = getScore(left, right - 1) - playTurn(stones, left, right - 1);\n \n mem[left][right] = Math.max(lScore, rScore);\n \n return mem[left][right];\n }\n```\n\n*Time Complexity* - `O(n*n)` - As we have lookup which is preventing repetitive calculations. \n\n# **Bottom Up DP - Space Optimized (Accepted) 27ms \u2705**\nLet\' try to tackle this problem from a different perspective. Let\'s try solving the problem starting with one element and slowly build up the final solution. Let\'s try to understand with an example and try to find the sub problems that can help find the overall solution.\n\n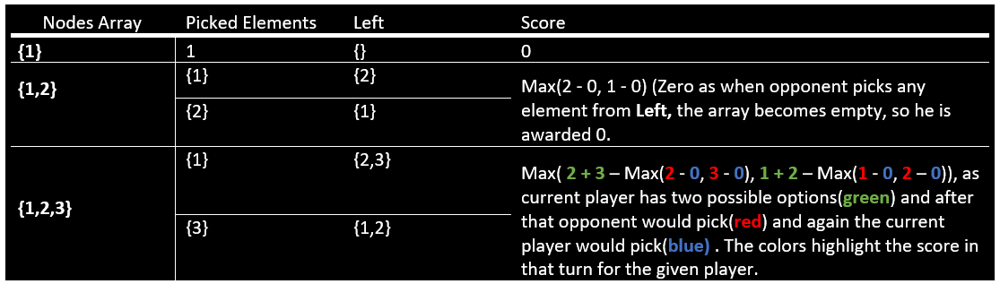\n\n\nAs we can see in the above image, when we have 3 elements the solution for that involves the solution when we had 2 elements. So, if we can leverage this pattern and try to find the solutions for sub-problems by linearly increasing the length of the array we can array at the final solution. \n\nDid we observe that? ..... let\'s try to find one more thing before scrolling down ...... it\'s would be interesting to juggle our brain horses.\n\nYes!! We observe that for a given length `L` we only need to look back at the `L - 1` which would already contain solution of the internal recursive solutions of decrement in lengths. So, as solution of `Length 2` would have already have optimum score using scores of `Length 1`. In that case when we move to `Length 3` we only need to look back at `Length 2` results. \nThis means we only need a `1-D array` to store the previous solutions.\n\nLet\'s look at the code and see if we get it. Even if there is any confusion, don\'y worry we would discuss the subtle interesting points in the solution.\n\n```\nprivate int[] preSum;\n private int[] dp;\n \n public int stoneGameVII(int[] stones) {\n int size = stones.length;\n preSum = new int[size + 1];\n dp = new int[size + 1];\n \n for(int i = 0; i < size; i++)\n preSum[i + 1] = preSum[i] + stones[i];\n \n for(int end = 1; end <= size; end++) {\n for(int i = 0; i < size - end; i++) {\n dp[i] = Math.max(\n getScore(i + 1, i + end) - dp[i + 1], // As if we pick i, we need to find solution of (i+1, end).\n getScore(i, i + end - 1) - dp[i] // As if we pick end, we need to find solution of (i, end - 1)\n ); \n }\n }\n \n return dp[0];\n }\n \n private int getScore(int left, int right) {\n return preSum[right + 1] - preSum[left];\n }\n```\n\nOnly thing that might have caused a confusion is the assignment of `dp[i]` which is below snippet.\n\n```\ndp[i] = Math.max(\n getScore(i + 1, i + end) - dp[i + 1],\n getScore(i, i + end - 1) - dp[i]\n ); \n```\n\nSo, basically `dp[i + 1]` for a given `end` and interval length `L` would mean score when `i + 1` is the start node and we have `L - 1` elements.This is what we need to add when the `i` element is picked. Remember our thinking that we need only the `L-1` length solution.\nSimilarly, `dp[i]` at that same very `end` and length `L` would mean that we picked `end` element and we need to find the solution for `L-1` elements where ending node was `end-1`.\n\n*Time Complexity* - `O(n*n)` - If we carefully look at the loops it would run for partial matrix and not exactly the full matrix. \n\nAlso, we improved so much on the space size from `O(n*n)` -> `O(n)`.\n\nHope that helps!! In case of any improvement or corrections please comment below. Thanks!! | 14 | 0 | ['Dynamic Programming', 'Java'] | 3 |
stone-game-vii | Python: Explained DP both Memoization(Top-Down) and Tabulation(Bottom-Up) | python-explained-dp-both-memoizationtop-f65zy | This problem cannot be solved using Greedy Approach as both Alice and Bob needs to play optimally and greedy always does not guarantee an optimal solution.\n\nS | meaditya70 | NORMAL | 2021-06-11T18:40:06.757842+00:00 | 2021-06-11T18:46:41.725893+00:00 | 1,053 | false | This problem cannot be solved using Greedy Approach as both Alice and Bob needs to play optimally and greedy always does not guarantee an optimal solution.\n\nSo, the only possible way to solve this is to enumerate all the possibilities Alice/Bob has in each turn. \nE.g.: stones = [5,3,1,4,2]\nAlice chooses both 5 and 2 parallely and removes them, when alice removes 5 bob has 2 options to remove 3 and 2 and bob tries both... but when alice removes 2 bob has two options 5 and 4 and bob will also try both and see which one is a better option... and so on...\n\nHere, each stone has two possibilites whether to be removed or not. Hence, total possibilites = O(2 ^ n) where n is the number of stones.\n\nThus by simple recurssion we will have Time = O(2^n) to go through all the possibilities and Space = O(n) owing to the depth of the binary tree (recursion stack).\n\nRecursion Tree Code: Sure TLE. ........ Time = O(2^n) and Space = O(n).\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n \n prefix = [0]\n for i in stones:\n prefix.append(prefix[-1]+i)\n \n def solve(left, right):\n if left == right:\n return 0\n \n leftScore = prefix[right+1] - prefix[left+1] - solve(left+1,right)\n rightScore = prefix[right] - prefix[left] - solve(left,right-1)\n return max(leftScore,rightScore)\n \n return solve(0,n-1)\n```\n\nif stones = [5,3,1,4,2], then prefix sum array = [0,5,8,9,13,15].... An additional zero is just added for better indexing.\n\nHere prefix sum array is needed so that we do not need to calculate sum every time, \nlike if alice removes 5 we can calulate the sum of rest of array as total sum of the array - sum upto the element 5 = prefix[n] - prefix[1] and so on.\n\nNow, why will the recursive equation hold?\n``` leftScore = prefix[right+1] - prefix[left+1] - solve(left+1,right) ```\nThis depicts a player\'s turn (may it be alice or bob), so if the player is removing the left stone we calulate the sum of stones values excluding the left most stone and ask the other player to play (solve(left+1,right)) with stones excluding the left most one. Then we get the difference of the scores of both the players.\n\nSimilar is the case when we exclude the rightmost stone and include the leftmost stone.\n\nIn this way we keep checking all the possibilities.\nAnd the base case is left == right as then we have only one element, so if we remove it the score/sum is zero and the game ends.\n\nI hope this recursive idea makes sense. \n\nNow, coming to the time complexity issue. T = O(2^n) will definitely give a TLE. \nCan we memoize? - Yes, due to overlapping subproblems.\nE.g.: stones = [5,1,3,4,2], one case of overlapping sub problems is [1,3,4] will be solved for both alice and bob. And there are many other overlaps.\n\nIf we memoize we will just have N^2 possible recurssion states, as both left and right has \'n\' possible values and the travel parallely. Hence Time = O(n^2) Space = O(n^2) owing to DP array.\n\nRecurssion + Memoization (Top - Down DP): Accepted ........... Time = O(n^2) Space = O(n^2)\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n \n prefix = [0]\n for i in stones:\n prefix.append(prefix[-1]+i)\n \n dp = [[-1]*n for _ in range(n)]\n \n def solve(left, right):\n if left == right:\n return 0\n \n if dp[left][right]!=-1:\n return dp[left][right]\n \n leftScore = prefix[right+1] - prefix[left+1] - solve(left+1,right)\n rightScore = prefix[right] - prefix[left] - solve(left,right-1)\n \n dp[left][right] = max(leftScore,rightScore)\n return dp[left][right]\n \n return solve(0,n-1)\n```\n\nAnd as we know, every memoized DP can be converted to Tabulation(Bottom-Up DP) by just converting the recurssion to Iteration. \n\nIn Top-Down DP (memoization), we traverse from the larger problem recursively to the smaller problem and we keep throwing the answer to the top/parent level.\n\nBut In Bottom-Up DP(Tabulation), we move from smaller problem to the larger problem iteratively(additively).\nThe main concept remains the same for both.\n\nBottom- Up DP: Accepted ........... Time = O(n^2) Space = O(n^2)\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n \n prefix = [0]\n for i in stones:\n prefix.append(prefix[-1]+i)\n \n dp = [[0]*n for _ in range(n)]\n \n for left in range(n-1,-1,-1):\n for right in range(n):\n if left == right:\n dp[left][right] = 0\n else:\n leftScore, rightScore = 0, 0\n if left+1 < n:\n leftScore = prefix[right+1] - prefix[left+1] - dp[left+1][right]\n if right - 1 >= 0:\n rightScore = prefix[right] - prefix[left] - dp[left][right-1]\n dp[left][right] = max(leftScore,rightScore) \n return dp[0][n-1]\n \n```\n\nHope it helps! | 13 | 1 | ['Dynamic Programming', 'Memoization', 'Python'] | 1 |
stone-game-vii | ✅ Stone Game VII | Dynamic Programming | Explanation | stone-game-vii-dynamic-programming-expla-gsdu | Intuition:\n\n1. Both Alice and Bob is playing optimally, so we need to consider the situation for one person.\n2. Let us say we are considering Alice case, if | shivaye | NORMAL | 2021-06-11T07:38:35.559606+00:00 | 2021-06-11T08:01:48.650296+00:00 | 989 | false | **Intuition:**\n```\n1. Both Alice and Bob is playing optimally, so we need to consider the situation for one person.\n2. Let us say we are considering Alice case, if Alice starts first then she has two options:\n* She can remove the first stone in the current stones.\n* She can remove the last stone in the current stones.\n\nIf Alice removed first stone,\nthen Bob can select from remaining stone but not the removed stone.\n\nLet us consider a simple case:\nStones: [1,2,3,4]\nAlice starts first:\nnow she can either remove 1 or 4\nif she removed 1 then Bob will have these options for his turn [2,3,4]\nif she removed 4 then Bob will have these options for his turn [1,2,3]\n\nNote: Bob and Alice both are playing optimally so Alice and Bob both want to obtain maximum points, or in simple term Alice want the difference between their scores i.e. AliceScore-BobScore as maximum and Bob wants the difference as minimum.\n\nIn below code I am considering the situation of Alice,\nSo she wants to maximize the difference between their scores,\nShe will try to see both possibilities and pick the possibility which is maximising the difference.\n\nIf Alice choose stone at index i,(i.e, taking stones from Front)\nthen the Points Alice will get is = Total Sum Of Stones Values - Stone[i];\n\nIf she choose stone at index j,(i.e, taking stones from Back)\nthen the Points Alice will get is = Total Sum Of Stones Values - Stone[j];\n\nAnd at every step Bob can form his score from min(Total Sum Of Stone Values-Stone[i],Total Sum Of Stones Values - Stone[j]);\n\nPlease see the below solution for more clarity.\n```\n\n```\nNote:\n1) Alice is always starting first according to question.\n2) We need to consider only that possibility which is yielding the best results for Alice i.e, maximising the difference between their scores.\n```\n**C++:**\n```\nclass Solution {\npublic:\n int dp[1002][1002];\n\tint getMaxDiff(vector<int> &v,int i,int j,int sum)\n {\n if(i>=j)\n return 0;\n if(sum<0)\n return 0;\n if(dp[i][j]!=-1)\n return dp[i][j];\n return dp[i][j]=max(sum-v[i]-getMaxDiff(v,i+1,j,sum-v[i]),sum-v[j]-getMaxDiff(v,i,j-1,sum-v[j]));\n \n }\n int stoneGameVII(vector<int>& stones) \n {\n memset(dp,-1,sizeof(dp));\n int sum=0;\n for(auto i:stones)\n sum+=i;\n return getMaxDiff(stones,0,stones.size()-1,sum); \n \n }\n};\n``` | 13 | 2 | ['C'] | 1 |
stone-game-vii | 🎨 The ART of Dynamic Programming | the-art-of-dynamic-programming-by-clayto-wovf | \uD83C\uDFA8 The ART of Dynamic Programming\n\n1. All possibilities are considered via top-down brute-force depth-first-search\n2. Remember each subproblem\'s o | claytonjwong | NORMAL | 2021-06-11T15:05:17.702028+00:00 | 2021-06-11T15:11:57.914706+00:00 | 858 | false | [\uD83C\uDFA8 The ART of Dynamic Programming](https://leetcode.com/discuss/general-discussion/712010/The-ART-of-Dynamic-Programming-An-Intuitive-Approach%3A-from-Apprentice-to-Master)\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n\n---\n\nWe use prefix sums `S` of the input array `A` to calculate each sum of `A` from `i..j` inclusive in O(1) time. For each player\'s turn there are 2 considerations:\n\n1. Take the right-most value at index `j`\n2. Take the left-most value at index `i`\n\nFor each consideration, we accumulate the sum of the sub-problem from `i..j` inclusive and subtract the sum of the optimal solution to the sub-problem without `j` xor without `i`.\n* Let `L` be the sum of the sub-problem `i..j - 1` (ie. `i..j` inclusive without `j`) minus the optimal solution to the sub-problem without `j`.\n* Let `R` be the sum of the sub-problem `i + 1..j` (ie. `i..j` inclusive without `i`) minus the optimal solution to the sub-problem without `i`.\n\nThen for the recursive case, we return the maximum of `L` and `R`. And the base case occurs when `i == j` for which the current player earns `0` points.\n\n---\n\n**Kotlin Solutions:**\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nclass Solution {\n fun stoneGameVII(A: IntArray): Int {\n var N = A.size\n var S = IntArray(N + 1) { 0 }\n for (i in 1..N)\n S[i] = S[i - 1] + A[i - 1]\n fun go(i: Int = 0, j: Int = N - 1): Int {\n if (i == j)\n return 0\n var L = S[j] - S[i] - go(i, j - 1)\n var R = S[j + 1] - S[i + 1] - go(i + 1, j)\n return Math.max(L, R)\n }\n return go()\n }\n}\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nclass Solution {\n fun stoneGameVII(A: IntArray): Int {\n var m = mutableMapOf<String, Int>()\n var N = A.size\n var S = IntArray(N + 1) { 0 }\n for (i in 1..N)\n S[i] = S[i - 1] + A[i - 1]\n fun go(i: Int = 0, j: Int = N - 1): Int {\n if (i == j)\n return 0\n var key = "$i,$j"\n if (m.contains(key))\n return m[key]!!\n var L = S[j] - S[i] - go(i, j - 1)\n var R = S[j + 1] - S[i + 1] - go(i + 1, j)\n m[key] = Math.max(L, R)\n return m[key]!!\n }\n return go()\n }\n}\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nclass Solution {\n fun stoneGameVII(A: IntArray): Int {\n var N = A.size\n var S = IntArray(N + 1) { 0 }\n for (i in 1..N)\n S[i] = S[i - 1] + A[i - 1]\n var dp = Array(N) { IntArray(N) { 0 } }\n for (i in N - 2 downTo 0) {\n for (j in i + 1 until N) {\n var L = S[j] - S[i] - dp[i][j - 1]\n var R = S[j + 1] - S[i + 1] - dp[i + 1][j]\n dp[i][j] = Math.max(L, R)\n }\n }\n return dp[0][N - 1]\n }\n}\n```\n\n---\n\n**Javascript Solutions:**\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nlet stoneGameVII = A => {\n let N = A.length;\n let S = Array(N + 1).fill(0);\n for (let i = 1; i <= N; ++i)\n S[i] = S[i - 1] + A[i - 1];\n let go = (i = 0, j = N - 1) => {\n if (i == j)\n return 0;\n let L = S[j] - S[i] - go(i, j - 1),\n R = S[j + 1] - S[i + 1] - go(i + 1, j);\n return Math.max(L, R);\n };\n return go();\n};\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nlet stoneGameVII = (A, m = new Map()) => {\n let N = A.length;\n let S = Array(N + 1).fill(0);\n for (let i = 1; i <= N; ++i)\n S[i] = S[i - 1] + A[i - 1];\n let go = (i = 0, j = N - 1) => {\n if (i == j)\n return 0;\n let key = `${i},${j}`;\n if (m.has(key))\n return m.get(key);\n let L = S[j] - S[i] - go(i, j - 1),\n R = S[j + 1] - S[i + 1] - go(i + 1, j);\n return m.set(key, Math.max(L, R))\n .get(key);\n };\n return go();\n};\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nlet stoneGameVII = A => {\n let N = A.length;\n let S = Array(N + 1).fill(0);\n for (let i = 1; i <= N; ++i)\n S[i] = S[i - 1] + A[i - 1];\n let dp = [...Array(N)].map(_ => Array(N).fill(0));\n for (let i = N - 2; 0 <= i; --i) {\n for (let j = i + 1; j < N; ++j) {\n let L = S[j] - S[i] - dp[i][j - 1],\n R = S[j + 1] - S[i + 1] - dp[i + 1][j];\n dp[i][j] = Math.max(L, R);\n }\n }\n return dp[0][N - 1];\n};\n```\n\n---\n\n**Python3 Solutions:**\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nclass Solution:\n def stoneGameVII(self, A: List[int]) -> int:\n N = len(A)\n S = [0] * (N + 1)\n for i in range(1, N + 1):\n S[i] = S[i - 1] + A[i - 1]\n def go(i = 0, j = N - 1):\n if i == j:\n return 0\n L = S[j] - S[i] - go(i, j - 1)\n R = S[j + 1] - S[i + 1] - go(i + 1, j)\n return max(L, R)\n return go()\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nclass Solution:\n def stoneGameVII(self, A: List[int]) -> int:\n N = len(A)\n S = [0] * (N + 1)\n for i in range(1, N + 1):\n S[i] = S[i - 1] + A[i - 1]\n @cache\n def go(i = 0, j = N - 1):\n if i == j:\n return 0\n L = S[j] - S[i] - go(i, j - 1)\n R = S[j + 1] - S[i + 1] - go(i + 1, j)\n return max(L, R)\n return go()\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nclass Solution:\n def stoneGameVII(self, A: List[int]) -> int:\n N = len(A)\n S = [0] * (N + 1)\n for i in range(1, N + 1):\n S[i] = S[i - 1] + A[i - 1]\n dp = [[0] * N for _ in range(N)]\n for i in range(N - 2, -1, -1):\n for j in range(i + 1, N):\n L = S[j] - S[i] - dp[i][j - 1]\n R = S[j + 1] - S[i + 1] - dp[i + 1][j]\n dp[i][j] = max(L, R)\n return dp[0][N - 1]\n```\n\n---\n\n**C++ Solutions:**\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using fun = function<int(int, int)>;\n int stoneGameVII(VI& A) {\n int N = A.size();\n VI S(N + 1);\n for (auto i{ 1 }; i <= N; ++i)\n S[i] = S[i - 1] + A[i - 1];\n fun go = [&](auto i, auto j) {\n if (i == j)\n return 0;\n auto L = S[j] - S[i] - go(i, j - 1),\n R = S[j + 1] - S[i + 1] - go(i + 1, j);\n return max(L, R);\n };\n return go(0, N - 1);\n }\n};\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using fun = function<int(int, int)>;\n using Map = unordered_map<string, int>;\n int stoneGameVII(VI& A, Map m = {}) {\n int N = A.size();\n VI S(N + 1);\n for (auto i{ 1 }; i <= N; ++i)\n S[i] = S[i - 1] + A[i - 1];\n fun go = [&](auto i, auto j) {\n if (i == j)\n return 0;\n stringstream key; key << i << "," << j;\n if (m.find(key.str()) != m.end())\n return m[key.str()];\n auto L = S[j] - S[i] - go(i, j - 1),\n R = S[j + 1] - S[i + 1] - go(i + 1, j);\n return m[key.str()] = max(L, R);\n };\n return go(0, N - 1);\n }\n};\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n int stoneGameVII(VI& A) {\n int N = A.size();\n VI S(N + 1);\n for (auto i{ 1 }; i <= N; ++i)\n S[i] = S[i - 1] + A[i - 1];\n VVI dp(N, VI(N, 0));\n for (auto i{ N - 2 }; 0 <= i; --i) {\n for (auto j{ i + 1 }; j < N; ++j) {\n auto L = S[j] - S[i] - dp[i][j - 1],\n R = S[j + 1] - S[i + 1] - dp[i + 1][j];\n dp[i][j] = max(L, R);\n }\n }\n return dp[0][N - 1];\n }\n};\n``` | 11 | 3 | [] | 0 |
stone-game-vii | [Python3] Easy code with explanation - DP | python3-easy-code-with-explanation-dp-by-wqny | The subproblem for the DP solution is that,\nFor n = 1, Alice or Bob picks the stone and nobody gets any score.\nFor n = 2, the person picks first stone and the | mihirrane | NORMAL | 2020-12-14T07:36:50.828904+00:00 | 2020-12-16T00:46:54.974428+00:00 | 1,500 | false | The subproblem for the DP solution is that,\nFor n = 1, Alice or Bob picks the stone and nobody gets any score.\nFor n = 2, the person picks first stone and the score equals second stone or vice versa.\nso on....\n\nNow, that we have the subproblem how do we fill the DP table and fill it with what?\nI thought of 3 choice for entries into the DP table - Alice\'s score, Bob\'s score or **difference of their scores**.\nIt gets messy for the rest so I chose difference of their scores. After zeroing on that, what should be the size of the table?\nEach table entry dp[i][j] signifies the difference in scores between the ith stone and jth stone.\nNow that we know what i and j mean its obvious that we have to find the difference of scores between the 0th stone and nth stone.\n\nOkay, next question that arises is, how do we fill the table entry when its Bob\'s turn and when its Alice\'s turn?\nNote that: the difference of scores is : (sum of scores obtained by Alice) - (sum of scores obtained by Bob)\nWhen its **Bob\'s turn**, his target is to minimize the difference:\n**dp[i][j] = min(dp[i][j-1] - (score after removing jth stone), dp[i+1][j] - (score after removing ith stone))**\n\ndp[i][j] -> Difference in score between ith and jth stone\ndp[i][j-1] -> Difference in score between ith and j-1 th stone\ndp[i+1][j] -> Difference in score between i+1 th and j th stone\n\nThe intuition is to make the negative part larger to minimize the difference.\n\nWhen its **Alice\'s turn**, her target is to maximize the difference:\n**dp[i][j] = min(dp[i][j-1] + (score after removing jth stone), dp[i+1][j] + (score after removing ith stone))**\n\ndp[i][j] -> Difference in score between ith and jth stone\ndp[i][j-1] -> Difference in score between ith and j-1 th stone\ndp[i+1][j] -> Difference in score between i+1 th and j th stone\n\nThe intuition is to make the positive part larger to maximize the difference.\n\nIf even number of stones were removed from the array then the upcoming turn is Alice\'s and similary for Bob odd number of stones must be removed.\n\nThe direction left to right and bottom to top.\n\nExample of DP table for : 5,3,1,4,2\n\n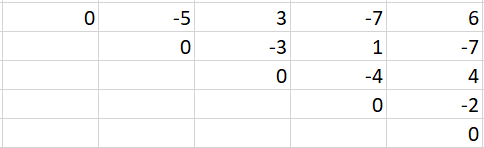\n\nRunning time: O(n^2)\nMemory : O(n^2)\n\nThis question is similar to: https://leetcode.com/problems/stone-game-vi/\n\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n dp = [[0 for _ in range(len(stones))] for _ in range(len(stones))] # dp table n x n\n run_sum = [0] # running sum -> sum [i..j] = run_sum[j] - run_sum[i]\n s = 0\n \n\t\t## Calculation of running sum\n for i in stones:\n s += i\n run_sum.append(s)\n\t\t\n n = len(stones) \n \n for k in range(1, n): # no. of stones left\n for i in range(0, n - k): # from each starting point\n remove_i_stone = (run_sum[i+k+1] - run_sum[i+1]) # score after removing i th stone\n remove_j_stone = (run_sum[i+k] - run_sum[i]) # score after removing j th stone\n \n if (n-(k+1))%2 == 0: # alice\'s move \n dp[i][i+k] = max(remove_i_stone + dp[i+1][i+k],\n remove_j_stone + dp[i][i+k-1])\n else: # bob\'s move\n dp[i][i+k] = min(-remove_i_stone + dp[i+1][i+k],\n - remove_j_stone + dp[i][i+k-1])\n \n return dp[0][n - 1]\n``` | 9 | 0 | ['Dynamic Programming', 'Memoization', 'Python', 'Python3'] | 0 |
stone-game-vii | C++| 100% | Detailed Explanation | DP Approach | c-100-detailed-explanation-dp-approach-b-gh07 | This is similar to Matrix Chain Multiplication Problem . The idea is to divide problem into subproblems and use them to constuct final solution using Dynamic Pr | prajwalroxman | NORMAL | 2020-12-15T12:54:06.586057+00:00 | 2020-12-15T14:46:37.743426+00:00 | 764 | false | This is similar to Matrix Chain Multiplication Problem . The idea is to divide problem into subproblems and use them to constuct final solution using Dynamic Programming .\n\nFor instance given input `[5,3,1,4,2]`\nUse the following `N x N` matrix to compute the result where `N is length of stones[]`\n```\n\t0 , 1 , 2 , 3 , 4 \n\t______________________\n0\t0 , -5 , 3 , -7 , 6 \n1\t0 , 0 , -3 , 1 , -7 \n2\t0 , 0 , 0 , -4 , 2 \n3\t0 , 0 , 0 , 0 , -4 \n4\t0 , 0 , 0 , 0 , 0 \n\n\t\n```\n\nWe construct the upper right triangle of Matrix, diagonally.\n```dP[i][j] represents score obtained if we have stones[i:j] only ```\nFor Alice\'s turn\n`dp[i][j] = max(sum[i+1:j] + dp[i+1][j] , sum[i:j-1] + dp[i][j-1] )`\nFor Bob\'s turn\n`dp[i][j] = min( -sum[i+1:j] + dp[i+1][j] , -sum[i:j-1] + dp[i][j-1] )`\n\nIn each iteration we use the results of previous iteration\n```\n\nSo first we initialise `1st Diagonal from left to right`\ndp[0][0] = 0\ndp[1][1] = 0\ndp[2][2] = 0\ndp[3][3] = 0\ndp[4][4] = 0\n\nThen in next iteration 2nd Diagonal\n\nIts Bob Turn\ndp[0][1] = min(-3+0 , -5+0) => -5 [5,3]\ndp[1][2] = min(-3+0 , -1+0) => -3 [3,1]\ndp[2][3] = min(-1+0 , -4+0) => -4 [1,4]\ndp[3][4] = min(-4+0 , -2+0) => -4 [4,2]\n\nThen in next iteration 3rd Diagonal\n\nIts Alice Turn\ndp[0][2] = max(4-3 , 8-5) => 3 [5,3,1]\ndp[1][3] = max(5-4 , 4-3) => 1 [3,1,4]\ndp[2][4] = max(5-4 , 6-4) => 2 [1,4,2]\n\nThen in next iteration 4th Diagonal\n\nIts Bob Turn \ndp[0][3] = min(-8+1 , -9+3) => -7 [5,3,1,4]\ndp[1][4] = min(-7+2 , -8+1) => -7 [3,1,4,2]\n\nThen in next iteration 5th Diagonal\n\nIts Alice Turn \ndp[0][4] = max(10-7 , 13-7) => 6 ANS [5,3,1,4,2]\n```\n\nWe have got the answer\n\n\n```\nclass Solution {\npublic:\n int stoneGameVII(vector<int>& stones) {\n ios::sync_with_stdio(false);\n cin.tie(NULL);\n int len = stones.size();\n \n int dp[1001][1001] = {0};\n \n /*Prefix Sum array for O(1) Sum calculation | sum (i to j inclusive) = pf[j+1] - pf[i] */\n int pf[1001+1] = {0};\n for(int i = 0;i < len; i++)\n pf[i+1] = pf[i] + stones[i];\n \n //last turn will be (Alice\'s[0]) or (Bob\'s[1])\n int turn = len%2 == 1;\n \n for(int k = 1;k < len;k++){\n int i = 0,j = k;\n while(i < len && j < len){\n if(turn%2 == 0){\n //alice\n dp[i][j] = max(dp[i][j-1] + (pf[j]-pf[i]) ,\n dp[i+1][j] + (pf[j+1]-pf[i+1]));\n } \n else{\n //bob\n //ij\n dp[i][j] = min(dp[i][j-1] - (pf[j]-pf[i]) ,\n dp[i+1][j] - (pf[j+1]-pf[i+1]));\n }\n i++;\n j++;\n }\n turn = turn^1;\n }\n return dp[0][len-1];\n }\n};\n``` | 8 | 0 | [] | 0 |
stone-game-vii | 2-Solutions Recursive and Top-Down DP | 2-solutions-recursive-and-top-down-dp-by-auqp | Intuition\nMaximization of the choices we pick and constraints were 1000 so N^2 could work\n\n# Approach\nWe have two choiches at a point :\n- Whether pick from | upadhyayabhi0107 | NORMAL | 2022-11-18T18:25:22.047518+00:00 | 2022-11-18T18:25:22.047552+00:00 | 995 | false | # Intuition\nMaximization of the choices we pick and constraints were 1000 so N^2 could work\n\n# Approach\nWe have two choiches at a point :\n- Whether pick from the start\n- Or pick from the end \n\nAnd for maintaining the profit sum we could directly subtract it from the sum that we make the call for the rest.\n\n# Complexity\n- Time complexity: O(2^N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(recursive stack)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code Recursive\n```\nclass Solution {\npublic:\n int dfs(int i , int j , int sum , vector<int>& stones){\n if(i >= j){\n return 0;\n }\n if(sum < 0){\n return 0;\n }\n int choose_front = sum - stones[i] - \n dfs(i + 1 , j , sum - stones[i] , stones);\n int choose_back = sum - stones[j] - \n dfs(i , j - 1 , sum - stones[j] , stones);\n int profit = max(choose_back , choose_front);\n return profit;\n }\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n int sum = 0 ;\n for(auto it : stones){\n sum += it;\n }\n return dfs(0 , n - 1 , sum , stones);\n }\n};\n```\n# Complexity\n- Time complexity: O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code Top - Down DP\n```\nclass Solution {\npublic:\n int dfs(int i , int j , int sum , vector<int>& stones ,\n vector<vector<int>>& dp){\n if(i >= j){\n return 0;\n }\n if(sum < 0){\n return 0;\n }\n if(dp[i][j] != -1){\n return dp[i][j];\n }\n int choose_front = sum - stones[i] - \n dfs(i + 1 , j , sum - stones[i] , stones , dp);\n int choose_back = sum - stones[j] - \n dfs(i , j - 1 , sum - stones[j] , stones , dp);\n int profit = max(choose_back , choose_front);\n return dp[i][j] = profit;\n }\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n vector<vector<int>> dp(n + 1 , vector<int>(n + 1 , -1));\n int sum = 0 ;\n for(auto it : stones){\n sum += it;\n }\n return dfs(0 , n - 1 , sum , stones , dp);\n }\n};\n``` | 7 | 0 | ['Dynamic Programming', 'Recursion', 'C++'] | 1 |
stone-game-vii | Detailed explanation, simple memoization using Java | detailed-explanation-simple-memoization-w4lo3 | Just think like a child. At every step there are 2 possibilities, \n\t1 .Picking the first stone.\n\t2. Picking the last stone.\n\nAt each step both of them wan | prakhar3agrwal | NORMAL | 2021-06-11T08:26:35.504440+00:00 | 2021-06-11T08:28:06.135917+00:00 | 358 | false | Just think like a child. At every step there are 2 possibilities, \n\t1 .Picking the first stone.\n\t2. Picking the last stone.\n\nAt each step both of them want to maximize the difference between their current score and the score that the other playes gets in the next step. This will be achieved by "maximizing the difference in the current score and the other player\'s score in the next step)\n\n**maximum(scoreOnRemovingFirstElement - score obtained on subsequent steps,**\n\t\t\t**scoreOnRemovingLastElement - score obtained on subsequent steps)**\n\n```\nclass Solution {\n \n int[][] dp = null;\n \n private int solve(int[] stones, int start, int end, int sum){\n if(start>=end){\n return 0;\n }\n if(dp[start][end] !=-1){\n return dp[start][end];\n }\n \n int scoreOnRemovingFirst = sum - stones[start];\n int scoreOnRemovingLast = sum - stones[end];\n \n dp[start][end] = Math.max(scoreOnRemovingFirst - solve(stones, start+1, end, scoreOnRemovingFirst),\n scoreOnRemovingLast - solve(stones, start, end-1, scoreOnRemovingLast));\n \n return dp[start][end];\n \n }\n \n public int stoneGameVII(int[] stones) {\n int n = stones.length;\n \n dp = new int[n][n];\n for(int i=0;i<n;i++){\n Arrays.fill(dp[i],-1);\n }\n \n int sum = 0;\n for(int num: stones){\n sum += num;\n }\n return solve(stones, 0, n-1, sum);\n \n }\n} | 7 | 1 | [] | 2 |
stone-game-vii | C++ DP MinMAX solution. N^2 | c-dp-minmax-solution-n2-by-chejianchao-f31v | dp[i][j] represent tha maximum different between i to j. and here we use val - dfs() to calculate different, this is a general way to calculate a MinMax value a | chejianchao | NORMAL | 2020-12-13T04:03:03.789595+00:00 | 2020-12-13T04:19:26.091618+00:00 | 731 | false | dp[i][j] represent tha maximum different between i to j. and here we use val - dfs() to calculate different, this is a general way to calculate a MinMax value and we don\'t need to consider whose turn now.\n```\nclass Solution {\npublic:\n int dp[1001][1001];\n int dfs(vector<int>& stones, int left, int right) {\n if(right == left) return 0;\n if(dp[left][right] >= 0) return dp[left][right];\n int res = stones[right] - stones[left] - dfs(stones, left + 1, right);\n res = max(res, stones[right - 1] - (left > 0 ? stones[left - 1] : 0) - dfs(stones, left, right - 1));\n return dp[left][right] = res;\n }\n int stoneGameVII(vector<int>& stones) {\n memset(dp, -1, sizeof(dp));\n for(int i = 1; i < stones.size(); ++i) {\n stones[i] += stones[i - 1];\n }\n return dfs(stones, 0, stones.size() - 1);\n }\n};\n``` | 7 | 0 | [] | 0 |
stone-game-vii | Easy to understand | dp solution | O(n^2) |CPP | easy-to-understand-dp-solution-on2-cpp-b-2mbm | let me firstly explain the logic involved:\nbasically we have to find the minimum difference bw Alice and Bobs overall score.\n\nlet us consider the scenario fo | suriansh | NORMAL | 2021-05-11T10:00:29.431765+00:00 | 2021-05-13T06:46:45.292422+00:00 | 589 | false | let me firstly explain the logic involved:\nbasically we have to find the minimum difference bw Alice and Bobs overall score.\n\nlet us consider the scenario for one move of alice:\nShe will have and array of stones from 0....n indices let it be A.Now she has 2 options:\n1) She takes the first element .Impact on her score would be as follows\n\t`score += (sum of array - A[0])`\n\tthis score would be further subtracted by the maximum possible difference bw score of alice and bob had the array been from 1...n\n\t\n\t\n\tOverall we might say that score_diff = **(sum of array - A[0]) - max. diff for A[1....n]** \n\t\n\t\n2) She takes the last element .Impact on her score would be as follows\n\t`score += (sum of array - A[n])`\nthis score would be further subtracted by the maxium possible difference bw score of alice and bob had the array been from 0...n-1\n\n\t\nOverall we might say that score_diff = **(sum of array - A[n]) - max. diff for A[0....n-1]** \n\nNow since we want to consider maximum option for our player, hence we consider the maximum so we consider the max of the above 2 options.\n\t\n\t\n\t\n```\n int stoneGameVII(vector<int>& stones) {\n \n vector<int> sums(stones.size()+1);\n \n for(int i=0;i<stones.size();i++){\n sums[i+1] = sums[i]+stones[i];\n }\n vector<vector<int>> dp(stones.size(),vector<int> (stones.size()));\n \n for(int len=2;len<=stones.size();len++){\n for(int i=0;i<=stones.size()-len;i++){\n \n int j = i+len-1;\n \n dp[i][j] = max(sums[j+1]-sums[i+1] -dp[i+1][j],sums[j]-sums[i]-dp[i][j-1] );\n \n }\n \n }\n \n \n return dp[0][stones.size()-1];\n \n \n }\n```\nLet dp[i][j] be the maximum difference the first player can get if the players play on A[i..j].\n\nIn the above code a prefix array has been used in order to find sum of the array efficiently.\n\nWe consider all the possible array with length ranging from 2 to N.\n```\ndp[i][j] = max(sums[j+1]-sums[i+1] -dp[i+1][j],sums[j]-sums[i]-dp[i][j-1] );\n```\nis the crux of the solution,\nhere ```sums[j+1]-sums[i+1]``` represents (sum of array - A[0]) and dp[i+1][j] represents the residual max difference bw scores.\n```sums[j]-sums[i]``` represents (sum of array - A[N]) and dp[i][j-1] represents the residual max difference bw scores.\n\nsince we are given an array of n elements dp[0][n-1] represents our answer.\n\n\n\n\n\n\t | 6 | 0 | ['Dynamic Programming', 'C++'] | 0 |
stone-game-vii | [Python3] Game Theory + Dynamic Programming - Simple Solution | python3-game-theory-dynamic-programming-v7tqz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dolong2110 | NORMAL | 2024-09-09T17:51:39.241471+00:00 | 2024-09-12T08:23:51.880698+00:00 | 152 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n ps = [0] + list(accumulate(stones))\n ops = [max, min]\n sign = [1, -1]\n \n @cache\n def dp(i: int, j: int) -> int:\n if i == j: return 0\n player = (i + n - j - 1) % 2\n return ops[player](\n sign[player] * (ps[j + 1] - ps[i + 1]) + dp(i + 1, j),\n sign[player] * (ps[j] - ps[i]) + dp(i, j - 1)\n )\n return dp(0, n - 1)\n```\n\n##### 2. Bottom-Up\n\n```python3 []\nn = len(stones)\n preSum = [0] * (n + 1)\n for i in range(n): preSum[i + 1] = preSum[i] + stones[i]\n\n def getSum(left, right):\n return preSum[right + 1] - preSum[left]\n\n dp = [[0] * n for _ in range(n)]\n for l in range(n - 1, -1, -1):\n for r in range(l + 1, n):\n scoreRemoveLeftMost = getSum(l + 1, r)\n scoreRemoveRightMost = getSum(l, r - 1)\n dp[l][r] = max(scoreRemoveLeftMost - dp[l + 1][r], scoreRemoveRightMost - dp[l][r - 1])\n return dp[0][n - 1]\n``` | 5 | 0 | ['Array', 'Math', 'Dynamic Programming', 'Game Theory', 'Python3'] | 1 |
stone-game-vii | Recursion->Memoization->Tabulation | recursion-memoization-tabulation-by-abhi-wbbn | Intuition\n Describe your first thoughts on how to solve this problem. \n\nAlice Turn\n [5 3 1 4 2]\n A = 5 + 3 + 1 + 4 = 13 \nBob Turn\n [ | abhisek_ | NORMAL | 2022-12-31T05:18:58.892710+00:00 | 2022-12-31T05:18:58.892755+00:00 | 774 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n```\nAlice Turn\n [5 3 1 4 2]\n A = 5 + 3 + 1 + 4 = 13 \nBob Turn\n [5 3 1 4]\n B = 3 + 1 + 4 = 8\nAlice Turn\n [3 1 4]\n A = 1 + 4 = 5\nBob Turn\n [1 4]\n B = 4 = 4\nResult\n A = 13 + 5 = 18\n - B = 8 + 4 = 12\n ------------------\n 6\n\n ---> 13 - 8 + 5 - 4 = 6\n can also be written as:\n ---> 13 -(8 - (5-(4)))\n 13 - 8 + (5-(4)) \n 13 - 8 + 5 - 4 = 6\nSo in recursive approach we will just keep subtracting the next Call\n```\n# Recursive Approach\n<!-- Describe your approach to solving the problem. -->\n```\ndef stoneGameVII(self, nums: List[int]) -> int:\n def f(start,end,total):\n if start>=end:return 0 //in recursion this line is not req. but converting this recursion to tabulation this is required\n if total == 0:\n return 0\n pickS = (total-nums[start]) - f(start+1,end,total-nums[start])\n pickE = (total-nums[end]) - f(start,end-1,total-nums[end])\n\n return max(pickS,pickE)\n return f(0,len(nums)-1,sum(nums))\n\n```\n\n# Memoization\n```\ndef stoneGameVII(self, nums: List[int]) -> int:\n def f(start,end,total,dp):\n if start>=end:return 0\n if total == 0:\n return 0\n if dp[start][end][total] != -1:return dp[start][end][total]\n pickS = (total-nums[start]) - f(start+1,end,total-nums[start],dp)\n pickE = (total-nums[end]) - f(start,end-1,total-nums[end],dp)\n\n dp[start][end][total] = max(pickS,pickE)\n return dp[start][end][total]\n\n n = len(nums)\n t = sum(nums)\n dp = [[[0]*(t+1) for _ in range(n+1)] for _ in range(n+1)]\n return f(0,n-1,t,dp)\n```\n\n# Tabulation\n```\nclass Solution:\n def stoneGameVII(self, nums: List[int]) -> int:\n n = len(nums)\n total = sum(nums)\n dp = [[0]*(n+1) for _ in range(n+1)]\n front = [0]*(n+1)\n back = [0]*(n+1)\n front[1] = nums[0]\n back[n-1] = nums[n-1]\n # Sum from start to end and end to start\n for i in range(1,n):\n front[i+1] = front[i] + nums[i]\n back[n-1-i] = back[n-i] + nums[n-i-1]\n # note front[0] = 0\n # back[n] = 0\n # for calculation purpose\n for start in range(n-1,-1,-1):\n for end in range(start+1,n,1):\n pickS = (total-(front[start+1]+back[end+1])) - dp[start+1][end]\n pickE = (total-(front[start]+back[end]))- dp[start][end-1]\n dp[start][end] = max(pickS,pickE)\n return dp[0][n-1]\n\n``` | 5 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Python3'] | 0 |
stone-game-vii | Simple c++ solution using Memoization | simple-c-solution-using-memoization-by-a-m9i2 | \nclass Solution {\npublic:\n int t[1001][1001];\n \n int solve(vector<int> &stones, int left, int right, int sum)\n {\n if(left>=right)\n | Amey_Joshi | NORMAL | 2021-06-11T13:43:38.262212+00:00 | 2021-06-11T13:43:38.262253+00:00 | 459 | false | ```\nclass Solution {\npublic:\n int t[1001][1001];\n \n int solve(vector<int> &stones, int left, int right, int sum)\n {\n if(left>=right)\n return 0;\n \n if(t[left][right]!=-1)\n return t[left][right];\n \n if(left-right==1)\n return t[left][right]=max(stones[left],stones[right]);\n \n int first=sum-stones[left]-solve(stones, left+1, right, sum-stones[left]);\n int second=sum-stones[right]-solve(stones, left, right-1, sum-stones[right]);\n \n return t[left][right]=max(first,second);\n \n }\n \n \n \n int stoneGameVII(vector<int>& stones) {\n int n=stones.size();\n int i,j,sum=0;\n for(i=0;i<n;i++)\n {\n sum+=stones[i];\n }\n \n for(i=0;i<=n;i++)\n {\n for(j=0;j<=n;j++)\n t[i][j]=-1;\n }\n \n return solve(stones,0,n-1,sum);\n \n \n \n }\n};\n``` | 5 | 0 | [] | 1 |
stone-game-vii | C++ Super Simple and Clear Solution | c-super-simple-and-clear-solution-by-yeh-rzph | \nclass Solution {\npublic:\n int rec(vector<int>& stones, int start, int end, int sum) {\n if (start == end) \n return 0;\n \n | yehudisk | NORMAL | 2021-06-11T09:10:34.599853+00:00 | 2021-06-11T09:10:34.599889+00:00 | 312 | false | ```\nclass Solution {\npublic:\n int rec(vector<int>& stones, int start, int end, int sum) {\n if (start == end) \n return 0;\n \n if (dp[start][end]) \n return dp[start][end];\n \n int remove_first = sum - stones[start] - rec(stones, start+1, end, sum-stones[start]);\n int remove_last = sum - stones[end] - rec(stones, start, end-1, sum-stones[end]);\n \n dp[start][end] = max(remove_first, remove_last);\n return dp[start][end];\n \n }\n int stoneGameVII(vector<int>& stones) {\n dp.assign(stones.size(), vector<int>(stones.size(), 0));\n int sum = 0;\n sum = accumulate(stones.begin(), stones.end(), sum);\n return rec(stones, 0, stones.size()-1, sum);\n }\n \nprivate:\n vector<vector<int>> dp;\n};\n``` | 5 | 1 | ['C'] | 0 |
stone-game-vii | Straight forward DP solution | Memoizaton | c++ | O(n*n) | straight-forward-dp-solution-memoizaton-qdcn4 | \nint pre[1005];\nint getsum(int l,int r){\n if(l > r)\n return 0;\n return pre[r] - (l>0?pre[l-1]:0);\n}\n\nint cache[1005][1005][2];\nint dp(int | ghoshashis545 | NORMAL | 2020-12-13T04:27:34.420403+00:00 | 2020-12-13T04:27:34.420443+00:00 | 328 | false | ```\nint pre[1005];\nint getsum(int l,int r){\n if(l > r)\n return 0;\n return pre[r] - (l>0?pre[l-1]:0);\n}\n\nint cache[1005][1005][2];\nint dp(int l,int r,int f)\n{\n if(l > r)\n return 0;\n int &ans = cache[l][r][f];\n if(ans != -1)\n return ans;\n int lsum = getsum(l,r-1) , rsum = getsum(l+1,r);\n if(f==0)\n ans = max(rsum + dp(l+1,r,f^1) , lsum + dp(l,r-1,f^1));\n else\n ans = min(-rsum + dp(l+1,r,f^1),-lsum + dp(l,r-1,f^1));\n return ans;\n}\nclass Solution {\npublic:\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n \n // initialize cache array\n for(int i =0;i < n; ++i){\n pre[i] = 0;\n for(int j =0;j < n; ++j)\n cache[i][j][0] = cache[i][j][1] = -1;\n }\n \n // build prefix sum array\n for(int i = 0;i < n; ++i){\n if(i > 0)\n pre[i] = pre[i-1];\n pre[i] += stones[i];\n }\n return dp(0,n-1,0);\n \n }\n};\n``` | 5 | 1 | ['Memoization'] | 0 |
stone-game-vii | C# Simple DP | c-simple-dp-by-leoooooo-n57f | \npublic class Solution\n{\n public int StoneGameVII(int[] stones)\n {\n int sum = stones.Sum();\n return Max(stones, 0, stones.Length - 1, | leoooooo | NORMAL | 2020-12-13T04:06:02.016077+00:00 | 2020-12-13T04:06:54.607874+00:00 | 301 | false | ```\npublic class Solution\n{\n public int StoneGameVII(int[] stones)\n {\n int sum = stones.Sum();\n return Max(stones, 0, stones.Length - 1, sum, new int[stones.Length, stones.Length]);\n }\n\n private int Max(int[] stones, int i, int j, int sum, int[,] memo)\n {\n if (i == j) return 0;\n if (memo[i, j] > 0) return memo[i, j];\n return memo[i, j] = Math.Max(\n sum - stones[i] - Max(stones, i + 1, j, sum - stones[i], memo), \n sum - stones[j] - Max(stones, i, j - 1, sum - stones[j], memo));\n }\n}\n``` | 5 | 0 | [] | 1 |
stone-game-vii | Python3. DP without prefix sum. | python3-dp-without-prefix-sum-by-yarosla-88f6 | Idea: make moves of two players as one dp step.\nThere are 4 cases. Consider [a, b, c, x, y, z]. \n1. Player one takes a. \n\t1.1. Player two takes b. Score sum | yaroslav-repeta | NORMAL | 2021-06-26T03:15:46.741081+00:00 | 2021-06-26T03:20:09.970263+00:00 | 170 | false | Idea: make moves of two players as one dp step.\nThere are 4 cases. Consider `[a, b, c, x, y, z]`. \n1. Player one takes `a`. \n\t1.1. Player two takes `b`. Score `sum(b, c, x, y, z) - sum(c, x, y, z) = b`.\n\t1.2. Player two takes `z`. Score `sum(b, c, x, y, z) - sum(b, c, x, y) = z`.\n2. Player one takes `z`.\n\t2.1. Player two takes `y`. Score `sum(a, b, c, x, y) - sum(a, b, c, x) = y`.\n\t2.2. Player two takes `a`. Score `sum(a, b, c, x, y) - sum(b, c, x, y) = a`.\n\nSo after two moves score equals to one element (that was taken by second player) from input array. Every two moves score increases by one of array elements. That way we don\'t need prefix sums.\n\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n @lru_cache(None)\n def dp(i, j):\n if i >= j:\n return 0\n\t\t\t# maximize by first player and minimize by the second one\n return max(\n min(stones[i + 1] + dp(i + 2, j), stones[j] + dp(i + 1, j - 1)),\n min(stones[j - 1] + dp(i, j - 2), stones[i] + dp(i + 1, j - 1))\n )\n return dp(0, len(stones) - 1)\n``` | 4 | 0 | [] | 2 |
stone-game-vii | Python "Numpy Is The King" solution (Runtime: 220 ms) | python-numpy-is-the-king-solution-runtim-x3nj | Just the same bottom-up solution as any other. But much faster with numpy:\n\n\nimport numpy as np\n\nclass Solution:\n def stoneGameVII(self, stones: List[i | agakishy | NORMAL | 2021-06-11T07:58:17.086160+00:00 | 2021-06-11T18:29:41.514165+00:00 | 250 | false | Just the same bottom-up solution as any other. But much faster with numpy:\n\n```\nimport numpy as np\n\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n stones = np.array(stones, dtype = int)\n score = np.zeros(n, dtype = int)\n summ = np.array(stones, dtype = int)\n for l in range(1, n):\n nxt = np.maximum(summ[:n-l]-score[:n-l], summ[1:n-l+1]-score[1:n-l+1])\n summ[:-l] += stones[l:]\n score = nxt\n \n return score[0]\n```\nThis is usual bottom-up approach: we start with n lines of stones of len 1 (starting at positions 0..n-1), and calculate for them score and sum. Score for them is 0 and sum is every stone. Then we are doing the same with (n-1) lines of len 2, and so on up to 1 line of len n. For every line of len m starting in in dex i the score in max of: sum(all stones except right) - score(of line of len m-1 starting at i) OR sum(all stones except left) - score(of line of len m-1 starting at i+1).\n\nAnd when we got to line of len n - this is our answer.\n\nThe speed comes from numpy using vector SIMD instructions. It is not the easiest thing to read and write, but works fast. Line `summ[:-l] += stones[l:]` for example adds one more stone to every position from 0 to -l and can be writen as equivalent cycle:\n```\nfor i in range(0, n-l):\n\t\tsumm[i] += stones[i+l]\n```\nBut in numpy it doesn\'t make this summs one by one. Its doing it in batches (or vectors) of up to 512 variables at ones. | 4 | 1 | [] | 1 |
stone-game-vii | C++, memozation, Minimax approach | c-memozation-minimax-approach-by-aditya_-o3tt | \n int memo(vector<vector<int>> & dp, vector<int>& stones, int sum, int start, int end){\n if(sum <= 0) return 0; \n if(start== end )return 0;\ | aditya_trips | NORMAL | 2021-01-16T13:26:49.377724+00:00 | 2021-01-16T13:26:49.377754+00:00 | 689 | false | ```\n int memo(vector<vector<int>> & dp, vector<int>& stones, int sum, int start, int end){\n if(sum <= 0) return 0; \n if(start== end )return 0;\n if(dp[start][end]!= -1)return dp[start][end]; \n \n int res = max(sum-stones[start]- memo(dp,stones, sum-stones[start], start+1, end),\n sum-stones[end]- memo(dp,stones, sum-stones[end], start, end-1)\n );\n return dp[start][end ] = res ;\n }\n int stoneGameVII(vector<int>& stones) {\n int sum = 0 ;\n int n = stones.size(); \n for(auto x:stones) sum +=x;\n vector<vector<int>> dp(n+1, vector<int>(n+1, -1)); \n return memo(dp , stones, sum, 0, n-1) ;\n }\n``` | 4 | 0 | ['Recursion', 'Memoization', 'C'] | 0 |
stone-game-vii | Java O(n^2) bottom up solution with detailed explanation. No prefix sum | java-on2-bottom-up-solution-with-detaile-wp17 | Considering array [a1,a2,...,an-1,an]\n\nIf Alice takes a1, then Alice gains sum(a2,...,an) score. Bob takes either a2 or an, which gives him either sum(a3,..., | datou12138 | NORMAL | 2020-12-29T12:50:36.506202+00:00 | 2020-12-29T12:50:36.506250+00:00 | 231 | false | Considering array [a1,a2,...,an-1,an]\n\nIf Alice takes `a1`, then Alice gains `sum(a2,...,an)` score. Bob takes either `a2` or `an`, which gives him either `sum(a3,...,an)` score or `sum(a2,...,an-1)` score, hence the difference is either `a2` or` an`. Since Bob wants to minimize the difference, he should take `min(a2, an)` given Alice took `a1`.\n\nIf Alice takes `an`, following a similar deduction, Bob should take `min(a1, an-1)` given Alice took `an`.\n\nNow that Alice want to maximize the difference, she should gain `max(min(a2, an), min(a1, an-1))`. \n\nThen they are back to the same problem with a smaller size.\n\nTo sum up, let\'s use `dp[i][j]` to represent the differece of their score for array `[ai,...aj]` if they both play optimally.\nThe initial state `dp[i][i]` is 0 since if Alice takes the only element she gains 0 score and so is Bob. `dp[i][i+1]` is `max(ai, ai+1)` since Alice must take the smaller element to gain the larger element\'s score. \nThe transfer equation is \n`dp[i][j]=max(`\n`min(dp[i+2][j]+a2 , dp[i+1][j-1]+an), ` when Alice takes a1\n`min(dp[i+1][j-1]+a1, dp[i][j-2]+an-1)` when Alice takes an\n`)`\n\n```\nclass Solution {\n public int stoneGameVII(int[] s) {\n int n = s.length;\n if(n==2) return Math.max(s[0],s[1]);\n int[][] dp = new int[n][n];\n\t\t// initial state setup\n for(int i=0; i<n-1; i++) {\n dp[i][i+1] = Math.max(s[i],s[i+1]);\n }\n\t\t// start from length 3, since length 2 is setup as initial state\n for(int len=3; len<=n; len++) {\n for(int i=0; i+len-1<n; i++) {\n int j = i+len-1;\n\t\t\t\t// if Alice takes left most stone\n int m1 = Math.min(dp[i+1][j-1]+s[j], dp[i+2][j]+s[i+1]);\n\t\t\t\t// if Alice takes right most stone\n int m2 = Math.min(dp[i+1][j-1]+s[i], dp[i][j-2]+s[j-1]);\n\t\t\t\t// choose the larger one\n dp[i][j] = Math.max(m1, m2);\n }\n }\n return dp[0][n-1];\n }\n}\n``` | 4 | 0 | [] | 0 |
stone-game-vii | DP SOLUTION W/O TURN TRACKING || EASY TO UNDERSTAND | dp-solution-wo-turn-tracking-easy-to-und-v9uf | At first glance this solution might look like we are just returning the max score by which Alice will win, \nHere Bob will follow the approach to maximise diffe | mehta_ | NORMAL | 2020-12-13T04:23:21.057898+00:00 | 2020-12-13T07:42:05.234203+00:00 | 736 | false | At first glance this solution might look like we are just returning the max score by which Alice will win, \nHere Bob will follow the approach to maximise difference at his play so he will then minimize Alice\'s score when she picked the stone before his turn.\nalicePreviousPickDiff = optimalPickByAlice - bobNextPickDiff\nHere to minimize alicePreviousPickDiff, bob has to maximize bobNextPickDiff.\nSo it results in a solution resembling, JUMP GAME 1\n\nEdit: Better explanation by [@fallenranger](http://https://leetcode.com/fallenranger/)\nBob is maximizing the difference on his turn, and since this is negated on a layer above, overall Bob is playing the optimal move to minimize the difference.\nAlice - (Bob - (Alice - Bob))\nBy selecting max between two options, Bob is doing it\'s best to minimize the above difference.\n\n```\nclass Solution {\n int dp[][];\n public int stoneGameVII(int[] stones) {\n dp = new int[stones.length][stones.length];\n return score(stones, 0, stones.length - 1, Arrays.stream(stones).sum());\n }\n int score(int[] stones, int l, int r, int sum) {\n if(l + 1 == r) return Math.max(stones[l], stones[r]);\n if(dp[l][r] != 0) return dp[l][r];\n int left = score(stones, l + 1, r, sum - stones[l]);\n int right = score(stones, l, r - 1, sum - stones[r]);\n dp[l][r] = Math.max(sum - stones[l] - left, sum - stones[r] - right);\n return dp[l][r];\n }\n}\n\n``` | 4 | 1 | ['Dynamic Programming', 'Java'] | 4 |
stone-game-vii | Recursion | Memoization | Tabulation ✅ | recursion-memoization-tabulation-by-shad-yaj6 | _____\n\nUp Vote if Helps\n\n_____\n\n# Recursion: 1 TLE \n\nclass Solution { \n public int stoneGameVII(int[] stones) {\n int totalSum=0;\n fo | Shadab_Ahmad_Khan | NORMAL | 2023-10-06T16:56:48.224404+00:00 | 2023-10-06T16:57:53.030974+00:00 | 359 | false | ______________________________________\n\n**Up Vote if Helps**\n\n______________________________________\n\n# Recursion: 1 *TLE* \n```\nclass Solution { \n public int stoneGameVII(int[] stones) {\n int totalSum=0;\n for(int i=0; i<stones.length ; i++){\n totalSum+=stones[i];\n }\n return stoneGameVII(stones,totalSum,0,stones.length-1,1);\n }\n public int stoneGameVII(int[] stones, int totalSum, int si, int ei, int isAlice) {\n if(si>ei){\n return 0;\n }\n if(isAlice==1){\n int a = totalSum-stones[si] + stoneGameVII(stones,totalSum-stones[si],si+1,ei,0);\n int b = totalSum-stones[ei] + stoneGameVII(stones,totalSum-stones[ei],si,ei-1,0);\n return Math.max(a,b);\n }else{ \n int a = stoneGameVII(stones,totalSum-stones[si],si+1,ei,1) - (totalSum-stones[si]); \n int b = stoneGameVII(stones,totalSum-stones[ei],si,ei-1,1) - (totalSum-stones[ei]);\n return Math.min(a,b);\n }\n } \n}\n```\n\n_________________________\n\n\n# Recursion : 2 *TLE* \n```\nclass Solution {\n public int stoneGameVII(int[] stones) {\n int totalSum=0;\n for(int i=0; i<stones.length ; i++){\n totalSum+=stones[i];\n }\n return stoneGameVII(stones,totalSum,0,stones.length-1);\n }\n public int stoneGameVII(int[] stones, int totalSum, int si, int ei) {\n if(si>ei || totalSum<=0){\n return 0;\n }\n int a = (totalSum-stones[si])-stoneGameVII(stones,totalSum-stones[si],si+1,ei);\n int b = (totalSum-stones[ei])-stoneGameVII(stones,totalSum-stones[ei],si,ei-1);\n return Math.max(a,b);\n } \n}\n```\n\n_________________________\n\n\n\n# Memoization\n```\nclass Solution {\n Integer[][] memo;\n public int stoneGameVII(int[] stones) {\n int totalSum=0;\n for(int i=0; i<stones.length ; i++){\n totalSum+=stones[i];\n }\n memo=new Integer[stones.length][stones.length];\n return stoneGameVII(stones,totalSum,0,stones.length-1);\n }\n public int stoneGameVII(int[] stones, int totalSum, int si, int ei) {\n if(si>ei || totalSum<=0){\n return 0;\n }\n if(memo[si][ei]!=null){\n return memo[si][ei];\n }\n int a = (totalSum-stones[si])-stoneGameVII(stones,totalSum-stones[si],si+1,ei);\n int b = (totalSum-stones[ei])-stoneGameVII(stones,totalSum-stones[ei],si,ei-1);\n return memo[si][ei] = Math.max(a,b);\n } \n}\n```\n\n_________________________\n\n# Tabulation\n```\nclass Solution {\n public int stoneGameVII(int[] stones) {\n int[] preSum=new int[stones.length];\n preSum[0]=stones[0];\n for(int i=1; i<stones.length ; i++){\n preSum[i]=preSum[i-1]+stones[i];\n }\n int[][] dp=new int[stones.length][stones.length]; \n for(int i=dp.length-1 ; i>=0 ; i--){\n for(int j=0; j<dp[0].length ; j++){\n if(i>=j){\n dp[i][j]=0;\n }else if(i+1==j){\n dp[i][j]=Math.max(stones[i],stones[j]);\n }else{\n int a =(preSum[j]-preSum[i])-dp[i+1][j];\n int b = (preSum[j-1]-(i==0 ? 0 : preSum[i-1]))-dp[i][j-1];\n dp[i][j] = Math.max(a,b);\n }\n }\n }\n return dp[0][dp.length-1];\n } \n}\n```\n\n______________________________________\n\n**Up Vote if Helps**\n\n______________________________________ | 3 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Java'] | 0 |
stone-game-vii | C++ || Memoization || Easy to Understand | c-memoization-easy-to-understand-by-yash-z9x9 | ```\nclass Solution {\npublic:\n int solve(vector &a,int i,int j,int sum,bool isAliceTurn,vector> &dp)\n {\n if(i>j)\n {\n // if | yashagrawal81930 | NORMAL | 2021-09-10T05:39:19.850344+00:00 | 2021-09-10T05:39:19.850379+00:00 | 236 | false | ```\nclass Solution {\npublic:\n int solve(vector<int> &a,int i,int j,int sum,bool isAliceTurn,vector<vector<int>> &dp)\n {\n if(i>j)\n {\n // if there is no element in array then Alice and Bob\'s scores are 0\n // So the difference is also 0\n return 0;\n }\n if(dp[i][j]!=-1)\n {\n //if ans is previously computed then return \n return dp[i][j];\n }\n if(isAliceTurn)\n {\n \n //the recursive function returns the score diff and Alice wants to maximise it so he will add his score in the diff\n \n \n int op1=solve(a,i+1,j,sum-a[i],!isAliceTurn,dp)+(sum-a[i]); //choose from start\n int op2=solve(a,i,j-1,sum-a[j],!isAliceTurn,dp)+(sum-a[j]); //choose from end\n return dp[i][j]=max(op1,op2); //return the max diff as Alice wants\n }\n else //it\'s Bob turn\n {\n //the recursive function returns the score diff and Bob wants to maximise it so he will subtract his score from the diff\n \n int op1=solve(a,i+1,j,sum-a[i],!isAliceTurn,dp)-(sum-a[i]); //choose from start\n int op2=solve(a,i,j-1,sum-a[j],!isAliceTurn,dp)-(sum-a[j]); //choose from end\n return dp[i][j]=min(op1,op2); //return the min diff as Bob wants\n }\n }\n int stoneGameVII(vector<int>& a) {\n int n=a.size();\n int sum=0;\n for(auto i:a)\n {\n sum+=i;\n }\n vector<vector<int>> dp(1001,vector<int>(1001,-1));\n return solve(a,0,n-1,sum,true,dp);\n \n }\n}; | 3 | 0 | [] | 1 |
stone-game-vii | C++ Solution || DP || Easy Understanding | c-solution-dp-easy-understanding-by-kann-jbwj | \nclass Solution {\npublic:\n int helper(int l, int r, vector<int>& stones, int sum, vector<vector<int>>& dp){\n if(l == r) return 0; //array has 1 el | kannu_priya | NORMAL | 2021-06-11T17:51:26.325475+00:00 | 2021-06-11T17:51:52.841082+00:00 | 391 | false | ```\nclass Solution {\npublic:\n int helper(int l, int r, vector<int>& stones, int sum, vector<vector<int>>& dp){\n if(l == r) return 0; //array has 1 element\n if(r-l == 1) return max(stones[l], stones[r]); // array has 2 elements\n if(dp[l][r] != -1) return dp[l][r]; //memorization\n int left_remove = sum - stones[l] - helper(l+1, r, stones, sum-stones[l], dp);\n int right_remove = sum - stones[r] - helper(l, r-1, stones, sum-stones[r], dp);\n return dp[l][r] = max(left_remove, right_remove);\n }\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size(), sum = 0;\n vector<vector<int>>dp(n,vector<int>(n, -1));\n for(int i = 0; i < n; i++) sum += stones[i];\n return helper(0, n-1, stones, sum, dp);\n } \n};\n``` | 3 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
stone-game-vii | [Python] O(n^2) Accepted Submission (with comments) | python-on2-accepted-submission-with-comm-mhj7 | \nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n if n==0:\n return 0\n total = sum(s | rajat499 | NORMAL | 2021-06-11T17:02:12.619184+00:00 | 2021-06-11T17:02:12.619228+00:00 | 115 | false | ```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n if n==0:\n return 0\n total = sum(stones)\n \n dp = [[-1]*n for _ in range(n)]\n ##Maximum difference the current player can achieve when stones[i:j](included) are left\n ##Curr is sum of all stones[i:j]\n def helper(i, j, curr):\n if i>=j:\n return 0\n if dp[i][j] != -1:\n return dp[i][j]\n ##The player picks ith stone and with remaining stones other player tries to maximize the difference from his/her perspective\n opt1 = (curr - stones[i]) - helper(i+1, j, curr-stones[i])\n ##The player picks jth stone and with remaining stones other player tries to maximize the difference from his/her perspective\n opt2 = (curr - stones[j]) - helper(i, j-1, curr-stones[j])\n dp[i][j] = max(opt1, opt2)\n return dp[i][j]\n \n return helper(0, n-1, total)\n``` | 3 | 0 | [] | 0 |
stone-game-vii | Whoever thought that I would see this day, that python wouldn't pass and java would make way. | whoever-thought-that-i-would-see-this-da-7yei | \nclass Solution {\n \n static int solve(int i,int j , int score,int [] stones,int [][] dp){\n if (i == stones.length || j < 0 ){\n retu | bismeet | NORMAL | 2021-06-11T08:54:45.870430+00:00 | 2021-06-11T08:54:45.870462+00:00 | 446 | false | ```\nclass Solution {\n \n static int solve(int i,int j , int score,int [] stones,int [][] dp){\n if (i == stones.length || j < 0 ){\n return 0;\n }\n if (dp[i][j]!=-1){\n return dp[i][j];\n }\n int best = 0;\n int op1 = score - stones[i] - solve(i+1,j,score - stones[i],stones,dp);\n int op2 = score - stones[j] - solve(i,j-1,score - stones[j],stones,dp);\n int best1 = Math.max(op1,op2);\n best = Math.max(best,best1);\n dp[i][j] = best;\n return dp[i][j];\n \n }\n \n public int stoneGameVII(int[] stones) {\n \n int N = stones.length;\n \n int [][] dp= new int [N][N];\n for(int i = 0; i < N; i++){\n for (int j = 0; j < N ;j++){\n dp[i][j] = -1;\n }\n }\n \n int total = 0;\n for (int i = 0 ; i < N ; i++){\n total+=stones[i];\n }\n \n return solve(0,N-1,total,stones,dp);\n \n \n }\n}\n``` | 3 | 0 | ['Java'] | 1 |
stone-game-vii | [JAVA] Dp + Memoization | java-dp-memoization-by-ziddi_coder-y3r5 | \tclass Solution {\n\t\tpublic int stoneGameVII(int[] stones) {\n\n\t\t\tint n = stones.length, sum = 0;\n\n\t\t\tint[][] dp = new int[n][n];\n\n\t\t\tfor(int i | Ziddi_Coder | NORMAL | 2020-12-13T08:40:41.381237+00:00 | 2020-12-13T08:41:03.894339+00:00 | 177 | false | \tclass Solution {\n\t\tpublic int stoneGameVII(int[] stones) {\n\n\t\t\tint n = stones.length, sum = 0;\n\n\t\t\tint[][] dp = new int[n][n];\n\n\t\t\tfor(int i = 0;i<n;i++) \n\t\t\t Arrays.fill(dp[i], -1);\n\n\t\t\tfor(int i = 0;i<n;i++) \n\t\t\t sum += stones[i];\n\n\t\t\treturn solve(0, n-1, stones, sum, dp);\n\t\t}\n\n\t\tpublic int solve(int i, int j, int[] stones, int sum, int[][] dp) {\n\t\t\tif(i >= j) \n\t\t\t return 0;\n\n\t\t\tif(j - i == 1) \n\t\t\t return Math.max(stones[i], stones[j]);\n\n\t\t\tif(dp[i][j] != -1) \n\t\t\t return dp[i][j];\n\n\t\t\treturn dp[i][j] = Math.max(sum - stones[i] - solve(i+1, j, stones, sum - stones[i], dp), \n\t\t\t\t\t\t\t\t\t sum - stones[j] - solve(i, j-1, stones, sum - stones[j], dp)); \n\t\t}\n\t} | 3 | 0 | [] | 0 |
stone-game-vii | Interval dynamic programming solution with tracing bottom-up approach | interval-dynamic-programming-solution-wi-sniz | IntuitionThis problem falls under Interval DP problem, where we progressively break down a larger interval into smaller intervals. The idea is to compute the op | MO-Harm | NORMAL | 2025-03-01T13:35:00.766696+00:00 | 2025-03-01T13:35:00.766696+00:00 | 83 | false | # Intuition
This problem falls under [Interval DP problem](https://algo.monster/problems/dp_interval_intro), where we progressively break down a larger interval into smaller intervals. The idea is to compute the optimal strategy for Alice and Bob as they remove stones from either end.
# Approach
1. Compute the prefix sum to efficiently calculate the sum of any subarray in $$O(1)$$.
1. Start processing subarrays of length 2 (the smallest playable intervals) and progressively increase the interval size.
1. Iterate over all possible subarrays:
1 - length 2 : [0,1] , [1,2] , [2,3] , [3,4]
2 - length 3 : [0,2], [1,3] , [2,4]
3 - length 4 : [0,3], [1,4]
4 - length 5 : [0,4]
Let’s assume Alice starts first with the entire array [0,4]. She can choose either the leftmost or rightmost stone, increasing her score by the remaining sum. Then, Bob plays optimally, removing another stone and maximizing his score.
Since both players are playing optimally, we need to compute their score difference recursively.
To solve this efficiently, we use dynamic programming:
# **Transition**:
- Option 1: Remove the leftmost stone → The score gained is sum of remaining elements, minus the best Bob can achieve.
- Option 2: Remove the rightmost stone → The score gained is sum of remaining elements, minus the best Bob can achieve.
- Take the maximum of the two options to get the optimal strategy.
# Complexity
- Time complexity:
$$O(n^2)$$
- Space complexity:
- $$O(n^2)$$ + $$O(n)$$ for the prefix sum.
```java []
class Solution {
public int stoneGameVII(int[] stones) {
int n = stones.length;
int [] prefix = new int[n + 1];
prefix[0] = 0;
for (int i = 1; i <= n; i++) {
prefix[i] = prefix[i - 1] + stones[i - 1];
}
int [][] dp = new int[n][n];
for(int IntervalSteps = 2; IntervalSteps <= n; IntervalSteps++){
for(int LeftPointer = 0; LeftPointer <= n - IntervalSteps; LeftPointer++){
int RightPointer = LeftPointer + IntervalSteps - 1;
int removeMostLeftItem = prefix[RightPointer + 1] - prefix[LeftPointer + 1] - dp[LeftPointer + 1][RightPointer];
int removeMostRightItem = prefix[RightPointer] - prefix[LeftPointer] - dp[LeftPointer][RightPointer - 1 ];
dp[LeftPointer][RightPointer] = Math.max(removeMostLeftItem , removeMostRightItem);
}
}
return dp[0][n - 1];
}
}
``` | 2 | 0 | ['Dynamic Programming', 'Java'] | 0 |
stone-game-vii | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-b1s3 | Recursion && Memoization\n\n Time Complexity :- O(N * N)\n\n Space Complexity :- O(N * N)\n\n\nclass Solution {\npublic:\n \n // declare a prefix array\n | __KR_SHANU_IITG | NORMAL | 2022-09-16T07:00:14.174220+00:00 | 2022-09-16T07:00:14.174262+00:00 | 1,303 | false | * ***Recursion && Memoization***\n\n* ***Time Complexity :- O(N * N)***\n\n* ***Space Complexity :- O(N * N)***\n\n```\nclass Solution {\npublic:\n \n // declare a prefix array\n \n vector<int> prefix_sum;\n \n // declare a dp\n \n vector<vector<int>> dp;\n \n int helper(vector<int>& stones, int start, int end)\n {\n // base case\n \n if(start >= end)\n {\n return 0;\n }\n \n // if already calculated\n \n if(dp[start][end] != -1)\n {\n return dp[start][end];\n }\n \n // remove from start\n \n int start_score = prefix_sum[end] - prefix_sum[start] - helper(stones, start + 1, end);\n \n // remove from end\n \n int end_score = 0;\n \n if(end - 1 >= 0)\n {\n end_score += prefix_sum[end - 1];\n }\n \n if(start - 1 >= 0)\n {\n end_score -= prefix_sum[start - 1];\n }\n \n end_score -= helper(stones, start, end - 1);\n \n // take the maximum from both start_score and end_score\n \n return dp[start][end] = max(start_score, end_score);\n }\n \n int stoneGameVII(vector<int>& stones) {\n \n int n = stones.size();\n \n // fill prefix_sum array\n \n prefix_sum.resize(n, 0);\n \n prefix_sum[0] = stones[0];\n \n for(int i = 1; i < n; i++)\n {\n prefix_sum[i] = prefix_sum[i - 1] + stones[i];\n }\n \n // resize dp\n \n dp.resize(n + 1);\n \n // initialize dp with -1\n \n dp.assign(n + 1, vector<int> (n + 1, -1));\n \n return helper(stones, 0, n - 1);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 0 |
stone-game-vii | C++ || RECURSION + MEMOIZATION + PREFIX_SUM | c-recursion-memoization-prefix_sum-by-ea-lafm | ```\nclass Solution {\npublic:\n int dp[1001][1001];\n \n \n int solve(vector& stones, int i, int j, vector& pre_sum){\n if(i >= j) return 0; | Easy_coder | NORMAL | 2022-03-29T15:55:24.248201+00:00 | 2022-03-29T15:55:24.248246+00:00 | 291 | false | ```\nclass Solution {\npublic:\n int dp[1001][1001];\n \n \n int solve(vector<int>& stones, int i, int j, vector<int>& pre_sum){\n if(i >= j) return 0;\n if(i + 1 == j) return max(stones[i], stones[j]);\n if(dp[i][j] != -1) return dp[i][j];\n // option 1 to choose the ith index value\n \n \n int op1;\n op1 = pre_sum[j] - pre_sum[i] - solve(stones, i + 1, j, pre_sum);\n \n \n \n \n // option 2 to choose the jth index value\n int op2;\n op2 = pre_sum[j-1] - (i == 0 ? 0 : pre_sum[i-1]) - solve(stones, i, j - 1, pre_sum);\n \n return dp[i][j] = max(op1, op2);\n }\n \n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n memset(dp, -1, sizeof(dp));\n vector<int> pre_sum(n,0);\n pre_sum[0] = stones[0];\n for(int i =1; i<n; i++){\n pre_sum[i] = stones[i] + pre_sum[i-1];\n } \n return solve(stones, 0, n - 1, pre_sum);\n }\n}; | 2 | 0 | ['Recursion', 'Memoization', 'C', 'Prefix Sum'] | 0 |
stone-game-vii | Cpp solution Recursion/DP (beats 98%/97%) | cpp-solution-recursiondp-beats-9897-by-d-le9x | Let the total sum of elements in array be "sum", then if Alice selects (say) i\'th element then Alice\'s current score is "sum-stones[i]". Now if Bob selects sa | dreamer4346 | NORMAL | 2021-06-12T09:57:52.065461+00:00 | 2021-06-12T09:58:52.273502+00:00 | 115 | false | Let the total sum of elements in array be "sum", then if Alice selects (say) i\'th element then Alice\'s current score is **"sum-stones[i]"**. Now if Bob selects say some k\'th element (which can be either i+1\'th or j\'th) then Bob\'s current score would be Alice\'s current-stones[k], i.e.**"sum-stones[i]-stones[k]"**. \nSo now the difference between their scores is, **(sum-stones[i])-(sum-stones[i]-stones[k])** which is equal to **stones[k]**, i.e. the stone that bob selected. So, ultimately the difference in scores is just the stones that bob selected and thus bob would want to minimize his stone selection score, which in turn means Alice will also want to minimize her score so that the difference could increase. So just finding what is the minimum score that Bob can get or subtracting the minimum score that ALice can get from total sum will give us the difference.\n```\nclass Solution {\npublic:\n int a[1001][1001];\n int solve(int i, int j, vector<int> &v)\n {\n if(i>j)\n return 0;\n if(a[i][j]!=0)\n return a[i][j];\n return a[i][j]=min(v[i]+max(solve(i+2, j, v), solve(i+1, j-1, v)), v[j]+max(solve(i+1, j-1, v), solve(i, j-2, v)));\n }\n int stoneGameVII(vector<int>& stones) {\n memset(a, 0, sizeof(a));\n int n=stones.size();\n int sum=accumulate(stones.begin(), stones.end(), 0);\n int small=solve(0, n-1, stones);\n //cout<<small<<endl;\n return sum-small;\n }\n};\n```\nAny suggestions and comments on improving the code would be welcomed. | 2 | 0 | [] | 0 |
stone-game-vii | Top Down, C++ | Simple | top-down-c-simple-by-digbick_17-r0nd | Calculate the difference directly by subtracting the optimal value chosen by the other player. Store the redundant states in a table.\n\nclass Solution {\npubli | DigBick_17 | NORMAL | 2021-06-11T19:24:59.394297+00:00 | 2021-06-12T05:57:43.090213+00:00 | 270 | false | Calculate the difference directly by subtracting the optimal value chosen by the other player. Store the redundant states in a table.\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n int stoneGameVII(vector<int>& stones) {\n dp.resize(stones.size(),vector<int>(stones.size(),-1));\n int total=0;\n for(int num:stones) total+=num;\n return stoneGameRec(0,stones.size()-1,total,stones);\n }\n int stoneGameRec(int i, int j, int total,vector<int>& stones) {\n if(i>=j) return 0;\n if(dp[i][j]!=-1) return dp[i][j];\n int op1=(total-stones[i]) - stoneGameRec(i+1,j,total-stones[i],stones);\n int op2=(total-stones[j]) - stoneGameRec(i,j-1,total-stones[j],stones);\n return dp[i][j]=max(op1,op2);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
stone-game-vii | Python [Top-down DP] | python-top-down-dp-by-gsan-4j50 | I think this is a quite difficult question even if the code itself is short. We need to use dynamic programming and in order to avoid tracking the solution path | gsan | NORMAL | 2021-06-11T09:11:32.550211+00:00 | 2021-06-11T09:12:50.615928+00:00 | 143 | false | I think this is a quite difficult question even if the code itself is short. We need to use dynamic programming and in order to avoid tracking the solution path for both Alice and Bob the DP should be on differences. \n\nIf we let `dp(i, j)` to be the best possible move for any player\'s turn, then this depends on selecting the max possible score based on current stones minus the min possible score for the subsequent interval. So unlike most other interval DP problems of sort `dp(i, j) = ... + f(dp(i + 1, j), dp(i, j-1))` here we have `dp(i, j) = ... - f(dp(i + 1, j), dp(i, j-1)` and this sign keeps flipping between calls, making it a max-min problem as expected.\n\nTime: `O(N^2)`\nSpace: `O(N^2)`\nThe complexity is quadratic, as there are N-choose-2 intervals.\n\n**Caution:** There seems to be a platform-specific issue when it comes to python top-down DP using lru_cache. Below I was able to get AC using `lru_cache(65536)` instead of `lru_cache(None)`. \n\n```python\nclass Solution:\n def stoneGameVII(self, stones):\n prefix = list(accumulate(stones, initial = 0))\n \n @lru_cache(65536)\n def dp(i, j):\n if i == j: \n return 0\n return max(prefix[j + 1] - prefix[i + 1] - dp(i + 1, j), \\\n prefix[j] - prefix[i] - dp(i, j - 1))\n \n return dp(0, len(stones) - 1)\n``` | 2 | 2 | [] | 1 |
stone-game-vii | [Python] Space optimized DP: 99% speed | python-space-optimized-dp-99-speed-by-kc-9vjb | This problem is almost equivalent to problem 486, and even has the same DP equation:\nDP[i][j] is the difference in scores between the next player to move and t | kcsquared | NORMAL | 2021-03-27T14:01:02.172873+00:00 | 2021-03-27T14:01:02.172912+00:00 | 275 | false | This problem is almost equivalent to [problem 486](https://leetcode.com/problems/predict-the-winner/), and even has the same DP equation:\nDP[i][j] is the difference in scores between the next player to move and the other player on the array stones[i .. j]. Then we get\nDP[i][j] = max(score for choosing i - DP[i+1][j], score for choosing j - DP[i][j-1]).\nThe only difference is that score for choosing i is now sum(stones[i..j]) - stones[i]: we still want to know DP[0][n-1]\n\nUsing the 1D dp trick (only store the last row) and computing prefix sums on the fly, we get O(n^2) time, O(n) space:\n\n```python\ndef stoneGameVII(self, stones: List[int]) -> int:\n\tn = len(stones)\n\tdp = [0] * n\n\n\tfor i in range(n - 1, -1, -1):\n\t\tv = stones[i]\n\t\trun_sum = 0\n\n\t\tfor j in range(i + 1, n):\n\t\t\tnew_run = run_sum+stones[j]\n\t\t\tdp[j] = max(new_run - dp[j], run_sum+v - dp[j - 1])\n\t\t\trun_sum = new_run\n\treturn dp[n - 1]\n``` | 2 | 0 | ['Dynamic Programming', 'Python'] | 0 |
stone-game-vii | C++ with logic explanation | c-with-logic-explanation-by-apun_ko_leve-h6cp | Both players want to MAXIMISE difference. \nIt says B wants to minimize absolute difference wrt A, but if consider max() on negative numbers, the lower absolute | apun_ko_level_badhane_ka | NORMAL | 2021-01-29T10:42:16.377369+00:00 | 2021-01-29T11:20:52.223220+00:00 | 218 | false | Both players want to MAXIMISE difference. \nIt says B wants to minimize absolute difference wrt A, but if consider max() on negative numbers, the lower absolute difference gets picked anyway. \n\nSince both players have the same objective (to maximize difference in score), whose chance it is does not matter.\n\nAssuming only the stones in (i,j) range are left.\nif we know the optimal difference for (i,j-1) range and (i+1,j) range respectively, we can find out whether we should pick the ith stone or the jth stone.\n\nTo Calculate for any i to j interval, what will be the optimal stone to pick:\n j==i -> pick ith stone\n j==i+1 -> pick the smaller stone\n j==i+2 -> pick between i and j based on max(sum(i+1,j) - diff(i+1,j) , sum(i,j-1) - diff(i,j-1))\n where diff(i+1,j) is the optimal score difference when only stones in (i+1,j) range are left and both play optimally. \n\tsum(i+1,j) are the points obtained on picking ith stone(sum of remaining stones).\n\nSo now build diff(i,j) using dynamic programming and then return diff(0,n-1) which will be the answer\n\n```\nclass Solution {\npublic:\n /*\n\n */\n int stoneGameVII(vector<int>& stones) {\n \n int n = stones.size();\n \n int diff[n][n];\n memset(diff,0,sizeof(diff));\n \n int sum[n][n];\n for(int i=0;i<n;i++) sum[i][i] = stones[i];\n \n \n // for(int i=0;i)\n for(int l=2;l<=n;l++)\n {\n for(int i=0;i<=n-l;i++)\n {\n int j = i+l-1;\n sum[i][j] = stones[j] + sum[i][j-1];\n }\n }\n \n for(int l=2;l<=n;l++)\n {\n for(int i=0;i<=n-l;i++)\n {\n int j = i+l-1;\n diff[i][j] = max(sum[i+1][j]-diff[i+1][j],sum[i][j-1]-diff[i][j-1]);\n }\n }\n\n return diff[0][n-1];\n \n }\n};\n``` | 2 | 0 | [] | 0 |
stone-game-vii | java memo | java-memo-by-prateekvortex-r4rs | \nclass Solution {\n int dp[][];\n int help(int arr[],int start,int end,int total){\n if(start>end)\n return 0;\n if(dp[start][en | prateekvortex | NORMAL | 2021-01-20T12:18:22.647327+00:00 | 2021-01-20T12:18:22.647357+00:00 | 336 | false | ```\nclass Solution {\n int dp[][];\n int help(int arr[],int start,int end,int total){\n if(start>end)\n return 0;\n if(dp[start][end]!=-1)\n return dp[start][end];\n \n \n return dp[start][end]= Math.max(total-arr[start]-help(arr,start+1,end,total-arr[start]),total-arr[end]-help(arr,start,end-1,total-arr[end]));\n }\n public int stoneGameVII(int[] stones) {\n dp=new int[stones.length][stones.length];\n for(int i[]:dp){\n Arrays.fill(i,-1);\n }\n int sum=0;\n for(int i:stones){\n sum+=i;\n }\n return help(stones,0,stones.length-1,sum);\n }\n}\n``` | 2 | 0 | ['Memoization', 'Java'] | 1 |
stone-game-vii | Javascript | Simple DP (no prefix sum needed) Solution | beats 100% | javascript-simple-dp-no-prefix-sum-neede-m6y9 | Create a dynamic programming solution matrix dp filled with solutions dp[i][j] where i and j represent the left and right positions of the remaining stones.\n\n | sgallivan | NORMAL | 2020-12-29T19:31:20.112300+00:00 | 2020-12-29T19:36:10.859678+00:00 | 208 | false | Create a dynamic programming solution matrix **dp** filled with solutions **dp[i][j]** where **i** and **j** represent the left and right positions of the remaining stones.\n\nIterate through **i** backwards in order to avoid having to build a prefix sum array beforehand, as you can just increment the **sum** value as you loop through **j**.\n\nFor each new **dp** value, find the max option between the next two possible **dp** values (**dp[i+1][j]** or **dp[i][j+1]**), but use the *difference* from the next **dp** value instead of the *sum* of both to adjust for the fact that successive turns represent competing scores.\n\n```\n\nvar stoneGameVII = function(s) {\n let len = s.length, dp = new Array(len).fill().map(_ => new Array(len).fill(0))\n for (let i = len - 2; ~i; i--)\n for (let j = i + 1, sum = s[i] + s[j]; j < len; sum += s[++j])\n dp[i][j] = Math.max(sum - s[i] - dp[i+1][j], sum - s[j] - dp[i][j-1])\n return dp[0][len-1]\n};\n``` | 2 | 0 | ['Dynamic Programming', 'JavaScript'] | 0 |
stone-game-vii | Javascript Memoization with clear code | javascript-memoization-with-clear-code-b-uzis | The main point is spotting the subproblem.\n\nOptimal diff with array between i, j = Max(\n Score when i + 1 is removed - Optimal diff with array between i + | itssumitrai | NORMAL | 2020-12-14T19:09:53.205052+00:00 | 2020-12-14T19:10:29.295924+00:00 | 148 | false | The main point is spotting the subproblem.\n\nOptimal diff with array between i, j = Max(\n Score when i + 1 is removed - Optimal diff with array between i + 1,j,\n Score when j - 1 is removed - Optimal diff with array between i, j - 1\n);\nIts a simple recursion equation at this point, and there would be alot of duplicate calls so better apply memoization.\n\n```js\n/**\n * Returns sum between start index & end index\n */\nconst getSum = (start, end, prefixSums) => {\n return prefixSums[end + 1] - prefixSums[start];\n}\n\n/**\n * calculates optimal diff between start index & end index\n **/\nconst calculateDiff = (start, end, prefixSums, dp) => {\n if (start === end) {\n // if start & end is the same diff would always be 0 as the player would remove the stone and score won\'t change.\n return 0;\n }\n\n if (!dp[start]) {\n dp[start] = [];\n }\n\n if (!dp[start][end]) {\n dp[start][end] = Math.max(\n getSum(start + 1, end, prefixSums) - calculateDiff(start + 1, end, prefixSums, dp),\n getSum(start, end - 1, prefixSums) - calculateDiff(start, end - 1, prefixSums, dp)\n );\n }\n\n return dp[start][end];\n}\n\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar stoneGameVII = function(stones) {\n // First calculate prefix sums\n const prefixSums = [0];\n for (let i = 1;i <= stones.length;i++) {\n prefixSums[i] = stones[i - 1] + prefixSums[i - 1];\n }\n\n // Now calculate optimal diff between 0 and stones.length - 1\n return calculateDiff(0, stones.length - 1, prefixSums, []);\n};\n``` | 2 | 0 | [] | 0 |
stone-game-vii | [Python] Clear DFS Solution with Video Explanation | python-clear-dfs-solution-with-video-exp-hia8 | Video with clear visualization and explanation:\nhttps://youtu.be/MwLSDvmkGGY\n\n\n\nIntuition: dfs+memo\n\n\nCode\nInspired by https://leetcode.com/problems/st | iverson52000 | NORMAL | 2020-12-13T21:38:31.193235+00:00 | 2020-12-13T21:38:31.193288+00:00 | 371 | false | Video with clear visualization and explanation:\nhttps://youtu.be/MwLSDvmkGGY\n\n\n\nIntuition: dfs+memo\n\n\n**Code**\nInspired by https://leetcode.com/problems/stone-game-vii/discuss/970268/C%2B%2BPython-O(n-*-n)\n```\nfrom itertools import accumulate\n\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n memo = [[0]*n for _ in range(n)]\n sums = [0]+list(accumulate(stones))\n \n def dfs(l, r) -> int:\n if l == r: return 0\n if memo[l][r] == 0:\n range_sum = sums[r+1]-sums[l]\n memo[l][r] = max(range_sum-stones[l]-dfs(l+1, r), range_sum-stones[r]-dfs(l, r-1))\n \n return memo[l][r]\n \n res = dfs(0, n-1)\n return res\n```\n\nTime: O(n*n)\n\n\nFeel free to subscribe to my channel. More LeetCoding videos coming up! | 2 | 0 | ['Python'] | 1 |
stone-game-vii | C++, Top-Down DP, O(n*n), Basic logic of game solving | c-top-down-dp-onn-basic-logic-of-game-so-iue5 | Logic used - \n1. Every time a player has to make a turn, he/she has 2 choices i.e whether to start from leftmost element or the rightmost element.\n2. Alice is | kakashi_98 | NORMAL | 2020-12-13T08:20:02.344915+00:00 | 2020-12-13T08:20:02.344951+00:00 | 213 | false | Logic used - \n1. Every time a player has to make a turn, he/she has 2 choices i.e whether to start from leftmost element or the rightmost element.\n2. Alice is trying to increase the difference so his score at every step will always be to "add" to the overall difference, so take the MAX of the 2 next states, choosing leftmost or choosing rightmost.\n3. Bob is trying to decrease the differenec so his score at every step will always be to "reduce" the overall difference, so take the MIN of the 2 next states, choosing leftmost or choosing rightmost.\n4. The total number of states are ```number of possible subarrays*2 ``` . Multiplies by 2 because every [start,end] can come for each player.\n\nprefix array is used to get the score[start-end] in O(1) time;\nturn = true means that alice is playing\nturn = false means that bob is playing\n\nPS : if you use ```vector<vector<vector<int>>> dp```, you will get TLE, that is way I used arrays.\n\n```\nclass Solution {\npublic:\n int dp[1001][1001][2] = {};\n int prefix[1001];\n int fn(int s,int e,bool turn){\n if(s==e) return 0;\n \n int curr = 0;\n if(!turn) curr = 1;\n if(dp[s][e][curr]!=0) return dp[s][e][curr];\n \n if(turn){\n int first = fn(s+1,e,!turn) + prefix[e]-prefix[s];\n int second = fn(s,e-1,!turn) + prefix[e-1]-((s-1>=0) ? prefix[s-1] : 0);\n dp[s][e][0] = max(first,second);\n return dp[s][e][0];\n }\n else{\n int first = fn(s+1,e,!turn) - (prefix[e]-prefix[s]);\n int second = fn(s,e-1,!turn) - (prefix[e-1]-((s-1>=0) ? prefix[s-1] : 0));\n dp[s][e][1] = min(first,second);\n return dp[s][e][1];\n }\n }\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n prefix[0] = stones[0];\n for(int i=1;i<n;i++) prefix[i] = prefix[i-1] + stones[i];\n return fn(0,n-1,true);\n } \n};\n``` | 2 | 1 | ['Dynamic Programming', 'C'] | 2 |
stone-game-vii | JAVA | DP | 6% | | java-dp-6-by-idbasketball08-n21l | ```\nclass Solution {\n public int stoneGameVII(int[] stones) {\n //strategy: DP\n //precompute the sum\n int sum = 0;\n for (int | idbasketball08 | NORMAL | 2020-12-13T04:20:05.641427+00:00 | 2020-12-14T04:32:28.142491+00:00 | 228 | false | ```\nclass Solution {\n public int stoneGameVII(int[] stones) {\n //strategy: DP\n //precompute the sum\n int sum = 0;\n for (int stone : stones) {\n sum += stone;\n }\n int n = stones.length;\n Integer[][][] dp = new Integer[n][n][2];\n return helper(stones, dp, 0, n - 1, sum, 0);\n }\n public int helper(int[] stones, Integer[][][] dp, int f, int b, int sum, int person) {\n //reached base case\n if (f > b) {\n return 0;\n }\n //seen before\n if (dp[f][b][person] != null) {\n return dp[f][b][person];\n }\n //Alice is taking her turn\n if (person == 0) {\n //Alice chooses the first stone and gets the remaining sum\n int x = helper(stones, dp, f + 1, b, sum - stones[f], 1) + (sum - stones[f]);\n //Alice chooses the last stone and gets the remaining sum\n int y = helper(stones, dp, f, b - 1, sum - stones[b], 1) + (sum - stones[b]);\n //find max that Alice can get\n return dp[f][b][person] = Math.max(x, y);\n //Bob is taking his turn\n } else {\n //Bob chooses the first stone and gets the remaining sum\n int x = helper(stones, dp, f + 1, b, sum - stones[f], 0) - (sum - stones[f]);\n //Bob chooses the last stone and gets the remaining sum\n int y = helper(stones, dp, f, b - 1, sum - stones[b], 0) - (sum - stones[b]);\n //find min so that we can subtract from Alice\'s score\n return dp[f][b][person] = Math.min(x, y);\n }\n }\n} | 2 | 0 | [] | 1 |
stone-game-vii | Python -- recursion approach | python-recursion-approach-by-zebratiger4-n35q | def helper(self,stone,tmp=0):\n \n if not stone:\n return 0\n \n \n \n left = tmp - stone[-1] - self.helper | zebratiger4 | NORMAL | 2020-12-13T04:17:45.672975+00:00 | 2020-12-13T04:17:45.673020+00:00 | 163 | false | def helper(self,stone,tmp=0):\n \n if not stone:\n return 0\n \n \n \n left = tmp - stone[-1] - self.helper(stone[:-1],tmp - stone[-1]) \n right = tmp - stone[0] - self.helper(stone[1:], tmp - stone[0])\n \n \n return max(left,right) \n \n \n def stoneGameVII(self, stones):\n """\n :type stones: List[int]\n :rtype: int\n """\n\n \n if not stones:\n return 0\n \n tmp = sum(stones)\n res = self.helper(stones,tmp)\n \n \n return res | 2 | 0 | [] | 0 |
stone-game-vii | Python 3 Simple DP Solution in O(n^2) | python-3-simple-dp-solution-in-on2-by-d_-vg10 | Similar to what we saw in previous Stone Game, we can take use of choosing from the left/right margin. In each turn, no matter who is choosing, we want to find | d_8023_k | NORMAL | 2020-12-13T04:08:57.504555+00:00 | 2020-12-13T04:08:57.504589+00:00 | 110 | false | Similar to what we saw in previous Stone Game, we can take use of choosing from the left/right margin. In each turn, no matter who is choosing, we want to find the optimal case:\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n length = len(stones)\n csum = [0 for _ in range(length+1)]\n for i in range(length):\n csum[i+1] = csum[i] + stones[i]\n dp = [[0 for _ in range(length)] for _ in range(length)]\n for j in range(1, length):\n for i in range(j-1, -1, -1):\n left = csum[j+1] - csum[i+1] - dp[i+1][j]\n right = csum[j] - csum[i] - dp[i][j-1]\n dp[i][j] = max(left, right)\n return dp[0][length-1]\n``` | 2 | 1 | [] | 1 |
stone-game-vii | [Python] O(n^2) Dynamic Programming | python-on2-dynamic-programming-by-delphi-p48v | Python code:\npython\ndef stoneGameVII(self, A: List[int]) -> int:\n n = len(A)\n pref_s = A.copy() # prefix sum\n for i in range(1, n):\n pref | delphih | NORMAL | 2020-12-13T04:01:26.804372+00:00 | 2020-12-13T04:01:26.804421+00:00 | 600 | false | ## Python code:\n```python\ndef stoneGameVII(self, A: List[int]) -> int:\n n = len(A)\n pref_s = A.copy() # prefix sum\n for i in range(1, n):\n pref_s[i] += pref_s[i-1]\n pref_s.append(0)\n dp = [0] * n\n for step in range(2, n+1):\n for i in range(n-1, step-2, -1):\n dp[i] = max(pref_s[i-1] - pref_s[i-step] - dp[i-1],\n pref_s[i] - pref_s[i-step+1] - dp[i])\n return dp[-1]\n``` | 2 | 0 | ['Dynamic Programming', 'Python'] | 0 |
stone-game-vii | Minimax Approach with Dual Caching for Stone Game VII | minimax-approach-with-dual-caching-for-s-umov | \n# Approach\n Describe your approach to solving the problem. \nThis solution applies a minimax algorithm to solve the Stone Game VII problem, utilizing distinc | _LaVa | NORMAL | 2024-08-21T10:09:02.330021+00:00 | 2024-08-21T10:09:02.330062+00:00 | 153 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis solution applies a minimax algorithm to solve the Stone Game VII problem, utilizing distinct caches for Alice and Bob. The approach involves:\n\n- **Prefix Sum Array:** To efficiently calculate the total sum of stones between any two indices.\n- **Dual Caching:** Separate caching (cacheA and cacheB) for Alice and Bob, improving efficiency by storing results of subproblems based on which player is currently making a move.\n- **Minimax Strategy:** Alice tries to maximize the score difference, while Bob tries to minimize it, using a top-down recursion with memoization to avoid redundant computations.\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n\n prefix = [0]\n for i in range(n):\n prefix.append(prefix[-1] + stones[i])\n \n has_cacheA = [[False] * n for _ in range(n)]\n has_cacheB = [[False] * n for _ in range(n)]\n cacheA = [[0] * n for _ in range(n)]\n cacheB = [[0] * n for _ in range(n)]\n \n def dfs(isAlice, l, r):\n if l > r: \n return 0\n\n if has_cacheA[l][r]:\n return cacheA[l][r]\n if has_cacheB[l][r]:\n return cacheB[l][r]\n\n\n res = float("-inf") if isAlice else float("inf")\n # Total sum of the stones between indices l and r\n total = prefix[r + 1] - prefix[l]\n\n if isAlice:\n res = max(\n res, \n dfs(False, l + 1, r) + total - stones[l],\n dfs(False, l, r - 1) + total - stones[r]\n )\n has_cacheA[l][r] = True\n cacheA[l][r] = res\n\n else:\n res = min(\n res,\n dfs(True, l + 1, r) - (total - stones[l]),\n dfs(True, l, r - 1) - (total - stones[r])\n )\n has_cacheB[l][r] = True\n cacheB[l][r] = res\n\n return res\n\n return dfs(True, 0, n - 1)\n \n``` | 1 | 0 | ['Python3'] | 0 |
stone-game-vii | Easy to Unuderstand || Top Down Solution || Game Theory | easy-to-unuderstand-top-down-solution-ga-m8ag | Intuition\nThe problem at hand involves finding the maximum score difference between two players, Alice and Bob, in a game where they take turns selecting stone | tinku_tries | NORMAL | 2024-06-03T07:12:11.467066+00:00 | 2024-06-03T07:12:11.467086+00:00 | 380 | false | # Intuition\nThe problem at hand involves finding the maximum score difference between two players, Alice and Bob, in a game where they take turns selecting stones from either end of a row. The score for each player is determined by the sum of the stones they select. To solve this, we can use dynamic programming to compute the maximum score difference efficiently.\n\n# Approach\n1. **Dynamic Programming**: Utilize a 2D `dp` array where `dp[st][end]` represents the maximum score difference between two players when the array is restricted to the segment from index `st` to index `end`.\n2. **Recursive Function**: Define a recursive function `f` to compute the maximum score difference for a given segment. The function will:\n - Calculate the score difference between selecting the first or last stone and the remaining segment, recursively calling itself on the updated segment.\n - Use memoization to avoid redundant calculations and improve performance.\n\n# Complexity\n- **Time complexity**: The time complexity is $$O(n^2)$$ because for each pair `(st, end)` we might iterate through all possible split points.\n- **Space complexity**: The space complexity is $$O(n^2)$$ for storing the `dp` array.\n\n# Beats\n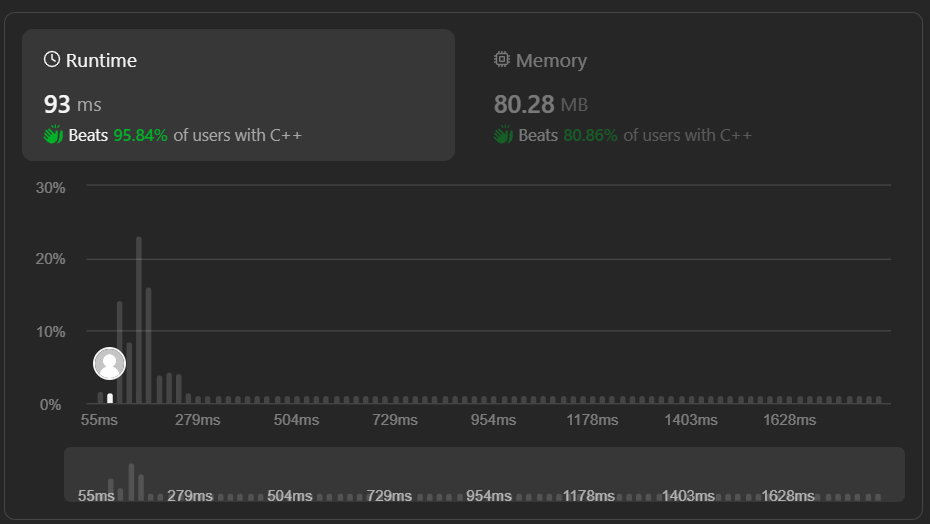\n\n\n# Code\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> dp ;\n int f(vector<int> &v, int st, int end,int sum) {\n if (st >= end || sum <= 0) return 0; // If there is only one stone, the score difference is 0.\n if (dp[st][end] != -1) return dp[st][end]; \n int front_score , end_score ;\n\n front_score = sum - v[st] - f(v , st+1 , end , sum-v[st]) ;\n end_score = sum - v[end] - f(v , st , end-1 , sum-v[end]) ;\n return dp[st][end] = max(front_score , end_score);\n }\n int stoneGameVII(vector<int>& v) {\n int n = v.size() , sum = 0 ;\n for(auto a : v) sum += a ;\n dp.clear() ;\n dp.resize(n + 1, vector<int>(n + 1, -1));\n return f(v , 0 , n-1,sum) ;\n }\n};\n```\n# Note\nThis solution effectively utilizes dynamic programming to calculate the maximum score difference between two players, ensuring optimal performance for larger inputs. | 1 | 0 | ['Array', 'Math', 'Dynamic Programming', 'Game Theory', 'C++'] | 0 |
stone-game-vii | Simple Recursion, there are 2 choices || Hindi Comments | simple-recursion-there-are-2-choices-hin-e128 | Intuition\n Describe your first thoughts on how to solve this problem. \nGame theory ka yhi basics h ki apna max bnao aur saamne wle se expect kro ki vo tumhe w | vaibhavsingh18 | NORMAL | 2023-10-07T06:24:50.320240+00:00 | 2023-10-07T06:24:50.320261+00:00 | 133 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGame theory ka yhi basics h ki apna max bnao aur saamne wle se expect kro ki vo tumhe worst ans laake dega, uske baad bs recursion h \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int dp[1001][1001];\n int solve(vector<int>&nums,int l,int r,int sum)\n {\n if(l>r)\n {\n return 0;\n }\n if(dp[l][r]!=-1)\n {\n return dp[l][r];\n }\n //phle se lia\n int val1=sum-nums[l]-solve(nums,l+1,r,sum-nums[l]);\n //dusre se lia\n int val2=sum-nums[r]-solve(nums,l,r-1,sum-nums[r]);\n //subtract islie qki bob ka score sub krna pdhega, baaki bachi hui array me kah diya bob ko ki apna max utha laa\n return dp[l][r]=max(val1,val2);\n }\n int stoneGameVII(vector<int>& nums) {\n memset(dp,-1,sizeof(dp));\n int l=0;\n int r=nums.size()-1;\n int sum=accumulate(nums.begin(),nums.end(),0);\n return solve(nums,l,r,sum);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Game Theory', 'C++'] | 1 |
stone-game-vii | Time 100% and Memory 100% | time-100-and-memory-100-by-fredrick_li-64qz | Intuition\nNotice that the difference of scores is the sum of all the stones that Bob takes, so for both Alice and Bob, their optimal strategy is to minimize th | Fredrick_LI | NORMAL | 2023-07-27T06:21:20.516288+00:00 | 2023-07-27T06:21:20.516311+00:00 | 151 | false | # Intuition\nNotice that the difference of scores is the sum of all the stones that Bob takes, so for both Alice and Bob, their optimal strategy is to minimize their own sums of stones.\n\n# Approach\nUse dynamic programming from the last step to the first.\n\n# Complexity\n- Time complexity:\n$O(n^2)$\n\n- Space complexity:\n$O(n)$\n\n# Code\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n flag = 1\n lis = list(stones)\n for i in range(1,n):\n for j in range(n - i):\n if flag:\n lis[j] = max(lis[j],lis[j+1])\n else:\n lis[j] = min(lis[j] + stones[j + i],lis[j+1] + stones[j])\n flag ^= 1\n #print(lis)\n return lis[0] if not flag else sum(stones) - lis[0]\n \n``` | 1 | 0 | ['Python3'] | 1 |
stone-game-vii | C++ || Bawaal Question || Fully Explained Intuitions || Memoization || DP | c-bawaal-question-fully-explained-intuit-gnxi | \n// Bawwal Question \n \n // A -> only one element , ans = 0;\n \n // AB -> if we will remove A , we will take B \n // if we will remove | KR_SK_01_In | NORMAL | 2022-08-19T07:18:31.747718+00:00 | 2022-08-19T07:19:53.187869+00:00 | 340 | false | ```\n// Bawwal Question \n \n // A -> only one element , ans = 0;\n \n // AB -> if we will remove A , we will take B \n // if we will remove B , we will take A , ans=max(A , B) in this case\n \n // ABC -> Case 1 if we will remove A , then it will be like B + C - max(func(BC))\n // Case 2 If we will remove C , then it will be like A + C -max(func(AB))\n // answer will be max(case1 , case2) in this .\n\t \n\t // ABCD-> Case 1 if we will remove A , then it will be like B + C + D - max(func(BCD))\n // Case 2 If we will remove D , then it will be like A + B + C -max(func(ABC))\n\t\t // answer will be max(case1 , case2) in this .\n \n // See there are 2 components First -> Adding B+C , Second -> Substracting \n \n //max(its smaller subproblem) , First Components represents taking Alice sum by\n //removing the value , Bob wants to minimise the diff thus by taking max value of \n //its smaller problem(func(BC)) , Our answer will be max (of all the \n //possibiliies) as Alice wants to maximise the diff of the scores , ans will be \n //max( B + C - max(func(BC)) , A + C -max(func(AB)) ). \n \n \n int dp[1004][1004];\n \n \n int func(vector<int> &nums , int i , int j , vector<int> &psum , int n)\n {\n if(i==j)\n {\n // only one stone left , so we have to remove it \n // diff will be zero in this case \n \n return 0;\n }\n \n if(dp[i][j]!=-1)\n {\n return dp[i][j];\n }\n \n // Alice remove from left side \n int Alice_pos1 = psum[j]-psum[i] - func(nums , i+1 , j , psum , n);\n // this func calls which we a re substracting doing the job of BOb , \n //(substracting maximal value of the smaller problem)\n \n // Alice removes from end\n \n int Alice_pos2 = psum[j-1]-psum[i]+nums[i] - func(nums , i , j-1 , psum , n);\n \n int ans=max(Alice_pos1 , Alice_pos2);// Alice wants will take max of 2 possibilty\n \n return dp[i][j]=ans;\n \n }\n \n int stoneGameVII(vector<int>& nums) {\n \n int n=nums.size();\n \n vector<int> psum(n , 0);\n \n psum[0]=nums[0];\n \n for(int i=1;i<n;i++)\n {\n psum[i]=psum[i-1]+nums[i];\n }\n \n memset(dp , -1 , sizeof(dp));\n \n int res=func(nums , 0 , n-1 , psum , n );\n \n return res;\n \n \n }\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 2 |
stone-game-vii | C++ || Top down || Bottom up || Detailed Explanation || Beginner Friendly | c-top-down-bottom-up-detailed-explanatio-pgqq | Code:\n\nTop-Down:\n\n\nclass Solution\n{\npublic:\n vector<vector<int>> memo;\n vector<int> preSum;\n int getSum(int i, int j)\n {\n return | anis23 | NORMAL | 2022-07-20T04:47:18.298285+00:00 | 2022-07-20T04:49:19.909025+00:00 | 457 | false | **Code:**\n\n**Top-Down:**\n\n```\nclass Solution\n{\npublic:\n vector<vector<int>> memo;\n vector<int> preSum;\n int getSum(int i, int j)\n {\n return preSum[j + 1] - preSum[i];\n }\n int dp(int i, int j)\n {\n if (i == j)\n return 0; // only 1 stone, score = 0 -> difference = 0 as well\n if (memo[i][j] != INT_MAX)\n return memo[i][j];\n int s1 = getSum(i + 1, j); // choose ith stone\n int s2 = getSum(i, j - 1); // choose jth stone\n int ans = max(s1 - dp(i + 1, j), s2 - dp(i, j - 1));\n return memo[i][j] = ans;\n }\n int stoneGameVII(vector<int> &stones)\n {\n int n = stones.size();\n memo.assign(n, vector<int>(n, INT_MAX));\n preSum.assign(n + 1, 0);\n for (int i = 0; i < n; i++)\n preSum[i + 1] = preSum[i] + stones[i];\n return dp(0, n - 1);\n }\n};\n```\n\n**Bottom-Up:**\n\n```\nclass Solution\n{\npublic:\n vector<int> preSum;\n int getSum(int left, int right)\n {\n return preSum[right + 1] - preSum[left];\n }\n int stoneGameVII(vector<int> &stones)\n {\n int n = stones.size();\n preSum.assign(n + 1, 0);\n for (int i = 0; i < n; i++)\n preSum[i + 1] = preSum[i] + stones[i];\n\n vector<vector<int>> dp(n, vector<int>(n, 0));\n for (int i = n - 1; i >= 0; i--)\n {\n for (int j = i + 1; j < n; j++)\n {\n int s1 = getSum(i + 1, j); // choose ith stone\n int s2 = getSum(i, j - 1); // choose jth stone\n dp[i][j] = max(s1 - dp[i + 1][j], s2 - dp[i][j - 1]);\n }\n }\n return dp[0][n - 1];\n }\n};\n```\n\n**Method:**\n* alice is trying to maximize the difference\n * in otherwords, she is trying to maximize her score\n* bob is trying to minimize the difference\n * in otherwords, he is trying to maximize his score\n* So, in this problem at any given point both alice and bob are trying to get the maximum score possible\n* Let\'s say there are n=5 stones\n * now, alice starts first\n * so for the whole process\n * ```alice gain = a1 + a3 + a5```\n * ```bob gain = b2 + b4```\n * where\n * ```a1 = sum obtained by alice in the 1st round```\n * ```b2 = sum obtained by bob in the 2nd round```\n * Now,\n * ```diff = (a1+a3+a5)-(b2+b4) for stones[1,5]```\n * Note that,\n * ```a1>b2>a3>b4>a5```\n * why?\n * because each stone[i]>=1\n * so if,\n * ```a1 = stone[i]+....+stone[j]```\n * ```b2 = stone[i+1]+....stone[j] or stone[i]+...stone[j-1]```\n * so it is clear that b2<a1\n * getting back at diff\n * we can rewrite it as\n * ```diff = a1-(b2+b4 -a3-a5)```\n * i.e a1 - (diff for stones[2,5])\n * again,\n * ```diff = a1-(b2-(a3+a5 - b4))```\n * i.e = a1-(b2- (diff for stones[3,5]))\n * so,\n * ```diff = a1-(b2-(a3-(b4-a5)))```\n* in general we can say that,\n* **```diff = current_round_gain - (sub_problem_diff)```**\n* Also, Note that,\n* **we don\'t have to keep track of turns**\n* why?\n * ```Alice goal: maximize the final diff```\n * ```Bob goal : minimuze the final diff```\n * From this\n * **```final diff = a1-(b2-(a3-(b4-a5))) = a1-(subproblem)```**\n * we can see that\n * Alice wants to\n * maximize a1-subproblem,\n * so Alice wants to maximize a3-subproblem due to the double negation.\n * The same goes for Bob.\n * Bob wants to minimize a1-subproblem = final_diff,\n * so Bob wants to maximize b2-subproblem = diff at bob turn,\n * then maximize b4-subproblem due to double negation.\n * (i.e we can say bob will try to maximize the diff at his turn so that the final diff is as min as possible)\n* So,\n* we can conclude that\n* **goal of bob = minimize the final diff**\n* **goal of alice = maximize the final diff**\n* **but at each round both will try to maximize the current diff**\n\n\n**Implementation:**\n\n* ```dp[i][j] = alex_sum - bob_sum = difference```\n* we create a prefixSum array to store the prefixSum\n * ```prefixSum(i) = sum of all the elements from 0 to i(i not included)```\n * ```prefixSum(j) = sum of all the elements from 0 to j(j not included)```\n* so if we want to find sum from index i to j\n * ```sum = prefixSum(j+1)-prefixSum(i)```\n* if alice chooses ith pile:\n * ```diff = sum(i-1,j) - dp[i+1][j]```\n* if alice chooses jth pile:\n * ```diff = sum(i-1,j) - dp[i+1][j]```\n* **ans = dp[0][n-1]**\n | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 0 |
stone-game-vii | C++ Fully Explained | Without Prefix Sum | c-fully-explained-without-prefix-sum-by-bl915 | There is no need to calculate prefix sum.\nFor.eg. Let\'s say the array is\n a1, a2, a3, a4\n\nNow consider alice picks a1\n Again consider bob picks a2, | mjustboring | NORMAL | 2022-07-15T19:56:41.700744+00:00 | 2022-07-15T20:00:39.128460+00:00 | 150 | false | There is no need to calculate prefix sum.\nFor.eg. Let\'s say the array is\n a1, a2, a3, a4\n\nNow consider alice picks a1\n Again consider bob picks a2, then diff will be\n (a2 + a3 + a4) - (a3 + a4) = a2\n i.e. the element which bob picked.\n\nIt can also be checked for others that the difference\nwill always be the value that bob picked.\n\n```\nstruct Solution {\n \n int n, *a;\n int dp[1000][1000];\n \n int f(int i, int j) {\n \n if (i >= j) return 0;\n \n if (dp[i][j] != -1) return dp[i][j];\n/*\n Alice will try to maximize and bob will try to minimize.\n Hence result will be\n max(f(i+1, j), f(i, j-1))\n i.e. max of if she pick left most, or if she pick right most\n\n if alice picks left most (i.e. i)\n then bob can pick either i+1 or j\n i.e. f(i+1, j) will be min( f(i+2, j) + a[i+1], f(i+1, j-1) + a[j] )\n \n \n if alice picks right most (i.e. j)\n then bob can pick either i or j-1\n i.e. f(i, j-1) will be min( f(i+1, j-1) + a[i], f(i, j-2) + a[j-1] )\n*/\n return dp[i][j] = max(\n min( f(i+2, j) + a[i+1], f(i+1, j-1) + a[j] ),\n min( f(i+1, j-1) + a[i], f(i, j-2) + a[j-1] ));\n }\n\n int stoneGameVII(vector<int> &a) {\n \n memset(dp, -1, sizeof dp);\n \n this->a = a.data();\n this->n = a.size();\n \n return f(0, n-1);\n }\n};\n```\nCleaned Solution\n```\nstruct Solution {\n \n int n, *a;\n int dp[1000][1000];\n \n int f(int i, int j) {\n \n if (i >= j) return 0;\n \n if (dp[i][j] != -1) return dp[i][j];\n\n return dp[i][j] = max(\n min( f(i+2, j) + a[i+1], f(i+1, j-1) + a[j] ),\n min( f(i+1, j-1) + a[i], f(i, j-2) + a[j-1] ));\n }\n\n int stoneGameVII(vector<int> &a) {\n \n memset(dp, -1, sizeof dp);\n \n this->a = a.data();\n this->n = a.size();\n \n return f(0, n-1);\n }\n};\n```\n\nTC: O(n\xB2)\nSC: O(n\xB2) (It can be optimized using Tabulation to O(n))\n\nPS: Upvote if found helpful :) | 1 | 0 | [] | 0 |
stone-game-vii | Java Top Down DP Solution | java-top-down-dp-solution-by-zaidzack-jynp | \nclass Solution {\n int[][] dp;\n public int stoneGameVII(int[] stones) {\n int len = stones.length;\n dp = new int[len][len];\n \n | zaidzack | NORMAL | 2022-07-04T18:48:14.494161+00:00 | 2022-07-04T18:48:14.494199+00:00 | 70 | false | ```\nclass Solution {\n int[][] dp;\n public int stoneGameVII(int[] stones) {\n int len = stones.length;\n dp = new int[len][len];\n \n int sum = 0;\n for(int n: stones)\n sum += n;\n \n for(int[] row: dp)\n Arrays.fill(row, -1);\n \n return helper(stones, 0, len - 1, sum, 0);\n }\n \n private int helper(int[] piles, int start, int end, int sum, int player)\n {\n if(start == end) return 0;\n if(dp[start][end] != -1) return dp[start][end];\n // if current player is Alice, we will try to Maximize Alice\'s Score \n if(player == 0)\n { \n int choice1 = sum - piles[start] + helper(piles, start + 1, end, sum - piles[start], 1);\n int choice2 = sum - piles[end] + helper(piles, start, end - 1, sum - piles[end], 1);\n dp[start][end] = Math.max(choice1, choice2);\n }\n\t\t// else we will Minimize Bob\'s Score from the remaining Score\n else\n {\n int choice1 = helper(piles, start + 1, end, sum - piles[start], 0) - (sum - piles[start]);\n int choice2 = helper(piles, start, end - 1, sum - piles[end], 0) - (sum - piles[end]);\n dp[start][end] = Math.min(choice1, choice2);\n }\n \n return dp[start][end];\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 1 |
stone-game-vii | C++ || EASY TO UNDERSTAND || Memoization | c-easy-to-understand-memoization-by-aari-c8ii | \nclass Solution {\npublic:\n int helper(int i,int j,int sum,vector<int> &stones,vector<vector<int>> &dp)\n {\n if(i>j)\n return 0;\n | aarindey | NORMAL | 2022-04-14T13:47:02.390058+00:00 | 2022-04-14T13:47:21.102585+00:00 | 137 | false | ```\nclass Solution {\npublic:\n int helper(int i,int j,int sum,vector<int> &stones,vector<vector<int>> &dp)\n {\n if(i>j)\n return 0;\n if(dp[i][j]!=-1)\n {\n return dp[i][j];\n }\n return dp[i][j]=max(sum-stones[i]-helper(i+1,j,sum-stones[i],stones,dp),sum-stones[j]-helper(i,j-1,sum-stones[j],stones,dp));\n \n return 0;\n }\n int stoneGameVII(vector<int>& stones) {\n int sum=accumulate(stones.begin(),stones.end(),0);\n int n=stones.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n int ans=helper(0,n-1,sum,stones,dp);\n return ans;\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome** | 1 | 0 | [] | 0 |
stone-game-vii | c++|| DP || memoization || Easy to understand | c-dp-memoization-easy-to-understand-by-s-llja | \nclass Solution {\npublic:\n int fun(vector<int>& stones,int i,int j,int sum,vector<vector<int>>&dp)\n {\n if(i>j) return 0;\n \n if | soujash_mandal | NORMAL | 2022-04-14T13:36:14.567387+00:00 | 2022-04-14T13:36:14.567432+00:00 | 76 | false | ```\nclass Solution {\npublic:\n int fun(vector<int>& stones,int i,int j,int sum,vector<vector<int>>&dp)\n {\n if(i>j) return 0;\n \n if(dp[i][j]!=-1) return dp[i][j];\n \n int res=0;\n res=max(res,(sum-stones[i])-fun(stones,i+1,j,sum-stones[i],dp));\n res=max(res,(sum-stones[j])-fun(stones,i,j-1,sum-stones[j],dp));\n dp[i][j]=res;\n return res;\n }\n int stoneGameVII(vector<int>& stones) {\n int sum=accumulate(stones.begin(),stones.end(),0);\n int n=stones.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n return fun(stones,0,stones.size()-1,sum,dp);\n }\n};\n``` | 1 | 0 | [] | 1 |
stone-game-vii | C++ || Bottom-up DP || Beats 99% time and 97% memory | c-bottom-up-dp-beats-99-time-and-97-memo-f0es | Regardless of the problem description, both the strategies of Alice and Bob are the same.\nMaximize the difference(From Bob\'s perspective, difference is define | walaohye | NORMAL | 2022-04-04T04:49:45.187469+00:00 | 2022-04-04T05:08:40.775795+00:00 | 57 | false | Regardless of the problem description, both the strategies of Alice and Bob are the same.\n**Maximize the difference(From Bob\'s perspective, difference is defined as Bob\'s score - Alice\'s score) given the remaing stones**\n```\nint stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n\t\t// Initialize 2 arrays to swap in each iteration\n int *diff = new int[n], *diff2 = new int[n];\n memset(diff, 0, n*sizeof(int));\n\t\t\n\t\t// Calculate prefix sum in order to calculate range sums;\n vector<int> prefix_sum(n+1, 0);\n for (int i=1; i<=n; ++i)\n prefix_sum[i] = stones[i-1] + prefix_sum[i-1];\n\t\t\n for (int i=1; i<n; ++i) {\n for (int j=0; j<n-i; ++j) {\n\t\t\t// new diff[j] would be:\n\t\t\t// max(result of choosing (j+i)th stone, result of choosing jth stone)\n\t\t\t// max(sum(j...j+i-1) - diff(j...j+i-1), sum(j+1...j+i) - diff(j+1...j+i))\n diff2[j] = max((prefix_sum[j+i] - prefix_sum[j] - diff[j]), (prefix_sum[j+i+1] - prefix_sum[j+1] - diff[j+1]));\n }\n swap(diff, diff2);\n }\n\t\t\n return diff[0];\n }\n``` | 1 | 0 | [] | 0 |
stone-game-vii | C++| Topdown Tree Traversal + Memoization | Lots of explanation. | c-topdown-tree-traversal-memoization-lot-38qh | The result of the each turns follows a decision tree:\n\n each turn\'s result is the value of piles[left] or piles[right]\n left, right value follows a patterns | freewind1986 | NORMAL | 2022-03-17T04:50:44.103708+00:00 | 2022-03-17T06:21:39.328788+00:00 | 64 | false | The result of the each turns follows a decision tree:\n\n* each turn\'s result is the value of piles[left] or piles[right]\n* left, right value follows a patterns: if a left stone is taken, the next left is left+1; if a right stone is taken, the next right is right-1\n* each turn is called recursively:\n```\nscore = player\'s score in current turn + recursivefunction (data set, next left, next right, cache, prefixSum)\n```\nIllustration of decision tree\n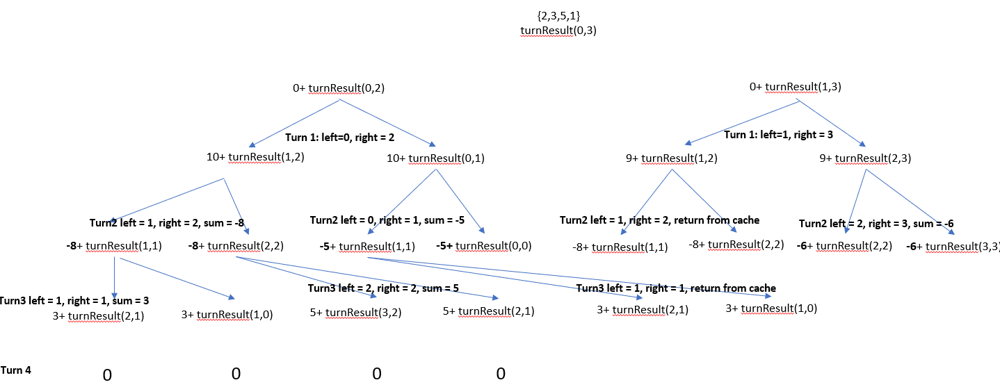\n\n* player\'s score in current turn is calculate by `prefixSum` - that way we don\'t have to run for loop to calculate score.\n```\nfor example: for data set { 5,2,3,1 }\nThe value {5,2,3}, if a player takes 1 is: 5+ 2 + 3 = 10 = (5+2+3+1) - 1 =prefixSum[4] - prefixSum[3]\nThe value {2,3,1} if a player takes 5 is: 2+3+1 = 6 = (5+2+3+1) - 5 = prefixSum[4] - prefixSum[0]\nprefixSum[0] = 0\nprefixSum[1] = 5\nprefixSum[2] = 5+2=7\nprefixSum[3] = 5+2+3=10\nprefixSum[4] = 5+2+3+1=11 // note that prefix sum has size + 1\n``` \n\n* the player turn is identified by even/odd values: Zero turn: game starts; Odd turn: Alice plays, Even turn: Bob plays.\n* the result of each turns is the different = Alice score - Bob score. Thus when Alice plays, score += AliceScore; and when Bob plays, score -=BobScore\n* the final score is returned to original call of recursive funtion , turn 0. \n\nMemoization is implemented: an array cache[left][right] saved a value for later retrieval. It helps pruning the tree: the branch that are repeated will not be visited again; instead, its value is returned from saved cache. Cache is initialized to INT_MAX (must use #include #include <bits/stdc++.h>)\n\nTraversing the tree is topdown. Top = root of tree = turn index = 0 (left =0, right = size of piles -1)\n\nTo further optimizing the run-time, pass by reference is used in recursive function; it saves time from making copy of piles, cache etc while invoking functions.\n\nThe code could be further optimized by not declaring local variables, but I used them anyway, for better code reading. \n\n```\n// Tree traversing + memoization\nclass Solution {\npublic:\n \n int turnScore (vector<int>&piles, int left, int right, int turn, vector<vector<int>>&cache, vector<int>&prefixSum){\n // cout<<"turn: "<<turn<<" (left,right="<<left<<","<<right<<")"<<endl;\n int sum = 0, a=0,b=0;\n // base case\n if (left>right) return 0; // must have because if not, for case left=0, right=-1, if(cache[left][right]) return segfault \n // if (left== right) // no neccessary since it is included in recursive case \n // memoization - return via cache\n if (cache[left][right] !=INT_MAX ){\n // cout<<"return cache["<<left<<"]["<<right<<"]="<<cache[left][right]<<endl;\n return cache[left][right];\n }\n // starting, no one play yet.\n if (turn == 0){ \n int sum = 0;\n int a = turnScore(piles, left, right-1, turn+1, cache, prefixSum);\n int b = turnScore(piles, left+1, right, turn+1, cache, prefixSum); \n int c = max(a,b);\n // cout<<"sum:"<<sum<<" a:"<<a<<" b:"<<b<<" c:"<<c<<endl;\n return c;\n } \n \n // both players scores when left <= right \n // input left, right indicates the range of remaining cards after the player removes a card\n // score = sum (left -> right) + turnResult (leftNext, rightNext, nextTurn)\n else if ((left <= right) && (turn %2 == 0)){ // Bob plays \n sum = prefixSum[right+1]-prefixSum[left];\n \n a = turnScore(piles, left+1, right, turn+1, cache, prefixSum); \n b = turnScore(piles, left, right-1, turn+1, cache, prefixSum); \n cache[left][right] = -sum + max(a,b); // max(a,b) is the score of the next player, Alice \n // cout<<"return value recursively"<<endl;\n // cout<<"turn: "<<turn<<" (left,right="<<left<<","<<right<<")"<<endl;\n // cout<<"sum:"<<sum<<endl;\n // cout <<"total "<< cache[left][right] <<endl;\n return cache[left][right];\n } \n else if ((left <= right) && (turn %2 != 0)){ // Alice plays\n sum = prefixSum[right+1]-prefixSum[left];\n a = turnScore(piles, left+1, right, turn+1, cache, prefixSum); \n b = turnScore(piles, left, right-1, turn+1, cache, prefixSum); \n cache[left][right] = sum + min(a,b); // min(a,b) is the score of the next player, Bob \n // cout<<"return value recursively"<<endl;\n // cout<<"turn: "<<turn<<" (left,right="<<left<<","<<right<<")"<<endl;\n // cout<<"sum:"<<sum<<endl;\n // cout <<"total "<< cache[left][right] <<endl;\n return cache[left][right];\n }\n else\n return 0;\n }\n\n int stoneGameVII(vector<int> &piles)\n {\n int left = 0;\n int right = piles.size()-1;\n int n = piles.size();\n int turn = 0;\n vector<vector<int>> cache (n,vector<int>(n, INT_MAX));\n vector<int> prefixSum(n + 1);\n for (int i = 0; i < n; i++) {\n prefixSum[i + 1] = prefixSum[i] + piles[i];\n }\n int score = turnScore(piles, left, right, turn, cache, prefixSum); // total score at top of tree\n // total score = Alice score - Bob score\n return score;\n }\n};\n``` | 1 | 0 | [] | 0 |
stone-game-vii | Simple and Precise | Simple | Recursive | Intuitive | Beginners Game Strategy | simple-and-precise-simple-recursive-intu-3cjj | ```\nclass Solution {\npublic:\n vector> dp;\n int fun(int i,int j,vector &arr,vector &pre){\n //Base Case \n if(i +1== j){\n ret | njcoder | NORMAL | 2022-03-06T13:44:21.185229+00:00 | 2022-03-06T13:44:21.185268+00:00 | 102 | false | ```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n int fun(int i,int j,vector<int> &arr,vector<int> &pre){\n //Base Case \n if(i +1== j){\n return max(arr[i],arr[i+1]);\n }\n if(i == j) return 0;\n if(i > j) return 0;\n if(dp[i][j] != -1) return dp[i][j];\n int L = pre[j] - pre[i];\n int R = (j == 0 ? 0 : pre[j-1]) - (i == 0 ? 0 : pre[i-1]);\n \n int L1 = fun(i+2,j,arr,pre);\n int L2 = fun(i+1,j-1,arr,pre);\n \n int R1 = fun(i+1,j-1,arr,pre);\n int R2 = fun(i,j-2,arr,pre);\n \n \n int l1 = pre[j] - pre[i+1]; \n int l2 = (j == 0 ? 0 : pre[j-1]) - pre[i];\n int r1 = (j - 1 < 0 ? 0 : pre[j-1]) - pre[i];\n int r2 = (j-2 <0 ? 0 : pre[j-2]) - (i-1<0 ? 0 : pre[i-1]);\n \n int ans = max(L + min(L1-l1,L2-l2),R + min(R1-r1,R2-r2));\n \n return dp[i][j] = ans;\n }\n \n int stoneGameVII(vector<int>& arr) {\n int n = arr.size();\n vector<int> pre(n);\n pre[0] = arr[0];\n for(int i=1;i<n;i++) pre[i] = pre[i-1] + arr[i];\n dp = vector<vector<int>> (n,vector<int> (n,-1));\n return fun(0,n-1,arr,pre);\n }\n}; | 1 | 0 | ['Dynamic Programming', 'Recursion'] | 0 |
stone-game-vii | From Recursion to Memoization | CPP | Extremely Simple | from-recursion-to-memoization-cpp-extrem-tw22 | \nint f(vector<int>stones, int i,int j,int sum){\n if(sum<=0 || i==j) return 0;\n \n return max((sum-stones[i])- f(stones,i+1,j,sum-stones[ | sarora160 | NORMAL | 2022-01-19T08:54:41.930204+00:00 | 2022-01-19T08:54:41.930293+00:00 | 154 | false | ```\nint f(vector<int>stones, int i,int j,int sum){\n if(sum<=0 || i==j) return 0;\n \n return max((sum-stones[i])- f(stones,i+1,j,sum-stones[i]),\n (sum-stones[j]) - f(stones,i,j-1, sum-stones[j]));\n }\n int stoneGameVII(vector<int>& stones) {\n int sum{accumulate(stones.begin(),stones.end(),0)};\n return f(stones,0,stones.size()-1,sum);\n }\n```\n\n\n\n```\nclass Solution {\npublic:\n int memo(vector<vector<int>> & dp, vector<int>& stones, int sum, int start, int end){\n if(sum <= 0) return 0; \n if(start== end )return 0;\n if(dp[start][end]!= -1)return dp[start][end]; \n \n int res = max(sum-stones[start]- memo(dp,stones, sum-stones[start], start+1, end),\n sum-stones[end]- memo(dp,stones, sum-stones[end], start, end-1)\n );\n return dp[start][end ] = res ;\n }\n int stoneGameVII(vector<int>& stones) {\n int sum = 0 ;\n int n = stones.size(); \n for(auto x:stones) sum +=x;\n vector<vector<int>> dp(n+1, vector<int>(n+1, -1)); \n return memo(dp , stones, sum, 0, n-1) ;\n }\n}; | 1 | 0 | ['C', 'C++'] | 0 |
stone-game-vii | Go | DP | Beat 100% | go-dp-beat-100-by-linhduong-wztp | \nfunc stoneGameVII(stones []int) int {\n sum := buildPrefixSum(stones) \n \n var (\n prev, current [2][]int\n n = len(stones)\n )\n | linhduong | NORMAL | 2021-12-14T12:16:06.043192+00:00 | 2021-12-14T12:16:06.043227+00:00 | 86 | false | ```\nfunc stoneGameVII(stones []int) int {\n sum := buildPrefixSum(stones) \n \n var (\n prev, current [2][]int\n n = len(stones)\n )\n \n\t// prev and current is pivot dp slice which store difference of each state\n\t//\n\t// 0: Alice move\n\t// 1: Bob move\n prev[0], prev[1] = make([]int, n), make([]int, n)\n current[0], current[1] = make([]int, n), make([]int, n)\n \n for ln := 2; ln <= n; ln++ {\n for i := 0; i <= n - ln; i++ {\n s1 := rangeSum(sum, i, i + ln - 2)\n s2 := rangeSum(sum, i + 1, i + ln - 1)\n \n\t\t\t// 0: Alice move -> try to maximize the difference, she knows that next move is Bob\n current[0][i] = max(prev[1][i] + s1, prev[1][i+1] + s2)\n\t\t\t\n\t\t\t// 1: Bob move -> try to minimize the difference, he knows that next move is Alice\n current[1][i] = min(prev[0][i] - s1, prev[0][i+1] - s2)\n }\n \n prev, current = current, prev\n } \n \n return prev[0][0]\n}\n\nfunc buildPrefixSum(v []int) (sum []int) {\n sum = make([]int, len(v))\n \n s := 0\n for i := range v {\n s += v[i] \n sum[i] = s\n }\n \n return\n}\n\n// inclusive\nfunc rangeSum(prefixSum []int, from, to int) int {\n if from == 0 {\n return prefixSum[to]\n }\n return prefixSum[to] - prefixSum[from - 1]\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n``` | 1 | 0 | ['Go'] | 0 |
stone-game-vii | [JAVA] Easy and Clean DP (Tabulation) Solution | java-easy-and-clean-dp-tabulation-soluti-97zd | Time Complexity - O(N^2)\nSpcae Complexity - O(N^2)\nRuntime - 37ms - Faster than 90.16%\n.\n\nclass Solution {\n public int stoneGameVII(int[] stones) {\n | Dyanjno123 | NORMAL | 2021-11-27T17:29:52.470039+00:00 | 2021-11-27T17:30:26.020147+00:00 | 151 | false | Time Complexity - O(N^2)\nSpcae Complexity - O(N^2)\nRuntime - 37ms - Faster than 90.16%\n.\n```\nclass Solution {\n public int stoneGameVII(int[] stones) {\n int[][] dp = new int[stones.length][stones.length];\n int[] pre = new int[stones.length];\n pre[0] = stones[0];\n for(int i = 1; i < pre.length; i++)\n pre[i] = pre[i - 1] + stones[i];\n for(int g = 0; g < dp.length; g++){\n for(int i = 0, j = g; j < dp.length; i++, j++){\n if(g == 0)\n dp[i][j] = 0;\n else if(g == 1) \n dp[i][j] = Math.max(stones[i], stones[j]);\n else\n dp[i][j] = Math.max((pre[j] - pre[i] - dp[i + 1][j]), (pre[j-1] - (i == 0 ? 0 : pre[i-1]) - dp[i][j - 1]));\n }\n }\n return dp[0][stones.length - 1];\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Java'] | 0 |
stone-game-vii | C++ || TWO METHODS || RECURSION + MEMOIZATION || BOTTOM-UP DP | c-two-methods-recursion-memoization-bott-3moz | METHOD --> 1 \n\nint dp[1005][1005];\n \n int func(vector&nums,vector&prefix,int i,int j){\n \n if(i>=j){\n return 0;\n }\ | anu_2021 | NORMAL | 2021-11-07T18:49:12.398384+00:00 | 2021-11-07T18:49:12.398417+00:00 | 114 | false | # **METHOD --> 1 **\n\nint dp[1005][1005];\n \n int func(vector<int>&nums,vector<int>&prefix,int i,int j){\n \n if(i>=j){\n return 0;\n }\n \n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n \n return dp[i][j]=max(prefix[j+1]-prefix[i+1]-func(nums,prefix,i+1,j) , prefix[j]-prefix[i]-func(nums,prefix,i,j-1));\n \n \n }\n \n int stoneGameVII(vector<int>& stones) {\n \n int n=stones.size();\n \n memset(dp,-1,sizeof(dp));\n \n vector<int>prefix(n+1,0);\n \n for(int i=1;i<=n;i++){\n prefix[i]=prefix[i-1]+stones[i-1];\n }\n \n return func(stones,prefix,0,n-1);\n \n }\n\t\n\t\n# **\tMETHOD --> 2**\n\t\n\tint stoneGameVII(vector<int>& nums) {\n \n int n=nums.size();\n \n vector<int>prefix(n+1,0);\n \n for(int i=1;i<=n;i++){\n prefix[i]=prefix[i-1]+nums[i-1];\n }\n \n vector<vector<int>>dp(n,vector<int>(n,0));\n \n for(int i=0;i<n-1;i++){\n dp[i][i+1]=max(nums[i],nums[i+1]);\n }\n \n for(int L=3;L<=n;L++){\n \n \n for(int i=0;i<n-L+1;i++){\n \n int j=i+L-1;\n \n int val1=prefix[j+1]-prefix[i+1]-dp[i+1][j];\n int val2=prefix[j]-prefix[i]-dp[i][j-1];\n \n dp[i][j]=max(val1,val2);\n \n }\n \n \n }\n \n return dp[0][n-1];\n \n } | 1 | 1 | [] | 0 |
stone-game-vii | C++ DP with explanation (easy) | c-dp-with-explanation-easy-by-uttu_dce-ipot | \n\t\nf(i, j, stones) : denotes the maximum lead that the current player can take while playing in the subarray stones[i...j] / or how ahead can the current pl | uttu_dce | NORMAL | 2021-10-17T08:58:58.184870+00:00 | 2021-10-17T09:00:40.050829+00:00 | 145 | false | \n\t\n**f(i, j, stones) : denotes the maximum lead that the current player can take while playing in the subarray stones[i...j] / or how ahead can the current player reach from the opponent given that both play optimally**\n\t\nAt any instant, the player whose turn it is currently, will try and take maximum lead (means he will try to make the difference in the scores (or how much ahead he is of the opponent will be maximized))\n\t\n\nas soon as we pick a stone from an end , lets say we pick up the stone at index i, so we immediattely take a lead of sum(i+1, j) (means we are now sum(i +1, j) ahead of the first guy)\nnow the second guy will take a lead of f(i + 1, j) \nso \n**the overall lead that we took in this case is sum(i + 1, j) - f(i+1, j)**\n\nsimilarly if i pick up the stone at index j (the right end) we immediattely take a lead of sum(i, j-1) and now it\'s the opponents turn\n**so he will take a lead of f(i, j-1), so again the lead in this case is sum(i, j-1) - f(i, j-1)**\n\n**all we have to do is, go for the maximum of the above two cases**\n\n```\nclass Solution {\npublic:\n\tvector<int> prefixSum;\n\tvector<vector<int>> dp;\n\tint sum(int i, int j) {\n\n\t\treturn (j >= 0 ? prefixSum[j] : 0) - (i >= 1 ? prefixSum[i - 1] : 0 );\n\t}\n\n\tint f(int i, int j, vector<int> &stones) {\n\n\t\tif (i >= j) return 0;\n\t\tif (dp[i][j] != -1) return dp[i][j];\n\n\t\treturn dp[i][j] = max(sum(i + 1, j) - f(i + 1, j, stones), sum(i, j - 1) - f(i, j - 1, stones));\n\t}\n\tint stoneGameVII(vector<int>& stones) {\n\t\tint n = stones.size();\n\t\tprefixSum.resize(n, 0);\n\t\tdp.resize(n, vector<int> (n, -1));\n\t\tint s = 0;\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\ts += stones[i];\n\t\t\tprefixSum[i] = s;\n\t\t}\n\n\t\treturn f(0, n - 1, stones);\n\t}\n};\n``` | 1 | 0 | [] | 0 |
stone-game-vii | Python, C++ || DP || Prefix Sum || O(N^2) | python-c-dp-prefix-sum-on2-by-in_sidious-j2ms | Python ->\n\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n=len(stones)\n prefix_Sum={-1:0}\n for i,val in enum | iN_siDious | NORMAL | 2021-08-23T09:06:37.987246+00:00 | 2021-08-23T09:07:16.222133+00:00 | 290 | false | Python ->\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n=len(stones)\n prefix_Sum={-1:0}\n for i,val in enumerate(stones):\n prefix_Sum[i]=prefix_Sum[i-1]+val\n dp=[[0]*n for _ in range(n)]\n for i in range(n-1,-1,-1):\n for j in range(i,n):\n if i!=j:\n dp[i][j]=max(prefix_Sum[j]-prefix_Sum[i]-(dp[i+1][j] if i+1<n else 0),prefix_Sum[j-1]-prefix_Sum[i-1]-(dp[i][j-1] if j-1>=0 else 0))\n return dp[0][n-1]\n \n```\n\nC++ ->\n```\nclass Solution {\npublic:\n int stoneGameVII(vector<int>& stones) {\n int n=stones.size();\n map <int,int> prefix_Sum;\n vector<vector<int>> dp(n,vector<int>(n,0));\n prefix_Sum[-1]=0;\n for (int i=0;i<n;i++){\n prefix_Sum[i]=prefix_Sum[i-1]+stones[i];\n }\n for (int i=n-1;i>=0;i--){\n for (int j=i;j<n;j++){\n if (i!=j){\n dp[i][j]=max(prefix_Sum[j]-prefix_Sum[i]-((i+1<n)?dp[i+1][j]:0),prefix_Sum[j-1]-prefix_Sum[i-1]-((j-1>=0)?dp[i][j-1]:0));\n }\n }\n }\n return dp[0][n-1];\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'C', 'Prefix Sum', 'Python'] | 1 |
stone-game-vii | ✔️ [C++] [DP] Simple, Concise and easy to understand code. | c-dp-simple-concise-and-easy-to-understa-o0g9 | null | f20180944 | NORMAL | 2021-08-12T14:30:37.065336+00:00 | 2021-08-12T14:33:14.366413+00:00 | 238 | false | [<iframe src="https://leetcode.com/playground/8HxADGfL/shared" frameBorder="0" width="900" height="409"></iframe>](http://) | 1 | 0 | ['Dynamic Programming', 'Memoization'] | 1 |
stone-game-vii | C++ Solution explained and commented | c-solution-explained-and-commented-by-pr-bpey | \nclass Solution {\npublic:\n /*\nLogic:Alice and Bob have to choose from either of the left or right most part \nand then his score will become sum of the r | pragya_anand | NORMAL | 2021-08-11T14:43:47.537048+00:00 | 2021-08-11T14:43:47.537097+00:00 | 261 | false | ```\nclass Solution {\npublic:\n /*\nLogic:Alice and Bob have to choose from either of the left or right most part \nand then his score will become sum of the remainning stone .So for this we \nneed to first calculate sum for the stones vector and then you have two choices--->\n 1)choose left stone and then score will be total sum-choosen stone and recur for remainning stone but sum will become total sum-choosen stone.\n 2)choose right stone and then score will be total sum-choosen stone and recur for remainning stone but sum will become total sum-choosen stone.\n Now you need to maximize the score difference so just maximum between these two.\n */\n //initialize table for memorization\n int dp[1005][1005];\n int solve(vector<int>&v,int i,int j,int sum)\n {\n //base case\n if(i>j)\n return 0;\n //memorized step\n else if(dp[i][j]!=-1)\n return dp[i][j];\n //ans will max between your two choices i.e left or right one\n int ans=max(sum-v[i]-solve(v,i+1,j,sum-v[i]),sum-v[j]-solve(v,i,j-1,sum-v[j]));\n return dp[i][j]=ans;\n }\n int stoneGameVII(vector<int>& v) {\n //initialize sum \n int n=v.size(),sum=0;\n //calculate sum\n for(int i=0;i<n;i++)\n sum+=v[i];\n memset(dp,-1,sizeof(dp));\n //call solve to return ans.\n return solve(v,0,n-1,sum);\n }\n};\ndo upvote if you find it useful.......\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 0 |
stone-game-vii | kotlin - dp using memo | kotlin-dp-using-memo-by-sandeep549-9p3e | \n fun stoneGameVII(stones: IntArray): Int {\n val sum = stones.sum()\n val memo = Array(stones.size){IntArray(stones.size){-1} }\n retu | sandeep549 | NORMAL | 2021-08-07T17:04:10.182556+00:00 | 2021-08-07T17:04:10.182599+00:00 | 47 | false | ```\n fun stoneGameVII(stones: IntArray): Int {\n val sum = stones.sum()\n val memo = Array(stones.size){IntArray(stones.size){-1} }\n return play(stones, 0, stones.lastIndex, sum, memo)\n }\n\n fun play(stones: IntArray, l:Int, r: Int, sum: Int, memo: Array<IntArray>) : Int {\n if(l == r) return 0\n if (memo[l][r] != -1) return memo[l][r]\n val a = sum - stones[l] - play(stones, l+1, r, sum - stones[l], memo)\n val b = sum - stones[r] - play(stones, l, r-1, sum - stones[r], memo)\n memo[l][r] = maxOf(a, b)\n return memo[l][r]\n }\n``` | 1 | 0 | [] | 0 |
stone-game-vii | C++ | O(n2) | DP solution | c-on2-dp-solution-by-sp140-q9ls | dp[i][j].first = maximum difference we can get for the sub-array of [i, j], it is Alice\'s turn.\n\ndp[i][j].second = min difference we can get for the sub-arra | sp140 | NORMAL | 2021-07-24T10:04:29.922236+00:00 | 2021-07-24T10:04:29.922291+00:00 | 119 | false | dp[i][j].first = maximum difference we can get for the sub-array of [i, j], it is Alice\'s turn.\n\ndp[i][j].second = min difference we can get for the sub-array of [i, j], it is Bob\'s turn.\n\nhence, \ndp[i][j].first = max(dp[i+1][j].second + (sum of the elements[i+1 to j]), dp[i][j-1] + (sum of the elements[i to j-1]))\ndp[i][j].second = min(dp[i+1][j].first - (sum of the elements[i+1 to j]), dp[i][j-1] + (sum of the elements[i to j-1]))\n\n\'+\' for maximizing difference - i.e. adding score to Alice\n\'-\' for minimizing difference - i.e. adding score to Bob\n\n**** In terms of fast execution\n3D vector < 2D vector of pair of ints < 2D array of pair of ints. in increasing order of speed of execution.\nArrays are faster than vectors.\n\n\n```\nclass Solution {\n\npublic:\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n pair<int,int> dp[n][n];\n int pfs[n];\n for(int i=0;i<n;i++)\n pfs[i] = stones[i] + ((i>0)?pfs[i-1]:0);\n \n for(int l=2;l<=n;l++){\n for(int i=0;i<n-l+1;i++){\n int j = i+l-1;\n if(l == 2){\n int pos = max(stones[i], stones[j]);\n dp[i][j].first = pos;\n dp[i][j].second = -1*pos;\n }else{\n int a_ = pfs[j]-pfs[i];\n int b_ = pfs[j-1]-((i==0)?0:pfs[i-1]);\n dp[i][j].first = max(dp[i+1][j].second + a_, \n dp[i][j-1].second + b_);\n dp[i][j].second = min(dp[i+1][j].first - a_, \n dp[i][j-1].first - b_);\n }\n }\n }\n return dp[0][n-1].first;\n }\n};\n``` | 1 | 0 | [] | 0 |
stone-game-vii | [C++] Easy to understand clean & concise dynamic programming one pass O(n*n) | c-easy-to-understand-clean-concise-dynam-7lsx | Please upvote if it helps!\n\nclass Solution {\npublic:\n int sum(vector<int>& a, int i, int j)\n {\n if(i>j)\n return 0;\n if(i= | somurogers | NORMAL | 2021-06-21T02:30:20.213321+00:00 | 2021-06-21T02:30:20.213353+00:00 | 267 | false | Please upvote if it helps!\n```\nclass Solution {\npublic:\n int sum(vector<int>& a, int i, int j)\n {\n if(i>j)\n return 0;\n if(i==0)\n return a[j];\n return a[j]-a[i-1];\n }\n \n int stoneGameVII(vector<int>& stones) {\n int n=stones.size();\n for(int i=1;i<n;i++)\n stones[i]+=stones[i-1];\n \n vector<vector<int>> dp(n+1, vector<int>(n+1,0));\n for(int i=n-1;i>=0;i--)\n for(int j=i+1;j<=n;j++)\n dp[i][j] = max(sum(stones,i+1,j-1) - dp[i+1][j], sum(stones,i,j-2) - dp[i][j-1]);\n \n return dp[0][n];\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
stone-game-vii | C++ SOLUTION WITH DP(MEMOIZATION) | c-solution-with-dpmemoization-by-shruti_-w7hc | \nclass Solution {\npublic:\n int check(vector<int> &s,int i,int n,int sum,vector<vector<int>> &dp)\n {\n if(i==n)\n return(0);\n | shruti_mahajan | NORMAL | 2021-06-18T19:40:27.269542+00:00 | 2021-06-20T09:50:50.930455+00:00 | 125 | false | ```\nclass Solution {\npublic:\n int check(vector<int> &s,int i,int n,int sum,vector<vector<int>> &dp)\n {\n if(i==n)\n return(0);\n if(dp[i][n]!=-1)\n return(dp[i][n]);\n return(dp[i][n]=max(sum-s[i]-check(s,i+1,n,sum-s[i],dp),sum-s[n]-check(s,i,n-1,sum-s[n],dp)));\n }\n int stoneGameVII(vector<int>& s) {\n int n=s.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n int sum=accumulate(s.begin(),s.end(),0);\n return(check(s,0,n-1,sum,dp));\n }\n};\n``` | 1 | 1 | [] | 2 |
stone-game-vii | Python | Recursive DP | Min Max | Two Pointer | with Explaination | python-recursive-dp-min-max-two-pointer-bopb4 | This is an application of Min/Max algorithm where one of competitor alice, tries to maximize the difference, while other bob tries to minimize it.\n\nSo the DP | PuneethaPai | NORMAL | 2021-06-12T15:43:56.315818+00:00 | 2021-06-13T05:30:23.991994+00:00 | 187 | false | This is an application of Min/Max algorithm where one of competitor `alice`, tries to maximize the difference, while other `bob` tries to minimize it.\n\nSo the DP or recursive solution you write, depending on, which players turn it is, you maximize or minimize the return value.\n\n## Step 1: Identifying sub-problem:\nWe will be using two pointers left `l` and right `r` to identify sub-array, thus sub-problem to solve. Solving sub-problem we will compute the solution to the whole `(0, N]`.\n\n## Step 2: Identifying which players turn it is:\nWe could have passed `bool` valirable around to identify which players turn it is. \nThis is redundant as we can deduce it from `l` and `r` values itself, i.e after each turn either `l -> l + 1` or `r -> r - 1`. Thus after each turn, `l` and `r` comes closer to each other by `1-step`. Depending on how many stones are remaining, i.e `remaining = (N - (r - l))`, we can tell if remaining is odd => `alice`\'s else `bob`\'s turn.\n\nThus to know which players turn it is:\n```python\nis_alice = (N - (r - l)) & 1\n```\n\n## Step 3: Computing difference in players score:\n\nTo compute answer, we need to take difference in total scores b/w two players accumulated over each turn.\n\nLooks complecated, but it can be reduced to sum of stone values picked by loosing player, i.e `Bob`. Here is the proof for the same.\n\nFor example:\n```\nConsider you have 4 stones: [a, b, c, d] with sum S = (a + b + c + d)\nLet Stone choices be:\nAlice: a, c\nBob : b, d\n\n| Turn | 1 | 2 |\n|:-----:|:----------------:|:-:|\n| Alice | a1 = S - a | d |\n| Bob | b1 = a1 - b | 0 |\n| Diff | b = a1 - b1 | d |\n```\n**Thus Final result = sum of diffs = b + d == sum of `Bobs` stone values**\n\n> ### All we need to do is add the values of stones picked by `bob` which will be diffs in two player scores.\n\n---\n\n# FInal solution looks like this:\n- Time: O(N), because of caching sub-problem solution. _Correct me if I am wrong_\n- Space: O(N * N), because of `lru_cache` saving results for all `nC2` pairs of `(l, r)`.\n\n```python\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n N = len(stones)\n\n @lru_cache(maxsize=2000)\n def dfs(l: int, r: int) -> int:\n is_alice = (N - r + l) & 1\n if l == r:\n return (1 - is_alice) * stones[l]\n if is_alice:\n return max(dfs(l + 1, r), dfs(l, r - 1))\n return min(stones[l] + dfs(l + 1, r), stones[r] + dfs(l, r - 1))\n\n return dfs(0, N - 1)\n```\n\n**Runtime: 4676 ms\nMemory Usage: 21 MB** | 1 | 0 | ['Two Pointers', 'Dynamic Programming', 'Recursion', 'Python'] | 0 |
stone-game-vii | C++ no prefix sum O(n^2) | c-no-prefix-sum-on2-by-divyanshu41-itpt | We look at turns as both Alice and Bob choosing a stone each with Alice choosing first.\n\nThere are 4 options\n Alice leftmost Bob rightmost -> lr\n Alice left | divyanshu41 | NORMAL | 2021-06-12T05:29:30.518343+00:00 | 2021-06-12T05:29:30.518387+00:00 | 79 | false | We look at turns as both Alice and Bob choosing a stone each with Alice choosing first.\n\nThere are 4 options\n* Alice leftmost Bob rightmost -> lr\n* Alice leftmost then Bob leftmost from remaining -> ll\n* Alice rightmost then Bob leftmost -> rl\n* Alice leftmost then Bob rightmost -> lr\n\nWe calculate for all 4 options, the difference in scores.\n\nThen as we know, Alice has the first turn, so she will try to minimise the difference.\n\nlet\'s say lr = 6, rl = 7, ll = 5, rr = 10\n\nNow you can see, if Alice choose the left stone, Bob will choose the next left stone to minimise diff.\nif Alice choose rightmost, bob will choose the leftmost\n\nfor alice, best case option is she choose right and then Bob will for sure choose leftmost.\n\n\n```class Solution {\npublic:\n vector<vector<int>> dp;\n int minDiff(vector<int> &stones, int left, int right) {\n if( left == right )\n return 0;\n if( right < left )\n return 0;\n \n if( dp[left][right] != INT_MAX)\n return dp[left][right];\n int ll = stones[left + 1] + minDiff(stones, left + 2, right );\n int rr = stones[right - 1] + minDiff(stones, left, right - 2 );\n int minlr = minDiff( stones, left + 1, right - 1 );\n int lr = stones[right] + minlr;\n int rl = stones[left] + minlr;\n \n if( min(ll,lr) < min(rr,rl) )\n dp[left][right] = min(rr, rl);\n else\n dp[left][right] = min(ll, lr);\n \n return dp[left][right];\n }\n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n dp = vector<vector<int>>(n, vector<int>(n,INT_MAX));\n return minDiff(stones, 0, stones.size() - 1);\n }\n};\n``` | 1 | 1 | [] | 0 |
stone-game-vii | Stone Game VII | Dynamic Programming C++ | Beats 99.68% of runtime | stone-game-vii-dynamic-programming-c-bea-wefh | Runtime: 84 ms\nMemory Usage: 14 MB\n\nclass Solution {\npublic:\n int dp[1002][1002] ={0};\n \n \n int stoneGameVII(vector<int>& stones) {\n | simarjot_kaur | NORMAL | 2021-06-11T22:56:16.024490+00:00 | 2021-06-11T23:17:23.517539+00:00 | 86 | false | Runtime: 84 ms\nMemory Usage: 14 MB\n```\nclass Solution {\npublic:\n int dp[1002][1002] ={0};\n \n \n int stoneGameVII(vector<int>& stones) {\n int n = stones.size();\n int total = 0;\n for (int i = n-2; i >=0; i--){\n total = stones[i]+stones[i+1];\n dp[i][i+1] = max(stones[i], stones[i+1]);\n for (int j = i+2; j < n; j++){\n total += stones[j];\n dp[i][j] = max(total-stones[i]-dp[i+1][j], \n total-stones[j]-dp[i][j-1]);\n }\n }\n return dp[0][n-1];\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.